Возведение в степень — Википедия
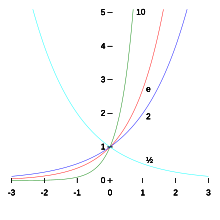Графики четырёх функций вида y=ax{\displaystyle y=a^{x}}, a{\displaystyle a} указано рядом с графиком функцииВозведе́ние в сте́пень — арифметическая операция, первоначально определяемая как результат многократного умножения числа на себя. Степень с основанием a{\displaystyle a} и натуральным показателем b{\displaystyle b} обозначается как
- ab=a⋅a⋅…⋅a⏟b,{\displaystyle a^{b}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{b},}
где b{\displaystyle b} — количество множителей (умножаемых чисел)[1][К 1].
Например, 32=3⋅3=9;24=2⋅2⋅2⋅2=16{\displaystyle 3^{2}=3\cdot 3=9;\quad 2^{4}=2\cdot 2\cdot 2\cdot 2=16}
В языках программирования, где написание ab{\displaystyle a^{b}} невозможно, применяются альтернативные обозначения[⇨].
Возведение в степень может быть определено также для отрицательных[⇨], рациональных[⇨], вещественных[⇨] и комплексных[⇨] степеней[1].
Извлечение корня — одна из операций, обратных возведению в степень, она по известным значениям степени c=ab{\displaystyle c=a^{b}} и показателя b{\displaystyle b} находит неизвестное основание a=cb{\displaystyle a={\sqrt[{b}]{c}}}. Вторая обратная операция — логарифмирование, она по известным значениям степени c=ab{\displaystyle c=a^{b}} и основания a{\displaystyle a} находит неизвестный показатель b=logac{\displaystyle b=log_{a}c}. Задача нахождения числа по известному его логарифму (потенцирование, антилогарифм) решается с помощью операции возведения в степень[⇨]).
Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.
Запись an{\displaystyle a^{n}} обычно читается как «a в n{\displaystyle n}-й степени» или «a в степени n». Например, 104{\displaystyle 10^{4}} читается как «десять в четвёртой степени», 103/2{\displaystyle 10^{3/2}} читается как «десять в степени три вторых (или: полтора)».
Для второй и третьей степени существуют специальные названия: возведение в квадрат и в куб соответственно. Так, например, 102{\displaystyle 10^{2}} читается как «десять в квадрате», 103{\displaystyle 10^{3}} читается как «десять в кубе». Такая терминология возникла из древнегреческой математики. Древние греки формулировали алгебраические конструкции на языке геометрической алгебры. В частности, вместо употребления слова «умножение» они говорили о площади прямоугольника или об объёме параллелепипеда: вместо a2{\displaystyle a^{2}}, a3{\displaystyle a^{3}} древние греки говорили «квадрат на отрезке a», «куб на a». По этой причине четвёртую степень и выше древние греки избегали[2].
Основные свойства[править | править код]
Все приведенные ниже основные свойства возведения в степень выполняются для натуральных, целых, рациональных и вещественных чисел[3]. Для комплексных чисел, в силу многозначности комплексной операции, они выполняются только в случае натурального показателя степени[⇨].
Запись anm{\displaystyle a^{n^{m}}} не обладает свойством ассоциативности (сочетательности), то есть, в общем случае,(an)m≠a(nm){\displaystyle (a^{n})^{m}\neq a^{\left({n^{m}}\right)}} Например, (22)3=43=64{\displaystyle (2^{2})^{3}=4^{3}=64}, а 2(23)=28=256{\displaystyle 2^{\left({2^{3}}\right)}=2^{8}=256}. В математике принято считать запись anm{\displaystyle a^{n^{m}}} равнозначной a(nm){\displaystyle a^{\left({n^{m}}\right)}}, а вместо (an)m{\displaystyle (a^{n})^{m}} можно писать просто anm{\displaystyle a^{nm}}, пользуясь предыдущим свойством. Впрочем, некоторые языки программирования не придерживаются этого соглашения.
Возведение в степень не обладает свойством коммутативности (переместительности): вообще говоря, ab≠ba{\displaystyle a^{b}\neq b^{a}}, например, 25=32{\displaystyle 2^{5}=32}, но 52=25.{\displaystyle 5^{2}=25.}
Таблица натуральных степеней небольших чисел[править | править код]
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2 187 | 6 561 | 19 683 | 59 049 |
| 4 | 16 | 64 | 256 | 1024 | 4 096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5 | 25 | 125 | 625 | 3125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6 | 36 | 216 | 7 776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 | |
| 7 | 49 | 343 | 2401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 40 353 607 | 282 475 249 |
| 8 | 64 | 512 | 4096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9 | 81 | 729 | 6561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
Целая степень[править | править код]
Операция обобщается на произвольные целые числа, включая отрицательные и ноль[4]::
- az={az,z>01,z=0,a≠01a|z|,z<0,a≠0{\displaystyle a^{z}={\begin{cases}a^{z},&z>0\\1,&z=0,a\neq \;0\\{\frac {1}{a^{|z|}}},&z<0,a\neq \;0\end{cases}}}
Результат не определён при a=0{\displaystyle a=0} и z⩽0{\displaystyle z\leqslant 0}.
Рациональная степень[править | править код]
Возведение в рациональную степени p/q,{\displaystyle p/q,} где p{\displaystyle p} — целое число, а q{\displaystyle q} — натуральное, определяется следующим образом[4]:
- apq=(aq)p{\displaystyle a^{p \over q}=({\sqrt[{q}]{a}})^{p}}.
Результат не определён при a=0{\displaystyle a=0} и p/q⩽0.{\displaystyle p/q\leqslant 0.} Для отрицательных a{\displaystyle a} в случае нечётного p{\displaystyle p} и чётного q{\displaystyle q} в результате вычисления степени получаются комплексные числа.
Следствие: an=a1/n.{\displaystyle {\sqrt[{n}]{a}}=a^{1/n}.} Таким образом, понятие рациональной степени объединяет возведение в целочисленную степень и извлечение корня в единую операцию.
Вещественная степень[править | править код]
Если a⩾0,r{\displaystyle a\geqslant 0,r} — вещественные числа, причём r{\displaystyle r} — иррациональное число, возможно определить ar{\displaystyle a^{r}} следующим образом: поскольку любое вещественное число можно приблизить, сверху и снизу, двумя рациональными числами, то есть можно подобрать для r{\displaystyle r} рациональный интервал [p,q]{\displaystyle [p,q]} с любой степенью точности, то общая часть всех соответствующих интервалов [ap,aq]{\displaystyle [a^{p},a^{q}]} состоит из одной точки, которая и принимается за ar{\displaystyle a^{r}}.
Полезные формулы:
- xy=aylogax{\displaystyle x^{y}=a^{y\log _{a}x}}
- xy=eylnx{\displaystyle x^{y}=e^{y\ln x}}
- xy=10ylgx{\displaystyle x^{y}=10^{y\lg x}}
Последние две формулы используют для возведения положительных чисел в произвольную степень на электронных калькуляторах (включая компьютерные программы), не имеющих встроенной функции xy{\displaystyle x^{y}}, и для приближённого возведения в нецелую степень или для целочисленного возведения в степень, когда числа слишком велики для того, чтобы записать результат полностью.
Комплексная степень[править | править код]
Возведение комплексного числа в натуральную степень выполняется обычным умножением, и результат однозначен (см. формулу Муавра). Основой для более общего определения комплексной степени служит экспонента ez{\displaystyle e^{z}}, где e{\displaystyle e} — число Эйлера, z=x+iy{\displaystyle z=x+iy} — произвольное комплексное число[5].
Определим комплексную экспоненту с помощью такого же ряда, как и вещественную:
- ez=1+z+z22!+z33!+z44!+⋯.{\displaystyle e^{z}=1+z+{\frac {z^{2}}{2!}}+{\frac {z^{3}}{3!}}+{\frac {z^{4}}{4!}}+\cdots .}
Этот ряд абсолютно сходится для любого комплексного z,{\displaystyle z,} поэтому его члены можно как угодно перегруппировывать. В частности, отделим от него часть для eiy{\displaystyle e^{iy}}:
- eiy=1+iy+(iy)22!+(iy)33!+(iy)44!+⋯=(1−y22!+y44!−y66!+⋯)+i(y−y33!+y55!−⋯).{\displaystyle e^{iy}=1+iy+{\frac {(iy)^{2}}{2!}}+{\frac {(iy)^{3}}{3!}}+{\frac {(iy)^{4}}{4!}}+\cdots =\left(1-{\frac {y^{2}}{2!}}+{\frac {y^{4}}{4!}}-{\frac {y^{6}}{6!}}+\cdots \right)+i\left(y-{\frac {y^{3}}{3!}}+{\frac {y^{5}}{5!}}-\cdots \right).}
В скобках получились известные из вещественного анализа ряды для косинуса и синуса, и мы получили формулу Эйлера:
- ez=exeyi=ex(cosy+isiny){\displaystyle e^{z}=e^{x}e^{yi}=e^{x}(\cos y+i\sin y)}
Общий случай ab{\displaystyle a^{b}}, где a,b{\displaystyle a,b} — комплексные числа, определяется через представление a{\displaystyle a} в показательной форме: a=rei(θ+2πk){\displaystyle a=re^{i(\theta +2\pi k)}} согласно определяющей формуле[5]:
- ab=(eLn(a))b=(eln(r)+i(θ+2πk))b=eb(ln(r)+i(θ+2πk)).{\displaystyle a^{b}=(e^{\operatorname {Ln} (a)})^{b}=(e^{\operatorname {ln} (r)+i(\theta +2\pi k)})^{b}=e^{b(\operatorname {ln} (r)+i(\theta +2\pi k))}.}
Здесь Ln{\displaystyle \operatorname {Ln} } — комплексный логарифм, ln{\displaystyle \ln } — его главное значение.
При этом комплексный логарифм — многозначная функция, так что, вообще говоря, комплексная степень определена неоднозначно[5]. Неучёт этого обстоятельства может привести к ошибкам. Пример: возведём известное тождество e2πi=1{\displaystyle e^{2\pi i}=1} в степень i.{\displaystyle i.} Слева получится e−2π,{\displaystyle e^{-2\pi },} справа, очевидно, 1. В итоге: e−2π=1,{\displaystyle e^{-2\pi }=1,} что, как легко проверить, неверно. Причина ошибки: возведение в степень i{\displaystyle i} даёт и слева, и справа бесконечное множество значений (при разных k{\displaystyle k}), поэтому правило (ab)c=abc{\displaystyle \left(a^{b}\right)^{c}=a^{bc}} здесь неприменимо. Аккуратное применение формул определения комплексной степени даёт слева и справа e−2πk;{\displaystyle e^{-2\pi k};} отсюда видно, что корень ошибки — путаница значений этого выражения при k=0{\displaystyle k=0} и при k=1.{\displaystyle k=1.}
Потенцирование (от нем. potenzieren[К 2]) — нахождение числа по известному значению его логарифма, то есть решение уравнения logax=b{\displaystyle \log _{a}x=b}. Из определения логарифма вытекает, что x=ab{\displaystyle x=a^{b}}, таким образом, возведение a{\displaystyle a} в степень b{\displaystyle b} может быть названо другими словами «потенцированием b{\displaystyle b} по основанию a{\displaystyle a}».
Антилогарифм — вычислительная операция нахождения числа по известному значению логарифма, как самостоятельное понятие используется в логарифмических таблицах, логарифмических линейках, микрокалькуляторах. Вычисление антилогарифма по основанию a{\displaystyle a} для числа b{\displaystyle b} соответствует возведению в степень ab.{\displaystyle a^{b}.}
Разновидности[править | править код]
Поскольку в выражении xy{\displaystyle x^{y}} используются два символа (x{\displaystyle x} и y{\displaystyle y}), то его можно рассматривать как одну из трёх функций.
- Функция переменной x{\displaystyle x} (при этом y{\displaystyle y} — постоянная-параметр). Такая функция называется степенной. Обратная функция — извлечение корня.
- Функция переменной y{\displaystyle y} (при этом x{\displaystyle x} — постоянная-параметр). Такая функция называется показательной (частный случай — экспонента). Обратная функция — логарифм.
- Функция двух переменных f(x,y)=xy.{\displaystyle f(x,y)=x^{y}.} Отметим, что в точке (0,0){\displaystyle (0,0)} эта функция имеет неустранимый разрыв. В самом деле, вдоль положительного направления оси X,{\displaystyle X,} где y=0,{\displaystyle y=0,} она равна единице, а вдоль положительного направления оси Y,{\displaystyle Y,} где x=0,{\displaystyle x=0,} она равна нулю.
Ноль в степени ноль[править | править код]
Выражение 00{\displaystyle 0^{0}} (ноль в нулевой степени) многие учебники считают неопределённым и лишённым смысла, поскольку, как указано выше, функция f(x,y)=xy{\displaystyle f(x,y)=x^{y}} в точке (0, 0) разрывна. Некоторые авторы предлагают принять соглашение о том, что это выражение равно 1. В частности, тогда разложение в ряд экспоненты:
- ex=1+∑n=1∞xnn!{\displaystyle e^{x}=1+\sum _{n=1}^{\infty }{x^{n} \over n!}}
можно записать короче:
- ex=∑n=0∞xnn!.{\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}.}
Следует предостеречь, что соглашение
определения, обозначение, примеры, степень с отрицательным показателем
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a), а в качестве показателя – натуральное (обозначим буквой n).
Определение 1Степень числа a с натуральным показателем n – это произведение n-ного числа множителей, каждый из которых равен числу а. Записывается степень так: an, а в виде формулы ее состав можно представить следующим образом: 
Например, если показатель степени равен 1, а основание – a, то первая степень числа a записывается как a1. Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a1=a.
В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида 8·8·8·8 можно сократить до 84. Примерно так же произведение помогает нам избежать записи большого числа слагаемых (8+8+8+8=8·4); мы это уже разбирали в статье, посвященной умножению натуральных чисел.
Как же верно прочесть запись степени? Общепринятый вариант – «a в степени n». Или можно сказать «n-ная степень a» либо «an-ной степени». Если, скажем, в примере встретилась запись 812, мы можем пр
степень — Викисловарь
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | сте́пень | сте́пени |
| Р. | сте́пени | степене́й |
| Д. | сте́пени | степеня́м |
| В. | сте́пень | сте́пени |
| Тв. | сте́пенью | степеня́ми |
| Пр. | сте́пени | степеня́х |
сте́-пень
Существительное, неодушевлённое, женский род, 3-е склонение (тип склонения 8e по классификации А. А. Зализняка).
Произношение[править]
- МФА: ед. ч. [ˈsʲtʲepʲɪnʲ] мн. ч. [ˈsʲtʲepʲɪnʲɪ]
Семантические свойства[править]
Значение[править]
- сравнительная мера, безразмерный количественный показатель ◆ Антимонопольное ведомство намерено определить степень конкуренции на российском рынке железорудного сырья.
- звание, статус в какой-либо системе ценностей ◆ Учёная степень.
- разряд, категория ◆ Наградить орденом Славы первой степени.
- матем. величина, полученная умножением другой величины, называемой основанием, самой на себя определенное число раз, называемое показателем; также сам показатель при такой операции ◆ Возведение в степень.
- лингв. степень сравнения, грамматическая категория прилагательного или наречия ◆ Категории сравнительной и превосходной степени прилагательного характерны для индоевропейских языков, включая балто-славянские.
Синонимы[править]
- мера, ступень, показатель, уровень
- —
- —
- —
- степень сравнения
Антонимы[править]
- —
- —
- —
- корень, логарифм
- —
Гиперонимы[править]
- —
- —
- —
- произведение
- грамматическая категория
Гипонимы[править]
- —
- —
- —
- положительная степень, превосходная степень, сравнительная степень
Родственные слова[править]
Этимология[править]
Происходит от др.-русск. степень, ст.-слав. степень (др.-греч. βαθμός), ср.: болг. сте́пен; с др. ступенью чередования гласных: белор. сто́пень, польск. stopień «ступень, степень, градус», в.-луж. stopjeń — то же, stopjeno «ступенька, скамеечка, след». Родственно сущ. стопа́. Родственно также лит. stẽpas «апоплексический удар», латышск. stepis «карапуз», более далеки др.-в.-нем. stuof(f)a «ступень», ср.-в.-нем. stuofe, нидерл. stоер «крыльцо», а также др.-в.-нем. stapfo «след ноги», нидерл. stap «ступенька», англ. step — то же, с и.-е. -b-. Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
Значение слова СТЕПЕНЬ. Что такое СТЕПЕНЬ?
СТЕ́ПЕНЬ, -и, род. мн. —е́й, ж.
1. Сравнительная величина, характеризующая что-л., мера чего-л. Степень сжатия газа. Степень продуктивности животноводства. Степень точности вычислений. □ Степень развития производительных сил определяет меру власти человека над природой. Плеханов, К вопросу о развитии монистического взгляда на историю.
2. только ед. ч. (с определением и предлогами „в“, „до“). Мера, предел; отношение. В слабой степени. В значительной степени. В равной степени. В достаточной степени. До известной степени.
3. (в сочетании с числительным). Разряд, категория, класс. Матрос порвал историю болезни и справку врачей, дававшую ему вторую степень ограничения военной годности. Борзенко, Повинуясь законам Отечества. | О наградах, орденах. Орден Отечественной войны второй степени. Диплом сельскохозяйственной выставки третьей степени. □ Кто-то умер: на красной подушке Первой степени Анна лежит. Н. Некрасов, Утро. || Стадия (об ожоге, обморожении).
4. Уровень, ступень, на которой находится, которой достигает кто-, что-л. [Наша литература] находится уже на той степени, когда изящная форма почитается не достоинством, а условием необходимым. Н. Некрасов, <Из статьи «Русские второстепенные поэты»>. Трудно пересчитать все ее [женщины] «домашние обязанности», которые низводят ее, человека, на степень домашнего животного. М. Горький, О женщине. Комнатные переживания, мир только литературных ассоциаций, споры о книгах, заседания, редакции —, — все это сводит поэзию на степень упражнения, где обыгрывается слово ради слова.
262
5. Устар. Служебный ранг, чин. Радищев должен был достигнуть одной из первых степеней государственных. Но судьба готовила ему иное. Пушкин, Александр Радищев. Соломонов не сомневался, что — он быстро достигнет высших степеней, доступных военному человеку. Славин, Дело под Картамышевом.
6. Ученое звание. Магистерская степень. Присудить степень кандидата наук.
7. Мат. Произведение нескольких равных сомножителей, результат повторного умножения числа на самого себя. Возвести десять в пятую степень.
◊
Возведение в степень: правила, примеры, дробная степень
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Пример 2Вычислите значение 3272
Решение
Данную запись можно переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327
СТЕПЕНЬ — это… Что такое СТЕПЕНЬ?
СТЕПЕНЬ — жен. ступень, ряд, разряд, порядок, от дел по качеству, достоинству; место и самое собранье однородного, равного во всем, где полагается лествичный порядок, восходящий и нисходящий. Царство ископаемых, растений и животных, это три степени… … Толковый словарь Даля
степень — Ступень, разряд, ряд, стадия, фазис, высота, точка, градус, уровень, ординар, достоинство, ранг, чин. Последовательность степеней лестница, иерархия. Образовательный, имущественный ценз. Дело вступило в новый фазис. Чахотка в последнем градусе … Словарь синонимов
СТЕПЕНЬ — произведение нескольких равных сомножителей (напр., 24=2.2.2.2=16). число, повторяющееся сомножителем (в примере число2), называют основанием степени; число, показывающее, сколько раз повторяется сомножитель (в примере число4), называют… … Большой Энциклопедический словарь
СТЕПЕНЬ — СТЕПЕНЬ, и, мн. и, ей, жен. 1. Мера, сравнительная величина чего н. С. подготовленности. С. загрязнения. 2. То же, что звание (в 1 знач.), а также (устар.) ранг, чин. Учёная с. доктора наук. Достичь высоких степеней. 3. обычно с поряд. числ.… … Толковый словарь Ожегова
степень — • степень диссоциации степень окисления степень поглощения … Химические термины
СТЕПЕНЬ — (power) Показатель, указывающий определенное количество умножений числа самого на себя, n я степень х означает х; умноженное само на себя n раз; n является показателем степени. Степени могут быть положительными и отрицательными: х n означает, что … Экономический словарь
СТЕПЕНЬ — СТЕПЕНЬ, в математике, результат умножения числа или ПЕРЕМЕННОЙ на себя определенное число раз. Так, а2 ( = а 3 а) является второй степенью а; а3 третьей степенью; а4 четвертой и т.д. Умножаемое число (в данном примере а) называется основанием… … Научно-технический энциклопедический словарь
степень — степень, мн. степени, род. степеней (неправильно степеня) … Словарь трудностей произношения и ударения в современном русском языке
СТЕПЕНЬ — (1) диссоциации величина, характеризующая состояние равновесия реакции (см.) в однородных (газообразных и жидких) системах; выражается отношением числа молекул, распавшихся (диссоциировавших) на своп составные части (атомы, молекулы, ноны), к… … Большая политехническая энциклопедия
Степень — Термин «степень» может означать: В математике Возведение в степень Декартова степень Корень n й степени Степень множества Степень многочлена Степень дифференциального уравнения Степень отображения Степень точки в геометрии Степени тысячи… … Википедия
Степень с натуральным показателем
Математика – точная наука, и математический язык приветствует употребление более кратких записей.
Вместо записи 5 + 5 + 5 + 5 + 5 + 5, математик использует запись 5 · 6, потому что у нас шесть одинаковых слагаемых.
А запись 5 · 5 · 5 · 5 · 5 · 5 математик заменит записью 56, потому что шесть одинаковых множителей. Конечно, при необходимости можно использовать обратные записи.
Мы знаем, что 76 есть произведение шести множителей, каждый из которых равен 7:
76 = 7 · 7 · 7 · 7 · 7.
Число 7 – основание степени, число 6 – показатель степени, выражение 76 – степень.
Дадим определение степени для любого основания и любого натурального показателя.
Степенью числа а с натуральным показателем n большим 1, называется произведение n множителей, каждый из которых равен а.
Для степени числа а с показателем n принято обозначение: аn.
По определению аn = а · а · а · а… а. (n раз)
В определение не включён случай, когда показатель n = 1, так как не имеет смысла говорить о произведении, состоящем из одного множителя. Степень с показателем 1 определяется особо.
Степенью числа а с показателем 1 называется само число а: а1 = а.
Вычисление значения степени называют действием возведения в степень. Это действие выполняется первым при вычислении значения выражения.
Рассмотрим примеры вычислений значений выражений, содержащих степени.
Пример 1. Найдём значение степеней (-4)4 (-4)3.
(-4)4 = (-4) · (-4) · (-4) · (-4) = 256
(-4)3 = (-4) · (-4) · (-4) = -64
Обратим внимание, при возведении в степень отрицательного числа, положительное число получается, если число возводится в чётную степень, если же отрицательное число возводится в нечётную степень, то получается отрицательное число.
Пример 2. Вычислим (3/4)3.
(3/4)3 = 3/4 · 3/4 · 3/4 = 27/64.
Пример 3. Найдем значение выражения 6 · 33.
Чтобы найти значение этого выражения, достаточно сначала найти значение степени 33, а затем выполнить умножение:
1) 33 = 3 · 3 · 3 = 27
2) 6 · 27 = 162.
Значение степени можно найти с помощью вычислительной техники, а можно воспользоваться таблицей степеней.
Пример 4. Рассмотрим ещё один пример. Найдём значение выражения 0,5 · 482.
0,5 · 482 = 0,5 · 2304 = 1152
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.