Что называют угловой скоростью: 404 — Страница не найдена — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Угловая скорость — это… Что такое Угловая скорость?

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
Производная угловой скорости по времени есть угловое ускорение.

Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где — радиус-вектор точки (из начала координат), — скорость этой точки. — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор).

При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .

Связь с конечным поворотом в пространстве

Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве . Тогда угловая скорость, соответствующая этому повороту, равна

Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .

См. также

Литература

Лурье А. И. Аналитическая механика\\ А. И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136

Часть 6 — Кинематика свободного твердого тела. Природа угловой скорости / Хабр

Что такое тензор и для чего он нужен?
Векторные и тензорные операции. Ранги тензоров
Криволинейные координаты
Динамика точки в тензорном изложении
Действия над тензорами и некоторые другие теоретические вопросы
Кинематика свободного твердого тела. Природа угловой скорости
Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
О свертках тензора Леви-Чивиты
Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
Получаем вектор угловой скорости. Работаем над недочетами
Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
Параметры Родрига-Гамильтона в кинематике твердого тела
СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
Нестандартное введение в динамику твердого тела
Движение несвободного твердого тела
Свойства тензора инерции твердого тела
Зарисовка о гайке Джанибекова
Математическое моделирование эффекта Джанибекова

Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.

Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.

Угловая скорость твердого тела — это первая производная от угла поворота тела по времени

А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении

обычно дается следующее определение

Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки

Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат.

И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».

При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.

Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.

Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.

Думаю для затравки вполне достаточно, а поэтому — начнем!

Итак, как известно из традиционного вузовского курса теормеха

Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным

Это — самый общий случай движения тела.

Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом

и сферического вокруг полюса.

Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.

Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.

Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна считается неподвижной и называется

базовой, другая жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.

Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.

Рис. 2. Ориентация твердого тела в локальном базисе.

Пусть положение полюса задается вектором

Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.

В точке O₁ задан локальный репер базовой системы координат, образованный тройкой векторов . С движущимся телом связан подвижный репер . Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства

Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор неподвижный относительно связанного репера. Его можно разложить по векторам этого репера

и по векторам базового репера

Каждый вектор связанного репера можно разложить через векторы базового репера

Подставляем (4) в (2) и сравниваем с (3)

Из (5) понятно, что компоненты вектора

в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора

или в безиндексной форме

где столбцы матрицы

– контравариантные компоненты векторов связанного репера по отношению к базовому.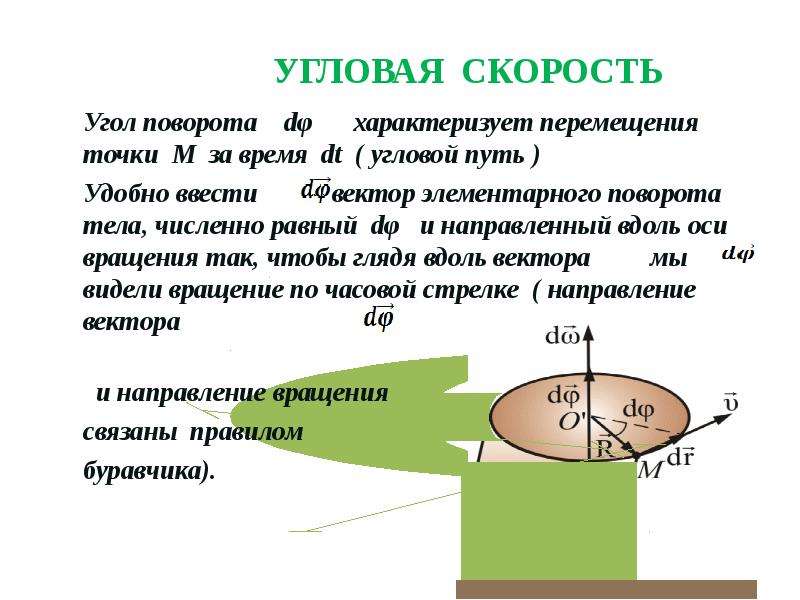 Точка, как мы уже отмечали в

прошлой статье

, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор

действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется

ортогональным

. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат

Правая часть (8) — это локальный метрический тензор

или

Оператор

является по сути обыкновенной матрицей поворота координатной системы. И (10) утверждает, что если транспонированную матрицу поворота умножить на метрический тензор, а результат умножить на матрицу поворота мы получим снова метрический тензор. Можно сделать вывод, что

Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.

В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в

самой первой статье цикла

Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.

Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.

Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть . Что же, посмотрим. Для этого умножим (10) слева на и справа на

откуда незамедлительно получаем

Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.

Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений

При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый

тензором поворота

Вычислим скорость точки

, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами

Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении

где

— скорость полюса;

— скорость точки вокруг полюса.

Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать

Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)

Перейдем в (16) к связанной системе координат, домножив (15) слева на

где

— компонента оператора обратного преобразования

Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева

Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости

при этом замечая, что

антисимметричный тензор второго ранга, о котором мы говорили в

прошлой статье<

. Таким образом, нам бы доказать, что

является антисимметричным тензором второго ранга. Для этого придется доказать, что (19) меняет знак при перестановка индексов (транспонировании). При этом будем учитывать, что метрический тензор — абсолютно симметричный тензор второго ранга и при транспонировании он не меняется. Поэтому исследуем взаимосвязи между матрицами поворота, для чего нам потребуются выражения (10) и (11). Но прежде чем приступить, докажем ещё одно вспомогательное утверждение

Ковариантная производная метрического тензора равна нулю

Обратимся к понятию ковариантной производной вектора, о которой упоминалось в

третьей статье

. Тогда мы вывели выражения для контравариантных компонент ковариантной производной от вектора

Как как и любой вектор, компоненты данного вектора можно трансформировать в ковариантные умножением и сверткой с метрическим тензором

А можно продифференцировать ковариантные компоненты непосредственно

Сравнивая (21) и (20) мы приходим к выводу, что равенство возможно лишь в случае если верно утверждение леммы

Теперь, перепишем (19) в безиндексном виде, учтя уравнение (11)

Далее, нам нужна связь между оператором поворота и его производной — дифференцируем (10) по времени

или, собирая производные от метрического тензора в правой части

Но, производные от метрического тензора в (24) будут равны нулю, в силу равенства нулю ковариантной производной метрического тензора.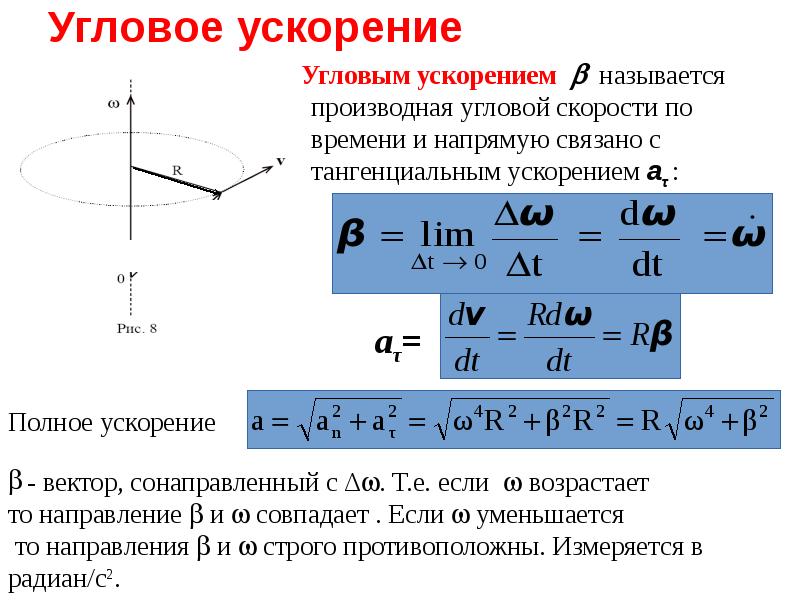 Значит правая часть (24) равна нулю

Пользуясь свойствами операции транспонирования, преобразуем (25)

Так как

и с учетом (23), получаем

Из (26) непосредственно следует антисимметричность тензора (19)

Ну а коль скоро (19) антисимметричный тензор, то мы смело переписываем (18)

Таким образом мы приходим к выводу, что (19) и (23) есть ни что иное как

антисимметричный тензор угловой скорости

Любому антисимметричному тензору можно поставить в соответствие псевдовектор, который мы уже получали в предыдущей статье. Повторим этот результат для тензора угловой скорости

Возможно читателю знаком распространенный подход замены векторного произведения на умножение кососимметричной матрицы, построенной из первого вектора по определенному правилу, на второй вектор. Так вот это правило получается естественным путем, если в качестве инструмента использовать тензорное исчисление. Действительно, вот эта кососимметричная матрица, которой в матричном изложении механики заменяют угловую скорость

Возможно, внимательный читатель увидит, что в полученной матрице знаки противоположны тем, что мы получали в статье, посвященной антисимметричным тензорам. Да, все верно, ведь в той статье мы сворачивали вектор с тензором Леви-Чивиты по его третьему индексу

, тут мы выполняем свертку по среднему индексу

что дает прямо противоположные знаки.

Матрица (30) частенько встречается в литературе, в частности в трудах Д. Ю. Погорелова, но там она вводится как мнемоническое правило. Формула (29) дает четкую связь между вектором угловой скорости и кососимметричной матрицей. Она же дает возможность перейти от (28) к формуле

Что, внезапно, эквивалентно векторному соотношению

В этой статье было много математики. И я вынужден пока ограничится этим материалом — статья вышла длинной и насыщенной формулами. Данная тема будет продолжена и углублена в следующих статьях цикла.

Какой же вывод мы можем сделать сейчас? А вот какой

Угловая скорость твердого тела есть антисимметричный тензор, или, соответствующий ему псевдовектор, порождаемый тензором поворота тела относительно базовой системы координат

Для того чтобы написать эту работу потребовалось перелопатить гору литературы. Основные выкладки выполнены автором самостоятельно. Камнем преткновения были матрицы поворота для случая косоугольных координат. Я не сразу разглядел в соотношении (10) преобразование, оставляющее метрику инвариантной, хотя с учетом ранее написанных статей — следовало бы. Понять эту связь мне помог ужасный по оформлению, но очень толковый сайт

«На что похожа математика»

. Кстати видно, что все соотношения переходят в известные для ортогональных матриц, если метрический тензор сделать единичным.

Разговор о механике твердого тела будет продолжен, а пока — всё. Спасибо за внимание!

Продолжение следует…

Угловая скорость — Справочник химика 21

U — угловая скорость вращения барабана в сек. п — число оборотов барабана в минуту [c.130]

Угловая скорость вращения [c.47]

О — угловая скорость вращения в рад сек [c.44]

Расчет валов на виброустойчивость, а также уточненный расчет на прочность выполняются по РД РТМ 26-01-72—75. Расчет на виброустойчивость сводится к определению критической частоты вращения и сравнению ее с принятой, Фактические угловые скорости вала не должны совпадать с критическими. В зависимости от соотношения рабочей и первой [c.239]

Угловая скорость радиан в секунду рад/с (1 рад) (1 с) [c.351]

Угловая скорость рад/с теплоты [c.12]

Если оба подшипника жесткие, то критическую угловую скорость вала определяют по формуле [c.274]

Одинарные уплотнения. Принципиальное устройство этих уплотнений показано на рпс. 54. На валу насоса (или на специальной гильзе) устанавливают втулку 4, вращающуюся вместе с ним с такой же угловой скоростью (см. рпс. 54). Крутящий момент от вала к втулке передается через устройство 2. [c.144]

Валы центрифуг по характеру работы разделяют на гибкие и жесткие. Гибкими называют валы, работающие при угловых скоростях, превышающих критическую (со > ю,,р), жесткими — валы, рабочая угловая скорость которых меньше критической (со[c.267]

Для определения первой критической угловой скорости вала Т еобходимо значение коэффициентов (корней частотного уравнения) аь которые -находят по графикам (рис. 225, а, б) в зависимости от приведенной массы Шпр, а 1,ля консольных валов — также и от относительной длины пролета Ь = 1 1, где I — длина пролета между опорами вала 1 — длина консоли. [c.240]

Примечание. Допускается использование смесей пластичных смазок Литол-24 и АМ Карданная с трансмиссионными маслами (50%+50%) для шарниров равных угловых скоростей грузовых автомобилей. [c.25]

В качестве функции отклика обычно выбирают такой параметр, который имеет ясный физический смысл и легко определяется количественно. В ряде случаев функция отклика, как и входные факторы, может представлять собой безразмерный комплекс параметров. Так, при исследовании центробежно-вихревого измельчителя в качестве функции отклика можно выбрать степень измельчения или относительную мощность Л/отн Л /( ы срР), в качестве входных факторов — критерий Фруда, безразмерный комплекс, характеризующий степень загрузки измельчителя материалом (3/((и/ срр), относительный зазор между роторами п т. д. М — мош,ность измельчения, ш — угловая скорость, Q — производительность, 7 ,, — средний радиус верхнего и нижнего роторов, р — плотность материала). [c.18]

Напряжения изгиба, обусловленные действием центробежных сил инерции при вращении вала, можно найти, если известны положения центров масс дисков, закрепленных на валу. При заданной угловой скорости со вала, не совпадающей с критической, рассчитывают деформации у вала, например для вала с двумя дисками по выражениям (3.48)—(3.50), и силы инерции P по формулам, аналогичным [c.77]

Рассмотрим движение диска, консольно закрепленного на валу (расчетная схема — см. рис. 3.11), последний вращается с угловой скоростью 03. В системе координат Хъ Ух, связанной с диском, моменты инерции массы диска относительно осей J= J 2 1 — = [c.78]

Из теоретической механики известно, что центробежная сила равна произведению массы на 1 вадрат угловой скорости и на радиус вращения [c.46]

Номинальная мощность и угловая скорость выходного вала п]1Ивода аппарата с мешалкой должны соответствовать значени-Я14, указанным в табл. 2.24. [c.108]

Сушилки и холодильники с диаметром барабана более 1200 мм допускается изготовлять с номинальной угловой скоростью 0,85 рал/с (табл. 3.16). Углы наклона барабанов сушилок и холо-дил ) 1иков составляют 1—4″, печей — 1—3°. Число опор у су)иилок две у печей и холодильников может быть две — четыре (в зависимости от длины барабана и его диаметра). [c.144]

Вращающийся дисковый электрод. Особенность вращающегося дискового. электрода (см. рис. 15.6), как это было показано рядом авторов, заключается в постоянстве толщины диффузионного слоя в любыз точках его поверхности, если только бдискового электрода, В то же время величина б является функцией угловой скорости вращения дискового электрода [c.313]

Валы машин, эксплуатируемые в докритической области (угловая скорость которых меньше частоты собственных колебаний), называются жесткими, а валы, эксплуатируемые в закритнческой области ((О > 01 )), — гибкими. Свойством самоцентрирования обладают 7- [c.74]

Центробежные пылеотделители той или иной формы встречаются обычно на многих предприятиях. В центробежных пылеосади-телях (циклонах) поток газа, содержащий пыль, движется с больщой скоростью, при этом угловая скорость твердых частиц достигает значительной величины, что приводит к увеличению центробежной силы. Характерная опасность центробежных пылеосадите-лей обусловлена тем, что в присутствии кислорода нельзя избежать образования зоны взрывоопасной концентрации пыли, так как осаждение твердых частиц сопровождается последовательным уплотнением среды в различных зонах циклона в зависимости от величины частиц. Кроме того, при высоких скоростях пыли в системе сухих центробежных аппаратов образуются большие заряды статического электричества, которые могут служить источником воспламенения горючей и взрывоопасной среды. [c.278]

Для данного насоса угловая скорость и радиус кривошипа — величины постоянные, а изменяется при работе насоса угол поворота кривошипа. Поэтому скорость поршня изменяется на протяжении двойного хода по закону синуса и графически может быть пред-ставл- па в виде синусоиды (рис. 54). [c.103]

Общее требование для всех конструкции центрифуг — хорошая урагшовешенность ротора и устойчивая работа вала. Нарушение устойчивой работы вала происходит в момент, когда угловая скорость вращення становится равной критической угловой скорости вращения, эквивалентной собственной круговой частоте вала. В этот момент наступает резонанс. [c.266]

В ряде случаев, особеипо для гибклх валов, в центрифугах применяют упругие опоры, назначение и сущность которых видны из следующего примера [31. Пусть вал (рис. 227) нагружен массами т, которые расположены с эксцентриситетом е относительно оси вращения. Тогда при вращении вала с некоторой угловой скоростью возникает центробежная сила тсо (е + //), которая изгибает вал и стремится увеличить иервоначальпый эксцентриситет на величину у. По мере приближения угловой скорости вала со к критической величина смещения масс возрастает и становится максимальной при со со р. Дальнейшее увеличение со приводит к тому, что из-за большей устойчивости движения вал займет такое положение, при котором центр масс т окажется на оси вращения, а сам вал будет вращаться около линии, соединяющей оиоры. При этом ирогиб 227. Схема работы ва.ла вала будет равен по величине п про- центрифуги [c.267]

Расчет критической угловой скорости вала центрифуги. Устойчивая работа вала нарушается при приближении его скорости к критической. При этом увеличивается прогиб вала. На рис. 232 приведена схема вала для наиболее типичного случая консольного закреилепия ротора центрифуги. Вал центрифуги совершает двойное вращательное движение. Кроме вращательного движения около собственной изогнутой оси, вал совершает вращательное [c.274]

Рабочая угловая скорость должна быть не более 0,7о)нр для аппаратов, работающих с системами жидкость — жидкость жи, кос1ь — твердое тело , а для систем жидкость — газ —не более 0,6сокр для всех типов мешалок, кроме лопастных, и 0,4о)ьр для лопастных мешалок. Для двухлопастной мешалки, кроме того, не допускается работа в интервале (0,454-0,55)о)кр. [c.241]

Мсследованиямп Б. Г. Холпна установлено, что вращающаяся совместно с перфорпроваппой оболочкой жидкость имеет малую угловую скорость, а для вытекающих из отверстий струй характерно интенсивное сжатие, возрастающее с увеличением частоты вращения. [c.115]

Энергия вращательного движешт е р является функцией угловой скорости ш и момента инерции J [см. уравнение (1,5)1 [c.18]

Характерная особенность рассматриваемой системы — вращение вала, изогнутого в плоскости действия силы инерции, вместе с этой плоскостью. Как следует из формулы (3.43), при угловой скорости вала, равной угловой частоте его собственных колебаний, прогиб вала стремится к бесконечности. Эта скорость называется критической. При угловой скорости вала, превышающей критическую (в закритнческой области), центр масс диска располагается между изогнутой осью вала и осью его вращения и при неограниченном увеличении угловой скорости диска стремится занять положение на оси вращения (рис. 3.19, б) при этом коэффициент и -> (—1). Это явление называется самоцентрированием вала деформация вала при этом уменьшается. [c.74]

Воздействие гироскоиического момента. При большой угловой скорости вала и значительном моменте инерции диска, закрепленного на валу, необходимо учитывать влияние гироскопического момента на критическую скорость вала. [c.78]

Скорость тела угловая — Энциклопедия по машиностроению XXL

Угловая скорость тела 0) = 7 рад/с, мгновенная ось его составляет в данный момент с неподвижными координатными осями острые углы а, р и у. Найти величину скорости и и проекции ее их, Ьу, Иг на координатные оси для точки тела, координаты которой, выраженные в метрах, в данный момент равны о, 2, о, а также расстояние й этой точки от мгновенной оси, если соз а = 2/7, соз у = 6/7. [c.142]

Движение тела вокруг неподвижной точки задано при помощи углов Эйлера следующими уравнениями ф == nt, i[i = я/2 -f ant, о == я/3. Определить проекции угловой скорости и углового ускорения тела на неподвижные оси, если а и п постоянные величины. Указать также то значение параметра а, при котором неподвижным аксоидом тела будет плоскость Оху. [c.150]

Т ело» движется в пространстве, причем вектор угловой скорости тела равен о) и направлен в данный момент по оси z. Скорость точки О тела равна vo и образует с осями (/, Z одинаковые углы, равные [c.189]

Мощность силы, приложенной к вращающемуся вокруг неподвижной оси твердому телу, равно произведению угловой скорости тела на момент силы относительно оси вращения тела. [c.331]

Если за промежуток времени —t тело совершает поворот на угол Дф=ф1—ф, то численно средней угловой скоростью тела за -этот промежуток времени будет Шср=Дф/Д/. В пределе при А/-Ч) найдем, что [c.120]

Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени —t угловая скорость тела изменяется на величину Дм = = oi—(О, то числовое значение среднего углового ускорения тела за этот промежуток времени будет В пределе при Д ->0 [c.121]

Скорость V в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М. [c.123]

Для определения искомых кинематических характеристик (угловой скорости тела или скоростей его точек) надо знать модуль и направление скорости какой-нибудь одной точки и направление скорости другой точки сечения этого тела (кроме случаев а) и в), рассмотренных в конце 56). С определения этих характеристик по данным задачи и следует начинать решение. [c.136]

Угловая скорость тела. При изменении угла ф тело совершает вращение вокруг оси Ог (собственное вращение) с угловой скоростью й)1=ф, при изменении угла — вращение вокруг оси Ozi (прецессия) с угловой скоростью o2=ii5 и при изменении [c.148]

Поскольку значения i, oj, со, со временем изменяются, вектор ш будет при движении тела тоже изменяться и численно, и по направлению. По этой причине со называют еще мгновенной угловой скоростью тела. [c.148]

Задачей кинематики в этом случае является нахождение зависимостей между характеристиками относительного, переносного и абсолютного движений. Основными кинематическими характеристиками движения тела, как мы знаем, являются его поступательные и угловые скорости и ускорения. Мы ограничимся в дальнейшем определением зависимостей только между поступательными и угловыми скоростями тела (кроме одного случая, рассмотренного в 71). [c.169]

Из того, что пара вращений эквивалентна поступательному движению, следует и обратный вывод поступательное движение твердого тела эквивалентно паре вращений, у которой момент угловых скоростей этих вращений равен поступательной скорости тела. [c.172]

Проделанными операциями (рис. 210, б) мы перешли от полюса А к полюсу С. Результат подтверждает (см. 63), что в общем случае движения твердого тела угловая скорость при перемене полюса не изменяется ((й =ш), а меняется только поступательная скорость (w y). [c.179]

Таким образом, кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела. [c.291]

Вращательное движение. Если тело вращается вокруг какой-нибудь оси Oz (см. рис. 295), то скорость любой его точки где /ift — расстояние точки от оси вращения, а ы — угловая скорость тела. Подставляя это значение в формулу (41) и вынося общие множители за скобки, получим [c.302]

Общий случай движения. Если выбрать центр масс С тела в качестве полюса (рис. 304), то движение тела в общем случае будет слагаться из поступательного со скоростью V полюса и вращательного вокруг мгновенной оси СР, проходящей через этот полюс (см. 63). При этом, как показано в 63, скорость Vk любой точки тела слагается из скорости V полюса и скорости, которую точка получает при вращении тела вокруг полюса (вокруг оси СР) и которую мы обозначим и, т. е. v =V — -v f,. При этом по модулю = где h), — расстояние точки от оси СР, а со — угловая скорость тела, которая (см. 63) не зависит от выбора полюса. Тогда [c.303]

Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощности вращающий момент будет тем больше, чем меньше угловая скорость. [c.306]

Условимся обозначать угловую скорость тела в начале удара через со, а в конце удара — через Q. Тогда Kiz=Jz и окончательно получим [c.405]

Обозначим соответственно ш, и угловую скорость тела, угловую скорость осей XYZ и скорость центра масс С относительно неподвижной системы координат Охуг. Скорость произвольной частицы тела, определяемой по отношению к системе XYZ радиусом-вектором р,, выразится согласно формуле (9.32) на стр. 93 следующим образом [c.601]

Зная скорости изменения углов Эйлера, определить угловую скорость тела и ее проекции на оси неподвижной 0 т1 и подвижной Oxyz систем отсчета. [c.145]

Углы Эйлера, определяющие положение тела, и.з-мсняются по закону (регулярная прецессия) г1 = г11о + П1/ 9 == Оо, ф = фо + 2 , где тро, 00, фо — начальные значения углов, а п и П2—постоянные числа, равные соответствующим угловым скоростям. Определить угловую скорость и тела, неподвижный и подвижный аксоиды. [c.150]

Введем поиятия векторов угловой скорости и углового ускорения тела, Рхли к единичный вектор оси вращения, направленный в ее положительную сторону, го векюры угловой скорости (Г) и углового ускорения е определяют выражениями [c.141]

Следовательно, кинетическая энергия тела при вращательном движении вокруг ненодвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела. [c.176]

Рассмотрим вращательное и осестремительное ускорения но отдельности. Вращательное ускорение вычисляют по формуле (9), аналогичной формуле (2) для скорости точки. Только здесь вместо угловой скорости ш входит угловое ускорение Г . Поэтому вранигтельное ускорение а р направлено аналогично скорости V, если тело вран1ается в рассматриваемый момент времени с угловой скоростью, равной угловому ускорению ё. [c.185]

Угловую скорость и упювое ускорение опюсительного вращательного движения вокруг какой-либо точки тела называют в общем случае угловой скоростью и угловым ускорением свободного твердого тела. Эти величины не зависят [c.320]

Таким образом, числозое значение угловой скорости тела а данный момент времени равно первой производной от, угла поворота по времени. Равенство (37) показывает также, что величина со равна отношению элементарного угла поворота ёф к соответствующ е.му промежутку времени d . Знак ш определяет направление вращения [c.120]

Угловую скорость тела можно изобразить в виде вектора , модуль которого равен 1ю1 и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис. 135). Такой вектор определяет сразу и модуль угло- jgg [c.121]

Если угловая скорость тела остается во все время движения постоянной ((О= onst), то вращение тела называется равномерным. Найдем закон равномерного вращения. Из формулы (37) имеем [c.121]

Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости телана расстояние от этой точки до оси вращения. [c.123]

Ураяненпя (73) называются кинематическими уравнениями Эйлера. Они определяют проекции вектора угловой скорости тела to па подвижные оси Одгуг через [c.150]

Определение Кг- У любой точки тела, отстоящей от оси вращения на расстоянии hk, скорость v, =(siHfi а — угловая скорость тела). Следовательно, для этой точки Тогда для всего тела, вынося общий множитель со за скобки, получим [c.291]

Формула (167) определяет изменение угловой скорости тела при ударе. Из нее следует, что угловая скорость тела за время удара изменяежя на величину, равную отношению момента ударного импульса к моменту инерции тела относительно оси вращения. [c.405]

Аналог угловой скорости — Энциклопедия по машиностроению XXL

Таким образом, действительная угловая скорость со равна произведению угловой скорости со начального звена на аналог угловой скорости

[c.70]

Для определения аналогов угловых скоростей со,, и (О4 звеньев 3 и 4 дифференцируем уравиеиия (5.19) по обобщенной координате фз. Получаем [c.116]

Имея в виду, что с(фз/й(ф2 = 32 есть аналог угловой скорости 0)3 звена 3 и ф4/ фг = ть аналог угловой скорости а>4 звена 4 (см. 16), получаем [c.116]

Аналоги угловой скорости ф2 и углового ускорения ф2 по обобщенной координате а>,- могут быть получены путем двукратного дифференцирования выражения (5.52) или (5.53). [c.121]

Для механизма, показанного на рис. 6.4, будем иметь аналоги угловых скоростей и ускорений [c.135]

Аналоги угловых скоростей и ,34 определяются так же, как и г с и г а. [c.357]

Между аналогом угловой скорости и угловой скоростью = dt Jdt звена существует зависимость = ф,ш. [c.103]

Частные передаточные отношения и u rj называют также аналогами угловых скоростей звена п. Смысл этого термина вытекает из следующего представления если о>2=0, а wi = l рад/с, то можно рассматривать как угловую скорость звена п при неподвижном звене 2 [c.62]

Дважды дифференцируя это выражение по фь получаем аналоги угловой скорости и углового ускорения [c.281]

Для определения аналогов угловой скорости кулисы 4 и скорости перемещения ползуна вдоль направляющей кулисы (V a)(p, уравнения (III.1.1), (III.1.2) дифференцируем по обобщенной координате ф2 [c.76]

Из (111.1.10) — (111.1.11) получаем формулы для расчета аналогов угловой скорости и скорости перемещения ползуна [c.76]

Аналоги угловой скорости и ускорения шатуна, а также аналоги скорости и ускорения ползуна получаем дифференцированием (III.1.1) и (III.1.2) по обобщенной координате ф в виде [c.80]

Дифференцируя дважды (3.1) по углу поворота кривошипа ф, получаем зависимости для расчета аналогов угловой скорости Р и углового ускорения Р» кулисы [c.43]

Для качающегося толкателя аналоги угловой скорости и ускорения звена = = угловые скорости и ускорения [c.61]

Величины фй, и фт аналогичны угловой скорости и угловому ускорению, вследствие чего мы будем называть их аналогами угловых скорости и ускорения. Равным образом и величины 1 т и 1 т называются аналогами линейной скорости и линейного ускорения. Следует иметь в виду, что аналоги угловых скорости и ускорения являются величинами отвлеченными, а аналоги линейных скорости и ускорения — величинами линейными. [c.145]

Величины 31 и 31 являются аналогами угловых скоростей звена 3, причем 34 можно рассматривать как угловую скорость звена 3 при (В4 = 0 н со, = 1 сек» , а 34 можно считать угловой скоростью звена 3 при №4=0 и 0)4 = 1 сек . Из этого следует, что для определения аналогов д, и 34 можно применить такой же способ, какой был применен для определения аналогов и и . Имеем [c.257]

Дифференцируя формулу (3.16) по ф, можно определить аналог угловой скорости Р == 1р/ ф и далее аналог углового ускорения Р» = Ц2р/с(ф2 коромысла. [c.79]

Как видно, она равна аналогу угловой скорости толкателя 3 (рис. 4.23, 6). [c.140]

Это поясняет название величины w угловой переменной. За один цикл величина w изменяется на 2тг, и налицо полная аналогия с вращением тела вокруг оси (частота и — аналог угловой скорости тела, w — аналог угла его поворота вокруг оси). [c.373]

Напомним, что I21, ы, к)., Ы представляют собой аналоги угловых скоростей и являются безразмерными величинами. Как определять эти аналоги, указывалось в 24, п. 3. [c.170]

Если ф4 = 0,5я или 1,5я, то 5 = m Аналог угловой скорости кулисы 42 [c.143]

Ряс. 4. Зависимость аналогов угловой скорости кулисы от угла поворота кривошипа механизма с вращающейся кулисой [c.147]

Графики экстремальных значений аналогов угловой скорости и ускорения кулисы, аналогов скорости и ускорения ползуна, а также его коэффициента динамической мощности /Сз4 для различных величин относительных параметров приведены на рис. 8—11. [c.157]

Рис. 3. Зависимость аналогов угловой скорости кривошипа ъц от угла поворота кулисы

Графики функций угла поворота ведомого звена, аналогов угловой скорости и ускорения в зависимости от угла поворота ведущего звена позволяют без проведения трудоемких вычислений производить кинетостатический и динамический расчет механизмов, определять приведенный момент инерции неравномерно движущихся звеньев с использованием известных методик и зависимостей. [c.168]

Даны схемы плоских кулисных механизмов и построены кинематические диаграммы углов поворота ведомой кулисы, аналогов угловой скорости и ускорения, а также коэффициента динамической мощности для наиболее часто встречающихся относительных размеров, по которым можно подобрать кулисный механизм в зависимости от вида функции передаточного отношения, заданного значения максимальной величины аналогов угловой скорости, ускорения я коэффициента динамической мощности. [c.171]

Угловая скорость (о креста будет максимальной и равной — (шах), когда угол ф будет равен pf = О, т. е. в положении, когда ось паза совпадает с прямой 0)0 (рис. 25.2). Из формулы (25 10) следует, что в этом положении аналог угловой скорости Ф2пт равен [c.509]

В этих уравнениях w,2 = — 0Sф //l2 0S(fпередаточная функция) звена 2 еаналог углового ускорения звена 2 [c.191]

Для определения аналога угловой скорости кривошипа /34 и аналога скорости (o jip, скольжения кулисы вдоль ползуна 3 дифференцируем по обобщенной координате Ф4 уравнения (111.1.1) и (111.1.2) [c.79]

На рис. 121 показано определение положения центра вращения кулачка О для кулачково-коромыслового механизма при геометрическом замыкании, считая известным длину коромысла I. Сначала находим аналог скорости центра ролика с15д/с1ф = /ф, где = = с1 ф/с1ф — аналог угловой скорости коромысла. Затем по зависимости ф(ф) в пределах заданного угла размаха фтах строим несколько положений коромысла ВС и откладываем от точки Во вдоль этих положений значения /ф, принимая масштабный коэффициент для /ф равным масштабному коэффициенту длин ц/. Значения /ф откладываются на фазе подъема от центра вращения С, если кулачок и коромысло вращаются в противоположных направлениях, н к центру С, если они вращаются в одну сторону. [c.220]

Рис. 8. Зависимость аналогов угловой скорости и ускорения кулисы центрального кулисного люха-низма с качающейся кулисой от поворота кривошипа

24 Угловая скорость и угловое ускорение тела, вращающегося вокруг неподвижной оси

Угловая скорость и угловое ускорение тела, вращающегося вокруг неподвижной оси

1. За весьма малый промежуток времени t угол поворота (или угловое перемещение) изменится на величину . Отношение к называется средней угловой скоростью и обозначается т. е.

Угловая скорость тела в данный момент характеризует скорость изменения во времени угла поворота и равна первой производной по времени от угла поворота:

или

Угловая скорость измеряется в радианах в секунду (. В технике угловую скорость часто задают числом n оборотов в минуту (n об/мин). Тогда |

Угловая скорость | Медицинские журналы

В физике угловая скорость относится к тому, насколько быстро объект вращается или вращается относительно другой точки, то есть насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и угловая скорость вращения. Угловая скорость вращения означает, насколько быстро твердое тело вращается относительно центра вращения. Орбитальная угловая скорость относится к тому, насколько быстро точечный объект вращается вокруг фиксированной точки начала координат, т.е.е. скорость изменения его углового положения относительно начала координат. Угловая скорость вращения не зависит от выбора начала координат, в отличие от орбитальной угловой скорости, которая зависит от выбора начала координат.

Обычно угловая скорость измеряется в углах в единицу времени, например радиан в секунду (угол, заменяющий расстояние от линейной скорости от времени в общем). Единица измерения угловой скорости в системе СИ выражается в радианах в секунду, причем радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ обозначаются как 1 / с или с − 1.Угловая скорость обычно обозначается символом омега (ω, иногда Ω). По соглашению, положительная угловая скорость означает вращение против часовой стрелки, а отрицательная — по часовой стрелке.

Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = (360 °) / (24 ч) = 15 ° / ч, или (2π рад) / (24 ч) ≈ 0,26 рад / ч. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega} {\ displaystyle v = r \ omega}.При радиусе орбиты 42000 км от центра Земли скорость спутника в космосе составляет v = 42000 км × 0,26 / ч ≈ 11000 км / ч. Угловая скорость положительна, поскольку спутник движется на восток вместе с вращением Земли (против часовой стрелки от северного полюса). В трех измерениях угловая скорость является псевдовектором, величина которого измеряет скорость вращения или вращения объекта, и его направление перпендикулярно плоскости мгновенного вращения или углового смещения.Ориентация угловой скорости условно задается правилом правой руки.

Актуальные темы общих наук

Формула и единицы измерения угловой скорости | Как определить угловую скорость — стенограмма видео и урока

Формула угловой скорости

Прежде чем мы рассмотрим формулу для угловой скорости, давайте сначала разберемся с более фундаментальными концепциями углового положения и углового смещения.Рассмотрим рисунок ниже.

Угловая скорость частицы — это ее угловое перемещение в единицу времени.

Твердое тело вращается вокруг оси z с угловой скоростью {eq} \ omega {/ eq}. Каждая частица твердого тела вращается вокруг оси z и очерчивает круг, лежащий в плоскости, перпендикулярной оси вращения (оси z), с центром на этой оси. Теперь рассмотрим частицу твердого тела на расстоянии {eq} r {/ eq} от оси.Его угловое положение относительно базовой линии (ось x) равно {eq} \ theta {/ eq}. По прошествии времени частица вращается вокруг оси z, и по прошествии времени {eq} \ Delta t {/ eq} ее угловое положение становится {eq} \ theta ‘{/ eq}. Таким образом, угловое смещение частицы, {eq} \ Delta \ theta = \ theta ‘- \ theta {/ eq}.

Угловая скорость определяется как угловое смещение в единицу времени. Следовательно, угловая скорость частицы

Угловое положение (и угловое смещение) измеряется в радианах (рад).{\ circ} {/ eq}.

В таблице ниже показаны некоторые меры углов в радианах и градусах.

Единицы угловой скорости

Угловая скорость — это угловое смещение тела в единицу времени. Поскольку радианы (рад) и секунды (с) являются единицами измерения углового смещения и времени в системе СИ, соответственно, единица измерения угловой скорости в системе СИ составляет радиан в секунду (рад / с) .Угловая скорость также иногда выражается в единицах оборотов в секунду (об / с) . Другая единица угловой скорости — это та, которая обычно использовалась, когда были виниловые пластинки, единица оборотов в минуту (об / мин) , обычно называемая об / мин .

Мы знаем, {eq} 1 \: rev = 2 \ pi \: rad {/ eq}. Таким образом, {eq} 1 \: rev / s = 2 \ pi \: rad / s {/ eq}.

Опять же, {eq} 1 \: s = \ frac {1} {60} \: min {/ eq}. Таким образом, {eq} 1 \: rpm = \ frac {2 \ pi} {60} \: rad / s {/ eq}.

Как найти угловую скорость

Теперь, когда мы изучили формулу и единицы измерения угловой скорости, давайте рассмотрим несколько интересных примеров.

Пример 1

Рассмотрим колесо обозрения на карнавале. Если колесо обозрения совершает один оборот за {eq} 3 \: min {/ eq}, какова его угловая скорость в рад / с и об / мин?

У нас есть,

Здесь {eq} \ Delta \ theta = 2 \ pi {/ eq} (один полный оборот) и {eq} \ Delta t = 3 \: min = \ left (3 \ times 60 \ right) \ : s = 180 \: s {/ eq}.

Таким образом, угловая скорость колеса обозрения в рад / с равна,

Сейчас,

Пример 2

Горный велосипед имеет колеса диаметром {eq} 61 \: см {/ eq}.Байкер-любитель проезжает {eq} 1,22 \: m {/ eq}, чтобы проверить байк, и обнаруживает, что на это у него уходит {eq} 2 \: s {/ eq}. Какая угловая скорость колеса велосипеда?

Имеем, угловая скорость

Здесь {eq} arc = 1.22 \: m = 122 \: cm {/ eq}, {eq} radius = 61/2 \: cm {/ eq} и {eq} t = 2 \: с {/ экв}.

Пример 3

Какой должна быть минимальная угловая скорость гоночного автомобиля, чтобы он имел скорость {eq} 150 \: mph {/ eq} или выше при движении по круговой трассе с радиусом {eq} 0.3 \: мили {/ eq}?

У нас

Здесь {eq} v = 150 \: mph {/ eq} и {eq} r = 0,3 \: мили {/ eq}.

Таким образом, гоночная машина должна иметь минимальную угловую скорость {eq} 500 \: рад / ч {/ eq}.

Как используется угловая скорость

Возможно, вы помните, как в начале урока мы говорили, что угловая скорость включает как величину, так и направление.В приведенных выше примерах определяемая нами угловая скорость на самом деле была величиной угловой скорости. Направление вектора угловой скорости может быть определено правилом правой руки .

Правило для правой руки

Согласно правилу для правой руки , если вы согнете правую руку вокруг оси вращения вращающегося тела с пальцами, указывающими в направлении вращения, направление вашего вытянутого большого пальца изменится. направление вектора угловой скорости.Таким образом, здесь твердое тело вращается вокруг направления вектора угловой скорости.

Крутящий момент и угловая скорость

Чтобы понять взаимосвязь между крутящим моментом и угловой скоростью, давайте сначала разберемся, что означает крутящий момент. Крутящий момент или момент силы — это сила, участвующая во вращении объекта. Крутящий момент при вращательном движении эквивалентен силе при поступательном движении. Рассмотрим рычаг, который вращается вокруг фиксированной точки. Чтобы повернуть этот рычаг, вам нужно приложить силу в любой точке по длине рычага; эта сила, вызывающая вращательное движение рычага, называется крутящим моментом.Величина крутящего момента является произведением количества приложенной силы и расстояния по перпендикуляру между точкой приложения силы и фиксированной точкой, вокруг которой вращается рычаг.

Как упоминалось ранее, крутящий момент аналогичен простой силе. Аналогичный характер крутящего момента и силы очевиден из формул мощности во вращательном и поступательном движениях.

По определению, мощность {eq} P {/ eq} — это работа, выполненная {eq} W {/ eq} за единицу времени {eq} t {/ eq}. В математической форме:

Теперь проделанная работа может быть выражена как произведение силы {eq} F {/ eq} и смещения {eq} d {/ eq}; кроме того, смещение в единицу времени дает скорость {eq} v {/ eq}.

Поскольку связь между линейной скоростью {eq} v {/ eq} и угловой скоростью {eq} \ omega {/ eq} дается формулой {eq} v = \ omega R {/ eq}, выражение мощности во вращательном движении становится {eq} P = F \ omega R {/ eq}.

Теперь мы можем ввести здесь крутящий момент {eq} \ tau {/ eq} (который является произведением силы и перпендикулярного расстояния). Таким образом, имеем

{eq} P = \ tau \ omega {/ eq}.

Здесь показано, как связаны крутящий момент и угловая скорость, и это выражение аналогично

{eq} P = Fv {/ eq},

, где крутящий момент {eq} \ tau {/ eq} заменяется простым сила {eq} F {/ eq} и угловая скорость {eq} \ omega {/ eq} заменяются линейной скоростью {eq} v {/ eq}.

Угловое ускорение

При вращательном движении угловое ускорение {eq} \ alpha {/ eq} — это изменение угловой скорости {eq} \ omega {/ eq} в единицу времени {eq} t {/ eq}. В математической форме:

Кинетическая энергия вращения

Кинетическая энергия, связанная с вращательным движением, называется кинетической энергией вращения . Это зависит от угловой скорости {eq} \ omega {/ eq} и момента инерции {eq} I {/ eq} вращающегося тела.

Центробежная сила

Когда тело массой {eq} m {/ eq} вращается вокруг фиксированной точки, которая находится на расстоянии {eq} r {/ eq} от него, тело чувствует внешнюю силу, действующую на . Эта сила называется центробежной силой и действует вдали от фиксированной точки, вокруг которой вращается тело. Центробежная сила определяется соотношением

Эффект Кориолиса

Когда Земля вращается вокруг своей оси, циркулирующий воздух в атмосфере отклоняется вправо в северном полушарии и влево в южном полушарии.Это отклонение воздушных потоков из-за вращательного движения Земли называется эффектом Кориолиса , а сила, связанная с ним, называется силой Кориолиса. Величина этой силы определяется как

Система шкивов

Шкив — это небольшое колесо с рифленым ободом, к которому можно прикрепить нить или веревку. Когда к одному концу каната прикреплен тяжелый груз, его можно легко подтянуть вверх, приложив направленную вниз силу к другому (свободному) концу каната, прикрепленному к шкиву.Более чем один шкив может быть соответствующим образом скомпонован для образования системы шкивов , что еще больше упрощает перемещение тяжелого груза.

Когда колесо шкива вращается, оно имеет соответствующую угловую скорость {eq} \ omega {/ eq}. Угловая скорость, связанная со шкивом, может быть определена путем приравнивания потенциальной и кинетической энергии системы следующим образом.

Подставляя выражения для трех энергий, получаем

Резюме урока

Подводя итоги этого урока, давайте вернемся к некоторым важным концепциям, которые были обсуждены. Вращение можно определить как твердое тело , движущееся вокруг фиксированной оси , при этом все частицы тела зафиксированы на месте. Скорость, связанная с вращательным движением тела, называется угловой скоростью . Угловая скорость вращающегося тела определяется как изменение его углового смещения в единицу времени. Угловая скорость является важным понятием в механике и определяет несколько физических величин, таких как угловое ускорение , кинетическая энергия вращения , центробежная сила , сила Кориолиса и движение системы шкивов .

Вот некоторые основные моменты урока:

Угловая скорость {eq} \ omega {/ eq} имеет несколько связанных формул, которые можно использовать в разных контекстах: {eq} \ omega = \ frac {\ Delta \ theta} {\ Delta t} = \ frac {arc} {radius} \ times \ frac {1} {t} = \ frac {v} {r} {/ eq}

Угловая скорость {eq} \ omega {/ eq} связана с линейной скоростью {eq} v {/ eq} по формуле {eq} v = \ omega r {/ eq}

Единица измерения угловой скорости в системе СИ — рад / с , а другие ее единицы — об / с и об / мин (или об / мин )

Формула для угловой скорости

.Определение, лучший пример и многое другое

Формула угловой скорости описывает, насколько быстро объект вращается или движется относительно другой стадии, то есть как быстро угловое положение или ориентация объекта изменяется со временем. Угловая скорость вращения описывает, насколько быстро твердое тело вращается относительно своего центра вращения. Орбитальная угловая скорость относится к тому, насколько быстро точечный объект вращается вокруг заданной точки начала координат, то есть периодической скорости изменения его углового положения относительно начала координат.

Обычно угловая скорость измеряется в углах в единицу времени, например радиан в минуту. Единица измерения угловой скорости в системе СИ выражается в радианах / сек вместе с радианом, имеющим безразмерное значение, равное единице, и, следовательно, единицы измерения угловой скорости в системе СИ записываются как 1 / сек.

\ Угловая скорость обычно обозначается символом омега (ω, иногда Ω). Угловая скорость — это скорость, с которой предмет или частица наклоняются вокруг центра или определенной точки в заданный период времени.Ее еще называют скоростью вращения. Угловая скорость измеряется в углах в единицу времени или в радианах в секунду (рад / с). Давайте узнаем более подробно о связи между угловой скоростью и линейной скоростью, угловым смещением и угловым ускорением.

Формула для угловой скорости

Что такое угловая скорость?

Угловая скорость — это векторная величина, называемая скоростью изменения углового смещения, которая определяет угловую скорость или скорость вращения объекта и ось, по которой объект вращается.Величина изменения углового смещения частицы за определенный промежуток времени известна как угловая скорость. Траектория вектора угловой скорости перпендикулярна плоскости вращения в направлении, которое обычно указывается числовым правилом.

Формула угловой скорости

Для начала, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-то другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругу или их части.Вы можете вспомнить из геометрии или тригонометрии, что длина окружности окружности равна ее диаметру, т.е. представляет собой константу пи или πd. (Значение пи составляет около 3,14159.) Это гораздо чаще выражается в отношении радиуса круга r, который составляет половину диаметра, что составляет длину окружности 2πr.

Кроме того, вы, вероятно, уже где-то слышали, что кольцо состоит из 360 градусов (360 °). Если вы переместите расстояние S по окружности, то угловое смещение θ эквивалентно S / r.Таким образом, один полный оборот дает 2πr / r, что оставляет 2π. Это означает, что углы меньше 360 ° могут быть выражены относительно пи или, другими словами, в радианах. Также прочтите — Правила и определение горизонтальной асимптоты

Взяв все эти части данных вместе, вы можете передавать углы или части круга в единицах, отличных от уровней:

360 ° = (2π) радиан.

1 радиан = (360 ° / / 2π) = 57,3 °,

В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно каждую минуту.

Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r в середине этого круга, причем направление v постоянно перпендикулярно радиусу круга, тогда угловая скорость может быть равна письменный

Единицы угловой скорости — радианы в минуту; вы также можете рассматривать эту единицу как «обратные моменты», поскольку v / r дает м / с, деленные на m, или с-1, что означает, что радианы технически являются безразмерной величиной.

Формулировка угловой скорости в оборотах в минуту

Оборотов в минуту Программы

Обороты в минуту также используются для выражения того, насколько быстро вращается круговой объект, такой как колесо.Поскольку один оборот равен одному полному обороту или вращению вокруг центральной ступени, говорят, что колесо, совершающее один полный оборот вокруг своего центра за минуту, вращается вокруг своего центра со скоростью 1 оборот в секунду или один оборот в минуту. Поскольку следующей стрелке часов требуется 1 минута, чтобы сделать один полный оборот вокруг своего центра, ее скорость вращения составляет 1 оборот в секунду или один оборот в минуту. Предложение — буквенно-цифровой символ | Определение и символы

Угловая скорость — обзор

3.09.4.1.1 Вековой тренд, приливная диссипация и ледниковая изостатическая корректировка

Приливная диссипация вызывает уменьшение угловой скорости Земли и, следовательно, углового момента вращения ( см. Глава 3.07). Поскольку угловой момент системы Земля-Луна сохраняется, орбитальный угловой момент Луны должен увеличиваться, чтобы уравновесить уменьшение углового момента вращения Земли. Увеличение орбитального углового момента Луны достигается за счет увеличения радиуса орбиты Луны и уменьшения орбитальной угловой скорости Луны.Но ранние наблюдения за положением Луны показали, что она явно ускоряется, а не замедляется на своей орбите. Это кажущееся ускорение Луны было результатом предположения, что Земля вращается с постоянной, а не уменьшающейся угловой скоростью при прогнозировании положения Луны. Если угловая скорость Земли на самом деле уменьшается, но предполагается, что она постоянна при прогнозировании положения Луны, то наблюдаемое положение Луны будет опережать ее прогнозируемое положение, то есть Луна будет казаться ускоряющейся в его орбита.То, что Луна явно ускоряется по своей орбите, было впервые отмечено Галлеем (1695). Но только в 1939 году Спенсер Джонс (1939) смог убедительно продемонстрировать, что угловая скорость Земли на самом деле уменьшается и что видимое ускорение Луны на ее орбите было артефактом предположения, что угловая скорость Земли был постоянным.

Галлей (1695) также, кажется, был первым, кто оценил важность древних и средневековых записей о лунных и солнечных затмениях для определения видимого ускорения Луны и соответствующего уменьшения угловой скорости Земли за последние несколько лет. тысяча лет.Изменение скорости вращения Земли можно вывести из несоответствия между тем, когда и где должны были наблюдаться затмения, если бы угловая скорость Земли была постоянной, а когда и где они действительно наблюдались, как записано на вавилонских глиняных табличках и на китайских, европейских и арабские книги и рукописи (Stephenson, 1997).

При использовании наблюдений за затмениями для определения векового изменения продолжительности дня за последние несколько тысяч лет необходимо точно знать положение Солнца и Луны.Первостепенное значение в этом отношении имеет значение приливного ускорения n ̇ Луны, поскольку оно определяет долгосрочное поведение Луны. Приливное ускорение Луны может быть определено из наблюдений за временем прохождения Меркурия (например, Spencer Jones, 1939; Morrison and Ward, 1975), а также из спутниковых и лунных лазерных измерений. Приливные силы искажают фигуру Земли и, следовательно, ее гравитационное поле, которое, в свою очередь, нарушает орбиты искусственных спутников.Измерения SLR могут обнаруживать эти приливные возмущения на орбитах спутников и, следовательно, могут использоваться для построения моделей приливов и, следовательно, определения приливного ускорения Луны. Используя этот подход, Christodoulidis et al. (1988) сообщает о величине -25,27 ± 0,61 угловой секунды в столетие ² (″ / cy ²) для приливного ускорения n ̇ Луны из-за рассеяния твердой Землей и океанскими приливами. Другие полученные из SLR значения для n ̇ были сообщены Cheng et al. (1990, 1992), Marsh et al. (1990, 1991), Dickman (1994), Lerch et al. (1994) и Рэй (1994).

Подобно орбитам искусственных спутников, орбита Луны также подвержена влиянию приливных сил. Поскольку измерения LLR могут обнаруживать приливные возмущения на орбите Луны, их можно использовать для определения приливного ускорения Луны. Помимо чувствительности к орбитальным возмущениям, вызванным приливами на Земле, измерения LLR, в отличие от измерений SLR, также чувствительны к орбитальным возмущениям, вызванным приливами на Луне.Используя измерения LLR, Williams et al. (2001) сообщают о значении -25,73 ± 0,5 ″ / cy ² для приливного ускорения Луны, что по закону Кеплера соответствует увеличению на 3,79 ± 0,07 см / год ⁻¹ в большой полуоси Луны. Орбита Луны, которая включает вклад +0.29 ″ / cy ² из-за рассеяния внутри самой Луны. В настоящее время изучена лишь половина расхождения между значениями, полученными из SLR и LLR для n ̇ из-за рассеяния справедливыми приливами на Земле (Williams et al., 2001). Другие полученные значения LLR для n ̇ были представлены Newhall et al. (1988), Dickey et al. (1994a) и Chapront et al. , (2002).

По a priori принимая значение приливного ускорения n ̇ Луны, наблюдения за лунными и солнечными затмениями могут быть использованы для определения векового увеличения продолжительности дня за последние несколько тысяч лет. Самые последние повторные редукции наблюдений за лунными и солнечными затмениями на предмет изменений LOD сделаны Стефенсоном и Моррисоном (1995) и Моррисоном и Стивенсоном (2001).Помимо наблюдений за затмениями в период с 700 г. до н.э. до 1600 г. н.э., они также использовали наблюдения за лунным затмением в период 1600–1955,5 гг. И оптические астрометрические и космически-геодезические измерения за период 1955,5–1990 гг. Приняв значение -26,0 ″ / cy ² для n ̇, Моррисон и Стивенсон (2001) обнаружили, что LOD увеличивался со скоростью +1,80 ± 0,1 мс / цикл в среднем за последние 2700 лет (см. Рисунок 3 ). В дополнение к вековой тенденции Стефенсон и Моррисон (1995) и Моррисон и Стефенсон (2001) также нашли доказательства флуктуации LOD с размахом около 8 мс и периодом около 1500 лет ( Рисунок 3 ).

Рис. 3. Вековые изменения LOD за последние 2500 лет, оцененные по данным лунных и солнечных затмений, затмения Луны, оптических астрометрических и космических геодезических наблюдений. Разница между наблюдаемым вековым трендом и трендом, вызванным приливным трением, обусловлена эффектами изостатической регулировки ледников и другими процессами, такими как изменение массы ледяного покрова и сопутствующее нестерическое изменение уровня моря. Из Моррисона Л.В. и Стивенсона FR (2001) Исторические затмения и изменчивость вращения Земли. Журнал геодинамики 32: 247–265.

При сохранении углового момента приливное ускорение Луны на -26,0 ″ / cy ² должно сопровождаться увеличением продолжительности дня на +2,3 мс / cy (Stephenson and Morrison, 1995). Поскольку наблюдаемое увеличение продолжительности дня составляет всего +1,8 мс / с (Morrison and Stephenson, 2001), должен действовать какой-то другой механизм или комбинация механизмов, чтобы изменить продолжительность дня на -0,5 мс / с. Согласно уравнениям [43] и [58], изменения как осевой составляющей относительного углового момента, так и полярного момента инерции Земли могут вызвать изменение LOD.Вековая тенденция общей циркуляции флюидов, таких как атмосфера и океаны, и, следовательно, атмосферного и океанического углового момента, вряд ли сохранится в течение нескольких тысяч лет. Фактически, используя результаты 100-летнего прогона модели общей циркуляции атмосферы Центра Хэдли, de Viron et al. (2004) обнаружил, что смоделированный вековой тренд атмосферного углового момента (AAM) в течение 1870–1997 гг. Вызывает вековой тренд LOD только +0,08 мс / с.

Одним из наиболее важных механизмов, вызывающих вековой тренд LOD во временных масштабах в несколько тысяч лет, является изостатическое регулирование ледникового покрова (GIA).Изостатическая регулировка твердой Земли в ответ на уменьшающуюся нагрузку на нее после последней дегляциации вызывает изменение фигуры Земли и, следовательно, изменение LOD. Поскольку твердая Земля отскакивает в регионах на высоких широтах, где раньше находилась ледяная нагрузка, фигура Земли становится менее сжатой, вращение Земли ускоряется, а LOD уменьшается. Модели GIA показывают, что его влияние на LOD очень чувствительно к предполагаемому значению вязкости нижней мантии (например.g., Wu and Peltier, 1984; Пельтье и Цзян, 1996; Vermeersen et al. , 1997; Митровица и Милн, 1998; Джонстон и Ламбек, 1999; Tamisea et al. , 2002; Сабадини и Вермеерсен, 2004). Но, создав модель для профиля радиальной вязкости Земли, которая соответствует как временам послеледникового распада, так и аномалиям силы тяжести в свободном воздухе, связанным с мантийной конвекцией, Митровица и Форте (1997) обнаружили, что GIA должна вызывать вековую тенденцию в LOD, составляющую — 0,5 мс / цикл, значение, которое замечательно согласуется с тем, что необходимо для объяснения разницы между наблюдаемым вековым трендом продолжительности дня и трендом, вызванным приливной диссипацией.

Однако GIA — не единственный механизм, который вызовет вековой тренд продолжительности дня. Современное изменение массы ледников и ледникового покрова и сопутствующее изменение нестерического уровня моря также вызовут вековую тенденцию в LOD (например, Peltier, 1988; Trupin et al. , 1992; Mitrovica and Peltier, 1993; Trupin , 1993; Джеймс и Айвинс, 1995, 1997; Накада и Окуно, 2003; Този и др. , 2005). Но влияние этого механизма на LOD очень чувствительно к неизвестному в настоящее время массовому изменению ледников и ледяных щитов, особенно антарктического ледяного покрова.Принимая различные сценарии массового изменения Антарктиды, модели предсказывают, что только ее массовое изменение должно вызвать вековой тренд LOD в диапазоне от -0,72 до +0,31 мс / с (Джеймс и Айвинс, 1997). Другие механизмы, которые могут вызывать вековой тренд LOD, включают тектонические процессы, происходящие в неизостатических условиях (Vermeersen and Vlaar, 1993; Vermeersen et al. , 1994; Sabadini and Vermeersen, 2004), субдукция плит (Alfonsi and Spada, 1998). землетрясения (Chao, Gross, 1987) и деформация мантии, вызванная колебаниями давления на границе ядро-мантия, связанными с движением флюидного ядра (Fang et al., 1996; Дамберри и Блоксхэм, 2004; Greff-Lefftz et al. , 2004).

Колебание LOD за 1500-летний период, обнаруженное Стефенсоном и Моррисоном (1995) и Моррисоном и Стивенсоном (2001), в настоящее время имеет неизвестное происхождение. Однако, учитывая его большую амплитуду, которая слишком велика, чтобы быть вызванной атмосферными и океаническими процессами, но сравнима по размеру с амплитудой десятилетних вариаций, она, вероятно, вызвана (Dumberry and Bloxham, 2006) тем же ядром и мантией. взаимодействия ( см. Глава 8.12), такие как гравитационное взаимодействие (Rubincam, 2003), которые, как известно, вызывают десятилетние вариации LOD.

Формула угловой скорости — определение, пример и многое другое

Формула угловой скорости относится к тому, насколько быстро объект вращается или вращается относительно другой точки, то есть насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и угловая скорость вращения. Угловая скорость вращения означает, насколько быстро твердое тело вращается относительно центра вращения.Орбитальная угловая скорость относится к тому, насколько быстро точечный объект вращается вокруг фиксированного начала координат, то есть скорость изменения его углового положения относительно начала координат во времени. Как правило, угловая скорость измеряется в углах в единицу времени, например. радиан в секунду. Единица измерения угловой скорости в системе СИ выражается в радианах / сек, причем радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ обозначаются как 1 / сек.

\ Угловая скорость обычно обозначается символом омега (ω, иногда Ω).По соглашению, положительная угловая скорость означает вращение против часовой стрелки, а отрицательная — по часовой стрелке. Угловая скорость — это скорость, с которой объект или частица вращается вокруг центра или определенной точки в заданный период времени. Это также известно как скорость вращения. Угловая скорость измеряется в углах в единицу времени или в радианах в секунду (рад / с). Скорость изменения угловой скорости — это угловое ускорение. Давайте узнаем более подробно о связи между угловой скоростью и линейной скоростью, угловым смещением и угловым ускорением.

Формула угловой скорости

Что такое угловая скорость?

Угловая скорость — это векторная величина, описываемая как скорость изменения углового смещения, которая определяет угловую скорость или скорость вращения объекта и ось, вокруг которой объект вращается. Величина изменения углового смещения частицы за определенный период времени называется угловой скоростью. Траектория вектора угловой скорости вертикальна к плоскости вращения в направлении, которое обычно указывается правилом правой руки.

Формула угловой скорости

Уравнение угловой скорости

Во-первых, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-либо другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругам или их частям. Вы можете вспомнить из геометрии или тригонометрии, что длина окружности равна его диаметру, умноженному на константу пи, или πd . (Значение пи составляет около 3,14159.) Это чаще всего выражается в терминах радиуса круга r , который составляет половину диаметра, в результате чего окружность 2πr .

Угловое смещение

Кроме того, вы, вероятно, где-то по пути узнали, что круг состоит из 360 градусов (360 °). Если вы переместитесь на расстояние S по окружности, то угловое смещение θ будет равно S / r. Таким образом, один полный оборот дает 2πr / r, что оставляет 2π. Это означает, что углы меньше 360 ° могут быть выражены в единицах пи или, другими словами, в радианах.

Взяв всю эту информацию вместе, вы можете выразить углы или части круга в единицах, отличных от градусов:

1 радиан = (360 ° / 2π) = 57.3 °,

Формула угловой скорости

В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно в секунду.

Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r от центра круга, причем направление v всегда перпендикулярно радиусу круга, тогда угловую скорость можно записать

, где ω — греческая буква омега.Единицы угловой скорости — радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v / r дает м / с, деленные на m, или с ^-1, что означает, что радианы технически являются безразмерной величиной.

Формула угловой скорости в об / мин

Оборотов в минуту Использует

оборотов в минуту также используются для выражения скорости вращения круглого объекта, такого как колесо. Поскольку один оборот эквивалентен одному полному обороту или вращению вокруг центральной точки, говорят, что колесо, которое совершает один полный оборот вокруг своего центра за минуту, вращается вокруг своего центра со скоростью 1 оборот в минуту или 1 оборот в минуту.Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 1 минуту, ее скорость вращения составляет 1 оборот в минуту или 1 оборот в минуту.

Формула угловой скорости в об / мин

Преобразование угловой скорости в число оборотов в минуту

Угловая скорость в градусах в секунду может быть преобразована в число оборотов в минуту путем умножения угловой скорости на 1/6, поскольку один оборот равен 360 градусам, а есть 60 секунд в минуту. Если угловая скорость задана равной 6 градусам в секунду, частота вращения будет 1 оборот в минуту, поскольку 1/6, умноженная на 6, будет равна 1.

об / мин для преобразования угловой скорости

Оборотов в минуту можно преобразовать в угловую скорость в градусах в секунду, умножив число оборотов в минуту на 6, поскольку один оборот составляет 360 градусов, а это 60 секунд в минуту. Если частота вращения равна 1 об / мин, угловая скорость в градусах в секунду будет равна 6 градусам в секунду, так как 6 умноженное на 1 дает 6.

Какая единица измерения угловой скорости?

Единица измерения угловой скорости в системе СИ — радианы в секунду.Но он может быть измерен и в других единицах (например, градусах в секунду, градусах в час и т. Д.). Угловая скорость обычно обозначается символом омега (Ω или ω).

Какая формула для скорости?

Уравнение или формула для скорости аналогична скорости. Чтобы вычислить скорость, вы делите расстояние на время, необходимое для прохождения того же расстояния, а затем добавляете к нему свое направление.

Какая формула углового момента?

p = m * v.С небольшим упрощением, угловой момент (L) определяется как расстояние объекта от оси вращения, умноженное на количество движения: L = r * p или L = mvr.

Какова формула угловой скорости?

Это изменение угла движущегося объекта (измеряется в радианах), деленное на время. Угловая скорость имеет величину (значение) и направление. (360 градусов — это 2π рад). Время, необходимое для того, чтобы секундная стрелка повернулась на 180 градусов, составляет 30 секунд, поэтому t = 30 секунд.Теперь мы можем вычислить угловую скорость.

Какой пример угловой скорости?

Угловая скорость, обозначенная буквой w, представляет собой скорость изменения этого угла во времени. Угловая скорость. Например, колесо обозрения может каждую минуту вращаться на пи / 6 радиан. Следовательно, угловая скорость колеса обозрения будет равна пи / 6 радиан в минуту.

Сообщение навигации

Угловая скорость

Введение

В физике угловая скорость — это векторная величина (точнее, псевдовектор), которая определяет угловую скорость объекта и ось, вокруг которой объект вращается.Единица (метрическая система) угловой скорости — радианы в секунду, хотя она может быть измерена в других единицах, таких как градусы в секунду, обороты в секунду, обороты в минуту, градусы в час и т. Д. Иногда его также называют вращением . скорость и ее величина — скорость вращения, обычно измеряемая в циклах или оборотах в единицу времени (например, оборотов в минуту). Угловая скорость обычно обозначается символом омега ( ω , редко Ω ).

Радиан в секунду определяется как изменение ориентации объекта в радианах каждую секунду.

Угловая частота ω	(Обычная) частота ν = ω / 2π
2π радиан в секунду	ровно 1 герц (Гц)
1 радиан в секунду	примерно 0.159155 Гц
1 радиан в секунду	примерно 57,29578 градусов в секунду
1 радиан в секунду	примерно 9,5493 об / мин

Другое — Radian

Радиан описывает плоский угол, образованный дугой окружности, как длину дуги, деленную на радиус дуги. Один радиан — это угол, образуемый в центре окружности дугой, длина которой равна радиусу окружности.В более общем смысле величина такого вытянутого угла в радианах равна отношению длины дуги к радиусу круга; то есть θ = s / r, где θ — угол наклона в радианах, s — длина дуги, а r — радиус. И наоборот, длина замкнутой дуги равна радиусу, умноженному на величину угла в радианах; то есть s = rθ. Полный оборот составляет 2π радиан (здесь показан круг радиуса один и окружность 2π).

Отсюда следует, что величина в радианах одного полного оборота (360 градусов) равна длине всей окружности, деленной на радиус, или 2πr / r, или 2π.Таким образом, 2π радиан равняется 360 градусам, что означает, что один радиан равен 180 / π градусам.

Ссылки и ресурсы

Википедия — http://en.wikipedia.org/wiki/Angular_velocity
Википедия — http://en.wikipedia.org/wiki/Radians_per_second

Угловая скорость Земли — Вселенная сегодня

[/ caption]
Планета Земля совершает три движения: она вращается вокруг своей оси, что дает нам день и ночь; он вращается вокруг Солнца, давая нам времена года, и проходит через Млечный Путь вместе с остальной частью Солнечной системы.В каждом случае ученые пытались рассчитать не только время, необходимое для этого, но и соответствующие относительные скорости. Когда речь идет о вращении Земли вокруг своей оси, процесс, который занимает 23 часа 56 минут и 4,09 секунды, этот процесс известен как звездные сутки, а скорость, с которой она движется, известна как угловая скорость Земли. Это в равной степени относится к Земле, вращающейся вокруг оси Солнца и центра Галактики Млечный Путь.

В физике угловая скорость — это векторная величина, которая определяет угловую скорость объекта и ось, вокруг которой объект вращается.Единица измерения угловой скорости в системе СИ — радианы в секунду, хотя она может быть измерена в других единицах, таких как градусы в секунду, обороты в секунду и т. Д., И обычно обозначается символом омега (ω, реже Ω). Радиан по определению — это единица измерения, которая связывает радиус дуги, длину дуги и угол, образованный дугой. Полный радиан равен 360 градусам, следовательно, мы знаем, что Земля совершает два радиана при полном вращении вокруг оси. Однако иногда ее также называют скоростью вращения, и ее величина — скорость вращения — обычно измеряется в циклах или оборотах в единицу времени (например,грамм. обороты в минуту). Кроме того, когда объект вращается вокруг оси, каждая точка объекта имеет одинаковую угловую скорость.

Математически средняя угловая скорость объекта может быть представлена следующим уравнением: ω _{среднее значение} = Δθ / Δt, где ω — радианы / обороты в секунду (в среднем), Δ — изменение количества, θ — скорость, а t — время. При вычислении угловой скорости Земли, когда она совершает полный оборот вокруг своей оси (солнечные сутки), это уравнение представляется как: ω _avg = 2πrad / 1day (86400 секунд), что соответствует умеренным угловым значениям. скорость 7.2921159 × 10 ^-5 радиан / сек. В случае солнечного года, где ω _avg = 2πрад / 1 год (3,2 × 10 ⁷ секунд), мы видим, что угловая скорость составляет 2,0 × 10 ^-7 рад / с.

Мы написали много статей об угловой скорости Земли для Universe Today. Вот статья об угловой скорости, а вот статья о том, почему Земля вращается.

Если вам нужна дополнительная информация об угловой скорости Земли, ознакомьтесь со следующими статьями:
Угловая скорость Земли
Вращение Земли

Мы также записали серию Astronomy Cast, посвященную планете Земля.

Что называют угловой скоростью: 404 — Страница не найдена

Угловая скорость — это… Что такое Угловая скорость?

Связь с конечным поворотом в пространстве

См. также

Литература

Часть 6 — Кинематика свободного твердого тела. Природа угловой скорости / Хабр

Угловая скорость — Справочник химика 21

Скорость тела угловая — Энциклопедия по машиностроению XXL

Аналог угловой скорости — Энциклопедия по машиностроению XXL

24 Угловая скорость и угловое ускорение тела, вращающегося вокруг неподвижной оси

Рекомендуемые файлы

Угловая скорость | Медицинские журналы

Актуальные темы общих наук

Формула и единицы измерения угловой скорости | Как определить угловую скорость — стенограмма видео и урока

Формула угловой скорости

Единицы угловой скорости

Как найти угловую скорость

Пример 1

Пример 2

Пример 3

Как используется угловая скорость

Правило для правой руки

Крутящий момент и угловая скорость

Угловое ускорение

Кинетическая энергия вращения

Центробежная сила

Эффект Кориолиса

Система шкивов

Резюме урока

.Определение, лучший пример и многое другое

Что такое угловая скорость?

Формула угловой скорости

Оборотов в минуту Программы

Угловая скорость — обзор

3.09.4.1.1 Вековой тренд, приливная диссипация и ледниковая изостатическая корректировка

Формула угловой скорости — определение, пример и многое другое

Сообщение навигации

Угловая скорость

Введение

Другое — Radian

Ссылки и ресурсы

Угловая скорость Земли — Вселенная сегодня

Добавить комментарий Отменить ответ