Падение напряжения: расчет, формула, как найти
Чтобы понять, что такое падение напряжения, следует вспомнить, какие виды напряженности в цепи бывают. Их всего два: напряженность источника питания (при этом источник питания должен быть подключен к контуру) и, собственно, снижение напряжения, которое рассматривается отдельно или в отношении контура. В этом материале будет рассмотрено, как найти падение напряжения, и дана формула расчета падения напряжения в кабеле.
Что означает падение напряжения
Падение происходит, когда происходит перенос нагрузки на всем участке электрической цепи. Действие этой нагрузки напрямую зависит от параметра напряженности в ее узловых элементах. Когда определяется сечение проводника, важно участь, что его значение должно быть таким, чтобы в процессе нагрузки сохранялось в определенных границах, которые должны поддерживаться для нормального выполнения работы сети.
Мнемоническая диаграмма для закона ОмаБолее того, нельзя пренебрегать и характеристикой сопротивляемости проводников, из которых состоит цепь.
Важно! Предел допустимого значения рассматриваемой характеристики отличается от страны к стране. Забывать это нельзя. Если она снижается ниже значений, которые определены в определенной стране, следует использовать провода с большим сечением.
Любой электроприбор будет работать полноценно, если к нему подается то значение, на которое он рассчитан. Если провод взят неверно, то из-за него происходят большие потери электронапряжения, и оборудование будет работать с заниженными параметрами. Особенно актуально это для постоянного тока и низкой напряженности. Например, если оно равно 12 В, то потеря одного-двух вольт уже будет критической.
Допустимое падение напряжение в кабеле
Значение потери электронапряжения регламентируется и нормируется сразу несколькими правилами и инструкциями устройства электроустановок. Так, согласно правилу СП 31-110-2003, суммарная потеря напряжения от входной точки в помещении до максимально удаленного от нее потребителя электроэнергии не должно быть больше 7.5 %. Это правило работает на всех электроцепях с напряжением не более 400 вольт. Данное правило используется при монтаже и проектировке сетей, а также при их проверке службами Ростехнадзора.
Так, согласно правилу СП 31-110-2003, суммарная потеря напряжения от входной точки в помещении до максимально удаленного от нее потребителя электроэнергии не должно быть больше 7.5 %. Это правило работает на всех электроцепях с напряжением не более 400 вольт. Данное правило используется при монтаже и проектировке сетей, а также при их проверке службами Ростехнадзора.
Важно! Этот документ обобщает и отклонение электронапряжения в сетях однофазного тока бытового назначения. Оно должно быть не более 5 % при нормальной работе и 10 % после аварийной ситуации. Если сеть низковольтная, то есть до 50 вольт, то нормальным падением считается +-10 %.
Для кабелей питающей сети используют правило РД 34.20.185-94. Оно допускает параметр потерь не более 6 %, если напряжение составляет 10 кВ и не более 4–6 % при электронапряжении 380 вольт. Чтобы одновременно соблюсти эти правила и инструкции, добиваются потерь 1.5 % для малоэтажных знаний и 2.5 % для многоэтажных.
Проверка кабеля по потере напряжения
Всем известно, что протекание электрического тока по проводу или кабелю с определенным сопротивлением всегда связано с потерей напряжения в этом проводнике.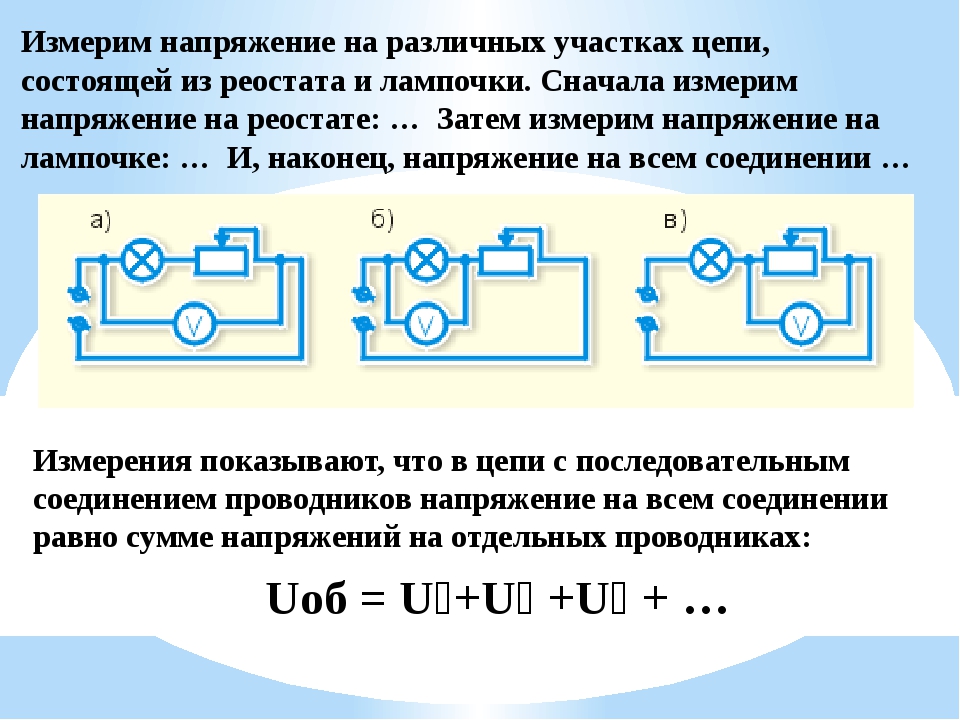
Согласно правилам Речного регистра, общая потеря электронапряжения в главном распределительном щите до всех потребителей не должна превышать следующие значения:
- при освещении и сигнализации при напряжении более 50 вольт – 5 %;
- при освещении и сигнализации при напряжении 50 вольт – 10 %;
- при силовых потреблениях, нагревательных и отопительных систем вне зависимости от электронапряжения – 7 %;
- при силовых потреблениях с кратковременным и повторно-кратковременным режимами работы вне зависимости от электронапряжения – 10 %;
- при пуске двигателей – 25 %;
- при питании щита радиостанции или другого радиооборудования или при зарядке аккумуляторов – 5 %;
- при подаче электричества в генераторы и распределительный щит – 1 %.
Исходя из этого и выбирают различные типы кабелей, способных поддерживать такую потерю напряжения.
Пример калькулятора для автоматизации вычисленийКак найти падение напряжения и правильно рассчитать его потерю в кабеле
 Для проводки от станции или щитка к помещению используются медные или алюминиевые провода. Их удельные сопротивления равны 0,0175 Ом*мм2/м для меди и 0,0280 Ом*мм2/м для алюминия.
Для проводки от станции или щитка к помещению используются медные или алюминиевые провода. Их удельные сопротивления равны 0,0175 Ом*мм2/м для меди и 0,0280 Ом*мм2/м для алюминия.Рассчитать падение электронапряжения для цепи постоянного тока в 12 вольт можно следующими формулами:
- определение номинального тока, проходящего через проводник. I = P/U, где P – мощность, а U – номинальное электронапряжение;
- определение сопротивления R=(2*ρ*L)/s, где ρ – удельное сопротивление проводника, s – сечение провода в миллиметрах квадратных, а L – длина линии в миллиметрах;
- определение потери напряженности ΔU=(2*I*L)/(γ*s), где γ – это величина, которая равна обратному удельному сопротивлению;
- определение требуемой площади сечения провода: s=(2*I*L)/(γ*ΔU).
Важно! Благодаря последней формуле можно рассчитать необходимую площадь сечения провода по нагрузке и произвести проверочный расчет потерь.
Таблица значений индуктивных сопротивленийВ трехфазной сети
Для обеспечения оптимальной нагрузки в трехфазной сети каждая фаза должна быть нагружена равномерно.
Потеря электронапряжения в каждом проводе трехфазной линии с учетом индуктивного сопротивления проводов подсчитывается по формуле
Формула расчетаПервый член суммы – это активная, а второй – пассивная составляющие потери напряженности. Для удобства расчетов можно пользоваться специальными таблицами или онлайн-калькуляторами. Ниже приведен пример такой таблицы, где учтены потери напряжения в трехфазной ВЛ с алюминиевыми проводами электронапряжением 0,4 кВ.
Пример таблицыПотери напряжения определены следующей формулой:
ΔU = ΔUтабл * Ма;
Здесь ΔU—потеря напряжения, ΔUтабл — значение относительных потерь, % на 1 кВт·км, Ма — произведение передаваемой мощности Р (кВт) на длину линии, кВт·км.
Однолинейная схема линии трехфазного токаНа участке цепи
Для того, чтобы провести замер потери напряжения на участке цепи, следует:
- Произвести замер в начале цепи.

- Выполнить замер напряжения на самом удаленном участке.
- Высчитать разницу и сравнить с нормативным значением. При большом падении рекомендуется провести проверку состояния проводки и заменить провода на изделия с меньшим сечением и сопротивлением.
Важно! В сетях с напряжением до 220 в потери можно определить при помощи обычного вольтметра или мультиметра.
Базовым способом расчета потери мощности может служить онлайн-калькулятор, который проводит расчеты по исходным данным (длина, сечение, нагрузка, напряжение и число фаз).
Образец калькулятора для вычисления потерьТаким образом, вычислить и посчитать потери напряжения можно с помощью простых формул, которые для удобства уже собраны в таблицы и онлайн-калькуляторы, позволяющие автоматически вычислять величину по заданным параметрам.
Напряжение на участке цепи
Содержание:
Напряжение на участке цепи
Сетевое напряжение.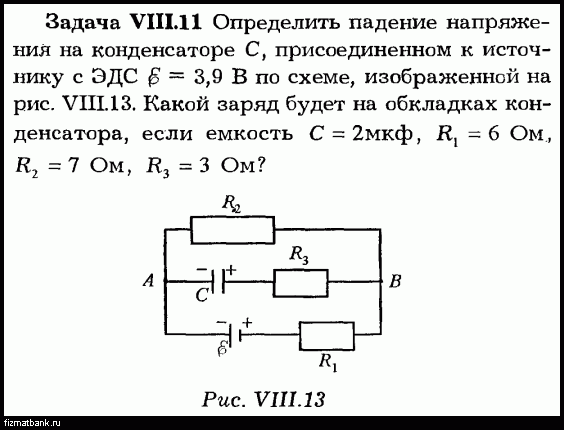 Напряжение определенного участка электрической цепи будет понимать разность потенциалов между крайними значениями этого участка. На Рис. 5 показано сопротивление R, E не являющееся участком цепи. D. s. крайние точки этого раздела обозначены буквами a и B. ток потока I из точки a в точку B. в области цепи без Э. Д. ток s течет от высокого потенциала к низкому потенциалу.
Напряжение определенного участка электрической цепи будет понимать разность потенциалов между крайними значениями этого участка. На Рис. 5 показано сопротивление R, E не являющееся участком цепи. D. s. крайние точки этого раздела обозначены буквами a и B. ток потока I из точки a в точку B. в области цепи без Э. Д. ток s течет от высокого потенциала к низкому потенциалу.
- Таким образом, потенциал точки a (fv) выше на величину, равную произведению тока/сопротивления R, чем потенциал точки b (fv). Ф. = Ф» + ’ Я- По определению, напряжение между точкой a и точкой b равно Uab = f. — f. *- Итак, Uob = IR.
В электротехнике разность потенциалов на обоих концах резистора обычно является «напряжением сопротивления»(например, L. 2 * в целом) или» падением напряжения » (L. 1 в a и B обычно называют).
То есть напряжение на резисторе равно произведению тока, протекающего по резистору, на величину этого резистора. Людмила Фирмаль
В дальнейшем разность потенциалов между двумя концами резистора, то есть продукта называется падение напряжения.
Теперь рассмотрим задачу о напряжении в секции схемы, которая включает в себя не только резисторы, но и Э. Д. С. Обозначают участок некоторых цепей, по которым протекает ток I. 、は 、ind найти разность потенциалов (напряжение) между точками A и C в этих разделах.
- Потенциал точки А выражается через потенциал точки С. При переходе из точки c в точку b (рис. 6, а) переходите к счетчику E. d. s следовательно, потенциал точки b ниже (меньше) потенциала точки c на величину e. d. s E, я имею в виду Φ » =Φ< — E.
Для рисунка 6b, при перемещении из точки c в точку b, она движется в соответствии с ЭДС E, поэтому потенциал точки b только выше (больше), чем потенциал точки c, величина ЭДС E, т. е. величина ЭДС. ФГ » = Фе +Е. Ранее было сказано, что в цепном сечении без Э. Д. ток s течет от высокого потенциала к низкому потенциалу.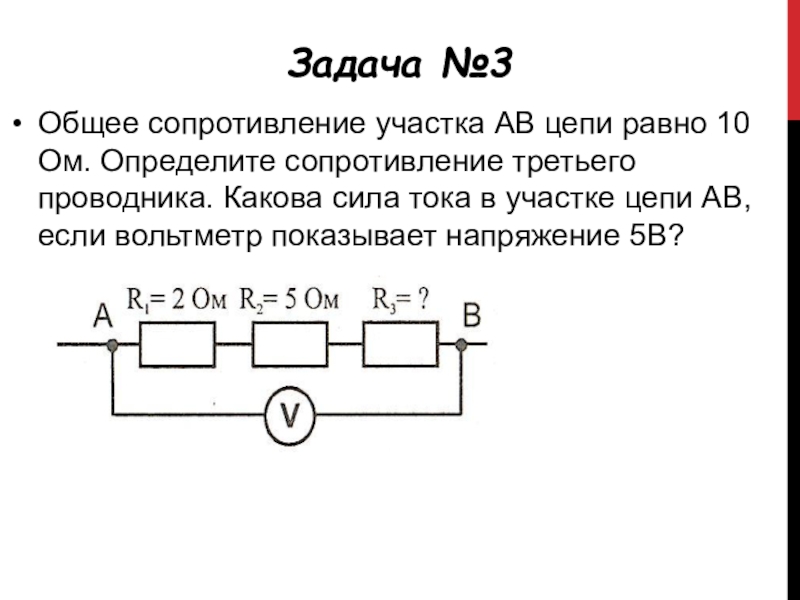 = ФА-ФС = //?+ E. (1.26) * Буква L с цифрой справа указывает на ссылку на литературу, список которой находится в конце книги. Из определения самого напряжения, это также Uca-=Фг-фа. So Uca == — Uac. In другими словами, изменение чередования (последовательности) индекса соответствует изменению знака этого напряжения.
= ФА-ФС = //?+ E. (1.26) * Буква L с цифрой справа указывает на ссылку на литературу, список которой находится в конце книги. Из определения самого напряжения, это также Uca-=Фг-фа. So Uca == — Uac. In другими словами, изменение чередования (последовательности) индекса соответствует изменению знака этого напряжения.
Из вышесказанного видно, что напряжение может быть как положительным, так и отрицательным. Положительное направление напряжения указано стрелкой на рисунке. Стрелка должна быть направлена от первой буквы указателя ко второй букве. Таким образом, положительное направление напряжения UAC является представленная стрелкой от А К А.
Смотрите также:
Предмет электротехника тоэ
Падение напряжения
Deprecated: Non-static method Date_TimeZone::getDefault() should not be called statically, assuming $this from incompatible context in /home/carkey/hitech/hardtech/kernel/pear/date/Date.php on line 201
Deprecated: Non-static method Date_TimeZone::isValidID() should not be called statically, assuming $this from incompatible context in /home/carkey/hitech/hardtech/kernel/pear/date/Date. php on line 576
php on line 576
Notice: Undefined offset: 1 in /home/carkey/hitech/hardtech/kernel/common/common/common.class.php on line 343
Notice: Undefined offset: 1 in /home/carkey/hitech/hardtech/kernel/common/common/common.class.php on line 343
Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead.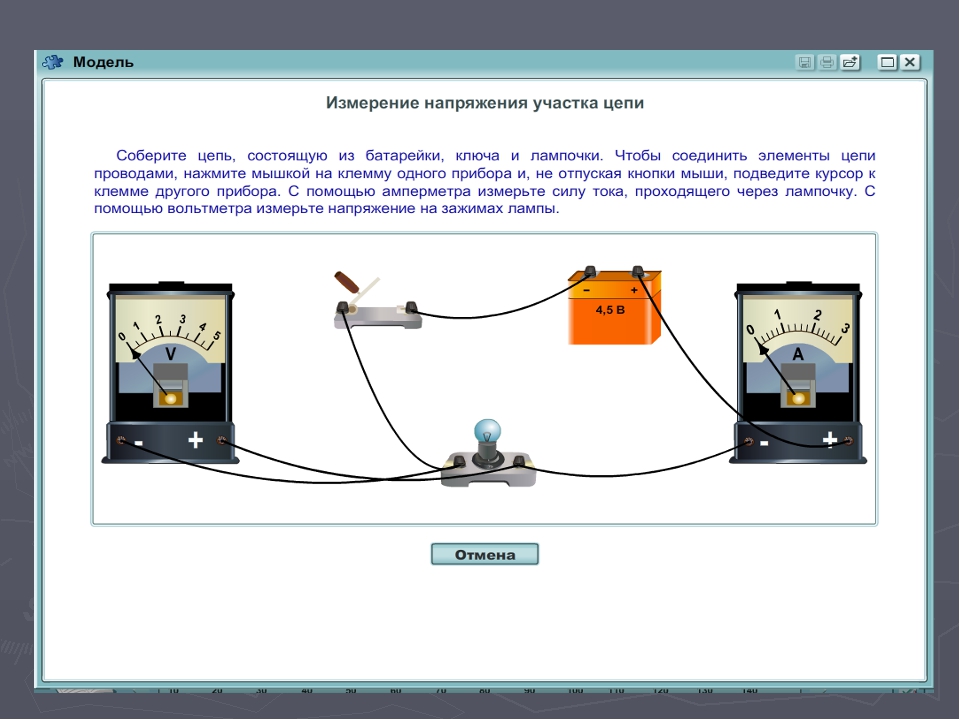 in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
Рассмотрим схему электрической цепи, состоящую из нескольких участков. Вольтметр подключен к зажимам источника тока. Он измеряет напряжение, приложенное к цепи. Вольтметры подключены к участкам цепи. Каждый из этих вольтметров показывает некоторое напряжение, меньшее напряжения источника тока. Напряжение, действующее на участке цепи, называется падением напряжения. Падение напряжения представляет собой часть напряжения источника, которая затрачивается на преодоление сопротивления данного участка цепи. Между падением напряжения на — участке и напряжением на источнике имеется существенное различие. Напряжение на источнике существует независимо от того, подключена к нему электрическая цепь или не подключена, замкнута она или разомкнута.
Падение напряжения на участках существует только тогда, когда по цепи течет ток. Если разомкнуть цепь в определенной точке, вольтметр будет по-прежнему показывать напряжение источника, а вольтметры никакого напряжения не покажут, как снимок УЗИ на первых днях беременности (см. беременность по неделям). Исходя из этого, считают, что падение напряжения на участке цепи создается током, текущим по этому участку. Выше сказано, что напряжение на источнике почти не зависит от величины тока в цепи; падение же напряжения на участке цепи зависит от величины тока и сопротивления участка. Падение напряжения на участке цепи тем больше, чем больше ток, текущий по этому участку, и чем больше сопротивление участка. Величину падения напряжения можно подсчитать, пользуясь законом Ома. Падение напряжения на участке цепи равно величине тока в участке, умноженной на сопротивление участка. Если по участку течет ток и на нем создается падение напряжения, то на концах этого участка часто ставят знаки «+» и «-». Расставлять эти знаки нужно, сообразуясь с направлением тока в участке, помня, что ток течет от плюса к минусу.
беременность по неделям). Исходя из этого, считают, что падение напряжения на участке цепи создается током, текущим по этому участку. Выше сказано, что напряжение на источнике почти не зависит от величины тока в цепи; падение же напряжения на участке цепи зависит от величины тока и сопротивления участка. Падение напряжения на участке цепи тем больше, чем больше ток, текущий по этому участку, и чем больше сопротивление участка. Величину падения напряжения можно подсчитать, пользуясь законом Ома. Падение напряжения на участке цепи равно величине тока в участке, умноженной на сопротивление участка. Если по участку течет ток и на нем создается падение напряжения, то на концах этого участка часто ставят знаки «+» и «-». Расставлять эти знаки нужно, сообразуясь с направлением тока в участке, помня, что ток течет от плюса к минусу.
Наша продукция
…
Warning: Unknown: write failed: Disk quota exceeded (122) in Unknown on line 0
Warning: Unknown: Failed to write session data (files). Please verify that the current setting of session.save_path is correct (/opt/alt/php56/var/lib/php/session) in Unknown on line 0
Please verify that the current setting of session.save_path is correct (/opt/alt/php56/var/lib/php/session) in Unknown on line 0
Падение напряжения на внешнем участке цепи U = 12 В, при внешнем сопротивлении R1 =10 Ом. При
2.4.* Нагрівник потужністю 400 Вт нагріває 400 г води від 10 до 90 °С за 10 хв. Визнач, за який час ця вода остигне на 10 °C, якщо нагрівник вимкнути. … Уважати кількість те- плоти, яку втрачає вода щосекунди, сталою.
1). яка ціна поділки мірного циліндра? 2). визначте об’єм зануреного в рідину тіла3) обчисліть довжину ланцюжка кубиків (у км) з ребром 1 см якщо їхні … й загальний об’єм дорівнює 1м кубічний4). об’єм акваріума що має форму прямокутного паралелепіпеда становить 0,0675м обчисліть площу основи в акваріума якщо його висота дорівнює 45 смпомогите даю 50
СРОЧНО! ПОМОГИТЕ ПРОШУ! БЫСТРЕЕ!
8 класс
1. В алюминиевый калориметр массой 140 г налили 250 г воды при температуре 15 градусов по Цельсию.После того,
… как брусок из свинца массой 100 г ,нагретый до 100 градусов по Цельсию,поместили в калориметр в водой,там установилась температура 16 градусов по Цельсию. Определите теплоемкость свинца.
2. 1) Два одинаковых стальных шарика, нагретые до одной и той же температуры, опустили: один в калориметр с водой, другой в калориметр с таким же количеством керосина. Какая жидкость нагреется до более высокой температуры после установления теплового равновесия?
2) В алюминиевый калориметр массой 40 г, содержащий 810г воды при температуре 15 градусов по цельсию, опустили металлический цилиндр массой 0,5 кг вынутый из кипятка. После установления теплового равновесия температура в калориметре стала равной 26 градусов по цельсию
3. В алюминиевый калориметр массой 100 г налита вода массой 240 г при температуре 15 градусов по цельсию. В калориметр погружают вынутый из кипятка маталлический брусок массой 30 г, и температура в калориметре после установления теплового равновесия повышается на 1 градус по цельсию.
а) Какое кол-во теплоты получила вода?
б) Какое кол-во теплоты отдал брусок?
в) Из какого металла может быть изготовлен брусок?
Определите теплоемкость свинца.
2. 1) Два одинаковых стальных шарика, нагретые до одной и той же температуры, опустили: один в калориметр с водой, другой в калориметр с таким же количеством керосина. Какая жидкость нагреется до более высокой температуры после установления теплового равновесия?
2) В алюминиевый калориметр массой 40 г, содержащий 810г воды при температуре 15 градусов по цельсию, опустили металлический цилиндр массой 0,5 кг вынутый из кипятка. После установления теплового равновесия температура в калориметре стала равной 26 градусов по цельсию
3. В алюминиевый калориметр массой 100 г налита вода массой 240 г при температуре 15 градусов по цельсию. В калориметр погружают вынутый из кипятка маталлический брусок массой 30 г, и температура в калориметре после установления теплового равновесия повышается на 1 градус по цельсию.
а) Какое кол-во теплоты получила вода?
б) Какое кол-во теплоты отдал брусок?
в) Из какого металла может быть изготовлен брусок?
О. Визначте об’єм (у дм3) пластини, площа основи якої дорівнює 450 см,
4 мм. а висота
а висота
помогите с физикой пожалуйста
Кроме электронамерительных приборов магнито электрической системы существуют измерительные приборы электродинамической и электромагнитной систем. В на … мерительных приборах электродинами ческой системы (рис. 2) вместо постоянного магнита используется электромагнит. Действие измеритель» ных приборов электромагнитной системы (рис. 3) основано на втягивании ферромагнитного диска в зазор неподвисной катушки с током. Рассмотрите рис. 2 и 3 и попробуйте объяснить, как работают данные приборы. При необходимости обратитесь *даю 30 баллов
2,3 Пожалуйста дам много балов
пж помогите срочно, ДАЮ 30 БАЛЛОВ
Дерев’яна куля радіусом R і масою М утримується під водою за допомогою сталевого ланцюга, який лежить на дні водоймища та прикріплений одним кінцем до
… кулі (див. рис.). Знайти довжину ланцюга l між кулею та дном. Маса одного метра ланцюга дорівнює m. Об’ємом ланцюга знехтувати. Густина води дорівнює ρ.
як взаємодіють постійний магніт та соленоїд, який приеднано до джерела струму
Напряжение на концах участка цепи прямо пропорционально. Электрическое сопротивление участка цепи
Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов. Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни. Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.
Историческая справка
Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
Закон Ома для участка цепи
Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:
Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.
Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.
Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.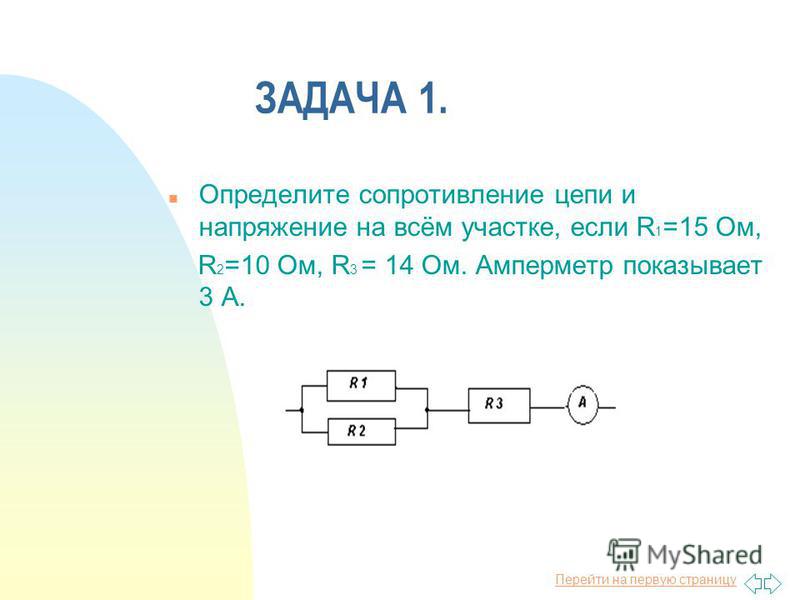
Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:
f(x) = ky или f(u) = IR или f(u)=(1/R)*I
Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:
I=12 В/6 Ом=2 А
Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.
Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.
Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:
R провод =ρ(L/S)
Где ρ – удельное сопротивление в Ом*мм 2 /м, L – длина в м, S – площадь поперечного сечения.
Закон Ома для параллельной и последовательной цепи
В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:
Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:
При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:
U эл =I*R элемента
Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:
1/R=1/R1+1/R2
Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
Закон Ома для полной цепи
Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:
- напряжение, если это источник ЭДС;
- силу тока, если это источник тока;
Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.
В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.
Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:
I=ε/(R+r)
Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.
На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.
Закон Ома в дифференциальной и интегральной форме
Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.
Это называется Закон Ома в дифференциальной форме.
Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.
В интегральной форме:
Закон Ома для переменного тока
При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки R a и реактивное сопротивление X (или R r). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:
- Ток в цепи с индуктивностью не может измениться мгновенно.
- Напряжение в цепи с ёмкостью не может измениться мгновенно.
Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.
X L и X C – это реактивные составляющие нагрузки.
В связи с этим вводится величина cosФ:
Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.
Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.
При этом сопротивление представляют в комплексной форме:
Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.
Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».
Как запомнить закон Ома
Чтобы запомнить Закон Ома – можно заучить формулировку простыми словами типа:
Чем больше напряжение – тем больше ток, чем больше сопротивление – тем меньше ток.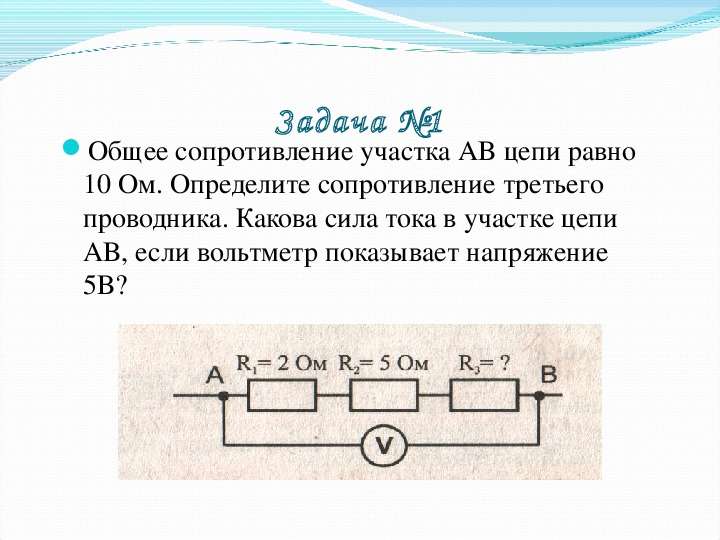
Или воспользоваться мнемоническими картинками и правилами. Первая это представление закона Ома в виде пирамиды – кратко и понятно.
Мнемоническое правило – это упрощенный вид какого-либо понятия, для простого и легкого его понимания и изучения. Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:
Вторая – это карикатурное представление. Здесь показано: чем больше старается Ом, тем труднее проходит Ампер, а чем больше Вольт – тем легче проходит Ампер.
Закон Ома – один из основополагающих в электротехнике, без его знания невозможна бОльшая часть расчетов. И в повседневной работе часто приходится переводить или по сопротивлению определять ток. Совершенно не обязательно понимать его вывод и происхождение всех величин – но конечные формулы обязательны к освоению. В заключении хочется отметить, что есть старая шуточная пословица у электриков: «Не знаешь Ома – сиди дома». И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.
И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.
Нравится(0 ) Не нравится(0 )
Здравствуйте, уважаемые читатели сайта «Заметки электрика»..
Сегодня открываю новый раздел на сайте под названием .
В этом разделе я постараюсь в наглядной и простой форме объяснить Вам вопросы электротехники. Скажу сразу, что далеко углубляться в теоретические знания мы не будем, но вот с основами познакомимся в достаточном порядке.
Первое, с чем я хочу Вас познакомить, это с законом Ома для участка цепи. Это самый основной закон, который должен знать каждый .
Знание этого закона позволит нам беспрепятственно и безошибочно определять значения силы тока, напряжения (разности потенциалов) и сопротивления на участке цепи.
Кто такой Ом? Немного истории
Закон Ома открыл всем известный немецкий физик Георг Симон Ом в 1826 году. Вот так он выглядел.
Вот так он выглядел.
Всю биографию Георга Ома я рассказывать Вам не буду. Про это Вы можете узнать на других ресурсах более подробно.
Скажу только самое главное.
Его именем назван самый основной закон электротехники, который мы активно применяем в сложных расчетах при проектировании, на производстве и в быту.
Закон Ома для однородного участка цепи выглядит следующим образом:
I – значение тока, идущего через участок цепи (измеряется в амперах)
U – значение напряжения на участке цепи (измеряется в вольтах)
R – значение сопротивления участка цепи (измеряется в Омах)
Если формулу объяснить словами, то получится, что сила тока пропорциональная напряжению и обратно пропорциональна сопротивлению участка цепи.
Проведем эксперимент
Чтобы понять формулу не на словах, а на деле, необходимо собрать следующую схему:
Цель этой статьи — это показать наглядно, как использовать закон Ома для участка цепи.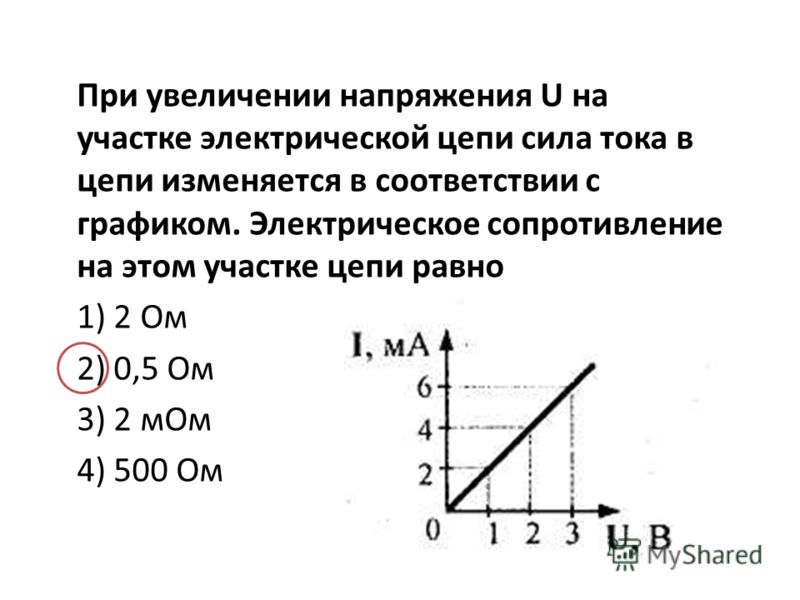 Поэтому я на своем рабочем стенде собрал эту схему. Смотрите ниже как она выглядит.
Поэтому я на своем рабочем стенде собрал эту схему. Смотрите ниже как она выглядит.
С помощью ключа управления (избирания) можно выбрать, либо постоянное напряжение, либо переменное напряжение на выходе. В нашем случае используется постоянное напряжения. Уровень напряжения я меняю с помощью лабораторного автотрансформатора (ЛАТР).
В нашем эксперименте я буду использовать напряжение на участке цепи, равное 220 (В). Контроль напряжения на выходе смотрим по вольтметру.
Теперь мы полностью готовы провести самостоятельно эксперимент и проверить закон Ома в действительности.
Ниже я приведу 3 примера. В каждом примере мы будем определять искомую величину 2 методами: с помощью формулы и практическим путем.
Пример № 1
В первом примере нам нужно найти ток (I) в цепи, зная величину источника постоянного напряжения и величину сопротивления светодиодной лампочки.
Напряжение источника постоянного напряжения составляет U = 220 (В) .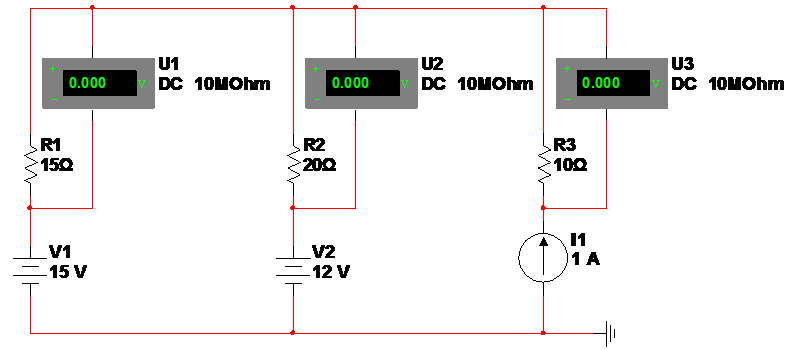 Сопротивление светодиодной лампочки равно R = 40740 (Ом) .
Сопротивление светодиодной лампочки равно R = 40740 (Ом) .
С помощью формулы найдем ток в цепи:
I = U/R = 220 / 40740 = 0,0054 (А)
Подключаем последовательно светодиодной лампочке , включенный в режиме амперметр, и замеряем ток в цепи.
На дисплее мультиметра показан ток цепи. Его значение равно 5,4 (мА) или 0,0054 (А), что соответствует току, найденному по формуле.
Пример № 2
Во втором примере нам нужно найти напряжение (U) участка цепи, зная величину тока в цепи и величину сопротивления светодиодной лампочки.
I = 0,0054 (А)
R = 40740 (Ом)
С помощью формулы найдем напряжение участка цепи:
U = I*R = 0,0054 *40740 = 219,9 (В) = 220 (В)
А теперь проверим полученный результат практическим путем.
Подключаем параллельно светодиодной лампочке мультиметр, включенный в режиме вольтметр, и замеряем напряжение.
На дисплее мультиметра показана величина измеренного напряжения. Его значение равно 220 (В), что соответствует напряжению, найденному по формуле закона Ома для участка цепи.
Пример № 3
В третьем примере нам нужно найти сопротивление (R) участка цепи, зная величину тока в цепи и величину напряжения участка цепи.
I = 0,0054 (А)
U = 220 (В)
Опять таки, воспользуемся формулой и найдем сопротивление участка цепи:
R = U/ I = 220/0,0054 = 40740,7 (Ом)
А теперь проверим полученный результат практическим путем.
Сопротивление светодиодной лампочки мы измеряем с помощью или мультиметра.
Полученное значение составило R = 40740 (Ом) , что соответствует сопротивлению, найденному по формуле.
Как легко запомнить Закон Ома для участка цепи!!!
Чтобы не путаться и легко запомнить формулу, можно воспользоваться небольшой подсказкой, которую Вы можете сделать самостоятельно.
Нарисуйте треугольник и впишите в него параметры электрической цепи, согласно рисунка ниже. У Вас должно получится вот так.
Как этим пользоваться?
Пользоваться треугольником-подсказкой очень легко и просто. Закрываете своим пальцем, тот параметр цепи, который необходимо найти.
Если оставшиеся на треугольнике параметры расположены на одном уровне, то значит их необходимо перемножить.
Если же оставшиеся на треугольнике параметры расположены на разном уровне, то тогда необходимо разделить верхний параметр на нижний.
С помощью треугольника-подсказки Вы не будете путаться в формуле. Но лучше все таки ее выучить, как таблицу умножения.
Выводы
В завершении статьи сделаю вывод.
Электрический ток — это направленный поток электронов от точки В с потенциалом минус к точке А с потенциалом плюс. И чем выше разность потенциалов между этими точками, тем больше электронов переместится из точки В в точку А, т. е. ток в цепи увеличится, при условии, что сопротивление цепи останется неизменным.
е. ток в цепи увеличится, при условии, что сопротивление цепи останется неизменным.
Но сопротивление лампочки противодействует протеканию электрического тока. И чем больше сопротивление в цепи (последовательное соединение нескольких лампочек), тем меньше будет ток в цепи, при неизменном напряжении сети.
P.S. Тут в интернете нашел смешную, но поясняющую карикатуру на тему закона Ома для участка цепи.
Зависит величина воздействия, которое ток может оказывать на проводник, будь то тепловое, химическое или магнитное действие тока . То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток , в свою очередь – это упорядоченное движение частиц под действием электрического поля .
Зависимость силы тока и напряжения
Очевидно, что чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением . Следовательно, мы приходит к выводу, что сила тока зависит от напряжения.
И действительно, опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.
Связь с сопротивлением
Однако любая цепь или участок цепи характеризуются еще одной немаловажной величиной, называемой сопротивлением электрическому току . Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.
Формула закона Ома для участка цепи
Сопоставив две эти зависимости, можно прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 г. Он связал воедино три вышеуказанные физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:
Закон Ома для участка цепи гласит:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
где I – сила тока,
U – напряжение,
R – сопротивление.
Применение закона Ома
Закон Ома – один из основополагающих законов физики . Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».
U=IR и R=U/I
Правда, следует понимать, что в собранной цепи величина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.
Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.
Соберём электрическую цепь, состоящую из источника тока (который позволяет плавно менять напряжение), амперметра, спирали из никелиновой проволоки (проводника), ключа и параллельно присоединённого к спирали вольтметра (схема этой цепи показана рядом, прямоугольником условно обозначен проводник).
Замкнём цепь и отметим показания приборов. Затем при помощи источника тока плавно изменим напряжение (лучше всего увеличить его вдвое). Напряжение на спирали при этом тоже увеличится вдвое, и амперметр покажет вдвое большую силу тока. Увеличивая напряжение в \(3\) раза, напряжение на спирали увеличивается втрое, во столько же раз увеличивается сила тока.
Таким образом, опыт показывает, что во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нём. Другими словами:
Другими словами:
Обрати внимание!
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника.
Эту зависимость можно изобразить графически. Её называют зависимостью силы тока в проводнике от напряжения между концами этого проводника.
Включая в электрическую цепь источника тока различные проводники и амперметр, можно заметить, что при разных проводниках показания амперметра различны, т.е. сила тока в данной цепи различна.
Графики тоже будут отличаться.
Вольтметр, поочерёдно подключаемый к концам этих проводников, показывает одинаковое напряжение. Значит, сила тока в цепи зависит не только от напряжения, но и от свойств проводников, включённых в цепь. Зависимость силы тока от свойств проводника объясняется тем, что разные проводники обладают различным электрическим сопротивлением.
Обрати внимание!
Электрическое сопротивление — физическая величина. Обозначается оно буквой R.
За единицу сопротивления принимают \(1\) ом — сопротивление такого проводника, в котором при напряжении на концах \(1\)вольт сила тока равна \(1\) амперу .
Кратко это записывают так: 1 Ом = 1 В 1 А.
Применяют и другие единицы сопротивления: миллиом (мОм), килоом (кОм), мегаом (МОм).
\(1\) мОм = \(0,001\) Ом;
\(1\) кОм = \(1000\) Ом;
\(1\) МОм = \(1 000 000\) Ом.
Причина сопротивления заключается в следующем: электроны взаимодействуют с ионами кристаллической решётки металла. При этом замедляется упорядоченное движение электронов, и сквозь поперечное сечение проводника проходит за \(1\) с меньшее их число. Соответственно, уменьшается и переносимый электронами за \(1\) с заряд, т.е. уменьшается сила тока. Таким образом, каждый проводник как бы противодействует электрическому току, оказывает ему сопротивление. Итак:
Обрати внимание!
Причиной сопротивления является взаимодействие движущихся электронов с ионами кристаллической решётки.
Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту.
На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор. В эту цепь по очереди включают проводники, обладающие различным сопротивлением. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром. Ниже приведены результаты опытов с тремя различными проводниками.
Обобщая результаты опытов, приходим к выводу, что:
Обрати внимание!
Сила тока в проводнике обратно пропорциональна сопротивлению проводника.
Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома — по имени немецкого учёного Георга Ома, открывшего этот закон в \(1827\) году.
Закон Ома читается так:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
И записывается так:
где \(I\) — сила тока в участке цепи, \(U\) — напряжение на этом участке, \(R\) — сопротивление участка.
Зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах может быть показана графически:
Найти сопротивление экспериментально можно несколькими способами:
При помощи амперметра и вольтметра | При помощи омметра |
Электрическое сопротивление для участка цепи определяется при помощи закона Ома. Для того, чтобы понять процессы, происходящие в элементах электрической цепи постоянного тока, необходимо дать общее определение закона Ома.
Закон Ома
Сила тока на участке цепи всегда прямо пропорциональна напряжению на данном участке и обратно пропорциональна сопротивлению участка.
Подобное определение будет верно также для растворов электролитов. Общий закон Ома характерен при описании однородного участка цепи, который не содержит источников тока.
При составлении формул вводятся дополнительные характеристики. Среди них коэффициент пропорциональности. Его записывают в виде $1=R$. Отсюда следует, что $I = \frac{U}{R}$.
$R$ – сопротивление проводника.
Сопротивление принято измерять в омах (Ом).
Закон Ома является главным законом в электротехнике. С помощью его:
- изучаются и рассчитываются электрические цепи;
- устанавливается логическое соотношение между сопротивлением и напряжением.
Определение 1
Вольтамперная характеристика – функциональная зависимость элемента участка цепи. Она является очень важной величиной электрических свойств элемента. Такую зависимость можно представить в виде $I = I(U)$.
Подобные характеристики в зависимости от ситуации могут приобретать различные формы и выражения. Наиболее простой вид вольтамперной характеристики выразил в формуле Георг Ом, в честь которого была названа единица сопротивления тока. Ученый подтвердил свою теорию многочисленными экспериментами, применяя опыты к металлическому проводнику.
Закон Ома необходимо понимать на теоретическом и практическом уровне, чтобы решать различные задачи. Если неправильно применять основные параметры закона, то результат приобретает неправильные черты, поэтому допускаются многочисленные ошибки.
Применение закона Ома для участка цепи
Каждый участок электрической цепи можно описать с помощью трех основных величин:
- сопротивления;
- напряжения;
- тока.
Такое сочетание также называют «треугольником Ома», поскольку величины характеризуют все процессы электротехники.
Все производимые расчеты имеют смысл только в тех случаях, когда напряжение на участке цепи выражается в вольтах (В), сопротивление — в омах (Ом), а ток – в амперах (А). При использовании иных единиц измерений или их кратных значений необходимо осуществлять дополнительный ряд действий, чтобы искомый результат полностью соответствовал задачам и целям расчетов. Для этого кратные единицы используемых величин переводят в традиционные величины.
Кратные единицы измерений:
- милливольты;
- миллиамперы;
- мегаомы.
При произведении расчетов в кратных единицах измерений величин напряжение всегда выражается в вольтах.
Для расчета сопротивления на участке цепи по закону Ома необходимо сначала определить ток на заданном участке цепи. Напряжение при этом делят на сопротивление конкретного участка цепи. Эти действия можно производить на любом участке без погрешности.
Для определения напряжения в цепи используют формулу $U = IR$.
Согласно указанной формуле, напряжение на обоих концах участка электрической цепи прямо пропорционально сопротивлению и току. Иными словами, если не стремиться все время изменять сопротивление на данном участке, то при увеличении тока применяется способ увеличения напряжения.
Значительному напряжению в цепи будет соответствовать больший ток. Эти правила действуют при постоянном сопротивлении. Для получении одинакового тока при различных сопротивлениях большее напряжение должно соответствовать большему сопротивлению.
Падение напряжения – это напряжение на определенном участке цепи. Это означает, что напряжение и падение напряжения – идентичные понятия, а слово «падение» никак не связано с потерей некоторого количества напряжения в цепи. Потерю напряжения следует различать от падения напряжения.
Расчет сопротивления
Сопротивление на участке цепи рассчитывается по классической формуле $R = \frac{U}{I}$. Для этого необходимо установить значения напряжения и тока. Сопротивление – отношение напряжения к току.
При многократном увеличении или уменьшении напряжения ток также изменяется в несколько раз в ту или иную сторону. Отношение напряжения к току, которое равно сопротивлению, всегда остается на неизменном уровне.
Сопротивление определенного проводника не зависит от напряжения и тока. Оно будет лежать в зависимости от материала проводника, его длины и площади сечения. Формула для расчета сопротивления на участке цепи очень похожа на формулу для определения тока, однако существует между ними принципиальное различие.
Оно состоит в том, что ток на конкретном участке цепи зависит от напряжения и сопротивления, поэтому изменяется таким же образом. Сопротивление на данном участке цепи – постоянная величина. Она не зависит от изменения значений тока и напряжения, однако равно отношению этих величин.
Вольтамперная характеристика
Закон Ома представляют в виде вольтамперной характеристики. Зависимость между двумя пропорциональными величинами выражается прямой линией на графике. Она проходит через начало координат. Подобную прямую пропорциональную зависимость величин также называют линейной зависимостью.
В графическом выражении закона Ома для участка цепи при отрицательных значениях напряжения и тока также рисуют прямую линию. Это означает, что ток в цепи проходит в разных направлениях одинаково. При большем сопротивлении меньшее значение имеет ток с таким же напряжением.
Вольтамперную характеристику составляют при помощи специальных приборов. Линейными называют такие приборы, у которых характеристика выражается прямой линией, и она проходит через начало координат.
Специалисты при составлении вольтамперной характеристики применяют также понятия линейные сопротивления и линейные цепи.
Определение 2
Нелинейными называют приборы, у которых сопротивление меняется при изменении тока или напряжения. Для таких случаев уже не действует закон Ома.
Закон Ома для участка цепи
Пожалуй, закон Ома для участка цепи является основой электротехники и электроники. Любое Пособие по физике для поступающих в вузы описывает Закон Ома и любой инженер должен его знать. Этот закон настолько прост, что его, по идее, должен знать и понимать каждый школьник. Однако я встречал людей с высшим техническим образованием, которые не знали как рассчитать простейшую электрическую цепь из двух резисторов. И это не шутка. Именно поэтому я решил написать небольшую статью, посвящённую Закону Ома для участка цепи. Постараюсь сделать это понятными словами.Закон Ома для участка цепи определяет зависимость между силой тока в проводнике и напряжением (разностью потенциалов) между двумя точками этого проводника. Эти точки ещё называют сечениями. Почему? Проводник, каким бы он ни был (круглым, квадратным или любой другой формы) можно мысленно рассечь (см. рис. 1). Это и будет сечение. А ещё есть понятие площадь поперечного сечения (обычно, когда говорят «сечение» по отношению к проводнику, то как раз и подразумевают площадь поперечного сечения, но это уже другая тема).
Рис. 1. Сечение проводника.
В 1826 г. немецким учёным Георгом Омом (1787-1854) было замечено, что отношение разности потенциалов (напряжения) на концах металлического проводника к силе тока является величиной постоянной, то есть:
U/I = R = constЭта величина зависит от геометрических свойств проводника (то есть от его размеров, в частности, от площади поперечного сечения), а также от его электрических свойств и температуры. Эта величина называется омическим (активным) сопротивлением, или просто сопротивлением.
Определение закона Ома для участка цепи следующее
Сила тока прямо пропорциональна разности потенциалов (напряжению) на концах участка
цепи и обратно пропорциональна сопротивлению этого участка:I = U/R
|
Единица измерения омического сопротивления в СИ – ом (Ом). Проводник имеет сопротивление 1 Ом, если при силе тока в этом проводнике 1 А разность потенциалов (напряжение) на его концах равна 1 В, то есть
1 Ом = 1 В / 1 АИными словами, если взять проводник, по которому течёт ток силой 1 А, отмерить отрезок этого проводника таким образом, чтобы напряжение на концах этого отрезка было равно 1 В, то сопротивление этого отрезка будет 1 Ом (рис. 2).
Рис. 2. Сопротивление проводника.
Как говаривал один известный товарищ – теория без практики мертва. Надеюсь, что всё прочитанное выше вы поняли. Но остался один вопрос – зачем это надо? Где можно применить полученные знания на практике? Приведу два простых примера, которые, однако, используются очень часто в электронике.Делитель напряжения
Довольно часто приходится сталкиваться с необходимостью понизить напряжение, например, с 12 до 3 вольт. Сделать это можно с помощью двух резисторов (см. рис. 3). Если вы не знаете, что такое резисторы, то советую ознакомиться со статьёй РЕЗИСТОРЫ. Ну а если знаете, то дальше можете прочитать о том, как это сделать.Задача, в общем-то, не сложная. Требуется подобрать два резистора таким образом, чтобы падение напряжения на одном из них составляло 3 вольта, а на втором – (12 – 3) = 9 вольт (для нашего примера). Кроме того, необходимо знать ток, который должен протекать в цепи. Допустим, что в нашем случае ток должен быть равен 50 мА (0,05 А). Тогда, используя закон Ома для участка цепи, вычислим полное сопротивление цепи, то есть общее сопротивление резисторов R1 и R2:
R = U/I = 12 В / 0,05 А = 240 ОмНапомню, что все единицы измерения должны соответствовать принятым в СИ, то есть напряжение измеряется в ВОЛЬТАХ, ток – в АМПЕРАХ, а сопротивление – в ОМАХ.
Поскольку на любом участке цепи из последовательно включенных элементов ток одинаков, то вычислить сопротивление резисторов R2 и R1 не составит труда:
R1 = U1 / I = 9 / 0,05 = 180 Ом R2 = U2 / I = 3 / 0,05 = 60 ОмНу вот и всё. Задача решена. Однако использовать такой делитель нужно с умом. Ведь любая нагрузка имеет своё сопротивление, которое называется входным сопротивлением. Это значит, что, подключив нагрузку к выходу делителя, мы тем самым уменьшим сопротивление цепи, а это, в свою очередь, увеличит ток в цепи и падение напряжения на резисторе R1 увеличится, а на нагрузке, соответственно, уменьшится. Что из этого следует? А следует из этого тот печальный факт, что сколь-нибудь мощную нагрузку подключать к выходу делителя нецелесообразно. Поэтому такие делители используются в основном, в электронных схемах, где протекают относительно небольшие токи.
Если интересно, то вы можете немного поэкспериментировать с делителем напряжения при помощи представленного ниже флэш-ролика (рис. 3). Для изменения входного напряжения и сопротивления резисторов воспользуйтесь соответственными «ползунками» или непосредственно введите данные в поля жёлтого цвета. Если флэш-ролик не отображается или не работает, то вам придётся настроить (или заменить) ваш браузер и/или установить (обновить) флэш-плеер.
Рис. 3. Делитель напряжения.
Как зажечь (но не сжечь) светодиод?
Светодиоды в наше время применяются очень широко – от простых устройств индикации до автомобильных фонарей и светофоров. Возможно, у вас возникала мысль поменять лампочки в автомобиле на светодиоды. Как бывалый автомобилист я вам этого делать не советую – возни много, а смысла мало. А вот как электронщик – помогу разобраться в премудростях включения светодиодов в электрическую цепь. Дело это несложное, но многие просто понятия не имеют, что и здесь нужно всё делать «по науке». А потом говорят, что светодиоды – вещь ненадёжная, хотя, как правило, выходят из строя светодиоды при правильной эксплуатации очень и очень редко. А вот при неправильной – ещё как. При желании сжечь светодиод можно моментально.Надо сказать, что сейчас в магазинах довольно много разных «мигающих» и прочих светодиодов, которые на самом деле являются электронными устройствами, встроенными в корпус светодиодов. Такие устройства можно подключать непосредственно к источнику питания, без гасящего резистора. Однако мы здесь будем говорить об обычных светодиодах.
Схема включения светодиода показана на рис. 4. При включении светодиода в цепь постоянного тока необходимо соблюдать полярность (см. документацию на светодиод).
Итак, главное, что нам нужно знать:
- Максимальное напряжение
- Максимально допустимый ток светодиода
Итак, допустим, что мы зачем-то хотим установить светодиод на автомобиль. Напряжение бортовой сети автомобиля при исправном оборудовании не может превышать 15 В. На это напряжение и будем рассчитывать. Допустим, что максимальный ток нашего светодиода составляет 20 мА (0,02 А). Далее нам необходимо учесть тот факт, что на любом полупроводнике (коим является и светодиод) падает какое-то напряжение. Для светодиодов это обычно 1,5…2 В. Примем его для нашего случая равным 2 В.
Поскольку резистор и светодиод будут подключены последовательно, то максимально возможное напряжение на резисторе для нашего примера будет
U1 = U – Ud = 15 – 2 = 13
- Где
- U1 – напряжение на гасящем резисторе R1
- U – входное напряжение
- Ud – напряжение, падающее на светодиоде
- U – входное напряжение
R = U1 / I = 13 / 0,02 = 650 ОмНу вот и всё. Задача решена – для включения светодиода с заданными характеристиками нам потребуется резистор сопротивлением 650 Ом. Однако сопротивление – это не единственный параметр резистора. Резистор ещё должен иметь подходящую мощность. Кроме того, промышленностью не выпускаются резисторы сопротивлением 650 Ом (точнее, выпускаются, но для особых случаев). Но это уже другая история. Хотите знать больше? Читайте статью РЕЗИСТОРЫ.
Ну и кроме того предоставлю вам возможность закрепить полученный материал с помощью флэш-ролика (рис. 4).
Рис. 4. Подключение светодиода.
См. также:
Как на резисторах, конденсаторах и индуктивностях делить напряжение
Как на резисторах, конденсаторах и индуктивностях делить напряжение
Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B.
С целью получения фиксированного значения напряжения, равного доле от исходного значения, в электрических цепях применяют делители напряжения. Делители напряжения могут состоять из двух или более элементов, которыми могут служить резисторы либо реактивные сопротивления (конденсаторы или катушки индуктивности).
В простейшем виде делитель напряжения представляется парой участков электрической цепи, соединенных последовательно друг с другом, которые и называются плечами делителя. Верхним плечом называется тот участок, который расположен между точкой положительного напряжения и выбранной точкой соединения участков, а нижним плечом — участок между точкой соединения (выбранной точкой, нулевой точкой) и общим проводом.
Делители напряжения на резисторах
Конечно, делители напряжения могут применяться как в цепях постоянного тока, так и в цепях тока переменного. Делители на резисторах подходят и для тех, и для других цепей, однако используются они только в цепях низкого напряжения. Для питания устройств делители напряжения на резисторах не применяют.
В простейшем виде резистивный делитель напряжения состоит всего из пары резисторов, соединенных последовательно. Делимое напряжение подается на делитель, в результате на каждом резисторе падает определенная доля этого напряжения, пропорциональная номиналу резистора. Сумма падений напряжений равна здесь напряжению подаваемому на делитель.
Согласно закону Ома для участка электрической цепи, на каждом резисторе падение напряжения будет прямо пропорционально току и величине сопротивления резистора. А согласно первому правилу Кирхгофа, ток через данную цепь будет везде один и тот же. Так, на каждый резистор придутся падения напряжения:
И напряжение на концах участка цепи будет равно:
А ток в цепи делителя составит:
Теперь если подставить выражение для тока в формулы для падений напряжений на резисторах, то получим формулы для нахождения величин напряжений на каждом из резисторов делителя:
Используя делитель напряжения на резисторах для тех или иных целей, важно понимать, что присоединенная к одному из плеч делителя нагрузка, будь то измерительный прибор или что-нибудь другое, должна иметь собственное сопротивление значительно большее, чем общее сопротивление резисторов, образующих делитель. В противном случае сопротивление нагрузки само должно учитываться в расчетах, будучи рассмотрено как параллельный плечу резистор, входящий в состав делителя.
Пример: есть источник постоянного напряжения 5 вольт, необходимо подобрать к нему резисторы для делителя напряжения, чтобы снимать с делителя измерительный сигнал величиной в 2 вольта. Допустимая рассеиваемая на делителе мощность не должна превышать 0,02 Вт.
Решение: Пусть максимальная мощность, рассеиваемая на делителе, равна 0,02 Вт, тогда минимальное общее сопротивление делителя при 5 вольтах найдем из закона Ома, оно получится равно 1250 Ом. Пусть 1,47 кОм — выбранное нами общее сопротивление делителя, тогда 2 вольта упадет на 588 омах. Выберем постоянный резистор на 470 Ом и переменный на 1 кОм. Установим на переменном резисторе значение в 588 Ом.
Делители напряжения на резисторах широко применяются сегодня в электронных схемах. На этих схемах значения величин резисторов для делителей выбираются исходя из параметров активных элементов схем. Как правило, делители стоят в измерительных цепях схем, в цепях обратной связи преобразователей напряжения и т. д. Минус таких решений заключается в том, что резисторы рассеивают на себе мощность в виде тепла, однако целесообразность оправдывает эти малые потери энергии.
Делители напряжения на конденсаторах
В цепях переменного тока, в высоковольтных схемах, применяют делители напряжения на конденсаторах. Здесь используется реактивный характер сопротивления конденсаторов в цепях переменного тока. Величина реактивного сопротивления конденсатора в цепи переменного тока зависит от электроемкости конденсатора и от частоты напряжения. Вот формула для нахождения этого сопротивления:
Формула свидетельствует о том, что чем больше электроемкость конденсатора — тем его реактивное (емкостное) сопротивление меньше и чем выше частота — тем так же меньше реактивное сопротивление. Такие делители используются в измерительных схемах цепей переменного тока, падения напряжений на плечах считается аналогично случаю с постоянными активными сопротивлениями (резисторами, см. выше).
Достоинство конденсаторов, применяемых в делителях, состоит в том, что рассеивание энергии в форме тепла получается минимальным, и зависит только от качества диэлектрика.
Делитель напряжения на индуктивностях
Индуктивный делитель напряжения — еще один вид делителей, применяемых в измерительной электронике переменного тока, особенно в низковольтных схемах, работающих на высоких частотах. Сопротивление катушек для переменного тока высокой частоты носит преимущественно реактивный (индуктивный) характер, оно находится по формуле:
Формула свидетельствует о том, что чем больше индуктивность и чем выше частота — тем выше сопротивление катушки переменному току. Здесь важно понимать, что провод катушки имеет активное сопротивление, поэтому мощность, рассеиваемая в виде тепла, свойственная делителю на индуктивностях, значительно выше, чем у делителей на конденсаторах.
В любительской электронике делители напряжения часто используются при подключении аналоговых датчиков к модулям Ардуино.
Ранее ЭлектроВести писали, что немецкие инженеры разработали полевой транзистор на основе оксида галлия с пробивным напряжением 1,8 кВ и рекордной добротностью — 155 МВт на квадратный сантиметр. Такие показатели приближают элемент к теоретическому лимиту оксида галлия.
По материалам: electrik.info.
Падение напряжения— обзор
6.17.4.3 Определение размера аккумуляторной батареи
Определение размера аккумуляторной батареи состоит из следующих двух технических вариантов:
- i.
Напряжение аккумулятора.
- ii.
Емкость аккумулятора.
Расчет напряжения аккумуляторной батареи выполняется с целью минимизировать падение напряжения в кабелях и избежать перегрева кабелей. Последние на практике ведут себя как электрическое сопротивление, которое вызывает падение напряжения между двумя концами.Падение напряжения выражается формулой. (6.42):
(6.42) ɛ = ρ⁎L⁎IS⁎UBat.
Падение напряжения ( ɛ ) не должно быть слишком большим между местом, где генерируется напряжение (аккумуляторная батарея), и местом, в котором оно подается (регулятор). Однако это падение напряжения зависит от следующих параметров, в том числе:
- i.
Напряжение ( U ) от кабелей, в данном случае напряжение батареи U Bat .
- ii.
Удельное сопротивление проводящего материала ( ρ ) (медь или алюминий) в рабочих температурных условиях, выраженное в Ом ( 2 мм / м).
- iii.
Длина кабеля ( L ), выраженная в метрах.
- iv.
Электрическая мощность, проходящая через кабели ( P ), выраженная в Вт.
- v.
Сечение кабелей ( S ), выраженное в мм 2 .
Напряжение батареи рассчитывается по формуле. (6.43):
(6.43) UBat = ρ⁎2⁎L⁎IS⁎ɛ.
Фактор 2 в уравнении. (6.43) позволяет учесть внешние и обратные расстояния кабеля. Чем больше длина L , тем выше напряжение аккумуляторной батареи. Близкое расположение аккумуляторной батареи к инвертору более выгодно. Обратите внимание, что регулятор не должен располагаться менее чем в 50 см от аккумуляторной батареи по соображениям безопасности.Увеличивая сечение кабелей, можно снизить напряжение аккумуляторной батареи.
При расчете напряжения аккумуляторной батареи необходимо учитывать наиболее неблагоприятную конфигурацию. То есть все электрооборудование дома работает одновременно. В этом исследовании электрическая мощность, которую должны обеспечивать батареи, равна P, = 6000 Вт. Для обеспечения оптимальной работы блока батарей падение напряжения между блоком батарей и инвертором должно составлять не более 1%. , я.е., ɛ = 0,01, и типичная длина должна составлять L = 3 м. Кабели, использованные в этом исследовании, изготовлены из меди с ρ 0 = 0,01851 Ом · мм 2 / м. Принимая во внимание влияние температуры на кабель, удельное сопротивление становится:
ρ = ρ0 × 1,25 = 0,02314 Ом.мм2 / м.
И уравнение. (6.42) принимает следующий вид:
S = ρ⁎2⁎L⁎PUBat2⁎ɛ = 0,02314⁎2⁎3⁎6000UBat2⁎0.01 = 83304UBat2.
Кабельное сечение кабелей не должно превышать 50 мм 2 , то есть S ≤ 50 мм 2 .Это дает U Bat ≥ 40,8 В [(83,304) / (UBat2) ≤ 50 мм 2 ].
Следовательно, используется напряжение аккумуляторной батареи 48 В. Сечение кабеля, проложенного между аккумуляторной батареей и инвертором, будет равно S = 50 мм 2 . Важно убедиться, что кабель длиной 50 мм 2 выдерживает ток, протекающий по нему. Действительно, при напряжении 48 В и мощности 6000 Вт результирующий ток возрастает до IBat = PBatUBat = 600048 = 125A.Допустимый ток для медного кабеля диаметром 50 мм 2 составляет 194 А, что намного выше расчетных 125 А.
Второй параметр, который необходимо определить при определении размеров аккумуляторной батареи, — это ее емкость. Емкость — это индикатор, используемый для оценки количества энергии, хранящейся в батарее. Обычно выражается в Ah. Емкость аккумуляторной батареи рассчитывается по формуле. (6.44):
(6.44) CTd≥Nd⁎EneedDP⁎KT.
C T d — емкость аккумулятора, связанная со временем разряда (Ач), N d — резервная автономия (сутки), D P — максимальная глубина разряда, E потребность — дневная потребляемая энергия (кВтч / день), равная Eneed = IneedUBat, K T — температурный коэффициент емкости K T = N d ⁎ 24 (час).
Суточная потребность в энергии составляет 19,3795 кВтч / день. Это значение должно быть выражено в Ач / день. При напряжении 48 В суточная потребность составляет:
19379,5Втч / день / 48В = 404Ач / день
Солнечные батареи по-прежнему очень дороги. Была выбрана только однодневная автономия, потому что дом будет подключен к сети с низким напряжением. Это означает, что батареи могут питать, независимо от фотоэлектрического поля, электрооборудование, указанное в Таблице 6.3, в течение 1 дня. Глубокие разряды вредны для срока службы свинцово-кислотных аккумуляторов.Была использована максимальная глубина разгрузки 90%, т.е. D P = 90%. В этом исследовании батареи будут работать при температуре -10 ° C зимой, и необходимо применить поправочный коэффициент K T (C) = 0,85, согласно таблице 6.4 (с использованием данных производителя) [42 ]:
Таблица 6.4. Различный коэффициент коррекции соответствует рабочей температуре аккумуляторной батареи.
| Рабочая температура аккумулятора (° C) | — 20 | — 10 | 0 | 10 | 20 | 30 | 40 | 50 |
| Корректирующий коэффициент (применяется к C Корректирующий коэффициент 24 ) | 0.8 | 0,85 | 0,9 | 0,95 | 1 | 1,04 | 1,1 | 1,13 |
Применяя уравнение По формуле (6.44) рассчитана емкость аккумулятора:
C1⁎24≥1⁎4040,9⁎0,85Ah = 528Ah.
Таким образом, у C 24 емкость аккумулятора должна быть не менее 528 Ач. Значение номинальной емкости C 10 можно вывести, используя соотношение: C 10 ≈ 71% × C 24 , что равно 375 Ач.Таким образом, в корпусе используются четыре последовательно соединенных свинцовых аккумулятора на 12 В и 100 Ач.
Сопротивление — Элементы схемы — Содержание MCAT
Согласно закону Ома, падение напряжения В на резисторе при протекании через него тока рассчитывается по формуле V = IR, где I — ток в амперах (А), а R — сопротивление в Ом (Ом).
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В .Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению. Многие вещества, для которых действует закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R, которое не зависит от напряжения V и тока I. Объект с простым сопротивлением называется резистором, даже если его сопротивление невелико.
Резисторы серии
Резисторывключены последовательно всякий раз, когда поток заряда или ток должен проходить через компоненты последовательно.
Общее сопротивление в цепи равно сумме отдельных сопротивлений.
Параллельные резисторы
Резисторывключены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения посредством соединения проводов, имеющих незначительное сопротивление.Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор в цепи имеет полное напряжение. По закону Ома токи, протекающие через отдельные резисторы, равны I1 = VR1
.Общее сопротивление в параллельной цепи равно сумме обратных величин каждого отдельного сопротивления.
Удельное сопротивление — это свойство материала, которое количественно определяет, насколько сильно он сопротивляется или проводит электрический ток.Низкое удельное сопротивление указывает на материал, который легко пропускает электрический ток, и наоборот. Рассчитывается как:
ρ = R • A / L
R — электрическое сопротивление однородного образца материала
л — длина экземпляра
А — площадь поперечного сечения образца
Практические вопросы
Ханская академия
Анализ сигналов напряжения электрокардиограммы
Официальная подготовка MCAT (AAMC)
Физика — карточки онлайн Вопрос 1
Physics Question Pack Отрывок 9 Вопрос 54
Physics Question Pack Отрывок 9 Вопрос 56
Пакет вопросов по физике, вопрос 117
Секция банка C / P Вопрос 15 секции
Секция банка C / P Вопрос 17 секции
Образец теста C / P Раздел Отрывок 7 Вопрос 35
Практический экзамен 1 Секция C / P Отрывок 10 Вопрос 52
Практический экзамен 2 Раздел C / P, вопрос 59
Практический экзамен 3 Раздел C / P Отрывок 7 Вопрос 39
Ключевые точки
• Падение напряжения V на резисторе при протекании через него тока рассчитывается по формуле V = IR
• Общее сопротивление в цепи равно сумме отдельных сопротивлений.
• Общее сопротивление в параллельной цепи равно сумме обратных величин каждого отдельного сопротивления.
• Удельное сопротивление измеряет, насколько сильно материал сопротивляется или проводит электрический ток.
Ключевые термины
ток : количество заряда, перемещающегося через поперечное сечение за период времени.
напряжение : Разность электрических потенциалов, выраженная в вольтах
сопротивление : сопротивление — это мера сопротивления току, протекающему в электрической цепи.
удельное сопротивление: свойство материала, которое количественно определяет, насколько сильно он сопротивляется или проводит электрический ток
Расчет падения напряжения Майк Холт
Часть ВТОРАЯ
Электрооборудование предназначено для работы в заданном диапазоне напряжений, обычно не менее 10% и не более 5% от номинального напряжения.
Пример: Типичная нагрузка 230 В рассчитана на работу при напряжении не менее 207 В (-10%). и не более 242 вольт (+ 5%), рисунок 1.
Комментарий автора: Рисунки не размещаются в Интернете.
Фактическое рабочее напряжение зависит от выходного напряжения от электросети. и падение напряжения на проводниках цепи. Помните, что напряжение от электроснабжение непостоянно; его меньше во время пиковой нагрузки и выше во время периоды внепиковой нагрузки.
Как правило, перенапряжение в электрической системе не является проблемой, если нет проводки. ошибка в электрической системе1, однако пониженное или пониженное напряжение может вызвать неудобства мерцающим светом2, неустойчивой работой электромеханических устройств, таких как реле контакторы, пожары и отказы оборудования.В частности, чувствительное электронное оборудование работа при пониженном напряжении не будет иметь достаточной «сквозной» способности из-за провалов напряжения, и оборудование пожарных насосов могло выйти из строя из-за недостаточного напряжения.
Электроэнергетические предприятия требуются комиссиями по коммунальным услугам для подачи электроэнергии с достаточным напряжением и мощностью для обслуживаемых нагрузок и для большинства установок, это не проблема. Пониженное или пониженное напряжение часто бывает вызвано чрезмерно длительным сроком службы, проводники фидера и / или ответвления.Размер этих проводов важен. для обеспечения надлежащего рабочего напряжения для безопасных и эффективных электрических систем.
Фактическое рабочее напряжение оборудования зависит от исходного напряжения, проводника размер (собственно его сопротивление) и величина тока, протекающего по цепи проводники. Возникающее напряжение в разы можно увеличить, регулируя отводы на трансформатор и падение напряжения в цепи можно уменьшить, уменьшив нагрузку или увеличение круглой миловой площади проводника.
В прошлом месяце я объяснил, что примечания к мелкому шрифту (FPN) в NEC о падении напряжения не подлежит исполнению как правило Кодекса. Однако Национальный электротехнический кодекс требует наличия проводников. должен быть рассчитан на падение напряжения для следующих целей:
- Заземляющие провода — Секция 250-122 б)
- Кино / телевизионные студии — Раздел 530-71 (d)
- Пожарные насосы — Раздел 695-7
Следующие формулы можно использовать для определения правильного размера проводов, чтобы предотвратить чрезмерное напряжение.
падение:
CM (однофазный) = (2 x K x I x D) / VD
CM (трехфазный) = (1.732 x K x I x D) / VD
Комментарий автора: Загрузите бесплатный калькулятор падения напряжения для Windows 95 с сайта www.mikeholt.com.
«CM» = Круглые милы: Круговые милы проводника цепи, указанные в Глава 9, Таблица 8.
«K» = Постоянный постоянный ток: постоянное значение постоянного тока, которое используется для медь — 12,9 Ом, а для алюминиевых проводников — 21,2 Ом.
«Q» = Регулировка переменного тока: Цепи переменного тока No.2/0 и большее значение должно быть скорректировано с учетом эффектов самоиндукции (скин-эффекта). «Q» поправочный коэффициент определяется путем деления сопротивления переменному току, как указано в NEC, глава 9, таблица 9, по сопротивлению постоянному току, как указано в главе 9, таблица. 8.
«I» = Амперы: нагрузка в амперах при 100 процентах, а не 125 процентах для двигателей. или постоянные нагрузки.
«D» = Расстояние: Расстояние, на котором нагрузка находится от источника питания, а не общая длина проводников цепи.
«VD» = падение напряжения: падение напряжения на проводниках цепи, как выражено. в вольтах.
Пример — однофазный
Двигатель мощностью 5 лошадиных сил расположен в 100 футах от панели управления напряжением 120/240 В. Какого размера проводник следует использовать, если на паспортной табличке двигателя указано, что диапазон напряжения составляет 208–230 вольт. Ограничьте падение напряжения до 7,2 В (3% от источника напряжения), и клеммы должны быть номинальными. 75ºC, рис. 2.
(а) № 10 THHN (б) № 8 THHN (c) No. 6 THHN (d) No. 4 THHN
• Ответ: (а) № 10 THHN
Раздел 430-22 (а) требует, чтобы провода двигателя были сечения не менее 125 процентов от ток полной нагрузки двигателя (28 ампер), как указано в Таблице 430-148. № 10 имеет рейтинг 35 ампер при 75ºC [Таблица 310-16 и Раздел 110-14 (c)], и он соответствует требованиям Требования NEC (28 ампер x 1.25 = 35 ампер). Кроме того, проводник № 10 ограничивает падение напряжения, соответствующее нормативам ограничения напряжения производителя [110-3 (b)].
Необходим проводник для ограничения падения напряжения до 3%
CM = (2 x K x I x D) / VD
CM = размер провода, глава 9, таблица 8
K = 12,9 Ом, медь
I = 28 ампер
D = 100 футов
В = 240 В x 3% = 7,2 В
CM = (2 x 12,9 Ом x 28 ампер x 100 футов) / 7.2 вольта
CM = 10033, № 10, Глава 9, Таблица 8
Пример — трехфазный
Пример: трехфазный двигатель пожарного насоса мощностью 25 лошадиных сил, 208 В расположен в 175 футах от услуга. Контроллер мотора пожарного насоса расположен в 150 футах от места обслуживания (мотор 25 футов от контроллера). Провод какого сечения должен быть проложен к двигателю пожарного насоса? Примечание: Клеммы рассчитаны на 75ºC, рис. 3.
(а) №4 THHN (б) № 3 THHN (c) No. 2 THHN (d) No. 1 THHN
• Ответ: (б) № 3 THHN
При выборе размеров проводов для двигателей пожарных насосов необходимо учитывать следующие правила.
Расчет 1.
Раздел 695-6 (c) (2) — № 3. Размер проводов ответвительной цепи должен быть не менее 125 процентов тока полной нагрузки двигателя пожарного насоса, как указано в Таблице 430-148 или 430-150, на основе номинальных значений клемм 75 ° C [110-14 (c) (1)], как указано в Таблице 310-16.
74,8 ампера x 1,25 = 93,4 ампера, № 3 THHN при 75 ° C рассчитан на 100 ампер
Расчет 2.
Раздел 695-7 — № 3. Рабочее напряжение на клеммах контроллера мотора должно при запуске двигателя не должно падать более чем на 15 процентов ниже номинального напряжения контроллера. (ток заторможенного ротора).
CM = (1,732 x K x I x D) / VD
CM = размер провода, глава 9, таблица 8
К = 12.9 Ом, медь
I = 404 ампер (с заторможенным ротором, таблица 430-151B)
D = 150 футов
VD = 31,2 В (208 В x 15%)
CM = (1,732 x 12,9 Ом x 404 ампер x 150 футов) / 31,2 В
CM = 43 396, Глава 9, Таблица 8 = № 3
Расчет 3.
Раздел 695-7 — № 4. Рабочее напряжение на выводах двигателя не должно падение более чем на 5 процентов ниже номинального напряжения двигателя во время работы двигателя при 115% номинального тока двигателя при полной нагрузке.
CM = (1,732 x K x I x D) / VD
CM = размер провода, глава 9, таблица 8
K = 12,9 Ом, медь
I = 86 ампер (74,8 ампера при 115%), Таблица 430-150
D = 175 футов
VD 5% = 10,4 В (208 В x 5%)
CM = (1,732 x 12,9 Ом x 86 ампер x 175 футов) / 10,4 В
CM = 32,332, Глава 9, Таблица 8 = No. 4
Внимание! При падении напряжения провод № 4 от контроллера к двигателю подходит, но Раздел 695-6 (c) (2) требует, чтобы проводники ответвленной цепи имели сечение не менее No.3.
Надеюсь, это краткое резюме было полезным. Если вы хотите узнать больше по этой теме, пожалуйста, посетите наш семинар или закажите видеопрограмму домашнего обучения сегодня.
ОСНОВНЫЕ КОНЦЕПЦИИ И ОТНОШЕНИЯ — Прикладное промышленное электричество
Столетия назад было обнаружено, что определенные типы материалов могут загадочным образом притягиваться друг к другу после того, как они натерты друг о друга. Например, если протереть кусок шелка о кусок стекла, шелк и стекло будут иметь тенденцию слипаться.Действительно, сила притяжения могла быть продемонстрирована, даже когда два материала были разделены:
Рис. 2.1.Стекло и шелк — не единственные материалы, которые, как известно, ведут себя подобным образом. Любой, кто когда-либо касался латексного шара только для того, чтобы обнаружить, что он пытается прилипнуть к нему, испытал то же самое явление. Парафин и шерстяная ткань — еще одна пара материалов, которые ранние экспериментаторы признали проявляющими силу притяжения после трения друг о друга:
Фигура 2.2Это явление стало еще более интересным, когда было обнаружено, что идентичные материалы после протирания их соответствующей тканью всегда отталкивают друг друга:
Рис. 2.3Также было отмечено, что когда кусок стекла, натертый шелком, подвергается воздействию куска воска, натертого шерстью, два материала будут притягиваться друг к другу:
Рисунок 2.4Кроме того, было обнаружено, что любой материал, демонстрирующий свойства притяжения или отталкивания после трения, может быть отнесен к одной из двух различных категорий: притягиваемый к стеклу и отталкиваемый воском или отталкиваемый стеклом и притягиваемый воском.Было либо одно, либо другое: не было обнаружено материалов, которые могли бы притягиваться или отталкиваться как стеклом, так и воском, или которые реагировали бы на одно, не реагируя на другое.
Больше внимания было обращено на куски ткани, используемые для растирания. Было обнаружено, что после протирания двух кусков стекла двумя кусками шелковой ткани не только кусочки стекла отталкивались друг от друга, но и ткани. То же самое произошло с кусочками шерсти, которыми натирали воск:
Фигура 2.5Это было действительно странно наблюдать. В конце концов, ни один из этих предметов не претерпел видимых изменений в результате трения, но они определенно вели себя иначе, чем до того, как их натерли. Какое бы изменение ни произошло, заставив эти материалы притягиваться или отталкивать друг друга, было незаметно.
Некоторые экспериментаторы предположили, что невидимые «жидкости» переходили от одного объекта к другому в процессе трения и что эти «жидкости» были способны воздействовать на физическую силу на расстоянии.Чарльз Дюфай был одним из первых экспериментаторов, которые продемонстрировали, что существует определенно два разных типа изменений, вызванных трением определенных пар предметов друг о друга. Тот факт, что в этих материалах проявлялось более одного типа изменений, был очевиден тем фактом, что были созданы два типа сил: притяжения и отталкивания . Гипотетический перенос жидкости стал известен как заряд .
Один исследователь-новатор, Бенджамин Франклин, пришел к выводу, что между натертыми предметами происходил обмен только одной жидкостью, и что два разных «заряда» были не чем иным, как избытком или недостатком этой жидкости.После экспериментов с воском и шерстью Франклин предположил, что грубая шерсть удаляет часть этой невидимой жидкости из гладкого воска, вызывая избыток жидкости на шерсти и недостаток жидкости на воске. Возникающее в результате несоответствие содержания жидкости между шерстью и воском могло вызвать силу притяжения, поскольку жидкость пыталась восстановить прежний баланс между двумя материалами.
Постулирование существования единой «жидкости», которая была получена или потеряна в результате трения, лучше всего объясняло наблюдаемое поведение: все эти материалы аккуратно попадали в одну из двух категорий при трении и, что наиболее важно, что два активных материала трулись о друг друга всегда попадали в противоположные категории , о чем свидетельствует их неизменное влечение друг к другу.Другими словами, никогда не было времени, когда два материала трулись друг о друга , и оба становились либо положительными, либо отрицательными.
После предположения Франклина о том, что шерсть что-то стирает с воска, тип заряда, который был связан с натертым воском, стал известен как «отрицательный» (поскольку предполагалось, что он имеет недостаток жидкости), в то время как тип заряда, связанный с натирание шерсти стало называться «положительным» (поскольку предполагалось, что в ней будет избыток жидкости).Он и не подозревал, что его невинное предположение в будущем вызовет много путаницы у изучающих электричество!
Точные измерения электрических зарядов были выполнены французским физиком Шарлем Кулоном в 1780-х годах с помощью устройства, называемого крутильными весами , для измерения силы, создаваемой между двумя электрически заряженными объектами. Результаты работы Кулона привели к разработке единицы электрического заряда, названной в его честь, кулонов .Если бы два «точечных» объекта (гипотетические объекты, не имеющие заметной площади поверхности) были бы одинаково заряжены величиной в 1 кулон и поместили их на расстоянии 1 метра (примерно 1 ярд) друг от друга, они бы генерировали силу примерно в 9 миллиардов ньютонов (примерно 2 миллиарда фунтов), либо притягивая, либо отталкивая в зависимости от типа задействованных зарядов. Рабочее определение кулона как единицы электрического заряда (в терминах силы, генерируемой между точечными зарядами) оказалось равным избытку или недостатку примерно в 6 250 000 000 000 000 000 электронов.Или, говоря наоборот, один электрон имеет заряд около 0,00000000000000000016 кулонов. Поскольку один электрон является наименьшим известным носителем электрического заряда, последняя величина заряда электрона определяется как элементарный заряд .
Гораздо позже было обнаружено, что эта «жидкость» на самом деле состоит из очень маленьких кусочков материи, названных электронов , названных так в честь древнегреческого слова, обозначающего янтарь: другого материала, проявляющего заряженные свойства при трении тканью.
Эксперименты с тех пор показали, что все объекты состоят из чрезвычайно маленьких «строительных блоков», известных как атомов , и что эти атомы, в свою очередь, состоят из более мелких компонентов, известных как частиц . Три основных частицы, составляющие большинство атомов, называются протонами , нейтронами и электронами . Хотя большинство атомов состоит из протонов, нейтронов и электронов, не все атомы имеют нейтроны; Примером является изотоп протия (1h2) водорода (Водород-1), который является самой легкой и наиболее распространенной формой водорода, которая имеет только один протон и один электрон.Атомы слишком малы, чтобы их можно было увидеть, но если бы мы могли взглянуть на один, он мог бы выглядеть примерно так:
Несмотря на то, что каждый атом в куске материала имеет тенденцию держаться вместе как единое целое, на самом деле между электронами и кластером протонов и нейтронов, находящимся посередине, остается много пустого пространства.
Рис. 2.6Эта грубая модель представляет собой модель элемента углерода с шестью протонами, шестью нейтронами и шестью электронами. В любом атоме протоны и нейтроны очень прочно связаны друг с другом, что является важным качеством.Плотно связанный сгусток протонов и нейтронов в центре атома называется ядром , и количество протонов в ядре атома определяет его элементарную идентичность: измените количество протонов в ядре атома, и вы измените тип атома, который он есть. Фактически, если бы вы могли удалить три протона из ядра атома свинца, вы осуществили бы мечту старых алхимиков о создании атома золота! Тесное связывание протонов в ядре отвечает за стабильную идентичность химических элементов и неспособность алхимиков осуществить свою мечту.
Нейтроны гораздо меньше влияют на химический характер и идентичность атома, чем протоны, хотя их так же трудно добавить в ядро или удалить из него, поскольку они так прочно связаны. Если добавить или получить нейтроны, атом все равно сохранит ту же химическую идентичность, но его масса немного изменится, и он может приобрести странные ядерные свойства , такие как радиоактивность.
Однако электроны обладают значительно большей свободой передвижения в атоме, чем протоны или нейтроны.Фактически, они могут быть выбиты из своего положения (даже полностью покинув атом!) С гораздо меньшей энергией, чем та, которая требуется для смещения частиц в ядре. Если это произойдет, атом по-прежнему сохраняет свою химическую идентичность, но возникает важный дисбаланс. Электроны и протоны уникальны тем, что они притягиваются друг к другу на расстоянии. Именно это притяжение на расстоянии вызывает притяжение между натертыми объектами, когда электроны удаляются от своих первоначальных атомов и располагаются вокруг атомов другого объекта.
Электроны имеют тенденцию отталкивать другие электроны на расстоянии, как и протоны с другими протонами. Единственная причина, по которой протоны связываются вместе в ядре атома, заключается в гораздо более сильной силе, называемой сильной ядерной силой , которая действует только на очень коротких расстояниях. Считается, что из-за такого поведения притяжения / отталкивания между отдельными частицами электроны и протоны имеют противоположные электрические заряды. То есть каждый электрон имеет отрицательный заряд, а каждый протон — положительный.В равных количествах внутри атома они противодействуют присутствию друг друга, так что общий заряд внутри атома равен нулю. Вот почему изображение атома углерода имеет шесть электронов: чтобы уравновесить электрический заряд шести протонов в ядре. Если электроны уйдут или появятся дополнительные электроны, общий электрический заряд атома будет разбалансирован, в результате чего атом останется «заряженным» в целом, заставив его взаимодействовать с заряженными частицами и другими заряженными атомами поблизости. Нейтроны не притягиваются и не отталкиваются электронами, протонами или даже другими нейтронами и, следовательно, классифицируются как не имеющие никакого заряда.
Процесс прибытия или ухода электронов — это именно то, что происходит, когда определенные комбинации материалов трются друг о друга: электроны от атомов одного материала вынуждаются трением покинуть свои соответствующие атомы и переходить к атомам другого материала. Другими словами, электроны составляют «жидкость», выдвинутую Бенджамином Франклином.
Что такое статическое электричество?Результат дисбаланса этой «жидкости» (электронов) между объектами называется статическим электричеством .Это называется «статическим», потому что смещенные электроны имеют тенденцию оставаться неподвижными после перемещения из одного изоляционного материала в другой. В случае воска и шерсти путем дальнейших экспериментов было установлено, что электроны в шерсти фактически передаются атомам воска, что прямо противоположно гипотезе Франклина! В честь того, что Франклин назвал заряд воска «отрицательным», а заряд шерсти «положительным», электроны, как говорят, обладают «отрицательным» зарядным влиянием.Таким образом, объект, атомы которого получили избыток электронов, считается заряженным на отрицательно, , в то время как объект, атомы которого не имеют электронов, считается заряженным положительно на , на , как бы сбивает с толку эти обозначения. К тому времени, когда была открыта истинная природа электрической «жидкости», номенклатура электрического заряда Франклина была слишком хорошо установлена, чтобы ее можно было легко изменить, и так остается по сей день.
Майкл Фарадей доказал (1832 г.), что статическое электричество такое же, как у батареи или генератора.Статическое электричество по большей части доставляет неудобства. В черный порох и бездымный порох добавлен графит для предотвращения возгорания из-за статического электричества. Это вызывает повреждение чувствительной полупроводниковой схемы. Хотя возможно производство двигателей с питанием от статического электричества с высоким напряжением и низким током, это неэкономично. Немногочисленные практические применения статического электричества включают ксерографическую печать, электростатический воздушный фильтр и высоковольтный генератор Ван де Граафа.
- Все материалы состоят из крошечных «строительных блоков», известных как атомов .
- Все встречающиеся в природе атомы содержат частицы, называемые электронами , протонами и нейтронами , за исключением изотопа протия ( 1 H 1 ) водорода.
- Электроны имеют отрицательный (-) электрический заряд.
- Протоны имеют положительный (+) электрический заряд.
- Нейтроны не имеют электрического заряда.
- Электроны можно удалить из атомов намного легче, чем протоны или нейтроны.
- Количество протонов в ядре атома определяет его идентичность как уникального элемента.
Электроны атомов разных типов имеют разную степень свободы передвижения. В некоторых типах материалов, таких как металлы, внешние электроны в атомах настолько слабо связаны, что они хаотично перемещаются в пространстве между атомами этого материала не более чем под влиянием тепловой энергии комнатной температуры.Поскольку эти практически несвязанные электроны могут свободно покидать свои соответствующие атомы и плавать в пространстве между соседними атомами, их часто называют свободными электронами .
Проводники и изоляторыВ других типах материалов, таких как стекло, электроны атомов имеют очень небольшую свободу передвижения. Хотя внешние силы, такие как физическое трение, могут заставить некоторые из этих электронов покинуть свои соответствующие атомы и перейти к атомам другого материала, они не очень легко перемещаются между атомами внутри этого материала.
Эта относительная подвижность электронов в материале известна как электрическая проводимость . Электропроводность определяется типами атомов в материале (количество протонов в ядре каждого атома определяет его химическую идентичность) и тем, как атомы связаны друг с другом. Материалы с высокой подвижностью электронов (много свободных электронов) называются проводниками , в то время как материалы с низкой подвижностью электронов (мало или совсем нет свободных электронов) называются изоляторами .
Вот несколько распространенных примеров проводников и изоляторов:
| Проводники | Изоляторы |
| серебристый | стекло |
| медь | резина |
| золото | масло |
| алюминий | асфальт |
| утюг | стекловолокно |
| сталь | фарфор |
| латунь | керамика |
| бронза | кварц |
| ртуть | (сухое) хлопок |
| графит | (сухая) бумага |
| грязная вода | (сухое) дерево |
| бетон | пластик |
| воздух | |
| алмаз | |
| чистая вода |
Следует понимать, что не все проводящие материалы имеют одинаковый уровень проводимости, и не все изоляторы одинаково устойчивы к движению электронов.Электропроводность аналогична прозрачности некоторых материалов для света: материалы, которые легко «проводят» свет, называются «прозрачными», а те, которые этого не делают, — «непрозрачными». Однако не все прозрачные материалы одинаково светопроводят. Оконное стекло лучше, чем большинство пластиков, и, конечно, лучше, чем «прозрачное» стекловолокно. Так и с электрическими проводниками, одни лучше других.
Например, серебро является лучшим проводником в списке «проводников», предлагая более легкий проход для электронов, чем любой другой упомянутый материал.Грязная вода и бетон также считаются проводниками, но эти материалы обладают значительно меньшей проводимостью, чем любой металл.
Также следует понимать, что некоторые материалы изменяют свои электрические свойства в различных условиях. Например, стекло является очень хорошим изолятором при комнатной температуре, но становится проводником при нагревании до очень высокой температуры. Такие газы, как воздух, обычно изолирующие материалы, также становятся проводящими при нагревании до очень высоких температур.Большинство металлов при нагревании становятся хуже проводниками, а при охлаждении — лучше. Многие проводящие материалы становятся идеально проводящими (это называется сверхпроводимостью , ) при чрезвычайно низких температурах.
Электронный поток / электрический токВ то время как нормальное движение «свободных» электронов в проводнике является случайным, без определенного направления или скорости, электроны могут скоординированно перемещаться через проводящий материал. Это равномерное движение электронов мы называем электричеством или электрическим током .Чтобы быть более точным, его можно было бы назвать динамическим электричеством в отличие от статического электричества , которое представляет собой неподвижное накопление электрического заряда. Так же, как вода, текущая через пустоту трубы, электроны могут перемещаться в пустом пространстве внутри и между атомами проводника. На наш взгляд проводник может показаться твердым, но любой материал, состоящий из атомов, по большей части представляет собой пустое пространство! Аналогия с потоком жидкости настолько уместна, что движение электронов через проводник часто называют «потоком».”
Здесь можно сделать примечательное наблюдение. Поскольку каждый электрон равномерно движется через проводник, он толкает проводник впереди, так что все электроны движутся вместе как группа. Начало и остановка потока электронов по длине проводящего пути происходит практически мгновенно от одного конца проводника к другому, даже если движение каждого электрона может быть очень медленным. Примерная аналогия — трубка, заполненная встык мрамором:
Фигура 2.7Трубка полна шариков, как проводник полон свободных электронов, готовых к перемещению под воздействием извне. Если один шарик внезапно вставляется в эту полную трубку с левой стороны, другой шарик немедленно попытается выйти из трубки справа. Несмотря на то, что каждый шарик прошел лишь небольшое расстояние, передача движения через трубку происходит практически мгновенно от левого конца к правому концу, независимо от длины трубки. С электричеством общий эффект от одного конца проводника до другого происходит со скоростью света: быстрые 186 000 миль в секунду !!! Однако каждый отдельный электрон проходит через проводник на , намного медленнее.
Электронный поток через проводЕсли мы хотим, чтобы электроны текли в определенном направлении в определенное место, мы должны обеспечить им правильный путь для движения, точно так же, как водопроводчик должен установить трубопровод, чтобы вода текла туда, где он или она хочет, чтобы она текла. Чтобы облегчить это, провода изготовлены из металлов с высокой проводимостью, таких как медь или алюминий, самых разных размеров.
Помните, что электроны могут течь только тогда, когда у них есть возможность перемещаться в пространстве между атомами материала.Это означает, что электрический ток может присутствовать только там, где существует непрерывный путь из проводящего материала, обеспечивающий канал для прохождения электронов. В аналогии с мрамором шарики могут течь в левую сторону трубки (и, следовательно, через трубку) тогда и только тогда, когда трубка открыта с правой стороны, чтобы шарики могли вытекать. Если трубка заблокирована с правой стороны, шарики будут просто «скапливаться» внутри трубки, и мраморный «поток» не произойдет.То же самое верно и для электрического тока: непрерывный поток электронов требует наличия непрерывного пути, позволяющего этот поток. Давайте посмотрим на диаграмму, чтобы проиллюстрировать, как это работает:
Рис. 2.8Тонкая сплошная линия (как показано выше) является условным обозначением непрерывного отрезка провода. Поскольку проволока сделана из проводящего материала, такого как медь, составляющие ее атомы имеют много свободных электронов, которые могут легко перемещаться по проволоке. Однако в этом проводе никогда не будет непрерывного или равномерного потока электронов, если им не будет откуда взяться и куда пойти.Добавим гипотетические «Источник» и «Назначение» электрона:
. Рис. 2.9.Теперь, когда Источник электронов проталкивает новые электроны в провод с левой стороны, может возникнуть поток электронов через провод (на что указывают стрелки, указывающие слева направо). Однако поток будет прерван, если токопроводящий путь, образованный проволокой, будет нарушен:
Рисунок 2.10 Целостность цепиПоскольку воздух — изолирующий материал, а два куска провода разделяет воздушный зазор, некогда непрерывный путь был прерван, и электроны не могут течь от источника к месту назначения.Это похоже на разрезание водопроводной трубы на две части и закрытие ее сломанных концов: вода не может течь, если нет выхода из трубы. С точки зрения электричества, у нас было состояние электрической цепи , , когда провод был цельным, а теперь эта непрерывность прервана из-за того, что провод был разрезан и отделен.
Если бы мы возьмем другой кусок провода, ведущего к Пункту назначения, и просто вступим в физический контакт с проводом, ведущим к Источнику, у нас снова будет непрерывный путь для движения электронов.Две точки на схеме обозначают физический контакт (металл-металл) между кусочками провода:
Рисунок 2.11Теперь у нас есть непрерывность от Источника до вновь созданного соединения, вниз, вправо и вверх до Назначения. Это аналогично установке тройника в одну из закрытых труб и направлению воды через новый сегмент трубы к месту назначения. Обратите внимание, что по обрыву провода с правой стороны нет электронов, проходящих через него, потому что он больше не является частью полного пути от Источника к Пункту назначения.
Интересно отметить, что из-за этого электрического тока внутри проводов не происходит «износа», в отличие от водопроводных труб, которые в конечном итоге подвергаются коррозии и изнашиваются из-за продолжительных потоков. Однако при движении электроны сталкиваются с некоторым трением, и это трение может генерировать тепло в проводнике. Это тема, которую мы рассмотрим более подробно позже.
- В проводящих материалах внешние электроны в каждом атоме могут легко приходить или уходить и называются свободными электронами.
- В изоляционных материалах внешние электроны не так свободно перемещаются.
- Все металлы электропроводны.
- Динамическое электричество или электрический ток — это равномерное движение электронов по проводнику.
- Статическое электричество — это неподвижное (если на изоляторе) накопленный заряд, образованный избытком или недостатком электронов в объекте. Обычно он образуется путем разделения зарядов путем контакта и разделения разнородных материалов.
- Для того, чтобы электроны могли непрерывно (бесконечно) течь через проводник, должен быть полный, непрерывный путь, по которому они могут двигаться как внутрь, так и из этого проводника.
Вы, возможно, задавались вопросом, как заряды могут непрерывно течь в одинаковом направлении по проводам без использования этих гипотетических Источников и Назначений. Чтобы схема источника и назначения работала, оба должны иметь бесконечную емкость для зарядов, чтобы поддерживать непрерывный поток!
Используя аналогию с мрамором и трубкой из предыдущего раздела о проводниках, изоляторах и потоке электронов, мраморный источник и мраморные приемные ведра должны быть бесконечно большими, чтобы вместить достаточно мрамора для «потока» мрамора. выдержанный.
Что такое цепь?Ответ на этот парадокс можно найти в концепции цепи : бесконечный петлевой путь для носителей заряда. Если мы возьмем провод или несколько проводов, соединенных встык, и закрутим его так, чтобы он образовал непрерывный путь, у нас есть средства для поддержки равномерного потока заряда без необходимости прибегать к бесконечным источникам и назначениям:
Рисунок 2.12Каждый носитель заряда, движущийся по часовой стрелке в этой цепи, толкает носитель перед ним, который толкает носитель перед ним, и так далее, и так далее, точно так же, как хула-хуп, наполненный шариками.Теперь у нас есть возможность поддерживать непрерывный поток заряда бесконечно без необходимости в бесконечных запасах и свалках. Все, что нам нужно для поддержания этого потока, — это постоянные средства мотивации для этих носителей заряда, о которых мы поговорим в следующем разделе этой главы, посвященном напряжению и току.
Wha t Означает ли это, что цепь b раскачивается?Непрерывность в цепи так же важна, как и в прямом проводе.Как и в примере с прямым отрезком провода между Источником и Назначением, любой разрыв в этой цепи не позволит заряду проходить через нее:
Рис. 2.13Здесь важно понимать, что не имеет значения, где происходит разрыв . Любое нарушение непрерывности в цепи предотвратит поток заряда по всей цепи. Если не существует непрерывной непрерывной петли из проводящего материала, через которую проходят носители заряда, устойчивый поток просто не может поддерживаться.
Рисунок 2.14- Цепь представляет собой непрерывную петлю из проводящего материала, которая позволяет носителям заряда непрерывно проходить через нее без начала и конца.
- Если цепь «разорвана», это означает, что ее проводящие элементы больше не образуют полный путь, и в ней не может происходить непрерывный поток заряда.
- Местоположение разрыва цепи не имеет отношения к ее неспособности поддерживать непрерывный поток заряда. Любой обрыв , где-нибудь в цепи предотвращает поток носителей заряда по цепи.
Как упоминалось ранее, нам нужно нечто большее, чем просто непрерывный путь (т. Так же, как мрамор в трубе или вода в трубе, для инициирования потока требуется некоторая сила воздействия. В случае электронов эта сила — это та же сила, которая действует в статическом электричестве: сила, создаваемая дисбалансом электрического заряда.
Если мы возьмем примеры воска и шерсти, которые были натерты друг с другом, мы обнаружим, что избыток электронов в воске (отрицательный заряд) и недостаток электронов в шерсти (положительный заряд) создают дисбаланс заряда между ними.Этот дисбаланс проявляется как сила притяжения между двумя объектами:
Рисунок 2.15Если между заряженным парафином и шерстью поместить проводящую проволоку, электроны будут проходить через нее, так как некоторые из избыточных электронов воска устремляются через провод, чтобы вернуться к шерсти, восполняя там недостаток электронов:
Рис. 2.16Дисбаланс электронов между атомами воска и атомами шерсти создает силу между двумя материалами. Поскольку электроны не могут перетекать от воска к шерсти, все, что может сделать эта сила, — это притягивать два объекта вместе.
Теперь, когда проводник перекрывает изолирующий зазор, сила заставит электроны течь в однородном направлении через провод, хотя бы на мгновение, пока заряд в этой области не нейтрализуется и сила между воском и шерстью не уменьшится.
Электрический заряд, образованный между этими двумя материалами при трении их друг о друга, служит для хранения определенного количества энергии. Эта энергия мало чем отличается от энергии, накопленной в высоком резервуаре с водой, который выкачивается из пруда нижнего уровня:
Фигура 2.17Влияние силы тяжести на воду в резервуаре создает силу, которая пытается снова опустить воду на более низкий уровень. Если подходящая труба проложена от резервуара обратно к пруду, вода под действием силы тяжести потечет вниз из резервуара по трубе:
Рис. 2.18.Требуется энергия, чтобы перекачивать воду из пруда с низким уровнем в резервуар с высоким уровнем, и движение воды по трубопроводу обратно к исходному уровню представляет собой высвобождение энергии, накопленной от предыдущей откачки.
Если вода перекачивается на еще более высокий уровень, для этого потребуется еще больше энергии, таким образом, будет сохранено больше энергии, и больше энергии будет высвобождено, если воде будет позволено снова течь по трубе обратно вниз:
Рис. 2.19.Электроны мало чем отличаются. Если мы протираем воск и шерсть вместе, мы «выкачиваем» электроны с их нормальных «уровней», создавая условия, при которых существует сила между парафином и шерстью, поскольку электроны стремятся восстановить свои прежние положения (и балансировать внутри своего тела). соответствующие атомы).Сила, притягивающая электроны обратно в исходное положение вокруг положительных ядер их атомов, аналогична силе гравитации, действующей на воду в резервуаре, пытаясь вернуть ее к прежнему уровню. Подобно тому, как перекачка воды на более высокий уровень приводит к накоплению энергии, «перекачка» электронов для создания дисбаланса электрического заряда приводит к накоплению определенного количества энергии в этом дисбалансе. И точно так же, как предоставление возможности воде стекать обратно с высоты резервуара приводит к высвобождению этой накопленной энергии, предоставление возможности электронам течь обратно к их первоначальным «уровням» приводит к высвобождению накопленной энергии.
Когда носители заряда находятся в этом статическом состоянии (точно так же, как вода, неподвижная, высоко в резервуаре), энергия, хранящаяся там, называется потенциальной энергией , потому что у нее есть возможность (потенциал) высвобождения, которая не была полностью исчерпана. понял еще.
Понимание концепции напряженияКогда носители заряда находятся в статическом состоянии (как вода, неподвижная, высоко в резервуаре), энергия, хранящаяся там, называется потенциальной энергией, потому что у нее есть возможность (потенциал) высвобождения, которая еще не полностью реализована. .
Когда вы терзаете обувь с резиновой подошвой о тканевый ковер в сухой день, вы создаете дисбаланс электрического заряда между вами и ковром. При царапании ногами накапливается энергия в виде дисбаланса зарядов, вытесняемых из их первоначальных мест. Этот заряд (статическое электричество) является стационарным, и вы вообще не заметите, что энергия накапливается. Однако, как только вы положите руку на металлическую дверную ручку (с большой подвижностью электронов для нейтрализации вашего электрического заряда), эта накопленная энергия будет высвобождена в виде внезапного потока заряда через вашу руку, и вы будете воспринимать ее как поражение электрическим током!
Эта потенциальная энергия, накопленная в виде дисбаланса электрического заряда и способная спровоцировать прохождение носителей заряда через проводник, может быть выражена термином, называемым напряжением, которое технически представляет собой меру потенциальной энергии на единицу заряда или что-то вроде того, что физик назвал бы удельную потенциальную энергию.
Определение напряженияОпределяемое в контексте статического электричества, напряжение — это мера работы, необходимой для перемещения единичного заряда из одного места в другое, против силы, которая пытается сохранить баланс электрических зарядов. В контексте источников электроэнергии напряжение — это количество доступной потенциальной энергии (работы, которую необходимо выполнить) на единицу заряда для перемещения зарядов по проводнику. Поскольку напряжение является выражением потенциальной энергии, представляющей возможность или потенциал высвобождения энергии при перемещении заряда с одного «уровня» на другой, на него всегда ссылаются между двумя точками.Рассмотрим аналогию с водохранилищем:
. Рис. 2.20Из-за разницы в высоте падения существует вероятность того, что гораздо больше энергии будет выпущено из резервуара через трубопровод в точку 2, чем в точку 1. Принцип можно интуитивно понять, бросив камень: что приводит к при более сильном ударе камень упал с высоты одного фута или тот же камень упал с высоты одной мили?
Очевидно, падение с большей высоты приводит к высвобождению большей энергии (более сильный удар).Мы не можем оценить количество накопленной энергии в водном резервуаре, просто измерив объем воды, точно так же, как мы можем предсказать серьезность удара падающей породы, просто зная вес породы: в обоих случаях мы также должны учитывать, как далекие эти массы упадут со своей начальной высоты. Количество энергии, высвобождаемой при падении массы, зависит от расстояния между его начальной и конечной точками. Точно так же потенциальная энергия, доступная для перемещения носителей заряда из одной точки в другую, зависит от этих двух точек.Следовательно, напряжение всегда выражается как величина между двумя точками.
Интересно, что аналогия массы, потенциально «падающей» с одной высоты на другую, является настолько удачной моделью, что напряжение между двумя точками иногда называют падением напряжения .
Генерирующее напряжениеНапряжение можно генерировать другими способами, кроме трения материалов определенных типов друг о друга. Химические реакции, лучистая энергия и влияние магнетизма на проводники — вот несколько способов создания напряжения.Соответствующими примерами этих трех источников напряжения являются батареи, солнечные элементы и генераторы (например, «генератор переменного тока» под капотом вашего автомобиля). На данный момент мы не будем вдаваться в подробности того, как работает каждый из этих источников напряжения — более важно то, что мы понимаем, как источники напряжения могут применяться для создания потока заряда в электрической цепи.
Давайте возьмем символ химической батареи и поэтапно построим схему:
Рисунок 2.21 Как работают источники напряжения?Любой источник напряжения, включая аккумуляторные батареи, имеет две точки электрического контакта.В этом случае у нас есть точка 1 и точка 2 на приведенной выше диаграмме. Горизонтальные линии различной длины указывают на то, что это батарея, и дополнительно указывают направление, в котором напряжение этой батареи будет пытаться протолкнуть носители заряда по цепи. Тот факт, что горизонтальные линии в символе батареи кажутся разделенными (и, таким образом, не могут служить в качестве пути для потока заряда), не вызывает беспокойства: в реальной жизни эти горизонтальные линии представляют собой металлические пластины, погруженные в жидкий или полутвердый материал. который не только проводит заряды, но и генерирует напряжение, чтобы подтолкнуть их, взаимодействуя с пластинами.
Обратите внимание на маленькие знаки «+» и «-» непосредственно слева от символа батареи. Отрицательный (-) конец батареи всегда является концом с самым коротким тире, а положительный (+) конец батареи всегда является концом с самым длинным тире. Положительный конец батареи — это конец, который пытается вытолкнуть из нее носители заряда (помните, что по традиции мы думаем, что носители заряда заряжены положительно, хотя электроны заряжены отрицательно). Точно так же отрицательный конец — это конец, который пытается привлечь носители заряда.
Если концы «+» и «-» батареи ни к чему не подключены, между этими двумя точками будет напряжение, но не будет потока заряда через батарею, потому что нет непрерывного пути, по которому могут перемещаться носители заряда. .
Рисунок 2.22Тот же принцип справедлив и для аналогии с резервуаром для воды и насосом: без возвратной трубы обратно в пруд накопленная энергия в резервуаре не может быть выпущена в виде потока воды. Когда резервуар полностью заполнен, поток не может возникнуть, независимо от того, какое давление может создать насос.Должен существовать полный путь (контур), по которому вода течет из пруда в резервуар и обратно в пруд для обеспечения непрерывного потока.
Мы можем обеспечить такой путь для батареи, соединив кусок провода от одного конца батареи к другому. Формируя цепь с петлей из проволоки, мы инициируем непрерывный поток заряда по часовой стрелке:
Рисунок 2.23 Понимание концепции электрического токаПока батарея продолжает вырабатывать напряжение и непрерывность электрического пути не нарушена, носители заряда будут продолжать течь в цепи.Следуя метафоре воды, движущейся по трубе, этот непрерывный, равномерный поток заряда через цепь называется током и . Пока источник напряжения продолжает «толкать» в одном направлении, носители заряда будут продолжать двигаться в том же направлении в цепи. Этот однонаправленный поток тока называется постоянного тока, или постоянного тока. Во втором томе этой серии книг исследуются электрические цепи, в которых направление тока переключается взад и вперед: переменного тока, или переменного тока.Но пока мы просто займемся цепями постоянного тока.
Поскольку электрический ток состоит из отдельных носителей заряда, текущих в унисон через проводник, перемещаясь и толкая носители заряда впереди, точно так же, как шарики через трубу или вода через трубу, величина потока через одну цепь будет равна то же самое в любой момент. Если бы мы отслеживали поперечное сечение провода в одной цепи, считая протекающие носители заряда, мы бы заметили точно такое же количество в единицу времени, что и в любой другой части цепи, независимо от длины проводника или проводника. диаметр.
Если мы нарушим непрерывность цепи в любой точке , электрический ток прекратится во всей петле, и полное напряжение, произведенное батареей, будет проявляться через разрыв, между концами проводов, которые раньше были соединены:
Рисунок 2.24 Что такое полярность падения напряжения?Обратите внимание на знаки «+» и «-», нарисованные на концах разрыва цепи, и то, как они соответствуют знакам «+» и «-» рядом с выводами аккумулятора.Эти маркеры указывают направление, в котором напряжение пытается протолкнуть ток, это направление потенциала, обычно называемое полярностью , . Помните, что напряжение всегда относительно между двумя точками. По этой причине полярность падения напряжения также является относительной между двумя точками: будет ли точка в цепи помечена знаком «+» или «-», зависит от другой точки, к которой она относится. Взгляните на следующую схему, где каждый угол петли отмечен номером для справки:
Фигура 2.25При нарушении целостности цепи между точками 2 и 3, полярность падения напряжения между точками 2 и 3 будет «+» для точки 2 и «-» для точки 3. Полярность батареи (1 «+» и 4 « — ”) пытается протолкнуть ток через петлю по часовой стрелке от 1 до 2, от 3 до 4 и снова обратно до 1.
Теперь посмотрим, что произойдет, если мы снова соединим точки 2 и 3 вместе, но сделаем разрыв цепи между точками 3 и 4:
Рисунок 2.26При разрыве между 3 и 4 полярность падения напряжения между этими двумя точками будет «-» для 4 и «+» для 3.Обратите особое внимание на тот факт, что «знак» точки 3 противоположен знаку в первом примере, где разрыв был между точками 2 и 3 (где точка 3 была помечена «-»). Мы не можем сказать, что точка 3 в этой цепи всегда будет либо «+», либо «-», потому что полярность, как и само напряжение, не зависит от одной точки, а всегда относительна между двумя точками!
- Носители заряда могут двигаться через проводник с помощью той же силы, которая проявляется в статическом электричестве.
- Напряжение — это мера удельной потенциальной энергии (потенциальной энергии на единицу заряда) между двумя точками. С точки зрения непрофессионала, это мера «толчка», позволяющая мотивировать обвинение.
- Напряжение, как выражение потенциальной энергии, всегда является относительным между двумя местоположениями или точками. Иногда это называют «падением напряжения».
- Когда источник напряжения подключен к цепи, напряжение вызывает равномерный поток носителей заряда через эту цепь, называемый током , .
- В одиночной (однопетлевой) схеме величина тока в любой точке такая же, как и величина тока в любой другой точке.
- Если цепь, содержащая источник напряжения, разорвана, полное напряжение этого источника появится в точках разрыва.
- +/- ориентация падения напряжения называется полярностью . Это также относительное значение между двумя точками.
Схема из предыдущего раздела не очень практична.На самом деле, это может быть довольно опасно строить (прямое соединение полюсов источника напряжения с помощью одного куска провода). Причина, по которой это опасно, заключается в том, что величина электрического тока может быть очень большой в таком коротком замыкании , и выделение энергии может быть очень значительным (обычно в виде тепла).
Обычно электрические цепи строятся таким образом, чтобы максимально безопасно использовать высвобождаемую энергию на практике.
Ток, протекающий через нить накала лампыОдно из практических и популярных применений электрического тока — это электрическое освещение.Самая простая форма электрической лампы — это крошечная металлическая «нить» внутри прозрачной стеклянной колбы, которая накаляется добела («накаляется») тепловой энергией, когда через нее проходит достаточный электрический ток. Как и аккумулятор, он имеет две токопроводящие точки подключения: одна для подачи тока, а другая — для вывода тока.
При подключении к источнику напряжения электрическая цепь лампы выглядит примерно так:
Рис. 2.27Когда ток проходит через тонкую металлическую нить накала лампы, он встречает большее сопротивление движению, чем обычно в толстом куске провода.Это сопротивление электрическому току зависит от типа материала, его площади поперечного сечения и температуры. Технически он известен как сопротивление . (Можно сказать, что у проводников низкое сопротивление, а у изоляторов очень высокое сопротивление.) Это сопротивление служит для ограничения количества тока, проходящего через цепь с заданным значением напряжения, подаваемого батареей, по сравнению с «коротким замыканием», когда у нас не было ничего, кроме провода, соединяющего один конец источника напряжения (батареи) с другим.
Когда ток движется против сопротивления сопротивления, возникает «трение». Точно так же, как механическое трение, трение, создаваемое током, протекающим против сопротивления, проявляется в виде тепла. Концентрированное сопротивление нити накала лампы приводит к тому, что на нити рассеивается относительно большое количество тепловой энергии. Этой тепловой энергии достаточно, чтобы нить накаливания стала раскаленной добела, производя свет, в то время как провода, соединяющие лампу с батареей (которые имеют гораздо меньшее сопротивление), едва ли нагреваются, проводя такое же количество тока.
Как и в случае короткого замыкания, если непрерывность цепи нарушена в любой точке, ток прекращается по всей цепи. Если лампа установлена, это означает, что она перестанет светиться:
Рисунок 2.28.Как и раньше, при отсутствии тока, весь потенциал (напряжение) батареи доступен через разрыв, ожидая возможности подключения, чтобы перемыть этот разрыв и позволить току снова течь. Это состояние известно как обрыв цепи , , когда разрыв цепи предотвращает ток повсюду.
Все, что требуется, — это однократное прерывание непрерывности, чтобы «разомкнуть» цепь. После повторного подключения любых разрывов и восстановления непрерывности цепи она называется замкнутой цепью , .
Основа для включения лампТо, что мы видим здесь, является основой для включения и выключения ламп с помощью дистанционных выключателей. Поскольку любой разрыв непрерывности цепи приводит к остановке тока по всей цепи, мы можем использовать устройство, предназначенное для преднамеренного разрыва этой непрерывности (называемое переключателем), установленное в любом удобном месте, к которому мы можем провести провода, для управления потоком ток в цепи:
Фигура 2.29Таким образом, выключатель, установленный на стене дома, может управлять лампой, установленной в длинном коридоре или даже в другой комнате, вдали от выключателя. Сам переключатель состоит из пары проводящих контактов (обычно сделанных из какого-либо металла), соединенных механическим рычажным приводом или кнопкой. Когда контакты соприкасаются друг с другом, ток может течь от одного к другому, и устанавливается непрерывность цепи. Когда контакты разделены, ток от одного к другому предотвращается воздушной изоляцией между ними, и непрерывность цепи нарушается.
Ножевой переключательПожалуй, лучший вид переключателя, который можно показать для иллюстрации основного принципа, — это «ножевой» переключатель:
Рис. 2.30Рубильник — это не что иное, как токопроводящий рычаг, свободно поворачивающийся на шарнире, вступающий в физический контакт с одной или несколькими неподвижными точками контакта, которые также являются токопроводящими.
Переключатель, показанный на иллюстрации выше, построен на фарфоровой основе (отличный изоляционный материал) с использованием меди (отличный проводник) для «лезвий» и точек контакта.Ручка сделана из пластика, чтобы изолировать руку оператора от токопроводящего лезвия переключателя при его открытии или закрытии.
Вот еще один тип рубильника, с двумя неподвижными контактами вместо одного:
Рис. 2.31Конкретный рубильник, показанный здесь, имеет одно «лезвие», но два неподвижных контакта, что означает, что он может включать или отключать более одной цепи. На данный момент это не так важно, чтобы знать, просто базовая концепция того, что такое переключатель и как он работает.Рубильные переключатели отлично подходят для иллюстрации основного принципа работы переключателя, но они представляют определенные проблемы безопасности при использовании в электрических цепях большой мощности. Открытые проводники рубильника делают случайный контакт с цепью, и любая искра, которая может возникнуть между движущимся лезвием и неподвижным контактом, может воспламенить находящиеся поблизости легковоспламеняющиеся материалы. В большинстве современных конструкций переключателей подвижные проводники и точки контакта герметично закрыты изолирующим кожухом, чтобы уменьшить эти опасности.Фотография нескольких современных типов переключателей показывает, что механизмы переключения гораздо более скрыты, чем в конструкции ножа:
Рисунок 2.32 Открытые и закрытые контурыВ соответствии с терминологией «разомкнутой» и «замкнутой» цепей, переключатель, который устанавливает контакт от одной клеммы подключения к другой (пример: рубильник с лезвием, полностью касающимся неподвижной точки контакта), обеспечивает непрерывность подачи тока в протекает и называется переключателем , замкнутым, .
И наоборот, выключатель, который нарушает целостность цепи (пример: рубильник с лезвием , не касающимся неподвижной точки контакта), не пропускает ток и называется выключателем , разомкнутым . Эта терминология часто сбивает с толку новичков, изучающих электронику, потому что слова «открытый» и «закрытый» обычно понимаются в контексте двери, где «открытый» приравнивается к свободному проходу, а «закрытый» — к блокировке. В случае электрических переключателей эти термины имеют противоположные значения: «разомкнутый» означает отсутствие потока, в то время как «замкнутый» означает свободное прохождение электрического тока.
- Сопротивление — это мера сопротивления электрическому току.
- Короткое замыкание — электрическая цепь, оказывающая небольшое сопротивление протеканию тока или не имеющая его. Короткие замыкания опасны для источников питания высокого напряжения, поскольку возникающие высокие токи могут вызвать выделение большого количества тепловой энергии.
- Разрыв цепи — это цепь, в которой непрерывность была нарушена из-за прерывания пути прохождения тока.
- Замкнутая цепь — это полная цепь с хорошей непрерывностью на всем протяжении.
- Устройство, предназначенное для размыкания или замыкания цепи в контролируемых условиях, называется переключателем .
- Термины «разомкнут», и «замкнут», относятся как к переключателям, так и ко всем цепям. Открытый переключатель — это переключатель без непрерывности: ток не может течь через него. Замкнутый переключатель — это переключатель, который обеспечивает прямой (с низким сопротивлением) путь для прохождения тока.
Поскольку соотношение между напряжением, током и сопротивлением в любой цепи настолько регулярное, мы можем надежно контролировать любую переменную в цепи, просто управляя двумя другими. Возможно, самой простой переменной в любой цепи для управления является ее сопротивление. Это можно сделать, изменив материал, размер и форму проводящих компонентов (помните, как тонкая металлическая нить накала лампы создавала большее электрическое сопротивление, чем толстый провод?).
Что такое резистор?Специальные компоненты, называемые резисторами, производятся специально для создания точного количества сопротивления для вставки в цепь.Обычно они изготавливаются из металлической проволоки или углерода и спроектированы так, чтобы поддерживать стабильное значение сопротивления в широком диапазоне условий окружающей среды. В отличие от ламп, они не излучают свет, но выделяют тепло, поскольку электрическая энергия рассеивается ими в рабочем контуре. Однако, как правило, резистор предназначен не для выработки полезного тепла, а просто для обеспечения точного количества электрического сопротивления.
Условные обозначения и значения на схеме резистораНаиболее распространенным условным обозначением резистора на схеме является зигзагообразная линия:
Фигура 2.33Значения резисторов в омах обычно отображаются как смежные числа, и если в цепи присутствует несколько резисторов, они будут помечены уникальным идентификационным номером, например R 1 , R 2 , R 3 , и т.д. Как видите, символы резисторов могут отображаться как по горизонтали, так и по вертикали:
Рис. 2.34.Реальные резисторы не похожи на зигзагообразный символ. Вместо этого они выглядят как маленькие трубки или цилиндры с двумя торчащими проводами для подключения к цепи.Вот образцы резисторов разных типов и размеров:
Рис. 2.35В соответствии с их внешним видом, альтернативный схематический символ резистора выглядит как небольшая прямоугольная коробка:
Рис. 2.36. Можно также показать, что резисторыимеют переменное, а не фиксированное сопротивление. Это может быть сделано с целью описания реального физического устройства, разработанного с целью обеспечения регулируемого сопротивления, или может быть для того, чтобы показать какой-то компонент, который просто случайно имеет нестабильное сопротивление:
Фигура 2.37
Фактически, каждый раз, когда вы видите символ компонента, нарисованный через диагональную стрелку, этот компонент имеет переменную, а не фиксированное значение. Этот «модификатор» символа (диагональная стрелка) является стандартным условным обозначением электронных символов.
Переменные резисторы должны иметь какие-либо физические средства регулировки, либо вращающийся вал, либо рычаг, который можно перемещать для изменения величины электрического сопротивления. На фотографии показаны некоторые устройства, называемые потенциометрами, которые можно использовать как переменные резисторы:
Фигура 2.38 Номинальная мощность резисторовПоскольку резисторы рассеивают тепловую энергию, поскольку электрические токи через них преодолевают «трение» их сопротивления, резисторы также оцениваются с точки зрения того, сколько тепловой энергии они могут рассеять без перегрева и повреждений. Естественно, эта номинальная мощность указывается в физических единицах измерения «ватты». Большинство резисторов, используемых в небольших электронных устройствах, таких как портативные радиоприемники, рассчитаны на 1/4 (0,25) Вт или меньше. Номинальная мощность любого резистора примерно пропорциональна его физическому размеру.Обратите внимание на первую фотографию резистора, как номинальная мощность соотносится с размером: чем больше резистор, тем выше его номинальная рассеиваемая мощность. Также обратите внимание, что сопротивление (в омах) не имеет ничего общего с размером!
Хотя сейчас может показаться бессмысленным иметь устройство, которое ничего не делает, кроме сопротивления электрическому току, резисторы — чрезвычайно полезные устройства в схемах. Поскольку они просты и широко используются в мире электричества и электроники, мы потратим значительное количество времени на анализ схем, состоящих только из резисторов и батарей.
Чем полезны резисторы?Для практической иллюстрации полезности резисторов, рассмотрите фотографию ниже. Это изображение печатной платы или печатной платы: сборка, состоящая из прослоенных слоев изоляционной фенольной волокнистой платы и проводящих медных полос, в которые можно вставлять компоненты и закреплять их с помощью процесса низкотемпературной сварки, называемого «пайкой». Различные компоненты на этой печатной плате обозначены печатными этикетками. Резисторы обозначаются любой этикеткой, начинающейся с буквы «R».
Рис. 2.39.Эта конкретная печатная плата представляет собой компьютерный аксессуар, называемый «модемом», который позволяет передавать цифровую информацию по телефонным линиям. На плате этого модема можно увидеть как минимум дюжину резисторов (все с мощностью рассеиваемой мощности 1/4 Вт). Каждый из черных прямоугольников (называемых «интегральными схемами» или «микросхемами») также содержит собственный массив резисторов для своих внутренних функций. Другой пример печатной платы показывает резисторы, упакованные в еще меньшие блоки, называемые «устройствами для поверхностного монтажа».Эта конкретная печатная плата является нижней стороной жесткого диска персонального компьютера, и снова припаянные к ней резисторы обозначены этикетками, начинающимися с буквы «R»:
Рисунок 2.40На этой печатной плате более сотни резисторов для поверхностного монтажа, и это количество, конечно, не включает количество резисторов, встроенных в черные «микросхемы». Эти две фотографии должны убедить любого, что резисторы — устройства, которые «просто» препятствуют прохождению электрического тока, — очень важные компоненты в области электроники!
«Нагрузка» на принципиальных схемахНа схематических диаграммах символы резисторов иногда используются для иллюстрации любого общего типа устройства в цепи, выполняющего что-то полезное с электрической энергией.Любое неспецифическое электрическое устройство обычно называется нагрузкой, поэтому, если вы видите схематическую диаграмму, показывающую символ резистора с пометкой «нагрузка», особенно в учебной принципиальной схеме, объясняющей некоторые концепции, не связанные с фактическим использованием электроэнергии, этот символ может просто быть своего рода сокращением чего-то еще более практичного, чем резистор.
Анализ цепей резисторовЧтобы обобщить то, что мы узнали в этом уроке, давайте проанализируем следующую схему, определив все, что мы можем, исходя из предоставленной информации:
Фигура 2.41Все, что нам здесь дано для начала, — это напряжение батареи (10 вольт) и ток цепи (2 ампера). Нам неизвестно сопротивление резистора в омах или рассеиваемая им мощность в ваттах. Изучая наш массив уравнений закона Ома, мы находим два уравнения, которые дают нам ответы на основе известных величин напряжения и тока:
Закон Ома[латекс] R = \ frac {E} {I} \ tag {2.1} [/ латекс]
Уравнение мощности[латекс] P = IE \ tag {2.2} [/ латекс]
Подставляя известные величины напряжения (E) и тока (I) в эти два уравнения, мы можем определить сопротивление цепи (R) и рассеиваемую мощность (P):
Закон Ома:[латекс] R \: = \ frac {10V} {2A} = 5 \ Omega [/ latex]
Степенной закон:[латекс] P = (2A) (10 В) = (20 Вт) [/ латекс]
Для условий цепи 10 В и 2 А сопротивление резистора должно быть 5 Ом.Если бы мы проектировали схему для работы при этих значениях, нам пришлось бы указать резистор с минимальной номинальной мощностью 20 Вт, иначе он перегреется и выйдет из строя.
Материалы резистора Резисторымогут быть изготовлены из самых разных материалов, каждый из которых имеет свои свойства и специфические области применения. Большинство инженеров-электриков используют указанные ниже типы:
Резисторы с проволочной обмоткой (WW) Резисторы с проволочной обмоткойизготавливаются путем намотки резистивного провода вокруг непроводящего сердечника по спирали.Обычно они производятся для высокоточных и силовых приложений. Сердечник обычно изготавливается из керамики или стекловолокна, а резистивный провод из никель-хромового сплава не подходит для приложений с частотами выше 50 кГц. Низкий уровень шума и устойчивость к колебаниям температуры являются стандартными характеристиками проволочных резисторов. Доступны значения сопротивления от 0,1 до 100 кВт с точностью от 0,1% до 20%.
Металлопленочные резисторыНитрид тантала или нихрома обычно используется для изготовления металлопленочных резисторов.Комбинация керамического материала и металла обычно составляет резистивный материал. Значение сопротивления изменяется путем вырезания спирального рисунка в пленке, очень похоже на углеродную пленку с помощью лазера или абразива. Металлопленочные резисторы обычно менее устойчивы к температуре, чем резисторы с проволочной обмоткой, но лучше справляются с более высокими частотами.
Металлооксидные пленочные резисторыВ металлооксидных резисторах используются оксиды металлов, такие как оксид олова, что немного отличает их от металлических пленочных резисторов.Эти резисторы надежны и стабильны и работают при более высоких температурах, чем металлопленочные резисторы. Из-за этого металлооксидные пленочные резисторы используются в приложениях, требующих высокой прочности.
Фольгированные резисторыРазработанный в 1960-х годах резистор из фольги по-прежнему остается одним из самых точных и стабильных типов резисторов, которые вы найдете и используются в приложениях с высокими требованиями к точности. Керамическая подложка, к которой приклеена тонкая объемная металлическая фольга, составляет резистивный элемент.Фольговые резисторы имеют очень низкотемпературный коэффициент сопротивления.
Резисторы из углеродного состава (CCR)До 1960-х годов резисторы из углеродного состава были стандартом для большинства приложений. Они надежны, но не очень точны (их допуск не может быть лучше примерно 5%). Смесь мелких частиц углерода и непроводящего керамического материала используется для резистивного элемента резисторов CCR. Вещество формуют в форме цилиндра и запекают.Размеры корпуса и соотношение углерода и керамики определяют величину сопротивления. Использование большего количества углерода в процессе означает меньшее сопротивление. Резисторы CCR по-прежнему полезны для определенных приложений из-за их способности выдерживать импульсы высокой энергии, хорошим примером применения может быть источник питания.
Резисторы углеродные пленочныеУглеродные пленочные резисторы имеют тонкую углеродную пленку (со спиралью, вырезанной в пленке для увеличения резистивного пути) на изолирующем цилиндрическом сердечнике.Это позволяет получить более точное значение сопротивления, а также увеличивает значение сопротивления. Резисторы из углеродной пленки намного точнее, чем резисторы из углеродной композиции. Специальные углеродные пленочные резисторы используются в приложениях, требующих высокой импульсной стабильности.
Показатели эффективности (КПЭ)Ключевые показатели эффективности для каждого материала резистора можно найти ниже:
| Характеристика | Металлическая пленка | Толстая металлическая пленка | Прецизионная металлическая пленка | Углеродный состав | Углеродная пленка |
|---|---|---|---|---|---|
| Темп.диапазон | -55 + 125 | -55 + 130 | -55 + 155 | -40 + 105 | ,55 + 155 |
| Макс. темп. коэфф. | 100 | 100 | 15 | 1200 | 250-1000 |
| Vмакс. | 200-350 | 250 | 200 | 350-500 | 350-500 |
| Шум (мкВ на вольт приложенного постоянного тока) | 0,5 | 0,1 | 0.1 | 4 (100 КБ) | 5 (100 КБ) |
| R Insul. | 10000 | 10000 | 10000 | 10000 | 10000 |
| Припой (изменение значения сопротивления в%) | 0,20% | 0,15% | 0,02% | 2% | 0,50% |
| Влажное тепло (изменение значения сопротивления в%) | 0,50% | 1% | 0,50% | 15% | 3.50% |
| Срок годности (изменение значения сопротивления,%) | 0,10% | 0,10% | 0,00% | 5% | 2% |
| Полный рейтинг (2000 ч при 70 ° C) | 1% | 1% | 0,03% | 10% | 4% |
- Устройства, называемые резисторами, созданы для обеспечения точного значения сопротивления в электрических цепях. Резисторы оцениваются как по их сопротивлению (Ом), так и по их способности рассеивать тепловую энергию (ватты). Номинальное сопротивление резистора
- не может быть определено по физическому размеру резистора (ов), о котором идет речь, хотя приблизительные номинальные значения мощности могут. Чем больше резистор, тем большую мощность он может рассеять без повреждений.
- Любое устройство, которое выполняет некоторые полезные задачи с помощью электроэнергии, обычно называют нагрузкой. Иногда символы резисторов используются на принципиальных схемах для обозначения неспецифической нагрузки, а не для обозначения фактического резистора.
Поскольку требуется энергия, чтобы заставить заряд течь вопреки сопротивлению, напряжение будет проявляться (или «падать») между любыми точками в цепи с сопротивлением между ними.
Важно отметить, что, хотя величина тока (т. Е. Количество заряда, проходящего мимо заданной точки каждую секунду) в простой схеме одинакова, величина напряжения (потенциальная энергия на единицу заряда) между различными наборами точек в одном контуре могут значительно отличаться:
Рисунок 2.42Возьмем эту схему в качестве примера. Если мы обозначим четыре точки в этой цепи номерами 1, 2, 3 и 4, мы обнаружим, что количество тока, проводимого через провод между точками 1 и 2, точно такое же, как количество тока, проводимого через лампу. (между пунктами 2 и 3).Такое же количество тока проходит по проводу между точками 3 и 4 и через батарею (между точками 1 и 4).
Однако мы обнаружим, что напряжение, возникающее между любыми двумя из этих точек, прямо пропорционально сопротивлению в пределах проводящего пути между этими двумя точками, учитывая, что величина тока на любой части пути цепи одинакова (что, для этой простой схемы это так).
В обычной цепи лампы сопротивление лампы будет намного больше, чем сопротивление соединительных проводов, поэтому следует ожидать появления значительного напряжения между точками 2 и 3 и очень небольшого напряжения между точками 1 и 2, или от 3 до 4.Напряжение между точками 1 и 4, конечно, будет полной «силой», обеспечиваемой батареей, которая будет лишь немного больше, чем напряжение на лампе (между точками 2 и 3).
Это, опять же, аналог системы резервуаров для воды:
Рисунок 2.43Между точками 2 и 3, где падающая вода высвобождает энергию в водяном колесе, существует разница давлений между двумя точками, отражающая противодействие потоку воды через водяное колесо.От точки 1 до точки 2 или от точки 3 до точки 4, где вода свободно течет через резервуары с небольшим сопротивлением, разница давлений мала или отсутствует (нет потенциальной энергии). Однако скорость потока воды в этой непрерывной системе одинакова везде (при условии, что уровни воды в пруду и водохранилище неизменны): через насос, через водяное колесо и через все трубы.
То же самое и с простыми электрическими цепями: ток одинаков в каждой точке цепи, хотя напряжения могут различаться в разных наборах точек
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивлениеЭлектрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда через проводники цепи называется током , и его часто называют «потоком», как поток жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» в цепи, называется напряжением .Напряжение — это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенном количестве напряжения, присутствующем в цепи, мы имеем в виду измерение того, сколько потенциальной энергии существует для перемещения носителей заряда из одной конкретной точки в этой цепи в другую конкретную точку. Без ссылки на , две конкретные точки , термин «напряжение» не имеет значения.
Ток имеет тенденцию проходить через проводники с некоторой степенью трения или противодействия движению.Это противодействие движению правильнее называть сопротивлением . Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление — это величина, относительная между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» или «поперек» двух точек в цепи.
Единицы измерения: вольт, ампер и омЧтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любой другой вид физической величины.Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. Вот стандартные единицы измерения электрического тока, напряжения и сопротивления:
Таблица 2.1«Символ», данный для каждой величины, представляет собой стандартную буквенную букву, используемую для представления этой величины в алгебраическом уравнении. Подобные стандартизированные буквы распространены в физических и технических дисциплинах и признаны во всем мире.«Аббревиатура единицы» для каждой величины представляет собой алфавитный символ, используемый в качестве сокращенного обозначения для ее конкретной единицы измерения. И да, этот странно выглядящий символ «подкова» — это заглавная греческая буква Ω, просто символ иностранного алфавита (извинения перед читателями-греками).
Каждая единица измерения названа в честь известного экспериментатора в области электричества: А в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта и Ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя, тогда как «I» для тока кажется немного странным. Считается, что буква «I» должна представлять «интенсивность» (потока заряда), а другой символ напряжения, «E», означает «электродвижущую силу». Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые споры по поводу значения слова «я». Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах зарезервировано «E» для обозначения напряжения на источнике (таком как батарея или генератор) и «V» для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (называемого «мгновенным» значением). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», в то время как пик напряжения при ударе молнии в тот самый момент, когда он попадает в линию электропередачи, скорее всего, будет обозначается строчной буквой «е» (или строчной буквой «v»), чтобы обозначить это значение как имеющееся в один момент времени.То же самое соглашение о нижнем регистре справедливо и для тока, строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений постоянного тока (DC), которые стабильны во времени, будут обозначены заглавными буквами.
Кулон и электрический зарядОдной из основных единиц измерения электрического тока, которую часто преподают в начале курсов электроники, но редко используют впоследствии, является единица кулонов , которая представляет собой меру электрического заряда, пропорционального количеству электронов в несбалансированном состоянии.Один кулон заряда равен 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается заглавной буквой «C». Бывает так, что единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этих терминах ток — это скорость движения электрического заряда по проводнику.
Как указывалось ранее, напряжение является мерой потенциальной энергии на единицу заряда , доступной для стимулирования протекания тока из одной точки в другую.Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общая метрическая единица для энергии любого вида — джоулей, , что равняется количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В британских подразделениях это чуть меньше 3/4 фунта силы, приложенной на расстоянии 1 фута. Проще говоря, требуется около 1 джоуля энергии, чтобы поднять гирю весом 3/4 фунта на 1 фут от земли или перетащить что-то на расстояние 1 фут, используя параллельную тяговую силу 3/4 фунта.В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленный на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Уравнения закона Ома Основное открытиеОма заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, прямо пропорциональна напряжению, приложенному к нему при любой заданной температуре.Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
[латекс] E = IR \ tag {2.3} [/ латекс]
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя методы алгебры, мы можем преобразовать это уравнение в два варианта, решая для I и R соответственно:
[латекс] I = \ frac {E} {R} \ tag {2.4} [/ латекс]
[латекс] R = \ frac {E} {I} \ tag {2.5} [/ латекс]
Анализ простых схем с помощью закона ОмаДавайте посмотрим, как эти уравнения могут работать, чтобы помочь нам анализировать простые схемы:
Рисунок 2.44В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применять закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы рассчитаем величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Рисунок 2.45Какая величина тока (I) в этой цепи?
[латекс] I = \ frac {E} {R} [/ latex] [латекс] = \ frac {12V} {3 \ Omega} = 4A [/ latex]
В этом втором примере мы рассчитаем величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Какое сопротивление (R) дает лампа?
[латекс] R = \ frac {E} {I} [/ latex] [latex] = \ frac {36V} {4A} = 9 \ Omega [/ latex]
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Фигура 2.46Какое напряжение обеспечивает аккумулятор?
[латекс] E = IR [/ латекс] [латекс] = (2A) (7 \ Omega) = 14V [/ латекс]
Техника треугольника закона Ома ЗаконОма — очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что серьезный студент должен запомнить его. Для тех, кто еще не знаком с алгеброй, есть уловка, позволяющая вспомнить, как найти любую одну величину, учитывая две другие.Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 2.45
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
В конце концов, вам придется быть знакомым с алгеброй, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений.Если вам удобна алгебра, все, что вам нужно сделать, это зафиксировать E = IR в памяти и вывести из нее две другие формулы, когда они вам понадобятся!
- Напряжение измеряется в вольт , обозначается буквами «E» или «V».
- Ток измеряется в ампер , обозначается буквой «I».
- Сопротивление измеряется в Ом. обозначается буквой «R».
- [латекс] \ text {Закон Ома:} E = IR [/ latex]; [латекс] I = \ frac {E} {R} [/ latex]; [латекс] R = \ frac {E} {I} [/ latex]
Мы видели формулу для определения мощности в электрической цепи: умножая напряжение в вольтах на ток в амперах, мы получаем ответ в ваттах.»Давайте применим это к примеру схемы:
В приведенной выше схеме мы знаем, что у нас напряжение батареи 18 В и сопротивление лампы 3 Ом. Используя закон Ома для определения силы тока, получаем:
[латекс] I = \ frac {E} {R} [/ latex] [latex] = \ frac {18V} {3 \ Omega} = 6A [/ latex]
Теперь, когда мы знаем ток, мы можем взять это значение и умножить его на напряжение, чтобы определить мощность:
[латекс] P = IE [/ латекс] [латекс] = (6A) (18 В) = 108 Вт [/ латекс]
Это говорит нам о том, что лампа рассеивает (выделяет) 108 Вт мощности, скорее всего, в форме света и тепла.
Повышение напряжения батареиДавайте попробуем взять ту же схему и увеличить напряжение батареи, чтобы увидеть, что произойдет. Интуиция подсказывает нам, что ток в цепи будет увеличиваться с увеличением напряжения, а сопротивление лампы останется прежним. Аналогично увеличится и мощность:
Теперь напряжение батареи 36 вольт вместо 18 вольт. Лампа по-прежнему обеспечивает электрическое сопротивление 3 Ом для прохождения тока. Текущий сейчас:
[латекс] I = \ frac {E} {R} [/ latex] [латекс] = \ frac {36V} {3 \ Omega} = 12A [/ латекс]
Это понятно: если I = E / R, и мы удваиваем E, а R остается неизменным, ток должен удвоиться.Действительно, есть: теперь у нас 12 ампер тока вместо 6. А что насчет мощности?
[латекс] P = IE [/ латекс] [латекс] = (12A) (36V) = 432W [/ латекс]
Как повышение напряжения батареи влияет на мощность?Обратите внимание, что мощность увеличилась, как мы и предполагали, но она увеличилась немного больше, чем ток. {2} R [/ latex]
Джоуля Закон против.Закон ОмаИсторическая справка: именно Джеймс Прескотт Джоуль, а не Георг Саймон Ом первым открыл математическую связь между рассеиваемой мощностью и током через сопротивление. Это открытие, опубликованное в 1841 году, имело форму последнего уравнения (P = I 2 R) и широко известно как закон Джоуля. Однако эти уравнения мощности настолько часто связаны с уравнениями закона Ома, связывающими напряжение, ток и сопротивление (E = IR; I = E / R; и R = E / I), что они часто приписываются Ому.{2}} {R} [/ латекс]
До сих пор мы анализировали схемы с одной батареей и одним резистором без учета соединительных проводов между компонентами, пока формируется полная цепь. Имеет ли значение для наших расчетов длина провода или «форма» цепи? Давайте посмотрим на несколько принципиальных схем и узнаем:
Рис. 2.49Когда мы рисуем провода, соединяющие точки в электрической цепи, мы обычно предполагаем, что эти провода имеют незначительное сопротивление. Как таковые, они не вносят заметного влияния на общее сопротивление цепи, и поэтому единственное сопротивление, с которым нам приходится бороться, — это сопротивление компонентов.В приведенных выше схемах единственное сопротивление исходит от резисторов 5 Ом, так что это все, что мы будем учитывать в наших расчетах. В реальной жизни металлические провода – имеют сопротивление (как и источники питания!), Но эти сопротивления, как правило, намного меньше, чем сопротивление, присутствующее в других компонентах схемы, что их можно безопасно игнорировать. Исключения из этого правила существуют в электропроводке энергосистемы, где даже очень небольшое сопротивление проводника может вызвать значительные падения напряжения при нормальных (высоких) уровнях тока.
Электрически общие точки в цепиЕсли сопротивление соединительного провода очень мало или отсутствует, мы можем рассматривать соединенные точки в цепи как электрически общие . То есть точки 1 и 2 в вышеуказанных схемах могут быть физически соединены близко друг к другу или далеко друг от друга, и это не имеет значения для любых измерений напряжения или сопротивления относительно этих точек. То же самое касается точек 3 и 4. Это как если бы концы резистора были присоединены непосредственно к клеммам батареи, что касается наших расчетов по закону Ома и измерений напряжения.Это полезно знать, потому что это означает, что вы можете заново нарисовать принципиальную схему или повторно подключить схему, сокращая или удлиняя провода по желанию, не оказывая заметного влияния на работу схемы. Важно только то, что компоненты прикрепляются друг к другу в одинаковой последовательности.
Это также означает, что измерения напряжения между наборами «электрически общих» точек будут одинаковыми. То есть напряжение между точками 1 и 4 (непосредственно на батарее) будет таким же, как напряжение между точками 2 и 3 (непосредственно на резисторе).Внимательно посмотрите на следующую схему и попытайтесь определить, какие точки являются общими друг для друга:
Рисунок 2.50Здесь у нас есть только 2 компонента, не считая проводов: батарея и резистор. Хотя соединительные провода образуют законченную цепь извилистым путем, на пути тока есть несколько электрически общих точек. Точки 1, 2 и 3 являются общими друг для друга, потому что они напрямую связаны друг с другом проводом. То же самое касается точек 4, 5 и 6.
Напряжение между точками 1 и 6 составляет 10 вольт, идущее прямо от батареи.Однако, поскольку точки 5 и 4 являются общими для 6, а точки 2 и 3 являются общими для 1, те же 10 вольт также существуют между этими другими парами точек:
- Между точками 1 и 4 = 10 вольт
- Между точками 2 и 4 = 10 вольт
- Между точками 3 и 4 = 10 В (непосредственно через резистор)
- Между точками 1 и 5 = 10 В Между точками 2 и 5 = 10 В
- Между точками 3 и 5 = 10 В Между точками 1 и 6 = 10 В (непосредственно на батарее)
- Между точками 2 и 6 = 10 В Между точками 3 и 6 = 10 В
Поскольку электрически общие точки соединены вместе проводом (нулевого сопротивления), между ними нет значительного падения напряжения, независимо от величины тока, проводимого от одной к другой через этот соединительный провод.Таким образом, если бы мы считали напряжения между общими точками, мы должны были бы показать (практически) ноль:
- Между точками 1 и 2 = 0 вольт
- Точки 1, 2 и 3 между точками 2 и 3 = 0 вольт электрически общие
- Между точками 1 и 3 = 0 вольт
- Между точками 4 и 5 = 0 вольт
- Точки 4, 5 и 6 находятся между точками 5 и 6 = 0 вольт электрически общий
- Между точками 4 и 6 = 0 вольт
Это тоже имеет смысл математически.С батареей на 10 В и резистором 5 Ом ток в цепи будет 2 ампера. Если сопротивление провода равно нулю, падение напряжения на любом непрерывном участке провода можно определить с помощью закона Ома как такового:
[латекс] E = IR [/ латекс]
[латекс] E = (2A) (0 \ Omega) [/ латекс]
[латекс] \ textbf {E = 0V} [/ латекс]
Должно быть очевидно, что рассчитанное падение напряжения на любой непрерывной длине провода в цепи, где предполагается, что провод имеет нулевое сопротивление, всегда будет равно нулю, независимо от величины тока, поскольку ноль, умноженный на что-либо, равен нулю.
Поскольку общие точки в цепи будут иметь одинаковые значения относительного напряжения и сопротивления, провода, соединяющие общие точки, часто помечаются одним и тем же обозначением. Это не означает, что точки подключения клеммы обозначены одинаково, только соединительные провода. Возьмем для примера эту схему:
Рисунок 2.56.Точки 1, 2 и 3 являются общими друг для друга, поэтому точки подключения проводов 1–2 обозначены так же (провод 2), что и точки подключения проводов 2–3 (провод 2).В реальной схеме провод, тянущийся от точки 1 до 2, может даже не быть того же цвета или размера, что и провод, соединяющий точку 2 и 3, но они должны иметь точно такую же метку. То же самое касается проводов, соединяющих точки 6, 5 и 4.
Падение напряжения должно равняться нулю в общих точкахЗнание того, что электрически общие точки имеют нулевое падение напряжения, является ценным принципом поиска и устранения неисправностей. Если я измеряю напряжение между точками в цепи, которые должны быть общими друг для друга, я должен прочитать ноль.Если, однако, я обнаружил значительное напряжение между этими двумя точками, то я с уверенностью знаю, что они не могут быть напрямую соединены друг с другом. Если предполагается, что эти точки , являются электрически общими, но они регистрируются иначе, то я знаю, что между этими точками существует «открытый сбой».
Нулевое напряжение технически означает незначительное напряжениеПоследнее замечание: для большинства практических целей можно предположить, что проводники имеют нулевое сопротивление от конца до конца.В действительности, однако, всегда будет небольшое сопротивление по длине провода, если только это не сверхпроводящий провод. Зная это, мы должны помнить, что изученные здесь принципы, касающиеся общих электрических точек, в значительной степени действительны, но не до абсолютных градусов. То есть правило, согласно которому между электрически общими точками гарантированно будет нулевое напряжение, более точно сформулировано как таковое: между электрически общими точками будет очень небольшое падение напряжения .Этот небольшой, практически неизбежный след сопротивления, обнаруживаемый в любом куске соединительного провода, должен создавать небольшое напряжение по всей его длине при прохождении тока. Если вы понимаете, что эти правила основаны на идеальных условиях, , вы не будете недоумевать, когда столкнетесь с каким-либо условием, которое кажется исключением из правила.
- Предполагается, что соединительные провода в цепи имеют нулевое сопротивление, если не указано иное.
- Провода в цепи можно укорачивать или удлинять, не влияя на работу схемы — все, что имеет значение, — это то, что компоненты подключены друг к другу в одной и той же последовательности.
- Точки, напрямую соединенные в цепь нулевым сопротивлением (проводом), считаются электрически общими .
- Электрически общие точки с нулевым сопротивлением между ними будут иметь нулевое падение напряжения между ними, независимо от величины тока (в идеале).
- Показания напряжения или сопротивления между наборами электрически общих точек будут одинаковыми.
- Эти правила применяются к идеальным условиям , где предполагается, что соединительные провода имеют абсолютно нулевое сопротивление.В реальной жизни это, вероятно, не так, но сопротивление проводов должно быть достаточно низким, чтобы общие принципы, изложенные здесь, оставались в силе.
Напряжение в последовательной цепи
Напряжение в последовательной цепи
Напряжение, падающее на резисторе в цепи, состоящей из одного резистора и источника напряжения, представляет собой полное напряжение в цепи и равно приложенному напряжению.Общее напряжение в последовательной цепи, состоящей из более чем одного резистора, также равно приложенному напряжению, но состоит из суммы падений напряжения отдельных резисторов. В любой последовательной схеме сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рисунке 3-17. В этой цепи потенциал источника (E T ) в 20 вольт падает на последовательную цепь, состоящую из двух резисторов сопротивлением 5 Ом. Общее сопротивление цепи (R T ) равно сумме двух отдельных сопротивлений или 10 Ом.Используя закон Ома, ток в цепи можно рассчитать следующим образом:
Рисунок 3-17. — Расчет отдельных падений напряжения в последовательной цепи.
Поскольку известно, что номинал резисторов составляет 5 Ом, а ток через резисторы равен 2 амперам, падение напряжения на резисторах может быть рассчитано. Таким образом, напряжение (E 1 ) на R 1 составляет:
. Осмотрев цепь, вы можете увидеть, что резистор R 2 имеет такое же омическое значение, что и R 1 , и пропускает тот же ток.Падение напряжения на R 2 , следовательно, также равно 10 вольт. Если сложить эти два падения по 10 вольт, общее падение составит 20 вольт, что в точности равно приложенному напряжению. Для последовательной схемы тогда:
E T = E 1 = E 2 + E 3 =. . . E n
Пример: последовательная цепь состоит из трех резисторов, имеющих номиналы 20 Ом, 30 Ом и 50 Ом соответственно. Найдите приложенное напряжение, если ток через резистор 30 Ом равен 2 ампера.(Аббревиатура amp обычно используется для обозначения ампер.)
Для решения проблемы сначала рисуется принципиальная схема и маркируется (рис. 3-18).
Рисунок 3-18. — Решение для приложенного напряжения в последовательной цепи.
Замена:
ПРИМЕЧАНИЕ. При использовании закона Ома величины для уравнения ДОЛЖНЫ быть взяты из ОДНОЙ части схемы. В приведенном выше примере напряжение на R 2 было вычислено с использованием тока через R 2 и сопротивления R 2 .
Величина падения напряжения на резисторе определяется приложенным напряжением и пропорционально сопротивлению цепи. Падения напряжения, возникающие в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток — чем больше сопротивление резистора, тем больше падение напряжения на нем.
Последовательная цепь, состоящая из трех резисторов, имеет ток 3 ампера. Если R 1 = 20 Ом, R 2 = 60 Ом и R 3 = 80 Ом, каковы (а) полное сопротивление и (б) напряжение источника цепи?
Какое напряжение падает на каждом резисторе цепи, описанной в вопросе 17?
Если бы ток был увеличен до 4 ампер, каким было бы падение напряжения на каждом резисторе в цепи, описанной в вопросе 17?
Что нужно сделать со схемой, описанной в вопросе 17, чтобы увеличить ток до 4 ампер?
% PDF-1.5 % 1 0 obj> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 4 0 obj> поток конечный поток эндобдж xref 0 5 0000000000 65535 ф 0000000016 00000 н. 0000000075 00000 н. 0000000120 00000 н. 0000000210 00000 н. трейлер ] >> startxref 3379 %% EOF 1 0 obj> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 5 0 obj null эндобдж 6 0 obj> эндобдж 7 0 obj> эндобдж 8 0 obj> эндобдж 9 0 obj> / Font> / XObject> / ProcSet [/ PDF / Text / ImageB] / ExtGState >>> эндобдж 10 0 obj> эндобдж 11 0 obj> эндобдж 12 0 obj> эндобдж 13 0 obj> эндобдж 14 0 obj> / Ширина 661 / Высота 221 / BitsPerComponent 1 / ImageMask true / Type / XObject / Subtype / Image >> stream & M‚Ck
Падение напряжения | Gorgeous Group Limited
Падение напряжения описывает, как подаваемая энергия источника напряжения уменьшается при прохождении электрического тока через пассивные элементы (элементы, которые не подают напряжение) электрической цепи.
Всякий раз, когда протекает ток, он встречается с динатроном, который препятствует его протеканию, величине потери напряжения во всей цепи или даже ее части — падению напряжения. В системах освещения низкого напряжения, таких как светодиодные ленты, падение напряжения происходит из-за того, что входное напряжение от источника питания постепенно уменьшается по длине полосы.
Чем длиннее гибкая светодиодная лента, тем большее сопротивление должен преодолевать ток; следовательно, он теряет напряжение по пути.Если гибкая светодиодная лента работает от источника питания 12 вольт, то вначале у вас будет 12 вольт, идущих на систему ленточного освещения, но на другом конце не будет 12 вольт из-за падения напряжения.
Падение напряжения зависит от длины провода, толщины провода и общей мощности, потребляемой гибкими светодиодными лентами. Снижение яркости и точности цветопередачи в более длинных гибких светодиодных лентах происходит из-за чрезмерного падения напряжения. Чрезмерное падение напряжения может привести к неудовлетворительной работе и повреждению электрических розеток и гибких светодиодных лент.Расстояние от источника питания до желаемого конечного расстояния гибкой светодиодной ленты называется пробегом. Более короткие и / или более толстые провода повысят яркость и однородность цвета до полного потенциала полосовых ламп.
Какое падение напряжения допустимо? В сноске (NEC 210-19 FPN No. 4) в Национальном электротехническом кодексе говорится, что падение напряжения на 5% в самой дальней розетке в цепи ответвления является приемлемым для нормальной эффективности. В цепи на 120 вольт и 15 ампер это означает, что падение напряжения на самом дальнем выходе при полной нагрузке цепи не должно превышать 6 вольт (114 вольт).Это также означает, что схема имеет сопротивление, не превышающее 0,4 Ом.
Каковы последствия «избыточного» падения напряжения в цепи? Чрезмерное падение напряжения может вызвать следующие состояния:
1. Низкое напряжение на оборудовании, на которое подается питание, что приводит к неправильной, неустойчивой работе или ее отсутствию — и повреждению оборудования.
2. Низкая эффективность и потери энергии.
3. Нагревание в месте соединения / сращивания с высоким сопротивлением может привести к возгоранию при высоких амперных нагрузках.
При каком% падении напряжения цепь становится опасной? Трудно сказать, в какой момент чрезмерное падение напряжения вызовет пожар, потому что это зависит от того, какой ток протекает через соединение с высоким сопротивлением, каково сопротивление этого соединения и потому что необходимо учитывать множество факторов относительно того, в какой момент произойдет возгорание, например:
1. Контакт с высоким сопротивлением соприкасается с горючим материалом?
2. Есть ли воздушный поток для отвода тепла?
3.Изолирована ли область вокруг соединения, чтобы тепло не выходило.
РЕКОМЕНДАЦИИ
Для энергоэффективности рекомендуется стандарт NEC, согласно которому максимальное падение напряжения составляет 5%.
С точки зрения безопасности, поскольку электрические соединения в некоторых домах со временем ухудшаются (особенно в домах, в которых используется алюминиевая проводка для силовых цепей), а модификации, сделанные своими руками, могут быть менее профессиональными, чрезмерное падение напряжения является проблемой из-за потенциальная опасность пожара в соединениях с высоким сопротивлением, особенно в цепях, питающих электродвигатели, когда обитатели дома спят, e.грамм. кондиционеры, холодильники, печные вентиляторы, вытяжные вентиляторы и т. д.
Некоторые агентства произвольно устанавливают критерии максимального падения напряжения в 10%, что считается неприемлемым и опасным. Автор считает, что любая разница падения напряжения> 1% от соседней розетки должна быть исследована, что любая разница падения напряжения> 2% от соседней розетки должна рассматриваться как опасность, и что использование критериев максимального падения напряжения более чем 8% (на 3% выше рекомендации «эффективность») склоняются к катастрофе.Падение напряжения 3% (3,6 В в цепи 120 В) на одном соединении с потоком 15 А создает 54 Вт тепла, что может вызвать возгорание при определенных условиях.
.



