Единицы измерения

Этот урок не будет новым для новичков. Все мы слышали со школы такие вещи как сантиметр, метр, километр. А когда речь заходила о массе, обычно говорили грамм, килограмм, тонна.

Сантиметры, метры и километры; граммы, килограммы и тонны носят одно общее название — единицы измерения физических величин.

В данном уроке мы рассмотрим наиболее популярные единицы измерения, но не будем сильно углубляться в эту тему, поскольку единицы измерения уходят в область физики. Сегодня мы вынуждены изучить часть физики, поскольку нам это необходимо для дальнейшего изучения математики.

Единицы измерения длины

Для измерения длины предназначены следующие единицы измерения:

• миллиметры;
• сантиметры;
• дециметры;
• метры;
• километры.

Самая маленькая единица измерения это миллиметр (мм). Миллиметры можно увидеть даже воочию, если взять линейку, которой мы пользовались в школе каждый день

Подряд идущие друг за другом маленькие линии это и есть миллиметры.  Точнее, расстояние между этими линиями равно одному миллиметру (1 мм):

---

Следующая единица измерения это сантиметр (см). На линейке каждый сантиметр обозначен числом. К примеру наша линейка, которая была на первом рисунке, имела длину 15 сантиметров. Последний сантиметр на этой линейке выделен числом 15.

В одном сантиметре 10 миллиметров. Между одним сантиметром и десятью миллиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 см = 10 мм

Вы можете сами убедиться в этом, если посчитаете количество миллиметров на предыдущем рисунке. Вы обнаружите, что количество миллиметров (расстояний между линиями) равно 10.

---

Следующая единица измерения длины это дециметр (дм). В одном дециметре десять сантиметров. Между одним дециметром и десятью сантиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 дм = 10 см

Вы можете убедиться в этом, если посчитаете количество сантиметров на следующем рисунке:

Вы обнаружите, что количество сантиметров равно 10.

---

Следующая единица измерения это метр (м). В одном метре десять дециметров. Между одним метром и десятью дециметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 м = 10 дм

К сожалению, метр нельзя проиллюстрировать на рисунке, потому что он достаточно великоват. Если вы хотите увидеть метр в живую, возьмите рулетку. Она есть у каждого в доме. На рулетке один метр будет обозначен как 100 см. Это потому что в одном метре десять дециметров, а в десяти дециметрах сто сантиметров:

1 м = 10 дм = 100 см

100 получается путём перевода одного метра в сантиметры. Это отдельная тема, которую мы рассмотрим чуть позже. А пока перейдём к следующей единице измерения длины, которая называется километр.

Километр считается самой большой единицей измерения длины. Есть конечно и другие более старшие единицы, такие как мегаметр, гигаметр тераметр, но мы не будем их рассматривать, поскольку для дальнейшего изучения математики нам достаточно и километра.

В одном километре тысяча метров. Между одним километром и тысячью метрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 км = 1000 м

В километрах измеряются расстояния между городами и странами. К примеру, расстояние от Москвы до Санкт-Петербурга около 714 километров.

---

Международная система единиц СИ

Международная система единиц СИ — это некоторый набор общепринятых физических величин.

Основное предназначение международной системы единиц СИ — достижение договоренностей между странами.

Мы знаем, что языки и традиции стран мира различны. С этим  ничего не поделать. Но законы математики и физики одинаково работают везде. Если в одной стране «дважды два будет четыре», то и в другой стране «дважды два будет четыре».

Основная проблема заключалась в том, что для каждой физической величины существует несколько единиц измерения. К примеру, мы сейчас узнали, что для измерения длины существуют миллиметры, сантиметры, дециметры, метры и километры. Если несколько ученых, говорящих на разных языках, соберутся в одном месте для решения какой-нибудь задачи, то такое большое многообразие единиц измерения длины может породить между этими учеными противоречия.

Один ученый будет заявлять, что в их стране длина измеряется в метрах. Второй может сказать, что в их стране длина измеряется в километрах. Третий может предложить свою единицу измерения.

Поэтому была создана международная система единиц СИ. СИ это аббревиатура от французского словосочетания Le Système International d’Unités, SI (что в переводе на русский означает — международная система единиц СИ). 

В СИ приведены наиболее популярные физические величины и для каждой из них определена своя общепринятая единица измерения. К примеру, во всех странах при решении задач условились, что длину будут измерять в метрах. Поэтому, при решении задач, если длина дана в другой единице измерения (например, в километрах), то её обязательно нужно перевести в метры. О том, как переводить одну единицу измерения в другую, мы поговорим немного позже. А пока нарисуем свою международную систему единиц СИ.

Наш рисунок будет представлять собой таблицу физических величин. Каждую изученную физическую величину мы будем включать в нашу таблицу и указывать ту единицу измерения, которая принята во всех странах. Сейчас мы изучили единицы измерения длины и узнали, что в системе СИ для измерения длины определены метры. Значит наша таблица будет выглядеть так:

---

Единицы измерения массы

Масса – это величина, обозначающая количество вещества в теле. В народе массу тела называют весом. Обычно, когда что-либо взвешивают, говорят «это весит столько-то килограмм»

, хотя речь идёт не о весе, а о массе этого тела.

Вместе с тем, масса и вес это разные понятия. Вес — это сила с которой тело действует на горизонтальную опору. Вес измеряется в ньютонах. А масса это величина, показывающая количество вещества в этом теле.

Но ничего страшного нет в том, если вы назовёте массу тела весом. Даже в медицине говорят «вес человека», хотя речь идёт о массе человека. Главное быть в курсе, что это разные понятия

Для измерения массы используются следующие единицы измерения:

• миллиграммы;
• граммы;
• килограммы;
• центнеры;
• тонны.

Самая маленькая единица измерения это

миллиграмм (мг). Миллиграмм скорее всего вы никогда не примените на практике. Их применяют химики и другие ученые, которые работают с мелкими веществами. Для вас достаточно знать, что такая единица измерения массы существует.

Следующая единица измерения это грамм (г). В граммах принято измерять количество того или иного продукта при составлении рецепта.

В одном грамме тысяча миллиграммов. Между одним граммом и тысячью миллиграммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 г = 1000 мг

Следующая единица измерения это килограмм (кг). Килограмм это общепринятая единица измерения. В ней измеряется всё что угодно. Килограмм включен в систему СИ. Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «масса»:

В одном килограмме тысяча граммов. Между одним килограммом и тысячью граммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 кг = 1000 г

Следующая единица измерения это центнер (ц). В центнерах удобно измерять массу урожая, собранного с небольшого участка или массу какого-нибудь груза.

В одном центнере сто килограммов. Между одним центнером и ста килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 ц = 100 кг

Следующая единица измерения это тонна (т). В тоннах обычно измеряются большие грузы и массы больших тел. Например, масса космического корабля или автомобиля.

В одной тонне тысяча килограмм. Между одной тонной и тысячью килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 т = 1000 кг

---

Единицы измерения времени

Что такое время думаем объяснять не нужно. Каждый знает что из себя представляет время и зачем оно нужно. Если мы откроем дискуссию на то, что такое время и попытаемся дать ему определение, то начнем углубляться в философию, а это нам сейчас не нужно. Лучше начнём с единиц измерения времени.

Для измерения времени предназначены следующие единицы измерения:

• секунды;
• минуты;
• часы;
• сутки.

Самая маленькая единица измерения это секунда (с). Есть конечно и более маленькие единицы такие как миллисекунды, микросекунды, наносекунды, но их мы рассматривать не будем, поскольку на данный момент в этом нет смысла.

В секундах измеряются различные показатели. Например, за сколько секунд спортсмен пробежит 100 метров. Секунда включена в международную систему единиц СИ для измерения времени и обозначается как «с». Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «время»:

Следующая единица измерения времени это

минута (м). В одной минуте 60 секунд. Между одной минутой и шестьюдесятью секундами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 м = 60 с

Следующая единица измерения это час (ч). В одном часе 60 минут. Между одним часом и шестьюдесятью минутами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 ч = 60 м

К примеру, если мы изучали этот урок один час и нас спросят сколько времени мы потратили на его изучение, мы можем ответить двумя способами: «мы изучали урок один час» или так «мы изучали урок шестьдесят минут». В обоих случаях, мы ответим правильно.

Следующая единица измерения времени это сутки. В сутках 24 часа. Между одними сутками и двадцатью четырьмя часами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 сут = 24 ч

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Метр — Википедия

Метр (русское обозначение: м; международное: m; от др.-греч. μέτρον «мера, измеритель») — единица измерения длины в Международной системе единиц (СИ), одна из семи основных единиц СИ. Также является единицей длины и относится к числу основных единиц в системах МКС, МКСА, МКСК, МКСГ, МСК, МКСЛ, МСС, МКГСС и МТС. Кроме того, во всех упомянутых системах метр — единица коэффициента трения качения, длины волны излучения, длины свободного пробега, оптической длины пути, фокусного расстояния, комптоновской длины волны, длины волны де Бройля и других физических величин, имеющих размерность длины^[1].

Согласно действующему определению, метр есть длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды^[2][3].

Современное определение метра в терминах времени и скорости света было принято XVII Генеральной конференцией по мерам и весам (ГКМВ) в 1983 году^[2][3].

Метр — длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды.

Из этого определения следует, что в СИ скорость света в вакууме принята равной в точности 299 792 458 м/с. Таким образом, определение метра, как и два столетия назад, вновь привязано к секунде, но на этот раз с помощью универсальной мировой константы.

Изменения определений основных единиц СИ 2018—2019 годов не затронуло метр с содержательной точки зрения, однако из стилистических соображений было принято формально новое определение, полностью эквивалентное предыдущему^[4]:

Метр, обозначение м, является единицей длины в СИ; его величина устанавливается фиксацией численного значения скорости света в вакууме c{\displaystyle c} равным в точности 299 792 458, когда она выражена единицей СИ м·с⁻¹, где секунда определена через частоту перехода в цезии ΔνCs{\displaystyle \Delta \nu _{\text{Cs}}}.

В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы метра образуются с помощью стандартных приставок СИ^[5]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в РФ тех же приставок^[6].

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 м	декаметр	дам	dam	10−1 м	дециметр	дм	dm
102 м	гектометр	гм	hm	10−2 м	сантиметр	см	cm
103 м	километр	км	km	10−3 м	миллиметр	мм	mm
106 м	мегаметр	Мм	Mm	10−6 м	микрометр	мкм	µm
109 м	гигаметр	Гм	Gm	10−9 м	нанометр	нм	nm
1012 м	тераметр	Тм	Tm	10−12 м	пикометр	пм	pm
1015 м	петаметр	Пм	Pm	10−15 м	фемтометр	фм	fm
1018 м	эксаметр	Эм	Em	10−18 м	аттометр	ам	am
1021 м	зеттаметр	Зм	Zm	10−21 м	зептометр	зм	zm
1024 м	иоттаметр	Им	Ym	10−24 м	иоктометр	им	ym
применять не рекомендуется      не применяются или редко применяются на практике

Соотношение с другими единицами длины[править | править код]

Метрическая единица, выраженная через единицу, не входящую в СИ					Единица, не входящая в СИ, выраженная через метрическую единицу
1 метр	≈	39,37	дюйма		1 дюйм	≡	0,0254	метра
1 сантиметр	≈	0,3937	дюйма		1 дюйм	≡	2,54	сантиметра
1 миллиметр	≈	0,03937	дюйма		1 дюйм	≡	25,4	миллиметра
1 метр	≡	1⋅1010	ангстрем		1 ангстрем	≡	1⋅10−10	метра
1 нанометр	≡	10	ангстрем		1 ангстрем	≡	100	пикометров

Один из публичных эталонов метра, установленных на улицах Парижа в 1795—1796 гг.

В Европе со времён распада империи Карла Великого не существовало общих стандартных мер длины: они могли быть стандартизированы в пределах одной юрисдикции (которая зачастую имела размеры одного торгового городка), но единых мер не было, и каждый регион мог иметь свои собственные. Причиной этого служило в какой-то мере то, что меры длины использовались в налогообложении (налог, например, мог измеряться в определённой длине полотна), а поскольку каждый местный правитель вводил свои налоги, то для соответствующей местности законами устанавливались свои единицы измерений^[8].

С развитием науки в XVII веке стали раздаваться призывы к введению «универсальной меры» (universal measure, как назвал её английский философ и лингвист Джон Уилкинс в своём эссе 1668 года^[9]) или «католического метра» (metro cattolico) итальянского учёного и изобретателя Тито Ливио Бураттини из его работы Misura Universale 1675 года^{[Комм. 1][10]}), меры, которая бы основывалась на каком-либо естественном явлении, а не на постановлении властьдержащей персоны, и которая была бы десятичной, что заменило бы множество разнообразных систем счисления, например, распространённую двенадцатеричную, одновременно существовавших в то время.

Метр — длина маятника[править | править код]

Идея Уилкинса заключалась в том, чтобы выбрать для единицы длины длину маятника с полупериодом колебаний равным 1 с. Подобные маятники были незадолго до этого продемонстрированы Христианом Гюйгенсом, и их длина была весьма близка к длине современного метра (так же, как к единицам длины, использовавшимся в те времена, например, ярду). Однако, вскоре было обнаружено, что длина, измеренная таким способом, различается в зависимости от места измерений. Французский астроном Жан Рише во время экспедиции в Южную Америку (1671—1673) обнаружил увеличение периода колебаний секундного маятника по сравнению с тем, который наблюдался в Париже. Выверенный в Париже маятник в процессе наблюдений им был сокращён на 1,25 французской линии (~ 2,81 мм), дабы избежать отставания во времени на 2 минуты в день. Это было первое прямое доказательство уменьшения силы тяжести по мере приближения к экватору, и это дало разницу в 0,3 % длины между Кайенной (во французской Гвиане) и Парижем^[11].

Вплоть до французской революции 1789 года в вопросе установления «универсальной меры» не было никакого прогресса. Франция была озабочена вопросом распространения единиц измерений длины, необходимость реформы в этой области поддерживали самые различные политические силы. Талейран возродил идею о секундном маятнике и предложил её Учредительному собранию в 1790 году, с тем уточнением, что эталон длины будет измерен на широте 45° N (примерно между Бордо и Греноблем). Таким образом, метр получал следующее определение: метр — это длина маятника с полупериодом колебаний на широте 45°, равным 1 с (в единицах СИ эта длина равна g/π² · (1 с)² ≈ 0,994 м).

Первоначально за основу было принято это определение (8 мая 1790, Французское Национальное собрание). Но несмотря на поддержку собрания, а также поддержку Великобритании и новообразованных Соединённых Штатов, предложение Талейрана так и не было осуществлено^{[12][Комм. 2]}.

Метр — часть Парижского меридиана[править | править код]

Крепость Монжуик — южный конец дуги меридиана

Вопрос реформы единиц измерения был отдан на рассмотрение Французской академии наук, которая создала специальную комиссию, возглавляемую инженером и математиком Жаном-Шарлем де Борда. Борда был ярым приверженцем перехода на десятичную систему исчисления: он усовершенствовал лимб повторительного теодолита, который позволял намного улучшить точность измерения углов на местности, и настаивал, чтобы инструмент калибровался в градах (¹⁄₁₀₀ четверти круга), а не в градусах, чтобы град делился на 100 минут, а минута — на 100 секунд^[13]. Для Борда метод секундного маятника был неудовлетворительным решением, поскольку он основывался на существовавшей в то время секунде — недесятичной единице, которая не подходила для предлагавшейся к внедрению системы десятичного времени — системе, когда в одних сутках 10 часов, в часе 100 минут, а в минуте 100 секунд.

Вместо метода секундного маятника комиссия — среди членов которой были Жозеф Луи Лагранж, Пьер-Симон Лаплас, Гаспар Монж и Кондорсе — решила, что новая единица измерения должна быть равна одной десятимиллионной расстояния от Северного полюса до экватора (четверть земной окружности), измеренного вдоль меридиана, проходящего через Париж^[12]. Помимо той выгоды, что это решение давало лёгкий доступ для французских геодезистов, существовало такое важное достоинство, что часть расстояния от Дюнкерка до Барселоны (около 1000 км, то есть одна десятая от общего расстояния) могла быть проложена от начальных и конечных точек, расположенных на уровне моря, а как раз эта часть находилась в середине четверти окружности, где влияние формы Земли, которая не является правильным шаром, а сплюснута, было бы наибольшим^[12].

30 марта 1791 предложение определить метр через длину меридиана было принято следующим: одна сорокамиллионная часть Парижского меридиана (то есть одна десятимиллионная часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа). Интересно, что в современных единицах это 11,00000000005{\displaystyle {\frac {1}{1{,}000\,000\,000\,05}}} метра. Идея привязать единицу измерения длины к меридиану Земли была не нова: аналогичным образом ранее были определены морская миля и лье.

Вновь определённая единица получила наименование «метр подлинный и окончательный» (фр. metre vrai et définitif)^[1].

7 апреля 1795 Национальный Конвент принял закон о введении метрической системы во Франции и поручил комиссарам, в число которых входили Ш. О. Кулон, Ж. Л. Лагранж, П.-С. Лаплас и другие учёные, выполнить работы по экспериментальному определению единиц длины и массы. В 1792—1797 годах по решению революционного Конвента французские учёные Деламбр (1749—1822) и Мешен (1744—1804) за 6 лет измерили дугу парижского меридиана длиной в 9°40′ от Дюнкерка до Барселоны, проложив цепь из 115 треугольников через всю Францию и часть Испании. Впоследствии, однако, выяснилось, что из-за неправильного учёта полюсного сжатия Земли эталон оказался короче на 0,2 мм; таким образом, длина меридиана лишь приблизительно равна 40 000 км.

Первый прототип эталона метра был изготовлен из латуни в 1795 году.

Следует отметить, что единица массы (килограмм, определение которого было основано на массе 1 дм³ воды), тоже была привязана к определению метра.

В 1799 году был изготовлен из платины эталон метра, длина которого соответствовала одной сорокамиллионной части Парижского меридиана^[14].

Во время правления Наполеона метрическая система распространилась по многим странам Европы. Выгода от её применения была столь очевидна, что и после отстранения Наполеона от власти принятие метрических единиц продолжалось^[15]:

• 1816 — Бельгия и Голландия;
• 1832 — Португалия;
• 1849 — Испания и Греция;
• 1870 — Германия;
• 1873 — Австрия;
• 1875 — Швейцария.

К концу XIX века из крупных стран только в Великобритании (и её колониях), США, России, Китае и Османской империи остались традиционные меры длины.

На метре как единице длины и килограмме как единице массы была основана метрическая система, которая была введена «Метрической конвенцией», принятой на Международной дипломатической конференции 17 государств (Россия, Франция, Великобритания, США, Германия, Италия и др.) 20 мая 1875 года^[16].

В 1889 году был изготовлен более точный международный эталон метра. Этот эталон изготовлен из сплава 90 % платины и 10 % иридия^[17] и имеет поперечное сечение в виде буквы «X». Его копии были переданы на хранение в страны, в которых метр был признан в качестве стандартной единицы длины.

Дальнейшее развитие[править | править код]

В 1960 было решено отказаться от использования изготовленного людьми предмета в качестве эталона метра, и с этого времени по 1983 год метр определялся как число 1 650 763,73, умноженное на длину волны оранжевой линии (6 056 Å) спектра, излучаемого изотопом криптона ⁸⁶Kr в вакууме. После принятия нового определения платино-иридиевый прототип метра продолжают хранить в Международном бюро мер и весов в тех условиях, что были определены в 1889 году. Однако теперь его статус стал иным: длина прототипа перестала считаться в точности равной 1 м и её фактическое значение должно определяться экспериментально. По своему первоначальному назначению прототип больше не используется.

К середине 1970-х годов был достигнут значительный прогресс в определении скорости света. Достаточно сказать, что если в 1926 году погрешность наиболее точных на то время измерений, выполненных А. Майкельсоном, составляла 4000 м/с^[18], то в 1972 году сообщалось о снижении погрешности вплоть до 1,1 м/с^[19]. После многократной проверки полученного результата в различных лабораториях XV Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать в качестве значения скорости света в вакууме величину, равную 299 792 458 м/с с относительной погрешностью 4·10⁻⁹, что соответствует абсолютной погрешности 1,2 м/с^[20]. Впоследствии в 1983 году именно это значение XVII Генеральная конференция по мерам и весам положила в основу нового определения метра^[2].

Определения метра с 1795 года^[21]

Основа	Дата	Абсолютная погрешность	Относительная погрешность
1⁄10 000 000 часть четверти Парижского меридиана, определённая по результатам измерений, проведённых Деламбром и Мешеном	1795	0,5—0,1 мм	10−4
Первый эталон Metre des Archives из платины	1799	0,05—0,01 мм	10−5
Платино-иридиевый профиль при температуре таяния льда (1-я ГКМВ)	1889	0,2—0,1 мкм	10−7
Платино-иридиевый профиль при температуре таяния льда и атмосферном давлении, поддерживаемый двумя роликами (VII ГКМВ)	1927	неизв.	неизв.
1 650 763,73 длины волны оранжевой линии (6056 Å) спектра, излучаемого изотопом криптона 86Kr в вакууме (XI ГКМВ)	1960	4 нм	4·10−9[2]
Длина пути, проходимого светом в вакууме за (1/299 792 458) секунды (XVII ГКМВ)	1983	0,1 нм	10−10

Погонный метр — единица измерения количества длинномерных объектов (так называемых погонажных изделий, материалов и т. п.), соответствующая куску или участку длиной 1 метр. Погонный метр ничем не отличается от обычного метра, это единица, которой измеряют длину материала независимо от ширины. Погонным метром могут, например, измерять кабельные каналы, доски, листы металла, трубы, плинтусы, оконные уплотнители, ткани. Хотя для тканей правильнее было бы измерять их площадь, но если ширина ткани подразумевается известной и постоянной — используется понятие «погонный метр» (как правило, ширина ткани составляет 1,4 м, и, таким образом, погонный метр ткани является куском 1,0×1,4 м). Говоря строго, в быту чаще используется понятие именно погонного метра, информация о ширине или высоте предметов подразумевается известной или не важной. Наименование погонного метра выделяется в специальной литературе либо для создания различной экспрессивной окраски речи.

Метрологическая литература не рекомендует использовать термин «погонный метр». Общее правило заключается в том, что в случае необходимости поясняющие слова должны входить в наименование физической величины, а не в наименование единицы измерения. Поэтому, например, следует писать «погонная длина равна 10 м», а не «длина равна 10 пог. м»^[22].

Комментарии

1. ↑ metro cattolico (lit. «catholic [в значении „универсальная“] мера»), заимствовано из греческого μέτρον καθολικόν (métron katholikón)
2. ↑ Идея секундного маятника для назначения стандартной длины тем не менее окончательно не умерла, и такой стандарт был использован для определения длины ярда в Великобритании в период 1843—1878 годов.

Источники

1. ↑ ^{1 2} Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5.
2. ↑ ^{1 2 3 4} Определение метра (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
3. ↑ ^{1 2} Положение о единицах величин, допускаемых к применению в Российской Федерации. Основные единицы Международной системы единиц (СИ) (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018. Архивировано 18 сентября 2017 года.
4. ↑ SI base units (неопр.) (недоступная ссылка). BIPM. Дата обращения 22 июня 2019. Архивировано 23 декабря 2018 года.
5. ↑ SI brochure Официальное описание СИ на сайте Международного бюро мер и весов
6. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Десятичные множители, приставки и обозначения приставок… (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018. Архивировано 18 сентября 2017 года.
7. ↑ Окунь Л. Б. Слабое взаимодействие // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 552—556. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
8. ↑ Nelson, Robert A. (1981), «Foundations of the international system of units (SI)», Phys. Teacher: 596–613, <http://plato.if.usp.br/1-2009/fmt0159n/PDFFiles/ThePhysTeacher_FoundationsOfTheSI.pdf>  Архивная копия от 6 июля 2011 на Wayback Machine.
9. ↑ Wilkins, John (1668), An Essay Towards a Real Character, And a Philosophical Language, London: Gillibrand, <http://www.metricationmatters.com/docs/WilkinsTranslationLong.pdf> .
10. ↑ Misura Universale, 1675 .
11. ↑ Poynting, John Henry & Thompson, Joseph John (1907), A Textbook of Physics: Properties of Matter (4th ed.), London: Charles Griffin, с. 20, <https://books.google.com/books?id=TL4KAAAAIAAJ&pg=PA20> .
12. ↑ ^{1 2 3} Grand dictionnaire universel du XIXe siècle, Paris: Pierre Larousse, 1866—1877, p. 163—164.
13. ↑ Jean Charles de Borda, MacTutor, <http://www-history.mcs.st-andrews.ac.uk/Biographies/Borda.html>. Проверено 13 августа 2010. .
14. ↑ Brief history of the SI (англ.). International Bureau of Weights and Measures. Дата обращения 12 июля 2010. Архивировано 21 августа 2011 года.
15. ↑ Гевара И., Карлес П. Измерение мира. Календари, меры длины и математика.. — М.: Де Агостини, 2014. — С. 125—126. — 160 с. — (Мир математики: в 45 томах, том 38). — ISBN 978-5-9774-0733-5.
16. ↑ Метрическая система мер (неопр.) (недоступная ссылка). История измерений. Дата обращения 12 июля 2010. Архивировано 27 октября 2011 года.
17. ↑ ПЛАТИНА — статья из энциклопедии «Кругосвет»
18. ↑ Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 387. — ISBN 5-9221-0314-8.
19. ↑ Evenson K. M., Wells J. S., Petersen F. R., Danielson B. L., Day G. W. Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser (англ.) // Phys. Rev. Lett.. — 1972. — Vol. 29, no. 19. — P. 1346—1349. — DOI:10.1103/PhysRevLett.29.1346.
20. ↑ Рекомендованное значение скорости света (англ.) Резолюция 2 XV Генеральной конференции по мерам и весам (1975)
21. ↑ Encydopaedia of scientific units, weights, and measures: their SI equivalences and origins. — Springer, 2004. — P. 5. — ISBN 1-85233-682-X.
22. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 78. — 240 с. — ISBN 5-7050-0118-5.

• Cardarelli, Francois (2003). Encydopaedia of scientific units, weights, and measures: their SI equivalences and origins, Springer-Verlag London Limited, ISBN 1-85233-682-X, page 5, table 2.1, data from Giacomo, P., Du platine a la lumiere, Bull. Bur. Nat. Metrologie, 102 (1995) 5-14.
• Humerfelt, Sigurd. (26 October 2010).
• Layer, H.P. (2008). Length—Evolution from Measurement Standard to a Fundamental Constant. Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 18 August 2008.
• Mohr, P., Taylor, B.N., and David B. Newell, D. (13 November 2012). CODATA Recommended Values of the Fundamental Physical Constants: 2010. Gaithersburg, MD: National Institute of Standards and Technology.
• National Institute of Standards and Technology. (December 2003). The NIST Reference on Constants, Units, and Uncertainty: International System of Units (SI) (web site):
• National Institute of Standards and Technology. (27 June 2011). NIST-F1 Cesium Fountain Atomic Clock. Author.
• National Physical Laboratory. (25 March 2010). Iodine-Stabilised Lasers. Author.
• Naughtin, Pat. (2008). Spelling metre or meter. Author.
• Taylor, B.N. and Thompson, A. (Eds.). (2008a). The International System of Units (SI). United States version of the English text of the eighth edition (2006) of the International Bureau of Weights and Measures publication Le Système International d’ Unités (SI) (Special Publication 330). Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 18 August 2008.
• Taylor, B.N. and Thompson, A. (2008b). Guide for the Use of the International System of Units (Special Publication 811). Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 23 August 2008.
• Tibo Qorl. (2005) The History of the Meter (Translated by Sibille Rouzaud). Retrieved 18 August 2008.
• Zagar, B.G. (1999). Laser interferometer displacement sensors in J.G. Webster (ed.). The Measurement, Instrumentation, and Sensors Handbook. CRC Press. isbn=0-8493-8347-1.
• Белобров В.А. (2019). История метра (короткая версия), История метра (полная версия)

Измерение величин, меры, единицы измерения

Величина – это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.

Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин. Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.

Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна – это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например, 5 см = 50 мм (длина), 1 ч = 60 мин (время), 2 кг = 2000 г (вес).

Измерить какую-нибудь величину – значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.

Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.

В результате измерения величины получается или именованное число, например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом.

Меры

В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.

Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм – меры однородные, так как они служат для измерения веса.

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы

• 1 тонна = 10 центнеров
• 1 центнер = 100 килограмм
• 1 килограмм = 1000 грамм
• 1 грамм = 1000 миллиграмм

Меры длины

• 1 километр = 1000 метров
• 1 метр = 10 дециметров
• 1 дециметр = 10 сантиметров
• 1 сантиметр = 10 миллиметров

Меры площади (квадратные меры)

• 1 кв. километр = 100 гектарам
• 1 гектар = 10000 кв. метрам
• 1 кв. метр = 10000 кв. сантиметров
• 1 кв. сантиметр = 100 кв. миллиметрам

Меры объёма (кубические меры)

• 1 куб. метр = 1000 куб. дециметров
• 1 куб. дециметр = 1000 куб. сантиметров
• 1 куб. сантиметр = 1000 куб. миллиметров

Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).

Меры времени

• 1 век (столетие) = 100 годам
• 1 год = 12 месяцам
• 1 месяц = 30 суткам
• 1 неделя = 7 суткам
• 1 сутки = 24 часам
• 1 час = 60 минутам
• 1 минута = 60 секундам
• 1 секунда = 1000 миллисекундам

Кроме того, используют такие единицы измерения времени, как квартал и декада.

• квартал – 3 месяца
• декада – 10 суток

Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь – 31 день. Февраль в простом году – 28 дней, февраль в високосном году – 29 дней. Апрель, июнь, сентябрь, ноябрь – 30 дней.

Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый – в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней – простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Сокращённые наименования мер

Сокращённые наименования мер принято записывать без точки:

Меры длины Километр – км Метр – м Дециметр – дм Сантиметр – см Миллиметр – мм	Меры веса/массы тонна – т центнер – ц килограмм – кг грамм – г миллиграмм – мг
Меры площади (квадратные меры) кв. километр – км2 гектар – га кв. метр – м2 кв. сантиметр – см2 кв. миллиметр – мм2	Меры объёма (кубические меры) куб. метр – м3 куб. дециметр – дм3 куб. сантиметр – см3 куб. миллиметр – мм3
Меры времени век – в год – г месяц – м или мес неделя – н или нед сутки – с или д (день) час – ч минута – м секунда – с миллисекунда – мс	Мера вместимости сосудов

	1 мм	1 см	1 дм	1 м	1 км
	1 мм2	1 см2	1 дм2	1 м2	1 км2
	1 мм3	1 см3	1 дм3	1 м3	1 км3

Измерительные приборы

Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.

Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.

Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:

Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы измерительного прибора.

Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

1. Найти два ближайших штриха шкалы, возле которых написаны значения величины.
2. Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.

Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).

Например, штрихи с обозначениями 20 °С и 30 °С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:

(30 °С — 20 °С) : 10 = 1 °С

Следовательно, термометр показывает 47 °С.

Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.

«Единицы измерения» — Яндекс.Знатоки

Единиц измерения сущетвует огромное количество. Во-первых, для разных измерений используются разные системы единиц, которые нельзя сравнивать между собой. Что больше – грамм или метр? Что меньше – литр или секунда? На эти вопросы нельзя дать ответ. Поэтому не может быть одной наименьшей единицы измерения вообще. Можно только говорить о наименьшей единице длины, наименьшей единице времени и т.д.

Но и для конкретного измерения, скажем, длины, всё не так просто. Если мы найдём наименьшую единицу, что помешает нам или кому-либо ещё придумать новую единицу ещё меньше? Ничего! А может быть, такая единица уже существует и где-то используется, просто она пока не получила широкой известности? Всё может быть!

Тем не менее, давайте попробуем найти ответ, например, для единиц днины. Возьмём систему СИ (международную систему единиц). В этой системе основной единицей длины является метр. К названию единицы можно приписывать стандартные префиксы, которые уменьшают или увеличивают эту единицу. Например, префикс «кило» даёт нам километр (1000 метров), а префикс «микро» даёт микрометр (0.001 метр). Чтобы получить наименьшую единицу, надо использовать префикс йокто. Один йоктометр равен 10⁻²⁴ метра или, если записать это в виде десятичной дроби, 0.000000000000000000000001 метра.

Но есть известная единица длины ещё меньше йоктометра. В далёком 1899г немецкий физик Макс Планк придумал систему единиц, основанную только на фундаментальных свойствах и постоянных нашей вселенной, таких, как скорость света. Вот, что писал Планк о своей системе:

…мы получаем возможность установить единицы длины, массы, времени и температуры, которые не зависели бы от выбора каких-либо тел или веществ и обязательно сохраняли бы своё значение для всех времен и для всех культур, в том числе и внеземных и нечеловеческих, и которые поэтому можно было бы ввести в качестве «естественных единиц измерений»

Система планковских единиц не используется широко, потому что все единицы в ней получились очень малы, их неудобно использовать на практике. Однако, если искать наименьшие единицы измерения, именно планковские единицы могут быть ответом на вопрос.

И правда, планковская длина равна 1,616 229(38)⋅10⁻³⁶ метра, т.е. почти в 600 миллиардов раз меньше йоктометра.

Похоже, победителем в конкурсе за звание наименьшей единицы длины с большим отрывом побеждает планковская длина.

Что измеряется в децибелах? Децибел: определение и области применения

Децибел — это относительная единица измерений, она не похожа на остальные известные величины, поэтому ее не включили в систему общепринятых единиц измерения СИ. Однако во многих расчетах допускается использование децибелов наравне с абсолютными единицами измерений и даже применение их в качестве опорной величины.

Децибелы определяются принадлежностью к физическим величинам, поэтому их нельзя относить к математическим понятиям. Это легко представить, если провести параллель с процентами, с которыми децибелы имеют много общего. Они не имеют конкретных размеров, но при этом очень удобны при сопоставлении 2-х одноименных величин, даже если они различны по своей природе. Таким образом, не сложно представить, что измеряется в децибелах.

История возникновения

Как выяснилось в результате длительных исследований, восприимчивость не находится в прямой зависимости от абсолютного уровня распространения звука. Она является показателем мощности, примененным к заданной единице площади, которая находится в зоне воздействия звуковых волн, что и измеряют в децибелах сегодня. В результате установили любопытную пропорцию – чем больше места принадлежит полезной площади человеческого уха, тем к лучшему восприятию минимальных мощностей оно расположено.

Таким образом, исследователю Александру Грэхему Беллу удалось установить, что предел восприятия человеческого уха равен от 10 до 12 Вт на метр квадратный. Полученные данные охватывали слишком широкий диапазон, который представлялся всего несколькими значениями. Это создавало определенные неудобства и исследователю пришлось создать собственную шкалу измерений.

В первоначальном варианте безымянная шкала имела 14 значений — от 0 до 13, где человеческий шепот имел значение «3», а разговорная речь – «6». Впоследствии эта шкала нашла широкое применение, а ее единицы назвали белами. Для получения более точных данных в логарифмическом масштабе исходную единицу увеличили в 10 раз – так сформировались децибелы.

Общие сведения

Прежде всего, следует отметить, что децибел — это одна десятая Бела, который является десятичной формой логарифма, определяющего отношение меж 2-мя мощностями. Природа мощностей, подлежащих сравнению, избирается произвольно. Главное, чтобы соблюдалось правило, представляющее сравниваемые мощности в равных единицах, например, в Ваттах. Благодаря этой особенности, обозначения децибелов применяют в разных областях:

• механической;
• электрической;
• акустической;
• электромагнитной.

Так как практическое применение показало, что Бел оказался довольно крупной единицей, то для лучшей наглядности было предложено его значение умножить на десять. Таким образом, появилась общепринятая единица – децибел, в чем измеряется звук сегодня.

Несмотря на обширную зону применения, большинству людей известно, что децибелы применяются для определения степени громкости. Эта величина характеризует интенсивность звуковой волны на метр квадратный. Таким образом, увеличение громкости на 10 децибел сопоставимо с возрастанием силы звука вдвое.

В законодательстве децибел был признан расчетной величиной зашумленности помещения. Он явился определяющей характеристикой для исчисления допустимой силы шума в жилых строениях. Эта величина дает возможность измерить допустимый уровень шума в децибелах в квартире и выявить факты нарушения в случае необходимости.

Область применения

Сегодня проектировщики телекоммуникаций используют децибел в качестве базовой единицы для проведения сравнительных характеристик устройств, отраженных в логарифмическом масштабе. Такие возможности предоставляет конструктивная особенность данной величины, которая является логарифмической единицей разных уровней, используемых при затуханиях или, наоборот, усилениях мощностей.

Децибел получил широкое распространение в разнообразных областях современной техники. Что измеряется в децибелах сегодня? Это различные величины, изменяющиеся в обширном диапазоне, которые могут применяться:

• в системах, связанных с передачей информации;
• радиотехнике;
• оптике;
• антенной технике;
• акустике.

Таким образом, децибелы применяют при измерении характеристик динамического диапазона, к примеру, ими можно измерить громкость звучания определенного музыкального инструмента. А также открывается возможность исчислять затухающие волны в момент их прохождения через поглощающую среду. Децибелы позволяют определить коэффициент усиления или зафиксировать коэффициент шума, создаваемого усилителем.

Использовать эти безразмерные единицы возможно как для физических величин, относящихся ко второму порядку – энергия или мощность, так и для величин, имеющих отношение к первому порядку – сила тока или напряжение. Децибелы открывают возможности измерения отношений между всеми физическими величинами, а кроме этого, с их помощью сопоставляют абсолютные значения.

Громкость звука

Физическая составляющая громкости звукового воздействия определяется уровнем имеющегося звукового давления, воздействующего на единицу контактной площади, что измеряется в децибелах. Формируется уровень шума из хаотического слияния звуков. На низкие частоты или, наоборот, звуки высокой частоты человек реагирует как на более тихие звуки. А звуки средних частот будут восприняты как более громкие, несмотря на одинаковую интенсивность.

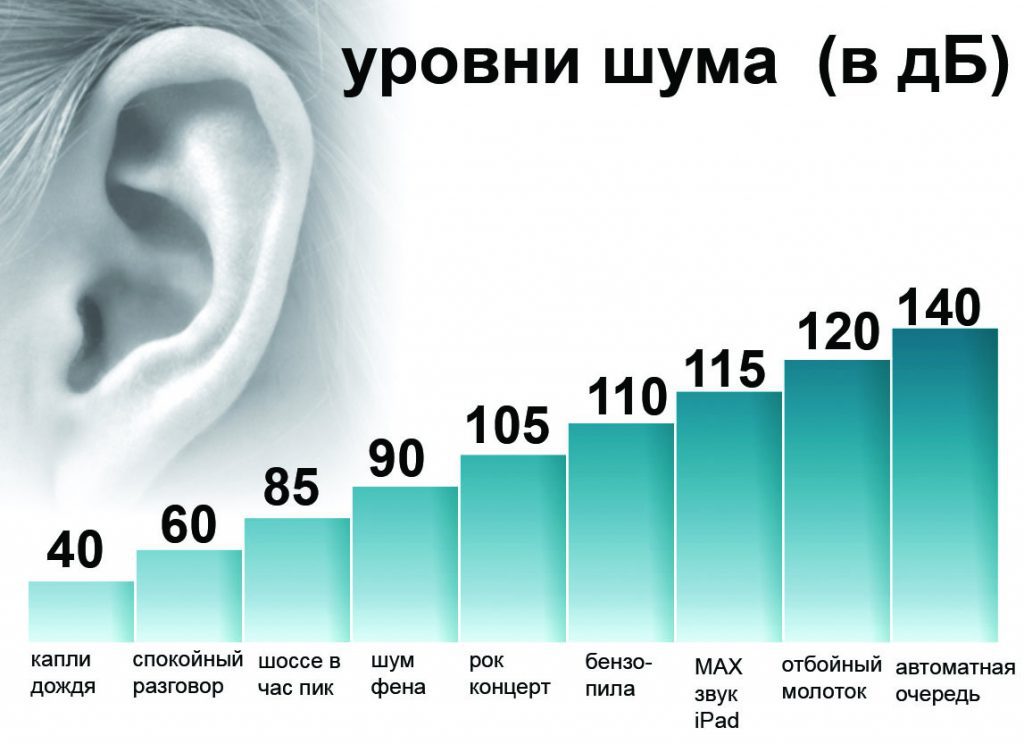
Учитывая неравномерное восприятие звуков различной частоты человеческим ухом, на электронной базе был создан частотный фильтр, способный передавать эквивалентную степень звука с единицей измерения, которая выражается в дБа – где «а» обозначает применение фильтра. Этот фильтр, по итогам нормирования измерений, способен моделировать взвешенное значение уровня звука.

Способность разных людей воспринимать звуки находится в пределах громкости от 10 до 15 дБ, а в отдельных случаях даже выше. Воспринимаемые пределы интенсивности звука составляют частоты от 20 до 20 тыс. Герц. Наиболее легкие для восприятия звуки располагаются в частотном диапазоне от 3-х до 4-х кГц. Такую частоту принято использовать в телефонах, а также при радиовещании на средних и длинных волнах.

С годами диапазон воспринимаемых звуков сужается, особенно это касается высокочастотного спектра, где восприимчивость может снижаться до 18 кГц. Это приводит к общему ухудшению слуха, которому подвержены многие пожилые люди.

Допустимые показатели уровня шума в жилых помещениях

С использованием децибелов появилась возможность определить более точную шкалу шумов для окружающих звуков. Она отражает превосходящие по точности характеристики по сравнению с исходной шкалой, созданной в свое время Александром Беллом. С использованием этой шкалы законодательными органами определен уровень шума, норма которого действует в пределах жилых помещений, предназначенных для отдыха граждан.

Таким образом, значение «0» дБ означает полнейшую тишину, от которой раздается звон в ушах. Следующее значение 5 дБ также определяет полную тишину при наличии небольшого звукового фона, заглушающего внутренние процессы организма. При 10 дБ становятся различимы нечеткие звуки – всевозможные шорохи или шуршание листвы.

Значение в 15 дБ находится в диапазоне четкой слышимости самых тихих звуков, таких как тиканье наручных часов. При силе звука в 20 дБ можно разобрать осторожный шепот людей на расстоянии 1 метра. Отметка 25 дБ позволяет слышать более отчетливо разговор шепотом и шорох от трения мягких тканей.

30 дБ определяет, сколько децибел разрешено в квартире ночью и сопоставляется с беззвучным разговором или тиканьем настенных часов. При 35 дБ можно отчетливо слышать приглушенную речь.

Уровень в 40 децибел определяет силу звука обычного разговора. Это достаточная громкость, позволяющая свободно общаться в пределах помещения, смотреть телевизор или прослушивать музыкальные треки. Данная отметка определяет, сколько децибел разрешено в квартире днем.

Уровень шума, допустимый в рабочих условиях

По сравнению с допустимым уровнем шума в децибелах в квартире, на производстве и в офисной деятельности в рабочее время допускаются другие нормы уровня звука. Здесь действуют ограничения иного прядка, четко отрегулированные для каждого рода занятий. Основное правило в данных условиях — не допускать уровня шума, который способен отрицательно повлиять на здоровье человека.

В офисах

Значение уровня шума в 45 дБ находится в пределах хорошей слышимости и сопоставимо с шумом работы дрели или электродвигателя. Шум в 50 дБ также характеризуется пределами отличной слышимости и совпадает по силе со звуком печатающей машинки.

Уровень шума в 55 децибел остается в пределах превосходной слышимости, его можно представить на примере одновременного звучного разговора сразу нескольких людей. Этот показатель принимают в качестве верхней отметки, допустимой для офисных помещений.

В животноводстве и канцелярской деятельности

Сила шума в 60 дБ считается повышенной, такой уровень зашумленности можно встретить в конторах, где одновременно работает много печатных машинок. Показатель в 65 дБ также считают повышенным и его можно зафиксировать при работе типографского оборудования.

Уровень шума, достигающий отметки 70 дБ, сохраняет значение повышенного и встречается на животноводческих фермах. Значение шума в 75 дБ — это предельное значение повышенного уровня шума, его можно отметить на птицефабриках.

В производстве и транспорте

С отметкой в 80 дБ наступает уровень громкого звука, длительное воздействие которого станет следствием частичной утраты слуха. Поэтому, при работе в таких условиях рекомендуется применять защитные наушники. Сила шума в 85 дБ также находится в пределах уровня громкого звука, такие показания можно сопоставить с работой оборудования ткацкой фабрики.

Показатель шума в 90 дБ сохраняется в пределах громкого звука, такую силу зашумленности можно зарегистрировать при движении железнодорожного состава. Величина шума в 95 дБ достигает крайних пределов громкого звука, такой силы шум можно зафиксировать в металлопрокатном цеху.

Предельный уровень шума

Уровень шума на отметке 100 дБ достигает пределов чрезмерно громкого звука, его можно сравнить с раскатами грома. Работа в таких условиях считается вредной для здоровья и выполняется в рамках определенного стажа, по истечении которого человек считается непригодным для вредных работ.

Значение шума в 105 дБ также находится в пределах чрезмерно громкого звука, шум такой силы создает бензорезка при порезке металла. Сила шума в 110 дБ остается в границах чрезмерно громкого звука, такой показатель фиксируется при взлете вертолета. Величина шума в 115 дБ считается предельной для границ чрезмерно громкого звука, такой шум издает пескоструйный аппарат.

Уровень шума 120 дБ считается невыносимым, его можно сравнить с работой отбойного молотка. Шумовая отметка в 125 дБ также характеризуется невыносимым уровнем шума, такой отметки достигает самолет на старте. Максимальный уровень шума в дБ считается предельным на отметке 130, после чего наступает болевой порог, вынести который способен далеко не каждый.

Критический уровень шума

Сила шума на отметке 135 дБ считается недопустимой, человек, оказавшийся в зоне действия звука такой силы, получает контузию. Уровень шума в 140 дБ также приводит к контузии, таким звуком сопровождается старт реактивного самолета. При величине шума в 145 дБ разрывается осколочная граната.

Достигает отметки 150-155 дБ разрыв кумулятивного снаряда на танковой броне, звук такой силы приводит к контузии и травмам. После отметки 160 дБ наступает звуковой барьер, звук, превышающий этот предел, приводит к разрыву ушных барабанных перепонок, распаду легких и множественным травмам, нанесенным ударной волной, что вызывает мгновенную смерть.

Воздействие на организм неслышимых звуков

Звук, частота которого ниже 16 Гц, называют инфракрасным, а если частота его превышает 20 тыс. Гц, то такой звук называют ультразвуком. Барабанные перепонки человеческого уха не способны воспринимать звуки такой частоты, поэтому они находятся за пределами человеческого слуха. Децибелы, в чем измеряется звук сегодня, также определяют значения не слышимых звуков.

Звуки низкой частоты, находящиеся в пределах от 5-ти до 10-ти Гц, плохо переносятся человеческим организмом. Такое воздействие способно активизировать сбои в работе внутренних органов и отражаться на мозговой активности. Кроме этого, интенсивность низких частот оказывает воздействие на костные ткани, провоцируя суставные боли у людей, страдающих различными заболеваниями или перенесших травмы.

Повседневными источниками ультразвука являются различные транспортные средства, также ими могут служить раскаты грома или работа электронной аппаратуры. Такие воздействия выражаются в нагреве тканей, а сила их влияния находится в зависимости от расстояния до действующего источника и от степени звука.

Для общедоступных мест работы, обладающих источниками звуков неслышимого диапазона, также существуют определенные ограничения. Максимальная сила инфракрасного звука должна удерживаться в пределах 110 дБа, а сила ультразвука ограничивается отметкой в 125 дБа. Строго запрещено даже кратковременное нахождение в зонах, где звуковое давление превышает 135 дБ любой частоты.

Влияние шума, исходящего от оргтехники, и способы защиты

Шум, который издает компьютер и прочая организационная техника, может быть выше значения в 70 дБ. В связи с этим специалисты не рекомендуют устанавливать большое количество данной аппаратуры в одном помещении, особенно, если оно не большое. Шумные агрегаты рекомендуется устанавливать за пределами помещения, в котором находятся люди.

Для снижения уровня зашумленности в отделочных работах применяют материалы, обладающие шумопоглощающими свойствами. Кроме этого, можно использовать шторы из плотной ткани или, в крайнем случае, бируши, закрывающие от воздействия барабанные перепонки.

Сегодня при строительстве современных зданий существует новая норма, определяющая степень звукоизоляции помещений. Стены и перекрытия корпусов многоквартирных домов проверяют на устойчивость к воздействию шума. Если уровень звукоизоляции находится ниже допустимого предела, здание не может быть сдано в эксплуатацию до устранения неполадок.

Кроме всего, сегодня устанавливают ограничения по силе звука для различных сигнальных и оповещающих устройств. Для противопожарных систем, к примеру, сила звука оповещающего сигнала должна находиться в рамках от 75 дБа до 125 дБа.

Давайте разберемся, что измеряется в джоулях

Физика — наука естественного направления. Наверное, именно поэтому ей уделяется большое внимание в школьном курсе. Часто ученики сталкиваются с вопросом о том, что измеряется в джоулях. Это вполне ожидаемо, так как разные разделы физики могут включать в себя эту величину. Однако если попробовать немного разобраться в теме, то сразу станет все на свои места. Где же вы можете встретить то, что измеряется в джоулях? Ответ не прост, но понятен.

Все начинается с простой формулы A=F*S. На подобную зависимость контрольная работа может попасться уже после первого месяца знакомства с физикой. Если сразу понять, что к чему, то можно начать вполне успешное знакомство с наукой. F — сумма всех действующих сил, приложенных к телу, которая повлияла на изменение положения тела. Она измеряется в ньютонах. Суждение о том, что сила измеряется в джоулях, неверно. S — путь, которое прошло тело. В единицах СИ оно обозначено метрами. Таким образом, 1 Дж = 1 Н * 1 м. То есть фактически мы нашли работу с физической точки зрения. И совершенно неважно, кем и при каких обстоятельствах она была совершена.

Далее, как правило, в восьмом классе изучаются тепловые процессы. Здесь вводится много новых понятий. Основная формула: Q=cm(t1-t2). Здесь опять возникает вопрос о том, что измеряется в джоулях в данной зависимости. И, кстати, заметим, что возникла какая-то непонятная переменная c. На самом деле это удельная теплоемкость вещества. Стоит отметить, что это, как правило, величина постоянная, измеренная уже давно. Ее размерность: Дж/(Кг*Градусов Цельсия). Отсюда легко заметить, что стоит перемножить эту величину на массу и на некоторую температуру, то получатся джоули. То есть буква Q. Она-то и измеряется в них. Стоит сказать, что на самом деле тепло — энергия. Например, в двигателях внутреннего сгорания сначала выделяется Q, которая затем с некоторым КПД переходит в A=F*S. На этом, в принципе, могут быть основаны некоторые олимпиадные задачи для 7-8 класса.

Еще одним большим разделом, который следует рассмотреть для того, чтобы узнать, что измеряется в джоулях, является «Электричество». Конечно, в более глобальных рамках называется он несколько иначе, но для школьной трактовки подойдет и такое обозначение. Многие знают, на каком принципе основаны лампы накаливания. Откуда же появляется тепловая энергия? Да, электрический ток совершает некоторую работу, которую можно рассчитать по формуле A=I*I*T*t. Здесь t — время, I — сила тока, R — сопротивление. Здесь работа также измеряется в джоулях.

Нельзя не сказать о механике, в которой рассматриваемая величина имеет немалое применение. Часто в школьных задачах имеет смысл Закон сохранения энергии. Так вот эта энергия как раз и измеряется в Джоулях. Основной смысл формулировки закона заключается в том, что тело имеет какую-то энергию при движении, тепловых процессах и других физических процессах. И если, например, деревянный брусок скользит по поверхности и останавливается, то это не значит, что он теряет энергию. Просто она уходит на работу силы трения.

Таким образом, вы узнали, что измеряется в джоулях. Как видно, эта характеристика используется во многих совершенно различных разделах физики. Однако если понять суть, то станет намного легче.