Таблица КОСИНУСОВ для углов от 0° до 360° градусов
КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos α (Косинус) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
…
| Угол в градусах | Cos (Косинус) |
|---|---|
| 0° | 1 |
| 1° | 0.9998 |
| 2° | 0.9994 |
| 3° | 0. |
| 4° | 0.9976 |
| 5° | 0.9962 |
| 6° | 0.9945 |
| 7° | 0.9925 |
| 8° | 0.9903 |
| 9° | 0.9877 |
| 10° | 0.9848 |
| 11° | 0.9816 |
| 12° | 0.9781 |
| 13° | 0.9744 |
| 14° | 0.9703 |
| 15° | 0.9659 |
| 16° | 0.9613 |
| 17° | 0.9563 |
| 18° | 0.9511 |
| 19° | 0.9455 |
| 20° | 0.9397 |
| 21° | 0.9336 |
| 22° | 0.9272 |
| 23° | 0.9205 |
| 24° | 0.9135 |
| 25° | 0.9063 |
| 26° | 0.8988 |
| 27° | 0.891 |
| 28° | 0.8829 |
| 29° | 0.8746 |
| 30° | 0. 866 866 |
| 31° | 0.8572 |
| 32° | 0.848 |
| 33° | 0.8387 |
| 34° | 0.829 |
| 35° | 0.8192 |
| 36° | 0.809 |
| 37° | 0.7986 |
| 38° | 0.788 |
| 39° | 0.7771 |
| 40° | 0.766 |
| 41° | 0.7547 |
| 42° | 0.7431 |
| 43° | 0.7314 |
| 44° | 0.7193 |
| 45° | 0.7071 |
| 46° | 0.6947 |
| 47° | 0.682 |
| 48° | 0.6691 |
| 49° | 0.6561 |
| 50° | 0.6428 |
| 51° | 0.6293 |
| 52° | 0.6157 |
| 53° | 0.6018 |
| 54° | 0.5878 |
| 55° | 0.5736 |
| 56° | 0.5592 |
| 57° | 0. 5446 5446 |
| 58° | 0.5299 |
| 59° | 0.515 |
| 60° | 0.5 |
| 61° | 0.4848 |
| 62° | 0.4695 |
| 63° | 0.454 |
| 64° | 0.4384 |
| 65° | 0.4226 |
| 66° | 0.4067 |
| 67° | 0.3907 |
| 68° | 0.3746 |
| 69° | 0.3584 |
| 70° | 0.342 |
| 71° | 0.3256 |
| 72° | 0.309 |
| 73° | 0.2924 |
| 74° | 0.2756 |
| 75° | 0.2588 |
| 76° | 0.2419 |
| 77° | 0.225 |
| 78° | 0.2079 |
| 79° | 0.1908 |
| 80° | 0.1736 |
| 81° | 0.1564 |
| 82° | 0.1392 |
| 83° | 0.1219 |
| 84° | 0. 1045 1045 |
| 85° | 0.0872 |
| 86° | 0.0698 |
| 87° | 0.0523 |
| 88° | 0.0349 |
| 89° | 0.0175 |
| 90° | 0 |
…
| Угол | cos (Косинус) |
|---|---|
| 91° | -0.0175 |
| 92° | -0.0349 |
| 93° | -0.0523 |
| 94° | -0.0698 |
| 95° | -0.0872 |
| 96° | -0.1045 |
| 97° | -0.1219 |
| 98° | -0.1392 |
| 99° | -0.1564 |
| 100° | -0.1736 |
| 101° | -0.1908 |
| 102° | -0.2079 |
| 103° | -0.225 |
| 104° | -0.2419 |
| 105° | -0.2588 |
| 106° | -0. 2756 2756 |
| 107° | -0.2924 |
| 108° | -0.309 |
| 109° | -0.3256 |
| 110° | -0.342 |
| 111° | -0.3584 |
| 112° | -0.3746 |
| 113° | -0.3907 |
| 114° | -0.4067 |
| 115° | -0.4226 |
| 116° | -0.4384 |
| 117° | -0.454 |
| 118° | -0.4695 |
| 119° | -0.4848 |
| 120° | -0.5 |
| 121° | -0.515 |
| 122° | -0.5299 |
| 123° | -0.5446 |
| 124° | -0.5592 |
| 125° | -0.5736 |
| 126° | -0.5878 |
| 127° | -0.6018 |
| 128° | -0.6157 |
| 129° | -0.6293 |
| 130° | -0.6428 |
| 131° | -0.6561 |
| 132° | -0.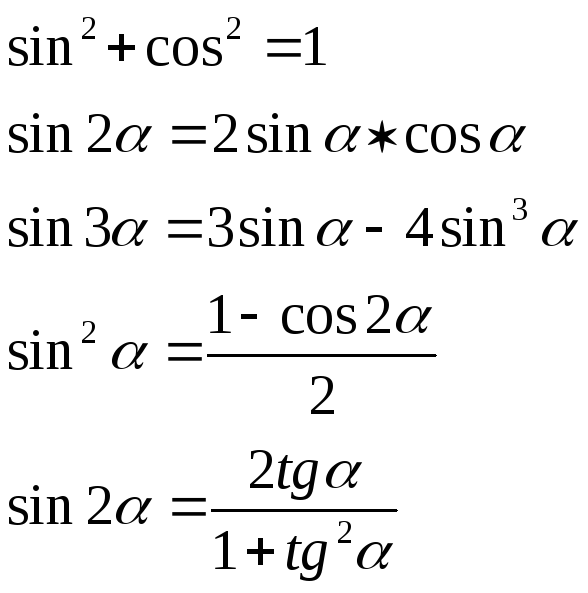 6691 6691 |
| 133° | -0.682 |
| 134° | -0.6947 |
| 135° | -0.7071 |
| 136° | -0.7193 |
| 137° | -0.7314 |
| 138° | -0.7431 |
| 139° | -0.7547 |
| 140° | -0.766 |
| 141° | -0.7771 |
| 142° | -0.788 |
| 143° | -0.7986 |
| 144° | -0.809 |
| 145° | -0.8192 |
| 146° | -0.829 |
| 147° | -0.8387 |
| 148° | -0.848 |
| 149° | -0.8572 |
| 150° | -0.866 |
| 151° | -0.8746 |
| 152° | -0.8829 |
| 153° | -0.891 |
| 154° | -0.8988 |
| 155° | |
| 156° | -0.9135 |
| 157° | -0.9205 |
| 158° | -0.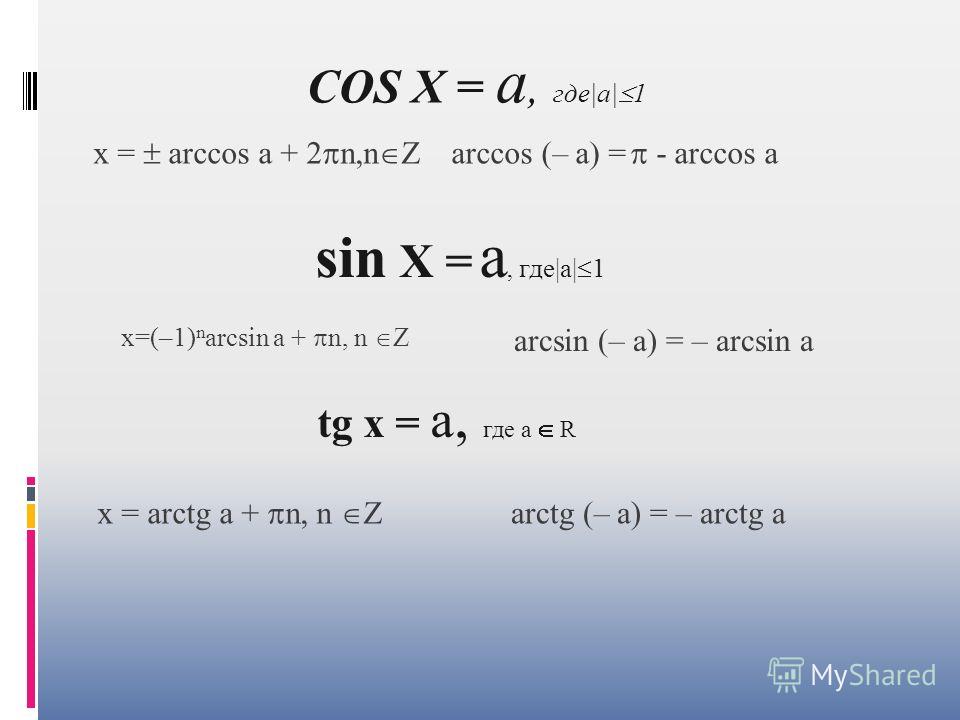 9272 9272 |
| 159° | -0.9336 |
| 160° | -0.9397 |
| 161° | -0.9455 |
| 162° | -0.9511 |
| 163° | -0.9563 |
| 164° | -0.9613 |
| 165° | -0.9659 |
| 166° | -0.9703 |
| 167° | -0.9744 |
| 168° | -0.9781 |
| 169° | -0.9816 |
| 170° | -0.9848 |
| 171° | -0.9877 |
| 172° | -0.9903 |
| 173° | -0.9925 |
| 174° | -0.9945 |
| 175° | -0.9962 |
| 176° | -0.9976 |
| 177° | -0.9986 |
| 178° | -0.9994 |
| 179° | -0.9998 |
| 180° | -1 |
…
| Угол | cos (косинус) |
|---|---|
| 181° | -0. 9998 9998 |
| 182° | -0.9994 |
| 183° | -0.9986 |
| 184° | -0.9976 |
| 185° | -0.9962 |
| 186° | -0.9945 |
| 187° | -0.9925 |
| 188° | -0.9903 |
| 189° | -0.9877 |
| 190° | -0.9848 |
| 191° | -0.9816 |
| 192° | -0.9781 |
| 193° | -0.9744 |
| 194° | -0.9703 |
| 195° | -0.9659 |
| 196° | -0.9613 |
| 197° | -0.9563 |
| 198° | -0.9511 |
| 199° | -0.9455 |
| 200° | -0.9397 |
| 201° | -0.9336 |
| 202° | -0.9272 |
| 203° | -0.9205 |
| 204° | -0.9135 |
| 205° | -0.9063 |
| 206° | -0.8988 |
| 207° | -0. 891 891 |
| 208° | -0.8829 |
| 209° | -0.8746 |
| 210° | -0.866 |
| 211° | -0.8572 |
| 212° | -0.848 |
| 213° | -0.8387 |
| 214° | -0.829 |
| 215° | -0.8192 |
| 216° | -0.809 |
| 217° | -0.7986 |
| 218° | -0.788 |
| 219° | -0.7771 |
| 220° | -0.766 |
| 221° | -0.7547 |
| 222° | -0.7431 |
| 223° | -0.7314 |
| 224° | -0.7193 |
| 225° | -0.7071 |
| 226° | -0.6947 |
| 227° | -0.682 |
| 228° | -0.6691 |
| 229° | -0.6561 |
| 230° | -0.6428 |
| 231° | -0.6293 |
| 232° | -0.6157 |
| 233° | -0.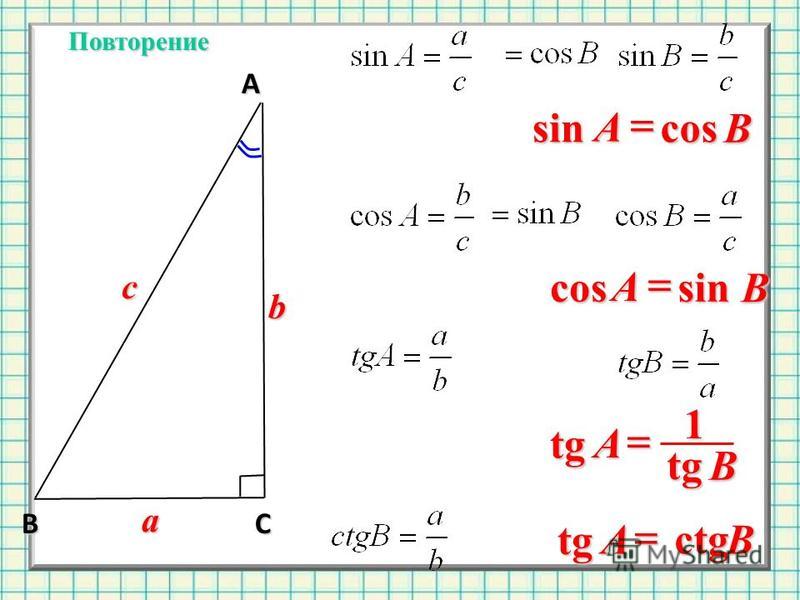 6018 6018 |
| 234° | -0.5878 |
| 235° | -0.5736 |
| 236° | -0.5592 |
| 237° | -0.5446 |
| 238° | -0.5299 |
| 239° | -0.515 |
| 240° | -0.5 |
| 241° | -0.4848 |
| 242° | -0.4695 |
| 243° | -0.454 |
| 244° | -0.4384 |
| 245° | -0.4226 |
| 246° | -0.4067 |
| 247° | -0.3907 |
| 248° | -0.3746 |
| 249° | -0.3584 |
| 250° | -0.342 |
| 251° | -0.3256 |
| 252° | -0.309 |
| 253° | -0.2924 |
| 254° | -0.2756 |
| 255° | -0.2588 |
| 256° | -0.2419 |
| 257° | -0.225 |
| 258° | -0.2079 |
| 259° | -0.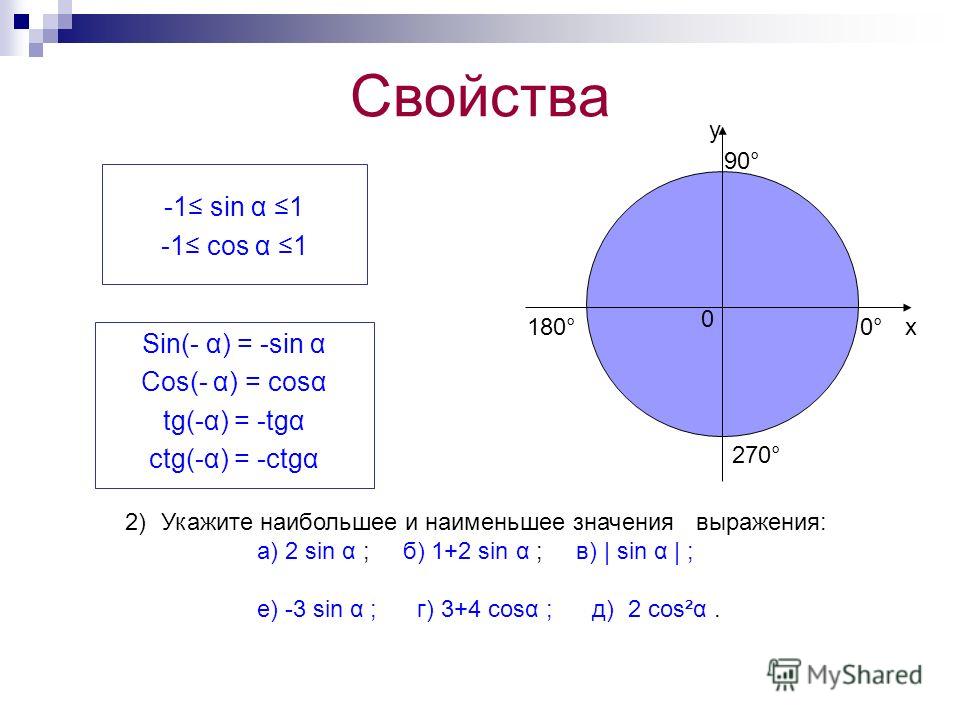 1908 1908 |
| 260° | -0.1736 |
| 261° | -0.1564 |
| 262° | -0.1392 |
| 263° | -0.1219 |
| 264° | -0.1045 |
| 265° | -0.0872 |
| 266° | -0.0698 |
| 267° | -0.0523 |
| 268° | -0.0349 |
| 269° | -0.0175 |
| 270° | 0 |
…
| Угол | Cos (Косинус) |
|---|---|
| 271° | 0.0175 |
| 272° | 0.0349 |
| 273° | 0.0523 |
| 274° | 0.0698 |
| 275° | 0.0872 |
| 276° | 0.1045 |
| 277° | 0.1219 |
| 278° | 0.1392 |
| 279° | 0.1564 |
| 280° | 0.1736 |
| 281° | 0. 1908 1908 |
| 282° | 0.2079 |
| 283° | 0.225 |
| 284° | 0.2419 |
| 285° | 0.2588 |
| 286° | 0.2756 |
| 287° | 0.2924 |
| 288° | 0.309 |
| 289° | 0.3256 |
| 290° | 0.342 |
| 291° | 0.3584 |
| 292° | 0.3746 |
| 293° | 0.3907 |
| 294° | 0.4067 |
| 295° | 0.4226 |
| 296° | 0.4384 |
| 297° | 0.454 |
| 298° | 0.4695 |
| 299° | 0.4848 |
| 300° | 0.5 |
| 301° | 0.515 |
| 302° | 0.5299 |
| 303° | 0.5446 |
| 304° | 0.5592 |
| 305° | 0.5736 |
| 306° | 0.5878 |
| 307° | 0.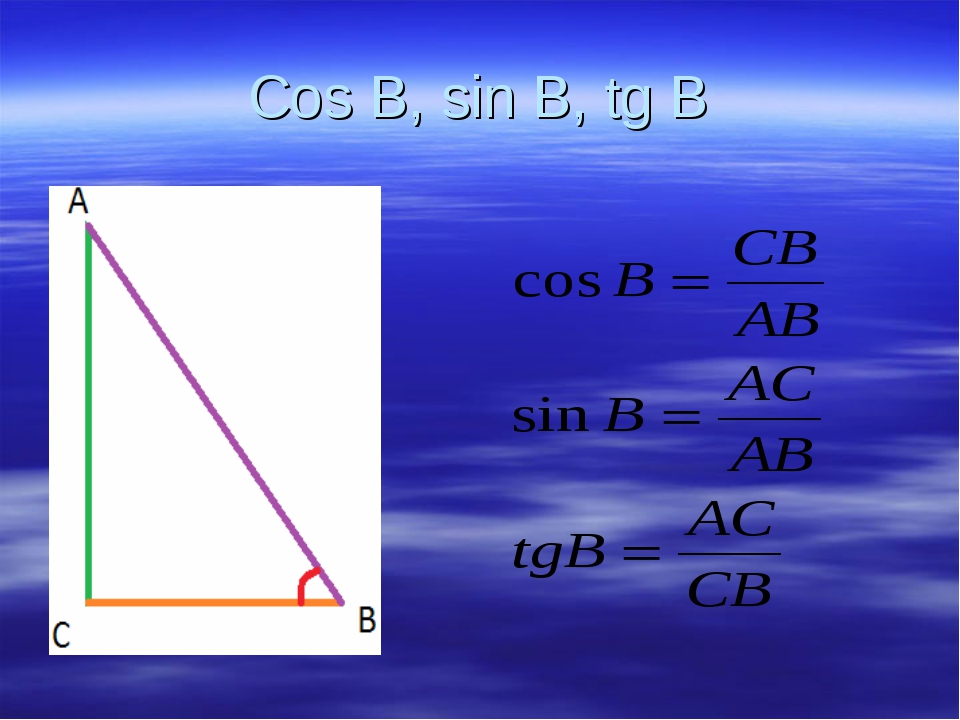 6018 6018 |
| 308° | 0.6157 |
| 309° | 0.6293 |
| 310° | 0.6428 |
| 311° | 0.6561 |
| 312° | 0.6691 |
| 313° | 0.682 |
| 314° | 0.6947 |
| 315° | 0.7071 |
| 316° | 0.7193 |
| 317° | 0.7314 |
| 318° | 0.7431 |
| 319° | 0.7547 |
| 320° | 0.766 |
| 321° | 0.7771 |
| 322° | 0.788 |
| 323° | 0.7986 |
| 324° | 0.809 |
| 325° | 0.8192 |
| 326° | 0.829 |
| 327° | 0.8387 |
| 328° | 0.848 |
| 329° | 0.8572 |
| 330° | 0.866 |
| 331° | 0.8746 |
| 332° | 0.8829 |
| 333° | 0. 891 891 |
| 334° | 0.8988 |
| 335° | 0.9063 |
| 336° | 0.9135 |
| 337° | 0.9205 |
| 338° | 0.9272 |
| 339° | 0.9336 |
| 340° | 0.9397 |
| 341° | 0.9455 |
| 342° | 0.9511 |
| 343° | 0.9563 |
| 344° | 0.9613 |
| 345° | 0.9659 |
| 346° | 0.9703 |
| 347° | 0.9744 |
| 348° | 0.9781 |
| 349° | 0.9816 |
| 350° | 0.9848 |
| 351° | 0.9877 |
| 352° | 0.9903 |
| 353° | 0.9925 |
| 354° | 0.9945 |
| 355° | 0.9962 |
| 356° | 0.9976 |
| 357° | 0.9986 |
| 358° | 0.9994 |
| 359° | 0.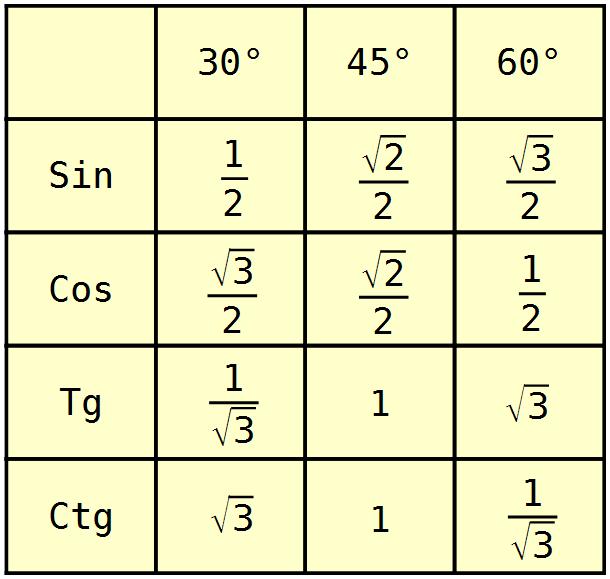 9998 9998 |
| 360° | 1 |
…
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Пример
Чему равен косинус 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.866
Автор: Bill4iam
Косинус — что это такое
Обновлено 21 июля 2021 Просмотров: 447925 Автор: Дмитрий Петров- Косинус — это …
- История изучения
- Таблица косинусов
- Вместо заключения
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое КОСИНУС.
Это слово, уверены, многим знакомо. Хотя бы потому что его проходят в школе. И многие наверняка точно определят, что это некий математический термин.
Но лишь единицы, которые действительно увлечены алгеброй и геометрией, вспомнят определение КОСИНУСА.
А между тем, без этих знаний не обойтись при сдаче ЕГЭ. Так что для старшеклассников это статья будет наиболее интересна. А для остальных – это хорошая возможность вспомнить подзабытые знания.
Косинус — это …
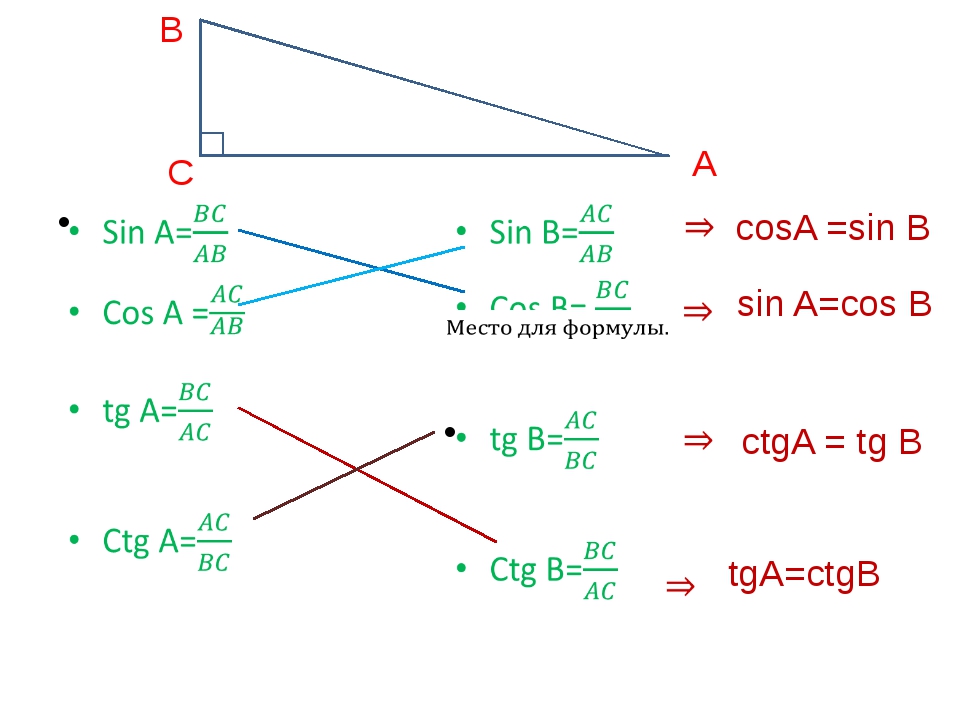
Со словом КОСИНУС школьники впервые знакомятся в 8 классе. И происходит это, когда проходят тему прямоугольных треугольников. Напомним, это такие треугольники, у которых две стороны пересекаются под прямым углом (90 градусов).
Выглядят они вот так:
У этого треугольника стороны АВ и ВС образуют между собой прямой угол. И напомним, по научному они называются КАТЕТАМИ. Этот термин имеет древнегреческие корни, произошло от «káthetos» и дословно переводится как «отвесный, опущенный, перпендикуляр».
А линия АС, которая соединяет два катета между собой, как многие знают из школьного курса, называется ГИПОТЕНУЗА. Этот термин также родом из Древней Греции. Слово «ὑποτείνουσα» переводится как «натянутая».
К чему мы так подробно это рассказали? Ну, во-первых, никогда не бывает лишним освежить в памяти старые знания. А во-вторых, это имеет непосредственное отношение к нашей теме.
А во-вторых, это имеет непосредственное отношение к нашей теме.
Косинус – это отношения прилежащего катета к гипотенузе.
Так звучит официальное определение КОСИНУСА. Но у внимательных читателей может возникнуть вопрос, а что такое «прилежащий катет»? И к чему он собственно «прилегает»?
Вопрос правильный. Дело в том, что КОСИНУС имеет прямое отношение к углам. А точнее, является их тригонометрической функцией. И в данном случае, надо просто понимать, о каком угле идет речь.
Вновь вернемся к нашему треугольнику АВС.
Если нам надо найти КОСИНУС угла с вершиной в точке А, то он будет равен отношению АВ (прилежащий катет) к АС (гипотенуза). А если нужно найти КОСИНУС угла с вершиной в точке С, то для него прилежащим катетом будет уже СВ, и уже его надо соотносить с гипотенузой АС.
Вот так это будет выглядеть более наглядно:
И если описывать формулы для конкретного примера, то выглядеть они будут так:
youtube.com/embed/hwpWTkdh-BA» allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>История изучения
Всегда интересно, откуда взялось то или иное слово. И как раз у КОСИНУСА это весьма интересная история. Она начинается еще в IV веке, и связана с именем индийского астронома и математика Ариабхты.
Он ввел специальный термин, которым называл дугу. Это было слово «ардхаджива», образованное от «ардха» (половина) и «джива» (тетива лука).
Спустя 500 лет уже арабские математики решили заменить этот сложный для их произношения термин на привычное себе слово «джайб». В переводе оно обозначало «выпуклость».
И наконец, еще немного позднее европейцы стали переводить арабские математические тексты и встретили этот термин. Для них слово «джайб» также было чужеродным, поэтому они заменили его на латинское «Sinus», что в переводе означает «кривизна, изгиб».
А вот слово КОСИНУС – это производное от СИНУС. Оно возникло от выражения «completely sinus», что в переводе означает «дополнительный синус» или «синус дополнительной дуги».
Оно возникло от выражения «completely sinus», что в переводе означает «дополнительный синус» или «синус дополнительной дуги».
Фактически уже тогда математики установили главную зависимость между синусом и косинусом. И выражается она в следующей формуле:
Таблица косинусов
Для каждого угла можно найти и рассчитать свой косинус.
Приведем самые популярные значения:
- 0 градусов – COS=1
- 30 градусов – COS=√3/2
- 45 градусов – COS=√2/2
- 60 градусов – COS=½
- 90 градусов – COS=0
- 180 градусов – COS=-1
- 270 градусов – COS=0
- 360 градусов – COS=-1
И еще одна важная зависимость. Если мы возьмем плоскость в 180 градусов:
В этом случае между углами α и β существует простая зависимость:
И тогда можно представить следующую формулу:
Данное утверждение будет верно при любых углах.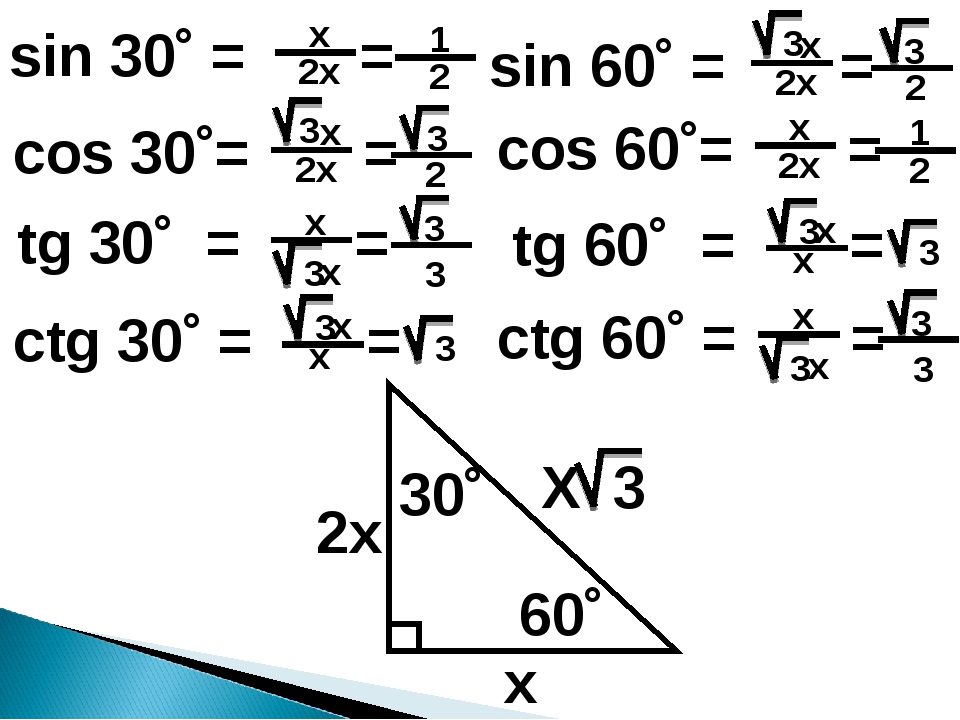
Вместо заключения
Есть еще две тригонометрические функции, которые широко используются в математике и изучаются в школе. Это ТАНГЕНС и КОТАНГЕНС.
Тангенс – это отношение противоположного катета к прилежащему. Также его можно представить как деление синуса на косинус.
Котангенс – это противоположная тангенсу функция, то есть отношение прилежащего катета к противолежащему. Или деление косинуса на синус.
Вот и все, что мы хотели рассказать про КОСИНУС.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Sin, cos — это отношения сторон в прямоугольном треугольнике
Тригонометрия — математическая наука о тригонометрических функциях sin и cos. Эти отношения — базовые понятия, без их понимания не получится изучать что-то новое в этой области. Это не сложно, главное понимать, откуда берутся значения косинусов и синусов и как их рассчитать.
Это не сложно, главное понимать, откуда берутся значения косинусов и синусов и как их рассчитать.
Из истории появления
В работах древнегреческих математиков уже в III веке до нашей эры встречаются отношения отрезков треугольников. В древнем Риме их исследовал Менелай. Математик Ариабхата из Индии также дал определения этим понятиям. Вычисления синуса он связывал с «архадживами» (дословный перевод — половина тетивы лука) — полухордами окружности. Позднее понятие сократилось до слова «джива». Арабские математики использовали термин «джайб» (выпуклость).
А что насчет cos? Это отношение значительно моложе. Понятие представляет собой сокращение от латинского выражения completely sinus, что в переводе звучит как дополнительный синус (синус дополнительной дуги).
Современные краткие латинские обозначения sin и cos введены Уильямом Отредом в VII веке и закреплены в трудах Эйлера.
Что такое прямоугольный треугольник?
Поскольку sin и cos — это отношения величин этой фигуры, то необходимо знать, что она собой представляет.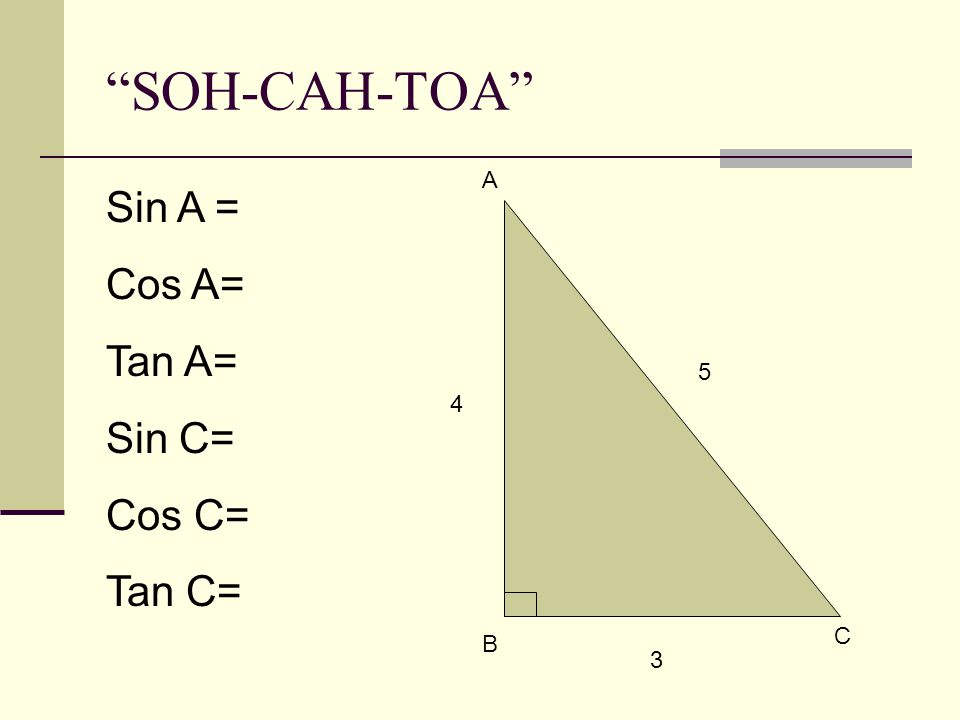 Это вид треугольника, у которого один из углов прямой, то есть составляет 90 градусов. Катетами называют стороны, прилежащие к прямому углу (лежат напротив острых), а гипотенузой — противолежащую сторону.
Это вид треугольника, у которого один из углов прямой, то есть составляет 90 градусов. Катетами называют стороны, прилежащие к прямому углу (лежат напротив острых), а гипотенузой — противолежащую сторону.
Они связаны между собой теоремой Пифагора.
sin — это отношение противолежащего катета к гипотенузе.
cos — это отношение прилежащего катета к гипотенузе.
Зная численные значения сторон треугольника можно определить обе эти величины.
Если рассмотреть единичную окружность с центром в точке (0,0) декартовой системы координат, тогда, взяв точку на оси абсцисс и повернув ее на острый угол альфа, опустим перпендикуляр на ось абсцисс. Длина катета, прилежащего к гипотенузе в полученном прямоугольном треугольнике, будет равна абсциссе точки.
Следовательно, определение через отношение сторон cos(sin) острого угла в этой фигуре эквивалентно нахождению косинуса (синуса) угла поворота при альфа, лежащем в пределах от 0 до 90 градусов.
Для чего нужны данные тригонометрические функции?
Известно, что сумма углов в прямоугольном треугольнике равна 180 градусам.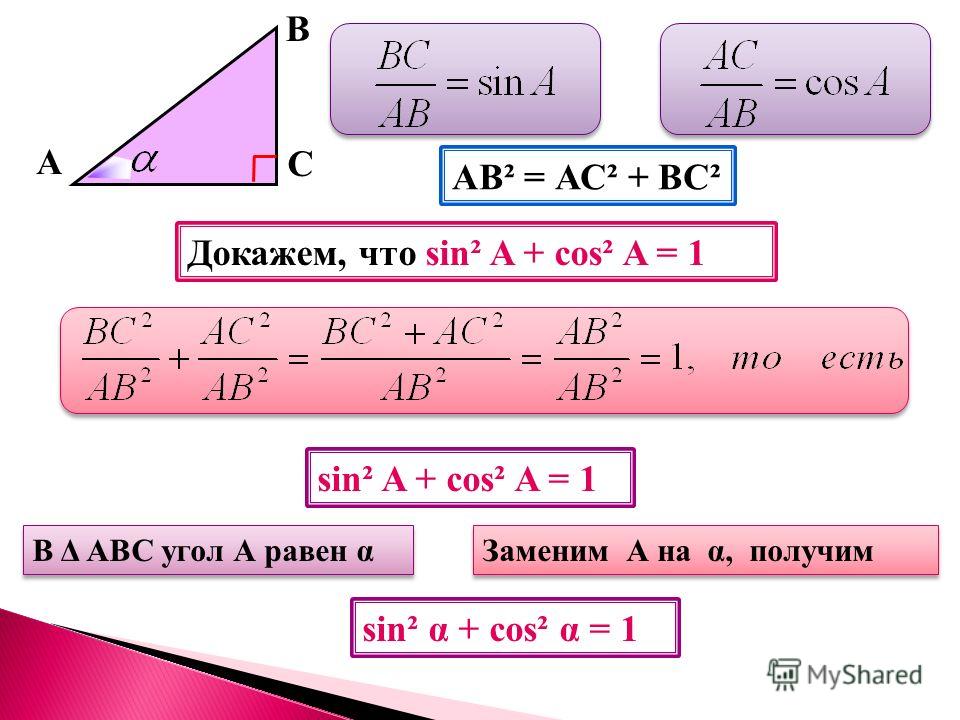 Значит, зная два угла, можно найти третий. С помощью теоремы Пифагора находят значение любой из сторон по двум другим. А их отношения через sin и cos помогут, если известен один угол и одна любая сторона.
Значит, зная два угла, можно найти третий. С помощью теоремы Пифагора находят значение любой из сторон по двум другим. А их отношения через sin и cos помогут, если известен один угол и одна любая сторона.
Вопрос решения такой задачи возник при составлении карт звездного неба, когда точно невозможно было измерить все величины.
С другой стороны, отношения sin и cos — это тригонометрические функции угла. Если известно его значение, то с помощью специальных таблиц получится найти все необходимые показатели.
Sin Cos Tan: Введение в тригонометрию
На колесе есть две точки, где вы будете находиться на нужной высоте (две красные точки на рисунке). Следовательно, существует два нужных нам угла α
1 и α2. Обратите внимание на два прямоугольных треугольника, выделенных зелёным цветом. Они одинаковые, так как являются зеркальным отображением друг друга. Давайте так же зеркально отобразим правый треугольник, но уже «вверх». Этот треугольник, выделенный красным цветом, имеет гипотенузу равную 1 (радиус колеса) и противолежащий катет (высота над центром) равный 1/2. В силу того, что все три треугольника одинаковые, они имеют одинаковые острые углы. Давайте найдём острый угол красного треугольника, при котором его синус равен 1/2. Поступим также, как древние астрономы, и заглянем в таблицу значений синуса для различных углов. Итак, sin α = 1/2 при = 30°. Интуитивно понятно, что наши три угла и значения их синусов связаны. Но как?
Этот треугольник, выделенный красным цветом, имеет гипотенузу равную 1 (радиус колеса) и противолежащий катет (высота над центром) равный 1/2. В силу того, что все три треугольника одинаковые, они имеют одинаковые острые углы. Давайте найдём острый угол красного треугольника, при котором его синус равен 1/2. Поступим также, как древние астрономы, и заглянем в таблицу значений синуса для различных углов. Итак, sin α = 1/2 при = 30°. Интуитивно понятно, что наши три угла и значения их синусов связаны. Но как?
Полный круг составляет 360°. Разделим его на четыре четверти по 90° и пронумеруем их. Первая точка находится в третьей четверти. Так как две четверти в общем дают 180°, а угол α = 30°, то искомый угол α
1 = 210°. Нашли первый угол. Вторая точка находится в четвертой четверти. Три четверти в общем дают 270°, но прибавлением 30° тут не отделаешся, так как нужно прибавить угол β, а не угол α. Так как угол α + β= 90°, то угол β = 90°− 30°=60°. И второй искомый угол равен 270°+ 60°=330°. Остался один маленький ньюанс. Помните, как мы говорили о том, что тригонометрические функции описывают повторяющиеся процессы? Если наше колесо не остановится после того, как совершит полный оборот в 360°, то с каждым новым оборотом вы будет проходить через две точки, находящиеся на уровне –1/2. Эти точки определяются простым прибавлением 360° к найденным нами углам.
И второй искомый угол равен 270°+ 60°=330°. Остался один маленький ньюанс. Помните, как мы говорили о том, что тригонометрические функции описывают повторяющиеся процессы? Если наше колесо не остановится после того, как совершит полный оборот в 360°, то с каждым новым оборотом вы будет проходить через две точки, находящиеся на уровне –1/2. Эти точки определяются простым прибавлением 360° к найденным нами углам.
При этом n – любое целое число, то есть, на нашем примере это количество оборотов колеса. Стоит заметить, что число n может быть и отрицательным, если колесо крутится в обратную сторону.
Равенстно sin α=−1/2 мы решили. Перейдем к неравенству
sin α ≥ −1/2. Если для решения равенства мы нашли значения углов, при которых наша высота над центром колеса равна −1/2, то для решения неравенства нам нужно найти все углы, при которых наша высота больше либо равна −1/2. Помните мы говорили о том, что угол может быть отрицательным? Сейчас нам это пригодится. Определим угол α2 не как 330°, а как −30° (330°−360°) На рисунке эта область выделена зелёным цветом.
Определим угол α2 не как 330°, а как −30° (330°−360°) На рисунке эта область выделена зелёным цветом.
Для того, чтобы правильно записать решение неравенства, обратите внимание на рисунок синусоиды и прямой y=−1/2(высота). Нас интересуют области синусоиды, которые выше прямой y=−1/2. На рисунке они заштрихованы красным цветом. Обратите внимание на точки, которые выделяют эти отрезки. Это те же точки, которые мы получили при решении равенства sin α=−1/2 и они повторяются каждые 360°. Ответ можно записать так:
Дело осталось за малым. Во-первых, вспомнить, что математики обозначают 180° как π, когда записывают формулы с углами, и переписать решение так:
Во-вторых, произвести обратную замену α на 3x − π/4.
Путём нехитрых алгебраических преобразований, а именно прибавления π/4 и деления на 3 ко всем частям неравенства, получаем:
Ответ:
Миссия выполнена!
| (1) | Основное тригонометрическое тождество | sin2(α) + cos2(α) = 1 | ||
| (2) | Основное тождество через тангенс и косинус | 1 + tg2(α) = 1/cos2(α) | ||
| (3) | Основное тождество через котангенс и синус | 1 + ctg2(α) = 1/sin2(α) | ||
| (4) | Соотношение между тангенсом и котангенсом | tg(α)ctg(α) = 1 | ||
| (5) | Синус двойного угла | sin(2α) = 2sin(α)cos(α) | ||
| (6) | Косинус двойного угла | cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α) | ||
| (7) | Тангенс двойного угла |
| ||
| (8) | Котангенс двойного угла |
| ||
| (9) | Синус тройного угла | sin(3α) = 3sin(α)cos2(α) – sin3(α) | ||
| (10) | Косинус тройного угла | cos(3α) = cos3(α) – 3cos(α)sin2(α) | ||
| (11) | Косинус суммы/разности | cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β) | ||
| (12) | Синус суммы/разности | sin(α±β) = sin(α)cos(β) ± cos(α)sin(β) | ||
| (13) | Тангенс суммы/разности | tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β)) | ||
| (14) | Котангенс суммы/разности | ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β)) | ||
| (15) | Произведение синусов | sin(α)sin(β) = ½(cos(α–β) – cos(α+β)) | ||
| (16) | Произведение косинусов | cos(α)cos(β) = ½(cos(α+β) + cos(α–β)) | ||
| (17) | Произведение синуса на косинус | sin(α)cos(β) = ½(sin(α+β) + sin(α–β)) | ||
| (18) | Сумма/разность синусов | sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β)) | ||
| (19) | Сумма косинусов | cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β)) | ||
| (20) | Разность косинусов | cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β)) | ||
| (21) | Сумма/разность тангенсов | tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β) | ||
| (22) | Формула понижения степени синуса | sin2(α) = ½(1 – cos(2α)) | ||
| (23) | Формула понижения степени косинуса | cos2(α) = ½(1 + cos(2α)) | ||
| (24) | Сумма/разность синуса и косинуса | sin(α) ± cos(α) = &sqrt;2sin(α±π/4) | ||
| (25) | Сумма/разность синуса и косинуса с коэффициентами | Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²))) | ||
| (26) | Основное соотношение арксинуса и арккосинуса | arcsin(x) + arccos(x) = π/2 | ||
| (27) | Основное соотношение арктангенса и арккотангенса | arctg(x) + arcctg(x) = π/2 |
Основное Тригонометрическое Тождество — Доказательство
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin2α + cos2α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Если развернуть точку A на угол α, то точка A становится на место точки A1.
- По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.

- Опускаем перпендикулярную прямую A1B на x0 из точки A1.
Образовался прямоугольный треугольник OA1B.
|A1B| = |у|
|OB| = |x|.
- Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
- Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B|2 + |OB|2 = |OA1|2.
- Записываем в виде: |y|2 + |x|2 = 12.
Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x - Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1 - Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Немного вводных:
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
Выражение
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению:
tg α = y/x
ctg α = x/y
- Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем и ,
получаем:
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Какие, какие числа?🤯
Взаимно обратные числа — это два числа, произведение которых равно 1.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg2α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg2α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
- Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.
- В результате деления получаем формулу tg2α + 1 =
- Если обе части основного тригонометрического тождества sin2α + cos2α = 1 разделить на sin2α, где синус не равен нулю, то получим тождество:
1 + ctg2α = .
- Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg2α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
1 | sin2α + cos2α = 1 |
2 | |
3 | |
4 | tgα * ctgα = 1 |
5 | tg2α + 1 = |
6 | 1 + ctg2α = |
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.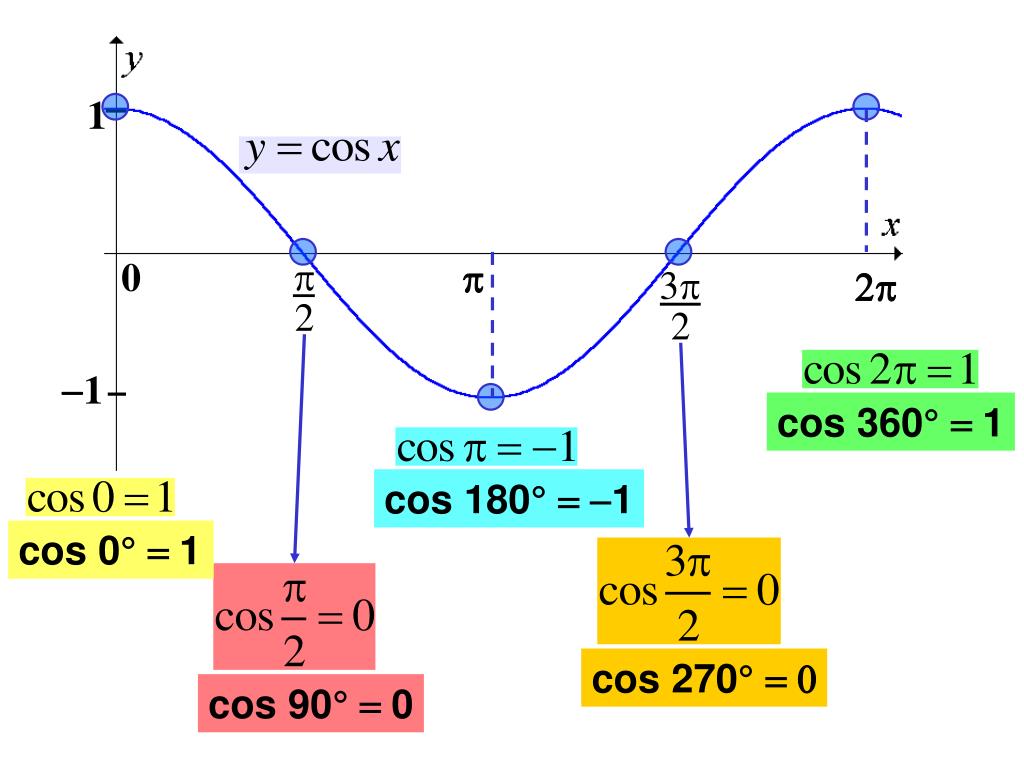
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
- Таким же образом, используя формулу, вычисляем значение котангенса:
Ответ:
Задачка 2. Найдите значение cos α,
если:
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- То же самое проделываем со вторым значение sin α
Подставляем значения sin α:
- Вычисляем:
Ответ:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Бренд COS показал коллекцию на Неделе моды в Лондоне: что это значит для бренда и чем она нам запомнилась
Бренд COS, входящий в компанию H&M Group., провел офлайн-показ новой коллекции осень-зима 2021/2022 в рамках Недели моды в Лондоне. Для бренда это не просто важный этап развития, но и своего рода заявление о том, что в будущем марку ждут серьезные изменения. В рамках этой стратегии COS уже обновил логотип, а теперь перемены можно заметить и на примере модных образов.
С момента своего основания в 2007 году бренд целенаправленно держал фокус на создании функциональных и практичных вещей в минималистичном стиле, которые можно комбинировать между собой и которые легко представить в любом базовом гардеробе. И, по словам креативного директора марки Карин Густафссон, главные ценности бренда останутся неизменными, но теперь центр внимания сместится на создание дизайна вещей, которые «влюбляют в себя».
Так, в новой осенне-зимней коллекции представлены классические пальто, выполненные в главных цветах сезона, по версии Института цвета Pantone, – оптимистичном желтом, насыщенном голубом и классическом синем. Темно-синий двубортный тренчкот, который Густафссон называет любимой вещью в новой коллекции, будет идеально сочетаться с костюмом-двойкой в песочном оттенке, а блейзеры и свитера, представленные на подиуме, выполнены в монохромных базовых цветах и легко впишутся в любой гардероб.
Однако в новой коллекции можно найти не только базовые вещи. С учетом главных трендов 2021 года дизайнер представляет платье-сетку, струящийся комбинезон в лавандовом оттенке, блузки с объемными рукавами и главный аксессуар показа, который вполне может составить конкуренцию знаменитой сумке-пельмень, – яркую пушистую сумку.
Больше новостей из мира моды вы найдете в нашем Telegram-канале. Подписывайтесь!
Главный бьюти-тренд 2020/2021: Исамайя Френч показала, как делать макияж с обесцвеченными бровями
Подробнеекосинусов
Затем рассмотрим углы 30 ° и 60 °. В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения
сторон равны 1: √3: 2. Отсюда следует, что
sin 30 ° = cos 60 ° = 1/2, и
sin 60 ° = cos 30 ° = √3 / 2.
В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения
сторон равны 1: √3: 2. Отсюда следует, что
sin 30 ° = cos 60 ° = 1/2, и
sin 60 ° = cos 30 ° = √3 / 2.
Эти результаты занесены в эту таблицу.
| Угол | Градус | Радианы | косинус | синус |
|---|---|---|---|---|
| 90 ° | π /2 | 0 | 1 | |
| 60 ° | π /3 | 1/2 | √3 / 2 | |
| 45 ° | π /4 | √2 / 2 | √2 / 2 | |
| 30 ° | π /6 | √3 / 2 | 1/2 | |
| 0 ° | 0 | 1 | 0 |
Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой. 30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. b = 6,4, c = 7,8. Найдите A, и a.
36. A = 23 ° 15 ‘, c = 12.15. Найдите a, и b.
Подсказки
30. Косинус A связывает b с гипотенузой c, , поэтому вы можете сначала вычислить c. Как только вы узнаете b и c, , вы сможете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух сторон, которых вы не знаете, а именно a / c. Тем не менее, это дает вам уравнение, с которым можно работать: 1/3 = a / c. Тогда c = 3 a. Тогда из теоремы Пифагора следует, что a 2 + 144 = 9 a 2 . Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
Ответы
30. c = b / cos A = 2,25 / 0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a составляет 4,24 ‘или 4’3 дюйма.
c = 3 a , что равно 12.73 ‘или 12’9 «.
35. cos A = b / c = 6,4 / 7,8 = 0,82. Следовательно, A = 34,86 ° = 34 ° 52 ‘, или около 35 °.
a 2 = 7,8 2 — 6,4 2 = 19,9, поэтому a составляет около 4,5.
36. a = c sin A = 12,15 sin 23 ° 15 ‘= 4,796.
b = c cos A = 12,15 cos 23 ° 15 ‘= 11. 17.
17.
Что такое диаграмма Sin Cos Tan? — MVOrganizing
Что такое диаграмма Sin Cos Tan?
В тригонометрии значения sin cos и tan являются основными функциями, которые мы учитываем при решении тригонометрических задач. Эти значения тригонометрии используются для измерения углов и сторон прямоугольного треугольника. Помимо значений синуса, косинуса и тангенса, три других основных значения — это котангенс, секанс и косеканс.
Какой период греха?
Период синусоиды — это длина одного цикла кривой.Собственный период синусоиды равен 2π. Таким образом, коэффициент при b = 1 эквивалентен периоду 2π. Чтобы получить период синусоиды для любого коэффициента b, просто разделите 2π на коэффициент b, чтобы получить новый период кривой.
Где загар равен 1?
Важные углы: 30 °, 45 ° и 60 °
| Уголок | Загар = Sin / Cos |
|---|---|
| 30 ° | 1 √3 = √3 3 |
| 45 ° | 1 |
| 60 ° | √3 |
Как называется tan-1?
Арктангенс также называется арктангенсом и обозначается \ begin {align *} \ tan ^ {- 1} \ end {align *} или арктангенсом. «-1» означает обратное. Обратный синус: если вы знаете противоположную сторону угла и гипотенузу в прямоугольном треугольнике, вы можете использовать обратный синус, чтобы найти меру угла.
«-1» означает обратное. Обратный синус: если вы знаете противоположную сторону угла и гипотенузу в прямоугольном треугольнике, вы можете использовать обратный синус, чтобы найти меру угла.
Где Cos равно?
Косинус угла определяется как синус дополнительного угла. Дополнительный угол равен заданному углу, вычтенному из прямого угла, 90 °. Например, если угол равен 30 °, то его дополнение составляет 60 °.
Является ли детская кроватка грехом?
tan x = sin x cos x.Котангенс x определяется как косинус x, деленный на синус x: cot x = cos x sin x. Секанс x равен 1, деленному на косинус x: sec x = 1 cos x, а косеканс x определяется как 1, деленный на синус x: csc x = 1 sin x.
Почему загар 90 не определен?
Почему Tan 90 не определен? Поскольку мы получили результат как бесконечность, и мы не можем определить бесконечность, значение tan 90 не определено.
Что такое cos в математике?
В прямоугольном треугольнике косинус угла равен: длине прилегающей стороны, деленной на длину гипотенузы. Сокращение — cos. cos (θ) = смежный / гипотенуза.
Сокращение — cos. cos (θ) = смежный / гипотенуза.
Какая формула Cos?
Закон косинусов обобщает формулу Пифагора на все треугольники. Он говорит, что c2, квадрат одной стороны треугольника, равен a2 + b2, сумме квадратов двух других сторон минус 2ab cos C, удвоенное их произведение на косинус противоположного угла.
Как вы находите грех, данный Cos?
треугольников! Узоры из прямоугольных треугольников. У всех треугольников есть 3 угла, которые в сумме составляют 180 градусов.Следовательно, если один угол равен 90 градусам, мы можем вычислить Sin Theta = Cos (90 — Theta) и Cos Theta = Sin (90 — Theta).
Как рассчитать cos?
В любом прямоугольном треугольнике для любого угла:
- Синус угла = длина противоположной стороны. длина гипотенузы.
- Косинус угла = длине прилегающей стороны. длина гипотенузы.
- Тангенс угла = длина противоположной стороны.-1 как в некоторых учебниках это обозначено) — это математика.
 метод acos (обозначение дуги). двойной АВ = 125; двойной AC = 150; двойной угол A = Math.
метод acos (обозначение дуги). двойной АВ = 125; двойной AC = 150; двойной угол A = Math.Что такое cos 120 градусов?
Значение Cos 120 составляет -½.
Как выполнить COS 1 на калькуляторе?
Пояснение:
- Нажмите кнопку «2nd», чтобы получить доступ к функции cos − 1. Слово «2nd» появится в нижнем левом углу экрана.
- Нажмите кнопку «COS», чтобы получить доступ к функции cos − 1.
- Введите свой номер с цифровой клавиатуры.
- Нажмите клавишу «Enter =», чтобы вернуть результат.
Какой угол равен cos1?
270 °
Какое значение греха равно 0?
Ответ) В математике значение степени sin 0 всегда равно 0.
Что такое COS 1 с точки зрения пи?
Значение Cos 1 равно 0 градусам.
Что такое COS 1 на единичной окружности?
Косинус — это длина смежной стороны (которая является координатой x), деленная на длину гипотенузы (которая равна 1).
 Итак, косинус — это просто координата x! Точно так же синус — это длина противоположной стороны (которая является длиной координаты y), деленная на длину гипотенузы (которая равна 1).
Итак, косинус — это просто координата x! Точно так же синус — это длина противоположной стороны (которая является длиной координаты y), деленная на длину гипотенузы (которая равна 1).Arccos — это то же самое, что 1 cos?
Арккосинус x определяется как функция, обратная косинусу x, когда -1≤x≤1. (Здесь cos-1 x означает обратный косинус, а не косинус в степени -1).
Является ли SEC обратной величиной cos?
Секанс — величина, обратная косинусу.Это отношение гипотенузы к стороне, прилегающей к заданному углу в прямоугольном треугольнике.
Как узнать, находится ли точка на единичной окружности?
Объяснение: Единичный круг по определению является кругом с радиусом, равным 1, и центром (0,0), поэтому расстояние от точек (x, y) в этом круге до центра равно 1, следовательно, на расстояние формула: √a2 + b2 = 1⟺a2 + b2 = 1. Если он равен 1, он находится на единичной окружности.
Sin Cos Tan — значения, формулы, таблица, примеры
В тригонометрии sin, cos и tan являются основными тригонометрическими отношениями, используемыми для изучения взаимосвязи между углами и сторонами треугольника (особенно прямоугольного треугольника).
 Пифагор работал над взаимосвязью между сторонами прямоугольного треугольника с помощью теоремы Пифагора, в то время как Гиппаркус работал над установлением взаимосвязи между сторонами и углами прямоугольного треугольника, используя концепции тригонометрии. Формулы sin, cos и tan в тригонометрии используются для нахождения недостающих сторон или углов прямоугольного треугольника.
Пифагор работал над взаимосвязью между сторонами прямоугольного треугольника с помощью теоремы Пифагора, в то время как Гиппаркус работал над установлением взаимосвязи между сторонами и углами прямоугольного треугольника, используя концепции тригонометрии. Формулы sin, cos и tan в тригонометрии используются для нахождения недостающих сторон или углов прямоугольного треугольника.Давайте разберемся с sin, cos и tan в тригонометрии, используя формулы и примеры.
Что такое Sin Cos Tan в тригонометрии?
Sin, cos и tan — это три основных тригонометрических отношения, а именно синус, косинус и тангенс соответственно, где каждое из которых дает отношение двух сторон прямоугольного треугольника.Мы знаем, что самая длинная сторона прямоугольного треугольника известна как «гипотенуза», а две другие стороны известны как «катеты». Это означает, что в тригонометрии самая длинная сторона прямоугольного треугольника все еще известна как «гипотенуза», но два других катета имеют следующие названия:
- противоположная сторона и
- смежная сторона
Мы определяем «противоположную» и «смежную» стороны, исходя из угла, о котором мы говорим.

- «Противоположная сторона» или перпендикуляр — это сторона, которая просто «противоположна» углу.
- «Смежная сторона» или основание — это сторона (кроме гипотенузы), которая «касается» угла.
Sin Cos Tan Значения
Значения Sin, Cos и Tan в тригонометрии относятся к значениям соответствующей тригонометрической функции для данного угла. Мы можем найти значения sin, cos и tan для данного прямоугольного треугольника, найдя необходимое соотношение сторон. Давайте разберемся с формулами, чтобы найти эти соотношения подробно в следующих разделах.
Sin Cos Tan Формула для загара
Функции Sin, cos и tan в тригонометрии определяются в терминах двух из трех сторон (противоположной, смежной и гипотенузы) прямоугольного треугольника.Вот формулы sin, cos и tan.
sin θ = Противоположно / Гипотенуза
cos θ = Соседний / Гипотенуза
tan θ = напротив / рядом
Помимо этих трех тригонометрических соотношений, у нас есть еще три отношения, называемые csc, sec и cot, которые являются обратными величинами sin, cos и tan соответственно.
 Давайте разберемся с этими формулами sin, cos и tan на примере, приведенном ниже.
Давайте разберемся с этими формулами sin, cos и tan на примере, приведенном ниже.Пример: Найдите sin, cos и tan треугольника для заданного угла θ.
Решение:
В треугольнике самая длинная сторона (или) сторона, противоположная прямому углу, является гипотенузой. Сторона, противоположная θ, является противоположной стороной или перпендикулярной. Сторона, смежная с θ, является смежной стороной или основанием.
Теперь мы находим sin θ, cos θ и tan θ, используя приведенные выше формулы:
sin θ = Противоположно / Гипотенуза = 3/5
cos θ = прилегающая / гипотенуза = 4/5
тангенс угла θ = напротив / рядом = 3/4
Уловка для запоминания формул sin cos tan в тригонометрии: Вот уловка для запоминания формул sin, cos и tan.Мы можем использовать аббревиатуру «SOHCAHTOA», как показано ниже,
Стол Sin Cos Tan
Тригонометрические отношения sin, cos и tan не зависят в точности от длин сторон треугольника, а, скорее, от угла, потому что в конечном итоге мы берем соотношение сторон.
 Таблица Sin, cos и tan используется для нахождения значений этих тригонометрических функций для стандартных углов. Во время расчетов с использованием синусоидальных, косинусных или тангенциальных соотношений мы можем напрямую обращаться к триггерной диаграмме, приведенной в следующем разделе, чтобы упростить выводы.
Таблица Sin, cos и tan используется для нахождения значений этих тригонометрических функций для стандартных углов. Во время расчетов с использованием синусоидальных, косинусных или тангенциальных соотношений мы можем напрямую обращаться к триггерной диаграмме, приведенной в следующем разделе, чтобы упростить выводы.Sin Cos Tan Диаграмма
Sin cos tan диаграмма / таблица — это диаграмма с тригонометрическими значениями синуса, косинуса и тангенса для некоторых стандартных углов 0 o , 30 o , 45 o , 60 o и 90 o . Мы можем обратиться к приведенной ниже таблице триггеров, чтобы напрямую выбрать значения sin, cos и tan для стандартных углов.
Советы, чтобы помнить Sin Cos Tan Table
Советы, которые вам нужно запомнить из этой таблицы:
- Углы 0 o , 30 o , 45 o , 60 o и 90 o по порядку.
- Первую строку (sin) можно запомнить так: 0/2, √1 / 2, √2 / 2, √3 / 2.

- Это все, что вам нужно запомнить, потому что:
Строка cos такая же, как и строка sin, только в обратном порядке. - Каждое значение в строке tan получается делением соответствующих значений sin на cos, поскольку tan = sin / cos.
Вы можете увидеть, как tan = sin / cos здесь:
sin θ / cos θ = (Противоположный / Гипотенуза) ÷ (Соседний / Гипотенуза) = (Противоположный / Гипотенуза) × (Гипотенуза / Соседний) = Противоположный / Соседний = tan θ
Sin Cos Tan на единичном круге
Значения sin, cos и tan могут быть вычислены для любого заданного угла с использованием единичной окружности.Единичный круг в координатной плоскости — это круг единичного радиуса 1, часто с центром в начале координат (0, 0) в декартовой системе координат в евклидовой плоскости, особенно в тригонометрии. Для любой точки на единичной окружности, заданной с координатами (x, y), отношения sin, cos и tan могут быть заданы как
- грех θ = y / 1
- cos θ = x / 1
- тангенс угла θ = y / x
где θ — это угол, который линия, соединяющая точку и начало координат, образует с положительной осью x.

Применение Sin Cos Tan в реальной жизни
Тригонометрические соотношения sin, cos, tan находят применение в нашей повседневной жизни для определения высоты и расстояния. Мы используем sin, cos и tan для решения многих реальных проблем. Вот пример, чтобы понять, как применяются слова sin, cos и tan.
Пример: Лестница прислоняется к кирпичной стене под углом 50 o к горизонту. Если лестница находится на расстоянии 10 футов от стены, то до какой высоты стены она достигает?
Решение:
Предположим, что лестница достигает x футов стены.
Используя предоставленную информацию:
Здесь мы знаем соседнюю сторону (которая составляет 10 футов), и мы должны найти противоположную сторону (которая равна x ft). Таким образом, мы используем отношение между противоположной и соседней сторонами, которое является желтовато-коричневым.
загар 50 o = x / 10
x = 10 загар 50 o
x ≈ 11.
 9 футов
9 футовЗдесь tan 50 o вычисляется с помощью калькулятора, а окончательный ответ округляется до 1 десятичного знака. Следовательно, лестница доходит до 11.9 футов стены.
Темы, связанные с Sin Cos Tan:
Часто задаваемые вопросы о Sin Cos Tan
Что означает Sin Cos Tan в тригонометрии?
Sin, cos и tan — основные тригонометрические соотношения в тригонометрии, используемые для изучения взаимосвязи между углами и сторонами треугольника (особенно прямоугольного).
Как использовать Sin Cos Tan?
Мы можем использовать sin cos и tan для решения реальных проблем.Чтобы решить любую проблему, мы сначала рисуем фигуру, описывающую проблему, и используем соответствующее тригонометрическое соотношение для решения проблемы.
Как найти ценности Sin Cos Tan?
Чтобы найти sin, cos и tan, мы используем следующие формулы:
- sin θ = Противоположно / Гипотенуза
- cos θ = Соседний / Гипотенуза
- tan θ = напротив / рядом
Чтобы найти sin, cos и tan стандартных углов, вы можете использовать таблицу тригонометрии.
Что такое таблица синуса, косинуса и тангенса в тригонометрии?
Таблица или диаграмма тригонометрии для sin, cos и tan используются для нахождения этих тригонометрических значений для стандартных углов 0 o , 30 o , 45 o , 60 o и 90 o . Используя таблицу sin cos tan, мы можем напрямую найти значения sin cos tan для этих углов и использовать их в задачах.
Как найти ценность загара с помощью греха и созидания?
Значение функции загара для любого угла θ в терминах sin и cos может быть задано с использованием формулы: tan θ = sin θ / cos θ.
Каков трюк, чтобы запомнить формулу для поиска греха Кос Тан?
Мы можем вспомнить формулы sin cos tan, используя слово «SOHCAHTOA». Это слово можно использовать для запоминания соотношений соответствующих сторон, участвующих в вычислении значений sin, cos и tan в тригонометрии, как указано ниже,
- S дюйм θ = O pposite / H ypotenuse
- C os θ = A djacent / H ypotenuse
- T an θ = O pposite / A djacent
Где используется Sin Cos Tan?
Sin, cos и tan находят применение в тригонометрии для вычисления значений этих функций при установлении взаимосвязи между углами и сторонами треугольника (особенно прямоугольного).
Что такое формула для Sin, Cos и Tan?
Формулы для нахождения sin, cos и tan для любого угла θ в любом прямоугольном треугольнике приведены ниже:
- sin θ = Противоположно / Гипотенуза
- cos θ = Соседний / Гипотенуза
- tan θ = напротив / рядом
Что такое косинусный коэффициент в тригонометрии?
Тригонометрические отношения
правило косинуса
Правило косинуса говорит нам, что когда у нас есть прямоугольный треугольник, косинус = ahcosine = \ frac {a} {h} cosine = ha.« a » в данном случае означает смежный. « h » обозначает гипотенузу, которую можно найти с помощью теоремы Пифагора. Все, что вам нужно, чтобы найти косинус, — это прилегающая сторона и гипотенуза.
правило синуса
Когда вы сталкиваетесь с синусом, вы можете найти ответ в прямоугольном треугольнике, взяв противоположную сторону над гипотенузой в виде sine = ohsine = \ frac {o} {h} sine = ho.
линейка касательной
Для правила касательной, когда у вас есть прямоугольный треугольник, вы можете использовать противоположное значение для смежных сторон треугольника, чтобы найти свое отношение.Это означает, что tan = oatan = \ frac {o} {a} tan = ao.
SohCahToa
Когда вы слышите SohCahToa, не сразу понятно, что это значит. Но на самом деле это более простой способ запомнить, как использовать синус, косинус и тангенс, который мы только что выучили. Это три основные функции, с которыми вы будете иметь дело в задачах тригонометрии.
Soh Cah Toa означает:
Стол Soh Cah ToaЭто может помочь вам найти длину стороны прямоугольного треугольника, если у вас есть угол θ \ thetaθ и некоторая информация о других сторонах треугольника.
Примеры задач
В этой главе мы сосредоточимся на правиле косинуса. Это означает, что мы будем работать только с частью SohCahToaSohCahToaSohCahToa «CahCahCah». Попробуйте вместе с нами следующие триггерные задачи, чтобы узнать, как решать вопросы с помощью правила косинуса.
Вопрос 1
Определите каждое косинусное отношение с помощью калькулятора
а) cos \ coscos 50 °
Просто введите число в свой калькулятор, и вы получите 0.640.640.64.
б) cos \ coscos -50 °
Просто введите число в свой калькулятор, и вы получите 0,640,640,64.
cos \ coscos 50 ° и cos \ coscos -50 ° оба = 0,640,640,64. Почему?
График ASTCПриведенная выше диаграмма ASTC помогает определить, какой коэффициент срабатывания положительный в каком квадранте. cos \ coscos 50 ° лежит в квадранте I, где все триггерные отношения положительны. cos \ coscos -50 ° лежит в квадранте 4, где косинус положительный. Вот почему мы получаем 0,640,640,64 как для cos \ coscos 50 °, так и для cos \ coscos -50 °.
Вопрос 2
Определить угол с точностью до градуса
Раствор
а) cosθ = 0,24 \ cos \ theta = 0,24 cosθ = 0,24
Используйте в калькуляторе обратный косинус, у которого рядом с coscoscos стоит немного −1-1−1:
arccos (0,24) = 76 \ arccos (0,24) = 76arccos (0,24) = 76 °
б) cosθ = −0,45 \ cos \ theta = -0,45 cosθ = −0,45
Используйте обратный косинус в калькуляторе, чтобы найти:
arccos (−0.45) = 117 \ arccos (-0,45) = 117arccos (-0,45) = 117 °
Вопрос 3
Определите углы и стороны с помощью косинуса
Раствор:
a) Найдите угол AAA и BBB:
Найдите угол A и Bcosθ = смежная гипотенуза \ cos \ theta = \ frac {соседняя} {гипотенуза} cosθ = смежная гипотенуза
Уголок AAA
cosA = 817 \ cos A = \ frac {8} {17} cosA = 178
Решить на вашем калькуляторе
arccos817 = 62 \ arccos \ frac {8} {17} = 62arccos178 = 62 °
Уголок BBB
cosB = 1517 \ cos B = \ frac {15} {17} cosB = 1715
Решить на вашем калькуляторе
arccos1517 = 28 \ arccos \ frac {15} {17} = 28arccos1715 = 28 °
б) Найдите значение «ххх», используя косинус
. Найдите x, используя косинус / figcaption>cosθ = смежная гипотенуза \ cos \ theta = \ frac {соседняя} {гипотенуза} cosθ = смежная гипотенуза
cos \ coscos 32 ° = 25 (x) \ frac {25} {(x)} (x) 25
x = 25cos32x = \ frac {25} {\ cos 32} x = cos3225
х = 29х = 29х = 29
Все еще интересуетесь правилом косинуса? Попробуйте этот онлайн-калькулятор закона косинусов!
Далее вы узнаете больше о законе косинусов, о том, как найти точные тригонометрические отношения, и коснитесь того, что такое единичная окружность в тригонометрии.
Что означает COS?
COS Косинус
Академия и наука »Математика — и не только …
Оцените: COS Церковь Саентологии
Сообщество »Религия
Оцените: COS Co-sine (Kosinüs)
Международный» Турецкий
COS Class of Service
Computing »Networking — and more…
Оцените: COS Начальник штаба
Правительственный »Военный — и многое другое …
Оцените: COS Корсиканский
Региональные »Коды языков (3 буквы)
Оцените: CoS Тайная комната
Вычислительная техника »Игры и многое другое…
Оцените: COS Сообщество науки
Академические и научные »Университеты
Оцените: 90 COS Изменение состояния
Академия и наука »Физика
Оцените: COS Стоимость обслуживания
Вычислительная техника» Сеть — — и более…
Оценить: COS Церковь Сатаны
Сообщество »Религия
COS Колледж наук
Академия и наука »Колледжи
Оцените: COS Операционная система компьютера
Вычислительная техника» Программное обеспечение
Оцените его: COS Спектрограф космического происхождения
Правительственный »НАСА
Оцените COS Common Object Services
Вычислительная техника » Нетворкинг — и многое другое…
Оцените: COS Корпорация открытых систем
Правительственные »Военные — и многое другое …
Оцените: COS Поддержка корпуса
Правительство »Военное дело
Оцените: COS Христос Спаситель
Сообщество »Религия
Оцените: COS Смена темы
Интернет» Чат
Оцените: COS Муниципальный аэропорт города Колорадо-Спрингс
9 0025 Правительственный »ТранспортОцените: COS Город Стерлинг
Государственный и местный
COS Центральная операционная система
Вычислительная техника »Сети
Оцените: COS Начальник службы безопасности
Бизнес» Должности
Оцените: COS Сержант компании
Правительственный »Военный
Оцените: COS Банка Общество онкологов adian
Медицина »Онкология
Оцените: Acos, Acot, Asin, Atan, Atan2, Cos, Cot, Degrees, Pi, Radians, Sin и Функции загара в Power Apps — Power Apps
- 2 минуты на чтение
В этой статье
Вычисляет тригонометрические значения.
Описание
Основные функции
Функция Cos возвращает косинус своего аргумента, угол, указанный в радианах.
Функция Cot возвращает котангенс своего аргумента, угол, указанный в радианах.
Функция Sin возвращает синус своего аргумента, угол, указанный в радианах.
Функция Tan возвращает тангенс своего аргумента, угол, указанный в радианах.
Обратные функции
Функция Acos возвращает арккосинус или обратный косинус своего аргумента. Арккосинус — это угол, косинус которого является аргументом. Возвращаемый угол указывается в радианах в диапазоне от 0 (ноль) до π.
Функция Acot возвращает главное значение арккотангенса или обратного котангенса своего аргумента. Возвращаемый угол указывается в радианах в диапазоне от 0 (ноль) до π.
Функция Asin возвращает арксинус или обратный синус своего аргумента.Арксинус — это угол, синус которого является аргументом. Возвращаемый угол указывается в радианах в диапазоне от -π / 2 до π / 2.
Функция Atan возвращает арктангенс или арктангенс своего аргумента. Арктангенс — это угол, тангенс которого является аргументом. Возвращаемый угол указывается в радианах в диапазоне от -π / 2 до π / 2.
Функция Atan2 возвращает арктангенс или арктангенс заданных координат x и y в качестве аргументов.Арктангенс — это угол от оси x до линии, которая содержит начало координат (0, 0) и точку с координатами ( x , y ). Угол указывается в радианах между -π и π, исключая -π. Положительный результат представляет собой угол против часовой стрелки от оси x ; отрицательный результат представляет собой угол по часовой стрелке. Atan2 ( a , b ) равно Atan ( b / a ) , за исключением того, что a может равняться 0 (нулю) с функцией Atan2 .
Вспомогательные функции
Функция градусов преобразует радианы в градусы. π радиан равняется 180 градусам.
Функция Pi возвращает трансцендентное число π, которое начинается с 3,141592 …
Функция Radians конвертирует градусы в радианы.
Банкноты
Если вы передадите в эти функции одно число, возвращаемое значение будет единственным результатом. Если вы передаете таблицу с одним столбцом, содержащую числа, возвращаемое значение представляет собой таблицу результатов с одним столбцом, по одному результату для каждой записи в таблице аргументов.Если у вас есть таблица с несколькими столбцами, вы можете преобразовать ее в таблицу с одним столбцом, как описано в работе с таблицами.
Если аргумент приведет к неопределенному значению, результатом будет пустое значение . Это может произойти, например, при использовании обратных функций с аргументами, выходящими за пределы допустимого диапазона.
Синтаксис
Основные функции
Cos ( Radians )
Детская кроватка ( Radians )
Sin ( Radians )
Tan ( Radians )- Radians — Обязательно.Угол действия.
Cos ( SingleColumnTable )
Cot ( SingleColumnTable )
Sin ( SingleColumnTable )
Tan ( SingleColumnTable)- SingleColumnTable — Обязательно. Одноколоночная таблица углов для работы.
Обратные функции
Acos ( номер )
Acot ( номер )
Asin ( номер )
Atan ( номер )- Номер — Обязательно.Номер для работы.
Acos ( SingleColumnTable )
Acot ( SingleColumnTable )
Asin ( SingleColumnTable )
Atan ( SingleColumn)- SingleColumnTable — Обязательно. Таблица чисел, состоящая из одного столбца.
Атан2 ( X , Y )
- X — Обязательно. X — координата оси.
- Y — Обязательно. Y — координата оси.
Вспомогательные функции
градусов ( радиан )
- Radians — Обязательно. Угол в радианах для преобразования в градусы.
Pi ()
Радианы ( градуса )
- Градусы — Обязательно. Угол в градусах для преобразования в радианы.
Примеры
Единый номер
Формула Описание Результат Cos (1.047197) Возвращает косинус 1,047197 радиан или 60 градусов. 0,5 Детская кроватка (Pi () / 4) Возвращает котангенс 0,785398 … радиан или 45 градусов. 1 Sin (Pi () / 2) Возвращает синус 1.570796 … радиан или 90 градусов. 1 Желто-коричневый (радианы (60)) Возвращает тангенс 1,047197 … радиан или 60 градусов. 1.732050 … Acos (0,5) Возвращает арккосинус 0,5 в радианах. 1,047197 … Acot (1) Возвращает арккотангенс 1 в радианах. 0,785398 … Асин (1) Возвращает арксинус 1 в радианах. 1,570796 … Атан (1.732050) Возвращает арктангенс 1,732050 в радианах. 1,047197 … Атан2 (5, 3) Возвращает арктангенс угла от оси x линии, содержащей начало координат (0,0), и координату (5,3), которая составляет приблизительно 31 градус. 0,540419 … Атан2 (4, 4) Возвращает арктангенс угла от оси x линии, содержащей начало координат (0,0) и координату (4,4), что составляет ровно π / 4 радиан или 45 градусов. 0,785398 … Градусов (1.047197) Возвращает эквивалентное количество градусов для 1,047197 радиана. 60 Pi () Возвращает трансцендентное число π. 3,141592 … Радианы (15) Возвращает эквивалентное количество радианов для 15 градусов. 0,261799 … Стол с одним столбцом
В примерах в этом разделе используется источник данных с именем ValueTable , который содержит следующие данные.Последняя запись в таблице — π / 2 радиан или 90 градусов.
Каково это быть майором COS?
Отвечу на самый часто задаваемый вопрос от абитуриентов: это супер круто!
По сути, специальность «Компьютерные науки» (COS) означает, что я должен пройти восемь факультетских классов, то есть классов COS уровня 300 или выше. Курсы COS обычно представляют собой лекционные занятия, а курсовая работа включает в себя задания по программированию, наборы задач и заключительные проекты.Не существует единого курса, который требовалось бы пройти всем специальностям COS, и приятно иметь так много вариантов занятий. (См. Список классов COS здесь.)
Потому что я получаю A.B. степень (в отличие от BSE — читайте о различиях здесь), мне нужно провести четыре семестра самостоятельной работы, что означает, что я могу работать над проектами по своему выбору, узнавать обо всем, о чем я хочу узнать, а затем писать отчет об этом. В подростковом возрасте я хотел научиться делать мобильное приложение, поэтому я создал приложение для Android, которое использует геозону для доставки push-уведомлений о публичных мероприятиях, происходящих в близлежащих парках.Ранней весной я хотел освежить свои навыки веб-разработки, поэтому я сделал веб-сайт, который сделал URL-адреса удобочитаемыми, а затем провел исследование пользователей. В старших классах я хотел больше общаться с людьми, поэтому я беру у них интервью и пишу об этом свою диссертацию! Если вам интересно, мой тезис об умных домах, конфиденциальности и Интернете вещей. 🙂
С тех пор, как я объявил COS своей главной весной второкурсника, я посещал два класса COS каждый семестр плюс самостоятельную работу. Около половины моих занятий посвящено COS, а другая половина посвящена тому, что я хочу изучать — английскому, французскому, китайскому, танцам, музыке и всему, что поражает мое воображение, чтобы завершить мое гуманитарное образование.
Кроме того, я очень благодарен за то, что получение специализации COS в буквальном смысле привело меня к местам: последние два лета я работал в Сан-Франциско и Сиэтле, а младшую весну я провел, обучаясь за границей в Эдинбургский университет в Шотландии.




 Математика (при поддержке «Ветвистого древа») 2009—2016
Математика (при поддержке «Ветвистого древа») 2009—2016

 метод acos (обозначение дуги). двойной АВ = 125; двойной AC = 150; двойной угол A = Math.
метод acos (обозначение дуги). двойной АВ = 125; двойной AC = 150; двойной угол A = Math.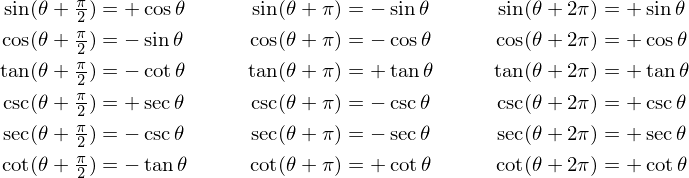 Итак, косинус — это просто координата x! Точно так же синус — это длина противоположной стороны (которая является длиной координаты y), деленная на длину гипотенузы (которая равна 1).
Итак, косинус — это просто координата x! Точно так же синус — это длина противоположной стороны (которая является длиной координаты y), деленная на длину гипотенузы (которая равна 1).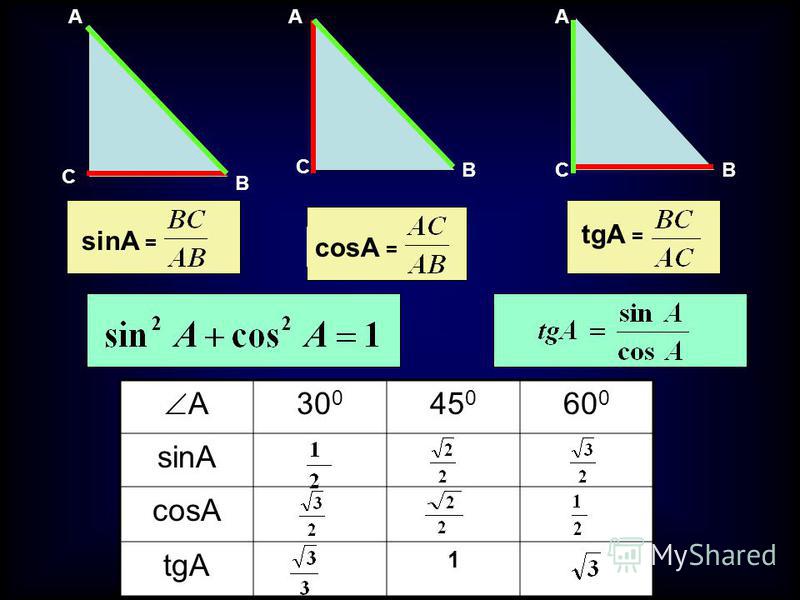 Пифагор работал над взаимосвязью между сторонами прямоугольного треугольника с помощью теоремы Пифагора, в то время как Гиппаркус работал над установлением взаимосвязи между сторонами и углами прямоугольного треугольника, используя концепции тригонометрии. Формулы sin, cos и tan в тригонометрии используются для нахождения недостающих сторон или углов прямоугольного треугольника.
Пифагор работал над взаимосвязью между сторонами прямоугольного треугольника с помощью теоремы Пифагора, в то время как Гиппаркус работал над установлением взаимосвязи между сторонами и углами прямоугольного треугольника, используя концепции тригонометрии. Формулы sin, cos и tan в тригонометрии используются для нахождения недостающих сторон или углов прямоугольного треугольника.
 Давайте разберемся с этими формулами sin, cos и tan на примере, приведенном ниже.
Давайте разберемся с этими формулами sin, cos и tan на примере, приведенном ниже. Таблица Sin, cos и tan используется для нахождения значений этих тригонометрических функций для стандартных углов. Во время расчетов с использованием синусоидальных, косинусных или тангенциальных соотношений мы можем напрямую обращаться к триггерной диаграмме, приведенной в следующем разделе, чтобы упростить выводы.
Таблица Sin, cos и tan используется для нахождения значений этих тригонометрических функций для стандартных углов. Во время расчетов с использованием синусоидальных, косинусных или тангенциальных соотношений мы можем напрямую обращаться к триггерной диаграмме, приведенной в следующем разделе, чтобы упростить выводы.

 9 футов
9 футов