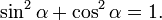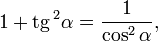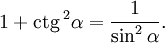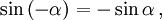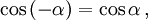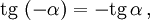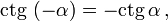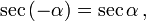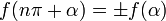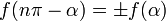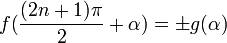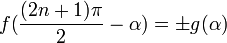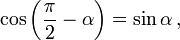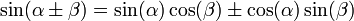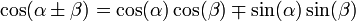COS — шведская марка одежды | История бренда COS

COS – бренд-ответвление скандинавского гиганта одежды H&M. Под названием марки выпускаются мужские, женские и детские коллекции стильной одежды, обуви и аксессуаров. В отличие от своего «старшего брата», компания совершенно не копирует одежду с модных показов, а предоставляет свое видение современной моды.
Одежда COS (расшифровывается как Collection of Style) понравится тем, кто устал гнаться за модой и предпочитает наряды вне сезонов и трендов. За столь короткое время модная марка успела зарекомендовать себя, как компания, выпускающая качественную классическую продукцию. Она выглядит совершенно не скучно и останется в гардеробе модниц на долгое время.

COS – история бренда и быстрый путь к успеху
Релиз торговой марки совпал с открытием именного модного бутика в Лондоне в 2007 году. Первая выпущенная коллекция отображала классику и минимализм кроя. Одежда очень отличается от марки H&M не только стилем исполнения, но и ценовой политикой. Первая коллекция марки COS имела успех, создавая модную одежду собственной философии.

Создание коллекций всегда сопровождается четким контролем отбора качественных тканей. Для изготовления одежды COS используют хлопок, шерсть, джерси и некоторые синтетические ткани. Цветовая палитра также довольно приглушенная или нейтральная. Одежда из коллекций COS составят стильный базовый гардероб жительницам мегаполиса.
Наш покупатель интересуется искусством и дизайном, и мы считаем, что хороший дизайн должен быть доступным каждому. Мы стремимся создавать вещи, которые не нужно менять каждый сезон. То, что хочется носить пусть не каждый день, но годами. Качество, которое не теряется со временем.
Еще одной фишкой компании COS является одинаковый ассортимент продукции в магазинах разных стран. Креативный директор компании Карин Густафссон отмечает, что она любит наблюдать как одни и те же вещи в разных странах носят по-разному.

Особое внимание ведущего дизайнера COS приковано к белой рубашке, которую она считает «душой бренда». По мнению Карин, белая рубашка не имеет ни возраста, ни определенного стиля. Так, она прекрасно подходит молодым девушкам, женщинам в возрасте. Способная подчеркнуть классический, морской или повседневный стиль casual. Белая рубашка каждый раз выглядит по-особенному – дополните ее аксессуарами, добавьте яркий акцент в образе и все заиграет по-новому.

Основной особенностью одежды бренда COS является гендерная нейтральность. Один и тот же элемент коллекции подходит мужчинам и женщинам. Представительницы прекрасного пола уже давно прогуливаются по мужским отделам и подбирают себе там одежду. По мнению Карин Густафссон, для их ритейлов это нормальная практика. Очень часто мужчины присматриваются к женским моделям пальто, свитеров или свободных брюк.

Создатели одежды марки COS черпают свое вдохновение из искусства и архитектуры. На сегодняшний день компания сотрудничает с архитектором Соу Фудзимото, художницей Агнес Мартин и рядом музеев. Создавая силуэты, дизайнеры марки ориентируются на современную архитектуру, которая взаимодействует с природой и показывает красоту окружающего мира.

Кроме прочего, философия компании COS полностью поддерживает течение Sustainable fashion, что означает «сознательная мода». Экологическое направление в моде, где модные бренды контролируют весь жизненный цикл производства от создания до его завершения. Важно не только изготовлять одежду из натуральных материалов, но и понимать, что соблюдены все трудовые и эко-нормы при ее пошиве. Марка одежды COS стремится производить продукцию, которая будет носиться годами и передаваться из поколения в поколение.
осознанность выбора – наше будущее,
а осознанное потребление – будущее моды
Одежда COS: что входит в модный каталог
Главное достоинство бренда – нет ограничений по возрасту и полу. Изделия не разделяются по статусу и подходят как менеджерам компании, так и студентам университетов. Наряды COS станут отличным решением для офисных работников, так как одежда гармонично вписывается в деловой дресс-код.

Размерная сетка продукции COS полностью соответствуют принятым Европейским стандартом. Стоит учитывать, что вся одежда пошита со свободным силуэтом, поэтому, чтобы наряд сидел более плотно, следует останавливать свой выбор на меньший размер.
Основой женского гардероба составляют платья. Модный бренд COS предлагает представительницам прекрасного пола наряды с широкой размерным рядом и выполненных из хлопка, шерсти, а также из атласа, шифона, гипюра и полиэстра. Фасон платьев COS – классический прямой силуэт, иногда с минималистическим дизайном в виде драпировки, объемных рукавов или добавлением пояса.

Особую категорию каталога COS занимают шифоновые и атласные блузки. Идеальный покрой, высокое качество, пастельная цветовая палитра делают блузы и женские рубашки COS классикой моды. Модели представлены с рукавами и без них. Они гармонично сочетаются с брюками, юбками и даже джинсами.

Трендовые модели штанов COS выполнены с учетом последних модных тенденций. Прямые, чинос, облегающие скинни, кюлоты и брюки с лампасами – каталог включает широкий ассортимент стильных моделей. Могут быть выполнены как из натуральных тканей, так и из вискозы и полиэстера высокого качества.

Архитектурный крой прослеживается и в юбках марки COS. Классические модели подчеркнут офисный стиль и сочетаются с любым верхом из модной коллекции бренда. Цветовая гамма представлена нейтральными цветами, иногда встречаются экспериментальные яркие модели.

Пальто бренда COS перезимует с вами ни одну зиму. Наряд для холодного времени года выполнен из шерсти удлиненного силуэта. Лаконичный дизайн сочетается с любой обувью, сумкой и зимними аксессуарами. Цветовая палитра, преимущественно, темных оттенков.

Обувь и аксессуары бренда COS также созданы в стиле минимализм и отличаются своим безупречным качеством. Иногда прослеживается грубый скандинавский характер исполнения, сочетая в себе простоту и изящество.

Одежда бренда COS должна быть обязательно в гардеробе каждой модницы. Она незаменима, чтобы составить городской look. Станьте частью творческой тусовки в одежде COS. Минималистический дизайн моделей существует вне сезонов и вне времени. И хотя, продукция компании имеет более высокий ценовой сегмент, чем H&M, руководство компании объясняет это более качественным пошивом изделий, которые прослужат долгое время своей обладательнице.

Вдохновившись архитектурным кроем и лаконичным дизайном новой коллекции COS, я отправляюсь на поиски модных новинок, ведь мне по-прежнему ✭ Нечего Надеть ✭
Mia Pas
Cos — Википедия

Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 апреля 2015; проверки требуют 7 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 апреля 2015; проверки требуют 7 правок. Перейти к навигации Перейти к поиску- Аббревиатура COS может означать
- Consequence of Sound — американский музыкальный сайт, публикующий новости, обзоры альбомов и концертов, редакционные статьи
- Chippewa Operating System — операционная система, разработанная Control Data Corporation для суперкомпьютера CDC 6600
- Cray Operating System — проприетарная операционная система для суперкомпьютеров, разработанная компанией Cray Research
- Crypto Operating System — название Mac-совместимой операционной системы, созданной Omega GmbH в конце 1990-х
- Алгоритм COS — субэкспоненциальный алгоритм дискретного логарифмирования в кольце вычетов по модулю простого числа
- China Operating System — China Operating System (Китайская национальная операционная система)
- Class of service (CoS) — метод приоритизации сетевого трафика в соответствии с IEEE 802.1p в рамках QoS, а так же непосредственно значение поля priority code point (PCP) в теге IEEE 802.1Q заголовка кадра Ethernet
- Caché ObjectScript — язык программирования и API для СУБД Caché, развитие языка программирования MUMPS
- Слово Cos может означать
- Cos — бельгийская группа, образованная в 1974 году
- Cos-B — орбитальная обсерватория Европейского космического агентства
cos — Перевод на русский — примеры английский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
You’re prejudiced cos you like me.
У тебя предвзятый взгляд, потому что я тебе нравлюсь.Well, you can’t quit cos I fired you.
Ну, ты не можешь уволиться, потому что я тебя уволила.I like pancakes cos they’re stackable.
Люблю оладьи, потому что их можно складывать в стопку.You don’t see them cos they’re shadowing.
Fresh air would do you good cos proper policing happens on the street.
Свежий воздух пойдёт тебе на пользу, потому что должная охрана правопорядка всегда происходит на улице.And bring your handcuffs cos I can be quite a troublesome prisoner.
И можешь взять с собой наручники, потому что я могу быть довольно беспокойным узником.Get the bearings, cos no-one knows where we’re heading.
Чтобы быть уверенным, потому что никто не знает, куда мы направляемся.You hate Nan cos she bullied you into keeping me.
Ты ненавидишь Нэн, потому что это она заставила тебя меня родить.Don’t say no immediately cos it could sound crazy.
Не говори сразу «нет», потому что это может показаться безумием.I don’t blame you cos they’re great.
Я не виню тебя, потому что они действительно очень милые.Mainly cos he doesn’t exist.
Just please stop pretending cos I know it was him.
Пожалуйста, просто перестань претворяться, потому что я знаю, что это был он.Yeah, only cos you disturbed him.
Good, cos it really wasn’t.
We called him Napoleon cos he was so little.
Мы звали его Наполеон, потому что он был таким маленьким.And I must’ve looked good, cos she was like…
Возможно, я выглядел слишком хорошо, потому что она…That’s not gonna happen is it, cos you’ve ruined it for me.
Sir didn’t get crazes, cos he went to a posh boys school.
Сэр не поддался мании, потому что ходил в элитную школу.Ask me, cos I have to get out of here.
That’s cos you’re a raving alcoholic, James.
Косинус — это… Что такое Косинус?

Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Способы определения
Геометрическое определение
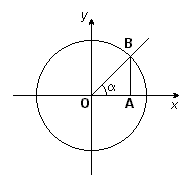
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
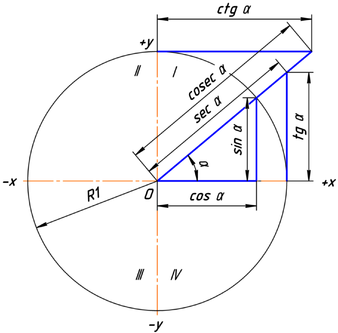
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
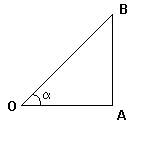
Рис. 4.
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений: 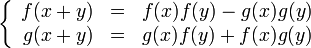
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Пользуясь этими формулами, а также уравнениями 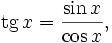
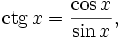
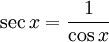 и
и 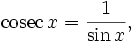 можно найти разложения в ряд Тейлора и других тригонометрических функций:
можно найти разложения в ряд Тейлора и других тригонометрических функций:
 где Bn — числа Бернулли.
где Bn — числа Бернулли. где En — числа Эйлера.
где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
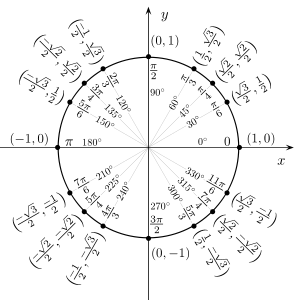
Значения косинуса и синуса на окружности.
Значения тригонометрических функций нестандартных углов
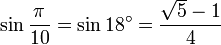
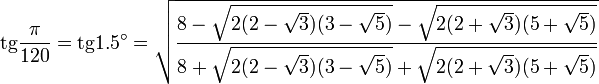
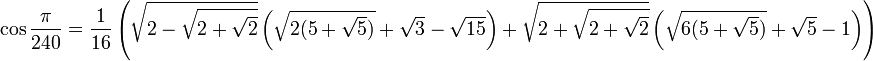
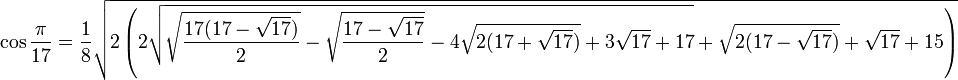
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
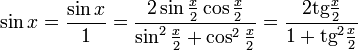
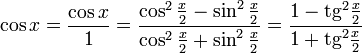
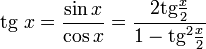
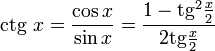
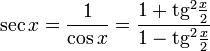
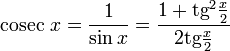
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
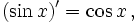
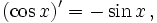
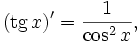
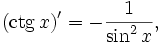
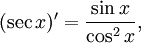
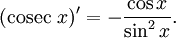
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
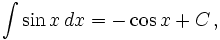
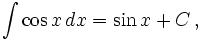
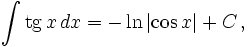
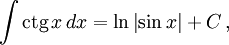
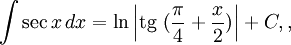
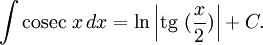
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
Ссылки
Wikimedia Foundation. 2010.
Косинус — что это такое? Определение, значение, перевод

Косинус (ударение на «о») это тригонометрическая функция, которая для острого угла в прямоугольном треугольнике определяется как отношение прилежащего катета к гипотенузе. На системе единичной окружности косинус угла является абсциссой (координатой x) точки на окружности, соответствующей данному углу. Эта функция обозначается латинскими буквами cos.
Как следует из его определения, косинус угла в прямоугольном треугольнике может принимать значения от нуля до единицы, а на единичной окружности — от (-1) до единицы. Аргумент косинуса в прямоугольном треугольнике принимает значения от нуля до (π/2), а в случае с единичной окружностью он может быть любым рациональным числом, в том числе и отрицательным.
Косинус и синус связаны через теорему Пифагора следующей формулой. Для любого угла α выполняется:
sin2(α) + cos2(α) = 1
Примеры значений косинуса для некоторых углов:
cos(0) = 1
cos(π/6) = √3/2
cos(π/4) = √2/2
cos(π/3) = 1/2
cos(π/2) = 0
cos(π) = -1
Косинус находится в списке: Математика
Вы узнали, откуда произошло слово Косинус, его объяснение простыми словами, перевод, происхождение и смысл.
Пожалуйста, поделитесь ссылкой «Что такое Косинус?» с друзьями:
И не забудьте подписаться на самый интересный паблик ВКонтакте!
Сайт новых и хорошо забытых слов Что-это-такое.ru
Добавить слово | Помочь проекту
Псст… Совесть есть?
А если найду?
cos — Викисловарь
 | См. также coś. |
Содержание
- 1 Международное обозначение
- 1.1 Семантические свойства
- 1.1.1 Значение
- 1.2 Смотреть также
- 1.1 Семантические свойства
- 2 Ирландский
- 2.1 Морфологические и синтаксические свойства
- 2.2 Произношение
- 2.3 Семантические свойства
- 2.3.1 Значение
- 2.3.2 Синонимы
- 2.3.3 Антонимы
- 2.3.4 Гиперонимы
- 2.3.5 Гипонимы
- 2.4 Родственные слова
- 2.5 Этимология
- 2.6 Фразеологизмы и устойчивые сочетания
- 2.7 Библиография
- 3 Каталанский
- 3.1 Морфологические и синтаксические свойства
- 3.2 Произношение
- 3.3 Семантические свойства
- 3.3.1 Значение
- 3.3.2 Синонимы
- 3.3.3 Антонимы
- 3.3.4 Гиперонимы
- 3.3.5 Гипонимы
- 3.4 Родственные слова
- 3.5 Этимология
- 3.6 Фразеологизмы и устойчивые сочетания
- 3.7 Библиография
Семантические свойства[править]
Значение[править]
- матем. косинус, тригонометрическая функция, безразмерная ◆ cos α
Смотреть также[править]
- sin, tg, tan, ctg
- arcsin, arccos, arctg, arcctg
- sec, csc
 | Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства[править]
cos
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- Это слово или выражение пока не переведено. Вы можете предложить свой вариант перевода. ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
 | Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства[править]
cos
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- Это слово или выражение пока не переведено. Вы можете предложить свой вариант перевода. ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
 | Для улучшения этой статьи желательно:
|
Косинус — это… Что такое Косинус?

Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Способы определения
Геометрическое определение
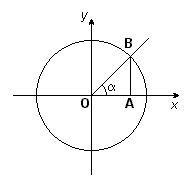
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
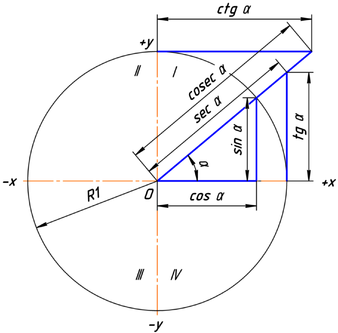
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
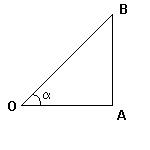
Рис. 4.
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений: 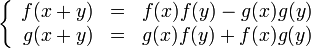
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Пользуясь этими формулами, а также уравнениями 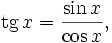
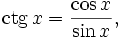
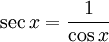 и
и 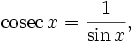 можно найти разложения в ряд Тейлора и других тригонометрических функций:
можно найти разложения в ряд Тейлора и других тригонометрических функций:
 где Bn — числа Бернулли.
где Bn — числа Бернулли. где En — числа Эйлера.
где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
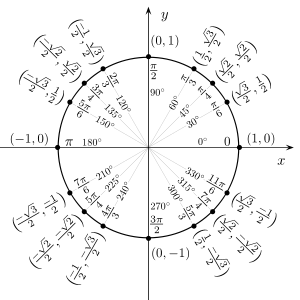
Значения косинуса и синуса на окружности.
Значения тригонометрических функций нестандартных углов
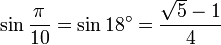
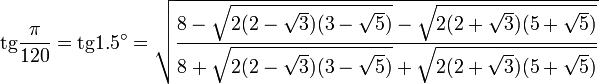
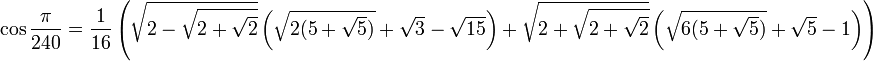
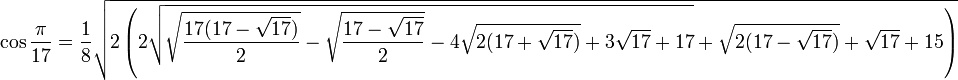
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
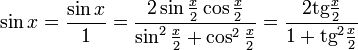
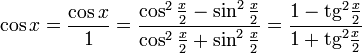
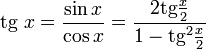
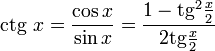
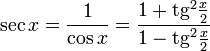
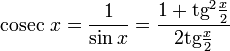
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
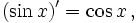
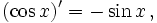
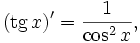
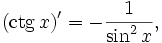
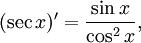
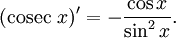
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
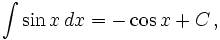
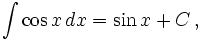
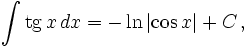
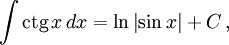
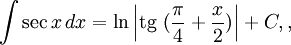
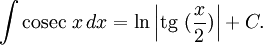
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
Ссылки
Wikimedia Foundation. 2010.




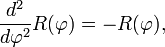
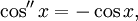
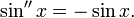
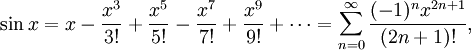
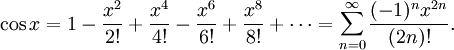
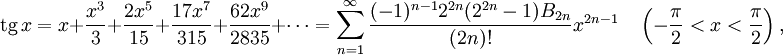 где Bn — числа Бернулли.
где Bn — числа Бернулли.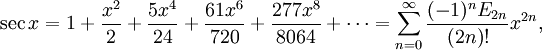 где En — числа Эйлера.
где En — числа Эйлера.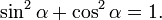
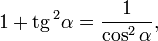
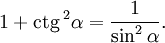
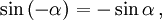
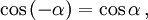
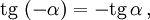
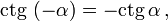
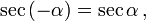
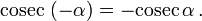
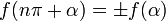
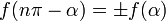
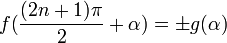
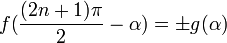
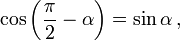
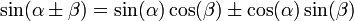
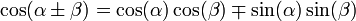
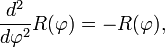
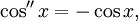
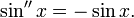
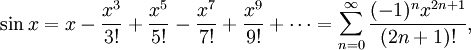
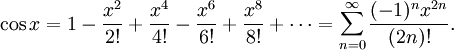
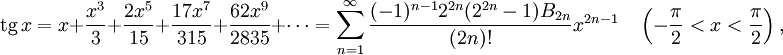 где Bn — числа Бернулли.
где Bn — числа Бернулли.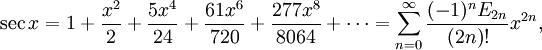 где En — числа Эйлера.
где En — числа Эйлера.