7. Анализ цепей с неисправными компонентами | 4. Последовательные и параллельные цепи | Часть1
7. Анализ цепей с неисправными компонентами
Анализ цепей с неисправными компонентами
Работа радиомастера часто связана с поиском и устранением неполадок в неисправных цепях. Анализ неисправных цепей требует от радиолюбителя глубокого понимания фундаментальных основ электроники, умения формулировать гипотезы, способность оценивать значимость различных гипотез (почему одна причина может быть вероятнее другой), а так же творческий подход в применении решений для устранения проблемы. Несмотря на то, что все эти навыки можно свести в научную методологию, многие мастера по ремонту радиоаппаратуры согласятся, что устранение неполадок — это искусство, для овладения которым могут понадобится годы.
Любому радиолюбителю очень важно интуитивное понимание того, как неисправные компоненты влияют на различные конфигурации цепей. В данной статье мы исследуем только некоторые эффекты воздействия неисправных компонентов на последовательные и параллельные цепи, более подробно эта тема будет раскрыта позднее, в статьях про последовательно-параллельные цепи.
Давайте начнем с простой последовательной цепи:
Если все компоненты функционируют должным образом, то мы математически можем определить все токи и напряжения этой схемы:
Теперь предположим, что резистор R
При закороченном резисторе R2 общее сопротивление цепи уменьшится. Так как напряжение, производимое батареей, является величиной постоянной, снижение общего сопротивления вызовет увеличение общей силы тока.
Поскольку сила тока в цепи увеличилась с 20 до 60 миллиампер, увеличится и напряжение на резисторах R1 и R3 (которые не изменили своего сопротивления). Резистор R2, закороченный перемычкой, фактически устраняется из цепи, так как его сопротивление равно нулю. Напряжение на этом резисторе так же будет иметь нулевое значение.
Если резистор R2 будет не замкнут а «оборван», то его сопротивление увеличится до бесконечности:
При бесконечном сопротивлении резистора R2 общее сопротивление последовательной цепи так же будет бесконечно (для последовательной цепи Rобщ = R1 + R2 + …. Rn). Общая сила тока в этом случае будет иметь нулевое значение, что означает отсутствие в цепи потока электронов, способного произвести напряжение на резисторах R1 и R3. Полное напряжение батареи проявится на выводах оборванного резистора R
Аналогичный метод анализа можно применить и к параллельной цепи. Для начала мы проанализируем «исправную» параллельную цепь:
Если предположить, что резистор R2 в этой цепи «оборван», то последствия будут следующими:
Заметьте, что «оборванная» ветвь нашей параллельной цепи влияет только на ток этой ветки и на общий ток схемы. В связи с тем, что напряжение в параллельной цепи одинаково на всех ее компонентах, вышедший из строя резистор R
Такая ситуация аналогична домашней системе освещения, в которой все лампочки получают рабочее напряжение от силовых проводов, смонтированных параллельным способом. Включение и выключение лампочки в одной комнате этой системы (включается и выключается одна ветвь параллельной цепи) не влияет на работу ламп в других комнатах. Данное действие затрагивает только ток этой лампы, и общий ток системы освещения:
Теперь давайте рассмотрим короткое замыкание одного из резисторов в простой параллельной цепи. В идеальном случае (с идеальным источником напряжения и нулевым сопротивление соединительных проводов), короткозамкнутый резистор в одной из ветвей этой цепи не повлияет на другие ее ветви. Но это в идеале, в реальности же эффект будет не совсем таким, а почему, мы увидим в следующих примерах:
Короткозамкнутый резистор (сопротивление которого равно 0 Ом) теоретически потребляет бесконечный ток от любого источника напряжения (I = U/0). В нашем случае нулевое сопротивление резистора R2 уменьшает общее сопротивление цепи до нуля, увеличивая тем самым общую силу тока до бесконечности. Пока источник напряжения поддерживает свою величину на уровне 9 вольт, токи оставшихся двух ветвей цепи (R1 и R3) не изменятся.
Внутренние сопротивления источников питания превращают простые параллельные цепи в последовательно-параллельные. Такие сопротивления как правило очень малы чтобы оказывать заметное влияние на работу схемы, но при больших токах, которые возникают вследствие замыкания компонентов, их влияние многократно увеличивается. В нашем случае, короткое замыкание резистора R2 приведет к тому, что практически все напряжение сосредоточится на внутреннем сопротивлении источника, а резисторы R1, R2 и R3 останутся почти без напряжения:
Следует отметить, что намеренное короткое замыкание через контакты любого источника напряжения — это плохая идея. Даже если полученный в результате такого замыкания ток (высокая температура, вспышки и искры) не причинит вреда находящимся поблизости людям, источник питания, скорее всего, будет поврежден, если он не был специально разработан для обработки коротких замыканий.
В последующих статьях мы подведем вас к анализу схем с неизвестными величинами, т. е. к анализу последствий отказов компонентов схем, в которых вам неизвестны значения напряжений источников питания, сопротивлений резисторов и т.д. Данная статья служит первым шагом к такому анализу.
В то время как обычный анализ (с применением Закона Ома и принципов последовательных и параллельных цепей), базирующийся на численных величинах — является количественным анализом, анализ схем с неизвестными величинами можно назвать качественным анализом. Другими словами, мы будем анализировать качественное влияние неисправностей на цепь, а не точные величины. В конечном итоге вы добьетесь глубокого интуитивного понимания работы электрической схемы.
Почему при резонансе напряжение на резисторе равно напряжению источника переменного тока
потому что больше нет сопротивления
резистор имеет активное сопростивление. к резонансу не имеет никакого отношения
Реактивные сопротивления катушки и кондёра равны, но с разным знаком, при сложении получается ноль, вот по этому и всё напряжение на резисторе.
Резистор. Падение напряжения на резисторе. Мощность. Закон Ома — МикроПрогер
Итак, резистор… Базовый элемент построения электрической цепи.
Работа резистора заключается в ограничении тока, протекающего по цепи. НЕ в превращении тока в тепло, а именно в ограничении тока. То есть, без резистора по цепи течет большой ток, встроили резистор – ток уменьшился. В этом заключается его работа, совершая которую данный элемент электрической цепи выделяет тепло.
Пример с лампочкой
Рассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток, проходящий через цепь. И Резистор. Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток, например, 0,75А. Лампочка горит ярко. Встроили в цепь резистор — у тока появился труднопреодолимый барьер, протекающий по цепи ток снизился до 0,2А. Лампочка горит менее ярко. Стоит отметить, что яркость, с которой горит лампочка, зависит так же и от напряжения на ней. Чем выше напряжение — тем ярче.
Ограничение тока резистором
Кроме того, на резисторе происходит падение напряжения. Барьер не только задерживает ток, но и «съедает» часть напряжения, приложенного источником питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт. На всякий случай амперметр, два вольтметра про запас, лампочку и резистор. Включаем цепь без резистора(слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр(снизу на схеме справа) показывает 5В. На лампочку остались остальные 12В-5В=7В. Вольтметр на лампочке показал 7В.
Падение напряжение на резистореРазумеется, оба примера являются абстрактными, неточными в плане чисел и рассчитаны на объяснение сути процесса, происходящего в резисторе.
Основная характеристика резистора — сопротивление. Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление, тем больший ток он способен ограничить, тем больше тепла он выделяет, тем больше напряжения падает на нем.
Основной закон всего электричества. Связывает между собой Напряжение(V), Силу тока(I) и Сопротивление(R).
V=I*R
Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте используем Закон Ома для нашей цепи с резистором и лампочкой, рассмотренной выше, и рассчитаем сопротивление резистора, при котором ток от источника питания на 12В ограничится до 0,2. При этом считаем сопротивление лампочки равным 0.
V=I*R => R=V/I => R= 12В / 0,2А => R=60Ом
Итак. Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи, будет составлять 0,2А.
Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении схем для реальных устройств.
Мощность электрического тока на каком-либо участке цепи равна произведению силы тока, протекающую по этому участку на напряжение на этом участке цепи. P=I*U. Единица измерения 1Вт.
При протекании тока через резистор совершается работа по ограничению электрического тока. При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающую среду. Но если резистор будет совершать слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.
Характеристика мощности резистора — это максимальная мощность тока, которую он способен выдержать и не перегреться.
Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток, проходящий по цепи(а значит и через резистор), равный 0,2А. Падение напряжения на резисторе равно 5В (не 12В, не 7В, а именно 5 — те самые 5, которые вольтметр показывает на резисторе). Это значит, что мощность тока через резистор равна P=I*V=0,2А*5В=1Вт. Делаем вывод: резистор для нашей цепи должен иметь максимальную мощность не менее(а лучше более) 1Вт. Иначе он перегреется и выйдет из строя.
Соединение резисторов
Резисторы в цепях электрического тока имеют последовательное и параллельное соединение.
Последовательное соединение резисторов
При последовательном соединении общее сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:
Последовательное соединение резисторов
Параллельное соединение резисторов
При параллельном соединении общее сопротивление резисторов рассчитывается по формуле:
Параллельное соединение резисторов
Остались вопросы? Напишите комментарий. Мы ответим и поможем разобраться =)
Автор публикации
не в сети 5 месяцев
wandrys
877 Комментарии: 0Публикации: 31Регистрация: 17-03-2016ФИЗИКА: ЗАДАЧИ на Закон Ома с решениями
Задачи на Закон Ома с решениями
Формулы, используемые на уроках «Задачи на Закон Ома».
Название величины | Обозначение | Единица измерения | Формула |
Сила тока | I | А | I = U / R |
Напряжение | U | В | U = IR |
Сопротивление | R | Ом | R = U/I |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?

Задача № 2. Сопротивление проводника 6 Ом, а сила тока в нем 0,2 А. Определите напряжение на концах проводника.

Задача № 3. Определите сопротивление проводника, если при напряжении 110 В сила тока в нем 2 А.

Задача № 4. По графикам зависимости силы тока от напряжения определите сопротивление каждого проводника.

Решение:
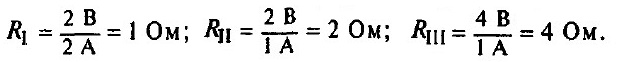
Задача № 5. Чему равна сила тока в электрической лампе карманного фонаря, если сопротивление нити накала 16,6 Ом и лампа подключена к батарейке напряжением 2,5 В?

Задача № 6. Электрический утюг включен в сеть с напряжением 220 В. Какова сила тока в нагревательном элементе утюга, если сопротивление его равно 48,4 Ом?
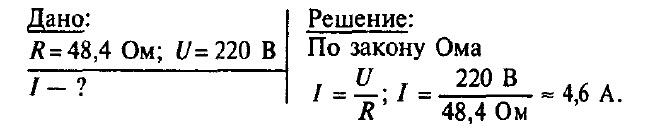
Задача № 7. При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?

Задача № 8. Чему равно сопротивление спирали электрической лампы в рабочем состоянии, у которой на цоколе написано 6,3 В, 0,22 А?
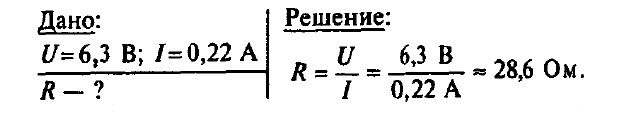
Задача № 9. Показание вольтметра, присоединенного к горящей электрической лампе накаливания, равно 120 В, а амперметра, измеряющего силу тока в лампе, 0,5 А. Чему равно сопротивление лампы? Начертите схему включения лампы, вольтметра и амперметра.

Задача № 10. ОГЭ Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.

Краткая теория для решения Задачи на Закон Ома.
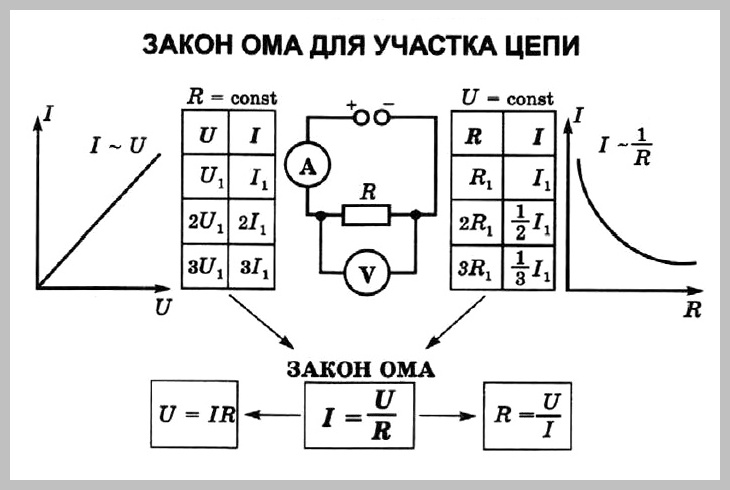
Это конспект по теме «ЗАДАЧИ на Закон Ома». Выберите дальнейшие действия:



