Центробежная сила • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Во вращающейся системе отсчета наблюдатель испытывает на себе действие силы, уводящей его от оси вращения.

Вам, наверное, доводилось испытывать неприятные ощущения, когда машина, в которой вы едете, входила в крутой вираж. Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)

Стороннему наблюдателю, однако, всё будет представляться иначе. Когда машина закладывает вираж, наблюдатель сочтет, что вы просто продолжаете прямолинейное движение, как это и делало бы любое тело, на которое не оказывает действия никакая внешняя сила; а автомобиль отклоняется от прямолинейной траектории. Такому наблюдателю покажется, что это не вас прижимает к дверце машины, а, наоборот, дверца машины начинает давить на вас.

Впрочем, никаких противоречий между этими двумя точками зрения нет. В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета.

Поскольку не все наблюдатели видят действие этой силы, физики часто называют центробежную силу фиктивной силой

или псевдосилой. Однако мне кажется, что такая интерпретация может вводить в заблуждение. В конце концов, едва ли можно назвать фиктивной силу, которая ощутимо придавливает вас к дверце автомобиля. Просто всё дело в том, что, продолжая двигаться по инерции, ваше тело стремится сохранить прямолинейное направление движения, в то время как автомобиль от него уклоняется и из-за этого давит на вас.

Чтобы проиллюстрировать эквивалентность двух описаний центробежной силы, давайте немного поупражняемся в математике. Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v²/r, где

v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv²/r.

Теперь обобщим сказанное: любое тело, движущееся по криволинейной траектории, — будь то пассажир в машине на вираже, мяч на веревочке, который вы раскручиваете над головой, или Земля на орбите вокруг Солнца — испытывает на себе действие силы, которая обусловлена давлением дверцы автомобиля, натяжением веревки или гравитационным притяжением Солнца. Назовем эту силу F. С точки зрения того, кто находится во вращающейся системе отсчета, тело не движется. Это означает, что внутренняя сила 

F уравновешивается внешней центробежной силой:

    F = mv²/r

Однако с точки зрения наблюдателя, находящегося вне вращающейся системы отсчета, тело (вы, мяч, Земля) движется равноускоренно под воздействием внешней силы. Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим:

    F = ma = mv²/r

Но тем самым мы получили в точности уравнение для наблюдателя, находящегося во вращающейся системе отсчета. Значит, оба наблюдателя приходят к идентичным результатам относительно величины действующей силы, хотя и исходят из разных предпосылок.

Это очень важная иллюстрация того, что представляет собою механика как наука. Наблюдатели, находящиеся в различных системах отсчета, могут описывать происходящие явления совершенно по-разному. Однако, сколь бы принципиальными ни были различия в подходах к описанию наблюдаемых ими явлений, уравнения, их описывающие, окажутся идентичными. А это — не что иное, как принцип инвариантности законов природы, лежащий в основе теории относительности.

Центробежная сила — Википедия

Центробе́жная си́ла^[1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.

Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно неё, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.

Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося

по круговой траектории тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.

Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный^[2].

Формулы

Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).

По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.

Для материальной точки центробежная сила выражается формулой:

F→=−m[ω→×[ω→×R→]]=m(ω2R→−(ω→⋅R→)ω→),{\displaystyle {\vec {F}}=-m\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right]=m\left(\omega ^{2}{\vec {R}}-\left({\vec {\omega }}\cdot {\vec {R}}\right){\vec {\omega }}\right),}

где:

F→{\displaystyle {\vec {F}}} — центробежная сила приложенная к телу,

 m{\displaystyle \ m} — масса тела,

ω→{\displaystyle {\vec {\omega }}} — угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),

R→{\displaystyle {\vec {R}}} — радиус-вектор тела во вращающейся системе координат.

Эквивалентное выражение для центробежной силы можно записать как

F→=mω2R0→{\displaystyle {\vec {F}}=m\omega ^{2}{\vec {R_{0}}}}

если использовать обозначение R0→{\displaystyle {\vec {R_{0}}}} для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.

Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.

Вывод

Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью v→n,{\displaystyle {\vec {v}}_{n},} а сама система движется поступательно с линейной скоростью v→0{\displaystyle {\vec {v}}_{0}} в инерциальной системе координат и одновременно вращается с угловой скоростью ω→.{\displaystyle {\vec {\omega }}.}

Тогда линейная скорость тела в инерциальной системе координат равна:

v→=v→0+[ω→×R→]+v→n,{\displaystyle {\vec {v}}={\vec {v}}_{0}+\left[{\vec {\omega }}\times {\vec {R}}\right]+{\vec {v}}_{n},}

где R→{\displaystyle {\vec {R}}} — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:

ddtv→=ddtv→0+ddt[ω→×R→]+ddtv→n.{\displaystyle {\frac {d}{dt}}{\vec {v}}={\frac {d}{dt}}{\vec {v}}_{0}+{\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]+{\frac {d}{dt}}{\vec {v}}_{n}.}

Найдём значение каждого слагаемого в инерциальной системе координат:

ddtv→0=a→0,{\displaystyle {\frac {d}{dt}}{\vec {v}}_{0}={\vec {a}}_{0},}

ddtv→n=a→n+[ω→×v→n],{\displaystyle {\frac {d}{dt}}{\vec {v}}_{n}={\vec {a}}_{n}+\left[{\vec {\omega }}\times {\vec {v}}_{n}\right],}

ddt[ω→×R→]=[ε→×R→]+[ω→×ddtR→]=[ε→×R→]+[ω→×v→n]+[ω→×[ω→×R→]],{\displaystyle {\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+\left[{\vec {\omega }}\times {\frac {d}{dt}}{\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+\left[{\vec {\omega }}\times {\vec {v}}_{n}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right],} где a→n{\displaystyle {\vec {a}}_{n}} — линейное ускорение относительно системы, ε→{\displaystyle {\vec {\varepsilon }}} — угловое ускорение.

Таким образом, получаем:

ddtv→=a→=a→0+a→n+[ε→×R→]+2[ω→×v→n]+[ω→×[ω→×R→]].{\displaystyle {\frac {d}{dt}}{\vec {v}}={\vec {a}}={\vec {a}}_{0}+{\vec {a}}_{n}+\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+2\left[{\vec {\omega }}\times {\vec {v}}_{n}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right].}

Последнее слагаемое и будет центростремительным ускорением.

Раскрыв двойное векторное произведение и положив R→{\displaystyle {\vec {R}}} перпендикулярным оси вращения, получим:

a→c=ω→(ω→R→)−R→ω→2=−R→ω→2.{\displaystyle {\vec {a}}_{c}={\vec {\omega }}({\vec {\omega }}{\vec {R}})-{\vec {R}}{\vec {\omega }}^{2}=-{\vec {R}}{\vec {\omega }}^{2}.}

Элементарное рассмотрение и мотивировка

Вращение с точки зрения инерциальной системы отсчета

Рассмотрим спицу, вращающуюся вокруг перпендикулярной к ней вертикальной оси с угловой скоростью ω{\displaystyle \omega }. Вместе со спицей вращается надетый на неё шарик, соединённый с осью пружиной.

Согласно второму закону Ньютона шарик займёт положение равновесия на таком расстоянии R{\displaystyle R} от центра диска, на котором сила натяжения пружины Fpr{\displaystyle F_{\mathrm {pr} }} оказывается равной произведению массы шарика m{\displaystyle m} на его ускорение^[3]an=ω2R{\displaystyle a_{n}=\omega ^{2}R}:

Fpr=−mω2R=−mv2R{\displaystyle F_{\mathrm {pr} }=-m\omega ^{2}R=-m{\frac {v^{2}}{R}}}.^[4]

Связанная со спицей система отсчёта вращается по отношению к инерциальной системе. Относительно системы отсчёта, связанной со спицей, шарик покоится, хотя на него действует сила упругости пружины. Это не противоречит второму закону Ньютона, так как вращающаяся система отсчёта не является инерциальной и соотношение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} в ней не выполняется.

Вращение с точки зрения неинерциальной системы отсчёта. Сила инерции

Для практических целей, однако, удобнее считать, что второй закон Ньютона выполняется и с точки зрения вращающейся системы отсчёта, введя для этого формально силу инерции Fcf=−Fpr=mω2R{\displaystyle F_{\mathrm {cf} }=-F_{\mathrm {pr} }=m\omega ^{2}R}^[4], действующую на шарик вдоль радиуса от центра диска наряду с реальной силой Fpr{\displaystyle F_{\mathrm {pr} }}.

Силу инерции Fcf{\displaystyle F_{\mathrm {cf} }}, вводимую во вращающейся системе отсчёта, называют центробежной силой. Эта сила действует на тело во вращающейся системе отсчёта, независимо от того, покоится тело в этой системе или движется относительно неё со скоростью v{\displaystyle v}’.

Следует иметь в виду, что для правильного описания движения тел во вращающихся системах отсчёта, кроме центробежной силы следует также вводить силу Кориолиса.

В литературе встречается и совсем другое понимание термина «центробежная сила». Так иногда называют реальную силу, приложенную не к совершающему вращательное движение телу, а действующую со стороны тела на ограничивающие его движение связи. В рассмотренном выше примере так называли бы силу, действующую со стороны шарика на пружину. (См., например, ниже ссылку на БСЭ.)

Центробежная сила как реальная сила

Центростремительная и центробежная силы при движении тел по круговым траекториям с общей осью вращения

Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин «центробежная сила» (букв. сила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющая его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона)^[5] в форме:

Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы

Или ещё^[6]:

Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.

Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так^[7].

Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной форме его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Ньютон связывал её с эфиром, заполняющим всё пространство)^[5], остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.

Рассматриваемое тело с массой (точнее — инертной массой) m{\displaystyle m} приобретает отличающееся от нуля ускорение a{\displaystyle a} в тот же момент t=0{\displaystyle t=0}, когда начинает действовать на него сила F{\displaystyle F} (Второй закон Ньютона:F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}). Однако для достижения отличающейся от нуля скорости v{\displaystyle v} требуется некоторое время t{\displaystyle t} в соответствии с определением импульса силы: t=mv/F{\displaystyle t=mv/F}. Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила^[8].

Использование термина «центробежная сила» правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле центробежная сила представляет собой один из членов в формулировке третьего закона Ньютона, антагониста центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направления движения тела (материальной точки).

Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины M1{\displaystyle {M_{1}}} и M2{\displaystyle {M_{2}}}, находящихся на расстоянии R{\displaystyle R} друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и R{\displaystyle R} есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения FG:GM1M2/R2{\displaystyle {F_{G}}:{GM_{1}M_{2}/R^{2}}}, где G{\displaystyle G}- гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями v1{\displaystyle {v_{1}}} = ω1{\displaystyle {\omega }_{1}} R1{\displaystyle {R_{1}}} и v2{\displaystyle {v_{2}}} = ω2{\displaystyle {\omega _{2}}} R2{\displaystyle {R_{2}}}, то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: ω1{\displaystyle {\omega _{1}}} = ω2{\displaystyle {\omega _{2}}} = ω{\displaystyle \omega }, а расстояния от центра вращения (центра масс) будут соотноситься, как: M1/M2{\displaystyle {M_{1}/M_{2}}} = R2/R1{\displaystyle {R_{2}/R_{1}}}, причём R2+R1=R{\displaystyle {R_{2}}+{R_{1}}=R}, что непосредственно следует из равенства действующих сил: F1=M1a1{\displaystyle {F_{1}}={M_{1}}{a_{1}}} и F2=M2a2{\displaystyle {F_{2}}={M_{2}}{a_{2}}}, где ускорения равняются соответственно: a1{\displaystyle {a_{1}}}= ω2R1{\displaystyle {\omega ^{2}}{R_{1}}} и a2=ω2R2{\displaystyle {a_{2}}={\omega ^{2}}{R_{2}}}^[9].

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): F1{\displaystyle {F_{1}}} =F2{\displaystyle {F_{2}}} =FG{\displaystyle ={F_{G}}}. При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствии с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы тяготения. То же самое справедливо и в отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел, и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

См. также

Примечания

1. ↑ Вне контекста физики/механики/математики, например, в философии, публицистике или художественной литературе, а также иногда и в разговорной речи, слова центробежная сила могут нередко употребляться просто как обозначение некоего влияния, направленного прочь от некоторого «центра»; в таком употреблении это может быть никак не связано не только с каким-либо вращением, но и с понятием силы, как оно употребляется в физике.
2. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
3. ↑ Воспользуемся формулой центростремительного ускорения.
4. ↑ ^{1 2} Физическая энциклопедия, т.4 — М.:Большая Российская Энциклопедия стр.494 и стр.495
5. ↑ ^{1 2} Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
6. ↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей . Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
7. ↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, апеллируя к тому, что он становится сладким не сам по себе, а лишь после того, что в него положен сахар.
8. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
9. ↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Ссылки

Центростремительная сила — Википедия

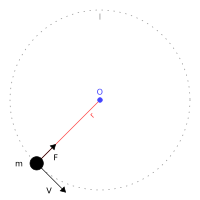Центростремительная сила F поворачивает тело массой m, движущееся со скоростью V вокруг точки O по круговой траектории радиуса r

Центростреми́тельная си́ла — это название той составляющей действующих на тело сил, которая заставляет тело поворачивать (то есть двигаться по траектории, радиус кривизны которой в точке, где находится тело, не может быть принят равным бесконечности). Это составляющая, направленная перпендикулярно мгновенному вектору скорости тела^[1].

Для образования траектории с радиусом кривизны в данной точке r{\displaystyle r}, требуется центростремительная сила Fc=mac=mv2r=mω2r{\displaystyle F_{c}=ma_{c}=m{\frac {v^{2}}{r}}=m\omega ^{2}r}, где ac{\displaystyle a_{c}} — центростремительное ускорение в данной точке, m{\displaystyle m} — масса тела, v{\displaystyle v} — его скорость в данной точке, а ω{\displaystyle \omega } — его угловая скорость в данной точке.

Если обратить внимание на поворот траектории тела, можно выделить ускорение ac→{\displaystyle {\vec {a_{c}}}}, перпендикулярное скорости. Именно это ускорение изменяет направление движения тела, поворачивая траекторию, и для образования кривизны радиуса r{\displaystyle r} на скорости v{\displaystyle v} это ускорение должно быть равно v2r{\displaystyle {\frac {v^{2}}{r}}}, или, что то же самое, ω2r{\displaystyle \omega ^{2}r}, где ω{\displaystyle \omega } — угловая скорость тела в данной точке относительно мгновенного центра поворота (связь между первой формулой и второй очевидна, учитывая что v=ωr{\displaystyle v=\omega r}). Эта составляющая ускорения называется центростремительным ускорением. Согласно второму закону Ньютона, наблюдаемое ускорение тела соответствует сумме действующих на него сил. Это верно в инерциальных системах отсчёта, а согласно принципу Д’Аламбера это, при введении соответствующих сил инерции, верно и в неинерциальных. Составляющая действующих на тело сил, соответствующая центростремительному ускорению, называется центростремительной силой (Fc→=mac→{\displaystyle {\vec {F_{c}}}=m{\vec {a_{c}}}}).

Центростремительная сила не является самостоятельной силой и представляет собой лишь результат формального разложения суммы всех действующих на тело сил на две составляющие — вдоль и поперёк касательной к траектории движения. В случае установившегося (то есть при постоянной угловой скорости) движения тела по круговой траектории за счёт единственной силы, действующей в направлении центра вращения (например, силы натяжения нити, связывающей тело с центром, или при движении по круговой орбите в поле силы гравитации), вся эта сила является центростремительной. Она направлена перпендикулярно к вектору скорости, работы за полный круг не совершает, кинетическая энергия тела не изменяется. Такое движение может продолжаться неограниченно долго.

В общем случае, при движении по любой траектории, отличающейся от круговой, центр поворота не лежит на направлении суммы действующих на тело сил. Так, например, при движении Земли вокруг Солнца по своей эллиптической орбите, действующая на Землю сила взаимного тяготения Земли и Солнца полностью становится центростремительной лишь в афелии и перигелии. При этом тангенциальная составляющая силы реакции связи, совершает работу, ведущую к увеличению кинетической энергии тела (при разгоне) или уменьшению её (при торможении). Это периодически имеет место во Вселенной при движении небесных тел по кеплеровским эллиптическим орбитам вокруг общего центра тяготения, поскольку работа сил связи за полный оборот равна нулю. Так же, за счёт систематического опережения мгновенного центра вращения смещением точки приложения силы, раскручивают, например, пращу.

Так же как скорости, ускорения и траектории тел зависят от выбранной системы отсчёта, от выбора системы отсчёта зависит и то, какую часть суммы сил понадобится считать центростремительной. В частности, переходя в систему отсчёта, связанную непосредственно с движущимся телом, мы естественным образом сводим траекторию в неподвижную точку в центре системы отсчёта, и, соответственно, не можем в контексте этой системы отсчёта говорить ни о центростремительном ускорении данного тела, ни о соответствующей силе. И наоборот, перейдя в систему отсчёта, вращающуюся относительно тел, мы в ней получаем криволинейные траектории этих тел, соответствующие центростремительные ускорения и, соответственно, центростремительные силы.

С понятием «центростремительная сила» и переходом из инерциальной системы отсчёта во вращающуюся неинерциальную, тесно связано понятие «центробежная сила».

В связи со сложностью понимания переходов из одной системы отсчёта в другую, особенно если они движутся относительно друг друга с динамически меняющимся ускорением, понятия центростремительной и центробежной сил вызывают многочисленные споры и недоразумения.

1. Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. М.: ГИТТЛ, 1957

Физические основы механики

Представим себе диск, равномерно вращающийся с угловой скоростью . Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).

Рис. 8.3. Центробежная сила инерции в системе отсчета, связанной с вращающимся диском

Шарик покоится относительно диска и занимает на спице такое положение, при котором сила натяжения пружины оказывается равной произведению массы шарика на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)

где — радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3). Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета. Свяжем с диском вращающуюся неинерциальную систему отсчета К’, в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:

Наблюдатель во вращающейся системе отсчета объясняет равновесие шарика наличием силы инерции

направленной от центра диска 0′ по радиус-вектору .

Сила инерции, действующая на материальную точку в равномерно вращающейся с угловой скоростью ω системе отсчета, называется центробежной силой инерции:

Здесь — вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.

Видео 8.4. Центробежная сила инерции: подвешенные шарики

При произвольном положении начала отсчета на оси вращения, радиус-вектор некоторой материальной точки всегда можно представить в виде

где _парал.— параллельная оси вращения, более того, лежащая на оси вращения (напомним: начинается вектор на оси вращения) составляющая радиус вектора , а — перпендикулярная к оси вращения его составляющая, начинающаяся на оси вращения, в центре той окружности, по которой движется рассматриваемая точка. С помощью известной формулы

учитывая, что векторное произведение и скалярное произведение равны нулю всегда, можно показать, что выражение для центробежной силы инерции представляется в виде

Таким образом, в общем случае, при произвольном выборе начала отсчета на оси вращения, для любого положения материальной точки, действующую на неё центробежную силу инерции, можно записать в виде

Видео 8.5. «Поразительное» поведение цепи — и здесь не обошлось без центробежной силы инерции. Цепь легкая, почти без трения между звеньями

Видео 8.6. «Поразительное» поведение цепи 2. Цепь тяжелая, с большим трением между звеньями

Пример. Сосуд с жидкостью вращается с угловой скоростью вокруг вертикальной оси (рис. 8.4). Найдем форму поверхности жидкости.

Рис. 8.4. Форма поверхности вращающейся жидкости

Задачу решаем в системе отсчета, вращающейся вместе с жидкостью. В этой системе жидкость неподвижна, но кроме силы тяжести на нее действует центробежная сила инерции. Поверхность жидкости симметрична относительно оси вращения. Рассмотрим сечение этой поверхности какой-нибудь вертикальной плоскостью, содержащей ось вращения, которую мы примем за ось .

Возьмем на поверхности элемент жидкости массой , расположенный в точке с координатой . На него действует сила тяжести и центробежная сила инерции (здесь координата есть расстояние от оси вращения, а и — единичные орты). Результирующая этих сил наклонена к вертикали под углом таким, что

Поверхность жидкости, описываемая функцией , всегда располагается ортогонально линии действия внешних сил. Как известно, тангенс того же угла можно найти как отношение приращений

то есть как производную. Получаем уравнение

которое легко интегрируется:

Это уравнение, как известно, описывает параболу. Вращение этой параболы задает параболоид вращения. Таким образом, поверхность вращающейся жидкости принимает форму параболоида вращения. При имеем , то есть плоскую горизонтальную поверхность.

Видео 8.7. Циркулярная «пила» из бумаги – неожиданное применение центробежной силы инерции

Видео 8.8. Сила Кориолиса: траектория движения шарика по вращающейся платформе

Дополнительная информация

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.–— стр.349–353 (§66): детально обсуждается вес тел и проблема взвешивания на Земле.

Центробежная сила — это… Что такое Центробежная сила?

Центробе́жная си́ла^[1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.

Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно нее, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.

Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося по круговой траектории тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.

Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный.

[2]

Формулы

Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).

По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.

Для материальной точки центробежная сила выражается формулой:

где:

 — центробежная сила приложенная к телу,

 — масса тела,

 — угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),

 — радиус-вектор тела во вращающейся системе координат.

Эквивалентное выражение для центробежной силы можно записать как

если использовать обозначение для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.

Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.

Вывод

Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью а сама система движется поступательно с линейной скоростью в инерциальной системе координат и одновременно вращается с угловой скоростью

Тогда линейная скорость тела в инерциальной системе координат равна:

где  — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:

Найдём значение каждого слагаемого в инерциальной системе координат:

где  — линейное ускорение относительно системы,  — угловое ускорение.

Таким образом, получаем:

Последнее слагаемое и будет центростремительным ускорением.

Раскрыв двойное векторное произведение и положив перпендикулярным оси вращения, получим:

Элементарное рассмотрение и мотивировка

Вращение с точки зрения инерциальной системы отсчета

Рассмотрим спицу, вращающуюся вокруг перпендикулярной к ней вертикальной оси с угловой скоростью ω. Вместе со спицей вращается надетый на неё шарик, соединённый с осью пружиной.

Согласно второму закону Ньютона шарик займёт положение равновесия на таком расстоянии R от центра диска, на котором сила натяжения пружины F_pr оказывается равной произведению массы шарика m на его ускорение^[3]:

.^[4]

Связанная со спицей система отсчёта вращается по отношению к инерциальной системе. Относительно системы отсчёта, связанной со спицей, шарик покоится, хотя на него действует сила упругости пружины. Это не противоречит второму закону Ньютона, так как вращающаяся система отсчёта не является инерциальной и соотношение в ней не выполняется.

Вращение с точки зрения неинерциальной системы отсчёта. Сила инерции

Для практических целей, однако, удобнее считать, что второй закон Ньютона выполняется и с точки зрения вращающейся системы отсчёта, введя для этого формально силу инерции ^[4], действующую на шарик вдоль радиуса от центра диска наряду с реальной силой F_pr.

Силу инерции F_cf, вводимую во вращающейся системе отсчёта, называют центробежной силой. Эта сила действует на тело во вращающейся системе отсчёта, независимо от того, покоится тело в этой системе или движется относительно неё со скоростью v’.

Следует иметь в виду, что для правильного описания движения тел во вращающихся системах отсчёта, кроме центробежной силы следует также вводить силу Кориолиса.

В литературе встречается и совсем другое понимание термина «центробежная сила». Так иногда называют реальную силу, приложенную не к совершающему вращательное движение телу, а действующую со стороны тела на ограничивающие его движение связи. В рассмотренном выше примере так называли бы силу, действующую со стороны шарика на пружину. (См., например, ниже ссылку на БСЭ.)

Центробежная сила как реальная сила

Центростремительная и центробежная силы при движении тел по круговым траекториям с общей осью вращения

Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин «центробежная сила» (букв. cила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющего его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона)^[5] в форме:

Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы

Или ещё^[6]:

Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.

Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так^[7].

Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной форме его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Ньютон связывал её с эфиром, заполняющим всё пространство)^[5], остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.

Рассматриваемое тело с массой (точнее — инертной массой) приобретает отличающееся от нуля ускорение в тот же момент , когда начинает действовать на него сила (Второй закон Ньютона:). Однако для достижения отличающейся от нуля скорости требуется некоторое время в соответствии с определением импульса силы: . Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила^[8].

Использование термина «центробежная сила» правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле центробежная сила представляет собой один из членов в формулировке третьего закона Ньютона, антагониста центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направление движения тела (материальной точки).

Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины и , находящихся на расстоянии друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения , где — гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями = и = , то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: = = , а расстояния от центра вращения (центра масс) будут соотноситься, как: = , причём , что непосредственно следует из равенства действующих сил: и , где ускорения равняются соответственно: = и ^[9].

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): =. При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствии с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы тяготения. То же самое справедливо и в отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел, и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

См. также

Примечания

1. ↑ Вне контекста физики/механики/математики, например, в философии, публицистике или художественной литературе, а также иногда и в разговорной речи, слова центробежная сила могут нередко употребляться просто как обозначение некоего влияния, направленного прочь от некоторого «центра»; в таком употреблении это может быть никак не связано не только с каким-либо вращением, но и с понятием силы, как оно употребляется в физике.
2. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука».Главная редакция физико-математической литературы.
3. ↑ Воспользуемся формулой центростремительного ускорения.
4. ↑ ^{1 2} Физическая энциклопедия, т.4 — М.:Большая Российская Энциклопедия стр.494 и стр.495
5. ↑ ^{1 2} Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
6. ↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей . Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
7. ↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким апеллируя к тому, что оно становится сладким не само по себе, а лишь после того, что в него положен сахар.
8. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
9. ↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Ссылки

Центростремительная и центробежная силы — это… Что такое Центростремительная и центробежная силы?

Центростремительная и центробежная силы

Центростремительная и центробежная силы

В буквальном смысле эти силы выглядят как определённым способом ориентированные по отношению к центру — некой точке, равноудалённой от всех точек траектории движущегося тела. В двумерном пространстве (на плоскости) такой траекторией является окружность, а в трехмерном — тоже окружность, образованная пересечением сферической поверхности плоскостью, в общем случае не проходящей через её центр.
Все остальные траектории любого вида центром в этом смысле не обладают, и потому применительно к движущемуся по не круговым траекториям телу использование представления о центростремительной и центробежной силах не оправдано и ведёт к многочисленным недомолвкам и недоразумениям.

Центростремительная и центробежная силы

Центростремительная сила — сила, действующая со стороны неких связей, ограничивающих свободу движения тела, и вызывающая его поворот вокруг центра поворота. Природа связей может быть любой, если они обладают свойством увеличивать потенциальную энергию системы тело-связь при удлинении последней.

Реально существующей является лишь сила реакции связи. Центростремительная, равно как и центробежная сила, как самостоятельная сила, не существует и представляет собой лишь результат формального разложения реальной силы на две составляющие.

В случае установившегося движения тела (вращения) центростремительная сила совпадает с силой, представляющей собой реакцию связи , она направлена перпендикулярно к вектору его скорости, работы не совершает, кинетическая энергия движения тела не изменяется и такое движение может продолжаться неограниченно долго.

В случае неустановившегося движения по кривой (например при раскрутке пращи), траектория движения тела представляет собой спираль и центростремительная сила, по определению нормальная по касательной к траектории, направлена в сторону мгновенного центра вращения и представляет собой результат формального разложения реальной силы реакции связи на две. При этом работу совершает тангенциальная составляющая силы реакции связи, ведущая к изменению кинетической энергии тела (при разгоне) или уменьшению её (при торможении). Это периодически имеет место в Мировом пространстве при движении небесных дел по кеплеровским эллиптическим орбитам вокруг общего центра тяготения

Центробе́жная си́ла — сила, действующая со стороны испытывающего поворот тела на вызывающие этот поворот связи, равная по модулю центростремительной силе и всегда направленная в противоположную ей сторону (Третий закон Ньютона). Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин Центробежная сила (букв. Сила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющего его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона) ^[1] в форме :

Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы

Или ещё^[2]:

Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.

Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так. ^[3]

Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной формы его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Нютон связывал её с эфиром, заполняющим всё пространство)^[4], остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.

Рассматриваемое тело с массой (точнее — инертной массой) m приобретает отличающееся от нуля ускорение a в тот же момент t = 0, когда начинает действовать на него сила F. (Второй закон Ньютона 🙂 Однако для достижения отличающейся от нуля скорости v требуется некоторое время t в соответствие с определением импульса силы : t = mv / F .Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила. ^[5]

Использование термина Центробежная сила правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле Центробежная сила представляет собой один из членов в формулировке Третьего закона Ньютона, антагониста Центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направление движения тела (материальной точки).

Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины M₁ и M₂, находящихся на расстоянии R друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и R есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения F_G:GM₁M₂ / R², где G— гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями v₁ = ω₁ R₁ и v₂ = ω₂ R₂, то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: ω₁ = ω₂ = ω, а расстояния от центра вращения (центра масс) будут соотноситься, как: M₁ / M₂ = R₂ / R₁, причём R₂ + R₁ = R, что непоcредственно следует из равенства действующих сил: F₁ = M₁a₁ и F₂ = M₂a₂, где ускорения равняются соответственно: a₁= ω²R₁ и a₂ = ω²R₂ ^[6]

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): F₁ =F₂ = F_G . При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствие с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы Всемирного тяготения. То же самое справедливо и отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

Переписывая Второй закон в виде F − ma = 0 и заменяя второй член слева на некую силу F_i = − ma, получаем новую запись Второго закона: F + F_i = 0.Здесь обе силы действуют на одно и то же тело, причём их сумма равна нулю, из чего следует, что данное тело в системе отсчёта, связанной с этим телом, покоится, хотя сама система вместе с ним движется ускоренно. Эта сила F_i, ничем не отличается по своему происхождению от силы F (о чём говорит знак равенства в канонической записи закона). Существует предложение называть её Ньютоновской силой инерции. Никакого отношения к центробежной силе эта сила не имеет. ^[5]

Литература

• Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
  
• С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
  
• Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. М.: ГИТТЛ, 1957
  
• «Центробежная сила» в Большой советской энциклопедии

См. также

Примечания

1. ↑ Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
2. ↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей . Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
3. ↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким апеллируя к тому, что оно становится сладким не само по себе, а лишь после того, что в него положен сахар.
4. ↑ Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
5. ↑ ^{1 2} С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
6. ↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Центробежная сила — Википедия. Что такое Центробежная сила

Центробе́жная си́ла^[1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.

Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно неё, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.

Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося по круговой траектории тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.

Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный^[2].

Формулы

Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).

По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.

Для материальной точки центробежная сила выражается формулой:

F→=−m[ω→×[ω→×R→]]=m(ω2R→−(ω→⋅R→)ω→),{\displaystyle {\vec {F}}=-m\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right]=m\left(\omega ^{2}{\vec {R}}-\left({\vec {\omega }}\cdot {\vec {R}}\right){\vec {\omega }}\right),}

где:

F→{\displaystyle {\vec {F}}} — центробежная сила приложенная к телу,

 m{\displaystyle \ m} — масса тела,

ω→{\displaystyle {\vec {\omega }}} — угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),

R→{\displaystyle {\vec {R}}} — радиус-вектор тела во вращающейся системе координат.

Эквивалентное выражение для центробежной силы можно записать как

F→=mω2R0→{\displaystyle {\vec {F}}=m\omega ^{2}{\vec {R_{0}}}}

если использовать обозначение R0→{\displaystyle {\vec {R_{0}}}} для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.

Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.

Вывод

Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью v→n,{\displaystyle {\vec {v}}_{n},} а сама система движется поступательно с линейной скоростью v→0{\displaystyle {\vec {v}}_{0}} в инерциальной системе координат и одновременно вращается с угловой скоростью ω→.{\displaystyle {\vec {\omega }}.}

Тогда линейная скорость тела в инерциальной системе координат равна:

v→=v→0+[ω→×R→]+v→n,{\displaystyle {\vec {v}}={\vec {v}}_{0}+\left[{\vec {\omega }}\times {\vec {R}}\right]+{\vec {v}}_{n},}

где R→{\displaystyle {\vec {R}}} — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:

ddtv→=ddtv→0+ddt[ω→×R→]+ddtv→n.{\displaystyle {\frac {d}{dt}}{\vec {v}}={\frac {d}{dt}}{\vec {v}}_{0}+{\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]+{\frac {d}{dt}}{\vec {v}}_{n}.}

Найдём значение каждого слагаемого в инерциальной системе координат:

ddtv→0=a→0,{\displaystyle {\frac {d}{dt}}{\vec {v}}_{0}={\vec {a}}_{0},}

ddtv→n=a→n+[ω→×v→n],{\displaystyle {\frac {d}{dt}}{\vec {v}}_{n}={\vec {a}}_{n}+\left[{\vec {\omega }}\times {\vec {v}}_{n}\right],}

ddt[ω→×R→]=[ε→×R→]+[ω→×ddtR→]=[ε→×R→]+[ω→×v→n]+[ω→×[ω→×R→]],{\displaystyle {\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+\left[{\vec {\omega }}\times {\frac {d}{dt}}{\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+\left[{\vec {\omega }}\times {\vec {v}}_{n}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right],} где a→n{\displaystyle {\vec {a}}_{n}} — линейное ускорение относительно системы, ε→{\displaystyle {\vec {\varepsilon }}} — угловое ускорение.

Таким образом, получаем:

ddtv→=a→=a→0+a→n+[ε→×R→]+2[ω→×v→n]+[ω→×[ω→×R→]].{\displaystyle {\frac {d}{dt}}{\vec {v}}={\vec {a}}={\vec {a}}_{0}+{\vec {a}}_{n}+\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+2\left[{\vec {\omega }}\times {\vec {v}}_{n}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right].}

Последнее слагаемое и будет центростремительным ускорением.

Раскрыв двойное векторное произведение и положив R→{\displaystyle {\vec {R}}} перпендикулярным оси вращения, получим:

a→c=ω→(ω→R→)−R→ω→2=−R→ω→2.{\displaystyle {\vec {a}}_{c}={\vec {\omega }}({\vec {\omega }}{\vec {R}})-{\vec {R}}{\vec {\omega }}^{2}=-{\vec {R}}{\vec {\omega }}^{2}.}

Элементарное рассмотрение и мотивировка

Вращение с точки зрения инерциальной системы отсчета

Рассмотрим спицу, вращающуюся вокруг перпендикулярной к ней вертикальной оси с угловой скоростью ω{\displaystyle \omega }. Вместе со спицей вращается надетый на неё шарик, соединённый с осью пружиной.

Согласно второму закону Ньютона шарик займёт положение равновесия на таком расстоянии R{\displaystyle R} от центра диска, на котором сила натяжения пружины Fpr{\displaystyle F_{\mathrm {pr} }} оказывается равной произведению массы шарика m{\displaystyle m} на его ускорение^[3]an=ω2R{\displaystyle a_{n}=\omega ^{2}R}:

Fpr=−mω2R=−mv2R{\displaystyle F_{\mathrm {pr} }=-m\omega ^{2}R=-m{\frac {v^{2}}{R}}}.^[4]

Связанная со спицей система отсчёта вращается по отношению к инерциальной системе. Относительно системы отсчёта, связанной со спицей, шарик покоится, хотя на него действует сила упругости пружины. Это не противоречит второму закону Ньютона, так как вращающаяся система отсчёта не является инерциальной и соотношение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} в ней не выполняется.

Вращение с точки зрения неинерциальной системы отсчёта. Сила инерции

Для практических целей, однако, удобнее считать, что второй закон Ньютона выполняется и с точки зрения вращающейся системы отсчёта, введя для этого формально силу инерции Fcf=−Fpr=mω2R{\displaystyle F_{\mathrm {cf} }=-F_{\mathrm {pr} }=m\omega ^{2}R}^[4], действующую на шарик вдоль радиуса от центра диска наряду с реальной силой Fpr{\displaystyle F_{\mathrm {pr} }}.

Силу инерции Fcf{\displaystyle F_{\mathrm {cf} }}, вводимую во вращающейся системе отсчёта, называют центробежной силой. Эта сила действует на тело во вращающейся системе отсчёта, независимо от того, покоится тело в этой системе или движется относительно неё со скоростью v{\displaystyle v}’.

Следует иметь в виду, что для правильного описания движения тел во вращающихся системах отсчёта, кроме центробежной силы следует также вводить силу Кориолиса.

В литературе встречается и совсем другое понимание термина «центробежная сила». Так иногда называют реальную силу, приложенную не к совершающему вращательное движение телу, а действующую со стороны тела на ограничивающие его движение связи. В рассмотренном выше примере так называли бы силу, действующую со стороны шарика на пружину. (См., например, ниже ссылку на БСЭ.)

Центробежная сила как реальная сила

Центростремительная и центробежная силы при движении тел по круговым траекториям с общей осью вращения

Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин «центробежная сила» (букв. сила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющая его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона)^[5] в форме:

Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы

Или ещё^[6]:

Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.

Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так^[7].

Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной форме его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Ньютон связывал её с эфиром, заполняющим всё пространство)^[5], остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.

Рассматриваемое тело с массой (точнее — инертной массой) m{\displaystyle m} приобретает отличающееся от нуля ускорение a{\displaystyle a} в тот же момент t=0{\displaystyle t=0}, когда начинает действовать на него сила F{\displaystyle F} (Второй закон Ньютона:F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}). Однако для достижения отличающейся от нуля скорости v{\displaystyle v} требуется некоторое время t{\displaystyle t} в соответствии с определением импульса силы: t=mv/F{\displaystyle t=mv/F}. Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила^[8].

Использование термина «центробежная сила» правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле центробежная сила представляет собой один из членов в формулировке третьего закона Ньютона, антагониста центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направления движения тела (материальной точки).

Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины M1{\displaystyle {M_{1}}} и M2{\displaystyle {M_{2}}}, находящихся на расстоянии R{\displaystyle R} друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и R{\displaystyle R} есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения FG:GM1M2/R2{\displaystyle {F_{G}}:{GM_{1}M_{2}/R^{2}}}, где G{\displaystyle G}- гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями v1{\displaystyle {v_{1}}} = ω1{\displaystyle {\omega }_{1}} R1{\displaystyle {R_{1}}} и v2{\displaystyle {v_{2}}} = ω2{\displaystyle {\omega _{2}}} R2{\displaystyle {R_{2}}}, то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: ω1{\displaystyle {\omega _{1}}} = ω2{\displaystyle {\omega _{2}}} = ω{\displaystyle \omega }, а расстояния от центра вращения (центра масс) будут соотноситься, как: M1/M2{\displaystyle {M_{1}/M_{2}}} = R2/R1{\displaystyle {R_{2}/R_{1}}}, причём R2+R1=R{\displaystyle {R_{2}}+{R_{1}}=R}, что непосредственно следует из равенства действующих сил: F1=M1a1{\displaystyle {F_{1}}={M_{1}}{a_{1}}} и F2=M2a2{\displaystyle {F_{2}}={M_{2}}{a_{2}}}, где ускорения равняются соответственно: a1{\displaystyle {a_{1}}}= ω2R1{\displaystyle {\omega ^{2}}{R_{1}}} и a2=ω2R2{\displaystyle {a_{2}}={\omega ^{2}}{R_{2}}}^[9].

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): F1{\displaystyle {F_{1}}} =F2{\displaystyle {F_{2}}} =FG{\displaystyle ={F_{G}}}. При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствии с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы тяготения. То же самое справедливо и в отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел, и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

См. также

Примечания

1. ↑ Вне контекста физики/механики/математики, например, в философии, публицистике или художественной литературе, а также иногда и в разговорной речи, слова центробежная сила могут нередко употребляться просто как обозначение некоего влияния, направленного прочь от некоторого «центра»; в таком употреблении это может быть никак не связано не только с каким-либо вращением, но и с понятием силы, как оно употребляется в физике.
2. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
3. ↑ Воспользуемся формулой центростремительного ускорения.
4. ↑ ^{1 2} Физическая энциклопедия, т.4 — М.:Большая Российская Энциклопедия стр.494 и стр.495
5. ↑ ^{1 2} Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
6. ↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей . Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
7. ↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, апеллируя к тому, что он становится сладким не сам по себе, а лишь после того, что в него положен сахар.
8. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
9. ↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Ссылки