Почему внутри источника существует внутреннее сопротивление. Реактивное внутреннее сопротивление

Внутреннее сопротивление источников тока пренебрежимо мало.
Внутреннее сопротивление источника тока пренебрежимо мало.
Внутреннее сопротивление источника тока, рассчитанное по данной формуле, будет, строго говоря, действительно только для данного интервала нагрузок вследствие того, что поляризация не пропорциональна плотности тока.
Внутреннее сопротивление источника тока — сопротивление, которым обладает, источник тока. Это важная характеристика всякого источника тока, определяющая его внутреннее падение напряжения, напряжение, которое может создать источник на концах питаемой им цепи, и тот наибольший ток, который может дать источник при коротком замыкании.
Внутреннее сопротивление источника тока — сопротивление, которым обладает источник тока.
Внутренним сопротивлением источника тока, сопротивлениями соединительных проводов и контактов в ключах пренебречь.

Чему равно внутреннее сопротивление источника тока, ЭДС которого равна 30 В, если после включения внешней цепи сопротивлением 6 Ом напряжение на зажимах батареи стало равным 18 В.
Отсюда находим внутреннее сопротивление источника тока.
Здесь и далее внутренним сопротивлением источника тока и подводящих проводов следует пренебречь, если оно не задано в условии.
Здесь тэар при небольшом внутреннем сопротивлении источника тока и соответственно небольшом сопротивлении лампы rgK относительно невелико. Соответственно тзар, определяющееся в основном высоким сопротивлением RgK (получающимся в результате того, что при разряде потенциал сетки оказывается под отрицательным потенциалом относительно катода), становится во много раз больше, чем тзар и длина экспоненциального импульса на выходе (считая продолжительность для половины амплитуды) в несколько десятков раз превышает длительность импульса, по-данного на вход.

Определить электродвижущую силу и внутреннее сопротивление источника тока, если при одном положении движка реостата амперметр показывает 0 2 А, вольтметр — 1 8 В, а при другом положении движка — 0 4 Аи 1 6 В соответственно.
Обозначим через г — внутреннее сопротивление источника тока, через R — сопротивление каждого из вольтметров.
Ничем, так как внутреннее сопротивление источника тока бесконечно велико.
Сначала определим ЭДС и внутреннее сопротивление источника тока.

Для определения ЭДС и внутреннего сопротивления источника тока к его выходу был подключен сначала резистор сопротивлением Д 2 Ом, затем — резистор сопротивлением Л2 4 Ом.
Наклон этих кривых определяется внутренним сопротивлением источника тока. В это понятие включается обычно как собственно омическое сопротивление, так и сопротивление, обусловленное поляризацией.
Здесь пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.
Для создания такого режима необходимо, чтобы внутреннее сопротивление источника тока было больше сопротивления базо-эмиг-терного перехода как в открытом, так и в закрытом состоянии. Чаще всего это условие выполняется при включении последовательно входу транзнсюра индуктивной катушки, которая одновременно является контурной катушкой.

При прохождении тока часть мощности выделяется на внутреннем сопротивлении источника тока.
К каким отрицательным последствиям приводит то, что внутреннее сопротивление источника тока дифференциального каскада имеет конечное значение.
Цепь из двух параллельных ветвей. U (в в течение t сек. равна.| Соотношения между единицами энергии. Мощность, передаваемая нагрузке, будет максимальной при раввщ ве внутреннего сопротивления источника тока и сопротивления нагрузки.
Зачастую серьезные недоразумения возникают у учащихся из-за неумения правильно учитывать влияние внутреннего сопротивления источников тока на режим работы всей электрической цепи. Ряд задач параграфа (например, 383, 385, 386, 392 — 395 и др.) посвящен специально выяснению этого вопроса, а также выяснению вопроса о выборе наиболее выгодных условий работы источников тока.
Кристаллы аммиаката цинка не-электропроводны, и образование этого соединения приводит к увеличению внутреннего сопротивления источника тока.
В любом замкнутом контуре (например, а ] 6, с алгебраическая сумма электродвижущих сил равна алгебраической сумме произведений величин токов на сопротивления отдельных участков цепи. Вычисляя сумму произведений токов на сопротивления отдельных участков цепи, следует учитывать также и внутренние сопротивления источников тока.
Если предположить, что емкость C0z пренебрежимо мала или включить ее в схему четырехполюсника Q, то внутреннее сопротивление источника тока / g можно считать действительным и равным У.
Получили, что максимальная мощность выделяется на нагрузке при условии, что величина внешнего сопротивления цепи R равна внутреннему сопротивлению источника тока.
Здесь под R понимается сопротивление всех резисторов, образующих цепь (сопротивление нагрузки), а под г — внутреннее сопротивление источника тока.

Здесь под R понимается сопротивление всех резисторов, образующих цепь (сопротивление нагрузки), а под т — внутреннее сопротивление источника тока.

Механическая система и ее электрические модели (метод четырехполюсников. Как уже указывалось выше, внутреннее сопротивление источника напряжения (первая система аналогий) должно быть весьма малым, а внутреннее сопротивление источника тока (вторая система аналогий) — весьма большим, по сравнению с сопротивлением модели.
К положительным качествам рассматриваемого преобразователя следует отнести то, что в нем не предъявляется особо жестких требований к переходному сопротивлению ключей, так как величина их переходного сопротивления составляет лишь незначительную часть внутреннего сопротивления источника тока и не оказывает влияния на точность преобразования.
Итак, при последовательном включении п одинаковых источников тока электродвижущая сила образующейся батареи в п раз превышает электродвижущую силу отдельного источника тока, однако в этом случае складываются не только электродвижущие силы, но также и внутренние сопротивления источников тока. Такое включение является выгодным, когда внешнее сопротивление цепи весьма велико в сравнении с внутренним сопротивлением.
Следует отметить, что схема рис. 1 — 2 6 эквивалентна схеме рис. 1 — 1 а только в отношений энергии, выделяющейся в сопротивлении нагрузки R, и не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника тока.
Но Сумма разностей потенциалов замкнутой цепи равна нулю, сумма сопротивлений всех участков замкнутой цепи — это ее суммарное сопротивление, которое обычно записывают в виде двух слагаемых: R — внешнее (по отношению к источникам) сопротивление иг — внутреннее сопротивление источников тока.
Второй [ IMAGE ] Схема к примеру. В этом уравнении г и г % — внутренние сопротивления источни-ков тока е и е2 — на схеме не показаны; IR, IR2 и IRS — падения напряжения на внешних сопротивлениях цепи; / г, и / г2 — падения напряжений на внутренних сопротивлениях источников тока.
Внутреннее сопротивление источника тока может быть как чисто активным, так и реактивным.
Зависимость р / ро — отношения (выраженного в децибелах звукового давления на поверхности жесткого цилиндра (с высотой, равной его диаметру, куба, сферы к звуковому давлению, имевшему место в поле до их внесения, от отношения dA (или. /. — диаметра цилиндра или сферы (или ребра куба к длине волны. Параметр семейства кривых — угол Ф между осью цилиндра, куба, сферы и направлением прихода звука. При расчете микрофонных усилителей исходят из следующих соображений. Номинальное сопротивление микрофона является внутренним сопротивлением источника тока на входе усилителя, входное сопротивление усилителя — сопротивлением нагрузки микрофона.
В качестве источников тока в потенциометрии чаще всего применяют аккумуляторы или сухие элементы, значительно реже — стабилизированные источники постоянного тока. Современные потенциометры устроены таким образом, что внутреннее сопротивление источника тока не отражается на работе потенциометра. При работе с сухими батареями и аккумуляторами необходимо учитывать зависимость разрядного тока от времени, которая имеет минимальную крутизну через 10 — 15 мин после включения.
Распределение электрического напряжения вдоль обмотки сверхпроводящего магнита при образовании в нем нормальной зоны.

На самом деле (рис. 9.2) высокий потенциал развивается внутри обмотки, где существует активная компонента напряжения, направленная навстречу индуктивной. Небольшая разность потенциалов между подводящими проводами обусловлена внутренним сопротивлением источника тока, который обычно автоматически отключается при переходе магнита в нормальное состояние. Но даже если это не произойдет, напряжение на источнике тока будет составлять всего лишь несколько вольт по сравнению с сотнями и, возможно, тысячами вольт в нормальной зоне. Поэтому напряжением источника можно пренебречь, но источник тока следует по возможности быстро отключить, чтобы не допустить длительного тепловыделения в обмотке и криостате.

Символом Rt на рис. 5.12, а обозначено внутреннее сопротивление источника тока.
Ключ, закорачивающий точку А на землю, с малым сопротивлением в открытом состоянии. Сопротивление открытого ключа обычно пренебрежимо мало по срав-нению с внутренним сопротивлением источника тока. Поэтому падение напряжения на ключе вызывает ничтожную погрешность.
Зависимость зарядного тока гео. На рис. 3 показана зависимость зарядного тока геометрической емкости от времени без учета токов абсорбции. Необходимо отметить, что спад тока в этом случае определяется внутренним сопротивлением источника тока, а не состоянием изоляции.
Хорошо, что при решении задачи Вы воспользовались методом эквивалентного активного двухполюсника. К сожалению, Вы ошиблись в определении значения сопротивления активного двухполюсника R3K: внутреннее сопротивление источника тока бесконечно велико, поэтому пассивный двухполюсник, к которому преобразуется схема рис. 6.13 а, при определении R3K будет содержать два резис-тивных элемента, соединенных последовательно.
К, так как в противном случае в выражении (5.1) должно быть учтено также напряжение непосредственно на входе усилителя. Вторым ограничивающим условием при выводе соотношения (5.1) является предположение о том, что внутреннее сопротивление источника тока весьма мало.
Таким образом, трансформатор изменяет величину сопротивления R в k2 раз.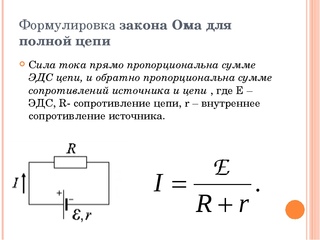 Этим широко пользуются при разработке различных электрических схем для согласования сопротивлений нагрузки с внутренним сопротивлением источников тока.
Основные типы однофазных трансформаторов.| Однофазные трансформаторы большой мощности. Таким образом, трансформатор изменяет величину сопротивления г в k2 раз. Этим свойством широко пользуются ьри разработке различных электрических схем для согласования сопротивлений нагрузки с внутренним сопротивлением источников тока.
Простей-шая электрическая цепь. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.
Цепь постоянного тока. Напряжение, действующее во внешней электрической цепи источника тока, может быть представлено в виде суммы падений напряжения на отдельных элементах этой цепи.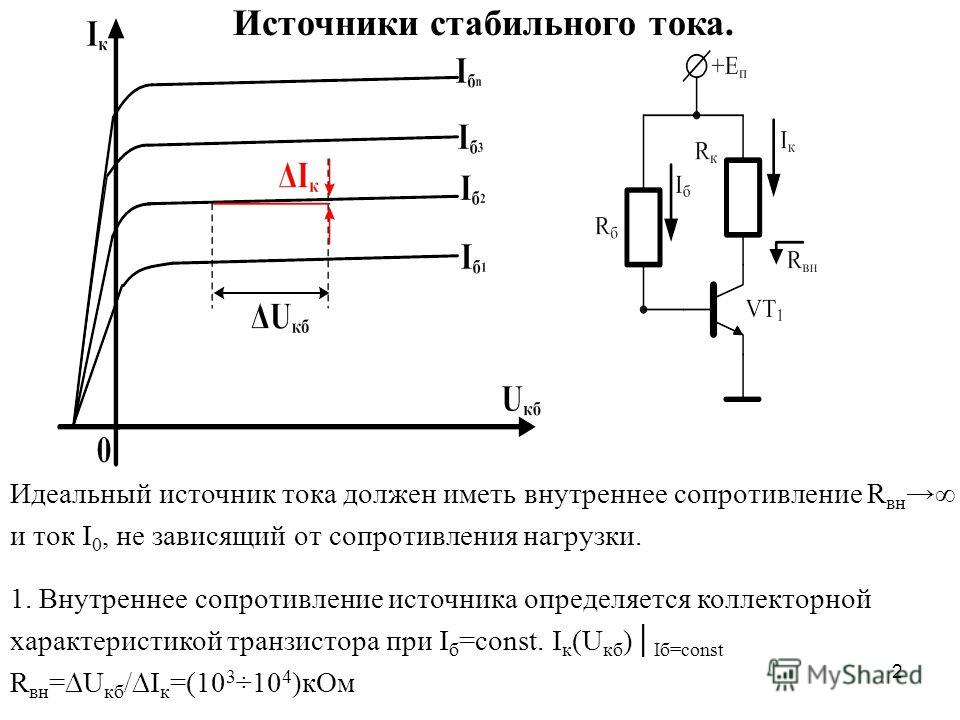 Но ведь ток, циркулирующий в цепи, протекает и через источник тока, который имеет свое сопротивление, называемое внутренним сопротивлением источника тока.

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.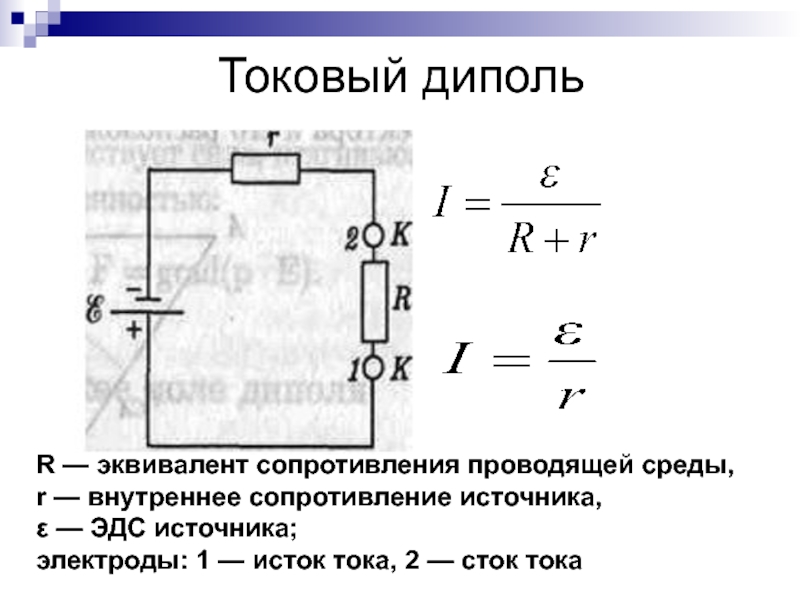

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

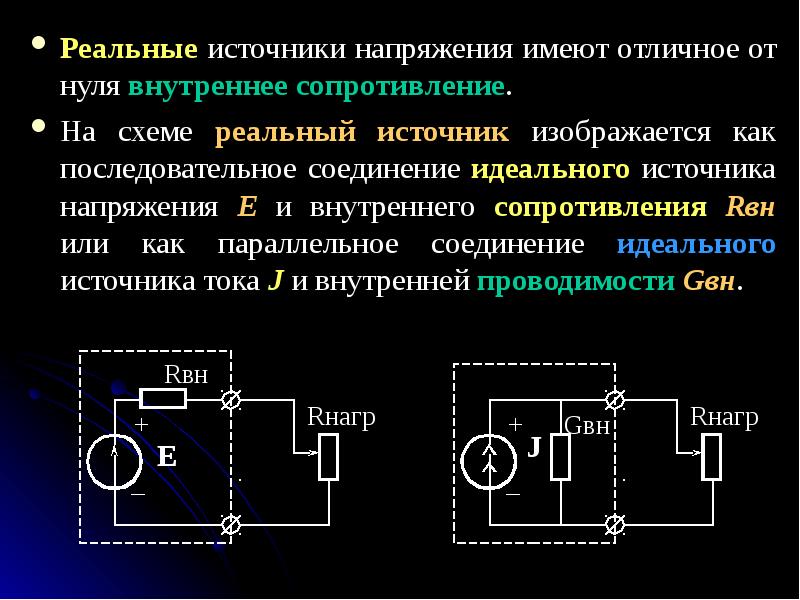
На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен . Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Введение

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление , то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности , отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1 ) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где U out1 I 1 , U out2 — выходное напряжение при токе I 2 . Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:

где U oc — выходное напряжение в режиме холостого хода (англ. open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём.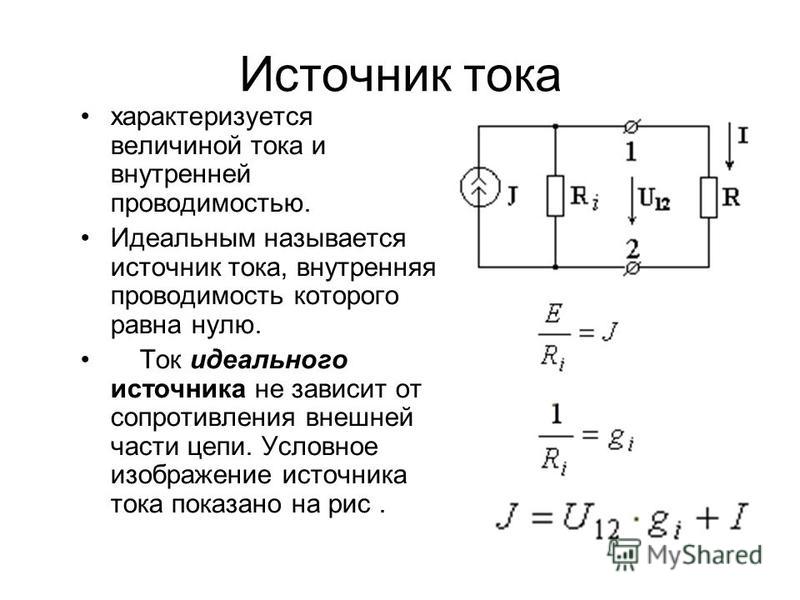 Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы . Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

Большое внутреннее сопротивление

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов .

См. также

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5

Примечания

Wikimedia Foundation . 2010 . Политехнический терминологический толковый словарь

Чему равно внутреннее сопротивление источника эдс. Внутреннее сопротивление — источник

Введение

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

• Автомобильный свинцово-кислотный аккумулятор напряжением 12 вольт и ёмкостью 55 А·ч
• Восемь батареек типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление , то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности , отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1 ) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где U out1 I 1 , U out2 — выходное напряжение при токе I 2 . Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:

где U oc — выходное напряжение в режиме холостого хода (англ. open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём. Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы . Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора.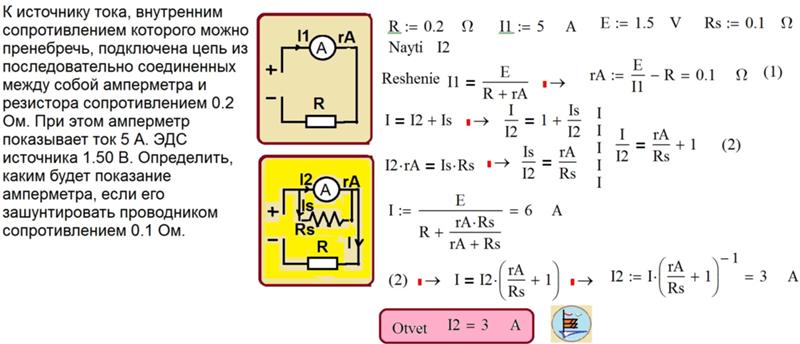 Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

Большое внутреннее сопротивление

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

• элементов с отрицательным дифференциальным сопротивлением , например, туннельных диодов

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов .

См. также

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5

Примечания

Wikimedia Foundation . 2010 . Политехнический терминологический толковый словарь

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен . Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Внутреннее сопротивление источников тока пренебрежимо мало.
Внутреннее сопротивление источника тока пренебрежимо мало.
Внутреннее сопротивление источника тока, рассчитанное по данной формуле, будет, строго говоря, действительно только для данного интервала нагрузок вследствие того, что поляризация не пропорциональна плотности тока.
Внутреннее сопротивление источника тока — сопротивление, которым обладает, источник тока. Это важная характеристика всякого источника тока, определяющая его внутреннее падение напряжения, напряжение, которое может создать источник на концах питаемой им цепи, и тот наибольший ток, который может дать источник при коротком замыкании.
Внутреннее сопротивление источника тока — сопротивление, которым обладает источник тока.
Внутренним сопротивлением источника тока, сопротивлениями соединительных проводов и контактов в ключах пренебречь.
Чему равно внутреннее сопротивление источника тока, ЭДС которого равна 30 В, если после включения внешней цепи сопротивлением 6 Ом напряжение на зажимах батареи стало равным 18 В.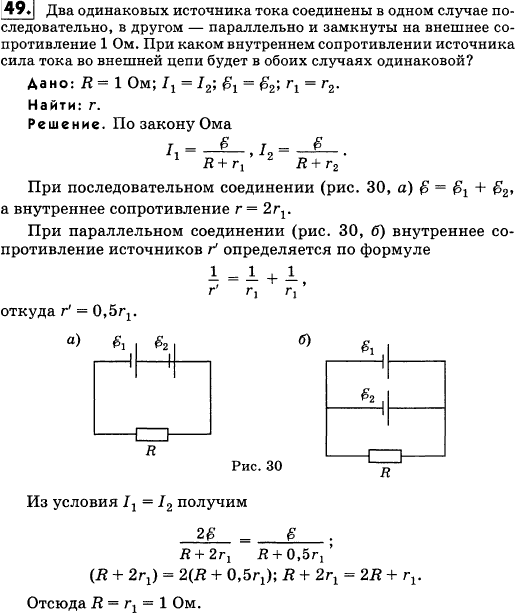
Отсюда находим внутреннее сопротивление источника тока.
Здесь и далее внутренним сопротивлением источника тока и подводящих проводов следует пренебречь, если оно не задано в условии.
Здесь тэар при небольшом внутреннем сопротивлении источника тока и соответственно небольшом сопротивлении лампы rgK относительно невелико. Соответственно тзар, определяющееся в основном высоким сопротивлением RgK (получающимся в результате того, что при разряде потенциал сетки оказывается под отрицательным потенциалом относительно катода), становится во много раз больше, чем тзар и длина экспоненциального импульса на выходе (считая продолжительность для половины амплитуды) в несколько десятков раз превышает длительность импульса, по-данного на вход.
Определить электродвижущую силу и внутреннее сопротивление источника тока, если при одном положении движка реостата амперметр показывает 0 2 А, вольтметр — 1 8 В, а при другом положении движка — 0 4 Аи 1 6 В соответственно.
Обозначим через г — внутреннее сопротивление источника тока, через R — сопротивление каждого из вольтметров.
Ничем, так как внутреннее сопротивление источника тока бесконечно велико.
Сначала определим ЭДС и внутреннее сопротивление источника тока.

Для определения ЭДС и внутреннего сопротивления источника тока к его выходу был подключен сначала резистор сопротивлением Д 2 Ом, затем — резистор сопротивлением Л2 4 Ом.
Наклон этих кривых определяется внутренним сопротивлением источника тока. В это понятие включается обычно как собственно омическое сопротивление, так и сопротивление, обусловленное поляризацией.
Здесь пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.
Для создания такого режима необходимо, чтобы внутреннее сопротивление источника тока было больше сопротивления базо-эмиг-терного перехода как в открытом, так и в закрытом состоянии. Чаще всего это условие выполняется при включении последовательно входу транзнсюра индуктивной катушки, которая одновременно является контурной катушкой.
При прохождении тока часть мощности выделяется на внутреннем сопротивлении источника тока.
К каким отрицательным последствиям приводит то, что внутреннее сопротивление источника тока дифференциального каскада имеет конечное значение.
Цепь из двух параллельных ветвей. U (в в течение t сек. равна.| Соотношения между единицами энергии. Мощность, передаваемая нагрузке, будет максимальной при раввщ ве внутреннего сопротивления источника тока и сопротивления нагрузки.
Зачастую серьезные недоразумения возникают у учащихся из-за неумения правильно учитывать влияние внутреннего сопротивления источников тока на режим работы всей электрической цепи. Ряд задач параграфа (например, 383, 385, 386, 392 — 395 и др.) посвящен специально выяснению этого вопроса, а также выяснению вопроса о выборе наиболее выгодных условий работы источников тока.
Кристаллы аммиаката цинка не-электропроводны, и образование этого соединения приводит к увеличению внутреннего сопротивления источника тока.
В любом замкнутом контуре (например, а ] 6, с алгебраическая сумма электродвижущих сил равна алгебраической сумме произведений величин токов на сопротивления отдельных участков цепи. Вычисляя сумму произведений токов на сопротивления отдельных участков цепи, следует учитывать также и внутренние сопротивления источников тока.
Если предположить, что емкость C0z пренебрежимо мала или включить ее в схему четырехполюсника Q, то внутреннее сопротивление источника тока / g можно считать действительным и равным У.
Получили, что максимальная мощность выделяется на нагрузке при условии, что величина внешнего сопротивления цепи R равна внутреннему сопротивлению источника тока.
Здесь под R понимается сопротивление всех резисторов, образующих цепь (сопротивление нагрузки), а под г — внутреннее сопротивление источника тока.

Здесь под R понимается сопротивление всех резисторов, образующих цепь (сопротивление нагрузки), а под т — внутреннее сопротивление источника тока.
Механическая система и ее электрические модели (метод четырехполюсников. Как уже указывалось выше, внутреннее сопротивление источника напряжения (первая система аналогий) должно быть весьма малым, а внутреннее сопротивление источника тока (вторая система аналогий) — весьма большим, по сравнению с сопротивлением модели.
К положительным качествам рассматриваемого преобразователя следует отнести то, что в нем не предъявляется особо жестких требований к переходному сопротивлению ключей, так как величина их переходного сопротивления составляет лишь незначительную часть внутреннего сопротивления источника тока и не оказывает влияния на точность преобразования.
Итак, при последовательном включении п одинаковых источников тока электродвижущая сила образующейся батареи в п раз превышает электродвижущую силу отдельного источника тока, однако в этом случае складываются не только электродвижущие силы, но также и внутренние сопротивления источников тока. Такое включение является выгодным, когда внешнее сопротивление цепи весьма велико в сравнении с внутренним сопротивлением.
Следует отметить, что схема рис. 1 — 2 6 эквивалентна схеме рис. 1 — 1 а только в отношений энергии, выделяющейся в сопротивлении нагрузки R, и не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника тока.
Но Сумма разностей потенциалов замкнутой цепи равна нулю, сумма сопротивлений всех участков замкнутой цепи — это ее суммарное сопротивление, которое обычно записывают в виде двух слагаемых: R — внешнее (по отношению к источникам) сопротивление иг — внутреннее сопротивление источников тока.
Второй [ IMAGE ] Схема к примеру. В этом уравнении г и г % — внутренние сопротивления источни-ков тока е и е2 — на схеме не показаны; IR, IR2 и IRS — падения напряжения на внешних сопротивлениях цепи; / г, и / г2 — падения напряжений на внутренних сопротивлениях источников тока.
Внутреннее сопротивление источника тока может быть как чисто активным, так и реактивным.
Зависимость р / ро — отношения (выраженного в децибелах звукового давления на поверхности жесткого цилиндра (с высотой, равной его диаметру, куба, сферы к звуковому давлению, имевшему место в поле до их внесения, от отношения dA (или. /. — диаметра цилиндра или сферы (или ребра куба к длине волны. Параметр семейства кривых — угол Ф между осью цилиндра, куба, сферы и направлением прихода звука. При расчете микрофонных усилителей исходят из следующих соображений. Номинальное сопротивление микрофона является внутренним сопротивлением источника тока на входе усилителя, входное сопротивление усилителя — сопротивлением нагрузки микрофона.
В качестве источников тока в потенциометрии чаще всего применяют аккумуляторы или сухие элементы, значительно реже — стабилизированные источники постоянного тока. Современные потенциометры устроены таким образом, что внутреннее сопротивление источника тока не отражается на работе потенциометра. При работе с сухими батареями и аккумуляторами необходимо учитывать зависимость разрядного тока от времени, которая имеет минимальную крутизну через 10 — 15 мин после включения.
Распределение электрического напряжения вдоль обмотки сверхпроводящего магнита при образовании в нем нормальной зоны. На самом деле (рис. 9.2) высокий потенциал развивается внутри обмотки, где существует активная компонента напряжения, направленная навстречу индуктивной. Небольшая разность потенциалов между подводящими проводами обусловлена внутренним сопротивлением источника тока, который обычно автоматически отключается при переходе магнита в нормальное состояние. Но даже если это не произойдет, напряжение на источнике тока будет составлять всего лишь несколько вольт по сравнению с сотнями и, возможно, тысячами вольт в нормальной зоне. Поэтому напряжением источника можно пренебречь, но источник тока следует по возможности быстро отключить, чтобы не допустить длительного тепловыделения в обмотке и криостате.

Символом Rt на рис. 5.12, а обозначено внутреннее сопротивление источника тока.
Ключ, закорачивающий точку А на землю, с малым сопротивлением в открытом состоянии. Сопротивление открытого ключа обычно пренебрежимо мало по срав-нению с внутренним сопротивлением источника тока. Поэтому падение напряжения на ключе вызывает ничтожную погрешность.
Зависимость зарядного тока гео. На рис. 3 показана зависимость зарядного тока геометрической емкости от времени без учета токов абсорбции. Необходимо отметить, что спад тока в этом случае определяется внутренним сопротивлением источника тока, а не состоянием изоляции.
Хорошо, что при решении задачи Вы воспользовались методом эквивалентного активного двухполюсника. К сожалению, Вы ошиблись в определении значения сопротивления активного двухполюсника R3K: внутреннее сопротивление источника тока бесконечно велико, поэтому пассивный двухполюсник, к которому преобразуется схема рис. 6.13 а, при определении R3K будет содержать два резис-тивных элемента, соединенных последовательно.
К, так как в противном случае в выражении (5.1) должно быть учтено также напряжение непосредственно на входе усилителя. Вторым ограничивающим условием при выводе соотношения (5.1) является предположение о том, что внутреннее сопротивление источника тока весьма мало.
Таким образом, трансформатор изменяет величину сопротивления R в k2 раз. Этим широко пользуются при разработке различных электрических схем для согласования сопротивлений нагрузки с внутренним сопротивлением источников тока.
Основные типы однофазных трансформаторов.| Однофазные трансформаторы большой мощности. Таким образом, трансформатор изменяет величину сопротивления г в k2 раз. Этим свойством широко пользуются ьри разработке различных электрических схем для согласования сопротивлений нагрузки с внутренним сопротивлением источников тока.
Простей-шая электрическая цепь. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.
Цепь постоянного тока. Напряжение, действующее во внешней электрической цепи источника тока, может быть представлено в виде суммы падений напряжения на отдельных элементах этой цепи. Но ведь ток, циркулирующий в цепи, протекает и через источник тока, который имеет свое сопротивление, называемое внутренним сопротивлением источника тока.

Вопрос №1. Электротехника — это область науки и техники, изучающая электрические и магнитные явления и их использование в практических целях.

Электрическая цепь — это совокупность устройств, предназначенных для производства, передачи, преобразования и использования электрического тока.

Все электротехнические устройства по назначению, принципу действия и конструктивному оформлению можно разделить на три большие группы .

Источники энергии , т.е. устройства, вырабатывающие электрический ток (генераторы, термоэлементы, фотоэлементы, химические элементы).

Приемники , или нагрузка, т.е. устройства, потребляющие электрический ток (электродвигатели, электролампы, электромеханизмы и т.д.).

Проводники, а также различная коммутационная аппаратура (выключатели, реле, контакторы и т.д.).

Направленное движение электрических зарядов называют электрическим током . Электрический ток может возникать в замкнутой электрической цепи. Электрический ток, направление и величина которого неизменны, называют постоянным током и обозначают прописной буквой I .

Электрический ток, величина и направление которого не остаются постоянными, называется переменным током. Значение переменного тока в рассматриваемый момент времени называют мгновенным и обозначают строчной буквой i .

Для работы электрической цепи необходимо наличие источников энергии. В любом источнике за счет сторонних сил неэлектрического происхождения создается электродвижущая сила . На зажимах источника возникает разность потенциалов или напряжение , под воздействием которого во внешней, присоединенной к источнику части цепи, возникает электрический ток.

Различают активные и пассивные цепи , участки и элементы цепей. Активными называют электрические цепи, содержащие источники энергии, пассивными — электрические цепи, не содержащие источников энергии. Электрическую цепь называют линейной , если ни один параметр цепи не зависит от величины или направления тока, или напряжения. Электрическая цепь является нелинейной , если она содержит хотя бы один нелинейный элемент. Параметры нелинейных элементов зависят от величины или направления тока, или напряжения.

Электрическая схема — это графическое изображение электрической цепи, включающее в себя условные обозначения устройств и показывающее соединение этих устройств. На рис. 1.1 изображена электрическая схема цепи, состоящей из источника энергии, электроламп 1 и 2, электродвигателя 3.

Для облегчения анализа электрическую цепь заменяют схемой замещения.

Схема замещения — это графическое изображение электрической цепи с помощью идеальных элементов, параметрами которых являются параметры замещаемых элементов.

На рисунке 1.2 показана схема замещения.

Простейшими пассивными элементами схемы замещения являются сопротивление, индуктивность и емкость.

В реальной цепи электрическим сопротивлением обладают не только реостат или резистор, но и проводники, катушки, конденсаторы и т.д. Общим свойством всех устройств, обладающих сопротивлением, является необратимое преобразование электрической энергии в тепловую. Тепловая энергия, выделяемая в сопротивлении, полезно используется или рассеивается в пространстве. В схеме замещения во всех случаях, когда надо учесть необратимое преобразование энергии, включается сопротивление.

Сопротивление проводника определяется по формуле

где l — длина проводника;

S — сечение;

r — удельное сопротивление.

Величина, обратная сопротивлению, называется проводимостью .

Сопротивление измеряется в омах (Ом), а проводимость — в сименсах (См). Сопротивление пассивного участка цепи в общем случае определяется по формуле

где P — потребляемая мощность;

I — ток. Сопротивление в схеме замещения изображается следующим образом:

Индуктивностью называется идеальный элемент схемы замещения, характеризующий способность цепи накапливать магнитное поле. Индуктивность катушки, измеряемая в генри [Гн], определяется по формуле

где W — число витков катушки;

Ф — магнитный поток катушки, возбуждаемый током i.

На рисунке показано изображение индуктивности в схеме замещения

Емкостью называется идеальный элемент схемы замещения, характеризующий способность участка электрической цепи накапливать электрическое поле. Емкостью обладают только конденсаторы. Емкостью остальных элементов цепи пренебрегают. Емкость конденсатора, измеряемая в фарадах (Ф ), определяется по формуле:

где q — заряд на обкладках конденсатора;

Uс — напряжение на конденсаторе.

На рисунке показано изображение емкости в схеме замещения

Любой источник энергии можно представить в виде источника ЭДС или источника тока. Источник ЭДС — это источник, характеризующийся электродвижущей силой и внутренним сопротивлением. Идеальным называется источник ЭДС, внутреннее сопротивление которого равно нулю.

изображен источник ЭДС, к зажимам которого подключено сопротивление R.

Ri — внутреннее сопротивление источника ЭДС.

Стрелка ЭДС направлена от точки низшего потенциала к точке высшего потенциала, стрелка напряжения на зажимах источника U12 направлена в противоположную сторону от точки с большим потенциалом к точке с меньшим потенциалом.

Ток (1.2)(1.3)

У идеального источника ЭДС внутреннее сопротивление Ri = 0, U12 = E.

Из формулы (1.3) видно, что напряжение на зажимах реального источника ЭДС уменьшается с увеличением тока. У идеального источника напряжение на зажимах не зависит от тока и равно электродвижущей силе.

Возможен другой путь идеализации источника: представление его в виде источника тока.

Источником тока называется источник энергии, характеризующийся величиной тока и внутренней проводимостью.

Идеальным называется источник тока, внутренняя проводимость которого равна нулю.

Поделим левую и правую части уравнения (1.2) на Ri и получим

где — ток источника тока; — внутренняя проводимость.

У идеального источника тока gi = 0 и J = I.

Ток идеального источника не зависит от сопротивления внешней части цепи . Он остается постоянным независимо от сопротивления нагрузки. Условное изображение источника тока показано на рис.

Любой реальный источник ЭДС можно преобразовать в источник тока и наоборот. Источник энергии, внутреннее сопротивление которого мало по сравнению с сопротивлением нагрузки, приближается по своим свойствам к идеальному источнику ЭДС.

Если внутреннее сопротивление источника велико по сравнению с сопротивлением внешней цепи, он приближается по своим свойствам к идеальному источнику тока.

Различают разветвленные и неразветвленные схемы .

На рис. 1.5 изображена неразветвленная схема.

На рис. 1.6 показана разветвленная схема, содержащая два источника ЭДС и 5 сопротивлений.

Сопротивления соединительных проводов принимают равными нулю.

Разветвленная схема — это сложная комбинация соединений пассивных и активных элементов.

Рис. 1.5 Участок электрической цепи, по которому проходит один и тот же ток, называется ветвью . Место соединения двух и более ветвей электрической цепи называется узлом . Узел, в котором сходятся две ветви, называется устранимым . Узел является неустранимым , если в нем соединены три и большее число ветвей. Узел в схеме обозначается точкой .

Последовательным называют такое соединение участков цепи, при котором через все участки проходит одинаковый ток. При параллельном соединении все участки цепи присоединяются к одной паре узлов, находятся под одним и тем же напряжением.

Любой замкнутый путь, включающий в себя несколько ветвей, называется контуром .

В зависимости от нагрузки различают следующие режимы работы : номинальный, режим холостого хода, короткого замыкания, согласованный режим.

При номинальном режиме электротехнические устройства работают в условиях, указанных в паспортных данных завода-изготовителя. В нормальных условиях величины тока, напряжения, мощности не превышают указанных значений.

Режим холостого хода возникает при обрыве цепи или отключении сопротивления нагрузки.

Режим короткого замыкания получается при сопротивлении нагрузки, равном нулю. Ток короткого замыкания в несколько раз превышает номинальный ток. Режим короткого замыкания является аварийным.

Согласованный режим — это режим передачи от источника к сопротивлению нагрузки наибольшей мощности. Согласованный режим наступает тогда, когда сопротивление нагрузки становится равным внутреннему сопротивлению источника. При этом в нагрузке выделяется максимальная мощность.

изображен участок цепи с сопротивлением R. Ток, протекающий через сопротивление R, пропорционален падению напряжения на сопротивлении и обратно пропорционален величине этого сопротивления.

Падением напряжения на сопротивлении называется произведение тока , протекающего через сопротивление, на величину этого сопротивления

Основными законами электрических цепей, наряду с законом Ома, являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа). В соответствии с первым законом Кирхгофа, алгебраическая сумма токов в любом узле цепи равна нулю:

Возьмем схему и запишем для нее уравнение по первому закону Кирхгофаили Токам, направленным к узлу, присвоим знак «плюс», а токам, направленным от узла — знак «минус».

Согласно второму закону Кирхгофа, алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжений в этом контуре

Возьмем схему и запишем для внешнего контура этой схемы уравнение по второму закону Кирхгофа. Для этого выберем произвольно направление обхода контура, например, по часовой стрелке. ЭДС и падения напряжений записываются в левую и правую части уравнения со знаком «плюс», если направления их совпадают с направлением обхода контура, и со знаком «минус», если не совпадают.

При определении тока в ветви, содержащей источник ЭДС, используют закон Ома для активной ветви. Возьмем ветвь, содержащую сопротивления и источники ЭДС. Ветвь включена к узлам a-b, известно направление тока в ветви Возьмем замкнутый контур, состоящий из активной ветви и стрелки напряжения Uab, и запишем для него уравнение по второму закону Кирхгофа. Выберем направление обхода контура по часовой стрелке. ПолучимИз этого уравнения выведем формулу для токаВ общем виде:где R — сумма сопротивлений ветви;

E — алгебраическая сумма ЭДС.

ЭДС в формуле записывается со знаком «плюс», если направление ее совпадает с направлением тока и со знаком «минус», если не совпадает.

Вопрос №2. Идеальный источник ЭДС представляет собой активный элемент с двумя выводами, напряжение на котором не зависит от сопротивления внешней цепи, т.е., не зависит от тока, проходящего через источник. Изображение идеального источника ЭДС приведено на рис. 1.8а

Предполагается, что внутри такого источника пассивные элементы (r, L, C) отсутствуют, и поэтому протекание тока через него не вызывает в нем падение напряжения. Внутреннее сопротивление идеального источника ЭДС равно нулю.

В отличие от пассивных элементов, где ток протекает от большего потенциала к меньшему, в источнике ЭДС этот процесс обратный вследствие действия внутренних сил источника. Работа, затрачиваемая на перемещение заряда от вывода “–” к выводу “+” и отнесенная к величине этого заряда, называется электродвижущей силой источника , и обозначатся в общем случае как e , а постоянная ЭДС, как Е. Соответственно, напряжение на выводах источника ЭДС равно u = e, т.е., положительное направление напряжения противоположно положительному направлению ЭДС.

Идеальных источников ЭДС в природе нет. Нет такого источника, короткое замыкание (соединение выводов проводником с сопротивлением, равным нулю) которого приводит к бесконечно большим токам iкз =. В любом источнике существует внутреннее сопротивление, падение напряжения на котором при коротком замыкании уравновешивает ЭДС источника, поэтому ток короткого замыкания имеет конечную величину.

Источник ЭДС конечной мощности изображается идеальным источником ЭДС и последовательно включенным пассивным элементом (рис. 1.8.б), параметры которого подбираются такими, чтобы отобразить реальные процессы на выводах источника. В цепях постоянного тока это, как правило, внутреннее сопротивление (на рис. 1.8б обозначено как Rвн), величина которого много меньше параметров внешней цепи. В некоторых случаях этим сопротивлением можно пренебречь (в зависимости от требуемой точности расчета). Вольтамперные характеристики идеального (1) и реального (2) источников ЭДС постоянного тока изображены на рис

Источник тока представляет собой активный элемент, ток которого практически не зависит от напряжения на его выводах. Это может быть, если сопротивление источника тока несоизмеримо больше сопротивления внешней цепи. Целесообразно ввести понятие идеального источника тока. Очевидно, что у идеального источника тока внутреннее сопротивление равно бесконечности.

Условное обозначение идеального источника тока приведено на рис. 1.9а. Двойная стрелка и знаки (+) и (–) указывают на положительное направление тока и полярность источника.

Если к идеальному источнику тока подключить сопротивление и увеличивать его до бесконечности, то напряжение на его выводах и соответственно мощность будут неограниченно возрастать. Поэтому идеальный источник тока, также как и идеальный источник ЭДС, рассматриваются как источники бесконечной мощности.

Источники тока конечной мощности (реальные) изображается в виде идеального с подключенным к нему пассивным элементом (рис. 1.9б), которым ограничивается мощность, выдаваемая во внешнюю цепь, и отражаются внутренние параметры источника. Ток реального источника меньше тока идеального на величину тока Iвн, протекающего по внутреннему сопротивлению Rвн.

Вопрос №3. Индуктивностью называется идеализированный элемент электрической цепи, в котором происходит запасание энергии магнитного поля. Запасания энергии электрического поля или преобразования электрической энергии в другие виды энергии в ней не происходит.

Наиболее близким к идеализированному элементу — индуктивности — является реальный элемент электрической цепи — индуктивная катушка. В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электрического поля и преобразование электрической энергии в другие виды энергии, в частности в тепловую.

Количественно способность реального и идеализированного элементов электрической цепи запасать энергию магнитного поля характеризуется параметром, называемым индуктивностью.

Таким образом термин «индуктивность» применяется как название идеализированного элемента электрической цепи, как название параметра, количественно характеризующего свойства этого элемента, и как название основного параметра индуктивной катушки.

Связь между напряжением и током в индуктивной катушке определяется законом электромагнитной индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости изменения потокосцепления катушки ψ и направленная таким образом, чтобы вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:

Потокосцепление катушки равно алгебраической сумме магнитных потоков пронизывающих ее отдельные витки:

где N — число витков катушки.

Индуктивность В системе единиц СИ магнитный поток и потокосцепление выражают в веберах (Вб).

Магнитный поток Ф, пронизывающий каждый из витков катушки, в общем случае может содержать две составляющие: магнитный поток самоиндукции Фси и магнитный поток внешних полей Фвп: Ф — Фси + Фвп.

Первая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, вторая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и постоянных магнитов. Если вторая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее называют магнитным потоком взаимоиндукции.

Потокосцепление катушки ψ, так же как и магнитный поток Ф, может быть представлено в виде суммы двух составляющих: ψ= ψси + ψвп

Индуктивность наведенная в индуктивной катушке ЭДС е, в свою очередь, может быть представлена в виде суммы ЭДС самоиндукции, которая вызвана изменением магнитного потока самоиндукции, и ЭДС, вызванной изменением магнитного потока внешних по отношению к катушке полей:

e = eси + eвп ,

здесь еси — ЭДС самоиндукции, евп — ЭДС внешних полей.

Если магнитные потоки внешних по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.

Потокосцепление самоиндукции зависит от протекающего по катушке тока. Эта зависимость, называемая вебер — амперной характеристикой индуктивной катушки, в общем случае имеет нелинейный характер (рис. 2, кривая 1).В частном случае, например для катушки без магнитного сердечника, эта зависимость может быть линейной (рис. 2, кривая 2).

Вебер-амперные характеристики индуктивной катушки: 1 — нелинейная, 2 — линейная.

В системе единиц СИ индуктивность выражают в генри (Гн).

При анализе цепей обычно рассматривают не значение ЭДС, наведенной в катушке, а напряжением на ее зажимах, положительное направление которого выбирают совпадающим с положительным направлением тока:Идеализированный элемент электрической цепи — индуктивность, можно рассматривать как упрощенную модель индуктивной катушки, отражающую способность катушки запасать энергию магнитного поля.

Для линейной индуктивности напряжение на ее зажимах пропорционально скорости изменения тока. При протекании через индуктивность постоянного тока напряжение на ее зажимах равно нулю, следовательно, сопротивление индуктивности постоянному току равно нулю.

Постоянный электрический ток. ЭДС источника тока и внутреннее сопротивление источника тока. Закон ома для полной цепи

Двухполюсник и его эквивалентная схема

Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включенных генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.

Введение

Рассмотрим пример. В легковом автомобиле запитаем бортовую сеть не от штатного свинцово-кислотного аккумулятора напряжением 12 вольт и ёмкостью 55 А·ч, а от последовательно соединённых восьми батареек (например, типоразмера АА, ёмкостью около 1 А·ч). Попробуем завести двигатель. Опыт показывает, что при питании от батареек вал стартера не повернётся ни на градус. Более того, не сработает даже втягивающее реле.

Интуитивно понятно, что батарейка «недостаточно мощная» для подобного применения, однако рассмотрение её заявленных электрических характеристик — напряжения и заряда (ёмкости) — не даёт количественного описания данного явления. Напряжение в обоих случаях одинаково:

Аккумулятор: 12 вольт

Гальванические элементы: 8·1,5 вольт = 12 вольт

Ёмкости также вполне достаточно: одного ампер·часа в батарейке должно хватить, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Казалось бы, в соответствии с законом Ома ток в одинаковой нагрузке при электрически одинаковых источниках также должен быть одинаковым. Однако в действительности это не совсем так. Источники вели бы себя одинаково, если бы были идеальными генераторами напряжения. Для описания степени отличия реальных источников от идеальных генераторов и применяется понятие внутреннее сопротивление.

Сопротивление и внутреннее сопротивление

Основной характеристикой двухполюсника является его сопротивление (или импеданс). Однако характеризовать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=Ir не выполняется.

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Входное сопротивление — внутреннее сопротивление двухполюсника, которым является вход системы.

Выходное сопротивление — внутреннее сопротивление двухполюсника, которым является выход системы.

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причем активное сопротивление, то есть резистор в нем присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведет себя так, словно в нем имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление чисто активное, оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определенный предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.

В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Внутреннее сопротивление невозможно убрать из двухполюсника

Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних условий.

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Если к источнику с ЭДС генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом.

Расчёт

Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).

Пусть, имеется двухполюсник, который может быть описан приведенной выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

ЭДС генератора напряжения U

Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (1) записывается следующим образом:

где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчета — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощенной формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Часто применяется следующий простой способ измерения, не требующий вычислений:

Измеряется напряжение холостого хода

В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нем составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:

Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.

Закон Ома для полной цепи, определение которого касается значения электрического тока в реальных цепях, находится в зависимости от источника тока и от сопротивления нагрузки. Этот закон носит и другое название — закон Ома для замкнутых цепей. Принцип действия данного закона заключается в следующем.

В качестве самого простого примера, электрическая лампа, являющаяся потребителем электрического тока, совместно с источником тока есть не что иное, как замкнутая . Данная электрическая цепь наглядно показана на рисунке.

Электроток, проходя через лампочку, также проходит и через сам источник тока. Таким образом, во время прохождения по цепи, ток испытает сопротивление не только проводника, но и сопротивление, непосредственно, самого источника тока. В источнике сопротивление создается электролитом, находящимся между пластинами и пограничными слоями пластин и электролита. Отсюда следует, что в замкнутой цепи, ее общее сопротивление будет состоять из суммы сопротивлений лампочки и источника тока.

Внешнее и внутреннее сопротивление

Сопротивление нагрузки, в данном случае лампочки, соединенной с источником тока, носит название внешнего сопротивления. Непосредственное сопротивление источника тока называется внутренним сопротивлением. Для более наглядного изображения процесса, все значения необходимо условно обозначить. I — , R — внешнее сопротивление, r — внутреннее сопротивление. Когда по электрической цепи протекает ток, то для того, чтобы поддерживать его, между концами внешней цепи должна присутствовать разность потенциалов, которая имеет значение IхR. Однако, протекание тока наблюдается и во внутренней цепи. Значит, для того, чтобы поддержать электроток во внутренней цепи, также необходима разность потенциалов на концах сопротивления r. Значение этой разности потенциалов равно Iхr.

Электродвижущая сила аккумулятора

Аккумулятор должен иметь следующее значение электродвижущей силы, способной поддерживать необходимый ток в цепи: Е=IхR+Iхr . Из формулы видно, что электродвижущая сила аккумулятора составляет сумму внешнего и внутреннего . Значение тока нужно вынести за скобки: Е=I(r+R) . Иначе можно представить: I=Е/(r+R) . Двумя последними формулами выражается закон Ома для полной цепи, определение которого звучит следующим образом: в замкнутой цепи сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна сумме сопротивлений этой цепи.

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен . Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Попробуем решить эту задачу на конкретном примере. Электродвижущая сила источника питания составляет 4,5 В. К нему подключили нагрузку, и через неё потёк ток, равный 0,26 А. Напряжение при этом стало равным 3,7 В. Первым делом, представим себе, что внутри источника спрятана последовательная цепь из идеального источника напряжения в 4,5 В, внутреннее сопротивление которого равно нулю, а также резистора, номинал которого и требуется найти. Понятно, что на самом деле это не так, но для расчётов аналогия вполне сойдёт.

2 шаг

Запомните, что буквой U обозначают только напряжение под нагрузкой. Для обозначения же электродвижущей силы зарезервирована другая буква – E. Абсолютно точно её измерить невозможно, потому что потребуется вольтметр с бесконечным входным сопротивлением. Даже у электростатического вольтметра (электрометра) оно огромно, но не бесконечно. Но одно дело – абсолютно точно, а другое – с точностью, приемлемой на практике. Второе вполне осуществимо: нужно лишь, чтобы внутреннее сопротивление источника было пренебрежимо мало по сравнению с внутренним сопротивлением вольтметра. А пока суть да дело, посчитаем разницу между ЭДС источника и его напряжением под нагрузкой, потребляющей ток в 260 мА. E-U = 4,5-3,7 = 0,8. Это и будет падение напряжения на том “виртуальном резисторе”.

3 шаг

Ну а дальше всё просто, ибо в дело вступает классический закон Ома. Помним, что ток через нагрузку и “виртуальный резистор” одинаков, ведь они соединены последовательно. Падение напряжения на последнем (0,8 В) делим на силу тока (0,26 А) и получаем 3,08 Ома. Вот и готов ответ! Можно ещё посчитать, какая мощность рассеивается на нагрузке, а какая – бесполезно на источнике. На нагрузке рассеивается: 3,7*0,26=0,962 Вт. На источнике: 0,8*0,26=0,208 Вт. Процентное соотношение между ними вычислите самостоятельно. Но эта не единственный вид задач на нахождение внутреннего сопротивления источника. Есть и такие, в которых вместо силы тока указано сопротивление нагрузки, а остальные исходные данные такие же. Тогда надо вначале проделать ещё одно вычисление. Приведённое в условии напряжение под нагрузкой (не ЭДС!) поделить на сопротивление нагрузки. И получится сила тока в цепи. После чего, как говорят физики, “задача сведена к предыдущей”! Попробуйте составить такую задачу и решить её.

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

• Автомобильный свинцово-кислотный аккумулятор напряжением 12 вольт и ёмкостью 55 А·ч
• Восемь батареек типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление , то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности , отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1 ) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где U out1 I 1 , U out2 — выходное напряжение при токе I 2 . Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:

где U oc — выходное напряжение в режиме холостого хода (англ. open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём. Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы . Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

Большое внутреннее сопротивление

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

• элементов с отрицательным дифференциальным сопротивлением , например, туннельных диодов

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов .

См. также

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5

Примечания

Wikimedia Foundation . 2010 .

• Политехнический терминологический толковый словарь
• 
  

Что называется внутренним сопротивлением. Как рассчитать внутреннее сопротивление источника питания

В век электричества, наверное, нет такого человека, что не знал бы о существовании электрического тока. Но мало кто помнит из школьного курса физики больше, чем название величин: сила тока, напряжение, сопротивление, закон Ома. И лишь очень немногие помнят, в чём заключается смысл этих слов.

В этой статье мы обсудим, как появляется электрический ток, как он передаётся по цепи и как использовать эту величину в расчётах. Но перед тем как перейти к основной части, обратимся к истории открытия электрического тока и его источников, а также определению того, чем является электродвижущая сила.

История

Электричество как источник энергии было известно ещё с древних времён, ведь сама природа генерирует его в огромных объёмах. Яркий пример — молния или электрический скат. Несмотря на такую близость к человеку, обуздать эту энергию удалось лишь в середине семнадцатого века: Отто фон Герике, бургомистр из Магдебурга, создал машину, позволяющую генерировать электростатический заряд. В середине восемнадцатого века Питер фон Мушенбрук — учёный из Голландии — создаёт первый в мире электрический конденсатор, названный Лейденской банкой в честь университета, где он работал.

Пожалуй, отсчёт эпохи настоящих открытий, посвящённых электричеству, принято начинать с работ Луиджи Гальвани и Алессандро Вольта, изучивших соответственно электрические токи в мышцах и возникновение тока в так называемых гальванических элементах. Дальнейшие исследования открыли нам глаза на связь электричества и магнетизма, а также на несколько очень полезных явлений (таких как электромагнитная индукция), без которых сегодня невозможно представить нашу жизнь.

Но мы не будем углубляться в магнитные явления и остановимся только на электрических. Итак, разберём, как же возникает электричество в гальванических элементах и что это вообще такое.

Что такое гальванический элемент?

Можно сказать, что это производящий электроэнергию за счёт химических реакций, происходящих между его компонентами. Самый простой гальванический элемент был изобретён Алессандро Вольтом и назван в его честь вольтовым столбом. Он состоит из нескольких слоёв, чередующихся между собой: медная пластина, проводящая прокладка (в домашнем варианте конструкции используется вата, смоченная солёной водой) и цинковая пластина.

Какие реакции протекают в нём?

Рассмотрим подробнее процессы, позволяющие нам получить электричество с помощью гальванического элемента. Таких превращений всего два: окисление и восстановление. При окислении одного элемента, восстановителя, происходит отдача им электронов другому элементу — окислителю. Окислитель, в свою очередь, восстанавливается, принимая электроны. Таким образом происходит движение заряженных частиц от одной пластины к другой, а это, как известно, и называется электрическим током.

А сейчас плавно перейдём к основной теме этой статьи — ЭДС источника тока. И для начала рассмотрим, что же представляет собой эта электродвижущая сила (ЭДС).

Что такое ЭДС?

Эту величину можно представить как работу сил (именно «работу»), совершаемую при перемещении заряда по замкнутой электрической цепи. Очень часто ещё делают уточнения, что заряд должен обязательно быть положительным и единичным. И это существенное дополнение, так как только при этих условиях можно считать электродвижущую силу точной измеримой величиной. Кстати, измеряется она в тех же единицах, что и напряжение: в вольтах (В).

ЭДС источника тока

Как известно, каждый аккумулятор или батарейка обладают своим значением сопротивления, которое они способны выдавать. Это значение, ЭДС источника тока, показывает, какую работу производят внешние силы для перемещения заряда по цепи, в которую включена батарейка или аккумулятор.

Уточнить стоит также и то, какой вид тока производит источник: постоянный, переменный или импульсный. Гальванические элементы, в том числе аккумуляторы и батарейки, производят всегда только постоянный электрический ток. ЭДС источника тока в таком случае будет равна по модулю выходному напряжению на контактах источника.

Сейчас пришла пора разобраться, для чего такая величина, как ЭДС, нужна вообще, как её использовать при расчётах других величин электрической цепи.

Формула ЭДС

Мы уже выяснили, что ЭДС источника тока равна работе сторонних сил по перемещению заряда. Для большей наглядности мы решили записать формулу этой величины: E=A сторонних сил /q, где A — работа, а q — заряд, над которым была совершена работа. Обратите внимание, что берётся общий заряд, а не единичный. Делается это потому, что мы считаем работу сил по перемещению всех зарядов в проводнике. И это отношение работы к заряду всегда будет постоянным для данного источника, так как какое количество заряженных частиц ни бери, удельная величина работы на каждый из них будет одинаковой.

Как видите, формула электродвижущей силы не так сложна и состоит всего из двух величин. Пришла пора перейти к одному из главных вопросов, вытекающих из этой статьи.

Зачем нужна ЭДС?

Уже было сказано, что ЭДС и напряжение — величины, фактически, одинаковые. Если мы знаем значения ЭДС и внутреннее сопротивление источника тока, то несложно будет подставить их в закон Ома для полной цепи, который выглядит следующим образом: I=e/(R+r), где I — сила тока, e — ЭДС, R — сопротивление цепи, r — внутреннее сопротивление источника тока. Отсюда мы можем находить две характеристики цепи: I и R. Следует обратить внимание, что все эти рассуждения и формулы справедливы лишь для цепи постоянного тока. В случае с переменным формулы будут совсем другие, так как он подчиняется своим колебательным законам.

Но всё же остаётся непонятным, какое применение имеет ЭДС источника тока. В цепи, как правило, очень много элементов, выполняющих свою функцию. В любом телефоне стоит плата, представляющая также не что иное, как электрическую цепь. А каждой такой схеме для работы требуется источник тока. И очень важно, чтобы его ЭДС подходила по параметрам для всех элементов цепи. Иначе схема либо перестанет работать, либо сгорит из-за высокого напряжения внутри неё.

Заключение

Думаем, для многих эта статья оказалась полезной. Ведь в современном мире очень важно знать как можно больше о том, что нас окружает. В том числе существенны знания о природе электрического тока и его поведении внутри цепей. И если вы думаете, что такая вещь, как электрическая цепь, применяется только в лабораториях и вы далеки от этого, то вы сильно ошибаетесь: все приборы, потребляющие электроэнергию, на самом деле состоят из цепей. И у каждой из них есть свой источник тока, создающий ЭДС.

Попробуем решить эту задачу на конкретном примере. Электродвижущая сила источника питания составляет 4,5 В. К нему подключили нагрузку, и через неё потёк ток, равный 0,26 А. Напряжение при этом стало равным 3,7 В. Первым делом, представим себе, что внутри источника спрятана последовательная цепь из идеального источника напряжения в 4,5 В, внутреннее сопротивление которого равно нулю, а также резистора, номинал которого и требуется найти. Понятно, что на самом деле это не так, но для расчётов аналогия вполне сойдёт.

2 шаг

Запомните, что буквой U обозначают только напряжение под нагрузкой. Для обозначения же электродвижущей силы зарезервирована другая буква – E. Абсолютно точно её измерить невозможно, потому что потребуется вольтметр с бесконечным входным сопротивлением. Даже у электростатического вольтметра (электрометра) оно огромно, но не бесконечно. Но одно дело – абсолютно точно, а другое – с точностью, приемлемой на практике. Второе вполне осуществимо: нужно лишь, чтобы внутреннее сопротивление источника было пренебрежимо мало по сравнению с внутренним сопротивлением вольтметра. А пока суть да дело, посчитаем разницу между ЭДС источника и его напряжением под нагрузкой, потребляющей ток в 260 мА. E-U = 4,5-3,7 = 0,8. Это и будет падение напряжения на том “виртуальном резисторе”.

3 шаг

Ну а дальше всё просто, ибо в дело вступает классический закон Ома. Помним, что ток через нагрузку и “виртуальный резистор” одинаков, ведь они соединены последовательно. Падение напряжения на последнем (0,8 В) делим на силу тока (0,26 А) и получаем 3,08 Ома. Вот и готов ответ! Можно ещё посчитать, какая мощность рассеивается на нагрузке, а какая – бесполезно на источнике. На нагрузке рассеивается: 3,7*0,26=0,962 Вт. На источнике: 0,8*0,26=0,208 Вт. Процентное соотношение между ними вычислите самостоятельно. Но эта не единственный вид задач на нахождение внутреннего сопротивления источника. Есть и такие, в которых вместо силы тока указано сопротивление нагрузки, а остальные исходные данные такие же. Тогда надо вначале проделать ещё одно вычисление. Приведённое в условии напряжение под нагрузкой (не ЭДС!) поделить на сопротивление нагрузки. И получится сила тока в цепи. После чего, как говорят физики, “задача сведена к предыдущей”! Попробуйте составить такую задачу и решить её.

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

• Автомобильный свинцово-кислотный аккумулятор напряжением 12 вольт и ёмкостью 55 А·ч
• Восемь батареек типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление , то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности , отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1 ) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где U out1 I 1 , U out2 — выходное напряжение при токе I 2 . Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:

где U oc — выходное напряжение в режиме холостого хода (англ. open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём. Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы . Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

Большое внутреннее сопротивление

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

• элементов с отрицательным дифференциальным сопротивлением , например, туннельных диодов

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов .

См. также

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5

Примечания

Wikimedia Foundation . 2010 .

• Политехнический терминологический толковый словарь
• 
  

ЭДС и напряжение. Внутреннее сопротивление источников питания.
Ликбез так ликбез!
Закон Ома. Вот я о чем.
О законе Ома мы уже говорили. Поговорим еще раз — с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.
Переведя сие заклинание на язык сухих формул получаем:

I=E/R

где:I — сила тока,E — Э.Д.С. — электродвижущая силаR — сопротивление
Ток измеряется в амперах, э.д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):

I=U/R

где:U — напряжение источника непосредственно на его клеммах.
Рассмотрим простой пример.
Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое — то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э.д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.Но, тем не менее именно эта величина и принимается за напряжение батарейки.
Формула конечного напряжения при этом будет иметь следующий вид:

U(бат)=E-U(внутр)

Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу!
Разобрались!
Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.
Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться — к просадке напруги.
Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.
Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.

На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .

Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).

Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.

При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).

В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:

— электростатическая — в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;

— термоэлектрическая — в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;

— фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;

— химическая — в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.

Электродвижущая сила (ЭДС) — характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:

ɛ = A ст /q ,

где ɛ — ЭДС источника тока, А ст — работа сторонних сил , q — количество перемещенного заряда.

Электродвижущую силу выражают в вольтах.

Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.

Внутреннее сопротивление источника тока.

Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R . Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r .

В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.

Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.

Внутреннее сопротивление — это… Что такое Внутреннее сопротивление?

Двухполюсник и его эквивалентная схема

Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.

Введение

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

В соответствии с законом Ома при источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведенном примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.

Эквивалентная схема активного двухполюсника

Реальные активные двухполюсники хорошо описываются математически, если их рассматривать как эквивалентную схему, состоящую из (см. рисунок) последовательно включённых генератора напряжения и сопротивления (в общем случае — комплексного импеданса). Генератор напряжения представляет собственно источник энергии, находящийся в этом двухполюснике. Этот генератор мог бы отдать в нагрузку сколь угодно большие мощность и ток. Однако сопротивление, включённое последовательно с генератором, ограничивает мощность, которую данный двухполюсник может отдать в нагрузку. Это воображаемое сопротивление и называется внутренним сопротивлением. Оно является лишь параметром абстрактной модели двухполюсника, то есть реального «резистора» внутри двухполюсников обычно нет. Хотя в реальных гальванических элементах это внутреннее сопротивление есть. Это суммарное сопротивления плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти реальные материалы имеют вполне конечное сопротивление, отличное от нуля. В прочих источниках эту функцию исполняют обмотки и контакты, которые также снижают характеристики источников напряжения. Контактные разности потенциалов имеют иную природу падения напряжения и носят неомический характер, то есть все затраты энергии идут на работу выхода носителей заряда.

Сопротивление и внутреннее сопротивление

Основной характеристикой двухполюсника является его сопротивление (или импеданс^[1]). Однако характеризовать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=Ir не выполняется^[2].

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников^[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

• Входное сопротивление — внутреннее сопротивление двухполюсника, которым является вход системы^{[источник не указан 147 дней]}.
• Выходное сопротивление — внутреннее сопротивление двухполюсника, которым является выход системы.

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

• Внутреннее сопротивление невозможно убрать из двухполюсника^[4]
• Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Если к источнику с ЭДС^[5] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:

Нахождение внутреннего сопротивления

Расчёт

Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).

Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U_out = φ₂ − φ₁) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

(Напряжения)

где U_out1 — выходное напряжение при токе I₁, U_out2 — выходное напряжение при токе I₂. Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:

где U_oc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; I_sc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

(ВнутрСопр)

Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:

• Рассчитать выходное напряжение двухполюсника в режиме холостого хода
• Рассчитать выходной ток двухполюсника в режиме короткого замыкания
• На основании полученных значений найти r и U по формуле (ВнутрСопр).

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

• Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями.
• Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен I_max=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
• Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной P_max=E²/(4r). В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
• Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём. Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы. Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

• Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
• Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
• Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от 0,05 Ом до 1 Ом и более (зависит от качества электропроводки). Сопротивление 1 Ом и более соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети может достигать 3 тысяч ампер, что требует применения автоматических предохранителей, выдерживающих подобные токовые удары.
• Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома^[6]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).

Большое внутреннее сопротивление

Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).

• Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
• Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать^[7] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
• Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.

См. также

Входной импеданс антенны

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5

Примечания

1. ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
2. ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣU_int, где ΣU_int — алгебраическая сумма ЭДС внутренних источников.
3. ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
4. ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
5. ↑ То же самое, что и напряжение
6. ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
7. ↑ В рабочем диапазоне частот
8. ↑ Похоже, что в графике ошибка: внутреннее сопротивление аккумулятора должно измеряться в миллиомах, а не в омах, как на графике.

Практическое занятие «Определение силы тока, ЭДС и внутреннего сопротивления источника электрической энергии»

 Практическое занятие.

Определение силы тока, ЭДС и внутреннего сопротивления источника электрической энергии.

Цель занятия: Научиться применять законы Ома для участка цепи и замкнутой цепи.

Пояснение к занятию:

Постоянный электрический ток – ток, значение и направление которого не изменяется с течением времени.

Сила тока – величина, характеризующая быстроту переноса заряда в проводнике через поперечное сечение.

[I] = А

Сопротивление проводника – величина, характеризующая противодействие электрическому току в проводнике, которое обусловлено внутренним строением проводника.

[R] = Ом

R = R0(1+α·t)- зависимость сопротивления проводника от его температуры.

R0 – сопротивление проводника при 00С, α – температурный коэффициент сопротивления.

ЭДС – величина, характеризующая отношение работы сторонних сил к значению положительного заряда, переносимого внутри источника.

[ε] = В

Закон Ома для участка цепи: сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.

Закон Ома для полной цепи: сила тока в цепи прямо пропорциональна ЭДС и обратно пропорциональна сумме сопротивлений внешней и внутренней цепей.

Задание на выполнение работы:

Необходимо найти все величины указанные в таблице знаком «?», если в таблице стоит знак « — » то эту величину находить ненужно.

По предложенным данным необходимо найти величины Ӏ, q, U, R и ℓ

Вариант	I, мА	q, Кл	t, с	U, В	R, Ом	ℓ , м	ρ, Ом·м	S, м2
1.	500	?	120	?	?	3	5,6·10-8	2·10-6
2.	?	?	300	30	5	?	2,6·10-8	3·10-6

По предложенным данным необходимо найти величины R, Αст, и q.

Вариант	R, Ом	R0, Ом	α, 0С-1	t, 0C	ε, В	Αст, Дж	q, Кл
1.	?	20	0,0045	1200	5	?	0,02
2.	?	30	0,0068	900	12	0,36	?

По предложенным данным необходимо найти величины R, и r.

Вариант	R, Ом	Ӏ, А	ε, В	r, Ом
1.	?	0,5	4,5	0,3
2.	6,5	0,8	5,6	?

ЭДС и внутреннего сопротивления источника.

Условные обозначения

R Ом. — внешнее сопротивление

I А. – сила тока

ε В. – электродвижущая сила

r Ом – сопротивление источника

Ответить на вопросы:

Как названа частица, которая обладает наименьшим ( неделимым) отрицательным электрическим зарядом?

Как электрический ток зависит от напряжения?

Как сопротивление зависит от длины и площади проводника?

Как определить ток короткого замыкания?

Вывод:

Как найти внутреннее сопротивление источника напряжения. Радиосвязь

Цель работы: изучить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.

Оборудование: металлический планшет, источник тока, амперметр, вольтметр, резистор, ключ, зажимы, соединительные провода.

Для измерения ЭДС и внутреннего сопротивления источника тока собирают электрическую цепь, схема которой показана на рисунке 1.

К источнику тока подключают амперметр, сопротивление и ключ, соединенные последовательно. Кроме того, непосредствен­но к выходным гнездам источника подключают еще и вольтметр.

ЭДС измеряют по показанию вольтметра при разомкнутом ключе. Этот прием определения ЭДС основан на следствии из за­кона Ома для полной цепи, согласно которому при бесконечно большом сопротивлении внешней цепи напряжение на зажимах источника равно его ЭДС. (См. параграф «Закон Ома для полной цепи» учебника «Физика 10»).

Для определения внутреннего сопротивления источника за­мыкают ключ К. При этом в цепи можно условно выделить два участка: внешний (тот, который подключен к источнику) и внутренний (тот, который находится внутри источника тока). Поскольку ЭДС источника равна сумме падения напряжений на внутрен­нем и внешнем участках цепи:

ε = U r +U R , то U r = ε -U R (1)

По закону Ома для участка цепи U r = I· r (2). Подставив равенство (2) в (1) получают:

I · r = ε — U r , откуда r = (ε — U R )/ J

Следовательно, чтобы узнать внутреннее сопротивление источника тока, необходимо пред­варительно определить его ЭДС, затем замкнуть ключ и измерить падение напряжения на внеш­нем сопротивлении, а также силу тока в нем.

Ход работы

1. Подготовьте таблицу для записи результатов измерений и вычислений:

ε ,в	U r , B	i,a	r , Ом

Начертите в тетради схему для измерения ЭДС и внутреннего сопротивления источника.

После проверки схемы соберите электрическую цепь. Ключ разомкните.

Измерьте величину ЭДС источника.

Замкните ключ и определите показания амперметра и вольтметра.

Вычислите внутреннее сопротивление источника.

1. Определение эдс и внутреннего сопротивления источника тока графическим методом

Цель работы: изучить измерения ЭДС, внутреннего сопротивления и тока короткого замы­кания источника тока, основанный на анализе графика зависимости напряже­ния на выходе источника от силы тока в цепи.

Оборудование: гальванический элемент, амперметр, вольтметр, резистор R 1 , переменный резистор, ключ, зажимы, металлический планшет, соединительные провода.

Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:

так как I =E/(R+r), то IR + Ir = Е, но IR = U, откуда U + Ir = Е или U = Е – Ir (1).

Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I К.З. — силу тока короткого замыкания (ток, который потечет в цепи источни­ка, когда внешнее сопротивление R станет равным нулю).

ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика со­ответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.

Силу тока короткого замыкания определяют по точке пересечения графика с осью токов. В этом случае внешнее сопротивление R = 0 и, следовательно, напряжение на выходе источника U = 0.

Внутреннее сопротивление источника находят по тангенсу угла наклона графика относи­тельно оси токов. (Сравните формулу (1) с математической функцией вида У = АХ +В и вспомни­те смысл коэффициента при X).

Ход работы

Для записи результатов измерений подготовьте таблицу:

1. После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источ­нику тока, будет максимальным.

Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.

Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.

Нанесите полученные в эксперименте точки на график. Напряжение откладывайте по верти­кальной оси, а силу тока — по горизонтальной. Проведите по точкам прямую линию.

Продолжите график до пересечения с осями координат и определите величины Е и, I К.З.

Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней це­пи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.

Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла на­клона построенного графика к оси токов. Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то практически это можно сделать, найдя отношение Е / I К.З

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен . Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Двухполюсник и его эквивалентная схема

Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включенных генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.

Введение

Рассмотрим пример. В легковом автомобиле запитаем бортовую сеть не от штатного свинцово-кислотного аккумулятора напряжением 12 вольт и ёмкостью 55 А·ч, а от последовательно соединённых восьми батареек (например, типоразмера АА, ёмкостью около 1 А·ч). Попробуем завести двигатель. Опыт показывает, что при питании от батареек вал стартера не повернётся ни на градус. Более того, не сработает даже втягивающее реле.

Интуитивно понятно, что батарейка «недостаточно мощная» для подобного применения, однако рассмотрение её заявленных электрических характеристик — напряжения и заряда (ёмкости) — не даёт количественного описания данного явления. Напряжение в обоих случаях одинаково:

Аккумулятор: 12 вольт

Гальванические элементы: 8·1,5 вольт = 12 вольт

Ёмкости также вполне достаточно: одного ампер·часа в батарейке должно хватить, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Казалось бы, в соответствии с законом Ома ток в одинаковой нагрузке при электрически одинаковых источниках также должен быть одинаковым. Однако в действительности это не совсем так. Источники вели бы себя одинаково, если бы были идеальными генераторами напряжения. Для описания степени отличия реальных источников от идеальных генераторов и применяется понятие внутреннее сопротивление.

Сопротивление и внутреннее сопротивление

Основной характеристикой двухполюсника является его сопротивление (или импеданс). Однако характеризовать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=Ir не выполняется.

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Входное сопротивление — внутреннее сопротивление двухполюсника, которым является вход системы.

Выходное сопротивление — внутреннее сопротивление двухполюсника, которым является выход системы.

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причем активное сопротивление, то есть резистор в нем присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведет себя так, словно в нем имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление чисто активное, оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определенный предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.

В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Внутреннее сопротивление невозможно убрать из двухполюсника

Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних условий.

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Если к источнику с ЭДС генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом.

Расчёт

Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).

Пусть, имеется двухполюсник, который может быть описан приведенной выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

ЭДС генератора напряжения U

Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (1) записывается следующим образом:

где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчета — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощенной формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Часто применяется следующий простой способ измерения, не требующий вычислений:

Измеряется напряжение холостого хода

В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нем составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:

Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

• Автомобильный свинцово-кислотный аккумулятор напряжением 12 вольт и ёмкостью 55 А·ч
• Восемь батареек типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление , то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности , отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1 ) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где U out1 I 1 , U out2 — выходное напряжение при токе I 2 . Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:

где U oc — выходное напряжение в режиме холостого хода (англ. open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём. Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы . Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

Большое внутреннее сопротивление

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

• элементов с отрицательным дифференциальным сопротивлением , например, туннельных диодов

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов .

См. также

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5

Примечания

Wikimedia Foundation . 2010 .

• Политехнический терминологический толковый словарь
• 
  

В век электричества, наверное, нет такого человека, что не знал бы о существовании электрического тока. Но мало кто помнит из школьного курса физики больше, чем название величин: сила тока, напряжение, сопротивление, закон Ома. И лишь очень немногие помнят, в чём заключается смысл этих слов.

В этой статье мы обсудим, как появляется электрический ток, как он передаётся по цепи и как использовать эту величину в расчётах. Но перед тем как перейти к основной части, обратимся к истории открытия электрического тока и его источников, а также определению того, чем является электродвижущая сила.

История

Электричество как источник энергии было известно ещё с древних времён, ведь сама природа генерирует его в огромных объёмах. Яркий пример — молния или электрический скат. Несмотря на такую близость к человеку, обуздать эту энергию удалось лишь в середине семнадцатого века: Отто фон Герике, бургомистр из Магдебурга, создал машину, позволяющую генерировать электростатический заряд. В середине восемнадцатого века Питер фон Мушенбрук — учёный из Голландии — создаёт первый в мире электрический конденсатор, названный Лейденской банкой в честь университета, где он работал.

Пожалуй, отсчёт эпохи настоящих открытий, посвящённых электричеству, принято начинать с работ Луиджи Гальвани и Алессандро Вольта, изучивших соответственно электрические токи в мышцах и возникновение тока в так называемых гальванических элементах. Дальнейшие исследования открыли нам глаза на связь электричества и магнетизма, а также на несколько очень полезных явлений (таких как электромагнитная индукция), без которых сегодня невозможно представить нашу жизнь.

Но мы не будем углубляться в магнитные явления и остановимся только на электрических. Итак, разберём, как же возникает электричество в гальванических элементах и что это вообще такое.

Что такое гальванический элемент?

Можно сказать, что это производящий электроэнергию за счёт химических реакций, происходящих между его компонентами. Самый простой гальванический элемент был изобретён Алессандро Вольтом и назван в его честь вольтовым столбом. Он состоит из нескольких слоёв, чередующихся между собой: медная пластина, проводящая прокладка (в домашнем варианте конструкции используется вата, смоченная солёной водой) и цинковая пластина.

Какие реакции протекают в нём?

Рассмотрим подробнее процессы, позволяющие нам получить электричество с помощью гальванического элемента. Таких превращений всего два: окисление и восстановление. При окислении одного элемента, восстановителя, происходит отдача им электронов другому элементу — окислителю. Окислитель, в свою очередь, восстанавливается, принимая электроны. Таким образом происходит движение заряженных частиц от одной пластины к другой, а это, как известно, и называется электрическим током.

А сейчас плавно перейдём к основной теме этой статьи — ЭДС источника тока. И для начала рассмотрим, что же представляет собой эта электродвижущая сила (ЭДС).

Что такое ЭДС?

Эту величину можно представить как работу сил (именно «работу»), совершаемую при перемещении заряда по замкнутой электрической цепи. Очень часто ещё делают уточнения, что заряд должен обязательно быть положительным и единичным. И это существенное дополнение, так как только при этих условиях можно считать электродвижущую силу точной измеримой величиной. Кстати, измеряется она в тех же единицах, что и напряжение: в вольтах (В).

ЭДС источника тока

Как известно, каждый аккумулятор или батарейка обладают своим значением сопротивления, которое они способны выдавать. Это значение, ЭДС источника тока, показывает, какую работу производят внешние силы для перемещения заряда по цепи, в которую включена батарейка или аккумулятор.

Уточнить стоит также и то, какой вид тока производит источник: постоянный, переменный или импульсный. Гальванические элементы, в том числе аккумуляторы и батарейки, производят всегда только постоянный электрический ток. ЭДС источника тока в таком случае будет равна по модулю выходному напряжению на контактах источника.

Сейчас пришла пора разобраться, для чего такая величина, как ЭДС, нужна вообще, как её использовать при расчётах других величин электрической цепи.

Формула ЭДС

Мы уже выяснили, что ЭДС источника тока равна работе сторонних сил по перемещению заряда. Для большей наглядности мы решили записать формулу этой величины: E=A сторонних сил /q, где A — работа, а q — заряд, над которым была совершена работа. Обратите внимание, что берётся общий заряд, а не единичный. Делается это потому, что мы считаем работу сил по перемещению всех зарядов в проводнике. И это отношение работы к заряду всегда будет постоянным для данного источника, так как какое количество заряженных частиц ни бери, удельная величина работы на каждый из них будет одинаковой.

Как видите, формула электродвижущей силы не так сложна и состоит всего из двух величин. Пришла пора перейти к одному из главных вопросов, вытекающих из этой статьи.

Зачем нужна ЭДС?

Уже было сказано, что ЭДС и напряжение — величины, фактически, одинаковые. Если мы знаем значения ЭДС и внутреннее сопротивление источника тока, то несложно будет подставить их в закон Ома для полной цепи, который выглядит следующим образом: I=e/(R+r), где I — сила тока, e — ЭДС, R — сопротивление цепи, r — внутреннее сопротивление источника тока. Отсюда мы можем находить две характеристики цепи: I и R. Следует обратить внимание, что все эти рассуждения и формулы справедливы лишь для цепи постоянного тока. В случае с переменным формулы будут совсем другие, так как он подчиняется своим колебательным законам.

Но всё же остаётся непонятным, какое применение имеет ЭДС источника тока. В цепи, как правило, очень много элементов, выполняющих свою функцию. В любом телефоне стоит плата, представляющая также не что иное, как электрическую цепь. А каждой такой схеме для работы требуется источник тока. И очень важно, чтобы его ЭДС подходила по параметрам для всех элементов цепи. Иначе схема либо перестанет работать, либо сгорит из-за высокого напряжения внутри неё.

Заключение

Думаем, для многих эта статья оказалась полезной. Ведь в современном мире очень важно знать как можно больше о том, что нас окружает. В том числе существенны знания о природе электрического тока и его поведении внутри цепей. И если вы думаете, что такая вещь, как электрическая цепь, применяется только в лабораториях и вы далеки от этого, то вы сильно ошибаетесь: все приборы, потребляющие электроэнергию, на самом деле состоят из цепей. И у каждой из них есть свой источник тока, создающий ЭДС.

Внутреннее сопротивление | Батареи и другие источники питания

Внутреннее сопротивление | Аккумуляторы и другие источники питания

В электрических цепях, которые мы рассмотрели до сих пор, мы рассматривали источник напряжения, питающий цепь, как идеальный источник напряжения. то есть:

• Мы предположили, что напряжение, подаваемое в цепь, остается постоянным, независимо от того, какой ток подается. поставляется.
• Мы также предположили, что энергия преобразуется в тепло только за счет сопротивления во внешней цепи.

На практике это не так:

1. Напряжение на клеммах батареи уменьшается по мере того, как ток, подаваемый в цепь, увеличивается.
   Это то же самое для всех реальных источников напряжения. (Однако разработчики блоков питания действительно производят стабилизированные блоки питания, в которых обратная связь схемы используются для поддержания относительно постоянного выходного напряжения).
2. Все блоки питания нагреваются во время использования, что свидетельствует о том, что часть выделяемой ими энергии фактически расходуется. преобразуется в тепло внутри самого блока питания!

Это показано на анимации ниже.

Это изменение напряжения питания потенциально трудно объяснить, особенно если учесть, что Причины отклонения будут зависеть от типа используемого источника питания.
Например:

• Для батареи: напряжение падает из-за скорости химических реакций, передающих заряд на клеммы батареи, не может соответствовать скорости, с которой заряд покидает клеммы, чтобы течь по цепи.
• Для генератора: ток создает более сильные магнитные поля внутри генератора, которые замедляют работу генератора и уменьшают напряжение питания.

К счастью, мы можем избежать этих деталей, и, независимо от фактического характера источника питания, мы можем представить его в виде модель блока питания, полностью состоящая из простых электрических компонентов.Один из способов сделать это — представить власть в качестве идеального источника напряжения (ЭДС) последовательно с внутренним сопротивлением. Когда эта модель источника питания применяется к внешней цепи, ток цепи также течет через внутреннее сопротивление. Это вызывает внутреннее падение напряжения внутри источника питания, что, следовательно, снижает напряжение на клеммах источника питания. Мощность, рассеиваемая внутренним сопротивлением, представляет собой тепло, выделяемое в источнике питания.Это показано на анимации ниже.

Напряжение на клеммах (В) равно ЭДС. напряжение (E) за вычетом внутреннего падения напряжения (Ir).
(используя закон Ома: внутреннее падение напряжения = ток (I) x внутреннее сопротивление (r)).

Чтобы смоделировать любой реальный источник питания, нам просто нужно определить правильные значения E и r для использования.

Когда источник питания не подключен к цепи, ток не протекает, поэтому:

• V = E — 0 x r.
• В = E.
• , то есть напряжение ЭДС, равно напряжению на клеммах холостого хода источника питания.

Внутреннее сопротивление можно определить, подключив цепь с известным сопротивлением и измерив протекающий ток.

• I = E / (R + r).
• поэтому r = (E / I) — R.

Мощность, подаваемая э.д.с., определяется как P = EI, а мощность, рассеиваемая в источнике питания, определяется как P = I ² r.
Энергия, обеспечиваемая ЭДС, определяется как W = EIt, а энергия, рассеиваемая в источнике питания, определяется как W = I ² rt.

Мощность и внутреннее сопротивление

Мощность и внутреннее сопротивление
Далее: Рабочие примеры Up: Электрический ток Предыдущая: Энергия в цепях постоянного тока

Мощность и внутреннее сопротивление Рассмотрим простую схему, в которой батарея ЭДС и внутренняя сопротивление управляет током через внешний резистор сопротивления (см. рис.17). Внешний резистор обычно называют как резистор нагрузки . Он мог обозначать либо электрический свет, либо электронагревательный элемент, а может и электродвигатель. В основная цель схема должна передавать энергию от батареи к нагрузке, где она фактически делает что-то полезное для нас ( например, , освещение лампочку или поднятие тяжести). Посмотрим, насколько внутреннее сопротивление батареи мешает этому процессу.

Эквивалентное сопротивление цепи (так как сопротивление нагрузки равно последовательно с внутренним сопротивлением), поэтому ток, протекающий в схема задается

(145)

Выходная мощность ЭДС просто

(146)

Мощность, рассеиваемая в виде тепла внутренним сопротивлением батареи, равна

(147)

Точно так же мощность, передаваемая нагрузке, равна

(148)

Обратите внимание, что

(149)

Таким образом, часть выходной мощности батареи немедленно теряется из-за рассеивания тепла внутреннее сопротивление батареи.Остаток передается в нагрузку.

Пусть а также . Это следует из Уравнение (148) что

(150)

Функция монотонно возрастает от нуля при увеличивая диапазон, достигает максимальное значение at, а затем монотонно убывает с увеличением В диапазоне . Другими словами, если сопротивление нагрузки изменяется на постоянная, а затем передаваемая мощность достигает максимума значение

(151)

когда .Это очень важный результат в электротехнике. Передача мощности между источником напряжения и внешней нагрузкой наиболее эффективна, когда сопротивление нагрузки соответствует внутреннему сопротивлению источника напряжения. Если сопротивление нагрузки слишком низкое, то большая часть выходной мощности напряжения источник рассеивается в виде тепла внутри самого источника. Если сопротивление нагрузки слишком велик, тогда ток, протекающий в цепи, слишком мал, чтобы передавать энергию нагрузке с заметной скоростью.Обратите внимание, что в оптимальном случае , только половина выходной мощности источника напряжения передается в нагрузку. Другая половина рассеивается внутри в виде тепла. источник. Между прочим, инженеры-электрики называют процесс, при котором сопротивление нагрузка согласована с нагрузкой источника питания , согласована импеданс (импеданс — это просто причудливое название сопротивления).

---

Далее: Рабочие примеры Up: Электрический ток Предыдущая: Энергия в цепях постоянного тока

Ричард Фицпатрик 2007-07-14

Внутреннее сопротивление

Любой источник электрической энергии, такой как аккумулятор или генератор, поставляет электроэнергию путем преобразования некоторой другой формы энергии в электрическую.В случае с батареей используется энергия, создаваемая какой-либо химической реакцией. Батарея обеспечивает электродвижущую силу (ЭДС), которая толкает электроны вокруг любой электрической цепи, к которой она подключена. Эта электродвижущая сила может быть выражена как напряжение и определяется как общее количество энергии (в джоулях) на единицу заряда (в кулонах), подаваемого в схему. Его можно представить с помощью следующей формулы:

куда:

E = энергия в джоулях

Q = заряд в кулонах

ℰ = электродвижущая сила

Разность потенциалов (pd) на каждом компоненте в цепи также выражается как напряжение, но определяется как энергия на единицу заряда, преобразованная компонентом в другие формы энергии.Полная ЭДС, обеспечиваемая батареей, по сути, является напряжением разомкнутой цепи, батареи, то есть напряжением, измеренным, когда к батарее не подключена нагрузка и не течет ток. На практике это можно измерить достаточно точно с помощью современного цифрового мультиметра, поскольку величина тока, потребляемого мультиметром, может считаться незначительной. В действительности разность потенциалов, измеренная на клеммах батареи, когда она подключена к нагрузке, будет меньше, чем ее напряжение холостого хода.Причина этого в том, что батарея не является идеальным источником напряжения , потому что, помимо протекания тока через нагрузку, батарея также должна пропускать ток через свое собственное внутреннее сопротивление , что приведет к рассеиванию энергии в виде тепла. .

Внутреннее сопротивление химической батареи обычно составляет от долей Ом до нескольких Ом и в основном связано с сопротивлением электролитических материалов, используемых при производстве батареи.Ток должен течь между электродами батареи и через эти материалы, когда батарея подключена к электрической цепи. Таким образом, источник напряжения, такой как батарея, можно рассматривать как идеальный источник напряжения (без внутреннего сопротивления), соединенный последовательно с резистором (внутреннее сопротивление батареи). Когда через батарею протекает ток, на внутреннем сопротивлении будет небольшое падение напряжения. Это падение напряжения можно рассчитать как умножение силы тока на внутреннее сопротивление (закон Ома).Когда к источнику напряжения приложена нагрузка, падение напряжения на сопротивлении нагрузки (напряжение на клеммах ) будет равно ЭДС источника минус падение напряжения на внутреннем сопротивлении, поскольку два сопротивления включены последовательно с друг друга. Схема ниже иллюстрирует принцип.

Внутреннее сопротивление батареи последовательно с сопротивлением нагрузки.

Внутреннее сопротивление батареи зависит от типа батареи (т.е.е. щелочной , свинцово-кислотный , никель-кадмиевый и т. Д.), И могут варьироваться в зависимости от нагрузки, температуры и возраста аккумулятора. Одноразовые батареи со временем подают меньшее напряжение, например, потому что их внутреннее сопротивление постоянно увеличивается. В конце концов, вырабатываемое напряжение будет настолько низким, что аккумулятор практически не будет использоваться, и его придется выбросить. Если ЭДС () батареи известна, ее внутреннее сопротивление ( R _{ВНУТРЕННЯЯ} ) можно определить путем измерения тока ( I _{НАГРУЗКА} ), протекающего через сопротивление нагрузки ( R _{НАГРУЗКА} ) с известным значением.Поскольку внутреннее сопротивление и сопротивление нагрузки включены последовательно, мы можем использовать закон Кирхгофа по напряжению и закон Ома, чтобы получить следующую формулу:

ℰ = ( R _{ВНУТРЕННЯЯ} + R _{НАГРУЗКА} ) × I _{НАГРУЗКА}

Решая для R _{ВНУТРЕННЯЯ} , получаем:

R ВНУТРЕННИЙ =	ℰ	— R НАГРУЗКА
	I НАГРУЗКА

Рассмотрим схему, показанную ниже, в которой батарея с известной ЭДС 1.5 В последовательно с лампой. Падение напряжения, измеренное на лампе В, _{НАГРУЗКА} , составляет 1,2 В, что означает, что мы «потеряли» 0,3 В на внутреннем сопротивлении R _{ВНУТРЕННИЙ} . Сопротивление проводов в цепи можно считать незначительным, тогда как сопротивление лампы R _{НАГРУЗКА} неизвестно. Ток –, протекающий по цепи, измеряется как 0,30 А. Как определить внутреннее сопротивление?

Какое внутреннее сопротивление батареи?

Поскольку мы знаем, что R = V / I (закон Ома), мы можем найти сопротивление нагрузки следующим образом:

R НАГРУЗКА =	V НАГРУЗКА	=	1.2 В	= 4 Ом
	I		0,3 A

Теперь, используя полученную ранее формулу для внутреннего сопротивления:

R ВНУТРЕННИЙ =	ℰ	— R НАГРУЗКА
	I НАГРУЗКА

ВНУТРЕННИЙ

1.5 В	— 4 Ом = 1 Ом
		0,3 А

Внутреннее сопротивление источника электрической энергии является важным фактором при рассмотрении вопроса о том, как получить от источника максимальную мощность для подключенного к нему электрического прибора (нагрузки). Хотя мы рассмотрим тему мощности более подробно в другом месте, теорема о максимальной мощности утверждает, что максимальная передача мощности происходит, когда внутреннее сопротивление источника равно сопротивлению нагрузки.Обратной стороной этого является то, что мощность, рассеиваемая в самом источнике, также равна мощности, передаваемой нагрузке ( Power = I ² × R ), что дает энергоэффективность всего 50%. Наиболее эффективная передача мощности происходит, когда внешнее (нагрузочное) сопротивление намного превышает внутреннее сопротивление источника. Поэтому при выборе наилучшего типа источника необходимо тщательно учитывать потребности приложения.Например, свинцово-кислотный автомобильный аккумулятор должен обеспечивать относительно высокие токи при сравнительно низком напряжении (большинство автомобильных аккумуляторов вырабатывают номинальную ЭДС 12,6 вольт). Его низкое внутреннее сопротивление позволяет ему обеспечивать такие высокие токи без значительного падения напряжения на клеммах. С другой стороны, высоковольтные источники питания должны иметь чрезвычайно высокое внутреннее сопротивление, чтобы ограничить ток, который может протекать в случае случайного короткого замыкания.

Проблемы

1. Батарея 9 В подключена последовательно к нагрузке, и напряжение на клеммах равно 8 В.Измеренный ток в цепи составляет 5 А. Какое внутреннее сопротивление батареи?
2. Какая ЭДС батареи в следующей цепи?
   
   
   
3. Какое внутреннее сопротивление батареи в следующей цепи?
   
   
   
4. Аккумулятор имеет внутреннее сопротивление 0,5 Ом и ЭДС 1.5 В. При последовательном подключении к сопротивлению нагрузки напряжение на клеммах падает до 1,45 В. Какой ток течет в цепи и каково значение сопротивления нагрузки?
5. Какое напряжение на клеммах аккумулятора с ЭДС 12 В и внутренним сопротивлением 0,5 Ом при последовательном подключении к резистору 10 Ом?

Ответы на проблемы

Измерение внутреннего сопротивления батарей

Добавлено в избранное Любимый 7

Внутреннее сопротивление

При проектировании схемы с аккумулятором мы часто предполагаем, что аккумулятор является идеальным источником напряжения.Это означает, что независимо от того, какую нагрузку мы прилагаем к аккумулятору, напряжение на выводах источника всегда остается неизменным.

Если мы моделируем эту батарею как идеальный источник напряжения, изменение значения R _L не влияет на напряжение между выводами батареи

На самом деле несколько факторов могут ограничить способность батареи действовать как идеальный источник напряжения. Размер батареи, химические свойства, возраст и температура — все это влияет на величину тока, которую батарея может выдавать.В результате мы можем создать лучшую модель батареи с идеальным источником напряжения и резистором, включенным в серию .

Батареи можно смоделировать как идеальный источник напряжения с последовательным резистором (обозначенным R _I )

Мы можем измерить напряжение аккумулятора на его выводах без подключенной нагрузки. Это известно как напряжение холостого хода (В _OC ).

Измерение напряжения щелочного элемента AA без нагрузки

Обратите внимание, что, поскольку через внутренний резистор не течет ток, падение напряжения на нем равно 0 В.Следовательно, можно предположить, что V _OC равно напряжению идеального источника напряжения в аккумуляторной батарее.

Если мы подключим нагрузку к аккумулятору, напряжение на выводах упадет.

Здесь мы измеряем падение напряжения на резисторе 4 Ом

Это падение напряжения вызвано внутренним сопротивлением батареи. Мы можем рассчитать внутреннее сопротивление, если снимем показания напряжения холостого хода и напряжения на клеммах батареи с подключенной нагрузкой.

Для начала создадим схему, показывающую нашу схему.

Вот наша схема. Мы хотим рассчитать R _I .

Мы можем подключить измеренное нами напряжение под нагрузкой (V _L ) и значение резистора (R _L ) в закон Ома, чтобы получить ток, протекающий по цепи (I).

Нам также нужно получить напряжение на внутреннем резисторе. Мы можем сделать это, используя закон напряжения Кирхгофа. Упрощенно для этой схемы, мы можем сказать, что падение напряжения на обоих резисторах должно составлять в сумме напряжение идеального источника напряжения.

Теперь, когда мы знаем падение напряжения на внутреннем резисторе и ток через него, мы можем снова использовать закон Ома, чтобы найти его сопротивление.

Из этого видно, что внутреннее сопротивление (в данный момент) элемента AA составляет 0,273 Ом .

ПРИМЕЧАНИЕ : С помощью этого метода мы можем только сделать снимок внутреннего сопротивления. Внутреннее сопротивление может варьироваться в зависимости от возраста батареи и температуры. Через 10 минут значение сопротивления может измениться! Обычная щелочная батарея AA может иметь где-то от 0.Внутреннее сопротивление 1 Ом и 0,9 Ом.

---

← Предыдущая страница
Введение

Влияние внутреннего импеданса — Тестеры батарей Neware

Практический источник электроэнергии, который представляет собой линейную электрическую цепь, может, согласно теореме Тевенина, быть представлен как идеальный источник напряжения, включенный последовательно с импедансом. Это сопротивление называется внутренним сопротивлением источника. Когда источник питания выдает ток, измеренное значение e.м.ф. (выходное напряжение) ниже, чем напряжение холостого хода; разница — это падение напряжения (произведение тока и сопротивления), вызванное внутренним сопротивлением. Понятие внутреннего сопротивления применимо ко всем видам электрических источников и полезно для анализа многих типов электрических цепей. Внутреннее сопротивление может быть вызвано рядом причин, хотя возможная причина — внутреннее химическое проникновение. Когда для обеспечения тока применяется тепловая энергия, эта приложенная энергия составляет большую часть энергии источника энергии, который производит химические вещества.Ток нагрузки передается по кругу и возвращается к батарее (источнику напряжения), а затем выполняет сопротивление.

Когда через элемент протекает ток, на внутреннем сопротивлении элемента возникает падение напряжения IR, которое снижает напряжение на выводах элемента во время разряда и увеличивает напряжение, необходимое для зарядки элемента, таким образом уменьшая его эффективную емкость, а также уменьшая его заряд. / эффективность разряда. Более высокие скорости разряда приводят к более высоким внутренним падениям напряжения, что объясняет более низкие кривые разряда напряжения при высоких скоростях C.

На внутренний импеданс влияют физические характеристики электролита: чем меньше размер гранул материала электролита, тем ниже полное сопротивление. Размер зерна контролируется производителем ячейки в процессе измельчения.

Спиральная конструкция электродов часто используется для увеличения площади поверхности и, таким образом, уменьшения внутреннего импеданса. Это снижает тепловыделение и обеспечивает более быструю зарядку и разрядку.

Внутреннее сопротивление гальванического элемента зависит от температуры и уменьшается с ростом температуры из-за увеличения подвижности электронов.

Внутреннее сопротивление большинства химических элементов ячеек также имеет тенденцию значительно увеличиваться к концу цикла разряда, поскольку активные химические вещества переводятся в свое разряженное состояние и, следовательно, эффективно израсходуются. Это в основном отвечает за быстрое падение напряжения на элементе в конце цикла разряда.

Внутреннее сопротивление также влияет на эффективную емкость ячейки. Чем выше внутреннее сопротивление, тем выше потери при зарядке и разрядке, особенно при более высоких токах.Это означает, что при высоких скоростях разряда доступная емкость ячейки ниже. И наоборот, если он разряжается в течение длительного периода, емкость в ампер-часах выше. Это важно, потому что некоторые производители указывают емкость своих батарей при очень низкой скорости разряда, что делает их намного лучше, чем они есть на самом деле.

Внутренний импеданс на WiKi: http://en.wikipedia.org/wiki/Internal_resistance

Neware имеет переносной продукт BVIR для теста ACIR батареи, а наш BTS4000 способен выполнять тест DCIR батареи.

Что такое внутреннее сопротивление? Как работает аккумулятор? »Science ABC

Внутреннее сопротивление можно определить как способность объекта препятствовать потоку электронов, проходящих через проводник. Резисторы сделаны из изоляторов, таких как углерод или пластмасса, материалов, которые препятствуют прохождению через них электронов. Эта способность заложена в их структуре.

Батарея аналогична двум ямкам электронов, которые соединены друг с другом, где объем электронов в одной яме больше, чем в другой.При подключении толчок естественным образом выталкивает лишние электроны из второй ямы в первую, пока их объемы не сравняются.

Однако по какой-то причине такая передача не обеспечивает абсолютной точности; не каждый электрон переходит на другую сторону. Похоже, что во время этого процесса теряется некоторая электрическая энергия. В случае реальных батарей эта потерянная энергия преобразуется в повышение температуры самой батареи.

Этот внутренний нагревательный элемент ведет себя как обычный резистор, который рассеивает мощность в виде тепла, когда через него проходит скачок тока.Мы называем этот элемент внутренним сопротивлением батареи . Чтобы понять, почему батареи не могут помочь, но сами вызывают разрушение, мы должны сначала понять, как батареи работают и распределяют энергию по цепи.

Как работает аккумулятор?

Аккумулятор имеет две клеммы, состоящие из разных металлов, и плавающий между ними электролит. Электролит — это химический раствор, который позволяет электронам проходить через него. Проще говоря, электролит проводит электричество.Электролит — это раствор, который бурно реагирует с металлами, разделяя их на составляющие ионы.

Один вывод представляет собой катод, предпочтительно из оксида металла, который содержит множество положительно заряженных объектов или ионов металлов с недостатком электронов. Другой вывод — это анод, металл, содержащий избыток отрицательно заряженных ионов, или ионы металла с избытком электронов.

Химическая реакция внутри электролита окисляет катод, заставляя его терять электроны, которые проходят через цепь и, следовательно, уменьшают анод, когда он наследует их.Этот аппарат формирует две наши ямы или потенциалы, соединенные средой, через которую проходят лишние электроны.

Система преобразует химическую энергию в электрическую до тех пор, пока не останутся реагенты для окислительно-восстановительной реакции. В этот момент батарея потухла. Однако мы можем добиться обратного с помощью внешних средств, например, преобразовать электрическую энергию из чужеродного источника в химическую.

Теперь аппарат пополняется новыми реагентами, и мы можем использовать эту пополненную химическую энергию, преобразовывая ее в электрическую.Аккумулятор теперь заряжен .

Это объяснение того, как батарея в идеале работает .

Внутреннее сопротивление

Сопротивление можно определить как способность объекта препятствовать потоку электронов, проходящих через проводник. Резисторы сделаны из изоляторов, таких как углерод или пластмасса, материалов, которые препятствуют прохождению через них электронов. Эта способность заложена в их структуре.

Проводники обладают кристаллической структурой, в которой несколько электронов прикреплены к определенным пустотам, в то время как многие свободные электроны роятся вокруг без колебаний.С другой стороны, изоляторы, такие как пластмассы, имеют кристаллическую структуру, которая прикрепляет свои электроны к местам, так что они полностью заняты. Нет электронов, которые могли бы свободно перемещаться и переносить ток.

Кристаллическая структура проводника, в которой несколько электронов свободно перемещаются. Справа: структура изолятора, в которой электроны склеены друг с другом.

Аналогичным образом батареи изготавливаются из материалов с ненулевым удельным сопротивлением. Внутреннее сопротивление компонента возникает из-за структурных недостатков или неровностей.Казалось бы, незаметные сопротивления всех компонентов в сумме дают общее сопротивление конечной ощутимой величины.

Нет кристаллической структуры идеальная. Даже металл имеет свойство обладать некоторым сопротивлением из-за различных факторов, таких как примеси или столкновение электронов в объеме проводника из-за случайного нагрева. Можно сделать вывод, что никакая настоящая батарея не является источником напряжения чистого .

Чтобы учесть это неизбежное препятствие, источник напряжения представлен последовательным напряжением ε с небольшим внутренним сопротивлением r .

Это напряжение официально известно как электродвижущая сила. Он обеспечивает силу, заставляющую электроны двигаться. Если мы подключим последовательно внешнее сопротивление R, нагрузку, чтобы замкнуть эту цепь, по закону Ома, мы находим:

Здесь В, — это падение напряжения на нагрузке R . Кроме того, из-за этого внутреннего сопротивления теперь уменьшается максимальный ток, который может потребляться от батареи.

Если значение I> I (0), , то значение V становится отрицательным, что означает отрицательное значение R.Это практически невозможно. Можно сделать вывод, что если эта цепь закорочена путем прямого соединения двух клемм проводом, максимальный ток, который будет потребляться, теперь ограничен до I (0).

Можно найти значение этих величин, вырезанных или напечатанных на батарее, чтобы пользователи могли предостеречь их от неправильного обращения с ними. Например, сухой элемент рассчитан на 1,5 В и 0,1 А. Конечно, такой короткозамкнутый сухой элемент не был бы опасен, но более мощный источник питания, рассчитанный, например, на 20 В и 200 А, потенциально опасен. .

Рассеиваемая мощность

Резистор рассеивает энергию в виде тепла. Мы можем наблюдать это и с внутренним сопротивлением. Можно показать, что небольшая часть мощности ε расходуется на внутреннее сопротивление r , а оставшаяся часть передается на нагрузку R .

Наличие внутреннего сопротивления говорит о том, что нет источников напряжения perfect . То есть они не идеальны в том смысле, что батареи не полностью эффективны, когда они передают свою электроэнергию во внешнюю цепь.Какой бы крошечной она ни была, она всегда будет рассеиваться и тратиться впустую в этом резисторе.

Статьи по теме

Статьи по теме

Здесь есть поразительное сходство с законами термодинамики, согласно которым никакая механическая машина не может преобразовывать и использовать всю входящую энергию для выполнения работы, не затрачивая на себя минимальное количество энергии. Эта энергия переводится как тепло — повышение собственной температуры машины.

Это один из самых фундаментальных законов Вселенной, независимо от того, применяется ли он к ревущему двигателю автомобиля или к лаконичной светодиодной лампе 5V.

Электродвижущая сила — Университетская физика, том 2

Цели обучения

К концу раздела вы сможете:

• Опишите электродвижущую силу (ЭДС) и внутреннее сопротивление батареи
• Объясните основную работу аккумулятора

Если вы забудете выключить автомобильные фары, они будут постепенно тускнеть по мере разрядки аккумулятора.Почему они не мигают внезапно, когда разрядился аккумулятор? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи. Причина снижения выходного напряжения для разряженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления. В этом разделе мы исследуем источник энергии и внутреннее сопротивление.

Введение в электродвижущую силу

Voltage имеет множество источников, некоторые из которых показаны на (Рисунок).Все такие устройства создают разность потенциалов и могут подавать ток, если подключены к цепи. Особый тип разности потенциалов известен как электродвижущая сила (ЭДС). ЭДС — это вовсе не сила, но термин «электродвижущая сила» используется по историческим причинам. Он был изобретен Алессандро Вольта в 1800-х годах, когда он изобрел первую батарею, также известную как гальваническая батарея. Поскольку электродвижущая сила не является силой, принято называть эти источники просто источниками ЭДС (произносимыми буквами «ee-em-eff»), а не источниками электродвижущей силы.

Разнообразные источники напряжения. а) ветряная электростанция Бразос в Флуванна, штат Техас; (б) Красноярская плотина в России; (c) солнечная ферма; (d) группа никель-металлогидридных батарей. Выходное напряжение каждого устройства зависит от его конструкции и нагрузки. Выходное напряжение равно ЭДС только при отсутствии нагрузки. (кредит a: модификация работы Стига Найгаарда; кредит b: модификация работы «vadimpl» / Wikimedia Commons; кредит c: модификация работы «The tdog» / Wikimedia Commons; кредит d: модификация работы «Itrados» / Wikimedia Commons)

Если электродвижущая сила вовсе не сила, то что такое ЭДС и что является источником ЭДС? Чтобы ответить на эти вопросы, рассмотрим простую схему лампы 12 В, подключенной к батарее 12 В, как показано на (Рисунок).Батарею можно смоделировать как устройство с двумя выводами, которое поддерживает один вывод с более высоким электрическим потенциалом, чем второй вывод. Более высокий электрический потенциал иногда называют положительной клеммой и обозначают знаком плюс. Клемму с более низким потенциалом иногда называют отрицательной клеммой и обозначают знаком минус. Это источник ЭДС.

Источник ЭДС поддерживает на одном выводе более высокий электрический потенциал, чем на другом выводе, действуя как источник тока в цепи.

Когда источник ЭДС не подключен к лампе, нет чистого потока заряда внутри источника ЭДС. Как только батарея подключена к лампе, заряды текут от одной клеммы батареи через лампу (в результате чего лампа загорается) и обратно к другой клемме батареи. Если мы рассмотрим протекание положительного (обычного) тока, положительные заряды покидают положительный вывод, проходят через лампу и попадают в отрицательный вывод.

Положительный поток тока полезен для большей части анализа схем в этой главе, но в металлических проводах и резисторах наибольший вклад в ток вносят электроны, протекающие в направлении, противоположном положительному потоку тока.Поэтому более реалистично рассмотреть движение электронов для анализа схемы на (рисунок). Электроны покидают отрицательную клемму, проходят через лампу и возвращаются к положительной клемме. Чтобы источник ЭДС поддерживал разность потенциалов между двумя выводами, отрицательные заряды (электроны) должны перемещаться с положительного вывода на отрицательный. Источник ЭДС действует как накачка заряда, перемещая отрицательные заряды от положительного вывода к отрицательному для поддержания разности потенциалов.Это увеличивает потенциальную энергию зарядов и, следовательно, электрический потенциал зарядов.

Сила, действующая на отрицательный заряд от электрического поля, действует в направлении, противоположном электрическому полю, как показано на (Рисунок). Чтобы отрицательные заряды переместились на отрицательный вывод, необходимо провести работу с отрицательными зарядами. Для этого требуется энергия, которая возникает в результате химических реакций в батарее. Потенциал поддерживается высоким на положительной клемме и низким на отрицательной клемме, чтобы поддерживать разность потенциалов между двумя клеммами.ЭДС равна работе, выполняемой над зарядом на единицу заряда при отсутствии тока. Поскольку единицей измерения работы является джоуль, а единицей заряда — кулон, единицей измерения ЭДС является

вольт.

Напряжение на клеммах батареи — это напряжение, измеренное на клеммах батареи, когда к клемме не подключена нагрузка. Идеальная батарея — это источник ЭДС, который поддерживает постоянное напряжение на клеммах, независимо от тока между двумя клеммами. Идеальная батарея не имеет внутреннего сопротивления, а напряжение на клеммах равно ЭДС батареи.В следующем разделе мы покажем, что у реальной батареи есть внутреннее сопротивление, а напряжение на клеммах всегда меньше, чем ЭДС батареи.

Источник потенциала батареи

ЭДС батареи определяется сочетанием химических веществ и составом выводов батареи. Свинцово-кислотные аккумуляторы, используемые в автомобилях и других транспортных средствах, представляют собой одну из наиболее распространенных комбинаций химических веществ. (Рисунок) показывает одну ячейку (одну из шести) этой батареи. Катодная (положительная) клемма ячейки соединена с пластиной из оксида свинца, а анодная (отрицательная) клемма подключена к свинцовой пластине.Обе пластины погружены в серную кислоту, электролит для системы.

Химические реакции в свинцово-кислотном элементе разделяют заряд, отправляя отрицательный заряд на анод, который соединен со свинцовыми пластинами. Пластины из оксида свинца подключаются к положительному или катодному выводу ячейки. Серная кислота проводит заряд, а также участвует в химической реакции.

Небольшое знание того, как взаимодействуют химические вещества в свинцово-кислотной батарее, помогает понять потенциал, создаваемый батареей.(Рисунок) показывает результат единственной химической реакции. На аноде помещаются два электрона, что делает его отрицательным, при условии, что катод снабжает два электрона. Это оставляет катод положительно заряженным, потому что он потерял два электрона. Короче говоря, разделение заряда было вызвано химической реакцией.

Обратите внимание, что реакция не происходит, если нет замкнутой цепи, позволяющей подавать два электрона на катод. Во многих случаях эти электроны выходят из анода, проходят через сопротивление и возвращаются на катод.Также обратите внимание, что, поскольку в химических реакциях участвуют вещества, обладающие сопротивлением, невозможно создать ЭДС без внутреннего сопротивления.

В свинцово-кислотной батарее два электрона вытесняются на анод элемента, а два электрона удаляются с катода элемента. В результате химической реакции в свинцово-кислотной батарее два электрона помещаются на анод и два электрона удаляются с катода. Для продолжения требуется замкнутая цепь, так как два электрона должны быть доставлены на катод.

Внутреннее сопротивление и напряжение на клеммах

Величина сопротивления прохождению тока внутри источника напряжения называется внутренним сопротивлением. Внутреннее сопротивление батареи r может вести себя сложным образом. Обычно она увеличивается по мере разряда батареи из-за окисления пластин или снижения кислотности электролита. Однако внутреннее сопротивление также может зависеть от величины и направления тока через источник напряжения, его температуры и даже его предыстории.Например, внутреннее сопротивление перезаряжаемых никель-кадмиевых элементов зависит от того, сколько раз и насколько глубоко они были разряжены. Простая модель батареи состоит из идеализированного источника ЭДС и внутреннего сопротивления r ((рисунок)).

Батарею можно смоделировать как идеализированную ЭДС с внутренним сопротивлением ( r ). Напряжение на клеммах аккумулятора.

Предположим, что внешний резистор, известный как сопротивление нагрузки R , подключен к источнику напряжения, например к батарее, как показано на (Рисунок).На рисунке показана модель батареи с ЭДС, внутренним сопротивлением R и нагрузочным резистором R , подключенным к ее клеммам. При обычном протекании тока положительные заряды покидают положительную клемму батареи, проходят через резистор и возвращаются к отрицательной клемме батареи. Напряжение на клеммах аккумулятора зависит от ЭДС, внутреннего сопротивления и силы тока и равно

.

При заданной ЭДС и внутреннем сопротивлении напряжение на клеммах уменьшается по мере увеличения тока из-за падения потенциала Ir внутреннего сопротивления.

Схема источника напряжения и его нагрузочного резистора R . Поскольку внутреннее сопротивление — последовательно с нагрузкой, оно может существенно повлиять на напряжение на клеммах и ток, подаваемый на нагрузку.

График разности потенциалов на каждом элементе цепи показан на (рисунок). По цепи проходит ток I , а падение потенциала на внутреннем резисторе равно Ir . Напряжение на клеммах равно падению потенциала на нагрузочном резисторе.Как и в случае с потенциальной энергией, важно изменение напряжения. Когда используется термин «напряжение», мы предполагаем, что это на самом деле изменение потенциала, или. Однако для удобства часто опускается.

График зависимости напряжения через цепь батареи и сопротивления нагрузки. Электрический потенциал увеличивает ЭДС батареи из-за химических реакций, выполняющих работу с зарядами. В аккумуляторе происходит снижение электрического потенциала из-за внутреннего сопротивления.Потенциал уменьшается из-за внутреннего сопротивления, в результате чего напряжение на клеммах аккумулятора равно. Затем напряжение уменьшается на ( IR ). Сила тока равна

Ток через нагрузочный резистор равен. Из этого выражения видно, что чем меньше внутреннее сопротивление r , тем больший ток подает источник напряжения на свою нагрузку R . По мере разряда батарей r увеличивается. Если r становится значительной частью сопротивления нагрузки, то ток значительно снижается, как показано в следующем примере.

Анализ цепи с батареей и нагрузкой У данной батареи есть ЭДС 12,00 В и внутреннее сопротивление. (a) Рассчитайте напряжение на его клеммах при подключении к нагрузке. (b) Какое напряжение на клеммах при подключении к нагрузке? (c) Какая мощность рассеивает нагрузка? (d) Если внутреннее сопротивление увеличивается до, найдите ток, напряжение на клеммах и мощность, рассеиваемую нагрузкой.

Стратегия Приведенный выше анализ дал выражение для тока с учетом внутреннего сопротивления.Как только ток будет найден, можно рассчитать напряжение на клеммах, используя уравнение. Как только ток будет найден, мы также сможем найти мощность, рассеиваемую резистором.

Решение

1. Если ввести данные значения ЭДС, сопротивления нагрузки и внутреннего сопротивления в выражение выше, получим
   

   
   Введите известные значения в уравнение, чтобы получить напряжение на клеммах:
   

   
   Напряжение на клеммах здесь лишь немного ниже, чем ЭДС, что означает, что ток, потребляемый этой легкой нагрузкой, не имеет значения.

2. Аналогично с, ток
   

   
   Напряжение на клеммах теперь
   

   
   Напряжение на клеммах значительно снизилось по сравнению с ЭДС, что означает большую нагрузку на эту батарею. «Сильная нагрузка» означает большее потребление тока от источника, но не большее сопротивление.

3. Мощность, рассеиваемую нагрузкой, можно найти по формуле. Ввод известных значений дает
   

   
   Обратите внимание, что эту мощность также можно получить с помощью выражения, где В, — напряжение на клеммах (10.0 В в данном случае).

4. Здесь внутреннее сопротивление увеличилось, возможно, из-за разряда батареи, до точки, в которой оно равно сопротивлению нагрузки. Как и раньше, мы сначала находим ток, вводя известные значения в выражение, что дает
   

   
   Теперь напряжение на клеммах
   

   
   , а мощность, рассеиваемая нагрузкой, составляет
   

   .

   
   Мы видим, что увеличившееся внутреннее сопротивление значительно снизило напряжение на клеммах, ток и мощность, подаваемую на нагрузку.

Значение Внутреннее сопротивление батареи может увеличиваться по многим причинам. Например, внутреннее сопротивление перезаряжаемой батареи увеличивается с увеличением количества раз, когда батарея перезаряжается. Повышенное внутреннее сопротивление может иметь двоякое влияние на аккумулятор. Сначала снизится напряжение на клеммах. Во-вторых, аккумулятор может перегреться из-за повышенной мощности, рассеиваемой внутренним сопротивлением.

Проверьте свое понимание Если вы поместите провод непосредственно между двумя выводами батареи, эффективно закоротив клеммы, батарея начнет нагреваться.Как вы думаете, почему это происходит?

Если к клеммам подсоединен провод, сопротивление нагрузки близко к нулю или, по крайней мере, значительно меньше внутреннего сопротивления батареи. Поскольку внутреннее сопротивление невелико, ток в цепи будет большим. Большой ток приводит к тому, что внутреннее сопротивление рассеивает большую мощность. Мощность рассеивается в виде тепла.

Тестеры батарей

Тестеры батарей

, такие как показанные на (Рисунок), используют малые нагрузочные резисторы, чтобы намеренно потреблять ток, чтобы определить, падает ли потенциал клемм ниже допустимого уровня.Хотя трудно измерить внутреннее сопротивление батареи, тестеры батареи могут обеспечить измерение внутреннего сопротивления батареи. Если внутреннее сопротивление велико, батарея разряжена, о чем свидетельствует низкое напряжение на клеммах.

Тестеры аккумуляторов измеряют напряжение на клеммах под нагрузкой, чтобы определить состояние аккумулятора. (a) Техник-электронщик ВМС США использует тестер аккумуляторов для проверки больших аккумуляторов на борту авианосца USS Nimitz .Тестер батарей, который она использует, имеет небольшое сопротивление, которое может рассеивать большое количество энергии. (b) Показанное небольшое устройство используется на небольших батареях и имеет цифровой дисплей для индикации допустимого напряжения на клеммах. (кредит А: модификация работы Джейсона А. Джонстона; кредит б: модификация работы Кейта Уильямсона)

Некоторые батареи можно заряжать, пропуская через них ток в направлении, противоположном току, который они подают в прибор. Это обычно делается в автомобилях и батареях для небольших электроприборов и электронных устройств ((рисунок)).Выходное напряжение зарядного устройства должно быть больше, чем ЭДС аккумулятора, чтобы ток через него реверсировал. Это приводит к тому, что напряжение на клеммах аккумулятора становится больше, чем ЭДС, поскольку и I теперь отрицательное.

Зарядное устройство для автомобильного аккумулятора меняет нормальное направление тока через аккумулятор, обращая вспять его химическую реакцию и восполняя ее химический потенциал.

Важно понимать последствия внутреннего сопротивления источников ЭДС, таких как батареи и солнечные элементы, но часто анализ цепей выполняется с помощью напряжения на клеммах батареи, как мы делали в предыдущих разделах.Напряжение на клеммах обозначается просто как В , без индекса «клемма». Это связано с тем, что внутреннее сопротивление батареи трудно измерить напрямую и может со временем измениться.

Сводка

• Все источники напряжения состоят из двух основных частей: источника электроэнергии с характеристической электродвижущей силой (ЭДС) и внутреннего сопротивления r . ЭДС — это работа, совершаемая за один заряд для поддержания постоянной разности потенциалов источника.ЭДС равна разности потенциалов на клеммах при отсутствии тока. Внутреннее сопротивление — источника напряжения влияет на выходное напряжение при протекании тока.
• Выходное напряжение устройства называется напряжением на его клеммах и выражается выражением, где I — электрический ток, положительный, когда он течет от положительного вывода источника напряжения, а r — внутреннее сопротивление.

Концептуальные вопросы

Как внутреннее сопротивление перезаряжаемой батареи повлияет на энергию, используемую для зарядки батареи?

Часть энергии, используемой для перезарядки батареи, будет рассеиваться в виде тепла за счет внутреннего сопротивления.

Батарея с внутренним сопротивлением r и эдс 10,00 В подключена к нагрузочному резистору. По мере старения батареи внутреннее сопротивление увеличивается втрое. Насколько уменьшен ток через нагрузочный резистор?

Покажите, что мощность, рассеиваемая нагрузочным резистором, максимальна, когда сопротивление нагрузочного резистора равно внутреннему сопротивлению батареи.

Проблемы

Автомобильный аккумулятор с ЭДС 12 В и внутренним сопротивлением заряжается током 60 А.Обратите внимание, что в этом процессе аккумулятор заряжается. а) Какова разность потенциалов на его выводах? (б) С какой скоростью рассеивается тепловая энергия в батарее? (c) С какой скоростью электрическая энергия преобразуется в химическую энергию?

Наклейка на радио с батарейным питанием рекомендует использовать никель-кадмиевый аккумулятор (никель), хотя он имеет ЭДС 1,25 В, тогда как щелочной элемент имеет ЭДС 1,58 В. У радио есть сопротивление. (а) Нарисуйте принципиальную схему радиоприемника и его батареи.Теперь рассчитайте мощность, подаваемую на радио (б) при использовании никадовых элементов, каждый из которых имеет внутреннее сопротивление, и (в) при использовании щелочных элементов, имеющих внутреннее сопротивление. (d) Кажется ли эта разница значительной, учитывая, что эффективное сопротивление радиоприемника уменьшается при увеличении громкости?

а.

г. 0,476 Вт; c. 0,691 Вт; d. При понижении разность мощностей уменьшается; следовательно, при более высоких объемах существенной разницы нет.

Автомобильный стартер имеет эквивалентное сопротивление и питается от батареи 12,0 В с внутренним сопротивлением. а) Какой ток у двигателя? б) Какое напряжение приложено к нему? (c) Какая мощность подается на двигатель? (d) Повторите эти расчеты, когда соединения батареи корродируют, и добавьте в цепь. (Существенные проблемы возникают из-за даже небольшого количества нежелательного сопротивления в низковольтных и сильноточных приложениях.)

(a) Каково внутреннее сопротивление источника напряжения, если его потенциал на клеммах падает на 2.00 В при увеличении подаваемого тока на 5,00 А? (b) Можно ли определить ЭДС источника напряжения с помощью предоставленной информации?

а. ; б. Нет, существует только одно независимое уравнение, поэтому можно найти только r .

Человек с сопротивлением тела между руками случайно схватился за клеммы источника питания 20,0 кВ. (НЕ делайте этого!) (A) Нарисуйте принципиальную схему, чтобы представить ситуацию. б) Если внутреннее сопротивление источника питания равно, то какой ток через его тело? в) Какая сила рассеивается в его теле? (d) Если источник питания должен быть безопасным за счет увеличения его внутреннего сопротивления, каким должно быть внутреннее сопротивление, чтобы максимальный ток в этой ситуации был равен 1.00 мА или меньше? (e) Снизит ли эта модификация эффективность источника питания для управления устройствами с низким сопротивлением? Объясните свои рассуждения.

Автомобильный аккумулятор с ЭДС 12,0 В имеет напряжение на клеммах 16,0 В при зарядке током 10,0 А. а) Каково внутреннее сопротивление аккумулятора? (б) Какая мощность рассеивается внутри батареи? (c) С какой скоростью (in) его температура будет увеличиваться, если его масса составляет 20,0 кг, а его удельная теплоемкость равна, при условии, что тепло не уходит?

а.; б. 40,0 Вт; c.

Глоссарий

электродвижущая сила (ЭДС)

энергия, производимая на единицу заряда, полученная из источника, производящего электрический ток

внутреннее сопротивление

величина сопротивления прохождению тока внутри источника напряжения

разность потенциалов

Разница электрического потенциала между двумя точками в электрической цепи, измеренная в вольтах

падение потенциала

Потеря электрической потенциальной энергии при прохождении тока через резистор, провод или другой компонент

напряжение на клеммах

разность потенциалов, измеренная на клеммах источника при отсутствии нагрузки

.