ГЕРЦ (единица частоты) — это… Что такое ГЕРЦ (единица частоты)?
- ГЕРЦ (единица частоты)
- ГЕРЦ (единица частоты) ГЕРЦ, единица частоты СИ (см. СИ (система единиц)) и СГС системы единиц (см. СГС СИСТЕМА ЕДИНИЦ), обозначается Гц. Названа в честь Генриха Герца. 1 Гц — частота периодического процесса, при которой за время 1 с происходит один цикл процесса. Широко применяются кратные единицы (см. КРАТНЫЕ ЕДИНИЦЫ) от Герца — килогерц (1 кГц = 103 Гц), мегагерц (1 МГц = 106 Гц) и др.
Энциклопедический словарь. 2009.
- ГЕРХАРТ Пауль
- ГЕРЦА
Смотреть что такое «ГЕРЦ (единица частоты)» в других словарях:
Герц (единица частоты) — Герц, единица частоты. Названа в честь Генриха Герца.
Сокращённое обозначение: русское гц, международное Hz. 1 Г. ≈ частота периодического процесса, при которой за время в 1 сек происходит один цикл процесса. Широко применяются кратные единицы от … Большая советская энциклопедияГерц (единица измерения) — У этого термина существуют и другие значения, см. Герц. Герц (русское обозначение: Гц, международное обозначение: Hz) единица измерения частоты периодических процессов (например, колебаний) в Международной системе единиц (СИ). Герц… … Википедия
Герц — а; м. Единица частоты периодических колебаний (Гц), равная одному колебанию в секунду. ● По имени немецкого физика Г. Герца (1857 1894). * * * Герц единица частоты СИ и СГС систем единиц, обозначается Гц. Названа по имени Г. Р. Герца. 1 Гц … … Энциклопедический словарь
герц — герц, а; р. мн. ев, счётн.ф. герц (единица частоты колебаний) … Русское словесное ударение
ГЕРЦ — единица частоты СИ и СГС системы единиц, обозначается Гц.
Названа в честь Генриха Герца. 1 Гц частота периодического процесса, при которой за время 1 с происходит один цикл процесса. Широко применяются кратные единицы от Герца килогерц (1 кГц =… … Большой Энциклопедический словарьГЕРЦ — единица частоты периодических колебаний; обозначается Гц. 1 Гц частота, при которой за время 1 с происходит один цикл периодического процесса … Большая политехническая энциклопедия
герц — (по имени нем. физика Генриха Герца (Hertz). 1857 1894) единица частоты периодических колебаний, равная одному колебанию в секунду, обозначается гц, hz; для измерения высоких частот употр. кратные единицы в тысячу, миллион н миллиард раз большие … Словарь иностранных слов русского языка
ГЕРЦ — • ГЕРЦ (Hertz) Генрих Рудольф (1857 94), немецкий физик, который открыл радиоволны. Был помощником Германа ГЕЛЬМГОДЬЦА, затем профессором университета в Карлсруэ, а позже Боннского университета.
Герц Генрих Рудольф — Херц (Hertz) (1857 1894), немецкий физик, один из основоположников электродинамики. Экспериментально доказал (1886 89) существование электромагнитных волн (используя вибратор Герца) и установил тождественность основных свойств электромагнитных и… … Энциклопедический словарь
Герц — Герц единица измерения частоты в системе СИ. Герц, Херц фамилия немецкого или еврейского происхождения. Этимология от нем. Herz сердце. Еврейская фамилия может также происходить от имени Герш. Густав Людвиг Герц (1887… … Википедия
Сокращённое обозначение: русское гц, международное Hz. 1 Г. ≈ частота периодического процесса, при которой за время в 1 сек происходит один цикл процесса. Широко применяются кратные единицы от … Большая советская энциклопедия
Названа в честь Генриха Герца. 1 Гц частота периодического процесса, при которой за время 1 с происходит один цикл процесса. Широко применяются кратные единицы от Герца килогерц (1 кГц =… … Большой Энциклопедический словарь
| Подборка ссылок из каталогов инструмента для словаря по машиностроению | |||||
| 1050 Преобразование основных единиц измерения Справочная таблица Сила Напряжение Давление Энергия Работа Мощность Удельная теплоемкость Частота вращения | 1082 Перевод единиц в системе СИ Таблица основных преобразований между старыми и новыми единицами измерения Основные приставки и их применение | ||||
| 1322 Международная единая система единиц СИ Справочные таблицы соотношения с другими произвольными единицами Давление Работа Энергия Мощность Напряжение | 1655 Unit conversion table for easier change into SI units Справочная переводная таблица перевода разных единиц измерения в единицы международной единой | ||||
См. | |||||
Предельные отклонения линейных размеров / Fit tolerance table | Основное машинное время обработки / Machining time | ||||
Формулы для расчета сверления / Formulas for drilling | Формулы точения / Turning formulas | ||||
Экономическая эффективность металлообработки / Machining economy | Формулы фрезерования / Milling formulas | ||||
Алфавит инструментов (Поисковые указатели) / Alphabet of tools (Index) | Фото режущих инструментов по металлу / Metal cutting tools images | ||||
| Примеры страниц из каталогов инструмента для металлообработки | |||||
1050 Каталог KORLOY 2016 Металлорежущий инструмент и станочная оснастка Стр. | |||||
Преобразование основных единиц измерения Справочная таблица Сила Напряжение Давление Энергия Работа Мощность Удельная теплоемкость Частота вращения Преобразование основных единиц измерения Справочная таблица Сила Напряжение Давление Энергия Работа Мощность Удельная теплоемкость Частота вращения _ кгс ДИН 1 1.Q1972X1Q-1 1X1Q-5 9.80665 1 9.8Q665X 1Q5 1X1Q-S 1.Q1972X1Q-6 1 Напряжение Па или Н/м2 МПа или Н/мм2 кгс/мм2 кгс/см2 кгс/м2 1 1X1Q-6 1.Q1972X1Q-7 1.Q1972X1Q-5 1.Q1972X1Q-1 1X1Q6 1 1.Q1972X1Q-1 1.Q1972X 1Q 1.Q1972X1Q5 9.8Q665X 1Q6 9.8Q665 1 1X1Q2 1X1Q6 9.8Q665X 1Q4 9.8Q665X 1Q-2 1X1Q-2 1 1X1Q4 9.8Q665 9.8Q665X 1Q-6 1X1Q-6 1X1Q-4 1 Давление Па кПа МПа Бар кгс/см2 1 1X1Q-3 1X1Q-6 1X1Q-5 1.Q1972X1Q-5 1X1Q3 1 1X1Q-3 1X1Q-2 1.Q1972X1Q-2 1X1Q6 1X1Q3 1 1X1Q 1.Q1972X1Q 1X1Q5 1X1Q2 1X1Q-1 1 1.Q1972 9.8Q665X 1Q4 9.8Q665X 1Q 9.8Q665X 1Q-2 9.8Q665X 1Q-1 1 Работа, Энергия, Калории Дж кВт КГС м ккал 1 2.77778X1Q-7 1.Q1972X1Q-1 2. | |||||
1082 Справочник HOFFMANN GROUP 2012 Обработка материалов резанием Garant ToolScout Стр. | |||||
Основные единицы СИ Величина Название Обозначение Длина Метр м Масса Килограмм кг Время Секунда с Сила тока Ампер A Сила Ньютон Н Вращающи Основные единицы СИ Величина Название Обозначение Длина Метр м Масса Килограмм кг Время Секунда с Сила тока Ампер A Сила Ньютон Н Вращающий момент Ньютон-метр Н м Мощность Ватт Вт Энергия (работа) Джоуль Дж Давление Паскаль Па Температура Кельвин К Перевод механических нагрузок Единица Н/мм2 Па кгс/мм2 1 Н/мм2 1 1 Па Ю’8 1 кгс/мм2 9,81 10° 1 9,81 — 0,102 0,102-1 O’6 1 В данном случае также на практике пересчет с достаточной точностью (погрешность 2 процента) производится следующим образом 1 Н/мм2 = 0,1 кгс/мм2 1 кгс/мм2 = 10 Н/мм2 Основные приставки СИ и их применение мега М 1 000 000 = 106 1 МВт = 1 000000 Вт кило к 000 = 103 1 кВт = 1 000 Вт гекто г 100 = 102 1 гл = 100 дека да 10 1 даН = 10 Н деци д 0,1 = 10’1 1 дм = 0,1 м санти с 0,01 = 10’2 1 см = 0,01 м милли м 0,001 = 10-3 1 мм = 0,001 м микро мк 0,000001 = 10-6 1 мкм = 0,000001 м Энергия/работа (в джоулях) Для единицы энергии приняты 3 эквивалентных обозначения 1.  с. кВт = 860 ккал/ч Дж = 0,102 кгс/м2 Дж = 0,239 кал Па = (1 N/m2) = 0,102 кгс/м2 К = «С + 273,15 старой единицы в единицу СИ 1 кгс 1 кгс м 1 кгс м/с 1 л. с. 1 ккал/ч 1 кгс/м2 1 кал 1 кгс/м2 9.81 Н 9.81 Н-м 9.81 Вт 0,736 кВт 1,16. 6 6’3 кВт= 0,00116 кВт 9.81 Дж 4 1Q Пж э з1 Па = 9,81 Н/м2 Согласно таблицам 1 кгс = 9,81 Н и 1 Н = 0,102 кгс. При норме погрешностей лишь 2 процента кгс и Н расходятся на коэффициент 10. Поэтому на практике используются следующие значения 1 кгс = 1 Н 10 Н 0,1 кгс Например 1. Нагрузка на балку составляет 10 кН 2. Балка весит 200 кг Шкала Кельвина начинается с абсолютного нуля = — 273,15 °С Следующая таблица отражает связь между °С и K Кельвин °С Абсолютный нуль О К -273,15°С Точка плавления льда 273,15 К 0°С Точка кипения воды 373,15 К + 100°С На практике сохраняется значение температуры воды, например, 20 °С . Только для разностей температур его следует давать в кельвинах K. В данном случае 1 °С точно соответствует 1 K. Например разность температур оконной рамы снаружи и изнутри составляет 15 K. Обозначение градуса ° не применяется при указании температуры в кельвинах. ) SI-System International d’Unites = Международная система единиц ) единицей температуры в системе СИ является кельвин. 1058 5 июля 1976 в ФРГ была введена система единиц СИ. По окончании переходного периода, с 1 января 1978 года, она стала обязательной. | |||||
1322 Каталог MITSUBISHI 2014 Металлорежущий инструмент токарный и вращающийся Стр.N040 | |||||
Международная единая система единиц СИ Справочные таблицы соотношения с другими произвольными единицами Давление Работа Энергия Мощность Напряжение Международная единая система единиц СИ Справочные таблицы соотношения с другими произвольными единицами Давление Работа Энергия Мощность Напряжение _ Па кПа МПа Бар кгс см2 атм. мм вод. ст. мм рт. ст. или Торр Напряжени дина кгс Па МПа или Н мм2 кгс мм2 кгс см2 1 1хЮ5 1. | |||||
| Пример иллюстрации инструмента из промышленного каталога (из подборки фото инструментов для металлообработки / Metal cutting tools images) | |||||
392 Каталог WALTER 2013 Дополнение к общему Стр. | |||||
Фото спирального метчика с винтовыми стружечными канавками Иллюстрация процесса нарезания внутренней метрической резьбы в глухом отверстии заготовки детали на станке Фото спирального метчика с винтовыми стружечными канавками Иллюстрация процесса нарезания внутренней метрической резьбы в глухом отверстии заготовки детали на станке _ метчиком Walter Prototyp Красочная иллюстрация из дополнительного каталога продукции немецкого производителя за 2013 год на русском языке Общий вид обработки на вертикально-фрезерном станке | |||||
Каталоги инструмента и оснастки для металлообработки на станках / | |||||
также / See also :
L7
1058
01972×10’1 1 1хЮ»б 1.01972×10’7 1.01972×10’5 1×10’5 1 1.01972×10- 1хЮ6 1 1.01972×10й 1.01972×10 9.80665 9.80665×105 1 9.80665×10е 9.80665 1 1×102 9.80665×104 9.80665×10’2 1×10’2 1 Работа Эн ергия Колич ество теплот (Примечание) 1 Мощность (Показ ЛПа1Н мм2 атель производитель носги Энергия) Koi мчество теплоты Дж кВтч КГСМ ккал Вт КГСм с л.с. ккал 1 2.77778×10’7 1.01972×10’1 2.38889×1 O’4 1 1.01972×10й 1.35962×1 O’3 8.6000 хЮ’1 3.600 хЮ6 1 3.67098×105 8.6000 хЮ2 9.80665 1 1.33333×1 о-2 8.43371 9.80665 2.72407Х10-6 1 2.34270×10-3 7.355 хЮ2 7.5 хЮ 1 6.32529×102 4.18605×103 1.16279×10’3 4.26858×102 1 1.16279 1.18572×10й 1.58095×1 O’3 1 (Примечание) 1Дж1ВтС 1Дж 1НМ (Примечание) 1Вт1Дж л.с. -лошадиная сила 1ккал4.18605Дж 1л.с.0.7355кВт (По закону мер и весо) 1 ккап4.18605Дж (По закону мер и весов) N040 ТЕХНИЧЕСКИЕ ДАННЫЕ ТЕХНИЧЕСКИЕ ДАННЫЕ МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ ЕДИНИЦЫ ИЗМЕРЕНИЯ В СИСТЕМЕ СИ ВЫДЕЛЕНЫ ЖИРНЫМ ШРИФТОМ (Жирный шрифт указывает единицу измерения СИ.) 1 1хЮ-3 1×10-6 1хЮ’5 1.01972×10″5 9.
86923×1 O’6 1.01972×10’1 7.50062×10’3 1х103 1 1×1 O’3 1×10-2 1.01972×10″2 9.86923×10’3 1.01972×102 7.50062 1хЮ6 1хЮ3 1 1×10 1.01972×10 9.86923 1.01972×105 7.50062×103 1хЮ5 1хЮ2 1×1 О-1 1 1.01972 9.86923×10й 1.01972×104 7.50062×102 9.80665×104 9.80665×10 9.80665×10’2 9.80665×10’1 1 9.67841×10й 1 хЮ4 7.35559×102 1.01325x10s 1.01325×102 1.01325×10й 1.01325 1.03323 1 1.03323×104 7.60000×102 9.80665 9.80665×10’3 9.80665×10-6 9.80665ХЮ-5 1ХЮ-4 9.67841×10’5 1 7.35559×10’2 1.33322×102 1.33322×10’1 1.33322×1 O’4 1.33322×10’3 1.35951×10’3 1.31579×10’3 1.35951×10 1 (Примечание) 1МПа1 Сила Н мм2Единицы измерения периода и частоты
Настоящие Правила распространяются на диапазон частот 100 кГц — 300 000 МГц.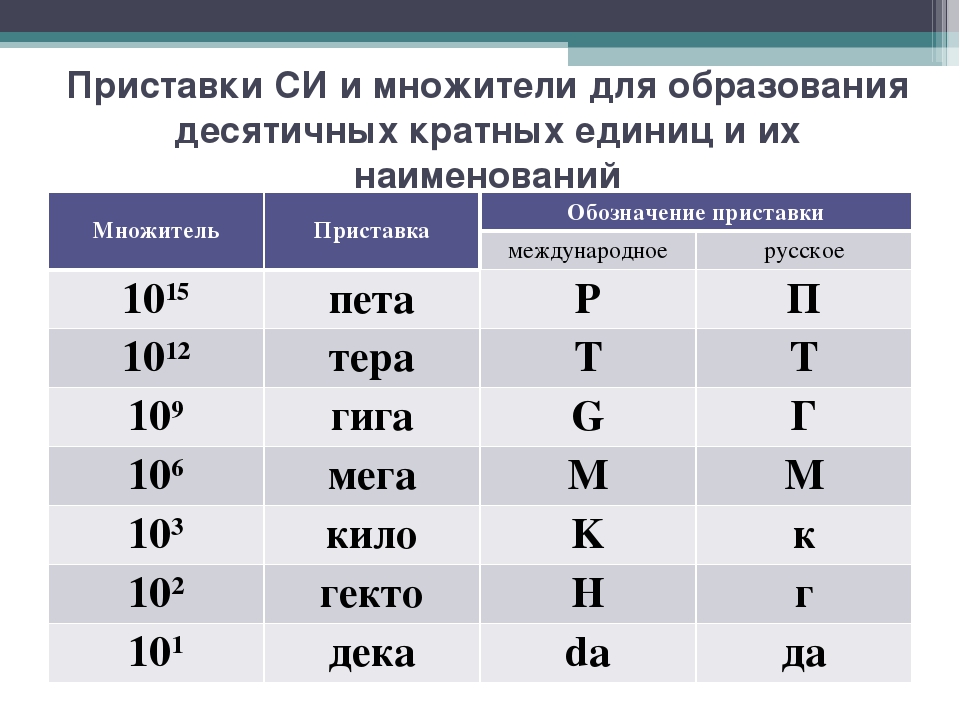
Единицей измерения частоты является герц (Гц)—частота переменного тока, меняющего направление со скоростью одного периода в секунду. В соответствии с международным регламентом радиосвязи действует следующая классификация радиочастот (табл. 1). [c.559]Единицей измерения частоты в системе СИ является герц (Гц). Его размер 1/с. Период Г измеряется в секундах (с). Длина [c.6]
Модуль G (oj) определяется как отношение составляюще напряжения, находящейся в фазе с синусоидально изменяющейся деформацией, к величине этой деформации. При сравнении различных систем при одинаковых амплитудах деформации он является мерой энергии, запасаемой и освобождаемой за период колебаний в единице объема данного материала. Зависимость упругого модуля от угловой частоты в логарифмических координатах представлена на фиг. 14. Поскольку как G(i), так и G (o>) определяют запасенную упругую энергию, а динамические нз.
мерения при частоте (О качественно эквивалентны измерениям неравновесных свойств при t = 1/о), 10 приведенные зависимости являются в первом приближении зеркальным отображением относительно оси. модуля соответствующих зависимостей, описывающих релаксацию напряжения. В частности, когда G(t) изменяется очень медленно, G(t) G (l//), так что значения Gg и Ge, характеризующие поведение материала при высоких и низких частотах, те же самые, что и значения, характеризующие поведение материала при малых и больших временах наблюдения соответственно. [c.46]В качестве основной единицы времени применяется продолжительность периода при частоте генератора. Выбор этой частоты ориентируется по скорости звука и по требуемой точности измерения времени прохождения или толщины стенки. [c.272]
Максимальная быстрота записи спектра достигается при развертке какого-либо участка спектра на экране катодного осциллоскопа [105]. Для получения максимальной чувствительности напряжение развертки (варьируемое пилообразно при помощи реостата, приводимого мотором) должно изменяться сравнительно медленно [106].
Наилучшие результаты для очень слабых ионных токов получены при периоде развертки от 1 до 30 сек. Для изображения спектра масс в диапазоне до 200 массовых единиц быJ i использован осциллоскоп с большим периодом послесвечения при желании любая часть спектра могла быть получена в большем масштабе. Сири [1071 описал компактный 180-градусный масс-работающий на переменном токе, в котором. т1ине11но растущее напряжение развертки от О до 200 в при частоте 200 гц накладывалось на постоянное ускоряющее напряжение, что позволяло одновременно выбирать как область спектра, так и масштаб развертки. Выходное напряжение из специальных усилителем подавалось на осциллоскоп. Разрешающая спла была достаточна до массового числа 65. Достигнута чувствительность в 2-10″ а на 1 см отклонения. Нри измерениях высоты пиков (с использованием делителя напряжения для приведения больших пиков к стандартной высоте), по словам автора, достигалась точность от 2 до 5%. Такие приборы, не будучи в такой же степени точными, как дрз гие регистрирующие установки д.
ля слабых токов, тем не менее имеют важное применение при изучении быстро проходящих эффектов (например, когда появление и исчезновение интересую-нюго исследователя компонента происходит очень быстро). Этим методом исследованы респираторные газы с целью наблюдения за быстро исчезающпми компонентами. [c.91]
Длина волны. Скорость распространения волн :: Класс!ная физика
ДЛИНА ВОЛНЫ
СКОРОСТЬ РАСПРОСТРАНЕНИЯ ВОЛН
Что ты должен знать и уметь?
1.Определение длины волны.
Длина волны — это расстояние между ближайшими точками, колеблющимися в одинаковых фазах.
2. Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [лямбда] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ ню ] = 1 Гц
3.
Расчетные формулы
4. Уметь показать графически длину волны ( для продольных и поперечных волн).
ЕЩЁ ОДНА ИГРУШКА
ДЛЯ УМНЕНЬКИХ И ЛЮБОЗНАТЕЛЬНЫХ
Ощути себя физиком-исследователем — нажми здесь.
ЭТО ИНТЕРЕСНО !
Сейсмические волны.
Сейсмическими волнами называются волны, распространяющиеся в Земле от очагов землетрясений или каких-нибудь мощных взрывов. Так как Земля в основном твердая, в ней одновременно могут возникать 2 вида волн — продольные и поперечные. Скорость этих волн разная: продольные распространяются быстрее поперечных. Например, на глубине 500 км скорость поперечных сейсмических волн 5км/с, а скорость продольных волн — 10км/с.
Регистрацию и запись колебаний земной поверхности, вызанных сейсмическими волнами, осуществляют с помощью приборов — сейсмографов.
Распространяясь от очага землетрясения, первыми на сейсмическую станцию приходят продольные волны, а спустя некоторое время — поперечные. Зная скорость распространения сейсмических волн в земной коре и время запаздывания поперечной волны, можно определить расстояние до центра землетрясения. Чтобы узнать точнее , где он находится , используют данные нескольких сейсмических станций.
Ежегодно на земном шаре регистрируют сотни тысяч землетрясений. Подавляющее большинство из них относится к слабым, однако время от времени наблюдаются и такие. которые нарушают целостность грунта, разрушают здания и ведут к человеческим жертвам.
Устали? — Отдыхаем!
Амплитуда, частота, период колебаний — урок. Физика, 11 класс.
Рассмотрим величины, с помощью которых можно охарактеризовать колебания.
Сравним колебания двух качелей на рисунке — пустых качелей и качелей с мальчиком.
Качели с мальчиком колеблются с большим размахом, т. е. их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.
Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний.
Обрати внимание!
Амплитуда колебаний, как правило, обозначается буквой \(А\) и в СИ измеряется в метрах (м).
Пример:
На рисунке ниже амплитудой колебания мальчика на качелях является дуга ОА.
Обрати внимание!
Амплитуду можно измерять также в единицах плоского угла, например в градусах, поскольку дуге окружности соответствует определённый центральный угол, т. е. угол с вершиной в центре окружности.
Колеблющееся тело совершает одно полное колебание, если от начала колебаний проходит путь, равный четырём амплитудам.Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Обрати внимание!
Период колебаний обозначается буквой \(Т\) и в СИ измеряется в секундах (с).
Пример:
Ударим по столу двумя линейками — металлической и деревянной. Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (А) сделает больше колебаний, чем деревянная (В).
Число колебаний в единицу времени называется частотой колебаний.
Обрати внимание!
Обозначается частота греческой буквой ν («ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).
Период колебания \(Т\) и частота колебаний ν связаны следующей зависимостью:
T=1ν.
Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.
Любая колебательная система имеет определённую собственную частоту, зависящую от параметров этой системы. Например, собственная частота пружинного маятника зависит от массы груза и жёсткости пружины.
Рассмотрим колебания двух одинаковых пустых качелей на рисунке выше.
В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зеленые качели из положения равновесия движутся назад. Качели колеблются с одной и той же частотой и с одинаковыми амплитудами. Однако эти колебания отличаются друг от друга: в любой момент времени скорости качелей направлены в противоположные стороны. В таком случае говорят, что колебания качелей происходят в противоположных фазах.
Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Скорости этих качелей в любой момент времени направлены одинаково. В этом случае говорят, что качели колеблются в одинаковых фазах.
Физическая величина, называемая фазой, используется не только при сравнении колебаний двух или нескольких тел, но и для описания колебаний одного тела.
Таким образом, колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой.
Источники:
Физика. 9 кл.: учебник / Перышкин А.В., Гутник Е.
М. — М.: Дрофа, 2014. — 319 с.
www.ru.depositphotos.com, сайт «Фотобанк с премиум-коллекцией фотографий, векторов и видео»
www.mognovse.ru, сайт «Можно все»
CSS — — CSS тип данных представляет собой измерение частоты, например, шаг г
<frequency> CSS тип данных представляет собой измерение частоты, например, шаг говорящего голосом. В настоящее время он не используется ни в каких свойствах CSS.
Syntax
Тип данных <frequency> состоит из <number> за которым следует одна из перечисленных ниже единиц. Как и во всех измерениях CSS, между литералом единицы и числом нет пробела.
Units
Hz- Представляет частоту в герцах. Примеры:
0Hz,1500Hz,10000Hz. kHz- Представляет частоту в килогерцах. Примеры: 0
0kHz,1.5kHz10kHz, 10 кГц .
Примечание. Хотя число 0 всегда одно и то же, независимо от единицы измерения, ее нельзя пропустить. Другими словами, 0 недействителен и не представляет 0Hz или 0 0kHz . Хотя единицы измерения не чувствительны к регистру, рекомендуется использовать заглавную букву «H» для Hz и kHz , как указано в системе СИ .
Examples
Действительные значения частоты
12Hz Positive integer 4.3Hz Non-integer 14KhZ The unit is case-insensitive, though non-SI capitalization is not recommended. +0Hz Zero, with a leading + and a unit -0kHz Zero, with a leading - and a unit
Недействительные значения частоты
12.0 This is a <number>, not an <frequency>, because it is missing a unit. 7 Hz No space is allowed between the number and the unit. 0 Although unitless zero is an allowable <length>, it
Specifications
Примечание.
Этот тип данных был первоначально введен в CSS Level 2 для устаревшего аудио типа мультимедиа , где он использовался для определения высоты голоса. Однако тип данных <frequency> был повторно введен в CSS3, хотя в данный момент ни одно свойство CSS не использует его.
Совместимость с браузерами
| Desktop | Mobile | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chrome | Edge | Firefox | Internet Explorer | Opera | Safari | WebView Android | Хромовый Android | Firefox для Android | Опера Андроид | Safari на IOS | Samsung Интернет | |
frequency | No | No | No | No | No | No | No | No | No | No | No | No |
hz | No | No | No | No | No | No | No | No | No | No | No | No |
khz | No | No | No | No | No | No | No | No | No | No | No | No |
См.
такжеУправление частотой будущих энергосистем: анализ и оценка проблем и новые методы управления
Гафури А., Милимонфаред Дж., Гарехпетян Г.Б. (2015) Скоординированное управление распределенными энергоресурсами и традиционными электростанциями для частотного управления энергосистемами. IEEE Trans Smart Grid 6 (1): 104–114
Статья Google ученый
Rui Y, Yingchen Z (2016) Скоординированная оптимизация распределенных энергоресурсов и интеллектуальных нагрузок в распределительных системах.In: Proceedings of the 2016 IEEE power and energy Society, Бостон, США, 17–21 июля 2016 г., 5 стр.
Ву Д., Ян Т., Стоорвогель А.А. и др. (2017) Оптимальная распределенная координация для распределенных энергоресурсы в энергосистемах. IEEE Trans Autom Sci Eng 14 (2): 414–424
Статья Google ученый
Chapman AC, Verbic G (2016) Динамическое распределенное распределение энергетических ресурсов для обеспечения аварийного резерва на стороне нагрузки.
In: Proceedings of IEEE Innovative Smart grid technologies — Asia, Melbourne, Australia, 28 ноября — 1 декабря 2016 г., 6 стр.
Георгиев М., Станев Р., Крустева А. (2016) Гибкое управление нагрузкой в электроэнергетических системах. с распределенными энергоресурсами и зарядкой электромобилей. В: Материалы международной конференции по силовой электронике и управлению движением IEEE, Варна, Болгария, 25–28 сентября 2016 г., 7 стр.
Huang S, Wu Q, Liu Z et al (2014) Обзор методов управления перегрузками для распределительных сетей с высокой степенью проникновения распределенных энергоресурсов.In: Proceedings of IEEE PES Innovative Smart grid technologies, Стамбул, Турция, 12–15 октября 2014 г., 6 стр.
Ян Дж, Ван И (2014) Обзор влияния распределенных энергоресурсов и электроэнергии. электронно управляемая нагрузка на устойчивость распределительной сети. В: Материалы конференции IEEE по промышленной электронике и приложениям, Ханчжоу, Китай, 9–11 июня 2014 г.
, 6 стр.
Апостолов А.П. (2011) Моделирование устаревших интеллектуальных электронных устройств для систем интеграции подстанций на базе УЦА.В: Материалы конференции по большим инженерным системам по энергетике, Галифакс, Канада, 11–13 июля 2001 г., 6 стр.
Cheng M, Sami SS, Wu J (2016) Преимущества использования виртуальной системы хранения энергии для АЧХ энергосистемы. Appl Energy 194: 376–385
Статья Google ученый
. Obaid ZA, Cipcigan LM, Muhssin MT (2017) Разработка гибридного иерархического управления частотой на стороне спроса на основе нечетких цепей / цепей Маркова.В: Proceedings of IEEE PES GM, Чикаго, США, 16–20 июля 2017 г., 5 стр.
Obaid ZA, Cipcigan LM, Sami SS et al (2017) Контроль совокупности аккумуляторных систем хранения энергии для динамический частотный регулятор институт энергетики. Диссертация, Кардиффский университет
Мухссин М.
Т., Ципсиган Л.М., Дженкинс Н. и др. (2016) Моделирование совокупности тепловых насосов как источника нагрузки в энергосистеме Великобритании. В: Материалы международной конференции по интеллектуальным системам и технологиям, Осиек, Хорватия, 12–14 октября 2016 г., 5 стр.
Lee SJ, Kim JH, Kim CH et al (2016) Алгоритм координированного управления для распределенной батареи системы накопления энергии для уменьшения отклонений напряжения и частоты.IEEE Trans Smart Grid 7 (3): 1713–1723
Статья Google ученый
Сами С.С., Мэн С., Цзяньчжун В. (2016) Моделирование и управление разнотипными накопителями энергии в масштабе сети для частотной характеристики энергосистемы. В: Материалы международной конференции по силовой электронике и управлению движением IEEE, Хэфэй, Китай, 22–26 мая 2016 г., 5 стр.
Стандарт безопасности и качества поставок NETS (2017 г.) По состоянию на февраль 2017 г.
plc NG (2017) АЧХ в энергосистеме Великобритании: общие описания.По состоянию на сентябрь 2017 г.
Ekanayake NJAJ (2017) Возобновляемая энергетика. Издательство Кембриджского университета, Кембридж
Google ученый
Grid N (2016) Структура работоспособности системы 2016. National Grid
Sami SS (2017) Виртуальный накопитель энергии для управления частотой и напряжением. Диссертация, Кардиффский университет
National Grid (2016) Структура работоспособности системы.http://www2.nationalgrid.com/UK/Industry-information/Future-of-Energy/System-Operability-Framework/. По состоянию на 15 февраля 2017 г.
Комиссия UGI (2016) Smart power
plc ”NG (2017) Частотная характеристика фирмы — FAQ. http://www2.nationalgrid.com/UK/Services/Balancing-services/Frequency-response/Firm-Frequency-Response/
Отчеты Firm Frequency Response Services Services (2017) Национальная сеть.
По состоянию на июнь 2017 г.
Obaid ZA (2018) Контроль частоты в будущих энергосистемах.Диссертация, Кардиффский университет
Grid N (2014) Расширенные возможности управления частотой (EFCC). https://www.ofgem.gov.uk/ofgem-publications//elecnicfullsubmissionproformaefccresubmission.pdf. По состоянию на 15 февраля 2017 г.
Obaid ZA, Cipcigan LM, Muhssin MT (2016) Оптимальное управление частотой в энергосистеме Великобритании на основе нечеткого иерархического подхода. Electric Power Syst Res 141: 529–537
Статья Google ученый
Mazin T, Muhssin LMC, Obaid ZA et al (2017) Новое адаптивное управление на основе непогоды для управления частотой нагрузки низкоинерционной системы в взаимосвязанных зонах к северу и югу от Шотландии.Int J Electric Power Energy Syst 89: 52–61
Статья Google ученый
Стрбак Г.
, Шакур А., Блэк М. и др. (2007) Влияние ветроэнергетики на работу и развитие электроэнергетических систем Великобритании. Electric Power Syst Res 77 (9): 1214–1227
Статья Google ученый
Обейд З.А., Сипсиган Л., Мухсин М.Т. (2015) Анализ энергосистемы Великобритании с электромобилями и системами хранения.В: Материалы международной конференции по применению интеллектуальных систем в электроэнергетических системах, Порту, Португалия, 11–16 сентября 2015 г., 6 стр.
Grid N (2015) Сценарии энергетики будущего. http://fes.nationalgrid.com/
Mu Y, Wu J, Ekanayake J et al (2013) Первичная частотная характеристика электромобилей в энергосистеме Великобритании. IEEE Trans Smart Grid 4 (2): 1142–1150
Статья Google ученый
Murrell W, Ran L, Wang J (2014) Моделирование частотной характеристики энергосистемы Великобритании при увеличении проникновения ветра.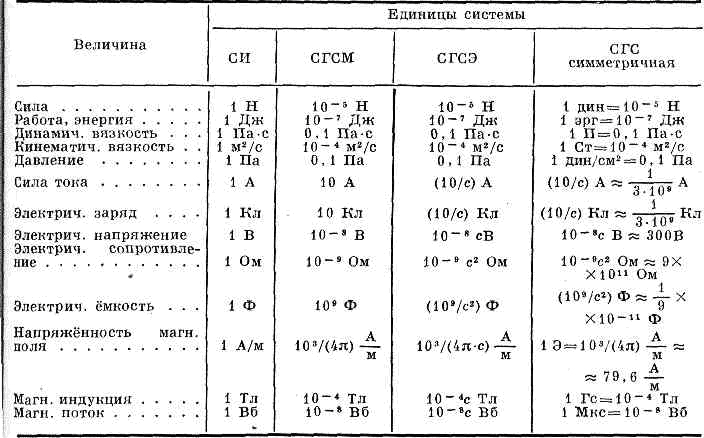
В: Proceedings of IEEE Innovative Smart grid technologies — Asia, Kuala Lumpur, Malaysia, 20–23 мая 2014 г., 6 стр.
Elizondo MA, Kalsi K, Calderon CM et al (2015) Спрос в зависимости от частоты в США модель западной энергосистемы. In: Proceedings of IEEE Power & Energy Society, Денвер, США, 26–30 июля 2015 г., 5 стр.
Kalsi JHK, Fuller J, Marinovici LD et al (2015) Нагрузки как ресурс, реагирующие на частоту потребность. Подготовлено к U.S. Министерство энергетики по контракту DE-AC05-76RL01830, Тихоокеанская северо-западная национальная лаборатория Ричленд, Вашингтон 99352
Калси К.Дж.Л., Мариновичи Л.Д., Элизондо М. и др. (2014) Нагрузки как ресурс, отвечающий частотно-зависимому спросу. Подготовлено для Министерства энергетики США по контракту DE-AC05-76RL01830, Тихоокеанская северо-западная национальная лаборатория Ричленд, Вашингтон 99352
Ван С., Ву Дж, Эканаяке Дж и др. (2017) Интеллектуальные распределительные сети.
CRC Press, Boca Raton
Книга Google ученый
Ли Б., Шен Дж., Ван Х и др. (2016) От контролируемых нагрузок к обобщенным ресурсам на стороне спроса: обзор развития ресурсов на стороне спроса. Renew Sustain Energy Rev 53: 936–944
Статья Google ученый
Патеракис Н.Г., Эрдинч О., Каталан, JP (2017) Обзор реакции на спрос: ключевые элементы и международный опыт.Renew Sustain Energy Rev 69: 871–891
Статья Google ученый
Western Power Distribution (2015) Проект FALCON: окончательный отчет о коммерческих испытаниях
Strbac G (2008) Управление спросом: преимущества и проблемы. Энергетическая политика 36 (12): 4419–4426
Статья Google ученый
Ченг М., Ву Дж., Голсуорси С.Дж. и др. (2016) Частотная характеристика энергосистемы от управления резервуарами с битумом.
IEEE Trans Power Syst 31 (3): 1769–1778
Статья Google ученый
Power Responsive (2016) Годовой отчет о гибкости спроса
Energyst (2015) Отчет о реакции на спрос
Energy (2012) внутренний сектор. Подготовлено для Ofgem
Cheng M, Wu J, Ekanayake J et al (2013) Первичная частотная характеристика в энергосистеме Великобритании от динамически регулируемых холодильников.В: Материалы международной конференции и выставки по распределению электроэнергии, Стокгольм, Швеция, 10–13 июня 213,4 стр.
Short JA, Infield DG, Freris LL (2007) Стабилизация частоты сети посредством динамического контроля спроса . IEEE Trans Power Syst 22 (3): 1284–1293
Статья Google ученый
Мухссин М.Т., Ципциган Л.М., Дженкинс Н. и др. (2016) Моделирование совокупности тепловых насосов как источника нагрузки в энергосистеме Великобритании.
В: Proceedings of smart systems and technologies, Osijek, Croatia, 12–14 октября 2016 г., 5 стр.
Koch S, Zima M, Andersson G (2009) Активная координация тепловых бытовых приборов для управления нагрузкой. IFAC Proc Vol 42 (9): 149–154
Статья Google ученый
Лу Н (2012) Оценка потенциала нагрузки HVAC для предоставления услуги балансировки нагрузки. IEEE Trans Smart Grid 3 (3): 1263–1270
Статья Google ученый
Cheng M, Wu J, Galsworthy SJ et al (2017) Характеристики промышленных плавильных котлов при обеспечении динамической частотной характеристики в энергосистеме Великобритании.Appl Energy 201: 245–256
Статья Google ученый
Cheng M, Wu J, Galsworthy S. et al (2014) Доступность нагрузки для обеспечения частотной характеристики в энергосистеме Великобритании.
In: Proceedings of the Power Systems Computing Conference, Wroclaw, Poland, 18–22 августа 2014, 7 pp
Vrettos E, Mathieu JL, Andersson G (2014) Реакция на спрос с оценкой подвижного горизонта отдельных состояний термостатической нагрузки по совокупным измерениям мощности.В: Материалы американской конференции по контролю, Портленд, США, 4–6 июня 2014 г., 8 стр.
Мэтью А.М., Менон Р. (2015) Оценка способности реагирования на спрос с помощью термостатических нагрузок в жилом секторе. In: Proceedings of the International Conference on Power, Instrumentation, Control and Computing, Thrissur, India, 9–11 декабря 2015 г., 5 стр.
Mathieu JL, Kamgarpour M, Lygeros J et al (2015) Внутридневный арбитраж рыночные цены на энергию с совокупностью термостатических нагрузок.IEEE Trans Power Syst 30 (2): 763–772
Статья Google ученый
Tindemans SH, Trovato V, Strbac G (2015) Децентрализованное управление термостатическими нагрузками для гибкого реагирования на спрос.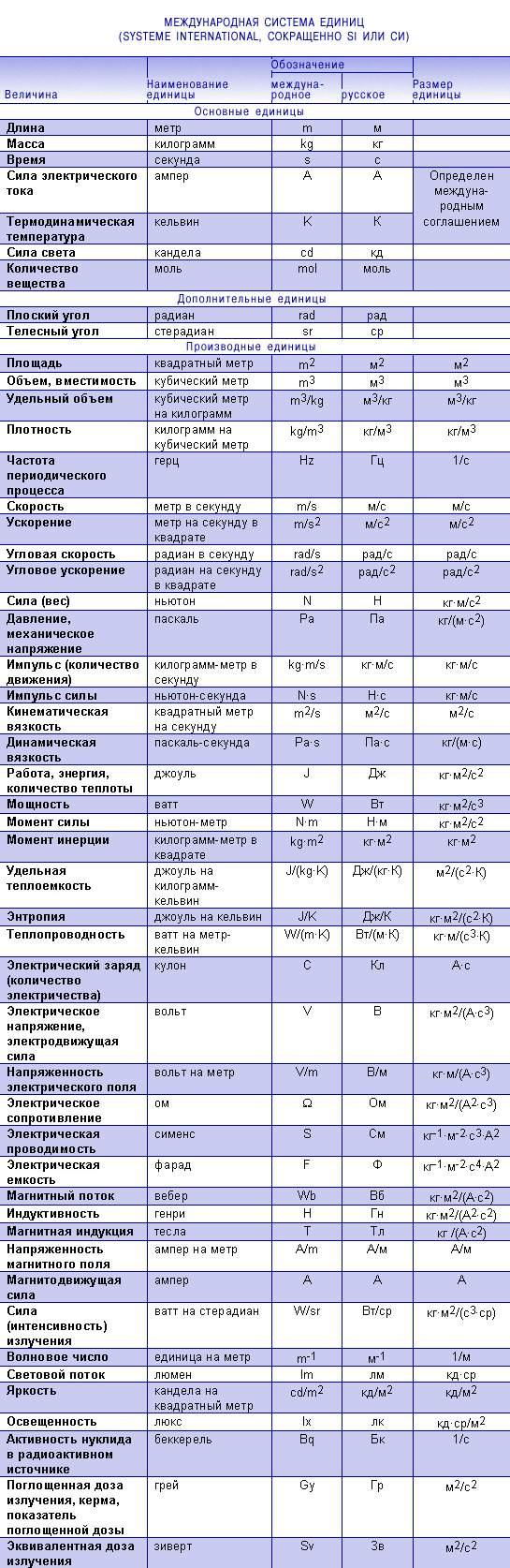
IEEE Trans Control Syst Technol 23 (5): 1685–1700
Статья Google ученый
Тровато В., Санс И.М., Чаудхури Б. и др. (2016) Расширенное управление термостатическими нагрузками для быстрой частотной характеристики в Великобритании.IEEE Trans Power Syst 32 (3): 2106–2117
Статья Google ученый
Тровато В., Тенг Ф., Стрбак Г. (2016) Значение термостатических нагрузок в будущей низкоуглеродистой системе Великобритании. В: Proceedings of the power systems computing conference, Генуя, Италия, 20–24 июня 2016 г., 7 стр.
Trovato V, Tindemans SH, Strbac G (2016) Модель утечки для оптимального распределения термостатических нагрузки. IET Gen Transm Distrib 10 (3): 585–593
Статья Google ученый
Тровато В., Мартинес-Санс И., Чаудхури Б. и др. (2017) Расширенное управление термостатическими нагрузками для быстрой частотной характеристики в Великобритании.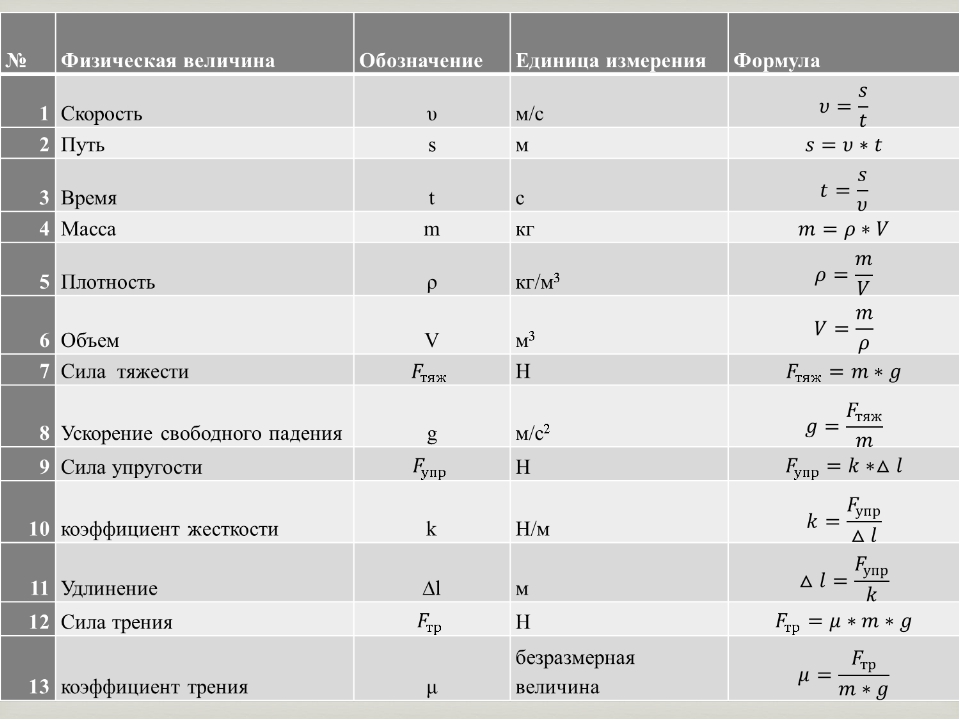
В: Proceedings of IEEE Manchester PowerTech, Манчестер, Великобритания, 18–22 июня 2017 г., 1 стр.
Латиф А., Хан С., Паленски П. и др. (2016) Платформа на основе совместного моделирования для термостатически регулируемых нагрузок, как частотный резерв. В: Материалы семинара по моделированию киберфизических энергетических систем, Вена, Австрия, 11 апреля 2016 г., 6 стр.
Trovato V, Teng F, Strbac G (2017) Роль и преимущества гибкого термостатирования контролируемые нагрузки в будущих низкоуглеродных системах.IEEE Trans Smart Grid. https://doi.org/10.1109/TSG.2017.2679133
Артикул Google ученый
Тровато В., Тиндеманс С.Х., Стрбак Г. (2013) Вклад реагирования на спрос в эффективную инерцию безопасности системы в сценарии перехода GB 2020 к экологии. В: Proceedings of IEEE PES ISGT Europe, Lyngby, Дания, 6–9 октября 2013 г., 5 стр.
Christian MWZ, Lian J, Karanjit K (2014) Иерархическая структура для управления частотой на стороне спроса.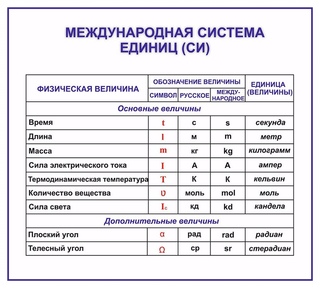
В: Материалы американской конференции по контролю, Портленд, США, 4–6 июня 2014 г., 6 стр.
Xu Z, Diao R, Lu S et al (2014) Моделирование электрических водонагревателей для реагирования на спрос: базовая модель PDE. IEEE Trans Smart Grid 5 (5): 2203–2210
Статья Google ученый
Cooper D, Cronje W (2016) Управление автономным водонагревателем для регулирования нагрузки в интеллектуальных сетях. В: Материалы международной энергетической конференции IEEE, Левен, Бельгия, 4–8 апреля 2016 г., 6 стр.
Масута Т., Йокояма А. (2012) Дополнительное регулирование частоты нагрузки с использованием ряда электромобилей и водонагреватели с тепловым насосом.IEEE Trans Smart Grid 3 (3): 1253–1262
Статья Google ученый
Ким Й.Дж., Фуэнтес Э., Норфорд Л.К. (2016) Экспериментальное исследование вспомогательной услуги регулирования частоты сети теплового насоса с регулируемой скоростью.
IEEE Trans Power Syst 31 (4): 3090–3099
Статья Google ученый
Ким Ю.Дж., Норфорд Л.К., Киртли Дж.Л. (2015) Моделирование и анализ теплового насоса с регулируемой скоростью для частотного регулирования посредством прямого управления нагрузкой.IEEE Trans Power Syst 30 (1): 397–408
Статья Google ученый
Power H (2017) Водонагреватели. По состоянию на 16 октября 2017 г.
Youngjin K (2016) Экспериментальное исследование вспомогательной услуги регулирования частоты сети теплового насоса с регулируемой скоростью. В: Proceedings of IEEE PESGM, Бостон, США, 17–21 июля 2016 г., 1 стр.
Vrettos E, Koch S, Andersson G (2012) Управление частотой нагрузки агрегатами термически стратифицированных электрических водонагревателей.In: Proceedings of IEEE PES Innovative Smart Grid Technologies Europe, Berlin, Germany, 14-17 October 2012, 8 pp
Masuta T, Yokoyama A, Tada Y (2011) Моделирование ряда водяных тепловых насосов нагреватели в качестве управляющего оборудования для регулирования частоты нагрузки в энергосистемах.
In: Proceedings of IEEE Trondheim powertech, Trondheim, Norway, 19–23 июня 2011 г., 7 стр.
Obaid ZA, Cipcigan L, Muhssin MT (2017) Дизайн гибридного иерархического спроса на основе нечетких цепей и цепей Маркова. — регулировка частоты боковая.В; Труды IEEE PES GM, Чикаго, США, 16–20 июля 2017 г., 5 стр.
Мухссин М.Т. (2018) Адаптивное управление и динамическое реагирование на спрос для стабилизации частоты гидратов. Диссертация, Кардиффский университет
Калси Дж.Л.К., Мариновичи Л.Д., Элизондо М. и др. (2014) Нагрузки как ресурс, отвечающий частотно-зависимому спросу. Министерство энергетики США по контракту DE-AC05-76RL01830, Тихоокеанская северо-западная национальная лаборатория Ричленд, Вашингтон 99352
Уильямс Т., Калси К., Элизондо М. и др. (2016) Управление и координация частотно-чувствительных бытовых водонагревателей.In: Proceedings of IEEE Power and Energy Society, Бостон, США, 17–21 июля 2016 г.
, 5 стр.
Karfopoulos EL, Hatziargyriou ND (2013) Многоагентная система для контролируемой зарядки большой популяция электромобилей. IEEE Trans Power Syst 28 (2): 1196–1204
Статья Google ученый
Qazi HW, Flynn D, Rather ZH (2016) Влияние изменения нагрузки электромобиля на стабильность частоты.In: Proceedings of IEEE PES Innovative Smart Grid Technologies Conference Europe, Любляна, Словения, 9–12 октября 2016 г., 6 стр.
Moghadam MRV, Zhang R, Ma RTB (2016) Распределенное управление частотой с помощью рандомизированного ответа электромобили в электросети. IEEE Trans Sustain Energy 7 (1): 312–324
Статья Google ученый
Li J, Xiong R, Yang Q et al (2016) Разработка / испытание гибридной системы накопления энергии для управления первичной частотой с использованием метода динамического спада в изолированной энергосистеме на базе микросети.
Appl Energy 201: 257–269
Статья Google ученый
Grid N (2017) Энергетический сценарий будущего. http://fes.nationalgrid.com/media/1253/final-fes-2017-updated-interactive-pdf-44-amended.pdf. По состоянию на 16 октября 2017 г.
Energy C (2017) Enel покупает прибыльный проект по хранению аккумуляторов за 17 миллионов фунтов стерлингов. По состоянию на 16 октября 2017 г.
Kim Y-J, Del-Rosario-Calaf G, Norford LK (2017) Анализ и экспериментальная реализация частотного регулирования в сети с использованием установленных за счетчиком батарей, компенсирующих быстрые изменения нагрузки.IEEE Trans Power Syst 32 (1): 484–498
Статья Google ученый
Иверсен Э.Б., Моралес Дж. М., Мэдсен Х. (2014) Оптимальная зарядка электромобиля с использованием марковского процесса принятия решений. Appl Energy 123: 1–12
Статья Google ученый
Сонг Дж.
, Кришнамурти В., Квасински А. и др. (2013) Разработка модели накопления энергии на основе цепей Маркова для оценки доступности электроснабжения фотоэлектрических электростанций.IEEE Trans Sustain Energy 4 (2): 491–500
Статья Google ученый
Tang Y, Zhong J, Bollen M (2016) Совокупное оптимальное управление зарядкой и подключением к сети для электромобилей при большом количестве электромобилей. IET Gen Transm Distrib 10 (8): 2012–2018
Статья Google ученый
Алхеджадж С.М., Гонсалес-Лонгатт Ф.М. (2016) Влияние управления имитацией инерции BESS сетевого масштаба на частотную характеристику энергосистемы.В: Материалы международной конференции для студентов по прикладной инженерии, Ньюкасл-апон-Тайн, Великобритания, 20–21 октября 2016 г., 5 стр.
Hatziargyriou N (2014) MicroGrids. Пресса Wiley-IEEE, США
Google ученый
Хубан М.
Х., Драгичевич Т., Блаабьерг Ф. и др. (2018) Судовые микросети: новый подход к управлению частотой нагрузки. IEEE Trans Sustain Energy 9 (2): 843–852
Статья Google ученый
Хубан М.Х., Никнам Т., Шасадеги М. и др. (2018) Управление частотой нагрузки в микросетях на основе стохастического нецелочисленного контроллера.IEEE Trans Sustain Energy 9 (2): 853–861
Статья Google ученый
Мохаммади Ф.Д., Ванаши Х.К., Фелиачи А. (2018) Моделирование в пространстве состояний, анализ и распределенное вторичное управление частотой изолированных микросетей. IEEE Trans Energy Convers 33 (1): 155–165
Статья Google ученый
Дехкорди Н.М., Садати Н., Хамзех М. (2017) Полностью распределенное кооперативное вторичное управление частотой и напряжением изолированных микросетей.IEEE Trans Energy Convers 32 (2): 675–685
Статья Google ученый
Пиллони А.
, Пизано А., Усай Э. (2018) Надежное восстановление частоты и напряжения за конечное время в микросетях на основе инвертора с помощью кооперативного управления в скользящем режиме. IEEE Trans Ind Electron 65 (1): 907–917
Статья Google ученый
Лунд П. (2007) Проект датской ячейки, часть 1: история вопроса и общий подход.В: Протоколы общего собрания энергетического общества, Тампа, США, 24–28 июня 2007 г., 6 стр.
Эканаяке Дж. Б., Дженкинс Н., Лиянаге К. и др. (2012) Интеллектуальные сети: технологии и приложения. Wiley, New York
Бронировать Google ученый
Pudjianto D, Ramsay C, Strbac G (2007) Виртуальная электростанция и системная интеграция распределенных энергоресурсов. IET Renew Power Gen 1 (1): 10–16
Статья Google ученый
Wu Z, Gao DW, Zhang H et al (2017) Стратегия скоординированного управления аккумуляторной системой хранения энергии и PMSG-WTG для улучшения возможностей регулирования частоты системы.
IEEE Trans Sustain Energy 8 (3): 1330–1343
Статья Google ученый
Перссон М., Чен П. (2017) Регулирование частоты с помощью ветряных турбин с регулируемой скоростью в изолированных энергосистемах с различным составом генерации. IET Renew Power Gen 11 (8): 1101–1109
Статья Google ученый
Wilches-Bernal F, Chow JH, Sanchez-Gasca JJ (2016) Фундаментальное исследование применения ветряных турбин для управления частотой энергосистемы.IEEE Trans Power Syst 31 (2): 1496–1505
Статья Google ученый
Zhang Y, Tomsovic K, Djouadi SM et al (2017) Гибридный контроллер для генераторов ветряных турбин для обеспечения адекватной частотной характеристики в электрических сетях. IEEE J Emerg Select Top Circuits Syst 7 (3): 359–370
Статья Google ученый
Ашури-Заде А., Тулаби М., Ранджбар А.М. (2016) Скоординированная разработка нечеткого регулятора скорости и вспомогательных контроллеров в ветряной турбине с регулируемой скоростью для улучшения управления частотой.IET Renew Power Gen 10 (9): 1298–1308
Статья Google ученый
Яо Дж, Ю М., Гао В. и др. (2017) Стратегия управления частотным регулированием для ветроэнергетической системы PMSG с маховиковым накопителем энергии. IET Renew Power Gen 11 (8): 1082–1093
Статья Google ученый
Wang J, Zhang H, Zhou Y (2017) Интеллектуальный метод сброса нагрузки при пониженной частоте и пониженном напряжении, основанный на активном участии интеллектуальных устройств.IEEE Trans Smart Grid 8 (1): 353–361
Статья Google ученый
Rudez U, Mihalic R (2016) Снижение нагрузки с пониженной частотой на основе WAMS с краткосрочным прогнозированием частоты. IEEE Trans Power Deliv 31 (4): 1912–1920
Статья Google ученый
Коэльо В.Н., Коэльо И.М., Коэльо Б.Н. и др. (2016) Коммунальная система планирования хранения данных в микросетях в рамках умного города.Appl Energy 201: 371–381
Статья Google ученый
Jin X, Mu Y, Jia H et al (2016) Динамическое экономическое управление гибридной энергетической микросетью с учетом виртуальной системы хранения энергии на базе здания. Appl Energy 194: 386–398
Статья Google ученый
Парра Д., Норман С.А., Уокер Г.С. и др. (2016) Оптимальная система накопления энергии в общине для переключения нагрузки по требованию.Appl Energy 174: 130–143
Статья Google ученый
Ломбарди П., Швабе Ф. (2017) Экономика совместного использования как новая бизнес-модель для систем хранения энергии. Appl Energy 188: 485–496
Статья Google ученый
Морстин Т., Момайезан М., Хредзак Б. и др. (2016) Распределенное управление для балансировки состояния заряда между модулями реконфигурируемой аккумуляторной системы хранения энергии.IEEE Trans Power Electron 31 (11): 7986–7995
Статья Google ученый
Cai H, Hu GQ (2016) Распределенная схема управления для балансировки состояния заряда на уровне пакета подключенной к сети аккумуляторной системы хранения энергии. IEEE Trans Ind Inform 12 (5): 1919–1929
Статья Google ученый
Сеть N (2014) Отчет по электроэнергии за десять лет. Передача электроэнергии Великобритании, Лондон
Google ученый
Моейни А., Камва И., Брунел П. и др. (2015) Испытательные системы IEEE с открытыми данными, реализованные в SimPowerSystems для обучения и исследований в области динамики и управления энергосистемой.В: Материалы международной университетской конференции по энергетике, Сток-он-Трент, Великобритания, 1–4 сентября 2015 г., 6 стр.
Hiskens RRAI (2015) Задача IEEE PES по тестовым системам для контроля стабильности — технический отчет
Vowles MGAD (2014) Упрощенная модель энергосистемы Юго-Восточной Австралии с 14 генераторами. Диссертация, Университет Аделаиды
Управление частотой нагрузки — обзор
11.3.1 Требования к связи
Все устройства, предоставляющие вспомогательные услуги, такие как управление частотой нагрузки [резерв удержания частоты (FCR), aFRR и mFRR], независимо от от того, являются ли они обычными электростанциями или системами VPP, используемыми агрегаторами, необходимо выполнить технические требования [e.g., емкость, время нарастания, время полной активации (FAT) и время отклика] и требования к обмену данными (например, время цикла передачи данных), как определено в руководстве по эксплуатации ENTSO-E (ENTSO-E, 2009).
В соответствии с руководящими указаниями для каждого действия по управлению частотой нагрузки предварительно определены параметры времени активации ( T A ) и времени цикла ( T C ) (Таблица 11.1). FAT, T A , определяется как время, необходимое для передачи сигнала уставки от TSO или DSO к VPP и ниже по потоку к DER, задействованным в процедуре для полной активации конкретной нагрузки. частотное регулирование воздействия.Время цикла, T C , указывает время для сбора данных измерений и их передачи обратно в TSO или DSO (ENTSO-E, 2009; Kolenc et al., 2018).
Таблица 11.1. Технические требования к регулированию частоты нагрузки (ENTSO-E, 2009)
| Регулировка частоты нагрузки | Время активации T A | Время цикла T C |
|---|---|---|
| FCR | 15–30 с | 1–2 с |
| aFRR | 5 мин – 15 мин | 1–5 с |
| mFRR | 1527 9034 | 1527 1 2734 1 |
Управление частотой нагрузки — важный механизм, позволяющий TSO поддерживать стабильную частоту энергосистемы в синхронной области.Он следует трехэтапной процедуре, в которой за FCR следует активация действий aFRR и mFRR. Каждое действие по управлению частотой нагрузки имеет свои собственные технические требования с точки зрения времени активации, времени цикла и т. Д. Указанные значения в таблице 11.1 даны в виде интервалов, поскольку разные национальные TSO корректируют значения в соответствии с характеристиками своей локальной системы (ENTSO-E, 2009). .
У каждого производителя / потребителя есть свой характерный рост. На рис. 11.6 показаны характеристики разгона для выбранных производителей (генераторов) и потребителей (нагрузки): (а) представлены батареи, (б) промышленные паровые или газовые турбины с горячим пуском, и (в) гидростанции речной электростанции. в группе производителей, за которыми следуют (d) ТЭЦ, (e) промышленные предприятия, такие как цементные заводы, и (f) сталелитейные заводы, представляющие группу потребителей.Шкала времени указывает приблизительное время, необходимое для 100% активации отдельного устройства. Значения на оси абсцисс указывают максимальный уровень гибкой мощности на уровне 100% и минимальный уровень, который может использоваться для сокращения, на уровне 0%.
Рис. 11.6. Примеры различных характеристик наращивания распределенных энергоресурсов (РЭР). (A) Аккумуляторные батареи, (B) промышленные паровые или газовые турбины с горячим пуском, (C) гидроэлектростанция с речным стоком, (D) ТЭЦ, (E) промышленные нагрузки и (F) сталелитейные заводы.
Эксплуатационные расходы на РЭД и их технические характеристики (время нарастания, предлагаемая мощность, надежность и т. Д.) Влияют на выбор РЭД для конкретной вспомогательной услуги. Время нарастания или период линейного нарастания определяется как период, когда выработка (или потребление) МЭД достигнет 100% от заданного значения, запрошенного VPP. Время разгона зависит от физико-технических характеристик блоков РЭД (таблица 11.2). Поскольку время нарастания влияет на общую задержку процесса активации VPP, оно может поставить под угрозу достижение целевого значения T A для конкретного действия по управлению частотой нагрузки.Следовательно, блоки DER должны быть тщательно рассмотрены при работе VPP, особенно для служб aFRR и FCR, где требования к связи и управлению являются значительно более высокими (таблица 11.1). Примеры типов МЭД из таблицы 11.2 с различными характеристиками линейного изменения и длительностями показаны на рис. 11.6.
Таблица 11.2. Время отклика блоков DER, используемых для агрегации (Klobasa et al., 2013; VDE-ETG, 2017)
| Тип ресурса | Время разгона | Классификация |
|---|---|---|
| Потребители | ||
| Сталелитейные, бумажные, цементные, нефтеперерабатывающие заводы | 15 мин. | Медленно |
| HVAC, чиллеры | 5–15 мин. Производители | |
| Паровая или газовая турбина | 10–15 мин (холодный старт) 5 мин (горячий старт) | Медленный |
| Малая гидроэнергетика, ветряные мельницы, фотоэлектрические установки, гидроаккумуляторы, комбинированные теплоэлектроцентрали (ТЭЦ), дизельные и бензиновые генераторы | 2–5 мин | Средняя |
| Батареи, аккумуляторные системы накопления энергии (BESS) | 1–10 s | Fast |
Услуги по частотной характеристике, предназначенные для хранения энергии
https: // doi.org / 10.1016 / j.apenergy.2017.06.046Получить права и контентОсновные моменты
- •
Выявлена потребность в улучшении частотной характеристики в будущих энергосистемах.
- •
Представлено исследование того, как накопители энергии могут удовлетворить эту потребность.
- •
Были разработаны новые экспериментальные методы с использованием силового оборудования в контуре.
- •
Анализ частотных данных высокого разрешения британской электроэнергетической системы.
- •
Анализ конкретного случая новой службы частотной характеристики, разработанной для хранения энергии.
Реферат
Ожидается, что системы накопления энергии (ESS) будут играть важную роль в регулировании частоты будущих электроэнергетических систем. Увеличение проникновения возобновляемой генерации и снижение инерции, обеспечиваемой большими синхронными генераторами, вероятно, увеличат серьезность и регулярность частотных событий в синхронных энергосистемах переменного тока.Поставляя или поглощая мощность в ответ на отклонения от номинальной частоты и дисбаланс между спросом и предложением, быстрая реакция ESS обеспечит форму стабильности, которая не может быть сопоставлена с обычными сетевыми активами. Однако возросшая сложность эксплуатационных требований и проектных спецификаций ESS создает проблемы, когда дело доходит до реализации их полного потенциала через существующие рынки услуг частотной характеристики: новые рынки услуг необходимо будет разработать, чтобы воспользоваться возможностями ESS.В этом документе представлены новые методы анализа и оценки производительности ESS в рамках существующих сервисных структур с использованием сетевого моделирования в реальном времени и силового оборудования в контуре. Эти методы можно использовать для внесения улучшений в существующие службы и, возможно, для создания новых. Были разработаны новые статистические методы для количественной оценки конструктивных и эксплуатационных требований ESS, предоставляющих услуги регулирования частоты. Эти новые методы демонстрируются посредством иллюстративного дизайна услуг и частотных данных с высоким разрешением из системы передачи Великобритании.
Ключевые слова
Энергоаккумулятор
Энергетические системы
Частотная характеристика
Аппаратное обеспечение в контуре
Моделирование в реальном времени
Рекомендуемые статьиЦитирующие статьи (0)
© 2017 Авторы. Опубликовано Elsevier Ltd.
Рекомендуемые статьи
Ссылки на статьи
Работа системы RAPS: (а) частота системы; (b) выходная мощность DFIG; (c) …
Контекст 1
… управление также отключено.Управление SOPPT также активируется при t = 45 с для согласования с тестом контроллера типа 1, и следует отметить, что этот переходный период, вызванный активацией SOPPT, не будет встречаться, когда SOPPT активируется во время инициализации DFIG. Характеристики контроллера Типа 2 показаны на Рис. 7 и Рис. 8. При частотном возмущении в t = 90 с, если управление спадом не реализовано, не обеспечивается первичная частотная характеристика, как показано на Рис. 7, который аналогичен контроллеру Типа 1 без контроля спада.При управлении спадом электромагнитный крутящий момент DFIG временно увеличивается, как показано на рисунке 8, в результате чего …
Контекст 2
… переходный период, вызванный активацией SOPPT, не будет встречаться, когда SOPPT активируется во время инициализация DFIG. Характеристики контроллера Типа 2 показаны на Рис. 7 и Рис. 8. При частотном возмущении в t = 90 с, если управление спадом не реализовано, не обеспечивается первичная частотная характеристика, как показано на Рис.7, который аналогичен контроллеру Типа 1 без контроля спада. При управлении спадом электромагнитный крутящий момент DFIG временно увеличивается, как показано на рис. 8, что приводит к увеличению выходной мощности DFIG и снижению скорости ротора, как показано на рис. 7- (b) и (c) соответственно. Следовательно, отклонение частоты во время управления …
Контекст 3
… не реализовано, первичная частотная характеристика не предоставляется, как показано на рисунке 7, который аналогичен контроллеру Типа 1 без спада. контроль.При управлении спадом электромагнитный крутящий момент DFIG временно увеличивается, как показано на рис. 8, что приводит к увеличению выходной мощности DFIG и снижению скорости ротора, как показано на рис. 7- (b) и (c) соответственно. Следовательно, колебание частоты во время переходного периода значительно уменьшается (см. Увеличенный график на рис. 7- (a)). В отличие от контроллера типа 1, DFIG с предлагаемым контроллером типа 2 восстанавливает рабочее состояние до возникновения возмущений, вместо того, чтобы постоянно изменять выходную мощность в соответствии со спадом…
Контекст 4
… контроль спада. При управлении спадом электромагнитный крутящий момент DFIG временно увеличивается, как показано на рис. 8, что приводит к увеличению выходной мощности DFIG и снижению скорости ротора, как показано на рис. 7- (b) и (c) соответственно. Следовательно, колебание частоты во время переходного периода значительно уменьшается (см. Увеличенный график на рис. 7- (a)). В отличие от контроллера типа 1, DFIG с предлагаемым контроллером типа 2 восстанавливает рабочее состояние до возникновения возмущений, а не постоянно меняет выходную мощность в соответствии с настройкой спада.На рис. 7- (b) видно, что выходная мощность DFIG после нарушения частоты такая же, как и до …
Контекст 5
… Следовательно, отклонение частоты во время переходного процесса период значительно сокращается (см. увеличенный график на рис. 7- (a)). В отличие от контроллера типа 1, DFIG с предлагаемым контроллером типа 2 восстанавливает рабочее состояние до возникновения возмущений, а не постоянно меняет выходную мощность в соответствии с настройкой спада.На рис. 7- (b) видно, что выходная мощность DFIG после частотного возмущения такая же, как и до появления частотного возмущения при t = 90 с. Следовательно, увеличение нагрузки полностью обеспечивается дизельным генератором, но ROCOP на дизельном генераторе во время переходных процессов снижается, как показано на рис. 7- (d). 3) Тип 3: управление спадом с дополнительным …
Контекст 6
… в соответствии с настройкой спада. На рис. 7- (b) видно, что выходная мощность DFIG после частотного возмущения такая же, как и до появления частотного возмущения при t = 90 с.Следовательно, увеличение нагрузки полностью обеспечивается дизельным генератором, но ROCOP на дизельном генераторе во время переходных процессов снижается, как показано на рис. 7- (d). 3) Тип 3: управление спадом с дополнительным контуром управления: как обсуждалось в Разделе IV-D- (2), контроллер первичной частотной характеристики типа 2 способен обеспечивать первичную частотную характеристику с KE, сохраненным во вращающейся массе, и запасом мощности, полученным через Управление SOPPT в DFIG. Однако у Типа 2 есть недостаток …
Контекст 7
… пик порыва, T1G — время начала порыва, а TG — период порыва. Параметры порыва и другие контрольные параметры, используемые в данном тематическом исследовании, перечислены в Таблице IV Приложения, а профиль порыва ветра показан на Рис. 16- (a). Используемое возмущение остается тем же самым, а именно резкое увеличение нагрузки на 0,2 МВт при t = 90 с. Как показано на рис. 17, результаты для DFIG с предложенным регулятором частоты Типа 3 или без него представлены при возникновении порыва ветра. Как видно на рис.17- (a), частотная характеристика доступна в оба момента, когда нагрузка увеличивается, а скорость ветра уменьшается. Однако из-за постоянного снижения скорости ветра механическая энергия ветра …
Контекст 8
… в Таблице IV Приложения, а профиль порыва ветра показан на Рис. 16- (а). Используемое возмущение остается тем же самым, а именно резкое увеличение нагрузки на 0,2 МВт при t = 90 с. Как показано на рис. 17, результаты для DFIG с предложенным регулятором частоты Типа 3 или без него представлены при возникновении порыва ветра.На рис. 17- (a) можно увидеть, что частотная характеристика доступна в оба момента, когда нагрузка увеличивается, а скорость ветра уменьшается. Однако из-за непрерывного снижения скорости ветра механическая мощность ветра быстро уменьшается, как показано на Рис. 17- (b), и выходная мощность DFIG уменьшается после обеспечения незначительной частотной характеристики. Следовательно, частота надира …
Контекст 9
… можно увидеть на рис. 17- (a), что частотная характеристика доступна в оба момента, когда нагрузка увеличивается, а скорость ветра уменьшается.Однако из-за непрерывного снижения скорости ветра механическая мощность ветра быстро уменьшается, как показано на Рис. 17- (b), и выходная мощность DFIG уменьшается после обеспечения незначительной частотной характеристики. Следовательно, нижний предел частоты для сценария с частотным регулятором ниже по сравнению со сценарием без частотного регулятора. …
Контекст 10
… Надир для сценария с частотным регулятором ниже по сравнению со сценарием без частотного регулятора.Тем не менее, в сценарии с частотным регулятором, момент, когда частота достигает своего надира, задерживается по сравнению со сценарием без частотного регулятора, и ROCOP на дизельном генераторе снижается (см. Рис. 17- (d)). Более того, система сохраняет стабильность и проходит через худшие условия, когда происходит внезапное увеличение нагрузки и уменьшение скорости ветра …
(PDF) Точный расчет частоты энергосистемы
366 IEEE TRANSACTIONS ON POWER POWER, VOL.16, № 3, ИЮЛЬ 2001
преимущества DFT, а также устраняет причину
ошибок девиации частоты, принимая во внимание гармоники
. Эти аспекты делают SDFT быстрым, точным и устойчивым к гармоникам методом
. Но мы не предлагаем принимать во внимание все
гармоник, так как это потребует слишком много времени для вычисления
. В качестве альтернативы, использование сглаживающего окна
для затухания гармоник высокого порядка и простой учет гармоник
низкого порядка будет более эффективным
и подходит для энергосистем в режиме реального времени.
R
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
[1] П. Дж. Мур, Р. Д. Карранса и А. Т. Джонс, «Модельные системные испытания нового числового метода измерения частоты энергосистемы
», IEEE
Trans. по энергоснабжению, т. 11, вып. 2, pp. 696–701, Apr. 1996.
[2] М. М. Бегович, П. М. Джурич, С. Данлап и А. Г. Фадке, «Отслеживание частоты
в электрических сетях при наличии гармоник», IEEE Trans.
Электроснабжение, т. 8, вып. 2, стр.480–486, Apr. 1993.
[3] К. Т. Нгуен и К. Сринивасан, «Новый метод быстрого отслеживания
отклонений частоты на основе пересечений уровней», IEEE Trans. по Power
Аппараты и системы, т. ПАС-103, вып. 8, pp. 2230–2236, Aug. 1984.
[4] И. Камва и Р. Грондин, «Быстрые адаптивные схемы для отслеживания вектора напряжения
и локальной частоты в системах передачи и распределения электроэнергии —
tems», IEEE Trans. по энергоснабжению, т. 7, вып.2, pp. 789–795, Apr.
1992.
[5] М. С. Сачдев и М. М. Гирей, «Метод наименьших квадратов ошибок для определения частоты энергосистемы
», IEEETrans. по энергетическим аппаратам
ии системам, т. ПАС-104, № 2, стр. 437–443, февраль 1985 г.
[6] М. М. Гирей и М. С. Сачдев, «Измерения частоты вне номинальной
в электроэнергетических системах», IEEE Trans. по энергоснабжению, т. 4, вып.
3, стр. 1573–1578, июль 1989 г.
[7] V.В. Терзия, М. Б. Джурич и Б. Д. Ковачевич, «Оценка вектора напряжения и
локальной системной частоты с использованием алгоритма типа Ньютона», IEEE
Trans. по энергоснабжению, т. 9, вып. 3, pp. 1368–1374, июль 1994.
[8] М. С. Сачдев, Х. К. Вуд и Н. Г. Джонсон, «Фильтрация Калмана
, применяемая к измерениям энергосистем для ретрансляции», IEEE Trans. на
Силовые аппараты и системы, т. ПАС-104, № 12, pp. 3565–3573,
Dec. 1985.
[9] A.А. Гиргис, Т.Л. Д. Хван, «Оптимальная оценка векторов напряжения
и девиации частоты с использованием линейного и нелинейного фильтра Калмана: теория
и ограничения», IEEE Trans. по энергетическим аппаратам и системам, т.
103, нет. 10, стр. 2943–2949, октябрь 1984 г.
[10] А.А. Гиргис и У.Л. Петерсон, «Адаптивная оценка девиации частоты энергосистемы
и скорости ее изменения для расчета внезапной мощности
перегрузок системы», IEEE Trans .по энергоснабжению, т. 5, вып. 2, pp.
585–594, апрель 1990 г.
[11] Т. Лобос и Дж. Резмер, «Определение частоты энергосистемы в реальном времени
», IEEETrans. по приборостроению и измерениям, т. 46, нет.
4, стр. 877–881, август 1997 г.
[12] AG Phadke, JS Thorp и MG Adamiak, «Новый метод измерения
для отслеживания векторов напряжения, частоты локальной системы и скорости
изменение частоты », IEEE Trans. по энергетическим аппаратам и системам,
т.102, нет. 5, pp. 1025–1038, May 1983.
[13] Ф. Дени, К. Кунан, Л. Хоссенлоп и К. Холвек, «Измерение
фазы напряжения для французского плана будущей защиты от потерь
».синхронизм », IEEE Trans. по энергоснабжению, т. 7, вып. 1, pp. 62–69,
Jan. 1992.
Jun-ZheYang родился в Тайнане, Тайвань, в 1971 году. степень
в области электротехники от Технологического института Татунг в 1994 году и
M.С. и к.т.н. В 1997 и 1999 годах окончил Национальный университет Тайваня.
В настоящее время он служит вторым лейтенантом в ВВС. Его интересующие исследования
включают передачу времени GPS и методику измерения в энергосистеме.
Чи-Вэнь Лю (M’94) родился на Тайване в 1964 году. Он получил степень бакалавра наук. de-
по электротехнике от Национального Тайваньского университета в 1987 году и
магистра наук. и к.т.н. Степень электротехники в Корнельском университете
в 1992 и 1994 годах.С 1994 года он работает в Национальном Тайваньском университете,
, где он является адъюнкт-профессором электротехники. Он является членом
IEEE и выступает в качестве рецензента IEEE T
RANSACTIONS ON CIRCUITS AND
SYSTEMS. Его основная область исследований — применение компьютерных технологий для мониторинга, эксплуатации, защиты и контроля энергосистем
. Его другие интересы
включают передачу времени GPS и хаотическую динамику, а также их применение
к системным проблемам.
Разрешенное лицензионное использование ограничено: Национальным университетом Тайваня. Загружено 9 марта 2009 г. в 04:33 с IEEE Xplore. Ограничения применяются.
Подход к разработке открытого программного комплекса для расчета частотной характеристики энергосистемы | Защита и управление современными энергосистемами
Модель DFR
Полное моделирование во временной области позволяет детально моделировать частотную характеристику энергосистем. Однако из-за связанной динамики активной мощности-частоты и динамики реактивной мощности-напряжения при изучении динамического поведения энергосистемы необходимо учитывать как частоту, так и напряжение.Влияние частоты и напряжения практически не различимо. Следовательно, в этой статье предлагается модель DFR для разделения динамики частоты и напряжения и учета влияния сети. В модели DFR сеть системы моделируется потоком мощности постоянного тока, поэтому можно учитывать перераспределение несбалансированной мощности между различными генераторами и пространственно-временные характеристики распределения частоты. Чтобы сосредоточиться на динамике активной мощности и частоты, делаются следующие предположения.(1) Система возбуждения и регулирования достаточно сильна, чтобы удерживать напряжение на клеммах генератора, и, таким образом, динамика систем возбуждения и регулирования и PSS может быть исключена из-за ее незначительного влияния на динамику активной промышленной частоты. (2) Уравнения качания генератора зарезервированы, в то время как влиянием переходного процесса внутренних обмоток на изменение частоты системы можно пренебречь из-за постоянного напряжения на клеммах генератора. Поскольку регуляторы турбины имеют существенное влияние на динамику частоты энергосистемы, детали регулятора турбины моделируются в модели DFR.
В модели DFR на динамическое поведение частоты влияет только изменение активной мощности. При постоянном напряжении на шине поток мощности постоянного тока вводится для моделирования сети при расчете потока активной мощности в начальных условиях эксплуатации [15]:
$$ \ mathbf {P} = \ mathbf {B} \ boldsymbol {\ uptheta} $ $
(1)
, где P — инжектируемая активная мощность, θ — угол напряжения всех шин, кроме шины провисания, а B — матрица чувствительности сети.
Допущение постоянного напряжения приводит к упрощению моделей нагрузки. При постоянном напряжении на клеммах можно игнорировать реактивную мощность нагрузки, а модель полиномиальной нагрузки [16] можно уменьшить как статическую активную мощность нагрузки с частотной зависимостью:
$$ {P} _L = {P} _0 \ left (1 + {K} _ {pf} \ varDelta f \ right) $$
(2)
где P л — фактическая нагрузка, P 0 — активная мощность нагрузки в исходном состоянии, К пф — коэффициент регулирования нагрузки, а Δ f — отклонение частоты.
Другие модели также можно упростить с соответствующими допущениями. Например, линии постоянного тока высокого напряжения (HVDC) могут быть представлены как нагрузки для передачи и приема с частотной зависимостью или без нее.
С упрощением генерирующих блоков, сети, нагрузок и другого оборудования, модель DFR может быть показана на рис. 1. Величины на рис. 1 указаны следующим образом. ω и , δ и , п. миль и P ei — частота вращения ротора, угол ротора, механическая мощность и электрическая мощность генераторного агрегата –.Δ f к и P к — частота шины и активная мощность нагрузки Дж .
Рис.1Принципиальная схема DFR модели
Подобно полному моделированию во временной области, модель DFR может быть выражена в терминах дифференциально-алгебраических уравнений (ДАУ) и может быть решена путем пошагового интегрирования, такого как неявное интегрирование трапеций.По сравнению с полным моделированием во временной области вычислительная нагрузка модели DFR значительно снижается, и она обеспечивает лучшую вычислительную эффективность с приемлемой точностью. Модель DFR может использоваться для анализа событий, связанных с изменением нагрузки, отключением генератора и т. Д. Ее также можно применять для быстрого расчета частотной характеристики для нарушений активной мощности и фильтрации событий.
С введением потока мощности постоянного тока модель DFR применима к системам, в которых реактивное сопротивление сети значительно превышает сопротивление, т.е.г., системы передачи высокого напряжения. Модель DFR в первую очередь полезна в тех случаях, когда стабильность частоты является основной проблемой, а угловая стабильность и стабильность напряжения могут быть сохранены.
Модель ASF
В реальных системах разница частот между шинами незначительна, если генераторы остаются синхронизированными во время переходного процесса [13]. Таким образом, частоту на разных шинах можно рассматривать как однородную, а пространственно-временным распределением частоты можно пренебречь. Пренебрегая сетью, модель DFR сводится к модели ASF, из которой может быть достигнута равномерная частота.Общая схема модели ASF показана на рис. 2 (а), где регуляторы турбин и нагрузки смоделированы в явном виде. -п м Σ и P e Σ — общая механическая мощность и общая активная мощность нагрузки системы. Δ ω — равномерная частота системы, которая генерируется из эквивалентного уравнения качания. Кроме того, все нагрузки могут быть объединены в эквивалентную модель нагрузки для упрощения модели ASF.Его можно применять в таких приложениях, как распределение вращающегося резерва, регулирование частоты нагрузки и т. Д. [17, 18].
Рис. 2Блок-схема ASF и модели с одной машиной. a Общая модель ASF. b Модель одной машины
Модель ASF может быть смоделирована с помощью DAE и решена с помощью пошаговой интеграции. Если пренебречь сетью, вычислительная нагрузка модели ASF намного меньше, чем у модели DFR.
Модель с одной машиной
Модель с одной машиной может рассматриваться как частный случай модели ASF, как показано на рис.2 (б). Он получается путем дальнейшего агрегирования всех регуляторов турбин и нагрузок в модели ASF. Нелинейность регуляторов турбины, такая как пределы клапана и зона нечувствительности, сохраняется. Структура агрегированных регуляторов турбины обычно такая же, как у обычных регуляторов турбины. Например, для автономной системы, в которой большая часть электроэнергии вырабатывается тепловыми генерирующими установками, паровая турбина-регулятор предпочтительнее для агрегированной модели. Пошаговая интеграция также используется для решения нелинейной модели отдельной машины.
Модель SFR
Нелинейность регуляторов турбин учитывается в модели DFR, модели ASF и модели отдельной машины. Непосредственно получить аналитическое выражение невозможно, и пошаговое интегрирование является наиболее популярным методом получения дискретного ответа. Пренебрегая нелинейными блоками и малыми постоянными времени, модель SFR была предложена в [14] для получения аналитического выражения частотной динамики для автономных систем, в которых в генераторах преобладают паровые турбины повторного нагрева.Блок-схема модели SFR представлена на рис. 3, где P д , п. м , H , D , R , F H , т р и K м — это возмущение, механическая мощность, инерция, демпфирование, спад, доля общей мощности, генерируемой турбиной высокого давления, постоянная времени подогревателя и коэффициент усиления механической мощности агрегированной системы.Используя аналитическое выражение, приведенное в [14], можно вычислить наибольшее отклонение частоты, соответствующее время и установившуюся частоту при заданном возмущении активной мощности. В нескольких исследованиях используется модель SFR для настройки UFLS [19, 20].
Рис.3Блок-схема модели SFR
Обсуждение
Частотные динамические характеристики можно категоризировать по-разному. Для приложений в зависимости от общих динамических характеристик частоты, например.g., регулирование частоты, обычно предполагается единообразная частота, и частота в разных местах рассматривается как одна и та же. В этом случае сетью можно пренебречь, и подходят модель ASF, модель одной машины и модель SFR. Функция пространственно-временного распределения частоты во время события представляет наибольший интерес для таких приложений, как определение местоположения события и обнаружение колебаний, где следует учитывать разницу между генераторами в разных местах. В этом случае необходимо сохранить влияние сети, чтобы получить пространственно-временные характеристики, и модель DFR подходит для таких приложений.
Для детального изучения динамических характеристик энергосистемы необходимо включить связь между динамикой активной мощности и частоты и динамикой реактивной мощности-напряжения, что приведет к комплексному моделированию во временной области. Однако для случаев, когда частотная динамическая характеристика вызывает наибольшее беспокойство, а динамика напряжения не представляет особого интереса или напряжение может поддерживаться на желаемых уровнях, для упрощения динамика активной мощности-частоты может быть отделена от динамики реактивной мощности-напряжения.Это делает активную мощность единственным фактором, влияющим на частоту, а приведенные выше приведенные модели подходят для изучения ключевого влияния активной мощности на частоту.
Границы | Эквивалентное управление компенсацией скорости вращения ротора ветряных турбин на основе PMSG для поддержки частоты в изолированных микросетях
Введение
В связи с быстрым развитием возобновляемых источников энергии в последние годы, технологии распределенного производства энергии, такие как фотоэлектрическая (PV), ветровая энергия и биогаз привлекают все больше внимания международного сообщества благодаря своей чистоте, низкому энергопотреблению и гибкости управления (Li et al., 2016). В то же время микросети, которые могут эффективно интегрировать распределенные источники энергии, постепенно стали важной частью современных электрических сетей.
Энергия ветра в основном подключается к сети через силовые электронные преобразователи, которым не хватает кинетической энергии (KE) ротора и которые не могут обеспечить инерцию сети. Ветровая энергия обычно работает в режиме слежения за точкой максимальной мощности (MPPT), а ее выходная мощность является случайной и непостоянной, что делает ее неспособной участвовать в регулировании частоты и напряжения в сети (Adam et al., 2015). Следовательно, сильное проникновение ветровой энергии вызывает проблему стабильности частоты из-за снижения общей инерции и способности первичной частоты (Zhao et al., 2019; Zhu et al., 2021a). Подход к решению вышеуказанных проблем заключается в том, что энергия ветра участвует в частотной характеристике сети.
Существующие подходы для ветряных турбин с регулируемой скоростью (VSWT) можно разделить на инерционное управление и управление без нагрузки. При инерционном управлении VSWT работают в режиме MPPT, и кинетическая энергия вращения (KE) высвобождается для обеспечения временной мощности для улучшения инерционного отклика.В основном инерционный контроль заключается в изменении активной мощности пропорционально скорости изменения частоты или девиации частоты или того и другого (Sun et al., 2019; Zeng et al., 2019). Для достижения компромисса в характеристиках частотного регулирования и безопасной эксплуатации скорости ротора были предложены некоторые методы адаптивного усиления (Zhang et al., 2012; Zhao et al., 2015; Wu et al., 2019; Zhao et al., 2020). В (Zhao et al., 2015) коэффициенты усиления схем частотного регулирования (FRS) при различных скоростях ветра регулируются в зависимости от скорости ветра.В (Wu et al., 2019) коэффициенты усиления дополнительных контуров девиации частоты адаптивно настраиваются в зависимости от измерения скорости ротора. В (Zhao et al., 2020) изменяющиеся во времени коэффициенты усиления, определенные на основе желаемого времени частотной характеристики, предназначены для повышения надира частоты и устранения второго падения частоты. В (Zhang et al., 2012) разработан адаптивный коэффициент усиления спада, который является функцией скорости ротора в реальном времени и уровня проникновения ветровой энергии.
Для управления разгрузкой часть активной мощности VSWT может быть зарезервирована через управление углом тангажа, управление превышением скорости или их комбинацию (Chang-Chien et al., 2011; Маргарис и др., 2012; Зертек и др., 2012; Wu et al., 2018; Луо и др., 2019; Tang et al., 2019).
Основываясь на управлении без нагрузки, управление спадом аналогично синхронным генераторам, которые могут обеспечивать поддержку первичной частоты в течение нескольких минут. В (Gao et al., 2019) предлагается комплексная схема частотного регулирования, сочетающая ступенчатое инерционное управление и управление с переменным спадом. Предлагается скоординированная схема управления, которая гибко переключается между дополнительным управлением мощностью, управлением кривой слежения и управлением регулировкой угла наклона на различных этапах запуска, что может эффективно улучшить недостаточную поддержку частоты.Схема управления с переменным наклоном, учитывающая дополнительный ротор KE, предложена в (Liu et al., 2019). Однако оценка KE ротора требовала информации о скорости ветра и параметрах ветряной турбины. Некоторые методы адаптивного усиления предложены в (Lee et al., 2016; Wu et al., 2019; Zhao et al., 2020), которые вводят дополнительное увеличение частоты управления инерцией в контур управления мощностью путем регулировки параметров дополнительный сигнал.
Из-за ограничения скорости вращения ротора регулирование разгруженного превышения скорости адаптировано только для районов с слабым ветром.Таким образом, в (Zhang et al., 2012) определены три области скорости ветра: область с низкой скоростью ветра, где работа без нагрузки осуществляется просто за счет управления скоростью ротора; область со средней скоростью ветра, в которой операция разгрузки осуществляется посредством комбинированного управления углом тангажа и управлением скоростью ротора; и область с высокой скоростью ветра, где управление измененным углом тангажа осуществляется отдельно. Однако для определения области скорости ветра требовалась точная информация о скорости ветра, а для расчета опорной мощности без нагрузки требуются как параметры ветряной турбины, так и скорость ветра.В (Chang-Chien et al., 2014), поскольку выходная мощность контролируется только регулировкой шага, они постоянно активируют регулировку шага во всем диапазоне скорости ветра. Таким образом, частая активация шага неизбежно увеличивает усталость сервопривода шага и напряжение лопасти. В (Tang et al., 2019) стратегия может в полной мере использовать инерционный отклик генераторов ветряных турбин (WTG) во всех положениях шага, чтобы поддерживать отправляемую активную мощность и уменьшать нагрузку на лопасти ветряных турбин.
По сравнению с генерацией ветряных турбин на основе индукционного генератора с двойным питанием (DFIG-WTG), генерация ветряных турбин на основе синхронных генераторов с постоянными магнитами (PMSG-WTG) может обеспечить гораздо более сильный инерционный отклик благодаря их преобразователю полной мощности, и он вмещает более широкий диапазон скорости вращения ротора (Wu et al., 2016). В большинстве публикаций FRS разработаны на основе управления отслеживанием мощности для DFIG-WTG. Дополнительная мощность от дополнительного контура управления добавляется к максимальной опорной мощности или опорной мощности без нагрузки, чтобы обеспечить поддержку частоты.
Однако для PMSG-WTG отслеживание скорости ротора является альтернативным привлекательным методом управления, при котором скорость ротора напрямую регулируется для захвата энергии ветра. Лишь несколько исследований сосредоточены на FRS, основанном на управлении скоростью ротора. В (Kayikci and Milanovic, 2009) предлагается алгоритм для извлечения максимального KE без остановки ветряной турбины (WT), в котором электрический крутящий момент увеличивается ступенчато за счет увеличения скорости ротора WT для обеспечения виртуальной инерции.Однако в этом исследовании механический крутящий момент был принят постоянным. В (LI et al., 2017) дополнительный опорный крутящий момент добавляется к опорному крутящему моменту преобразователя на стороне генератора, чтобы реагировать на изменение частоты системы. В (Zhu et al., 2021b) предлагается комплексная стратегия скоординированного управления, содержащая интегрированное инерционное управление с переменным коэффициентом и управление виртуальным конденсатором.
Целью данного исследования является изучение новой FRS для управления скоростью ротора на основе PMSG-WTG во всем диапазоне скорости ветра.Комбинированная переменная скорости ротора и угла наклона компенсации без нагрузки определяется и называется «эквивалентной скоростью ротора», что помогает реализовать управление без нагрузки во всей области скорости ветра. Инерционная и первичная частотная характеристика генерируется путем добавления виртуального отклонения скорости ротора, что приводит к тому, что регулировка скорости ротора или угла наклона соединяется с отклонением частоты сети для увеличения или уменьшения выходной активной мощности.
Остальная часть этой статьи организована следующим образом: в разделе «Традиционная схема регулирования частоты для PMSG-WTG » представлена традиционная структура управления скоростью ротора PMSG-WTG; в разделе «Предлагаемая схема регулирования частоты » подробно представлен базовый принцип предложенной схемы, включая кривую зависимости эквивалентной скорости ротора от мощности без нагрузки и схему расчета переменной виртуальной компенсации для изменения опорной скорости ротора; а в разделе Пример построена имитационная модель изолированной микросети, и предложенная схема сравнивается с методом, описанным в (LI et al., 2017). Проверена эффективность участия предложенной схемы управления в АЧХ системы при различных изменениях скорости ветра и нагрузки. Наконец, краткий вывод сделан в Разделе Заключение .
Традиционная схема регулирования частоты для PMSG-WTG
Схема моделирования стратегии управления скоростью ротора на основе PMSG-WTG (Hu et al., 2017) показана на рисунке 1, который в основном состоит из ветряных турбин, PMSG и мощности. электронные преобразователи.Аэродинамический ротор WT напрямую соединен с PMSG без какой-либо коробки передач. PMSG подключен к сети через преобразователь на стороне машины (MSC) и преобразователь на стороне сети (GSC) для управления скоростью и мощностью генератора.
РИСУНОК 1 . Блок-схема модели генераторов ветряных турбин на базе PMSG.
Уловленная механическая энергия ветра, P м , определяется как (Sun et al., 2019)
Pm = 12ρπR2vw3Cp (λ, β), (1), где ρ — плотность воздуха, R — радиус , v w — скорость ветра, λ — передаточное число конечных скоростей, λ = ω r R / v w , ω r — скорость ротора , β — угол наклона, а C p ( λ, β ) — коэффициент мощности.
Как и в (Ekanayake and Jenkins, 2004), C p ( λ, β ) может быть выражено как
Cp (λ, β) = (0,44−0,0167β) sin [π (λ − 3 ) 5−0,3β] −0,00184 (λ − 3) β. (2)Кривая характеристики скорости вращения ротора с максимальной механической мощностью предварительно задана, а эталонная скорость вращения ротора запрашивается в соответствии с измерением электромагнитной мощности (Sun et al. , 2019). Когда скорость ветра увеличивается, скорость вращения ротора БТ увеличивается за счет увеличения захваченной мощности P m .Чтобы достичь баланса системы, электромагнитная мощность P e , управляемая контроллером скорости ротора, увеличивается. Увеличенный P e течет в конденсатор промежуточного контура. Затем GSC вводит активную мощность, поставляемую MSC, в энергосистему, чтобы поддерживать постоянное напряжение звена постоянного тока. Когда скорость ветра продолжает увеличиваться и электромагнитная мощность достигает номинальной мощности, начинает действовать регулятор угла наклона, чтобы ветряная турбина работала с постоянной мощностью.
Однако этот тип ветряной турбины работает в режиме отслеживания максимальной мощности и не может реагировать на изменение частоты системы. В (LI et al., 2017) предлагается типичная схема регулирования частоты, в которой крутящий момент регулируется в соответствии с отклонением частоты, как показано на рисунке 2.
Рисунок 2 . Традиционная схема управления частотным регулированием.
Режим управления отслеживанием максимальной мощности используется вместо режима отслеживания мощности без нагрузки. Задание скорости вращения ротора без нагрузки, ω de , предоставляется для контроллера скорости, а выходной крутящий момент T r получается через PI-регулятор.Когда частота сети f s отклоняется от номинальной частоты f n , дополнительный опорный крутящий момент Δ T добавляет в зависимости от отклонения частоты Δ f добавляется к T r . Затем опорный крутящий момент T ref получается и передается во внутренний контур управления. Захваченная активная мощность регулируется откликом внутреннего контура, и скорость ротора отслеживает ω, de .Из-за эффектов быстрого регулирования системы управления GSC, GSC, а затем активная мощность от MSC немедленно вводятся в сеть, чтобы поддерживать постоянное напряжение звена постоянного тока.
Дополнительный опорный крутящий момент Δ T add определяется в соответствии с девиацией частоты Δ f и коэффициентом регулирования спада K pf , который может быть выражен как
Однако дополнительный Δ T add имеет конфликт с регулятором скорости. T r от регулятора скорости используется для регулирования скорости ротора, отслеживая опорное значение. Δ T добавить зависит от девиации частоты. Этот конфликт влияет как на регулирование скорости, так и на поддержку частоты. В то же время эта схема не учитывает согласование управления крутящим моментом и управлением углом тангажа. В зоне средней и высокой скорости ветра необходимо регулировать угол тангажа для регулирования активной мощности из-за ограничения скорости вращения ротора.Кроме того, K pf является фиксированным значением, которое не может быть изменено адаптивно при различных условиях скорости ветра. Когда скорость ветра находится в низкой области, дополнительный опорный крутящий момент Δ T add слишком велик, что приводит к слишком быстрому падению скорости ротора. Когда скорость ветра находится в высокой области, дополнительного опорного крутящего момента Δ T добавить для регулирования частоты будет недостаточно.
Предлагаемая схема регулирования частоты
Блок-схема предлагаемой схемы регулирования частоты
Блок-схема схемы, предложенной в этой статье, показана на рисунке 3.
РИСУНОК 3 . Предлагаемая схема частотного регулирования.
Чтобы реализовать управление без нагрузки для PMSG во всем диапазоне скоростей ветра, в этой статье определяется новая переменная, названная здесь эквивалентной скоростью ротора « ω b », которая объединяет скорость ротора и шаг без нагрузки. угол.
ω de — это скорость ротора без нагрузки в области низкой скорости ветра, а β de — угол тангажа без нагрузки в области средней и высокой скорости ветра.
Кроме того, кривая зависимости эквивалентной скорости ротора от мощности без нагрузки получается путем подбора данных моделирования ветряной турбины. В зависимости от этой кривой можно запросить соответствующий ω b в соответствии с электромагнитной мощностью P e . Подробности приведены в подразделе «Кривая эквивалентной скорости вращения ротора — активная мощность » ниже.
Чтобы напрямую связать частоту сети со скоростью ротора, на основе отклонения частоты получается компенсационная переменная Δ ω b .При добавлении Δ ω b к ω b получается эталонная скорость ротора ω ref
Поскольку эквивалентная скорость ротора ω b содержит сумму пер- единицы измерения скорости ротора и угла наклона, эти два значения должны быть разделены, чтобы получить опорную скорость ротора или опорный угол наклона для контроллера. К счастью, угол тангажа действует только тогда, когда частота вращения ротора достигает ω max (1.p.u в этой статье). Следовательно, за эквивалентной скоростью ротора ω ref добавлен ограничитель. Когда ω ref меньше ω max , ω ref непосредственно используется в качестве опорного значения контура управления скоростью ротора. Когда ω ref больше, чем ω max , задание скорости ротора составляет ω max , а задание угла наклона β ref может быть получено путем вычитания ω max. из ω исх. . Следовательно, угол тангажа может помочь разгрузке управления и реакции на изменение частоты, когда ω ref превышает ω max . Как получить Δ ω b объясняется в подразделе «Метод расчета скорости вращения ротора виртуальной компенсации » ниже.
Кривая эквивалентной скорости вращения ротора и активной мощности
Как и в (Zhang et al., 2012), скорость вращения ротора без нагрузки и угол тангажа без нагрузки могут быть рассчитаны с помощью следующих выражений:
{Cp, de (λde , 0) = (1 − d%) Cp, max (λopt, 0) v1При низкой скорости ветра λ opt и C p, max можно получить с помощью уравнения. 2. Следовательно, λ de можно рассчитать по формуле. 6, а затем мы можем вычислить ω de на λ de = ω de R / v .
В зоне среднего ветра λ ref = ω max R / v , λ opt и C p, max были получены с помощью уравнения.2. Угол наклона ( β de ) можно рассчитать по формуле. 6.
В области сильного ветра, мы можем вычислить C p, оцененный по формуле. 1. Тогда, поскольку λ ref было известно, β 0 может быть получено по формуле. 2. Следовательно, β de может быть получено по формуле. 6.
Следовательно, исходя из ур. 4 и уравнение. 6, могут быть получены данные автономной подгонки мощности без нагрузки P de и ω b при различных областях скорости ветра.Данные и аппроксимация кривой ω b -P de показаны на рисунке 4.
Рисунок 4 . Эквивалентная частота вращения ротора ω b активная мощность P de кривая.
РИСУНОК 5 . Активная мощность, эквивалентная скорости вращения ротора, ω b кривая во всей области скорости ветра.
В соответствии с областью скорости ветра кривую ω b — P de можно разделить на три сегмента.Первый сегмент — это область с низкой скоростью ветра, где P de меньше 0,53 о.е. Управление углом тангажа отключено; то есть β равно 0. Согласно формуле. 4, ω b равно ω de . Второй сегмент — это область средней скорости ветра, где мощность превышает 0,53 о.е. Третий — область высокой скорости ветра, где P de больше или равно 0,9 о.е. Во втором и третьем сегментах включено управление углом тангажа.
Учитывая точность и сложность, для аппроксимации кривой ω b — P de используется следующая кусочная функция:
ωb = {k1Pde3Pde≤0,53 puPde − b3k30,53 puМетод расчета скорости вращения ротора виртуальной компенсации
Скорость вращения ротора виртуальной компенсации Δ ω b введена для генерации как инерционных, так и первичных частотных характеристик. В разделе Кривая эквивалентной скорости вращения ротора-активной мощности , уравнение. 7, который описывает соотношение между мощностью без нагрузки P de и эквивалентной скоростью ω b ротора.Согласно обратной функции уравнения. 7, мы можем получить кривую P-ω b , как в
Pde = {k1ωb3ωmin <ωb≤ωblowk3ωb + b3ωblow <ω≤ωbmediumk4ωb + b4ω≥ωbmedium. (8), где ω 4 мин. скорость ротора включения WT и ω b low — это демаркационная эквивалентная скорость ротора между областью низкой скорости ветра и областью средней скорости ветра. Значение ω b low равно номинальной скорости вращения ротора ω max , что составляет 1 p.u. ω b средняя — демаркационная эквивалентная скорость ротора между областью средней скорости ветра и областью высокой скорости ветра, и ее значение составляет 2,6 о.е. Когда ω b превышает ω b средний , активная мощность должна оставаться постоянной.
Кривая максимальной мощности может быть приблизительно равна
Pmppt = {k2ωb3 ωmin <ωb≤ωblowk4ωb + b4k4 + 0,1 ωb≥ωblow. (9), где k 2 — максимальный коэффициент мощности, k 2 = 0.98.
Кривая P de -ω b и кривая P mppt -ω b кривая в области низкой скорости ветра показаны на рисунке 6. Предположим, что PMSG- Первоначально WTG работает в разгрузочной стабильной точке 1 ′.
РИСУНОК 6 . Активная мощность, эквивалентная скорости вращения ротора, ω b кривая в области низкой скорости ветра.
Обычно выходная активная мощность PMSG регулируется на основе девиации частоты Δf , и ее выражение составляет
ΔPe = −ΔPmax (fb-fa) Δf, (10), где Δ P max равно максимальная мощность регулирования частоты, f a и f b соответствуют интервалу регулирования частоты системы, а Δ P max является предельной мощностью регулирования частоты.
Чтобы предотвратить скорость вращения ротора ниже оптимальной во время процесса регулирования частоты, значение Δ P max представляет собой разницу между максимальной мощностью P mppt и мощностью без нагрузки с максимальной мощностью. частота вращения силового ротора ω b2 , то есть
ΔPmax = P2 − P3 = k2ωb23− k1ωb23, (11), где P 2 — максимальная мощность в рабочей точке ‘2’ и P 3 — мощность без нагрузки при максимальной скорости вращения ротора в точке «3».
Предполагая, что происходит падение частоты, электромагнитная мощность P e должна возрасти, что эквивалентно увеличению скорости ротора Δ ω b ′
P1 ′ = P1 + ΔPe = k1 (ωb1 + Δωb ′) 3 = k1 (ωb13 + 3ωb12Δωb ′ + 3ωb1Δωb′2 + Δωb′3) (12)Поскольку диапазон регулирования частоты вращения ротора невелик, 1> ω b1 >> Δ ω б ′ . Следовательно, члены более высокого порядка с Δ ω b ′ могут быть проигнорированы, и тогда уравнение.12 можно упростить
P1 ′ = P1 + ΔPe≈k1Δ (ωb13 + 3ωb12Δωb ′). (13)Объединение уравнения. 13 и уравнение. 9,
ΔPe = 3ωb12Δωb ′ = — ΔPmaxΔfmaxΔf (14)Начальная мощность без нагрузки P 1 и максимальная мощность P 2 может быть выражена как
Тогда, учитывая уравнение. 8, уравнение. 9 и уравнение. 15,
(1 − d%) k2ωb23 = k1ωb13. (16)Из уравнения. 16, следующее выражение может быть получено как
ωb2 = k1ωb13k2 (1-d%) 3. (17)Подставить уравнение. 17 в уравнение. 11 можно вывести следующее выражение:
ΔPmax = k2k1ωb13k2 (1 − d%) — k12ωb13k2 (1 − d%).(18)Далее подставляем уравнение. 18 в уравнение. 10, получается следующее выражение:
Δωb ′ = — k1 (k2 − k1) ωb13k2 (1 − d%) ΔfmaxΔf. (19)Наблюдая за рис. 6, Δ ω b ′ — разница между эквивалентная скорость ротора в точке «1» и эквивалентная скорость ротора в точке «1» после регулирования частоты.
Фактически, ω b1 трудно измерить в инженерных приложениях. Следовательно, ω b1 заменяется на ω b , и уравнение.19 можно записать как
Δωb = −k1 (k2 − k1) ωb3k2 (1 − d%) ΔfmaxΔf. (20)ω b всегда больше или равно ω b1 . Следовательно, при замене ω b1 на ω b , Δ ω b больше и приводит к высвобождению большей активной мощности.
В области средней скорости ветра, поскольку диапазон регулировки ω b увеличивается, Δ ω b ‘ больше не может игнорироваться.Когда происходит событие провала частоты, электромагнитная мощность может быть выражена как
P4 ′ = P4 + ΔPe = k3 (ωb4 + Δωb ′) + b3. (21)В области высокой скорости ветра Δ P max постоянная величина, 0,1 о.е.
Используя тот же подход к анализу в области низкой скорости ветра, можно вывести взаимосвязь между Δ ω b и Δ f при средней и высокой скорости ветра. Выражение Δ ω b -Δ f может быть получено как
Δωb = {- k1 (k2 − k1) ωb3k2 (1 − d%) (fb − fa) Δf ωb≤ωblow − k3 (k2 −k1) ωb + b3 (k2 − k1) (1 − d%) k2k3 (fb − fa) Δf ωblow <ωb≤ωbmedium − 0.1k4 (fb − fa) Δf ωb> ωbmedium. (22)Динамический процесс частотного регулирования предложенной схемы управления
Динамический отклик PMSG, участвующего в частотном регулировании, при падении частоты показан на рисунке 7. Траектория активного мощность и частота вращения ротора показаны на Рисунке 8.
РИСУНОК 7 . Процесс динамического отклика PMSG, участвующий в частотном регулировании.
РИСУНОК 8 .Траектория активной мощности P e и эквивалентной скорости ротора ω b .
На рисунке 7 область S 1 между механической мощностью и мощностью, захваченной ветряной турбиной, представляет KE вращения, выделяемую ветровой турбиной. Он в основном используется для обеспечения инерционного отклика и влияет на скорость изменения частоты и надиру частоты. Область S 2 представляет увеличение захваченной энергии ветряной турбиной, которая в основном используется для обеспечения первичного регулирования частоты и влияния на установившуюся частоту системы.
Динамический процесс частотного регулирования разделен на шесть периодов, и динамический процесс в каждом периоде анализируется, соответственно.
t
t 1 < t < t 2 : при t = t 1 нагрузка внезапно увеличивается, а частота падает.Согласно формуле. 22, Δ ω b убывает. Поскольку скорость ротора PMSG не связана с частотой сети, скорость ротора ω r остается неизменной в данный момент. Согласно формуле. 7, ω ref уменьшается, а отклонение Δ ω e между ω r и ω ref увеличивается. Следовательно, посредством ПИ-регулирования опорное значение электромагнитного момента T ref увеличивается.То есть P e PMSG увеличивается. Согласно механическому уравнению ротора, частота вращения ротора ω r уменьшается. Из-за уменьшения ω r увеличивается сила захвата ветра P m , а также увеличивается его крутящий момент T m .
t 2 < t < t 3 : по мере увеличения P e , в зависимости от P de — ω b кривой 905 b увеличивается.В течение этого периода, поскольку Δ f увеличивается, а диапазон изменения ω b мал, Δ ω b играет доминирующую роль в это время, так что ω ref уменьшается и его величина уменьшения больше, чем величина уменьшения ω r . Δ ω e увеличивается. Следовательно, T ref увеличивается после ПИ-регулятора, что приводит к увеличению P e . ω r продолжает уменьшаться из-за увеличения P e . Когда t = t 3 , Δ ω e достигает максимального значения, а P e достигает максимального значения. Исходя из кривой ω b — P de , ω b также достигает своего максимального значения.
t 3 < t < t 4 : в этот период, когда частота начинает восстанавливаться, Δ ω b начинает уменьшаться, а изменение ω ref меньше, чем ω r , что приводит к уменьшению Δ ω e . P e тоже начинает уменьшаться, но все равно больше P m . ω b также начинает убывать с уменьшением P e . Согласно формуле. 7, ω ref уменьшится. Согласно механическому уравнению ротора, ω r уменьшается. t 4 < t < t 5 : поскольку P e все еще больше, чем P m , согласно механическому уравнению ротора, ω r и ω ref продолжают уменьшаться, а отклонение Δ ω e продолжает уменьшаться, что приводит к уменьшению T ref и P e .По мере уменьшения ω r , P m увеличивается. Когда t = t 5 , P m впервые равно P e .
t > t 5 : поскольку уменьшение ω r немного медленнее, чем ω ref , P m немного больше P 4 e . Следовательно, ω r увеличивается.Когда t = t 6 , P m равно P e и ω r равно ω ref . В это время PMSG-WTG достигает новой установившейся рабочей точки.
Пример из практики
Создана имитационная модель изолированной микросети ветроэнергетических дизельных генераторов. Схема изолированной микросети представлена на рисунке 9. Номинальная мощность дизельного агрегата — 70 кВт.Номинальное действующее значение напряжения и частоты составляет 5 кВ и 50 Гц соответственно.
РИСУНОК 9 . Структурная схема модели независимой микросети.
Для проверки эффективности предложенной схемы регулирования частоты устанавливаются различные сценарии изменения скорости ветра и нагрузки. Следующие три схемы используются для сравнения с предлагаемой схемой управления.
1) Предлагаемая схема частотного регулирования.
2) Обычная схема частотного регулирования.
3) Схема управления переменным коэффициентом в (Zhu et al., 2021b).
4) Схема управления без нагрузки (PMSG не участвует в регулировании частоты).
Зона низкой скорости ветра
Случай 1: скорость ветра задана равной 9 м / с; нагрузка внезапно увеличивается на 15 кВт за 50 с. Результат моделирования показан на рисунке 10. Как видно на рисунке 10, когда PMSG принимает традиционную схему, скорость ротора не превышает нижний ограничитель. Когда PMSG принимает предложенную схему, надир частоты (FN) равен 59.84 Гц, что на 0,02 Гц больше, чем у PMSG-WTG, использующего традиционную схему, и на 0,01 Гц больше, чем у схемы управления с переменным коэффициентом. Установившаяся частота составляет 59,91 Гц, что на 0,01 больше, чем у двух других схем управления. По сравнению с традиционной схемой регулирования частоты и схемой управления с переменным коэффициентом предложенная схема показывает лучшие характеристики. Причина в том, что активная мощность для частотной опоры увеличивается с увеличением скорости ветра, что подтверждает, что предложенная схема управления имеет потенциальную адаптируемость к скорости ветра.
РИСУНОК 10 . Результаты для случая 1. (A) Системная частота; (В) Активная мощность PMSG; (C) Скорость вращения ротора PMSG; (D) Угол наклона.
Случай 2: задана скорость ветра 9 м / с; нагрузка внезапно снижается на 15 кВт за 50 с. Результат моделирования показан на рисунке 11. Наблюдая за результатами моделирования, когда PMSG принимает предложенную схему регулирования частоты, пик и девиация частоты системы меньше, чем у PMSG-WTG, использующего схему регулирования частоты. две другие схемы управления, которые подтверждают, что предложенная схема имеет лучшие характеристики регулирования частоты.
РИСУНОК 11 . Результаты для случая 2. (A) Системная частота; (В) Активная мощность PMSG; (C) Скорость вращения ротора PMSG; (D) Угол наклона.
Зона средней скорости ветра
Случай 3: скорость ветра установлена равной 11 м / с; нагрузка внезапно увеличивается на 15 кВт за 50 с. Результат моделирования показан на рисунке 12. Как показано на рисунке 12A, когда PMSG принимает предложенную схему, FN составляет 59,88 Гц, что на 0,11 Гц выше, чем при использовании PMSG. не участвуют в частотном регулировании и 0.На 1 Гц и 0,09 Гц выше, чем у традиционной схемы и схемы управления с переменным коэффициентом соответственно. Стабильная частота составляет 59,92 Гц, что на 0,03 Гц больше, чем когда PMSG не участвует в регулировании частоты, на 0,019 Гц больше, чем при использовании традиционной схемы, и на 0,019 Гц больше, чем в схеме управления с переменным коэффициентом. Как показано на рисунке 12B, дополнительная мощность предложенной схемы больше, чем у других схем частотного регулирования. Пониженная скорость ротора используется для поддержки инерции.Пиковая мощность, когда PMSG-WTG принимает традиционную схему, составляет 107,5 кВт, схема управления с переменным коэффициентом составляет 107,7 кВт, а мощность PMSG-WTG, использующая предложенную схему, составляет 116,1 кВт. В процессе регулирования частоты PMSG-WTG работает в безопасном диапазоне скоростей ротора, как показано на Рисунке 12C. Из-за потенциальной самоадаптации частота вращения ротора в предложенной схеме сходится к более низкому значению 0,9739 о.е. и больше KE высвобождается в течение этого периода. Как показано на рисунке 12D, управление углом тангажа активируется для обеспечения управления разгрузкой и поддержкой частоты.Перед изменением нагрузки PMSG-WTG работает в режиме без нагрузки, а угол тангажа составляет приблизительно 0,094 градуса. После изменения нагрузки угол тангажа уменьшается, чтобы высвободить дополнительную мощность для поддержки частоты. Фактически, управление углом тангажа и управление скоростью ротора трудно скоординировать для двух других схем управления в области средней скорости ветра. Когда PMSG принимает предложенную схему, угол тангажа падает глубже, чем при использовании других схем. Следовательно, предложенная схема может лучше использовать управление углом наклона и скоростью ротора для обеспечения частотной поддержки.
РИСУНОК 12 . Результаты для случая 3. (A) Системная частота; (В) Активная мощность PMSG; (C) Скорость вращения ротора PMSG; (D) Угол наклона.
Случай 4: скорость ветра установлена равной 11 м / с; нагрузка внезапно уменьшается на 15 кВт за 50 с. Результат моделирования показан на рисунке 13. Если нагрузка уменьшается, если ожидается, что PMSG-WTG будет регулировать частоту, скорость ротора должна увеличиться. Однако скорость ротора достигла максимального значения во время управления без нагрузки, как показано на Рисунке 13C.Таким образом, отклонение частоты может быть подавлено только путем увеличения угла тангажа, как показано на рисунке 13D. Когда PMSG принимает предложенную схему, может быть высвобождено больше активной мощности из-за его потенциальной самоадаптации, как показано на рисунке 13B. На рисунке 13A пиковая частота предложенной схемы составляет 60,195 Гц, что на 0,01 Гц ниже, чем у схемы управления с переменным коэффициентом, на 0,03 Гц ниже, чем у традиционной схемы, и на 0,04 Гц ниже, чем у PMSG- WTG, которая не участвует в частотном регулировании.Установившаяся частота составляет 60,08 Гц для предложенной схемы и схемы управления с переменным коэффициентом, что на 0,02 Гц ниже, чем у PMSG, использующего традиционную схему, и на 0,03 Гц ниже, чем у PMSG, не участвующего в регулировании частоты.
РИСУНОК 13 . Результаты для случая 4. (A) Системная частота; (В) Активная мощность PMSG; (C) Скорость вращения ротора PMSG; (D) Угол наклона.
Зона высокой скорости ветра
Случай 5: скорость ветра установлена равной 14 м / с; нагрузка внезапно увеличивается на 15 кВт за 50 с.Результат моделирования показан на рисунке 14. В зоне с высокой скоростью ветра частота регулируется с помощью регулятора угла тангажа. На рисунке 14C показано, что скорость ротора составляет 1 о.е. для всех схем управления. Когда PMSG принимает предложенную схему, наблюдается более глубокое падение угла тангажа, чем у двух других схем управления, как показано на рисунке 14D. Как показано на рисунке 14A, когда PMSG принимает предложенную схему, FN составляет 59,86 Гц, Более активная мощность может быть высвобождена из-за потенциальной самоадаптации схемы, предложенной на рисунке 14B.Что на 0,07 Гц выше, чем у традиционной схемы, и на 0,05 Гц выше, чем у схемы управления с переменным коэффициентом. Установившаяся частота предложенной схемы составляет 59,92 Гц, тогда как установившаяся частота традиционной схемы и традиционной схемы составляет 59,9 и 59,91 Гц соответственно. Благодаря адаптивности предложенной схемы происходит более глубокое уменьшение угла тангажа, чем у других схем.
РИСУНОК 14 . Результаты для случая 5. (A) Системная частота; (В) Активная мощность PMSG; (C) Скорость вращения ротора PMSG; (D) Угол наклона.
Radom Wind Speed
Случай 6: фактическая измеренная скорость ветра (область средней скорости ветра) в Северо-Восточном Китае вводится в имитационную модель, как показано на рисунке 15A. Из-за изменения скорости ветра выходная активная мощность увеличивается или уменьшается, что приводит к колебаниям частоты на стороне сети, как показано на рисунках 15A и 15B. Благодаря участию ветряных турбин в регулировании частоты, вся традиционная схема, схема управления с переменным коэффициентом и предложенная схема улучшают частотную характеристику.По сравнению с двумя другими схемами управления, предложенная схема имеет потенциальную адаптацию, а дополнительная мощность для поддержки частоты адаптивно изменяется с изменением скорости ветра. Как показано на рисунках 15D и 15E, когда PMSG принимает предложенную схему, скорость ротора и угол наклона уменьшаются больше, чем в других схемах, особенно когда скорость ветра находится на большом участке. Следовательно, PMSG высвобождает больше активной мощности. Предлагаемая схема обеспечивает лучшую поддержку активной мощности, поэтому колебания частоты малы.Результаты этих случаев ясно показывают, что предложенная схема может обеспечить лучшую частотную поддержку, чем другие схемы, для всего диапазона скоростей ветра, независимо от низкой, средней, высокой или случайной скорости ветра. Он может обеспечить адаптивную частотную поддержку для различных скоростей ветра.
РИСУНОК 15 . Результаты для случая 6. (A) Случайная скорость ветра; (В) Системная частота; (С) Активная мощность PMSG; (D) Обороты ротора PMSG; (E) Угол наклона.
Заключение
В этой статье предлагается эквивалентная схема управления компенсацией скорости ротора PMSG-WTG для поддержки частоты в изолированных микросетях. Определена новая эквивалентная переменная скорости ротора, состоящая из комбинированного угла наклона и скорости ротора, которая может найти опорную скорость ротора или опорную величину компенсации угла наклона в соответствии с измерением активной мощности. В результате ветряная турбина может просто регулировать скорость ротора и угол наклона для управления без нагрузки во всем диапазоне скорости ветра.
Обеспечивается виртуальная компенсация скорости ротора для визуализации скорости ротора PMSG-WTG, напрямую связанной с частотой сети, для генерации как инерционной, так и первичной частотной характеристики. Скорость вращения ротора виртуальной компенсации адаптивно регулируется в зависимости от отклонения частоты для поддержания надлежащего крутящего момента, включающего характеристики регулирования частоты и безопасную работу ветряной турбины. Кроме того, угол тангажа и крутящий момент координируются и регулируются для обеспечения поддержки частоты при средней и высокой скорости ветра.
Результаты моделирования в различных условиях показывают, что предложенная схема обладает потенциалом самоадаптации и обеспечивает адаптивную частотную поддержку для всей ветровой области.
Заявление о доступности данных
Исходные материалы, представленные в исследовании, включены в статью / дополнительный материал; дальнейшие запросы можно направить автору-корреспонденту.
Вклад авторов
CZ и YL внесли свой вклад в концепцию и дизайн исследования.CZ, YL и YZ написали первый черновик рукописи. HL написал разделы рукописи. Все авторы внесли свой вклад в доработку рукописи, прочитали и одобрили представленную версию.
Конфликт интересов
Автор YZ работал в государственной сетевой компании Shandong Electric Power Company.
Остальные авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Примечание издателя
Все претензии, выраженные в этой статье, принадлежат исключительно авторам и не обязательно относятся к их аффилированным организациям, либо к претензиям издателя, редакторов и рецензентов.Любой продукт, который может быть оценен в этой статье, или заявление, которое может быть сделано его производителем, не подлежат гарантии или одобрению со стороны издателя.
Ссылки
Adam, Milczarek., Mariusz, Malinowski., And Josep, M. Guerrero. (2015). Управление реактивной мощностью в Islandedmicrogrid — Пропорциональное распределение мощности в иерархическом управлении падением напряжения. IEEE Transaction on Smart Grid. 6 (4), 1631–1637. doi: 10.1109 / TSG.2015.2396639
CrossRef Полный текст | Google Scholar
Chang-Chien, L.-R., Lin, W.-T., and Yin, Y.-C. (2011). Улучшение управления частотной характеристикой с помощью DFIG в энергосистемах с сильным ветром. IEEE Trans. Power Syst. 26 (2), 710–718. doi: 10.1109 / tpwrs.2010.2052402
CrossRef Полный текст | Google Scholar
Chang-Chien, L.-R., Sun, C.-C., and Yeh, Y.-J. (2014). Моделирование участия ветряных электростанций в AGC. IEEE Trans. Power Syst. 29 (3), 1204–1211. doi: 10.1109 / tpwrs.2013.22
CrossRef Полный текст | Google Scholar
Ekanayake, J., и Дженкинс, Н. (2004). Сравнение реакции ветряных турбин индукционных генераторов с двойным питанием и индукционных генераторов с фиксированной скоростью на изменение частоты сети. IEEE Trans. Energ. Беседы. 19 (4), 800–802. doi: 10.1109 / tec.2004.827712
CrossRef Полный текст | Google Scholar
Гао, Д. В., Ву, З., Янь, В., Чжан, Х., Янь, С. и Ван, X. (2019). Комплексная схема регулирования частоты для ветроэнергетической установки на основе синхронного генератора с постоянным магнитом. IET Renew.Выработка энергии. 13 (2), 234–244. doi: 10.1049 / iet-rpg.2018.5247
CrossRef Полный текст | Google Scholar
Hu, J., Wang, S., Tang, W., and Xiong, X. (2017). Ветряная турбина полной мощности с инерционной опорой за счет регулировки отклика контура фазовой синхронизации. IET Renew. Энергетика 11 (1), 44–53. doi: 10.1049 / iet-rpg.2016.0155
CrossRef Полный текст | Google Scholar
Каикчи, М., Миланович, Дж. В. (2009). Динамический вклад ветряных установок на основе DFIG в частотные нарушения в системе. IEEE Trans. Power Syst. 24 (2), 859–867. doi: 10.1109 / tpwrs.2009.2016062
CrossRef Полный текст | Google Scholar
Lee, J., Jang, G., Muljadi, E., Blaabjerg, F., Chen, Z., and Cheol Kang, Y. (2016). Стабильная краткосрочная поддержка частоты с использованием адаптивных коэффициентов усиления для ветряной электростанции на базе DFIG. IEEE Trans. Energ. Беседы. 31 (3), 1068–1079. doi: 10.1109 / TEC.2016.2532366
CrossRef Полный текст | Google Scholar
Li, Shichun., Huang, Yuehua., и Ван, Линюнь., (2017). Моделирование вспомогательной системы управления первичной частотной модуляцией для ветряных турбин с двойным питанием на основе управления скоростью. Proc. CSEE 37 (24), 7077–7086.
Google Scholar
Li, Xialin., Guo, Li., Wang, Chengshan., And Li, Yunwei. (2016). Обзор исследований по ключевым технологиям микросетей постоянного тока. Proc. CSEE 36 (1), 2–17.
Google Scholar
Лю Т., Пань В., Цюань Р. и Лю М. (2019). Стратегия управления переменной частотой падения для ветроэлектростанций с учетом оптимальной кинетической энергии ротора. Доступ IEEE 7, 68636–68645. doi: 10.1109 / access.2019.26
CrossRef Полный текст | Google Scholar
Луо, Х., Ху, З., Чжан, Х. и Чен, Х. (2019). Скоординированная стратегия управления активной мощностью для разряженных ветряных турбин для улучшения характеристик регулирования в AGC. IEEE Trans. Power Syst. 34 (1), 98–108. doi: 10.1109 / tpwrs.2018.2867232
CrossRef Полный текст | Google Scholar
Margaris, I. D., Papathanassiou, S. A., Hatziargyriou, N.Д., Хансен, А. Д., и Соренсен, П. (2012). Контроль частоты в автономных энергосистемах с сильным проникновением ветровой энергии. IEEE Trans. Поддерживать. Energ. 3 (2), 189–199. doi: 10.1109 / tste.2011.2174660
CrossRef Полный текст | Google Scholar
Sun, C., Ali, S. Q., Joos, G., and Bouffard, F. (2019). «Улучшенное управление VSG для ветряных генераторов типа IV с учетом эксплуатационных ограничений», на конгрессе и выставке по преобразованию энергии (ECCE) 2019 IEEE, 29 сентября — 3 октября.2019 (Балтимор, Мэриленд, США: IEEE), 2085–2091. doi: 10.1109 / ecce.2019.83
CrossRef Полный текст | Google Scholar
Тан, X., Инь, М., Шен, К., Сюй, Ю., Дун, З. Ю., и Цзоу, Ю. (2019). Активное управление мощностью ветряных турбин посредством регулирования скорости вращения ротора и угла наклона. IEEE Trans. Поддерживать. Energ. 10 (2), 822–832. doi: 10.1109 / tste.2018.2848923
CrossRef Полный текст | Google Scholar
Wu, Y.-K., Yang, W.-H., Hu, Y.-L., and Dzung, P.В. (2019). Регулирование частоты на ветряной электростанции с использованием изменяющейся во времени инерции и регуляторов наклона. IEEE Trans. Ind. Applicat. 55 (1), 213–224. doi: 10.1109 / tia.2018.2868644
CrossRef Полный текст | Google Scholar
Wu, Z., Gao, W., Gao, T., Yan, W., Zhang, H., Yan, S., et al. (2018). Современный обзор частотных характеристик ветряных электростанций в энергосистемах. J. Mod. Power Syst. Чистый. Energ. 6 (1), 1–16. doi: 10.1007 / s40565-017-0315-y
CrossRef Полный текст | Google Scholar
Wu, Z., Гао, В., Ван, X., Кан, М., Хван, М., Кан, Ю.С. и др. (2016). Улучшенное инерционное управление для ветряных генераторов с синхронным генератором на постоянных магнитах. IET Renew. Энергетика 10 (9), 1366–1373. doi: 10.1049 / iet-rpg.2016.0125
CrossRef Полный текст | Google Scholar
Zeng, X., Liu, T., Wang, S., Dong, Y., and Chen, Z. (2019). Комплексная стратегия скоординированного управления ветряной турбиной на базе PMSG для предоставления услуг по регулированию частоты. Доступ IEEE 7, 63944–63953.doi: 10.1109 / access.2019.28
CrossRef Полный текст | Google Scholar
Зертек А., Вербич Г. и Пантос М. (2012). Новая стратегия участия ветряных турбин с переменной скоростью в первичном регулировании частоты. IEEE Trans. Поддерживать. Energ. 3 (4), 791–799. doi: 10.1109 / tste.2012.2199773
CrossRef Полный текст | Google Scholar
Zhang, Z.-S., Sun, Y.-Z., Lin, J., and Li, G.-J. (2012). Скоординированное регулирование частоты ветряными электростанциями на базе индукционных генераторов с двойным питанием. IET Renew. Генератор мощности. 6 (1), 38–47. doi: 10.1049 / iet-rpg.2010.0208
CrossRef Полный текст | Google Scholar
Zhao, Jingjing., Li, Min., And He, Xinqin. (2019). Схема скоординированного управления ветроэнергетикой и накоплением энергии при регулировании частоты на основе управления предельным крутящим моментом. Пер. China Electrotechnical Soc. 34 (23), 4982–4990.
Google Scholar
Zhao, J., Lv, X., and Fu, Y. (2015). «Технология регулировки частоты микросети ветро-солнечного дизельного топлива на основе виртуальной инерции с переменным коэффициентом и координации управления превышением скорости ветряных турбин с двойным питанием» ,. J. Electrotechnical Eng. 30 (5), 59–68. (На китайском языке).
Google Scholar
Чжао, X., Сюэ, Y., и Zhang, X.-P. (2020). Быстрая поддержка частоты от ветряных турбин путем удержания надира частоты, близкой к установочной частоте. IEEE Open J. Power Energ. 7, 191–202. doi: 10.1109 / oajpe.2020.2996949
CrossRef Полный текст | Google Scholar
Zhu, Xiaorong., Zheng, Li., And Meng, Fanqi. (2021 г.). Анализ устойчивости микросетей постоянного тока на основе различных сетевых структур. Пер. China Electrotechnical Soc. 36 (1), 166–178.
Google Scholar
Чжу, Ю., Лю, С., и Ван, В. (2021 г.). Комплексная стратегия скоординированного управления ветряной турбиной на основе PMSG для поддержки инерции системы.