Формула частоты колебаний пружинного маятника в физике
Частота колебаний
ОпределениеЧастота колебаний ($\nu$) является одним из параметров, которые характеризуют колебания Это величина обратная периоду колебаний ($T$):
\[\nu =\frac{1}{T}\left(1\right).\]Таким образом, частотой колебаний называют физическую величину, равную числу повторений колебаний за единицу времени.
\[\nu =\frac{N}{\Delta t}\left(2\right),\]где $N$ — число полных колебательных движений; $\Delta t$ — время, за которые произошли данные колебания.
Циклическая частота колебаний (${\omega }_0$) связана с частотой $\nu $ формулой:
\[\nu =\frac{{\omega }_0}{2\pi }\left(3\right).\]Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
\[\left[\nu \right]=с^{-1}=Гц.\]Пружинный маятник
ОпределениеПружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать горизонтальные движения груза (рис.1), то он движется под действием силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. При этом часто считают, что силы трения можно не учитывать.
Уравнения колебаний пружинного маятника
Пружинный маятник, который совершает свободные колебания — это пример гармонического осциллятора. Пусть он выполняет колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза запишем как:
\[\ddot{x}+{\omega }^2_0x=0\left(4\right),\]где ${\omega }^2_0=\frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решение уравнения (4) это функция синуса или косинуса вида:
\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(5\right),\]где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний пружинного маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.
Частота колебаний пружинного маятника
Из формулы (3) и ${\omega }_0=\sqrt{\frac{k}{m}}$, следует, что частота колебаний пружинного маятника равна:
\[\nu =\frac{1}{2\pi }\sqrt{\frac{k}{m}}\ \left(6\right).\]Формула (6) справедлива в случае, если:
- пружина в маятнике считается невесомой;
- груз, прикрепленный к пружине, является абсолютно твердым телом;
- крутильные колебания отсутствуют.
Выражение (6) показывает, что частота колебаний пружинного маятника увеличивается с уменьшением массы груза и увеличени
Формула циклической частоты колебаний в физике
Определение и формула циклической частоты колебаний
ОпределениеЦиклическая частота — это параметр, характеризующий колебательные движения. Обозначают эту скалярную величину как $\omega $, иногда ${\omega }_0$.
Напомним, что уравнение гармонических колебаний параметра $\xi $ можно записать как:
\[\xi \left(t\right)=A{\cos \left({\omega }_0t+{\varphi }_0\right)\ }\left(1\right),\]где $A={\xi }_{max}$ — амплитуда колебаний величины $\xi $; $\left({\omega }_0t+{\varphi }_0\right)$=$\varphi $ — фаза колебаний; ${\varphi }_0$ — начальная фаза колебаний.
Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($\varphi $) по времени ($t$):
Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:
\[{\omega }_0=\frac{2\pi }{T}\left(3\right).\]Циклическую частоту с частотой $?$$?$ связывает выражение:
\[{\omega }_0=2\pi \nu \ \left(4\right).\]Формулы для частных случаев нахождения циклической частоты
Пружинный маятник совершает гармонические колебания с циклической частотой равной:
\[{\omega }_0=\sqrt{\frac{k}{m}}\left(5\right),\]$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Гармонические колебания физического маятника происходят с циклической частотой равной:
\[{\omega }_0=\sqrt{\frac{mga}{J}}\left(6\right),\]где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:
\[{\omega }_0=\sqrt{\frac{g}{l}}\left(7\right),\]где $l$ — длина подвеса, на которой находится материальная точка.
Частота колебаний в электрическом контуре равна:
\[{\omega }_0=\frac{1}{\sqrt{LC}}\left(8\right),\]где $C$ — емкость конденсатора, который входит в контур; $L$ — индуктивность катушки контура.
Если колебаний являются затухающими, то их частоту находят как:
где $\delta $ — коэффициент затухания; в случае с затуханием колебаний, ${\omega }_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Пример 1Задание. В электрический колебательный контур (рис.1) входит соленоид, длина которого $l$, площадь поперечного сечения $S_1$, число витков $N\ $и плоский конденсатор с расстоянием между пластинами $d$, площадью пластин $S_2$. Какова частота соб
Частота колебаний | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени.
Разновидность частот колебаний :
Циклическая частота
Частота колебаний физического маятника
Частота пружинного маятника
Частота математического маятника
Частота электромагнитных колебаний
Частота колебаний крутильного маятника
В Формуле мы использовали :
— Частота колебаний
— Циклическая частота
— Период колебаний маятника
— Масса груза, или масса маятника
— Жесткость пружины
— Длина подвеса
— Ускорение свободного падения
— Момент инерции маятника относительно оси вращения
— Расстояние от оси вращения до центра масс
— Момент инерции тела
— Вращательный коэффициент жёсткости маятника
Колебания и волны | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Свободные колебания в реальных условиях не могут продолжаться вечно. Для механических систем всегда имеет место сопротивление среды, вследствие чего энергия движения объекта рассеивается при трении. В электромагнитных контурах колебания затухают за счет сопротивления проводников.
Уравнение затухающих колебаний описывает движение реальных колебательных систем. В дифференциальной форме оно записывается следующим образом:
![Rendered by QuickLaTeX.com \[\frac{\partial^2 x}{\partial t^2} +2\beta \frac{\partial x}{\partial t} +\omega_0^2 x=0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-11c9c1570354c5fa7e67fc58fe048710_l3.png)
Из этого выражения можно получить еще одну каноническую форму:
![Rendered by QuickLaTeX.com \[x=Ae^{-\beta t} \cos (\omega t +\varphi_0 )\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-aa4e45627a38f2749aa0a75e5cff65d5_l3.png)
либо
![Rendered by QuickLaTeX.com \[x=Ae^{-\beta t} \sin (\omega t +\varphi_0 )\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-eca9d4cd7c02cd12ceb04db6676e741e_l3.png)
.
Здесь x и t – координаты пространства и времени, А – первоначальная амплитуда.
![Rendered by QuickLaTeX.com \[\beta\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9dd9202d5c8ce4000957f0b13db4c135_l3.png)
– коэффициент затухания, который зависит от сопротивления среды r и массы колеблющегося объекта m:
![Rendered by QuickLaTeX.com \[\beta = \frac{r}{2m} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-62973b0048dcb3513a172c54ae086729_l3.png)
Чем больше сопротивление среды, тем больше энергии рассеивается при вязком трении. И наоборот – чем больше масса (а значит, инерционность) тела, тем дольше оно будет продолжать движение.
Циклическая частота свободных колебаний (такой же системы, но без трения) \omega_0 учитывает силу упругости в системе (например, жесткость пружины k):
![Rendered by QuickLaTeX.com \[\omega_0 =\frac{k}{m} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ac946e64b86b37396a125cd362eae542_l3.png)
Строго говоря, в случае затухающих колебаний нельзя говорить про период – время между повторяющимися движениями системы постоянно увеличивается. Однако если колебания затухают медленно, для них с достаточной точностью можно определить период Т:
![Rendered by QuickLaTeX.com \[T=\frac{2\pi}{\sqrt{\omega_0^2 -\beta^2}} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-3c5ec7cc423ee74d862df3b516713c2f_l3.png)
Циклическая частота затухающих колебаний
Еще одна характеристика затухающих колебаний – циклическая частота:
![Rendered by QuickLaTeX.com \[\omega =\sqrt{\omega_0^2 -\beta^2} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c47f5943d8f3f2a8777d24dba46e2146_l3.png)
Время релаксации – это коэффициент, показывающий, за какое время амплитуда колебаний уменьшится в е раз:
![Rendered by QuickLaTeX.com \[\tau = \frac{1}{\beta} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8a49613633ad905d37bfc6e7d7e1c15c_l3.png)
Отношение амплитуды изменяющейся величины в двух последовательных периодах называют декрементом затухания:
![Rendered by QuickLaTeX.com \[D= \frac{A(t)}{A(t+T)} =e^{\beta T} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-770a758e5c0e9995798fa4288856fa85_l3.png)
Эту же характеристику при расчетах часто представляют в виде логарифма:
![Rendered by QuickLaTeX.com \[\lambda =lnD=\beta T\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4e766ef9bd409d6768764d9fe77d8ce8_l3.png)
Добротность Q характеризует, насколько силы упругости системы превышают силы сопротивления среды, препятствуя диссипации энергии:
![Rendered by QuickLaTeX.com \[Q= \frac{\sqrt{mk}}{r} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-6730d1ba66bc4c55ec663e443114ac6e_l3.png)
Математический маятник. Частота колебаний математического маятника (формула).
Математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Если отклонить маятник от положения равновесия, то сила тяжести и сила упругости будут направлены под углом. Равнодействующая сила уже не будет равна нулю. Под воздействием этой силы маятник устремится к положению равновесия, но по инерции движение продолжится и маятник отклоняется в другую сторону. Равнодействующая сила его снова возвращает.
Частота математического маятника — Чем больше период колебаний математического маятника, тем меньше частота.


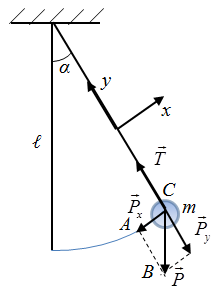
Важно где происходят колебания! На Луне и на Земле один и тот же математический маятник при одинаковых начальных условиях колебаться будет по-разному. Так как ускорение свободного падения на Луне отличается от ускорения свободного падения на Земле.
Линейная скорость материальной точки, линейное ускорение материальной точки, единицы измерения. Сложение скоростей.
линейная скорость — это производная от пройденного пути по времени.
Отдельные
точки вращающегося тела имеют различные
линейные скорости  (метр/сек).
Скорость каждой точки, будучи направлена
по касательной к соответствующей
окружности, непрерывно изменяет свое
направление. Величина
скорости
(метр/сек).
Скорость каждой точки, будучи направлена
по касательной к соответствующей
окружности, непрерывно изменяет свое
направление. Величина
скорости  определяется
скоростью вращения тела
определяется
скоростью вращения тела 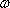 и
расстоянием R рассматриваемой точки от
оси вращения. Пусть за малый промежуток
времени
и
расстоянием R рассматриваемой точки от
оси вращения. Пусть за малый промежуток
времени 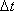 тело
повернулось на угол
тело
повернулось на угол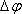 Точка, находящаяся на расстоянии R от
оси проходит при этом путь, равный :
Точка, находящаяся на расстоянии R от
оси проходит при этом путь, равный :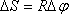
Линейная скорость точки по определению:
|
линейное ускорение — это производная от скорости по времени.
Формула линейного ускорения:
a = dv/dt = d2s/dt2, где s – путь,пройденный телом.
Сложение скоростей — с помощью данного закона определяется скорость движения тела относительно неподвижной системы отсчёта. Она равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы
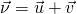
Для
того, чтоб было более понятно, как
работает закон сложения скоростей,
рассмотрим такой пример. Вагон движется
со скоростью 50 км\ч (это будет 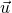 ),
в вагоне идет человек со скоростью 3
км\ч (это будет
),
в вагоне идет человек со скоростью 3
км\ч (это будет 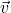 ),
найти скорость человека относительно
Земли.
),
найти скорость человека относительно
Земли.
 У
данной задачи будет два решения. Если
человек будет идти по направлению
движения вагона, то скорость человека
относительно Земли будет 53 км\ч.
У
данной задачи будет два решения. Если
человек будет идти по направлению
движения вагона, то скорость человека
относительно Земли будет 53 км\ч.

А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 км\ч.
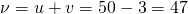
В Формуле мы использовали :
 —
Конечная
скорость тела
—
Конечная
скорость тела
— Скорость тел в различных инерциальных системах отчета
Свободные колебания. Пружинный маятник. Частота колебаний пружинного маятника (формула).
Колебания называются свободными (или собственными), если они совершаются за счет первоначальной сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания).
Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы
Частота
пружинного маятника — Чем больше
период колебаний пружинного маятника,
тем меньше частота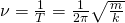
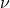 —
Частота
Пружинного маятника,
—
Частота
Пружинного маятника, 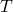 — Период
колебаний маятника
— Период
колебаний маятника
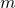 —
Масса
груза, или масса маятника,
—
Масса
груза, или масса маятника, 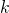
Угловая скорость, частота вращения, период вращения (определение, единицы измерения, связь между величинами). Связь между линейной и угловой скоростями.
Угловая скорость численно равна углу поворота радиуса за единицу времени.
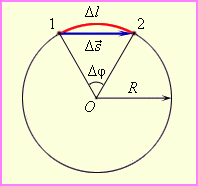
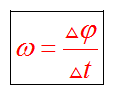

Период и частота
Период вращения
Частота вращение — это количество оборотов за одну секунду.

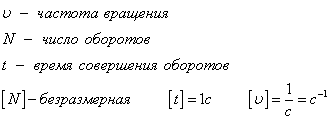
Частота
и период взаимосвязаны соотношением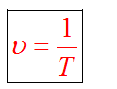
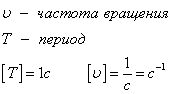
Связь
с угловой скоростью
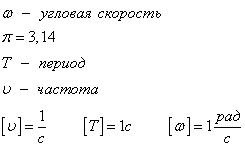
Линейная
скорость точки.
Направление вектора линейной скорости
всегда совпадает с касательной к
окружности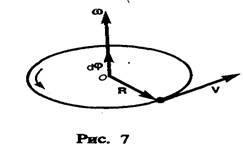 Точка,
лежащая на окружности радиусом R,
за один оборот пройдет путь
Точка,
лежащая на окружности радиусом R,
за один оборот пройдет путь 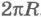 .
Поскольку время одного оборота тела
есть период T,
то модуль линейной скорости точки можно
найти так:
.
Поскольку время одного оборота тела
есть период T,
то модуль линейной скорости точки можно
найти так:
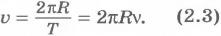
Так
как 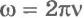

Условия возникновения затухающих колебаний (соотношение между собственной частотой и коэффициентом затухания). Амплитуда затухающих колебаний (формула).
Соотношение: 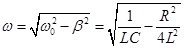 β — коэффициент затухания. Этот коэффициент
характеризует скорость затухания
колебаний, При наличии сил сопротивления
энергия колеблющейся системы будет
постепенно убывать, колебания будут
затухать.
β — коэффициент затухания. Этот коэффициент
характеризует скорость затухания
колебаний, При наличии сил сопротивления
энергия колеблющейся системы будет
постепенно убывать, колебания будут
затухать.
Амплитуда
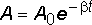 ,
где А0 –
начальная амплитуда. Зависимость
амплитуды показана на рис. 8.3.
,
где А0 –
начальная амплитуда. Зависимость
амплитуды показана на рис. 8.3.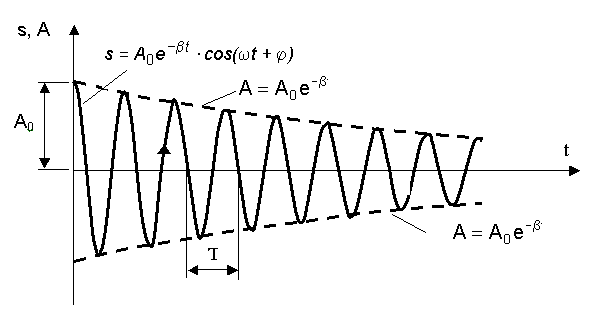 Рис.
8.3. График затухающих колебаний
Рис.
8.3. График затухающих колебаний
Механическая работа (определение, единицы измерения). Мощность силы (определение, единицы измерения).
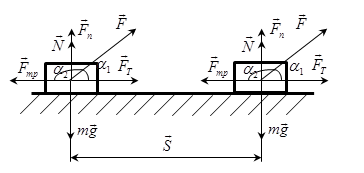
Механическая
рабоат — то
скалярная физическая величина, которая
характеризует процесс перемещения тела
под действием силы и равна произведению
модуля силы F на модуль перемещения S и
на косинус угла  между
ними
между
ними
Если
тело под действием силы 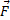 совершает
перемещение
совершает
перемещение 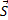 ,
работа А этой
силы равна скалярному произведению
силы на вектор перемещения. Работа силы
есть скалярная величинаА=
,
работа А этой
силы равна скалярному произведению
силы на вектор перемещения. Работа силы
есть скалярная величинаА=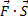
А=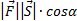
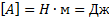
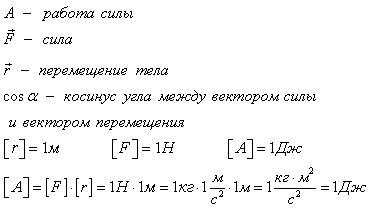
мощность
силы —
скалярная физическая величина N, равная
отношению работы А, совершаемой силой,
к промежутку времени 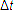 ,
в течение которого она совершается:
,
в течение которого она совершается:
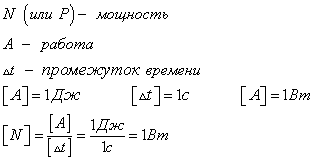 Работа
силы, совершаемая в единицу времени,
называется мощностью.
Мощность N это
физическая величина, равная отношению
работы A к
промежутку времени t,
в течение которого совершена эта
работа:
Работа
силы, совершаемая в единицу времени,
называется мощностью.
Мощность N это
физическая величина, равная отношению
работы A к
промежутку времени t,
в течение которого совершена эта
работа: 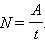
В
Международной системе (СИ) единица
мощности называется ватт
(Вт).
Ватт равен мощности силы, совершающей
работу в 1 Дж за время 1 с. 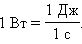
Если
тело движется прямолинейно и на него
действует постоянная сила, то она
совершает работу  .
Поэтому мощность этой силы
.
Поэтому мощность этой силы
Колебания и волны | Формулы и расчеты онлайн
Любые колебания представляют собой движение с переменным ускорением. Отклонение, скорость и ускорение в этом случае являются функциями времени. Для любых колебаний характерна периодичность, т.е. движение повторяется по истечении времени T, называемого длительностью или периодом колебания. Колебания возникают в тех случаях, когда системе способной совершать колебания, сообщается энергия.
Необходимо различать:
Незатухающие колебания
Незатухающие колебания, происходят с постоянной амплитудой Ym. Предполагается, что в данном случае подводимая энергия сохраняется. Приближенно такие условия имеют место при малых потерях энергии и малом времени наблюдения. Для получения действительно незатухающих колебаний необходимо регулярно восполнять теряемую энергию.
Затухающие колебания
Затухающие колебания, постепенно уменьшают свою амплитуду Ym. Без пополнения энергии любые колебания затухают.
Важные характеристики колебаний
| Отклонение | $ y = f(t) $ | Мгновенное перемещение относительно положения равновесия. |
| Амплитуда | $ Y_m $ | максимальное отклонение, размах колебаний. |
| Период | $ T = \frac[-1.5]{1}{f} $ | длительность полного колебания. |
| Частота | $ f = \frac[-1.5]{1}{T} $ | число колебаний в единицу времени. |
| Угловая Частота | $ ω = 2πf = \frac[-1.5]{2π}{T} $ | |
| Фаза | $ φ = ωt + φ_0 $ | |
| Начальная Фаза | $ φ_0 $ | значение фазы при t=0 (начало колебаний). |
| Время | $ t $ | Отсчитывается от момента начала колебаний. |
В помощь студенту
Колебания и волны |
стр. 530 |
|---|
По какой формуле найти ЧАСТОТУ КОЛЕБАНИЙ???
1/T T — период колебаний
Частота равна единицу делим на период. Смотря что тебе дано в задаче
это короче герцы (hz)
частота колебаний= количество колебаний делить на время колебаний! т. е ню= эн поделить на тэ
У нас такая формула — Частота=1\период (Т)
V=N/t или 1/T (герц)