ЧАСТОТА ВОЛНЫ — это… Что такое ЧАСТОТА ВОЛНЫ?
- ЧАСТОТА ВОЛНЫ
ЧАСТОТА ВОЛНЫ, число полных колебаний или циклов волны, совершенных в единицу времени; если за 1 секунду, то измеряется в ГЕРЦАХ. Ее можно вычислить, разделив скорость распространения волны на длину волны. Согласно КВАНТОВОЙ ТЕОРИИ, частота любого ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ (включая свет, радиоволны, рентгеновское излучение) пропорциональна энергии составляющих его фотонов. Многие характеристики электромагнитного излучения зависят от частоты.
Научно-технический энциклопедический словарь.
- ЧАСТИЧНОЕ ЗАТМЕНИЕ
- ЧАСТОТА
Смотреть что такое «ЧАСТОТА ВОЛНЫ» в других словарях:
частота волны — bangos dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikros bangos dažnis. atitikmenys: angl. wave frequency vok. Wellenfrequenz, f rus. частота волны, f pranc. fréquence d’une onde, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
частота волны — bangos dažnis statusas T sritis fizika atitikmenys: angl. wave frequency vok. Wellenfrequenz, f rus. частота волны, f pranc. fréquence d’onde, f … Fizikos terminų žodynas
ВОЛНЫ ЧАСТОТА — ВОЛНЫ ЧАСТОТА, см. ЧАСТОТА волны … Научно-технический энциклопедический словарь
Волны — Волна изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой… … Википедия
ЧАСТОТА — ЧАСТОТА, показатель, выражающий собой число повторений или возникновения событий (процессов). В статистике частота это цифра, показывающая, сколько раз за какой то период происходило некоторое событие, проявлялось определенное свойство объекта… … Научно-технический энциклопедический словарь
Частота периодического процесса — Частота физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах , или . Единицей частоты в Международной системе единиц (СИ) в общем случае… … Википедия
Частота ядра — Частота физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах , или . Единицей частоты в Международной системе единиц (СИ) в общем случае… … Википедия
Волны де Бройля — волны, связанные с любой движущейся микрочастицей, отражающие их квантовую природу. Впервые квантовые свойства были обнаружены у электромагнитного поля. После исследования М. Планком законов теплового излучения (См. Тепловое… … Большая советская энциклопедия
ЧАСТОТА — (Frequency) число периодов в одну секунду. Частота величина, обратная периоду колебаний; напр. если частота переменного тока f = 50 колебаниям в сек. (50 Н), то период Т = 1/50 сек. Частота измеряется в герцах. При характеристике излучения… … Морской словарь
ВОЛНЫ ДЕ БРОЙЛЯ — волны, связанные с любой микрочастицей и отражающие их квант. природу. В 1924 франц. физик Л. де Бройль (L. de Broglie) высказал гипотезу о том, что установленный ранее для фотонов корпускулярно волновой дуализм (заключающийся в том, что фотоны… … Физическая энциклопедия
Нормальные колебания — Википедия
Различные нормальные моды в 1D решётке.Норма́льные колеба́ния,
Общая теория[править | править код]
Потенциальная энергия взаимодействия атомов в молекулах является определённой функцией их обобщённых координат U(r1,…,ri,…,rN){\displaystyle U(\mathbf {r} _{1},\ldots ,\mathbf {r} _{i},\ldots ,\mathbf {r} _{N})}. Эта функция теоретически рассчитывается методами квантовой механики в адиабатическом приближении или задаётся определёнными модельными эмпирическими потенциалами. Равновесные положения атомов в молекулах ri0{\displaystyle \mathbf {r} _{i0}} задаются условием минимума этой функции:
- ∂U∂ri=0.{\displaystyle {\frac {\partial U}{\partial \mathbf {r} _{i}}}=0.}
При выводе конфигурации молекулы из равновесия так, что каждый атом сместится на некую величину δri{\displaystyle \delta \mathbf {r} _{i}}, в молекуле возникнут силы, которые стремятся вернуть атомы в положение равновесия, отвечающего минимуму потенциальной энергии, а потенциальная энергия возрастёт и станет равной:
- U(r1,…,ri,…,rN)=U0+12∑i,j=1N∑α,β=13aijαβδriαδrjβ+o(‖r‖2),{\displaystyle U(\mathbf {r} _{1},\ldots ,\mathbf {r} _{i},\ldots ,\mathbf {r} _{N})=U_{0}+{\frac {1}{2}}\sum _{i,j=1}^{N}\sum _{\alpha ,\beta =1}^{3}a_{ij}^{\alpha \beta }\delta r_{i}^{\alpha }\delta r_{j}^{\beta }+o(\left\|\mathbf {r} \right\|^{2}),},
- где i{\displaystyle i} и j{\displaystyle j} — индексы атомов,
- α{\displaystyle \alpha } и β{\displaystyle \beta } — индексы осей координат,
- U0{\displaystyle U_{0}} — потенциальная энергия молекулы в положении равновесия,
а коэффициенты aijαβ{\displaystyle a_{ij}^{\alpha \beta }} определяются разложением потенциальной энергии в ряд Тейлора в окрестности положения равновесия.
Коэффициенты в разложении в ряд, соответствующие первым производным равны нулю, так как в положение равновесия — минимум потенциальной энергии, то есть «дно» потенциальной ямы и поэтому первые производные по координатам обращаются в нуль.
- aijαβ=∂2U∂riα∂rjβ|ri=ri0+∂2U∂riα∂riβ|rj=rj0.{\displaystyle a_{ij}^{\alpha \beta }={\frac {\partial ^{2}U}{\partial r_{i}^{\alpha }\partial r_{j}^{\beta }}}{\bigg |}_{\mathbf {r} _{i}=\mathbf {r} _{i0}}+{\frac {\partial ^{2}U}{\partial r_{i}^{\alpha }\partial r_{i}^{\beta }}}{\bigg |}_{\mathbf {r} _{j}=\mathbf {r} _{j0}}.}
Уравнения движения для смещённых из положения равновесия атомов имеют следующий вид:
- mid2dt2δriα=−∑j=1N∑β=13aijαβδrjβ{\displaystyle m_{i}{\frac {d^{2}}{dt^{2}}}\delta r_{i}^{\alpha }=-\sum _{j=1}^{N}\sum _{\beta =1}^{3}a_{ij}^{\alpha \beta }\delta r_{j}^{\beta }},
- где mi{\displaystyle m_{i}} — масса i-го атома.
Если искать решения системы дифференциальных уравнений в виде
- δriα=biαeiωt.{\displaystyle \delta r_{i}^{\alpha }=b_{i}^{\alpha }e^{i\omega t}.}
то получим систему линейных уравнений:
- miω2biα−∑j=1N∑β=13aijαβbjβ=0.(A){\displaystyle m_{i}\omega ^{2}b_{i}^{\alpha }-\sum _{j=1}^{N}\sum _{\beta =1}^{3}a_{ij}^{\alpha \beta }b_{j}^{\beta }=0.\qquad ({\text{A}})}
Всего таких уравнений 3N−6{\displaystyle 3N-6} (3N−5{\displaystyle 3N-5} в случае линейных молекул), где N{\displaystyle N} — число атомов.
3 других уравнений описывают движение центра массы молекулы, а ещё три (два в случае линейных молекул) — вращения молекулы как целого[2]. Система этих дифференциальных уравнений однородная, а следовательно, имеет нетривиальное решение лишь при наборе определённых частот, называемых собственными частотами, которые находятся из решения уравнения равенства нулю детерминанта этой системы:
- |miω2δijδαβ−aijαβ|=0{\displaystyle \left|m_{i}\omega ^{2}\delta _{ij}\delta _{\alpha \beta }-a_{ij}^{\alpha \beta }\right|=0},
- где δij{\displaystyle \delta _{ij}} — символ Кронекера.
Данный детерминант является уравнением 3N−6{\displaystyle 3N-6}-ой степени относительно ω2{\displaystyle \omega ^{2}}, которое называется вековым или секулярным уравнением. Его корни определяют спектр собственных частот колебаний молекулы.
Собственные векторы bi{\displaystyle \mathbf {b} _{i}} уравнения (A) определяют 3N−6{\displaystyle 3N-6} нормальных мод колебаний молекулы.
Нормальные моды взаимно линейно независимы и взаимно ортогональны:
- ∑i=1Nbim⋅bin=0{\displaystyle \sum _{i=1}^{N}\mathbf {b} _{i}^{m}\cdot \mathbf {b} _{i}^{n}=0},
если m≠n{\displaystyle m\neq n}, где m{\displaystyle m} и n{\displaystyle n} — индексы, которыми обозначены различные собственные векторы. Именно этой особенности нормальные моды обязаны своим названием.
Собственные векторы матрицы вторых производных потенциальной энергии по масс-взвешенным декартовым координатам пропорциональны малым смещениям таких координат атомов относительно положения равновесия. Эти смещения должны быть достаточно малыми, чтобы соответствующие члены в разложении Тейлора потенциальной энергии по координатам были пренебрежимо малы. Поэтому нормальные колебания есть малые колебания, при нарастании амплитуды колебаний увеличивается ангармонизм колебаний, то есть при разложении колебаний в ряд Фурье в спектре появляются высшие гармоники, что делает теорию колебаний молекулы очень сложной.
Произведение вектора нормальной моды на вектор взвешенных по массе декартовых координат является т. н. нормальной координатой. Базис нормальных координат представляет собой направления колебательных движений молекулы.
В теории механизма химических реакций элементарный акт химической перестройки молекулы представляется как движение по одной из нормальных координат (она называется в таком случае естественной координатой реакции, англ. intrinsic reaction coordinate). При этом система преодолевает «горб» потенциальной энергии и колебательное движение перестаёт быть колебательным, а становится поступательным. В более сложных случаях акт перестройки молекулярной структуры описывается изменением не одной, а двух или более нормальных координат, в этом случае говорят о сильном взаимодействии колебательных мод и большой кривизне реакционного пути в поперечном направлении.
Дипольный момент[править | править код]
Если известны нормальные моды, которые задаются векторами bin{\displaystyle \mathbf {b} _{i}^{n}}, где индекс n — номер моды, а также частичные заряды атомов в молекулах, то можно образовать векторы:
- dn=∑iqibin,{\displaystyle \mathbf {d} ^{n}=\sum _{i}q_{i}\mathbf {b} _{i}^{n},}
которые называются дипольными моментами нормальных мод.
Во внешнем электрическом поле, например, в поле электромагнитной волны, энергия диполя определяется формулой:
- E⋅d.{\displaystyle \mathbf {E} \cdot \mathbf {d} .}
Поэтому те нормальные моды, которые имеют значительный дипольный момент сильно взаимодействуют с электромагнитными волнами (обычно их частоты лежат в инфракрасном диапазоне). Те нормальные моды, для которых дипольный момент пренебрежимо мал, не поглощают и не излучают инфракрасные волны.
Например, симметричная молекула O2 имеет равный электрический симметричный заряд на своих атомах, следовательно, нулевой дипольный момент и поэтому кислород в атмосфере не поглощает инфракрасное излучение и не является «парниковым» газом.
В молекуле углекислого газа CO2 атомы кислорода несколько подтягивают электроны общего электронного облака к себе от центрального атома углерода, поэтому все три атома имеют небольшой частичный заряд. В линейной молекуле углекислого газа присутствуют четыре (3N−5{\displaystyle 3N-5}) нормальные моды. Одна из них — это симметричные колебания атомов кислорода вдоль оси молекулы. Эта мода не имеет дипольного момента. Другая мода колебаний — асимметричные колебания атомов кислорода вдоль оси молекулы и изгибные колебания имеют ненулевой дипольный момент, — третья и четвёртая вырожденные моды, описывающие угловые колебания молекулы во взаимно перпендикулярных направлениях.
- Федорченко, А. М. Теоретическая механика. — Киев : Высшая школа, 1975. — 516 с.
Диапазон частот — это… Что такое Диапазон частот?
Диапазон частот — полоса излучаемых источником частот, которой зачастую присвоено условное наименование, одно из важнейших понятий радиотехники, а также физико-технических дисциплин в целом. Это понятие имеет общий характер, то есть можно говорить или о диапазоне частот какого-либо конкретного излучателя (природного или искусственного происхождения), или о диапазоне, выделенном какой-то радиослужбе, или, например, об обобщённой разбивке всей полосы радиочастот.
Примеры выделенных радиодиапазонов
- Диапазон средних волн с амплитудной модуляцией (530—1610 кГц).
- Различные диапазоны коротких волн (5,9—26,1 МГц).
- Гражданский диапазон (26,965—27,405 МГц).
- Частоты телевизионных каналов (48,5—862,0 МГц).
- Диапазон ультракоротких волн c частотной модуляцией (87,5—108 МГц, кроме 76—90 МГц в Японии; в России также 65,9—74 МГц).
- ISM диапазон.
- Диапазоны военных частот. 42-48 МГц , (224-280 МГц военная авиация)
- Диапазоны частот гражданской авиации (108-118 навигационные для ILS , VOR)(118—136,975 МГц).
- Международный морской диапазон 156,050-162,025 МГц. Речной диапазон (Россия) 300-337 МГц .
Диапазоны радиочастот в гражданской радиосвязи
В России для гражданской радиосвязи с использованием радиоэлектронных устройств, не требующих регистрации в территориальных гос. органах по надзору в сфере связи, выделены три диапазона частот:
- 27 МГц (гражданский диапазон), с разрешённой выходной мощностью передатчика до 10 Вт;
- 433 МГц (LPD), выделено 69 каналов для носимых радиостанций с выходной мощностью передатчика не более 0,01 Вт;
- 446 МГц (PMR), выделено 8 каналов для носимых радиостанций с выходной мощностью передатчика не более 0,5 Вт.
Данные диапазоны совершенно безнаказанно можно использовать в практических целях.
| |||||||
Диапазоны в акустике
- Инфразвуковой — ниже 20 Гц.
- Звуковой — от 20 Гц до 20 кГц (в него полностью укладывается диапазон слышимых человеческим ухом частот).
- Ультразвуковой — от 20 кГц до 1 ГГц.
- Гиперзвуковой — свыше 1 ГГц.
См. также
Ссылки
Длина волны — это… Что такое Длина волны?
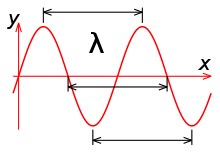Длина волны λ может быть измерена между любыми двумя точками волны с одинаковой фазой, максимумами, минимумами или узлами волны.Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой .[1] По аналогии с волнами, возникающими в воде от брошенного камня, длиной волны является расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.
Получить соотношение, связывающее длину волны с фазовой скоростью () и частотой () можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний , поэтому
Волнам де Бройля также соответствует определенная длина волны. Частице с энергией Е и импульсом p, соответствуют:
- частота:
- длина волны:
где h — постоянная Планка.
Примеры
Приближённо, с ошибкой около 0,07%, рассчитать длину радиоволны можно так: 300 делим на частоту в мегагерцах, получаем длину волны в метрах, например для 80 Гц, длина волны 3750 километра, для 89 МГц — 3,37 метра, для 2,4 ГГц — 12,5 см.
Точная формула для расчёта длины волны электромагнитного излучения в вакууме выглядит так:
где — скорость света, равная в Международной системе единиц (СИ) 299 792 458 м/с точно.
Для определения длины волны электромагнитного излучения в какой-либо среде следует использовать формулу:
где — показатель преломления среды для излучения с данной частотой.
Примечания
- ↑ Мякишев Г. Я., Буховцев Б. Б. Колебания и волны // Физика. Учебник для 11 класса общеобразовательных учреждений. — 12-е изд. — М.: Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1