51. Эквивалентные бесконечно малые функции. Таблица эквивалентных бесконечно малых функций.
Функции 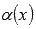 и
и 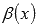 называют бесконечно
малыми при
называют бесконечно
малыми при 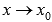 ,
если
,
если 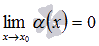 и
и 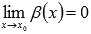
Функции 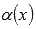 и
и 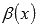 называют эквивалентными
бесконечно малыми при
называют эквивалентными
бесконечно малыми при 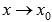 ,
если
,
если 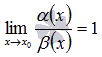
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть 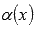 —
бесконечно малая при
—
бесконечно малая при 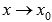 .
.

Эквивалентность
всех величин таблицы можно доказать,
основываясь на равенстве 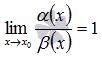
52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
При
вычислении пределов часто применяется
следующая Теорема.
Предел отношения двух бесконечно малых
(неопределенность  )
равен пределу отношения двух других
бесконечно малых, эквивалентных данным,
т.е.
)
равен пределу отношения двух других
бесконечно малых, эквивалентных данным,
т.е.
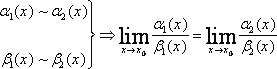
Отметим
также: если  ,
то
,
то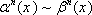
3.2. Основные формулы эквивалентности бесконечно малых.
Известна формула первого замечательного предела:
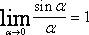
Используя это равенство, получим
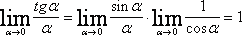
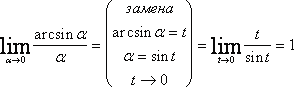
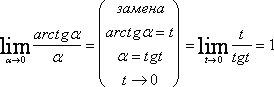
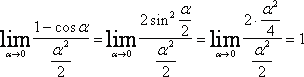
Отсюда получаем первую группу формул эквивалентности бесконечно малых.
При 
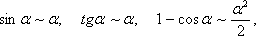
 . (1)
. (1)
Вторая группа формул связана с логарифмической функцией.
Имеем: 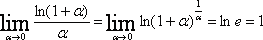
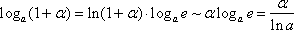
Если
при  ,
то
,
то
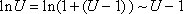
Получаем вторую группу формул:
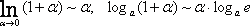
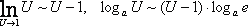 (2)
(2)
Третья группа формул связана с показательной функцией. Имеем:
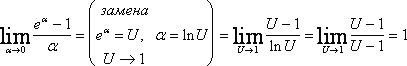 Отсюда
Отсюда 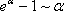
Тогда 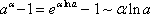
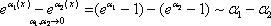
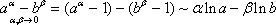
Итак, третья группа формул эквивалентности бесконечно малых
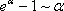
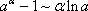
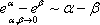 ,
, 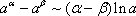 (3)
(3)
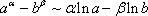
Четвертая группа формул связана со степенной функцией.
Имеем: 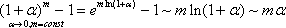
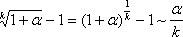
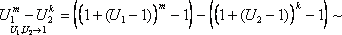
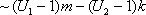
Итак, четвертая группа формул эквивалентности бесконечно малых
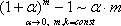 ,
, 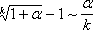
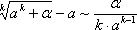
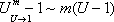 ,
, 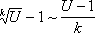
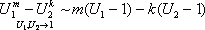 (4)
(4)
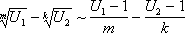
53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
Определение. Предела слева (справа)
Число
А(В) по определению называется пределом
функции f(x)
в точке х
>0 >0 : x из x0-<x<x0 (x0<x<x0+)
f(x)-A< (f(x)-B<),
при
этом пишут: 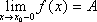
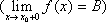
Пример.
Справедлив критерий 2 существования предела функции в точке.
Для того, чтобы у функции f(x) существовал предел при хх0 необходимо и достаточно, чтобы существовал левосторонний предел в т. х0, существовал правосторонний предел в т. х0 и они были бы равны между собой.
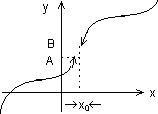
Определение. Непрерывности функции слева (справа).
Функция f(x) определенная в левосторонней окрестности т. х0 (или в правосторонней окрестности т.х0) и в самой точке х0 называется непрерывной в т. х0 слева (справа), если
>0 >0
: x из x0-<xx
f(x)-f(x0-0)< (f(x)-f(x0+0)<)
При этом значения f(x0-0) (f(x0+0)) называют значениями функции в точке х0 слева (справа).
Пример 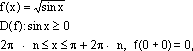 .
.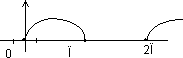
f(-0)=0.
Теорема. Критерий непрерывности функции в точке.
f(x0-0)=f(x0+0)=f(x0)
54. Точки разрыва функции и их классификация.
Определение. Разрывной функции в т. x0.
Функция f(x) не являющаяся непрерывной в т. x0 называется разрывной в т. x0.
При этом точки разрыва функции подразделяются на точки разрыва I рода и II рода.
Определение. Точка разрыва I рода.
Если
у функции f(x) 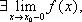
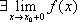 и
они конечны, то говорят, что точка x0—
точка разрыва первого рода.
и
они конечны, то говорят, что точка x0—
точка разрыва первого рода.
При
этом, если 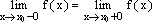 ,
то говорят, что точкаx0—
точка устранимого
разрыва.
,
то говорят, что точкаx0—
точка устранимого
разрыва.
Если
же 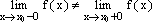 ,
то говорят, что точкаx0—
точка разрыва с конечным
скачком.
,
то говорят, что точкаx0—
точка разрыва с конечным
скачком.
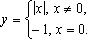 -разрывная
функция.
-разрывная
функция. 
Если
положить 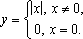 — то
произойдет устранение разрыва и функция
станет непрерывной.
— то
произойдет устранение разрыва и функция
станет непрерывной.
У
функции 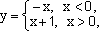 так
как
так
как
 —
имеется конечный скачок.
—
имеется конечный скачок.

Определение. Точка разрыва II рода.
Если у функции f(x) хотя бы один из односторонних пределов не существует или равен , то говорят, что т. х0— точка разрыва II рода.
Пример 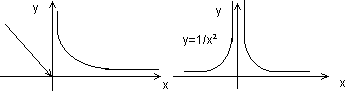

Если устремить х к 0 разными способами, то получим различные значения пределов:
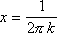 , kN, x0
, а ;
, kN, x0
, а ;
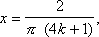 kN, x0
, а
kN, x0
, а 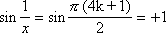 ,
,
значит функция f(x) не имеет предела â т. х0=0, то есть т. х0 точка разрыва II рода.
Применение эквивалентных функций при решении пределов
Метод решения
Применение эквивалентных функций позволяет упростить вычисление пределов. Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).
Все связанные с этим определения и теоремы приводятся на странице «О большое и о малое. Сравнение функций». Напомним некоторые из них.
Применяемые определения и теоремы
Определение эквивалентных функций
Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.
Если при , то ;
если , то .
При этом функцию называют главной частью при . См. теорему о связи эквивалентных функций с о малым
Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство
Отметим часто применяемое следствие этой теоремы. Пусть мы имеем частное, составленное из конечного произведения функций: . Тогда, при вычислении предела, эти функции можно заменить на эквивалентные:
,
где . Знак равенства означает, что если существует один из этих пределов, то существует и равный ему второй. Если не существует один из пределов, то не существует и второй. Разумеется, можно менять не все функции а только одну или некоторые из них.
Таблица эквивалентных функций
Далее приводится таблица функций, эквивалентных при . Здесь t может быть как переменной, так и бесконечно малой функцией при : ; .
| Эквивалентность при | Равенство при |
Предостережение
Как указывалось в самом начале, производить замену функций эквивалентными можно только в множителях дробей и произведений, предел которых мы хотим найти. В других выражениях, например в суммах, делать такую замену нельзя.
В качестве примера рассмотрим следующий предел:
.
При . Но если заменить в числителе на x, то получим ошибку:
.
Ошибки не будет, если выразить синус через эквивалентную функцию и о малое, :
.
Поскольку и , то мы снова получили неопределенность 0/0. Это указывает на то, что для вычисления этого предела применение эквивалентной функции не достаточно. Нужно применить другой метод.
Можно решить этот пример разложением в ряд Маклорена:
.
Также можно применить правило Лопиталя:
.
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов, упрощая вычисления с помощью эквивалентных функций.
⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Найти предел:
.
Решение
Из таблицы эквивалентных функций ⇑ имеем:
. Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.
Ответ
Пример 2
Все примеры ⇑ Найти предел:
.
Решение
Из таблицы эквивалентных функций ⇑ находим:
.
Преобразуем квадрат логарифма:
.
Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.
Ответ
Пример 3
Все примеры ⇑ Вычислить предел.
.
Решение
Здесь мы имеем неопределенность вида один в степени бесконечность. Приводим ее к неопределенности вида 0/0. Для этого воспользуемся тем, что экспонента и натуральный логарифм являются взаимно обратными функциями.
.
Теперь в показателе экспоненты у нас неопределенность вида 0/0.
Вычисляем предел:
.
Поскольку у нас дробь, то заменим некоторые множители в числителе и знаменателе эквивалентными функциями, пользуясь приведенной выше таблицей ⇑.
;
;
.
Поскольку экспонента непрерывна для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.
Ответ
Пример 4
Все примеры ⇑ Вычислить предел.
.
Решение
При . Выясним, к чему стремится . Поскольку здесь дробь, то заменим логарифм эквивалентной функцией: . Тогда
. Таким образом, мы имеем неопределенность вида ∞–∞.
Преобразуем ее к неопределенности вида 0/0. Для этого приводим дроби к общему знаменателю.
.
Здесь мы также воспользовались формулой . После преобразований, наш предел принимает следующий вид:
.
В знаменателе мы сразу можем заменить натуральный логарифм эквивалентной функцией, как это сделали выше:
.
В числителе имеется произведение двух множителей, каждый из которых тоже можно заменить эквивалентной функцией и, таким образом, упростить вычисления. В качестве эквивалентных, попробуем найти степенные функции:
.
Тогда . Считаем, что . Раскрываем неопределенность по правилу Лопиталя.
.
Если положить , то . Тогда
.
Тот же результат можно получить, применяя разложение в ряд Тейлора при :
.
Отсюда .
Найдем эквивалентную функцию для второго множителя, используя разложение в ряд Тейлора при :
.
Отсюда .
Теперь заменим множители эквивалентными функциями:
.
Заметим, что делать замену функций на эквивалентные можно, только если функция, от которой ищется предел, является дробью или произведением. Тогда часть множителей в числителе или знаменателе можно заменить эквивалентными функциями. Так, если бы мы с самого начала заменили \ln (1+x) на x, то получили бы ошибку.
Ответ
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Автор: Олег Одинцов. Опубликовано:
Таблица эквивалентности пределов — справочник для студентов и школьников
ОПРЕДЕЛЕНИЕ
Таблица эквивалентных функций используется для вычисления пределов и изучения числовых рядов для сходимости.
Пусть функция \(\ \alpha(x) \) — бесконечно малая функция в точке а, т. е.
\(\ \lim _{x \rightarrow a} \alpha(x)=0 \)
то имеют место следующие соотношения:
\(\ \sin \alpha(x) \sim \alpha(x) \), \(\ e^{\alpha(x)}-1 \sim \alpha(x) \)
\(\ \operatorname{tg} \alpha(x) \sim \alpha(x) \), \(\ a^{\alpha(x)}-1 \sim \alpha(x) \ln a \)
\(\ \arcsin \alpha(x) \sim \alpha(x) \), \(\ \ln (1+\alpha(x)) \sim \alpha(x) \)
\(\ \operatorname{arctg} \alpha(x) \sim \alpha(x) \), \(\ \log _{a}(1+\alpha(x)) \sim \frac{\alpha(x)}{\ln a} \)
\(\ 1-\cos \alpha(x) \sim \frac{\alpha^{2}(x)}{2} \), \(\ (1+\alpha(x))^{m}-1 \sim \operatorname{mo}(x) \)
Примеры решения проблем
ПРИМЕР
Используя таблицу эквивалентных бесконечно малых, вычислите предел
\(\ \lim _{x \rightarrow 0} \frac{x \arcsin x^{2}}{\sin x} \)
Этот предел имеет неопределенность.
\(\ \left[\frac{0 \cdot \arcsin 0^{2}}{\sin 0}=\frac{0}{0}\right] \)
Перейдем под знаком предела к эквивалентной бесконечно малой (это можно сделать, поскольку аргументы арксина и синуса стремятся к нулю):
\(\ \lim _{x \rightarrow 0} \frac{x \arcsin x^{2}}{\sin x}\left[\frac{0}{0}\right]=\lim _{x \rightarrow 0} \frac{x \cdot x^{2}}{x}=\lim _{x \rightarrow 0} x^{2}=0 \)
\(\ \lim _{x \rightarrow 0} \frac{x \arcsin x^{2}}{\sin x}=0 \)
ПРИМЕР
Найти предел
\(\ \lim _{x \rightarrow 1} \frac{\operatorname{tg}(x-1)}{x^{2}-1} \)
\(\ \left[\frac{\operatorname{tg}(1-1)}{1^{2}-1}=\frac{\operatorname{tg} 0}{0}=\frac{0}{0}\right] \)
То есть, мы имеем неопределенность типа \(\ \left[\frac{0}{0}\right] \) . Поскольку касательный аргумент стремится к нулю, когда х стремится к единице, можно заменить касательную на ее эквивалентное значение:
\(\ \operatorname{tg}(x-1)^{-} x-1 \)
Для знаменателя фракции применяйте сокращенную формулу умножения «разность квадратов»:
\(\ \lim _{x \rightarrow 1} \frac{\operatorname{tg}(x-1)}{x^{2}-1}\left[\frac{0}{0}\right]=\lim _{x \rightarrow 1} \frac{x-1}{(x-1)(x+1)}=\lim _{x \rightarrow 1} \frac{1}{x+1}=\frac{1}{1+1}=\frac{1}{2} \)
Эквивалентные электрические цепи
Определение 1
Последовательным соединением называют совокупность связанных элементов в электрической цепи. Во всех элементах последовательного соединения течет ток с одинаковыми показателями. Изменения тока происходят только в узлах электрической цепи.
Последовательное соединение электрической цепи
При последовательном соединении в цепь входит:
- любое количество источников;
- любое количество резисторов.
В то же время в подобное соединение не может входить более одного источника тока. Это противоречит определенным свойствам каждого источника, так как они не смогут создавать ток в цепи, который не будет зависеть от внешних элементов.
Эквивалентные преобразования
При падении напряжения между двумя точками цепи в их разность включают свободное число значений потенциалов, имеющих противоположные знаки. После чего их попарно объединяют.
$Uab = \phi a — \phi b$, где $a$ и $b$ – точки.
После преобразований у нас получается внушительная формула:
$U_{ab} = \phi a — \phi b = \phi a -\phi с +\phi с -\phi d +\phi d -…-\phi i +\phi i -\phi k +\phi k-… -\phi q +\phi q — \phi b = (\phi a -\phi с) + (\phi с-\phi d) + (\phi d -…-\phi i) + (\phi i -\phi k) + (\phi k-… -\phi q) + (\phi q — \phi b) = U_{ac}+ U_{cd} + U_{de} +…+ U_{ik} + U_{kl} + U_{lm} +…+ U_{qb} = Ir_1+ Ir_2 + … + Ir_m + E_1 + E_2 +… –E_n = I(r_1 + r_2 + r_3 + … + r_m) + ( E_1 + E_2 +… –E_n) = IR + E$
Всякое последовательное соединения электрической цепи можно преобразовать при помощи последовательного соединения:
- эквивалентного резистора;
- источника электродвижущей силы.
В нашем случае сопротивление эквивалентного резистора равняется сумме сопротивлений, которые входят в соединение. Электродвижущая сила эквивалентного источника будет равна сумме ЭДС источников, входящих в это соединение.
Определение 2
Любые элементы соединения цепи возможно переставлять в разном порядке. Все действия должны осуществляться в пределах соединения. Такой процесс называют свойством коммутативности последовательного соединения элементов.
Если взять за основу эквивалентное сопротивление ($R$), которое представляет собой сумму положительных слагаемых, тогда получим, что $R \geq r$, где $r$ — максимальное значение из всех сопротивлений, входящих в соединение.
При подключении последовательного соединения к узлам электрической цепи его значение будет равно определению ветви цепи. В этом случае ветвь образовывается исключительно последовательным соединением.
В параллельном соединении элементов совокупность частей электрической цепи не имеет связи с другими узлами, при этом объединена с двумя узлами. Параллельное соединение ветви и элементов параллельного соединения цепи существенно отличается от последовательного соединения.
В параллельное соединение входят также резисторы и источники тока, однако в цепи не могут присутствовать больше одного источника электродвижущей силы.
Преобразования цепей поддерживают еще одну особую задачу в физике. Она состоит в определении сопротивления цепи относительно точек разрыва. Такая ситуация возникает, когда используется метод эквивалентного генератора при анализе электрических цепей, находящихся в неподвижном режиме, а также при решении уравнения для анализа переходных процессов.
Эквивалентное сопротивление является входным сопротивлением определенной цепи. До начала эквивалентных преобразований необходимо в изучаемой цепи заменить источники электродвижущей силы на эквивалентное сопротивление тока и ЭДС. После этого нужно определить само эквивалентное сопротивление. При этом сопротивление источника электродвижущей силы равняется нулю. Сопротивление источника тока имеет бесконечные значения.
Простые электрические цепи содержат исключительно последовательное или параллельное соединение элементов.
Сложный участок цепи содержит последовательное и параллельное соединение элементов (смешанное соединение).
Эквивалентные преобразования имеют смысл, если при их выполнении токи и напряжения не изменяются на конкретных участках цепи. При преобразовании сложных электрических цепей пользуются последовательным методом. Он состоит в последовательном преобразовании участков цепи, которые имеют простое соединение элементов.
Эквивалентное преобразование при последовательном соединении
Подобный метод преобразования применяется при замещении электрической цепи из последовательных соединений другими отдельными элементами. Цепь состоит из контура, где через все элементы течет ток, который является общим. При преобразовании схемы к одному элементу должны сохраняться значения напряжения и тока на выводах схемы. Такой итог можно получить при равенстве сопротивления исходной и эквивалентной цепи.
Эквивалентное преобразование при параллельном соединении
При рассмотрении комплексной схемы замещения электрической цепи, состоящей из параллельного соединения отдельных элементов, можно сделать вывод о существовании двух узлов, между которыми включены все элементы. Общим для этих элементов является напряжение. В процессе преобразования схемы к одному элементу напряжение и ток на выводах схемы должны сохранять свои значения. Это возможно в случаях, когда сопротивление исходной и эквивалентной цепи обладают одинаковыми значениями.
Эквивалентная схема — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2015; проверки требуют 14 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2015; проверки требуют 14 правок.Эквивалентная схема (схема замещения, эквивалентная схема замещения) цепи — электрическая схема, в которой все реальные элементы заменены их эквивалентными схемами.
Эквивалентная схема (схема замещения, эквивалентная схема замещения) реального элемента цепи — электрическая схема цепи, состоящая из идеализированных элементов цепи, рассчитанные напряжения и токи на зажимах которой совпадают с какой-то погрешностью с измеренными токами и напряжениями на зажимах реального элемента. Уравнения для токов и напряжений эквивалентной схемы реального элемента являются его математической моделью.
Одной из основных задач электроники является расчет электрических цепей, то есть получение детальной количественной информации о процессах, происходящих в этой цепи. Однако рассчитать произвольную цепь, состоящую из реальных электронных компонент, практически невозможно. Мешает расчету то обстоятельство, что попросту не существует методик математического описания поведения реальных электронных компонентов (например, транзистора) как единого целого. Имеются значения отдельных параметров и экспериментально снятые зависимости, но связать их в единую точную формулу, полностью описывающую поведение компоненты, в большинстве случаев не представляется возможным.
С другой стороны, исключительно простым математическим аппаратом описываются идеализированные базовые элементы электронных схем (например, идеальный резистор). Однако они не существуют в реальном мире. Так, любой резистор (реальный элемент) имеет множество паразитных параметров: индуктивность, ёмкость, температурные зависимости и т. п.
Введение понятия эквивалентная схема позволяет «связать» мир реальных компонентов и мир их идеальных приближений. Эквивалентная схема представляет собой цепь только из идеальных компонент, которая функционирует примерно так же, как и исходная схема. В эквивалентной схеме реального элемента могут быть отражены, при необходимости, различные паразитные эффекты: утечки, внутренние сопротивления и т. д. В зависимости от требуемой точности разработаны и продолжают разрабатываться множество схем замещения одного и того же реального элемента. Например, известны сотни схем замещения (моделей) разных типов транзисторов.
В эквивалентных схемах используются перечисленные ниже идеальные элементы. Предполагается также, что геометрические размеры эквивалентной схемы настолько малы, что какие-либо эффекты длинных линий отсутствуют, то есть эквивалентная схема рассматривается как система с сосредоточенными параметрами.
Для любой электрической схемы можно составить сколько угодно различных эквивалентных схем — количество их ограничивается только соображениями целесообразности. Для одной схемы имеет смысл составлять несколько эквивалентных схем по следующим причинам:
- Учёт различных эффектов. Эквивалентная схема составляется тем или иным образом в зависимости от того, какие эффекты мы хотим с её помощью описать. Например, для нахождения рабочей точки по постоянному току требуется одна эквивалентная схема, а для расчета АЧХ — совершенно другая.
- Поэтапное упрощение. В процессе расчета схемы целесообразно заменять её сложные участки простыми эквивалентными цепями. Например, цепь из последовательно включенных резисторов можно заменить одним резистором с суммарным сопротивлением. В полученной упрощенной схеме можно вновь применить некоторую замену и т. д.
Эквивалентная схема является линейной системой, поэтому нелинейные эффекты реальных схем не могут быть смоделированы путём составления эквивалентных схем.
Частичным выходом из этого затруднения является рассмотрение нелинейной системы в малосигнальном приближении для конкретной рабочей точки, при этом нелинейные эффекты малы и ими можно пренебречь. Данный подход позволяет не описать нелинейные эффекты, а всего лишь ограничиться случаем, когда они пренебрежимо малы.
Эквивалентная схема реального элемента, описываемая дифференциальными уравнениями в обыкновенных производных, не может абсолютно точно соответствовать реальному элементу, электрические процессы в котором описываются дифференциальными уравнениями в частных производных (например, многие характеристики полупроводникового диода могут быть получены из решения уравнения Пуассона для p — n-перехода).
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Высшая школа, 1996. — 224 с. — ISBN 5-8297-0159-6
- Попов В. П. Основы теории цепей . — М.: Высшая школа, 2003. — 575 с. — ISBN 5-06-003949-8
Эквиваленция — Википедия
| Эквиваленция | |
|---|---|
| Исключающее ИЛИ-НЕ, EQ, XNOR | |
 Диаграмма Венна | |
| Определение | x=y{\displaystyle x=y} |
| Таблица истинности | (1001){\displaystyle (1001)} |
| Логический вентиль |  |
| Нормальные формы | |
| Дизъюнктивная | x⋅y+x¯⋅y¯{\displaystyle x\cdot y+{\overline {x}}\cdot {\overline {y}}} |
| Конъюнктивная | (x¯+y)⋅(x+y¯){\displaystyle ({\overline {x}}+y)\cdot (x+{\overline {y}})} |
| Полином Жегалкина | 1⊕x⊕y{\displaystyle 1\oplus x\oplus y} |
| Принадлежность предполным классам | |
| Сохраняет 0 | Нет |
| Сохраняет 1 | Да |
| Монотонна | Нет |
| Линейна | Да |
| Самодвойственна | Нет |
Логическая равнозначность или эквивале́нция (или эквивале́нтность[1]) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Двуместная логическая операция обычно обозначается символом ≡ или ↔.
Эквиваленция A⟺B{\displaystyle A\iff B} — это сокращённая запись для выражения (¬A∧¬B)∨(A∧B){\displaystyle (\neg A\land \neg B)\lor (A\land B)}
Задаётся следующей таблицей истинности:
| a{\displaystyle a} | b{\displaystyle b} | a≡b{\displaystyle a\equiv b} |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Таким образом, высказывание A ≡ B означает «A то же самое, что B», «A эквивалентно B», «A тогда и только тогда, когда B».
Не надо путать эквиваленцию — логическую операцию с логической эквивалентностью[en] высказываний — бинарным отношением. Связь между ними следующая:
Логические выражения A{\displaystyle A} и B{\displaystyle B} эквивалентны в том и только в том случае, когда эквиваленция A⟺B{\displaystyle A\iff B} истинна при всех значениях логических переменных.
Содержание
- 1 Примечания
- 2 См. также
- 3 Ссылки
- 4 Литература
- ↑ Алгебра логики — статья из Большой советской энциклопедии.
- Элемент XNOR (англ.) — физическая реализация эквиваленции.
- Математические основы информатики. Журнал 1 сентября
- Мендельсон Э. «Введение в математическую логику». — М. Наука, 1971.
| |
 | Это заготовка статьи по логике. Вы можете помочь проекту, дополнив её. |
4.3. Эквивалентные преобразования электрических цепей
Электрические цепи считают простыми, если они содержат только последовательное или только параллельное соединение элементов.
Участок цепи, содержащий и параллельное, и последовательное соединение элементов называют сложным или участком со смешанным соединением элементов.
Преобразования электрических цепей считают эквивалентными, если при их выполнении напряжения и токи на интересующих нас участках не изменяются.
При преобразовании сложных электрических цепей пользуются последовательным методом, то есть последовательно преобразуют участки цепи, имеющие простое соединение элементов.
4.3.1. Эквивалентное преобразование схемы при последовательном соединении элементов
Р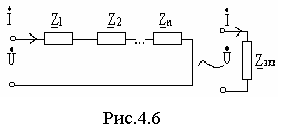 ассмотрим
комплексную схему замещения электрической
цепи, состоящей из последовательного
соединения отдельных элементов (рис.
4.6). Данная цепь представляет собой
контур, у которого через все элементы
протекает общий для всех элементов ток.
Эквивалентно преобразуем схему к одному
элементу, но так чтобы напряжение и ток
на выводах схемы сохранили свои значения.
Это возможно, когда сопротивление
исходной цепи и эквивалентной цепи
одинаковы. На основании закона Ома и
второго закона Кирхгофа в комплексной
форме можно записать уравнение
электрического равновесия
ассмотрим
комплексную схему замещения электрической
цепи, состоящей из последовательного
соединения отдельных элементов (рис.
4.6). Данная цепь представляет собой
контур, у которого через все элементы
протекает общий для всех элементов ток.
Эквивалентно преобразуем схему к одному
элементу, но так чтобы напряжение и ток
на выводах схемы сохранили свои значения.
Это возможно, когда сопротивление
исходной цепи и эквивалентной цепи
одинаковы. На основании закона Ома и
второго закона Кирхгофа в комплексной
форме можно записать уравнение
электрического равновесия
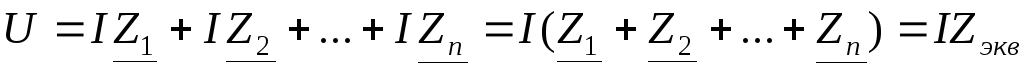
Напряжение и ток для обеих схем одинаковы, когда
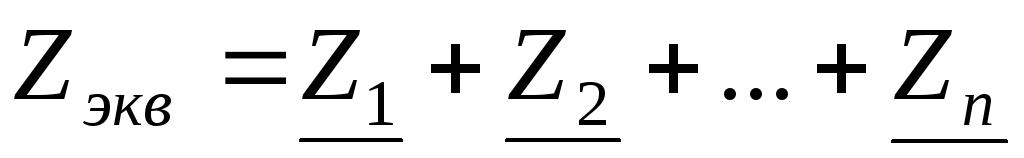 .
.
Вывод. При эквивалентном преобразовании, при последовательном соединении элементов их комплексные сопротивления складываются.
1) Эквивалентное преобразование сопротивлений
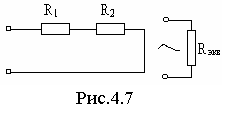 Рассмотрим
электрическую цепь схема, которой
приведена на рис.4.7. Эквивалентно
преобразуем сопротивления R1и
R2 к одному сопротивлению Rэкв.
Рассмотрим
электрическую цепь схема, которой
приведена на рис.4.7. Эквивалентно
преобразуем сопротивления R1и
R2 к одному сопротивлению Rэкв.
Учитывая, что ZR=R, и соотношение полученное выше, получим Rэкв=R1+R2.
2) Эквивалентное преобразование емкостей.
Р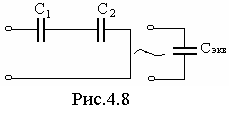 ассмотрим
электрическую цепь схема, которой
приведена на рис.4.8. Эквивалентно
преобразуем емкости С1и
С2 к одной эквивалентной емкости Сэкв.
ассмотрим
электрическую цепь схема, которой
приведена на рис.4.8. Эквивалентно
преобразуем емкости С1и
С2 к одной эквивалентной емкости Сэкв.
Учитывая, что ZС=1/(jωC), и соотношение полученное выше, получим
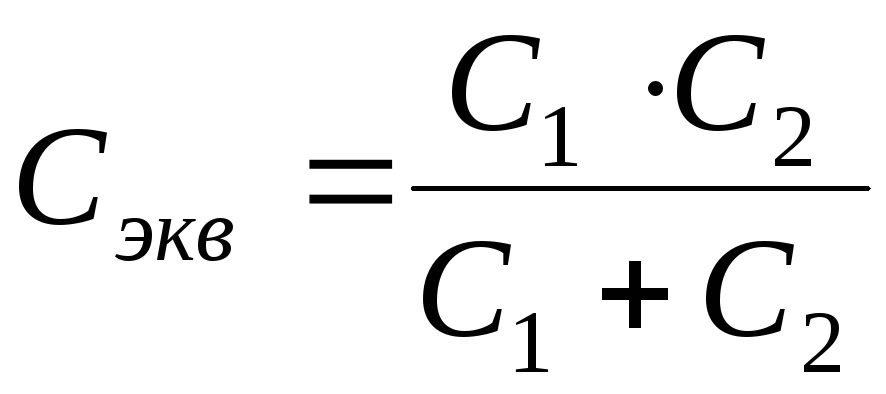 .
.
3) Эквивалентное преобразование индуктивностей
Р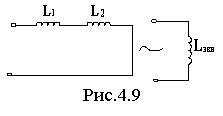 ассмотрим
электрическую цепь схема, которой
приведена на рис.4.9 . Эквивалентно
преобразуем индуктивностиL1и
L2 к одной эквивалентной индуктивности
Lэкв.
ассмотрим
электрическую цепь схема, которой
приведена на рис.4.9 . Эквивалентно
преобразуем индуктивностиL1и
L2 к одной эквивалентной индуктивности
Lэкв.
Учитывая, что ZL=jωL, и соотношение полученное выше, получим Lэкв=L1+L2.
4.3.2. Эквивалентное преобразование схемы при параллельном соединении элементов
Рассмотрим комплексную схему замещения электрической цепи, состоящей из параллельного соединения отдельных элементов (рис. 4.10). Данная цепь содержит два узла, между которыми включены все элементы. Общим для всех элементов является напряжение на них. Эквивалентно преобразуем схему к одному элементу, но так чтобы напряжение и ток на выводах схемы сохранили свои значения. Это возможно, когда сопротивление исходной цепи и эквивалентной цепи одинаковы. На основании закона Ома и первого закона Кирхгофа в комплексной форме можно записать уравнение электрического равновесия
I=I1+I2+…+In, или (U/Zэкв) = (U/Z1) + (U/Z2) + …(U/Zn) .
Отсюдаследует, что
(1/Zэкв) = (1/Z1) + (1/Z2) + … +(1/Zn), или Zэкв = 1/[(1/Z1) + (1/Z2) + … +(1/Zn)].
Учитывая, (1/Z) = Y – комплексная проводимость элемента, можно записать, что
Yэкв = Y1 + Y2 + … + Yn.
Вывод. При эквивалентном преобразовании, при параллельном соединении элементов их комплексные проводимости складываются.



