Цепь переменного тока с активным сопротивлением

Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как u = Um sin ωt, то изменение тока i также идет по синусоиде:

Активное сопротивление

 

 

i = Im sin ωt

При этом

Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.

Мощность, ток, напряжение

Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается: I = U/R.

Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного.

Электрическая мощность

Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения

U на мгновенное значение силы тока i в любой момент времени. Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt. Мощность изменяется по отношению к изменению тока с двойной частотой ωt. Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами. С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.

В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.

Относительно линии

АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине

P = Pmax / 2 = UI

Если использовать закон Ома, то можно выразить активную мощность в следующем виде:

P = I2R или P = U2/R.

Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.

Поверхностный эффект

Необходимо особо отметить такую особенность проводников, включенных в сеть

переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного. Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность. Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.

То, что переменный ток

распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему. Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.

Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника. Необходимо также отметить, что

сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.

Please enable JavaScript to view the comments powered by Disqus.

Цепь переменного тока с активным сопротивлением

Дата публикации: 27 марта 2015.
Категория: Электротехника.

Рассмотрим цепь (рисунок 1), состоящую из сопротивления r. Влиянием индуктивности и емкости для простоты пренебрегаем. К зажимам цепи приложено синусоидальное напряжение

Рисунок 1. Активное сопротивление в цепи переменного тока

u = U_m × sin ωt .

По закону Ома мгновенное значение тока будет равно:

где

или, переходя к действующим значениям, получаем:

и

Как следует из последнего выражения, вид закона Ома для цепи переменного тока, содержащей сопротивление, тот же, что для цепи постоянного тока. Кроме того, из закона Ома видна пропорциональность между мгновенным значением напряжения и мгновенным значением тока. Отсюда следует, что в цепи переменного тока, содержащей сопротивление r, напряжение и ток совпадают по фазе. На рисунке 2 даны кривые напряжения и тока и векторная диаграмма для рассматриваемой цепи, причем длины векторов обозначают действующие значения напряжения и тока. Сопротивление проводников переменному току несколько больше их сопротивления постоянному току. Это объясняется поверхностным эффектом, сущность которого изложена в статье «Поверхностный эффект». Поэтому сопротивление проводников переменному току называют

активным. Обозначается оно также буквой r.

Рисунок 2. Графики и векторная диаграмма для цепи переменного тока, содержащей активное сопротивление

В цепи, представленной на рисунке 1, приложенное внешнее напряжение уравновешивается падением напряжения в сопротивлении r, которое называется

активным падением напряжения и обозначается U_a.

U_a = I × r .

Мгновенное значение мощности в рассматриваемой цепи равно произведению мгновенных значений напряжения и тока:

p = u × i .

На рисунке 3 дана кривая мгновенной мощности за один период. Из чертежа видно, что мощность не является постоянной величиной, она пульсирует с двойной частотой ¹.

Рисунок 3. Кривая мгновенной мощности цепи с активным сопротивлением

Среднее за период значение мощности или просто средняя мощность обозначается буквой P и может быть определена по формуле, доказательство которой мы не приводим:

P = U × I × cos φ ,

где угол φ – угол сдвига фаз между напряжением и током.

Средняя мощность называется также активной мощностью. Данная формула активной мощности справедлива для любых цепей переменного тока.

Для цепи с активным сопротивлением напряжение и ток совпадают по фазе. Поэтому угол φ равен нулю, а cos φ = 1. Для активной мощности получим:

P = U × I

или

P = I² × r ,

то есть формула мощности для цепи переменного тока с активным сопротивлением такая же, как формула мощности для цепи постоянного тока. Активным сопротивлением обладают все проводники. В цепи переменного тока практически только одним активным сопротивлением обладают нити ламп накаливания, спирали электронагревательных приборов и реостатов, дуговые лампы, специальные бифилярные обмотки и прямолинейные проводники небольшой длины.

---

¹ Пульсацией называется изменение численного значения величины при постоянстве ее знака.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

Цепь переменного тока с активным и индуктивным сопротивлениями

Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости.

Таким образом. емкостное сопротивление:

где Хс — емкостное сопротивление, ом;

ώ — угловая частота переменного тока, рад/сек;

С —емкость, ф.

Известно, что угловая частота . Поэтому емкостное сопротивление можно определить так:

где f— частота переменного тока, гц.

Если включенная емкость измеряется в микрофарадах, то ем­костное сопротивление

Если емкость измеряется в пикофарадах, то

Следует подчеркнуть, что имеется существенное различие меж­ду емкостным и активным сопротивлениями. Как известно, актив­ная нагрузка безвозвратно потребляет энергию генератора пере­менного тока.

Если же к источнику переменного тока присоединена емкость, то, как было рассмотрено выше, энергия генератора расходуется при заряде конденсатора на создание электрического поля между пластинами и возвращается обратно генератору при разряде кон­денсатора.

Следовательно, емкостная нагрузка не потребляет энергию ге­нератора, а в цепи с емкостью происходит «перекачивание» энергии из генератора в конденсатор и обратно. По этой причине емкостное сопротивление, как и индуктивное, называется реактивным.

Пример. Конденсатор емкостью С=2 мкф включен в цепь переменного тока, частота которого 50 гц. Определить:

1)  его емкостное сопротивление при частоте f=50 гц;

2)  емкостное сопротивление этого конденсатора переменному току, частота которого 500 гц.

Решение. Емкостное сопротивление конденсатора переменному току при частоте f=50 гц

При частоте f=500 гц

 Из приведенного примера видно, что емкостное сопротивление конденсатора уменьшается с повышением частоты, а с уменьшением частоты переменного тока емкостное сопротивление возрастает. Для постоянного тока, когда напряжение на зажимах цепи не изме­няется, конденсатор практически обладает бесконечно большим со­противлением и поэтому он постоянного тока не пропускает.

§ 55. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ И ИНДУКТИВНЫМ СОПРОТИВЛЕНИЯМИ

Любая проволочная катушка, включенная в цепь переменного тока, обладает активным сопротивлением, зависящим от материала, Длины и сечения проволоки  ,  и индуктивным сопротивлением, которое зависит от  индуктивности катушки и частоты переменного тока, протекающего по ней (ХL=ωL=2πfL). Такую катушку можно рассматривать как приемник энергии, в котором активное и индуктивное сопротивления соединены последовательно.

Рассмотрим цепь переменного тока, в которую включена катуш­ка индуктивности (рис. 56, а) с активным r и индуктивным ХL со­противлением. Падение напряжения на  активном сопротивлении

Падение напряжения на индуктивном сопротивлении

Построим векторную диаграмму тока и напряжения (рис. 56, б) для рассматриваемой цепи.

Пример. Падение напряжения на активном сопротивлении Ua=15в. Напря­жение  на индуктивном сопротивлении UL=26 в. Вычислить общее напряжение, приложенное к цепи.

Решение. Общее напряжение на зажимах цепи переменного тока с после­довательно соединенными активным и индуктивным сопротивлениями.

Чтобы определить полное сопротивление цепи переменного тока с активным и индуктивным сопротивлениями, следует разделить векторы Ua=Ir и UL =IXL на число I, выражающее силу тока в цепи, и построить треугольник А’О’В’ (рис. 56, в), стороны которого меньше сторон треугольника напряжений в I раз. Образованный треугольник называется треугольником сопротивлений. Его сторо­нами являются сопротивления r и ХL и полное сопротивление цепи Z.

Пользуясь теоремой Пифагора, можно написать что,

отсюда полное сопротивление цепи

Пример. Активное сопротивление катушки r=7 ом, а ее индуктивное сопро­тивление ХL=24 ом. Вычислить полное сопротивление катушки.

Решение. Полное сопротивление катушки переменному току

Сила тока в цепи с  активным и  индуктивным сопротивлениями определяется по закону Ома:

На векторной диаграмме видно, что в цепи переменного тока с активным и индуктивным сопротивлениями ток и напряжение не совпадают по фазе. Ток отстает от напряжения — на угол .

Угол сдвига между током и напряжением можно определить, если известен косинус этого угла.

Из треугольника напряжений косинус угла сдвига фаз

Теперь можно, пользуясь таблицей тригонометрических функ­ций, определить угол .

Пример. Падение напряжения на активном сопротивлении катушки Ua =30 в. Общее напряжение на ее зажимах U=60в. Определить угол сдвига фаз между током и напряжением в цепи.

Решение. На основании данных найдем

По таблице тригонометрических функций угол сдвига фаз при со =0,5 составляет 60°.

Лекция по электротехнике по теме «Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью»

Лекция № 9

Тема1.3.Основные положения теории переменного тока. Цепи переменно тока

План

1. Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью.

1.Цепь переменного тока с активным сопротивлением. Рассмотрим цепь (рис, 4,3), в которой к активному сопротивлению (резистору) приложено синусоидальное напряжение:

Тогда по закону Ома ток в цепи будет равен:
                   
Мы видим, что ток и напряжение совпадают по фазе. Векторная диаграмма для этой цепи приведена на рис. 4.4, а зависимости тока и напряжения от времени (временная диаграмма) — на рис. 4.5:
Выясним, как изменяется со временем мощность в цепи переменного тока с резистором.

Мгновенное значение мощности равно произведению мгновенных значений тока и напряжения:

Из этой формулы мы видим, что мгновенная мощность всегда положительна и пульсирует с удвоенной частотой (рис4.5). I,U,p .
Это означает, что электрическая энергия необратимо превращается в теплоту независимо от направления тока в цепи.
Те элементы цепи, на которых происходит необратимое преобразование электрической энергии в другие виды энергии (не только в теплоту), называются активными сопротивлениями. Поэтому резистор представляет собой активное сопротивление.

Цепь переменного тока с индуктивностью. Рассмотрим цепь (рис. 4.6), в которой к катушке индуктивности L, не обладающей активным сопротивлением (R = 0), приложено синусоидальное напряжение (4.6).

Протекающий через катушку переменный ток создает в ней ЭДС самоиндукции , которая в соответствии с правилом Ленца направлена таким образом, что препятствует изменению тока. Другими словами, ЭДС самоиндукции направлена навстречу приложенному напряжению. Тогда в соответствии со вторым правилом Кирхгофа можно записать:

(4.9)
Согласно закону Фарадея ЭДС самоиндукции
         (4.10)
Подставив (4.10) в (4.9), получим:

Решение этого дифференциального уравнения имеет вид:
       (4.12), где           (4.13)
Деля обе части равенства (4.13) на , получим для действующих значений

             (4.14)
Соотношение (4.14) представляет собой закон Ома для цепи с идеальной индуктивностью, а величина  называется индуктивным сопротивлением. Индуктивное сопротивление измеряется в омах.
Мгновенная мощность в цепи с чисто индуктивным сопротивлением равна:
        (4.15)

Положительные значения мощности соответствуют потреблению энергии катушкой, а отрицательные — возврату запасенной энергии обратно источнику. Средняя за период мощность равна нулю. Следовательно, цепь с индуктивностью мощности не потребляет — это чисто реактивная нагрузка. В этой цепи происходит лишь перекачивание электрической энергии от источника в катушку и обратно. Индуктивное сопротивление является реактивным сопротивлением.

Цепь переменного тока с индуктивностью и активным сопротивлением. Реальные цепи, содержащие индуктивность, всегда имеют и активное сопротивление: сопротивление провода обмотки и подводящих проводов. Поэтому рассмотрим электрическую цепь (рис. 4.9), в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток
      (4.16)
Через катушку и резистор протекает один и же ток, поэтому в качестве основного выберем вектор тока и будем строить вектор напряжения, приложенного к этой цепи.
Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе:
      (4.17)
Напряжение на резисторе, как было показано выше, будет совпадать по фазе с током:

         (4.18)
а напряжение на индуктивности будет равно ЭДС самоиндукции со знаком минус (по второму правилу Кирхгофа):
.  (4.19)
Мы видим, что напряжение на индуктивности опережает ток на угол ?/2. Построив векторы и , и воспользовавшись формулой (4.17), найдем вектор  Векторная диаграмма показана на рис. 4.10. Мы видим, что в рассматриваемой цепи ток I отстает по фазе от приложенного напряжения U, но не на / 2, как в случае чистой индуктивности, а на некоторый угол . Этот угол может принимать значения от 0 до ? / 2 и при заданной индуктивности зависит от значения активного сопротивления: с увеличением R угол уменьшается.

Как видно из векторной диаграммы, модуль вектора  равен
 , где величина        называется полным сопротивлением цепи.
Сдвиг по фазе  между током и напряжением данной цепи также определяется из векторной диаграммы:
      (4.22)

Цепь переменного тока с емкостью Рассмотрим электрическую цепь, в которой переменное напряжение (4.6) приложено к емкости С.
Мгновенное значение тока в цепи с емкостью равно скорости изменения заряда на обкладках конденсатора:
     ; но поскольку q = СU, то
    , где      (4.25)
Мы видим, что в этой цепи ток опережает напряжение на 2. Переходя в формуле (4.25) к действующим значениям переменного тока

) , получим:          (4.26)

Это закон Ома для цепи переменного тока с емкостью, а величина — называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 4.12, а временная – на рис. 4.13
Мгновенная мощность в цепи, содержащей емкость:
     (4.27)

Мы видим, что мгновенная мощность изменяется с удвоенной частотой (рис. 4.13). При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные — его разряду и возврату запасенной энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергией между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность, является реактивным сопротивлением.

Вопросы для самопроверки:

1. Дать определение понятию « Активное сопротивление».

2. Выразить закон Ома для цепи переменного тока с активным сопротивлением.

3. Дать определение понятию « Индуктивность».

4. Выразить закон Ома для цепи переменного тока с индуктивностью.

5. Дать определение понятию « Емкость».

6. Описать основные параметры цепей переменного тока с активным сопротивлением, индуктивностью и емкостью.

7. Дать определение понятию « Активное сопротивление».

8. Дать определение понятию « Индуктивность».

9. Выразить закон Ома для цепи переменного тока.

Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями

По треугольнику сопротивлений можно также определить угол сдвига фаз между током и напряжением:

Пример.  Активное  сопротивление  катушки  составляет  5 ом,  а  ее  полное сопротивление Z=30 ом. Определить угол сдвига фаз.

Решение.

При соs =0,25 угол =75°.

§ 56. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ

На рис. 57, а изображена цепь переменного тока, в которую  включены  последовательно  активное  сопротивление r,  индуктивность L, обладающая индуктивным сопротивлением ХL, и емкость С, обладающая емкостным сопротивлением Хс.

Под действием переменного напряжения в этой цепи протекает переменный ток.

Выясним, чему равно общее напряжение на за­жимах цепи. Построим векторную диаграмму то­ка и напряжений для рас­сматриваемой цепи (рис. 57, б). Так как сопротив­ления соединены последовательно, то в них проте­кает одинаковый ток. Отложим по горизонтали, в  выбранном  масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпа­дают  по  фазе,  поэтому вектор напряжения Uа от­кладываем по вектору тока.

Напряжение на индуктивности опережает ток на угол  = 90°. Поэтому век­тор UL откладываем вверх

под углом 90° к вектору тока.

В цепи с емкостью, наоборот, напряжение отстает от тока на угол  = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.

Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы UL и UС. Для этого отнимем от большего вектора UL вектор UС и получим вектор UL-UC, выражающий вектор­ную сумму этих двух напряжений. Теперь сложим векторы (UL-UC) и Ua. Суммой этих векторов будет диагональ параллелограмма – вектор U, изображающий общее напряжение на за­жимах цепи.

На основании теоремы Пифагора из треугольника напряжений АО Б следует, что

отсюда общее напряжение

Определим полное сопротивление цепи переменного тока, со­держащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А’О’Б’ (рис. 57, в). Его сторонами являются сопро­тивления r, (ХL — Хс) и полное сопротивление цепи Z.

Пользуясь теоремой Пифагора, можно написать, что

Отсюда полное сопротивление цепи

Силу тока в цепи с активным, индуктивным и емкостным сопро­тивлениями определяют по закону Ома:

На векторной диаграмме (рис. 57, б) видно, что в рассматри­ваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что

Из треугольника сопротивлений

§ 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ

На рис. 58 изображена цепь переменного тока, в которую включены параллельно две катушки. Каждая из этих катушек обладает соответственно активным сопротивлением r1 и r2 и индуктивным сопротивлением XL1 и XL2.

Полное сопротивление первой катушки

Полное сопротивление второй катушки

Напряжение на  зажимах  катушек  равно  напряжению генератора.

Сила  тока в каждой  катушке  определяется  согласно  закону Ома:

Из этих равенств можно сделать вывод, что в такой цепи токи раз­ветвляются обратно пропорционально полным сопротивлениям ветвей.

Для определения угла сдвига фаз между напряжением и током

в каждой катушке вычисляют  и    и по таблице тригонометрических функций находят значения углов 1 и 2.

Чем больше угол сдвига фаз между напряжением и током, тем больше реактивный ток и меньше активный, тем хуже используется электрический ток в данной установке, ниже ее коэффициент мощ­ности (cos ).

Так как первый закон Кирхгофа справедлив для цепей перемен­ного тока, то в рассматриваемой цепи общий ток определяется гео­метрическим сложением векторов (рис. 58,6).

По горизонтали в выбранном масштабе отложим вектор напря­жения U. Так как ток в цепи с индуктивностью отстает от напря­жения, то вектор тока  I1 выбранном масштабе отложим с по­мощью транспортира под углом 1 к вектору напряжения U, а век­тор тока I2 и отложим под углом 2. Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбран­ного масштаба.

Чтобы найти общий ток, нужно воспользоваться тем, что актив­ная составляющая общего тока — общий активный ток равен сумме активных токов ветвей:

а общий реактивный ток — сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе или все опережаю­щие):

После чего определяют общий ток:

Угол сдвига фаз между общим током и напряжением ср находят по векторной диаграмме.

Пример. Три катушки соединены параллельно и к ним подключено перемен­ное напряжение U=100 в. Частота тока 50 гц. Активное сопротивление катушки r1=2 ом; r2=3 ом; r3=4 ом;

Индуктивность катушек L1=0,04 гн; L2=0,03 гн; L3=0, 01 гн.

Вычислить силу тока в каждой катушке и общий ток в цепи, а также угол сдвига фаз между током и напряжением.

Решение. Индуктивное сопротивление катушек:

Полное сопротивление катушек:

Сила тока в катушках:

2.2. Цепь переменного тока с активным сопротивлением

Известно, что сопротивление одного и того же проводника переменному току больше, чем постоянному току. Это объясняется явлением поверхностного эффекта, сущность которого заключается в следующем. Электрические заряды, обуславливающие постоянный ток, распределяются по сечению проводника равномерно, примерно так, как показано на рис. 2.3, а. При прохождении по проводнику переменного тока, создаваемый им переменный магнитный поток вытесняет электрические заряды из центральной части проводника к его периферийным слоям (рис. 2.3, б).

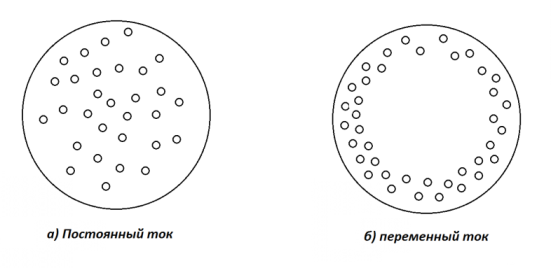
а) постоянный ток б) переменный ток

Рис. 2.3 Распределение электрических зарядов по сечению проводника

Чем выше частота тока в цепи, тем ближе к поверхности проводника располагаются электрические заряды. При этом плотность зарядов на поверхности проводника увеличивается и его сопротивление возрастает. Сопротивление проводника постоянному току называют омическим сопротивлением, а его сопротивление переменному току – активным сопротивлением. К активным сопротивлениям относят электрические лампы накаливания, электрические печи, различные нагревательные приборы и провода, где электрическая энергия почти целиком превращается в тепловую энергию.

Рассмотрим цепь, состоящую из активной нагрузки с сопротивлением R (рис. 2.4), к зажимам которой приложено переменное напряжение.

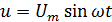(2.5)

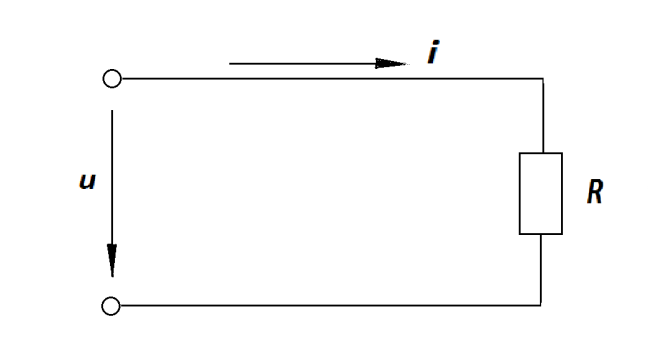
Рис. 2.4 Цепь переменного тока с активной нагрузкой.

Мгновенное значение тока в цепи определяется по закону Ома

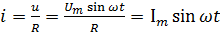(2.6)

где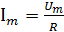

Сравнивая между собой выражения (2.5) и (2.6), отметим, что в цепи переменного тока с активным сопротивлением напряжение и ток совпадают по фазе друг с другом.

Мгновенная мощность такой цепи равна произведению мгновенных значений тока и напряжения.

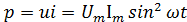(2.7)

Построим волновую и векторную диаграммы цепи переменного тока с активным сопротивлением (рис. 2.5).

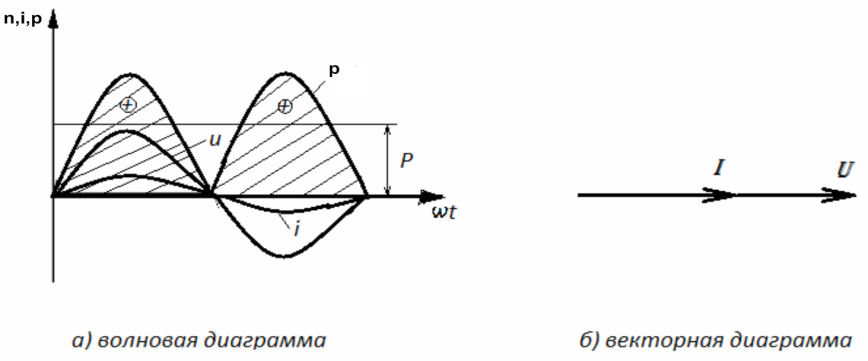
Рис. 2.5 Волновая и векторная диаграммы цепи переменного тока с активным сопротивлением.

Как видно из волновой диаграммы, потребление мощности в сети с активной нагрузкой периодически изменяется от нуля до максимального значения и опять до нуля. При этом знак мощности всё время остаётся положительным. Это означает, что в активной нагрузке происходит процесс необратимого преобразования электрической энергии в тепловую энергию.

Мощность цепи переменного тока принято оценивать по среднему значению мгновенной мощности за период:

=

Следовательно, в цепи переменного тока с активным сопротивлением активная мощность определяется как произведение действующих значений тока и напряжения: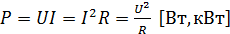

2.3 Цепь переменного тока с индуктивным сопротивлением.

Многие элементы электрических установок состоят из индуктивных катушек, обладающих индуктивностью L. При включении такой катушки в цепь переменного тока, в ней мгновенно проявляется действие ЭДС самоиндукции — 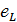, препятствующее изменению тока. Величина этой ЭДС настолько значительна, что на ее уравновешивание затрачивается основная часть напряжения, приложенного к катушке, и лишь его небольшая часть приходится на падение напряжения в активном сопротивлении катушки. Поэтому часто активное сопротивление катушки приравнивается к нулю, и такую катушку называют идеальной катушкой индуктивности. Цепь переменного тока с такой катушкой называется цепью с индуктивной нагрузкой (рис. 2.6).

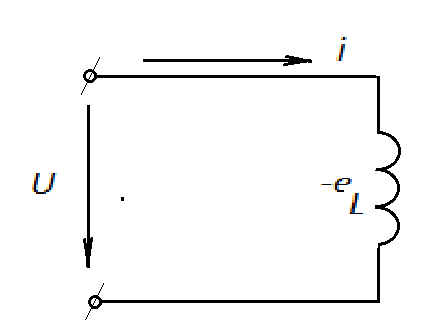
Рис. 2.6 Цепь переменного тока с индуктивной нагрузкой.

К зажимам цепи подведено синусоидальное напряжение u. Под действием этого напряжения в цепи возникает ток, мгновенное значение которого равно 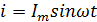(2.8.)

Ток возбуждает в катушке ЭДС самоиндукции, пропорциональную скорости изменения тока в цепи

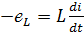(2.9)

В любой момент времени ЭДС самоиндукции —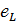 уравновешивается напряжением на зажимах цепи u

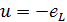(2.10)

Подставляя (2.8) и (2.10) в (2.9), имеем:

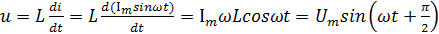(2.11)

где 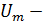амплитудное значение напряжения:

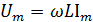(2.12)

Разделив обе части уравнения (2.12) на 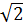, получим выражение закона Ома для цепи с идеальной катушкой индуктивности.

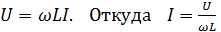(2.13)

Рассмотрим размерность знаменателя выражения (2.13)

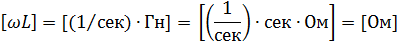
Обозначим 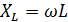и назовем индуктивным сопротивлением идеальной катушки. Его величина зависит от индуктивности катушки и частоты питающего тока.

Сравнивая между собой уравнения (2.8) и (2.11) делаем вывод: в цепи переменного тока с индуктивной нагрузкой напряжение опережает ток на угол в 90°.

Мгновенная мощность цепи определяется как произведение мгновенных значений тока и напряжения, т.е.

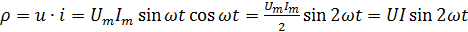
Таким образом, мгновенная мощность в цепи переменного тока с индуктивностью изменяется во времени с удвоенной частотой по отношению к частоте тока.

Построим векторную и волновую диаграммы цепи с индуктивным сопротивлением (рис. 2.7).

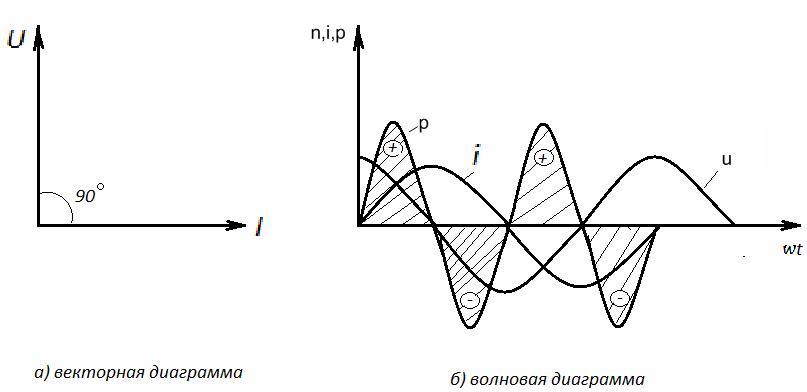
Рис. 2.7 Векторная и волновая диаграммы цепи переменного тока с индуктивным сопротивлением.

Анализ волновой диаграммы позволяет сделать следующие выводы:

В течение первой и третьей четвертей периода переменного тока при его изменении от нуля до амплитудного значения, мощность положительна. Это означает, что энергия, посылаемая источником во внешнюю цепь, запасается в катушке индуктивности в форме энергии магнитного поля

.

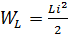В течении второй и четвёртой четвертей периода, при изменении тока от амплитудного значения до нуля, мощность отрицательна. Это означает, что катушка индуктивности возвращает запасенную энергию источнику.

Таким образом, в цепи переменного тока с идеальной катушкой индуктивности происходит периодический обмен энергией между внешним источником и магнитным полем катушки. Средняя активная мощность за период оказывается равной нулю, т.е. источник в такой цепи не расходует энергии и, следовательно, в индуктивности не происходит необратимого преобразования электрической энергии в другие виды энергии.

Мощность цепи с идеальной катушкой оценивают по величине индуктивной мощности Q_L, измеряемой в ВАр (вольт-ампер реактивный) и характеризующей интенсивность обмена энергией между генератором и магнитным полем катушки

.

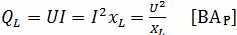
Индуктивная мощность в отличие от активной мощности не может быть использована в практических целях.

Цепь переменного тока с активным сопротивлением. Цепь с активным сопротивлением

Активным сопротивлением R обладают элементы, которые на­греваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).

Если к активному сопротивлению R приложено си­нусоидальное напряжение u= U_msinώt, то и ток в этой цепи изме­няется по синусоидальному закону (рис. 11.1 в):

где

Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (ψi = ψ_U = O).

М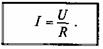атематическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка, к которому приложено напряжение U.

12. Цепь переменного тока с индуктивным сопротивлением.

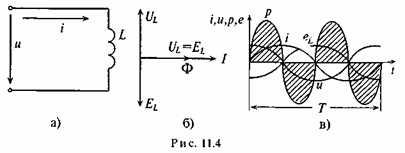
ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90°.

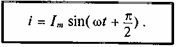
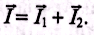Напряжение, приложенное к цепи с идеальной индуктивностью, как и ток в этой цепи, изменяется по синусоидальному закону, но опережает ток по фазе на угол 90°.

В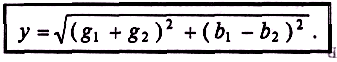ывод: для существования тока в цепи с идеальной индуктивностью необходимо приложить к цепи напряжение, которое в любой момент времени

равно по величине, но находится в противофазе с ЭДС, вызванной этим током (рис. 11.46, в).

Это уравнение и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением X_L.

Таким образом,

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление X_L — это противодействие, которое ЭДС самоиндукции e_L оказывает изменению тока.

12. Цепь переменного тока с емкостным сопротивлением.

Цепь с емкостью

Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжение на конденсаторе U_c отстает по фазе от напряжения источника при зарядке, и при разрядке конденсатора.

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда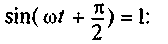

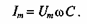
Тогда

Ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°

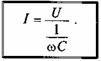
Это равенство и является математическим выражением закона Ома для цепи переменного тока с емкостью. Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Тогда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему.

12. Неразветвленная RL-цепь.

13. Неразветвленная RC-цепь.

14. Неразветвленная RLC-цепь.