Большое переходное сопротивление это: Большое переходное сопротивление это

Содержание

Зависимость величины переходного сопротивления в разборных электро контактах

Понятие переходного электрического сопротивления в электрических контактах

Переходным электрическим сопротивлением называется сопротивление, возникающее в местах перехода тока с одного провода на другой или с провода на какой-либо электрический аппарат, при наличии плохого контакта, например, в местах соединений и оконцеваний проводов, в контактах машин и аппаратов. При прохождении тока нагрузки в таких местах за единицу времени выделяется некоторое количество тепла, величина которого пропорциональна квадрату тока и сопротивлению места переходного контакта, которое может нагреваться до весьма высокой температуры. Если нагретые контакты соприкасаются с горючими материалами, то возможно их зажигание, а при наличии взрывчатой системы возможен взрыв. В этом и состоит пожарная опасность переходных контактных сопротивлений, которая усугубляется тем, что места с наличием переходного сопротивления трудно обнаружить, а защитные аппараты сетей и установок, даже правильно выбранные, не могут предупредить возникновение пожаров, так как ток в цепи не возрастает, а нагрев участка с переходным сопротивлением происходит только вследствие увеличения сопротивления.

От чего зависит величина переходного электрического сопротивления

Величина переходного сопротивления контактов зависит от материала, из которого они изготовлены, геометрической формы и размеров, степени обработки поверхностей контактов, силы нажатия контактов и степени окисления. Особенно интенсивное окисление происходит во влажной среде и с химически активными веществами, а также при нагреве контактов выше 70 — 75 С.

Величина переходного контактного сопротивления не должна превышать более чем на 20% величину сопротивления сплошного участка этой цепи примерно такой же длины.

Величина переходного электрического сопротивления контакта зависит от степени окисления соединяемых контактных поверхностей проводников. Металл контактов взаимодействует с окружающей средой, кислородом воздуха, агрессивными тазами и влагой и вступает с ними в химические реакции, вызывая химическую коррозию металла. Пленка окиси, образующаяся на поверхности металла (например, алюминия) от воздействия воздуха и окружающей среды, создается чрезвычайно быстро и обладает очень большим электрическим сопротивлением. Загрязненные или покрытые окислами контактные поверхности имеют более высокое переходное сопротивление, так как в этом случае в ряде точек нет непосредственного соприкосновения металлов. Окисление идет тем быстрее, чем выше температура контактных поверхностей и чем легче доступ воздуха к ним. Переходное сопротивление контактного соединения или контакта вследствие окисления может возрасти в десятки и сотни раз, так как окислы большинства металлов являются плохими проводниками. В результате реакции окисления проводящая конструкция постепенно разрушается. Если при этом она находится под нагрузкой, то уменьшение ее сечения приводит к дополнительному нагреву (закон Джоуля-Ленца), что в итоге может привести к ее расплавлению.

Величина переходного сопротивления контакта зависит от его конструкции, материала соприкасающихся частей и силы прижатия их друг к другу. Контактные поверхности всегда имеют микроскопические возвышения и впадины; поэтому соприкосновение происходит только в отдельных точках-небольших площадках. Действительная площадь касания увеличивается с ростом силы прижатия контактов друг к другу. Под влиянием силы прижатия металл в точках касания сминается и размеры площадок увеличиваются, возникает соприкосновение в новых точках. Это приводит к снижению переходного сопротивления.

Проверка расстояния. Величина переходного сопротивления контактов выключателей (на одну фазу) для масляных выключателей 200 а составляет не более 350 мком и для выключателей 1000 а-100 мком. Для всей цепи одной фазы воздушных выключателей сопротивление контактов должно быть не более 500 мком.

Величина переходных сопротивлений контактов выключателей зависит от их типа.

На величину переходного сопротивления контакта, как показывают опытные данные, оказывает влияние ряд причин. Оно зависит от материала контактного соединения, давления, испытываемого контактными элементами, величины поверхности их соприкосновения и ее состояния, а также температуры контакта.

Сопротивление зависит от материала контактного соединения, давления, испытываемого контактами, величины поверхности соприкосновения, состояния поверхности и температуры контакта.

Большое влияние на большие переходные сопротивления контактов оказывает их окисление. Контакты, помещенные в масло, подвергаются значительно меньшему окислению, чем работающие в воздухе.

Конструкция контактов должна быть такова, чтобы замыкание и размыкание контактов сопровождалось трением одной поверхности о другую, что способствует их очищению от оксидной пленки.

Когда не так важна величина переходного сопротивления контакта, как его постоянство (например, в измерительной аппаратуре), применяют гальваническое осаждение палладия, имеющего электропроводность в семь раз меньшую, чем у серебра, но весьма стойкого к химической коррозии и твердого.

При очень больших силах нажатия величина переходного сопротивления контактов меняется чрезвычайно не-значительно. Кроме того, слишком большие силы нажатия вызывают чрезмерные напряжения в материале контактных элементов, вследствие чего контакты утрачивают упругость и становятся менее прочными.

По виду касания различают размыкаемые контакты точечные, линейные и плоскостные. Поверхности контактов из-за шероховатости соприкасаются в ограниченном числе точек. Величина переходного сопротивления контакта зависит от силы сжатия контактов, пластичности их материала, качества обработки поверхности и ее состояния, а также от удельного сопротивления материала и вида касания.

Остались вопросы?
Проконсультируем по телефону

или пишите нам e-mail: [email protected]

Что такое переходное контактное сопротивление и почему так важно, чтобы оно было минимальным | Энергофиксик

Все мы с вами прекрасно знаем, что согласно ПУЭ существует несколько разрешенных способов соединения проводников, а именно: опрессовка, сварка, пайка или использование сжимов. И, по большому счету, неважно, какой именно вид соединения будет выбран в том или ином конкретном случае. Самое главное, чтобы было обеспечено соединение с минимальным переходным сопротивлением. А почему это так важно я и расскажу вам в этой статье.

yandex.ru

Что такое переходное контактное сопротивление

Итак, давайте разберемся, что же такое переходное контактное сопротивление, а для этого надо начать с контактного соединения.

Контактное соединение — это конструктивное устройство, в котором создается механическое и вследствие этого электрическое соединение двух и более проводников входящих в электрическую цепь.

В месте контакта двух проводников создается электрический контакт – токопроводящее соединение, в результате которого ток протекает из одного проводника в другой.

Причем если мы с вами просто приложим два проводника друг к другу, то это не обеспечит надежный контакт. Так как реальный контакт проводников осуществляется не по всей поверхности прислоненных пластин, а лишь в немногочисленных точках.

yandex.ru

А все из-за того, что на проводнике присутствуют микроскопические ямы и бугры и даже тщательная обработка (шлифовка) не устранит такие неровности.

Получается, что из-за столь незначительного контакта поверхностей в данном месте будет довольно большое сопротивление протеканию тока.

Сопротивление в месте перехода тока из одного проводника в другой и получило название «Переходное сопротивление контактов. «

Определение. Переходное контактное сопротивление – это активное сопротивление в месте перехода тока из одной детали в другую.

Величину такого сопротивления можно найти по формуле, которая была получена экспериментальным путем:

yandex.ru

Как вы, наверное, заметили, если внимательно изучить формулу, то становится очевидно, что сопротивление контакта не имеет прямой зависимости от размера контактных поверхностей. И в этом случае для переходного сопротивления гораздо важнее сила давления (контактного нажатия).

Теперь давайте разберемся, что такое контактное нажатие

Контактным нажатием называется усилие, с которым оказывается давление одной контактной поверхности на другую.

Число контактных точек начинает увеличиваться по мере того, как возрастает сила нажатия. Причем даже при малом давлении процесс деформации вершин и впадин в значительной степени увеличивает число точек соприкосновения.

И именно по этой причине для создания надежного контакта используют разнообразные способы сжатия и скрепления проводников:

1. Механическое соединение с помощью болтовых соединений.

2. Использование пружин для упругого нажатия (Wago клеммники).

3. Сварка, пайка и опрессовка.

Получается, что переходное контактное сопротивление тем меньше, чем больше сила нажатия, а, следовательно, больше реальная площадь соприкосновения проводников.

yandex.ru

Примечание. На первый взгляд кажется, что выше представленное утверждение не согласуется с экспериментально полученной формулой, но на самом деле все прекрасно согласуется. Ведь по формуле мы с вами высчитываем сопротивление в конкретной точке, но с ростом давления количество точек соприкосновения увеличивается, создавая в месте контакта все больше условно параллельных сопротивлений. А, как известно, при параллельном соединении суммарное сопротивление уменьшается.

Но при этом следует учесть, что увеличивать давление (тем самым снижая сопротивление) можно только до определенного уровня. Нельзя допускать пластических деформаций соединяемых проводников, ведь это может привести к их разрушению.

Также данное сопротивление зависит от температуры, ведь при нагреве проводника возрастает переходное контактное сопротивление. Еще следует учесть, что при росте температуры существенно быстрее изменяется удельное сопротивление материала, в результате чего переходное сопротивление наоборот уменьшается.

Получается, что небольшой нагрев не столь страшен, главное чтобы температура не превышала определенных рамок.

Изменение контактного сопротивления со временем

Как говорят классики: «Ничто не вечно под луной.» Так дела обстоят и с надежно выполненным контактом. Минимальное переходное сопротивление у него будет лишь в самом начале, а во время эксплуатации оно может существенно измениться и вот почему.

Сильное влияние на такое сопротивление оказывает температура. Так даже при температуре в 20 градусов по Цельсию медь окисляется, в результате чего на поверхности жилы формируется оксидная пленка, которую достаточно легко разрушить.

А вот если температура провода в результате сильно возросшей нагрузки или плохого контакта возрастет до +70 градусов и более, процесс формирования оксидной пленки ускорится многократно, что приведет к еще большему увеличению сопротивления, а, следовательно, увеличит нагрев, что может привести к плачевным последствиям. 12 Ом*см.

Отсюда следует вывод, что использовать алюминий для выполнения, например, домашней проводки, нежелательно. Ведь таким образом создать надежное контактное соединение со стабильно низким контактным сопротивлением будет достаточно сложно.

И, подводя итог всего вышенаписанного, хочу сказать, что какой бы вы не выбрали способ соединения проводов, самое главное, чтобы контакт был выполнен строго по всем правилам и требованиям, и тогда переходное контактное сопротивление будет минимально, и соединение при должном периодическом обслуживании (если это не сварка тут обслуживание не нужно) прослужит вам очень долго и безаварийно.

Понравилась статья, тогда ставим лайк. Если хотите высказать свои мысли, то прошу в комментарии и спасибо за уделенное время!

«Электрические» причины пожаров! | Опаринская Сорока

За 2019 год в Опаринском районе произошло 9 пожаров, причиной которых явился аварийный режим работы электрооборудования, а за истекший период 2020 года 2 таких пожара.

С физической точки зрения в быту можно выделить три основных пожароопасных процесса, характерных для авариных режимов работы электрооборудования: перегрузка по току, короткое замыкание, образование больших переходных сопротивлений. Указанные процессы имеют высокую пожарную опасность, они сопровождаются тепловыми эффектами, которые при определенных условиях могут стать источниками зажигания для большинства горючих материалов или вызвать новые повреждения в элементах электросети.

Рассмотрим подробнее каждый из процессов. Перегрузка по току – так принято называть аварийный режим работы электрических сетей, при котором проходящий ток превышает допустимую (расчетную) величину. Это возникает по следующим причинам:

Подключение к электросети неисправных бытовых электроприборов
Неправильное распределение нагрузки между линиями электрической сети
Проблемы с проводкой (несвоевременная замена, неправильный монтаж, ошибка при выборе сечения кабеля, неправильный выбор наминала автоматических выключателей и т. д.)
Превышение мощности потребителей
Низкое качество энергоснабжения

Короткое замыкание – это электрическое соединение разных фаз или потенциалов электроустановки между собой или с землей, не предусмотренное в нормальном режиме работы, при котором в проводниках, в месте контакта, резко возрастает сила тока, превышая максимально допустимые величины.

Если же говорить простым языком, короткое замыкание – это любое незапланированное, нештатное соединение электрических проводников с разным потенциалом, например, фазы и ноля, при котором образуются разрушительные токи.

В быту, чаще всего происходит дуговое короткое замыкание, при котором, между проводниками в месте КЗ, возникает мощнейший электрический разряд, который нередко воспламеняет окружающие предметы и горючие материалы.

Большое переходное сопротивление – это сопротивление участка электрической цепи в месте соединения отдельных элементов (места соединения проводов, подсоединения их к электроприемникам, контактным элементам и т.

п.) в которых, при неправильном их исполнении, сопротивление выше по сравнению с сопротивлением электрической цепи до этих участков и после их.

Наиболее часто большие переходные сопротивления возникают в следующих случаях:

в местах соединения проводов между собой, когда вместо пайки, сварки, опрессовки или зажимов под болты применяются скрутки проводов с алюминиевыми и медными жилами;
в местах подключения проводов к рубильникам, электродвигателям и другим аппаратам без специальных зажимов и наконечников;

в рубильниках, магнитных пускателях, выключателях, штепсельных разъемах (розетках, вилках) на контактных элементах при снижении прилагаемых для включения усилий, недовключения, подгорания и т.п.;
в местах контактов, выполненных с помощью резьбовых соединений в электрооборудовании, которое в процессе работы подвержено вибрации, и особенно в случаях отсутствия приспособлений против самоотвинчивания;
в местах соединения проводов, выполненных с помощью пайки, но с применением при подготовке поверхностей кислот, которые практически всегда остаются в месте пайки и впоследствии вызывают усиленное окисление мест соединения или близ расположенных участков проводов.

Большое переходное сопротивление может быть причиной возникновения короткого замыкания.

Так же пожар может возникнуть от неправильных действий при ремонте электросетей или электрооборудования. Помните: ремонт электрооборудования должен выполнять специалист.

Напоминаем, что несоблюдение следующих требований, является нарушением требований пожарной безопасности, за что предусмотрена административная ответственность в соответствии с ст. 20.4 КоАП РФ:

Запрещается оставлять по окончании рабочего времени не обесточенными электроустановки и бытовые электроприборы в помещениях, в которых отсутствует дежурный персонал, за исключением дежурного освещения, систем противопожарной защиты, а также других электроустановок и электротехнических приборов, если это обусловлено их функциональным назначением и (или) предусмотрено требованиями инструкции по эксплуатации.

Прокладка в пространстве воздушного зазора навесных фасадных систем открытым способом электрических кабелей и проводов не допускается.
Запрещается прокладка и эксплуатация воздушных линий электропередачи (в том числе временных и проложенных кабелем) над горючими кровлями, навесами, а также открытыми складами (штабелями, скирдами и др.) горючих веществ, материалов и изделий.

Запрещается:

а) эксплуатировать электропровода и кабели с видимыми нарушениями изоляции;

б) пользоваться розетками, рубильниками, другими электроустановочными изделиями с повреждениями;

в) обертывать электролампы и светильники бумагой, тканью и другими горючими материалами, а также эксплуатировать светильники со снятыми колпаками (рассеивателями), предусмотренными конструкцией светильника;

г) пользоваться электроутюгами, электроплитками, электрочайниками и другими электронагревательными приборами, не имеющими устройств тепловой защиты, а также при отсутствии или неисправности терморегуляторов, предусмотренных конструкцией;

д) применять нестандартные (самодельные) электронагревательные приборы и использовать несертифицированные аппараты защиты электрических цепей;

е) оставлять без присмотра включенными в электрическую сеть электронагревательные приборы, а также другие бытовые электроприборы, в том числе находящиеся в режиме ожидания, за исключением электроприборов, которые могут и (или) должны находиться в круглосуточном режиме работы в соответствии с инструкцией завода-изготовителя;

ж) размещать (складировать) в электрощитовых (у электрощитов), у электродвигателей и пусковой аппаратуры горючие (в том числе легковоспламеняющиеся) вещества и материалы;

з) при проведении аварийных и других строительно-монтажных и реставрационных работ, а также при включении электроподогрева автотранспорта использовать временную электропроводку, включая удлинители, сетевые фильтры, не предназначенные по своим характеристикам для питания применяемых электроприборов.

Уважаемые жители Опаринского района! Проявляйте бдительность, не подвергайте себя и окружающих людей смертельной опасности, соблюдайте элементарные меры пожарной безопасности!

При обнаружении пожара нужно незамедлительно сообщить о происшествии в пожарную охрану (01, 101) или в единую дежурно-диспетчерскую службу (112) для успешной работы соответствующих служб.

голоса

Рейтинг статьи

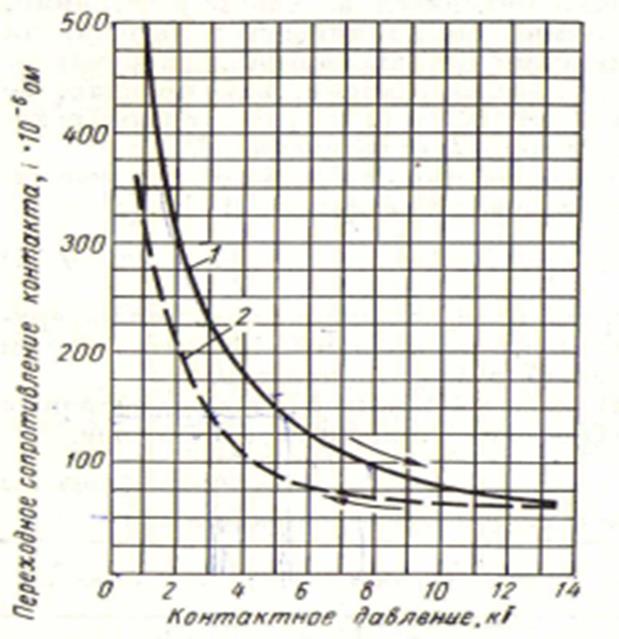
Зависимость изменения переходного сопротивления от момента силы сжатия контактов

25 декабря 2020

Статья опубликована в журнале «ЭЛЕКТРОЭНЕРГИЯ. Передача и распределение» № 2(59), март-апрель 2020 г.

Различные соединения электрических контактов имеют переходное сопротивление, которое зависит от многих факторов, например, таких как степень сжатия, материал или температура. Само же значение переходного сопротивления — важный показатель в любой электроустановке, поэтому оно нормируется и проверяется, т.к. его увеличение приводит к нарушению работы в энергосистеме и аварийным, а иногда даже опасным для жизни ситуациям.

Контактные поверхности имеют микроскопические возвышения и впадины, вследствие чего их соприкосновение происходит не по всей площади, а только на отдельных точках, которые называют точками соприкосновения (рис. 1). В точках с сильно суженным сечением ток с одной контактной поверхности переходит на другую, вследствие чего возникает большое электрическое сопротивление, называемое переходным.

Рис. 1. Соприкосновение двух контактных поверхностей:

1-2 Контактные поверхности; 3 Точки соприкосновения

Переходное сопротивление в контакте зависит, главным образом, от состояния контактных поверхностей и давления, с которым контакты прижаты друг к другу. В контактах, не испытывающих давление (усилий, прижимающих контакты друг к другу), число точек соприкосновения незначительно. При увеличении же давления, прижимающем контактные поверхности друг к другу, выступающие неровности деформируются, и первоначальные точки соприкосновения превращаются в небольшие площади.

Зависимость переходного сопротивления от давления контактов друг на друга объясняется тем, что при большом давлении легче смять выступающие на их поверхности точки и таким образом улучшить контакты между ними. При этом на контактных поверхностях создаются новые точки соприкосновения, улучшающие условия перехода тока, а, следовательно, и качества контакта.

Для доказательства описанных выше данных, опыт проводился на двух алюминиевых шинах 10 х 100 мм (болты М16), сжатие которых проводилось динамометрическим ключом (рис. 2).

Рис. 2. Алюминиевые шины и их соединение

Для данного доказательного эксперимента был выбран высокоточный микроомметр производства компании ООО «СКБ ЭП» — МИКО-21, который отличается от аналогов наилучшим сочетанием функционала с учетом потребностей Пользователей.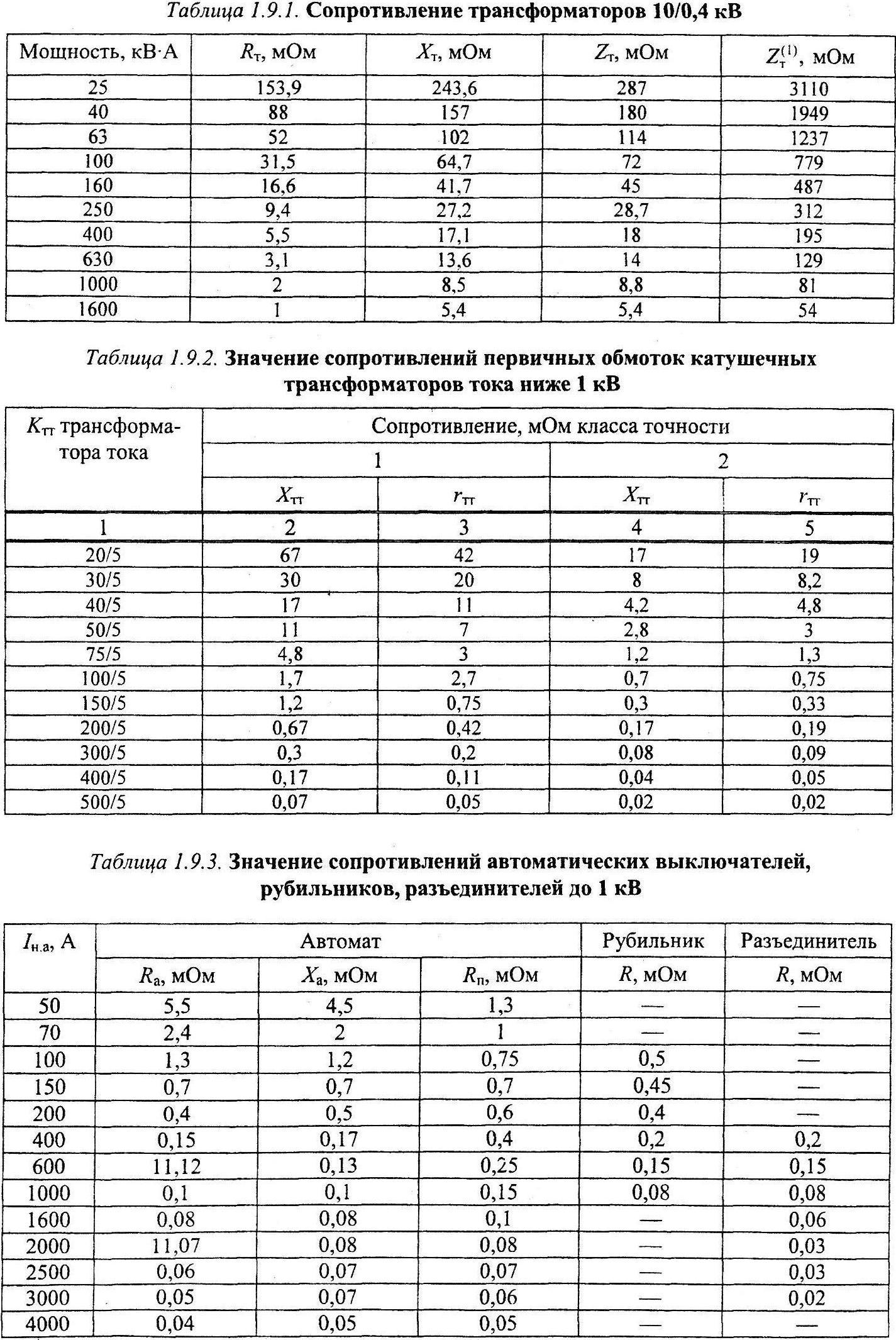

МИКО-21 предназначен для измерения переходных сопротивлений цепей электрооборудования в диапазоне 0,1 мкОм ÷ 2 Ом при рабочем токе до 200А с самой низкой погрешностью ±0,05% среди аналогичных российских и зарубежных разработок (рис. 3).

Рис. 3. Микроомметр МИКО-21

Площадь соприкосновения двух алюминиевых пластин предварительно была отчищена, т.к. результат переходного сопротивления в значительной мере зависит от обработки контактных поверхностей и их состояния, а степень сжатия проводилась согласно ВСН 164-82.

По данным документа ВСН 164-82 «Инструкция по проектированию и монтажу контактных соединений шин между собой и с выводами электротехнических устройств» и пункту 7.12. — затягивать болты контактных соединений необходимо индикаторными ключами со следующим крутящим моментом:

Диаметр болта	М10	М12	М16	М20
Крутящий момент, Н × м	40-50	60-70	90-100	120-130

Все замеры были проведены на токе 200А. Шаг увеличения момента силы сжатия составил 5 N*m при начальном значении 40 N*m. На графике 1 видно, что при увеличении момента силы сжатия данные измеренного переходного сопротивления снижаются, но при достижении момента силы сжатия более 100 H*m интенсивность падения замедляется.

График 1. Зависимость изменения переходного сопротивления от момента силы сжатия контактов

Чем больше число и площадь точек соприкосновения между контактными поверхностями, тем меньше переходное сопротивление между ними. Однако интенсивность процесса образования новых точек соприкосновения даже при дальнейшем возрастании давления в контактах постепенно замедляется. Это объясняется тем, что при повышении давления оно воспринимается большей площадью, удельное давление в точках соприкосновения контактов уменьшается, материал контактов сминается не так интенсивно, поэтому процесс увеличения числа и площади точек соприкосновения замедляется.

Переходное сопротивление, является основным показателем качества любого контакта и в значительной мере зависит от обработки контактных поверхностей и их состояния. Разумеется, что момент силы сжатия, ровно, как и показатели переходного сопротивления имеют свои нормы, на которые важно обращать внимание, т.к. даже минимальное излишнее усилие при сжатии может привести к деформации контакта и крепежного материала, что ухудшит переходное сопротивление.

Говоря же о приборах для измерения переходного сопротивления, следует делать выбор в сторону оборудования, которое соответствует следующим критериям:

Измерительный ток прибора должен быть близким к рабочему току контролируемого объекта, т.к. окисная пленка и неметаллические включения обуславливают повышенное переходное сопротивление (далее Rпер.) контактов, которое уменьшается при повышении измерительного тока.
Учет влияния встроенного трансформатора тока (ТТ) на измерение Rпер. баковых выключателей. ТТ баковых выключателей создают длительный переходной процесс при подаче измерительного тока, поэтому время измерения определяется параметрами ТТ, их числом и силой измерительного тока.
Электромагнитная обстановка на энергетических объектах. Игнорирование перечисленных выше особенностей может приводить к тому, что приборы, показывающие в условиях офиса отличные метрологические характеристики оказываются малопригодными для применения в условиях электрической подстанции.

Эти и другие особенности измерений электрического сопротивления в условиях подстанции известны компании ООО «СКБ ЭП» свыше 17 лет, с момента выпуска ее первого микроомметра. Сейчас компания успешно реализует приборы для измерения переходного сопротивления МИКО-10, МИКО-1, МИКО-21 и МИКО-2.3, сохраняя основные требования и внося новый функционал.

Если Вас заинтересовали приборы СКБ ЭП для измерения переходного сопротивления и Вы хотите получить больше информации, обращайтесь к менеджерам по тел. +7 (812) 500-25-48 или по почте [email protected].

Официальный сайт компании: www.skbpribor.ru

Instagram: skbep_ru

Нормативные документы:

1. Правила устройства электроустановок – ПУЭ, 7-е издание раздел 1, гл. Р.1.8, п.1.8.26, пп.2, п. 1.8.27, пп.3

2. ВСН 164-82 Инструкция по проектированию и монтажу контактных соединений шин между собой и с выводами электротехнических устройств

Переходное сопротивление контакта.

В месте перехода тока из одного проводника в

Рис. 3. Модель контакта другой возникает электрическое сопротивление, которое называется переходным сопротивлением контакта.

Переходное сопротивление контакта можно представить как результат резкого повышения плотности тока в местах соприкосновения контактных поверхностей по сравнению с плотностью тока в самом контакте (рис. 3). В местах соприкосновения проводников линии тока стягиваются к участкам с малым сечением, которые представляют большое сопротивление току. Это сопротивление называется сопротивлением стягивания и определяется по следующей формуле:

, (1)

где r – удельное сопротивление материала контактов, Ом. м; a – радиус площадки фактического касания, м; n – число точек касания.

Радиус фактического касания (рис. 4) зависит от вида деформации материала контактов. При упругой деформации радиус площадки

определяется формулой:

, (2)

где F_к – контактное нажатие, Н; Е – модуль уп-

ругости материала, Н/м.

При пластической деформации радиус пло-

щадки определяется формулой:

Рис. 4. Площадка касания

, (3)

где σ_см – предел прочности материала контактов на смятие, Н/м².

Таким образом, переходное сопротивление контакта можно представить следующим выражением:

R_п = R_ст + R_пл_. (4)

Здесь R_пл – сопротивление окисной пленки на поверхности контакта.

На основании опытных данных величина переходного сопротивления определяется выражением

. (5)

Здесь k_пх – коэффициент, завися-

Рис. 5. Зависимость переходного щий от материала и формы кон-

сопротивления от силы контактного такта, способа обработки и состоя-

нажатия ния контактной поверхности; n – показатель степени, характеризующий число точек соприкосновения, для различных контактов имеет следующие значения: точечный контакт n = 0,5; линейный контакт n = 0,5…0,7; поверхностный контакт n = 0,7…1,0.

С увеличением контактного нажатия переходное сопротивление уменьшается вследствие увеличения площади касания за счет смятия бугорков (рис. 5). Причем, после снятия F_к за счет остаточной деформации бугорков на поверхности контактов, переходное сопротивление становится меньше, чем при увеличении F_к.

Переходное сопротивление очень чувствительно к окислению поверхности в виду того, что окислы многих металлов являются плохими проводниками. Окисление поверхности контактов происходит под воздействием кислорода воздуха. Вследствие окисления переходное сопротивление может возрасти в сотни и тысячи раз. Возрастание переходного сопротивления приводит к увеличению мощности на R_п и возрастанию температуры контактного соединения. Для борьбы с окислением контактов их покрывают оловом, серебром или техническим вазелином.

Узнать еще:

§91. Контакты электрических аппаратов | Электротехника

Типы контактных соединений. Электрическим контактом называют место перехода тока из одной токоведущей части аппарата или иного токопровода в другую часть. В аппаратах контактом также называют конструктивный элемент, с помощью которого в процессе работы аппарата осуществляется периодическое замыкание и размыкание электрической цепи.

Контактная система электрического аппарата состоит в большинстве случаев из пары или нескольких пар подвижных и неподвижных элементов, при замыкании которых образуется электрическая цепь.

Различают две группы контактных соединений: неподвижные и подвижные. Неподвижные контактные соединения служат для жесткого присоединения внутренних токоведущих частей и внешнего присоединения соединительных проводов к аппарату. Во время работы аппарата такие соединения не разъединяются. Подвижные контактные соединения имеют один или несколько подвижных контактов, которые в процессе работы, соприкасаясь с неподвижными контактами, создают электрическую цепь. В зависимости от характера соприкосновения элементов контактного соединения контакты подразделяют на поверхностные (плоскостные), линейные и точечные. В поверхностных контактах электрический контакт осуществляется по плоскости ABCD (рис. 295, а), в линейных — по линии АВ (рис. 295,б), в точечных — в точке А (рис. 295, в).

Условия работы контактов. Полное сопротивление контактного соединения включает в себя сопротивления собственного материала контактных элементов и переходного сопротивления в месте их соприкосновения. Переходное сопротивление зависит от материала контактов, силы прижатия их друг к другу, площади контактной поверхности, ее состояния и температуры. При соприкосновении двух контактных поверхностей 1 и 2 (рис. 296) электрическое соединение происходит не по всей поверхности, а по точкам соприкосновения, которые образуются из-за неточностей обработки поверхностей и их износа в результате воздействия электрической дуги. При нажатии контактов происходит частичное смятие материала контакта в точках соприкосновения. Чем больше контактное нажатие F и мягче материал контакта, тем больше площадь реального соединения и меньше переходное сопротивление Rп (рис. 297, а).
Каждый контактный материал характеризуется некоторым пре-

Рис. 295. Формы контактных поверхностей

Рис. 296. Соприкасающиеся контактные поверхности

Рис. 297. Зависимости переходного сопротивления от нажатия (а) и от температуры (б)

дельным значением нажатия, свыше которого переходное сопротивление практически не снижается. Очень резкую зависимость переходного сопротивления от нажатия имеют угольные контакты. Это свойство угольного контакта широко используют в угольных регуляторах напряжения, осуществляющих регулирование тока возбуждения электрических машин.

Чрезмерное нагревание контактов приводит к их окислению, а окисные пленки большинства металлов не проводят электрический ток и резко повышают переходное сопротивление (рис. 297, б). На участке а — Ь переходное сопротивление растет вследствие все более интенсивного возникновения окисной пленки. На участке b — с сопротивление падает вследствие нарушения прочности материала и его размягчения, что приводит к увеличению площади соприкосновения. На участке c — d сопротивление вновь начинает расти вследствие резкого увеличения удельного сопротивления материала. Этот рост будет продолжаться до полного расплавления материала.

Особенно значительные повышения температуры контактов могут иметь место при прохождении через них тока короткого замыкания. Предельно допустимая температура при токах короткого замыкания для контактов из меди составляет 200—300 °С, а для алюминиевых — 150—200 °С. В случаях превышения предельной допустимой температуры механическая прочность материала контактов резко уменьшается.
Нагревание контактов проходящим током может привести к расплавлению и привариванию контактов друг к другу.

Cвойства аппаратов выдерживать определенные значения аварийных токов без повреждения характеризуются его электродинамической стойкостью. Она определяется наибольшим значением тока, который может выдержать аппарат во включенном состоянии, не повреждаясь и не отключаясь самопроизвольно.

Размеры контактной поверхности мало влияют на контактное сопротивление, поскольку с увеличением поверхности и соответственно числа точек соприкосновения снижаются нажатие на единицу площади и смятие. Однако от поверхности контакта зависят условия его нагрева и при том же сопротивлении большие по размеру контакты допускают большую нагрузку током.

Материал контакта должен обладать высокой механической прочностью, хорошей электропроводностью, теплостойкостью и антикоррозионной стойкостью. Широкое распространение получили контакты из меди и ее сплавов (латунь, бронза) для изготовления как подвижных, так и неподвижных контактных соединений. При длительной непрерывной работе во избежание окисления медные контакты покрывают слоем олова или выполняют с серебряными накладками.

Алюминий и сталь применяют, главным образом, для неподвижных контактных соединений. Для защиты от коррозии алюминиевые контакты иногда оцинковывают, а стальные покрывают слоем кадмия. Большой теплостойкостью и твердостью обладают вольфрамовые контакты.

Никель, платину и серебро используют для контактов маломощных аппаратов, где требуется точность и надежность срабатывания.

Серебряные контакты имеют проводящую окисную пленку с такой же электропроводностью, как и сам металл, а платиновые практически не покрываются окисной пленкой.

Широкое применение в электрических аппаратах получили металлокерамические контакты, выполненные путем прессования смеси порошков различных металлов.

На контакты электрических аппаратов в моменты их включения и отключения действуют возникающие электродинамические и механические силы, которые влияют на переходное сопротивление и приводят к механическому износу контактов. В первый момент включения аппарата, когда на контакты еще полностью не действует нажатие, соприкосновение происходит по отдельным точкам, через которые устремляется весь ток (рис. 298, а). При этом линии тока в месте контактного перехода искривляются, располагаются параллельно и имеют в нижнем и верхнем контактных элементах противоположное направление (рис. 298,б). Магнитные поля этих токов, взаимодействуя друг с другом, создают электродинамические усилия взаимного отталкивания F, которые стремятся разомкнуть контакты и вызывают их вибрацию.

Кроме электродинамических усилий, отталкиванию контактов способствуют механические силы, возникающие в момент упругого удара одного контакта о другой. Упругий удар при соприкосновении контактов вызывает ряд повторных отскоков и совместных перемещений обоих контактных элементов под действием нажатия и инерции. Такие вибрации приводят к расплющиванию и механическому разрушению контактов.

В момент размыкания контактов переходное сопротивление резко увеличивается, возрастает температура и возникает электрическая дуга, что приводит к электрическому износу контактов (их выгоранию и эрозии).

Механический и электрический износ контактов в основном определяет срок службы аппарата (выражаемый числом его срабатываний) и максимально допустимую частоту его включений.

Рис. 298. Распределение тока по площади сечения контактов в момент включения

Рис. 299. Перекатывающиеся контакты Т-образной формы в начале (а) и в конце (б) включения

Способы уменьшения износа контактов. В аппаратах, рассчитанных на большое число включений и отключений (выключатели, контакторы, контроллеры), применяют конструкции контактов с перекатывающимися поверхностями. Такие контакты замыкаются и размыкаются, соприкасаясь одним участком поверхности, где происходит горение электрической дуги и наблюдается повышенный механический износ, а затем в процессе работы передвигаются друг относительно друга, и в дальнейшем электрический контакт поддерживается между чистыми поверхностями (рис. 299). Эти контакты бывают Г- или Т-образной формы и изготовляются из профильной твердой меди.

Перекатывающиеся контакты износостойки, поскольку при их работе трение скольжения невелико. При перекатывании контактных элементов происходит их самозачистка от окисных пленок.

Другим методом защиты контактной поверхности от обгорания является использование дополнительных дугогасительных контактов 1, которые включены параллельно главным контактам 2 (рис. 300). Главные контакты рассчитывают на длительное протекание рабочего тока, а дугогасительные — на меньший ток, но их контактные поверхности выполняют из тугоплавкого материала. При включении сначала замыкаются дугогасительные контакты, и электрическая дуга, возникающая при отскоках этих контактов, может вызывать некоторый их подгар. Затем включаются главные контакты, шунтируя дугогасительные.

При отключении сначала размыкаются главные контакты, но цепь остается замкнутой через дугогасительные контакты, и только после полного отключения главных контактов начинают размыкаться дугогасительные, разрывая электрическую цепь. Таким образом, при включении и при отключении аппарата электрическая цепь создается и разрывается дугогасительными контактами, на которых возникает электрическая дуга и образуются подгар и окис-ные пленки. Во всех случаях электрической дуги между главными контактами не возникает, и они соприкасаются чистыми поверхностями.

В электрических аппаратах высокого напряжения широкое применение получили торцовые контакты, образуемые при соприкосновении плоских контактных элементов. Подвижный контакт представляет собой полую трубу 1 (рис. 301,а) с плоским торцом. Неподвижный контакт 2 выполнен в виде цилиндра с плоским основанием. Для надежного прижатия контактных элементов друг к другу неподвижный контакт 2 имеет возможность незначительного перемещения из-за сжатия пружины 3. Благодаря этому перемещению компенсируются перекосы контактов и их износ в процессе эксплуатации.

Щеточные контакты (рис. 301,б) применяются в реостатах, различных командоконтроллерах, переключателях и относятся к линейным соединениям. Подвижной контакт 4 (щетка) состоит из набора пластин из твердой меди или специальной бронзы, срезанного под определенным углом. Он соприкасается с основанием неподвижного контакта 2. Для усиления механической прочности набора верхнюю пластинку выполняют более толстой. Такой контакт имеет большую поверхность соприкосновения, чем аналогичный сплошной.

В аппаратах барабанного типа — контроллерах часто используют пальцевые контакты (рис. 302, а). Неподвижный контакт 2 (палец) прижимается к барабану, вращающемуся на оси 4, с помощью привода, пружиной 1. Подвижные контакты 3, 5, 6 укреплены на барабане в виде полос или сегментов, обычно выполненных из меди.

В зависимости от значения тока параллельно может устанавливаться несколько пальцев.

В различных рубильниках, разъединителях, плавких предохранителях применяют рубящие контакты (рис. 302,б), состоящие из плоского медного или латунного ножа 7 (подвижного контакта) и неподвижного контакта 8 в виде стоек из упругого металла. При больших токах стойки усиливаются дополнительными стальными пружинами 9.

Рис. 300. Главные и дугогасительные контакты аппарата

Рис. 301. Торцовые (а) и щеточные (б) контакты

Рис. 302. Пальцевый (а), рубящий (б) и мостиковый (в) контакты

В кнопках управления, реле, путевых выключателях применяют мостиковые контакты (рис. 302, в). Контактный мостик 10 с припаянными к нему контактами 11 и 13 устанавливается на подвижной части аппарата. При включении такой мостиковый контакт замыкает неподвижные контакты 14 и 15, создавая между ними электрическую цепь. Нажатие контактов зависит от пружины 12.

На одной подвижной части может быть установлено несколько замыкающих и размыкающих контактов, каждый из которых включает или отключает свою электрическую цепь.

ПЕРЕХОДНОЕ СОПРОТИВЛЕНИЕ КОНТАКТА

Механика ПЕРЕХОДНОЕ СОПРОТИВЛЕНИЕ КОНТАКТА

просмотров — 421

В зоне перехода тока из одного тела в другое имеет место относительно большое электрическое сопротивление, называемое переходным сопротивлением контакта.

По своей природе переходное сопротивление контакта есть обычное сопротивлению металлического проводника. Только данный проводник – микроскопический бугорок, в котором и происходит физическое контактирование двух проводников между собой. Переходное сопротивление контакта можно представить себе как результат сужения сечения материала в элементарных бугорках и резкого повышения плотности тока в площадках контактирования (рис. 4-1, г и д) по сравнению с плотностью тока в теле контакта.

С уточнениями на основании опытных данных значение переходного сопротивления определяется выражением.

(4-3)

где ε – некоторая величина, зависящая от материала и формы контакта͵ способа обработки и состояния контактной поверхности; Р – сила, сжимающая контакты; n – показатель степени, характеризующий число точек соприкосновения.

С увеличением числа точек соприкосновения переходное сопротивление контакта уменьшается. В выражении (4-3) показатель степени принимают: для одноточечного контакта n= 0,5, для многоточечных n = 0,7 ÷ 1 (для линейного контакта n = 0,7 ÷ 0,8, для поверхностного n = 1).

Значения величины ε зависят от состояния поверхности контактов, характера их обработки и особенно от степени окисления. Важно заметить, что для свежих, неокисленных и нормально обработанных одноточечных контактов (обработка на станке, окончательная отделка щлифным напильником и смазка вазелином) можно принимать следующие средние значения ε в омах на корень квадратный из ньютона (OM/H^0,5) [4]:

Зависимость переходного сопротивления от контактного нажатия. Эта зависимость в соответствии с уравнением (4-3) представлена на рис. 4-2. Кривая 1 соответствует процессу возрастания контактного нажатия, кривая 2 – снижению нажатия. Различный ход кривых объясняется наличием остаточных деформаций отдельных бугорков, по которым происходило соприкосновение.

Рис. 4-2. Зависимость переходного сопротивления от силы нажатия

Следует отметить, что при одном и том же нажатии переходное сопротивление одного и того же контакта при каждом замыкании может быть разным и отличаться в достаточно широких пределах: в больших при малых нажатиях и в меньших при больших нажатиях (более 100 Н). Объясняется это тем, что число и размер площадок контактирования при каждом замыкании бывают разными. Значение переходного сопротивления в зависимости от нажатия практически выражается не какой-то кривой, а областью, ограниченной двумя кривыми.

Рис. 4-3. Зависимость переходного сопротивления от температуры

Зависимость переходного сопротивления от температуры. Как указано выше, переходное сопротивление контакта есть сопротивление металла проводника, в связи с этим оно должно в той же мере зависеть от температуры. При этом с увеличением температуры меняется структура бугорков и площадок соприкосновения за счет изменения удельного сопротивления смятию σ. По этой причине температурный коэффициент здесь будет меньшим. Для меди и

(4-4)

С ростом температуры переходное сопротивление вначале растет (участок I кривой на рис. 4-3). Затем при некоторой температуре (для меди и серебра при 200 – 300 °С) происходит резкое падение механических свойств материала. При том же нажатии увеличивается площадка контактирования, переходное сопротивление (участок II) резко падает. В дальнейшем (участок III) оно снова возрастает линейно с ростом температуры, и при температуре плавления материала контакты свариваются, переходное сопротивление резко падает (участок IV).

Следует отметить, что исследования, выполненные О. Б. Броном [6], показали, что при длительном пребывании серебряных контактов под током их переходное сопротивление не возрастает с температурой, а наоборот, падает, и падает по линейному закону (опыты производились при температуре до 140°С). Отступление от соотношения (4-4) объясняется медленно происходящей в результате Длительного нагревания пластической деформацией материала в площадках контактирования, приводящей к росту этих площадок и уменьшению переходного сопротивления. Коэффициент α оказывается отрицательным.

Огромное магнитосопротивление и сверхострый метамагнитный переход в поликристаллическом Sm 0,5 Ca 0,25 Sr 0,25 MnO 3

Синтез и структурная характеристика

Высококачественный поликристаллический SCSMO был получен известным золь-гель методом (см. Подробности в методах). Кристаллическая структура и однофазность образца были изучены с помощью рентгеновской дифрактометрии при комнатной температуре и просвечивающей электронной микроскопии (ПЭМ). На дифрактограмме (см. Рис. 1а) (анализ обсуждается в дополнительном разделе I (A)) и на дифрактограмме ПЭМ (см. Рис.1д) демонстрируют ромбическую кристаллографическую симметрию (Pnma) образца. Химический анализ при комнатной температуре с использованием измерения EDS (см. Дополнительный раздел I (C)) показывает, что элементы распределены однородно и стехиометрически.

Рис. 1: XRD- и TEM-анализ

a , b показывают подгонку профиля данных XRD при комнатной температуре (RT) и низкой температуре (15 K) с использованием Pnma и (Pnma + P21 / m) пространства. группы. На вставках a и b показано соответствие пиков при 2θ = 47.5 °, где при низкой температуре появляется новая моноклинная фаза (P21 / m). c отображает эволюцию нового пика пространственной группы P21 / m с температурой. d показывает изменение ширины линии XRD в присутствии нулевого магнитного поля и магнитного поля 70 кЭ и после удаления поля. e отображает типичные (100) диаграммы ED по оси зоны при комнатной температуре. Шаблон был проиндексирован с использованием ромбической структуры (Pnma). f демонстрирует изображение в светлом поле (001), записанное при 100 К во время измерений ПЭМ.Для анализа HRTEM см. Дополнительный раздел I (B)

Мы также представляем XRD-анализ при нескольких низких температурах на рис. 1b – d. При понижении температуры ниже T ≤ 120 K появляется другая кристаллографическая фаза с моноклинной симметрией P21 / m наряду с симметрией Pnma при комнатной температуре, т. Е. Комбинация Pnma и P21 / m. Развитие нового пика, соответствующего моноклинная пространственная группа P21 / m показана на рис. 1в. Этот рисунок показывает, что ниже 120 К новый пик появляется при 2θ = 47.5 °, и его интенсивность остается почти постоянной ниже 100 К. Это означает, что ниже 100 К фаза P21 / m оказывается захваченной в основной фазе Pnma, создавая деформацию решетки в основной фазе Pnma. Деформация также очевидна из анализа ПЭМ (см. Рис. 1е) при 100 К. Ранее было показано, что антиферромагнитный переход связан со структурным переходом из орторомбической в орторомбическую + моноклинную фазу при 135 К в Sm _0,5 Sr _0,5 MnO ₃ ^40,41.Следовательно, моноклинная структура благоприятствует антиферромагнитной фазе в Sm _0,5 Sr _0,5 MnO ₃. В нашем случае соединение SCSMO также претерпевает такой же структурный переход при 120 К. В следующем разделе мы покажем, что система также претерпевает антиферромагнитный переход при 120 К. Таким образом, моноклинная фаза P21 / m (показанная на рис. 1б, в) связана с фазой CE-AFM.

Влияние внешнего магнитного поля (70 кЭ) на уширение линии XRD при 2 К (см.рис.1d) указывает на уменьшение ширины линии (полная ширина на полувысоте) при 2θ = 47,5 ° с 0,58 ° до 0,46 °, которая затем остается на том же значении даже после удаления поля. Это показывает, что деформация уменьшается во внешнем магнитном поле, а затем остается неизменной даже после снятия поля.

Измерения магнитного поля и магнитотранспорта

Температурно-зависимые намагниченность и удельное сопротивление для различных приложенных магнитных полей показаны на рис. 2a, b. Интересно, что ниже 60 К намагниченность увеличивается, но доля ферромагнетика очень мала для магнитного поля 100 Э, что подтверждается измерениями термоостаточной намагниченности (обсуждаются в дополнительном разделе I (D)).В результате система без какого-либо магнитного поля остается изолирующей при низкой температуре, как показано на рис. 2b, но стабильность состояния CO-AFM снижается (обсуждается в следующем абзаце). В этом отличие от ранее исследованных нами наноструктур типа ядро-оболочка (ферромагнитное ядро и антиферромагнитная оболочка) ²², для которых сравнительно небольшое удельное сопротивление (~ 10 ² Ом-см) было получено при низких температурах. Ниже определенной температуры ( T, <10 K) значение сопротивления составляет R ~ 10 ¹³ Ом для SCSMO, что является предельным значением для наших измерительных приборов (подробности см. В разделе о методах).Температуры заказа ( T _CO и T _N) указаны на вставке рис. 2a, b, и аналогичный T _CO также получается из измерения теплоемкости (см. Дополнительный раздел I (E)).

Рис. 2: Магнитотранспортные свойства

a Изменение намагниченности с температурой во внешних магнитных полях 100 и 30 кЭ. На вставке показана подпись упорядочения CO и AFM, указанная стрелками, из температурной производной данных M (T), взятых в протоколе нагрева с полевым охлаждением (FCW) в присутствии магнитного поля 100 Э. b Температурное сопротивление без (красный) и с (30 кЭ (синий), 50 кЭ (оливковый) и 90 кЭ (фиолетовый)) внешних магнитных полей. Пунктирные линии представляют данные удельного сопротивления, полученные во время цикла охлаждения в полевых условиях, а сплошные линии представляют собой цикл FCW. На вставке показано изменение энергии активации (E _A ∞ d [ln (ρ)] / dT ⁻¹) в зависимости от температуры, вычисленное из температурной зависимости данных удельного сопротивления в нулевом поле, и указаны температуры упорядочения. стрелками. c Зависимость MR от температуры магнитного поля для различных магнитных полей. d Зависимость намагниченности от магнитного поля и e удельного сопротивления от магнитного поля при различных температурах. На вставке в d показана температурная зависимость H _CR и намагниченности с охлаждением в нулевом поле (ZFC) в магнитном поле 100 Э. f Магнитосопротивление, зависящее от магнитного поля при трех различных температурах. См. Раздел «Материалы и методы» для объяснения предела-I и предела-II, упомянутых в b и e , соответственно

Магнитное поле 30 кЭ индуцирует большую долю ферромагнетика, и, как результат, удельное сопротивление уменьшается. значительно (от 10 ¹³ Ом-см до ρ ~ 17.5 Ом-см при Тл = 2,5 К) при низких температурах (см. Рис. 2а, б). Это показывает не только то, что T _CO уменьшается, но также то, что устойчивость состояния CO-AFM снижается в SCSMO. Наблюдается огромный гистерезис между циклами полевого охлаждения и нагрева для 30 кЭ в диапазоне температур 50 K < T <100 K как на кривых намагничивания, так и на кривых сопротивления, что является признаком индуцированного полем электронного разделения фаз ⁴². При дальнейшем увеличении приложенного магнитного поля это сосуществование подавляется, и низкотемпературное сопротивление достигает 10 ⁻² Ом-см (для 90 кЭ).

Для количественной оценки изменения удельного сопротивления, вызванного полем, мы строим график зависимости MR (= ( ρ ( H) — ρ (0)) / ρ (H) × 100) от температуры при различных магнитных полях. на рис. 2в. MR составляет ~ 10% для 20 кЭ, но удивительно увеличивается до 10 ¹³% для внешнего магнитного поля 30 кЭ и до ~ 10 ¹⁵% при 10 К для магнитного поля 90 кЭ. Значение MR до 10 ¹⁵% в поликристаллическом стабильном соединении SCSMO является уникальным наблюдением.

Изотермическая намагниченность, измеренная в протоколе с охлаждением в нулевом поле (ZFC) при различных температурах (представленная на рис. 2d), показывает индуцированные полем метамагнитные переходы. Полученный экспериментально магнитный момент насыщения (3,82 мкм _B) при 30 К близок к расчетному магнитному моменту для полного насыщения ионов Mn ³⁺ / Mn ⁴⁺ и Sm ³⁺ (3,85 мкм _В). Это ясно указывает на то, что состояние CO-AFM полностью трансформируется при приложении магнитного поля через метамагнитный переход вблизи критического магнитного поля H _CR.Изменение температуры H _CR, измеренное по изотермам M (H), противоположно изменению намагниченности ZFC, как показано на вставке к рис. 2d. Компоненты FM, присутствующие в образце ZFC, действуют как центры зародышеобразования и растут за счет компонентов AFM во внешнем магнитном поле, что приводит к метамагнитному переходу на H _CR. По мере увеличения намагниченности ZFC от 2 K до 50 K повышенная тепловая энергия снижает H _CR с 47,8 кЭ при 2 K до 34,5 кЭ при 50 K.При T> 50 K H _CR увеличивается за счет уменьшения намагниченности ZFC. В отсутствие AFM-компонентов выше T _N индуцированный полем метамагнитный переход исчезает.

На рис. 2д показаны изотермы зависимости удельного сопротивления от магнитного поля, измеренные при различных температурах. Интересно, что на изотермах, измеренных при более низкой температуре (10 К), наблюдается исключительно резкий метамагнитный скачок. С повышением температуры площадь петли между увеличивающейся и убывающей разверткой поля уменьшается, а при 100 К она практически исчезает.Таким образом, мы полагаем, что индуцированное полем сосуществование фаз поддерживается до ~ 120 K, что является температурой антиферромагнитного упорядочения. Также следует отметить, что система остается в состоянии с низким удельным сопротивлением даже после снятия поля для Тл <50 К. Из-за ограничения измерения удельного сопротивления сопротивление ограничено 10 ¹⁰ Ом-см во внешнем магнитное поле, и, как результат, мы можем измерить MR только при температурах выше 25 K. MR равно 10 ¹²% (10 ⁴%) при 25 K (80 K) для магнитного поля 45 кЭ. , как показано на рис.2f, а при более низких температурах будет еще больше.

Ультрарезкий метамагнитный переход

Интересно, что изотермы зависимости сопротивления (и намагниченности) от магнитного поля (см. Рис. 3а) при 2 К показывают исключительно резкие ступеньки шириной ~ 10 Э (наименьший шаг, используемый во время измерения, составляет 3 Э). Чтобы исследовать происхождение этого сверхострого метамагнитного перехода, мы теперь измеряем теплоемкость ( C ) с помощью магнитного поля. Во время цикла увеличения поля данные по теплоемкости показывают ступенчатое поведение при ~ 48 кЭ, как показано на рис.3б, что однозначно соответствует ступенчатому поведению, наблюдаемому на изотермах намагниченности и сопротивления. Это противоположно случаю, наблюдавшемуся в более ранних исследованиях, когда C резко уменьшалось с H в точке перехода, что было связано с повышением температуры системы из-за высвобождения энергии, которая способствовала резкому индуцированному полем переходу ^36,43. Резкое увеличение теплоемкости в магнитном поле 48 кЭ исключает возможность наблюдаемого в нашей системе экзотермического лавинно-метамагнитного перехода, вызванного температурой, и мы полагаем, что система изменяется мартенситно.

Рис. 3: Ультрарезкий метамагнитный переход

a Зависимость намагниченности (и удельного сопротивления) от магнитного поля при 2 К. См. Раздел «Материалы и методы» для объяснения ограничения-II. b Изменение теплоемкости с внешним магнитным полем при 2 К. Здесь красные и синие символы представляют данные C (H), полученные при увеличении и уменьшении полей, соответственно. c Влияние на изотермическую намагниченность различных полей охлаждения при 2 K

Чтобы установить мартенситную природу, мы также исследовали изотермическую намагниченность (при 2 K) для различных полей охлаждения 9 (см. Рис.3в). С увеличением охлаждающего поля увеличивается доля FM, и, как следствие, увеличивается межфазная упругая энергия. Благодаря этому критическое поле увеличивается с увеличением поля охлаждения. В то же время критическое поле немного уменьшается, когда мы увеличиваем скорость развертки с 10 Э / сек до 200 Э / сек для образца ZFC (подробности см. В дополнительном разделе I (F)). Это связано с тем, что решетка имеет достаточно времени, чтобы приспособиться к индуцированной межфазной деформации между AF- и FM-доменами при более низкой скорости развертки, а для преодоления энергетического барьера требуется большее магнитное поле.Оба этих сценария указывают на мартенситную природу перехода ^{43,44,45,46,47}. Наше исследование релаксации сопротивления (см. Дополнительный раздел I (G)) также подтверждает мартенситный характер метамагнитных переходов (рис. 2d, e) при более высоких температурах.

Теоретическое моделирование

В этом разделе мы обсуждаем физическое происхождение огромного МС, используя двухзонную модель двойного обмена, включая сверхобмен ( J ) и электрон-фононную связь ( λ ).Наш модельный гамильтониан ^{19,48,49,50,51} (подробности см. В дополнительном разделе II), эффективно представляющий собой решетку ионов Mn, качественно воспроизводит фазовую диаграмму манганитов. Для материалов типа SCMO (и SSMO), включающих два элемента A-типа ³⁰, обычно добавляют \ (\ mathop {\ sum} \ nolimits_i {\ varepsilon _in_i} \) так, чтобы \ (\ overline {\ varepsilon _i } = 0 \) для моделирования катионного беспорядка в A-сайте ^48,51. Учитывая тот факт, что ионы Sr ²⁺ случайным образом занимают A-позиции в поликристаллическом соединении SCSMO и имеют больший размер по сравнению с Sm ³⁺ и Ca ²⁺, создается химический беспорядок.Это также очевидно из изображений HRTEM при комнатной температуре, показанных в дополнительном разделе I (B) (рис. 1b, c). Поэтому для моделирования SCSMO мы пренебрегаем беспорядком между элементами Sm и Ca и включаем беспорядок Sr, добавляя \ (\ mathop {\ sum} \ nolimits_i {\ varepsilon _in_i} \) в каждый сайт Mn, выбранный из распределения \ (P \ left ({\ varepsilon _i} \ right) = \ frac {1} {4} \ delta \ left ({\ varepsilon _i — \ Delta} \ right) + \ frac {3} {4} \ delta \ left ( {\ varepsilon _i + \ Delta} \ right) \), где Δ — потенциал тушенного беспорядка.Мы добавляем член зеемановской связи — \ (\ mathop {\ sum} \ limits_i h \ cdot {\ boldsymbol {S}} _ i \) к гамильтониану во внешнем магнитном поле, где S _i — Mn t _2g спины, чтобы проанализировать MR. Мы измеряем Дж, , λ, Δ, h и температуру ( T ) в единицах кинетического параметра прыжка t . Расчетное значение t в манганитах составляет 0,2 эВ ⁴⁸.

Спин-фермионный метод Монте-Карло, основанный на приближении бегущих кластеров ⁵², используется на двумерной решетке 24 × 24 (подробности см. В дополнительном разделе II).Мы используем J / t = 0,1 и λ / t = 1,65, что воспроизводит фазу CE-CO-OO-I ¹⁹ при электронной плотности n = 1 — x = 0,5. В наших расчетах электронная плотность — это количество перемещающихся e _g электронов на узел Mn. Система, как показано на рис. 4а, б, остается изолирующей при низких температурах для Δ / t = 0,3 и h = 0, а фактор ферромагнитной структуры S (0,0) составляет ~ 0.001 (схему расчетов удельного сопротивления и структурного магнитного фактора см. В дополнительном разделе II).

Рис.4: Результаты Монте-Карло

Температурная зависимость a удельного сопротивления ρ в единицах га / 2 _Π ² e ² и b структурный фактор FM S (0, 0) при различных значениях внешнего магнитного поля h / t для λ / t = 1,65, Дж / t = 0,1 и Δ / t = 0.3 (материалы типа SCSMO). Легенды в a , b такие же. На всех рисунках плотность электронов зафиксирована на уровне n = 0,5. c Температурная зависимость ρ для λ / t = 1,73, Дж / t = 0,105 и Δ / t = 0 (материалы типа SCMO). d Температурная зависимость структурного фактора FM S (0,0) (вставка: удельное сопротивление) для трех наборов параметров (имитирующих SCMO, SCSMO и SSMO) в очень малом магнитном поле h = 0.002. См. Подробности в тексте

Удельное сопротивление при низких температурах уменьшается с увеличением магнитного поля h (Рис. 4a), аналогично нашим экспериментальным результатам. Это связано с увеличением корреляций ФМ при низких температурах (рис. 4б). С другой стороны, SCMO-подобные материалы (рис. 4в) остаются изоляционными при всех температурах, даже в течение ч = 0,03. Напомним, что SCSMO (SSMO) имеет меньшую (большую) пропускную способность, чем SCSMO. В наших модельных расчетах больший λ / t (и J / t ) соответствует меньшей полосе пропускания или наоборот.Для наглядности мы используем Δ / t = 0 (из-за небольшого несоответствия между ионными радиусами Sm и Ca) и устанавливаем λ / t = 1,73 и Дж / t = 0,105 для SCMO- нравятся материалы. Для SSMO-подобных материалов мы устанавливаем бинарный беспорядок ^48,51 с Δ / t = 0,3 и используем λ / t = 1,57 и J / t = 0,095. Корреляции FM при низких температурах увеличиваются, а удельное сопротивление уменьшается от SCMO-подобных материалов до SCSMO-подобных материалов (рис.4г), что качественно аналогично результатам экспериментов ^30,31,32.

Теперь мы переходим к пониманию MR в SCSMO путем построения снимков Монте-Карло, полученных при T = 0,01. При h = 0.002 система остается изолирующей (см. Рис. 4d) благодаря корреляциям CE-типа без каких-либо значительных ферромагнитных зон с разупорядоченным зарядом (см. Рис. 5a, c) в системе. При h = 0,02 ферромагнитные кластеры сосуществуют с зигзагообразными ферромагнитными цепочками, а концентрация электронов примерно однородна (~ 0.65) внутри ферромагнитных кластеров (см. Рис. 5б, г). Более того, ферромагнитные кластеры в SCSMO соединяются друг с другом в достаточно больших магнитных полях, в отличие от материалов, подобных SCMO, для которых удельное сопротивление уменьшается при более низких температурах. Следовательно, в целом беспорядок из-за присутствующих в SCSMO ионов Sr ослабляет состояние SCMO типа CE и зарождает ферромагнитные зарядово-разупорядоченные кластеры, но система остается изолирующей при низких температурах. Во внешнем магнитном поле ферромагнитные кластеры растут и соединяются, вызывая большое МС в образцах SCSMO.

Рис. 5

Снимки Монте-Карло a , b Компоненты z смоделированных спинов Mn (t _2g). c , d Электронная плотность для каждого узла на решетке 24 × 24 при T = 0,01 с использованием λ / t = 1,65, Дж / t = 0,1 и Δ / t = 0,3. В a , c h / t = 0,002, а в b , d h / t = 0.02.

Большие дискретные скачки, наблюдаемые при переходе между состояниями Черна в ферромагнитном топологическом изоляторе

ВВЕДЕНИЕ

В полупроводниках, известных как топологические изоляторы (на примере Bi ₂ Se ₃, Bi ₂ Te ₃ и Bi ₂ Te ₂ Se) ( 1 — 4 ), сильное спин-орбитальное взаимодействие вместе с инверсией зон приводит к электронным поверхностным состояниям, которые демонстрируют линейную дисперсию типа Дирака.На каждой поверхности состояния Дирака имеют только одну спиновую степень свободы, причем спин заблокирован поперек импульса. Узел конуса Дирака защищен от образования зазора, если преобладает симметрия обращения времени (TRS) (это ограничивает закрепление узлов при инвариантных импульсах относительно обращения времени).

Необычные свойства поверхностных состояний Дирака интенсивно исследуются с помощью фотоэмиссионной спектроскопии с угловым разрешением, сканирующей туннельной микроскопии и транспортных экспериментов.Возникает естественный вопрос: что происходит, когда TRS нарушается из-за намагничивания поверхности? Теория утверждает, что нарушение TRS открывает разрыв в узле Дирака повсюду на поверхности (включая поверхностное «объемное» состояние, а не краевые состояния) ( 1 — 4 ). Однако остается проводящее краевое состояние, которое проходит по периметру образца. Краевое состояние является киральным (оно движется вправо или влево в зависимости от вектора намагниченности) и бездиссипативным (обратное рассеяние электронов запрещено).Как и в квантовом эффекте Холла (QHE), краевое состояние отображает сопротивление Холла, которое строго квантовано ( R _yx = h / e ², где h — постоянная Планка, а e — заряд электрона), а продольное сопротивление R _xx исчезает ( 1 — 5 ). Однако квантование R _yx происходит, даже если внешнее магнитное поле H равно 0.Это явление известно как квантовый аномальный эффект Холла (QAH). Квантование R _yx в нулевом поле было впервые экспериментально установлено Чангом и др. . ( 6 ) с использованием ультратонких пленок легированного хромом (Bi, Sb) ₂ Te ₃. Подобные результаты в родственных пленках топологических изоляторов были впоследствии получены несколькими группами ( 7 — 13 ). Топологическая природа квантования Холла создает гистерезисную петлю в R _yx, которая отражает магнитный гистерезис, когда H (приложенное магнитное поле) медленно циклически выходит за пределы коэрцитивного поля H _c.Если система подготовлена с намагничиванием M || H || — z , хиральные краевые моды приводят к R _yx = — h / e ² = −25,812 кОм. Это состояние характеризуется числом Черна C = −1. Когда H меняет знак, система становится метастабильной; для выхода из метастабильного состояния он претерпевает очень резкий переход в состояние с C = 1 и R _yx = + h / e ².Здесь мы сосредоточимся на природе этого перехода при температурах в милликельвинах T . В обычных магнитах гистерезисный переход отражает постепенное диффузионное движение доменных стенок. Удивительно, но переход на самом деле происходит большими дискретными скачками в R _yx. Мы обнаружили, что небольшое увеличение T подавляет вероятность скачка. Подробное исследование того, как вероятность скачка изменяется с H и T , предполагает, что скачки отражают события квантового туннелирования при наличии диссипации.

РЕЗУЛЬТАТЫ

Характеристика и тесты

В эксперименте использовались образцы легированного хромом (Bi, Sb) ₂ Te ₃, выращенные на подложке SrTiO ₃ методом молекулярно-лучевой эпитаксии (МБЭ) до толщиной 10 нм и разрезать на стержни Холла (0,5 мм × 1 мм) [см. материалы и методы и исследование Kandala et al. ( 11 )]. После выращивания поверхностные состояния легированы n , с химическим потенциалом, лежащим высоко над поверхностным узлом Дирака.Большое отрицательное напряжение заднего затвора В _g = -80 В требуется для понижения μ до поверхностного узла Дирака. В пределах оптимального окна затвора −120 В < В _g <−80 В (пределы номинальные; в последовательных экспериментах они изменяются на ± 10%) сопротивление Холла R _yx достигает примерно идеальное квантование при температуре T = 10 мК. Рисунок 1A показывает, что при H _c ~ 0,14 Тл, R _yx претерпевает узкие переходы между -1 и +1 с узкими пиками сопротивления R _xx ширина Δ H ~ 20 мТл (здесь и далее сопротивление указывается в единицах h / e ²).

Рис. 1 Квантование холловского сопротивления в пленке легированного хромом (Bi, Sb) толщиной 10 нм ₂ Te ₃ при милликельвиновых температурах.

( A ) Плато Холла в сопротивлении Холла R _yx при 10 мК (синие кривые). Переход между состояниями Черна в коэрцитивном поле H _c (~ 0,14 Тл) почти вертикальный. Продольное сопротивление R _xx (красные кривые) демонстрирует сверхнизкое рассеяние, за исключением резких пиков при H, _c.( B ) Тестирование стабильности состояния Черна R _yx = h / e ² в течение длительного периода (от 8 до 9 часов), с H , установленным на 0, начиная с время указано вертикальными стрелками. Две кривые при 49 мК (серая кривая) и 72 мК (зеленая) показаны смещенными для ясности. ( C ) Расширенная шкала показывает, что R _yx отклоняется от h / e ² на несколько частей в 10 ⁴ в оптимальном окне стробирования — 110 _г <- 90.( D ) Расширенная шкала показывает, что R _xx падает до <3 × 10 ⁻⁴ h / e ² около H = 0. R _xx термически активируется с зазором Δ _R ~ 190 мК.

Важный вопрос — стабильность квантованных значений R _yx = ± 1. Если намагничивание на самом деле не является спонтанным, R _yx должно расслабиться от квантованных значений, когда H возвращается в 0, тогда как истинно намагниченное основное состояние с C = ± 1 не должно показывать никаких признаков релаксация.Чтобы проверить это, мы подготовили состояние в положительном поле H || z . Затем мы вернули H → 0 и контролировали R _yx в течение 8–9 часов. Как показано на рис. 1В, мы не обнаруживаем никаких признаков релаксации при 49 и 72 мК для В _г = -80 В. Для нас это показывает, что на плато Холла система находится в истинном состоянии. основное состояние с C = ± 1. Более того, он остается стабильным в пределах H → 0 не менее 8–9 часов.

Расширенная шкала на рис. 1C показывает, что R _yx отклоняется от 1,0000 примерно на четыре части из 10 ⁴ в пределах оптимального окна стробирования. На рис. 1D в увеличенном масштабе показано поведение R _xx вдали от пиков. Примечательно, что R _xx при H = 0 падает до значений <3 × 10 ⁻⁴ при 10 мК, что соответствует сверхнизкому рассеянию. Эти показатели сопоставимы с лучшими из достигнутых на сегодняшний день ( 9 , 10 ).

Чтобы обеспечить более широкое представление о поведении при транспортировке при 10 мК, мы показываем кривые R _yx и R _xx по сравнению с H на рис. 2, с V _g, установленное на значения от 0 до -120 В. Кривые Холла R _yx (рис. 2A) остаются очень близкими к 1,0000 в оптимальном окне затвора, но начинают монотонно падать как | V _г | уменьшается, достигая 0.03, когда V _g = 0 (поверхностные состояния сильно легированы n ). На всем интервале затвора от −70 до 0 В знак носителей типа n придает пологий наклон R _yx для полей | H | > H _c. Переходя к продольному сопротивлению, мы показываем в полулогарифмическом масштабе кривые R _xx в сравнении с H для тех же значений напряжения затвора (рис.2Б). Как отмечалось выше, R _xx падает до значений 3 × 10 ⁻⁴ (в терминах h / e ²) в окне поля | H | < H _c (см. Кривую при В _g = −90 В). Небольшие узкие всплески при H = ± 10 мТл вызваны гашением сверхпроводимости в индиевых контактах (в эксперименте, в котором индий заменен золотом во всех контактах, мы обнаружили, что всплески полностью отсутствуют).Когда | H | увеличивается за пределы H _c, рассеивание увеличивается экспоненциально. Когда мы настраиваем V _g за пределы оптимального окна затвора, кривые R _xx также увеличиваются экспоненциально, в конечном итоге достигая ~ 0,2, когда V _g приближается к 0. Схема экспоненциального увеличения | в рассеивании, когда либо V _g настроено за пределы своего оптимального окна, либо | H | Увеличивается выше коэрцитивного поля, подразумевает существование небольшой энергетической щели, которая «защищает» состояние без диссипации с точно квантованным R _yx.Мы оцениваем промежуток активации ниже (см. Раздел «Активация через небольшой промежуток»).

Рис.2 Зависимости R _yx и R _xx от напряжения затвора В _g при T = 10 мК.
( A ) Следы R _yx по сравнению с H при выбранном V _g от 0 до -120 V. когда | V _г | < 40 В относятся к типу n .( B ) График R _xx для тех же значений V _g в полулогарифмическом масштабе. Небольшие аномалии при H = — 10 мТл обусловлены тушением сверхпроводимости в контактах In. Коэрцитивное поле H _c, определяемое резкими пиками в R _xx, практически не зависит от V _g.
Прыжки в
R _xx и R _yx
Основные результаты (наблюдение больших прыжков в R _xx и R _{9039 ) описаны в этом подразделе.Для каждого T подготавливаем систему с числом Черна C = −1 ( H || — z ). Чтобы исследовать переход C : -1 → 1, мы очень медленно (от 1 до 10 мТл / мин) просканируем H через H _c (слева направо на всех рисунках). Начиная с самого низкого значения T (от 10 до 50 мК), R _yx показывает номинально гладкий профиль при изменении от -1 до 1 (рис. 3A). Плавное изменение, которое имеет профиль, который не зависит от T и имеет ширину до 580 мК, вероятно, связано с обычным движением доменной стенки.}
Рис. 3 Скачки в R _yx при переходе между состояниями Черна.
( A ) Следы R _yx при выбранном T (10 → 70 мК), поскольку H медленно проходит (10 мТ / мин) за H _c, как указано стрелками. Переход между состояниями Черна C = ± 1 номинально плавный ниже 40 мК. Начиная с T ₁ ~ 65 мК, в начале перехода появляются небольшие вертикальные скачки.( B ) R _yx против H в важном интервале 70 мК ≤ T ≤ 145 мК, в котором группируются большие скачки. Начиная с 83 мК, система «выходит» из состояния C = — 1 очень большим начальным скачком, за которым следует каскад более мелких. Сосредоточившись на начальном скачке, мы видим, что поле H _J ( T ), которое запускает скачок (характеристика излома), постоянно увеличивается по мере того, как T увеличивается до 142 мК.Выше 131 мК величина скачка Δ R _yx резко уменьшается, становясь неразрешенной выше T ₂ ~ 145 мК. ( C ) От T ₂ до 580 мК, R _yx изменяется плавно в течение (теперь расширенного) перехода. ( D ) Схема изменения кривых R _yx с V _g при 10 мК. При оптимальном стробировании ( В _g = -90 В) переход плавный, но по мере увеличения В _g до -10 В скачки появляются снова, подразумевая, что для посейте прыжок по самому низкому T .Экспериментальные постоянные времени равны 1 с на всех панелях, кроме (D), где постоянная равна 5 с.
В интервале от 50 до 65 мК небольшие ступеньки предвестника становятся различимы над начальным полем H _s. При характерной температуре T ₁ ~ 65 мК наблюдается появление очень больших скачков с величиной Δ R _yx ~ 1. В интервале T ₁ → T ₂ = 145 мК, скачки имеют стохастический, но систематический характер, как показано на рис.3Б. Их возникновение не зависит от принятой скорости развертки (от 1 до 10 мТл / мин). Мы сосредотачиваемся на первом прыжке, который всегда является самым большим (из более чем 50 записанных сканирований). Когда T поднимается выше T ₁, его величина Δ R _yx сначала увеличивается (кривые при 83 → 131 мК). Выше 138 мК Δ R _yx быстро уменьшается и становится неразрешенной. Как показано на фиг. 3C, все кривые выше T ₂ гладкие и лишены скачков.Хотя скачки не наблюдаются при 10 мК в состоянии сверхнизкого рассеяния, они снова появляются, когда мы настраиваем V _g для выхода из оптимального окна. На рис. 3D, R _yx при -90 В является плавным, но скачки появляются, когда V _g поднимается выше -40 В. Скачки воспроизводимо наблюдаются даже после многократного нагревания до 300 К. Они отличаются от скачков намагниченности, наблюдаемых в манганитах ниже 4,7 К (когда заряженные изолирующие области сосуществуют с ферромагнитными областями) ( 14 ).Скачки в манганитах появляются при характеристических полях, которые почти не зависят от T , хотя они сильно чувствительны к условиям охлаждения поля. Прыжки здесь качественно разные.
Скачки также заметны в диссипативном канале (кривые R _xx). При низком T (от 10 до 50 мК) R _xx демонстрирует номинально гладкий асимметричный профиль (рис. 4A). Выше T ₁ большие скачки появляются на переднем (левом) крае, тогда как задний край остается плавным при увеличении ширины до 38 мТл.Рисунок 4B следует этим кривым выше T ₂ до 216 мК.
Рис. 4 Профили сопротивления R _xx по сравнению с H при выбранном T , поскольку H медленно перемещается со скоростью 1 мТ / мин (стрелки).
( A ) Ниже 50 мК профиль номинально гладкий и асимметричный, тогда как небольшие вертикальные скачки появляются около передней кромки, когда T поднимается выше T ₁. ( B ) В интервале 83 → 216 мК гладкий профиль рассечен большими скачками Δ R _xx, которые положительны (вверх) у передней кромки и отрицательны у задней кромки.Выше T ₂ профиль снова гладкий, но в два раза шире, чем при 10 мК. ( C ) Мы строим график распределения начальной величины скачка Δ R _yx по сравнению с T в пределах оптимального окна стробирования. Выше T ₁, Δ R _yx сначала возрастает до значения ~ h / e ², а затем резко падает до 0 при T ₂. Скачки выше T ₂ не разрешаются.На вставке схематично изображена система (красный кружок), захваченная потенциалом U ( M ). ( D ) Поле выхода H _J ( T ) график начального прыжка в сравнении с T (сплошные символы), полученным из R _yx и R _xx как с подметанием, так и с подметанием. Ниже T ₁, H _J ( T ) заканчивается кривой H _s ( T ) (начальное поле для небольших ступеней предвестников, изображенных в виде открытых треугольников), который имеет тот же наклон, что и коэрцитивное поле H _c ( T ) (белые кружки). H _c определяется максимумом в R _xx (когда кривая плавная). H _c не определено между 100 мК и T ₂, но плавно распространяется на измерения выше T ₂.
Как отмечено для R _yx, поле выхода H _J ( T ) начального прыжка увеличивается с T . Однако в окне от 125 до 138 мК скачки теперь имеют противоположные знаки (положительные на переднем фронте).Скачки, наблюдаемые в R _yx и R _xx, очень похожи, когда H перемещается в противоположном направлении (рис. S2 и S3).
На рис. 4 (C и D) показано, как две важные величины (величина скачка и начальное поле) изменяются с T . Как уже отмечалось, величина скачка ΔR _yx изначально мала в пределах интервала предвестника, но быстро увеличивается при T ₁ до насыщения при значении плато ~ 1 (рис.4С). Поскольку T дополнительно поднимается выше T ₂, Δ R _yx сжимается до значения ниже нашего разрешения. Выше T ₂ (до 500 мК) кривые Холла плавно меняются по всей петле гистерезиса. В отличие от немонотонности Δ R _yx ( T ), поле убегания H _J ( T ) резко увеличивается от T ₁ до T ₂ (сплошные символы на рис.4D). Интересно, что H _J все еще растет с крутым наклоном, когда величина скачка падает ниже разрешения выше T ₂. Для сравнения мы также построим график плавного уменьшения H _c и H _s (открытые символы) на том же интервале T (полученный из кривых на рис. S4).
Пространственные корреляции
Интересный способ изучения скачков — одновременные измерения R _ij на хорошо разделенных парах контактов напряжения.Сопротивление R _{ij, mn} определяется как V _mn/ I _ij, где V _mn — напряжение, измеренное на контактах ( m , n ) с током I _ij, введенным в контакт с источником i и опущенным при j (см. вставку на рис. 5A). Типичная картина состоит в том, что скачок R _yx, измеренный на одной паре контактов, практически не влияет на сигнал на другой паре, но при немного большем H имеет место обратное.
Рис. 5 Скачки в R _yx (вверху) и R _xx (внизу), обнаруженные одновременными измерениями R _{14, mn}, как обозначено [ I , приложенное к контактам (1, 4) и напряжение, измеренное на ( м, n )].
Скорость развертки поля 1 т / мин. ( A и B ) Как при 105 мК (A), так и при 120 мК (B) начальный скачок сильно влияет на сигнал Холла ниже по потоку ( R _14,53), но почти не меняет восходящую пару ( R _14,62).Однако при втором скачке пара вверх по потоку сильно возмущается. На вставке в (A) показаны контакты и стенка, разделяющая состояние Черна C = — 1 (зеленый) от +1 (желтый) после первого скачка. ( C и D ) В сопротивлении (нижний ряд) первый прыжок увеличивает R _14,23, но уменьшает R _14,65 как при 105 мК (C), так и при 120 мК ( D). Знаки в обеих парах меняются местами при втором прыжке, что также соответствует движению стены вверх по потоку.
На рисунке 5 (A и B) показаны следы R _14,53 и R _14,62 по сравнению с H при T = 105 и 120 мК соответственно. На обеих панелях начальный скачок (при H, = 0,129 Тл) велик по паре Холла ниже по потоку ( 3 , 5 ), тогда как пара Холла выше по потоку ( 2 , 6 ) практически не затронута . При большем H (0,133 Тл) второй скачок заметен в паре выше по потоку, но намного меньше в паре ниже по потоку.При этом сопротивление R _14,23 в правой паре ( 2 , 3 ) сначала увеличивается, а затем уменьшается, а в левой паре ( 5 , 6 ) R _14,65 показывает обратную последовательность (рис. 5, C и D).
Несмотря на стохастическую природу скачков, общая картина систематична и воспроизводима, особенно для первых двух скачков в следе. На рис. 6 мы построили четыре последовательных сканирования трасс, сделанных последовательно, с T , установленным на 86 мК, и V _g = -80 В.Образец готовится таким же образом при каждом сканировании с фиксированной скоростью развертки 1 мТл / мин. На рисунке 6А показаны холловские сопротивления (кривые блеска для восходящей пары и жирные кривые для нисходящей пары). На рис. 6Б показаны соответствующие кривые продольного сопротивления (жирные кривые для левой пары и кривые блеска для правой пары). Первые два скачка воспроизводимы, хотя величины скачка и H _J могут отличаться на 10%. Показанные здесь изменения от одного скачка к другому типичны для воспроизводимости во всем исследованном диапазоне температур (от 10 до 580 мК).
Рис.6 Четыре кривой сопротивлений R _{14, mn}, измеренные последовательно при 86 мК с V _g = -80 В.
Для каждой кривой образец готовится в C = −1, и переход вызывается медленным перемещением H через H _c со скоростью 1 мТл / мин при мониторинге сопротивлений R _{14, mn}. ( A ) Холловское сопротивление выше по потоку R _14,26 (кривые блеска) и ниже по потоку сопротивление Холла R _14,53 (жирный шрифт).( B ) Соответствующие продольные левые контактные сопротивления R _14,65 (жирные кривые) и правые контактные сопротивления R _14,23 (светлые) графики. Хотя скачки являются стохастическими, общая картина первых двух скачков достаточно воспроизводима от одного запуска к другому.
Насколько быстрые прыжки? Чтобы свести к минимуму посторонние возмущения, все кривые, показанные выше, были сняты при очень низкой скорости развертки поля (обычно 1 мТл / мин). Мы попытались оценить длительность первого скачка Δ t , минимизируя емкостную нагрузку в измерительной схеме в холодильнике разбавления.Для этого мы последовательно удалили несколько каскадов фильтрующих элементов в схеме (что увеличивало шум на трассах), замедляя сканирование поля до 0,1 мТл / мин. Окончательная кривая в этом процессе измеряется только при наличии низкотемпературного фильтра. Зашумленный график (рис. 7) показывает, что Δ t короче 1 мс, постоянной времени оставшегося фильтра.
Рис.7 График времени скачка, наблюдаемого в R _xx, измеренный с удаленными фильтрами комнатной температуры в контуре (но не низкотемпературными фильтрами) при T = 117 мК и V _g = −85 В.
Скачок происходит в масштабе времени Δ t , который короче 1 мс, постоянной времени оставшегося фильтра. Скорость развертки поля составляла 0,1 мТл / мин. а.е., условные единицы.
Активация через небольшой промежуток
Расширяя измерения в широком диапазоне В, , _г, и T, , мы обнаруживаем, что состояние сверхнизкого рассеяния защищено мини-зазором Δ _R ~ 190 мК. Установка В _g в пределах оптимального окна стробирования (от −110 до −75 В) помещает μ внутри Δ _R (эти числа могут сдвигаться на 10% между запусками из-за захвата заряда на границе раздела).Как только μ выходит из мини-щели, рассеивание возрастает экспоненциально.
На рисунке 8A показаны изменения в R _yx и R _xx как V _g изменяется от -120 до 0 В, с T , фиксированным на 10 мК и H зафиксировано на ~ 0 T (сплошные треугольники) или 1 T (сплошные круги). Кривые Холла (красный и пурпурный символы) показывают, что при | V _г | уменьшается, R _yx остается близким к квантовому значению h / e ² (оптимальное окно стробирования) до тех пор, пока | V _г | уменьшается ниже 70 В в нулевом поле.После этого R _yx экспоненциально уменьшается до 0,03 при V _g → 0. [Нижний предел оптимального окна (-70 В на рис. 8A) меняется от цикла к запуску из-за гистерезиса, вызванного захватом заряда в подложке SrTiO ₃.] Сопротивление R _xx при H = 0 (синие треугольники) экспоненциально возрастает с более низким порогом, чем R _yx. Конечное поле (1 Тл; черные кружки) значительно снижает порог.Мы идентифицируем экспоненциальные изменения в R _yx и R _xx с увеличением μ выше верхнего предела зазора Δ _R путем стробирования.
Рис. 8 Зависимость напряжения затвора R _xx и R _yx и активационный зазор при различных магнитных полях.
( A ) Полугодовой график R _yx и R _xx как функция от V _g, с T , фиксированным при 10 мK и H фиксированным при 0 T (закрашенные треугольники) или 1 T (закрашенные кружки).As | V _г | уменьшается, экспоненциальное увеличение R _xx (синие и черные символы) означает, что μ поднимается над мини-щелью Δ _R. Сравнение R _xx при H = 0 T (синий) и 1 T (черный) показывает, что конечный H уменьшает Δ _R. Аналогично, кривые для R _yx (красный и пурпурный) показывают экспоненциальное отклонение от квантового значения h / e ² as | V _g | уменьшается.Кривые Холла сохраняются дольше при квантованном значении, чем кривые сопротивления. ( B ) Полулогарифмический график σ _xx в сравнении с 1 / T с V _г = -80 В показывает активированную проводимость как при H, = 0,5 Тл, так и при 33 мТл. Прямая линия соответствует значениям Δ _R ~ 190 мК (при H ≈ 0) и 155 мК (0,5 Тл).
Величина мини-щели Δ _R определяется путем подробного измерения проводимости σ _xx по сравнению с T .Из полулогарифмического графика σ _xx по сравнению с 1/ T на рис. 8B, мы заключаем, что Δ _R ~ 190 мК для H = 33 мТл (черные квадраты). При 0,5 Тл эквивалентный график дает немного меньшее значение Δ _R (155 мК), что соответствует более крутому увеличению кривой с черными символами на фиг. 8A. Оба графика показывают, что мини-щель заметно уменьшается с увеличением H . Это также согласуется с постепенным увеличением рассеяния фона, обсуждаемым в связи с рис.2Б.
Изменения кривых переноса, вызванные изменением V _g или T , предоставляют твердое свидетельство того, что состояние сверхнизкого рассеяния в состоянии QAH защищено мини-щелью Δ _R ~ 190 мК. Экспоненциальное увеличение рассеяния наблюдается, когда T увеличивается или когда мы выводим μ из оптимального окна с помощью стробирования. Размер зазора также уменьшается за счет увеличения H сверх 0,5 T. Постепенное увеличение фона с H вместе с отрицательным наклоном R _yx за пределами окна коэрцитивного поля предполагает, что популяция балкеров ( n -типа) постепенно увеличивается на H , когда μ выходит за пределы оптимального окна.Для обобщения результатов схематически построим поведение кривых Δ _R, T ₁ и T ₂ в плоскости V _g — T (рис.9). .
Рис.9 Границы кроссовера в плоскости ( V _g, T ) (A) и график масштабирования σ _xx по сравнению с σ _xx (B).
(A) Оптимальное окно стробирования находится слева от вертикальной пунктирной линии (-120 В _g <- 80 В).Зазор сопротивления Δ _R, который защищает состояние сверхнизкого рассеяния (ULD), равен ~ 190 мК в этом окне, но быстро падает за пределы окна. В заштрихованной области выше Δ _R система является рассеивающей (более темный оттенок указывает на больший R _xx). Скачки в R _xx и R _yx наблюдаются между двумя характеристическими температурами T ₁ и T ₂.Кривая T ₁ круто спадает за окном. В области сверхмалой диссипации ниже T ₁ скачки не наблюдаются на наших экспериментальных временных масштабах. (B) График масштабирования описывает почти идеальный полукруг выше T ₂ (кривые при 142 и 152 мК). В интервале ( T ₁, T ₂) появление скачков отбрасывает орбиты высоко над полукругом. Это означает нарушение двухпараметрического масштабного поведения (38).
ОБСУЖДЕНИЕ
Метастабильность и эффект
T
Изменение направления H от направления подготовки системы ( H || — z ) захватывает систему в метастабильном состоянии (вращение ↓) до тех пор, пока не произойдет побег вблизи коэрцитивного поля. Мы исследовали природу перехода в магнитном топологическом изоляторе при милликельвиновых температурах. В обычном ферромагнетике выход из метастабильного состояния соответствует постепенному движению доменных стенок, разделяющих домены вверх и вниз, что позволяет домену со спином ↑ расширяться.Это приводит к знакомой гладкой гистерезисной петле M — H . Однако здесь переход, который включает в себя как изменение числа Черна ( C = −1 → 1), так и среднее значение M , отображает богатый набор дополнительных функций, в первую очередь большие скачки в R _yx и R _xx в интервале T ₁ < T < T ₂ (рис.3 и 4). Скачки происходят на временах короче 1 мс. Первый скачок включает разворот M примерно на половине выборки. (Как уже упоминалось, мы идентифицируем плавное независимое от T изменение R _yx выше T ₂ с обычным перемещением доменной стенки. Ниже T ₂ плавное изменение сохраняется как фоновый канал между скачками.)
В двух недавних исследованиях ( 12 , 13 ) перехода C = −1 → 1 вариация R _yx намного шире, чем наблюдаемые здесь.Вместо скачков в R _yx наблюдается плечо при C = 0 (особенность нулевой холловской проводимости). По сравнению с настоящим образцом (толщина 10 нм) используемые образцы находятся в пределе ультратонких [5 нм в исследовании Kou et al. ( 12 ) и 6 нм в исследовании Feng et al. ( 13 )], где ожидается гибридизация между состояниями на двух поверхностях. Как наличие плеча с нулевым холлом, так и отсутствие скачков предполагают, что эти ультратонкие образцы находятся в совершенно другом режиме QAH-поведения по сравнению с настоящим образцом.Степень беспорядка оказывается выше в ультратонком режиме. Например, в образце с нулевым холлом ( 13 ) диссипация остается высокой при 50 мК ( R _xx ~ 4 при H = 0), тогда как точное квантование Холла не достигается ( R _yx ~ 0,9).
Мы начнем с применения стандартной теории зародышеобразования Кана-Хилларда к расширению пузыря истинного основного состояния (↑) внутри образца в метастабильном состоянии (↓).Свободная энергия двумерного (2D) пузырька радиуса R равна (1) где Δ F > 0 — это прирост свободной энергии в объеме пузырька. Поверхностное натяжение σ, которое выражает стоимость стены, пропорционально обменной энергии. Когда R превышает критический радиус R _c = σ / Δ F , пузырек расширяется без ограничений (если диссипация отсутствует), с радостью оплачивая стоимость стены, чтобы получить объемную энергию. И наоборот, если R < R _c, пузырек сжимается до 0.На критическом радиусе F _b имеет критическое значение F _b ^c = πσ ² / Δ F . Для чисто классического (термически активированного) процесса ухода время жизни метастабильного состояния равно (2) где 1 / τ ₀ — частота попыток. Ясно, что если σ и Δ F оба являются T -независимыми (что, как мы утверждаем, имеет место здесь при всех T <0,5 K), время жизни метастабильного состояния уменьшается экспоненциально с увеличением T .
Захват системы в метастабильном состоянии можно представить как частицу, расположенную в потенциальной яме U ( M ), где M — коллективная координата, представляющая локальную намагниченность M ( r ) (см. эскиз на рис. 4С, вставка). После подготовки системы с H || — z при температуре T ~ 100 мК, он остается в ловушке очень долгое время, если H настроен на положительное, но небольшое значение 0 < H < H _s ( T ) (~ 0.122 Тл при 70 мК). Как показано на фиг. 1B, стабильность для H = 0 превышает 8 часов при 10 мК. Увеличение H выше H _s приводит к понижению барьера и уменьшению t _E. Когда H равно H _J ( T ), мы заключаем, что t _E ( T ) попадает в временное окно наблюдения (от 1 до 3 минут), поэтому первый прыжок наблюдается. Измеряя, как H _J ( T ) изменяется с T , мы можем вывести влияние T на скорость эвакуации.
Кривая H _J ( T ) (рис. 4D) показывает, что H _J резко увеличивается с T . Эта тенденция противоречит здравому смыслу, если рассматривать побег как классический процесс. В таких процессах «через барьер» подъем T неизменно ускоряет эвакуацию. В общем, в формулировке Лангера ( 15 ) побег происходит, когда конкретная конфигурация вращения создает седловую точку в потенциальном ландшафте U ( M ( r )), которая пробивает барьер.Поскольку вероятность этого возрастает экспоненциально с T , повышение T должно привести к резкому снижению на t _E (и, следовательно, к меньшему H _J). Это противоположно наблюдаемой тенденции H _J ( T ). Вопреки общему ожиданию того, что «побег» должен стать легче, поскольку большее количество конфигураций вращения становится доступным при более высоких T , мы находим, что побег труднее.
Далее мы рассматриваем гибридный классический квантовый процесс, в котором ускользание происходит в результате термически поддерживаемого туннелирования.Поглощение бозонов (фононов или спиновых волн) из ванны приближает энергию системы к вершине барьера, тем самым увеличивая скорость туннелирования. Очевидно, что повышение T увеличивает фононную или спин-волновую популяцию, что приводит к увеличению скорости ускользания, что снова противоречит H _J ( T ).
Диссипативное квантовое туннелирование
Одним из способов получить скорость ухода, которая увеличивается с уменьшением T , является диссипативное квантовое туннелирование.Здесь важную роль играет рассеивание, отслеживаемое с помощью R _xx.
Квантовое туннелирование конфигурации намагниченности из метастабильного состояния тесно связано с распадом ложного вакуума, исследованным Коулманом ( 16 , 17 ) и Калланом и Коулманом ( 16 , 17 ). Посредством инстантонного процесса (см. Раздел S3) система туннелирует «под барьером», чтобы сформировать небольшой пузырек истинного основного состояния.После этого пузырь быстро неограниченно расширяется (если диссипация отсутствует) в классическом процессе Кана-Хилларда.
Чтобы учесть диссипацию, Калдейра и Леггетт ( 18 , 19 ) рассмотрели одиночную частицу массой м в наклонном двухъямном потенциале U ( q ) с динамикой, описываемой классическим уравнением Диссипация — вносимая линейной связью со многими классическими осцилляторами — проявляется как коэффициент затухания η (ω), который может зависеть от частоты ω.Они обнаружили, что увеличение диссипации сильно снижает вероятность туннелирования Γ. Фактически, каждый выбор (измерение) положения частицы осциллятором коллапсирует ее волновую функцию; это сбрасывает процесс туннелирования. В то время как η само по себе уменьшает Γ, повышение T дает противоположный эффект ( 20 ). Противоположные эффекты диссипации и T были исследованы экспериментально ( 21 ).
В пределах оптимального окна стробирования в нашем эксперименте, R _xx термически активируется с энергетической щелью Δ _R.Следовательно, рассеивание увеличивается быстрее, чем T (в 17 раз по сравнению с 4 в диапазоне от 50 до 200 мК). Мы считаем, что Γ должно уменьшаться в соответствии с наблюдаемой тенденцией в H _J.
При очень низком T изменения, вызванные увеличением η, конкурируют с чисто статистическими эффектами из-за T . Следуя Граберту и др. . ( 20 ), скорость туннелирования Γ ( T , η) при низком уровне T может быть выражена как (3) где B (η, 0) — показатель степени, зависящий от η при T = 0 .Коэффициент, зависящий от T , равен A ( T, η) = f (η) T ² (для омического рассеяния). Хотя аналитическое выражение для B (η, 0) неизвестно, численное интегрирование ( 22 ) показывает, что при очень большом η значение B (η, 0) асимптотически линейно по η, но приближается к константа при η → 0. Поскольку они аддитивны и имеют противоположные знаки, B (η, 0) и A ( T, η) конкурируют в показателе степени Γ ( T , η).К сожалению, теория дает лишь ограниченное представление об их относительной величине. Мы считаем, что при низких T и малых η A ( T, η) очень мало по сравнению с B (η, 0) [Grabert et al. ( 20 ) показывают, что A ( T, η) экспоненциально обращается в нуль как exp (- ħ ω ₀/ k _B T ) в пределе η → 0, где ω ₀ — характерная частота в минимуме скважины].Следовательно, B (η, 0) доминирует над показателем степени в Γ ( T , η), то есть Γ ( T , η) является общей убывающей функцией η с пренебрежимо малой зависимостью от T ( за исключением того, что повышение T в нашей ситуации приводит к экспоненциальному увеличению η). Когда мы увеличиваем T между T ₁ и T ₂, мы ожидаем, что Γ ( T , η) будет уменьшаться в соответствии с тенденцией в H _J ( T ) .Тесты макроскопического квантового туннелирования проводились в экспериментах с джозефсоновскими переходами ( 21 , 23 , 24 ), молекулярными магнитами ( 25 — 27 ) и динамикой доменных стенок ( 28 — ). 30 ).
Новой особенностью настоящего эксперимента является то, что величина скачка Δ R _yx и его пространственная корреляция также предоставляют информацию о быстром расширении стенки, которое происходит после туннелирования.Поскольку рассеяние отвлекает часть выигрыша в энергии, большое рассеяние сильно ограничит конечный размер пузырька, чрезмерно демпфируя расширение ( 31 , 32 ). Для нас это дает убедительное объяснение поведения Δ R _yx ( T ), наблюдаемого выше 120 мК (рис. 4C). Величина Δ R _yx обеспечивает меру размера областей с раскруткой вверх после расширения, соответствующего первому скачку.В интервале 80 мК < T <120 мК расширение истинного основного состояния распространяется примерно на половину образца. Когда T поднимается выше 120 мК, рассеивание все больше ограничивает расширение. Выше T ₂ конечный радиус (измеряемый размером скачка) оказывается ниже разрешения. Даже если туннелирование сохраняется (как следует из продолжающегося увеличения H _J около T ₂), последние пузырьки слишком малы, чтобы их можно было обнаружить с помощью R _yx.Повышение T в этом интервале открывает диссипативный канал, который резко ограничивает размер истинных пузырей основного состояния. [Поскольку активационная щель, защищающая квантованное состояние, аналогична по величине (Δ _R ~ 190 мК; активация участка через небольшой промежуток), мы предполагаем, что объемные электроны являются источником рассеяния, ограничивающего расширение стенки.]
Выше T ₂, плавные изменения R _yx по сравнению с H (рис.3C) подразумевают постепенное увеличение доменов с раскруткой вверх, связанных с движением доменной стенки, как в обычных магнитах. Во всех исследованных T эта плавная эволюция присутствует как фоновый процесс, существующий параллельно с интересующими скачками.
При более низком T главная разгадка заключается в неуклонном уменьшении Δ R _yx до очень малых шагов, когда T уменьшается ниже 70 до 10 мК для V _g = −80 V (рис.3B и 4C). Немонотонный профиль Δ R _yx по сравнению с T означает, что второй процесс, который подавляет скорость туннелирования, становится все более важным при очень низком T . Подчеркнем, что это подавление ограничено состоянием сверхмалого рассеяния (область -120 < В _g <-80 В на рис. 9). Как только диссипация активируется стробированием, скачки снова появляются при 10 мК. Как показано на рис. 3D, кривая при V _g = -90 V не показывает скачков, тогда как скачки снова появляются на кривых, когда V _g изменяется на (-40, -10) V ( все кривые при 10 мК).
Поучительно рассмотреть этот узор на плоскости V _g — T (рис. 9). Повторное появление скачков для V _g> -40 V означает, что граница T ₁ быстро уменьшается с 70 до <10 мК, как только V _g покидает оптимальное окно стробирования. Следовательно, большой зазор Δ _R (который сильно подавляет активацию навалочных судов) способствует большему T ₁, тогда как небольшой Δ _R снижает T ₁ до уровня ниже 10 мК.Схема подразумевает, что отсутствие скачков ниже T ₁ присуще состоянию сверхнизкого рассеяния.
Наблюдение позволяет предположить следующую (предварительную) картину. Поскольку нулевая диссипация приводит к резкому увеличению корреляционной длины ξ спинов в пределе T → 0, мы полагаем, что скорость туннелирования Γ снова будет подавлена, если N _s (количество спинов, которые туннелируют когерентно) увеличивается до макроскопических значений (например, размера всего образца).В приближении Вентцеля-Крамерса-Бриллюэна (ВКБ), где Γ ~ exp (- B / ħ ) с q в качестве коллективной координаты, большой N _s или большая масса m приводит к сильному подавлению Γ .
Когда μ находится внутри мини-щели, объемные электроны становятся незначительными в пределе T → 0, так что ξ распространяется на макроскопические области и Γ становится очень малым. Увеличение рассеивания путем изменения В _g на (-40, -10) В служит для уменьшения размера когерентной области.Следовательно, скачки могут появиться снова при 10 мК. Хотя этот аргумент является умозрительным, эксперимент потенциально предоставляет способ измерить ξ и его влияние на Γ в пределе T → 0.
Зарождение в сверхтекучем гелии
Другой известный пример, в котором скорость выхода увеличивается с уменьшением T является метастабильной фазой A сверхтекучей жидкости ³ He, полученной переохлаждением ниже перехода AB . Если ³ He охлаждается из нормального состояния в сверхтекучее при конечном давлении P (скажем, 30 бар), он сначала претерпевает переход второго рода в анизотропную фазу A при критической температуре ( Т _c ~ 2.3 мК). При несколько меньшем значении T (~ 2 мК) происходит переход первого рода в изотропную фазу B . Из-за природы перехода AB первого рода фаза A является метастабильной как переохлажденная жидкость, пока она не достигнет ~ 0,7 T _c при ~ 1,4 мК, когда пузырьки фазы B расширяются до заполнить весь образец.
Теория Кана-Хиллиарда (уравнение 1) предсказывает, что в 3D R _c = 2σ _AB / Δ F и F _b ^c = (2π / 3) R ³ Δ F , где σ _AB — поверхностное натяжение, а F _B — энергия конденсации фазы B .Используя известные величины, можно рассчитать, что F _b ^c будет чрезвычайно большим (10 ⁶ → 10 ⁷ k _B T при 0,7 T _c). Прогнозируемое время жизни фазы A τ _A должно во много раз превышать возраст Вселенной. Наблюдаемая температура нуклеации представляла собой глубокую загадку, пока Леггетт не предложил теорию (получившую название «запеченная Аляска») ( 33 ), согласно которой нуклеация запускается космическими лучами.Сильно стохастический и часто невоспроизводимый характер процесса зародышеобразования затруднял экспериментальные испытания. Впоследствии было показано, что τ _A уменьшается в 10–100 раз, если сверхтекучая жидкость подвергается воздействию гамма-излучения от источника ⁶⁰ Co, что является убедительным подтверждением теории космических лучей ( 34 ). Экспериментально наблюдается резкое уменьшение τ _A ( T ) с уменьшением T с эмпирической формой τ _A ~ exp ( a ( R _c/ R ₀) ⁿ), с n = от 3 до 5 ( a и R ₀ — подходящие параметры).
Несмотря на сходство тенденции срока службы с T , эти два эксперимента сильно различаются. В ³ He чрезвычайно большой барьер F _b ^c исключает термическую активацию в качестве важного фактора при 1 мК. Зависимость τ _A от T возникает из-за того, что в окрестности кривой T _c критическое расхождение σ _AB ( T ) приводит к расходящемуся увеличению R . _c (следовательно, из F _b ^c), поскольку T приближается к T _c снизу.Основным эффектом уменьшения T является сильное уменьшение высоты барьера F _b ^c. Ясно, что это зависит от близости к кривой перехода второго рода T _c (чтобы иметь сильно T -зависимый R _c). Кроме того, нам нужен промежуточный переход первого рода ( AB ), чтобы произошло переохлаждение.
В системе QAH обширные измерения R _ij по сравнению с H и T [сообщенные здесь и в предыдущих исследованиях ( 6 — 10 )] не обнаружили никаких доказательств термодинамических фазовых переходов. (первого или второго порядка) ниже 4 К (критическая температура ферромагнитного перехода находится в диапазоне от 15 до 30 К).Высота барьера в метастабильном состоянии (которая зависит от H _c и обменной энергии) контролируется H , но по существу не зависит от T ниже 0,5 К. Поскольку ручка ( H ) изменяется высота барьера не зависит от ручки, которая управляет рассеиванием ( T ), мы можем сделать вывод, что наблюдаемая тенденция H _J ( T ) отражает влияние рассеивания на скорость утечки. Обе причины убеждают нас, что теория переохлаждения ³ He здесь неприменима.
Множественные пути и модель сети
Характер корреляции между холловскими сигналами, наблюдаемый через пары холловских контактов, разделенных на 100 мкм (или более), предполагает, что скачки сильно нарушают картину намагничивания. В качестве иллюстрации мы начнем с одностенной модели, которая позволяет рассчитать R _{14; mn} для предполагаемых положений стены с использованием формализма Бюттикера (см. Раздел S4). Мы подсчитали, что пара Холла ниже по потоку R _{14; 53} претерпевает скачок, но не выше по потоку R _{14; 62} (рис.S5). R _{14; 23} подпрыгивает вверх, а R _{14; 65} прыгает вниз, в соответствии с рис.5 (C и D). Далее мы предполагаем, что стенка еще больше смещается, чтобы лежать между парой ( 2 , 6 ) и контактом 1 при втором прыжке. Рассчитанная пара Холла вверх по потоку претерпевает скачок, и пары сопротивлений теперь меняют направление скачка в соответствии с наблюдениями. Однако одностенная модель во многом неадекватна. Самая большая трудность заключается в том, что предсказанные скачки Δ R _yx всегда равны 2 (в единицах h / e ²), тогда как наблюдаемые величины примерно равны 1 или намного меньше.Этот недостаток, по-видимому, является неотъемлемой частью предположения об одной стене.
Мы обобщаем на многодоменную картину, в которой туннелирование начинается с множества начальных значений, распределенных по выборке. Естественной отправной точкой является тесно связанный переход плато в обычном целочисленном QHE (IQHE), которому уделяется значительное внимание (см. Раздел S5) ( 35 — 37 ). При изменении H химический потенциал μ пересекает центр уровня Ландау, расширенный потенциалом беспорядка V ( x ).Ток отводится от краевых мод без диссипации к очень небольшому подмножеству расширенных, но диссипативных объемных состояний в центре зоны (удаленные состояния локализованы по Андерсону). В балке центры циклотронных орбит описывают киральные траектории, которые отслеживают энергетические контуры V ( x ). Туннелирование происходит между сближающимися киральными траекториями (это приводит к рассеянию). Следовательно, переход R _yx с одного холловского плато на другое происходит одновременно с появлением диссипации (конечное σ _xx).
Сетевая модель, изученная Чалкером и соавторами (раздел S5) ( 35 , 36 ), обеспечивает элегантный способ обработки протекания тока по многосвязным путям. Образец моделируется как регулярная решетка из петель с разделением углов, определяемых направленными связями. В общих углах (узлах) входящие токи рассеиваются к одному из двух исходящих звеньев с амплитудами, параметризованными с помощью β (уравнения S10 и S11 в секции S5). Они обнаружили, что длина локализации ξ (β) расходится как | β — β _c | ^ν, при ν = 2.5, где β = β _c при максимальном рассеивании (где σ _xx пики).
Для перехода Черна в проблеме QAH (уравнение S13 в разделе S5), Ван и др. . ( 38 ) установили существование трех типов доменов с числом Черна C = 0, ± 1. Отождествление доменных границ числа Черна с контурами энергии в задаче IQHE, Ван и др. . сопоставьте переход Черна с сетевой моделью Чалкера и его коллег и получите расхождение по ξ с тем же показателем ν.Ван и др. . сделайте вывод, что σ _ij подчиняется двухпараметрическому соотношению масштабирования ( 39 ). Доказательства этого масштабирования в задаче QAH были получены путем построения графика зависимости σ _xx от σ _xy вблизи перехода числа Черна ( 7 , 8 ). Доказательства состояния QAH ν = 0 также были представлены Йошими и др. . ( 40 ).
Мы обсуждаем наши результаты в этом контексте.Непосредственно перед первым скачком в R _yx образец находится преимущественно в состоянии C = −1 (потому что R _xx является конечным и очень маленькими, небольшими областями с C = 0 существует). После первого скачка, который включает (по предположению) расширение из нескольких семян, распределенных по образцу, области C = 0 определяют многосвязную сеть проводящих путей, которые проходят по ширине образца.Наблюдение, что Δ R _yx близко к 1 (но никогда не 2), подсказывает нам, что преобразованные области имеют C = 0 [это обеспечивает поддержку трехдоменного предложения Wang et al. ( 38 )]. В этой сети связь между киральными модами опосредуется туннелированием в узлах, как в сетевой модели (микроскопическое туннелирование между киральными модами, возникающее в узлах, следует отличать от макроскопического квантового туннелирования, запускающего скачки).В объемной проводимости преобладают несколько магистральных путей (как в перколяционных сетях), которые проходят по ширине образца, давая Δ R _yx ~ 1. Мы ожидаем внезапного появления сети областей с C . = 0, чтобы сильно отклонить систему от двухпараметрического масштабного поведения. Это подтверждается интересным образом.
На рис. 9B мы показываем графики зависимости σ _xx от σ _xy при выбранном T для V _g, фиксированном при -80 В (в пределах оптимального окна стробирования).Выше T ₂ (кривые при 142 и 152 мК) измеренные значения σ _ij очерчивают почти идеальный полукруг (купол). В пределах интервала ( T ₁, T ₂) первый и последующие прыжки поднимают орбиту высоко над куполом — орбита возвращается только тогда, когда переход почти завершен (σ _xy → e ²/ h ). Примечательной закономерностью является то, что возмущенные орбиты простираются над куполом (исключение составляет небольшая полоса внутри купола для сегментов перед скачком при T <100 мК).Этот богатый шаблон предполагает, что поведение двухпараметрического масштабирования допустимо выше T ₂, но ниже T ₂, скачки уносят систему высоко над масштабным куполом.
Хотя двухпараметрическое масштабирование не может использоваться для получения σ _xy при возникновении скачков, кажется возможным вычислить σ _xy и σ _xx численно из больших сетей, как это выполнено для ξ Чалкер и его коллеги ( 35 , 36 ).Расчеты, уточняющие условия, при которых Δ R _yx меньше единицы, добавят ценную информацию о том, что происходит при прыжках.
Перспективы и выводы
Центральными обнаруженными особенностями являются большие скачки холловского сопротивления величиной ΔR _yx ~ h / e ² и R _xx когда система QAH находится в метастабильном состоянии с C = -1, в интервале T ₁ < T < T ₂.Ключевой вывод заключается в том, что скорость ухода резко снижается по мере увеличения T . Из термической активации R _xx мы сделали вывод, что увеличение рассеяния подавляет любой чисто тепловой эффект, связанный с увеличением T ; тогда повышенная диссипация подавляет вероятность туннелирования Γ. Следовательно, теория Кальдейры-Леггетта кажется наиболее привлекательным объяснением скачков.
Поскольку переходы включают туннелирование поля ϕ ( x , t ) со многими степенями свободы (в отличие от одной коллективной степени свободы), настоящий эксперимент обнаруживает дополнительные особенности, которые требуют дальнейшего исследования.Наиболее интересным представляется существование шкалы температур T ₁, ниже которой скачки не наблюдаются в пределах экспериментальной шкалы времени, что мы предварительно идентифицируем как еще один эффект диссипации. Как показано на рис. 9, состояние сверхнизкого рассеяния защищено небольшой энергетической щелью Δ _R от теплового возбуждения объемных электронов. Последний открывает диссипативный канал, который сильно влияет на процесс туннелирования. Выше T ₂ диссипация сильно ограничивает расширение пузыря после туннелирования.
Недавнее исследование намагниченности близких по размеру QAH-пленок при сканировании нанокварами при T вплоть до 300 мК ( 41 ) не обнаружило расширения пузырьков, соответствующих нашим прыжкам. Однако 300 мК вдвое превышают наш предел T ₂ для разрешения скачков. Расширение экспериментов с кальмарами до значений ниже 100 мК (где ΔR _yx ~ 1) позволит визуализировать макроскопические пузыри, соответствующие областям, преобразованным первым скачком в R _xy .Мы ожидаем, что статический размер областей с раскруткой вверх будет быстро увеличиваться до макроскопических длин (100 мкм) по мере того, как T снижается с T ₂ до 100 мК. Недавно был опубликован родственный эксперимент, показывающий совпадение суперпарамагнетизма и квантования в проблеме QAH ( 42 ). Исследование корреляций между скачками можно расширить до большого числа (~ 20) контактов, чтобы получить более подробную карту пространственного смещения стенки.
Роль диссипации в макроскопическом квантовом туннелировании (например, при определении N _s) остается проблемой как для теории, так и для эксперимента. Система QAH, в которой химический потенциал, диссипация, напряженность поля и температура могут изменяться независимо, представляет собой мощную систему для количественного исследования этих проблем.
Благодарности: Мы благодарим D. Goldhaber-Gordon, J. Wang, Y. Wang и S.-C. Чжан за ценные обсуждения. Финансирование: Мы выражаем признательность за поддержку со стороны Агентства перспективных оборонных исследовательских проектов / Космические и морские войны (N66001-11-1-4110) и награду Многопрофильной университетской исследовательской инициативы за топологические изоляторы (ARO W911NF-12-1-0461). N.P.O. благодарит за поддержку инициативы EPiQS Фонда Гордона и Бетти Мур в рамках гранта GBMF4539. Вклад авторов: M.L., N.S., A.Y. и N.P.O. разработал эксперимент. A.R.R. и Н.С. выросли образцы. M.L., W.W. и A.К. проводил измерения. M.L., W.W., J.L., A.Y. и N.P.O. провели анализ и моделирование результатов. М.Л. и N.P.O. написал рукопись при участии всех авторов. Конкурирующие интересы: Авторы заявляют, что у них нет конкурирующих интересов. Доступность данных и материалов: Необработанные данные для кривых на всех рисунках доступны в корреспонденции Dryad Correspondence, а запросы на материалы следует направлять к M.L. (minhaol {at} princeton.edu) и N.P.O.(npo {at} princeton.edu).
Отображение сопротивления датчика края сверхпроводящего перехода в зависимости от температуры, тока и приложенного магнитного поля
J Appl Phys. Авторская рукопись; доступно в PMC 2019 июля 29.
Опубликован в окончательной редакции как:
PMCID: PMC6662222
NIHMSID: NIHMS1031959
Shuo Zhang
¹ Физический факультет Университета Мэдисона, Университет Висконс , WI 53706, США
Меган Э.Эккарт
² НАСА Годдард, Центр космических полетов, Гринбелт, Мэриленд, 20771, США
Феликс Т. Джекель
¹ Физический факультет Университета Висконсин-Мэдисон 1150 Юниверсити-авеню, Мэдисон, Висконсин 53706, США
Кари Л. Криппс
¹ Физический факультет Университета Висконсин-Мэдисон 1150 University Avenue, Madison, WI 53706, USA
Dan McCammon
¹ Физический факультет Университета Висконсин-Мэдисон 1150 University Avenue, Madison , WI 53706, США
Келси М.Морган
¹ Физический факультет Университета Висконсин-Мэдисон 1150 University Avenue, Madison, WI 53706, USA
³ Национальный институт стандартов и технологий, Боулдер, CO 80305, США
Yu Zhou
¹ Физический факультет Университета Висконсин-Мэдисон 1150 University Avenue, Madison, WI 53706, USA
¹ Физический факультет, University of Wisconsin-Madison 1150 University Avenue, Madison, WI 53706, USA
² NASA Goddard, Центр космических полетов, Гринбелт, Мэриленд, 20771, США
³ Национальный институт стандартов и технологий, Боулдер, Колорадо 80305, США
Аннотация
Мы измерили сопротивление R ( T, I , B _ext) сверхпроводящего краевого датчика перехода по всей переходной области в мелком масштабе, создавая 4-мерную карту поверхности сопротивления.В каждой точке определены безразмерные температурная и токовая чувствительность (α≡∂logR / ∂logT | I и β≡∂logR / ∂logI | T) сопротивления ТЭС. α и β тесно связаны с характеристиками датчика, но демонстрируют большую сложную тонкую структуру с большой амплитудой на больших участках поверхности, которая чувствительна к приложенному магнитному полю. Мы обсуждаем связь этой структуры с наличием джозефсоновских полос «слабого звена».
Ключевые слова: TES, эффект слабой связи, сверхпроводящий переход
I.ВВЕДЕНИЕ
Детекторы, использующие сверхпроводящие датчики температуры, которые работают в переходной области, оказались весьма успешными в диапазоне мягкого рентгеновского излучения, продемонстрировав энергетическое разрешение до 100 раз лучше, чем это теоретически возможно с кремниевым ионизационным детектором. Однако предсказуемость новых конструкций и единообразие для больших массивов — постоянная проблема. ¹⁸ «Чрезмерный шум» в дополнение к ожидаемому шуму Джонсона часто наблюдается, особенно когда температурная чувствительность сопротивления датчика высока — в противном случае желательная цель.¹⁷ В наиболее эффективных датчиках обычно используются структуры, такие как обычные металлические «полоски зебры», основанные на эмпирических доказательствах улучшенных характеристик. ¹⁹, но причина улучшенных характеристик плохо изучена. В настоящее время нет полной модели поведения TES в переходной области, и поэтому пока невозможно рассчитать теоретические пределы производительности этих датчиков. ^1,7,14
Мы разрабатываем микрокалориметры большой площади (1 мм ²) с датчиками переходной кромки для изучения 0.1 — 1 кэВ диффузный рентгеновский фон. ¹² Большие пиксели необходимы для достижения требуемой общей области сбора с разумным количеством детекторов. Энергетическое разрешение идеального микрокалориметра с резистивным термометром приблизительно определяется выражением:
ΔEFWHM≈7kBT2C1 + 2βα,
(1)
где T и C — температура и теплоемкость детектора, а α и β — безразмерные чувствительности к температуре и току.^5,11 Для достижения требуемого разрешения <2 эВ с относительно высокой теплоемкостью C , связанной с этими большими поглотителями, нам нужен ТЭС с высокой температурной чувствительностью ( α ), низкой чувствительностью по току ( β ) и небольшой лишний шум. ^1,10
Выражение 1 предполагает оптимизированное значение теплопроводности между датчиком и подложкой G (которое зависит от мощности смещения TES в выбранной рабочей точке) и отсутствие избыточного шума.Член 1 + 2β объясняет увеличение первого порядка шума Джонсона из-за текущей зависимости сопротивления датчика. ⁴ В этом приближении одним из показателей энергетического разрешения TES в конкретной рабочей точке является высокое значение k≡α / 1 + 2β. Измеряя α и β над сверхпроводящим переходом в мелком масштабе, мы можем дополнительно исследовать корреляцию между этими величинами и увидеть, как они связаны с рабочей точкой, включая магнитное поле.Наша цель проектирования имеет более простую задачу оптимизации, чем большинство приложений TES с мягким рентгеновским излучением. Для массивов маленьких пикселей, которые покрывают диапазон энергий до 10 кэВ, требуется хорошо настроенный путь Δ T , который покрывает значительную часть резистивного перехода. Наши низкие значения энергии, представляющие интерес, и относительно высокая теплоемкость наших больших пикселей делают температурные отклонения небольшими, поэтому важны только значения локальной производной. Таким образом, нам нужно только найти локальную «золотую середину» в пространстве параметров операции TES.
II. УСТРОЙСТВО И ЦЕПЬ
Двухслойные устройства TES из Mo / Au, испытанные в этой статье, были изготовлены в Центре космических полетов имени Годдарда НАСА (GSFC). Двухслойный датчик имеет размер 140 мкм м × 140 мкм м и состоит из 50 нм Mo, покрытого 260 нм Au, что снижает температуру перехода в нулевой ток T _{c ₀} примерно с 900 мК до 105 мК из-за эффекта близости, и в результате получается нормальное сопротивление R _N = 11,2 мОм.Золотые банки толщиной 350 нм добавляются по обоим краям параллельно потоку тока, чтобы избежать сверхпроводящих коротких замыканий по краям, а три чередующихся золотых «зебровых полосы» одинаковой толщины отходят от банков перпендикулярно току, как показано на. Контактные электроды и электрические выводы изготовлены из ниобия 150 нм. ^2,6 Эти устройства обычно термически изолированы мембраной из нитрида кремния толщиной ~ 1 мкм, толщиной м, но для минимизации источников изменчивости в этом исследовании мы выбрали тестовое устройство с нитридом непосредственно на кремниевой подложке.Это дает устройству высокую теплопроводность по отношению к подложке G≈5,8 нВт / К при 100 мК. Схема смещения для TES также показана на рис. TES смещается с помощью нагрузочного резистора R _L, который мал по сравнению с нормальным сопротивлением TES, обеспечивая приблизительно постоянное смещение напряжения, за исключением нижней части перехода. Все соединения в контуре от нагрузочного резистора через входную катушку TES и SQUID и обратно являются сверхпроводящими.
слева: Устройство датчика ТЭС; справа: цепь смещения TES с нагрузочным резистором R _L = 260 мк Ом
Испытательный бокс TES экранирован с помощью 0.Свинцовая фольга толщиной 5 мм, окруженная девятью слоями металлического стекла толщиной 0,025 мм. Внешнее магнитное поле B _ext может быть приложено перпендикулярно к TES с помощью 60-витковой катушки NbTi. Поле как функция I _{катушки} моделировалось с учетом внешнего сверхпроводящего экрана, поскольку индуцированные токи значительно подавляют поле на детекторах.
III. ЭФФЕКТ СЛАБЫХ СВЯЗЕЙ
Хорошо известно, что TES могут проявлять эффекты слабых связей, которые становятся более выраженными при уменьшении размера TES.^3,14,15,20 Влияние этого на α и β было тщательно изучено Смитом и др., Которые качественно сопоставили свои данные с помощью модели резистивно-шунтированного перехода (RSJ) на TES. устройство аналогичного конструкции и размера с протестированными нами. ¹⁷ Наш TES показывает аналогичное поведение, но хуже соответствует модели RSJ.
показывает кривые I _TES и B _ext при разных температурах TES и постоянном смещении I для двух устройств с одинаковой геометрией на одной и той же пластине.После охлаждения от комнатной температуры в экранировании всегда остается некоторый остаточный захваченный поток, который приводит к B -полям при TES величиной 1 или 2 μ T. Это не изменяется в течение продолжительности цикла и составляет почти то же самое для соседних устройств, поэтому, по-видимому, оно довольно постоянное для отдельного TES. Его значение определяется эмпирически путем регулировки тока в катушке возбуждения для максимизации критической температуры нулевого тока TES, и эта точка определяется как B _ext = 0.Самые холодные следы плоские сверху, потому что ТЭС являются сверхпроводящими в низких полях для этих температур и токов. Оба устройства показывают небольшие полосы на трассах I и B _ext, которые, по нашему мнению, связаны с эффектами интерференции слабых звеньев. Смещение их положения с увеличением тока могло быть связано с добавлением собственного поля на B _ext. Для этого потребуется, чтобы текущее распределение изменилось с большими изменениями в B _ext, поскольку наклон текущего эффекта меняет знак.Возможно, более вероятно, что изменение распределения тока увеличивает эффективную площадь слабого звена по мере увеличения тока, делая его более чувствительным к полю обеих полярностей. В любом случае это подтверждает вывод Смита и др. О том, что распределение тока должно изменяться с температурой в устройствах со сложной геометрией.
I _TES vs B _ext кривые при разных температурах TES для двух устройств с одной пластины с одинаковой геометрией. I _{смещение} = 120 μ A для обоих. Базовая температура находится в диапазоне от 99,5 до 104,5 мК (слева) и от 100 до 106 мК (справа) с шагом 0,2 мК. Пунктирными линиями показано линейное смещение положения полос с увеличением тока TES
Устройство слева имеет систематически более высокое сопротивление, чем то, что справа, при любой заданной температуре, но все небольшие неровности в узоре полос по существу идентичны. (мы не понимаем разницы между устройствами при | Bext |> 3μT, где пропали полосы).Последующие данные, показанные в этом документе, относятся к устройству слева.
IV.
R ( T, I, B _ext) MAPPING
Базовая температура ( T _base), внешнее магнитное поле ( B _ext) и ток смещения ( I _{смещение}) — это три параметра, которыми можно управлять напрямую. Используя значение текущего I в TES, измеренное SQUID, мы можем затем вычислить V _TES, R _TES, P _TES и T _TES, для которые мы впредь используем V , R , P и T .
Используемая процедура заключалась в том, чтобы зафиксировать B _ext и просканировать I _{смещение} треугольной волной с периодом 2 с при нарастании T _base при 5,0 μ К / с. Сначала мы определили теплопроводность от TES к подложке G ( T ) из набора точек с тем же R , выбрав R в верхней части перехода, где у него почти нет I. -зависимость. ⁸ Таким образом, эти точки имеют постоянную величину T _TES, и зависимость мощности TES от T _base может использоваться для определения G ( T ).Этот G ( T ) использовался для расчета температуры TES T для каждой точки на кривых IV путем интегрирования рассеиваемой мощности, деленной на G ( T ) от известной температуры подложки до T _TES, в результате получается плотно измеренная поверхность T ( I, V ), как показано на. Это было повторено для различных значений B _ext с шагом ~ 0,05 μ T. Выполнение набора сканирований при ~ 1000 базовых температурах потребовало 33 минут для каждого значения B _ext.
слева: TES IV кривые для температур TES в диапазоне от 94 до 104 мК при B _ext = 0,05 μ T. справа: Расширенный вид
V. РАСЧЕТ
α И β ИЗ THE IV КРИВЫЕ
Температурная и токовая чувствительность сопротивления TES определяется:
α≡TR∂R∂T | I≈ΔRR / ΔTT | I, и
(2)
β≡IR∂R∂I | T≈ΔRR / ΔII | T.
(3)
Поскольку log R = log V — log I , Δ R / R можно выразить как Δ V / V — Δ I / I в уравнении.3 и
β можно рассчитать непосредственно по кривым IV с поправкой на температуру. Для I = константа, Δ R / R = Δ V / V и
α = ΔRR / ΔTT | I = TV / ΔTΔV | I.
(5)
Чтобы вычислить β , мы находим наклон Δ I / Δ V вдоль линии равных температур, при необходимости интерполируя между ближайшими доступными точками данных. Для расчета α мы можем взять T ( V ) при константе I , найти его наклон △ T / △ V | I в каждой точке V , а затем вычислить α из уравнения.5 с использованием обратной величины наклона.
VI. ОБСУЖДЕНИЕ
Карты α , β и наш номинальный показатель качества k≡α / 1 + 2β показаны как функции от V _TES и I _TES слева функции P _TES и R _TES с правой стороны. Эти данные были взяты на B _ext = 0,05 μ T. показаны те же карты на B _ext = –3.05 μ T. Хотя кривые IV выглядят довольно гладкими, небольшие колебания, возникающие из-за зависимости от тока положения полос, наблюдаемых на, создают большие отклонения и тонкую структуру в производных. Шум при измерениях IV очень мал, поэтому обширная структура, наблюдаемая в α и β , является стабильной и воспроизводимой, за исключением некоторых областей в больших V , где есть грубая нестабильность на кривых IV .
abc: Значения безразмерной чувствительности TES к температуре и току α и β и добротность k (цветные полосы) в зависимости от V _TES и I _TES для фиксированного B _ext = 0,05 μ T; d.e.f .: то же, что и a-c, но как функции P _TES и R _TES. Обратите внимание, что мощность точки смещения менее ~ 0,5 пВт требует непрактично низкой теплопроводности и больших постоянных времени.
То же, что и B _ext = — 3.05 μ T
VII. ЗАКЛЮЧЕНИЕ
Мы создали 4-мерные поверхности сверхпроводящего перехода Mo / Au TES и показали различные величины в виде разрезов при постоянном B _ext. Это разумно, поскольку обычно не изменяют намеренно B _ext. Однако Smith et al. показали, как полосы, подобные тем, которые видны на кривой I vs B , могут создавать большие разрывы в производных α и β при движении вверх по поверхности сопротивления с постоянным B _ext и I. _{смещение}.¹⁷ Они проиллюстрировали источник этого эффекта графиками a и β vs B _ext. Наши данные показывают k≡α / 1 + 2β как функцию от B _ext и I _bias для наших данных TES при двух разных температурах. Амплитуда и узость деталей на этих графиках согласуются с результатами Smith et al. Некоторые из наших устройств с очень похожими конструкциями TES показали гораздо большие полосы на кривых I-B и, вероятно, будут иметь еще более непредсказуемые значения α и β при наличии небольших вариаций в B _ext.Эта чувствительность к небольшим изменениям в общем поле означает, что значительные отклонения в производительности могут быть вызваны небольшими изменениями свойств материала или свинцового покрытия в массивах, незначительными конструктивными изменениями, которые изменяют распределение тока и собственные поля, или градиентами в паразитных внешних полях, которые варьироваться от запуска к запуску. ^13,16
Показатель качества k≡α / 1 + 2β по сравнению с B _ext при постоянной T. слева: T = 101,5 мК; справа: T = 103 мК
Нашим следующим шагом будет расширение этих измерений на большее количество устройств, чтобы увидеть, похоже ли основное поведение, хотя, очевидно, мы не можем ожидать, что детали останутся такими же.Нам также необходимо будет получить спектры шума в различных рабочих точках, поскольку наша добротность предполагает, что нет лишнего шума, кроме нелинейного шума Джонсона первого порядка, обязательно связанного с конечным значением β . ⁴ Широко известно, что избыточный шум коррелирует с желательными высокими рабочими точками α , но менее ясно, насколько это связано с сильной корреляцией α-β . Мы можем сопоставить избыточный шум с α / 1 + 2β, чтобы увидеть, действительно ли это полезный показатель качества.
Мы также попробуем взять наши данные I-V при амплитудной модуляции тока смещения на нескольких частотах, следуя методу, разработанному Lindeman et al. ^8,9 Это позволит непрерывно получать измерения проводимости A ( w ) в каждой рабочей точке. Результаты должны позволить нам получить α и β напрямую (отдельно определенный G ( T ) требуется для α ) без необходимости брать разности для получения производных.Затем мы сравним эти значения со значениями, полученными для поверхности T ( I , V , B _ext) с использованием метода, описанного в этой статье. Если мы сможем стабильно воспроизводить эти результаты, это устранит необходимость в такой плотной выборке, что позволит быстрее отображать устройства и облегчить исследование конструкций, которые могут иметь более выгодные рабочие точки.
VIII. БЛАГОДАРНОСТИ
Джеймс Червенак, Эдвард Васселл, Дженнетт Матео и Кэролайн Килбурн сыграли важную роль в разработке и изготовлении устройств, испытанных здесь.Мы благодарим двух анонимных рецензентов за их внимательное чтение и многие предложения, которые значительно улучшили статью. Мы благодарим НАСА за поддержку гранта NNX13Ah31G.
Ссылки
1. Беннет Дуглас А., Шмидт Даниэль Р., Свец Даниэль С. и Уллом Джоэл Н. Линии фазового сдвига как механизм сопротивления в датчиках с переходной кромкой. Applied Physics Letters, 104 (4), 2014. [Google Scholar] 2. Финкбайнер FM, Брекоски Р.П., Червенак Дж.А., Фигероа-Фелисиано Э., Ли М.Дж., Линдеман М.А., Стале К.К., Стале К.М. и Тралшавала Н.Изготовление массивов микрокалориметров TES с плотной упаковкой с использованием сверхпроводящих датчиков переходного края молибден / золото. Материалы конференции AIP, 605 (1): 215–218, 2002. [Google Scholar] 3. Готтарди Л., Козорезов А., Акамацу Х., ван дер Куур Дж., Брейн М. П., ден Хартог Р. Х., Хеймеринг Р., Хосропана П., Ламберт С., ван дер Линден А. Дж., Риддер М. Л., Сузуки Т. и Гао Дж. Эффекты Джозефсона в датчике края перехода со смещением переменного тока. Applied Physics Letters, 105 (16), 2014. [Google Scholar] 4. Ирвин К.Д.Термодинамика нелинейных болометров вблизи равновесия. Ядерные инструменты и методы в физических исследованиях Секция A: Ускорители, спектрометры, детекторы и связанное с ними оборудование, 559 (2): 718–720, 2006. Материалы 11-го международного семинара по низкотемпературным детекторам, LTD-11 11-го международного семинара по низкотемпературным детекторам. [Google Scholar] 5. Ирвин К.Д. и Хилтон Г.К. Обнаружение криогенных частиц, глава «Датчики переходного края», страницы 63–150. Springer Berlin Heidelberg, Берлин, Гейдельберг, 2005 г.[Google Scholar] 6. Iyomoto N, Bandler SR, Brekosky RP, Brown AD, Chervenak JA, Finkbeiner FM, Kelley RL, Kilbourne CA, Porter FS, Sadleir JE, Smith SJ и Figueroa-Feliciano E. микрокалориметры с высоким спектральным разрешением при 5.9кв. Applied Physics Letters, 92 (1), 2008. [Google Scholar] 7. Козорезов А., Голубов А.А., Мартин Д.Д., де Корте PAJ, Линдеман М.А., Хеймеринг Р.А., ван дер Куур Дж., Ховерс Х.Ф.С., Готтарди Л., Ю. М. Куприянов и Дж. К. Вигмор. Моделирование резистивного состояния в датчике переходной кромки.Applied Physics Letters, 99 (6), 2011. [Google Scholar] 8. Линдеман М.А., Баргер К.А., Брандл Д.Е., Краудер С.Г., Рокс Л. и Маккаммон Д. Точные измерения теплопроводности и импеданса датчиков края перехода. Journal of Low Temperature Physics, 151 (1): 180–184, 2008. [Google Scholar] 9. Lindeman MA, Barger KA, Brandl DE, Crowder SG, Rocks L, McCammon D и Hoevers HFC. Сверхпроводящий переход в 4-D: температура, ток, сопротивление и теплоемкость. Журнал физики низких температур, 151 (1): 190–194, 2008.[Google Scholar] 10. Линдеман Марк А., Бендлер Саймон, Брекоски Регис П., Червенак Джеймс А., Энектали Фигероа-Фелисиано Фред М. Финкбайнер, Ли Мэри Дж. И Килбурн Кэролайн А. Измерения импеданса и моделирование калориметра с переходным датчиком границы . Review of Scientific Instruments, 75 (5): 1283–1289, 2004. [Google Scholar] 11. Маккаммон Д. Криогенное обнаружение частиц, глава Тепловые равновесные калориметры — Введение, страницы 1–34. Springer Berlin Heidelberg, Берлин, Гейдельберг, 2005 г.[Google Scholar] 12. Morgan KM, Busch SE, Eckart ME, Kilbourne CA и McCammon D. Рентгеновские микрокалориметры с краевым датчиком перехода с большой площадью для исследований диффузного рентгеновского фона. Journal of Low Temperature Physics, 176 (3): 331–336, 2014. [Google Scholar] 13. Sadleir JE, Smith SJ, Bandler SR, Adams JS, Busch SE, Eckart ME, Chervenak JA, Kelley RL, Kilbourne CA, Porter FS, Porst JP и Clem JR. Сверхпроводящие краевые датчики с магнитной настройкой. Протоколы IEEE по прикладной сверхпроводимости, 23 (3): 2101405–2101405, июнь 2013.[Google Scholar] 14. Сэдлэйр Джон Э., Смит Стивен Дж., Бэндлер Саймон Р., Червенак Джеймс А. и Клем Джон Р. Эффекты продольной близости в сверхпроводящих датчиках на границе перехода. Phys. Rev. Lett., 104: 047003, январь 2010. [PubMed] [Google Scholar] 15. Сэдлэйр Джон Э., Смит Стивен Дж., Робинсон Ян К., Финкбейнер Фред М., Червенак Джеймс А., Бэндлер Саймон Р., Эккарт Меган Э. и Килбурн Кэролайн А. Эффекты близости и неравновесная сверхпроводимость на краю перехода датчики. Phys.Ред. B, 84: 184502, ноябрь 2011. [Google Scholar] 16. Smith SJ, Adams JS, Bandler SR, Busch SE, Chervenak JA, Eckart ME, Finkbeiner FM, Kelley RL, Kilbourne CA, Lee SJ, Porst JP, Porter FS и Sadleir JE. Характеристика датчиков переходной кромки Mo / Au с различными геометрическими конфигурациями. Journal of Low Temperature Physics, 176 (3): 356–362, 2014. [Google Scholar] 17. Смит Стивен Дж., Адамс Джозеф С., Бейли Кэтрин Н., Бэндлер Саймон Р., Буш Сара Э., Червенак Джеймс А., Эккарт Меган Э., Финкбайнер Фред М., Килбурн Кэролайн А., Келли Ричард Л., Ли Санг-Джун, Порст Ян-Патрик, Портер Фредерик С. и Сэдлэйр Джон Э. Влияние поведения слабых звеньев на производительность Mo / Au двухслойные датчики переходной кромки. Журнал прикладной физики, 114 (7), 2013. [Google Scholar] 18. Смит Стивен Дж., Адамс Джозеф С., Бэндлер Саймон Р., Бетанкур-Мартинес Габриэле, Червенак Джеймс А., Эккарт Меган Э., Финкбайнер Фред М., Келли Ричард Л., Килбурн Кэролайн А., Ли Санг-Джун, Портер Ф.Скотт, Сэдлэйр Джон Э. и Вассел Эдвард Дж. Единообразие массивов килопикселей датчиков переходного края для рентгеновской астрономии. IEEE Transactions по прикладной сверхпроводимости, 25 (3–1): 1–5, 2015. [Google Scholar] 19. Уллом Дж. Н., Дориэза В. Б., Хилтон Дж. К., Билл Дж. А., Дайкер С., Дункан В. Д., Феррейра Л., Ирвин К. Д., Рейнтсема С. Д. и Вейл Л. Р.. Определение характеристик и снижение необъяснимого шума в сверхпроводящих датчиках на границе перехода. Applied Physics Letters, 84 (21): 4206–4208, 2004. [Google Scholar] 20. Джоэл Н Уллом и Дуглас Беннетт.Обзор сверхпроводящих датчиков края перехода для рентгеновской и гамма-спектроскопии. Superconductor Science and Technology, 28 (8): 084003, 2015. [Google Scholar]
Наблюдаются большие дискретные скачки при переходе между состояниями Черна в ферромагнитном топологическом изоляторе — Penn State
TY — JOUR
T1 — Наблюдаются большие дискретные скачки при переходе между состояниями Черна в ферромагнитном топологическом изоляторе
AU — Liu, Minhao
AU — Wang, Wudi
AU — Richardella, Anthony R.
AU — Kandala, Abhinav
AU — Li, Jian
AU — Yazdani, Ali
AU — Samarth, Nitin
AU — Phuan Ong, N.
N1 — Информация о финансировании: Мы благодарим D. Goldhaber-Gordon, J. Wang, Y. Wang и S.-C. Чжан за ценные обсуждения. Финансирование: мы благодарим за поддержку Агентство перспективных оборонных исследовательских проектов / Космические и морские войны (N66001-11-1-4110) и награду Многопрофильной университетской исследовательской инициативы за топологические изоляторы (ARO W911NF-12-1-0461).N.P.O. благодарит за поддержку инициативы EPiQS Фонда Гордона и Бетти Мур в рамках гранта GBMF4539. Вклад авторов: M.L., N.S., A.Y. и N.P.O. разработал эксперимент. A.R.R. и Н.С. выросли образцы. M.L., W.W. и A.K. выполнил измерения. M.L., W.W., J.L., A.Y. и N.P.O. провели анализ и моделирование результатов. М.Л. и N.P.O. написал рукопись при участии всех авторов. Конкурирующие интересы: авторы заявляют, что у них нет конкурирующих интересов.Доступность данных и материалов: исходные данные для кривых на всех рисунках доступны в Dryad Correspondence, а запросы на материалы следует направлять к M.L. ([email protected]) и N.P.O. ([email protected]). Авторские права издателя: © 2016 Авторы.
PY — 2016
Y1 — 2016
N2 — Поразительным предсказанием топологических изоляторов является появление квантованного холловского сопротивления при намагничивании поверхностных состояний. Поверхностные дираковские состояния повсюду на поверхности становятся пустыми, но киральные краевые состояния остаются на краях.В приложенном токе краевые состояния создают квантованное сопротивление Холла, равное числу Черна C = ± 1 (в натуральных единицах), даже в нулевом магнитном поле. Этот квантовый аномальный эффект Холла наблюдали Чанг и др. При изменении направления магнитного поля система оказывается в метастабильном состоянии из-за магнитной анизотропии. Исследуем, как система выходит из метастабильного состояния при низких температурах (от 10 до 200 мК). Когда диссипация (измеряемая по продольному сопротивлению) сверхнизкая, мы обнаруживаем, что система ускользает, делая несколько очень быстрых переходов, что обнаруживается по большим скачкам холловского и продольного сопротивлений.Используя поле, при котором происходит начальный скачок, для оценки скорости убегания, мы обнаруживаем, что повышение температуры сильно подавляет скорость. Из подробной карты зависимости сопротивления от напряжения затвора и температуры, мы показываем, что рассеяние сильно влияет на скорость утечки. Мы сравниваем наблюдения с предсказаниями диссипативного квантового туннелирования. В режиме сверхмалой диссипации существуют две температурные шкалы (T1 ∼ 70 мК и T2 ∼ 145 мК), между которыми могут наблюдаться скачки. Скачки показывают пространственную корреляцию, которая распространяется на большую часть выборки.
AB — Поразительным предсказанием топологических изоляторов является появление квантованного холловского сопротивления при намагничивании поверхностных состояний. Поверхностные дираковские состояния повсюду на поверхности становятся пустыми, но киральные краевые состояния остаются на краях. В приложенном токе краевые состояния создают квантованное сопротивление Холла, равное числу Черна C = ± 1 (в натуральных единицах), даже в нулевом магнитном поле. Этот квантовый аномальный эффект Холла наблюдали Чанг и др. При изменении направления магнитного поля система оказывается в метастабильном состоянии из-за магнитной анизотропии.Исследуем, как система выходит из метастабильного состояния при низких температурах (от 10 до 200 мК). Когда диссипация (измеряемая по продольному сопротивлению) сверхнизкая, мы обнаруживаем, что система ускользает, делая несколько очень быстрых переходов, что обнаруживается по большим скачкам холловского и продольного сопротивлений. Используя поле, при котором происходит начальный скачок, для оценки скорости убегания, мы обнаруживаем, что повышение температуры сильно подавляет скорость. Из подробной карты зависимости сопротивления от напряжения затвора и температуры, мы показываем, что рассеяние сильно влияет на скорость утечки.Мы сравниваем наблюдения с предсказаниями диссипативного квантового туннелирования. В режиме сверхмалой диссипации существуют две температурные шкалы (T1 ∼ 70 мК и T2 ∼ 145 мК), между которыми могут наблюдаться скачки. Скачки показывают пространственную корреляцию, которая распространяется на большую часть выборки.
UR — http://www.scopus.com/inward/record.url?scp=85019457933&partnerID=8YFLogxK
UR — http://www.scopus.com/inward/citedby.url?scp=85019457933&partnerID=8YFLog
У2 — 10.1126 / sciadv.1600167
DO — 10.1126 / sciadv.1600167
M3 — Статья
C2 — 27482539
AN — ОБЛАСТЬ ПРИМЕНЕНИЯ: 85019457933
VL — 2
JO — Science Advances SN — 2375-2548
IS — 7
M1 — e1600167
ER —
% PDF-1.3 % 482 0 объект > эндобдж xref 482 84 0000000016 00000 н. 0000002031 00000 н. 0000002131 00000 п. 0000002604 00000 н. 0000002906 00000 н. 0000003402 00000 н. 0000003424 00000 н. 0000004085 00000 н. 0000004108 00000 п. 0000005665 00000 н. 0000005688 00000 п. 0000005958 00000 н. 0000007062 00000 н. 0000008538 00000 н. 0000008561 00000 п. 0000010007 00000 п. 0000010030 00000 п. 0000011609 00000 п. 0000011632 00000 п. 0000013145 00000 п. 0000013168 00000 п. 0000013452 00000 п. 0000015124 00000 п. 0000015147 00000 п. 0000015168 00000 п. 0000016592 00000 п. 0000016614 00000 п. 0000017260 00000 п. 0000017282 00000 п. 0000018023 00000 п. 0000018046 00000 п. 0000020034 00000 п. 0000020056 00000 п. 0000021201 00000 п. 0000021224 00000 п. 0000024801 00000 п. 0000024824 00000 п. 0000029399 00000 н. 0000029422 00000 н. 0000032836 00000 п. 0000032859 00000 п. 0000037539 00000 п. 0000037562 00000 п. 0000041274 00000 п. 0000041297 00000 п. 0000045589 00000 п. 0000045612 00000 п. 0000049294 00000 п. 0000049317 00000 п. 0000053713 00000 п. 0000053736 00000 п. 0000057534 00000 п. 0000057557 00000 п. 0000061555 00000 п. 0000061577 00000 п. 0000062600 00000 п. 0000062622 00000 п. 0000063085 00000 п. 0000063108 00000 п. 0000066634 00000 п. 0000066657 00000 п. 0000071713 00000 п. 0000071736 00000 п. 0000076930 00000 п. 0000076953 00000 п. 0000081965 00000 п. 0000081988 00000 п. 0000086522 00000 п. 0000086545 00000 п. 00000 00000 п. 00000
00000 п. 0000094856 00000 п. 0000094879 00000 п. 0000098579 00000 п. 0000098602 00000 п. 0000102206 00000 н. 0000102229 00000 н. 0000107290 00000 н. 0000107313 00000 п. 0000108801 00000 п. 0000108822 00000 н. 0000109149 00000 п. 0000002195 00000 н. 0000002582 00000 н. трейлер ] >> startxref 0 %% EOF 483 0 объект > эндобдж 484 0 объект > эндобдж 564 0 объект > поток Hb`pb`
Лаборатория экспериментальной космологии и астрофизики Массачусетского технологического института

Датчик переходной кромки — это термометр, изготовленный из сверхпроводящая пленка работает вблизи температуры перехода Tc.При переходе от сверхпроводника к нормальному металла, очень небольшое изменение температуры вызывает большое изменение сопротивления. Ширина перехода обычно составляет порядка милли-Кельвина. Много разных типов сверхпроводящие металлические пленки используются различными группами в качестве ТЭС. Мы используем тонкие бислои молибдена / золота для наших устройств. Наши ТЭС Mo / Au используют эффект близости, когда два металла ведут себя как одиночная пленка с температурой перехода между 800 мК (Tc Мо) и 0 К (Tc Au).Обычно наши фильмы настроен на Tc = 100 мК. Низкая температура необходима, потому что энергетическое разрешение этих устройств масштабируется с температура, поэтому криогенные температуры необходимы для высокоэнергетическое разрешение. Показатель заслуг для микрокалориметрические резистивные термометры — это параметр, называемый α, определенный как

где T — температура, а R — сопротивление ТЭС. Энергетическое разрешение TES может быть приблизительно равно

где k — постоянная Больцмана, T — температура ТЭС, C — теплоемкость микрокалориметра, α определено выше, а коэффициент 2.35 — это преобразование стандартного отклонения в полную ширину на половина максимума (FWHM) (просто более простой способ измерения разрешение наших устройств). Итак, для хорошего энергетического разрешения мы хотим, чтобы устройства работали как можно холоднее, теплоемкость и высокий α.
Важным ограничением является то, что TES работает ну как градусник только в переходе. Как только это пойдет нормально, его сопротивление больше не меняется с температурой (много) и
α → 0.Это подразумевает максимальную температуру изменение TES, что, в свою очередь, подразумевает максимальную энергию входящие фотоны:

Таким образом, параметры C и α связаны требуемая энергетическая полоса микрокалориметра. Тогда мы можем сформулировать теоретическое энергетическое разрешение микрокалориметр по простой формуле, которая зависит только от температура срабатывания и полоса пропускания устройства:

Для типичного рентгеновского применения полоса пропускания составляет от ~ 0.1 кэВ до 10 кэВ, а работа при 100 мК дает нам энергию разрешение ΔE = 1,4 эВ FWHM, почти на два порядка лучше, чем теоретические пределы для рентгеновских ПЗС. Это изображение матрицы микрокалориметров TES размером 8 x 8. построен в НАСА Центр космических полетов Годдарда. Каждый пиксель имеет размер 250 мкм на стороне и имеет Mo / Au TES и Поглотитель Bi / Cu для достижения эффективности остановки рентгеновского излучения 95% при 10 кэВ.Наша задача и цель — построить массивы гораздо большего размера. (десятки тысяч пикселей), стремясь к лучшему возможно энергетическое разрешение (4 эВ или лучше).
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера на прием файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:
В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Зависимость величины переходного сопротивления в разборных электро контактах

Понятие переходного электрического сопротивления в электрических контактах

От чего зависит величина переходного электрического сопротивления

Что такое переходное контактное сопротивление и почему так важно, чтобы оно было минимальным | Энергофиксик

Что такое переходное контактное сопротивление

Теперь давайте разберемся, что такое контактное нажатие

«Электрические» причины пожаров! | Опаринская Сорока

Зависимость изменения переходного сопротивления от момента силы сжатия контактов

Переходное сопротивление контакта.

Узнать еще:

§91. Контакты электрических аппаратов | Электротехника

ПЕРЕХОДНОЕ СОПРОТИВЛЕНИЕ КОНТАКТА

Механика ПЕРЕХОДНОЕ СОПРОТИВЛЕНИЕ КОНТАКТА

Читайте также

Огромное магнитосопротивление и сверхострый метамагнитный переход в поликристаллическом Sm 0,5 Ca 0,25 Sr 0,25 MnO 3

Синтез и структурная характеристика

Измерения магнитного поля и магнитотранспорта

Ультрарезкий метамагнитный переход

Теоретическое моделирование

Большие дискретные скачки, наблюдаемые при переходе между состояниями Черна в ферромагнитном топологическом изоляторе

ВВЕДЕНИЕ

РЕЗУЛЬТАТЫ

Характеристика и тесты

Прыжки в

Пространственные корреляции

Активация через небольшой промежуток

ОБСУЖДЕНИЕ

Метастабильность и эффект

Диссипативное квантовое туннелирование

Зарождение в сверхтекучем гелии

Множественные пути и модель сети

Перспективы и выводы

Отображение сопротивления датчика края сверхпроводящего перехода в зависимости от температуры, тока и приложенного магнитного поля

Shuo Zhang

Меган Э.Эккарт

Феликс Т. Джекель

Кари Л. Криппс

Dan McCammon

Келси М.Морган

Yu Zhou

Аннотация

I.ВВЕДЕНИЕ

II. УСТРОЙСТВО И ЦЕПЬ

III. ЭФФЕКТ СЛАБЫХ СВЯЗЕЙ

IV.

V. РАСЧЕТ

VI. ОБСУЖДЕНИЕ

VII. ЗАКЛЮЧЕНИЕ

VIII. БЛАГОДАРНОСТИ

Ссылки

Наблюдаются большие дискретные скачки при переходе между состояниями Черна в ферромагнитном топологическом изоляторе — Penn State

Лаборатория экспериментальной космологии и астрофизики Массачусетского технологического института

Произошла ошибка при настройке вашего пользовательского файла cookie

Настройка вашего браузера на прием файлов cookie

Почему этому сайту требуются файлы cookie?

Что сохраняется в файле cookie?

Добавить комментарий Отменить ответ