Бесконечно малая и бесконечно большая — Википедия
Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
В нестандартном анализе бесконечно малые и бесконечно большие определяются не как последовательности и не как переменные величины, а как особый вид чисел.
Исчисление бесконечно малых и больших[править | править код]
Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.
Бесконечно малая[править | править код]
Последовательность an{\displaystyle a_{n}} называется бесконечно малой, если limn→∞an=0{\displaystyle \lim \limits _{n\to \infty }a_{n}=0}. Например, последовательность чисел an=1n{\displaystyle a_{n}={\dfrac {1}{n}}} — бесконечно малая.
Функция называется бесконечно малой в окрестности точки x0{\displaystyle x_{0}}, если limx→x0f(x)=0{\displaystyle \lim \limits _{x\to x_{0}}f(x)=0}.
Функция называется бесконечно малой на бесконечности, если limx→+∞f(x)=0{\displaystyle \lim \limits _{x\to +\infty }f(x)=0} либо limx→−∞f(x)=0{\displaystyle \lim \limits _{x\to -\infty }f(x)=0}.
Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если limx→+∞f(x)=a{\displaystyle \lim \limits _{x\to +\infty }f(x)=a}, то f(x)−a=α(x){\displaystyle f(x)-a=\alpha (x)}, limx→+∞(f(x)−a)=0{\displaystyle \lim \limits _{x\to +\infty }(f(x)-a)=0}.
Подчеркнём, что бесконечно малую величину следует понимать как переменную величину (функцию), которая лишь в процессе своего изменения [при стремлении x{\displaystyle x} к a{\displaystyle a} (из limx→af(x)=0{\displaystyle \lim \limits _{x\to a}f(x)=0})] делается меньше произвольного числа (ε{\displaystyle \varepsilon }). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе [абсолютном значении] не имеет смысла говорить, что оно бесконечно малое.[1]
Бесконечно большая[править | править код]
Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsinx{\displaystyle x\sin x}, неограниченная с обеих сторон, не является бесконечно большой при x→+∞{\displaystyle x\to +\infty }.
Последовательность an{\displaystyle a_{n}} называется бесконечно большой, если limn→∞an=∞{\displaystyle \lim \limits _{n\to \infty }a_{n}=\infty }.
Функция называется бесконечно большой в окрестности точки x0{\displaystyle x_{0}}, если limx→x0f(x)=∞{\displaystyle \lim \limits _{x\to x_{0}}f(x)=\infty }.
Функция называется бесконечно большой на бесконечности, если limx→+∞f(x)=∞{\displaystyle \lim \limits _{x\to +\infty }f(x)=\infty } либо limx→−∞f(x)=∞{\displaystyle \lim \limits _{x\to -\infty }f(x)=\infty }.
Как и в случае бесконечно малых, необходимо отметить, что ни одно отдельно взятое значение бесконечно большой величины не может быть названо как «бесконечно большое» — бесконечно большая величина — это функция, которая лишь в процессе своего изменения может стать больше произвольно взятого числа.
Свойства бесконечно малых[править | править код]
- Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
- Произведение бесконечно малых — бесконечно малая.
- Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
- Если an{\displaystyle a_{n}} — бесконечно малая последовательность, сохраняющая знак, то bn=1an{\displaystyle b_{n}={\dfrac {1}{a_{n}}}} — бесконечно большая последовательность.
Определения[править | править код]
Допустим, у нас есть бесконечно малые при одном и том же x→a{\displaystyle x\to a} величины α(x){\displaystyle \alpha (x)} и β(x){\displaystyle \beta (x)} (либо, что не важно для определения, бесконечно малые последовательности).
Для вычисления подобных пределов удобно использовать правило Лопиталя.
Примеры сравнения[править | править код]
- С использованием О-символики полученные результаты могут быть записаны в следующем виде x5=o(x3){\displaystyle x^{5}=o(x^{3})}.
- limx→02×2+6xx=limx→02x+61=limx→0(2x+6)=6,{\displaystyle \lim \limits _{x\to 0}{\dfrac {2x^{2}+6x}{x}}=\lim \limits _{x\to 0}{\dfrac {2x+6}{1}}=\lim \limits _{x\to 0}(2x+6)=6,} то есть при x→0{\displaystyle x\to 0} функции f(x)=2×2+6x{\displaystyle f(x)=2x^{2}+6x} и g(x)=x{\displaystyle g(x)=x} являются бесконечно малыми величинами одного порядка.
- В данном случае справедливы записи 2×2+6x=O(x){\displaystyle 2x^{2}+6x=O(x)} и x=O(2×2+6x).{\displaystyle x=O(2x^{2}+6x).}
Определение[править | править код]
Если limx→aβα=1{\displaystyle \lim \limits _{x\to a}{\dfrac {\beta }{\alpha }}=1}, то бесконечно малые или бесконечно большие величины α{\displaystyle \alpha } и β{\displaystyle \beta } называются эквивалентными (обозначается как α∼β{\displaystyle \alpha \thicksim \beta }).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых (бесконечно больших) величин одного порядка малости.
При α(x)→x→x00{\displaystyle \alpha (x){\xrightarrow[{x\to x_{0}}]{}}0} справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):
- 1+α(x)n≈α(x)n+1{\displaystyle {\sqrt[{n}]{1+\alpha (x)}}\approx {\frac {\alpha (x)}{n}}+1}, где α(x)→x→x00{\displaystyle \alpha (x){\xrightarrow[{x\to x_{0}}]{}}0}.
Теорема[править | править код]
Предел частного (отношения) двух бесконечно малых или бесконечно больших величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.
Данная теорема имеет прикладное значение при нахождении пределов (см. пример).
Примеры использования[править | править код]
- Найти limx→0sin2xx.{\displaystyle \lim \limits _{x\to 0}{\dfrac {\sin 2x}{x}}.}
- Заменяя sin2x{\displaystyle \sin 2x} эквивалентной величиной 2x{\displaystyle 2x}, получаем
- limx→0sin2xx=limx→02xx=2.{\displaystyle \lim \limits _{x\to 0}{\dfrac {\sin 2x}{x}}=\lim \limits _{x\to 0}{\dfrac {2x}{x}}=2.}
- Найти limx→π2sin(4cosx)cosx.{\displaystyle \lim \limits _{x\to {\frac {\pi }{2}}}{\dfrac {\sin(4\cos x)}{\cos x}}.}
- Так как sin(4cosx)∼4cosx{\displaystyle \sin(4\cos x)\thicksim {4\cos x}} при x→π2{\displaystyle x\to {\dfrac {\pi }{2}}} получим
- limx→π2sin(4cosx)cosx=limx→π24cosxcosx=4.{\displaystyle \lim \limits _{x\to {\frac {\pi }{2}}}{\dfrac {\sin(4\cos x)}{\cos x}}=\lim \limits _{x\to {\frac {\pi }{2}}}{\dfrac {4\cos x}{\cos x}}=4.}
- Вычислить 1,2{\displaystyle {\sqrt {1{,}2}}}.
- Используя формулу: 1,2≈1+0,22=1,1{\displaystyle {\sqrt {1{,}2}}\approx 1+{\frac {0{,}2}{2}}=1{,}1}, тогда как, используя калькулятор (более точные вычисления), получили: 1,2≈1,095{\displaystyle {\sqrt {1{,}2}}\approx 1{,}095}, таким образом ошибка составила 0,005 (менее 1 %), то есть метод полезен, благодаря своей простоте, при грубой оценке арифметических корней близких к единице.
Понятие «бесконечно малое» обсуждалось ещё в античные времена в связи с концепцией неделимых атомов, однако в классическую математику не вошло. Вновь оно возродилось с появлением в XVI веке «метода неделимых» — разбиения исследуемой фигуры на бесконечно малые сечения.
В XVII веке произошла алгебраизация исчисления бесконечно малых. Они стали определяться как числовые величины, которые меньше всякой конечной (положительной) величины и всё же не равны нулю. Искусство анализа заключалось в составлении соотношения, содержащего бесконечно малые (дифференциалы), и затем — в его интегрировании.
Математики старой школы подвергли концепцию бесконечно малых резкой критике. Мишель Ролль писал, что новое исчисление есть «набор гениальных ошибок»; Вольтер ядовито заметил, что это исчисление представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Даже Гюйгенс признавался, что не понимает смысла дифференциалов высших порядков.
Споры в Парижской Академии наук по вопросам обоснования анализа приобрели настолько скандальный характер, что Академия однажды вообще запретила своим членам высказываться на эту тему (в основном это касалось Ролля и Вариньона). В 1706 году Ролль публично снял свои возражения, однако дискуссии продолжались.
В 1734 году известный английский философ, епископ Джордж Беркли выпустил нашумевший памфлет, известный под сокращённым названием «Аналитик». Полное его название: «Аналитик или рассуждение, обращённое к неверующему математику, где исследуется, более ли ясно воспринимаются или более ли очевидно выводятся предмет, принципы и умозаключения современного анализа, чем религиозные таинства и догматы веры». «Аналитик» содержал остроумную и во многом справедливую критику исчисления бесконечно малых. Метод анализа Беркли считал несогласным с логикой и писал, что, «как бы он ни был полезен, его можно рассматривать только как некую догадку; ловкую сноровку, искусство или скорее ухищрение, но не как метод научного доказательства». Цитируя фразу Ньютона о приращении текущих величин «в самом начале их зарождения или исчезновения», Беркли иронизирует: «это ни конечные величины, ни бесконечно малые, ни даже ничто. Не могли ли бы мы их назвать призраками почивших величин?.. И как вообще можно говорить об отношении между вещами, не имеющими величины?.. Тот, кто может переварить вторую или третью флюксию [производную], вторую или третью разность, не должен, как мне кажется, придираться к чему-либо в богословии».
Невозможно, пишет Беркли, представить себе мгновенную скорость, то есть скорость в данное мгновение и в данной точке, ибо понятие движения включает понятия о (конечных ненулевых) пространстве и времени.
Как же с помощью анализа получаются правильные результаты? Беркли пришёл к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Как ни странно, некоторые крупные математики (например, Лагранж) согласились с ним.
Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция. И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.
В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс. В настоящее время термин «бесконечно малая» математики в подавляющем большинстве случаев относят не к числам, а к функциям и последовательностям.
Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.
- ↑ Бесконечно малые и бесконечно большие величины // Справочник по математике (для ср. уч. заведений)/ Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 337—340. — 480 с.
Бесконечно малые функции (величины) и их свойства.
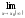 α(х)=0.
х0 может быть как число, так и -,+,.
α(х)=0.
х0 может быть как число, так и -,+,. Т.е. 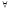 ε
> 0
ε
> 0 δ=δ(ε)>
0
δ=δ(ε)>
0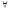 х:
0<|х–х
х:
0<|х–х |α(х)|<ε
|α(х)|<ε
Аналогично можно сформулировать определение бесконечно малой при х → ∞
 ε>0
ε>0  S=S(ε)>0
S=S(ε)>0  х : |х|
> S
х : |х|
> S 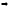 |α
|α
Например,
y=cos x — б/м при х→П/2, у=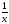 б/м при х→∞.
б/м при х→∞.
Связь бесконечно малых величин с пределами функций.
Теорема. Функция f(x) имеет при х→х0 (х → ∞) предел, равный А, тогда и только тогда, когда ее можно представить как сумму числа A и бесконечно малой функции α(х) при х → х0 (х → ∞).
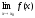 =А
=А 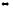 f(x)-A=α(x)
f(x)-A=α(x)
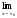 f(x)
= A. Это означает, что для любого ε > 0
существует такое число δ>0, что для
всех х≠х0 и удовлетворяющих условию |х–х0|<δ
будет верно неравенство |f(x)–A|<ε, или,
обозначив α(х)=f(x)–A, справедливо
неравенство |α(х)|<ε. Это и означает,
что α(х) есть бесконечно малая при х→
х0.
■
f(x)
= A. Это означает, что для любого ε > 0
существует такое число δ>0, что для
всех х≠х0 и удовлетворяющих условию |х–х0|<δ
будет верно неравенство |f(x)–A|<ε, или,
обозначив α(х)=f(x)–A, справедливо
неравенство |α(х)|<ε. Это и означает,
что α(х) есть бесконечно малая при х→
х0.
■ Достаточность.
□ По условию α(х)=f(x)–A есть бесконечно
малая при х→х0,
то для любого числа ε>0 существует
такое число δ>0, что при всех х≠х
Это
и означает, что 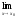 f(x)=A.
■
f(x)=A.
■
Доказательство
через последовательности. Необходимость. Возьмем последовательность х1,x2,…,xn,…
значений х любую, но такую, что xn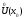 и xnx0 при n.
и xnx0 при n.
По
условию 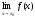
Т.к.
последовательность
х1,x2,…,xn,…-любая,
сходящаяся
к х0,
то 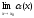 =0
=0
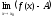 =0.
А последнее и означает, что разность
f(x)–A – б.м. при хх0.
=0.
А последнее и означает, что разность
f(x)–A – б.м. при хх0.
Достаточность.
Возьмем последовательность х1,x2,…,xn,…
значений х любую, но такую, что xn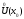 и xnx0 при n.
и xnx0 при n.
По
условию (х)=f(x)–A
– б.м. при хх0,
т.е. 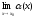 =
=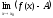 =0.
Но тогда
=0.
Но тогда
α(хn)0 при n(f(xn)-A)0 при n.
Т.к.
последовательность
х1,x2,…,xn,…-любая,
сходящаяся
к х0,
то 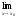 f(x)=A.
f(x)=A.
Свойства бесконечно малых величин:
Если одна из трех функций f(x), -f(x), f(x) является б.м. при х→х0, то и две другие функции также являются б.м. при х→х0.
Алгебраическая сумма конечного числа б/м величин есть величина б/м.
Произведение б/м величины на ограниченную функцию (в том числе на постоянную, на другую б/м) есть величина б/м.
Частное от деления б/м величины на функцию, предел которой отличен от нуля, есть величина б/м.
Доказательство через последовательности или через определение предела функции при А=0.
Пример. Доказать, что функция f(x)=(х-1)sin является бесконечно малой при х→1.
является бесконечно малой при х→1.
Т.к. 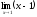 =0,
т.е. (х-1) – б.м. при х→1, а функция sin
=0,
т.е. (х-1) – б.м. при х→1, а функция sin ограничена (т.к.
ограничена (т.к.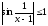 ),
то функция f(x) является произведением
б.м. функции на ограниченную. Следовательно,
функция f(x)=(х-1)sin
),
то функция f(x) является произведением
б.м. функции на ограниченную. Следовательно,
функция f(x)=(х-1)sin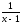 является бесконечно малой при х→1.
является бесконечно малой при х→1.
Бесконечно большие функции (величины).
Определение. Функция β(х) называется бесконечно
большой величиной (б/б) при х→х0,
если либо 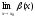 =∞,
либо
=∞,
либо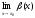 =+∞,
либо
=+∞,
либо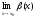 =-∞.
=-∞.
При
этом в случае, когда  =+∞,
говорят, что β(х) – положительная
бесконечно большая, а в случае, когда
=+∞,
говорят, что β(х) – положительная
бесконечно большая, а в случае, когда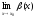 =-∞,
говорят, что β(х) – отрицательная
бесконечно большая функция при х→х0.
=-∞,
говорят, что β(х) – отрицательная
бесконечно большая функция при х→х0.
Например, функция у=tg x при х→П/2 – б/б;
Функция
у=х2+5
при х→∞ — б/б; у=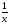 при х→0 – б/б. (На графике
показать определение)
при х→0 – б/б. (На графике
показать определение)
Замечание. х0 может означать и конечное число, и один из символов , +, -.
Любая б/б функция является неограниченной. Обратное неверно. Так, например, функция у=хcos х – неограниченная функция, но б/б не является, т.к. при х→∞ функция колеблется, переходя от отрицательных значений к положительным и наоборот, принимая значения 0.
4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
Пусть f1 (x)
и
f 2 (x)
бесконечно малые величины при 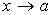 ,
т.е.
,
т.е.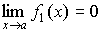 и
и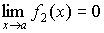 .
.
1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:
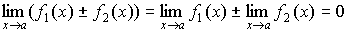 .
(4.17)
.
(4.17)
2. Произведение бесконечно малых величин есть величина бесконечно малая:
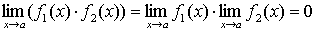 .
(4.18)
.
(4.18)
3.
Произведение бесконечно малой величины
на константу С или
на функцию, имеющую конечный предел 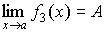 ,
есть величина бесконечно малая:
,
есть величина бесконечно малая:
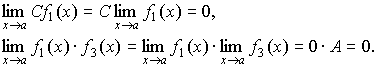 .
(4.19)
.
(4.19)
Пусть 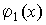 и
и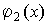 бесконечно
большие величины при
бесконечно
большие величины при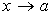 ,
т.е.
,
т.е.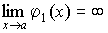 и
и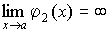 .
.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
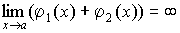 .
(4.20)
.
(4.20)
2. Произведение бесконечно больших величин есть величина бесконечно большая:
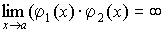 .
(4.21)
.
(4.21)
3.
Произведение бесконечно большой величины
на константу С,
или на функцию, имеющую конечный предел 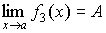 ,
есть величина бесконечно большая:
,
есть величина бесконечно большая:
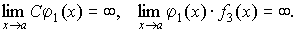 (4.22)
(4.22)
Связь бесконечно малой и бесконечно большой величины
Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.
Пусть 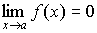 и
и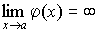 ,
тогда
,
тогда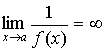 и
и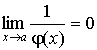 .
.
Символически можно записать:
 и
и
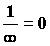
Примеры:
1) 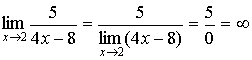 ;
;
2) 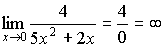 ;
;
3) 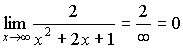 .
.
П р и м е ч а н и е. При вычислении пределов возможны следующие комбинации бесконечно малых и бесконечно больших величин, которые называются неопределенностями:
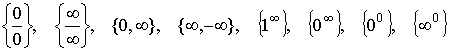 .
.
17.Арифметическое свойство придела.
Арифметические свойства предела функции. Пусть функции f и g определены на интервале ( a, b ), кроме быть может точки x0. Если существует пределы
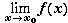 и
и 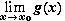 ,
,
то существуют пределы в левых частях равенств и имеют место эти равенства :
a. 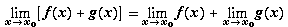 б.
б. 
Эти свойства вытекают из определения Гейне предела функции и соответствующих свойств сходящихся последовательностей. 2. Если
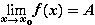 ,
,
то
существует проколатая окрестность 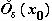 точки
точки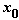 ,
где функцияf ( x ) ограничена.
Действительно,
если взять
,
где функцияf ( x ) ограничена.
Действительно,
если взять  =
1
=
1  0,
то из существования конечного предела
следует, что существует
0,
то из существования конечного предела
следует, что существует 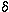
 0,
что для всех x :
0
0,
что для всех x :
0  |x — x0 |
|x — x0 | 
 ,
выполняется | f ( x )
— A |
,
выполняется | f ( x )
— A |  1,
отсюда, | f ( x )
| — | A |
1,
отсюда, | f ( x )
| — | A |  |f ( x )
— A |
|f ( x )
— A |  1,
т.е.
1,
т.е.
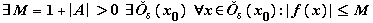
3. Если
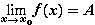 ,
,
то
существует проколотая окрестность 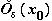 точки
точки ,
что для всехx
,
что для всехx 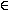
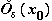 :
:

Действительно,
возьмем 
 0,
тогда из существования конечного
предела, следует, что существует окрестность
0,
тогда из существования конечного
предела, следует, что существует окрестность 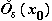 ,
что для всехx
,
что для всехx 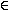
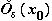 :
:
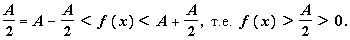
4. Свойства, связанные с неравенствами. Если
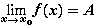 ,
, 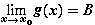
и
для всех x 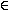
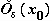 :f ( x )
:f ( x ) 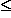 g ( x )
, то A
g ( x )
, то A 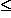 B Если
B Если
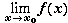 =
= 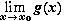 =A
=A
и
для всех x 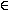
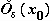 :
: ,то
существует
,то
существует
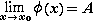
Доказательства этих свойств следуют из следующих свойств для сходящихся последовательностей и определения предела функции по Гейне.
18. Первый замечательный предел.
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Первый
замечательный предел имеет
вид: 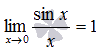
На
практике чаще встречаются модификации
первого замечательного предела в
виде 
где, k – коэффициент.
Пояснение: 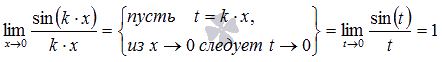
Следствия первого замечательного предела:
Эти следствия очень просто доказываются, если использовать правило Лопиталя или заменуэквивалентных бесконечно малых функций.
Разберем несколько примеров нахождения предела по первому замечательному пределу сподробным оприсанием решения.
Пример.
Найти
предел не пользуясь правилом Лопиталя 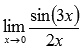
Решение.
Подставляем
значение: 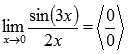
Пришли
к неопределенности ноль делить на ноль.
Смотрим в таблицу
неопределенностей для
определения метода решения. Комбинация
синуса и его аргумента подсказывает
нам о применении первого замечательного
предела, но для этого сначала нужно
немного преобразовать выражение.
Домножим на 3х и
числитель и знаменатель дроби. 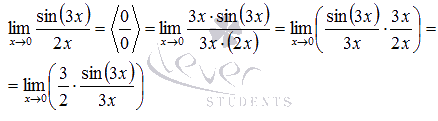
В
силу следствия из первого замечательного
предела 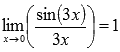 ,
поэтому приходим к результату:
,
поэтому приходим к результату: 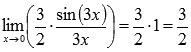
Ответ:
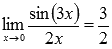
Пример.
Вычислить
предел 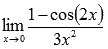
Решение.
Подставляем
значение: 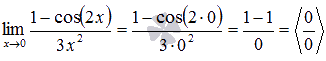
Пришли
к неопределенности ноль делить на ноль.
Преобразуем числитель, используя формулы
тригонометрии. 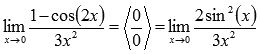
Стало
видно, что здесь можно применить первый
замечательный предел: 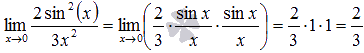
Ответ:
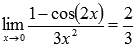
Пример.
Вычислить
предел 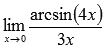
Решение.
Подставляем
значение: 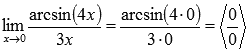
Пришли к неопределенности ноль делить на ноль. Сделаем замену.
Пусть 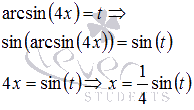
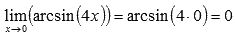 ,
следовательно,
,
следовательно,  при
при  .
.
Тогда
предел после замены переменной примет
вид: 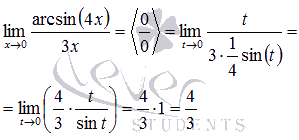
Ответ:
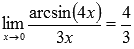
предел имеет
вид: 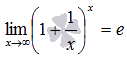
Бесконечно малые величины и их свойства — Мегаобучалка
Единственность предела и ограниченность сходящейся числовой последовательности
Определение 1. Числовая последовательность (1) называется ограниченной, если множество членов этой последовательности образует ограниченное множество.
В этом случае числовую последовательность (1) мы будем называть ограниченной величиной.
Определение 2. Числовая последовательность (1) сходится и имеет предел (Возможно использование записи ), если .
Давайте повторим это определение, используя в большей степени русский язык. Предел числовой последовательности существует и равен некоторому числу, если, начиная с некоторого номера, все члены последовательности удалены от этого предельного числа менее, чем любое, наперед заданное, сколь угодно малое положительное число. Можно это же самое сказать другими словами. Число будет пределом числовой последовательности (1) тогда и только тогда, когда для каждой -окрестности точки все члены последовательности, начиная с некоторого номера, лежат в этой –окрестности. Заметим, что интервал называется -окрестностью точки .
Теорема 1. Если предел числовой последовательности существует, то он единственный.
Доказательство. Доказательство теоремы проведем «методом от противного». Предположим, что теорема неверна и существует, как минимум, 2 числа и ( ), для которых выполнены условия определения 2. В этом определении возьмем . Тогда, после номера члены последовательности отличаются от числа меньше чем на , а после номера члены последовательности отличаются от числа меньше чем на . Покажем, что этого не может быть. В самом деле, при выполнены соотношения , , откуда для этих имеем . Теорема доказана.
Теорема 2. Если числовая последовательность имеет предел, то эта числовая последовательность ограничена.
Доказательство. Доказательство будет носить конструктивный характер. Возьмем и найдем соответствующее . Разобьем последовательность на 2 части: первые членов и остальные члены последовательности. Первая группа состоит из конечного числа членов и поэтому ограничена. Вторая группа состоит из чисел, удаленных от предельного значения не больше чем на 1, и поэтому также ограничена. Объединение двух ограниченных множеств есть множество ограниченное. Теорема доказана.
Бесконечно малые величины и их свойства
Определение 3. Числовая последовательность называется бесконечно малой величиной, если она имеет предел, равный 0.
Для бесконечно малых величин используются обозначение б. м.
Пусть заданы числовые последовательности и . Числовая последовательность с общим членом , называется суммой этих числовых последовательностей. Числовая последовательность с общим членом , называется суммой этих числовых последовательностей. Числовая последовательность с общим членом , называется суммой этих числовых последовательностей.
Теорема 3. Сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Доказательство. Достаточно доказать утверждение для суммы двух б. м. Пусть числовые последовательности и являются бесконечно малыми величинами, т. е. пределы этих последовательностей равны 0. Данный факт означает следующее. Если задано произвольное, скроль угодно малое положительное число , то для числа и числовой последовательности существует номер , обладающий тем свойством, что при выполнено соотношение . По той же причине для этого же числа и числовой последовательности существует номер , обладающий тем свойством, что при выполнено соотношение . Возьмем число , тогда при справедливы соотношения . Итак, для произвольного мы нашли номер , такой что при выполнено . Следовательно, предел последовательности , равен 0, и она является бесконечно малой величиной. Теорема доказана.
Теорема 4. Произведение бесконечно малой величины на ограниченную величину есть величина бесконечно малая.
Доказательство. Пусть числовая последовательность является бесконечно малой величиной, а числовая последовательность является ограниченной величиной. Это означает что, с одной стороны, , с другой стороны, существует число такое, что для каждого выполнено условие . Пусть теперь задано произвольное, скроль угодно малое положительное число . Рассмотрим числа , для него в числовой последовательности существует номер , обладающий тем свойством, что при выполнено соотношение . При этом будет выполнено условие , что и означает, что произведение этих двух величин – бесконечно малой и ограниченной есть величина бесконечно малая. Теорема доказана.
Свойства пределов
А как конкретно происходит вычисление пределов, в данном случае числовых последовательностей? Мы стараемся представить величину, предел которой надо найти, в виде суммы, разности, произведения, частного более простых величин, предел которых легко найти. Для обоснования такого подхода надо сформулировать и доказать свойства пределов.
Теорема 5. Числовая последовательность имеет предел, равный тогда и только тогда, когда последовательность , является бесконечно малой величиной.
Доказательство. Пусть , т.е. при для каждого при выполнено неравенство ( ). Но это неравенство равносильно тому, что , т. е. последовательность , имеет предел 0, т.е. является бесконечно малой величиной. Теорема доказана.
Теорема 6. (Свойства пределов) Пусть , , тогда , , , а если, кроме того, , , то .
Доказательство. Докажем в условиях теоремы формулу , т. е. мы докажем, что предел суммы последовательностей равен сумме их пределов, если каждый из пределов существует. Так как , то , где — б. м. Аналогично , где — б. м. Отсюда следует, что . В последней скобке сумма двух бесконечно малых величин есть величина б. м. Поэтому представляется в виде суммы и бесконечно малой величины . В силу теоремы 5 это означает, что . Первое утверждение теоремы доказана. Формула доказывается совершенно аналогично. Рассмотрим теперь формулу и используем для преобразования левой части те же обозначения. Поэтому …
Бесконечно малые функции (величины) и их свойства.
Определение. Функция α(х)
называется бесконечно малой (б/м) функцией
при х→х0,
или при х → ∞, если: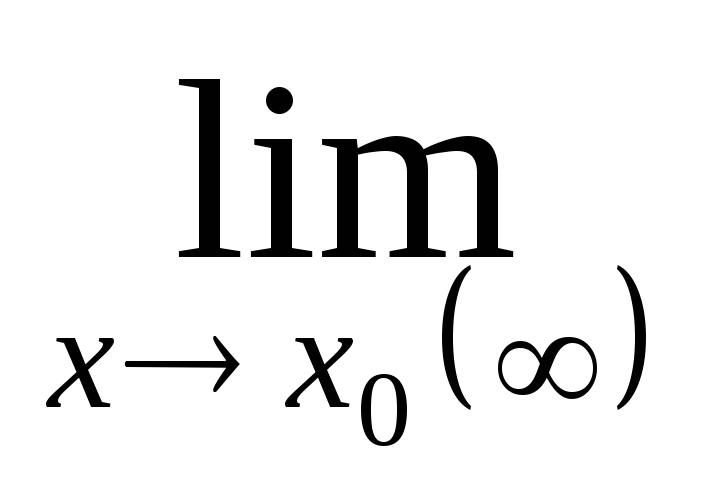 α(х)=0.
х0 может быть как число, так и -,+,.
α(х)=0.
х0 может быть как число, так и -,+,.
Т.е.  ε
> 0
ε
> 0  δ=δ(ε)>
0
δ=δ(ε)>
0  х:
0<|х–х0|<δ
х:
0<|х–х0|<δ  |α(х)|<ε
|α(х)|<ε
Аналогично можно сформулировать определение бесконечно малой при х → ∞
 ε>0
ε>0  S=S(ε)>0
S=S(ε)>0  х : |х|
> S
х : |х|
> S  |α(x)|<ε
|α(x)|<ε
Например,
y=cos x — б/м при х→П/2, у=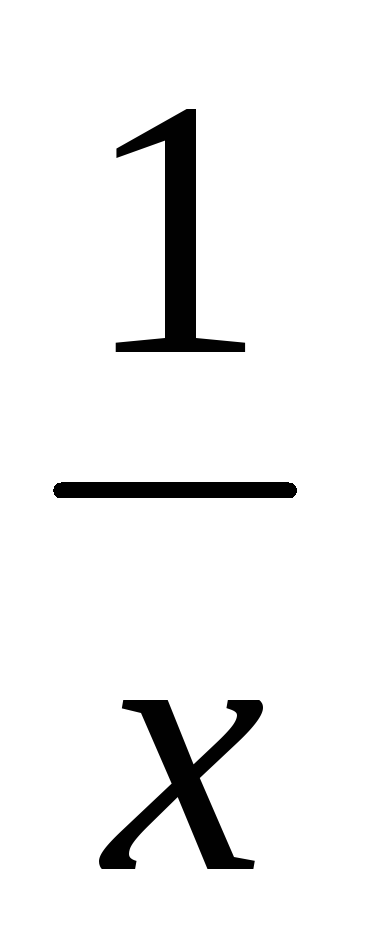 б/м при х→∞.
б/м при х→∞.
Связь бесконечно малых величин с пределами функций.
Теорема. Функция f(x) имеет при х→х0 (х → ∞) предел, равный А, тогда и только тогда, когда ее можно представить как сумму числа A и бесконечно малой функции α(х) при х → х0 (х → ∞).
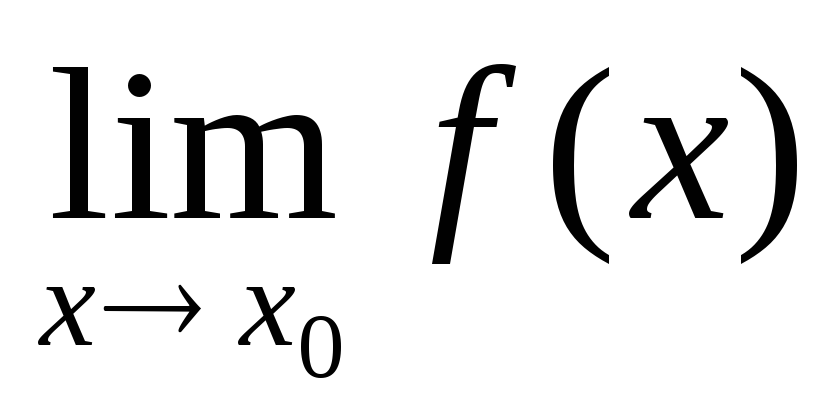 =А
=А  f(x)-A=α(x)
f(x)-A=α(x)
Доказательство. Необходимость. Докажем
теорему для любого случая х→х0.
По условию  f(x)
= A. Это означает, что для любого ε > 0
существует такое число δ>0, что для
всех х≠х0 и удовлетворяющих условию |х–х0|<δ
будет верно неравенство |f(x)–A|<ε, или,
обозначив α(х)=f(x)–A, справедливо
неравенство |α(х)|<ε. Это и означает,
что α(х) есть бесконечно малая при х→
х0.
■
f(x)
= A. Это означает, что для любого ε > 0
существует такое число δ>0, что для
всех х≠х0 и удовлетворяющих условию |х–х0|<δ
будет верно неравенство |f(x)–A|<ε, или,
обозначив α(х)=f(x)–A, справедливо
неравенство |α(х)|<ε. Это и означает,
что α(х) есть бесконечно малая при х→
х0.
■
Достаточность. □ По условию α(х)=f(x)–A есть бесконечно малая при х→х0, то для любого числа ε>0 существует такое число δ>0, что при всех х≠х0 и удовлетворяющих условию |х–х0|<δ верно неравенство |α(х)|=|f(x)–A|<ε.
Это
и означает, что 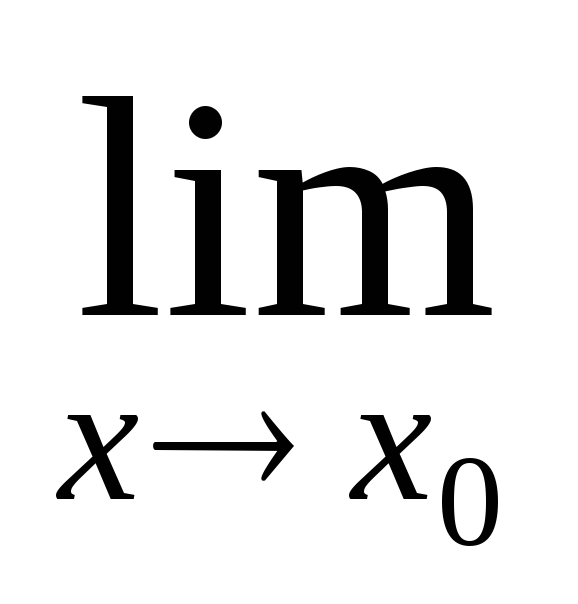 f(x)=A.
■
f(x)=A.
■
Доказательство
через последовательности. Необходимость. Возьмем последовательность х1,x2,…,xn,…
значений х любую, но такую, что xn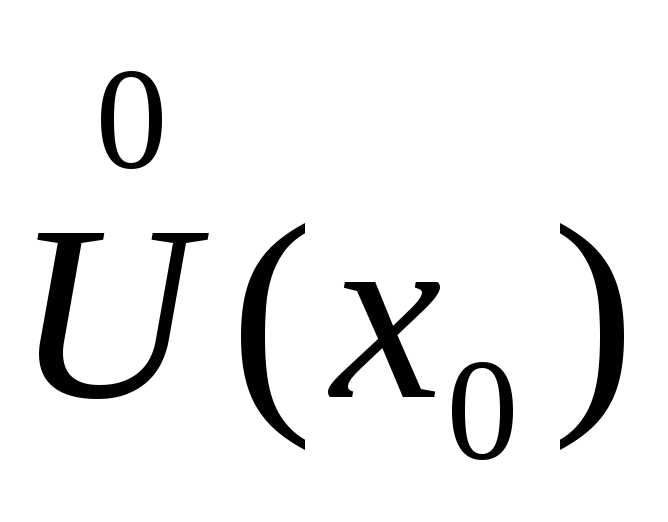 и xnx0 при n.
и xnx0 при n.
По
условию 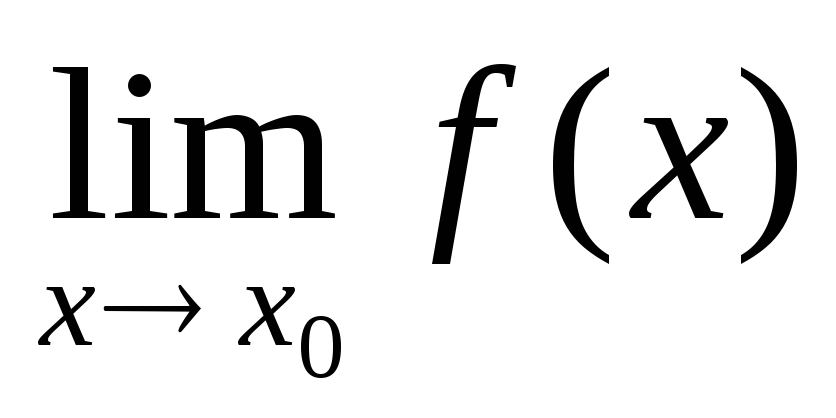 =А.
Тогда f(xn)A
при (f(xn)-A)=α(хn)0
при n.
=А.
Тогда f(xn)A
при (f(xn)-A)=α(хn)0
при n.
Т.к.
последовательность
х1,x2,…,xn,…-любая,
сходящаяся
к х0,
то 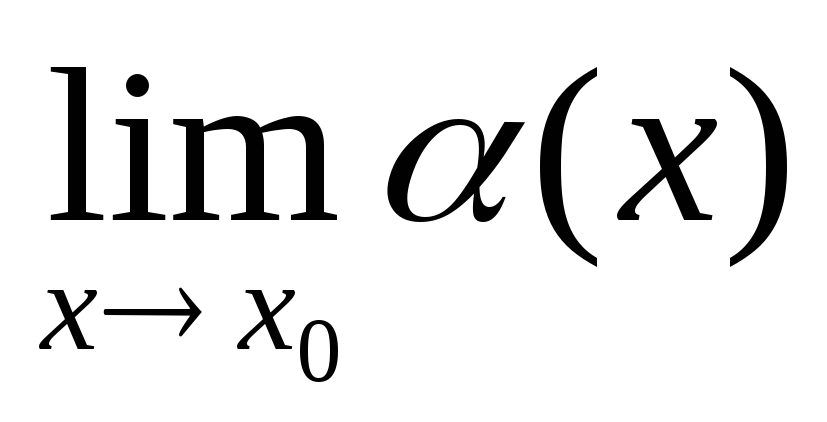 =0
=0
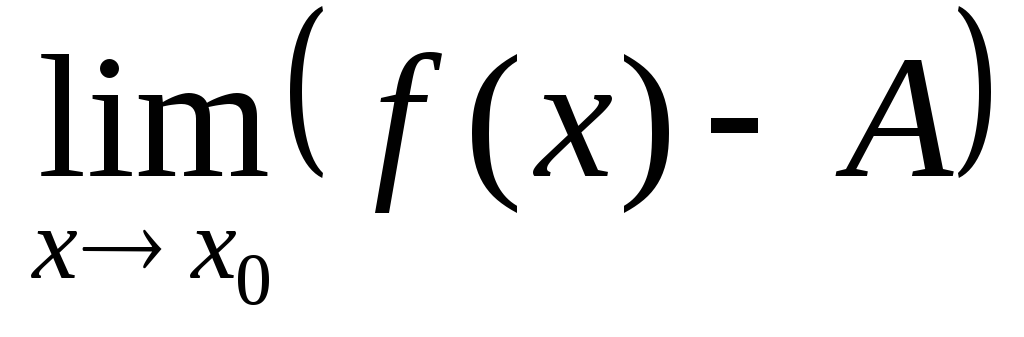 =0.
А последнее и означает, что разность
f(x)–A – б.м. при хх0.
=0.
А последнее и означает, что разность
f(x)–A – б.м. при хх0.
Достаточность.
Возьмем последовательность х1,x2,…,xn,…
значений х любую, но такую, что xn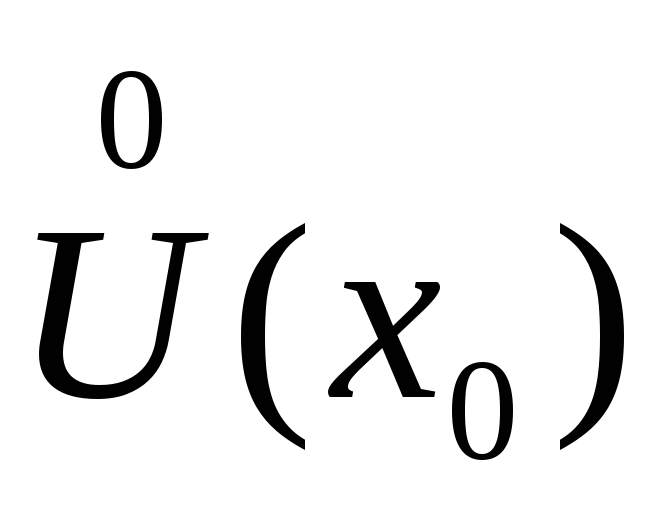 и xnx0 при n.
и xnx0 при n.
По
условию (х)=f(x)–A
– б.м. при хх0,
т.е.  =
= =0.
Но тогда
=0.
Но тогда
α(хn)0 при n(f(xn)-A)0 при n.
Т.к.
последовательность
х1,x2,…,xn,…-любая,
сходящаяся
к х0,
то 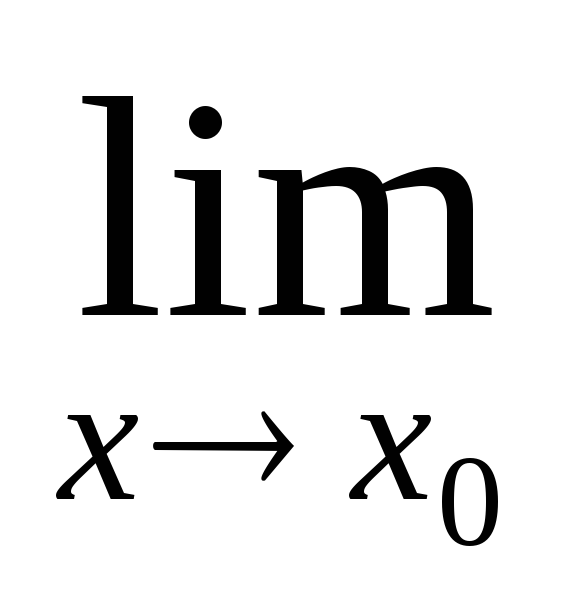 f(x)=A.
f(x)=A.
Свойства бесконечно малых величин:
Если одна из трех функций f(x), -f(x), f(x) является б.м. при х→х0, то и две другие функции также являются б.м. при х→х0.
Алгебраическая сумма конечного числа б/м величин есть величина б/м.
Произведение б/м величины на ограниченную функцию (в том числе на постоянную, на другую б/м) есть величина б/м.
Частное от деления б/м величины на функцию, предел которой отличен от нуля, есть величина б/м.
Доказательство через последовательности или через определение предела функции при А=0.
Пример. Доказать, что функция f(x)=(х-1)sin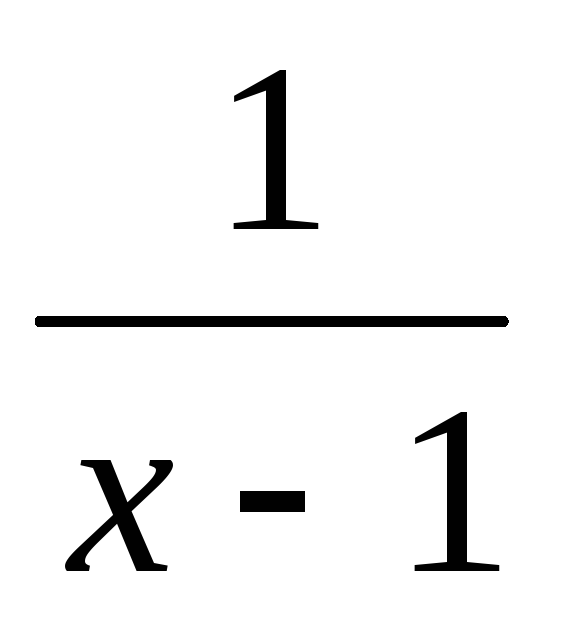 является бесконечно малой при х→1.
является бесконечно малой при х→1.
Т.к.  =0,
т.е. (х-1) – б.м. при х→1, а функция sin
=0,
т.е. (х-1) – б.м. при х→1, а функция sin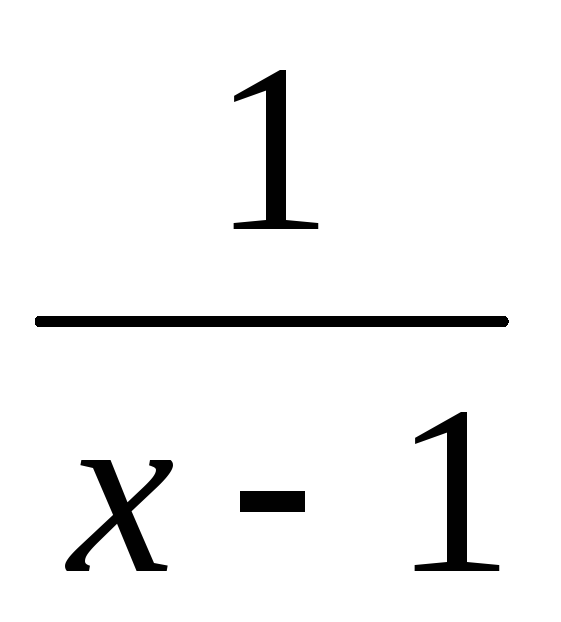 ограничена (т.к.
ограничена (т.к. 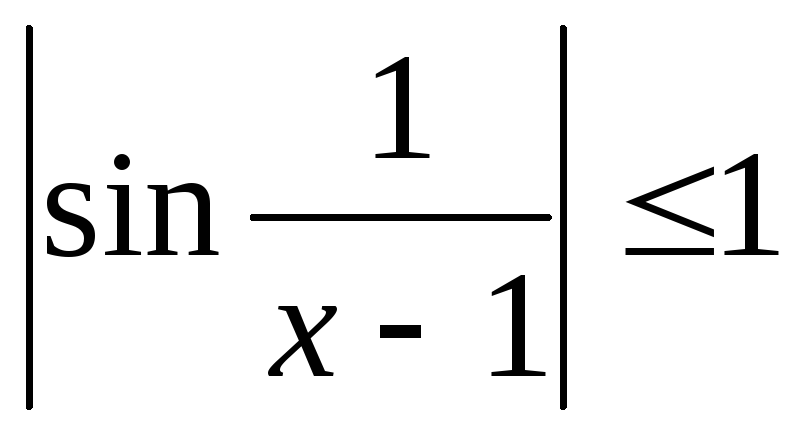 ),
то функция f(x) является произведением
б.м. функции на ограниченную. Следовательно,
функция f(x)=(х-1)sin
),
то функция f(x) является произведением
б.м. функции на ограниченную. Следовательно,
функция f(x)=(х-1)sin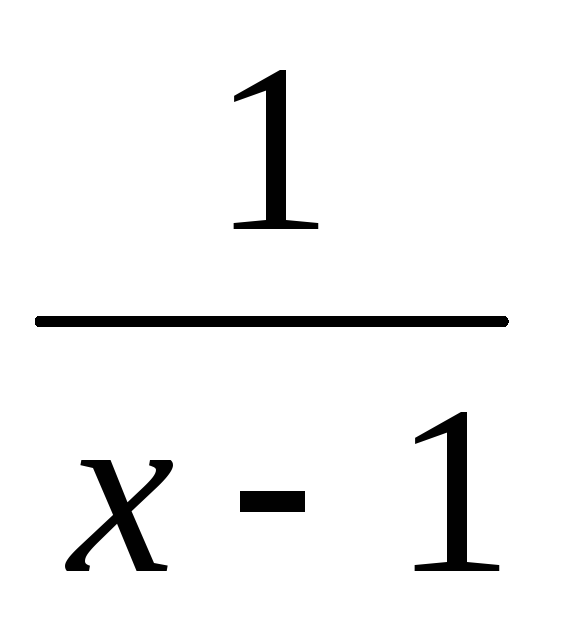 является бесконечно малой при х→1.
является бесконечно малой при х→1.
Бесконечно большие функции (величины).
Определение. Функция β(х) называется бесконечно
большой величиной (б/б) при х→х0,
если либо 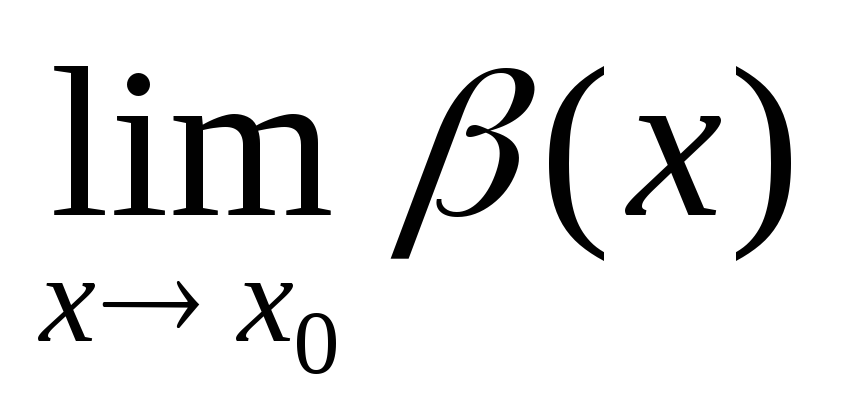 =∞,
либо
=∞,
либо 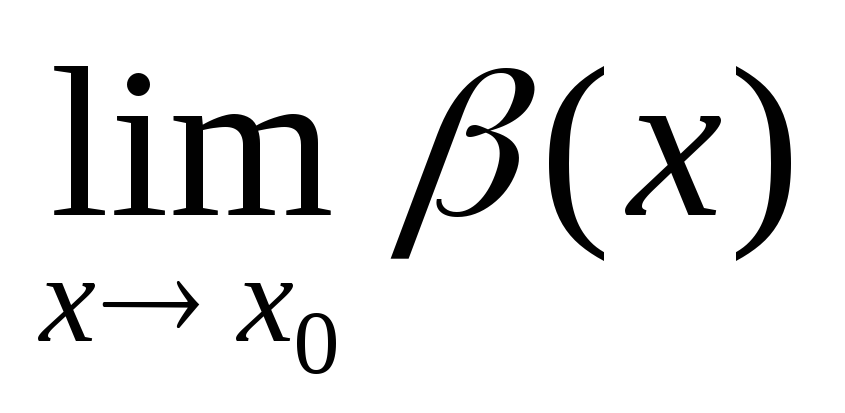 =+∞,
либо
=+∞,
либо  =-∞.
=-∞.
При
этом в случае, когда 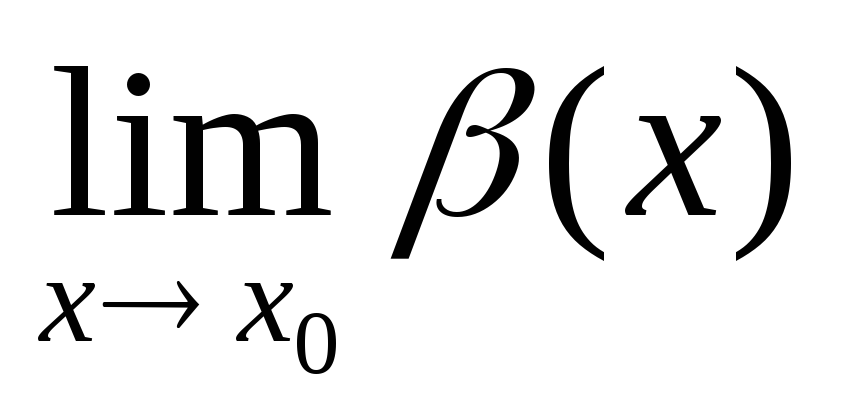 =+∞,
говорят, что β(х) – положительная
бесконечно большая, а в случае, когда
=+∞,
говорят, что β(х) – положительная
бесконечно большая, а в случае, когда 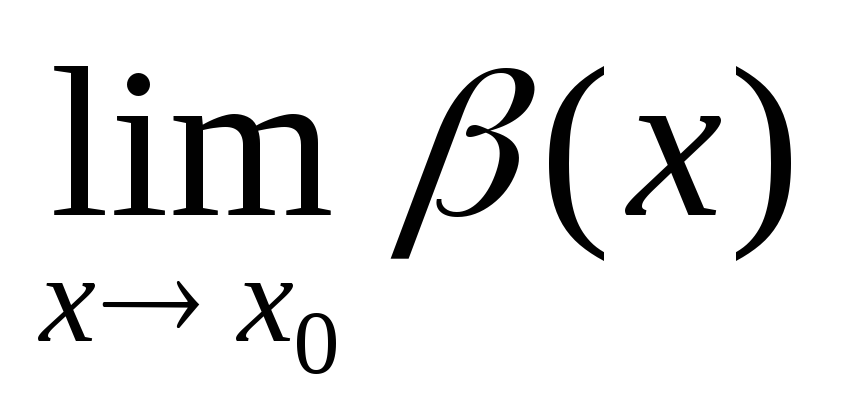 =-∞,
говорят, что β(х) – отрицательная
бесконечно большая функция при х→х0.
=-∞,
говорят, что β(х) – отрицательная
бесконечно большая функция при х→х0.
Например, функция у=tg x при х→П/2 – б/б;
Функция
у=х2+5
при х→∞ — б/б; у=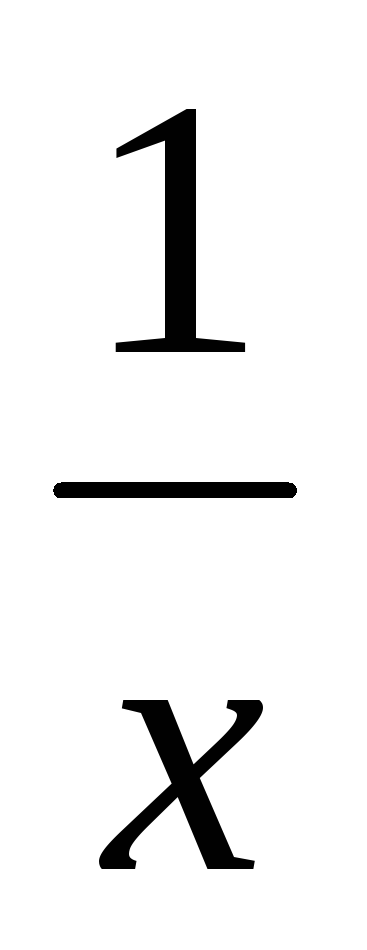 при х→0 – б/б. (На графике
показать определение)
при х→0 – б/б. (На графике
показать определение)
Замечание. х0 может означать и конечное число, и один из символов , +, -.
Любая б/б функция является неограниченной. Обратное неверно. Так, например, функция у=хcos х – неограниченная функция, но б/б не является, т.к. при х→∞ функция колеблется, переходя от отрицательных значений к положительным и наоборот, принимая значения 0.
Бесконечно малые величины.
Функция
называется бесконечно
малой при  ,
если
,
если  .
.
Примеры:
1)  функция
функция 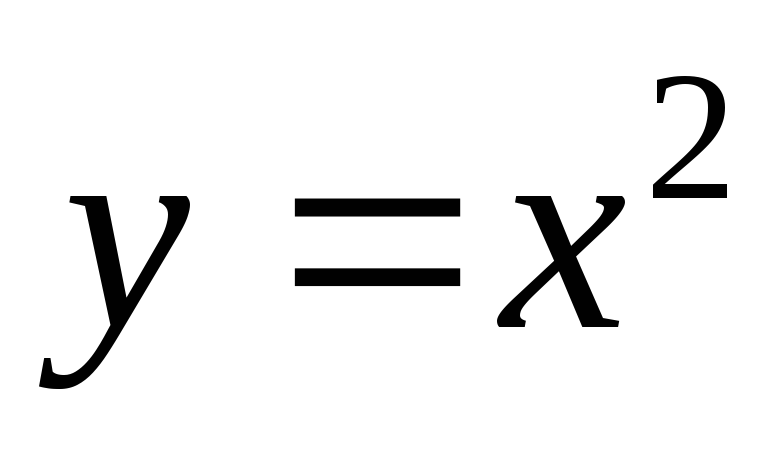 является бесконечно малой (б.м.) при
является бесконечно малой (б.м.) при 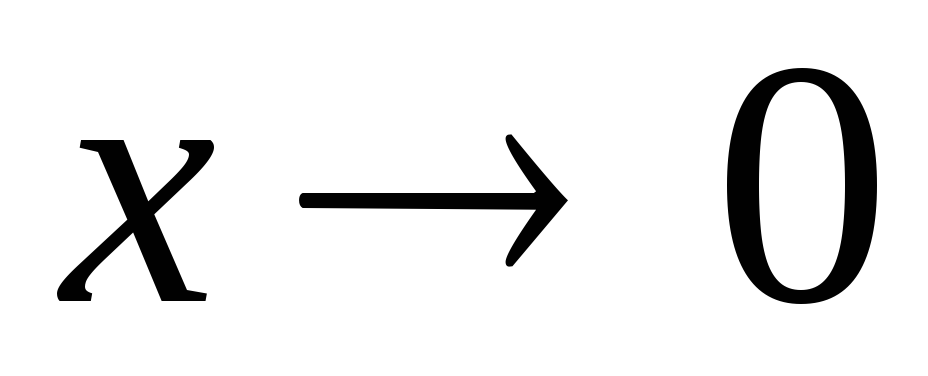 ;
;
2) 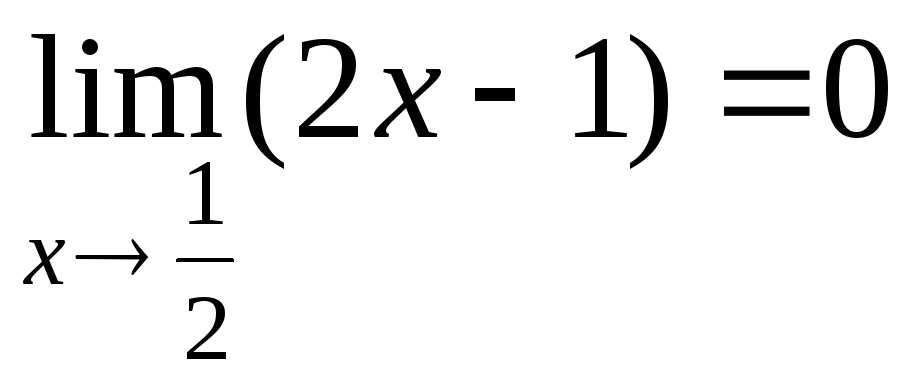 функция
функция 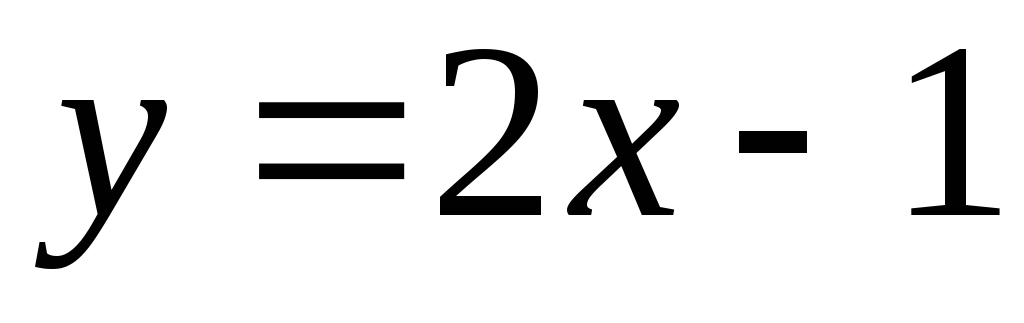 б.м. при
б.м. при  ;
;
3) 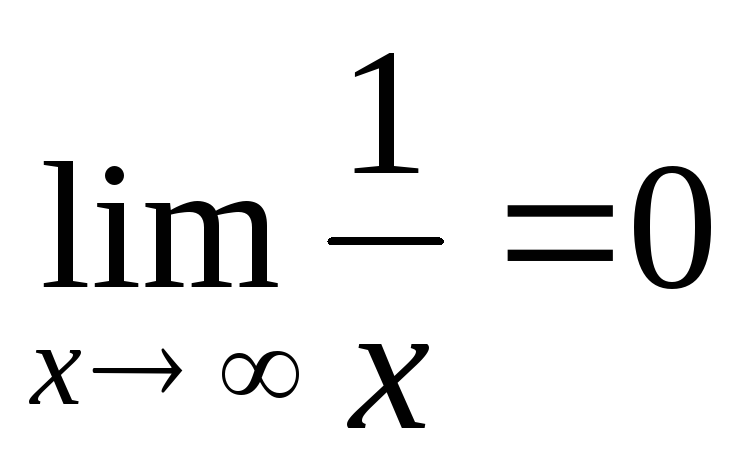 функция
функция 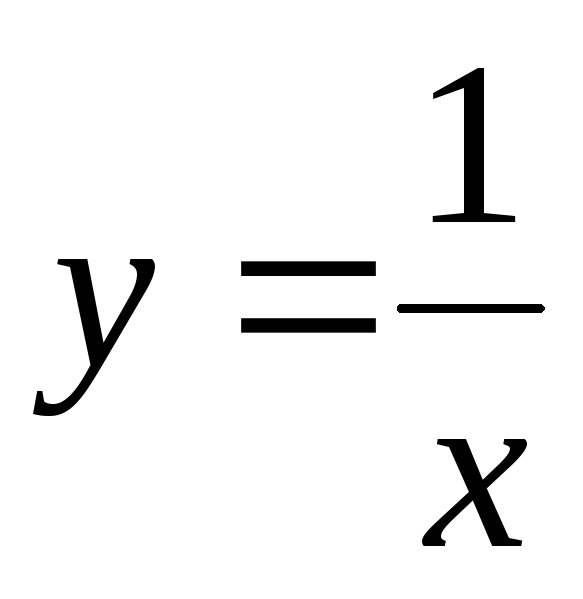 б.м. при
б.м. при  .
.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми, обозначают буквами α, β, γ, δ и т.д. (В природе – масса льдины находящейся в воде, в процессе таяния является бесконечно малой величиной.) суть б.м. в том, что в процессе изменения переменная величина стремится к нулю.
Теорема 1. Алгебраическая сумма любого конечного числа бесконечно малых величин есть так же бесконечно малая величина.
Теорема
2. Произведение бесконечно малой функции 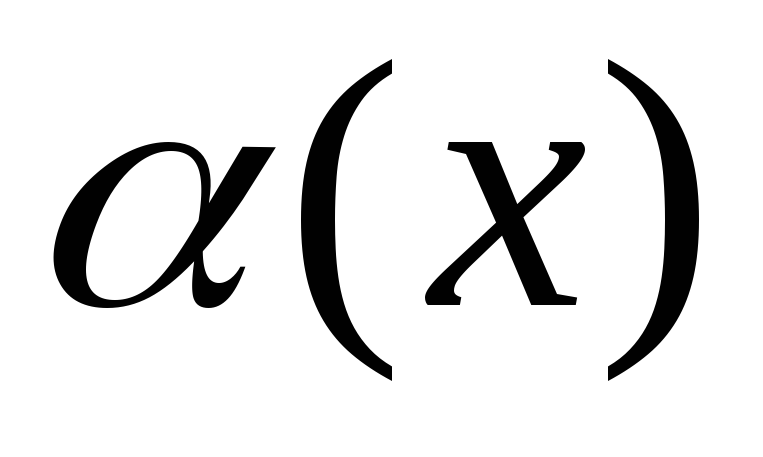 на ограниченную функцию
на ограниченную функцию 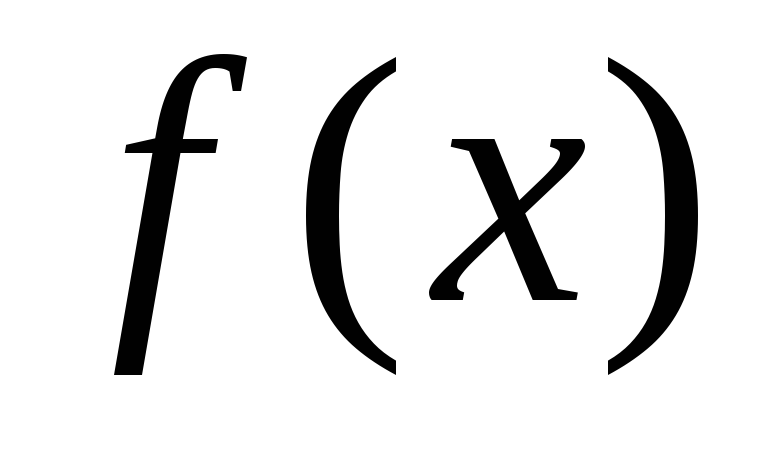 при
при 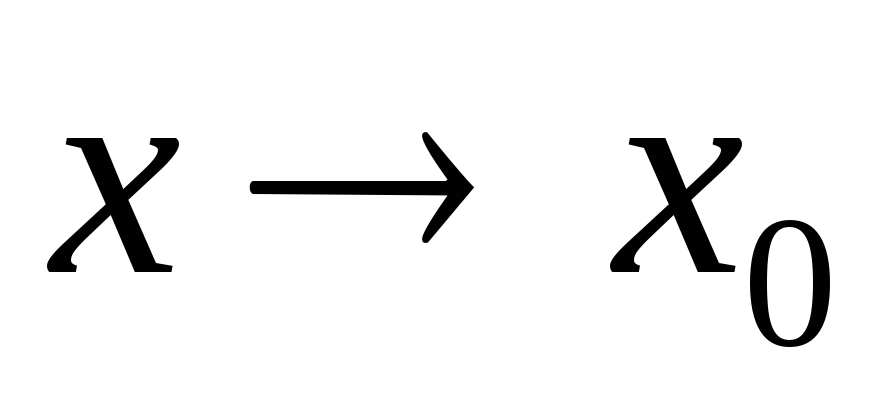 (или при
(или при  )
есть бесконечно малая функция.
)
есть бесконечно малая функция.
Доказательство.
Так как функция 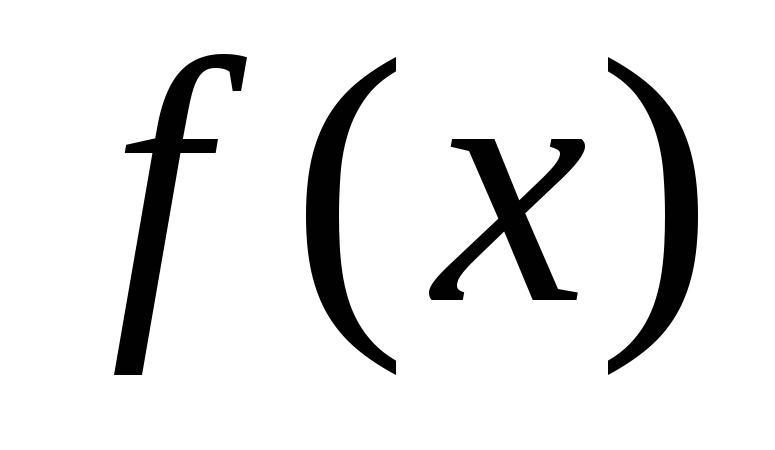 ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки
ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки 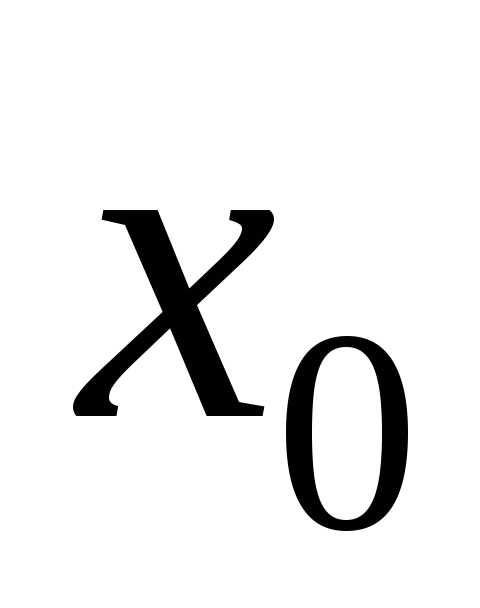
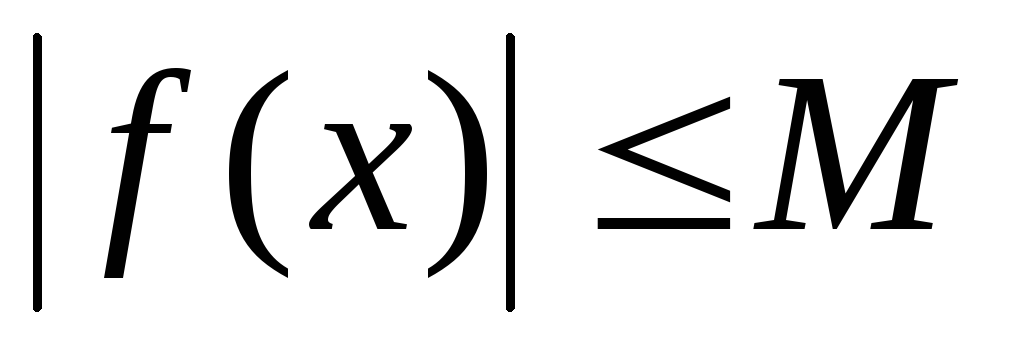 .
Кроме того, так как
.
Кроме того, так как  – бесконечно малая функция при
– бесконечно малая функция при  ,
то для произвольного
,
то для произвольного 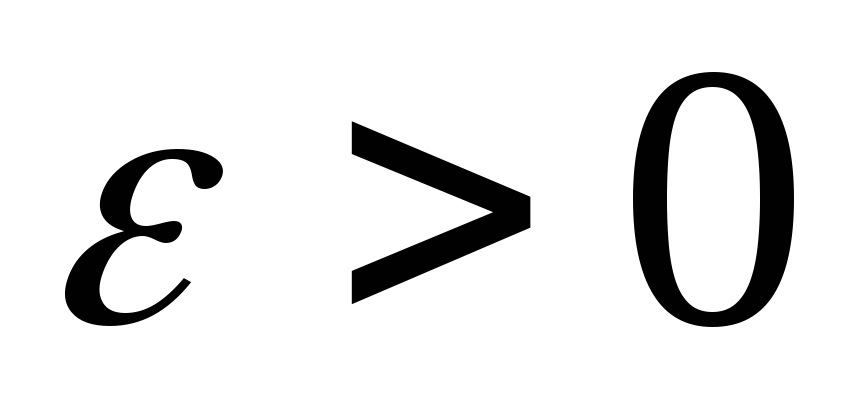 найдется окрестность точки
найдется окрестность точки  ,
в которой будет выполняться неравенство
,
в которой будет выполняться неравенство 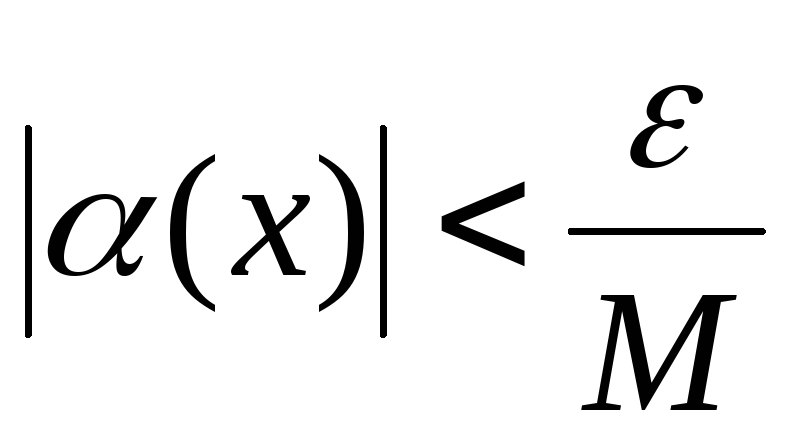 .
Тогда в меньшей из этих окрестностей
имеем
.
Тогда в меньшей из этих окрестностей
имеем 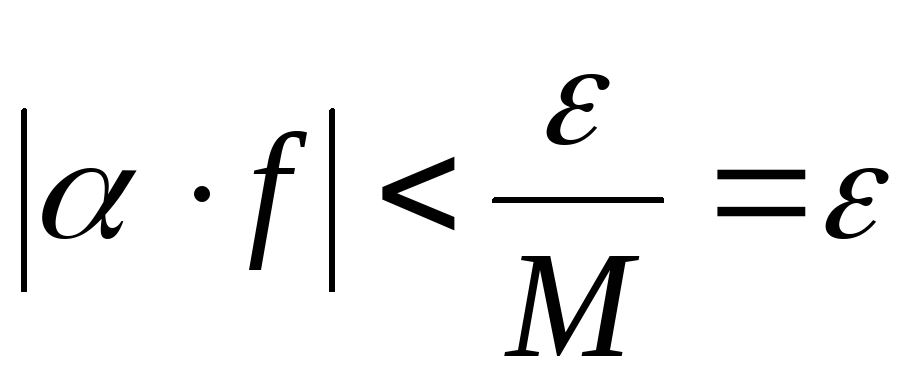 .
А это и значит, что
.
А это и значит, что  – бесконечно малая. Для случая
– бесконечно малая. Для случая доказательство проводится аналогично.
доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие
1. Если 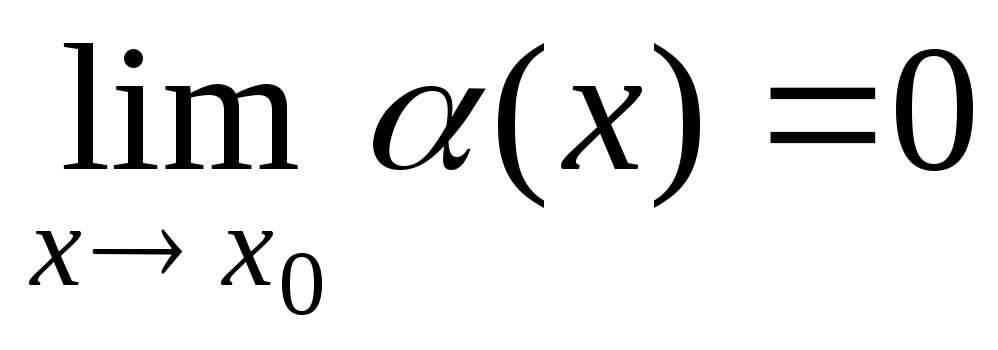 и
и  ,
то
,
то 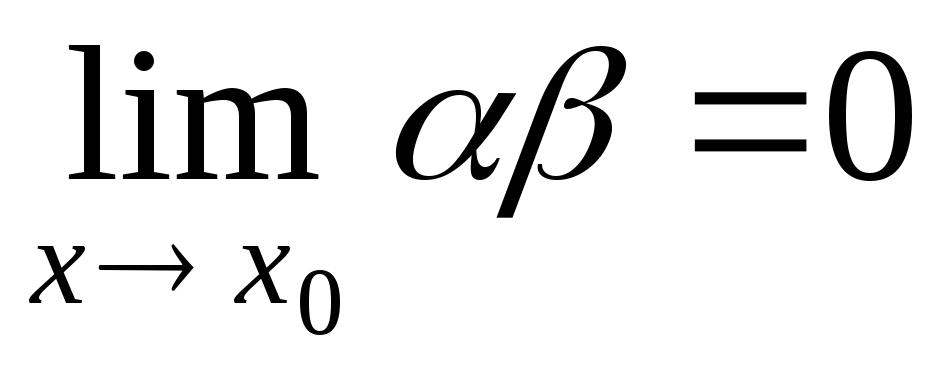 .
Произведение конечного числа б.м. величин
есть б.м. величина.
.
Произведение конечного числа б.м. величин
есть б.м. величина.
Следствие
2. Если 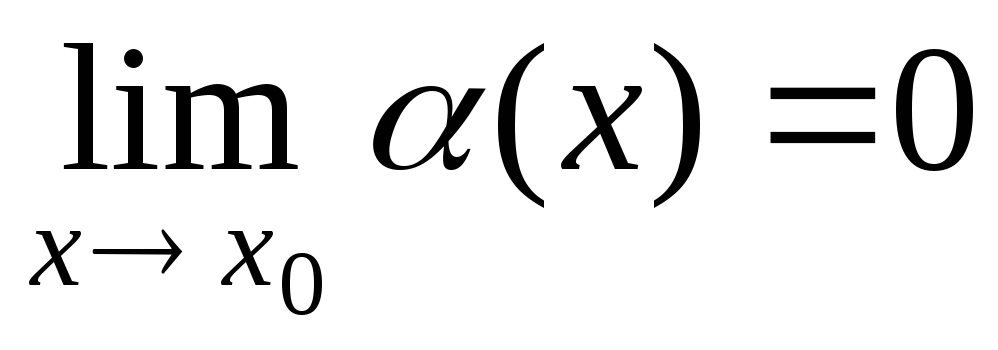 и c=const,
то
и c=const,
то 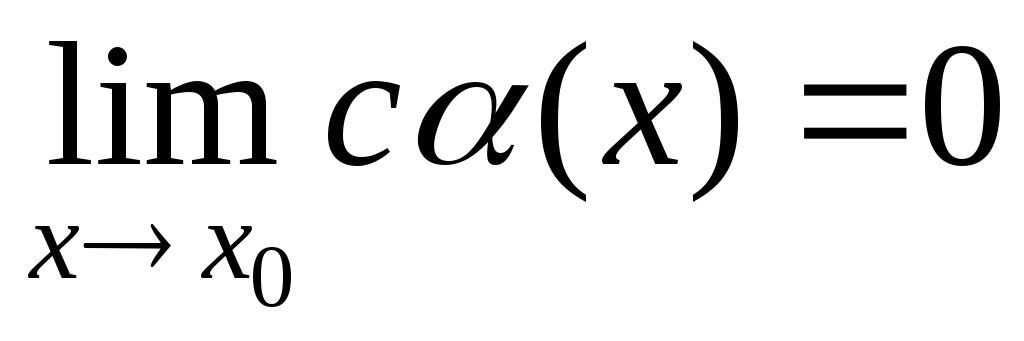 .
Произведение величины б.м. на величину
постоянную есть б.м. величина.
.
Произведение величины б.м. на величину
постоянную есть б.м. величина.
Теорема
3. Отношение бесконечно малой функции 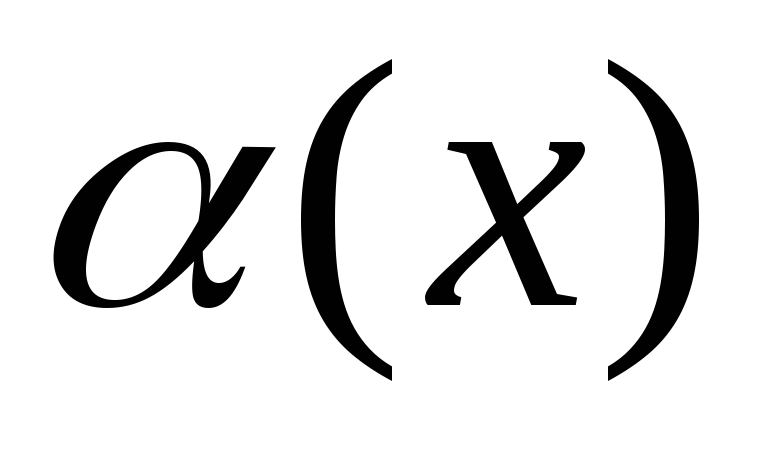 на функцию
на функцию 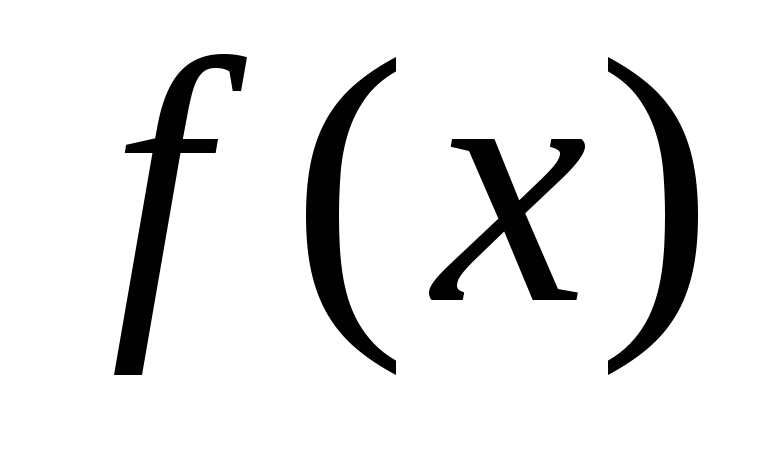 ,
предел которой отличен от нуля, есть
бесконечно малая функция.
,
предел которой отличен от нуля, есть
бесконечно малая функция.
Доказательство.
Пусть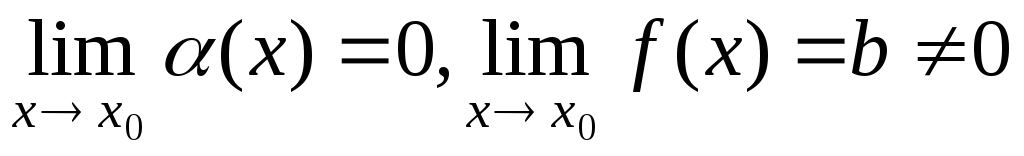 .
Тогда
.
Тогда 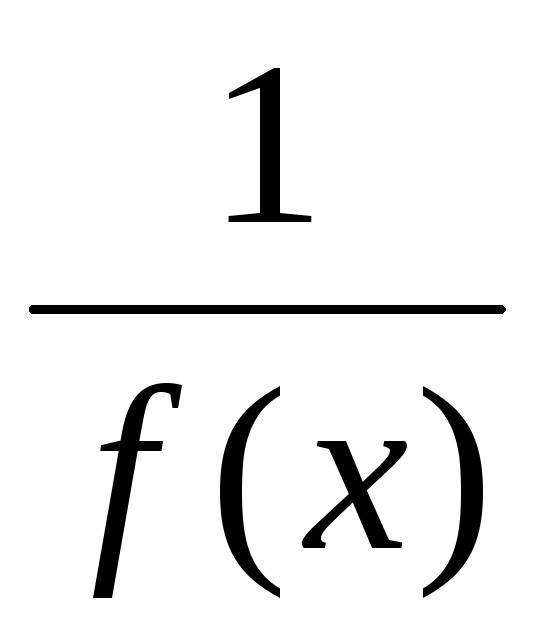 есть ограниченная функция. Поэтому
дробь
есть ограниченная функция. Поэтому
дробь 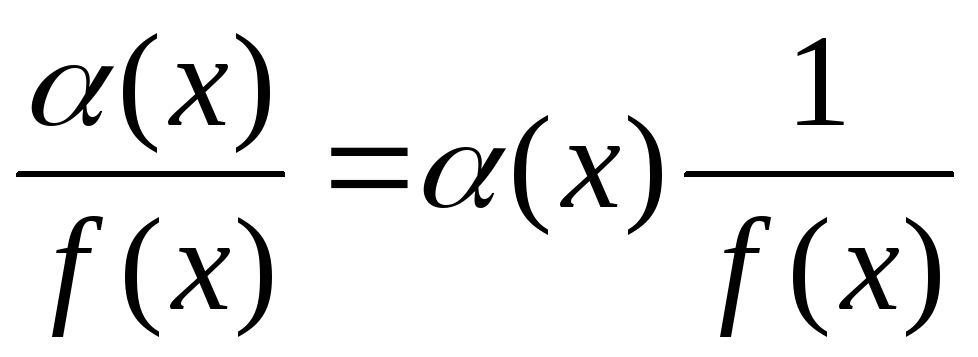 есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
Бесконечно большие функции.
Наряду с бесконечно малыми величинами существуют бесконечно большие. Например, время, отсчитываемое от некоторого начального момента, может возрастать неограниченно. Путь, который проходит точка числовой оси, неограниченно удаляясь от начала координат.
Опр.
Функция 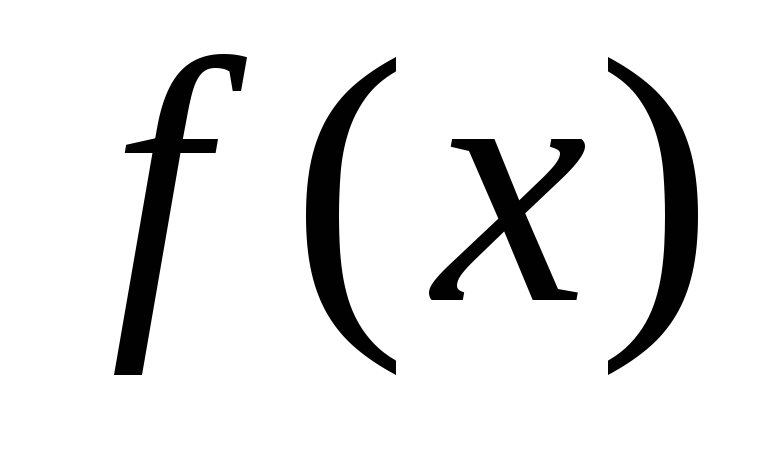 стремится к бесконечности при
стремится к бесконечности при  ,
т.е. является бесконечно
большой величиной, если для любого числа М,
как бы велико оно ни было, можно найти
такое
,
т.е. является бесконечно
большой величиной, если для любого числа М,
как бы велико оно ни было, можно найти
такое 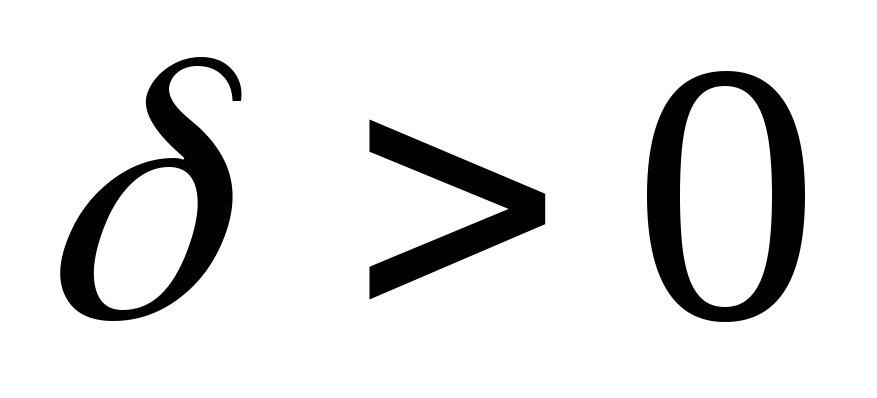 ,
что для всех значений
,
что для всех значений 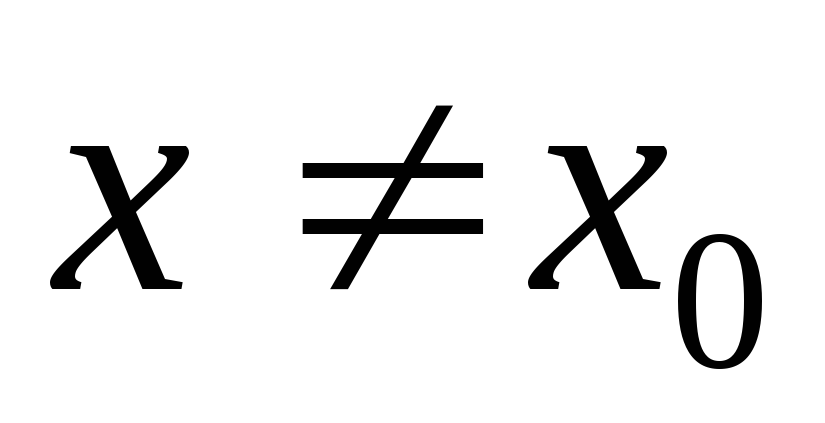 ,
удовлетворяющих условию
,
имеет место неравенство
,
удовлетворяющих условию
,
имеет место неравенство 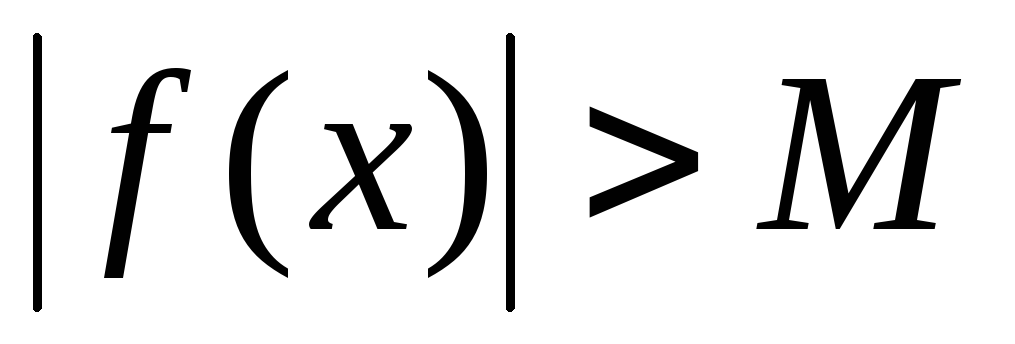 .
.
Обозначают 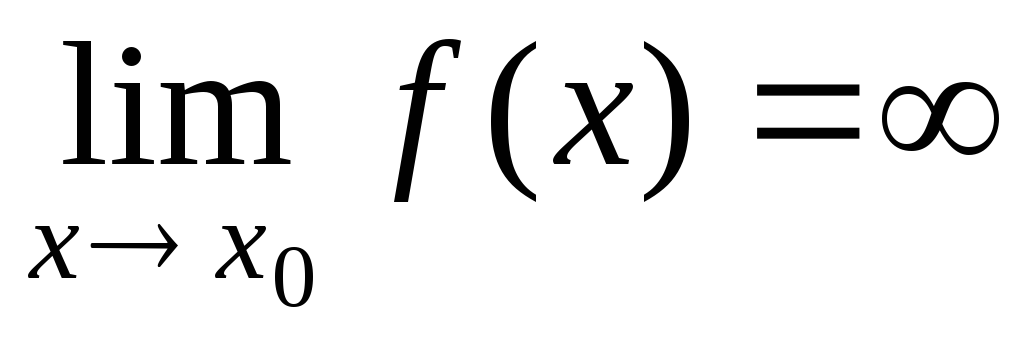 .
.
Если 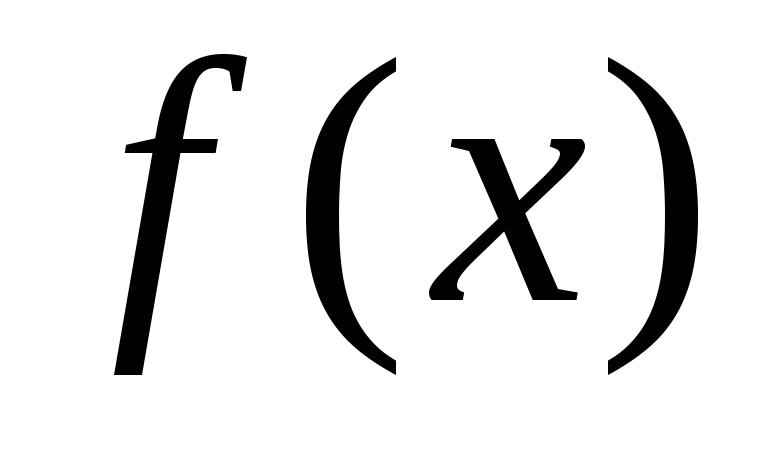 стремится к бесконечности при
стремится к бесконечности при 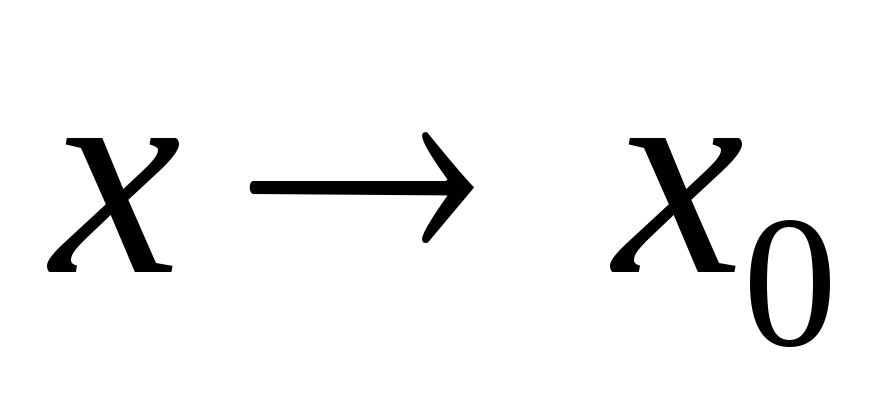 и при этом принимает только положительные
или только отрицательные значения,
соответственно пишут
и при этом принимает только положительные
или только отрицательные значения,
соответственно пишут 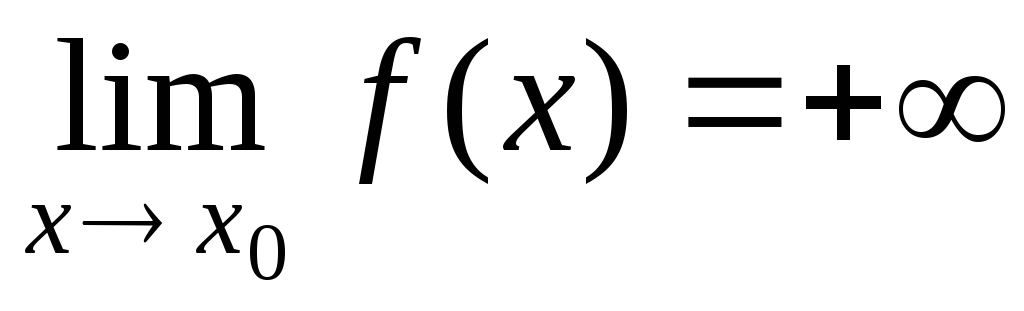 или
или 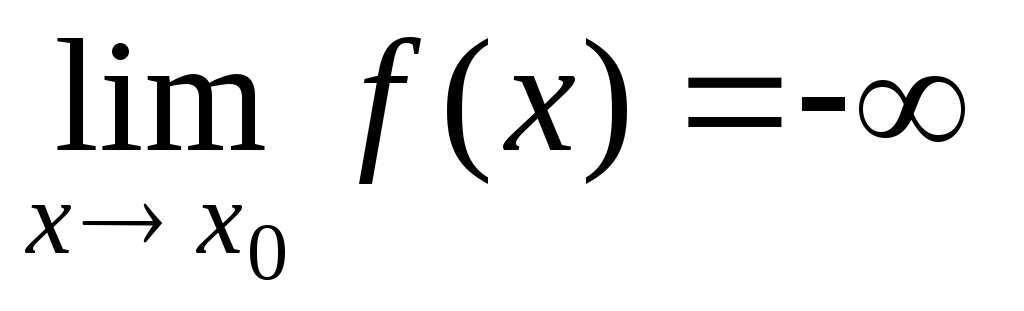 .
.
П римеры.
римеры.
 ,
, (см. рис.).
(см. рис.).

 .
.Функция
 при
при  не стремится ни к какому пределу (см.
рис.).
не стремится ни к какому пределу (см.
рис.).
Соотношение между бесконечно малыми и бесконечно большими функциями.
Теорема
1. Если функция 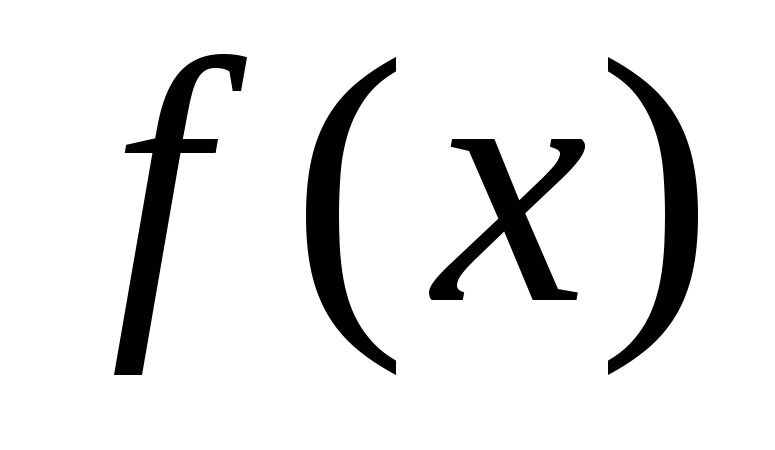 является бесконечно большой при
является бесконечно большой при  ,
то функция
,
то функция  является бесконечно малой при
является бесконечно малой при 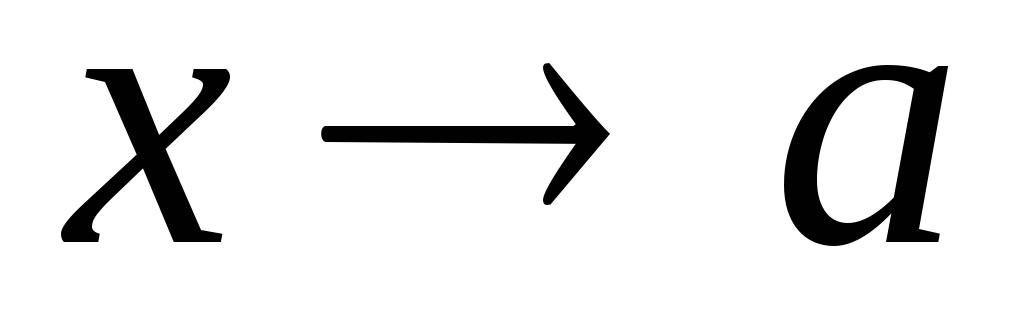 .
.
Пример.
Ясно,
что при 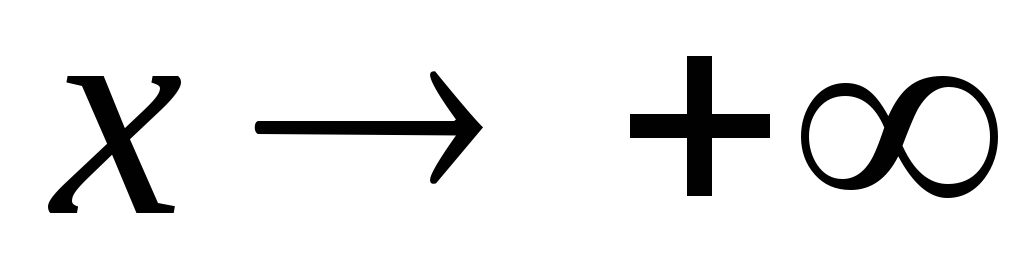 функция
функция 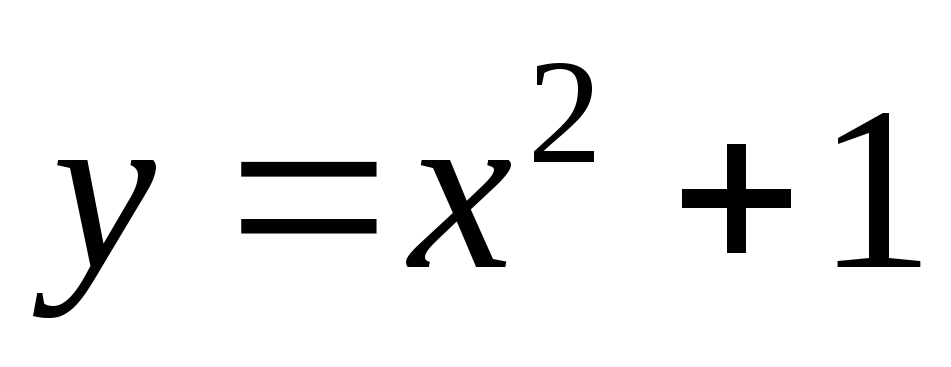 является бесконечно большой. Но тогда
согласно сформулированной выше теореме
функция
является бесконечно большой. Но тогда
согласно сформулированной выше теореме
функция 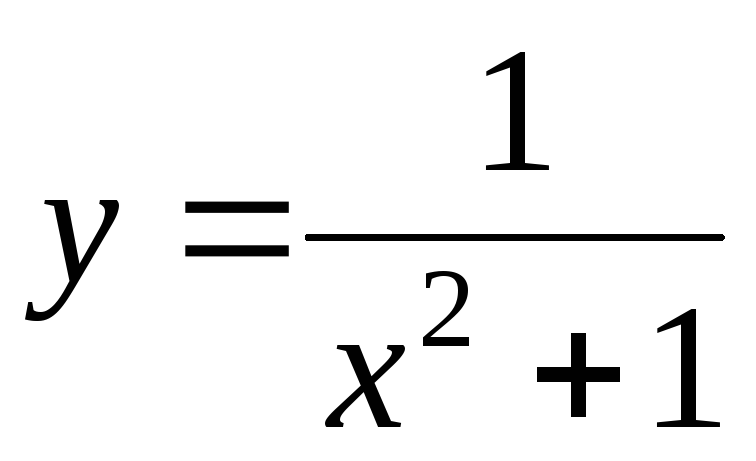 –
бесконечно малая при
–
бесконечно малая при 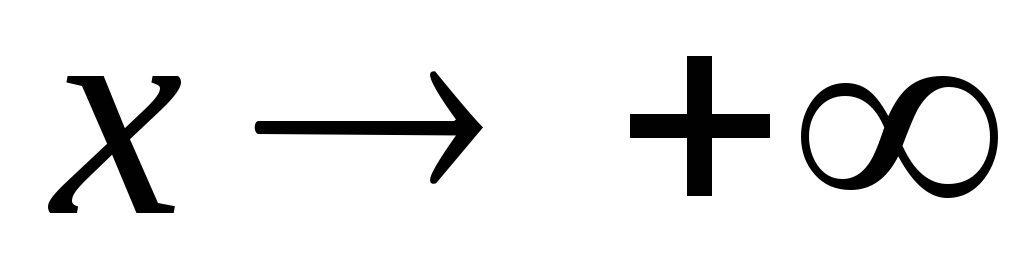 ,
т.е.
,
т.е. 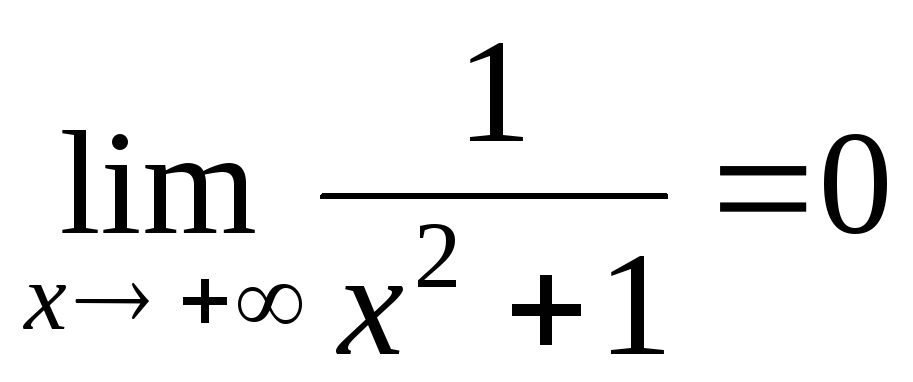 .
.
Теорема
2. Если функция 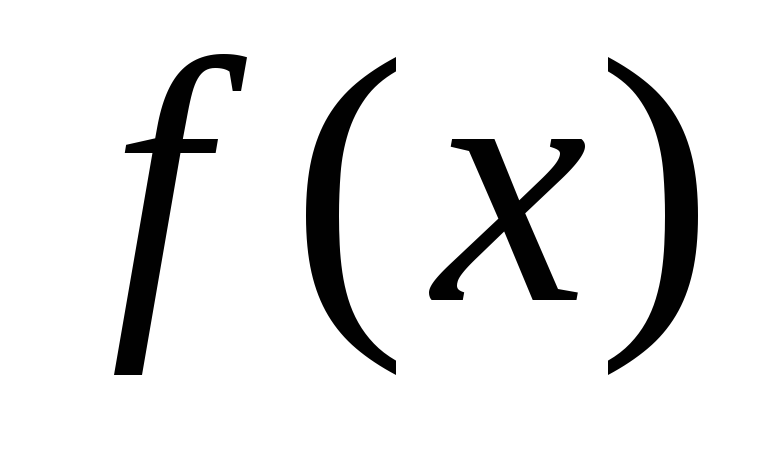 — бесконечно малая при
— бесконечно малая при 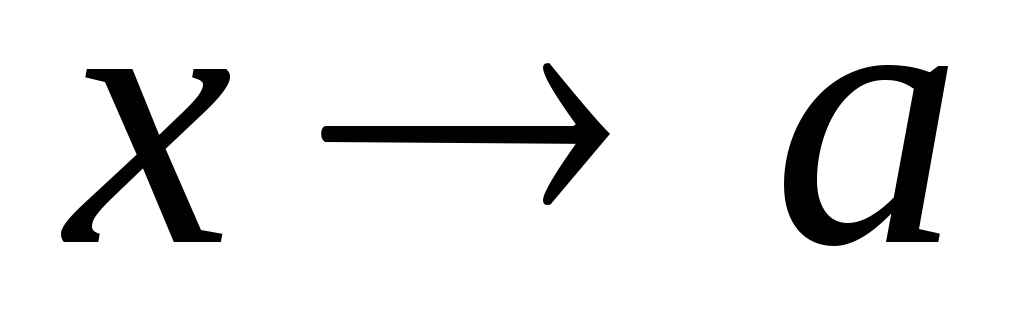 (или
(или ) и не обращается в нуль, то
) и не обращается в нуль, то 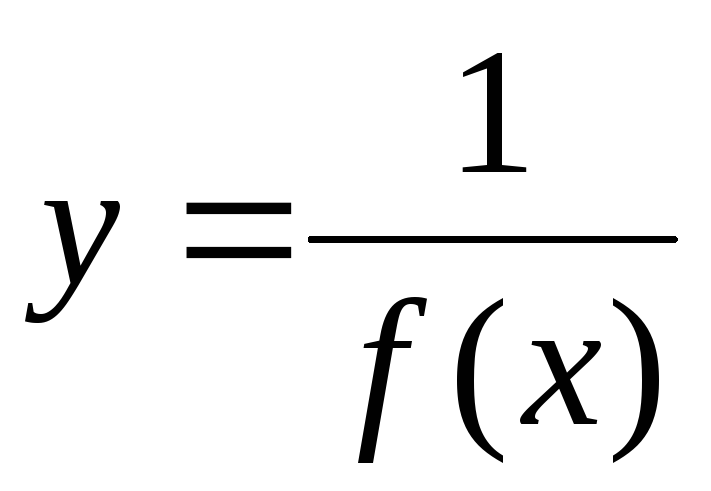 является бесконечно большой функцией.
является бесконечно большой функцией.
Примеры.
 .
. .
. ,
так как функции
,
так как функции  и
и  —
бесконечно малые при
—
бесконечно малые при  ,
то
,
то  ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же  является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
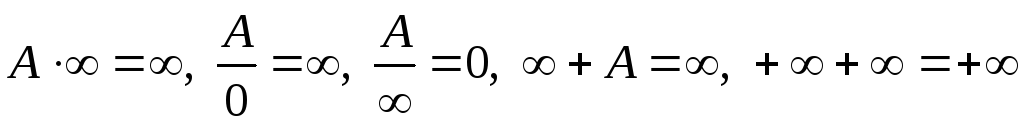 .
.
бесконечно малые величины и их свойства
Пусть функция 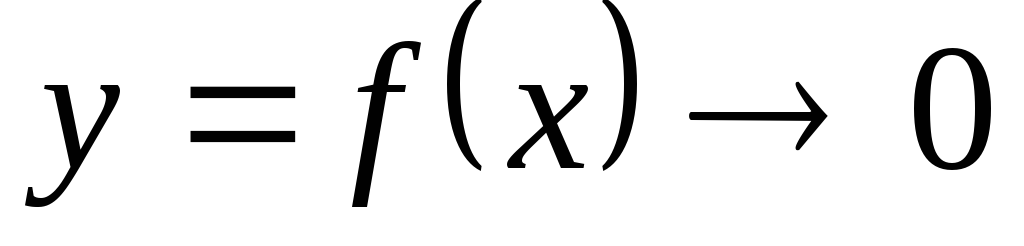 ,
при
,
при  ,
тогда эта функция называется бесконечно
малой величиной при
,
тогда эта функция называется бесконечно
малой величиной при  .
.
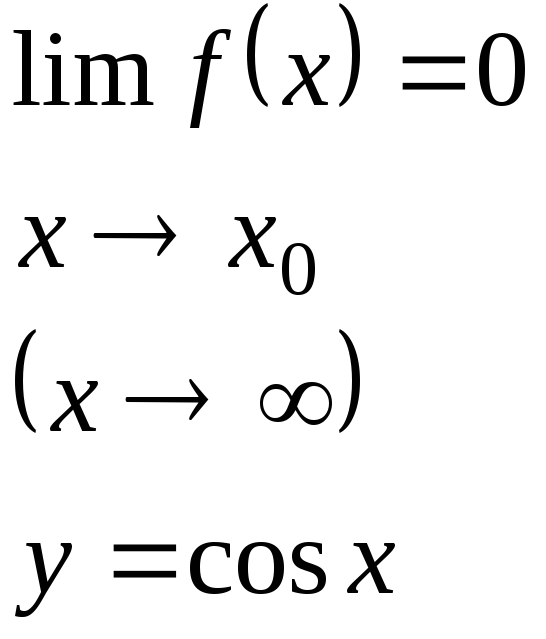
Если 
 ,
то функцию можно назвать бесконечно
малой величиной, но если
,
то функцию можно назвать бесконечно
малой величиной, но если 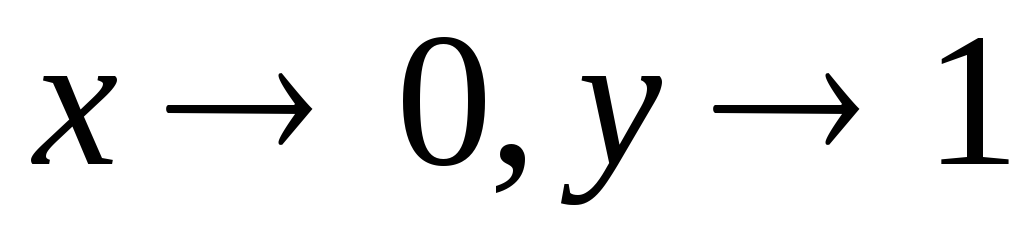 ,
то функцию нельзя назвать бесконечно
малой величиной.
,
то функцию нельзя назвать бесконечно
малой величиной.
Основные свойства
Пусть предел функции
 ,
при
,
при 
 ,
тогда в некоторой окрестности точки
,
тогда в некоторой окрестности точки  ,
справедливо равенство
,
справедливо равенство  ,
где
,
где  бесконечное,
при
бесконечное,
при  .
.Пусть в некоторой окрестности точки
 справедливо равенство
справедливо равенство 
При 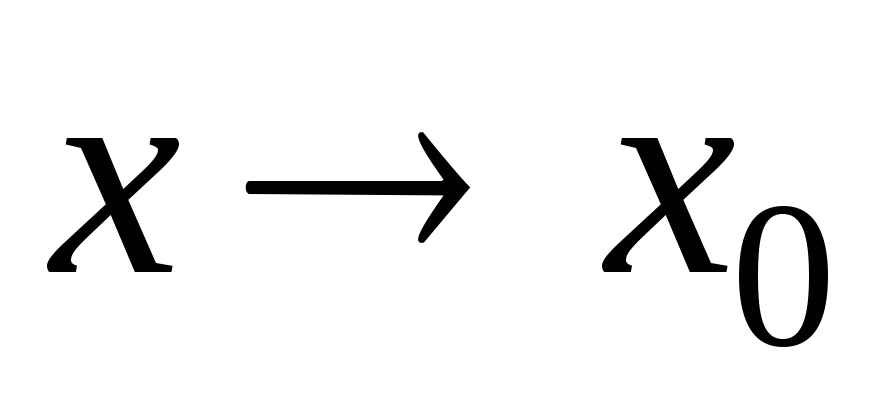 ,
тогда предел этой функции при
,
тогда предел этой функции при 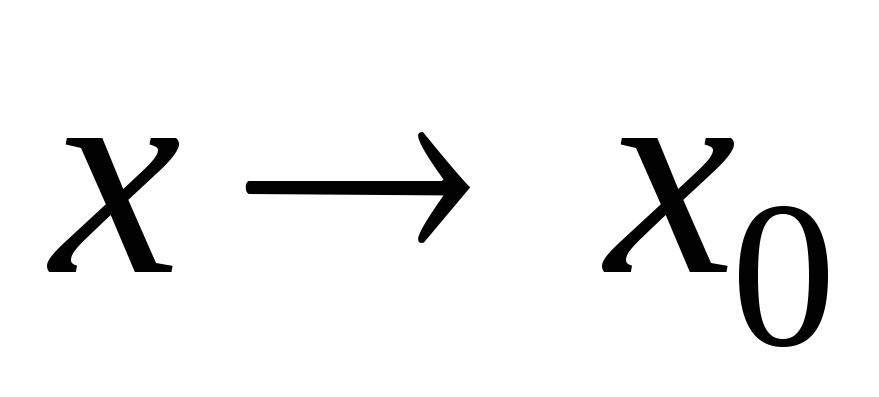 = b
= b 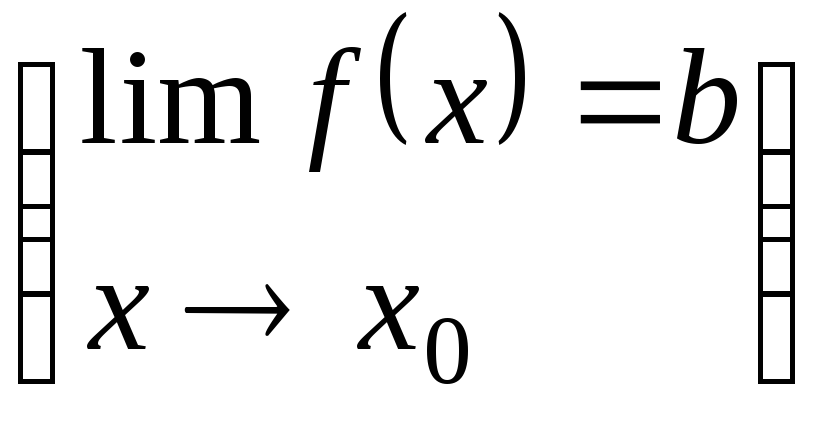
если
 ,
при
,
то
,
при
,
то  ,
стремится к бесконечности
,
стремится к бесконечностиАлгебраическая сума конечного числа точки
 M
величин есть также
M
величин есть также  Mb
MbПроизведение Mb на ограниченную функцию, есть
 Mb
Mb
Следствие
Произведение
 M
на постоянную величину есть
M
на постоянную величину есть  M
MПроизведение конечного числа
 Mb
есть
Mb
есть Mb
Mb
Тема: Основные теоремы о пределах
Теорема 1
Предел суммы или разности конечного числа слагаемых функций равен соответственно сумме или разности пределов каждой функции
Теорема 2
Предел произведения конечного числа функции равен произведению пределов сомножителей
Теорема 3
Предел частного двух функций равен отношению их пределов, если предел знаменателя отличен от 0
Теорема 4
Пусть функция 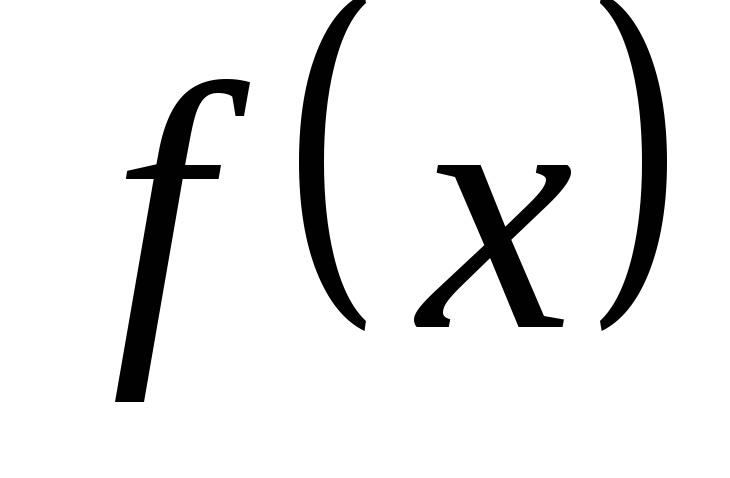 удовлетворяет условию:
удовлетворяет условию:
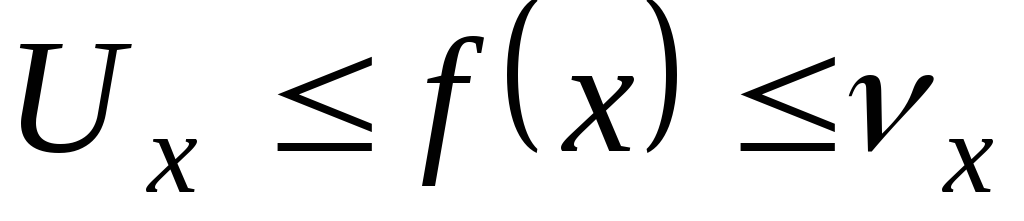 и пусть пределы крайних функций равны
друг другу и равны b, тогда
предел средней функции существует и
равен b
и пусть пределы крайних функций равны
друг другу и равны b, тогда
предел средней функции существует и
равен b
lim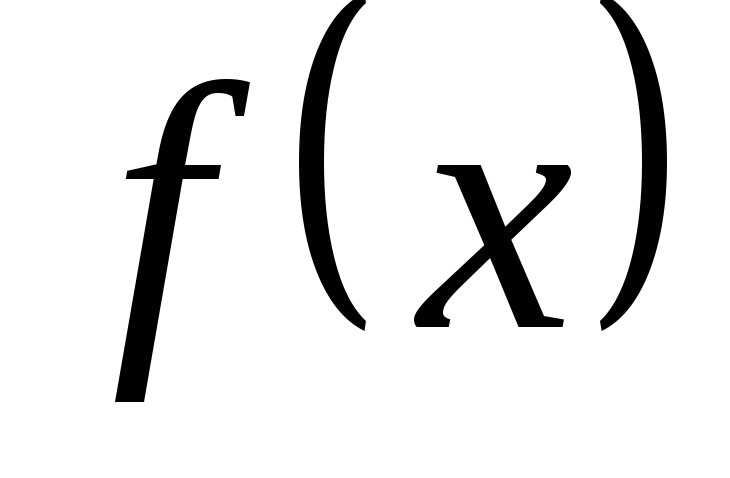 =
= 
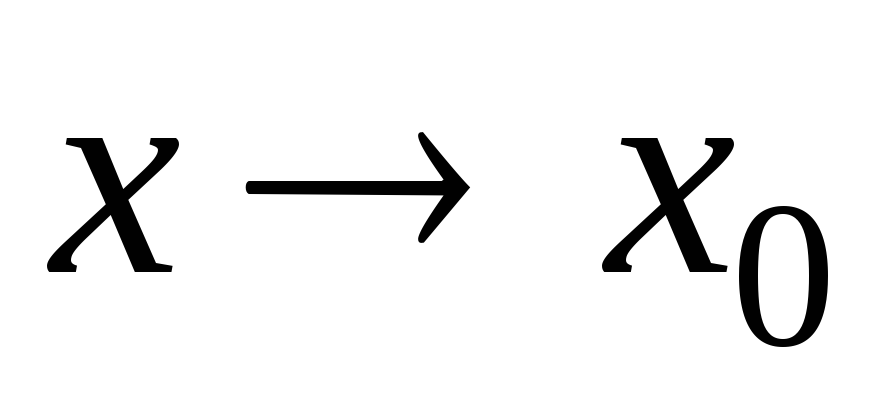
n! =1·2·3·4…………n
n- Факториал
0!=1, 2!=2
1!=1, 3!=1·2·3=6, 4!=24
Теорема 5
Пусть некоторая
функция y= при
при 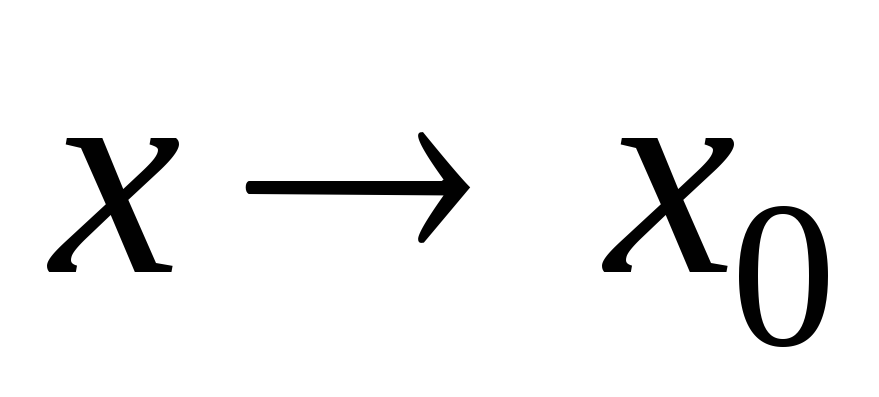 стремится
к пределу
стремится
к пределу  ,
принимая при этом все время не отрицательные
значения, тогда предел
,
принимая при этом все время не отрицательные
значения, тогда предел  ,
тогда b также не отрицателен
,
тогда b также не отрицателен 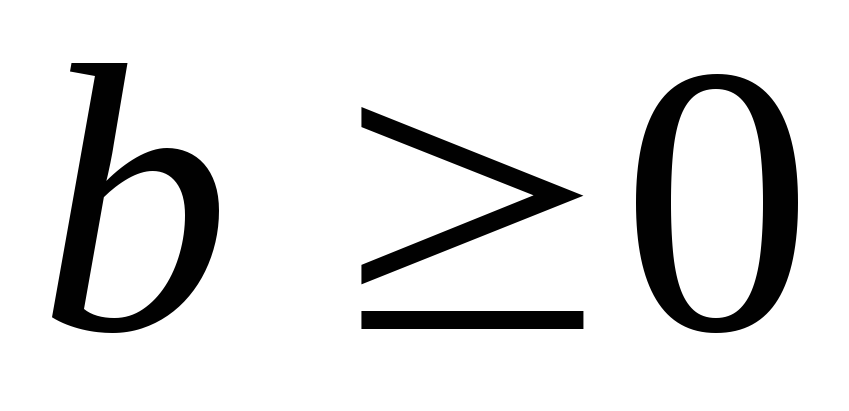
Теорема 6
Пусть при 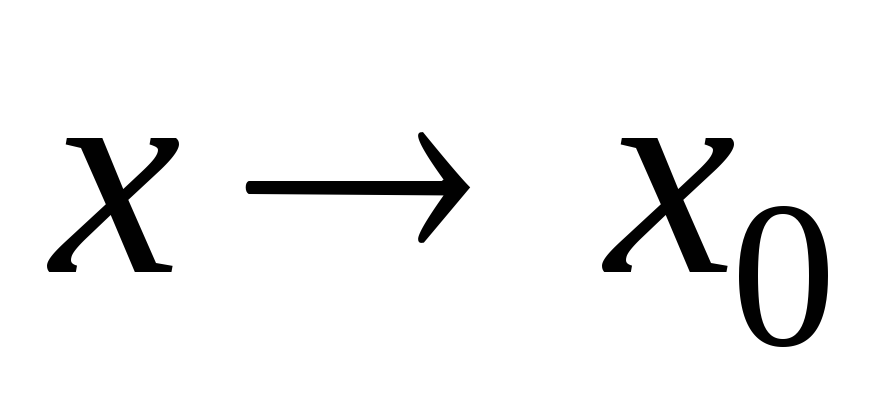 две функции связанные неравенством стремятся к
некоторым пределам, тогда
две функции связанные неравенством стремятся к
некоторым пределам, тогда 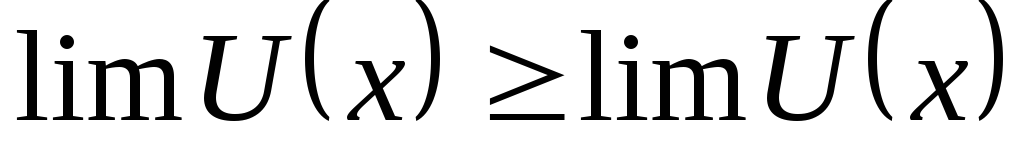 ,
их пределы связаны таким же неравенством
,
их пределы связаны таким же неравенством
Теорема 7
Если переменная величина монотонно возрастает и ограничено сверху числом М, то она имеет предел не превосходящий М.
Тема: Первый замечательный предел
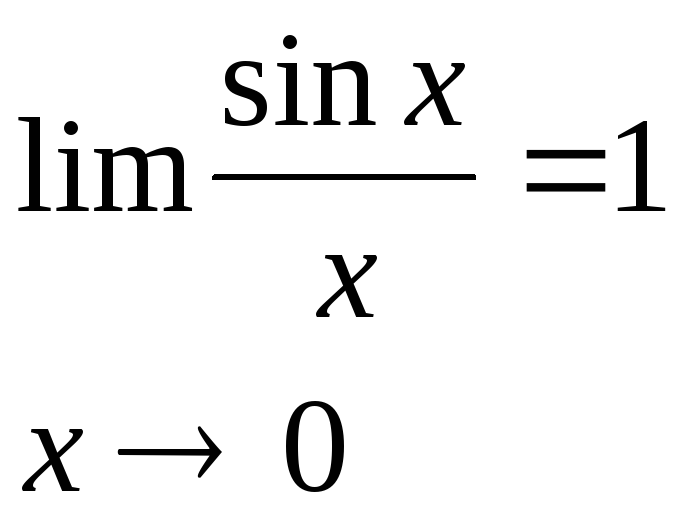
Рассмотрим
S

 y D
y D


 A
A
 0 xc B
x
0 xc B
x

Рассмотрим 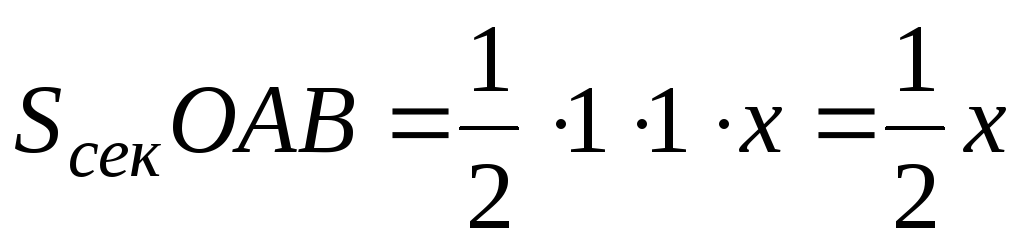

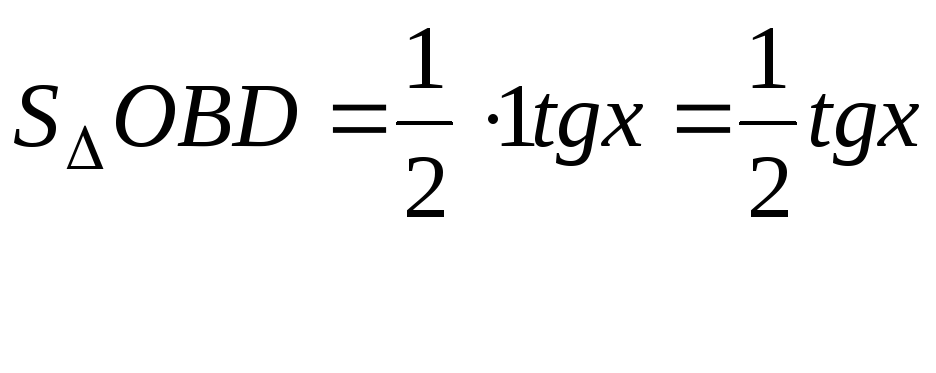
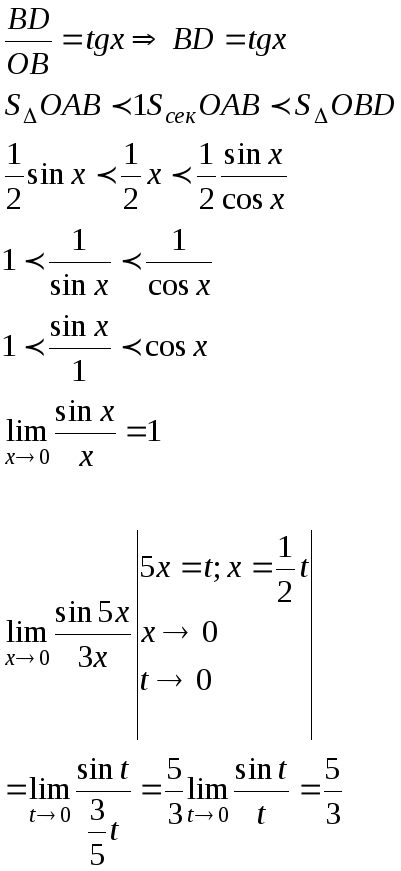
Тема: второй замечательный предел. Число e, натуральные логарифмы
Рассмотрим числовую последовательность
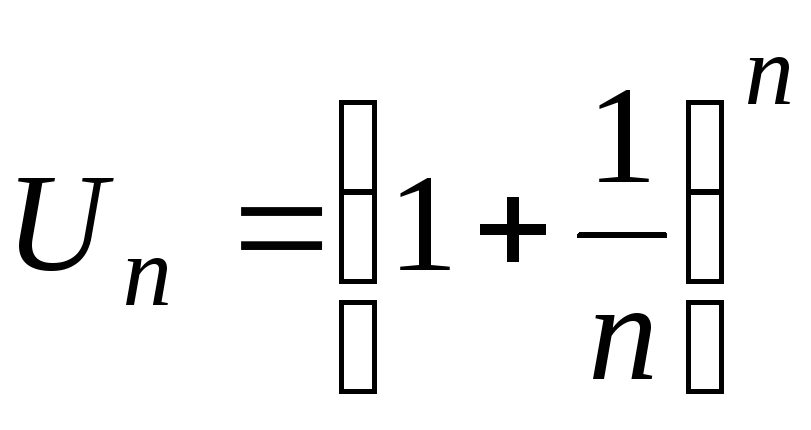
Теорема:
Предел
последовательности  при
при 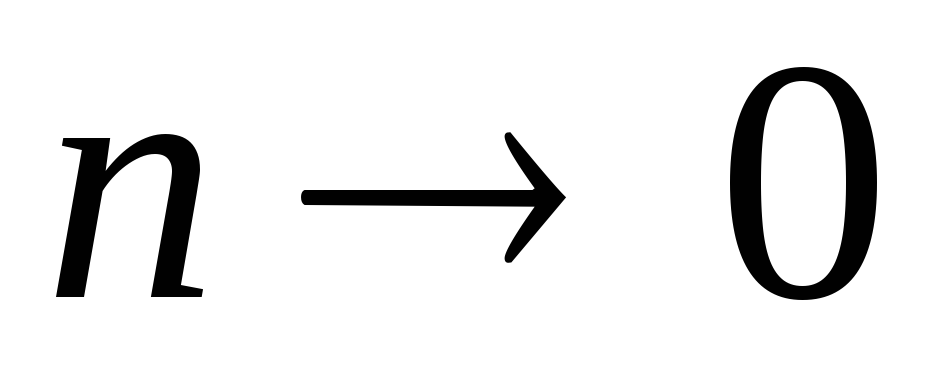 равен числу e
равен числу e 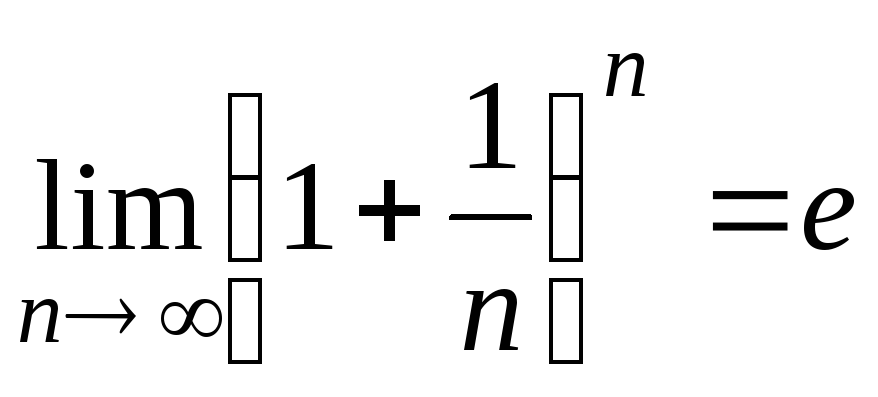 иррациональное число
иррациональное число
Теорема:
Рассмотрим
функцию 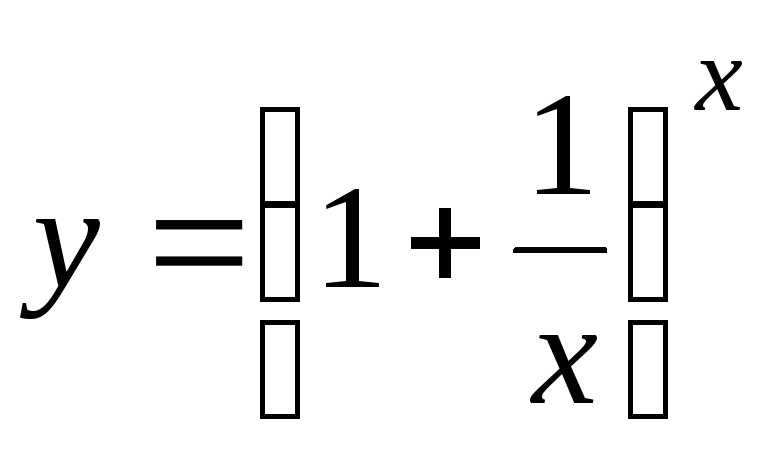 ,
пусть
,
пусть  принимая при этом иррациональные и
рациональные значения, т.е. непрерывно
принимая при этом иррациональные и
рациональные значения, т.е. непрерывно  ,
тогда можно доказать теорему
,
тогда можно доказать теорему 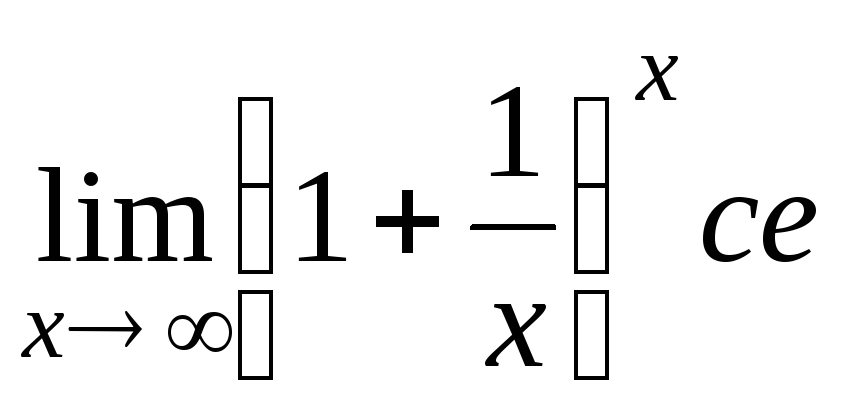
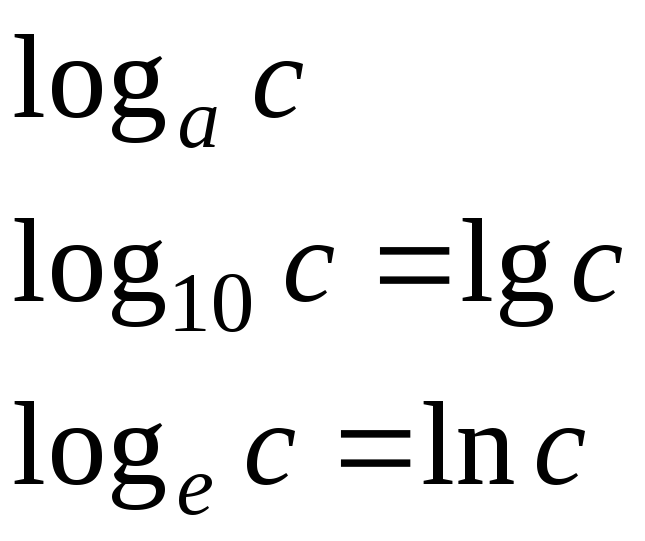
Натуральный логарифм
 экспонент
экспонент
Найти предел функции:
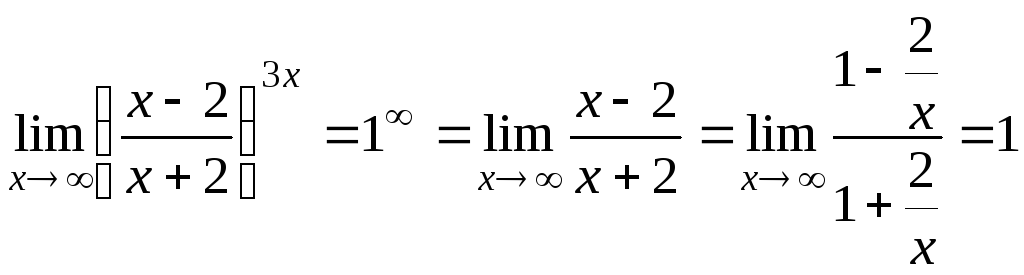
1 в любой конечной степени остается единицей
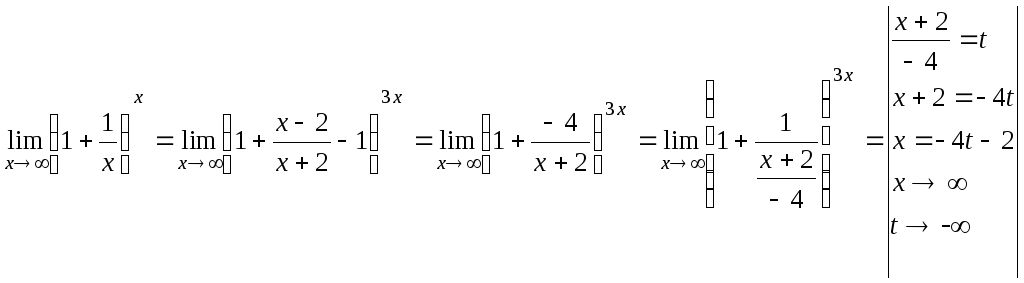 =
=
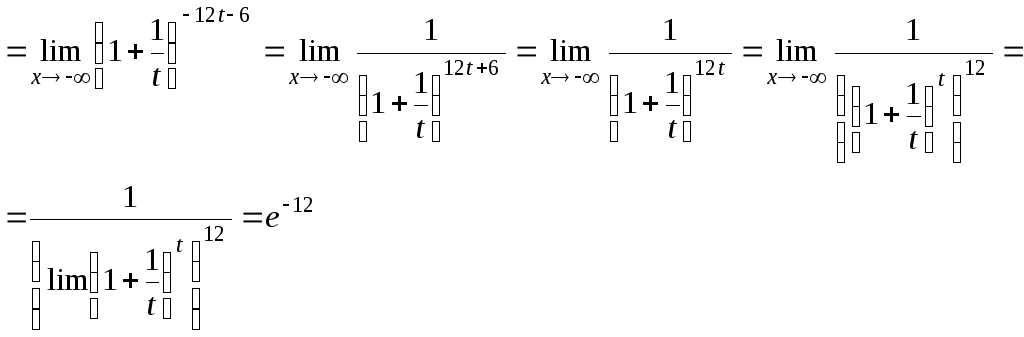
Тема: Сравнение бесконечно малых величин
Пусть даны две функции 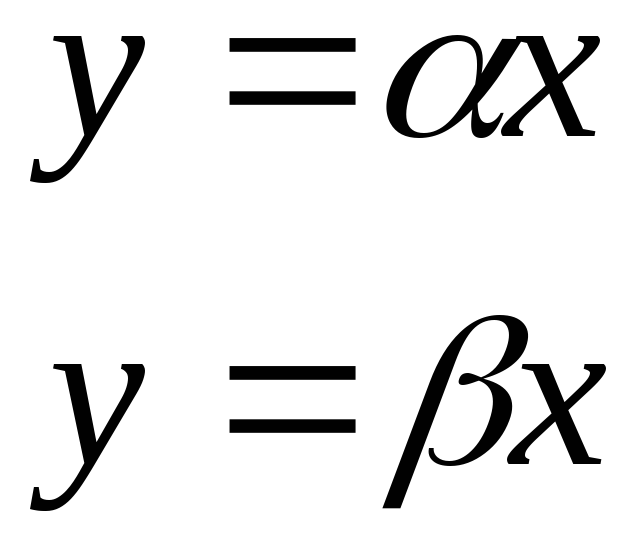
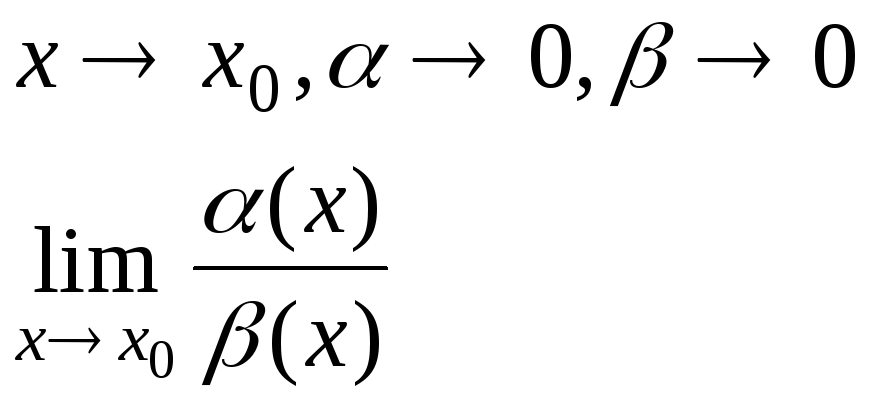
1) пусть этот предел равен случайному.
с≠0, тогда эти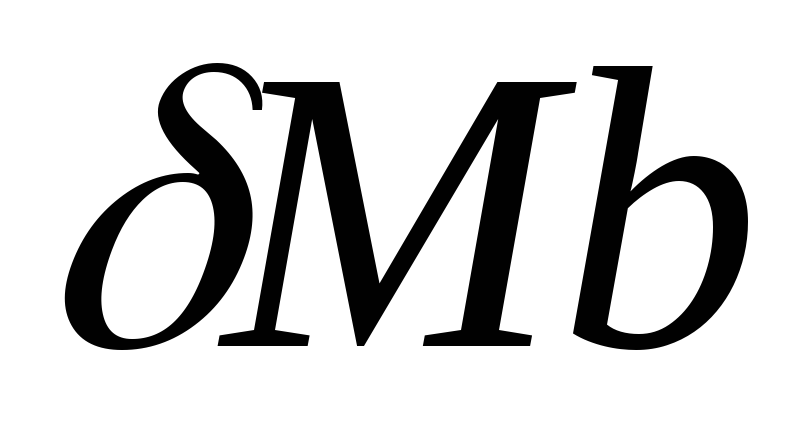 ,
называются бесконечно малыми
,
называются бесконечно малыми  одного
порядка малости или одного порядка.
одного
порядка малости или одного порядка.
Пусть с=1, тогда. 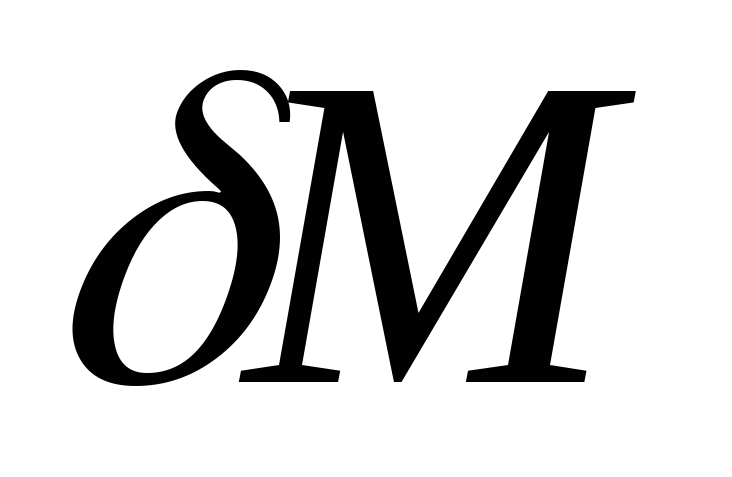 называются
эквивалентами
называются
эквивалентами


 при
при 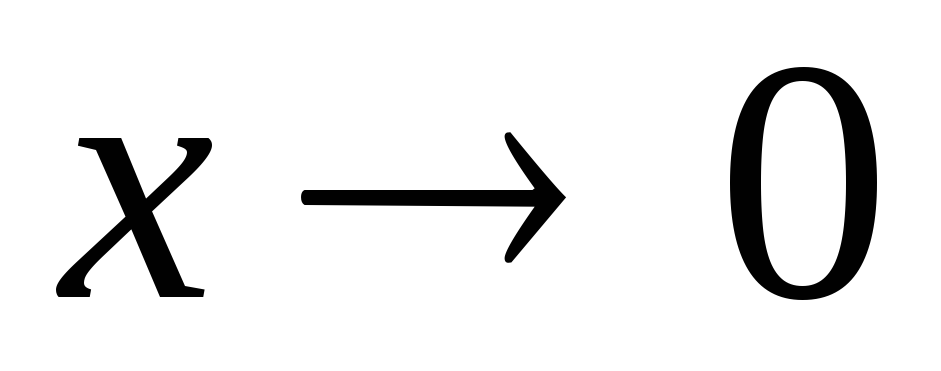
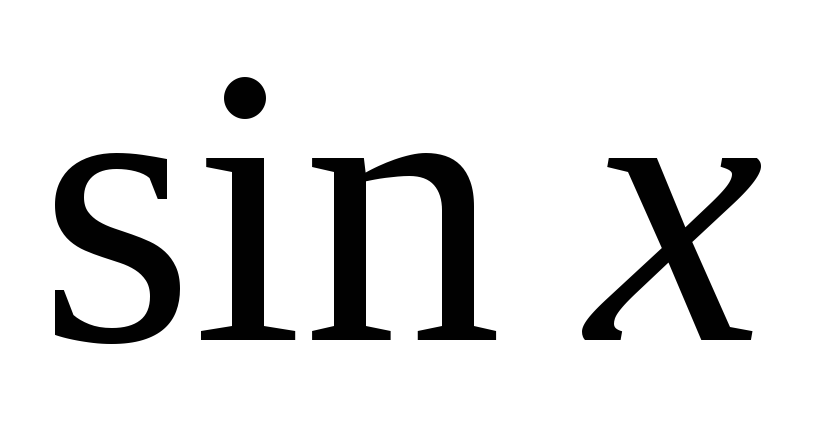
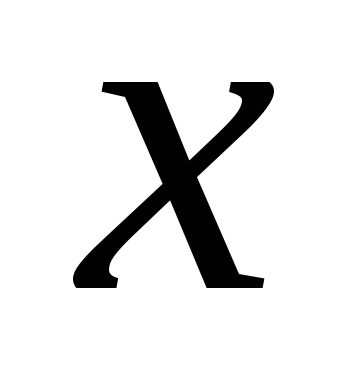
Пусть величина этого случайного предела =0, то
 называют
называют  более высокого порядка по сравнению с
более высокого порядка по сравнению с  ,
,  и
и  являются
одного порядка, тогда
являются
одного порядка, тогда  называют
называют
 катово порядка малости по сравнению с
катово порядка малости по сравнению с 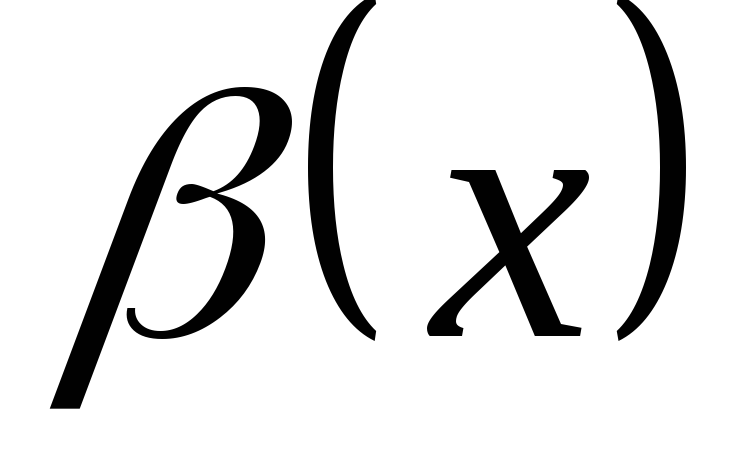 .
.
Непрерывность функции в точки и области
Пусть функция 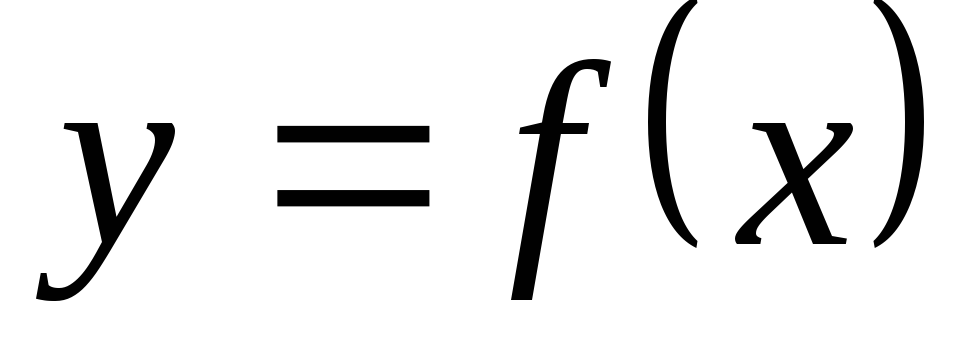 определяется в точке
определяется в точке  и в некоторой ее окрестности.
и в некоторой ее окрестности.
Функция 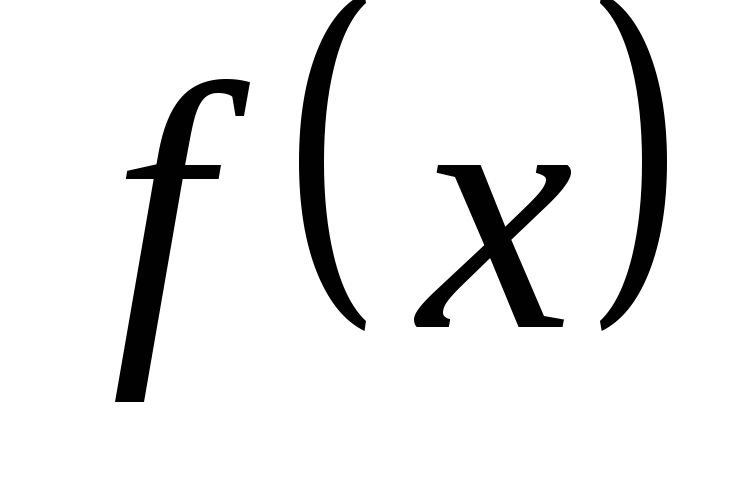 называется непрерывной в точке
называется непрерывной в точке  если справедливо равенство
если справедливо равенство
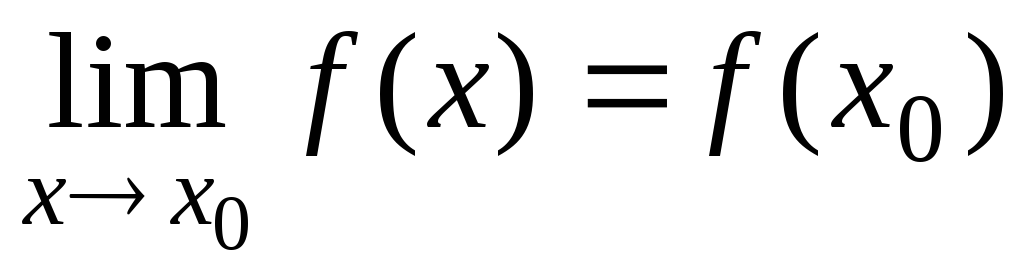
Функция 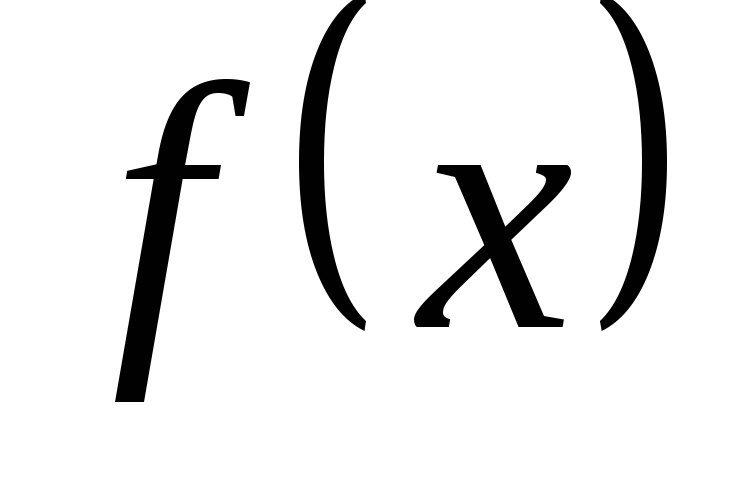 называется непрерывной, если
называется непрерывной, если 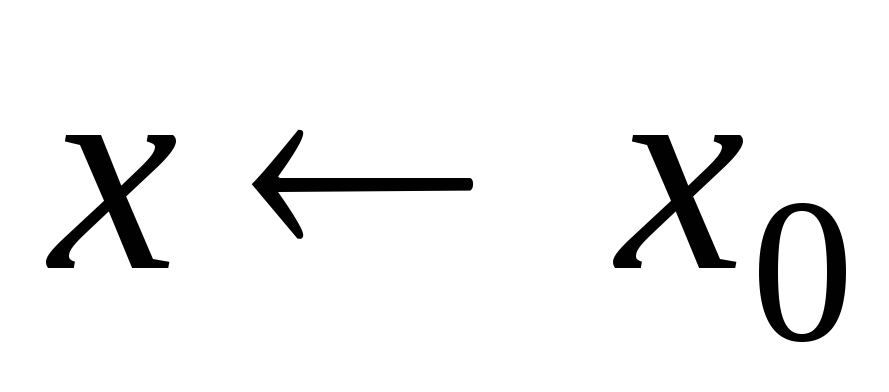 то предел этой функции совпадает со
значением в точки
то предел этой функции совпадает со
значением в точки 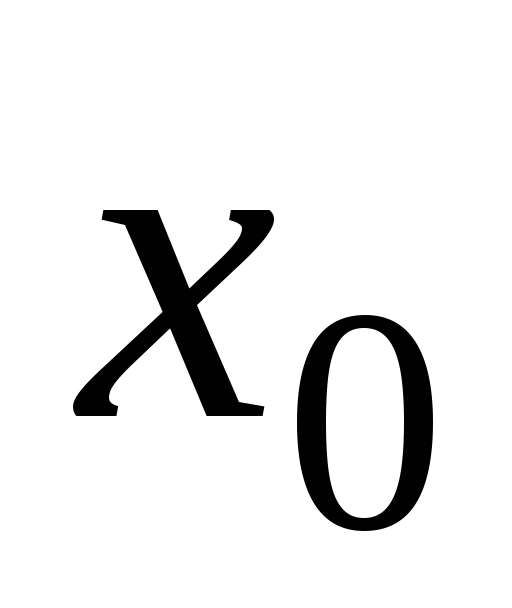
Если  ,
то
,
то 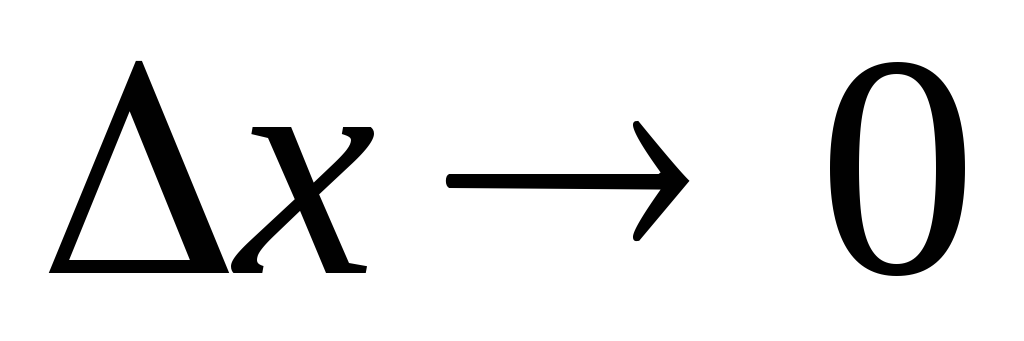
 (соответствующее
превращение функции)
(соответствующее
превращение функции)
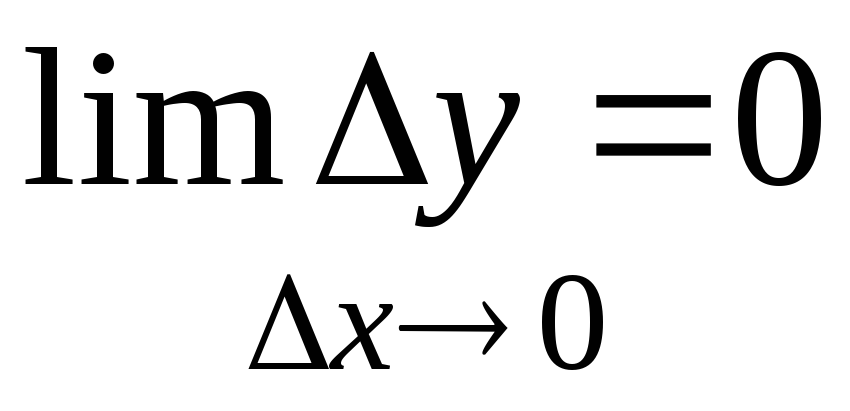
Функция  называется непрерывной в точке
называется непрерывной в точке 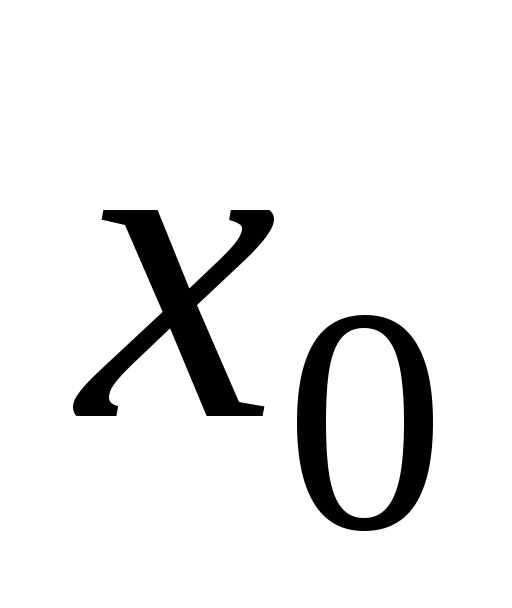 если
если  превращения
аргумента соответствует
превращения
аргумента соответствует  превращения функции.
превращения функции.
Пусть  ,
то
,
то 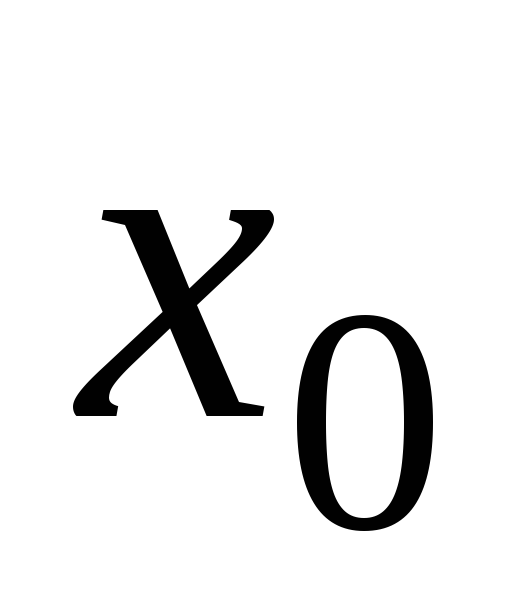 ,
первое неравенство
,
первое неравенство 
Если 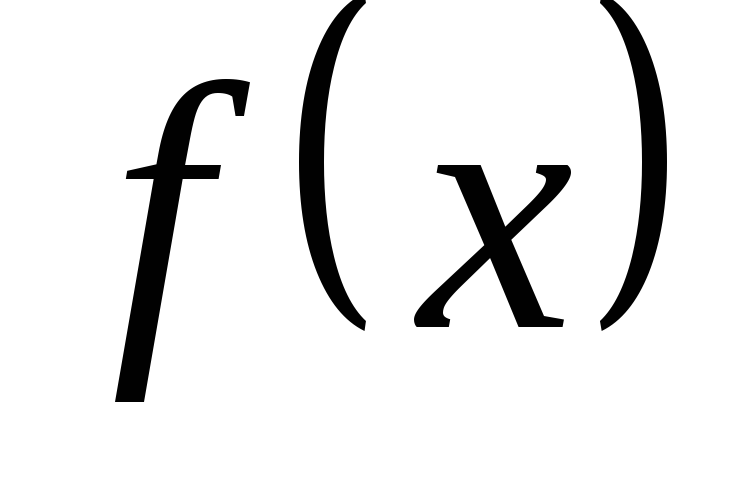 непрерывна в точке
непрерывна в точке 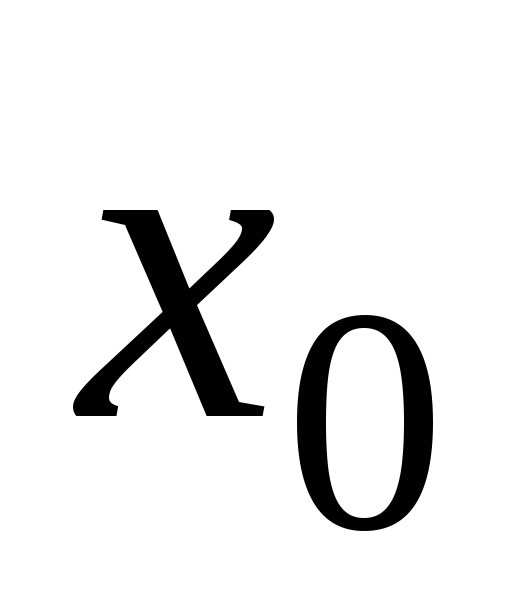 ,
то предел этой функции при
,
то предел этой функции при 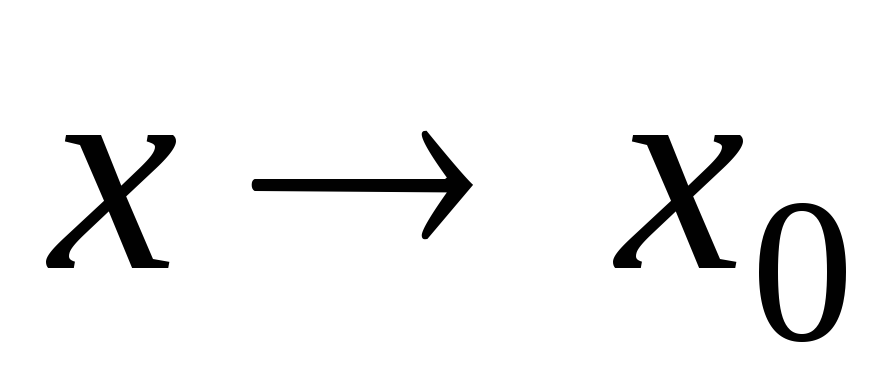 вычисляется
подстановкой предельного значения
аргумента в функциональное выражение.
вычисляется
подстановкой предельного значения
аргумента в функциональное выражение.
Если 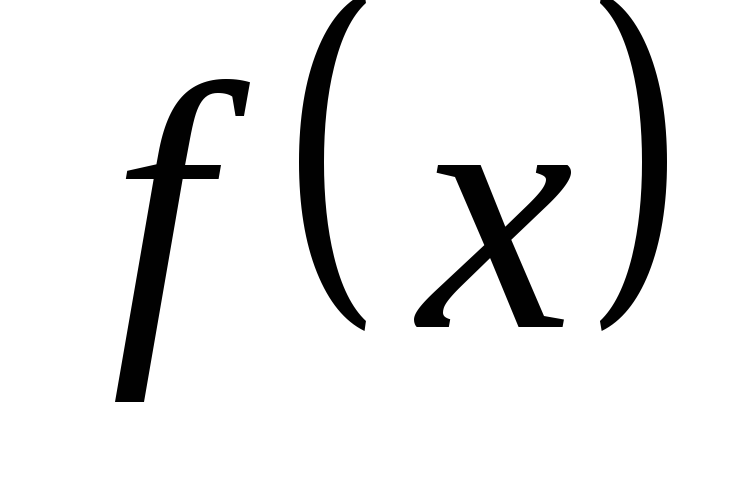 непрерывна во всех точках области, то
она называется непрерывное в этой
области.
непрерывна во всех точках области, то
она называется непрерывное в этой
области.
Если  непрерывна в некоторой области, то ее
график в этой области является сплошной
линией.
непрерывна в некоторой области, то ее
график в этой области является сплошной
линией.
Если график функции имеет разрывы, то такую функцию нельзя назвать непрерывной на этой области.




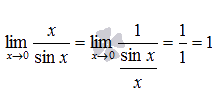
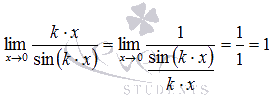
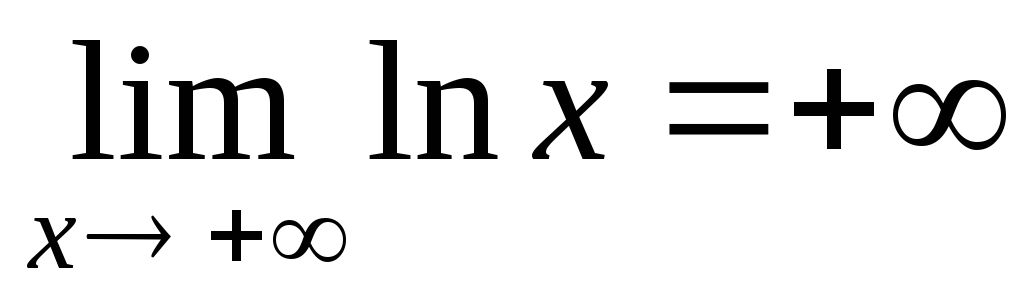 ,
,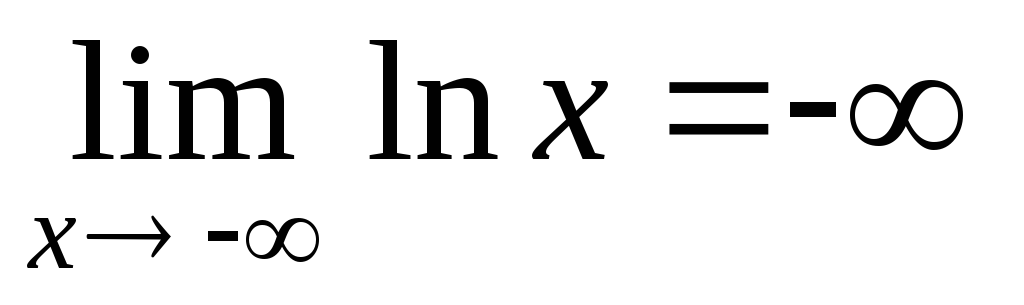 (см. рис.).
(см. рис.).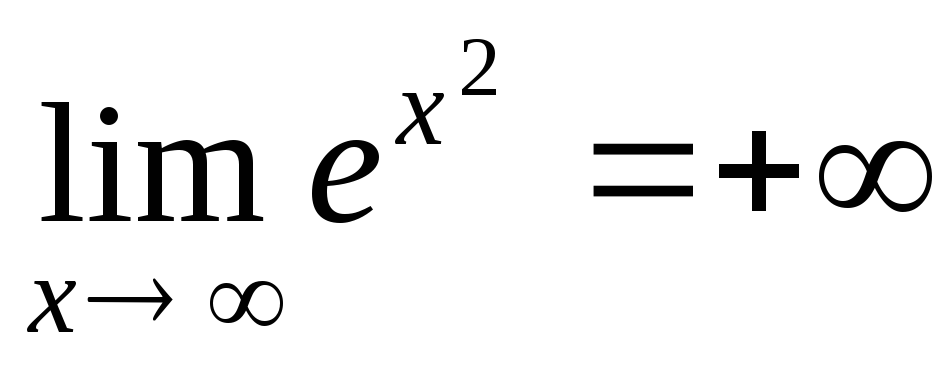
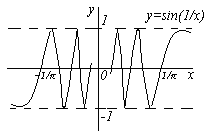 .
.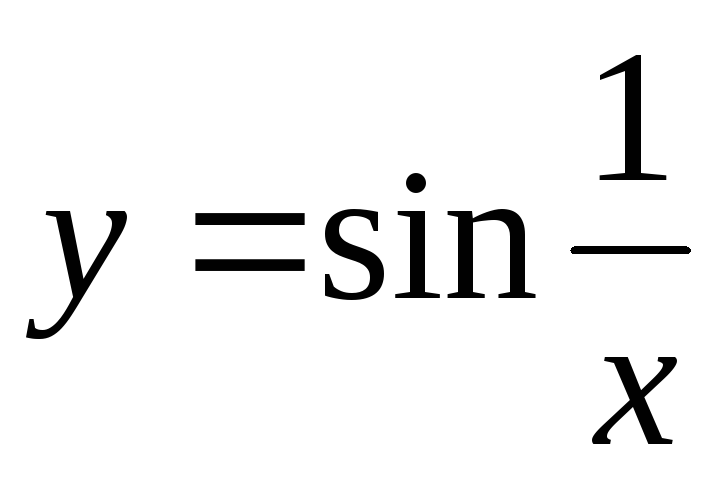 при
при  не стремится ни к какому пределу (см.
рис.).
не стремится ни к какому пределу (см.
рис.).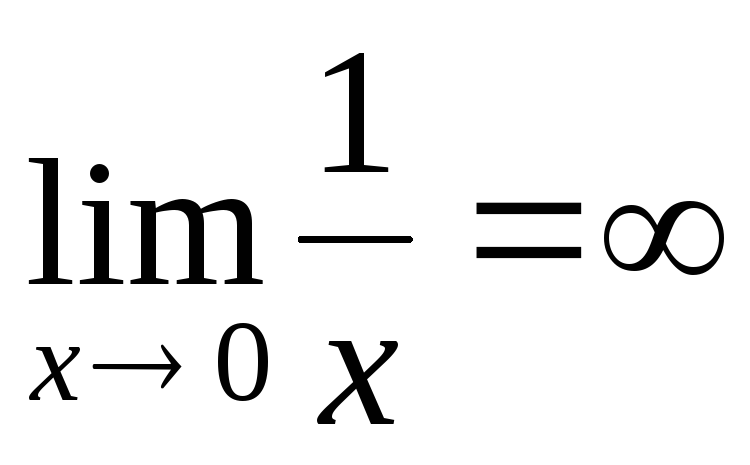 .
. .
.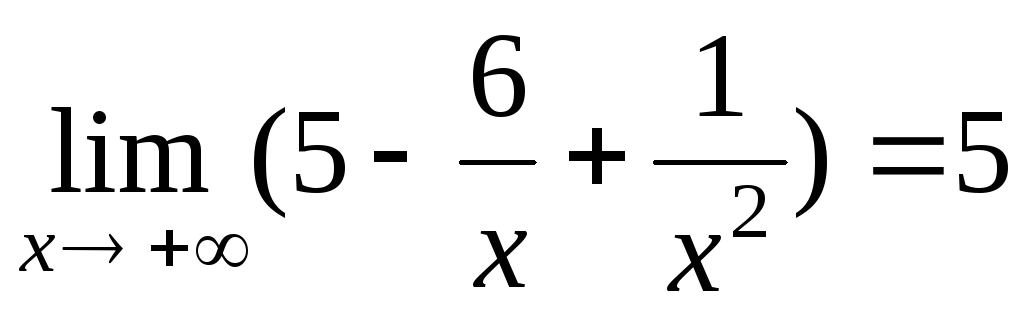 ,
так как функции
,
так как функции 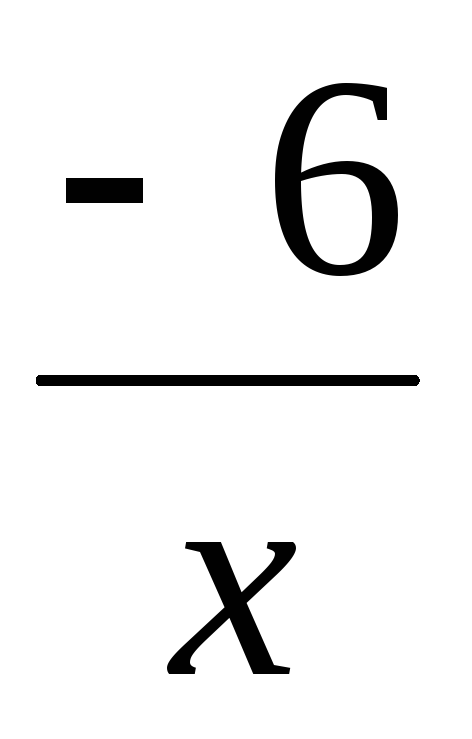 и
и 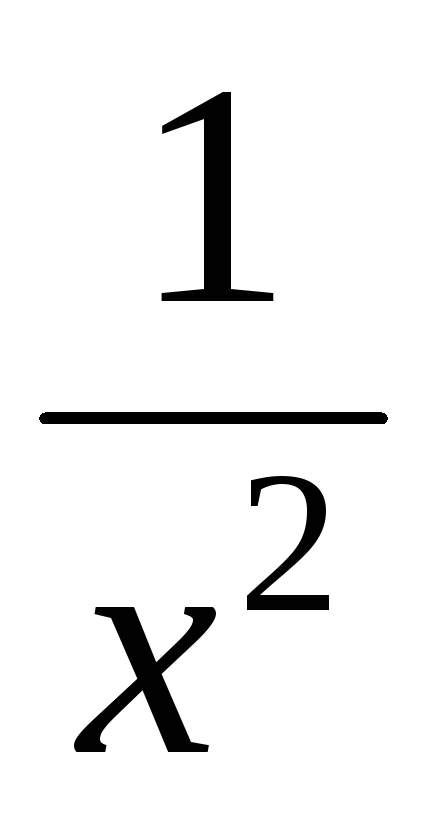 —
бесконечно малые при
—
бесконечно малые при 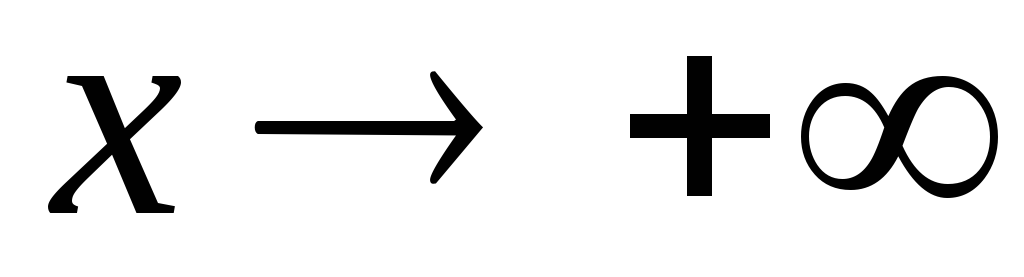 ,
то
,
то 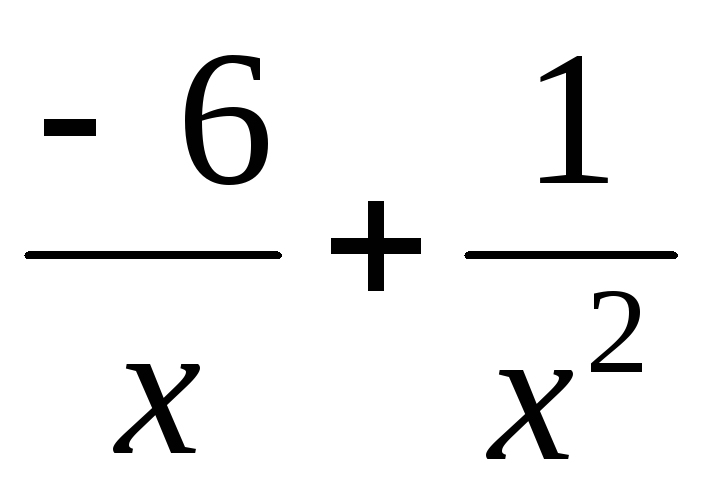 ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же 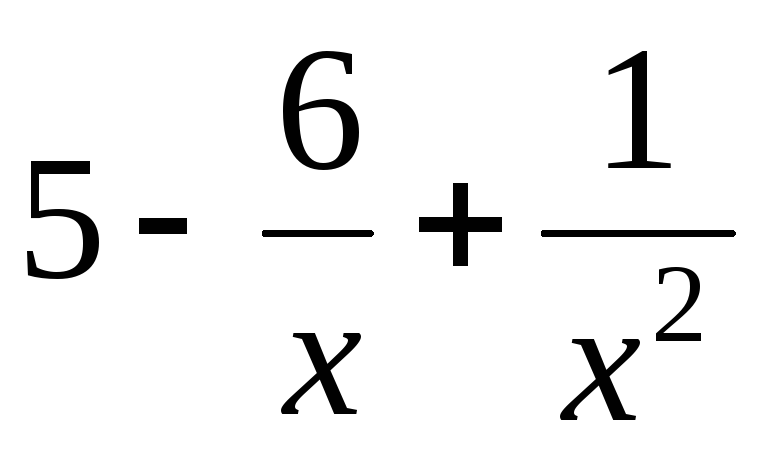 является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство. ,
при
,
при 
 ,
тогда в некоторой окрестности точки
,
тогда в некоторой окрестности точки 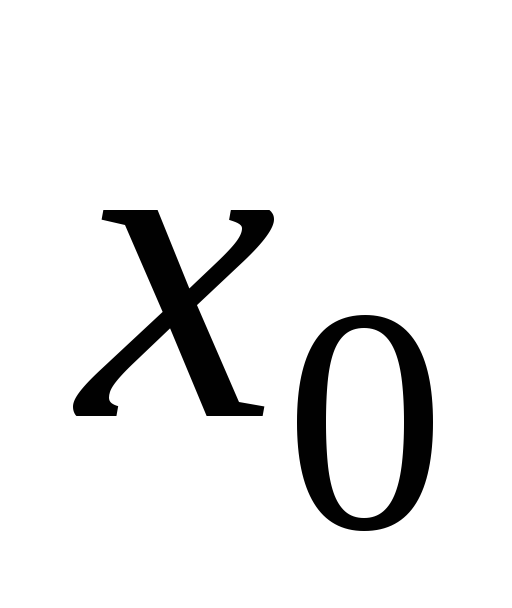 ,
справедливо равенство
,
справедливо равенство 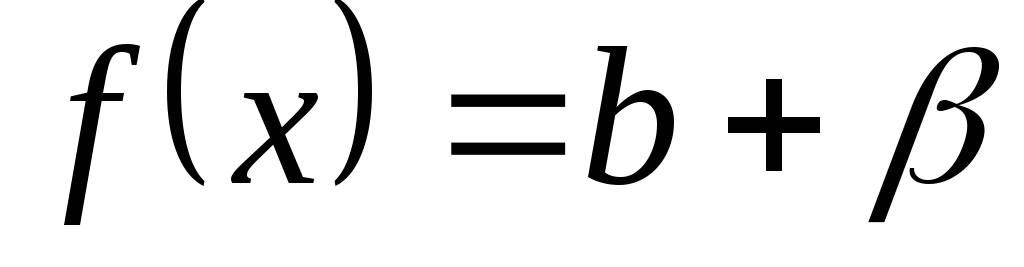 ,
где
,
где  бесконечное,
при
бесконечное,
при 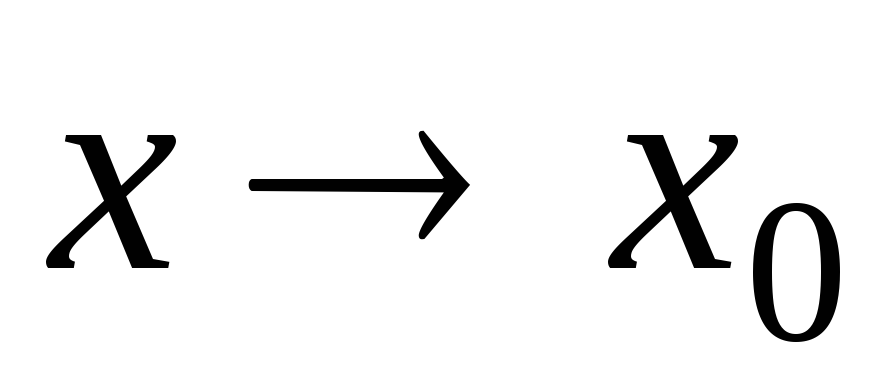 .
. справедливо равенство
справедливо равенство 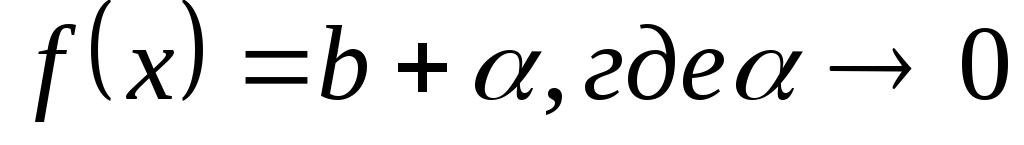
 ,
при
,
то
,
при
,
то 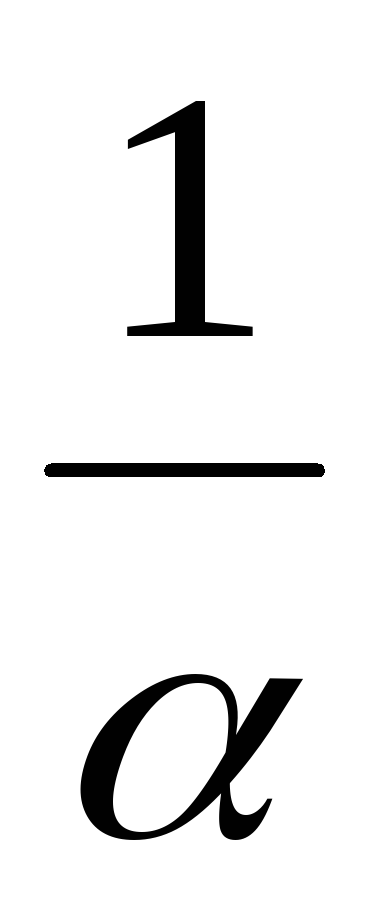 ,
стремится к бесконечности
,
стремится к бесконечности M
величин есть также
M
величин есть также  Mb
Mb Mb
Mb M
на постоянную величину есть
M
на постоянную величину есть  M
M Mb
есть
Mb
есть Mb
Mb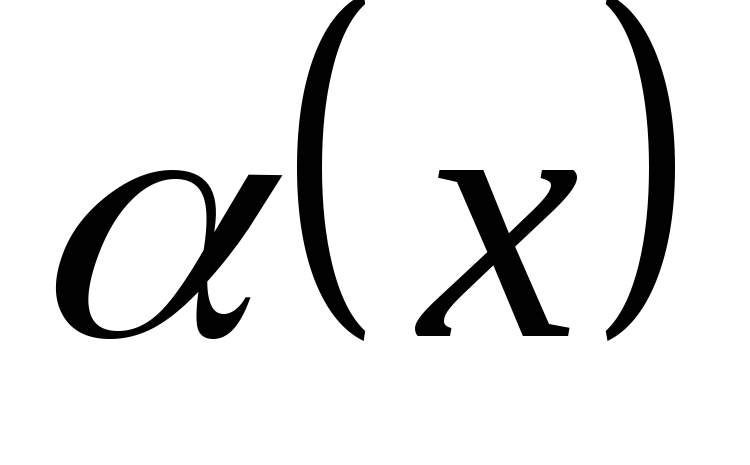 называют
называют  более высокого порядка по сравнению с
более высокого порядка по сравнению с 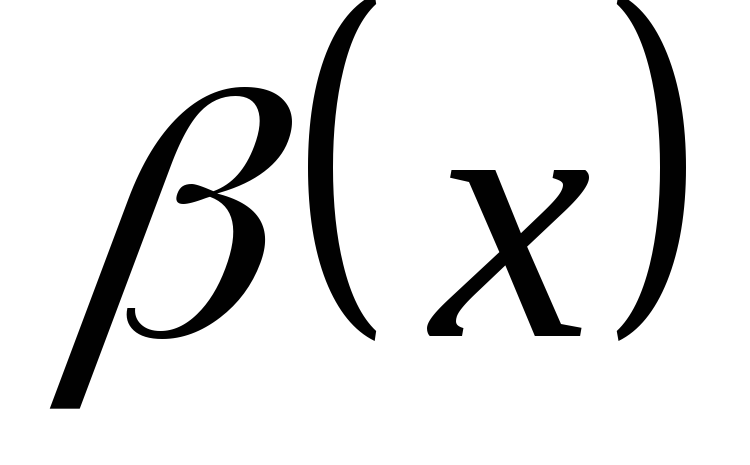 ,
, 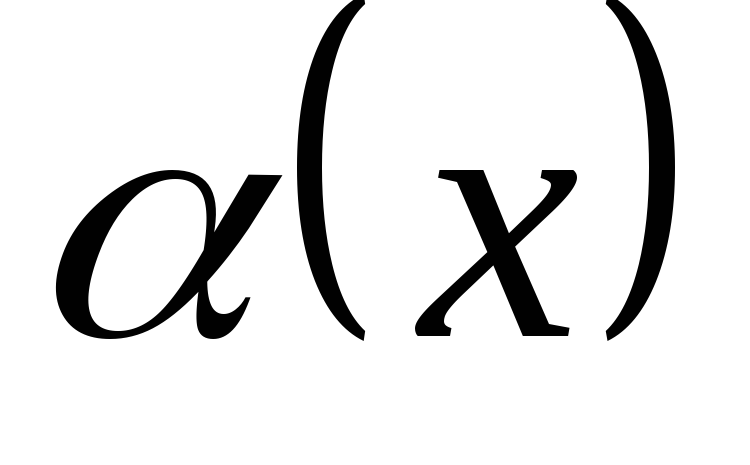 и
и  являются
одного порядка, тогда
являются
одного порядка, тогда 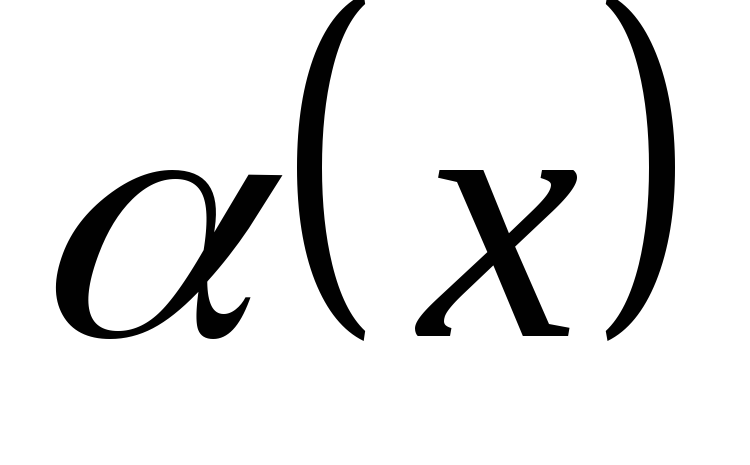 называют
называют