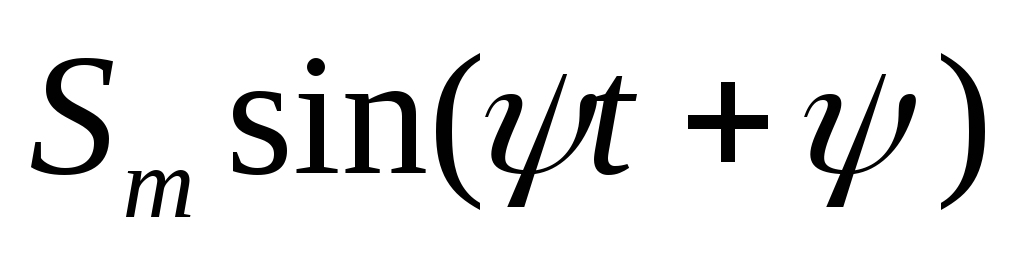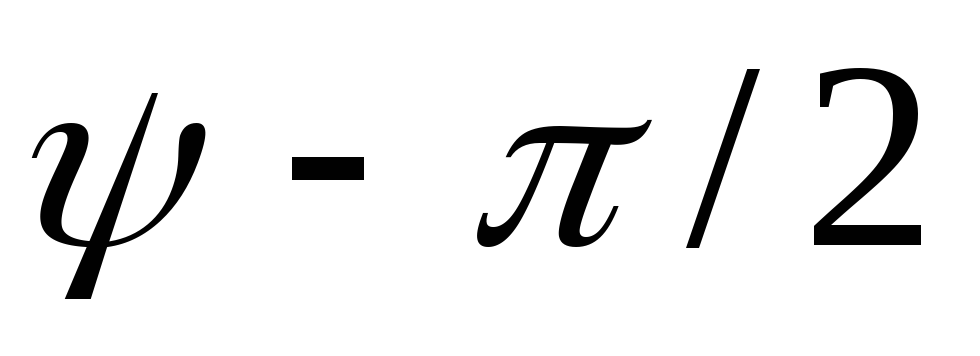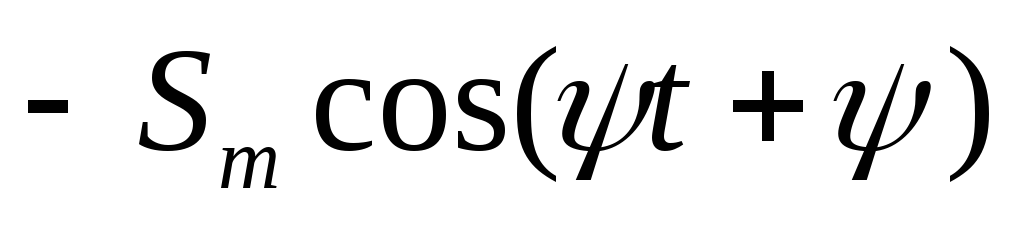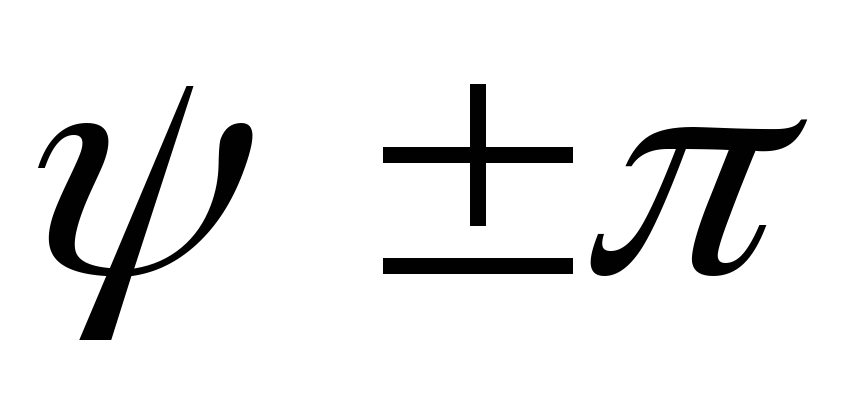Действующее, амплитудное, среднее значение величины на синусоиде
Синусоида (синус) — самый наш идеальный и необходимый вариант. Используется на выходе из генераторов для передачи на расстояния и затем используется вами из розетки (какой ток в розетке?). Самый распространенный сигнал, вероятно, если я чего-то не знаю. Рассмотрим основные элементы графика переменного тока:
Период — это время, через которое функция начинает повторяться, величина обратная частоте. Обозначается буквой Т. Т=2тт/w.
тт — так почему-то в интернетах принято обозначать число “пи”, против толпы не попрешь, так сказать, хотя можно просто 3,14 написать или “пи”. Дело вкуса.
Амплитудное значение (амплитуда) — значения, в которых график синусоиды достигает максимумов. То есть для синусоиды таких значения два на период — положительное и отрицательное.
Действующее значение — это 0,707 от амплитудного значения. Есть у нас цепь — в этой цепи за время Т1 постоянный ток определенной величины I1 выделит определенное количество тепла Q1, если в той же цепи пустить переменный ток, то за тоже время Т1 он выделит такое же количества тепла Q1 при действующем значении равном I1. И это значение I1 для синусоиды будет равно 0,707 от амплитудного — что означает единица делить на корень из двух. Если вам интересно, откуда это такое взялось, то плиз велком:
Мгновенное значение — значение величины в определенный момент времени. Если посмотреть на синусоиду, то видно, что мгновенное значение постоянно передвигается и на протяжении одного периода постоянно меняет свои значения. В следующем периоде опять идет тем же путем. Остановись мгновение =) Значение мгновенного значения определяется как Im*sin(wt) — амплитудное значение умноженное на “синус омега тэ” — где “омега тэ” — произведение угловой скорости на момент времени. Омега равно два пи делить на период Т.
Среднее значение — сумма всех мгновенных значений за полпериода. Для синусоиды равно 0,6366197730950255438113531364418 ~ 0,637 от амплитудного значения. Если вновь стало интересно, откуда число, то ответ ниже на примере переменного тока:
Если амплитудное значение разделить на действующее значение, то мы получим, правильно корень из двух для синусоиды — его еще называют коэффициентом амплитуды. Если же мы разделим действующее значение на среднее — то получим для синусоиды 1,11 — это отношение называется коэффициентом формы кривой
Сколько инженеров, столько и форм кривых в электронике, а если серьезно, то существуют например такие: Форма сигнала меандр — сигнал, в котором отсутствуют четные гармоники, имеет прямоугольную форму. В отличие от прямоугольного импульса, у которого длительность сигнала и длительность паузы могут отличаться, у меандра они равны. Сигнал такой формы может встречаться в импульсных источниках бесперебойного питания и прочих электронных схемах, ШИМ.
Пилообразный сигнал — сигнал пилообразной формы может идти и в одну сторону и в другую (знак минус в формуле функции). Для создания этой и других форм сигналов применяются генераторы сигналов. Применяются в старых осциллографах, мониторах, как и треугольные.
Треугольный сигнал — у треугольного сигнала длина роста и длина падения равны.
Каждая из этих форм может быть представлена через преобразование фурье, смысл которого в разбиении функции на гармонические составляющие от единицы до бесконечности с набором определенных гармоник — нечетных например, как для меандра. В функциях выше, которые были построены в маткаде, смысл построения в следующем, чем больше составляющих вы берете для построения (ближе к бесконечности), тем красивее получается график.
Сохраните в закладки или поделитесь с друзьями
Самое популярное

Список параметров напряжения и силы электрического тока — Википедия
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)[править | править код]
Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.
Мгновенное значение[править | править код]
Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u(t) ,i(t){\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.
Амплитудное значение[править | править код]
- Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):
- UM=max(|u(t)|) ,IM=max(|i(t)|){\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}
Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.
Среднеквадратичное значение[править | править код]
Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.
- U=1T∫0Tu2(t)dt ,I=1T∫0Ti2(t)dt{\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I{\displaystyle I} и U{\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение[править | править код]
Среднее значение (смещение) — постоянная составляющая напряжения или силы тока
- U=1T∫0Tu(t)dt ,I=1T∫0Ti(t)dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.
Средневыпрямленное значение[править | править код]
Средневыпрямленное значение — среднее значение модуля сигнала
- U=1T∫0T∣u(t)∣dt ,I=1T∫0T∣i(t)∣dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока — магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
- Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π/22≈1.11{\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11}.
- Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2{\displaystyle {\sqrt {2}}}.
- Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература[править | править код]
Нормативно-техническая документация[править | править код]
Лекция №6
8
ЛЕКЦИЯ №6
2. ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
2.1. Гармонические колебания
Электромагнитные процессы в электрической цепи, при которых мгновенные значения напряжений и токов повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, по истечении которого наблюдаются повторения мгновенных значений периодических величин, называется периодом. Если величину, являющуюся периодической функцией времени t, обозначить F(t), то для любого положительного или отрицательного значения аргумента t справедливо равенство
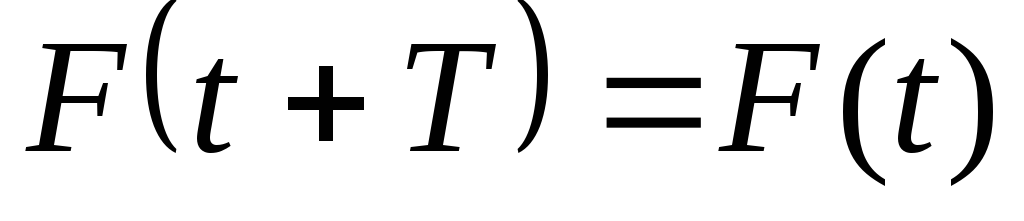 ,
,
где T – период.
Величина, обратная периоду, т.е. число периодов в единицу времени, называется частотой
f = 1 / T.
Частота имеет размерность с-1, а единицей измерения частоты служит Герц (Гц). Частота равна 1 Гц, если период равен 1 с.
Преобладающим видом периодического процесса в электрических цепях является синусоидальный режим. Он характеризуется тем, что все напряжения и токи являются синусоидальными функциями одинаковой частоты. Это возможно только при заданных синусоидальных ЭДС и токах источников и при линейных элементах электрической цепи. Синусоидальность обеспечивает наиболее выгодный режим работы электрических установок.
Синусоида является простейшей периодической функцией. Все другие несинусоидальные периодические функции могут быть разложены в бесконечный ряд синусоид, имеющих кратные частоты. Поэтому изучение цепей периодического тока начнем с анализа особенностей цепей синусоидального тока.
Колебания, описываемые синусоидальными (или косинусоидальными) функциями называются гармоническими.
На рис. 2.1. показаны основные элементы математического описания функции u = Umsin(t + ).
На рис. 2.1 приняты следующие обозначения:
u – мгновенное значение напряжения;
Um – максимальное значение напряжения или амплитуда;
– скорость изменения аргумента (угла), называемая угловой частотой, которая равна = 2pf [рад/с];
0 – начальная фаза, которая определяется величиной смещения гармонической функции относительно начала координат.

Рис. 2.1. Основные элементы функции u = Umsin(t + )
За аргумент записанной функции может быть принято время t или соответствующий ему угол t. Аргументу t соответствует период T, а аргументу t – период 2p. и t могут измеряться как в радианах, так и в градусах.
Величина t + , определяющая стадию изменения записанной функции, называется фазовым углом или фазой.
2.2. Генерирование синусоидальной ЭДС
Наиболее распространенным в промышленности способом получения синусоидального тока является применение электромагнитных машин, называемых синхронными генераторами, приводимых во вращение тепловыми, гидравлическими, газовыми или другими двигателями.
Синхронный генератор состоит из двух частей – неподвижного статора и вращающегося ротора. На одном из них (чаще на роторе) располагаются электромагниты, обмотки которых питаются от источника постоянного тока. На другом (обычно на статоре) расположена основная обмотка, в которой наводится ЭДС (рис. 2.2).

Генератор может иметь одну или несколько пар полюсов. На рис. 2.2а упрощенно показан генератор с двумя парами полюсов, размещенных на роторе. Иногда для удобства рассмотрения процессов цилиндрический воздушный зазор разворачивают на плоскости (рис. 2.2б).
В каждом проводе обмотки статора при вращении ротора по закону электромагнитной индукции наводится ЭДС
e = Blv,
где B – магнитная индукция, l – длина проводника, v – линейная скорость перемещения магнитного поля.
При постоянных значениях l и v закон изменения ЭДС e(t) определяется законом распределения индукции B в воздушном зазоре. Благодаря специальной форме полюсных наконечников закон изменения B вдоль воздушного зазора делается приблизительно синусоидальным: максимальное значение индукция имеет в середине и убывает к концам полюсных наконечников.
В момент времени, которому соответствует положение ротора на рис. 2.2, магнитная индукция над проводом равна нулю и ЭДС также равна нулю. При повороте ротора на 1/8 полного оборота (половина полюсного шага) ЭДС достигает максимума и будет направлена от зажима 2 к зажиму 1 (по правилу правой руки). При повороте ротора еще на 1/8 полного оборота ЭДС вновь обратится в ноль. Далее процесс повторяется, однако ЭДС будет отрицательна (направлена противоположно: от зажима 1 к зажиму 2). На зажимах генератора возникает синусоидальная ЭДС.
При числе пар полюсов p и частоте вращения ротора n частота переменной ЭДС f, Гц, равна
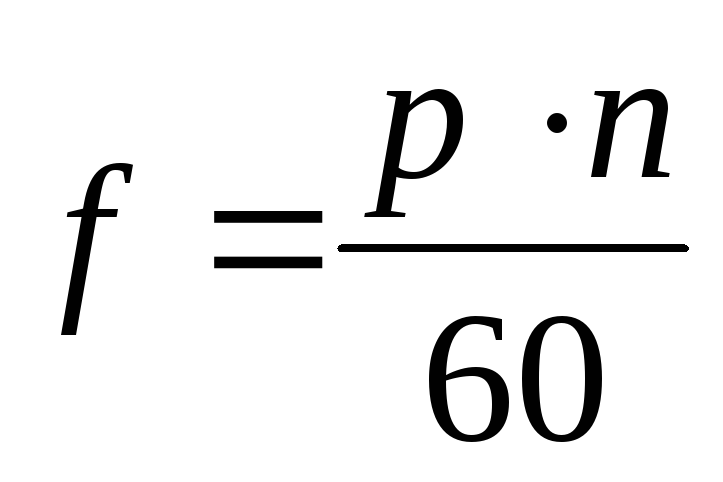 .
(2.2)
.
(2.2)
В энергосистемах России и большинства других стран принята промышленная частота тока – 50 Гц. В США принята частота 60 Гц. В авиации с целью уменьшения веса оборудования применяются машины с повышенной частотой вращения (в большинстве случаев 400 Гц). Проводная электросвязь использует частоты от
Начало практического внедрения переменного тока относится ко второй половине XIX века, когда выдающийся русский электротехник П.Н. Яблочков стал применять на практике изобретенные им электрические свечи.
2.3. Средние и действующие значения гармонических функций
Среднее значение периодической функции f(t) за период T определяется по формуле
 .
(2.3)
.
(2.3)
В случае гармонического колебания среднее значение за период равно нулю, поэтому здесь мы будем использовать понятие среднего значения абсолютной величины функции или среднего полупериодического значения.
Для
тока  среднее значение будет равно
среднее значение будет равно

Аналогично определяется среднее значение напряжения
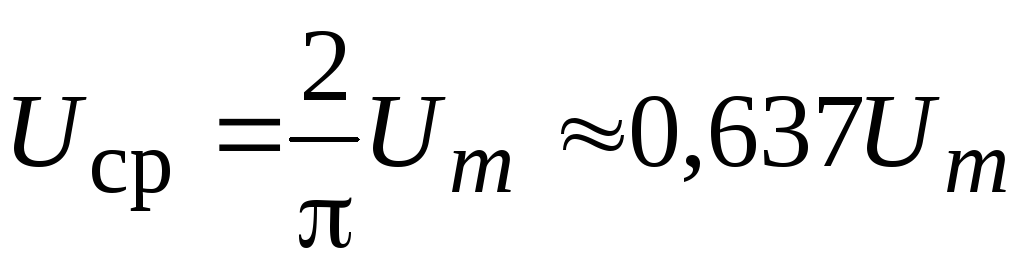 .
.
Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым проходит один и тот же ток, пропорциональны квадрату тока. Поэтому о величине тока судят обычно по так называемому действующему значению тока. Действующее значение – это среднеквадратичное значение величины за период. Оно определяется по формуле
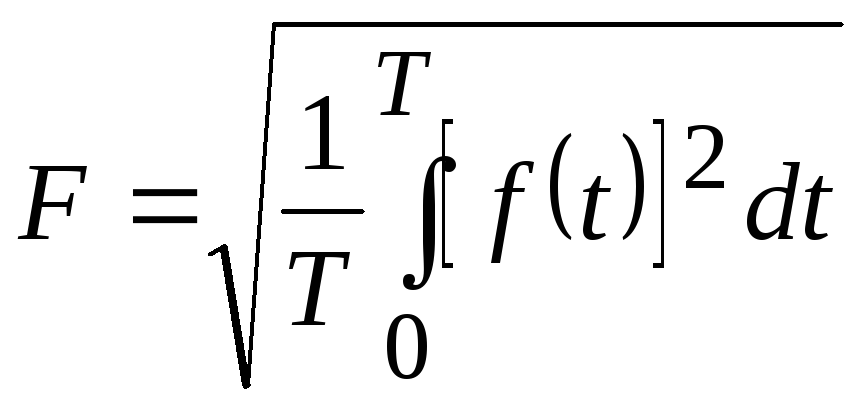 .
(2.5)
.
(2.5)
Действующее значение периодического тока
 .
(2.6)
.
(2.6)
Возведя (2.6) в квадрат и умножив обе части выражения на RT, получим:
 .
(2.7)
.
(2.7)
Это равенство показывает, что действующее значение периодического тока равно по величине такому постоянному току, который, проходя через неизменное сопротивление R за период времени Т, выделяет то же количество тепла, что и данный ток i.
При токе i = I
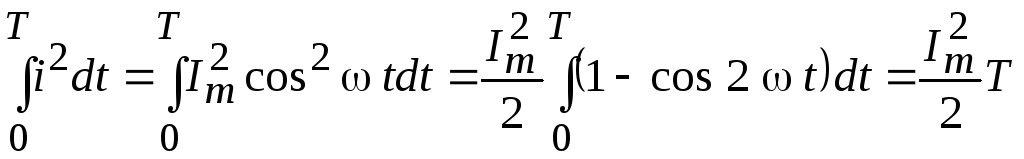 .
.
Следовательно, согласно (2.7) действующее значение равно
 .
(2.8)
.
(2.8)
Аналогично для действующего значения напряжения
 .
(2.9)
.
(2.9)
Номинальные токи и напряжения электротехнических устройств определяются, как правило, действующими значениями, поэтому действующие значения представляют наиболее распространенный электрический параметр. Чаще всего измерительные приборы градуируются также в действующих значениях.
2.4. Представление гармонических функций в виде проекций
вращающихся векторов
Мгновенное
значение функции 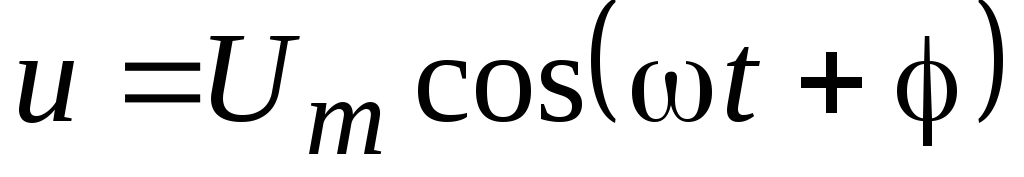 можно получить как проекцию на
горизонтальную ось отрезка длиной Um,
вращающегося относительно начала
прямоугольной системы координат с
угловой частотой =
2pf в положительном направлении (против
часовой стрелки) (рис. 2.3).
можно получить как проекцию на
горизонтальную ось отрезка длиной Um,
вращающегося относительно начала
прямоугольной системы координат с
угловой частотой =
2pf в положительном направлении (против
часовой стрелки) (рис. 2.3).
Вращающийся отрезок будем называть вектором.
В
момент t = 0 вектор образует с горизонтальной
осью угол ψ и его проекция на горизонтальную
ось равна Umcos ψ,
т.е. мгновенному значению функции  при t = 0. За время t = t1 вектор повернется на угол t1 и окажется повернутым относительно
горизонтальной оси на угол t1 +,
его проекция на ось будет равна
при t = 0. За время t = t1 вектор повернется на угол t1 и окажется повернутым относительно
горизонтальной оси на угол t1 +,
его проекция на ось будет равна  и т.д.
и т.д.
Таким образом, рассмотрение гармонических колебаний можно заменить рассмотрением вращающихся векторов. Для получения мгновенных значений условимся проектировать вектора на горизонтальную ось.
Если гармонические колебания имеют одну и ту же частоту, то соответствующие этим колебаниям векторы вращаются с одинаковой угловой частотой, и поэтому углы между ними сохраняются неизменными.
Зарисуем две гармонические функции
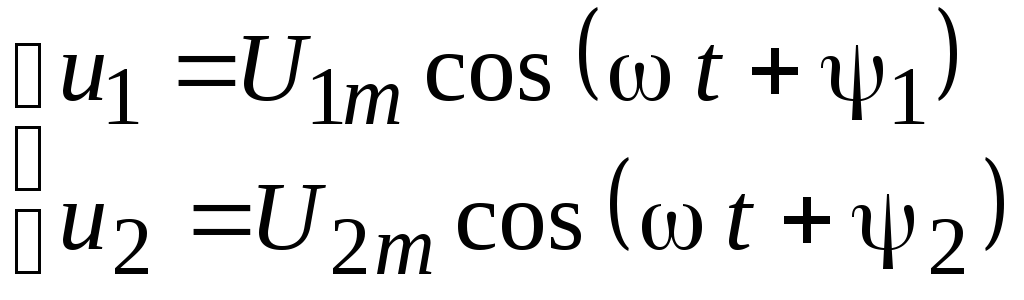 ,
(2.9)
,
(2.9)
и меющие
одинаковую угловую частоту
и начальные фазы 1 и 2 (рис. 2.4).
меющие
одинаковую угловую частоту
и начальные фазы 1 и 2 (рис. 2.4).
Кривая u1, смещенная влево относительно u2, возрастает от нуля до своего положительного максимума раньше, чем кривая u2. Поэтому говорят, что u1 опережает по фазе u2, или наоборот. Разность начальных фаз = 1 – (–2) называется фазовым сдвигом или углом сдвига u1 относительно u2. Этот угол и образуют векторы, показанные на верхней части рис. 2.4.
При равенстве начальных фаз, т.е. при = 0, векторы направлены в одну и ту же сторону, т.е. совпадают по фазе (синфазны). При фазовом сдвиге 180 векторы направлены в диаметрально противоположные стороны (находятся в противофазе).
Диаграмма, изображающая совокупность векторов, построенных с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой.
Векторное представление гармонических функций, частота которых одинакова, облегчает алгебраические операции с ними и дает возможность наглядно представить процессы, происходящие в цепи.
Например, операция сложения
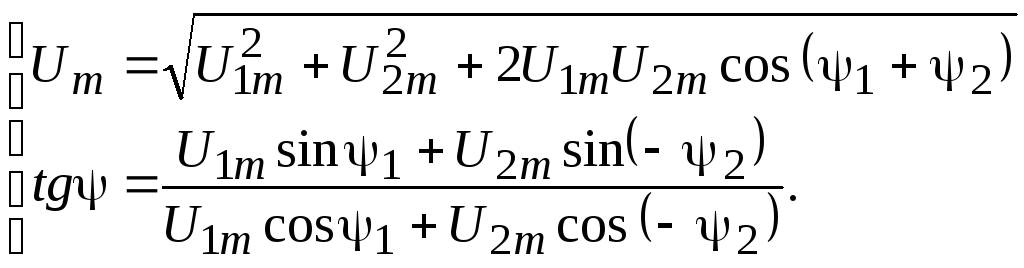 (2.10)
(2.10)
При использовании векторной диаграммы с целью установления фазовых сдвигов или амплитудных значений гармонических величин, имеющих одинаковую частоту, векторная диаграмма может считаться неподвижной. Это равносильно переходу во вращающуюся вместе с векторами систему координат.
Построение векторной диаграммы обычно не связано с определением мгновенных значений гармонических функций. В этом случае они строятся не для амплитуд, а для действующих значений. Кривые мгновенных значений называются временными диаграммами.
Прописные истины для новичков. — Начинающим — Теория
Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.
Закон Ома.
Основным законом, которым руководствуются радиолюбители — является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm, 1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.
Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.
I = U/R, где R — электрическое сопротивление проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.
Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля — Ленца. Звучит так;
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.
Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.
В центре искомые величины, а в секторах с соответствующими цветами — варианты решений в зависимости от известных величин.
Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье — треугольник Ома.
Выглядит она следующим образом:
В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
- ,
- — ЭДС цепи,
- I — сила тока в цепи,
- R — сопротивление всех элементов цепи,
- r — внутреннее сопротивление источника питания.
Закон Ома для полной цепи звучит так — Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Электрические измерения.
Нарисуем простейшую электрическую цепь, состоящую из батареи «В» и нагрузки «R», и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.
Что бы измерить протекающий в цепи ток, необходимо в разрыв источника питания и нагрузки включить измерительный прибор (амперметр).
Для того, что бы на измеряемую цепь было как можно меньше влияний и для повышения точности измерения, амперметры изготавливают с очень малым внутренним сопротивлением, то есть если включить амперметр в разрыв проверяемой цепи, то он практически не добавит к измеряемой цепи дополнительного сопротивления, и протекающий по цепи ток практически не изменится, или уменьшится на очень незначительную величину не оказывающую значительного влияния на конечный результат измерения.
Поэтому категорически нельзя измерять «ток приходящий на нагрузку» путём подключения амперметра параллельно нагрузке, или непосредственно у источника питания (без нагрузки) и таким образом попытаться замерить выходной ток выдаваемый источником питания или осветительной сетью.
Это равносильно тому, что подключить параллельно нагрузке или источнику питания обычный провод. Попросту сказать — закоротить цепь.
Если источник питания обладает хорошей мощностью — будет очень сильный Б А Х !!! Последствия могут быть самыми разными, от выхода из строя измерительного прибора (амперметра), что обычно и случается, и до выбитых пробок (АЗС) в квартире и обесточивания помещения и возможного поражения током.
Для измерения напряжения на нагрузке необходимо, что бы подключаемый к ней вольтметр не шунтировал нагрузку и не оказывал заметного влияния на результат измерения. Для этого вольтметры изготавливают с очень высоким входным сопротивлением и их наоборот подключают параллельно измеряемой цепи. Благодаря высокому входному сопротивлению вольтметра — сопротивление измеряемой цепи практически не изменяется, или изменяется очень не значительно, не оказывая заметного влияния на результат измерения.
На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.
Постоянный и переменный ток.
Кратко напомню — постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.
Переменный ток (AC) — это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению.
На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.
Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Возникает вопрос, как же его измерять? Для его измерения и введено понятие — «Действующее (или эффективное) значение» переменного тока.
Что же такое действующее (или эффективное) и амплитудное значение переменного тока?
Как Вам попроще объяснить, чтобы было понятно.
Действующее (эффективное) значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время, выделяет такое же количество энергии.
То есть если к какой либо активной нагрузке (нагревательный элемент, лампа накаливания, резистор и т.д.) подключить переменный ток, который за определённый промежуток времени (например 10 секунд) выделит на активной нагрузке то-же количество энергии, тепла на нагревательном элементе, резисторе, или разогреет спираль лампы накаливания до точно такой же светоотдачи, что и постоянный ток какой-то определённой величины за тот же промежуток времени (тоже 10 секунд) — то тогда действующее (эффективное) значение такого переменного тока будет равняться величине постоянного тока.
Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.
Что такое «Амплитудное значение» переменного тока?
Если объяснять попроще, то это самое максимальное значение (величина) синусоидального тока на самом пике (максимуме) синусоиды.
Амплитудное значение переменного тока можно измерить электронно — лучевым осциллографом, так как все осциллографы откалиброваны на измерение амплитудных значений.
Поскольку действующее значение переменного синусоидального тока пропорционально квадратному корню из площади, то оно получается в 1,41 раза меньше его амплитудного значения.
Проще говоря — если измерить величину переменного тока (напряжения) электроизмерительными приборами, отградуированными для измерения переменного синусоидального тока (напряжения), то есть например замерить величину переменного напряжения на вторичной обмотке трансформатора, — то амплитудное значение напряжения на этой обмотке будет соответственно в 1,41 раз больше замеренного.
Это справедливо только для переменного синусоидального тока (напряжения).
Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.
Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).
Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.
Для действующего значения переменного синусоидального напряжения (тока) — справедливы формулы для расчётов сопротивлений, мощности, действующих токов и напряжений — приведённые выше в Законе Ома для постоянного тока.
Ответим на вопросы в начале статьи;
Как рассчитать шунт для амперметра?
Большинство отечественных измерительных головок для амперметров, рассчитываются на полное отклонение при подведении к ним напряжения в 75 мВ (0,075 вольта). У них на шкале имеется надпись «НШ — 75 мВ», или «Наружный шунт 75 мв», или что-то подобное.
Нам стало известно две величины, а именно — необходимый нам ток полного отклонения и напряжение полного отклонения измерительной головки.
Например, нам нужно рассчитать шунт на 20 ампер. По Закону Ома 0,075 делим на 20 = 0,00375 Ом.
Изготовить такой шунт можно из медной проволоки, посмотрев её удельное сопротивление по таблице ЗДЕСЬ . Только необходимо брать проволоку, диаметром желательно не менее 1,5 мм, так как шунт при большом токе будет греться, и показания прибора будет изменяться (при нагреве проволоки увеличится её внутреннее сопротивление).
Почему из 12 вольт переменного напряжения, стало около 16 вольт постоянного — надеюсь Вам стало понятно. У переменного напряжения 12 вольт (действующее его значение) — амплитудное значение будет в 1,41 раз больше, то есть 16,92 вольта, минус около вольта падение напряжения на диодах. В итоге получается около 16 вольт — до которых и заряжаются электролитические конденсаторы фильтра.
Как правильно измерить мощность УНЧ?
Давайте для начала вспомним теорию.
Выходная мощность усилителей НЧ измеряется на синусоидальном сигнале. У идеального двухтактного выходного каскада, максимальное амплитудное значение синусоидального сигнала на выходе может приблизиться к величине равной половине напряжения источника питания.
У каскада по мостовой схеме, выходное напряжение может приблизиться к величине напряжения источника питания.
Говоря другими словами, у автомобильной магнитолы при напряжении питания 13,5 вольт, для двухтактного выходного каскада максимальное выходное напряжение (синус) будет 6,5 вольт, а его действующее значение 4,6 вольта, для мостовой схемы соответственно 13 В. и 9,2 вольта.
Возьмём минимальную нагрузку для этих усилителей 2 Ома, соответственно максимальная выходная мощность (исходя из Закона Джоуля — Ленца) для первой магнитолы, которую она выдаст теоретически — будет 10,6 ватта, для второй — 42,3 ватта (это для нагрузки 2 Ома). На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность.
В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными «цешками» или бытовыми «цифровиками», так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.
Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт — это развод, рекламный ход и т.д., если только для питания этого усилителя не применяется повышающий преобразователь.
Гармоника и частота гармоник в цепях переменного тока
В данной статье мы рассмотрим что такое гармоники, фундаментальную частоту и сложные формы волны из-за гармоник, в конце статьи подведем краткие итоги по этой теме.
Что такое гармоники
Гармоники — это нежелательные более высокие частоты, которые накладываются на основную форму волны, создавая искаженную волновую картину.
В цепи переменного тока сопротивление ведет себя точно так же, как в цепи постоянного тока. То есть ток, протекающий через сопротивление, пропорционален напряжению на нем. Это связано с тем, что резистор является линейным устройством, и если приложенное к нему напряжение представляет собой синусоидальную волну, ток, протекающий через него, также является синусоидальной, поэтому разность фаз между двумя синусоидами равна нулю.
Как правило, при работе с переменными напряжениями и токами в электрических цепях предполагается, что они имеют чистую и синусоидальную форму с присутствием только одного значения частоты, называемого «основной частотой», но это не всегда так.
В электрическом или электронном устройстве или цепи, которая имеет вольт-амперную характеристику, которая не является линейной, то есть ток, протекающий через нее, не пропорционален приложенному напряжению. Чередующиеся сигналы, связанные с устройством, будут отличаться в большей или меньшей степени от сигналов идеальной синусоидальной формы. Эти типы сигналов обычно называют несинусоидальными или сложными сигналами.
Сложные сигналы генерируются обычными электрическими устройствами, такими как индукторы с железной сердцевиной, переключающие трансформаторы, электронные балласты в люминесцентных лампах и другие такие сильно индуктивные нагрузки, а также формы выходного напряжения и тока генераторов переменного тока, генераторов и других подобных электрических машин. В результате форма волны тока не может быть синусоидальной, даже если форма волны напряжения есть.
Также большинство электронных схем переключения источников питания, таких как выпрямители, кремниевые выпрямители (SCR), силовые транзисторы, преобразователи питания и другие подобные твердотельные переключатели, которые отключают и измельчают источники питания синусоидальной формы волны для управления мощностью двигателя или преобразования синусоидального источника переменного тока в постоянный. Эти переключающие схемы имеют тенденцию потреблять ток только при пиковых значениях источника переменного тока, и, поскольку форма сигнала переключающего тока не является синусоидальной, результирующий ток нагрузки, как говорят, содержит гармоники.
Несинусоидальные сложные формы волны создаются путем «сложения» серии синусоидальных частот, известных как «гармоники». Гармоники — это обобщенный термин, используемый для описания искажения синусоидальной формы волны сигналами разных частот.
Тогда независимо от формы сложную форму волны можно математически разделить на отдельные компоненты, называемые основной частотой и рядом «гармонических частот». Но что мы понимаем под «фундаментальной частотой»?
Фундаментальная частота
Фундаментальные формы волны (или первая гармоника) является синусоидальным сигналом , который имеет частоту питания. Фундаментальным является самой низкой или базовой частотой, ƒ , на которой построен комплекс формы сигнала и в качестве такового периодического времени, Τ результирующего комплексного сигнала будет равен периоду основной частоты.
Давайте рассмотрим основной сигнал переменного тока первой гармоники, как показано на рисунке.

Где:
Vmax — пиковое значение в вольтах, а
ƒ — частота колебаний в герцах (Гц).
Мы можем видеть, что синусоидальная форма волны представляет собой переменное напряжение (или ток), которое изменяется как синусоидальная функция угла, 2πƒ . Частоты формы волны, ƒ определяется числом циклов в секунду. В Соединенном Королевстве эта основная частота установлена на 50 Гц, тогда как в Соединенных Штатах она составляет 60 Гц.
Гармоники — это напряжения или токи, которые работают на частоте, которая является целым (целым числом) кратным основной частоте. Таким образом, для основной формы волны 50 Гц это означает, что частота 2-й гармоники будет 100 Гц (2 x 50 Гц), 3-й гармоники будет 150 Гц (3 x 50 Гц), 5-й = 250 Гц, 7-й = 350 Гц и так далее. Аналогичным образом, с учетом основной формы волны 60 Гц частоты 2-й, 3-й, 4-й и 5-й гармоник будут равны 120 Гц, 180 Гц, 240 Гц и 300 Гц соответственно.
Другими словами, мы можем сказать, что «гармоники» являются кратными основной частоты и поэтому могут быть выражены как: 2ƒ , 3ƒ , 4ƒ и т.д.
Сложные формы волны

Обратите внимание, что красные формы волны, приведенные выше, являются фактическими формами сигналов, видимыми нагрузкой, из-за гармонического содержания, добавляемого к основной частоте.
Основной сигнал также можно назвать сигналом 1й гармоники. Поэтому вторая гармоника имеет частоту, в два раза превышающую частоту основной, третья гармоника имеет частоту, в три раза превышающую основную, а четвертая гармоника имеет частоту, в четыре раза превышающую основную, как показано в левом столбце.
Правый столбец показывает сложную форму волны, сгенерированную в результате эффекта между добавлением основной формы волны и форм гармонических колебаний на разных частотах гармоник. Обратите внимание, что форма результирующего сложного сигнала будет зависеть не только от количества и амплитуды присутствующих частот гармоник, но также и от соотношения фаз между основной или базовой частотой и отдельными частотами гармоник.
Мы можем видеть, что сложная волна состоит из основной формы волны плюс гармоники, каждая из которых имеет свое пиковое значение и фазовый угол. Например, если основная частота задана как: E = V MAX (2πƒt) или V MAX (ωt) , значения гармоник будут заданы:
Для второй гармоники:
Е 2 = V 2max (2 * 2πƒt) = V 2max (4πƒt) = V 2max (2ωt)
Для третьей гармоники:
E 3 = V 3max (3 * 2πƒt) = V 3max (6πƒt), = V 3max (3ωt)
Для четвертой гармоники:
E 4 = V 4max (4 * 2πƒt) = V 4max (8πƒt), = V 4max (4ωt)
и так далее.
Тогда уравнение, данное для значения сложной формы волны, будет иметь вид:

Гармоники обычно классифицируются по их названию и частоте, например, 2- й гармонике основной частоты при 100 Гц, а также по их последовательности. Гармоническая последовательность относится к векторному вращению гармонических напряжений и токов по отношению к основной форме волны в сбалансированной 3-фазной 4-проводной системе.
Гармоника прямой последовательности (4-й, 7-й, 10-й,…) будет вращаться в том же направлении (вперед), что и основная частота. Тогда как гармоника обратной последовательности (2-й, 5-й, 8-й,…) вращается в противоположном направлении (обратном направлении) основной частоты.
Как правило, гармоники прямой последовательности нежелательны, поскольку они ответственны за перегрев проводников, линий электропередач и трансформаторов из-за добавления сигналов.
С другой стороны, гармоники обратной последовательности циркулируют между фазами, создавая дополнительные проблемы с двигателями, поскольку противоположное вращение вектора ослабляет вращательное магнитное поле, необходимое для двигателей, и особенно асинхронных двигателей, заставляя их создавать меньший механический крутящий момент.
Другой набор специальных гармоник, называемых «тройками» (кратными трем), имеют нулевую последовательность вращения. Тройки — это кратные третьей гармоники (3-й, 6-й, 9-й, …) и т.д., отсюда и их название, и поэтому они смещены на ноль градусов. Гармоники нулевой последовательности циркулируют между фазой и нейтралью или землей.
В отличие от гармонических токов прямой и обратной последовательностей, которые взаимно компенсируют друг друга, гармоники третьего порядка не компенсируются. Вместо этого сложите арифметически в общем нейтральном проводе, который подвергается воздействию токов всех трех фаз.
В результате амплитуда тока в нейтральном проводе из-за этих тройных гармоник может быть в 3 раза больше амплитуды фазового тока на основной частоте, что делает его менее эффективным и перегретым.
Затем мы можем суммировать эффекты последовательности, кратные основной частоте 50 Гц:
| Название | Основная | Вторая | Третья | Четвертая | Пятая | Шестая | Седьмая | Восьмая | Девятая |
| Частота, Гц | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 |
| Последовательность | + | — | 0 | + | — | 0 | + | — | 0 |
Обратите внимание, что та же самая гармоническая последовательность также применяется к основным сигналам 60 Гц.
| Последовательность | Вращение | Гармонический эффект |
| + | Вперед | Чрезмерный эффект нагрева |
| — | Обратный ход | Проблемы с крутящим моментом двигателя |
| 0 | Нет | Добавляет напряжения и / или токи в нейтральный провод, вызывая нагрев |
Резюме по гармоникам
Гармоники — это высокочастотные сигналы, накладываемые на основную частоту, то есть частоту цепи, и которые достаточны для искажения формы волны. Величина искажения, применяемого к основной волне, будет полностью зависеть от типа, количества и формы присутствующих гармоник.
Гармоники были в достаточном количестве только в течение последних нескольких десятилетий с момента появления электронных приводов для двигателей, вентиляторов и насосов, цепей переключения электропитания, таких как выпрямители, преобразователи питания и тиристорные регуляторы мощности, а также большинства нелинейных электронных фаз с управлением нагрузки и высокочастотные (энергосберегающие) люминесцентные лампы. Это связано, главным образом, с тем фактом, что управляемый ток, потребляемый нагрузкой, не точно соответствует синусоидальным сигналам питания, как в случае выпрямителей или силовых полупроводниковых коммутационных цепей.
Гармоники в системе распределения электроэнергии в сочетании с источником основной частоты (50 Гц или 60 Гц) создают искажения формы сигналов напряжения и / или тока. Это искажения создают сложную форму волны, состоящую из ряда частот гармоник, которые могут оказать неблагоприятное воздействие на электрооборудование и линии электропередач.
Величина искажения формы волны, придающая сложной форме ее характерную форму, напрямую связана с частотами и величинами наиболее доминирующих гармонических компонентов, частота гармоник которых кратна (целым числам) основной частоты. Наиболее доминирующими гармоническими составляющими являются гармоники низкого порядка со 2- го по 19- е, причем тройки являются наихудшими.
Цепи с источниками гармонических воздействий Основные характеристики гармонических сигналов
59
Переменным током i(t) и напряжением u(t) называют токи и напряжения, изменяющиеся во времени.
Сигналы, мгновенные значения которых повторяются через определенный фиксированный промежуток времени, называются периодическими, а этот промежуток времени – периодом. Такие сигналы описываются следующим образом:
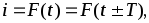 (3.1)
(3.1)
где Т – период [сек].
Величина,
обратная периоду, называется частотой  :
:
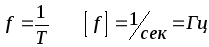 . (3.2)
. (3.2)
Также существует понятие угловой (циклической) частоты:

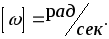 (3.3)
(3.3)
В электроэнергетике нашли широкое применение синусоидальные сигналы, как наиболее экономичные. Для передачи информации в технике связи и радиотехнике используют различные модуляции синусоидальных сигналов: амплитудную, частотную, фазовую. В общем случае любой несинусоидальный сигнал может быть представлен в виде суммы синусоидальных сигналов различной частоты с помощью разложения в ряд Фурье. И, таким образом, расчет подобных цепей может быть сведен к расчету цепей синусоидального тока и напряжения.
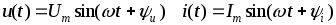 , (3.4)
, (3.4)
где 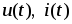 –мгновенное
значение;
–мгновенное
значение;
 –амплитуда переменного сигнала – максимальная по
модулю его величина;
–амплитуда переменного сигнала – максимальная по
модулю его величина;
 –фаза гармонического сигнала – аргумент при
синусе в каждый момент времени;
–фаза гармонического сигнала – аргумент при
синусе в каждый момент времени;
 –начальная
фаза – значение аргумента в начальный момент
времени (t
= 0).
Фаза измеряется в радианах или градусах.
–начальная
фаза – значение аргумента в начальный момент
времени (t
= 0).
Фаза измеряется в радианах или градусах.
В дальнейшим под переменным сигналом будем понимать гармонический (синусоидальный) сигнал.
или графически:
О значениях периодических токов и напряжений обычно судят по их среднеквадратических значениях за период, которые называют действующим значением тока и напряжения и обозначают I, U.
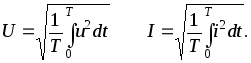 (3.5)
(3.5)
За период Т на резисторе с сопротивлением R при синусоидальном изменении тока выделится тепловая энергия:
 (3.6)
(3.6)
Таким образом, действующий ток численно равен такому постоянному току, который за время t = T выделяет в том же сопротивлении такое же количество тепла, что и переменный.
В действующих величинах градуируются (тарируются) амперметры и вольтметры электродинамической и электромагнитной системы. Приборы магнитоэлектрической системы показывают постоянную составляющую тока или напряжения, или среднее значение за период:
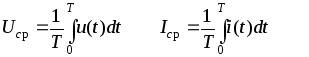 (3.7)
(3.7)
Установим
связь между действующим и амплитудным
значением гармонического сигнала на
примере тока. Если ток изменяется по
закону 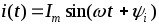 ,
то
,
то

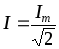 (3.8)
(3.8)
Произведя аналогичные действия для сигнала напряжения, получим
 (3.9)
(3.9)
Введем
понятие мощности
переменного тока.
Мгновенная мощность вычисляется как
произведение мгновенных значений
напряжения и тока  Тогда
Тогда
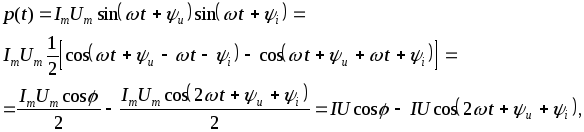 (3.10)
(3.10)
где  – сдвиг фазы тока по отношению к
напряжению;
– сдвиг фазы тока по отношению к
напряжению;
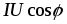 – постоянная составляющая мгновенной
мощности;
– постоянная составляющая мгновенной
мощности;
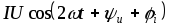 – гармоническая
составляющая, которая изменяется с
двойной угловой частотой.
– гармоническая
составляющая, которая изменяется с
двойной угловой частотой.
Средняя мощность за период называется активной мощностью:
 (3.11)
(3.11)


Элементы цепей гармонического тока
Электрическая цепь синусоидального тока кроме электротехнических устройств, назначение которых совпадает с назначением функционально аналогичных устройств цепи постоянного тока (источники энергии, измерительные приборы, коммутационные аппараты и др.), содержит также устройства, присущие только цепям синусоидального тока: конденсаторы и катушки индуктивности.
Для расчета режима работы электротехнических устройств необходимо перейти от принципиальной схемы цепи к ее схеме замещения (математической модели).
Элементами схем замещения цепей синусоидального тока являются источники синусоидальных тока и ЭДС (j(t), e(t)), резистивные (R), индуктивные (L) и емкостные (C) элементы.
Рассмотрим картину распределения тока и напряжения на реальных элементах.
1. Метод комплексных амплитуд
1.1. Гармонический сигнал
Гармонический
сигнал 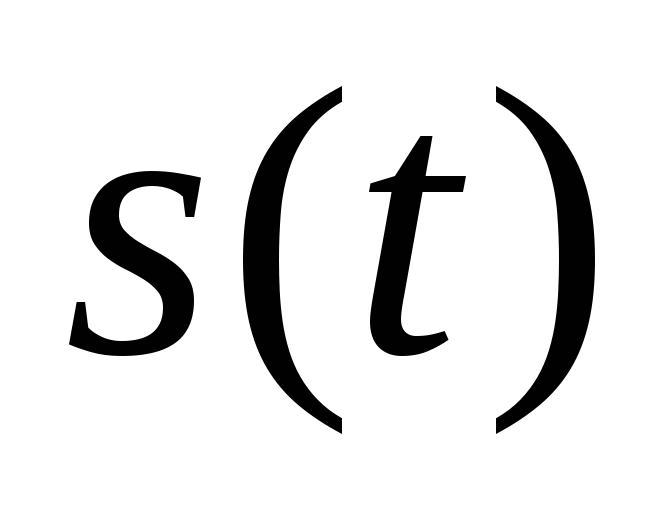 записывают в виде
записывают в виде
 ,
(1.1)
,
(1.1)
где 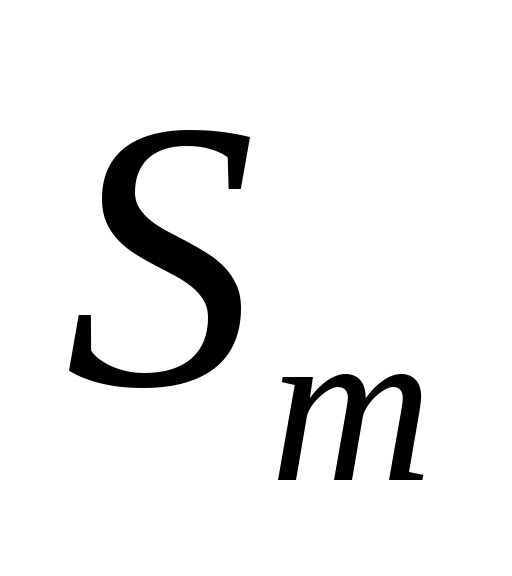 — амплитуда сигнала (индекс
— амплитуда сигнала (индекс от слова «максимум»),
от слова «максимум»), —
круговая частота, а
—
круговая частота, а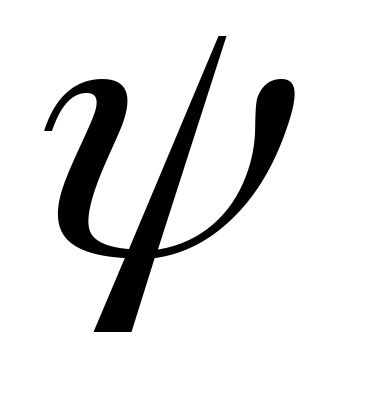 —
начальная фаза. Временная диаграмма
гармонического сигнала
—
начальная фаза. Временная диаграмма
гармонического сигнала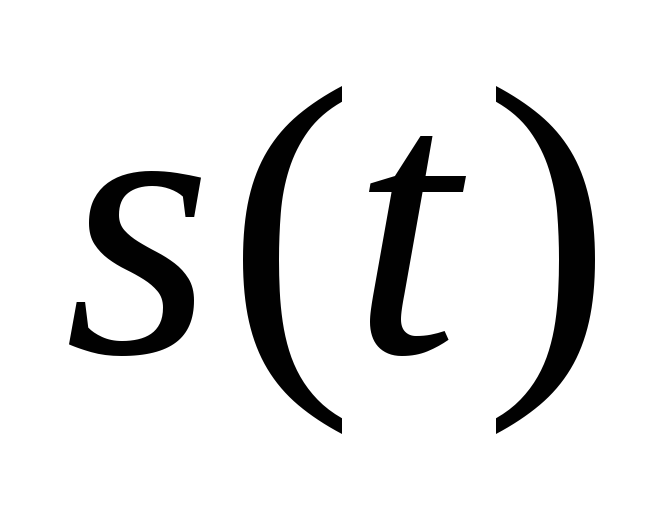 показана на рис. 1.1.
показана на рис. 1.1.
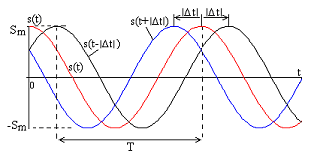
Рис. 1.1
Амплитуда гармонического сигнала – это его максимальное значение, она измеряется в единицах сигнала (вольтах для напряжения и амперах для тока).
Период сигнала  (рис. 1.1) определяетциклическую
частоту
(рис. 1.1) определяетциклическую
частоту  его повторения,
его повторения,
 ,
(1.2)
,
(1.2)
измеряемую в герцах (Гц). Ее физический смысл – число периодов колебаний в секунду.
Аргумент косинуса в (1.1) вида
4
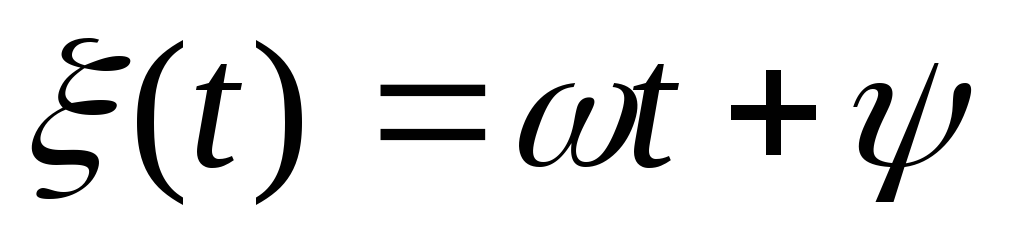 (1.3)
(1.3)
называют полной фазой колебания, она пропорциональна текущему времени и измеряется в радианах или градусах.
Круговая
частота  равна
равна
 (1.4)
(1.4)
и представляет собой число радиан, на которое изменяется полная фаза колебания в единицу времени (1 с).
При 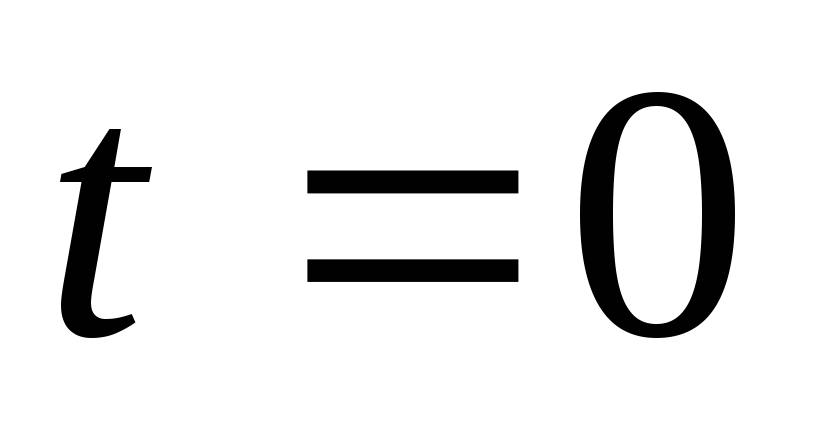 полная фаза равна
полная фаза равна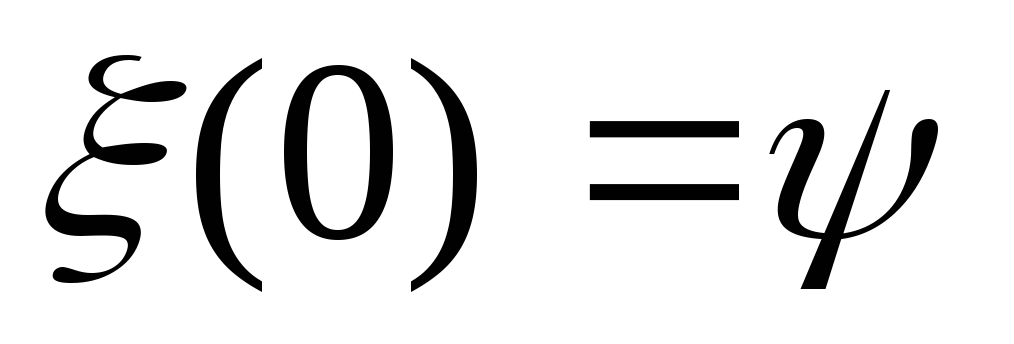 ,
поэтому параметр
,
поэтому параметр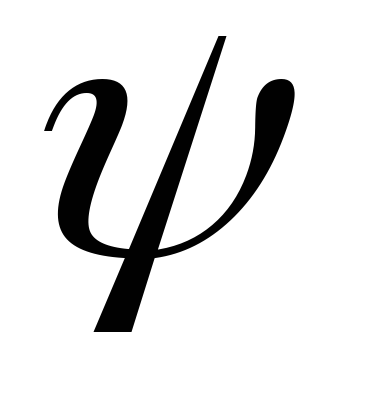 называютначальной
фазой гармонического сигнала. Она измеряется
в радианах или градусах. Так как период
функции
называютначальной
фазой гармонического сигнала. Она измеряется
в радианах или градусах. Так как период
функции  равен
равен или 3600,
то начальная фаза оказывается многозначной
величиной. Например, значения начальной
фазы 300 и (300+3600)=3900,
а также (300-3600)=-3300 оказываются эквивалентными. Для устранения
неоднозначности договариваются, что значения начальной
фазы должны находиться, например, в
интервале от 0 до
или 3600,
то начальная фаза оказывается многозначной
величиной. Например, значения начальной
фазы 300 и (300+3600)=3900,
а также (300-3600)=-3300 оказываются эквивалентными. Для устранения
неоднозначности договариваются, что значения начальной
фазы должны находиться, например, в
интервале от 0 до  ,
или от
,
или от до
до (аналогичные границы могут быть заданы
в градусах).
(аналогичные границы могут быть заданы
в градусах).
Начальная
фаза связана со смещением гармонического
сигнала во времени на величину  относительно функции
относительно функции ,
как показано на рис. 1.1. Функция
,
как показано на рис. 1.1. Функция смещена влево относительно
смещена влево относительно ,
а
,
а — вправо.Положительные значения
— вправо.Положительные значения  отсчитываются в сторонуувеличения
отсчитываются в сторонуувеличения 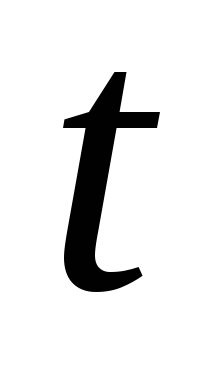 ,
а отрицательные – наоборот.
,
а отрицательные – наоборот.
Из (1.1) можно записать
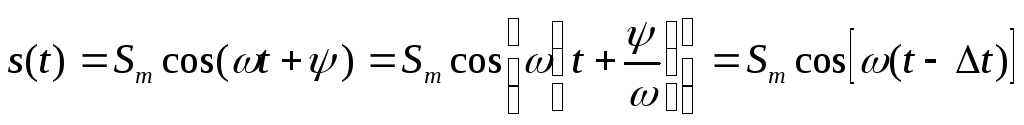 ,
(1.5)
,
(1.5)
5
где
смещение во времени  равно
равно
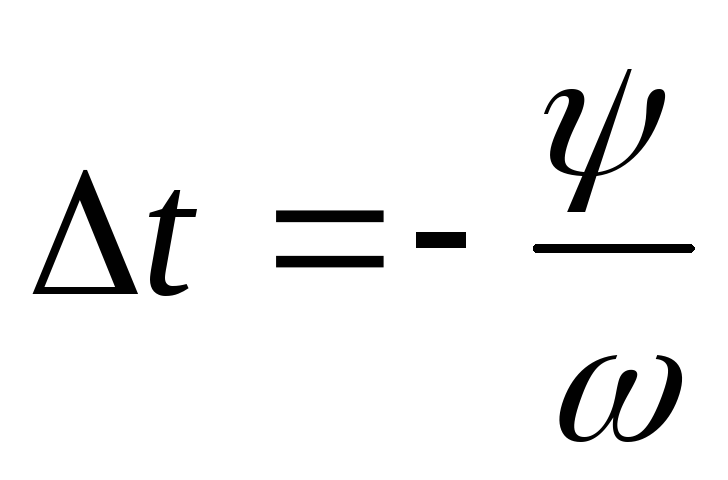 .
(1.6)
.
(1.6)
Тогда для начальной фазы получим
 .
(1.7)
.
(1.7)
Как
видно, начальная фаза определяется
временным сдвигом  гармонического сигнала относительно
функции
гармонического сигнала относительно
функции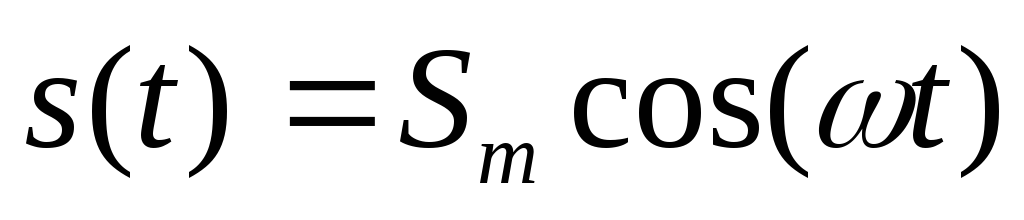 .
При
.
При сигнал
сигнал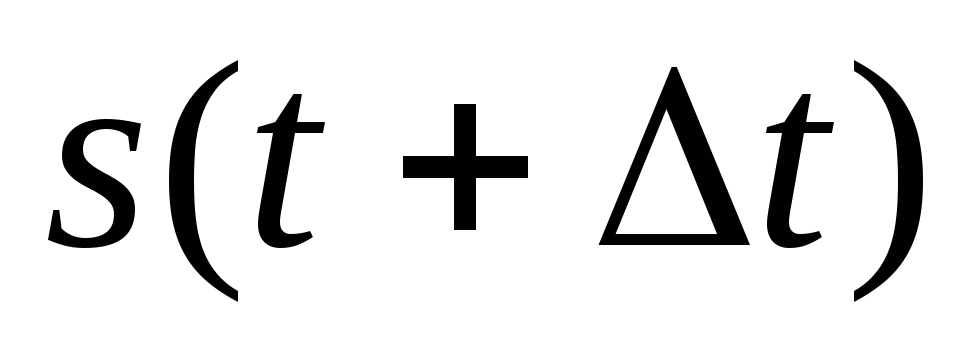 смещается вправо по оси времени, при
этом его начальная фаза
смещается вправо по оси времени, при
этом его начальная фаза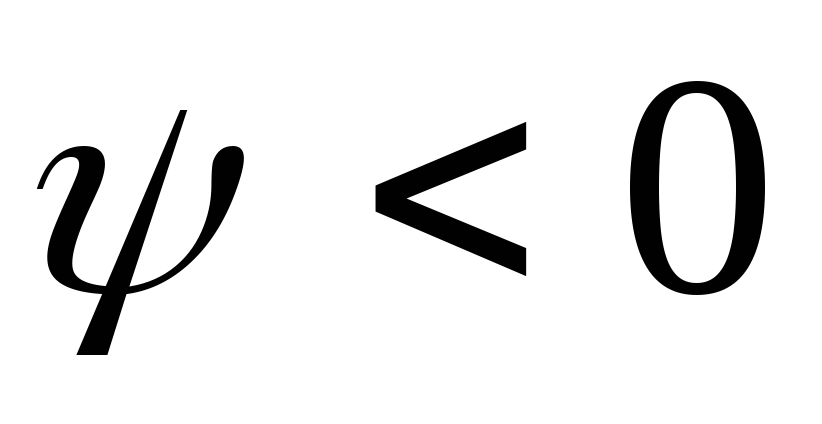 ,
а если
,
а если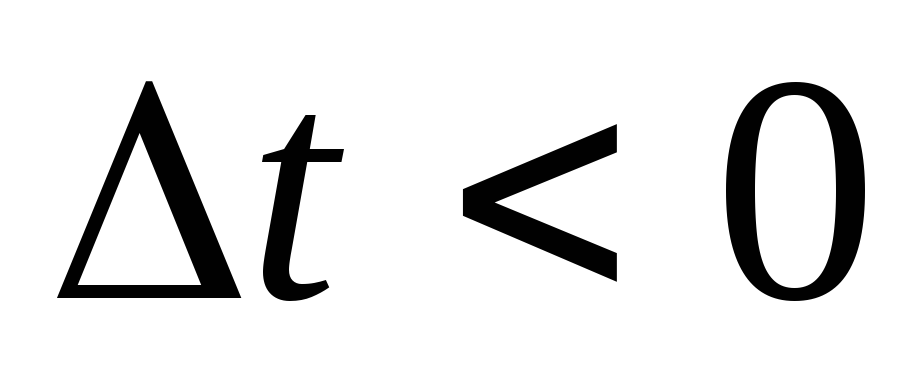 ,
то временная диаграмма смещается влево
по оси времени, а
,
то временная диаграмма смещается влево
по оси времени, а .
Величина начальной фазы зависит от
начала отсчета времени (положения точки
.
Величина начальной фазы зависит от
начала отсчета времени (положения точки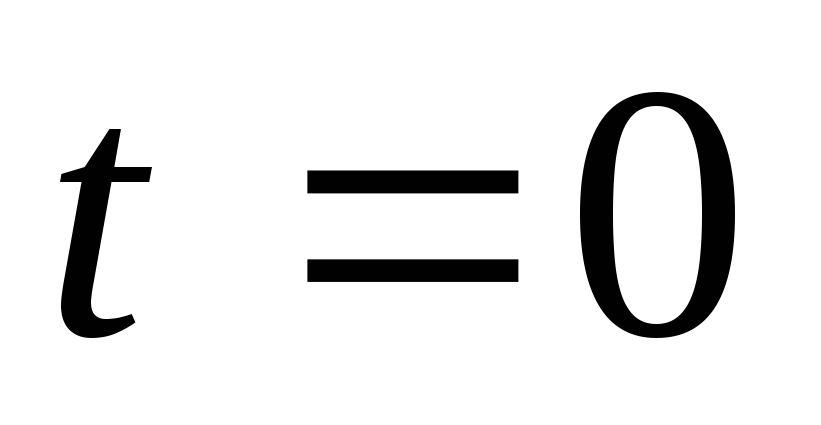 ).
При смещении начала отсчета времени
изменяется и начальная фаза.
).
При смещении начала отсчета времени
изменяется и начальная фаза.
Применительно
к двум гармоническим сигналам  и
и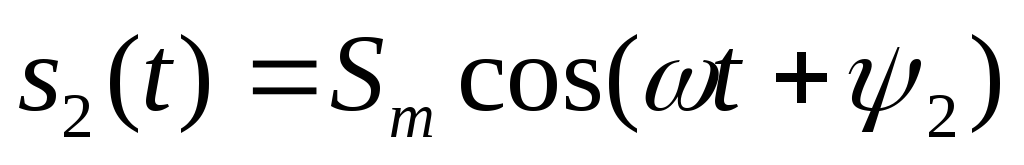 с разными начальными фазами
с разными начальными фазами и
и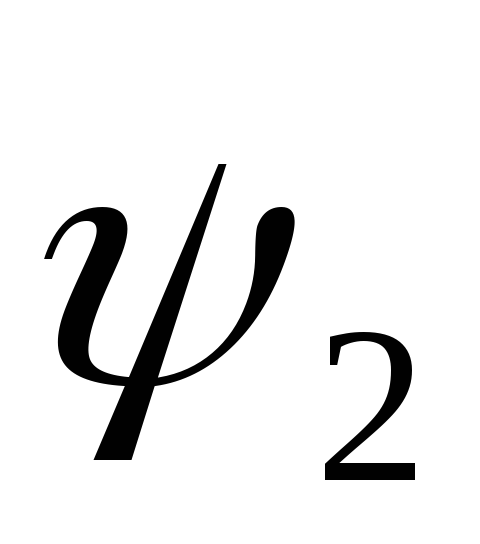 вводится в рассмотрениесдвиг
фаз между первым и
вторым сигналами,
вводится в рассмотрениесдвиг
фаз между первым и
вторым сигналами,
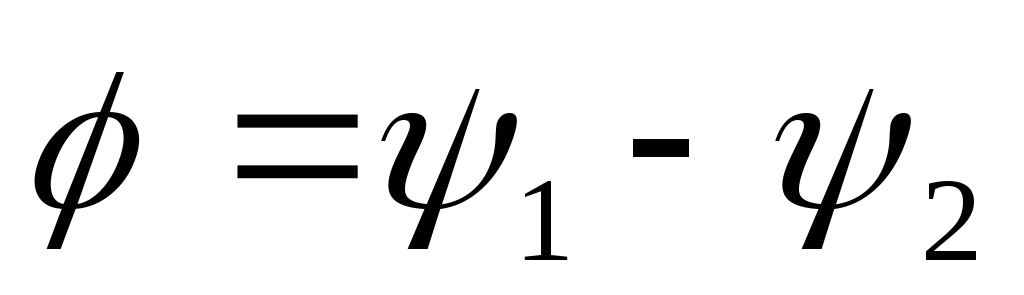 .
(1.8)
.
(1.8)
На
рис. 1.2 показаны два гармонических
сигнала с начальными фазами 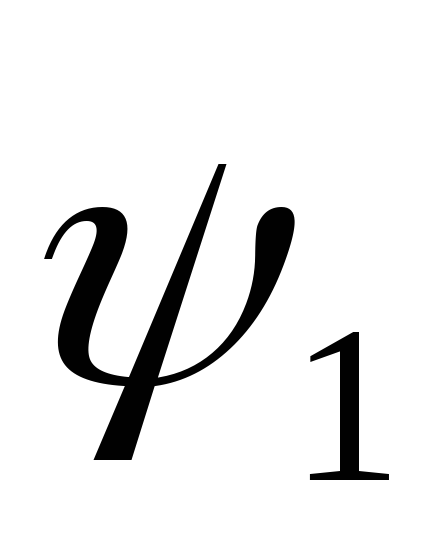 и
и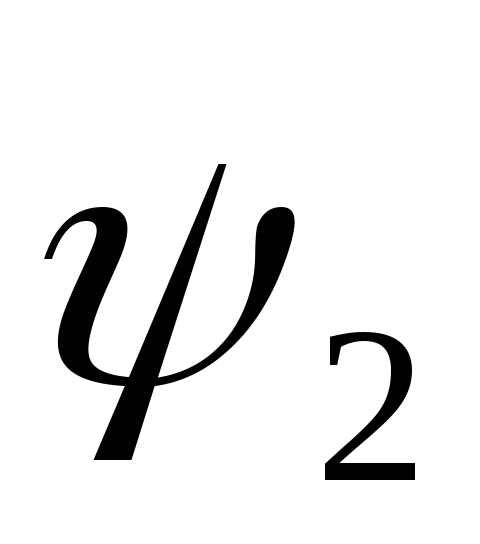 ,
причем
,
причем и
и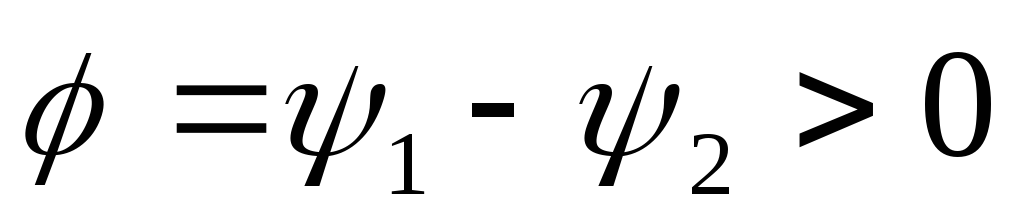 .
В этом случае говорят, что первый сигналопережает
по фазе второй или второй сигнал отстает
по фазе от
первого.
.
В этом случае говорят, что первый сигналопережает
по фазе второй или второй сигнал отстает
по фазе от
первого.
Сдвиг
фаз 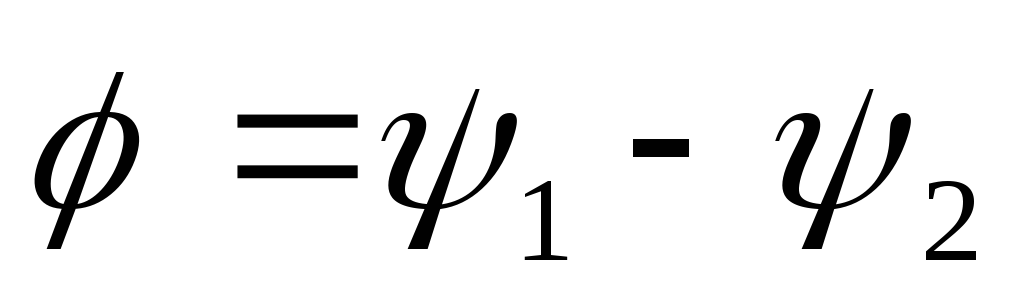 связан со смещением
связан со смещением сигналов во времени
сигналов во времени
 ,
(1.9)
,
(1.9)
6
п оложительные
значения временного сдвига отсчитываются
в направлении оси времени. Гармоническое
колебание может быть задано в нетипичной
форме, которую необходимо преобразовать
к виду (1.1), иначе начальная фаза
оложительные
значения временного сдвига отсчитываются
в направлении оси времени. Гармоническое
колебание может быть задано в нетипичной
форме, которую необходимо преобразовать
к виду (1.1), иначе начальная фаза
Рис. 1.2 оказывается неопреде-
ленной. Примеры преобразования показаны в табл. 1.1.
Таблица 1.1.
Исходный сигнал | Преобразованный сигнал | Начальная фаза |
| | |
| | |
| | |
1.2. Комплексная амплитуда гармонического сигнала
Для
гармонического сигнала (тока или
напряжения)  комплексная
амплитуда равна
комплексная
амплитуда равна
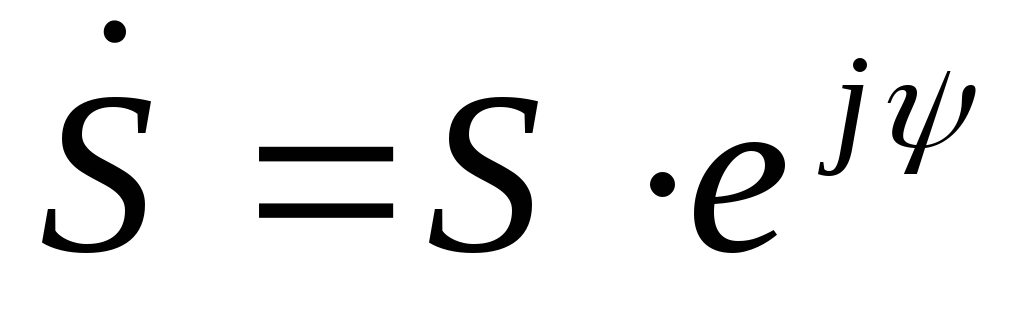 ,
,  .(1.10)
.(1.10)
Комплексная
амплитуда является комплексным числом ( —мнимая
единица) и
определяется только амплитудой
и начальной фазой сигнала и не
зависит от его час-
—мнимая
единица) и
определяется только амплитудой
и начальной фазой сигнала и не
зависит от его час-
7
тоты. Комплексная амплитуда обозначается тем же символом, что и амплитуда сигнала, но с точкой сверху.
Например,
если мгновенное значение гармонического
напряжения равно 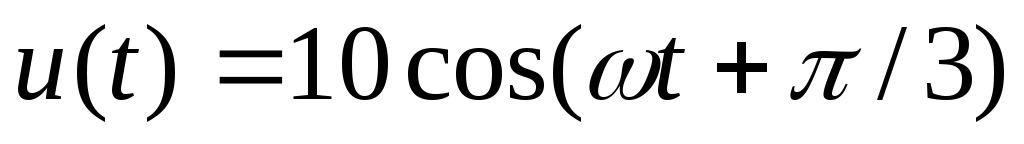 В,
то его комплексная амплитуда равна
В,
то его комплексная амплитуда равна В
или
В
или В.
В.

Если запись сигнала отличается от формы (5.1) то необходимо провести соответствующие тригонометрические преобразования, представленные в табл. 1.2.
Таблица 1.2.
Если
гармоническое напряжение имеет вид  мВ,
то после преобразования получим
мВ,
то после преобразования получим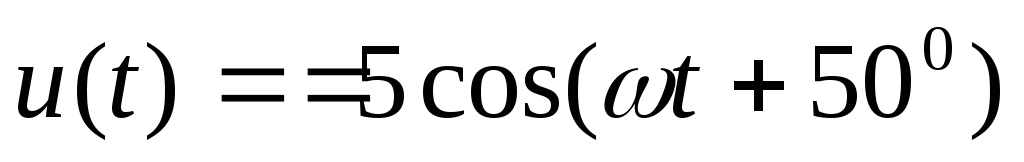 мВ,
а комплексная амплитуда будет равна
мВ,
а комплексная амплитуда будет равна мВ.
мВ.
1.3. Операции с комплексными числами
Комплексные
числа могут быть записаны в двух формах:
алгебраической и показательной. В алгебраической
форме комплексное число  (точка сверху используется для обозначения
комплексной амплитуды сигнала, а если
речь идет о комплексном сопротивлении
или проводимости, то используется
подчеркивание символа
(точка сверху используется для обозначения
комплексной амплитуды сигнала, а если
речь идет о комплексном сопротивлении
или проводимости, то используется
подчеркивание символа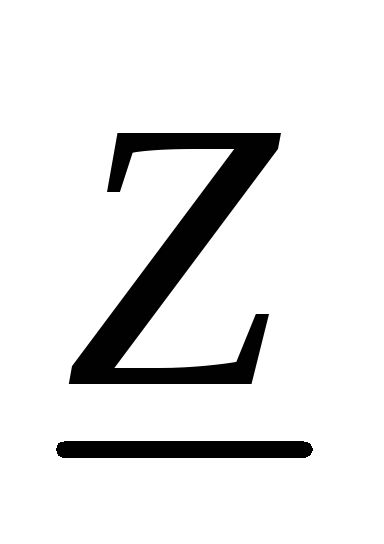 )
записывается в виде
)
записывается в виде
8
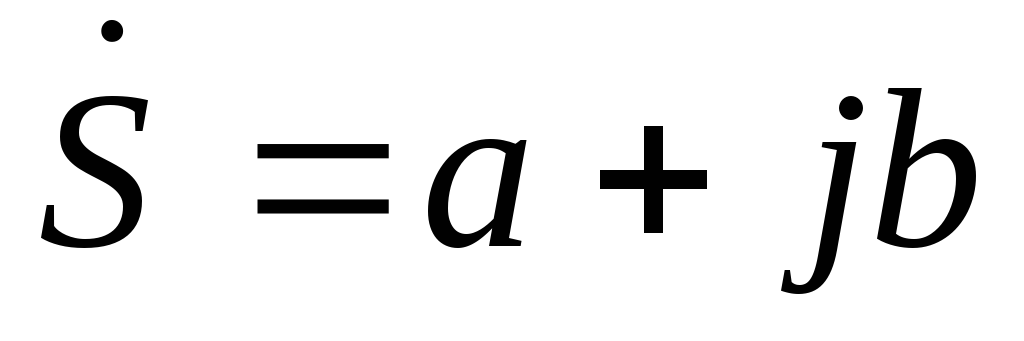 ,
(1.12)
,
(1.12)
где  —действительная,
а
—действительная,
а 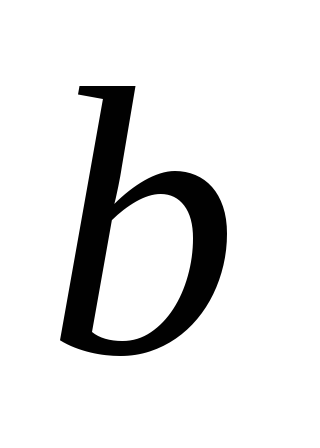 —мнимая части комплексного числа,
—мнимая части комплексного числа,  —мнимая
единица.
—мнимая
единица.
В показательной форме комплексное число представляется выражением
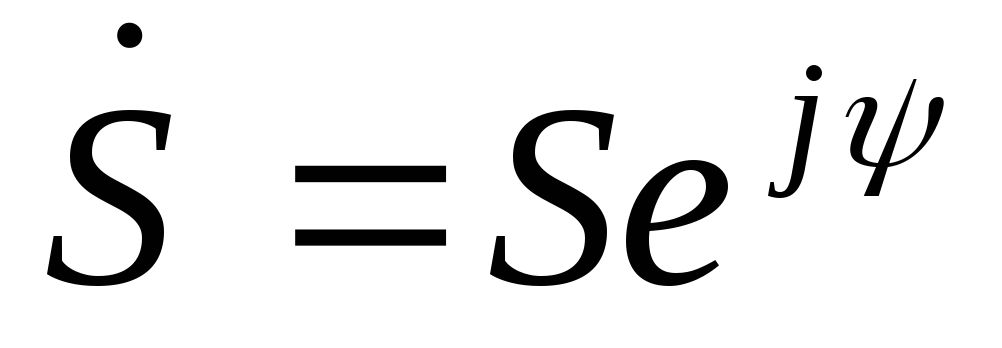 ,
(1.13)
,
(1.13)
величину  называютмодулем,
а
называютмодулем,
а 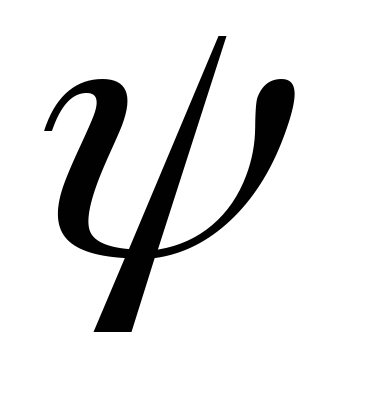 —аргументом комплексного числа. От алгебраической
формы можно перейти к показательной, модуль комплексного числа равен
—аргументом комплексного числа. От алгебраической
формы можно перейти к показательной, модуль комплексного числа равен
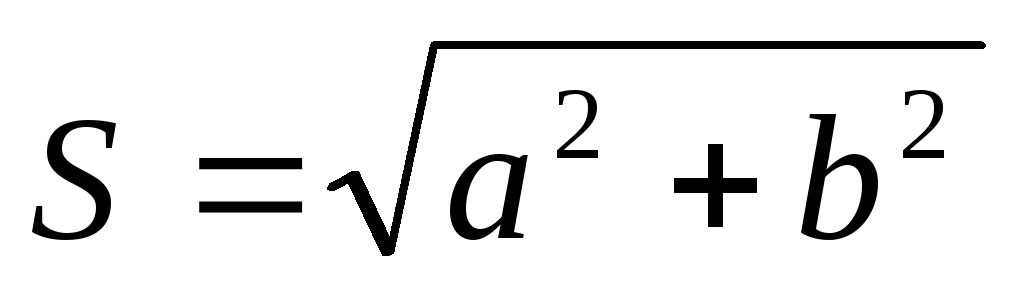 ,
(1.14)
,
(1.14)
а аргумент
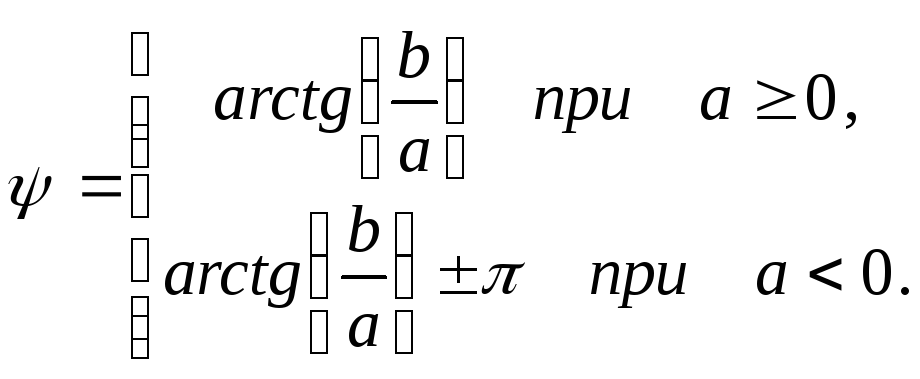 (1.15)
(1.15)
Аргумент
комплексного числа, как и начальная
фаза гармонического сигнала, величина многозначная,
к ней можно добавить (или вычесть)  любое число раз. Для обеспечения
однозначности аргумента комплексного
числа его значения выбирают в диапазоне,
например, от
любое число раз. Для обеспечения
однозначности аргумента комплексного
числа его значения выбирают в диапазоне,
например, от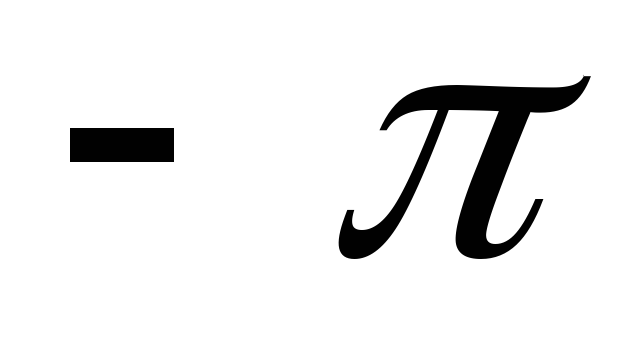 до
до или от 0 до
или от 0 до .
.
Показательную форму комплексного числа можно заменить алгебраической с помощью соотношений
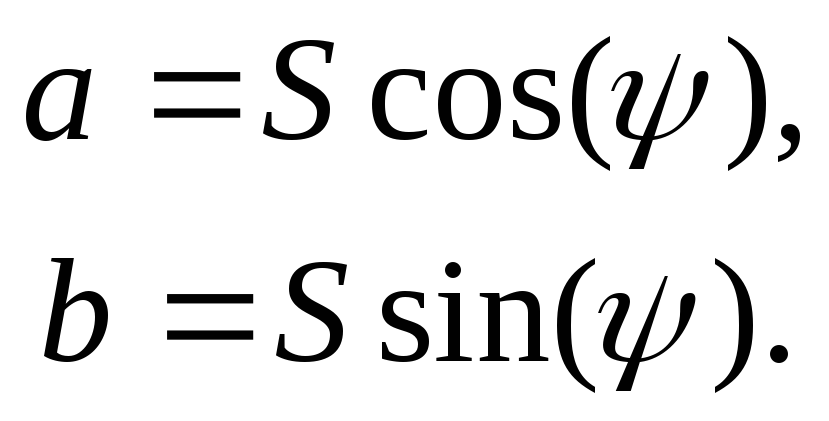 (1.16)
(1.16)
Они вытекают из известной в математике формулы Эйлера,
9
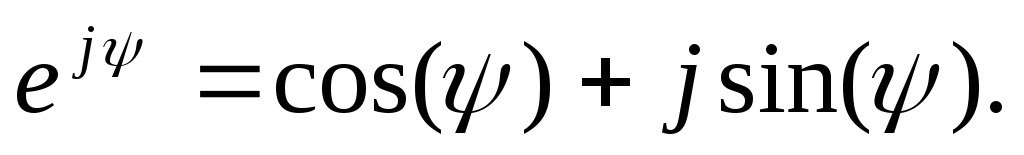 (1.17)
(1.17)
Например,
если комплексное число в алгебраической
форме равно 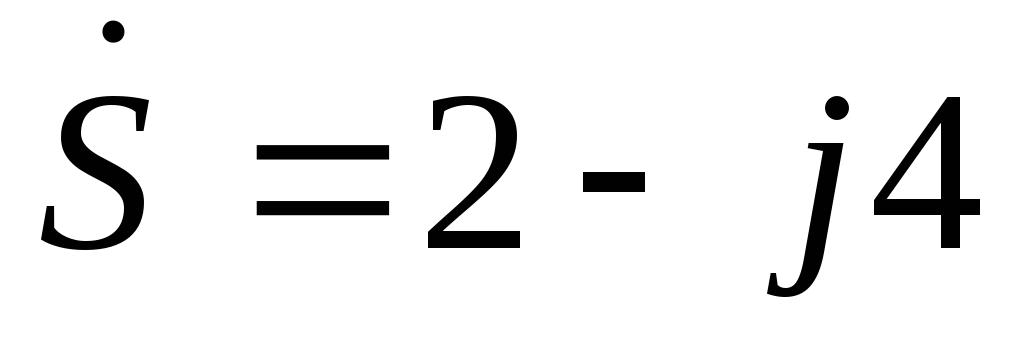 ,
то в показательной форме его можно
записать в виде
,
то в показательной форме его можно
записать в виде
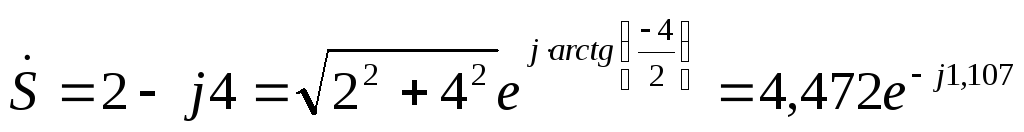 .
.
Если
комплексное число равно  ,
то в показательной форме получим
,
то в показательной форме получим
 .
.
Для
комплексного числа в показательной
форме в виде  его алгебраическая форма имеет вид
его алгебраическая форма имеет вид
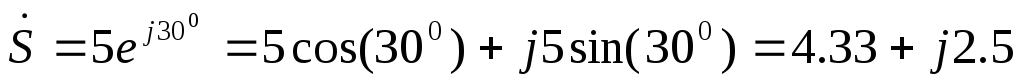 .
.
С комплексными числами проводятся все четыре арифметические действия.
При
сложении и вычитании комплексных чисел 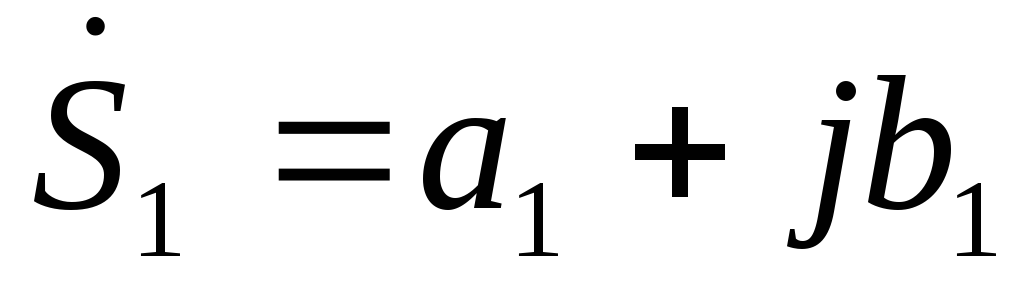 и
и в алгебраической форме получим
в алгебраической форме получим
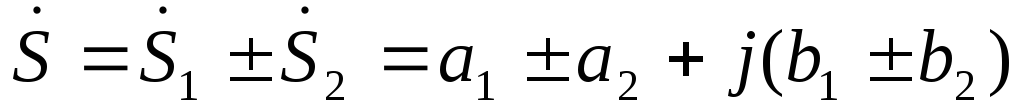 .
(1.18)
.
(1.18)
Если числа заданы в показательной форме, то перед сложением или вычитанием их необходимо преобразовать в алгебраическую форму.
Операции
умножения и деления удобнее выполнять
в показательной форме, когда 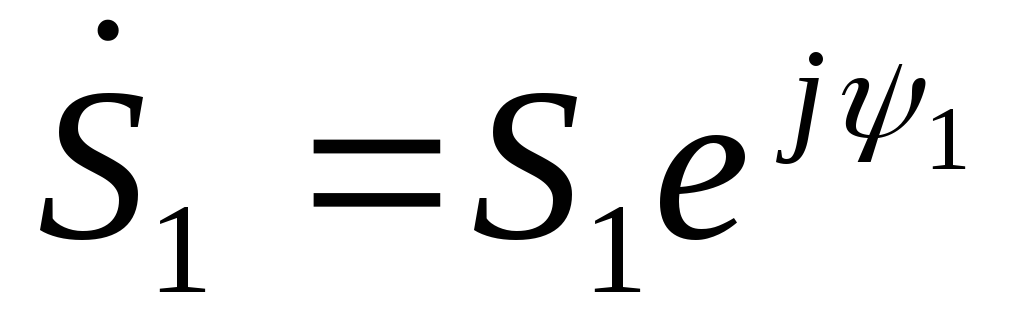 и
и ,
при этом при умножении комплексных
чисел их модули перемножаются, а аргументы
складываются
,
при этом при умножении комплексных
чисел их модули перемножаются, а аргументы
складываются
10
 ,
(1.19)
,
(1.19)
а при делении делятся модули и вычитаются аргументы числителя и знаменателя
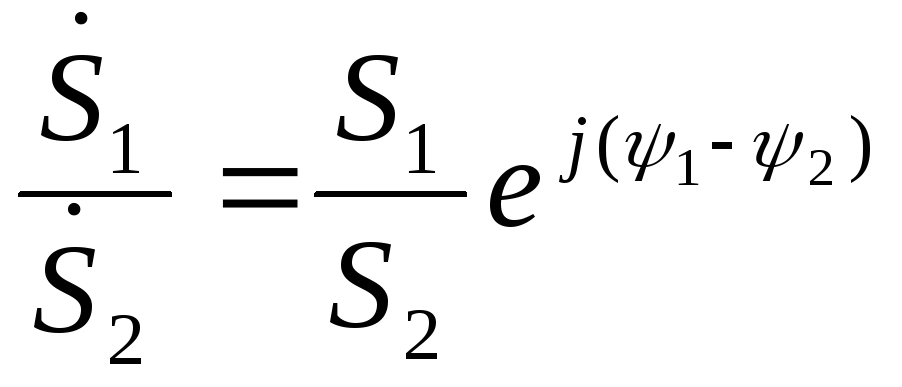 .
(1.20)
.
(1.20)
Умножение
можно провести и с алгебраической формой
сомножителей по известным правилам с
учетом того, что 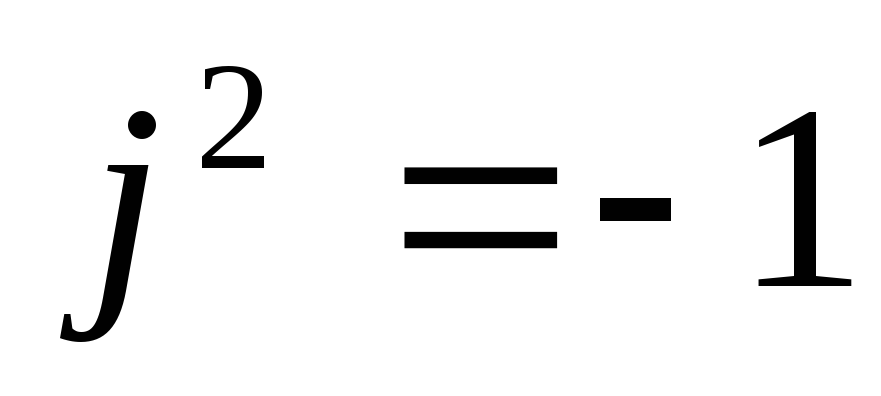 :
:
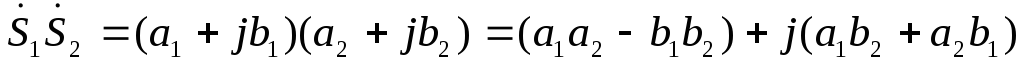 .
(1.21)
.
(1.21)
При
делении комплексных чисел в
алгебраической форме используется
операция устранения
комплексности в знаменателе путем умножения числителя и знаменателя
дроби на число, комплексно
сопряженное знаменателю. Для заданного числа 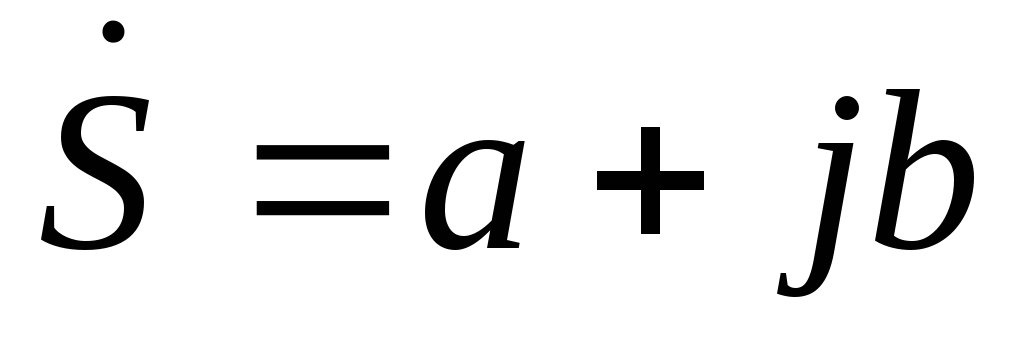 комплексно сопряженное число
комплексно сопряженное число равно
равно ,
то есть отличается от
,
то есть отличается от противоположным знаком примнимой
части.
Произведение двух комплексно сопряженных
чисел всегда равно квадрату их модуля,
противоположным знаком примнимой
части.
Произведение двух комплексно сопряженных
чисел всегда равно квадрату их модуля,
 .
(1.22)
.
(1.22)
Тогда при делении в алгебраической форме получим
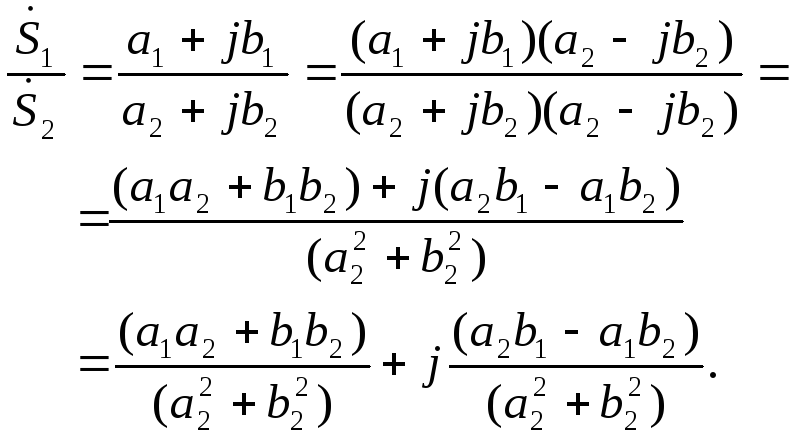 (1.23)
(1.23)
11
Рассмотрим
пример  и
и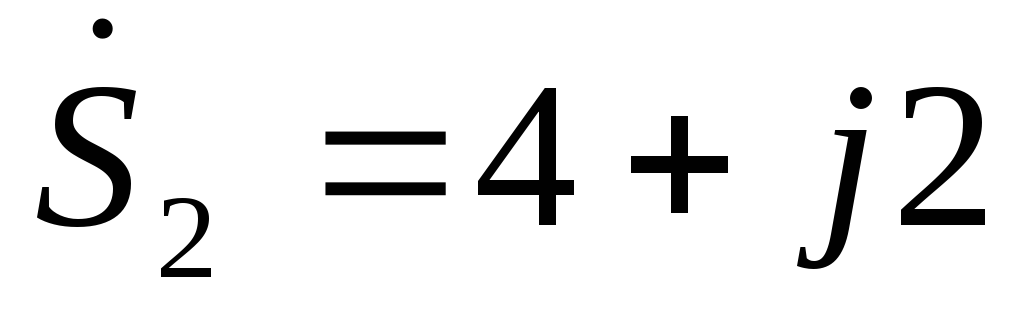 ,
тогда
,
тогда
 ,
,
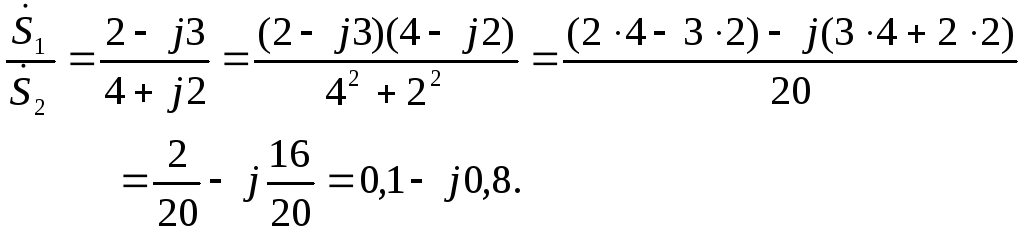
Эти операции можно провести и в показательной форме
 ,
,
 ,
,
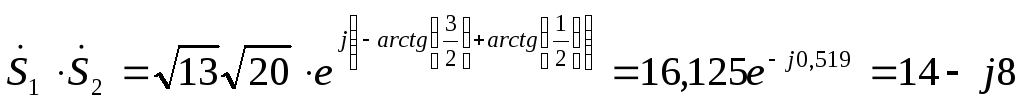 ,
,
 .
.
Как видно, полученные результаты совпадают.
Полезно запомнить следующие равенства (табл. 1.3.), вытекающие из формулы Эйлера,
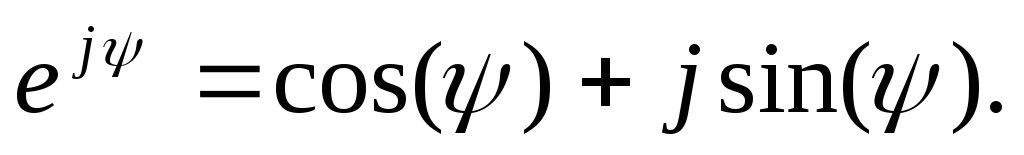 (1.24)
(1.24)
12
Таблица 1.3.
Вычисления с комплексными числами удобно проводить на персональной ЭВМ с помощью пакета программ MathCAD.
1.4. Законы Ома и Кирхгофа для комплексных
амплитуд токов и напряжений
Законы Ома и Кирхгофа применимы в своих классических формулировках для комплексных амплитуд токов и напряжений.
Закон Ома: комплексная амплитуда напряжения на участке цепи прямо пропорционально комплексной амплитуде протекающего через него тока. Для двухполюсного участка цепи его можно записать в виде
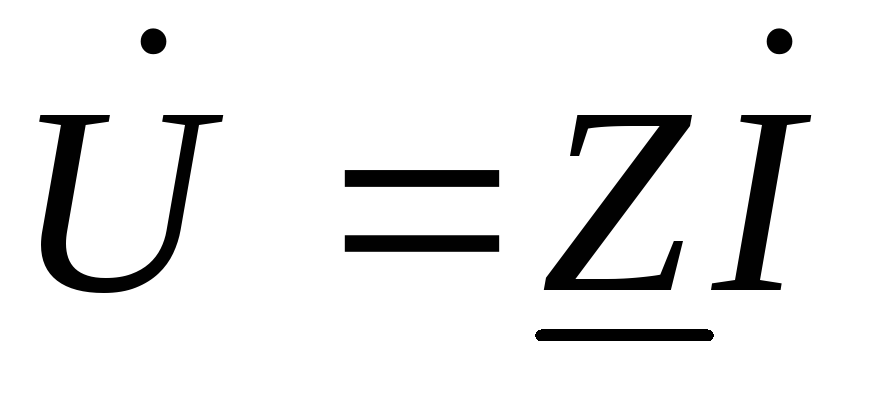 или
или  ,
(1.25)
,
(1.25)
где  —полное
комплексное сопротивление,
а
—полное
комплексное сопротивление,
а  —полная
комплексная проводимость участка цепи.
—полная
комплексная проводимость участка цепи.
Первый закон Кирхгофа: алгебраическая сумма комплексных амплитуд сходящихся в узле токов равна нулю,
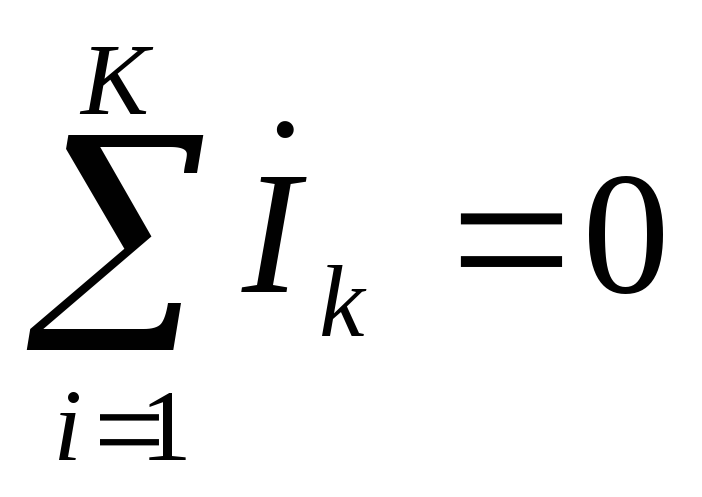 .
(1.26)
.
(1.26)
Второй закон Кирхгофа: алгебраическая сумма комплексных амплитуд падений напряжения на элементах замкнутого контура равна алгебраической сумме комплексных амплитуд ЭДС идеальных источников напряжения, включенных в этот контур,
13
 .
(1.27)
.
(1.27)
Знаки в алгебраических суммах определяются выбранными положительными направлениями токов и напряжений и направлением обхода контура.
1.5. Комплексные сопротивления и проводимости
элементов цепи
Значения
комплексных сопротивлений  и проводимостей
и проводимостей элементов цепиR,
L
и C
приведены в табл. 1.4 (запомните
эти формулы).
элементов цепиR,
L
и C
приведены в табл. 1.4 (запомните
эти формулы).
Таблица 1.4
Элемент | R | L | C |
Комплексное сопротивление |
| | |
Комплексная
проводимость |
| | |
Комплексные
сопротивление и проводимость сопротивления  всегдадействительны (мнимая часть равна нулю), а индуктивности
и емкости – мнимые (действительная
часть равна нулю).
всегдадействительны (мнимая часть равна нулю), а индуктивности
и емкости – мнимые (действительная
часть равна нулю).
Для
комплексного сопротивления  из закона Ома получим
из закона Ома получим
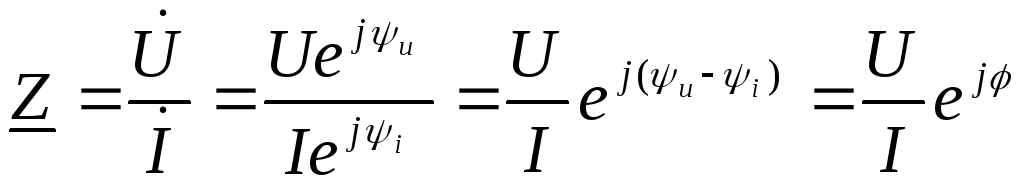 ,
(1.28)
,
(1.28)
где  —сдвиг фаз
между напряжением и током в
—сдвиг фаз
между напряжением и током в
14
элементе.
Для сопротивления 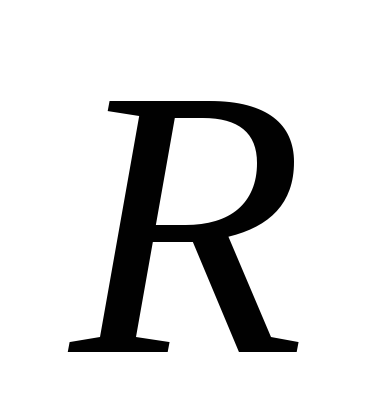 напряжение и ток совпадают по фазе, то
есть
напряжение и ток совпадают по фазе, то
есть и из (1.28) величина
и из (1.28) величина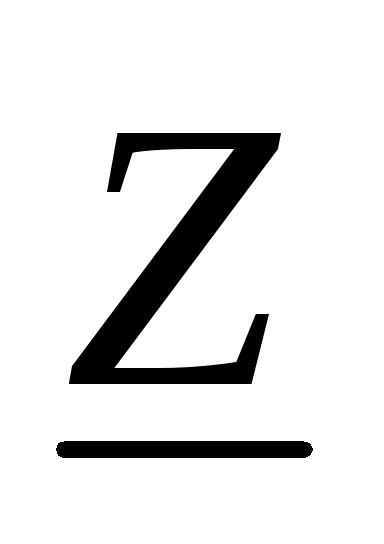 действительна.
действительна.
В
индуктивности напряжение опережает по
фазе ток на 900 (на 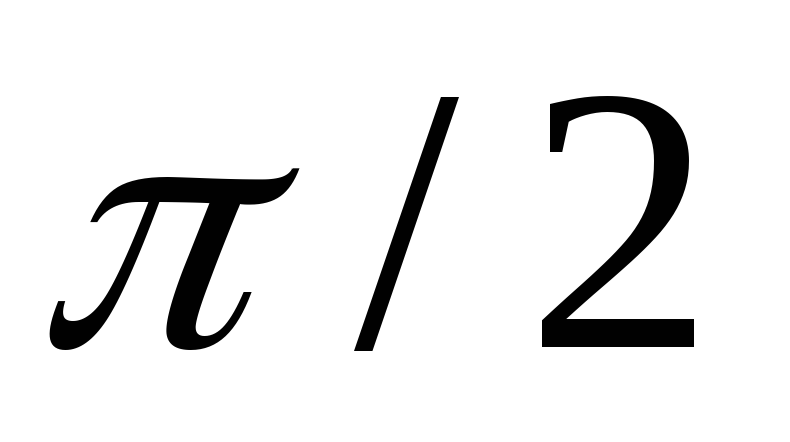 радиан), следовательно
радиан), следовательно ,
тогда
,
тогда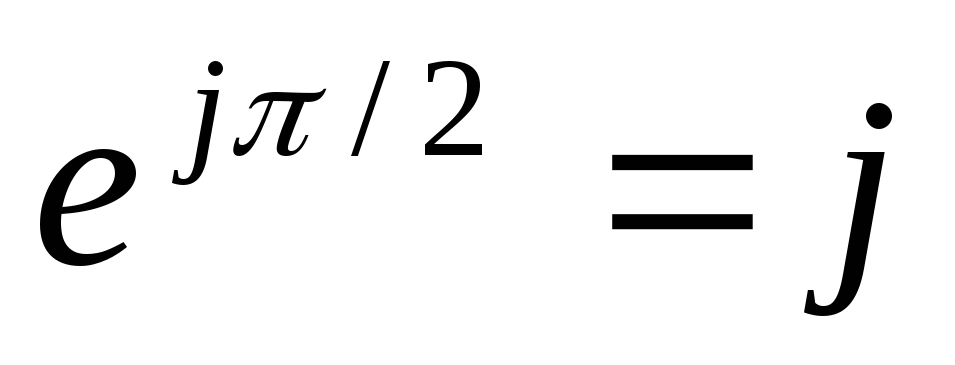 и величина комплексного сопротивления
индуктивности
и величина комплексного сопротивления
индуктивности оказывается снулевой действительной и положительной мнимой частями. В емкости
оказывается снулевой действительной и положительной мнимой частями. В емкости  ,
, и ее комплексное сопротивление имеетнулевую действительную и отрицательную мнимую части.
и ее комплексное сопротивление имеетнулевую действительную и отрицательную мнимую части.
1.6. Комплексные сопротивление и проводимость
участка цепи
Полные комплексные сопротивления (и проводимости) двухполюсного участка цепи с произвольным соединением элементов определяются по следующим правилам:
— комплексное сопротивление последовательного соединения двухполюсников равно сумме их комплексных сопротивлений;
— комплексная проводимость параллельного соединения двухполюсников равна сумме их комплексных проводимостей.
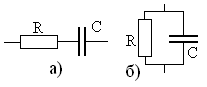 Например,
сопротивление последовательной цепи,
показанной на рис. 1.3а при
Например,
сопротивление последовательной цепи,
показанной на рис. 1.3а при кОм
ипФ
и частоте
кОм
ипФ
и частоте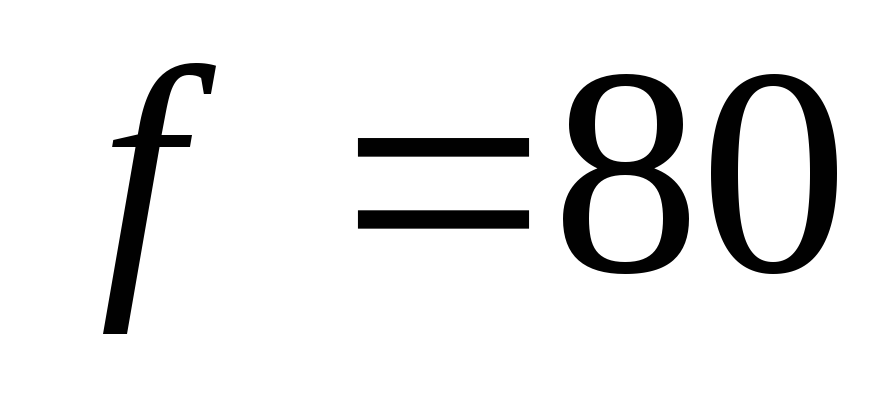 кГц равно
кГц равно
 кОм,
кОм,
Рис. 1.3 а проводимость параллельной це-
пи на рис 5.1б —
 Сим.
Сим.
Зная комплексное сопротивление цепи, можно определить ее комплексную проводимость и наоборот,
15
 (1.29)
(1.29)
Для последовательной цепи на рис. 1.3а ее проводимость равна
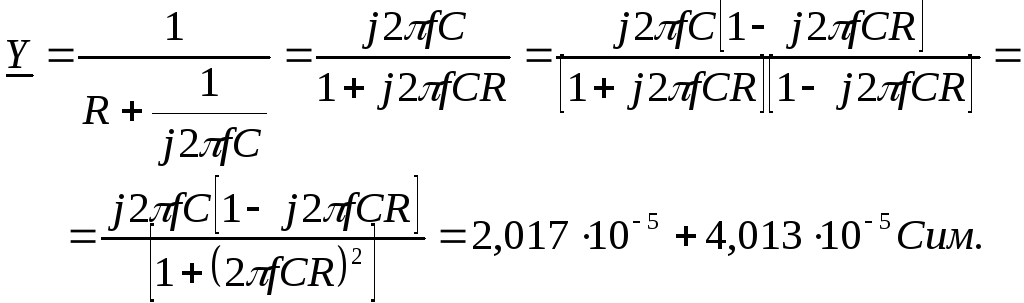
Расчет проведен методом устранения комплексности знаменателя путем умножения числителя и знаменателя дроби на множитель, комплексно-сопряженный знаменателю. Можно провести вычисление проводимости путем преобразования комплексного сопротивления из алгебраической формы в показательную,
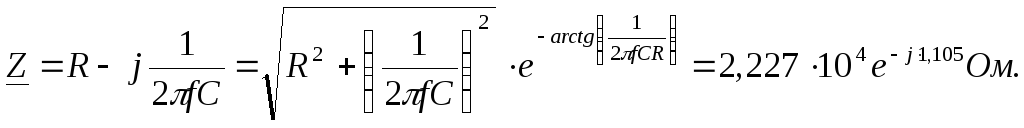 .
.
Тогда для проводимости получим
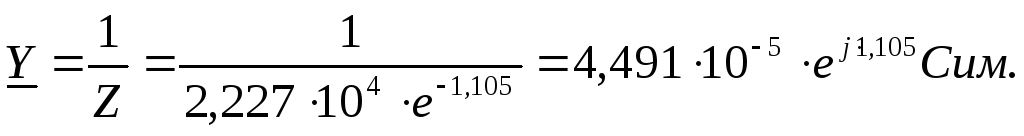

С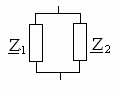 опротивлениепараллельного соединения двух элементов с сопротивлениями
опротивлениепараллельного соединения двух элементов с сопротивлениями  и
и определяется выражением
определяется выражением
 .
.
Комплексное сопротивление цепи со смешанным со-
16
единением элементов определяется следующим образом:
— в цепи выделяется фрагмент с простым (последовательным или параллельным) соединением элементов и определяется его сопротивление или проводимость;
— фрагмент заменяется эквивалентным элементом, в полученной цепи вновь выделяется простой фрагмент и повторяется предыдущее действие;
— эти действия повторяются до тех пор, пока цепь не трансформируется в один элемент с соответствующим сопротивлением или проводимостью.
 Рассмотрим
цепь, схема которой показана на рис. 1.4
при
Рассмотрим
цепь, схема которой показана на рис. 1.4
при кОм,
кОм,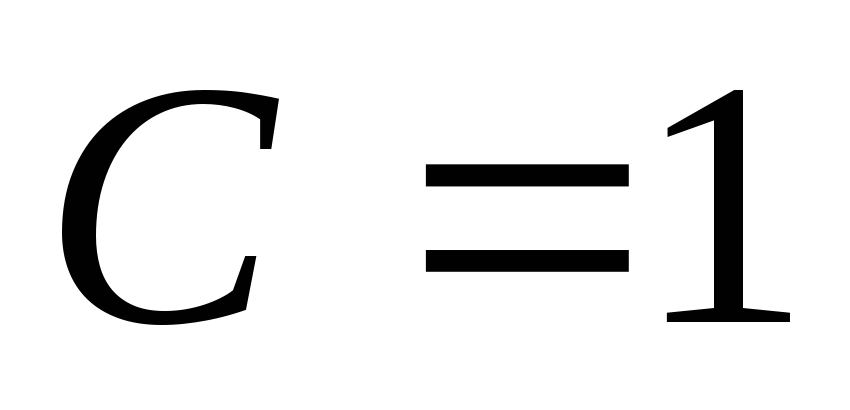 нФ,
нФ,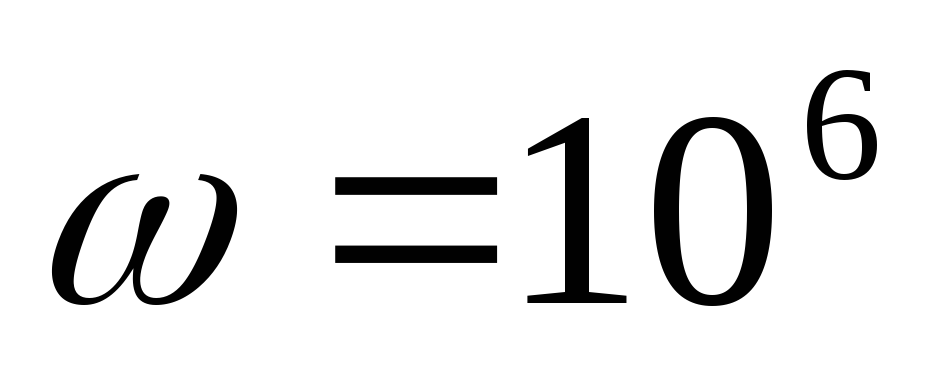 рад/с
и определим ее комплексное сопротивление
рад/с
и определим ее комплексное сопротивление 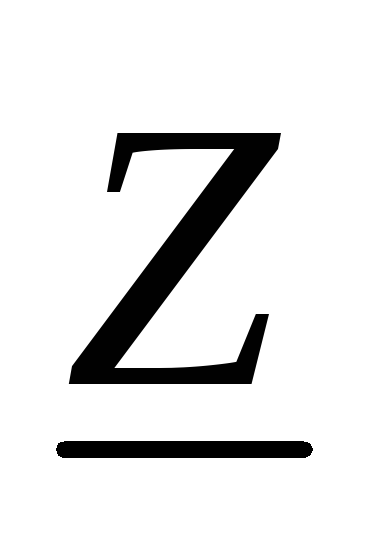 .
В цепи выделяется простой параллельный
фрагмент из элементов
.
В цепи выделяется простой параллельный
фрагмент из элементов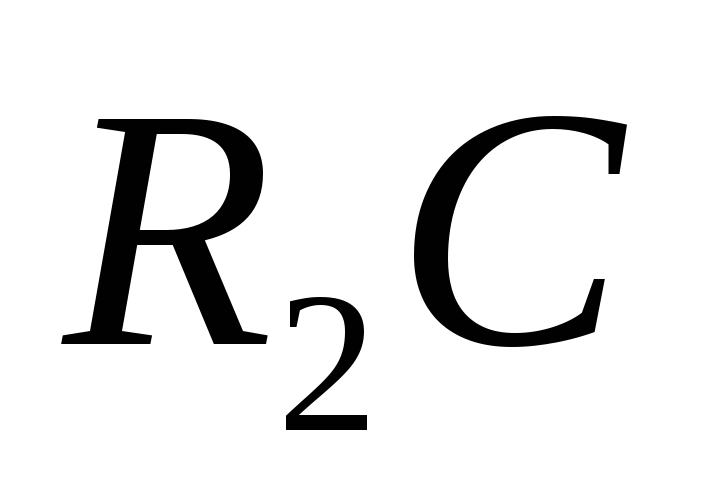 иопределяется
его сопротивление
иопределяется
его сопротивление 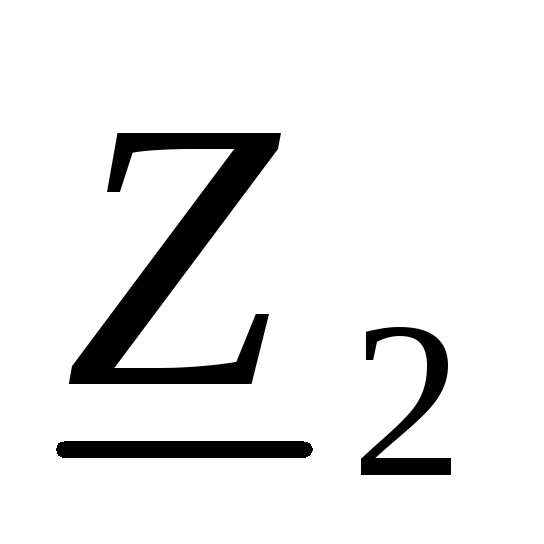 ,
равное
,
равное
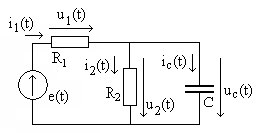 Рис.
1.4
Рис.
1.4  .
.
Тогда
параллельный фрагмент  заменяется эквивалентным элементом с
сопротивлением
заменяется эквивалентным элементом с
сопротивлением и схема цепи принимает вид, показанный
на рис. 1.5.
и схема цепи принимает вид, показанный
на рис. 1.5.
Для
полученной последовательной цепи ее
сопротивление равно
равно
 .
.
Подставляя исходные данные, получим
Рис. 1.5
 Ом.
Ом.
17