Сила Ампера: взаимодействие двух проводников

В этой статье предлагаю задачи на взаимодействие двух проводов с током, расположенных недалеко друг от друга. Сила взаимодействия – взаимная:  как первый провод, создавая поле, действует на второй, так и наоборот. В первой задаче приведен вывод формулы, с которой проводники взаимодействуют, в дальнейшем я просто использую ее.

Задача 1. Горизонтальные рельсы находятся на расстоянии м  друг от друга. На них перпендикулярно рельсам лежит стержень. Какой должна быть минимальная индукция магнитного поля, чтобы проводник двигался равномерно, если по нему пропускать электрический ток? Коэффициент трения стержня о рельсы . Масса стержня кг, сила тока А.

Чтобы проводник двигался равномерно, без ускорения, нужно, чтобы сила Ампера как минимум была равна силе трения. Тогда:

   

   

Откуда:

   

Ответ: Тл.

Задача 2. Проводящий стержень подвешен горизонтально на двух легких проводах в магнитном поле, индукция которого направлена вертикально вниз (рис.). К точкам крепления провода можно подключать конденсатор. Определить емкость конденсатора С1‚ при разрядке которого стержень отклонится от вертикали на угол , если при разрядке заряженного до такого же напряжения конденсатора емкостью мкФ угол отклонения . Сопротивление стержня и проводов не учитывать.

К задаче 2

Можем записать для отклонившегося проводника уравнения по второму закону Ньютона  по вертикальной и горизонтальной осям:

Рисунок 2. Детализация.

 

   

   

Разделим эти уравнения друг на друга:

   

Или

   

Вес проводника меняться не будет, поэтому при действии разных по модулю сил отклонение его тоже будет разным:

   

Распишем силы Ампера:

   

Но , следовательно,

   

А в силу малости углов можно перейти к ним самим:

   

Откуда

   

Ответ: 15 мкФ.

Задача 3. Сила тока в двух параллельных проводниках   А и А соответственно, длина каждого проводника м. Определить расстояние между проводниками , если они взаимодействуют с силой Н.

Сила взаимодействия двух проводников может быть определена следующим образом: первый находится в поле второго, на него действует сила

   

Второй находится в поле первого, на него действует сила

   

Силы равны (это одна и та же сила), следовательно,

   

Индукция, создаваемая протяженным проводником с током, равна

   

   

Подставляя, получим:

   

Откуда :

   

Ответ: 3 см.
Задача 4. Два параллельных проводника, сила тока в которых одинакова, находятся на расстоянии см друг от друга и притягиваются с силой Н. Определить силу тока в проводнике, если длина каждого проводника см.

По формуле из предыдущей задачи

   

   

   

Ответ: А.

Задача 5. Металлический стержень длиной м расположен параллельно бесконечно длинному прямому проводу. Сила тока в проводе А. Найти силу, действующую на стержень со стороны магнитного поля, которое создается проводом, если сила тока в стержне А. Расстояние от провода до стержня см.

Из задачи 3

   

Ответ: Н.

Задача 6. В вертикальной плоскости расположены два горизонтальных прямых, параллельных друг другу проводника. Сила тока в каждом проводнике А. Верхний проводник можно считать бесконечно
длинным. Нижний проводник имеет длину м и массу кг. Каково должно быть расстояние между проводниками, чтобы сила их взаимодействия уравновешивала силу тяжести нижнего проводника?

   

Откуда

   

Ответ: 20 см.

42. Взаимодействие проводников с током. Закон Ампера.

Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, ис­пытываемый рамкой, есть результат дейст­вия сил на отдельные ее элементы. Обоб­щая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находяще­гося в магнитном поле, прямо пропорцио­нальна силе тока I в проводнике и век­торному произведению элемента длиной dl проводника на магнитную индук­цию В: d

F = I[dl, В]. Направление вектора dF может быть найдено по общим пра­вилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы Ампера вычисляется по формуле dF = IBdlsin, где a — угол между векторами dl и В.

Закон Ампера применяется для опре­деления силы взаимодействия двух токов. Рассмотрим два бесконечных прямолиней­ных параллельных тока

I₁ и I₂ (направле­ния токов указаны на рис. 167), расстоя­ние между которыми равно R. Каждый из проводников создает магнитное поле, ко­торое действует по закону Ампера на дру­гой проводник с током. Рассмотрим, с ка­кой силой действует магнитное поле тока I₁ на элемент dl второго проводника с то­ком I₂. Ток I₁ создает вокруг себя магнит­ное поле, линии магнитной индукции кото­рого представляют собой концентрические окружности. Направление вектора В₁ за­дается правилом правого винта, его мо­дуль равен

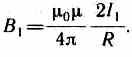
Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы с учетом того, что угол  между элементами тока I₂ и вектором B₁ прямой, равен dF₁=I₂B₁dl, или, подставляя значение для В₁, получим

Рассуждая аналогично, можно пока­зать, что сила dF₂

, с которой магнитное поле тока I₂ действует на элемент dl пер­вого проводника с током I₁, направлена в противоположную сторону и по модулю равна

Сравнение выражений показывает, что dF₁=dF₂, т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой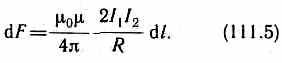

Если токи имеют противоположные на­правления, то, используя правило левой руки, можно показать, что между ними действует

сила отталкивания.

43. Магнитное поле движущегося заряда.

Каждый проводник с током создает в ок­ружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что лю­бой движущийся в вакууме или среде за­ряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий по­ле В точечного зарядаQ, свободно движу­щегося с нерелятивистской скоростью v. Под свободным движением заряда по­нимается его движение с постоянной ско­ростью. Этот закон выражается формулой

где r — радиус-вектор, проведенный от за­ряда Q к точке наблюдения М. Вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с на­правлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции вычисляется по формуле где а — угол между векторамиv и r.

Движущийся заряд по своим магнитным свойствам эквива­лентен элементу тока: Idl=Qv.

Приведенные закономерности справедливы лишь при малых скоростях (v<<c) движущихся зарядов, когда электрическое поле свободно движу­щегося заряда можно считать электроста­тическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени находится дви­жущийся заряд.

Формула 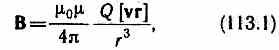определяет магнит­ную индукцию положительного заряда, движущегося со скоростьюv. Если дви­жется отрицательный заряд, то Q надо заменить на —Q. Скорость v — относительная скорость, т. е. скорость относи­тельно наблюдателя. Вектор В в рассмат­риваемой системе отсчета зависит как от времени, так и от положения точки

М на­блюдения.

Впервые поле движущегося заряда удалось обнаружить американскому физи­ку Г. Роуланду (1848—1901). Окончатель­но этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), изучившим магнит­ное поле конвекционного тока, а также магнитное поле связанных зарядов поля­ризованного диэлектрика. Магнитное поле свободно движущихся зарядов было из­мерено академиком А. Ф. Иоффе, доказав­шим эквивалентность, в смысле возбужде­ния магнитного поля, электронного пучка и тока проводимости.

§ 111. Закон Ампера. Взаимодействие параллельных токов

Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента дли-

ной dl проводника на магнитную индукцию В:

dF = I[dl, В]. (111.1)

Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (см. (111.1)) вычисляется по формуле

dF = IBdlsin, (111.2)

где a — угол между векторами dl и В.

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂ (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I₁ на элемент dl второго проводника с током I₂. Ток I₁ создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора b₁ задается правилом правого винта, его модуль по формуле (110.5) равен

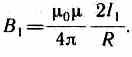
181

Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол  между элементами тока I₂ и вектором B₁ прямой, равен

dF₁=I₂B₁dl, или, подставляя значение для В₁, получим

Рассуждая аналогично, можно показать, что сила dF₂, с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направлена в противоположную сторону и по модулю равна

Сравнение выражений (111.3) и (111.4) показывает, что

dF₁=dF₂,

т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).

§112. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля

Если два параллельных проводника с током находятся в вакууме (=1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна

Для нахождения числового значения ₀ воспользуемся определением ампера, со-

гласно которому при I₁=I₂=1А и R=1 м

dF/dl=2•10^-7 Н/м. Подставив это значение в формулу (112.1), получим 0=4•10^-7 Н/А²=4•10^-7 Гн/м,

где генри (Гн) — единица индуктивности (см. §126).

Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде

dF=IBdl,

откуда

Единица магнитной индукции — тесла (Тл): 1 Тл—магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1 А:

1Тл=1Н/(А•м).

Так как ₀= 4•10^-7 Н/А², а в случае вакуума (=1), согласно (1.09.3), В =₀H, то для данного случая

H=В/₀.

Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4•10^-7 Тл.

Взаимодействие параллельных проводников с током

. (4)

Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников.

Эталон силы тока: 1Ампер – это сила постоянного тока при длине проводников и расстоянию между ними в 1 м в вакууме, равная 210^-7 Н.

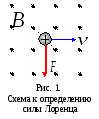
30. Действие магнитного поля на движущийся заряд. Сила Лоренца

Сила, действующая со стороны магнитного поля на движущийся заряд, называется силой Лоренца.

(1)

Направление силы Лоренца, действующей на положительно заряженную частицу, может быть найдено по правилу левой руки. Если расположить левую руку так, чтобы линии индукции магнитного поля входили в ладонь, а вытянутые пальцы были направлены вдоль скорости движения частицы, то отведенный большой палец укажет направление силы Лоренца.

Сила Лоренца всегда направлена перпендикулярно скорости, поэтому при движении заряженной частицы в магнитном поле сила Лоренца работы не совершает.

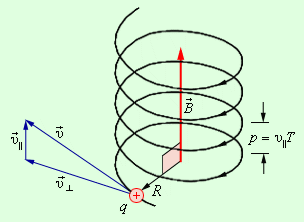
Рис. 2. Движение заряженной частицы по спирали

Движение частицы под углом  к линиям ().

Радиус спирали: ,

Шаг спирали: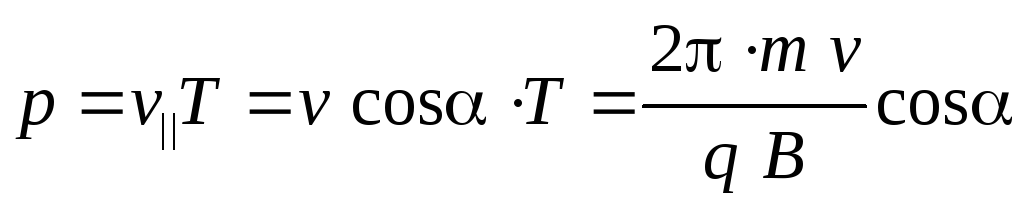

Угловая скорость движения заряженной частицы по круговой траектории

(2)

называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).

В общем случае, когда на заряженную частицу действуют электрическое и магнитное поля:

. (3)

Рис. 3. Радиационные пояса Земли

31. Магнитный поток. Работа перемещения проводника

с током в магнитном поле

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина

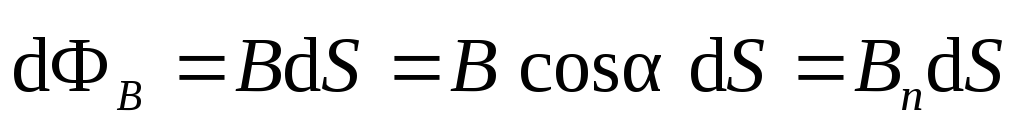, (1)

при , 1 Вб = 1 Тлм² , (2)

где — единичный вектор нормали к поверхности,— угол между направлением вектораи направлением нормали к поверхности. В системе СИ единица измерения магнитного потокаВебер (Вб).

Работа по перемещению проводника с током в магнитном поле

Сила Ампера: F = I B l ,

,

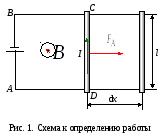
, (3)

т.е. работа по перемещению проводника с током в магнитном поле равна произ­ведению силы тока на магнитный поток, пересеченный движущимся проводником.

32. Явление электромагнитной индукции. ЭДС индукции.

Закон Фарадея. Правило Ленца. Практическая значимость

явления электромагнитной индукции

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает индукционный электрический ток.

Явление возбуждения тока с помощью магнитного поля открыто Фарадеем в 1831 году. «Магнетизм превратить в электричество» — такова была основная цель, к которой стремился Фарадей в течение 10 лет (1821-1831 г.г.), веривший в эту идею. Главный вывод, который он сделал: электрический ток возникает при движении катушки и магнита относительно друг друга. Вскоре после этого Фарадей создал первый генератор электрического тока. Индукционный ток в опытах Фарадея возникал при изменения магнитного потока.

(1)

Всякий раз при изменении полного магнитного потока через произвольный контур в контуре возникает электродвижущая сила, называемая электродвижущей силой индукции:

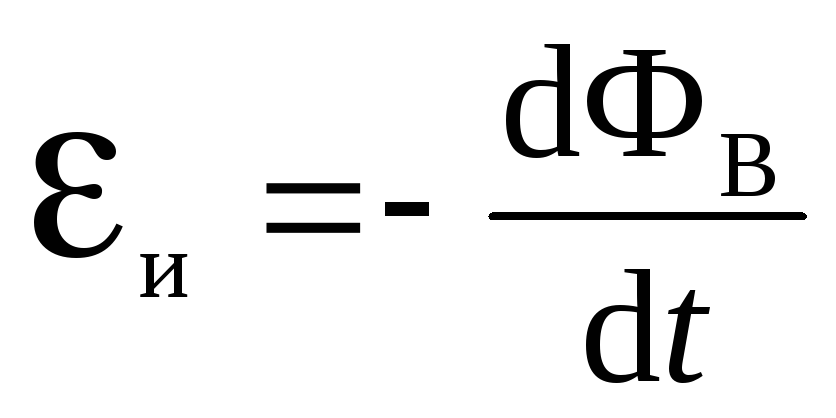, (2)

Правило Ленца

Индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.

1.4. Взаимодействие двух параллельных проводников с током.@

Законы Био – Савара – Лапласа и Ампера применяются для определения силы взаимодействия двух параллельных проводников с током. Рассмотрим два бесконечных прямолинейных проводника с токами I1 и I2 , расстояние между которыми равно а. На рис. 1.10 проводники расположены перпендикулярно чертежу. Токи в них направлены одинаково (из-за чертежа на нас) и обозначены точками. К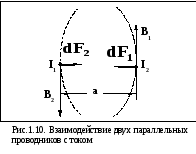аждый из проводников создает магнитное поле, которое действует на другой проводник. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направлениеопределяется правилом правого винта, а его модуль по закону Био – Савара – Лапласа . Согласно проведенным выше расчетам модуль равен сТогда, согласно закону Ампера, dF1=I2B1dl или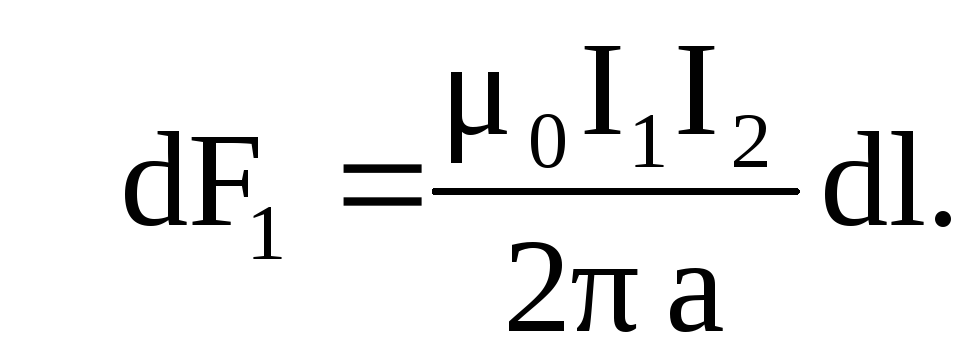и аналогично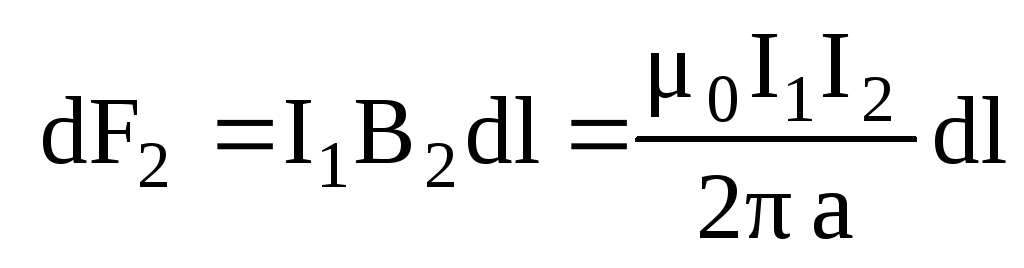. Направление силы , с которой поле действует на участокdℓ второго проводника с током I₂ (рис.1.10), определяется по правилу левой руки (см. разд. 1.2). Как видно из рис.1.10 и расчетов, силы 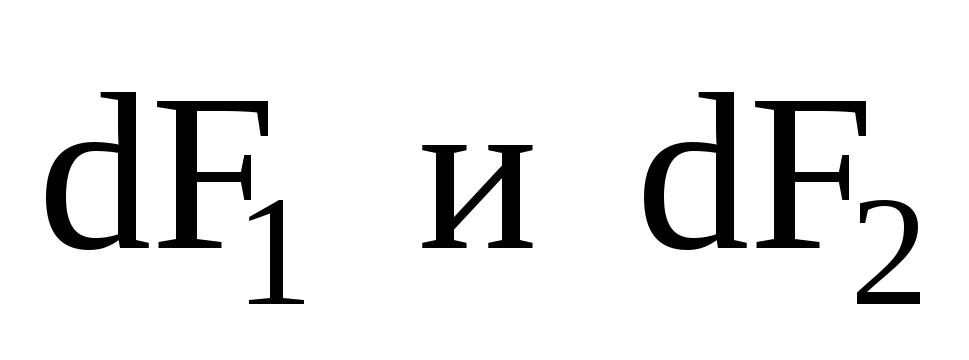одинаковы по модулю и противоположны по направлению. В нашем случае они направлены навстречу друг другу и проводники притягиваются. Если токи текут в противоположных направлениях, то возникающие между ними силы отталкивают проводники друг от друга. Итак, параллельные токи (одного направления) притягиваются, а антипараллельные ( противоположных направлений ) — отталкиваются. Для определения силы F, действующей на проводник конечной длины ℓ, необходимо проинтегрировать полученное равенство по ℓ от 0 до ℓ : 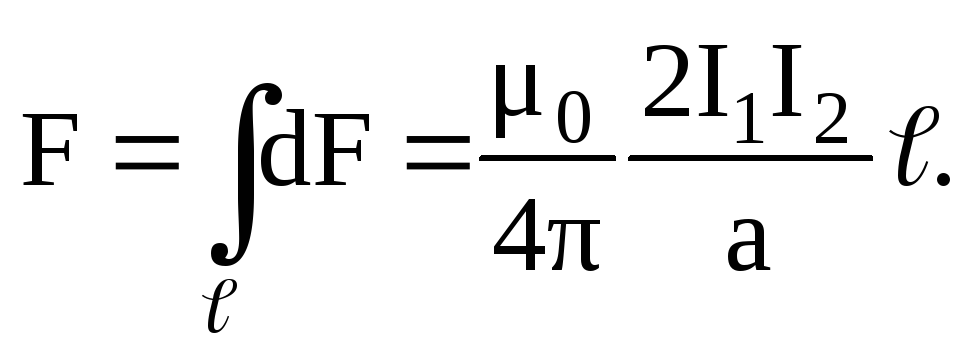При магнитном взаимодействии выполняется закон действия и противодействия, т.е. третий закон Ньютона:

.

1.5. Действие магнитного поля на движущуюся заряженную частицу.@

Как уже было отмечено, важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся электрические заряды. В результате опытов было установлено, что любая заряженная частица, движущаяся в магнитном поле, испытывает действие силы F, которая пропорциональна величине магнитного поля в этой точке. Направление этой силы всегда перпендикулярно скорости движения частицы и зависит от угла между направлениями 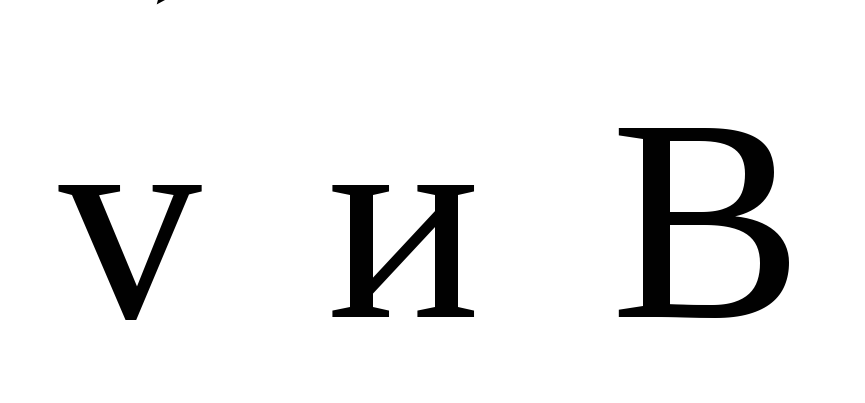. Эта сила называетсясилой Лоренца. Модуль данной силы равен 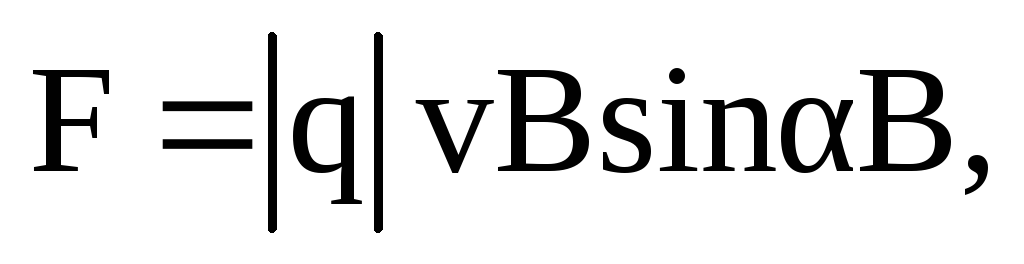гдеq – величина заряда; v – скорость его движения; – вектор магнитной индукции поля; α – угол между векторами и . В векторной форме выражение для силы Лоренца имеет вид.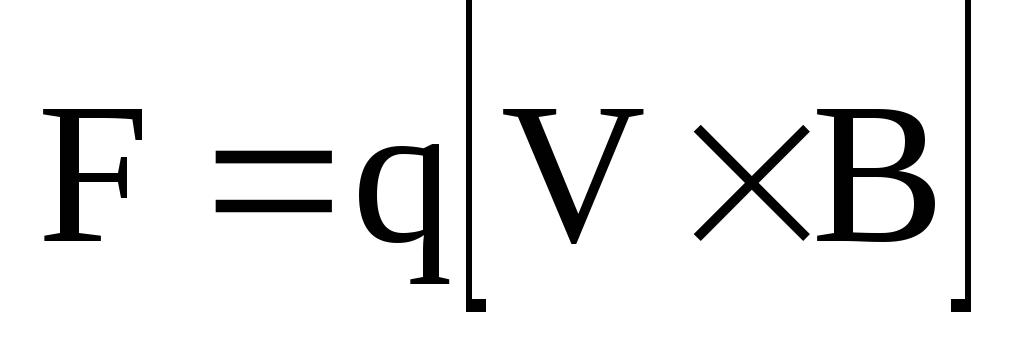

Для случая когда скорость заряда перпендикулярна вектору магнитной индукции, направление данной силы определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы векторвходил в ладонь, а пальцы направить вдоль (для q>0), то отогнутый под прямым углом большой палец укажет направление силы Лоренца для q>0 (рис.1.11, а). Для q < 0 сила Лоренца имеет противоположное направление (рис.1.11,б).

Поскольку данная сила всегда перпендикулярна скорости движения частицы, она изменяет только направление скорости, а не ее модуль, и поэтому сила Лоренца работы не совершает. То есть магнитное поле не совершает работы над движущейся в нем заряженной частицей и ее кинетическая энергия при таком движении не изменяется.

Вызываемое силой Лоренца отклонение частицы зависит от знака q. На этом основано определение знака заряда частиц, движущихся в магнитных полях. Магнитное поле не действует на заряженную частицу (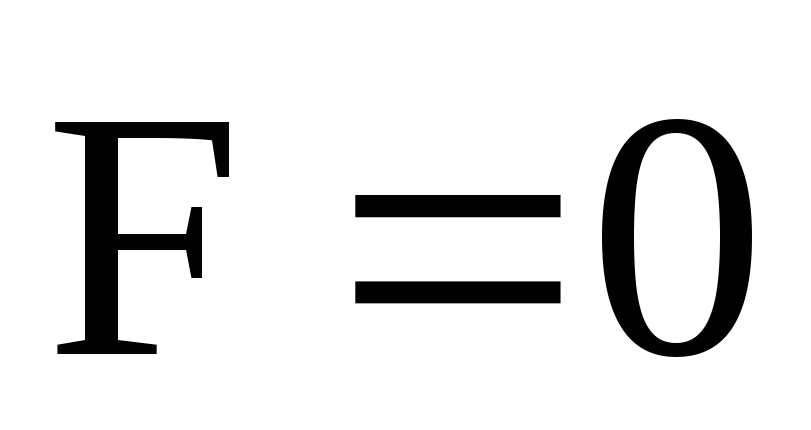) в двух случаях: если частица неподвижна () или если частица движется вдоль силовой линии магнитного поля. В этом случае векторыпараллельны иsinα=0. Если вектор скорости перпендикулярен, то сила Лоренца создает центростремительное ускорение и частица будет двигаться по окружности. Если скорость направлена под углом к, то заряженная частица движется по спирали, ось которой параллельна магнитному полю.

На данном явлении основана работа всех ускорителей заряженных частиц – устройств, в которых под действием электрических и магнитных полей создаются и ускоряются пучки высокоэнергетических частиц.

Действие магнитного поля Земли вблизи земной поверхности изменяет траекторию движения частиц, испускаемых Солнцем и звездами. Этим объясняется так называемый широтный эффект, заключающийся в том, что интенсивность космических лучей, доходящих до Земли, вблизи экватора меньше, чем в более высоких широтах. Действием магнитного поля Земли объясняется тот факт, что полярное сияние наблюдается только в самых высоких широтах, на Крайнем Севере. Именно в том направлении магнитное поле Земли отклоняет заряженные космические частицы, которые вызывают свечение атмосферы, называемое полярным сиянием.

Кроме магнитной силы, на заряд может действовать также уже знакомая нам электрическая сила 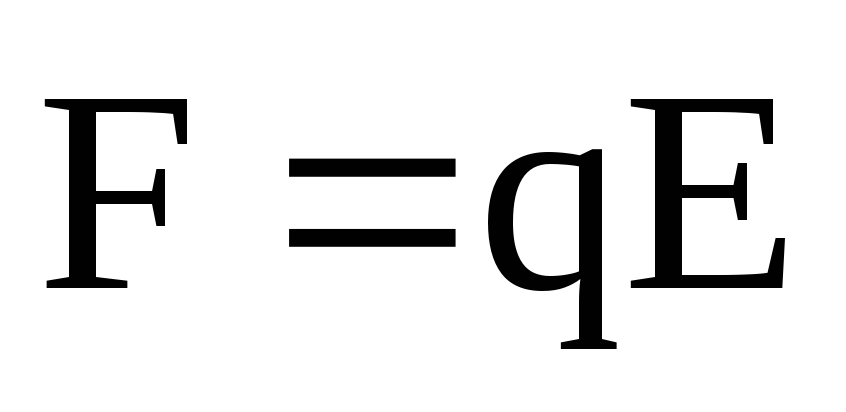, и результирующая электромагнитная сила, действующая на заряд, имеет вид

Эта формула называетсяформулой Лоренца. Действию такой силы подвергаются, например, электроны в электронно-лучевых трубках телевизоров, радиолокаторов, электронных осциллографов, электронных микроскопах.

7. Сила взаимодействия двух параллельных проводников с токами (вывод).Определение единицы силы тока.

Каждый из проводников создаёт магнитное поле, которое действует по закону Ампера на второй проводник. Ток создаёт вокруг себя магнитное поле, линии магнитной индукции которого

представляют собой концентрические окружности. Направление вектора В задаётся правилом правого винта, его модуль равен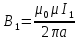

Направление силы d с которой поле с вектором действует на участокdL второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, с учётом того, что угол между элементами тока 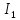и векторомпрямой, равен:

Аналогичными рассуждениями можно показать, что на участок dl первого проводника действует сила направленная в сторону, противоположную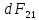и численно равна:

Сравнение выражений показывает, что 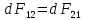т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой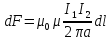

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания. Полагая имеем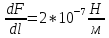

Магнитные линии двух проводников с токами разных направлений в пространстве между проводниками направлены в одну сторону. Магнитные линии, имеющие одинаковое направление, будут взаимно отталкиваться. Поэтому проводники с токами противоположного направления отталкиваются один от другого

За единицу силы тока 1 А принимают силу тока, при которой два параллельных проводника длиной 1м, расположенные на расстоянии 1м друг от друга, взаимодействуют с силой 0,0000002 Н.

8. Действие магнитного поля на движущийся заряд. Сила Лоренца. Определение направления силы Лоренца.

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.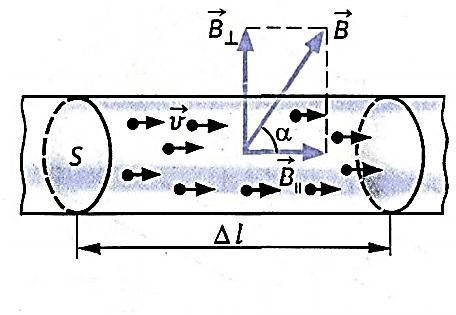

Сила Лоренца – сила, действующая со стороны магнитного поля на движущиеся в нем заряды. = q·V·B·sina

где q — величина движущегося заряда; V — модуль его скорости; B — модуль вектора индукции маг. поля; a — угол м/у вектором скорости заряда и вектором маг. инд.

Cила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно.

Сила Лоренца перпендикулярна векторам В и v , и её направление определяется по правилу: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.

Сила Лоренца зависит от модулей скорости частицы и индукции магнитного поля. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Частица равномерно движется по окружности радиуса r.

9. Движение заряженных частиц в однородном магнитном поле: а) вектор индукции параллелен вектору скорости частицы; б) перпендикулярен ему; в) составляет угол а с направлением скорости частицы. Вычисление радиуса окружности, периода обращения и шага винтовой линии.