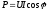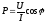Тема 4 Активная, реактивная и полная мощности. Коэффициент мощности
1.
Активная мощность при r
= XC = 20 Ом и показаниях амперметра 10 А,
вольтметра 200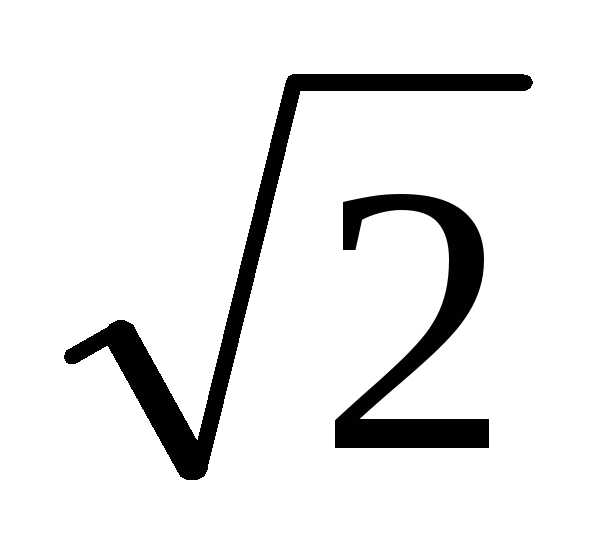 В,
равна
В,
равна
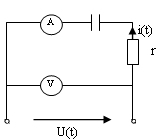
1) P = 2000 Вт 2) Р = 200 Вт
3) Р = 100 Вт 4) Р = 20 Вт
2. Формула
для определения мгновенной мощности 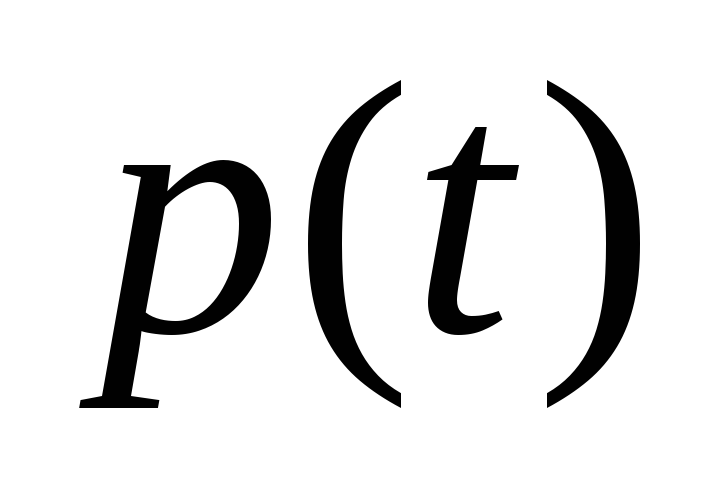 переменного тока
переменного тока
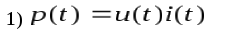
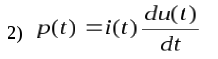
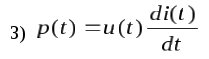

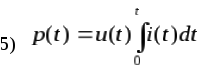
3. Выражение для энергии WL, накопленной в поле индуктивного элемента, имеет вид
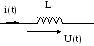

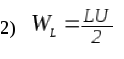
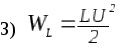 4)
4) 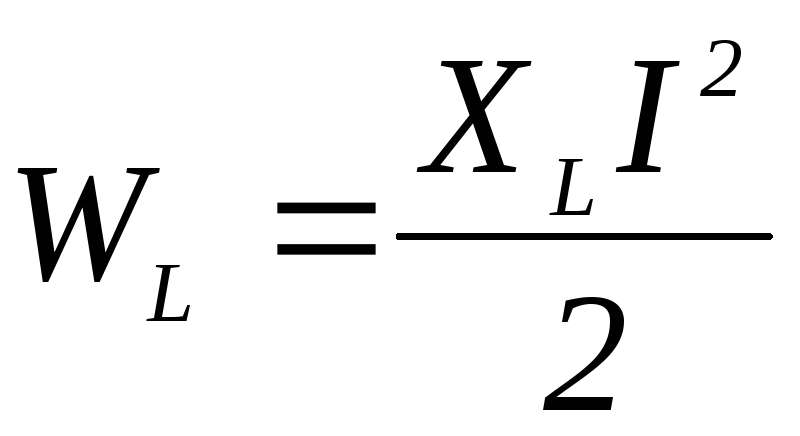
4. Формула полной мощности имеет вид
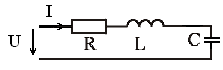
1) 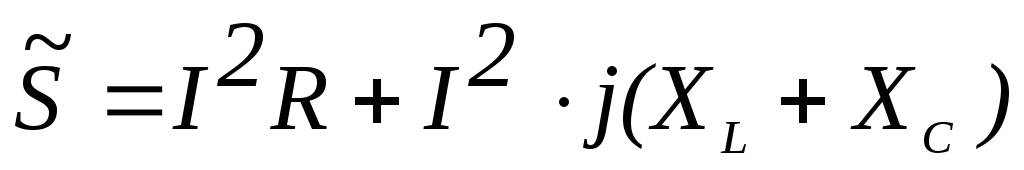 2)
2)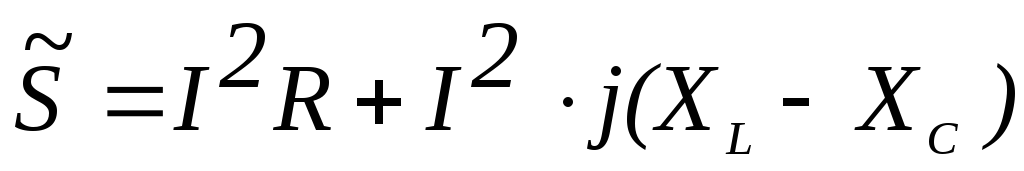
3) 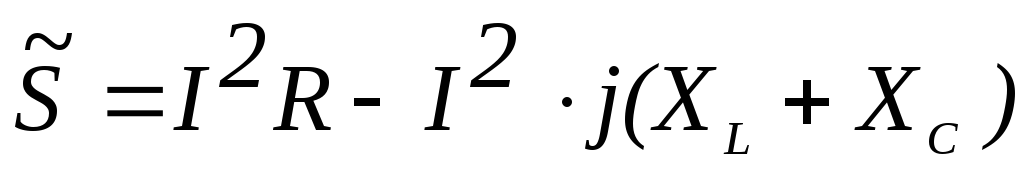 4)
4)
5. Формула активной мощности цепи имеет вид
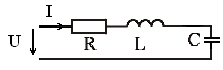
1) 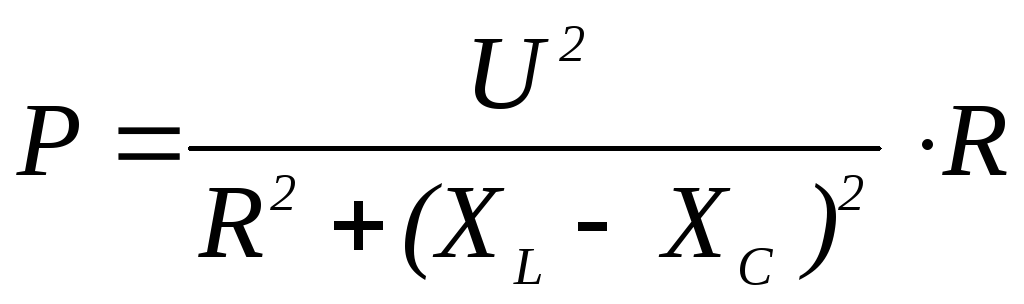
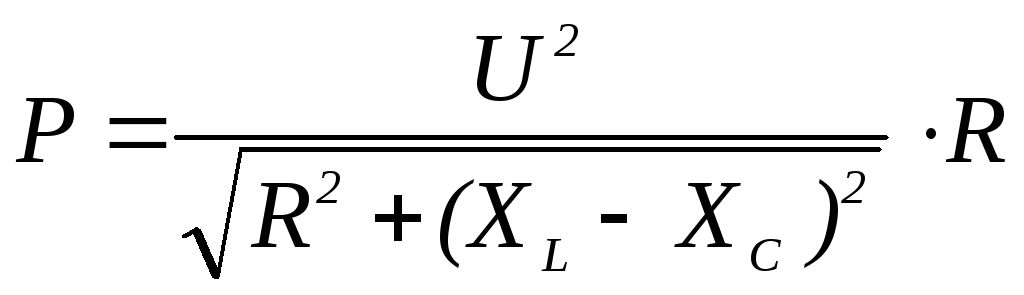
3)  4)
4)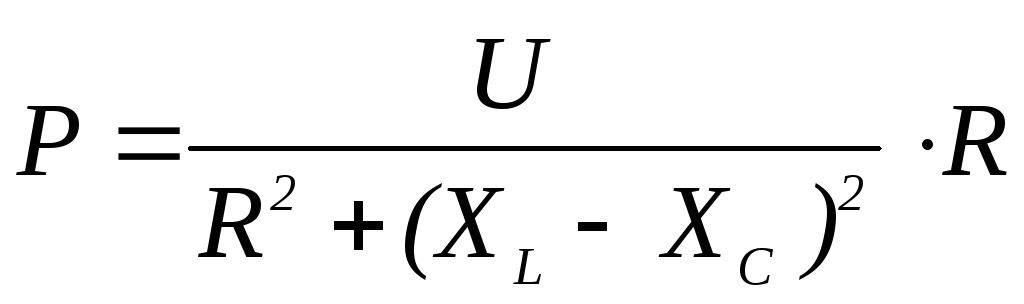
6. Полная
комплексная мощность  для цепи из последовательно соединенныхR,L,Cопределяется по формуле
для цепи из последовательно соединенныхR,L,Cопределяется по формуле

1) 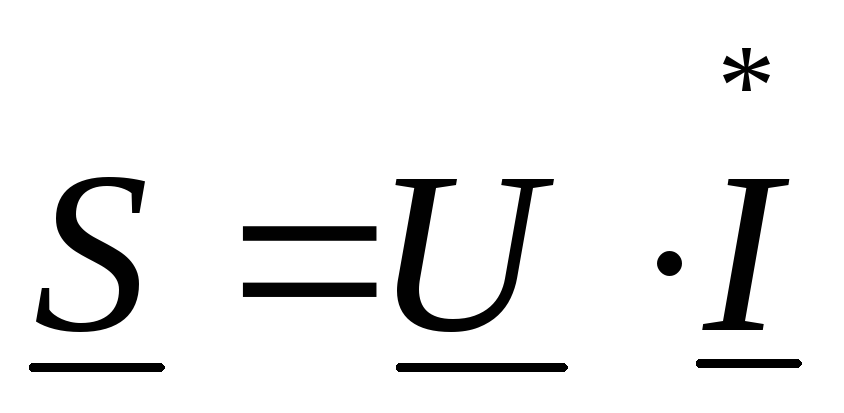

3) 4)
4)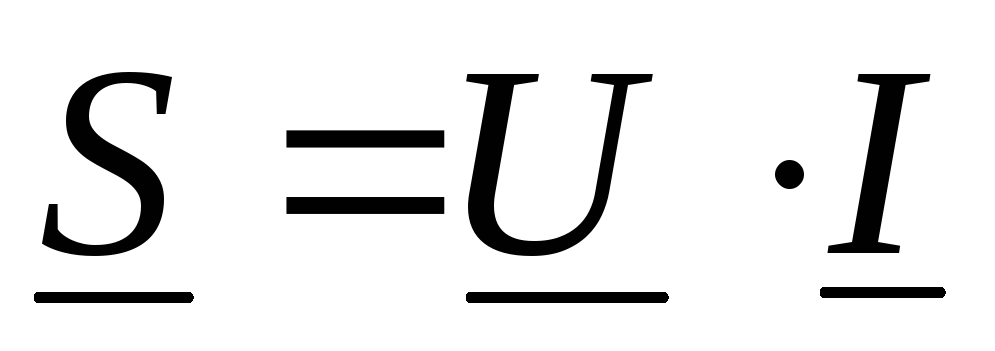
7. Формула реактивной мощности катушки индуктивности имеет вид
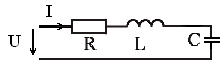
1) 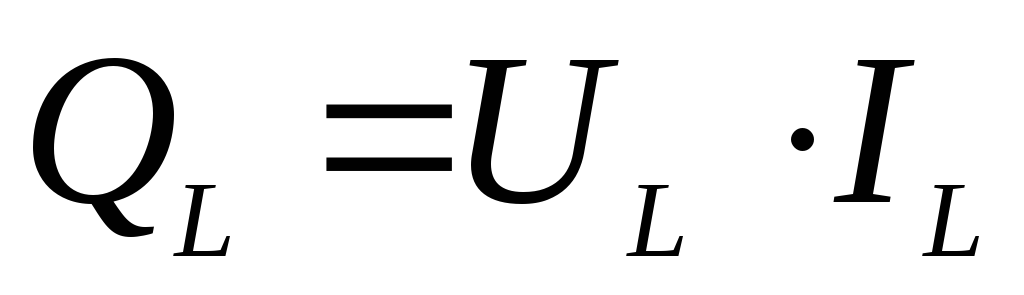 2)
2) 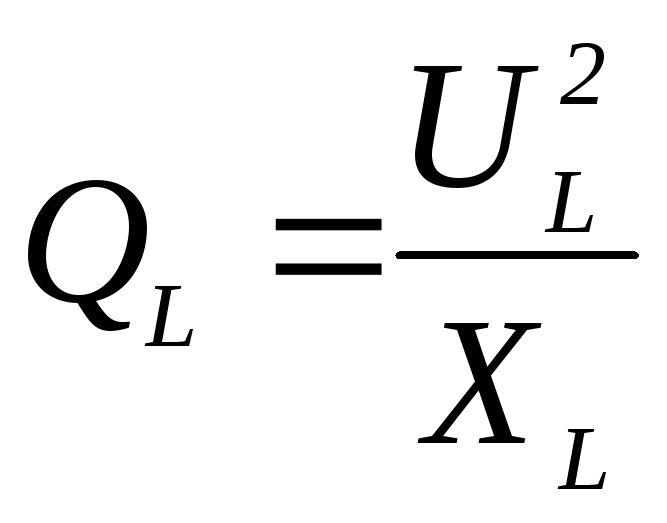
3) 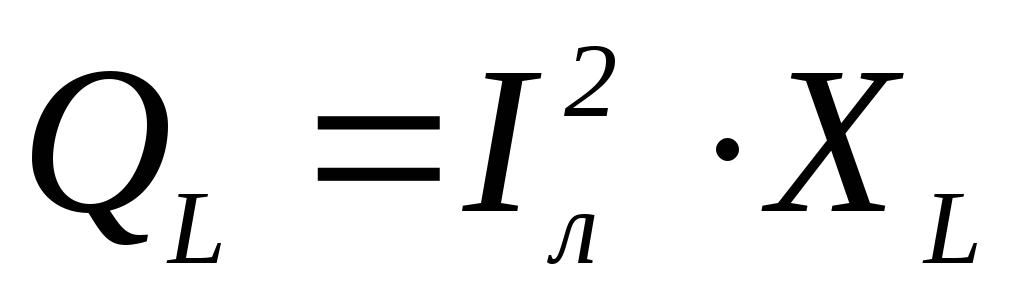 4)
4) 
8. Формула реактивной мощности QCконденсатора С в цепи имеет вид
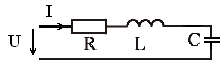
1) 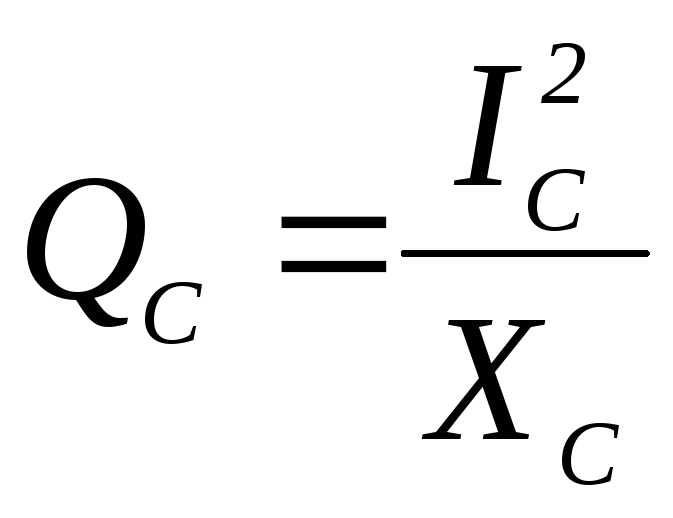 2)
2)
3) 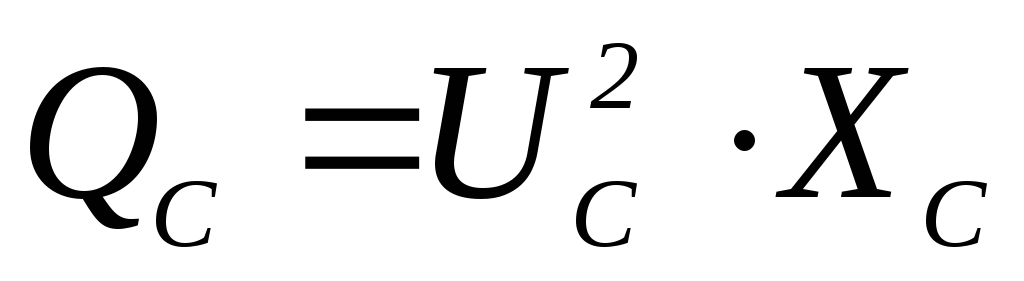 4)
4)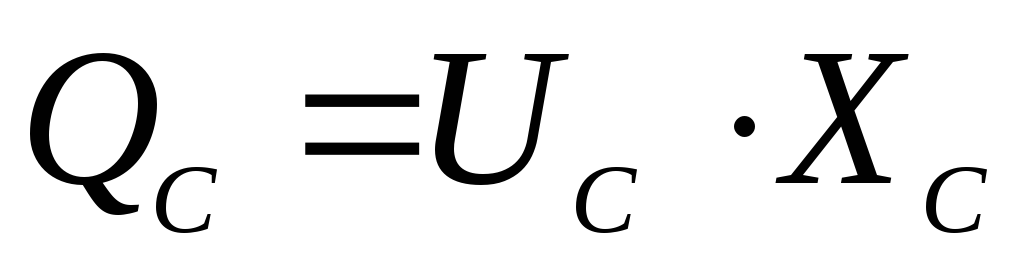
9. Выражение активной мощности Р пассивного двухполюсника в цепи переменного тока имеет вид
1)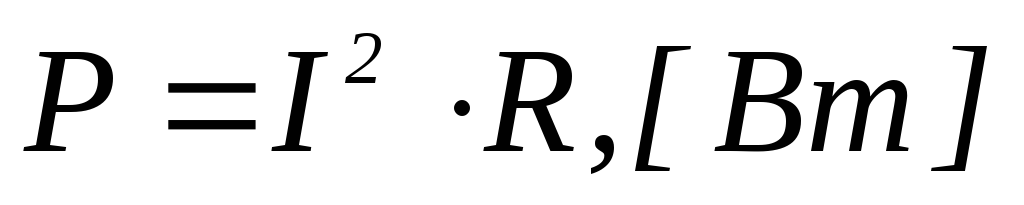 2)
2)
3) 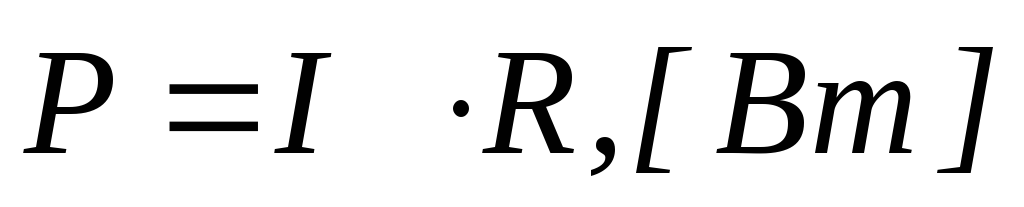 4)
4)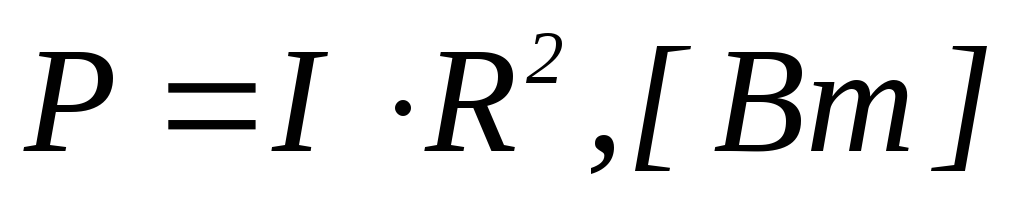
10. Каким свойством обладают индуктивные элементы схем
1) поглощать энергию2) создавать энергию
3) запасать энергию в виде электрического поля
4) запасать энергию в виде магнитного поля
11.Полная мощность цепи переменного тока
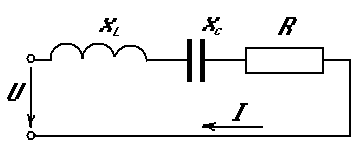
1)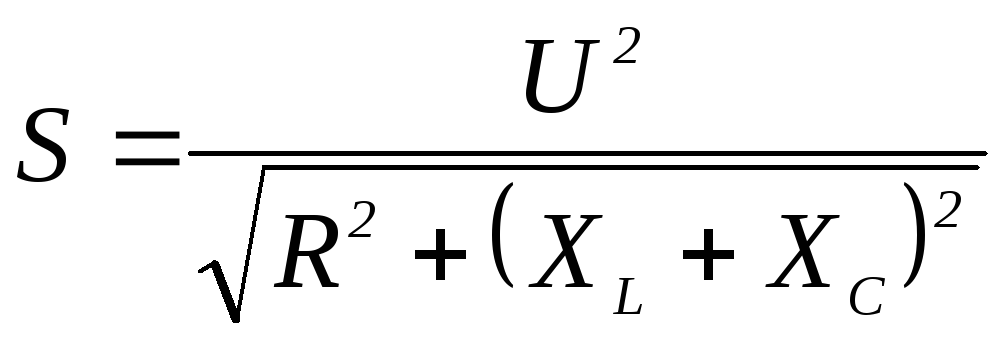 2)
2) 
3)  4)
4) 
12. Каким свойством обладают резистивные элементы схем
1) создавать энергию
2) запасать энергию в виде электрического поля
3) запасать в виде энергию магнитного поля
4) преобразовывать электрическую энергию
13. Формула для определения реактивной мощности QLна индуктивностиLв цепи переменного тока
1) 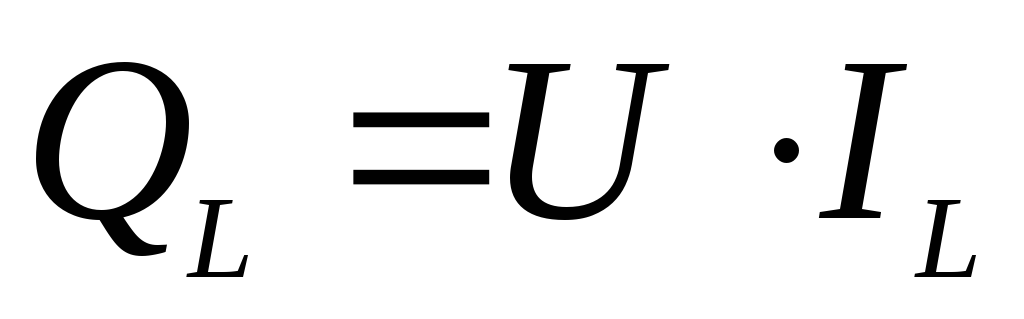 2)
2) 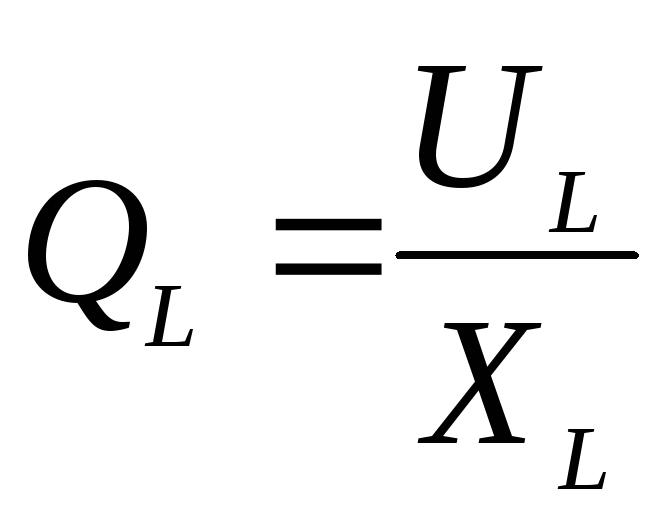 3)
3) 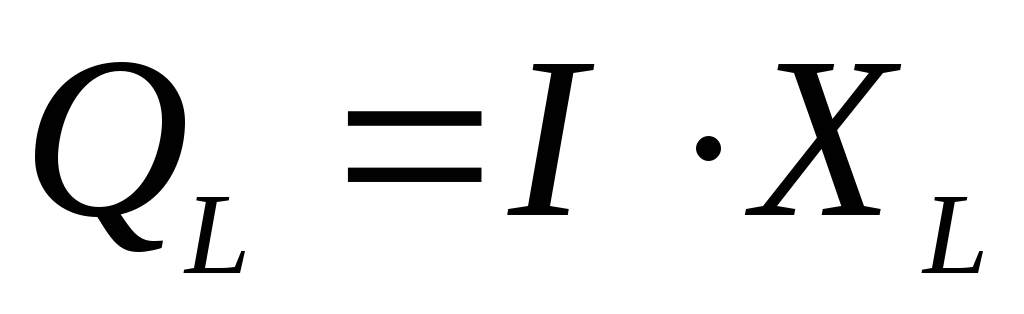 4)
4) 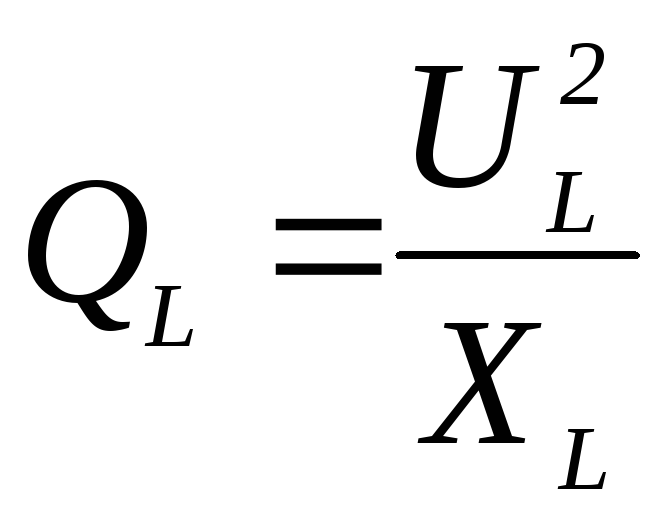
14. Формула, показывающая связь между активной, реактивной и полной мощностью
1) 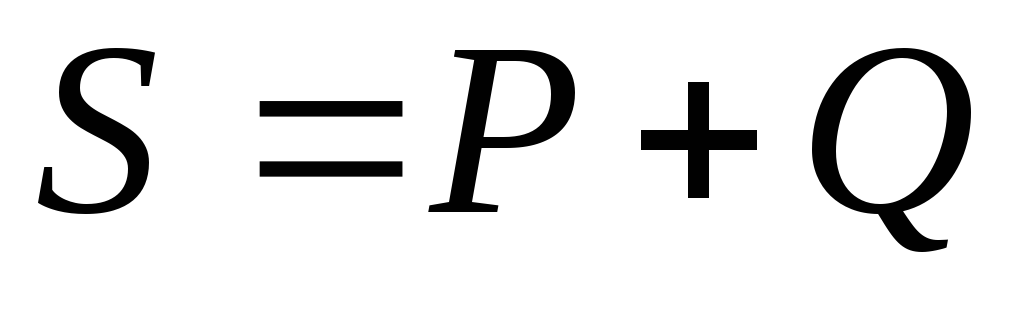 2)
2) 
3) 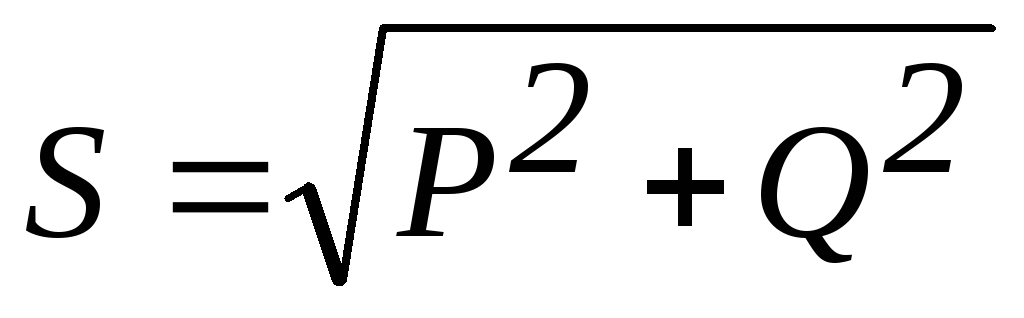 4)
4) 
15. Формула, показывающая связь между реактивной и полной мощностью
1) Q=S tg 2) Q=S/sin 3) Q=S/tg 4) Q=S sin
16. Выражение полной мощности S пассивного двухполюсника в цепи переменного тока имеет вид
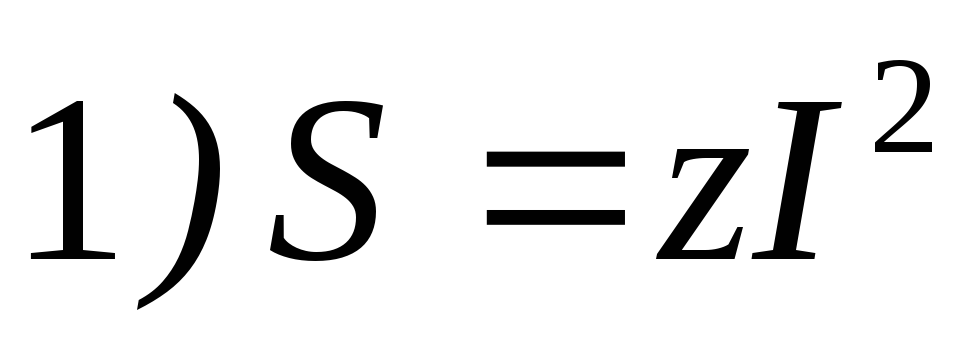
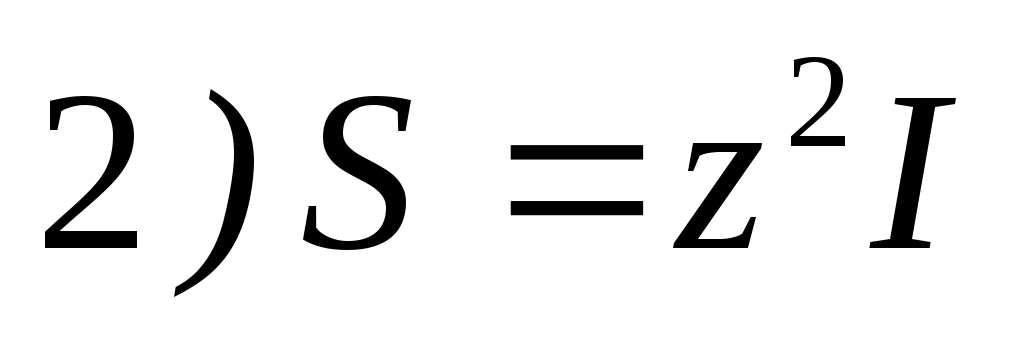

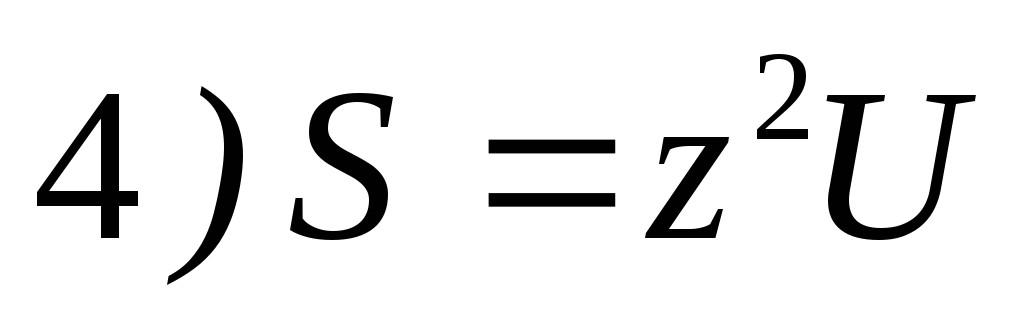
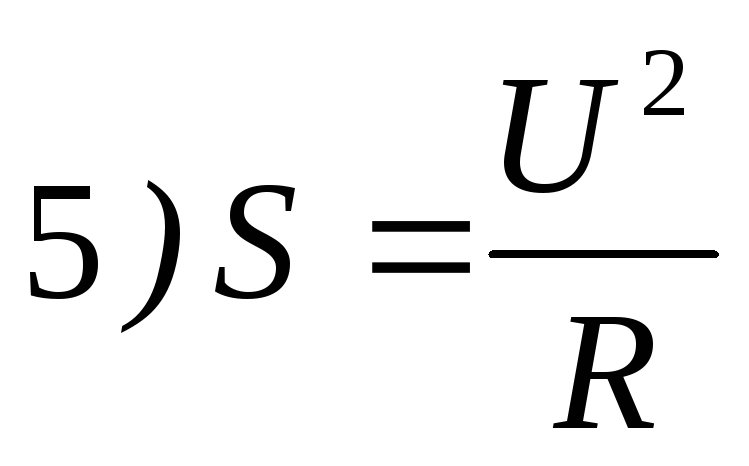
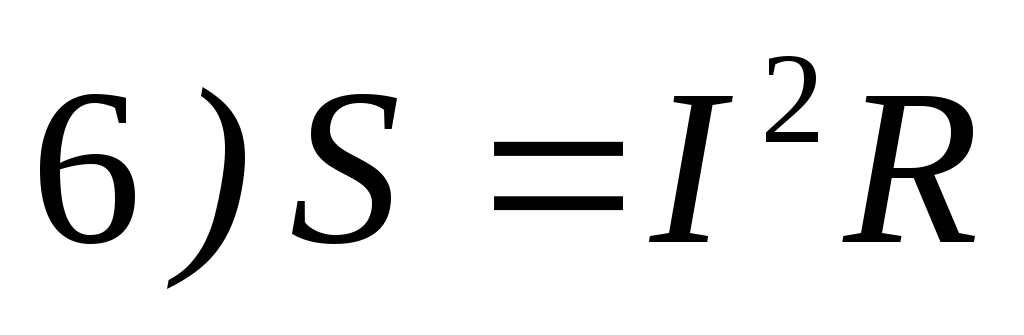
17.
Реактивная мощность при r
= XC = 20 Ом и показаниях амперметра 10 А,
вольтметра 200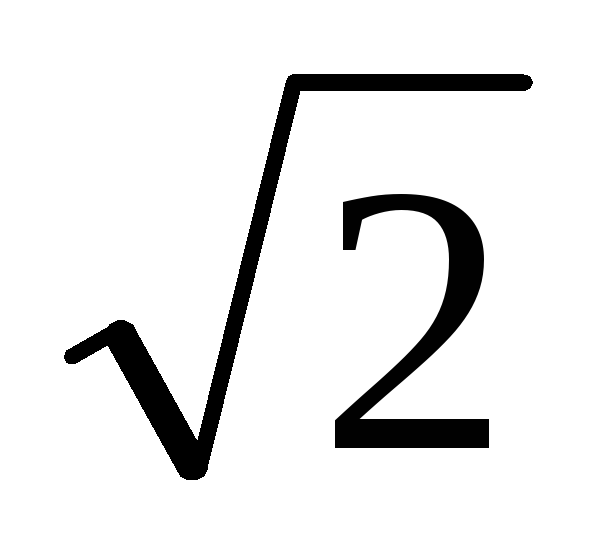 В,
равна
В,
равна
1 )
Q=20 вар 2) Q= 2000 вар
)
Q=20 вар 2) Q= 2000 вар
3) Q= 200 вар 4) Q= 2вар
1 8.
Полная мощность приr
= XC = 20 Ом и показаниях амперметра 10 А,
вольтметра 200
8.
Полная мощность приr
= XC = 20 Ом и показаниях амперметра 10 А,
вольтметра 200 В,
равна
В,
равна
1) S =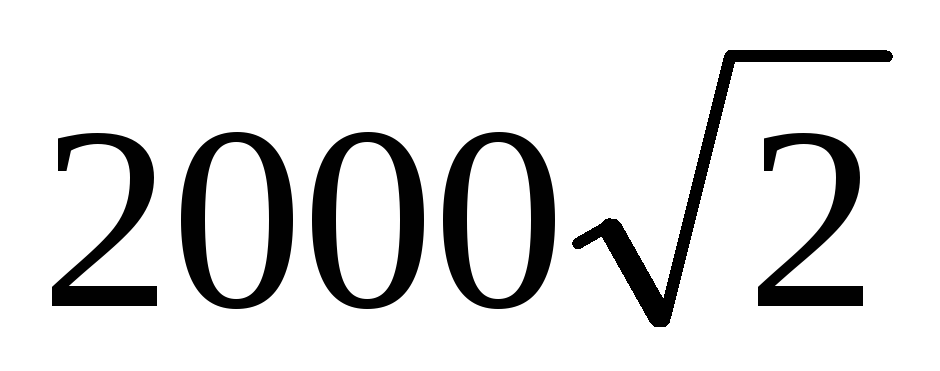
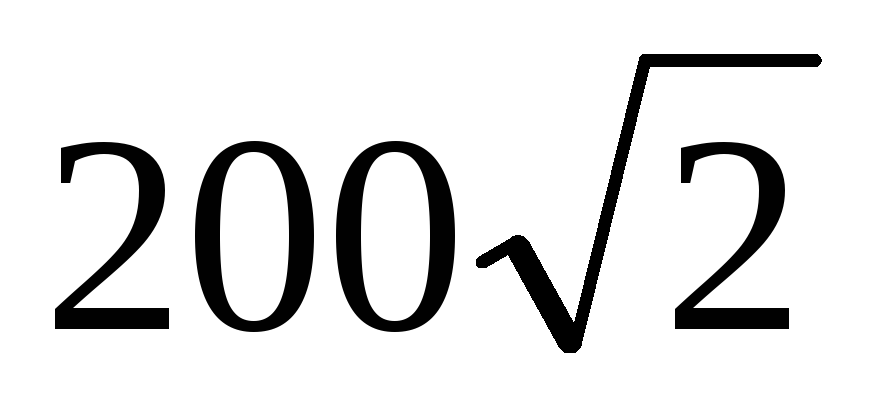 ВА 3) 200 ВА
4) 2000 ВА
ВА 3) 200 ВА
4) 2000 ВА19. Активная мощность цепи переменного тока

1) 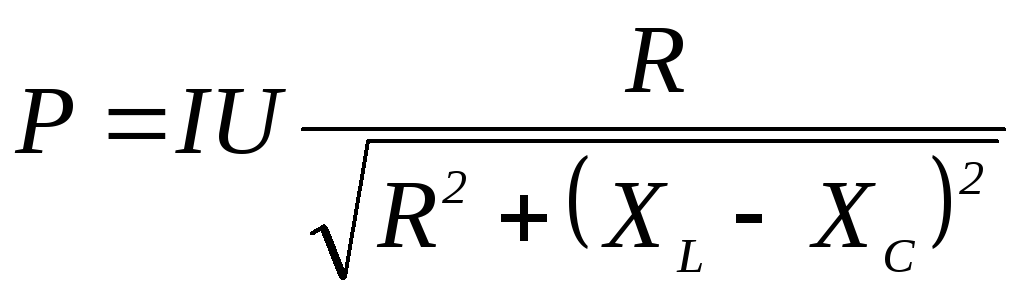 2)
2) 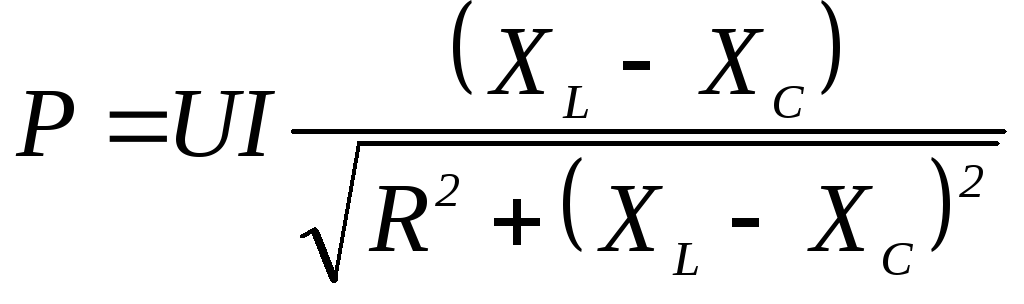
3) 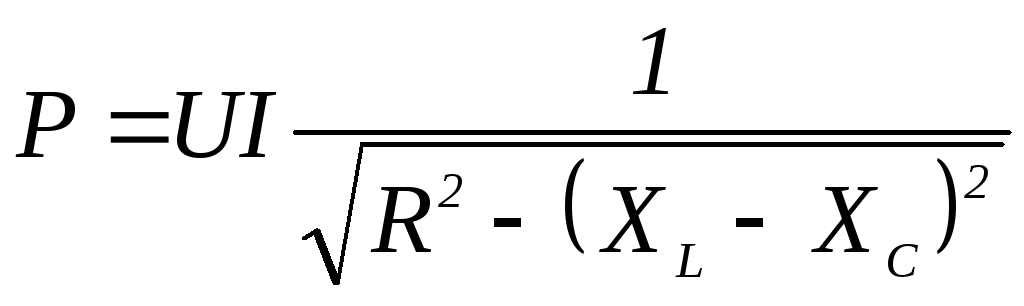 4)
4)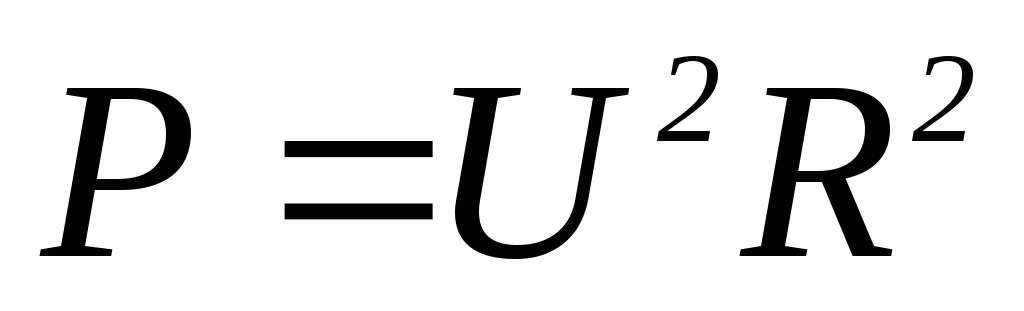
20. Реактивная мощность цепи переменного тока
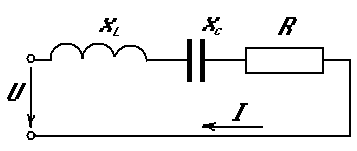
1) 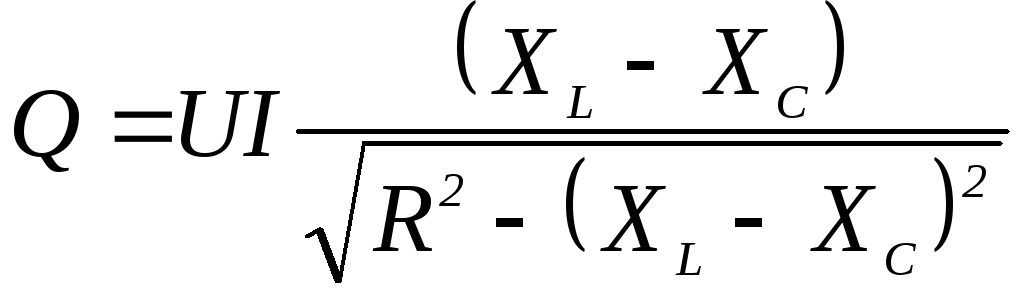 2)
2) 
3)  4)
4) 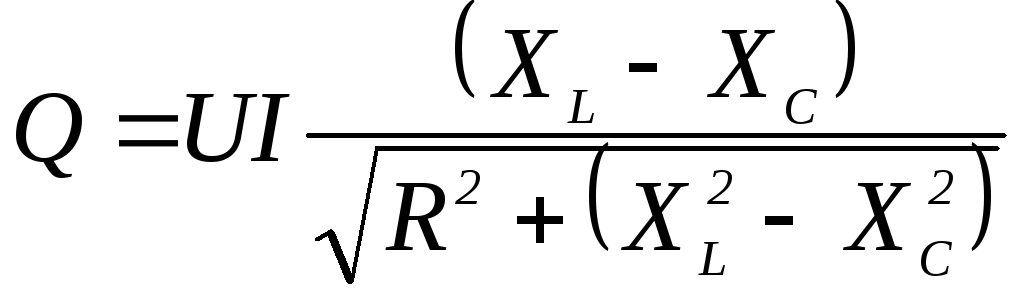
5. Частотные свойства электрической цепи. Резонанс
1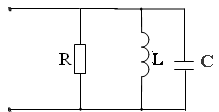 .
Резонансная частота0колебательного контура
.
Резонансная частота0колебательного контура


2. Резонансная частота — 0 колебательного контура

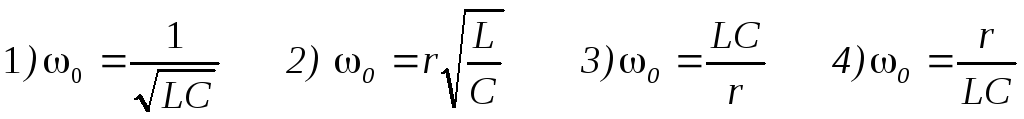
3 .
В режиме резонанса, приU=90
В,r=5 Ом,ХL =ХC= 20 Ом,
амперметр покажет
.
В режиме резонанса, приU=90
В,r=5 Ом,ХL =ХC= 20 Ом,
амперметр покажет
1) I=18A2)I=2A3)I=4,5A4)I=6A
4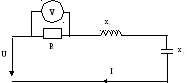 .
В режиме резонанса, приU=90
В,R=5 Ом,
.
В режиме резонанса, приU=90
В,R=5 Ом,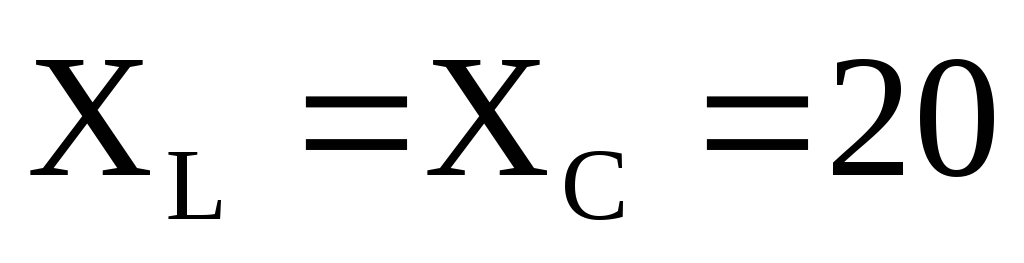 Ом,
вольтметр покажет:
Ом,
вольтметр покажет:
1) U=90 В 2) U=10 В 3) U=30 В 4) U=22,5 В
5. В
режиме резонанса, при U=90
В,R=5 Ом,  20
Ом, вольтметр покажет:
20
Ом, вольтметр покажет:
1 )
U=360 В 2) U=180 В 3) U=40 В 4) U=120 В
)
U=360 В 2) U=180 В 3) U=40 В 4) U=120 В
6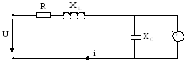 .
В режиме резонанса, приU=90
В,R=5 Ом,
.
В режиме резонанса, приU=90
В,R=5 Ом,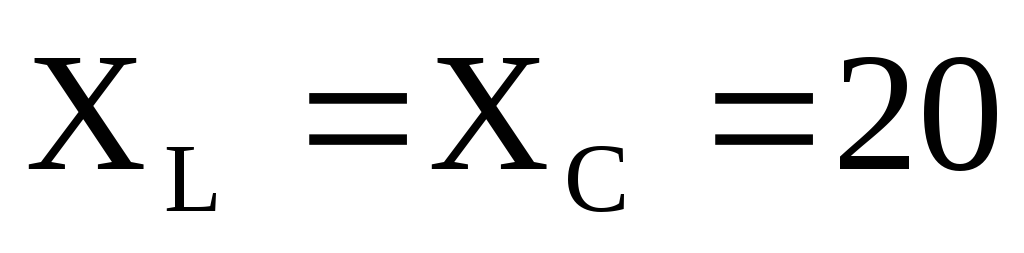 Ом, вольтметр покажет
Ом, вольтметр покажет
1) U=360 В 2) U=180 В 3) U=40 В 4) U=120 В
7 .
В режиме резонанса, приU=100
В,R=10 Ом,
.
В режиме резонанса, приU=100
В,R=10 Ом,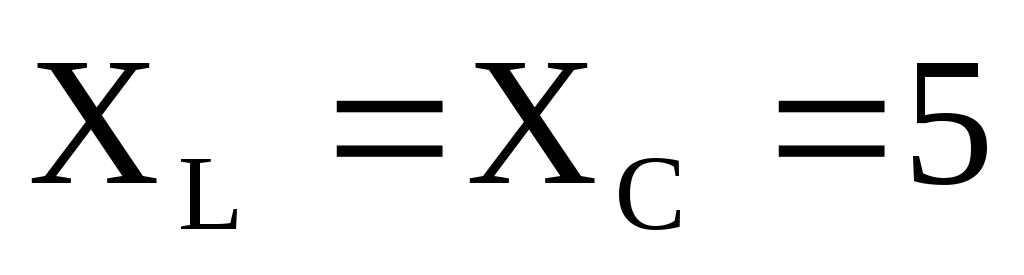 Ом,
амперметр покажет:
Ом,
амперметр покажет:
1) I=10A2)I=20A3)I=5A4)I=50A
8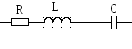 .
Резонансная частота контура при
уменьшении активного сопротивления в
4 раза
.
Резонансная частота контура при
уменьшении активного сопротивления в
4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
9 .
Резонансная частота контура при
увеличении активного сопротивления в
4 раза
.
Резонансная частота контура при
увеличении активного сопротивления в
4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
10. Резонансная частота контура при увеличении емкости в 4 раза
1 )
уменьшится в 2 раза 2) увеличится в
2 раза 3) не изменится
)
уменьшится в 2 раза 2) увеличится в
2 раза 3) не изменится
1 1.
Резонансная частота контура при
уменьшении емкости в 4 раза
1.
Резонансная частота контура при
уменьшении емкости в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
1 2.
Резонансная частота контура при
увеличении индуктивности в 4 раза
2.
Резонансная частота контура при
увеличении индуктивности в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
1 3.
Резонансная частота контура при
уменьшении индуктивности в 4 раза
3.
Резонансная частота контура при
уменьшении индуктивности в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
14. Условием возникновения резонанса напряжений в линейной электрической цепи является
1) равенство нулю активной составляющей полной мощности
2) равенство нулю активной и мнимой части комплексной проводимости
3) равенство нулю мнимой части комплексного сопротивления
4) равенство нулю активной составляющей комплексного сопротивления
15. Условием возникновения резонанса токов в линейной электрической цепи является
1) равенство нулю мнимой части комплексной проводимости
2)равенство нулю действительной и мнимой части комплексного сопротивления
3) равенство нулю активной мощности
4) равенство нулю разности мнимой и действительной части
16. Резонансом электрической цепи r, L, С называется режим работы, при котором
1) резонансная частота цепи равна частоте напряжения сети
2) активная мощность цепи равна нулю
3) цепь имеет чисто активный характер
4) цепь имеет индуктивный характер
5) цепь имеет емкостной характер
17. Электрическая цепь, в которой возможно возникновение резонанса напряжений, имеет вид
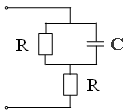


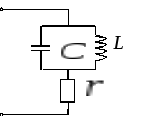
1) 2) 3) 4)
18. Электрическая цепь, в которой возможно возникновение резонанса токов, имеет вид


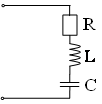

1) 2) 3) 4)
19. Цепь находится в режиме резонанса, когда
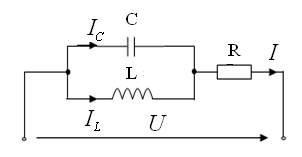
1) IL =IC 2) I = IL + IC 3) IC = I + IL 4) IL = I + IC
20. Цепь находится в режиме резонанса, когда

1) UL =UC 2) U = UL + UC 3) UC = Ur + UL 4) UL = Ur + UC
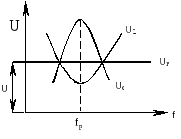
21.
Резонансные кривые ,
,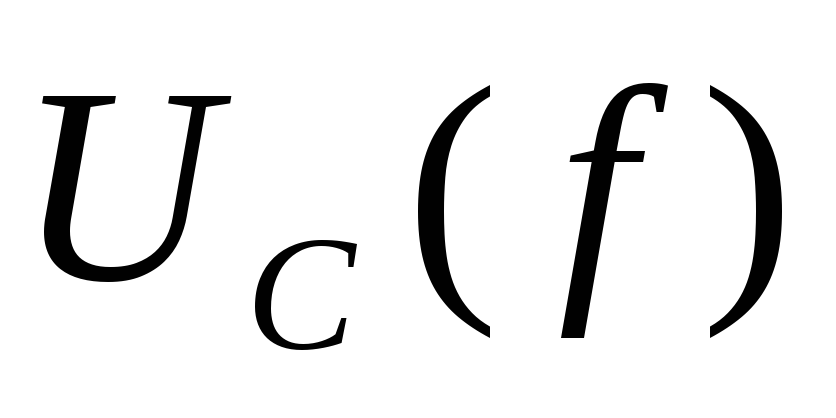 ,
,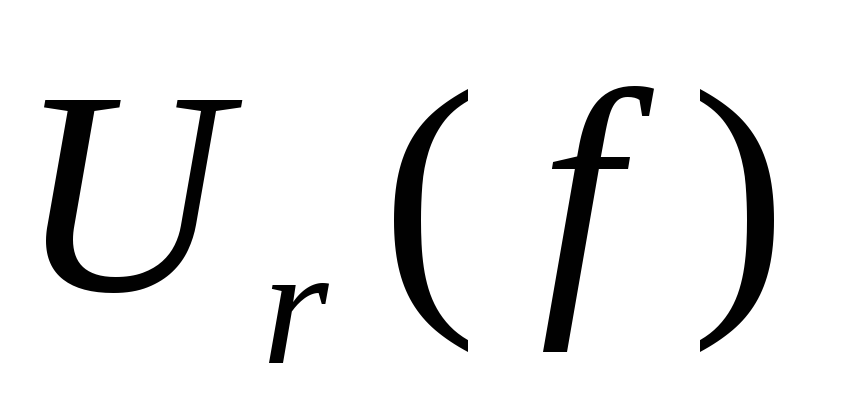 имеют вид
имеют вид



Резонанс токов
Резонанс токов возникает в электрических цепях переменного тока при параллельном соединении ветвей с разнохарактерными (индуктивными и емкостными) реактивными сопротивлениями. В режиме резонанса токов реактивная индуктивная проводимость цепи оказывается равной ее реактивной емкостной проводимости, т.е. BL=BC.
Простейшей электрической цепью, в
которой может наблюдаться резонанс
токов, является цепь с параллельным
соединением катушки индуктивности и
конденсатора. Данная схема соответствует
цепи, представленной на рис. 8, а, для
которойR2 =
0, а R1=Rк (здесьRк – активное сопротивление катушки
индуктивности). Полная проводимость
такой цепиY=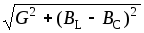 .
.
Условие резонанса токов (BL=BC)
можно записать через соответствующие
параметры электрической цепи. Так как
реактивная проводимость катушки, имеющей
активное сопротивлениеRк,
определяется выражениемBL=XL/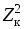 =L/(Rк2+2L2),
а проводимость конденсатора без учета
его активного сопротивления (RC= 0)BC=XC/
=L/(Rк2+2L2),
а проводимость конденсатора без учета
его активного сопротивления (RC= 0)BC=XC/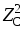 = 1/XC=C,
то условие резонанса может быть записано
в виде
= 1/XC=C,
то условие резонанса может быть записано
в виде
L/(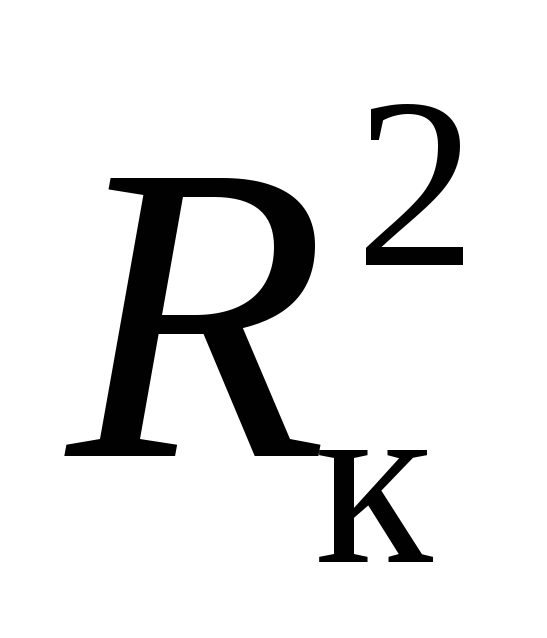 +2L2) = C.
+2L2) = C.
Из этого выражения следует, что резонанс токов в такой цепи можно получить при изменении одного из параметров Rк,L,Cипри постоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении указанных параметров.
Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяются в радиоэлектронике в качестве колебательных контуров, резонанс токов в которых достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала.
В лабораторных условиях наиболее часто резонанс токов достигается при неизменной индуктивности катушки L, путем изменения емкостиСбатареи конденсаторов. С изменением емкостной проводимостиBC=C, пропорциональной емкости конденсатора, происходит изменение полной проводимостиY, общего токаIи коэффициента мощности cos. Указанные зависимости приведены на рис. 10,a. Анализ этих зависимостей показывает, что при увеличении емкости от нуля полная проводимость электрической цепи сначала уменьшается, достигает при (BL=BC) своего минимума, а затем возрастает с увеличениемС, в пределе стремясь к бесконечности. Общий токI=YU, потребляемый цепью, пропорционален полной проводимости. Поэтому характер его изменения подобен характеру изменения проводимости.
Коэффициент мощности cosс увеличением емкости сначала возрастает, а затем уменьшается, в пределе стремясь к нулю, так как cos=G/Y. В результате анализа указанных зависимостей можно установить, что резонанс токов характеризуется следующими явлениями.
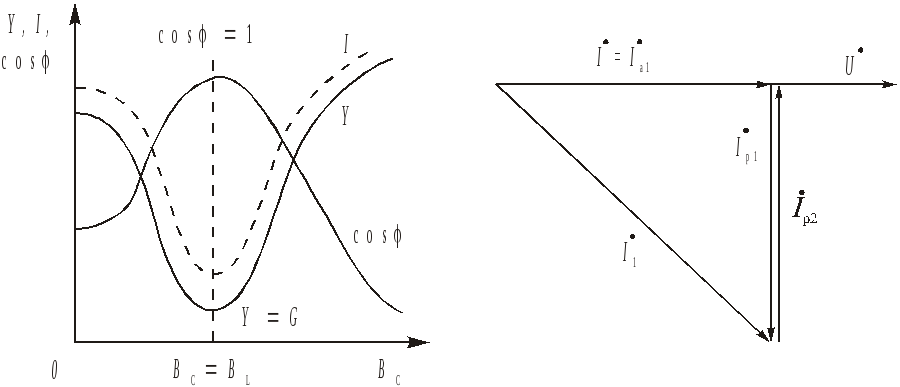
a)б)
Рис. 10
1. При резонансе токов полная проводимость всей электрической цепи приобретает минимальное значение и становится равной активной ее составляющей:
Y = 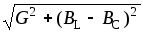 =G.
=G.
2. Минимальное значение проводимости обусловливает минимальное значение тока цепи:
I = YU = GU.
3. Емкостный ток ICи индуктивная составляющаяIL тока катушкиIкоказываются при этом равными по величине, а активная составляющая тока катушкиIа1 становится равной токуI, потребляемому из сети:
Iр1 = IL = BLU = BCU = IC = Iр2; Iа = Iа1 =GU = YU =I.
При этом реактивные составляющие токов IL иICв зависимости от значений реактивных проводимостей могут приобретать теоретически весьма большие значения и намного превышать токI, потребляемый электрической цепью из сети.
4. Реактивная составляющая полной мощности цепи при BL=BCоказывается равной нулю:
Q = BLU2 BCU2 = QL QC = 0.
При этом индуктивная и емкостная составляющие реактивной мощности также могут приобретать весьма большие значения, оставаясь равными друг другу.
5. Полная мощность цепи при резонансе равна ее активной составляющей:
S = YU 2 = GU 2 = P.
6. Коэффициент мощности всей цепи при резонансе:
cos = P/S = GU 2/YU 2 = 1.
Напряжение и ток электрической цепи при резонансе токов совпадают по фазе. Векторная диаграмма, построенная для условий резонанса токов и применительно к рассматриваемой цепи, представлена на рис. 10, б. В табл. 2 методических указаний по выполнению работы обозначениямIL, IK, IC соответствуют обозначенияIр1, I1, Iр2 на векторной диаграмме токов (рис. 10,б).
Резонанс токов находит широкое применение в силовых электрических цепях для повышения коэффициента мощности, так как это имеет большое технико-экономическое значение. Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер; некоторые из них работают с низким коэффициентом мощности и потребляют значительную реактивную мощность. К таким потребителям могут быть отнесены асинхронные двигатели (особенно работающие с неполной нагрузкой), установки электрической сварки, высокочастотной закалки и т.д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батарей снижает общую реактивную мощность установки и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах за счет снижения его реактивной составляющей и, соответственно, к уменьшению потерь энергии в генераторе и подводящих проводах.
Вопрос №4. Коэффициент мощности и его технико-экономическое значение (10 мин.)
Технико-экономическое значение коэффициента мощности cosφ заключается в том, что от его значения зависят эффективность использования электрических установок и, следовательно, капитальные и эксплуатационные расходы.

Активная мощность, развиваемая генератором при номинальном режиме
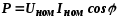
где UНОМ – номинальное напряжение генератора;
IНОМ – номинальный ток, который при длительном прохождении вызывает предельно допустимое нагревание генератора.
Полное использование мощности генератора происходит, когда cosφ=1. В этом случае активная мощность Р максимальна и равна номинальной полной мощности

Влияние значений cosφ на режим работы оборудования:
1) уменьшение cosφ, значение которого определяется характером нагрузки, приводит к неполному использованию генератора;
2) уменьшение cosφ при постоянной мощности потребителя Р приводит к увеличению тепловых потерь в линии передачи, которые растут обратно пропорционально квадрату коэффициента мощности
 . (16)
. (16)
где Р0 – потери в линии при cosφ=1.
Для полного использования номинальной мощности генераторов и уменьшения тепловых потерь необходимо повышать cosφ приемников энергии до значений, близких к единице (0,95–1,0). В этом случае потребитель меньше нагружает линию реактивной мощностью.
Способы повышения коэффициента мощности:
1) естественный – правильный выбор оборудования и его эксплуатация;
2) подключение параллельно приемнику батарей конденсаторов в случае индуктивной нагрузки (асинхронные двигатели). Благодаря этому источником реактивной энергии для приемника становится емкость и линия передачи разгружается от реактивного тока.
Разберем следующие вопросы:
Коэффициент мощности электрической цепи синусоидального тока называется …
отношение активной мощности Р к полной мощности S
отношение полной мощности S к активной мощности Р
произведение активной мощности Р на полную мощность S
активная мощность Р
Активную мощность Р цепи синусоидального тока можно определить по формуле…
Если Q и S – реактивная и полная мощности пассивной электрической цепи синусоидального тока, то отношение Q к S равно…


tg φ
arcsin φ
Вывод по четвертому вопросу: синусоидальные токи и напряжения как функции времени могут быть описаны различными способами: алгебраически, векторными диаграммами и комплексами.
5. Заключение (10 мин.)
1) Процессы, протекающие в однофазных цепях переменного тока со смешанным последовательным соединением приемников, характеризуются появлением понятий полного сопротивления, полной мощности, треугольников сопротивлений и мощностей, повторяющих треугольник напряжений. В них также необходимо учитывать взаимные фазовые сдвиги напряжений и токов. Умение анализировать однофазные цепи со смешанным соединением резисторов является важным при изучении трехфазных цепей, принципа действия и устройства электрических машин.
2) Для расчета параллельного соединения приемников используется метод проводимостей.
3) При резонансном режиме работы цепи, содержащей приемники различного характера, ее сопротивление является чисто активным. Различают резонансы токов и напряжений, которые используются в радиотехнике и повышения коэффициента мощности.
3) От значения коэффициента мощности зависят эффективность использования электрических установок и, следовательно, капитальные и эксплуатационные расходы. Для его повышения необходимо правильно выбирать оборудование и условия его эксплуатации.
2.4. Активная, реактивная и полная мощности. Баланс мощностей
Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток. Пусть напряжение и ток являются синусоидальными функциями времени:
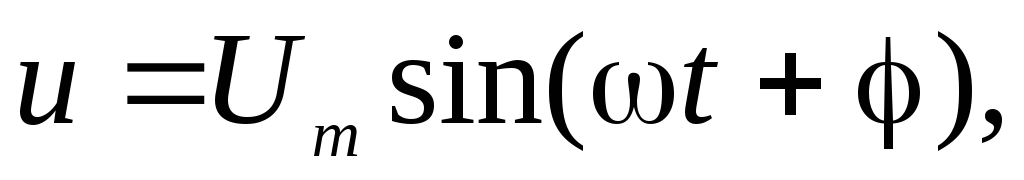
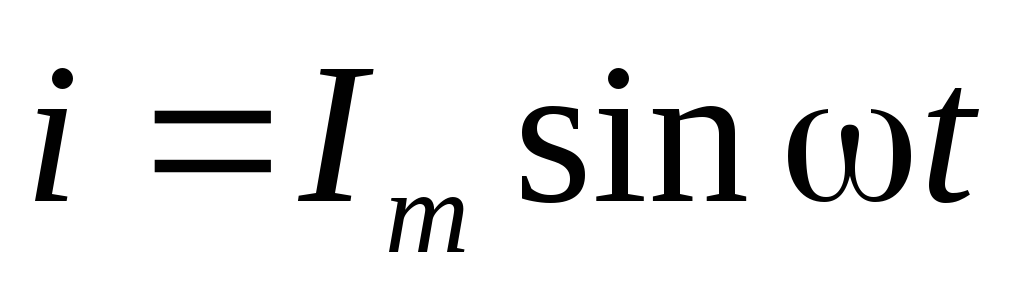 .
.
Получим
выражение для мгновенной мощности:  (2.29)
(2.29)
Из
(2.29) следует, мгновенная мощность
изменяется с частотой  ,
в два раза превышающей частоту тока и
напряжения.
,
в два раза превышающей частоту тока и
напряжения.
Среднее значение мгновенной мощности за период T называют активной мощностью и обозначают буквой P:
 (2.30)
(2.30)
При
выводе (2.30) учтено равенство 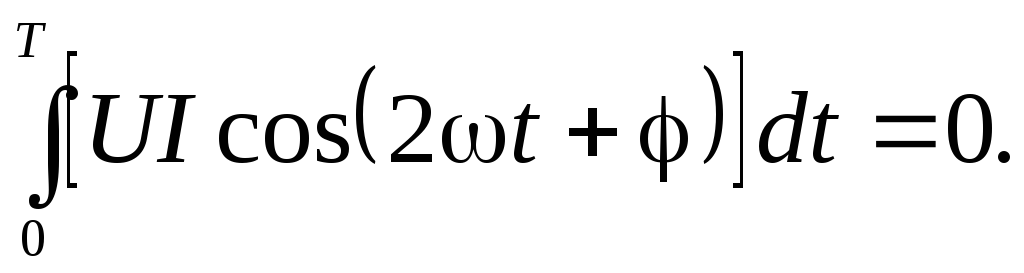
Учитывая
из треугольника сопротивлений (рис.2.15)
соотношение 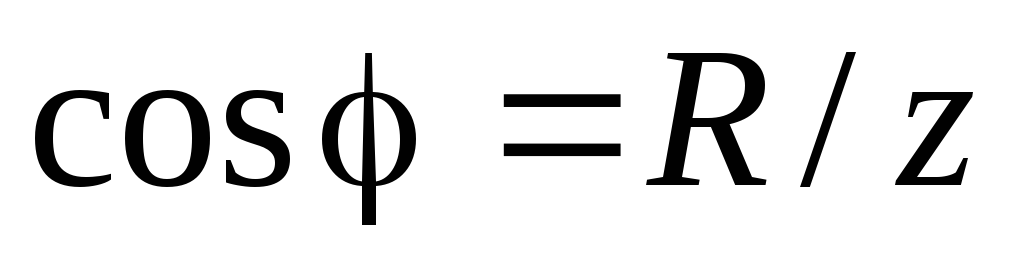 и из треугольника проводимостей
(рис.2.16)
и из треугольника проводимостей
(рис.2.16) ,
получаем из (2.30) следующие выражения
для активной мощности:
,
получаем из (2.30) следующие выражения
для активной мощности:
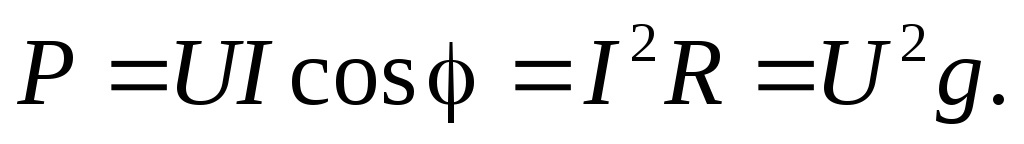 (2.31)
(2.31)
Активная мощность измеряется в ваттах (Вт) и характеризует необратимое преобразование электрической энергии, которая выделяется в виде теплоты на участках цепи в активных сопротивлениях. В электрических двигателях потребляемая из сети активная мощность преобразуется в механическую мощность (за вычетом потерь в процессе преобразования) и является их основной характеристикой.
Множитель 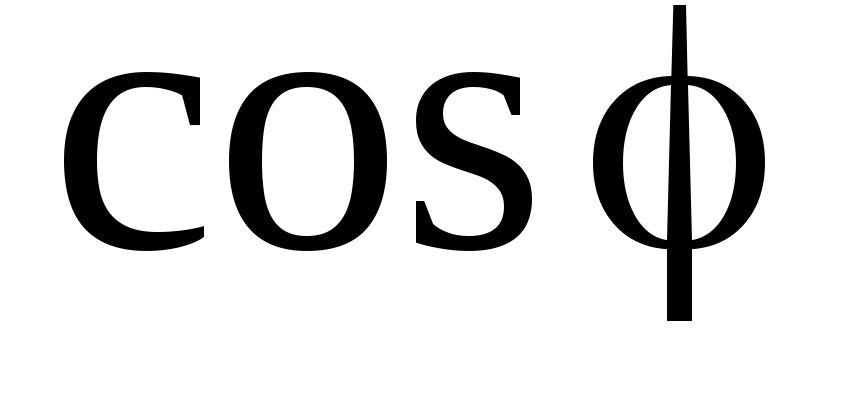 называется коэффициентом мощности.
Коэффициент мощности является
одной из важнейших характеристик
электротехнических устройств, и повышение
его до предельного значения
называется коэффициентом мощности.
Коэффициент мощности является
одной из важнейших характеристик
электротехнических устройств, и повышение
его до предельного значения остается одной из основных задач
энергосбережения.
остается одной из основных задач
энергосбережения.
Рассмотрим
идеальные реактивные элементы
(индуктивность и емкость). Активная
мощность в этих элементах равна нулю,
так как напряжение и ток в индуктивности
или емкости различаются по фазе на 90o и 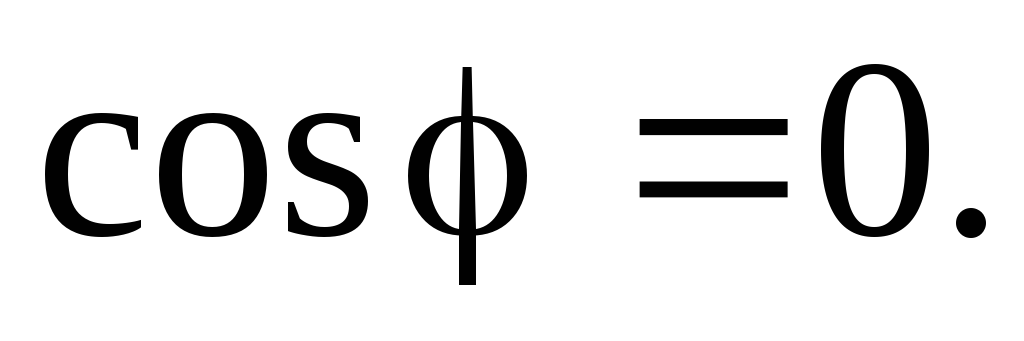
В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.
Преобразуем выражение (2.29) для мгновенной мощности:
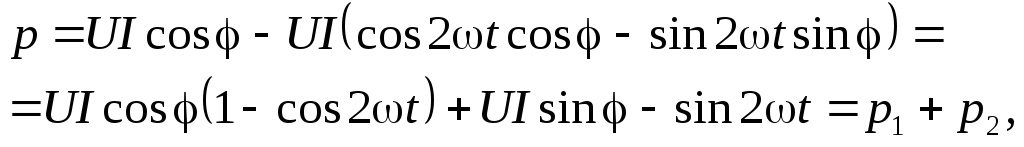
где 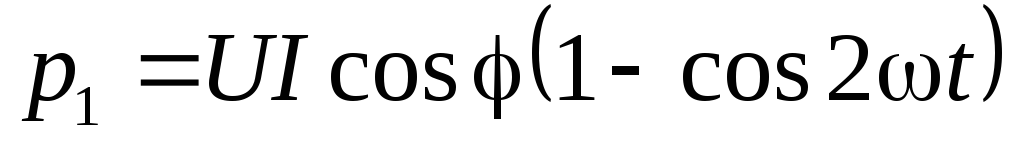 —
мгновенная мощность в активном
сопротивлении;
—
мгновенная мощность в активном
сопротивлении;
 —
мгновенная мощность в реактивном
элементе (в индуктивности или в емкости).
—
мгновенная мощность в реактивном
элементе (в индуктивности или в емкости).
Максимальное или амплитудное значение мощности p2 называется реактивной мощностью:
Q =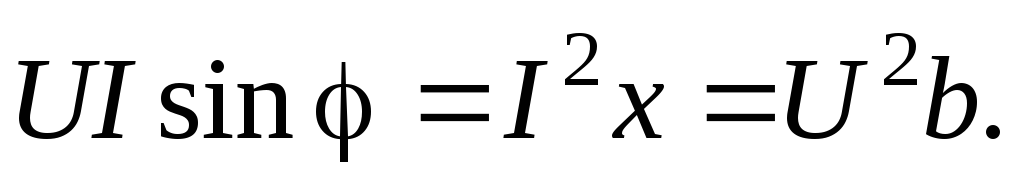
 (2.32)
(2.32)
где x, b – соответственно реактивные сопротивление и проводимость. Реактивная мощность измеряется в вольт-амперах реактивных (ВАр) и расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.
Амплитудное значение суммарной мощности p = p1 + p2 называется полной мощностью. Полная мощность, измеряемая в вольт-амперах (ВА), равна произведению действующих значений напряжения и тока:
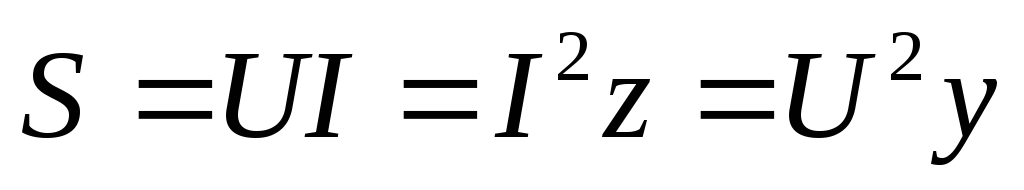 .
(2.33)
.
(2.33)
Возьмем треугольник сопротивлений (рис.2.15) и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 2.17).
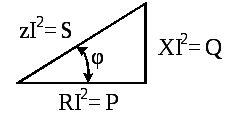
Рис. 2.17
Из треугольника мощностей получим соотношения между мощностями P, Q, S:
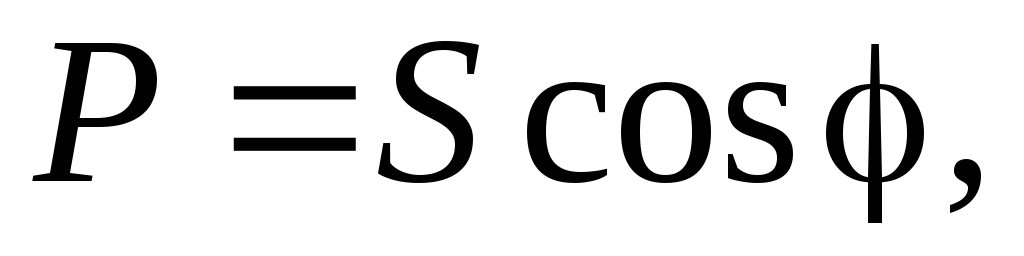 Q
=
Q
= ,
, 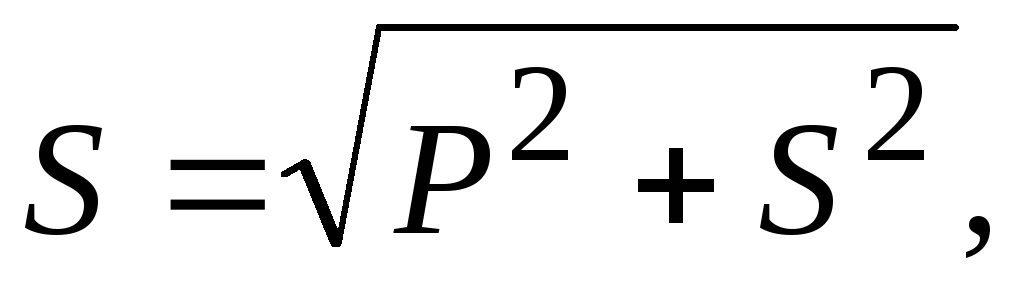
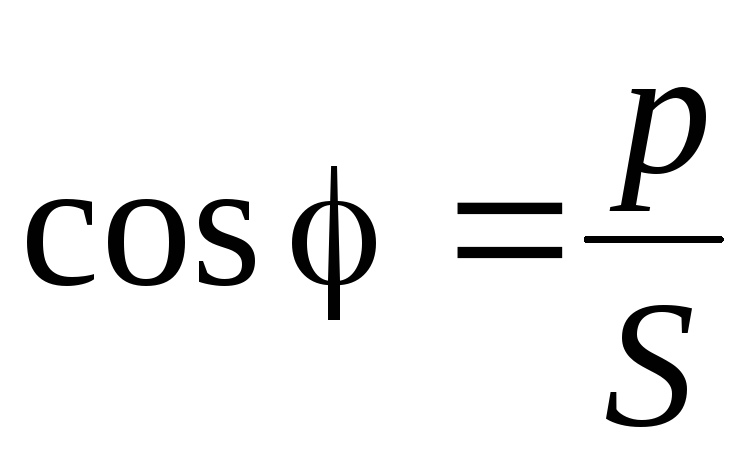 .
(2.34)
.
(2.34)
При
расчете электрических цепей комплексным
методом используют выражение комплексной
мощности, равное произведению комплексного
напряжения на сопряженный комплекс
тока. Для цепи, имеющей
активно-индуктивный характер, ток по
фазе отстает от напряжения на угол 
 ,
,
где
 —
комплекс напряжения;
—
комплекс напряжения;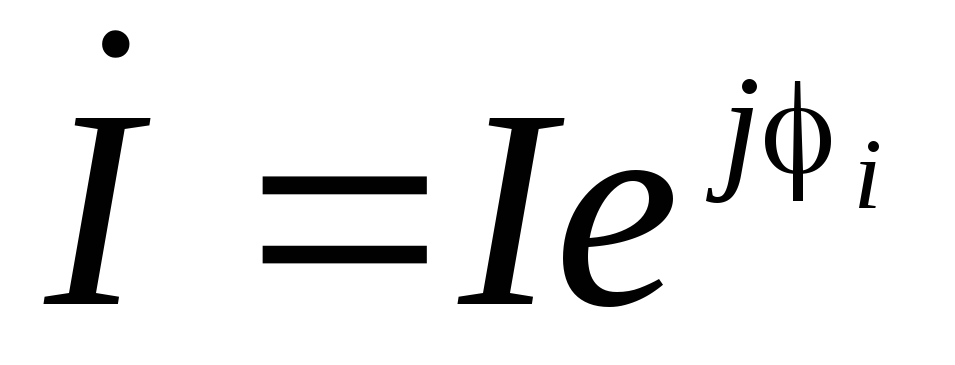 — комплекс тока;
— комплекс тока;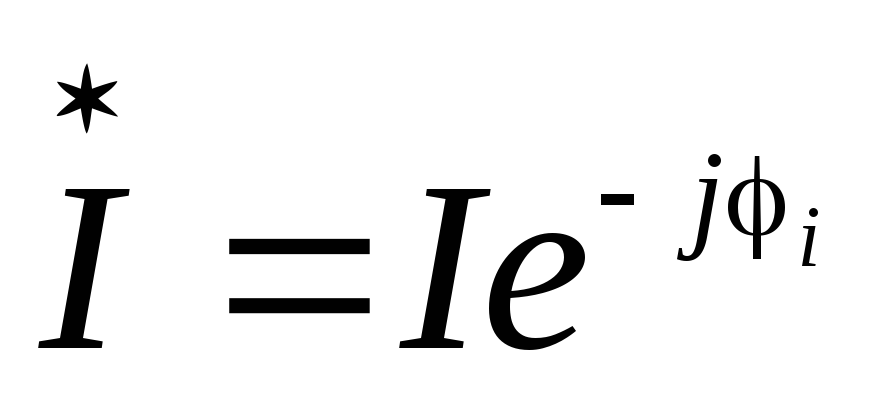 — сопряженный комплекс тока;
— сопряженный комплекс тока; — сдвиг по фазе между напряжением и
током.
Вещественной
частью полной комплексной мощности
является активная мощность, мнимой
частью комплексной мощности — реактивная
мощность:
— сдвиг по фазе между напряжением и
током.
Вещественной
частью полной комплексной мощности
является активная мощность, мнимой
частью комплексной мощности — реактивная
мощность:
 Q =
Q = 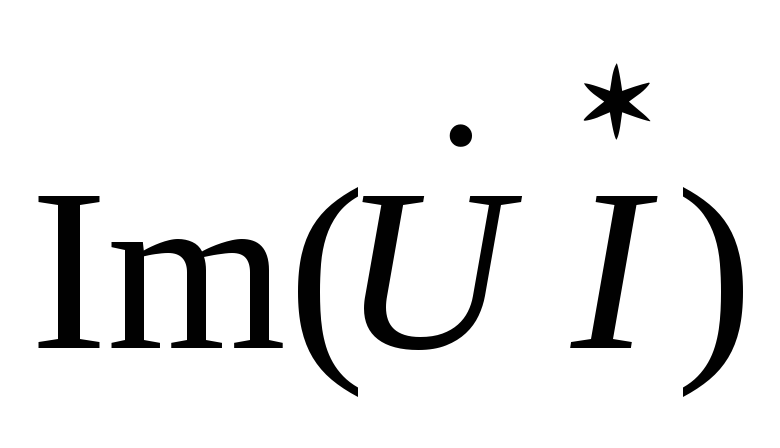 . (2.35)
. (2.35)
Для
цепи, имеющей активно-емкостной характер,
ток по фазе опережает напряжение  .
.

Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, — положительна, а в цепи с емкостным характером — отрицательна.
При выводе полученных соотношений предполагалось, что на зажимах цепи действует напряжение U. Если к зажимам цепи присоединен идеальный источник синусоидальной ЭДС с действующим значением E, то выражения (2.31)-(2.33), (2.35) для источника имеют следующий вид:
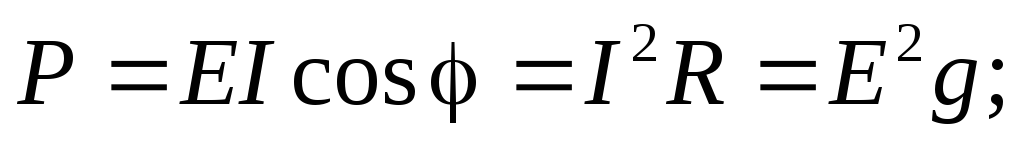 Q=
Q=
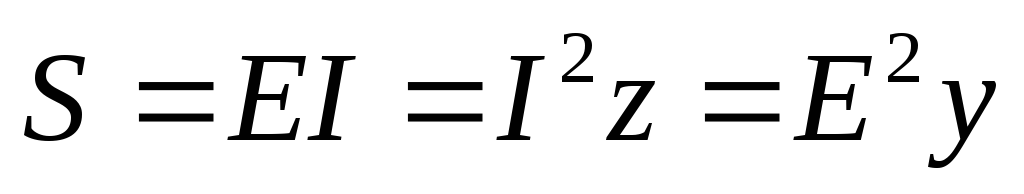 ;
;  Q =
Q = 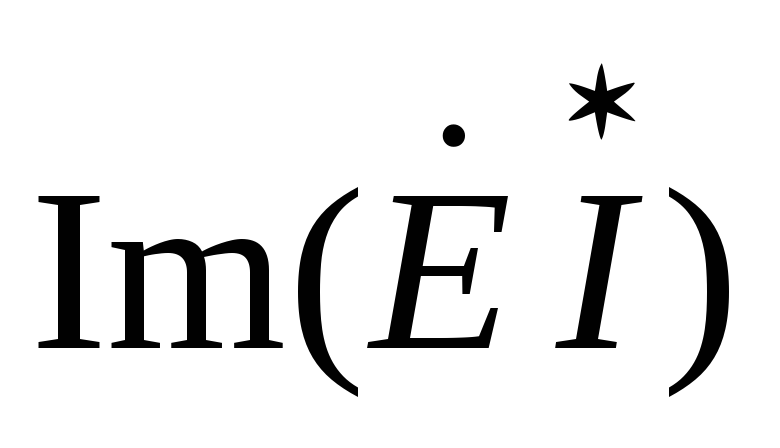 .
(2.36)
.
(2.36)
Из закона сохранения энергии следует, что для электрической цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источниками, равна активной мощности, потребляемой всеми приемниками.
Покажем, что соблюдается баланс и для комплексных, и, следовательно, для реактивных мощностей. Определим комплексные мощности для схемы (рис.2.7), содержащей идеальный источник синусоидальной ЭДС, последовательно соединенные активные и реактивные сопротивления приемника.
Запишем уравнение по второму закону Кирхгофа, умножим левую и правую части уравнения на сопряженный комплекс тока и учтем свойства произведения комплексно сопряженных чисел:
 ,
, 
 ,
,
где
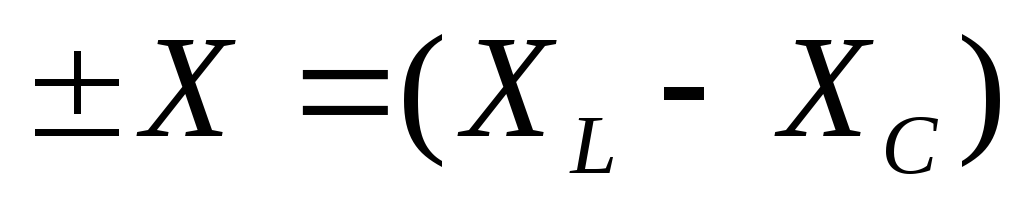 — результирующее реактивное сопротивление.
— результирующее реактивное сопротивление.
 ,
,
где
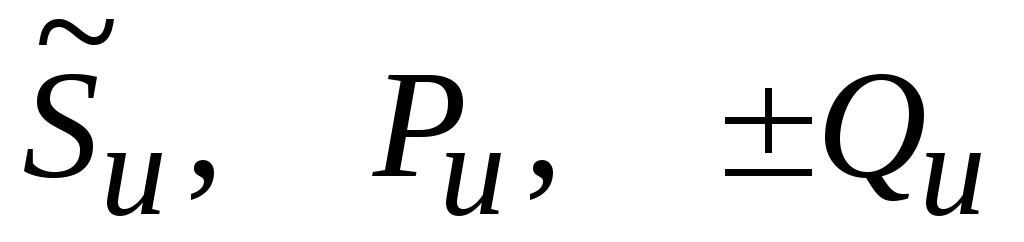 —
полная комплексная, активная и реактивная
мощности источника питания.
—
полная комплексная, активная и реактивная
мощности источника питания.
 ,
,
где 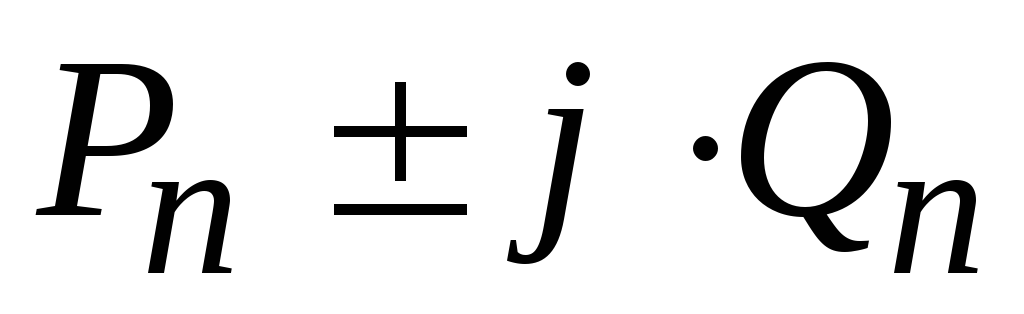 активная
и реактивная мощности, потребляемые
элементами схемы.
активная
и реактивная мощности, потребляемые
элементами схемы.
Получим уравнение для комплексных мощностей источника и приемника:
 (2.37)
(2.37)
Равенство (2.37) выражает баланс комплексных мощностей источника и приемника. При равенстве комплексных чисел равны по отдельности их вещественные и мнимые части, следовательно, уравнение (2.37) можно записать в следующей форме:
 .
(2.38)
.
(2.38)
Из следует (2.38), что для электрической цепи соблюдается закон баланса реактивных мощностей: реактивная мощность, отдаваемая источниками, равна реактивной мощности, потребляемой всеми приемниками.
Рассмотрим условие передачи источником максимальной мощности при заданном коэффициенте мощности приемника.
В
схеме на рис. 2.18 обозначены : 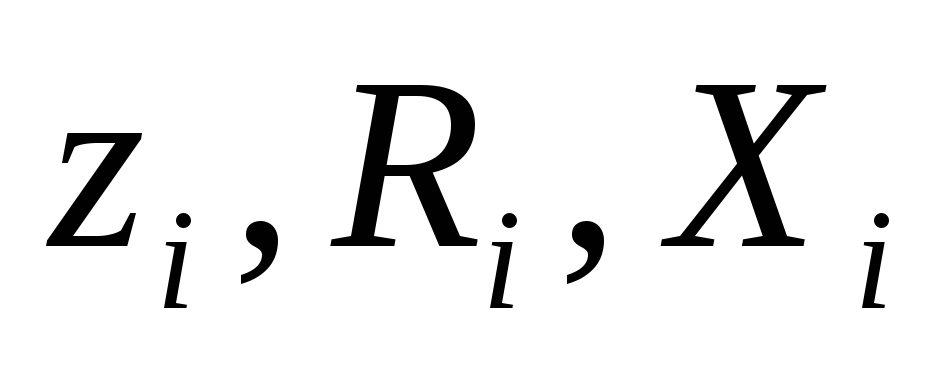 — полное, активное и реактивное
сопротивления источника ЭДС,
— полное, активное и реактивное
сопротивления источника ЭДС, — полное, активное и реактивное
сопротивления нагрузки.
— полное, активное и реактивное
сопротивления нагрузки.
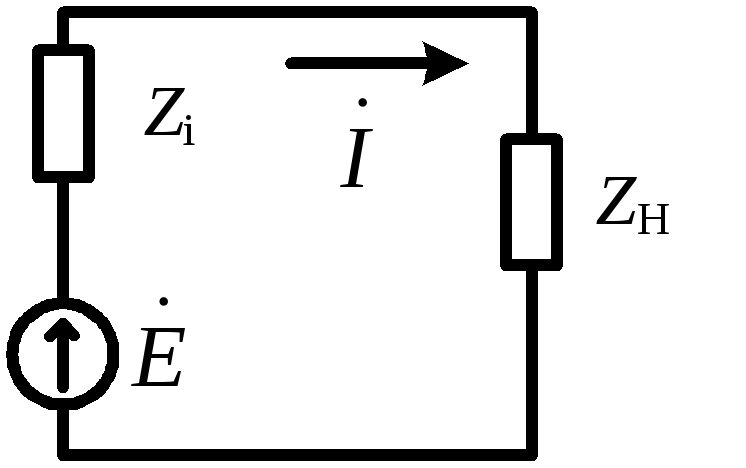
Рис. 2.18
Активная мощность может выделяться только в активных сопротивлениях цепи переменного тока. Активная мощность, выделяемая в нагрузке,
 .
(2.39)
.
(2.39)
Активная
мощность, развиваемая генератором 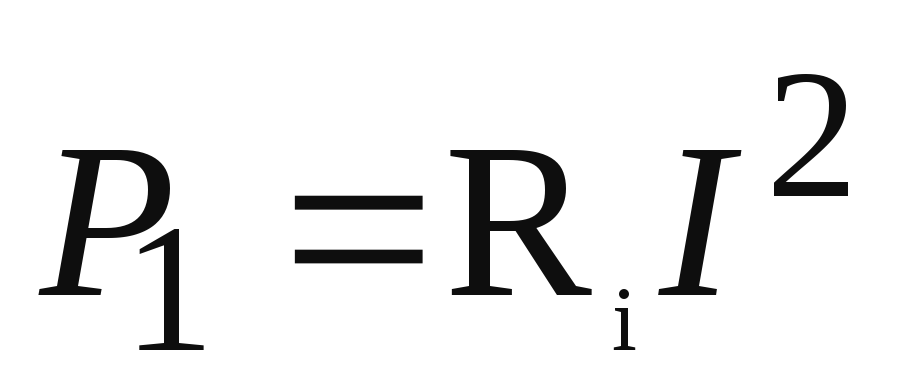 .
Коэффициент
полезного действия (КПД) для данной
схемы:
.
Коэффициент
полезного действия (КПД) для данной
схемы:
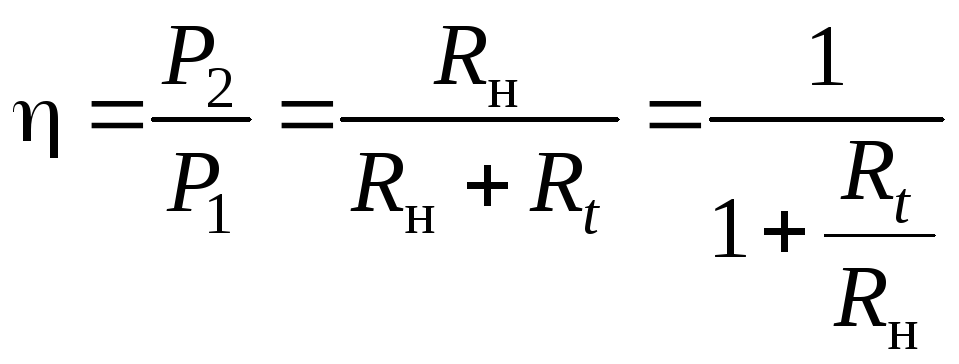 .
.
Из
(2.39) видно, что выделяемая в нагрузке
мощность будет максимальной, когда
знаменатель минимален. Последнее имеет
место при  ,
т.е. при
,
т.е. при .
Это означает, что реактивные сопротивления
источника и нагрузки должны быть
одинаковы по модулю и иметь разнородный
характер. При индуктивном характере
реактивного сопротивления источника
реактивное сопротивление нагрузки
должно быть емкостным, и наоборот:
.
Это означает, что реактивные сопротивления
источника и нагрузки должны быть
одинаковы по модулю и иметь разнородный
характер. При индуктивном характере
реактивного сопротивления источника
реактивное сопротивление нагрузки
должно быть емкостным, и наоборот:
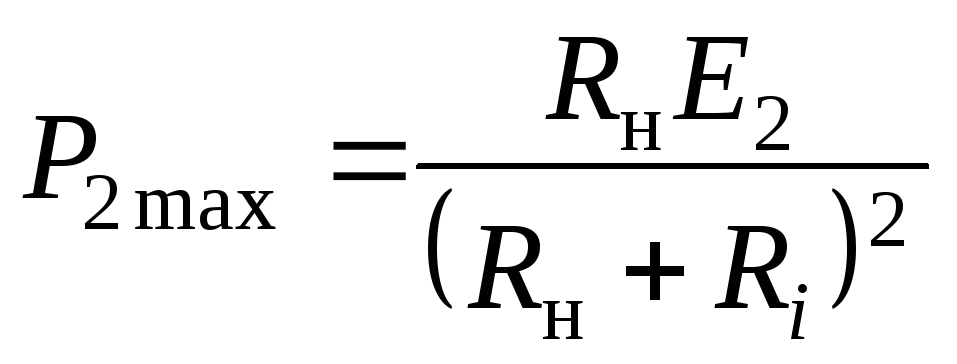 .
(2.40)
.
(2.40)
Установим условие, при котором от источника к нагрузке будет передаваться наибольшая мощность:
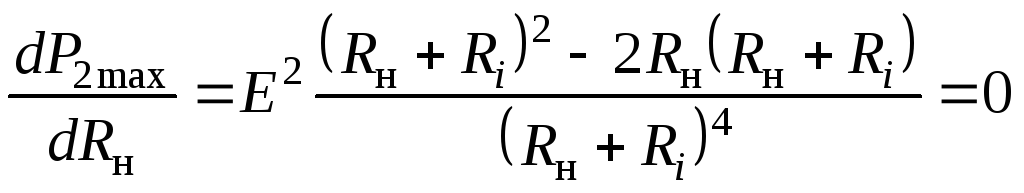 .
.
отсюда 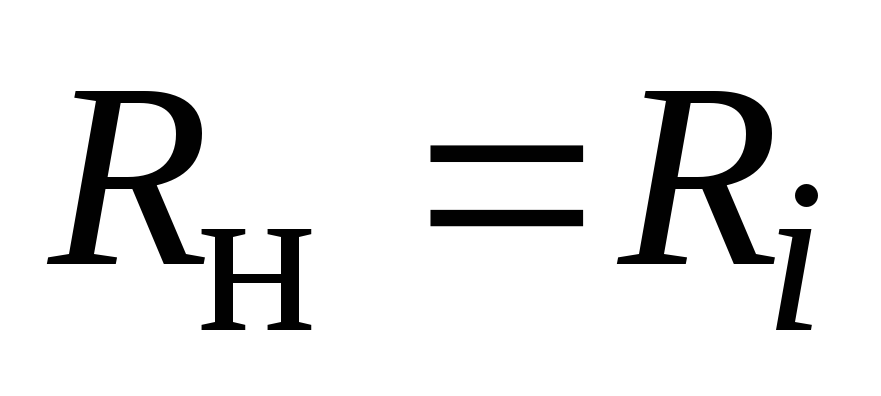 .
.
От источника к нагрузке передается наибольшая мощность, когда
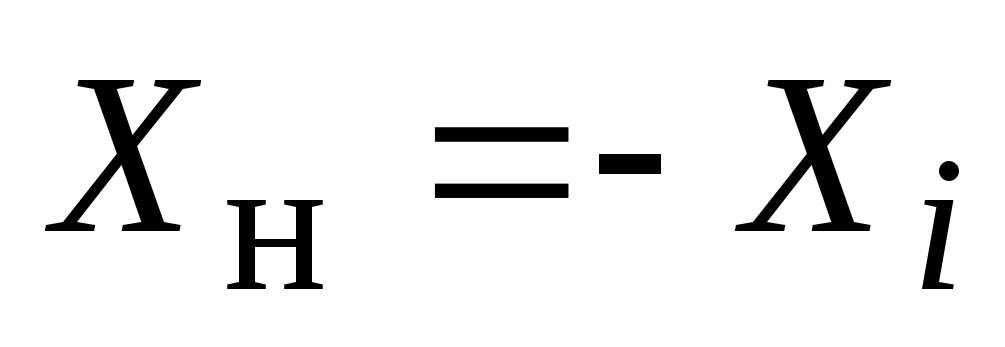 ;
;
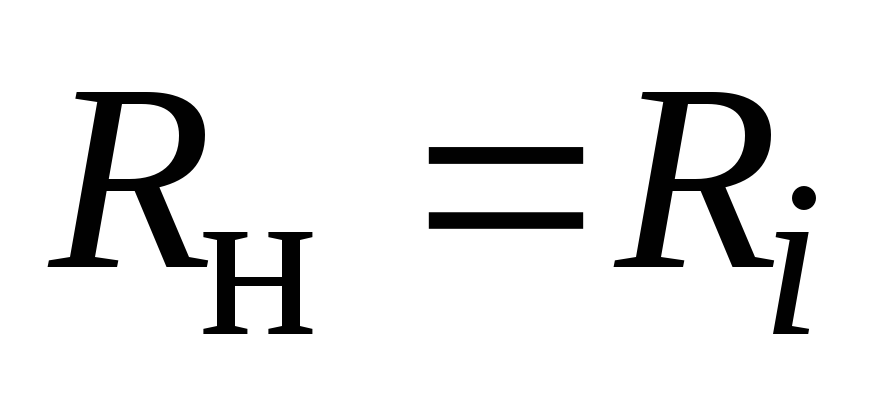 .
(2.41)
.
(2.41)
Величина наибольшей мощности
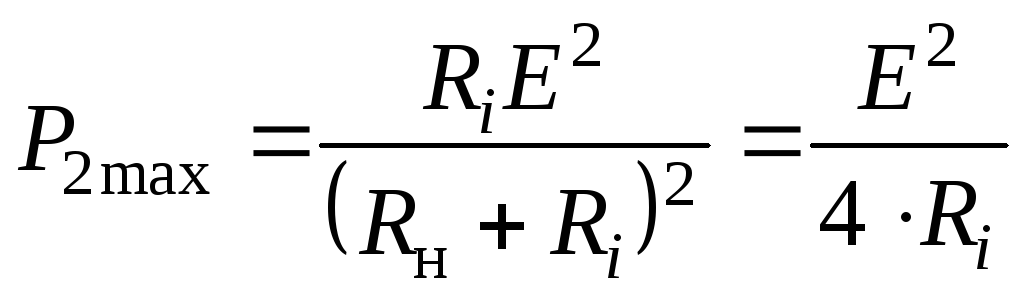 . (2.42)
. (2.42)
Режим передачи наибольшей мощности от источника к нагрузке называется согласованным режимом, а подбор сопротивлений согласно равенствам (2.41) — согласованием нагрузки с источником.
В согласованном режиме величина КПД составляет:
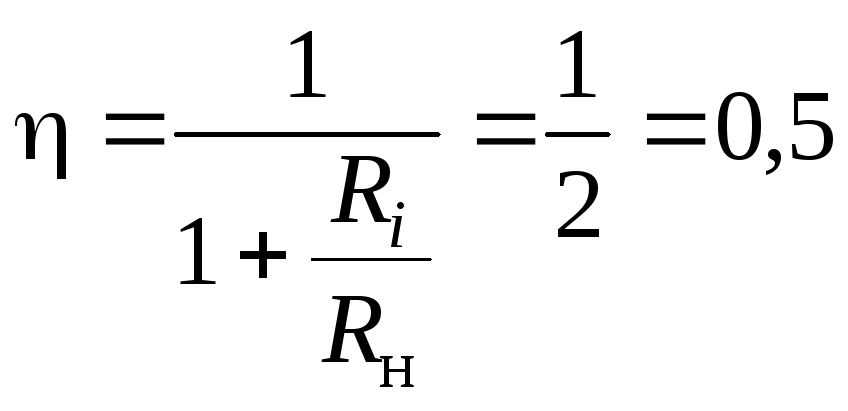 .
.
Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях. Этот режим используют в информационных цепях, где мощности могут быть малыми, и решающими являются не соображения экономичности передачи сигнала, а максимальная мощность сигнала в нагрузке.
Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. (Лекция №7)
Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:
| . | (1) |
Выражение для мгновенного значения мощности в электрических цепях имеет вид:
| . | (2) |
Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим:
| . | (3) |
Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.
Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.
Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна .
Среднее за период значение мгновенной мощности называется активной мощностью .
Принимая во внимание, что , из (3) получим:
| . | (4) |
Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому , т.е. на входе пассивного двухполюсника . Случай Р=0, теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.
1. Резистор (идеальное активное сопротивление).
Здесь напряжение и ток (см. рис. 2) совпадают по фазе , поэтому мощность всегда положительна, т.е. резистор потребляет активную мощность
2. Катушка индуктивности (идеальная индуктивность)
При идеальной индуктивности ток отстает от напряжения по фазе на .
Поэтому в соответствии с (3) можно записать
.
Участок 1-2: энергия , запасаемая в магнитном поле катушки, нарастает.
Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.
3. Конденсатор (идеальная емкость)
Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что . Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления ХL и ХС , в отличие от активного сопротивления R резистора, – реактивными.
Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.
В общем случае выражение для реактивной мощности имеет вид:
| (5) |
Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка- ). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).
В частности для катушки индуктивности имеем:
, так как .
.
Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:
.
Полная мощность
Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:
| . | (6) |
Активная, реактивная и полная мощности связаны следующим соотношением:
| . | (7) |
Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,
| . | (8) |
Комплексная мощность
Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:
| , | (9) |
где — комплекс, сопряженный с комплексом .
.
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:
Применение статических конденсаторов для повышения cos
Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению в силовых электрических цепях.
Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.
Если параллельно такой нагрузке (см. рис. 5), включить конденсатор С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов для повышения .
Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения до значения ?
Разложим на активную и реактивную составляющие. Ток через конденсатор компенсирует часть реактивной составляющей тока нагрузки :
| ; | (10) |
| ; | (11) |
| . | (12) |
Из (11) и (12) с учетом (10) имеем
,
но , откуда необходимая для повышения емкость:
| . | (13) |
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
а) Постоянный ток
Для любой цепи постоянного тока выполняется соотношение:
| (14) |
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
б) Переменный ток.
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
| (15) |
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:
| , | (16) |
где знак “+” относится к индуктивным элементам , “-” – к емкостным .
Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):
или
.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Что такое активная мощность?
- Что такое реактивная мощность, с какими элементами она связана?
- Что такое полная мощность?
- Почему необходимо стремиться к повышению коэффициента мощности ?
- Критерием чего служит баланс мощностей?
- К источнику с напряжением подключена активно-индуктивная нагрузка, ток в которой . Определить активную, реактивную и полную мощности.
- В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.
- Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XC элементов цепи.
Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.
Ответ: R=30 Ом; XL=40 Ом.
Ответ: R=10 Ом; XС=7,5 Ом.
| Коэффициент мощности — безразмерная физическая величина, характеризующая потребитель тока, с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, на сколько сдвинут по фазе ток, протекающий через потребитель электроэнергии, относительно приложенного к потребителю напряжения. Численно, коэффициент мощности равен косинусу этого фазового сдвига. Можно показать, что, если источник синусоидального сигнала (например розетка 220В, 50Гц) нагрузить на нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем сопротивлении источника, выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдинутыми напряжением и током, от электростанции требуется больше энергии, избыток выделяется в виде тепла на проводах и может быть довольно значительным. Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт). Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.
Коэффициент мощности позволяет судить о нелинейных искажениях, вносимых нагрузкой в электросеть. Чем он меньше, тем больше вносится нелинейных искажений. Кроме того, при одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.
Нелинейные искажения тока Потребители электроэнергии с нелинейной вольтамперной характеристикой (с коэффициентом мощности, меньшим единицы) создают ток, который меняется непропорционально мгновенному напряжению в сети (как правило, форма тока при этом отличается от синусоидальной). Соответственно искажается форма напряжения на данном участке электросети, что приводит к ухудшению качества электроэнергии. В зависимости от характера нагрузки можно выделить следующие основные виды нелинейных искажений тока: это фазовый сдвиг, вызванный реактивной составляющей в нагрузке, и несинусоидальность формы тока. Несинусоидальные искажения, в частности, имеют место, когда нагрузка несимметрична в разных полуволнах сетевого напряжения.
Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности.
|