Что такое активная, реактивная и полная мощность нагрузки стабилизатора?

В отличии от вычисления мощности при постоянном токе, формулы для вычисления мощности в цепях переменного тока достаточно сложны. В общем случае электрическая мощность в этом случае имеет интегральные зависимости.

Для определения полной мощности нагрузки необходимо вычислить активную и реактивную мощность. Полная мощность определяется как векторное сложение этих величин.

Активная мощность — это полезная часть мощности, та часть, которая определяет прямое преобразования электрической энергии в другие необходимые виды энергии. Для каждого электрического прибора вид преобразования энергии свой: в электрической лампочке электроэнергия преобразуется в свет и тепло, в утюге электроэнергия преобразуется в тепло, в электродвигателе электроэнергия преобразуется в механическую энергию. Фактически, активная мощность определяет скорость полезного потребления энергии.

Реактивная мощность — мощность определяемая электромагнитными полями, образующимися в процессе работы приборов. Реактивная мощность, как правило, является «вредной» или «паразитной». Реактивная мощность определяется характером нагрузки. Для такого прибора как лампочка она равна нулю, в процессе горения лампы электромагнитные поля практически не образуются. В процессе работы электродвигателя реактивная мощность может достигать больших значений. Понятие реактивной мощности тесно связано с понятием «пусковые токи».

При выборе стабилизатора напряжения необходимо определять полную мощность потребителей. Самый точный способ — найти значение полной мощности прибора в его паспорте. Если такой возможности нет, то для определения полной мощности приборов с большими «пусковыми токами» принято использовать повышающий коэффициент «4».

Следует также учитывать, что номинальная мощность стабилизатора напряжения может указываться разными производителями стабилизаторов и ИБП в различных диапазонах входных параметров тока. Китайские производители часто завышают реальную мощность устройства в два и более раз.

Особое внимание при выборе подходящего стабилизатора напряжения или источника бесперебойного питания следует обратить на возможность использования стабилизатора при реактивной нагрузке. Часто производители указывают, что номинальная мощность стабилизатора или ИБП указана без учета реактивной нагрузки. В паспортных данных стабилизаторов и источников питания можно найти фразу «устройство не может использоваться для реактивной нагрузки».

Для работы с приборами, имеющими большую реактивную мощность мы рекомендуем использовать специальные стабилизаторы напряжения и ИБП компании «Бастион». Эти приборы характеризуются большой перегрузочной мощностью и хорошей защитой от помех в сети по нагрузке.

Подробные ответы вы можете найти в следующих статьях:

Сравнение реальных мощностей стабилизаторов напряжения разных марок

Сравнение стабилизаторов напряжения Ресанта, APC, Voltron, Калибри, Teplocom

Стабилизаторы напряжения для котлов отопления

Преимущества релейных стабилизаторов напряжения «Бастион»

Стабилизатор напряжения для холодильника

Стабилизаторы напряжения для насосов

Стабилизатор напряжения для кондиционера и сплит-системы

Активная и реактивная мощность.

За что платим и работа

Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).

Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.

Активная и реактивная мощность

В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии.

Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю.

Активная мощность

Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.

Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность . Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).

Реактивная мощность

Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).

Реактивная емкостная мощность

Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке. Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.

Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т. е. на четверть периода.

Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.

Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.

Реактивная индуктивная мощность

Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.

На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.

Реальные потребители электрической энергии и полная электрическая мощность

Из рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно. Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга. Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации.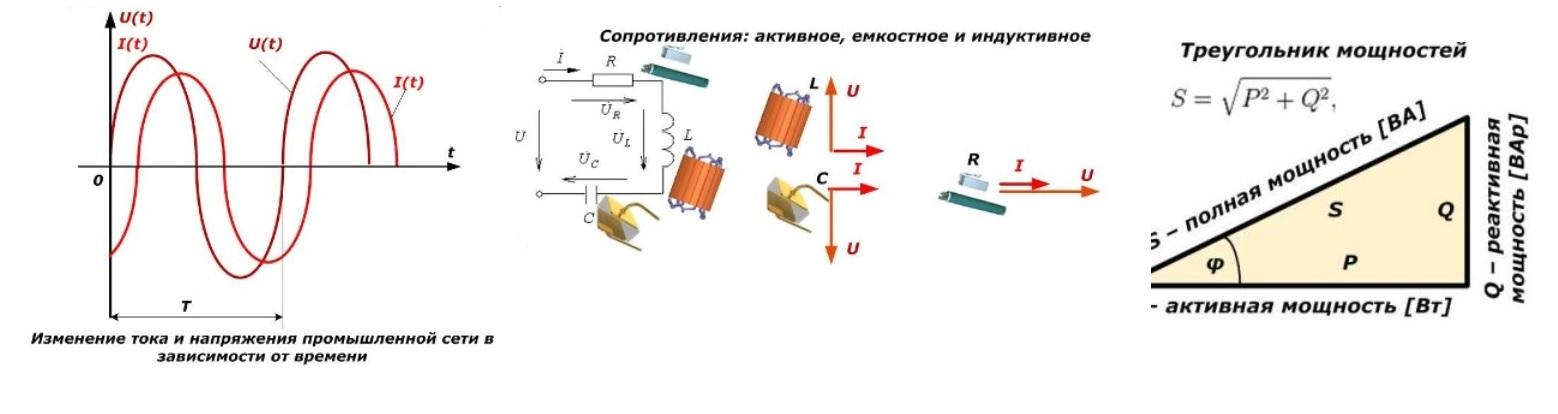 Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи. Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.

Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники. Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности. Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.

Таинственный «косинус фи»

Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.

В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1. Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.

За что платим?

И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем. Но бес, как известно, кроется в деталях. Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».

Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.

Потребитель находит возможность платить меньше

Если потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.

Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т.е. практически до единицы.

Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается.

Что же касается индивидуальных потребителей, то, ввиду сравнительно невысокой потребляемой ими мощности, разделять счета на оплату потребляемой электроэнергии на активную и реактивную не принято. Бытовые однофазные счетчики электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е. в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.

Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку. За электросчетчиком (перед счетчиком тоже, но за то потребитель не платит), что вызовет потребление активной мощности с соответствующим увеличением счета на оплату, а автоматические компенсаторы дороги и вряд ли оправдают затраты на их приобретение.

Другое дело, что производитель иногда устанавливает компенсационные конденсаторы на входе потребителей с индуктивной составляющей нагрузки. Эти конденсаторы, при правильном их подборе, несколько снизят потери энергии в подводящих проводах, при этом несколько повысив напряжение на подключенном электроприборе за счет уменьшения падения напряжения на подводящих проводах.

Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.

Похожие темы:

Типы электрических потребителей. Активная и реактивная нагрузка, активно-индуктивная и активно-емкостная, в чем различия?

Какие типы электрических потребителей бывают? Активная и реактивная нагрузка, активно-индуктивная и активно-емкостная, в чем различия?

В повседневной жизни и общениях с клиентами интернет-магазина Электрокапризам-НЕТ! мы выясняем множество технических вопросов и максимально точно подбираем оборудование под  инженерные задачи. Имея большой опыт работ и выбора технических решений  специалистами компании НТС-ГРУПП (ТМ Электрокапризам-НЕТ!) была собрана масса полезной информации, которую мы попытались структурировать и  в сжатом виде донести нашим клиентам путем публикации на сайте.  Ниже приведена своеобразная  классификация типа нагрузок с небольшими комментариями, а в следующей статье будут описаны особенности выбора мощности, запаса мощности и варианты использования источников бесперебойного питания, стабилизаторов напряжения и электрогенераторов в сетях с несбалансированным распределением потребителей, с различными видами активной и реактивной нагрузкок и др.

Применительно к выбору оборудования классифицируем типы нагрузок следующим образом

1. По типу электрического потребления нагрузки делятся на:

АКТИВНУЮ:  — Активная (или еще известную, как резистивная) нагрузка. В этом случае закон Ома выполняется в каждый момент времени и аналогичен закону Ома для схем постоянного тока. В качестве примеров : электрическая лампочка накаливания, нагревательный элемент (ТЭН), электрическая плита, бойлер и т.п.

РЕАКТИВНУЮ, которая также разделяется на такие:

—  Индуктивная нагрузка — нагрузка, через которую ток отстает от напряжения и нагрузка потребляет реактивную мощность. Примеры: асинхронные двигатели, электромагниты, катушки дросселей, трансформаторы, выпрямители, преобразователи построенные на тиристорах. Индуктивная (реактивная) нагрузка преобразует в течение одной половины полупериода энергию электрического тока в магнитное поле, а течении следующей половины преобразует энергию магнитного поля в электрический ток. При этом в индуктивной нагрузке кривая тока отстаёт от кривой напряжения на ту же половину полупериода. Примером для данного вида нагрузок может быть дроссель или катушка индуктивности.

—  Ёмкостная (реактивная) нагрузка преобразует в течение одной половины полупериода энергию электрического тока в электрическое поле, а течении следующей половины преобразует энергию электрического поля в электрический ток. При этом в ёмкостной нагрузке кривая тока опережает кривую напряжения на ту же половину полупериода. Примером данного вида нагрузок может быть конденсатор.

На практике  чистые реактивные нагрузки в электротехнике не встречаются. Вся электротехника работает с коэфициентом полезного действия ниже 100% вследствие рассеяния части энергии в виде тепловых потерь, потерь при излучении и др. побочных явлений. Таким образом в практической электротехнике применяется понятие активно-реактивной нагрузки. Активно-реактивная нагрузка также подразделяется на две: активно-индуктивная и активно-емкостная.

Активно-индуктивная нагрузка может рассматриваться как последовательное или параллельное соединение активного сопротивления и идеальной индуктивности. Примером таких нагрузок может быть обмоточный электромагнитный трансформатор, электродвигатель, электромагнитное пускорегулирующее устройство для люминесцентных ламп, катушка зажигания в автомобиле. Для этого вида нагрузок характерен бросок напряжения в момент размыкания электрической цепи.

Активно-ёмкостная нагрузка может рассматриваться как последовательное или параллельное соединение активного сопротивления и идеальной ёмкости. Примером таких нагрузок может быть конденсатор, электронные блоки питания галогенных или люминесцентных ламп. Для этих нагрузок характерен бросок тока в момент замыкания электрической цепи, особенно если он произошёл в тот момент, когда напряжение в сети максимально, или близко к максимальному.

При протекании тока через активно-реактивную нагрузку часть тока будет протекать через прибор, не производя никакой полезной работы.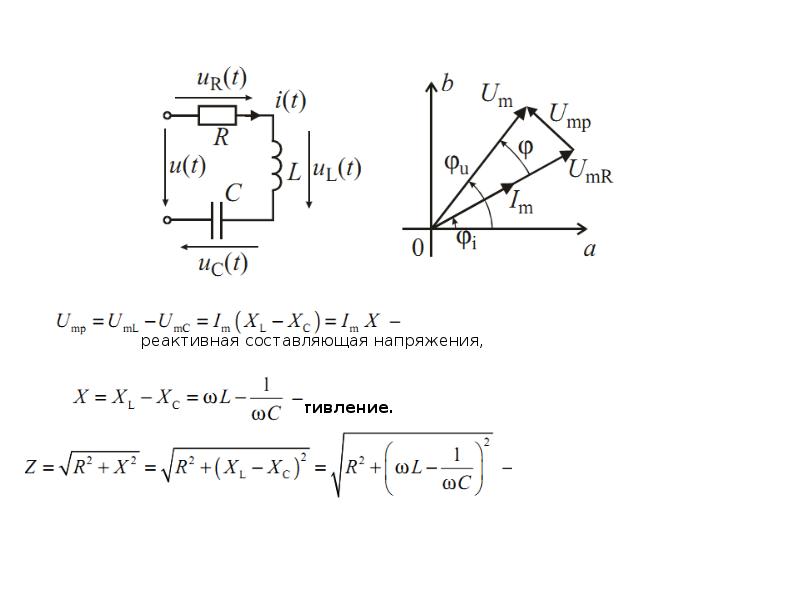 При этом максимумы и минимумы тока и напряжения будут достигаться в разное время, а кривые изменения по времени тока и напряжения будут не совпадать – оставаясь, при этом, периодическими функциями. Происходит сдвиг тока и напряжения по фазе.  Для обозначения зависимости такого сдвига применяется понятие Косинус угла между током и напряжением, и обозначается как cos(ϕ). Этот параметр является очень важным в электротехнике, которым не стоит пренебрегать при расчетах и выборе стабилизаторов напряжения, источников бесперебойного питания и электрогенераторов.

2. Фазность электропотребителей:

— однофазные –потребители рассчитанные на электропитание от 220/230В по схеме фаза-ноль-земля.

— трехфазные – потребители для которых необходимо подать напряжение 380В/400В в схеме с нейтралью и землей.

3. По способу распределения нагрузки (для трехфазных схем)

— Сбалансированные – сбалансированными считают такое распределение постребителей, когда на каждой фазе в трехфазной схеме мощности нагрузок распределены равномерно (с перекосом не более +/-20%). В качестве примера можно привести коттедж с трехфазным вводом электроснабжения, в котором при проектировании и монтаже электрических потребителей  15 кВт мощности равномерно распределили  по 5 кВт на каждую  фазу. Еще одним примером можно выделить промышленный цех, в котором преобладают трехфазные потребители и таким образом все три фазы будут нагружены равномерно.

— Несбалансированные – характеризуются как хаотично-нагруженные фазы, где нагруженность фаз может отличаться на 100% между собой. Примером может служить частный трехэтажный дом в котором на каждый этаж отводится одна фаза. Как показывает практика первый этаж дома (т.е. одна из фаз) обычно перегружена в силу того, что на первом этаже размещаются:  кухня, бойлерная и комната отдыха, а на остальных этажах спальни с бытовой техникой. В итоге одна фаза может быть  нагружена на 100%, а другие используются редко или не сильно нагружены. 

особенности оплаты, как найти формулу мощностей

Разбираясь в основных принципах электрики, важно понимать, что представляет собой активная и реактивная нагрузка.

Первый тип энергии считается полезным и идет непосредственно на нужды потребителя, например, на обогрев здания, приготовление еды и работу электрических приборов. Вторая разновидность, реактивная, определяет ту часть энергии, которая не применяется для выполнения полезной работы.

Активная и реактивная мощность

Понятия активной и полной мощности могут иметь ряд противоречивых интересов со стороны клиентов и поставщиков. Потребитель пытается сэкономить на электроэнергии, оплачивая счета за расходуемые ресурсы, а поставщик ищет выгодные пути для получения полной суммы за оба типа энергии. Но есть ли способы совмещения таких требований? Да, ведь если свести объемы реактивной мощности к нулю, то это позволит приблизиться к максимальной экономии денежных средств.

Не секрет, что у некоторых потребителей электричества показатели полной и активной мощности сопоставимы. Связано это с тем, что они используют специальные приборы, нагрузка которых осуществляется с помощью резисторов. В их числе:

1. Лампы накаливания.
2. Электрические плиты.
3. Жарочные шкафы и духовки.
4. Обогревательное оборудование.
5. Утюги.
6. Паяльники.

Для определения мощности нагрузок можно использовать знакомую со школьных времен формулу, умножив ток нагрузки на сетевое напряжение. В таком случае будут задействованы следующие единицы измерения:

1. Амперы (А) — указывают на силу тока.
2. Вольты (В) — характеризуют текущее напряжение.
3. Ватты (Вт) — указывают на показатель мощности.

В последнее время все чаще можно замечать такую картину, что на застекленных балконах расположена тонкая блестящая пленка. Ее создают из бракованных конденсаторов, которые раньше использовались на распределительных подстанциях. Как известно, конденсаторы являются главными потребителями реактивной нагрузки, которые состоят из диэлектрика, не проводящего электрический ток (в качестве главного элемента задействуется полимерная пленка или бумага, обработанная маслом).

Для сравнения, у потребителей активной мощности роль главного элемента выполняет проводящий ток материал, такой как вольфрамовый проводник, нихромовая спираль и другие.

Емкостные нагрузки

Пытаясь понять, как найти реактивную мощность, необходимо разбираться в особенностях и принципе действия конденсаторов

. Блестящие поверхности, которые расположены на балконе, являются обкладками конденсаторов из токопроводящего материала. Они отличаются способностью накапливать электроэнергию, а затем передавать ее для потребительских нужд. По сути, конденсаторы используются в качестве своеобразной аккумуляторной батареи.

А если присоединить конструкцию к источнику постоянного тока, это позволит зарядить ее кратковременным импульсом электротока, который со временем потеряет свою мощность. Для возвращения прежнего состояния конденсатора, достаточно отключить его от источника напряжения и подключить к обкладкам нагрузку.

В течение какого-либо времени через нагрузку будет подаваться ток. В идеале, конденсатор должен отдать столько энергии, сколько он получил вначале.

Если подключить его к лампочке, это позволит ей на короткое время вспыхнуть, при этом неосторожный человек может даже получить незначительный удар током, если коснется к открытым контактам. Более того, если показатели напряжения довольно высокие, это может привести к фатальному исходу — смерти.

При присоединении конденсаторов к переменному току ситуация выглядит немного иначе. Так как источник переменного напряжения характеризуется свойством постоянно менять полярность, конденсаторный элемент будет постоянно разряжаться и заряжаться, пропуская переменный ток. Однако его значения не будут совпадать с напряжением источника, а составят на четверть периода больше.

Конечные показатели будут выглядеть следующим образом: примерно половину периода конденсатор будет получать электроэнергию от источника, а другую половину — отдавать потребителю. Это значит, что суммарный показатель активной мощности составит нулевое значение. Однако из-за того, что через конденсатор постоянно протекает значительный ток, для измерения которого используется амперметр, его относят к потребителям реактивных мощностей. Формула реактивной мощности вычисляется как произведение тока на напряжение, но в этом случае единицей измерения становится вольт-ампер реактивный (ВАр), а не Вт.

Реальные потребители

Разбираясь, как найти активную мощность, люди задумываются, что будет, если попытаться подключить емкостную и индуктивную нагрузку одновременно и параллельно. В таком случае реакция будет осуществляться противоположным образом, а конечные значения начнут компенсировать себя.

При определенных обстоятельствах можно достичь идеальной компенсации, но выглядит это парадоксально: подключенные амперметры отреагируют на значительные токи, а также их полное отсутствие.

Но важно понимать, что идеальных конденсаторов не существует (то же самое касается катушек индуктивности), поэтому идеализация — это условная картина для расширенного понимания процессов.

Что касается реальной ситуации, то в бытовых условиях потребители расходуют чисто активную мощность, а также смешанную активно-индуктивную. В последнем случае основными потребителями являются такие приборы:

1. Электрические дрели.
2. Перфораторы.
3. Электрические двигатели.
4. Холодильники.
5. Стиральные машины.
6. Другая бытовая техника.

К тому же, к таким потребителям относятся электрические трансформаторы источников питания бытового оборудования и стабилизаторов напряжения. При смешанной нагрузке, кроме полезной, потребляется еще и реактивная, при этом ее значения могут превышать показатели активной мощности. В качестве единицы измерения полной мощности используется вольт-ампер.

В электротехнике присутствует такое понятие, как «косинус фи» или коэффициент мощности. Оно указывает на отношение активной мощности к реактивной. При использовании активных нагрузок, сопоставимых с реактивными, показатель cos φ равен 1. При совмещении емкостных и индуктивных нагрузок с нулевой активной мощностью значение «косинуса фи» будет составлять нулевое значение. Если речь идет о смешанных нагрузках, то коэффициент мощности будет варьироваться от 0 до 1.

Оплата электричества

Разобравшись, как найти активную и реактивную мощность, в чем может измеряться такое значение и как описать его простым языком, остается задать логичный вопрос, за что платит реальный потребитель, пользуясь электричеством. Оплачивать полную (реактивную) энергию нет смысла. Однако в этом вопросе существует множество подводных камней, которые кроются в незначительных деталях.

Как известно, смешанная нагрузка способствует повышению тока в электросети, в результате чего могут возникать разные трудности на электростанциях, где происходит выработка электричества синхронными генераторами. Дело в том, что индуктивные нагрузки вызывают «развозбуждение» генератора, а чтобы вернуть его в начальное состояние, придется потратить реальную активную энергию, то есть переплатить массу денежных средств. Есть смысл сделать реактивную мощность платной, так как это заставит клиента компенсировать полную составляющую нагрузок.

Если возникает необходимость оплачивать оба типа мощностей по отдельности, то потребитель может рассмотреть вариант монтажа специальных батарей конденсаторов, которые будут запускаться только по графику при достижении определенного уровня потребления электроэнергии. К тому же, есть возможность выполнить монтаж профессионального оборудования в виде компенсаторов реактивной энергии, которые подключают конденсаторы при росте количества потребляемой мощности. Они эффективно поднимают «косинус фи» с 0,6 до 0,97, то есть практически до отметки 1.

К тому же, согласно текущим нормам, если клиент использовал не больше 0,15 коэффициента мощности, то он освобождается от необходимости выполнять плату за полную нагрузку. Тем не менее, большинство индивидуальных потребителей используют совсем незначительный объем электричества, поэтому проводить разделение счетов на оплату двух типов энергии нецелесообразно.

К тому же, во многих зданиях установлены однофазные счетчики, которые не способны отслеживать расход реактивных электрических нагрузок, поэтому чек за электроэнергию выставляется с учетом израсходованной активной энергии.

Полезные советы

Заниматься компенсированием индуктивных нагрузок не совсем целесообразно, так как среднестатистический потребитель использует незначительное количество активной нагрузки. Да и обустройство приборов, разделяющих потоки, требует больших вложений и выглядит сложно в техническом плане.

Подключенные конденсаторы при отключении нагрузок бесполезно нагружают электропроводку. В некоторых случаях производители счетчиков оснащают их входы компенсационными конденсаторами с индуктивной нагрузкой. При правильной конфигурации такие элементы могут снизить энергопотери, а также немного поднять напряжение на приборе путем уменьшения падения напряжения на проводе подводки.

К тому же, компенсация реактивной энергии позволит снизить уровень токов по всей линии электропитания, что положительно скажется на экономии электричества и предотвратит чрезмерные энергопотери.

Понятие о реактивных и активных мощностях и нагрузках

Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Батареи статических конденсаторов

Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

P = U x I.

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

Реактивная нагрузка бывает двух видов:

1. Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
2. Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Емкостная и индуктивная нагрузка

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Треугольник мощностей

Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей. Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную. Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).

Треугольник мощностей

Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.

Полная мощность не находится как алгебраическая сумма активного и реактивного мощностного значения, это векторная сумма P и Q. Ее количественное значение вычисляется извлечением квадратного корня из суммы квадратов мощностных показателей: активного и реактивного. Измеряться полная мощность может в ВА (вольтампер) или производных от него: кВА, мВА.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:

cos φ = P/S.

Данный коэффициент находит эффективность работы сети.

Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.

Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.

Если, к примеру, имеется катушка, для которой:

• Р = 80 Вт;
• Q = 130 ВАр;
• тогда S = 152,6 BA как среднеквадратичный показатель;
• cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.

Принцип компенсации реактивной мощности

Главные потребители реактивной энергии:

1. Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
2. Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
3. Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
4. Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней. Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения. Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.

Как и где измеряют cos φ

Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

Фазометр

Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.

1. Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
2. При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
3. Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Синхронный компенсатор

Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.

Видео

Оцените статью:

Что такое активная и реактивная электроэнергия?

Расчет электрической энергии, используемой бытовым или промышленным электротехническим прибором, производится обычно с учетом полной мощности электрического тока, проходящего через измеряемую электрическую цепь.
При этом выделяются два показателя, отражающие затраты полной мощности при обслуживании потребителя. Эти показатели называются активная и реактивная энергия. Полная мощность представляет собой сумму этих двух показателей. 

Полная мощность.

По сложившейся практике потребители оплачивают не полезную мощность, которая непосредственно используется в хозяйстве, а полную, которую отпускает предприятие-поставщик. Различают эти показатели по единицам измерения – полная мощность измеряется в вольт-амперах (ВА), а полезная – в киловаттах. Активная и реактивная электроэнергия используется всеми запитанными от сети электроприборами.

Активная электроэнергия. 

Активная составляющая полной мощности совершает полезную работу и преобразовывается в те виды энергии, которые нужны потребителю. У части бытовых и промышленных электроприборов в расчетах активная и полная мощность совпадают. Среди таких устройств – электроплиты, лампы накаливания, электропечи, обогреватели, утюги и гладильные прессы и прочее. Если в паспорте указана активная мощность 1 кВт, то полная мощность такого прибора будет составлять 1 кВА.

Понятие реактивной электроэнергии. 

Этот вид электроэнергии присущ цепям, в составе которых имеются реактивные элементы. Реактивная электроэнергия — это часть полной поступаемой мощности, которая не расходуется на полезную работу. В электроцепях постоянного тока понятие реактивной мощности отсутствует. В цепях переменного тока реактивная составляющая возникает только в том случае, когда присутствует индуктивная или емкостная нагрузка. В таком случае наблюдается несоответствие фазы тока с фазой напряжения. Данный сдвиг фаз между напряжением и током обозначается символом «φ». При индуктивной нагрузке в цепи наблюдается отставание фазы, при емкостной – ее опережение. Поэтому потребителю приходит только часть полной мощности, а основные потери происходят из-за бесполезного нагревания устройств и приборов в процессе эксплуатации. Потери мощности происходят из-за наличия в электрических устройствах индуктивных катушек и конденсаторов. Из-за них в цепи в течение некоторого времени происходит накопление электроэнергии. После этого запасенная энергия поступает обратно в цепь. К приборам, в составе потребляемой мощности которых имеется реактивная составляющая электроэнергии, относятся переносные электроинструменты, электродвигатели и различная бытовая техника. Эта величина рассчитывается с учетом особого коэффициента мощности, который обозначается как cos φ.

Расчет реактивной электроэнергии. 

Коэффициент мощности лежит в пределах от 0,5 до 0,9; точное значение этого параметра можно узнать из паспорта электроприбора. Полная мощность должна быть определена как частное от деления активной мощности на коэффициент. Например, если в паспорте электрической дрели указана мощность в 600 Вт и значение 0,6, тогда потребляемая устройством полная мощность будет равна 600/06, то есть 1000 ВА. При отсутствии паспортов для вычисления полной мощности прибора коэффициент можно брать равным 0,7. Поскольку одной из основных задач действующих систем электроснабжения является доставка полезной мощности конечному потребителю, реактивные потери электроэнергии считаются негативным фактором, и возрастание этого показателя ставит под сомнение эффективность электроцепи в целом.

Значение коэффициента при учете потерь. 

Чем выше значение коэффициента мощности, тем меньше будут потери активной электроэнергии – а значит конечному потребителю потребляемая электрическая энергия обойдется немного дешевле. Для того чтобы повысить значение этого коэффициента, в электротехнике используются различные приемы компенсации нецелевых потерь электроэнергии. Компенсирующие устройства представляют собой генераторы опережающего тока, сглаживающие угол сдвига фаз между током и напряжением. Для этой же цели иногда используются батареи конденсаторов. Они подключаются параллельно к рабочей цепи и используются как синхронные компенсаторы.

Расчет стоимости электроэнергии для частных клиентов. 

Для индивидуального пользования активная и реактивная электроэнергия в счетах не разделяется – в масштабах потребления доля реактивной энергии невелика. Поэтому частные клиенты при потреблении мощности до 63 А оплачивают один счет, в котором вся потребляемая электроэнергия считается активной. Дополнительные потери в цепи на реактивную электроэнергию отдельно не выделяются и не оплачиваются. Учет реактивной электроэнергии для предприятий Другое дело – предприятия и организации. В производственных помещениях и промышленных цехах установлено огромное число электрооборудования, и в общей поступаемой электроэнергии имеется значительная часть энергии реактивной, которая необходима для работы блоков питания и электродвигателей. Активная и реактивная электроэнергия, поставляемая предприятиям и организациям, нуждается в четком разделении и ином способе оплаты за нее. Основанием для регуляции отношений предприятия-поставщика электроэнергии и конечных потребителей в этом случае выступает типовой договор. Согласно правилам, установленным в этом документе, организации, потребляющие электроэнергию свыше 63 А, нуждаются в особом устройстве, предоставляющем показания реактивной энергии для учета и оплаты. Сетевое предприятие устанавливает счетчик реактивной электроэнергии и начисляет оплату согласно его показаниям.

Коэффициент реактивной энергии. 

Как говорилось ранее, активная и реактивная электроэнергия в счетах на оплату выделяются отдельными строками. Если соотношение объемов реактивной и потребленной электроэнергии не превышает установленной нормы, то плата за реактивную энергию не начисляется. Коэффициент соотношения бывает прописан по-разному, его среднее значение составляет 0,15. При превышении данного порогового значения предприятию-потребителю рекомендуют установить компенсаторные устройства.

Реактивная энергия в многоквартирных домах. 

Типичным потребителем электроэнергии является многоквартирный дом с главным предохранителем, потребляющий электроэнергию свыше 63 А. Если в таком доме имеются исключительно жилые помещения, плата за реактивную электроэнергию не взимается. Таким образом, жильцы многоквартирного дома видят в начислениях оплату только за полную электроэнергию, поставленную в дом предприятием-поставщиком. Та же норма касается жилищных кооперативов.

Частные случаи учета реактивной мощности. 

Бывают случаи, когда в многоэтажном здании имеются и коммерческие организации, и квартиры. Поставка электроэнергии в такие дома регулируется отдельными Актами. Например, разделением могут служить размеры полезной площади. Если в многоквартирном доме коммерческие организации занимают менее половины полезной площади, то оплата за реактивную энергию не начисляется. Если пороговый процент был превышен, то возникают обязательства оплаты за реактивную электроэнергию. В ряде случаев жилые дома не освобождаются от оплаты за реактивную энергию. Например, если в доме установлены пункты подключения лифтов для квартир, начисление за использование реактивной электроэнергии происходит отдельно, лишь для этого оборудования. Владельцы квартир по-прежнему оплачивают лишь активную электроэнергию.

Назад к списку

как найти, формула расчёта, в чем измеряется

Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.

Мощность в цепи переменного электрического тока

Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.

Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.

В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.

Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.

При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.

Понятие активной мощности

Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).

Рассчитывается по формуле: P = U⋅I⋅cosφ,

где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.

ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73

Понятие реактивной мощности

Реактивная «вредная» мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.

Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.

Обозначается эта величина латинской буквой Q.

ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).

Рассчитывается по формуле:

Q = U⋅I⋅sinφ,

где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.

ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.

Емкостные и индуктивные нагрузки

Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.

Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.

ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.

Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.

ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.

Коэффициент мощности cosφ

Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.

Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.

ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.

Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.

Понятие полной мощности. Треугольник мощностей

Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.

Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.

S = U⋅I

ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).

Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.

Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.

Как найти активную, реактивную и полную мощности. Пример расчета

Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.

Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.

Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.

Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.

Как измеряют cosφ на практике

Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром. Также с этой задачей легко справится цифровой ваттметр.

Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.

1. Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору. Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
2. Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.

Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.

Разница между активной и реактивной мощностью (со сравнительной таблицей)

Наиболее существенная разница между активной и реактивной мощностью состоит в том, что активная мощность — это фактическая мощность, рассеиваемая в цепи. В то время как реактивная мощность — это бесполезная мощность, которая течет только между источником и нагрузкой. Другие различия между активной и реактивной мощностью поясняются ниже в сравнительной таблице.

Активная, полная и активная мощность индуцируется в цепи только тогда, когда их ток отстает от приложенного напряжения на угол Φ.Прямоугольный треугольник, показанный ниже, показывает соотношение между активной, реактивной и полной мощностью.

Где, S — полная мощность
Q — реактивная мощность
P — Активная мощность

Содержание: активная против реактивной мощности

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Заключение

Сравнительная таблица

Основа для сравнения	Активная мощность	Реактивная мощность
Определение	Активная мощность — это реальная мощность, которая рассеивается в цепи.	Мощность, которая движется назад и образует пену между нагрузкой и источником такого типа мощности, известна как реактивная мощность
Формула
Измерительный блок	Вт	VAR
Представлен	P	Q
Причины	Вырабатывает тепло в нагревателе, светится в лампах и крутящий момент в двигателе.	Измеряет коэффициент мощности цепи.
Измерительный прибор	Ваттметр	Измеритель VAR

Определение активной мощности

Мощность, которая рассеивается или выполняет полезную работу в цепи, известна как активная мощность. Он измеряется в ваттах или мегаваттах. Активная мощность обозначается заглавным алфавитом P. Среднее значение мощности в цепи дается выражением.

Активная мощность формирует цепь и нагрузку.

Определение реактивной мощности

Реактивная мощность перемещается между источником и нагрузкой цепи. Эта мощность не выполняет с нагрузкой никакой полезной работы. Q представляет собой реактивную мощность и измеряется в ВАр. Реактивная мощность сохраняется в цепи и разряжается асинхронным двигателем, трансформатором или соленоидами.

Ключевые различия между активной и реактивной мощностью

1. Активная мощность — это реальная мощность, потребляемая нагрузкой.А реактивная мощность — это бесполезная мощность.
2. Активная мощность — это произведение напряжения, тока и косинуса угла между ними. В то время как реактивная мощность — это произведение напряжения и тока и синуса угла между ними.
3. Активная мощность — это активная мощность, измеряемая в ваттах. Пока реактивная мощность измеряется в ВАР.
4. Буква P представляет активную мощность, а Q представляет реактивную мощность.
5. Крутящий момент, развивающийся в двигателе, тепло, рассеиваемое нагревателем, и свет, излучаемый лампами, — все это из-за активной мощности.Реактивная мощность определяет коэффициент мощности цепи.
6. Ваттметр измеряет активную мощность, а VAR-метр используется для измерения полной мощности.

Заключение

Активная мощность выполняет полезную работу в цепи. И реактивная мощность просто течет по цепи, не выполняя никакой полезной работы.

Активная, реактивная и полная мощность

Требуемый источник питания для электрической цепи зависит от

• активной мощности — фактическая потребляемая мощность электрического сопротивления в цепи
• реактивная мощность — мнимая индуктивная и емкостная потребляемая мощность в цепи

Требуемый источник питания называется полной мощностью , и представляет собой комплексное значение, которое может быть выражено в виде треугольника Пифагора, как показано на рисунке ниже.

Полная мощность — S

Полная мощность — это мощность, подаваемая в электрическую цепь (обычно от поставщика энергии в сеть) для покрытия реальной и реактивной мощности, потребляемой нагрузкой.

Полная мощность может быть рассчитана как

S = (Q ² + P ² ) ^1/2 (1)

, где

S = полное напряжение питания цепи ( вольт-ампер, ВА)

Q = потребляемая реактивная мощность в нагрузке (вольт-ампер, реактивная, вар)

P = активная мощность, потребляемая в нагрузке (ватт, Вт)

Полная мощность измеряется в вольт-амперах (ВА) — напряжение системы переменного тока, умноженное на текущий ток.Полная мощность — это комплексное значение и векторная сумма активной и реактивной мощности, как показано на рисунке выше.

Однофазный ток

S = UI (2a)

где

U = электрический потенциал (В)

I = ток (A)

Трехфазный ток

S

= 3 ^1/2 UI

= 1.732 U I (2b)

Активная мощность — P

Активная — или Реальная или Истинная — мощность выполняет фактическую работу в нагрузке. Активная мощность измеряется в Вт (Вт) и представляет собой мощность, потребляемую электрическим сопротивлением.

• Истинная мощность — это ток в фазе с напряжением, умноженный на напряжение

Однофазный ток

P = UI cos φ

= UI PF (3a)

где

φ = фазовый угол между электрическим потенциалом (напряжением) и током

PF = cos φ

= коэффициент мощности

Трехфазный ток

P = 3 ^1/2 UI cos φ

= 1.732 U I PF (3b)

Постоянный ток

P = U I (3c)

Реактивная мощность — Q

Реактивная мощность — это мнимая или комплексная мощность в емкостной или индуктивной нагрузке. Реактивная мощность представляет собой обмен энергией между источником питания и реактивными нагрузками, при котором полезная мощность не увеличивается и не теряется. Чистая средняя реактивная мощность равна нулю. Реактивная мощность накапливается и разряжается асинхронными двигателями, трансформаторами, соленоидами и конденсаторами.Чистая катушка индуктивности и чистый конденсатор не потребляют никакой энергии, поскольку в течение полупериода, какая бы мощность ни принималась от источника этими компонентами, та же самая мощность возвращается к источнику.

Реактивную мощность следует минимизировать, поскольку она увеличивает общий ток, протекающий в электрической цепи, не создавая работы для нагрузки. Повышенные реактивные токи приводят только к невосстановимым потерям мощности из-за сопротивления линии электропередачи.

Увеличение реактивной и полной мощности приведет к уменьшению коэффициента мощности — PF .

Реактивная индуктивная мощность измеряется в реактивных вольт-амперах (ВАР).

• Реактивная мощность — это ток, не совпадающий по фазе с напряжением, умноженным на напряжение

Однофазный ток

Q = UI sin φ (4a)

, где

φ = фазовый угол

Трехфазный ток

Q = 3 ^1/2 UI sin φ

= 1.732 UI sin φ (4b)

13 Разница между активной и реактивной мощностью

В предыдущем посте мы узнали о различных типах питания в электрических цепях с помощью принципиальной схемы. Теперь в этом посте мы собираемся изучить разницу между активной и реактивной мощностью.

В чем разница между активной и реактивной мощностью?

Давайте сравним две разные мощности с их спецификациями и примерами в табличной форме.

Старший №	Содержание	Активная мощность	Реактивная мощность
01	Базовый Определение	Активная мощность — это мощность, которая непрерывно поступает из источника загрузить в электрическую цепь.	Реактивная мощность — это мощность, которая непрерывно течет от источника к нагрузке , а возвращается обратно к источнику в электрической цепи.
02	Обозначается как	Активная мощность обозначается как « Реальная мощность » или « Вт при полной мощности », или « Истинная мощность » или Фактическая мощность .	Реактивная мощность называется « Мнимая мощность » или « Вт без мощности » или « Бесполезная мощность» или Комплексная мощность .
03	Обозначается как	Активная мощность обозначается заглавной буквой « P ».	Реактивная мощность обозначается заглавной буквой « Q ».
04	Формула (онлайн-калькулятор мощности)	Вы можете рассчитать активную мощность (P), используя приведенную ниже формулу. Активная мощность = [Напряжение * Ток * Cos (θ)]	Вы можете рассчитать реактивную мощность (Q), используя формулу ниже. Реактивная мощность = [Напряжение * Ток * Sin (θ)]
05	Измерительный блок	Измеряется в Вт (Вт) или Киловатт (кВт) или МВт (МВт) ) .	Он измеряется в вольт-ампер, реактивном (ВАр), или киловольт-ампер, реактивном (кВАр), или мегавольт-ампер, реактивном (МВАр).
06	Измерительные приборы (Как измерить активную и реактивную мощность?)	Для измерения активной мощности требуется ваттметр .	Для измерения реактивной мощности требуется VARmeter .
07	Мощность Направление	Эта мощность течет в только в одном направлении с обратным временем.	Эта мощность течет в в обоих направлениях с соответствующим временем.
08	Функция I	Активная мощность используется или рассеивается в цепи через подключенную резистивную нагрузку.	Реактивная мощность сохраняется в цепи через подключенную индуктивную нагрузку.
09	Функция II	Потребляет полезной мощности, нагрузка.	Потребляет энергии меньше потребляет по нагрузке.
10	Полезная цепь	Работает как в цепи AC , так и в цепи DC .	Работает в цепи AC .
11	Рабочая Роль	Преобразует электрическую энергию в другие формы энергии , такие как оптическая, тепловая, механическая.	Не преобразует энергию. Но он производит электрический или магнитный поток.
12	Мощность Вклад	В электрической цепи активная мощность вносит вклад в составляющую тока, которая составляет в фазе с напряжением цепи.	В электрической цепи реактивная мощность способствует составляющей тока, которая на не совпадает по фазе с напряжением цепи.
13	Использование	Активная мощность используется в лампе накаливания, духовке, кофеварке, утюге, тостере, нагревателе, машине и т. Д.	Реактивная мощность используется в вентиляторе, пылесосе, посудомоечной машине, стиральной машине, компрессор в холодильнике, кондиционеры, трансформатор и т. д.

С помощью основных концепций, функций и использования мы разграничили активную и реактивную мощности.

Прочитать похожие сравнения:

Если у вас есть какие-либо сомнения или вопросы относительно разницы между активной и реактивной мощностью, спросите меня в разделе комментариев ниже.

Спасибо за чтение!

Если вы цените то, что я делаю здесь, в DipsLab, вам следует принять во внимание:

DipsLab — это самый быстрорастущий и пользующийся наибольшим доверием сайт сообщества инженеров по электротехнике и электронике. Все опубликованные статьи доступны БЕСПЛАТНО всем.

Если вам нравится то, что вы читаете, пожалуйста, купите мне кофе (или 2) в знак признательности.

Это поможет мне продолжать оказывать услуги и оплачивать счета.

Я благодарен за вашу бесконечную поддержку.

Я получил степень магистра в области электроэнергетики. Я работаю и пишу технические руководства по ПЛК, программированию MATLAB и электрике на портале DipsLab.com.

Я счастлив, поделившись своими знаниями в этом блоге.А иногда вникаю в программирование на Python.

Установите пользовательское содержимое вкладки HTML для автора на странице профиля

Разница между активной и реактивной мощностью (активной и реактивной)

Наиболее важное различие между активной и реактивной мощностью состоит в том, что активная мощность — это реальная мощность, которая используется в цепи, в то время как реактивная мощность колеблется между нагрузкой и источником.

Прежде чем сравнивать активную и реактивную мощность, я хочу объяснить активную и реактивную мощность.Итак, давайте посмотрим на введение активной, реактивной мощности.

Активная мощность:

Активная мощность также называется фактической мощностью, активной мощностью или рабочей мощностью. Это мощность, которая фактически приводит оборудование в действие и выполняет полезную работу. Он измеряется в киловаттах (кВт) или МВт.

Реактивная мощность:

Реактивная мощность — это мощность, необходимая магнитному оборудованию (трансформатору, двигателю и реле) для создания намагничивающего потока. Он течет вперед и назад, что означает, что он движется в обоих направлениях контура.

Реактивная энергия вызывает перегрузку в линиях, трансформаторах и генераторах, не обеспечивая при этом полезной производительности. Однако это записано в счете, поэтому может значительно увеличить общую сумму к оплате. Реактивная мощность измеряется в киловольт-амперах, реактивная (кВАр) или мвар.

Давайте посмотрим на треугольник мощности, чтобы понять взаимосвязь между активной, реактивной и полной мощностью.

На упомянутом изображении вы можете видеть, что комплексная мощность представляет собой векторную сумму активной и реактивной мощности.Кажущаяся мощность — это величина комплексной мощности. давайте посмотрим на терминологию, которая была использована На изображении

• P => Активная мощность
• Q => Реактивная мощность
• S => Комплексная мощность
• | S | => Полная мощность
• φ => Фаза напряжения относительно тока

Следовательно, следующее выражение, показанное ниже, дает активную, реактивную и полную мощность соответственно.

• Активная мощность P = V x I cosϕ = V I cosϕ
• Реактивная мощность Pr или Q = V x I sinϕ = V I sinϕ
• Комплексная мощность S = P + jQ
• Полная мощность = | S | = √P² + Q²

Теперь я думаю, что мы можем увидеть разницу между активной и реактивной мощностью с помощью диаграммы.

Основа для сравнения	Активная мощность	Реактивная мощность
Определение	Активная мощность — это реальная мощность, рассеиваемая в цепи.	Мощность, которая движется вперед и назад между нагрузкой и источником такого типа мощности, известна как реактивная мощность
Формула	P = V x I cosϕ = V I cosϕ	Q = V x I sinϕ = V I sinϕ
Измерительный блок	Вт, кВт, МВт	ВАр, кВАр, МВАр
В лице	-P	Q
Причины	Вырабатывает тепло в нагревателе, свет в лампах и крутящий момент в двигателе.	Измеряет коэффициент мощности цепи.
Измерительный прибор	Ваттметр	Измеритель VAR

Рекомендуемое сообщение

О Amlendra

Я инженер-программист встраиваемых систем и корпоративный инструктор. В настоящее время я работаю старшим инженером-программистом в крупнейшей консалтинговой компании по программному обеспечению. Имею опыт работы с различными микроконтроллерами (stm32, LPC, PIC AVR и 8051), драйверами (USB и виртуальный com-порт), POS-устройством (VeriFone) и платежным шлюзом (глобальные и первые данные).

Что такое реактивная мощность? — Определение из Техопедии

Что означает реактивная мощность?

В системах электросетей реактивная мощность — это мощность, которая течет обратно от пункта назначения к сети в сценарии переменного тока.

В системе постоянного тока напряжение и нагрузка статичны, и, проще говоря, направление энергии «одностороннее», но в переменном токе есть разные фазы, связанные с элементами системы, такими как конденсаторы. и индукторы.

Реактивная мощность — это энергия, возвращаемая в сеть во время пассивных фаз.

Реактивная мощность также известна как фантомное питание.

Techopedia объясняет реактивную мощность

Другой способ объяснить это состоит в том, что реактивная мощность — это результирующая мощность в ваттах цепи переменного тока, когда форма волны тока не совпадает по фазе с формой волны напряжения, обычно на 90 градусов, если нагрузка является чисто реактивной, и является результатом емкостных или индуктивных нагрузок.

Фактическая работа выполняется только тогда, когда ток находится в фазе с напряжением, например, в резистивных нагрузках. Примером может служить лампа накаливания; в реактивной нагрузке энергия течет к нагрузке половину времени, тогда как в другой половине мощность течет от нее, что создает иллюзию, что нагрузка не рассеивает и не потребляет мощность.

Три вида мощности

Реактивная мощность — это один из трех типов мощности, присутствующих в нагруженных цепях.

Истинная мощность

Фактическая мощность в ваттах, рассеиваемая схемой

Реактивная мощность

Рассеиваемая мощность от индуктивных и емкостных нагрузок, измеренная в вольт-амперах реактивной (VAR)

Полная мощность

Комбинация измерения реактивной и истинной мощности в вольт-амперах (ВА)

Реактивная мощность также называется «фантомной мощностью», потому что неясно, куда она уходит.Общеизвестно, что реактивные нагрузки, такие как конденсаторы и катушки индуктивности, на самом деле не рассеивают мощность в том смысле, что она не используется для их питания, но измерение напряжения и тока вокруг них указывает на то, что они падают напряжение и потребляют ток.

Мощность, рассеиваемая при этом падении напряжения и потребляемом токе, находится в форме тепла или ненужной энергии и не выполняется как фактическая работа; поэтому инженеры искали способы уменьшить это. Из-за этого фантомного питания проводники и генераторы должны иметь соответствующий номинал и размер, чтобы выдерживать полный ток, включая потери, а не только ток, который выполняет фактическую работу.

Маятник часов

Некоторые эксперты в области энергетики говорят о реактивной мощности как о части движения конденсатора, которое напоминает движение маятника часов от зенита до надира. По этой аналогии, когда маятник качается вверх, переменный ток подает активную мощность на устройство назначения. По мере того, как маятник движется вниз, реактивная мощность возвращается в сеть для поглощения.

В таких определениях эксперты сказали бы, что реактивная энергия — это энергия, циркулирующая взад и вперед между источником и нагрузкой, а именно, что реактивная мощность «исчезает» обратно к источнику.В некотором смысле это связано с задержкой между током и напряжением. Помимо конденсаторов, статические компенсаторы VAr и синхронные конденсаторы могут использоваться для управления реактивной мощностью в системе.

Ключевым моментом является размещение оборудования реактивного тока рядом с силовыми нагрузками. Это уменьшает количество реактивного тока, который система доставки должна переносить на определенное расстояние.

Реактивная мощность в сети

Чтобы справиться с реалиями переменного тока и изменения путей передачи энергии, проектировщики принимают меры по контролю напряжения.Эксперты в области энергетики отмечают, что даже 5% -ное изменение напряжения в данной системе может вызвать отключение электроэнергии и другие проблемы.

С этой целью многие элементы электрической системы, такие как трансформаторы, могут переключаться с подачи на поглощение реактивной мощности по фазам. Но те, кто близок к отрасли, подчеркивают, что это станет еще более важным, когда мы переведем части американской электросети на возобновляемые источники энергии.

Реактивная мощность и возобновляемые источники

Реактивная мощность также очень важна в контексте меняющихся энергосистем.

По многим важным причинам возобновляемые источники энергии, такие как солнце и ветер, заменяют традиционные источники энергии, такие как уголь и природный газ. Но это может иметь разветвления для электросети в целом.

«Всплеск возобновляемых источников энергии в сети без достаточной вращающейся массы может вызвать серьезные проблемы: отключение электроэнергии в определенных областях, чтобы привести спрос в соответствие с предложением; и отключение крупных электростанций от сети, чтобы предотвратить их перегрузку », — пишет Арчи Робб из Renewable Energy World, описывая принцип« инерции сети »и то, как это применимо к управлению реактивной мощностью в системе, которая переходит на возобновляемые источники энергии. строить.

Поскольку возобновляемые источники энергии поставляют энергию в сеть по-разному, возникнет потребность в микроуправлении активной мощностью и реактивной мощностью соответственно.

Активная, реактивная и полная мощность

В этом блоге мы поймем концепцию активной, реактивной и полной мощности. Мы также изучим мгновенную мощность. Мы также увидим, как активная, реактивная и полная мощность связаны друг с другом, что объясняется треугольником мощности. Итак, в конце этого блога мы рассмотрим Треугольник власти.Следовательно, в этом блоге есть о чем рассказать. Итак, начнем.

Для инженера-электрика очень важно знать активную, реактивную и полную мощность, потому что этот раздел является одним из строительных блоков энергосистемы.

Активная, реактивная и полная мощность проявляется только в случае цепей переменного тока, а не в случае цепей постоянного тока, потому что все мы знаем, что формы сигналов напряжения и тока синусоидальны в случае цепей переменного тока.

Вот почему мы изучаем активную, реактивную и полную мощность в цепях переменного тока только не в цепях постоянного тока.В цепях постоянного тока мы изучаем мощность постоянного тока.

Прежде чем изучать активную, реактивную и полную мощность, мы должны знать, «что такое мгновенная мощность?»

МГНОВЕННАЯ СИЛА

Мощность, которая измеряется в определенный момент времени, известна как Мгновенная мощность.

(ИЛИ)

Умножение напряжения и тока в определенный момент времени известно как Мгновенная мощность.

Чтобы понять концепцию мгновенной мощности, давайте рассмотрим форму волны некоторой цепи, показанной на диаграмме ниже.

В момент t ₁

P ₁ = V ₁ (+ ve) * I ₁ (-ve) = -ve

Мгновенная мощность P ₁ в момент t ₁ отрицательна.

В момент t ₂

P ₂ = V ₂ (+ ve) * I ₂ (+ ve) = + ve

Мгновенная мощность P ₂ в момент t ₂ положительна.

Из приведенного выше примера мы можем сказать, что

• Мгновенная мощность может быть положительной и отрицательной.

Что такое положительная сила и отрицательная сила?

Положительная мощность

Когда мощность течет от источника к нагрузке в цепи, мощность называется положительной мощностью .

Отрицательная мощность

В некоторых ситуациях мощность может течь от нагрузки к источнику.В этом случае мощность известна как отрицательная мощность .

• Отрицательная мощность индуцируется в цепи в случае индуктивной нагрузки, емкостной нагрузки и при наличии некоторых нелинейных устройств, таких как выпрямительный мост.

АКТИВНАЯ МОЩНОСТЬ

Чтобы понять концепцию активной мощности, давайте возьмем пример чисто резистивной цепи.

На принципиальной схеме чисто резистивная нагрузка питается от источника переменного тока с напряжением В, и током в цепи I.

В случае чисто резистивной нагрузки напряжение и ток остаются в одной фазе, как показано на векторной диаграмме. Это означает, что формы сигнала как напряжения, так и тока достигают своего положительного и отрицательного пика одновременно, и обе формы сигнала пересекают нулевое значение в один и тот же момент времени, и это можно проверить на формах сигналов, приведенных ниже.

Теперь мы увидим полярность мгновенной мощности в разные моменты времени.

В момент t ₁

P ₁ = V ₁ (+ ve) * I ₁ (+ ve) = + ve

В момент t ₂

P ₂ = V ₂ (-ve) * I ₂ (-ve) = + ve

Следовательно, в случае чисто резистивной нагрузки мощность всегда положительна в каждый момент времени, что означает, что мощность всегда течет от источника к нагрузке.Этот тип мощности известен как активная мощность .

Свойства активной мощности

• Активная мощность всегда положительная.
• Активная мощность не меняет своего направления, как вы можете видеть на осциллограмме.
• Он всегда перетекает от источника к нагрузке.
• Активная мощность всегда отвечает за полезную работу, например: свет, звук, движение и т. Д.
• Обозначается буквой «P» и измеряется в «Вт».{\ circ}} \)
• \ (\ Rightarrow P = VI \ quad Вт \)

РЕАКТИВНАЯ МОЩНОСТЬ

Мы поймем концепцию реактивной мощности с помощью чисто индуктивной цепи.

На принципиальной схеме чисто индуктивная нагрузка питается от источника переменного тока с напряжением В, и током в цепи I.

В случае чисто индуктивной нагрузки ток отстает от напряжения питания на 90 ^o , как показано на векторной диаграмме.

Это означает, что форма волны тока достигает своего положительного пика, отрицательного пика и пересекает нулевое значение 90 ^o после формы волны напряжения. Ниже приведены кривые напряжения, тока и мощности для чисто индуктивной нагрузки.

Теперь мы увидим полярность мгновенной мощности в разные моменты времени.

В момент t ₁

P ₁ = V ₁ (+ ve) * I ₁ (-ve) = -ve

В момент t ₂

P ₂ = V ₂ (-ve) * I ₂ (-ve) = + ve

Следовательно, в случае чисто индуктивной нагрузки мощность может быть как положительной, так и отрицательной.Это означает, что мощность идет вперед и назад между источником и нагрузкой точно так же, как маятник, не выполняя никакой полезной работы в системе. Этот тип мощности известен как реактивная мощность .

Теперь давайте посмотрим, что происходит в случае чисто емкостной нагрузки .

В случае чисто емкостной нагрузки ток опережает напряжение на 90 ^o , что означает, что форма волны тока достигнет своего положительного пика, отрицательного пика и нулевого значения 90 ^o перед формой волны напряжения.Векторная диаграмма и формы сигналов для чисто емкостной нагрузки приведены ниже.

На графике мощности видно, что мощность также является положительной и отрицательной, что означает, что мощность колеблется между источником и нагрузкой, не выполняя никакой полезной работы. Этот тип мощности известен как реактивная мощность .

Если мы внимательно понаблюдаем за формами колебаний мощности как для чисто индуктивной, так и для чисто емкостной нагрузки, мы обнаружим, что величина положительной и отрицательной мощности абсолютно одинакова.

Следовательно, средняя мощность в случае чисто индуктивной нагрузки и чисто емкостной нагрузки равна нулю.

Почему мощность течет назад и вперед в случае индуктивных и емкостных нагрузок?

Во время положительного полупериода, когда мощность положительная, то есть мощность течет от источника к нагрузке, конденсатор накапливает энергию в виде электрического поля.

Во время отрицательного полупериода электрическое поле конденсатора схлопывается, и вся энергия, накопленная в конденсаторе, отправляется обратно к источнику, и мощность начинает течь от нагрузки к источнику.Следовательно, мы получаем отрицательную мощность.

Аналогичным образом, в случае индуктивной нагрузки, в течение положительного полупериода, когда мощность положительная, т. Е. Мощность течет от источника к нагрузке, индуктор накапливает энергию в виде магнитного поля.

Во время отрицательного полупериода магнитное поле индуктора схлопывается, и вся энергия, накопленная в индукторе, высвобождается и отправляется обратно к источнику, и мощность начинает течь от нагрузки к источнику. {\ circ}} \)

\ (\ Rightarrow Q = VI \ quad VAR \)

ВНЕШНЯЯ МОЩНОСТЬ

Случаи, которые мы видели до сих пор (чисто резистивная, чисто индуктивная и чисто емкостная нагрузка), являются стандартными случаями.

На самом деле, большинство нагрузок, которые мы используем в нашей повседневной жизни (например: электрический вентилятор, электрический утюг, асинхронный двигатель и т. Д.), Представляют собой комбинацию резистивной и индуктивной нагрузки. Некоторые нагрузки также могут представлять собой комбинацию резистивной и емкостной нагрузки, но большинство бытовых и промышленных нагрузок представляют собой смесь резистивной и индуктивной нагрузки.

Общая схема для смеси резистивной и индуктивной нагрузки показана на схеме.

Резистивный компонент потребляет активную мощность, а индуктивный компонент потребляет реактивную мощность.Таким образом, общая мощность, отдаваемая источником, представляет собой комбинацию активной и реактивной мощности, и эта мощность известна как полная мощность .

В случае комбинации резистивной и индуктивной нагрузки, ток отстает от напряжения питания на угол \ (\ phi \), что означает, что форма волны тока достигает своего положительного пика, отрицательного пика и нулевого значения с фазовой задержкой \ (\ phi \) От формы сигнала напряжения.

Векторная диаграмма и формы сигналов для смеси резистивной и индуктивной нагрузки приведены ниже.

На диаграмме формы сигнала мы можем видеть, что мощность бывает положительной и отрицательной из-за наличия активной и реактивной мощности в цепи. Кроме того, величина положительной мощности больше, чем величина отрицательной мощности.

Следовательно, средняя мощность в этом случае не будет равна нулю и, следовательно, мы получим некоторую мощность от системы. Но в этом случае средняя мощность меньше по сравнению со средней мощностью чисто резистивной цепи.

Свойства полной мощности

• Полная мощность — это комбинация активной и реактивной мощности.{2} \)

СИЛОВОЙ ТРЕУГОЛЬНИК

Треугольник мощности — это прямоугольный треугольник, который показывает соотношение между активной, реактивной и полной мощностью.

Основание, нормаль и гипотенуза прямоугольного треугольника представляют активную, реактивную и полную мощность соответственно.

Чтобы получить треугольник мощности, мы будем использовать векторную диаграмму смеси резистивной и емкостной нагрузки.

В случае сочетания резистивной и емкостной нагрузки ток опережает напряжение питания на некоторый угол \ (\ phi \).Теперь ток можно разделить на две перпендикулярные составляющие, которые равны

• \ (I \ cos {\ phi} \) = Составляющая тока (I), которая находится в фазе с напряжением питания (В).
  • \ (I \ cos {\ phi} \) известен как Активная или Ваттная составляющая тока (I)
• \ (I \ sin {\ phi} \) = Составляющая тока (I) который на 90 ^o не совпадает по фазе с напряжением питания (В).
  • \ (I \ sin {\ phi} \) известна как Реактивная или безватная составляющая тока (I)

Теперь, чтобы получить треугольник мощности, давайте отдельно нарисуем треугольник тока.{2} \)

Наблюдать за активной, реактивной и полной мощностью

Подробнее

Распределительное устройство и защита

Системы управления и виды систем управления

Мгновенная активная и реактивная мощность — обзор

3.2.1 0,

α, β Координаты

В этом подразделе формулировка так называемой исходной мгновенной реактивной мощности будет представлена ​​в координатах 0, α , β .В четырехпроводных трехфазных системах исходная формулировка определяет две мгновенные действительные мощности p ₀ и p _αβ и мгновенную воображаемую мощность q _αβ , как описано в (3.6)

(3.6) p0pαβqαβ = u0000uαuβ0 − uβuα i0iαiβ

Матричное уравнение (3.6) предполагает, что p ₀ (= v ₀ i ₀ i ₀ в фазовой цепи нулевой последовательности, и, с другой стороны, продукты v _α i _α и v _β i _β также соответствуют мгновенным мощностям, поскольку они определяются как произведение мгновенное напряжение в фазе мгновенным током в той же фазе.Таким образом, p _αβ считается мгновенной активной мощностью в фазной цепи α — и β с размерами ватт, Вт. Напротив, изделия v _α i _β и v _β i _α не являются мгновенными мощностями, поскольку они определяются как произведение мгновенного напряжения и мгновенного фазного тока в другой фазе. Соответственно, q _αβ , в α — и β -фазная цепь — это не мгновенная активная мощность, а новая переменная мощность, определенная в исходной формулировке, и единица измерения указана в [25] как мнимые ватты, IW.

Поскольку в (3.6) трехфазные напряжения u ₀ , u _α , u _β представляют собой набор из трех форм сигналов, налагаемых источником питания, уравнение (3.6 ) можно интерпретировать как геометрическое преобразование (иногда используется термин «отображение») трехмерного вектора текущего пространства в трехмерный вектор пространства мощности, и наоборот [24,25]. Хотя многие из этих матриц «сопоставления» возможны с теоретической точки зрения, лишь немногие из них могут предложить четкое значение с практической точки зрения; действительно, матрица, приведенная в (3.6) оказался полезным при управлении фильтрами активной мощности.

Матрица преобразования (3.6), впервые описанная в 1983 году, поддерживает обратное преобразование,

(3.7) i0iαiβ = 1u0⁡uαβ2 uαβ2000u0⁡uα − u0uβ0u0uβu0⁡uα p0pαβqαβ

, где

uβ2 .

Из (3.7) получаются члены составляющих мгновенных токов 0– α — β координаты

(3.9) i0 = 1u0p0ia = 1uaβ2uapaβ + 1uaβ2 − uβqaβ = iapua + iaqiβ = 1uaβ2βu iβp + iβq

, где i ₀ — мгновенный ток нулевой последовательности, i _αp — мгновенный активный ток фазы α , i _βp — мгновенный активный ток фазы β , i _αq — мгновенный реактивный ток фазы α , i _αq — мгновенный реактивный ток фазы β .

Вывод уравнения (3.9) из (3.7) возможен всякий раз, когда u ₀ ≠ 0, поскольку иначе было бы невозможно вычислить обратную матрицу. Однако i _α и i _β в (3.9) не зависят от u ₀ , даже если оно не равно нулю. Это означает, что исходная формулировка рассматривает цепь нулевой последовательности как однофазную цепь, независимую от цепей α — и β -фаз; следовательно, можно заменить на ₀ = 0, когда исходная формулировка применяется к четырехпроводным трехфазным системам без напряжения нулевой последовательности.

Из уравнений (3.6) и (3.9) следуют отношения степенных членов, (3.10) — (3.11):

(3.10) p (t) = p0 (t) + pa (t) + pβ (t ) = p0 (t) + pap (t) + pβp (t) + paq (t) + pβq (t) = u0i0 + ua2uaβ2paβ + uβ2uaβ2paβ + −uauβuaβ2qaβ + uauβuaβ2qaβ.

(3.11) 0 = uaiaq + uβiβq = ua1uaβ2 (−uβqaβ) + uβ1uaβ2uaqaβ = paq + pβq

Мгновенная активная и реактивная мощность в каждой фазе обозначается следующим образом:

901 u ₀ i ₀ : мгновенная мощность нулевой последовательности

p _αp = u _α i 90p52: фаза, мгновенная активная мощность

p _βp = u _β i _βp : β14 9153

фазная активная мощность _αq = u _α i _αq : α- мгновенная реактивная мощность фазы

90 153 p _βq = u _β i _βq : β- мгновенная реактивная мощность фазы

Рисунок 3.3a и b описывают поток мощности, основанный на исходной формулировке четырехпроводной трехфазной системы. В исходной структуре схема нулевой последовательности мгновенной реактивной мощности рассматривается как отдельная однофазная цепь фазной цепи α, — и β- .

Рисунок 3.3. Поток мощности основан на формулировке исходной мгновенной реактивной мощности.

Этот подход заимствован из метода симметричных компонентов, который делит четырехпроводную трехфазную цепь на схему нулевой последовательности, схему прямой последовательности и схему обратной последовательности; цепь нулевой последовательности рассматривается как независимая однофазная цепь от других цепей последовательности фаз.

Уравнение (3.11) означает, что сумма мгновенной реактивной мощности фазы α- , p _αq и β -фазная мгновенная реактивная мощность, p _βq , всегда равна нуль. Это предполагает, что оба они не участвуют в передаче энергии между источником и нагрузкой в ​​фазовой цепи α – β- . Однако p _αq участвует в передаче энергии в фазовой цепи α- , так же, как p _βq в фазовой цепи β- , увеличивая значение тока, протекающего через каждую из фаз.Таким образом, исходная формулировка, введенная стороной q _αβ как мгновенная мнимая мощность, которая определяет p _αq и p _βq , а вторая определяет два независимых мгновенных действительных мощности p ₀ и p _αβ ; три степенных переменных образуют трехмерное силовое пространство.

Пример 3.1

Определение переменных мощности для реактивной сбалансированной трехфазной нагрузки на Рисунке 3.4, который питается от сбалансированной трехфазной системы напряжения (3.12).

(3.12) u1 (t) = 2 VF cos ωtu2 (t) = 2 VF cos (ωt — 120) u3 (t) = 2 VF cos (ωt + 120)

Рисунок 3.4. Сбалансированная трехфазная нагрузка звездой, состоящая из трех индуктивностей.

Линейные токи, циркулирующие в индуктивной сбалансированной трехфазной нагрузке, имеют вид (3.13)

(3.13) i1 (t) = 2 IF cos (ωt − φ) i2 (t) = 2 IF cos (ωt − 120 −φ) i3 (t) = 2 IF cos (ωt + 120 − φ)

, где φ для нагрузки на Рисунке 3.4 — 90 °. Из (3.1) составляющие напряжения находятся в плоскости α, β .

(3,14) uα = 3VF cos ωt; uβ = 3VF sin ωt

Аналогично (3.2) составляющие тока, полученные в плоскости α, β , равны

(3.15) iα = 3IF sin ωt; iβ = −3IF cos ωt

Из (3.6) получаются три переменные мощности:

(3.16) p0 = 0pαβ = 0qαβ = −3VFIF sin90

Сбалансированная трехфазная нагрузка, показанная на рисунке 3.4, питаемая сбалансированной синусоидальной тройкой. -фазное напряжение фаз прямой последовательности поглощает мгновенную активную мощность, равную активной мощности (средней мощности).Активная мощность для чисто реактивной нагрузки равна нулю; в результате (3.16) становится (3.17),

(3.17) p (t) = p0 (t) + paβ (t) = P = 0

С другой стороны, (3.16) показывает, что мгновенная мнимая мощность для Нагрузка на Рисунке 3.4 для условий этого упражнения представляет собой среднее значение реактивной мощности противоположного знака,

(3.18) qaβ = −3VFIF = −Q

Из этого примера вытекают два наблюдения. Во-первых, описание потока энергии между источником и нагрузкой невозможно с помощью только мгновенной переменной реальной мощности, как это происходит в случае однофазных систем.Для трехфазной системы, рассматриваемой как глобальная система, необходимо определить новую переменную мощности. Формулировка исходной мгновенной реактивной мощности вводит мгновенную воображаемую мощность, чтобы завершить описание процесса передачи энергии между источником и нагрузкой. Во-вторых, определение, данное в (3.6), вводит мгновенную мнимую мощность, среднее значение которой является средней реактивной мощностью противоположного знака. Эта ситуация будет преодолена в разделе 3.2.2, где мгновенная мнимая мощность вводится с противоположным знаком; ну, его среднее значение принимает положительное значение для положительной последовательности фаз и отрицательное значение для отрицательной последовательности фаз.Эта модификация кажется более совместимой с условными обозначениями стандартных знаков.

Таким образом, в этом примере линейные токи включают только мгновенную составляющую реактивного тока.

Формулировка мгновенной реактивной мощности устанавливается с помощью того, что мы называем матрицей отображения, как было продемонстрировано при разработке этого подраздела, однако возможно развитие вектора. Фактически, как было заявлено в [17, 21], в трехмерном пространстве, определяемом осями 0 αβ, вектор пространства трех напряжений может быть определен как

(3.19) uαβ = 0uαuβ; u0 = u000; u − βα = 0 − uβuα

Пространственный вектор u _αβ — проекция пространственного вектора напряжения u _{0 αβ} в плоскости вектора αβ , u ₀ следует направлению оси 0 и вектора u _{— βα} называется ортогональным вектором напряжения, так как u _{αβ также 901 расположен в плоскости αβ .}

Три вектора перпендикулярны друг другу, поэтому скалярное произведение между любыми двумя из них равно нулю. В частности, проверяются следующие соотношения:

(3.20) u0αβ = u0uαuβt = uαβ + u0

(3.21) u − βα⋅u0αβ = 0

Текущий пространственный вектор i (3.22)

(3.22 ) i = i0iαiβt

можно разделить на три составляющие, которые являются проекциями вектора тока на три вектора напряжения (3.19). Фактически

(3.23) i = pαβ (t) uαβ⋅uαβuαβ + qαβ (t) u − βα⋅u − βαu − βα + p0 (t) u0⋅u0u0

Степенная переменная (3.6) появляется в числителе каждого текущего члена, мгновенная активная мощность в фазе αβ-

(3,24) pαβ (t) = uαβ. i

мгновенная активная мощность нулевой последовательности

(3,25) p0 (t) = u0. i

и мгновенная мнимая мощность в плоскости αβ- ,

(3,26) qαβ (t) = u − βα. i

В знаменателях каждой составляющей мгновенного тока фигурируют квадраты норм каждого вектора напряжения,

(3.