Конденсатор в цепи постоянного и переменного тока

Конденсатор в цепи постоянного тока

Итак, берем блок питания  постоянного напряжения и выставляем на его крокодилах напряжение в 12 Вольт.  Лампочку тоже берем на 12 Вольт. Теперь между одним щупом блока питания и лампочки вставляем конденсатор:

Не-а, не горит.

А  вот если напрямую сделать, то горит:

Отсюда напрашивается вывод: постоянный ток через конденсатор не течет!

Если честно, то в самый начальный момент подачи напряжения ток все-таки течет на доли секунды. Все зависит от емкости конденсатора.

Конденсатор в цепи переменного тока

Итак, чтобы узнать, течет ли переменный ток через конденсатор, нам нужен генератор переменного тока. Думаю, этот  генератор част оты вполне сойдет:

Так как китайский генератор у меня очень слабенький, то мы вместо нагрузки-лампочки будем использовать простой резистор на 100 Ом. Также возьмем и конденсатор емкостью в 1 микрофарад:

Спаиваем как-то вот так и подаем сигнал с генератора частоты:

Далее за дело берется Цифровой осциллограф OWON SDS 6062. Что такое осциллограф и с чем его едят, читаем зде   сь.  Будем использовать сразу два канала. На одном экране будут высвечиваться сразу два сигнала. Здесь на экранчике уже видны наводки от сети 220 Вольт. Не обращайте внимание.

Будем подавать переменное напряжение и смотреть сигналы, как говорят профессиональные электронщики, на входе и на выходе. Одновременно.

Все это будет выглядеть примерно вот так:

Итак, если у нас частота нулевая, то это значит постоянный ток. Постоянный ток, как мы уже видели, конденсатор не пропускает. С этим вроде бы разобрались. Но что будет, если подать синусоиду с частотой в 100 Герц? 

На дисплее осциллографа я вывел такие параметры, как частота сигнала и его амплитуда:  F – это частота, Ma – амплитуда (эти параметры пометил белой стрелочкой). Первый канал помечен красным цветом, а второй канал – желтым,  для удобства восприятия.

Красная синусоида показывает сигнал, который выдает нам китайский генератор частоты. Желтая синусоида – это то, что мы уже получаем на нагрузке. В нашем случае нагрузкой является резистор. Ну вот, собственно, и все.

Как вы видите на осциллограмме выше, с генератора я подаю синусоидальный сигнал с частотой в 100 Герц и амплитудой в 2 Вольта.  На резисторе мы уже видим сигнал с такой же частотой (желтый сигнал), но его амплитуда составляет каких-то 136 милливольт. Да еще и сигнал получился какой-то “лохматый”. Это связано с так называемыми “шумами“. Шум – это сигнал с маленькой амплитудой и беспорядочным изменением напряжения. Он может быть вызван самими радиоэлементами, а также это могут быть помехи, которые ловятся из окружающего пространства. Например очень хорошо “шумит” резистор. Значит “лохматость” сигнала – это сумма синусоиды и шума.

Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается влево, то есть опережает красный сигнал, или научным языком, появляется

сдвиг фаз. Опережает именно фаза, а не сам сигнал. Если бы опережал сам сигнал, то у нас бы тогда получилось, что сигнал на резисторе появлялся бы по времени раньше, чем сигнал, поданный на него через конденсатор. Получилось бы какое-те перемещение во времени :-), что конечно же, невозможно.

Сдвиг фаз – это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют,

разность фаз:

Давайте увеличим частоту  на генераторе до 500 Герц

На резисторе уже получили 560 милливольта. Сдвиг фаз уменьшается.

Увеличиваем частоту до 1 КилоГерца

На выходе у нас уже 1 Вольт.

Ставим частоту 5 Килогерц

Амплитуда 1,84 Вольта и сдвиг фаз явно стает меньше

Увеличиваем до 10 Килогерц

Амплитуда уже почти  такая же как и на входе. Сдвиг фаз менее заметен.

Ставим 100 Килогерц:

Сдвига фаз почти нет. Амплитуда почти такая же, как и на входе, то есть 2 Вольта.

Отсюда делаем глубокомысленные выводы:

Чем больше частота, тем меньшее сопротивление конденсатор оказывает переменному току. Сдвиг фаз убывает с увеличением частоты почти до нуля. На бесконечно низких частотах его величина составляет 90 градусов или π/2.

Если построить обрезок графика, то получится типа что-то этого:

По вертикали я отложил напряжение, по горизонтали –  частоту.

Итак, мы с вами узнали, что сопротивление конденсатора зависит от частоты. Но только ли от частоты? Давайте возьмем конденсатор емкостью в 0,1 микрофарад, то есть номиналом в 10 раз меньше, чем предыдущий и снова прогоним по  этим же частотам.

Смотрим и анализируем значения:

Внимательно сравните амплитудные значения желтого сигнала на одной и той же частоте, но с разными номиналами конденсатора. Например, на частоте в 100 Герц  и номиналом конденсатора в 1 мкФ амплитуда желтого сигнала равнялась 136 милливольт, а на этой же самой частоте амплитуда желтого сигнала, но с конденсатором в 0,1 мкФ уже была 101 милливольт( в реальности еще меньше из за помех). На частоте 500 Герц –  560 милливольт и 106 милливольт соответственно, на частоте в 1 Килогерц – 1 Вольт и 136 милливольт и так далее.

Отсюда вывод напрашивается сам собой: при уменьшении номинала конденсатора его сопротивление стает больше.

С помощью физико-математических преобразований физики и математики вывели формулу для расчета сопротивления конденсатора. Прошу любить и жаловать:

где, Х_С

  – это сопротивление конденсатора, Ом

П – постоянная и равняется приблизительно 3,14 

F – частота, измеряется в Герцах

С – емкость,  измеряется в Фарадах

Так вот, поставьте в эту формулу частоту в  ноль Герц. Частота в ноль Герц – это и есть постоянный ток. Что получится? 1/0=бесконечность или очень большое сопротивление. Короче говоря, обрыв цепи.

Заключение

Забегая вперед, могу сказать, что в данном опыте мы получили Фильтр Высокой Частоты (ФВЧ). С помощью простого конденсатора и резистора, применив где-нибудь в звуковой аппаратуре такой фильтр на динамик,  в динамике мы будет слышать только писклявые высокие тона.  А вот  частоту баса как раз и заглушит такой фильтр. Зависимость сопротивления конденсатора от частоты очень широко используется в радиоэлектронике, особенно в различных фильтрах, где надо погасить одну частоту и пропустить другую.

принцип работы устройства, реактивная электроэнергия

Конденсатор в цепи переменного тока или постоянного, который нередко называется попросту кондёром, состоит из пары обкладок, покрытых слоем изоляции. Если на это устройство будет подаваться ток, оно будет получать заряд и сохранять его в себе некоторое время. Емкость его во многом зависит от промежутка между обкладками.

Принцип работы

Конденсатор может быть выполнен по-разному, но суть работы и основные его элементы остаются неизменными в любом случае. Чтобы понять принцип работы, необходимо рассмотреть самую простую его модель.

У простейшего устройства имеются две обкладки: одна из них заряжена положительно, другая — наоборот, отрицательно. Заряды эти хоть и противоположны, но равны. Они притягиваются с определенной силой, которая зависит от расстояния. Чем ближе друг к другу располагаются обкладки, тем больше между ними сила притяжения. Благодаря этому притяжению заряженное устройство не разряжается.

Однако достаточно проложить какой-либо проводник между двумя обкладками и устройство мгновенно разрядится. Все электроны от отрицательно заряженной обкладки сразу же перейдут на положительно заряженную, в результате чего заряд уравняется. Иными словами, чтобы снять заряд с конденсатора, необходимо лишь замкнуть две его обкладки.

Описание конденсатора постоянного тока

Электрические цепи бывают двух видов — постоянными или переменными. Все зависит от того, как в них протекает электроток. Устройства в этих цепях ведут себя по-разному.

Чтобы рассмотреть, как будет вести себя конденсатор в цепи постоянного тока, нужно:

1. Взять блок питания постоянного напряжения и определить значение напряжения. Например, «12 Вольт».
2. Установить лампочку, рассчитанную на такое же напряжение.
3. В сеть установить конденсатор.

Никакого эффекта не будет: лампочка так и не засветится, а если убрать из цепи конденсатор, то свет появится. Если устройство будет включено в сеть переменного тока, то она попросту не будет замыкаться, поэтому и никакой электроток здесь пройти не сможет. Постоянный — не способен проходить по сети, в которую включен конденсатор. Всему виной обкладки этого устройства, а точнее, диэлектрик, который разделяет эти обкладки.

Убедиться в отсутствии напряжения в сети постоянного электротока можно и другими способами. Подключать к сети можно, что угодно, главное, чтобы в цепь был включен источник постоянного электротока. Элементом же, который будет сигнализировать об отсутствии напряжения в сети или, наоборот, о его присутствии, также может быть любой электроприбор. Лучше всего для этих целей использовать лампочку: она будет светиться, если электроток есть, и не будет гореть при отсутствии напряжения в сети.

Можно сделать вывод, что конденсатор не способен проводить через себя постоянный ток, однако это заключение неправильное. На самом деле электроток сразу после подачи напряжения появляется, но мгновенно и исчезает. В этом случае он проходит в течение лишь нескольких долей секунды. Точная продолжительность зависит от того, насколько емким является устройство, но это, как правило, в расчет не берется.

Особенности устройства с переменным электротоком

Чтобы определить, будет ли проходить переменный электроток, необходимо устройство подключить в соответствующую цепь. Основным источником электроэнергии в таком случае должно являться устройство, генерирующее именно переменный электроток.

Постоянный электрический ток не идет через конденсатор, а вот переменный, наоборот, протекает, причем устройство постоянно оказывает сопротивление проходящему через него электротоку. Величина этого сопротивления связана с частотой. Зависимость здесь обратно пропорциональная: чем ниже частота, тем выше сопротивление. Если к источнику переменного электротока подключить кондер, то наибольшее значение напряжения здесь будет зависеть от силы тока.

Убедиться в том, что конденсатор может проводить переменный электроток, наглядно поможет простейшая цепь, составленная из:

• Источника тока. Он должен быть переменным.
• Конденсатора.
• Потребителя электротока. Лучше всего использовать лампу.

Однако стоит помнить об одном: лампа загорится лишь в том случае, если устройство имеет довольно большую емкость. Переменный ток оказывает на конденсатор такое влияние, что устройство начинает заряжаться и разряжаться. А ток, который проходит по сети во время перезарядки, повышает температуру нити накаливания лампы. В результате она и светится.

От емкости устройства, подключенного к сети переменного тока, во многом зависит электроток перезарядки. Зависимость прямо пропорциональная: чем большей емкостью обладает, тем больше величина, характеризующая силу тока перезарядки. Чтобы в этом убедиться, достаточно лишь повысить емкость. Сразу после этого лампа начнет светиться ярче, так как нити ее будут больше накалены. Как видно, конденсатор, который выступает в качестве одного из элементов цепи переменного тока, ведет себя иначе, нежели постоянный резистор.

При подключении конденсатора переменного тока начинают происходить более сложные процессы. Лучше их понять поможет такой инструмент, как вектор. Главная идея вектора в этом случае будет заключаться в том, что можно представить значение изменяющегося во времени сигнала как произведение комплексного сигнала, который является функцией оси, отображающей время и комплексного числа, которое, наоборот, не связано со временем.

Поскольку векторы представляются некоторой величиной и некоторым углом, начертить их можно в виде стрелки, которая вращается в координатной плоскости. Напряжение на устройстве немного отстает от тока, а оба вектора, которыми они обозначаются, вращаются на плоскости против часовых стрелок.

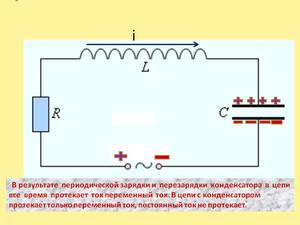Конденсатор в сети переменного тока может периодически перезаряжаться: он то приобретает какой-то заряд, то, наоборот, отдает его. Это означает, что кондер и источник переменного электротока в сети постоянно обмениваются друг с другом электрической энергией. Такой вид электроэнергии в электротехнике носит название реактивной.

Конденсатор не позволяет проходить по сети постоянному электротоку. В таком случае он будет иметь сопротивление, приравнивающееся к бесконечности. Переменный же электроток способен проходить через это устройство. В этом случае сопротивление имеет конечное значение.

Резистор и конденсатор в цепи генератора переменного напряжения

Решение

Запишем закон Ома для цепи переменного тока:

JR + Uc = 0 cos ωt.

Здесь J и U_c – мгновенные значения тока в цепи и напряжения на конденсаторе. Принимая во внимание, что где q – заряд конденсатора, получим

Мы получили линейное дифференциальное уравнение, описывающее процессы, происходящие в RC-цепях под действием синусоидального напряжения генератора. Будем искать решение в виде u_c = U_c cos (ωt + φ). Подставим это выражение в дифференциальное уравнение:

–ωRCUc sin (ωt + φ) + Uc cos (ωt + φ) = 0 cos ωt.

Полученное трансцендентное уравнение проще всего решать графически с помощью векторной диаграммы. Первый член этого уравнения по формулам тригонометрии можно преобразовать к виду:

–ωRCUc sin (ωt + φ) = ωRCUc cos (ωt + φ + π / 2).

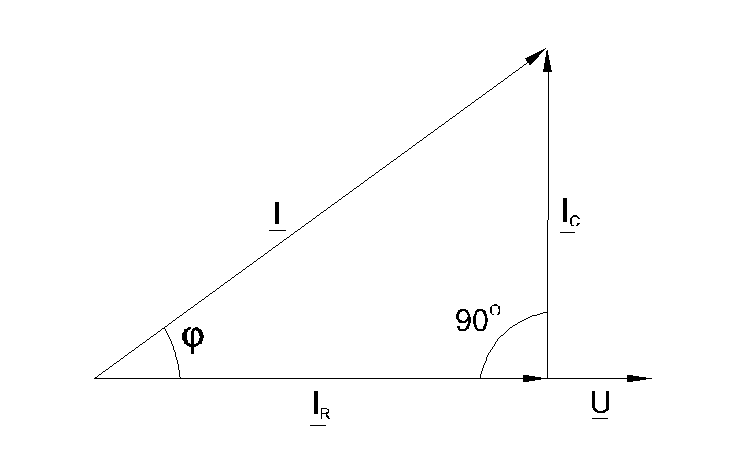
Отсюда следует, что колебания, описываемые первым и вторым членами в левой части уравнения, сдвинуты по фазе на угол π / 2. На векторной диаграмме эти колебания должны изображаться векторами, ориентированными перпендикулярно друг другу, и, следовательно, векторная диаграмма должна иметь вид прямоугольного треугольника (см. рис.).

• Из данных в условии задачи следует, что ωRC = 1, следовательно

• Фазовый сдвиг φ между напряжением генератора и напряжением на конденсаторе определяется соотношением

  tg φ = – ωRC = –1.

  Напряжение на конденсаторе отстает по фазе от напряжения генератора на угол π / 4.

39. Переменный ток. Резистор, конденсатор и катушка в цепи переменного тока.

14. Элементы цепи переменного тока

Резистор в цепи постоянного тока

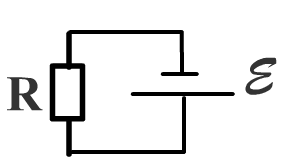
По закону Ома, в замкнутой цепи постоянного тока

напряжение на зажимах источника меньше ЭДС

U = IR; U = E — Ir

15. Резистор в цепи переменного тока

Р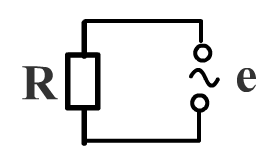ассмотрим схему, состоящую из источника переменного

тока, резистора и идеальных проводов.

Предположим, что напряжение на резисторе

изменяется по гармоническому закону

U = U₀ cos ω t .

Найдем силу тока, протекающего через резистор.

По закону Ома для участка цепи

I=U/R ==> I = I₀ cos ω t

Амплитуда силы тока I₀ = U₀/R

Ток и напряжение изменяются по одинаковому гармоническому закону (косинуса), то есть совпадают по фазе. Это означает, что, например, в тот момент времени, когда в цепи максимальна сила тока, напряжение на резисторе также максимально.

16. Конденсатор в цепи переменного тока

Включим конденсатор в цепь постоянного тока.Некоторый заряд перетечет от источника тока на обкладки конденсатора.В цепи возникает кратковременный импульс зарядного тока. Конденсатор заряжается до напряжения источника, после чего ток прекращается. Через конденсатор постоянный ток течь не может!

Р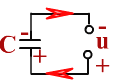ассмотрим процессы, происходящие при включении конденсатора в цепь переменного тока

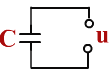
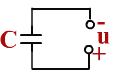
зарядный ток

.

Через диэлектрик, разделяющий обкладки конденсатора, электрический ток протекать, как и прежде, не может. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в цепи появится переменный ток.

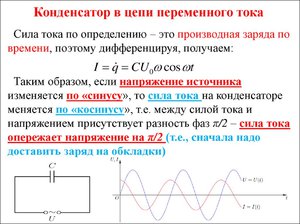
Если напряжение в цепи изменяется по гармоническому закону,

U = U₀cos ωt

то заряд на обкладках конденсатора изменяется

также погармоническому закону

q=Cu = CU₀cos ωt

и силу тока в цепи можно найти как производную заряда

i = q^/

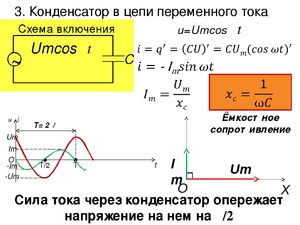
i= -CU₀ ω sin ωt = CU₀ω cos(ωt+π/2),

i= I₀ω cos(ωt+π/2)

Амплитуда силы тока I₀ = CU₀ω

Из полученной формулы видно, что в любой момент времени

фаза тока больше фазы напряжения на π/2.

В цепи переменного напряжение на конденсаторе тока отстает по фазе от тока на π/2, или на четверть периода.

Емкостное сопротивление

Величину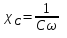

называют емкостным сопротивлением.

Связь между амплитудными значениями силы тока и напряжения формально совпадает с законом Ома для участка цепи

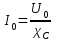
Такое же соотношение выполняется для действующих значений силы тока и напряжения.

Емкостное сопротивление конденсатора зависит от частоты переменного напряжения. С увеличением частоты колебаний напряжения емкостное сопротивление уменьшается, поэтому амплитуда силы тока увеличивается прямо пропорционально частоте I₀ = CU₀ω.

При уменьшении частоты амплитуда силы тока уменьшается и при ω=0 обращается в 0. Отметим, что нулевая частота колебаний означает, что в цепи протекает постоянный ток.

17. Катушка индуктивности в цепи переменного тока

Мы предполагаем, что катушка индуктивности обладает пренебрежимо малым активным сопротивлением R. Такой элемент включать в цепь постоянного тока нельзя, потому что произойдет короткое замыкание.

В цепи переменного тока мгновенному нарастанию силы тока препятствует ЭДС самоиндукции. При этом для сверхпроводника e_i+u=0.

Используя закон Фарадея для самоиндукции e_i= -Li^/ ,

можно показать, что, если сила тока в цепи изменяется по гармоническому закону

i= I₀cos(ωt),

то колебания напряжения на катушке описываются

уравнением

U = — I₀ Lωsin ωt = I₀ Lω cos(ωt+π/2),

то есть колебания напряжения опережают по фазе колебания силы тока на π/2.Произведение U₀ = I₀Lω является амплитудой напряжения:

U = U₀ cos(ωt+π/2)

Индуктивное сопротивление

Величину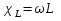

6.2. Параллельное соединение резистора и конденсатора

6.2.1. Общие сведения

Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.

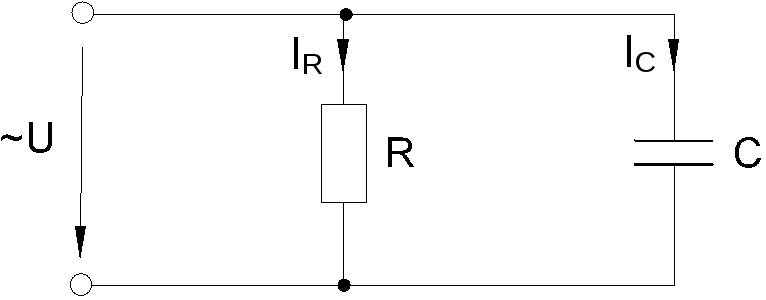
Рис. 6.2.1

Общий ток цепи Iразветвляется на ток в конденсатореI_C (емкостная составляющая общего тока) и ток в резистореI_R (активная составляющая).

Между токами I, I_CиI_Rсуществуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлениемX_Cконденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).

Рис. 6.2.2	Рис. 6.2.3

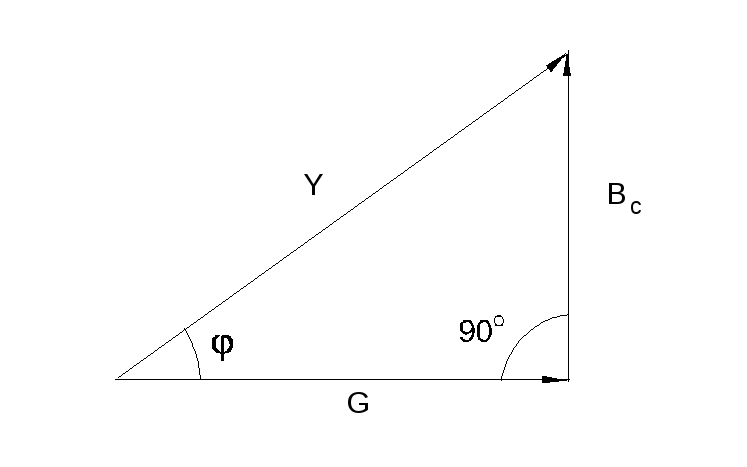
Фазовый сдвиг между напряжением Uцепи и током в резистореI_R отсутствует, тогда как между этим напряжением и током в конденсатореI_Cравен –90⁰(т.е. ток опережает напряжение на 90⁰). При этом сдвиг между полным токомI и напряжениемUцепи определяется соотношением между проводимостямиB_CиG. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.2.3).

В треугольнике проводимостей G=1/R,B_C=1/X_C, аYпредставляет собой так называемую полную проводимость цепи в См, тогда какG– активная, аB_C – реактивная (емкостная) проводимости.

Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:I = I_R +I_C.

Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:

Действующее значение полного тока цепи

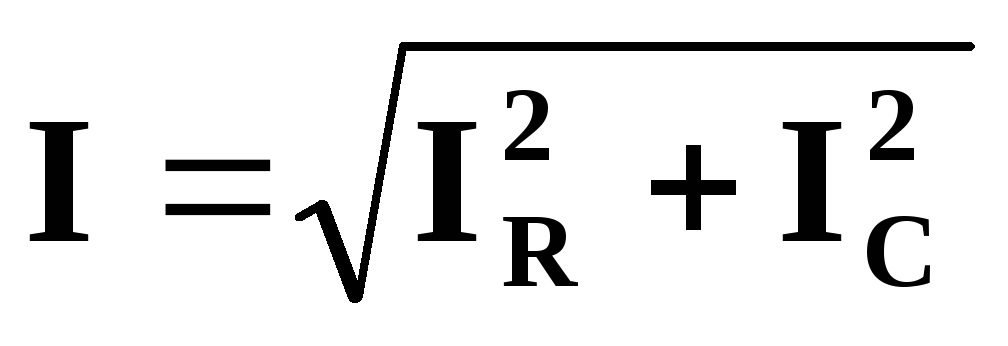; I = U  Z = UY.

Полная проводимость цепи

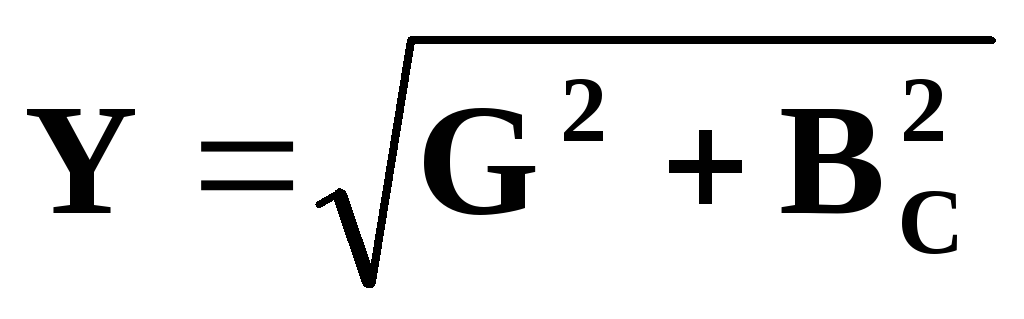; Y = I U = 1/Z ,

где Z — полное сопротивление цепи.

Угол сдвига фаз

 = arctg (I _C  I_R) = arctg (B_C  G).

Активная и реактивная проводимости

G = Y cos; B_C=Ysin.

6.2.2. Экспериментальная часть Задание

Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе I_Rи конденсатореI _C, полный токIи вычислите угол сдвига фаз, полное сопротивление цепиZи емкостную реактивную проводимостьB_C.

Порядок выполнения работы

• Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U= 5 В,f= 1 кГц.

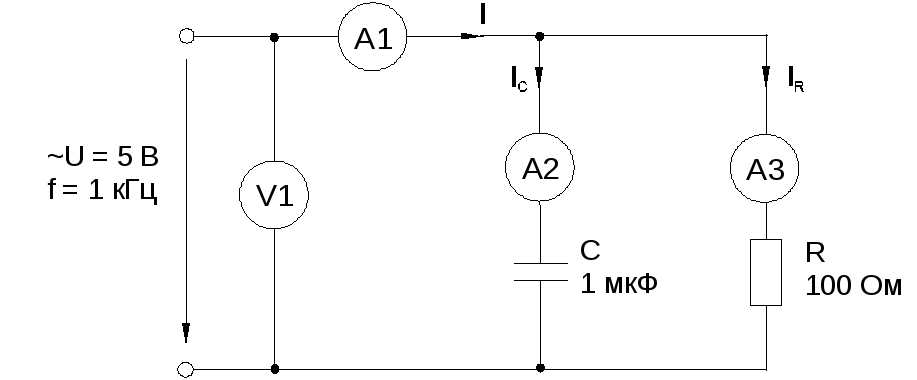
Рис. 6.2.4

• Выполните измерения U,I,I_C,I_Rи занесите результаты в табл. 6.2.1. Если измерения производите виртуальными приборами, то измерьте такжеR, , X_C, Z.

Таблица 6.2.1

U,B	I, мА	IС, мА	IR, мА	, град	R, Ом	XC, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

Фазовый угол

 = arctg (I _C  I _R) =

Активные проводимость цепи и сопротивление цепи

G = I_R  U ; R = U  I_R.

Емкостные реактивные проводимость и сопротивление цепи

B_C = I_C  U ; X_C = U  I_C.

Полные проводимость и сопротивление цепи

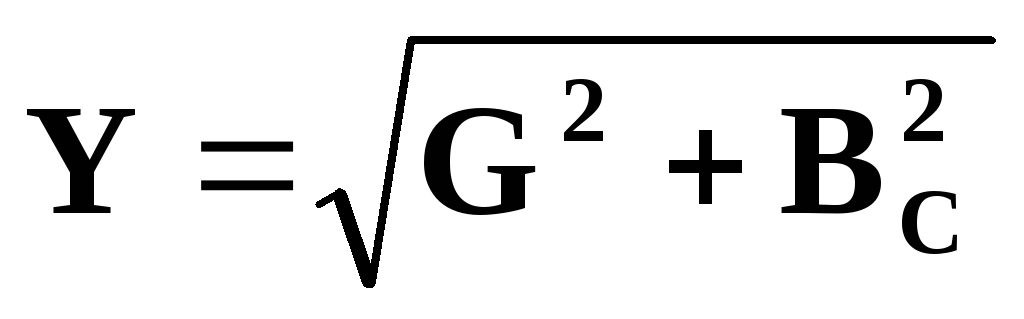; Z = 1  Y.

Рис. 6.2.5 Рис. 6.2.6

2.2. Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока

Составными элементами цепей синусоидального тока являются резистор, индуктивная катушка и конденсатор. Для упрощения исследования процессов в реальной электрической цепи переменного тока эту цепь, как и цепь постоянного тока, представляют схемой замещения, составленной из этих элементов. Эле­менты цепи переменного тока, в которых энергия выделяется в виде теплоты, на­зываются активными. Элементы цепи, в которых периодически запасается энер­гия в электрическом или магнитном поле, называются реактивными, а сопротив­ления, оказываемые ими переменному току –реактивными сопротивлениями. Реактивные сопротивления имеют катушки и конденсаторы.

Рассмотрим соотношения между токами и напряжениями в простейших цепях.

2.2.1. Резистор в цепи синусоидального тока

Если синусоидальное напряжение 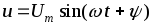(рис. 2.6 а) подклю­чить к резистору с сопротивлением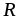, то через него будет протекать синусоидаль­ный ток

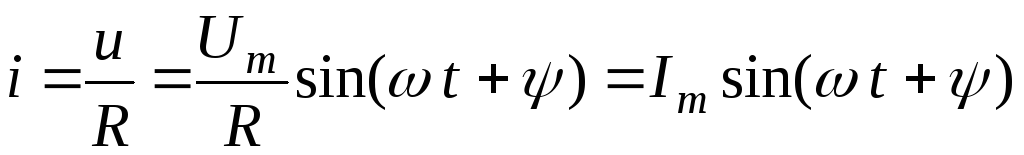(2.7)

Следовательно, напряжение на зажимах и ток, проходящий через резистор, имеют одинаковую начальную фазу, или, как говорят, совпадают по фазе– они одновременно достигают своих амплитудных значений и соответственно одно­временно проходят через нуль (рис. 2.6 б, в).

Разность начальных фаз двух синусоид называют углом сдвига фаз. В дан­ном случае угол сдвига фаз между напряжением и током равен нулю

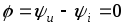. (2.8)

Амплитуды и действующие значения тока и напряжения связаны законом Ома

;.

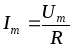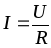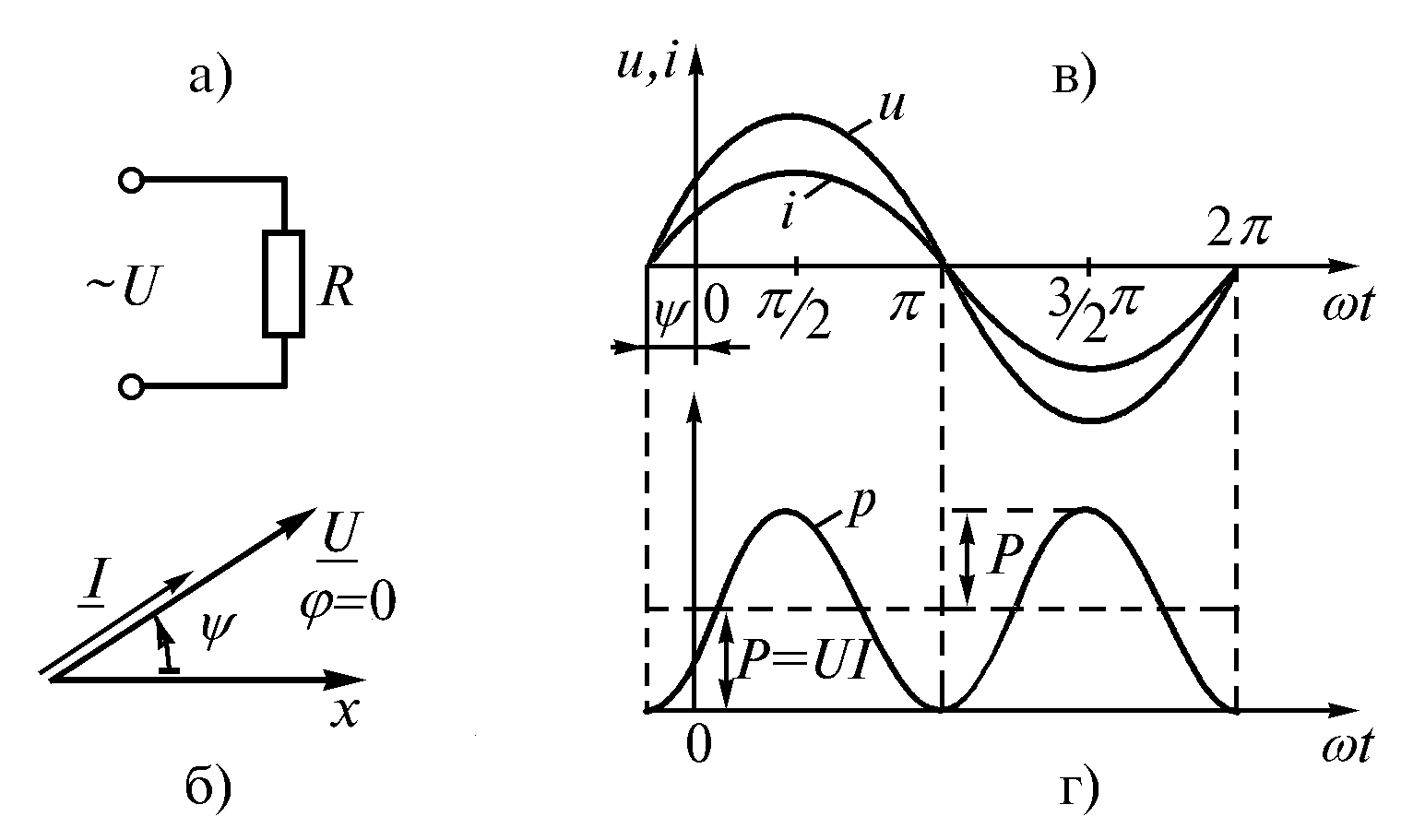
Рис. 2.6

Протекание тока через резистор сопровождается потреблением энергии от источников. Скорость поступления энергии характеризуется мощностью. Мгно­венная мощность, потребляемая резистором

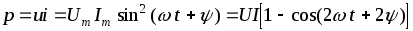, (2.9)

изменяется с угловой частотой, удвоенной по сравнению с частотой напряжения и тока. Мгновенная мощность имеет постоянную составляющую 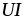и составляю­щую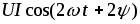, изменяющуюся с частотой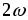(рис. 2.6 г). Так как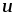и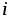совпадают по фазе, т.е. всегда имеют одинаковый знак, то их произведение всегда положительно, следовательно,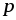> 0.

Среднее значение мгновенной мощности за период

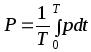(2.10)

называется активной мощностьюи измеряется в ваттах. В данном случае актив­ная мощность

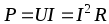. (2.11)

Отсюда активное сопротивление

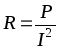. (2.12)

Известно, что сопротивление проводника переменному току больше, чем постоянному, вследствие явления поверхностного эффекта.

2.2.2. Индуктивная катушка в цепи синусоидального тока

Индуктивная катушка как элемент схемы замещения реальной цепи синусои­дального тока дает возможность учитывать при расчете явление самоиндук­ции и явление накопления энергии в ее магнитном поле. Пусть в цепь перемен­ного тока (рис 2.7 а) включена катушка с бесконечно малым сопро­тивлением провода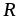= 0. Непрерывное во времени изменение тока вызывает появ­ление в витках катушки ЭДС самоиндукции. В соответствии с правилом Ленца эта ЭДС противодействует изменению тока.

Допустим, ток через катушку изменяется по закону

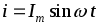. (2.13)

В этом случае ЭДС самоиндукции

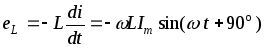. (2.14)

Поэтому напряжение на катушке

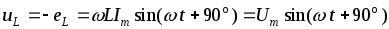. (2.15)

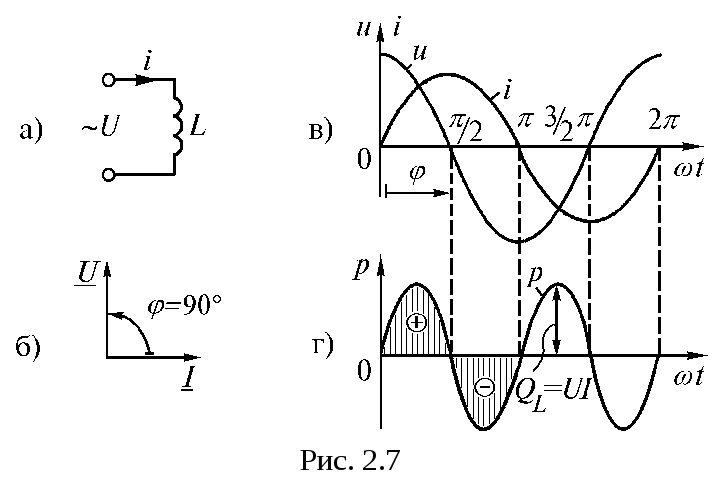Сравнивая формулы (2.13) и (2.15), можно сделать вывод о том, чтонапряже­ние на катушке опережает ток на угол 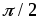или ток отстает от напряжения по фазе на угол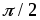(рис 2.7 б). Угол сдвига фаз в этом случае положительный (рис. 2.7 в).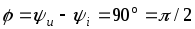

Параметр цепи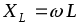–индуктивное сопротивление, имеющее размерностьОм. Оно зависит от частоты и представляет собой величину, с помо­щью которой учитывается явление самоиндукции.

Из анализа (2.14) видно, что амплитуды напряжения и тока связаны законом Ома:

.

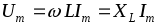Аналогично для действующих значений

.

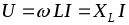Мгновенная мощность цепи с катушкой

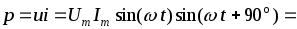
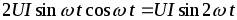. (2.16)

Из графика (рис 2.7 г), построенного по уравнению (2.16), видно, что за пер­вую четверть периода, когда 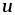> 0 и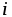> 0, площадь, ограниченная кривой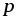и осью абсцисс, пропорциональна энергии, потребляемой катушкой на создание магнитного поля. Во вторую четверть периода (ток убывает от максимума до нуля) энергия магнитного поля катушки передается источнику питания. При этом мгновен­ная мощность отрицательна, а процесс повторяется. Таким образом, происходит колебание энергии между источником и катушкой, причемактивная мощность, поступающая в катушку, равна нулю. Амплитуду колебания мгновенной мощ­ности в цепи с катушкой называютреактивной (индуктивной) мощностью

.

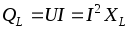Реактивную мощность в отличие от активной мощности измеряют в вар(вольт-ампер реактивный).

Конденсатор в цепи постоянного тока

Заряд конденсатора через резистор

При подключении конденсатора к источнику постоянного тока под действием электрического поля на нижнюю обкладку движутся электроны. В следствии, явления электростатической индукции с верхней обкладки конденсатора заряды уходят к положительному выводу источника питания в цепи возникает ток – ток заряда по мере накопления зарядов в конденсаторе, растёт напряжение , а ток заряда уменьшается, и так, – конденсатор подключённый к источнику тока, заряжается до Uист.

Конденсатор в цепи постоянного тока

 

 

Кратковременный ток в цепи называется ток заряда, а так как он существует короткое время, то говорят, конденсатор постоянный ток не пропускает.

Считается что конденсатор заряжается если напряжение на нём составляет 0,63 от Uист и это происходит за время
равное Τ

Ес – ЭДС ёмкости

Τ заряда – постоянная времени заряда конденсатора в секундах

Одна секунда – 1с = 103мс = 106мкс =1012нс

Rзар – сопротивление в Омах

С – ёмкость в Фарадах

Τ = Rзар × С

График заряда конденсатора

Разряд конденсатора через резистор

Работа конденсатора в цепи постоянного тока

Считается, что конденсатор разрядится если напряжение на нём составляет 0,37 от напряжения источника и это происходит за время Τ разряда.

Τразр = Rразр × С

График разряда конденсатора