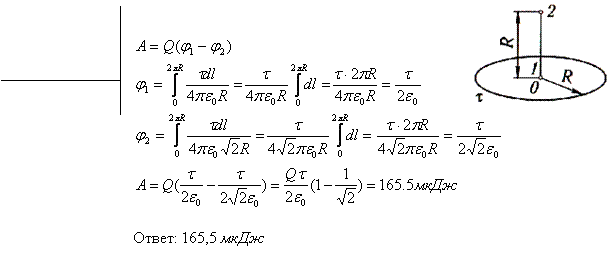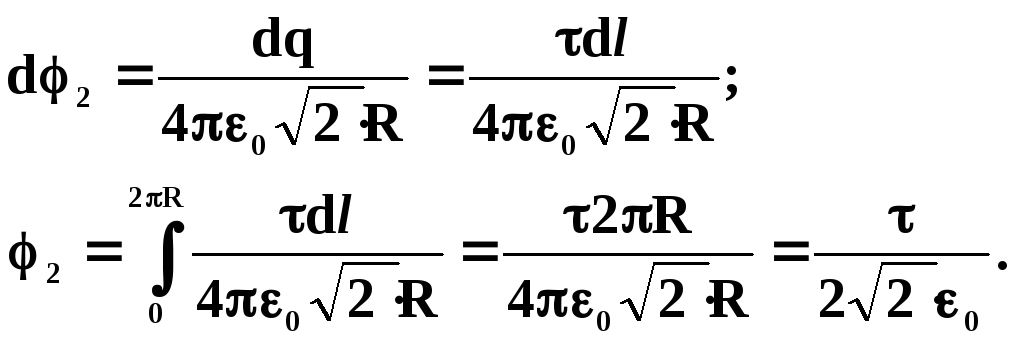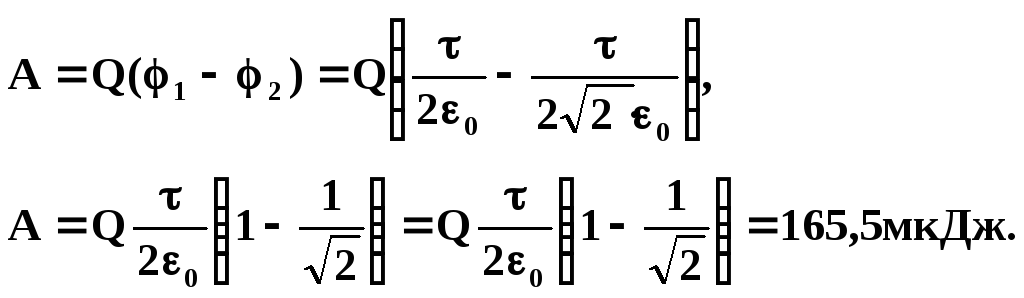Зєднання конденсаторів, Основи електроніки — Акумулятор

З’єднання конденсаторів

В електричних ланцюгах застосовуються різні способи з’єднання конденсаторів. З’єднання конденсаторів може здійснюватися: послідовно. паралельно і послідовно-паралельно (останнє іноді називають змішане з’єднання конденсаторів). Існуючі види з’єднання конденсаторів показано на малюнку 1.

Малюнок 1. Способи з’єднання конденсаторів.

Паралельне з’єднання конденсаторів.

Якщо група конденсаторів включена в ланцюг таким чином, що до точок включення безпосередньо приєднані пластини всіх конденсаторів, то таке з’єднання називається паралельним з’єднанням конденсаторів (малюнок 2.).

Малюнок 2. Паралельне з’єднання конденсаторів.

При заряді групи конденсаторів, з’єднаних паралельно, між пластинами всіх конденсаторів буде одна і та ж різниця потенціалів, так як всі вони заряджаються від одного і того ж джерела струму. Загальна ж кількість електрики на всіх конденсаторах буде дорівнює сумі кількостей електрики, лягають на кожному з конденсаторів, так як заряд кожного їх конденсаторів відбувається незалежно від заряду інших конденсаторів даної групи. Виходячи з цього, всю систему паралельно з’єднаних конденсаторів можна розглядати як один еквівалентний (рівноцінний) конденсатор. Тоді загальна ємність конденсаторів при паралельному з’єднанні дорівнює сумі ємностей всіх з’єднаних конденсаторів.

Позначимо сумарну ємність з’єднані у батарею конденсаторів буквою Собщ, ємність першого конденсатора С1 ємність другого С2 і ємність третього С3. Тоді для паралельного з’єднання конденсаторів буде справедлива наступна формула:

Останній знак » + » і три крапки вказують на те, що цією формулою можна користуватися при чотирьох, п’яти і взагалі при будь-якому числі конденсаторів.

Послідовне з’єднання конденсаторів.

Якщо ж з’єднання конденсаторів в батарею проводиться у вигляді ланцюжка і до точок включення в ланцюг безпосередньо приєднані пластини тільки першого і останнього конденсаторів, то таке

з’єднання конденсаторів називається послідовним (малюнок 3).

Малюнок 2. Послідовне з’єднання конденсаторів.

При послідовному з’єднанні всі конденсатори заряджаються однаковою кількістю електрики, так як безпосередньо від джерела струму заряджаються тільки крайні пластини (1 і 6), а інші пластини (2, 3, 4 і 5) заряджаються через вплив. При цьому заряд пластини 2 буде дорівнює за величиною і протилежний за знаком заряду пластини 1, заряд пластини 3 буде дорівнює за величиною і протилежний за знаком заряду пластини 2 і т. д.

Напруги на різних конденсаторах будуть, взагалі кажучи, різними, так як для заряду одним і тим же кількістю електрики конденсаторів різної ємності завжди потрібні різні напруги. Чим менше ємність конденсатора, тим більша напруга необхідно для того, щоб зарядити цей конденсатор необхідною кількістю електрики, і навпаки.

Таким чином, при заряді групи конденсаторів, з’єднаних послідовно, на конденсаторах малої ємності напруги будуть більше, а на конденсаторах великої ємності — менше.

Аналогічно попередньому випадку можна розглядати всю групу конденсаторів, з’єднаних послідовно, як один еквівалентний конденсатор, між пластинами якого існує напруга, що дорівнює сумі напруг на всіх конденсаторах групи, а заряд якого рівний заряду кожного з конденсаторів групи.

Візьмемо самий маленький конденсатор в групі. На ньому має бути найбільша напруга. Але напруга на цьому конденсаторі складає тільки частину загальної напруги, існуючого на всій групі конденсаторів. Напруга на всій групі більше напруги на конденсаторі, що має саму малу ємність. А звідси безпосередньо випливає, що загальна місткість групи конденсаторів, з’єднаних послідовно, менше ємності самого малого конденсатора в групі.

Для обчислення загальної ємності при послідовному з’єднанні конденсаторів найзручніше користуватися наступною формулою:

Для приватного випадку двох послідовно з’єднаних конденсаторів формула для обчислення їх загальної ємності буде мати вигляд:

Послідовно-паралельне (змішане) з’єднання конденсаторів

Послідовно-паралельним з’єднанням конденсаторів називається ланцюг має в своєму складі ділянки, як з паралельним, так і з послідовним з’єднанням конденсаторів.

На рисунку 4 наведено приклад ділянки ланцюга зі змішаним з’єднанням конденсаторів.

Малюнок 4. Послідовно-паралельне з’єднання конденсаторів.

При розрахунку загальної місткості такого ділянки кола з послідовно-паралельним з’єднанням конденсаторів цю ділянку розбивають на прості ділянки, що складаються тільки з груп з послідовним або паралельним з’єднанням конденсаторів. Далі алгоритм розрахунку має вигляд:

1. Визначають еквівалентну ємність ділянок з послідовним з’єднанням конденсаторів.

2. Якщо ці ділянки містять послідовно з’єднані конденсатори, то спочатку обчислюють їх ємність.

3. Після розрахунку еквівалентних ємностей конденсаторів перемальовували схему. Зазвичай виходить ланцюг з послідовно з’єднаних еквівалентних конденсаторів.

4. Розраховують ємність отриманої схеми.

Один з прикладів розрахунку ємності при змішаному з’єднанні конденсаторів наведено на малюнку 5.

Малюнок 5. Приклад розрахунку послідовно-паралельного з’єднання конденсаторів.

Детальніше про розрахунки з’єднання конденсаторів можна дізнатися у мультимедійному підручнику з основ електротехніки та електроніки:

Короткий опис статті: ємність батареї В електричних ланцюгах конденсатори можуть з’єднуватися різними способами. Розглянемо існуючі види з’єднань конденсаторів, співвідношення і методи для розрахунку ємності при з’єднанні конденсаторів батареї. конденсатор, ємність

Джерело: З’єднання конденсаторів — Основи електроніки

Post Views: 9 432

З’єднання конденсаторів

Конденсатори можуть з’єднуватися між собою, утворюючи батареї конденсаторів. При паралельному з’єднанні конденсаторів (рис. 3.16) напруги на конденсаторах однакові:

U₁ = U₂ = U, , а заряди різні q₁ = С₁ U і q₂ = С₂ U. Таку систему можна розглядати як єдиний конденсатор електроємності C, заряджений зарядом q=q₁+q₂ при напрузі між обкладками рівному U. Звідси слідує:

, (3.23)

Таким чином, при паралельному з’єднанні електроємності складаються.

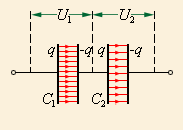
Рисунок 3.16. Рисунок 3.17.

При послідовному з’єднанні (рис. 3.17) однаковими виявляються заряди обох конденсаторів :q₁=q₂=q, а напруга на них різна U

1 =q/C₁ і U₂ =q/C₂ Таку систему можна розглядати як єдиний конденсатор, заряджений зарядом q при напрузі між обкладками U = U₁ + U₂. Отже,

(3.24)

При послідовному з’єднанні конденсаторів складаються зворотні величини ємностей.

Формули для паралельного і послідовного з’єднання залишаються справедливими при будь-якому числі конденсаторів, сполучених в батарею.

§43. Енергія електричного поля

Дослід показує, що заряджений конденсатор містить запас енергії.

Енергія зарядженого конденсатора дорівнює роботі зовнішніх сил, яку необхідно витратити, щоб зарядити конденсатор.

Процес зарядки конденсатора можна представити як послідовне перенесення досить малих порцій зарядуdq > 0 з однієї обкладки на іншу (рис. 3.18). При цьому одна обкладка поступово заряджається позитивним зарядом, а інша — негативним. Кожна порція dq переноситься в умовах, коли на обкладках вже є деякий заряд q, а між ними існує деяка різниця потенціалів. Тоді при перенесенні кожної порції dq зовнішні сили повинні виконати роботу

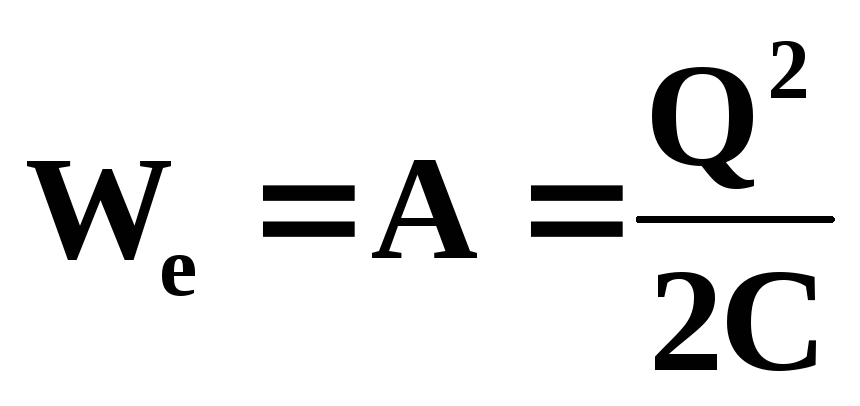Енергія конденсатора ємностіC, зарядженого зарядом Q, може бути знайдена шляхом інтегрування цього виразу в межах від 0 до Q:

. (3.25)

Рисунок 3.18.

Формулу, що виражає енергію зарядженого конденсатора, можна переписати в іншій формі, якщо скористатися співвідношеннямQ = CU.

(3.26)

Електричну енергію W_e слід розглядати як потенціальну енергію, запасену в зарядженому конденсаторі.

Р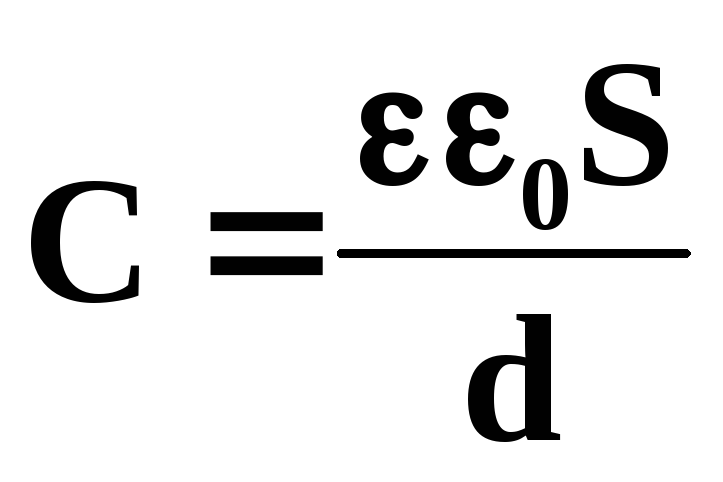озглянемо плоский конденсатор. Напруженість однорідного поля в плоскому конденсаторі рівна

E = U/d, а його ємність , тоді

(3.27)

деV = Sd — об’єм простору між обкладками, зайнятий електричним полем. З цього співвідношення виходить, що фізична величина

(3.28)

є електричною (потенціальною) енергією одиниці об’єму простору, в якому створено електричне поле. Її називають об’ємною густиною електричної енергії.

Приклад розв’язку задачі :

Електричне поле створене рівномірно розподіленим по кільцю зарядом (=1 мкКл/м).Визначити роботу сил поля по переміщенню заряду Q=10 нКл з точки 1 (у центрі кільця) в точку 2, що знаходиться на перпендикулярі до площини кільця (Рисунок нижче).

  

Дано: τ= 1мкКл/м Q=10 нКл А1, 2 -?

Розв’язку: Робота сил електричного поля по переміщенню заряду дорівнює: А12= Q(φ1 — φ2), де φ1 і φ2 — відповідно потенціали електричного поля в точках 1 і 2. Потенціали поля в центрі кільця φ1 і на перпендикулярі до площини кільця φ2 створюється зарядом рівномірно розподіленому по кільцю.

Питання і завдання

1. Що таке електричне поле? Яка фізична величина є характеристикою електричного поля? Що таке лінійна, поверхнева і об’ємна густини зарядів?

2. Що називається силовими лініями електричного поля, як вони проводяться?

3. Що таке потік вектора напруженості електричного поля. Сформулюйте теорему Гауса.

4. Як довести, що електричне поле є потенціальним? Дайте визначення потенціалу даної точки електричного поля і різниці потенціалів.

5. Що таке еквіпотенціальна поверхня. Чому дорівнює робота сил електричного поля по переміщенню заряду уздовж еквіпотенціальної поверхні?

6. Що таке поляризація діелектриків. У чому відмінність поляризації діелектриків з полярними і не полярними молекулами?

7. Що відбувається з провідниками при внесенні їх в електричне поле?

8. На двох тонких нитках завдовжки 1м, підвішених до одного гачка,висять дві маленькі кульки однакової маси. Після передачі кулькам однакових зарядів 2,5·10^-6 Кл вони розійшлися, причому нитки утворили кут 60°. Знайти масу кульок. (10 г).

9. Який заряд має порошинка вагою 6·10^-11Н, якщо вона урівноважена в електричному полі, напруженість якого дорівнює 3·10⁵ В/м?(2·10^-16 Кл).

10. У двох вершинах рівностороннього трикутника із стороною 10 см знаходяться однакові точкові заряди 1 нКл. Знайти напруженість електричного поля в третій вершині.(1566 В/м).

11. Розрахувати напруженість електричного поля в точці, віддаленій на 1 см від кінця рівномірно зарядженого тонкого стержня завдовжки 1 м Заряд стержня дорівнює 1 нКл.( 891 В/м).

12. Використовуючи теорему Гауса розрахуйте напруженість електричного поля на відстані 1 см від нескінченної зарядженої нитки з лінійною густиною заряду 10 мкКл/м (1,8·107 В/м).

13. З якою силою взаємодіє точковий заряд 1 нКл з нескінченною зарядженою ниткою? Лінійна густина заряду нитки 8 мкКл/м, відстань між ниткою і зарядом 2 см (7,2 мкН).

14. Використовуючи теорему Гауса розрахуйте напруженість електричного поля рівномірно зарядженої кулі з об’ємною густиною заряду 5 нКл/м³ і радіусом 10 см на відстані 2см і 12 см від центра кулі. Побудувати графік залежності Е(r)? (3,8В/м, 13 В/м).

15. Використовуючи теорему Гауса розрахуйте напруженість електричного поля рівномірно зарядженої сфери з поверхневою густиною заряду 0,5 мкКл/м² і радіусом 10 см на відстані 2см і 12 см від центра сфери. Побудувати графік залежності Е(r). (0, 393 В/м).

16. Електричне поле утворене зарядженою сферою радіусом 4 см, рівномірно зарядженою з поверхневою густиною заряду 1 нКл/м². Визначити різницю потенціалів між двома точками поля, віддалених на відстані 6 і 10 см від поверхні сфери.

17. Електрон рухається у вакуумі по напряму силової лінії однорідного електричного поля. Його початкова швидкість 10⁶ м/с. Яка різниця потенціалів початкової точки і точки, в якій швидкість електрона стане рівною нулю.(2,84 В).

18. Конденсатори ємністю С і 2С сполучені паралельно. Знайти заряд на другому конденсаторі, якщо заряд на першому дорівнює 2 мкКл. (4 мкКл).

19. Два конденсатори ємністю 5 і 10 мкФ підключені паралельно до джерела постійної напруги 100 В. Який заряд на пластинах кожного конденсатора?(500 мкКл, 1000 мкКл).

20. Різниця потенціалів між пластинами плоского конденсатора дорівнює 200 В. Площа кожної пластини 100 см², відстань між пластинами 1 мм, простір між пластинами заповнений парафіном (ε=2). Визначити енергію зарядженого конденсатора.(3,54·10-6 Дж).

Послідовне з’єднання конденсаторів.

При послідовному з’єднанні конденсаторів негативно заряджену обкладку першого конденсатора з’єднують з позитивно зарядженою обкладкою другого і т.д. (рис. 144).

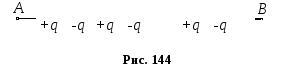
Якщо на батарею подати напругу , то до такої різниці потенціалів зарядяться тільки крайні обкладки першого і останнього конденсатора, причому

.

Провідник, що з’єднує негативно заряджену обкладку першого та позитивно заряджену обкладку другого конденсатора, можна розглядати разом з обкладками як одне провідне тіло. Внаслідок явища електростатичної індукції вільні заряди цього тіла під дією поля прикладеної напруги перерозподіляються так, що на одній обкладці з’являється негативний заряд 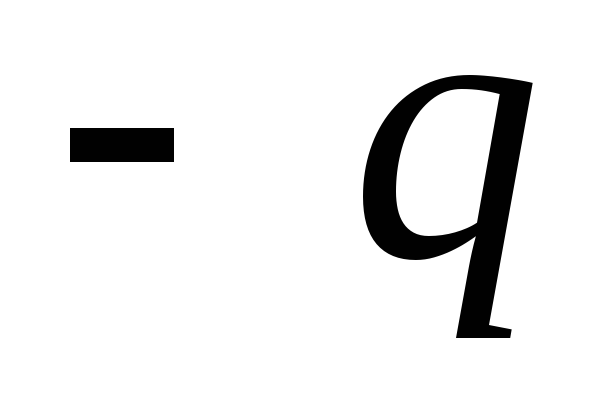, а на інший – позитивний . Тому можна зробити висновок, що заряди на всіх послідовно з’єднаних конденсаторах, незалежно від їх ємності, однакові і дорівнюють заряду всієї батареї, тобто

.

Ємність батареї послідовно з’єд­наних конденсаторів

,

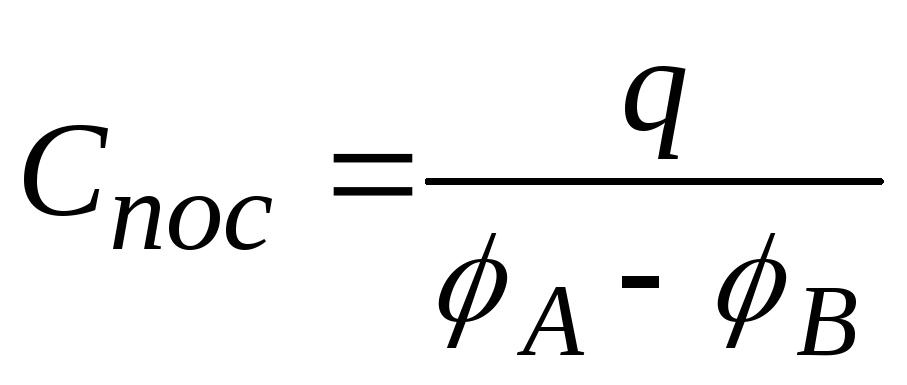звідки

.

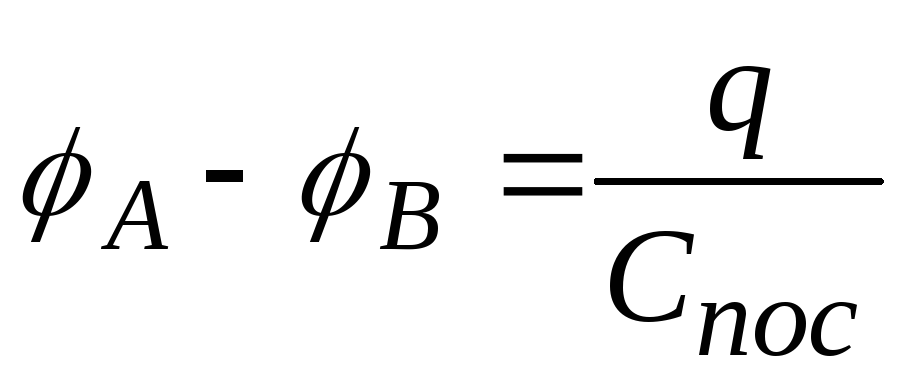Для першого конденсатора ,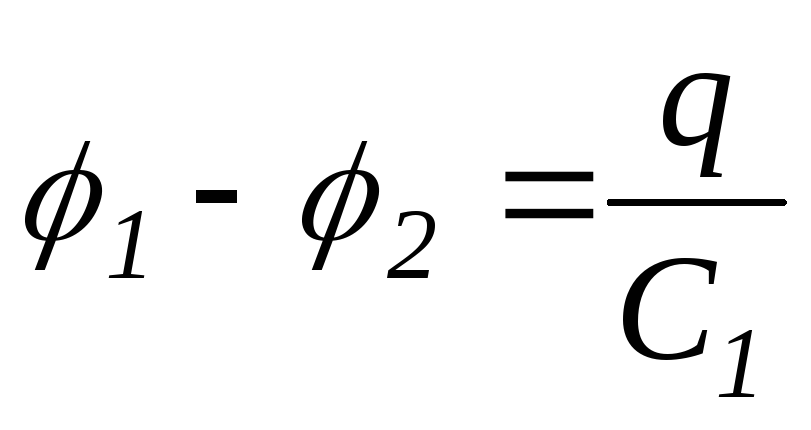

для другого і т.д. Тоді

.

Після скорочення на qотримуємо формулу для обчислення електроємності батареї послідовно з’єднаних конденсаторів:

.

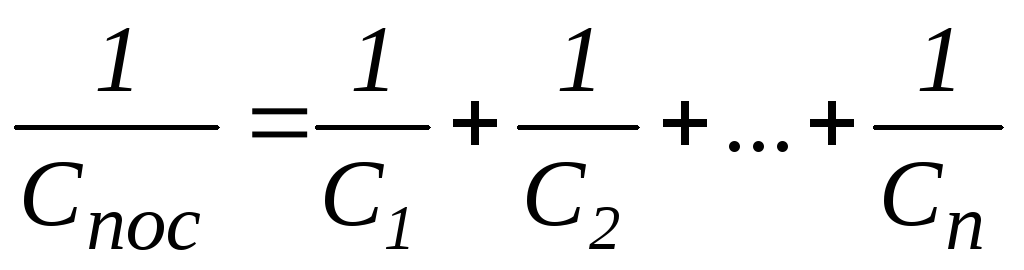Якщо послідовно з’єднано nоднакових конденсаторів з ємністюCкожен, то

.

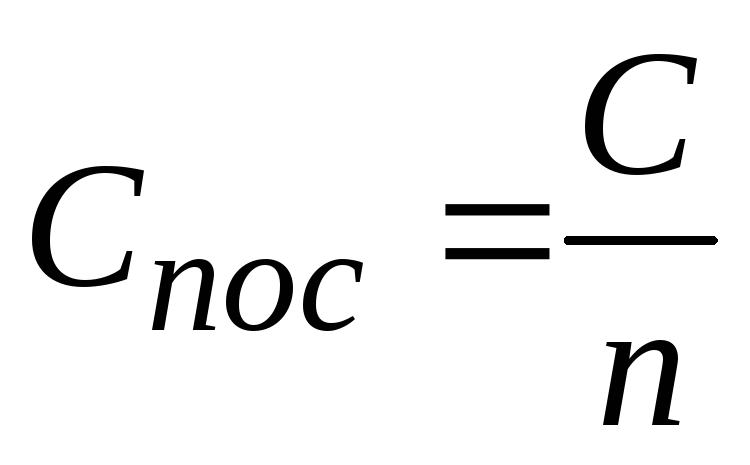Послідовно з’єднують конденсатори для підвищення робочої напруги, яку можна подати на батарею конденсаторів.

§57. Енергія зарядженого відокремленого провідника, конденсатора. Енергія електростатичного поля.

Нехай в однорідному ізотропному середовищі знаходиться відокремлений провідник, заряд якого q, потенціалі електроємністьС.Для збільшення заряду цього провідника наdq, треба перенести цей заряд з нескінченості до поверхні провідника. При цьому треба виконати роботу проти сил електростатичного поля, яка дорівнює

.

Щоб зарядити провідник від нульового заряду до q, треба виконати роботу

.

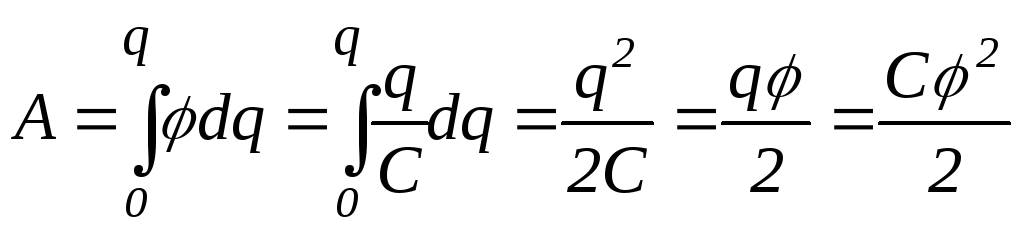Енергія зарядженого провідника числово дорівнює тій роботі, яку треба виконати, щоб зарядити цей провідник,

тобто

.

Під час зарядження конденсатора витрачається робота із перенесення електричних зарядів з однієї обкладки на іншу. Енергію зарядженого конденсатора визначають за формулою:

,

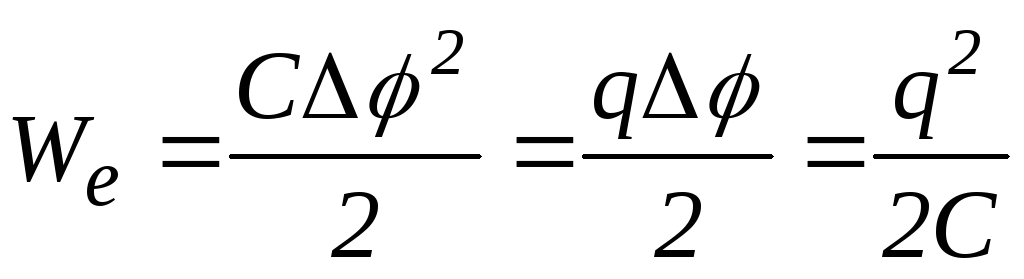де – різниця потенціалів між обкладками конденсатора.

Енергію зарядженого конденсатора можна визначити через величини, які характеризують електричне поле в проміжку між обкладками плоского конденсатора. Для цього у формулу

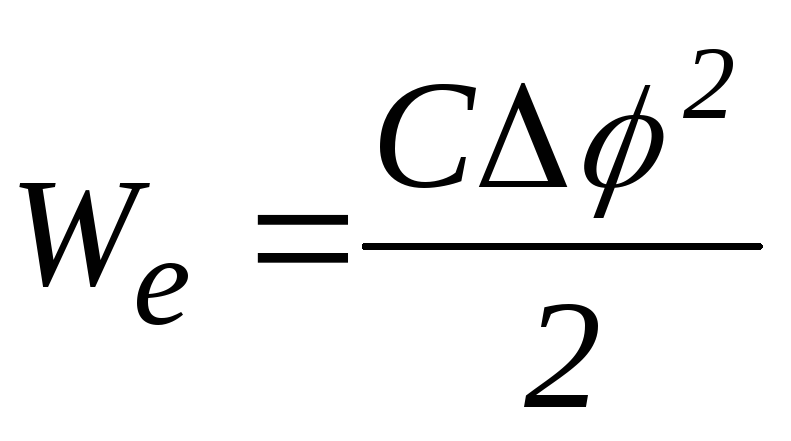
підставимо значення Сі:

,.

Тоді

,

де V=Sd– об’єм конденсатора.

Отже, енергія конденсатора виражається через величину, яка характеризує електростатичне поле – напруженість поля .

Електростатичне поле як одна з форм матерії існує в часі і просторі. Енергія є однією з характеристик стану матерії. Тому енергія нерозривно пов’язана з її матеріальним носієм – електричним полем. Енергія електричного поля локалізована у просторі, де існує це поле.

Вираз відповідає положенням теорії далекодії, деWрозглядається як потенціальна енергія заряджених тіл, що притягуються або відштовхуються один від одного. Формулавідповідає уявленням теорії поля (теорії близькодії), де вважається, що енергія, подібно до речовини, розподілена у просторі зоб’ємною густиною

.

В ізотропному діелектрику напрямки векторів іспівпадають. Тому

.

Враховуючи, що електричне зміщення 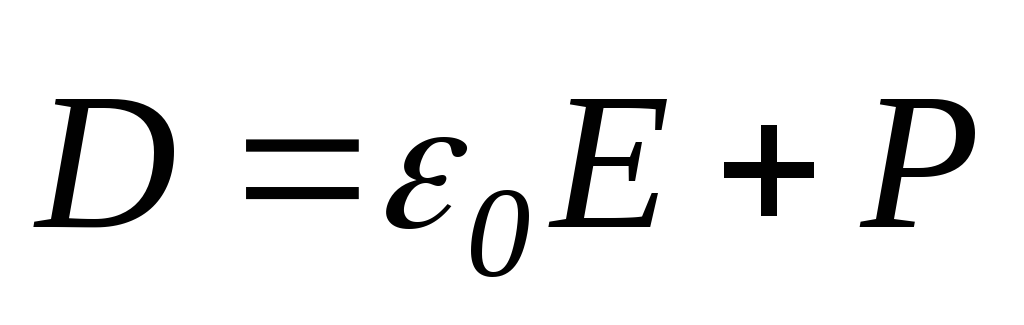, отримуємо длянаступний вираз:

.

Перший доданок відповідає густині енергії поля у вакуумі. Другий доданок – це густина енергії, яка витрачається на поляризацію діелектрика.

Дослідження неоднорідних елек­тричних полів, утворених довільними зарядженими тілами, показали, що для них формула незастосовна, бо

, а вираз длявизначає об’ємну густину енергії в кожній точці будь-якого електричного поля.

У випадку неоднорідного електричного поля енергія нескінченно малого об’ємуdVполя дорівнює

.

Інтегруючи по всьому об’ємуVполя, знаходимо повну енергію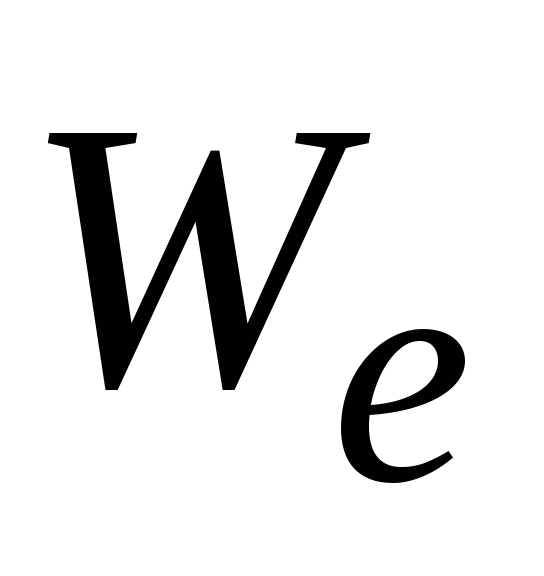електростатичного поля:

.

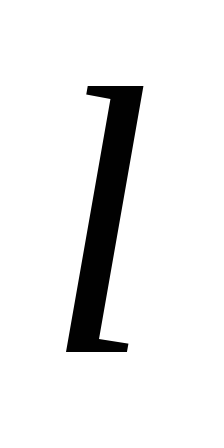
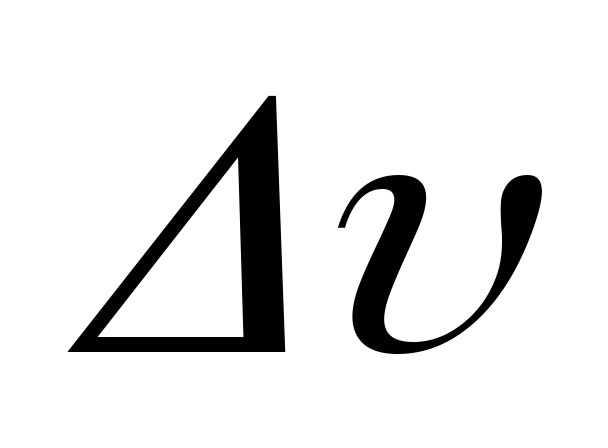
Рис. 7

140

Контрольні запитання

1. Дайте визначення основних характеристик електричного поля.

2. В яких одиницях вимірюють напруженість та потенціал електричного поля?

3. Яке поле називають однорідним ?

4. Що називають еквіпотенціальною поверхнею?

5. Як розташований вектор напруженості в кожній точці електростатичного поля по відношенню до еквіпотенціальної поверхні ?.

6. Який зв’язок існує між напруженістю та різницею потенціалів електростатичного поля ?

7. Яке поле називають потенціальним ?

8. Доведіть, що електростатичне поле є потенціальним.

Література: [1, §2.1 – 2.3; § 3.1 – 3.4; 2, § 85 – 89; § 92 – 94 ]

Лабораторна робота EП 2

Визначення електричної ємності конденсатора та батареї конденсаторів

Мета й завдання роботи – навчитись вимірювати ємність конденсаторів різними методами; перевірити на досліді формули, за якими обчислюється ємність батареї конденсаторів при їх послідовному і паралельному з’єднанні.

Основні теоретичні відомості

Найпростіший конденсатор являє собою сукупність двох електропровідних (металевих) тіл, розташованих так, що за наявності на них рівних за величиною і протилежних за знаком зарядів електричне поле буде зосереджене практично повністю між ними. Тому електрична ємність такої системи тіл не буде залежати від наявності оточуючих тіл.

Провідники, що утворюють конденсатор, називаються обкладками конденсатора.

Залежно від форми обкладок конденсатори бувають плоскими, циліндричними, сферичними.

Для збільшення ємності конденсатора між обкладками розташовують діелектрик.

Залежно від роду діелектрика розрізняють конденсатори повітряні, слюдяні, керамічні, паперові, електролітичні тощо. Конденсатори бувають з фіксованою і змінною ємностями. Для всіх конденсаторів, крім електролітичних, немає значення, яким полюсом (плюс чи мінус) до нього приєднане джерело струму.

Ємність конденсатора визначають за формулою

C = 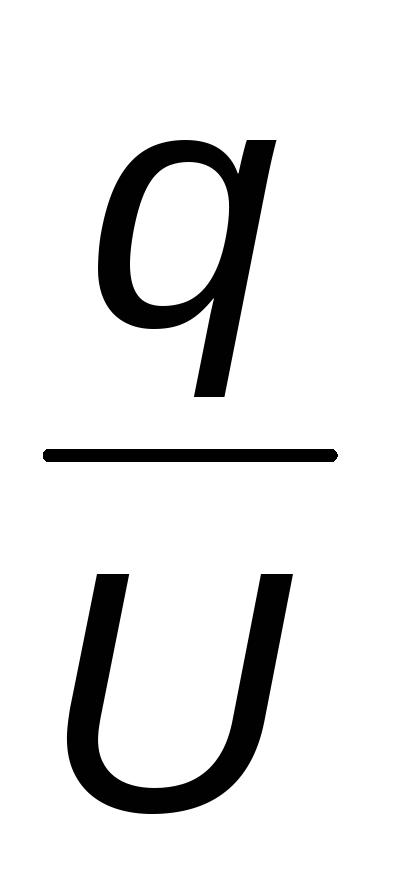, (ЕП 2.1)

де q – заряд на одній з обкладок конденсатора, U = φ₁ — φ₂ – різниця потенціалів між обкладками, або напруга на конденсаторі, U.

Електрична ємність конденсатора не залежить ні від заряду q, ні від напруги U. С являє собою коефіцієнт пропорційності між величиною заряду і напругою на конденсаторі.

Ємність залежить від форми, розмірів конденсатора, діелектричної проникності діелектрика між його обкладками. Приміром, ємність плоского конденсатора

C = ,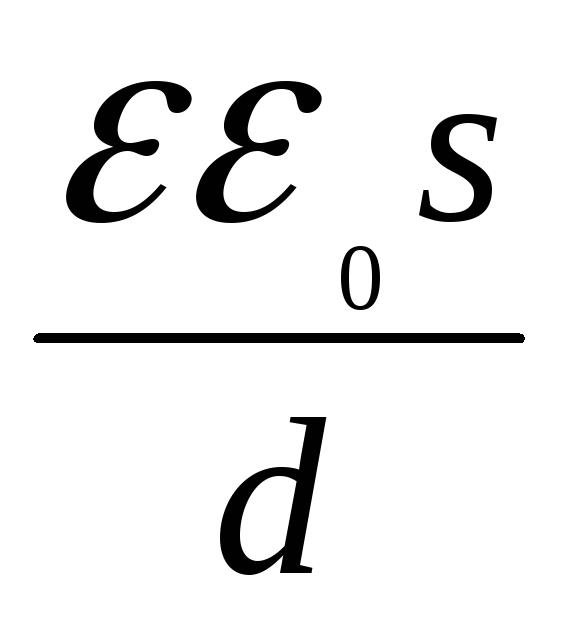

де ε – діелектрична проникність; ε₀ – електрична стала, S – площа обкладок конденсатора; d — відстань між обкладками конденсатора.

Ємність конденсатора вимірюється у фарадах (Ф). 1 Ф – це ємність такого конденсатора, кожній обкладці якого треба надати заряд 1 Кл, щоб напруга змінилась на 1 В.

Ємність 1 Ф – дуже велике значення ємності, тому на практиці частіше використовують конденсатори з ємностями порядку мікрофарад (мкФ), нанофарад (нФ), пікофарад (пФ).

З’єднання конденсаторів у батареї

При практичному використанні у конкретній схемі конденсаторів повинні мати необхідну електричну ємність і електричну міцність, що характеризується напругою пробою. Якщо один конденсатор не відповідає цим вимогам, використовують кілька конденсаторів, з’єднуючи їх у батареї .

5.Конденсатори. З*єднання конденсаторів. Енергія електричного поля. Густина енергії.

Ємність конденсатора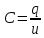

За природою речовини конденсатори бувають: повітряні, паперові, слюдяні, керамічні, електролітичні, а залежно від форми обкладок:

Плоскі, сферичні, циліндричні.

З*єднання конденсаторів:

Електричне поле викликає переміщення вільних зарядів і може виконувати роботу, а це значить, що воно має енергію.

Енергія електричного поля W задається формулою

Відповідно, густина енергії електричного поля задається формулою

6)

6.Діелектрики. Електричний диполь. Полярні та неполярні молекули. Зв*язані заряди на поверхні провідника.

Діелектрики – речовини які погано проводять ел. Струм.

Електричний диполь – сукупність двох однакових за значенням, але протилежних за знаком зарядів, розміщених на деякій відстані

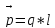
Неполярні молекули – ті в яких за відсутності зовн. Ел. Поля рухомі електрони зберігають у часі сферичну симетрію просторового розміщення відносно ядер.

Полярні молекули – (це атоми інертних газів) атоми які являють собою електричні диполі.

Зв*язані заряди – заряди які входять до складу нейтральних атомів і молекул, і під дією зовн. Ел. Поля можуть зміщуватись на мікроскопічні відстані в межах своїх атомів, а по об.єму або поверхні діелектрика переміщуватися неможуть.

7.Поляризація діелектриків. Вектор поляризації. Діелектрична сприйнятливість та проникність. Вектор електростатичної індукції. Сегнето- та п’єзоелектрики.

Поляризація – явище зміщення зв*язаних ел. Зарядів під дією зовн. Ел. Поля.

Вектор поляризації

Діелектрична проникність діелектрика

Сегнетоелектрики – це речовини які мають спонтанний дипольний в одній із кристалічних фа. Що існує в певному діапазоні температур.

Прикладом є сіль.

Завдяки велицій діелектричній проникності сегнетоелектрики широко використовуються при виготовленні конденсаторів.

П*єзоелектрики – це речовини що змінюють свої розміри пр. подачі до них електричного поля .

Приклади: п8єзоелектричні детонатори, джерела звуку, генератори високих напруг.

8.Електричний струм. Сила струму та його густина. Рівняння неприривності в інтегральній та диф. Формі.

Ел. Струм- упорядкований рух ел. Зарядів.

Сила струму – це складна фіз.. вел. Яка чисельно дорівнює величині заряду, що переноситься через поперечний переріз провідника за одиницю часу.

G – густина струму, це векторна величина, напрям якої збігається з напрямом струму, що чисельно = відношенню сили струму d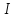, що проходить через перпендикулярну до напрямку руху носіїв поверхню 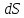до площі цієї поверхні.

9.Закон Ома для ділянки кола.Опір провідника. Закон Ома в дифер. Формі.

Закон ома для ділянки кола

I=U/R

Опят металевого провыдника обумовлений електричною провыдныстю на теплових коливаннях ы структурних неоднорыдностях ккристалічної решітки.

Опір однорідного провідника при не дуже великих струмах не залежить від сили струму а визначається :

1) геометричними розмірами

2) хімічною природою матеріалу

3) фізичним станом.

R= po*l / S

Закон ома у диференціальній формі – J=сигма Е.

10. Послідовне та паралельне з’єднання конденсаторів.

Щоб підібрати потрібну електроємність для заданої робочої напруги, конденсатори з’єднують у батареї. Можливими є три типи з’єднань конденсаторів: послідовне, паралельне і змішане.

Нехай послідовно з’єднано N конденсаторів. На обкладках кожного конденсатора буде однаковий за модулем заряд, тобто, q₁ = q₂ = … =  q_N = Q, де Q — заряд обкладок всієї батареї. Напруга на клемах такої батареї дорівнюватиме сумі напруг на всіх послідовно з’єднаних конденсаторах, тобто:

U = U₁ + U₂ + … +  U_N.     

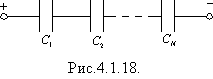
Ураховуючи, що ,,, …,, знайдемо формулу розрахунку електроємності батареї послідовно з’єднаних конденсаторів:

.

Нехай N конденсаторів з’єднано паралельно За такого з’єднання напруга на кожному конденсаторі однакова і дорівнює напрузі на клемах батареї:

U = U₁ = U₂ = … =  U_N.

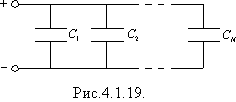
Заряд такої батареї Q дорівнює сумі зарядів на всіх паралельно з’єднаних конденсаторах: Q = q₁ + q₂ + … +  q_N.

Враховуючи, що Q = CU, Q₁ = C₁U, Q₂ = C₂U, …, Q_N = C_NU, знаходимо вираз для розрахунку електричної ємності батареї паралельно з’єднаних конденсаторів:

C = C₁ + C₂ + … +  С_N.

З’єднання конденсаторів, зображене на рис. 4.1.20, називають змішаним.

11. Енергія електричного поля.

Унаслідок уведення діелектрика між обкладками конденсатора його електроємність збільшується в e разів. Для того, щоб зарядити конденсатор, треба виконати роботу з розділення позитивних і негативних зарядів. Згідно із законом збереження енергії ця робота дорівнює енергії конденсатора. Розрахуємо її. Напруженість поля, створеного зарядом однієї з пластин, дорівнює E/2, де E — напруженість поля в конденсаторі. В однорідному полі однієї пластини знаходиться заряд q, розміщений по всій поверхні другої пластини. Згідно із формулою для потенціальної енергії енергія конденсатора:

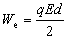, де q — заряд конденсатора; d — відстань між пластинами; E — напруженість електричного поля. Оскільки Ed = U, то .

Замінивши у формулі різницю потенціалів чи заряд за допомогою формул для електроємності конденсатора, отримуємо

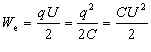. Підставимо у формулу значення електроємності плоского конденсатора і напруги. Тоді енергія конденсатора дорівнюватиме:

.

Поділивши на об’єм Sd, що його займає поле, дістанемо енергію, яка припадає на одиницю об’єму, тобто густину енергії:

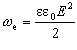
Формула справедлива не тільки для однорідного поля плоского конденсатора, а й для будь-якого іншого електростатичного поля. Одержаний вираз для густини енергії справедливий і для змінних електричних полів.

Енергія конденсаторів звичайно не дуже велика, зате вони здатні накопичувати її впродовж тривалого часу, а під час розрядження віддають її майже миттєво. Саме ці якості конденсаторів використовують найбільше на практиці. Основне застосування конденсатори знаходять в радіотехніці. Їх використовують як згладжувачі пульсацій у випрямлячах змінного струму, в електромагнітних коливальних контурах, для накопичення великої кількості енергії, під час проведення експериментів у галузі ядерної техніки і керованого термоядерного синтезу.

Приклади розв’язування задач

1. В однорідному електричному полі, напруженість якого 1 кВ/м, перемістили на 2см в напрямі силової лінії заряд – 25нКл. Визначити роботу поля, зміну потенціальної енергії взаємодії заряду з полем і різницю потенціалів між початковою і кінцевою точками переміщення. 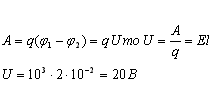Відповідь: -0,5 мкДж; 0,5мкДж; 20В.

2. Електрон вилітає з точки, потенціал якої 300 В, із швидкістю 0,6·10⁷ м/с у напрямі силових ліній поля. Визначити потенціал точки поля, у якій швидкість електрона дорівнюватиме нулю.

Розв’язання:

Робота електричного поля по переміщенні заряду (електрона):

. З іншого боку (теорема про кінетичну енергію):

Оскільки

Обчислення:

Відповідь: 198 В.

Як поєднати конденсатори | Ремонт та вироби своїми руками

У попередніх статтях було розглянуто питання роботи та характеристики конденсаторів. Зараз Я розповім про всіх методах з’єднання конденсаторів для підключення в схему. Відразу скажу, що в житті практично скрізь, за винятком рідкісних випадків використовується тільки паралельна схема підключення.

Слід знати, що в ланцюзі змінного струму конденсатор виступає ще як ємнісне опір. При чому з збільшенням величини ємності конденсатора зменшується опір в колі змінного струму.

Паралельне з’єднання конденсаторів

При паралельній схемі підключення все обкладки конденсаторів з’єднуються в дві групи, причому один висновок з кожного конденсатора з’єднується в одну групу з іншими, а другий — в іншу. Наочний приклад паралельного з’єднання і схема на картинці.

Все паралельно з’єднані конденсатори підключаються до одного джерела напруги, тому існує на них дві точки різниці потенціалів або напруги. На всіх висновках конденсаторів буде абсолютно однакову напругу.

При підключенні паралельно всі конденсатори разом, утворюють принципово одну ємність, величина якої буде дорівнювати сумі всіх ємностей підключених в ланцюзі конденсаторів.

При паралельному підключенні через кожен з конденсаторів потече різний струм, який буде залежати від величини ємності кожного з них. Чим вища ємність, тим більший струм потече через неї.

Паралельне з’єднання дуже часто зустрічається в житті. З його допомогою можна з групи конденсаторів зібрати будь-яку необхідну ємність. Наприклад, для запуску 3 фазного електродвигуна в однофазної мережі 220 Вольт в результаті розрахунків Ви отримали що необхідна робоча ємність 125 мкФ. Такої ємності конденсаторів Ви не знайдете у продажу. Для того, що б отримати необхідну ємність доведеться купити і з’єднати паралельно 3 конденсатора один на 100 мкФ, другий – на 20, і третій на 5 мкФ.

З’єднання конденсаторів послідовно

При послідовному з’єднанні конденсаторів кожна з обкладок з’єднується тільки в одній точці з однією обкладкою іншого конденсатора. Виходить ланцюжок конденсаторів. Крайні два висновки підключаються до джерела струму, в результаті чого відбувається перерозподіл між ними електричних зарядів. Заряди на всіх проміжних обкладках однакові величиною з чергуванням по знаку.

Через всі сполучені конденсатори послідовно протікає однакової величини струм, тому що у нього немає іншого шляху проходження.
Загальна ж місткість буде обмежуватися площею обкладок найменшого за розміром, тому що як тільки повністю зарядиться конденсатор з найменшою ємністю – весь ланцюжок перестане пропускати струм і заряд інших перерветься. Вираховується ж ємність по цій формулі:

Але при послідовному з’єднанні збільшується відстань (або ізоляція) між обкладками до величини дорівнює сумі відстаней між обкладками всіх послідовно підключених конденсаторів. Наприклад, якщо взяти два конденсатори з робочою напругою 200 Вольт і з’єднати послідовно, то ізоляція між обкладками зможе витримати 1000 Вольт при підключенні в схему.

З вище сказаного можна зробити висновок, що послідовно з’єднувати необхідно:

Для отримання еквівалентного меншого ємності конденсатора.

Якщо необхідна ємність, яка працює на більш високих напругах.

Для створення ємнісного дільника напруги, який дозволяє отримати меншої величини напруження з більш високого.

Практично, для одержання першого та другого достатньо просто купити один конденсатор з необхідною величиною ємності або робочою напругою. Тому даний метод з’єднання в житті не зустрічається.

Змішане з’єднання конденсаторів

Зустрічається змішане з’єднання тільки на різних платах. Для нього характерна наявність в одного ланцюга паралельного і послідовного з’єднання конденсаторів. При чому змішане з’єднання може бути як послідовного, так паралельного характеру.

В житті докладні знання про змішаному сполученні можуть тільки нагоді радіоаматорам, тому не буду на цьому детально зупинятися.

У цій статті Ви дізнаєтеся як правильно перевірити і визначити ємність конденсатора.

Я давно працюю в сфері ремонтних послуг, тому я розумію всі важливі моменти в будівництві і ремонті будинків, квартир і все що з ним повязано. Раніше я працював за кордоном, і встиг зробити багато роботи, стаж більше 15 років в сфері будівництва та в напрямку Сад та Город.

Якщо Вам не важко, то діліться в соц-мережах і оцінюйте статті!!!

Залишилися питання, пишіть нам, використовуючи на сайті форму “Зворотній зв’язок”