Ёмкость цилиндрического конденсатора | Все формулы

Ёмкость цилиндрического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.

Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), один вставлен в другой, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками, так же пренебрегаем краевыми эффектами. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l. При наличии диэлектрика между обкладками разность потенциалов

Подставим в формулу электроемкости конденсатора и у нас получится формула для цилиндрического конденсатора:

Так же есть:

Энергия цилиндрического конденсатора:

Ёмкость конденсатора :

Ёмкость плоского конденсатора :

Емкость сферического конденсатора :

В формуле мы использовали :

— Ёмкость цилиндрического конденсатора

— Линейная плотность

— Относительная диэлектрическая проницаемость

— Электрическая постоянная

— Длина цилиндрического конденсатора

— Больший радиус (от центра, до края конденсатора)

— Малый радиус (Его может и не быть — это пустота)

— Потенциал проводника

— Точечный заряд

— Напряжение

2.4.2. Емкость цилиндрического конденсатора

Цилиндрический конденсатор представляет собой устройство из двух цилиндрических обкладок, имеющих общую ось (коаксиальных цилиндров), разделенных слоем диэлектрика цилиндрической формы (рис. 2.5).

Электрическое поле такого конденсатора представляет собой суперпозицию двух полей цилиндрических поверхностей, имеющих равные по величине, но противоположные по знаку заряды.

Напряженность такого электрического поля

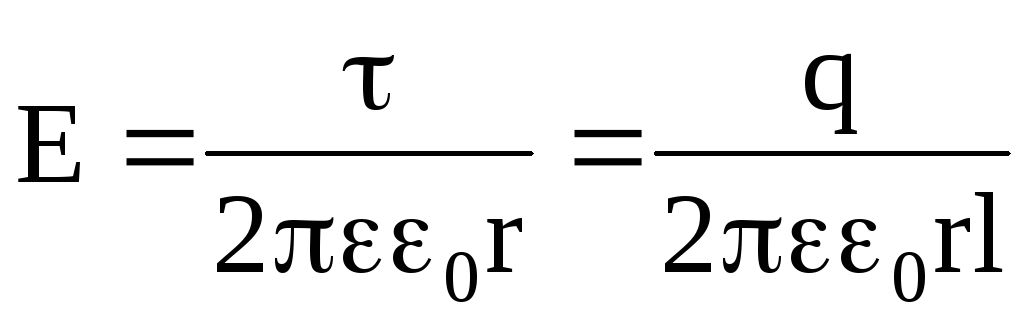. (2.18)

Разность потенциалов между обкладками

, (2.19)

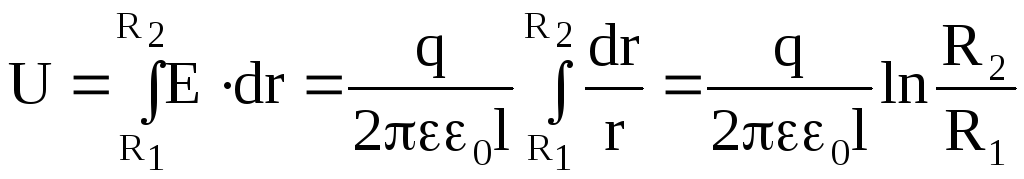
где R₁ и R₂ – соответственно радиусы внутренней и внешней обкладок.

Таким образом,

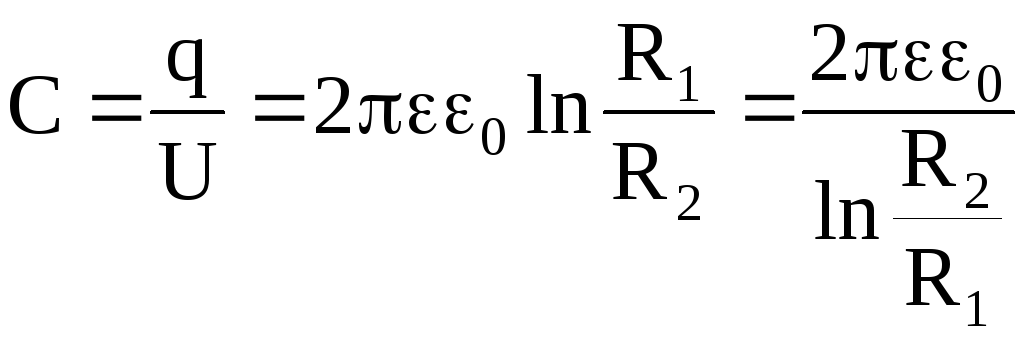. (2.20)

При d = R₂ — R₁ << R₁

,

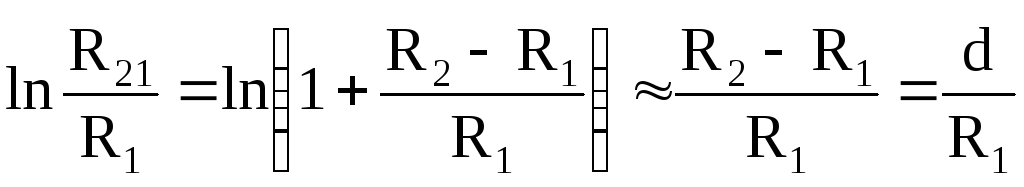где d = R₂ — R₁ – расстояние между обкладками.

Тогда

. (2.21)

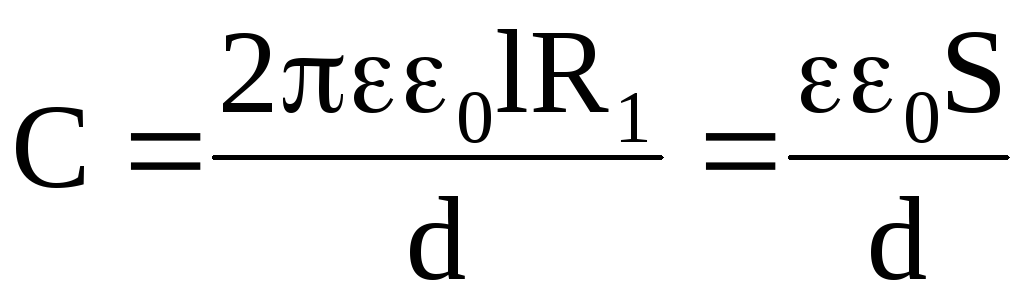
Следовательно, при указанных условиях емкость цилиндрического конденсатора можно рассчитывать по формуле емкости плоского конденсатора.

2.4.3. Емкость сферического конденсатора

С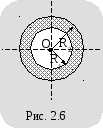ферический конденсатор представляет собой устройство, состоящее из двух сферических поверхностей, которые имеют общий центр различных радиусов, разделенных сферическим слоем диэлектрика (рис. 2.6).

Напряженность электрического поля между обкладками такого конденсатора

. (2.22)

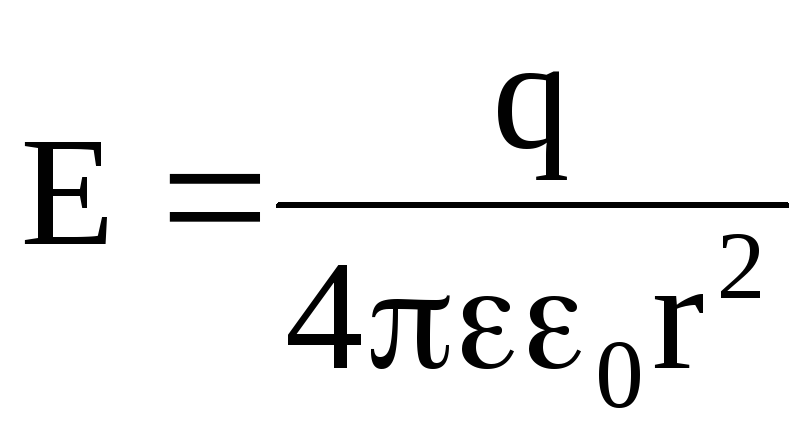
Разность потенциалов между обкладками

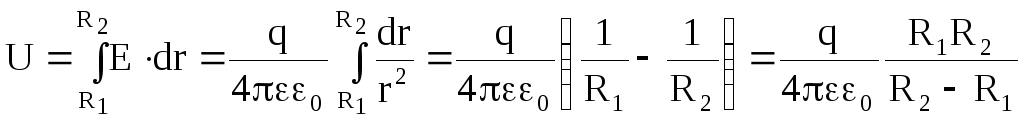.(2.23)

Таким образом,

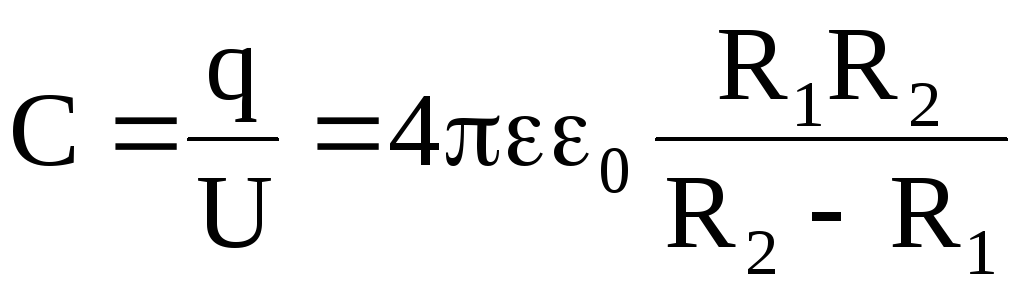. (2.24)

При R₂ — R₁ = d << R₁R₂

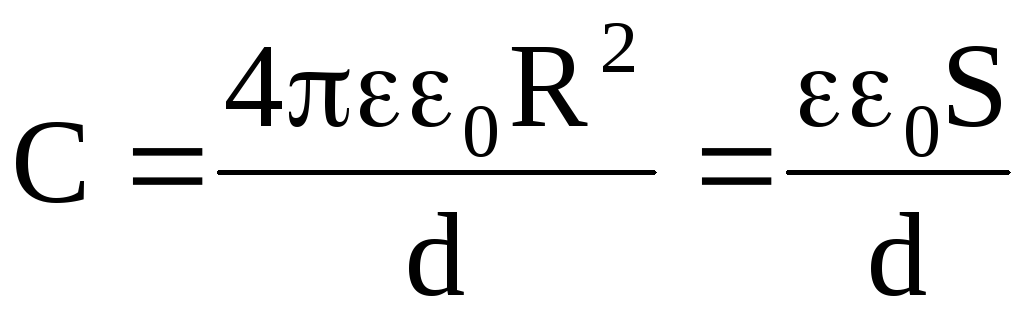. (2.25)

Следовательно, при указанных условиях емкость сферического конденсатора можно рассчитывать по формуле емкости плоского конденсатора.

2.5. Соединения конденсаторов

Отдельные конденсаторы обладают определенной емкостью и могут работать только при подключении их к характерным для них напряжениям, которые определяются свойствами и толщиной диэлектрика. Если напряжение превышает допустимое — происходит пробой конденсатора. Поэтому очень часто из имеющихся в наличии конденсаторов собирают батарею необходимой емкости, предназначенную для работы при более высоких напряжениях. Существует следующие виды соединения конденсаторов: последовательное, параллельное и смешанное.

2.5.1. Последовательное соединение конденсаторов

П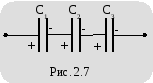

ри последовательном соединении каждая из обкладок какого-либо конденсатора соединяется только с одной обкладкой другого конденсатора, образуется цепочка конденсаторов (рис. 2.7). К крайним обкладкам такой цепочки прикладывается соответствующее напряжение, под действием которого происходит перераспределение электрических зарядов, при этом заряды на всех промежуточных обкладках равны по величине, но чередуются по знаку.

В результате перераспределения зарядов заряд батареи (цепочки) равен заряду одного конденсатора. Напряжение между обкладками отдельно взятого конденсатора обратно пропорционально его емкости, а напряжение батареи равно сумме напряжений каждого из входящих в батарею конденсаторов.

Такое соединение конденсаторов применяется в тех случаях, когда необходимо получить емкость, работающую при высоких напряжениях.

Так как в рассматриваемом случае

,

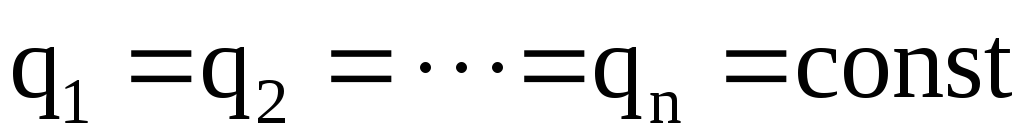а ,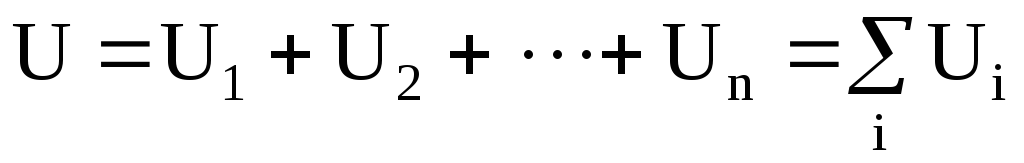

то будем иметь

или

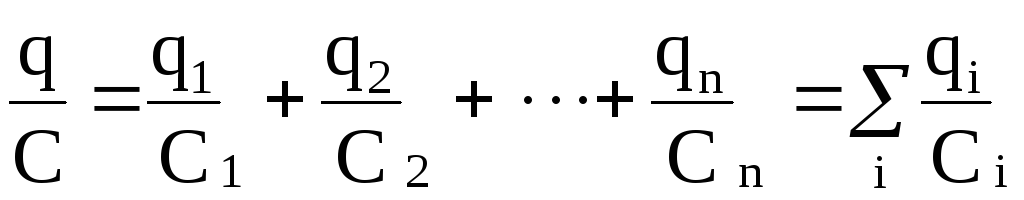
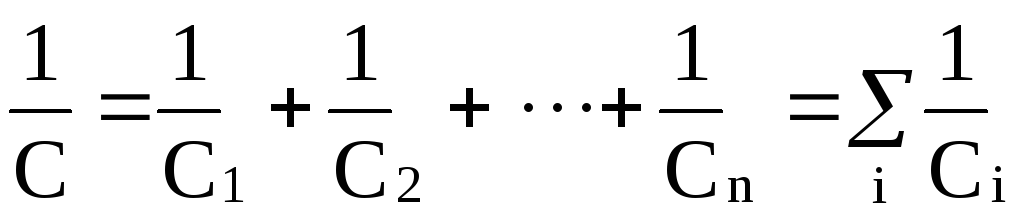. (2.26)

Таким образом, при последовательном соединении конденсаторов величина, обратная емкости батареи, равна сумме обратных величин емкостей отдельных конденсаторов.

Если емкости отдельных конденсаторов равны:

C₁ = C₂ = C₃ = C_n,

то

,

, (2.27)

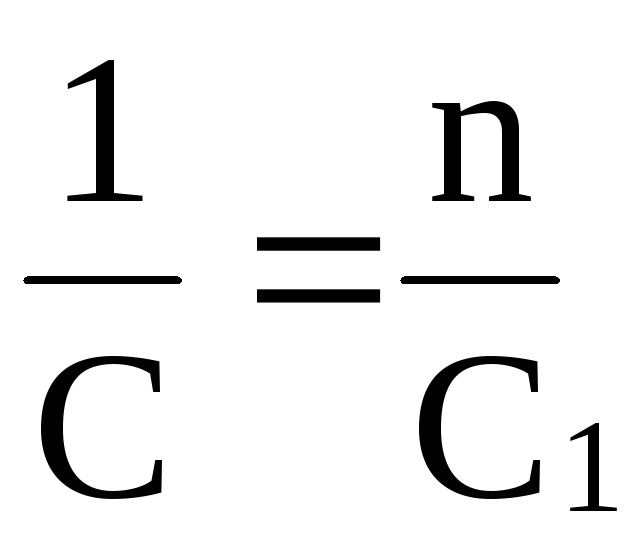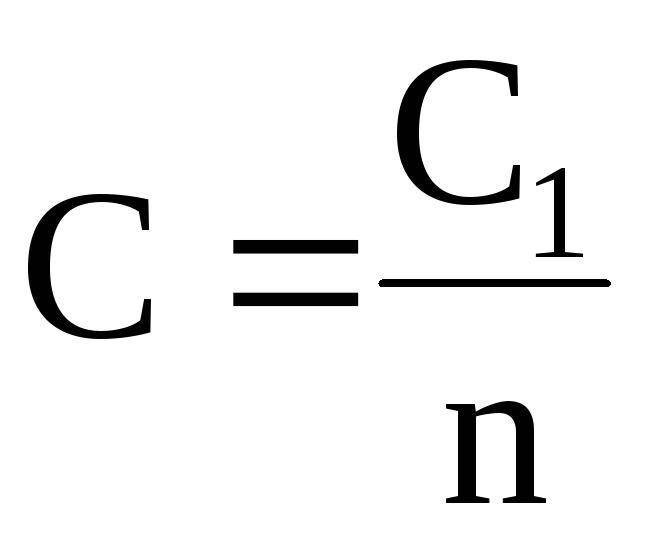
т. е. при последовательном соединении n одинаковых конденсаторов, емкость батареи в n раз меньше емкости одного конденсатора.

Емкость плоского и других конденсаторов

Конфигурация конденсатора такова, что поле, которое создается зарядами, локализовано между обкладками. В общем случае электроемкость конденсатора равна:

\[C=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{U}\left(1\right),\]

где ${\varphi }_1-{\varphi }_2=U$ — разность потенциалов обкладок, которую называют напряжением и обозначают $U$. Емкость по определению считается положительной величиной. Она зависит только от геометрии обкладок конденсатора их взаиморасположения и диэлектрика. Форму обкладок и их расположение подбирают так, чтобы внешние поля минимально влияли на внутреннее поле конденсатора. Силовые линии поля конденсатора начинались на проводнике с положительным зарядом и заканчивались на проводнике с отрицательным зарядом. Конденсатор может быть проводником, который помещен в полость, окруженную замкнутой оболочкой.

В соответствии с конфигураций конденсаторов можно выделить три большие группы: плоские, сферические и цилиндрические (по форме обкладок). Вычисление емкости конденсатора сводится к определению $напряжения$ конденсатора при известном заряде на его обкладках.

Плоский конденсатор

Плоский конденсатор (рис.1) — это две разноименно заряженные пластины, разделенные тонким слоем диэлектрика. Формула для расчета емкости такого конденсатора представляет собой выражение:

\[С=\frac{\varepsilon {\varepsilon }_0S}{d}\left(2\right),\]

где $S$ — площадь обкладки, $d$ — расстояние между обкладками, $\varepsilon $ — диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (2), с реальной емкостью.

Рис. 1

Электроемкость плоского конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равна $d_i$, диэлектрическая проницаемость этого слоя ${\varepsilon }_i$ вычисляется по формуле:

\[C=\frac{{\varepsilon }_0S}{\frac{d_1}{{\varepsilon }_1}+\frac{d_2}{{\varepsilon }_2}+\dots +\frac{d_N}{{\varepsilon }_N}}\ \left(3\right).\]

Сферический конденсатор

В том случае, если внутренний проводник шар или сфера, внешняя замкнутая оболочка — концентрическая ему сфера, то конденсатор является сферическим. Сферический конденсатор (рис.2) состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком. Емкость его можно рассчитать по формуле:

\[C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(4\right),\]

где $R_1{\ и\ R}_2$ — радиусы обкладок.

Рис. 2

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равна:

\[C=\frac{2\pi \varepsilon {\varepsilon }_0l}{{ln \left({R_2}/{R_1}\right)\ }}\left(5\right),\]

где $l$ — высота цилиндров, $R_1$ и $R_2$ — радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).

Рис. 3

Еще одной, но не маловажной характеристикой всех конденсаторов является пробивное напряжение ($U_{max}$)— это напряжение, при котором происходит электрический разряд через слой диэлектрика. $U_{max}$ зависит от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Помимо одиночных конденсаторов применяют их соединения. Для того чтобы увеличить емкость используют параллельное соединение конденсаторов (соединение одноименными обкладками). В этом случае результирующая емкость такого соединения может быть найдена как сумма${\ С}_i$ где $С_i$ — емкость конденсатора с номером i:

\[C=\sum\limits^N_{i=1}{С_i}\ \left(6\right).\]

Если конденсаторы соединить последовательно (обкладками с разными знаками заряда), то суммарная емкость соединения будет всегда меньше, чем минимальная емкость любого конденсатора, который входит в систему. В этом случаем для того чтобы рассчитать результирующую емкость складывают величины, обратные к емкостям отдельных конденсаторов:

\[\frac{1}{C}=\sum\limits^N_{i=1}{{\frac{1}{C_i}}_i}\left(7\right).\]

Пример 2

Задание: Какова напряженность электростатического поля сферического конденсатора на расстоянии x=1 см=${10}^{-2}м$ от поверхности внутренней обкладки, если внутренний радиус обкладки конденсатора $R_1=$1 см${=10}^{-2}м$, внешний $R_2=$ 3 см=${3\cdot 10}^{-2}м$. Напряжение на обкладках равно ${10}^3В$.

Решение:

Напряженность поля, которое создается проводящей заряженной сферой, вычисляется в соответствии с формулой:

\[E=\frac{1}{4\pi \varepsilon {\varepsilon }_0}\frac{q}{r^2}\ \left(2.1\right),\]

где $q$ — заряд внутренней сферы (обкладки конденсатора), $r=R_1+x$ —расстояние от центра сферы.

Заряд сферы найдем из определения емкости конденсатора (С):

\[q=CU\ \left(2.2\right).\]

Емкость сферического конденсатора определяется как:

\[C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(2.3\right),\]

где $R_1{\ и\ R}_2$ — радиусы обкладок конденсатора.

Подставим выражения (2.2) и (2.3) в (2.1), получим искомую напряженность:

\[E=\frac{1}{4\pi \varepsilon {\varepsilon }_0}\frac{U}{{(x+R_1)}^2}4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}=\frac{U}{{(x+R_1)}^2}\frac{R_1R_2}{R_2-R_1}.\]

Так как все данные в задаче уже переведены в систему СИ, проведем вычисления:

\[E=\frac{{10}^3}{{{(1+1)}^2\cdot 10}^{-4}}\cdot \frac{{{10}^{-2}\cdot 3\cdot 10}^{-2}}{{3\cdot 10}^{-2}-{10}^{-2}}=\frac{3\cdot {10}^{-1}}{8\cdot 10^{-6}}=3,75\cdot {10}^4\left(\frac{В}{м}\right).\]

Ответ: $E=3,75\cdot {10}^4\frac{В}{м}.$

2.3. Электроемкость уединенного проводника и ее физический смысл

Опыты показывают, что изменение заряда проводника приводит к изменению его потенциала, а отношение изменения заряда dq (q) к изменению потенциала d () для данного проводника остается величиной постоянной. Это отношение и называют электрической емкостью (электроемкостью) уединенного проводника. Следовательно, каждый проводник можно характеризовать электроемкостью (отношением)

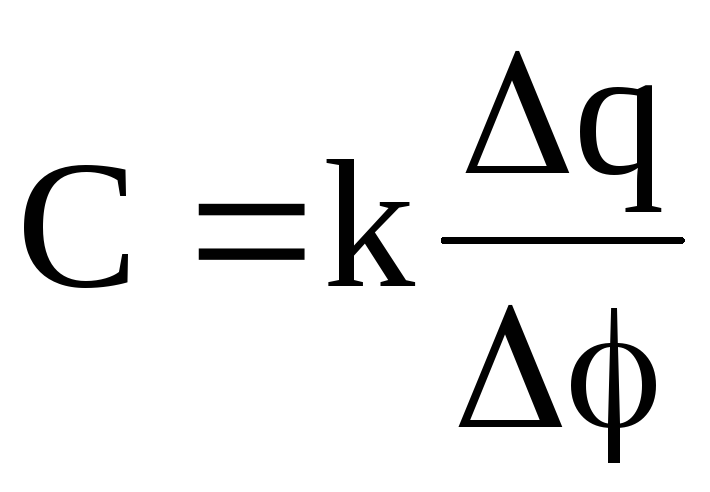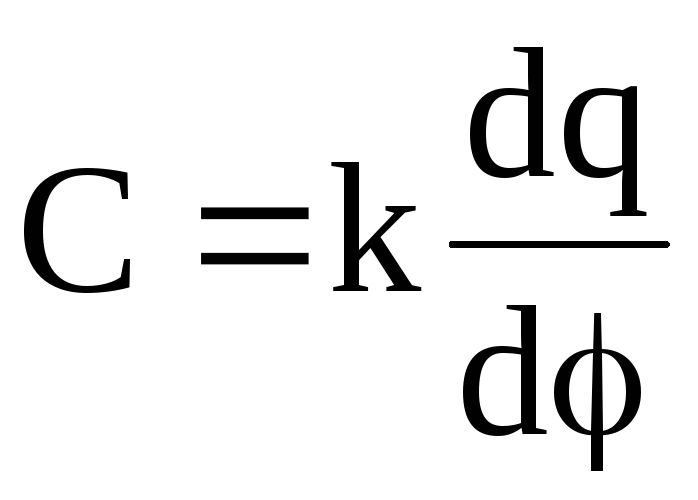или , (2.9)

где k — коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин.

В системе СИ k = 1, поэтому

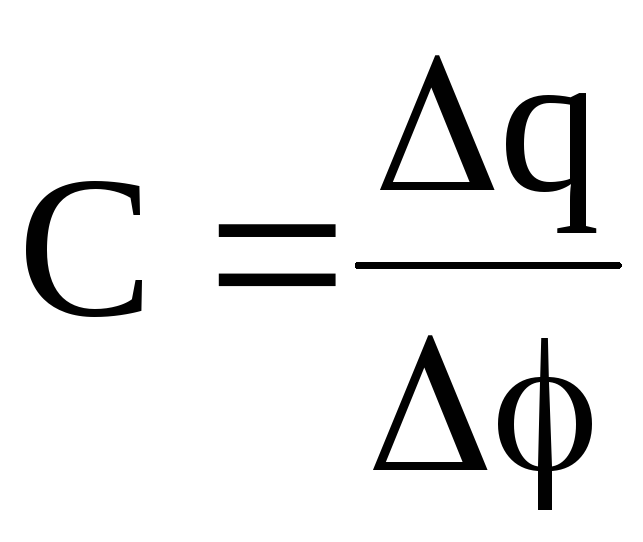или 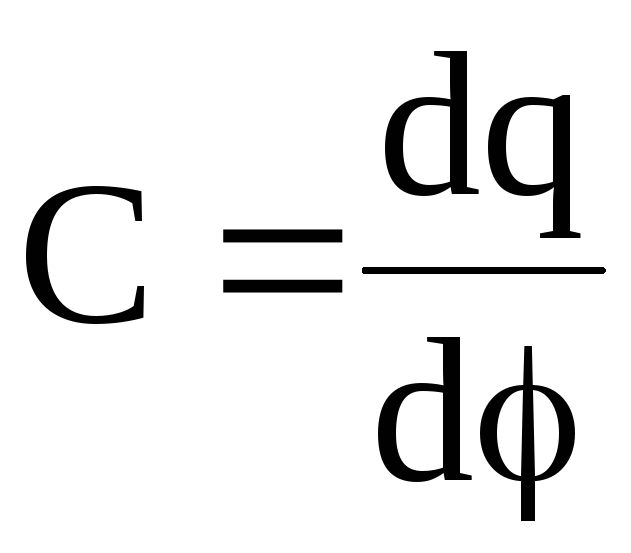. (2.10)

Таким образом, электроемкость уединенного проводника – это физическая величина, численно равная количеству электричества, на которое необходимо изменить заряд проводника, чтобы его потенциал изменился на единицу. В этом и заключается физический смысл электроемкости уединенного проводника.

Так как при q = 0,  = 0, а изменение заряда проводника q пропорционально изменению его потенциала , то и заряд проводника q пропорционален его потенциалу . Следовательно,

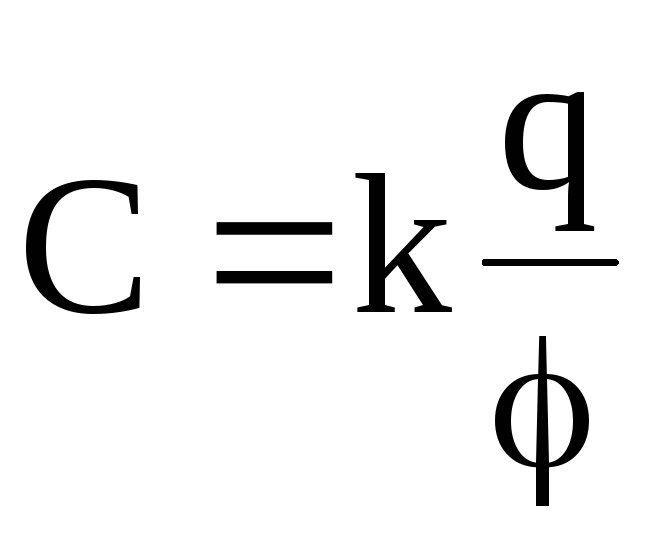. (2.11)

В системе СИ

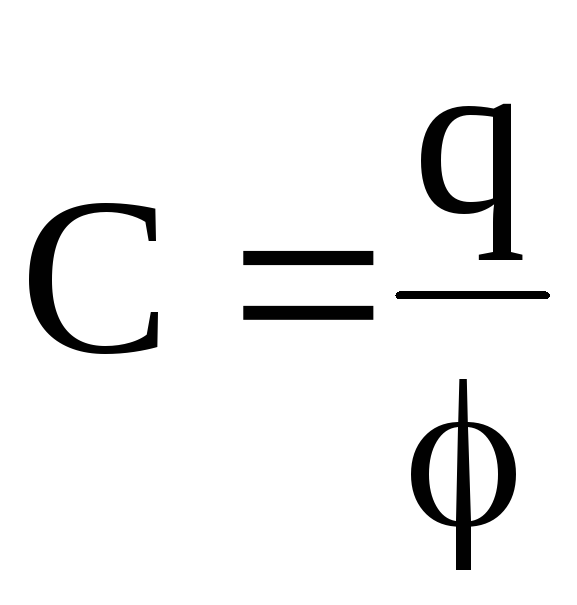. (2.12)

Экспериментальные данные говорят о том, что электроемкость (емкость) проводника зависит только от формы его поверхности, линейных размеров, расположения проводника относительно других проводников и диэлектрической проницаемости среды, окружающей проводник.

За единицу емкости принимается емкость такого проводника, потенциал которого изменяется на единицу при изменении его заряда на единицу.

В системе СИ единицей емкости является Фарада. 1 Ф = 1 Кл/В = = 10^-6 мкФ = 10^-12 пФ.

2.4. Конденсаторы и их емкость

Отдельно взятые проводники обладают малой емкостью. Увеличить емкость проводника можно, приблизив к нему другой проводник. Полученное устройство называют «конденсатор». Конденсаторы принебольших потенциалах способны накапливать («конденсировать») значительные по величине заряды. Образующие конденсатор проводники называют обкладками или пластинами. На обкладках конденсаторов накапливаются равные по величине, но противоположные по знаку заряды.

Под электроемкостью (емкостью) конденсатора подразумевают физическую величину, численно равную отношению величины заряда одного знака к разности потенциалов между обкладками:

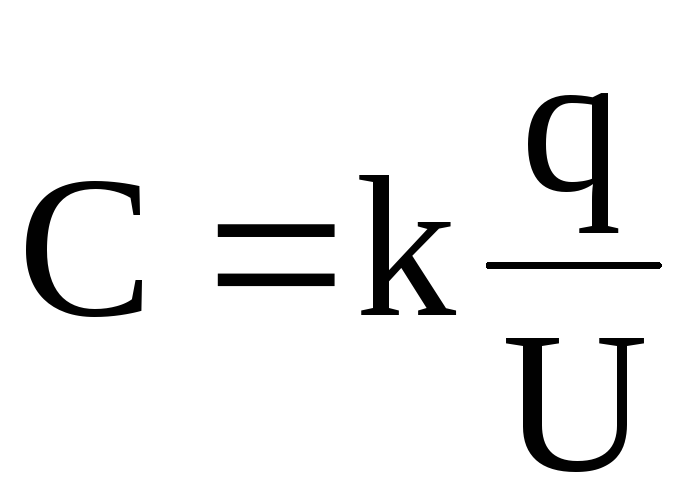, (2.13)

где k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин.

В системе СИ

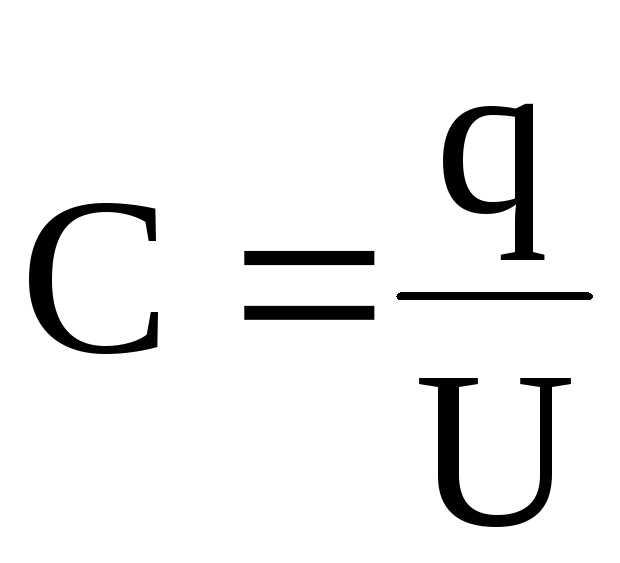. (2.14)

Емкость конденсаторов измеряется в тех же единицах, что и емкость проводника.

Величина емкости конденсатора определяется его геометрическими размерами, формой и диэлектрической проницаемостью среды, заполняющей пространство между обкладками.

Наибольшее распространение получили плоские, цилиндрические и сферические конденсаторы.

2.4.1. Емкость плоского конденсатора

Плоский конденсатор представляет собой две пластины, расположенные на некотором расстоянии друг от друга. Пространство между пластинами заполнено слоем диэлектрика. Схематическое устройство плоского конденсатора представлено на рис. 2.4.

Если площадь одной из обкладок равна S, а заряд на ней q равномерно распределен с поверхностной плотность , то напряженность электрического поля между обкладками

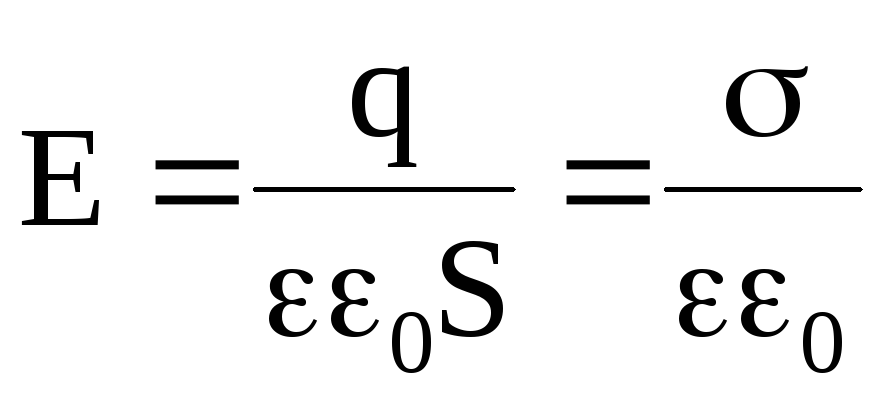, (2.15)

но

,

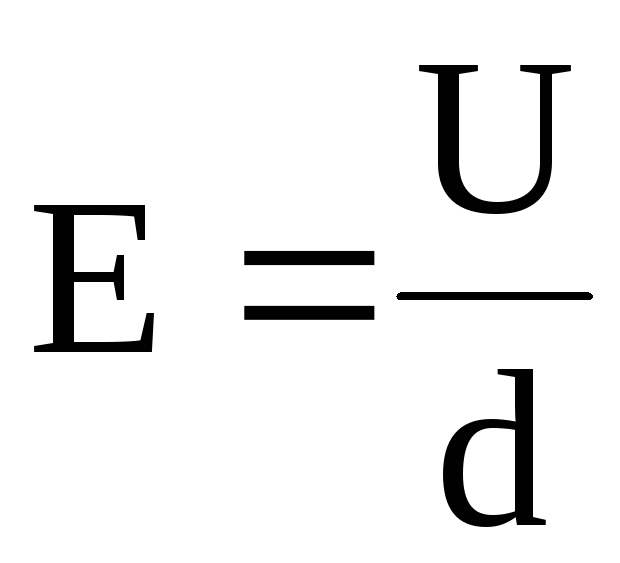где d – расстояние между обкладками.

Следовательно,

.

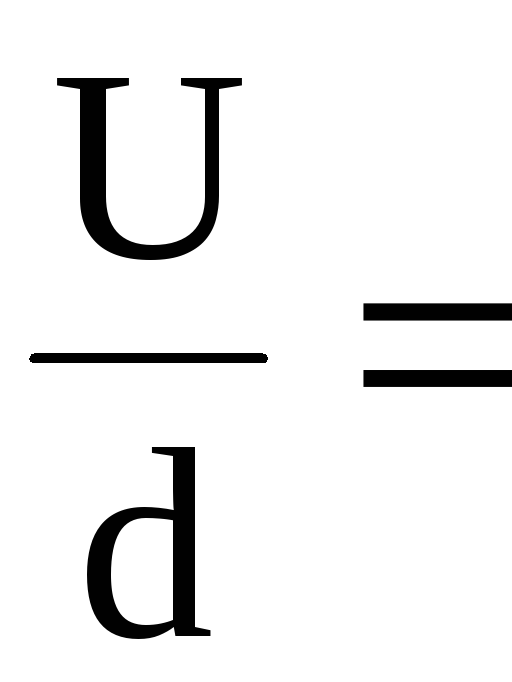
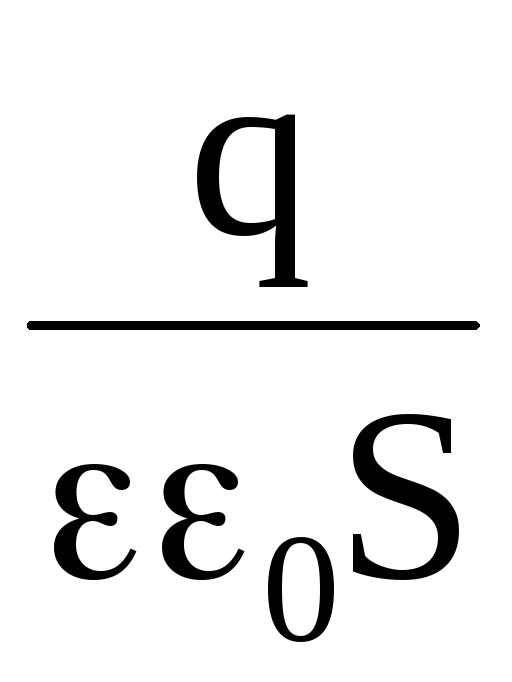Откуда

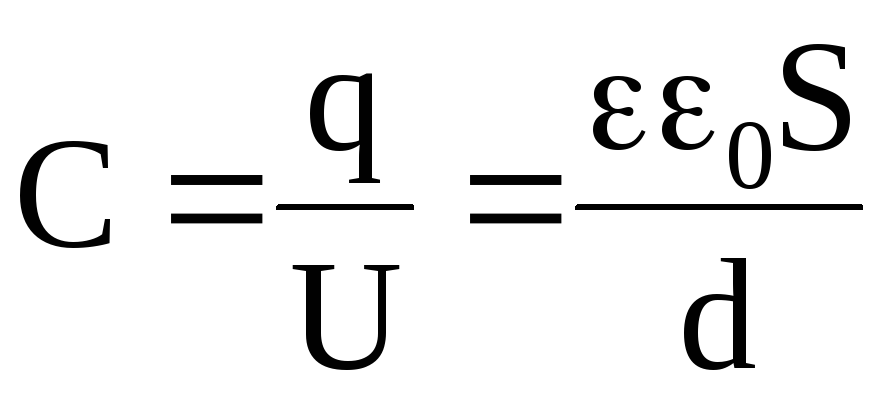. (2.16)

Из (2.15) видно, что емкость плоского конденсатора действительно зависит от его геометрических размеров и диэлектрической проницаемости среды, заполняющей пространство между обкладками. Кроме того, из нее можно получить размерность диэлектрической проницаемости вакуума (электрической постоянной) ₀. Так как

,

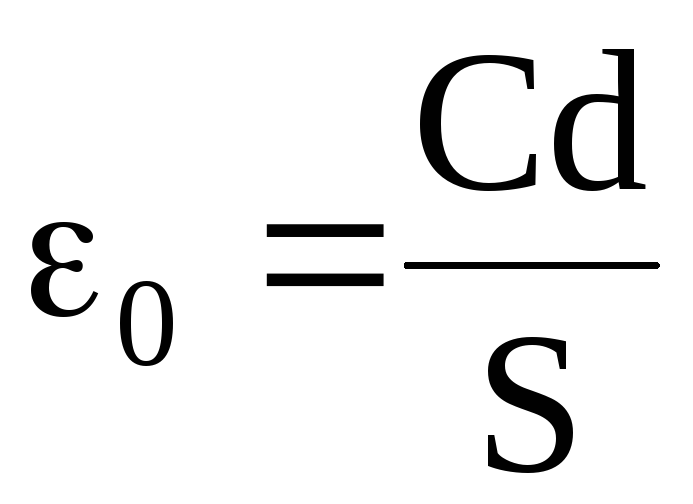то

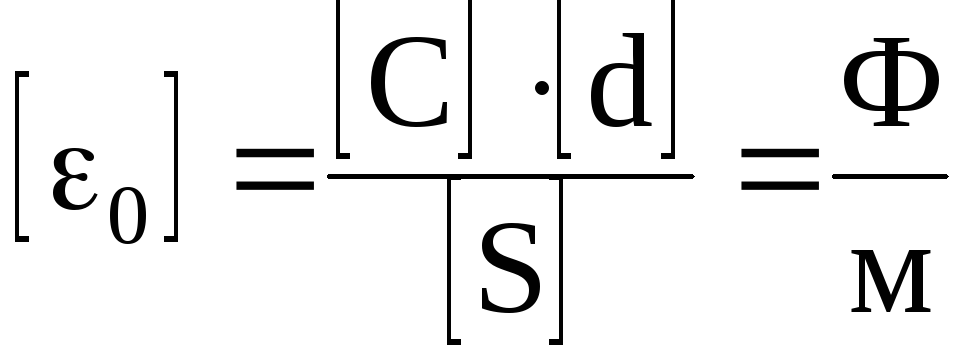. (2.17)

Упражнение 2. Исследование поля цилиндрического конденсатора.

При помощи электролитической ванны можно исследовать поля, обладающие осевой симметрией, т.е. поля, не зависящие от угловой координаты в цилиндрической системе координат (r,,Z).

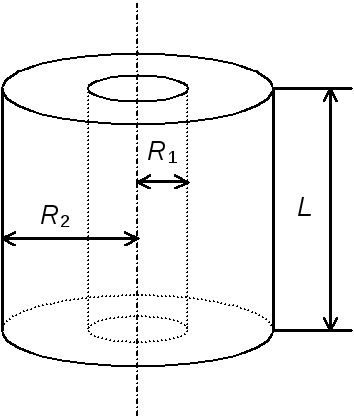
Рис.2.

Ёмкость цилиндрического конденсатора, пропорциональная длине конденсатора, диэлектрической проницаемости среды, заполняющей конденсатор, а также зависит от отношения радиусов цилиндров, возрастая с уменьшением этого отношения (рис.2):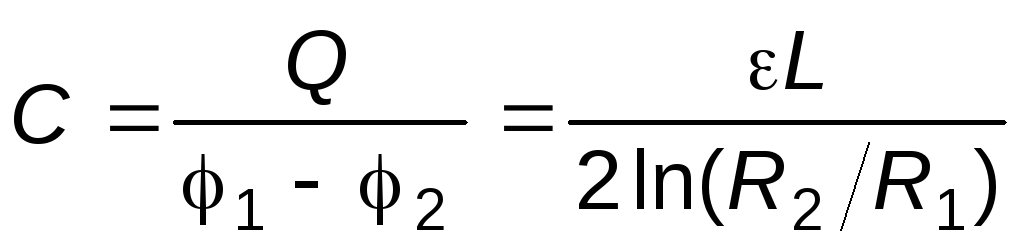

.

Из формулы ёмкости цилиндрического конденсатора можно получить выражение для разности потенциалов между его обкладками:

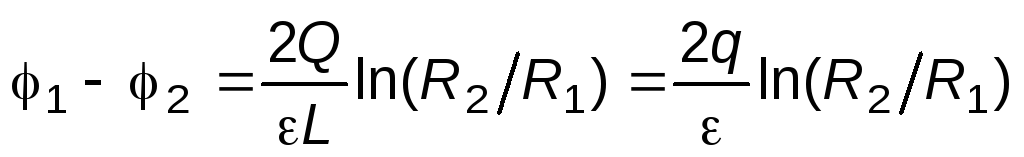, (7)

где q=Q/L— заряд, приходящийся на единицу длины цилиндра.

Проверка формулы (7) составляет содержание данного упражнения.

Порядок выполнения.

Расположите два коаксиальных цилиндрических электрода как показано на рис. 3.

Рис.3.

Определите форму эквипотенциальных поверхностей и исследуйте распределение потенциалов вдоль радиуса цилиндра. Сравните найденное распределение потенциалов с теоретической формулой (7).

Сравнение проведите с помощью графиков. Сначала на основе результатов измерений постройте график экспериментальной зависимости U_x=f(R_x), откладывая по оси абсцисс значенияR_xрасстояние от оси цилиндра до той точки поля, где определялся потенциал.

Затем в этих же осях координат постройте теоретический график функции

.

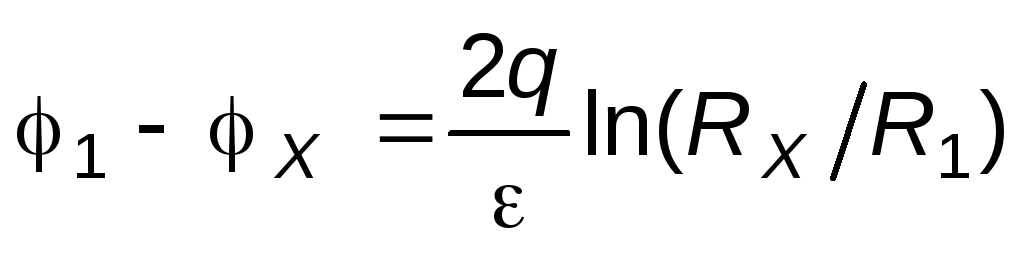Для того чтобы не определять величину 2q/, масштаб по оси ординат для теоретического графика следует выбрать таким, чтобы для какого-либо одного значенияR_xмасштабные отрезки в относительных единицах разности потенциалов и в вольтах были одинаковыми.

Если формула (7) справедлива, то теоретический и опытный графики функции должны совпасть.

Контрольные вопросы.

1. Какова связь между напряженностью электростатического поля и потенциалом? Как экспериментально эта связь может быть проверена?

2. Чему равна циркуляция напряженности по любому замкнутому контуру в потенциальном электрическом поле? Как обосновать справедливость соответствующего уравнения?

3. Сформулируйте закон Кулона и теорему Гаусса.

4. Обоснуйте возможность моделирования электростатического поле в вакууме с помощью слабопроводящей жидкости?

5. Выполняются ли граничные условия на электродах ванны?

6. Почему необходимо, чтобы электроды касались дна ванны и выступали над поверхностью жидкости?

7. Чему равна напряженность электрического поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью?

8. Вывести формулу емкости цилиндрического конденсатора.

Лабораторная работа №3

Изучение вынужденных колебаний и явления резонанса в последовательном колебательном контуре

Цельработы:построение резонансных кривых для колебательного контура, определение добротности и её зависимости от параметров контура.

Оборудование:исследуемый контур, набор резисторов, вольтметр переменного тока или осциллограф в качестве измерителя напряжения, генератор сигналов, соединительные проводники и кабели.

Краткая теория

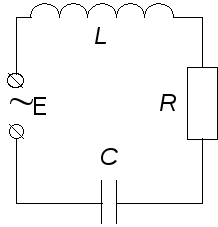
Рис.1. Последовательный колебательный контур.

В работе исследуются вынужденные колебания в колебательном контуре, соединенном с источником электродвижущей силы переменной частоты. В зависимости от того, как источник соединен с колебательным контуром, различаютпоследовательныеипараллельныеколебательные контуры. В данной работе исследуется последовательный колебательный контур (рис.1).

При исследовании вынужденных колебаний большой интерес представляет изучение зависимости интенсивности колебаний от соотношения между частотой внешнего воздействия и собственной частотой незатухающих колебаний в системе.

Вынужденные электромагнитные колебания в контуре могут быть количественно охарактеризованы разными величинами: силой тока; напряжением на конденсаторе; напряжением на катушке индуктивности контура и т.д. Амплитуда каждой из этих величин выражается особой функцией частоты, имеющей характерный максимум при определённом значении частоты _р, называемойрезонанснойчастотой. График такой функции называетсярезонансной кривой(рис.2).

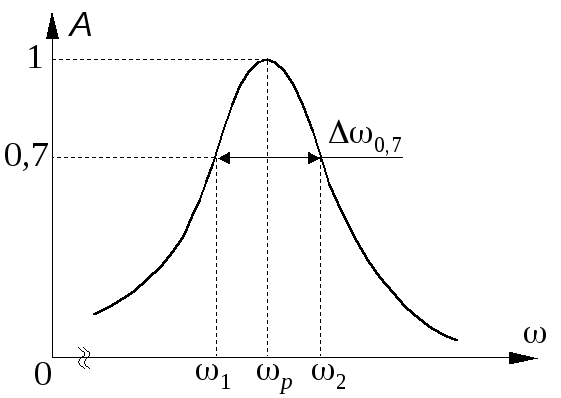
Рис.2. Резонансная кривая (А– относительная амплитуда).

Уравнение для резонансной кривой может быть получено следующим образом.

Запишем, на основании второго закона Кирхгофа, уравнение вынужденных колебаний в последовательном колебательном контуре:

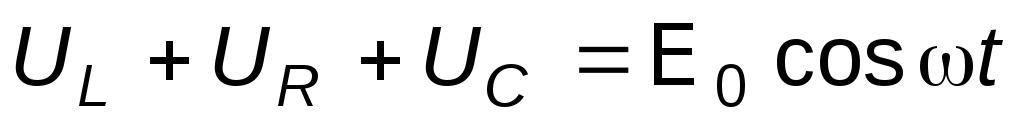, (1)

или

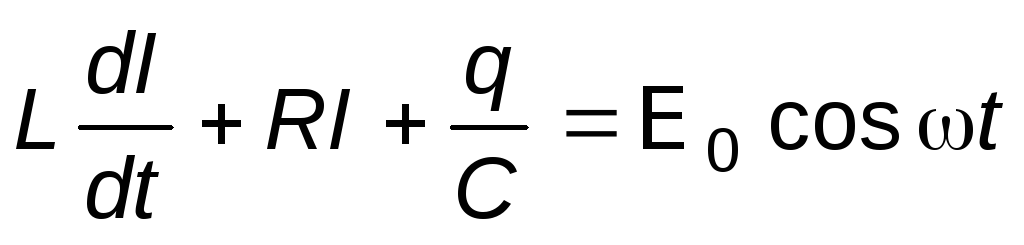. (2)

где E₀— амплитуда э.д.с. генератора, включенного в контур. Учитывая, что сила тока

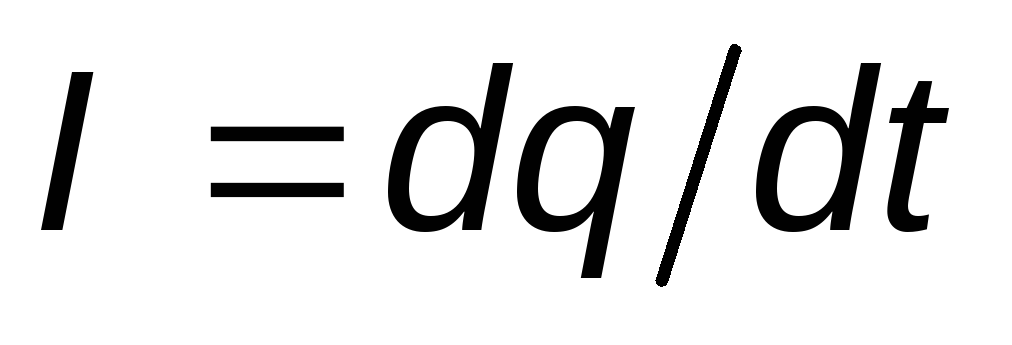, (3)

где q— заряд на конденсаторе, уравнение (2) можно записать в виде:

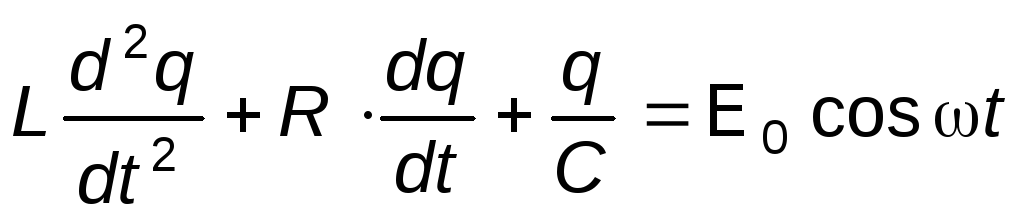. (4)

Поделив обе части уравнения (4) на L, можно привести его к стандартному виду уравнения вынужденных колебаний гармонического осциллятора:

,

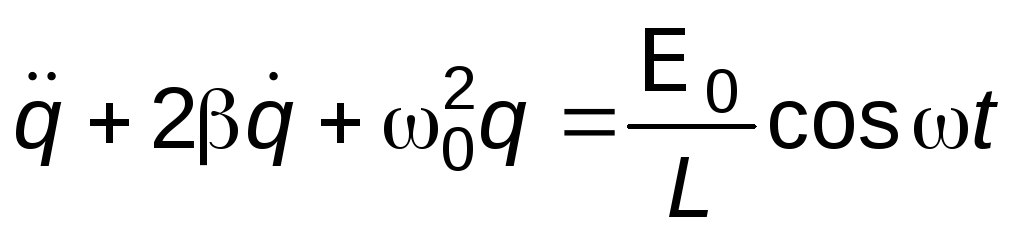где 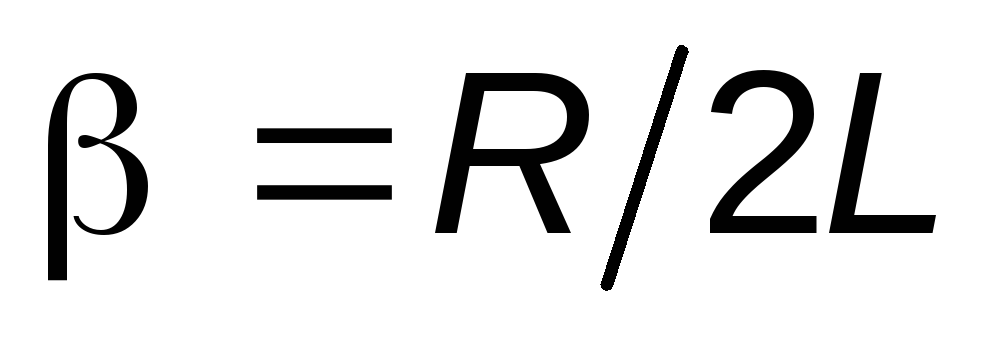– коэффициент затухания, характеризующий потери энергии;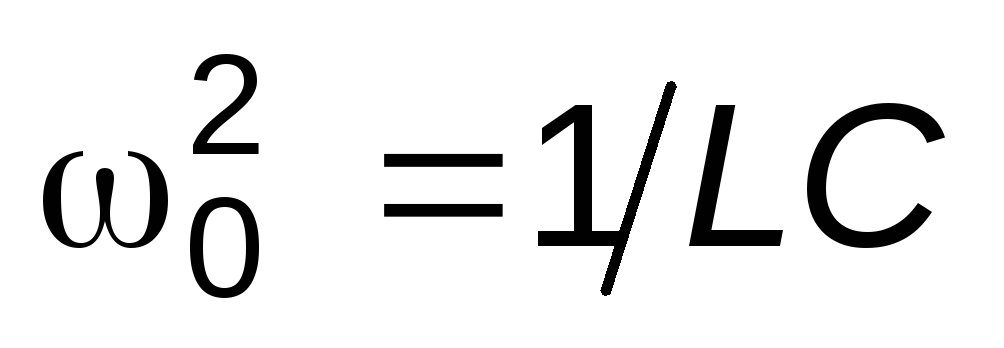– квадрат собственной частоты колебательного контура.

Решение этого линейного неоднородного дифференциального уравнения второго порядка в режиме установившихся вынужденных колебаний будет иметь вид

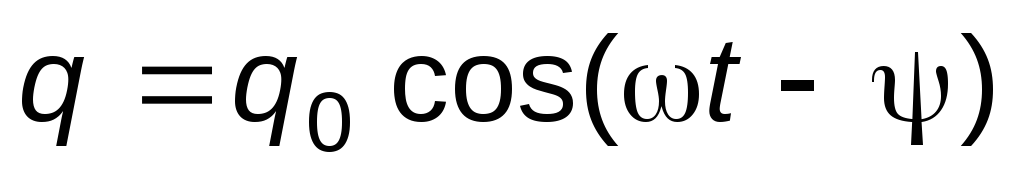, (5)

где q­₀– амплитуда заряда конденсатора,­– разность фаз между колебаниями заряда и внешней э.д.с.E.

Удобнее перейти от выражения для заряда (5) к выражению для тока I, воспользовавшись соотношением (3):

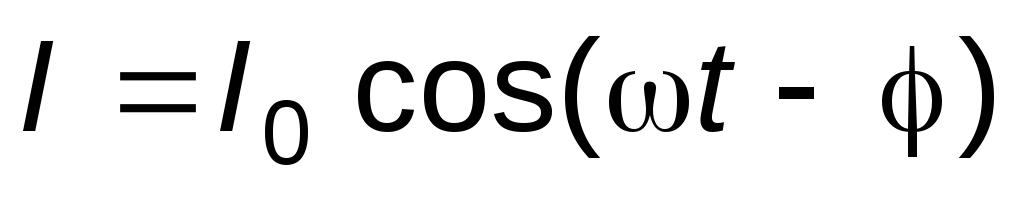, (6)

где I₀— амплитуда тока,- сдвиг по фазе между током и внешней э.д.с.E:

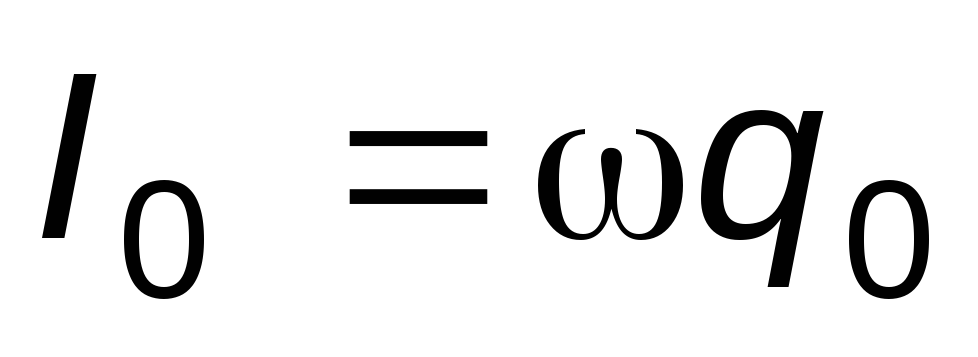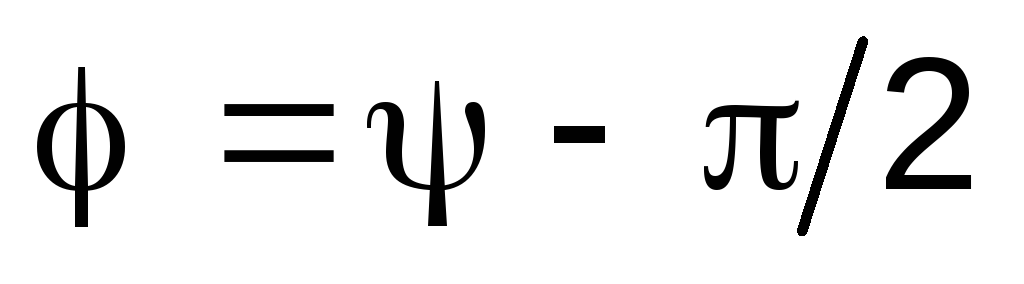,. (7)

С учётом этого, можно получить выражения для напряжений на сопротивлении R, ёмкостиCи индуктивностиL:

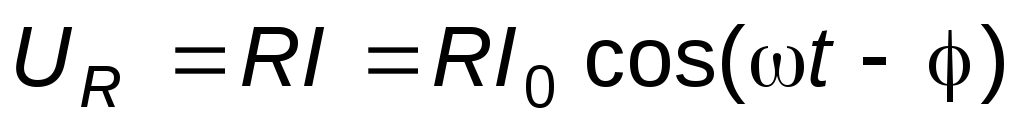, (8)

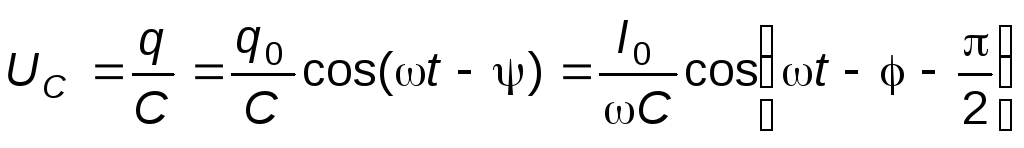, (9)

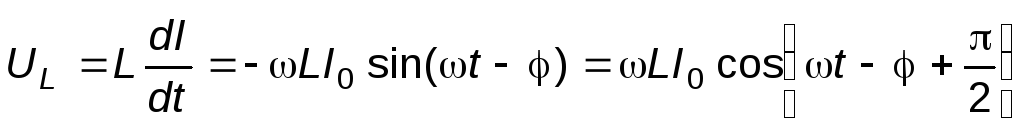, (10)

На основании выражений (8), (9) и (10) можно построить векторную диаграммудля амплитуд напряжений, векторная сумма которых должна быть равна, согласно (1), вектору величинойE₀(рис.2).

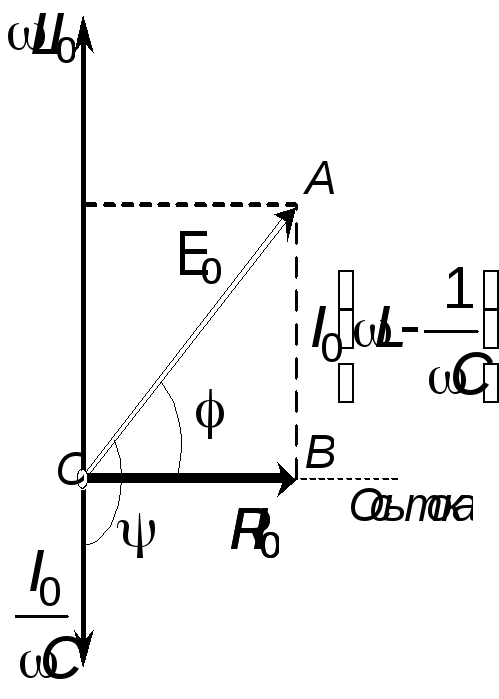
Рис.2. Векторная диаграмма для колебательного контура.

Из треугольника OABэтой диаграммы можно получить выражения дляI₀и:

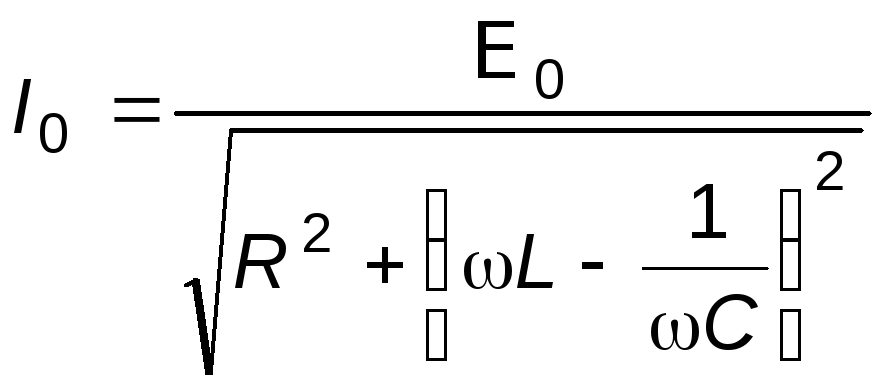, (11)

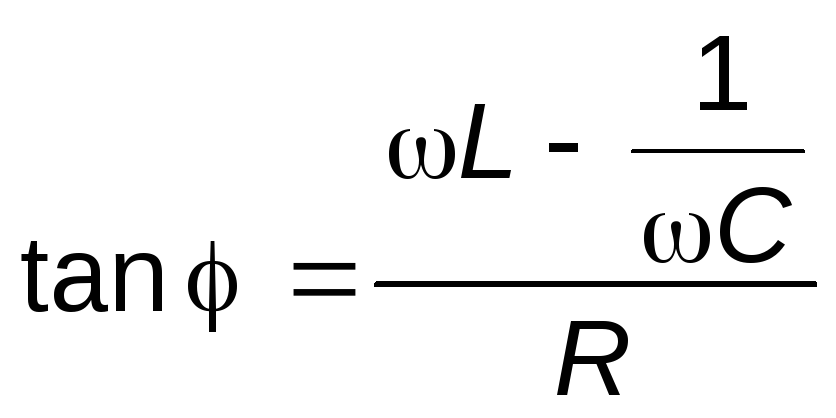. (12)

Как видно из выражения (11), максимальное значение силы тока достигается при 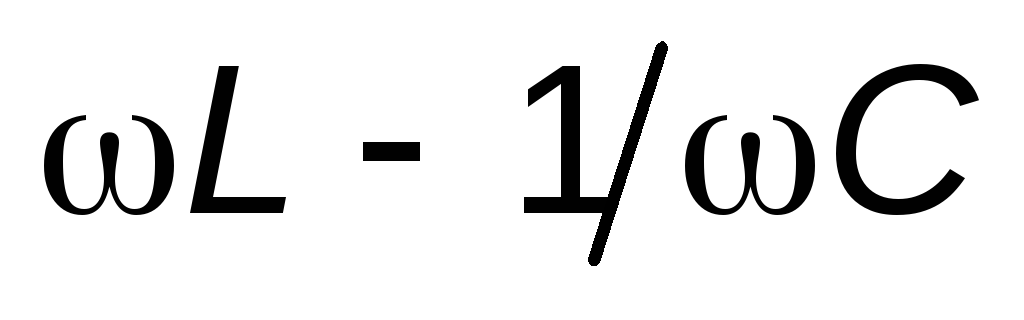= 0. Таким образом,резонансная частота для силы тока равна собственной частоте колебательного контура:

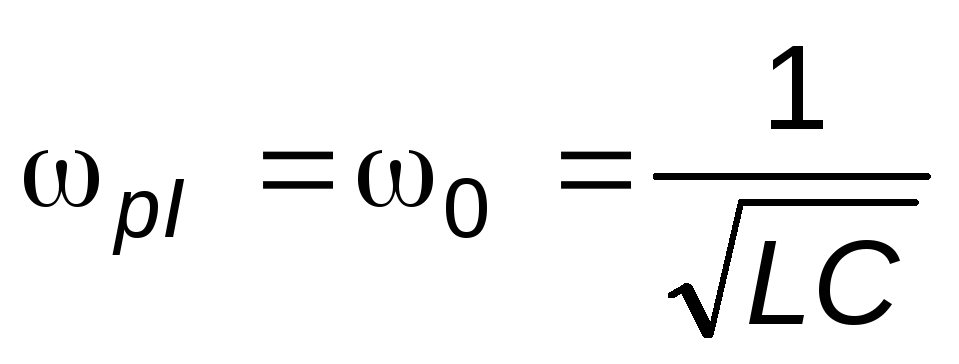(13)

Очевидно, что для напряжения на сопротивлении U_Rчастота максимальной амплитуды колебаний_рRтакже совпадает с₀. Однако, для напряжений на ёмкости и на индуктивности это не так. Выражения для резонансных частот_рCи_рLможно получить, приравняв нулю первые производные подля соответствующих выражений амплитудU_0CиU_0L из (9) и (10):

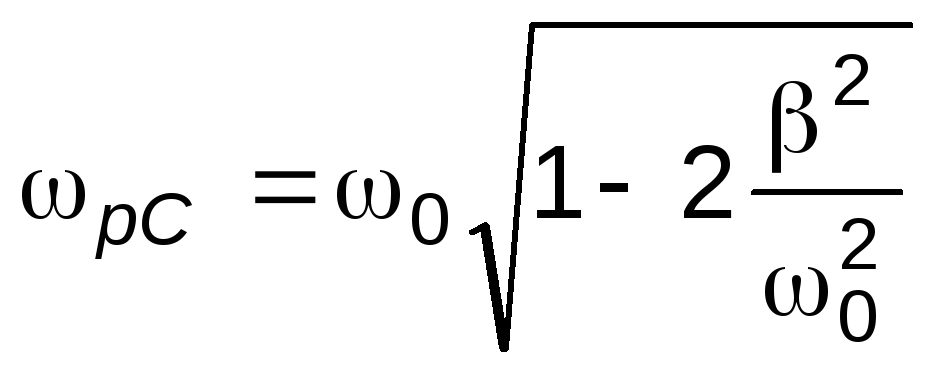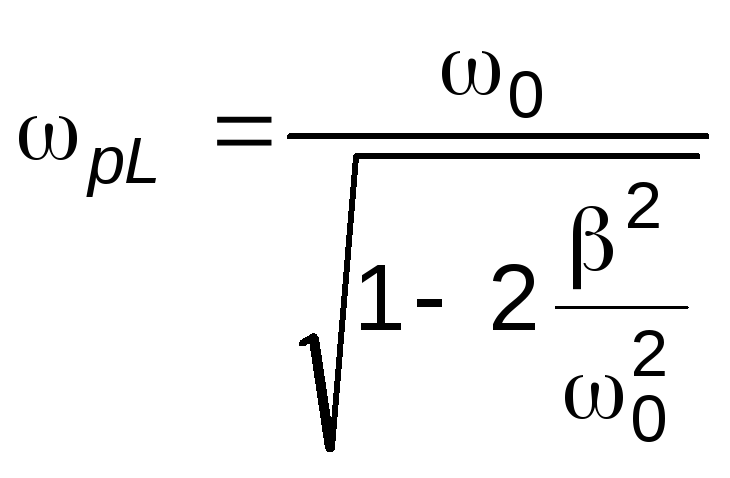,. (14)

Как видно, из формул (14), резонансная частота для напряжения на ёмкости меньше, а для напряжения на индуктивности – больше по сравнению с собственной частотой колебательного контура. Однако, чем меньше коэффициент затухания (т.е., чем меньше потери энергии, обусловленные, в рамках модели, наличием активного сопротивления), тем ближе резонансные частоты_рCи_рLк значению₀. Привсе три резонансные частоты практически одинаковы.

Графики зависимости амплитуд напряжений U_0R,U_0CиU_0Lот частотыпоказаны на рис.3.

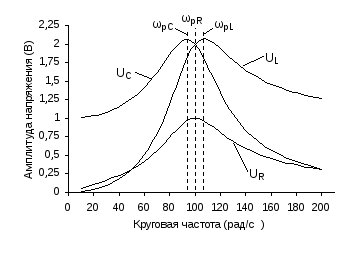
Рис.3. Резонансные кривые колебательного контура со следующими параметрами: R= 1 Ом,C= 0,005 Ф, L= 0,02 Гн,E₀= 1 В.

Важным параметром колебательного контура, характеризующим его резонансные свойства, является добротностьQ. Для колебательного контура с малым затуханием () добротность может быть определена как отношение энергииW, запасённой в контуре, к энергииW, теряемой контуром за один период колебаний:

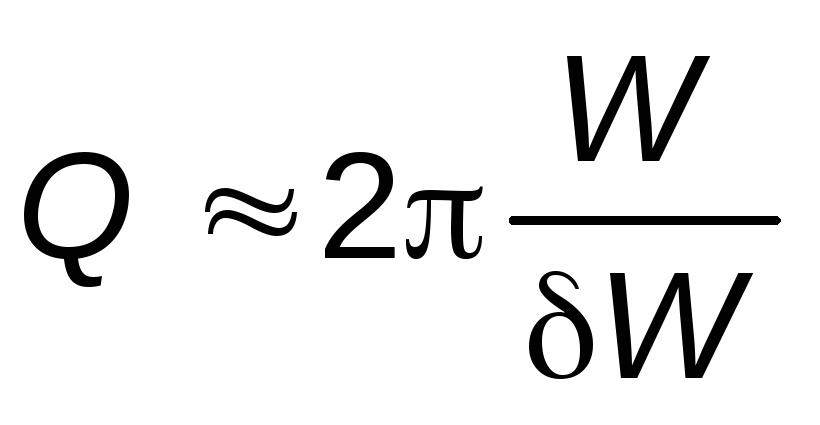
Величина добротности связана с коэффициентом затухания следующим образом:

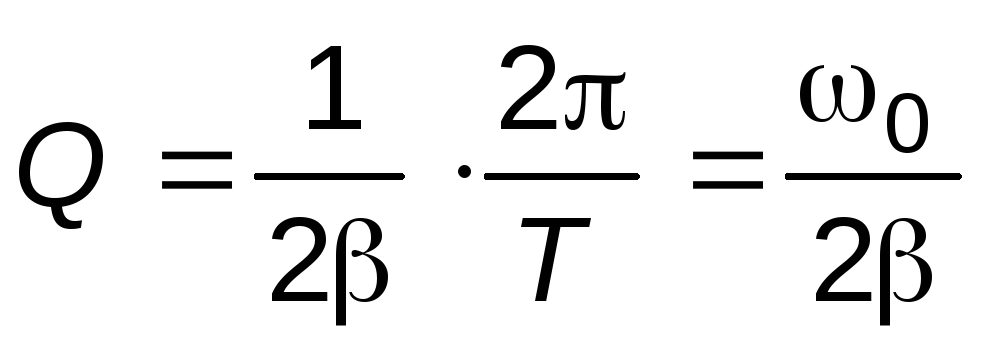(15).

Подставляя выражения для ₀и, получим:

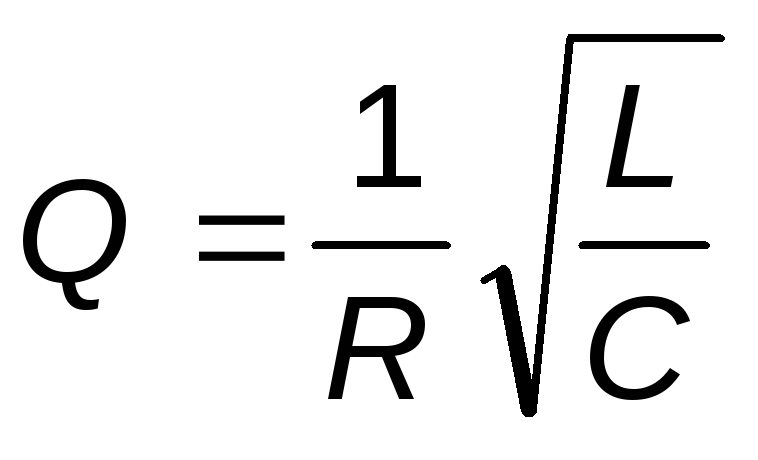. (16)

Выразим отношение амплитуды напряжения на конденсаторе U_0Cк амплитуде внешней э.д.с.E₀на резонансной частоте в случае малого затухания (_рC₀), используя (9) и (11):

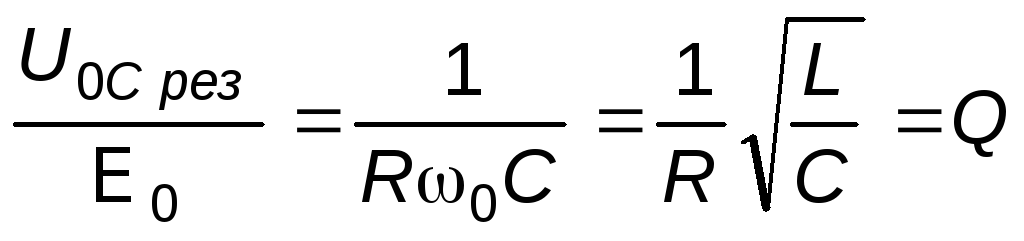(17)

Таким образом, при резонансе в последовательном колебательном контуре амплитуда напряжения на конденсаторе в Q раз превышает амплитуду выходного напряжения генератора. Аналогичный результат можно получить и для амплитуды напряжения на индуктивности. Поэтому резонанс в последовательном колебательном контуре называютрезонансом напряжений.

Добротность контура связана также с ещё одной важной характеристикой резонансной кривой – её шириной. Можно показать, что при малом затухании

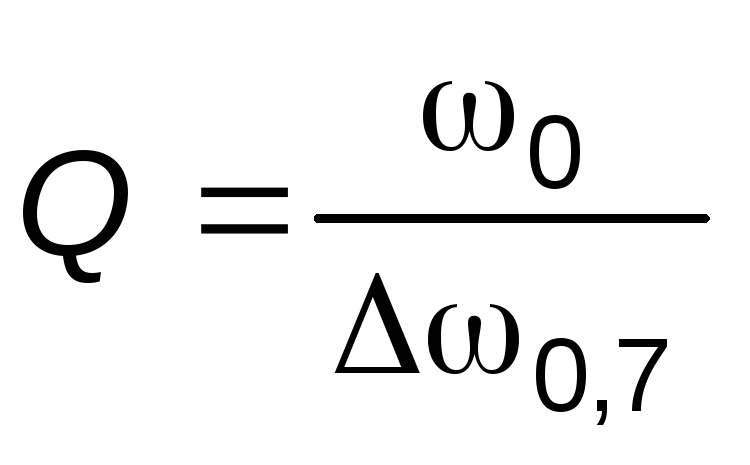, (18)

где _0,7– ширина резонансной кривой на уровне 0,7 (точнее,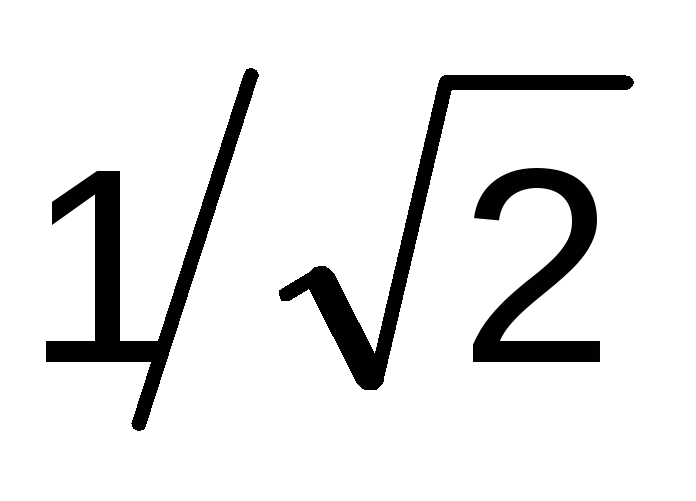) от максимума (см. рис. 2). Формула (18) даёт практический способ определения добротности колебательного контура по измеренной резонансной кривой.