Нахождение емкости конденсатора. Наука техника технологии
Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком.
Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками:
Используя определение емкости конденсатора, получаем:
Отметим, что полученная формула является приближенной, так как выведена без учета искажения поля у краев пластин. Расчет по этой формуле дает завышенное значение ёмкости и тем точнее, чем меньше зазор по сравнению с линейными размерами пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет собой систему двух концентрических сфер с радиусами и. Электрическое поле между обкладками сферического конденсатора согласно теореме Гаусса определяется зарядом внутренней сферы. Напряжение между обкладками равно:
.
Для ёмкости сферического конденсатора получаем:
Это формула точная.
Если , полученная формула переходит в выражение для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
..
Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора.
Соединение конденсаторов.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного соединения конденсаторов.
Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует:
Если
,
то(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении).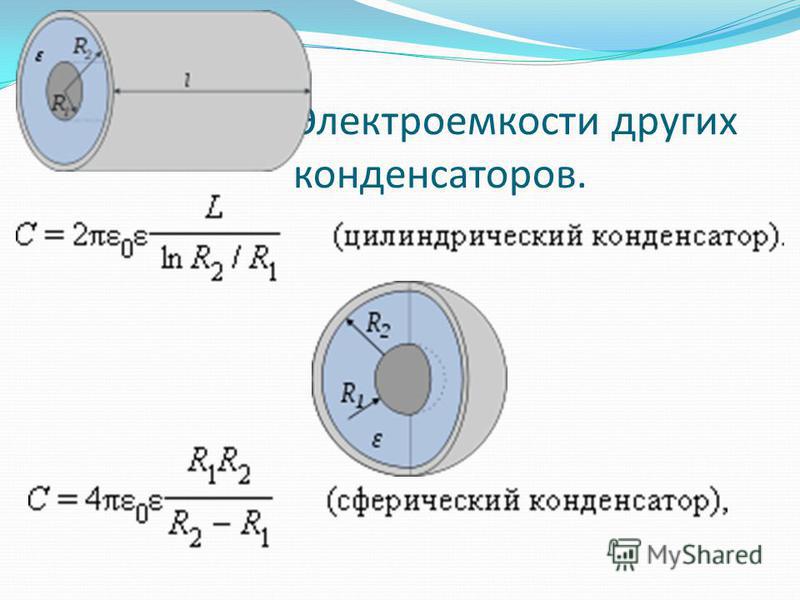
Для последовательно соединенных конденсаторов емкость вычисляется по формуле:
Ёмкость параллельного соединения конденсаторов.
Заряд батареи равен сумме зарядов:
а напряжение . По определению емкости получаем:
Для параллельно соединенных конденсаторов:.
В случае одинаковых конденсаторов: .
Оценить емкость батареи (см. рисунок) .
Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок).
Для расчета ёмкости батареи получаем:
Откуда: , так как, то.
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных
молекул, либо из ионов, находящихся в
узлах кристаллической решетки. Сами же
молекулы могут быть полярными инеполярными.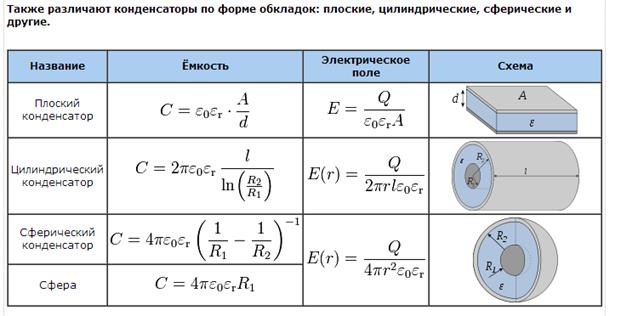
Поляризация.
В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных » зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично.
Под действием электрического поля
диполи ориентируются преимущественно
в направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара сил
исоздает
вращательный момент равный,
где-
дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.
В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.
Отметим, что существуют диэлектрики, поляризованные даже при отсутствии внешнего поля (электреты, сегнетоэлектрики). Мы остановимся на рассмотрении только однородных диэлектриков, в которых отсутствует остаточная поляризация, а объемный и «связанный» заряд всегда равен нулю .
Плоский конденсатор – это физическое упрощение, взявшее начало из ранних исследований электричества, представляющее собой конструкцию, где обкладки имеют форму плоскостей и в каждой точке параллельны.
Формулы
Многие ищут формулы, описывающие ёмкость плоского конденсатора. Если это так, то не читайте ниже любопытные и малоизвестные факты, потому что сухие математические знаки, конечно же, важнее.
Первым определил ёмкость плоского конденсатора Вольта. В его распоряжении ещё не было такой величины, как разница потенциалов, именуемая напряжением, но интуитивно он совершенно правильно объяснил суть явления. Что касается количества зарядов, то он трактовал её, как объем электрического флюида атмосферы – не совсем правильно, но в конечном итоге похоже на правду. Согласно этому мировоззрению ёмкость плоского конденсатора может быть найдена, как отношение объёма накопленного электрического флюида к разнице атмосферных потенциалов, то есть:
Эта формула применима к любому конденсатору, вне зависимости от его конструкции. То есть, является универсальной. Специально для плоских конденсаторов имеется формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры:
В этой формуле через S обозначена площадь обкладок, вычисляемая через произведение сторон, а d – показывает расстояние между обкладками. Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика, да простит Тот столь откровенные тавтологии.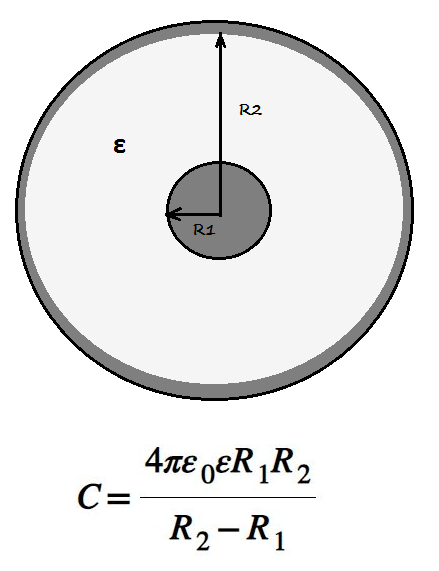 Электролитические конденсаторы обладают столь большой ёмкостью по той причине, что проводящий раствор отделен от металла очень тонким слоем оксида. Следовательно, d в этом случает будет минимальным. Единственный минус в том, что электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на каждом анод или катод обозначены значками плюса или минуса.
Электролитические конденсаторы обладают столь большой ёмкостью по той причине, что проводящий раствор отделен от металла очень тонким слоем оксида. Следовательно, d в этом случает будет минимальным. Единственный минус в том, что электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на каждом анод или катод обозначены значками плюса или минуса.
Плоские конденсаторы сегодня редко встречаются, и это преимущественно плёночные микроскопические технологии, где такой род поверхностей является доминирующим. Все пассивные и активные элементы образуются через трафарет. И, следовательно, имеют вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст.
От материала диэлектрика ёмкость зависит по той причине, что у каждого из них структура своя. Считается, что аморфное вещество состоит из неориентированных диполей, упруго укреплённых на своих местах. При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость.
Из истории
Исторически первым начал исследовать накопление заряда великий Алессандро Вольта. В докладе Королевскому научному обществу за 1782 год он впервые озвучил слово конденсатор. В понимании Вольты электрофорус, представляющий собой две параллельные обкладки, выкачивал из эфира электрический флюид.
В то время все познания сводились к тому, что учёные думали, будто атмосфера Земли содержит в себе нечто, что не может быть определено приборами. Существовали только простейшие электроскопы, способные определить знак заряда и его наличие, но не дававшие представления о количестве. Учёные просто натирали мехом поверхность тела и подносили его для исследования в область влияния прибора. Ещё Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием.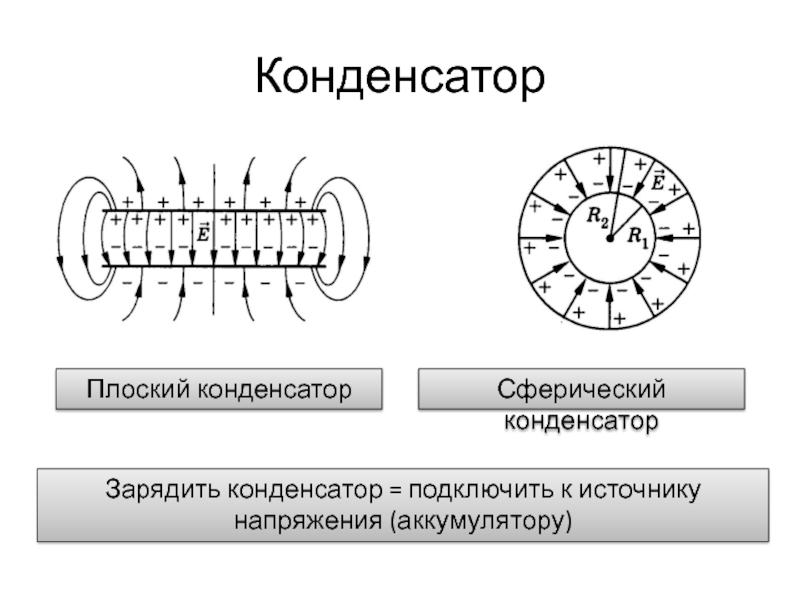
Гипотеза об атмосферном электричестве высказана Бенджамином Франклином. Он активно исследовал молнии и пришёл к выводу, что это проявления все той же единой силы. Запуская воздушного змея в небо, он соединял его шёлковой нитью с землёй и наблюдал дуговой разряд. Это были достаточно опасные опыты, и Бенджамин много раз рисковал своей жизнью ради развития науки. О том, что шёлковая нить проводит статический заряд, было известно от Стивена Грея, первым собравшего в 1732 году электрическую цепь.
Уже через 20 лет (1752 год) Бенджамин Франклин предложил конструкцию первого громоотвода, осуществлявшего молниезащиты близлежащих построек. Только вдуматься! – до этого всякий мог ожидать того, что его дом сгорит от случайного удара. Именно Бенджамин Франклин предложил один из видов заряда называть положительным (стеклянный), а другой отрицательным (смоляной). Так физики были введены в заблуждение относительно истинного направления движения электронов.
К началу исследования Вольтой электрических явлений, таким образом, были уже известны статические заряды и факт наличия у них двух знаков, кроме того люди упорно считали, что весь «флюид» берётся из воздуха. На эту мысль их натолкнули опыты с натиранием янтаря шерстью, которые не могли быть проведены под водой. Следовательно, логичным было предположить, что электричество может происходить только из атмосферы Земли, что, конечно же, совершенно неверно. В частности, многие растворы, исследованные Хампфри Дэви, могут проводить электрический ток.
Причина, следовательно, была в другом – при натирании янтаря под водой силы трения снижались в десятки и сотни раз, а заряд рассеивался по всему объёму жидкости. Следовательно, этот процесс был всего лишь неэффективным. Но сегодня каждый добытчик знает, что нефть прекрасно электризуется трением о трубы и без воздуха. Следовательно, атмосфера для «флюида» не является обязательным компонентом.
Но сегодня каждый добытчик знает, что нефть прекрасно электризуется трением о трубы и без воздуха. Следовательно, атмосфера для «флюида» не является обязательным компонентом.
Самый большой в мире плоский конденсатор
Столь систематизированные, но в корне неверные толкования все-таки не смогли остановить Вольту на его исследовательском пути. Он упорно изучал электрофорус, как один из самых совершенных генераторов, существовавших в то время. Вторым был серный шар Отто фон Герике, изобретённый более чем за век до этого (1663 год). С тех самых пор его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. В частности, в для этого служат металлические гребёнки-нейтрализаторы.
Долгое время учёные ходили вокруг да около. Электрофорная машина 1880 года может считаться первым мощным генератором разряда, позволявшим получить дугу, но своей настоящей силы электроны достигли в генераторе Ван де Граафа (1929 год), где разница потенциалов составила единицы мегавольта. Для сравнения грозовое облако, согласно данным Википедии, может иметь потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Для сравнения грозовое облако, согласно данным Википедии, может иметь потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Суммируя сказанное, можно с определённой долей уверенности сказать, что природные процессы используют в качестве принципа своего действия электризацию трением, влиянием и некоторые другие её виды, а мощный циклон является самым большим из известных нам плоских конденсаторов. Молния показывает, что бывает, когда диэлектрик (атмосфера) не выдерживает приложенной разницы потенциалов и пробивается. В точности то же самое происходит в любом плоском конденсаторе, созданном человеком, если вольтаж оказывается для него непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя.
Электрофорус
Итак, Вольта взялся за исследование модели природных процессов. Первый электрофорус появился в 1762 году сконструированный Йоханом Карлом Вильке.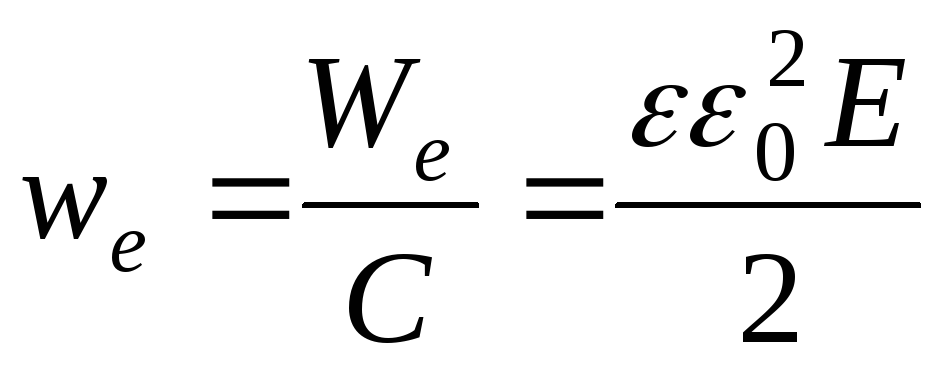 По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта же и дал прибору его нынешнее название.
По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта же и дал прибору его нынешнее название.
Электрофорус способен накапливать электростатический заряд, образованный трением резины куском шерсти. Он состоит из двух плоских, параллельных друг другу обкладок:
- Нижняя представляет собой тонкий кусок резины. Толщина его выбирается из соображений эффективности устройства. Если выбрать кусок более солидный, то значительная часть энергии будет накапливаться внутри диэлектрика на ориентацию его молекул. Что и наблюдается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.
- Верхняя пластина из тонкой стали кладётся сверху, когда заряд уже накоплен трением. За счёт влияния на верхней поверхности образуется избыток отрицательного заряда, и он должен быть снят на заземлитель, чтобы при расстыковке двух обкладок не произошло взаимной компенсации.

Принцип действия этого плоского конденсатора должен быть уже понятен. Оператор трёт резину шерстью, оставляя на ней отрицательный заряд. Затем сверху кладётся кусок металла. Из-за значительной шероховатости поверхностей они не соприкасаются, но находятся на некотором расстоянии друг от друга. В результате металл электризуется влиянием. Электроны отталкиваются поверхностным зарядом резины и уходят на внешнюю плоскость, где оператор их снимает через заземлитель лёгким кратковременным прикосновением.
Низ металлической обкладки остаётся заряженным положительно. При расстыковке двух поверхностей этот эффект сохраняется, потому что в материале наблюдается дефицит электронов. И можно наблюдать искру, если дотронуться до металлической обкладки. Этот опыт можно на одном и том же заряде резины проделывать сотни раз, поскольку её поверхностное статическое сопротивление весьма велико. Это не даёт заряду растекаться. Демонстрируя этот опыт, Вольта привлёк внимание всего научного мира, но исследования никак не двигались вперёд, если не считать открытий Шарля Кулона.
В 1800 году сам Алессандро даёт толчок развитию изысканий в области электричества, изобретя свой знаменитый гальванический источник питания.
Конструкция плоского конденсатора
Электрофорус по сути представляет собой первый из когда-либо сконструированных плоских конденсаторов. Его обкладки способны хранить только статический заряд, потому что иначе наэлектризовать резину невозможно. Поверхность очень долго хранит электроны. Вольта даже предлагал снимать их пламенем свечи через ионизированный воздух или ультрафиолетовым излучением Солнца. Сегодня каждый школьник знает, что то же самое можно проделать и водой. Правда, электрофорус нужно будет после этого высушить.
В современном мире нижней обкладкой может служить тефлоновое покрытие или пластик. Они тоже хорошо набирают статический заряд. Диэлектриком здесь служит воздух. Чтобы перейти к конструкции современного конденсатора, нужно обе обкладки сделать металлическими. Тогда при возникновении на одной из них заряда влиянием электризация распространится на вторую, и если другой контакт заземлён, накопленная энергия может храниться какое-то время.
Запас электронов напрямую зависит от материала диэлектриков. Так например, среди современных конденсаторов встречаются:
- Слюдяные.
- Воздушные.
- Электролитические (оксидные).
- Керамические.
В эти названия как раз и заложен материал диэлектрика. От его состава зависит напрямую ёмкость, которая может быть увеличена во много раз. Роль диэлектриков объяснялась выше, в частности их параметры определяются непосредственно строением вещества. Однако многие материалы, обладающие высокими характеристиками, использовать не удаётся по причине их непригодности. Так например, вода обладает высокой диэлектрической проницаемостью.
КОНДЕНСАТОР — означает накопитель. В радио и электронной
аппаратуре конденсатор является накопителем электрических
зарядов. Простейший конденсатор состоит из двух металлических
пластинок разделенных слоем диэлектрика. Диэлектрик — это
материал который не проводит электрического тока и обладает
определенными свойствами о которых поговорим чуть позже.
Так как конденсатор является накопителем, то он должен
обладать определенной емкостью (объемом для накопления
зарядов). На емкость конденсатора влияют площадь пластин
(еще их называют «обкладками»), расстояние между обкладками
и качество диэлектрика. К хорошим диэлектрикам
относятся вакуум, эбонит, фарфор, слюда, полиэтилен,
текстолит и много других синтетических материалов.
На рисунке изображен простейший конденсатор
с двумя параллельными обкладками площадью S
(S = m * n), которые находятся в вакууме на расстоянии d друг
от друга.
Если между верхней и нижней обкладками конденсатора
приложить напряжение Uab, то на верхней и нижней обкладках
конденсатора накопятся одинаковые положительный +q и
отрицательный -q заряды, которые называют свободными. Между
обкладками возникает электрическое поле обозначенное на рисунке
буквой Е.
Емкость нашего конденсатора (обозначается буквой С) будет:
С = Eo*S/d, где Ео — электрическая постоянная (для вакуума)
Ео=8,854 * 10 -12 Ф/м (Фарад на метр).
Если между обкладками поместить диэлектрик,
то ёмкость конденсатора
будет: С = Er * Eo *S / d. В формуле расчета ёмкости добавилась
величина Er — относительная диэлектрическая проницаемость
введённого диэлектрика.
Из формулы следует, что емкость конденсатора увеличивается на
величину Er проницаемости диэлектрика. Итак, чем больше площадь
S пластин конденсатора, больше значение Er и меньше расстояние
d между пластинами, тем больше емкость конденсатора.
Основной единицей емкости в системе единиц СИ является фарад
(Ф). Емкость 1Ф очень велика. В электротехнике обычно
используют дольные единицы емкости:
микрофарада (мкФ), 1мкФ = 1*10 -6 Ф,
нанофарада (нФ), 1нФ = 1*10 -9 Ф, и
пикофарада (пФ), 1пФ = 1*10 -12 Ф.
При выборе диэлектрика для конденсаторов, кроме относительной
диэлектрической проницаемости диэлектрика, учитывают еще два
важных параметра:
1) Электрическую прочность — прочность диэлектрика при подаче
на прокладки конденсатора высокого напряжения. При низкой
электрической прочности может произойти электрический пробой,
и диэлектрик станет проводником электрического тока;
При низкой
электрической прочности может произойти электрический пробой,
и диэлектрик станет проводником электрического тока;
2) Удельное объемное сопротивление — электрическое
сопротивление диэлектрика постоянному току. Чем больше удельное
сопротивление диэлектрика, тем меньше утечка накопленных
зарядов в конденсаторе.
КОНДЕНСАТОР В ЦЕПИ ПОСТОЯННОГО ТОКА. На графике накопление заряда конденсатором выглядит как показано на рисунке 1.
Время заряда конденсатора зависит от ёмкости конденсатора (при одинаковом приложенном напряжении). Чем больше ёмкость конденсатора, тем больше время заряда. Аналогичная картина (Рис. 2) наблюдается при разрядке конденсатора на сопротивление. При одинаковом сопротивлении время разряда больше у конденсатора с большей ёмкостью.
КОНДЕНСАТОР В ЦЕПИ ПЕРЕМЕННОГО ТОКА. Если напряжение приложенное к емкостному элементу, будет
изменяться по амплитуде (переменное напряжение),то будет
изменяться и заряд конденсатора, то есть в емкостном элементе
появится ток.
Ток Ic проходящий через конденсатор зависит от
частоты f приложенного переменного напряжения и ёмкости С
конденсатора. Если для постоянного тока сопротивление
конденсатора можно считать равным бесконечности, то для
переменного тока конденсатор обладает определённым
сопротивлением. Сопротивление конденсатора переменному току
Rc рассчитывается по формуле показанной на рисунке.
В формуле расчета емкостного сопротивления переменному току
частота выражается в герцах, а емкость конденсатора в
фарадах. Из формулы видно, что с увеличением частоты f при
неизменной емкости конденсатора сопротивление Rc снижается,
аналогично с увеличением емкости конденсатора при неизменной
частоте сопротивление Rc так же снижается.
Конденсаторы, так же как и резисторы, для получения заданной
емкости Со можно включать параллельно и последовательно.
Формулы расчета результирующей емкости показаны на рисунке.
КОНСТРУКЦИЯ, ПАРАМЕТРЫ И ТИПЫ КОНДЕНСАТОРОВ. Предположим, что мы конструируем конденсатор и попробуем,
уже обладая определенными знаниями, рассчитать емкость
конденсатора.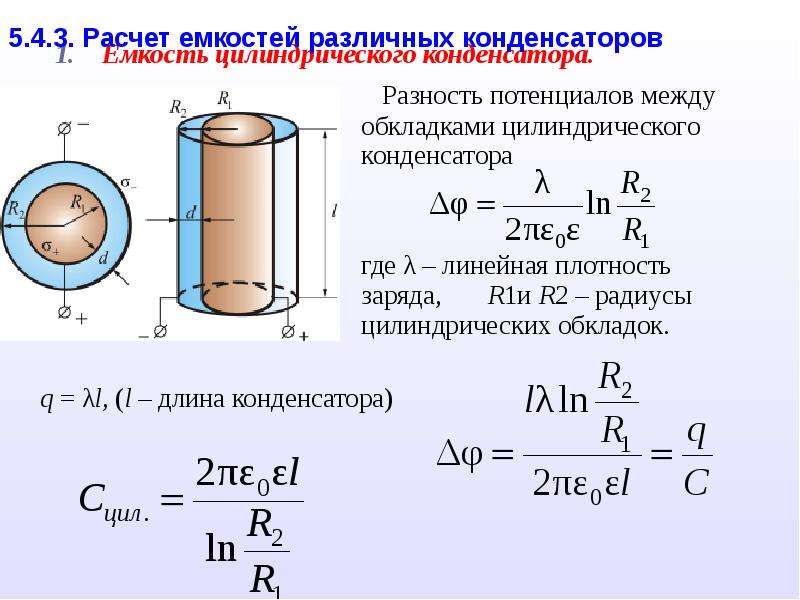 Как известно, емкость конденсатора зависит от
площади обкладок S, расстояния между обкладками d и
диэлектрической проницаемости применяемого диэлектрика Er.
Обкладки конденсатора изготавливаются из металлов с хорошей
электрической проводимостью — алюминий, медь, серебро, золото.
Емкость конденсатора не зависит от толщины обкладок, поэтому
чем тоньше обкладки конденсатора, тем лучше — экономим металл
и уменьшаем геометрический объём конденсатора.
Как известно, емкость конденсатора зависит от
площади обкладок S, расстояния между обкладками d и
диэлектрической проницаемости применяемого диэлектрика Er.
Обкладки конденсатора изготавливаются из металлов с хорошей
электрической проводимостью — алюминий, медь, серебро, золото.
Емкость конденсатора не зависит от толщины обкладок, поэтому
чем тоньше обкладки конденсатора, тем лучше — экономим металл
и уменьшаем геометрический объём конденсатора.
Расстояние d не должно быть слишком малым, во избежание
электрического пробоя диэлектрика.
Выберем в качестве диэлектрика наиболее распространенный
материал — гетинакс с Er равной 6 … 8. Примем Er для
нашего конденсатора равной 7.
Площадь S вычисляется для одной обкладки конденсатора при условии,
что линейные размеры обкладок одинаковы.
Если одна из обкладок имеет меньшие длину или ширину то площадь
вычисляется для меньшей обкладки.
Все размеры — длина и ширина обкладок и расстояние между ними
должны быть выражены в метрах. Примем размеры такие, какие
показаны на рисунке. Подставим в формулу расчета емкости
конденсатора наши данные: C = Er * Eo * S / d;
Примем размеры такие, какие
показаны на рисунке. Подставим в формулу расчета емкости
конденсатора наши данные: C = Er * Eo * S / d;
C = 7 * 8.854*10 -12 * 0.0025 / 0.001= 0.000000000155Ф (фарады).
Возведем полученный результат в 12 степень чтобы получить
значение емкости в пикофарадах:
C = 0.000000000155 12 = 155пФ.
Полученная нами ёмкость конденсатора 155пф очень мала, обычно
такие ёмкости используются в аппаратуре работающей на высоких
частотах переменного тока порядка 1 — 600 МГц (мегагерц).
Представьте себе, что мы разрабатываем миниатюрный карманный
радиоприемник в котором требуется порядка 30 таких конденсаторов.
Если мы установим в схему 30 разработанных нами конденсаторов,
не считая других необходимых радиодеталей, то наш радиоприемник
никак не получится миниатюрным. Все дело в том, что объём
только наших конденсаторов получится таким, что его никак
нельзя будет назвать приемлемым.
Объем одного конденсатора Vc равен Vc = 5см * 5см * 0,1см
Vc = 2,5см в кубе. Тогда объем 30 конденсаторов будет равен:
Тогда объем 30 конденсаторов будет равен:
V = 30 * 2,5 = 75см в кубе.
Что делать, как быть, как уменьшить геометрический объем
конденсатора для применения в миниатюрной радиоаппаратуре?
Для решения этой проблемы максимально уменьшают расстояние
между обкладками, тогда увеличивается емкость и уменьшается
геометрический объем конденсатора. Но расстояние уменьшают
до определенных пределов иначе конденсатор будет пробиваться
даже при низком напряжении подаваемом на конденсатор. В связи
с этим на каждом конденсаторе указывается напряжение которое
он может выдержать.
Для уменьшения площади обкладок конденсатор делают многослойным
состоящим как бы из нескольких параллельно включенных конденсаторов
(вспомните формулу параллельного включения конденсаторов).
В качестве диэлектрика в миниатюрных конденсаторах используют
тонкие пленки из синтетических материалов, а в качестве обкладок
металлическую фольгу, чаще всего из алюминия.
На корпусе конденсатора, обычно, указывается его тип, емкость и
рабочее напряжение. Остальные параметры конденсатора
определяются из справочников. Емкость конденсатора указывается
не так, как на электрических схемах. Например емкость 2,2пФ
обозначается 2П2, емкость 1500 пФ — 1Н5, емкость 0,1 мкФ — М1,
емкость 2,2 мкФ — 2М2, емкость 10 мкФ — 10М.
Остальные параметры конденсатора
определяются из справочников. Емкость конденсатора указывается
не так, как на электрических схемах. Например емкость 2,2пФ
обозначается 2П2, емкость 1500 пФ — 1Н5, емкость 0,1 мкФ — М1,
емкость 2,2 мкФ — 2М2, емкость 10 мкФ — 10М.
У обычных конденсаторов КМ, КД, МБМ и так далее трудно получить
большую ёмкость при малых габаритах поэтому были разработаны
так называемые электролитические конденсаторы у которых в
качестве диэлектрика используется специальная электролитическая
жидкость с очень большим Er. Ёмкость таких конденсаторов может
достигать сотен тысяч микрофарад. К недостатку таких конденсаторов
следует отнести низкое рабочее напряжение (до 500V) и обязательное
соблюдение полярности при включении в схему.
Для настройки и подстройки некоторых типов радиоаппаратуры,
например радиоприемник или телевизор, применяют специальные конденсаторы
с изменяемой ёмкостью.
В зависимости от назначения такие конденсаторы называют «подстроечные»
и «конденсаторы переменной емкости».
Емкость переменных и подстроечных конденсаторов изменяется
механическим способом, путем изменения расстояния между
обкладками или изменения площади пластин. В качестве
диэлектрика в таких конденсаторах используется воздух или
фарфор.
В заключение следует отметить, что в настоящее время, в связи
с бурным развитием радиоэлектроники подстроечные и переменные
конденсаторы практически не применяются. Их с успехом заменяют
специальные фильтры и полупроводниковые приборы которые не
требуют механического изменения параметров.
Площадь обкладки конденсатора. Наука техника технологии
Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком.
Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками:
Используя определение емкости конденсатора, получаем:
Отметим, что полученная формула является
приближенной, так как выведена без учета
искажения поля у краев пластин.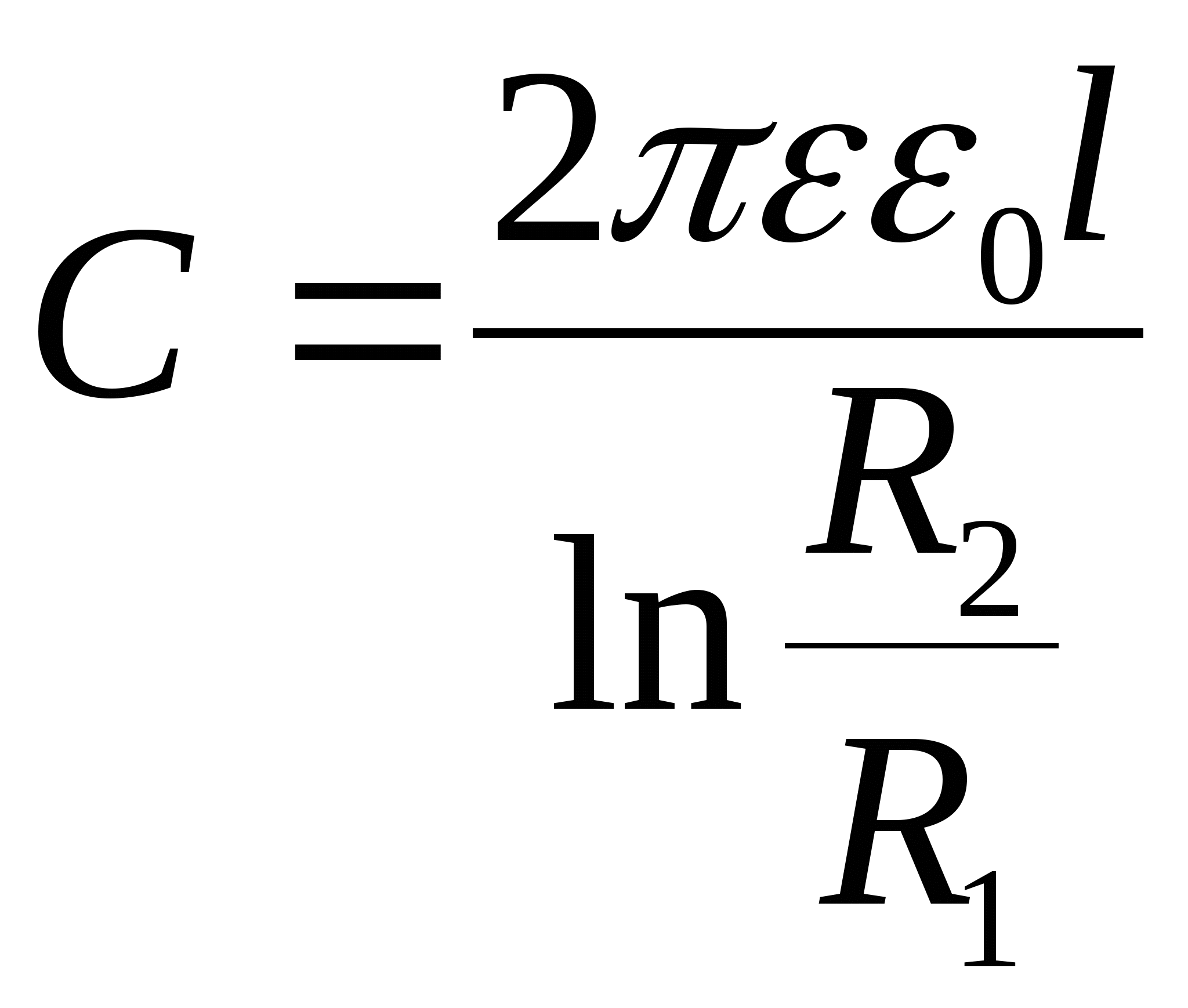 Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор
по сравнению с линейными размерами
пластин.
Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор
по сравнению с линейными размерами
пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет собой систему двух концентрических сфер с радиусами и. Электрическое поле между обкладками сферического конденсатора согласно теореме Гаусса определяется зарядом внутренней сферы. Напряжение между обкладками равно:
.
Для ёмкости сферического конденсатора получаем:
Это формула точная.
Если , полученная формула переходит в выражение для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
..
Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора.
Соединение
конденсаторов.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного соединения конденсаторов.
Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует:
Если , то(ёмкость последовательного соединения меньше наименьшей ёмкости в последовательном соединении).
Для последовательно соединенных конденсаторов емкость вычисляется по формуле:
Ёмкость параллельного соединения конденсаторов.
Заряд батареи равен сумме зарядов:
а напряжение . По определению емкости получаем:
Для параллельно соединенных конденсаторов:.
В случае одинаковых конденсаторов: .
Оценить емкость батареи (см. рисунок) .
Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок).
Для расчета ёмкости батареи получаем:
Откуда:
,
так как,
то.
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярными инеполярными. Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики
поляризуются. Это явление связано с
появлением в объеме и на поверхности
диэлектрика «связанных » зарядов.
При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т. е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.
е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.
Под действием электрического поля диполи ориентируются преимущественно в направлении поля. Рассмотрим подробнее этот механизм (см. рисунок). Пара сил исоздает вращательный момент равный, где- дипольный момент молекулы. Этот момент стремится ориентировать диполь вдоль поля. В ионных кристаллах под действием электрического поля все положительные ионы смещаются по полю, отрицательные – против поля. Отметим, что смещение зарядов очень малы даже по сравнению с размерами молекул. Это связано с тем, что напряженность внешнего электрического поля обычно много меньше напряженности внутренних электрических полей в молекулах.
Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю
.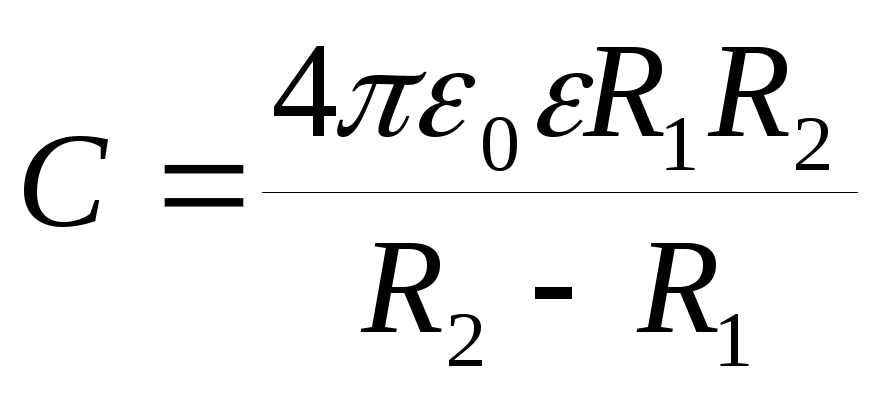
Плоский конденсатор – это физическое упрощение, взявшее начало из ранних исследований электричества, представляющее собой конструкцию, где обкладки имеют форму плоскостей и в каждой точке параллельны.
Формулы
Многие ищут формулы, описывающие ёмкость плоского конденсатора. Если это так, то не читайте ниже любопытные и малоизвестные факты, потому что сухие математические знаки, конечно же, важнее.
Первым определил ёмкость плоского конденсатора Вольта. В его распоряжении ещё не было такой величины, как разница потенциалов, именуемая напряжением, но интуитивно он совершенно правильно объяснил суть явления. Что касается количества зарядов, то он трактовал её, как объем электрического флюида атмосферы – не совсем правильно, но в конечном итоге похоже на правду. Согласно этому мировоззрению ёмкость плоского конденсатора может быть найдена, как отношение объёма накопленного электрического флюида к разнице атмосферных потенциалов, то есть:
Эта формула применима к любому конденсатору, вне зависимости от его конструкции. То есть, является универсальной. Специально для плоских конденсаторов имеется формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры:
То есть, является универсальной. Специально для плоских конденсаторов имеется формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры:
В этой формуле через S обозначена площадь обкладок, вычисляемая через произведение сторон, а d – показывает расстояние между обкладками. Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика, да простит Тот столь откровенные тавтологии. Электролитические конденсаторы обладают столь большой ёмкостью по той причине, что проводящий раствор отделен от металла очень тонким слоем оксида. Следовательно, d в этом случает будет минимальным. Единственный минус в том, что электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на каждом анод или катод обозначены значками плюса или минуса.
Плоские конденсаторы сегодня редко встречаются, и это преимущественно плёночные микроскопические технологии, где такой род поверхностей является доминирующим. Все пассивные и активные элементы образуются через трафарет. И, следовательно, имеют вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст.
Все пассивные и активные элементы образуются через трафарет. И, следовательно, имеют вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст.
От материала диэлектрика ёмкость зависит по той причине, что у каждого из них структура своя. Считается, что аморфное вещество состоит из неориентированных диполей, упруго укреплённых на своих местах. При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость. В результате заряд продолжает накапливаться, пока этот процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на свои места, делая возможным следующий рабочий цикл. Так функционирует плоский электрический конденсатор.
Из истории
Исторически первым начал исследовать накопление заряда великий Алессандро Вольта. В докладе Королевскому научному обществу за 1782 год он впервые озвучил слово конденсатор. В понимании Вольты электрофорус, представляющий собой две параллельные обкладки, выкачивал из эфира электрический флюид.
В то время все познания сводились к тому, что учёные думали, будто атмосфера Земли содержит в себе нечто, что не может быть определено приборами. Существовали только простейшие электроскопы, способные определить знак заряда и его наличие, но не дававшие представления о количестве. Учёные просто натирали мехом поверхность тела и подносили его для исследования в область влияния прибора. Ещё Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием. Поэтому учёные примерно знали, что нужно делать, но исследования не продвигались ни на йоту.
Гипотеза об атмосферном электричестве высказана Бенджамином Франклином. Он активно исследовал молнии и пришёл к выводу, что это проявления все той же единой силы. Запуская воздушного змея в небо, он соединял его шёлковой нитью с землёй и наблюдал дуговой разряд. Это были достаточно опасные опыты, и Бенджамин много раз рисковал своей жизнью ради развития науки. О том, что шёлковая нить проводит статический заряд, было известно от Стивена Грея, первым собравшего в 1732 году электрическую цепь.
Уже через 20 лет (1752 год) Бенджамин Франклин предложил конструкцию первого громоотвода, осуществлявшего молниезащиты близлежащих построек. Только вдуматься! – до этого всякий мог ожидать того, что его дом сгорит от случайного удара. Именно Бенджамин Франклин предложил один из видов заряда называть положительным (стеклянный), а другой отрицательным (смоляной). Так физики были введены в заблуждение относительно истинного направления движения электронов. Но как они могли думать иначе, когда в 1802 году на примере опытов нашего соотечественника Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, вот только это были ионы воздушной плазмы.
К началу исследования Вольтой электрических явлений, таким образом, были уже известны статические заряды и факт наличия у них двух знаков, кроме того люди упорно считали, что весь «флюид» берётся из воздуха. На эту мысль их натолкнули опыты с натиранием янтаря шерстью, которые не могли быть проведены под водой. Следовательно, логичным было предположить, что электричество может происходить только из атмосферы Земли, что, конечно же, совершенно неверно. В частности, многие растворы, исследованные Хампфри Дэви, могут проводить электрический ток.
Следовательно, логичным было предположить, что электричество может происходить только из атмосферы Земли, что, конечно же, совершенно неверно. В частности, многие растворы, исследованные Хампфри Дэви, могут проводить электрический ток.
Причина, следовательно, была в другом – при натирании янтаря под водой силы трения снижались в десятки и сотни раз, а заряд рассеивался по всему объёму жидкости. Следовательно, этот процесс был всего лишь неэффективным. Но сегодня каждый добытчик знает, что нефть прекрасно электризуется трением о трубы и без воздуха. Следовательно, атмосфера для «флюида» не является обязательным компонентом.
Самый большой в мире плоский конденсатор
Столь систематизированные, но в корне неверные толкования все-таки не смогли остановить Вольту на его исследовательском пути. Он упорно изучал электрофорус, как один из самых совершенных генераторов, существовавших в то время. Вторым был серный шар Отто фон Герике, изобретённый более чем за век до этого (1663 год). С тех самых пор его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. В частности, в для этого служат металлические гребёнки-нейтрализаторы.
С тех самых пор его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. В частности, в для этого служат металлические гребёнки-нейтрализаторы.
Долгое время учёные ходили вокруг да около. Электрофорная машина 1880 года может считаться первым мощным генератором разряда, позволявшим получить дугу, но своей настоящей силы электроны достигли в генераторе Ван де Граафа (1929 год), где разница потенциалов составила единицы мегавольта. Для сравнения грозовое облако, согласно данным Википедии, может иметь потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Суммируя сказанное, можно с определённой долей уверенности сказать, что природные процессы используют в качестве принципа своего действия электризацию трением, влиянием и некоторые другие её виды, а мощный циклон является самым большим из известных нам плоских конденсаторов. Молния показывает, что бывает, когда диэлектрик (атмосфера) не выдерживает приложенной разницы потенциалов и пробивается. В точности то же самое происходит в любом плоском конденсаторе, созданном человеком, если вольтаж оказывается для него непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя.
В точности то же самое происходит в любом плоском конденсаторе, созданном человеком, если вольтаж оказывается для него непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя.
Электрофорус
Итак, Вольта взялся за исследование модели природных процессов. Первый электрофорус появился в 1762 году сконструированный Йоханом Карлом Вильке. По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта же и дал прибору его нынешнее название.
Электрофорус способен накапливать электростатический заряд, образованный трением резины куском шерсти. Он состоит из двух плоских, параллельных друг другу обкладок:
- Нижняя представляет собой тонкий кусок резины. Толщина его выбирается из соображений эффективности устройства. Если выбрать кусок более солидный, то значительная часть энергии будет накапливаться внутри диэлектрика на ориентацию его молекул.
 Что и наблюдается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.
Что и наблюдается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости. - Верхняя пластина из тонкой стали кладётся сверху, когда заряд уже накоплен трением. За счёт влияния на верхней поверхности образуется избыток отрицательного заряда, и он должен быть снят на заземлитель, чтобы при расстыковке двух обкладок не произошло взаимной компенсации.
Принцип действия этого плоского конденсатора должен быть уже понятен. Оператор трёт резину шерстью, оставляя на ней отрицательный заряд. Затем сверху кладётся кусок металла. Из-за значительной шероховатости поверхностей они не соприкасаются, но находятся на некотором расстоянии друг от друга. В результате металл электризуется влиянием. Электроны отталкиваются поверхностным зарядом резины и уходят на внешнюю плоскость, где оператор их снимает через заземлитель лёгким кратковременным прикосновением.
Низ металлической обкладки остаётся заряженным положительно. При расстыковке двух поверхностей этот эффект сохраняется, потому что в материале наблюдается дефицит электронов.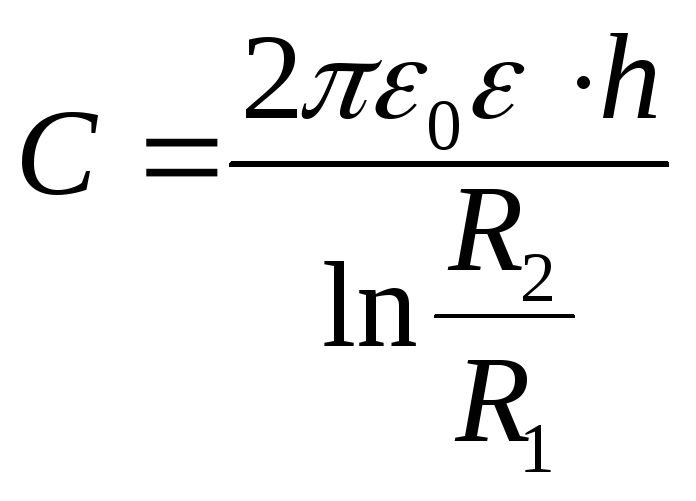 И можно наблюдать искру, если дотронуться до металлической обкладки. Этот опыт можно на одном и том же заряде резины проделывать сотни раз, поскольку её поверхностное статическое сопротивление весьма велико. Это не даёт заряду растекаться. Демонстрируя этот опыт, Вольта привлёк внимание всего научного мира, но исследования никак не двигались вперёд, если не считать открытий Шарля Кулона.
И можно наблюдать искру, если дотронуться до металлической обкладки. Этот опыт можно на одном и том же заряде резины проделывать сотни раз, поскольку её поверхностное статическое сопротивление весьма велико. Это не даёт заряду растекаться. Демонстрируя этот опыт, Вольта привлёк внимание всего научного мира, но исследования никак не двигались вперёд, если не считать открытий Шарля Кулона.
В 1800 году сам Алессандро даёт толчок развитию изысканий в области электричества, изобретя свой знаменитый гальванический источник питания.
Конструкция плоского конденсатора
Электрофорус по сути представляет собой первый из когда-либо сконструированных плоских конденсаторов. Его обкладки способны хранить только статический заряд, потому что иначе наэлектризовать резину невозможно. Поверхность очень долго хранит электроны. Вольта даже предлагал снимать их пламенем свечи через ионизированный воздух или ультрафиолетовым излучением Солнца. Сегодня каждый школьник знает, что то же самое можно проделать и водой. Правда, электрофорус нужно будет после этого высушить.
Правда, электрофорус нужно будет после этого высушить.
В современном мире нижней обкладкой может служить тефлоновое покрытие или пластик. Они тоже хорошо набирают статический заряд. Диэлектриком здесь служит воздух. Чтобы перейти к конструкции современного конденсатора, нужно обе обкладки сделать металлическими. Тогда при возникновении на одной из них заряда влиянием электризация распространится на вторую, и если другой контакт заземлён, накопленная энергия может храниться какое-то время.
Запас электронов напрямую зависит от материала диэлектриков. Так например, среди современных конденсаторов встречаются:
- Слюдяные.
- Воздушные.
- Электролитические (оксидные).
- Керамические.
В эти названия как раз и заложен материал диэлектрика. От его состава зависит напрямую ёмкость, которая может быть увеличена во много раз. Роль диэлектриков объяснялась выше, в частности их параметры определяются непосредственно строением вещества. Однако многие материалы, обладающие высокими характеристиками, использовать не удаётся по причине их непригодности. Так например, вода обладает высокой диэлектрической проницаемостью.
Так например, вода обладает высокой диэлектрической проницаемостью.
Характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.
Под зарядом конденсатора понимают заряд одной пластины.
Так же есть:
Энергия конденсатора:
Ёмкость цилиндрического конденсатора:
Емкость сферического конденсатора:
В формуле мы использовали:
Электрическая ёмкость (ёмкость конденсатора)
Относительная диэлектрическая проницаемость
Электрическая постоянная
3.1.9 Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора
Видеоурок 1: Емкость конденсатора — Физика в опытах и экспериментах
Видеоурок 2: Емкость плоского конденсатора. Классификация конденсаторов
Лекция: Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора
Для определения понятия конденсатора, необходимо воспользоваться всеми знаниями по поводу проводников и диэлектриков, поскольку и те, и другие одновременно используются для изготовления конденсаторов.
Ёмкость конденсатора
Во время изучения понятия конденсаторов будем использовать термин «уединенный конденсатор». Он значит, что данное проводящее тело находится вне поля действия других тел. Рассмотрим проводник, у которого имеется какой-то определенный потенциал «фи». Данный потенциал является пропорциональным к величине заряда проводника. Данный коэффициент принято обозначать 1/С. В данном случае величина, что находится в знаменателе, является электрической ёмкостью имеющегося проводника.
Если рассматривать некоторый объемный шар в виде проводника, то его ёмкость можно определить по следующей формуле:
Эпсилон нулевое — это электрическая постоянная.
Судя из данной формулы, можно сделать вывод, что емкость сферического проводника зависит исключительно от внешнего диэлектрика, а также от радиуса сферы, то есть её размера. То есть, чем больше сфера, тем больше её емкость. Иными словами можно сказать, что ёмкость — это некая тара, которая вмещает в себя величину заряда.
Итак,
Ёмкость — это некая ФВ, позволяющая определить величину заряда, необходимую для изменения потенциала проводника на 1 В.
Ёмкость измеряется в фарадах (Ф).
Самым главным для нас сферическим проводником является Земля. Посчитать её емкость достаточно просто. Если принять радиус за 6400 км, а окружающую диэлектрическую среду мы знаем — это воздух, то получим:
Плоский конденсатор
Самым простым примером для исследования конденсаторов являются плоские конденсаторы. Структура плоского конденсатора достаточно проста. Он состоит из двух металлических плоскостей (обкладок), которые параллельно расположены друг к другу, и располагаются на некотором расстоянии. Между данными пластинами имеется диэлектрик.
Самым простым примером плоского конденсатора является тот, у которого в виде диэлектрика воздух, то есть Ɛ = 1.
Обе обкладки имеют противоположный заряд -q, +q. Схематически конденсатор изображают следующим образом:
Следует отметить, что поле в конденсаторе показывается линиями, выходящими из положительно заряженной пластины, и входящими в отрицательно заряженную пластину.
Для определения его ёмкости следует воспользоваться следующей формулой:
Как уже говорилось раньше, ёмкость зависит исключительно от геометрических размеров конденсатора, а также от диэлектрика между пластинами.
в чём измеряется и от чего зависит величина, как её определить, формулы расчёта
Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.
История накопителей заряда
Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.
Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.
Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.
Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
- 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
- 1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
- 1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
- конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
- начало XX в. — изобретение слюдяных и керамических конденсаторов.
Физика ёмкостных характеристик
Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.
Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.
Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.
Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:
- геометрия пластин;
- расстояние между ними;
- диэлектрический материал между пластинами.
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
- пикофарад — 10—12 Ф;
- нанофарад — 10—9 Ф;
- микрофарад — 10—6 Ф.
Диэлектрическая проницаемость
Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
- А — площадь меньшей пластины;
- d — расстояние между ними;
- ε — абсолютная проницаемость используемого диэлектрического материала.
Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:
- 1,0006 — воздух;
- 2,5—3,5 — бумага;
- 3—10 — стекло;
- 5—7 — слюда.
Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Идея суперконденсатора
Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.
Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:
- непродолжительный жизненный цикл;
- невысокая удельная мощность;
- узкий диапазон температур зарядки и разрядки;
- неспособность быстро отдать весь запас энергии.
Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.
Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.
Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.
2}}} $, $ {\ text {E}} = — \ dfrac {{d {\ text {V}}}} {{dr}} $ и $ {\ text {C}} = \ dfrac {{ \ text {Q}}} {{\ Delta {\ text {V}}}} $.Полное пошаговое решение:
Рассмотрим сферический конденсатор, имеющий заряд + Q на внутренней поверхности и –Q на внешней поверхности. Пусть R и r радиусы внешней и внутренней поверхности соответственно. Эти две заряженные поверхности разделены радиальным расстоянием (R-r). Пусть потенциал на внутренней сферической поверхности равен $ {{\ text {V}} _ 1} $, а потенциал на внешней сферической поверхности равен $ {{\ text {V}} _ 2} $.R \\
\ Rightarrow {{\ text {V}} _ 2} — {{\ text {V}} _ 1} = \ left ({\ dfrac {{\ text {Q}}} {{4 \ pi {\ varepsilon _0}}} \ right) \ left [{\ dfrac {1} {R} — \ dfrac {1} {r}} \ right] \\
\ Rightarrow \ Delta {\ text {V}} = \ left ({\ dfrac {{\ text {Q}}} {{4 \ pi {\ varepsilon _0}}}} \ right) \ left [{\ dfrac {1} {R} — \ dfrac {1} {r }} \ right] {\ text {}} \ to {\ text {(3)}} \\
\]
, где \ [\ Delta {\ text {V}} = {{\ text {V}} _ 2 } — {{\ text {V}} _ 1} \] представляет увеличение потенциала, возникающее при перемещении от внутренней сферической поверхности к внешней сферической поверхности
Кроме того, емкость любого конденсатора определяется как
$ {\ text {C} } = \ dfrac {{\ text {Q}}} {{\ Delta {\ text {V}}}} $
Подставляя уравнение (3) в приведенное выше уравнение, мы получаем
\ [
\ Rightarrow {\ text {C}} = \ dfrac {{\ text {Q}}} {{\ left ({\ dfrac {{\ text {Q}}} {{4 \ pi {\ varepsilon _0}}}} \ right) \ left [{\ dfrac {1} {R} — \ dfrac {1} {r}} \ right]}} \\
\ Rightarrow {\ text {C}} = \ dfrac {{{\ text {Q}} \ left ({4 \ pi {\ varepsilon _0}} \ right)}} {{ {\ text {Q}} \ left [{\ dfrac {1} {R} — \ dfrac {1} {r}} \ right]}} = \ dfrac {{{\ text {Q}} \ left ({ 4 \ pi {\ varepsilon _0}} \ right)}} {{{\ text {Q}} \ left [{\ dfrac {{r — R}} {{rR}}} \ right]}} = \ dfrac {{{\ text {Q}} \ left ({4 \ pi {\ varepsilon _0}} \ right) rR}} {{{\ text {Q}} \ left ({r — R} \ right)}} \\
\ Rightarrow {\ text {C}} = 4 \ pi {\ varepsilon _0} \ left ({\ dfrac {{rR}} {{r — R}}} \ right) \\
\]
Вышеприведенное уравнение дает выражение для емкости сферического конденсатора с радиусом внутренней поверхности как r и радиусом внешней поверхности как R.
Примечание. Важно отметить, что в любом конденсаторе две заряженные поверхности (с равными и противоположными зарядами) разделены некоторым расстоянием. Конденсаторы обычно используются для хранения электрического заряда. В этой конкретной задаче интеграция выполняется от внутренней сферической поверхности к внешней сферической поверхности.
Физика для науки и техники II
5.6 Сферический конденсатор от Office of Academic Technologies на Vimeo.
5.06 Сферический конденсатор
Сферический конденсатор состоит из двух концентрических сферических проводящих пластин. Скажем, это представляет собой внешнюю сферическую поверхность или сферическую проводящую пластину, а эта представляет собой внутреннюю сферическую поверхность. Давайте снова зарядим эти поверхности так, чтобы соединить внутреннюю поверхность с положительной клеммой источника питания батареи, а внешнюю поверхность с отрицательной клеммой источника питания. При этом внутренняя поверхность будет заряжена положительно до некоторого количества кулонов плюс q, а внешняя поверхность будет заряжена отрицательно до некоторого количества кулонов минус q.Затем дайте нам некоторые размеры, скажем, внутренний радиус равен a, а внешний радиус равен b. Таким образом, зарядив конденсатор, мы завершили первый шаг по вычислению емкости этого сферического конденсатора.
На втором этапе мы рассчитаем электрическое поле между пластинами; поэтому выбираем произвольную точку между пластинами. Так как геометрия является сферической геометрией, мы выберем сферическую гауссовскую поверхность так, чтобы она проходила через интересующую точку.Допустим, эта точка находится на расстоянии r от центра сферического конденсатора. Закон Гаусса гласит, что интеграл E dot dA по этой замкнутой поверхности s равен q, заключенному в ноль эпсилона, который представляет собой чистый заряд внутри области, окруженной гауссовой поверхностью.
Итак, электрическое поле, после того как мы зарядим эти пластины, будет исходить от положительно заряженной пластины и входить в отрицательно заряженную пластину, поэтому оно будет направлено радиально наружу, заполняя область между этими двумя заряженными пластинами. .Следовательно, электрическое поле будет направлено радиально наружу от положительной пластины к отрицательной. Вектор площади поверхности, который представляет собой вектор увеличивающейся площади поверхности, перпендикулярен этой дополнительной поверхности на этой гауссовой сфере. Следовательно, это тоже будет в радиальном направлении наружу и перпендикулярно поверхности, как эта, так что угол между E и dA в каждой точке вдоль этой поверхности будет равен нулю градусов.
E dA Косинус нуля будет явной формой этого скалярного произведения, интегрированного по этой замкнутой поверхности, равному q, заключенному в ноль эпсилона.Косинус нуля равен 1, и пока мы находимся на поверхности этой гауссовой сферы, мы будем находиться на таком же расстоянии от источника заряда, который она окружает. Так что это будет постоянным на этой поверхности. Мы можем вынести его за пределы интеграла, что, таким образом, даст нам E, умноженное на интеграл от dA по этой гауссовой сфере.
Это будет равно q, заключенному в ноль Epsilon. Интеграл dA, опять же, добавляя все эти инкрементальные поверхности вдоль этой гауссовой сферической поверхности, в конечном итоге даст нам площадь поверхности этой сферы, которая равна 4 Pi, умноженному на квадрат радиуса, r в квадрате.Суммарный заряд, заключенный внутри области, окруженной этой сферой, представляет собой общий заряд, распределенный вдоль этой внутренней сферы, потому что он полностью охватывает эту сферу. Таким образом, это будет количество заряда вдоль внутренней сферы, равное q. У нас будет q над нулем Эпсилона.
Решение для электрического поля, отсюда между пластинами, окажется равным q больше 4 Пи эпсилон ноль r в квадрате. Если вы посмотрите на это выражение, мы увидим, что оно идентично электрическому полю точечного заряда.Как вы помните, мы упоминали, что сферическое распределение заряда, будь то твердая сфера или сферическая оболочка, ведет себя как точечный заряд для всех внешних областей. Итак, эта точка p, представляющая интерес здесь, является внешней точкой для этого сферического распределения. Следовательно, он ведет себя как точечный заряд, как будто весь заряд q сконцентрирован в его центре, так что в конечном итоге электрическое поле равно q на 4 Пи эпсилон ноль r в квадрате.
Теперь, как только мы определим величину электрического поля, которое направлено радиально наружу, мы можем продолжить и вычислить или применить третий шаг, который заключается в том, что разность потенциалов между пластинами равна интегралу от положительной пластины к отрицательной в точке E. дл.Опять же, как и в случае с цилиндрическим конденсатором, мы собираемся выбрать путь в этом случае, чтобы вычислить этот интеграл по пути, в радиальном направлении. А поскольку наше электрическое поле направлено радиально наружу, мы выберем путь для получения интеграла также и в радиальном направлении, и, следовательно, dl будет равно dr для этого пути радиально наружу.
Другими словами, вектор инкрементного смещения dl будет заменен вектором инкрементного смещения в радиальном направлении. Тогда разность потенциалов между пластинами становится величиной E, которая равна q на 4 Pi Epsilon ноль r в квадрате.Величина dl будет равна величине dr, умноженной на косинус угла между этими двумя векторами.
Опять же, мы выбираем этот путь так, чтобы он совпадал с вектором электрического поля, так что угол между этими двумя векторами станет нулевым. Косинус нуля равен 1. Здесь q и 4 Пи Эпсилон ноль, они постоянны, поэтому мы можем взять его за пределы интеграла, и это оставляет нам разность потенциалов между пластинами этого конденсатора как q над 4 Пи Эпсилон нулевой интеграл. из dr над r в квадрате.Теперь интеграл берется от положительной пластины к отрицательной. Для этой области, если мы посмотрим на изменение в радиальном направлении, мы начнем от внутреннего радиуса до внешнего радиуса, поэтому границы интеграла будут идти от a до b.
Далее, разность потенциалов будет равна q в течение 4 Пи. Нулевой интеграл эпсилона от dr по квадрату равен минус 1 по r, который будет оцениваться в точках a и b. Подставляя границы, разность потенциалов будет равна q на 4 Pi Epsilon zero, и у нас будет минус 1 над b минусом, а еще один минус будет исходить от функции, сделает эту 1 положительной над a.Если у вас есть общий знаменатель, мы можем записать это выражение как q над 4 Пи Эпсилон ноль b минус a над ab. Это разность потенциалов между пластинами сферического конденсатора.
В последнем шаге говорится, что емкость рассчитывается по ее определению, которое представляет собой отношение величины заряда в конденсаторе к разности потенциалов между пластинами конденсатора, которая тогда будет равна — для разности потенциалов — мы имеем q больше 4 Пи ноль Эпсилона, умноженное на b минус a больше ab.
Заряды прекратятся, и емкость сферического конденсатора окажется равной 4 Pi Epsilon, умноженному на ноль ab над b минус a. Как и в предыдущих случаях, для параллельного конденсатора и цилиндрического конденсатора, здесь мы снова видим, что емкость напрямую зависит от физических свойств конденсатора. В данном случае для сферического конденсатора внутренний и внешний радиус конденсатора.
Здесь мы рассмотрим частный случай. Если вы рассматриваете заряженный цилиндр, мы всегда можем рассматривать этот цилиндр как конденсатор, так что его внешняя пластина расположена на бесконечности.Другими словами, мы можем сказать, что пусть a равно R, а b стремится к бесконечности. Итак, мы переносим внешнюю сферу на бесконечность и говорим о заряженной изолированной сфере. Этот случай соответствует заряженной изолированной сфере. Тогда мы можем выразить это выражение, емкость, как ноль 4 Pi Epsilon. И давайте, скажем, заменим a на большое R, оставим на мгновение b как b и запишем знаменатель в скобках b. Итак, возьмите b снаружи, 1 минус, замените a на R, R над b.
Буквы «b» в числителе и знаменателе сократятся, и по мере того, как b стремится к бесконечности, R над b будет приближаться к нулю, так что емкость изолированной заряженной сферы окажется равной 4 Pi Epsilon ноль, принимая R над b до нуля.Мы закончим просто буквой r, что указывает на то, что емкость изолированной заряженной сферы равна 4 Пи эпсилону, умноженному на ноль радиуса этой сферы.
Емкость сферического проводника
Емкость сферического проводника
Емкость — это способность накапливать электрическую энергию. Почти все вещи, включая вас, могут накапливать электрическую энергию и, следовательно, иметь емкость. Когда вы трете ногами ковер, заряженные частицы, называемые электронами, могут переноситься с ковра на вас.Емкость сферического проводника прямо пропорциональна его радиусу.
Сферический конденсатор — это емкость для сферических или цилиндрических проводников, которая может быть получена путем оценки разности напряжений между проводниками при заданном заряде каждого из них. Это своего рода конденсатор, который имеет одну или несколько тонких полых сферических пластин / проводников. Сферические конденсаторы могут быть различных типов, а именно: изолированный сферический конденсатор, концентрические сферические конденсаторы с двумя сферами и т. Д.Тогда это зависит от внутреннего и внешнего радиуса каждой сферы.
Предположим, что центр сферического проводника A радиуса r (м), помещенного в вакуум или в воздух, равен O и содержит заряд + Q [рисунок]. Пусть емкость сферы равна C, а ее поверхностный потенциал — V. Теперь, согласно определению емкости,
C = Q / V или V = Q / C……. …. (1)
Мы знаем, что заряды равномерно распределяются по всей поверхности проводника. Таким образом, будет казаться, что все силовые линии исходят из центра сферы.Даже если мы рассмотрим величину заряда Q в центре сферы O, силовые линии будут выходить аналогичным образом. Таким образом, в случае заряженного сферического проводника можно считать, что все заряды сосредоточены в центре.
Потенциал на поверхности сферического проводника,
V = 1 / 4πε 0 x Q / r……… (2)
Из уравнений (1) и (2) получаем,
Q / C = 1 / 4πε 0 x Q / r
, поэтому C = 4πε 0 r…….(3)
(1) Для среды с диэлектрической проницаемостью ε r , потенциал на сфере, V = Q / 4πε 0 r
так, C = Q / V = 4πε 0 ε r r……… (4)
Здесь ε 0 = 8,854 x 10 -12 Кулон 2 / Ньютон-метр 2 (C 2 / Нм 2 ).
(2) «Емкость проводника 1 Фарад» означает, что для увеличения его потенциала на 1 вольт требуется 1 кулон заряда, а емкость проводника равна емкости сферического проводника в вакууме. или в воздухе радиусом 9 x 10 9 м.
(3) Из уравнения (3), единица измерения ε 0 Фарад / метр (Ф / м).
Рабочее упражнение: Из двух металлических сфер одного радиуса одна полая, а другая сплошная. Если их поменять при том же потенциале, в каком останется еще один заряд?
Емкость для сферических проводников может быть получена путем оценки разности напряжений между проводниками при заданном заряде каждого из них. Емкость любой сферы (C = 4πε 0 R), полой или твердой, будет одинаковой, если такая же окружающая среда.Опять же, если окружающей средой является воздух, то емкость C = 4πε 0 R, где R = радиус сферы. Две вышеуказанные сферы имеют равный радиус. Значит, их емкости будут одинаковыми. Если приложенный потенциал равен V, то заряд каждой из сфер будет Q = CV. Итак, в двух сферах останется равное количество заряда.
Пешаварский университет
Автор (ы): Латиф-ур-Рахман, Анвар-уль-Хак Али Шах, Афзал Шах, Сайед Мухаммад Салман, Абдул Халик Янв
Год: 2022
Журнал: Biointerface Res.Прил. Chem.
Объем: 12
Выпуск: 1
Страниц: 377-390
Автор (ы): 2. Парвин, С., Л. Бадшах, А. Уллах, С.Г. Али, С.М. Шах, А. Заман и С. Х. Сиддики.
Год: 2021
Журнал: Этноботанические исследования и приложения
Том: 22
Выпуск: 30
Страниц: 1-16
Ссылка: Скачать
Автор (ы): 1.Аббас, К., С. Батул, С. В. Хан, А. Хуссейн, Су Дин, М. А. Нафис, С. Али, М. А. Файзи и А.
Год: 2021
Журнал: Пакистанский журнал серии научных и промышленных исследований Биологические науки,
Том: 64
Выпуск: 3
Страниц: 251-255
Ссылка: Скачать
Автор (ы): Раис Хан, Башир Хан, Абдур Рашид, Асад Уллах и Шейх Заин Ул Абидин
Год: 2021
Журнал: Microscopy Research & Technique
Volume: 84
Выпуск: 12
Страниц: 1-7
Ссылка: Скачать
Автор (ы): Муджиб Ур Рахман, З.Мухаммад, Р. Уллах, В. М. Хан, А. Уллах, Т. Уллах, Х. Али, Г. Джелани и И. А.
Год: 2021
Журнал: Mitteilungen Klosterneuburg
Том: 71
Выпуск: 5
Страниц: 20-40
Ссылка: Скачать
Вычислитель емкости сферического конденсатора
Емкость сферического конденсатора Формула
емкость = Диэлектрическая проницаемость * Радиус сферы * Радиус оболочки / ([Кулон] * (Радиус оболочки-Радиус сферы))
C = k * R * a / ([Кулон] * (a-R))
Как найти сферический проводник?
Емкость для сферических проводников может быть получена путем оценки разности напряжений между проводниками при заданном заряде каждого из них.Применив закон Гаусса к заряженной проводящей сфере, можно найти электрическое поле снаружи. Напряжение между сферами можно найти, интегрировав электрическое поле по радиальной линии. Таким образом, емкость можно найти, взяв отношение Q / V (заряд / разность потенциалов).
Как рассчитать емкость сферического конденсатора?
В калькуляторе емкости сферического конденсатора используется емкость = Диэлектрическая проницаемость * Радиус сферы * Радиус оболочки / ([Кулон] * (Радиус оболочки-Радиус сферы)) для расчета емкости. Емкость сферического конденсатора равна проводящая сфера радиуса «а», окруженная концентрически проводящей сферической оболочкой с внутренним радиусом «b».Внутренняя оболочка имеет общий заряд + Q, а внешняя оболочка имеет заряд -Q. Емкость обозначается символом C и .
Как рассчитать емкость сферического конденсатора с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для определения емкости сферического конденсатора, введите диэлектрическую проницаемость (k) , радиус сферы (R) и радиус оболочки (a) и нажмите кнопку «Рассчитать». Вот как можно объяснить расчет емкости сферического конденсатора с заданными входными значениями -> -2.667E-9 = 1 * 12 * 8 / ([Кулон] * (8-12)) .
Сферический конденсатор
Показать решение
Сначала мы рассчитаем решение для указанной диэлектрической проницаемости, используя закон Гаусса таким же образом, как в «Коаксиальном конденсаторе с двумя встроенными диэлектриками». Поняв этот пример, мы обобщим наш результат на угловую диэлектрическую проницаемость.
Удельное угловое изменение диэлектрической проницаемости
Определение металла (в электростатике) говорит нам, что электрическое поле всегда перпендикулярно металлической границе.В противном случае заряды текли бы внутри металла, пока мы не обнаружим именно такое поведение. Конечно, это подразумевает постоянный электростатический потенциал металла . Теперь, если мы немного углубимся в диэлектрик, это все равно должно быть верно, если диэлектрик не изменяется вдоль силовых линий. Это означало бы, что поверхностные заряды изменяют электрическое поле. Для нашей задачи это означает, что диэлектрическая проницаемость может иметь угловое изменение, но электрическое поле все еще должно быть постоянным для данного радиуса.И поскольку на радиусе внутренней сферы может быть только радиальная составляющая, это должно быть верно для всего конденсатора! С математической точки зрения \ [\ mathbf {E} \ left (\ mathbf {r} \ right) = E_r \ left (r \ right) \ mathbf {e} _r \, \], что значительно упростит наши вычисления!
Рассмотрим сферическую гауссову поверхность вокруг внутренней металлической сферы с радиусом \ (R_i
Если бы у нас теперь была радиальная зависимость диэлектрической проницаемости , это привело бы к поверхностным зарядам, ослабляющим электрическое поле. Таким образом, в этой более общей формулировке проблемы можно было бы разделить диэлектрическое разделение на части без радиальных отклонений, поскольку мы уже знаем решение в этом случае.Для предполагаемых радиальных скачков диэлектрической проницаемости мы должны использовать граничные условия для электрического поля. Для действительно произвольной диэлектрической проницаемости мы могли бы быть вынуждены решать проблему численными методами.
Какова емкость системы двух сфер? — Реабилитацияrobotics.net
Какова емкость системы двух сфер?
(a) Две сферы имеют радиусы a и b, а их центры находятся на расстоянии d друг от друга. Покажите, что емкость этой системы равна C = 4 π ϵ 0 1 a + 1 b — 2 d при условии, что d больше по сравнению с a и b.
Что такое взаимная емкость?
Взаимная емкость C между двумя проводниками определяется как количество заряда, которое может храниться на каждой плоскости, Q, на единицу разности напряжений между плоскостями, В.
Как рассчитывается взаимная емкость?
Отношение Q2 / V1 = C21 называется взаимной емкостью. Поскольку силовые линии всегда заканчиваются зарядами противоположной полярности, это соотношение всегда отрицательно.
Какова емкость сферического конденсатора?
Пусть потенциал на внутренней сферической поверхности равен V1, а потенциал на внешней сферической поверхности равен V2.Пусть C — требуемая емкость предполагаемого сферического конденсатора. В приведенном выше уравнении заряд (Q) постоянен, и, следовательно, Q4πε0 можно вынести за пределы интегрирования, поскольку он постоянен.
Какие бывают типы конденсаторов?
Наиболее распространенные типы конденсаторов:
- Керамические конденсаторы имеют керамический диэлектрик.
- Пленочные и бумажные конденсаторы названы в честь их диэлектриков.
- Алюминиевые, танталовые и ниобиевые электролитические конденсаторы названы в честь материала, используемого в качестве анода, и конструкции катода (электролита)
Что означает емкость?
Ф
Какие бывают 3 типа конденсаторов?
Конденсаторы различных типов
- Конденсатор электролитический.
- Конденсатор слюдяной.
- Бумажный конденсатор.
- Пленочный конденсатор.
- Неполяризованный конденсатор.
- Керамический конденсатор.
Какая формула конденсатора?
Основное уравнение для конструкции конденсатора: C = εA / d, В этом уравнении C — емкость; ε — диэлектрическая проницаемость, термин, обозначающий, насколько хорошо диэлектрический материал сохраняет электрическое поле; А — площадь параллельной пластины; и d — расстояние между двумя проводящими пластинами.
Что такое единица измерения конденсатора в системе СИ?
фарад
Для чего нужен конденсатор?
Конденсатор — это электронный компонент, который накапливает и выделяет электричество в цепи.Он также пропускает переменный ток, не пропуская постоянный ток. Конденсатор является неотъемлемой частью электронного оборудования и поэтому почти всегда используется в электронных схемах.
Для чего нужен конденсатор?
Чаще всего конденсаторы используются для накопления энергии. Дополнительные области применения включают согласование мощности, объединение или развязку сигналов, электронную фильтрацию шума и дистанционное зондирование. Из-за разнообразия применения конденсаторы используются в самых разных отраслях промышленности и стали жизненно важной частью повседневной жизни.
Конденсаторы замыкаются накоротко?
Цепи переменного тока o Цепь в установившемся состоянии. Все напряжения и токи в цепи постоянного тока синусоидальны на частоте источников. Конденсаторы не действуют как разомкнутые цепи, а индукторы не действуют как короткие замыкания.
Используются ли в ноутбуках конденсаторы?
Да, в ноутбуках будут конденсаторы. «Конденсатор» было бы немного преуменьшением; на плате их будет много. Многие из них будут сглаживающими конденсаторами для обеспечения стабильного питания.В простейшей форме конденсаторы накапливают энергию.
Используются ли в компьютерах конденсаторы?
Конденсаторы большой емкости используются в блоках питания компьютеров. При обработке сигнала конденсатор и резистор сглаживают всплески и острые края сигнала. В микросхемах DRAM конденсаторы представляют собой микроскопические ячейки, в которых хранятся нули и единицы (биты). Логические схемы, которые в основном представляют собой транзисторы и резисторы, также могут содержать конденсаторы.
Почему конденсаторы используются в материнских платах?
С точки зрения непрофессионала, конденсатор — это крошечный электрический компонент, припаянный к материнской плате.Конденсаторы выполняют несколько разных функций. Во-первых, конденсатор создает постоянное напряжение для других компонентов (например, видеокарты, жесткого диска, звуковой карты и т. Д.), Чтобы обеспечить постоянный поток энергии.
Конденсатор — это программное обеспечение?
Capacitor: кроссплатформенная среда выполнения для веб-приложений.
Что лучше конденсатор или Кордова?
В качестве альтернативы Cordova Capacitor обеспечивает те же кроссплатформенные преимущества, но с более современным подходом к разработке приложений, использующим преимущества новейших веб-API и встроенных возможностей платформы.В конце концов, приложения Capacitor — это нативные приложения.
Конденсатор — это батарея?
Батарея — это электронное устройство, которое преобразует химическую энергию в электрическую, чтобы обеспечить статический электрический заряд для питания. В то время как конденсатор — это электронный компонент, который накапливает электростатическую энергию в электрическом поле.
Конденсатор — это программное или аппаратное обеспечение?
Конденсатор — это небольшое электрическое оборудование, которое может удерживать электрическую энергию в цепи или поле.Эксперты иногда называют конденсаторы типом внутренней батареи или держателя энергии, хотя конденсаторы и батареи работают по-разному.
Что вы имеете в виду под конденсатором?
Конденсатор, устройство для хранения электрической энергии, состоящее из двух проводников, расположенных в непосредственной близости и изолированных друг от друга.
Что подразумевается под стандартным конденсатором?
[‘stan · dərd kə′pas · əd · ər] (электричество) Конденсатор, сконструированный таким образом, что его значение емкости вряд ли зависит от температуры и известно с высокой степенью точности.Также известен как эталон емкости.
Что подразумевается под емкостью конденсатора?
Емкость выражается как отношение электрического заряда на каждом проводе к разности потенциалов (т. Е. Напряжению) между ними. Значение емкости конденсатора измеряется в фарадах (Ф), единицах, названных в честь английского физика Майкла Фарадея (1791–1867). Фарад — это большая емкость.
Чему равна емкость?
Определение емкости дается следующим уравнением: емкость C, измеренная в фарадах, равна заряду Q, измеренному в кулонах, деленному на напряжение V, измеренному в вольтах.Таким образом, он представляет, сколько кулонов заряда будет храниться в конденсаторе на один вольт, который вы приложите к нему.
В чем разница между емкостью и конденсатором?
Емкость — это не что иное, как способность конденсатора накапливать энергию в виде электрического заряда. Другими словами, емкость — это запоминающая способность конденсатора. Измеряется в фарадах.
.



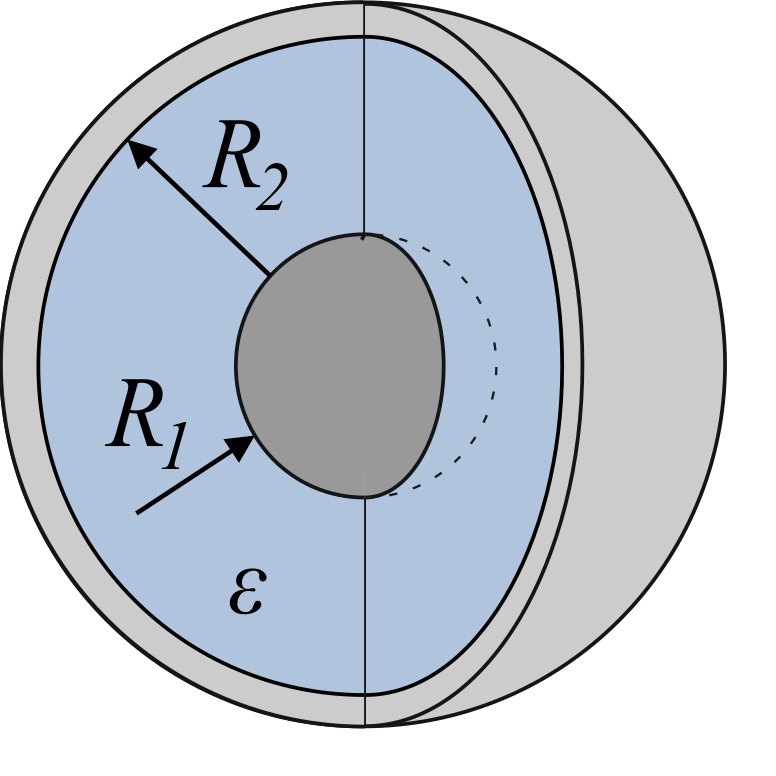
 Что и наблюдается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.
Что и наблюдается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.