Ёмкость сферического конденсатора | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
![Rendered by QuickLaTeX.com \[\Large C=4\pi \varepsilon \varepsilon _0(\frac{1}{R_1} - \frac{1}{R_2})^{-1}= 4\pi \varepsilon \varepsilon _0\frac{r_1r_2}{r_2-r_1}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-faa4aaf02d4d30dc11a36efdf5252fd7_l3.png)
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
![Rendered by QuickLaTeX.com \[\Large\varphi _1-\varphi _2=\frac{q}{4\pi \varepsilon \varepsilon _0}(\frac{1}{r_1}-\frac{1}{r_2})\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9d0e83fb311f5b6362242bcc6132892d_l3.png)
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
![Rendered by QuickLaTeX.com \[\Large C=4\pi \varepsilon \varepsilon _0(\frac{1}{R_1} - \frac{1}{R_2})^{-1}= 4\pi \varepsilon \varepsilon _0\frac{r_1r_2}{r_2-r_1}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-faa4aaf02d4d30dc11a36efdf5252fd7_l3.png)
При малой величине зазора, то есть
![Rendered by QuickLaTeX.com \[r_2-r_1\ll r_1 \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8e60804c97a6e1f3dd6717bd192a6b0a_l3.png)
, а следовательно можно считать, что
![Rendered by QuickLaTeX.com \[r_1\approx r_2\approx r\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c3882e1af4bffd53cbaf0481dd3e0f7a_l3.png)
емкость сферического конденсатора будет равна
![Rendered by QuickLaTeX.com \[\frac{4\pi r^2\varepsilon \varepsilon _2}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-aa0085e6255ca24869842faf994c1a5a_l3.png)
Площадь сферы
![Rendered by QuickLaTeX.com \[S=4\pi r^2\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-61dc71bd1581396bc6941cd241ab0d23_l3.png)
следовательно формула будет совпадать с формулой емкости плоского конденсатора
![Rendered by QuickLaTeX.com \[\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4bf7cc165579770f830fec36debdc793_l3.png)
Так же есть:
Энергия конденсатора:
![Rendered by QuickLaTeX.com \[\large W_p=\frac{U q}{2}=\frac{q^2}{2C}=\frac{CU^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c48185fd72204f7932e94ce28f23e7c3_l3.png)
Ёмкость конденсатора :
![Rendered by QuickLaTeX.com \[\large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-65907405fbd131bc9587b0b2750da723_l3.png)
Ёмкость цилиндрического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=2\pi \varepsilon \varepsilon _0\frac{l}{ln(\frac{R_2}{R_1})} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-53c9846a6d69f2a5b024b7b42f38ecc7_l3.png)
Емкость плоского конденсатора :
![Rendered by QuickLaTeX.com \[\large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-65907405fbd131bc9587b0b2750da723_l3.png)
В Формуле мы использовали :
C — Электроемкость сферического конденсатора
![Rendered by QuickLaTeX.com \[\varepsilon\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bb5ae93f2a2e84cf68e4653cb1b294fe_l3.png)
— Относительная диэлектрическая проницаемость
![Rendered by QuickLaTeX.com \[ \varepsilon _0 = 8.854185\times 10^{-12}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-380ba968da8291bc8d0b0977ed36fa7d_l3.png)
— Электрическая постоянная
![Rendered by QuickLaTeX.com \[r_2\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-e155ec80cb932611bd8750b0b7253c16_l3.png)
— Больший радиус (от центра, до края конденсатора)
![Rendered by QuickLaTeX.com \[ r_1\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-2c6af0c2e0781e22b928b7d99318cd3c_l3.png)
— Малый радиус (Его может и не быть — это пустота)
Ёмкость сферического конденсатора | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
При малой величине зазора, то есть , а следовательно можно считать, что емкость сферического конденсатора будет равна . Площадь сферы следовательно формула будет совпадать с формулой емкости плоского конденсатора
Так же есть:
Энергия конденсатора:
Ёмкость цилиндрического конденсатора :
Емкость плоского конденсатора : ;
В Формуле мы использовали :
— Электроемкость сферического конденсатора
— Относительная диэлектрическая проницаемость
— Электрическая постоянная
— Больший радиус (от центра, до края конденсатора)
— Малый радиус (Его может и не быть — это пустота)
14. Электрическая емкость. Конденсаторы (плоский, сферический, цилиндрический), их емкости.
Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создавается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на
Так
как поле сосредоточено внутри конденсатора,
то линии напряженности начинаются на
одной обкладке и кончаются на другой,
поэтому свободные заряды, которые
возникают на разных обкладках, равны
по модулю и противоположны по знаку.
Под емкостьюконденсатора
понимается физическая величина, равная
отношению заряда Q, накопленного в
конденсаторе, к разности потенциалов
(φ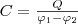 (1)
(1)
Найдем
емкость плоского конденсатора, который
состоит из двух параллельных металлических
пластин площадью S каждая, расположенных
на расстоянии d друг от друга и имеющих
заряды +Q и –Q. Если считать, что расстояние
между пластинами мало по сравнению с
их линейными размерами, то краевыми
эффектами на пластинах можно пренебречь
и поле между обкладками считать
однородным. Его можно найти используя
формулу потенциала поля двух бесконечных
параллельных разноименно заряженных
плоскостей φ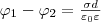 (2)
(2)
где
ε — диэлектрическая проницаемость.
Тогда из формулы (1), заменяя Q=σS, с учетом
(2) найдем выражение для емкости плоского
конденсатора: 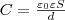 (3)
(3)
Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2(r2 > r1), один вставлен в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/
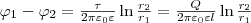 (4)
(4) Подставив
(4) в (1), найдем выражение для емкости
цилиндрического конденсатора: 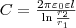 (5)
(5)
Чтобы
найти емкость сферического конденсатора,
который состоит из двух концентрических
обкладок, разделенных сферическим слоем
диэлектрика, используем формулу для
разности потенциалов между двумя
точками, лежащими на расстояниях r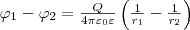 (6)
(6)
Подставив
(6) в (1), получим 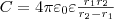
Электрическая
ёмкость —
характеристика проводника, мера его
способности накапливать электрический
заряд.
В теории электрических цепей ёмкостью
называют взаимную ёмкость между двумя
проводниками; параметр ёмкостного
элемента электрической схемы,
представленного в виде двухполюсника.
Такая ёмкость определяется как отношение
величины электрического заряда к
В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах.
Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
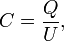 где
где 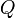
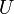 —
потенциал проводника.
—
потенциал проводника.Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса Rравна (в системе СИ):
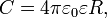
где ε0 — электрическая постоянная, ε — относительная диэлектрическая проницаемость.
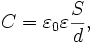
где S —
площадь одной обкладки (подразумевается,
что они равны), d —
расстояние между обкладками, ε — относительная
диэлектрическая проницаемость среды
между обкладками, ε0 =
8.854·10
Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Ёмкость цилиндрического конденсатора | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Ёмкость цилиндрического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
![Rendered by QuickLaTeX.com \[\Large C=2\pi \varepsilon \varepsilon _0\frac{l}{ln(\frac{R_2}{R_1})}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4424de47bb73ab5ac208af482bc56a58_l3.png)
Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), один вставлен в другой, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками, так же пренебрегаем краевыми эффектами. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l. При наличии диэлектрика между обкладками разность потенциалов
![Rendered by QuickLaTeX.com \[ \Large \varphi _1-\varphi _2=\frac{\tau}{2\pi\varepsilon \varepsilon _0 }ln\frac{r_2}{r_1}=\frac{q}{2\pi\varepsilon \varepsilon _0 }ln\frac{r_2}{r_1} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-1e07e0218ad8f87db05fddaedd778207_l3.png)
Подставим в формулу электроемкости конденсатора и у нас получится формула для цилиндрического конденсатора:
![Rendered by QuickLaTeX.com \[\large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =2\pi \varepsilon \varepsilon _0\frac{l}{ln(\frac{R_2}{R_1})}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-2f5aecbc66675440d5b6c91a84199ad2_l3.png)
Так же есть:
Энергия цилиндрического конденсатора:
![Rendered by QuickLaTeX.com \[\large W_p=\frac{U q}{2}=\frac{q^2}{2C}=\frac{CU^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c48185fd72204f7932e94ce28f23e7c3_l3.png)
Ёмкость конденсатора :
![Rendered by QuickLaTeX.com \[\large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-65907405fbd131bc9587b0b2750da723_l3.png)
Ёмкость плоского конденсатора :
![Rendered by QuickLaTeX.com \[\large C=\varepsilon \varepsilon _0\frac{S}{d} = \frac{q}{U}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-48bd8eac0f29d42fe03ae9cb607237a7_l3.png)
Емкость сферического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=4\pi \varepsilon \varepsilon _0(\frac{1}{R_1} - \frac{1}{R_2})^{-1}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-3895a2e647055e3e48eaa26d8db6c3cd_l3.png)
В формуле мы использовали:
C — Ёмкость цилиндрического конденсатора
![Rendered by QuickLaTeX.com \[ τ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ad08fe670c80c178c7a9cd6d72b8ea90_l3.png)
— Линейная плотность
![Rendered by QuickLaTeX.com \[\varepsilon \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d45054fdfb62d237dd41e4ab3c4cbb44_l3.png)
— Относительная диэлектрическая проницаемость
![Rendered by QuickLaTeX.com \[ \varepsilon _0 = 8.854185\times 10^{-12} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-975e0568bd14221b8dd50df4bdf44cff_l3.png)
— Электрическая постоянная
l — Длина цилиндрического конденсатора
![Rendered by QuickLaTeX.com \[ R_2\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-53995bd5c66c281c50dd8d7aa95a3dc0_l3.png)
— Больший радиус (от центра, до края конденсатора)
![Rendered by QuickLaTeX.com \[ R_1\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-955a08e77ffee71547f9241733dd9303_l3.png)
— Малый радиус (Его может и не быть — это пустота)
![Rendered by QuickLaTeX.com \[\varphi \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-2687d595c74c1faba992b8fd2b1257b5_l3.png)
— Потенциал проводника
q — Точечный заряд
U — Напряжение
Поле сферического конденсатора
Обкладками сферического конденсатора являются две концентрические сферы (R1иR2). Сообщим этим поверхностям одинаковые по величине, но разноимённые заряды+qи–qи вычислим электрическое поле, создаваемое этими зарядами в пространстве (рис. 2.10.).
Сферы делят пространство на 3 области:
I— внутри первой сферы (r1<R1),
II— между обкладками (R1r2<R2),
III— за пределами конденсатора (r3>R2).
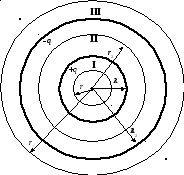
Рис. 2.10.
Область I.
Выберем замкнутую гауссову поверхность внутри первой области. Разумно, руководствуясь соображениями симметрии, эту поверхность выбрать сферической (r1).
Поток вектора напряжённости через эту поверхность (по определению потока) равен:
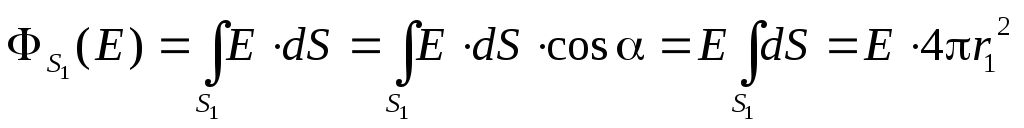
Этот поток, согласно теореме Гаусса, пропорционален заряду, заключённому внутри поверхности. Но внутри сферы радиуса r1заряд отсутствует. Поэтому и поток равен нулю
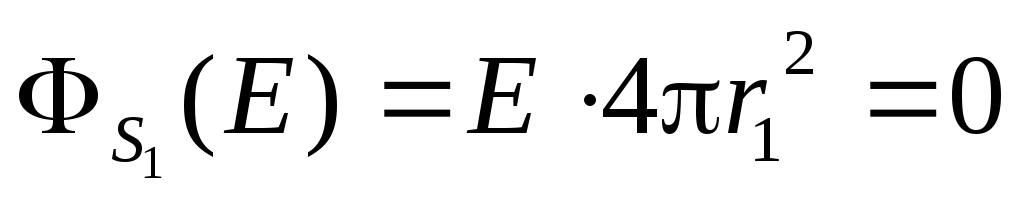 (!)
(!)
Отсюда заключаем, что в области Iполе равно нулю
0 < r<R1,E= 0 (2.18)
Область II.
Вновь в качестве замкнутой поверхности выберем сферу, но теперь её радиус r2лежит в пределах отR1доR2.
Вычислим поток вектора напряжённости поля через эту гауссову поверхность.
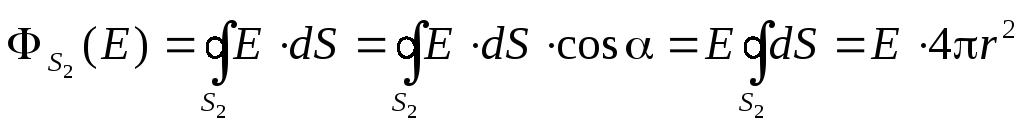
Воспользуемся теорией Гаусса: 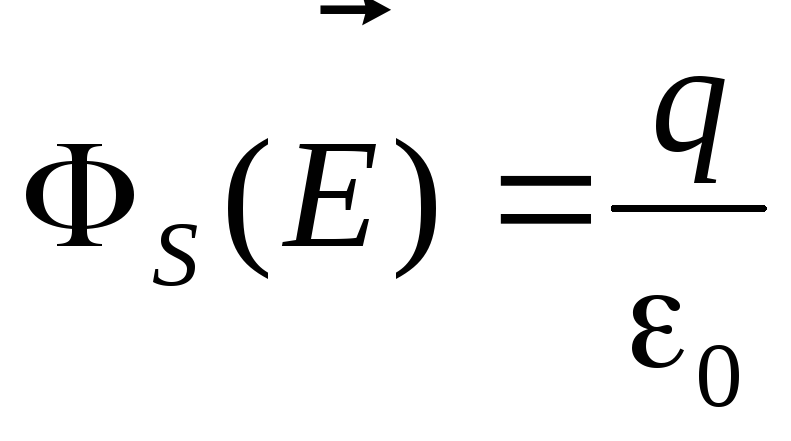 :
:
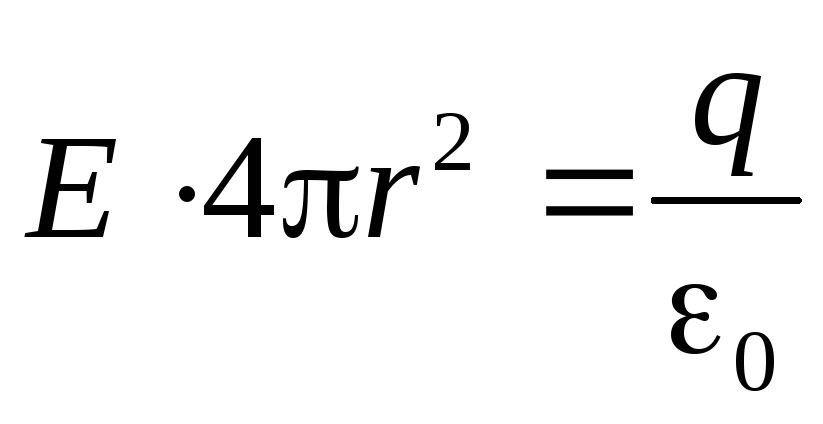
Оказывается, что электрическое поле между обкладками сферического конденсатора неотличимо от поля точечного заряда
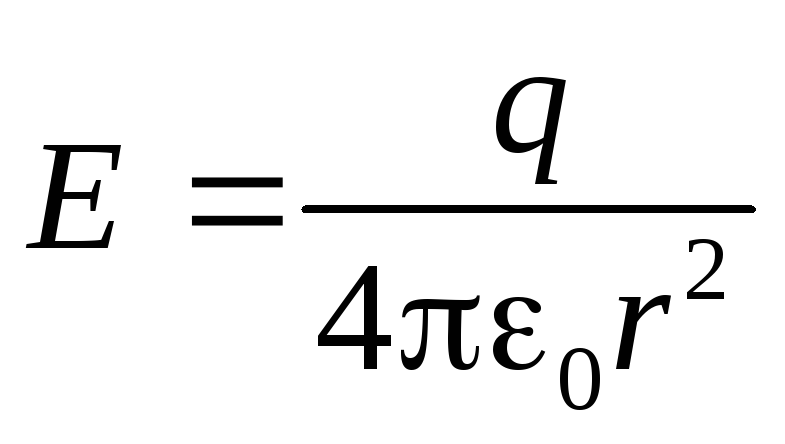 . (2.19)
. (2.19)
Посмотрим теперь, как выглядит поле в области III.
Вновь выберем замкнутую гауссову сферическую поверхность (радиус r3>R2). Вычисляем поток вектора напряжённости
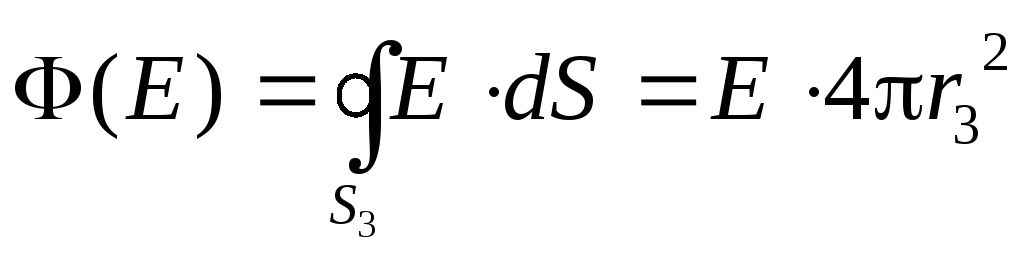
Этот поток равен нулю, так как он пропорционален алгебраической сумме зарядов, заключённых внутри этой поверхности. Но алгебраическая сумма одинаковых разноимённых зарядов равна нулю
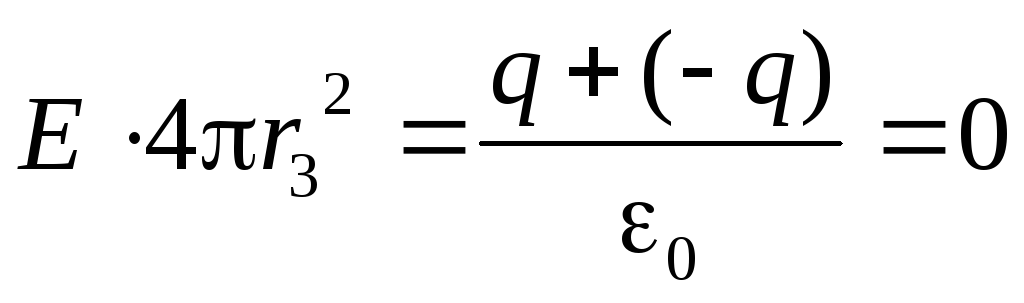
Отсюда следует, что Е = 0 (r3R2)/
График Е=Е(r) приведён на рисунке 2.11.

Рис. 2.11.
Лекция 3 «Потенциал электростатического поля»
План лекции
3.1. Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
3.2. Теорема о циркуляции вектора напряжённости электростатического поля.
3.3. Связь напряжённости и потенциала электростатического поля.
3.4. Примеры расчёта потенциала электростатического поля.
3.4.1. Потенциал поля точечного заряда.
3.4.2. Разность потенциалов на обкладках сферического конденсатора.
Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика.
Потенциал — энергетическая характеристика поля, связанная и с энергией заряда в электростатическом поле и с работой, совершаемой электрической силой при перемещении заряда.
Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
Рассмотрим произвольное перемещение (1–а–2) зарядаqв электростатическом поле. Пусть поле создаётся неподвижным точечным зарядомQ(рис. 3.1.). В процессе перемещения на зарядq действует кулоновская сила:
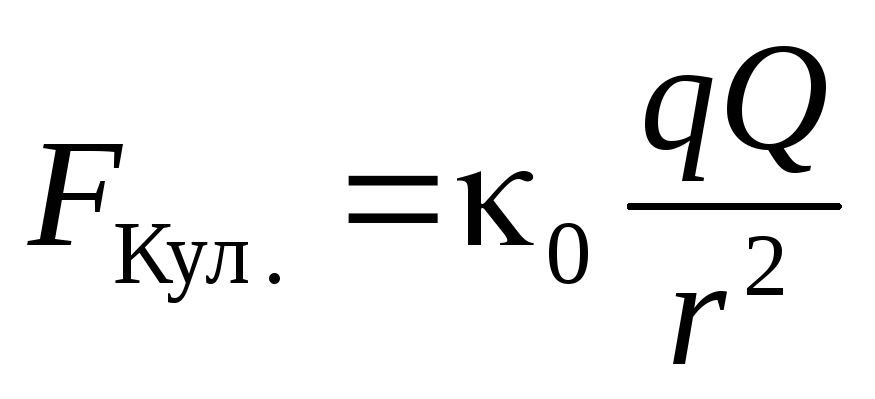 . (3.1)
. (3.1)

Рис. 3.1.
Её работа на перемещении  равна:
равна:
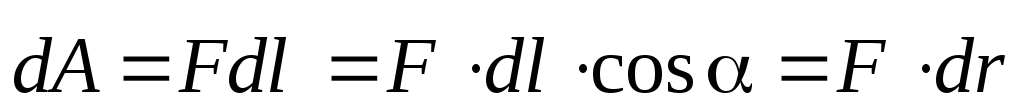 . (3.2)
. (3.2)
Здесь dr=dlсos— толщина сферической оболочки, окружающей зарядQ. Полная работа электрической силы равна сумме работ на всех участках траектории:
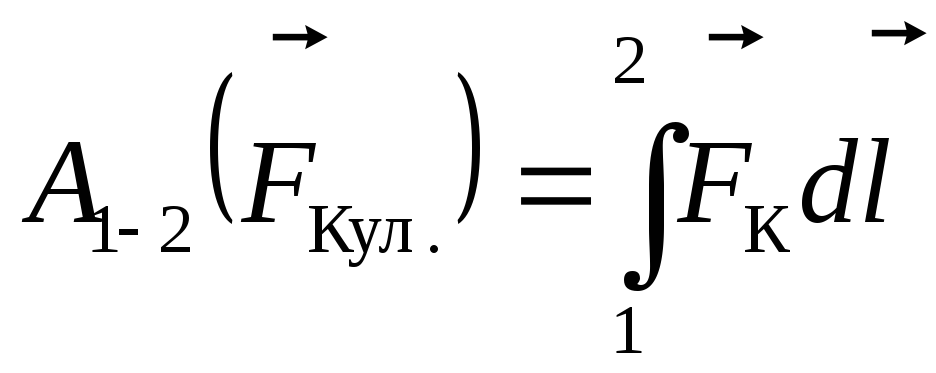 . (3.3)
. (3.3)
Теперь несложно показать, что эта работа
не зависит от формы траектории и остаётся
неизменной, если начальная и конечная
точки траектории не меняют своего
положения. Рассмотрим, например,
перемещение того же заряда q из начальной точки 1 в конечную 2 по
новой траектории 1–b–2.
При преодолении прежнего сферического
слоя на перемещении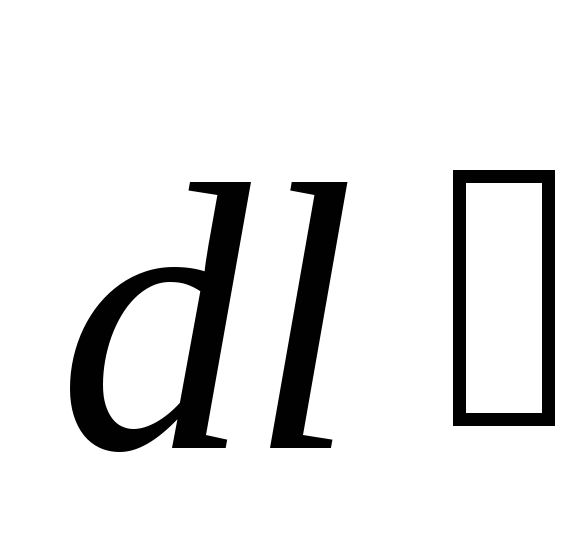 электрическая сила совершит работу:
электрическая сила совершит работу:
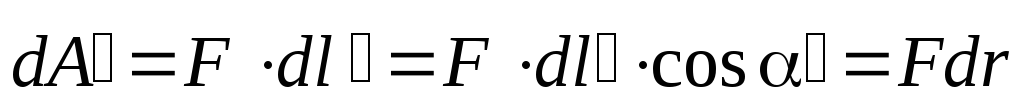 . (3.4)
. (3.4)
Но ведь эта работа в точности совпадает с работой на перемещении dl(3.2) по первоначальной траектории 1–а–2.
Полная работа, равная сумме элементарных работ на всех участках новой траектории, будет равна работе электрической силы на траектории 1–а–2:
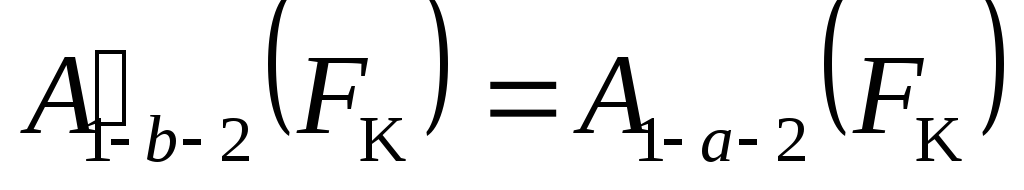 . (3.5)
. (3.5)
Вспомним, что силы, работа которых не зависит от вида траектории и определяется только положением её начальной и конечной точек, называются консервативными.
Мы пришли к выводу, что кулоновская сила консервативна. Впрочем, ничего неожиданного в этом выводе нет: ведь сила взаимодействия двух точечных зарядов может быть отнесена к классу центральных сил, а все центральные силы, как было установлено в механике, консервативны.
Итак, вычислим работу кулоновской силы при перемещении заряда qиз точки 1 в положение 2 (по любой траектории):
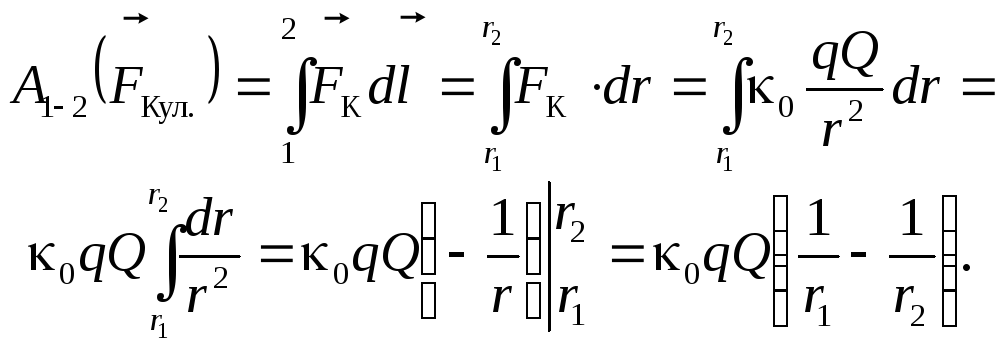 (3.6)
(3.6)
Как и следовало ожидать, величина работы никак не связана с видом траектории. Она зависит только от положения её начальной (r1) и конечной (r2) точек.
В механике было показано, что работа консервативной силы равна убыли потенциальной энергии системы:
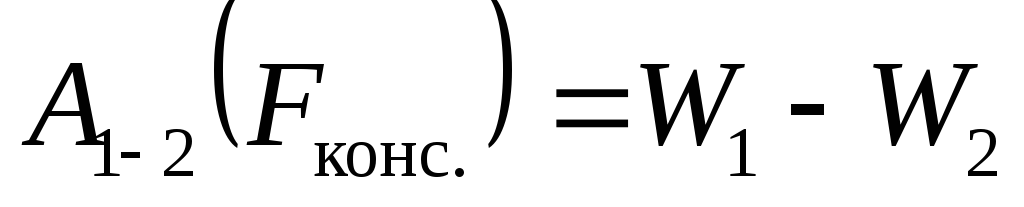 . (3.7)
. (3.7)
Присмотримся внимательнее к результату (3.6):
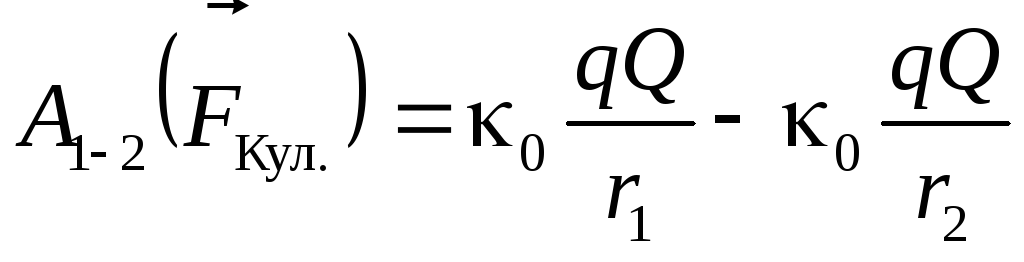 .
.
Сопоставив этот результат с теоремой о работе консервативной силы (3.7), запишем уравнение:
 ,
,
из которого следует, что потенциальная энергия системы:
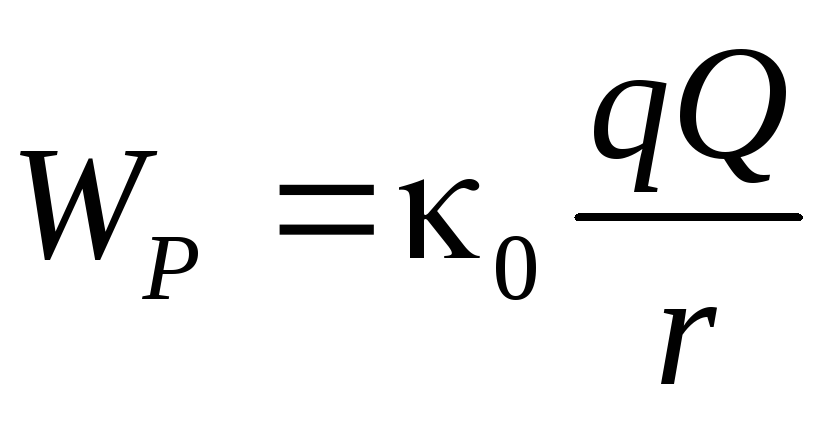 +const. (3.9)
+const. (3.9)
Это потенциальная энергия системы двух точечных зарядов, или, что то же самое, энергия заряда qв электрическом поле точечного зарядаQ.
Константа в выражении (3.9) принимается
обычно равной нулю. Это означает, что
принимается равной нулю энергия
взаимодействия зарядов qиQна бесконечном удалении
их друг от друга (приr= ∞).Тогда на расстоянииrэнергия взаимодействия равна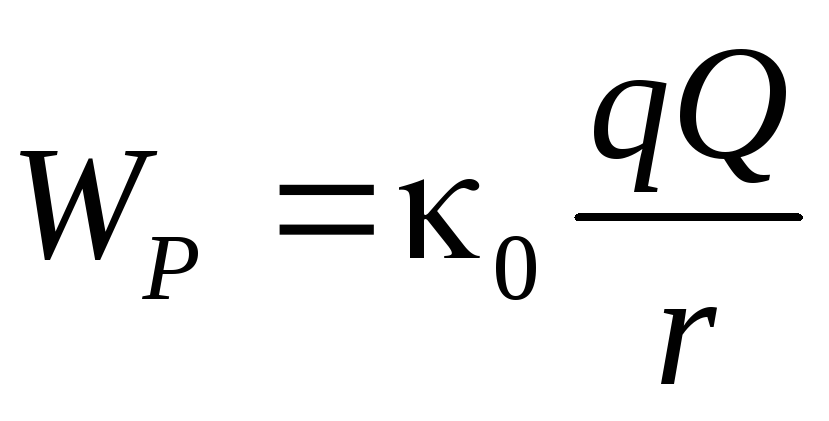 . (3.10)
. (3.10)
Потенциальная энергия заряженной частицы в электрическом поле зависит, таким образом, от величины заряда qи от его положения в поле относительно зарядаQ, создающего поле.
Энергия единичного (q= 1) точечного заряда уже не будет связана с величиной этого пробного зарядаqи может быть принята в качестве энергетической характеристики данной точки электростатического поля:
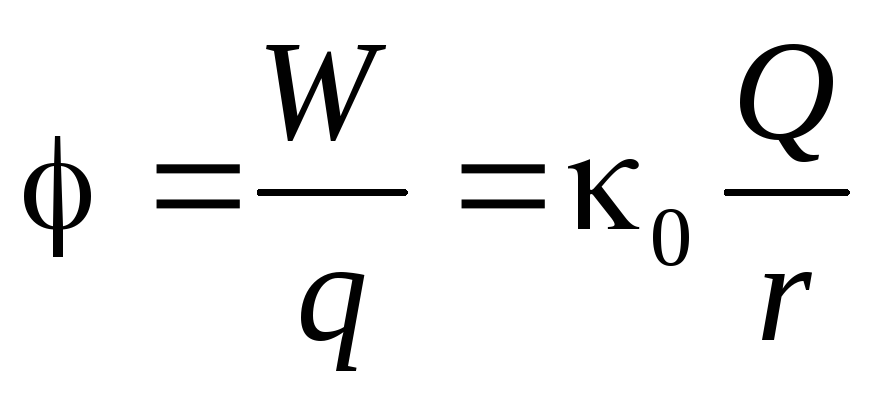 .
.
Эта энергетическая характеристика поля получила название потенциал — .
Потенциал произвольной точки электростатического поля равен энергии единичного положительного заряда, помещённого в эту точку.
Можно придать потенциалу и иной физический смысл.
Поместим заряд qв поле точечного зарядаQ. Первоначально расстояние между зарядами —r. Отпустим зарядq. Под действием электрической силы отталкивания зарядqудалится в бесконечность (рис. 3.2.). На этом перемещении кулоновская сила совершит работу:
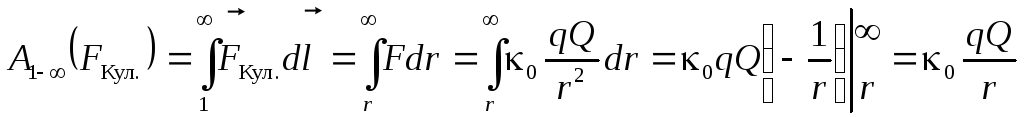 . (3.11)
. (3.11)
Эта работа не зависит от формы траектории, поэтому мы её вычислили, считая, что заряд qудаляется по радиусу.
Рис. 3.2.
Сравнивая (3.10) и (3.11), заключаем, что:
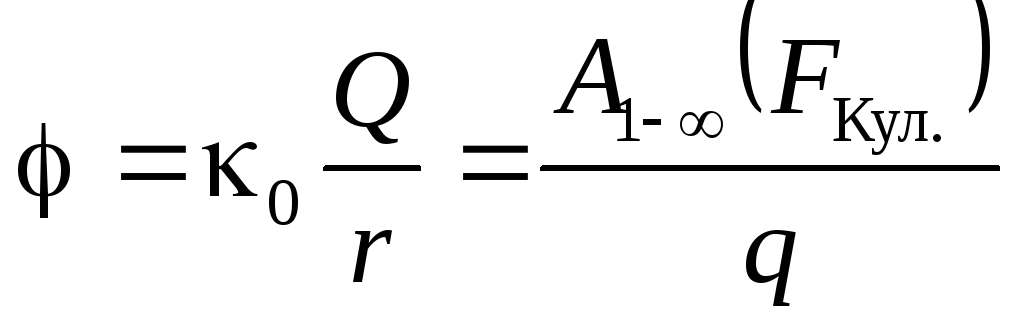 . (3.12)
. (3.12)
Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при эвакуации единичного положительного заряда из этой точки в бесконечность.
Теперь вычислим потенциал поля, созданного системой точечных зарядов Q1,Q2, …,QN.
При перемещении заряда qиз точки 1 в бесконечность электрическая сила совершит работу, равную алгебраической сумме работ сил, действующих на движущийся заряд со стороны зарядовQ1,Q2, …,QN(рис. 3.3.):


Рис. 3.3.
Согласно (3.12) работа каждой силы равна:
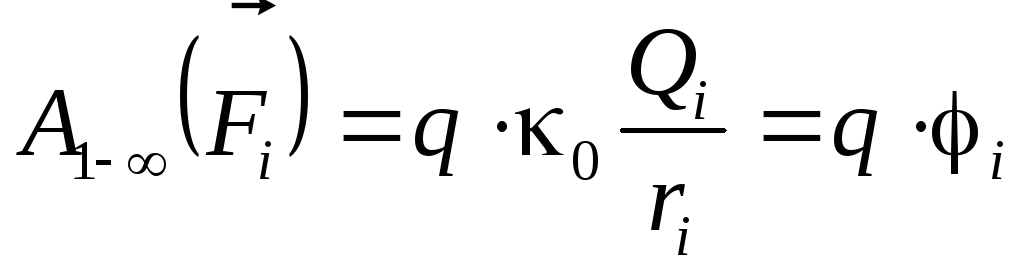 . (3.13)
. (3.13)
Здесь 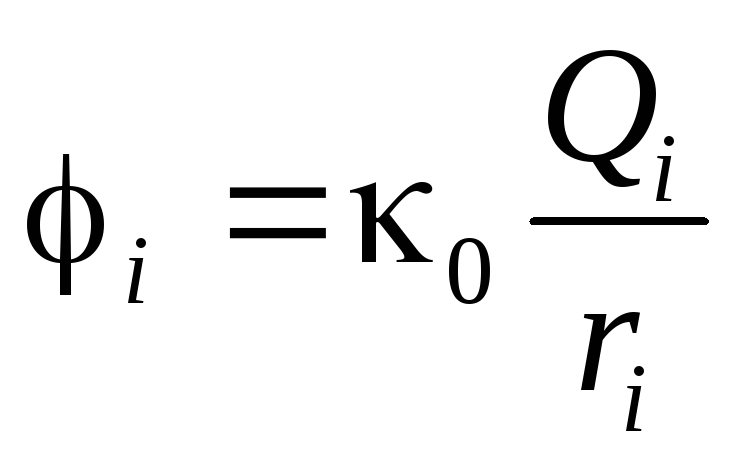 — потенциал поля, создаваемого в точке
1 зарядомQi.
— потенциал поля, создаваемого в точке
1 зарядомQi.
Таким образом, суммарная работа равна:
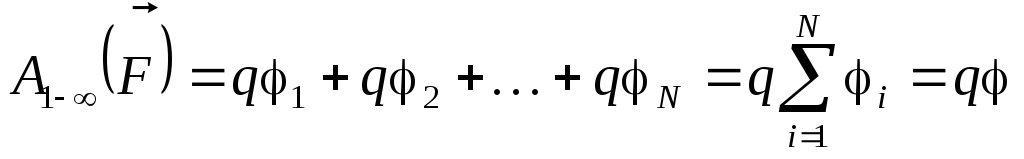 ,
,
где 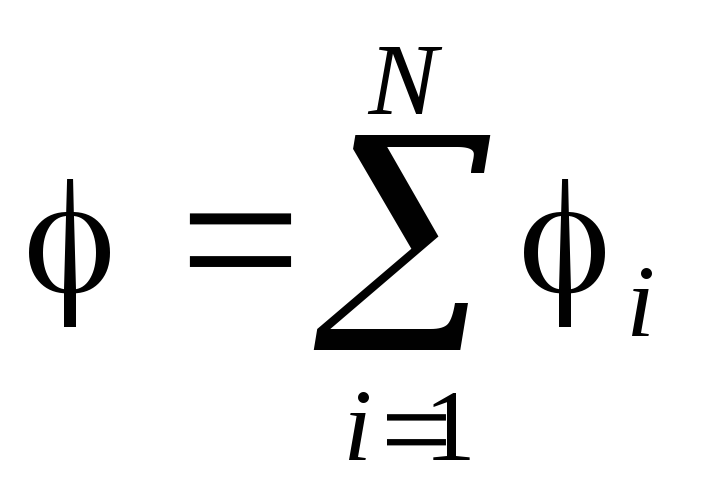 .
.
Потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов в отдельности:
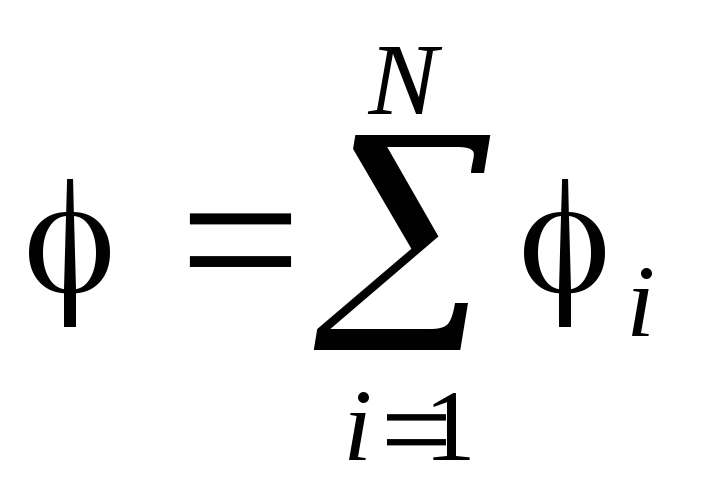 . (3.14)
. (3.14)
Результат (3.14) известен как «принцип суперпозиции для потенциала». Это очень важный вывод, позволяющий использовать понятие потенциала не только для характеристики полей точечных зарядов, но и для любых произвольных электростатических полей.
Ещё раз обратимся к вычислению работы электрической силы при перемещении заряда qиз точки 1 теперь уже произвольного электростатического поля в бесконечность. Поскольку эта работа не зависит от формы траектории, унося заряд в бесконечность, пройдём предварительно точку 2 электростатического поля (рис. 3.4.).
Рис. 3.4.
Ясно, что вся работа на этом перемещении складывается из двух частей:
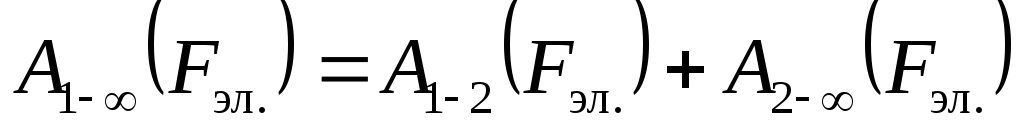 .
.
Разделив это равенство на величину переносимого заряда q, получим:
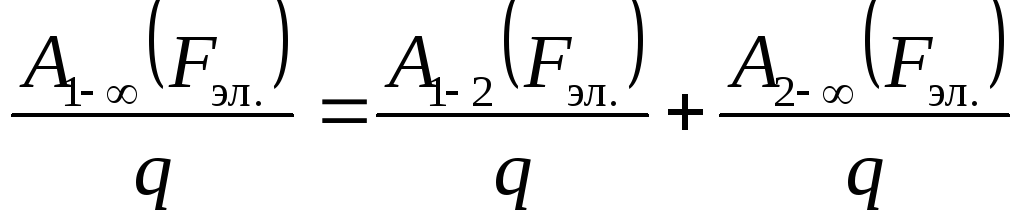 ,
,
или:
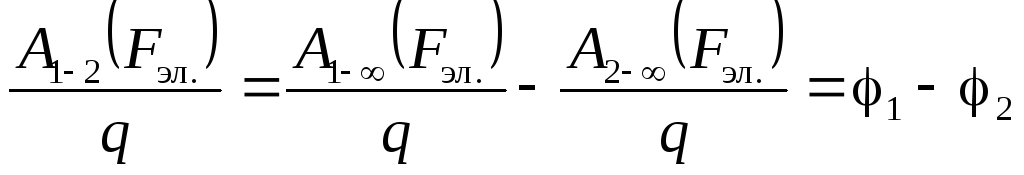 . (3.15)
. (3.15)
Здесь  —разность потенциаловдвух точек
поля. Она равна работе, совершаемой
электрической силой при перемещении
единичного заряда из первой точки во
вторую:
—разность потенциаловдвух точек
поля. Она равна работе, совершаемой
электрической силой при перемещении
единичного заряда из первой точки во
вторую:
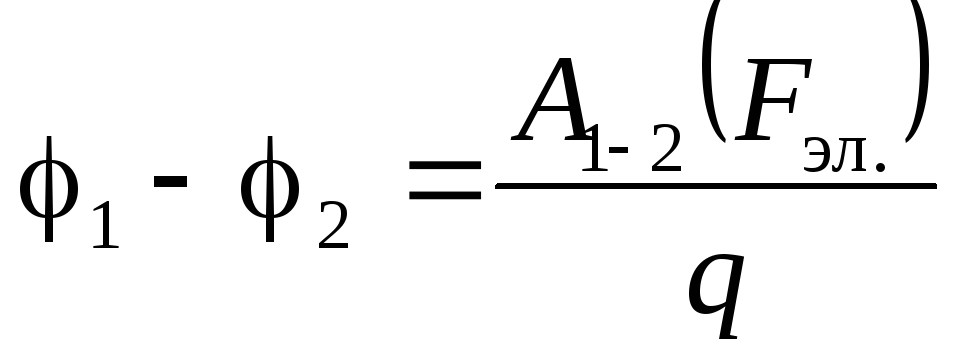 . (3.16)
. (3.16)
Таким образом, зная разность потенциалов двух точек поля, легко вычислить работу электрического поля, совершаемую при перемещении заряда qмежду этими точками:
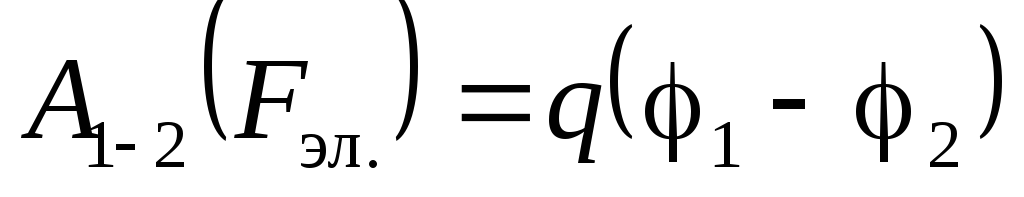 . (3.17)
. (3.17)
В международной системе единиц СИ потенциал (и разность потенциалов) измеряется в вольтах:
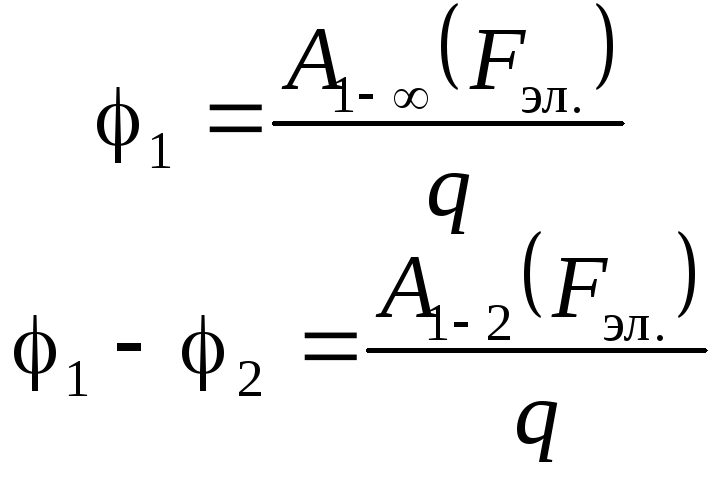
 .
.
Разность потенциалов двух точек электростатического поля равна одному вольту, если при переносе заряда q= 1Кл между этими точками, электрическая сила совершает работуА(Fэл.) = 1 Дж.
Ответы На Защиту К Лабам 2, 6
ЛАБОРАТОРНАЯ РАБОТА 2.
1. Конденсатор- система из двух проводников форма и взаимное расположение которых таковы, что электростатическое поле этих проводников при сообщении им равных по абсолютному значению и противоположных по знаку электрических зарядов полностью или почти полностью локализовано в ограниченной области пространства. В конденсаторе накапливается электрический заряд и соответственно энергия электростатического поля. Способность конденсатора к накоплению заряда характеризуется его электроемкостью, представляющей собой взаимную электрическую емкость его обкладок. Электрическая емкость конденсатора равна отношению его заряда к разности потенциалов между обкладками, измеряется в Фарадах:
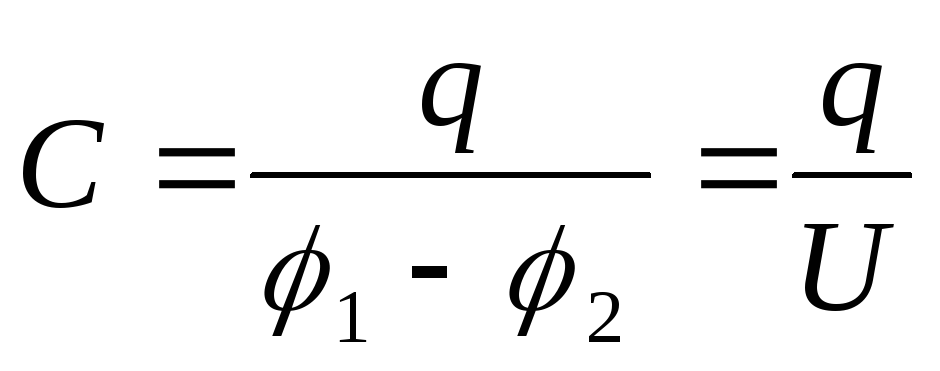 .
.
2. Емкость
плоского конденсатора зависит от его геометрических характеристик: площади
пластин  и
расстояния между ними
и
расстояния между ними  .
Если же присутсвует диэлектрик, то и от
его диэлектрической проницаемости
.
Если же присутсвует диэлектрик, то и от
его диэлектрической проницаемости  .
При изменении разности потенциалов
между обкладками, электроемкость
конденсатора не меняется.
.
При изменении разности потенциалов
между обкладками, электроемкость
конденсатора не меняется.
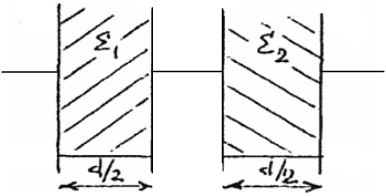 3. Данный
конденсатор можно представить как 2
последовательно соединенных конденсатора:
3. Данный
конденсатор можно представить как 2
последовательно соединенных конденсатора:
Тогда,
по формуле для последовательного
соединения: 
 .
.
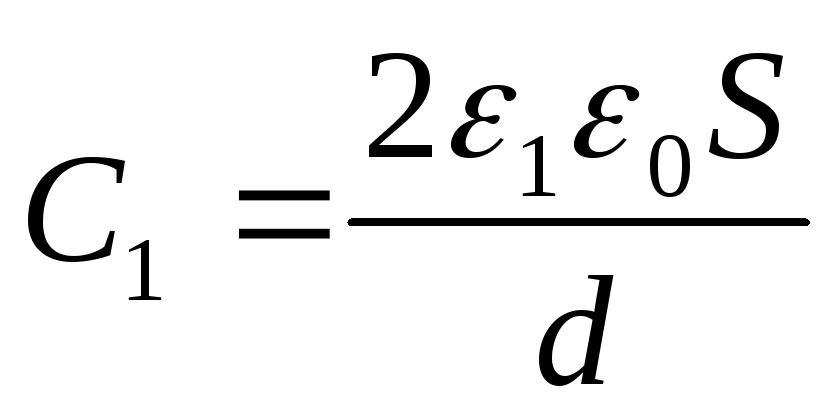 ,
, 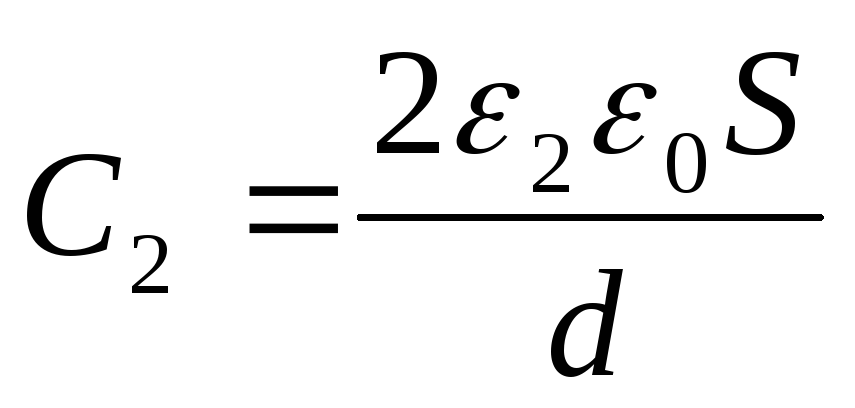 . Подставляем
в формулу и получаем:
. Подставляем
в формулу и получаем:
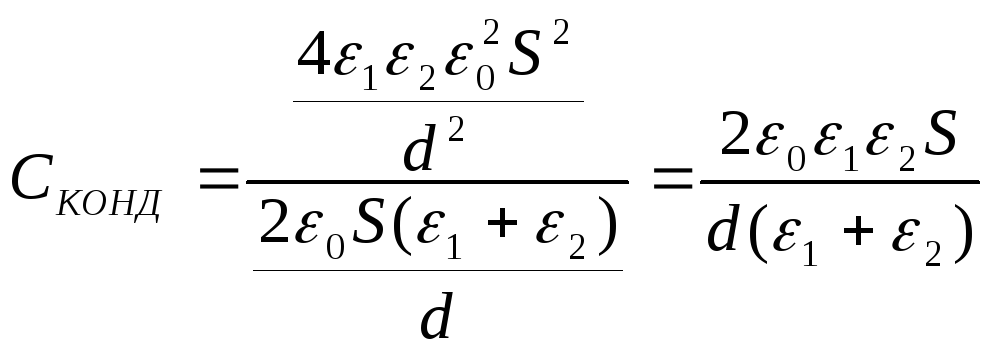
Постройте графики зависимости Er(r) и φ(r).
4. Формула емкости сферического конденсатора:
Пусть
имеется сферический конденсатор,
состоящий из двух концентрических
металлических обкладок 1 и 2 сферической
формы, радиусы которых соответственно
равны  и
и 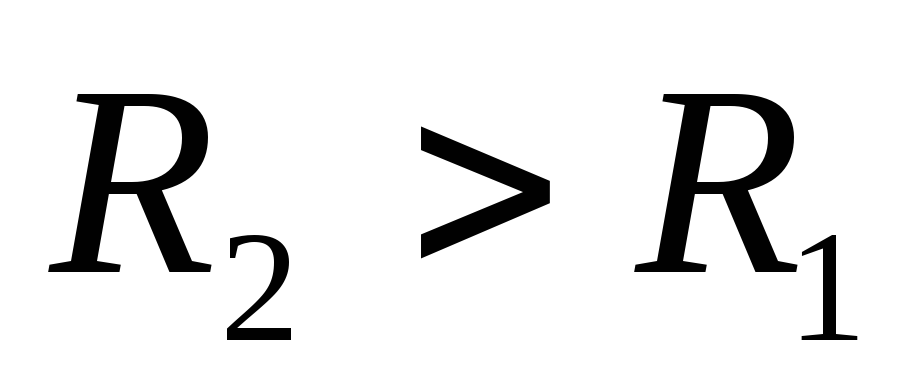 .
Пусть
.
Пусть 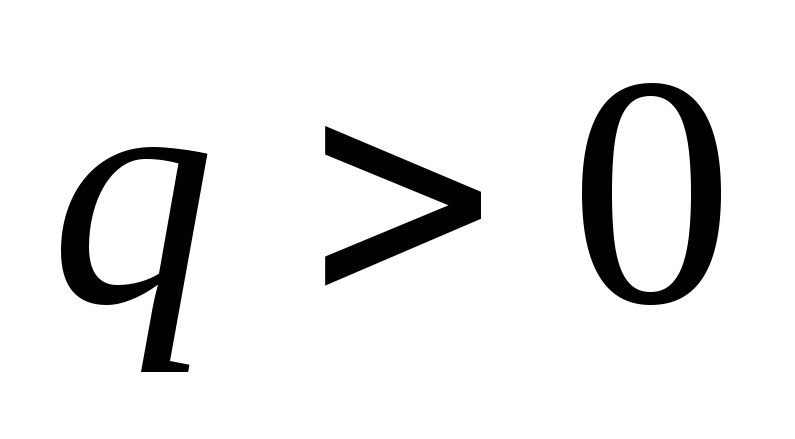 —
заряд обкладки 1, а
—
заряд обкладки 1, а  —
заряд обкладки 2. Равномерно заряженная
сфера создает электростатическое поле
только в области пространства вне этой
сферы. Напряженность поля в конденсаторе
направлена радиально:
—
заряд обкладки 2. Равномерно заряженная
сфера создает электростатическое поле
только в области пространства вне этой
сферы. Напряженность поля в конденсаторе
направлена радиально: 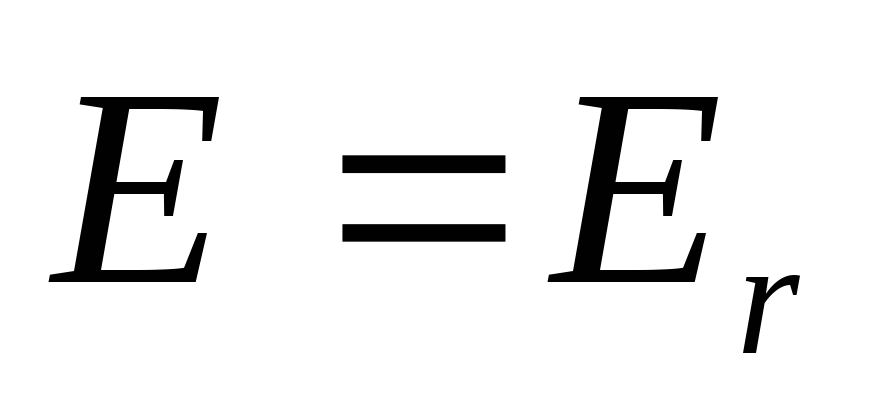 ,
причем
,
причем
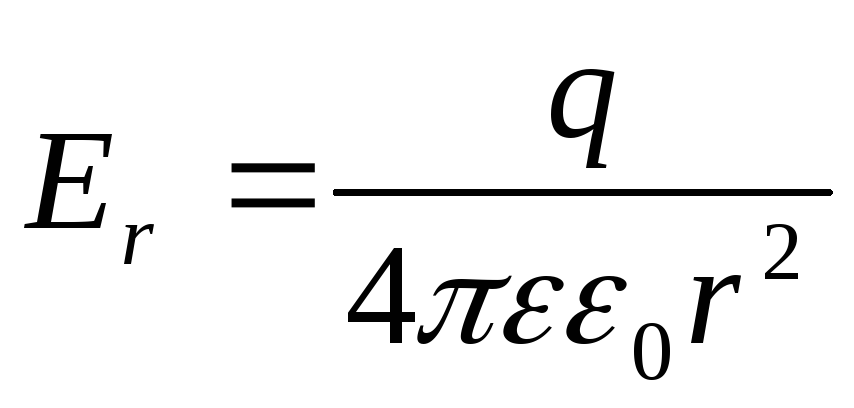 ,
,
где  —
относительная диэлектрическая
проницаемость среды, заполняющей
конденсатор. Так как
—
относительная диэлектрическая
проницаемость среды, заполняющей
конденсатор. Так как

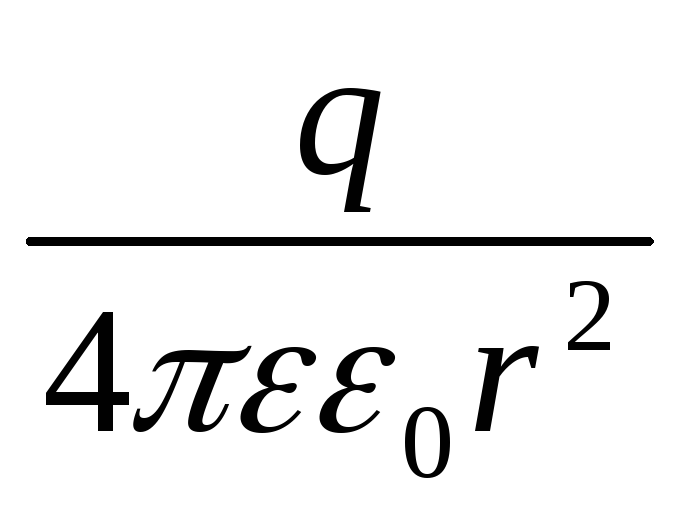 ,
,
то разность потенциалов обкладок
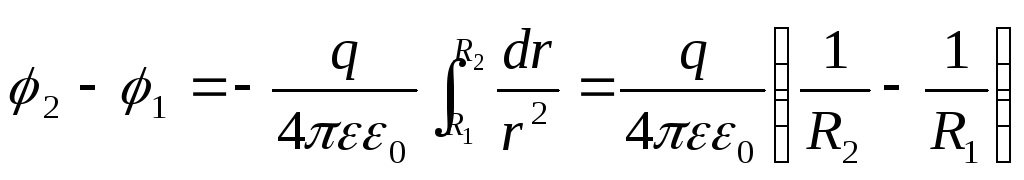
Электрическая емкость сферического конденсатора:
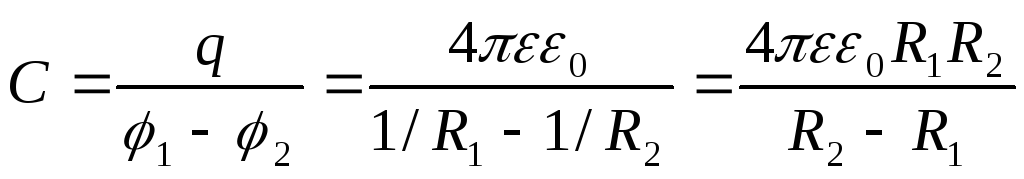 .
.
Если  ,
то
,
то 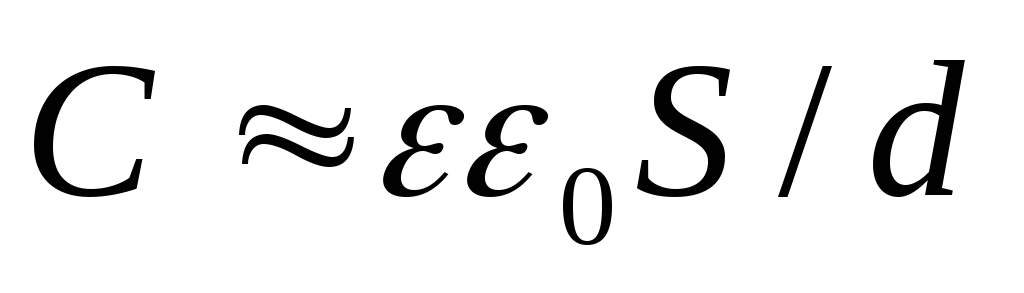 ,
где
,
где 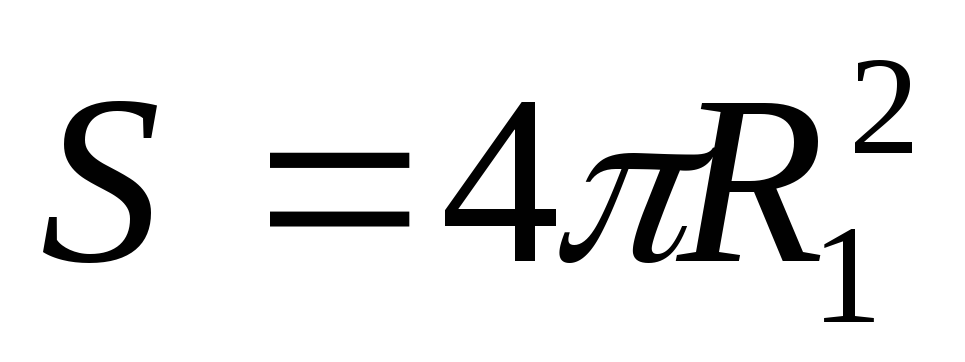 —
площадь внутренней обкладки.
—
площадь внутренней обкладки.
5. При
последовательном соединении конденсаторов
в батарею заряды всех конденсаторов
одинаковы и равны заряду  батареи.
Разность потенциалов
батареи.
Разность потенциалов  клемм батареи равна сумме разностей
потенциалов на каждом конденсаторе
порознь:
клемм батареи равна сумме разностей
потенциалов на каждом конденсаторе
порознь:
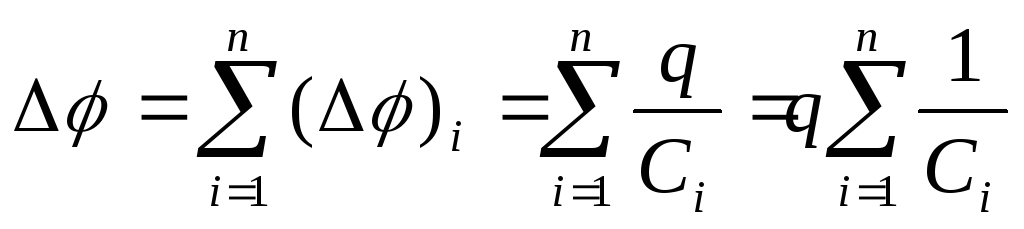 .
.
С
другой стороны 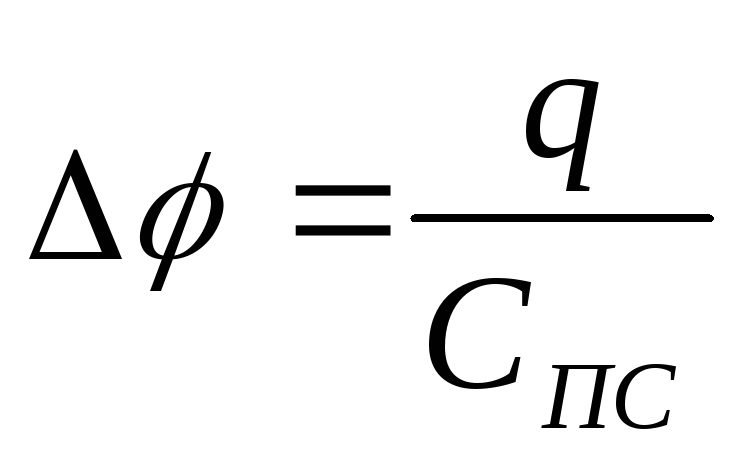 ,
где
,
где 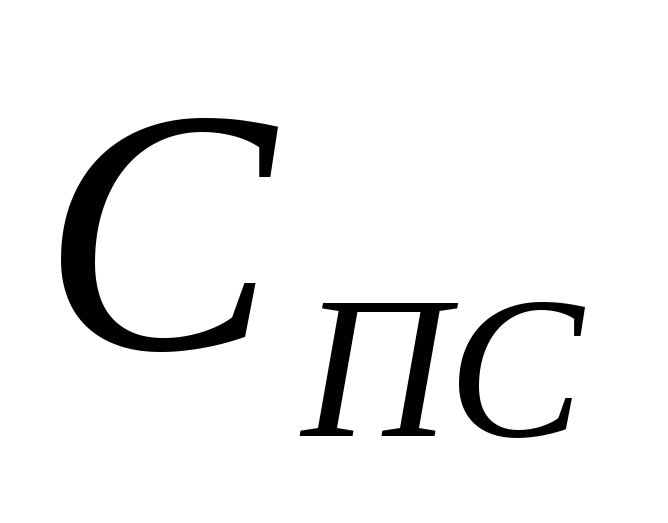 —
электрическая емкость батареи. Таким
образом,
—
электрическая емкость батареи. Таким
образом,

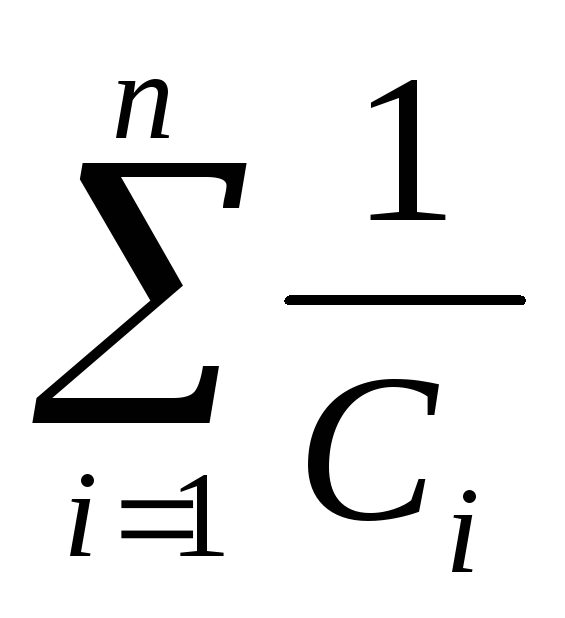
6. Для получения батареи конденсаторов,
имеющей большую электрическую емкость,
конденсаторы соединяют в батарею
параллельно. Все конденсаторы такой
батареи заряжаются до одной и той же
разности потенциалов  клемм батареи. Если
клемм батареи. Если  —
емкость
—
емкость 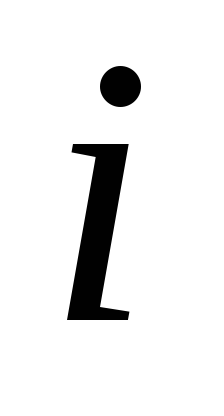 -го
конденсатора, а
-го
конденсатора, а 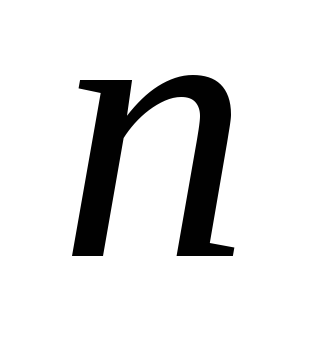 —
общее число конденсаторов в батарее,
то заряд
—
общее число конденсаторов в батарее,
то заряд 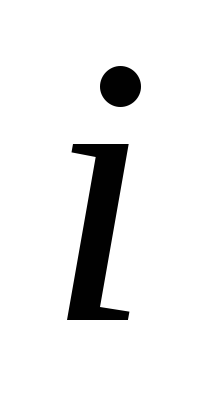 -го
конденсатора
-го
конденсатора 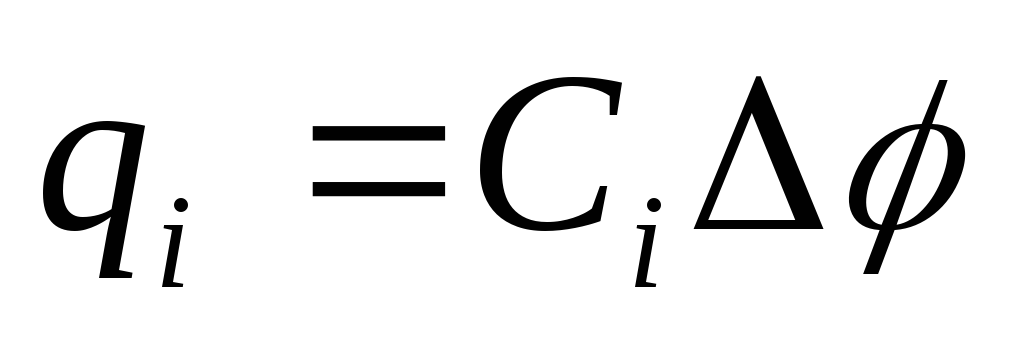 ,
а заряд всей батареи равен сумме зарядов
всех конденсаторов:
,
а заряд всей батареи равен сумме зарядов
всех конденсаторов:

С
другой стороны,  ,
где
,
где 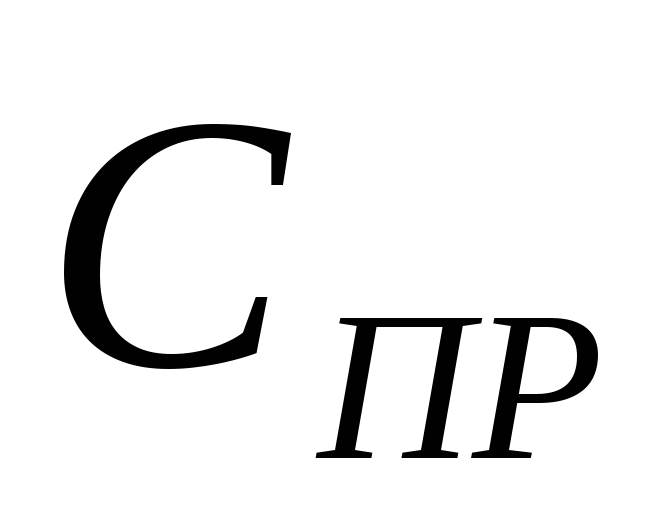 —
общая электроемкость всей батареи.
Таким образом,
—
общая электроемкость всей батареи.
Таким образом,
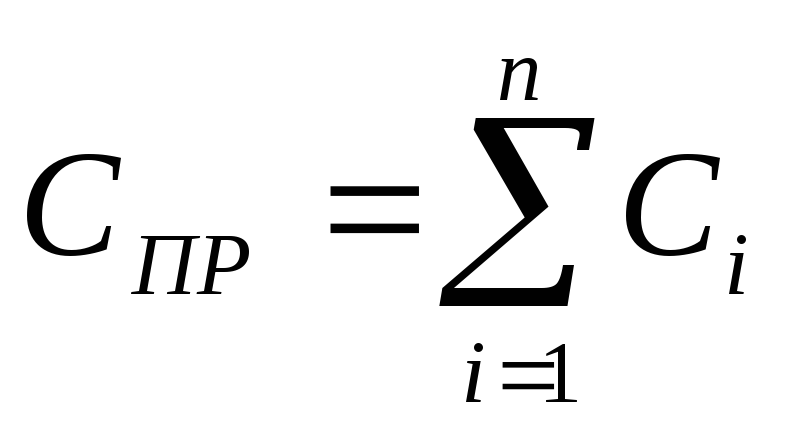 .
.
7. При последовательном соединении.
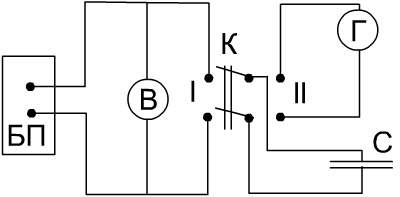 8. Мы
в положении переключателя I
заряжаем конденсатор, включенный в
цепь, при определенной разности
потенциалов, измеряемой вольтметром.
Далее переводим переключатель в положение
II
и смотрим на гальванометре отброс
светового пятна по шкале.
8. Мы
в положении переключателя I
заряжаем конденсатор, включенный в
цепь, при определенной разности
потенциалов, измеряемой вольтметром.
Далее переводим переключатель в положение
II
и смотрим на гальванометре отброс
светового пятна по шкале.
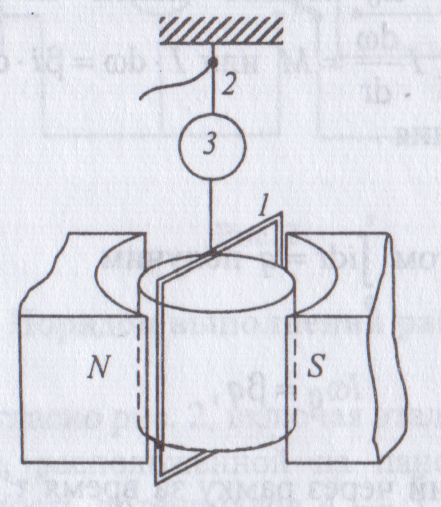
9. Заряд конденсатора измеряют с помощью
баллистического гальванометра.
Баллистический гальванометр относится
к приборам магнито-электрической
системы.
Его схематичное устройство показано
на рисунке.
Между полюсами
постоянного магнита N,S,
имеющими
цилиндрическую форму, неподвижно
закреплен стальной цилиндр. В зазоре
возникает однородное
радиально направленное магнитное поле.
Между полюсами магнита и цилиндром
может свободно вращаться рамка
1 с
обмоткой из тонкой проволоки, подвешенная
на металлической или кварцевой нити 2.
Для
отсчета углов поворота рамки служит
зеркальце 3,
на
которое
падает свет от осветительного устройства.
После отражения от зеркальца, свет
попадает на прозрачную шкалу.
Баллистический
гальванометр используется для измерения
заряда q,
время
протекания которого через обмотку
подвижной рамки мало по сравнению с
периодом Т
собственных
колебаний рамки . Он отличается от
обычных зеркальных гальванометров
увеличенным значением момента инерции 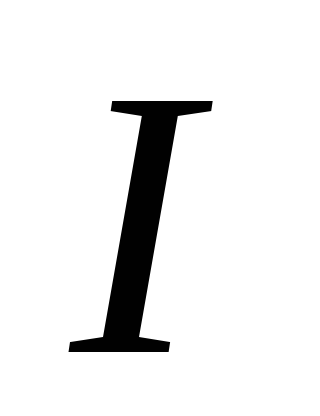 его подвижной системы.
его подвижной системы.
10. Для измерения отброса светового пятна в делениях, чтобы потом по значениям делений и по заряду для каждого случая построить график зависимости заряда от количества делений, из которого потом находят заряд неизвествного конденсатора; для расчета баллистической постоянной.
11. 
12. 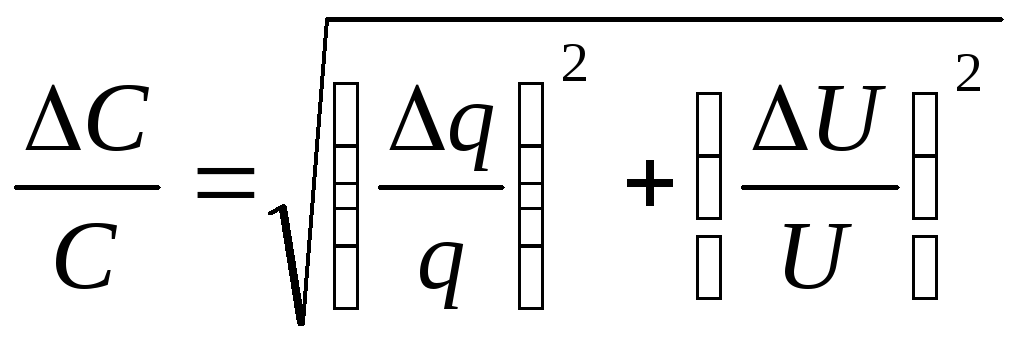 , где
, где  определяют
по градуировочному графику, а
определяют
по градуировочному графику, а
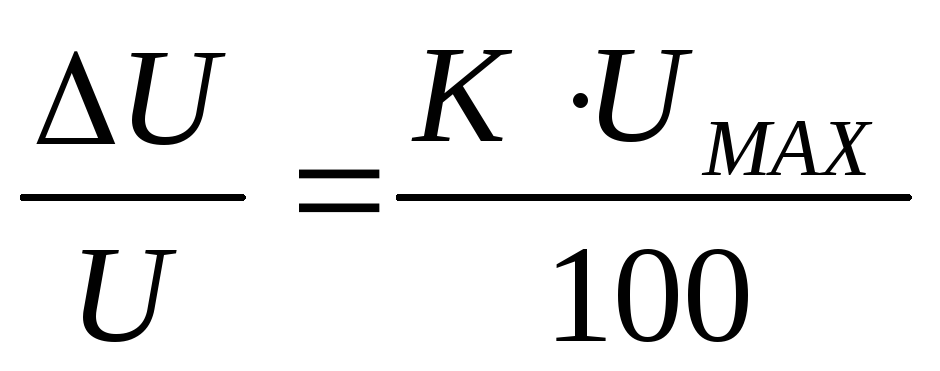 .
.
ЛАБОРАТОРНАЯ РАБОТА 6.
1. Относительной диэлектрической проницаемостью среды называется число, показывающее, во сколько раз напряженность электростатического поля в однородном диэлектрике меньше, чем напряженность в вакууме:
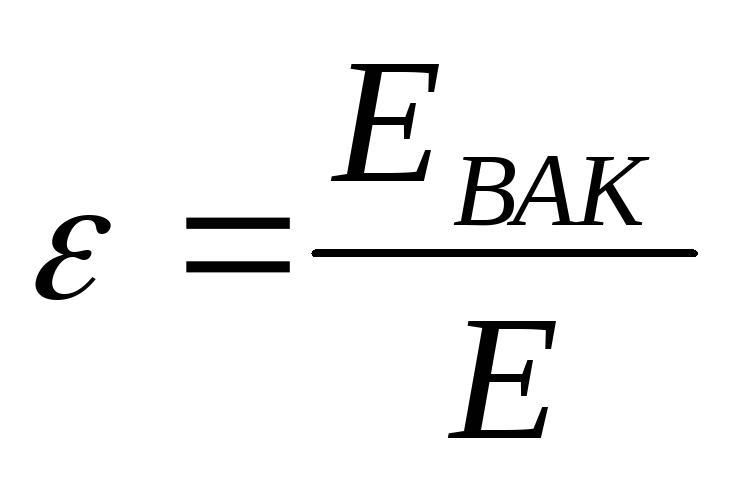
Связь: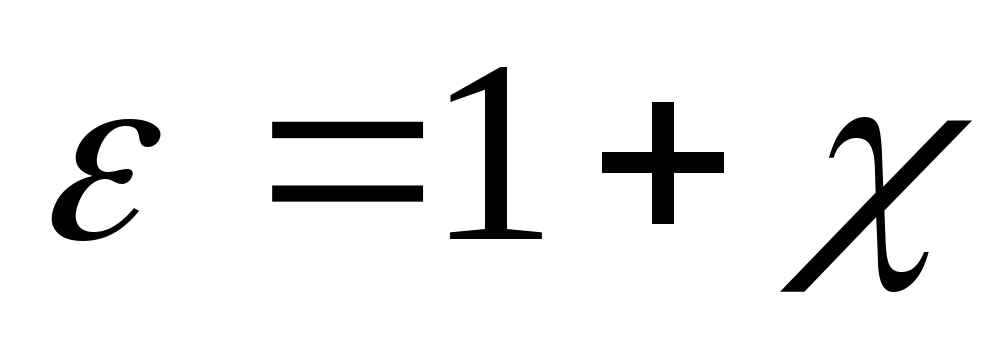 ,
где
,
где 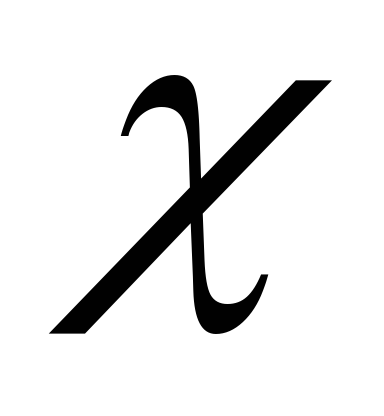 —
диэлектрическая
восприимчивость среды:
—
диэлектрическая
восприимчивость среды: 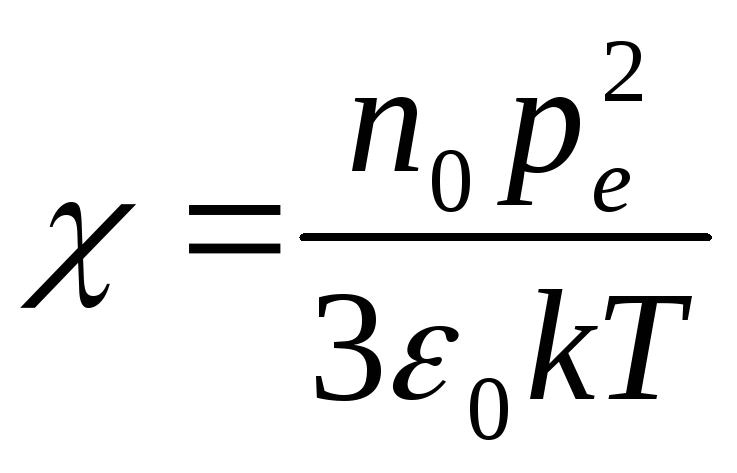 (где
(где 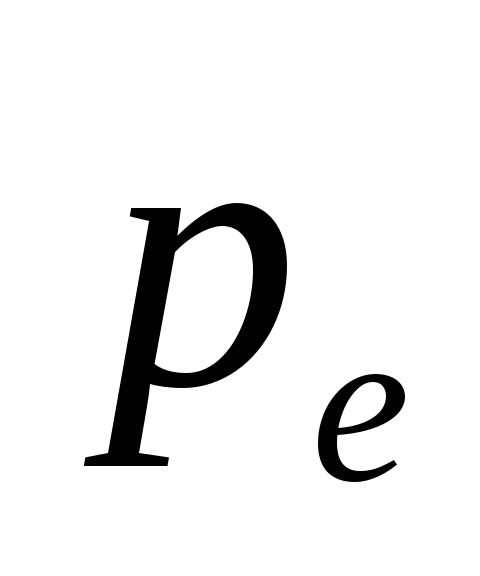 -дипольный
электрический момент,
-дипольный
электрический момент, 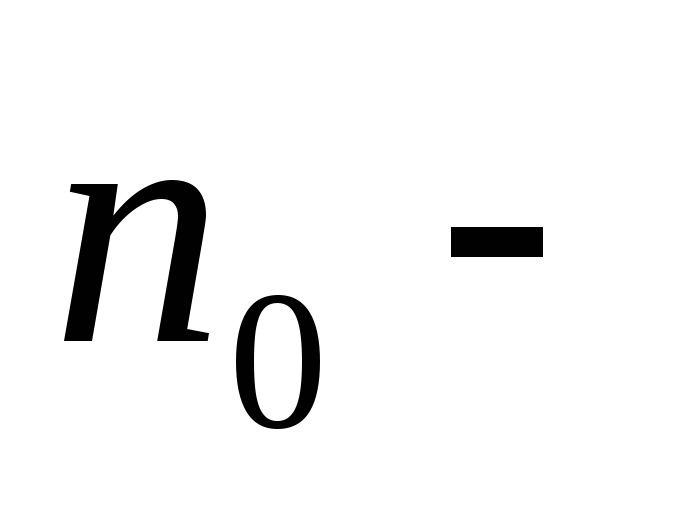 концентрация молекул)
концентрация молекул)
2. В данной работе определяется диэлектрическая проницаемость среды с помощью явления втягивания жидкого диэлектрика внутрь плоского конденсатора.
Выведение формулы:
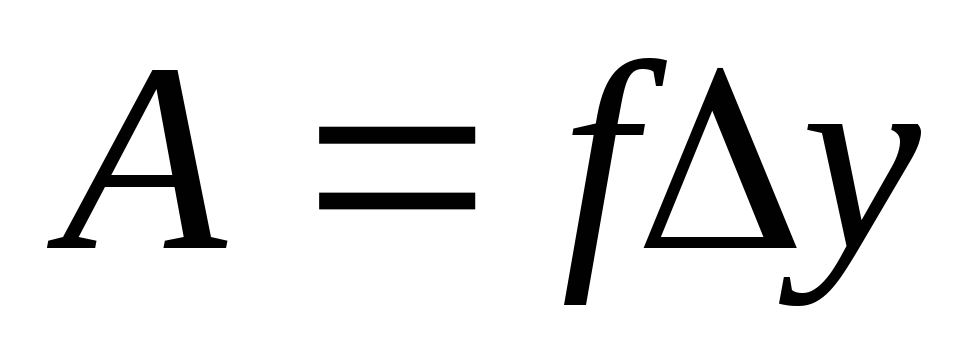
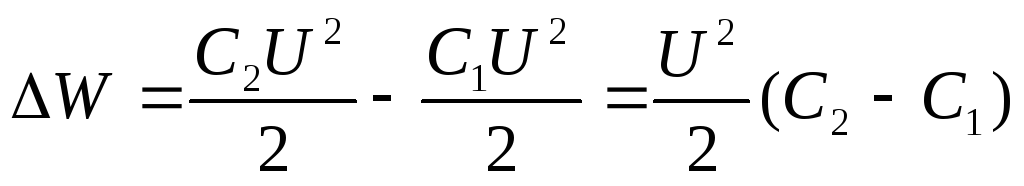
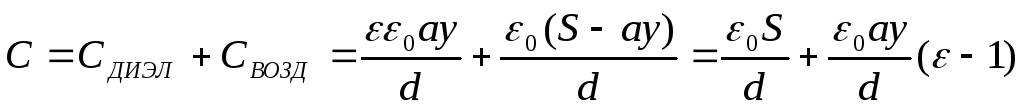

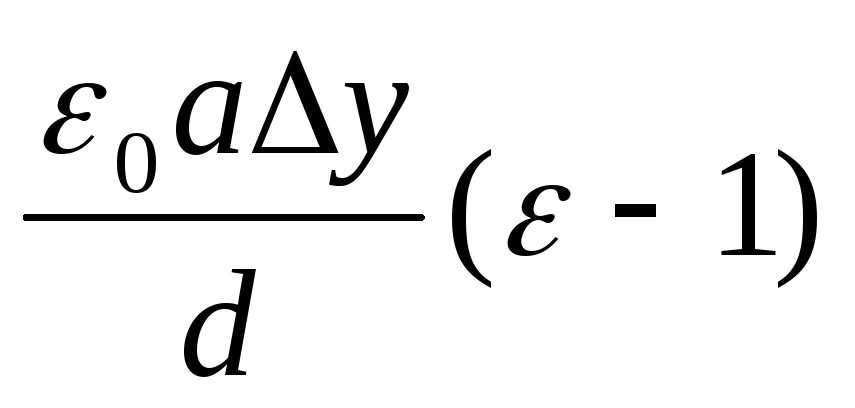

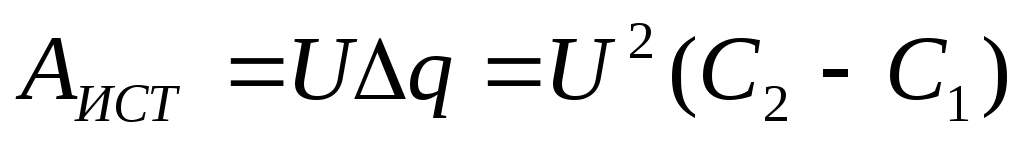
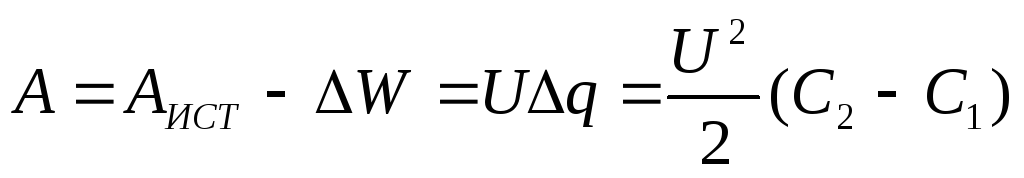
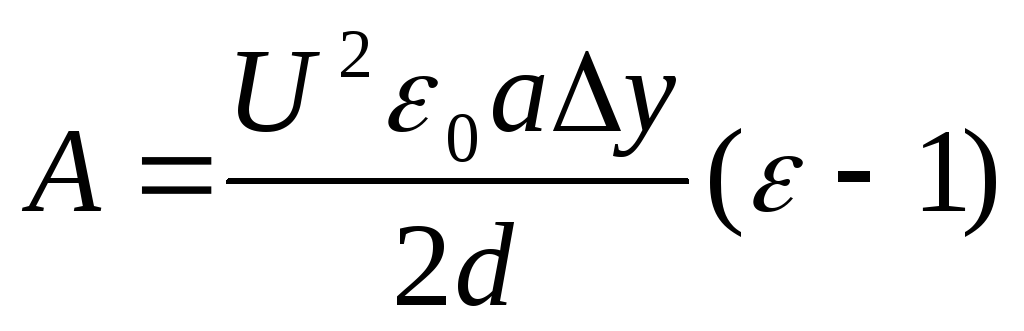
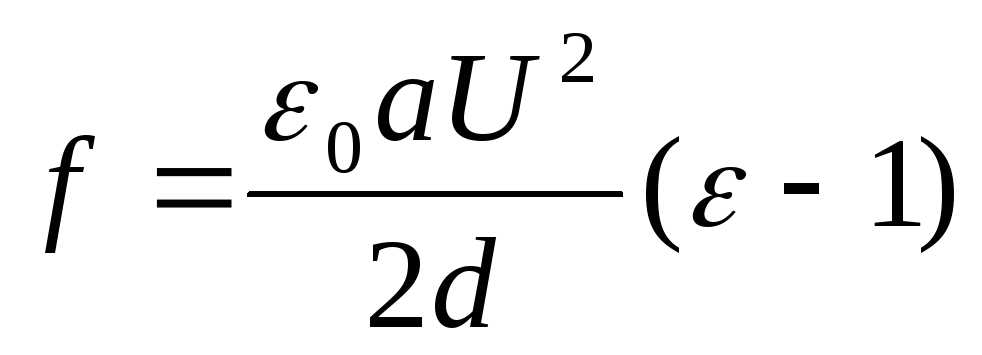
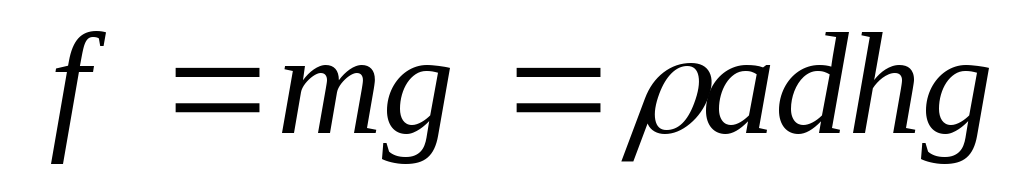
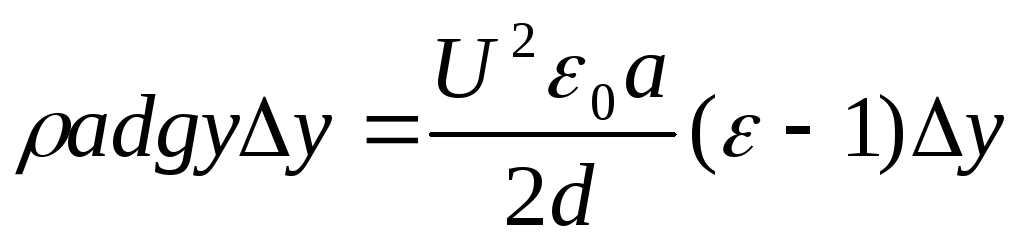
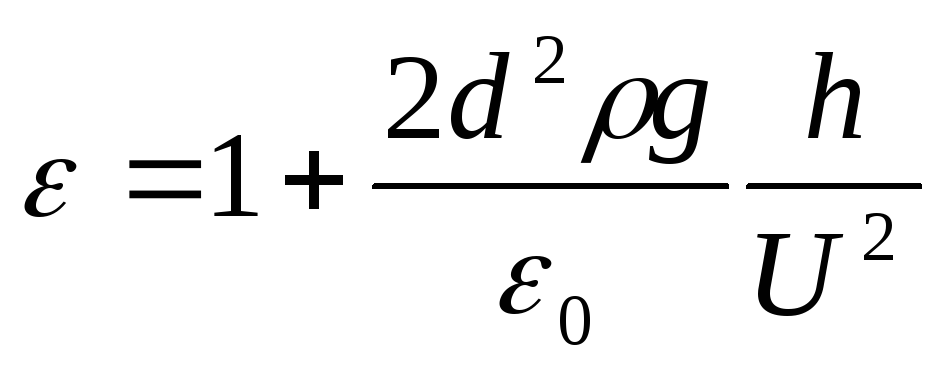
3. Незаряженный
диэлектрик, помещенный в электрические
поле, поляризуется. Этот процесс состоит
в образовании диполей. Рассмотрим
поведение такого диполя в неоднородном
электрическом поле. Пусть в направлении
оси Х напряженность поля Е возрастает.
Силы, действующие на заряды диполя
неодинаковы. 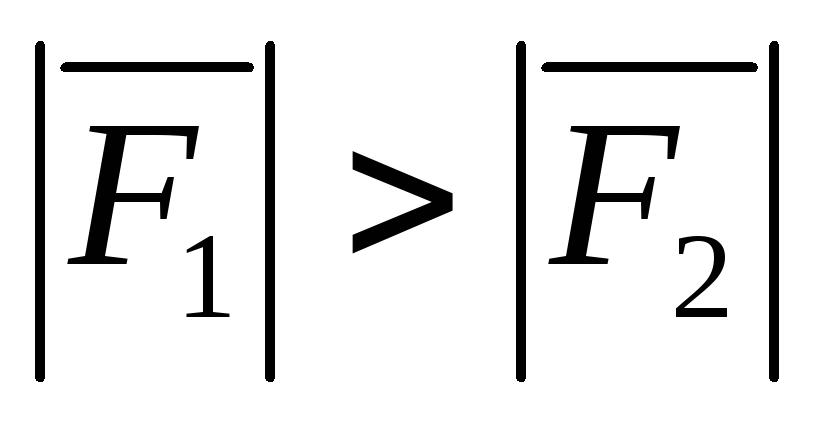 ,
так как
,
так как  в той точке, где находится положительный
заряд больше, чем
в той точке, где находится положительный
заряд больше, чем 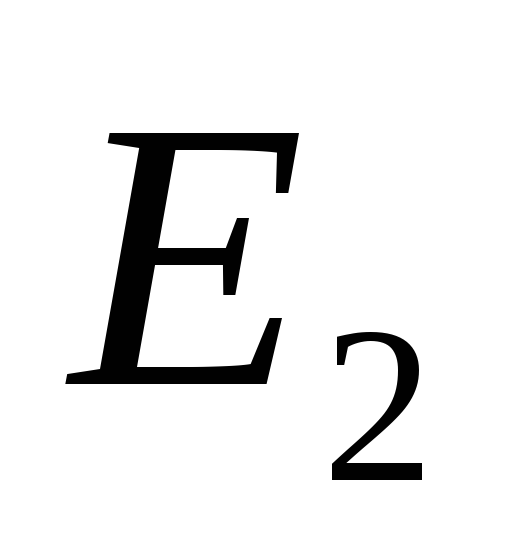 в точке, где расположен отрицательный
заряд. Следовательно, диполь под действием
результирующей силы
перемещается
в область более сильного поля. Поэтому
диэлектрик втягивается внутрь плоского
конденсатора.
в точке, где расположен отрицательный
заряд. Следовательно, диполь под действием
результирующей силы
перемещается
в область более сильного поля. Поэтому
диэлектрик втягивается внутрь плоского
конденсатора.
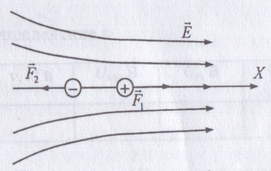
4. По мере втягивания диэлектрика заряд на обкладках конденсатора увеличивается. Напряженность вроде-бы тоже возрастает.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма. / / Электростатика. / / Электроемкость. Емкость заряженного конденсатора (плоского, циллиндрического и коаксиального провода, сферического, двухпроводной линии). Энергия. Поделиться:
| ||||



