Конденсатор в цепи постоянного тока для чего

При подключении конденсатора к источнику постоянного тока под действием электрического поля на нижнюю обкладку движутся электроны. В следствии, явления электростатической индукции с верхней обкладки конденсатора заряды уходят к положительному выводу источника питания в цепи возникает ток – ток заряда по мере накопления зарядов в конденсаторе, растёт напряжение , а ток заряда уменьшается, и так, – конденсатор подключённый к источнику тока, заряжается до U_ист .

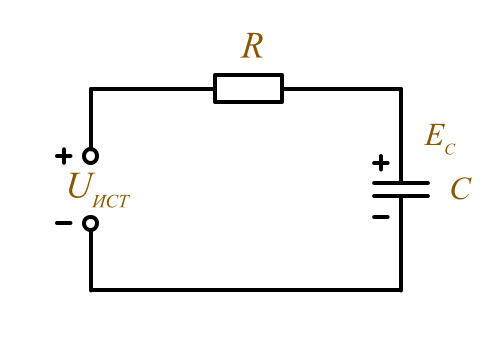
Конденсатор в цепи постоянного тока

Кратковременный ток в цепи называется ток заряда, а так как он существует короткое время, то говорят, конденсатор постоянный ток не пропускает.

Считается что конденсатор

заряжается если напряжение на нём составляет 0,63 от U_ист и это происходит за время
равное Τ

Τ заряда – постоянная времени заряда конденсатора в секундах

Одна секунда – 1с = 10 3 мс = 10 6 мкс =10 12 нс

R_зар – сопротивление в Омах

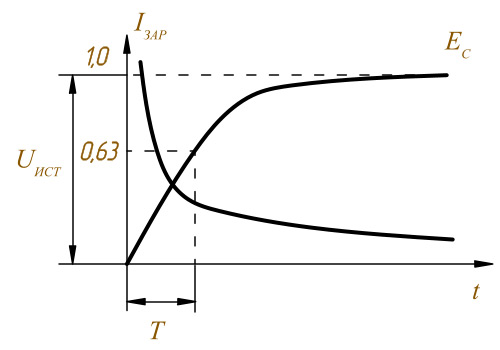
График заряда конденсатора

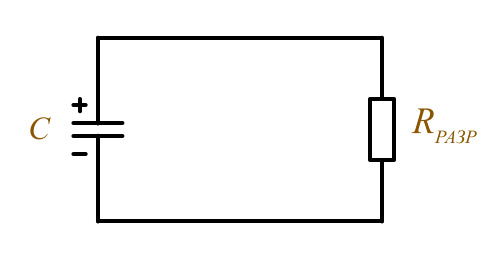
Работа конденсатора в цепи постоянного тока

Считается, что конденсатор разрядится если напряжение на нём составляет 0,37 от напряжения источника и это происходит за время Τ разряда.

Во всех радиотехнических и электронных устройствах кроме транзисторов и микросхем применяются конденсаторы. В одних схемах их больше, в других меньше, но совсем без конденсаторов не бывает практически ни одной электронной схемы.

При этом конденсаторы могут выполнять в устройствах самые разные задачи. Прежде всего, это емкости в фильтрах выпрямителей и стабилизаторов. С помощью конденсаторов передается сигнал между усилительными каскадами, строятся фильтры низких и высоких частот, задаются временные интервалы в выдержках времени и подбирается частота колебаний в различных генераторах.

Свою родословную конденсаторы ведут от лейденской банки, которую в середине XVIII века в своих опытах использовал голландский ученый Питер ван Мушенбрук. Жил он в городе Лейдене, так что нетрудно догадаться, почему так называлась эта банка.

Собственно это и была обыкновенная стеклянная банка, выложенная внутри и снаружи оловянной фольгой – станиолем. Использовалась она в тех же целях, как и современная алюминиевая, но тогда алюминий открыт еще не был.

Единственным источником электричества в те времена была электрофорная машина, способная развивать напряжение до нескольких сотен киловольт. Вот от нее и заряжали лейденскую банку. В учебниках физики описан случай, когда Мушенбрук разрядил свою банку через цепь из десяти гвардейцев взявшихся за руки.

В то время никто не знал, что последствия могут быть трагическими. Удар получился достаточно чувствительным, но не смертельным. До этого не дошло, ведь емкость лейденской банки была незначительной, импульс получился очень кратковременным, поэтому мощность разряда была невелика.

Как устроен конденсатор

Устройство конденсатора практически ничем не отличается от лейденской банки: все те же две обкладки, разделенные диэлектриком. Именно так на современных электрических схемах изображаются конденсаторы. На рисунке 1 показано схематичное устройство плоского конденсатора и формула для его расчета.

Рисунок 1. Устройство плоского конденсатора

Здесь S – площадь пластин в квадратных метрах, d – расстояние между пластинами в метрах, C — емкость в фарадах, ε – диэлектрическая проницаемость среды. Все величины, входящие в формулу, указаны в системе СИ. Эта формула справедлива для простейшего плоского конденсатора: можно просто расположить рядом две металлические пластины, от которых сделаны выводы. Диэлектриком может служить воздух.

Из этой формулы можно понять, что емкость конденсатора тем больше, чем больше площадь пластин и чем меньше расстояние между ними. Для конденсаторов с другой геометрией формула может быть иной, например, для емкости одиночного проводника или электрического кабеля. Но зависимость емкости от площади пластин и расстояния между ними та же, что и у плоского конденсатора: чем больше площадь и чем меньше расстояние, тем больше емкость.

На самом деле пластины не всегда делаются плоскими. У многих конденсаторов, например металлобумажных, обкладки представляют собой алюминиевую фольгу свернутую вместе с бумажным диэлектриком в плотный клубок, по форме металлического корпуса.

Для увеличения электрической прочности тонкая конденсаторная бумага пропитывается изолирующими составами, чаще всего трансформаторным маслом. Такая конструкция позволяет делать конденсаторы с емкостью до нескольких сотен микрофарад. Примерно так же устроены конденсаторы и с другими диэлектриками.

Формула не содержит никаких ограничений на площадь пластин S и расстояние между пластинами d. Если предположить, что пластины можно развести очень далеко, и при этом площадь пластин сделать совсем незначительной, то какая-то емкость, пусть небольшая, все равно останется. Подобное рассуждение говорит о том, что даже просто два проводника, расположенные по соседству, обладают электрической емкостью.

Этим обстоятельством широко пользуются в высокочастотной технике: в некоторых случаях конденсаторы делаются просто в виде дорожек печатного монтажа, а то и просто двух скрученных вместе проводков в полиэтиленовой изоляции. Обычный провод–лапша или кабель также обладают емкостью, причем с увеличением длины она увеличивается.

Кроме емкости C, любой кабель обладает еще и сопротивлением R. Оба этих физических свойства распределены по длине кабеля, и при передаче импульсных сигналов работают как интегрирующая RC – цепочка, показанная на рисунке 2.

На рисунке все просто: вот схема, вот входной сигнал, а вот он же на выходе. Импульс искажается до неузнаваемости, но это сделано специально, для чего и собрана схема. Пока же речь идет о влиянии емкости кабеля на импульсный сигнал. Вместо импульса на другом конце кабеля появится вот такой «колокол», а если импульс короткий, то он может и вовсе не дойти до другого конца кабеля, вовсе пропасть.

Исторический факт

Здесь вполне уместно вспомнить историю о том, как прокладывали трансатлантический кабель. Первая попытка в 1857 году потерпела неудачу: телеграфные точки – тире (прямоугольные импульсы) искажались так, что на другом конце линии длиной 4000 км разобрать ничего не удалось.

Вторая попытка была предпринята в 1865 году. К этому времени английский физик У. Томпсон разработал теорию передачи данных по длинным линиям. В свете этой теории прокладка кабеля оказалась более удачной, сигналы принять удалось.

За этот научный подвиг королева Виктория пожаловала ученого рыцарством и титулом лорда Кельвина. Именно так назывался небольшой город на побережье Ирландии, где начиналась прокладка кабеля. Но это просто к слову, а теперь вернемся к последней букве в формуле, а именно, к диэлектрической проницаемости среды ε.

Немножко о диэлектриках

Эта ε стоит в знаменателе формулы, следовательно, ее увеличение повлечет за собой возрастание емкости. Для большинства используемых диэлектриков, таких как воздух, лавсан, полиэтилен, фторопласт эта константа практически такая же, как у вакуума. Но вместе с тем существует много веществ, диэлектрическая проницаемость которых намного выше. Если воздушный конденсатор залить ацетоном или спиртом, то его емкость возрастет раз в 15…20.

Но подобные вещества обладают кроме высокой ε еще и достаточно высокой проводимостью, поэтому такой конденсатор заряд держать будет плохо, он быстро разрядится сам через себя. Это вредное явление называется током утечки. Поэтому для диэлектриков разрабатываются специальные материалы, которые позволяют при высокой удельной емкости конденсаторов обеспечивать приемлемые токи утечки. Именно этим и объясняется такое разнообразие видов и типов конденсаторов, каждый из которых предназначен для конкретных условий.

Электролитический конденсатор

Наибольшей удельной емкостью (соотношение емкость / объем) обладают электролитические конденсаторы. Емкость «электролитов» достигает до 100 000 мкФ, рабочее напряжение до 600В. Такие конденсаторы работают хорошо только на низких частотах, чаще всего в фильтрах источников питания. Электролитические конденсаторы включаются с соблюдением полярности.

Электродами в таких конденсаторах является тонкая пленка из оксида металлов, поэтому часто эти конденсаторы называют оксидными. Тонкий слой воздуха между такими электродами не очень надежный изолятор, поэтому между оксидными обкладками вводится слой электролита. Чаще всего это концентрированные растворы кислот или щелочей.

На рисунке 3 показан один из таких конденсаторов.

Рисунок 3. Электролитический конденсатор

Чтобы оценить размеры конденсатора рядом с ним сфотографировался простой спичечный коробок. Кроме достаточно большой емкости на рисунке можно разглядеть еще и допуск в процентах: ни много ни мало 70% от номинальной.

В те времена, когда компьютеры были большими и назывались ЭВМ, такие конденсаторы стояли в дисководах (по-современному HDD). Информационная емкость таких накопителей теперь может вызвать лишь улыбку: на двух дисках диаметром 350 мм хранилось 5 мегабайт информации, а само устройство весило 54 кг.

Основным назначением показанных на рисунке суперконденсаторов был вывод магнитных головок из рабочей зоны диска при внезапном отключении электроэнергии. Такие конденсаторы могли хранить заряд несколько лет, что было проверено на практике.

Чуть ниже с электролитическими конденсаторами будет предложено проделать несколько простых опытов, чтобы понять, что может делать конденсатор.

Для работы в цепях переменного тока выпускаются неполярные электролитические конденсаторы, вот только достать их почему-то очень непросто. Чтобы как-то эту проблему обойти, обычные полярные «электролиты» включают встречно-последовательно: плюс-минус-минус-плюс.

Если полярный электролитический конденсатор включить в цепь переменного тока, то сначала он будет греться, а потом раздастся взрыв. Отечественные старые конденсаторы разлетались во все стороны, импортные же имеют специальное приспособление, позволяющее избежать громких выстрелов. Это, как правило, либо крестовая насечка на донышке конденсатора, либо отверстие с резиновой пробкой, расположенное там же.

Очень не любят электролитические конденсаторы повышенного напряжения, даже если полярность соблюдена. Поэтому никогда не надо ставить «электролиты» в цепь, где предвидится напряжение близкое к максимальному для данного конденсатора.

Иногда в некоторых, даже солидных форумах, начинающие задают вопрос: «На схеме означен конденсатор 470µF * 16V, а у меня есть 470µF * 50V, можно ли его поставить?». Да, конечно можно, вот обратная замена недопустима.

Конденсатор может накапливать энергию

Разобраться с этим утверждением поможет простая схема, показанная на рисунке 4.

Рисунок 4. Схема с конденсатором

Главным действующим лицом этой схемы является электролитический конденсатор C достаточно большой емкости, чтобы процессы заряда – разряда протекали медленно, и даже очень наглядно. Это дает возможность наблюдать работу схемы визуально с помощью обычной лампочки от карманного фонаря. Фонари эти давно уступили место современным светодиодным, но лампочки для них продаются до сих пор. Поэтому, собрать схему и провести простые опыты очень даже просто.

Может быть, кто-то скажет: «А зачем? Ведь и так все очевидно, да если еще и описание почитать…». Возразить тут, вроде, нечего, но любая, даже самая простая вещь остается в голове надолго, если ее понимание пришло через руки.

Итак, схема собрана. Как она работает?

В положении переключателя SA, показанном на схеме, конденсатор C заряжается от источника питания GB через резистор R по цепи: +GB __ R __ SA __ C __ -GB. Зарядный ток на схеме показан стрелкой с индексом iз. Процесс заряда конденсатора показан на рисунке 5.

Рисунок 5. Процесс заряда конденсатора

На рисунке видно, что напряжение на конденсаторе возрастает по кривой линии, в математике называемой экспонентой. Ток заряда прямо-таки зеркально отражает напряжение заряда. По мере того, как напряжение на конденсаторе растет, ток заряда становится все меньше. И только в начальный момент соответствует формуле, показанной на рисунке.

Через некоторое время конденсатор зарядится от 0В до напряжения источника питания, в нашей схеме до 4,5В. Весь вопрос в том, как это время определить, сколько ждать, когда же конденсатор зарядится?

Постоянная времени «тау» τ = R*C

В этой формуле просто перемножаются сопротивление и емкость последовательно соединенных резистора и конденсатора. Если, не пренебрегая системой СИ, подставить сопротивление в Омах, емкость в Фарадах, то результат получится в секундах. Именно это время необходимо для того, чтобы конденсатор зарядился до 36,8% напряжения источника питания. Соответственно для заряда практически до 100% потребуется время 5* τ.

Часто, пренебрегая системой СИ, подставляют в формулу сопротивление в Омах, а емкость в микрофарадах, тогда время получится в микросекундах. В нашем случае результат удобнее получить в секундах, для чего придется микросекунды просто умножить на миллион, а проще говоря, переместить запятую на шесть знаков влево.

Для схемы, показанной на рисунке 4, при емкости конденсатора 2000мкФ и сопротивлении резистора 500Ω постоянная времени получится τ = R*C = 500 * 2000 = 1000000 микросекунд или ровно одна секунда. Таким образом, придется подождать приблизительно 5 секунд, пока конденсатор зарядится полностью.

Если по истечении указанного времени переключатель SA перевести в правое положение, то конденсатор C разрядится через лампочку EL. В этот момент получится короткая вспышка, конденсатор разрядится и лампочка погаснет. Направление разряда конденсатора показано стрелкой с индексом iр. Время разряда также определяется постоянной времени τ. График разряда показан на рисунке 6.

Рисунок 6. График разряда конденсатора

Конденсатор не пропускает постоянный ток

Убедиться в этом утверждении поможет еще более простая схема, показанная на рисунке 7.

Рисунок 7. Схема с конденсатором в цепи постоянного тока

Если замкнуть переключатель SA, то последует кратковременная вспышка лампочки, что свидетельствует о том, что конденсатор C зарядился через лампочку. Здесь же показан и график заряда: в момент замыкания переключателя ток максимальный, по мере заряда конденсатора уменьшается, а через некоторое время прекращается совсем.

Если конденсатор хорошего качества, т.е. с малым током утечки (саморазряда) повторное замыкание выключателя к вспышке не приведет. Для получения еще одной вспышки конденсатор придется разрядить.

Конденсатор в фильтрах питания

Конденсатор ставится, как правило, после выпрямителя. Чаще всего выпрямители делаются двухполупериодными. Наиболее распространенные схемы выпрямителей показаны на рисунке 8.

Рисунок 8. Схемы выпрямителей

Однополупериодные выпрямители также применяются достаточно часто, как правило, в тех случаях, когда мощность нагрузки незначительна. Самым ценным качеством таких выпрямителей является простота: всего один диод и обмотка трансформатора.

Для двухполупериодного выпрямителя емкость конденсатора фильтра можно рассчитать по формуле

C = 1000000 * Po / 2*U*f*dU, где C емкость конденсатора мкФ, Po мощность нагрузки Вт, U напряжение на выходе выпрямителя В, f частота переменного напряжения Гц, dU амплитуда пульсаций В.

Большое число в числителе 1000000 переводит емкость конденсатора из системных Фарад в микрофарады. Двойка в знаменателе представляет собой число полупериодов выпрямителя: для однополупериодного на ее месте появится единица

C = 1000000 * Po / U*f*dU,

а для трехфазного выпрямителя формула примет вид C = 1000000 * Po / 3*U*f*dU.

Суперконденсатор – ионистор

В последнее время появился новый класс электролитических конденсаторов, так называемый ионистор. По своим свойствам он похож на аккумулятор, правда, с несколькими ограничениями.

Заряд ионистора до номинального напряжения происходит в течение короткого времени, буквально за несколько минут, поэтому его целесообразно использовать в качестве резервного источника питания. По сути ионистор прибор неполярный, единственное, чем определяется его полярность это зарядкой на заводе – изготовителе. Чтобы в дальнейшем эту полярность не перепутать она указывается знаком +.

Большую роль играют условия эксплуатации ионисторов. При температуре 70˚C при напряжении 0,8 от номинального гарантированная долговечность не более 500 часов. Если же прибор будет работать при напряжении 0,6 от номинального, а температура не превысит 40 градусов, то исправная работа возможна в течение 40 000 часов и более.

Наиболее распространенное применение ионистора это источники резервного питания. В основном это микросхемы памяти или электронные часы. В этом случае основным параметром ионистора является малый ток утечки, его саморазряд.

Достаточно перспективным является использование ионисторов совместно с солнечными батареями. Здесь также сказывается некритичность к условию заряда и практически неограниченное число циклов заряд-разряд. Еще одно ценное свойство в том, что ионистор не нуждается в обслуживании.

Пока получилось рассказать, как и где работают электролитические конденсаторы, причем, в основном в цепях постоянного тока. О работе конденсаторов в цепях переменного тока будет рассказано в другой статье — Конденсаторы для электроустановок переменного тока.

Практически во всех электронных устройствах, от самых простых до высокотехнологичных, таких как материнские платы компьютеров, можно встретить один неизменно присутствующий элемент, являющийся пассивным компонентом. Но к сожалению, мало кто знает как устроен и для чего нужен конденсатор, и какие виды этого накопителя бывают.

Просто о сложном

Итак, это небольшое устройство для накопления электрического поля или заряда похоже на обычную банку, ту, в которой маринуют помидоры или хранят муку. Она точно так же в себе накапливает сухое вещество или жидкость, которую в неё поместят. Аналогия проста: по цепи бегут электроны, а на своей дороге встречают проводников, которые ведут их в «банку», где они и накапливаются, усиливая заряд.

Для того чтобы выяснить, много ли элекрончиков так можно собрать, и в какой момент накопление прекратится (банка лопнет), электрический процесс обычно сравнивают с водопроводом. Если представить трубу, в которой течёт вода, закачиваемая туда насосом, то где-то в центре трубопровода нужно вообразить мягкую мембрану, растягивающуюся под давлением жидкости. Очевидно, что она будет растягиваться до определённого предела, пока не разорвётся или, если попалась очень крепкая, не уравновесит силу насоса.

Такой пример показывает, как работает конденсатор, только мембрана заменяется электрическим полем, которое увеличивается по мере зарядки накопителя (работы насоса), уравновешивая напряжение источника питания. Очевидно, что этот процесс не бесконечный, и предельный заряд существует, по достижении которого «банка» выйдет из строя и перестанет выполнять свои функции.

Устройство и принцип работы

Конденсатор — устройство, состоящее из двух пластин (обкладок), имеющих между собой пустоту. Напряжение к нему подаётся через проводки, подсоединённые к пластинкам. Современные приборы, по сути, не сильно отличаются от макетов на уроках физики, они также состоят из диэлектрика и обкладок. Следует отметить, что именно вещество или его отсутствие (вакуум), плохо проводящее электричество, изменяет характеристики накопителя.

Суть принципа работы конденсатора проста: дали напряжение, и заряд начал накапливаться. Для примера следует рассмотреть как ведёт себя накопитель в двух вариантах электрической цепи:

• Постоянный ток. Если в цепь с подключённым к ней конденсатором подать ток, то можно увидеть, что стрелка на амперметре начнёт двигаться, а потом быстро вернётся в исходное положение. Это объясняется просто: устройство быстро зарядилось, то есть источник питания был уравновешен обкладками накопителя, и тока не стало. Поэтому часто говорят, что в условиях постоянного тока конденсатор не работает. Такое утверждение неправильное, всё функционирует, но очень непродолжительное время.
• Переменный ток — это когда электроны двигаются сначала в одну, а затем в другую сторону. Если представить такую цепь с подключённым к ней накопителем, то на обеих обкладках конденсатора будут попеременно накапливаться положительные и отрицательные заряды. Это говорит о том, что переменный ток свободно протекает через устройство.

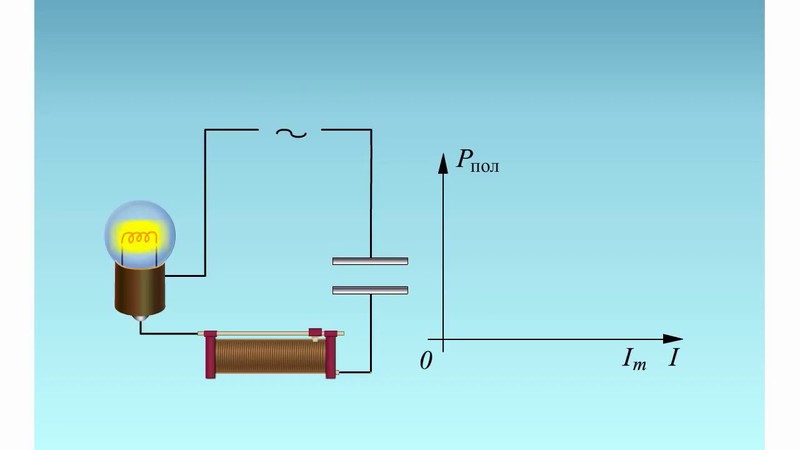
Поскольку конденсатор задерживает постоянный ток, но пропускает переменный, отсюда формируются и сферы его назначения, например, для устройств, в которых нужно убрать постоянную составляющую в сигнале. Вполне очевидно, что накопитель обладает сопротивлением, а вот мощность на нём не выделяется, поэтому он не греется.

Основные виды

Рядовой пользователь не всегда знает о том, каким конденсатором снабжено его устройство. А ведь каждый вид имеет свои недостатки и преимущества, а также эксплуатационные особенности. Существуют две большие группы этих устройств, предназначенные для электрической цепи с переменным и постоянным током. Но всё-таки основная классификация ведётся по типу диэлектрика, который находится между облатками конденсатора. Основные виды:

• Керамические. Имеют маленький размер, малый ток утечки и небольшую индуктивность. Отлично работают в условиях высоких частот, в цепях пульсирующего, постоянного и переменного тока. Представлены в различном диапазоне напряжений и ёмкостей, в зависимости от того, для чего конденсатор предназначен.
• Слюдяные. В настоящее время почти не используются и не выпускаются. В накопителях такого типа диэлектриком служит слюда. Рабочее напряжение таких конденсаторов в диапазоне — 200−1500 В.
• Бумажные. В алюминиевых облатках заключена конденсаторная бумага. Выдерживают напряжение 160−1500 В.
• Полиэстеровые. Максимальная ёмкость не превышает 15 мФ, рабочее напряжение — 50−1500 В.
• Полипропиленовые. Выгодно выделяются на фоне остальных собратьев двумя преимуществами. Первое — маленький допуск ёмкости (+/- 1%), второе — до 3 кВ рабочего напряжения.

Отдельно стоит отметить электролитические конденсаторы. Главное их отличие от других видов — подключения только к цепи постоянного или пульсирующего тока. Такие накопители имеют полярность — это особенность их конструкции, поэтому неправильное подключение ведёт к вздутию или взрыву устройства. Они обладают большой ёмкостью, что делает конденсатор электролитический пригодным для применения в выпрямительных цепях.

Сферы применения

Можно смело сказать, что конденсаторы используют практически во всех электронных и радиотехнических схемах. Чтобы иметь представление о том, где и зачем нужен конденсатор, следует вспомнить его способность сохранять заряд и разряжаться в нужное время, а также пропускать переменный ток и не пропускать постоянный. А это значит, что такие устройства используются во многих технических сферах, например:

• телефонии;
• в производстве счётных и запоминающих устройств;
• автоматике;
• при создании измерительных приборов и многих других.

Электрические накопители можно встретить как в телевизорах, так и в приборах радиолокации, где необходимо формировать импульс большой мощности, для чего и служит конденсатор. Невозможно встретить блок питания без этих устройств или сетевой фильтр.

Нужно сказать, что накопители применяют и в сферах, не связанных с электрикой, например, в производстве металла и добыче угля, где используют конденсаторные электровозы.

Постоянный ток не проходит через конденсатор. Почему переменный ток проходит через конденсатор, а постоянный не проходит

>>Физика 11 класс >> Конденсатор в цепи переменного тока

§ 33 КОНДЕНСАТОР В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком .

Переменный же ток может идти по цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.

Пусть у нас имеются источники постоянного и переменного напряжений, причем постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 4.13), соединенных последовательно. При включении постоянного напряжения (переключатель повернут влево, цепь подключена к точкам АА») лампа не светится. Но при включении переменного напряжения (переключатель повернут вправо, цепь подключена к точкам ВВ») лампа загорается, если емкость конденсатора достаточно велика.

Как же переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Все дело в том, что происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, идущий в цепи при перезарядке конденсатора , нагревает нить лампы.

Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь (рис. 4.14).

Напряжение на конденсаторе

Сила тока, представляющая собой производную заряда по времени, равна:

Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на (рис. 4.15).

Амплитуда силы тока равна:

I m = U m C. (4.29)

Если ввести обозначение

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим

Величину X c , обратную произведению С циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома (см. формулу (4.17)). Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока. Это и позволяет рассматривать величину Х с как сопротивление конденсатора переменному току (емкостное сопротивление).

Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение X c . С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты .

В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.

Сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на .

1. Как связаны между собой действующие значения силы тока и напряжения на конденсаторе в цепи переменного тока!
2. Выделяется ли энергия в цепи, содержащей только конденсатор, если активным сопротивлением цепи можно пренебречь!
3. Выключатель цепи представляет собой своего рода конденсатор. Почему же выключатель надежно размыкает цепь!

Что такое переменный ток

Если рассматривать постоянный ток, то он не всегда может быть идеально постоянным: напряжение на выходе источника может зависеть от нагрузки или от степени разряда аккумулятора или гальванической батареи. Даже при постоянном стабилизированном напряжении ток во внешней цепи зависит от нагрузки, что и подтверждает закон Ома. Получается, что это тоже не совсем постоянный ток, но переменным такой ток назвать тоже нельзя, поскольку направления он не меняет.

Переменным обычно называют напряжение или ток, направление и величина которого меняются не под действием внешних факторов, например нагрузки, а вполне «самостоятельно»: именно таким его вырабатывает генератор. К тому же, эти изменения должны быть периодическими, т.е. повторяющимися через определенный п

Занимательная радиотехника. Проходит ли ток через конденсатор?

Проходит электрический ток через конденсатор или не проходит? Повседневный радиолюбительский опыт убедительно говорит, что постоянный ток не проходит, а переменный проходит.

Это легко подтвердить опытами. Можно зажечь лампочку, присоединив ее к сети переменного тока через конденсатор. Громкоговоритель или телефонные трубки будут продолжать работать, если их присоединить к приемнику не непосредственно, а через конденсатор.

Конденсатор представляет собой две или несколько металлических пластин, разделенных диэлектриком. Этим диэлектриком чаще всего бывает слюда, воздух или керамика, являющиеся наилучшими изоляторами. Вполне естественно, что постоянный ток не может пройти через такой изолятор. Но почему же проходит через него переменный ток? Это кажется тем более странным, что такая же самая керамика в виде, например, фарфоровых роликов прекрасно изолирует провода переменного тока, а слюда прекрасно выполняет функции изолятора в паяльниках, электроутюгах и других нагревательных приборах, исправно работающих от переменного тока.

Посредством некоторых опытов мы могли бы «доказать» еще более странный факт: если в конденсаторе заменить диэлектрик со сравнительно плохими изоляционными свойствами другим диэлектриком, который является лучшим изолятором, то свойства конденсатора изменятся так, что прохождение переменного тока через конденсатор будет не затруднено, а, наоборот, облегчено. Например, если включить лампочку в цепь переменного тока через конденсатор с бумажным диэлектриком и затем заменить бумагу таким прекрасным изолятором; как стекло или фарфор такой же толщины, то лампочка начнет гореть ярче. Подобный опыт позволит прийти к заключению, что переменный ток не только проходят через конденсатор, но что он к тому же проходит тем легче, чем лучшим изолятором является его диэлектрик.

Однако, несмотря на всю кажущуюся убедительность подобных опытов, электрический ток — ни постоянный, ни переменный — через конденсатор не проходит, Диэлектрик, разделяющий пластины конденсатора, служит надежной преградой на пути тока, каким бы он ни был — переменным или постоянным. Но это еще не означает, что тока не будет и во всей той цепи, в которую включен конденсатор.

Конденсатор обладает определенным физическим свойством, которое мы называем емкостью. Это свойство состоит в способности накапливать на обкладках электрические заряды. Источник электрического тока можно грубо уподобить насосу, перекачивающему в цепи электрические заряды. Если ток постоянный, то электрические заряды перекачиваются все время в одну сторону.

Как же будет вести себя в цепи постоянного тока конденсатор?

Наш «электрический насос» будет качать заряды на одну его обкладку и откачивать их с другой обкладки. Способность конденсатора удерживать на своих обкладках (пластинах) определенную разницу количества зарядов и называется его емкостью. Чем больше емкость конденсатора, тем больше электрических зарядов может быть на одной обкладке по сравнению с другой.

В момент включения тока конденсатор не заряжен — количество зарядов на его обкладках одинаково. Но вот ток включен. «Электрический насос» заработал. Он погнал заряды на одну обкладку и начал откачиватьихс Другой. Раз в цепи началось движение зарядов, значит в ней начал протекать ток. Ток будет течь до тех пор, пока конденсатор не зарядится полностью. По достижении этого предела ток прекратится.

Следовательно, если в цепи постоянного тока есть конденсатор, то после ее замыкания ток в ней будет течь столько времени сколько нужно для полного заряда конденсатора.

Если сопротивление цепи, через которую заряжается конденсатор, сравнительно невелико, то время заряда оказывается очень коротким: оно длится ничтожные доли секунды, после чего течение тока прекращается.

 

Иное дело в цепи переменного тока. В этой цепи «насос» перекачивает электрические заряды то в одну, то в другую сторону. Едва создав на одной обкладке конденсатора превышение количества зарядов по сравнению с количеством их на другой обкладке, насос начинает перекачивать их в обратно направлении. Заряды будут циркулировать в цепи непрерывно, значит в ней, несмотря на присутствие не проводящего ток конденсатора, будет существовать ток — ток заряда и разряда конденсатора.

От чего будет зависеть величина этого тока?

Под величиной тока мы понимаем количество электрических зарядов, протекающих в единицу времени через поперечное сечение проводника. Чем, больше емкость конденсатора, тем больше зарядов потребуется для его «заполнения», значит тем сильнее будет ток в цепи. Емкость конденсатора зависит от ве-, личины пластин, расстояния между ними и рода разделяющего их диэлектрика, его диэлектрической проницаемости. У фарфора диэлектрическая проницаемсклъ больше, чем у бумаги, поэтому при замене в конденсаторе бумаги фарфором ток в цепи увеличивается, хотя фарфор является лучшим изолятором, чем бумага.

Величина тока зависит также от его частоты. Чем выше частота, тем больше будет ток. Легко понять, почему это происходит, представив себе, что мы наполняем водой через трубку сосуд емкостью, например, 1 л и затем выкачиваем ее оттуда. Если этот процесс будет повторяться 1 раз в секунду, то по трубке в секунду будет проходить 2 л воды: 1 л в одну сторону и 1 л — в другую. Но если мы удвоим частоту^ процесса: будем наполнять и опорожнять сосуд 2 раза в секунду, то по трубке в секунду пройдет уже 4 л воды — увеличение частоты процесса при неизменной емкости сосуда привело к соответствующему увеличению количества воды, протекающей по трубке.

Из всего сказанного можно сделать следующие выводк: электрический ток — ни постоянный, ни переменный — через конденсатор не проходит. Но в цепи, соединяющей источник переменного тока с конденсатором, течет ток заряда и разряда этого конденсатора. Чем больше емкость конденсатора и выше частота тока, тем сильнее будет этот ток.

Эта особенность переменного тока чрезвычайно широко используется в радиотехнике. На ней основано и излучение радиоволн. Для этого мы возбуждаем в передающей антенне высокочастотный переменный ток. Но почему же ток течет в антенне, ведь она не представляет собой замкнутую цепь? Он течет потому, что между проводами антенны и противовеса или землей существует емкость. Ток в антенне представляет собой ток заряда и разряда этой емкости, этого конденсатора.

 

Л. В. Кубаркин и Е. А. Левитин, Занимательная радиотехника, Госэнергоиздат, 1956.

2. Конденсаторы и расчеты | 12. Конденсаторы | Часть1

2. Конденсаторы и расчеты

Конденсаторы и расчеты

Конденсаторы, в отличие от проводников, не обладают стабильным сопротивлением. Однако, у них существует определенная математическая зависимость между напряжением и током:

 

 

Прописная буква «i» (мгновенный ток) характеризует величину тока через конденсатор в определенный момент времени. Этот ток резко контрастирует с постоянным током (заглавная буква «I»), величина которого не меняется с течением времени. Выражение «du/dt» обозначает мгновенную величину изменения напряжения во времени, или скорость изменения напряжения (вольт в секунду) в определенный момент времени.

В данном уравнении вы можете увидеть нечто новое  — переменную времени. В резистивных цепях эта переменная не имеет никакого значения, так как все величины там постоянны. Для цепей, содержащих конденсаторы, переменная времени очень важна, потому что ток в них связан с изменением напряжения во времени. Чтобы понять эту связь в полной мере, давайте рассмотрим несколько иллюстраций. Предположим, что мы подключили конденсатор к источнику переменного напряжения, состоящему из потенциометра и батареи:

 

 

Пока механизм потенциометра находится в одном положении (ползунок неподвижен), вольтметр, подключенный к конденсатору, будет регистрировать постоянное (неизменное) напряжение, а амперметр будет показывать 0 ампер. Объяснить это можно следующим образом. Так как напряжение на конденсаторе постоянно, то и скорость изменения напряжения (dv/dt) на нем будет равна нулю. Посмотрев внимательно на вышеприведенное уравнение можно сделать вывод, что при нулевом значении dv/dt мгновенный ток через конденсатор так же будет равен нулю.

 

 

Если ползунок потенциометра медленно переместить вверх, то напряжение на конденсаторе постепенно возрастет. Данное повышение напряжения можно увидеть на индикаторе вольтметра:

 

 

Если предположить, что ползунок потенциометра перемещается таким образом, что скорость увеличения напряжения на конденсаторе имеет равномерный характер (например, напряжение растет с постоянной скоростью 2 вольта в секунду), то отношение dv/dt в формуле будет иметь фиксированное значение. В соответствии с уравнением, это фиксированное значение, умноженное на емкость конденсатора, даст нам постоянный ток некоторой величины. С точки зрения физики, увеличивающееся напряжение на конденсаторе приведет к увеличению заряда между его пластинами. Таким образом, для равномерного темпа увеличения напряжения необходим равномерный темп накопления заряда в конденсаторе, который приравнивается к равномерной (постоянной) скорости потока электронов, или к электрическому току. В этом случае конденсатор действует как нагрузка: электроны входят в его отрицательную пластину и выходят из положительной, накапливая энергию в электрическом поле.

 

 

Если ползунок потенциометра перемещать в том же направлении, но с большей скоростью, то скорость изменения напряжения (dv/dt) будет больше, а соответственно больше будет и ток через конденсатор:

 

 

 

Из всего выше сказанного можно сделать вывод, что ток через конденсатор является производной от напряжения на нем во времени. Если говорить проще, то ток через конденсатор прямопропорционален скорости изменения напряжения. Применительно к нашей схеме, в которой напряжение на конденсаторе устанавливается положением ручки потенциометра, можно сказать, что ток через конденсатор прямопропорционален скорости перемещения этой ручки.

Если  бы мы могли двигать ползунок потенциометра в том же направлении, но с различной скоростью, то получили бы следующий график:

 

 

Обратите внимание: ток через конденсатор в любой момент времени пропорционален скорости изменения  (наклону линии) напряжения. Когда линия напряжения на графике растёт быстро (крутой подъем), ток имеет большое значение. Когда линия напряжения растет медленно (пологий подъем), ток имеет маленькое значение. В одном месте графика можно увидеть строго горизонтальный отрезок линии напряжения (нулевой наклон, представляющий период времени, когда ползунок потенциометра не двигался вообще), при котором ток упал до нулевой отметки.

Если мы будем двигать ползунок потенциометра вниз, то напряжение на конденсаторе будет уменьшаться, порождая ток противоположного направления. Объяснить такое положение дел можно следующим образом. Уменьшение напряжения на конденсаторе приведет к уменьшению заряда между его пластинами. Единственным способом уменьшения заряда является изменение направления потока электронов (разрядка конденсатора). В этом состоянии (с электронами выходящими из отрицательной пластины конденсатора и входящими — в положительную) конденсатор будет выступать в качестве источника питания, высвобождая запасенную энергию в остальную часть схемы.

 

 

В обоих случаях величина тока через конденсатор прямопропорциональна скорости изменения напряжения. Единственной разницей между увеличением и уменьшением напряжения является направление потока электронов. Математически, уменьшение напряжения выразится в отрицательном значении выражения dv/dt, а следовательно, и в отрицательном значении мгновенного тока.