Соединение конденсаторов

Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.

Параллельное соединение конденсаторов

Параллельное соединение конденсаторов

Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.

При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.

Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах. Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.

Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.

На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.

Последовательное соединение конденсаторов

Последовательное соединение конденсаторов

При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.

Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле

а трех –

Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.

При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение, чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.

Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения.

Смешанное соединение конденсаторов

Пример смешанного соединения конденсаторов

Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.

Оцените качество статьи:

Соединение конденсаторов — схемы | white-santa.ru

Все наверняка уже знают, что собой представляют последовательное и параллельное соединения.
Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным.

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов, получаемая цепь выглядит следующим образом:

Эта схема состоит из следующих элементов:                                                                                          трех конденсаторов C1, C2, С3 и источника электрической энергии E.

Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора

C2, ну а конец конденсатора C2 соединен с началом третьего конденсатора C3.
Стоит обратить внимание на то, как распределяются ёмкости каждого.

При таком соединении, все ёмкостя следующим образом.

Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад.
Общую емкость можно рассчитать по следующей формуле:

Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:

Параллельное соединение конденсаторов

При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже:

Так при параллельном соединении, емкости всех конденсаторов складываются:

То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.

Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме.

Смешанное соединение конденсаторов

Смешанное соединение конденсаторов выглядит следующим образом:

И представляет с собой различные сочетания параллельного и последовательного соединений.
Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.
Например, дана следующая схема и следующие данные:

C1=0.4Ф
C2=0.8Ф
C3=0,73Ф
Необходимо найти общую емкость всех трех конденсаторов.
Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.
Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.

Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.

Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.

§ 12.12 Электрическая ёмкость. Конденсаторы. Соединение конденсаторов

Сообщённый проводнику заряд q распределяется по его поверхности так, что напряжённость поля внутри проводника равна нулю. Если проводнику сообщить такой же заряд q, то он распределится по поверхности проводника. Отсюда вытекает, что потенциал проводника пропорционален находящемуся на нём заряду:

q = Cφ (12.49)

Коэффициент пропорциональности С называют электроёмкостью:

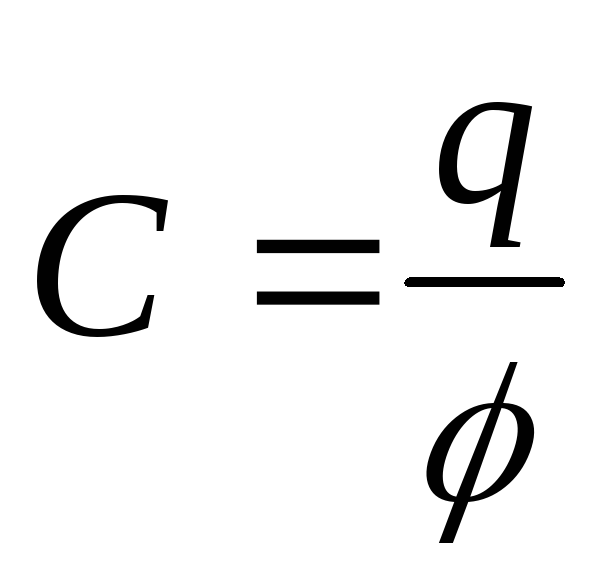(12.50)

Электроёмкость проводника или системы проводников – физическая величина, характеризующая способность проводника или системы проводников накапливать электрические заряды.

Для примера рассчитаем электроёмкость уединённого проводника, имеющего форму сферы. Используя соотношение между потенциалом и напряжённостью электростатического поля, запишем

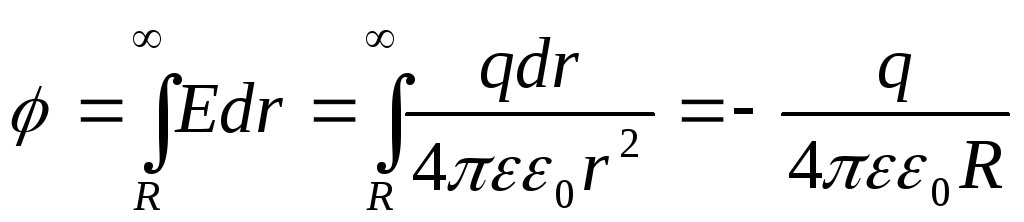(12.51)

R – радиус сферы.

При вычислении полагаем, что φ_∞=0. Получаем, что электроёмкость уединённой сферы равна

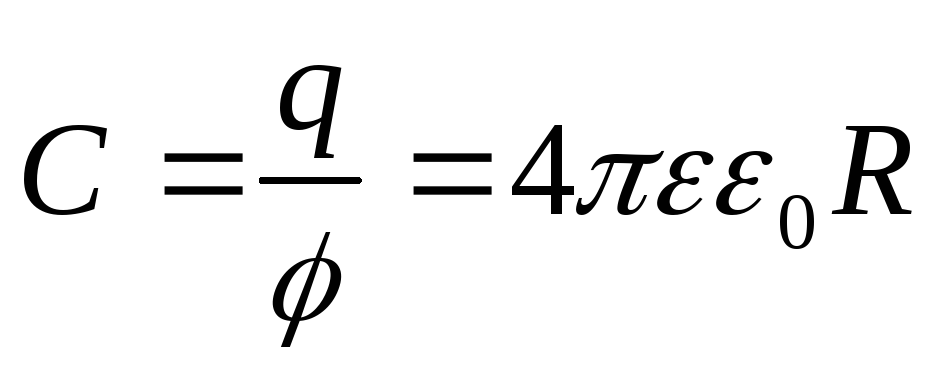(12.52)

Из соотношения видно, что электроёмкость зависит как от геометрии проводника, так и от относительной диэлектрической проницаемости среды.

Конденсаторы – это система из двух проводников, обкладок, разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Тогда электрическое поле, создаваемое зарядами на конденсаторе, будет практически целиком сосредоточено между его обкладками (рис.12.33). Электроёмкость определяется геометрией конденсатора и диэлектрическими свойствами среды, заполняющей пространство между обкладками.

По форме исполнения различают плоские, цилиндрические, сферические и слоистые конденсаторы.

(12.53)

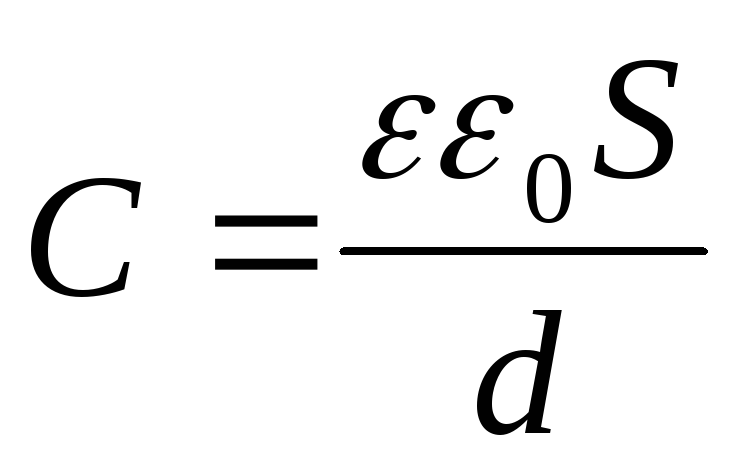
(S – площадь обкладка конденсатора, d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды, заполняющая пространство между обкладками).

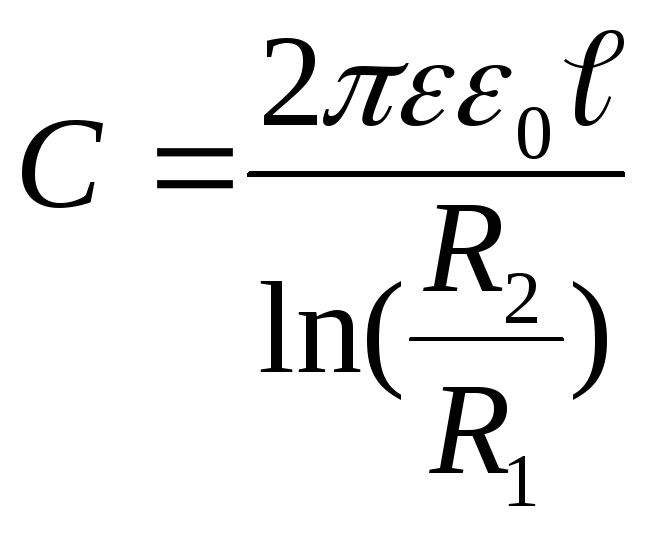(12.54)

(R₁ и R₂ – радиусы аксиальных цилиндров, ℓ- длина образующей цилиндров).

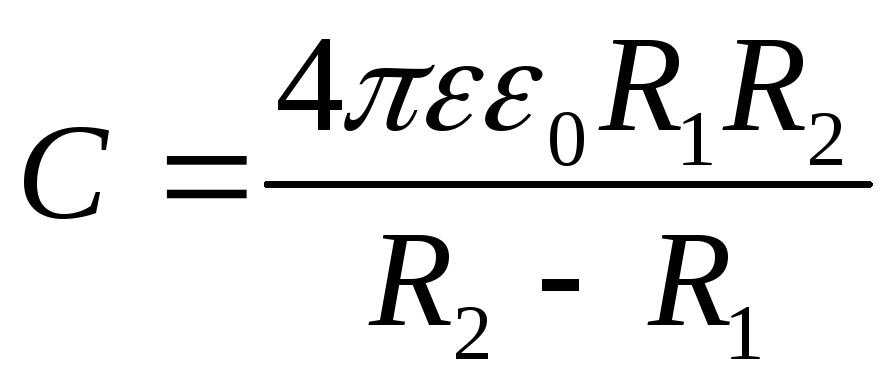(12.55)

(R₂ и R₁ – радиусы сферы; ε — относительная диэлектрическая проницаемость среды, заполняющей пространство между сферами).

• Слоистые конденсаторы. Электроёмкость слоистого конденсатора, т.е. конденсатора, имеющего слоистый диэлектрик,

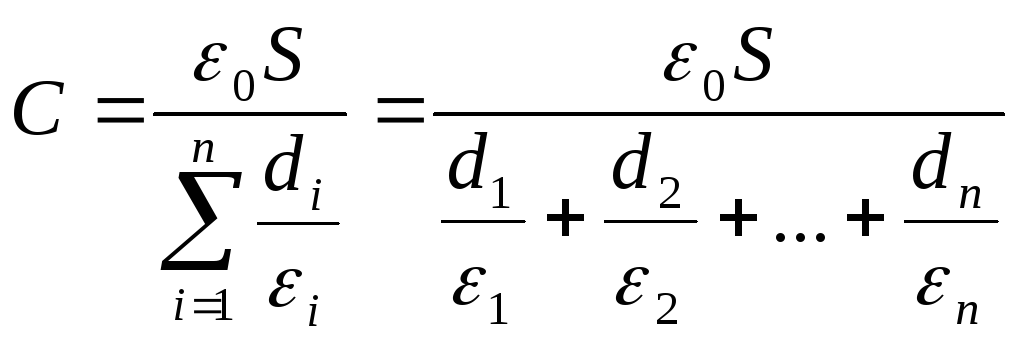(12.56)

Для получения необходимой электроёмкости конденсаторы соединяют в батарею. Различают два соединения конденсаторов: параллельное и последовательное.

q = q₁+q₂+q₃, но так как q₁

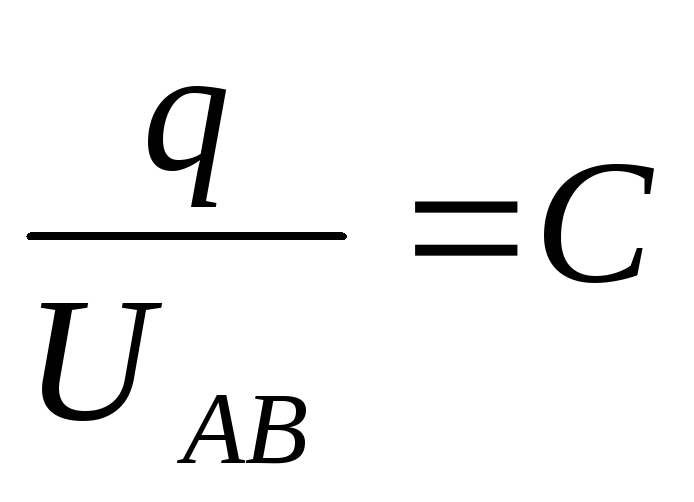= U_ABC₁; q₂ = U_ABC₂; q_n= U_ABC_n, то q= U_AB(C₁+ C₂+…+ C_n), откуда т.е.

С= C₁+ C₂+ C₃

При параллельном соединении конденсаторов электроёмкость батареи равна сумме электроёмкостей, включённых в неё:

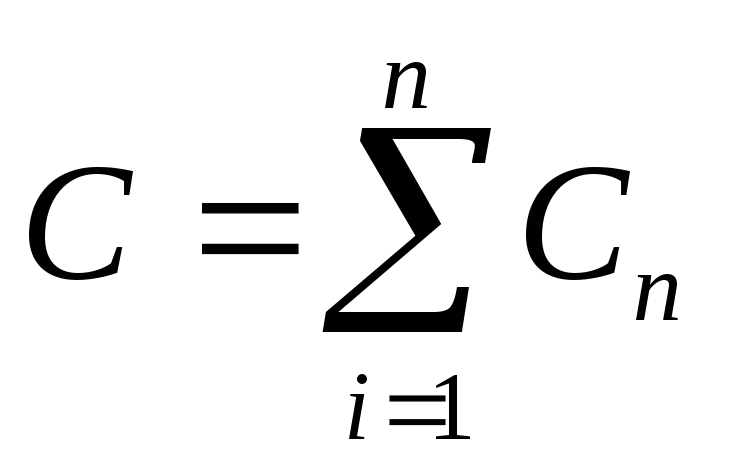(12.57)

q = q₁= q₂= q₃

напряжению между точками А и В

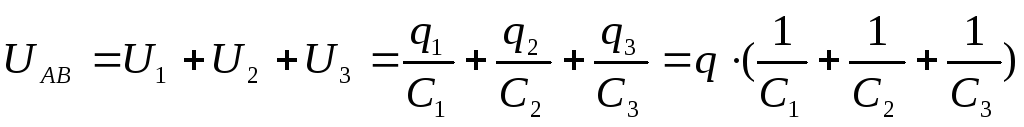откуда

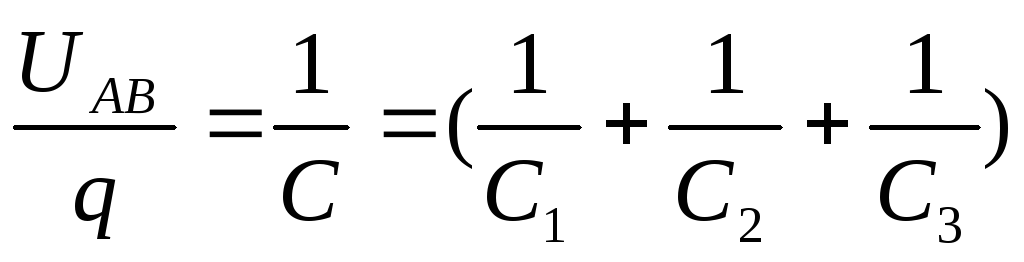
При последовательном соединении конденсаторов электроёмкость батареи

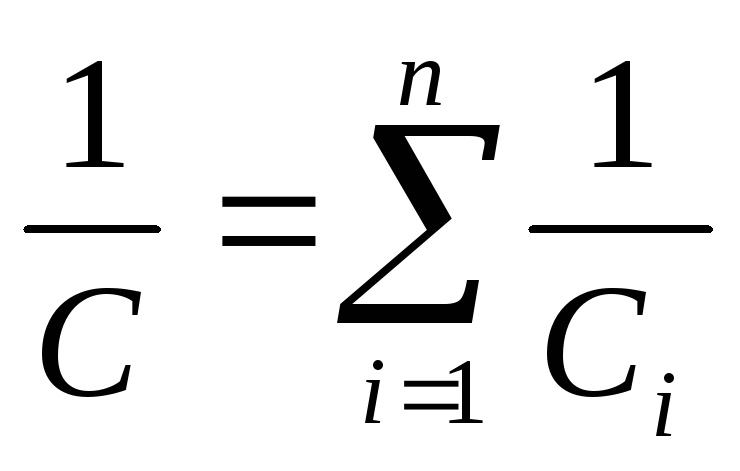(12.58)

конденсаторы, виды соединений, расчет емкости законом Гаусса

В статье мы расскажем про электроемкость, емкость конденсатора, про последовательное и параллельное соединение конденсаторов, а также как использовать закон Гаусса для расчета емкости конденсаторов с примерами и решениями.

Конденсатор (Электроемкость) –элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается – С. Напряжение и ток на его контактах связано зависимостью:

Величина ёмкости измеряется в фарадах (Ф).

1 фарада – это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон.

1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10^-12; нанофарад – 10^-9; микрофарад – 10^-6.

Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке.

Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома.

Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой.

---

Дифференцирующая цепочка применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке.

Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.

Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качестве фильтра высоких частот (ФВЧ). Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют реактивным сопротивлением конденсатора, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается Xc или Zc и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением:

Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора.

Теперь представьте, что дифференцирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.

То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.

Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр высокой частоты на конденсаторе и резисторе.

Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим – интегрирующую цепочку. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f1.

Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности.

Емкость конденсатора

Как мы уже видели, изолированный проводник может накапливать электрический заряд. Однако на практике мы используем устройства, называемые конденсаторами, для хранения нагрузки. Конденсатор представляет собой систему из двух произвольно изолированных проводников, зарядка конденсатора состоит не в отдельной зарядке каждого из проводников, а в переносе заряда (одинакового на обоих проводниках, но с противоположными знаками) от одного проводника к другому.

Мы определяем электрическую емкость C конденсатора точно так же, как емкость изолированного проводника.

Конденсаторы очень часто используются в технике. Они обычно строятся как система из двух поверхностей с разной изолированной поверхностью, которые обычно располагаются параллельно друг другу. Как будет видно далее, емкость такого конденсатора пропорциональна размеру поверхности пластин и обратно пропорциональна расстоянию между ними. Таким образом, конденсатор большой емкости имеет большие поверхностные панели, которые расположены как можно ближе друг к другу. Простейшим таким конденсатором является плоский конденсатор, схематически показанный на рисунке ниже.

Пример двух конденсаторов, соединенных вместе, как показано на рисунке ниже (параллельно), может служить иллюстрацией постоянства заряда на крышках конденсаторов, не подключенных к источнику напряжения. Первоначально система нагрузки , которая охватывает один конденсатор заряда Q₁ и на крышке второго заряда Q₂. Потенциал, на котором расположены верхние крышки, одинаков для обоих (крышки связаны с лампочкой). Когда мы начнем изменять расстояния между крышками одного из конденсаторов, то мы изменим его емкость — чем меньше зазор между крышками, тем больше емкость конденсатора. Поскольку общий заряд обоих конденсаторов неизменен, это изменение емкости вызовет перенос заряда между конденсаторами. Если конденсаторы заряжены достаточно большим зарядом, лампочка может светиться во время потока между крышками, образующими верхнюю пару. Энергия, необходимая для освещения лампы, исходит от работы, которую мы выполняем при перемещении крышки (верхняя и нижняя крышки заряжены противоположными знаками и поэтому притягиваются).

Схемы соединения конденсаторов

Существует множество различных схем соединения конденсаторов: последовательное подключение, параллельное, мостовое. И меняется абсолютно все показатели (Емкость, разность потенциалов, общая нагрузка) при различных видах подключения

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов, как показано на рисунке ниже, значения зарядов на всех крышках всех конденсаторов одинаковы.

Разность потенциала в последовательной цепи конденсаторов равно сумме разностей потенциалов на отдельных конденсаторах:

Следовательно, совокупная емкость С последовательной системы определяется по формуле

Параллельное соединение конденсаторов

В параллельном соединении конденсаторов

общая нагрузка Q, накопленная в системе, равна сумме зарядов на крышках всех конденсаторов.

Уменьшение потенциала одинаково на каждом из конденсаторов и, следовательно,

Следовательно, общая емкость C параллельной системы равна сумме емкостей всех конденсаторов.

Мостовое соединение конденсаторов

Последовательные и параллельные соединения не исчерпывают всех возможных конфигураций, которые могут быть получены при подключении конденсаторов. Мы сможем описать все возможные конфигурации только после завершения предыдущих соединений с мостовым соединением, схема которых показана на левом рисунке ниже.

Мы не можем напрямую заменить мостовые комбинации любой комбинацией последовательных и параллельных соединений. Чтобы рассчитать запасную емкость системы моста, используйте изменение треугольника конденсатора на эквивалентную звезду, как показано на среднем и правом рисунках выше.

Емкости между точками 1-2, 2-3 и 3-1, которые мы обозначаем как C ₁₂, C₂₃ и C₃₁, должны быть одинаковыми в обеих конфигурациях. На основе значений емкости C₁, C₂ и C₃ рассчитывают C_x, C_y и C_z. Условия равной емкости в обеих конфигурациях, для треугольника и для звезды, запишем как

Отсюда мы получаем искомые значения C_x, C_y и C_z:

После замены треугольника на звезду мостовое соединение исчезает, и на его месте мы получаем простую и удобную для вычисления комбинацию последовательных и параллельных конденсаторов.

Использование закона Гаусса для расчета емкости конденсаторов

Имея емкость конденсатора с заданной геометрией для расчета, мы используем следующую схему:

Мы исходим из определения емкости конденсатора. Вставьте разность потенциалов Vab в формулу, определяющую эту емкость. Нагрузка Q уменьшается.

но нам не хватает разности потенциалов Vab, которую мы находим из соотношения между полями E и V,

3. Однако сначала мы должны знать E, и для этого мы будем использовать универсальный инструмент, который является законом Гаусса:

Примеры закона Гаусса для расчета емкости конденсаторов

Закон Гаусса выполняется для каждой замкнутой поверхности А. Однако такую ​​поверхность следует выбирать так, чтобы интегрирование было как можно более простым. В примерах, представленных ниже, форма предложенной поверхности Гаусса для обсуждаемых случаев обозначена контуром, нарисованным пунктирной кривой. Расчеты выполнены в соответствии с представленной схемой и не содержат дополнительных пояснений. ε₀ — электрическая проницаемость вакуума.

Плоский конденсатор

Отсюда мы получаем емкость для плоского конденсатора

Цилиндрический конденсатор

Отсюда мы получаем емкость для цилиндрического конденсатора:

Сферический конденсатор

Отсюда мы получаем емкость для сферического конденсатора:

Цель представленных примеров — показать, как схема расчета работает на практике. Вы должны помнить только образец для емкости плоского конденсатора, который часто будет использоваться в дальнейшем вашем обучении.

Энергия заряженного конденсатора

Энергия заряженного конденсатора U равна той работе, которую мы будем выполнять при зарядке. Вся энергия U содержится в электрическом поле между крышками конденсатора.

При зарядке конденсатора разность потенциалов между его крышками V (q) зависит от заряда q, который в настоящее время находится на крышках. Работа по переносу между крышками дополнительной нагрузки составляет

Энергия поля в конденсаторе, полностью заряженном зарядом Q, становится

или

Плотность энергии электрического поля

Плотность энергии электрического поля u будет рассчитываться путем деления энергии U на объем, занимаемый полем. Используя простую геометрию плоского конденсатора с площадью крышки A и расстояние между крышками d, мы находим значение u, действительное для поля E любой геометрии:

Схемы соединения конденсаторов в батареях

Страница 34 из 53

Важным признаком, характеризующим схему соединений конденсаторной установки, является схема соединения конденсаторов в батарее. От нее зависит работа защиты батареи и некоторые другие процессы как в конденсаторной установке, так и в сети, к которой последняя присоединена.

Рис. 6-3. Схема параллельного соединения трехфазных конденсаторов в батарее.

Трехфазные конденсаторы всегда соединяются в батареях параллельно независимо от схемы их внутренних соединений (треугольник или звезда). Номинальное напряжение батареи Uб при этом равно номинальному напряжению конденсатора Uк. Примером этой схемы соединений может служить изображенная на рис. 6-3 схема конденсаторной батареи, выполненной из трехфазных конденсаторов, соединенных треугольником.
Теоретически возможна и изображенная на рис. 6-4 схема соединения трех трехфазных конденсаторов в группу, номинальное напряжение которой равно 2Uк, т. е. удвоенному номинальному напряжению конденсатора. Такая группа эквивалентна одному трехфазному конденсатору, емкость фазы которого равна 0,6 емкости фазы каждого из трех конденсаторов, входящих в группу (если схемы соединения фаз одинаковы в обоих случаях). Вывод этого соотношения произведен путем последовательных преобразований треугольника емкостей в эквивалентную звезду емкостей и обратно. Мощность такой группы, присоединенной к сети с напряжением 2Uк, равна 0,8 суммы номинальных мощностей тех же трех конденсаторов.

Рис. 6-4. Схема группы из трех трехфазных конденсаторов, в которой номинальное напряжение группы равно удвоенному номинальному напряжению конденсатора.

Однофазные конденсаторы соединяются в каждой фазе трехфазной батареи или параллельно, или параллельно — последовательно. Возможно и последовательное соединение, когда все конденсаторы, составляющие фазу батареи, соединены последовательно («цепочкой») один с другим. Его можно считать частным случаем параллельно — последовательного соединения при числе параллельно соединенных конденсаторов в группе, равном единице. Еще одним вариантом является последовательно-параллельное соединение, когда несколько «цепочек» конденсаторов соединены параллельно в фазе батареи. Оба последних варианта встречаются очень редко и здесь не рассматриваются.

При параллельном соединении однофазных конденсаторов номинальное напряжение Uб батареи равно их номинальному напряжению Uк, если фазы батареи соединены треугольником, или превышает его в 1,73 раза при соединении звездой. Если соотношение между Uб и Uкпревышает 1,73, то батарея должна быть выполнена путем параллельно-последовательного соединения конденсаторов в каждой фазе. В § 2-2 приведены выражения для определения Uб в зависимости от Uк и от схемы соединения конденсаторов в батарее.
В трехфазных батареях, состоящих из однофазных конденсаторов, фазы могут быть соединены или треугольником, или звездой. При соединении звездой нейтральная точка последней может быть или изолирована от земли, или заземлена (рис. 6-5).
Различные комбинации трех схем соединения фаз в батарее (треугольник, звезда с изолированной нейтралью и звезда с заземленной нейтралью) с двумя схемами соединения конденсаторов в фазе (параллельное или параллельно-последовательное) дают шесть возможных схем соединения однофазных конденсаторов в трехфазной батарее.

Рис. 6-5. Варианты схем соединения фаз В, трехфазной батарее.
Ниже указаны условные обозначения, применяемые для этих схем в дальнейшем изложении:

Преимущества и недостатки различных схем соединения фаз батареи рассмотрены отдельно в § 6-3.
Номинальные напряжения однофазных конденсаторов отечественного производства равны увеличенным на 5% номинальным линейным напряжениям электрических сетей. Это значит, что отечественные однофазные конденсаторы рассчитаны на соединение фаз батареи треугольником с параллельным соединением конденсаторов в каждой фазе (схема Δ-l). В Советском Союзе по этой схеме соединено подавляющее большинство конденсаторных установок с однофазными конденсаторами, т. е. номинальным напряжением 3—10 кВ (рис. 6-6).
Соединение фаз батареи звездой при параллельном соединении однофазных конденсаторов в каждой фазе (схемы Υ-1 и Yз-l) встречается в Советском Союзе очень редко, а именно тогда, когда номинальное напряжение конденсаторов почему-либо равно не линейному, а фазному напряжению сети или близко к последнему.
Например, соединение конденсаторов 6,3 кВ по схеме Υ-1 или Y3-l позволяет получить батарею номинальным напряжением 1,73 · 6,3=10,9 кВ, т. е. пригодную к установке в сети 10 кВ.
В зарубежных конденсаторных установках с параллельным соединением однофазных конденсаторов фазы батареи соединяются иногда треугольником и иногда звездой (см. § 6-3).

Рис. 6-6. Схема параллельного соединения однофазных конденсаторов в каждой фазе трехфазной батареи, соединенной треугольником.
Рис. 6-7. Схема параллельно-последовательного соединения однофазных конденсаторов в одной фазе трехфазной батареи.

При параллельно-последовательном соединении однофазных конденсаторов фазы батареи соединяются, как правило, звездой (схемы Y-2 и Y3-2). Такие батареи напряжением до 110 кВ получили значительное распространение за рубежом, в особенности в США, а наивысшее напряжение батареи для параллельного присоединения, находящейся там в эксплуатации, составляет 230 кВ (Л.3-21).

На рис. 6-7 приведена схема одной фазы батареи с параллельно-последовательным соединением однофазных конденсаторов. В пределах каждой группы конденсаторы соединены параллельно, и все группы соединены последовательно. Число таких групп в одной фазе батареи доходит до 15 при напряжении батареи 110 кВ.
Параллельно-последовательное соединение встречается и при напряжении батареи 6—10 кВ, если она собрана из конденсаторов напряжением около 1 кВ. Несколько таких батарей было выполнено в Советском Союзе из конденсаторов типа КМ напряжением 1 000 В [Л. 6-1] и 1 050 в. Существует также несколько батарей для параллельного присоединения, выполненных из конденсаторов для продольной компенсации типа КПМ. В этих батареях конденсаторы номинальным напряжением 600 В соединены, параллельно-последовательно.
В последние годы некоторые западноевропейские фирмы сократили шкалу напряжений изготовляемых ими конденсаторов, комплектуя из конденсаторов 1— 2 кВ батареи более высоких напряжений, например 10 кВ [Л. 1-16].
Переход от параллельного к параллельно-последовательному соединению конденсаторов в батареях 3—10 кВ позволил бы выполнять эти батареи из одних и тех же конденсаторов напряжением около 1 кВ (например, 910 в), что является одним из преимуществ этой схемы соединений [Л. 5]. Недостаток ее заключается в том, что изменение проектной мощности батареи происходит при параллельно-последовательном соединении большими ступенями, чем при параллельном соединении. В первом случае мощность одной ступени равна 3nQK и во втором — 3Qк (здесь QK — мощность одного конденсатора и п—число последовательно соединенных групп в фазе батареи).
Соединение фаз батареи треугольником при параллельно-последовательном соединении однофазных конденсаторов (схема Δ-2) в Советском Союзе не применяется, а за рубежом встречается, по-видимому, значительно реже соединения звездой.
Однофазные конденсаторные батареи распространены очень мало. Одной из областей их применения является компенсация однофазных индуктивных приемников значительной мощности, например, некоторых видов электрических печей. Однофазные батареи малой мощности встречаются за рубежом и в сельских электрических сетях. В зарубежной практике известен также случай применения однофазной конденсаторной установки 10,8 кВ в тяговой сети 25 Гц. Мощность этой установки при той же частоте составляла 10 000 кВАр.

Для однофазных батарей возможны те же схемы соединений конденсаторов, что и для каждой фазы трехфазной батареи, т. е. или параллельное, или параллельно-последовательное.
Например, одна отечественная однофазная батарея мощностью около 4 000 кВАр была выполнена из четырех последовательно соединенных групп номинальным напряжением по 10,5 кВ. Номинальное напряжение батареи составило, таким образом, 4 · 10,5=42 кВ, что позволило присоединить ее на линейное напряжение сети 35 кВ.