1.4. Способы соединения конденсаторов
Возможны параллельное и последовательное соединения конденсаторов.
П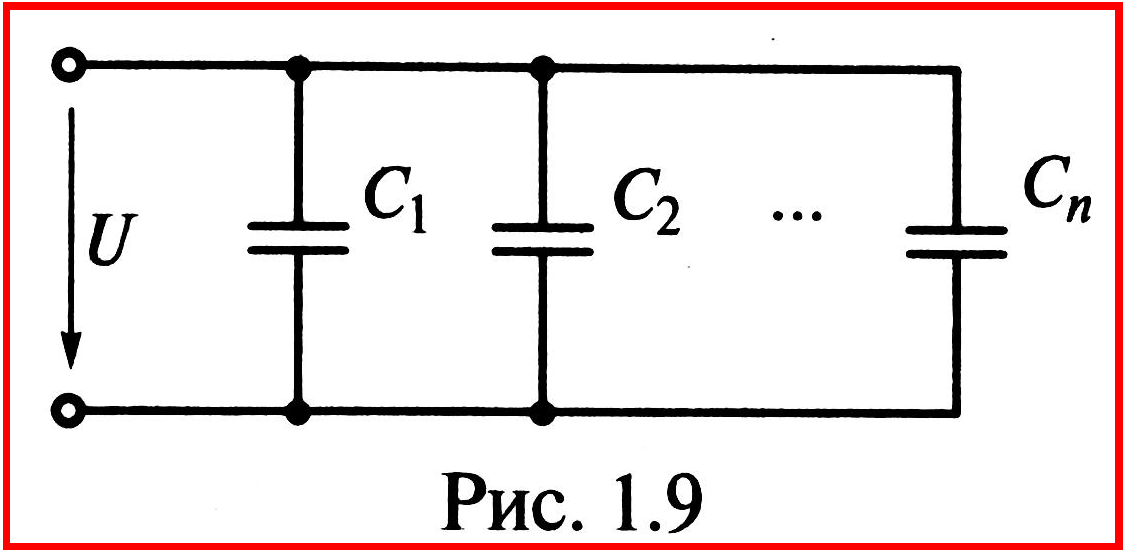 рипараллельном соединении (рис. 1.9) все конденсаторы находятся под
одним напряжением U, а
заряд, который они получают от источника
энергии, равен сумме зарядов отдельных
конденсаторов
рипараллельном соединении (рис. 1.9) все конденсаторы находятся под
одним напряжением U, а
заряд, который они получают от источника
энергии, равен сумме зарядов отдельных
конденсаторов
г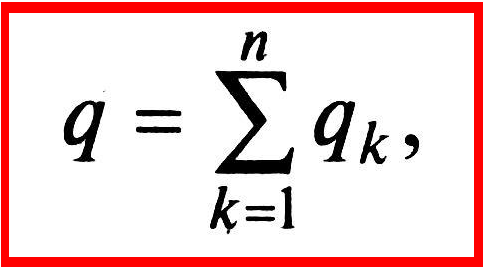 деп —
число конденсаторов;
деп —
число конденсаторов;
к — порядковый номер конденсатора.
Следовательно, общая емкость параллельно соединенных конденсаторов по (1.9)равна сумме емкостей отдельных конденсаторов.
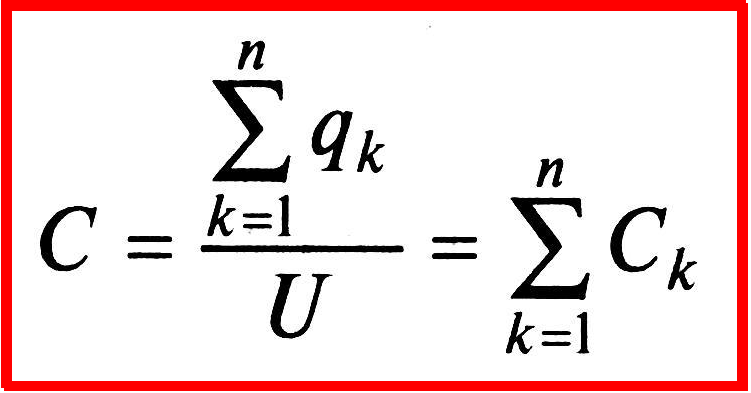
П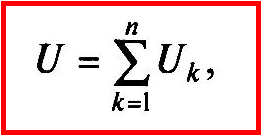 рипоследовательном соединении
конденсаторов (рис. 1.10) общее напряжение равно сумме
напряжений на отдельных конденсаторах
рипоследовательном соединении
конденсаторов (рис. 1.10) общее напряжение равно сумме
напряжений на отдельных конденсаторах
где п — число конденсаторов;
к — порядковый номер конденсатора.
Н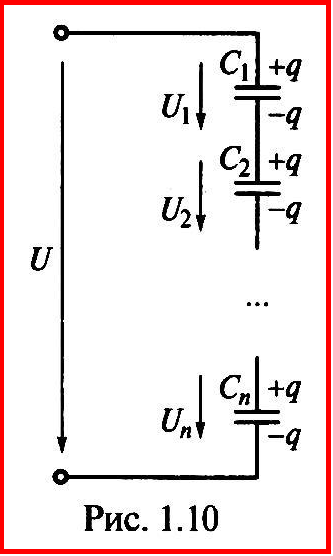 о
заряд от источника энергии получают
лишь внешние электроды двух крайних
конденсаторов. На остальных попарно
электрически
соединенных электродах заряды создаются
переносом положительного заряда на
один электрод и отрицательного — на
второй, которые равны между собой. Таким
образом,
о
заряд от источника энергии получают
лишь внешние электроды двух крайних
конденсаторов. На остальных попарно
электрически
соединенных электродах заряды создаются
переносом положительного заряда на
один электрод и отрицательного — на
второй, которые равны между собой. Таким
образом,
Так как заряд конденсатора равен произведению его емкости на приложенное к нему напряжение
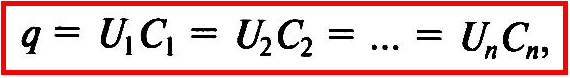
то напряжения на конденсаторах равны
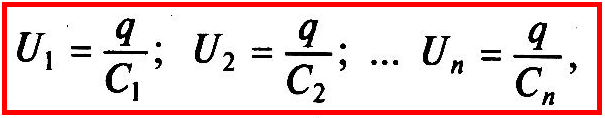
а общая емкость последовательно соединенных конденсаторов — Собщ
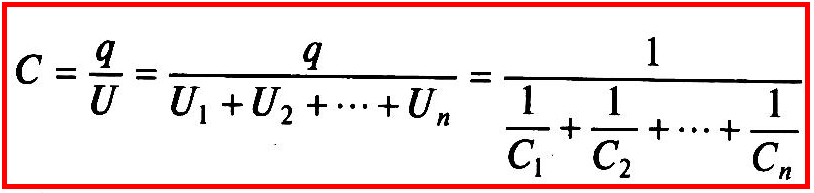
Если последовательно соединены n одинаковых конденсаторов каждый емкостью С0, то их общая емкость будет равна
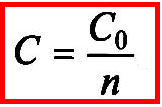
1.5. Зарядка и разрядка конденсатора
Ч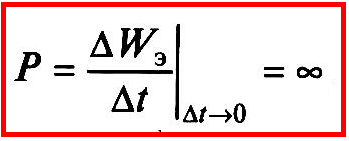 тобы
изменить скачком энергию конденсатора,
необходим источник бесконечной мощности
что невозможно.
тобы
изменить скачком энергию конденсатора,
необходим источник бесконечной мощности
что невозможно.
Поэтому при зарядке и разрядке конденсатора его энергия, а следовательно, и напряжение на нем Uс не могут изменяться скачком. Это условие называется
(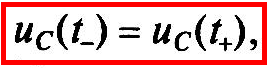 1.16)
1.16)
где 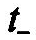 и
и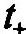 — моменты времени, непосредственно
предшествующий моменту времени
— моменты времени, непосредственно
предшествующий моменту времени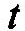 и непосредственно следующий за моментом
времениt, в
который начинается зарядка или разрядка
конденсатора.
и непосредственно следующий за моментом
времениt, в
который начинается зарядка или разрядка
конденсатора.
Зарядка конденсатора.
Рассмотрим процесс зарядки конденсатора от источника постоянного напряжения Е=U (см. подразд. 2.7) через резистор сопротивлением R (см. подразд. 2.4) при замыкании в момент времени t=0 ключа К (рис. 1.11, а).
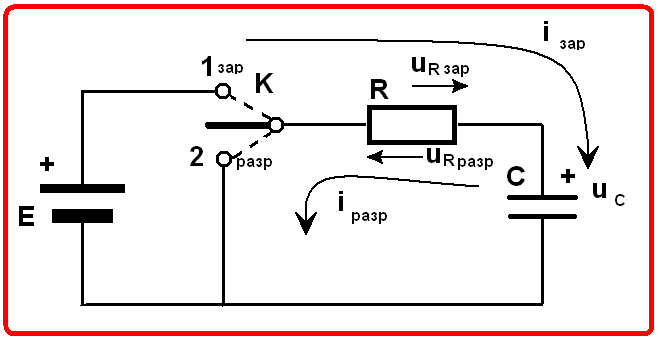
Напряжение источника равно сумме напряжений на резисторе и конденсаторе
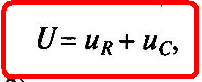
или с учетом (2.1) и (1.13)
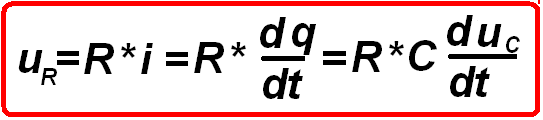
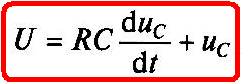 (1.17)
(1.17)
Разделим переменные в (1.17)
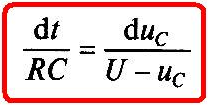
(1.18)
и проинтегрируем (1.18)
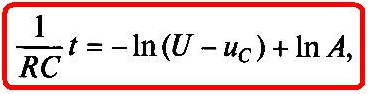 (1.19)
(1.19)
где неизвестная постоянная интегрирования записана в виде In
Умножив обе части равенства (1.19) на (-1) и заменив разность логарифмов логарифмом частного, после потенцирования получим
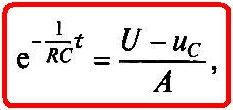
или
 (1.20)
(1.20)
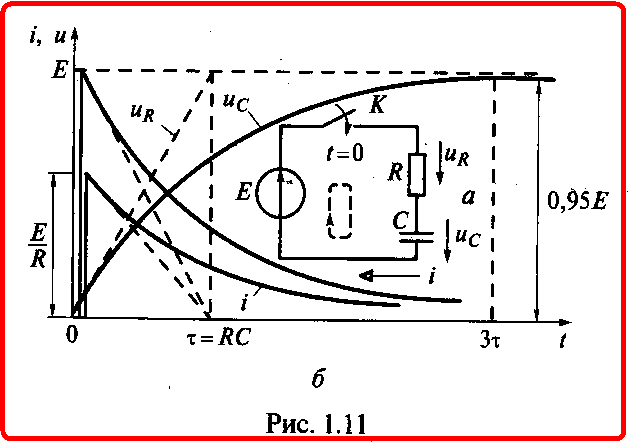
Для определения постоянной А в (1.20) обратимся к закону коммутации для емкостного элемента (1.16). Примем, что емкостный элемент до замыкания ключа, т. е. и в момент времени /= 0_, не был заряжен. Поэтому
ис(0_) = 0 = ис(0+) = Е+А, откуда А = -Е.
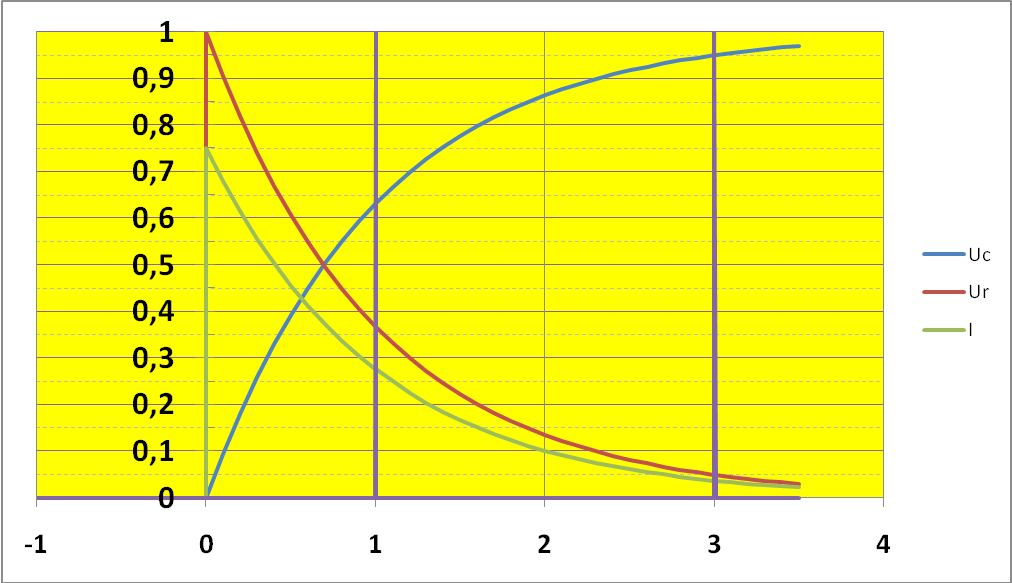
Подставив значение постоянной А в (1.20), найдем напряжение на емкостном элементе во время его зарядки (рис. 1.11, б):
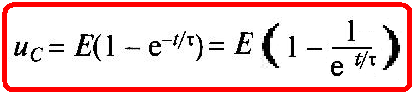
где τ = RC имеет размерность времени (Ом • Ф = Ом • А • с/В = с) и называется постоянной времени цепи. Она определяет скорость переходного процесса.
Напряжение на емкостном элементе (1.21) определяет зависимости от времени тока зарядки и напряжения на резисторе (рис. 1.11,5):
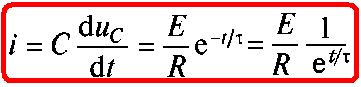
тогда
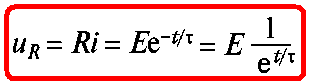
В
от нуля i (0_) = 0
до i (0+) = E/R.
При малом сопротивлении R в цепи может наблюдаться значительный скачок тока.
Процесс зарядки можно считать практически закончившимся через интервал времени Зτ, (при этом
Разрядка конденсатора.
В электрическом поле заряженного емкостного элемента сосредоточена энергия (1.15), за счет которой емкостный элемент в течение некоторого времени сам может служить источником энергии. После подключения емкостного элемента, предварительно заряженного до напряжения
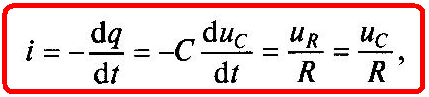 (1.22)
(1.22)
где знак минус указывает на то, что ток i — это ток разрядки в контуре цепи, обозначенном на рисунке штриховой линией, направленный навстречу напряжению на емкостном элементе.
Разделим переменные в (1.22)
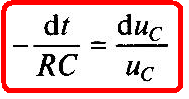
и проинтегрируем (1.23)
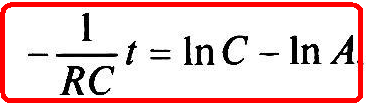 (1.24)
(1.24)
где неизвестная постоянная интегрирования записана в виде (-In А).
После потенцирования (1.24) получим
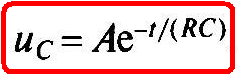 (1.25)
(1.25)
Для определения постоянной А в (1.25) обратимся к закону коммутации для емкостного элемента (1.16). Так как до коммутации, т.е. и в момент времени t=0_, емкостный элемент был заряжен до напряжения источника, то
ис (0_) = Е=ис (0+)=А.
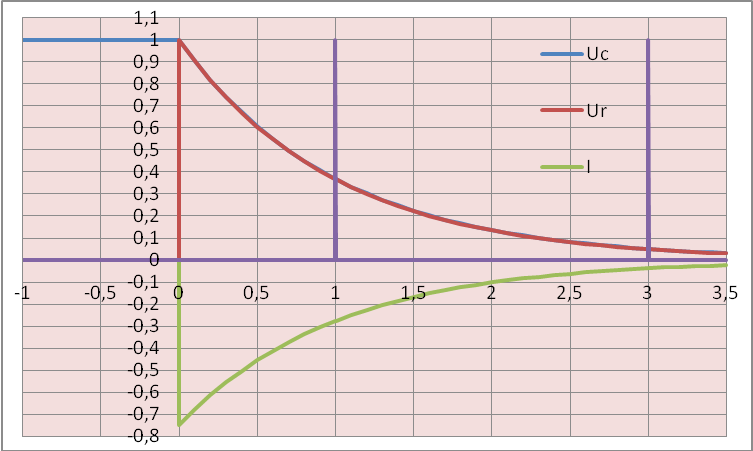
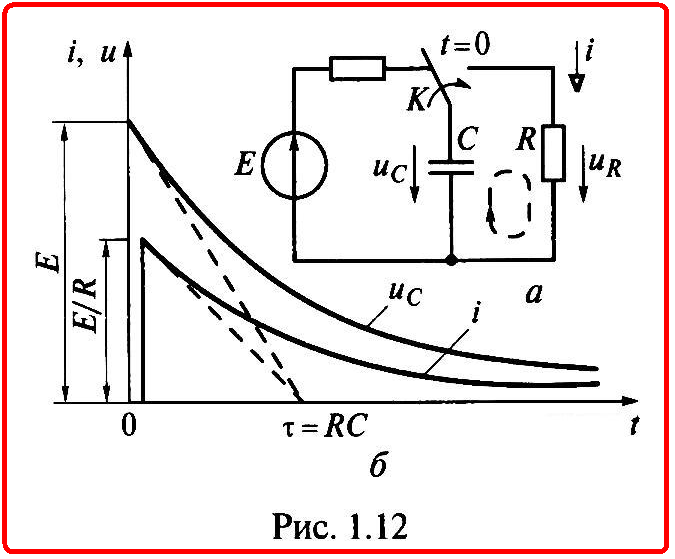
Подставив значение постоянной А в (1.25), получим зависимость изменения напряжения на емкостном элементе при его разрядке (рис. 1.12, б):
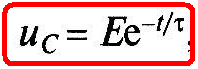 (1.26)
(1.26)
где τ = RC — постоянная времени цепи.
Ток разрядки найдем по (1.22):
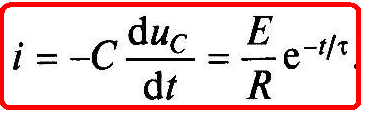
Ток разрядки скачком возрастает от нуля
i(0_) = 0 до i(0+) = E/R, а затем убывает экспоненциально (см. рис. 1.12, б).
Зарядка конденсатора при малых значениях тока и больших значениях ЭДС Ев цепи на рис. 1.12, а позволяет накопить в нем большую энергию, которая может использоваться при разрядке большим током в импульсных источниках.
ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1.1. Конденсатор емкостью С = 1 Ф, имеющий заряд q = 1 Кл, в момент времени t= 0 начинает разряжаться через резистор сопротивлением R= 1 Ом (см. рис. 1.12). Определите ток в резисторе в момент времени i=0,5 с.
Ответ: 0,6065 А.
1.2. Сохранив условия задачи 1.1, определите энергию конденсатора в момент времени t=0,5 с.
Ответ: 0,183 Дж.
1.3. Сохранив условия задачи 1.1, определите, какое количество энергии выделится в виде тепла в резисторе к моменту времени t= 0,5 с.
Ответ: 0,317 Дж.
1.4. Плоский конденсатор (см. рис. 1.7, а) состоит из двух листов фольги каждый площадью 20 см2, разделенных слоем парафина (см. табл. 1.1) толщиной 0,05 мм с относительной диэлектрической проницаемостью εr = 2,1. Определите емкость конденсатора.
Ответ: 0,745 нФ.
Дайте определения электрического потенциала и разности электрических потенциалов.
Дайте определения линейных и нелинейных емкостных элементов.
Определите общую емкость двух конденсаторов, включенных параллельно, емкостью 1 мкФ каждый (см. рис. 1.9).
Ответ: 2 мкФ.
1.8. Определите общую емкость двух конденсаторов, включенных последовательно, емкостью 2 мкФ каждый (см. рис. 1.10).
Ответ: 1 мкФ.
3
Соединение конденсаторов: формулы
Содержание:
- Последовательное соединение
- Онлайн калькулятор
- Смешанное соединение
- Параллельное соединение
- Видео
В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.
Последовательное соединение
При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.
Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.
Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.
Смешанное соединение

Параллельное соединение конденсаторов
Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.
Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.
15. Соединение конденсаторов (параллельное и последовательное)
Помимо показанного на рис. 60 и 61, а также на рис. 62, а параллельного соединения конденсаторов, при котором соединены между собой все положительные и все отрицательные обкладки, иногда соединяют конденсаторы последовательно, т. е. так, чтобы отрицательная обкладка
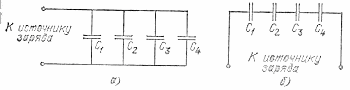
Рис. 62. Соединение конденсаторов: а) параллельное; б) последовательное
первого
конденсатора была соединена с положительной
обкладкой второго, отрицательная
обкладка второго — с положительной
обкладкой третьего и т. д. (рис. 62, б). В
случае параллельного соединения все
конденсаторы заряжаются до одной и той
же разности потенциалов U, но заряды на
них могут быть различными. Если емкости
их равны С1, С2,…, Сn, то соответствующие
заряды будут 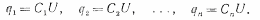
Общий
заряд на всех конденсаторах 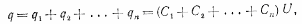
и,
следовательно, емкость всей системы
конденсаторов 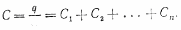 (35.1)
(35.1)
Итак, емкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов. В случае последовательно соединенных конденсаторов (рис. 62, б) одинаковы заряды на всех конденсаторах. Действительно, если мы поместим, например, заряд +q на левую обкладку первого конденсатора, то вследствие индукции на правой его обкладке возникнет заряд —q, а на левой обкладке второго конденсатора — заряд +q. Наличие этого заряда на левой обкладке второго конденсатора опять-таки вследствие индукции создает на правой его обкладке заряд —q, а на левой обкладке третьего конденсатора — заряд +q и т. д. Таким образом, заряд каждого из последовательно соединенных конденсаторов равен q. Напряжение же на каждом из этих конденсаторов определяется емкостью соответствующего конденсатора:
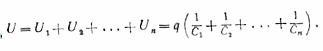 где
Сi — емкость одного конденсатора.
Суммарное напряжение между крайними
(свободными) обкладками всей группы
конденсаторов
где
Сi — емкость одного конденсатора.
Суммарное напряжение между крайними
(свободными) обкладками всей группы
конденсаторов
Следовательно,
емкость всей системы конденсаторов 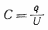 определяется
выражением
определяется
выражением 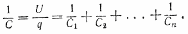 (35.2)
(35.2)
Из этой формулы видно, что емкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.
16. Энергия электрического поля и её объёмная плотность.
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
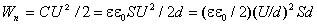
Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,
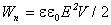
Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна
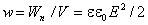
C
учетом соотношения 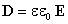 можно
записать
можно
записать
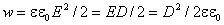
В
изотропном диэлектрике направления
векторов D и E совпадают
и 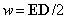 .Подставим
выражение
.Подставим
выражение 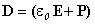 ,
получим
,
получим
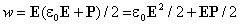
Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов qi на величину dri, составляет
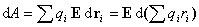
Выражение
в скобках есть дипольный момент единицы
объема или поляризованность диэлектрика Р.
Следовательно, 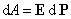 .
.
Вектор P связан
с вектором E соотношением 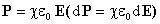 .
Подставив это выражение в формулу для
работы, получим
.
Подставив это выражение в формулу для
работы, получим
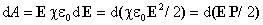
Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика
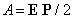 .
.
Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:
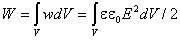
17. Постоянный электрический ток, его характеристики и условия существования. Закон Ома для однородного участка цепи (интегральная и дифференциальная формы)
Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.
Источник тока — устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают при движении проводника в магнитном поле, в фотоэлементах — при действия света на электроны в металлах и полупроводниках.
Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.
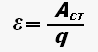
Сила тока — скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.
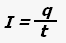
где I — сила тока, q — величина заряда (количество электричества), t — время прохождения заряда.
Плотность тока — векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.
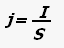
где j -плотность тока, S — площадь сечения проводника.
Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.
Напряжение — скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.
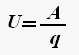
где A — полная работа сторонних и кулоновских сил, q — электрический заряд.
Электрическое сопротивление — физическая величина, характеризующая электрические свойства участка цепи.
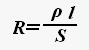
где ρ — удельное сопротивление проводника, l — длина участка проводника, S — площадь поперечного сечения проводника.
Проводимостью называется величина, обратная сопротивлению
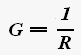
где G — проводимость.
Закон Ома для однородного участка цепи.
Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.
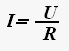
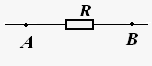
где U — напряжение на участке, R — сопротивление участка.
Закон Ома для однородного участка цепи, все точки которого имеют одинаковую температуру, выражается формулой (в современных обозначениях):
В таком виде формула закона Ома справедлива только для проводников конечной длины, так как входящие в это выражение величины I и U измеряются приборами, включенными на этом участке.
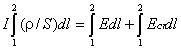 ,
,
где 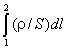 представляет
собой суммарное сопротивление участка
цепи, первый интеграл в правой части —
разность потенциалов
представляет
собой суммарное сопротивление участка
цепи, первый интеграл в правой части —
разность потенциалов 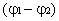 на
концах участка, а второй интеграл
определяет ЭДС
на
концах участка, а второй интеграл
определяет ЭДС 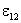 ,
действующую на участке цепи. Таким
образом
,
действующую на участке цепи. Таким
образом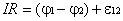 .
.
Соединение конденсаторов в батарею
Система из нескольких конденсаторов называется батареей. Рассмотрим два типа соединения конденсаторов в батарею.
Параллельное соединение (рис. 90).
У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна (φА – φВ ). Если емкости конденсаторов С1 , С2 , …Сn , то
Q1 = C1 (φА – φВ )
Q2 = C2 (φА – φВ )
Q3 = C3 (φА – φВ )
. . . . . . . . . . . . .
Qn = Cn (φА – φВ ).
Заряд
батареи будет равен сумме зарядов Q
= 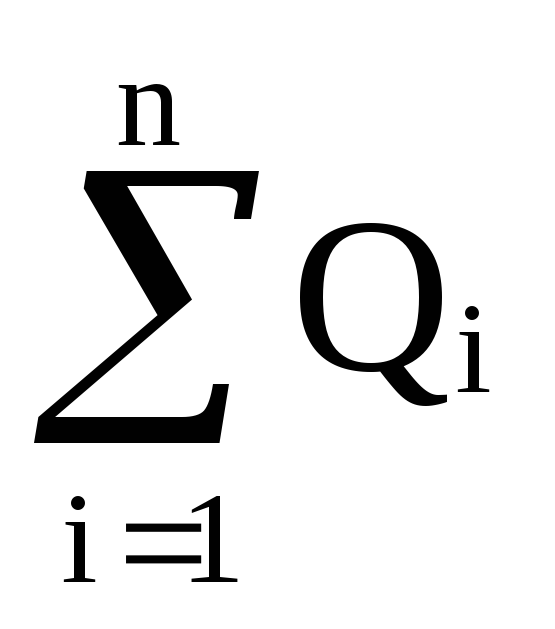 =
(C1+C2+.
. .+Cn)(φА–φВ).
=
(C1+C2+.
. .+Cn)(φА–φВ).
Полная емкость батареи будет равна
С
= 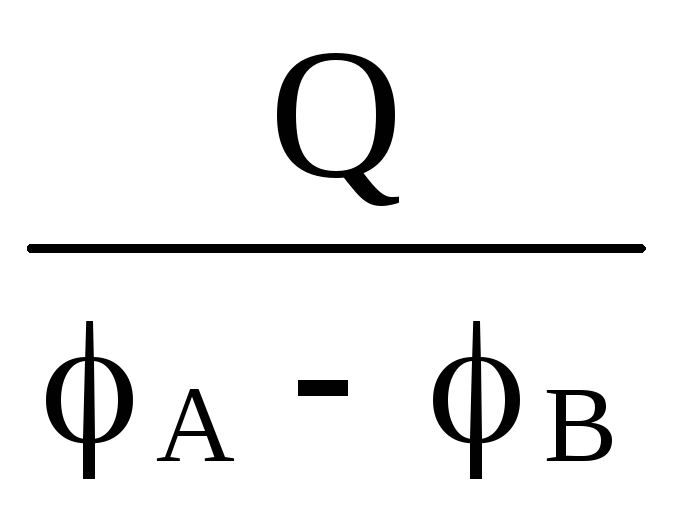 = (C1 + C2 + . . . + Cn ) =
= (C1 + C2 + . . . + Cn ) = 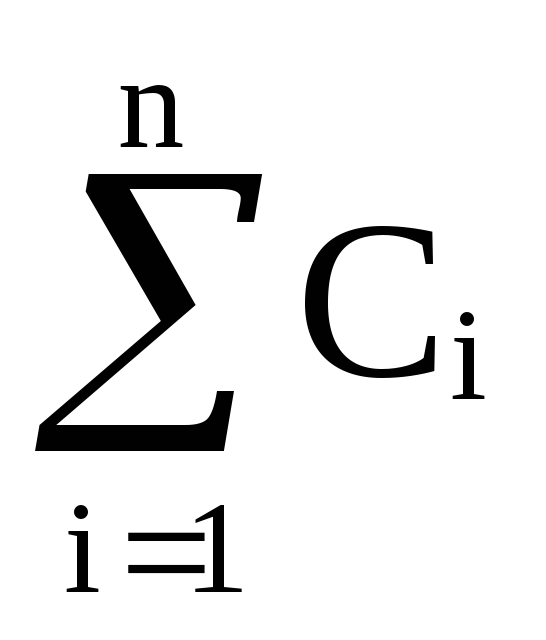 .
.

Последовательное соединение (рис. 91)
У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи Δφ равна
Δφ
= 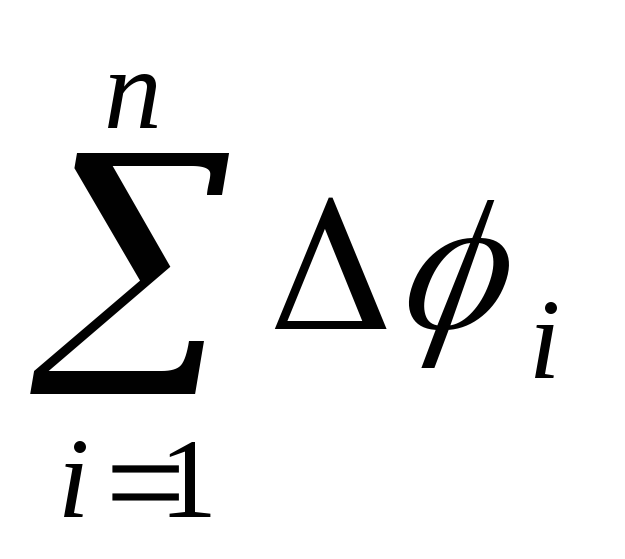 ,
,
где 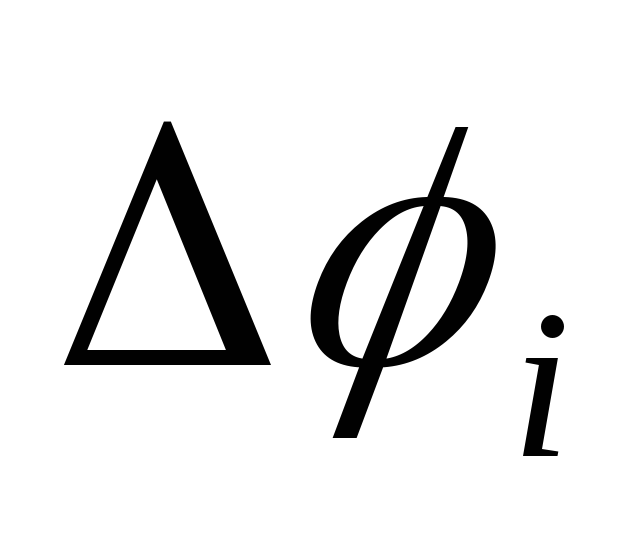 разность потенциалов для любого из
рассматриваемых конденсаторов равна
разность потенциалов для любого из
рассматриваемых конденсаторов равна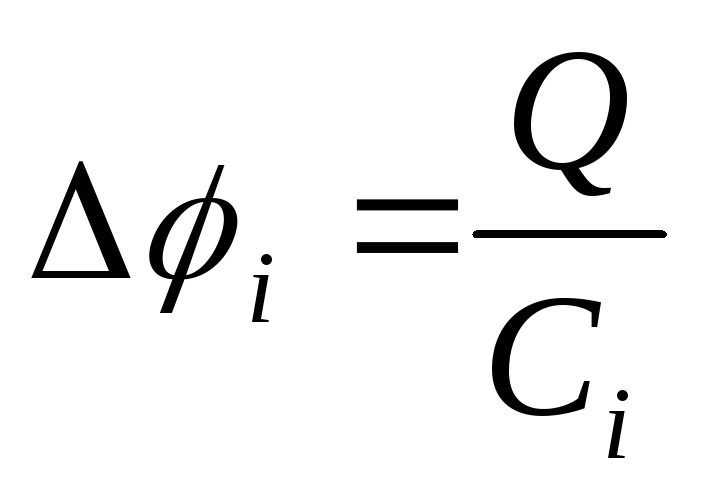 .
.
Таким образом, разность потенциалов батареи конденсаторов будет
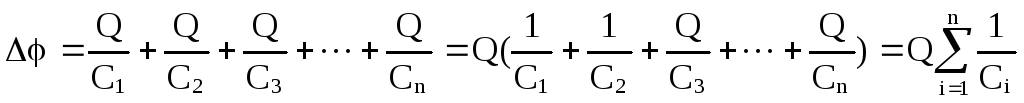
По
определению 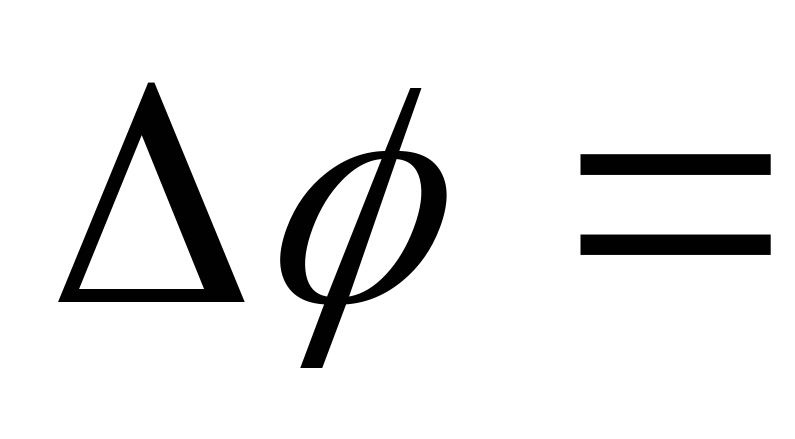
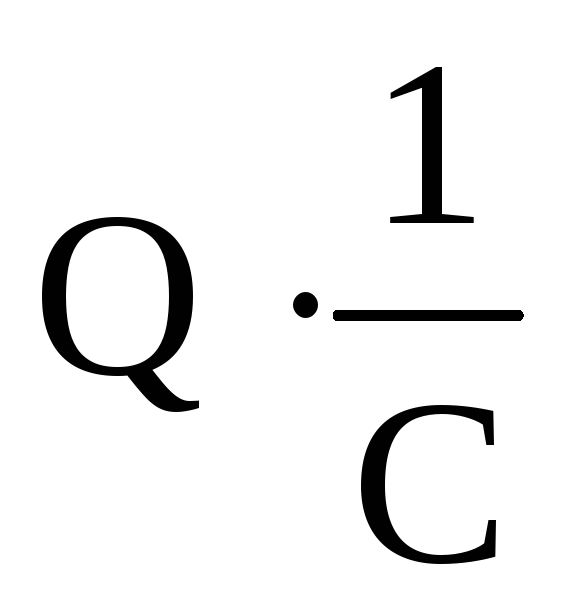 ,
откуда получаем
,
откуда получаем
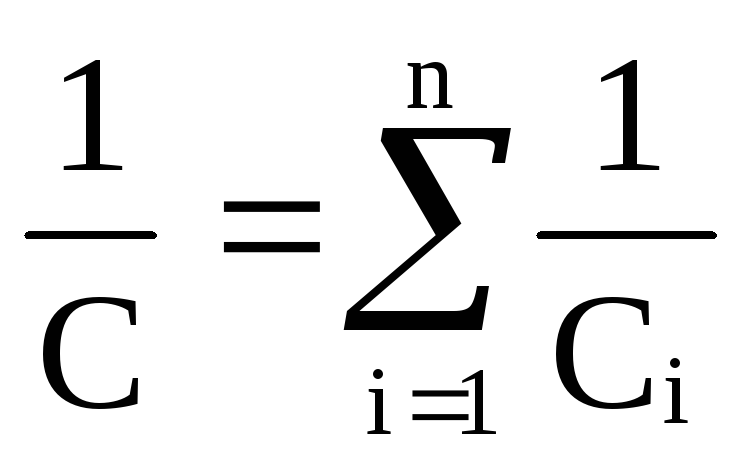
При последовательном соединении суммируются обратные величины емкостей и результирующая емкость батареи С всегда меньше наименьшей емкости, используемой в батарее.
Энергия зарядов, проводников, конденсаторов и электростатического поля. Объемная плотность энергии
Энергия системы точечных неподвижных зарядов. Электростатические силы консервативны и система зарядов обладает потенциальной энергией. Пусть заряды Q1 и Q2 находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией
 ,
,
где φ12 и φ21 – соответственно потенциалы, создаваемые зарядом Q2 в точке нахождения заряда Q1 , и наоборот.
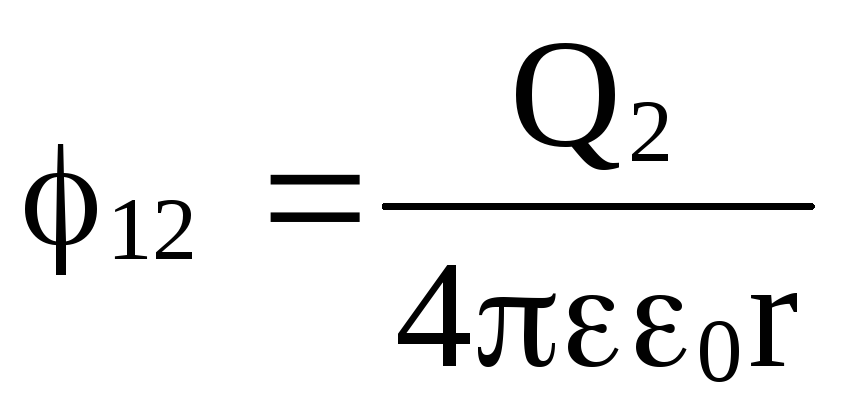 ;
; 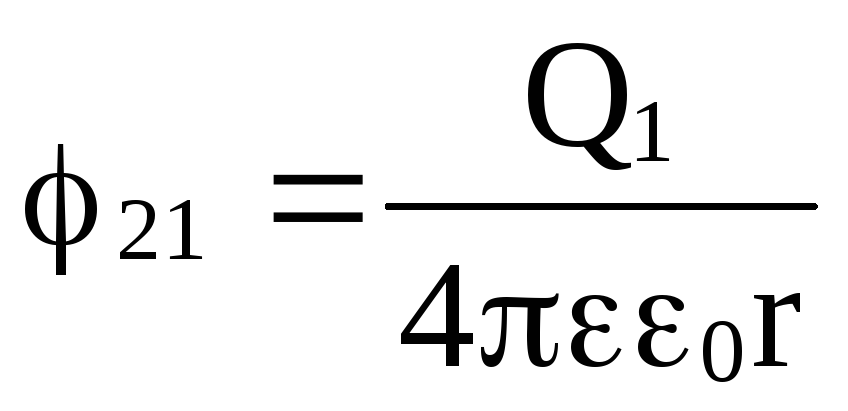 .
.
Поэтому W1 = W2 =W = Q1 φ12 = Q2 φ21 = ½ (Q1 φ12 + Q2 φ21).
Добавляя к системе из двух зарядов последовательно заряды Q3 , Q4 , …, Qn, можно убедиться, что энергия взаимодействия системы зарядов равна
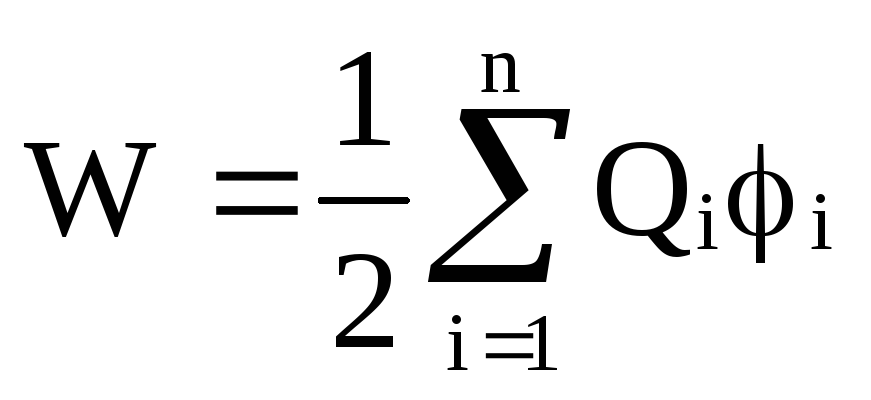 ,
,
где φi – потенциал, создаваемый в той точке, где находится заряд Qi , всеми зарядами, кроме i-го.
Энергия заряженного уединенного проводника. Пусть имеется уединенный проводник, заряд, емкость и потенциал которого Q, C, φ.
Увеличим заряд на dQ. Для этого необходимо перенести заряд dQ из бесконечности к поверхности проводника, затратив на это работу, равную
dA = φdQ = C φd φ
Чтобы зарядить тело от нулевого потенциала до потенциала равного φ необходимо совершить работу
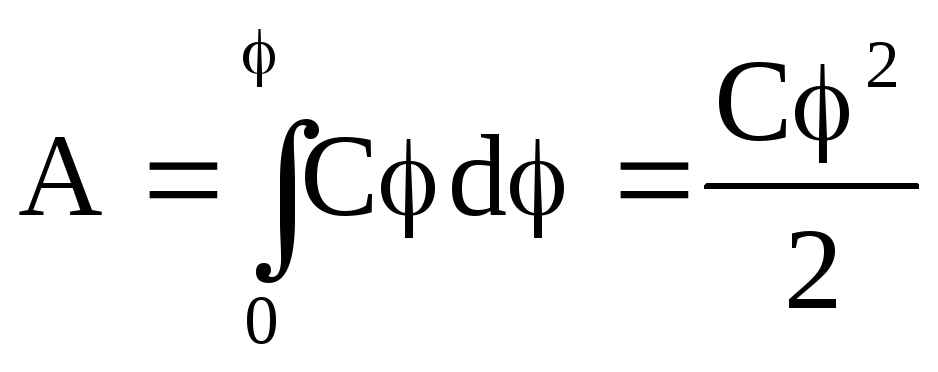
Энергия заряженного проводника будет равна этой работе
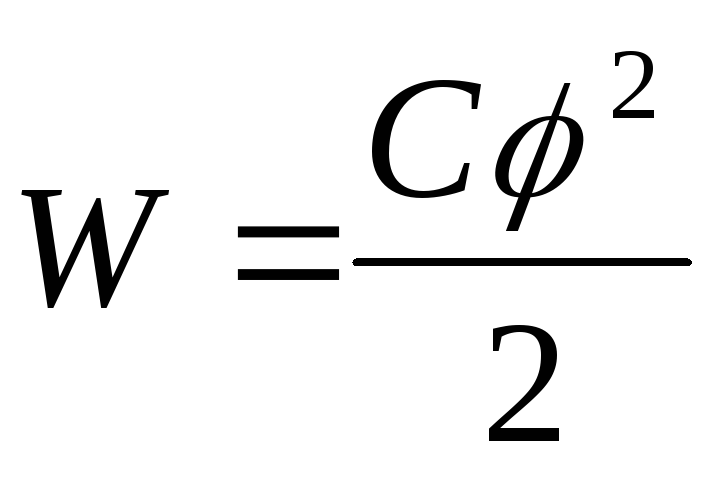
Учитывая,
что 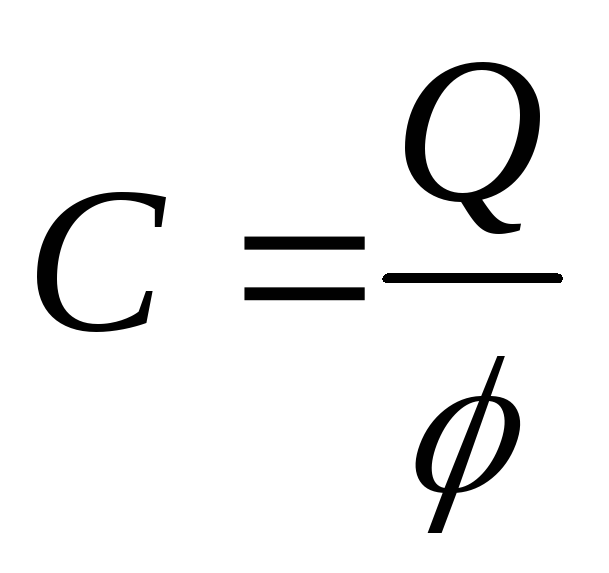 ,
эту энергию можно представить в виде
,
эту энергию можно представить в виде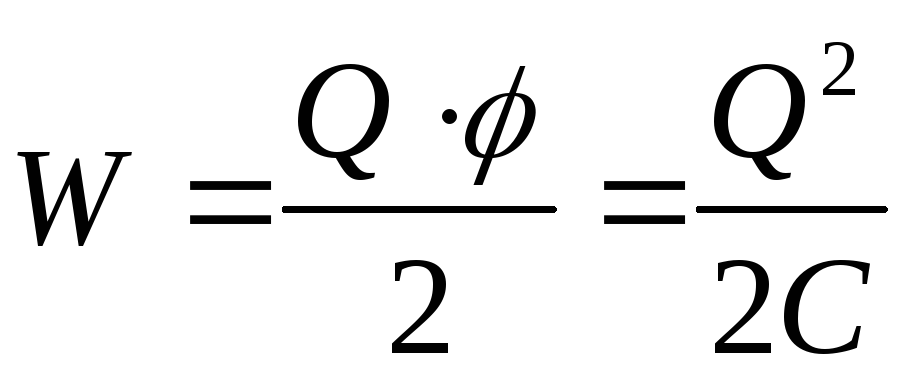
Энергия заряженного конденсатора. Как всякий заряженный проводник, конденсатор обладает энергией
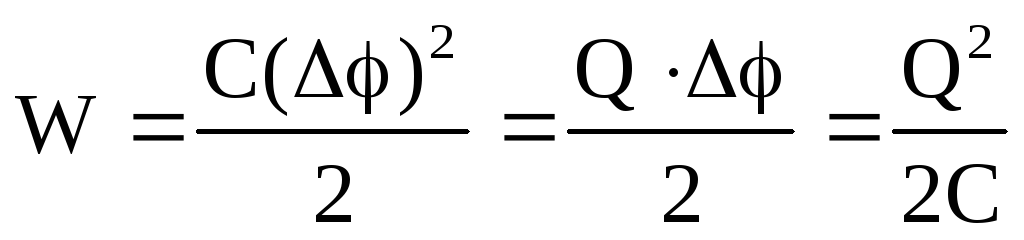
где Q — заряд конденсатора, С – его емкость и Δφ – разность потенциалов между обкладками.
Используя
выражение для энергии, можно найти
механическую (пондеромоторную) силу, с
которой пластины конденсатора притягивают
друг друга. Для этого предположим, что
расстояние х между пластинами меняется
на величину dx.
Тогда действующая сила совершает работу
равную dA
=Fdx
за счет уменьшения потенциальной энергии
Fdx
= — dW,
откуда 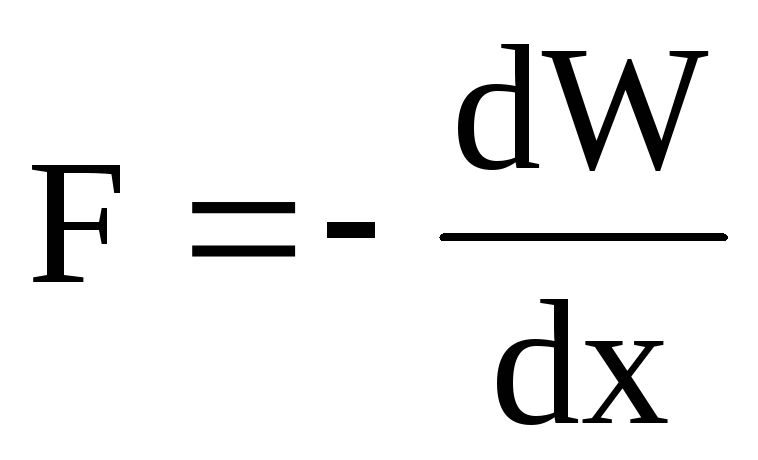 .
.
Подставляя
в формулу энергии 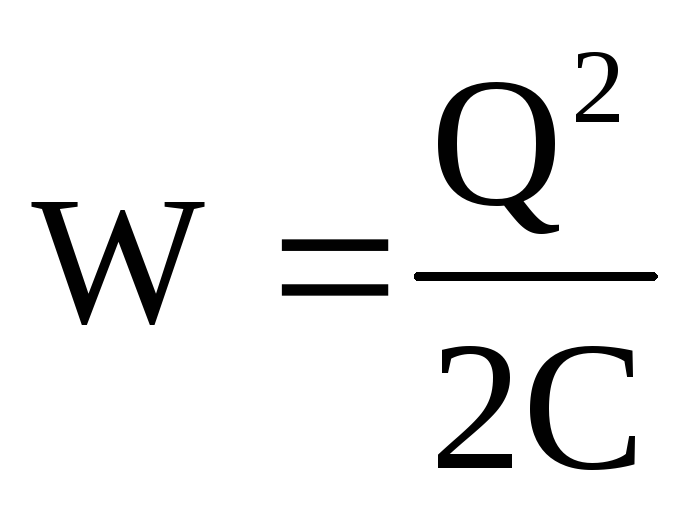 выражение емкости
выражение емкости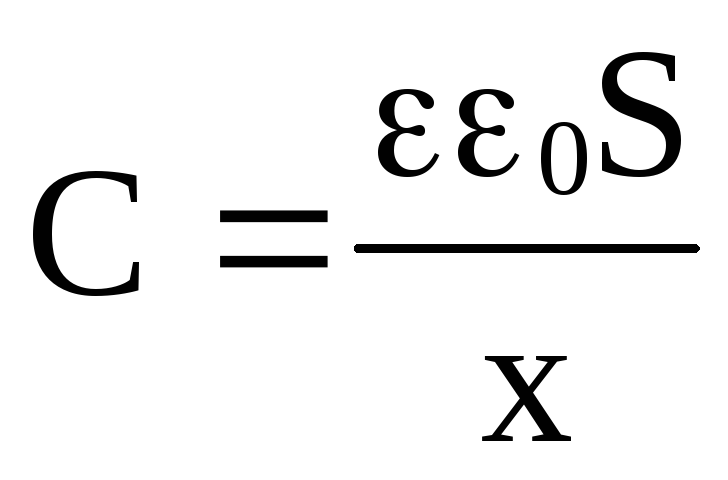 ,
получим
,
получим
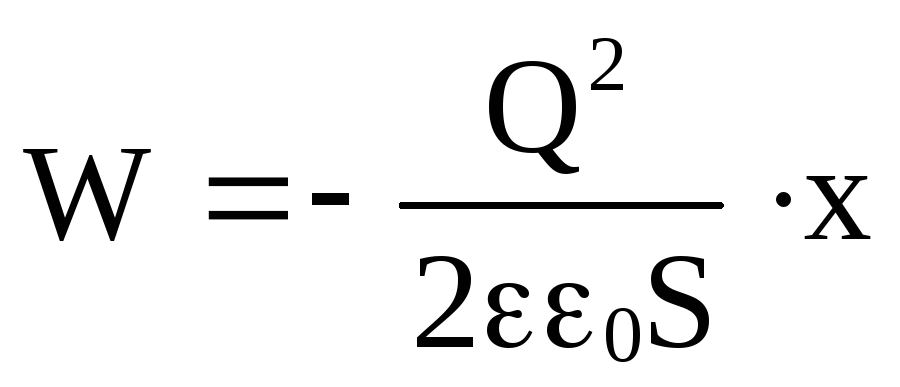 .
.
Дифференцируя W по х, найдем силу F
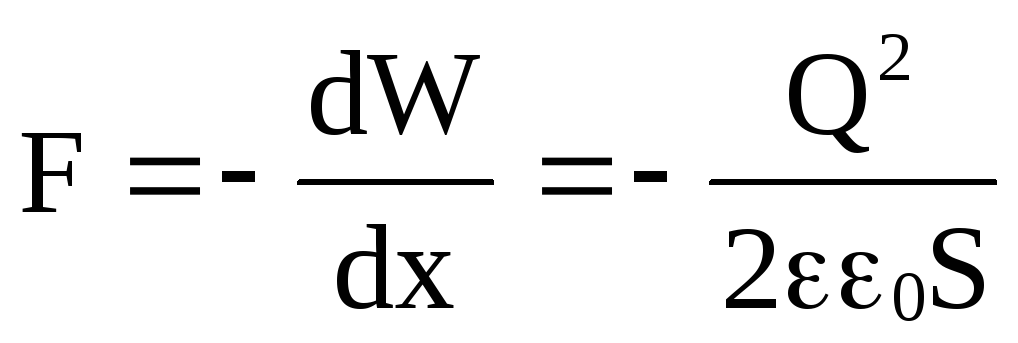 ,
,
где
знак “минус“ указывает, что сила F
стремится уменьшить расстояние между
пластинами, т.е. является силой притяжения.
Подставляя выражение плотности зарядов
на пластинках 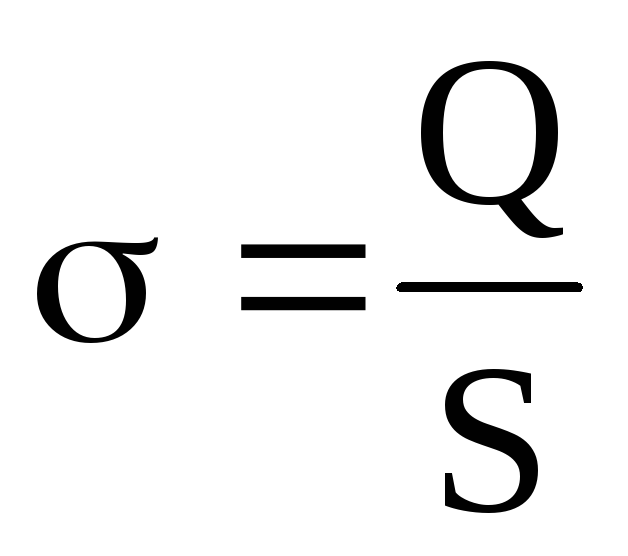 ,
получим
,
получим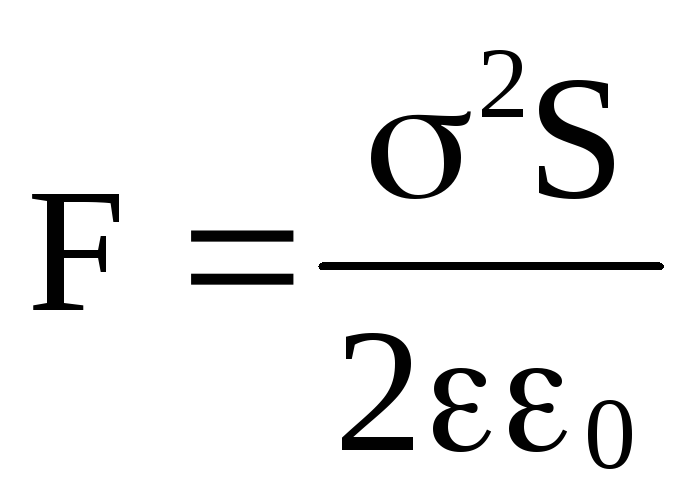 .
.
Учитывая
напряжённость поля, что Е = 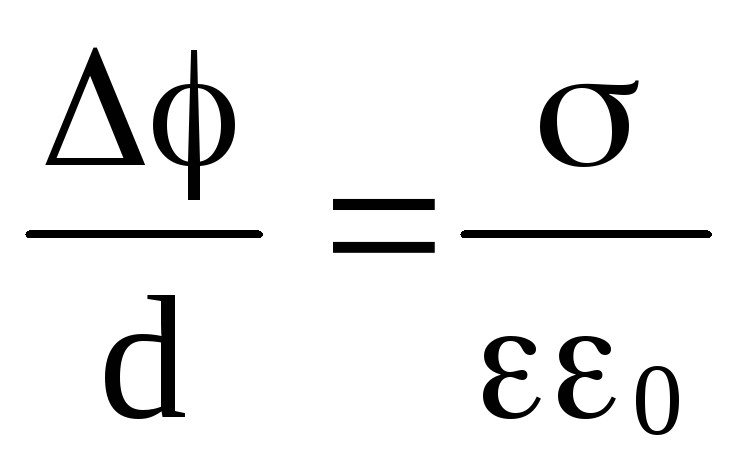 ,
получим
,
получим
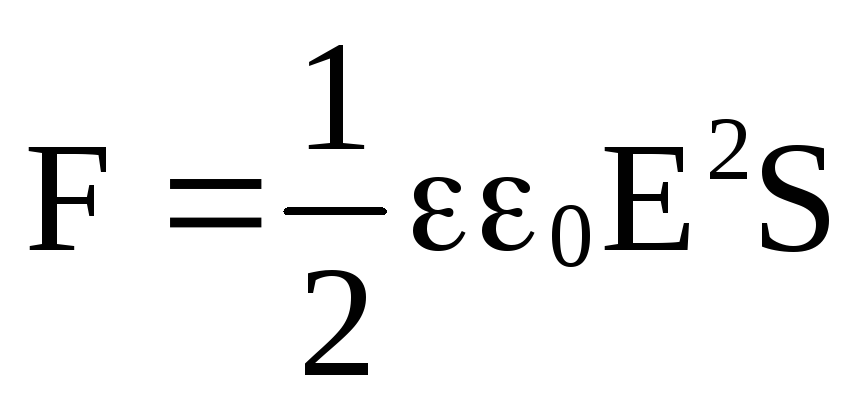 .
.
Давление на пластины диэлектрика, помещенные в зазоре конденсатора, будет
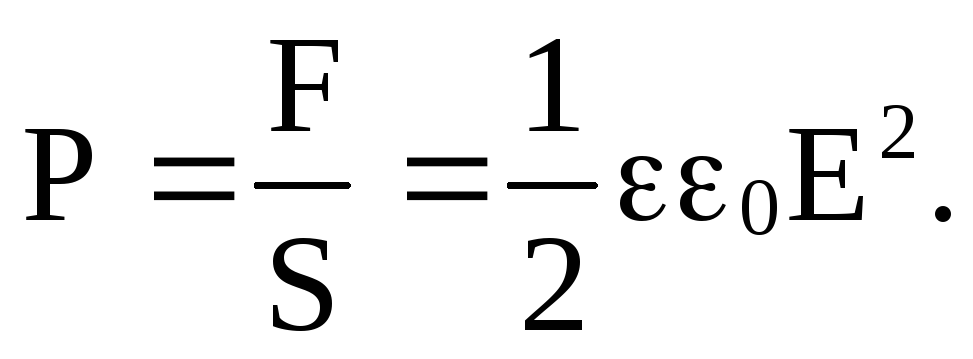
Энергия электростатического поля. Преобразуем формулу энергии плоского конденсатора
 ,
используя формулы
,
используя формулы и Δφ = Еd.
и Δφ = Еd.
Получим 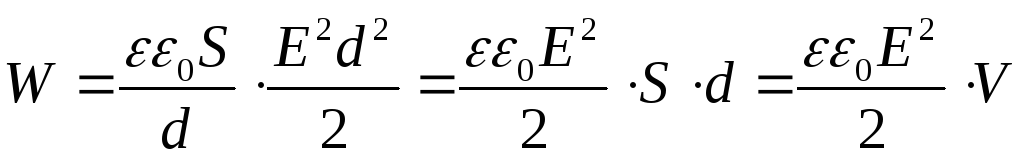 ,
,
где V – объем пространства между пластинами конденсатора, в котором сосредоточена энергия его поля W.
Объемная плотность энергии поля w – это энергия, заключённая в единице объёма электрического поля и она равна
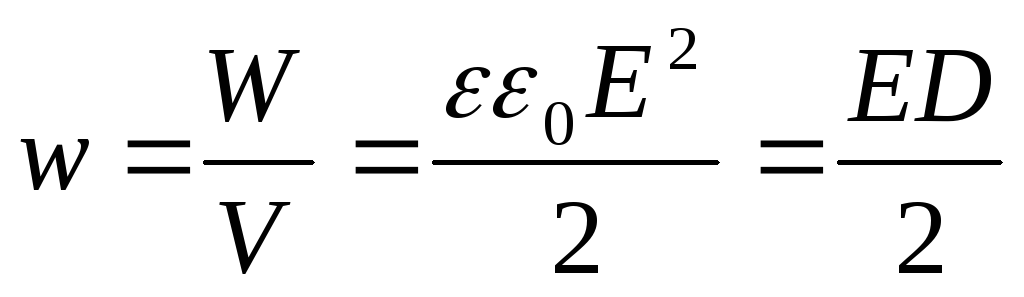 .
.
Единица измерения [Дж/м3].
Видно, что объемная плотность энергии поля зависит только от характеристик поля и среды.




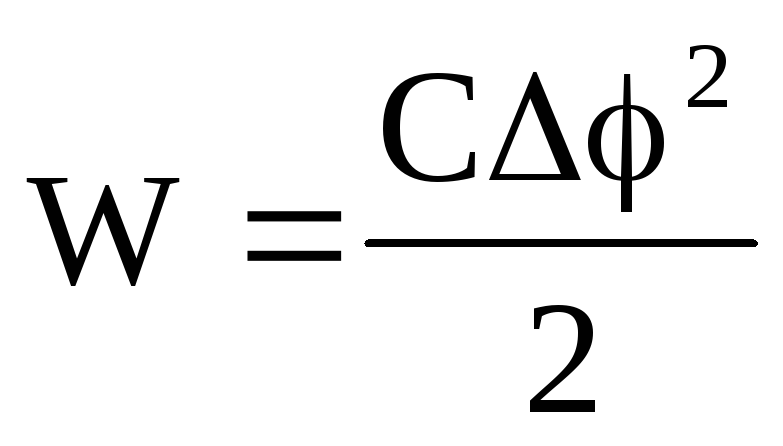 ,
используя формулы
,
используя формулы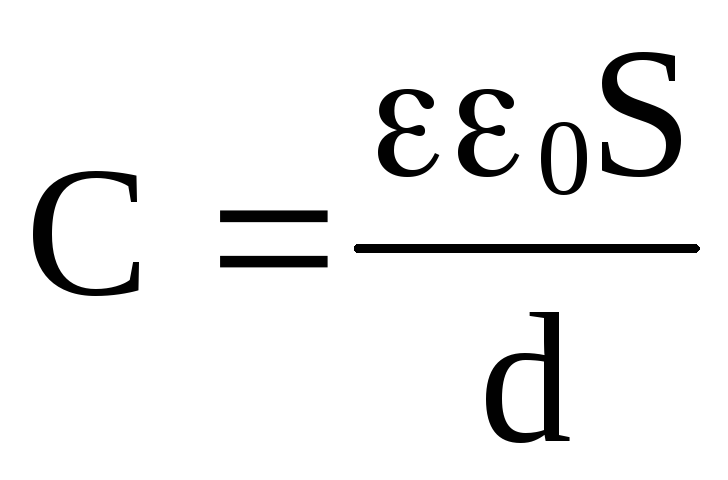 и Δφ = Еd.
и Δφ = Еd.