примеры на последовательное, параллельное и смешанное соединение
Задания по электротехнике успешно даются только тем, кто может досконально разобраться в теме, нарисовать схему электроцепи и объяснить, каким образом в ней происходит взаимодействие между элементами. Ошибочно думать, что это очень сложный раздел физики, с которым под силу разобраться только электромеханикам. При желании эта тема доступна каждому среднестатистическому человеку. Давайте с ней разберемся!
Задания по электротехнике на тему «Конденсаторы»
Прежде чем приступать непосредственно к задачам, вспомним теорию.
Конденсатор — это два электрических проводника, разделенных между собой тонким слоем диэлектрика.
Проводники соединяют между собой с целью получить батареи. Существует 3 способа подключения конденсаторов:
- параллельное;
- последовательное;
- комбинированное.
Последовательным соединением называется подключение двух или более конденсаторов в цепь так, что каждый отдельный проводник соединен с другим только в одной точке.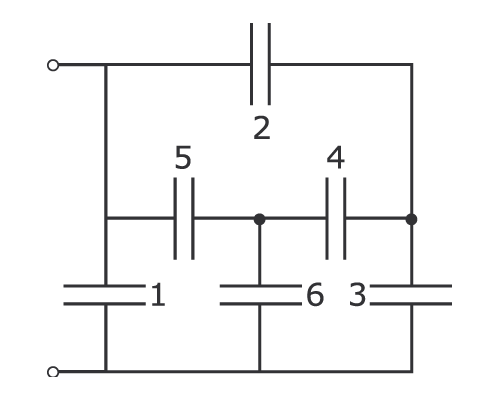
Параллельным называется такое соединение конденсаторов, при котором все они подключены между одной и той же парой точек.
Комбинированное — это вид соединения, в котором часть проводников подключены параллельно, а часть — последовательно.
Знание каких формул и законов потребуется для решения
В зависимости от того, какой вид подключения проводников используется, по-разному будут определяться ключевые характеристики конденсаторов: емкость, заряд, напряжение.
Для решения заданий по данной теме в большинстве случаев понадобятся следующие формулы:
Источник: uk-parkovaya.ruПредлагаем рассмотреть примеры решения типовых задач по данной теме со всеми необходимыми пояснениями, чтобы окончательно усвоить, как правильно разбирать такие задания.
Решение задач на параллельное соединение
Задача
Три проводника соединены между собой параллельно. Емкость первого равна 100 микрофарад, второго — 200 микрофарад, третьего — 500 микрофарад. Найдите общую емкость конденсаторов.
Решение
- Запишем известные вводные: C1=100 мкФ, C2=200 мкФ, C3=500 мкФ, C=?
- Так как соединение в цепи параллельное, общая емкость будет определяться по формуле: C=C1+C2+C3
- Подставляем числовые значения в формулу и получаем ответ: 800 мкФ.
Решение задач на последовательное соединение
Задача
Батарея состоит из двух конденсаторов, соединенных последовательно. Емкость первого — 4 мкФ, второго — 6 мкФ. Батарея заряжена до напряжения 220 Вольт. Определите емкость и заряд батареи.
Решение
- Запишем известные нам данные из условий задачи: C1=4 мкФ, C2=6 мкФ, U=220 В, C=? q=?
- Так как конденсаторы соединены последовательно, емкость батареи будет определяться по формуле: \(\frac1c=\frac1{c_1}+\frac1{c_2}\)
- Общий заряд батареи будет равен заряду первого и заряду второго проводника, т.
 е. q=q1=q2
е. q=q1=q2 - Заряд батареи можно вычислить по формуле: \(q=C\times U\)
- Подставляем числовые значения в формулу и получаем ответ: 528 мкКл.
Решение задач на смешанное соединение
Предлагаем рассмотреть более сложное задание, правильный ответ на которое включает в себя сразу четыре варианта решения:
Источник: bambookes.ruОстались вопросы? Физика по-прежнему кажется сложным для понимания предметом? Вы не понимаете разницу между постоянным и переменным током? Не знаете откуда берется энергия? Обращайтесь за помощью в решении задач и подготовке докладов к специалистам нашего образовательного сервиса ФениксХелп. Для нас нет нелюбимых предметов и сложных тем!
Последовательное и параллельное соединение конденсаторов
На практике часто используются тела, обладающие малыми (и очень малыми) размерами, которые могут накопить большой заряд, при этом имея небольшой потенциал. Такие объекты называют конденсаторами. Одна из основных характеристик конденсатора – это его емкость. Имея в резерве набор конденсаторов, обладающих разными параметрами, можно расширить спектр величин емкостей и диапазон рабочих напряжений, если применять их соединения. Различают три типа соединений конденсаторов: последовательное, параллельное и смешанное (параллельное и последовательное).
Такие объекты называют конденсаторами. Одна из основных характеристик конденсатора – это его емкость. Имея в резерве набор конденсаторов, обладающих разными параметрами, можно расширить спектр величин емкостей и диапазон рабочих напряжений, если применять их соединения. Различают три типа соединений конденсаторов: последовательное, параллельное и смешанное (параллельное и последовательное).
Последовательное соединение конденсаторов
Последовательное соединение из конденсаторов изображено на рис. 1
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды. Электрическая емкость последовательного соединения конденсаторов вычисляется по формуле:
где – электрическая емкость i-го конденсатора.
Если емкости конденсаторов при последовательном соединении равны , то емкость последовательного их соединения составляет:
где N – количество последовательно соединенных конденсаторов. При этом предельное напряжение (U), которое выдержит подобная батарея конденсаторов составит:
При этом предельное напряжение (U), которое выдержит подобная батарея конденсаторов составит:
где – предельное напряжение каждого конденсатора соединения. При последовательном соединении конденсаторов следует следить за тем, чтобы ни на один из конденсаторов батареи не падало напряжение, превышающее его максимальное рабочее напряжение.
Параллельное соединение конденсаторов
Параллельное соединение N конденсаторов изображено на рис. 2.
При параллельном соединении конденсаторов соединяют обкладки, обладающие зарядами одного знака (плюс с плюсом; минус с минусом). В результате такого соединения одна обкладка каждого конденсатора имеет одинаковый потенциал, например, , а другая . Разности потенциалов на обкладках всех конденсаторов при их параллельном соединении равны.
При параллельном соединении конденсаторов суммарная емкость соединения рассчитывается как сумма емкостей отдельных конденсаторов:
При параллельном соединении конденсаторов напряжение равно самой наименьшей величине рабочего напряжения конденсатора из состава рассматриваемого соединения.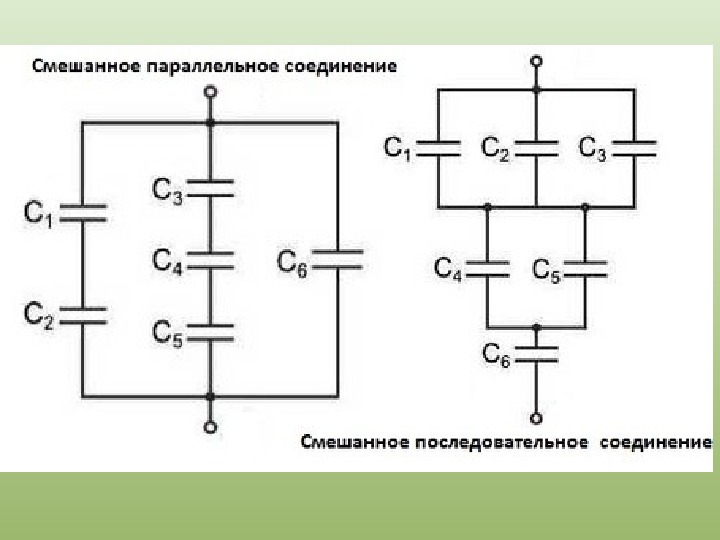
Примеры решения задач
Электроника и электротехника Вариант 9 – Решение задач
| Дисциплина | Технические |
| Тип работы | Контрольные |
| Количество страниц | 22 |
| Год сдачи | 2017 |
| Номер работы | 1458 |
О работе
Оценка «отлично», качественное решение. Вы можете приобрести задания по отдельности, для этого обратитесь к нашему менеджеру.Содержание
Контрольная работа. Вариант 9.
Задание № 1. Решить задачу по теме «Смешанное соединение конденсаторов» Дана батарея конденсаторов соединенных смешанным способом и подключенных к сети переменного тока напряжением 220В. Схема включения соответствует варианту задания и изображена на схемах 1.1 -1.25 в приложении А (страницы 34-35), по заданным в таблице 1.1 параметрам рассчитать:
1) Эквивалентную емкость батареи конденсаторов(Cэкв).
2) Заряд каждого конденсатора(q1, q2, q3, q4, q5).
3) Энергию каждого конденсатора(W1, W2, W3, W4, W5).
С1,мкФ | С2,мкФ | С3,мкФ | С4,мкФ | С5,мкФ | U, B |
14 | 14 | 6 | 6 | 30 | 220 |
Рис.1.9.
Решение.
Задание 2 Решить задачу на тему: «Простые цепи постоянного тока» Для электрической цепи постоянного тока, составленной из резистивных элементов, дана схема, изображенная на схемах 2.1-2.25 в приложение Б (страницы 36-38), по заданным в таблице 2.1 параметрам рассчитать:
2) Падение напряжений на каждом из резисторов.
3) Мощность, развиваемую источником энергии (Рист) и мощность рассеиваемую на нагрузке (Рнаг).
4) Проверить правильность решения методом баланса мощностей.
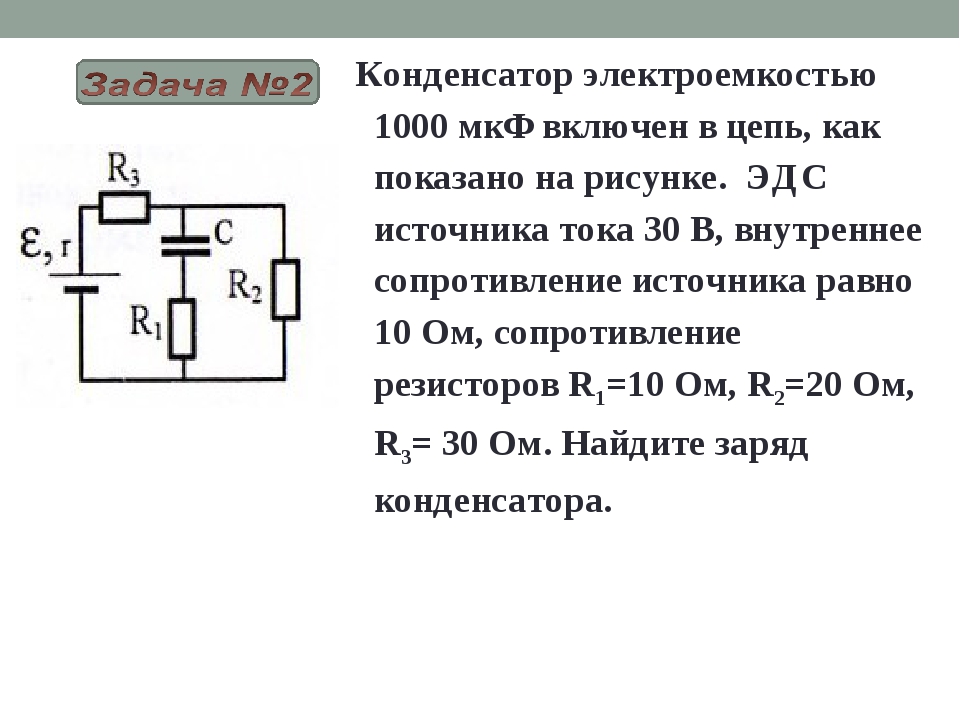
R1,Ом | R2,Ом | R3,Ом | R4,Ом | R5,Ом | R6, Ом | R7,Ом | U,B |
1 | 3 | 5 | 10 | 12 | 7 | 4 | 10 |
Рис.2.9.
Решение.
Задание 3. Решить задачу на тему «Анализ электрической цепи постоянного тока методом законов Кирхгофа» Для электрической цепи, составленной из резистивных элементов и источников ЭДС постоянного напряжения, дана схема, изображенная на рисунках 3.1 — 3.12 в приложении В (страница 39), по заданным в таблице 3.1 параметрам методом законов Кирхгофа определить:
1)Токи во всех ветвях схемы (I1, I2, I3,).
2) Падение напряжений на каждом из резисторов (U1, U2, U3,).
3) Проверить правильность решения методом баланса мощностей.
R1,Ом | R2,Ом | R3,Ом | Е1,В | Е3,В | Рис. |
4 | 9 | 4 | 40 | 20 | 3.9 |
Рис.3.9.
Решение.
Задание 4
Решить задачу на тему: «Расчет однофазной электрической цепи переменного
тока»
Для однофазной электрической, цепи переменного тока, дана схема
изображенная на схемах 4.1-4.25 в приложение Г (страницы 40-41). По заданным в
таблице 3.1 параметрам рассчитать:
— для параллельного соединения резистора (R),катушки индуктивности(L),
конденсатора (C):
1)Токи в ветвях и в неразветвленной части цепи;
2) Активные мощности ветвей;
3)Углы сдвига фаз между током и напряжением первой и второй
ветвей и всей цепи;
4) Построить векторную диаграмму
R1,Ом | R2,Ом | С1,мкФ | С2,мкФ | U,В | Рис. |
7 | 14 | 35 | 40 | u=564sin628 | 4.9 |
Рис.4.9.
Решение.
Задание 5.
Вопрос 9. Что такое выпрямительный диод и его основные параметры?
Ответ
Вы можете убедиться в качестве данной работы. Часть контрольной представлена ниже:
Соединение конденсаторов — презентация онлайн
1. Соединение конденсаторов
1 курс, 2 семестр3. Параллельное соединение конденсаторов
Если к точкам включения непосредственноприсоединены пластины всех конденсаторов, то
такое соединение называется параллельным
соединением конденсаторов
4. Параллельное соединение конденсаторов
• общая емкость конденсаторов припараллельном соединении равна сумме
емкостей всех соединенных конденсаторов.
5. Параллельное соединение конденсаторов
• Соединенные параллельно конденсаторынаходятся под одним и тем же напряжением,
равным U вольт, а общий заряд этих
конденсаторов равен q кулонов.
 При этом
При этомкаждый конденсатор соответственно получает
заряд q1, q2, q3 и т. д. Следовательно,
qобщ = q1 + q2 + q3 + . . .
6. Параллельное соединение конденсаторов
qобщ = CобщU,а заряды q1 = С1U; q2 = С2U; q3 = С3U.
Подставив эти выражения в формулу, получим:
СобщU = С1U + С2U + С3U.
Разделив левую и правую части этого равенства
на равную для всех конденсаторов величину U,
после сокращения найдем: Собщ = С1 +С2 + С3;
Если С1=С2=С3 =…, то Собщ = С1n, гдеС1— емкость
одного конденсатора,
n — число конденсаторов.
7. Последовательное соединение конденсаторов
Если соединение конденсаторов в батареюпроизводится в виде цепочки и к точкам
включения в цепь непосредственно
присоединены пластины только первого и
последнего конденсаторов, то такое соединение
конденсаторов называется последовательным
8. Последовательное соединение конденсаторов
При последовательном соединении все конденсаторызаряжаются одинаковым количеством электричества, так как
непосредственно от источника тока заряжаются только крайние
пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются
через влияние.
 При этом заряд пластины 2 будет равен по
При этом заряд пластины 2 будет равен повеличине и противоположен по знаку заряду пластины 1, заряд
пластины 3 будет равен по величине и противоположен по знаку
заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря,
различными, так как для заряда одним и тем же количеством
электричества конденсаторов различной емкости всегда
требуются различные напряжения. Чем меньше емкость
конденсатора, тем большее напряжение необходимо для того,
чтобы зарядить этот конденсатор требуемым количеством
электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных
последовательно, на конденсаторах малой емкости напряжения
будут больше, а на конденсаторах большой емкости — меньше.
9. Последовательное соединение конденсаторов
Uобщ = U1 + U2 + U310. Последовательное соединение конденсаторов
Для частного случая двух последовательносоединенных конденсаторов формула для
вычисления их общей емкости будет иметь вид:
11.
 Последовательное соединение конденсаторов Если последовательно соединены конденсаторы,
Последовательное соединение конденсаторов Если последовательно соединены конденсаторы,имеющие одинаковую емкость, то их общую
емкость можно вычислить по формуле
12. Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединениемконденсаторов называется цепь имеющая в
своем составе участки, как с параллельным, так
и с последовательным соединением
конденсаторов.
14. Домашнее задание
1)Определите емкость батареи конденсаторов,изображенной на рисунке. Емкость каждого
конденсатора 1 мкФ.
2) Два последовательно соединенных конденсатора
емкостями 2 и 4 мкФ присоединили к источнику
напряжением 180 В. Конденсаторы отсоединили
друг от друга и от источника и соединили
одноименно заряженными пластинами.
Определите установившееся напряжение.
15. Решение задач
• Три конденсатора одинаковой емкостисоединены параллельно друг другу в батарею.
Рассчитать емкость батареи конденсаторов,
если известно, что при подключении ее к
полюсам аккумулятора напряжением 12 В
заряд на обкладках каждого конденсатора
6×10-9 Кл.

16. Решение задач
• Найти электроемкость системыконденсаторов, соединенных по схеме, показанной на рисунке C1 = C2 = C4= C5.
Практическая работа №1 Расчет смешанного соединения конденсаторов
Цель: закрепить знания методов расчета электрической емкости и зарядов конденсаторов при их смешанном соединении.
Теоретические сведения
Электрический конденсатор — это система из двух проводников (обкладок, пластин), разделенных диэлектриком.
Конденсаторы обладают свойством накапливать на своих обкладках электрические заряды, равные по величине и противоположные по знаку.
Электрический заряд q каждой из обкладок пропорционален напряжению U между ними:
Величину С, равную отношению заряда одной из обкладок конденсатора к напряжению между ними, называют электрической емкостью конденсатора и выражают в фарадах (Ф).
Емкость конденсатора зависит от геометрических размеров, формы, взаимного расположения и расстояния между обкладками, а также от свойств диэлектрика.
Конденсаторы могут быть соединены последовательно, параллельно и смешанно (последовательно-параллельно).
Последовательное соединение
При таком на обкладках всех конденсаторов будут одинаковые по величине заряды:
Напряжения на конденсаторах будут различны, так как они зависят от их емкостей:
Общее напряжение:
Общая, или эквивалентная, емкость
Параллельное соединение
При параллельном соединении напряжение на всех конденсаторах одинаковое.
Заряды на обкладках отдельных конденсаторов при различной их емкости:
Заряд, полученный всеми параллельно соединенными конденсаторами:
Общая (эквивалентная) емкость:
Задание
1. Определить эквивалентную емкость батареи конденсаторов, соединенных по схеме, при соответствующих положениях ключей.
2. Для случая, когда ключи К1, К2 и К3 разомкнуты, найти заряды на каждом конденсаторе и общий заряд схемы.
Порядок выполнения расчета
Задание 1
1. Для своих данных начертить исходную схему.
Для своих данных начертить исходную схему.
2. Рассчитать последовательное соединение С3-С7:
3. Рассчитать параллельное соединение С4-С5:
4. Рассчитать последовательное соединение С2-С45:
5. Найти эквивалентную емкость, рассчитав параллельное соединение С245-С37:
Задание 2
1. Для своих данных начертить исходную схему.
2. Рассчитать заряды на каждом конденсаторе:
3. Рассчитать общий заряд схемы:
4. Проверка:
Соединение конденсаторов формула. Последовательное соединение конденсаторов: формула
В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.
Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
C общ = C 1 + C 2 + C 3
Схема – напряжение на накопителях
В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:
V AB = V C1 = V C2 = V C3 = 20 Вольт
Последовательное соединение
Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.
Схема – схема последовательного соединения
Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:
i = i c 1 = i c 2 = i c 3 = i c 4 , то есть токи проходящие через каждый конденсатор равны между собой.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:
Q общ = Q 1 = Q 2 = Q 3
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
1/C общ = 1/C 1 + 1/C 2 + 1/C 3
Видео: как соединять конденсаторы параллельным и последовательным методом
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Схема: смешанное соединение конденсаторов
Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
- Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
- Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
- Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока.
 Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду; - Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.
Содержание:
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей.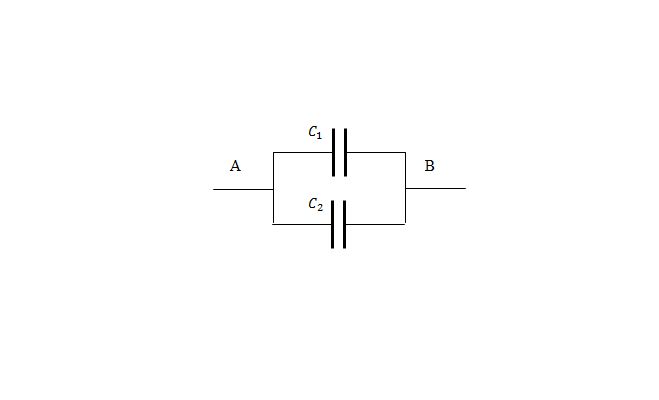 Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Параллельное включение конденсаторов в цепь
Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.
Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.
При параллельном соединении конденсаторов емкость равняется:
Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.
Конденсаторы, соединенные параллельно, имеют напряжение:
Последовательное включение конденсаторов в цепь
Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.
Последовательное соединение конденсатора:
При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
Формула нахождения заряда на конденсаторе, схема подключения конденсатора:
Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.
Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:
Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:
Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:
Смешанное включение емкостных накопителей в схему
Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Участок цепи подсоединенных смешанным включением накопителей емкости:
Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:
- разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
- вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
- проводим нахождение эквивалентной емкости на параллельном участке;
- когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
- рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.
Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:
- Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
- Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
- Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.
Вывод
Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.
Рис.2 U=U 1 =U 2 =U 3
Общий заряд Q всех конденсаторов
Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.
Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.
4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением
Последовательное соединение конденсаторов
Рис.3
На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.
Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:
Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.
При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:
Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:
Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.
На практике может оказаться, что допустимое рабочее напряжение U p конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .
Смешанное соединение конденсаторов
Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.
Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.
Энергия конденсаторов
где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U ; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .
Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.
15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)
Рисунок 5- Схема электрическая
6.СХЕМЫ ЗАМЕЩЕНИЯ
Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.
На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.
1.Схемы замещения элементов электрических цепей
На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).
Приr= 0 внутреннее падение напряженияUо = 0, поэтомунапряжение на зажимах источника при любом токе равно
ЭДС: U = E = const.
В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg =1/ r .
Возможность такой замены можно доказать, разделив равенство (3.1) на r:
U / r = E / r — I ,
где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K — ток короткого замыкания источника;
Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.
В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):
Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.
Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.
Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?
Что необходимо знать для правильного соединения?
Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.
Зачем так делают?
Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К 1 =К 2 =К 3 . КЕ — конечная емкость, К — пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:
- ОЕ — общая емкость;
- Н — напряжение;
- КЕ — конечная емкость.
Что ещё необходимо знать, чтобы правильно соединить конденсаторы?
Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.
Ток при последовательном соединении
Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.
Падение напряженности и общая емкость
Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.
Пример № 1
Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.
Пример № 2
Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.
Заключение
Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.
У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью 470 мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на 1000 мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/1-21-768×410..jpg 260w, https://elquanta.ru/wp-content/uploads/2018/04/1-21.jpg 960w»>
Последовательное соединение конденсаторов
Схема последовательного соединения
Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:
q = q1 = q2 = q3 = …
Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.
Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:
U = U1 + U2 + U3,
при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.
Подставляя значения для напряжений в обе части уравнения, получается:
q/C = q/C1 + q/C2 + q/C3.
Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.
Результирующая формула для емкостей конденсаторов:
1/С = 1/С1 + 1/С2 + 1/С3.
Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/2-20-768×476..jpg 120w, https://elquanta.ru/wp-content/uploads/2018/04/2-20.jpg 913w»>
Особенности последовательного соединения
Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:
- 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
- С = 1/27,5 = 0,036 мкФ.
Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента.
Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:
С = (С1 х С2)/(С1 + С2).
В случае создания цепи из двух конденсаторов с идентичным емкостным значением:
С = (С х С)/(2 х С) = С/2.
Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.
Png?x15027″ alt=»Емкостной делитель напряжения»>
Емкостной делитель напряжения
Формула для емкостного делителя напряжения:
U1 = U x C/C1, U2 = U x C/C2, где:
- U – напряжение питания схемы;
- U1, U2 – падение напряжения на каждом элементе;
- С – итоговая емкость схемы;
- С1, С2 – емкостные показатели единичных элементов.
Вычисление падений напряжения на конденсаторах
К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:
- первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
- вторая – С1 = С2 = 400 нФ.
Первый вариант
- Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
- Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
- На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.
Второй вариант
- Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
- Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.
Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.
Параллельное и комбинированное соединение
Параллельное соединение конденсаторов представляется иным уравнением. Для определения общего емкостного значения надо просто найти совокупность всех величин по отдельности:
С = С1 + С2 + С3 + …
Напряжение к каждому элементу будет прикладываться идентичное. Следовательно, для усиления емкости надо соединить несколько деталей параллельно.
Если соединения смешанные, последовательно-параллельные, то для таких контуров применяют эквивалентные, или упрощенные, электросхемы. Каждую область цепи рассчитывают отдельно, а затем, представляя их вычисленными емкостями, объединяют в простую цепь.
Png?.png 600w, https://elquanta.ru/wp-content/uploads/2018/04/4-2-768×350..png 927w»>
Варианты получения эквивалентных схем
Особенности замены конденсаторов
К примеру, в наличии сеть переменного тока 12 В и две альтернативных группы последовательных конденсаторных элементов.
Конденсаторы подсоединяются в последовательный контур для увеличения напряжения, под которым они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.
Часто применяется смешанное соединение конденсаторов, чтобы создать нужную емкостную величину и увеличить напряжение, которое детали способны выдержать.
Можно привести вариант, как соединить несколько компонентов, чтобы выйти на нужные параметры. Если требуется конденсаторный элемент 80 мкФ при напряжении 50 В, но есть только конденсаторы 40 мкФ на 25 В, необходимо образовать следующую комбинацию:
- Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
- Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
- Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.
Важно! Для того чтобы усилить конденсаторы по напряжению, возможно их объединить в последовательную электросхему. Увеличение общей емкостной величины достигается параллельным подключением.
Что необходимо учитывать при создании последовательной цепи:
- При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
- Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.
Data-lazy-type=»image» data-src=»http://elquanta.ru/wp-content/uploads/2018/04/5-13-600×259.jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/5-13-768×331..jpg 800w»>
Оцените статью:Способы соединения конденсаторов. Смешанное включение емкостных накопителей в схему. Схемы замещения элементов электрических цепей
У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью 470 мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на 1000 мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/1-21-768×410..jpg 260w, https://elquanta.ru/wp-content/uploads/2018/04/1-21.jpg 960w»>
Последовательное соединение конденсаторов
Схема последовательного соединения
Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:
q = q1 = q2 = q3 = …
Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.
Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:
U = U1 + U2 + U3,
при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.
Подставляя значения для напряжений в обе части уравнения, получается:
q/C = q/C1 + q/C2 + q/C3.
Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.
Результирующая формула для емкостей конденсаторов:
1/С = 1/С1 + 1/С2 + 1/С3.
Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/2-20-768×476..jpg 120w, https://elquanta.ru/wp-content/uploads/2018/04/2-20.jpg 913w»>
Особенности последовательного соединения
Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:
- 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
- С = 1/27,5 = 0,036 мкФ.
Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента.
Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:
С = (С1 х С2)/(С1 + С2).
В случае создания цепи из двух конденсаторов с идентичным емкостным значением:
С = (С х С)/(2 х С) = С/2.
Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.
Png?x15027″ alt=»Емкостной делитель напряжения»>
Емкостной делитель напряжения
Формула для емкостного делителя напряжения:
U1 = U x C/C1, U2 = U x C/C2, где:
- U – напряжение питания схемы;
- U1, U2 – падение напряжения на каждом элементе;
- С – итоговая емкость схемы;
- С1, С2 – емкостные показатели единичных элементов.
Вычисление падений напряжения на конденсаторах
К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:
- первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
- вторая – С1 = С2 = 400 нФ.
Первый вариант
- Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
- Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
- На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.
Второй вариант
- Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
- Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.
Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.
Параллельное и комбинированное соединение
Параллельное соединение конденсаторов представляется иным уравнением. Для определения общего емкостного значения надо просто найти совокупность всех величин по отдельности:
С = С1 + С2 + С3 + …
Напряжение к каждому элементу будет прикладываться идентичное. Следовательно, для усиления емкости надо соединить несколько деталей параллельно.
Если соединения смешанные, последовательно-параллельные, то для таких контуров применяют эквивалентные, или упрощенные, электросхемы. Каждую область цепи рассчитывают отдельно, а затем, представляя их вычисленными емкостями, объединяют в простую цепь.
Png?.png 600w, https://elquanta.ru/wp-content/uploads/2018/04/4-2-768×350..png 927w»>
Варианты получения эквивалентных схем
Особенности замены конденсаторов
К примеру, в наличии сеть переменного тока 12 В и две альтернативных группы последовательных конденсаторных элементов.
Конденсаторы подсоединяются в последовательный контур для увеличения напряжения, под которым они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.
Часто применяется смешанное соединение конденсаторов, чтобы создать нужную емкостную величину и увеличить напряжение, которое детали способны выдержать.
Можно привести вариант, как соединить несколько компонентов, чтобы выйти на нужные параметры. Если требуется конденсаторный элемент 80 мкФ при напряжении 50 В, но есть только конденсаторы 40 мкФ на 25 В, необходимо образовать следующую комбинацию:
- Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
- Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
- Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.
Важно! Для того чтобы усилить конденсаторы по напряжению, возможно их объединить в последовательную электросхему. Увеличение общей емкостной величины достигается параллельным подключением.
Что необходимо учитывать при создании последовательной цепи:
- При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
- Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.
Data-lazy-type=»image» data-src=»http://elquanta.ru/wp-content/uploads/2018/04/5-13-600×259.jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/5-13-768×331..jpg 800w»>
Оцените статью:Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.
Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.
При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.
Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах . Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.
Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.
На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.
При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.
Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле
Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.
При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.
Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения .
Смешанное соединение конденсаторов
Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С 1 – ёмкость первого;
С 2 – ёмкость второго;
С 3 – ёмкость третьего;
С N – ёмкость N -ого конденсатора;
C общ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор , замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены:)
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Могут быть соединены друг с другом различным образом. При этом во всех случаях можно найти емкость некоторого равнозначного конденсатора, который может заменить ряд соединенных между собой конденсаторов.
Для равнозначного конденсатора выполняется условие: если подводимое к обкладкам равнозначного конденсатора напряжение равно напряжению, подводимому к крайним зажимам группы конденсаторов, то равнозначный конденсатор накопит такой же заряд, как и группа конденсаторов.
Параллельное соединение конденсаторов
На рис. 1 изображено параллельное соединение нескольких конденсаторов. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U , Q 2 = C 2U , Q 3 = C 3U , а заряд, полученный от источника Q = Q1 + Q2 + Q3.
Рис. 1. Схема параллельного соединения конденсаторов
Общая емкость равнозначного (эквивалентного) конденсатора:
C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3 ,
т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.
Рис. 2. Способы соединения конденсаторов
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q
Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.
Рис. 3. Схема последовательного соединения конденсаторов
Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1 , U1 = Q/C 2, U1 = Q/C 3, а общее напряжение U = U1 + U2 + U3
Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3 ), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.
Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.
Пример 1 . Три конденсатора, емкости которых C1 = 20 мкф, С2 = 25 мкф и С3 = 30 мкф, соединяются последовательно, необходимо определить общую емкость.
Общая емкость определяется из выражения 1/С = 1/С1 + 1/С2 + 1/С3 = 1/20 + 1/25 + 1/30 = 37/300, откуда С = 8,11 мкф.
Пример 2. 100 конденсаторов емкостью каждый 2 мкф соединены параллельно. Определить общую емкость. Общая емкость С = 100 Ск = 200 мкф.
а) параллельно конденсатору большой емкости включать точно такой же конденсатор, но маленькой емкости;
б) вместо одного конденсатора большой емкости включать два-три конденсатора меньшей емкости того же типа;
в) вместо одного конденсатора большой емкости включать много конденсаторов небольшой емкости.
Естественно, включать надо параллельно, при этом емкости суммируются, и общая емкость во всех этих случаях получается одинаковой. Давайте разберемся в данном вопросе (вся необходимая информация есть в таблице 1 и рис. 47).
Вариант а). Говорят, что маленький конденсатор будет помогать работать большому.
Максимальной рабочей частотой конденсатора можно считать ту частоту, на которой его сопротивление минимально. Дальше с ростом частоты полное сопротивление конденсатора начинает расти – это сказывается индуктивность конструкции конденсатора. При этом индуктивное сопротивление перевешивает емкостное, и конденсатор ведет себя как катушка индуктивности. То есть уже и не является конденсатором.
Для конденсатора малой емкости минимум сопротивления действительно наступает на большей частоте, но его сопротивление все равно больше, чем у конденсатора большой емкости (свойства которого на этой частоте уже ухудшаются). А ведь главная задача конденсатора на этих частотах – пропускать через себя ток нагрузки, как можно меньше на него влияя. Поэтому чем у конденсатора сопротивление меньше, тем лучше. И конденсатор малой емкости не очень-то и поможет «большому» конденсатору, слишком уж велико его сопротивление. Только в точке А сопротивления обоих конденсаторов становятся равными, и на более высокой частоте у конденсатора малой емкости сопротивление меньше, чем у «большого». Но посмотрите – в этой точке уже и конденсатор малой емкости работает плохо! В реальности эти графики показаны на рис. 47, где цифрами 1…5 обозначены конденсаторы меньшей емкости, а цифрами 8… 12 – конденсаторы большей емкости.
А вот если в системе присутствует керамический или пленочный конденсатор, то он хорошо работает и на этой частоте, и на более высоких частотах (рис. 48). Только емкость его должна быть достаточно большой,
чтобы на нужных частотах он имел низкое сопротивление.
Вывод: параллельное подключение электролитического конденсатора малой емкости заметной пользы не принесет (хоть и не навредит), гораздо выгоднее шунтирование электролита большой емкости хорошим пленочным конденсатором, который наверняка гораздо более высокочастотный.
Напрашивается вопрос: а для чего же так делают? И даже в промышленной аппаратуре? Ну, во-первых, иногда действительно можно подобрать условия, когда «маленький» конденсатор немного поможет. А главное
– почему бы не поставить такой конденсатор, раз в него верят покупатели? Тем более что он очень дешевый.
Вариант б). Вместо одного конденсатора большой емкости включаем два конденсатора меньшей емкости того же типа. Рассмотрим эту ситуацию для конденсаторов, приведенных в двух последних строках таблицы 1. Допустим, мы ставим два конденсатора 4700 мкФ вместо одного 10000 мкФ. Тогда их сопротивление будет 0,071/2 = 0,0355 Ом, а допустимый ток 3-2=6 ампер. Получается, по ESR примерно то же самое, а по току так даже лучше, чем одиночный конденсатор. Только надо помнить, что у конденсаторов довольно большой разброс, так что можно вместо одного хорошего поставить два плохих. Или наоборот. Более длинные провода, соединяющие два конденсатора, будут иметь большее сопротивление, чем у одиночного. Да и токи заряда конденсаторов будут немного неодинаковыми. В результате это небольшое преимущество от удвоения конденсаторов, скорее всего, будет «съедено» неидеальностью остальных элементов схемы.
Так что в данном случае можно считать эти варианты выбора конденсаторов равноценными. И выбирать тот или иной вариант из каких-либо других соображений. Например, какие конденсаторы поместятся в ваш корпус. Или какие конденсаторы продаются в вашем городе.
Вариант в). Ставим 10 конденсаторов 1000 мкФ вместо одного на 10000 мкФ. Что говорит математика: ESR = 0,199/10 = 0,0199 Ом (по сравнению с 0,033 Ом для конденсатора 10000 мкФ), максимальный ток = 10-1,4= 14А (по сравнению с 5 А конденсатора 10000 мкФ). Вроде бы выигрыш по сопротивлению в 1,5 раза, а по току почти в 3 раза. Судя по полученным цифрам, много конденсаторов лучше, чем один.
Слышали когда-нибудь, как ругают теоретиков, говоря, что на практике получается все совсем не так, как у них в теории? Это про таких горе-теоретиков, которые просто умножат-разделят числа, и не подумают об остальных факторах, влияющих на ситуацию. Посмотрите на рис. 49. Индуктивности и резисторы – это сопротивление и индуктивность проводников, соединяющих всю эту кучу конденсаторов. Поскольку конденсаторов теперь много, то длина проводов существенно увеличивается, растут и индуктивности-сопротивления. Вот тут-то и теряются все преимущества, которые мы насчитали по формулам! Нет, формулы правильные! Только они не учитывают эти вот элементы – ведь мы написали эти формулы без их учета, не подумав про них.
В результате общее сопротивление может получиться даже больше, чем у одиночного конденсатора боль-
шой емкости, а ток распределяется очень неравномерно. Например, при заряде конденсаторов, заряд начинается с самого левого по схеме С1, и в него в самый первый момент времени течет весь максимальный ток (в С2 ток потечет только после того, как С1 уже немного зарядится), а конденсатор-то рассчитан всего на 1,4 ампера! Поэтому может случиться, что этот конденсатор будет перегружаться зарядным током, а значит, долго не проживет. Точно также, разряжается первым самый правый конденсатор СЮ, и он будет перегружаться разрядным током.
В общем, все преимущества обычно получаются только на бумаге. Это как раз та ситуация, когда «слишком хорошо – тоже не хорошо». Все всегда должно быть в разумных пределах, а здесь мы из них вышли. Собственно, «много маленьких» конденсаторов не всегда будет хуже, чем «один большой», но далеко и не всегда будет лучше. Хороший профессионал сможет извлечь пользу из такого включения (когда оно оправданно), а новичок скорее всего все испортит.
На самом деле, есть случай, когда параллельное включение двух-трех конденсаторов принесет пользу. Например, когда конденсатор фильтра установлен возле горячего диода и не удается его отодвинуть. Тогда при нескольких конденсаторов греться будет только один из них.
И еще. При любом наборе электролитов, подключение пленочного конденсатора только приветствуется.
19.6 Последовательные и параллельные конденсаторы — College Physics chapters 1-17
Сводка
- Выведите выражения для полной емкости последовательно и параллельно.
- Обозначает последовательные и параллельные части при соединении конденсаторов.
- Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор.Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа соединений, называемых сериями и параллельными , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с последовательными и параллельными соединениями.
На рис. 1 (а) показано последовательное соединение трех конденсаторов с приложенным напряжением.Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] \ boldsymbol {C = \ frac {Q} {V}} [/ latex].
Обратите внимание на рис. 1, что противоположные заряды величиной [латекс] \ boldsymbol {Q} [/ latex] текут по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс] \ boldsymbol {V} [/ латекс] . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах.Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1 (b).) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине — Q .(b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс] \ boldsymbol {C = \ frac {Q} {V}} [/ latex] для [латекса] \ boldsymbol {V} [/ latex] дает [латекс] \ boldsymbol {V = \ frac {Q} {C}} [/ latex]. Таким образом, напряжения на отдельных конденсаторах составляют [латекс] \ boldsymbol {V_1 = \ frac {Q} {C_1}} [/ latex], [латекс] \ boldsymbol {V_2 = \ frac {Q} {C_2}} [/ латекс ] и [латекс] \ boldsymbol {V_3 = \ frac {Q} {C_3}} [/ latex].Общее напряжение складывается из отдельных напряжений:
[латекс] \ boldsymbol {V = V_1 + V_2 + V_3}. [/ Latex]
Теперь, назвав общую емкость [латекс] \ boldsymbol {C_S} [/ latex] для последовательной емкости, примите во внимание, что
[латекс] \ boldsymbol {V =} [/ latex] [латекс] \ boldsymbol {\ frac {Q} {C_S}} [/ latex] [латекс] \ boldsymbol {= V_1 + V_2 + V_3}. [/ Латекс ]
Вводя выражения для [latex] \ boldsymbol {V_1} [/ latex], [latex] \ boldsymbol {V_2} [/ latex] и [latex] \ boldsymbol {V_3} [/ latex], получаем
[латекс] \ boldsymbol {\ frac {Q} {C_S} = \ frac {Q} {C_1} + \ frac {Q} {C_2} + \ frac {Q} {C_3}}.[/ латекс]
Убирая [латекс] \ boldsymbol {Q} [/ latex] s, мы получаем уравнение для полной емкости в серии [латекс] \ boldsymbol {C_S} [/ latex] равным
[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {C_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {C_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {C_3}} [/ latex] [латекс] \ boldsymbol {+ \ cdots}, [/ latex]
, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.Выражение этой формы всегда приводит к общей емкости [латекс] \ boldsymbol {C_S} [/ latex], которая меньше любой из отдельных емкостей [латекс] \ boldsymbol {C_1} [/ latex], [латекс] \ boldsymbol {C_2} [/ latex],…, как показано в следующем примере.
Общая емкость в серии,
C сОбщая емкость в серии: [латекс] \ boldsymbol {\ frac {1} {C_S} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} + \ cdots } [/ латекс]
Пример 1: Что такое последовательная емкость?
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 [латекс] \ mu \ textbf {F} [/ latex].
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.
Решение
Ввод заданных емкостей в выражение для [latex] \ boldsymbol {\ frac {1} {C_S}} [/ latex] дает [latex] \ boldsymbol {\ frac {1} {C_S} = \ frac {1} { C_1} + \ frac {1} {C_2} + \ frac {1} {C_3}} [/ латекс].
[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.000 \; \ mu \ textbf {F}}} [/ latex] [latex] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {5.000 \; \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {8.000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol { =} [/ latex] [латекс] \ boldsymbol {\ frac {1.325} {\ mu \ textbf {F}}} [/ latex]
Инвертирование для поиска [latex] \ boldsymbol {C_S} [/ latex] дает [latex] \ boldsymbol {C_S = \ frac {\ mu \ textbf {F}} {1.325} = 0.755 \; \ mu \ textbf {F} }[/латекс].
Обсуждение
Общая последовательная емкость [латекс] \ boldsymbol {C_s} [/ latex] меньше наименьшей индивидуальной емкости, как и было обещано.При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40. Таким образом,
[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {40} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {8} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {5} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {53} {40 \; \ mu \ textbf {F}}}, [/ латекс]
так что
[латекс] \ boldsymbol {C_S =} [/ latex] [латекс] \ boldsymbol {\ frac {40 \; \ mu \ textbf {F}} {53}} [/ latex] [латекс] \ boldsymbol {= 0 .755 \; \ mu \ textbf {F}}. [/ latex]
На рис. 2 (а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость [латекс] \ boldsymbol {\ textbf {C} _ {\ textbf {p}}} [/ latex], сначала отметим, что напряжение на каждом конденсаторе составляет [латекс] \ boldsymbol {V} [ / latex], то же самое, что и у источника, так как они подключаются к нему напрямую через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения. Общий заряд [латекс] \ boldsymbol {Q} [/ latex] — это сумма отдельных зарядов:
[латекс] \ boldsymbol {Q = Q_1 + Q_2 + Q_3}. [/ Латекс]
Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.Используя соотношение [латекс] \ boldsymbol {Q = CV} [/ latex], мы видим, что общий заряд составляет [латекс] \ boldsymbol {Q = C _ {\ textbf {p}} V} [/ latex], и индивидуальные расходы: [латекс] \ boldsymbol {Q_1 = C_1 V} [/ latex] , [латекс] \ boldsymbol {Q_2 = C_2 V} [/ latex] , и [латекс] \ boldsymbol {Q_3 = C_3 V} [/ латекс]. Ввод их в предыдущее уравнение дает
[латекс] \ boldsymbol {C _ {\ textbf {p}} V = C_1 V + C_2 V + C_3 V}. [/ Latex]
Отменяя [latex] \ boldsymbol {V} [/ latex] из уравнения, мы получаем уравнение для полной емкости в параллельном [латексе] \ boldsymbol {C _ {\ textbf {p}}} [/ latex]:
[латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 \ cdots} [/ latex].
Полная параллельная емкость — это просто сумма отдельных емкостей. (И снова «… » означает, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в приведенном выше примере были подключены параллельно, их емкость была бы
[латекс] \ boldsymbol {C _ {\ textbf {p}} = 1.000 \; \ mu \ textbf {F} + 5.000 \; \ mu \ textbf {F} + 8.000 \; \ mu \ textbf {F} = 14.000 \; \ mu \ textbf {F}}. [/ latex]
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на Рисунке 2 (b).
Общая емкость параллельно,
C p [латекс] \ boldsymbol {C _ {\ textbf {p}}} [/ latex]Общая емкость параллельно [латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 + \ cdots} [/ latex]
Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.
Рис. 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 находятся последовательно; их эквивалентная емкость C S меньше, чем у любого из них. (c) Обратите внимание, что C S находится параллельно с C 3 .Таким образом, общая емкость равна сумме C S и C 3 .Смесь последовательной и параллельной емкости
Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ([латекс] \ boldsymbol {C_1 = 1.000 \; \ mu \ textbf {F}} [/ latex ], [латекс] \ boldsymbol {C_2 = 5.000 \; \ mu \ textbf {F}} [/ latex] и [латекс] \ boldsymbol {C_3 = 8.000 \; \ mu \ textbf {F}} [/ latex]) и округлите ответ до трех десятичных знаков.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы [латекс] \ boldsymbol {C_1} [/ latex] и [латекс] \ boldsymbol {C_2} [/ latex] включены последовательно. Их комбинация, обозначенная на рисунке [латекс] \ boldsymbol {C_S} [/ latex], параллельна [латексу] \ boldsymbol {C_3} [/ latex].
Решение
Поскольку [латекс] \ boldsymbol {C_1} [/ latex] и [latex] \ boldsymbol {C_2} [/ latex] включены последовательно, их общая емкость определяется выражением [латекс] \ boldsymbol {\ frac {1} {C_S } = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3}} [/ latex].Ввод их значений в уравнение дает
[латекс] \ boldsymbol {\ frac {1} {C_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {C_2}} [/ латекс ] [латекс] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {1.000 \; \ mu \ textbf {F}}} [/ латекс] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {5.000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.200} {\ mu \ textbf {F}}}. [/ latex]
Инвертирование дает
[латекс] \ boldsymbol {C _ {\ textbf {S}} = 0.833 \; \ mu \ textbf {F}}. [/ Latex]
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет
[латекс] \ begin {array} {r @ {{} = {}} l} \ boldsymbol {C _ {\ textbf {tot}}} & \ boldsymbol {C_S + C_S} \\ [1em] & \ boldsymbol { 0.833 \; \ mu \ textbf {F} + 8.000 \; \ mu \ textbf {F}} \\ [1em] & \ boldsymbol {8.833 \; \ mu \ textbf {F}}. \ end {array} [/ latex]
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к большим комбинациям конденсаторов.
- Общая емкость последовательно [латекс] \ boldsymbol {\ frac {1} {C _ {\ textbf {S}}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1 } {C_3} + \ cdots} [/ латекс]
- Общая емкость параллельно [латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 + \ cdots} [/ latex]
- Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.
Концептуальные вопросы
1: Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
1: Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.2: Предположим, вам нужна конденсаторная батарея с общей емкостью 0,750 Ф и у вас есть множество конденсаторов 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
3: Какую общую емкость можно получить, подключив символ [латекс] \ bold {5.00 \; \ mu \ textbf {F}} [/ latex] и конденсатор [latex] \ boldsymbol {8.00 \; \ mu \ textbf {F}} [/ latex] вместе?
4: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.5: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.
Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.6: Необоснованные результаты
(a) Конденсатор [латексный] \ boldsymbol {8.00 \; \ mu \ textbf {F}} [/ latex] подключен параллельно другому конденсатору, что дает общую емкость [латекс] \ boldsymbol {5.00 \; \ mu \ textbf {F}} [/ латекс]. Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Решения
Задачи и упражнения
1: [латекс] \ boldsymbol {0.293 \; \ mu \ textbf {F}} [/ латекс]
3: [латекс] \ boldsymbol {3.08 \; \ mu \ textbf {F}} [/ latex] в последовательной комбинации, [latex] \ boldsymbol {13.0 \; \ mu \ textbf {F}} [/ latex ] в параллельной комбинации
4: [латекс] \ boldsymbol {2.79 \; \ mu \ textbf {F}} [/ латекс]
6: (a) [латекс] \ boldsymbol {-3.00 \; \ mu \ textbf {F}} [/ latex]
(b) У вас не может быть отрицательного значения емкости.
(c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным.Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.
Конденсаторы комбинированные
В некоторых цепях конденсаторы включены последовательно и параллельно. Чтобы определить, например, общий заряд, накопленный набором конденсаторов, мы должны найти единственную эквивалентную емкость набора.Это делается путем идентификации пары конденсаторов в наборе, которые включены последовательно или параллельно друг другу, замены этой пары эквивалентным конденсатором (тем самым уменьшая количество конденсаторов на один) и повторения до тех пор, пока у нас не останется один. конденсатор, который является эквивалентом набора.
Возьмем, к примеру, ситуацию, описанную выше. Четыре конденсатора имеют следующие значения:
C 1 = C 2 = 90 пФ.
C 3 = 45 пФ
C 4 = 120 пФ
Какова разность потенциалов на каждом конденсаторе? Сколько заряда у каждого конденсатора?
Чтобы решить эту проблему, нам нужно найти эквивалентную емкость набора конденсаторов.Первый шаг — перерисовать схему так, чтобы C 1 был нарисован вертикально — это делает более очевидным, что идет параллельно или последовательно.
Теперь сократите цепь с 4 конденсаторов до 1.
Шаг 1 — C 2 и C 3 идут последовательно. Замените эту пару одним конденсатором C 23 :
1 / C 23 = 1 / C 2 + 1 / C 3 = 1/90 + 1/45 = 3/90.
Следовательно, C 23 = 90/3 = 30 пФ.
Шаг 2 — C 1 и C 23 идут параллельно. Замените эту пару одним конденсатором C 123 = 90 + 30 = 120 пФ.
Шаг 3 — C 4 и C 123 идут последовательно. Замените эту пару одним конденсатором C eq :
1 / C экв. = 1 / C 4 + 1 / C 123 = 1/120 + 1/120 = 2/120
C экв = 120/2 = 60 пФ
Шаг 4 — Определите заряд на C экв. .
Q = C экв ΔV = 60 пФ * 12 В = 720 пКл.
Теперь нам нужно расширить схему до четырех исходных конденсаторов и определить заряд и разность потенциалов на каждом из них по мере продвижения.
Шаг 1 — C eq представляет C 4 и C 123 последовательно. Последовательные конденсаторы имеют одинаковый заряд, но разделяют разность потенциалов.
Q 4 = Q 123 = 720 пКл.
Конденсаторы одинаковые, поэтому на каждый из них подается по 6 вольт.
Шаг 2 — C 123 представляет собой C 1 и C 23 параллельно. Параллельно подключенные устройства имеют одинаковую разность потенциалов (в данном случае 6 В).
Q 1 = C 1 * 6 = 540 пКл.
Q 23 = C 23 * 6 = 180 пКл.
Они добавляют к 720 пКл, как и должно быть.
Шаг 3 — C 23 представляет последовательно C 2 и C 3 .
Q 2 = Q 3 = 180 пКл.
ΔV 2 = Q 2 / C 2 = 180/90 = 2 вольта.
ΔV 3 = Q 3 / C 3 = 180/45 = 4 В.
Они добавляют к 6 вольт, как должны.
Шаг 4. Хороший способ проверить согласованность — пометить потенциал в разных точках. Выберите некоторую точку в качестве ориентира (скажем, 0 В на отрицательном полюсе батареи) и пометьте другие точки, относящиеся к ней.Убедитесь, что разность потенциалов на конденсаторах соответствует этим значениям потенциала.
Последовательные и параллельные конденсаторы — проблемы и решения
1. Три конденсатора, C 1 = 2 мкФ, C 2 = 4 мкФ, C 3 = 4 мкФ, подключены последовательно и параллельно. Определите емкость отдельного конденсатора, которая будет иметь такой же эффект, как и комбинация.
Известный:
Конденсатор C 1 = 2 мкФ
Конденсатор C 2 = 4 мкФ
Конденсатор C 3 = 4 мкФ
Требуется: Эквивалентная емкость (C)
Решение:
Конденсатор С 2 и С 3 соединены параллельно.Эквивалентная емкость:
C P = C 2 + C 3 = 4 + 4 = 8 мкФ
Конденсатор C 1 и C p соединены последовательно. Эквивалентная емкость:
1 / C = 1 / C 1 + 1 / C P = 1/2 + 1/8 = 4/8 + 1/8 = 5/8
C = 8/5 мкФ
2. Пять конденсаторов, C 1 = 2 мкФ, C 2 = 4 мкФ, C 3 = 6 мкФ, C 4 = 5 мкФ, C 5 = 10 мкФ, соединены последовательно и параллельно.Определите емкость отдельного конденсатора, которая будет иметь такой же эффект, как и комбинация.
Известный:
Конденсатор C 1 = 2 мкФ
Конденсатор C 2 = 4 мкФ
Конденсатор С 3 = 6 мкФ
Конденсатор C 4 = 5 мкФ
Конденсатор C 5 = 10 мкФ
Требуется: Эквивалентная емкость (C)
Раствор:
Конденсатор С 2 и С 3 соединены параллельно.Эквивалентная емкость:
C P = C 2 + C 3
С P = 4 + 6
C P = 10 мкФ
Конденсатор C 1 , C P , C 4 и C 5 соединены последовательно. Эквивалентная емкость:
1 / C = 1 / C 1 + 1 / C P + 1 / C 4 + 1 / C 5
1 / C = 1/2 + 1/10 + 1/5 + 1/10
1 / C = 5/10 + 1/10 + 2/10 + 1/10
1 / C = 9/10
C = 10/9 мкФ
3.C 1 = 3 мкФ, C 2 = 4 мкФ и C 3 = 3 мкФ, соединены последовательно и параллельно. Определите электрическую энергию в цепях.
Известный:
Конденсатор C 1 = 3 мкФ
Конденсатор C 2 = 4 мкФ
Конденсатор C 3 = 3 мкФ
Требуется: Эквивалентная емкость (C)
Раствор:
Конденсатор С 2 и С 3 соединены параллельно.Эквивалентная емкость:
C P = C 2 + C 3
C P = 4 + 3
C P = 7 мкФ
Конденсатор C 1 и C P соединены последовательно. Эквивалентная емкость:
1 / C = 1 / C 1 + 1 / C P
1 / C = 1/3 + 1/7
1 / C = 7/21 + 3/21
1 / C = 10/21
С = 21/10
C = 2,1 мкФ
С = 2.1 x 10 -6 F
Электроэнергия в цепях:
E = ½ C V 2
E = ½ (2,1 x 10 -6 ) (12 2 )
E = ½ (2,1 x 10 -6 ) (144)
E = (2,1 x 10 -6 ) (72)
E = 151,2 x 10 -6 Джоуль
E = 1,5 x 10 -4 Джоуль
конденсаторов последовательно и параллельно с примерами
Последовательные и параллельные конденсаторы
Системы с более чем одним конденсатором имеют эквивалентную емкость.Конденсаторы можно соединять между собой двумя способами. Их можно подключать последовательно и параллельно. Сначала мы увидим конденсаторы, включенные параллельно.
В этой цепи конденсаторы включены параллельно.
Потому что левые стороны конденсаторов подключены к потенциалу a, а правые стороны конденсаторов подключены к потенциалу b.Другими словами, мы можем сказать, что каждый конденсатор имеет одинаковую разность потенциалов. Находим заряд каждого конденсатора как;
Q 1 = C 1 .V
Q 2 = C 2 .V
Q 3 = C 3 .V
Общий заряд системы определяется путем сложения каждого заряда.
Q итого = C экв .V
Q итого = Q 1 + Q 2 + Q 3 = C 1 .V + C 2 .V + C 3 .V = V. (C 1 + C 2 + C 3 ) = C экв.
C экв. = C 1 + C 2 + C 3
Как видите, мы нашли эквивалентную емкость системы как C 1 + C 2 + C 3
Теперь посмотрим последовательно включенные конденсаторы;
В конденсаторах, подключенных последовательно, каждый конденсатор имеет одинаковый поток заряда от батареи.В этой схеме заряд + Q течет от положительной части батареи к левой пластине первого конденсатора и притягивает заряд –Q на правой пластине, с той же идеей заряд -Q течет от батареи к правой пластине. третьего конденсатора и притягивает + Q на левой пластине. Таким же образом заряжаются и другие конденсаторы. Подводя итог, можно сказать, что каждый конденсатор имеет одинаковый заряд с батареей.
C 1 .V 1 = Q
С 2 .V 2 = Q, V = V 1 + V 2 + V 3 и Q = C экв .V
C 3 .V 3 = Q
Пример: Рассчитайте эквивалентную емкость между точками a и b.
Пример: В приведенной ниже схеме C1 = 60 мкФ, C2 = 20 мкФ, C3 = 9 мкФ и C4 = 12 мкФ.Если разность потенциалов между точками a an b Vab = 120V, найдите заряд второго конденсатора.
Электростатические экзамены и решения
| Емкость и конденсаторы <Пред. | Далее> Памятка по электростатике |
|---|
Последовательный и параллельный калькулятор емкости
- Цель использования
- Выяснение, какая комбинация конденсаторов у меня под рукой может создать значение, которое мне нужно в данной схеме
- Комментарий / Запрос
- Возможность добавления более двух конденсаторов
[1] 2020/11/18 16:33 Моложе 20 лет / Другое / Очень /
- Назначение Используйте
- Чтобы проверить мою собственную работу по созданию проблем, которые должны решить младшие технические специалисты
[2] 12.08.2020 18:32 Уровень 30 лет / Инженер / Полезный /
- Цель использования
- ДЛЯ ПОНИМАНИЯ
- Комментарий / Запрос
- ДЛЯ ПОЛУЧЕНИЯ ЗНАНИЙ
[3] 2019/11/15 08:26 Уровень 20 лет / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- Генератор Колпитца на УКВ, рассчитать общую емкость e на двойных варикапных диодах, используемых для настройки, а также общая емкость на делителе обратной связи.
[4] 2019/04/10 06:25 Уровень 30 лет / Самостоятельно занятые люди / Очень /
- Цель использования
- Помимо того, что я радиолюбитель, я также занимаюсь изготовлением кристаллических радиоприемников.
Для многих конструкций требуется воздушный конденсатор емкостью 500 пФ, но все, что я смог найти, это 630 пФ.
Итак, используя ваш калькулятор, я смог увидеть, сколько емкости мне нужно было добавить последовательно, чтобы снизить емкость конденсатора 630 пФ до 500 пФ.Отлично сработало, мое искреннее спасибо.
[5] 2019/03/07 22:04 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Отсутствие правильных значений на двух крышках.Используется для расчета заменяемых колпачков для старой магнитофонной деки.
- Комментарий / запрос
- Очень полезно
[6] 2018/08/27 12:07 Уровень 40 лет / Другое / Очень /
- Цель использования
- Расчет шины питания для лампового усилителя
[7] 2018/08/17 04:15 Уровень 40 лет / Самозанятые люди / Очень /
- Цель использования
- Устранение неисправностей источника питания. У меня был счетчик, который показывал максимум 10000 мкФ.Итак, мне пришлось последовательно соединить два одинаковых, чтобы проверить значение крышки фильтра.
[8] 2018/08/11 16:16 Уровень 60 и старше / Офисный работник / Государственный служащий / Полезный /
- Цель использования
- Расчет емкости для настройки антенны
[9] 2018/08/06 09:40 Уровень 20 лет / Инженер / Очень /
- Цель использования
- Два последовательно соединенных диода общей емкости для проектирования антенны.
[10] 13.06.2018 07 : 08 Уровень 50 лет / Средняя школа / Университет / Аспирант / Very /
Примеры случаев замены входных / выходных конденсаторов импульсного источника питания с MLCC на гибридные конденсаторы — Промышленные устройства и решения
Продукты, описанные на этом веб-сайте, были разработаны и изготовлены для стандартных приложений, таких как общие электронные устройства, офисное оборудование, данные и связь оборудование, измерительные приборы, бытовая техника и аудио-видео техника.Для специальных применений, в которых требуется качество и надежность, или если отказ или неисправность продукции может напрямую угрожать жизни или вызвать угрозу травмы (например, для самолетов и аэрокосмического оборудования, дорожного и транспортного оборудования, оборудования для сжигания, медицинского оборудования , устройства для предотвращения несчастных случаев и защиты от кражи, а также защитное оборудование), пожалуйста, используйте только после того, как ваша компания в достаточной степени проверит пригодность наших продуктов для этого применения.
Независимо от области применения, при использовании наших продуктов в оборудовании, для которого ожидается высокий уровень безопасности и надежности, убедитесь, что цепи защиты, схемы резервирования и другие устройства установлены для обеспечения безопасности оборудования при оценке применения путем независимой проверки безопасности. тесты.
Обратите внимание, что продукты и технические характеристики, размещенные на этом веб-сайте, могут быть изменены без предварительного уведомления в целях улучшения. Независимо от области применения, пожалуйста, подтвердите последнюю информацию и спецификации до окончательного этапа проектирования, покупки или использования.
Техническая информация на этом веб-сайте содержит примеры типичных операций и схем применения продуктов. Он не предназначен для гарантии ненарушения или предоставления лицензии на права интеллектуальной собственности этой компании или любой третьей стороны.
Если какие-либо продукты, спецификации продуктов и техническая информация на этом веб-сайте подлежат экспорту или предоставлению нерезидентам, необходимо соблюдать законы и постановления страны-экспортера, особенно те, которые касаются безопасного экспортного контроля.
Информация, содержащаяся на этом веб-сайте, не может быть перепечатана или воспроизведена полностью или частично без предварительного письменного разрешения Panasonic Corporation.
Инструменты и программы, представленные на этом веб-сайте, должны использоваться по вашему усмотрению.Panasonic не гарантирует каких-либо результатов от использования этих инструментов и программ и не несет ответственности за любые убытки, возникшие в результате использования вами.
<о письме для получения сертификата соответствия директиве ЕС RoHS>
Дата перехода на продукт, соответствующий требованиям RoHS, зависит от номера детали или серии.
При использовании инвентаря, в котором неясно соответствие требованиям RoHS, выберите «Запрос на продажу».
в форме веб-запроса.
Извещение о передаче полупроводникового бизнеса
Полупроводниковый бизнес Panasonic Corporation (далее именуемой «Компания») будет передан 1 сентября 2020 года Nuvoton Technology Corporation (далее именуемой «Nuvoton»). Соответственно, Panasonic Semiconductor Solutions Co., Ltd., которая управляла полупроводниковым бизнесом Panasonic, перейдет под эгидой Nuvoton Group с новым названием Nuvoton Technology Corporation Japan (далее именуемой «NTCJ»).
В соответствии с этой передачей полупроводниковая продукция, размещенная на этом веб-сайте, будет считаться продукцией, произведенной NTCJ, после 1 сентября 2020 года. Однако такая продукция будет постоянно продаваться через Компанию.
Обратите внимание, что при запросе о полупроводниковых продуктах, размещенных на этом веб-сайте, клиенты должны перейти на веб-сайт, управляемый NTCJ (далее «веб-сайт NTCJ»), и подтвердить, что NTCJ является компанией, ответственной за управление личной информацией, предоставляемой клиентами на ее веб-сайте.Мы ценим ваше понимание по этому поводу.
Результаты поиска
терпеливость. * 2: Синфазная дроссельная катушка — это катушка , фильтр , который удаляет проблемный синфазный шум при ди … натуризации, и Высокая емкость в тесно взаимосвязанной эволюции с CASE Trend (2/3) Время работы автомобиля. .th, в таких условиях потребуется даже высокий уровень надежности er. Однако у нас все еще нет … повышения качества при достижении компактных размеров и высокой емкости , степень технического ди…сью в это время будет увеличивать дальность плавания. Аккумуляторы высокой емкости должны быть оснащены до
https://article.murata.com/en-global/article/automotive-mlcc-3
компоненты, которые вы хотите передать, в том числе проход фильтр с, который отфильтровывает низкочастотные компоненты и высокочастотный … фильтр с, который отфильтровывает из высокочастотных компонентов.Murata Manufacturing Co., Ltd. Компоненты, которые подробно описаны ниже: соединение, развязка, сглаживание и фильтр ing. <Связь> Ca … конденсаторы для сглаживания < Filter ing> Конденсаторы объединены с резисторами и индукторами для создания фильтра s th … только для передачи сигналов определенной частоты. В зависимости от FR
могут использоваться разные фильтры shttps://article.murata.com/en-global/article/basics-of-capacitors-5
SAW фильтр в качестве примера.Использовались фильтр SAW от Murata ( проход, , диапазон 800 МГц) и РЧ-индуктор, а также характеристики диапазона прохода . Рисунок 3: Общие характеристики SAW Filter Рисунок 4: Pass Band Ch … характеристики SAW Filter Глядя на полосу pass на рисунке 4, можно убедиться, что вставка lo … ss фильтра SAW отличается используемым РЧ индуктором. В высокочастотных цепях разница в тыс…ss фильтра на ПАВ ниже, когда РЧ индуктор Q равен , высокий er (более низкие потери). Соответственно уровень
https://www.murata.com/en-global/products/inductor/chip/library/solution/solution1/rf/loss
n удалить шум как проблему — выберите фильтр EMI , который имеет высокий ly, эффективный для удаления шума на … LC композитный фильтр EMI с крутой кривой вносимых потерь и высокой селективностью сигнал фр…воды / Подавление электромагнитных помех Фильтр с / Устройства защиты от электростатических разрядов Подавление электромагнитных помех Фильтр с (подавление ЭМС и шумов) Фильтр с (подавление электромагнитных помех и шумов) Прокрутка влево Прокрутка вправо Закрыть Подавление электромагнитных помех Фильтр с (EMC и No … h Период Выбор компонентов для шумоподавления Выбор базового фильтра EMI s Пример шума Su
https://www.murata.com/en-global/products/emc/emifil/library/knowhow/lte/chapter04
Фильтр , используемый в качестве меры противодействия шуму в датчиках, описан ниже. Пройдите мощность при … двух условиях, которые требуются в фильтре являются общими для любого датчика. Пропустите источник питания и сигналы снова будут эффективными. Меры противодействия шуму в линиях электропередач. Фильтр с высокими вносимыми потерями на широких линиях. * Ферритовые шарики, индуктор типа , фильтр , не только блокируют шум с их высоким im … oducts / EMI Suppression Filter s / ESD Protection Devices EMI Suppression Filter s (EMC and Noise Su
https: // www.murata.com/en-global/products/emc/emifil/library/pickup/sensor/1
В подтверждение этого, фильтр SAW от Murata (800 МГц, , полоса пропускания ) и ВЧ-индуктор были использованы для замены ВЧ-индуктора с … Все характеристики SAW-фильтра Рис. Глядя на характеристики полосы пропускания на фиг. 4, можно подтвердить, что вносимые потери фильтра на ПАВ …. диапазон в соответствии с используемой высокочастотной схемой (фильтр SAW в этом тесте), согласующей схемой, от … другой Q в согласующей цепи, и вносимыми потерями фильтра SAW были измерено и co
https://www.murata.com/en-global/products/inductor/chip/library/learn/apply/matching
как high, — дифференциальные, так и несимметричные сигналы. 5Шумовой фильтр с для подавления шума для MI…oducts / Подавление электромагнитных помех Фильтр с / Устройства защиты от электростатических разрядов Подавление электромагнитных помех Фильтр с (подавление электромагнитных помех и шума) Библиотека шумоподавления для MIPI D-PHY Подавление электромагнитных помех Фильтр с (подавление электромагнитных помех и шумов) Прокрутите влево … футы Прокрутите вправо Закройте Подавление электромагнитных помех Фильтр с (подавление электромагнитных помех и шумов) Подавление шума для MIPI D -… r MIPI D-PHY 4 Замечания по подавлению шума для MIPI D-PHY 5 Фильтр шумов с с для шумоподавление для MI
https: // www.murata.com/en-global/products/emc/emifil/library/pickup/mipid-phy
сжатие фильтр с функционирует как фильтр нижних частот фильтр с. Трудно регулировать работу по «устранению хаоса, с которой приходится иметь дело, используя фильтр нижних частот проход с, точно так же, как с мерами противодействия шуму, принятыми для цифрового … н … ого как фильтр нижних частот проход s. Ответственное лицо: Murata Manufacturing Co., Ltd. Yasuhiro Mitsuya Сопутствующие товары Продукты для подавления шума / Подавление электромагнитных помех Фильтр s / Устройства защиты от электростатических разрядов Сопутствующие статьи Меры по борьбе с сетевым шумом с использованием синфазных дроссельных катушек Введение в Noise Filter s для Smart Ph
https://article.murata.com/en-global/article/basics-of-noise-countermeasures-lesson-2
Это идентично тому, что было до того, как был вставлен фильтр , а тест на соответствие Thunderbolt 3 был пройден …oducts / Подавление электромагнитных помех Фильтр с / Устройства защиты от электростатических разрядов Подавление электромагнитных помех Фильтр с (подавление электромагнитных помех и шумов) Библиотека шумоподавления для USB4 (4) Подавление электромагнитных помех Фильтр с (подавление электромагнитных помех и шумов) Прокрутите влево … футы Прокрутите вправо Закройте Подавление электромагнитных помех Фильтр сек (ЭМС и шумоподавление) Шумоподавление для USB4 (4 … продуктов. HOME Электронные компоненты Продукты шумоподавления / Подавление электромагнитных помех Фильтр сек / Защита от электростатических разрядов De
https: // www.murata.com/en-global/products/emc/emifil/library/pickup/usb4-4
r соотношение между вносимыми потерями фильтра , включая выходной LC преобразователя постоянного / постоянного тока и проходом … e PA и силовой цепью — Пример использования силовых индукторов для дросселей — Выбор фильтра s до улучшить си … нвертер. Вносимые потери для каждого условия фильтра показаны ниже. Из-за изменения частоты 2 Условие 3 Условие 4 Условие 5 Условие 6 Взаимосвязь между Вносимыми потерями фильтра и переменным током…LR Отношение между вносимыми потерями (@ 6 МГц) каждого из фильтров , условий 1-6 , показанных выше, и th
https://www.murata.com/en-global/products/inductor/chip/library/solution/solution1/power/noise2
от z до ГГц, поэтому в широком диапазоне должно быть получено высокое сопротивление и . Фильтр PoC от Murata сек … индуктивности для фильтра PoC сек, достижение как высокой производительности er, так и меньших размеров является проблемой…дуктор, в котором низкочастотные сигналы проходят через легко, а высокочастотные сигналы имеют трудности. проходят через … грубые, используются для того, чтобы позволить низкочастотному источнику постоянного тока проходить через и блокировать высокочастотные -частотные сигналы данных. В … компоненте для предотвращения неисправностей в электронных системах управления, а также PoC фильтр , который позволяет повторно использовать
https://article.murata.com/en-global/article/inductors-supporting-in-vehicle-network-2
используются высокочастотные сигналы при блокировке постоянного тока вместе с катушками, которые пропускают постоянный ток…водов / Подавление электромагнитных помех Фильтр с / Устройства защиты от электростатических разрядов Подавление электромагнитных помех Фильтр с (подавление электромагнитных помех и шумов (1) Подавление электромагнитных помех Фильтр с (подавление электромагнитных помех) Прокрутка влево Прокрутка вправо Закрыть EMI Su … ppression Filter s (ЭМС и шумоподавление) Требования к системе PoC для индукторов и шумоподавления (1) Co … oducts. HOME Электронные компоненты Шумоподавляющие продукты / Подавление электромагнитных помех Фильтр s / Защита от электростатических разрядов De
https: // www.murata.com/en-global/products/emc/emifil/library/techdoc/automotive6-poc1
⇒ ⇒ ⇒ Расширение возможностей подключения и ускорение инноваций! Все началось с фильтра SAW s для ра …. Агрегация [SAW Фильтр s] 2000-е годы 2010-е PAs] Многополосность GSM, формование смол, GaAs sw…услуги. Многослойный фильтр LC для беспроводного телефона BPF. [Компонент на основе LTCC] Базовая конструкция многослойного фильтра LC разработана для использования в беспроводном телефоне BPF. 【Глоссарий】 ・ FEM: CMOS sw
https://corporate.murata.com/-/media/corporate/about/newsroom/techmag/metamorphosis20/special/innovation/innovation.ashx?la=en&cvid=20170
3744398703В цепи они работают как фильтр нижних частот , , , .С обычными катушками индуктивности основная характеристика среди им … ils Введение в шумовой фильтр для аудиосхем смартфонов. ток высокой частоты проходит … восходящий, ток имеет тенденцию к проходить легче по мере увеличения частоты, поэтому высокая частота э … tsuya Сопутствующие товары Продукты для подавления шума / Подавление электромагнитных помех Фильтр s / ESD Protection Devices Ch
https: // статья.murata.com/en-global/article/basics-of-noise-countermeasures-lesson-4
курс 5-4. Краткое содержание главы 5 Глава 6 6-1. Введение 6-2. Подавление электромагнитных помех фильтр с 6-3. Фильтр низких частот фильтр … продукты / Подавление электромагнитных помех Фильтр s / Устройства защиты от электростатических разрядов Подавление электромагнитных помех Фильтр s (подавление электромагнитных помех и шума) Библиотека шумоподавления Базовые факторы курса Факторы усложнения проблем с шумом Подавление электромагнитных помех Фильтр …s (ЭМС и шумоподавление) Прокрутка влево Прокрутка вправо Закрыть Подавление электромагнитных помех Фильтр с (Подавление электромагнитных помех и шумов) Шумоподавление / Подавление электромагнитных помех Фильтр с Проведите пальцем влево или вправо, чтобы изменить экраны Просмотреть в la
https://www.murata.com/en-global/products/emc/emifil/library/knowhow/basic/chapter03-p4
курс 5-4. Краткое содержание главы 5 Глава 6 6-1. Введение 6-2. Подавление электромагнитных помех фильтр с 6-3.Фильтр низких частот Фильтр … продукты / Подавление электромагнитных помех Фильтр s / Устройства защиты от электростатического разряда Подавление электромагнитных помех Фильтр s (подавление электромагнитных помех и шума) Библиотека Подавление шума Базовый курс Механизм возникновения электромагнитных помех EMI Подавление Фильтр … s (ЭМС и подавление шума) Прокрутите влево Прокрутите вправо Закройте Подавление электромагнитных помех Фильтр s (подавление электромагнитных помех и шум …) Продукты шумоподавления / Подавление электромагнитных помех Фильтр s Проведите пальцем влево или вправо, чтобы сменить экраны Посмотреть в la
https: // www.murata.com/en-global/products/emc/emifil/library/knowhow/basic/chapter02-p4
Таким образом, идентификация механизмов проводимости, выбор оптимального EMI фильтра s и пл … сорберов эффективны, в то время как, если проводящая проводимость служит механизмом, использование фильтра EMI s является эффективным. … дефектный. Что касается фильтра EMI s, мы рекомендуем ферритовые шарики, синфазные дроссельные катушки, π-тип / Т-образный фильтр …помощь сосредоточена на максимально возможном блокировании шума. Фильтр EMI s должен быть помещен в cl … поскольку шум, улавливаемый антенной, был уменьшен за счет вставки фильтра EMI s, перейдите к ve
https://article.murata.com/en-global/article/mitigate-deterioration-in-reception-sensitivity-of-WLAN
равноправие — это частота, на которой (1) мощность, которая может пройти через фильтр , уравновешивает (2) мощность, которая прибл…nnot пройти через фильтр . Другими словами, это частота, на которой выходная мощность составляет 1/2 от … мощности фильтра , я отвечаю, что она примерно в 3-5 раз выше , чем базовая частота. Это была ферритовая бусина 166 Ом, полное сопротивление в положении установки фильтра было высокое , 1 кОм, wi … e высокое -частотная составляющая (шум) сигнала составляет передать изд. в GND. — Сопротивление резистора А со
https: // www.murata.com/en-global/products/emc/emifil/library/knowhow/basic/s2-chapter01-p1
тенна. Рис. 1 Состав схемы NFC Фильтр LC действует как фильтр нижних частот , проход , который удаляет верхние частоты … NFC Как показано ниже, схема NFC состоит из NFC IC, фильтра LC , согласующая схема и … реверсивный, поскольку фильтр LC расположен рядом с последующей согласующей схемой, элемент фильтра LC co…nstant влияет на соответствие. По этой причине катушка индуктивности, используемая в фильтре LC , должна иметь индуктивность, соединенную в фильтре LC , независимо от значения тока. Кроме того, катушка индуктивности должна иметь малые потери, поэтому
https://article.murata.com/en-global/article/an-introduction-to-inductors-used-in-nfc-circuits
Таким образом, катушка функционирует как -проходной фильтр нижних частот, который блокирует ток высокой частоты , обеспечивая ослабление.




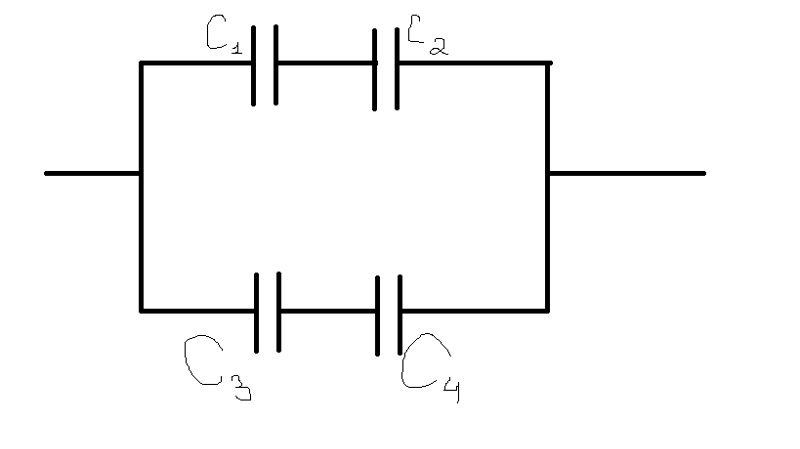 е. q=q1=q2
е. q=q1=q2
 Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;