Решение задач смешанное соединение конденсаторов – Пример решения задачи по теме «Соединение конденсаторов» | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Как решать задачи со смешанным соединением конденсаторов — MOREREMONTA

Преподаватель междисциплинарного курса

Практическое занятие №4

Тема: Расчет общей емкости конденсатора

Цель: рассчитать напряжение, заряд, емкость конденсаторов и их энергию в электрических цепях постоянного тока с последовательным, параллельным и смешанным соединением конденсаторов.

1. Изучить краткие теоретические сведения.

2. Рассмотреть примеры выполнения задания.

3. Выполнить индивидуальное задание.

1. Краткие теоретические сведения

Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).

где С емкость конденсатора, Ф

Q – заряд конденсатора, Кл

U – напряжение на конденсаторе, В

Энергия конденсатора зависит от его емкости. Поэтому при изменении емкости заряженного конденсатора будем изменяться его энергия:

где W – энергия конденсатора, Дж

В электрических цепях применяются различные способы соединения конденсаторов.

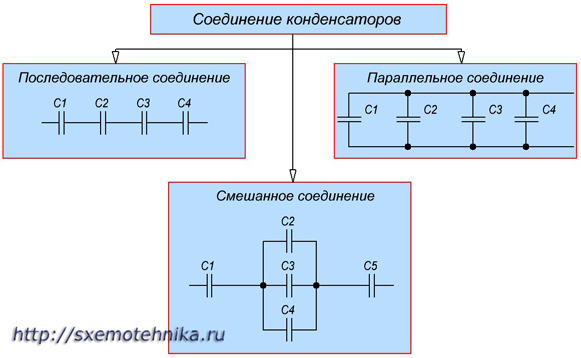
Соединение конденсаторов может производиться: последовательно, параллельно и смешанно (то есть последовательно-параллельно). Существующие виды соединения конденсаторов показаны на рисунке 1.

Рисунок 1. Способы соединения конденсаторов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока.

U = UC1 = UC2 = UC3 = …

Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы:

Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Собщ = С1 + С2 + С3 + …

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.

Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Рисунок 3. Последовательное соединение конденсаторов.

При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д. Всю группу конденсаторов, соединенных последовательно, можно рассмотреть как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Напряжения на различных конденсаторах будут различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.

U = UC1 + UC2 + UC3 + …

Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:

Для частного случая двух последовательно соединенных конденсаторов рисунок 4

Рисунок 4. Последовательное соединение двух конденсаторов

Формула для вычисления их общей емкости будет иметь вид:

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 5 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 5. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов.

Всякое смешанное соединение конденсаторов путем упрощений может быть сведено либо к параллельному соединению, либо к последовательному.

Алгоритм расчета имеет вид:

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 6.

Рисунок 6. Алгоритм сворачивания схемы при смешанном соединении конденсаторов

Пример выполнения задания

Дано: Решение:

U = 36 В 1. Конденсаторы С1 и С2 соединены параллельно:

Собщ, q1, q2, q3, С1,2 = С1 + С2 = 8×10-6 + 4×10-6 = 12×10-6 Ф = 12 мкФ

q4, q, W1, W2, 2. Конденсаторы С3 и С4 соединены последовательно:

W3, W4, W — ?

3. Общая емкость:

Собщ =

4. Определим заряд цепи:

q = Собщ×U = 2×10-6×36 = 72×10-6 Кл = 72 мкКл

При последовательном соединении конденсаторов:

q = q1,2 = q3 = q4 = 72 мкКл

Тогда, напряжение на участках цепи

U1,2 =

U3 =

U4 =

U1,2 = U1 = U2 = 6 В, тогда

q1 = C1×U1 = 8×10-6×6 = 48×10-6 Кл = 48 мкКл

q2 = C2×U2 = 4×10-6×6 = 24×10-6 Кл = 24 мкКл

5. Энергия всей цепи:

W = = 1,29 мДж

Энергия электрического поля каждого конденсатора:

W1 =

W2 =

W3 =

W4 =

Ответ: Собщ = , q1 = 48 мкКл, q2 = 24 мкКл, q = q3 = q4 = 72 мкКл,

W1 , W2 , W3

, W4

Эквивалентная емкость верхней ветви

Эквивалентная емкость нижней цепи

Теперь это смешанное соединение конденсаторов может быть приведено к параллельному соединению. Эквивалентная емкость всей батареи конденсаторов

Эквивалентная емкость между точками 1 и 2:

Эквивалентная емкость между точками 2 и 3

Теперь это смешанное соединение конденсаторов может быть приведено к последовательному соединению

Эквивалентная емкость батареи конденсаторов

Конденсатор емкостью С=2 мкф и номинальным рабочим напряжением Up=600 в вышел из строя.

Составить схему замены его конденсаторами емкостью С=1 мкФ и номинальным рабочим напряжением Up=200 В.

Р е ш е н и е. Конденсаторы с номинальным рабочим напряжением 200 В нельзя включать под напряжение 600 В. Поэтому прежде всего необходимо обеспечить электрическую прочность батареи. Для этого конденсаторы надо соединить последовательно. Число последовательно соединенных конденсаторов должно быть

Емкость такой ветви

Для обеспечения емкости батареи необходимо соединить несколько параллельных ветвей. Число параллельных ветвей

Общая схема замены конденсатора

3. Индивидуальные задания для обучающихся

Задание: Определить эквивалентную емкость цепи, напряжение на каждом конденсаторе, заряд и энергию электрического поля в цепи и для каждого конденсатора.

Варианты задания, номера схемы и исходные данные для расчета приведены в таблице 1.

Попроси больше объяснений
Следить
Отметить нарушение

VeronikaRov 13.09.2016

Ответ

Проверено экспертом

Конденсаторы С₂ и С₃ соединены ПОСЛЕДОВАТЕЛЬНО, поэтому
С₂₃ = 0,45*0,15/(0,45+0,15)=0,1125 мкФ

Конденсаторы С₄ и С₅ тоже соединены последовательно, поэтому
С₄₅ = 0,2*0,6/(0,2+0,6) = 0,15 мкФ

Конденсаторы С₁, С₂₃ и С₄₅ соединены ПАРАЛЛЕЛЬНО, поэтому
С₀ = 0,35+0,1125+0,15 ≈0,61 мкФ = 0,61*10⁻⁶ Ф

Общий заряд
Q = C₀*U = 0,61*10⁻⁶*75 ≈ 0,46 мкКл

Теперь осталось «обратным» ходом вычислить заряды на каждом конденсаторе. Вот и всё!

Лабораторная работа №3

Тема: «Соединение конденсаторов»

Цель: изучить параллельное, последовательное и смешанное соединение конденсаторов.

Оборудование: мультиметр, источник переменного напряжения, конденсаторы.

Теоретический материал

Электроемкость — это скалярная величина, характеризующая способность проводника накапливать электрический заряд

Электроемкость зависит от формы проводника.

Поэтому для каждого вида существует своя формула расчета электроемкости.

Конденсатор — это система, состоящая из двух или более проводников.

Плоский конденсатор — две параллельные металлические пластины (обкладки), между которыми находится диэлектрик.

В быту можно встретить подобные конденсаторы

На схеме конденсатор обозначается следующим образом:

Электроемкость плоского конденсатора

Используя общую формулу нахождения электроемкости, можно получить

Поле между обкладками конденсатора однородно, поэтому напряжение можно определить как

Несколько конденсаторов, соединенных вместе, образуют батарею конденсаторов.

Различают последовательное, параллельное и смешанное соединение конденсаторов

Порядок выполнения

Задание 1. Последовательное соединение конденсаторов

1. Собрать схему:

2. Емкость конденсаторов С_конд и напряжение U_ист на источнике переменного тока установить по указанию преподавателя.

3. Измерьте напряжение U_конд с помощью вольтметра на каждом конденсаторе.

4. Вычислите заряд каждого конденсатора q_конд

5. Вычислите общую емкость С_общ батареи конденсаторов.

6. Найдите общее напряжение U_общ и сравните его с напряжением источника U_ист переменного напряжения.

7. Заполните таблицу:

№ конд

С_конд, Ф

U_конд, В

q_конд, Кл

С_общ, Ф

U_общ, В

U_ист, В

Задание 2. Параллельное соединение конденсаторов

1. Собрать схему:

3. Измерьте напряжение U_конд с помощью вольтметра на каждом конденсаторе.

4. Вычислите заряд каждого конденсатора q_конд

5. Вычислите общую емкость С_общ батареи конденсаторов.

6. Найдите общий заряд на конденсаторах q_общ

7. Заполните таблицу:

№ конд

С_конд, Ф

U_конд, В

q_конд, Кл

С_общ, Ф

q_общ, Кл

U_ист, В

Задание 3. Смешанное соединение конденсаторов

1. Собрать схему:

2. Емкость конденсаторов С_конд установить по указанию преподавателя, напряжение U_ист на источнике переменного тока установить самостоятельно.

3. Измерьте напряжение U_конд с помощью вольтметра на каждом конденсаторе.

4. Вычислите заряд каждого конденсатора q_конд

5. Вычислите общую емкость С_общ батареи конденсаторов.

6. Найдите общий заряд на конденсаторах q_общ

7. Найдите общее напряжение U_общ и сравните его с напряжением источника U_ист переменного напряжения.

Конденсаторы — задачи

В задачах с присутствием конденсаторов очень часто нужно уметь находить емкость последовательного и параллельного соединения емкостей. С параллельным соединением емкостей все просто: при параллельном соединении емкости складываются. Почему это так? Дело в том, что при параллельном соединении на всех конденсаторах одинаковое напряжение, а их заряды пропорциональны емкостям:

и т.д.

Общий заряд на конденсаторах:

Тогда емкость системы конденсаторов: .

С последовательным соединением все сложнее. Кстати, когда готовила эту статью, наткнулась на такой вот перл, который не могла не процитировать:

Заряды при последовательном соединении одинаковы на всех конденсаторах:

и т.д.

Тогда напряжение между крайними точками равно:

$U=U_1+ U_2+... +U_n=q(1/{C_1}+1/{C_2}+...+1/{C_n})$

Емкость всей системы: $C=q/U=1/(1/{C_1}+1/{C_2}+...+1/{C_n})$ , или $1/C=(1/{C_1}+1/{C_2}+...+1/{C_n})$

1. Разность потенциалов между точками А и В U=9 В. Емкость конденсаторов соответственно равна C_1=3 мкФ и C_2=6 мкФ. Определите заряды Q_1 и Q_2 и разности потенциалов U_1 и U_2 на обкладках первого и второго конденсаторов.

Задача 1

Определим общую емкость такого соединения: $1/{C_Sigma}=1/{C_1}+1/{C_2}$ ,

мкФ (сразу считаем в микрофарадах, чтобы не расписывать степени десятки)

Тогда заряд равен:

мкКл.

Заряды при последовательном соединении на всех конденсаторах одинаковые, значит для первого:

, для второго .

Напряжения на конденсаторах:

$U_1=q_1/{C_1}=18*10^{-6}/{3*10^{-6}}=6$ В, $U_2=q_2/{C_2}=18*10^{-6}/{6*10^{-6}}=3$ В.

Ответ: 18 мкКл, 6 В, 3 В.

2. Определите емкость батареи конденсаторов, изображенной на рисунке. Емкость каждого конденсатора C=1 мкФ.

Задача 2

Емкости C_3 и C_4 , поскольку они соединены параллельно, необходимо сложить: мкФ. Тогда получим последовательное соединение трех одинаковых емкостей и C_34 , емкость которой вдвое больше. При последовательном соединении емкостей их эквивалентная емкость вычисляется по формуле: $1/{C_Sigma}=sum{1}{n}{1/{C_i}}$ . Тогда получим: $1/{C_Sigma}=1/1+1/1+1/2+1/1=3,5$ , ${C_Sigma}=1/{3,5}=0,286$ мкФ.

Ответ: 286 нФ

3. Емкость батареи конденсаторов, образованной двумя последовательно включенными конденсаторами, 100 пФ, а заряд 20 нКл. Определите емкость второго конденсатора, а также разность потенциалов на обкладках каждого из них, если C_1=200 пФ.

Воспользуемся . Тогда (считаем в пикофарадах)

Отсюда , , C_2=200 пФ.

При последовательном соединении заряд на конденсаторах равный: нКл.

Напряжения также получатся одинаковыми:

$U_1=q_1/{C_1}=20*10^{-9}/{200*10^{-12}}=100$ В, В.

Ответ: В, нКл.

4. Наибольшая емкость конденсатора 60 мкФ. Какой заряд он накопит при подключении источника постоянного напряжения 60В?

Так как q=C*U , то $q=60*10^{-6}*60=0,36$ мКл.

Ответ: 0,36 мКл

5. При введении в пространство между пластинами воздушного конденсатора твердого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 100 В. Какова диэлектрическая проницаемость диэлектрика?

Рассмотрим сначала конденсатор до введения диэлектрика: q=C_1*U , . Заряд остался тем же при введении диэлектрика, а напряжение изменилось: .

Тогда , или $C_1/{C_2}=1/4$

Емкость конденсатора, как известно, зависит от площади пластин и расстояния между ними, а также от диэлектрика:

$C={varepsilon*varepsilon_0*S}/d$

В первом случае, без диэлектрика: $C_1={varepsilon_0*S}/d$ , а во втором $C_2={varepsilon*varepsilon_0*S}/d$

Найдем и в этом случае отношение емкостей: $C_1/{C_2}=1/varepsilon$ , или $varepsilon=C_2/{C_1}=4$

Ответ: Кл*Кл/Н*м*м

6. Площадь пластин конденсатора равна 520 см кв. На каком расстоянии нужно разместить пластины в воздухе, чтобы емкость конденсатора была равна 50 пФ?

Емкость конденсатора без диэлектрика:

$C={varepsilon_0*S}/d$

Площадь нужно выразить в кв. метрах: $S=520*10^{-4}=0,052$

Электрическая постоянная $varepsilon_0=8,85*10^{-12}$ .

Выразим из первого выражения нужную нам величину: $d={varepsilon_0*S}/C={8,85*10^{-12}*0,052}/{50*10^{-12}}=0,0092$ м, или 9,2 мм.

Ответ: 9,2 мм

7. Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора?

Энергию электрического поля, накопленную конденсатором, можно вычислить по формуле:

$W=CU^2/2=q^2/{2C}$ – и в этой задаче как раз хорошо будет воспользоваться второй записью.

Тогда: $W=q^2/{2C}=(5*10^{-6})^2/{2*20*10^{-6}}=25/40=0,625*10^{-6}$ мкДж

8. Расстояние между пластинами плоского конденсатора с диэлектриком из бумаги, пропитанной парафином, равно 2 мм, а напряжение 200 В. Найти плотность энергии поля.

Чтобы найти плотность энергии, нужно сначала определить энергию поля, а потом посчитать, в каком объеме она сосредоточена.

, с другой стороны, емкость $C={varepsilon*varepsilon_0*S}/d$ , тогда $W={{varepsilon*varepsilon_0*S}U^2}/{2d}$ . Объем пространства между пластинами конденсатора – это произведение площади пластин на расстояние между ними: V=Sd . Тогда плотность энергии поля равна $W/V={{varepsilon*varepsilon_0}U^2}/{2d^2}$

Посмотрим в справочнике, какова диэлектрическая проницаемость бумаги с парафином, выразим расстояние между пластинами в метрах, и подставим цифры:

$W/V={{2,2*8,85*10^{-12}}200^2}/{2(0,002)^2}=9,7$ мДж

Задачи с конденсаторами: сборная солянка

В эту статью вошли задачи всех типов: здесь и определение эквивалентных емкостей, и напряжений между определенными точками схемы, и бесконечные цепочки, и даже исчезновение конденсаторов из схем (бесследное и без последствий).

Задача 1. Плоский конденсатор разрезают на n = 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторов соединяют последовательно. Чему равна емкость полученной батaреи конденсаторов, если емкость исходного конденсатора мкФ?

К задаче 1

Площадь исходного конденсатора:

$C_{0}=\frac{\varepsilon_0 \varepsilon S }{d}$

Площадь нового конденсатора (одного) – в 4 раза меньше исходного (так как площадь меньше):

$C_{mal}=\frac{\varepsilon_0 \varepsilon S }{4d}=\frac{ C_{0}}{4}$

Теперь соединяем последовательно:

$\frac{1}{C_{bat}}=\frac{1}{C_{mal}}\cdot 4$

$C_{bat}=\frac{C_{mal}}{4}=\frac{\varepsilon_0 \varepsilon S }{16d}=\frac{ C_{0}}{16}=\frac{16}{16}=1$

Ответ: 1 мкФ.

Задача 2. Два плоских конденсатора, емкостью каждый, соединили параллельно. В один из них вставили диэлектрическую пластину с проницаемостью $\varepsilon$ , заполнившую весь объем конденсатора. Какой емкости и как необходимо подключить третий конденсатор, чтобы емкость системы стала равной ?

Так как первые два конденсатора соединены параллельно, то их емкости надо сложить, чтобы получить эквивалентную емкость:

$C_1=C+C=2C$

После введения пластины емкость такого конденсатора стала равна $C\varepsilon$ , а эквивалентная емкость стала равна

$C_2=C+ C\varepsilon=C(1+\varepsilon )$

Теперь к этой конструкции будем присоединять еще один конденсатор. Попробуем присоединить параллельно, тогда

$C(1+\varepsilon )+C_x=3C$

$C_x=2C- C\varepsilon=C(2- \varepsilon)$

Так как C_x > 0 , то $2- \varepsilon > 0$ , $\varepsilon < 2$ .

Теперь присоединяем последовательно, тогда:

$\frac{1}{ C(1+\varepsilon )}+ \frac{1}{ C_x}=\frac{1}{3C}$

$\frac{ CC_x(1+\varepsilon )}{ C(1+\varepsilon )+C_x}=3C$

$\frac{ C_x(1+\varepsilon )}{ 1+\varepsilon +\frac{C_x}{C}}=3C$

$C_x(1+\varepsilon )=3C(1+\varepsilon+\frac{C_x}{C} )$

$C_x(1+\varepsilon )-3C_x=3C(1+\varepsilon)$

$C_x(\varepsilon-2 )=3C(1+\varepsilon)$

$C_x=\frac{3C(1+\varepsilon)}{ \varepsilon-2}$

Решим неравенство:

$\frac{3C(1+\varepsilon)}{ \varepsilon-2}>0$

Решение – $\varepsilon<-1$ – это решение не имеет смысла, $\varepsilon>2$ .

Ответ: $C_x=C(2- \varepsilon)$ , при $\varepsilon < 2$ , параллельно.

$C_x=\frac{3C(1+\varepsilon)}{ \varepsilon-2}$ , при $\varepsilon>2$ , последовательно.

Задача 3. Разность потенциалов между точками А и В равна . Емкости конденсаторов известны. Определить заряды конденсаторов и разность потенциалов U_1 между точками А и D.

К задаче 3

Так как емкости C_2 и C_3 соединены параллельно, то напряжение на них одинаковое. Кроме того, заряды на емкостях C_1 и системе конденсаторов C_2-C_3 одинаковы, так как они соединены последовательно. Поэтому

$q_1=q_2+q_3~~~~~~~~~~~~~~~~~~~~~~(1)$

$U_2=U_3$

$\frac{q_3}{C_3}=\frac{q_2}{C_2}$

$q_3=\frac{q_2C_3}{C_2}$

Эквивалентная емкость $C_{23}=C_2+C_3$ , поэтому эквивалентная емкость всей схемы – произведение на сумму – $C_e=\frac{C_1(C_2+C_3)}{C_1+ C_2+C_3}$ .

Тогда заряд

$q=C_eU=\frac{UC_1(C_2+C_3)}{C_1+ C_2+C_3}$

Но вследствие (1)

$q_1=\frac{UC_1(C_2+C_3)}{C_1+ C_2+C_3}$

Тогда

$U_1=\frac{q_1}{C_1}=\frac{U(C_2+C_3)}{C_1+ C_2+C_3}$

Находим U_2=U_3 :

$U_2= U_3=U-U_1=\frac{UC_1}{C_1+ C_2+C_3}$

Определим заряды q_2 и q_3 :

$q_2= \frac{UC_1C_2}{C_1+ C_2+C_3}$

$q_3= \frac{UC_1C_3}{C_1+ C_2+C_3}$

Ответ: $U_1=\frac{U(C_2+C_3)}{C_1+ C_2+C_3}$ , $q_1=\frac{UC_1(C_2+C_3)}{C_1+ C_2+C_3}$ , $q_2= \frac{UC_1C_2}{C_1+ C_2+C_3}$ , $q_3= \frac{UC_1C_3}{C_1+ C_2+C_3}$ .
Задача 4. Определить емкость батареи конденсаторов, показанной на рисунке, если C_1 = 4 мкФ, мкФ, C_3 = 2 мкФ.

К задаче 4

Сначала два конденсатора C_1 подключены параллельно, при этом емкости складываются: 2C_1 . В конце параллельное соединение C_1 и C_3 : C_1+C_3 . Теперь имеем последовательное соединение емкостей 2C_1 , C_2 и C_1+C_3 . Тогда

$\frac{1}{C_e}=\frac{1}{2C_1}+\frac{1}{C_2}+\frac{1}{ C_1+C_3}$

Можно подставить числа и довести решение до конца:

$\frac{1}{C_e}=\frac{1}{8}+\frac{1}{10}+\frac{1}{6}=\frac{15+12+20}{120}=\frac{47}{120}$

$C_e=\frac{120}{47}=2,55$

Ответ: мкФ.

Задача 5. Найти емкость системы конденсаторов, изображенной на рисунке.

К задаче 5

На рисунке a) емкость C_3 оказывается незаряженной, так как схема совершенно симметрична и $U_{AB}=U_1+U_2$ , поэтому $U_{CD}=U_1-U_1=U_2-U_2=0$ .

Рисунок 2 (задача 5)

Поэтому конденсатор C_3 не заряжен – разность потенциалов на его выводах нулевая. Следовательно, имеем две веточки, включенные в параллель: в каждой последовательное соединение C_1 и C_2 .

Рисунок 3 (к задаче 5)

Сопротивление одной ветки (емкость двух последовательно включенных конденсаторов – произведение, деленное на сумму):

$C_{e1}=\frac{C_1C_2}{C_1+C_2}$

А двух таких веток в параллель (емкости, включенные параллельно, складываются): $\frac{2C_1C_2}{C_1+C_2}$ .

На рисунке б) – если приглядеться, та же самая ситуация:

К задаче 5 – рисунок 4

Так что, аналогично первой схеме, сопротивление одной ветки с двумя последовательно включенными конденсаторами – $\frac{C}{2}$ , а две такие емкости в параллель дадут .

Ответ: а) $\frac{2C_1C_2}{C_1+C_2}$ ; б) .

Задача 6. Определить емкость Сх бесконечно длинной системы одинаковых конденсаторов, емкостью С каждый, соединенных друг с другом, как показано на рисунке.

К задаче 6, рисунок 1

Выделим в этой цепи повторяющийся элемент:

К задаче 6, рисунок 2

Эти элементы соединены параллельно. Так как емкость цепи бесконечна, то от нее не убудет, если мы один элемент удалим, или выделим. Тогда справа от выделенного элемента цепь с емкостью C_x , и слева – тоже.

К задаче 6, рисунок 3

Можем записать для последовательно включенных емкостей:

$\frac{1}{C}+\frac{1}{C+C_x}=\frac{1}{C_x}$

$C_x=\frac{C(C+C_x)}{C+C+C_x}$

$C_x^2-CC_x-C^2=0$

$D=5C^2$

$C_x=\frac{-C\pm c\sqrt{5}}{2}=C\left(\frac{\sqrt{5}-1}{2}\right)$

Задача 7. Найти разность потенциалов между точками А и В в схеме, изображенной на рисунке. Емкость C_1 = 1 мкФ, C_2 =2 мкФ, C_3 = 3 мкФ. Напряжение источника U = 100 В.

К задаче 7

Емкость верхней ветки:

$C_v=\frac{C_1C_3}{C_1+C_3}=\frac{3}{1+3}=\frac{3}{4}$

Емкость нижней ветки:

$C_n=\frac{C_2C_3}{C_2+C_3}=\frac{2\cdot3}{2+3}=\frac{6}{5}$

Заряд верхней ветви (мкКл):

$q_v=UC_v=\frac{3}{4}\cdot100=75$

Заряд нижней ветви (мкКл):

$q_n=UC_n=\frac{6}{5}\cdot100=120$

Но C_1 соединен последовательно с C_3 , поэтому q_1=q_3 , и

$U_1=\frac{q_1}{C_1}=\frac{q_v}{C_1}=75$

$U_3=\frac{q_1}{C_3}=\frac{q_v}{C_3}=25$

Аналогично в нижней ветви:

$U_2=\frac{q_2}{C_2}=\frac{q_n}{C_2}=60$

$U_4=\frac{q_2}{C_4}=\frac{q_n}{C_4}=40$

В сумме .

Найдем разность потенциалов между точками и :

$U_{AB}=U_2-U_1=U_3-U_4=60-75=25-40=-15$

Ответ: $U_{BA}=15$ B.

Соединение конденсаторов, теория и примеры задач

Для получения большего спектра емкостей конденсаторы часто соединяют между собой, получают, так называемые батареи конденсаторов. Соединение при этом может быть параллельным, последовательным или комбинированным (смешанным). Рассмотрим случай с двумя конденсаторами.

Последовательное соединение конденсаторов

Последовательное соединение конденсаторов показано на рис. 1

Здесь (рис.1) обкладка одного конденсатора, имеющая отрицательный заряд соединяется с положительной обкладкой следующего конденсатора. При последовательном соединении средние пластины конденсаторов электризуются через влияние, следовательно, их заряды по величине равны и противоположны по знаку. Заряды на этих конденсаторах одинаковы. При этом соединении разности потенциалов складываются:

При этом имеем:

Получаем, что при последовательном соединении конденсаторов емкость соединения находят как:

Обобщив формулу (3) для N конденсаторов, получаем:

где – электрическая емкость i-го конденсатора.

Последовательное соединение конденсаторов используют тогда, когда для избегания пробоя конденсатора необходимо разность потенциалов распределить между несколькими конденсаторами.

Параллельное соединение конденсаторов

Последовательное соединение конденсаторов показано на рис. 2

При параллельном соединении разности потенциалов между обкладками конденсаторов одинаковы. Суммарный заряд системы равен сумме зарядов на каждом из конденсаторов:

Из сказанного выше получим:

Для батареи из N параллельно соединенных конденсаторов имеем:

Параллельное соединение конденсаторов используют тогда, когда необходимо увеличить емкость конденсатора.

Примеры решения задач

Практическая работа по дисциплине Электротехника и электроника на тему «Расчет электрической цепи при смешанном соединении конденсаторов»

Практическая работа №1

Тема: Расчет электрической цепи при смешанном соединении конденсаторов.

Цель: Изучить методы соединения конденсаторов в электрических цепях постоянного тока. Рассчитать эквивалентную емкость, напряжение и заряд батареи конфденсаторов при смешанном соединении конденсаторов.

Ход работы:

Изучить свойства конденсаторов, способы соединения, формулы для определения основных величин.
Рассчитать эквивалентную емкость, напряжение и заряд батареи конденсаторов при смешанном соединении конденсаторов по заданному варианту.
Оформить отчет.

Теоретическая часть:

Сообщение электрического заряда проводнику называется электризацией. Чем больший заряд принял проводник, тем больше его электризация, или, иначе говоря, тем выше его электрический потенциал.

Между количеством электричества и потенциалом данного уединенного проводника существует линейная зависимость: отношение заряда проводника к его потенциалу есть величина постоянная:

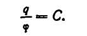
Для какого-либо другого проводника отношение заряда к потенциалу есть также величина постоянная, но отличная от этого отношения для первого проводника.

Одной из причин, влияющих на эту разницу, являются размеры самого проводника. Один и тот же заряд, сообщенный различным проводникам, может создать различные потенциалы. Чтобы повысить потенциал какого-либо проводника на одну единицу потенциала, необходим определенный заряд.

Свойство проводящих тел накапливать и удерживать электрический заряд, измеряемое отношением заряда уединенного проводника к его потенциалу, называется электрической емкостью, или просто емкостью, и обозначается буквой С.

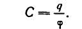
Приведенная формула позволяет установить единицу емкости.

Практически заряд измеряется в кулонах, потенциал в вольтах, а емкость в фарадах:

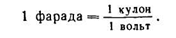
Емкостью в 1 фараду обладает проводник, которому сообщают заряд в 1 кулон и при этом потенциал проводника увеличивается на 1 вольт.

Единица емкости — фарада (обозначается ф или F) очень велика. Поэтому чаще пользуются более мелкими единицами — микрофарадой (мкф или 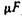), составляющей миллионную часть фарады:

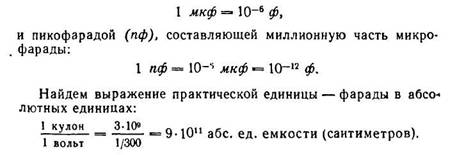
Устройство, предназначенное для накопления электрических зарядов, называется электрическим конденсатором. Конденсатор состоит из двух металлических пластин (обкладок), разделенных между собой слоем диэлектрика. Чтобы зарядить конденсатор, нужно его обкладки соединить с полюсами электрической машины. Разноименные заряды, скопившиеся на обкладках конденсатора, связаны между собой электрическим полем. Близко расположенные пластины конденсатора, влияя одна на другою, позволяют получить на обкладках большой электрический заряд при относительно невысокой разности потенциалов между обкладками. Емкость конденсатора есть отношение заряда конденсатора к разности потенциалов между его обкладками:

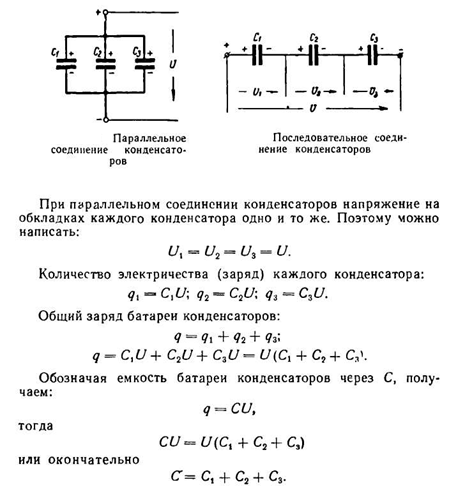
Следовательно, при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. При параллельном соединении каждый конденсатор окажется включенным на полное напряжение сети.
Рассмотрим последовательное соединение конденсаторов:

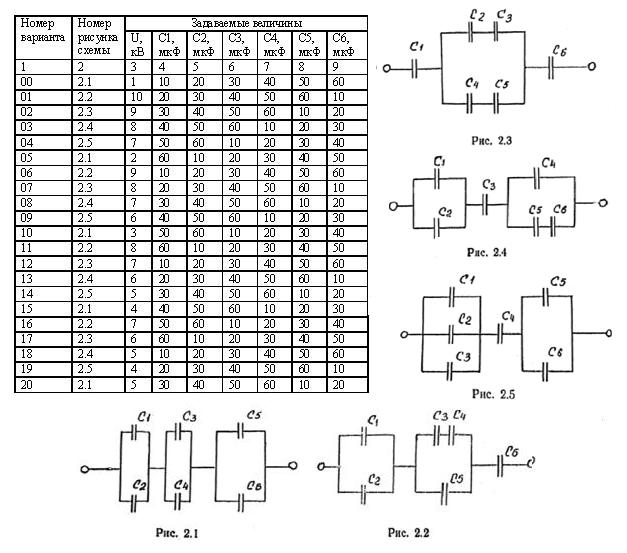
Практическое задание:

Определить заряд, напряжение, энергию электрического поля каждого конденсатора, эквивалентную емкость цепи.

Практическая работа «Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы»

Практическая работа № 24

Раздел 3 Электродинамика

Тема 3.1 Электростатика

Название практической работы: Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы

Учебная цель: изучить распределение напряжения, зарядов в схемах с последовательным и параллельным соединением конденсаторов

Учебные задачи: определять эквивалентную ёмкость, заряд и энергию батареи конденсаторов по схеме. Определить напряжения и заряды на конденсаторах.

Правила безопасности: правила проведения в кабинете во время выполнения практического занятия

Норма времени: 2 часа

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь: вычерчивать схемы, определять эквивалентную ёмкость и заряд конденсаторов. Рассчитывать энергию батареи конденсаторов

знать: законы последовательного и параллельного соединения конденсаторов в батарею. Расчётные формулы ёмкости, заряда, напряжения, единицы измерения. Применение конденсаторов

Обеспеченность занятия:

— методические указания по выполнению практического занятия

— лабораторно-практическая тетрадь, карандаш, линейка

Порядок проведения занятия:

Для выполнения практической работы учебная группа распределяется по вариантам.

Теоретическое обоснование

Конденсатор – система двух проводников (обкладок) разделённых слоем диэлектрика. Служит для накопления (конденсации) разделённых зарядов.

Плоский конденсатор – две плоские металлические пластины, расположенные параллельно и разделённые слоем диэлектрика. Обозначение конденсатора на электрических схемах соответствует его принципиальному устройству.

Электроёмкость конденсатора показывает, как много заряда может «натечь» в конденсатор, подключённый к источнику, разделяющему заряды.

Если это источник ЭДС равный ,то при соединении конденсатора и источника тока по схеме, рисунок 1, натекание заряда прекратиться,

когда напряжение на обкладках станет равно

Коэффициент пропорциональности между зарядом на конденсаторе Q и разностью потенциалов U на его обкладках называется электрической ёмкостью конденсатора С. Заряд на обкладках конденсатора тем больше, чем больше ЭДС источника

Важнейшей характеристикой любого конденсатора является его электрическая ёмкость С – физическая величина, равная отношению заряда Q конденсатора к разности потенциалов U между его обкладками:

Выражается в СИ в фарадах (Ф).

Ёмкость реальных конденсаторов гораздо меньше, и для её измерения обычно используют более мелкие единицы: 1 микрофарада (мкФ),

1нанофарада (нФ), 1 пикофарада (пФ)

Эквивалентной ёмкостью батареи конденсаторов называют такую ёмкость

С _общ которая при подключении к тому же источнику тока принимает на себя такой же заряд, что и батарея конденсаторов.

Два конденсатора соединены параллельно, если обкладки обоих попарно соединены друг с другом, рисунок 2

Рисунок 2 Рисунок 4

У параллельного соединения конденсаторов ёмкости и заряды складываются, рисунок 2:

Для последовательного соединения конденсаторов, рисунок 4.

На практике конденсаторы включают только параллельно, можно представить это так, как будто площади их пластин складываются, складываются и их ёмкости. Последовательное соединение не имеет практического смысла, знание сложения необходимо только при анализе цепей переменного тока.

Проверка конденсаторов – перед проверкой конденсатор разряжают, то есть закорачивают его выводы на металлический предмет.

Энергия конденсатора. При зарядке конденсатора между обкладками скапливаются разделённые заряды (энергия электрического поля)

Эта энергия может быть высвобождена, если обкладки заряжённого конденсатора соединить через лампу накаливания. После того, как все заряды противоположного знака, скопленные на обкладках, протекут через спираль лампочки и прорекомбинируют, лампочка погаснет. Энергия конденсатора перейдёт во внутреннюю и световую энергию.

Для увеличения ёмкости радиотехнические конденсаторы изготавливают в виде двух слоёв алюминиевой фольги, проложенных промасленной бумагой (диэлектрик) и скрученных в многослойную пачку, упакованную в прочный корпус

Важной характеристикой конденсатора является максимальное напряжение U_макс указанное на корпусе, при котором он сохраняет работоспособность. При больших напряжениях диэлектрик, проложенный между обкладками, пробивается, и обкладки замыкаются накоротко, составляя единый проводник. Чем больше напряжение, тем меньше ёмкость. В электролитических конденсаторах важно соблюдать полярность, иначе конденсатор выйдет из строя или возможен разрыв корпуса.

Использование конденсаторов

Конденсаторы используются в радиотехнике (излучение и приём электромагнитных волн, преобразование электромагнитных колебаний). В устройствах, где нужно медленно накопить энергию, а затем быстро высвободить (фотовспышка, импульсный лазер).

Вопросы для закрепления теоретического материала к занятию:

1.Что такое эквивалентная ёмкость батареи конденсаторов?

2.Что значит, если два конденсатора соединены параллельно, последовательно?

3. Как рассчитываются ёмкости и заряды при параллельном и последовательном соединении конденсаторов?

4. Как рассчитывается энергия конденсатора?
5. Что значит закоротить конденсатор?

6. В каком случае необходимо применять последовательное соединение конденсаторов?

7. Что является важной характеристикой конденсатора, как технического устройства?

8. Где используется конденсатор?

9. Виды конденсаторов.

Содержание и Последовательность выполнения практической работы:

Задачи практической работы:

Задание 1

Вычертить схему №1 с учётом данных в таблице для своего варианта.

Определить эквивалентную ёмкость С, заряд Q батареи и энергию W, накопленную батареей.

Вычислить напряжение и заряд на каждом конденсаторе. Как изменятся найденные величины, если один из конденсаторов закоротить? Напряжение на зажимах цепи U, взять из таблицы №1

Схема №1

Таблица №1

№ варианта	U В	C₁ _мкФ	C₂ _мкФ	C₃ _мкФ	C₄ _мкФ	C₅ _мкФ	Закоротить конденсатор
1	150	10	20	30	60	—	С4
2	60	20	—	90	15	30	С3
3	150	15	15	30	20	40	С5
4	60	—	20	90	40	5	С3
5	150	20	10	30	—	60	С5
6	60	10	10	90	45	—	С4
7	150	30	—	30	10	50	С3
8	60	—	20	90	25	20	С5
9	150	—	30	30	30	30	С4
10	60	15	20	90	—	45	С5
11	150	10	5	45	25	15	С3
12	60	15	45	15	10	20	С4

Пример выполнения и оформления

Для решения задач необходимо изучить, как располагаются напряжения и заряды в схемах с последовательным и параллельным соединением конденсаторов, а также формулы определения эквивалентной ёмкости

Таблица №2

Параметры Схема цепи		Таблица №2
Напряжение	U = U₁+U₂	U = U₁_{= U₂}
Заряд	Q = Q₁+Q₂	Q = Q₁= Q₂
Ёмкость	C =	C = C₁+ C₂

Пример №1

Определить эквивалентную ёмкость, заряд батареи конденсаторов, схема №3

Дано:

С₁=16мкФ

С₂ = 6мкФ

U = 120B

C- ? Q – ?

W-?

схема №3

Решение

Показать на схеме №3 полярность (+ или –) зарядов на обкладках конденсаторов.

Задачу решать методом эквивалентных замен. Выделить участки с последовательным соединением или параллельным соединением конденсаторов и заменим их одним эквивалентным конденсатором, ёмкость которого определяется по формулам в таблице №2

1.Конденсаторы С₂ и С₃соединены последовательно, заменим их одним, эквивалентным С₂₃ и начертим на схеме №4

= = = 4мкФ

схема №5

схема №4

2. Конденсаторы С₂₃ и С₁ соединены параллельно.

Определить эквивалентную ёмкость С по схеме №5

С=С₁₂₃ = 16+4 =20мкФ

3. Определить эквивалентный заряд батареи

Q = C₁₂₃·U

Q = 20·10^-6 ·120 = 2400·^10-6 Кл

4. Энергия электрического поля батареи определить по формуле:

= = =0,144 Дж

5. Определить напряжение и заряды на конденсаторах. Так как конденсаторы С₂₃и С₁ соединены последовательно схема №3 то:

Q₂₃ = Q₂ = Q₃ = C₂₃·U

Q₂₃ = 4·10^-6·120 =480·10^-6 Кл

U₂ = = =8В

U₃ = = =40В

По окончанию практической работы студент должен представить:— Выполненную в рабочей тетради практическую работу в соответствии с вышеуказанными требованиями.
Список литературы:

Физика для профессий и специальностей технического профиля В. Ф. Дмитриева М.: ИД Академия – 2015
http://elektt.blogspot.ru/2016/05/tipy-kondensatorov.html
www.ugtfilmiit.ru

Открытый урок по физике Соединение конденсаторов и их признаки

ПЛАН УРОКА

Тема: «Соединение конденсаторов»

Класс: 10

Тип урока: Комбинированный урок

Цель урока:

Образовательная:

— Формирование умения решать задачи при различных способах соединения конденсаторов

Развивающая: развитие умения формулировать проблему, предлагать способы ее решения
Воспитывающая: воспитание дисциплинированности в ходе проведения урока

Оборудование: раздаточный материал

Ход урока:

1.Организационный момент

Приветствие, запись даты и темы в журнале, отметить отсутствующих, объявление целей и хода урока

2.Постановка цели и задачи урока перед учениками:

Цель – освоить принципы нахождения параметров электрической цепи при различных способах соединения ее элементов

3.Проверка домашнего задания:

Проверка домашнего задания в виде взаимной проверки с помощью учителя.

Объяснение нового материала:

ПЛАН:

1.Последовательное соединение конденсаторов

2.Параллельное соединение конденсаторов

3.Смешанное соединение конденсаторов

4. примеры решения задач

5.Решение задач

6. Рефлексия

ВОПРОС 1 Последовательное Соединение конденсаторов

Если соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 1).

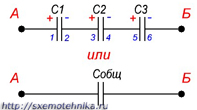
Рисунок 1. Последовательное соединение конденсаторов.

В случае последовательно соединенных конденсаторов одинаковы заряды на всех конденсаторах Q₁ = Q₂ =…= Q_n Действительно, если мы поместим, например, заряд 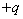на левую обкладку первого конденсатора, то вследствие индукции на правой его обкладке возникнет заряд 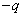, а на левой обкладке второго конденсатора – заряд 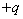. Наличие этого заряда на левой обкладке второго конденсатора опять-таки вследствие индукции создает на правой его обкладке заряд 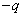, а на левой обкладке третьего конденсатора – заряд 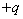и т. Д. Таким образом, заряд каждого из последовательно соединенных конденсаторов равен 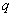. Напряжение же на каждом из этих конденсаторов определяется емкостью соответствующего конденсатора:

, , …, ,

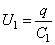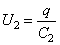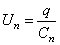где 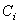– емкость одного конденсатора. Суммарное напряжение между крайними (свободными) обкладками всей группы конденсаторов

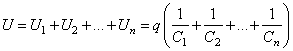Следовательно, емкость всей системы конденсаторов

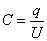
определяется выражением

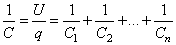Вопрос 2.

РИСУНОКМ 2

В случае параллельного соединения все конденсаторы заряжаются до одной и той же разности потенциалов 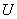, но заряды на них могут быть различными. Если емкости их равны 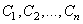, то соответствующие заряды будут

, , …, .

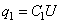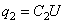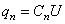Общий заряд на всех конденсаторах

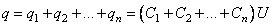и, следовательно, емкость всей системы конденсаторов

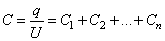Итак, емкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.

Из этой формулы видно, что емкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.

ВОПРОС 3

На рисунке 3 приведен пример участка цепи со смешанным соединением конденсаторов.

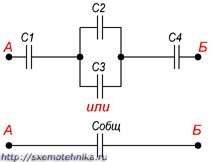
Рисунок 3. Последовательно-параллельное соединение конденсаторов.

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 4.

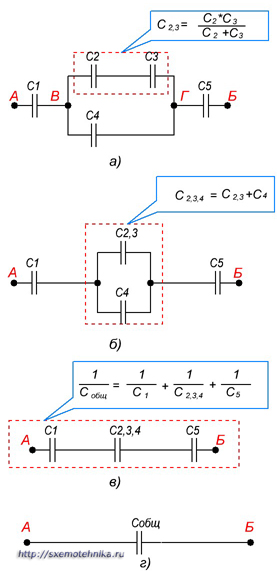
Закрепление материала

Рассчитать ёмкость конденсаторов (раздать по два конденсатора каждой группе.

Рефлексия: самооценка

Домашнее задание_______________________

РАБОЧАЯ КАРТА УРОКА.

Фамилия, имя, группа.____________________________________________________

Домашнее

Задание

Изучение нового

материала.

Решение

задач.

Парная, групповая

работа.

Всего

баллов.

Оценка.

Как решать задачи со смешанным соединением конденсаторов — MOREREMONTA

Ответ

Проверено экспертом

Конденсаторы — задачи

Задачи с конденсаторами: сборная солянка

Соединение конденсаторов, теория и примеры задач

Последовательное соединение конденсаторов

Параллельное соединение конденсаторов

Примеры решения задач

Практическая работа по дисциплине Электротехника и электроника на тему «Расчет электрической цепи при смешанном соединении конденсаторов»

Практическая работа «Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы»

Открытый урок по физике Соединение конденсаторов и их признаки

Добавить комментарий Отменить ответ