3.1. Разряд конденсатора через активное сопротивление
Разряд предварительно заряженного конденсатора через активное сопротивление (через резистор) является простейшим переходным процессом.
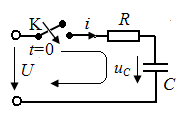
Пусть конденсатор ёмкостью С заряжен до напряжения U. В момент t=0 замыкается ключ К и конденсатор начинает разряжаться через активное сопротивление R. Так как здесь внешнего воздействия нет, то в цепи будет только свободный процесс.
В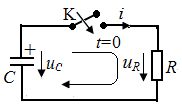 ыбрав
направление обхода, запишем для этой
цепи второе уравнение Кирхгофа:
ыбрав
направление обхода, запишем для этой
цепи второе уравнение Кирхгофа:
uR−uC=0,
или
iR−uC=0. (1)
А так как для конденсатора ток
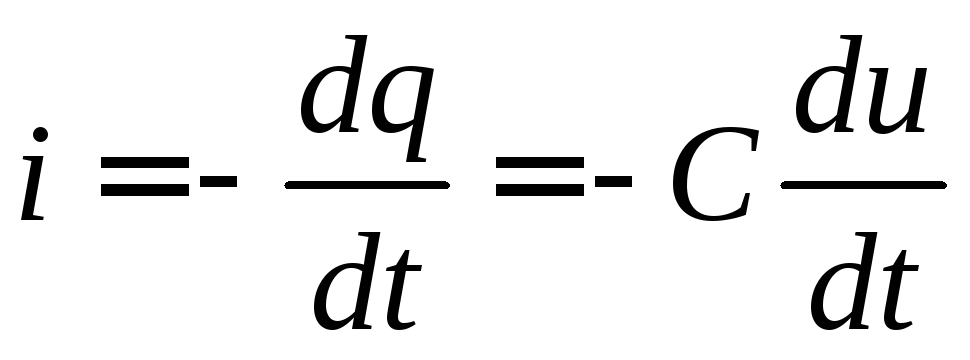 ,
и тогда
,
и тогда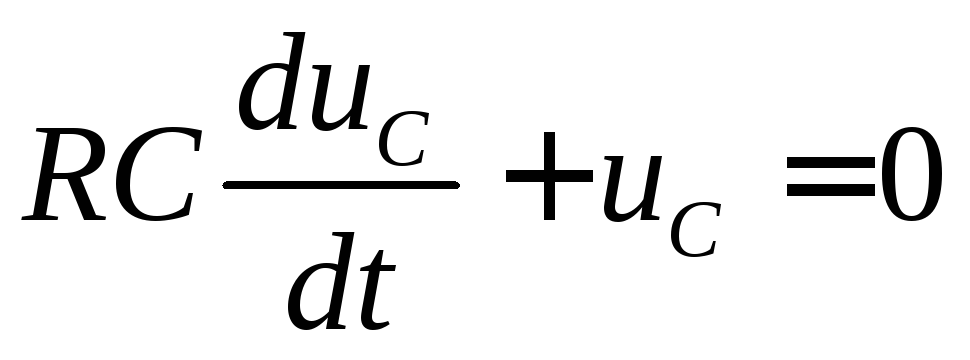 ,
(2)
,
(2) или 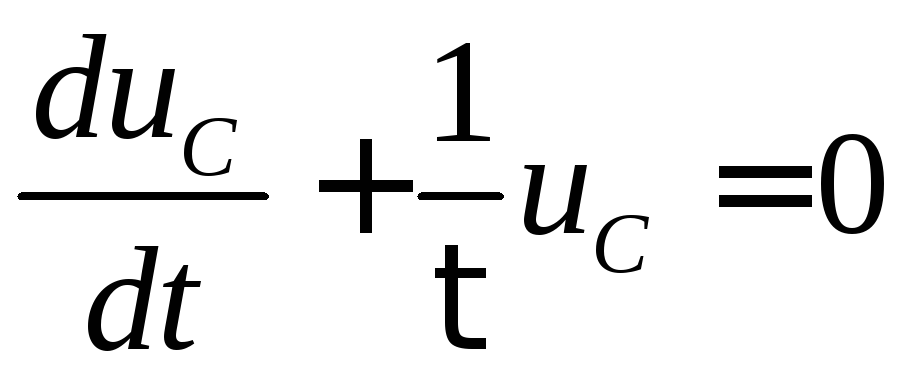 ,
,
где  −постоянная
времени RC-цепочки.
−постоянная
времени RC-цепочки.
Общее решение этого однородного уравнения имеет вид (проинтегрировать самостоятельно; однако,
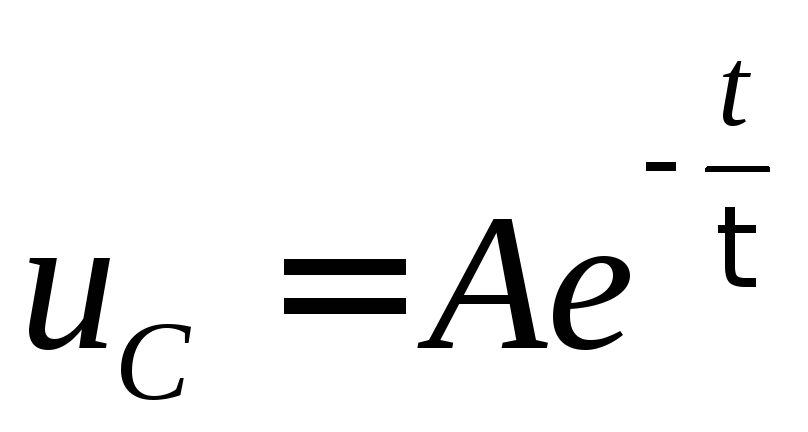 ,
,
где А – коэффициент, определяемый начальным
условием,
т.е. 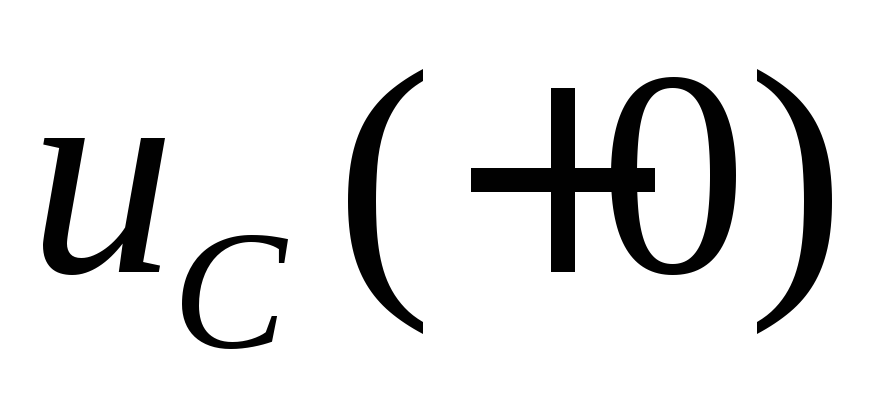 − напряжением на конденсаторев
первый момент после замыкания ключа К.
Так как, по условию, до замыкания
напряжение
− напряжением на конденсаторев
первый момент после замыкания ключа К.
Так как, по условию, до замыкания
напряжение 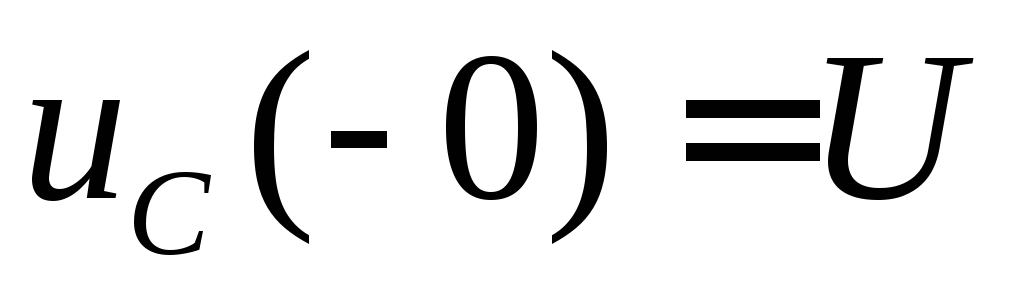 ,
а напряжение на конденсаторе скачком
измениться не может (это привело бы к
тому, что
,
а напряжение на конденсаторе скачком
измениться не может (это привело бы к
тому, что
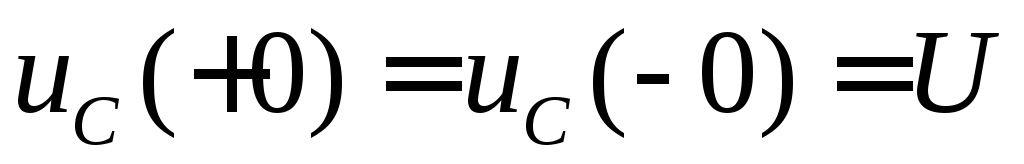 (это второе правило
коммутации).
(это второе правило
коммутации).
Это даёт: А=U, и, следовательно,
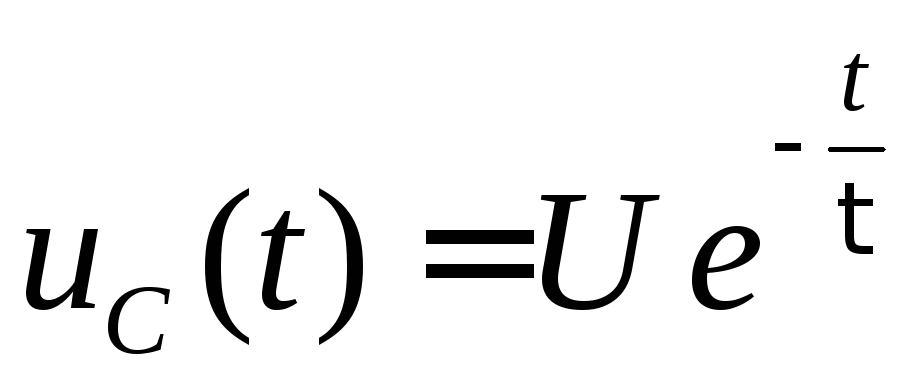
 .
(3)
.
(3)
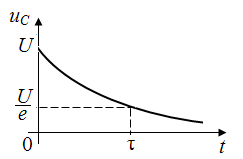
Отсюда видно, что τ – это время, за которое напряжение на конденсаторе убывает в е раз:
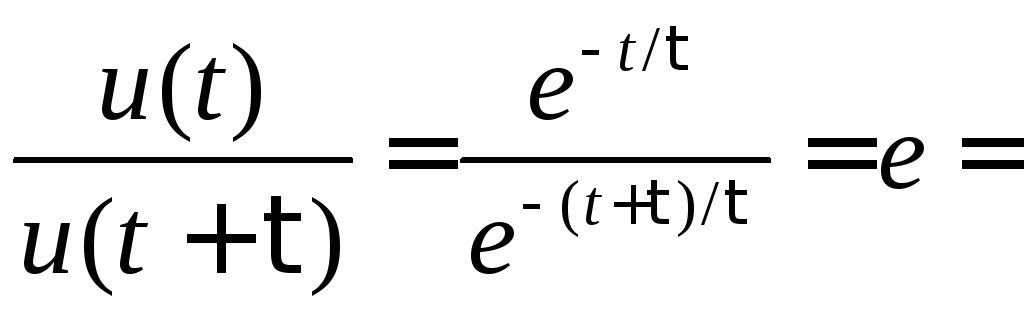 2,7.
2,7.Реально время переходного процесса оценивается примерно в 3τ, когда напряжение уменьшается в е3 = 20 раз, или когда до установившегося значения осталось лишь 1/20 = 5 % от исходного напряжения U.
Пример. Пусть С=1 мкФ, R=1 кОм. Тогда время переходного процесса Δtперх.=3τ=3RC=3 мс.
Теперь легко получить закон убывания тока в цепи:
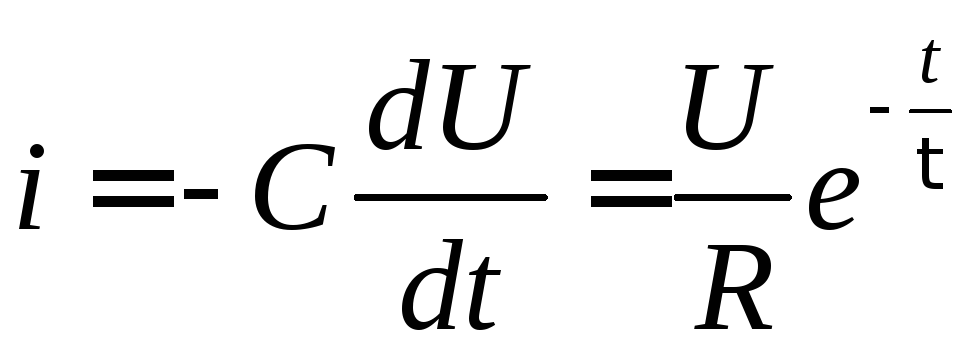 .
.
3.2. Включение постоянного напряжения
в последовательную цепь RC
Рассмотрим теперь процесс заряда конденсатора через активное сопротивление R от генератора с постоянным напряжением U.
Пусть в момент t=0 замыкается ключ К. Тогда второе уравнение Кирхгофа для выбранного направления обхода контура будет таким:
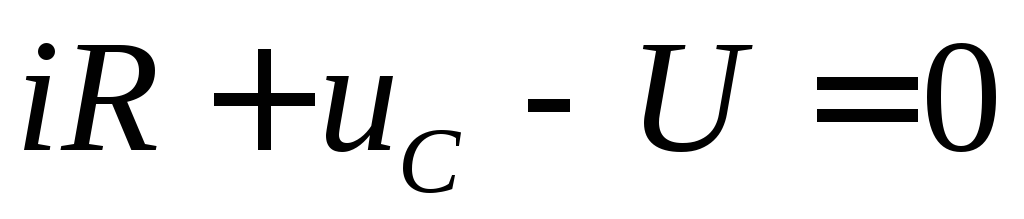
 ,
,
или, так как i = C (
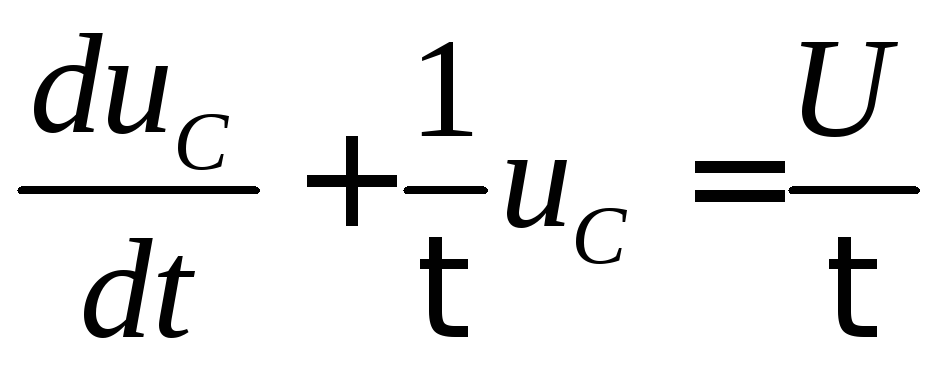 ,
(4)
,
(4)
где 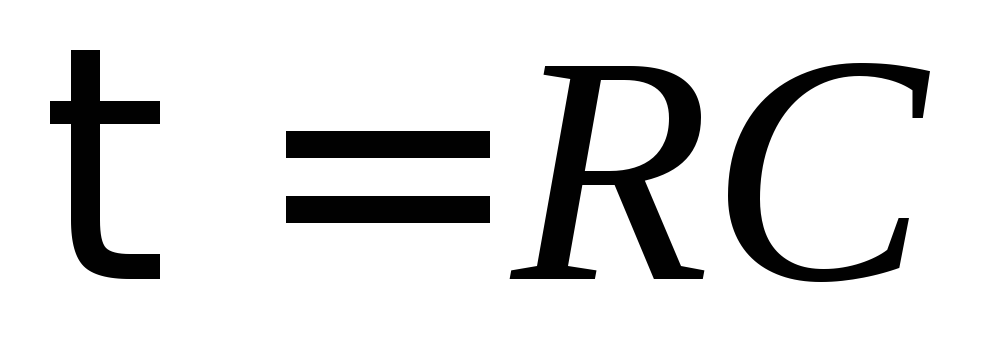 −постоянная
времени RC-цепочки.
−постоянная
времени RC-цепочки.
Общее решение этого неоднородного уравнения равно сумме его частного решения и общего решения соответствующего однородного. Частное решение легко угадывается: иС частн.=U (оно проверяется простой подстановкой). Тогда

 .
.Коэффициент А определяется из начального условия: иС(+0)=иС(−0)=0. Это даёт: А=−U; и тогда
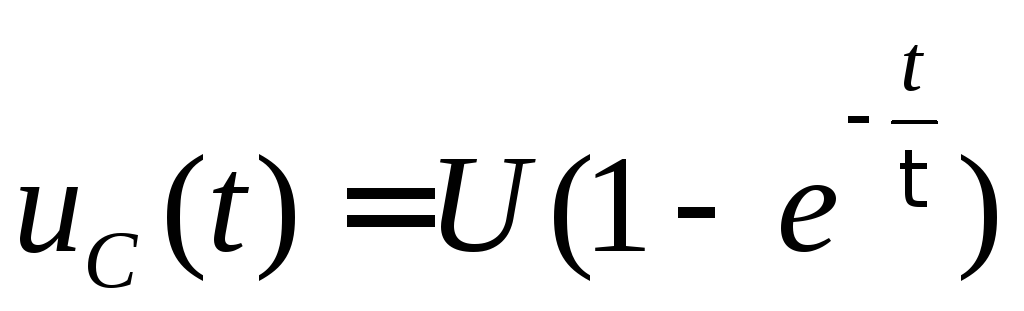
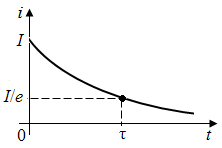 .
.
Ток заряда
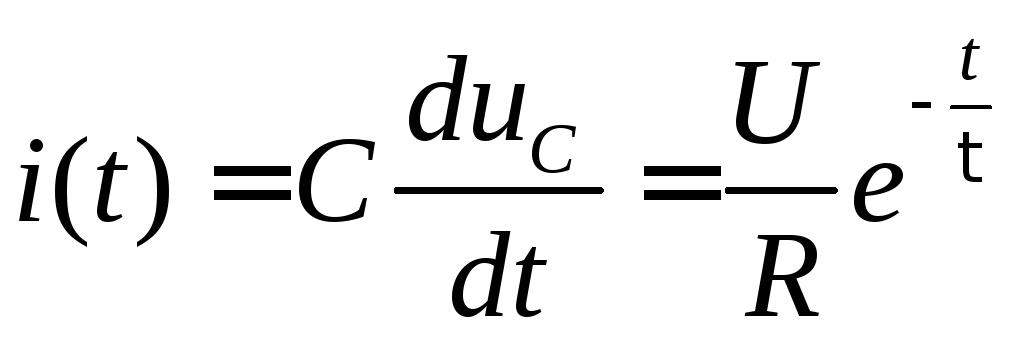 .
.
3.3. Включение постоянного напряжения
в последовательную цепь RL
Процессы при коммутациях в цепи RL описываются такими же дифференциальными уравнениями, как и (2) или (4), поэтому подробнее остановимся лишь на некоторых специфических особенностях.
В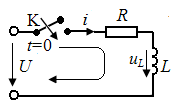 торое
уравнение Кирхгофа:
торое
уравнение Кирхгофа:
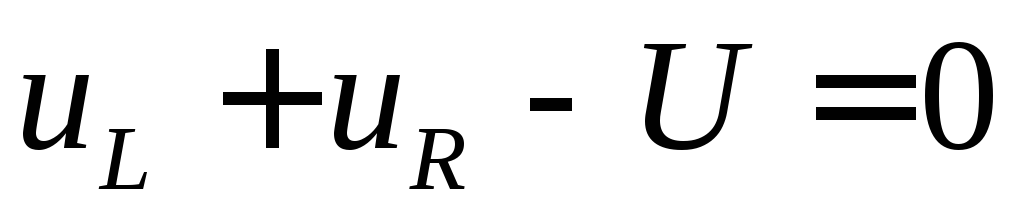 ,
или:
,
или:  .
.
Или: 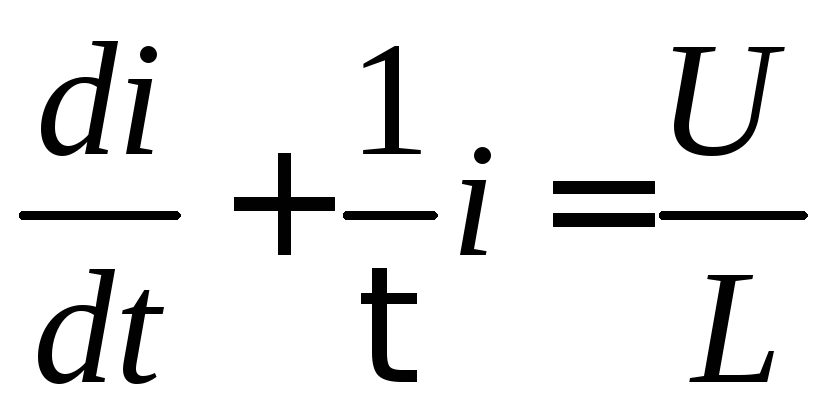
где 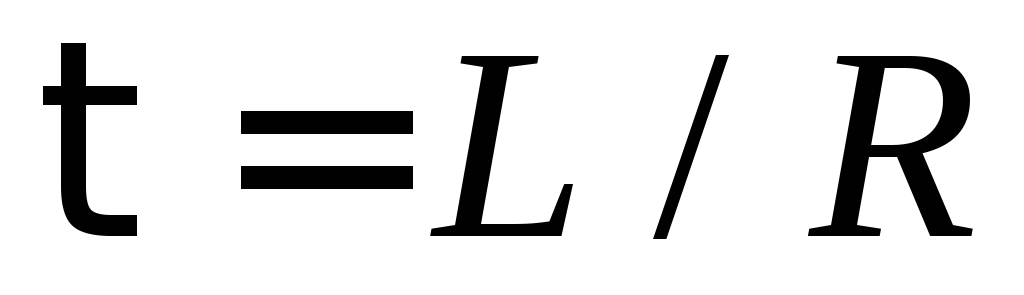 −постоянная
времени цепи RL.
−постоянная
времени цепи RL.
Общее решение
неоднородного уравнения (5): i = iоднор.+iчастн.= .
.
Н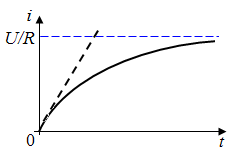 ачальное
условие:i(+0)
= i(−0)=0
(ток через индуктивность скачком
измениться не может, так как это
противоречило бы уравнению (5)). Отсюда
ачальное
условие:i(+0)
= i(−0)=0
(ток через индуктивность скачком
измениться не может, так как это
противоречило бы уравнению (5)). Отсюда
 .
(6)
.
(6)
Замечание 1.
При R=0
(подключение напряжения U к идеальной индуктивности) уравнение
(5) принимает вид:  ,
откуда
,
откуда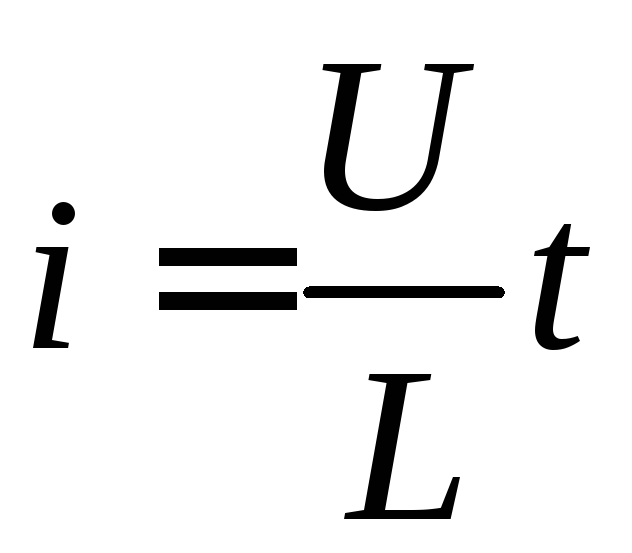 ,
т.е. ток в катушке линейно и бесконечно
растёт (наклонный пунктир на рисунке).
Это следует и из (6) при разложении
экспоненты в ряд Тейлора по малому
параметру (t/τ):
,
т.е. ток в катушке линейно и бесконечно
растёт (наклонный пунктир на рисунке).
Это следует и из (6) при разложении
экспоненты в ряд Тейлора по малому
параметру (t/τ): 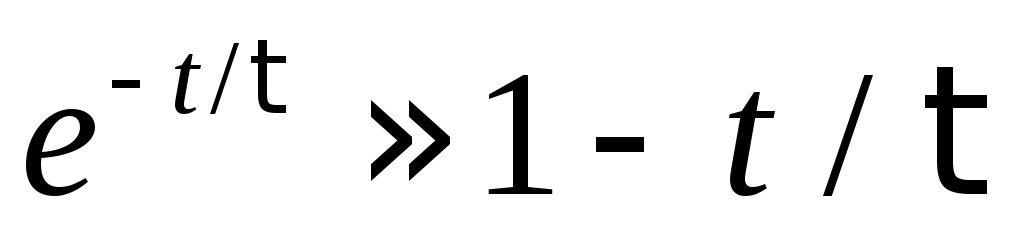
Замечание 2. Если скачки тока через индуктивности и скачки напряжения на ёмкости запрещены, то скачки напряжения на катушке и тока на конденсаторе не противоречат уравнениям Кирхгофа.
Конденсатор в цепи постоянного тока
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.

Заряд конденсатора от источника постоянной ЭДС
Точность вычисленияЗнаков после запятой: 2
Постоянная времени RC-цепи, миллисекунд
Время зарядки конденсатора до 99.2%, миллисекунд
Начальный ток, Ампер
Максимальная рассеиваемая мощность, Ватт
Напряжение на конденсаторе, Вольт
Заряд на конденсаторе, микроКулон
Энергия конденсатора, миллиДжоуль
Работа, совершенная источником, миллиДжоуль
save Сохранить share Поделиться extension Виджет

Разряд конденсатора через сопротивление
Начальное напряжение на конденсаторе, Вольт
Точность вычисленияЗнаков после запятой: 2
Начальная энергия конденсатора, миллиДжоуль
Начальный заряд конденсатора, микроКулон
Постоянная времени RC-цепи, миллисекунд
Начальный ток, Ампер
Максимальная рассеиваемая мощность, Ватт
Конечный заряд конденсатора, микроКулон
Конечная энергия конденсатора, миллиДжоуль
Конечное напряжение конденсатора, Вольт
save Сохранить share Поделиться extension Виджет
Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):
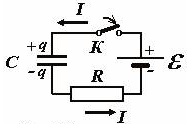
Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:
При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.
Во время зарядки конденсатора, напряжение на нем изменяется по закону
где величину
называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:
Энергия, запасенная в конденсаторе:
Работа, выполненная источником ЭДС:
Заряд и разряд конденсатора через сопротивление
| Полученные характеристики ЗАРЯДА конденсатора через сопротивление |
Заряд конденсатора емкостью
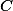 от источника тока через наружное сопротивление
от источника тока через наружное сопротивление 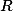 происходит в соответствии с формулой
происходит в соответствии с формулой
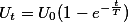
при этом мгновенный зарядный ток:
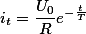
где
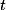 — рассматриваемый момент времени в секундах от момента начала заряда;
— рассматриваемый момент времени в секундах от момента начала заряда; 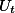 — напряжение на обкладках конденсатора момент времени t в Вольтах;
— напряжение на обкладках конденсатора момент времени t в Вольтах; 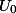 — напряжение источника, от которого производится заряд конденсатора в Вольтах
— напряжение источника, от которого производится заряд конденсатора в Вольтах 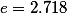
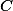 — емкость конденсатора в Фарадах
— емкость конденсатора в Фарадах 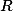 — сопротивление последовательной цепи в Омах
— сопротивление последовательной цепи в Омах 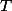 — постоянная времени в секундах (
— постоянная времени в секундах (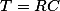 ).
).Разряд конденсатора емкостью
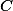 , заряженного до разности потенциалов
, заряженного до разности потенциалов 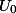 через сопротивление
через сопротивление 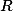 представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой
представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой
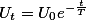
Мгновенная величина разрядного тока
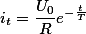
где
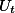 — напряжение между обкладками конденсатора через
— напряжение между обкладками конденсатора через 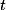 секунд после начала разряда,
секунд после начала разряда,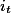 — ток в цепи (внешней или внутренней) конденсатора существующей через
— ток в цепи (внешней или внутренней) конденсатора существующей через 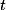 секунд после начала разряда.
секунд после начала разряда.
| Полученные характеристики РАЗРЯДА конденсатора через сопротивление |
Процессы заряда и разряда конденсаторов рассматриваются обычно в зависимости от постоянной времени цепи
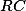 . Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в
. Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в 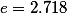 раз,
раз,от рассматриваемого напряжения. При заряде конденсатора постоянная времени указывает время (в секундах), в течение которого напряжение на обкладках повышается на 63% от разницы между имевшимся напряжением и напряжением источника тока заряда.
В связи с тем что заряд и разряд до полных значений конечных напряжений длятся неопределенно долгий срок, часто удобнее считать режим заряда законченным при доведении напряжения на обкладках до 99% от заряжающего напряжения (или до 1% от первоначальной величины напряжения при разряде).
Синтаксис
Для пользователей XMPP клиентов, используется команда
fiz ключи
где ключи это известные параметры, параметра=значение, разделенные точкой с запятой
Обязателен ключ key=razryad при расчете разаряда конденсатора
и zaryad при расчете заряда
Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.
Заметьте, чем данный калькулятор отличается от других:
Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)
Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.
Примеры использования бота
Определим время заряда конденсатора ёмкостью 1микроФарад, до 5 Вольт, если сопротивление цепи 1 килоОм.
Напряжение внешнего источника питания 12 Вольт, а на обкладках конденсатора напряжение, в момент подключения источника питания, составляло 1 Вольт.
Что бы сразу хотелось бы заметить. Как видно из задачи у нас есть остаточное напряжение на конденсаторе в размере 1 Вольт, которое надо учитывать в расчетах времени заряда.
Данные, которые мы будем вводить следующие:
U0=12-1 =11В
Ut=5-1=4В
R=1кОм
С=1мкФ
пишем запрос fiz U0=11В;Ut=4В;R=1кОм;C=1мкФ;key=zaryad
и получаем ответ
U0 = 11 Вольт
Ut = 4 Вольт
R = 1 килоОм
C = 1 микрофарад
T = 1 милисекунда
tt = 0.4519851237 милисекунда
То есть решение = 451.98 мкс
Теперь давайте проверим наши расчеты. Если бы конденсатор был бы в момент подключения источника питания полностью разряжен
То при условии зарядки его до 1 Вольта наш запрос был бы таким
fiz U0=12В;Ut=1В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 87.011377 микросекунда
а при зарядки до 5 Вольт был бы таким
fiz U0=12В;Ut=5В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 538.9965007 микросекунда
То время заряда конденсатора с 1В до 5 Вольт составило бы 538.9965007 микросекунда минус 87.011377 микросекунда = 451.98 мкс
Что несомненно говорит о правильности наших расчетов по изначальным условиям.
- Из звезды в треугольник. Эквивалентная схема. >>
5 3 51
Расчет параметров заряда и разряда конденсатора через сопротивление онлайн. Определение всех необходимых параметров | заряд, конденсатор, разряд, время, онлайнКонденсатор
Данный элемент используется как фильтр переменного тока, так как при большой ёмкости конденсатора сопротивление последнего подавляет его низкие частоты, а при малой высокие.
В постоянном токе конденсатор используется как сглаживающий элемент, так как в момент заряда пропускает ток, а в момент завершения заряда и далее нет, и по мере заполнения его ёмкости ток так же плавно перестаёт течь.
Ёмкость считается самым важным элементом в конденсаторе и измеряется в Фарадах.
1 Фарад (ф) = 1 000 000 Микрофарад (мкФ)
1 мкФ = 1 000 000 Пикофарад (пФ)
Вторым по важности параметром конденсаторов, после ёмкости, является его рабочее напряжение. Превышение этого параметра может привести к выходу конденсатора из строя, поэтому при построении реальных схем принято применять конденсаторы с удвоенным значением рабочего напряжения.
Для увеличения значений ёмкости или рабочего напряжения используют приём объединения конденсаторов в батареи. При последовательном соединении двух однотипных конденсаторов рабочее напряжение удваивается, а суммарная ёмкость уменьшается в два раза. При параллельном соединении двух однотипных конденсаторов рабочее напряжение остаётся прежним, а суммарная ёмкость увеличивается в два раза.
Третьим по важности параметром конденсаторов является температурный коэффициент изменения ёмкости (ТКЕ). Он даёт представление об изменении ёмкости в условиях изменения температур.
При подключении конденсатора к источнику постоянного тока под действием электрического поля на нижнюю обкладку движутся электроны. В следствии, явления электростатической индукции с верхней обкладки конденсатора заряды уходят к положительному выводу источника питания и в цепи возникает ток – ток заряда, по мере накопления зарядов в конденсаторе, растёт напряжение, а ток заряда уменьшается, и так, – конденсатор подключённый к источнику тока, заряжается до Uист
Конденсатор в цепи постоянного тока
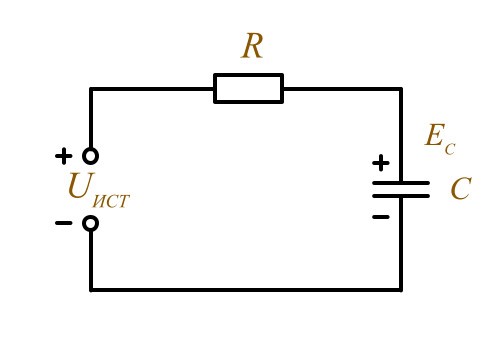
Кратковременный ток в цепи называется ток заряда, а так как он существует короткое время, то говорят, конденсатор постоянный ток не пропускает.
Считается что конденсатор заряжается если напряжение на нём составляет 0,63 от Uист и это происходит за время равное Τ
Ес – ЭДС ёмкости
Τ заряда – постоянная времени заряда конденсатора в секундах
Одна секунда – 1с = 103мс = 106мкс = 1012нс
Rзар – сопротивление в Омах
С – ёмкость в Фарадах
Τ = Rзар × С
График заряда конденсатора
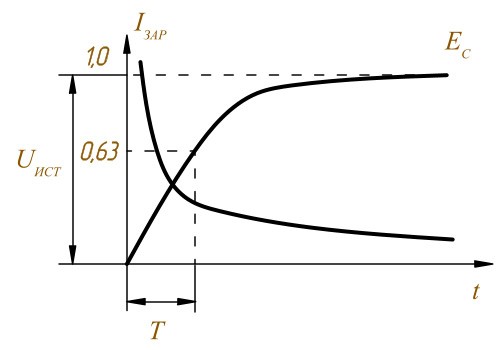
Работа конденсатора в цепи постоянного тока
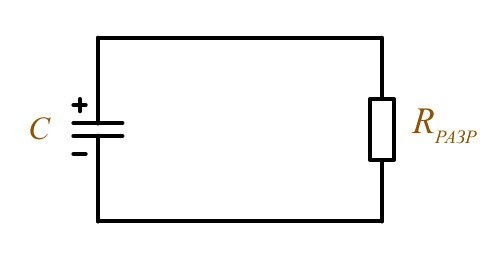
Считается, что конденсатор разрядится если напряжение на нём составляет 0,37 от напряжения источника и это происходит за время Τ разряда.
Τразр = Rразр × С
График разряда конденсатора
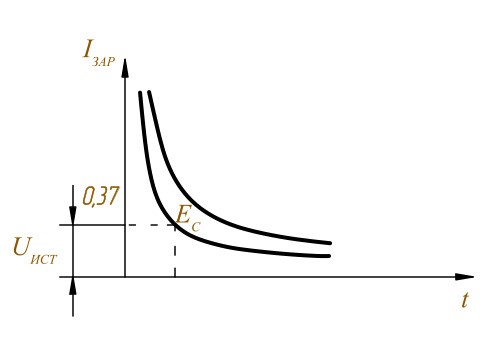
http://digitrode.ru/articles/1312-kakie-kondensatory-ispolzovat-v-proektah-s-arduino-i-drugih-elektronnyh-proektah.html
Конденсатор и RC цепочка | Электроника для всех
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.
О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:
Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R, где U напряжение на выводах резистора, R — его сопротивление.
Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.
Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!
Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.
Емкость конденсатора. Что это?
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.
Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.
Залить то можно сколько угодно, но напряжение будет разным.
Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник 🙂
А как быстро заряжается конденсатор?
В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.
Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.
В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону.
А у этого закона есть пара характерных величин:
- Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max—1/e*max.
- 3T — а при троекратной постоянной значение достигнет 95% своего максимума.
Постоянная времени для RC цепи Т=R*C.
Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.
Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:
T= C*R = 10-6 * 103 = 0.001c
3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.
Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.
Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.
Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.
Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:
Видишь как колбасится 🙂 Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!
А до какой величины конденсатор можно зарядить?
В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.
Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.
А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!
Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.
Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.
Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.
Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?
Переменная и постоянная составляющие сигнала легко разделяются!
Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.
Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T
Возможны два вида включения RC цепочки:
Интегрирующая и дифференцирующая. Они же фильтр низких частот и фильтр высоких частот.
Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.
Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.
Как здесь вычисляется постоянная составляющая? А с виду и не скажешь, но надо помнить, что любой периодически сигнал раскладывается в ряд Фурье, превращаясь в сумму из постоянной составляющей и пачки синусоид разной частоты и амплитуды.
Фильтр высоких частот работает наоборот. Он не пускает постоянную составляющую (т.к. ее частота слишком низка — 0) — ведь конденсатор для нее равносилен обрыву, а вот переменная пролазит через кондер без проблем.
А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.
- На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
- На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
- На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
- Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.
А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:
Вверху идет осциллограма того что на входе, внизу то что на выходе дифференциальной цепи.
Как видишь, тут мощные всплески на фронтах. Оно и понятно, в этом месте функция меняется резко, а значит производная (скорость изменения) этой функции велика, на пологих участках сигнал константа и его производная, скорость изменения, равна нулю — на графике ноль.
А если загнать в дифференциатор пилу, то на выходе получим…
прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.
Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер 🙂 Препод будет в шоке 🙂
Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь 🙂
А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:
И вот что получилось на осциллографе:
Вот, чуть покрупней один участок:
| > |
Как видишь, на одном срезало постоянную составляющую, на другом переменную.
Ладно, что то мы отвлеклись от темы.
Как еще можно применить RC цепь?
Да способов много. Часто ее используют не только в качестве фильтров, но и как формирователи импульсов. Например, на сбросе контроллера AVR, если надо чтобы МК стартанул не сразу после включения питания, а с некоторой выдержкой:
При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.
Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0
Аналоговые измерения
Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.
Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.
Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.
Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.
Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.
По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!
Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.
Теперь, думаю, ты понял за что я так люблю RC цепочки и почему на моей отладочной плате PinBoard их несколько и с разными параметрами 🙂
Заряд и разряд конденсатора через сопротивление
| Полученные характеристики ЗАРЯДА конденсатора через сопротивление |
Заряд конденсатора емкостью
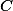 от источника тока через наружное сопротивление
от источника тока через наружное сопротивление 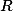 происходит в соответствии с формулой
происходит в соответствии с формулой
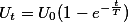
при этом мгновенный зарядный ток:
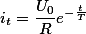
где
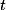 — рассматриваемый момент времени в секундах от момента начала заряда;
— рассматриваемый момент времени в секундах от момента начала заряда; 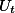 — напряжение на обкладках конденсатора момент времени t в Вольтах;
— напряжение на обкладках конденсатора момент времени t в Вольтах; 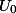 — напряжение источника, от которого производится заряд конденсатора в Вольтах
— напряжение источника, от которого производится заряд конденсатора в Вольтах 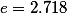
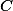 — емкость конденсатора в Фарадах
— емкость конденсатора в Фарадах 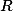 — сопротивление последовательной цепи в Омах
— сопротивление последовательной цепи в Омах 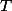 — постоянная времени в секундах (
— постоянная времени в секундах (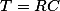 ).
).Разряд конденсатора емкостью
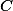 , заряженного до разности потенциалов
, заряженного до разности потенциалов 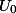 через сопротивление
через сопротивление 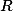 представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой
представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой
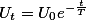
Мгновенная величина разрядного тока
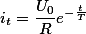
где
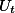 — напряжение между обкладками конденсатора через
— напряжение между обкладками конденсатора через 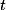 секунд после начала разряда,
секунд после начала разряда,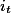 — ток в цепи (внешней или внутренней) конденсатора существующей через
— ток в цепи (внешней или внутренней) конденсатора существующей через 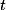 секунд после начала разряда.
секунд после начала разряда.
| Полученные характеристики РАЗРЯДА конденсатора через сопротивление |
Процессы заряда и разряда конденсаторов рассматриваются обычно в зависимости от постоянной времени цепи
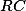 . Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в
. Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в 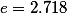 раз,
раз,от рассматриваемого напряжения. При заряде конденсатора постоянная времени указывает время (в секундах), в течение которого напряжение на обкладках повышается на 63% от разницы между имевшимся напряжением и напряжением источника тока заряда.
В связи с тем что заряд и разряд до полных значений конечных напряжений длятся неопределенно долгий срок, часто удобнее считать режим заряда законченным при доведении напряжения на обкладках до 99% от заряжающего напряжения (или до 1% от первоначальной величины напряжения при разряде).
Синтаксис
Для пользователей XMPP клиентов, используется команда
fiz ключи
где ключи это известные параметры, параметра=значение, разделенные точкой с запятой
Обязателен ключ key=razryad при расчете разаряда конденсатора
и zaryad при расчете заряда
Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.
Заметьте, чем данный калькулятор отличается от других:
Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)
Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.
Примеры использования бота
Определим время заряда конденсатора ёмкостью 1микроФарад, до 5 Вольт, если сопротивление цепи 1 килоОм.
Напряжение внешнего источника питания 12 Вольт, а на обкладках конденсатора напряжение, в момент подключения источника питания, составляло 1 Вольт.
Что бы сразу хотелось бы заметить. Как видно из задачи у нас есть остаточное напряжение на конденсаторе в размере 1 Вольт, которое надо учитывать в расчетах времени заряда.
Данные, которые мы будем вводить следующие:
U0=12-1 =11В
Ut=5-1=4В
R=1кОм
С=1мкФ
пишем запрос fiz U0=11В;Ut=4В;R=1кОм;C=1мкФ;key=zaryad
и получаем ответ
U0 = 11 Вольт
Ut = 4 Вольт
R = 1 килоОм
C = 1 микрофарад
T = 1 милисекунда
tt = 0.4519851237 милисекунда
То есть решение = 451.98 мкс
Теперь давайте проверим наши расчеты. Если бы конденсатор был бы в момент подключения источника питания полностью разряжен
То при условии зарядки его до 1 Вольта наш запрос был бы таким
fiz U0=12В;Ut=1В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 87.011377 микросекунда
а при зарядки до 5 Вольт был бы таким
fiz U0=12В;Ut=5В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 538.9965007 микросекунда
То время заряда конденсатора с 1В до 5 Вольт составило бы 538.9965007 микросекунда минус 87.011377 микросекунда = 451.98 мкс
Что несомненно говорит о правильности наших расчетов по изначальным условиям.
Заряд и разряд конденсатора через сопротивление | 2014-06-23 10:12:35 | Варламов Дмитрий | Электротехника онлайн |
5 3 51
Расчет параметров заряда и разряда конденсатора через сопротивление онлайн. Определение всех необходимых параметров | заряд, конденсатор, разряд, время, онлайн4.2. Заряд и разряд конденсатора через резистор
4.2.1. Процесс заряда
Р
U – постоянное напряжение источника.
До замыкания ключа «К» напряжение на емкости uC = 0.
ассматривается цепь, представленная на рис. 4.1. 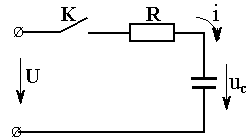
Рис. 4.1
После замыкания ключа в цепи протекает ток i, который согласно 2-му закону Кирхгофа:
RI + uc = U.
Ток в конденсаторе:
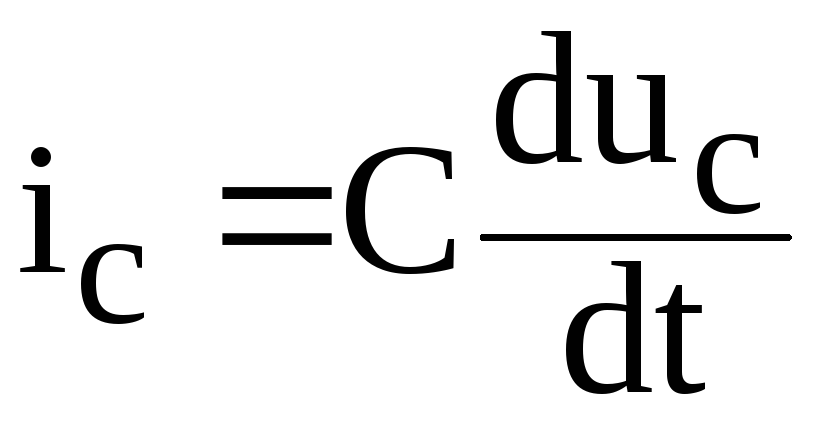 .
.
Тогда уравнение, описывающее изменение напряжения на конденсаторе в процессе его заряда, приобретает вид:
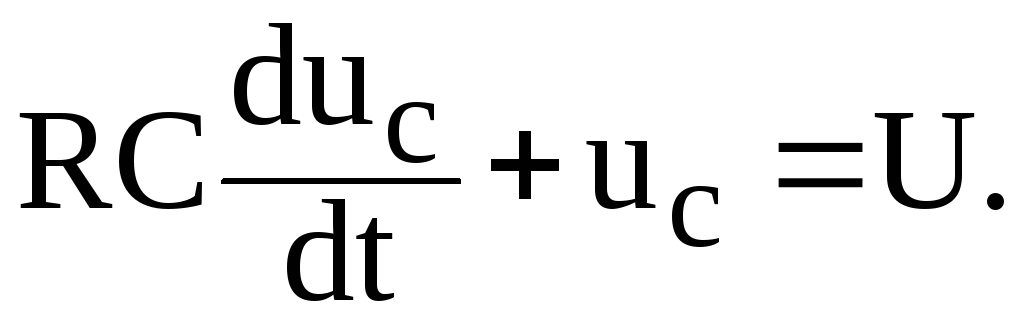 (4.2)
(4.2)
Напряжение на емкости в свободном режиме:

или 
Характеристическое уравнение
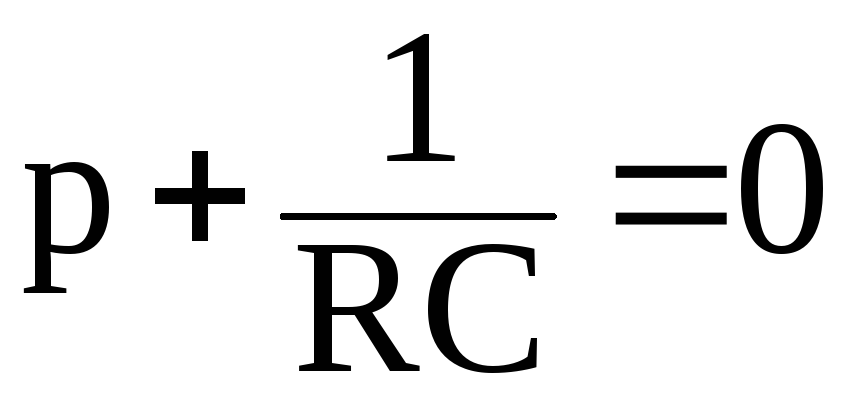

Результат решения характеристического уравнения:
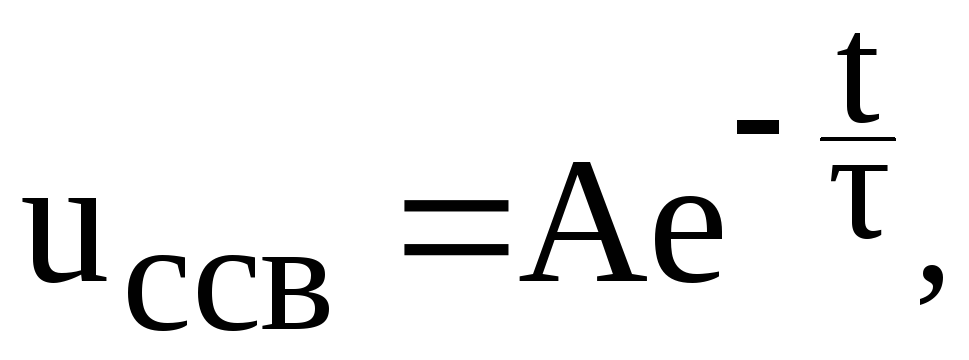 где τ
= RC,
где τ
= RC,
где τ – постоянная переходного процесса, имеющая размерность времени и характеризующая длительность протекания переходного процесса. Считается, что он завершается за t = 4τ, когда изменяющееся напряжение составляет 2% от установившегося значения.
Процесс заряда конденсатора заканчивается, когда напряжение на нем достигает величины U. Т.е. в установившемся режиме uсу = U.
Таким образом, решение уравнения (4.2):
uc = uссв + uсу = U + Ae—t/τ.
Постоянная «А» определяется, исходя из 2-го закона коммутации (при t = 0, uc = 0).
0 = U + A. A = -U.
uc = U (1 — e—t/τ).
Ток в цепи после замыкания ключа:

Результаты решения отражены на рис. 4.3.

Рис. 4.3
Ток в цепи после
замыкания мгновенно увеличивается до
величины, равной 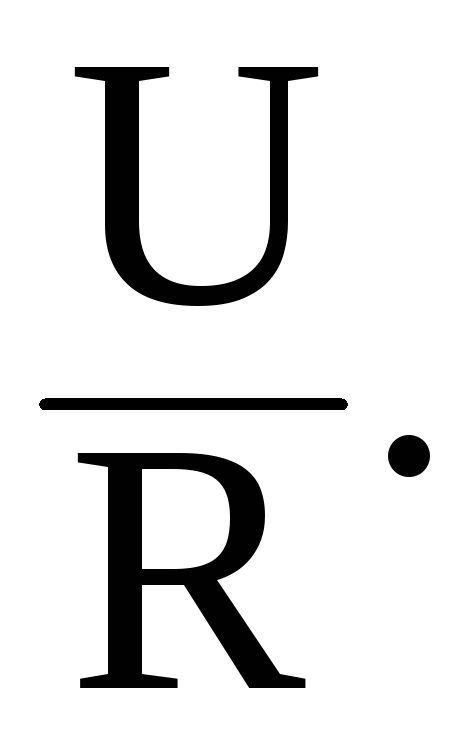 Это необходимо
учитывать при малых величинах
сопротивления.
Это необходимо
учитывать при малых величинах
сопротивления.
4.2.2. Процесс разряда
Рассматриваемая цепь представлена на рис. 4.4.
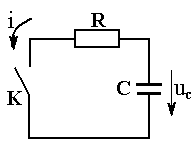
Полагается, что напряжение на конденсаторе до замыкания ключа «К»:
uc = U.
Рис. 4.4
При замыкании ключа направление тока разряда противоположно направлению тока заряда

Согласно второму закону Кирхгофа:
uc – Ri = 0.
Тогда уравнение, описывающее изменение напряжения на конденсаторе в процессе разряда, имеет вид:
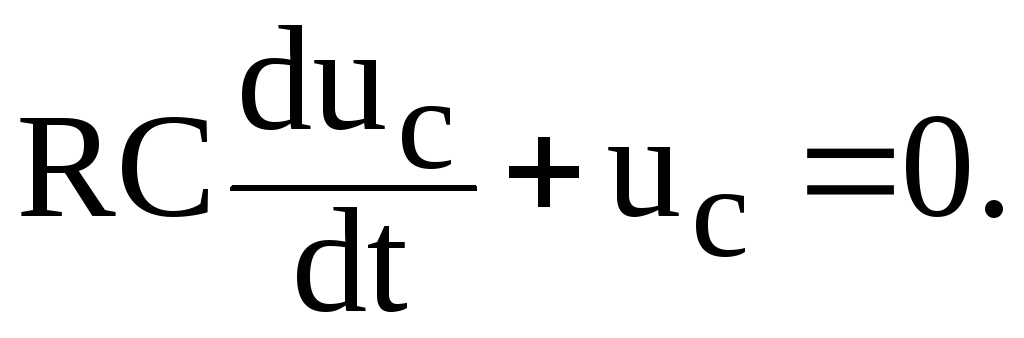 (4.4)
(4.4)
Его решение
uc = ucсв = Ае-t/τ
uc (0) = U A = U uc = Ue-t/τ
Ток разряда
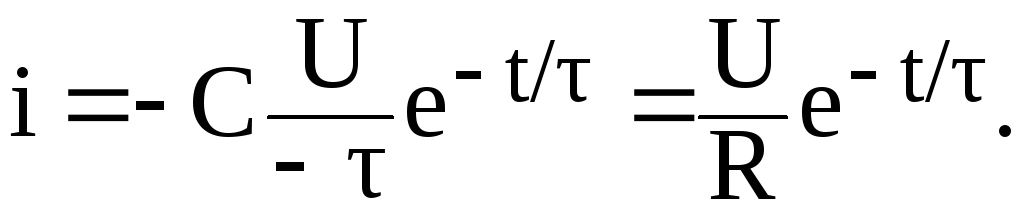
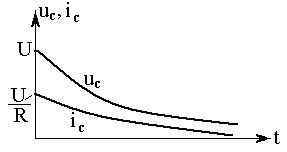
Рис. 4.5
Результаты решения отражены на рис. 4.5.
При разряде конденсатора энергия электрического поля, запасенная в нем, трансформируется в тепловую энергию в резисторе.
4.2.3. Уравнение, описывающее процессы заряда и разряда
конденсатора в общем случае
Пусть до замыкания ключа напряжение на конденсаторе, т.е. в начальный момент времени равно uc (0).
Тогда после определении постоянной «А»:
uc (0) = U + A. A = [u(0) – u(∞)].
где u(∞) — напряжение на конденсаторе при полном окончании переходного процесса (u(∞) = U).
Откуда по аналогии с решением уравнения (4.2):
uc (t) = uc(∞) — [uc(∞) – uc(0)]e-t/τ. (4.5)
Проверим справедливость соотношения (4.5) для случая разряда конденсатора.
В начальный момент времени uc (0) = U.
После окончания переходного процесса
uc(∞) = 0
После подстановки в уравнение (4.5) получается:
uc (t) = Ue—t/τ,
что совпадает с ранее полученным решением уравнения (4.4).
Пример расчета. Определить продолжительность переходного процесса Тпр в цепи с конденсатором С = 80 мкФ и резистором R = 10000 Ом.
τ = RC = 10000 · 80·10-6 = 0,8 c.
Тпр = 4τ = 4 · 0,8 = 3,2 с.
Пример применения.
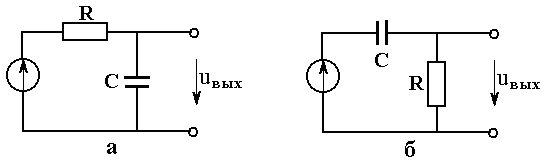
Рис. 4.6
Источник в схемах рис. 4.6 вырабатывает прямоугольные импульсы длительностью τ. Процессы в этих цепях представляют собой последовательно чередующиеся процессы заряда и разряда конденсаторов, которые происходят на переднем и заднем фронтах импульсов соответственно. В схеме рис. 4.6,б ток при заряде и разряде конденсаторов проходит через резисторR1. Создаваемое на нем падение напряжения является выходным. В схеме рис. 4.6,а выходным напряжением является напряжение на конденсаторе.
Схема рис. 4.6,а рассматривается для случая, когда:
τ >> Tимп.
Tимп – длительность импульса. В этом случае, как видно из рис. 4.7, процесс заряда конденсатора происходит медленно, так что в момент окончания импульса выходное напряжение достигает величины:
Uвыхmax = Uвхmax (1 – eTимп/RC).
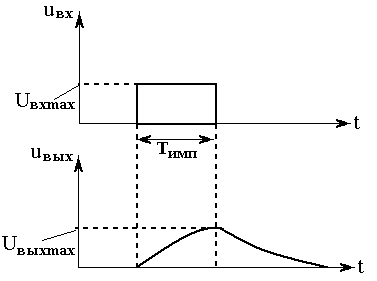
Рис. 4.7
После окончания импульса происходит медленный разряд конденсатора, а, следовательно, медленное уменьшение напряжения до нуля.
Схема рис. 4.6,б рассматривается в случае, когда:
τ << Tимп.
В этом случае конденсатор заряжается очень быстро, что обуславливает в начале импульса скачок тока до Uвхmax/R. Поэтому выходное напряжение представляет собой короткий импульс положительной полярности, амплитуда которого равна:
Uвыхmax = i R = Uвхmax.
Это иллюстрируется рис. 4.8.
Второй импульс на выходе, аналогичный первому, но отрицательной полярности, соответствует окончанию импульса напряжения источника. Его отрицательная полярность обусловлена разрядом конденсатора.
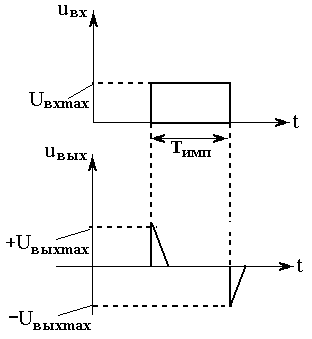
Рис. 4.8



