Расчёт реактивного сопротивления конденсатора и индуктивности. Он-лайн калькулятор сопротивлений ёмкости Xc и индуктивности Xl переменному току.
Прежде, чем мы приступим к расчётам разнообразных пассивных и активных фильтров, не плохо было бы сориентироваться в пространстве и задуматься — а за счёт чего происходит процесс частотной фильтрации сигналов, какой неведомый зверь должен выбежать на свист царевича после преобразования частотно-зависимыми цепями, и что это за цепи такие — частотно-зависимые?
Большая Энциклопедия Нефти и Газа учит нас, что частотно-зависимыми цепями называются электрические цепи с использованием емкостных и резистивных элементов. Спасибо, господа нефтяники и газовики — будем знать. От себя добавлю, что индуктивные элементы в частотно-зависимом хозяйстве также иногда пригождаются.
Для постоянного тока ни конденсаторы, ни катушки индуктивности никакого интереса не представляют. Сопротивление идеального конденсатора — бесконечность, индуктивности — ноль. Другое дело — переменный ток, тут наши частотно-зависимые элементы, начинают приобретать определённые значения сопротивлений, называемые реактивными сопротивлениями. Ясен пень, значения этих сопротивлений зависят от частоты протекающего тока. Для особо продвинутых, вымучаю из себя умную фразу — «Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах».
Графики, фазовые сдвиги, интегралы и прочие атрибуты студенческих знаний, как правило, мало кого интересуют. Если я не прав, пусть первыми бросят в меня камень и с лёгкостью найдут необходимую информацию на других сайтах. А мы ребята весёлые, поэтому сразу перейдём к делу и напишем всего пару формул:
Xс = 1 / 2πƒС, Xl = 2πƒL, где
Xc — сопротивление конденсатора переменному току, а Xl — сопротивление индуктивности переменному току.
РИСУЕМ ТАБЛИЧКУ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ КОНДЕНСАТОРА
ТО ЖЕ САМОЕ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ ИНДУКТИВНОСТИ
В реальной жизни конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлениями и индуктивностью, а катушки индуктивности — омическим сопротивлением провода обмотки и межвитковой паразитной ёмкостью.
Нужно Вам вооружаться этими знаниями, или нет, судить не возьмусь, а вот то, что электролитические конденсаторы имеют обыкновение
иногда взрываться при превышении допустимых уровней напряжений, либо перегреве, вызванным утечками вследствие старения —
знать надо обязательно.
Так что, если не хотите превратиться в одноглазого шахматиста из Васюков, соблюдайте технику безопасности, покупайте электролиты приличных производителей.


Онлайн расчет сопротивления конденсатора Xc и индуктивности Xl переменному току | hardware
Удобные методы онлайн-расчета сопротивления емкости C и индуктивности L переменному току с частотой F.
[Xc — сопротивление конденсатора переменному току]
Формула для расчета: Xc = 1/(2*pi*F*C), где Xc — сопротивление конденсатора переменному току в Омах, F — частота в Герцах, C — емкость в Фарад
[Xl — сопротивление индуктивности переменному току]
Формула для расчета: Xl = 2*pi*F*L, где Xl — сопротивление индуктивности переменному току в Омах, F — частота в Герцах, L — индуктивность в Генри. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах — Гц, мкГн, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).
[Общие замечания по использованию калькуляторов
1. 1 микрофарад (мкф) = 1000000 пикофарад (пФ). 1 фарад (Ф) = 1000000 микрофарад (мкФ) = 1012 пикофарад (пФ).
2. Десятичные значения с точкой нужно вводить с точкой, а не с запятой, иначе скрипт будет выдавать «infinity». Например, емкость 50 пФ следует ввести как 0.00005.
[Ссылки]
1. Микрофарад, Электрическая ёмкость site:convertworld.com. Очень удобный калькулятор для преобразования физических величин.
2. Расчёт резонансной частоты колебательного контура.
3. Расчет начальной магнитной проницаемости ферритовых колец по пробной обмотке.
4. Расчет дросселей на резисторах МЛТ.
Формула расчета реактивного сопротивления, калькулятор расчетов
В цепь переменного электрического тока входят активные (содержащие внутренние источники энергии) и пассивные элементы (потребители энергии). К пассивным элементам относят резисторы и реактивные устройства.

Пассивные элементы
Виды пассивных элементов
В электротехнике рассматривают два типа резисторов: активное и реактивное сопротивление. Активным – обладают приборы, в которых энергия электрического тока преобразуется в тепловую. В физике оно обозначается символом R. Единица измерения – Ом.
Рассчитать его можно, используя закон Ома:
R = U/I.
Этой формулой можно пользоваться для расчёта по мгновенным значениям тока и напряжения, максимальным или действующим.
Реактивные устройства энергию не рассеивают, а накапливают. К ним относятся:
- катушка индуктивности;
- конденсатор.
Реактивное сопротивление обозначается символом Х. Единица измерения – Ом.
Катушка индуктивности
Представляет собой проводник, выполненный в форме спирали, винта или винтоспирали. Благодаря высокой инерционности, прибор используют в схемах, которые применяются для уменьшения пульсаций в цепях переменного тока и колебательных контурах, для создания магнитного поля и т.д. Если она имеет большую длину при небольшом диаметре, то катушку называют соленоидом.

Схема включения
Для вычисления падения напряжения (U) на концах катушки используют формулу:
U = –L·DI/Dt, где:
- L – индуктивность прибора, измеряется в Гн (генри),
- DI – изменение силы тока (измеряется в амперах) за промежуток времени Dt (измеряется в секундах).
Внимание! При любом изменении тока в проводнике возникает ЭДС самоиндукции, которая препятствует этому изменению.
Вследствие этого в катушке возникает сопротивление, которое называется индуктивным.
В электротехнике обозначается ХL и рассчитывается по формуле:
ХL = w · L,
где w – угловая частота, измеряется в рад/с.
Угловая частота является характеристикой гармоничного колебания. Связана с частотой f (количество полных колебаний в секунду). Частота измеряется в колебаниях в секунду (1/с):
w = 2 · p · f.
Если в схеме используется несколько катушек, то при их последовательном соединении общее ХL для всей системы будет равно:
XL = XL1 + XL2 + …
В случае параллельного соединения:
1/XL = 1/XL1 + 1/XL2 + …
Закон Ома для такого соединения имеет вид:
XL=UL/I,
где UL – падение напряжения.
Помимо индуктивного, устройство обладает и активным R.
Электрический импеданс в этом случае равен:
Z = XL + R.
Емкостной элемент
В проводниках и обмотке катушки, кроме индуктивного и активного сопротивлений, присутствует и емкостное, которое обусловлено наличием ёмкости в этих приборах. Кроме резистора и катушки, в схему может быть включен конденсатор, который состоит из двух металлических пластин, между которыми размещён слой диэлектрика.
К сведению. Электрический ток протекает за счёт того, что в устройстве проходят процессы заряда и разряда пластин.
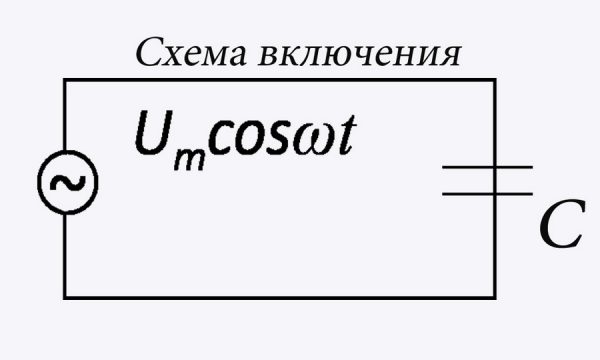
Схема подключения
При максимальном заряде на пластинах прибора:
U = max, I = 0.
За счёт того, что резистивное устройство может накапливать энергию, его используют в приборах, которые стабилизируют напряжение в цепи.
Возможность накапливать заряд характеризуется ёмкостью.
Реактивное сопротивление конденсатора (ХС) можно рассчитать по формуле:
XC = 1/(w·C), где:
- w – угловая частота,
- С – ёмкость конденсатора.
Единица измерения ёмкости – Ф (фарада).
Учитывая, что угловая частота связана с циклической частотой, расчет значения реактивного сопротивления конденсатора можно выполнить по формуле:
XC=1/(2·p·f·C).
Если в цепи последовательно соединены несколько устройств, то общее XС системы будет равно:
XС = XС1 + XС2 + …
Если соединение объектов параллельное, то:
1/XC = 1/XC1 + 1/XC2+…
Закон Ома для этого случая записывается следующим образом:
XC = UC/I,
где UС – падение напряжения на конденсаторе.
Расчёт цепи
При последовательном соединении I = const в любой точке и, согласно закону Ома, его можно рассчитать по формуле:
I = U/R,
где Z – электрический импеданс.

Последовательное соединение элементов
Напряжение на устройствах рассчитывается следующим образом:
UR = I · R, UL = I · XL, UC = I · XC.
Вектор индуктивной составляющей напряжения направлен в противоположную сторону от вектора емкостной составляющей, поэтому:
UX = UL – UC,
следовательно, согласно расчётам:
X = XL – XC.
Внимание! Для вычисления значения импеданса можно воспользоваться «треугольником сопротивлений», в котором гипотенузой является значение Z, а катетами – значения X и R.
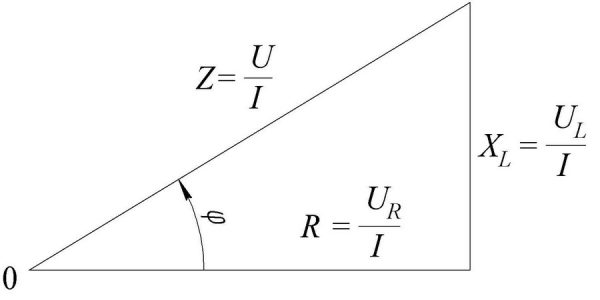
Треугольник сопротивлений
Если в цепь подключены и конденсатор, и катушка индуктивности, то, согласно теореме Пифагора, гипотенуза (Z) будет равна:
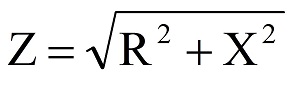
Так как X = XL – XC, то:

При решении электротехнических задач часто импеданс записывают в виде комплексного числа, в котором действительная часть соответствует значению активной составляющей, а мнимая – реактивной. Таким образом, выражение для импеданса в общем виде имеет вид:
Z = R + X·i,
где i – мнимая единица.
Для онлайн расчёта реактивного сопротивления можно использовать программу – калькулятор, которую можно найти в сети Интернет. Подобных сервисов достаточно много, поэтому вам не составит труда подобрать удобный для вас калькулятор.

Онлайн калькулятор для расчёта емкостных и индуктивных характеристик
Благодаря таким Интернет сервисам, можно быстро выполнить нужный расчёт.
Видео
Оцените статью:Реактивное сопротивление | Формулы и расчеты онлайн
Цепи переменного тока часто содержат как емкостные, так и индуктивные сопротивления. Их сложение подчиняется определенным правилам.
Если
| U | полное напряжение (эффективное значение), | Вольт |
|---|---|---|
| UC | напряжение на емкостном сопротивлении, | Вольт |
| UL | напряжение на индуктивном сопротивлении, | Вольт |
| I | полный ток (эффективное значение), | Ампер |
| IC | ток через емкостное сопротивление, | Ампер |
| I | ток через индуктивное сопротивление, | Ампер |
| XC | емкостное сопротивление, | Ом |
| XL | индуктивное сопротивление, | Ом |
| X | полное реактивное сопротивление, | Ом |
| B = 1/Х | реактивная проводимость, | сименс |
то
Реактивное сопротивление индуктивности и конденсатора при последовательном соединении L и С
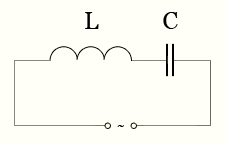
Реактивное сопротивление индуктивности и конденсатора при последовательном соединении L и С
\[ U = U_{L} — U_{C} = IX_{L} — IX_{C} = IX \]
Определить, найти реактивное сопротивление индуктивности и конденсатора при последовательном соединении
Реактивное сопротивление индуктивности и конденсатора при параллельном соединении L и С

Реактивное сопротивление индуктивности и конденсатора при параллельном соединении L и С
\[ B = B_{C} — B_{L} = \frac{1}{X_{C}} — \frac{1}{X_{L}} = ωC — \frac{1}{ωL} \]
\[ X = \frac{ωL}{ω^{2}LC-1} \]
\[ I = I_{C} — I_{L} = \frac{U}{X_{C}} — \frac{U}{X_{L}} = \frac{U}{X} = UB \]
Определить, найти реактивное сопротивление индуктивности и конденсатора при параллельном соединении
В помощь студенту
Реактивное сопротивление |
стр. 688 |
|---|
влияние на переменный и постоянный ток, формулы для расчета
 Конденсатор используется в схемах для разделения переменной и постоянной составляющей напряжения, при этом он хорошо проводит высокочастотный сигнал, и плохо — низкочастотный. Находясь в цепи постоянного тока, его импеданс принимается бесконечно большим. Для переменного тока ёмкостное сопротивление конденсатора не имеет постоянной величиной. Поэтому расчёт этого значения крайне важен при проектировании различных радиоэлектронных приборов.
Конденсатор используется в схемах для разделения переменной и постоянной составляющей напряжения, при этом он хорошо проводит высокочастотный сигнал, и плохо — низкочастотный. Находясь в цепи постоянного тока, его импеданс принимается бесконечно большим. Для переменного тока ёмкостное сопротивление конденсатора не имеет постоянной величиной. Поэтому расчёт этого значения крайне важен при проектировании различных радиоэлектронных приборов.
Общее описание
Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.
Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).
На схемах конденсатор изображается в виде двух прямых, соответствующих проводящим пластинам прибора, и перпендикулярно к их серединам нарисованными отрезками — выводами устройства.
 Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.
Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.
Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.
Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
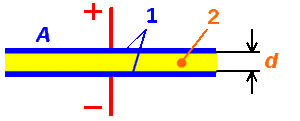
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.

Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.
Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
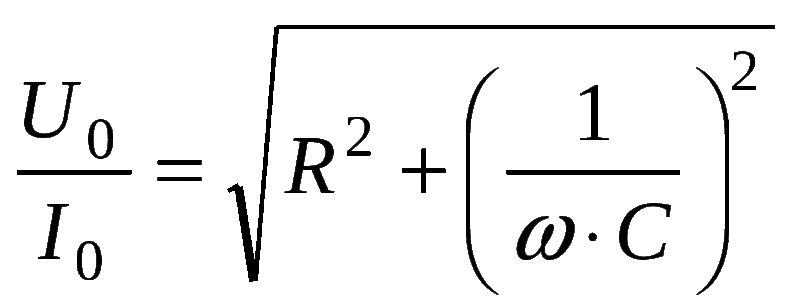
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное — с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Ёмкостное сопротивление
Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.

Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.
Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:
- Xc = 1/w*C = ½*p*f*C. Единица измерения — ом.
Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.
На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.
Индуктивная составляющая
При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .
Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность.
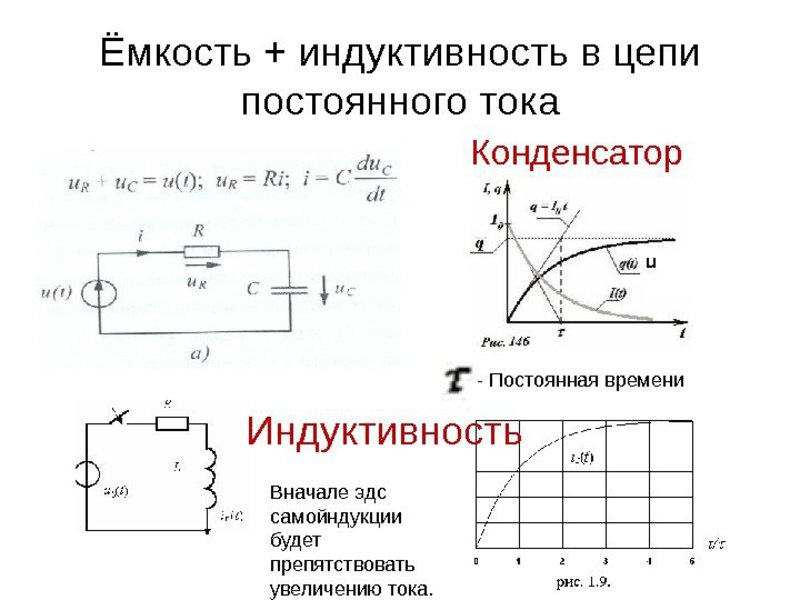
Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.
Таким образом, индуктивное сопротивление будет равно Xl = w * L, измеряется оно также в омах. Из полученного выражения видно, что чем больше частота сигнала, тем сильнее будет сопротивление прохождению тока.
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R

Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.

Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.
Содержание:
Реактивным называется сопротивление, препятствующее прохождению переменного электротока в цепи под действием конденсатора или катушки индуктивности, включенных в эту цепь. Это связано со свойствами индуктивности, которая выступает в качестве обычного проводника для постоянного тока с бесконечно малым сопротивлением. В тех же условиях конденсатор уже становится диэлектриком с возрастающим сопротивлением. При переменном токе реактивное сопротивление конденсатора оказывает влияние на такие параметры, как частота самого тока, индуктивность катушки или емкость. Из-за этого свойства конденсатор получил наименование реактивного элемента или реактивного электронного компонента. Свойства реактивного сопротивления конденсатораВ каждом заряженном конденсаторе присутствует электрический ток. В этих условиях он является составной частью процесса зарядки и разрядки, когда электрическое поле, образующееся между обкладками, накапливает или отдает энергию.
Установленный в цепь переменного тока, конденсатор будет накапливать энергию, то есть заряжаться, до определенного максимума, пока направление тока не изменится на противоположное. Поэтому при амплитудном значении напряжения, ток в конденсаторе будет иметь нулевое значение. В результате, ток и напряжение конденсатора будут постоянно расходиться во времени на четверть периода. Таким образом, падение напряжения на конденсаторе ограничивает ток во всей цепи, создавая реактивное сопротивление. Его значение обратно пропорционально частоте тока и емкости конденсатора.
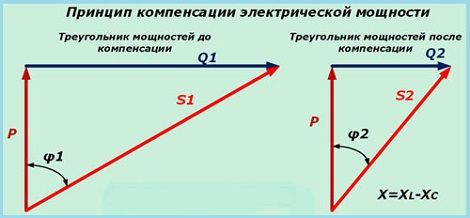
Если к конденсатору подвести напряжение U, в этом случае начнется уменьшение тока от максимума до нуля. Одновременно, напряжение на его выводах будет возрастать от нулевого до максимального значения. В этом случае напряжение на обкладках конденсатора отстает по фазе от тока на угол, равный 90 градусам. Данное явление получило название отрицательного сдвига фаз. Практическое использование реактивного сопротивленияС помощью конденсаторных установок осуществляется компенсация реактивной мощности. Через электрические сети высоковольтная электроэнергия передается на большие расстояния. В большинстве случаев она потребляется электродвигателями с резистивными элементами и значительным индуктивным сопротивлением.
Полная мощность, поступающая к потребителям, включает в себя активную составляющую Р, с помощью которой совершается полезная работа, и реактивную составляющую Q, приводящую к нагреву обмоток электродвигателей и трансформаторов. Качество электроэнергии существенно снижается под действием реактивной составляющей, возникающей на индуктивных сопротивлениях. Для того чтобы ликвидировать ее негативное воздействие, была разработана специальная схема компенсации. С этой целью подключались конденсаторные батареи, емкостное сопротивление которых способствовало понижению косинуса угла ф. Установка таких конденсаторных батарей практиковалась в основном на подстанциях, осуществляющих непосредственную поставку электроэнергии проблемным потребителям. Данное мероприятие позволяло эффективно регулировать качество поставляемой энергии. Снижение уровня реактивной компоненты способствует существенному уменьшению нагрузки на установленное оборудование, хотя активная мощность остается на одном и том же уровне. Используя реактивное сопротивление конденсатора, удалось добиться экономии электроэнергии на предприятиях промышленного производства и объектах жилищно-коммунального хозяйства, повысить надежность работы энергетических систем. Расчет онлайн |
2. Конденсатор в цепи переменного тока | 4. Реактивное сопротивление и импеданс — Емкость | Часть2
2. Конденсатор в цепи переменного тока
Конденсатор в цепи переменного тока
Конденсатор в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то конденсаторы противостоят изменению напряжения («тормозя» или добавляя ток во время зарядки или разрядки до нового уровня напряжения). Проходящий через конденсатор ток прямопропорционален скорости изменения напряжения. Это противостояние изменению напряжения является еще одной формой реактивного сопротивления, которое по своему действию противоположно реактивному сопротивлению катушки индуктивности.
Математическая взаимосвязь между проходящим через конденсатор током и скоростью изменения напряжения на нем выглядит следующим образом:
Отношение du/dt представляет собой скорость изменения мгновенного напряжения (u) с течением времени, и измеряется в вольтах в секунду. Емкость (С) измеряется в Фарадах, а мгновенный ток (i) — в амперах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую емкостную схему:
Простая емкостная цепь: напряжение конденсатора отстает от тока на 90o.
Если мы построим график тока и напряжения для этой простой цепи, то он будет выглядеть примерно так:
Как вы помните, проходящий через конденсатор ток является реакцией на изменение напряжения на этом конденсаторе. Отсюда можно сделать вывод, что мгновенный ток равен нулю всякий раз, когда мгновенное значение напряжения находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны напряжения), и мгновенный ток равен своему пиковому значению всякий раз, когда мгновенное напряжение находится в точках максимального изменения (точки самого крутого наклона волны напряжения, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на -90o не совпадает по фазе с волной тока. На графике видно, как волна тока дает «фору» волне напряжения: ток «ведет» напряжение, а напряжение «запаздывает» за током.
Как вы уже догадались, такая же необычная волна мощности, которую мы видели в простой индуктивной цепи, присутствует и в простой емкостной цепи:
Как и в случае с простой индуктивной цепью, фазовый сдвиг 90 градусов между напряжением и током приводит к равномерному чередованию волны мощности между положительными и отрицательными значениями. Это означает, что конденсатор не рассеивает мощность (когда реагирует на изменения напряжения), а просто поглощает и высвобождает ее (поочередно).
Сопротивление конденсатора, изменяющее напряжение, интерпретируется как сопротивление переменному напряжению в целом, у которого по определению постоянно меняется мгновенная величина и направление. Для любой заданной величины переменного напряжения на заданной частоте, конденсатор заданного размера будет «проводить» определенную величину переменного тока. Так же, как ток через резистор является функцией напряжения на этом резисторе и его сопротивления, переменный ток через конденсатор является функцией переменного напряжения на этом конденсаторе и его реактивного сопротивления. Как и в случае с катушками индуктивности, реактивное сопротивление конденсатора измеряется в Омах, и обозначается буквой Х (или ХС, если быть более точным).
Поскольку проходящий через конденсатор ток пропорционален скорости изменения напряжения, он будет больше для быстро меняющихся напряжений, и меньше — для напряжений с более медленным изменением. Это означает, что реактивное сопротивление любого конденсатора (в Омах) обратно пропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления конденсатора выглядит следующим образом:
Если на конденсатор емкостью 100 мкФ воздействовать частотами 60, 120 и 2500 Гц, то его реактивное сопротивление примет следующие значения:
| Частота (Гц) | Реактивное сопротивление (Ом) |
|---|---|
| 60 | 26.5258 |
| 120 | 13.2629 |
| 2500 | 0.6366 |
Обратите внимание на то, что отношение емкостного реактивного сопротивления к частотам точно противоположно отношению индуктивного реактивного сопротивления к тем же частотам. Емкостное реактивное сопротивление уменьшается с увеличением частоты переменного тока, а индуктивное реактивное сопротивление наоборот, увеличивается с ростом частоты переменного тока. Если катушки индуктивности выступают против быстрого изменения тока, производя большее напряжение, то конденсаторы выступают против быстрого изменения напряжения, производя больший ток.
По аналогии с катушками индуктивности, выражение 2πf в уравнении реактивного сопротивления конденсатора может быть заменено на строчную греческую букву ω (Омега), которую иначе называют угловой (циклической) частотой переменного тока. Таким образом, уравнение XC = 1/(2πfC) может быть записано как XC = 1/(ωC), где ω выражается в радианах в секунду.
Переменный ток в простой емкостной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление конденсатора (в Омах). Это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:
Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, ток имеет фазовый сдвиг +90o по отношению к напряжению. Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что реактивное сопротивление конденсатора переменному току обладает следующим фазовым углом:
Математически можно сказать, что фазовый угол сопротивления конденсатора переменному току составляет -90o. Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).