Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов

При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на Q, получим знакомую формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

Так как заряд конденсатора

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

Пример 1

Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С₁ = 10 мкФ, C₂ = 2 мкФ, C₃ = 5 мкФ, а C₄ = 1 мкФ?

При последовательном соединении общая емкость равна:

При параллельном соединении общая емкость равна:

Пример 2

Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С₁ = 7 мкФ, С₂ = 2 мкФ, С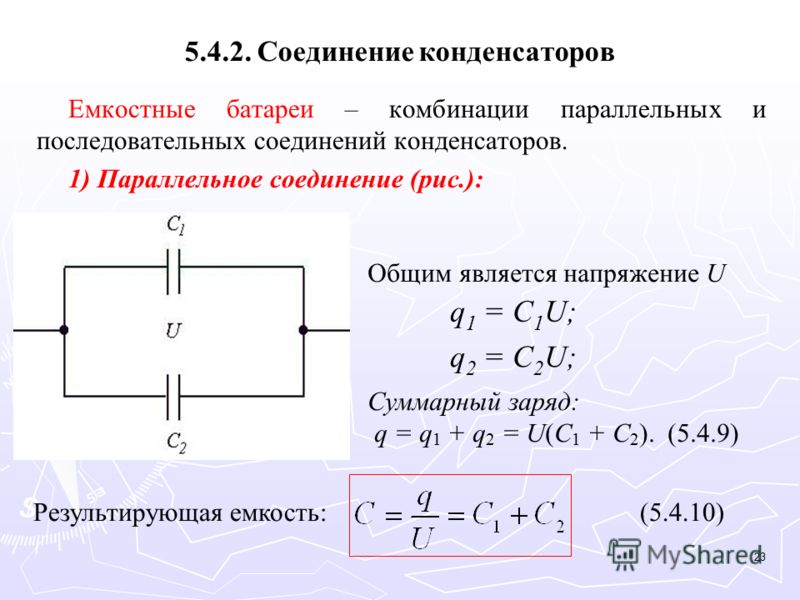

3 = 1 мкФ.

Сначала найдем общую емкость параллельного участка цепи:

Затем найдем общую емкость для всей цепи:

По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Советуем прочесть — Заряд и разряд конденсатора

Просмотров:

Соединения конденсаторов. Энергия электрического поля конденсатора.

Соединения конденсаторов .
Параллельное соединение конденсаторов
Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора
Вывод: При параллельном соединении конденсаторов заряды складываются, напряжения одинаковые, емкости складываются. Т.о.,  общая емкость больше емкости любого из параллельно соединенных конденсаторов
Последовательное соединение конденсаторов
Производят только одно соединение, а две оставшиеся обкладки — одна от конденсатора С1 другая от конденсатора С2 — играют роль обкладок нового конденсатора.
Вывод: При последовательном соединении конденсаторов напряжения складываются, заряды одинаковы, складываются величины, обратные емкости.    Т.о.,  общая емкость меньше емкости любого из последовательно соединенных конденсаторов.
Энергия электрического поля конденсатора. Под  энергией электрического поля конденсатора будем понимать энергию одной его обкладки, находящейся в поле, созданном другой  обкладкой. Тогда:   Формулы справедливы для любого конденсатора.	Пример: С=2мкФ; U=1000В . t=10-6c.W=1 Дж  — опасно для жизни!
Плотность энергии.   — плотность энергии (энергия единицы объема). Формула справедлива для полей любых конденсаторов и, кроме того, для полей, меняющихся со временем (неэлектростатических).

Последовательное соединение конденсаторов: особенности и примеры

Последовательное соединение конденсаторов – батарея, образованная цепочкой конденсаторов. Отсутствует ветвление, выход одного элемента подключается к входу следующего.

Физические процессы при последовательном соединении

При последовательном соединении конденсаторов заряд каждого равноценен. Обусловлено природным принципом равновесия. С источником соединены только крайние обкладки, другие заряжаются путем перераспределения меж ними зарядов. Используя равенство, находим:

q = q1 = q2 = U1 C1 = U2 C2, откуда запишем:

U1/U2 = C2/C1.

Напряжения меж конденсаторами распределяются обратно пропорционально номинальным емкостям. В сумме оба составляют вольтаж питающей сети. При разряде конструкция способна отдать заряд q вне зависимости от того, сколько конденсаторов включено последовательно. Емкость батареи найдем из формулы:

C = q/u = q/(U1 + U2), подставляя выражения, приведенные выше, приводя к общему знаменателю:

1/С = 1/С1 + 1/С2.

Вычисление общей емкости батареи

При последовательном соединении конденсаторов в батарею складываются величины, обратные номинальным емкостям. Приводя последнее выражение к общему знаменателю, переворачивая дроби, получаем:

С = C1C2/(C1 + C2).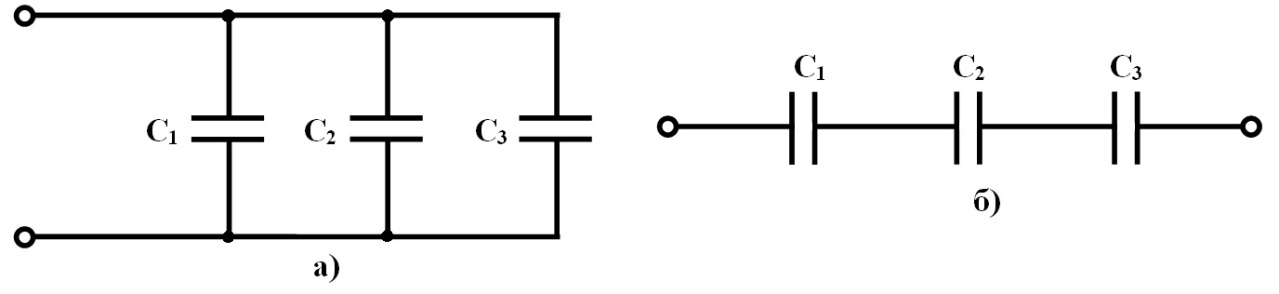

Выражение используется для нахождения емкости батареи. Если конденсаторов более двух, формула усложняется. Для нахождения ответа номиналы перемножаются меж собой, выходит числитель дроби. В знаменатель ставят попарные произведения двух номиналов, перебирая комбинации. Практически иногда удобнее вести вычисление через обратные величины. Полученным результатом разделить единицу.

Соединение последовательное конденсаторов

Формула сильно упрощается, если номиналы батареи одинаковы. Требуется просто цифру поделить общим числом элементов, получая результирующее значение. Напряжение распределится равномерно, следовательно, достаточно номинал питающей сети разбить поровну на общее число. При питании аккумулятором 12 вольт, 4-х емкостях, на каждой упадет 3 вольта.

Одно упрощение сделаем для случая, когда номиналы равны, одна емкость включена переменная, чтобы подстраивать результат. Тогда максимальное напряжение каждого элемента удастся приближенно найти, разделив вольтаж источника уменьшенным на единицу количеством.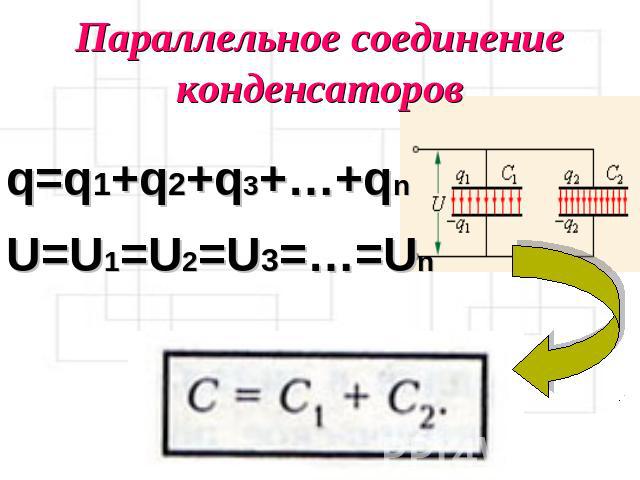 Получится результат с заведомым запасом. Что касается переменной емкости, требования намного жёстче. В идеале рабочее значение перекрывает вольтаж источника.

Необходимость в последовательном соединении

На первый взгляд идея соединения конденсаторов батареей последовательным образом покажется лишенной смысла. Первое преимущество очевидно: падают требования к максимальному напряжению обкладок. Больше рабочий вольтаж, дороже изделие. Подобным образом мир видит радиолюбитель, владеющий рядом низковольтных конденсаторов, желающий применить железо составной частью высоковольтной цепи.

Рассчитывая по приведенным выше формулам действующие напряжения элементом, можно легко решить поставленную задачу. Рассмотрим для пущей наглядности пример:

Пусть установлены аккумулятор напряжением 12 вольт, три емкости номиналами 1, 2 и 4 нФ. Найдем напряжение при последовательном соединении элементов батареей.

Решение:

Для нахождения трех неизвестных потрудитесь составить равное количество уравнения. Известно из курса высшей математики. Результат будет выглядеть следующим образом:

1. U1 + U2 + U3 = 12;
2. U1/U2 = 2/1 = 2, откуда запишем: U1 = 2U2;
3. U2/U3 = 4/2 = 2, откуда видно: U2 = 2U

Не сложно заметить, последние два выражения подставим первому, выразив 12 вольт через вольтаж третьего конденсатора. Получится следующее:

4U3 + 2U3 + U3 = 12, откуда находим, напряжение третьего конденсатора составляет 12/7 = 1,714 вольта, U2 – 3,43 вольта, U1 – 6,86 вольта. Сумма чисел дает 12, каждое меньше напряжения питающего аккумулятора. Причем тем больше разница, чем меньший номинал у соседей. Из этого правила следует: в последовательном соединении конденсаторы низкой емкости показывают большее рабочее напряжение. Найдем для определенности номинал составленной батареи, заодно проиллюстрируем формулу, поскольку выше описана чисто словесно:

С = С1С2С3/(С1С2 + С2С3 + С1С3) = 8/(2 + 8 + 4) = 8/14 = 571 пФ.

Результирующий номинал меньше каждого конденсатора, составляющего последовательное соединение.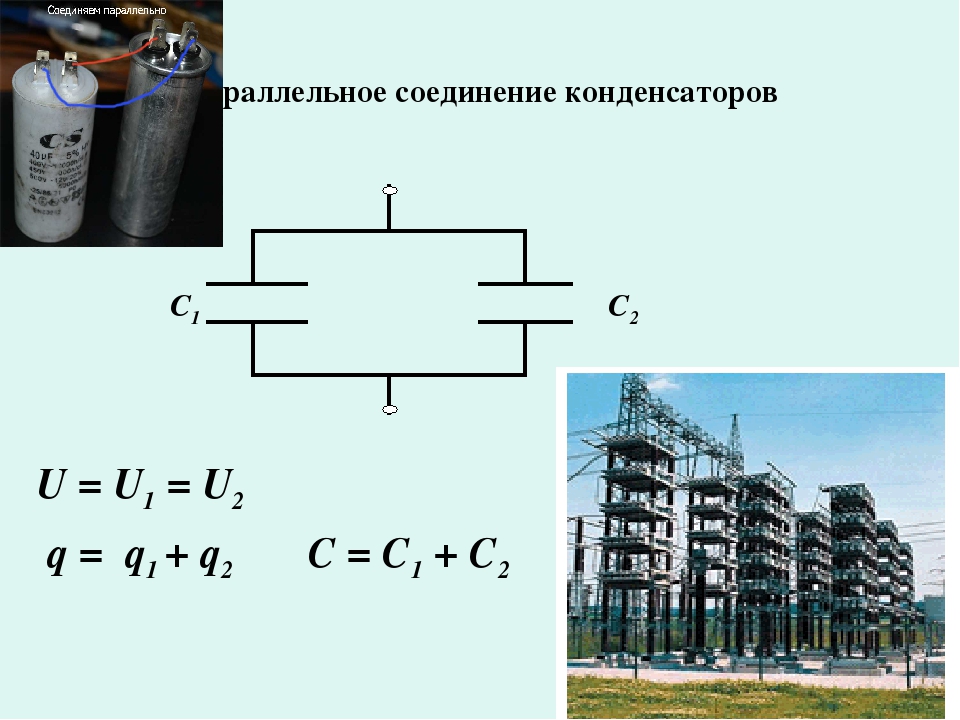 Из правила видно: максимальное влияние на суммарную емкость оказывает меньший. Следовательно, при необходимости подстройки полного номинала батареи должен быть переменный конденсатор. В противном случае поворот винта не окажет большого влияния на конечный результат.

Видим очередной подводный камень: после подстройки распределение напряжений по конденсаторам изменится. Просчитайте крайние случаи, дабы вольтаж не превысил рабочее значение для составляющих батарею элементов.

Программные пакеты исследования электрических цепей

Помимо онлайн- калькуляторов расчета последовательного соединения конденсаторов присутствуют и инструменты помощнее. Большой минус общедоступных средств объясняется нежеланием сайтов проверять программный код, значит, содержат ошибки. Плохо, если одна емкость выйдет из строя, сломленная процессом испытаний неправильно собранной схемы. Не единственный недостаток. Иногда схемы гораздо сложнее, разобраться комплексно невозможно.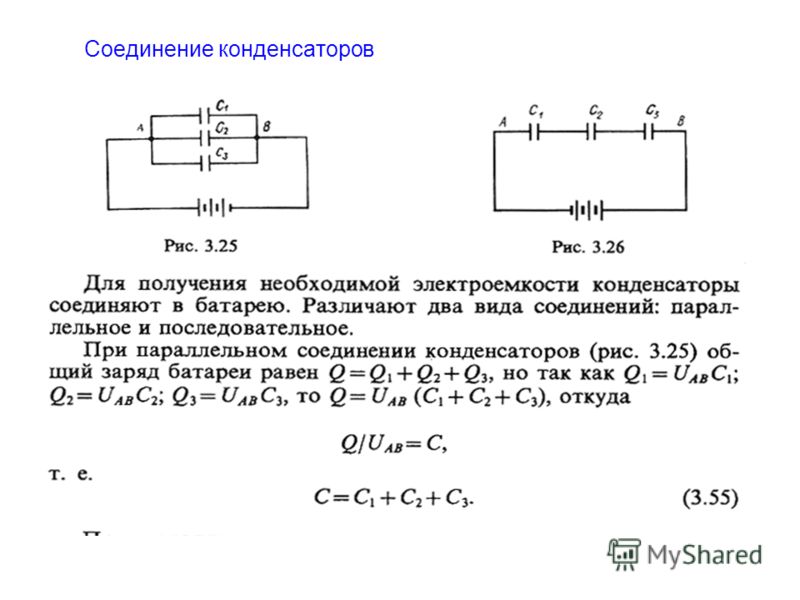

В отдельных приборах встречаются фильтры высокой частоты, использующие конденсатор, включенные каскадами. Тогда на схеме помимо замыкания через резистор на землю образуется последовательное соединение емкостей. Обычно не применяют формулу, показанную выше. Принято считать, каждый каскад фильтра существует отдельно, результат прохождения сигнала описывается амплитудно-частотной характеристикой. Графиком, показывающим, как сильно обрежет на выходе спектральную составляющую сигнала.

Желающим провести ориентировочные расчеты рекомендуется ознакомиться с программным пакетом персонального компьютера Electronics Workbench. Конструктив выполнен по английским стандартам, потрудитесь учитывать нюанс: обозначение резисторов на электрической схеме изломанным зигзагом. Номиналы, названия элементов будут изложены на иностранный манер. Не мешает пользоваться оболочкой, предоставляющей оператору гору источников питания различного толка.

И главное – Electronics Workbench позволит задать контрольные точки на каждой, в режиме реального времени посмотреть напряжение, ток, спектр, форму сигнала. Полагается дополнить проект амперметром, вольтметром, прочими аналогичного толка приборами.

При помощи такого программного пакета смоделируете ситуацию, посмотрите, сколько падает напряжения на элементе батареи. Уберегает от громоздких расчетов, намного ускоряя процесс проектирования схемы. Одновременно исключаются ошибки. Легко и просто становится добавлять, удалять конденсаторы с немедленной оценкой результата.

Рабочий пример

Скрин показывает рабочий стол Electronics Workbench 5.12 с собранной электрической схемой последовательного соединения конденсаторов. Каждый емкостью 1 мкФ, одинаковые элементы взяты для целей демонстрации. Чтобы каждый мог без труда проверить правильность.

Последовательная батарея конденсаторов

Обратим вначале внимание на источник. Переменное напряжение частотой 60 Гц. В стране разработчика действует иной стандарт, нежели российские. Рекомендуется правой кнопкой мыши щелкнуть источник, посетить свойства, выставить:

1. Частоту (frequency) 50 Гц вместо 60 Гц.
2. Действующее значение напряжения (voltage) 220 вольт вместо 120.
3. Фазу (phase – имитация реактивности) взять согласно своим нуждам.

Для буквоедов будет полезно полистать свойства элементов цепи. У источника вольны задать допустимое отклонение напряжения (voltage tolerance) в процентах. Достаточно добавить один резистор размером 1 кОм, цепь становится фильтром верхних частот. Рекомендуется не упрощать действия. Поставить правильно знак заземления, убедиться: схема полностью тривиальна. В противном случае результаты заставят надолго поломать голову.

Построение графиков

Проиллюстрированный скрином фильтр верхних частот обнаруживает подъем амплитудно-частотной характеристики в районе 1 кГц. При нахождении полосы пропускания необходимо учесть: вертикальная шкала логарифмическая. Посему срез на уровне 70% максимума не соответствует семи десятым высоты пологой части пика. Заядлым любителям будет интересна фазочастотная характеристика, в окне расположенная снизу.

Тот и другой график строятся из меню Analysis раздел AC Frequency. А еще тут… Fourier. Доступно посмотреть спектр выходного сигнала. В нашем случае не будет ничего интересного, поскольку собрали унылый пассивный фильтр, колебание на входе гармоническое. Гораздо интереснее наблюдать спектр импульсного сигнала.

График отклика

Раздел Transient показывает отклик на подачу фронта питающего напряжения. На графике фактически представлен процесс заряда батареи, откуда найдем постоянную времени по уровню 0,7 максимума. Тонкости понятны желающим собрать сглаживающий фильтр амплитудного детектора. Как видно из графика, значение составляет 250 мкс. Параметр определяется из окна следующим образом:

1. Считается, за три постоянные времени цепи заряд конденсаторов, разряд производится приблизительно на 95%.
2. Легко заметить, точка находится в районе 800 мкс.
3. Следует разделить значение на три, получится постоянная времени батареи последовательно соединенных конденсаторов.

По-другому постоянная времени вычисляется произведением сопротивления на общую емкость батареи. Пользуясь приведенными выше формулами, вычислим: С = 1 мкФ / 4 = 250 нФ. Осталось умножить значение на 1000 Ом, получится 250 мкс. Программный пакет Electronics Workbench 5.12 при умелом использовании высвобождает уйму свободного времени.

Версия ПО

Раздобыть программный пакет расчета электрики

В интернете бытует мнение: автором Electronics Workbench выступает дочерняя компания корпорации National Instruments, разрабатывающая программное обеспечение. Неправда. Из окна авторских прав упомянутого приложения видно: разработка выполнена отделом Interactive Image Technologies.

Вышеозначенное подразделение обрело самостоятельность в 1995 году. Отдел направленно занимался рекламными и обучающими материалами. Electronics Workbench разработан для целей обучения студентов Канады. Потом программный продукт распространился всемирно, с некоторых пор именуется Multisim.

Обновленный программный продукт продают официальные дилеры, перечень представлен официальным сайтом компании National Instruments: russia.ni.com/contact. На момент исследования счастливчиками, получившими право купить ПО не выезжая за город, назовем жителей Москвы, Санкт-Петербурга. Удачи решившимся связаться с официальными представителями, в Multisim добавлены новые фишки:

1. Более 36000 схемных элементов.
2. Возможность разработки печатных плат на основе собранной электрической схемы.
3. Продвинутые опции анализа вместо убогости, демонстрируемой скринам, версии 20-летней давности.

Соединение конденсаторов: последовательное, параллельное и смешанное

В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.

Параллельное соединение

Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи.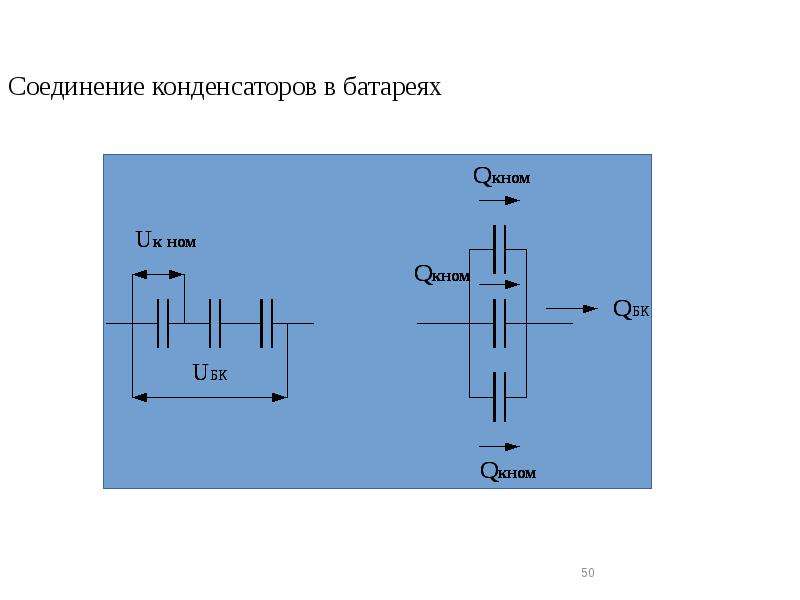 В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии

Схема параллельного крепления

 

Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.

C_общ = C₁ + C₂ + C₃

Схема — напряжение на накопителях

 

В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:

V_AB = V_C1 = V_C2 = V_C3 = 20 Вольт

Последовательное соединение

Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.

Схема — схема последовательного соединения

 

Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.

Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:

i = i_c1 = i_c2 = i_c3

= i_c4, то есть токи проходящие через каждый конденсатор равны между собой.

Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:

Q_общ= Q₁ = Q₂ = Q₃

А так определяется общая суммарная емкость конденсаторов при последовательном соединении:

1/C_общ = 1/C₁ + 1/C₂ + 1/C₃

Видео: как соединять конденсаторы параллельным и последовательным методом

Смешанное подключение

Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.

Схема: смешанное соединение конденсаторов

Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:

1. Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
2. Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
3. Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
4. Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.

Последовательное и параллельное соединение конденсаторов (ёмкостей)

Практически ни одно электронное устройство не обходится без конденсатора. Он может стоять на входе или выходе устройства, перед или после некоторых элементов. Применяется последовательное и параллельное соединение конденсаторов. Как и для чего их подключать тем или иным способом и будем обсуждать.

Содержание статьи

Что такое конденсатор и его основные характеристики

Конденсатор — это радиодеталь, которая работает как накопитель электрической энергии. Чтобы понятнее было, как он работает, его можно представить как своего рода небольшой аккумулятор. Обозначается двумя параллельными чёрточками.

Обозначения различных типов конденсаторов на схемах. Чаще всего из строя выходят электролитические конденсаторы, так что стоит запомнить их обозначение

Основная характеристика конденсатора любого типа — ёмкость. Это то количество заряда, которое он в состоянии накопить. Измеряется в Фарадах (сокращенно просто буква F или Ф), а вернее, в более «мелких» единицах:

• микрофарадах — мкФ это 10^-6 фарада,
• нанофарадах — нФ это 10^-9 фарада;
• пикофарадах — пФ это 10^-12 фарада.

Вторая важная характеристика — номинальное напряжение. Это то напряжение, при котором гарантирована длительная безотказная работа. Например, 4700 мкФ 35 В, где 35 В — это номинальное напряжение 35 вольт.

У крупных по размеру конденсаторов, ёмкость и напряжение указаны на корпусе

Нельзя ставить конденсатор в цепь с более высоким напряжением чем то, которое на нём указано. В противном случае он быстро выйдет из строя.

Можно использовать конденсаторы на 50 вольт вместо конденсаторов на 25 вольт. Но это порой нецелесообразно, так как те, которые рассчитаны на более высокое напряжение, дороже, да и габариты у них больше.

Что он из себя представляет и как работает

В самом простейшем случае конденсатор состоит из двух токопроводящих пластин (обкладок), разделённых слоем диэлектрика.

Между обкладками находится слой диэлектрика — материала плохо проводящего электрический ток

На пластины подаётся постоянный или переменный ток. Вначале, пока энергия накапливается, потребление энергии конденсатором высокое. По мере «наполнения» ёмкости оно снижается. Когда заряд набран полностью, токопотребления вообще нет, источник питания как бы отключается. В это время конденсатор сам начинает отдавать накопленный заряд. То есть, он на время становится своеобразным источником питания. Поэтому его и сравнивают с аккумулятором.

Где и для чего используются

Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:

• Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
• Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом.

  Часто можно увидеть электролитические цилиндрические конденсаторы

• Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец. Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
• Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
• Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
• Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
• В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.

Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.

Как подключать конденсаторы

В электротехнике есть два основных вида соединения деталей — параллельное и последовательное. Конденсаторы также можно подключать по любому из указанных способов. Есть ещё особая — мостовая схема. Она имеет собственную область использования.

В схеме может быть последовательное и параллельное соединение конденсаторов

Параллельное подключение конденсаторов

При параллельном соединении все конденсаторы объединены двумя узлами. Чтобы параллельно подключить конденсаторы, скручиваем попарно их ножки, обжимаем пассатижами, потом пропаиваем. У некоторых конденсаторов большие корпуса (банки), а выводы маленькие. В таком случае используем провода (как на  рисунке ниже).

Так физически выглядит параллельное подключение конденсаторов

Если конденсаторы электролитические, следите за полярностью. На них должны стоять «+» или «-«. При их параллельном подключении соединяем одноимённые выводы — плюс к плюсу, минус — к минусу.

Расчёт суммарной ёмкости

При параллельном подключении конденсаторов их номинальная ёмкость складывается. Просто суммируете номиналы всех подключённых элементов, сколько бы их ни было. Два, три, пять, тридцать. Просто складываем. Но следите, чтобы размерность совпадала. Например, складывать будем в микрофарадах. Значит, все значения переводим в микрофарады и только после этого суммируем.

Расчёт ёмкости при параллельном подключении конденсаторов

Когда на практике применяют параллельное соединение конденсаторов? Например, тогда, когда надо заменить «пересохший» или сгоревший, а нужного номинала нет и бежать в магазин некогда или нет возможности. В таком случае подбираем из имеющихся в наличии. В сумме они должны дать требуемое значение. Все их проверяем на работоспособность и соединяем по приведенному выше принципу.

Пример расчёта

Например, включили параллельно два конденсатора — 8 мкФ и 12 мкФ. Следуя формуле, их номиналы просто складываем. Получаем 8 мкФ + 12 мкФ = 20 мкФ. Это и будет суммарная ёмкость в данном случае.

Пример расчёта конденсаторов при параллельном подключении

Последовательное соединение

Последовательным называется соединение, когда выход одного элемента соединяется со входом другого. Сравнить можно с вагонами или цепочкой из лампочек. По такому же принципу последовательно соединяют и конденсаторы.

Вот что значит последовательно соединить конденсаторы

При подключении полярных электролитических «кондеров» надо следить за соблюдением полярности. Плюс первого конденсатора подаете на минус второго и так далее. Выстраиваете цепочку.

Существуют неполярные (биполярные) электролитические конденсаторы. При их соединении нет необходимости соблюдать полярность.

Как определить ёмкость последовательно соединенных конденсаторов

При последовательном соединении конденсаторов суммарная ёмкость элементов будет меньше самого маленького номинала в цепочке. То есть, ёмкость последовательно соединённых конденсаторов уменьшается. Это также может пригодиться при ремонте техники — замена конденсатора требуется часто.

Последовательно соединённые конденсаторы

Использовать формулу расчёта приведённую выше не очень удобно, поэтому её обычно используют в преобразованном виде:

Формула расчёта ёмкости при последовательном соединении

Это формула для двух элементов. При увеличении их количества она становится значительно сложнее. Хотя, редко можно встретить больше двух последовательных конденсаторов.

Пример расчёта

Какая суммарная ёмкость будет если конденсаторы на 12 мкФ и 8 мкФ соединить последовательно? Считаем: 12*8 / (12+8) = 96 / 20 = 4,8 мкФ. То есть, такая цепочка соответствует номиналу 4,8 мкФ.

Пример расчета ёмкости при последовательном подключении конденсаторов

Как видите, значение меньше чем самый маленький номинал в последовательности. А если подключить таким образом два одинаковых конденсатора, то результат будет вполовину меньше номинала. Например, рассчитаем для двух ёмкостей по 12 мкФ. Получим: 12*12 / (12 + 12) = 144 / 24 = 6 мкФ. Проверим для 8 мкФ. Считаем: 8*8 / (8+8) = 64 / 16 = 4 мкФ. Закономерность подтвердилась. Это правило можно использовать при подборе номинала.

Почему электролитические конденсаторы выходят из строя и что делать

Зачастую, чтобы отремонтировать вышедшую из строя электронную технику, достаточно найти и заменить вздувшиеся конденсаторы. Дело в том, что срок жизни их небольшой — 1000-2000 тысячи рабочих часов. Потом он обычно выходит из строя и требуется его замена. И это при нормальном напряжении не выше номинального. Так происходит потому, что диэлектрик в конденсаторах, чаще всего, жидкий. Жидкость понемногу испаряется, меняются параметры и, рано или поздно, конденсатор вздувается.

Электролитические конденсаторы имеют специальные насечки на верхушке корпуса, чтобы при выходе из строя избежать взрыва

Высыхает электролит не только во время работы. Даже просто «от времени». Это конструктивная особенность электролитических конденсаторов. Поэтому не стоит ставить выпаянные из старых схем конденсаторы или те, которые несколько лет (или десятков лет) хранятся в мастерской. Лучше купить «свежий», но проверьте дату производства.

Можно ли продлить срок эксплуатации конденсаторов? Можно. Надо улучшить теплоотвод. Чем меньше греется электролит, тем медленнее высыхает. Поэтому не стоит ставить аппаратуру вблизи отопительных приборов.

Для улучшения отвода тепла ставят радиаторы

Второе — надо следить за тем, чтобы хорошо работали кулера. Третье — если рядом стоят детали, которые активно греются во время работы, надо конденсаторы каким-то образом от температуры защитить.

Как подобрать замену

Если часто приходится менять один и тот же конденсатор, его лучше заменить на более «мощный» — той же ёмкости, но на большее напряжение. Например, вместо конденсатора на 25 вольт, поставить конденсатор на 35 вольт. Только надо иметь в виду, что более мощные конденсаторы имеют большие размеры. Не всякая плата позволяет сделать такую замену.

Конденсатор той же ёмкости, но рассчитанный на большее напряжение, имеет больший размер

Можно поставить параллельно несколько конденсаторов с тем же напряжением, подобрав номиналы так, чтобы получить требуемую ёмкость. Что это даст? Лучшую переносимость пульсаций тока, меньший нагрев и, как следствие, более продолжительный срок службы.

Что будет, если поставить конденсатор большей ёмкости?

Часто приходит в голову идея поставить вместо сгоревшего или вздувшегося конденсатор большей ёмкости. Ведь он должен меньше греться. Так, во всяком случае, кажется. Ёмкость практически никак не связана со степенью нагрева корпуса. И в этом выигрыша не будет.

Устройство электролитического конденсатора

По нормативным документам отклонение номинала конденсаторов допускается в пределах 20%. Вот на эту цифру можете спокойно ставить больше/меньше. Но это может привести к изменениям в работе устройства. Так что лучше найти «родной» номинал. И учтите, что не всегда можно ставить большую ёмкость. Можно если конденсатор стоит на входе и сглаживает скачки питания. Вот тут большая ёмкость уместна, если для её установки достаточно места. Это точно нельзя делать там, где конденсатор работает как фильтр, отсекающий заданные частоты.

Можно менять на ту же ёмкость, но чуть более высокое напряжение. Это имеет смысл. Но размеры такого конденсатора будут намного больше. Не в любую плату получится его установить. И учтите, что корпус его не должен соприкасаться с другими деталями.

Формула расчета последовательного соединения конденсатора

У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью 470 мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на 1000 мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.

Последовательное соединение конденсаторов

Схема последовательного соединения

Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:

q = q1 = q2 = q3 = …

Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.

Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U  на основании закона Кирхгофа:

U = U1 + U2 + U3,

при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.

Подставляя значения для напряжений в обе части уравнения, получается:

q/C = q/C1 + q/C2 + q/C3.

Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.

Результирующая формула для емкостей конденсаторов:

1/С = 1/С1 + 1/С2 + 1/С3.

Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей.

Особенности последовательного соединения

Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:

1. 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
2. С = 1/27,5 = 0,036 мкФ.

Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента.

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

С = (С1 х С2)/(С1 + С2).

В случае создания цепи из двух конденсаторов с идентичным емкостным значением:

С = (С х С)/(2 х С) = С/2.

Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.

Емкостной делитель напряжения

Формула для емкостного делителя напряжения:

U1 = U x C/C1, U2 = U x C/C2, где:

• U – напряжение питания схемы;
• U1, U2 – падение напряжения на каждом элементе;
• С – итоговая емкость схемы;
• С1, С2 – емкостные показатели единичных элементов.

Вычисление падений напряжения на конденсаторах

К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:

• первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
• вторая – С1 = С2 = 400 нФ.

Первый вариант

1. Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
2. Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
3. На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант

1. Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
2. Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.

Параллельное и комбинированное соединение

Параллельное соединение конденсаторов представляется иным уравнением. Для определения общего емкостного значения надо просто найти совокупность всех величин по отдельности:

С = С1 + С2 + С3 + …

Напряжение к каждому элементу будет прикладываться идентичное. Следовательно, для усиления емкости надо соединить несколько деталей параллельно.

Если соединения смешанные, последовательно-параллельные, то для таких контуров применяют эквивалентные, или упрощенные, электросхемы. Каждую область цепи рассчитывают отдельно, а затем, представляя их вычисленными емкостями, объединяют в простую цепь.

Варианты получения эквивалентных схем

Особенности замены конденсаторов

К примеру, в наличии сеть переменного тока 12 В и две альтернативных группы последовательных конденсаторных элементов.

Конденсаторы подсоединяются в последовательный контур для увеличения напряжения, под которым они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.

Часто применяется смешанное соединение конденсаторов, чтобы создать нужную емкостную величину и увеличить напряжение, которое детали способны выдержать.

Можно привести вариант, как соединить несколько компонентов, чтобы выйти на нужные параметры. Если требуется конденсаторный элемент 80 мкФ при напряжении 50 В, но есть только конденсаторы 40 мкФ на 25 В, необходимо образовать следующую комбинацию:

1. Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
2. Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
3. Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.

Важно! Для того чтобы усилить конденсаторы по напряжению, возможно их объединить в последовательную электросхему. Увеличение общей емкостной величины достигается параллельным подключением.

Что необходимо учитывать при создании последовательной цепи:

1. При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
2. Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.

Получение неполярного конденсатора

Включение в последовательную цепь всегда должно происходить с соблюдением «плюса» и «минуса» конденсаторов. Если их соединить одноименными полюсами, то такое сочетание уже теряет поляризованность. При этом емкость созданной группы будет равна половине от емкостного значения одной из деталей. Такие конденсаторы возможно применять в качестве пусковых на электромоторах.

Видео

Оцените статью:

ПАРАЛЛЕЛЬНОЕ И ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ

Когда в нашем распоряжении нет конденсатора нужной емкости или напряжение на конденсаторе превышает допускаемое, возникает необходимость использовать параллельное и последовательное соединение конденсаторов.

Последовательное соединение конденсаторов

Сообщим равные по величине разноименные заряды крайним обкладкам (внешним электродам) цепочке из двух последовательно соединенных конденсаторов с емкостью С1 и С2.

В результате взаимодействия зарядов на соединенных проводником внутренних обкладках возникнут также равные по величине и обратные по знаку заряды, так что на каждой из четырех обкладок будут одинаковые по величине заряды Q. Согласно формуле C = Q/U напряжения между обкладками каждого конденсатора будут:
U = Q/C1 и U2 = Q/C2,
т. е. при различных значениях емкостей напряжения на конденсаторах будут различны.
Сложив напряжения U1 и U2, мы получим напряжение U между внешними обкладками (напряжение на зажимах цепочки). Таким образом,
U = U1 + U2. (1-9)
Подставив в выражение (1-9) вместо напряжений отношение зарядов к емкостям, получим:
Q/C = Q/C1 + Q/C2
где С — общая или эквивалентная емкость.
Сокращая на Q, будем иметь:
1/C = 1/C1 + 1/C2,                          (1-10)
откуда емкость конденсатора, заменяющая цепочку, или общая емкость двух последовательно соединенных конденсаторов.
1/C = C2 + C1 / C1C2 или C = C1C2 / C1+C2               (1-11)

В случае последовательного соединения трех конденсаторов общую емкость можно найти из формулы, аналогичной (1-10):
1/C = 1/C1 + 1/C2 + 1/C3                   (1-12)
Тем же путем можно вычислить общую емкость любого числа последовательно соединенных конденсаторов.

 

Параллельное соединение конденсаторов

При параллельном соединении, например, трех конденсаторов (рис. 1-11) получаются две группы обкладок разных конденсаторов. Каждая группа обкладок представляет собой равнопотенциальное проводящее тело, поэтому разности потенциалов (или напряжения) между обкладками отдельных конденсаторов будут одинаковы. Заряды на обкладках при неодинаковых емкостях конденсаторов имеют разные значения:
Ql = C1U;  Q2 = C2U;  Q3 = C3U.
Заряд на группе объединенных обкладок
Q = Q1 + Q2 + Q3,
откуда емкость конденсатора, заменяющего три параллельно соединенных конденсатора, или общая емкость
С = Q/U = Q1 + Q2 + Q3/U = C1 + C2 + C3, (1-13)
т. е. равна сумме емкостей отдельных конденсаторов. Это и есть формула при параллельном соединение конденсаторов.

При другом числе параллельно соединенных конденсаторов общая емкость вычисляется аналогично.
Пример:
Определить общую емкость двух конденсаторов при последовательном и параллельном их соединении, если С1 = 2 мкф, а С2 = 4 мкф.
Емкость при последовательном соединении
C = C1C2/C1+C2 = 2×4/2+4 = 1,33 мкф.
Емкость при параллельном соединении
С = С1 + С2 = 2 + 4 = 6 мкф.

Видеофильм о последовательном и параллельном их соединении конденсаторов смотрите ниже:

Конденсаторы, подключенные параллельно и последовательно

Конденсаторы, подключенные параллельно

Конденсаторы могут быть подключены параллельно:

Эквивалентная емкость для конденсаторов, подключенных параллельно, может быть рассчитана как

C = C ₁ + C ₂ +. . + C _n (1)

, где

C = эквивалентная емкость для параллельно соединенной цепи (Фарад, Ф, мкФ)

C _1..n = емкостные конденсаторы (Фарад, Ф, мкФ)

Обычно в качестве единицы измерения емкости используют мкФ .

Конденсаторы серии

Конденсаторы могут быть подключены последовательно:

Эквивалентная емкость для последовательно соединенных конденсаторов может быть рассчитана как

1 / C = 1 / C ₁ + 1 / C ₂ +. . + 1 / C _n (2)

Для особого случая с двумя последовательно включенными конденсаторами — емкость может быть выражена как

1 / C = ( C ₁ + C ₂ ) / (C ₁ C ₂ ) (2b)

— или преобразовано в

C = C ₁ C ₂ / (C ₁ + C ₂ ) (2c)

Пример — конденсаторы, подключенные параллельно и последовательно

Эквивалентная емкость двух конденсаторов с емкостью 10 мкФ и 20 мкФ может быть рассчитана как

параллельно

C = (10 мкФ) + (20 мкФ)

= 30 (мкФ)

последовательно

1 / C = 1 / (10 мкФ) + 1 / (20 мкФ)

= 0.15 (1 / мкФ)

или

C = 1 / 0,15 (1 / мкФ)

= 6,7 (мкФ)

Конденсаторы серии

Три конденсатора C ₁ = 3 мкФ, C ₂ = 6 мкФ и C ₃ = 12 мкФ подключены последовательно, как показано на рисунке выше. Напряжение питания цепи составляет 230 В.

Емкость эквивалентной цепи можно рассчитать по формуле (2)

1 / C = 1 / ( 3 мкФ ) + 1 / (6 мкФ ) + 1/ _{( 12 мкФ )}

= (4 + 2 + 1) / 12

= 0.58 1 / мкФ

— или преобразованное

C = 12 / (4 + 2 + 1)

= 1,7 мкФ

Общий заряд в цепи может рассчитывается с использованием

Q = UC

, где

Q = заряд (кулон, Кл)

U = электрический потенциал (В)

— или значениями

Q = (230 В) (1.7 10 ^-6 F)

= 3,91 10 ^-4 C

= 391 мкКл

Поскольку конденсаторы соединены последовательно — заряд 391 мкКл на каждом из них.

Можно рассчитать напряжение на конденсаторе 1

U ₁ = Q / C ₁

= (391 мкКл) / (3 мкФ)

= 130 В

Напряжение на конденсаторе 2 можно рассчитать

U ₂ = Q / C ₂

= (391 мкКл) / (6 мкФ)

= 65 В

Напряжение на конденсаторе 3 можно рассчитать

U ₃ = Q / C ₃

= (391 мкКл) / (12 мкФ)

= 33 В

Емкость двух коаксиальных Цилиндры

Емкость двух коаксиальных цилиндров, как показано на рисунке, можно рассчитать как

C = 2 π ε _o ε _r л / л (r ₂ / r ₁ ) (3)

, где

ε _o = абсолютная диэлектрическая проницаемость, диэлектрическая проницаемость вакуума (8.85 10 ^-12 Ф / м, Фарад / м)

ε _r = относительная диэлектрическая проницаемость

l = длина цилиндров

r ₂ = радиус внутреннего цилиндра

r ₁ = радиус внешнего цилиндра

Последовательные и параллельные конденсаторы

Последовательные и параллельные конденсаторы
Далее: Энергия, запасенная в конденсаторах Up: Емкость Предыдущая: Диэлектрики Конденсаторы — один из стандартных компонентов электронных схем.Кроме того, часто встречаются сложные комбинации конденсаторов. в практических схемах. Это, поэтому полезно иметь набор правил для определения эквивалентной емкости некоторого общего расположения конденсаторов. Оказывается, всегда можно найти эквивалентная емкость при повторном применение двух простых правил . Эти правила относятся к подключенным конденсаторам. последовательно и параллельно.

Рисунок 15: Два конденсатора подключены параллельно.

Рассмотрим два конденсатора, подключенных параллельно : , т. Е. , с положительно заряженные пластины подключены к общему « входному » проводу, а отрицательно заряженные пластины присоединены к общему « выходному » проводу — см. рис. 15. Какая эквивалентная емкость между входным и выходным проводами? В этом случае потенциал разница между двумя конденсаторами одинакова и равна разность потенциалов между входным и выходным проводами.Общий заряд однако, хранящиеся в двух конденсаторах делятся между конденсаторы, так как он должен распределяться так, чтобы напряжение на два то же самое. Поскольку конденсаторы могут иметь разную емкость, и, и сборы тоже могут быть разными. Эквивалентная емкость пары конденсаторов — это просто соотношение, где — общий накопленный заряд. Следует, что

(113)

давая

(114)

Здесь мы воспользовались тем фактом, что напряжение является общим для всех трех конденсаторы.Таким образом, правило таково:

Эквивалентная емкость двух конденсаторов, соединенных параллельно представляет собой сумму отдельных емкостей.

Для конденсаторов, соединенных параллельно, уравнение. (114) обобщает на .

Рисунок 16: Два конденсатора соединены последовательно.

Рассмотрим два конденсатора, подключенных в серию : , т. Е. , в линию так, что положительная пластина одного прикреплена к отрицательной пластине другого — см. Инжир.16. Фактически, предположим, что положительная обкладка конденсатора 1 подключена к проводу « вход » отрицательная обкладка конденсатора 1 подключается к положительная пластина конденсатора 2 и отрицательная пластина конденсатора 2 подключается к проводу « выход ». Какая эквивалентная емкость между входными и выходными проводами? В этом случае важно понимать, что заряд, хранящийся в два конденсатора одинаковые. Это легче всего увидеть, если рассмотреть « внутренние » пластины: i.е. , отрицательная пластина конденсатора 1, и положительная пластина конденсатора 2. Эти пластины физически отключены. от остальной части схемы, поэтому общий заряд на них должен Остаются неизменными. Если предположить, что кажется разумным, что эти пластины несут нулевой заряд когда к двум конденсаторам приложена нулевая разность потенциалов, следует что при наличии ненулевой разности потенциалов заряд на положительном пластина конденсатора 2 должна быть уравновешена равным и противоположным зарядом на отрицательной пластине конденсатора 1.Поскольку отрицательная пластина Конденсатор 1 несет заряд, положительная пластина должна нести заряд. Аналогичным образом, поскольку положительная пластина конденсатора 2 несет заряд, отрицательная пластина должна нести заряд. В итоге оба конденсатора обладают таким же накопленным зарядом. Потенциал падает, и два конденсатора, как правило, разные. Однако сумма этих падение равняется общему падению потенциала, приложенному на входе и выходе провода: т.е. ,. Эквивалентная емкость пары конденсаторы снова .Таким образом,

(115)

давая

(116)

Здесь мы воспользовались тем фактом, что заряд является общим для всех трех конденсаторы. Следовательно, правило таково:

Величина, обратная эквивалентной емкости двух конденсаторов, подключенных в серия — это сумма обратных величин отдельных емкостей.

Для конденсаторов, соединенных последовательно, уравнение.(116) обобщает на

---

Далее: Энергия, запасенная в конденсаторах Up: Емкость Предыдущая: Диэлектрики

Ричард Фицпатрик 2007-07-14

Физика для науки и техники II

Подключение конденсаторов серии 5.8 от Office of Academic Technologies на Vimeo.

• Демонстрация: энергия, запасенная в конденсаторе
• Пример: подключение конденсаторов

5.Подключение конденсаторов серии 08

Хорошо. Теперь займемся последовательным соединением конденсаторов. В этом случае, опять же, давайте рассмотрим три конденсатора с емкостью C1, C2 и C3. А для того, чтобы соединить их последовательно, соединяем их друг за другом. Чтобы конденсаторы были установлены последовательно, сумма разностей потенциалов на каждом конденсаторе должна быть равна разности потенциалов, приложенной ко всей комбинации. Следовательно, мы говорим, что конденсаторы соединены последовательно, если сумма разностей потенциалов на каждом конденсаторе равна разности потенциалов, приложенной к комбинации.

Итак, как я упоминал ранее, в этом случае мы подключаем конденсаторы C1, C2 и C3 один за другим, как это. Подобно сцепке вагонов поезда на одном рельсе или пути. Затем мы применяем разность потенциалов к комбинации, подключая эти два конца к клеммам источника питания, скажем, батареи, которая вырабатывает разность потенциалов V вольт, и вводим здесь переключатель. Здесь у нас есть конденсатор с емкостью C1, конденсатор 2 с емкостью C2 и C3 для третьего конденсатора.

Как только мы здесь замкнем переключатель, опять же, как и в предыдущем случае, так как эти заряды постоянно отталкивают друг друга, скажем, на выводах источника питания батареи, и положительные заряды будут проходить по этому доступному пути чтобы как можно дальше уйти друг от друга. И они будут собраны на левой пластине конденсатора C1 как q1 плюс q1. Точно так же отрицательные будут продолжаться по этому пути и собираться на выводах правой пластины конденсатора C3 как минус, скажем, q.

Но поскольку они подключены, эти пластины подключены к клеммам источника питания, поэтому эти заряды, величина заряда q1, и если вы назовете его как q3, все они будут равны друг другу, и все они будут быть равным, скажем, заряду q. Поэтому, давайте обозначим этот вот здесь как плюс q, а другой как минус q. Опять же, они напрямую подключены к клеммам этого источника питания.

Итак, как мы помним из конструкции конденсатора, мы сказали, что это устройство, которое состоит из двух проводящих пластин, разделенных изолирующей средой.Таким образом, эти среды между пластинами каждого из этих конденсаторов являются изолирующими средами. Другими словами, они не являются средой для легкого перемещения зарядов. Они изоляторы. Итак, когда мы смотрим на эту схему в целом, на самом деле это разомкнутая цепь. Другими словами, у нас нет полностью замкнутого пути для движения зарядов.

Тогда мы можем легко задать вопрос, хорошо, мы можем понять, почему пластина конденсатора C1 заряжается положительно, и почему пластина конденсатора C3 получает отрицательный заряд, потому что они напрямую подключены к клеммам источника питания. тогда как эта пластина, другая пластина C3 и затем другая пластина C1, а также конденсатор C2 будут заряжаться во время этого процесса, потому что у них нет прямой проводящей связи с клеммами источника питания.

Что ж, когда мы посмотрим — давайте рассмотрим вот это устройство. Как мы видим, эта единица здесь является пластиной конденсатора C2 и этой пластиной конденсатора C3, и почему вся эта область здесь является проводящей средой. Он разделен этими изолирующими точками. Эта проводящая среда, кусок проволоки и, скажем, металлические пластины этих конденсаторов, имеют большое количество свободных электронов. Итак, как только эта другая пластина заряжена до значения минус q, эти отрицательные заряды будут отталкивать эти свободные электроны в этой среде от самих себя.Таким образом, эти свободные электроны будут двигаться как можно дальше для них, и это другая граница этой области, и они будут собираться и собираться, следовательно, на правой боковой пластине конденсатора C2.

Следовательно, поскольку мы собираемся иметь это избыточное количество отрицательного заряда, свободных электронов, отталкиваемых этим минус q, мы получим минус q заряда, который будет собираться на этой пластине, на правой боковой пластине. этот конденсатор С2. Поскольку эти заряды будут перемещаться от этого конца к этой области, то на другом конце здесь не будет такого большого количества отрицательного заряда.Следовательно, эта пластина будет заряжена положительным q.

И, конечно же, аналогичный тип зарядки будет иметь место и для другого устройства. Этот отрицательный заряд будет отталкивать такое же количество свободных электронов как можно дальше от этой области. Таким образом, эта пластина будет заряжена минус q, и поскольку, следовательно, они покинут другую область, не имеющую такого большого отрицательного заряда, эта пластина будет заряжена положительно q. Следовательно, другие пластины и конденсаторы, которые не подключены напрямую к источнику питания, будут заряжаться в результате индукции.

Итак, в качестве первого свойства этого соединения или комбинации мы можем сказать, что заряды, накопленные на каждом конденсаторе в последовательной комбинации, будут равны друг другу. Другими словами, q1 будет равно q2, что будет равно q3, и все они будут равны количеству заряда, полученному от источника питания, то есть q. Опять же, это напрямую связано с принципом сохранения заряда.

И если вы посмотрите на второе свойство, и оно напрямую проистекает из общей характеристики последовательной комбинации, как мы заявили здесь выше, разность потенциалов по всей комбинации будет равна сумме разностей потенциалов на каждом конденсаторе.Другими словами, если вы просто возьмете наш вольтметр и измеряете разность потенциалов во всей комбинации, подключив наш вольтметр к этим двум точкам, через комбинацию, мы собираемся считывать V вольт независимо от напряжения, подаваемого источником питания. Так что это будет считывать нас вольт.

И затем, если мы измеряем разность потенциалов на первом конденсаторе, мы получим V1 вольт. На C2 мы будем читать V2 вольт, а на C3 мы будем читать V3 вольт. И мы увидим, что разность потенциалов во всей комбинации, которая составляет V вольт, будет равна V1 плюс V2 плюс V3.И это общее свойство последовательного соединения. Разность потенциалов по всей комбинации равна сумме разностей потенциалов по каждому компоненту в последовательном соединении.

Теперь, как и в случае параллельного соединения, мы собираемся упростить эту схему, заменив все эти 3 конденсатора при последовательном соединении одним конденсатором. И давайте назовем это эквивалентом C, так что этот единственный конденсатор будет выполнять ту же работу в цепи, которую эти три выполняли в последовательной комбинации.Опять же, давайте представим здесь наш переключатель. Та же батарея обеспечивает такую ​​же разность потенциалов в вольт, что и в предыдущем случае, и как только мы включим переключатель, как только мы его закроем, эти положительные заряды снова будут двигаться по этому пути и собираться вдоль левой боковой пластины. эквивалентного конденсатора. А положительные будут двигаться по другому пути и собираться на правой боковой пластине эквивалента C. И, конечно же, зарядка будет продолжаться до тех пор, пока мы не достигнем высокой плотности заряда, чтобы они создавали достаточно сильную силу отталкивания для входящих зарядов.И в это время конденсатор будет полностью заряжен.

Если мы запишем эквивалент конденсатора C, емкость этого конденсатора, эквивалентного C, по его определению, она будет равна общему заряду, хранящемуся на месте конденсатора, который равен q, деленному на разность потенциалов между пластинами. этого конденсатора. И это будет равно любой разности потенциалов, генерируемой этой батареей. А это V.

Отсюда, если вы решите для разности потенциалов, мы можем записать это выражение как q в эквиваленте C, количество заряда, хранящегося в конденсаторе, деленное на емкость конденсатора.Конечно, мы можем записать аналогичные выражения для конденсаторов C1, C2 и C3. Разность потенциалов относительно C1, которая была V1, будет равна q1 над C1. Но поскольку в последовательной комбинации количество заряда, хранящегося в каждом конденсаторе, одинаково, q1 равно q. Следовательно, для V1 у нас будет q над C1. И аналогично, V2 будет равно q2 над C2, и это тоже будет равно q над C2, так как снова q2 равно q. В дальнейшем V3 будет равно q3 над C3. И снова, поскольку q3 равно q из свойства 1, у нас будет q больше C3 для этого конденсатора.

Используя свойство 2 из свойства 2, поскольку V равно V1 плюс V2 плюс V3, а в терминах заряда и емкости, мы можем записать V как q в эквиваленте C. Это будет равно для V1. У нас будет q над V1, плюс для V2 у нас будет q над C2, плюс для V3 у нас будет q над C3. Поскольку заряд является общим для каждого из этих членов, делящих обе части уравнения на q, мы можем исключить qs и получить окончательное выражение, в котором 1 по сравнению с эквивалентом C равняется 1 по C1 плюс 1 по C2 плюс 1 по C3 .

Теперь мы можем легко увидеть тренд. Если мы соединим конденсаторы последовательно, то мы увидим, что обратное значение эквивалентных конденсаторов становится суммой обратных значений конденсаторов или емкостей в последовательной комбинации. Мы можем обобщить это для числа N конденсаторов, подключенных последовательно, один по сравнению с эквивалентом C, эквивалентная емкость всей комбинации становится равной сумме инверсий каждой емкости в комбинации или последовательной комбинации. Здесь также легко увидеть, что после последовательного подключения конденсаторов результирующая емкость становится меньше наименьшей емкости в комбинации.Другими словами, общая емкость цепи уменьшается, когда мы соединяем конденсаторы последовательно.

Одна вещь, которую вы всегда должны быть очень осторожны, используя это уравнение для вычисления эквивалентной емкости цепи, это выражение дает вам обратную величину эквивалентной емкости. Таким образом, чтобы получить эквивалент C или эквивалентную емкость, после того, как мы вычислим правую часть этого уравнения, вы должны сделать обратное, чтобы получить эквивалентную емкость этих конденсаторов.

Цепи конденсаторов серии

и параллельные

Разница между Кулоном и Фарадом

Раньше переходя к последовательным и параллельным цепям конденсаторов, сначала посмотрите на разница между кулоном и фарадом, потому что многие люди запутаться в определении разницы между кулоном и Фарад.

Электрический заряд измеряется в кулонах.Один кулон (1С) равен равно количеству заряда, передаваемого за одну секунду Текущий одного Ампера (1А).

Емкость является способность тела или устройства накапливать электрический заряд. Емкость измеряется в фарадах (Ф). Устройство с большим Емкость (96F) сохранит большой заряд. Точно так же устройство с малой емкостью (1F) будет хранить небольшая сумма заряда.

серии конденсаторная цепь

А последовательный конденсатор схема — это электронная схема, в которой все конденсаторы подключаются друг за другом по одному и тому же пути, поэтому что к каждому конденсатору протекает одинаковый заряд или ток.

общая емкость цепи последовательного конденсатора получается как сложение обратных величин (1 / C) значений емкости отдельных конденсаторов, а затем взяв обратную величину Общая.

Для Например, если три конденсатора соединены последовательно. Тогда общая емкость цепи

Все ток или заряд, протекающий через первый конденсатор, другого пути нет. Следовательно, он также должен проходить через второй конденсатор, третий конденсатор, четвертый конденсатор и т. д. на.

Пример:

А Схема последовательного конденсатора показана на рисунке ниже. В схема состоит из трех конденсаторов, которые включены в последовательный и источник постоянного напряжения.

емкости из трех конденсаторов: C ₁ = 2F, C ₂ = 4F, C ₃ = 6F и постоянное напряжение = 10 В.

как как показано на рисунке, положительный полюс батареи постоянного тока подключается к правой боковой пластине конденсатора С ₃ отрицательная клемма батареи постоянного тока подключена к Левая боковая пластина конденсатора С ₁ .

Когда а напряжение приложено к цепи, отрицательные заряды в правой боковой пластине конденсатора С ₃ находятся притянул к плюсовой клемме аккума.Это вызывает Недостаток отрицательных зарядов в правой боковой пластине C ₃ . В итоге правая боковая пластина конденсатора С ₃ заряжен положительно.

Аналогично, в положительные заряды в левой боковой пластине конденсатора С ₁ притягиваются к отрицательной клемме аккумулятора. Этот вызывает нехватку положительных зарядов в левой боковой пластине из C ₁ .В результате левая боковая пластина Конденсатор С ₁ заряжен отрицательно.

отрицательные заряды в левой боковой пластине конденсатора С ₁ отталкивать отрицательные заряды в правой боковой пластине конденсатор С ₁ . Это вызывает отрицательные заряды. сток с правой боковой пластины конденсатора С ₁ к левой боковой пластине конденсатора С ₂ .Как В результате правая боковая пластина конденсатора С ₁ оказывается положительно заряжена и левая боковая пластина конденсатора С ₂ заряжен отрицательно.

отрицательные заряды в левой боковой пластине конденсатора С ₂ отталкивать отрицательные заряды в правой боковой пластине конденсатор С ₂ .Это вызывает отрицательные заряды. сток с правой боковой пластины конденсатора С ₂ к левой боковой пластине конденсатора С ₃ . Как В результате правая боковая пластина конденсатора С ₂ оказывается положительно заряжена и левая боковая пластина конденсатора С ₃ заряжен отрицательно.

Таким образом, все три конденсатора заряжаются.

ср знайте, что ток означает поток заряда. С того же ток течет через все три конденсатора, поэтому каждый конденсатор будет удерживать такой же заряд. Это означает, что если один конденсатор держит заряд 2C, тогда остальные конденсаторы тоже держит такой же заряд 2С.

Так если вы обнаружите заряд на одном из конденсаторов, у вас нашел заряд на всех оставшихся конденсаторах.

В чтобы найти заряд на каждом конденсаторе, сначала нам нужно найти общую емкость или эквивалентную емкость.

общая емкость эквивалентного конденсатора

Автор используя формулу C = Q / V, легко найти заряд хранится на эквивалентном конденсаторе.

Начисление на каждого физ. конденсаторы, подключенные последовательно, такие же, как заряд на эквиваленте конденсатор.

Итак, так как заряд на эквивалент конденсатор был 10,91 кулонов, заряд на каждой из отдельные конденсаторы, включенные последовательно, будут иметь 10,91 кулонов.

Следовательно,

Сбор за C ₁ = 10.91 C

Заряд на C ₂ = 10.91 C

Заряд на C ₃ = 10.91 C

Однако в цепи последовательного конденсатора напряжение на каждом индивидуальный конденсатор разный.

ср легко найти напряжение на каждом отдельном конденсаторе по формуле C = Q / V

емкость и заряд на каждом отдельном конденсаторе известны. Итак, мы нужно найти неизвестное напряжение.

В = Q / C

напряжение на конденсаторе (C ₁ ) составляет В ₁ = Q / C ₁ = 10,91 / 2 = 5,455 В

напряжение на конденсаторе (C ₂ ) составляет В ₂ = Q / C ₂ = 10,91 / 4 = 2,727 В

напряжение на конденсаторе (C ₃ ) составляет В ₃ = Q / С ₃ = 10.91/6 = 1,818 В

полное напряжение в цепи последовательного конденсатора равно сумма всех отдельных напряжений, сложенных вместе.

Т.е. V = V ₁ + V ₂ + V ₃ = 5,455 + 2,727 + 1,818 = 10 В

Параллельно конденсаторная цепь

А параллельная конденсаторная схема — это электронная схема, в которой все конденсаторы соединены бок о бок в разных пути, чтобы тот же заряд или ток не проходили через каждый конденсатор.

Когда на параллельную цепь подается напряжение, каждый конденсатор получит другой заряд. Конденсатор с высоким емкость получит больший заряд, тогда как конденсатор с чем меньше емкость, тем меньше будет заряда. Например, восьмерка Фарадный конденсатор (8F) получит больше заряда, чем четыре фарада конденсатор (4Ф) попадает.

Путь конденсаторы параллельно будет увеличиваться размер пластин конденсатора без увеличения расстояния между ними. Итак, общая емкость параллельной конденсаторной цепи получается просто суммируя значения емкости отдельных конденсаторы.

Пример:

А Схема параллельного конденсатора показана на рисунке ниже.В схема состоит из трех конденсаторов, которые включены в параллельный и источник постоянного напряжения.

Если Значения трех конденсаторов: C ₁ = 8F, C ₂ = 4F, C ₃ = 2F и батарея постоянного тока = 10 В, тогда

общая емкость составляет C _T = C ₁ + C ₂ + C ₃ = 8 + 4 + 2 = 14F

В Принципиальная схема, нижние обкладки трех конденсаторов напрямую подключены к положительной клемме аккумулятора а верхние обкладки трех конденсаторов непосредственно подключен к отрицательной клемме аккумуляторной батареи.Следовательно, напряжение на всех трех конденсаторах одинаковое, что составляет равно напряжению АКБ постоянного тока (10 В).

Однако в параллельной цепи конденсаторов заряд сохраняется на каждом конденсатор будет другим.

Автор используя формулу емкости, легко найти заряд хранится на каждом конденсаторе.

И.е. C = Q / V

Q = C × V

заряд, накопленный в конденсаторе (C ₁ ), составляет Q ₁ = С ₁ × V = 8 × 10 = 80 С

заряд, накопленный в конденсаторе (C ₂ ), составляет Q ₂ = С ₂ × V = 4 × 10 = 40 С

Заряд, накопленный в конденсаторе (C ₃ ), составляет Q ₃ = C ₃ × V = 2 × 10 = 20 С

Общий заряд, хранящийся в параллельном конденсаторная цепь равна сумме всех отдельных заряды конденсатора складываются.

Т.е. Q _T = Q ₁ + Q ₂ + Q ₃ = 80 + 40 + 20 = 140 C

Конденсаторы в последовательной и параллельной комбинациях с примерами

Конденсатор является накопителем энергии.Они классифицируются как электролитические и неэлектролитические конденсаторы в зависимости от диэлектриков и полярностей. Он должен быть включен в схему таким образом, чтобы получить необходимое значение емкости. Существуют и другие комбинации конденсаторов, используемых при его включении в схему. Среди которых ряд и параллель являются основными.

Несколько подключенных конденсаторов действуют как «один эквивалентный конденсатор». Общая емкость в цепи зависит от количества отдельных конденсаторов, соединенных последовательно в цепи, и будет меньше, чем у любого из конденсаторов в цепи.Расстояние между пластинами конденсатора также влияет на емкость конденсатора.

В системах распределения электроэнергии, где уровень напряжения падает ниже указанного уровня. Эти компоненты, называемые конденсаторами, используются для поддержания линии напряжения. Эти компоненты могут минимизировать потерю мощности. С помощью базовых последовательных и параллельных комбинаций можно получить более сложные соединения.

Что такое последовательный конденсатор?

Соединение между конденсаторами, помещенными в одну линию, можно определить как конденсаторы, соединенные последовательно.Пластина положительных зарядов одного конденсатора соединена с пластиной отрицательного заряда другого конденсатора. В этом типе подключения каждый конденсатор имеет одинаковую величину заряда и зарядный ток.

Хотя зарядный ток такой же, но отличается от падения напряжения. На каждом конденсаторе разное падение напряжения. Но общее падение напряжения, которое применяется между входной и выходной линиями, совпадает с суммой напряжений отдельных падений.

Последовательные конденсаторы, работа и уравнение

Конденсатор, подключенный последовательно, обычно имеет меньшую емкость. Когда эти соединения выполнены, ток, протекающий по цепи, будет одинаковым. Следовательно, заряд, накопленный вокруг каждого из конденсаторов, также одинаков.

Конденсаторы, подключаемые последовательно

Обычно конденсаторы подключаются по схеме «гирляндной цепи». В таких схемах ток для зарядки будет одинаковым.Это потому, что путь устанавливается таким же.

Общий ток = Ток на C1 = Ток на C2

Вместо емкости заряд в каждом конденсаторе одинаков. Потому что обкладки каждого конденсатора соединены смежным образом.

Общий заряд = Заряд на C1 = Заряд на C2

Когда конденсаторы следуют последовательному соединению и подключено более трех конденсаторов. C1 обеспечивается источником питания, а C3 подключается к выходному концу.В то время как C2 в середине изолирован от прямого взаимодействия источника напряжения (DC). Из-за этого падения напряжения на каждом конденсаторе разные. Это зависит от индивидуальных емкостей каждого конденсатора.

Обычно заряд, емкость и падение напряжения связаны как

Q = CV

Формулу можно переписать как

C = Q / V

Напряжение на конденсаторах можно рассчитать как

Общее напряжение = Напряжение на C1 + напряжение на C2

Общее напряжение (Q / C) = Q1 / C1 + Q2 / C2

Последовательный заряд будет равен Q1 = Q2

Наконец, разделив уравнение на Q с обеих сторон

1 / C = 1 / C1 + 1 / C2

Следовательно, приведенное выше уравнение предназначено для расчета емкости для последовательного соединения конденсаторов.

Пример

Два конденсатора, соединенных последовательно, номиналом 10 мкФ и 20 мкФ. Найти значение емкости в цепи?

решение : дано C1 = 10 мкФ

C2 = 20 мкФ

Общая емкость может быть рассчитана как обратная величина для отдельных емкостей.

1 / C = 1/10 +1/20

1 / C = 0,15 микрофарад

Что такое конденсатор, подключенный параллельно?

Поскольку в конденсаторах две пластины, первая пластина конденсатора соединена с первой пластиной второго конденсатора.Это называется параллельным подключением конденсаторов. Следовательно, конденсаторы при параллельном соединении имеют одинаковое количество значений напряжения. Общее значение емкости — это сумма отдельных емкостей.

Конденсаторы при параллельной работе и уравнении

При параллельном подключении конденсаторов. Каждый из конденсаторов в цепи имеет прямое взаимодействие с проводником. Это приводит к тому, что потенциал конденсатора остается прежним. Заряд будет таким же, как и у каждого конденсатора, имеющего индивидуальное соединение с предоставленным источником питания.

Общая стоимость может быть рассчитана как сумма отдельных платежей.

Общая сумма начислений (Q) = Q1 + Q2 + …….

Если два конденсатора подключены параллельно.

Тогда Q = Q1 + Q2. Где Q = CV

CV = C1V1 + C2V2

В параллельной комбинации V = V1 = V2

CV = (C1 + C2) V

Следовательно, C = C1 + C2

Пример

Найдите значение итога емкость, если в цепь включены два конденсатора по 10 мкФ и 20 мкФ?

Решение:

При C1 = 10 мкФ

C2 = 20 мкФ

В параллельной комбинации общую емкость можно рассчитать как

C = C1 + C2

C = 10 + 20 = 30 мкФ

На основании приведенных выше формул можно рассчитать значение емкости.

Конденсаторы можно подключать последовательно и параллельно. В таких ситуациях соединение должно быть идентифицировано. На основе идентификации используются подходящие формулы последовательного и параллельного сочетания.

Пример

Найдите значение емкости, когда в цепь включены три конденсатора по 10 мкФ?

Конденсаторы, соединенные последовательно и параллельно

Решение:

Данная схема состоит из конденсаторов C1, C2 и C3.

Из анализа схемы конденсаторы C1 и C2 соединены последовательно.

Эквивалентную емкость C1 и C2 можно рассчитать по формуле

1 / C = 1 / C1 + 1 / C2

1 / C = 1/10 + 1/10

1 / C = 2/10

Наконец, C = 10/2 = 5 мкФ.

Далее этот C подключен параллельно конденсатору C3.

Эквивалентную емкость схемы можно найти по формуле

C (Всего) = C + C3 = 5 + 10 = 15 микрофарад

Пожалуйста, обратитесь по этой ссылке, чтобы узнать больше о конденсаторах MCQ

Следовательно, значение емкости может реализовываться на основе последовательного и параллельного анализа.Отмечается, что значение емкости уменьшается при последовательном соединении. В параллельной комбинации увеличивается значение емкости. Но в случае сопротивления все наоборот. Из приведенного выше анализа можете ли вы определить, если вам нужно хранить огромное количество энергии, то какая комбинация подключения предпочтительнее?

4.2 Последовательные и параллельные конденсаторы — Введение в электричество, магнетизм и схемы

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Объясните, как определить эквивалентную емкость конденсаторов, соединенных последовательно и параллельно
• Вычислить разность потенциалов на пластинах и заряд на пластинах для конденсатора в сети и определить полезную емкость сети конденсаторов

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях.Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серия и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

Рисунок 4.2.1 иллюстрирует последовательную комбинацию трех конденсаторов, расположенных в ряд внутри схемы. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 4.1.1. Когда эта последовательная комбинация подключена к аккумулятору с напряжением В, , каждый из конденсаторов получает одинаковый заряд. Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме аккумулятора, есть, а заряд на пластине, подключенной к отрицательной клемме.Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала на одном конденсаторе может отличаться от падения потенциала на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд в последовательной цепи снимается с пластины первого конденсатора (который мы обозначаем как), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как), и так далее.

(рисунок 4.2.1)

Рисунок 4.2.1 (a) Три конденсатора соединены последовательно. Величина заряда на каждой пластине. (б) Сеть конденсаторов в (а) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей в (а), и заряд на его пластинах равен.

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах, и равны соответственно,, и ,. Эти потенциалы должны суммироваться с напряжением батареи, давая следующий баланс потенциалов:

Потенциал измеряется на эквивалентном конденсаторе, который держит заряд и имеет эквивалентную емкость.Вводя выражения для, и, получаем

Отменяя заряд, получаем выражение, содержащее эквивалентную емкость трех последовательно соединенных конденсаторов:

Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.

КОМБИНАЦИЯ СЕРИИ

---

Для конденсаторов, включенных в комбинацию серии , величина, обратная эквивалентной емкости, является суммой обратных величин индивидуальных емкостей:

(4.2.1)

ПРИМЕР 4.2.1

---

Эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны, и.

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.1 с тремя членами.

Решение

Мы вводим указанные емкости в уравнение 4.2.1:

Теперь инвертируем этот результат и получаем.

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке 4.2.2 (а). Поскольку конденсаторы подключены параллельно, , все они имеют одинаковое напряжение на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость параллельной сети, отметим, что общий заряд, накопленный в сети, представляет собой сумму всех отдельных зарядов:

В левой части этого уравнения используется соотношение, которое справедливо для всей сети. В правой части уравнения мы используем соотношения, и для трех конденсаторов в сети.Таким образом получаем

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

ПАРАЛЛЕЛЬНАЯ КОМБИНАЦИЯ

---

Для конденсаторов, соединенных в параллельную комбинацию , эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

(4.2.2)

(рисунок 4.2.2)

Рисунок 4.2.2 (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

ПРИМЕР 4.2.2

---

Эквивалентная емкость параллельной сети

Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая их индивидуальные емкости, и.

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.2 с тремя членами.

Решение

Ввод заданных емкостей в уравнение 4.2.2 дает

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательного и параллельного подключения, как показано на рисунке 4.2.3. Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

(рисунок 4.2.3)

ПРИМЕР 4.2.4

---

Сеть конденсаторов

Определите полезную емкость комбинации конденсаторов, показанной на рисунке 4.2.4 при емкостях,,. Когда в комбинации сохраняется разность потенциалов, найдите заряд и напряжение на каждом конденсаторе.

(рисунок 4.2.4)

Рисунок 4.2.4 (a) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.

Стратегия

Сначала мы вычисляем полезную емкость параллельного соединения и. Тогда — чистая емкость последовательного соединения и. Мы используем соотношение, чтобы найти заряды, и, и напряжения,, и на конденсаторах, и, соответственно.

Решение

Эквивалентная емкость для и составляет

Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 4.2.4 (b). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд,. Кроме того, конденсаторы разделяют разность потенциалов, поэтому

Теперь разность потенциалов на конденсаторе

.

Поскольку конденсаторы и подключены параллельно, они имеют одинаковую разность потенциалов:

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

Значение

Как и ожидалось, чистая плата за параллельную комбинацию и составляет.

ПРОВЕРЬТЕ ПОНИМАНИЕ 4.5

---

Кандела Цитаты

Лицензионный контент

CC, особая атрибуция

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

Работа конденсаторов в последовательной и параллельной цепях

Конденсаторы — стандартные компоненты электронных схем.В схемах практически используются разные комбинации конденсаторов. В этой статье рассказывается о последовательной и параллельной комбинациях конденсаторов.

Конденсаторы серийные

Как подключить конденсаторы последовательно?

«Последовательные конденсаторы» означает два или более конденсатора, соединенных в одну линию. Положительная пластина одного конденсатора соединена с отрицательной пластиной следующего конденсатора.

Здесь,

QT = Q1 = Q2 = Q3 = ———- = Q

IC = I1 = I2 = I3 = ——— = IN

При последовательном соединении конденсаторов Заряд и ток на всех конденсаторах одинаковые.

Почему заряд последовательно соединенных конденсаторов одинаков?

Для последовательных конденсаторов одинаковое количество электронов будет проходить через каждый конденсатор, потому что заряд на каждой пластине исходит от соседней пластины. Итак, кулоновский заряд такой же. Поскольку ток — это не что иное, как поток электронов, ток такой же.

Какая эквивалентная емкость?

Эквивалентная емкость — это общая емкость конденсаторов. Давайте посмотрим, как рассчитать емкость, когда они включены последовательно.

На рисунке ниже показаны три конденсатора, последовательно подключенные к батарее. Когда конденсаторы соединены последовательно, соседние пластины заряжаются за счет электростатической индукции.

Каждая пластина будет иметь разный потенциал. Но величина заряда на пластинах такая же.

Первая пластина C1 будет иметь потенциал V1, равный напряжению батареи, а вторая пластина будет иметь потенциал меньше V1. Пусть это будет V2.

Теперь первая пластина C2 будет иметь потенциал, равный V2, а вторая пластина будет иметь потенциал меньше V3, пусть это будет V4.
Первая пластина C3 будет иметь потенциал V5 (V5 = V4), а потенциал второй пластины меньше V5. Пусть это будет V6.

Но общая разность потенциалов между пластинами равна ЭДС АКБ.

Итак, VT = V1 + V2 + V3

Но мы знаем, что Q = CV

C = Q / V

Ceq = Q / V1 + Q / V2 + Q / V3 (как заряд такой же)

1 / Ceq = (V1 + V2 + V3) / Q

VT = Q / Ceq = Q / C1 + Q / C2 + Q / C3

Следовательно, 1 / Ceq = 1 / C1 + 1 / C2 + 1 / C3

Если N конденсаторов подключены последовательно, эквивалентная емкость может быть указана ниже.

1 / Ceq = 1 / C1 + 1 / C2 + ……… + 1 / CN

Таким образом, когда конденсаторы включены последовательно, величина, обратная эквивалентной емкости, равна сумме обратных величин индивидуальной емкости конденсаторов в цепи.

Конденсаторы в серии Пример

Рассчитайте эквивалентную емкость, и отдельные падения напряжения на наборе из двух последовательно соединенных конденсаторов имеют 0,1 мкФ и 0,2 мкФ соответственно при подключении к источнику переменного тока 12 В. поставка.

Эквивалентная емкость,

1 / Ceq = 1 / C1 + 1 / C2

Ceq = (C1C2) / (C1 + C2)

Ceq = (0.1 мкФ * 0,2 мкФ) / (0,1 мкФ + 0,2 мкФ)

Ceq = 0,066 мкФ = 66 нФ

Падение напряжения на двух последовательно соединенных конденсаторах составляет,

В1 = (C2 * VT) / (C1 + C2) = (0,2 мкФ * 12 В) / (0,1 мкФ + 0,2 мкФ) = 8 Вольт

V2 = (C1 * VT) / (C1 + C2) = (0,1 мкФ * 12 В) / (0,1 мкФ + 0,2 мкФ) = 4 В

Из этих результатов мы заметили, что эквивалентная емкость 66 нФ меньше наименьшей емкости 0,1 мкФ из данных двух конденсаторов. Отдельные падения напряжения на данных двух конденсаторах различны.

Но сумма индивидуальных падений напряжения обоих конденсаторов равна общему напряжению. т.е. 8 В + 4 В = 12 В.

Теперь посчитаем заряд, накопленный в отдельном конденсаторе,

Q1 = V1 * C1 = 8 В * 0,1 мкФ = 0,8 мкКл

Q2 = V2 * C2 = 4 В * 0,2 мкФ = 0,8 мкК

Здесь мы заметили, что одинаковый заряд 0,8 мкКл хранится в обоих конденсаторах C1 и C2, которые соединены последовательно.

Конденсаторы в серии Сводка

• Заряд конденсаторов при последовательном включении одинаков.

• Эквивалентная емкость конденсаторов меньше наименьшей емкости в серии.

• Эквивалентная емкость последовательно подключенных n конденсаторов равна

.

1 / Ceq = 1 / C1 + 1 / C2 + ……… + 1 / CN

Конденсаторы в параллельных цепях

Почему мы подключаем конденсаторы параллельно?

Есть преимущество подключения конденсаторов параллельно, чем последовательно. При параллельном подключении конденсаторов общее значение емкости увеличивается.В некоторых приложениях требуются более высокие значения емкости.

Как подключить конденсаторы параллельно?

На рисунке ниже показано параллельное соединение конденсаторов. Все положительные клеммы подключены к одной точке, а отрицательные клеммы — к другой точке.

Какая эквивалентная емкость конденсаторов, подключенных параллельно?

• Все конденсаторы, которые соединены параллельно, имеют одинаковое напряжение и равное ТН, приложенному между входными и выходными клеммами схемы.
• Тогда на параллельные конденсаторы подается «общее напряжение». VT = V1 = V2 и т. Д.
• Эквивалентная емкость Ceq цепи, в которой конденсаторы соединены параллельно, равна сумме всех индивидуальных емкостей конденсаторов, сложенных вместе.
• Это связано с тем, что верхняя пластина каждого конденсатора в цепи соединена с верхней пластиной соседних конденсаторов. Таким же образом нижняя пластина каждого конденсатора в цепи соединена с нижней пластиной соседних конденсаторов.

Давайте посмотрим, как рассчитать эквивалентную емкость конденсаторов при параллельном подключении. Рассмотрим два конденсатора, подключенных, как показано на схеме ниже.

Общий заряд (Q) в цепи делится между двумя конденсаторами, это означает, что заряд Q распределяется между конденсаторами, подключенными параллельно. Заряд Q равен сумме всех зарядов отдельных конденсаторов.

Таким образом, Q = Q1 + Q2

Где Q1, Q2 — заряды на конденсаторах C1 и C2.

Мы знаем это,

Q = Ceq VT

Здесь Q = Q1 + Q2

Ceq VT = C1xV1 + C2xV2

Так как VT = V1 = V2 = V

Ceq VT = C1xV + C2xV

Ceq VT = (C1 + C2) В

Следовательно, Ceq = C1 + c2

Если N конденсаторов подключены параллельно, то Ceq = C1 + C2 + C3 + —— Cn

Таким образом, эквивалентная емкость конденсаторов, соединенных параллельно, равна сумме индивидуальных емкостей конденсаторов в цепи.

Конденсаторы в параллельном образце №1

Рассмотрим значения емкости двух конденсаторов C1 = 0,2 мкФ и C2 = 0,3 мкФ, которые показаны на рисунке 4 выше. Теперь вычислите эквивалентную емкость цепи.

Мы знаем, что эквивалентная емкость,

Ceq = C1 + C2

Ceq = 0,2 мкФ + 0,3 мкФ

Ceq = 0,5 мкФ

Один важный момент, который следует помнить о параллельно соединенных цепях конденсаторов, эквивалентная емкость (Ceq) любых двух или более конденсаторов, соединенных вместе параллельно, всегда будет больше, чем значение самого большого конденсатора в цепи, поскольку мы складываем значения.Таким образом, в нашем примере выше Ceq = 0,5 мкФ, тогда как емкость самого большого конденсатора в цепи составляет всего 0,3 мкФ.

Когда конденсаторы подключены параллельно?

Вот несколько приложений, в которых конденсаторы подключаются параллельно.

• В некоторых источниках постоянного тока для лучшей фильтрации используются конденсаторы небольшой емкости с превосходным коэффициентом пульсации.