Последовательное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = Imsinωt.
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цели
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
u = u1R + uL + uC + u2R,
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
Для построения векторной диаграммы находим:
U1R = IR1; U2R = IR2; UL = IXL; UC = IXC.
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U
Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: 
При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
где R = R1 + R2 и X = XL — XC
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Из треугольников напряжения и сопротивлений определяют следующие величины:
Угол сдвига по фазе между напряжением и током в цепи положительный (φ

2. ХL< ХC Векторная диаграмма изображена на рис. 14.3, где UL<UC , поэтому общее напряжение отстает от тока на угол φ<0.
Реактивное сопротивление цепи носит емкостный характер.
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы:
Общее напряжение совпадает по фазе с током и равно по величине активной
составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
U = IR, или I = U/R.
В случае XL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи с последовательном соединении конденсатора и катушки
Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0; при φ<0 Q<0.
Активная мощность положительна при любом угле, так как cosφ = cos(-φ).
Полная мощность также всегда положительна.
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задачи по теме и пример решения задачи для схемы с последовательным соединением конденсатора и катушки
Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс
Физика, 11 класс
Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока
Перечень вопросов, рассматриваемых на уроке:
Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;
Устройство и принцип действия генератора переменного тока и трансформатора;
Автоколебания;
Проблемы передачи электроэнергии и способы повышения эффективности её использования.
Глоссарий по теме
Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами.
Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.
Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.
Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:
N- число витков.
Возникает ЭДС индукции который меняется по гармоническому закону.
ЭДС индукции в рамке равна:
Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.
В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.
Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т. к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
Величину ХC, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.
Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.
Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.
Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.
Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.
Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.
Для потребления электрической энергии нужно доставить его от источника к потребителю. Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:
Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.
Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».
k– коэффициент трансформации.
U1 иU2 – напряжения на первичной и на вторичной обмотке.
N1 и N2— число витков на первичной и на вторичной обмотке.
Если k < 1 — трансформатор повышающий,
k > 1 — трансформатор понижающий.
КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:
Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.
Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.
Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.
Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.
Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция
Разбор тренировочных заданий
1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м2.
Дано:
N=50
ω=180 рад/с
B=0,4 Тл
S=0,02 м2
_________
Ԑm=?
Решение:
Ответ: 72 В.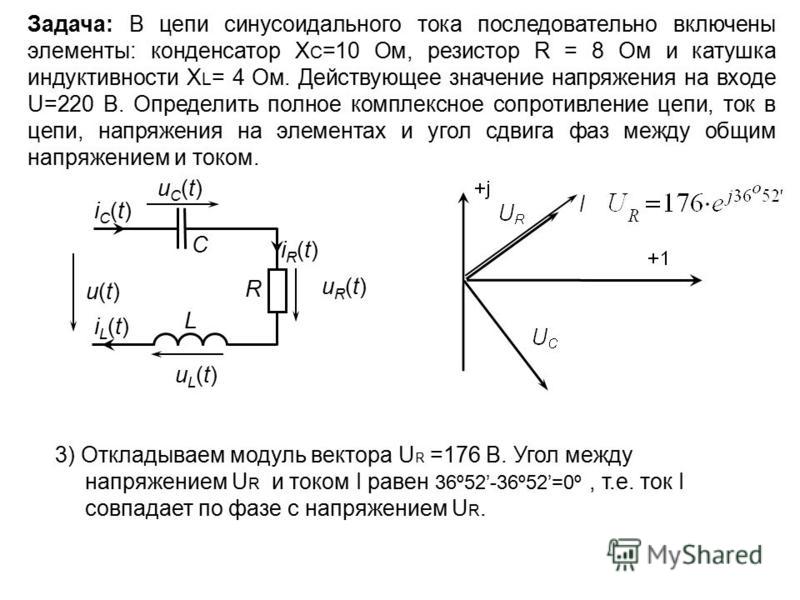
2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.
Дано:
L=0,08 Гн
ν= 1000 Гц
U=100 В
__________
Im=?
Решение:
Напишем закон Ома для переменного тока
Т.к. ХC и R равны нулю, то
Учитывая, что , получаем:
Найдем амплитудное значение напряжения:
Подставим числовые данные в формулу для расчета амплитуды силы тока:
Ответ: Im = 0,3 А.
Конденсатор и катушка соединены последовательно емкостное сопротивление
Конденсатор и катушка соединены последовательно. Емкостное сопротивление конденсатора 5 кОм. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте колебаний силы тока 20 кГц?
Лучший ответ:
Дано: СИ
Xc = 5 кОм 5*10³ Ом
f = 20 КГц 20*10³ Ом
___________
L — ?
1)
При резонансе:
XL = Xc
2π*f*L = Xc
L = Xc / (2π*f) = 5*10³ / (6,28*20*10³) = 5 / (6,28*20) ≈ 0,04 Гн
Другие вопросы:
урале почти нет угля , истощаются запасы руды. Тем не менее уральская металлургическая база остается главной в стране. Почему?
Тем не менее уральская металлургическая база остается главной в стране. Почему?
Переведите пожалуйста на татарский ОЧЕЕНЬ НУЖНО СРОЧНО !! 1.он к нам оказывается приходил а я не знал.2 она оказывается вернулась а я не видела.3 она оказывается оставила лекарственные травы а я сейчас только увидела. 4 он об этом оказывается говорил а я не слышала
ПОМОГИТЕ ПОЖАЛУЙСТА*-*большинство людей в обществе одновременно выступают в роли производителей и потребителей.подумайте и приведите примеры конкретных ситуаций, в которых человек является производителем и потребителем.
«Раз счастье, два раза счастье — помилуй Бог!
Надо же когда-нибудь и немножко умения » А.В. Суворов
Скачать:
| Вложение | Размер |
|---|---|
| 8 класс КР №1 Тепловые явления | 401.5 КБ |
| 9 класс КР №1 Кинематика | 401.5 КБ |
| 10класс КР №1 Кинематика | 740.5 КБ |
| 11 класс КР №1 МП ЭМ индукция | 324. 5 КБ 5 КБ |
| 9 класс ДКЗ Основы динамики | 421 КБ |
| 10 класс КР №2 Динамика | 351 КБ |
| 11 класс КР №2 ЭМ Колебания | 33 КБ |
Предварительный просмотр:
Предварительный просмотр:
9КЛ Контрольная работа № 1 «Основы кинематики» 1 вариант
9КЛ Контрольная работа № 1 «Основы кинематики» 2 вариант
Предварительный просмотр:
10 кл Контрольная работа №1 Кинематика материальной точки
10 кл Контрольная работа №1 Кинематика материальной точки
Предварительный просмотр:
11 кл Подготовка к К.Р. «Магнитное поле. Электромагнитная индукция»
- Правильно ли утверждение, что явление электромагнитной индукции проявляется лишь в замкнутом контуре?
- некорректная постановка вопроса
- правильно, так как только в замкнутом контуре может идти ток
- не совсем правильно, так как при движении замкнутого проводника в магнитном поле происходит разделение зарядов и между концами проводника возникает разность потенциалов
Предварительный просмотр:
Предварительный просмотр:
Контрольная работа «ДИНАМИКА» 1 вариант
В. Под действием силы 150 Н тело движется прямолинейно так, что его координата
Под действием силы 150 Н тело движется прямолинейно так, что его координата
изменяется по закону х = 100 + 5t + 0,5t 2 . Какова масса тела?
С. В шахту равноускоренно опускается лифт, масса которого 300 кг. В первые 5с он
проходит 25 м. Определить силу натяжения каната, к которому подвешен лифт.
Контрольная работа «ДИНАМИКА» 2 вариант
В. Скорость материальной точки изменяется по закону v x = 5 — 3t под действием силы
6 Н. Какова масса точки?
С . Грузовик взял на буксир легковой автомобиль массой 2,4 т и, двигаясь равноускоренно,
за 40 с проехал путь 200 м. На сколько удлинился во время буксировки трос,
соединяющий автомобили, если его жесткость 2∙ 10 6 Н/м.
Предварительный просмотр:
КР-2. “Электромагнитные колебания» Вариант 3
1. Определите емкость конденсатора, сопротивление которого в цепи переменного тока частотой 50 Гц равно 800Ом.
2. В рамке, равномерно вращающейся в однородном магнитном поле, индуцируется ток, мгновенное значение которого выражается формулой А. Определите амплитуду, действующее значение, круговую частоту колебаний и начальную фазу колебаний силы тока.
Определите амплитуду, действующее значение, круговую частоту колебаний и начальную фазу колебаний силы тока.
3. Рассчитайте период собственных колебаний в колебательном контуре при емкости конденсатора 2 мкФ и индуктивности катушки 0,5 мГн.
4. Рамка площадью 150 см 2 , содержащая 50 витков проволоки, равномерно вращается со скоростью 120 об/мин в однородном магнитном поле с магнитной индукцией 0,8 Тл. Найдите амплитуду ЭДС индукции в рамке.
5. Амплитуда напряжения в колебательном контуре 100 В, частота колебаний 5 МГц. Через какое время напряжение будет 71 В?
6. Конденсатор емкостью 10 мкФ зарядили до напряжения 400 В и подключили к катушке. После этого возникли затухающие электрические колебания. Какое количество теплоты выделится в контуре за время, в течение которого амплитуда колебаний уменьшится вдвое?
7. Электроплитка сопротивлением 50 Ом включена в сеть переменного тока с частотой 50 Гц и напряжением 220 В. Запишите уравнения, выражающие зависимость напряжения и силы тока от времени для электроплитки. Чему равно мгновенное значение силы тока и напряжения через 1/100 с, если колебания происходят по закону синуса?
Чему равно мгновенное значение силы тока и напряжения через 1/100 с, если колебания происходят по закону синуса?
КР-2. “Электромагнитные колебания» Вариант 4
1. Какой индуктивности катушку надо включить в колебательный контур, чтобы при емкости конденсатора 2 мкФ получить частоту 1 кГц?
2. Сила тока в электрической цепи изменяется по закону А. Определите амплитуду силы тока, действующее значение силы тока, круговую частоту колебаний и начальную фазу колебаний.
3. Рассчитайте сопротивление конденсатора емкостью 250 мкФ, включенного в цепь переменного тока с частотой 200 Гц.
4. Индуктивность колебательного контура равна 0,01 Гн, а емкость 1 мкФ. Конденсатор зарядили до разности потенциалов 200 В. Какой наибольший ток возникает в контуре в процессе электромагнитных колебаний?
5. Конденсатор и катушка соединены последовательно. Емкостное сопротивление конденсатора 5 кОм. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте колебаний силы тока 20 кГц?
6. В колебательном контуре с индуктивностью 0,4 Гн и емкостью 20 мкФ амплитудное значение силы тока равно 0,1 А. Каким будет напряжение в момент, когда энергия электрического и энергия магнитного полей будут равны? Колебания считать незатухающими.
В колебательном контуре с индуктивностью 0,4 Гн и емкостью 20 мкФ амплитудное значение силы тока равно 0,1 А. Каким будет напряжение в момент, когда энергия электрического и энергия магнитного полей будут равны? Колебания считать незатухающими.
7. В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0,1 Гн. Определите, какой ёмкости конденсатор надо включить в эту цепь, чтобы осуществился резонанс.
Здесь легко и интересно общаться. Присоединяйся!
Условие резонанса X(L)=X(C)
X(C)=5 ком=5000 ом
f=20 кГц=20000 Гц
Тогда
X(L)=2pi*f*L
L=X/(2pi*f)=5000/(6,28*20000)=0.04 Генри
Удачи.
А ты типа-пока на дискотеке оторвёшься Вот потом такие ИТР и приходят-что за них работают другие
| гл.1 Электрические цепи однофазного электрического тока | |||
| глава 2| глава 3| глава 4| глава 5| глава 6| глава 7| глава 8| глава 9| глава 10| глава 11| | |||
Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока
Лекция № 4 Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока.

Термин «сопротивление» для цепей переменного тока, оказывается недостаточно полным, поскольку сопротивление переменному току оказывают не только те элементы цепи, в которых выделяется энергия в виде теплоты (их называют активными сопротивлениями), но и те элементы цепи, в которых энергия периодически запасается в электрическом или магнитном полях. Такие элементы цепи называют реактивными сопротивлениями. Реактивными сопротивлениями обладают индуктивности и емкости.
Активное сопротивление в цепи синусоидального тока.
Если по активному сопротивлению течет ток тогда
по закону Ома
или
где
Т. е. в активном сопротивлении элемента цепи комплекс тока совпадает с комплексом напряжения
Рис. 4.1 – Графики мгновенных значений
Мгновенная мощность
=
или
т. е. мгновенная мощность имеет постоянную составляющую и переменную составляющую меняющуюся с частотой равной (на рис. 4.1)
4.1)
Индуктивность в цепи переменного синусоидального тока.
Практически любая обмотка (катушка) обладает некоторой индуктивностью и активным сопротивлением .
Схема замещения катушки может быть представлена в виде последовательного соединения индуктивности и активного сопротивления .
Выделим из схемы одну индуктивность
Рис. 4.2
Если через индуктивность течет ток , то в катушке наводится ЭДС самоиндукции — .
Для прохождения переменного тока через индуктивность необходимо, чтобы на ее зажимах было напряжение , равное и противоположно направленное .
,
где — индуктивное сопротивление
где — частота, Гц,
— индуктивность, Гн.
Движению переменного тока через индуктивность оказывается сопротивление за счет накопления энергии , это сопротивление называется индуктивным.
Размерность индуктивного сопротивления
.
Значение тока в цепи с индуктивностью опережает ЭДС самоиндукции на 90°, но т. к. вектор напряжения на катушке индуктивности направлен в противоположную сторону ЭДС.
к. вектор напряжения на катушке индуктивности направлен в противоположную сторону ЭДС.
т. е.
т. о. в цепи с индуктивностью вектор тока отстает от вектора напряжения на угол 90°.
Действующее значение тока в цепи с индуктивностью равно действующему значению напряжения, деленному на индуктивное сопротивление.
т. е.
Приведенная формула похожа на закон Ома. Это внешнее сходство позволяет определить ток в цепи с индуктивностью, подобно тому, как в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения с обычным сопротивлением ничего общего не имеет.
Понятие об индуктивном сопротивлении формально введено для облегчения расчета.
Оно заменяет фактическое влияние ЭДС самоиндукции на ток в цепи.
Мгновенная и реактивная мощность
Мгновенное значение мощности или
График изменения мощности представляет собой синусоиду двойной частоты с амплитудой
.
Наибольшее значение мощности в цепи с индуктивностью равно произведению действующих значений напряжения и тока.
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии: ток направлен против ЭДС самоиндукции.
Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику). Направление ЭДС самоиндукции и тока совпадают. Катушка является источником энергии.
В следующую половину периода процесс повторяется.
Средняя активная мощность за период равна нулю , т. к. в цепи с индуктивностью преобразования электрической энергии в другие виды энергии не происходит.
Цепь с емкостью –
К конденсатору с идеальным диэлектриком, т. е. в нем нет потерь энергии, подведено напряжение
Определим ток и мощность
Ток в цепи.
Заряд конденсатора пропорционален напряжению между его обкладками, поэтому изменение напряжения сопровождается изменением заряда.
Скорость изменения заряда пропорциональна скорости изменения напряжения.
но скорость изменения заряда равна электрическому току
т. к.
то
Сопоставляя:
получаем, что ток через конденсатор по фазе опережает напряжение на конденсаторе на угол 90°. На векторной диаграмме вектор тока опережает вектор напряжения на угол 90°.
Амплитуда тока
Действующее значение тока
или
где — реактивное сопротивление конденсатора
Построение графика мгновенной мощности конденсатора выполняют также как и для индуктивной катушки.
т. к.
В первую четверть периода, когда напряжение на конденсаторе возрастает, энергия накапливается в электрическом поле конденсатора за счет работы источника, конденсатор в это время заряжается, т. е. является приемником энергии. Направления тока и напряжения совпадают.
Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть к источнику. Ток направлен против напряжения сети – конденсатор является источником энергии ( разряжается ) и так в 3й и 4й части периода.
Активная мощность равна нулю, а реактивная
Установившийся режим в простейшей неразветвленной цепи с сосредоточенными параметрами.
Электрические цепи характеризуются двумя режимами: переходным и установившимся.
Переходные режимы возникают в результате перераспределения энергии электрических и магнитных полей в и при резком изменении параметров электрической цепи.
Простейшая электрическая цепь переменного тока с
Общее сопротивление такой цепи
где — реактивное сопротивление
или
где
Если по цепи протекает ток, то:
или
в комплексной форме
Отсюда или
— закон Ома в комплексной форме
где — комплексное сопротивление
— модуль комплексного сопротивления
Величина обратная комплексному сопротивлению называется комплексной проводимостью.
(сименс)
Умножая на сопряженный комплекс получаем
где — активная проводимость,
— реактивная проводимость.
,
по модулю
Умножив сопротивление на ток получим треугольник U.
Напряжение можно представить в виде двух составляющих
Цепь
Пусть
По второму закону Кирхгофа
где и — синусоидальные напряжения
В комплексной форме
тогда
или
где — комплекс полного сопротивления индуктивной катушки (цепи )
Показательная форма записи
где — модуль комплекса полного сопротивления цепи
— аргумент.
Если , а ,
тогда
где , а
Если ток , то .
— Комплекс тока в цепи с равен комплексу напряжения деленному на комплекс полного сопротивления катушки.
Умножив треугольники на получим:
– полная мощность (ВА)
— реактивная мощность (ВАp)
— активная мощность (Вт)
или
— коэффициент мощности, зависит от соотношения и по его величине судят о том, какую часть полной мощности цепи составляет активная мощность.
Активную мощность измеряют ваттметром.
Цепь
Пусть .
По второму закону Кирхгофа
, т. к. напряжение отстает от тока
или
– комплекс полного сопротивления
— модуль комплекса
— аргумент
Напряжение на входе цепи отстает от тока на угол сдвига фаз
т. о. , т. к.
Аналогично цепи
или
Сложные цепи, состоящие из последовательных и параллельных участков
Расчет
1. При расчете цепи определяют активные и реактивные проводимости параллельных ветвей
; ; ; .
2. Далее определяют активную и реактивную проводимость разветвления аb
3.Преобразуют схему в эквивалентную
4.Определяют активное и реактивное сопротивление всей цепи
тогда ; ; ; ,
где , а .
Построение векторной диаграммы (по активным и реактивным составляющим).
Лучше построение векторной диаграммы начать с последней ветви и идти к началу цепи, т. е.к общему току и напряжению.
В нашем случае построение начнем с напряжения — откладываем его произвольно в масштабе.
Топографическая диаграмма:
при последовательном соединении напряжений и параллельных токов.
Топографическая диаграмма – такая векторная диаграмма, каждая точка которой соответствует определенной точке электрической цепи.
Резонанс при последовательном и параллельном соединении элементов
Резонанс – такой режим цепи содержащей , индуктивность и емкость, при котором ее входное сопротивление (или проводимость) имеет активный характер.
В зависимости от вида цепи (последовательное или параллельное соединение) существует резонанс напряжений и токов.
1. Последов. соединение R, L,C.
Условие резонанса:
или
т. к. , а , т. о.
, т. е. или
где — резонансная угловая частота.
при резонансе
При последовательном соединении и в резонансном режиме , т. е. имеется резонанс напряжений.
При резонансе значения и могут значительно превышать напряжения на зажимах.
Ток при резонансе
или , т. к. , а
т. о. , делим на , сокращаем
,
где — характеристическое (волновое) сопротивление контура имеет размерность сопротивления.
т. к. ; ; .
Отношение напряжения на индуктивности (или емкости) к напряжению на зажимах цепи при резонансе называется добротностью контура.
.
Величина обратная называется затуханием ()
Параллельное соединение
Условие резонанса: , т. е .
При равенстве реактивных проводимостей ветвей противоположные по фазе реактивные составляющие токов и равны по величине.
Такой режим работы цепи называют резонансом токов.
,
,
тогда
или ,
т. к. , то .
т. е. общий ток носит чисто активный характер (совпадает с ) и может быть меньше и .
Символический метод анализа электрических цепей синусоидального тока.
В режиме синусоидального тока можно перейти от уравнений составленных для мгновенных значений (дифференциальных уравнений) к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС.
Например ,
Для схемы:
или
,
т. к. амплитуда действующего напряжения на , то знак говорит о том, что опережает на 90°.
Для емкости — напряжение отстает от тока на 90°.
Если – комплексная амплитуда действующей ЭДС, то
и ,
т. о.умножение на равносильно повороту вектора на 90°, а на — на “-90°”.
Три формы записи комплексных чисел:
— алгебраическая форма,
— показательная форма,
— тригонометрическая.
Операции с комплексными числами
Сложение и вычитание комплексных чисел производится в алгебраической форме.
.
Деление и умножение производится в показательной форме:
;.
,
где , а .
Калькулятор емкости последовательного соединения конденсаторов • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор позволяет рассчитать емкость нескольких конденсаторов, соединенных последовательно.
Пример. Рассчитать эквивалентную емкость двух соединенных последовательно конденсаторов 10 мкФ и 5 мкФ.
Входные данные
Добавить конденсатор
Выходные данные
Эквивалентная емкость
C микрофарад (мкФ)
Введите значения емкости в поля C1 и C 2, добавьте при необходимости новые поля, выберите единицы емкости (одинаковые для всех полей ввода) в фарадах (Ф), миллифарадах (мФ), микрофарадах (мкФ), пикофарадах (пФ), нанофарадах (нФ) и нажмите на кнопку Рассчитать.
1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.
В соответствии со вторым правилом Кирхгофа, падения напряжения V₁, V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:
По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость Ceq всех трех конденсаторов, соединенных последовательно, определяется как
или
Для группы из n соединенных последовательно конденсаторов эквивалентная емкость Ceq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:
или
Эта формула для Ceq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:
Если конденсаторов только два, то их общая емкость определяется по формуле
или
Если имеется n соединенных последовательно конденсаторов с емкостью C, их эквивалентная емкость равна
Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов.
Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.
Конденсаторы на печатной плате
Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки. На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.
Выравнивающие резисторы уменьшают разброс напряжений на отдельных конденсаторах
Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.
Если несколько конденсаторов соединены параллельно, разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁, Q₂ and Q₃ тоже будут различными. Общий заряд определяется как
Конденсаторы, соединенные параллельно
По определению емкости, эквивалентная емкость группы конденсаторов равна
отсюда
или
Для группы n включенных параллельно конденсаторов
То есть, если несколько конденсаторов включены параллельно, их эквивалентная емкость определяется путем сложения емкостей всех конденсаторов в группе.
Возможно, вы заметили, что конденсаторы ведут себя противоположно резисторам: если резисторы соединены последовательно, их общее сопротивление всегда будет выше сопротивлений отдельных резисторов, а в случае конденсаторов всё происходит с точностью до наоборот.
Конденсаторы на печатной плате
Автор статьи: Анатолий Золотков
Чему равны реактивные сопротивления катушки и конденсатора. Параллельное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = I m sinωt .
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цели
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
u = u 1R + u L + u C + u 2R ,
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
U = U 2R + U L + U C +U 2R
Для построения векторной диаграммы находим:
U 1R = IR 1 ; U 2R = IR 2 ; U L = IX L ; U C = IX C .
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
1. Х L >Х C . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U 1 и U 2 на этих элементах.
Векторная сумма напряжений U 1 + U 2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (U а и U р ). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: U a = U 1R + U 2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: U р = U L — U C .
При одинаковом токе во всех элементах цепи U L >U C . Ток отстает от общего напряжения по фазе на угол φ . Из треугольника напряжений следует
где R = R 1 + R 2 и X = X L — X C общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Из треугольников напряжения и сопротивлений определяют следующие величины:
Угол сдвига по фазе между напряжением и током в цепи положительный (φ >0) (фазовые токи отсчитываются от вектора тока).
2. Х L Векторная диаграмма изображена на рис. 14.3, где U L φ
Р е активное сопротивление цепи носит емкостный характер .
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. X L = Х C . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: U L = U C (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.
Общее напряжение совпадает по фазе с током и равно по величине активной
составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
U = IR, или I = U/R.
В случае X L = Х C в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи с последовательном соединении конденсатора и катушки
Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0 ; при φ
Активная мощность положительна при любом угле, так как cosφ = cos(-φ ).
Полная мощность также всегда положительна. На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии (Р ≠ 0) и обменный процесс между генератором и приемником (Q ≠ 0 при φ ≠ 0).
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при X L = Х С .
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задачи по теме и пример решения задачи для схемы с последовательным соединением конденсатора и катушки
Рис. 4.12. Рис. 4.13
если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L , единицей ее измерения является генри (Гн).
Постоянная времени RС -цепи
На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е т. е. ЭДС или напряжения источника питания.
Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е , называется постоянной времени контура или цепи.
Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.
Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени.
Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой
где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах.
Например, для случая С = 10мкФ и R = 10 кОм постоянная времени цепи равна
На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.
Рис. 4.15.
Постоянная времени RL -цепи
Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R , имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R станет равным приложенному напряжению Е. Установившееся значение тока равно
E/ R = 20 В/1 кОм = 20 мА.
Скорость изменения тока в цепи зависит от конкретных значений R и L . Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/ R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R , указанные на рисунке, получаем
Следует заметить, что, чем больше R , тем меньше L/R и тем быстрее изменяется ток в цепи.
Рис. 4.16.
Рис. 4.17.
Сопротивление по постоянному токуКатушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.
Векторное представление
Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω = 2πf , где f – частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω = 2πf . Это означает, что угол между этими векторами
Рис. 4.18.
Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ
(или вектор ОВ отстает от вектора ОА) на угол θ .
изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ , а вектор ОВ отстает от вектора ОА на угол в. На рис. 4.19(б) эти сигналы развернуты во времени.
Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f , но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.
В этом видео рассказывается о катушке индуктивности:
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
На схеме рис. 14.1.1, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, BL и конденсатора G2, BC, а также напряжение u = Umsinωt
При последовательном: индуктивность складывается. С емкостью 1/Cобщ=1/С1+1/C2+1/С3
При параллельном: емкости складываются, с индуктивностями, как с конденсаторами при последовательном соединении
Вариант 2. ёмкость при параллельном соединении складывается (напряжение пробоя остается тем же) , при последовательном высчитывается по формуле как параллельные сопротивления, напряжение просто складывается.
а индуктивность при последовательном складывается, а при параллельном как сопротивления параллельные высчитывается.
40.Метод комплексных амплитуд.
Метод комплексных амплитуд состоит в следующем:
1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:
а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.
б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е. х (t ) = Xm cos(w0t – jx ) ® Xm = Xm e–j jx.
Z L=j wL
Z C= 1/(j wC )
Z R=R
Рис. 4.27
2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождению комплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е.Ym = Ym e–j jy.
3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.
Ym =Ym e –j jy ® y (t ) = Ym cos(w0t – jy ).
Пример 1. Алгоритм метода рассмотрим на примере анализа цепи, схема которой приведена на рис. 4.29.
Рис. 4.29. RLC -цепь второго порядка
На вход цепи подается синусоидальное воздействие. Параметры воздействия и элементов цепи известны: Um =1 В, ω =1 с-1 , φ u =900 , R =1 Ом, L =1 Гн, C =1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.
1. Представим воздействие в комплексной форме:
2. Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.
Рис. 4.30. Схема замещения цепи в частотной области
3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:
51.41. Элементы R , L и С в цепях переменного тока. Импеданс.
Физическими элементами реальной электрической цепи являются резисторы, катушки индуктивности, конденсаторы, трансформаторы, транзисторы и другие компоненты электроники. При изучении электрических цепей реальные элементы заменят их математическими моделями, которые с нужной точностью воспроизводят свойства и параметры физических элементов.
Рис. 1.1. Условные обозначения резистивного (а), емкостного (б) и индуктивного (в) элементов.
К пассивным элементам относятся резистивные R, индуктивные L, и емкостные C элементы, условные обозначения которых показаны на рис. 1.1.
Резистивным элементом (рис. 1.1,а) называют такой элемент, который обладает только свойством рассеивания энергии. Математическая модель резистивного элементаR определяется законом Ома, который устанавливает зависимость напряжения u от тока i, протекающего через сопротивление R. Такую зависимость называют вольт-амперной характеристикой (ВАХ) резистивного элемента и записывают в следующем виде:
Если в (1.6) u = 1В, i = 1А, то R = 1Ом. Более крупными единицами измерения величины сопротивления являются килоом (1кОм = 103Ом) и мегоом (1мОм = 106Ом). Величина, обратная сопротивлению, называется проводимостью резистора. Она обозначается G и измеряется в сименсах (См). ВАХ для линейного и нелинейного резистивных элементов показаны на рис. 1.2.
Рис. 1.2. ВАХ линейного (а) и нелинейного (б) резистивных элементов.
Согласно уравнению (1.5) мощность, рассеиваемая резистивным элементом в виде тепла, равна:
Источником напряжения (Рис. 1.3,а и б) называют идеализированный двухполюсный элемент, напряжение на зажимах (полюсах) которого не зависит от протекающего через него тока. Часто источник напряжения называют генератором напряжения и в качестве характеристики используют напряжение или электродвижущую силу генератораuг или eг.
Электри?ческий импеда?нс (комплексное сопротивление , полное сопротивление ) — комплексное сопротивление двухполюсника для гармонического сигнала.
В отличие от резистора, электрическое сопротивление которого характеризует соотношение напряжения к току на нём, попытка применения термина электрическое сопротивление к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что сопротивление идеальной катушки индуктивности стремится к нулю, а сопротивление идеального конденсатора — к бесконечности.
Сопротивление правильно описывает свойства катушки и конденсатора только на постоянном токе. В случае же переменного тока свойства реактивных элементов существенно иные: напряжение на катушке индуктивности и ток через конденсатор не равны нулю. Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Было бы удобно иметь некоторую характеристику и для реактивных элементов, которая бы при любых условиях связывала ток и напряжение на них подобно сопротивлению. Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при гармонических воздействиях на них. В этом случае ток и напряжение оказываются связаны некоей стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название электрический импеданс (или просто импеданс ). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно оно позволяет одновременно учитывать и амплитудные, и фазовые характеристики сигналов и систем.
42.Мощность, рассеиваемая элементами R , L и С .
Рассеиваемая (поглощаемая) мощность элемента электрической цепи – значение мощности рассеиваемой на элементе цепи, которую элемент может поглотить (выдержать) без изменения его номинальных параметров (выхода из строя). Рассеиваемая мощность резисторов обозначается в его названии (например: двух ваттный резистор — ОМЛТ-2, десяти ваттный проволочный резистор – ПЭВ-10). При расчёте принципиальных схем, значение необходимой рассеиваемой мощности элемента цепи рассчитывается по формулам:
Для надёжной работы, определённое по формулам значение рассеиваемой мощности элемента умножается на коэффициент 1,5 , учитывающий то, что должен быть обеспечен запас по мощности.
Так как напряжение u и ток i могут совпадать или не совпадать по направлению, то согласно (1.14) мощность p может быть как положительной, так и отрицательной.
При p > 0 емкостной элемент накапливает энергию, а при p
43.Расчёт цепей переменного тока. Характер импеданса (емкостной и индуктивный).
// Первую половину вопросов вытащить из методички по первой лабе.
Любой ток изменяющийся по величине является переменным. Но на практике под переменным током понимают такой ток, закон изменения которого во времени есть синусоидальная функция.
Математическое выражение для синусоидального тока можно записать в виде:
где, i — мгновенное значение тока, показывающее величину тока в конкретный момент времени, Im — амплитудное (максимальное) значение тока, выражение в скобках есть фаза, которая определяет значение тока в момент времени t, f — частота переменного тока, это величина, обратная периоду изменения синусоидальной величины Т, ω — угловая частота, ω = 2πf = 2π / T, α — начальная фаза, показывает значение фазы в момент времени t = 0.
Индуктивное сопротивление () обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:
Ёмкостное сопротивление (). Величина ёмкостного сопротивления зависит от ёмкости элемента и также частоты протекающего тока:
Здесь — циклическая частота, равная.
44.Четырёхполюсники. Передаточная характеристика и её измерение.
Четырёхпо?люсник — электрическая цепь, разновидность многополюсника, имеющая четыре точки подключения. Как правило, две точки являются входом, две другие — выходом.
При анализе электрических цепей очень часто бывает удобным выделить фрагмент цепи, имеющий две пары зажимов. Поскольку электрические (электронные) цепи очень часто связаны с передачей энергии или обработкой и преобразованием информации, одну пару зажимов обычно называют «входными», а вторую — «выходными». На входные зажимы подаётся исходный сигнал, с выходных снимается преобразованный.
Такими четырёхполюсниками являются, например, трансформаторы, усилители, фильтры, стабилизаторы напряжения, телефонные линии, линии электропередачи и т. д.
Передаточная характеристика, где Uвых, UВХ – соответственно напряжение на выходе и входе схемы. Характеристика снимается для одного входа (нагрузкой элемента являются аналогичные элементы).
На входах х2, х3 будет уровень напряжения U0ВХ, а на входе х1 – напряжение UВХ. Изменяя напряжение на входе х1 от Uвх U0вх до Uвх U1вх и измеряя напряжение на входе х1 и на выходах схемы у1 и у2, получим передаточную характеристику.
45.Четырёхполюсники. Переходная, импульсная и частотная характеристики.
Четырёхпо́люсник — электрическая цепь, разновидность многополюсника, имеющая четыре точки подключения . Как правило, две точки являются входом, две другие — выходом.
Симметричный четырёхполюсник — четырёхполюсник, у которого схема одинакова относительно его входных и выходных зажимов. Тогда для симметричного четырёхполюсника Z11 = Z22. Ещё: если при перемене местами источника и приемника энергии их токи не меняются, то такой четырёхполюсник называется симметричным.
Пассивный четырёхполюсник — это четырёхполюсник, который не содержит источников энергии, либо содержит скомпенсированные источники энергии.
Активный четырёхполюсник — это четырёхполюсник, который содержит нескомпенсированные источники энергии.
Обратимый четырёхполюсник — четырёхполюсник, у которого выполняется теорема обратимости, то есть передаточное сопротивление входных и выходных контуров не зависят от того, какая пара зажимов входная, а какая выходная: U1/I2=U2/I1
Частотные характеристики. Бывают АЧХ и ФЧХ. Поскольку при подаче на вход линейной системы синусоидального сигнала на выходе также появляется синусоидальный сигнал той же частоты, частотные характеристики связывают амплитуды и фазы этих сигналов. АЧХ – отношение амплитуды выходного сигнала к амплитуде входного сигнала в зависимости от частоты. ФЧХ – сдвиг фаз между входным и выходным сигналами в зависимости от частоты.
Интегрирующая RC-цепь:
— Комплексная частотная характеристика
— АЧХ
— ФЧХ
АЧХ и ФЧХ интегрирующей цепи:
Частотные характеристики показывают как преобразуется синусоидальный сигнал в данной системе. Следовательно, воспользовавшись разложением Фурье для входного сигнала можно получить спектр выходного сигнала. Для этого спектр амплитуд умножают на АЧХ почастотно, а спектр фаз складывают также почастотно.
Связь между частотными, переходными и импульсными характеристиками. Импульсная характеристика связана с переходной интегрирования, потому что импульс — это производная от ступеньки. Частотная характеристика связана c импульсной преобразованием Фурье, так как частотная характеристика строится в частотной области, а импульсная — во временной.
Связь между частотной, переходной и импульсной характеристиками:
46.АЧХ и ФЧХ четырёхполюсников.
//обратиться к методичке от первой лабы
47.Основные типы электрических фильтров.
Электрический фильтр — это устройство, предназначенное для выделения или подавления электрических сигналов заданных частот.
По характеру полосы пропускаемых частот фильтры делятся на шесть типов:
1) ФНЧ (фильтр нижних частот) — пропускает сигналы с частотой от 0 до f в (f в =ω в /2π).
2) ФВЧ (фильтр верхних частот) — пропускает сигналы с частотой от f н до ∞
3) ФПП (полосовой фильтр) — пропускает сигналы с частотой от f н до f в.
4) РФ (режекторный фильтр) — не пропускает сигналы заданной частоты или полосы частот
5) ГПФ (гребенчатый фильтр) — фильтр, имеющий несколько полос пропускания.
6) РГФ (режекторный гребенчатый фильтр) — фильтр, имеющий несколько полос подавления.
48.Последовательный колебательный контур, его основные свойства.
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
последовательный колебательный контур, сопротивление которого на резонансной частоте стремится к нулю.
Последовательный колебательный контур является простейшей резонансной (колебательной) цепью. Состоит последовательный колебательный контур, из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина которого вычисляется по закону Ома: I = U / Х Σ , где Х Σ — сумма реактивных сопротивлений последовательно включенных катушки и конденсатора (используется модуль суммы).
Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое (или волновое) сопротивление ρ и добротность контура Q . Характеристическим (волновым) сопротивлением контура ρ называется величина реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = Х L = Х C при ω =ω р . Характеристическое сопротивление может быть вычислено следующим образом: ρ = √(L/C) . Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура — катушкой (энергия магнитного поля) W L = (LI 2)/2 и конденсатором (энергия электрического поля) W C =(CU 2)/2 . Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает «качество». Добротность колебательного контура — характеристика, определяющая амплитуду и ширину АЧХ резонанса и показывающая, во сколько раз запасы энергии в контуре больше, чем потери энергии за один период колебаний. Добротность учитывает наличие активного сопротивления нагрузки R .
Для последовательного колебательного контура в RLC цепях, в котором все три элемента включены последовательно, добротность вычисляется:
где R , L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно. Величину, обратную добротности d = 1 / Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q = ρ / R , где R -сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р = I 2 R . Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.
Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ), при этом сами цепи рассматривают как четырёхполюсники.
49.Параллельный колебательный контур, его основные свойства.
В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рисунке приведена принципиальная схема параллельного колебательного контура. Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя — можно лишь складывать проводимости. На рисунке приведены графические зависимости реактивных проводимостей катушки индуктивности B L = 1/ωL , конденсатора В C = -ωC , а также суммарной проводимости В Σ , этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току.
50.RC -цепь и её характерное время.
RC-цепь — электрическая цепь, состоящая из конденсатора и резистора. Её можно рассматривать как делитель напряжения с одним из плеч, обладающих ёмкостным сопротивлением переменному току.
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.
Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R , где U напряжение на выводах резистора, R — его сопротивление.
Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.
«В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону.»
и там же, в этой же статье:
«А у этого закона есть пара характерных величин:
Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max–1/e*max.
3T — а при троекратной постоянной значение достигнет 95% своего максимума.
Постоянная времени для RC цепи Т=R*C.»
51.RL -цепь и её характерное время.
LR-цепь — электрическая цепь, состоящая из резистора и индуктивности. Её можно рассматривать как делитель напряжения, в котором одно из плеч представляет собой индуктивное сопротивление переменному току.
Рассмотрим цепь, состоящую из последовательно соединенных резистора R и катушки L, в электротехнике такая цепь часто называетсяпоследовательной RL-цепью .
В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.
Простейшие
.
В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.
52.Дифференцирующие и интегрирующие RLC -цепи и условия их работы.
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.
LR-цепь дифференцирующего типа является фильтром верхних частот. Фильтр верхних частот (ФВЧ ) — электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала ниже частоты среза. Степень подавления зависит от конкретного типа фильтра.
Не так давно, мы с вами рассматривали, как ведет себя конденсатор в цепи постоянного и переменного тока . А в этой статье рассмотрим, как ведет себя катушка индуктивности , если на нее подать постоянный и переменный ток. Хочу вам напомнить, что постоянный ток — это ток, который течет всегда в одном направлении, а переменный ток — это ток, который меняет свое направление с какой-то частотой.
Катушка индуктивности в цепи постоянного тока.
Итак, для этого опыта нам понадобится блок питания , который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.
Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:
Намотать на него лакированного медного провода и зачистить выводы:
Замеряем индуктивность нашей катушки с помощью LC метра :
132 микроГенри.
Теперь собираем все это вот по такой схеме:
где
L — катушка индуктивности
La — лампочка накаливания на напряжение 12 Вольт
Bat — блок питания, с выставленным напряжением 12 Вольт
Лампочка засветилась!
Как вы помните, конденсатор у нас не пропускал постоянный электрический ток:
Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам провод, из которого сделана катушка.
Катушка индуктивности в цепи переменного тока.
Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф , генератор частоты , собственно сама катушка индуктивности и резистор на 100 Ом. Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.
Собираем все это дело по такой схеме:
Получилось как то так:
Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал — желтым. Следовательно, красная синусоида — это частота, которую нам выдает генератор частоты, а желтая синусоида — это сигнал, который снимается с резистора.
Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.
Кто до сих пор не знает что такое осциллограф, можно прочитать про него . Что такое цифровой осциллограф, можно прочитать . Про автоматическое измерение параметров с помощью цифрового осцилла, читаем Кто уже читал и все знает, идем дальше.
Для начала подаем сигнал с частотой в 1 КилоГерц.
Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф
Красный кружок с цифрой «1» — это замеры «красного»канала. Как мы видим, F (частота) =1 КилоГерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой «2». F =1 КилоГерц, а Ма =1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.
Увеличиваем частоту до 10 КилоГерц
Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.
Увеличиваем до 100 КилоГерц
Видели да? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз . Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.
Сдвиг фаз — это разность между начальными фазами двух измеряемых величин . В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота . Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз :
Увеличиваем частоту до 200 КилоГерц
На частоте 200 КилоГерц амплитуда упала вдвое, да и разность фаз стала больше.
Увеличиваем частоту до 300 КилоГерц.
Амплитуда желтого сигнала упала уже до 720 миллиВольт. Разность фаз стала еще больше.
Увеличиваем частоту до 500 КилоГерц
Амплитуда уменьшилась до 480 миллиВольт.
Добавляем еще частоту до 1 МегаГерца
Амплитуда желтого канала стала 280 миллиВольт .
Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 МегаГерца
Амплитуда «желтого» сигнала стала настолько маленькой, что мне пришлось ее даже увеличить на осцилле в 5 раз.
И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.
Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:
Так какой вывод можно сделать?
С увеличением частоты сопротивление катушки растет, а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.
Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микроГенри.
Итак, прогоняем все по тем же значениям частоты
При частоте в 1 КилоГерц у нас значение почти не изменилось.
10 КилоГерц
Здесь тоже ничего не изменилось.
100 КилоГерц
Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонька сдвигаться.
200 КилоГерц
Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.
300 КилоГерц
Сдвиг фаз стал больше и амплитуда просела еще больше
500 КилоГерц
Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.
1 МегаГерц
Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉
2 МегаГерца, предел моего генератор частоты
Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.
Обратите внимание на амплитуду в Вольтах на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.
Отсюда вывод напрашивается сам собой:
При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.
С помощью нехитрых умозаключений, физиками была выведена формула:
где
Х L — сопротивление катушки, Ом
П — постоянная и равна приблизительно 3,14
F — частота, Гц
L — индуктивность
В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.
домашних заданий и упражнений — индуктор и конденсатор параллельно
Я смотрел на это 10 минут и ооочень сбит с толку. Надеюсь, вы, ребята, сможете помочь!
Итак, допустим, мы замыкаем переключатель. Насколько я понимаю, конденсатор будет заряжаться до 10 В почти мгновенно, при этом ток не будет течь через катушку индуктивности. В самом начале через резистор будет протекать 0,2 А $.
Но что будет, если оставить выключатель замкнутым на долгое время?
В моей книге написано, что ток через катушку индуктивности может подняться до 0 долларов.2A $, а ток через конденсатор упадет до $ 0A $.
Эта первая часть имеет смысл.
Однако в книге говорится, что через бесконечное время конденсатор будет на 10 вольт.
Мне это кажется неправильным … если ток через катушку индуктивности когда-либо перестанет изменяться, индуктор будет вести себя как закороченный участок цепи, верно? Разве через него не разрядится конденсатор?
Что касается падения напряжения — если ток через резистор когда-либо достигнет нуля.2A $, это будет означать, что все напряжение падает через резистор. На дросселе нет падения напряжения.
Buuut, поскольку катушка индуктивности и конденсатор включены параллельно, не означает ли это автоматически, что на конденсаторе НЕ ДОЛЖНО быть заряда?
Моя книга ошибается, говоря, что по прошествии бесконечного времени с замкнутым переключателем на конденсаторе будет разница в 10 вольт?
Изменить:
Это редактирование после прочтения некоторых ваших ответов и комментариев — они были великолепны.Я недостаточно подробно остановился на том, что конкретно было сказано в моей книге в моем исходном посте, так что это редактирование предназначено только для решения этой проблемы. Однако суть вопроса остается прежней.
Точный вопрос:
Через очень долгое время переключатель размыкается. Какой максимальный ток?
Тогда их объяснение таково:
Мы создали схему $ LC $, и максимальный ток составляет $ 0,44A $. Поскольку ток через катушку индуктивности должен оставаться непрерывным, начальный ток через катушку индуктивности равен 0 долларов США.2} {2}
долл. СШАПодключив начальный ток в 0,2 А $, я понял, что максимальное напряжение на конденсаторе на самом деле составляет 5,16 В $.
ЦепиRL — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Анализировать цепи, в которых последовательно соединены индуктор и резистор
- Опишите, как ток и напряжение экспоненциально растут или затухают в зависимости от начальных условий.
Цепь с сопротивлением и самоиндукцией известна как цепь RL .(Рисунок) (a) показывает схему RL , состоящую из резистора, катушки индуктивности, постоянного источника ЭДС и переключателей, а в замкнутом состоянии схема эквивалентна одноконтурной цепи, состоящей из резистора и катушки индуктивности. подключен через источник ЭДС ((Рисунок) (б)). Когда открыт и закрыт, схема становится одноконтурной схемой только с резистором и катушкой индуктивности ((Рисунок) (c)).
Сначала рассмотрим схему RL (рисунок) (b).Когда он замкнут и разомкнут, источник ЭДС создает ток в цепи. Если бы в цепи не было самоиндукции, ток немедленно повысился бы до постоянного значения. Однако, согласно закону Фарадея, возрастающий ток вызывает на катушке индуктивности ЭДС. В соответствии с законом Ленца наведенная ЭДС противодействует увеличению тока и направлена, как показано на рисунке. В результате I (t) начинается с нуля и асимптотически увеличивается до своего конечного значения.
Применяя к этой схеме правило петли Кирхгофа, получаем
, которое является дифференциальным уравнением первого порядка для I (t) . Обратите внимание на его сходство с уравнением для последовательно соединенных конденсатора и резистора (см. RC Circuits). Точно так же решение (рисунок) можно найти, сделав замены в уравнениях, связывающих конденсатор с катушкой индуктивности. Это дает
где
— индуктивная постоянная времени цепи.
Текущее значение I (t) показано на (Рисунок) (а).Он начинается с нуля, и по мере того, как I (t) приближается к асимптотически. Индуцированная ЭДС прямо пропорциональна dI / dt или наклону кривой. Следовательно, в то время как наивысшая сразу после включения переключателей, наведенная ЭДС уменьшается до нуля со временем, когда ток приближается к своему конечному значению. Схема становится эквивалентной резистору, подключенному к источнику ЭДС.
Изменение во времени (а) электрического тока и (б) величины индуцированного напряжения на катушке в цепи (рисунок) (б).Энергия, запасенная в магнитном поле индуктора, составляет
.Таким образом, по мере того, как ток приближается к максимальному, запасенная в катушке индуктивности энергия увеличивается от нуля и асимптотически приближается к максимуму
.Постоянная времени показывает, насколько быстро ток увеличивается до своего конечного значения. При токе в цепи, начиная с (рисунок),
, который имеет окончательное значение. Чем меньше индуктивная постоянная времени, тем быстрее приближается ток.
Мы можем найти временную зависимость индуцированного напряжения на катушке индуктивности в этой цепи, используя и (рисунок):
Величина этой функции показана на (Рисунок) (b). Наибольшее значение имеет место, когда dI / dt является наибольшим, то есть сразу после закрытия и открытия. При приближении к установившемуся состоянию значение dI / dt уменьшается до нуля. В результате напряжение на катушке индуктивности также обращается в нуль как
Постоянная времени также говорит нам, как быстро спадает наведенное напряжение.По величине наведенного напряжения
Таким образом, напряжение на катушке индуктивности падает примерно до своего начального значения после одной постоянной времени. Чем короче постоянная времени, тем быстрее падает напряжение.
По прошествии достаточного количества времени, чтобы ток практически достиг своего конечного значения, положения переключателей на (Рисунок) (a) меняются местами, давая нам схему в части (c). При токе в цепи согласно правилу петли Кирхгофа получаем
Решение этого уравнения аналогично решению уравнения для разряжающегося конденсатора с аналогичными заменами.Текущее значение на момент времени t равно
.Ток начинается и уменьшается со временем по мере того, как энергия, запасенная в катушке индуктивности, истощается ((рисунок)).
Зависимость напряжения на катушке индуктивности от времени можно определить из
Это напряжение изначально, и оно спадает до нуля, как и ток. Энергия, запасенная в магнитном поле индуктора, также экспоненциально уменьшается со временем, поскольку она рассеивается за счет джоулева нагрева в сопротивлении цепи.
Изменение во времени электрического тока в цепи RL (Рисунок) (c). Индуцированное напряжение на катушке также экспоненциально спадает.Проверьте свое понимание Убедитесь, что RC и L / R имеют измерения времени.
а. 2,2 с; б. 43 H; c. 1.0 с
Проверьте свое понимание Для схемы на (Рисунок) (b), покажите, что при достижении устойчивого состояния разница в полных энергиях, производимых батареей и рассеиваемых в резисторе, равна энергии, накопленной в магнитном поле. поле катушки.
Концептуальные вопросы
Используйте закон Ленца, чтобы объяснить, почему начальный ток в цепи RL (рисунок) (b) равен нулю.
По мере того, как ток течет через катушку индуктивности, по закону Ленца возникает обратный ток, который создается, чтобы поддерживать чистый ток на уровне нуля ампер, начальном токе.
Когда ток в цепи RL (рисунок) (b) достигает своего конечного значения, каково напряжение на катушке индуктивности? Через резистор?
Зависит ли время, необходимое для достижения током в цепи RL какой-либо части своего установившегося значения, от ЭДС батареи?
Катушка индуктивности подключена к клеммам батареи.Зависит ли ток, который в конечном итоге протекает через катушку индуктивности, от внутреннего сопротивления батареи? Зависит ли время, необходимое для того, чтобы ток достиг своего конечного значения, от этого сопротивления?
В какое время напряжение на катушке индуктивности цепи RL (рисунок) (b) является максимальным?
При первом включении переключателя.
В простой схеме RL (Рисунок) (b), может ли ЭДС, индуцированная на катушке индуктивности, когда-либо быть больше, чем ЭДС батареи, используемой для создания тока?
Если ЭДС батареи (рисунок) (b) уменьшается в 2 раза, насколько изменится установившаяся энергия, запасенная в магнитном поле индуктора?
Постоянный ток течет по цепи с большой индуктивной постоянной времени.Когда переключатель в цепи размыкается, на выводах переключателя возникает большая искра. Объяснять.
Обсудите возможные практические применения схем RL .
Глоссарий
- индуктивная постоянная времени
- , обозначенное как, характерное время, заданное количеством L / R конкретной серии RL цепи
Катушка индуктивности подключена последовательно к полностью заряженному конденсатору. 2} E = 21 LI2 + 21 CV2
Здесь первый член указывает накопленную энергию магнитного поля в катушке индуктивности, а второй член указывает накопленную энергию электрического поля в конденсаторе.2} E = 21 LI2 + 21 CV2
Первый член в приведенном выше выражении указывает накопленную энергию магнитного поля в катушке индуктивности, а второй член указывает накопленную энергию электрического поля в конденсаторе. Эти две энергии независимы и могут быть меньше, больше или равны друг другу, но общая энергия должна оставаться постоянной.
Следовательно, накопленная энергия электрического поля может быть равна накопленной энергии магнитного поля, но общая энергия должна оставаться постоянной.
Ответ: Часть 1Данное утверждение неверно.
Часть 2Данное утверждение верно.
Часть 3Данное утверждение верно.
Часть 4Данное утверждение верно.
Часть 5Данное утверждение верно.
Проще говоря, что такое индуктор | ОРЕЛ
Можете ли вы назвать тройку пассивных компонентов для электронных устройств? Мы говорим о резисторах (R), конденсаторах (C) и индукторах (L). Это трио составляет основу всех наших электронных устройств, открывая путь к созданию удивительных вещей с такими простыми концепциями.Итак, в то время как резисторы сопротивляются потоку электричества, а конденсаторы изо всех сил стараются удерживать заряд, что вообще делают катушки индуктивности? Этот компонент немного загадочнее других, он использует магию магнетизма. Хотите знать, какие секреты внутри? Давайте разберемся!
Как яблоки к яблокам, сорт
Прежде чем мы углубимся в детали индуктора, давайте сначала начнем с того, что нам знакомо. Как и конденсатор, индуктор хранит электрическую энергию.За исключением того, что вместо накопления энергии в электрическом поле, как это делает конденсатор, индуктор накапливает энергию в магнитном поле.
Вся энергия индуктора накапливается в магнитном поле. (Источник изображения)
Когда вы смотрите на трио пассивных компонентов, конденсаторы и катушки индуктивности похожи на братьев-близнецов. Они оба занимаются схожей деятельностью, накапливая энергию, просто у них есть своя уникальная личность и способ выполнять эту работу. Если конденсатор любит поддерживать постоянное напряжение, катушка индуктивности предпочитает поддерживать постоянный ток.Они оба по-своему достигают одной и той же конечной цели — накапливать и препятствовать потоку энергии.
В отличие от сложной физической структуры конденсатора, катушки индуктивности немного проще и состоят из простой катушки с проволокой вокруг магнита или даже воздуха. Но почему форма катушки? Если есть что-то, что нужно знать об электромагнетизме, так это то, что, посылая электрический ток по куску меди, создается магнитное поле.
Катушки индуктивностииспользуют это естественное свойство, увеличивая величину магнитного поля с помощью витого провода.Когда ток проходит по медному проводу индуктора, вы получаете магнитное поле, которое намного больше и намного сильнее, чем то, которое вы получили бы на прямом пути из меди.
Катушки индуктивности бывают всех форм и размеров, каждый со своим сердечником и медью. (Источник изображения)
Это настоящая красота индуктора. Создавая магнитное поле, вы можете преобразовывать электрическую энергию в магнитную и хранить ее там до тех пор, пока она не понадобится!
Еще одна аналогия с водой для понимания
Теперь, когда вы знаете, что такое индуктор, как именно он работает в цепи? Индукторы работают на основе свойства, называемого индуктивностью, которое представляет собой просто способность хранить некоторое количество энергии в магнитном поле.
Давайте подумаем на простом примере, таком как водяное колесо, чтобы понять, что здесь происходит. Допустим, у вас есть река с плотиной, в русле которой находится водяное колесо, готовое вырабатывать электричество. Теперь предположим, что вы открыли этот барьер и направили воду, льющуюся сквозь водяное колесо. Когда он ударяется о колесо, вода сначала замедляется, поскольку водяное колесо работает, чтобы соответствовать скорости воды. Именно здесь происходит процесс «зарядки» индуктора, когда через него проходит ток.
Водяное колесо готово к «зарядке», как и наш индуктор! (Источник изображения)
А затем представьте, что вы решили снова перекрыть реку плотиной. Это водяное колесо будет медленно замедляться, пока снова не остановится. И так же, как в индукторе, процесс сжатия магнитного поля при отсутствии тока происходит постоянно, а не сразу.
Звучит достаточно просто, правда? Но какова польза от накопления и высвобождения электрического заряда? Вот несколько примеров:
Сглаживающий ток
Когда вам нужен очень плавный ток для чего-то вроде источника постоянного тока, то магнитное поле в индукторе помогает стабилизировать ток, когда он движется по цепи.И если у вас есть уменьшающийся ток в цепи, которая должна оставаться стабильной, вы можете использовать резервы в магнитном поле индуктора, чтобы накачать ток обратно до исходного уровня.
Действует как датчик
Вы также найдете индукторы, используемые в светофорах. Поместив индуктор под дорогой с датчиком, а затем проведя по нему большим металлическим предметом, например автомобилем, вы добавили сердечник к индуктору, создавая большее магнитное поле! Затем датчик в стоп-сигнале может использовать эти данные, чтобы узнать, что вас ждет машина, и поэтому свет изменится.
Ток передачи
Когда вы перейдете к большему семейству индукторов, вы также обнаружите, что они используются в системах передачи энергии. Здесь они несут ответственность за стабилизацию огромного количества тока и следят за тем, чтобы ток оставался стабильным во время транспортировки.
Существует множество других применений индукторов в электронных устройствах, некоторые из которых зависят от определенного номинала индуктивности, например:
- Индукторы нано-генри .Эти катушки индуктивности отфильтровывают очень высокие частоты, и вы обнаружите, что они используются в радиосхемах.
- Индукторы микрогенри . Эти катушки индуктивности фильтруют частоты от 50 кГц до нескольких МГц, и вы обнаружите, что они сглаживают напряжения в источниках питания.
- Катушки индуктивности Миллигенри . Эти индукторы предназначены для разделения низкочастотных и высокочастотных звуков в схемах кроссовера аудио.
Измерительные индукторы с индуктивностью
Катушки индуктивности измеряются по их индуктивности и представляют собой группу сопротивлений, когда нужно пропускать ток.Пока индуктор не получит полный магнитный заряд, он никогда не пропустит ток! Но сколько им нужно заряда? Емкость индуктивности катушки индуктивности может определяться несколькими факторами, в том числе:
Проницаемость ядра
Если у вас есть металлический сердечник в катушке индуктивности с низкой проницаемостью, такой как воздух, то вы получите и индуктивность с низкой проницаемостью. А если у вас высокая магнитная проницаемость, как у железного сердечника, то и индуктивность тоже будет высокой.
Чем выше проницаемость, тем выше индуктивность. (Источник изображения)
Площадь поверхности катушки
Наконец, если вы разделите магнитную катушку пополам и произведете измерение ее общей площади поверхности, то катушка с большей площадью поверхности будет иметь большую индуктивность и магнитное поле.
Чем больше площадь поверхности, тем выше индуктивность. (Источник изображения)
Длина катушки
У вас может быть как можно больше скручиваний в катушке, но если вы растягиваете катушку все дальше и дальше, вы обнаружите, что индуктивность уменьшается.Чем больше длина вашей катушки, тем меньше будет ваше магнитное поле.
Чем дальше вы его растянете, тем меньше индуктивность! (Источник изображения)
Скручивания в катушке
По мере того, как количество витков в медном проводе увеличивается, увеличивается и индуктивность в вашей катушке индуктивности. Эта плотность медного провода в катушке индуктора также дает вам гораздо большее магнитное поле.
В вашей катушке больше витков? Вы получите более высокую индуктивность.(Источник изображения)
Все эти коэффициенты индуктивности собраны вместе, чтобы сформировать измерение для катушек индуктивности, называемое Генри. 1 Генри — это большая индуктивность, поэтому обычно используются единицы меньшего размера, например:
Префикс Символ Множитель Сила десяти милли м 1/1000 10-3 микро µ 1/1 000 000 10-6 нано n 1/1 000 000 000 10-9 Поиск индукторов на схеме
Как выглядит один из этих символов индуктивности на схеме? Они удивительно похожи по своей физической форме и организованы на основе своего внутреннего ядра.Обычно вы видите символы индуктивности для воздушных сердечников, железных сердечников и ферритовых сердечников. Посмотрите их ниже:
Некоторые из множества символов индуктивности, которые вы встретите на схеме.
Теперь определить все катушки индуктивности на принципиальной схеме — это одно, но что произойдет, если вы захотите узнать общую величину индуктивности для всех ваших катушек индуктивности? Это просто, и работает он так же, как резисторы. Вот как это сделать:
Катушки индуктивности серииКогда у вас есть группа катушек индуктивности, соединенных последовательно, общая индуктивность — это просто сумма всех индивидуальных индуктивностей:
Катушки индуктивности параллельные
А если у вас есть группа катушек индуктивности, соединенных параллельно, то вы можете найти свою общую индуктивность с помощью следующего уравнения:
Заметили сходство? Определение полной индуктивности для ваших катушек индуктивности похоже на определение общего сопротивления для резисторов!
Трио создателей индукторов
Да, когда-то было время, когда магия магнитных полей и индустрий была полной загадкой для мира науки.Индуктивность была впервые обнаружена еще в 1830 году Майклом Фарадеем. Фарадей наткнулся на свое открытие, обмотав бумажный цилиндр проволокой и соединив концы проволоки с помощью прибора, который мог измерять электрический ток, называемого гальванометром.
Когда магнит входил и выходил из цилиндра, устройство регистрировало небольшой ток, и так родилась теория индуктивности! После этого открытия преподобный Николас Каллан изобрел простую, но прочную катушку индуктивности, и так вошла история.
Но, конечно, нельзя забывать и о нашем дорогом Джозефе Генри, который первым открыл электромагнитное свойство самоиндукции. Он смог измерить, как катушка с проволокой может вызвать изменение напряжения в цепи за счет магнитной силы. Если бы только он опубликовал свои открытия до Фарадея, и сегодня он мог бы быть известен как отец самой индуктивности. Однако Генри продолжал создавать большие и лучшие вещи, такие как электрический дверной звонок и электрические реле.А измерение индуктивности Генри? Он назван в его честь.
Человек, миф, легенда, Джозеф Генри. (Источник изображения)
Гладкий оператор
Когда дело доходит до сглаживания тока в цепи, нет лучшего выбора, чем наш верный старый индуктор. Этот компонент использует силу магнетизма для хранения электрического заряда, формируя основу для некоторых из наших наиболее важных электронных устройств, таких как аудиокроссоверы, источники питания постоянного тока, радиочастотные цепи и многое другое.А когда вы соберете вместе три пассивных компонента, у вас под рукой окажется опасный арсенал электронного волшебства. Эти три элемента составляют основу всех наших крупных электронных изобретений, и без них наш мир никогда не был бы прежним.
У нас есть множество бесплатных библиотек индукторов, которые вы можете использовать в своей собственной конструкции электроники. Попробуйте Autodesk EAGLE бесплатно сегодня!
Цепьпеременного тока содержит омическое сопротивление, конденсатор и индуктивную катушку, соединенные последовательно (RLC-цепь)
ИмпедансВ электрической цепи, содержащей источник питания переменного тока вместе с индуктивными катушками, конденсаторами и резисторами, переменному току будет противодействовать реактивное сопротивление (индуктивное реактивное сопротивление или емкостное реактивное сопротивление) в дополнение к сопротивлению резисторов и проводов, сопротивление и реактивное сопротивление вместе называются импедансом, обозначаются символом (Z) и измеряются в Ом (Ом).
Импеданс (Z) эквивалентен сопротивлению, емкостному реактивному сопротивлению и индуктивному реактивному сопротивлению вместе в цепи переменного тока, Когда полное сопротивление цепи RLC = 300 Ом, это означает, что полное сопротивление электрическому току в этой цепи из-за сопротивления и реактивного сопротивления как катушки, так и конденсатора = 300 Ом.
Цепь переменного тока содержит последовательно включенные омическое сопротивление и индуктивную катушку (RL — цепь)Практически невозможно построить индуктивную катушку с нулевым сопротивлением, потому что любая катушка должна иметь сопротивление из-за проводов, используемых при ее изготовлении.
Когда электрическая цепь содержит индуктивную катушку, омическое сопротивление и источник переменного тока, соединенные последовательно, мы заметили, что ток, проходящий через каждое из сопротивлений и индукционную катушку, одинаков по величине и фазе, поскольку они соединены последовательно.
Но напряжение в катушке (V L ) опережает ток (I) на цикла (фазовый угол 90 °) в индукционной катушке, напряжение на сопротивлении (V R ) синфазно с током (I ) в омическом сопротивлении.
Разность потенциалов на катушке (V L ) опережает разность потенциалов на сопротивлении (V R ) на фазовый угол 90 °, таким образом, общая разность потенциалов не совпадает по фазе с силой тока (I) .
Общее напряжение можно найти с помощью векторов из отношения:
V² = V² R + V² L
V = I Z, V R = I R, V L = I X L
(I Z) ² = I² R² + I² X² L = I² (R² + X² L )
Z² = (R² + X² L )
Фазовый угол может быть определен между общим напряжением (В) и напряжением резистора (В R ) из соотношения:
tan θ = V L / V R , tan θ = IX L / I R, Итак, tan θ = X L / R
Цепь переменного тока содержит омическое сопротивление и последовательно включенный конденсатор (RC-цепь)Когда электрическая цепь содержит конденсатор, омическое сопротивление и источник переменного тока, соединенные последовательно, мы замечаем, что ток, проходящий через каждое из сопротивлений и конденсатор, одинаков по величине и фазе, поскольку они соединены последовательно.
Но напряжение в конденсаторе (В C ) отстает от тока (I) на цикла (фазовый угол 90 °) в конденсаторе. Напряжение на сопротивлении (В R ) синфазно с током (I) в конденсаторе. омическое сопротивление.
Разность потенциалов на конденсаторе (V C ) отстает от разности потенциалов на сопротивлении (V R ) на фазовый угол 90 °, таким образом, общая разность потенциалов (V) не совпадает по фазе с силой тока (I ).
Общее напряжение можно найти с помощью векторов из отношения:
V² = V² R + V² C
V = I Z, V R = I R, V C = I X C
I² Z² = I² R² + I² X² C
I² Z² = I² (R² + X² C )
Z² = (R² + X² C )
Фазовый угол (θ) можно определить между общей разностью напряжений (В) и напряжением резистора (В R ) из соотношения:
tan θ = — V C / V R , tan θ = — IX C / I R, Итак, tan θ = — X C / R
Знак минус означает, что разность потенциалов (V C ) отстает от разности потенциалов (V R ) на угол 90 °.
Цепь переменного тока
Цепь переменного тока содержит омическое сопротивление, индукционную катушку и конденсатор, соединенные последовательно (RLC — цепь)
Когда электрическая цепь содержит конденсатор, омическое сопротивление, индукционную катушку и источник переменного тока, подключенные последовательно, мы заметили, что ток, проходящий через каждое из сопротивлений, индукционную катушку и конденсатор, одинаковы по величине и фазе, поскольку они подключены в серия, Но:
- В индукционной катушке напряжение (V L ) опережает ток (I) с фазовым углом 90 °.
- В омическом сопротивлении напряжение (V R ) находится в фазе с током (I).
- В конденсаторе напряжение (В c ) отстает от тока (I) на фазовый угол 90 °.
Напряжение катушки (V L ) опережает напряжение сопротивления (V R ) на угол 90 °, а напряжение конденсатора (V c ) отстает от напряжения сопротивления (V R ) на угол 90 °. и, таким образом, разность фаз между (V L ) и (V c ) составляет 180 °.
Общее напряжение (В) можно найти с помощью векторов из соотношения:
V² = V² R + (V L — V c ) ²
Где: V = I Z, V R = I R, V L = I X L , V C = I X C
I² Z² = (I R) ² + (I X L — I X C ) ² = I² [(R) ² + (X L — X C ) ²]
Z² = (R) ² + (X L — X C ) ²
Из предыдущего рисунка фазовый угол можно определить из соотношения:
tan θ = (V L — V C ) / V R
tan θ = (X L — X C ) / R
На фазовый угол θ влияет изменение значений емкостного и индуктивного реактивного сопротивления, тогда когда:
- V L > V C , X L > X C , Фазовый угол (θ) положительный, полное напряжение (V) опережает ток (I) на угол (θ) , Это означает индуктивное поведение цепи.
- V L = V C , X L = X C , фазовый угол (θ) равен нулю, полное напряжение (V) находится в фазе с током (I), что означает омическое сопротивление поведение сопротивления.
- V L
C , X L C , Фазовый угол (θ) отрицательный, полное напряжение (V) отстает от тока (I) на угол (θ), Это означает поведение емкостной цепи. Реальная потребляемая мощность (P w ) в цепи переменного тока, RL, RC или RLC, — это только мощность, потребляемая в омическом сопротивлении в виде тепловой энергии.
P w = I² R = V² R / R
Емкостное реактивное сопротивление сети конденсаторов, переменный ток и переменное напряжение в конденсаторной цепи
Колебательный контур, Настроечный или резонансный контур в радиоприемниках радиосвязи
Индуктивность серии— обзор
41.2.1.3 Линии передачи и кабели
Линии передачи и кабели поглощают переменные в зависимости от их последовательной индуктивности. Им также присуща способность генерировать переменные токи за счет своей шунтирующей емкости, которая вызывает прохождение реактивного «зарядного тока» в линии.И последовательная индуктивность, и шунтирующая емкость распределены по длине линии.
С аналитической точки зрения кабели неотличимы от воздушных линий, за исключением того, что соотношение между шунтирующей емкостью и последовательным реактивным сопротивлением значительно выше. Использование кабелей в высоковольтных сетях увеличивается из-за трудностей со строительством новых воздушных линий для передачи электроэнергии в городские районы и, в меньшей степени, для линий переменного тока. подводные ссылки; использование кабелей по-прежнему очень мало по сравнению с воздушными линиями из-за недостатков стоимости.Если кабели используются в любом количестве, их высокая шунтирующая емкость снижает потребность в дополнительном генерировании переменной мощности в периоды пиковой нагрузки, но увеличивает потребность в ее поглощении в условиях низкой нагрузки.
Когда нет тока нагрузки, протекающего по линии или кабелю, обнаруживается, что напряжение на приемном конце линии выше, чем на передающем конце; это вызвано протеканием емкостного зарядного тока через последовательную индуктивность и известно как эффект Ферранти.Величина повышения напряжения очень быстро увеличивается с увеличением длины линии, от всего лишь примерно 3% для 200 км до примерно 50% для 800 км. Величина такого повышения напряжения в системе передачи должна быть ограничена (обычно на 5 или 10% выше номинального напряжения), чтобы избежать превышения безопасных пределов эксплуатации для изоляции самой линии или кабеля, а также безопасные пределы для различного оборудования, подключенного к системе передачи. Очень длинные линии обычно делятся на участки длиной от 200 до 300 км; При необходимости на промежуточных подстанциях могут быть применены меры по управлению напряжением или переменным током.
По мере увеличения мощности, протекающей через линию, также увеличивается поглощение реактивной мощности в последовательном реактивном сопротивлении. Существует критический ток, при котором величина «последовательных переменных», поглощаемых в линии, достаточно, чтобы уравновесить «шунтирующие переменные», генерируемые шунтирующей емкостью линии. При таком уровне потока мощности линейное напряжение будет иметь одинаковое значение по всей линии (без учета резистивных потерь). Когда происходит дальнейшее увеличение мощности, протекающей по линии, поглощенные переменные будут перевешивать генерируемые переменные, и напряжение на принимающем конце линии начнет очень быстро падать с увеличением нагрузки и может достигнуть точки полного коллапса.
Импеданс линии передачи, имеющей последовательную индуктивность L и шунтирующую емкость C , представляет собой сопротивление, равное ( L / C ). Если нагрузка, имеющая это значение сопротивления, подключена к концу линии, мощность, которая течет в нагрузку, называется нагрузкой импульсного сопротивления или SIL. Это упомянутая выше нагрузка, при которой поглощение var в последовательном реактивном сопротивлении равно генерации var в шунтирующей емкости, и для которой напряжение вдоль линии постоянно.При заданном импульсном сопротивлении SIL увеличивается пропорционально квадрату линейного напряжения.
Значение импульсного сопротивления для линии 132 кВ составляет около 400 Ом. Для систем с более высоким напряжением обычно используются несколько проводников, отчасти для уменьшения эффектов коронного разряда, а последовательная индуктивность также несколько ниже, что дает импульсное сопротивление примерно от 250 до 300 Ом для линии 400 кВ. Одним из следствий выбора повышенного напряжения передачи является снижение потерь при передаче при заданном потоке мощности, но другой эффект заключается в обеспечении улучшенной способности передачи мощности на полосе отвода.Поэтому при выборе напряжения передачи необходимо соблюдать баланс между затратами на оборудование, эксплуатационными расходами и будущей мощностью.
Уровень SIL типичных кабелей обычно превышает их номинальные значения, поэтому кабели генерируют больше переменных, чем поглощают, и часто требуется компенсация. Это накладывает ограничение на длину непрерывного кабеля, который можно использовать; например, для подводных кабелей предел обычно составляет 50–75 км, прежде чем емкостный зарядный ток достигнет номинального тока кабеля.
Теперь доступны кабели с изоляцией из сшитого полиэтилена (XLPE) для напряжений передачи 400–500 кВ; для кабеля с изоляцией из сшитого полиэтилена мощностью 400 кВ и 1100 МВА SIL составляет около 2500 МВт, что все же намного выше номинального значения. Тем не менее, эти кабели генерируют гораздо меньший зарядный ток, чем предыдущие типы, и обеспечивают непрерывную длину до 100 км. Если требуются большие расстояния, необходимо другое решение, например, h.v.d.c. или ЛЭП с элегазовой изоляцией (ЛЭП).
В большинстве стран есть два или три уровня напряжения передачи в своих системах, самый высокий обычно находится в диапазоне 400-500 кВ, при этом несколько стран в Северной и Южной Америке и СССР эксплуатируют или устанавливают сети в диапазоне 750 кВ. Хотя использование сверхвысокого напряжения на 1000–1500 кВ технически возможно, затраты высоки, и его коммерческое применение, вероятно, будет ограничено в обозримом будущем.
Последовательные и параллельные индукторы | Энергия, накопленная в индукторе
Когда через проводник проходит ток, он оказывается окруженным электромагнитным полем.Это поле приводит к свойству, известному как индуктивность , , , (L), которое препятствует любому изменению тока. Индукторы — это компоненты, которые обладают этим свойством. В этом модуле мы обсудим основную конструкцию катушек индуктивности, как их можно комбинировать последовательно и параллельно, и как они ведут себя в цепях.
Катушка индуктивности представляет собой электрический компонент, образованный катушкой с проволокой, которая проявляет свойство индуктивности.Величина индуктивности, которую демонстрирует катушка, измеряется в генри (H) .
Генри определяется как скорость изменения тока в один ампер в секунду, индуцирующего один вольт на катушке.
Однако Генри — довольно большая единица измерения, и индуктивность чаще всего измеряется в миллигенри (мГн) или микрогенри (мкГн).
Основная конструкция индуктораНа рисунке 1 показан основной индуктор с магнитными силовыми линиями и направлением тока.Сила тока, протекающего через катушку, пропорциональна величине поля; следовательно, изменяющийся ток вызовет изменение магнитного поля вокруг индуктора. Это изменяющееся поле вызывает на катушке наведенное напряжение . Это напряжение противоположно току и препятствует изменению тока.
Рисунок 1 — Базовый индуктор
На индуктивность катушки сильно влияет материал, вокруг которого наматывается провод.Внутренний материал, известный как сердечник , может быть либо немагнитным (воздух, дерево и т. Д.), Либо магнитным (железо, сталь и т. Д.). Проницаемость , , , сердечника является мерой его сопротивления магнитным силовым линиям. Поскольку силовые линии контролируют величину индуктивности, проницаемость сердечника (µ) напрямую связана с индуктивностью.
Другими характеристиками индуктора, которые регулируют величину индуктивности, являются площадь поперечного сечения сердечника (A), количество витков в катушке (N) и длина катушки (l).{2}} \ times \ mu \ times A} {l} \]
Две другие характеристики индукторов — это сопротивление обмотки и емкость обмотки. Сопротивление обмотки является мерой сопротивления постоянного тока провода, составляющего катушку. Емкость обмотки , , , — это побочный эффект, вызванный множеством витков провода, находящихся в непосредственной близости. Они могут повлиять на цепь, если катушка индуктивности слишком велика или частота очень высока; однако в большинстве схем их можно не учитывать при расчетах.{-5}} \ right)} {\ left (0,015 \ right)} = 40 мГн $
Серия индукторовНа картинке в вашей голове несколько индукторов, соединенных встык. Если сдвинуть их все ближе и ближе друг к другу, они в конечном итоге будут похожи на большую катушку проволоки. {d {{i} _ {t}}} / {} _ {dt}} \ text {} \ cdots \ текст {(b)} \]
Левая часть уравнения (b) представляет собой полное напряжение, деленное на скорость изменения тока.{d {{i} _ {t}}} / {} _ {dt}} = {{L} _ {3}} \]
Итак, общая индуктивность будет,
$ {{L} _ {T}} = {{L} _ {1}} + {{L} _ {2}} + {{L} _ {3}} \ text {} \ cdots \ text {(c)}
долл. СШАУравнение (c) утверждает, что при последовательном соединении катушек индуктивности общая индуктивность является суммой индивидуальных индуктивностей.
Если есть две или более катушки индуктивности одинаковой величины, соединенные последовательно, общая индуктивность может быть определена как;
$ {{L} _ {T}} = NL $
Где N — количество одинаковых катушек индуктивности, а L — значение одной индуктивности.
Параллельные индукторыКатушки индуктивности также могут быть объединены в параллельные цепи. Последовательное подключение катушек индуктивности увеличивало общую индуктивность; Таким образом, вполне очевидно, что параллельное подключение катушек индуктивности должно уменьшить общую индуктивность.
Подобно тому, как последовательные индукторы действуют как последовательные резисторы, параллельные индукторы действуют как параллельные резисторы. Формула для определения полной индуктивности в параллельной цепи очень похожа на формулу для определения полного сопротивления в параллельной цепи.
Применяя закон Кирхгофа к следующему рисунку, мы можем определить, как соединяются параллельно включенные индукторы;
$ ~ {{i} _ {T}} = {{i} _ {1}} + {{i} _ {2}} + {{i} _ {3}} \ text {} \ cdots \ text {(d)} $
Чтобы выразить вышеприведенное уравнение как скорость изменения текущей производной с обеих сторон;
\ [\ frac {d {{i} _ {T}}} {dt} = \ frac {d {{i} _ {1}}} {dt} + \ frac {d {{i} _ { 2}}} {dt} + \ frac {d {{i} _ {3}}} {dt} \ text {} \ cdots \ text {(e)} \]
Поскольку напряжение на катушке индуктивности равно
$ {{V} _ {L}} = L \ frac {di} {dt} $
А также, поскольку V T — это полное напряжение на параллельной индуктивности,
$ \ frac {{{V} _ {T}}} {{{L} _ {T}}} = \ frac {{{V} _ {T}}} {{{L} _ {1}}} + \ frac {{{V} _ {T}}} {{{L} _ {2}}} + \ frac {{{V} _ {T}}} {{{L} _ {3}}} \ text {} \ cdots \ text { (f)} $
Разделив обе части уравнения (c) на V T , мы получили бы следующее уравнение;
$ \ frac {1} {{{L} _ {T}}} = \ frac {1} {{{L} _ {1}}} + \ frac {1} {{{L} _ {2 }}} + \ frac {1} {{{L} _ {3}}} \ text {} \ cdots \ text {(g)} $
Уравнение (g) утверждает, что обратная величина полной индуктивности равна сумма обратных величин отдельных индуктивностей, соединенных параллельно.
Если две или более параллельных катушки индуктивности равны. Полная индуктивность может быть определена путем деления значения одной из катушек индуктивности на количество равных катушек индуктивности.
$ {{L} _ {T}} = \ frac {L} {N} $
Где L — значение одного из равных показателей, а N — количество равных индукторов.
Снова представьте несколько катушек индуктивности, соединенных вместе, но на этот раз они включены параллельно. В параллельной цепи ток делится между ветвями; Таким образом, через каждую катушку индуктивности проходит меньше тока.Это приводит к меньшему наведенному напряжению, что приводит к меньшей общей индуктивности.
Энергия, запасенная в катушке индуктивностиМощность, поступающая в катушку индуктивности в любой момент времени, равна;
$ P = Vi = Li \ frac {di} {dt} $
Когда ток постоянный, производная равна нулю и в индукторе не накапливается дополнительная энергия. Когда ток увеличивается, производная тока имеет положительное значение, а мощность — положительное значение.






 Из треугольника напряжений следует
Из треугольника напряжений следует 14.3, где UL емкостный характер.
14.3, где UL емкостный характер.
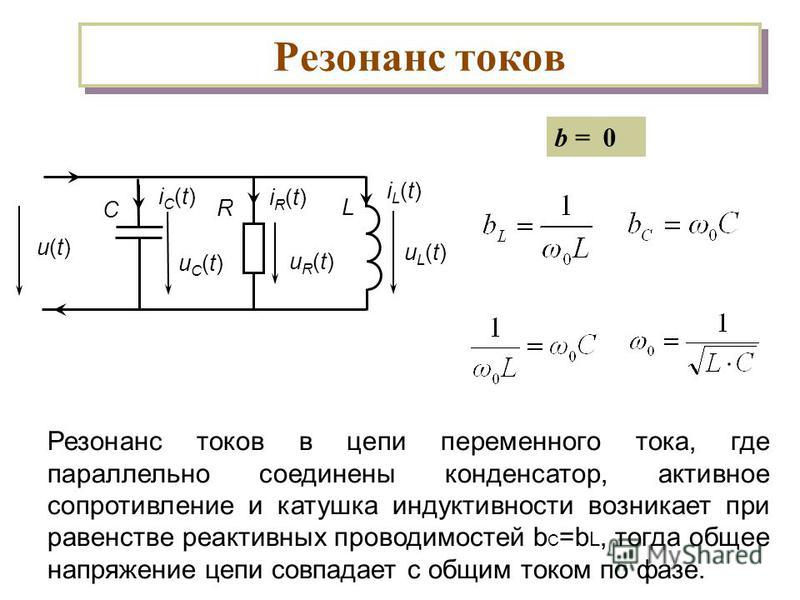 Обозначаются мгновенные значения малыми буквами: i, u, e, p.
Обозначаются мгновенные значения малыми буквами: i, u, e, p. Тогда начальная фаза будет опережающей или отстающей.
Тогда начальная фаза будет опережающей или отстающей. При наличии R и L значение суммарного сопротивления Z подсчитывается по формуле:
При наличии R и L значение суммарного сопротивления Z подсчитывается по формуле:
 1.4.1).
1.4.1). 1.4.3)
1.4.3) 



 + С n и 1/L = 1/L 1 + 1/L 2 +. + 1/L n для параллельных цепей и
+ С n и 1/L = 1/L 1 + 1/L 2 +. + 1/L n для параллельных цепей и