Последовательное соединение катушки и конденсатора


При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.

Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = Imsinωt.
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цели
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
u = u1R + uL + uC + u2R,
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
U = U2R + UL + UC +U2R
Для построения векторной диаграммы находим:
U1R = IR1; U2R = IR2; UL = IXL; UC = IXC.
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
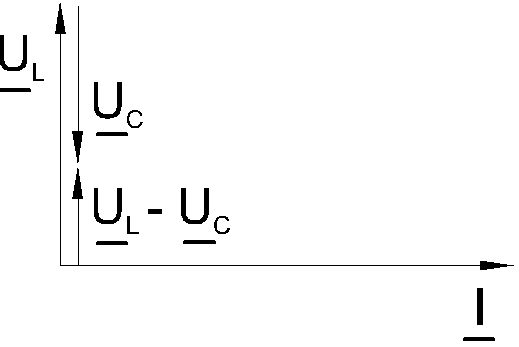
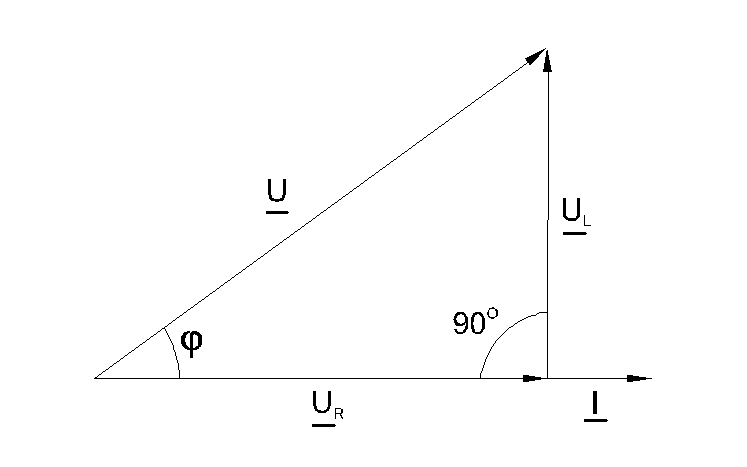
1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.

Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: Uр = UL — UC .
При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует

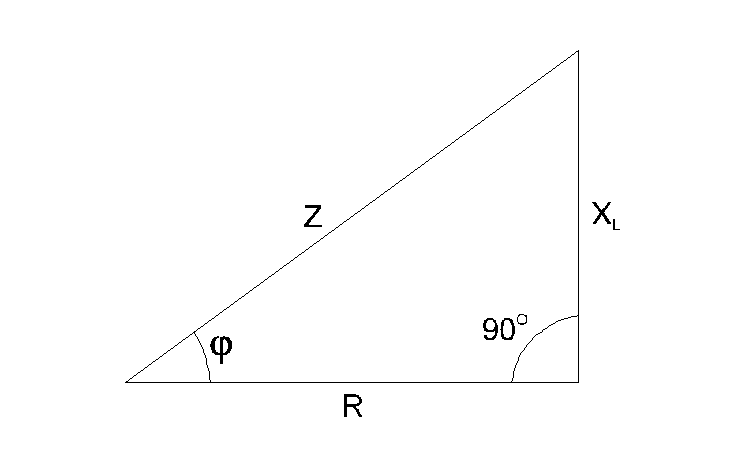
где R = R1 + R2 и X = XL — XC общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Из треугольников напряжения и сопротивлений определяют следующие величины:

Угол сдвига по фазе между напряжением и током в цепи положительный (φ>0) (фазовые токи отсчитываются от вектора тока).
2. ХL< ХC Векторная диаграмма изображена на рис. 14.3, где UL<UC , поэтому общее напряжение отстает от тока на угол φ<0.
Реактивное сопротивление цепи носит емкостный характер.
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: UL = UC (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.


Общее напряжение совпадает по фазе с током и равно по величине активной
составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
U = IR, или I = U/R.
В случае XL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи с последовательном соединении конденсатора и катушки
Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:

Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0; при φ<0 Q<0.
Активная мощность положительна при любом угле, так как cosφ = cos(-φ).
Полная мощность также всегда положительна. На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии (Р ≠ 0) и обменный процесс между генератором и приемником (Q ≠ 0 при φ ≠ 0).
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при XL = ХС.

Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задачи по теме и пример решения задачи для схемы с последовательным соединением конденсатора и катушки
6.5. Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений
6.5.1. Общие сведения
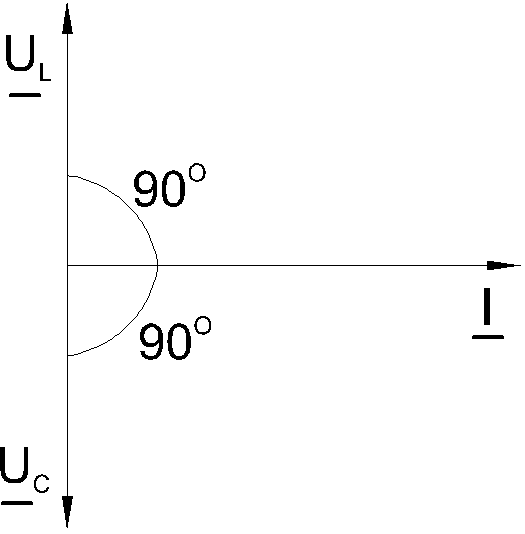
Когда по цепи (рис. 6.5.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на конденсатореUCотстает от токаIна 900, а напряжение на катушке индуктивностиULопережает ток на 900. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 1800).
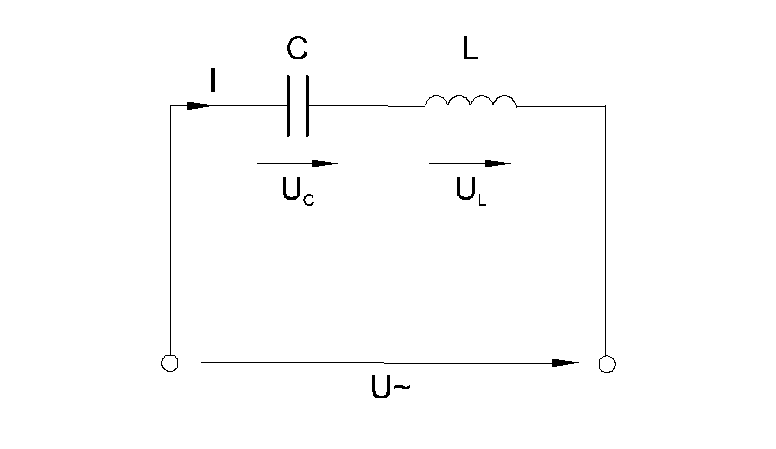
Рис. 6.5.1
Когда одно из напряжений больше другого,
цепь оказывается либо преимущественно
индуктивной (рис. 6.5.2), либо преимущественно
емкостной (рис. 6.5.3). Если напряжения U
|
|
|
Рис. 6.5.2 | Рис. 6.5.3 | Рис. 6.5.4 |
При резонансе напряжений реактивное сопротивление цепи
X = XL – XC
оказывается равным нулю. При заданных значениях LиCрезонанс может быть получен путем изменения частоты.
Поскольку XL=L, аXC= 1 /C, то резонансная частота
0L – 1 / 0C = 0,
откуда
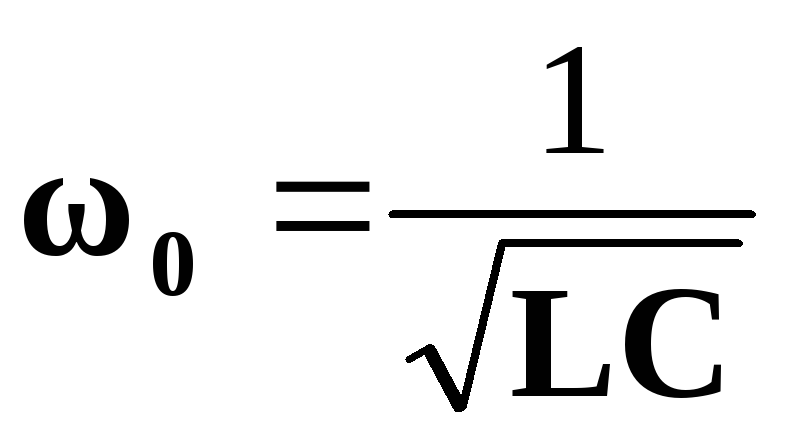 и
и .
.
Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения U
6.5.2. Экспериментальная часть Задание
Для цепи с последовательным соединением конденсатора и катушки индуктивности измерьте действующие значения тока Iи напряженийU,UC,UL при = 0, <0 и >0. Постройте векторные диаграммы.
Порядок выполнения работы
Соберите цепь согласно схеме (рис. 6.5.5), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2 В и частоту 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
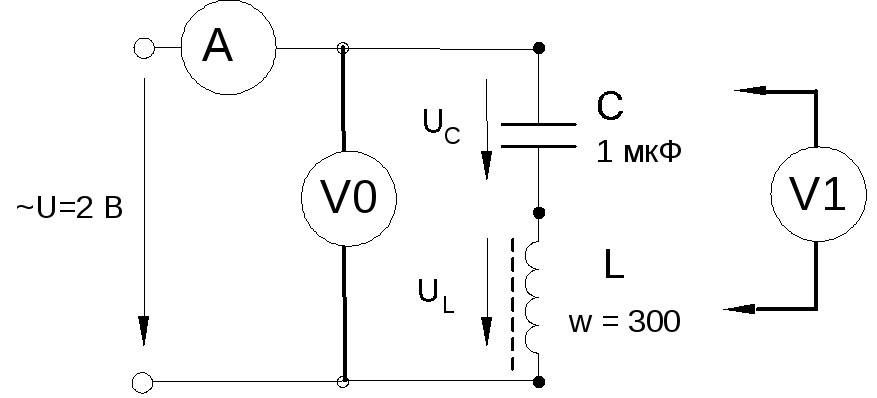
Рис. 6.5.5
Изменяя частоту приложенного напряжения, добейтесь резонанса по максимальному току. Для точной настройки по максимуму тока необходимо поддерживать неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входными напряжением и током. Тогда нет необходимости поддерживать входное напряжение неизменным.
Произведите измерения и запишите в табл. 6.5.1 результаты измерений при резонансе f=f0 при f1 0,75f0 и f2 1,25f0.
Таблица 6.5.1
f, Гц
I, мА
U, B
UC, B
f0 =
f1 =
f2 =
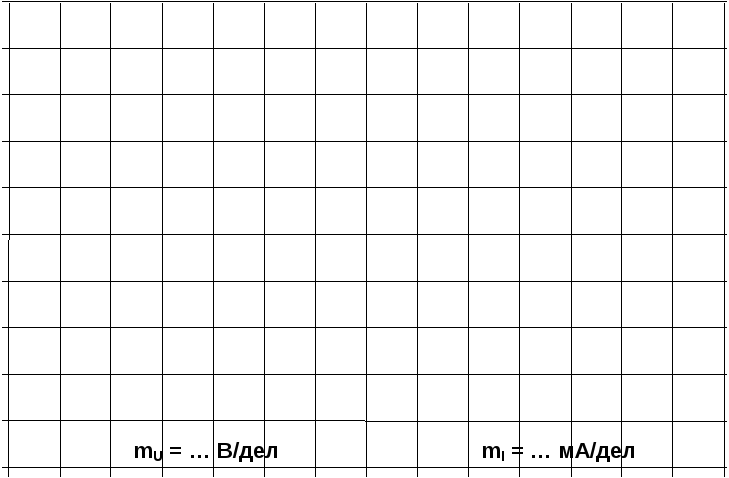
Рис. 6.5.6
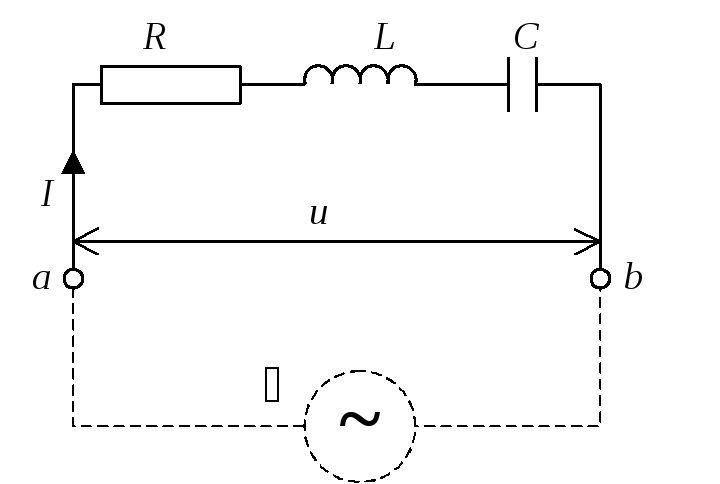
Последовательное соединение резистора, конденсатора и катушки индуктивности
Рис.8. Последовательное соединение резистора, конденсатора и катушки индуктивности |
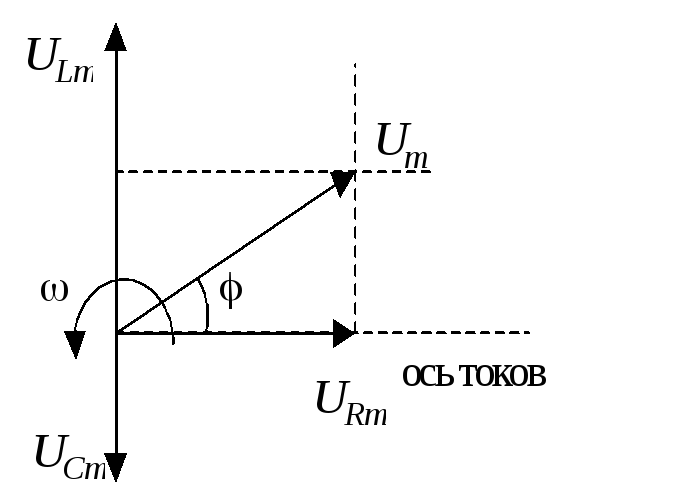
Рис.9. Векторная диаграмма |
Положим по-прежнему, что ток в цепи изменяется по закону
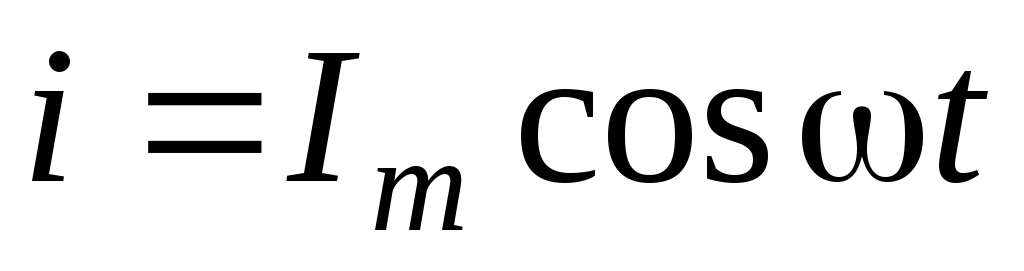 ,
,
и
вычислим напряжение между концами цепи u.
Так как при последовательном соединении
проводников складываются напряжения,
то искомое напряжение u есть сумма
трех напряжений: на сопротивлении 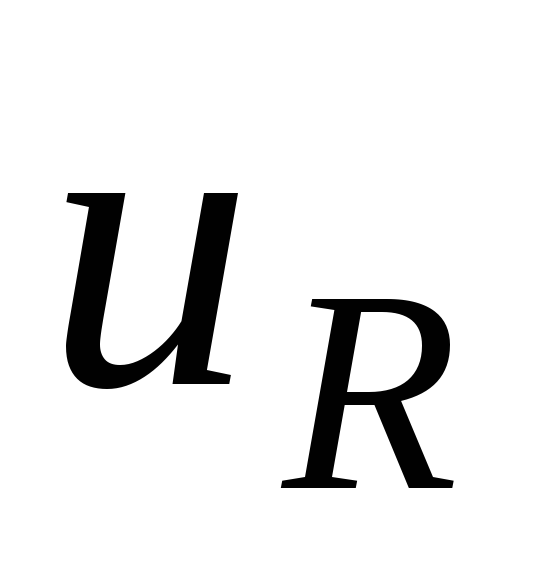 ,
на емкости
,
на емкости 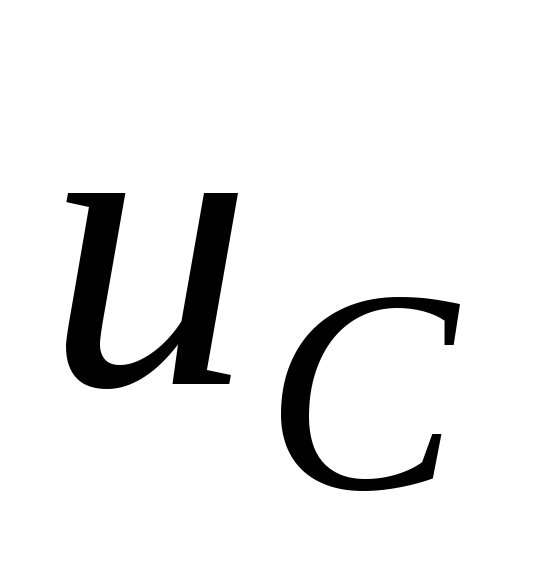
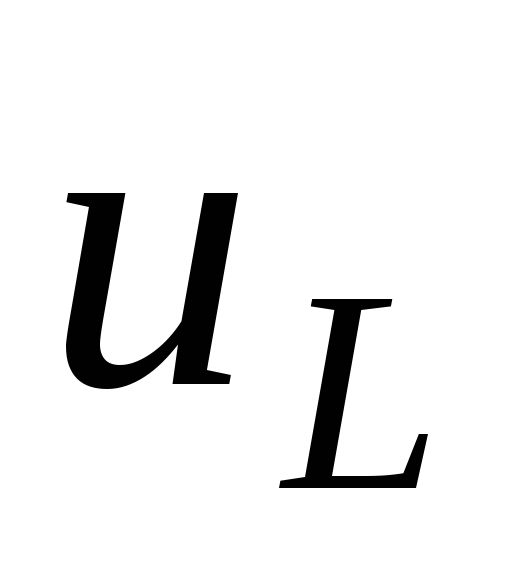 ,
причем каждое из этих напряжений, как
мы видели, изменяется со временем по
закону косинуса:
,
причем каждое из этих напряжений, как
мы видели, изменяется со временем по
закону косинуса: 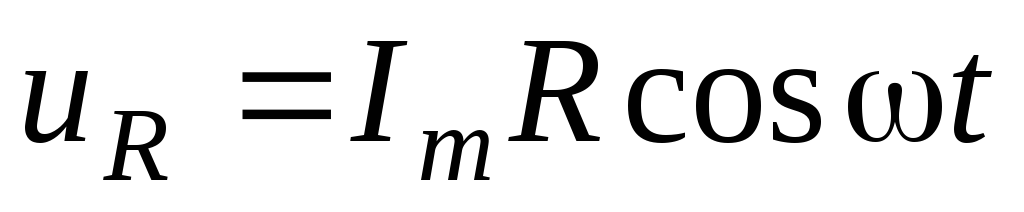 ,
(5)
,
(5)
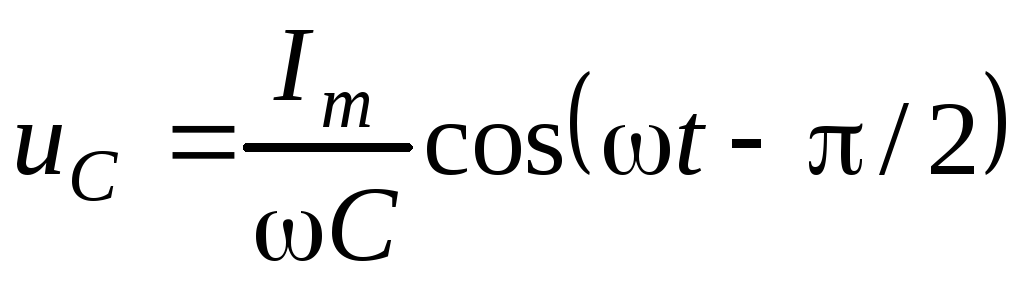 ,
(6)
,
(6)
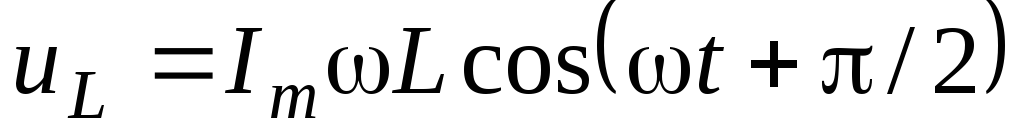 .
(7)
.
(7)
Для
сложения этих трех колебаний воспользуемся
векторной диаграммой напряжений.
Колебания напряжения на сопротивлении
изображаются на ней вектором 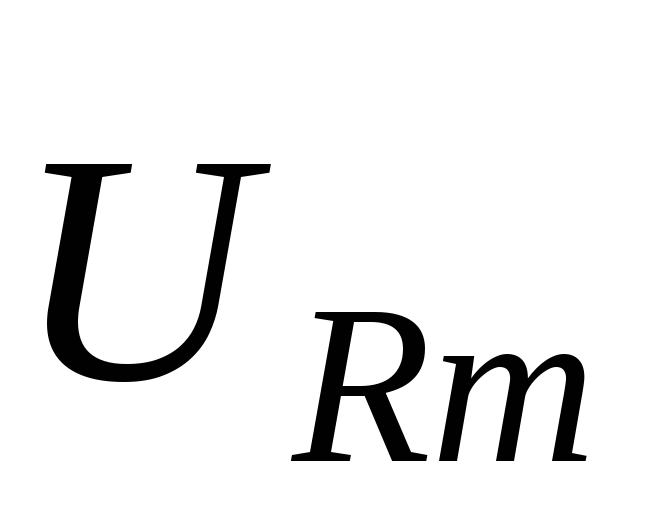 ,
направленным вдоль оси токов и имеющим
длину
,
направленным вдоль оси токов и имеющим
длину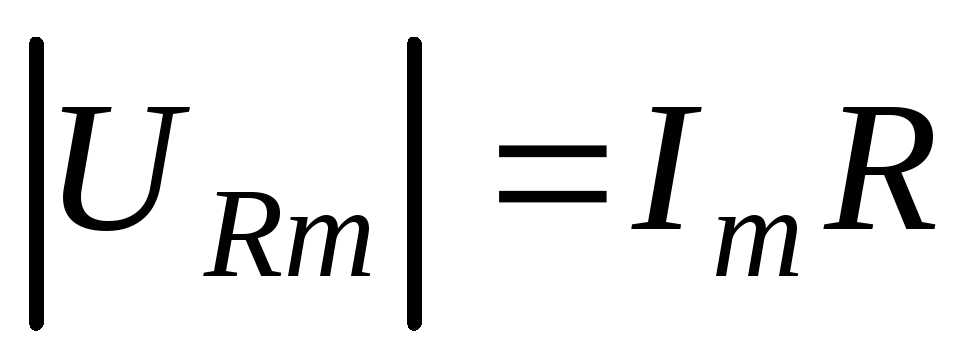 ,
колебания же напряжений на емкости и
индуктивности — векторами
,
колебания же напряжений на емкости и
индуктивности — векторами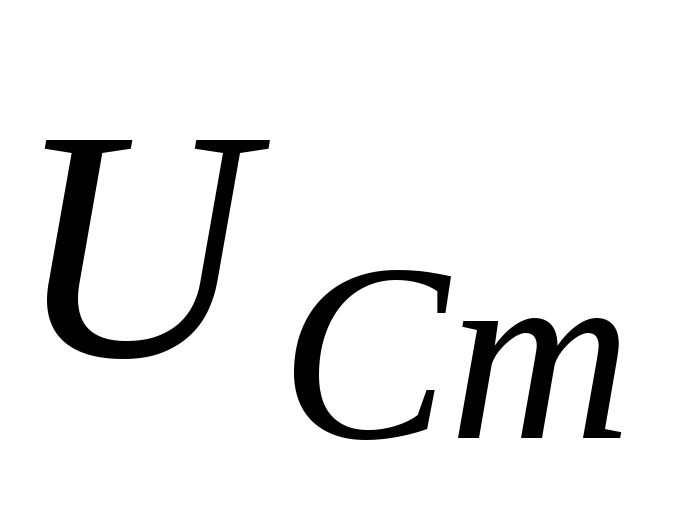 и
и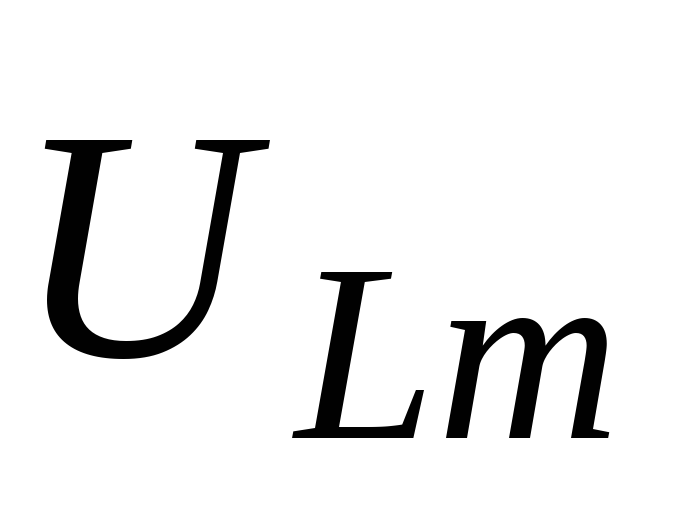 ,
перпендикулярными к оси токов, с длинами
(Im
,
перпендикулярными к оси токов, с длинами
(Im
 ,
, и
и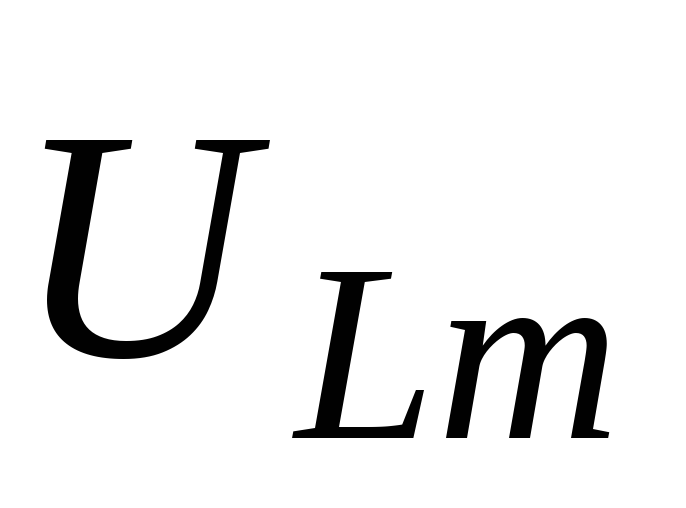 ,
будут описываться соответственно
формулами (5)-(7). Очевидно, что проекция
на ось токов суммарного вектора
,
будут описываться соответственно
формулами (5)-(7). Очевидно, что проекция
на ось токов суммарного вектора 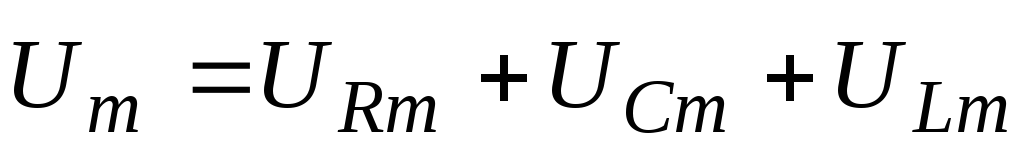
равна
сумме 
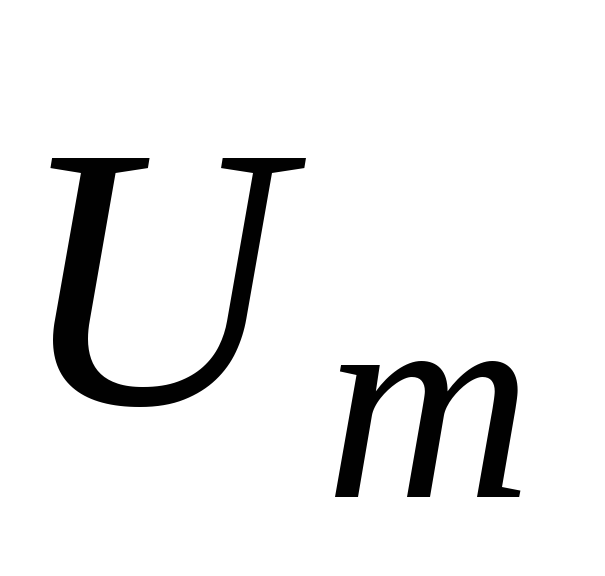 .
Эта величина легко определяется
геометрически. Сначала целесообразно
найти модуль вектора
.
Эта величина легко определяется
геометрически. Сначала целесообразно
найти модуль вектора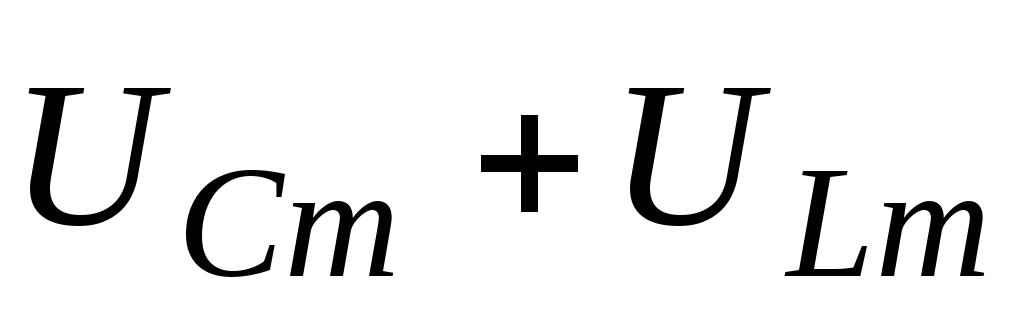 :
: 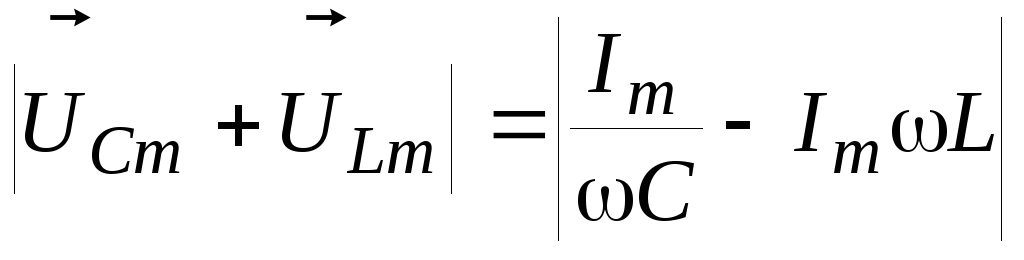 ,
,
а затем по теореме Пифагора:
 .
(8)
.
(8)
Из рисунка также видно, что
 .
(9)
.
(9)
Для напряжения на участке цепи можно записать
 ,
,
где
амплитуда напряжения и фазовый сдвиг
между током и напряжением определяются
формулами (8), (9). Если 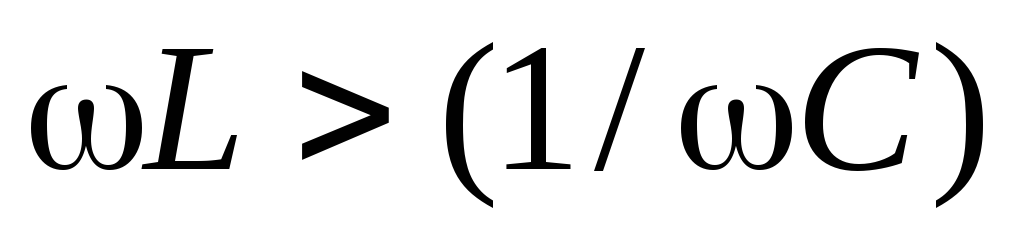 ,
то напряжение по фазе опережает ток, в
противном случае — напряжение отстает
по фазе.
,
то напряжение по фазе опережает ток, в
противном случае — напряжение отстает
по фазе.
Формула
(8) имеет сходство с законом Ома в том
смысле, что амплитуда напряжения
пропорциональна амплитуде тока. Поэтому
ее иногда называют законом Ома для
переменного тока. Однако нужно помнить,
что эта формула относится только к
амплитудам, но не к мгновенным значениям  и
и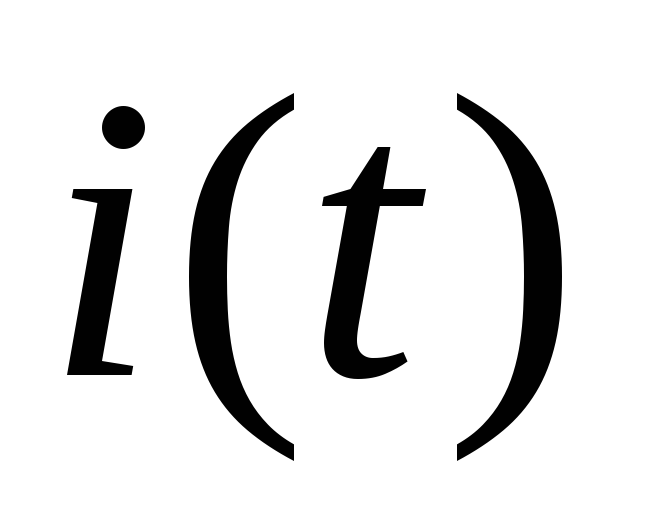 .
Величину
.
Величину

называют сопротивлением цепи для переменного тока, величину
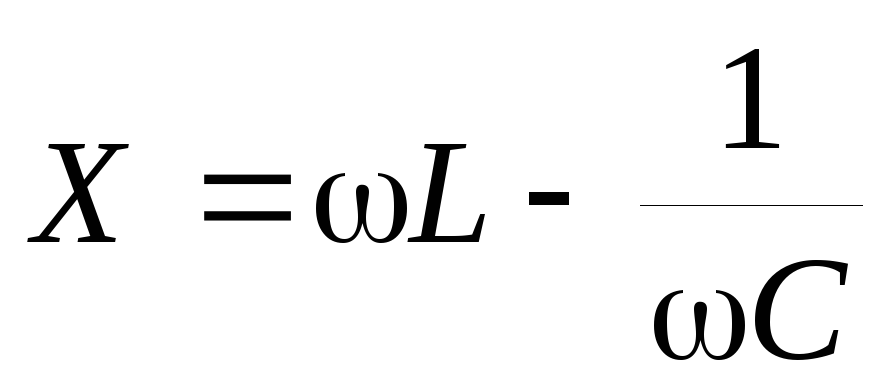
называют реактивным сопротивлением цепи, а величину R — активным сопротивлением.
Полученные
формулы справедливы и для замкнутой
цепи, включающей в себя генератор
переменного напряжения, если под R, C и L понимать их значения для всей цепи
(например R представляет собой суммарное активное
сопротивление цепи, включая и внутреннее
сопротивление генератора). В этом случае
во всех формулах следует заменить u на ЭДС генератора.
Действительно,
для всех наших рассуждений было
безразлично, в каком именно месте
сосредоточены емкость, индуктивность
и сопротивление, поэтому в замкнутой
цепи (рис.8) мы можем считать, что  представляет собой суммарное активное
сопротивление цепи, включая и внутреннее
сопротивление генератора, а
представляет собой суммарное активное
сопротивление цепи, включая и внутреннее
сопротивление генератора, а и
и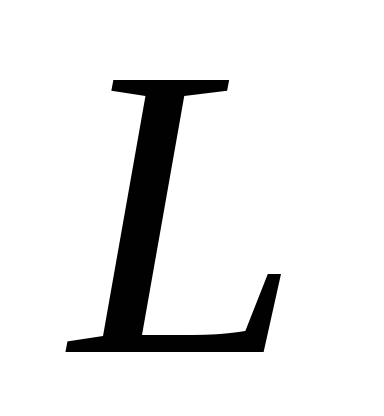 — емкость и индуктивность цепи, и заменить
реальный генератор воображаемым, у
которого внутреннее сопротивление
равно нулю. При этом напряжениеu между точками a и b будет равно ЭДС генератора
— емкость и индуктивность цепи, и заменить
реальный генератор воображаемым, у
которого внутреннее сопротивление
равно нулю. При этом напряжениеu между точками a и b будет равно ЭДС генератора 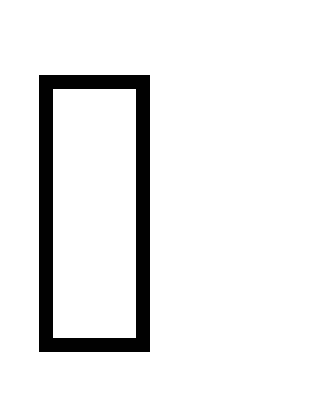 .
Отсюда следует, что формулы (8), (9)
справедливы и для замкнутой цепи
переменного тока, если под
.
Отсюда следует, что формулы (8), (9)
справедливы и для замкнутой цепи
переменного тока, если под ,
, ,
и
,
и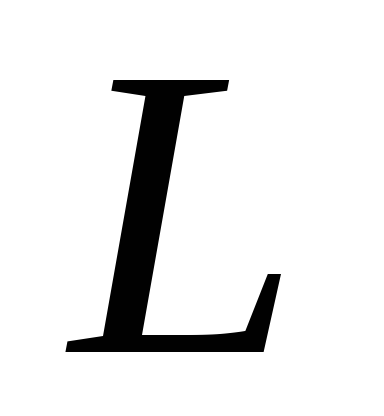 понимать их значения для всей цепи и
заменить во всех формулахu на ЭДС генератора
понимать их значения для всей цепи и
заменить во всех формулахu на ЭДС генератора  .
.
Задачи для схемы с последовательным соединением катушки и конденсатором с решением


Пример решения
Теоретический материал для решения задач.
Задача 14,1
Конденсатор емкостью С = 3,4 мкФ и катушка с активным сопротивлением R = 50 Ом и индуктивностью L = 29,8 мГн подключены последовательно к генератору с напряжением U = 200 В (рис. 14.6).

Определить ток, активную, реактивную и полную мощности катушки, конденсатора и всей цепи при неизменном напряжении генератора и трех значениях частоты: f=fp;
f<fp; f>fр. где fр — резонансная частота.
Решение.
Для примера далее приведен расчет при частоте f = 250 Гц.
Реактивное сопротивление индуктивности





Сделать аналогичный подсчет для f=fp; f<fp; f>fр
Задача решается легко оставляйте свои ответы в комментариях.
Задача 14,2
В сеть переменного тока частотой 50 Гц включены последовательно катушка с активным R = 30 Ом и индуктивным XL = 50 Ом сопротивлениями и конденсатор с емкостью С = 318 мкФ. Напряжение на конденсаторе Uc = 100 В.
Определить ток в цепи, напряжение на катушке и в сети, активную и реактивную мощности цепи. Построить векторную диаграмму.
Оставляем свои ответы в комментариях

 Загрузка …
Загрузка …6.3. Последовательное соединение резистора и катушки индуктивности
6.3.1. Общие сведения
Когда к цепи (рис. 6.3.1) с последовательным соединением резистора и катушки индуктивности подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.

Рис. 6.3.1
Между напряжениями UR, UL иU существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлениемXL катушки. Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 6.3.2).
|
|
Рис. 6.3.2 | Рис. 6.3.3 |
Фазовый сдвиг между током I и напряжением на резистореUR отсутствует, тогда как сдвиг между этим током и падением напряженияULна катушке индуктивности равен 900(ток отстает от напряжения). При этом сдвиг между полным напряжениемUцепи и током определяется соотношением между сопротивлениями XLиR. Разделив все стороны треугольника напряжений на ток, получим треугольник сопротивлений (рис. 6.3.3), в котором Zпредставляет собой так называемое полное сопротивление цепи.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение напряжений на отдельных элементах как в последовательной чисто резистивной цепи, невозможно. Только в векторной форме U = UR +UL. Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника сопротивлений.
Действующее значение полного напряжения цепи
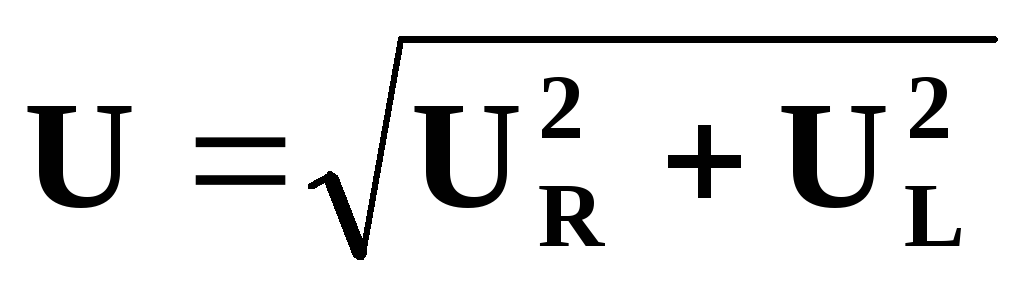
U = Z I
Полное сопротивление цепи
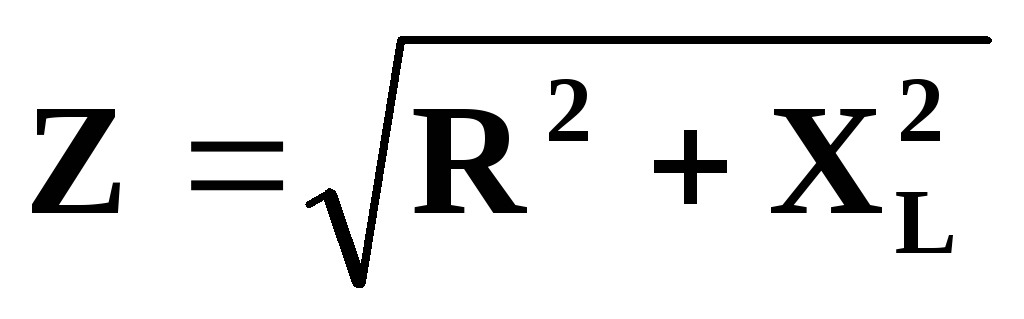 ;
;
Z = U I
Активное сопротивление цепи
R = Z cos
Индуктивное реактивное сопротивление цепи
XL = Z sin
Угол сдвига фаз
= arctg (ХL R)
6.3.2. Экспериментальная часть Задание
Для цепи с последовательным соединением резистора и катушки индуктивности измерьте действующие значения падений напряжения на резисторе URи катушкеULи токI. Вычислите фазовый угол, полное сопротивление цепиZ, индуктивное реактивное сопротивлениеXL и фазовый сдвиг между полным напряжением цепиUи падением напряжения на катушкеUL. Активным сопротивлением катушки ввиду его малой величины можно при этом пренебречь.
Порядок выполнения работы
Соберите цепь согласно схеме (рис. 6.3.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U= 5 В,f= 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
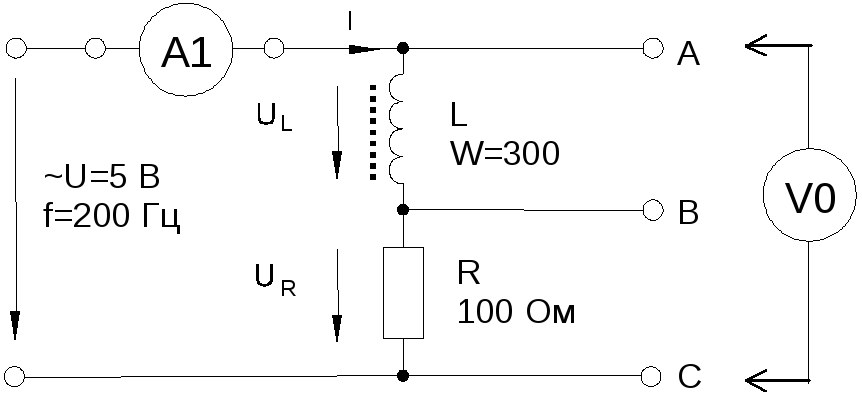
Рис. 6.3.4
Выполните измерения тока и напряжений, указанных в табл. 6.3.1. Если измерения производятся виртуальными приборами, то измерьте также R, , XL, Z.
Таблица 6.3.1.
U,B
UL, B
UC, B
I, мА
, град
R, Ом
XL, Ом
Z, Ом
Примечание
Расчет
Вирт. Изм
Вычислите = arctg (UL R), Z = U I, XL = UL I, занесите результаты вычислений в табл. 6.3.1 и сравните с результатами виртуальных измерений, если они есть.
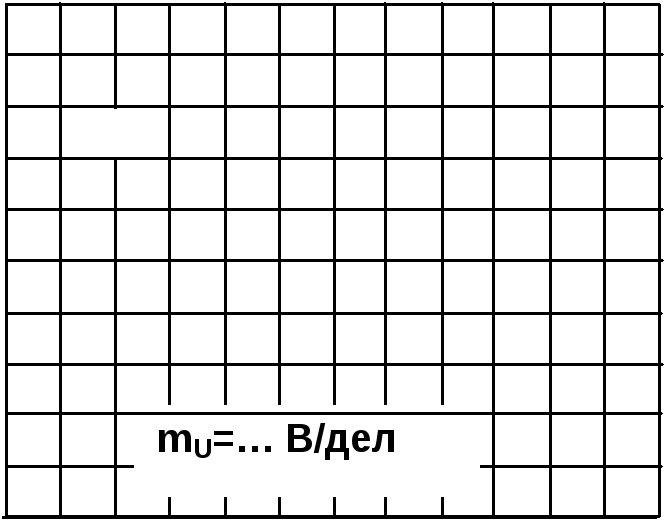
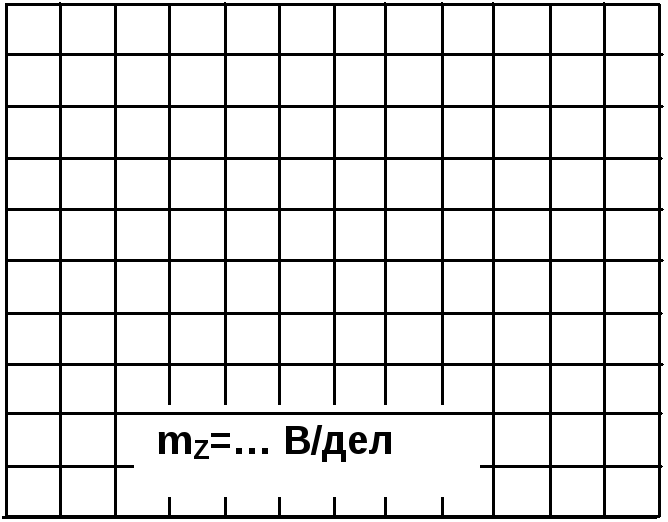
Рис. 6.3.5 Рис. 6.3.6
6.7. Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока
Катушка с активным сопротивлением Rи индуктивностьюLи конденсатор емкостьюСвключены последовательно(рис.7.8). В схеме протекает синусоидальный ток
 .
.
Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа,

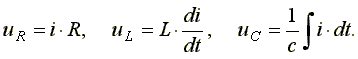 (7.15)
(7.15)
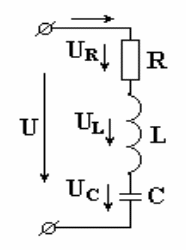
Рис. 7.8
Подставим эти формулы в уравнение (7.15). Получим:
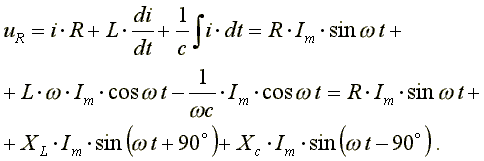 (7.16)
(7.16)
Из выражения (7.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o. Запишем уравнение (7.16) в комплексной форме:
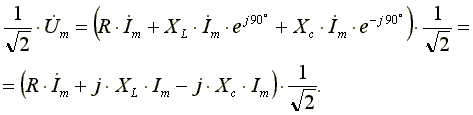 (7.17)
(7.17)
Поделим левую и правую части уравнения (7.17) на √2. Получим уравнение для комплексов действующих значений токов и напряжений
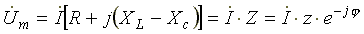 ,
(7.18)
,
(7.18)
Где  — комплексное сопротивление цепи;
— комплексное сопротивление цепи; — модуль комплексного сопротивления,
или полное сопротивление цепи;
— модуль комплексного сопротивления,
или полное сопротивление цепи;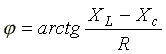 —
начальная фаза комплексного сопротивления.
—
начальная фаза комплексного сопротивления.
При построении векторных диаграмм цепи рассмотрим три случая.
XL> XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока(рис.7.9).
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.7.10).
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.7.11).
Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

Условие возникновения резонанса:
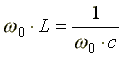 ,
,
отсюда резонансная частота равна
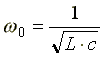 .
.
Из формулы следует, что режима резонанса можно добиться следующими способами:
— изменением частоты;
— изменением индуктивности;
— изменением емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0(а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).
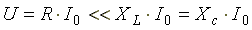 .
.
 Рис. 7.9
Рис. 7.10 Рис. 7.11
Рис. 7.9
Рис. 7.10 Рис. 7.11
7.8. Параллельно соединенные индуктивность, емкость и активное сопротивление в цепи синусоидального тока
К схеме на рис. 7.12 подключено синусоидальное
напряжение 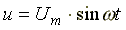 .
Схема состоит из параллельно включенных
индуктивности, емкости и активного
сопротивления.
Определим ток на входе
схемы.
.
Схема состоит из параллельно включенных
индуктивности, емкости и активного
сопротивления.
Определим ток на входе
схемы.
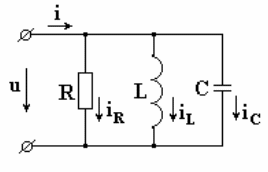
Рис. 7.12
В соответствии с первым законом Кирхгофа:
 ,
(7.19)
,
(7.19)
где 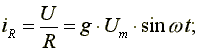
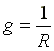 — активная проводимость.
— активная проводимость.
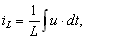
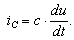
Подставим эти формулы в уравнение (7.19). Получим:
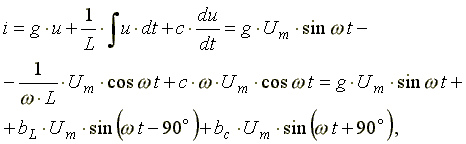 ,
(7.20)
,
(7.20)
Где 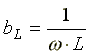 — индуктивная проводимость;
— индуктивная проводимость;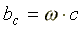 — емкостная проводимость.
— емкостная проводимость.
Из уравнения (7.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90o. Запишем уравнение (6.20) в комплексной форме.
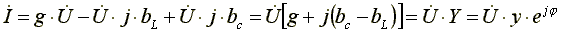 ,
(7.21)
,
(7.21)
где 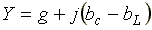 — комплексная проводимость;
— комплексная проводимость;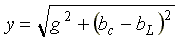 — полная проводимость;
— полная проводимость;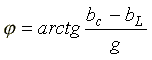 — начальная фаза комплексной
проводимости.
— начальная фаза комплексной
проводимости.
Построим векторные диаграммы, соответствующие комплексному уравнению (7.21).
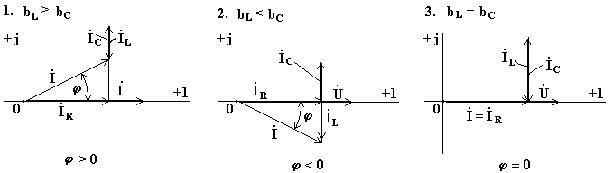 Рис. 7.13
Рис. 7.14 Рис. 7.15
Рис. 7.13
Рис. 7.14 Рис. 7.15
В схеме на рис. 7.12может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. Из условия возникновения резонанса токаполучим формулу для резонансной частоты тока
 .
.
В режиме резонанса тока полная проводимость
цепи  —
минимальна, а полное сопротивление
—
минимальна, а полное сопротивление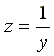 —
максимально. Ток в неразветвленной
части схемы
—
максимально. Ток в неразветвленной
части схемы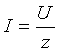 в
резонансном режиме имеет минимальное
значение. В идеализированном случае R
= 0,
в
резонансном режиме имеет минимальное
значение. В идеализированном случае R
= 0,
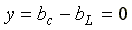 и
и .
.
Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр — пробкой.
Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты.
«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно.
Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным
да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»
Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему.
Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи
равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для
всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.
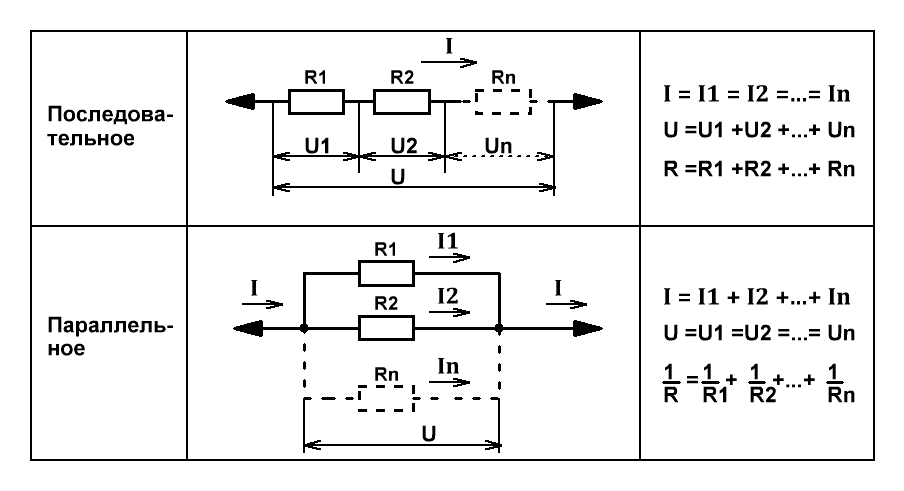
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то
оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном
соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
Короче, все вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение
напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность,
а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную
зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и
параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
С = С1+ С2+….+ Сn и
1/L = 1/L1+ 1/L2 +…+ 1/Ln
для параллельных цепей и
L = L1 + L2 +….+ Ln и
1/С = 1/С1+ 1/С2+…+ 1/Сn для последовательных.
Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов
Ну и в завершении ещё одна таблица.
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.