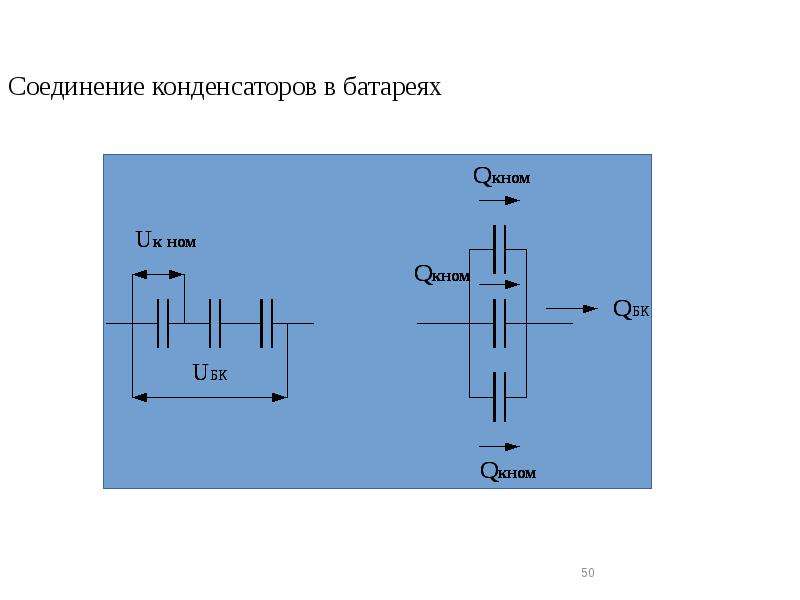
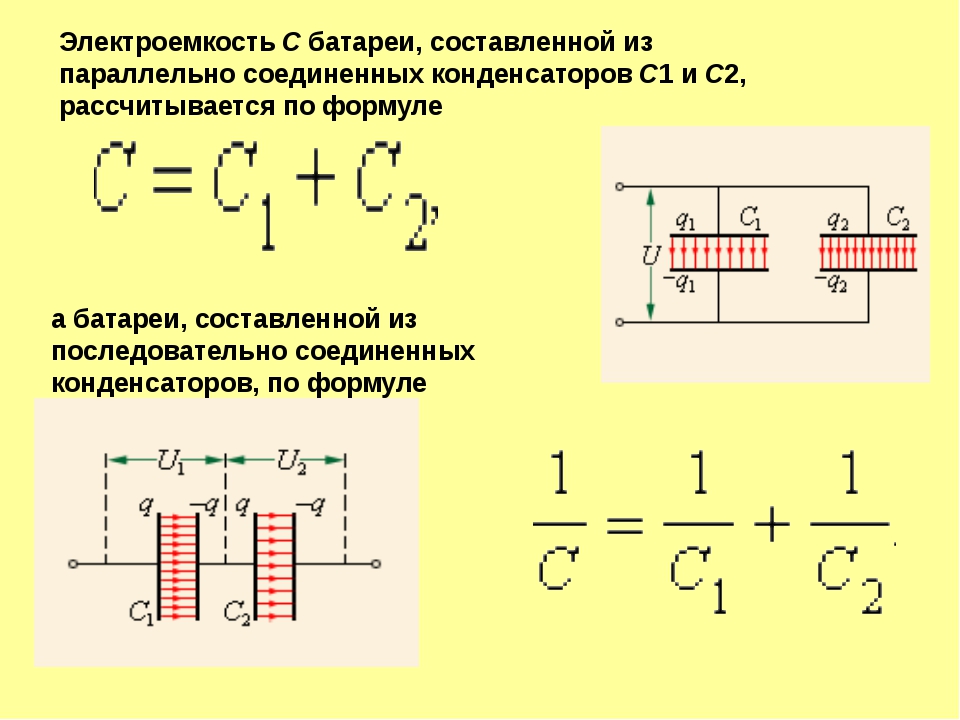
Параллельное и последовательное соединение конденсаторов

В предыдущих статьях были рассмотрены вопросы работы и характеристики конденсаторов. Сейчас Я расскажу о всех методах соединения конденсаторов для подключения в схему. Сразу скажу, что в жизни практически везде, за исключением редких случаев используется только параллельная схема подключения.

Следует знать, что в цепи переменного тока конденсатор выступает еще как емкостное сопротивление. При чем с увеличением величины емкости конденсатора- уменьшается сопротивление в цепи переменного тока.

Параллельное соединение конденсаторов

При параллельной схеме подключения все обкладки конденсаторов соединяются в две группы, причем один вывод с каждого конденсатора соединяется в одну группу с другими, а второй — в другую. Наглядный пример параллельного соединения и схема на картинке.
Все параллельно соединенные конденсаторы подключаются к одному источнику напряжения, поэтому существует на них две точки разности потенциалов или напряжения.

На всех выводах конденсаторов будет абсолютно одинаковое напряжение.

При  подключении параллельно все конденсаторы вместе, образуют принципиально одну емкость, величина которой будет равняться сумме всех емкостей подключенных в цепи конденсаторов.При параллельном подключении через каждый из конденсаторов потечет разный ток, который будет зависеть от величины емкости каждого из них. Чем выше емкость, тем больший ток потечет через неё.

Параллельное соединение очень часто встречается в жизни. С его помощью можно из группы конденсаторов собрать любую необходимую емкость. Например, для запуска 3 фазного электродвигателя в однофазной сети 220 Вольт в результате расчетов Вы получили что необходима рабочая емкость 125 мкФ. Такой емкости конденсаторов Вы не найдете в продаже. Для того, что бы получить необходимую емкость придется купить и соединить параллельно 3 конденсатора один на 100 мкФ, второй- на 20, и третий на 5 мкФ.

Соединение конденсаторов последовательно

При последовательном соединении конденсаторов каждая из обкладок соединяется только в одной точке с одной обкладкой другого кон­денсатора. Получается цепочка конденсаторов. Крайние два вывода подключаются к источнику тока, в результате чего происходит перераспределение между ними электрических зарядов. Заряды на всех промежуточных обкладках одинаковые величине с чередованием по знаку. 

Через все соединенные конденсаторы последовательно протекает одинаковой величины ток, потому что у него нет другого пути прохождения.
Общая же емкость будет ограничиваться площадью обкладок самого маленького по величине, потому что как только зарядится полностью конденсатор с самой маленькой емкостью- вся цепочка перестанет пропускать ток и заряд остальных прервется. Высчитывается же емкость по этой формуле:Но при последовательном соединении увеличивается расстояние (или изоляция) между обкладками до величины равной сумме расстояний между обкладками всех последовательно подключенных конденсаторов. Например, если взять два конденсатора с рабочим напряжением 200 Вольт и соединить последовательно, то изоляция между их обкладками сможет выдержать 1000 Вольт при подключении в схему.

Из выше сказанного можно сделать вывод, что последовательно соединять необходимо:

1. Для получения эквивалентного меньшего по емкости конденсатора.
2. Если необходима емкость, работающая на более высоких напряжениях.
3. Для создания емкостного делителя напряжения, который позволяет получить меньшей величины напряжение из более высокого.

Практически, для получения первого и второго достаточно просто купить один конденсатор с необходимой величиной емкости или рабочим напряжением. Поэтому данный метод соединения в жизни не встречается.

Смешанное соединение конденсаторов

Встречается смешанное соединение только на различных платах. Для него характерно наличие в одной цепи параллельного и последовательного соединения конденсаторов. При чем смешанное соединение может быть как последовательного, так параллельного характера.

В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям, поэтому не буду на этом подробно останавливаться.

Из следующей статьи Вы узнаете как правильно проверить и определить емкость конденсатора.

Параллельное включение конденсаторов | Техника и Программы

Иногда рекомендуют параллельное соединение конденсаторов в фильтрах. Причем предлагают следующие варианты:

а)         параллельно конденсатору большой емкости включать точно такой же конденсатор, но маленькой емкости;

б)         вместо одного конденсатора большой емкости включать два-три конденсатора меньшей емкости того же типа;

в)         вместо одного конденсатора большой емкости включать много конденсаторов небольшой емкости.

Естественно, включать надо параллельно, при этом емкости суммируются, и общая емкость во всех этих случаях получается одинаковой. Давайте разберемся в данном вопросе (вся необходимая информация есть в таблице 1 и рис. 47).

Вариант а). Говорят, что маленький конденсатор будет помогать работать большому.

Это не всегда так.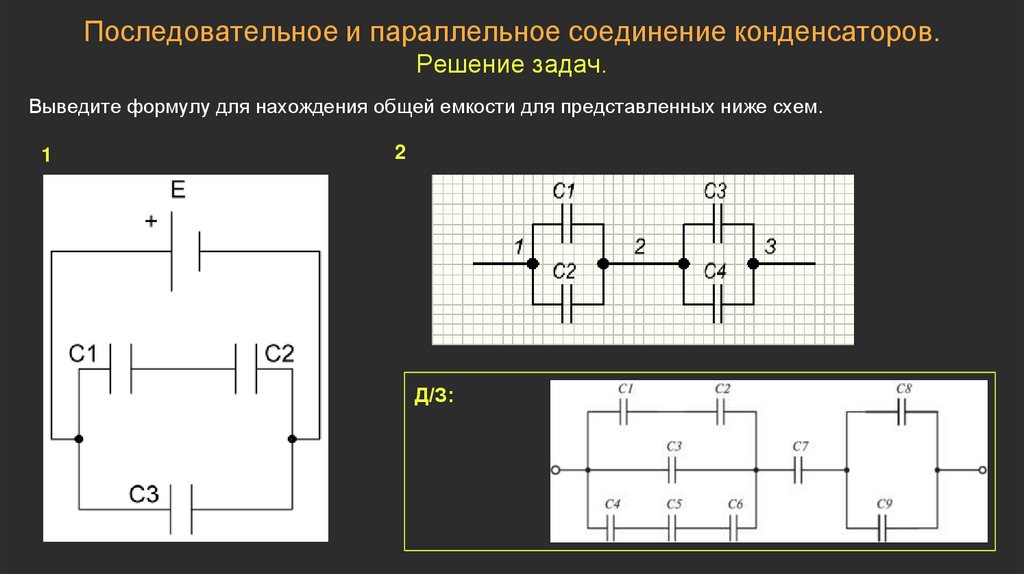 У конденсатора меньшей емкости действительно паразитная индуктивность обычно меньше, поэтому частотные свойства зачастую могут быть лучше (а если у конденсатора малой емкости частотные свойства не лучше, то и говорить не о чем). Рассмотрим эту ситуацию. На рис. 48 показана зависимость модуля полного сопротивления конденсаторов разной емкости от частоты.

Максимальной рабочей частотой конденсатора можно считать ту частоту, на которой его сопротивление минимально. Дальше с ростом частоты полное сопротивление конденсатора начинает расти – это сказывается индуктивность конструкции конденсатора. При этом индуктивное сопротивление перевешивает емкостное, и конденсатор ведет себя как катушка индуктивности. То есть уже и не является конденсатором.

Для конденсатора малой емкости минимум сопротивления действительно наступает на большей частоте, но его сопротивление все равно больше, чем у конденсатора большой емкости (свойства которого на этой частоте уже ухудшаются). А ведь главная задача конденсатора на этих частотах – пропускать через себя ток нагрузки, как можно меньше на него влияя.

Поэтому чем у конденсатора сопротивление меньше, тем лучше. И конденсатор малой емкости не очень-то и поможет «большому» конденсатору, слишком уж велико его сопротивление. Только в точке А сопротивления обоих конденсаторов становятся равными, и на более высокой частоте у конденсатора малой емкости сопротивление меньше, чем у «большого». Но посмотрите – в этой точке уже и конденсатор малой емкости работает плохо! В реальности эти графики показаны на рис. 47, где цифрами 1…5 обозначены конденсаторы меньшей емкости, а цифрами 8… 12 – конденсаторы большей емкости.

А вот если в системе присутствует керамический или пленочный конденсатор, то он хорошо работает и на этой частоте, и на более высоких частотах (рис. 48). Только емкость его должна быть достаточно большой,

чтобы на нужных частотах он имел низкое сопротивление.

Вывод: параллельное подключение электролитического конденсатора малой емкости заметной пользы не принесет (хоть и не навредит), гораздо выгоднее шунтирование электролита большой емкости хорошим пленочным конденсатором, который наверняка гораздо более высокочастотный.

Напрашивается вопрос: а для чего же так делают? И даже в промышленной аппаратуре? Ну, во-первых, иногда действительно можно подобрать условия, когда «маленький» конденсатор немного поможет. А главное

–               почему бы не поставить такой конденсатор, раз в него верят покупатели? Тем более что он очень дешевый.

Вариант б). Вместо одного конденсатора большой емкости включаем два конденсатора меньшей емкости того же типа. Рассмотрим эту ситуацию для конденсаторов, приведенных в двух последних строках таблицы 1. Допустим, мы ставим два конденсатора 4700 мкФ вместо одного 10000 мкФ. Тогда их сопротивление будет 0,071/2 = 0,0355 Ом, а допустимый ток 3-2=6 ампер. Получается, по ESR примерно то же самое, а по току так даже лучше, чем одиночный конденсатор. Только надо помнить, что у конденсаторов довольно большой разброс, так что можно вместо одного хорошего поставить два плохих. Или наоборот. Более длинные провода, соединяющие два конденсатора, будут иметь большее сопротивление, чем у одиночного.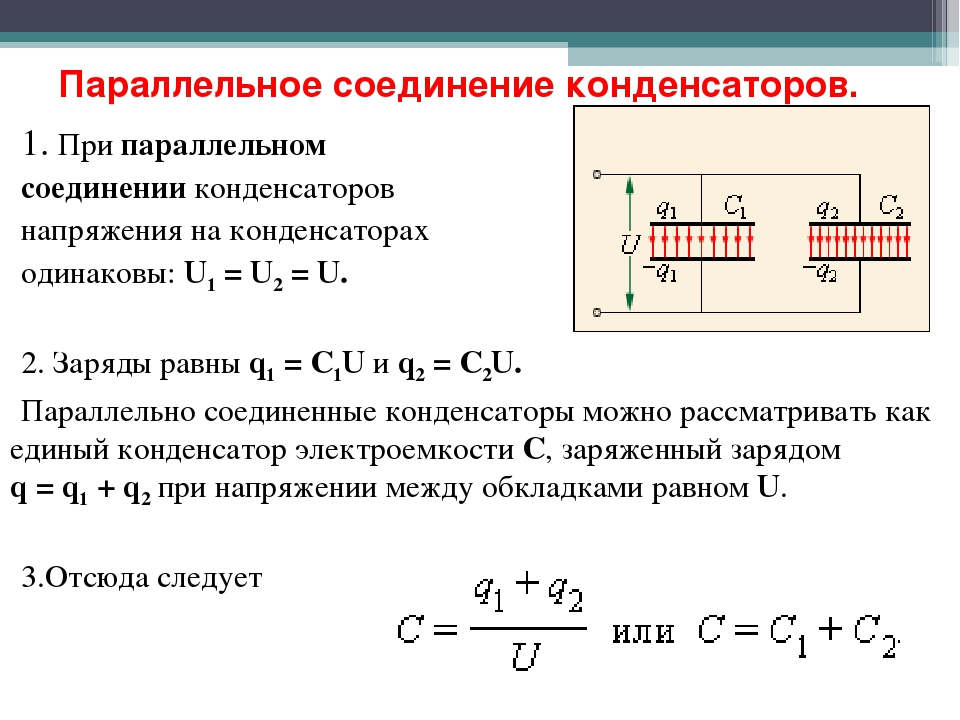

Да и токи заряда конденсаторов будут немного неодинаковыми. В результате это небольшое преимущество от удвоения конденсаторов, скорее всего, будет «съедено» неидеальностью остальных элементов схемы.

Так что в данном случае можно считать эти варианты выбора конденсаторов равноценными. И выбирать тот или иной вариант из каких-либо других соображений. Например, какие конденсаторы поместятся в ваш корпус. Или какие конденсаторы продаются в вашем городе.

Вариант в). Ставим 10 конденсаторов 1000 мкФ вместо одного на 10000 мкФ. Что говорит математика: ESR = 0,199/10 = 0,0199 Ом (по сравнению с 0,033 Ом для конденсатора 10000 мкФ), максимальный ток = 10-1,4= 14А (по сравнению с 5 А конденсатора 10000 мкФ). Вроде бы выигрыш по сопротивлению в 1,5 раза, а по току почти в 3 раза. Судя по полученным цифрам, много конденсаторов лучше, чем один.

Слышали когда-нибудь, как ругают теоретиков, говоря, что на практике получается все совсем не так, как у них в теории? Это про таких горе-теоретиков, которые просто умножат-разделят числа, и не подумают об остальных факторах, влияющих на ситуацию. Посмотрите на рис. 49. Индуктивности и резисторы – это сопротивление и индуктивность проводников, соединяющих всю эту кучу конденсаторов. Поскольку конденсаторов теперь много, то длина проводов существенно увеличивается, растут и индуктивности-сопротивления. Вот тут-то и теряются все преимущества, которые мы насчитали по формулам! Нет, формулы правильные! Только они не учитывают эти вот элементы – ведь мы написали эти формулы без их учета, не подумав про них.

В результате общее сопротивление может получиться даже больше, чем у одиночного конденсатора боль-

шой емкости, а ток распределяется очень неравномерно. Например, при заряде конденсаторов, заряд начинается с самого левого по схеме С1, и в него в самый первый момент времени течет весь максимальный ток (в С2 ток потечет только после того, как С1 уже немного зарядится), а конденсатор-то рассчитан всего на 1,4 ампера! Поэтому может случиться, что этот конденсатор будет перегружаться зарядным током, а значит, долго не проживет. Точно также, разряжается первым самый правый конденсатор СЮ, и он будет перегружаться разрядным током.

В общем, все преимущества обычно получаются только на бумаге. Это как раз та ситуация, когда «слишком хорошо – тоже не хорошо». Все всегда должно быть в разумных пределах, а здесь мы из них вышли. Собственно, «много маленьких» конденсаторов не всегда будет хуже, чем «один большой», но далеко и не всегда будет лучше. Хороший профессионал сможет извлечь пользу из такого включения (когда оно оправданно), а новичок скорее всего все испортит.

На самом деле, есть случай, когда параллельное включение двух-трех конденсаторов принесет пользу. Например, когда конденсатор фильтра установлен возле горячего диода и не удается его отодвинуть. Тогда при нескольких конденсаторов греться будет только один из них.

Или если у вас имеются конденсаторы LowESR, или Lowlmpedance, но их емкости недостаточно. Тогда вы ставите этот хороший конденсатор параллельно с «обыкновенным» и полностью используете его преимущества.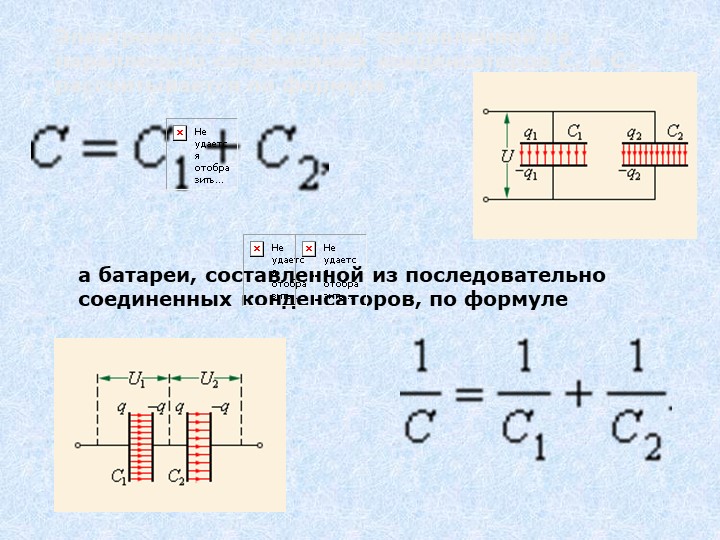 Все равно ведь низкое-сопротивление получается на достаточно больших частотах, а там конденсатор даже не очень большой емкости хорошо сработает и принесет пользу. Я так сделал в одном своем блоке питания – поставил обычный конденсатор 10000 мкФ и параллельно ему низкоимедансный 4700 мкФ (интересно, что они оказались одинаковые по размерам). В результате получились хорошими и суммарная емкость, и высокочастотные свойства, и сопротивление. Лучше всего устанавливать высокочастотные и низкоимпе- дансные конденсаторы прямо на плате усилителя, где сведены к минимуму все паразитные индуктивности и сопротивления.

И еще. При любом наборе электролитов, подключение пленочного конденсатора только приветствуется.

Источник: Рогов И.Е. Конструирование источников питания звуковых усилителей. – Москва: Инфра- Инженерия, 2011. – 160 с.

Параллельное соединение конденсаторов | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

В условиях массового применения кон­денсаторов невозможно организовать изготов­ление конденсаторов всех возможных зна­чений электроемкости и рабочей разности потенциалов на обкладках. Для получения необходимых параметров стандартные кон­денсаторы определенным образом соединя­ют между собой. На практике применяют параллельное, последовательное и смешан­ное соединение конденсаторов.

Рис. 4.76. Параллельное соединение кон­денсаторов

При параллельном соединении конден­саторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рис. 4.76 изображена схема такого соеди­нения. Каждая группа обкладок имеет оди­наковый потенциал.

Если полученную батарею параллельных конденсаторов зарядить, то между обклад­ками каждого конденсатора будут одина­ковые разности потенциалов

Δφ₁ = Δφ₂ = Δφ₃ = … = Δφ_n.

Общий заряд на пластинах будет равен сумме зарядов каждого конденсатора:

Q = Q₁ + Q₂ + Q₃ + … + Q_n.

Учитывая, что Q = CΔφ, получим

CΔφ = C₁Δφ + C₂Δφ + C₃Δφ + … + C_nΔφ,

или

C = C₁ + C₂ + C₃ + …+ C_n.

Электроемкость батареи параллельно со­единенных конденсаторов равна сумме элект­роемкостей всех конденсаторов.

Рис. 4.78. Строение и схема плоского конденсатора с несколькими пластина­ми

Если батарея состоит из n конденсаторов емкостью Q каждый, то емкость батареи

C = nC₀.

Увеличение емкости при параллельном соединении конденсаторов можно объяс­нить также тем, что при этом увеличивается площадь пластин, которые имеют одина­ковые потенциалы.

Емкость конденсаторов можно увеличить путем их параллельно­го соединения. Материал с сайта http://worldofschool.ru

Примером параллельного соединения кон­денсаторов является плоский конденсатор, имеющий n пластин, разделенных диэлект­риком (рис. 4.78). Пластины этого конден­сатора через одну соединены между собой. Но количество этих конденсаторов всегда на один меньше, чем пластин. Из рис. 4.78, а видно, что шесть пластин образуют пять кон­денсаторов, соединенных параллельно (рис. 4.78, б). Каждая внутренняя пластина яв­ляется одновременно обкладкой двух кон­денсаторов. Поэтому при вычислении элект­роемкости плоского сложного конденсатора пользуются формулами:

C = (n — 1)C₀,

C = (εε₀S / d) • (n — 1).

где C — общая электроемкость; Q — элект­роемкость конденсатора из двух пластин; n — общее количество пластин.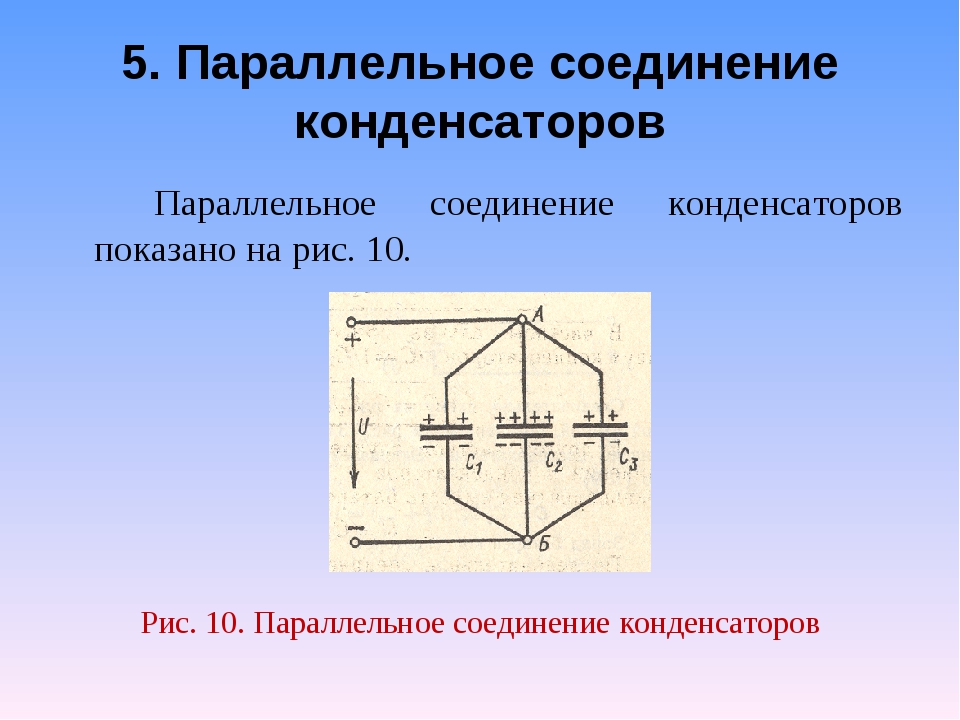

На этой странице материал по темам:

• Чего достигают соединенияя конденсаторы паралельно? посдедоватильно?

• Физика параллельное соединение катушки и конденсатора лабораторная работа

• Сообщение по физике применение конденсатора

• Последовательное и параллельное соединение конденсаторов реферат

• Физика -параллельное соединение нескольких конденсаторов

Вопросы по этому материалу:

• С какой целью конденсаторы объединяют в батареи?

• Чего достигают, соединяя конденсаторы параллельно?

• Чему равна общая электроемкость соединенных параллельно кон­денсаторов?

• Как рассчитать емкость плоского конденсатора из многих пластин?

Зачем нужен конденсатор на электромоторчике? И что будет если его удалить

Если вы когда-нибудь разбирали детскую машинку и вынимали из нее небольшие моторчики, то могли заметить, что на каждом из них напаян небольшой конденсатор к выводам питания.
Если его отпаять и проверить работу мотора, то практически ничего не изменится. Так зачем он нужен?
Конденсаторы емкостью 0,1-0,01 мкФ обычно припаиваются параллельно выводам коллекторных электродвигателей.

Проверим на опыте

Давайте возьмем двигатель и отпаяем конденсатор. Возьмем вольтметр и подключим параллельно выводам мотора. Для питания будем использовать две пальчиковые батарейки включенные последовательно, общим напряжением 3 В.

При включении и отключении мотора от питания появляются импульсы высокого напряжение до 1000 В

Это нормально, ЭДС самоиндукции еще никто не отменял. Причем с конденсатором таких скачков не наблюдалось.
Такие импульсы называю еще обратным током, они обычно губительный для любой цепи где есть электроника. Это первое для чего устанавливают этот конденсатор.

Изменения в работе

Теперь давайте подключим каждый двигатель по отдельности и послушаем на слух их работу.


Изменения конечно не очевидные, но мотор без конденсатора работает с дребезгами и более не устойчиво. Это второе зачем ставят конденсатор: искрогашение, благодаря чему увеличивается ресурс щеток и двигателя в целом.
И наконец третье, для чего используют конденсатор, это помехозащищенность. Если во время работы моторчика без конденсатора включить любой радиоприемник, то в нем будут отчетливо слышны помехи издаваемые коллектором двигателя.

Итог: зачем нужен электродвигателю нужен конденсатор?

У коллекторного мотора во время работы происходи постоянная коммутация обмоток якоря. Использование конденсатора в цепи питания мотора решает следующие проблемы:

• Первое — это искрогашение на щетках коллектора.
  
• Второе — помехозащита.
  
• Третье — защита питающей цепи от обратного тока.

Смотрите видео

B14: Последовательные и параллельные конденсаторы

Метод все более простых схем, который мы использовали для схем с более чем одним резистором, также можно использовать для схем, содержащих более одного конденсатора. Идея состоит в том, чтобы заменить элемент комбинированной схемы, состоящий из более чем одного конденсатора, на один эквивалентный конденсатор. Эквивалентный конденсатор должен быть эквивалентным в том смысле, что при том же потенциале на нем он будет иметь такой же заряд, как и элемент комбинированной схемы.

Конденсаторы серии

Начнем со случая, когда элемент комбинированной схемы состоит из двух конденсаторов, последовательно соединенных друг с другом:

Мы рассматриваем два конденсатора как двухконтактный комбинированный элемент схемы:

Напряжение на элементе комбинированной схемы явно является напряжением ЭДС V, поскольку как для места расположения ЭДС, так и для элемента комбинированной схемы мы говорим о разности потенциалов между одними и теми же двумя проводниками:

Напряжение на каждом отдельном конденсаторе, однако, неизвестно.

Но подумайте вот о чем: после того, как последний провод подключен к цепи, процесс зарядки (который практически не занимает времени) можно понять следующим образом (где для простоты понимания мы описываем вещи, которые происходят одновременно, как если бы они произошли последовательно):

Гнездо ЭДС вытягивает некоторый положительный заряд с нижней пластины нижнего конденсатора и толкает его на верхнюю пластину верхнего конденсатора.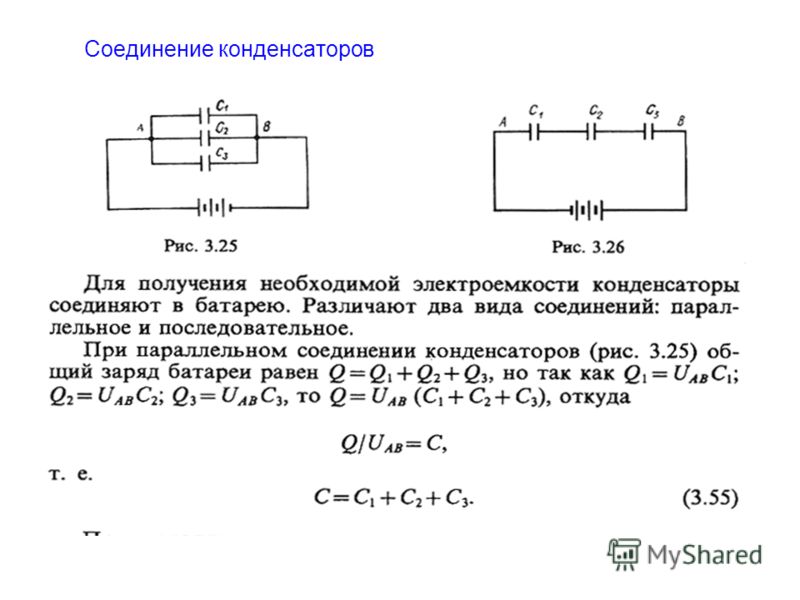

Ключевым моментом в этом движении заряда является то, что количество положительного заряда на верхней пластине верхнего конденсатора в точности равно количеству отрицательного заряда на нижней пластине нижнего конденсатора (потому что именно отсюда происходит положительный заряд. !)

Теперь положительный заряд на верхней пластине верхнего конденсатора отталкивает положительный заряд (помните, каждый нейтральный объект состоит из огромного количества зарядов обоих типов, и, согласно нашему соглашению о носителях положительного заряда, положительные заряды свободны. перемещаться) на нижней пластине верхнего конденсатора, и этот заряд имеет проводящий путь к верхней пластине нижнего конденсатора, к которому он (положительный заряд) притягивается отрицательным зарядом на нижней пластине нижнего конденсатора.

Конечный результат — оба конденсатора имеют одинаковый заряд \ (q \):

, что, в свою очередь, заставляет конденсатор \ (C_1 \) иметь напряжение \ (V_1 = \ frac {q} {C_1} \), а конденсатор \ (C_2 \) иметь напряжение \ (V_2 = \ frac {q} {C_2} \).

По правилу цикла,

КВЛ 1

\ [V-V_1-V_2 = 0 \]

\ [V = V_1 + V_2 \]

\ [V = \ frac {q} {C_1} + \ frac {q} {C_2} \]

\ [V = q (\ frac {1} {C_1} + \ frac {1} {C_2}) \]

\ [q = \ frac {1} {\ frac {1} {C_1} + \ frac {1} {C_2}} V \]

Итак, мы говорим, что когда вы прикладываете напряжение \ (V \) к двухконтактному элементу схемы

количество заряда \ (q = \ frac {1} {\ frac {1} {C_1} + \ frac {1} {C_2}} V \) перемещается с нижнего вывода элемента комбинированной схемы вокруг цепи к верхнему выводу.Затем заряд перестает двигаться. Напомним, что мы определили емкость конденсатора как отношение \ (\ frac {q} {V} \) заряда конденсатора к соответствующему напряжению на конденсаторе. \ (\ frac {q} {V} \) для нашего двухконтактного комбинированного элемента схемы, таким образом, является эквивалентной емкостью двухконтактного элемента схемы. Решение \ (q = \ frac {1} {\ frac {1} {C_1} + \ frac {1} {C_2}} V \) для отношения \ (\ frac {q} {V} \) дает \ ( \ frac {q} {V} = \ frac {1} {\ frac {1} {C_1} + \ frac {1} {C_2}} \), поэтому наша эквивалентная емкость для двух последовательно соединенных конденсаторов равна \ (C_s = \ frac {1} {\ frac {1} {C_1} + \ frac {1} {C_2}} \)

Посредством логической индукции мы можем расширить этот аргумент, чтобы охватить любое количество конденсаторов, последовательно соединенных друг с другом, получив:

\ [C_s = \ frac {1} {\ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +. ..} \ label {14-1} \]

Что касается упрощения запоминания, то просто плохо, как иногда все складывается. Это выражение математически идентично выражению для резисторов , включенных параллельно. Но это выражение относится к конденсаторам , включенным последовательно.

Конденсаторы параллельно

Предположим, мы подаем напряжение \ (В \) на элемент комбинированной схемы, состоящий из пары конденсаторов, включенных параллельно друг другу:

Из диаграммы видно, что напряжение на каждом конденсаторе — это просто ЭДС \ (В \), поскольку напряжение на каждом компоненте в цепи представляет собой разность потенциалов между теми же двумя проводниками.

Итак, что происходит (почти мгновенно), когда мы устанавливаем это последнее соединение? Ответ: Заряд ЭДС снимает заряд с нижних пластин двух конденсаторов и проталкивает его на верхние пластины до тех пор, пока заряд на \ (C_1 \) не станет \ (q_1 = C_1V \), а заряд на \ (C_2 \) не станет равным.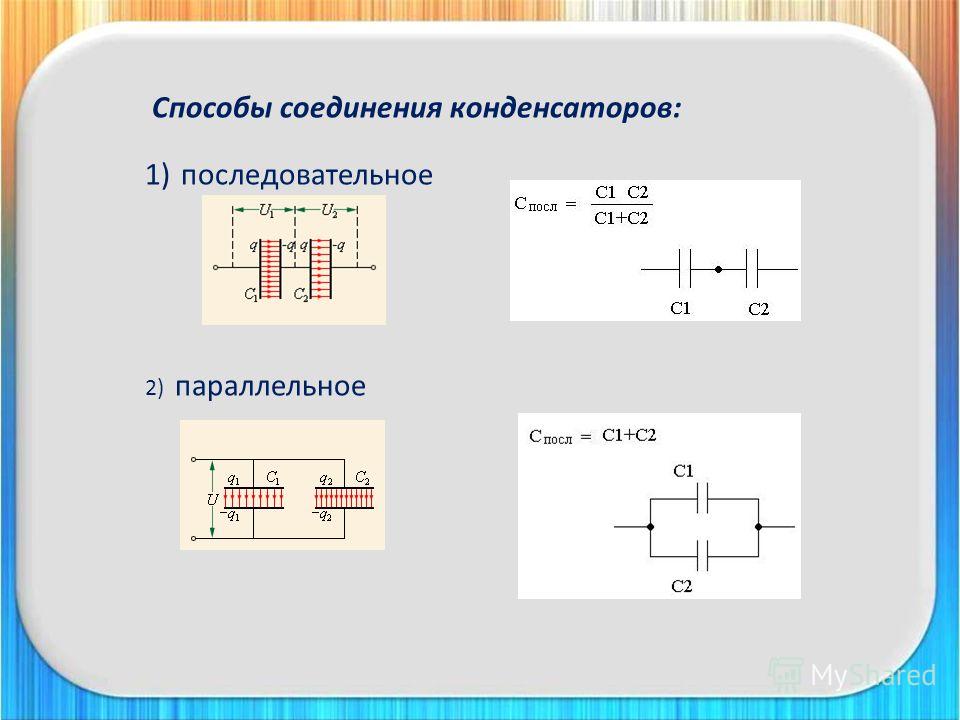 \ (q_2 = C_2V \).

Для этого кресло EMF должно переместиться на общую сумму

\ [q = q_1 + q_2 \]

\ [q = C_1V + C_2V \]

\ [q = (C_1 + C_2) V \]

Решение последнего уравнения \ (q = (C_1 + C_2) V \) для эквивалентной емкости \ (C_P \), определенной как \ (q / V \), дает:

\ [\ frac {q} {V} = C_1 + C_2 \]

\ [C_p = C_1 + C_2 \]

Другими словами:

Таким образом, эквивалентная емкость конденсаторов, подключенных параллельно, является просто суммой отдельных емкостей.(Таким образом комбинируются последовательно соединенные резисторы и ). С помощью индуктивных соображений результат можно распространить на любое количество конденсаторов, получив:

\ [C_P = C_1 + C_2 + C_3 + … \ label {14-2} \]

Заключительные замечания

Тот факт, что напряжение одинаково для конденсаторов, подключенных параллельно, и заряд одинаков для конденсаторов, подключенных последовательно, важны, но если вы посмотрите на это как на еще две вещи, которые вы должны сохранить в памяти, то вы не собираетесь этого делать. правильное изучение физики.Вы должны быть в состоянии «видеть», что заряд последовательно соединенных конденсаторов должен быть одинаковым, потому что заряд одного конденсатора исходит от его (изначально нейтрального) соседа. Вы должны быть в состоянии «видеть», что напряжение на конденсаторах, подключенных параллельно, должно быть одинаковым, потому что для каждого конденсатора напряжение — это разность потенциалов между двумя одинаковыми проводниками.

Авторы и авторство

Серия

и параллельные конденсаторы — стенограмма видео и урока

Параллельные конденсаторы

Если два или более конденсатора соединяются параллельно, каждый конденсатор независимо подключается к одному и тому же источнику напряжения, которым часто является батарея.Это означает, что каждый конденсатор имеет одинаковое напряжение на пластинах.

Параллельные конденсаторы: каждый конденсатор независимо подключается к батарее, поэтому каждый конденсатор имеет одинаковое напряжение на своих пластинах.

Основываясь на конфигурации конденсаторов, вы можете рассчитать эквивалентную емкость для всей цепи. Поскольку мы знаем, что каждый конденсатор имеет одинаковое напряжение на пластинах, мы можем рассчитать эквивалентную емкость по формуле, которую вы сейчас видите на экране:

Эквивалентная емкость конденсаторов, включенных параллельно (Ceq), равна C1 + C2 + C3, и так далее, пока вы не просуммируете все переменные.Это означает, что эквивалентная емкость любого количества конденсаторов, подключенных параллельно, является просто суммой всех индивидуальных емкостей. Эквивалентная емкость больше, чем емкость любого из отдельных конденсаторов.

Если бы у вас была цепь с двумя параллельно включенными конденсаторами, один с емкостью 12 Ф, а другой с емкостью 8 Ф, какова емкость одного конденсатора, который можно было бы использовать для замены обоих?

Чтобы ответить на этот вопрос, вам необходимо рассчитать эквивалентное сопротивление цепи, которое вы можете увидеть на своем экране прямо сейчас:

Как видите, после выполнения переменных по формуле эквивалентная емкость составляет 20 F.

Конденсаторы в серии

Помимо параллельного соединения, конденсаторы также могут быть соединены последовательно в электрическую цепь. Если два конденсатора подключены последовательно друг к другу, они находятся в одной ветви цепи. Поскольку они не подключены к источнику напряжения независимо, каждый конденсатор может иметь разное напряжение на пластинах. Однако, поскольку все они подключены напрямую друг к другу, каждый последовательно включенный конденсатор будет накапливать одинаковое количество заряда.

Последовательные конденсаторы: каждый конденсатор подключается к следующему в той же ветви схемы, поэтому каждый конденсатор сохраняет одинаковое количество заряда.

Еще раз, мы можем рассчитать эквивалентную емкость группы конденсаторов, включенных последовательно, используя определение емкости, которое вы можете видеть на своем экране прямо сейчас:

Таким образом, эквивалентная емкость конденсаторов, включенных последовательно, равна 1 / C1 + 1 / C2 + 1 / C3. Следовательно, эквивалентная емкость нескольких конденсаторов, соединенных последовательно, меньше емкости любого отдельного конденсатора.

Давайте рассмотрим конкретный пример, чтобы увидеть, как это работает. Какова эквивалентная емкость цепи, содержащей три последовательно соединенных конденсатора с емкостями 10 Ф, 5 Ф и 2 Ф?

Как мы и ожидали (и теперь вы можете видеть на экране), эквивалентное сопротивление (1,25 Ф) меньше, чем емкость любого из отдельных конденсаторов.

Последовательные и параллельные конденсаторы

Что произойдет, если у вас будет более сложная схема, в которой одни конденсаторы подключены последовательно, а другие — параллельно? В этом случае вам нужно разбить схему на несколько частей. Объедините все конденсаторы, которые включены последовательно, и любые, которые включены параллельно. Затем перерисуйте схему и повторяйте этот процесс, пока не получите только одно окончательное эквивалентное сопротивление.

Рассмотрим пример. Какая эквивалентная емкость цепи, показанной сейчас на вашем экране?

Сначала найдите эквивалентную емкость двух последовательно соединенных конденсаторов (12 Ф и 6 Ф):

Теперь у вас есть цепь с двумя конденсаторами, включенными параллельно.Вы можете сложить емкости этих двух вместе, чтобы получить эквивалентную емкость всей цепи.

Эквивалентная емкость всей этой схемы составляет 12 F.

Краткое содержание урока

Конденсатор — это электрическое устройство, которое используется в схемах для хранения заряда и электрической энергии. Емкость конденсатора определяется как его способность накапливать заряд, а емкость рассчитывается как отношение величины накопленного заряда к приложенному напряжению:

Когда конденсаторы включены в цепь параллельно, каждый конденсатор имеет одинаковое напряжение на своих пластинах.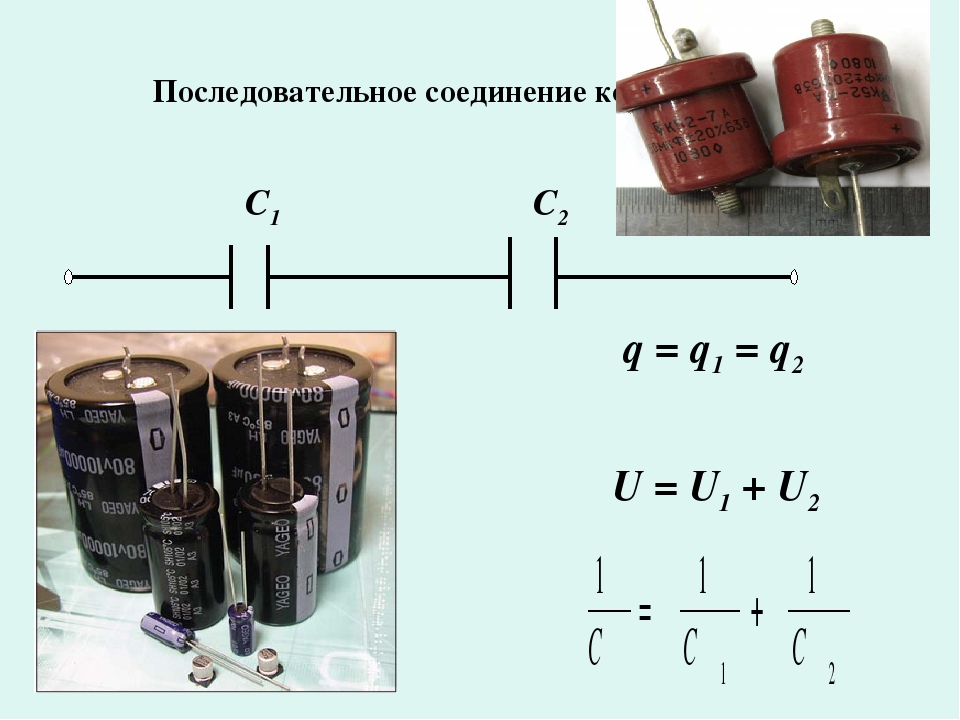 Когда конденсаторы соединены последовательно, каждый конденсатор сохраняет одинаковое количество заряда.

Эквивалентная емкость цепи — это емкость одного конденсатора, который может заменить все остальные конденсаторы в цепи. На экране вы увидите, что формула для конденсаторов, подключенных параллельно, выглядит следующим образом. Также на экране вы можете видеть, что формула для конденсаторов, соединенных последовательно, выглядит следующим образом:

Конденсаторы серии

и параллельные конденсаторы серии

и конденсаторы параллельной работы

Последовательные и параллельные конденсаторы

Конденсатор — это устройство для хранения разделенного заряда и поэтому накапливается электростатическая потенциальная энергия.Цепи часто содержат более одного конденсатора.

Рассмотрим два конденсатора в параллельно , как показано справа

Когда батарея подключена, электроны будут течь до тех пор, пока потенциал точка A совпадает с потенциалом положительной клеммы аккумулятора и потенциал точки B равен потенциалу отрицательной клеммы аккумулятор. Таким образом, разность потенциалов между пластинами обоих конденсаторов равна V _A — V _B = V _bat .Имеем C ₁ = Q ₁ / V _bat и C ₂ = Q ₂ / V _bat , где Q ₁ — заряд конденсатора C ₁ , а Q ₂ — заряд конденсатора С ₂ . Пусть C — эквивалентная емкость двух конденсаторов в параллельно, то есть C = Q / V _bat , где Q = Q ₁ + Q ₂ . Тогда C = (Q ₁ + Q ₂ ) / V _bat = C ₁ + C ₂ .

Для конденсаторов, включенных параллельно, емкости складываются.

Для более двух конденсаторов имеем

C = C ₁ + C ₂ + C ₃ + C ₄ + ….

---

Рассмотрим два конденсатора серии , как показано справа.

Пусть Q представляет собой общий заряд на верхней пластине C ₁ , который затем индуцирует заряд -Q на своей нижней пластине.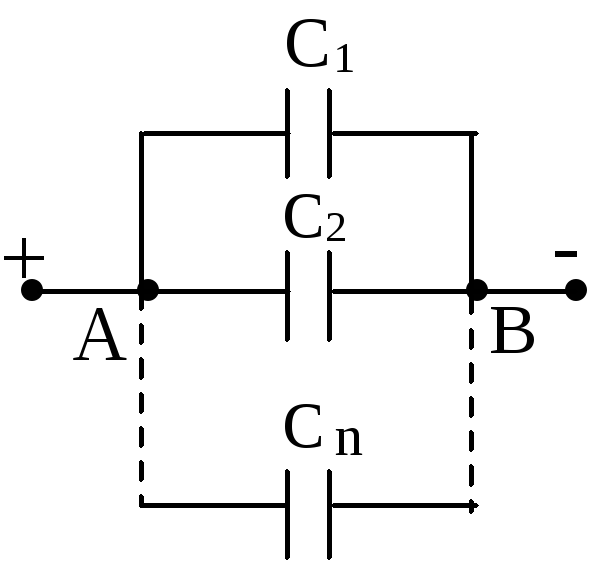 Заряд на нижняя пластина C ₂ будет -Q, что, в свою очередь, вызывает заряд + Q на верхней пластине, как показано.
Пусть V ₁ и V ₂ представляют разности потенциалов между обкладками конденсаторов С ₁ и С ₂ соответственно. потом V ₁ + V ₂ = V _bat , или (Q / C ₁ ) + (Q / C ₂ ) = Q / C или (1 / C ₁ ) + (1 / C ₂ ) = 1 / C. Более двух конденсаторы последовательно имеем

1 / C = 1 / C ₁ + 1 / C ₂ + 1 / C ₃ + 1 / C ₄ +….

, где C — эквивалентная емкость двух конденсаторов.

Для конденсаторов, соединенных последовательно, величина, обратная их эквивалентная емкость равна сумме обратных величин их индивидуальных емкости.

Проблема:

Какую общую емкость можно получить, подключив 5 мкФ и 8 мкФ конденсатор вместе?

Решение:

• Рассуждение:
  Мы можем подключать конденсаторы последовательно или параллельно.
  Чтобы получить наибольшую емкость, мы необходимо подключить конденсаторы параллельно.
  Чтобы получить наименьшую емкость, мы должны подключить конденсаторы последовательно.
• Детали расчета:
  Параллельное подключение конденсаторов:
  C _{наибольший} = (5 + 8) мкФ = 13 мкФ.
  Последовательное соединение конденсаторов.
  1 / C _{наименьшее} = (1/5 + 1/8) (мкФ) ^-1 = 13 / (40 мкФ) = 0,325 / мкФ.
  C _{наименьший} = 40/13 мкФ = 3.077 мкФ.

конденсаторов, подключенных параллельно — видео по физике от Brightstorm

Параллельно подключенные конденсаторы позволяют заряжать конденсаторы на выбор. Потенциальная разница такая же, как и для нескольких параллельных конденсаторов, но увеличивается заряд. Подобно последовательному сопротивлению, добавление конденсаторов параллельно увеличивает эффективную емкость. Формула для определения эффективной емкости: эффективная емкость = емкость 1 + емкость 2 .

Хорошо, давайте поговорим о параллельном добавлении конденсаторов. Как мы все знаем, параллельность означает, что у тока есть выбор. Теперь, когда мы говорим о конденсаторах, вместо того, чтобы говорить о токе, имеющем выбор, мы говорим о заряде, имеющем выбор. Итак, мы напишем параллельную комбинацию конденсаторов точно так же, поэтому, если я начну заряжать эту комбинацию, посылая сюда некоторый заряд, этот заряд может идти по 2 разным ветвям.Таким образом, он может заряжать этот конденсатор или он может заряжать тот. Хорошо, разность потенциалов будет такой же, как всегда, с параллельными комбинациями, но заряд будет увеличиваться. Итак, идея состоит в том, что если я хочу, чтобы только один эффективный конденсатор c был параллелен, чтобы представить эту параллельную комбинацию, заряд, который я должен поместить параллельно c, будет суммой этих двух зарядов.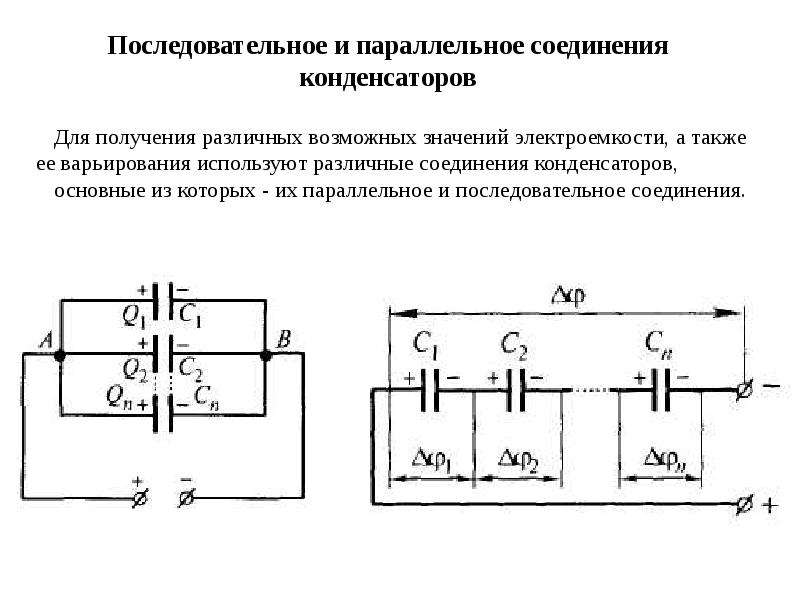 Потому что, когда я пытаюсь зарядить c параллельно, весь заряд, который я поставил либо на c1, либо на c2, перешел на cp.

Хорошо, заряд добавляет, разность потенциалов такая же. Хорошо, давайте посмотрим, что произойдет, q равно q1 плюс q2, поэтому, поскольку q равно емкости, умноженной на разность потенциалов, мы пишем c, параллельная дельта v равна c1 дельта v плюс c2 дельта v, разность потенциалов одинакова, поэтому дельта v сокращается. И это дает нам удивительно простую формулу, в которой добавление конденсаторов параллельно, c параллельно просто равно c1 плюс c2. Это означает, что все, что мне нужно сделать, это просто добавить, что всегда приятно. Это похоже на резисторы, включенные последовательно, поэтому, если я добавлю больше конденсаторов параллельно, емкость увеличится.И это действительно очень часто использовалось при создании компьютеров; вы бы поместили кучу конденсаторов параллельно, и тогда вы могли бы получить гораздо большую емкость, чем можно было бы получить любым другим способом.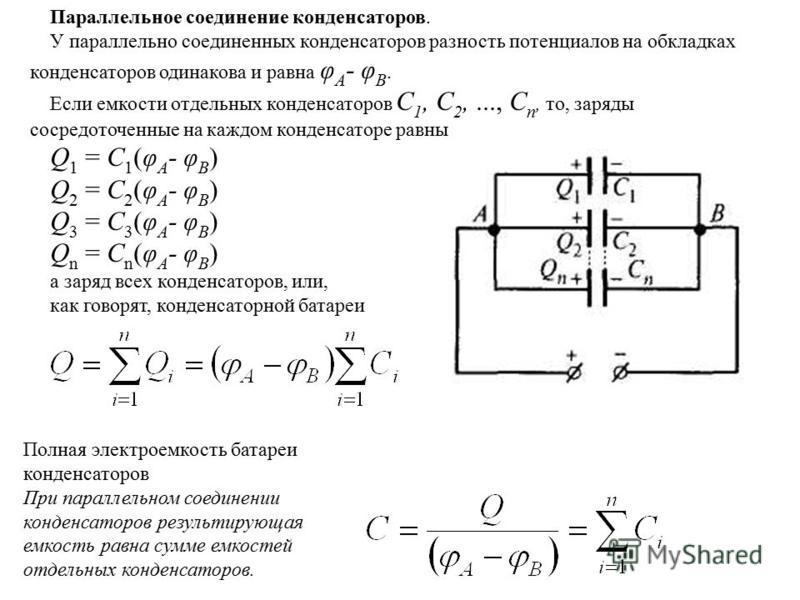 Итак, мы собираемся добавить эти 2 конденсатора параллельно, и я хочу определить общий заряд, если разность потенциалов на этих конденсаторах составляет 6 вольт.

Хорошо, давайте сделаем это двумя разными способами, если разность потенциалов составляет 6 вольт, тогда это должна быть разность потенциалов на конденсаторе 3 Фарада, так что это означает, что заряд, удерживаемый на конденсаторе 3 Фарада, будет равен разности потенциалов, умноженной на емкость 18 джоули.Хорошо, и заряд, удерживаемый конденсатором 2 Фарада, снова будет равен емкости, умноженной на разность потенциалов, в 2 раза 6,12 джоулей. Итак, общая сумма, извините, не джоули, кулоновские, поэтому общая сумма заряда, которую я собираюсь удерживать, составляет 18 плюс 12, что составляет 30 кулонов. Хорошо, теперь давайте сделаем это, добавив их сначала параллельно. Ну, я добавляю их параллельно, а затем говорю, что вы знаете, что я действительно просто хочу рассмотреть один конденсатор емкостью 5 Фарад. Если разность потенциалов на нем составляет 6 вольт, намного проще. Хорошо, теперь еще одна вещь, о которой нужно подумать, когда у вас есть конденсаторы, подключенные параллельно, самый большой конденсатор будет хранить больше всего энергии, и это потому, что конденсаторы, подключенные параллельно треугольнику v, одинаковы. Итак, мы говорим, что энергия равна половине c дельта v в квадрате, это постоянная величина, поэтому большая c самая большая энергия, и таким образом конденсаторы складываются параллельно.

конденсаторов, подключенных параллельно — формула и решенные примеры

Конденсаторы, подключенные параллельно

Конденсатор — это устройство, которое накапливает энергию (электрическую) путем накопления заряда.Конденсатор имеет две клеммы. Это пассивный электрический компонент. Конденсатор раньше назывался конденсатором. По сравнению с батареей, конденсатор имеет меньшую емкость, но зарядка и разрядка конденсатора происходят быстро. Внутри конденсатора есть две фольги, катодная фольга (-) и анодная фольга (+). Эффект конденсатора известен как емкость. Емкость конденсатора — это отношение величины заряда к величине разности потенциалов между двумя проводниками.

C = Q / V

Единица измерения емкости в системе СИ — фарад (Ф)

1 фарад = 1 кулон / 1 вольт

Параллельные конденсаторы

Конденсаторы могут быть подключены последовательно и параллельно. Если конденсаторы подключены друг за другом в виде цепочки, то это последовательно. В серии емкость меньше.

Когда конденсаторы подключаются между двумя общими точками, они должны быть подключены параллельно.

При параллельном соединении пластин размер пластин увеличивается вдвое, из-за чего удваивается емкость.Таким образом, при параллельном соединении конденсаторов мы получаем большую емкость.

Конденсаторы в формуле параллельности

Работа конденсаторов параллельно

[Изображение будет загружено в ближайшее время]

Пусть на приведенной выше принципиальной схеме C1, C2, C3, C4 будут емкостью четырех параллельных пластин конденсатора. C1, C2, C3, C4 подключены параллельно друг другу.

Если напряжение V приложено к цепи, следовательно, в параллельной комбинации конденсаторов, разность потенциалов на каждом конденсаторе будет одинаковой.Но заряд на каждом конденсаторе разный.

Когда батарея подключена к цепи, ток течет от положительной клеммы батареи к переходу. Итак, по контуру начинает течь заряд.

Этот сбор распределяется как Q1, Q2, Q3, Q4. Одна пластина конденсатора C1 получает заряд + Q1, в то время как другая пластина конденсатора C1 приобретает заряд -Q1. Это по индукции.

Одна пластина конденсатора C2 имеет заряд + Q2, в то время как другая пластина конденсатора C2 имеет заряд -Q2, это также происходит за счет индукции.

Аналогично, для конденсатора C3 одна пластина имеет заряд + Q3, а другая пластина конденсатора C3 имеет индукционный заряд -Q3.

Аналогично для конденсатора C4 одна пластина имеет заряд + Q4 другая пластина имеет заряд -Q4

Теперь согласно закону сохранения заряда

Q = Q1 + Q2 + Q3 + Q4 — (1)

Мы знаем, что C = Q / V

Q = CV

Q1 = C1V

Q2 = C2V

Q3 = C3V

Q4 = C4V

Q = CpV — (2)

Из уравнений (1) и (2) мы можем написать,

CpV = C1V + C2V + C3V + C4V

CpV = (C1 + C2 + C3 + C4) V

Cp = C1 + C2 + C3 + C4

Cp — выражение для эквивалентная емкость при параллельном подключении четырех конденсаторов.

Если есть три конденсатора, подключенных параллельно, то эквивалентная емкость составляет,

Cp = C1 + C2 + C3

Если имеется n конденсаторов, подключенных параллельно, то эквивалентная емкость составляет

Cp = C1 + C2 + C3 + ………. + Cn

Решенные примеры

1. Три конденсатора 10, 20, 25 мкФ подключены параллельно к источнику питания 250 В. Рассчитайте эквивалентную емкость.

Решение —

C1 = 10 мкФ = 10 × 10-6 F

C2 = 20 мкФ = 20 × 10-6 F

C3 = 25 мкФ = 25 × 10-6 F

Эквивалентная емкость параллельной комбинации составляет,

Cp = C1 + C2 + C3

Cp = 10 + 20 + 25

Cp = 55 мкФ

2.Два конденсатора емкостью 10 мкФ и 25 мкФ заряжаются на 12 В и 24 В соответственно. Каков общий потенциал при параллельном подключении?

Раствор —

C1 = 10 мкФ

C2 = 25 мкФ

V1 = 12 В

V2 = 24 В

V =?

Заряд на 1-м конденсаторе,

Q1 = C1V1 = 10 × 10-6 × 12 = 120 × 10-6 C

Заряд на 2-м конденсаторе,

Q2 = C2V2 = 25 × 10-6 × 24 = 600 × 10-6 C

Общий заряд Q = Q1 + Q2 = 120 × 10-6 + 600 × 10-6

Q = 720 × 10-6 C

Эквивалентная емкость параллельной комбинации составляет,

Cp = C1 + C2 = 10 + 25 = 35 мкФ

Если V — общий потенциал,

Q = CV

V = Q / C

V = 720/35 = 20. 57 В

Параллельный пластинчатый конденсатор | Физика и астрономия

Конденсатор состоит из двух проводящих пластин, разделенных изолятором, и используется для хранения электрического заряда. Если на конденсатор подается напряжение, одна пластина становится отрицательно заряженной, а другая — положительно заряженной.

Для пластин, у которых d << A , емкость C определяется по формуле:

C = ε ₀ A / d

, где A — площадь каждой пластины, d — расстояние между пластинами, а ε ₀ — диэлектрическая проницаемость свободного пространства (= 8.854X10 ^-12 ).

Для конденсатора с параллельными пластинами Паско A = π (0,085 м) ² = 2,27X10 ^-2 м ²

и d = 1,5X10 ^-3 м для минимального расстояния между плитами. Следовательно,

C _{теорема} = 1,34X10 ^-10 F или 0,134 нФ

По мере того, как вы перемещаете правую пластину дальше от неподвижной пластины, емкость изменяется как 1 / d , поэтому она быстро падает, а затем остается довольно постоянной примерно через 3 см.

В качестве демонстрации можно провести два разных измерения:

1. Цифровой мультиметр с диапазоном емкости может быть подключен к конденсатору (рис. 1 ниже). Сам измеритель обеспечивает зарядный ток, измеряет разность потенциалов и преобразует ее в значение емкости. Если пластины установлены на минимальное расстояние между ними, счетчик покажет:

C _{измерено} = 0,33 нФ

Это измерение примерно в два раза выше расчетного значения емкости и может быть объяснено «вручную» добавлением краевых эффектов, поскольку пластины полностью покрыты проводящим металлом (края и задняя часть), что увеличивает емкость измерение, которое не входит в рассчитанное значение.

Также обратите внимание, что недорогой цифровой измеритель емкости, используемый в этой демонстрации, не имеет возможности компенсировать емкость измерительного провода. Использование более сложного измерителя импеданса дает результат измерения C = 0,27 нФ.

Вы можете увеличить расстояние между пластинами и отметить, что уменьшение измеренной емкости изменяется на 1/ d .

2. Вместо измерителя емкости можно использовать отдельный источник питания для зарядки пластин и электрометр для измерения напряжения на пластинах.

Подключите оборудование, как показано на Рис. 2 ниже.

Установите неподвижную пластину слева в положение 0. После этого шкала на оптической скамье покажет фактическое расстояние между пластинами в сантиметрах. Установите подвижную пластину справа на минимальное расстояние 0,15 см.

Подсоедините черный провод электрометра к подвижной пластине, а черный (заземляющий) провод источника питания к гнезду заземления на боковой стороне электрометра.

Присоедините красный провод электрометра и красный (положительный провод с изображением аллигатора) от источника питания к неподвижной пластине.

При выключенном источнике питания и напряжении 0 установите ДИАПАЗОН электрометра на 10 вольт и включите его.

Нажмите кнопку ZERO на электрометре, чтобы удалить остаточный заряд.

Включите источник питания и медленно увеличивайте напряжение, пока электрометр не покажет 5 вольт. Затем отсоедините зажим «крокодил». Электрометр должен по-прежнему показывать 5 вольт, если вы мало двигаетесь — вы можете двигать рукой ровно настолько, чтобы отсоединить зажим из крокодиловой кожи, но не отодвигайте дальше нескольких сантиметров от клеммы.

Установите переключатель ДИАПАЗОНА электрометра на 100 В. Переместите подвижную пластину на расстояние 0,5 см и отметьте напряжение электрометра. Убедитесь, что вы не касаетесь металлической части пластины. Измените расстояние между пластинами на 1,0 и обратите внимание на напряжение. Продолжайте увеличивать расстояние между пластинами шагами от 1,0 см до примерно 10,0 см (рис. 3 ниже). Верните подвижную пластину на минимальное расстояние 0,15; напряжение должно вернуться к 5 вольт.

Поскольку Q = CV и заряд остается постоянным при изменении разделения пластин, если емкость C уменьшается как 1 / d , то напряжение В на пластинах должно увеличиваться как 1 / d .

Акриловые диэлектрические пластины могут быть вставлены между проводящими пластинами для увеличения емкости. Диэлектрическая пластина изначально должна быть бесплатной и не должна касаться металлических пластин при установке, чтобы не создавался дополнительный статический заряд.

Когда конденсатор хранит больше энергии при последовательном или параллельном подключении?

Эй, в этой статье мы узнаем, когда конденсатор будет хранить больше энергии при последовательном или параллельном подключении. Эта статья расширит ваши знания об основах конденсаторов.Если вы хотите стать гением, сначала очистите свои базовые знания в области электротехники. Однако давайте узнаем.

Конденсатор — это пассивное устройство, которое может накапливать электрическую энергию в виде заряда. Формула накопления энергии конденсатора:

здесь C = емкость
V = приложенное напряжение на конденсаторе

Таким образом, накопление электрической энергии зависит от значения емкости конденсатора и квадрата приложенного напряжения.

При последовательном соединении 4-х конденсаторов общая емкость составит

.
При параллельном соединении 4-х конденсаторов общее значение емкости составит:
Так убирается, что при параллельном подключении значение емкости будет больше.

Поскольку накопление энергии зависит от значения емкости и напряжения, конденсатор будет накапливать гораздо больше энергии при параллельном соединении, чем при последовательном соединении для того же уровня приложенного напряжения, потому что при параллельном соединении значение емкости больше.

Поясним это на примере

. Предположим, мы берем 4 одинаковых конденсатора номиналом 4 фарада, 4 вольта.

Последовательное подключение, накопитель энергии,

При параллельном подключении накопитель энергии,

Итак, теперь вы можете понять, что при параллельном соединении конденсатор может хранить, сколько энергии, чем при последовательном соединении.

Теперь, если мы подумаем практически, когда несколько конденсаторов подключены параллельно, все они будут иметь одинаковое напряжение, поэтому каждый из них будет накапливать энергию в соответствии с их значением емкости, а чистый накопитель энергии будет суммой всех отдельных накопителей энергии. .

Когда несколько конденсаторов соединены последовательно, все они не будут получать одинаковое напряжение, потому что напряжение будет падать в зависимости от распределения номиналов конденсаторов. Таким образом, они не могут заряжаться полностью или не могут хранить максимум энергии.

Таким образом, можно сделать вывод, что конденсатор будет хранить больше энергии при параллельном соединении, чем при последовательном соединении.

Спасибо, что посетили сайт. продолжайте посещать для получения дополнительных обновлений. .