емкость, напряжение, напряженность и прочее
В этой статье мы начнем разбирать конденсаторы “по косточкам”. Мы узнаем, как зависит напряжение на конденсаторе от расстояния между пластин, в чем отличие поведения конденсатора в случаях, когда он подключен к источнику и когда нет. В последующих статьях – продолжение.
Задача 1. Найти емкость сферического конденсатора, состоящего из двух концентрических сфер радиусами  м и
м и  м. Пространство между сферами заполнено маслом. Какого радиуса должен быть изолированный шар, чтобы он имел емкость, равную емкости такого конденсатора?
м. Пространство между сферами заполнено маслом. Какого радиуса должен быть изолированный шар, чтобы он имел емкость, равную емкости такого конденсатора?
Как известно,
![Rendered by QuickLaTeX.com \[C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9f2319a451c55645871235800035a863_l3.png)
Запишем потенциалы сфер:
![Rendered by QuickLaTeX.com \[\varphi_1=\frac{k q}{\varepsilon r_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b62c50d992afeb0c928f5ac244c63ea6_l3.png)
![Rendered by QuickLaTeX.com \[\varphi_2=\frac{k q}{\varepsilon r_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-15bb6281fed6a285357cfb9ff2fed1d0_l3.png)
Разность потенциалов:
![Rendered by QuickLaTeX.com \[\varphi_1-\varphi_2=\frac{k q}{\varepsilon}\left(\frac{1}{r_1}-\frac{1}{r_2}\right)= \frac{k q(r_2-r_1)}{\varepsilon r_1 r_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-47d277b7486a5144e894fd5d4180453a_l3.png)
Тогда емкость конденсатора равна (диэлектрическая проницаемость масла равна  ):
):
![Rendered by QuickLaTeX.com \[C=\frac{q\varepsilon r_1 r_2}{ k q(r_2-r_1) }=\frac{\varepsilon r_1 r_2}{ k(r_2-r_1) }=\frac{2,2\cdot0,01\cdot 0,0105}{9\cdot10^9(0,0105-0,01)}=5,1\cdot10^{-11}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d123a29ae737c7c612e0095561060afb_l3.png)
А радиус шара был бы равен
![Rendered by QuickLaTeX.com \[R=\frac{ r_1 r_2}{ r_2-r_1}=\frac{ 0,01\cdot 0,0105}{ 0,0105-0,01}=0,21\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7a12dbd89911efc7704e8f300fda0b4b_l3.png)
Ответ:  пФ,
пФ,  м.
м.
Задача 2. Найти емкость плоского конденсатора, состоящего из двух круглых пластин диаметром  см, разделенных парафиновой прослойкой толщиной
см, разделенных парафиновой прослойкой толщиной  мм.
мм.
Диэлектрическая проницаемость парафина  .
.
По формуле
![Rendered by QuickLaTeX.com \[C=\frac{\varepsilon \varepsilon_0 S}{d}=\frac{\varepsilon \varepsilon_0 \pi D^2 }{4d}=\frac{2\cdot8,85 \cdot10^{-12}\cdot3,14 \cdot0,2^2}{4\cdot10^{-3}}=556\cdot10^{-6}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ccd93f023e32b99c1ecb79610cfdfda7_l3.png)
Ответ: 556 мкФ
Задача 3. Площадь каждой пластины плоского конденсатора  см
см . На каком расстоянии друг от друга надо расположить в воздухе пластины, чтобы емкость конденсатора была
. На каком расстоянии друг от друга надо расположить в воздухе пластины, чтобы емкость конденсатора была  пФ?
пФ?
Диэлектрическая проницаемость воздуха  .
.
Из формулы
![Rendered by QuickLaTeX.com \[C=\frac{\varepsilon \varepsilon_0 S}{d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-07473c5fa4574eaa54a823cf0612cb18_l3.png)
«вытащим»  :
:
![Rendered by QuickLaTeX.com \[d=\frac{\varepsilon \varepsilon_0 S}{C}=\frac{8,85 \cdot10^{-12} \cdot520 \cdot10^{-4}}{46\cdot 10^{-12}}=0,01\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-55b56be355a985b4b5f731a5089519fc_l3.png)
Ответ: 1 см
Задача 4. Расстояние между обкладками плоского конденсатора увеличивают. Как изменится: а) электроемкость конденсатора; б) напряженность электрического поля; в) напряжение? Рассмотреть два случая: 1) конденсатор заряжен и отключен от источника тока; 2) конденсатор подключен к источнику тока.
Здесь необходимо запомнить: если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Действительно, куда ему деваться? А если начать что-либо менять, то будут меняться емкость и напряжение.
Если же конденсатор подключен к источнику, то напряжение на нем постоянно, и при любых вмешательствах (раздвинули пластины, вложили диэлектрик) будет меняться емкость и заряд.
Тогда в первом случае (заряд постоянен!): так как  зависимость емкости от
зависимость емкости от  обратная, то емкость будет падать при увеличении расстояния между пластинами. Напряженность
обратная, то емкость будет падать при увеличении расстояния между пластинами. Напряженность  – никак не зависит от расстояния между обкладками, она не изменится; напряжение
– никак не зависит от расстояния между обкладками, она не изменится; напряжение  – увеличится, оно от величины
– увеличится, оно от величины  зависит прямо.
зависит прямо.
Во втором случае (напряжение постоянно): напряженность поля уменьшится; емкость уменьшится.
Задача 5. Плоский конденсатор состоит из двух пластин, площадью  см
см каждая, расположенных на расстоянии
каждая, расположенных на расстоянии  мм друг от друга, между которыми находится слой слюды. Какой наибольший заряд можно сообщить конденсатору, если допустимое напряжение
мм друг от друга, между которыми находится слой слюды. Какой наибольший заряд можно сообщить конденсатору, если допустимое напряжение  кВ?
кВ?
Диэлектрическая проницаемость слюды  .
.
![Rendered by QuickLaTeX.com \[q=CU\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-85df9f01aff96575f694c0205e9bfe9b_l3.png)
![Rendered by QuickLaTeX.com \[q=\frac{\varepsilon \varepsilon_0 S U}{d}=\frac{6 \cdot 8,85 \cdot10^{-12} \cdot200 \cdot10^{-4} \cdot 3000}{2\cdot10^{-3}}=1,59\cdot10^{-6}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0955f7deeb20f1a8484e9b208f1a320f_l3.png)
Ответ: 1,59 мкКл
Задача 6. Плоский воздушный конденсатор, расстояние между пластинами которого  мм, заряжен до напряжения
мм, заряжен до напряжения  В и отключен от источника. Каким будет напряжение
В и отключен от источника. Каким будет напряжение  , если пластины раздвинуть до расстояния
, если пластины раздвинуть до расстояния  мм?
мм?
Если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Тогда
![Rendered by QuickLaTeX.com \[q=CU=\frac{\varepsilon \varepsilon_0 S U_1}{d_1}=\frac{\varepsilon \varepsilon_0 S U_2}{d_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3b7991916e49809400ae3c0e4b78bb67_l3.png)
![Rendered by QuickLaTeX.com \[\frac{U_1}{d_1}=\frac{U_2}{d_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a4b0269a4dc47fef78930f06873db88b_l3.png)
![Rendered by QuickLaTeX.com \[U_2=\frac{ U_1 d_2}{ d_1}=\frac{10\cdot5}{0,5}=100\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9e368a7fec4ae93743e216e2f964e9bf_l3.png)
Ответ:  В
В
Задача 7. С какой силой взаимодействуют пластины плоского воздушного конденсатора площадью  м
м , если напряжение на пластинах
, если напряжение на пластинах  В и расстояние между ними
В и расстояние между ними  м?
м?
Сила взаимодействия пластин может быть вычислена как произведение заряда пластины на напряженность поля пластины:  – делим пополам, потому что напряженность поля одной пластины вдвое меньше напряженности поля конденсатора – там пластин две штуки.
– делим пополам, потому что напряженность поля одной пластины вдвое меньше напряженности поля конденсатора – там пластин две штуки.
![Rendered by QuickLaTeX.com \[E=\frac{U}{d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6b6be7764ba0b2038d217fbfef26c51a_l3.png)
![Rendered by QuickLaTeX.com \[F=\frac{qE}{2}=\frac{CU\cdot U}{2d}=\frac{U^2\varepsilon_0 S }{2d^2}=\frac{500^2\cdot 8,85 \cdot10^{-12} \cdot 0,01 }{2\cdot 9 \cdot10^{-6}}=1229\cdot10^{-6}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-12ee72e92634a3deb74c2cd24662b6f2_l3.png)
Ответ:  мН.
мН.
электричекое поле и плотность энергии
В статье мы расскажем про диэлектрики и их роль в конденсаторе, электрическое поле в диэлектрике и плотность энергии электрического поля в диэлектрике.
Диэлектрик — это газ, жидкость или твердое тело, которое не является проводником электричества. Это означает, что электрические заряды, содержащиеся в каждом теле, связаны в диэлектрике в том смысле, что они могут перемещаться только внутри диэлектрика. Если электрическое поле приложено к диэлектрику, смещение нагрузок под этим полем приведет к поляризации диэлектрика, то есть, давая ему ненулевой дипольный момент. Это означает, что между крышками заряженного конденсатора поверхность диэлектрика, примыкающая к положительно заряженной крышке, получит отрицательный заряд. И наоборот, отрицательно заряженная крышка будет притягиваться к положительно заряженной поверхности диэлектрика. Наиболее важным эффектом диэлектрической поляризации является то, что часть заряда на крышках конденсатора нейтрализуется и больше не способствует генерации электрического поля между крышками.
Частичная, но не полная нейтрализация (компенсация) заряда электрода диэлектрическим слоем связана с тем фактом, что полярность диэлектрика обусловлена ориентацией диполей, существующих внутри диэлектрика. Такие диполи можно условно разделить на постоянные и индуцированные диполи. Постоянные диполи встречаются в веществах, молекулы которых имеют стабильный дипольный момент. Здесь наглядным примером является вода, которая подвергается очень сильной поляризации в электрическом поле. Индуцированные диполи не возникают при отсутствии приложенного электрического поля и появляются в атоме или молекуле только под действием этого поля. Внешнее поле деформирует электронный заряд атомов и молекул, в результате чего центр отрицательного заряда электронов больше не совпадает с центром положительного заряда ядра и, таким образом, появляется дипольный момент, который сразу исчезает после выключения поля. Примером может быть бензол С6H 6, не имеющий постоянного дипольного момента и получающий этот момент только под действием поля. Конечно, также вещества, состоящие из молекул, имеющих постоянные дипольные моменты, подвергаются слабой дополнительной индуцированной поляризации. Поляризация ионных кристаллов состоит в том, что положительные и отрицательные ионы смещаются относительно друг друга под воздействием приложенного поля, и в некоторых веществах поляризация движущегося пространственного заряда (например, ионных примесей) также может играть роль.
Ориентация диполя в диэлектрике никогда не бывает идеальной, и поэтому мы не имеем полной компенсации заряда конденсатора конденсатора, заполненного диэлектриком. Причиной отсутствия полной ориентации диполей является, главным образом, дезорганизация тепловых движений, а также ограничения, налагаемые кристаллической структурой диэлектрического слоя и препятствиями при вращении молекул из других молекул. Таким образом, полная ориентация диполя, то есть полная поляризация диэлектрика, не достигается до напряжения пробоя диэлектрика.
Роль диэлектрика в конденсаторе
Что происходит с емкостью конденсатора, если пространство между его крышками заполнено диэлектриком?
Оказывается, емкость конденсатора, заполненного диэлектриком, во много раз превышает емкость пустого конденсатора (наполненного воздухом). Давайте посмотрим, в чем причина этого очень важного явления. Емкость зарядного конденсатора С с разностью потенциалов между крышками основана на определении

Хотя все рассуждения, представленные ниже, действительны для каждого типа конденсатора, мы ограничимся далее простейшим случаем плоского конденсатора.

Ранее мы получили, используя закон Гаусса, формулу для емкости такого конденсатора

Если в этом примере плоский конденсатор заряжен постоянным зарядом Q, обозначенным на левом рисунке ниже двумя знаками плюс и двумя минусами (заряды на крышках создаются смещением заряда и должны быть одинаковыми), то интенсивность поля E будет обозначаться двумя векторами, начинающимися с заряда плюс и конец на заряде минус. Количество загрузок на крышках, представленных на рисунке, является только символическим — на самом деле это число исчисляется многими миллиардами.

Натяжение между крышками, удаленными друг от друга, определяется уже известным нам шаблоном («шаговое напряжение»)

Если теперь мы поместим диполь между крышками, как на правом рисунке выше, то один из E-векторов будет удален из пространства между электродами противоположно направленным дипольным полем. Поле Е уменьшилось вдвое, и поэтому натяжение между крышками также уменьшится вдвое. Поскольку конденсатор отключен от источника питания, заряд на электродах не может быть изменен, и при применении формулы, определяющей емкость

Затем мы обнаруживаем, что емкость конденсатора стала вдвое больше. Если мы обозначим емкость левого конденсатора как Сслева , а справа как Ссправа, то мы сразу увидим, что

и
другими словами, в этом символическом случае емкость конденсатора с диэлектриком удвоилась

На самом деле работа диэлектрика намного эффективнее, и увеличение емкости конденсатора, заполненного диэлектриком, может достигать нескольких, нескольких десятков или даже нескольких сотен раз.
Совершенно аналогично, мы получаем увеличение емкости конденсатора после заполнения его диэлектриком, когда конденсатор подключен к источнику постоянного напряжения V. Ситуация в «воздушном» конденсаторе показана ниже

На этом символическом рисунке каждый плюс-заряд порождает вектор поля E, который заканчивается минус-зарядом. Если теперь мы поместим диполь между крышками, как на рисунке ниже, то теперь также один из векторов E будет удален из пространства между электродами противоположно направленным дипольным полем.

Возникла ситуация, которую невозможно поддерживать. Когда источник постоянного напряжения V подключен, напряженность поля E должна быть такой, чтобы зависимость выполнялась. Для этого от источника напряжения должен вытекать дополнительный заряд, который заменит заряд, компенсируемый наличием диэлектрика. С другой стороны, у нас есть три вектора E, как на рисунке ниже, и это столько, сколько необходимо для удовлетворения требования, выраженного в формуле.

Теперь, при неизменном напряжении, на конденсаторе появляется больший заряд, что означает, что емкость конденсатора соответственно увеличилась. Чтобы количественно оценить влияние диэлектрика на емкость конденсатора, мы вводим материальную постоянную для этого диэлектрика, которую мы называем относительной электрической проницаемостью ε и которую мы определяем, как отношение емкости конденсатора, заполненного диэлектриком C, к емкости пустого конденсатора C0

E, D и P векторы
Более точное формальное описание поведения диэлектрика в конденсаторе получается путем введения двух дополнительных векторов: вектора P — поляризации и вектора D — смещения. Вектор P уже появился на скриншоте выше. Обратите особое внимание на вектор D, длина которого равна общей плотности заряда σ, накопленной на крышках конденсатора, и которая входит в уравнения Максвелла, записанные в компактной, элегантной форме. Когда пустой конденсатор поддерживается под постоянным напряжением V, а плотность заряда на крышках этого конденсатора обозначается σ0, то поле E между крышками таково, что

Механизм диэлектрической поляризации теперь будет работать. После установки диэлектрика между крышками конденсатора электрическое поле между крышками вызывает поляризацию диэлектрика, что означает перемещение к крышкам зарядов с противоположными знаками. Часть нагрузок на покрытиях, имеющих плотность σ0, будет «замаскирована» противоположным индуктивным зарядом с плотностью σi. Затем источник напряжения должен перезарядить конденсатор до такой плотности заряда, чтобы снова напряженность поля между крышками удовлетворяла условию V = Ed. Таким образом, σ = σ0 + σi , то есть плотность полного заряда на крышках конденсатора с диэлектриком равна сумме плотности заряда на конденсаторе без диэлектрика и плотности поляризационного заряда.
Если мы имеем в виду
σ 0 = ε 0 E,
σ i = P
σ = D
и мы применим закон Гаусса к конденсатору с диэлектриком, тогда мы сразу получим соединение

Эта связь между векторами D, E и P записана в векторной форме


Напомним, что D — вектор смещения, E — вектор поля, а P — вектор поляризации. Вектор Р (показано ниже обозначена красным) проходит внутри диэлектрика и сделать его в виде стрелки от «негативного» на «позитивный», то есть противоположно вектору Е .


Как уже было сказано, диэлектрическая проницаемость ε определяется как отношение емкости С и диэлектрическим заполнением конденсатора пустых C0.

Помните, что конденсатор постоянно подключен к источнику напряжения, т.е. V = Q/C = const. Емкость конденсатора с диэлектриком будет

и емкость пустого конденсатора будет

Исходя из этого, мы можем написать

Подставив выражение, мы получим эквивалентное определение вектора D:

Электрическое поле в диэлектрике
Если конденсатор НЕ подключен к источнику питания, заряд Q = CV на его крышках будет оставаться постоянным независимо от того, помещен ли диэлектрик между ними. Если мы обозначим C0 и E0 соответственно, емкость пустого конденсатора и значение электрического поля между его крышками, а C и E аналогичные значения для конденсатора, заполненного диэлектриком, мы можем записать

Отсюда и на основании определения диэлектрической проницаемости ε получаем

Таким образом, видно, что напряженность поля в диэлектрике в ε раз меньше, чем в вакууме.

Это соотношение является общим и применяется в каждом фиксированном поле E, независимо от его источника.
Плотность энергии электрического поля в диэлектрике
Плотность энергии электрического поля E в диэлектрике в ε раз больше, чем в вакууме, и равна

Используя выражение зависимости от плотности энергии, мы можем записать в компактном векторном виде

Это выражение всегда применимо, в том числе и для кристаллов, где векторы E и D обычно не параллельны друг другу.
1. Вставка и снятие диэлектрика с крышек конденсатора с постоянной суммарной нагрузкой, как на чертеже, вызывает передачу нагрузки от одного конденсатора к другому. Лампочка может светить.

2. Плотность заряда на крышке конденсатора, частично заполненного диэлектриком, не постоянна.

Гауссовский обобщенный закон
Описывая кулоновскую силу между точечными зарядами в диэлектрике, электрическая проницаемость вакуума умножалась на диэлектрическую проницаемость и вместо ε 0 мы использовали произведение ε 0 ε. Мы можем обобщить эту процедуру и применить ее к закону Гаусса, где центром, через который проникает поле, является не вакуум, а диэлектрик. Тогда мы знаем закон Гаусса

мы сможем написать в форме

мы получим окончательную форму обобщенного закона Гаусса

Закон Гаусса в таком виде применяется в вакууме, где ε = 1, и в диэлектриках. Заряд Q в этом уравнении, как и прежде, представляет собой результирующий заряд, содержащийся внутри замкнутой поверхности, после чего происходит интегрирование.
В конденсаторе с диэлектриком результирующий заряд представляет собой разницу между нагрузкой, накопленной на крышке q1 = σA, и поляризационным зарядом (с противоположным знаком), индуцированным в диэлектрике поверхностного слоя q2 = -σ и A. Если мы используем закон Гаусса для этой структуры, то мы предполагаем, что заряды они накапливаются на соседних поверхностях крышки и диэлектрика, и это поле не выходит за пределы крышек конденсатора. Естественным выбором гауссовой поверхности, после которой мы интегрируем поток, является прямоугольная призма или поверхность цилиндра. Основание прямоугольной призмы А параллельно поверхности крышки. Одна база находится снаружи крышки (там, где нет поля), а другая находится внутри диэлектрика.

Закон Гаусса в представленной выше форме является одним из четырех уравнений Максвелла, описывающих все электрические, магнитные и оптические явления. Уравнения Максвелла являются фундаментальными законами электродинамики, и ни одно из них не может быть выведено из более простых законов. Если бы существовали еще более фундаментальные права, они, безусловно, были бы представлены здесь. Эти уравнения являются результатом творческого вдохновения, просвещения их создателей Гаусса, Фарадея и Ампера. Максвелл представил им гениальную концепцию «тока смещения», о которой мы поговорим чуть позже, которая позволила унифицировать структуру этих уравнений и распространить их на случай электромагнитных и, следовательно, световых волн.
Глава 20. Конденсаторы
Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.
Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):
(20.1) |
Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.
Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):
(20.2) |
Разность потенциалов между пластинами равна
(20.3) |
где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора
(20.4) |
Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает
(20.5) |
Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.
Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов
(20.6) |
Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .
Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов
(20.7) |
Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна
(20.8) |
С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:
(20.9) |
Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.
Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (
Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).
Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в
(ответ 4).
Согласно определению электрической емкости имеем в задаче 20.1.5
(ответ 2).
Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).
При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул
где и — новый заряд конденсатора (ответ 3).
Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).
В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)
то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что
произведение от расстояния между пластинами не зависит (см. формулу (20.4)).
Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.
При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ
Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.8)
(1) |
Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ
В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)
Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)
В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)
Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).
В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).
Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ
Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:
где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора
(ответ 4).
Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):
Ёмкость плоского конденсатора
Сообщим обкладкам плоского конденсатора
заряды +Qи –Q.
Плотность заряда на обкладках станет
равной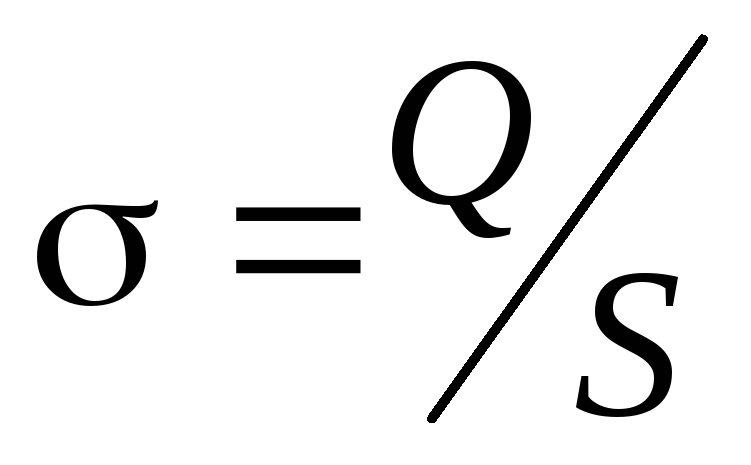 ,
а напряжённость однородного электрического
поля, возникшего в конденсаторе (см.
2.17):
,
а напряжённость однородного электрического
поля, возникшего в конденсаторе (см.
2.17):
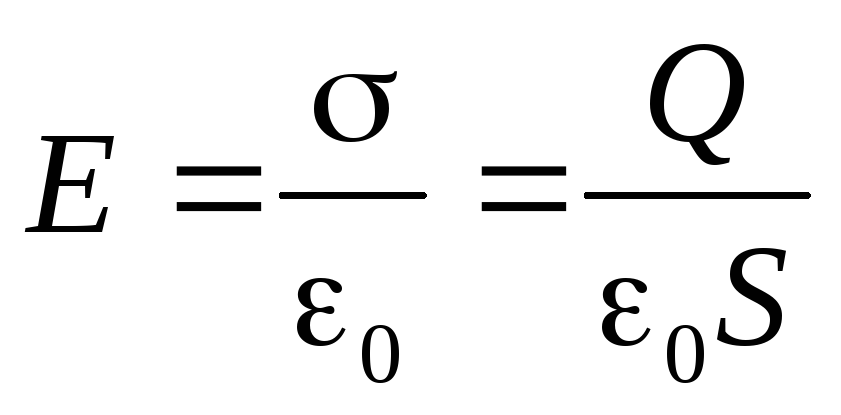 .
.
Воспользовавшись связью напряжённости и потенциала в электрическом поле, вычислим разность потенциалов на обкладках конденсатора:
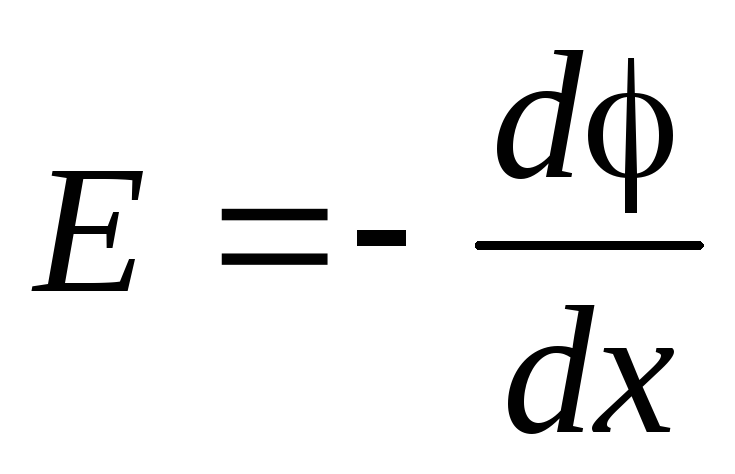 ;
;
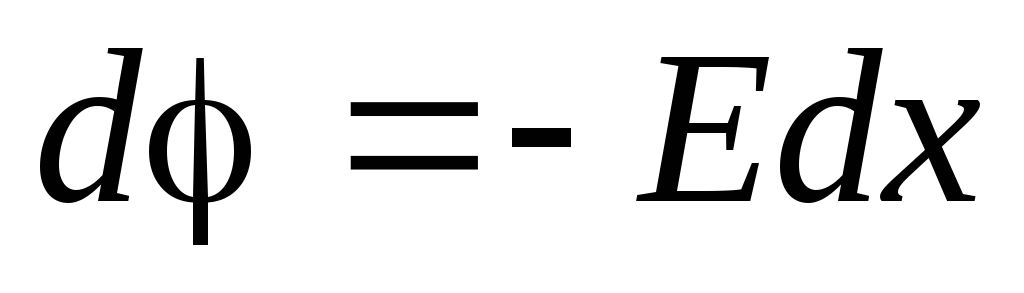 .
. . (4.6)
. (4.6)
Это соотношение и позволяет определить ёмкость плоского конденсатора
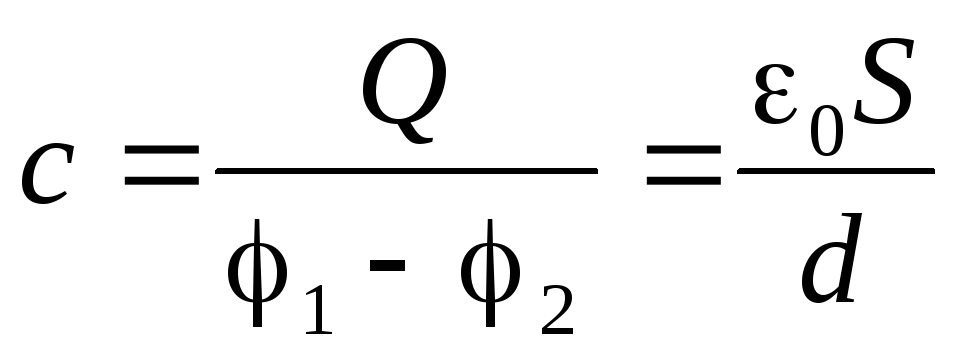 (4.7)
(4.7)
Ёмкость этого конденсатора прямо пропорциональна площади его обкладок (S) и обратно пропорциональна расстоянию (d) между ними.
Напомним, что разность потенциалов между обкладками была вычислена в предположении, что поле между ними однородное. Это означает, что результат (4.7) в известном смысле идеализация. Мы вычислили ёмкость плоского конденсатора, пренебрегая краевыми искажениями поля.
Ёмкость сферического конденсатора
Обкладками такого конденсатора являются две концентрические сферы радиусами R1иR2(рис. 4.10,b).
На прошлой лекции была вычислена разность потенциалов между обкладками сферического конденсатора. Она оказалась пропорциональна заряду конденсатора (см. 3.27).

Ёмкость, равная по определению отношению заряда к разности потенциалов, для сферического конденсатора, составит следующую величину
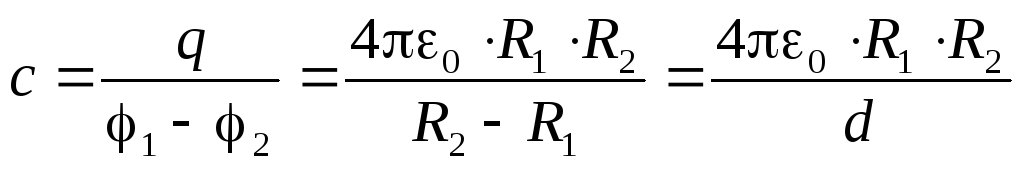 (4.8)
(4.8)
Этот результат свидетельствует о том, что ёмкость сферического конденсатора зависит от размеров сфер (R1иR2) и от величины зазораd(d=R1–R2) между ними.
Интересно, что при достаточно малом зазоре d, когдаR1R2 = R, можно записать ёмкость сферического конденсатора так:
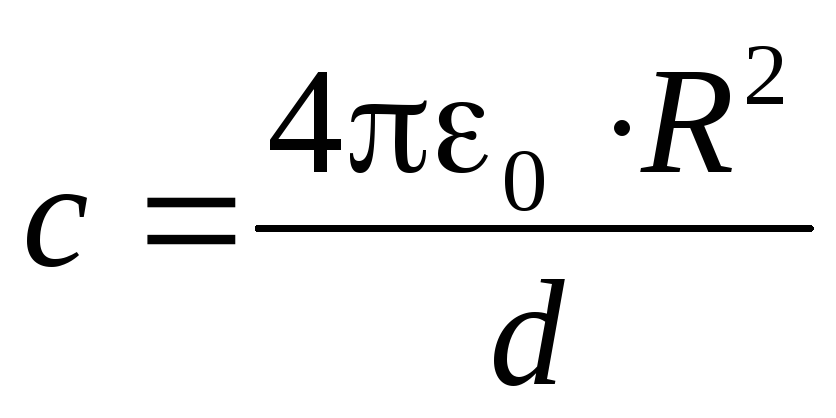
Но 4R2=S— площадь поверхности сферы. Поэтому
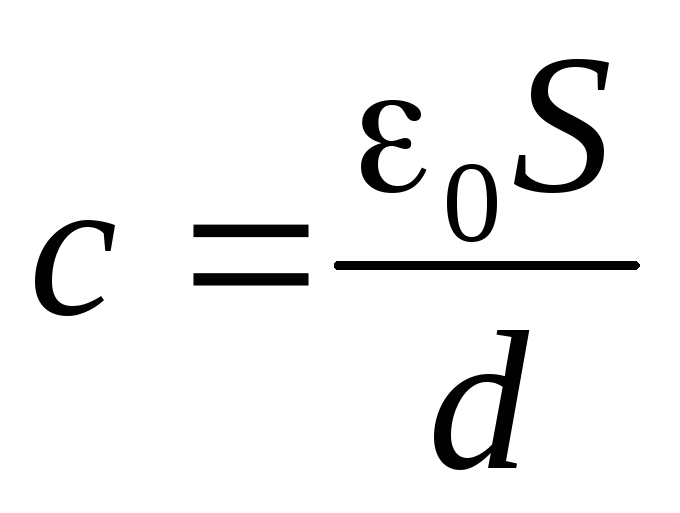
и ёмкость сферического конденсатора оказывается равной ёмкости «эквивалентного» плоского конденсатора.
Ёмкость цилиндрического конденсатора
Сообщим обкладкам цилиндрического конденсатора заряды (+q) и (–q) (рис. 4.11.). Вычислим напряжённость поля между обкладками. Для этого выберем гауссову замкнутую поверхность в виде цилиндра радиусомR1<r<R2и высотойl. Пренебрегая краевыми эффектами (!), запишем уравнение теоремы Гаусса
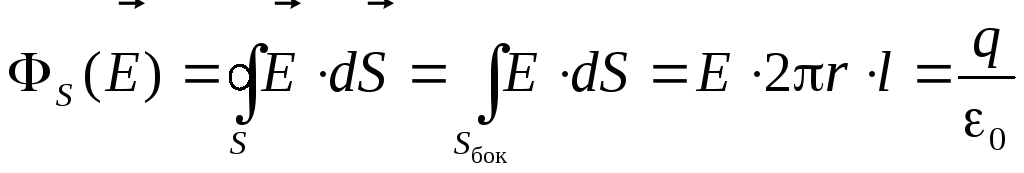
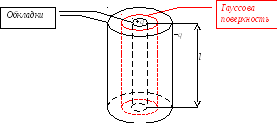
Рис. 4.11.
Из последнего равенства заключаем, что
 (4.9)
(4.9)
Теперь, воспользовавшись связью
напряжённости и потенциала электрического
поля  ,
вычислим разность потенциалов между
обкладками цилиндрического конденсатора
,
вычислим разность потенциалов между
обкладками цилиндрического конденсатора
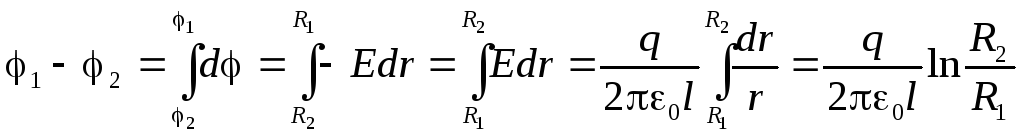
Как и в случае других конденсаторов, разность потенциалов на обкладках цилиндрического конденсатора оказалась пропорциональной заряду q. Поэтому ёмкость конкретного цилиндрического конденсатора оказывается величиной постоянной, зависящей только от размеров этого конденсатора
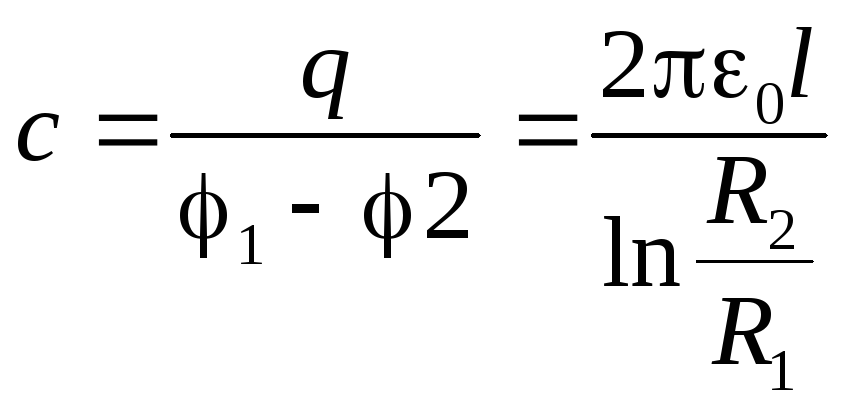 (4.10)
(4.10)
Энергия электрического поля. Плотность энергии.
Будем заряжать плоский конденсатор, перенося малые порции заряда dqс одной обкладки на другую (рис. 4.12.) Для того чтобы перенести зарядdqмежду обкладками с разностью потенциалов (1–2) необходимо совершить работу
dA= (1–2)dq (4.11)

Рис. 4.12.
Учитывая, что 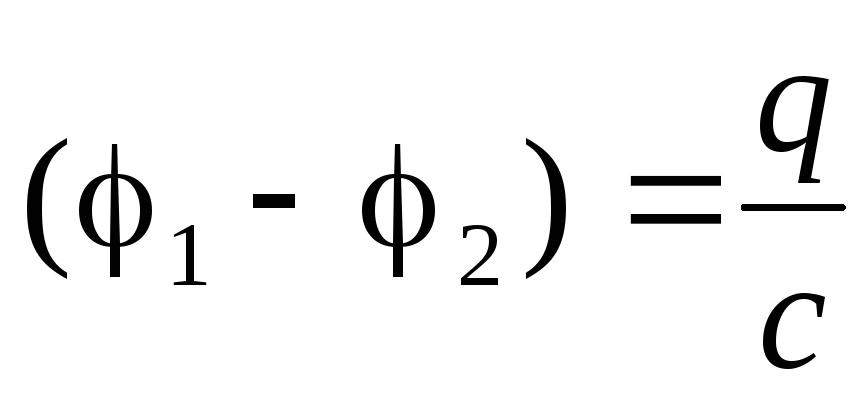 ,
эту работу можно записать ещё и так
,
эту работу можно записать ещё и так

Для того чтобы первоначально незаряженному конденсатору сообщить заряд Q, необходимо совершить работу
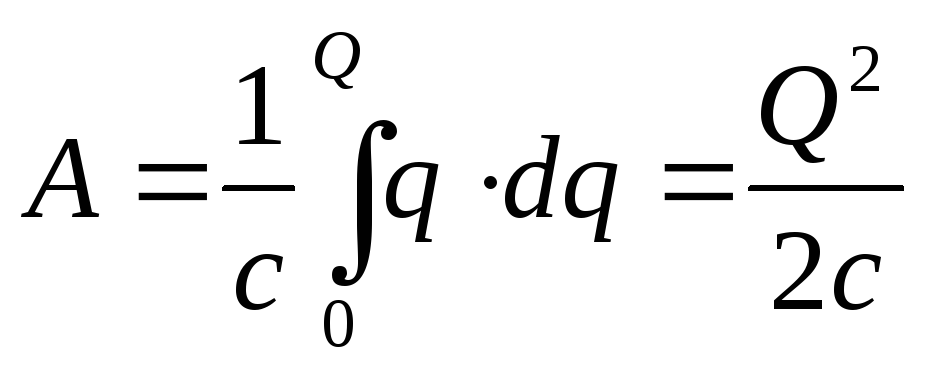
Эта работа равна энергии заряженного конденсатора
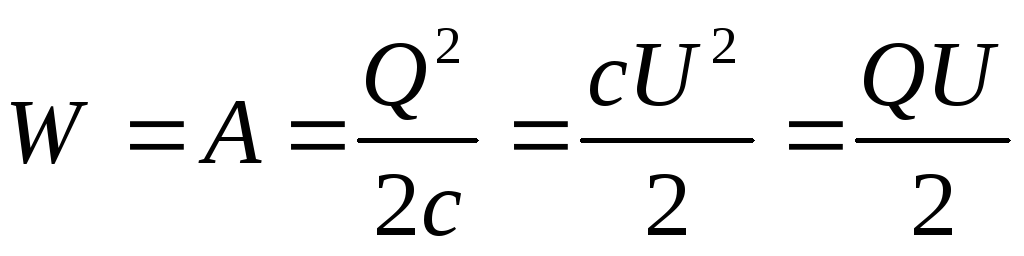 (4.12)
(4.12)
Здесь 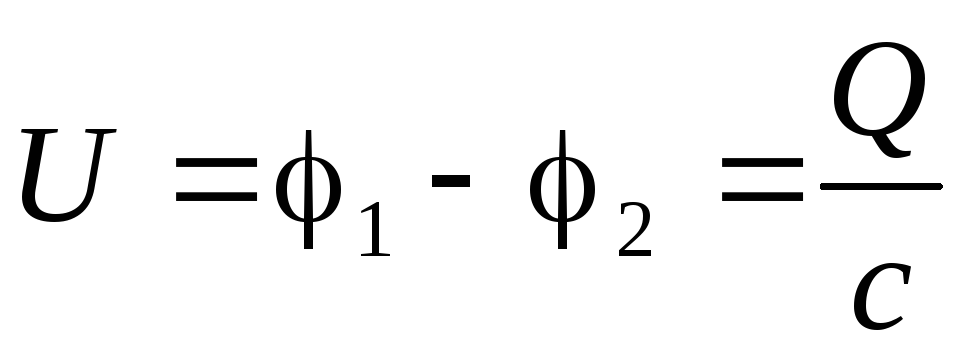 — напряжение на конденсаторе, равное
разности потенциалов на его обкладках.
— напряжение на конденсаторе, равное
разности потенциалов на его обкладках.
Продолжим преобразования уравнения (4.12).
Вспомним, что ёмкость плоского конденсатора
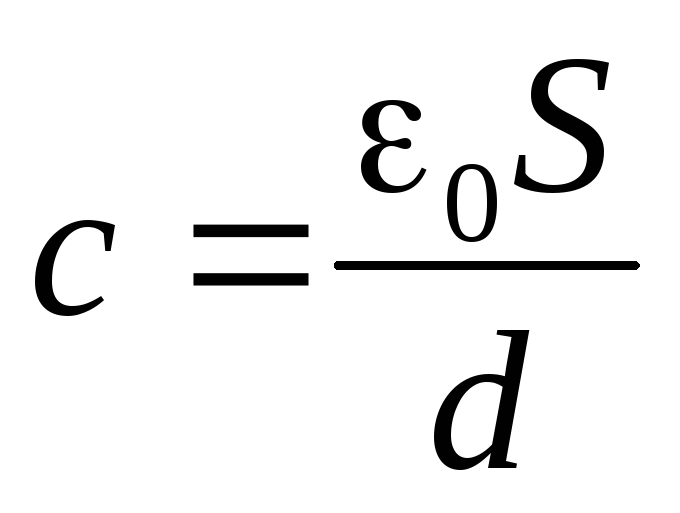 ,
,
а напряжение связано с напряжённостью электрического поля
U=E∙d
Воспользовавшись этими соотношениями, запишем энергию заряженного конденсатора в таком виде
 (4.13)
(4.13)
Эти два выражения энергии конденсатора

приводят к следующему принципиальному вопросу: где в конденсаторе располагается энергия? Где она «локализована»?
Если она связана с электрическими зарядами, то она находиться на обкладках конденсатора. Если же это энергия электрического поля, то она занимает пространство между обкладками, объем которого равен объему конденсатора V=S∙d.
Для ответа на этот вопрос нужно было бы заряд с обкладок убрать, а поле при этом оставить. Тогда можно было бы посмотреть: осталась энергия — значит, она связана с полем, исчезла — значит, она располагалась вместе с зарядом на обкладках.
Но проблема-то в том, что при удалении зарядов исчезает, конечно, и их электростатическое поле. Поэтому вопрос о локализации энергии в рамках электростатики не может быть решён.
В электродинамике переменныеэлектрические и магнитные поля, как известно, могут существовать и без электрических зарядов. Причем такие поля обладают энергией, что является прямым экспериментальным доказательством того, что эта энергия связана с электрическими полями и локализована в объёме, занятом полем. Теперь становиться понятнее последнее выражение энергии заряженного конденсатора:

Энергия конденсатора связана с его электрическим полем и поэтому пропорциональна объёму конденсатора (V), то есть объёму поля.
Отношение 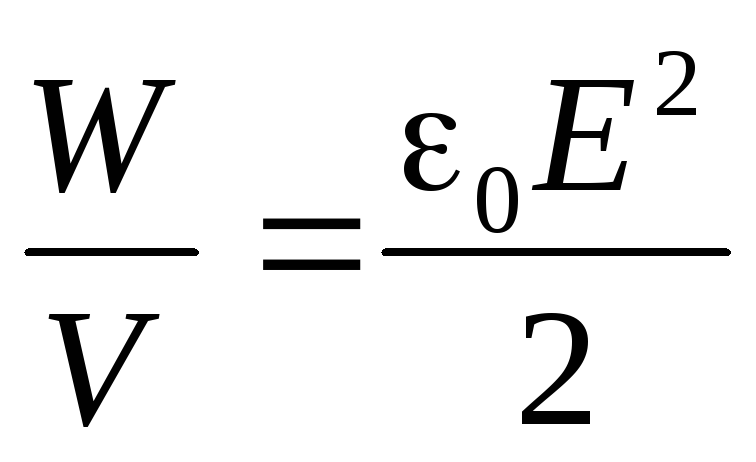 представляет собой среднее значение
энергии, приходящейся на единичный
объём поля
представляет собой среднее значение
энергии, приходящейся на единичный
объём поля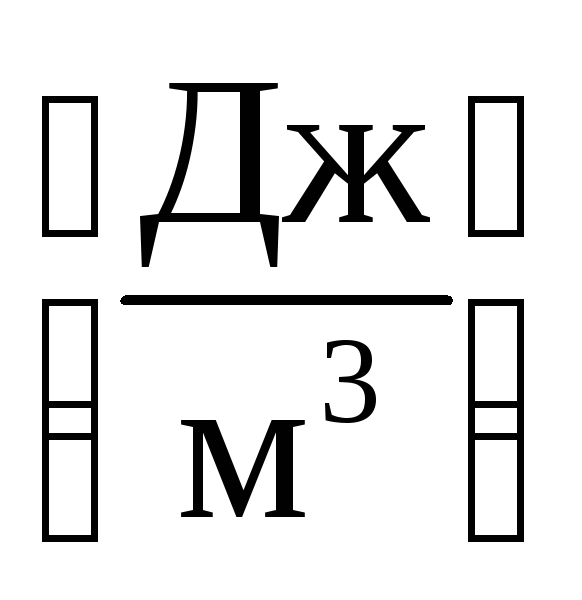 .
.
Эта характеристика энергетической насыщённости поля получила название «объёмная плотность энергии».
Обычно эта характеристика носит точечный, локальный характер. Вокруг заданной точки выбирают элементарный объём dVи вычисляют энергетическую плотность, деля энергию этой областиdWна её объём
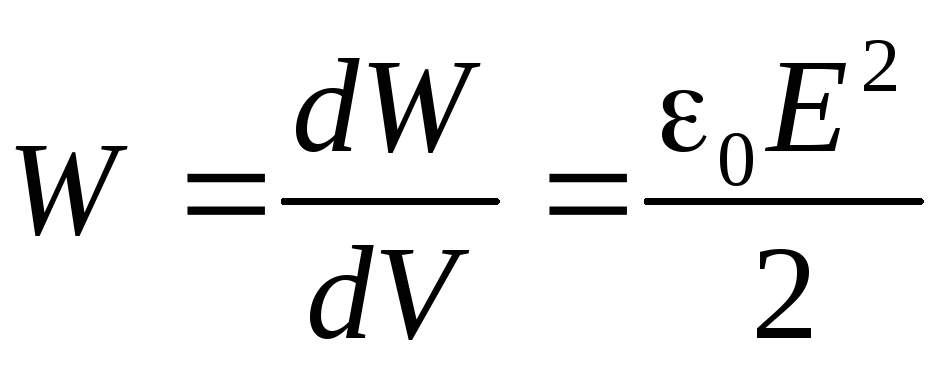 (4.14)
(4.14)
Объёмная плотность энергии в заданной точке электрического поля пропорциональна квадрату напряжённости поля в этой точке. Измеряется объёмная плотность энергии, конечно, в Дж/м3:
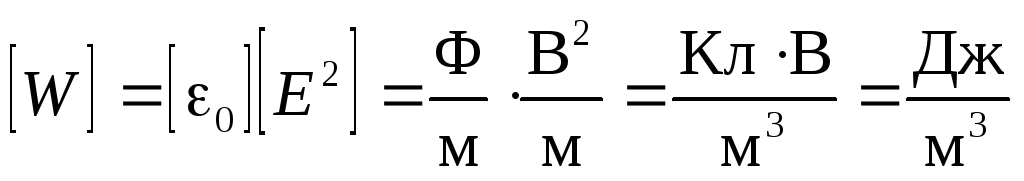 .
.
Зная, как меняется плотность энергии в пространстве, можно вычислить энергию, сосредоточенную в объёме V, электрического поля:
 .
.
Пример.
Проводящий шар радиусом Rнесет зарядQ. Какова энергия электрического поля этого шара?
Поле внутри заряженного шара отсутствует, а вне шара оно совпадает с полем точечного заряда:
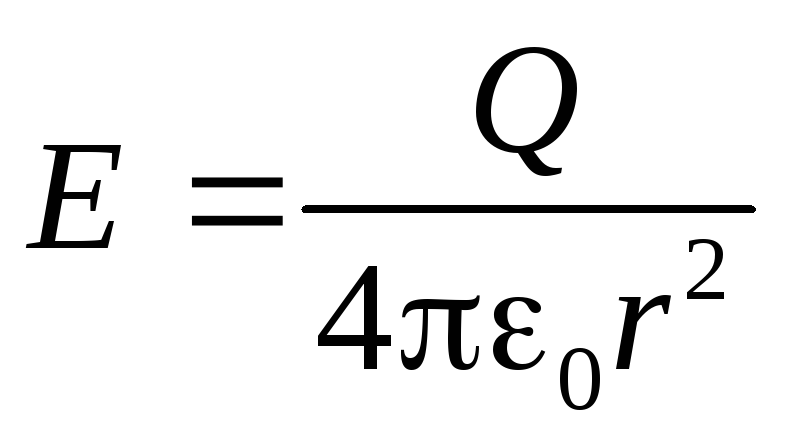 ,rR
,rR
Объёмная плотность энергии такого поля
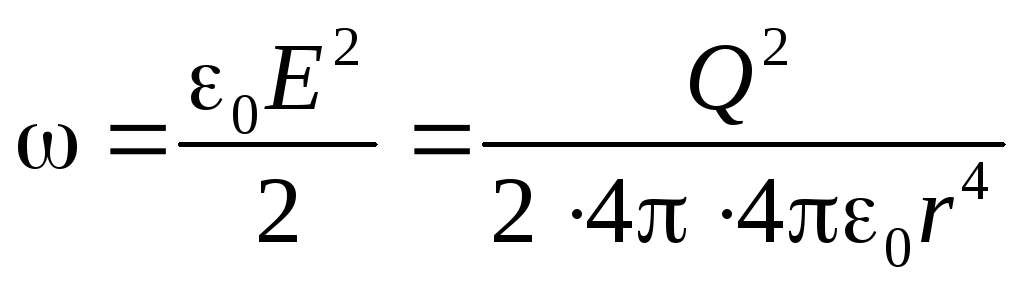
Вычислим энергию, сосредоточенную в сферическом слое толщиной dr(рис. 4.13.)
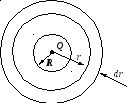
Рис. 4.13.
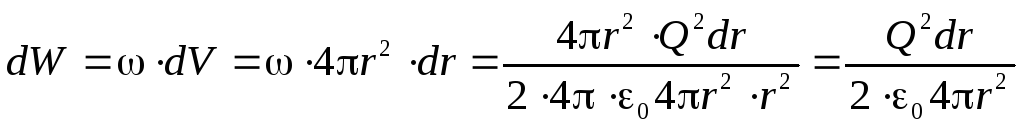
Теперь просуммируем энергии всех слоёв от Rдо

Вспомним, что 40R=с— ёмкость шара (см. 4.4.), а — его потенциал. Тогда:
— его потенциал. Тогда:
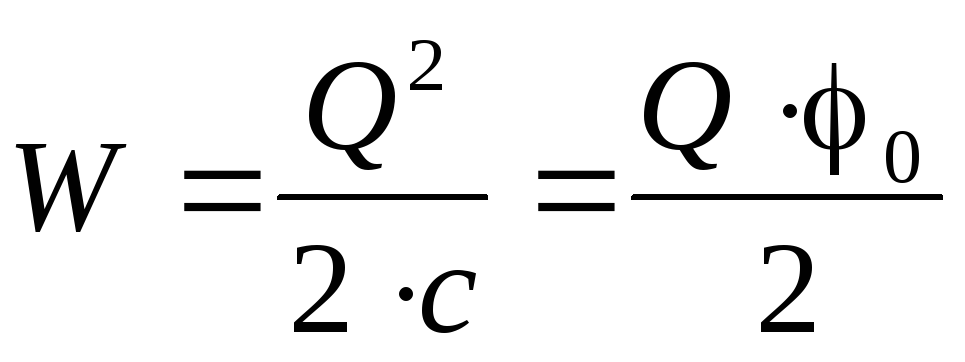 .
(4.15)
.
(4.15)
Эта энергия поля равна работе, которая
была совершена при зарядке шара до
потенциала 0= .
Покажем это.
.
Покажем это.
Начнем заряжать шар, перенося на него
из бесконечности электрические заряды
малыми порциями dq.
Если в некоторый момент времени заряд
шара окажется равнымq,
а его потенциал —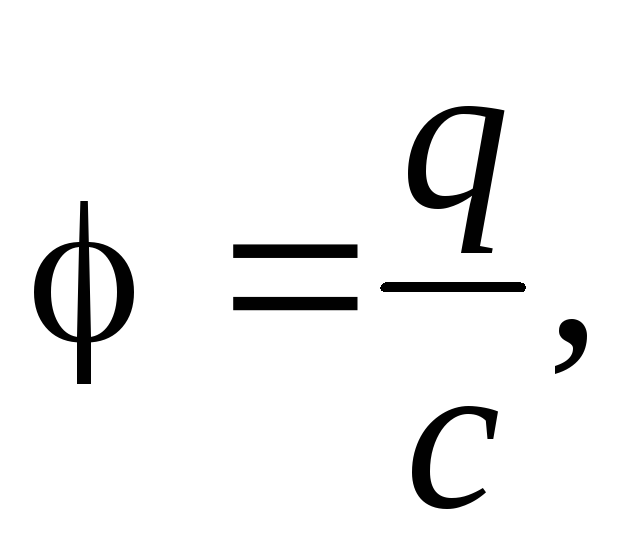 то при переносе следующей порции зарядаdqпридется совершить
работу против сил электрического поля
то при переносе следующей порции зарядаdqпридется совершить
работу против сил электрического поля
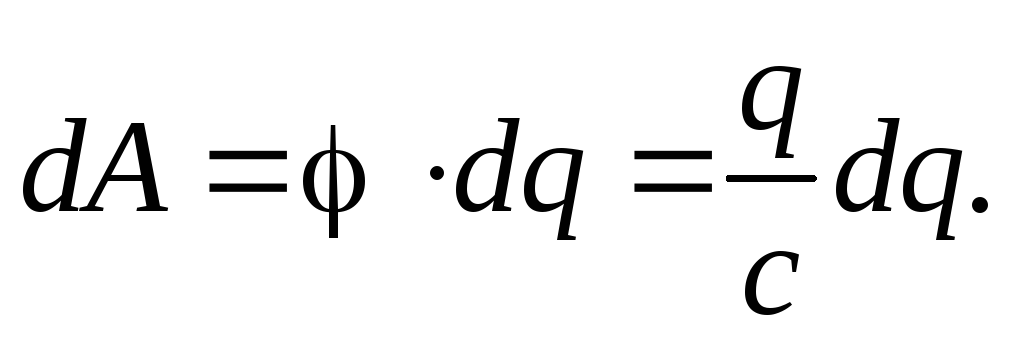
Теперь легко вычислить полную работу, которую необходимо проделать, чтобы передать первоначально незаряженному шару заряд Q:
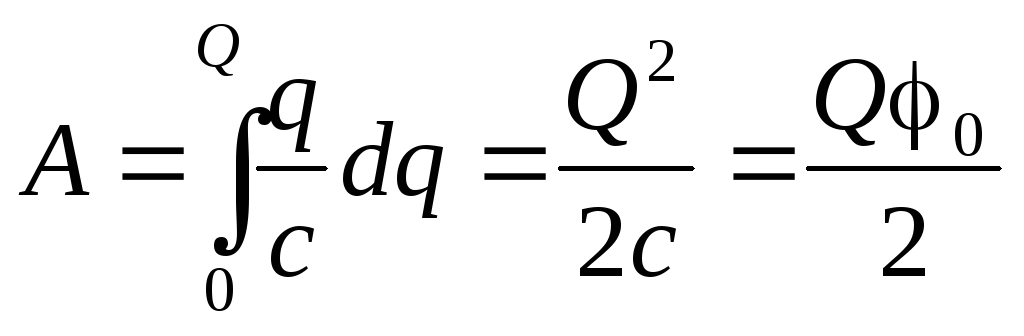
Эта работа, как и ожидалось, равна энергии электрического поля, созданного нами при зарядке шара (см. 4.15).
Материал презентаций по физике / Часть 2 / Лекция 5 / Лекция 5
8
Лекция 5
Проводники в электрическом поле
Вопросы
Проводники в электростатическом поле.
Электроемкость заряженного проводника. Конденсаторы.
Энергия заряженного проводника, конденсатора и электростатического поля.
1. Проводники в электростатическом поле
Проводником называется среда, в которой имеется достаточное число свободных электрических зарядов. Например, в металлах в 1 см3 содержится около 1023 свободных электронов. В диэлектриках свободных электронов менее 106 в 1 см3, а в хороших диэлектриках менее 103 в 1 см3.
Хорошими проводниками электрического тока являются не только металлы, но еще растворы электролитов и ионизованные газы.
Металлы имеют кристаллическую структуру. В узлах кристаллических решеток металлов находятся положительно заряженные ионы, а валентные электроны могут свободно передвигаться между ними в различных направлениях по всему объему. Совокупность свободных электронов в металле называют электронным газом.
 и
и 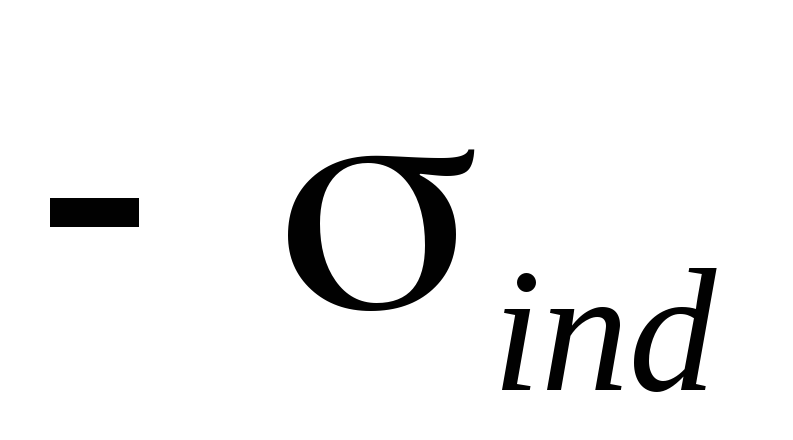 .
Электрическое поле индуцированных
зарядов компенсирует внешнее электрическое
поле, т.е.
.
Электрическое поле индуцированных
зарядов компенсирует внешнее электрическое
поле, т.е. 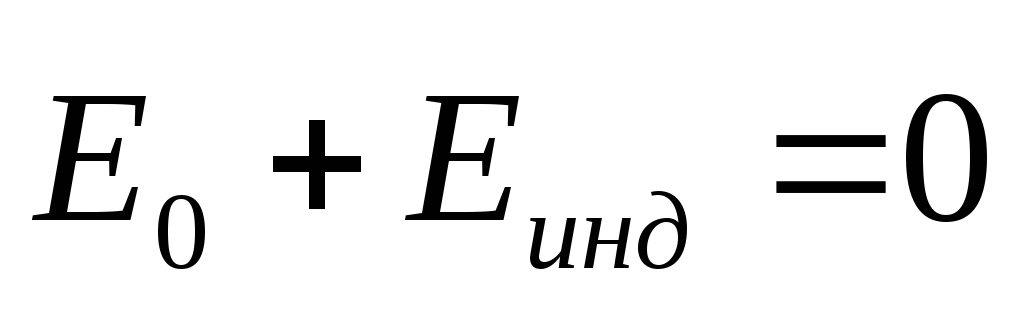 ,
т.к.
,
т.к. 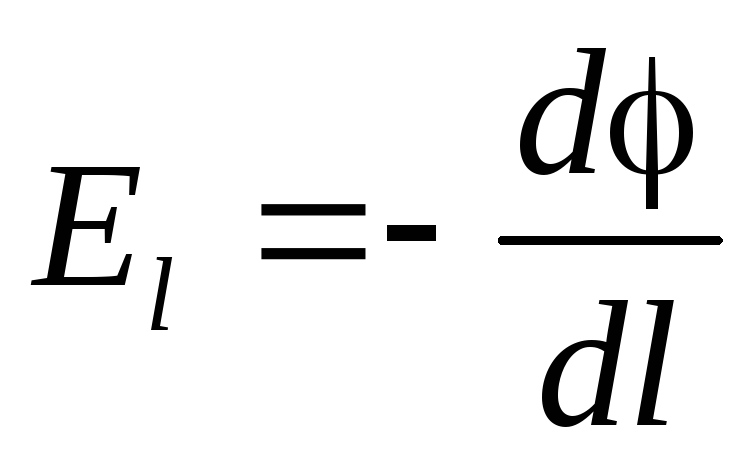 , то
, то 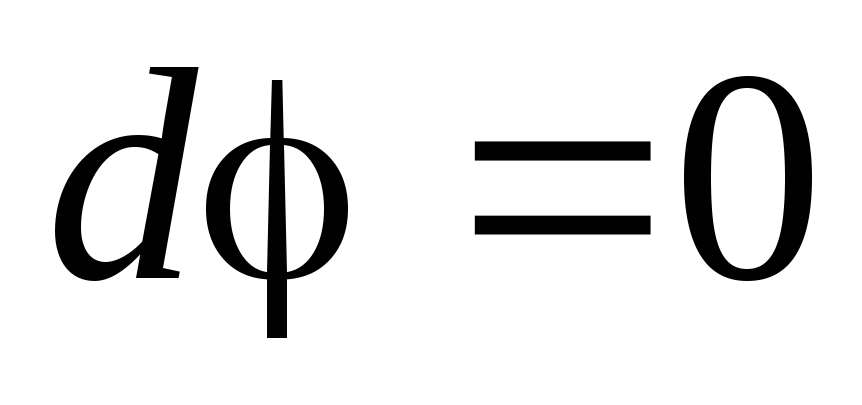
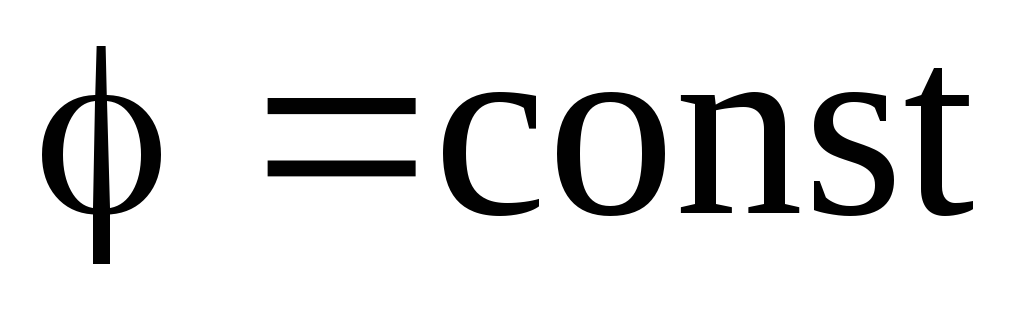 , (1)
, (1)
т.е. электростатическое поле внутри проводника отсутствует, а потенциал проводника является постоянным (проводник эквипотенциален).
У криволинейной поверхности проводника
силовая линия напряженности
электростатического поля должна быть
направлена по нормали к этой поверхности,
иначе под действием тангенциальной
составляющей поля 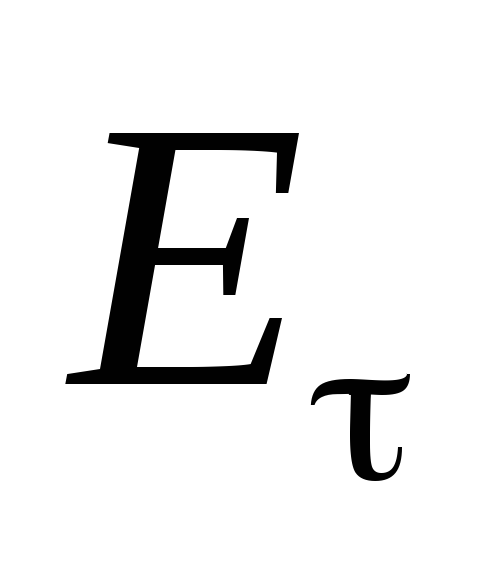 заряды перемещались бы по проводнику,
что противоречит условию (1).
заряды перемещались бы по проводнику,
что противоречит условию (1).
В заряженном проводнике избыточный заряд располагается только на поверхности, т.к. согласно теореме Гаусса для замкнутой области S внутри проводника заряд отсутствует.
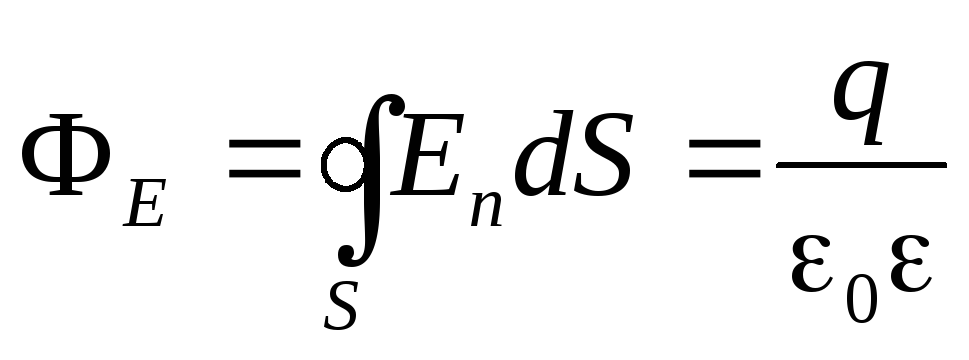

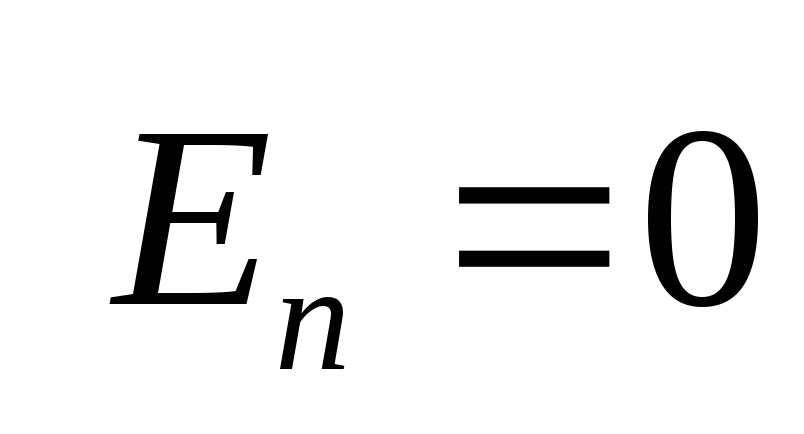

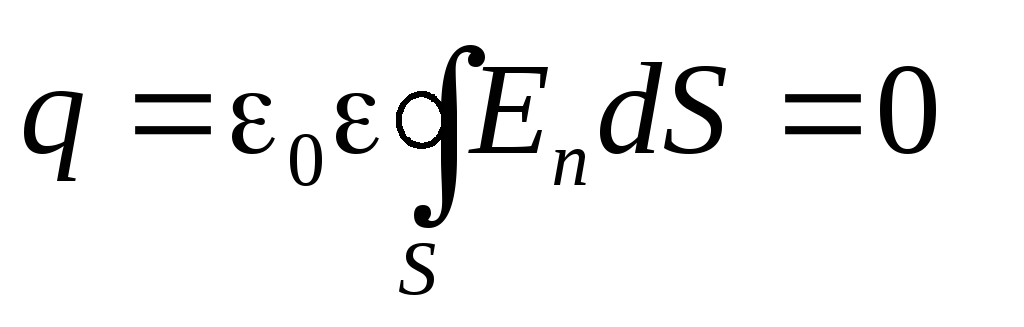 .
(2)
.
(2)
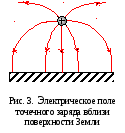
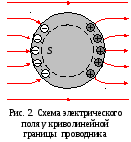
Пример. Точечный заряд у поверхности Земли. Поскольку силовые линии перпендикулярны эквипотенциальным поверхностям, электрическое поле вблизи проводника должно быть нормально к его поверхности. (Это понятно, так как если бы поле имело касательную составляющую, то электроны двигались бы вдоль поверхности проводника). В качестве примера на рис. 3 показано электрическое поле точечного заряда вблизи поверхности Земли (Земля – проводник).
Электростатическая индукция
При внесении незаряженного проводника в электростатическое поле носители зарядов приходят в движение. Перераспределение идет до тех пор, пока внутри проводника не будет Е=0, а на поверхности Е=Еn.
Явление, состоящее в электризации незаряженного проводника во внешнем электростатическом поле путем разделения в этом проводнике уже имеющихся в нем в равных количествах положительных и отрицательных зарядов, называется электризацией через влияние или электростатической индукцией.
И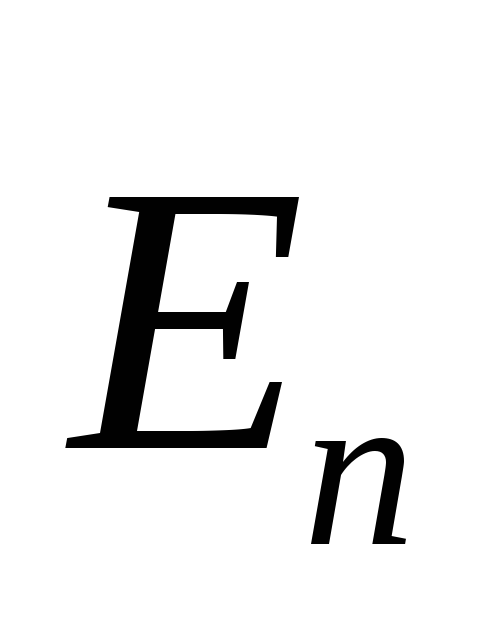
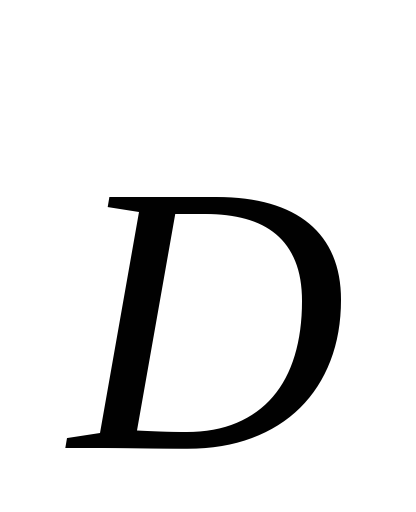 ндуцированные
заряды появляются на проводнике
вследствие смещения их под действием
поля. При замыкании концов проводника
с разноименными зарядами может появиться
ток смещения, поэтому вектор на
поверхности проводника называется
вектором электрического смещения .
ндуцированные
заряды появляются на проводнике
вследствие смещения их под действием
поля. При замыкании концов проводника
с разноименными зарядами может появиться
ток смещения, поэтому вектор на
поверхности проводника называется
вектором электрического смещения .
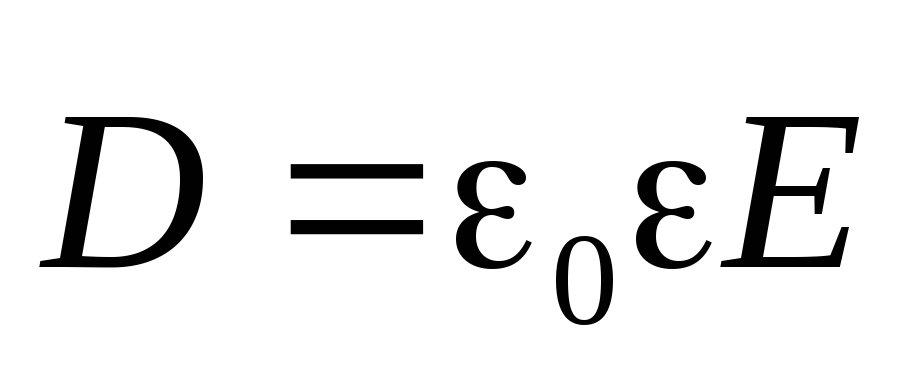 .
(2)
.
(2)
Электростатическая защита
Э лектростатическая
защита объектов (например, приборов)
от влияния внешних электростатических
полей основана на том, что заряды
располагаются на поверхности, а полость
в замкнутом проводнике не заряжена
(экранирована от
внешнего поля). Для электростатической
защиты можно использовать не сплошной
проводник, а металлическую сетку,
которую заземляют, т.е. соединяют с
нулевым потенциалом Земли.
лектростатическая
защита объектов (например, приборов)
от влияния внешних электростатических
полей основана на том, что заряды
располагаются на поверхности, а полость
в замкнутом проводнике не заряжена
(экранирована от
внешнего поля). Для электростатической
защиты можно использовать не сплошной
проводник, а металлическую сетку,
которую заземляют, т.е. соединяют с
нулевым потенциалом Земли.
Свойство зарядов располагаться на внешней поверхности используется в электростатических генераторах, применяемых в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.
2. Электроемкость заряженного проводника. Конденсаторы
Электроемкостью заряженного проводника называется скалярная физическая величина С, характеризующая способность проводника накапливать заряды и численно равная заряду, изменяющему потенциал проводника на один Вольт.
 , 1 Фарад = 1 Кулон / 1 Вольт
. (3)
, 1 Фарад = 1 Кулон / 1 Вольт
. (3)
Так как заряды в проводнике располагаются только на поверхности, то электроемкость не зависит от материала проводника, его агрегатного состояния, но зависит от формы и размеров.
Фарад – большая единица. Например, используя потенциал проводящей поверхностно заряженной сферы и формулу (3), получим
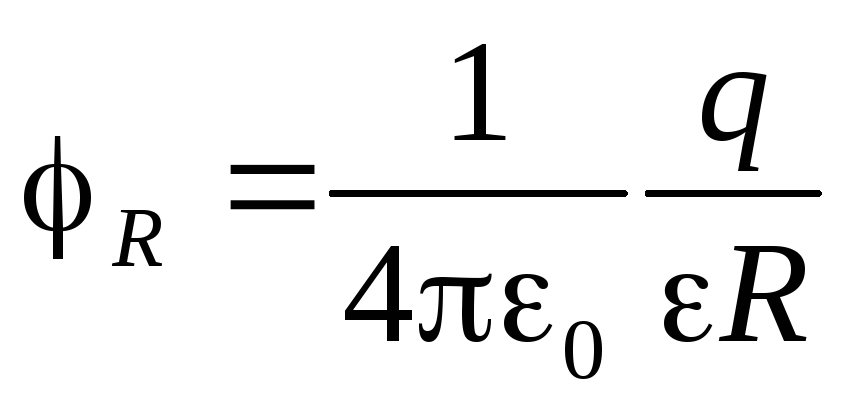


 ,
,
что в 1400 раз больше радиуса Земли. Электроемкость Земли — 711 мкФ.
Единицы измерения в технике:
1 мФ = 10-3Ф; 1 мкФ = 10-6Ф; 1 нФ = 10-9Ф; 1 пФ = 10-12Ф.
Конденсатором называется система из двух изолированных
друг от друга проводников. Эти проводники
обычно называют пластинами, хотя они
могут иметь любую форму. На практике
конденсаторы используются как «накопители
зарядов» или «резервуары», в которых
содержится энергия электрического
поля. Если на пластины поместить
одинаковые по величине, но противоположные
по знаку заряды  и
и 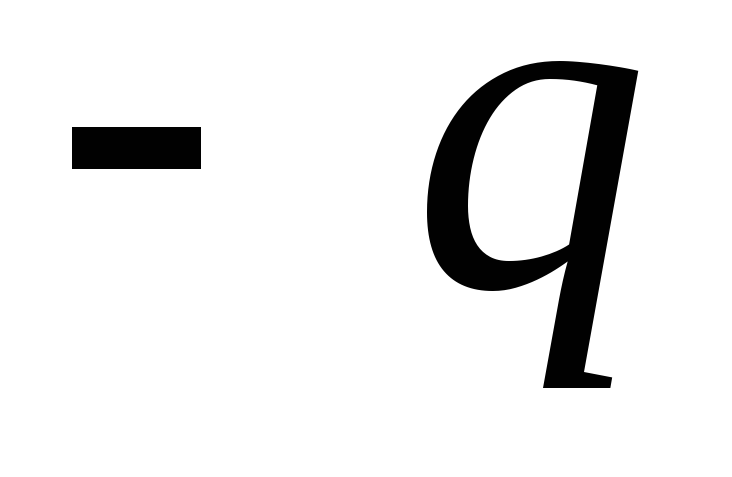 ,
то между пластинами возникнет разность
потенциалов
,
то между пластинами возникнет разность
потенциалов 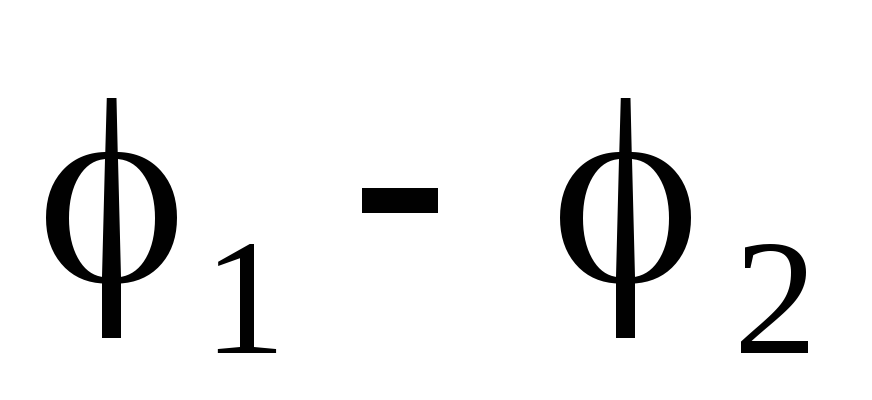 . Емкостью конденсатора называется величина:
. Емкостью конденсатора называется величина:
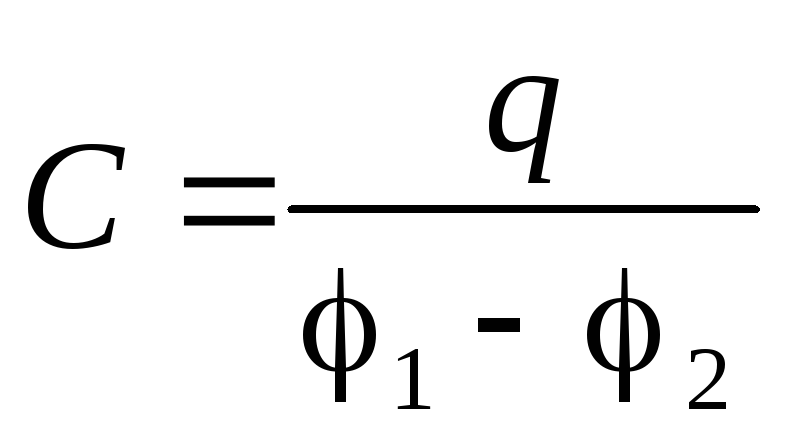 . (4)
. (4)
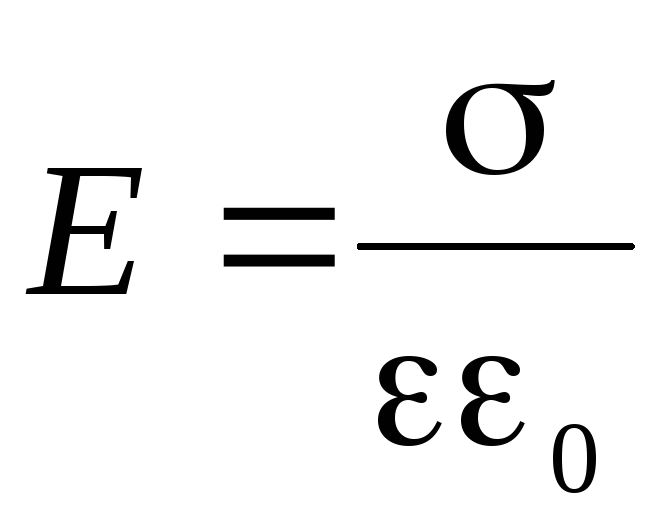 ;
; 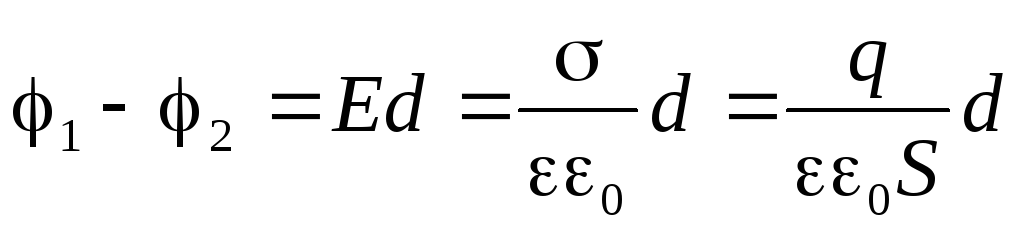 ;
;
, (5)
т.е. ёмкость конденсатора зависит только от его геометрических характеристик, вида диэлектрика между пластинами, и не зависит от сообщаемых ему зарядов.
Для того чтобы получить заданную емкость, можно использовать не один, а несколько конденсаторов. Систему из нескольких конденсаторов называют батареей конденсаторов. Емкостью батареи конденсаторов называется величина
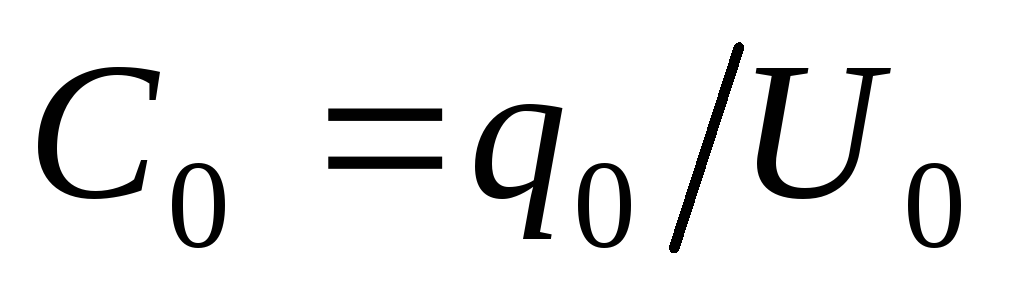 ,
,
где 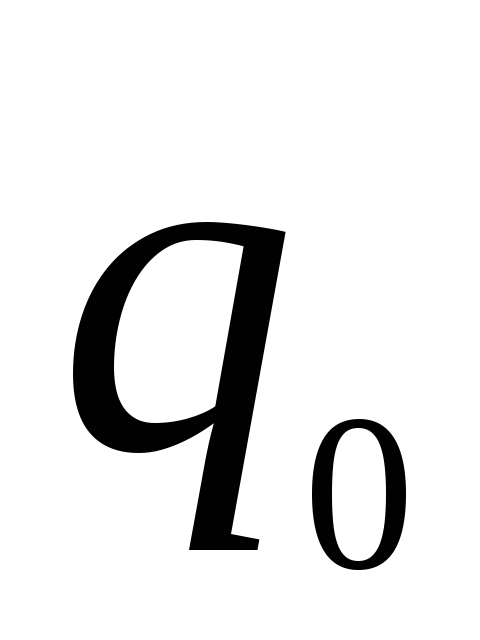 — полный заряд батареи, полученный от
источника, а
— полный заряд батареи, полученный от
источника, а 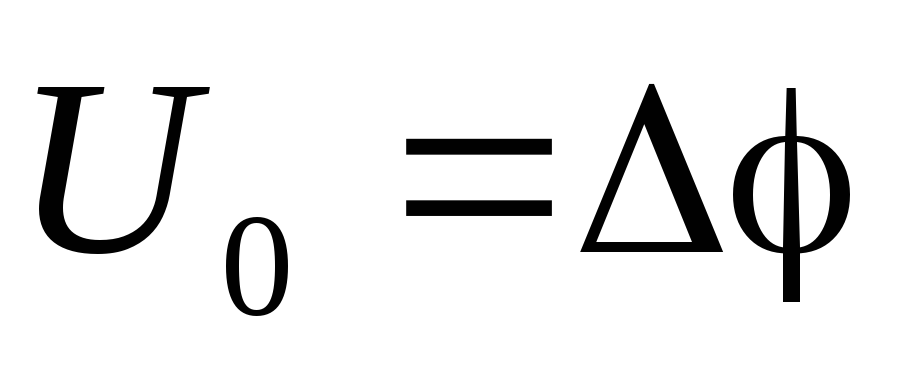 — напряжение, поданное на батарею
конденсаторов.
— напряжение, поданное на батарею
конденсаторов.
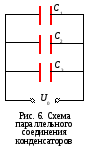
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов
между собой соединены все положительные
и отрицательные обкладки. В этом случае
все конденсаторы заряжаются до одной
и той же разности потенциалов 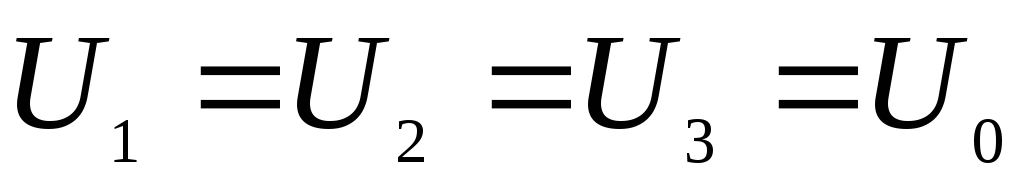 ,
общий заряд такой батареи:
,
общий заряд такой батареи:
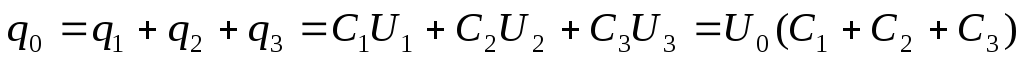
и, следовательно, емкость всей системы:
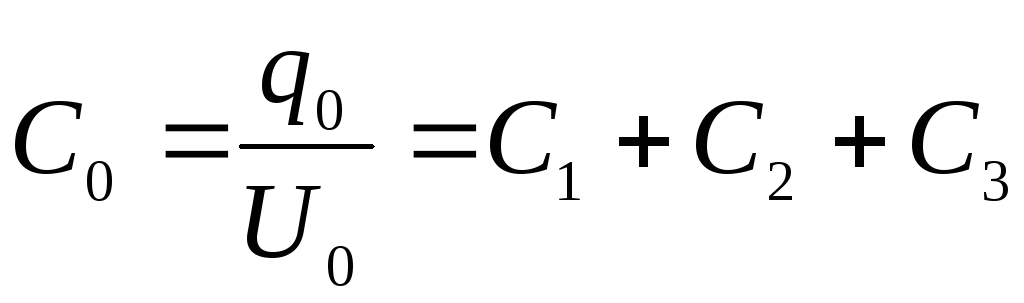

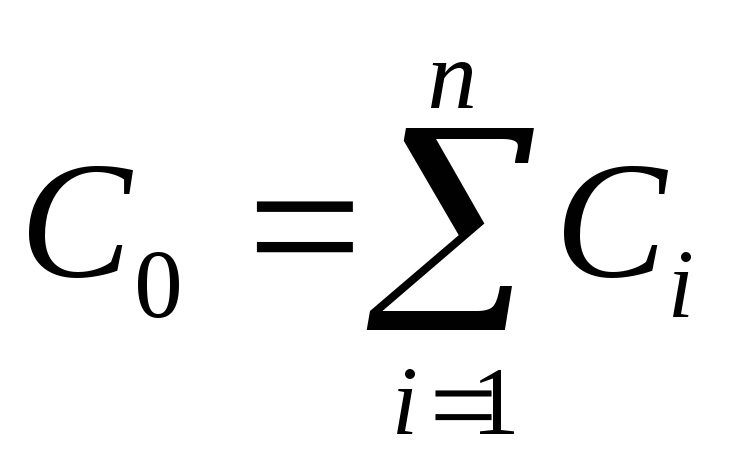 . (6)
. (6)
Ёмкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов. При С1 = С2 = С3 = 1 С0= 3.
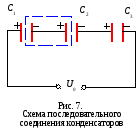
При последовательном соединении конденсаторов отрицательная обкладка первого конденсатора соединена с положительной обкладкой второго и т. д. В этом случае на всех конденсаторах заряды одинаковы:
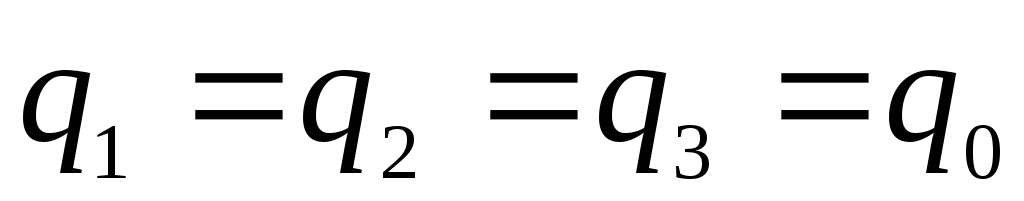 ,
,
а выделенная часть цепи нейтральна, так как она не соединена с источником напряжения.
Общее напряжение на батарее конденсаторов складывается из напряжений на каждом конденсаторе:
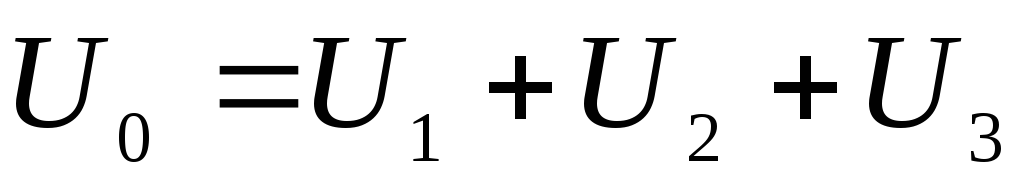

 .
.
Из-за равенства зарядов


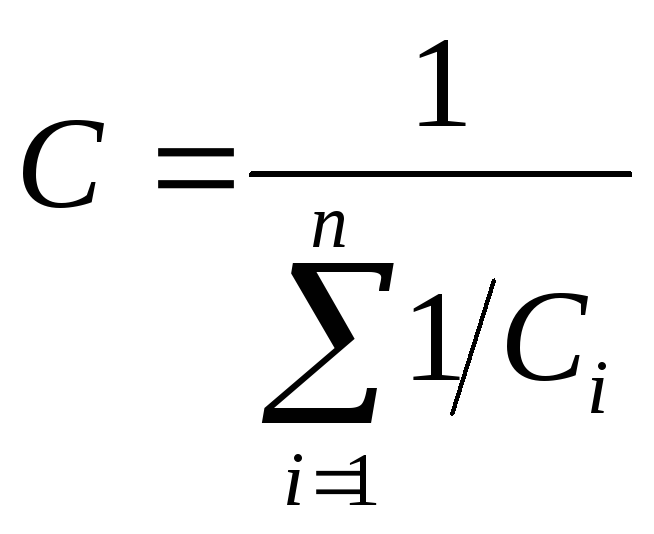 . (7)
. (7)
При С1 = С2 = С3 = 1 С0 = 1/3, т.е. ёмкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.
3. Энергия заряженного проводника, конденсатора
и электростатического поля
Для зарядки проводника нужно совершить работу против сил кулоновского отталкивания одноименных зарядов.
Если незаряженному проводнику сообщать
заряд малыми порциями dq,
переносимыми из бесконечности, где
0=0. По мере
зарядки проводника ёмкостью 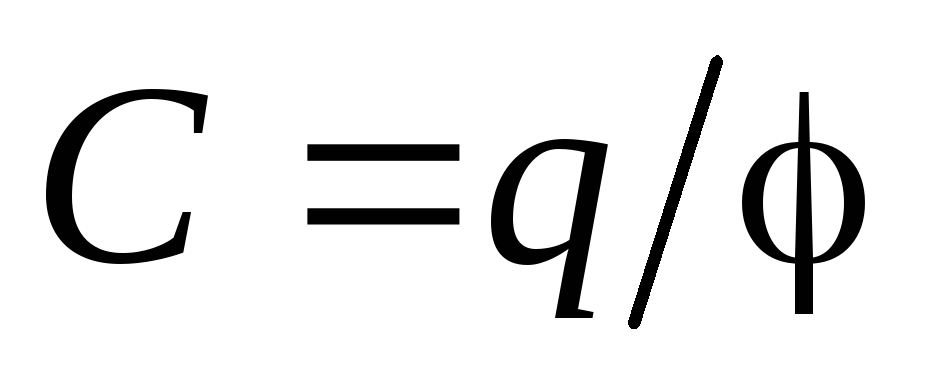 его потенциал возрастает
его потенциал возрастает


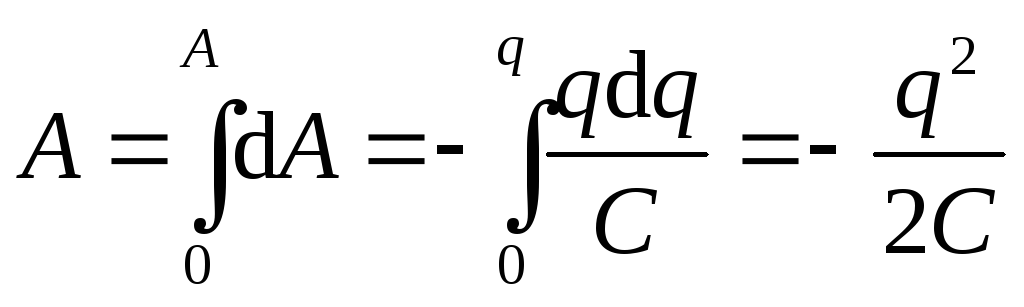 .
.
Энергия заряженного проводника равна совершенной работе
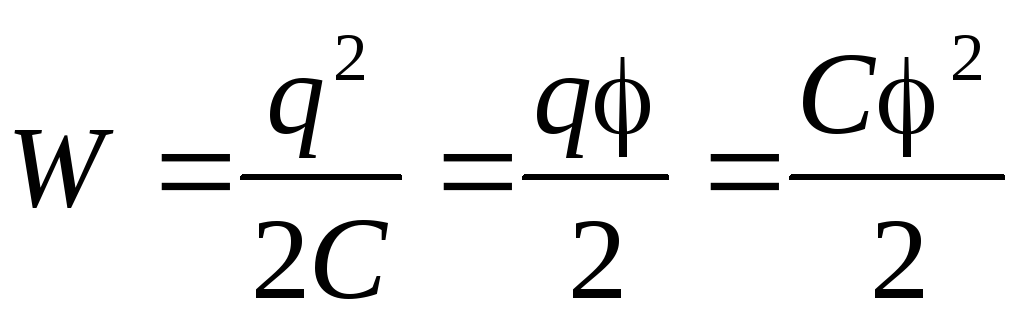 . (8)
. (8)
При зарядке конденсатора малыми
порциями 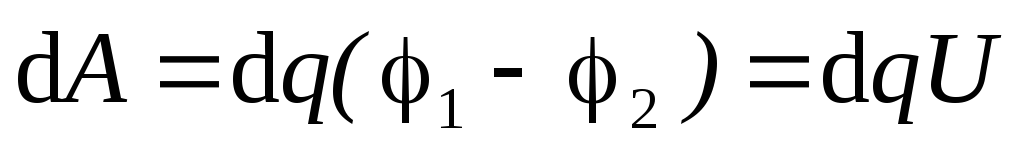 по аналогии с зарядкой проводника имеем
энергию заряженного конденсатора
по аналогии с зарядкой проводника имеем
энергию заряженного конденсатора
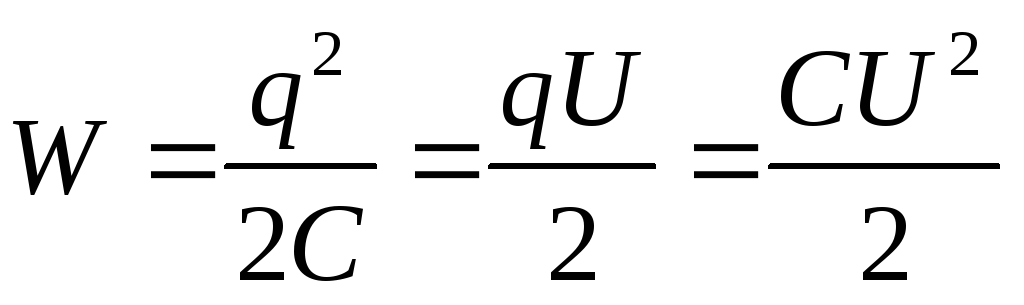 . (9)
. (9)
Используя формулу (9), можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. При изменении расстояния x между пластинами эта сила совершает работу

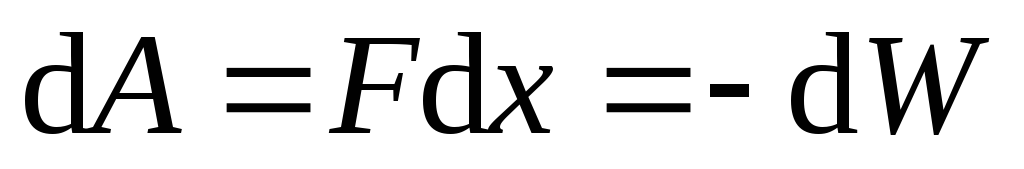

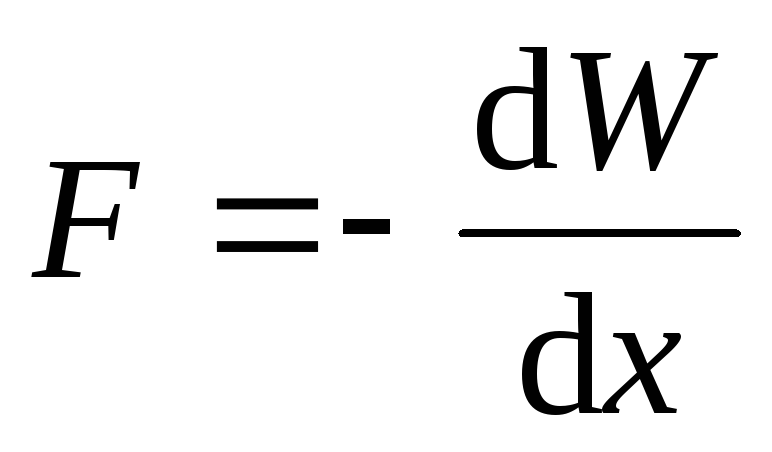


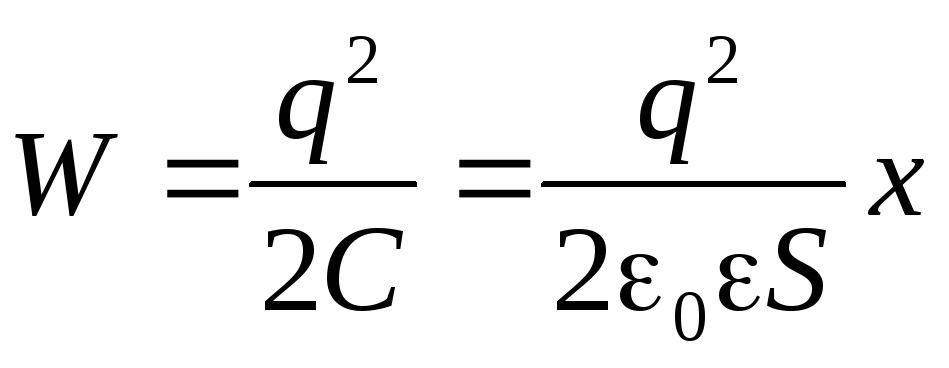
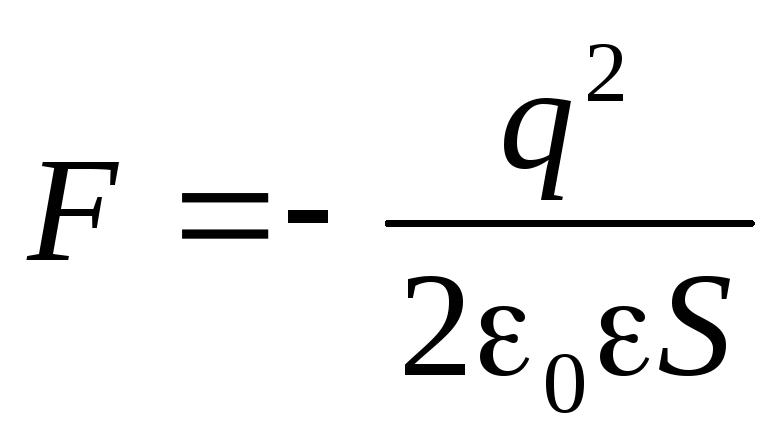 .
.
Выразим энергию (9) через характеристики электростатического поля
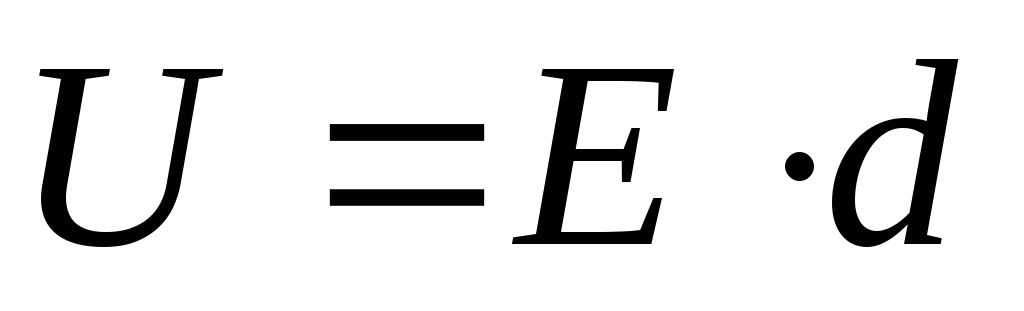 ,
, 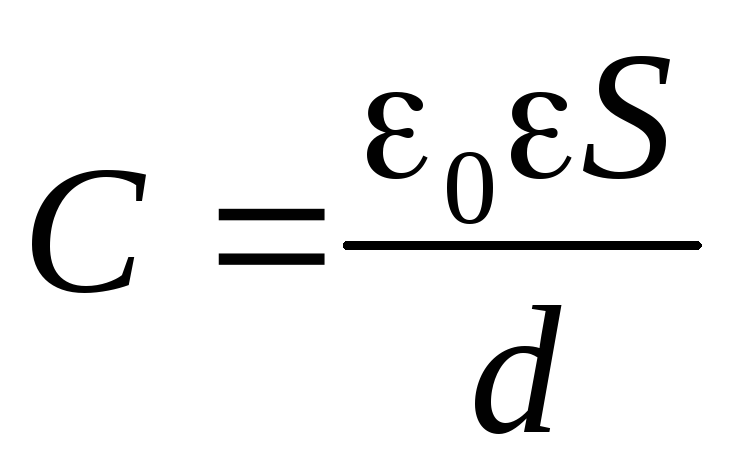 ,
,
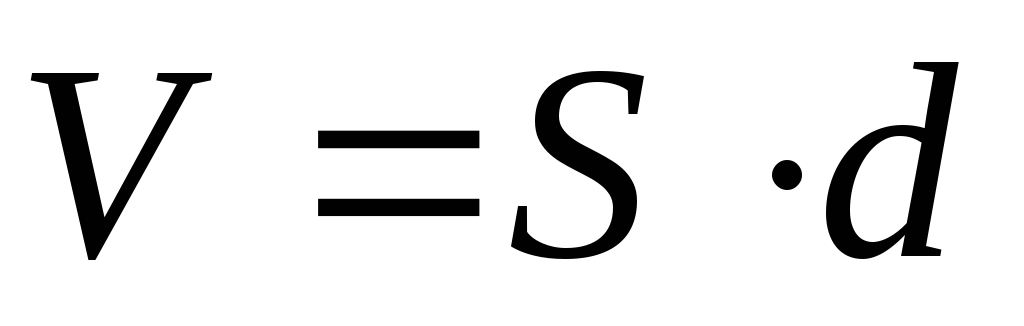 — объём между обкладками конденсатора.
— объём между обкладками конденсатора.
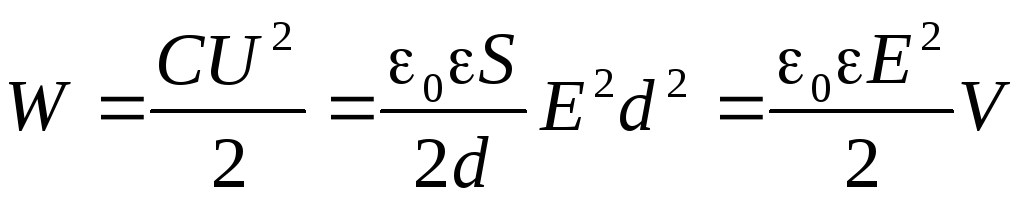

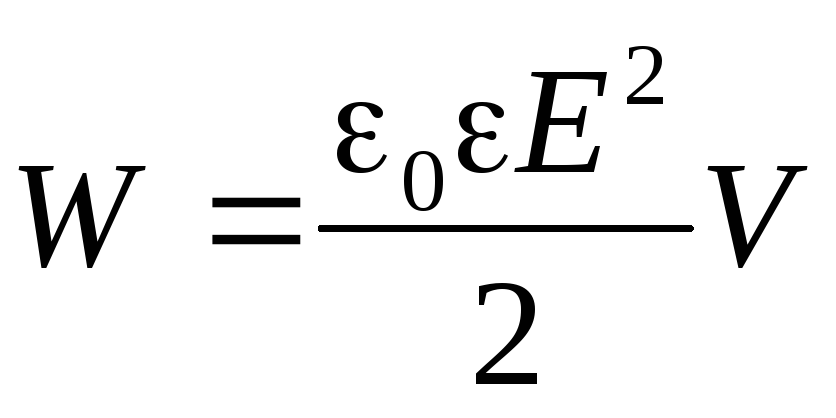 . (10)
. (10)
Объёмная плотность энергии
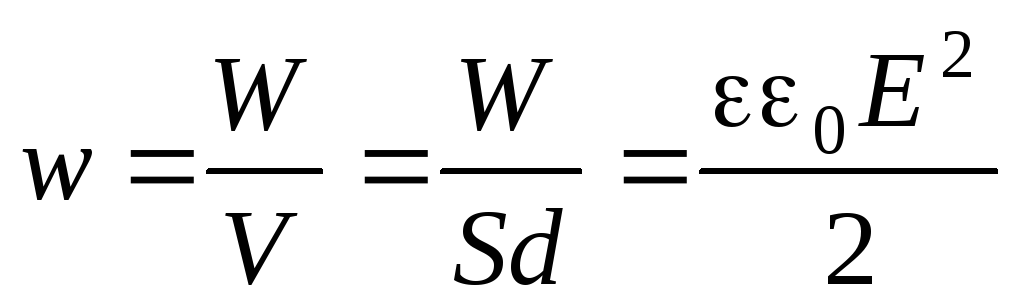 .
.
Используя связь (2) между напряженностью
электрического поля  и вектором электрического смещения
и вектором электрического смещения  полученный результат можно записать
так:
полученный результат можно записать
так:
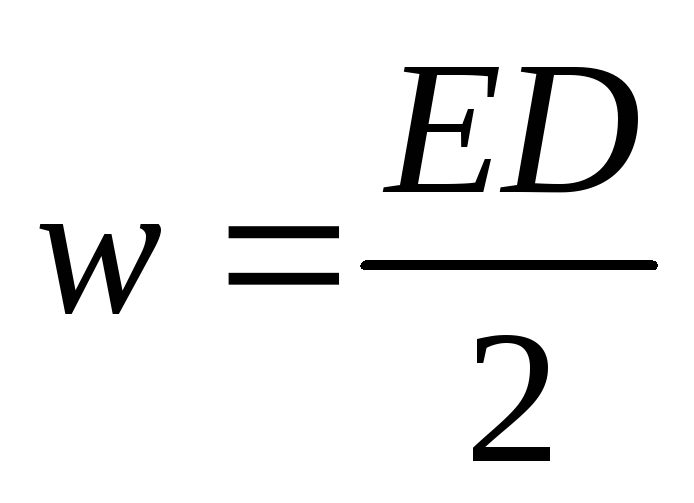 .
(11)
.
(11)
Объемная плотность энергии конденсатора уже не зависит от каких-либо его геометрических характеристик. Она выражается лишь через характеристики электрического поля конденсатора. Таким образом, энергия конденсатора – это энергия электрического поля, заключенного между его обкладками.
Выражение (11) для плотности электрического поля в какой-либо точке пространства, доказанное нами в случае электрического поля конденсатора, является универсальным. В общем случае энергия неоднородного электрического поля, заключенная в некотором объеме V, рассчитывается через объемный интеграл:
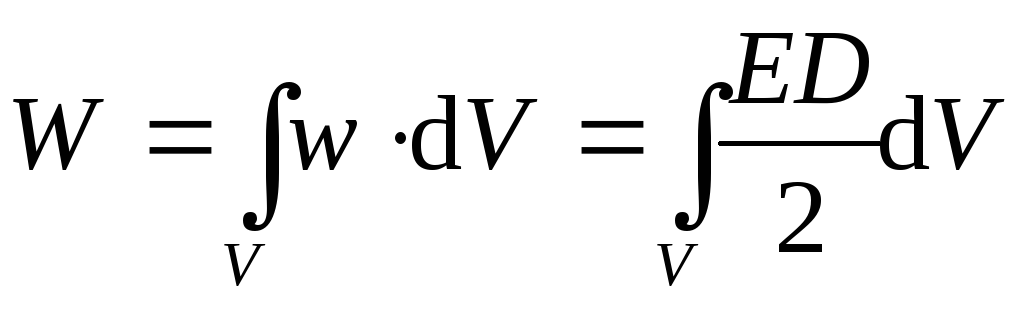 ,
(12)
,
(12)
т.е. носителем энергии является электростатическое поле.
1. Электрическое поле и конденсатор | 12. Конденсаторы | Часть1
1. Электрическое поле и конденсатор
Электрическое поле и конденсатор
Если к двум отдельным проводам приложить напряжение, то в пределах пространства между ними возникнет электрическое поле. До этого момента мы с вами изучали взаимодействие тока, напряжения и сопротивления в пределах электрических цепей, которые служат проводящими путями для потока электронов. Теперь, когда мы говорим о полях, мы имеем дело с взаимодействиями, происходящими в пространстве.
Понятие «поле» несколько абстрактно. Если электрический ток представить себе не так уж сложно (крошечные частицы, называемые электронами, передвигаются между ядрами атомов внутри проводника), то с полем дела обстоят совершенно иначе.
Несмотря на абстрактный характер полей, каждый из вас не раз с ними сталкивался, по крайней мере в виде магнитов. Если вы когда-нибудь играли с парой магнитов, то не могли не заметить, что они притягиваются или отталкиваются друг от друга в зависимости от относительной ориентации. Между двумя магнитами существует неоспоримая сила, и сила эта нематериальна. Она не имеет ни массы, ни цвета, ни запаха, и проявляется только на самих магнитах, совершенно не действуя на человеческое тело. Физики описывают взаимодействие магнитов с точки зрения магнитных полей в пространстве между ними. Если возле магнита рассыпать металлические опилки, то они сориентируются вдоль линий поля, визуально указывая на его присутствие.
Темой данного раздела являются электрические поля (у которых много общего с магнитными), и устройства которые их используют — конденсаторы. С электрическими полями вы скорее всего тоже сталкивались. Вспомните самое начало нашего обучения, в котором мы рассматривали статическое электричество. Если воск и шерсть потереть дуг о друга, то между ними возникнет физическая сила притяжения. Физики описали бы такое взаимодействие с точки зрения электрических полей, создаваемых двумя объектами в результате дисбаланса электронов. Сейчас достаточно будет сказать, что при наличии напряжения между двумя точками, в пространстве между ними всегда проявится электрическое поле.
Электрическое поле обладает запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные тела. По значению силы, с которой притягивается или отталкивается некоторый электрический заряд, принятый за единицу, можно судить об интенсивности электрического поля. Сила и интенсивность поля примерно аналогичны напряжению (сила) и току (интенсивность) в электрической цепи. Однако, поле может существовать в совершенно пустом пространстве, в то время как ток существует только там, где есть свободные электроны. Характер среды пространства (тип изоляционного материала, расположенный между двумя проводниками) может оказывать сопротивление интенсивности поля точно так же, как материал проводника оказывает сопротивление электрическому току. Интенсивность, с которой поле распространяется в пространстве, пропорциональна его силе поделенной на сопротивление среды.
Обычно электроны не могут войти в провод, если не существует пути для выхода равного количества электронов. Вот почему, для создания потока электронов, провода объединяются в замкнутую электрическую цепь. Однако, существует возможность «втиснуть» дополнительные электроны в незамкнутый провод. Для этого рядом с ним нужно разместить еще один провод, что приведет к возникновению электрического поля. Количество дополнительных свободных электронов, вошедших в незамкнутый провод, будет прямо пропорционально напряженности данного поля.
Сущность этого явления используется в устройствах, называемых конденсаторами. Конденсаторы состоят из двух проводящих пластин (обычно металлических), расположенных в непосредственной близости дуг от друга. Существует большое количество разновидностей конденсаторов, предназначенных для выполнения различных задач. Для конденсаторов маленькой емкости достаточно двух круглых пластин, между которыми расположен диэлектрический материал. Для конденсаторов большой емкости «пластины» изготавливаются из свернутых полосок металлической фольги, между которыми проложен гибкий изолирующий материал. Наиболее высокие значения емкости получаются при использовании микроскопического слоя изолирующего оксида, разделяющего две проводящие поверхности. Несмотря на различия в конструктивном исполнении конденсаторов, в них заложена общая идея: два проводника разделены диэлектриком.
Условное обозначение конденсатора выглядит следующим образом:
При подаче напряжения на пластины конденсатора, между ними возникает электрическое поле, которое способствует образованию значительной разницы в количестве свободных электронов на каждой из пластин. Если говорить проще, то принцип действия конденсаторов основан на способности накапливать на обкладках электрические заряды при приложении между ними напряжения:
Поскольку электрическое поле создается приложенным напряжением, свободные электроны «забираются» у положительной пластины конденсатора и скапливаются на отрицательной. Эта разница зарядов приравнивается к хранению энергии в конденсаторе. Чем больше разница электронов на противоположных пластинах, тем больше интенсивность (напряженность) поля, и тем больший «заряд» энергии будет хранить конденсатор.
Поскольку конденсаторы хранят потенциальную энергию накопленных электронов в виде электрического поля, в цепи они ведут себя несколько иначе, чем резисторы (которые просто рассеивают энергию в виде тепла). Аккумулирование энергии в конденсаторе является функцией напряжения между его пластинами, а так же других факторов, которые мы рассмотрим позже. Способность конденсатора сохранять энергию в зависимости от приложенного напряжения приводит к тому, что он стремится поддерживать напряжение на постоянном уровне. Иными словами, конденсатор сопротивляется изменениям напряжения. Когда напряжение на конденсаторе увеличивается или уменьшается, он «сопротивляется» этим изменениям, забирая или отдавая ток источнику изменения напряжения.
Для сохранения в конденсаторе большей энергии, напряжение на его пластинах должно быть увеличено. Это приведет к тому, что больше электронов будет отнято от положительной (+) пластины и добавлено к отрицательной (-). Ток при этом должен течь от (-) к (+). И наоборот, для высвобождения энергии из конденсатора, напряжение на нем должно быть уменьшено. Это приведет к тому, что некоторые из избыточных электронов будут возвращены от отрицательной (-) пластины к положительной (+). Направление тока при этом изменится на противоположное.
Вспомните Первый закон Ньютона, который гласит что всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. С конденсаторами ситуация примерно аналогичная: «Заряженный конденсатор стремится оставаться заряженным, а разряженный имеет тенденцию оставаться разряженным». Гипотетически, при отсутствии внешнего воздействия заряженный конденсатор будет бесконечно долго сохранять накопленный заряд, который сможет изменить только внешний источник тока:
На практике же, благодаря внутренним путям утечки электронов из одной пластины в другую, конденсаторы со временем теряют сохраненный заряд. Это время зависит от конкретного типа конденсатора и может составлять несколько лет.
Когда напряжение на конденсаторе увеличивается, он начинает забирать ток у схемы, действуя в качестве нагрузки. В этом случае можно сказать что конденсатор «заряжается», поскольку большее количество энергии сохраняется в его электрическом поле. Обратите внимание на направление тока с учетом полярности напряжения:
И наоборот, когда напряжение на конденсаторе уменьшается, он отдает ток остальной части схемы, действуя в качестве источника питания. В этом случае можно сказать что конденсатор «разряжается». Его запас энергии, сохраненный в электрическом поле, уменьшается, а энергия отдается в схему:
Если к незаряженному конденсатору подключить источник питания (внезапное увеличение напряжения), то он будет потреблять ток из этого источника до тех пор, пока их напряжения не сравняются. Как только напряжение конденсатора сравнивается с напряжением источника питания, его ток становится равным нулю. И наоборот, если нагрузочное сопротивление подключить к заряженному конденсатору, то он будет поставлять ток этой нагрузке до тех пор, пока не истратит всю запасенную энергию, и его напряжение не упадет до нуля. Как только напряжение конденсатора достигает нулевого значения, ток через него прекращается. Благодаря своей способности заряжаться и разряжаться, конденсаторы можно рассматривать как вторичные источники питания.
Тип изоляционного материала между пластинами конденсатора, как уже отмечалось ранее, оказывает большое влияние на величину накапливаемого заряда при любом приложенном напряжении. Не все изоляционные (диэлектрические) материалы одинаковы. Величина, характеризующая реакцию диэлектрического материала на электрическое поле, называется диэлектрической проницаемостью.
Основной характеристикой конденсатора является его электрическая емкость. Емкость конденсатора характеризует количество электрической энергии, которую он способен запасти. Иными словами, чем больше электронов способен уместить в себе конденсатор, тем больше его емкость, и наоборот. В математических уравнениях емкость обозначается заглавной буквой «C» и измеряется в Фарадах (сокращенно — «ф»).



