Как найти напряжение в конденсаторе. Что такое конденсатор

ОПРЕДЕЛЕНИЕ

Емкость — один из основных параметров характеризующих конденсатор.

Если q — величина заряда одной из обкладок конденсатора, а — разность потенциалов между его обкладками, то величина C, равная:

называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.

Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():

где — диэлектрическая проницаемость диэлектрика.

За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).

Формула электрической емкости плоского конденсатора

Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:

где — электрическая постоянная; S — площадь каждой (или наименьшей) пластины; d — расстояние между пластинами.

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:

Формула электрической емкости цилиндрического конденсатора

Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:

где l — высота цилиндров; — радиус внешней обкладки; — радиус внутренней обкладки.

Формула электрической емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

где — радиусы обкладок конденсатора.

Примеры решения задач по теме «Емкость конденсатора»

ПРИМЕР 1

Задание	Какова электрическая емкость плоского двуслойного конденсатора? Один из слоев диэлектрика — фарфор с толщиной =2мм; второй слой — эбонит ( мм). Площадь пластин конденсатора равна 0,01 м 2 .
Решение	Для решения этой задачи проще всего применить формулу для расчета емкости слоистого плоского конденсатора, учитывая, что мы имеем всего два слоя:

Конденсатор — это элемент электрической цепи, способный, при небольшом размере, накапливать электрические заряды достаточно большой величины . Самой простой моделью конденсатора является два электрода, между которыми находится любой диэлектрик. Роль диэлектрика в нем выполняют бумага, воздух, слюда и другие изолирующие материалы, задача которых не допустить соприкосновения обкладок.

Свойства

Емкость . Это основное свойство конденсатора. Измеряется в Фарадах и вычисляется по следующей формуле (для плоского конденсатора):

где С, q, U — это соответственно емкость, заряд, напряжение между обкладками, S –площадь обкладок, d – расстояние между ними, — диэлектрическая проницаемость, — диэлектрическая постоянная, равная 8,854*10^-12 Ф/м..

Полярность конденсатора ;

Номинальное напряжение ;

Удельная емкость и другие .

Величина емкости конденсатора зависит от

Площадь пластин . Это понятно из формулы: емкость прямо пропорциональна заряду. Естественно, увеличив площадь обкладок, получаем большее количество заряда.

Расстояния между обкладками . Чем они ближе расположены, тем больше напряженность получаемого электрического поля.

Устройство конденсатора

Наиболее распространенные конденсаторы — это плоские и цилиндрические. Плоские состоят из пластин, удаленных друг от
друга на небольшое расстояние. Цилиндрические, собираются при помощи цилиндров равной длины и разного диаметра. Все конденсаторы, в принципе, устроены одинаково. Разница, в основном, в том, какой материал используется в качестве диэлектрика. По типу диэлектрической среды и классифицируют конденсаторы, которые бывают жидкими, вакуумными, твердыми, воздушными.

Как заряжается и разряжается конденсатор?

При подключении к источнику постоянного тока, обкладки конденсатора заряжаются, одна приобретает положительный потенциал, а другая отрицательный. Между обкладками противоположные по знаку, но равные по значению, электрические заряды создают электрическое поле. Когда напряжения станут одинаковыми и на обкладках, и на источнике подаваемого тока, движение электронов прекратится и зарядка конденсатора закончится. Определенный промежуток времени конденсатор сохраняет заряды и выполняет функции автономного источника электроэнергии. В таком состоянии он может находиться достаточно долгое время. Если вместо источника, включить в цепь резистор, то конденсатор разрядится на него.

Процессы, происходящие в конденсаторе

При подключении прибора к переменному или постоянному току в нем будут происходить разные процессы. Постоянный ток не пойдет по цепи с конденсатором. Так как между его обкладками находится диэлектрик, цепь фактически разомкнута.

Переменный ток , за счет того что периодически меняет направление, может проходить через конденсатор. При этом происходит периодический разряд и заряд конденсатора. На протяжении первой четверти периода заряд идет до максимума, в нем запасается электроэнергия, в следующую четверть конденсатор разряжается и электрическая энергия возвращается обратно в сеть. В цепи переменного тока, конденсатор обладает кроме активного сопротивления, еще и реактивной составляющей. Кроме того, в конденсаторе, ток опережает напряжение на 90 градусов, это важно учитывать, при построении векторных диаграмм .

Применение

Конденсаторы используются в радиотехнике, электронике, автоматике. Конденсатор –незаменимый элемент, который применяется во многих отраслях электротехники, на предприятиях, в научных разработках. Как пример, при необходимости, выступает в качестве разделителя токов: переменного и постоянного, применяется в конденсаторных установках, если необходимо компенсировать реактивную мощность , применяется как накопитель электричества в электросетях.

Емкость C есть способность конденсатора принять (накопить и удержать) количество электричества Q в ампер-секундах или заряд Q в кулонах. Если сообщить какому-либо телу, например шару, электрический заряд (количество электричества) Q, то электроскоп, включенный между этим телом и землей, покажет напряжение U (рис. 1). Это напряжение пропорционально заряду и зависит также от формы и размеров тела.

Конденсатор: формулы для конденсаторов

Содержание:

1. Формула емкости конденсатора
2. Формула энергии конденсатора
3. Формула заряда конденсатора
4. Формула тока утечки конденсатора

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов емкости плоского конденсатора используется формула:
в которой ε₀ = 8,854187817 х 10^-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде:

W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU²/2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U_c = E.

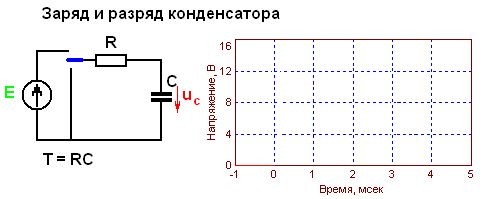
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I

ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.

Электрический конденсатор — Википедия

Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик Слева — конденсаторы для поверхностного монтажа; справа — конденсаторы для объёмного монтажа; сверху — керамические; снизу — электролитические. На танталовых конденсаторах (слева) полоской обозначен «+», на алюминиевых (справа) маркируют «-». SMD-конденсатор на плате, макрофотография Различные конденсаторы для объёмного монтажа

Конденса́тор (от лат. condensare — «уплотнять», «сгущать» или от лат. condensatio — «накопление») — двухполюсник с постоянным или переменным значением ёмкости^[1] и малой проводимостью; устройство для накопления заряда и энергии электрического поля.

Конденсатор является пассивным электронным компонентом. Ёмкость конденсатора измеряется в фарадах.

В 1745 году в Лейдене немецкий каноник Эвальд Юрген фон Клейст и независимо от него голландский физик Питер ван Мушенбрук изобрели конструкцию-прототип электрического конденсатора — «лейденскую банку»^[2]. Первые конденсаторы, состоящие из двух проводников, разделенных непроводником (диэлектриком), упоминаемые обычно как конденсатор Эпинуса или электрический лист, были созданы ещё раньше^[3].

Конденсатор является пассивным электронным компонентом^[4]. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).

Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит зарядка или перезарядка конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.

В методе гидравлических аналогий конденсатор — это гибкая мембрана, вставленная в трубу. Анимация демонстрирует мембрану, которая растягивается и сокращается под действием потока воды, что аналогично заряду и разряду конденсатора под действием электрического тока

С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом

Z^C=1jωC=−jωC=−j2πfC,{\displaystyle {\hat {Z}}_{C}={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}=-{\frac {j}{2\pi fC}},}

где j{\displaystyle j} — мнимая единица, ω{\displaystyle \omega } — циклическая частота (радиан/с) протекающего синусоидального тока, f{\displaystyle f} — частота в герцах, C{\displaystyle C} — ёмкость конденсатора (фарад). Отсюда также следует, что реактивное сопротивление конденсатора равно XC=1ωC.{\displaystyle \scriptstyle X_{C}={\tfrac {1}{\omega C}}.} Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).

При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью C{\displaystyle C}, собственной индуктивностью Lc{\displaystyle L_{c}} и сопротивлением потерь Rn{\displaystyle R_{n}}.

Резонансная частота конденсатора равна

fp=12πLcC{\displaystyle f_{p}={\frac {1}{2\pi {\sqrt {L_{c}C}}}}}

При f>fp{\displaystyle f>f_{p}} конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f<fp{\displaystyle f<f_{p}}, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.

Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:

W=CU22=qU2=q22C{\displaystyle W={CU^{2} \over 2}={qU \over 2}={q^{2} \over 2C}}

где U{\displaystyle U} — напряжение (разность потенциалов), до которого заряжен конденсатор, q{\displaystyle q} — электрический заряд на одной из обкладок.

Обозначение конденсаторов на схемах[править | править код]

В России для условных графических обозначений конденсаторов на схемах рекомендуется использовать ГОСТ 2.728-74^[5] либо стандарт международной ассоциации IEEE 315—1975:

На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 1·10⁶ пФ = 1·10⁻⁶ Ф) и пикофарадах (1 пФ = 1·10⁻¹² Ф), но нередко и в нанофарадах (1 нФ = 1·10⁻⁹ Ф). При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения. Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мкФ × 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10—180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, то есть на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.

Характеристики[править | править код]

Ёмкость[править | править код]

Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.

Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга, в системе СИ выражается формулой C=εε0Sd{\displaystyle C={\tfrac {\varepsilon \varepsilon _{0}S}{d}}}, где ε{\displaystyle \varepsilon } — диэлектрическая проницаемость среды, заполняющая пространство между пластинами (в вакууме равна единице), ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная, численно равная 8,854187817⋅10⁻¹² Ф/м. Эта формула справедлива, лишь когда d намного меньше линейных размеров пластин.

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

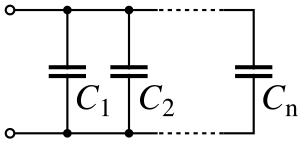
C=∑i=1nCi{\displaystyle C=\sum _{i=1}^{n}C_{i}} или C=C1+C2+…+Cn.{\displaystyle C=C_{1}+C_{2}+\ldots +C_{n}.}

Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.

При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна

1C=∑i=1n1Ci⇒C=(∑i=1n1Ci)−1{\displaystyle {\tfrac {1}{C}}=\sum _{i=1}^{n}{\tfrac {1}{C_{i}}}\Rightarrow C={\begin{pmatrix}\sum _{i=1}^{n}{\tfrac {1}{C_{i}}}\end{pmatrix}}^{-1}} или 1C=1C1+1C2+…+1Cn.{\displaystyle {\tfrac {1}{C}}={\tfrac {1}{C_{1}}}+{\tfrac {1}{C_{2}}}+\ldots +{\tfrac {1}{C_{n}}}.}

Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.

Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.

Удельная ёмкость[править | править код]

Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.

Плотность энергии[править | править код]

Плотность энергии электролитического конденсатора зависит от конструктивного исполнения. Максимальная плотность достигается у больших конденсаторов, где масса корпуса невелика по сравнению с массой обкладок и электролита. Например, у конденсатора EPCOS B4345 с ёмкостью 12 000 мкФ, максимально допустимым напряжением 450 В и массой 1,9 кг плотность энергии при максимальном напряжении составляет 639 Дж/кг или 845 Дж/л. Особенно важен этот параметр при использовании конденсатора в качестве накопителя энергии, с последующим мгновенным её высвобождением, например, в пушке Гаусса.

Номинальное напряжение[править | править код]

Другой не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах.

Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. Эксплуатационное напряжение на конденсаторе должно быть не выше номинального.

Полярность[править | править код]

Современные конденсаторы, разрушившиеся без взрыва благодаря специальной разрывающейся конструкции верхней крышки. Разрушение возможно из-за нарушения режима эксплуатации (температуры, напряжения, полярности) или старения. Конденсаторы с разорванной крышкой практически неработоспособны и требуют замены, а если она просто вздувшаяся, но ещё не разорвана, то, скорее всего, скоро он выйдет из строя или сильно изменятся параметры, что сделает его использование невозможным.

Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.

Опасность разрушения (взрыва)[править | править код]

Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). В современных компьютерах перегрев конденсаторов — частая причина выхода их из строя вследствие близкого расположения с источниками тепла, например, рядом с радиатором охлаждения.

Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают вышибной предохранительный клапан или выполняют надсечку корпуса (часто её можно заметить в виде креста или в форме букв X, K или Т на торце цилиндрического корпуса, иногда, на больших конденсаторах, она покрыта пластиком). При повышении внутреннего давления вышибается пробка клапана или корпус разрушается по насечке, пары электролита выходят в виде едкого газа и, даже, брызг жидкости. При этом разрушение корпуса конденсатора происходит без взрыва, разбрасывания обкладок и сепаратора.

Взорвавшийся электролитический конденсатор на печатной плате жидкокристаллического монитора. Видны волокна бумажного сепаратора обкладок и развернувшиеся фольговые алюминиевые обкладки.

Старые электролитические конденсаторы выпускались в герметичных корпусах и в конструкции их корпусов не предусматривалась взрывобезопасность. Скорость разлёта осколков при взрыве корпуса устаревших конденсаторов может быть достаточной для того, чтобы травмировать человека.

В отличие от электролитических, взрывоопасность оксиднополупроводниковых (танталовых) конденсаторов связана с тем, что такой конденсатор фактически представляет собой взрывчатую смесь: в качестве горючего служит тантал, а в качестве окислителя — двуокись марганца, и оба этих компонента в конструкции конденсатора перемешаны в виде тонкого порошка. При пробое конденсатора или при его случайной переполюсовке выделившееся при протекании тока тепло инициирует реакцию между данными компонентами, протекающую в виде сильной вспышки с хлопком, что сопровождается разбрасыванием искр и осколков корпуса. Сила такого взрыва довольно велика, особенно у крупных конденсаторов, и способна повредить не только соседние радиоэлементы, но и плату. При тесном расположении нескольких конденсаторов возможен прожог корпусов соседних конденсаторов, что приводит к одновременному взрыву всей группы.

Паразитные параметры[править | править код]

Реальные конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлением и индуктивностью. С достаточной для практики точностью, эквивалентную схему реального конденсатора можно представить как показано на рисунке, где все двухполюсники подразумеваются идеальными.

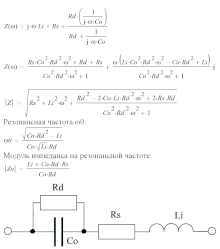Эквивалентная схема реального конденсатора и некоторые формулы.
C₀ — собственная ёмкость конденсатора;
R_d — сопротивление изоляции конденсатора;
R_s — эквивалентное последовательное сопротивление;
L_i — эквивалентная последовательная индуктивность. Зависимость модуля импеданса реального конденсатора от частоты и формула импеданса.

Электрическое сопротивление изоляции диэлектрика конденсатора, поверхностные утечки и саморазряд[править | править код]

Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением R_d = U / I_ут, где U — напряжение, приложенное к конденсатору, I_ут — ток утечки.

Из-за тока утечки, протекающего через слой диэлектрика между обкладками и по поверхности диэлектрика, предварительно заряженный конденсатор с течением времени теряет заряд (саморазряд конденсатора). Часто, в спецификациях на конденсаторы, сопротивление утечки определяют через постоянную времени T саморазряда конденсатора, которая численно равна произведению ёмкости на сопротивление утечки:

T=RdC0{\displaystyle T=R_{d}C_{0}}

T — время, за которое начальное напряжение на конденсаторе, неподключенном ко внешней цепи уменьшится в e раз.

Хорошие конденсаторы с полимерными и керамическими диэлектриками имеют постоянные времени саморазряда достигающие многих сотен тысяч часов.

Эквивалентное последовательное сопротивление — R_s[править | править код]

Эквивалентное последовательное сопротивление (англ. Equivalent series resistance; ESR, ЭПС, внутреннее сопротивление) обусловлено, главным образом, электрическим сопротивлением материала обкладок и выводов конденсатора и контактов между ними, а также учитывает потери в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор, вследствие поверхностного эффекта.

В большинстве практических случаев этим параметром можно пренебречь, но, иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания), достаточно малое его значение существенно для надёжности и устойчивости работы устройства. В электролитических конденсаторах, где один из электродов является электролитом, этот параметр при эксплуатации со временем деградирует, вследствие испарения растворителя из жидкого электролита и изменения его химического состава, вызванного взаимодействием с металлическими обкладками, что происходит относительно быстро в низкокачественных изделиях («конденсаторная чума»^[en]).

Некоторые схемы (например, стабилизаторы напряжения) критичны к диапазону изменения ЭПС конденсаторов в своих цепях. Это связано с тем, что при проектировании таких устройств инженеры учитывают этот параметр в фазочастотной характеристике (ФЧХ) обратной связи стабилизатора. Существенное изменение со временем ЭПС применённых конденсаторов изменяет ФЧХ, что может привести к снижению запаса устойчивости контуров авторегулирования, и, даже, к самовозбуждению.

Существуют специальные приборы (ESR-метр (англ.)) для измерения этого достаточно важного параметра конденсатора, по которому можно часто определить пригодность его дальнейшего использования в определённых целях. Этот параметр, кроме собственно ёмкости (ёмкость — это основной параметр) — часто имеет решающее значение в исследовании состояния старого конденсатора и принятия решения, стоит ли использовать его в определённой схеме, или он прогнозируемо выйдет за пределы допустимых отклонений.

Эквивалентная последовательная индуктивность — L_i[править | править код]

Эквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. Результатом этой распределенной паразитной индуктивности является превращение конденсатора в колебательный контур с характерной собственной частотой резонанса. Эта частота может быть измерена и обычно указывается в параметрах конденсатора либо в явном виде либо в виде рекомендованной максимальной рабочей частоты.

Саморазряд[править | править код]

Предварительно заряженный конденсатор с течением времени теряет запасённую энергию за счёт тока утечки, протекающего через слой диэлектрика между обкладками. Часто в справочниках на конденсаторы приводится постоянная времени саморазряда конденсатора, численно равная произведению ёмкости на сопротивление утечки. Это время, за которое начальное напряжение на отключенном конденсаторе уменьшится в e раз.

Тангенс угла диэлектрических потерь[править | править код]

Тангенс угла диэлектрических потерь — отношение мнимой и вещественной части комплексной диэлектрической проницаемости. tgδ=εimεre=σωεa.{\displaystyle {\rm {{tg}\,\delta ={\frac {\varepsilon _{im}}{\varepsilon _{re}}}={\frac {\sigma }{\omega \varepsilon _{a}}}.}}}

Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол φ=π2−δ,{\displaystyle \scriptstyle \varphi ={\tfrac {\pi }{2}}-\delta ,} где δ — угол диэлектрических потерь. При отсутствии потерь δ = 0. Тангенс угла потерь определяется отношением активной мощности P_а к реактивной P_р при синусоидальном напряжении определённой частоты. Величина, обратная tg δ, называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.

Температурный коэффициент ёмкости (ТКЕ)[править | править код]

ТКЕ — относительное изменение ёмкости при изменении температуры окружающей среды на один градус Цельсия (кельвин). ТКЕ определяется так:

TKE=ΔCCΔT{\displaystyle TKE={\frac {\Delta C}{C\Delta T}}}.

где ΔC{\displaystyle \Delta C} — изменение ёмкости, вызванное изменением температуры на ΔT{\displaystyle \Delta T}.
Таким образом, изменение ёмкости от температуры (при не слишком больших изменениях температуры) выражается линейной функцией:

C(T)=CH.y.+TKE⋅CH.y.⋅ΔT,{\displaystyle \scriptstyle C(T)=C_{H.y.}+TKE\cdot C_{H.y.}\cdot \Delta T,},

где ΔT{\displaystyle \Delta T} — изменение температуры в °C или К относительно нормальных условий, при которых специфицировано значение ёмкости, CH.y.{\displaystyle C_{H.y.}} — ёмкость при нормальных условиях. TKE применяется для характеристики конденсаторов с практически линейной зависимостью ёмкости от температуры. Однако ТКЕ указывается в спецификациях не для всех типов конденсаторов.

Для конденсаторов, имеющих существенно нелинейную зависимость ёмкости от температуры и для конденсаторов с большими изменениями ёмкости от воздействия температуры окружающей среды в спецификациях нормируются относительное изменение ёмкости в рабочем диапазоне температур или в виде графика зависимости ёмкости от температуры.

Диэлектрическая абсорбция[править | править код]

Если заряженный конденсатор быстро разрядить до нулевого напряжения путём подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то мы увидим, что напряжение на обкладках снова появится как если бы мы разрядили конденсатор не до нуля. Это явление получило название диэлектрическая абсорбция (диэлектрическое поглощение). Конденсатор ведёт себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора.

Подобный эффект можно наблюдать практически на всех типах диэлектриков. В электролитических конденсаторах он особенно ярок и является следствием химических реакций между электролитом и обкладками. У конденсаторов с твердым диэлектриком (например, керамических и слюдяных) эффект связан с остаточной поляризацией диэлектрика. Наименьшим диэлектрическим поглощением обладают конденсаторы с неполярными диэлектриками: тефлон (фторопласт), полистирол, полипропилен и т. п.

Эффект зависит от времени зарядки конденсатора, времени закорочения, иногда от температуры. Количественное значение абсорбции принято характеризовать коэффициентом абсорбции, который определяется в стандартных условиях.

Особое внимание в связи с эффектом следует уделять измерительным цепям постоянного тока: прецизионным интегрирующим усилителям, устройствам выборки-хранения, некоторым схемам на переключаемых конденсаторах.

Паразитный пьезоэффект[править | править код]

Многие керамические материалы, используемые в качестве диэлектрика в конденсаторах (например, титанат бария, обладающий очень высокой диэлектрической проницаемостью в не слишком сильных электрических полях) проявляют пьезоэффект — способность генерировать напряжение на обкладках при механических деформациях. Это характерно для конденсаторов с пьезоэлектрическими диэлектриками. Пьезоэффект ведёт к возникновению электрических помех, в устройствах, где использованы такие конденсаторы при воздействии акустического шума или вибрации на конденсатор. Это нежелательное явление иногда называют «микрофонным эффектом».

Также подобные диэлектрики проявляют и обратный пьезоэффект — при работе в цепи переменного напряжения происходит знакопеременная деформация диэлектрика, генерирующая акустические колебания, порождающие дополнительные электрические потери в конденсаторе.

Самовосстановление[править | править код]

Конденсаторы с металлизированным электродом (бумажный и пленочный диэлектрик) обладают важным свойством самовосстановления (англ. self-healing, cleaning) электрической прочности после пробоя диэлектрика. Механизм самовосстановления заключается в отгорании металлизации электрода после локального пробоя диэлектрика посредством микродугового электрического разряда.

Слюдяной герметичный конденсатор в металлостеклянном корпусе типа «СГМ» для навесного монтажа

Основная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др.

По виду диэлектрика различают:

• Конденсаторы вакуумные (между обкладками находится вакуум).
• Конденсаторы с газообразным диэлектриком.
• Конденсаторы с жидким диэлектриком.
• Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные (стеклоэмалевые, стеклокерамические, стеклоплёночные), слюдяные, керамические, тонкослойные из неорганических плёнок.
• Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные, комбинированные — бумажноплёночные, тонкослойные из органических синтетических плёнок.
• Электролитические и оксидно-полупроводниковые конденсаторы. Такие конденсаторы отличаются от всех прочих типов прежде всего большой удельной ёмкостью. В качестве диэлектрика используется оксидный слой на металлическом аноде. Вторая обкладка (катод) — это или электролит (в электролитических конденсаторах), или слой полупроводника (в оксидно-полупроводниковых), нанесённый непосредственно на оксидный слой. Анод изготовляется, в зависимости от типа конденсатора, из алюминиевой, ниобиевой или танталовой фольги или спечённого порошка. Время наработки на отказ типичного электролитического конденсатора 3000—5000 часов при максимально допустимой температуре, качественные конденсаторы имеют время наработки на отказ не менее 8000 часов при температуре 105 °С^[6]. Рабочая температура — основной фактор, влияющий на продолжительность срока службы конденсатора. Если нагрев конденсатора незначителен из-за потерь в диэлектрике, обкладках и выводах, (например, при использовании его во времязадающих цепях при небольших токах или в качестве разделительных), можно принять, что интенсивность отказов снижается вдвое при снижении рабочей температуры на каждые 10 °C вплоть до +25 °C. При работе конденсаторов в импульсных сильноточных цепях (например, в импульсных источниках питания) такая упрощённая оценка надёжности конденсаторов некорректна и расчёт надёжности более сложен^[7].
• Твердотельные конденсаторы — вместо традиционного жидкого электролита используется специальный токопроводящий органический полимер или полимеризованный органический полупроводник. Время наработки на отказ около 50 000 часов при температуре 85 °С. ЭПС меньше чем у жидко-электролитических и слабо зависит от температуры. Не взрываются.

Керамический подстроечный конденсатор

• Тонкопленочные конденсаторы

Кроме того, конденсаторы различаются по возможности изменения своей ёмкости:

• Постоянные конденсаторы — основной класс конденсаторов, не меняющие своей ёмкости (кроме как в течение срока службы).
• Переменные конденсаторы — конденсаторы, которые допускают изменение ёмкости в процессе функционирования аппаратуры. Управление ёмкостью может осуществляться механически, электрическим напряжением (вариконды, варикапы) и температурой (термоконденсаторы). Применяются, например, в радиоприёмниках для перестройки частоты резонансного контура.
• Подстроечные конденсаторы — конденсаторы, ёмкость которых изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры. Их используют для подстройки и выравнивания начальных ёмкостей сопрягаемых контуров, для периодической подстройки и регулировки цепей схем, где требуется незначительное изменение ёмкости.

В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляющие, дозиметрические, пусковые и другие конденсаторы.

Также различают конденсаторы по форме обкладок: плоские, цилиндрические, сферические и другие.

Название	Ёмкость	Электрическое поле	Схема
Плоский конденсатор	C=ε0εr⋅Ad

Емкость конденсаторов: определение, формулы, примеры.

Определение 1

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C=qφ1-φ2=qU.

Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Определение 2

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.

Формула для расчета электроемкости записывается как

C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

Рисунок 1

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:

C=ε0Sd1ε1+d2ε2+…+dNεN.

Сферический конденсатор

Определение 3

Конденсатор

Конденсатор состоит из двух пластин (или обкладок), находящихся одна перед другой и сделанных из проводящего материала. Между пластинами находится изолирующий материал, называемый диэлектриком (рис. 4.1). Простейшими диэлектриками являются воздух, бумага, слюда и т. д.

Рис. 4.1. Конденсатор

 

Зарядка конденсатора

Основным свойством конденсатора является его способность запасать электрическую энергию в виде электрического заряда.
На рис. 4.2(а) изображена схема, в которой конденсатор соединяется через ключ с источником питания. Когда ключ замкнут (рис. 4.2(б)), положительный полюс источника «откачивает» электроны с обкладки А, и она приобретает положительный заряд. Отрицательный полюс источника питания тем временем «поставляет» электроны на обкладку В, в результате чего она приобретает отрицательный заряд, по абсолютной величине равный положительному заряду обкладки А. Такой поток электронов называется током заряда. Он продолжает течь до тех пор, пока напряжение на конденсаторе не сравняется с ЭДС источника питания. В этом случае говорят, что конденсатор полностью заряжен. Электрический заряд обозначается буквой Q, а его величина измеряется в кулонах (Кл).

 

 

Рис. 4.2. Заряд и разряд конденсатора

 

Когда конденсатор заряжен, между его обкладками возникает разность потенциалов, а следовательно, и электрическое поле.
Если в момент, когда конденсатор уже зарядился, разомкнуть ключ (рис. 4.2(в)), конденсатор будет хранить заряд. В этом случае внутри диэлектрика между обкладками возникает электрическое поле. При разряде конденсатора через сопротивление нагрузки (рис. 4.2(г)) электрическое ноле исчезает.

 

Емкость конденсатора

Способность конденсатора накапливать электрический заряд называется емкостью, а величина этой емкости обозначается буквой С и измеряется в фарадах (Ф). Фарада — очень большая единица емкости, и поэтому она практически не используется. Чаще используются дробные единицы:

                         1 микрофарада (мкФ) =  Ф = 10^-6 Ф,

                         1 пикофарада (пФ) =   мкФ = 10^-6 мкФ = 10^-12 Ф.

 

Емкость конденсатора возрастает с увеличением площади обкладок и убывает с увеличением расстояния между ними.
Например, при возрастании площади обкладок вдвое емкость также увеличивается в два раза. Если же увеличить вдвое расстояние между обкладками, емкость станет вдвое меньше.

 

Связь заряда, емкости и напряжения

Если конденсатор заряжен до разности потенциалов V , его заряд определяется формулой Q=CV

где С выражается в фарадах, V – в вольтах, а Q – в кулонах. Преобразовав эту формулу, получим:

 

Энергия заряженного конденсатора

Энергия W, запасенная конденсатором, определяется формулой

где W выражается в джоулях, С – в фарадах, а V — в вольтах.

 

Параллельное и последовательное соединение конденсаторов

Если два конденсатора, С1 и С2, соединены параллельно (рис. 4.3(а)), результирующая емкость СТ такого соединения равна сумме емкостей этих конденсаторов:

Если конденсаторы соединены последовательно (рис. 4.3(б)), результирующая емкость СТ оказывается меньше емкости любого из конденсаторов я выражается формулой

Например, если С1 = С2, то результирующая емкость СТ последовательного соединения равна половине емкости любого из конденсаторов:

 

Напряжение на последовательно соединенных конденсаторах

На схеме, показанной на рис. 4.4, конденсаторы С1 и С2 соединены последовательно и подключены к источнику постоянного напряжения VТ. Полное напряжение VТ будет поделено между С1 и С2 таким образом, что на конденсаторе меньшей емкости установится большее напряжение,

Рис. 4.3. Параллельное (а) и последовательное (б) соединение конденсаторов.

Рис. 4.4. Напряжение на конденсаторах при их последовательном соединении

и наоборот.

Сумма V1 (напряжения на С1) и V2 (напряжения на С2) всегда равна полному напряжению VТ.
В общем случае, когда несколько конденсаторов, соединенных последовательно, подключено к источнику постоянного тока, напряжение на каждом из конденсаторов обратно пропорционально его емкости. При последовательном соединении двух конденсаторов напряжения на С1 и С2 соответственно равны

 

Пример 1

Определим результирующую емкость цепи, изображенной на рис. 4.5. Результирующая емкость параллельного соединения равна

С2 + С3 = 10 + 20 = 30 пФ

Поскольку емкость С1 также равна 30 пФ, то результирующая емкость всей цепи равна ½*30 = 15 пФ.

Рис. 4.6.                                                                                                   Рис. 4.7.

 

Пример 2

На рис. 4.6 напряжение на конденсаторе С1 равно

откуда напряжение на С2 равно 30 – 20 = 10 В.

 

Рабочее напряжение

Любой конденсатор характеризуется некоторым максимальным напряжением, при превышении которого наступает пробой диэлектрика. Это напряжение называется рабочим, или номинальным, напряжением конденсатора, и подаваемое на конденсатор напряжение ни в коем случае не должно его превышать. При использовании конденсатора в цепях переменного тока амплитудное значение напряжения в цепи также не должно превышать рабочего напряжения конденсатора. Рабочим напряжением для батареи конденсаторов, соединенных параллельно, является наименьшее из рабочих напряжений конденсаторов, входящих в схему, Например, рабочее напряжение для цепи, изображенной на рис. 4.7, равно 25 В.
Для конденсаторов, соединенных последовательно, рабочее напряжение подбирать труднее. Рассмотрим схему на рис. 4.8. Конденсатор С1 (1 мкФ, рабочее напряжение Vраб = 25 В) соединен последовательно с конденсатором С2 (10 мкФ, Vраб = 10 В). Поскольку на конденсаторе С1, обладающем меньшей емкостью, установится большее напряжение, чем на С2, то при расчетах следует прежде всего иметь в виду рабочее напряжение конденсатора С1, равное 25 В. Таким образом, V1 = 25 В. соотношения V1/ V2 = С1/ С2 следует, что

Поскольку рабочее напряжение конденсатора С2 выше, чем V2, рабочее напряжение данной батареи конденсаторов равно 25 + 2,5 = 27,5 В.
Следует заметить, что если бы рабочее напряжение конденсатора было равно, например, 2 В, как показано на рис. 4.9, то он зарядился бы

 

                      Рис. 4.8.                                                                          Рис. 4.9.

                           Рис. 4.10.                                     Рис. 4.11. Катушка индуктивности

 

до уровня рабочего напряжения прежде, чем напряжение на конденсаторе С1 достигло бы 25 В. Вот расчет для этого случая:
V2 = 2 В, тогда.

Следовательно, рабочее напряжение такой батареи будет составлять 20 + 2 = 22 В.

 

Пример 3

Конденсаторы С1 и С2, изображенные на рис. 4.10, имеют каждый рабочее напряжение 60 В. Какое максимальное напряжение может быть приложено к этой схеме?

 

Решение
Поскольку на конденсаторе С1 установится более высокое напряжение, чем на конденсаторе С2, то напряжение на нем раньше достигнет уровня рабочего напряжения. При V1 = 60 В

Максимальное напряжение, которое может быть подано на данную схему, составляет 60 + 20 = 80 В.

 

В этом видео рассказывается о понятии конденсатора:

Добавить комментарий

Как определить емкость конденсатора: 4 рабочих способа

Основной характеристикой конденсатора является его емкость. Очень часто замеры емкости требуется проводить в электролитическом конденсаторе. В отличие от керамических и оксидных конденсаторов, которые редко выходят из строя (разве что в результате пробоя диэлектрика), электролитическим деталям свойственна потеря ёмкости из-за высыхания электролита. Поскольку работа электронных схем сильно зависит от емкостных характеристик, то необходимо знать, как определить емкость конденсатора.

Существуют разные способы определения ёмкости:

• по кодовой или цветной маркировке деталей;
• с помощью измерительных приборов;
• с использованием формулы.

Измерить емкость проще всего с помощью измерителя C и ESR. Для этого контакты измерительных щупов подсоединяют к выводам конденсатора, соблюдая полярность электролитических деталей. При этом результаты измерений выводятся на дисплей. (Рисунок 1). Радиолюбители, которым часто приходится делать измерения, приобретают такой прибор или изготавливают его самостоятельно.

Рис. 1. Измерение ёмкости с помощью измерителя C и ESR

С использованием мультиметра и формул

Если в вашем распоряжении есть мультиметр с функцией измерения параметра «Cx», то измерить ёмкость конденсатора довольно просто: следует переключить прибор в режим «Сх», после чего выбрать оптимальный диапазон измерения, соответствующий параметрам конденсатора. Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.

Режим «Сх» в мультиметре

Менее точно можно определить ёмкость с помощью тестера, у которого нет режима «Сх». Для этого потребуется источник питания, к которому подключают конденсатор по простой схеме (рис. 2).

Рис. 2. Схема подключения конденсатора

Алгоритм измерения следующий:

1. Измерьте напряжение источника питания щупами контактов измерительного прибора.
2. Образуйте RC-цепочку с конденсатором и выводами резистора номиналом 1 – 10 кОм.
3. Закоротите выводы конденсатора и подключите RC-цепочку к источнику питания.
4. Замерьте напряжение образованной цепи с помощью мультиметра.
5. Если напряжение изменилось, необходимо подогнать его до значения, близкого к тому, которое вы получили на выходе источника питания.
6. Вычислите 95% от полученного значения. Запишите показатели измерений.
7. Возьмите секундомер и включите его одновременно с убиранием закоротки.
8. Как только мультиметр покажет значение напряжения, которое вы вычислили (95%), остановите секундомер.
9. По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.

Рис. 3. Измерение с помощью тестера. Проверка

Подчеркнём ещё раз, что точность измерения ёмкости данным способом не слишком высока, но определить работоспособность радиоэлемента на основании такого измерения вполне возможно. Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.

Таким же методом можно вычислить параметры керамического радиоэлемента. Для этого необходимо подключить RC-цепочку через трансформатор и подать переменное напряжение. Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*X_c , где f – частота тока, а X_c – ёмкостное сопротивление.

Осциллографом

С приемлемой точностью можно определить ёмкость конденсатора с помощью цифрового или обычного электронного осциллографа. Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = U_R / U_C* ( 1 / 2*π*f*R ).

Рис. 4. Простая схема

Алгоритм вычисления простой:

1. Подключите осциллограф к электрической схеме. При подключении щупов прибора к электролитам соблюдайте полярность электрического тока.
2. Измерьте амплитуды напряжений на конденсаторе и на резисторе.
3. Путём подстройки частоты генератора добивайтесь, чтобы значения амплитуд на обоих элементах сравнялись (хотя бы приблизительно).
4. Подставьте полученные значения в формулу и вычислите ёмкость конденсатора.

При измерении ёмкостей неполярных конденсаторов часто вместо RC-цепочки собирают мостовую схему с частотным генератором (показано на рис. 5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r₄ / C_x = r₂ / C₀.

Рисунок 5. Мостовая схема

Гальванометром

При наличии баллистического гальванометра также можно определить ёмкость конденсатора.  Для этого используют формулу:

C = α * C_q / U , где α –  угол отклонения гальванометра, C_q – баллистическая постоянная прибора, U – показания гальванометра.

Из-за падения сопротивления утечки ёмкость конденсаторов уменьшается. Энергия теряется вместе с током утечки.

Описанные выше методики определения ёмкости позволяют определить исправность конденсаторов. Значительное отклонение от номиналов говорит, что конденсаторы неисправны. Пробитый электролитический радиоэлемент легко определяется путём измерения сопротивления. Если сопротивление стремится к 0 – изделие закорочено, а если к бесконечности – значит, есть обрыв.

Следует опасаться сильного электрического разряда при подключениях щупов к большим электролитам. Они могут накапливать мощный электрический заряд от постоянного тока, который молниеносно высвобождается током разряда.

По маркировке

Напомним, что единицей емкости в системе СИ является фарада ( обозначается F или Ф). Это очень большая величина, поэтому на практике используются дольные величины:

• миллифарады (mF, мФ ) = 10^-3 Ф;
• микрофарады (µF, uF, mF, мкФ) = 10^-3 мФ = 10^-6 Ф;
• нанофарады (nF, нФ) = 10^-3 мкФ =10^-9 Ф;
• пикофарады (pF, mmF, uuF) = 1 пФ = 10^-3 нФ = 10^-12 Ф.

Мы перечислили название единиц и их сокращённое обозначение потому, что они часто встречаются в маркировке крупных конденсаторов (см. рис. 6).

Рис. 6. Маркировка крупных конденсаторов

Обратите внимание на маркировку плоского конденсатора (второй сверху): после трёхзначной цифры стоит буква М. Данная буква не обозначает единицы измерения «мегафарад» – таких просто не существует. Буквами обозначены допуски, то есть, процент отклонения от ёмкости, обозначенной на корпусе. В нашем случае отклонение составляет 20% в любую сторону. Надпись 102М на большом корпусе можно было бы написать: 102 нФ ± 20%.

Теперь расшифруем надпись на корпусе третьего изделия. 118 – 130 MFD обозначает, что перед нами конденсатор, ёмкость которого находится в пределах 118 – 130 микрофарад. В данном примере буква М уже обозначает «микро». FD – обозначает «фарады», сокращение английского слова «farad».

На этом простом примере видно, какая большая путаница в маркировке. Особенно запутана кодовая маркировка, применяемая для крохотных конденсаторов. Дело в том, что можно встретить конденсаторы, маркировка которых выполнена старым способом и детали с современной кодировкой, в соответствии со стандартом EIA. Одни и те же символы можно по-разному интерпретировать.

По стандарту EIA:

1. Две цифры и одна буква. Цифры обозначают ёмкость, обычно в пикофарадах, а буква – допуски.
2. Если буква стоит на первом или втором месте, то она обозначает либо десятичную запятую (символ R), либо указывает на название единицы измерения («p» – пикофарад, «n» – нанофарад, «u» – микрофарад). Например: 2R4 = 2.4 пФ; N52 = 0,52 нФ; 6u1 = 6,1 мкф.
3. Маркировка тремя цифрами. В данном коде обращайте внимание на третью цифру. Если её значение от 0 до 6, то умножайте первые две на 10 в соответствующей степени. При этом 10⁰ =1; 10¹ = 10; 10² = 100 и т. д. до 10⁶.

Цифры от 7 до 9 указывают на показатель степени со знаком «минус»: 7 условно = 10^-3; 8 = 10^-2; 9 = 10^-1.

Пример:

• 256 обозначает: 25× 10⁵ = 2500 000 пФ = 2,5 мкФ;
• 507 обозначает: 50 × 10^-3 = 50 000 пФ = 0, 05 мкФ.

Возможна и такая надпись: «1B253». При расшифровке необходимо разбить код на две части – «1B» (значение напряжения) и 253 = 25 × 10³ = 25 000 пФ = 0,025 мкФ.

В кодовой маркировке используются прописные буквы латинского алфавита, указывающие допуски. Один пример мы рассмотрели, анализируя маркировку на рис. 6.

Приводим полный список символов:

• B = ± 0,1 пФ;
• C = ± 0,25 пФ;
• D = ± 0,5 пФ или ± 0,5% (если емкость превышает 10 пФ).
• F = ± 1 пФ или ± 1% (если емкость превышает 10 пФ).
• G = ± 2 пФ или ± 2% (для конденсаторов от 10 пФ»).
• J = ± 5%.
• K = ± 10%.
• M = ± 20%.
• Z = от –20% до + 80%.

Изделия с кодовой маркировкой изображены на рис. 7.

Рис. 7. Пример кодовой маркировки

Если в кодировке отсутствует символ из приведённого выше списка, а стоит другая буква, то она может единицу измерения емкости.

Важным параметром является его рабочее напряжение конденсатора. Но так как в данной статье мы ставим задачу по определению ёмкости, то пропустим описание маркировки напряжений.

Отличить электролитический конденсатор от неполярного можно по наличию символа «+» или «–» на его корпусе.

Цветовая маркировка

Описывать значение каждого цвета не имеет смысла, так как это понятно из следующей таблицы (рис. 8):

Рис. 8. Цветовая маркировка

Запомнить символику кодовой и цветовой маркировки довольно трудно. Если вам не приходится постоянно заниматься подбором конденсаторов, то проще пользоваться справочниками или обратиться к информации, изложенной в данной статье.

Видео в помощь

Конденсатор | Класс робототехники

Электрический конденсатор (англ. capacitor) — это устройство, которое может накапливать электрический заряд и хранить его некоторое время. Конденсаторы можно найти практически в любом электронном устройстве. Они бывают разных типов и размеров. На электрических схемах конденсаторы обозначают двумя параллельными черточками. При этом, у полярных конденсаторов около положительного электрода дополнительно ставится плюсик.

Для чего нужен конденсатор?

У этого прибора есть множество применений. Мы не будем перечислять их все, отметим лишь некоторые. 1) Фильтрация пульсаций в цепях питания. Конденсаторы часто ставят на входе и выходе преобразователей напряжения, на входе питания микросхем. В этом случае конденсаторы служат своего рода амортизаторами, которые могут сгладить неровности напряжения, подобно амортизаторам автомобиля, сглаживающим неровности дороги. 2) Времязадающие электрические цепи. Конденсаторы разной ёмкости заряжаются и разряжаются за разное время. Эту особенность используют в устройствах, где необходимо отсчитывать определенные промежутки времени. Например, с помощью резистора и конденсатора задается период и скважность импульса в микросхеме таймера 555 (урок про таймер 555). 3) Датчики прикосновения. В роли одной из обкладок конденсатора может выступить человек. Эту особенность нашего тела используют в своей работе сенсорные кнопки, тачскрины и тачпады некоторых видов. 4) Хранение данных. Конденсаторы применяются для хранения данных в оперативной памяти — ОЗУ (SRAM). Каждый модуль такой памяти содержит миллиарды отдельных конденсаторов, которые могут быть заряжены или разряжены, что интерпретируется как единица или ноль. И это далеко не все варианты применения этого незаменимого прибора. Попробуем разобраться, как устройство конденсатора позволяет ему выполнять столько полезных функций!

Устройство простейшего конденсатора

Конденсатор состоит их двух металлических пластин — электродов, называемых также обкладками, между которыми находится тонкий слой диэлектрика. Собственно, все конденсаторы устроены именно таким (или почти таким) образом, разве что меняется материал обкладок и диэлектрика. Чтобы увеличить ёмкость конденсатора, не увеличивая его размеры, применяют разные хитрости. Например, если мы возьмем две обкладки в виде длинных полосок фольги, проложим между ними хотя бы тот же полиэтилен и свернем все это как рулет, то получится очень компактный прибор с большой ёмкостью. Именно так устроены плёночные конденсаторы. Если вместо полиэтилена взять бумагу и пропитать её электролитом, то на поверхности фольги образуется тонкий слой оксида, который не проводит ток. Такой конденсатор будет называться электролитическим. Существует много разных видов конденсаторов: бумажные, плёночные, оксидные алюминиевые и танталовые, вакуумные и т.п. В нашем уроке мы будем использовать оксидные электролитические конденсаторы из-за их большой ёмкости и доступности.

Полярные и неполярные конденсаторы

Очень важным является разделение конденсаторов на полярные и неполярные. Приборы на основе оксидов: электролитические алюминиевые и танталовые обычно являются полярными, а значит если перепутать их полярность — они выйдут из строя. Причём этот выход из строя будет сопровождаться бурной электрохимической реакций вплоть до взрыва конденсатора. На полярных конденсаторах всегда имеется маркировка. Как правило на электролитических конденсаторах на корпусе контрастной полосой отмечается отрицательный вывод (катод), у танталовых (в желтых прямоугольных корпусах) полоской помечается положительный вывод (анод). Если есть сомнения в маркировке, то лучше найти документацию на этот конденсатор и убедиться. Неполярные же конденсаторы можно включать в цепь какой угодно стороной. К примеру, многослойные керамические конденсаторы — неполярные.

Ёмкость и напряжение конденсатора

Теперь обратим внимание на две важные характеристики конденсатора: ёмкость и номинальное напряжение. Ёмкость конденсатора характеризует способность конденсатора накапливать заряд. Это как ёмкость банки, в которой хранится, к примеру, вода. Кстати, не зря одним из первых электрических конденсаторов была так называемая Лейденская банка. Она представляла собой обыкновенную стеклянную посуду, снаружи обмотанную фольгой. В банку была налита токопроводящая жидкость — электролит. Фольга и электролит играли роль обкладок, а стекло банки служило тем самым диэлектрическим барьером. Ёмкость электрического конденсатора измеряют в фарадах. В схемах ёмкость обозначают латинской буквой C. Как правило, ёмкость классических конденсаторов варьируется от нескольких пикофарад (пФ) до нескольких тысяч микрофарад (мкФ). Ёмкость указывается на корпусе конденсатора. Если единицы не указаны — то это пикофарады. Микрофарады часто обозначают как uF — так как буква u внешне похожа на греческую букву мю, которую используют вместо приставки микро. Существует и особый вид конденсаторов, называемых ионисторами (англ. supercapacitor), которые имеют ёмкость в несколько фарад!  Чем больше ёмкость конденсатора, тем больше энергии в нём может храниться и тем дольше он заряжается, при прочих равных условиях. Номинальное напряжение — второй важный параметр. Это такое напряжение, при котором конденсатор будет работать весь срок службы без критичного изменения своих параметров. Нельзя применять в 12-вольтовой цепи конденсатор на 6 вольт — он быстро выйдет из строя. Именно эти два параметра обычно наносят на поверхность корпуса конденсатора. На фотографии ниже изображён электролитический конденсатор ёмкостью 470 мкФ и номинальным напряжением 16 Вольт. А вот на керамических конденсаторах часто указывают только ёмкость. На картинке ниже конденсатор имеет маркировку 104. Что бы это значило? Последняя цифра в этом коде — количество нулей после двухзначного числа в начале. 104 = 10 0000 пФ = 100 нФ = 0,1 мкФ

Параллельное и последовательное подключение конденсаторов

Как и в случае резисторов, конденсаторы можно составлять в цепочки. Это бывает нужно, когда в схеме необходима какая-то конкретная ёмкость, а у вас нет такого конденсатора. Параллельное подключение В отличие от резисторов, при параллельном подключении конденсаторов их ёмкости складываются. Например, если нам нужно получить ёмкость 3000 мкФ, а у нас есть два конденсатора по 1000 мкФ, и 10 штук по 100 мкФ, смело ставим их параллельно и получаем: 1000*2+100*10 = 2000 + 1000 = 3000 мкФ Последовательно подключение При последовательном подключении конденсаторы ведут себя как резисторы, соединённые параллельно. Например, посчитаем суммарную ёмкость двух конденсаторов на 100 мкФ, соединённых последовательно: Суммарная ёмкость Ctot = 50 мкФ.

Заряд и разряд конденсатора — RC-цепочка

Теперь разберёмся с процессами, происходящими внутри конденсатора во время заряда и разряда. Для этого рассмотрим самую простую электрическую цепь с конденсатором. С левой стороны схемы подключим источник питания. Сверху разместим ключ и резистор, а справа сам конденсатор. Участок цепи, на котором есть конденсатор и резистор называют RC-цепью. При замыкании ключа, в такой цепи образуется электрический ток, сила которого зависит от сопротивления резистора и внутреннего сопротивления самого конденсатора. Заряженные частицы устремятся к конденсатору, но не смогут преодолеть слой диэлектрика (по крайней мере все разом). Вследствие чего, с одной стороны конденсатора накопятся отрицательно заряженные частицы, а с другой стороны — положительно заряженные. Концентрация заряженных частиц на обкладках создаст мощное электрическое поле между ними. С течением времени, напряжение на конденсаторе растет, а сила тока падает. После завершения процесса заряда, ток в цепи упадет почти до нуля. Останется только очень маленький ток утечки, который образуется благодаря тому, что некоторым заряженным частицам всё же удается проскочить через слой диэлектрика. Напряжение, напротив, станет практически равным напряжению источника. Когда мы отключим конденсатор от источника питания, этот самый ток утечки постепенно разрядит конденсатор. Эта особенность электрических конденсаторов не даёт нам сделать из них контейнер для длительного хранения энергии. Хотя частично эту проблему решают ионисторы.

Резистор и время заряда конденсатора

Зачем в цепи нужен резистор? Что на мешает подключить его напрямую к источнику? Тому есть две причины. Резистор ограничивает ток, протекающий через конденсатор. Чем меньше заряженных частиц за единицу времени прибывает в конденсатор, тем больше времени для заряда ему потребуется. Конденсатор заряжается и разряжается по экспоненциальному закону. Зная это, мы можем легко рассчитать время заряда/разряда в зависимости от его ёмкости и от сопротивления резистора. По картинке можно понять, что за время T конденсатор заряжается на 63,2%. А вот за время 3T уже на 95%. Время T здесь равно произведению ёмкости конденсатора C на сопротивление R, последовательно соединенного резистора: Например, у нас есть конденсатор ёмкостью 100 мкФ, соединенный с резистором 1 кОм. Посчитаем за сколько секунд он зарядится хотя бы до 95%: Теперь умножаем это на 3 и получаем 3T = 0,3 секунды — за такое время конденсатор почти полностью будет заряжен. Таким образом, меняя ёмкость конденсатора и резистора мы можем управлять временем его заряда, что нам ещё пригодится в будущем. Вторая важная причина, по которой в цепи присутствует резистор — защита источника питания. Дело в том, что разряженные конденсаторы имеют очень низкое внутреннее сопротивление, которое составляет доли Ома. По сути, их можно рассматривать как обычные проводники. А что будет, если замкнуть выводы питания проводником? Будет короткое замыкание! Такой режим работы цепи является аварийным для источника питания, и его нужно всячески избегать.

Плавное выключение светодиода при помощи конденсатора

Проведем небольшой опыт. Для этого соберем на макетной плате цепь с кнопкой, конденсатором и светодиодом. В качестве источника питания используем контакты питания Ардуино Уно. Принципиальная схема Внешний вид макета Подключим Ардуино  к питанию. Затем, нажмем кнопку и светодиод практически мгновенно загорится. Отпустим кнопку — светодиод медленно начнет гаснуть. Почему так происходит? Сразу после подключения нашей схемы к источнику питания, в ней начинают происходит интересные процессы. Как уже говорилось ранее, пока конденсатор пустой, ток через него максимален. Следовательно, конденсатор начинает стремительно набирать заряд. При этом светодиоду, который подключен параллельно, ничего не достается 🙁 Напряжение на нем близко к нулю. С течением времени конденсатор насыщается, благодаря чему ток начинает постепенно переходить в параллельную цепь — через светодиод. Напряжение на светодиоде начинает расти. Наступает момент, когда напряжение на светодиоде принимает критическое значение (для красного светодиода около 1,8 В), при котором он стремительно отбирает остатки тока у конденсатора и вспыхивает! Когда мы отпускаем кнопку, ситуация становится гораздо проще. Конденсатор становится источником питания для светодиода с резистором. Светодиод начинает медленно высасывать заряд из конденсатора, пока тот не разрядится. Тут мы и наблюдаем медленно угасание. Меняя сопротивление R1, мы можем влиять на скорость вспыхивания светодиода. Однако, следует учитывать, что увеличивая R1 мы будем снижать ток в цепи, тем самым уменьшая максимальный заряд конденсатора и яркость светодиода. Увеличивая C1, мы получим более длительное время работы светодиода после выключения источника. Это как поставить более ёмкую батарейку. Наконец, меняя R2 можно регулировать яркость светодиода, и соответственно, время его работы. Ведь чем меньше тока мы забираем из конденсатора, тем на большее время его хватит.

Заключение

Итак, мы познакомились с конденсатором — интересным и порой опасным жителем любой электронной платы. В следующих уроках уделим внимание резистору и индуктивности, а также более сложному их собрату — транзистору.

Вконтакте

Facebook

Twitter