Напряжение конденсатора как найти: как определить напряжение, вольтаж конденсаторов

Содержание

как определить напряжение, вольтаж конденсаторов

Конденсатор – один из самых важных элементов электрической цепи. Он накапливает внутри себя электрический заряд и передает его другим элементам электрической цепи. О том, что представляет собой конденсатор и как определить на нём напряжение, рассказывается ниже.

Что такое конденсатор

Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.

Конденсатор

Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).

Термин из учебного пособия

Характеристики конденсаторов

Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.

Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.

Емкость

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.

В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.

В чем измеряется напряжение конденсаторов

Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.

Измерение силы заряда двухполюсника

Что влияет на напряжение конденсаторов

Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд.

Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.

Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.

Описание влияния на показатель

Как вычислить напряжение и вольтаж

Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.

Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.

Вычисление мультиметром

Формулы измерения напряжения конденсаторов

Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.

Основные формулы для расчета

В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.

<center><div class="lazy lazy-hidden advv"><ins class="lazy lazy-hidden adsbygoogle" style="display:inline-block;width:336px;height:280px" data-ad-client="ca-pub-1812626643144578" data-ad-slot="9935184599"></ins> <script>(adsbygoogle=window.adsbygoogle||[]).push({});</script></div></center>

Как найти напряжение на конденсаторе формула

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант.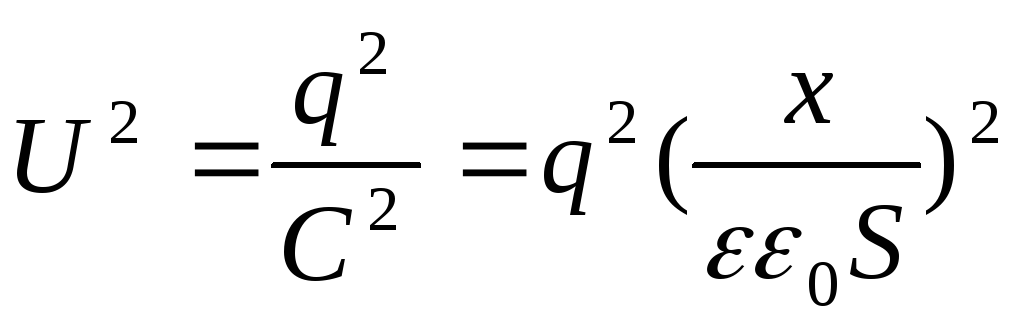 Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки.

С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed.

Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU 2 /2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U

c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R.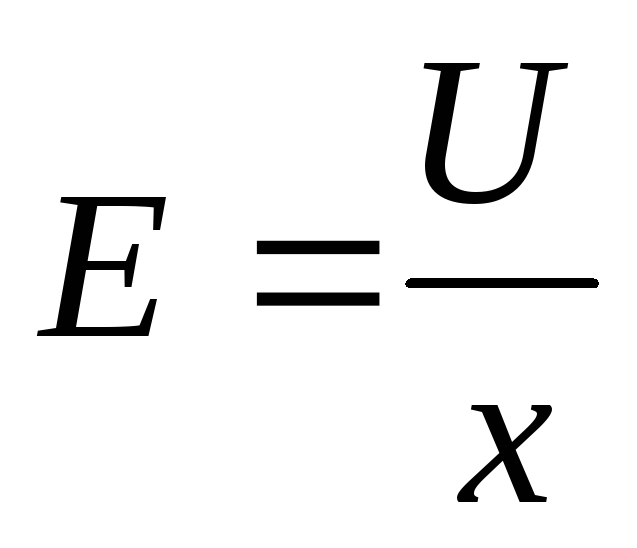 Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I_ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.

Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

где – радиусы обкладок конденсатора.

Заряд конденсатора связан с энергией поля (W) внутри него:

Из формулы (6) следует, что заряд можно выразить как:

Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

Примеры решения задач по теме «Заряд конденсатора»

Задание

Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис.3)? Чему равен суммарный заряд соединения?

РешениеРазности потенциалов на обкладках конденсаторов будут при таком соединении равны:

Заряд на первом конденсаторе при этом равен:

Заряд на обкладках второго конденсатора:

Суммарный заряд системы можно найти как:

Тогда суммарный заряд равен:

Ответ Кл; Кл; Кл

Задание	Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора?
Решение	При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем:

Энергию найдем как:

Энергию электрического поля конденсатора будет удобнее выразить:

Подставим в выражение (2.1) правые части (2.2) и (2.3), имеем:

Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.

История накопителей заряда

Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.

Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.

Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.

Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:

1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
начало XX в. — изобретение слюдяных и керамических конденсаторов.

Физика ёмкостных характеристик

Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.

Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.

Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.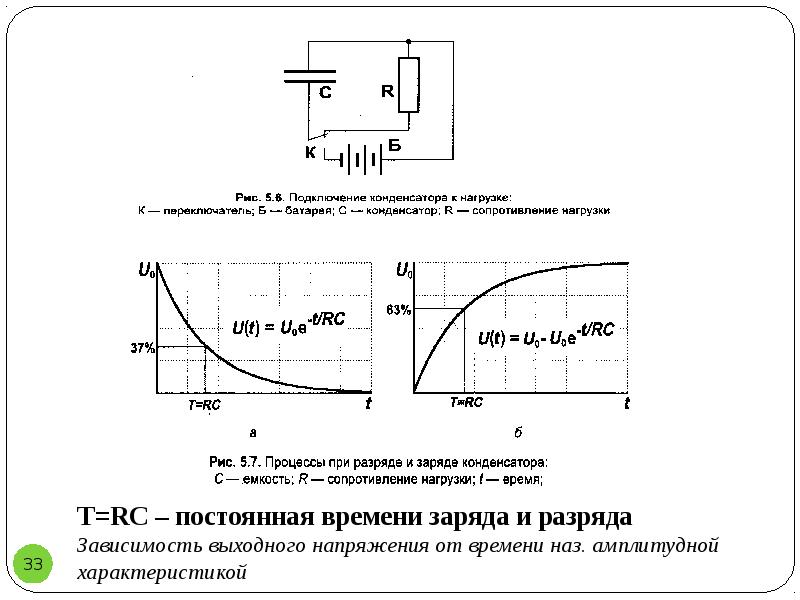

Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:

геометрия пластин;
расстояние между ними;
диэлектрический материал между пластинами.

Единица и формулы расчёта

Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.

Математическое выражение фарада

Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.

Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:

пикофарад — 10—12 Ф;
нанофарад — 10—9 Ф;
микрофарад — 10—6 Ф.

Диэлектрическая проницаемость

Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:

А — площадь меньшей пластины;
d — расстояние между ними;
ε — абсолютная проницаемость используемого диэлектрического материала.

Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.

На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:

Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.

Практические измерения

Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.

Идея суперконденсатора

Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.

Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:

непродолжительный жизненный цикл;
невысокая удельная мощность;
узкий диапазон температур зарядки и разрядки;
неспособность быстро отдать весь запас энергии.

Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.

Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.

Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.

Глава 20. Конденсаторы

Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.

Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):

(20.1)

Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.

Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):

(20.2)

Разность потенциалов между пластинами равна

(20.3)

где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора

(20.4)

Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает

(20.5)

Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.

Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов

(20.6)

Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .

Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов

(20.7)

Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна

(20.8)

С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:

(20.9)

Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.

Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).

Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).

Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4

(ответ 4).

Согласно определению электрической емкости имеем в задаче 20.1.5

(ответ 2).

Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).

При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул

где и — новый заряд конденсатора (ответ 3).

Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).

В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)

то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что

произведение от расстояния между пластинами не зависит (см. формулу (20.4)).

Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.

При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).

Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.8)

(1)

Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).

В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)

Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)

В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)

Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).

Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).

В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).

Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).

Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:

где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора

(ответ 4).

Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):

Как определить рабочее напряжение конденсатора

Правила маркировки конденсаторов постоянной ёмкости

При сборке самодельных электронных схем поневоле сталкиваешься с подбором необходимых конденсаторов.

Притом, для сборки устройства можно использовать конденсаторы уже бывшие в употреблении и поработавшие какое-то время в радиоэлектронной аппаратуре.

Естественно, перед вторичным использованием необходимо проверить конденсаторы, особенно электролитические, которые сильнее подвержены старению.

При подборе конденсаторов постоянной ёмкости необходимо разбираться в маркировке этих радиоэлементов, иначе при ошибке собранное устройство либо откажется работать правильно, либо вообще не заработает. Встаёт вопрос, как прочитать маркировку конденсатора?

У конденсатора существует несколько важных параметров, которые стоит учитывать при их использовании.

Первое, это номинальная ёмкость конденсатора. Измеряется в долях Фарады.

Второе – допуск. Или по-другому допустимое отклонение номинальной ёмкости от указанной. Этот параметр редко учитывается, так как в бытовой радиоаппаратуре используются радиоэлементы с допуском до ±20%, а иногда и более. Всё зависит от назначения устройства и особенностей конкретного прибора. На принципиальных схемах этот параметр, как правило, не указывается.

Третье, что указывается в маркировке, это допустимое рабочее напряжение. Это очень важный параметр, на него следует обращать внимание, если конденсатор будет эксплуатироваться в высоковольтных цепях.

Итак, разберёмся в том, как маркируют конденсаторы.

Одни из самых ходовых конденсаторов, которые можно использовать – это конденсаторы постоянной ёмкости K73 – 17, К73 – 44, К78 – 2, керамические КМ-5, КМ-6 и им подобные. Также в радиоэлектронной аппаратуре импортного производства используются аналоги этих конденсаторов. Их маркировка отличается от отечественной.

Конденсаторы отечественного производства К73-17 представляют собой плёночные полиэтилентерефталатные защищённые конденсаторы. На корпусе данных конденсаторов маркировка наноситься буквенно-числовым индексом, например 100nJ, 330nK, 220nM, 39nJ, 2n2M.

Конденсаторы серии К73 и их маркировка

Правила маркировки.

Ёмкости от 100 пФ и до 0,1 мкФ маркируют в нанофарадах, указывая букву H или n.

Обозначение 100n – это значение номинальной ёмкости. Для 100n – 100 нанофарад (нФ) – 0,1 микрофарад (мкФ). Таким образом, конденсатор с индексом 100n имеет ёмкость 0,1мкФ. Для других обозначений аналогично. К примеру:
330n – 0,33 мкФ, 10n – 0,01 мкФ. Для 2n2 – 0,0022 мкФ или 2200 пикофарад (2200 пФ).

Можно встретить маркировку вида 47HC. Данная запись соответствует 47nK и составляет 47 нанофарад или 0,047 мкФ. Аналогично 22НС – 0,022 мкФ.

Для того чтобы легко определить ёмкость, необходимо знать обозначения основных дольных единиц – милли, микро, нано, пико и их числовые значения. Подробнее об этом читайте здесь.

Также в маркировке конденсаторов К73 встречаются такие обозначения, как M47C, M10C.
Здесь, буква М условно означает микрофарад. Значение 47 стоит после М, т.е номинальная ёмкость является дольной частью микрофарады, т.е 0,47 мкФ. Для M10C – 0,1 мкФ. Получается, что конденсаторы с маркировкой M10С и 100nJ обладают одинаковой ёмкостью. Различия лишь в записи.

Таким образом, ёмкость от 0,1 мкФ и выше указывается с буквой M, m вместо десятичной запятой, незначащий ноль опускается.

Номинальную ёмкость отечественных конденсаторов до 100 пФ обозначают в пикофарадах, ставя букву П или p после числа. Если ёмкость менее 10 пФ, то ставиться буква R и две цифры. Например, 1R5 = 1,5 пФ.

На керамических конденсаторах (типа КМ5, КМ6), которые имеют малые размеры, обычно указывается только числовой код. Вот, взгляните на фото.

Керамические конденсаторы с нанесённой маркировкой ёмкости числовым кодом

Например, числовая маркировка 224 соответствует значению 220000 пикофарад, или 220 нанофарад и 0,22 мкФ. В данном случае 22 это числовое значение величины номинала. Цифра 4 указывает на количество нулей. Получившееся число является значением ёмкости в пикофарадах. Запись 221 означает 220 пФ, а запись 220 – 22 пФ. Если же в маркировке используется код из четырёх цифр, то первые три цифры – числовое значение величины номинала, а последняя, четвёртая – количество нулей. Так при 4722, ёмкость равна 47200 пФ – 47,2 нФ. Думаю, с этим разобрались.

Допускаемое отклонение ёмкости маркируется либо числом в процентах (±5%, 10%, 20%), либо латинской буквой. Иногда можно встретить старое обозначение допуска, закодированного русской буквой. Допустимое отклонение ёмкости аналогично допуску по величине сопротивления у резисторов.

Буквенный код отклонения ёмкости (допуск).

Так, если конденсатор со следующей маркировкой – M47C, то его ёмкость равна 0,047 мкФ, а допуск составляет ±10% (по старой маркировке русской буквой). Встретить конденсатор с допуском ±0,25% (по маркировке латинской буквой) в бытовой аппаратуре довольно сложно, поэтому и выбрано значение с большей погрешностью. В основном в бытовой аппаратуре широко применяются конденсаторы с допуском H, M, J, K. Буква, обозначающая допуск указывается после значения номинальной ёмкости, вот так 22nK, 220nM, 470nJ.

Таблица для расшифровки условного буквенного кода допустимого отклонения ёмкости.

Допуск в %	Буквенное обозначение
лат.	рус.
± 0,05p	A
± 0,1p	B	Ж
± 0,25p	C	У
± 0,5p	D	Д
± 1,0	F	Р
± 2,0	G	Л
± 2,5	H
± 5,0	J	И
± 10	K	С
± 15	L
± 20	M	В
± 30	N	Ф
-0. +100	P
-10. +30	Q
± 22	S
-0. +50	T
-0. +75	U	Э
-10. +100	W	Ю
-20. +5	Y	Б
-20. +80	Z	А

Маркировка конденсаторов по рабочему напряжению.

Немаловажным параметром конденсатора также является допустимое рабочее напряжение. Его стоит учитывать при сборке самодельной электроники и ремонте бытовой радиоаппаратуры. Так, например, при ремонте компактных люминесцентных ламп необходимо подбирать конденсатор на соответствующее напряжение при замене вышедших из строя. Не лишним будет брать конденсатор с запасом по рабочему напряжению.

Обычно, значение допустимого рабочего напряжения указывается после номинальной ёмкости и допуска. Обозначается в вольтах с буквы В (старая маркировка), и V (новая). Например, так: 250В, 400В, 1600V, 200V. В некоторых случаях, буква V опускается.

Иногда применяется кодирование латинской буквой. Для расшифровки следует пользоваться таблицей буквенного кодирования рабочего напряжения.

Номинальное рабочее напряжение, B	Буквенный код
1,0	I
1,6	R
2,5	M
3,2	A
4,0	C
6,3	B
10	D
16	E
20	F
25	G
32	H
40	S
50	J
63	K
80	L
100	N
125	P
160	Q
200	Z
250	W
315	X
350	T
400	Y
450	U
500	V

Таким образом, мы узнали, как определить ёмкость конденсатора по маркировке, а также по ходу дела познакомились с его основными параметрами.

Маркировка импортных конденсаторов отличается, но во многом соответствует изложенной.

У меня не возникало вопросов к метало-плёночным конденсаторам. Большинство из них имеют напряжение 63 В, а некоторые — и более. А я до недавнего времени работал с устройствами, у которых напряжения были ниже этого значения.

630В, 0.47 мкф, 10%

Но вот, пришла пора разрабатывать импульсные источники питания, и понеслось! Конденсаторов (выдранных из трупов старых телевизоров) много, а вот на какое они напряжение — хрен его знает! Риск спалить не только сам конденсатор, но и всю схему, оказался очень большой. Пришлось копать Большую Помойку — Интернет.

Стыдно признаться, но я таки не смог в интернете найти готовую таблицу кодов напряжения для конденсаторов. Пришлось её составлять самостоятельно по крупицам скудной информации.

В общем, выношу на суд общественности таблицу кодов напряжения для конденсаторов.

Юзайте на здоровье, а если есть чем дополнить — присылайте коды!

Буква	0x	1x	2x	3x
A	10	100	1000
B	12,5	125
C	16	160
D	2	20	200
E	2,5	25	250
F	315
G	4	400
H	50	500
I
J	6,3	63	630
K	8	80
L	5,5
M
N
O
P	220
Q	110
R
S
T	(50)
U
V	35	350
W	450
X
Y
Z	180

Как правило на конденсаторы наносится значение ёмкости, допуск и номинальное напряжение.

Напряжение может указываться как явно, например, 100V, 250В, 630 В. так и в виде кода. Причем, следует заметить, что в мире действуют две системы кодирования напряжения.

Первая система имеет одно-буквенное значение. Обычно так кодируется напряжение на метало-плёночных конденсаторах. (Возможно и на керамических, но в этом я не уверен.)

Вот эта таблица:

Напр В	Букв. обозн.	Напр. В	Букв. обозн.	Напр. В	Букв. обозн.	Напр. В	Букв. обозн	Напр. В	Букв. обозн
1,0	I	6.3	B	40	S	100	N	350	T
2,5	M	10	D	50	J	125	P	400	Y
3.2	A	16	E	63	K	160	Q	450	U
4.0	C	20	F	80	L	315	X	500	V

Найти в интернете эту таблицу не составляет особого труда.

Вторая система имеет двух-символьный код напряжения. Вот как раз её-то найти и не удалось.

Напряжение в этой системе может обозначаться как: 1J, 2A, 2G, 2J, что соответствуют напряжению 63В, 100В, 400В, 630В.

Эти обозначения также наносятся на метало-плёночные (и, возможно, керамические) конденсаторы.

А вот коды напряжения на танталовых конденсаторах я встречал только второй системы. Первую систему ни видел ни разу. Ну, иногда бывает, что на танталовых конденсаторах указывают напряжение непосредственно.

Я специально заговорил о танталовых конденсаторах. У них, как правило, небольшое напряжение. Я много раз видел, когда указывается только одна буква, например, — «D». В этом случае подразумевается, что ей предшествует отсутствующая единичка. Нетрудно догадаться, что такой конденсатор рассчитан на напряжение 20 В. Или вместо «1A» или «1E» стоит просто «A» или «E», что означает, что конденсатор рассчитан на напряжение 10 В или 25 В.

«E» = 25 В, «j» = 6.3 В

Здесь очень легко ошибиться, перепутав «J» и «j». Будьте внимательны! Просто подумайте, что танталовый конденсатор 10 мкФ и напряжением 63 В, не может быть меньше конденсатора 10 мкФ и напряжением 25 В. И к тому же, танталовых SMD-конденсаторов на напряжение более 50 В пока не выпускают.

Но там где указывается прописная буква, например, — «e», то следует понимать, что перед ней должен стоять нулик. То есть полное обозначение должно быть «0e», что соответствует напряжению 2.5 В.

«A» = 10 В, «C» = 16 В

В таблице я указал напряжение для кода «1T» в скобочках. Код этого напряжения я увидел в интернете всего один раз, причем, увидел его не в официальных документах. Возможно, это ошибка, так как согласно таблице напряжению 50 В должен соответствовать код «1H». Тем более, что коду «2H» соответствует напряжение 500 В.

Вы видите, что таблица не полная. Поэтому, я обращаюсь ко всем заинтересованным товарищам — не стесняйтесь присылать мне отсутствующую в таблице информацию. Единственная просьба: информация должна быть достоверной. Например, было бы логично установить в клеточку «1H» значение напряжения 5.0 В. Но я это не сделал, так как еще не встречал этого. Поэтому пусть лучше в клеточке будет «ничего», чем будет указано ошибочное значение.

Таблицу допусков (точности изготовления) тоже относительно легко найти в интернете. Я ее продублирую здесь чтобы вам (да и мне тоже!) не рыть интернет в её поисках. Пусть будет всё в одном месте.

630В, 0.47 мкф, 10%

В общем, выношу на суд общественности таблицу кодов напряжения для конденсаторов.

Юзайте на здоровье, а если есть чем дополнить — присылайте коды!

Буква	0x	1x	2x	3x
A	10	100	1000
B	12,5	125
C	16	160
D	2	20	200
E	2,5	25	250
F	315
G	4	400
H	50	500
I
J	6,3	63	630
K	8	80
L	5,5
M
N
O
P	220
Q	110
R
S
T	(50)
U
V	35	350
W	450
X
Y
Z	180

Как правило на конденсаторы наносится значение ёмкости, допуск и номинальное напряжение.

Вот эта таблица:

Напр В	Букв. обозн.	Напр. В	Букв. обозн.	Напр. В	Букв. обозн.	Напр. В	Букв. обозн	Напр. В	Букв. обозн
1,0	I	6.3	B	40	S	100	N	350	T
2,5	M	10	D	50	J	125	P	400	Y
3.2	A	16	E	63	K	160	Q	450	U
4.0	C	20	F	80	L	315	X	500	V

Найти в интернете эту таблицу не составляет особого труда.

Вторая система имеет двух-символьный код напряжения. Вот как раз её-то найти и не удалось.

Напряжение в этой системе может обозначаться как: 1J, 2A, 2G, 2J, что соответствуют напряжению 63В, 100В, 400В, 630В.

Эти обозначения также наносятся на метало-плёночные (и, возможно, керамические) конденсаторы.

«E» = 25 В, «j» = 6.3 В

«A» = 10 В, «C» = 16 В

Как найти напряжение между пластинами конденсатора

Одним из разделов физики, лежащих в основе знания, посвященного процессам, связанным с электричеством, является электростатика. Она изучает взаимодействие неподвижных электрических зарядов. Поэтому одной из типичных задач, которую может потребоваться решить школьникам и студентам младших курсов ВУЗ-ов, является нахождение напряжения между пластинами конденсатора на основании знания различных параметров.Вам понадобится

Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C — емкость, а U — напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).

Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества электричества) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q — заряд). Следовательно, зная энергию и заряд конденсатора, можно вычислить напряжение между его пластинами по формуле: U=2∙W/q.

Поскольку заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C∙U), то, зная заряд и емкость, можно найти и напряжение.-12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.

По какой формуле найти ёмкость (объем) конденсаторов

Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.

Конденсаторы

Расчёт конденсаторов

Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:

C=q/U, где:

C – ёмкость,
q – заряд одной из обкладок элемента,
U – разность потенциалов между обкладками.

В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».

Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:

С=Co*ε, где:

С – реальная ёмкость,
Со – идеальная, при условии, что между пластинами вакуум или воздух,
ε – диэлектрическая проницаемость материала между ними.

Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.

Устройство конденсатора

Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).

Расчет плоской конструкции

Если нужно рассчитать плоский конденсатор, то необходимо учесть площадь обкладок и расстояние между ними. Это отражено в формуле, по которой рассчитывается ёмкость плоского конденсатора:

C=ε/d, где:

ε – диэлектрическая проницаемость изолирующего материала,
d – расстояние между пластинами.

Расчет конструкции цилиндрической формы

Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.

Вычисляются параметры такого устройства по формуле:

C=(2π*l*R*ε)/d, где:

l – длина устройства,
R – радиус цилиндра,
ε – диэлектрическая проницаемость изолятора,
d – его толщина.

Расчёт сферической конструкции

Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:

C=(4π*l*R1*R2*ε)/(R2-R1), где:

R1 – радиус внутренней сферы,
R2 – радиус внешней сферы,
ε – диэлектрическая проницаемость.

Формулы ёмкости конденсаторов различной формы

Ёмкость одиночного проводника

Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:

C=Q/φ, где:

Q – заряд,
φ – потенциал проводника.

Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.

Способы соединения элементов

Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.

Соединение конденсаторов

Параллельное соединение

Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.

При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:

C=C1+C2+…Cn,

где C1-Cn – параметры деталей, участвующих в параллельном соединении.

Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.

Последовательное соединение

Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.

При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.

Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.

Рассчитываются эти параметры следующим образом:

Допустимое напряжение:

Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;

Общая ёмкость:

1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.

Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).

Смешанное соединение

Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:

определяются группы элементов, соединённые параллельно;
для каждой группы в отдельности рассчитывается эквивалентные значения;
рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.

Видео

Оцените статью:

Электрическая емкость (страница 1)

Решение:
При перемещении пластины емкость конденсатора в данный момент времени определяется той частью площади пластин, по которой они перекрывают друг друга. В моменты времени t₁ и t₂ площади

где l=10 см-длина стороны пластины. В эти моменты времени конденсатор имеет емкости

а заряды на его пластинах

11 Найти заряд, который нужно сообщить двум параллельно соединенным конденсаторам с емкостями C₁ = 2 мкФ и С₂=1 мкФ, чтобы зарядить их до разности потенциалов V=20кВ.

Решение:
Общий заряд параллельно соединенных конденсаторов

12 Два одинаковых плоских конденсатора соединены параллельно и заряжены до разности потенциалов V₀ = 6 В. Найти разность потенциалов V между пластинами конденсаторов, если после отключения конденсаторов от источника тока у одного конденсатора уменьшили расстояние между пластинами вдвое.

Решение:

13 Два конденсатора с емкостями С₁ = 1 мкФ и С₂ = 2мкФ зарядили до разностей потенциалов V₁=20B и V₂ = 50 В. Найти разность потенциалов V после соединения — конденсаторов одноименными полосами.

Решение:

14 Конденсатор емкости C₁ = 20 мкФ, заряженный до разности потенциалов V₁ = 100B, соединили параллельно с заряженным до разности потенциалов V₁=40 В конденсатором, емкость которого С₂ неизвестна (соединили одноименно заряженные обкладки конденсаторов). Найти емкость С₂ второго конденсатора, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=80 В.

Решение:

15 Конденсатор емкости С₁=4мкФ, заряженный до разности потенциалов V₁ = 10B, соединен параллельно с заряженным до разности потенциалов V₂ = 20 В конденсатором емкости С₂ = 6 мкФ (соединили разноименно заряженные обкладки конденсаторов). Какой заряд окажется на пластинах первого конденсатора после соединения?

Решение:
Заряды конденсаторов до их соединения q₁ = C₁V₁ и q₂ = C₂V₂. После соединения разноименно заряженных обкладок конденсаторов общий заряд q = |q₂-q₁| = (C₁ + C₂)V и заряд первого конденсатора где V-разность потенциалов между обкладками конденсаторов после соединения; отсюда

16 Конденсатор, заряженный до разности потенциалов V₁ = 20 В, соединили параллельно с заряженным до разности потенциалов V₂ = 4 В конденсатором емкости С₂ = 33 мкФ (соединили разноименно заряженные обкладки конденсаторов). Найти емкость С1 первого конденсатора, если разность потенциалов между обкладками конденсаторов после их соединения V=2 В.

Решение:
После соединения разноименных обкладок общий заряд q = CV равен разности зарядов q₁ = C₁V₁ и q₂ = C₂V₂ отдельных конденсаторов, где С=С₁ + С₂ — общая емкость после соединения. Таким образом,

17 Конденсатор емкости С₁ = 1 мкФ, заряженный до разности потенциалов V₁ = 100B, соединили с конденсатором емкости С₂ = 2 мкФ, разность потенциалов V₂ на обкладках которого неизвестна (соединили разноименно заряженные обкладки конденсаторов). Найти разность потенциалов V₂, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=200 В.

Решение:
До соединения заряды первого и второго конденсаторов

После соединения разноименных обкладок общий заряд

Двойной знак мы здесь поставили потому, что заранее не известно, какой из зарядов, q₂ или q₁ больше; отсюда

Решение со знаком минус соответствует случаю, когда знаки зарядов на пластинах первого конденсатора после соединения пластин не меняются, а со знаком плюс-случаю, когда эти знаки становятся обратными. Так как в нашем случае , а величина |V₂| должна быть всегда положительной, то существует лишь одно решение-со знаком плюс. В результате |V₂| = 350 В.

18 Два проводящих шара с радиусами R₁ и R₂ расположены так, что расстояние между ними во много раз больше радиуса большего шара. На шар радиуса R₁ помещен заряд q. Каковы будут заряды на шарах после соединения их проводником, если второй шар не был заряжен? Емкостью проводника, соединяющего шары, пренебречь.

Решение:

19 Два проводящих шара с радиусами R₁ = 8см и R₂ = 20 см, находящихся на большом расстоянии друг от друга, имели электрические заряды q₁=40 нКл и q₂=— 20 нКл. Как перераспределятся заряды, если шары соединить проводником? Емкостью проводника, соединяющего шары, пренебречь.

Решение:
Соединение шаров проводником эквивалентно параллельному соединению конденсаторов. После соединения

20 Два проводящих шара с радиусами R₁ = 10см и R₂ = 5см, заряженных до потенциалов φ₁=20B и φ₂=10В, соединяются проводником. Найти поверхностные плотности зарядов на шарах σ₁ и σ₂ после их соединения. Расстояние между шарами велико по сравнению с их радиусами. Емкостью проводника, соединяющего шары, пренебречь.

Решение:
Заряды на шарах до и после соединения Общий потенциал шаров после соединения определим из условия сохранения заряда
Заряды на первом и втором шарах после соединения

Поверхностные плотности зарядов на шарах

21 Плоский воздушный конденсатор, заряженный до разности потенциалов V₀ = 800 В, соединили параллельно с таким же по размерам незаряженным конденсатором, заполненным диэлектриком. Какова диэлектрическая проницаемость e диэлектрика, если после соединения разность потенциалов между пластинами конденсаторов оказалась равной V=100В?

Решение:

22 Найти емкость С трех плоских воздушных конденсаторов, соединенных параллельно. Размеры конденсаторов одинаковы: площадь пластины S=314 см², расстояние между пластинами d=1 мм. Как изменится емкость трех конденсаторов, если пространство между пластинами одного конденсатора заполнить слюдой (диэлектрическая проницаемость ε₁ = 7), а другого — парафином (диэлектрическая проницаемость ε₂ = 2)?

Решение:
Емкость трех конденсаторов без диэлектрика При заполнении двух конденсаторов диэлектриками емкость трех конденсаторов

23 В заряженном плоском конденсаторе, отсоединенном от источника тока, напряженность электрического поля равна Е₀. Половину пространства между пластинами конденсатора заполнили диэлектриком с диэлектрической проницаемостью ε (толщина диэлектрика равна расстоянию между пластинами). Найти напряженность электрического поля Е в пространстве между пластинами, свободном от диэлектрика.

Решение:
Если d-расстояние между пластинами и С₀— емкость конденсатора без диэлектрика, то разность потенциалов между пластинами конденсатора (без диэлектрика) и заряд на пластинах Конденсатор, половина которого заполнена диэлектриком, можно рассматривать как два соединенных параллельно конденсатора (рис. 341), причем один не содержит диэлектрика и имеет емкость а в другом все пространство между пластинами заполнено диэлектриком, и поэтому его емкость Полная емкость конденсатора, половина которого заполнена диэлектриком, При отключенном источнике тока заряд на пластинах сохраняется, поэтому разность потенциалов между пластинами V=q/C, и напряженность электрического поля в пространстве между пластинами, свободном от диэлектрика,

24 Два последовательно соединенных конденсатора с емкостями C₁ = 1 мкФ и С₂ = 3 мкФ подключены к источнику тока с напряжением V =220 В. Найти напряжение на каждом конденсаторе.

Решение:
Если V₁ и V₂ — напряжения на первом и втором конденсаторах, то V= V₁ + V₂, а заряды на них одинаковы и равны
q=C₁V₁=C₂V₂; отсюда

При последовательном соединении конденсаторов на конденсаторе меньшей емкости напряжение больше, чем на конденсаторе большей емкости.

25 Два последовательно соединенных конденсатора с емкостями C₁ = 1 мкФ и С₂ = 2 мкФ подключены к источнику тока с напряжением V =900 В. Возможна ли работа такой схемы, если напряжение пробоя конденсаторов V_пр = 500 В?

Решение:
Напряжения на первом и втором конденсаторах (см. задачу 24). Работать при указанном в условии задачи напряжении пробоя конденсаторов нельзя, ибо произойдет пробой первого, а затем и второго конденсаторов.

26 Два последовательно соединенных конденсатора подключены к источнику тока с напряжением V= 200 В (рис. 79). Один конденсатор имеет постоянную емкость C₁ = 0,5 мкФ, а другой — переменную емкость С₂ (от Cmin = 0,05 мкФ до Сmах = 0,5 мкФ). В каких пределах изменяется напряжение на переменном конденсаторе при изменении его емкости от минимальной до максимальной?

Решение:
При изменении емкости переменного конденсатора С₂ от Cmin до Сmax, напряжение на нем V изменяется в пределах (см. задачу 24)

27 При последовательном соединении трех различных конденсаторов емкость цепи С₀ = 1 мкФ, а при параллельном соединении емкость цепи С=11мкФ. Найти емкости конденсаторов С₂ и С₃, если емкость конденсатора С₁ = 2 мкФ.

Решение:

28 При последовательном соединении трех различных конденсаторов емкость цепи С₀ = 0,75 мкФ, а при параллельном соединении емкость цепи С = 7 мкФ. Найти емкости конденсаторов С₂ и С₃ и напряжения на них V₂ и V₃ (при последовательном соединении), если емкость конденсатора C₁ = 3 мкФ, а напряжение на нем V₁= 20B.

Решение:
При последовательном соединении конденсаторов имеем

при параллельном

Из этих уравнений находим

Согласно теореме Виета С2 и С3 должны быть корнями квадратного уравнения

Решая его, найдем

Заряды на всех конденсаторах при последовательном соединении равны между собой:

29 Три последовательно соединенных конденсатора с емкостями С₁ = 100пФ, С₂ = 200 пФ, С₃ = 500 пФ подключены к источнику тока, который сообщил им заряд q=10нКл. Найти напряжения на конденсаторах V₁, V₂ и V₃, напряжение источника тока V и емкость всех конденсаторов С₀.

Решение:
При последовательном соединении конденсаторов заряд каждого конденсатора равен q, поэтому

Напряжение источника тока равно полному напряжению на всех конденсаторах:

Так как при последовательном соединении
то

30 Три последовательно соединенных конденсатора с емкостями С₁=0,1мкФ, С₂ = 0,25 мкФ и С₃ = 0,5 мкФ подключены к источнику тока с напряжением V =32 В. Найти напряжения V₁, V₂ и V₃ на конденсаторах.

Решение:

31 Два одинаковых воздушных конденсатора емкости С=100пФ соединены последовательно и подключены к источнику тока с напряжением V= 10 В. Как изменится заряд на конденсаторах, если один из них погрузить в диэлектрик с диэлектрической проницаемостью ε = 2?

Решение:
При последовательном соединении конденсаторов заряды на конденсаторах равны. До погружения одного из них в диэлектрик заряд на каждом конденсаторе

после погружения одного из них в диэлектрик заряды конденсаторов будут

Учитывая, что

Изменение заряда на конденсаторах

32 Два плоских воздушных конденсатора с одинаковыми емкостями соединены последовательно и подключены к источнику тока. Пространство между пластинами одного из конденсаторов заполняют диэлектриком с диэлектрической проницаемостью ε = 9. Во сколько раз изменится напряженность электрического поля Е в этом конденсаторе?

Решение:
Первоначальная напряженность электрического поля в каждом конденсаторе

где d-расстояние между пластинами конденсатора. После заполнения одного конденсатора диэлектриком напряженность электрического поля в нем

Отношение напряженностей

33 Решить предыдущую задачу для случая, когда конденсаторы после зарядки отключаются от источника тока.

Решение:
После отключения конденсатора от источника тока и заполнения его диэлектриком заряд на нем не изменяется:

Напряженность электрического поля в конденсаторе, заполненном диэлектриком,

Отношение напряженностей

34 Два плоских воздушных конденсатора с одинаковыми емкостями С=10пФ соединены последовательно. Насколько изменится емкость конденсаторов, если пространство между пластинами одного из них заполнить диэлектриком с диэлектрической проницаемостью ε = 2?

Решение:
Изменение емкости соединенных конденсаторов

35 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а ее толщина намного меньше d. Найти емкость конденсатора с проводящей пластинкой, если пластинка расположена на расстоянии l от одной из обкладок конденсатора.

Решение:
После введения пластинки образовалось два последовательно включенных конденсатора с емкостями

(рис. 342). Их общую емкость определим из соотношения

где С-первоначальная емкость конденсатора. Таким образом, после введения пластинки при любом ее положении С₀ = С.

36 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а толщина d_п = d/3

Решение:
Введение проводящей пластинки между обкладками конденсатора приводит к образованию двух последовательно включенных конденсаторов с расстояниями между обкладками d₁ и d₂ и емкостями

(рис.343). Их общую емкость находим из соотношения

При -первоначальная емкость конденсатора.

37 Плоский воздушный конденсатор заряжен до разности потенциалов V₀ = 50 В и отключен от источника тока. После этого в конденсатор параллельно обкладкам вносится проводящая пластинка толщины d_п= 1 мм. Расстояние между обкладками d=5 мм, площади обкладок и пластинки одинаковы. Найти разность потенциалов V между обкладками конденсатора с проводящей пластинкой.

Решение:
Емкости конденсатора до и после внесения проводящей пластинки толщины d_п (см. задачу 36)
Заряд конденсатора, отключенного от источника тока, не изменяется:

отсюда разность потенциалов между обкладками конденсатора после внесения проводящей пластинки

38 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d вводится параллельно обкладкам диэлектрическая пластинка толщины d₁<d/ Диэлектрическая проницаемость пластинки равна ε, площади обкладок и пластинки одинаковы и равны S. Найти емкость конденсатора с диэлектрической пластинкой.

Решение:

Цепи постоянного тока

, содержащие резисторы и конденсаторы

1. Устройство синхронизации в системе стеклоочистителей прерывистого действия автомобиля основано на постоянной времени RC и использует конденсатор емкостью 0,500 мкФ и переменный резистор. В каком диапазоне R должно изменяться для достижения постоянных времени от 2,00 до 15,0 с?

2. Кардиостимулятор срабатывает 72 раза в минуту, каждый раз, когда конденсатор емкостью 25,0 нФ заряжается (батареей, включенной последовательно с резистором) до 0,632 от его полного напряжения.В чем ценность сопротивления?

3. Продолжительность фотографической вспышки связана с постоянной времени RC , которая составляет 0,100 мкс для определенной камеры. (а) Если сопротивление импульсной лампы составляет 0,0400 Ом во время разряда, каков размер конденсатора, обеспечивающего его энергию? (б) Какова постоянная времени зарядки конденсатора, если сопротивление зарядки составляет 800 кОм?

4. Конденсатор емкостью 2,00 и 7,50 мкФ можно подключать последовательно или параллельно, как и конденсатор емкостью 25 мкФ.0- и резистор 100 кОм. Вычислите четыре постоянные времени RC , которые можно получить при последовательном соединении полученной емкости и сопротивления.

5. После двух постоянных времени, какой процент конечного напряжения, ЭДС, находится на первоначально незаряженном конденсаторе C , заряженном через сопротивление R ?

6. Резистор 500 Ом, незаряженный конденсатор 1,50 мкФ и ЭДС 6,16 В соединены последовательно. а) Каков начальный ток? (b) Какова постоянная времени RC ? (c) Какой ток будет через одну постоянную времени? (d) Какое напряжение на конденсаторе после одной постоянной времени?

7.Дефибриллятор сердца, используемый на пациенте, имеет постоянную времени RC 10,0 мс из-за сопротивления пациента и емкости дефибриллятора. (a) Если дефибриллятор имеет емкость 8,00 мкФ, каково сопротивление пути, проходящего через пациента? (Вы можете пренебречь емкостью пациента и сопротивлением дефибриллятора.) (B) Если начальное напряжение составляет 12,0 кВ, сколько времени потребуется, чтобы упасть до 6,00 × 10 ² В?

8. У монитора ЭКГ постоянная времени RC должна быть меньше 1.00 × 10 ² мкс, чтобы иметь возможность измерять изменения напряжения за небольшие промежутки времени. (а) Если сопротивление цепи (в основном из-за сопротивления груди пациента) составляет 1,00 кОм, какова максимальная емкость цепи? (б) Будет ли сложно на практике ограничить емкость до значения, меньшего, чем значение, указанное в (а)?

9. На рис. 7 показано, как истекающий резистор используется для разряда конденсатора после отключения электронного устройства, что позволяет человеку работать с электроникой с меньшим риском поражения электрическим током.а) Что такое постоянная времени? (b) Сколько времени потребуется, чтобы снизить напряжение на конденсаторе до 0,250% (5% от 5%) от его полного значения после начала разряда? (c) Если конденсатор заряжен до напряжения В ₀ через сопротивление 100 Ом, рассчитайте время, необходимое для повышения до 0,865 В ₀ (это примерно две постоянные времени).

Рисунок 7.

10. Используя точную экспоненциальную обработку, найдите, сколько времени требуется, чтобы разрядить конденсатор емкостью 250 мкФ через резистор 500 Ом до 1.00% от исходного напряжения.

11. Используя точную экспоненциальную обработку, найдите, сколько времени требуется для зарядки первоначально незаряженного конденсатора 100 пФ через резистор 75,0 МОм до 90,0% от его конечного напряжения.

12. Integrated Concepts Если вы хотите сфотографировать пулю, летящую со скоростью 500 м / с, то очень короткая вспышка света, производимая разрядом RC через импульсную лампу, может ограничить размытие. Предполагая, что перемещение 1,00 мм за одну постоянную RC является приемлемым, и учитывая, что вспышка приводится в действие конденсатором емкостью 600 мкФ, какое сопротивление в импульсной лампе?

13. Integrated Concepts Мигающая лампа в рождественской серьге основана на разряде конденсатора RC через его сопротивление. Эффективная продолжительность вспышки составляет 0,250 с, в течение которых она дает в среднем 0,500 Вт при среднем 3,00 В. а) Какую энергию она рассеивает? б) Сколько заряда проходит через лампу? (c) Найдите емкость. (г) Какое сопротивление лампы?

14. Integrated Concepts Конденсатор емкостью 160 мкФ, заряженный до 450 В, разряжается через 31.Резистор 2 кОм. (а) Найдите постоянную времени. (b) Рассчитайте повышение температуры резистора, учитывая, что его масса составляет 2,50 г, а его удельная теплоемкость [латекс] 1,67 \ frac {\ text {кДж}} {\ text {кг} \ cdotº \ text {C}} \\ [/ latex], учитывая, что большая часть тепловой энергии сохраняется за короткое время разряда. (c) Рассчитайте новое сопротивление, предполагая, что это чистый углерод. (d) Кажется ли это изменение сопротивления значительным?

15. Необоснованные результаты (a) Рассчитайте емкость, необходимую для получения постоянной времени RC , равной 1.00 × 10 ³ с резистором 0,100 Ом. б) Что неразумного в этом результате? (c) Какие допущения ответственны?

16. Создай свою проблему Рассмотрим вспышку фотоаппарата. Постройте задачу, в которой вы вычисляете размер конденсатора, который накапливает энергию для лампы-вспышки. Среди факторов, которые необходимо учитывать, — это напряжение, приложенное к конденсатору, энергия, необходимая для вспышки, и соответствующий заряд, необходимый для конденсатора, сопротивление импульсной лампы во время разряда и желаемая постоянная времени RC .

17. Создайте свою проблему Рассмотрим перезаряжаемый литиевый элемент, который будет использоваться для питания видеокамеры. Постройте задачу, в которой вы вычисляете внутреннее сопротивление элемента во время нормальной работы. Кроме того, рассчитайте минимальное выходное напряжение зарядного устройства, которое будет использоваться для зарядки литиевого элемента. Среди факторов, которые следует учитывать, — ЭДС и полезное напряжение на клеммах литиевого элемента, а также ток, который он должен обеспечивать в видеокамере.

Заряд, разделение пластин и напряжение

Dynamics Track
Наклонная плоскость
Импульс

Конденсатор
Пластина Sep
Пластина Sep / Volt
Диэлектрики

Цепи
Закон Ома
Последовательный / Параллельный

Wave Tank
Частота / длина волны
Two Pt Interf.

Оптическая скамья
Refraction
Фокусное расстояние

Конденсатор с параллельными пластинами

Заряд конденсаторов, разделение пластин и напряжение

Конденсатор используется для хранения электрического заряда. Чем большее напряжение (электрическое давление) вы прикладываете к конденсатору, тем больше заряда нагнетается в конденсатор. Кроме того, чем большей емкостью обладает конденсатор, тем больший заряд будет вызван данным напряжением.Это соотношение описывается формулой q = CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение.

Глядя на эту формулу, можно спросить, что бы произошло, если бы заряд оставался постоянным, а емкость изменялась. Ответ, разумеется, таков, что напряжение изменится! Это то, что вы будете делать в этой лаборатории.

Лабораторный конденсатор

Конденсатор с параллельными пластинами — это устройство, используемое для изучения конденсаторов.Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно скручены по спирали в небольших корпусах, поэтому конденсатор с параллельными пластинами значительно упрощает привязку функции к устройству.

Этот конденсатор работает, накапливая противоположные заряды на параллельных пластинах, когда напряжение подается с одной пластины на другую. Количество заряда, который перемещается в пластины, зависит от емкости и приложенного напряжения в соответствии с формулой Q = CV, где Q — заряд в кулонах, C — емкость в фарадах, а V — разность потенциалов между пластинами в вольт.

Конденсаторы накапливают энергию

Если напряжение подается на конденсатор, а затем отключается, заряд, накопленный в конденсаторе, сохраняется до тех пор, пока конденсатор каким-либо образом не разрядится. Между пластинами возникает электрическое поле, которое позволяет конденсатору накапливать энергию. Это один из полезных аспектов конденсаторов, способность накапливать энергию в электрическом поле, чтобы ее можно было использовать позже.

От чего зависит емкость?

Количество заряда, которое может храниться на один приложенный вольт, определяется площадью поверхности пластин и расстоянием между ними.Чем больше пластины и чем ближе они расположены, тем больше заряда может храниться на каждый вольт разности потенциалов между пластинами. Заряд, накопленный на приложенный вольт, представляет собой емкость, измеряемую в фарадах.

Может ли изменение емкости заряженного конденсатора изменить его напряжение?

Лабораторный конденсатор можно регулировать, поэтому мы можем провести интересный эксперимент с емкостью и напряжением. Если конденсатор имеет постоянный заряд, изменение емкости должно вызвать изменение напряжения.Раздвигание пластин приведет к уменьшению емкости, поэтому напряжение должно увеличиться.

Как можно математически определить емкость нашего конденсатора?
Для конденсатора с параллельными пластинами емкость определяется по следующей формуле:

C = ε 0 А / сут

Где C — емкость в Фарадах, ε 0 — постоянная диэлектрической проницаемости свободного пространства (8,85×10 -12), A — площадь пластин в квадратных метрах, а d — расстояние между пластинами в метрах.

Фарада — это очень большая величина емкости, поэтому мы будем использовать метрические префиксы для получения более удобных чисел. Емкость обычно измеряется в микрофарадах (мкФ), что составляет 1,0×10 -6F, или пикофарадах (пФ), что составляет 1,0×10 -12F. 1.0F = 1,000,000 мкФ = 1,000,000,000,000 пФ! Будьте очень внимательны с расчетами!

Этот расчет даст вам приблизительное значение емкости лабораторного конденсатора. Однако есть и другие факторы, которые вносят ошибки в реальные измерения емкости и напряжения.Вам нужно внимательно учитывать эти факторы.

Лабораторное оборудование:

Для получения хороших результатов эта лабораторная деятельность требует специального оборудования. Вам нужен хороший стабилизированный источник питания, чтобы напряжение, подаваемое на конденсатор, было одинаковым при каждом испытании.

Вам также понадобится очень точный способ измерения напряжения между пластинами без резистивной нагрузки на конденсатор. Количество накопленного заряда очень мало, поэтому обычный вольтметр не подойдет.Мельчайший заряд, накопленный в конденсаторе, просто разрядится через счетчик, делая любые измерения бесполезными. Вы будете использовать специальный прибор для измерения напряжения, называемый электрометром, который измеряет напряжение без разряда конденсатора.

Одна из проблем электрометра заключается в том, что он имеет некоторую собственную емкость. Поскольку эта емкость параллельна емкости конденсатора, встроенная емкость выводов должна быть добавлена к емкости конденсатора.

Назначение:

Целью данной лабораторной работы является исследование взаимосвязи между разделением пластин и напряжением в конденсаторе с параллельными пластинами, который поддерживается постоянным зарядом.

Оснащение:

Конденсатор переменной емкости
Электрометр
Регулируемый источник питания
Поводки для перемычек
Выводы для электрометра

Предупреждения:

Это хрупкое оборудование. Все должно сочетаться с легчайшими прикосновениями. Ничего не заставляйте!

Ваша первая задача — предсказать, что произойдет с напряжением конденсатора, когда вы зарядите его источником 10 В, а затем раздвинете пластины (что уменьшит емкость). Вы сделаете это в следующем разделе.

Теоретические расчеты:

Сначала необходимо рассчитать теоретическую емкость для каждого расстояния между пластинами. Мы сделаем первое, а потом вы сможете сделать все остальное! Самая сложная часть этого — правильно настроить юниты. Проще всего сложить все в метрах для расчетов:

Измерьте диаметр пластин конденсатора в сантиметрах. Ваш размер должен быть около 17,8 см
Разделите диаметр на 100, чтобы получить размер в метрах.Результат — 0,178 м. Разделите это на два, чтобы получить радиус: 0,089 м
Площадь пластины определяется по общей формуле A = πr 2. Подставьте числа, чтобы получить A = π (0,089) 2 = 0,0249м 2
Преобразуйте расстояние между пластинами (1 мм) в метры, разделив на 1000. 1/1000 = 0,001 м.
Используйте это число в формуле C = ε 0A / d, чтобы определить расчетную емкость, таким образом: C = 8,85×10 -12 (0,0249) / 0,001 = 2,20×10 -10. Это равно 220×10 -12F или 220pF
Добавьте встроенную емкость электрометра (50 пФ) к теоретической емкости, чтобы получить 270 пФ.
Запишите этот результат (270 пФ) в столбец «Расчетная емкость» и в строку 1 мм.
Повторите этот процесс для других расстояний между пластинами. Обратите внимание, что площадь пластины одинакова для всех, поэтому все, что вам нужно сделать, это повторить шаги 5, 6 и 7, вставляя правильные значения для интервала в каждом случае.
Теперь вы рассчитаете теоретическое напряжение для каждого интервала. Предположим, что для шага 1,0 мм напряжение составляет 10 В, поэтому вы можете просто указать это значение в таблице.Во-первых, вы определяете количество заряда в конденсаторе при таком расстоянии и напряжении. Используйте формулу Q = CV, чтобы определить заряд, таким образом: Q = 270×10 -12F (10V) = 2700×10 -12C. Этот заряд остается неизменным на всех расстояниях между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец Расчетный заряд! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V = Q / C, таким образом: V = 2700×10 -12C / 94,0×10 -12F = 28,7V. Введите это значение в столбец «Расчетное напряжение» в строке 5 мм.
Повторите тот же расчет напряжения для оставшихся расстояний между пластинами. Используйте рассчитанную емкость и постоянный заряд для каждого промежутка и введите значение напряжения в столбец «Расчетное напряжение» таблицы.
Поздравляем! Вы закончили предварительные расчеты! Все, что вам нужно сделать сейчас, это произвести измерения!

В следующих разделах вы проведете реальный эксперимент для проверки (или, возможно, не проверки!) Ваших теоретических расчетов.

Процедура настройки переменного конденсатора (если лаборатория уже настроена, переходите к следующему разделу!)

Поместите переменный конденсатор в середину лабораторного стола так, чтобы отметка 0 см находилась слева от вас. Не ставьте конденсатор слишком близко к краю стола!
Поместите блок питания за конденсатором переменной емкости. Подключите блок питания, но не включайте его.
Подключите красный и черный перемычки к красной и черной клеммам источника питания. Просто прикрепите зажим «крокодил» к отверстию и оставьте другой конец проводов свободным.
Поместите электрометр слева от конденсатора.
Присоедините плоские клеммы выводов электрометра к клеммам на задней стороне каждой пластины конденсатора. Красный провод идет к правой пластине, черный провод идет к левой пластине.
Вставьте разъем BNC в электрометр.
Поместите пластины на расстоянии минимум 1 мм.Белые бамперы предотвращают сближение пластин. Если пластины не параллельны друг другу, используйте регулировочные ручки в центре правой опоры, чтобы выровнять пластины. Левый край пластикового язычка, выступающий в сторону шкалы, должен быть совмещен с отметкой 1 мм.

Сбор экспериментальных данных

Убедитесь, что оборудование настроено правильно и полностью.
Поверните все четыре регулятора на блоке питания против часовой стрелки до упора.
Поверните крайнюю левую ручку (Fine Current) в положение на 12 часов (прямо вверх!)
Включите источник питания. Дисплеи должны загореться.
Используйте ручки Fine и Coarse Voltage (две крайние правые ручки), чтобы установить напряжение на 10,0 В.
Установите пластины на минимальное значение
Установите электрометр на шкалу 30 В.
Нажмите кнопку питания на электрометре. Должен загореться светодиод 30 В.
Нажмите кнопку нуля на электрометре. Обнуляет счетчик и обеспечивает нулевое напряжение на пластинах относительно друг друга.
На мгновение прикоснитесь к проводам от источника питания к пластинам, черный к левой пластине и красный к правой пластине.
Электрометр должен показывать 12 В в этой точке (12 В — это первая маленькая отметка над «1» на нижней шкале. Если он не проверяет вашу настройку, попробуйте еще раз.Иногда вам нужно несколько раз прикоснуться проводами к пластинам, чтобы получить правильные показания 12 В.
С этого момента вы должны быть осторожны, чтобы не прикасаться к пластинам. Прикоснувшись к ним, вы измените заряд в пластинах и испортите данные!
Следите за электрометром, чтобы убедиться, что заряд сохраняется. Если вы видите падение напряжения более чем на вольт за 30 секунд, остановитесь и выясните, что не так, прежде чем продолжить.
Переключите электрометр на настройку 100 В. Счетчик должен по-прежнему показывать 12 В, но по шкале 100 В.
Осторожно раздвиньте пластины на расстояние 5 мм.
Снимите показание электрометра и запишите его в таблицу под столбцом «Измеренное напряжение».
Повторите два предыдущих шага для других расстояний между пластинами и запишите соответствующие данные.

Разделение пластин (мм)	Расчетная емкость (пФ)	Расчетный сбор (пКл)	Расчетное напряжение (В)	Измеренное напряжение (В)
1
5
10
15
20
25
30
35
40

Анализ данных:

На миллиметровой бумаге постройте расчетную емкость по оси x (горизонтальная) в зависимости от напряжения на оси y (вертикальная).Нанесите на график рассчитанное и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различать две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначили оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»).
Изучите свой график и ответьте на следующие вопросы:

Подтверждают ли ваши измеренные данные измеренные значения?

Две кривые имеют одинаковую форму? Если да, то на что это указывает?

Что бы вы сделали, чтобы повысить точность собираемых данных?
Формула для энергии, запасенной в конденсаторе, U e = ½CV 2.Сохраняется ли энергия, запасенная в конденсаторе, постоянной при изменении расстояния между пластинами? Он идет вверх или вниз? Обсудите, откуда пришла или ушла энергия.

Напряжение на конденсаторе — Электротехническая стековая биржа

Решение ckt # 3 сложным путем с использованием дифференциальных уравнений:

Начнем с того, что уравнение всегда выполняется для любого конденсатора. $$ i = CdV / dt $$

В схеме, которую вы предоставили, у нас есть два неизвестных напряжения (V1 на C1 и V2 на C2).Их можно решить, применяя текущие законы Кирхгофа к двум узлам.

Для узла V1: $$ (V_s-V_1) / R_1 = C_1 dV_1 / dt + (V_1-V_2) / R_2

А для узла V2: $$ (V_1-V_2) / R_2 = C_2 dV_2 / dt

Теперь у нас есть два дифференциальных уравнения с двумя неизвестными. Решите их одновременно, и мы получим выражения для V1 и V2. После вычисления V1 и V2 вычисление токов в ответвлениях становится тривиальным.

Конечно, решение дифференциальных уравнений нетривиально, поэтому обычно мы используем преобразование Лапласа или преобразование Фурье, чтобы преобразовать их в простые алгебраические уравнения в частотной области, решить для неизвестных, а затем выполнить обратное преобразование Лапласа / Фурье, чтобы вернуть неизвестные. во временную область.

Метод 2: Используйте правило делителя напряжения:

Если мы вспомним, что импеданс конденсатора C равен $$ Z = 1 / jwC $$ и обозначив импедансы двух конденсаторов C1 и C2 как Z1 и Z2, мы можем вычислить V2, используя формулу для деления напряжения на два импеданса (http://en.wikipedia.org/wiki/Voltage_divider): $$ V_2 = V_1 R_2 / (R_2 + Z_2) $$ V1 также можно рассчитать с использованием того же правила, единственная проблема заключается в том, что импеданс на правой стороне узла 1 немного сложен: это параллельная комбинация Z1 и (R2 + Z2).V1 теперь становится $$ V_1 = V_s (Z_1 * (R_2 + Z_2) / (Z_1 + R_2 + Z_2)) / (R_1 + (Z_1 * (R_2 + Z_2) / (Z_1 + R_2 + Z_2))) $$

Что делать дальше, так это расширить Z1 и Z2, используя формулу емкостного импеданса, чтобы получить V1 и V2 через w. Если вам нужен полный временной отклик переменных, вы можете выполнить обратное преобразование Фурье и получить V1 и V2 как функции времени. Однако, если вам нужно только окончательное (установившееся) значение, просто установите $$ w = 0 $$ и оцените V1 и V2.

Более простой способ:

Этот метод может дать только окончательные установившиеся значения, но он удобен для быстрых вычислений.Загвоздка в том, что как только цепь перешла в устойчивое состояние, ток через каждый конденсатор будет равен нулю. Возьмем, к примеру, первую схему (простой RC). Тот факт, что ток через C равен нулю, диктует, что ток через R (и, следовательно, падение напряжения на нем) также равняется нулю. Следовательно, напряжение на C будет равно Vs.

Для второй цепи весь ток должен проходить по пути R1-> R2-> R3, если конденсатор не потребляет ток. Это означает, что напряжение на C (равное напряжению на R2) составляет $$ V_s R_2 / (R_1 + R_2 + R_3) $$

В последней схеме ток через C2, равный нулю, означает, что ток через R2 равен нулю (и, следовательно, любое падение напряжения на нем).Это означает, что любой протекающий ток должен проходить по пути R1-> C1. Однако ток через C1 также равен нулю, что означает, что R1 также не пропускает ток. Таким образом, оба напряжения V1 и V2 будут равны Vs в установившемся режиме

Конденсаторы 101 — iFixit

Вот немного сухого материала, просто чтобы помочь понять, что такое конденсатор и что он обычно делает. Конденсатор — это небольшой (в большинстве случаев) электрический / электронный компонент на большинстве печатных плат, который может выполнять различные функции.Когда конденсатор помещается в цепь с активным током, электроны с отрицательной стороны накапливаются на ближайшей пластине. Отрицательный перетекает к положительному, поэтому отрицательный является активным проводом, хотя многие конденсаторы не поляризованы. Как только пластина больше не может удерживать их, они выталкиваются через диэлектрик на другую пластину, тем самым вытесняя электроны обратно в цепь. Это называется разрядом. Электрические компоненты очень чувствительны к колебаниям напряжения, и поэтому скачок мощности может убить эти дорогостоящие детали.Конденсаторы создают постоянное напряжение для других компонентов и, таким образом, обеспечивают стабильное питание. Переменный ток выпрямляется диодами, поэтому вместо переменного тока есть импульсы постоянного тока от нуля до пика. Когда конденсатор от линии питания подключен к земле, и постоянный ток не проходит, но по мере того, как импульс заполняет конденсатор, он снижает ток и эффективное напряжение. Пока напряжение питания падает до нуля, конденсатор начинает вытекать из своего содержимого, это сглаживает выходное напряжение и ток.Таким образом, конденсатор размещается линейно к компоненту, что позволяет поглощать выбросы и дополнять впадины, что, в свою очередь, поддерживает постоянное питание компонента.

Существует множество различных типов конденсаторов. Часто они по-разному используются в схемах. Все слишком знакомые конденсаторы в виде круглых жестяных банок обычно являются электролитическими конденсаторами. Они сделаны из одного или двух листов металла, разделенных диэлектриком. Диэлектрик может быть воздухом (простейший конденсатор) или другими непроводящими материалами.Металлические пластины из фольги, разделенные диэлектриком, затем скручиваются, как Fruit Roll-up, и помещаются в банку. Они отлично подходят для объемной фильтрации, но не очень эффективны на высоких частотах.

Вот конденсатор, который некоторые, возможно, еще помнят со времен старого радио. Это многосекционный баночный конденсатор. Этот конкретный конденсатор представляет собой четырехсекционный конденсатор. Все это означает, что в одной емкости содержится четыре отдельных конденсатора с разными номиналами.

Керамические дисковые конденсаторы идеально подходят для более высоких частот, но не подходят для объемной фильтрации, поскольку керамические дисковые конденсаторы становятся слишком большими по размеру для более высоких значений емкости.В схемах, где жизненно важно поддерживать стабильный источник напряжения, обычно имеется большой электролитический конденсатор, параллельный керамическому дисковым конденсаторам. Электролитик будет делать большую часть работы, тогда как небольшой керамический дисковый конденсатор будет отфильтровывать высокую частоту, которую пропускает большой электролитический конденсатор.

Еще есть танталовые конденсаторы. Они маленькие, но имеют большую емкость по сравнению с керамическими дисковыми конденсаторами. Они более дорогие, но находят широкое применение на печатных платах небольших электронных устройств.

Старые бумажные конденсаторы, хотя и неполярные, имели черные полосы на одном конце. Черная полоса показывала, на каком конце бумажного конденсатора была металлическая фольга (которая действовала как экран). Конец с металлической фольгой был подключен к земле (или к самому низкому напряжению). Основное назначение экрана из фольги — продлить срок службы бумажного конденсатора.

Вот тот, который нас, скорее всего, интересует больше всего, когда речь идет об iDevices. Они очень маленькие по сравнению с перечисленными выше конденсаторами.Это крышки для устройств поверхностного монтажа (SMD). Несмотря на то, что они миниатюрны по размеру по сравнению с предыдущими конденсаторами, функция остается той же. Одной из важных особенностей этих конденсаторов является их «упаковка». Размеры этих компонентов стандартизированы, например, упаковка 0201 — 0,6 мм x 0,3 мм (0,02 дюйма x 0,01 дюйма). Размер корпуса керамических конденсаторов SMD соответствует размеру корпуса резисторов SMD. Это делает практически невозможным определить, конденсатор это или резистор, с помощью визуализации.Вот хорошее описание индивидуальных размеров на основе номеров пакетов.

Определить значение конденсатора можно несколькими способами. Номер один, конечно же, это маркировка на самом конденсаторе.

Этот конкретный конденсатор имеет емкость 220 мкФ (микрофарад) с допуском 20%. Это означает, что оно может находиться в диапазоне от 176 мкФ до 264 мкФ. Он имеет номинальное напряжение 160 В. Расположение выводов показывает, что это радиальный конденсатор.Оба вывода выходят с одной стороны, в отличие от осевого расположения, когда один вывод выходит с обеих сторон корпуса конденсатора. Кроме того, полоса со стрелками на стороне конденсатора указывает полярность, стрелки указывают на отрицательный вывод .

Теперь главный вопрос здесь — как проверить конденсатор на предмет необходимости его замены.

Для проверки конденсатора, когда он все еще установлен в цепи, потребуется измеритель ESR. Если конденсатор удален из схемы, то можно использовать мультиметр, установленный в качестве омметра, , но только для выполнения теста «все или ничего» .Этот тест покажет только, полностью ли разряжен конденсатор. , а не будет определять, в хорошем или плохом состоянии конденсатор. Чтобы определить, работает ли конденсатор при правильном значении (емкости), потребуется тестер конденсатора. Конечно, это также верно для определения номинала неизвестного конденсатора.

Счетчик, используемый для этой Wiki, является самым дешевым из всех доступных в любом универмаге. Для этого теста также рекомендуется использовать аналоговый мультиметр.Он покажет движение более наглядно, чем цифровой мультиметр, отображающий только быстро меняющиеся числа. Это должно позволить любому выполнять эти тесты, не тратя целое состояние на что-то вроде глюкометра Fluke.

Всегда разряжайте конденсатор перед тестированием, если этого не сделать, будет шокирующим сюрпризом. Конденсаторы очень маленькой емкости можно разрядить, переставив оба вывода отверткой. Лучше всего это сделать, разрядив конденсатор через нагрузку.В этом случае это выполнят кабели из крокодиловой кожи и резистор. Вот отличный сайт, показывающий, как построить инструменты для разряда.

Чтобы проверить конденсатор с помощью мультиметра, установите показание измерителя в диапазоне высоких сопротивлений, где-то выше 10 кОм и 1 м Ом. Прикоснитесь к выводам измерителя к соответствующим выводам на конденсаторе, красный к плюсу и черный к минусу. Измеритель должен начинать с нуля, а затем медленно приближаться к бесконечности. Это означает, что конденсатор находится в рабочем состоянии.Если счетчик остается на нуле, конденсатор не заряжается через батарею счетчика, что означает, что он не работает.

Это также будет работать с заглушками SMD. Тот же тест, когда стрелка мультиметра медленно движется в том же направлении.

Еще одно испытание конденсатора — это испытание напряжением. Мы знаем, что конденсаторы накапливают на своей пластине разность потенциалов зарядов, это напряжения. Конденсатор имеет анод с положительным напряжением и катод с отрицательным напряжением.Один из способов проверить, работает ли конденсатор, — это зарядить его напряжением, а затем измерить напряжение на аноде и катоде. Для этого необходимо зарядить конденсатор напряжением и подать напряжение постоянного тока на выводы конденсатора. В этом случае очень важна полярность. Если у этого конденсатора есть положительный и отрицательный вывод, это поляризованные конденсаторы (электролитические конденсаторы). Положительное напряжение пойдет на анод, а отрицательное — на катод конденсатора. Не забудьте проверить маркировку на тестируемом конденсаторе.Затем на несколько секунд подайте напряжение, которое должно быть меньше номинального напряжения конденсатора. В этом примере конденсатор 160 В будет заряжаться от батареи постоянного тока 9 В в течение нескольких секунд.

По окончании заряда отсоедините аккумулятор от конденсатора. Воспользуйтесь мультиметром и снимите напряжение на выводах конденсатора. Напряжение должно быть около 9 вольт. Напряжение будет быстро уменьшаться до 0 В, потому что конденсатор разряжается через мультиметр. Если конденсатор не сохраняет это напряжение, он неисправен и его следует заменить.

Проще всего конечно будет проверить конденсатор емкостным измерителем. Вот осевой GPF 1000 мкФ 40 В FRAKO с допуском 5%. Проверить этот конденсатор с помощью измерителя емкости очень просто. На этих конденсаторах отмечен положительный вывод. Подключите положительный (красный) провод от мультиметра к нему, а отрицательный (черный) — к противоположному. Этот конденсатор показывает 1038 мкФ, что явно в пределах допуска.

Тестирование конденсатора SMD может быть затруднено с помощью громоздких пробников.Можно либо припаять иглы к концам этих зондов, либо купить умный пинцет. Лучше всего использовать умный пинцет.

Некоторые конденсаторы не требуют проверки для определения неисправности. Если визуальный осмотр конденсаторов обнаруживает какие-либо признаки вздутия верхних частей, их необходимо заменить. Это наиболее частая неисправность блоков питания. При замене конденсатора крайне важно заменить его конденсатором того же или более высокого номинала. Никогда не субсидируйте конденсатор меньшей стоимости.

Если конденсатор, который собираются заменить или проверить, не имеет маркировки, потребуется схема. На изображении ниже показано несколько символов конденсаторов, которые используются на схеме.

В этом отрывке из схемы iPhone указаны символы конденсаторов, а также их значения.

Эта Wiki — это в значительной степени только основы того, что искать в конденсаторах, она никоим образом не является полной. Чтобы узнать больше о любых распространенных электронных компонентах, существует множество хороших онлайн-курсов и офлайн-курсов.

Eaton Electronics

Максвелл

Digikey

Конденсаторы Mouser

— learn.sparkfun.com

Добавлено в избранное Любимый 73

Введение

Конденсатор — это двухконтактный электрический компонент. Наряду с резисторами и катушками индуктивности они являются одними из самых фундаментальных пассивных компонентов , которые мы используем. Вам придется очень внимательно поискать схему, в которой не содержит конденсатора.

Особенностью конденсаторов является их способность накапливать энергию ; они похожи на полностью заряженную электрическую батарею. Колпачки , как мы их обычно называем, имеют самые разные критические приложения в схемах. Общие приложения включают локальное накопление энергии, подавление скачков напряжения и комплексную фильтрацию сигналов.

рассматривается в этом учебном пособии

В этом руководстве мы рассмотрим всевозможные темы, связанные с конденсаторами, в том числе:

Как делается конденсатор
Как работает конденсатор
Единицы емкости
Типы конденсаторов
Как распознать конденсаторы
Как емкость сочетается последовательно и параллельно
Применение конденсаторов общего назначения

Обозначения и единицы

Условные обозначения цепей

Есть два распространенных способа изобразить конденсатор на схеме. У них всегда есть две клеммы, которые подключаются к остальной цепи. Символ конденсаторов состоит из двух параллельных линий, которые могут быть плоскими или изогнутыми; обе линии должны быть параллельны друг другу, близко друг к другу, но не соприкасаться (это фактически показывает, как сделан конденсатор.Сложно описать, проще показать:

(1) и (2) — стандартные обозначения конденсаторной цепи. (3) представляет собой пример символов конденсаторов в действии в цепи регулятора напряжения.

Символ с изогнутой линией (№2 на фото выше) указывает, что конденсатор поляризован, что означает, что это, вероятно, электролитический конденсатор. Подробнее об этом в разделе о типах конденсаторов этого руководства.

Каждый конденсатор должен сопровождаться названием — C1, C2 и т. Д.. — и стоимость. Значение должно указывать на емкость конденсатора; сколько там фарадов. Кстати о фарадах …

Единицы измерения емкости

Не все конденсаторы одинаковы. Каждый конденсатор имеет определенную емкость. Емкость конденсатора говорит вам, сколько заряда он может хранить , большая емкость означает большую емкость для хранения заряда. Стандартная единица измерения емкости называется фарад, , сокращенно F .

Получается, что фарад — это лот емкости, даже 0,001 Ф (1 миллифарад — 1 мФ) — это большой конденсатор. Обычно вы увидите конденсаторы с номиналом от пико- (10 ^-12) до микрофарад (10 ^-6).

Имя префикса	Сокращение	Вес	Эквивалентные фарады
Пикофарад	pF	10 ^-12	0,000000000001 F			0.000000001 F
Микрофарад	мкФ	10 ^-6	0.000001 F
Милифарад	mF	10 ^-3 0,003		10 ³	1000 Факс

Когда вы переходите к диапазону емкости от фарада до килофарада, вы начинаете говорить о специальных конденсаторах, которые называются super или ultra -конденсаторы.

Теория конденсаторов

Примечание : Материал на этой странице не совсем критичен для понимания новичками в электронике … и к концу все становится немного сложнее. Мы рекомендуем прочитать раздел Как делается конденсатор , остальные, вероятно, можно пропустить, если они вызывают у вас головную боль.

Как делается конденсатор

Схематический символ конденсатора на самом деле очень похож на то, как он сделан.Конденсатор состоит из двух металлических пластин и изоляционного материала, называемого диэлектриком . Металлические пластины расположены очень близко друг к другу, параллельно, но между ними находится диэлектрик, чтобы они не соприкасались.

Ваш стандартный конденсаторный сэндвич: две металлические пластины, разделенные изолирующим диэлектриком.

Диэлектрик может быть изготовлен из любых изоляционных материалов: бумаги, стекла, резины, керамики, пластика или всего, что препятствует прохождению тока.

Пластины изготовлены из проводящего материала: алюминия, тантала, серебра или других металлов. Каждый из них подключен к клеммному проводу, который в конечном итоге подключается к остальной части схемы.

Емкость конденсатора — сколько в нем фарад — зависит от того, как он устроен. Для большей емкости требуется конденсатор большего размера. Пластины с большей площадью перекрытия поверхности обеспечивают большую емкость, в то время как большее расстояние между пластинами означает меньшую емкость. Материал диэлектрика даже влияет на то, сколько фарад имеет колпачок.Полная емкость конденсатора может быть рассчитана по формуле:

где ε _r — относительная диэлектрическая проницаемость диэлектрика (постоянное значение, определяемое материалом диэлектрика), A — площадь перекрытия пластин друг с другом, а d — расстояние между пластинами.

Как работает конденсатор

Электрический ток — это поток электрического заряда, который электрические компоненты используют, чтобы загораться, вращаться или делать то, что они делают.Когда ток течет в конденсатор, заряды «застревают» на пластинах, потому что они не могут пройти через изолирующий диэлектрик. Электроны — отрицательно заряженные частицы — засасываются одной из пластин, и она становится в целом отрицательно заряженной. Большая масса отрицательных зарядов на одной пластине отталкивает, как заряды, на другой пластине, делая ее заряженной положительно.

Положительный и отрицательный заряды на каждой из этих пластин притягиваются друг к другу, потому что это то, что делают противоположные заряды.Но с диэлектриком, сидящим между ними, как бы они ни хотели соединиться, заряды навсегда останутся на пластине (до тех пор, пока им не будет куда-то идти). Неподвижные заряды на этих пластинах создают электрическое поле, которое влияет на электрическую потенциальную энергию и напряжение. Когда заряды группируются на конденсаторе таким образом, крышка накапливает электрическую энергию так же, как батарея может хранить химическую энергию.

Зарядка и разрядка

Когда на пластинах конденсатора сливаются положительный и отрицательный заряды, конденсатор становится на заряженным .Конденсатор может сохранять свое электрическое поле — удерживать свой заряд, потому что положительный и отрицательный заряды на каждой из пластин притягиваются друг к другу, но никогда не достигают друг друга.

В какой-то момент обкладки конденсатора будут настолько заряжены, что просто не смогут больше принимать их. На одной пластине достаточно отрицательных зарядов, чтобы они могли отразить любые другие, которые попытаются присоединиться. Здесь в игру вступает емкость (фарады) конденсатора, которая говорит вам о максимальном количестве заряда, которое может хранить конденсатор.

Если в цепи создается путь, который позволяет зарядам найти другой путь друг к другу, они выйдут из конденсатора, и разрядит .

Например, в схеме ниже можно использовать батарею для создания электрического потенциала на конденсаторе. Это вызовет накопление одинаковых, но противоположных зарядов на каждой из пластин, пока они не станут настолько полными, что оттолкнут ток от протекания. Светодиод, расположенный последовательно с крышкой, может обеспечивать путь для тока, а энергия, запасенная в конденсаторе, может использоваться для кратковременного освещения светодиода.

Расчет заряда, напряжения и тока

Емкость конденсатора — сколько в нем фарад — говорит вам, сколько заряда он может хранить. Сколько заряда конденсатора хранит в настоящее время , зависит от разности потенциалов (напряжения) между его пластинами. Это соотношение между зарядом, емкостью и напряжением можно смоделировать с помощью следующего уравнения:

Заряд (Q), накопленный в конденсаторе, является произведением его емкости (C) и приложенного к нему напряжения (V).

Емкость конденсатора всегда должна быть постоянной известной величиной. Таким образом, мы можем регулировать напряжение, чтобы увеличивать или уменьшать заряд крышки. Больше напряжения означает больше заряда, меньше напряжения … меньше заряда.

Это уравнение также дает нам хороший способ определить значение одного фарада. Один фарад (F) — это способность хранить одну единицу энергии (кулоны) на каждый вольт.

Расчет тока

Мы можем пойти дальше по уравнению заряда / напряжения / емкости, чтобы выяснить, как емкость и напряжение влияют на ток, потому что ток — это скорость потока заряда.Суть отношения конденсатора к напряжению и току такова: величина тока , проходящего через конденсатор , зависит как от емкости, так и от того, как быстро напряжение растет или падает . Если напряжение на конденсаторе быстро растет, через конденсатор будет индуцироваться большой положительный ток. Более медленный рост напряжения на конденсаторе означает меньший ток через него. Если напряжение на конденсаторе стабильное и неизменное, через него не будет проходить ток.

(Это некрасиво, и касается вычислений. Это не все, что нужно, пока вы не перейдете к анализу во временной области, разработке фильтров и прочим грубым вещам, так что переходите к следующей странице, если вам не нравится это уравнение. .) Уравнение для расчета тока через конденсатор:

Часть этого уравнения dV / dt является производной (причудливый способ сказать мгновенная скорость ) напряжения во времени, это эквивалентно выражению «насколько быстро напряжение растет или падает в этот самый момент».Большой вывод из этого уравнения заключается в том, что если напряжение стабильно, , производная равна нулю, что означает, что ток также равен нулю . Вот почему ток не может течь через конденсатор, поддерживающий постоянное постоянное напряжение.

Типы конденсаторов

Существуют всевозможные типы конденсаторов, каждый из которых имеет определенные особенности и недостатки, которые делают его лучше для одних приложений, чем для других.

При выборе типа конденсатора необходимо учитывать несколько факторов:

Размер — Размер как по физическому объему, так и по емкости.Конденсатор нередко является самым большим компонентом в цепи. Также они могут быть очень маленькими. Для большей емкости обычно требуется конденсатор большего размера.
Максимальное напряжение — Каждый конденсатор рассчитан на максимальное падение напряжения на нем. Некоторые конденсаторы могут быть рассчитаны на 1,5 В, другие — на 100 В. Превышение максимального напряжения обычно приводит к разрушению конденсатора.
Ток утечки — Конденсаторы не идеальны.Каждая крышка склонна пропускать небольшое количество тока через диэлектрик от одного вывода к другому. Эта крошечная потеря тока (обычно наноампер или меньше) называется утечкой. Утечка заставляет энергию, накопленную в конденсаторе, медленно, но верно истощаться.
Эквивалентное последовательное сопротивление (ESR) — Выводы конденсатора не на 100% проводящие, они всегда будут иметь крошечное сопротивление (обычно менее 0,01 Ом). Это сопротивление становится проблемой, когда через колпачок проходит большой ток, вызывая потери тепла и мощности.
Допуск — Конденсаторы также не могут иметь точную, точную емкость. Каждая крышка будет рассчитана на свою номинальную емкость, но, в зависимости от типа, точное значение может варьироваться от ± 1% до ± 20% от желаемого значения.

Конденсаторы керамические

Наиболее часто используемый и производимый конденсатор — керамический конденсатор. Название происходит от материала, из которого сделан их диэлектрик.

Керамические конденсаторы обычно бывают как физически, так и по емкости малыми .Трудно найти керамический конденсатор больше 10 мкФ. Керамический колпачок для поверхностного монтажа обычно находится в крошечных корпусах 0402 (0,4 мм x 0,2 мм), 0603 (0,6 мм x 0,3 мм) или 0805. Керамические колпачки со сквозными отверстиями обычно выглядят как маленькие (обычно желтые или красные) лампочки с двумя выступающими клеммами.

Две крышки в радиальном корпусе со сквозным отверстием; конденсатор 22 пФ слева и 0,1 мкФ справа. Посередине — крошечная крышка 0,1 мкФ 0603 для поверхностного монтажа.

По сравнению с не менее популярными электролитическими крышками керамические конденсаторы являются более близкими к идеальным (гораздо более низкое последовательное последовательное сопротивление и токи утечки), но их небольшая емкость может быть ограничивающей.Обычно они также являются наименее дорогим вариантом. Эти колпачки хорошо подходят для высокочастотной связи и развязки.

Электролитический алюминий и тантал

Электролитики
хороши тем, что они могут упаковать много емкости в относительно небольшой объем. Если вам нужен конденсатор емкостью от 1 мкФ до 1 мФ, вы, скорее всего, найдете его в электролитической форме. Они особенно хорошо подходят для высоковольтных приложений из-за их относительно высокого максимального номинального напряжения.
Алюминиевые электролитические конденсаторы, самые популярные из семейства электролитических, обычно выглядят как маленькие жестяные банки с обоими выводами, выходящими снизу.
Ассортимент электролитических конденсаторов сквозного и поверхностного монтажа. Обратите внимание, что у каждого из них есть метод маркировки катода (отрицательный вывод).
К сожалению, электролитические колпачки обычно поляризованы . У них есть положительный вывод — анод — и отрицательный вывод, называемый катодом.Когда напряжение подается на электролитический колпачок, анод должен иметь более высокое напряжение, чем катод. Катод электролитического конденсатора обычно обозначается знаком «-» и цветной полосой на корпусе. Ножка анода также может быть немного длиннее, как еще один признак. Если на электролитический колпачок подать обратное напряжение, они выйдут из строя ( лопнет и разорвется) и навсегда. После лопания электролитик будет вести себя как короткое замыкание.
Эти колпачки также известны утечкой — позволяя небольшим токам (порядка нА) проходить через диэлектрик от одного вывода к другому. Это делает электролитические колпачки менее чем идеальными для хранения энергии, что, к сожалению, с учетом их высокой емкости и номинального напряжения.
Суперконденсаторы
Если вы ищете конденсатор, предназначенный для хранения энергии, не ищите ничего, кроме суперконденсаторов. Эти колпачки имеют уникальную конструкцию, позволяющую иметь очень высоких емкостей в диапазоне фарад.
Суперконденсатор 1Ф (!). Высокая емкость, но рассчитана только на 2,5 В. Обратите внимание, что они также поляризованы.
Несмотря на то, что они могут хранить огромное количество заряда, суперкаперы не могут работать с очень высокими напряжениями. Этот суперконденсатор 10F рассчитан только на максимальное напряжение 2,5 В. Более того, это уничтожит его. Суперэлементы обычно устанавливаются последовательно для достижения более высокого номинального напряжения (при уменьшении общей емкости).
Основное применение суперконденсаторов в — хранение и выделение энергии , как и батареи, которые являются их основным конкурентом.Хотя суперконденсаторы не могут удерживать столько энергии, сколько батарея такого же размера, они могут высвобождать ее намного быстрее и обычно имеют гораздо больший срок службы.
прочие
Электролитические и керамические крышки покрывают около 80% типов конденсаторов (а суперкапсы только около 2%, но они супер!). Другой распространенный тип конденсатора — пленочный конденсатор , который отличается очень низкими паразитными потерями (ESR), что делает их идеальными для работы с очень высокими токами.
Есть много других менее распространенных конденсаторов. Переменные конденсаторы могут производить различные емкости, что делает их хорошей альтернативой переменным резисторам в схемах настройки. Скрученные провода или печатные платы могут создавать емкость (иногда нежелательную), потому что каждый состоит из двух проводников, разделенных изолятором. Лейденские банки — стеклянная банка, наполненная проводниками и окруженная ими — это О. семейства конденсаторов. Наконец, конечно, конденсаторы потока (странная комбинация катушки индуктивности и конденсатора) имеют решающее значение, если вы когда-нибудь планируете вернуться в дни славы.
Последовательные / параллельные конденсаторы
Подобно резисторам, несколько конденсаторов могут быть объединены последовательно или параллельно для создания комбинированной эквивалентной емкости. Конденсаторы, однако, складываются таким образом, что полностью противоположны резисторам.
Параллельные конденсаторы
Когда конденсаторы размещаются параллельно друг другу, общая емкость равна сумме всех емкостей .Это аналогично тому, как резисторы добавляются последовательно.
Так, например, если у вас есть три конденсатора номиналом 10 мкФ, 1 мкФ и 0,1 мкФ, подключенные параллельно, общая емкость будет 11,1 мкФ (10 + 1 + 0,1).
Конденсаторы серии
Подобно тому, как резисторы сложно добавить параллельно, конденсаторы становятся странными при установке в серии . Общая емкость последовательно соединенных конденсаторов Н и является обратной суммой всех обратных емкостей.
Если у вас есть только и два конденсатора , соединенных последовательно, вы можете использовать метод «произведение над суммой» для расчета общей емкости:
Если продолжить это уравнение, если у вас два конденсатора с одинаковым номиналом, соединенные последовательно , общая емкость будет вдвое меньше их значения.Например, два суперконденсатора по 10 Ф, соединенные последовательно, дадут общую емкость 5 Ф (это также позволит удвоить номинальное напряжение всего конденсатора с 2,5 В до 5 В).
Примеры применения
Существует множество приложений для этого изящного маленького (на самом деле, обычно они довольно большие) пассивного компонента. Чтобы дать вам представление об их широком диапазоне использования, вот несколько примеров:
Конденсаторы развязки (байпаса)
Многие конденсаторы, которые вы видите в схемах, особенно те, которые имеют интегральную схему, развязаны.Задача развязывающего конденсатора — подавить высокочастотный шум в сигналах источника питания. Они снимают с источника напряжения крошечные колебания напряжения, которые в противном случае могли бы нанести вред чувствительным микросхемам.
В каком-то смысле развязывающие конденсаторы действуют как очень маленький локальный источник питания для ИС (почти как источник бесперебойного питания для компьютеров). Если в источнике питания очень быстро падает напряжение (что на самом деле довольно часто, особенно когда цепь, которую он питает, постоянно переключает требования к нагрузке), разделительный конденсатор может кратковременно подавать питание с правильным напряжением.Вот почему эти конденсаторы также называются шунтирующими конденсаторами , конденсаторами; они могут временно действовать как источник питания в обход источника питания.
Разделительные конденсаторы подключаются между источником питания (5 В, 3,3 В и т. Д.) И землей. Нередко для обхода источника питания используют два или более конденсаторов с разным номиналом или даже разных типов, потому что некоторые номиналы конденсаторов будут лучше, чем другие, при фильтрации определенных частот шума.
На этой схеме три развязывающих конденсатора используются для уменьшения шума в источнике напряжения акселерометра.Два керамических 0,1 мкФ и один танталовый электролитический 10 мкФ разделенные функции развязки.
Хотя кажется, что это может привести к короткому замыканию между питанием и землей, только высокочастотные сигналы могут проходить через конденсатор на землю. Сигнал постоянного тока поступит на ИС, как и нужно. Другая причина, по которой они называются шунтирующими конденсаторами, заключается в том, что высокие частоты (в диапазоне кГц-МГц) обходят ИС, а не проходят через конденсатор, чтобы добраться до земли.
При физическом размещении развязывающих конденсаторов они всегда должны располагаться как можно ближе к ИС.Чем дальше они находятся, тем менее эффективны.
Вот схема физической схемы из схемы выше. Крошечная черная ИС окружена двумя конденсаторами по 0,1 мкФ (коричневые крышки) и одним электролитическим танталовым конденсатором 10 мкФ (высокая прямоугольная крышка черного / серого цвета).
В соответствии с передовой инженерной практикой всегда добавляйте хотя бы один развязывающий конденсатор к каждой ИС. Обычно хорошим выбором является 0,1 мкФ или даже дополнительные конденсаторы на 1 мкФ или 10 мкФ. Это дешевое дополнение, и они помогают убедиться, что микросхема не подвергается сильным провалам или скачкам напряжения.
Фильтр источника питания
Диодные выпрямители
могут использоваться для преобразования переменного напряжения, выходящего из вашей стены, в постоянное напряжение, необходимое для большинства электронных устройств. Но сами по себе диоды не могут превратить сигнал переменного тока в чистый сигнал постоянного тока, им нужна помощь конденсаторов! При добавлении параллельного конденсатора к мостовому выпрямителю выпрямленный сигнал выглядит следующим образом:
Может быть преобразован в сигнал постоянного тока близкого к уровню, например:
Конденсаторы — упрямые компоненты, они всегда будут пытаться противостоять резким перепадам напряжения.Конденсатор фильтра будет заряжаться по мере увеличения выпрямленного напряжения. Когда выпрямленное напряжение, поступающее в конденсатор, начинает быстро снижаться, конденсатор получит доступ к своему банку накопленной энергии, и он будет очень медленно разряжаться, передавая энергию нагрузке. Конденсатор не должен полностью разрядиться, пока входной выпрямленный сигнал не начнет снова увеличиваться, заряжая конденсатор. Этот танец разыгрывается много раз в секунду, многократно, пока используется источник питания.
Цепь питания переменного тока в постоянный.Крышка фильтра (C1) имеет решающее значение для сглаживания сигнала постоянного тока, посылаемого в цепь нагрузки.
Если вы разорвите любой блок питания переменного тока в постоянный, вы обязательно найдете хотя бы один довольно большой конденсатор. Ниже показаны внутренности настенного адаптера постоянного тока на 9 В. Заметили там конденсаторы?
Конденсаторов может быть больше, чем вы думаете! Имеется четыре электролитических колпачка, напоминающих жестяную банку, в диапазоне от 47 мкФ до 1000 мкФ. Большой желтый прямоугольник на переднем плане — это высоковольтный 0.Крышка из полипропиленовой пленки 1 мкФ. И синяя дискообразная крышка, и маленькая зеленая посередине — керамические.
Хранение и поставка энергии
Кажется очевидным, что если конденсатор накапливает энергию, одно из множества его применений — подача этой энергии в цепь, как аккумулятор. Проблема в том, что конденсаторы имеют гораздо более низкую плотность энергии , чем батареи; они просто не могут вместить столько же энергии, как химическая батарея того же размера (но этот разрыв сокращается!).
Положительным моментом конденсаторов является то, что они обычно служат дольше, чем батареи, что делает их лучшим выбором с экологической точки зрения. Они также способны выдавать энергию намного быстрее, чем аккумулятор, что делает их подходящими для приложений, которым требуется короткий, но большой всплеск мощности. Вспышка камеры может получать питание от конденсатора (который, в свою очередь, вероятно, заряжался от аккумулятора).
Батарея или конденсатор?
910 Срок службы 910 Срок службы
Батарея Конденсатор
Емкость ✓
Плотность энергии ✓
910 Срок службы ✓
Фильтрация сигналов
Конденсаторы
обладают уникальной реакцией на сигналы различной частоты.Они могут блокировать низкочастотные компоненты или составляющие сигнала постоянного тока, позволяя при этом проходить более высоким частотам. Они как вышибалы в очень эксклюзивном клубе только для высоких частот.
Фильтрация сигналов может быть полезна во всех видах приложений обработки сигналов. Радиоприемники могут использовать конденсатор (среди других компонентов) для отключения нежелательных частот.
Другой пример фильтрации сигнала конденсатора — это пассивные схемы кроссовера внутри громкоговорителей, которые разделяют один аудиосигнал на множество.Последовательный конденсатор блокирует низкие частоты, поэтому оставшиеся высокочастотные части сигнала могут идти на твитер динамика. При прохождении низких частот в цепи сабвуфера высокие частоты в основном могут быть шунтированы на землю через параллельный конденсатор.
Очень простой пример схемы кроссовера аудио. Конденсатор блокирует низкие частоты, а катушка индуктивности блокирует высокие частоты. Каждый из них может использоваться для доставки нужного сигнала настроенным аудиодрайверам.
Снижение рейтинга
При работе с конденсаторами важно проектировать схемы с конденсаторами, которые имеют гораздо более высокий допуск, чем потенциально самый высокий скачок напряжения в вашей системе.
Вот отличное видео от инженера SparkFun Шона о том, что происходит с различными типами конденсаторов, когда вы не можете снизить номинальные параметры конденсаторов и превысить их максимальное напряжение. Вы можете прочитать больше о его экспериментах здесь.

Покупка конденсаторов
Храните на этих маленьких компонентах накопителя энергии или используйте их в качестве начального блока питания.
Наши рекомендации:
Комплект конденсаторов SparkFun
Нет на складе КОМПЛЕКТ-13698
Это комплект, который предоставляет вам базовый ассортимент конденсаторов, чтобы начать или продолжить возиться с электроникой. Нет мес…
10
Конденсатор керамический 0.1 мкФ
В наличии COM-08375
Это очень распространенный конденсатор емкостью 0,1 мкФ. Используется во всевозможных приложениях для разъединения микросхем от источников питания. 0,1 дюйма с интервалом…
1
Суперконденсатор — 10Ф / 2.5В
В наличии COM-00746
Да, вы правильно прочитали — конденсатор 10 Фарад. Этот маленький колпачок можно заряжать, а затем медленно рассеивать в течение…
3
Ресурсы и дальнейшее развитие
Уф.Почувствуйте себя экспертом по конденсаторам ?! Хотите узнать больше об основах электроники? Если вы еще этого не сделали, подумайте о прочтении некоторых других распространенных электронных компонентов:
Или, может быть, некоторые из этих руководств привлекут ваше внимание?
Как измерить емкость с помощью цифрового мультиметра
Мультиметр определяет емкость, заряжая конденсатор известным током, измеряя результирующее напряжение и затем вычисляя емкость.
Предупреждение: Хороший конденсатор сохраняет электрический заряд и может оставаться под напряжением после отключения питания. Перед тем, как прикасаться к нему или проводить измерение: а) выключите все питание, б) используйте мультиметр, чтобы убедиться, что питание отключено, и в) осторожно разрядите конденсатор, подключив резистор к его проводам (как указано в следующем абзаце). Обязательно используйте соответствующие средства индивидуальной защиты.
Для безопасной разрядки конденсатора: После отключения питания подключите 5-ваттный резистор 20 000 Ом к клеммам конденсатора на пять секунд.Используйте мультиметр, чтобы убедиться, что конденсатор полностью разряжен.
Используйте цифровой мультиметр (DMM), чтобы убедиться, что питание цепи отключено. Если конденсатор используется в цепи переменного тока, настройте мультиметр на измерение переменного напряжения. Если он используется в цепи постоянного тока, установите цифровой мультиметр на измерение постоянного напряжения.
Осмотрите конденсатор. Если утечки, трещины, вздутия или другие признаки износа очевидны, замените конденсатор.
Поверните циферблат в режим измерения емкости.Символ часто разделяет точку на циферблате с другой функцией. В дополнение к регулировке шкалы обычно необходимо нажать функциональную кнопку, чтобы активировать измерение. За инструкциями обратитесь к руководству пользователя мультиметра.
4. Для правильного измерения необходимо удалить конденсатор из цепи. Разрядите конденсатор, как описано в предупреждении выше.
Примечание: Некоторые мультиметры поддерживают относительный (REL) режим. При измерении малых значений емкости можно использовать относительный режим для удаления емкости измерительных проводов.Чтобы перевести мультиметр в относительный режим измерения емкости, оставьте измерительные провода открытыми и нажмите кнопку REL. Это удаляет значение остаточной емкости измерительных проводов.
Подключите измерительные провода к клеммам конденсатора. Оставьте измерительные провода подключенными в течение нескольких секунд, чтобы мультиметр автоматически выбрал правильный диапазон.
Прочтите отображаемое измерение. Если значение емкости находится в пределах диапазона измерения, мультиметр отобразит значение конденсатора.Он будет отображать OL, если а) значение емкости выше диапазона измерения или б) конденсатор неисправен.
Обзор измерения емкости
Устранение неисправностей однофазных двигателей — одно из наиболее практичных применений функции емкости цифрового мультиметра.
Однофазный двигатель с конденсаторным запуском, который не запускается, является признаком неисправного конденсатора. Такие двигатели будут продолжать работать после запуска, что затрудняет поиск и устранение неисправностей. Отказ конденсатора жесткого пуска компрессоров HVAC — хороший пример этой проблемы.Двигатель компрессора может запуститься, но вскоре перегреется, что приведет к срабатыванию выключателя.
Однофазные двигатели с такими проблемами и шумные однофазные двигатели с конденсаторами требуют мультиметра для проверки правильности работы конденсаторов. Почти все моторные конденсаторы имеют значение в микрофарадах, указанное на конденсаторе.
Трехфазные конденсаторы коррекции коэффициента мощности обычно защищены плавкими предохранителями. Если один или несколько из этих конденсаторов выйдут из строя, это приведет к неэффективности системы, скорее всего, увеличатся счета за коммунальные услуги и могут произойти непреднамеренные отключения оборудования.Если предохранитель конденсатора перегорел, необходимо измерить предполагаемое значение микрофарад конденсатора и убедиться, что оно находится в пределах диапазона, указанного на конденсаторе.
Стоит знать о некоторых дополнительных факторах, связанных с емкостью:
Конденсаторы имеют ограниченный срок службы и часто являются причиной неисправности.
Неисправные конденсаторы могут иметь короткое замыкание, разрыв цепи или могут физически выйти из строя до точки отказа.
При коротком замыкании конденсатора может перегореть предохранитель или повредить другие компоненты.
Когда конденсатор размыкается или выходит из строя, цепь или ее компоненты могут не работать.
Износ может также изменить значение емкости конденсатора, что может вызвать проблемы.
Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.
Связанные ресурсы
Как рассчитать заряд конденсатора — Onlinecomponents.com
Конденсатор — это устройство, которое используется для хранения электрического заряда и электрической энергии.Основной конденсатор состоит из двух металлических пластин, разделенных некоторым изолятором, называемым диэлектриком. Способность конденсатора удерживать заряд называется емкостью.
Когда клеммы батареи соединены через конденсатор, потенциал батареи перемещает заряд, и он начинает накапливаться на пластинах конденсатора. Клемма конденсатора, подключенная к катоду батареи, будет заряжена положительно (+ Q), а клемма, которая подключена к аноду батареи, будет заряжена отрицательно (-Q).Конденсатор в целом остается нейтральным, но заряды разделены на противоположных пластинах, которые находятся на заданном расстоянии друг от друга с расстоянием (d). Базовый конденсатор показан на рис. 1
.
Рис.1
Заряд, накопленный на пластинах конденсатора, прямо пропорционален приложенному напряжению, поэтому [1]
В α Q
Где
В = Напряжение
Q = Заряд
Конденсаторы с разными физическими параметрами могут удерживать разное количество заряда, когда на конденсаторы подается одинаковое напряжение.Эта способность конденсатора называется емкостью. Емкость конденсатора можно определить как отношение количества максимального заряда (Q), который конденсатор может хранить, к приложенному напряжению (V).
V = C Q
Q = C / V
Таким образом, количество заряда конденсатора можно определить по вышеупомянутой формуле.
Конденсаторы заряжаются предсказуемым образом, и для зарядки конденсатора требуется время. Рассматривая зарядку как функцию времени, мы также можем определить количество заряда конденсатора через определенный период времени, когда он подключен к батарее, как показано на рис.2
Рис.2 Конденсатор, включенный в RC-цепочку
Предположим, что конденсатор (C) полностью разряжен, а переключатель разомкнут, конденсатор не заряжается. Эта ситуация представляет собой сценарий, когда при t = 0, I = 0, и заряд, накопленный на конденсаторе C, также будет равен нулю.
Теперь, как только переключатель замкнут, ток начнет течь через цепь, максимальное количество тока, которое будет протекать через цепь, ограничивается резистором (R), подключенным последовательно с конденсатором.Ток, который будет протекать через цепь, можно найти с помощью закона напряжения Кирхгофа [2]
V = I (t) R + V _C Q = C / V _C и V _C = Q / C
где
В = Напряжение
I (t) = Ток в цепи в любой момент времени
Vc = напряжение на конденсаторе
Q = Заряд
C = Емкость, включенная в цепь
R = Сопротивление, подключенное в цепи
В = I (t) R + Q / C
Q = CV [1-e ^{-t / RC}]
Количество заряда в любой момент можно найти с помощью вышеупомянутого уравнения.График зарядки конденсатора показан на рис. 3
.
Рис.3 Заряд конденсатора по времени
Из графика можно сказать, что первоначально зарядный ток будет максимальным, и конденсатор начнет быстро изменяться, а после одноразовой постоянной, равной T = RC, конденсатор будет заряжаться примерно на 63% от своего общего значения.

как определить напряжение, вольтаж конденсаторов

Что такое конденсатор

Характеристики конденсаторов

В чем измеряется напряжение конденсаторов

Что влияет на напряжение конденсаторов

Как вычислить напряжение и вольтаж

Формулы измерения напряжения конденсаторов

Как найти напряжение на конденсаторе формула

В чем измеряется емкость конденсатора

Формула энергии конденсатора

Формула заряда конденсатора

Формула тока утечки конденсатора

Формула заряда конденсатора

Примеры решения задач по теме «Заряд конденсатора»

История накопителей заряда

Физика ёмкостных характеристик

Единица и формулы расчёта

Математическое выражение фарада

Диэлектрическая проницаемость

Практические измерения

Идея суперконденсатора

Глава 20. Конденсаторы

Как определить рабочее напряжение конденсатора

Правила маркировки конденсаторов постоянной ёмкости

Маркировка конденсаторов по рабочему напряжению.

Как найти напряжение между пластинами конденсатора

По какой формуле найти ёмкость (объем) конденсаторов

Расчёт конденсаторов

Расчет плоской конструкции

Расчет конструкции цилиндрической формы

Расчёт сферической конструкции

Ёмкость одиночного проводника

Способы соединения элементов

Параллельное соединение

Последовательное соединение

Смешанное соединение

Видео

Электрическая емкость (страница 1)

, содержащие резисторы и конденсаторы

Заряд, разделение пластин и напряжение

Напряжение на конденсаторе — Электротехническая стековая биржа

Решение ckt # 3 сложным путем с использованием дифференциальных уравнений:

Метод 2: Используйте правило делителя напряжения:

Более простой способ:

Конденсаторы 101 — iFixit

— learn.sparkfun.com

Введение

рассматривается в этом учебном пособии

Рекомендуемая литература

Обозначения и единицы

Условные обозначения цепей

Единицы измерения емкости

Теория конденсаторов

Как делается конденсатор

Как работает конденсатор

Зарядка и разрядка

Расчет заряда, напряжения и тока

Расчет тока

Типы конденсаторов

Конденсаторы керамические

Электролитический алюминий и тантал

Суперконденсаторы

прочие

Последовательные / параллельные конденсаторы

Параллельные конденсаторы

Конденсаторы серии

Примеры применения

Конденсаторы развязки (байпаса)

Фильтр источника питания

Хранение и поставка энергии

Фильтрация сигналов

Снижение рейтинга

Покупка конденсаторов

Наши рекомендации:

Комплект конденсаторов SparkFun

Конденсатор керамический 0.1 мкФ

Суперконденсатор — 10Ф / 2.5В

Ресурсы и дальнейшее развитие

Как измерить емкость с помощью цифрового мультиметра