Конденсатор в цепи переменного тока

Конденсатор в цепи переменного тока

«Физика — 11 класс»

Постоянный ток не может идти по цепи, содержащей конденсатор, так как обкладки конденсатора разделены диэлектриком.
Переменный же ток может идти по цепи, содержащей конденсатор.

Есть источники постоянного и переменного напряжений, в которых постоянное напряжение на зажимах источника равно действующему значению переменного напряжения.
Цепь состоит из конденсатора и лампы накаливания, соединенных последовательно.
При включении постоянного напряжения (переключатель влево) лампа не светится.
При включении переменного напряжения (переключатель вправо) лампа загорается, если емкость конденсатора достаточно велика.

Под действием переменного напряжения происходит периодическая зарядка и разрядка конденсатора.
Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.

Если сопротивлением проводов и обкладок конденсатора можно пренебречь,

то напряжение на конденсаторе равно напряжению на концах цепи.

Следовательно,

Заряд конденсатора меняется по гармоническому закону:

q = CU_m cos ωt

Сила тока, представляющая собой производную заряда по времени, равна:

Колебания силы тока опережают по фазе колебания напряжения на конденсаторе на .

Амплитуда силы тока равна:

I_m = U_mCω

Если ввести обозначение

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим

Величину Х_с, обратную произведению

ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением.
Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.
Это и позволяет рассматривать величину Х_с как сопротивление конденсатора переменному току (емкостное сопротивление).

Чем больше емкость конденсатора, тем больше ток перезарядки.
Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.

В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х_с.
С увеличением емкости оно уменьшается.
Уменьшается оно и с увеличением частоты ω.

На протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля.
В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.

Итак,
сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на .

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

Переменный ток. Резистор, конденсатор и катушка в цепи переменного тока.

⇐ ПредыдущаяСтр 8 из 11Следующая ⇒

Элементы цепи переменного тока

 

 

 

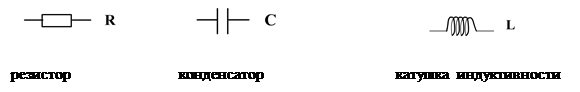
Резистор в цепи постоянного тока

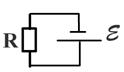По закону Ома, в замкнутой цепи постоянного тока

напряжение на зажимах источника меньше ЭДС

U = IR; U = E — Ir

 

Резистор в цепи переменного тока

 

Рассмотрим схему, состоящую из источника переменного

тока, резистора и идеальных проводов.

Предположим, что напряжение на резисторе

изменяется по гармоническому закону

U = U₀ cos ω t .

Найдем силу тока, протекающего через резистор.

По закону Ома для

участка цепи

I=U/R ==> I = I₀ cos ω t

Амплитуда силы тока I₀ = U₀/R

Ток и напряжение изменяются по одинаковому гармоническому закону (косинуса), то есть совпадают по фазе. Это означает, что, например, в тот момент времени, когда в цепи максимальна сила тока, напряжение на резисторе также максимально.

Конденсатор в цепи переменного тока

Включим конденсатор в цепь постоянного тока. Некоторый заряд перетечет от источника тока на обкладки конденсатора. В цепи возникает кратковременный импульс зарядного тока. Конденсатор заряжается до напряжения источника, после чего ток прекращается. Через конденсатор постоянный ток течь не может!

 

 

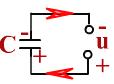Рассмотрим процессы, происходящие при включении конденсатора в цепь переменного тока

зарядный ток

.

 

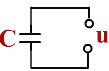Через диэлектрик, разделяющий обкладки конденсатора, электрический ток протекать, как и прежде, не может. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в цепи появится переменный ток.

 

Если напряжение в цепи изменяется по гармоническому закону,

U = U₀cos ωt

то заряд на обкладках конденсатора изменяется

также погармоническому закону

q=Cu = CU₀cos ωt

 

и силу тока в цепи можно найти как производную заряда

i = q^/

i= -CU₀ ω sin ωt = CU₀ω cos(ωt+π/2),

i= I₀ω cos(ωt+π/2)

Амплитуда силы тока I₀ = CU₀ω

Из полученной формулы видно, что в любой момент времени

фаза тока больше фазы напряжения на π/2.

В цепи переменного напряжение на конденсаторе тока отстает по фазе от тока на π/2, или на четверть периода.

 

Емкостное сопротивление

 

Величину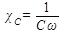

называют емкостным сопротивлением.

Связь между амплитудными значениями силы тока и напряжения формально совпадает с законом Ома для участка цепи

 

 

Такое же соотношение выполняется для действующих значений силы тока и напряжения.

Емкостное сопротивление конденсатора зависит от частоты переменного напряжения. С увеличением частоты колебаний напряжения емкостное сопротивление уменьшается, поэтому амплитуда силы тока увеличивается прямо пропорционально частоте I₀ = CU₀ω.

При уменьшении частоты амплитуда силы тока уменьшается и при ω=0 обращается в 0. Отметим, что нулевая частота колебаний означает, что в цепи протекает постоянный ток.

 

Катушка индуктивности в цепи переменного тока

Мы предполагаем, что катушка индуктивности обладает пренебрежимо малым активным сопротивлением R. Такой элемент включать в цепь постоянного тока нельзя, потому что произойдет короткое замыкание.

В цепи переменного тока мгновенному нарастанию силы тока препятствует ЭДС самоиндукции. При этом для сверхпроводника e_i+u=0.

 

Используя закон Фарадея для самоиндукции e_i= -Li^/ ,

 

можно показать, что, если сила тока в цепи изменяется по гармоническому закону

i= I₀cos(ωt),

 

то колебания напряжения на катушке описываются

уравнением

U = — I₀ Lωsin ωt = I₀ Lω cos(ωt+π/2),

то есть колебания напряжения опережают по фазе колебания силы тока на π/2. Произведение U₀ = I₀Lω является амплитудой напряжения:

U = U₀ cos(ωt+π/2)

 

 

Индуктивное сопротивление

Величину

Трансформатор. Производство, передача и потребление электроэнергии.

Трансформаторы

Переменное напряжение можно преобразовывать — повышать или понижать.

Устройства, с помощью которых можно преобразовывать напряжение называются трансформаторами. Работа трансформаторов основана на явлении электромагнитной индукции.

 

Устройство трансформатора

Трансформатор состоит из ферромагнитного сердечника, на который надеты две катушки.

Первичной обмоткой называется катушка, подключенная к источнику переменного напряжения U₁.

Вторичной обмоткой называется катушка, которую можно подключать к приборам, потребляющим электрическую энергию.

Приборы, потребляющие электрическую энергию, выполняют роль нагрузки, и на них создается переменное напряжение U₂.

Если U₁ > U₂, то трансформатор называется понижающим, а если U₂ > U₁ — то повышающим.

Принцип работы

В первичной обмотке создается переменный ток, следовательно, в ней создается переменный магнитный поток. Этот поток замыкается в ферромагнитном сердечнике и пронизывает каждый виток обеих обмоток. В каждом из витков обеих обмоток появляется одинаковая ЭДС индукции e_i0

Если n₁ и n₂ — число витков в первичной и вторичной обмотках соответственно, то

ЭДС индукции в первичной обмотке e_i1=n₁*e_i0
ЭДС индукции во вторичной обмотке e_i2 = n₁*e_i0

где e_i0 — ЭДС индукции, возникающая в одном витке вторичной и первичной катушки.

Передача электроэнергии

Передача электрической энергии от электростанций до больших городов или промышленных центров на расстояния тысяч километров является сложной научно-технической проблемой. Потери энергии (мощности) на нагревание проводов можно рассчитать по формуле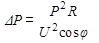

Для уменьшения потерь на нагревания проводов необходимо увеличить напряжение. Обычно линии электропередачи строятся в расчете на напряжение 400–500 кВ, при этом в линияхиспользуется переменный ток частотой 50 Гц. На рисунке представлена схема линии передачи электроэнергии от электростанции до потребителя. Схема дает представление об использовании трансформаторов при передаче электроэнергии



Как заколебать ток. Конденсаторы и катушки

РадиоКот >Обучалка >Аналоговая техника >Основы электроники >

Как заколебать ток. Конденсаторы и катушки

Начинаем с первого и самого главного блока — ГВЧ (Генератор Высокой частоты).

Как вы помните, генератор обязан преобразовать постоянный ток батарейки в переменный ток ВЧ. Для этого обычно используют транзистор и еще две детали, с которыми мы пока что не знакомы: конденсатор и катушку индуктивности.

Конденсатор — это элемент, способный накапливать в себе электрическую энергию. Конденсатор состоит из двух металлических пластин, изолированных между собой непроводящим материалом (диэлектриком). Эти пластины называют обкладками конденсатора.

Обозначение конденсатора на схеме полностью объясняет его конструкцию:

Конденсатор можно сравнить с батарейкой. Вот только, в нем нет той силы, которая перекидывает заряд в обратную сторону.
Если вспомнить нашу научно-экспериментальную установку с бутылками, то сначала (пока мы не стали вычерпывать воду из в одной бутылки в другую) ее можно было сравнить именно с конденсатором. То есть: наливаем воду в одну бутылку, вторая пуста. Пускаем воду по шлангу. Вторая бутылка — заполняется, первая — опустошается. Это происходит до тех пор, пока уровни в двух бутылках не сравняются, и ток не прекратится.

Так же и в конденсаторе. Когда он заряжен — на одной обкладке электронов больше, чем на другой. То есть, у них разные заряды, а значит — есть разность потенциалов (напряжение). Если к заряженному конденсатору подключить нагрузку, скажем, резистор — потечет ток, и через определенное время заряды двух обкладок сравняются, ток прекратится. То есть — конденсатор разрядится. Чтобы ток пошел снова, нужно опять создать разность потенциалов — то есть, зарядить конденсатор.

Вот так, в общем, все несложно.

Катушка индуктивности — это такая обычная катушка из металлической проволоки.

Можно на что угодно намотать кусок проволоки — это уже будет катушка индуктивности.
На схеме она изображается так:

Катушка обладает некоторыми полезными электрическими свойствами. Какими? Сейчас разберемся.

Итак, коль уж вспомнилась нам лабораторная установка из бутылок — давайте ее апгрейдить.
На сей раз нам понадобится водяная турбина. Честно говоря, я не пробовал ее делать, поэтому — не скажу рецепт приготовления =). Однако, если кто-то решится, и у него получится — можете поделиться с народом своим счастьем… и технологией.
Водяная турбина состоит из лопастей, сидящих на оси. Все это находится внутри герметичного кожуха, но ось выводится наружу. При протекании воды, лопасти начинают вращаться. Такие турбины используют, например, на гидроэлектростанциях. На их оси сидят электрогенераторы.

У нас же все проще и меньше. И на ось мы посадим не мощный генератор, а просто какое-нибудь тяжелое круглое колесико, чтобы воде было трудно его вращать.

Кстати! Протекающая вода вращает турбину. Но возможно и обратное: вращающаяся турбина может вызывать ток воды. Помним об этом…

Ну, в общем, всобачим эту турбину между двумя бутылками, и нальем в левую бутылку воды. Смотрим, что происходит.
А вот что происходит. Поскольку есть разность потенциалов (то есть, давлений) — вода хочет течь из левой бутылки в правую. Но на пути — турбина! Ничего не остается, как ее крутить. Хочешь жить — умей вертеться. =)

Однако, турбина начинает крутиться не сразу, а постепенно, потому что на ее оси — тяжелое колесо, которое создает инерцию. Поэтому, сначала вода течет медленно, и постепенно, своим током разгоняет турбину. Чем быстрее крутится турбина — тем быстрее перетекает вода в правую бутылку. Перетекает, перетекает… И вот — уровни сравнялись! Казалось бы, пора остановиться. Куда там! Турбина раскрутилась до таких оборотов, что и не думает остановиться, и продолжает по инерции гнать воду из левой бутылки в правую. Однако, постепенно ее скорость снижается, и через некоторое время, она, все же, останавливается.

Но теперь уже в правой бутылке воды больше, чем в левой. И она хочет течь обратно. Турбина начинает крутиться в обратную сторону. Сначала — нехотя, потом — все быстрее и быстрее. В момент, когда уровни равны, турбина опять несется на полных оборотах, и продолжает гнать. Останавливается она, когда в левой бутылке уровень снова больше, чем в правой. Все повторяется заново.

То, что мы видим, называется простым и знакомым нам словом — «колебания».

В идеальных условиях (отсутствие трения и т.п.), этот колебательный процесс длится бесконечно. В реальности — через несколько циклов (периодов), он затухнет. То есть, уровни таки сравняются. Но не в этом суть. Главное, что мы только что познакомились с принципом работы самого распространенной в радиотехнике схемы — колебательного контура. На водяной его модели. =)

Так вот, турбина в нашей научно-экспериментальной мегаустановке — это и есть катушка индуктивности.

У катушки индуктивности, надо сказать, весьма скверный характер. Она, по русски выражаясь, «тормозит». То есть, когда ток, текущий через нее начинает увеличиваться — она всячески препятствует его увеличению. А когда ток уменьшается — она наоборот, «подгоняет» его, не давая уменьшаться. Ну чем не турбина?!

Однако, в счастливом союзе с конденсатором, катушка образует тот самый колебательный контур, без которого не смог бы работать ни один радиоприемник и передатчик.

Вот как выглядит колебательный контур:

Если зарядить конденсатор, а потом подключить к нему катушку — ток в катушке начнет мотаться туда-сюда точно так же, как вода — в турбине.

Как вы, может быть, уже догадались — именно колебательный контур мы будем использовать для преобразования постоянного тока в переменный в нашем генераторе. Однако, прежде чем преступить к преобразованию, познакомимся еще с одним элементом. Без него ничего не получится.

<<—Вспомним пройденное—-Поехали дальше—>>

---

Как вам эта статья?	Заработало ли это устройство у вас?

Конденсатор и катушка индуктивности в цепи переменного тока

Как мы с вами говорили, в цепи переменного тока, содержащей активное сопротивление, происходят постоянные потери энергии, сопровождающиеся выделением тепла. При этом, количество теплоты, выделяющееся на активном сопротивление при прохождении по нему переменного тока, можно рассчитать, как и в случае с постоянным током, по закону Джоуля — Ленца:

Однако быстрое изменение величины и направления переменного тока обусловливает ряд особенностей, отличающих его действия от действий тока постоянного. Так, например, переменный ток не годится для технических применений электролиза. Дело в том, что величина переменного тока зависит не только от напряжения и сопротивления цепи, но и от индуктивности проводников, включённых в цепь. В этом можно убедиться на следующем опыте. Включим в цепь постоянного тока катушку, содержащую большое количество витков медной проволоки и амперметр.

Снимем показания амперметра. А теперь вдвинем в катушку железный сердечник — ток при этом не изменился.

Посмотрим, что будет происходить в этой же цепи, но при включении в неё источника переменного тока с действующим напряжением, равным напряжению постоянного тока.

Нетрудно заметить, что ток в катушке уменьшился. Введение же в катушку железного сердечника приведёт к ещё большему ослаблению тока. Следовательно, индуктивность цепи переменного тока уменьшает величину тока.

Причиной этого является возникающая в цепях переменного тока ЭДС самоиндукции, которая препятствует нарастанию тока. Вследствие ЭДС самоиндукции в момент, когда напряжение в цепи достигает максимума, ток не успевает достигнуть той величины, которую он достиг бы в отсутствие самоиндукции.

Например, представим, что у нас есть катушка, на которую намотано 600 витков медной проволоки, диаметром 1 мм. Предположим, что на эту катушку пошло 150 метров этой проволоки. Тогда, исходя из определения, её сопротивление примерно равно 3,2 Ом. Но если измерить сопротивление этой катушки в цепи переменного тока частотой 50 Гц, то оно окажется равным примерно 20 Ом.

Это говорит нам о том, что индуктивность в цепи переменного тока действует в отношении величины тока так же, как и активное сопротивление.

Сопротивление, которым обладает цепь вследствие наличия в ней индуктивности, называется индуктивным сопротивлением. Узнаем от чего оно зависит. Итак, пусть в цепи, содержащей катушку индуктивности, протекает переменный ток, сила которого изменяется по гармоническому закону:

Тогда, ЭДС самоиндукции будет равна произведению индуктивности катушки и первой производной силы тока по времени, взятому с обратным знаком:

Если активное сопротивление катушки равно нулю, то и напряжённость электрического поля внутри проводника в любой момент времени должна быть равна нулю. В противном случае сила тока была бы бесконечно большой (это следует из закона Ома). Равенство нулю напряжённости поля оказывается возможным потому, что напряжённость, вихревого электрического поля, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряжённости кулоновского поля, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Следовательно, удельная работа вихревого поля (то есть ЭДС самоиндукции) равна по модулю и противоположна по знаку удельной работе кулоновского поля.

Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение в цепи переменного тока, будет обратно по знаку ЭДС самоиндукции:

Произведение величин, стоящих перед функцией косинуса, является амплитудой напряжения:

Давайте перепишем уравнение для мгновенного напряжения, воспользовавшись введённым обозначением, а также заменим косинус на синус, воспользовавшись формулой приведения:

Отсюда следует, что колебания напряжения на катушке опережают колебания силы тока на π/2:

Давайте выразим из формулы для амплитуды напряжения амплитуду силы тока в катушке:

Величина, равная произведению циклической частоты и индуктивности катушки и есть индуктивное сопротивление:

Тогда можно записать, что амплитудное значение силы тока в цепи переменного тока, содержащую только катушку индуктивности, прямо пропорционально амплитудному напряжению и обратно пропорционально индуктивному сопротивлению.

А теперь давайте определим мгновенную мощность в данной цепи:

Как видим, потребляемая идеальной катушкой, периодически изменяется с двойной частотой, а её среднее значение за период равно нулю, так как равно нулю среднее значение синуса двойного аргумента. Следовательно, так же как активное сопротивление, индуктивное сопротивление ограничивает силу тока в цепи, но в отличие от активного сопротивления на нём электрическая энергия не превращается необратимо в другие виды энергии.

Теперь давайте с вами соберём цепь постоянного тока, содержащую последовательно соединённые конденсатор и лампочку. Замкнув цепь, мы обнаружим, что никакого тока в цепи нет. Это вполне понятно, так как пластины конденсатора отделены друг от друга изолятором. Поэтому через конденсатор постоянный ток течь не может.

А теперь заменим источник постоянного тока на источник переменного напряжения. Лампочка горит. Объясняется это достаточно просто. В цепи переменного тока электроны совершают колебательное движение. Это приводит к тому, что обкладки конденсаторов попеременно заряжаются то положительно, то отрицательно. Электроны же в проводах цепи движутся то в одном, то в другом направлении, нагревая спираль лампы. Если выключить конденсатор из цепи, то лампочка будет гореть ярче. Следовательно, наличие конденсатора в цепи переменного тока увеличивает сопротивление цепи.

Сопротивление, которым обладает цепь вследствие наличия в ней ёмкости, называется ёмкостным сопротивлением.

Выясним, от чего оно зависит. Для этого рассмотрим цепь, состоящую из генератора переменного напряжения, конденсатора и проводов, сопротивление которых пренебрежимо мало.

Пусть напряжение на конденсаторе изменяется синусоидально:

Следовательно, и заряд конденсатора будет изменяться со временем по закону синуса:

Найдём силу тока в цепи, как первую производную заряда по времени:

Произведение величин, стоящих перед функцией синуса, является амплитудой силы тока:

Перепишем предыдущее уравнение с учётом введённых обозначений, и воспользуемся формулой приведения для перехода от функции косинуса к функции синус:

 

Отсюда следует, что колебания силы тока опережают по фазе колебания напряжения на конденсаторе на π/2:

Теперь давайте перепишем уравнение для амплитуды силы тока так, как это показано на экране:

Величина, обратная произведению ёмкости конденсатора и циклической частоты является ёмкостным сопротивлением:

Подставив данное уравнение в предыдущее равенство, найдём, что амплитудное значение силы тока в цепи переменного тока, содержащую только конденсатор, прямо пропорционально амплитудному напряжению и обратно пропорционально ёмкостному сопротивлению:

Теперь определим мгновенную мощность в данной цепи:

Как и в предыдущем случае, при наличии в цепи только ёмкостного сопротивления частота изменения мощности вдвойне больше частоты изменения силы тока, а её среднее значение за период равно нулю. Следовательно, на ёмкостном сопротивлении электрическая энергия не превращается необратимо в другие виды. Поэтому ёмкостное и индуктивное сопротивления в отличие от активного называют реактивными.

Теперь рассмотрим цепь, содержащую все элементы: резистор, катушку индуктивности, конденсатор и источник переменного напряжения.

Так как электромагнитные взаимодействия распространяются со скоростью света, то во всех последовательно включённых элементах цепи изменения силы тока происходят практически одновременно. Однако колебания мгновенных значений напряжения на каждом из элементов не совпадают по фазе с колебаниями силы тока. Но в любой момент времени сумма мгновенных значений напряжений на последовательно включённых элементах цепи равна ЭДС источника:

Учитывая, что на активном сопротивлении колебания силы тока совпадают, на ёмкостном опережают, а на индуктивном отстают от колебаний напряжения, то последнее равенство можно записать так:

Амплитуду колебаний напряжения в цепи можно выразить через амплитудные значения напряжения на отдельных её элементах, воспользовавшись методом векторных диаграмм.

Амплитудное значение силы тока в цепи совпадает по фазе с амплитудным значением напряжения на резисторе. Из этой диаграммы можно найти амплитуду приложенного напряжения, которая равна геометрической сумме этих амплитуд.

Используя теорему Пифагора, выразим квадрат амплитуды колебаний напряжения в цепи:

Далее, используя закон Ома для участка цепи, выразим амплитудные значения напряжений, стоящих в правой части равенства, через амплитудное значение силы тока и реактивные сопротивления:

Выражая из полученного уравнение амплитудное значение силы тока, получим закон Ома для участка цепи переменного тока:

Величина, стоящая в знаменателе формулы, называется полным сопротивлением цепи:

Величина же, стоящая в скобках под знаком корня, называется реактивным сопротивлением.

Таблица «Резистор, конденсатор и катушка в цепи переменного тока» (11 класс)

Резистор, конденсатор и катушка в цепи переменного тока.

I – сила тока

U — напряжение

Вывод

Дополнительная информация

R – активное сопротивление

i = I_m cos ωt

I_{m =}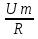

I =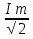

u = U_m cos ωt

U_{m =} I_m R

U =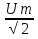

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения.

Мощность

P = I_m²R / 2

C — конденсатор

i = I_m cos (ωt+ )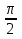

I_{m =} U_mCω

I =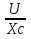

u = U_m cos ωt

Колебания силы тока опережают по фазе колебания напряжения на

на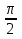

Емкостное сопротивление

Xc =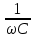

L — катушка

i = I_m sin ωt

I_{m =} U_m /ωL

I =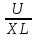

u = U_m (sin ωt +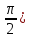

U_m = LωI_m

Колебания силы тока отстают по фазе от колебаний напряжения на на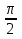

Индуктивное сопротивление

X_L = ωL

Емкостное и индуктивное сопротивления в цепи переменного тока

называют реактивными сопротивлениями.

При последовательном соединении катушки индуктивностью L и конденсатора емкостью C реактивное сопротивление X участка цепи равно X_L — X_C.

При параллельном соединении катушки индуктивностью L и конденсатора емкостью C реактивное сопротивление участка цепи

определяется по формуле 1/ X_C – 1/ X_L.

Резонанс в колебательном контуре: резкое возрастание амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура

ω = ω₀ =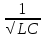

Конденсатор и катушка в цепи переменного тока

Почему конденсатор хорошо пропускает высокие частоты и плохо низкие, а катушка наоборот? Не факт вообще.

смотря какой емкости конденсатор и какой проницаемости катушка) ) в принципе я с вами согласен. конденсатор режет низкие частоты, катушка верхние. если честно, не знаю почему

Не знаю как емкость в гидравлике обозначена, может простой бочкой с жидкостью. А вот индуктивность в гидравлике — это такая штука, как «трубка Перкинса», так, кажется, называется. Обычно, ставится между трубопроводом и манометром, чтобы сгладить толчки давления. Так вот катушки индуктивности тоже сглаживают подобные толчки тока. И чем выше их частота, а витков в катушке больше, тем лучше сглаживает.

Почему конденсатор вообще не пропускает постоянного тока — надеюсь, понятно. Это тупо кусок диэлектрика, т. е. разрыв в цепи. На переменном токе не всё так просто.. . Изменение электрического поля норовит распространиться в пространстве. Причём что там в этом пространстве — ему по фигу, потому что это не ток проводимости (перенос зарядов с место на место) , а ток смещения. Передаётся именно изменение поля. И передаётся оно тем лучше, чем быстрее поле изменяется, математически это выражается тем, что плотность тока смещения пропорциональна производной от напряжённости электрического поля по времени. Для синуса производная пропорциональна частоте. Так что чем выше частота — тем выше производная (точнее — максимум производной, мы ж имеем дело с периодической функцией…) , а значит — больше ток смещения. С индуктивностью другая фигня. Магнитное поле обладает энергией, поэтому оно инерционно. Оно не может мгновенно появиться и мгновенно исчезнуть. В этом случае аналогом магнитного поля можно считать массу, а аналогом напряжения — силу. Если у нас есть фиксированная сила, то мы может этой массе сообщить фиксированное ускорение, и за определённое время она «сдвинется» (т. е. поле изменится) на определённую величину. Но если это время уменьшается (с повышением частоты) , то — ясень пень — будет уменьшаться и «смещение массы», т. е. изменение поля. Поскольку поле катушки однозначно связано с током, который через неё протекает, то, значит, и ток будет изменяться тем меньше, чем быстрее мы будем пытаться его дёргать туда-сюда. ========== Отмазка: возникает вполне закономерный вопрос: электрическое поле в конденсаторе тоже обладает энергией, а значит — инерцией. Почему такое неравенство? ! Почему через конденсатор ток растёт, а через катушку — падает? Прикол в том, что мы неявно ставим их в ОДИНАКОВЫЕ условия — подключение к источнику напряжения (а не источнику тока; в электротехнике это разные вещи) . У источника напряжения нулевое выходное сопротивление. Это означает, что теоретически он способен выдавать сколь угодно большой ток. Что эквивалентно бесконечно большой мощности источника. А раз у него бесконечно большая мощность — значит, он может за любое сколь угодно малое время совершать ЛЮБУЮ работу. Сколь угодно большую. В частности, работу по изменению электрического поля в конденсаторе на противоположное. Ровно то же можно было бы проделать и с катушкой, если подключить её не к источнику напряжения, а к источнику тока (с бесконечно большим внутренним сопротивлением) . При таком подключении ток в катушке тоже будет тот, который идёт от источника, то есть этот источник тоже способен совершать работу по изменению поля на противоположное за любое сколь угодно малое время. Просто напряжение будет неограниченно расти…

Чем больше ёмкость конденсатора, тем более он способен пропускать низкие частоты. Пропускание тока в конденсаторе заключается в том, что увеличивающееся количество электронов на одной его обкладке, начинает отталкивать электроны со второй его обкладки, причём процесс накопления электронов в обкладке конденсатора не линейный, потому что электроны отталкиваются при сближении обратно пропорционально квадрату расстояния между ними. Главный момент торможения накопления электронов на обкладке заключается в том, что диэлектрический зазор в конденсаторе постоянная величина. Если этот зазор уменьшать, то конденсатор будет более линейно передавать изменение состояния своих электронов с одной обкладки на другую. Более лучшая линейность передачи будет и при увеличении площади обкладок. В катушке переменный ток вырабатывает магнитное поле, которое вследствие большой инерции тормозит колебательный процесс.

Резистор, конденсатор и катушка в цепи переменного тока. Переменный ток

При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.

Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.

Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = I m sinωt .

Требуется определить напряжение на участках цепи и мощность.

Векторная диаграмма и полное сопротивление цели

Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:

u = u 1R + u L + u C + u 2R ,

Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:

U = U 2R + U L + U C +U 2R

Для построения векторной диаграммы находим:

U 1R = IR 1 ; U 2R = IR 2 ; U L = IX L ; U C = IX C .

В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:

1. Х L >Х C . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U 1 и U 2 на этих элементах.

Векторная сумма напряжений U 1 + U 2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (U а и U р ). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: U a = U 1R + U 2R.

Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: U р = U L — U C .

При одинаковом токе во всех элементах цепи U L >U C . Ток отстает от общего напряжения по фазе на угол φ . Из треугольника напряжений следует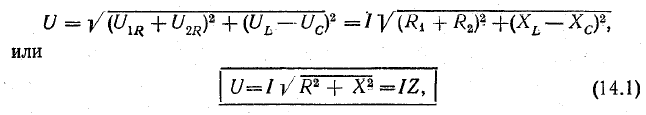

где R = R 1 + R 2 и X = X L — X C общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.

Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.

Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:

U = IZ; I = U/Z; Z = U/I.

Из треугольников напряжения и сопротивлений определяют следующие величины:

Угол сдвига по фазе между напряжением и током в цепи положительный (φ >0) (фазовые токи отсчитываются от вектора тока).

2. Х L Векторная диаграмма изображена на рис. 14.3, где U L φ

Р е активное сопротивление цепи носит емкостный характер .

Расчетные формулы для первого случая остаются без изменения и для второго случая.

3. X L = Х C . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: U L = U C (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.

Общее напряжение совпадает по фазе с током и равно по величине активной

составляющей напряжения.

Угол φ сдвига фаз между током и общим напряжением равен нулю.

Ток в цепи и общее напряжение связаны формулой

U = IR, или I = U/R.

В случае X L = Х C в цепи имеет место явление резонанса напряжений.

Энергетический процесс в цепи с последовательном соединении конденсатора и катушки

Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:

Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.

В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0 ; при φ

Активная мощность положительна при любом угле, так как cosφ = cos(-φ ).

Полная мощность также всегда положительна. На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии (Р ≠ 0) и обменный процесс между генератором и приемником (Q ≠ 0 при φ ≠ 0).

Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.

Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при X L = Х С .

Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
и конденсатором.

Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.

Задачи по теме и пример решения задачи для схемы с последовательным соединением конденсатора и катушки

Рассмотрим цепь, содержащую в себе катушку индуктивности , и предположим, что активное сопротивление цепи, включая провод катушки, настолько мало, что им можно пренебречь. В этом случае подключение катушки к источнику постоянного тока вызвало бы его короткое замыкание, при котором, как известно, сила тока в цепи оказалась бы очень большой.

Иначе обстоит дело, когда катушка присоединена к источнику переменного тока. Короткого замыкания в этом случае не происходит. Это говорит о том. что катушка индуктивности оказывает сопротивление проходящему по ней переменному току .

Каков характер этого сопротивления и чем оно обусловливается?

Чтобы ответить ил этот вопрос, вспомним . Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна и скорости изменения тока в ней. Но так как непрерывно изменяется, то непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току.

Для уяснения процессов, происходящих в с катушкой индуктивности, обратимся к графику. На рисунке 1 построены кривые линии, характеризующие соответственно тик в цепи, напряжение на катушке и возникающую в ней ЭДС самоиндукции. Убедимся в правильности произведенных па рисунке построений.

С момента t = 0, т. е. с начального момента наблюдения за током, он начал быстро возрастать, но по мере приближения к своему максимальному значению скорость нарастания тока уменьшалась. В момент, когда ток достиг максимальной величины, скорость его изменения на мгновение стала равной нулю, т. е. прекратилось изменение тока. Затем ток начал сначала медленно, а потом быстро убывать и по истечении второй четверти периода ум