Емкость плоского и других конденсаторов

Конфигурация конденсатора такова, что поле, которое создается зарядами, локализовано между обкладками. В общем случае электроемкость конденсатора равна:

\[C=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{U}\left(1\right),\]

где ${\varphi }_1-{\varphi }_2=U$ — разность потенциалов обкладок, которую называют напряжением и обозначают $U$. Емкость по определению считается положительной величиной. Она зависит только от геометрии обкладок конденсатора их взаиморасположения и диэлектрика. Форму обкладок и их расположение подбирают так, чтобы внешние поля минимально влияли на внутреннее поле конденсатора. Силовые линии поля конденсатора начинались на проводнике с положительным зарядом и заканчивались на проводнике с отрицательным зарядом. Конденсатор может быть проводником, который помещен в полость, окруженную замкнутой оболочкой.

В соответствии с конфигураций конденсаторов можно выделить три большие группы: плоские, сферические и цилиндрические (по форме обкладок).

Вычисление емкости конденсатора сводится к определению $напряжения$ конденсатора при известном заряде на его обкладках.

Плоский конденсатор

Плоский конденсатор (рис.1) — это две разноименно заряженные пластины, разделенные тонким слоем диэлектрика. Формула для расчета емкости такого конденсатора представляет собой выражение:

\[С=\frac{\varepsilon {\varepsilon }_0S}{d}\left(2\right),\]

где $S$ — площадь обкладки, $d$ — расстояние между обкладками, $\varepsilon $ — диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (2), с реальной емкостью.

Рис. 1

Электроемкость плоского конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равна $d_i$, диэлектрическая проницаемость этого слоя ${\varepsilon }_i$ вычисляется по формуле:

\[C=\frac{{\varepsilon }_0S}{\frac{d_1}{{\varepsilon }_1}+\frac{d_2}{{\varepsilon }_2}+\dots +\frac{d_N}{{\varepsilon }_N}}\ \left(3\right). \]

Сферический конденсатор

В том случае, если внутренний проводник шар или сфера, внешняя замкнутая оболочка — концентрическая ему сфера, то конденсатор является сферическим. Сферический конденсатор (рис.2) состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком. Емкость его можно рассчитать по формуле:

\[C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(4\right),\]

где $R_1{\ и\ R}_2$ — радиусы обкладок.

Рис. 2

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равна:

\[C=\frac{2\pi \varepsilon {\varepsilon }_0l}{{ln \left({R_2}/{R_1}\right)\ }}\left(5\right),\]

где $l$ — высота цилиндров, $R_1$ и $R_2$ — радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).

Рис.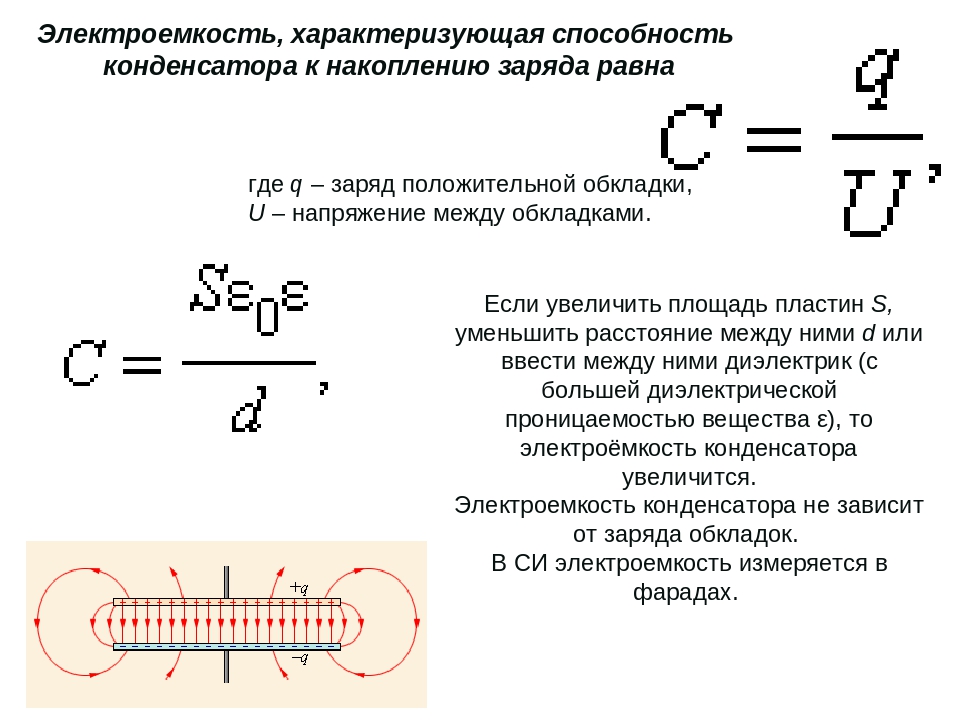

4\frac{В}{м}.$

Плоский конденсатор: формулы, особенности, конструкция

Плоский конденсатор – физическое упрощение, взявшее начало из ранних исследований электричества, представляющее собой конструкцию, где обкладки носят форму плоскостей и в любой точке параллельны.

Формулы

Люди ищут формулы, описывающие ёмкость плоского конденсатора. Читайте ниже любопытные и малоизвестные факты, сухие математические знаки также важны.

Первым определил ёмкость плоского конденсатора Вольта. В его распоряжении ещё не было величины – разница потенциалов, именуемая напряжением, но интуитивно учёный правильно объяснил суть явления. Величину количества зарядов трактовал как объем электрического флюида атмосферы – не совсем правильно, но похоже на правду. Согласно озвученному мировоззрению ёмкость плоского конденсатора находится как отношение объёма накопленного электрического флюида к разнице атмосферных потенциалов:

С = q/U.

Формула применима к любому конденсатору, вне зависимости от конструкции. Признана универсальной. Специально для плоских конденсаторов разработана формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры:

В этой формуле через S обозначена площадь обкладок, вычисляемая через произведение сторон, а d – показывает расстояние между обкладками. Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика. Электролитические конденсаторы обладают столь большой ёмкостью по понятной причине: проводящий раствор отделен от металла крайне тонким слоем оксида. Следовательно, d оказывается минимальным. Единственный минус – электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на аноде или катоде обозначены значками плюса или минуса.

Плоские конденсаторы сегодня редко встречаются, это преимущественно плёночные микроскопические технологии, где указанный род поверхностей считается доминирующим. Все пассивные и активные элементы образуются через трафарет, образуя вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст.

От материала диэлектрика зависит ёмкость, у каждого собственная структура. Считается, что аморфное вещество состоит из неориентированных диполей, упруго укреплённых на своих местах. При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость. В результате заряд накапливается, пока процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на места, делая возможным новый рабочий цикл. Так функционирует плоский электрический конденсатор.

Конденсатор для уроков

Из истории

Первым начал исследовать накопление заряда великий Алессандро Вольта. В докладе Королевскому научному обществу за 1782 год впервые озвучил слово конденсатор. В понимании Вольты электрофорус, представляющий две параллельные обкладки, выкачивал из эфира электрический флюид.

В давнее время все познания сводились к мнению учёных, будто атмосфера Земли содержит нечто, не определяемое приборами. Присутствовали простейшие электроскопы, способные определить знак заряда и его наличие, не дававшие представления о количестве. Учёные просто натирали мехом поверхность тела и подносили для исследования в область влияния прибора. Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием. Учёные примерно знали, что делать, но исследования не продвигались.

Гипотеза об атмосферном электричестве высказана Бенджамином Франклином. Он активно исследовал молнии и пришёл к выводу, что это проявления прежней единой силы. Запуская воздушного змея в небо, он соединял игрушку шёлковой нитью с землёй и наблюдал дуговой разряд. Это опасные опыты, и Бенджамин многократно рисковал собственной жизнью ради развития науки. Шёлковая нить проводит статический заряд – это доказал Стивен Грей, первый собравший в 1732 году электрическую цепь.

Уже через 20 лет (1752 год) Бенджамин Франклин предложил конструкцию первого громоотвода, осуществлявшего молниезащиты близлежащих построек. Только вдуматься! – прежде любой ожидал, что дом сгорит от случайного удара. Бенджамин Франклин предложил один вид заряда называть положительным (стеклянный), а второй отрицательным (смоляной). Так физики оказались введены в заблуждение относительно истинного направления движения электронов. Но откуда возьмётся иное мнение, когда в 1802 году на примере опытов россиянина Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, но в действительности это оказались ионы воздушной плазмы.

К началу исследования Вольтой электрических явлений уже известны статические заряды и факт наличия у них двух знаков. Люди упорно считали, что «флюид» берётся из воздуха. На эту мысль натолкнули опыты с натиранием янтаря шерстью, не воспроизводимые под водой. Следовательно, логичным стало предположить, что электричество может происходить исключительно из атмосферы Земли, что, конечно же, неверно. К примеру, многие растворы, исследованные Хампфри Дэви, проводят электрический ток.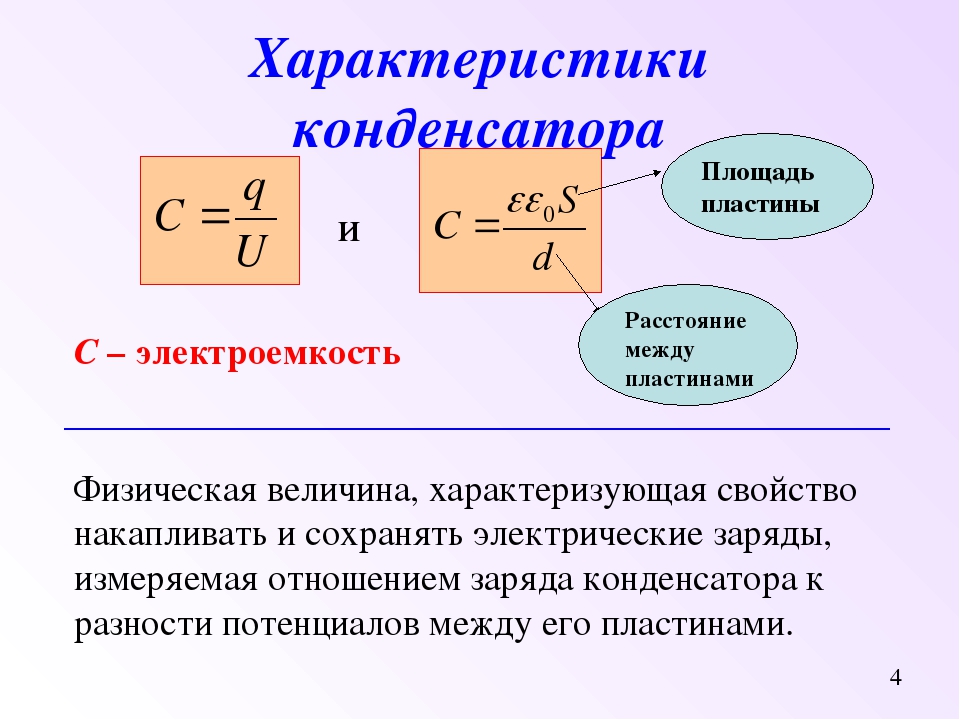

Причина, следовательно, иная – при натирании янтаря под водой силы трения снижались в десятки и сотни раз, а заряд рассеивался по объёму жидкости. Следовательно, процесс лишь оказывался неэффективным. Сегодня каждый добытчик знает, что нефть электризуется трением о трубы без воздуха. Следовательно, атмосфера для «флюида» не считается обязательным компонентом.

Самый большой в мире плоский конденсатор

Столь систематизированные, но в корне неверные толкования не остановили Вольту на исследовательском пути. Он упорно изучал электрофорус, как совершенный генератор того времени. Вторым был серный шар Отто фон Герике, изобретённый на век раньше (1663 год). Его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. К примеру, в электрофорной машине применяются металлические гребёнки-нейтрализаторы.

Долгое время учёные раскачивались. Электрофорная машина 1880 года вправе считаться первым мощным генератором разряда, позволявшим получить дугу, но истинной силы электроны достигли в генераторе Ван де Граафа (1929 год), где разница потенциалов составила единицы мегавольта. Для сравнения – грозовое облако, согласно данным Википедии, обнаруживает потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).

Суммируя сказанное, с определённой долей уверенности скажем, что природные процессы используют в качестве принципа действия электризацию трением, влиянием и прочие виды, а мощный циклон считается самым большим из известных плоских конденсаторов. Молния показывает, что случается, когда диэлектрик (атмосфера) не выдерживает приложенной разницы потенциалов и пробивается. В точности аналогичное происходит в плоском конденсаторе, созданном человеком, если вольтаж оказывается непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя.

Электрофорус

Итак, Вольта взялся за исследование модели природных процессов. Первый электрофорус появился в 1762 году сконструированный Йоханом Карлом Вильке. По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта дал прибору нынешнее название.

Вид электрофоруса

Электрофорус способен накапливать электростатический заряд, образованный трением резины куском шерсти. Состоит из двух плоских, параллельных друг другу обкладок:

• Нижняя представляет тонкий кусок резины. Толщина выбирается из соображений эффективности устройства. Если выбрать кусок солиднее, значительная часть энергии станет накапливаться внутри диэлектрика на ориентацию его молекул. Что отмечается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.
• Верхняя пластина из тонкой стали кладётся сверху, когда заряд уже накоплен трением. За счёт влияния на верхней поверхности образуется избыток отрицательного заряда, снимаемого на заземлитель, чтобы при расстыковке двух обкладок не произошло взаимной компенсации.

Принцип действия плоского конденсатора уже понятен. Оператор трёт резину шерстью, оставляя на ней отрицательный заряд. Сверху кладётся кусок металла. Из-за значительной шероховатости поверхностей они не соприкасаются, но находятся на расстоянии друг от друга. В результате металл электризуется влиянием. Электроны отталкиваются поверхностным зарядом резины и уходят на внешнюю плоскость, где оператор их снимает через заземлитель лёгким кратковременным прикосновением.

Низ металлической обкладки остаётся заряженным положительно. При расстыковке двух поверхностей этот эффект сохраняется, в материале наблюдается дефицит электронов. И заметно искру, если дотронуться до металлической обкладки. Этот опыт допускается на единственном заряде резины проделывать сотни раз, её поверхностное статическое сопротивление крайне велико. Это не даёт заряду растекаться. Демонстрируя описанный опыт, Вольта привлёк внимание научного мира, но исследования не двигались вперёд, если не считать открытий Шарля Кулона.

В 1800 году Алессандро даёт толчок развитию изысканий в области электричества, изобретя знаменитый гальванический источник питания.

Конструкция плоского конденсатора

Электрофорус представляет собой первый из сконструированных плоских конденсаторов. Его обкладки способны хранить только статический заряд, иначе наэлектризовать резину невозможно. Поверхность чрезвычайно долго хранит электроны. Вольта даже предлагал снимать их пламенем свечи через ионизированный воздух или ультрафиолетовым излучением Солнца. Сегодня каждый школьник знает, что явление проделывается водой. Правда, электрофорус потом потребуется высушить.

В современном мире нижней обкладкой служит тефлоновое покрытие или пластик. Они хорошо набирают статический заряд. Диэлектриком становится воздух. Чтобы перейти к конструкции современного конденсатора, нужно обе обкладки сделать металлическими. Тогда при возникновении на одной заряда электризация распространится на вторую, и если другой контакт заземлён, накопленная энергия хранится определённое время.

Конструкция в деталях

Запас электронов напрямую зависит от материала диэлектриков. К примеру, среди современных конденсаторов встречаются:

1. Слюдяные.
2. Воздушные.
3. Электролитические (оксидные).
4. Керамические.

В эти названия заложен материал диэлектрика. От состава зависит напрямую ёмкость, способная увеличиваться многократно. Роль диэлектриков объяснялась выше, их параметры определяются непосредственно строением вещества. Однако многие материалы, обладающие высокими характеристиками, использовать не удаётся по причине их непригодности. К примеру, вода характеризуется высокой диэлектрической проницаемостью.

Плоский конденсатор, теория и примеры задач

Большое число конденсаторов, которые применяют в технике, приближены по типу к плоскому конденсатору. Это конденсатор, который представляет собой две параллельные проводящие плоскости (обкладки), которые разделяет небольшой промежуток, заполненный диэлектриком. На обкладках сосредоточены равные по модулю и противоположные по знаку заряды.

Электрическая емкость плоского конденсатора

Электрическая емкость плоского конденсатора очень просто выражается через параметры его частей.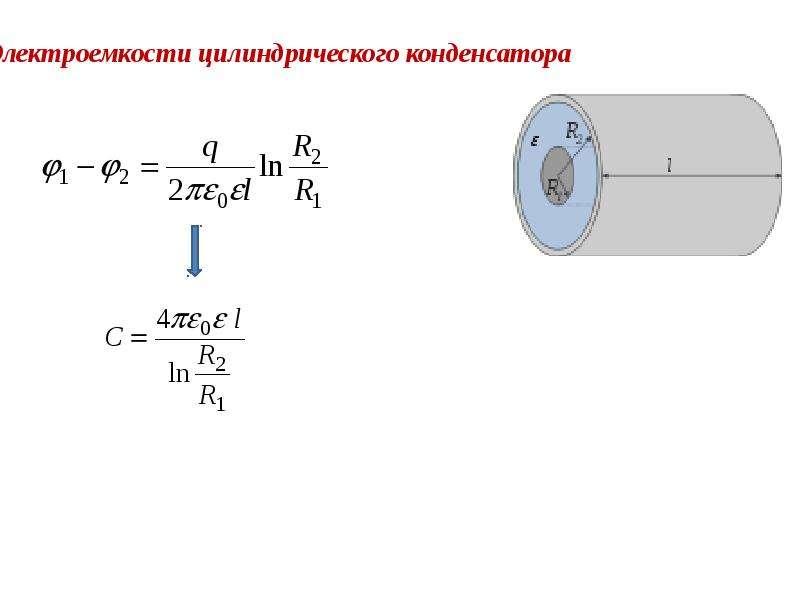 Изменяя площадь пластин конденсатора и расстояние между ними легко убедиться, что электрическая емкость плоского конденсатора прямо пропорциональна площади его пластин (S) и обратно пропорциональна расстоянию между ними (d):

   

Формулу для расчета емкости плоского конденсатора просто получить при помощи теоретических расчетов.

Положим, что расстояние между пластинами конденсатора много меньше, чем их линейные размеры. Тогда краевыми эффектами можно пренебречь, и электрическое поле между обкладками считать однородным. Поле (E), которое создают две бесконечные плоскости, несущие одинаковый по модулю и противоположный по знаку заряд, разделенные диэлектриком с диэлектрической проницаемостью , можно определить при помощи формулы:

   

где — плотность распределения заряда по поверхности пластины. Разность потенциалов между рассматриваемыми обкладками конденсатора, находящимися на расстоянии d будет равна:

   

Подставим правую часть выражения (3) вместо разности потенциалов в (1) учитывая, что , имеем:

   

Энергия поля плоского конденсатора и сила взаимодействия его пластин

Формула энергии поля плоского конденсатора записывается как:

   

где – объем конденсатора; E – напряженность поля конденсатора. Формула (5) связывает энергию конденсатора с зарядом на его обкладках и напряженностью поля.

Механическую (пондемоторную) силу, с которой пластины плоского конденсатора взаимодействуют между собой можно найти, если использовать формулу:

   

В выражении (6) минус показывает, что пластины конденсатора притягиваются друг к другу.

Примеры решения задач

Плоский конденсатор. Заряд и емкость конденсатора.

Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются! Давайте, в  первую очередь, рассмотрим устройство и принцип работы конденсаторов. А затем плавно перейдем к основным свойствам и характеристикам – заряду, энергии и, конечно же, емкости конденсатора. Как видите, нам сегодня предстоит изучить много интересных моментов 🙂

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E = \frac{\sigma}{2\varepsilon_0\thinspace\varepsilon}

Здесь \sigma– это поверхностная плотность заряда: \sigma = \frac{q}{S}, а \varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора.

Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S}

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S} + \frac{q}{2\varepsilon_0\thinspace\varepsilon S} = \frac{q}{\varepsilon_0\thinspace\varepsilon S}

А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0 🙂

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как видите, здесь нет ничего сложного 🙂

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:

C = \frac{q}{\Delta\varphi} = \frac{q}{U}

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). 2}{2C}

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!

Электроёмкость плоского конденсатора | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Плоским конденсатором обычно называ­ют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Про­стота конструкции такого конденсатора по­зволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.

Рис. 4.71. Плоский конденсатор на элект­рометре

Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электромет­ра, а вторая — к его металлическому кор­пусу (рис. 4.71). При таком соединении электрометр будет измерять разность по­тенциалов между пластинами, которые об­разуют плоский конденсатор из двух пла­стин. Проводя исследования, необходимо пом­нить, что

при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроем­кости конденсатора, и наоборот.

Сообщим пластинам разноименные заря­ды и отметим отклонение стрелки электро­метра. Приближая пластины друг к другу (уменьшая расстояние между ними), заме­тим уменьшение разности потенциалов. Та­ким образом, при уменьшении расстояния между пластинами конденсатора его элект­роемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельст­вом уменьшения электроемкости.

Электроемкость плоского конденсатора об­ратно пропорциональна расстоянию между его обкладками.

C ~ 1 / d,

где d — расстояние между обкладками.

Рис. 4.72. График зависимости емкости плоского конденсатора от расстояния между пластинами

Рис. 4.73. При расчетах емкости плоских конденсаторов учитывают площадь пере­крытия пластин

Эту зависимость можно изобразить гра­фиком обратной пропорциональной зависи­мости (рис. 4.72).

Будем смещать пластины одну относи­тельно другой в параллельных плоскостях, не изменяя расстояния между ними.

При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об умень­шении электроемкости.

Увеличение площади перекрытия пластан приведет к увеличению емкости.

Электроемкость плоского конденсатора про­порциональна площади пластин, которые пере­крываются.

C ~ S,

где S — площадь пластин.

Рис. 4.74. График зависимости емкости плоского конденсатора от площади его пластин

Эту зависимость можно представить гра­фиком прямой пропорциональной зависи­мости (рис. 4.74). 

Возвратив пластины в начальное поло­жение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увели­чении электроемкости конденсатора. Если между пластинами поместить другой диэлек­трик, то изменение электроемкости будет иным.

Электроемкость плоского конденсатора за­висит от диэлектрической проницаемости ди­электрика.

C ~ ε,

где ε — диэлектрическая проницаемость ди­электрика. Материал с сайта http://worldofschool.ru

Рис. 4.75. График зависимости емкости плоского конденсатора от диэлектри­ческой проницаемости диэлектрика

Такая зависимость показана на графике рис. 4.75.

Результаты опытов можно обобщить в ви­де формулы ёмкости плоского конденсатора:

C = εε₀S / d,

где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая прони­цаемость диэлектрика; ε₀ — электрическая постоянная.

Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.

На этой странице материал по темам:

• График зависимости электроемкости плоского конденсатора от площади его пластин

• Примеры решения задач поизменению энергии в плоском конденсаторе

• График зависимости емкости c плоского конденсатора

• График зависимости электроемкости от расстояния

• При увеличении площади перекрывания пластин конденсатора

Вопросы по этому материалу:

• Какое строение плоского конденсатора?

• По изменению какой величины в опыте можно делать заключение об изменении электроемкости?

• В какой последовательности проводится опыт, в котором устанавли­валась зависимость электроемкости конденсатора от его параметров?

• Как зависит электроемкость плоского конденсатора от активной площади пластин?

• Как зависит электроемкость плоского конденсатора от расстояния между пластинами?

• Как влияет диэлектрик на электроемкость конденсатора?

Как изменяется электроемкость плоского конденсатора.

Что такое электроемкость конденсатора? Электрическая емкость цилиндрического конденсатора

Одним их важнейших параметров, при помощи которого характеризуют конденсатор, является его электроёмкость (C). Физическая величина C, равная:

называется емкостью конденсатора. Где q — величина заряда одной из обкладок конденсатора, а — разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Для конденсаторов с одинаковым устройством и при равных зарядах на его обкладках разность потенциалов воздушного конденсатора будет в раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Значит емкость конденсатора с диэлектриком (C) в раз больше, чем электроемкость воздушного конденсатора ():

где — диэлектрическая проницаемость диэлектрика.

Единицей емкости конденсатора считают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) является фарад (Ф).

Электроемкость плоского конденсатора

Поле между обкладками плоского конденсатора в большинстве случаев считают однородным. Однородность нарушается только около краев. При расчете емкости плоского конденсатора данными краевыми эффектами обычно пренебрегают. Это возможно, если расстояние между пластинами мало в сравнении с их линейными размерами. В таком случае емкость плоского конденсатора вычисляют как:

где — электрическая постоянная; S — площадь каждой (или наименьшей) пластины; d — расстояние между пластинами.

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:

Электрическая емкость цилиндрического конденсатора

Конструкция цилиндрического конденсатора включает две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость такого конденсатора находят как:

где l — высота цилиндров; — радиус внешней обкладки; — радиус внутренней обкладки.

Емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

где — радиусы обкладок конденсатора.

Примеры решения задач

ПРИМЕР 1

Задание	Пластины плоского воздушного конденсатора несут заряд, который равномерно распределен с поверхностной плотностью . При этом расстояние между его обкладками, равно . На какую величину изменится разность потенциалов на обкладках этого конденсатора, если его пластины раздвинуть до расстояния ?
Решение	Сделаем рисунок. В задаче при изменении расстояния между пластинами конденсатора заряд на его обкладках не изменяется, изменяются емкость и разность потенциалов на обкладках. Емкость плоского воздушного конденсатора равна: где . Емкость этого же конденсатора можно определить как: где U — разность потенциалов на обкладках конденсатора. Для конденсатора в первом случае имеем: Для того же конденсатора, но после того как пластины раздвинули, имеем: Используя формулу (1.3) и применяя соотношение: выразим разность потенциалов Следовательно, для конденсатора во втором состоянии получим: Найдем изменение разности потенциалов:
Ответ

Рассмотрим два заряженных проводника. Предположим, что все силовые линии, начинающиеся на одном из них, заканчиваются на другом. Для этого, разумеется, они должны иметь равные и противоположные по знаку заряды. Такая система двух проводящих тел называется конденсатором.

Примеры конденсаторов. Примерами конденсаторов могут служить две концентрические проводящие сферы (сферический, или шаровой, конденсатор), две параллельные плоские проводящие пластины при условии, что расстояние между ними мало по сравнению с размерами пластин (плоский конденсатор), два коаксиальных проводящих цилиндра при условии, что их длина велика по сравнению с зазором между цилиндрами (цилиндрический конденсатор).

Два проводника, образующие конденсатор, называются его обкладками.

Рис. 41. Электрическое поле в сферическом, плоском и цилиндрическом конденсаторах

Во всех таких системах при сообщении обкладкам равных по модулю и противоположных по знаку зарядов электрическое поле практически целиком заключено в пространстве между обкладками (рис. 41). Внешний вид некоторых используемых в технике конденсаторов показан на рис. 42.

Основная характеристика конденсатора — электроемкость или просто емкость С, определяемая как отношение заряда одной из

обкладок к разности потенциалов т. е. к напряжению, между ними:

Распределение зарядов на обкладках будет одинаковым независимо от того, большой или малый заряд им сообщен. Это значит, что напряженность поля, а следовательно, и разность потенциалов между обкладками, пропорциональны сообщенному конденсатору заряду. Поэтому емкость конденсатора не зависит от его заряда.

Рис. 42. Устройство, внешний вид и условные обозначения на электрических схемах некоторых конденсаторов

В вакууме емкость определяется исключительно геометрическими характеристиками конденсатора, т. е. формой, размерами и взаимным расположением обкладок.

Единицы емкости. В СИ за единицу электроемкости принят фарад Емкостью 1 Ф обладает конденсатор, между обкладками которого устанавливается напряжение 1 В при сообщении заряда 1 Кл:

В абсолютной электростатической системе единиц СГСЭ электроемкость имеет размерность длины и измеряется в сантиметрах:

На практике обычно приходится иметь дело с конденсаторами, емкость которых значительно меньше 1 Ф. Поэтому используются доли этой единицы — микрофарад (мкФ) и пикофарад . Соотношение между фарадом и сантиметром легко установить, учитывая, что

Электроемкость и геометрия конденсатора. Зависимость емкости конденсатора от его геометрических характеристик легко проиллюстрировать простыми опытами. Воспользуемся для этого электрометром, подключенным к двум плоским пластинам, расстояние между которыми можно изменять (рис. 43). Чтобы заряды пластин были одинаковы и все поле было сосредоточено только между ними, следует заземлить вторую пластину и корпус электрометра. Отклонение стрелки электрометра пропорционально напряжению между обкладками. Если сдвигать или раздвигать пластины конденсатора, то при неизменном заряде напряжение будет соответственно уменьшаться или увеличиваться: емкость тем больше, чем меньше расстояние между пластинами. Аналогично можно убедиться в том, что емкость конденсатора тем больше, чем больше площадь его пластин. Для этого можно просто сдвигать пластины при неизменном зазоре между ними.

Рис. 43. Емкость конденсатора зависит от расстояния между пластинами

Емкость плоского конденсатора. Получим формулу для емкости плоского конденсатора. Поле между его обкладками однородно за исключением небольшой области вблизи краев пластин. Поэтому напряжение между обкладками равно произведению напряженности поля Е на расстоянии между ними: Для нахождения напряженности поля Е можно воспользоваться формулой (1) § 6, которая связывает Е вблизи поверхности проводника с поверхностной плотностью зарядов с: Выразим а через заряд конденсатора и площадь пластины, считая распределение заряда равномерным, что согласуется с используемым предположением об однородности поля: Подставляя приведенные соотношения в общее определение емкости (1), находим

В СИ, где емкость плоского конденсатора имеет вид

В системе единиц СГСЭ k = 1 и

Емкость сферического конденсатора. Совершенно аналогично можно вывести формулу для емкости сферического конденсатора, рассматривая электрическое поле в промежутке между двумя заряженными концентрическими сферами радиусов Напряженность поля там такая же, как в случае уединенного заряженного шара радиуса Поэтому для напряжения между обкладками радиусов справедливо

Выражение для емкости получаем, подставляя в формулу (1):

Емкость уединенного проводника. Иногда вводят понятие емкости уединенного проводника, рассматривая предельный случай конденсатора, одна из обкладок которого удалена на бесконечность. В частности, емкость уединенного проводящего шара получается из (5) в результате предельного перехода что соответствует неограниченному увеличению радиуса внешней обкладки при неизменном радиусе внутренней

В системе единиц СГСЭ, где емкость уединенного шара равна его радиусу. Если проводник имеет несферическую форму, его емкость по порядку величины равна характерному линейному размеру, хотя, конечно же, зависит и от его формы. В отличие от уединенного проводника, емкость конденсатора гораздо больше его линейных размеров. Например, у плоского конденсатора характерный линейный размер равен причем Как видно из формулы (4), при этом

Конденсатор с диэлектриком. В рассмотренных выше примерах конденсаторов пространство между обкладками считалось пустым. Тем не менее полученные выражения для емкости справедливы и тогда, когда это пространство заполнено воздухом, как это было в описанных простых опытах. Если пространство между обкладками заполнить каким-либо диэлектриком, емкость конденсатора увеличивается. В этом легко убедиться на опыте, вдвигая диэлектрическую пластину в промежуток между обкладками заряженного конденсатора, подключенного к электрометру (рис. 43). При неизменном заряде конденсатора напряжение между обкладками уменьшается, что свидетельствует о возрастании емкости.

Уменьшение разности потенциалов между обкладками при внесении туда диэлектрической пластины свидетельствует о том, что напряженность электрического поля в зазоре становится меньше. Это уменьшение зависит от того, какой именно диэлектрик используется в опыте.

Диэлектрическая проницаемость. Для характеристики электрических свойств диэлектрика вводят физическую величину, называемую диэлектрической проницаемостью. Диэлектрическая проницаемость — это безразмерная величина, показывающая, во сколько раз напряженность электрического поля в заполненном диэлектриком конденсаторе (или напряжение между его обкладками) меньше, чем в отсутствие диэлектрика при том же заряде конденсатора. Другими словами, диэлектрическая проницаемость показывает, во сколько раз увеличивается емкость конденсатора при заполнении его диэлектриком. Например, емкость плоского конденсатора, заполненного диэлектриком с проницаемостью равна

Приведенное здесь определение диэлектрической проницаемости соответствует феноменологическому подходу, при котором рассматриваются только макроскопические свойства вещества в электрическом поле. Микроскопический подход, основанный на рассмотрении поляризации атомов или молекул, из которых состоит вещество, предполагает исследование какой-либо конкретной модели и позволяет не только подробно описывать электрические и магнитные поля внутри вещества, но и понять, как протекают макроскопические электрические и магнитные явления в веществе. На этом этапе мы ограничиваемся только феноменологическим подходом.

Рис. 44. Параллельное соединение конденсаторов

У твердых диэлектриков значение лежит в пределах от 4 до 7, а у жидких — от 2 до 81. Такой аномально большой диэлектрической проницаемостью обладает обыкновенная чистая вода. Кроме воздушного конденсатора переменной емкости (см. рис. 42), используемого для настройки радиоприемников, все другие применяемые в технике конденсаторы заполнены диэлектриком.

Батареи конденсаторов. При использовании конденсаторов их иногда соединяют в батареи. При параллельном соединении (рис. 44) напряжения на конденсаторах одинаковы, а полный заряд батареи равен сумме зарядов конденсаторов для каждого из которых, очевидно, справедливо Рассматривая батарею как один

конденсатор, имеем

С другой стороны,

Сравнивая (8) и (9), получаем, что емкость батареи параллельно соединенных конденсаторов равна сумме их емкостей:

Рис. 45. Последовательное соединение конденсаторов

При последовательном соединении предварительно незаряженных конденсаторов (рис. 45) заряды на всех конденсаторах одинаковы, а полное напряжение равно сумме напряжений на отдельных конденсаторах:

С другой стороны, рассматривая батарею как один конденсатор, имеем

Сравнивая (11) и (12), видим, что при последовательном соединении конденсаторов складываются обратные емкостям величины:

При последовательном соединении емкость батареи меньше самой малой из емкостей соединенных конденсаторов.

В каком случае два проводящих тела образуют конденсатор?

Что называется зарядом конденсатора?

Как установить связь между единицами емкости СИ и СГСЭ?

Объясните качественно, почему емкость конденсатора увеличивается при уменьшении зазора между обкладками.

Получите формулу для емкости плоского конденсатора, рассматривая электрическое поле в нем как суперпозицию полей, создаваемых двумя плоскостями, заряженными разноименно.

Получите формулу для емкости плоского конденсатора, рассматривая его как предельный случай сферического конденсатора, у которого стремятся к бесконечности так, что разность остается постоянной.

Почему нельзя говорить о емкости уединенной бесконечной плоской пластины или отдельного бесконечно длинного цилиндра?

Охарактеризуйте кратко различие между феноменологическим и микроскопическим подходами при исследовании свойств вещества в электрическом поле.

Каков смысл диэлектрической проницаемости вещества?

Почему при расчете емкости батареи последовательно соединенных конденсаторов оговаривалось условие, чтобы они предварительно не были заряжены?

В чем смысл последовательного соединения конденсаторов, если оно приводит лишь к уменьшению емкости?

Поле внутри и вне конденсатора. Чтобы подчеркнуть различие между тем, что называют зарядом конденсатора, и полным зарядом обкладок, рассмотрим следующий пример. Пусть наружная обкладка сферического конденсатора заземлена, а внутренней сообщен заряд д. Весь этот заряд равномерно распределится по внешней поверхности внутренней обкладки. Тогда на внутренней поверхности наружной сферы индуцируется заряд , следовательно, заряд конденсатора равен . А что будет на внешней поверхности наружной сферы? Это зависит от того, что окружает конденсатор. Пусть, например, на расстоянии от поверхности внешней сферы находится точечный заряд (рис. 46). Этот заряд никак не повлияет на электрическое состояние внутреннего пространства конденсатора, т. е. на поле между его обкладками. В самом деле, внутреннее и внешнее пространства разделены толщей металла наружной обкладки, в которой электрическое поле равно нулю.

Рис. 46. Сферический конденсатор во внешнем электрическом поле

Заряд на внешней поверхности обкладки. Но характер поля во внешнем пространстве и заряд, индуцированный на наружной поверхности внешней сферы, зависят от величины и положения заряда Это поле будет точно таким же, как и в случае, коща заряд находится на расстоянии от поверхности сплошного заземленного металлического шара, радиус которого равен радиусу внешней сферы конденсатора (рис. 47). Таким же будет и индуцированный заряд.

Для нахождения величины индуцированного заряда будем рассуждать следующим образом. Электрическое поле в любой точке пространства создается зарядом и зарядом, индуцированным

на поверхности шара, который распределен там, разумеется, неравномерно — как раз так, чтобы обратилась в нуль результирующая напряженность поля внутри шара. Согласно принципу суперпозиции потенциал в любой точке можно искать в виде суммы потенциалов полей, создаваемых точечным зарядом и точечными зарядами, на которые можно разбить распределенный по поверхности шара индуцированный заряд. Поскольку все элементарные заряды на которые разбит индуцированный на поверхности шара заряд находятся на одинаковом расстоянии от центра шара, то потенциал создаваемого им поля в центре шара будет равен

Рис. 47. Поле точечного заряда вблизи заземленного проводящего шара

Тогда полный потенциал в центре заземленного шара равен

Знак минус отражает тот факт, что индуцированный заряд всегда противоположного знака.

Итак, мы видим, что заряд на наружной поверхности внешней сферы конденсатора определяется тем окружением, в котором находится конденсатор, и не имеет никакого отношения к заряду конденсатора д. Полный заряд внешней обкладки конденсатора, разумеется, равен сумме зарядов ее внешней и внутренней поверхностей, однако заряд конденсатора определяется только зарядом внутренней поверхности этой обкладки, который связан силовыми линиями поля с зарядом внутренней обкладки.

В разобранном примере независимость электрического поля в пространстве между обкладками конденсатора и, следовательно, его емкости от внешних тел (как заряженных, так и незаряженных) обусловлена электростатической защитой, т. е. толщей металла внешней обкладки. К чему может привести отсутствие такой защиты, можно увидеть на следующем примере.

Плоский конденсатор с экраном. Рассмотрим плоский конденсатор в виде двух параллельных металлических пластин, электрическое поле которого практически целиком сосредоточено в пространстве между пластинами. Заключим конденсатор в незаряженную плоскую металлическую коробку, как показано на рис. 48. На первый взгляд может показаться, что картина поля между обкладками конденсатора не изменится, так как все поле сосредоточено между пластинами, а краевым эффектом мы пренебрегаем. Однако легко видеть, что это не так. Снаружи конденсатора напряженность поля равна нулю, поэтому во всех точках слева от конденсатора потенциал одинаков и совпадает с потенциалом левой пластины. Точно так же потенциал любой точки справа от конденсатора совпадает с потенциалом правой пластины (рис. 49). Поэтому, заключая конденсатор в металлическую коробку, мы соединяем проводником точки, имеющие разный потенциал.

В результате в металлической коробке будет происходить перераспределение зарядов до тех пор, пока не выравняются потенциалы всех ее точек. На внутренней поверхности коробки индуцируются заряды, и появится электрическое поле внутри коробки, т. е. снаружи конденсатора (рис. 50).

Рис. 48. Конденсатор в металлической коробке

Рис. 49. Электрическое поле заряженного плоского конденсатора

Рис. 50. Электрическое поле заряженного конденсатора, помещенного в металлическую коробку

Но это означает, что на внешних поверхностях пластин конденсатора тоже появятся заряды. Так как при этом полный заряд изолированной пластины не меняется, то заряд на ее внешней поверхности может возникнуть только за счет перетекания заряда с внутренней поверхности. Но при изменении заряда на внутренних поверхностях обкладок изменится напряженность поля между пластинами конденсатора.

Таким образом, заключение рассмотренного конденсатора в металлическую коробку приводит к изменению электрического состояния внутреннего пространства.

Изменение зарядов пластин и электрического поля в этом примере может быть легко рассчитано. Обозначим заряд изолированного конденсатора через Заряд, перетекающий на наружные поверхности пластин при надевании коробки, обозначим через Такой же заряд противоположного знака будет индуцирован на внутренних поверхностях коробки. На внутренних поверхностях пластин конденсатора останется заряд Тогда в пространстве между пластинами напряженность однородного поля будет равна в единицах СИ, а вне конденсатора поле направлено в противоположную сторону и его напряженность равна где — площадь пластины. Требуя, чтобы разность потенциалов между противоположными стенками металлической коробки была равна нулю, и считая для простоты расстояния между всеми пластинами одинаковыми и равными то

Этот результат легко понять, если учесть, что после надевания коробки поле существует во всех трех промежутках между пластинами, т. е. фактически имеются три одинаковых конденсатора, эквивалентная схема включения которых показана на рис. 51. Вычисляя емкость получившейся системы конденсаторов, получаем .

Надетая на конденсатор металлическая коробка осуществляет электростатическую защиту системы. Теперь мы можем подносить снаружи к коробке любые заряженные или незаряженные тела и при этом электрическое поле внутри коробки не изменится. Значит, не изменится и емкость системы.

Обратим внимание на то, что в разобранном примере, выяснив все, что нас интересовало, мы тем не менее обошли стороной вопрос о том, какие же силы осуществили перераспределение зарядов. Какое электрическое поле вызвало движение электронов в материале проводящей коробки?

Очевидно, что это может быть только то неоднородное поле, которое выходит за пределы конденсатора вблизи краев пластины (см. рис. 39). Хотя напряженность этого поля мала и не принимается во внимание при расчете изменения емкости, именно она определяет суть рассматриваемого явления — перемещает заряды и этим вызывает изменение напряженности электрического поля внутри коробки.

Почему под зарядом конденсатора следует понимать не полный заряд обкладки, а только ту его часть, что находится на ее внутренней стороне. обращенной к другой обкладке?

В чем проявляется роль краевых эффектов при рассмотрении электростатических явлений в конденсаторе?

Как изменится емкость батареи конденсаторов, если замкнуть между собой обкладки одного из них?

Формула электроемкости следующая.

Измеряется эта величина в фарадах. Как правило, емкость элемента очень мала и измеряется в пикофарадах.

В задачах часто спрашивается, как изменится электроемкость конденсатора, если увеличить заряд или напряжение. Это вопрос с подвохом. Проведем другую аналогию.

Представьте, что речь идет про обычную банку, а не конденсатор. Например, у вас она трехлитровая. Аналогичный вопрос: что произойдет со вместимостью банки, если туда налить 4 литра воды? Разумеется, вода просто выльется, но при этом размеры банки никак не изменятся.

То же самое с конденсаторами. Заряд и напряжение никак не влияют на емкость. Этот параметр зависит только от реальных физических размеров.

Формула будет следующей

Только эти параметры влияют на реальную электроемкость конденсатора.

На любом конденсаторе есть маркировка с техническими параметрами.

Разобраться несложно. Достаточно минимальных знаний по электричеству.

Соединение конденсаторов

Конденсаторы, так же как и сопротивления, можно подключать последовательно и параллельно. Кроме этого, в схемах бывают и смешанные соединения.

Как видите, электроемкость конденсатора в обоих случаях считается по-разному. Это также относится к напряжению и заряду. По формулам видно, что электроемкость конденсатора, вернее, их совокупности в схеме, будет наибольшей при параллельном соединении. При последовательном общая емкость значительно уменьшается.

При подключении последовательно заряд размещается равномерно. Он будет везде одинаков — как суммарный, так и на каждом конденсаторе. А когда соединение параллельное, суммарный заряд складывается. Это важно помнить при решении задач.

Напряжение считается наоборот. При последовательном соединении складываем, а при параллельном оно равно везде.

Здесь приходится выбирать: если вам нужно больше напряжения, тогда жертвуем емкостью. Если емкость, то огромного напряжения не будет.

Виды конденсаторов

Существует огромное количество конденсаторов. Они отличаются как по размеру, так и по форме.

Разумеется, емкость вычисляется у всех по-разному.

Электроемкость плоского конденсатора

Электроемкость плоского конденсатора определяется проще всего. Эту формулу в основном все и помнят, в отличии от других.

Здесь всё зависит от физических параметров и среды между пластинами.

Здесь также большое значение имеет, какой диэлектрик или материал помещен внутрь. Так как деталь имеет размер сферы, ее емкость зависит от радиуса.

В случае с цилиндрической формой, кроме среды внутри, значение имеют радиусы и длина цилиндра.

Подумайте, как изменится электроемкость плоского конденсатора, если на нем будут повреждения? Существуют различные сбои, которые могут повлиять на работоспособность конденсаторов.

Например, они рассыхаются или вздуваются. После этого они становятся непригодными для нормальной работы устройства, куда установлены.

Рассмотрим примеры повреждений и выхода из строя конденсаторов. Вздуться могут все сразу.

Иногда из строя выходят только несколько. Такое бывает, когда конденсаторы разных параметров или качества.

Наглядный пример порчи (вздутие, разрыв и выход наружу содержимого).

Если вы увидите вот такие ленты, это крайняя степень повреждения. Хуже и быть не может.

Если вы заметите на устройстве (например на видеокарте в компьютере) такие вздутые конденсаторы, это повод задуматься о замене детали.

Подобные проблемы можно устранить только заменой на аналогичную деталь. У вас должны совпадать все параметры один в один. Иначе работа может быть некорректной или очень кратковременной.

Менять конденсаторы нужно аккуратно, не повредив платы. Выпаивать нужно быстро, не допуская перегрева. Если вы не умеете этого делать, лучше отнесите деталь в ремонт.

Основной причиной разрушения является перегрев, который возникает в случае старения или большого сопротивления в цепи.

Рекомендуется не затягивать с ремонтом. Поскольку у поврежденных конденсаторов изменяется емкость, устройство, где они расположены, будет работать с отклонением от нормы. И со временем это может стать причиной выхода из строя.

Если у вас на видеокарте вздулись конденсаторы, то их своевременная замена может исправить ситуацию. В противном случае может сгореть микросхема или что-то еще. В таком случае ремонт будет стоить очень дорого или вовсе окажется невозможным.

Меры предосторожности

Выше был приведен пример с банкой воды. Там говорилось, что если воды налить больше, то воды выльется. А теперь подумайте, куда могут «вылиться» электроны в конденсаторе? Ведь он запечатан полностью!

Если вы подадите в цепи больше тока, чем тот, на который рассчитан конденсатор, то как только он зарядится, его излишек попытается выйти куда-то. А пространства свободного нет. Результатом будет взрыв. В случае незначительного превышения заряда хлопок будет небольшой. Но если подать колоссальное количество электронов на конденсатор, его просто разорвет, и диэлектрик вытечет.

Будьте аккуратны!

Плоским конденсатором обычно называ-ют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Про-стота конструкции такого конденсатора по-зволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.

Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электромет-ра, а вторая — к его металлическому кор-пусу (рис. 4.71). При таком соединении электрометр будет измерять разность по-тенциалов между пластинами, которые об-разуют плоский конденсатор из двух пла-стин. Проводя исследования, необходимо пом-нить, что

при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроем-кости конденсатора, и наоборот.

Сообщим пластинам разноименные заря-ды и отметим отклонение стрелки электро-метра. Приближая пластины друг к другу (уменьшая расстояние между ними), заме-тим уменьшение разности потенциалов. Та-ким образом, при уменьшении расстояния между пластинами конденсатора его элект-роемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельст-вом уменьшения электроемкости.

об-ратно пропорциональна расстоянию между его обкладками.

C ~ 1 / d ,

где d — расстояние между обкладками.

Эту зависимость можно изобразить гра-фиком обратной пропорциональной зависи-мости (рис. 4.72).

Будем смещать пластины одну относи-тельно другой в параллельных плоскостях, не изменяя расстояния между ними.

При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об умень-шении электроемкости.

Увеличение площади перекрытия пластан приведет к увеличению емкости.

Электроемкость плоского конденсатора про-порциональна площади пластин, которые пере-крываются.

C ~ S,

где S — площадь пластин.

Эту зависимость можно представить гра-фиком прямой пропорциональной зависи-мости (рис. 4.74).

Возвратив пластины в начальное поло-жение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увели-чении электроемкости конденсатора. Если между пластинами поместить другой диэлек-трик, то изменение электроемкости будет иным.

Электроемкость плоского конденсатора за-висит от диэлектрической проницаемости ди-электрика.

C ~ ε ,

где ε — диэлектрическая проницаемость ди-электрика. Материал с сайта

Такая зависимость показана на графике рис. 4.75.

Результаты опытов можно обобщить в ви-де формулы ёмкости плоского конденсатора :

C = εε 0 S / d,

где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая прони-цаемость диэлектрика; ε 0 — электрическая постоянная.

Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.

На этой странице материал по темам:

• Решение задач по теме электроемкость плоского конденсатора

• Как влияет диэлектрик на электроёмкость?

• Теория плоских конденсаторов

• График электроемкости плоского конденсатора от площади его пластин

• Заключение по электроемкости

Вопросы по этому материалу:

• Какое строение плоского конденсатора?

• По изменению какой величины в опыте можно делать заключение об изменении электроемкости?

По какой формуле найти ёмкость (объем) конденсаторов

Емкостный показатель является одной из основных характеристик не только батареек и аккумуляторных элементов, но и конденсаторных устройств. Любому человеку, работающему с электросхемами, необходимо знать, от чего зависит эта величина, может ли она уменьшиться или увеличиться под влиянием внешних факторов (как, например, период времени, зарядка элемента или частота напряжения), и как выглядит выражающая емкость конденсатора формула для разных типов элементов.

Измерение емкостных данных мультиметром

Расчёт конденсаторов

В общем случае емкостной показатель С определяется по формуле:

C=q/U,

где q – заряд конденсатора на одной из его пластин, U – значение напряжения на конденсаторе.

Из этого выражения можно вывести формулу заряда конденсатора, величину которого можно найти, измерив два других показателя с помощью мультиметра.

Часто возникает вопрос, может ли этот параметр измениться. Он является постоянной величиной, присущей данному элементу и зависящей от его габаритов и устройства. Узнать емкостное значение можно с помощью мультиметра. Пользуясь этими данными, можно рассчитать целевую индуктивность дросселя для колебательного контура или параметры резистора.

В чем измеряется емкость? За измерительную единицу принимается параметр конденсаторного устройства, который можно зарядить 1 Кл до состояния, когда разница потенциалов будет равной 1 вольту. Название этой единицы – фарад (Ф).

Важно! Если сравнить два устройства, идентичных по габаритам, но различающихся тем, что у одного в зазоре между пластинами находится диэлектрический материал, а у другого – воздушное пространство, то при помещении одинаковых зарядов потенциальная разница первой детали будет в Е раз больше. Е – это число, равное диэлектрической проницаемости материала, из которого состоит использованный слой.

Ниже приведены формулы для конденсаторных элементов разной конфигурации. Рассчитанные по ним значения соответствуют идеальным устройствам, но релевантны и для реальных в тех случаях, когда емкостными потерями можно пренебречь.

Формула электрической емкости плоского конденсатора

В основном электрополе пластин плоского конденсатора бывает однородным, за исключением боковых частей, влиянием которых обычно принято пренебрегать. Однако, если пространство между обкладками велико в сопоставлении с их габаритами, краевые искажения нужно учитывать. В общем случае, чтобы высчитать, сколько фарад составит емкость плоского конденсатора, пользуются выражением:

C=E*E0*S/d, где S – площадь меньшей обкладки, E0 – электрическая константа, d – длина пространства между пластинами.

Плоский конденсаторный элемент

Формула электрической емкости цилиндрического изделия

Такой компонент состоит из пары разных по размеру коаксиальных цилиндрических элементов проводника, в пространстве между которыми расположили диэлектрический материал. В этом случае для нахождения емкостной величины не нужно узнавать значение заряда на обкладках конденсатора. Можно воспользоваться следующей формулой емкости:

С=2 π *E*E0*l / ln(R2/R1).

Здесь R1 и R2 – радиусы, соответственно, внутреннего и наружного цилиндров, l – их высота (она одинакова, в то время как радиальные параметры отличаются).

Цилиндрическое изделие

Формула для сферического изделия

Сферическая деталь состоит из двух проводниковых сфер с диэлектрическим слоем между ними. Вот как найти емкость круглого конденсатора:

C=4 π *E*E0* R1* R2 / R2 — R1.

Буквами R обозначены, как и в предыдущем примере, радиусы компонентов.

Ёмкость одиночного проводника

Это характеристика способности твердого проводникового компонента к удержанию электрозаряда.  Она определяется особенностями средового окружения (в частности, диэлектрической проницаемостью), взаиморасположением тел, имеющих на себе заряд, размерами детали. От силы тока и величины заряда она не зависит.

Способы соединения элементов

Монтаж изделия на плату может быть вертикальным или горизонтальным. При использовании нескольких изделий они могут быть соединены между собой разными способами.

Параллельное соединение

Для его организации нужно подключить группу  деталей к электроцепи так, чтобы обкладки всех деталей были подсоединены напрямую к местам включения. Поскольку все компоненты получают заряд от одного источника тока, у них будет одинаковая разность потенциалов. Но так как заряд копится на каждом изделии отдельно, количество электричества на группе можно выразить как сумму количеств на ее деталях. Это справедливо и для емкостных данных – значение для конфигурации равно сумме значений каждой единицы. Поэтому такую группу можно считать равной одному конденсатору, емкостной параметр которого равен сумме таковых для всех частей.

Параллельное подключение

Последовательное соединение

Эта схема подразумевает соединение устройств одно за другим, когда к местам подключения к цепи подсоединены только два крайних изделия. Количество электричества для каждой детали будет одинаковым. При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.

Важно! Емкостной показатель такой системы будет еще меньше, чем у устройства, обладающего наименьшим его значением. Соотношение выглядит так: 1/С = 1/С1 + 1/С2 + 1/С3 + … Опираясь на него, можно произвести вывод непосредственно формулы С. Для двух элементов: С = С1*С2 / С1+С2.

Последовательное подключение

Смешанное соединение

Такая сложная конструкция содержит фрагменты с двумя вышеприведенными типами соединений. Чтобы подсчитать полную емкость, схему делят на простые блоки, состоящие только из деталей, соединенных каким-то одним образом. Находят эквивалентные значения для каждого блока и затем рисуют схему заново в упрощенном виде. Рассчитывают  данные для получившейся системы.

Чтобы суметь подобрать подходящий конденсаторный набор, нужно уметь узнавать емкостные данные. Важно также знать, как рассчитывается показатель для конфигурации из нескольких деталей, соединенных между собой тем или иным образом.

Видео

Конденсаторы и диэлектрики | Физика II

Цели обучения

К концу этого раздела вы сможете:

• Опишите действие конденсатора и определите емкость.
• Объясните, что такое конденсаторы с параллельными пластинами и их емкости.
• Обсудите процесс увеличения емкости диэлектрика.
• Определите емкость при заданном заряде и напряжении.

Конденсатор — это устройство, используемое для хранения электрического заряда.Конденсаторы имеют разные применения: от фильтрации статического электричества при радиоприеме до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 1. (В большинстве случаев между двумя пластинами используется изолятор для обеспечения разделения — см. Обсуждение диэлектриков ниже). Клеммы батареи подключены к первоначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, + Q и — Q , разделены на его две пластины.Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд Q .

Рис. 1. Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них разделены заряды + Q и — Q на двух половинах. (а) Конденсатор с параллельными пластинами. (b) Скрученный конденсатор с изоляционным материалом между двумя проводящими листами.

Конденсатор

Конденсатор — это устройство, используемое для хранения электрического заряда.

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Количество заряда

Q конденсатор может хранить

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Рис. 2. Линии электрического поля в этом конденсаторе с параллельными пластинами, как всегда, начинаются с положительных зарядов и заканчиваются отрицательными.Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.

Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как на рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для конденсатора с параллельными пластинами, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поля будет больше. линии, если есть больше заряда.(Рисование одной силовой линии для каждого заряда — это только удобство. Мы можем нарисовать много силовых линий для каждого заряда, но их общее количество пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна Ом. .

Поле пропорционально начислению:

E ∝ Q ,

, где символ ∝ означает «пропорционально». Из обсуждения в разделе «Электрический потенциал в однородном электрическом поле» мы знаем, что напряжение на параллельных пластинах равно

.

V = Ed .

Таким образом, V ∝ E . Отсюда следует, что V ∝ Q , и, наоборот,

Q ∝ V .

В целом это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.

Различные конденсаторы будут накапливать разное количество заряда для одного и того же приложенного напряжения, в зависимости от их физических характеристик. Мы определяем их емкость C так, чтобы заряд Q , хранящийся в конденсаторе, был пропорционален C .Заряд, накопленный в конденсаторе, равен

.

Q = CV .

Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Переставляя уравнение, мы видим, что емкость C — это количество заряда, сохраненного на вольт, или

.

[латекс] C = \ frac {Q} {V} \\ [/ latex].

Емкость

Емкость C — это количество хранимого заряда на вольт, или

[латекс] C = \ frac {Q} {V} \\ [/ latex]

Единица измерения емкости — фарад (Ф), названная в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или

.

[латекс] 1 \ text {F} = \ frac {1 \ text {C}} {1 \ text {V}} \\ [/ latex].

Конденсатор емкостью 1 фарад может хранить 1 кулон (очень большое количество заряда) при подаче всего 1 вольт. Таким образом, одна фарада — это очень большая емкость. Типичный диапазон конденсаторов составляет от долей пикофарада (1 пФ = 10 ⁻¹² Ф) до миллифарадов (1 мФ = 10 ⁻³ Ф).

На рисунке 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.

Рисунок 3. Некоторые типичные конденсаторы. Размер и значение емкости не обязательно связаны. (Источник: Windell Oskay)

Конденсатор с параллельными пластинами

Рис. 4. Конденсатор с параллельными пластинами, разделенные пластинами на расстояние d. Каждая пластина имеет площадь A.

Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности A, , разделенных расстоянием d (без материала между пластинами).Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость зависит от A и d , рассмотрев характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, в отличие от зарядов притягиваются, и сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут расходиться больше. Таким образом, C должен быть больше для большего A .Точно так же, чем ближе пластины друг к другу, тем сильнее на них притяжение противоположных зарядов. Таким образом, C должно быть больше для меньшего d .

Можно показать, что для конденсатора с параллельными пластинами есть только два фактора ( A, и d ), которые влияют на его емкость C . Емкость конденсатора с параллельными пластинами в форме уравнения равна

.

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].

Емкость параллельного пластинчатого конденсатора

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex]

A — это площадь одной пластины в квадратных метрах, а d — это расстояние между пластинами в метрах.Константа ε ₀ — диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε ₀ = 8,85 × 10 ⁻¹² Ф / м. Единицы измерения Ф / м эквивалентны C ² / Н · м ² . Небольшое числовое значение ε ₀ связано с большим размером фарада. Конденсатор с параллельными пластинами должен иметь большую площадь, чтобы его емкость приближалась к фарадам. (Обратите внимание, что приведенное выше уравнение действительно, когда параллельные пластины разделены воздухом или свободным пространством.Когда между пластинами помещается другой материал, уравнение изменяется, как обсуждается ниже.)

Пример 1. Емкость и заряд в параллельном пластинчатом конденсаторе

1. Какова емкость конденсатора с параллельными пластинами, каждая из которых имеет площадь 1,00 м ² , разделенных расстоянием 1,00 мм?
2. Какой заряд хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 10 ³ В?

Стратегия

Определение емкости C представляет собой прямое приложение уравнения [латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].{-9} \ text {F} = 8.85 \ text {nF} \ end {array} \\ [/ latex]

Обсуждение части 1

Это небольшое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонких пленок очень большой площади, расположенных близко друг к другу.

Решение для Части 2

Заряд любого конденсатора определяется уравнением Q = CV . Ввод известных значений в это уравнение дает

[латекс] \ begin {array} {lll} Q & = & CV = \ left (8.{3} \ text {V} \ right) \\\ text {} & = & 26.6 \ mu \ text {C} \ end {array} \\ [/ latex]

Обсуждение части 2

Этот заряд лишь немного больше, чем у обычного статического электричества. Поскольку воздух разрывается при примерно 3,00 × 10 ⁶ В / м, на этом конденсаторе не может быть накоплено больше заряда за счет увеличения напряжения.

Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. {6} \ text {V / m} \\ [/ latex]

Этого электрического поля достаточно, чтобы вызвать пробой в воздухе.

Диэлектрик

Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если d сделать меньше, чтобы обеспечить большую емкость, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс] E = \ frac {V} {d} \\ [/ latex]). Важным решением этой проблемы является размещение изоляционного материала, называемого диэлектриком , между пластинами конденсатора и обеспечение минимально возможного размера d .Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем сломаться.

Есть еще одно преимущество использования диэлектрика в конденсаторе. В зависимости от используемого материала емкость больше, чем заданная уравнением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], на коэффициент κ , называемый диэлектрическая проницаемость . Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex] (конденсатор с параллельными пластинами с диэлектриком).

Значения диэлектрической проницаемости κ для различных материалов приведены в таблице 1. Обратите внимание, что κ для вакуума равно 1, поэтому приведенное выше уравнение справедливо и в этом случае. Если использовать диэлектрик, например, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в κ раз, что для тефлона составляет 2,1.

Эксперимент на вынос: создание конденсатора

Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут из алюминиевой фольги, а разделитель (диэлектрик) между ними — из бумаги.

Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC
Материал	Диэлектрическая проницаемость κ	Электрическая прочность (В / м)
Вакуум	1,00000	–
Воздух	1.00059	3 × 10 6
Бакелит	4,9	24 × 10 6
Плавленый кварц	3.78	8 × 10 6
Неопреновый каучук	6,7	12 × 10 6
Нейлон	3,4	14 × 10 6
Бумага	3,7	16 × 10 6
Полистирол	2,56	24 × 10 6
Стекло Pyrex	5,6	14 × 10 6
Кремниевое масло	2.5	15 × 10 6
титанат стронция	233	8 × 10 6
Тефлон	2,1	60 × 10 6
Вода	80	–

Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится равной. слишком большой.(Напомним, что [латекс] E = \ frac {V} {d} \\ [/ latex] для конденсатора с параллельными пластинами.) В таблице 1 также показаны максимальные напряженности электрического поля в В / м, которые называются диэлектрической прочностью , для нескольких материалов. Это поля, над которыми материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного расстояния между пластинами. 6 \ text {V / m} \ right) \ left ( 1.{-3} \ text {m} \ right) \\\ text {} & = & 3000 \ text {V} \ end {array} \\ [/ latex]

Однако предел для расстояния в 1,00 мм, заполненного тефлоном, составляет 60 000 В, поскольку диэлектрическая прочность тефлона составляет 60 × 10 ⁶ В / м. Таким образом, тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для конденсатора с параллельными пластинами, заполненного воздухом, мы обнаружили, что конденсатор с тефлоновым заполнением может хранить максимальный заряд

[латекс] \ begin {array} {lll} Q & = & CV \\\ text {} & = & \ kappa {C} _ {\ text {air}} V \\\ text {} & = & (2.4 \ text {V}) \\\ text {} & = & 1.1 \ text {mC} \ end {array} \\ [/ latex]

Это в 42 раза больше заряда того же конденсатора, заполненного воздухом.

Диэлектрическая прочность

Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется его диэлектрической прочностью.

Микроскопически, как диэлектрик увеличивает емкость? За это отвечает поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость κ .Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды обуславливает ее относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации лучше всего объясняется характеристиками кулоновской силы. На рис. 5 схематично показано разделение зарядов в молекулах диэлектрического материала, помещенных между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень сильна, поскольку они расположены очень близко друг к другу.Это притягивает больше заряда к пластинам, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии d друг от друга.

Рис. 5. (a) Молекулы изоляционного материала между пластинами конденсатора поляризованы заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (б) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к уменьшению напряжения между пластинами при одинаковом заряде.Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.

Другой способ понять, как диэлектрик увеличивает емкость, — это рассмотреть его влияние на электрическое поле внутри конденсатора. На рисунке 5 (b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются зарядами в диэлектрике, их меньше, идущих от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, даже если бы на пластинах был одинаковый заряд.Напряжение между пластинами составляет В, = Ед, , поэтому оно тоже снижается за счет диэлектрика. Таким образом есть меньшее напряжение В, для того же заряда Q ; поскольку [латекс] C = \ frac {Q} {V} \\ [/ latex], емкость C больше.

Диэлектрическая проницаемость обычно определяется как [латекс] \ kappa = \ frac {E_0} {E} \\ [/ latex], или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и в конечном итоге связанные с поляризуемостью материала.

Великие и малые вещи: субмикроскопическое происхождение поляризации

Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома описывает его как имеющее положительное ядро, вращающееся вокруг отрицательных электронов, аналогично планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в других местах, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.

Рис. 6. Художественное представление о поляризованном атоме. Орбиты электронов вокруг ядра слегка смещены внешними зарядами (показаны в преувеличении). Получающееся разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что непохожий заряд теперь ближе к внешним зарядам, вызывая поляризацию.

В атомной физике мы обнаружим, что орбиты электронов более правильно рассматривать как электронные облака с плотностью облака, связанной с вероятностью обнаружения электрона в этом месте (в отличие от определенных положений и путей движения планет на их орбитах). вокруг Солнца).Это облако сдвигается кулоновской силой, так что в среднем атом имеет разделенный заряд. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.

Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому они называются полярными молекулами. На рисунке 7 показано разделение зарядов в молекуле воды, которая имеет два атома водорода и один атом кислорода (H ₂ O).Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец слегка положительным. Внутреннее разделение зарядов в полярных молекулах облегчает их выравнивание с внешними полями и зарядами. Следовательно, полярные молекулы проявляют более сильные поляризационные эффекты и имеют более высокие диэлектрические проницаемости.Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды собирают ионы гораздо эффективнее, потому что у них есть электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как было показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

Рис. 7. Художественная концепция молекулы воды. Существует внутреннее разделение зарядов, поэтому вода — полярная молекула.Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда около двух ядер водорода. (Обратите внимание, что схема справа является приблизительной иллюстрацией распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)

Исследования PhET: лаборатория конденсаторов

Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.Измените напряжение и посмотрите, как на пластинах накапливаются заряды. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

• Конденсатор — это устройство для накопления заряда.
• Количество заряда Q , которое может хранить конденсатор, зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
• Емкость C, — это количество заряда, накопленного на вольт, или [латекс] C = \ frac {Q} {V} \\ [/ latex].
• Емкость конденсатора с параллельными пластинами составляет [латекс] C = {\ epsilon} _ {0} \ frac {A} {d} \\ [/ latex], когда пластины разделены воздухом или свободным пространством. [latex] {\ epsilon} _ {\ text {0}} [/ latex] называется диэлектрической проницаемостью свободного пространства.
• Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], где κ — диэлектрик. константа материала.
• Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется электрической прочностью.

Концептуальные вопросы

1. Зависит ли емкость устройства от приложенного напряжения? А как насчет хранящегося в нем заряда?
2. Используйте характеристики кулоновской силы, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора. Аналогичным образом объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
3. Объясните причину, по которой диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора.Какова независимая причина того, что диэлектрический материал также позволяет приложить большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C и допускает более V .)
4. Как полярный характер молекул воды помогает объяснить относительно высокую диэлектрическую проницаемость воды? (См. Рисунок 7.)
5. Искры возникают между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем когда сухой. Объясните почему, учитывая полярный характер молекул воды.
6. Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
7. Мембраны в живых клетках, в том числе в человеческих, характеризуются разделением заряда через мембрану. Таким образом, мембраны представляют собой заряженные конденсаторы, важные функции которых связаны с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизм пищевой энергии или каким-либо другим источником?

Рисунок 8.Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K ⁺ (калий) и Cl ^— (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Это приводит к слою положительного заряда снаружи, слою отрицательного заряда внутри и, следовательно, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na ⁺ (ионы натрия).

Задачи и упражнения

1. Какой заряд сохраняется в конденсаторе 180 мкФ, когда к нему приложено 120 В?
2. Найдите накопленный заряд, когда 5.50 В подается на конденсатор емкостью 8,00 пФ.
3. Какой заряд хранится в конденсаторе в Примере 1?
4. Рассчитайте напряжение, приложенное к конденсатору 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
5. Какое напряжение необходимо подать на конденсатор емкостью 8,00 нФ для накопления заряда 0,160 мкКл?
6. Какая емкость необходима для хранения заряда 3,00 мкКл при напряжении 120 В?
7. Какая емкость терминала большого генератора Ван-де-Граафа, учитывая, что он хранит 8?00 мкКл заряда при напряжении 12,0 МВ?
8. Найдите емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 5,00 м ² , разделенных слоем тефлона 0,100 мм.
9. (a) Какова емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 1,50 м ² , разделенных 0,0200 мм неопреновой резины? (b) Какой заряд он держит, когда к нему приложено 9,00 В?
10. Интегрированные концепции. Шутник подает 450 В на 80.Конденсатор 0 мкФ, а затем бросает его ничего не подозревающей жертве. Палец пострадавшего обгорел от разряда конденсатора через 0,200 г мяса. Какое повышение температуры мяса? Разумно ли предполагать отсутствие изменения фазы?
11. Необоснованные результаты. (a) Конденсатор с параллельными пластинами имеет площадь пластин 4,00 м ² , разделенных нейлоном толщиной 0,0100 мм, и накапливает 0,170 Кл заряда. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие допущения являются ответственными или противоречивыми?

Глоссарий

конденсатор: устройство, накапливающее электрический заряд

емкость: количество заряда на единицу вольт

диэлектрик: изоляционный материал

диэлектрическая прочность: максимальное электрическое поле, выше которого изоляционный материал начинает разрушаться и проводить

Конденсатор с параллельными пластинами: две идентичные проводящие пластины, разделенные расстоянием

полярная молекула: молекула с внутренним разделением заряда

Избранные решения проблем и упражнения

1.21,6 мК

3. 80.0 мС

5. 20,0 кВ

7. 667 пФ

9. (а) 4,4 мкФ; (б) 4.0 × 10 ⁻⁵ C

11. (а) 14,2 кВ; (b) Напряжение неоправданно велико, более чем в 100 раз больше напряжения пробоя нейлона; (c) Предполагаемый заряд неоправданно велик и не может храниться в конденсаторе таких размеров.

Формулы и калькуляторы емкости

На этой странице представлены формулы и калькуляторы емкостей различные формы или типы конденсаторов.Это также полезно, если вы собираетесь использовать свой конденсатор в Танк LC резонансный схема.

Емкость конденсаторов с параллельными пластинами

Конденсатор с параллельными пластинами состоит из двух плоских параллельных пластин, которые электроды, разделенные диэлектрик или изолятор. Для формулы и калькулятора здесь пластины могут быть любой формы, если они плоские, параллельные и вы знаете площадь тарелки или что-то еще, что нужно, чтобы найти этот район.

Конденсатор с параллельными пластинами — пластины прямоугольной формы.

Конденсатор с параллельными пластинами — круглые пластины.

Формула емкости конденсатора с параллельными пластинами:

Где:

• ε _r = относительная диэлектрическая проницаемость диэлектрика (реже К, диэлектрическая проницаемость)
• ε ₀ = 8.854×10 ^-12 Ф / м (фарад / метр) = диэлектрическая проницаемость вакуума или диэлектрическая проницаемость свободного пространства

На схемах показаны конденсаторы с параллельными пластинами разной формы. пластины, одна прямоугольная и одна круглая. Формула для расчета площадь прямоугольника:

а формула для вычисления площади круга:

Где π — это число пи, равное 3,14159.

Емкость цилиндрических конденсаторов

Цилиндрический конденсатор состоит из двух цилиндров, также называемых пластины, которые являются электродами, разделены диэлектрик или изолятор.

Цилиндрический конденсатор.

Формула емкости цилиндрического конденсатора:

Где:

• ε _r = относительная диэлектрическая проницаемость диэлектрика (реже К, диэлектрическая проницаемость)
• ε ₀ = 8,854×10 ^-12 Ф / м (фарад / метр) = диэлектрическая проницаемость вакуума или диэлектрическая проницаемость свободного пространства

Видео — Как сделать конденсаторы — Низкое напряжение

В этом видео не только показано, как делать конденсаторы, но и формула емкости в более динамичном формате, чем указано выше.После всего, если вы делаете конденсатор, вам сначала нужно знать, как спроектировать конденсатор.

Видео — Как сделать конденсаторы — Высокое напряжение

В этом видео показано, как разработать конденсаторы для высокого напряжения, объясняя, измерение и построение для напряжения пробоя / диэлектрической прочности, чтобы что конденсатор может выдерживать желаемое высокое напряжение.

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследовательская работа
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О Массачусетском технологическом институте
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О Массачусетском технологическом институте

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

Емкость двух параллельных пластин

Емкость двух параллельных пластин

Емкость из двух параллельных пластин

Самый распространенный Конденсатор состоит из двух параллельных пластин.Емкость конденсатор с параллельными пластинами зависит от площади пластин А и их разделение d . По мнению Гаусса закон, электрическое поле между двумя пластинами:

Поскольку емкость определяется тем, что емкость:

Таким образом, вы получите максимум емкость, когда пластины большие и расположены близко друг к другу. Большой емкость означает, что конденсатор хранит большое количество заряжать.

Если диэлектрик материал вставлен между пластинами, микроскопический диполь моменты материала будут экранировать заряды на пластинах и изменить отношение. Материалы имеют проницаемость e, который задается относительной величиной проницаемость k, e = ke ₀ . Таким образом, емкость дается по:

Все материалы имеют относительную проницаемость k больше единицы, поэтому емкость можно увеличить, вставив диэлектрик.Иногда k равно называется диэлектрической проницаемостью материала. В электрическое поле вызывает некоторую часть диполей в материала, чтобы ориентироваться вдоль E-поля, в отличие от обычная случайная ориентация. Фактически это выглядит так, как если бы отрицательный заряд выстраивается напротив положительной пластины, и положительный заряд против отрицательной пластины. На рисунке к справа синий материал — это диэлектрик.

---

Примеры Конденсаторы главная Список лекций

Конденсатор

Конденсатор — это устройство, используемое для хранения электрической энергии.

Пластины конденсатора заряжены, и между ними существует электрическое поле. Конденсатор разрядится, если пластины соединить вместе через резистор.

Заряд конденсатора

Заряд конденсатора можно выразить как

Q = I t (1)

где

Q = заряд конденсатора (кулон, Кл, мкКл)

I = ток (А)

t = время (с)

Количество заряда (количество электронов) измеряется в кулонах — C — , где

1 кулон = 6.24 10 ¹⁸ электронов

Наименьший существующий заряд — это заряд, переносимый электроном, равный -1,602 10 ^-19 кулонов .

Пример — количество переданной электроэнергии

Если ток 5 А протекает в течение 2 минут, количество электроэнергии — кулонов — можно рассчитать как

Q = (5 А) (2 мин. ) (60 с / мин)

= 600 C

или, в электронах:

(600 C) ( 6.24 10 ¹⁸ электронов / C)

= 3,744 10 ²¹ электронов

Напряженность электрического поля (диэлектрическая прочность)

Если две заряженные пластины разделены изолирующей средой — диэлектрик — напряженность электрического поля (градиент потенциала) между двумя пластинами может быть выражена как

E = U / d (2)

, где

E = напряженность электрического поля (вольт / м)

U = электрический потенциал (вольт)

d = толщина диэлектрика, расстояние между пластинами (м)

Пример — напряженность электрического поля

Напряжение между двумя пластинами составляет 230 В, и расстояние между ними. их 5 мм .Напряженность электрического поля может быть рассчитана как

E = (230 В) / ((5 мм) (10 ^-3 м / мм))

= 46000 вольт / м

= 46 кВ / м

Плотность электрического потока

Плотность электрического потока — это соотношение между зарядом конденсатора и площадью поверхности пластин конденсатора:

D = Q / A (3)

, где

D = плотность электрического потока (кулон / м ² )

A = площадь поверхности конденсатора (м ² )

Заряд и приложенное напряжение

Заряд в конденсаторе пропорционален приложенное напряжение и может быть выражено как

Q = CU (4)

, где

C = константа пропорциональности или емкость (фарад, Ф, 90 027 мкФ )

Емкость

Из (4) емкость можно выразить как

C = Q / U (5)

Один фарад определяется как емкость конденсатора, когда существует разность потенциалов на пластинах в один вольт при удерживании заряда в один кулон.

Обычно используется мкФ (10 ^-6 F) .

Пример — Напряжение на конденсаторе

Конденсатор 5 мкФ заряжен конденсатором 10 мКл . Напряжение на конденсаторе можно рассчитать, изменив (4) на

U = Q / C

= (10 мКл) (10 ^-3 Кл / мКл) / ((5 мкФ) ( 10 ^-6 Ф / мкФ)

= 2000 В

= 2 кВ

Абсолютная диэлектрическая проницаемость

Отношение плотности электрического потока к электрическому полю называется абсолютной диэлектрической проницаемостью — ε — диэлектрическая проницаемость и может быть выражена как

ε = D / E (6)

где

ε = абсолютная диэлектрическая проницаемость (Ф / м)

Абсолютная диэлектрическая проницаемость свободного пространства или вакуума — также называемая электрической постоянной — ε ₀ — это 8.85 10 ^-12 Ф / м .

Относительная диэлектрическая проницаемость

Относительная диэлектрическая проницаемость, также называемая диэлектрической проницаемостью ε _r , представляет собой отношение между плотностью потока поля в реальном диэлектрике — ε — и плотностью потока поля в абсолютном выражении. вакуум — ε ₀ .

ε _r = ε / ε ₀ (7a)

Фактическая диэлектрическая проницаемость может быть рассчитана путем преобразования (7a) в

ε = ε _r ε ₀ ( 7b)

Параллельный пластинчатый конденсатор

Емкость пластинчатого конденсатора — как показано на рисунке выше — пропорциональна площади А пластины.Емкость может быть выражена как

C = ε _r ε ₀ A / d (8)

, где

A = площадь пластины (м ² )

d = толщина диэлектрика, расстояние между пластинами (м)

Для пластинчатого конденсатора с несколькими пластинами емкость можно выразить как

C = ε _r ε ₀ A (n — 1) / d (8b)

, где

n = количество пластин

Пример — емкость пластинчатого конденсатора

Емкость пластинчатого конденсатора площадью 5 см ² , 10 пластин и расстояние 0.1 мм между пластинами — с керамическим диэлектриком с относительной диэлектрической проницаемостью 30 между пластинами — можно рассчитать как

C = ( 8,85 10 ^-12 Ф / м ) _{(30) (5 см ² ) (10 ^-4 м ² / см ² ) (10-1) / ((0,1 мм) (10 ^-3 м / мм))}

= 11 10 ^{— 9} F

= 11 пФ

Типичные обычно используемые конденсаторы

Типичные конденсаторы —

• конденсаторы переменного воздуха
• конденсаторы слюдяные
• бумажные конденсаторы
• керамические конденсаторы
9000 пластмассовые конденсаторы пластиковые 9000 конденсаторы
• электролитические конденсаторы

Конденсаторы: все, что вам нужно знать | ОРЕЛ

Нет, мы здесь не говорим о Grand Theft Auto! Закрывание крышки в мире электроники нехорошо, если вам не нравится видеть, как ваш электролитический конденсатор горит в огне.Конденсаторы играют важную роль в семействе пассивных электронных компонентов, и их можно использовать повсюду.

Помните вспышку в вашей цифровой камере? Конденсаторы делают это возможным. Или возможность переключать канал на телевизоре? Опять конденсаторы. Эти ребята — маленькие батарейки, которые «могут», и вам нужно знать все, что о них известно, прежде чем вы начнете работать над своим первым проектом в области электроники.

Это как бутерброд с мороженым

Для простоты — конденсатор накапливает электрический заряд , как и батарея.Также называемые caps , вы найдете этих парней в приложениях, требующих накопления энергии, подавления напряжения и даже фильтрации сигналов. А как они выглядят? Ну бутерброд с мороженым!

Что бы вы сделали с баром «Клондайк»? Сравните это, конечно, с конденсатором! (Источник изображения)

Подумайте о том восхитительном бутерброде с мороженым, который вам понравился в тот знойный летний день. У вас есть восхитительная корочка с двух сторон и кремовый кусок ванильного мороженого посередине.Эта композиция из двух внешних слоев и одного внутреннего слоя — это то, как выглядит конденсатор. Вот из чего они сделаны:

• Запуск снаружи. Сверху и снизу конденсатора вы найдете набор металлических пластин, также называемых проводниками. Электрический заряд находит эти металлические пластины очень привлекательными.
• Сидит посередине. Среди этих двух металлических пластин вы найдете изолятор или материал, к которому не притягивается электричество.Этот изолятор обычно называют диэлектриком и может быть изготовлен из бумаги, стекла, резины, пластика и т. Д.
• Соединяем вместе. Две металлические пластины сверху и снизу крышки соединены двумя электрическими клеммами, которые соединяют ее с остальной частью цепи. Один конец конденсатора подключается к источнику питания, а другой течет к земле.

Внутренняя структура конденсатора, у нас есть две металлические пластины, внутренний диэлектрик и соединительные клеммы.

Конденсаторы всех форм и размеров

Конденсаторы

бывают разных форм и размеров, каждый из которых определяет, насколько хорошо они могут удерживать заряд. Три наиболее распространенных типа конденсаторов, с которыми вы столкнетесь, включают керамический конденсатор, электролитический конденсатор и суперконденсатор:

Конденсаторы керамические

Это конденсаторы, с которыми вы, вероятно, будете работать в своем первом электронном проекте с использованием макета. В отличие от своих электролитических аналогов, керамические конденсаторы удерживают меньший заряд, но и меньше пропускают ток.Они также оказываются самыми дешевыми конденсаторами из всей группы, так что запасайтесь! Вы можете быстро определить керамический конденсатор со сквозным отверстием, посмотрев на маленькие желтые или красные лампочки с двумя торчащими из них выводами.

Три типа керамических конденсаторов, вы будете использовать их на макетных платах. (Источник изображения)

Конденсаторы электролитические

Эти парни выглядят как маленькие консервные банки, которые вы найдете на печатной плате, и в их крошечном следе могут удерживаться огромные электрические заряды.Это также единственный тип конденсатора, который поляризован, а это означает, что они будут работать только при подключении с определенной ориентацией. На этих электролитических конденсаторах есть положительный вывод, называемый анодом, и отрицательный вывод, называемый катодом. Анод всегда нужно подключать к более высокому напряжению. Если вы подключите его наоборот, когда на катоде будет более высокое напряжение, приготовьтесь к взрыву крышки!

Электролитический конденсатор, обратите внимание на положительный вывод и более длинный (анод) и более короткий отрицательный вывод (катод).(Источник изображения)

Несмотря на то, что электролитические колпачки способны удерживать большое количество электрического заряда, они также хорошо известны тем, что пропускают ток быстрее, чем керамические колпачки. Из-за этого они не лучший выбор, когда вам нужно хранить энергию.

Суперконденсаторы

Supercaps — супергерои семейства конденсаторных, они могут хранить большое количество энергии! К сожалению, суперкапс не очень хорошо справляется с повышенным напряжением, и вы окажетесь без колпачка, если превысите максимальное напряжение, указанное в таблице данных.ПОП!

В отличие от электролитических конденсаторов, вы обнаружите, что суперконденсаторы используются для хранения и разряда энергии, как и батареи. Но в отличие от батареи, суперкапсы высвобождают свой заряд сразу, и вы никогда не получите такой же срок службы, как обычный аккумулятор.

Посмотрите на этот мощный supercap ! Он имеет огромную емкость 3000F. (Источник изображения)

Обозначения конденсаторов

Идентифицировать конденсатор на вашей первой схеме очень просто, так как они бывают только двух типов: стандартные и поляризованные.Обратите внимание на символ стандартного конденсатора ниже. Вы заметите, что это всего лишь две простые линии с пробелом между ними. Это две металлические пластины, которые вы найдете сверху и снизу физического конденсатора.

Поляризованный конденсатор выглядит немного иначе и имеет дугообразную линию в нижней части, а также положительный вывод наверху. Этот положительный вывод очень важен и указывает, как этот поляризованный конденсатор должен быть подключен. Положительная сторона всегда подключается к источнику питания, а сторона дуги подключается к земле.

Два наиболее распространенных типа конденсаторов, которые вы увидите на схеме для США, стандартные и поляризованные.

Кто это изобрел?

Хотя многие считают английского химика Майкла Фарадея пионером современного конденсатора, он не был первым, кто его изобрел. То, что сделал Фарадей, было важно — он продемонстрировал первые практические примеры конденсатора и то, как использовать его для хранения электрического заряда в своих экспериментах. И благодаря Фарадею у нас также есть способ измерить заряд, который может удерживать конденсатор, известный как емкость, который измеряется в Фарадах!

Гениальный английский химик Майкл Фарадей, пионер конденсаторов, которые мы используем сегодня.(Источник изображения)

До Майкла Фарадея некоторые записи указывают на то, что покойный немецкий ученый Эвальд Георг фон Клейст изобрел первый конденсатор в 1745 году. Несколько месяцев спустя голландский профессор по имени Питер ван Мушенбрук придумал похожий дизайн, теперь известный как Лейденская банка. Странное время, правда? Однако все это было просто совпадением, и оба ученых в равной степени получили признание за свои первоначальные изобретения конденсатора.

Самый ранний образец конденсатора, лейденская банка.(Источник изображения)

Знаменитый Benjamin Franklin позже усовершенствовал дизайн Лейденской банки, созданный Musschenbroek. Франклин также смог обнаружить, что использование плоского куска стекла было отличной альтернативой целой банке. Так родился первый плоский конденсатор, получивший название площади Франклина.

Колпачки в действии — как они работают

Давайте подробно рассмотрим, как работают эти мощные конденсаторы, на практическом примере. Вы ведь раньше пользовались цифровым фотоаппаратом? Тогда вы знаете, что есть несколько коротких моментов между нажатием кнопки, чтобы сделать снимок, и моментом срабатывания вспышки.

Что здесь происходит? К вспышке прикреплен конденсатор, который заряжается после того, как вы нажмете кнопку, чтобы сделать снимок. Как только этот конденсатор полностью заряжается аккумулятором камеры, вся эта энергия взрывается наружу в ослепляющей вспышке света!

Обратите внимание, конденсатор, который делает возможной вспышку в этой камере. (Источник изображения)

Так как же все это произошло? Заглянем изнутри в загадочный мир конденсатора:

1. Начинается с зарядки. Электрический ток от источника питания сначала течет в конденсатор и застревает на первой пластине. Почему застревает? Потому что есть изолятор, который не пропускает отрицательно заряженную электронику.
2. Накопление сборов. По мере того, как все больше и больше электронов прилипает к этой первой пластине, она становится отрицательно заряженной и в конечном итоге отталкивает все лишние электроны, с которыми не может справиться, к другой пластине. Затем эта вторая пластина становится положительно заряженной.
3. Заряд сохраняется. По мере того, как две пластины конденсатора продолжают заряжаться, отрицательные и положительные электроны отчаянно пытаются соединиться, но этот надоедливый изолятор посередине не позволяет им, создавая электрическое поле. Вот почему колпачок продолжает удерживать и накапливать заряд, потому что существует бесконечный источник напряжения между отрицательной и положительной сторонами двух пластин, которые не разрешены.
4. Заряд высвобождается. Рано или поздно две пластины в нашем конденсаторе не смогут удерживать заряд, так как они на пределе емкости.Но что происходит сейчас? Если в вашей цепи есть путь, по которому электрический заряд может течь в другом месте, то все электроны в вашей крышке разрядятся, и , наконец, прекратят свое напряжение, когда они будут искать другой путь друг к другу.

Измерение заряда

Как можно измерить, сколько заряда хранится в конденсаторе? Каждый колпачок рассчитан на определенную емкость. Он измеряется в фарадах по имени английского химика Майкла Фарадея. Поскольку в одном фараде содержится тонна электрического заряда, вы обычно видите конденсаторы, измеряемые в пикофарадах или микрофарадах.Вот полезная диаграмма, которая показывает, как разбиваются эти измерения:

Имя	Сокращение	Фарады
Пикофарад	пФ	0,000000000001 Факс
нанофарад	нФ	0,000000001 Факс
Микрофарад	мкФ	0,000001 Факс
Милифарад	мФ	0.001 F
Килофарад	кФ	1000 Факс

Теперь, чтобы выяснить, сколько заряда в настоящее время хранит конденсатор, вам понадобится это уравнение:

В этом уравнении общий заряд представлен как (Q) , и соотношение этого заряда можно найти, умножив емкость конденсатора ( C ) на приложенное к нему напряжение ( В ). Следует отметить, что емкость конденсатора напрямую зависит от его напряжения.Таким образом, чем больше вы увеличиваете или уменьшаете источник напряжения в цепи, тем больший или меньший заряд будет у вашего конденсатора.

Емкость в параллельных и последовательных цепях

Когда вы размещаете конденсаторы в цепи параллельно, вы можете определить общую емкость, сложив все отдельные емкости вместе.

Получить общую емкость в параллельной цепи так же просто, как 1 + 1, просто сложите их все вместе! (Источник изображения)

При последовательном размещении конденсаторов общая емкость вашей цепи является обратной величиной всех ваших суммированных емкостей.Вот краткий пример. Если у вас есть два конденсатора по 10 Ф, соединенные последовательно, то общая емкость будет равна 5 Ф.

Получить общую емкость в последовательной цепи немного сложнее. Емкость уменьшается вдвое. (Источник изображения)

Начало работы

Теперь, когда у нас есть четкое представление о том, что такое конденсаторы, как они работают и как измеряются, давайте рассмотрим три распространенных применения конденсаторов. Сюда входят такие приложения, как развязывающие конденсаторы, накопители энергии и емкостные сенсорные датчики.

Конденсатор развязки

В наши дни вам будет сложно найти схему, в которой нет интегральной схемы или ИС. В этих типах схем конденсаторы должны выполнять критически важную работу, удаляя весь высокочастотный шум, обнаруживаемый в сигналах источника питания, которые питают ИС.

Почему это необходимая работа для нашего конденсатора? Любые колебания напряжения могут быть фатальными для ИС и даже могут привести к неожиданному отключению питания микросхемы. Помещая конденсаторы между ИС и источником питания, они успокаивают колебания напряжения, а также действуют как второй источник питания, если первичная мощность падает до уровня, достаточного для выключения ИС.

Разделительный конденсатор для контроля колебаний напряжения.

Накопитель энергии

Конденсаторы

имеют много общих характеристик с батареями, включая их способность накапливать энергию. Однако, в отличие от батареи, конденсаторы не выдерживают такой большой мощности. Но хотя они не могут угнаться за количеством, они компенсируют свое стремление разрядиться как можно быстрее! Конденсаторы могут поставлять энергию намного быстрее, чем аккумулятор, что делает их идеальными для питания вспышки в камере, настройки радиостанции или переключения каналов на телевизоре.

Емкостные сенсорные датчики

Одно из последних достижений в области применения конденсаторов связано с бурным ростом технологий сенсорных экранов. Стеклянные экраны, из которых состоят эти сенсорные датчики, имеют очень тонкое прозрачное металлическое покрытие. Когда ваш палец касается экрана, это вызывает падение напряжения, определяющее точное местоположение вашего пальца!

Емкостные сенсорные датчики в действии с защитной накладкой и печатной платой. (Источник изображения)

Практика — выбор конденсатора

Давайте перейдем к сфере практичности и поговорим о том, на что обращать внимание при выборе следующего конденсатора.Необходимо учитывать пять переменных, в том числе:

• Размер — сюда входит как физический размер вашего конденсатора, так и его общая емкость. Не удивляйтесь, если выбранный вами конденсатор будет самой большой частью вашей печатной платы, так как чем больше вам потребуется емкости, тем больше они станут.
• Допуск — Конденсаторы, как и их аналоги с резисторами, имеют переменный допуск. Вы найдете допуск для конденсаторов от ± 1% до ± 20% от заявленного значения.
• Максимальное напряжение — Каждый конденсатор имеет максимальное допустимое напряжение. В противном случае он взорвется! Вы найдете максимальное напряжение от 1,5 до 100 В.
• Эквивалентное последовательное сопротивление (ESR) — Как и любой другой физический материал, выводы конденсатора имеют очень маленькое сопротивление. Это может стать проблемой, если вам нужно помнить о потерях тепла и энергии.
• Leakage Current — В отличие от наших батарей, в конденсаторах происходит утечка накопленного заряда.И пока он истощается медленно, вам стоит обратить внимание на то, насколько сильно протекает ваш конденсатор, если его основная функция — накопление энергии.

Все заряжено

Вот и все, что вам нужно знать о конденсаторах, чтобы полностью зарядиться для вашего следующего электронного проекта! Конденсаторы — это очаровательная небольшая группа, способная накапливать электрический заряд для множества применений, и они даже могут выступать в качестве вторичного источника питания для этих чувствительных интегральных схем.При работе с конденсаторами внимательно следите за максимально возможным напряжением. В противном случае вы получите несколько взрывающихся крышек, как вы увидите на видео:

Знаете ли вы, что Autodesk EAGLE бесплатно включает тонну библиотек конденсаторов? Начните со своего следующего проекта в области электроники и забудьте о создании собственных деталей! Попробуйте Autodesk EAGLE бесплатно сегодня.

Изменится ли емкость при подаче постоянного напряжения на керамические конденсаторы? Есть ли какие-то моменты, которые следует учитывать при изменении емкости?

Фарад (Ф) — это единица измерения емкости керамических конденсаторов.
Он показывает, сколько заряда хранится в конденсаторе. Емкость часто описывается в описании продукта как «номинальное значение».

Обратите внимание, что емкость керамических конденсаторов, особенно конденсаторов с высокой диэлектрической проницаемостью (характеристика B / X5R, R / X7R), может отличаться от номинального значения при подаче напряжения постоянного тока.

Например, как показано на диаграмме, чем больше напряжение постоянного тока, приложенное к конденсаторам с высокой диэлектрической проницаемостью, тем более эффективная емкость уменьшается.

На следующей диаграмме горизонтальная ось показывает напряжение постоянного тока, приложенное к конденсатору (В), а вертикальная ось показывает отношение изменения емкости к начальному значению. *

Таким образом, характеристика изменения емкости в зависимости от приложенного напряжения называется «характеристикой смещения постоянного тока».

Исходя из вышеизложенного, при использовании конденсаторов с высокой диэлектрической проницаемостью следует тщательно учитывать характеристики. Кроме того, следует подтверждать целесообразность использования на основании фактических условий, а также фактического оборудования.

К вашему сведению, не только наши продукты имеют смещение постоянного тока; это явление обычно наблюдается в конденсаторах с высокой диэлектрической проницаемостью.

Характеристики смещения, температурные характеристики, частотные характеристики и т. Д. Могут быть подтверждены с помощью этого программного обеспечения. (SimSurfing)
SimSurfing
Как использовать

Механизм характеристики смещения постоянного тока

В керамических конденсаторах с высокой диэлектрической проницаемостью в настоящее время в основном используется BaTiO3 (титанат бария) в качестве основного компонента высокого диэлектрика.
Как показано ниже, BaTiO3 имеет кристаллическую структуру в форме перовскита, а выше температуры Кюри он приобретает кубическую форму с ионами Ba2 + в вершинах, ионами O2- в направлении к центру и ионами Ti4 + в центрированном положении.

Кристаллическая структура керамики BaTiO3

При температуре Кюри (около 125 ° C) или выше он имеет кубическую кристаллическую структуру, а ниже температуры Кюри и в диапазоне температур окружающей среды одна ось (ось C) растягивается, а другие оси сжимаются и превращаются в тетрагональный кристалл. структура.

В этом случае поляризация возникает в результате сдвига единицы вытянутого в осевом направлении кристалла иона Ti4 +. Эта поляризация возникает без приложения внешнего электрического поля или давления и известна как «спонтанная поляризация». Как объяснялось выше, характеристика, которая имеет спонтанную поляризацию и свойство изменять ориентацию спонтанной поляризации внешним электрическим полем на обратную, называется «сегнетоэлектричеством».