Плоский конденсатор, теория и примеры задач
Большое число конденсаторов, которые применяют в технике, приближены по типу к плоскому конденсатору. Это конденсатор, который представляет собой две параллельные проводящие плоскости (обкладки), которые разделяет небольшой промежуток, заполненный диэлектриком. На обкладках сосредоточены равные по модулю и противоположные по знаку заряды.
Электрическая емкость плоского конденсатора
Электрическая емкость плоского конденсатора очень просто выражается через параметры его частей. Изменяя площадь пластин конденсатора и расстояние между ними легко убедиться, что электрическая емкость плоского конденсатора прямо пропорциональна площади его пластин (S) и обратно пропорциональна расстоянию между ними (d):
Формулу для расчета емкости плоского конденсатора просто получить при помощи теоретических расчетов.
Положим, что расстояние между пластинами конденсатора много меньше, чем их линейные размеры. Тогда краевыми эффектами можно пренебречь, и электрическое поле между обкладками считать однородным. Поле (E), которое создают две бесконечные плоскости, несущие одинаковый по модулю и противоположный по знаку заряд, разделенные диэлектриком с диэлектрической проницаемостью , можно определить при помощи формулы:
где — плотность распределения заряда по поверхности пластины. Разность потенциалов между рассматриваемыми обкладками конденсатора, находящимися на расстоянии d будет равна:
Подставим правую часть выражения (3) вместо разности потенциалов в (1) учитывая, что , имеем:
Энергия поля плоского конденсатора и сила взаимодействия его пластин
Формула энергии поля плоского конденсатора записывается как:
где – объем конденсатора; E – напряженность поля конденсатора. Формула (5) связывает энергию конденсатора с зарядом на его обкладках и напряженностью поля.
Механическую (пондемоторную) силу, с которой пластины плоского конденсатора взаимодействуют между собой можно найти, если использовать формулу:
В выражении (6) минус показывает, что пластины конденсатора притягиваются друг к другу.
Примеры решения задач
2.4.2. Емкость цилиндрического конденсатора
Ц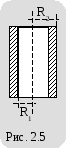 илиндрический
конденсатор представляет собой
устройство из двух цилиндрических
обкладок, имеющих общую ось (коаксиальных
цилиндров), разделенных слоем диэлектрика
цилиндрической формы (рис. 2.5).
илиндрический
конденсатор представляет собой
устройство из двух цилиндрических
обкладок, имеющих общую ось (коаксиальных
цилиндров), разделенных слоем диэлектрика
цилиндрической формы (рис. 2.5).
Электрическое поле такого конденсатора представляет собой суперпозицию двух полей цилиндрических поверхностей, имеющих равные по величине, но противоположные по знаку заряды.
Напряженность такого электрического поля
 .
(2.18)
.
(2.18)
Разность потенциалов между обкладками
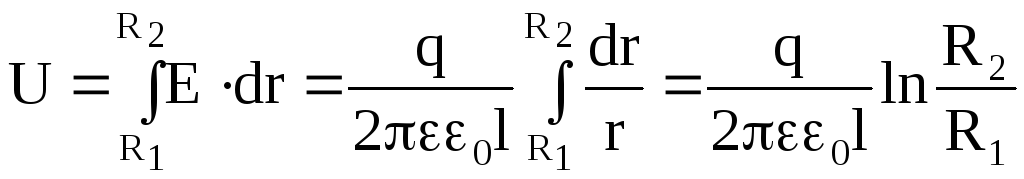 ,
(2.19)
,
(2.19)
где R1 и R2 – соответственно радиусы внутренней и внешней обкладок.
Таким образом,
. (2.20)
При d = R2 — R1 << R1
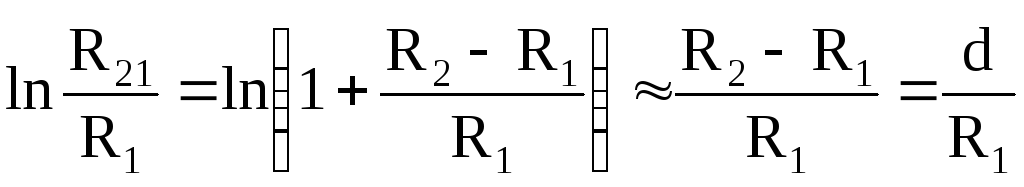 ,
,
где d = R2 — R1 – расстояние между обкладками.
Тогда
 .
(2.21)
.
(2.21)
Следовательно, при указанных условиях емкость цилиндрического конденсатора можно рассчитывать по формуле емкости плоского конденсатора.
2.4.3. Емкость сферического конденсатора
С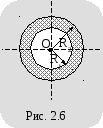 ферический
конденсатор представляет собой
устройство, состоящее из двух сферических
поверхностей, которые имеют общий центр
различных радиусов, разделенных
сферическим слоем диэлектрика (рис.
2.6).
ферический
конденсатор представляет собой
устройство, состоящее из двух сферических
поверхностей, которые имеют общий центр
различных радиусов, разделенных
сферическим слоем диэлектрика (рис.
2.6).
Напряженность электрического поля между обкладками такого конденсатора
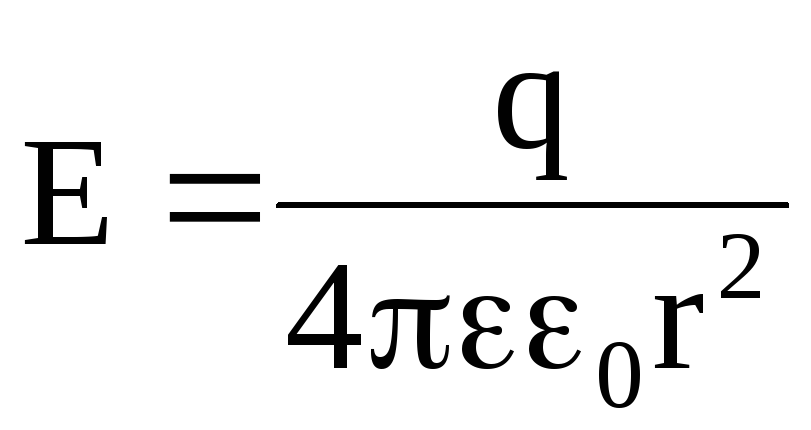 . (2.22)
. (2.22)
Разность потенциалов между обкладками
 .(2.23)
.(2.23)Таким образом,
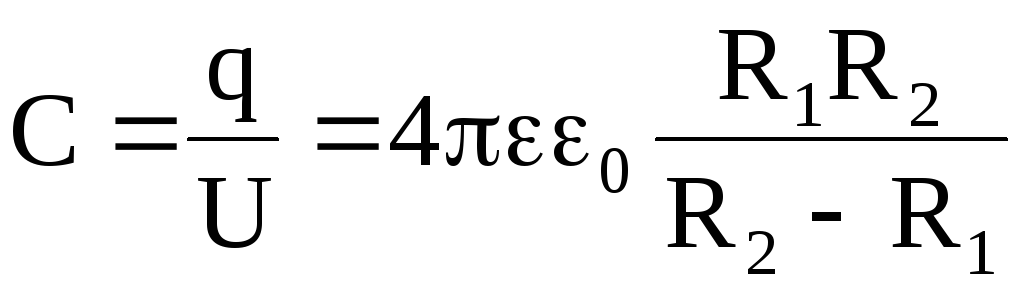 .
(2.24)
.
(2.24)
При R2 — R1 = d << R1R2
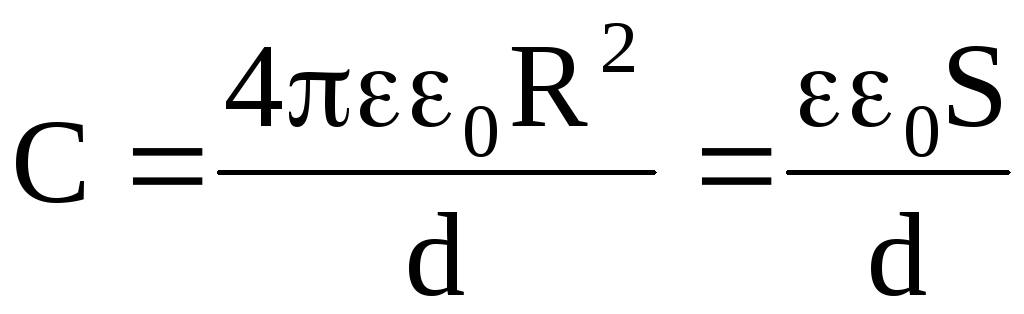 . (2.25)
. (2.25)
Следовательно, при указанных условиях емкость сферического конденсатора можно рассчитывать по формуле емкости плоского конденсатора.
2.5. Соединения конденсаторов
Отдельные конденсаторы обладают определенной емкостью и могут работать только при подключении их к характерным для них напряжениям, которые определяются свойствами и толщиной диэлектрика. Если напряжение превышает допустимое — происходит пробой конденсатора. Поэтому очень часто из имеющихся в наличии конденсаторов собирают батарею необходимой емкости, предназначенную для работы при более высоких напряжениях. Существует следующие виды соединения конденсаторов: последовательное, параллельное и смешанное.
2.5.1. Последовательное соединение конденсаторов
П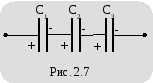 ри
последовательном соединении каждая
из обкладок какого-либо конденсатора
соединяется только с одной обкладкой
другого конденсатора, образуется
цепочка конденсаторов (рис. 2.7). К крайним
обкладкам такой цепочки прикладывается
соответствующее напряжение, под
действием которого происходит
перераспределение электрических
зарядов, при этом заряды на всех
промежуточных обкладках равны по
величине, но чередуются по знаку.
ри
последовательном соединении каждая
из обкладок какого-либо конденсатора
соединяется только с одной обкладкой
другого конденсатора, образуется
цепочка конденсаторов (рис. 2.7). К крайним
обкладкам такой цепочки прикладывается
соответствующее напряжение, под
действием которого происходит
перераспределение электрических
зарядов, при этом заряды на всех
промежуточных обкладках равны по
величине, но чередуются по знаку.
В результате перераспределения зарядов заряд батареи (цепочки) равен заряду одного конденсатора. Напряжение между обкладками отдельно взятого конденсатора обратно пропорционально его емкости, а напряжение батареи равно сумме напряжений каждого из входящих в батарею конденсаторов.
Такое соединение конденсаторов применяется в тех случаях, когда необходимо получить емкость, работающую при высоких напряжениях.
Так как в рассматриваемом случае
 ,
,
а 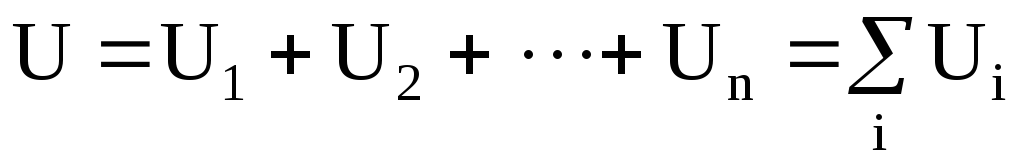 ,
,
то будем иметь

или
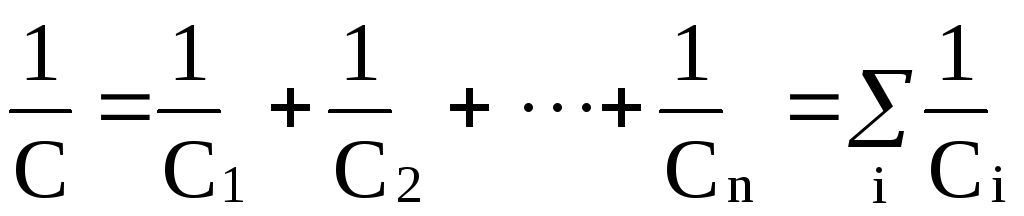 .
(2.26)
.
(2.26)
Таким образом, при последовательном соединении конденсаторов величина, обратная емкости батареи, равна сумме обратных величин емкостей отдельных конденсаторов.
Если емкости отдельных конденсаторов равны:
C1 = C2 = C3 = Cn,
то
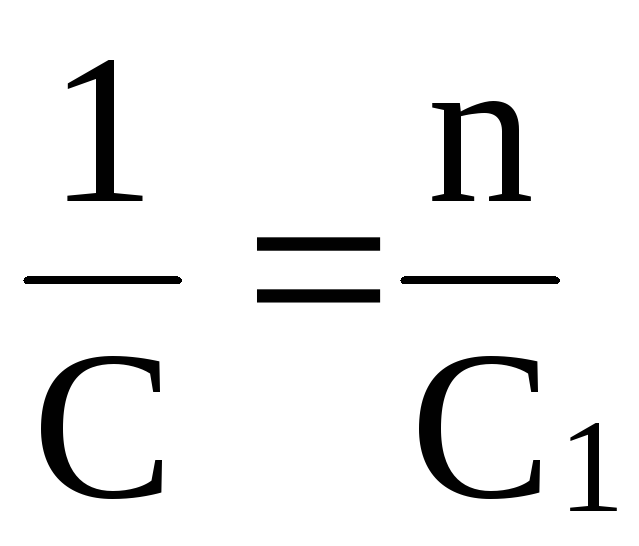 ,
,
(2.27)
,
,
(2.27)
т. е. при последовательном соединении n одинаковых конденсаторов, емкость батареи в n раз меньше емкости одного конденсатора.
Плоские конденсаторы, особенности, емкость и энергия плоских конденсаторов
Плоский конденсатор – это очень простое устройство для Емкость плоского конденсатора, зависит от его размеров, а именно от поверхности его обкладок. Также влияет диэлектрик. Основное удобство плоских моделей – их компактность. Они занимают меньше места на плате и схеме, тем сам экономя драгоценное пространство. Выглядит такая радиодеталь в виде двух пластинок, помещенных в тонкий плоский корпус. Электроны движутся с одной обкладки к плюсовому полюсу, то есть противоположный электрод. Преградой является диэлектрик.
В статье содержится вся полезная информация по определению плоского конденсатора, расчету его емкости и отличиям от конденсаторов, имеющие иную форму. В качестве бонуса читателю предложен файл с интересной лекцией, а также видеоролик на данную тему.

Плоский конденсатор.
Электрическая емкость плоского конденсатора
Электрическая емкость плоского конденсатора очень просто выражается через параметры его частей. Изменяя площадь пластин конденсатора и расстояние между ними легко убедиться, что электрическая емкость плоского конденсатора прямо пропорциональна площади его пластин (S) и обратно пропорциональна расстоянию между ними (d).

Емкость плоского конденсатора прямо пропорциональна площади его обкладок и диэлектрической проницаемости материала диэлектрика, разделяющего обкладки, и обратно пропорциональна расстоянию между ними:
C=εε0SdC=εε0Sd
Плоский конденсатор представляет из себя две плоские проводящие пластины, разделенные диэлектриком. Расстояние между пластинами много меньше характерного размера пластин. Поле вдали от краев пластин можно представить в виде суперпозиции полей бесконечно заряженных плоскостей.
Поле вдали от краев обкладок конденсатора
 Так как обкладки заряжены равными по величине разноименными зарядами, напряженность поля между обкладками складывается из напряженностей полей каждой из обкладок. Вне обкладок конденсатора их поля противоположно направлены и результирующее поле становится нулевым. Таким образом:
Так как обкладки заряжены равными по величине разноименными зарядами, напряженность поля между обкладками складывается из напряженностей полей каждой из обкладок. Вне обкладок конденсатора их поля противоположно направлены и результирующее поле становится нулевым. Таким образом:
Eрез=E++E−=2⋅σ2εε0Eрез=E++E-=2⋅σ2εε0
Используем связь между напряженностью и напряжением и напряженностью и определение поверхностной плотности заряда
E=UdE=Ud
σ=qSσ=qS
Получаем$
Ud=qεε0SUd=qεε0S
Откуда
C=qU=εε0Sd
Плоский конденсатор
 Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин. Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин. Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора.
Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле, изображенное стрелками на нашей схеме. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит. Для определения величины этого поля рассмотрим еще одно изображение плоского конденсатора:

Плоские конденсаторы
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина (+q) создает поле, напряженность которого равна
- отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_
Здесь – это поверхностная плотность заряда: . А – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой. Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0.
Процессы зарядки и разрядки конденсаторов
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить? Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника, в связи с чем на обкладке возникнет недостаток отрицательно заряженных частиц и она станет положительно заряженной.

В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора, в результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов.
Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока, после этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

Емкость и энергия конденсатора.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом.
Материал в тему: все о переменном конденсаторе.
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Емкость и энергия конденсатора
 Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора одного из проводников к разности потенциалов между проводниками. Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ).
Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора одного из проводников к разности потенциалов между проводниками. Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ).
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом.

Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение – то есть величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные
заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками. В таблице ниже приведем основные параметры конденсаторов.

Стоит почитать: все об электолитических конденсаторах.
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин. Под зарядом конденсатора понимают заряд одной пластины.
Заключение
Более подробно о том, что такое плоский конденсатор и как рассчитать его электроемкость, можно узнать из статьи “Электроемкость“. Если у вас остались вопросы, можно задать их в комментариях на сайте. Также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов.
Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vк.coм/еlеctroinfonеt. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.sverh-zadacha.ucoz.ru
www.ru.solverbook.com
www.xn--80ancbkzagjllo.xn--p1ai
www.microtechnics.ru
www.energetik.com.ru
www.easy-physic.ru
Ёмкость плоского конденсатора | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Ёмкость плоского конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
![Rendered by QuickLaTeX.com \[\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-09d765c50887987e2330b40f79a68e3e_l3.png)
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
![Rendered by QuickLaTeX.com \[\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-25394e74f3d757cdf9d8353c32d600aa_l3.png)
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.
Под зарядом конденсатора понимают заряд одной пластины.
Так же есть:
Энергия конденсатора:
![Rendered by QuickLaTeX.com \[\large W_p=\frac{U q}{2}=\frac{q^2}{2C}=\frac{CU^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c48185fd72204f7932e94ce28f23e7c3_l3.png)
Ёмкость конденсатора :
![Rendered by QuickLaTeX.com \[\large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-65907405fbd131bc9587b0b2750da723_l3.png)
Ёмкость цилиндрического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=2\pi \varepsilon \varepsilon _0\frac{l}{ln(\frac{R_2}{R_1})} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-53c9846a6d69f2a5b024b7b42f38ecc7_l3.png)
Емкость сферического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=4\pi \varepsilon \varepsilon _0(\frac{1}{R_1} - \frac{1}{R_2})^{-1} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8000dcae1c6bc4a3b16bcb4bd7933302_l3.png)
В формуле мы использовали :
C — Электрическая ёмкость (ёмкость конденсатора)
![Rendered by QuickLaTeX.com \[\varepsilon\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bb5ae93f2a2e84cf68e4653cb1b294fe_l3.png)
— Относительная диэлектрическая проницаемость
![Rendered by QuickLaTeX.com \[\varepsilon _0 = 8.854185\times 10^{-12}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-6904ff3687cf7fd22eff67df52e5007f_l3.png)
— Электрическая постоянная
S — Площадь одной обкладки
d — Расстояние между обкладками
U — Напряжение на обкладках
q — Заряд конденсатора
3 Конденсаторы. Расчет электроемкостей конденсаторов
Конденсаторы – это приборы, обладающие
большой электроемкостью, которые
способны накапливать большие заряды.
Простейший конденсатор состоит из двух
проводников (обкладок), расположенных
на малом расстоянии друг от друга.
Практически очень важно, чтобы
электрическое поле было сосредоточено
внутри конденсатора. Для этого заряды
на обкладках должны быть одинаковы по
модулю и противоположны по знаку ( и
и ).
).
Электроемкостью конденсатора называют
величину  ,
пропорциональную заряду
,
пропорциональную заряду конденсатора, и обратно пропорциональную
разности потенциалов между обкладками:
конденсатора, и обратно пропорциональную
разности потенциалов между обкладками:
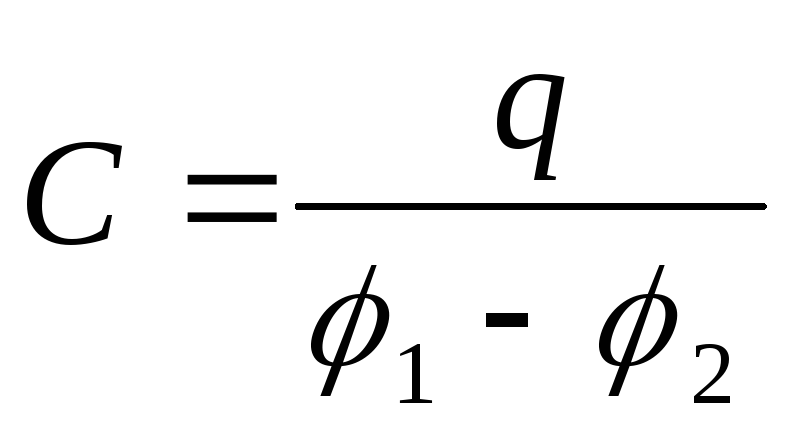 (2.7)
(2.7)
Разность потенциалов 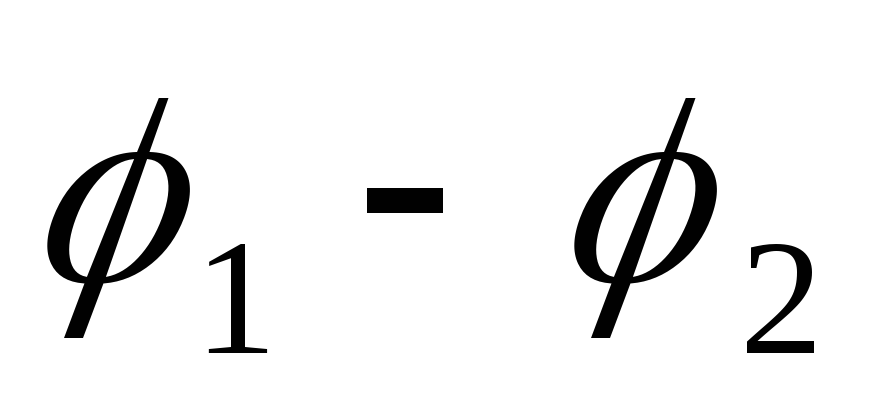 называют напряжением и обозначают
называют напряжением и обозначают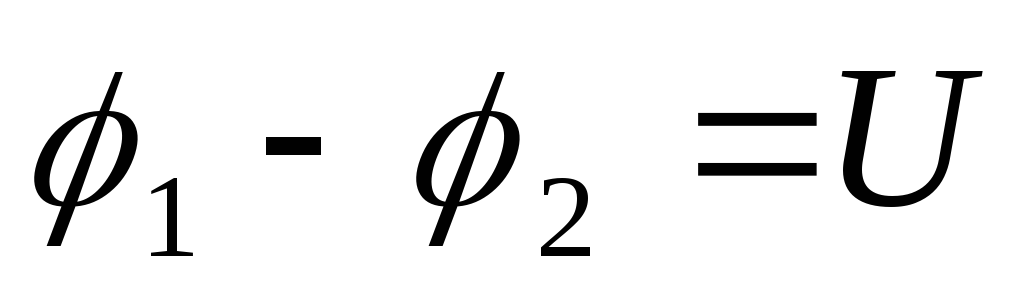 .
Поэтому формулу (2.7) можно представить
в виде:
.
Поэтому формулу (2.7) можно представить
в виде:
 (2.8)
(2.8)
Размерность емкости конденсатора  = ФАРАД.
= ФАРАД.
Емкость конденсатора зависит от размеров и формы обкладок, от расстояния между ними и от диэлектрика, заполняющего конденсатор.
Примеры вычисления электроемкостей различных конденсаторов
1 Электроемкость плоского конденсатора(рис. 4)
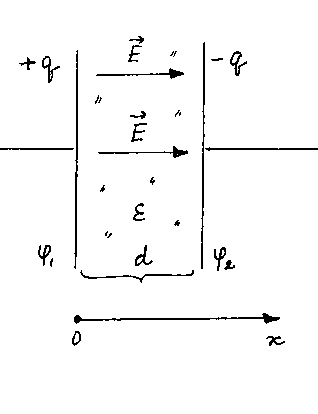
Рис. 4
Пусть  — площадь обкладок,
— площадь обкладок, —
расстояние между обкладками, зазор
между обкладками заполнен диэлектриком
с проницаемостью
—
расстояние между обкладками, зазор
между обкладками заполнен диэлектриком
с проницаемостью .
Если
.
Если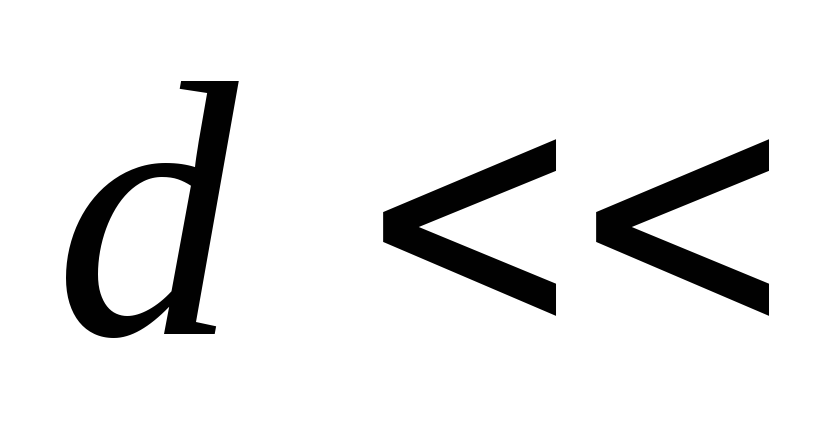 линейных размеров обкладок, можно
пренебречь краевыми эффектами и считать
электрическое поле
линейных размеров обкладок, можно
пренебречь краевыми эффектами и считать
электрическое поле внутри конденсатора практически
однородным, а заряд
внутри конденсатора практически
однородным, а заряд распределенным по пластинам равномерно
с поверхностной плотностью
распределенным по пластинам равномерно
с поверхностной плотностью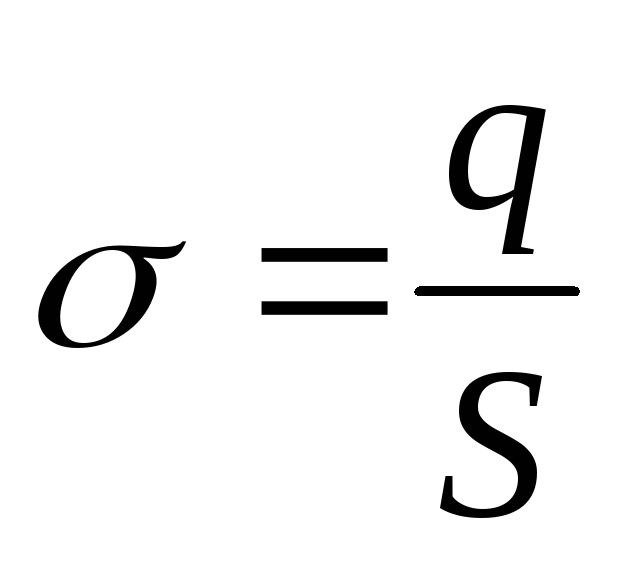 .
.
Напряженность поля в конденсаторе:
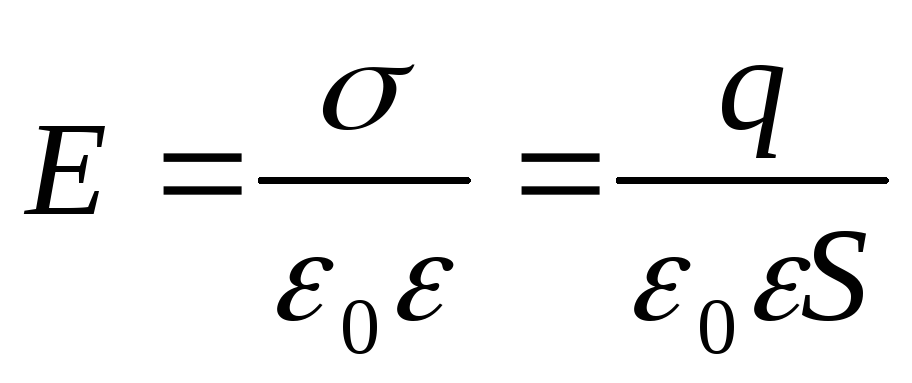
Напряжение между обкладками:
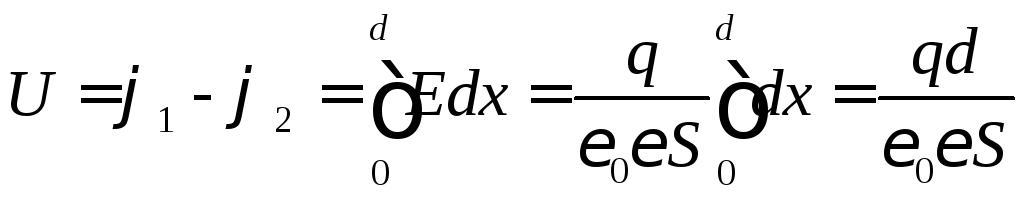 .
.
Отсюда емкость плоского конденсатора равна:
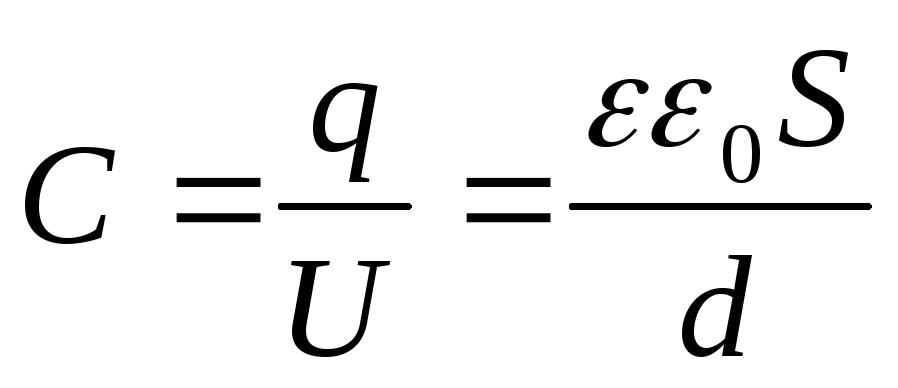 (2.9)
(2.9)
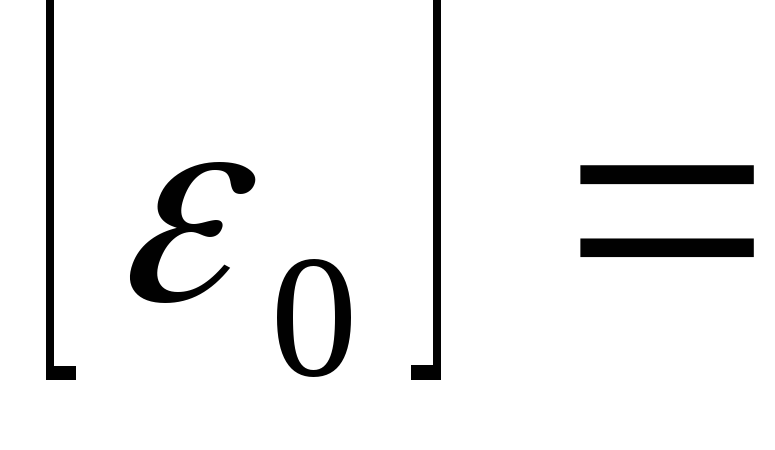 Ф/м
Ф/м
2 Электроемкость цилиндрического конденсатора(рис. 5)
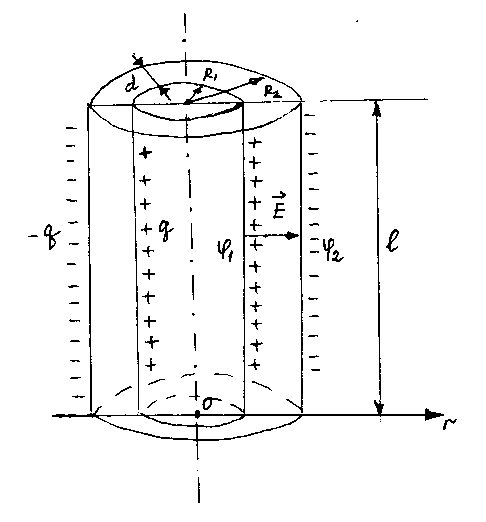
Рис. 5
Пусть  ,
, — радиусы внутренней и внешней
цилиндрических обкладок,
— радиусы внутренней и внешней
цилиндрических обкладок,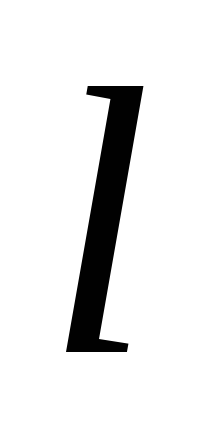 — длина конденсатора,
— длина конденсатора, —
зазор между обкладками.
—
зазор между обкладками.
Если 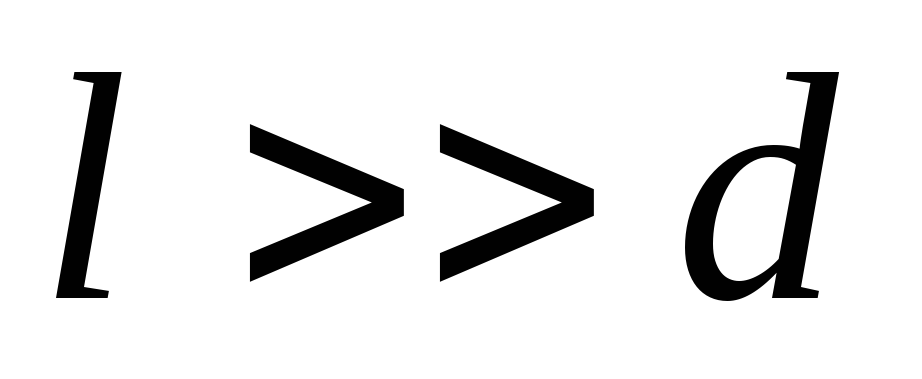 ,
то рассеянием поля вблизи краев обкладок
можно пренебречь и вычислить поле в
зазоре по формуле
,
то рассеянием поля вблизи краев обкладок
можно пренебречь и вычислить поле в
зазоре по формуле
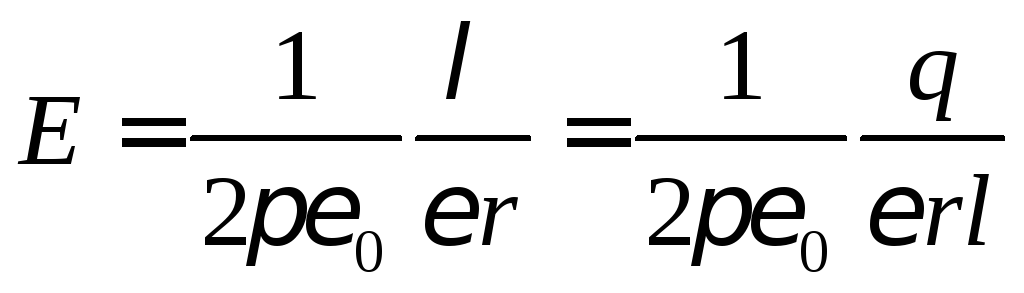 .
.
(см. 1.24 и 1.13).
Напряжение между обкладками
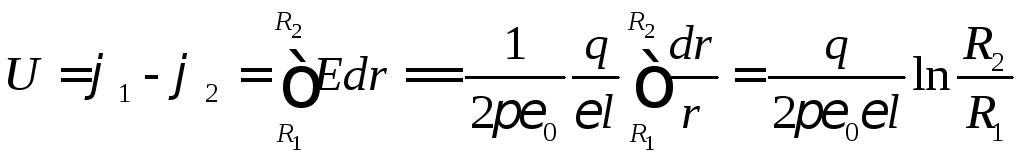 .
.
Следовательно, емкость цилиндрического конденсатора равна
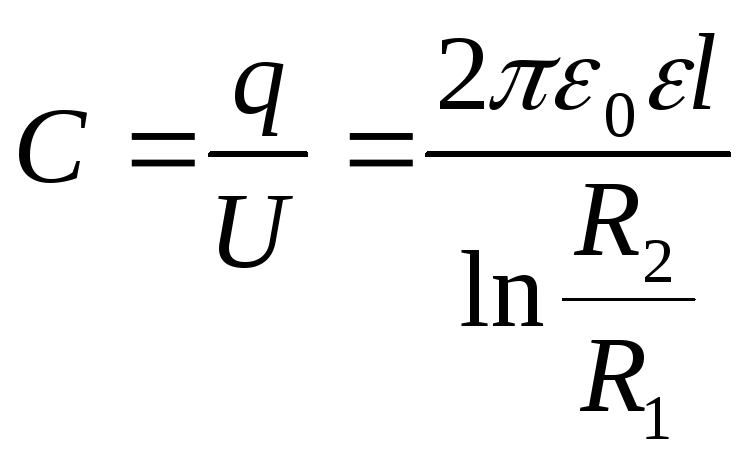 . (2.10)
. (2.10)
Предположив, что  ,
преобразуем
,
преобразуем по формуле
по формуле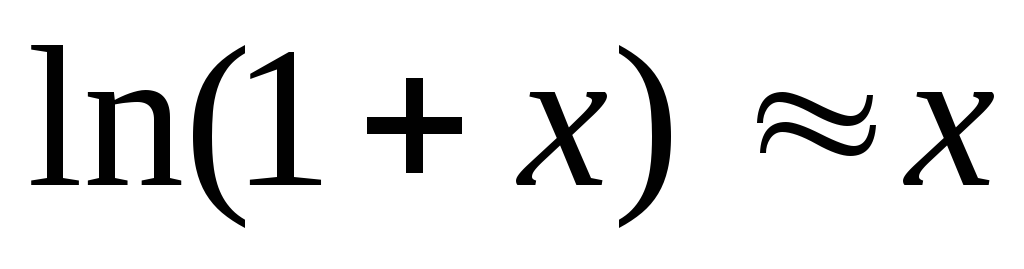 ,
справедливой для
,
справедливой для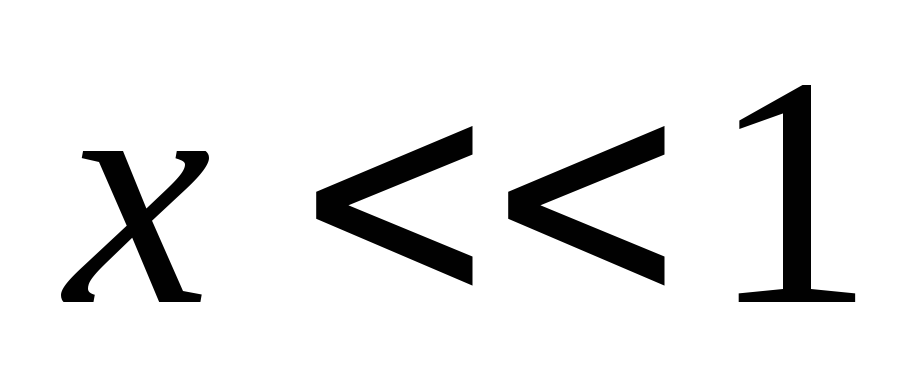 :
:
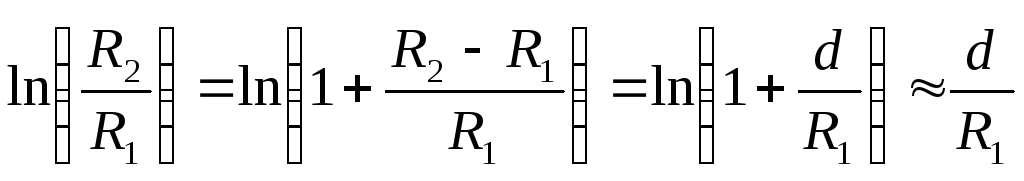
Подставив в (2.10) и учтя, что 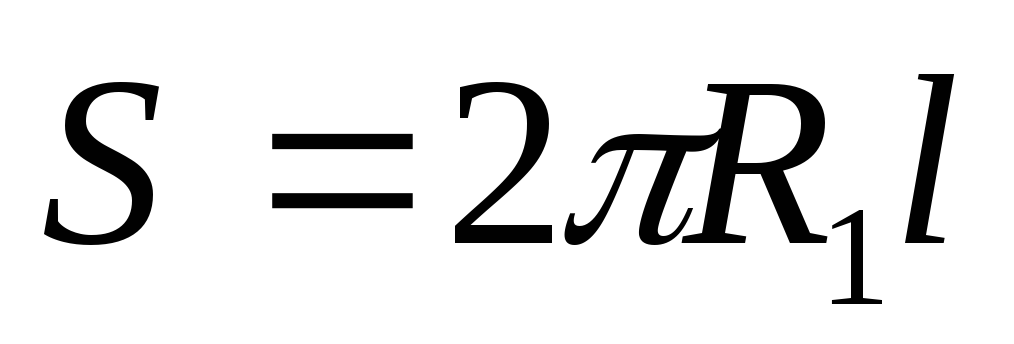 —
площадь обкладки, получим
—
площадь обкладки, получим
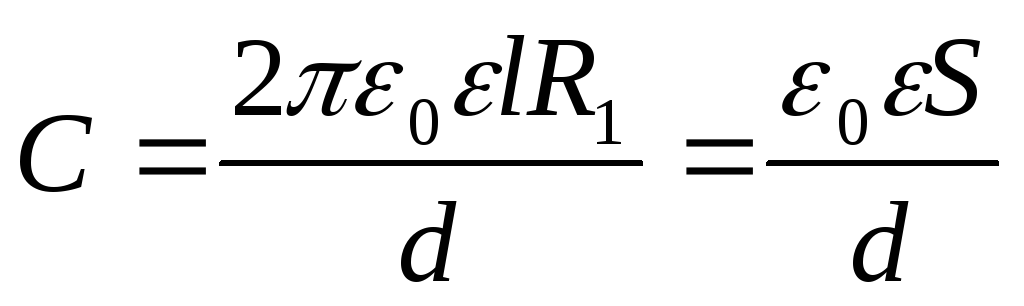 ,
,
Что совпадает с формулой (2.9) для емкости плоского конденсатора.
3 Электроемкость сферического конденсатора (рис. 6)
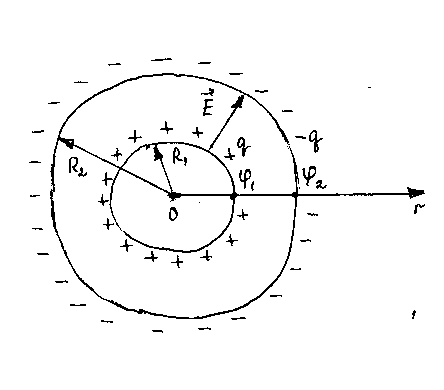
Рис. 6
Пусть  ,
,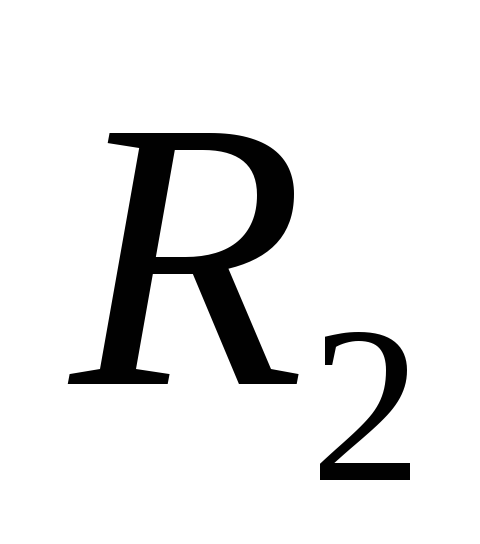 — радиусы внутренней и внешней сферических
обкладок,-
зазор между обкладками. Если заряд
конденсатора
— радиусы внутренней и внешней сферических
обкладок,-
зазор между обкладками. Если заряд
конденсатора ,
то напряженность поля между обкладками
(
,
то напряженность поля между обкладками
(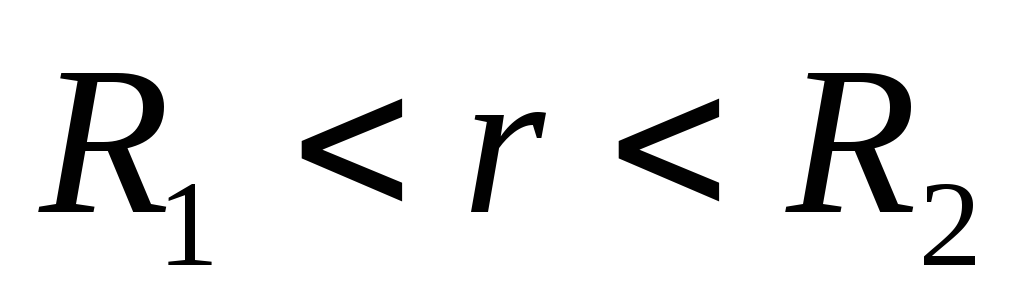 )
определяется по теореме Гаусса:
)
определяется по теореме Гаусса:
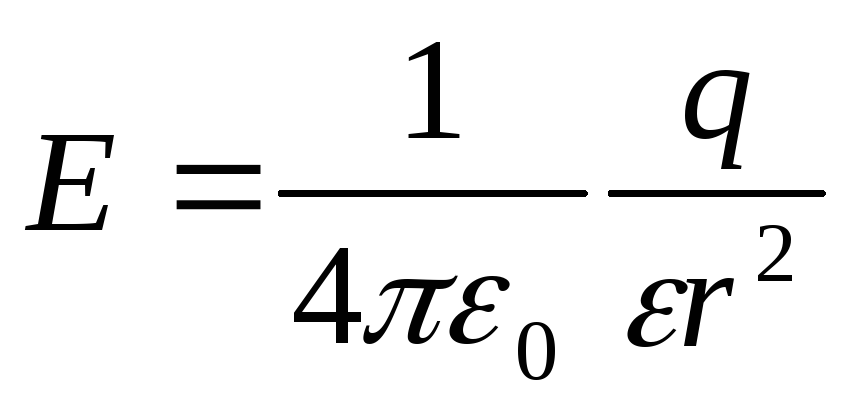
Напряжение на конденсаторе
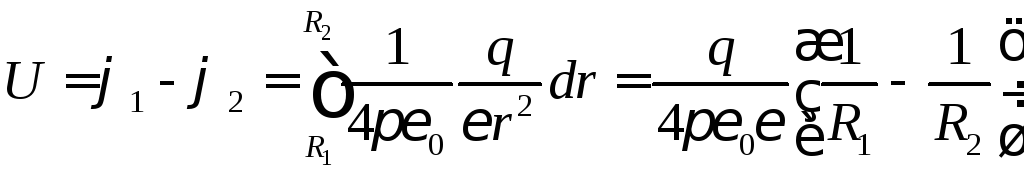
Отсюда следует, что емкость сферического конденсатора
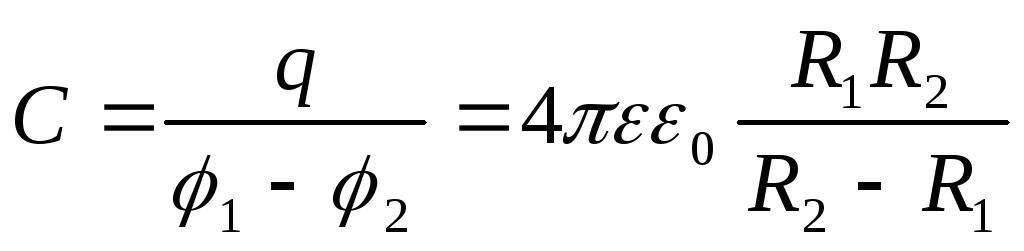 (2.11)
(2.11)
Если 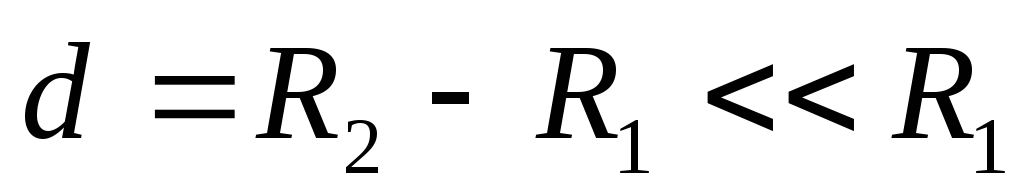 ,
то
,
то
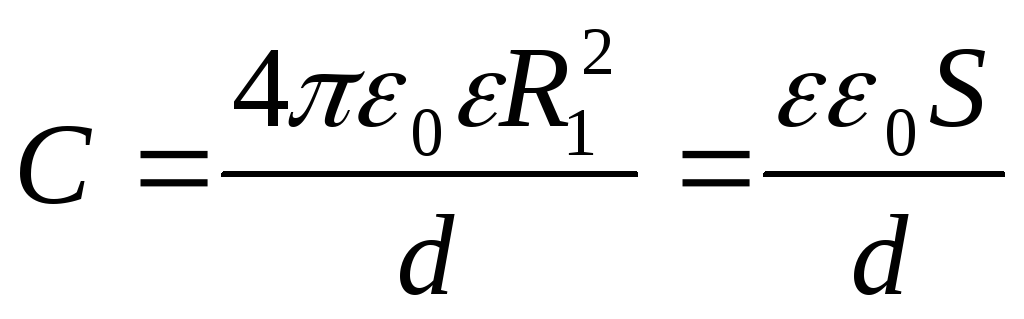 ,
совпадает с формулой (2.9)
,
совпадает с формулой (2.9)
Соединение конденсаторов
1 Параллельное соединение конденсаторов (рис. 7)
Напряжение на конденсаторах одинаково
 ,
,
заряд различен 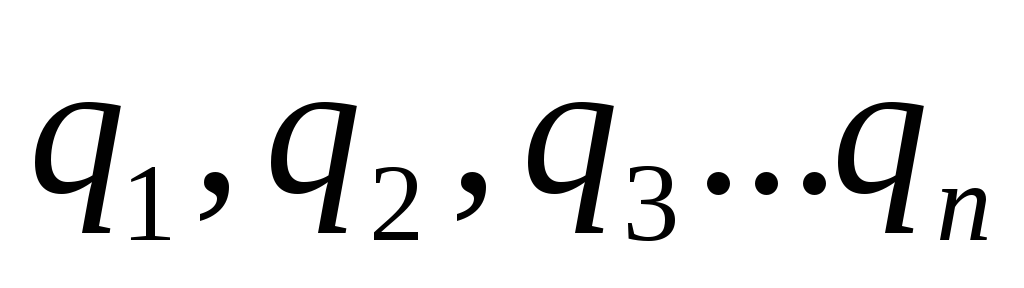 .
.
Общий заряд  всей батареи равен
всей батареи равен
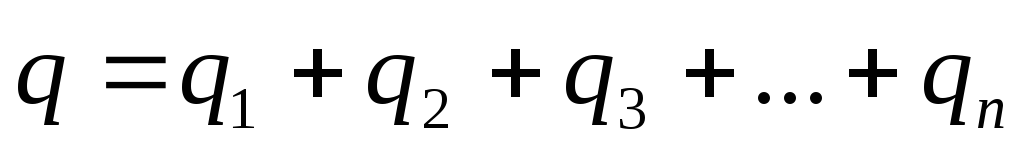
Емкость батареи
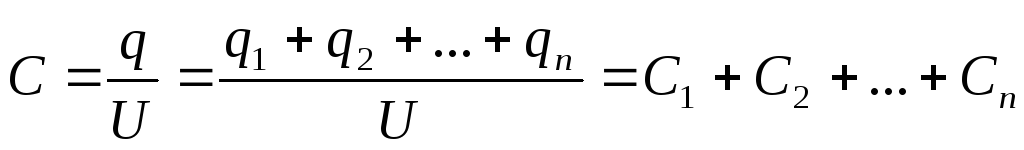
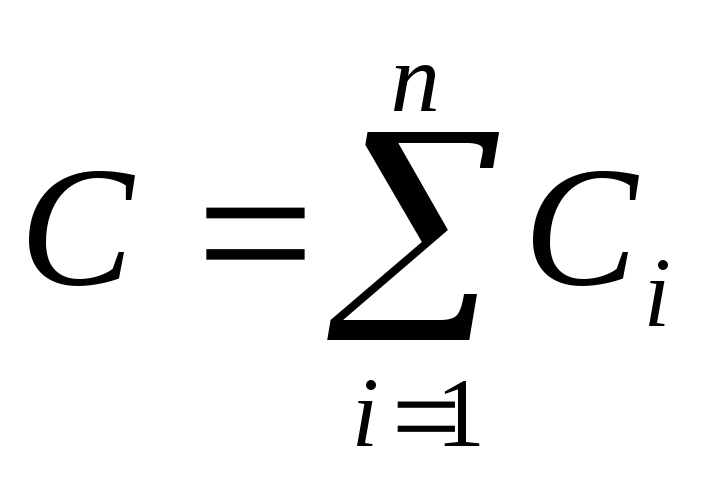 (2.12)
(2.12)
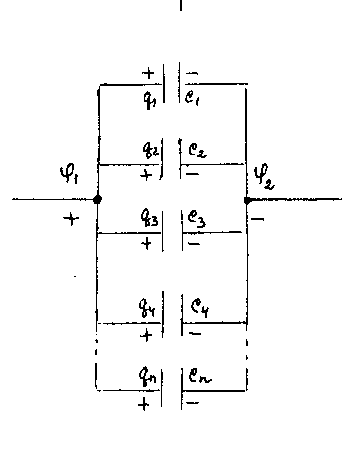
Рис. 7
Таким образом, при параллельном соединении конденсаторов емкости складываются.
2. Последовательное соединение(рис. 8)
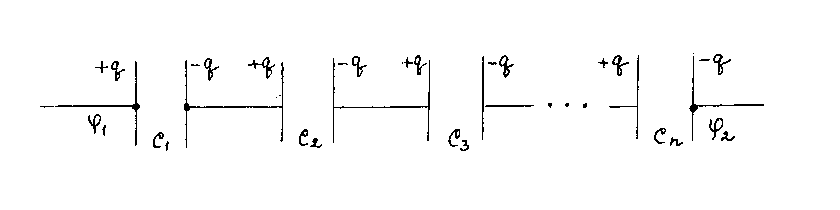
Рис. 8
Напряжение на батарее
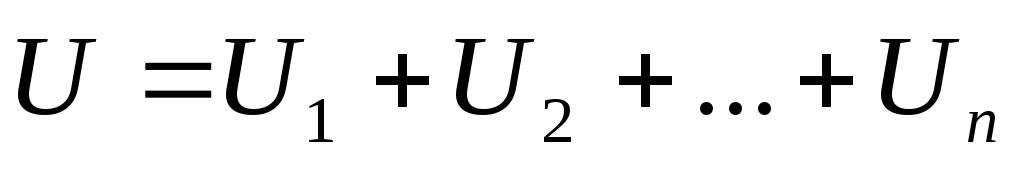
Заряд на конденсаторах одинаков
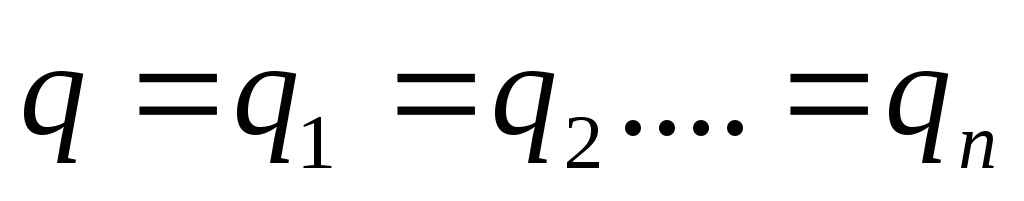
Поэтому напряжение на каждом из конденсаторов:
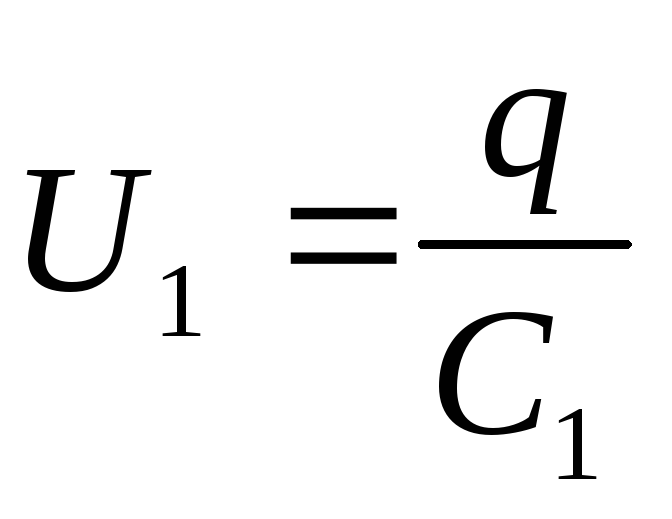 ;
;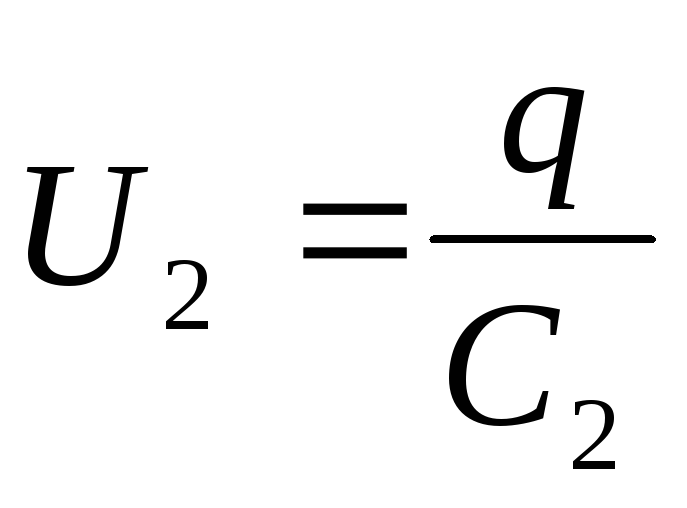 ;….
;….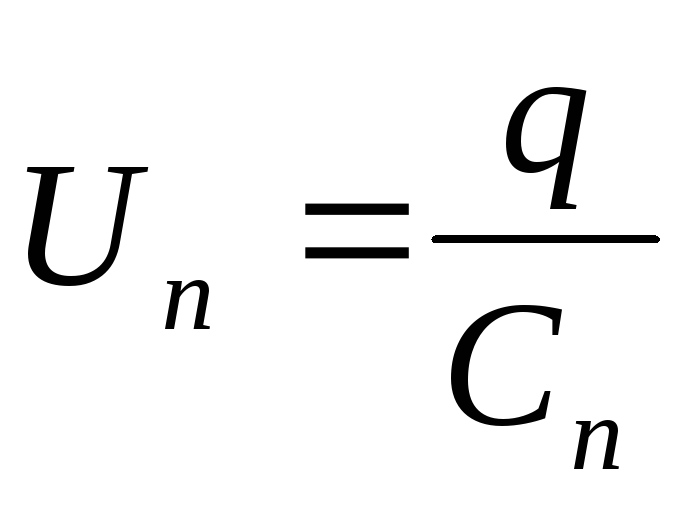
Отсюда
 ,
или
,
или

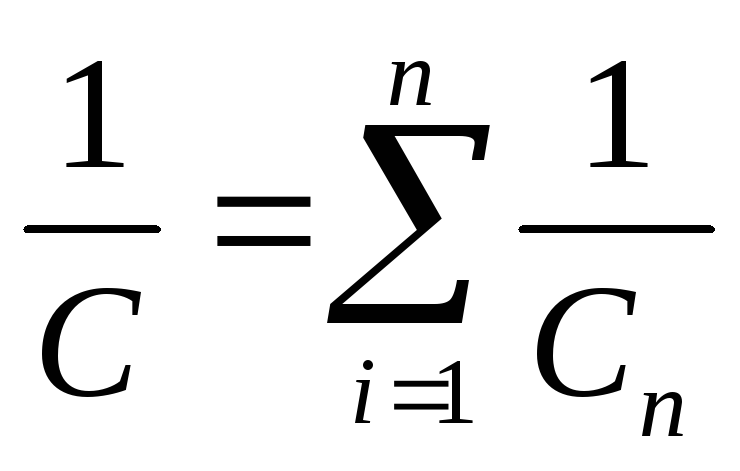 (2.13)
(2.13)
При последовательном соединении конденсаторов складываются величины, обратные емкости.
Задачи
1. На два последовательно соединенных
конденсатора, имеющих емкости  =100
пФ и
=100
пФ и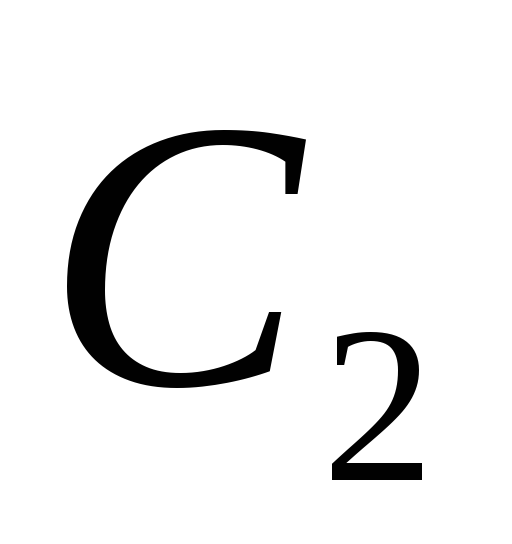 =200
пФ, подано постоянное напряжение
=200
пФ, подано постоянное напряжение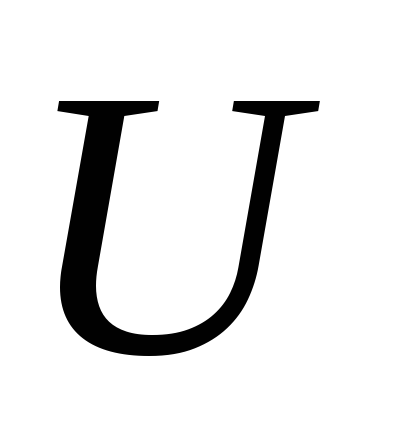 =300
В. Определить напряжения
=300
В. Определить напряжения и
и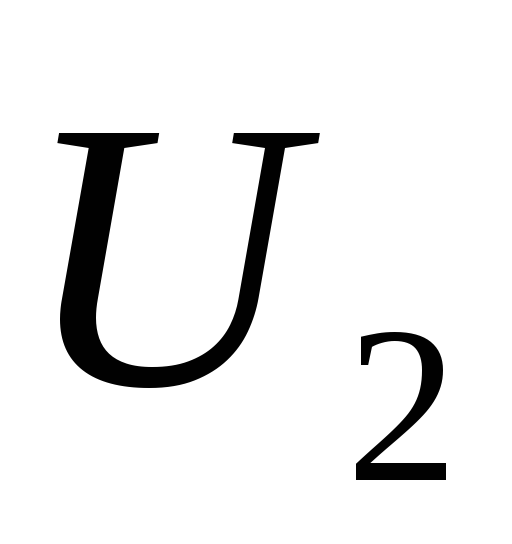 на конденсаторах и заряд
на конденсаторах и заряд на
их обкладках.
на
их обкладках.
Решение:

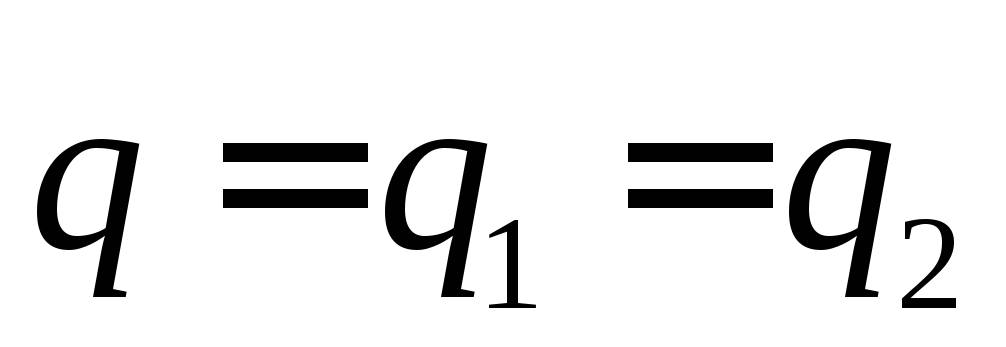
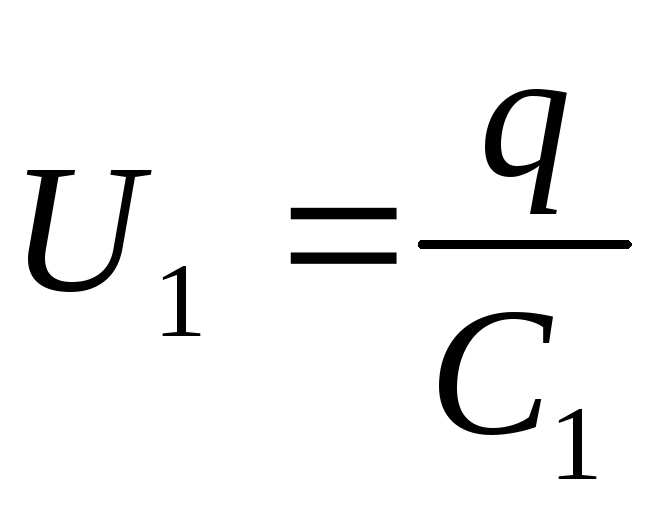 ,
,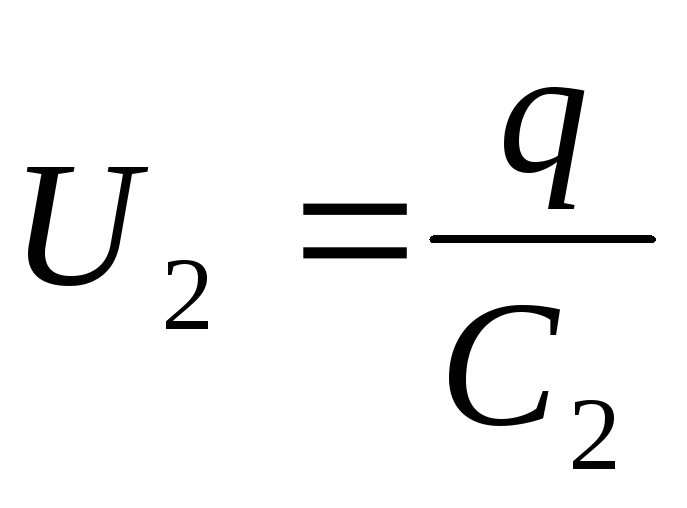
Отсюда следует равенство
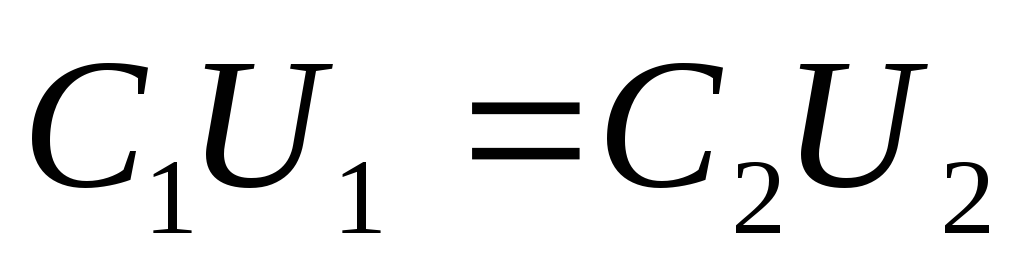
Кроме того,
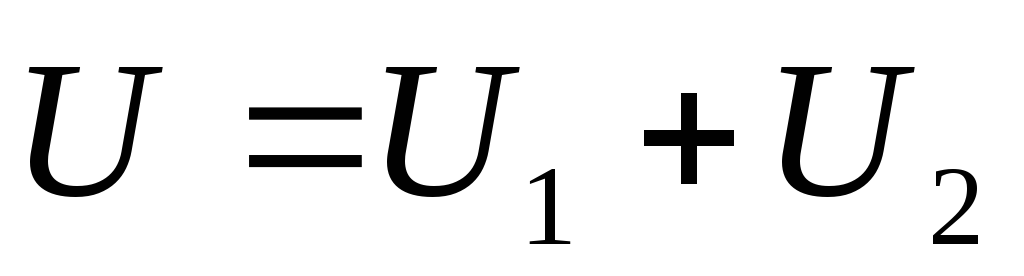
Отсюда получим, что
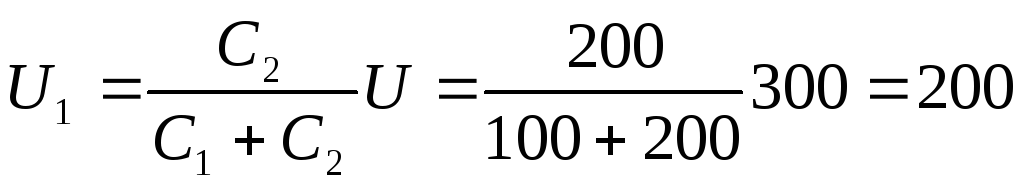 В
В
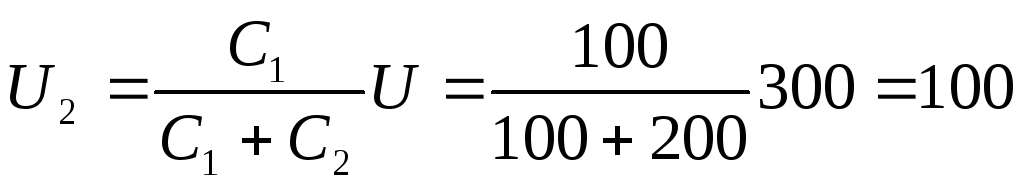 В
В
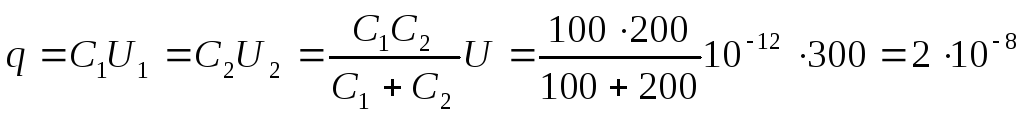 Кл
Кл
Формула емкости конденсатора, С
Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:
называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():
где – диэлектрическая проницаемость диэлектрика.
За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).
Формула электрической емкости плоского конденсатора
Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Формула электрической емкости цилиндрического конденсатора
Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Формула электрической емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач по теме «Емкость конденсатора»
77. Конденсатори. Ємність плоского конденсатора.
Конденсáтор— система з двох чи більше електродів (обкладок), які розділені діелектриком, товщина якого менша у порівнянні з розміром обкладок. Така система має взаємну електричну ємність і здатна зберігати електричний заряд.
Прикладання електричної напруги до обкладок конденсатора спричиняє накопичення на них електричного заряду.
Основною характеристикою конденсатора є його електрична ємність (точніше номінальна ємність), яка визначає накопичений заряд. Ємність виражається у фарадах. Типові значення ємності конденсаторів складають від одиниць пікофарад до сотень мікрофарад. Але існують конденсатори з ємністю десятків фарад.
Ємність плоского конденсатора, яка складається з двох паралельних металічних пластин площиною S кожна, які розташовані на відстані d одна від одної, в системі СІ виражена
формулою
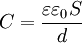 ,
,
де ε — відносна діелектрична проникність середовища, яке заповнює простір між пластинами.
Для отримання великих ємностей конденсатори з`єднують паралельно. Загальна ємність батареї паралельно з`єднаних конденсаторів дорівнює сумі ємностей всіх конденсаторів, які входять у батарею.
При послідовному з`єднанні конденсаторів заряди усіх конденсаторів однакові.
78. Паралельне та послідовне з’єднаня конденсаторів.
Конденсатором називається сукупність двох провідників, в яких накопичуються заряди, рівні по величині і різні за знаком.
Для отримання великих ємностей конденсатори з’єднують паралельно. Загальна ємність батареї паралельно з’єднаних конденсаторів дорівнює сумі ємностей всіх конденсаторів, які входять у батарею.

Заряди розподіляються прямопропорційно ємності конденсаторів.
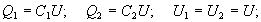
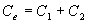
При послідовному з`єднанні в результаті електростатичної індукції на конденсаторах будуть однакові заряди:Q1=Q2=Q
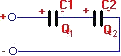
Напруги розподіляються обернено пропорційно величині їх ємностей
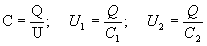
Загальна ємність батареї послідовно з’єднаних конденсаторів дорівнює
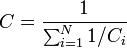
Ця ємність завжди менша мінімальної ємності конденсатора, який входить в батарею. Але при послідовному з’єднанні зменшується загроза пробою конденсаторів, оскільки на кожний конденсатор надходить лише частина різниці потенціалів джерела напруги.
Еквівалентна ємність
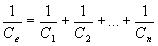
Конденсатори також характеризуються питомою ємністю — відношення ємності до об`єму (або маси) конденсатора.
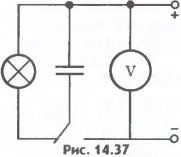
79 .Як і будь-яка система заряджених тіл, конденсатор має енергією. Обчислити енергію зарядженого плоского конденсатора з однорідним полем всередині нього нескладно. Енергія зарядженого конденсатора. Для того щоб зарядити конденсатор, треба виконати роботу з розділення позитивних і негативних зарядів. Відповідно до закону збереження енергії ця робота дорівнює енергії конденсатора. У тому, що заряджений конденсатор володіє енергією, можна переконатися, якщо розрядити його через ланцюг, що містить лампу розжарювання, розраховану на напругу в кілька вольт (ріс.14.37). При розрядці конденсатора лампа спалахує. Енергія конденсатора перетворюється в тепло та енергію світла
Виведемо формулу для енергії плоского конденсатора. Напруженість поля, створеного зарядом однієї з пластин, дорівнює Е / 2, де Е-напруженість поля в конденсаторі. В однорідному полі однієї пластини знаходиться заряд q, розподілений по поверхні іншої пластини (ріс.14.38). Відповідно до формули (14.14) для потенційної енергії заряду в однорідному полі енергія конденсатора дорівнює
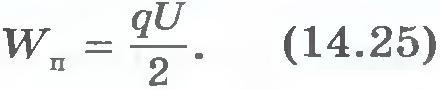
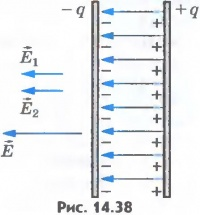
де
q
—
заряд
конденсатора,
а
d
—
відстань
між
пластинами.
Так
як
Ed
=
U,
де
U
—
різниця
потенціалів
між
обкладками
конденсатора,
то його
енергія
дорівнює: 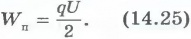 Ця
енергія
дорівнює
роботі,
яку
здійснить
електричне
поле
при
зближенні
пластин
впритул.
Замінивши
у
формулі
(14.25)
різниця потенціалів
або
заряд
за
допомогою
виразу
(14.22)
для електроємності
конденсатора,
отримаємо:
Ця
енергія
дорівнює
роботі,
яку
здійснить
електричне
поле
при
зближенні
пластин
впритул.
Замінивши
у
формулі
(14.25)
різниця потенціалів
або
заряд
за
допомогою
виразу
(14.22)
для електроємності
конденсатора,
отримаємо: 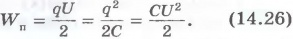 Можна
довести,
що
ці
формули
справедливі
для
будь-якого
конденсатора,
а
не
тільки
для
плоского.
Енергія
електричного
поля.
Відповідно
до теорії
близькодії
вся
енергія
взаємодії
заряджених
тіл
сконцентрована
в
електричному
полі
цих
тіл.
Значить,
енергія може
бути
виражена
через
основну
характеристику
поля
—
напруженість.
Так
як
напруженість
електричного
поля
прямо
пропорційна
різниці
потенціалів
(U
=
Ed,
то згідно
з формулою
Можна
довести,
що
ці
формули
справедливі
для
будь-якого
конденсатора,
а
не
тільки
для
плоского.
Енергія
електричного
поля.
Відповідно
до теорії
близькодії
вся
енергія
взаємодії
заряджених
тіл
сконцентрована
в
електричному
полі
цих
тіл.
Значить,
енергія може
бути
виражена
через
основну
характеристику
поля
—
напруженість.
Так
як
напруженість
електричного
поля
прямо
пропорційна
різниці
потенціалів
(U
=
Ed,
то згідно
з формулою 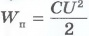 енергія
конденсатора
прямопропорційна
квадрату
напруженості
електричного
поля
всередині
нього:
енергія
конденсатора
прямопропорційна
квадрату
напруженості
електричного
поля
всередині
нього: 
80. Електричний струм – це упорядкований потік електрично заряджених частинок. Хаотичний рух заряджених частинок не створює електричного струму. За напрям електричного струму умовно беруть напрям руху позитивно заряджених частинок. Для виникнення електричного струму потрібні такі умови 1) наявність вільно рухомих заряджених частинок; 2) наявність електричного поля, під дією якого утворився б упорядкований потік заряджених частинок. За цих умов на будь-якій ділянці всередині провідника існуватиме електричне поле, напруженість якого Е=-Δφ/Δl. Електричне поле виконуватиме роботу переміщення зарядженої частинки ΔА=qΔφ. Постійний електричний струм — електричний струм, незмінний у часі. Насправді для постійного струму незмінним є перш за все знач. напруги (вимір.у вольтах), а не значення струму,хоча значення струму також може бути незмінним. Тому термін постійний струм, слід розуміти,як постійну напругу. Щоб добути неперервний струм у провіднику, треба весь час поповнювати енергію електричного поля. Для цього до кінців провідника приєднують джерело електричного струму.



