Ёмкость плоского конденсатора.
Плоский конденсатор состоит из двух
параллельных пластин, разделённых
небольшим зазором шириной 
,
заполненным однородным диэлектриком.
Нам известно, что поле между двумя
разноимённо заряженными пластинами с
одинаковой по величине поверхностной
плотностью 
равно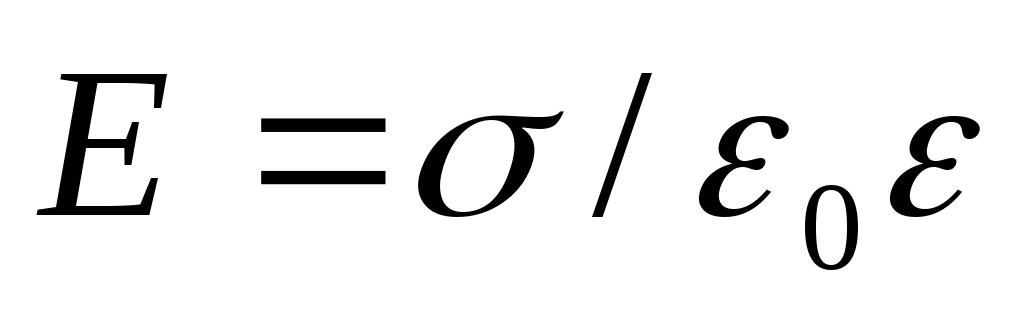
,
где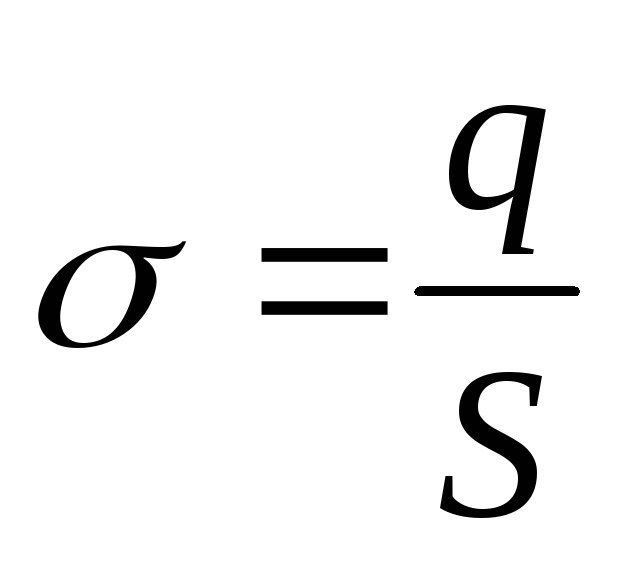
,S– площадь каждой пластины.
Напряжение между обкладками:
.
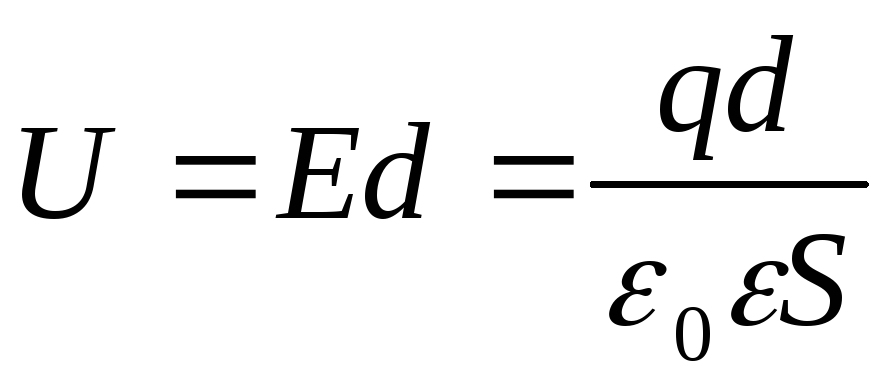Используя определение емкости конденсатора, получаем:
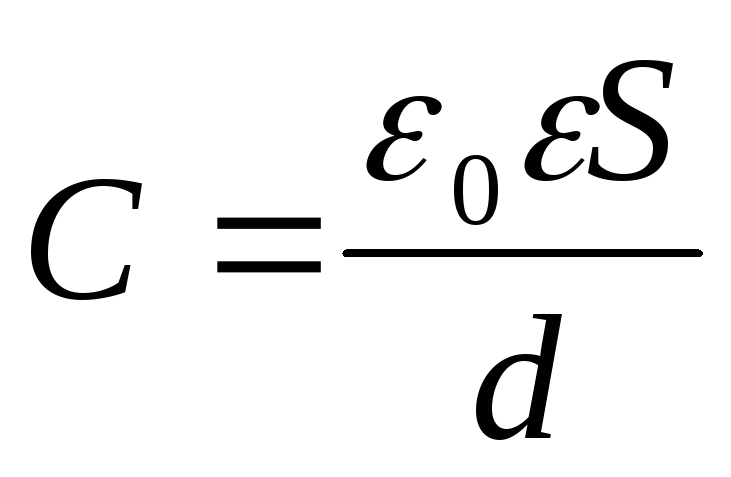
Отметим, что полученная формула является
приближенной, так как выведена без учета
искажения поля у краев пластин. Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор 
по сравнению с линейными размерами
пластин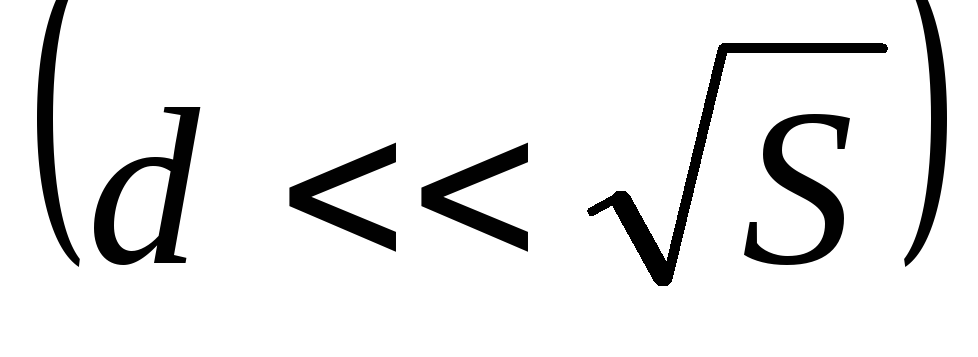
.
Ёмкость сферического конденсатора.
С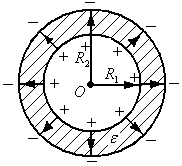
ферический
конденсатор представляет собой систему
двух концентрических сфер с радиусами
.
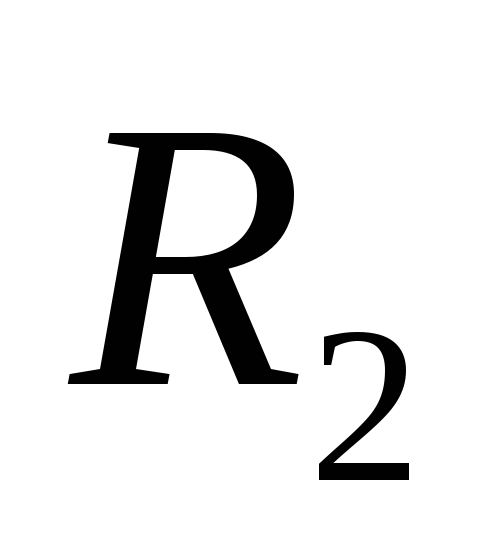Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы. Напряжение между
обкладками равно: 
.
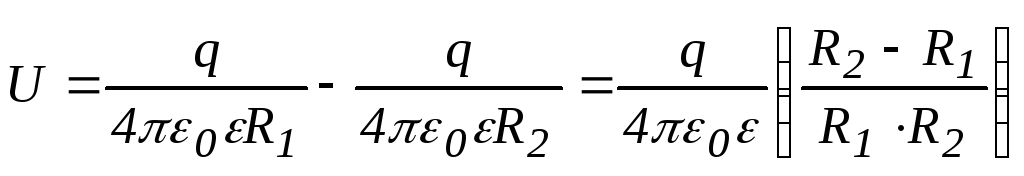Для ёмкости сферического конденсатора получаем:
.
Это формула точная.
Если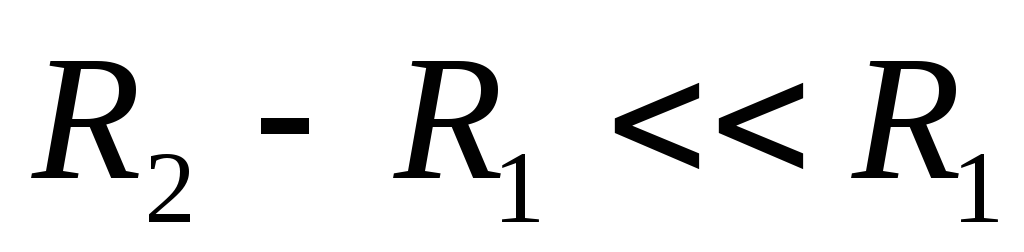 
,
полученная формула переходит в выражение
для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет
систему двух коаксиальных цилиндров с
радиусами 
и
,
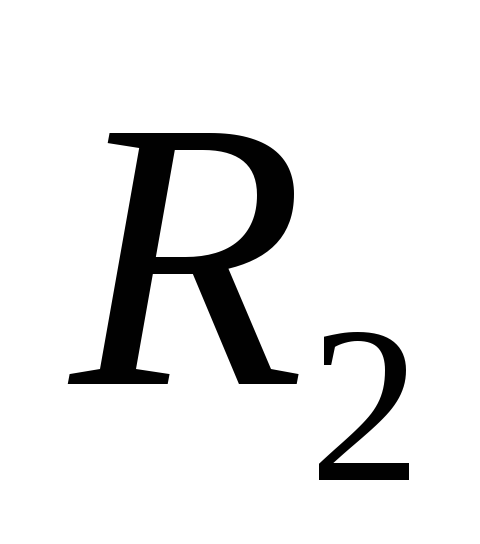длиной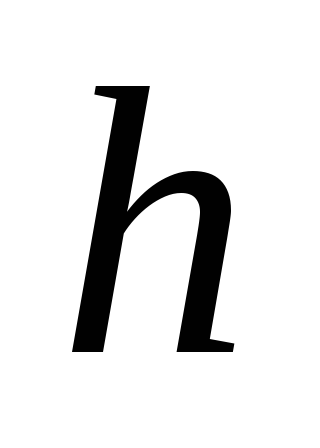
.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
.
.
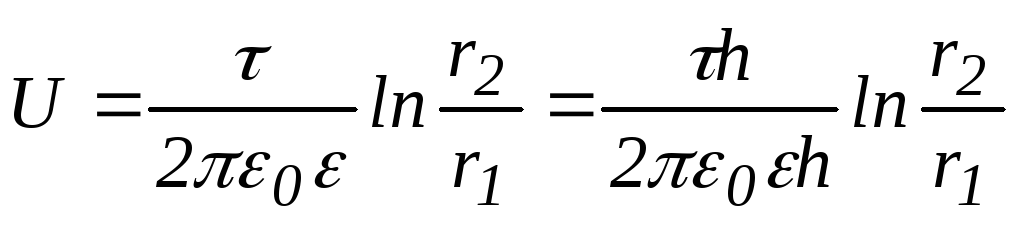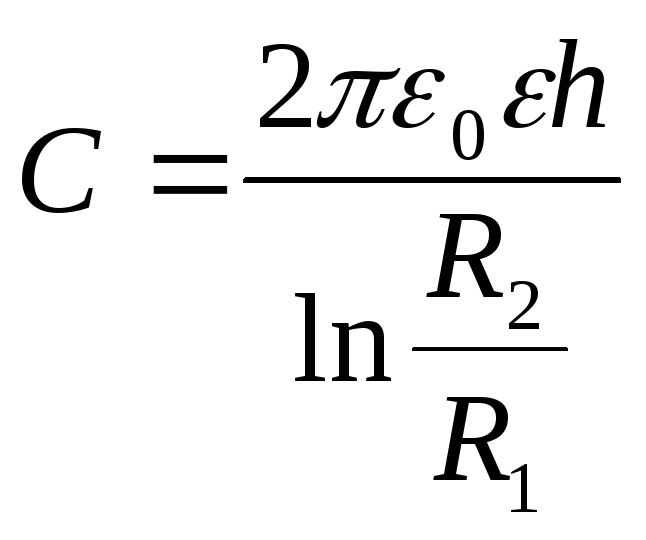Полученная формула является приближенной
и при малом зазоре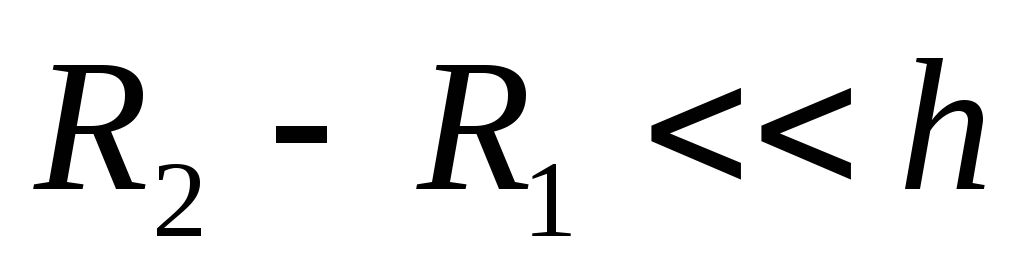 
переходит в формулу емкости плоского
конденсатора.
Соединение конденсаторов.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного соединения конденсаторов.
Заряды последовательно соединенных
конденсаторов равны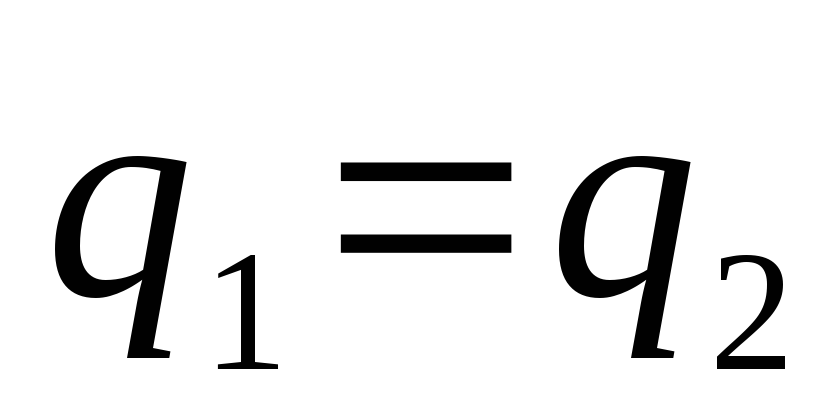 
,
а напряжение на батарее
.
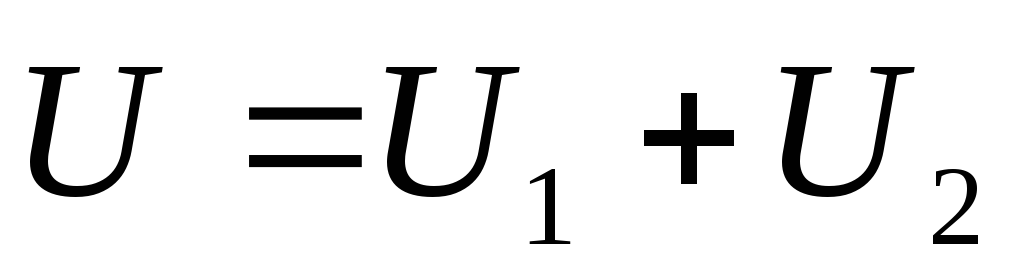Из определения емкости следует:
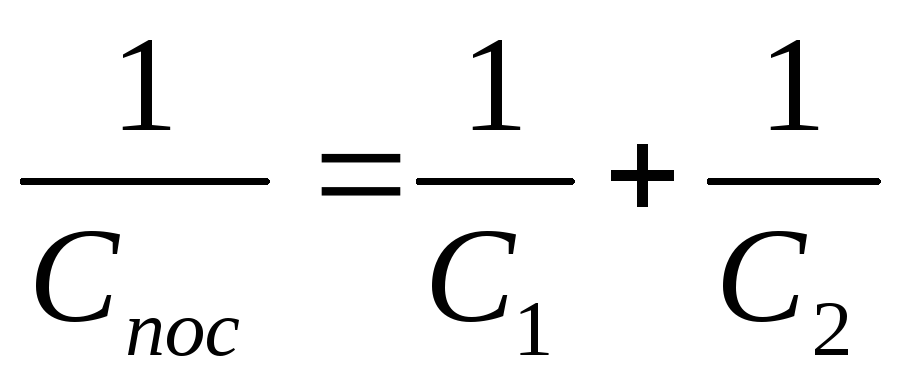
или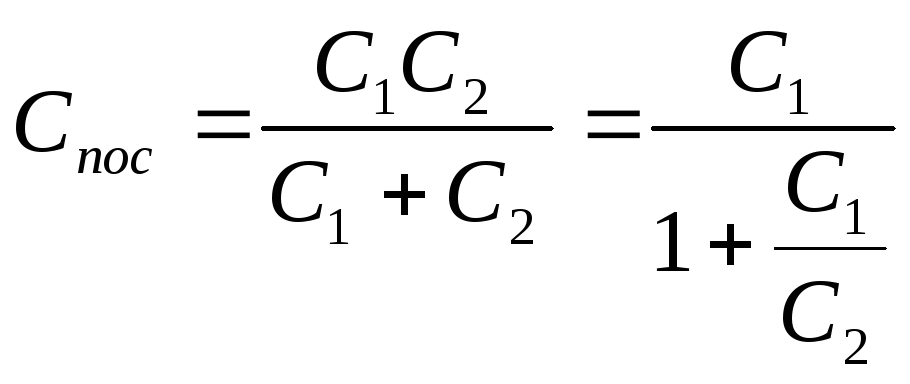 
.
,
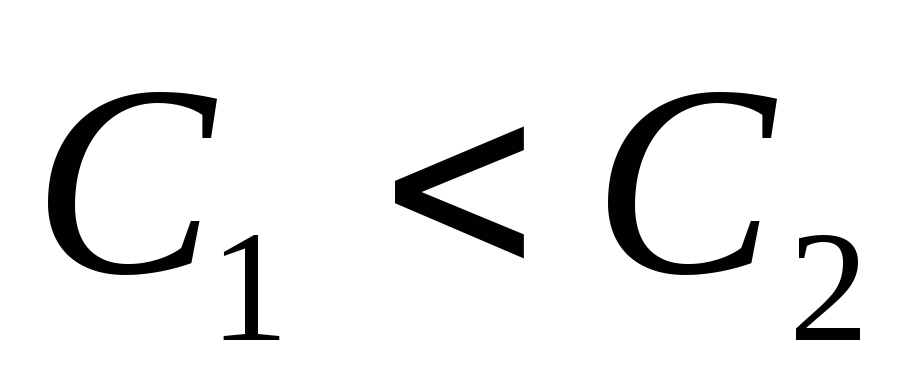то
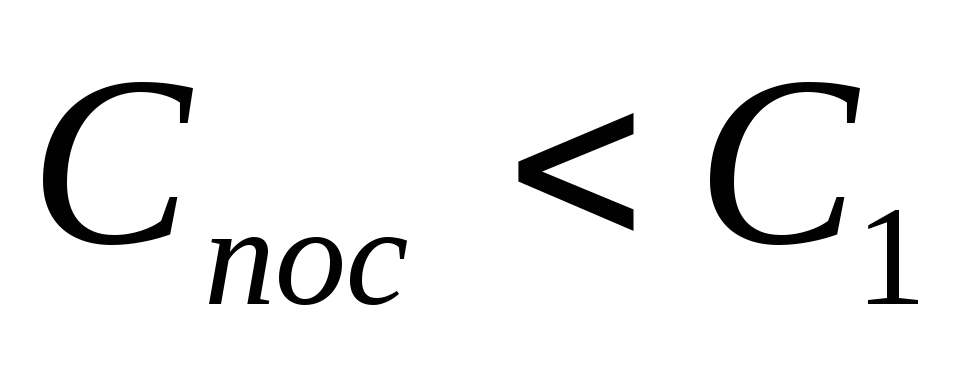(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении). Для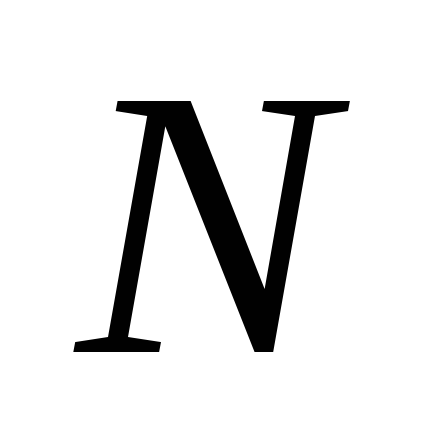 
последовательно соединенных конденсаторов
емкость вычисляется по формуле:
.
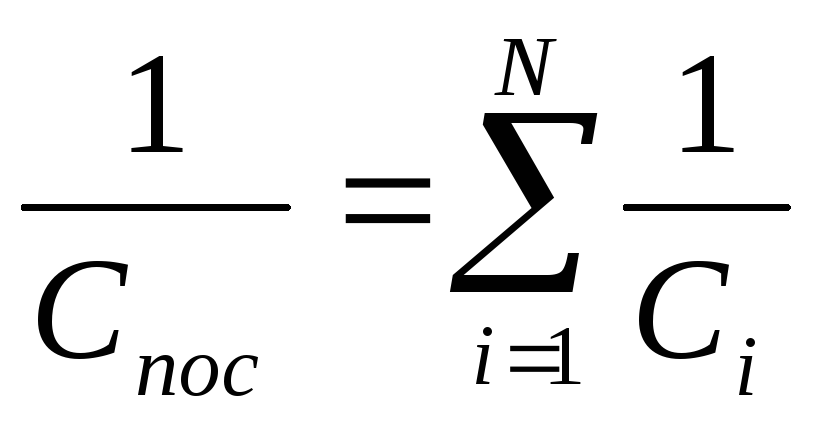В случае одинаковых конденсаторов: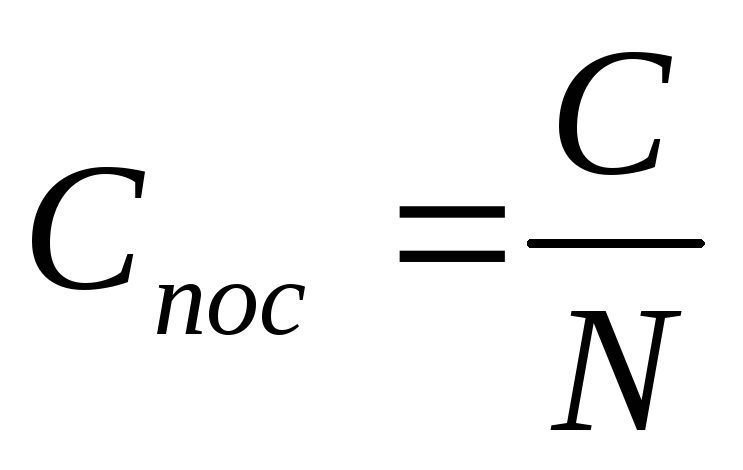 
.
Заряд батареи равен сумме зарядов:
,
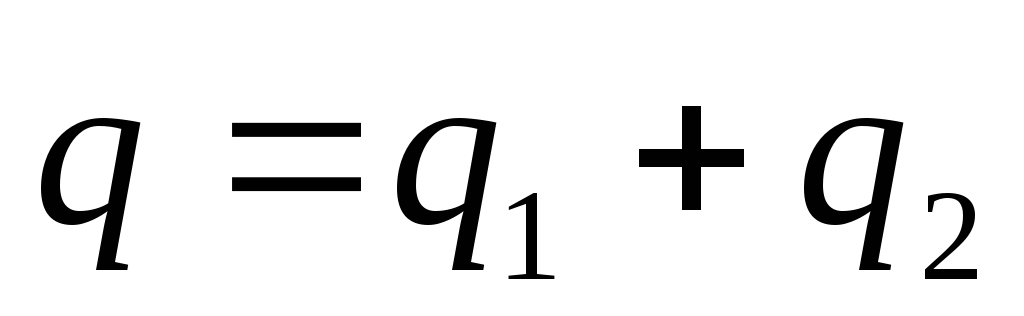а напряжение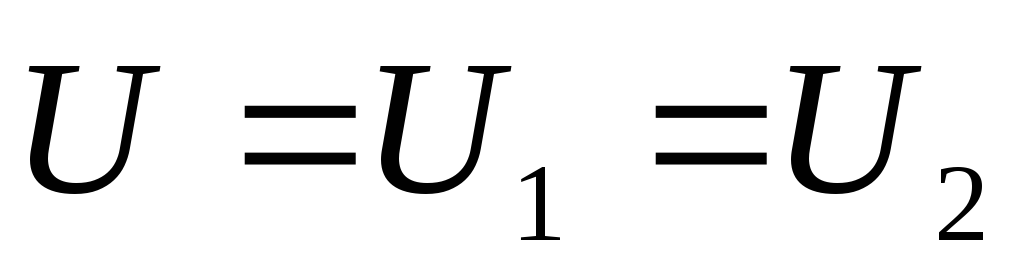 
.
По определению емкости получаем:
.
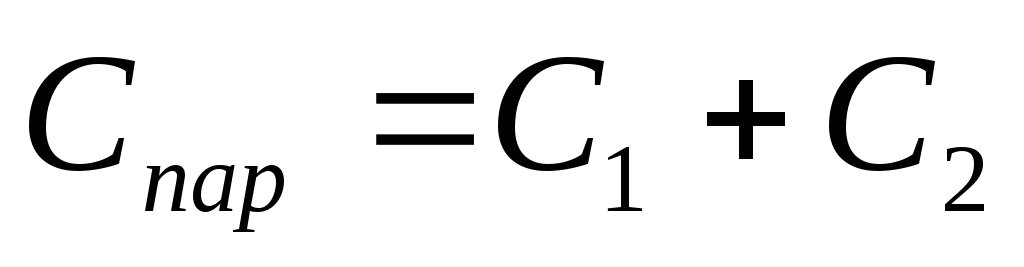Для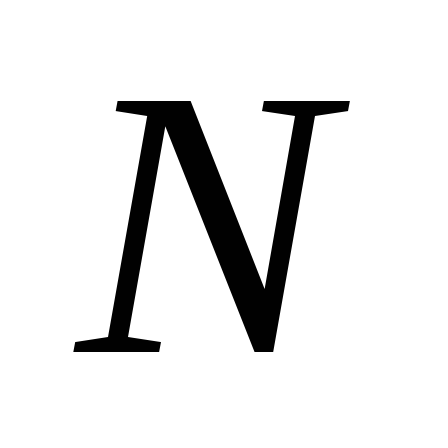 
параллельно соединенных конденсаторов: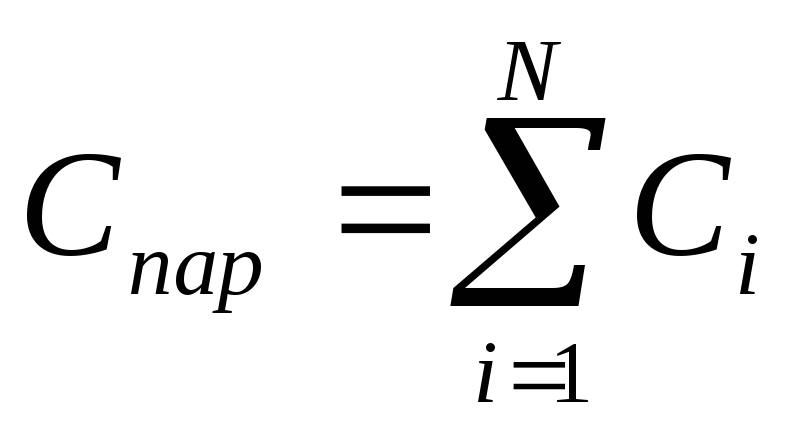
В случае одинаковых конденсаторов: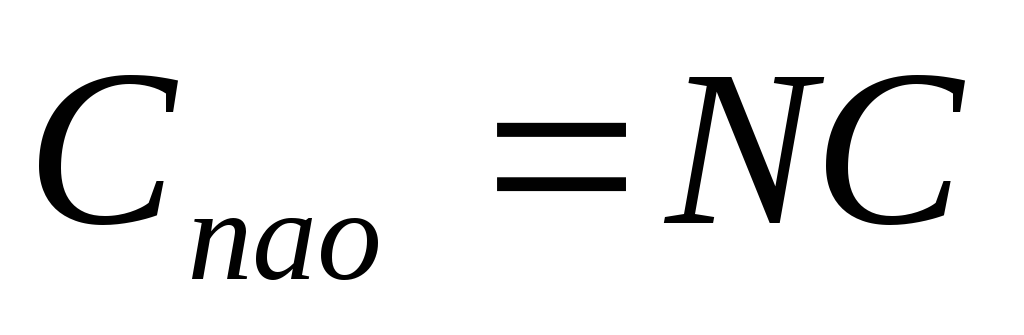 
.
Пример.
О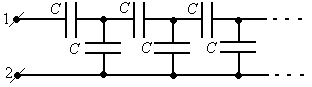
ценить
емкость батареи (см. рисунок)
.
.
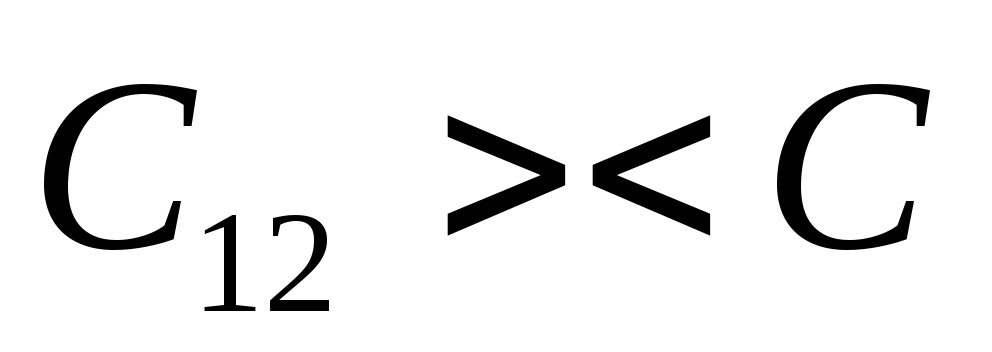Ответ: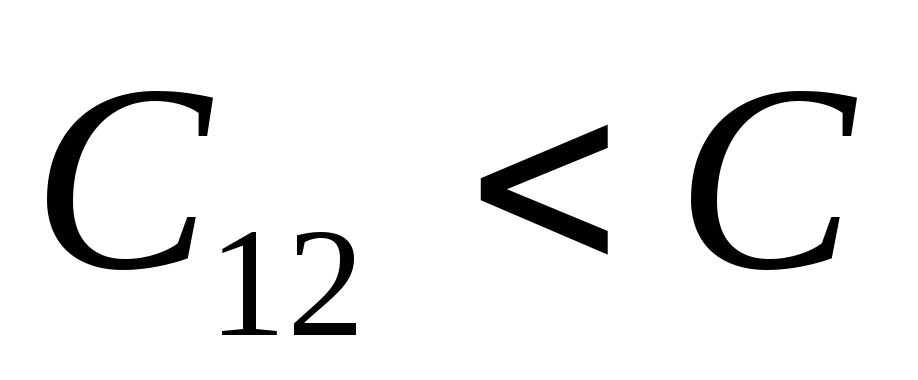
.
Д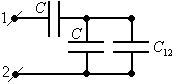
ля
расчета ёмкости батареи получаем:
,
.
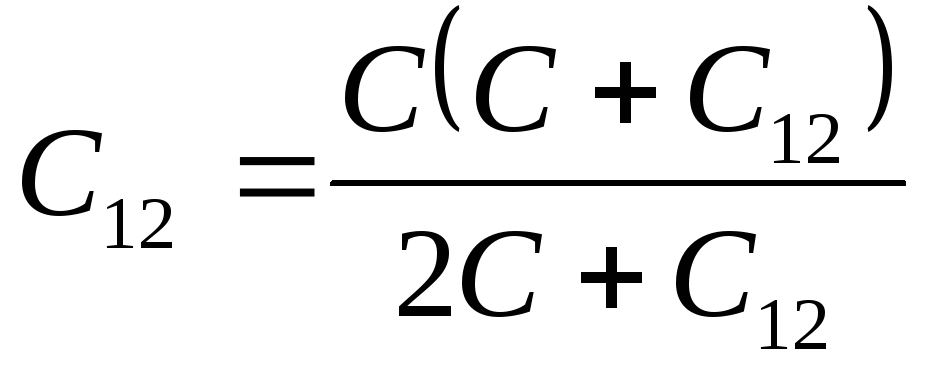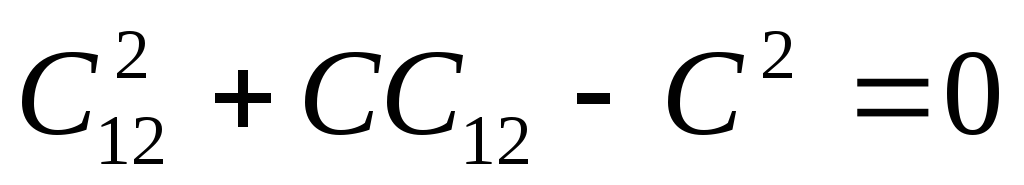Откуда: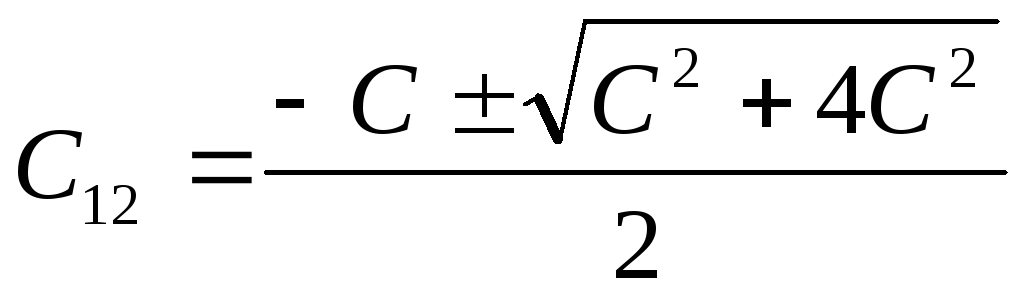 
,
так как
,
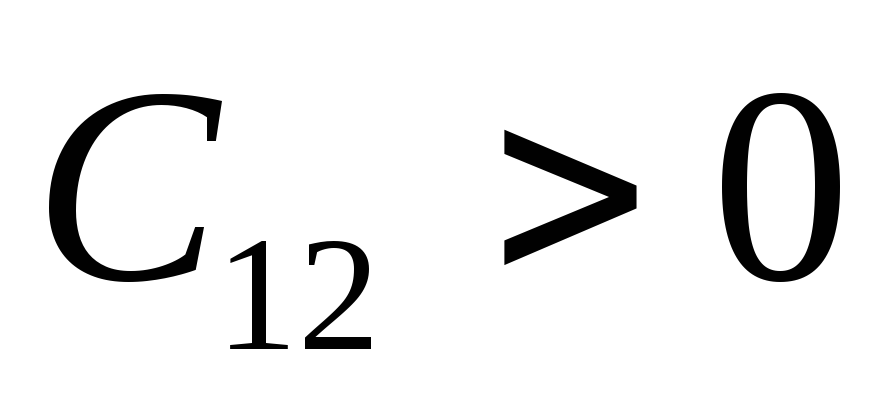то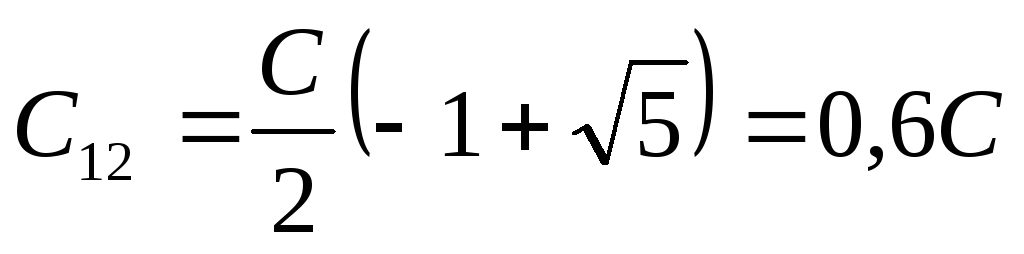
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярнымиинеполярными.Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю.
В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных» зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично.
П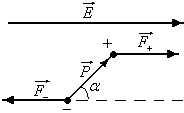
и
создает
вращательный момент равный
,
где
—
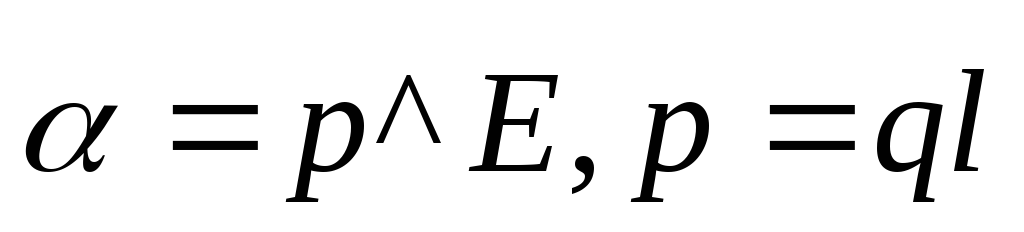дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах. Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю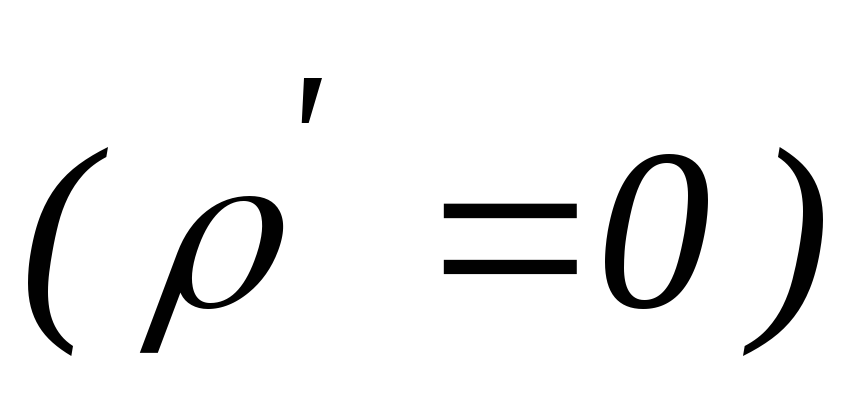 
.
Плоский конденсатор: формулы, особенности, конструкция
Плоский конденсатор – физическое упрощение, взявшее начало из ранних исследований электричества, представляющее собой конструкцию, где обкладки носят форму плоскостей и в любой точке параллельны.
Формулы
Люди ищут формулы, описывающие ёмкость плоского конденсатора. Читайте ниже любопытные и малоизвестные факты, сухие математические знаки также важны.
Первым определил ёмкость плоского конденсатора Вольта. В его распоряжении ещё не было величины – разница потенциалов, именуемая напряжением, но интуитивно учёный правильно объяснил суть явления. Величину количества зарядов трактовал как объем электрического флюида атмосферы – не совсем правильно, но похоже на правду. Согласно озвученному мировоззрению ёмкость плоского конденсатора находится как отношение объёма накопленного электрического флюида к разнице атмосферных потенциалов:
С = q/U.
Формула применима к любому конденсатору, вне зависимости от конструкции. Признана универсальной. Специально для плоских конденсаторов разработана формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры:
В этой формуле через S обозначена площадь обкладок, вычисляемая через произведение сторон, а d – показывает расстояние между обкладками. Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика. Электролитические конденсаторы обладают столь большой ёмкостью по понятной причине: проводящий раствор отделен от металла крайне тонким слоем оксида. Следовательно, d оказывается минимальным. Единственный минус – электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на аноде или катоде обозначены значками плюса или минуса.
Плоские конденсаторы сегодня редко встречаются, это преимущественно плёночные микроскопические технологии, где указанный род поверхностей считается доминирующим. Все пассивные и активные элементы образуются через трафарет, образуя вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст.
От материала диэлектрика зависит ёмкость, у каждого собственная структура. Считается, что аморфное вещество состоит из неориентированных диполей, упруго укреплённых на своих местах. При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость. В результате заряд накапливается, пока процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на места, делая возможным новый рабочий цикл. Так функционирует плоский электрический конденсатор.
Конденсатор для уроков
Из истории
Первым начал исследовать накопление заряда великий Алессандро Вольта. В докладе Королевскому научному обществу за 1782 год впервые озвучил слово конденсатор. В понимании Вольты электрофорус, представляющий две параллельные обкладки, выкачивал из эфира электрический флюид.
В давнее время все познания сводились к мнению учёных, будто атмосфера Земли содержит нечто, не определяемое приборами. Присутствовали простейшие электроскопы, способные определить знак заряда и его наличие, не дававшие представления о количестве. Учёные просто натирали мехом поверхность тела и подносили для исследования в область влияния прибора. Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием. Учёные примерно знали, что делать, но исследования не продвигались.
Гипотеза об атмосферном электричестве высказана Бенджамином Франклином. Он активно исследовал молнии и пришёл к выводу, что это проявления прежней единой силы. Запуская воздушного змея в небо, он соединял игрушку шёлковой нитью с землёй и наблюдал дуговой разряд. Это опасные опыты, и Бенджамин многократно рисковал собственной жизнью ради развития науки. Шёлковая нить проводит статический заряд – это доказал Стивен Грей, первый собравший в 1732 году электрическую цепь.
Уже через 20 лет (1752 год) Бенджамин Франклин предложил конструкцию первого громоотвода, осуществлявшего молниезащиты близлежащих построек. Только вдуматься! – прежде любой ожидал, что дом сгорит от случайного удара. Бенджамин Франклин предложил один вид заряда называть положительным (стеклянный), а второй отрицательным (смоляной). Так физики оказались введены в заблуждение относительно истинного направления движения электронов. Но откуда возьмётся иное мнение, когда в 1802 году на примере опытов россиянина Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, но в действительности это оказались ионы воздушной плазмы.
К началу исследования Вольтой электрических явлений уже известны статические заряды и факт наличия у них двух знаков. Люди упорно считали, что «флюид» берётся из воздуха. На эту мысль натолкнули опыты с натиранием янтаря шерстью, не воспроизводимые под водой. Следовательно, логичным стало предположить, что электричество может происходить исключительно из атмосферы Земли, что, конечно же, неверно. К примеру, многие растворы, исследованные Хампфри Дэви, проводят электрический ток.
Причина, следовательно, иная – при натирании янтаря под водой силы трения снижались в десятки и сотни раз, а заряд рассеивался по объёму жидкости. Следовательно, процесс лишь оказывался неэффективным. Сегодня каждый добытчик знает, что нефть электризуется трением о трубы без воздуха. Следовательно, атмосфера для «флюида» не считается обязательным компонентом.
Самый большой в мире плоский конденсатор
Столь систематизированные, но в корне неверные толкования не остановили Вольту на исследовательском пути. Он упорно изучал электрофорус, как совершенный генератор того времени. Вторым был серный шар Отто фон Герике, изобретённый на век раньше (1663 год). Его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. К примеру, в электрофорной машине применяются металлические гребёнки-нейтрализаторы.
Долгое время учёные раскачивались. Электрофорная машина 1880 года вправе считаться первым мощным генератором разряда, позволявшим получить дугу, но истинной силы электроны достигли в генераторе Ван де Граафа (1929 год), где разница потенциалов составила единицы мегавольта. Для сравнения – грозовое облако, согласно данным Википедии, обнаруживает потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Суммируя сказанное, с определённой долей уверенности скажем, что природные процессы используют в качестве принципа действия электризацию трением, влиянием и прочие виды, а мощный циклон считается самым большим из известных плоских конденсаторов. Молния показывает, что случается, когда диэлектрик (атмосфера) не выдерживает приложенной разницы потенциалов и пробивается. В точности аналогичное происходит в плоском конденсаторе, созданном человеком, если вольтаж оказывается непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя.
Электрофорус
Итак, Вольта взялся за исследование модели природных процессов. Первый электрофорус появился в 1762 году сконструированный Йоханом Карлом Вильке. По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта дал прибору нынешнее название.
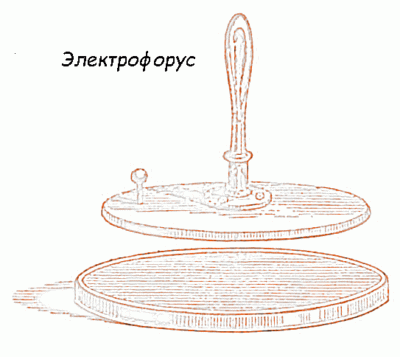
Вид электрофоруса
Электрофорус способен накапливать электростатический заряд, образованный трением резины куском шерсти. Состоит из двух плоских, параллельных друг другу обкладок:
- Нижняя представляет тонкий кусок резины. Толщина выбирается из соображений эффективности устройства. Если выбрать кусок солиднее, значительная часть энергии станет накапливаться внутри диэлектрика на ориентацию его молекул. Что отмечается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.
- Верхняя пластина из тонкой стали кладётся сверху, когда заряд уже накоплен трением. За счёт влияния на верхней поверхности образуется избыток отрицательного заряда, снимаемого на заземлитель, чтобы при расстыковке двух обкладок не произошло взаимной компенсации.
Принцип действия плоского конденсатора уже понятен. Оператор трёт резину шерстью, оставляя на ней отрицательный заряд. Сверху кладётся кусок металла. Из-за значительной шероховатости поверхностей они не соприкасаются, но находятся на расстоянии друг от друга. В результате металл электризуется влиянием. Электроны отталкиваются поверхностным зарядом резины и уходят на внешнюю плоскость, где оператор их снимает через заземлитель лёгким кратковременным прикосновением.
Низ металлической обкладки остаётся заряженным положительно. При расстыковке двух поверхностей этот эффект сохраняется, в материале наблюдается дефицит электронов. И заметно искру, если дотронуться до металлической обкладки. Этот опыт допускается на единственном заряде резины проделывать сотни раз, её поверхностное статическое сопротивление крайне велико. Это не даёт заряду растекаться. Демонстрируя описанный опыт, Вольта привлёк внимание научного мира, но исследования не двигались вперёд, если не считать открытий Шарля Кулона.
В 1800 году Алессандро даёт толчок развитию изысканий в области электричества, изобретя знаменитый гальванический источник питания.
Конструкция плоского конденсатора
Электрофорус представляет собой первый из сконструированных плоских конденсаторов. Его обкладки способны хранить только статический заряд, иначе наэлектризовать резину невозможно. Поверхность чрезвычайно долго хранит электроны. Вольта даже предлагал снимать их пламенем свечи через ионизированный воздух или ультрафиолетовым излучением Солнца. Сегодня каждый школьник знает, что явление проделывается водой. Правда, электрофорус потом потребуется высушить.
В современном мире нижней обкладкой служит тефлоновое покрытие или пластик. Они хорошо набирают статический заряд. Диэлектриком становится воздух. Чтобы перейти к конструкции современного конденсатора, нужно обе обкладки сделать металлическими. Тогда при возникновении на одной заряда электризация распространится на вторую, и если другой контакт заземлён, накопленная энергия хранится определённое время.
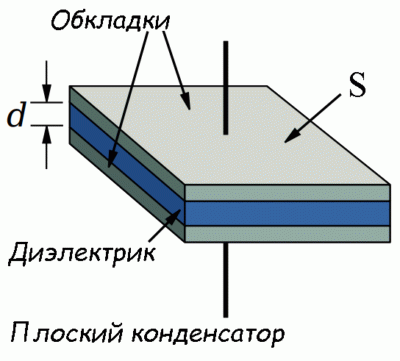
Конструкция в деталях
Запас электронов напрямую зависит от материала диэлектриков. К примеру, среди современных конденсаторов встречаются:
- Слюдяные.
- Воздушные.
- Электролитические (оксидные).
- Керамические.
В эти названия заложен материал диэлектрика. От состава зависит напрямую ёмкость, способная увеличиваться многократно. Роль диэлектриков объяснялась выше, их параметры определяются непосредственно строением вещества. Однако многие материалы, обладающие высокими характеристиками, использовать не удаётся по причине их непригодности. К примеру, вода характеризуется высокой диэлектрической проницаемостью.
Ёмкость плоского конденсатора | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Ёмкость плоского конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.
Под зарядом конденсатора понимают заряд одной пластины.
Так же есть:
Энергия конденсатора:
Ёмкость конденсатора :
Ёмкость цилиндрического конденсатора :
Емкость сферического конденсатора :
В формуле мы использовали :
— Электрическая ёмкость (ёмкость конденсатора)
— Относительная диэлектрическая проницаемость
— Электрическая постоянная
— Площадь одной обкладки
— Расстояние между обкладками
— Напряжение на обкладках
— Заряд конденсатора
Ёмкость плоского конденсатора.
Плоский конденсатор состоит из двух
параллельных пластин, разделённых
небольшим зазором шириной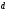 
,
заполненным однородным диэлектриком.
Нам известно, что поле между двумя
разноимённо заряженными пластинами с
одинаковой по величине поверхностной
плотностью 
равно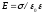
,
где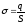
,S– площадь каждой пластины.
Напряжение между обкладками:
.
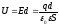Используя определение емкости конденсатора, получаем:
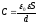
Отметим, что полученная формула является
приближенной, так как выведена без учета
искажения поля у краев пластин. Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор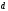 
по сравнению с линейными размерами
пластин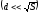
.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет
собой систему двух концентрических
сфер с радиусам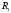и 
и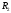
.
Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы. Напряжение между
обкладками равно: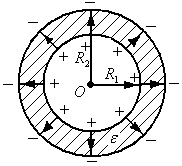
.
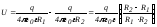Для ёмкости сферического конденсатора получаем:
.
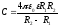Это формула точная.
Если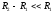 
,
полученная формула переходит в выражение
для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет
систему двух коаксиальных цилиндров с
радиусам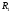и 
и
,
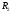длиной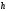
.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
.
.
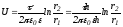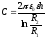Полученная формула является приближенной
и при малом зазоре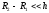 
переходит в формулу емкости плоского
конденсатора.
Соединение конденсаторов.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного соединения конденсаторов.
Заряды последовательно соединенных
конденсаторов равны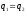 
,
а напряжение на батарее
.
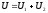Из определения емкости следует:
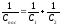
или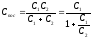 
.
Если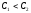 
,
то
(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении).
Для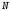 
последовательно соединенных конденсаторов
емкость вычисляется по формуле:
.
В
случае одинаковых конденсаторов: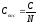 
.
Ёмкость параллельного соединения конденсаторов.
Заряд батареи равен сумме зарядов:
,
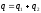а
напряжение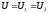 
.
По определению емкости получаем:
.
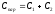Для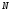 
параллельно соединенных конденсаторов:
.
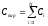В
случае одинаковых конденсаторов: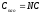 
.
Пример.
Оценить
емкость батареи (см. рисунок)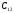 
.
.
Ответ:
.
Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок).
Для
расчета ёмкости батареи получаем: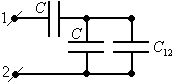
,
.
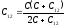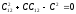Откуда: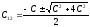 
,
так как
,
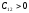то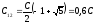
.
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярнымиинеполярными.Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных» зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично.
Под действием электрического поля
диполи ориентируются преимущественно
в направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара сил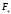 
и
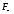создает
вращательный момент равный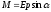
,
где
—
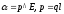дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.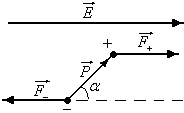
Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю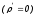 
.
6. Электроемкость. Конденсаторы. Емкость плоского конденсатора
Потенциал уединенного проводника пропорционален сообщенному ему заряду, поэтому отношение заряда проводника к его потенциалу не зависит от заряда и является характеристикой данного проводника.
Электроемкостью уединенного проводника называют величину, равную отношению заряда проводника к потенциалу этого проводника.
.
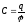
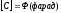
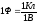На
практике применяются 
Электроемкость проводника не зависит от вещества, из которого он изготовлен, а зависит от его формы, размеров и диэлектрической проницаемости среды, в которой находится этот проводник.
Используя формулу потенциала электрического поля, созданного равномерно заряженным шаром
,
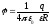для емкости шара получим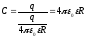 
.
КОНДЕНСАТОРЫ
Уединенные проводники обладают малой емкостью. На практике возникает потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе значительные заряды.
Конденсатором называют систему, состоящую из двух разделенных диэлектриком проводников, на которых могут накапливаться заряды противоположных знаков.
Проводники, образующие конденсатор, называют обкладками.
Чтобы внешние тела не влияли на емкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было полностью сосредоточено внутри конденсатора. Этому условию удовлетворяют две близко расположенные пластины, два коаксиальных цилиндра и две концентрические сферы.
Емкостью конденсатора называют величину, равную отношению заряда конденсатора к разности потенциалов (напряжению) между его обкладками
=
.
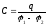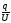ЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
Напряженность поля между обкладками плоского конденсатора
.
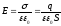Для однородного поля справедливо соотношение
.
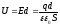Следовательно, емкость плоского конденсатора
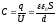
(S – площадь обкладок, d – расстояние между обкладками).
7. Соединение конденсаторов. Энергия заряженного конденсатора
При параллельном соединении конденсаторов напряжения на каждом конденсаторе одинаковы и равны напряжению на клеммах батареи
.
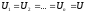Заряд батареи
.
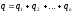Исходя
из того, что 
,
имеем
,
поэтому
.
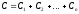При последовательном соединении конденсаторов
, 
.
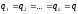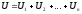Учитывая,
что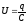 
,
имеем
,
поэтому при последовательном соединении конденсаторов
.
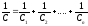ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
При
зарядке конденсатора совершается работа
по перемещению электрических зарядов
против сил электрического поля. При
перемещении заряда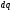 
совершается работа
.
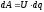Учитывая, что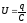
,
получим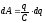
.
Следовательно,
.
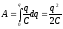По закону сохранения энергии эта работа равна энергии заряженного конденсатора, т.е.
.
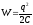Используя
формулы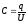 
и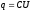
,
получим
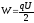и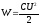 
.
8. Закон Ома для однородного участка цепи. Сопротивление проводников
Участок цепи, на котором не действуют сторонние силы, приводящие к возникновению ЭДС, называется однородным.
Согласно закону Ома для однородного участка цепи постоянного тока: сила тока в однородном проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению данного проводника.
.
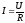Опыты показывают, что сопротивление R проводника пропорционально его длине, обратно пропорционально площади его поперечного сечения и зависит от вещества, из которого изготовлен проводник. Для однородного проводника длиной l и неизменной площадью поперечного сечения S эту зависимость выражают формулой
,
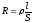где 
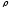— коэффициент пропорциональности,
называемый удельным электрическим
сопротивлением. Удельное сопротивление
равно сопротивлению проводника,
изготовленного из данного вещества и
имеющего единичную длину и единичную
площадь поперечного сечения. Удельное
сопротивление есть свойство проводника
и зависит от его состояния.
Сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений этих проводников.
.
Сопротивление цепи, состоящей из параллельно соединенных проводников можно определить из формулы
Конденсаторы
Электрическая емкость
При сообщении проводнику заряда на его поверхности появляется потенциал φ, но если этот же заряд сообщить другому проводнику, то потенциал будет другой. Это зависит от геометрических параметров проводника. Но в любом случае потенциал φ пропорционален заряду q.
| . | (5.4.1) |
Коэффициент пропорциональности С называют электроемкостью – физическая величина, численно равная заряду, который необходимо сообщить проводнику для того, чтобы изменить его потенциал на единицу.
| . | (5.4.2) |
Единица измерения емкости в СИ – фарада. 1 Ф = 1Кл/1В.
Если потенциал поверхности шара
| (5.4.3) |
то
| (5.4.4) |
По этой формуле можно рассчитать емкость Земли. Если диэлектрическая проницаемость среды ε = 1 (воздух, вакуум) и то имеем, что CЗ = 7·10–4 Ф или 700 мкФ.
Чаще на практике используют более мелкие единицы емкости: 1 нФ (нанофарада) = 10–9 Ф и 1пкФ (пикофарада) = 10–12 Ф.
Необходимость в устройствах, накапливающих заряд, есть, а уединенные проводники обладают малой емкостью. Опытным путем было обнаружено, что электроемкость проводника увеличивается, если к нему поднести другой проводник – за счет явления электростатической индукции.
Конденсатор – это два проводника, называемые обкладками, расположенные близко друг к другу.
Конструкция такова, что внешние, окружающие конденсатор тела, не оказывают влияние на его электроемкость. Это будет выполняться, если электростатическое поле будет сосредоточено внутри конденсатора, между обкладками.
Конденсаторы бывают плоские, цилиндрические и сферические.
Так как электростатическое поле находится внутри конденсатора, то линии электрического смещения начинаются на положительной обкладке, заканчиваются на отрицательной, и никуда не исчезают. Следовательно, заряды на обкладках противоположны по знаку, но одинаковы по величине.
Емкость конденсатора равна отношению заряда к разности потенциалов между обкладками конденсатора:
| (5.4.5) |
Помимо емкости каждый конденсатор характеризуется Uраб (или Uпр.) – максимальное допустимое напряжение, выше которого происходит пробой между обкладками конденсатора.
Соединение конденсаторов
Емкостные батареи – комбинации параллельных и последовательных соединений конденсаторов.
1) Параллельное соединение конденсаторов (рис. 5.9):
Рис. 5.9
В данном случае общим является напряжение U:
.
Суммарный заряд:
Результирующая емкость:
Сравните с параллельным соединением сопротивлений R:
.
Таким образом, при параллельном соединении конденсаторов суммарная емкость
.
Общая емкость больше самой большой емкости, входящей в батарею.
2) Последовательное соединение конденсаторов (рис. 5.10):
Общим является заряд q.
Рис. 5.10
или , отсюда
| (5.4.6) |
Сравните с последовательным соединением R:
Таким образом, при последовательном соединении конденсаторов общая емкость меньше самой маленькой емкости, входящей в батарею:
Расчет емкостей различных конденсаторов
1. Емкость плоского конденсатора
Напряженность поля внутри конденсатора (рис. 5.11):
Рис. 5.11
Напряжение между обкладками:
где – расстояние между пластинами.
Так как заряд , то
| . | (5.4.7) |
Как видно из формулы, диэлектрическая проницаемость вещества очень сильно влияет на емкость конденсатора. Это можно увидеть и экспериментально: заряжаем электроскоп, подносим к нему металлическую пластину – получили конденсатор (за счет электростатической индукции, потенциал увеличился). Если внести между пластинами диэлектрик с ε, больше, чем у воздуха, то емкость конденсатора увеличится.
Из (5.4.6) можно получить единицы измерения ε0:
| (5.4.8) |
.
2. Емкость цилиндрического конденсатора
Разность потенциалов между обкладками цилиндрического конденсатора, изображенного на рисунке 5.12, может быть рассчитана по формуле:
где λ – линейная плотность заряда,R1 иR2 – радиусы цилиндрических обкладок,l– длина конденсатора, .
Рис. 5.12
Тогда, так как , получим
| (5.4.9) |
Понятно, что зазор между обкладками мал: то есть
Тогда
| (5.4.10) |
3. Емкость шарового конденсатора (рис. 5.13)
Рис. 5.13
Из п. 3.6 мы знаем, что разность потенциала между обкладками равна:
Тогда, так как , получим
.
Это емкость шарового конденсатора, где R1 и R2 – радиусы шаров.
В шаровом конденсаторе – расстояние между обкладками. Тогда
| (5.4.11) |
Таким образом, емкость шарового конденсатора с достаточной степенью точности можно рассчитать так же, как и емкость плоского, и цилиндрического конденсаторов.
Формулы конденсатора
Формулы емкости конденсаторов
Для любого конденсатора справедлива формула:
где C – емкость конденсатора; q – величина заряда одной из обкладок конденсатора; – разность потенциалов между его обкладками.
Емкость конденсатора, между пластинами которого находится диэлектрик (C) (диэлектрическая проницаемость которого равна в раз больше, чем емкость такого же воздушного конденсатора ():
Для расчета емкости плоского конденсатора применяют формулу:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Емкость плоского конденсатора, содержащего N слоев диэлектрика (толщина i-го слоя равна , диэлектрическая проницаемость i-го слоя , определяется как:
Электрическая емкость цилиндрического конденсатора вычисляют как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Емкость сферического (шарового) конденсатора находят по формуле:
где – радиусы обкладок конденсатора.
Формулы для расчета емкости соединения конденсаторов
При параллельном соединении конденсаторов суммарная емкость батареи (C) равна сумме емкостей отдельных конденсаторов (), ее составляющих:
Электрическая емкость последовательного соединения конденсаторов может быть вычислена по формуле:
Если последовательно соединены N конденсаторов, с емкостями то емкость батареи вычислим как:
Сопротивление конденсатора
При включении конденсатора в цепь с постоянным током сопротивление конденсатора считают бесконечно большим.
Если конденсатор включен в цепь переменного тока, то его сопротивление называют емкостным и вычисляют при помощи формулы:
где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.
Формула энергии поля конденсатора
где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.
Энергия поля плоского конденсатора: