Энергия запасенная в конденсаторе « Учи физику!

Конденсаторы изготовляют для разных целей. В некоторых электрических цепях применение конденсаторов позволяет пропускать быстрые изменения потенциалов, но задерживать их медленные изменения. (Иначе говоря, как будет видно ниже, переменный ток может проходить через конденсаторы, в то время как постоянный — нет.) В других устройствах конденсаторы используются для того, чтобы накапливать на короткое время заряд, или электрическую энергию. На рисунке показан высоковольтный конденсатор, предназначенный для накопления энергии. Он имеет емкость в 1 микрофараду и рассчитан на разность потенциалов в 2000 вольт. В качестве диэлектрика в нем используется масло, что обеспечивает более высокую диэлектрическую проницаемость, чем воздух, и позволяет предотвратить проскакивание искр между пластинами.

Работа, совершаемая при переносе очередной небольшой порции заряда от нижней пластины к верхней, равна произведению имеющейся разности потенциалов на переносимый заряд: A

2=U₁Δq_2,

Когда переносится последняя порция заряда от нижней пластины к верхней, совершаемая работа равна произведению этого заряда на полную разность потенциалов в конденсаторе. Среднее значение разности потенциалов, через которую переносились заряды, равна половине окончательной разности потенциалов. Поэтому работа, совершаемая при зарядке конденсатора, равна qU/2, где U — разность потенциалов между пластинами, часто называемая «электрическое напряжение». Эта работа равна энергии W запасенной в конденсаторе.

 

Автор Кл. Э. Суорц “Необыкновенная физика обыкновенных явлений”

Интересные научные игрушки

Вывод формулы энергии запасенной в конденсаторе. Как работает ионистор. Ионистор

Вся энергия заряженного конденсатора накапливается в электрическом поле между его пластинами. Энергию, сосредоточенную в конденсаторе, можно вычислить следующим методом. Давайте представим себе, что мы заряжаем емкость не сразу, а потихоньку, перенося электрические заряды с одной его металлической пластины на другую.

Во время переноса первого заряда работа, совершенная нами, будет относительно небольшой. На уже на перенос второго электрического заряда мы истратим больше энергии, так как из-за переноса первого заряда, между металлическими пластинами конденсатора возникнет разность потенциалов, которую нам необходимо преодолевать, третий, четвертый и каждый последующий за ними одиночный заряд будет переносить значительно труднее и на их перенос придется расходовать все больше и больше энергии. Пусть мы перекинем таким образом некоторое определенное количество зарядов, которое мы условно обозначим латинской буквой

Q .

На прототипе мембраны исследовательская группа продемонстрировала отличные показатели энергопотребления. Се исследует возможность работы с инвесторами венчурного капитала для коммерциализации мембраны. Несколько рискованных инвесторов проявили интерес к этой мембранной технологии.

С появлением нашей новой мембраны хранение энергии будет намного более доступным, более доступным, и можно будет производить эту технологию в больших масштабах. Мембрана является экологически чистой и предлагает возможность изменять текущее состояние энергетических технологий, — говорит д-р.

Энергия поля конденсатора — обучающий видео фильм

Вся энергия, потраченная при заряде конденсатора, скопиться в электрическом поле между его металлическими пластинами. Напряжение между пластинами конденсатора в конце процесса заряда мы условно обозначим латинской буквой U .

Как мы уже поняли, разность потенциалов в процессе заряда емкости не остается постоянной, а постепенно возрастает от нуля — в начале заряда — до своего конечного значения напряжения. Для упрощения расчета энергии поля допустим, что мы перенесли полностью весь электрический заряд Q с одной пластины на другую не маленькими частями, а сразу. Но при этом мы считаем, что напряжение между металлическими пластинами было не ноль, как в начальный момент, и не какое-то значение

U , как в конце процесса заряда, а равнялось какому-то среднему значению от нуля и до U, т. е. половине U . Таким образом, энергия, накопленная в электрическом поле емкости, будет равна половине напряжения U, умноженной весь заряд перенесенного электричества Q .

Новейшая энергоемкая мембрана: производительность превосходит существующие аккумуляторные батареи и суперконденсаторы. Хм, поэтому мы сохраним полистирольную фольгу! Полистирол — это легковоспламеняющееся и термически не очень устойчивое вещество, не так ли? Формула для расчета конденсатора показывает, что чем ближе мы соединяем электроды, тем большая емкость мы получаем. Когда они производят полистирол «нанофолия», он может иметь вполне приличную емкость. Поэтому вам нужно искать не только конденсатор с большой емкостью, но прежде всего с наивысшим рабочим напряжением, а просто рискнуть венчурному капиталу.

Так как напряжение измеряется в вольтах, а количество электричества — в кулонах, то энергия W будет в джоулях. Так как заряд, накопленный между пластинами емкости, равен Q = C×U , то формулу можно перезаписать в следующей форме:

Эта получившееся формула говорит нам о том, что энергия, накопленная в поле конденсатора, равна половине произведения емкости на квадрат напряжения между его металлическими пластинами

.

Спасибо автору за Сиань Нин Се! Мембрана является ионно-проводящей, а энергия осаждается конденсацией подвижных катионов на мембране. Против декондиционирования освобождается заряд. Проблема в том, что у мембраны должна быть «красная куча» вокруг нее, которая заряжает ее. Поэтому вы не можете делать миниатюрные многослойные колпачки.

Но открытие весьма воодушевляет, если способность эффективно масштабироваться, одна из больших проблем человечества — эффективное хранение электроэнергии — решена. В этих электродах он рисовал колеса, которые были сильно раздуты в сторону изолятора и вдали от изолятора. В одном электро, он нарисовал плюсовые колеса, а другой минус. И выражение «конденсация подвижных катионов на мембране» переводит «кластеризацию положительных частиц в диэлектрики», т.е. описывает эту часть изображения с накопленным «плюсом».

Думаю данный вывод мы еще вспомним при изучении материала о колебательных контурах.

Энергия заряженной емкости

Конденсатор — это простой электротехнический прибор, обладающий свойством накопления энергией поля

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА

энергия поля конденсатора — занимательный опыт из курса физики и лекций по электротехнике с основами электроники.

В заряженном конденсаторе накоплена (аккумулирована) электрическая энергия. Эта энергия конденсатора равна работе, необходимой для зарядки конденсатора.
Процесс зарядки конденсатора состоит, по сути, в том, что заряд с одной пластины переносится на другую. Именно это совершает источник напряжения, когда его подключают к конденсатору. Сначала, когда конденсатор не заряжен, для переноса первой порции заряда не требуется работы.
Но когда на каждой из пластин уже имеется заряд, для пополнения его приходится совершать работу против сил электрического отталкивания. Чем больше накопленный пластинами заряд, тем большую работу, необходимо совершить для его увеличения. Если на пластинах существует разность потенциалов

V , работа по переносу элемента заряда dq равна dW = V dq . Поскольку V= q/C , где С — емкость конденсатора, тогда работа по его заряду составит:

Таким образом, этот принцип является нормальным конденсатором. Укажите электролитический конденсатор, когда ему нужен «красный бык» или электролит. Это чудесное 7 Вт будет потеряно, преж

Формула энергии конденсатора. Энергия запасенная в конденсаторе

Энергия запасенная в конденсаторе « Учи физику!

Конденсаторы изготовляют для разных целей. В некоторых электрических цепях применение конденсаторов позволяет пропускать быстрые изменения потенциалов, но задерживать их медленные изменения. (Иначе говоря, как будет видно ниже, переменный ток может проходить через конденсаторы, в то время как постоянный — нет.) В других устройствах конденсаторы используются для того, чтобы накапливать на короткое время заряд, или электрическую энергию. На рисунке показан высоковольтный конденсатор, предназначенный для накопления энергии. Он имеет емкость в 1 микрофараду и рассчитан на разность потенциалов в 2000 вольт. В качестве диэлектрика в нем используется масло, что обеспечивает более высокую диэлектрическую проницаемость, чем воздух, и позволяет предотвратить проскакивание искр между пластинами.

Работа, совершаемая при переносе очередной небольшой порции заряда от нижней пластины к верхней, равна произведению имеющейся разности потенциалов на переносимый заряд: A2=U1Δq2,

Когда переносится последняя порция заряда от нижней пластины к верхней, совершаемая работа равна произведению этого заряда на полную разность потенциалов в конденсаторе. Среднее значение разности потенциалов, через которую переносились заряды, равна половине окончательной разности потенциалов. Поэтому работа, совершаемая при зарядке конденсатора, равна qU/2, где U — разность потенциалов между пластинами, часто называемая «электрическое напряжение». Эта работа равна энергии W запасенной в конденсаторе.

 

Автор Кл. Э. Суорц “Необыкновенная физика обыкновенных явлений”

Интересные научные игрушки

uchifiziku.ru

Формула расчета энергии конденсаторов, как зарядить плоский конденсатор

Конденсаторы являются неотъемлемой частью электрических схем. В большинстве случаев оперируют такими понятиями, как емкость и рабочее напряжение. Эти параметры являются основополагающими.

Конденсаторы различных типов

В некоторых случаях для более полного понимания работы упомянутого элемента необходимо иметь представление, что означает энергия заряженного конденсатора, как она вычисляется и от чего зависит.

Определение понятия энергии

Наиболее просто вести рассуждения применительно к плоскому конденсатору. В основе его конструкции лежат две металлических обкладки, разделенные тонким слоем диэлектрика.

Плоский конденсатор

Если подключить емкость к источнику напряжения, то нужно обратить внимание на следующее:

• На разделение зарядов по обкладкам электрическим полем затрачивается определенная работа. В соответствии с законом сохранения энергии, эта работа равняется энергии заряженного конденсатора;
• Разноименно заряженные обкладки притягиваются друг к другу. Энергия заряженного конденсатора в этом случае равняется работе, затраченной на сближение пластин друг к другу вплотную.

Данные соображения позволяют сделать вывод, что формулу энергии заряженного конденсатора можно получить несколькими способами.

Вывод формулы

Энергия заряженного плоского конденсатора наиболее просто определяется, исходя из работы по сближению обкладок.

Рассмотрим силу притяжения единичного заряда одной из обкладок к противоположной:

F=q0E.

В данном выражении q0 – величина заряда, E – напряженность поля обкладки.

Поскольку напряженность электрического поля определяется из выражения:

E=q/(2ε0S), где:

• q – величина заряда,
• ε0 – электрическая постоянная,
• S – площадь обкладок,

формулу силы притяжения можно записать как:

F=q0 q/(2ε0S).

Для всех зарядов сила взаимодействия между обкладками, соответственно, составляет:

F=q2/(2ε0S).

Работа по сближению пластин равняется произведению силы взаимодействия на пройденное расстояние. Таким образом, энергия заряженного конденсатора определяется выражением:

W=A=Fd.

Важно! В приведенном выражении должна быть разница в положениях пластин. Записывая только одну величину d, подразумеваем, что конечным результатом будет полное сближение, то есть d2=0.

С учетом предыдущих выражений можно записать:

W=d q2/(2ε0S).

Известно, что емкость плоского конденсатора определяется из такого выражения:

C=d/(ε0S).

В результате энергия определяется как:

W=q2/(2С).

Полученное выражение неудобно тем, что вызывает определенные затруднения определения заряда на обкладках. К счастью, заряд, емкость и напряжение имеют строгую взаимосвязь:

q = С U.

Теперь выражение принимает полностью понятный вид:

W=CU2/2.

Полученное выражение справедливо для конденсаторов любых типов, не только плоских, и позволяет без затруднений в любой момент времени определять накопленную энергию. Емкость обозначается на корпусе и является величиной постоянной. В крайнем случае ее несложно измерять, используя специальные приборы. Напряжение измеряется вольтметром с необходимой точностью. К тому же очень просто зарядить конденсатор не полностью (меньшим напряжением), снизив, таким образом, запасенную энергию.

Для чего необходимо знать энергию

В большинстве случаев применения емкостей в электрических цепях понятие энергии не употребляется. Особенно это относится к время,- и частотозадающим цепям, фильтрам. Но есть области, где необходимо использовать накопители энергии. Наиболее яркий пример –фотографические вспышки. В накопи

Накопление электрической энергии

Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.

В заряженном конденсаторе накоплена (аккумулирована) электрическая энергия. Эта энергия конденсатора равна работе, необходимой для зарядки конденсатора.
Процесс зарядки конденсатора состоит, по сути, в том, что заряд с одной пластины переносится на другую. Именно это совершает источник напряжения, когда его подключают к конденсатору. Сначала, когда конденсатор не заряжен, для переноса первой порции заряда не требуется работы.

Но когда на каждой из пластин уже имеется заряд, для пополнения его приходится совершать работу против сил электрического отталкивания. Чем больше накопленный пластинами заряд, тем большую работу, необходимо совершить для его увеличения. Если на пластинах существует разность потенциалов V, работа по переносу элемента заряда dq равна dW = V_dq. Поскольку V= q/C , где С — емкость конденсатора, тогда работа по его заряду составит:

Итак, мы можем сказать, что энергия, запасенная, или аккумулированная, конденсатором, равна

если заряды обкладок конденсатора емкостью С равны соответственно +Q и -Q. А так как Q = СV, где V — разность потенциалов между обкладками, мы можем написать

Пример 25.5. Конденсатор емкостью 20 мкФ подключен к батарее напряжением 12 В. Какую энергию может запасти конденсатор?

Решение. Согласно (25.5),

Энергия не является «вещественной субстанцией», поэтому она вовсе не должна быть где-то сосредоточена. Тем не менее принято считать, что она запасена электрическим полем между пластинами.

Для примера выразим энергию плоского конденсатора через напряженность электрического поля. Мы показали [см. (24.3)], что между параллельными пластинами существует приблизительно однородное электрическое поле Е и его напряженность связана с разностью потенциалов соотношением V = Ed, где d — расстояние между пластинами.
Кроме того, согласно (25.2), емкость плоского конденсатора равна С = s₀ A/d. Тогда

Произведение Ad характеризует объем, занимаемый электрическим полем Е. Разделив обе части формулы на объем, получим выражение для энергии, запасенной в единице объема, или плотности энергии u:

Плотность электростатической энергии, запасенной в любой части пространства, пропорциональна квадрату напряженности электрического поля в этой области.

Выражение (25.6) получено для частного случая плоского конденсатора. Можно показать, однако, что оно справедливо для любой области пространства, в которой существует электрическое поле.

Продолжение следует. Коротко о следующей публикации:

Диэлектрики.
В конденсаторах между пластинами проложен изолирующий материал (диэлектрик), например слюда или пластмассовая пленка. Этим достигается сразу несколько целей. Во-первых, диэлектрики лучше противостоят электрическому пробою, чем воздух, и к конденсатору можно приложить более высокое напряжение. Во-вторых, при наличии диэлектрика пластины можно расположить ближе друг к другу без опасения, что они могут соприкасаться. В третьих, ёмкость конденсатора увеличится в несколько раз благодаря электрической поляризации диэлектрика.

Альтернативные статьи: Переменный ток, Закон Ома.

---

Замечания и предложения принимаются и приветствуются!

Разряд конденсатора с выделением тепла

Переходные процессы – сложная тема, сложная даже для студентов, тем более – для школьников. Помните: постоянный ток не протекает через конденсатор. Напряжение на конденсаторе определяется его подключением: если параллельно резистору – то напряжение такое же, как на резисторе, если последовательно с источником – то конденсатор зарядится до ЭДС источника, после чего ток исчезнет. Если дать конденсатору возможность разрядиться – то энергия, запасенная в нем, превратится в тепло на резисторе.

Задача 1. Источник постоянного тока с ЭДС В и внутренним сопротивлением Ом подсоединен к параллельно соединенным резисторам Ом, Ом и конденсатору. Определите емкость конденсатора С, если энергия электрического поля конденсатора равна мкДж.

К задаче 1

Определить емкость легко из энергии конденсатора, только надо знать напряжение:

   

Объединим резисторы в один:

   

Ток в неразветвленной части цепи равен

   

Напряжение на внутреннем сопротивлении тогда равно

   

Тогда на резисторах и конденсаторе напряжение

   

Емкость равна

   

Ответ: мкФ.
Задача 2. Источник постоянного напряжения с ЭДС 100 В подключен через резистор к конденсатору переменной емкости, расстояние между пластинами которого можно изменять (см. рис.). Пластины медленно раздвинули. Какая работа была совершена против сил притяжения пластин, если за время движения пластин на резисторе выделилось количество теплоты 10 мкДж и заряд конденсатора изменился на 1 мкКл?

К задаче 2

У конденсатора была энергия до того, как пластины раздвинули – пусть . И после тоже была – пусть . В процессе раздвижения пластин совершили работу (которую надо найти), и, так как заряд уменьшился (а он именно уменьшился, так как напряжение осталось тем же), то источник тоже совершил работу. Поэтому закон сохранения энергии запишется так:

   

   

   

Заряд на конденсаторе сначала: , потом – . Тогда изменение заряда равно

   

Работа источника

   

Тогда наш закон сохранения можно переписать:

   

   

Ответ: 60 мкДж

Задача 3. Заряженный конденсатор мкФ включен в последовательную цепь из резистора Ом, незаряженного конденсатора мкФ и разомкнутого ключа К (см. рис.). После замыкания ключа в цепи выделяется количество теплоты  мДж. Чему равно первоначальное напряжение на конденсаторе ?

К задаче 3

Первоначально на конденсаторе есть заряд:

   

После замыкания ключа заряд разделится:

   

Но напряжение на конденсаторах одно и то же:

   

   

Тогда

   

Откуда:

   

   

Энергия до замыкания, запасенная в конденсаторе , сохраняется:

   

   

   

   

   

   

   

Ответ:

Задача 4. В электрической схеме, показанной на рисунке, ключ К замкнут. ЭДС батарейки В, сопротивление резистора Ом, заряд конденсатора 2 мкКл. После размыкания ключа К в результате разряда конденсатора на резисторе выделяется количество теплоты 20 мкДж. Найдите внутреннее сопротивление батарейки .

К задаче 4

Сначала на конденсаторе напряжение такое же, как на резисторе (потому что они включены параллельно):

   

Определим ток. Он замыкается в контуре , потому что постоянный ток не течет через конденсатор:

   

Тогда напряжение на резисторе и конденсаторе:

   

С другой стороны, когда ключ разомкнется, вся энергия, запасенная в конденсаторе, рассеется в виде тепла через резистор:

   

То есть

   

Приравняем:

   

   

А внутреннее сопротивление равно

   

Ответ:

Энергия заряженного конденсатора

Задание: Два конденсатора имеют емкости $C_1\ и\ C_2$. Они заряжены до напряжений $U_1\ и\ U_2$ соответственно. Конденсаторы соединили параллельно. Определите, какое количество тепла выделится при таком соединении?

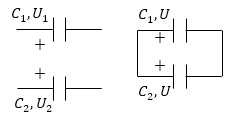
Рис. 1

Решение:

Потенциалы обкладок, которые соединили стали одинаковыми. По закону сохранения сумма заряда на обкладках конденсаторов сохранилась.

Значит можно записать следующее:

\[q_1+q_2=\widetilde{q_1}+\widetilde{q_2}\left(1.1\right),\]

где $q_1; q_2$ заряды конденсаторов до того как их соединили, соответственно $\widetilde{q_1};;\widetilde{q_2}$ — заряды конденсаторов после их соединения. Причем:

\[q_1=C_1U_1,\] \[q_2=C_2U_2\ \left(1.2\right).\]

Количество тепла, которое выделится при соединении конденсаторов равно:

\[Q=W_1-W_2\left(1.3\right),\]

где $W_1$ — суммарная энергия конденсаторов до соединения, $W_2$ — сумма энергий полей конденсаторов после соединения. Причем:

\[W_1=\frac{1}{2}\left(C_1{U_1}^2+C_2{U_2}^2\right)\left(1.4\right).\] \[W_2=\frac{С U^2}{2}\ \left(1.5\right).\]

Подставим (1.5) и (1.4) в уравнение (1.3), получим:

\[Q=\frac{1}{2}\left(C_1{U_1}^2+C_2{U_2}^2\right)-\frac{СU^2}{2}\ \left(1.6\right).\]

Емкость параллельного соединения конденсаторов (С) найдем как:

\[С=C_1+C_2\left(1.7\right).\]

Если уравнение (1.1) переписать, заменив заряды, на соответствующие произведения емкостей и разностей потенциалов, то получим:

\[C_1U_1+C_2U_2=C_1U+C_2U\ \left(1.8\right).\]

Выразим из (1.8) разность потенциалов на конденсаторах после их соединения:

\[\frac{C_1U_1+C_2U_2}{C_1+C_2}=U\ \left(1.9\right).\]

Подставим (1.9) в (1.6) найдем искомую теплоту:

\[Q=\frac{C_1C_2{\left(U_1-U_2\right)}^2}{2{(C}_1+C_2)}.\]

Ответ: $Q=\frac{C_1C_2{\left(U_1-U_2\right)}^2}{2{(C}_1+C_2)}.$

КОНДЕНСАТОР КАК АВТОНОМНЫЙ ИСТОЧНИК ЭНЕРГИИ

УДК 621.314 КОНДЕНСАТОР КАК АВТОНОМНЫЙ ИСТОЧНИК ЭНЕРГИИ Викторова И.В., студентка 3-го курса; Чашко М.В., канд. техн. наук, доц (Донецкий национальный технический университет г. Донецк, Украина) Работа посвящена электропитанию потребителей, удаленных от магистральных электрических сетей. Актуальность темы обусловлена возможностью снизить стоимость энергопитания удаленных потребителей использованием автономного питания на основе суперконденсатора. Проблемы, которые возникают для использования автономных источников энергии, например, солнечной или энергии ветра – это  неравномерность солнечного излучения или скорости ветра. Эта проблема решается применением накопителя электроэнергии большой емкости, например, суперконденсатора или сверхпороводникового накопителя. Цель настоящей работы – предложить схемы и оценить количественно параметры энергоблока для потребителя, удаленного от магистральной электрической сети. На рисунке представлена схема питания потребителя переменного тока. Рисунок – Структурная схема комбинированного энергоблока. Она содержит солнечную батарею 1, регулятор  отбора энергии от батареи 2, который состоит из коммутатора и устройства, повышающего  напряжение. Последнее необходимо, т.к. количество энергии, запасенной конденсатором, пропорционально квадрату напряжения. В качестве запасника энергии применен электрический конденсатор 3 ИКЭ «ЭКОНД» большой емкости Его энергоемкость составляет 108 Дж/м3 при  КПД заряда – разряда 90%. Предусмотрен регулятор 4 передачи энергии в систему, который согласует напряжение конденсатора с напряжением, которое необходимо потребителю. Как правило, потребителем является трехфазная нагрузка переменного тока, поэтому в схему введен автономный инвертор 5, от которого питается нагрузка 6. Питание потребителя происходит следующим образом. Облучение солнечной батареи 1 вызывает в ее цепи электрический ток, пропорциональный световому потоку. Напряжение каждой ячейки батареи приблизительно 0,5 В, ячейки в батарее могут быть собраны последовательно для увеличения выходного напряжения, но по электрической прочности полупроводниковых элементов выходное напряжение батареи не превышает десятков вольт.  Ток батареи поступает в регулятор 2, который повышает его напряжение до сотен вольт и обеспечивает экономичный режим заряда конденсатора 3. В электрическом поле конденсатора энергия накапливается и сохраняется до востребования потребителем. Когда энергию нужно передать в нагрузку, напряжение конденсатора преобразователем 4 снижается до значения напряжения, номинального для потребителя и подается на инвертор 5, которым оно преобразуется в 3-х фазное переменное стандартной частоты. Специфика солнечной и ветровой энергетики в неравномерности поступления энергии по часам суток и по временам года. Поэтому энергоблок должен быть снабжен еще одним автономным источником. Дополнительно к солнечной батарее энергоблок содержит ветровую турбину с генератором 7 и преобразователь 8, согласующий напряжения этого генератора и конденсатора.  При длительном отсутствии солнечного излучения потребитель получает энергию от ветрового генератора. Для этого генератор 7 вырабатывает энергию на номинальном для него напряжении, преобразователь 8 изменяет напряжение до значения, необходимого для заряда конденсатора, далее процесс передачи энергии потребителю происходит как и при питании от солнечной батареи.  Пространственные параметры солнечной батареи определены для батареи SolarGen. За год на широте Украины батарея может выработать 200 кВт·ч/(год· м2). Считаем, что установленная мощность потребителя 10 кВт и работает 10 часов в сутки. Тогда годовая потребность в электроэнергии потребителя составляет 30 тыс. кВт·ч. Из этого следует, что площадь батареи, необходимая для удовлетворения годовой потребности составляет 150 м2 или квадрат со стороной приблизительно 12 м. Такой размер позволяет расположить солнечную батарею на крыше дома или подсобного помещения.  Выводы. Существует возможность снабжать электроэнергией удаленные от магистральных линий электропередач объекты от солнечных энергоблоков. Целесообразно выполнять энергоблок комбинированным, содержащим, кроме солнечного, электромеханический преобразователь энергии.