Калькулятор резистивно-емкостной цепи • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Данный калькулятор позволяет рассчитывать максимальный ток I_max в начале заряда конденсатора, максимальную энергию E_max и максимальный заряд конденсатора Q_max, когда он полностью заряжен при данном напряжении, а также постоянную времени RC-цепи.

Пример. Рассчитать постоянную времени, максимальную энергию, максимальный ток и максимальный заряд для цепи, состоящей из последовательно соединенных резистора 2 кОм и конденсатора 5 мкФ. Цепь подключена к источнику постоянного напряжения 10 V. Обратите внимание: напряжение не нужно для расчета постоянной времени RC-цепи.

Входные данные

Напряжение V

микровольт (мкВ)милливольт (мВ)вольт (В)киловольт (кВ)мегавольт (МВ)

Емкость C

фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)

Сопротивление R

миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)

Выходные данные

Постоянная времени

τ с

Макс.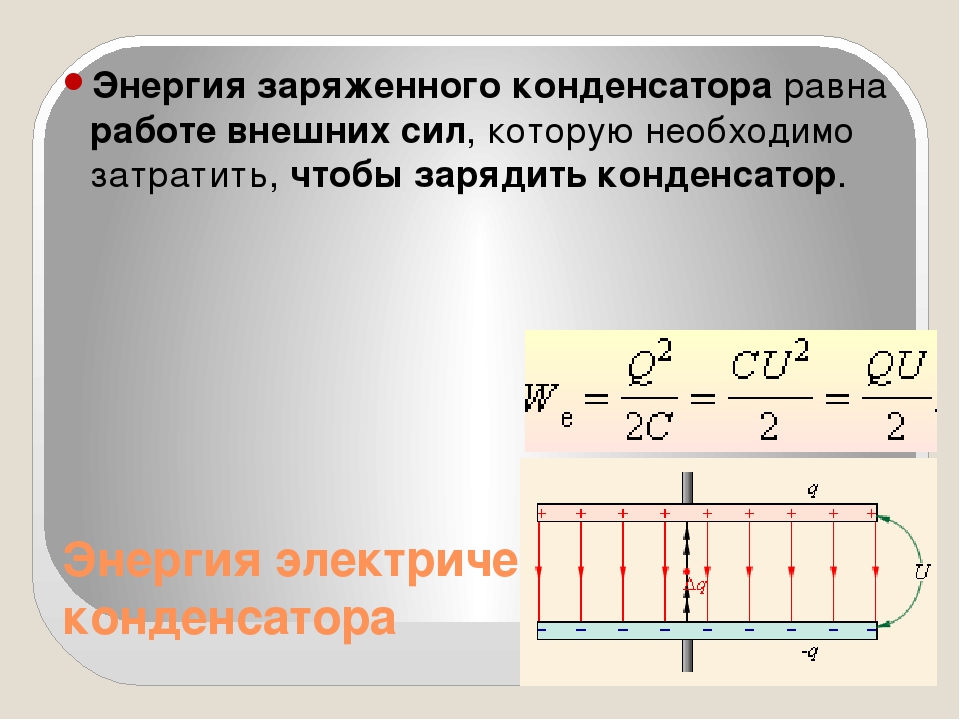 энергия

E Дж

Макс. ток

I А

Макс заряд

Q Кл

Введите величины в поля для ввода, выберите единицы измерения и нажмите кнопку Рассчитать.

Постоянная времени определяется по формуле

где τ — постоянная времени в секундах, R — сопротивление в омах и C — емкость в фарадах. Постоянная времени RC-цепи определяется как время, которое требуется, чтобы конденсатор зарядился до 63,2% его максимально возможного заряда при условии, что начальный заряд нулевой. Отметим, что конденсатор зарядится до 63,2% за время τ и почти полностью (до 99,3%) зарядится за время 5τ.

Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой

где C — емкость в фарадах и V — напряжение в вольтах.

Максимальный ток I определяется по закону Ома:

Максимальный заряд Q определяется по формуле

где C — емкость в фарадах и V — напряжение в вольтах.

Фильтрующие электролитические конденсаторы на системной плате компьютера

Применение

Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе

Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор. Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.

Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.

Резистивно-емкостные фильтры нижних частот

Пример двухкаскадного RC-фильтра нижних частот с неинвертирующим операционным усилителем с единичным коэффициентом передачи, который используется в качестве буфера между двумя каскадами фильтра

Фильтры нижних частот пропускают только низкочастотные сигналы и подавляют высокочастотные сигналы. Частота среза определяется компонентами фильтра.

Такие фильтры широко используются в электронике. Например, их используют в сабвуферах для того, чтобы не подавать на них звуки высоких частот, которые они не могут воспроизводить. Фильтры нижних частот используются также в радиопередатчиках для блокировки нежелательных высокочастотных составляющих в передаваемом сигнале. У тех, кто пользуется ADSL подключением к Интернету, всегда установлены частотные разделители с такими фильтрами нижних частот, которые предотвращают возникновение помех в аналоговых устройствах (телефонах) от сигналов DSL и воздействия помех от аналоговых устройств на оборудование DSL, подключенное к обычной телефонной линии.

Фильтры нижних частот используются для обработки сигналов перед их аналого-цифровым преобразованием. Такие фильтры улучшают качество аналоговых сигналов при их дискретизации и необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста таким образом, чтобы он удовлетворял требованиям теоремы Котельникова для данной частоты дискретизации, то есть максимальная частота не должна быть выше половины частоты выборки.

На верхнем рисунке показан простой фильтр нижних частот. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот (ФНЧ). В более сложных пассивных ФНЧ используются также катушки индуктивности.

В отличие от пассивных фильтров нижних частот, в активных фильтрах используются усилительные устройства, например, транзисторы или операционные усилители. В пассивные фильтрах также часто имеются операционные усилители, применяемые для развязки. В зависимости от количества конденсаторов и катушек индуктивности, влияющих на крутизну частотной характеристики фильтра, они обычно называются «фильтрами первого порядка», «второго порядка» и так далее. Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.

Простой пассивный RC-фильтр верхних частот

RC-фильтры верхних частот

Фильтры верхних частот пропускают только высокочастотные составляющие сигналов и ослабляют низкочастотные составляющие. Фильтры верхних частот используются, например, в разделительных фильтрах звуковых частот (кроссоверах) для подавления низкочастотных составляющих в сигналах, подаваемых на высокочастотные динамики («пищалки»), которые не могут воспроизводить такие сигналы и к тому же обладают малой мощностью по сравнению с мощностью низкочастотных сигналов.

Активный фильтр верхних частот с операционным усилителем

Фильтры верхних частот часто используются для блокировки постоянной составляющей сигналов в тех случаях, когда она нежелательна. Например, в профессиональных микрофонах очень часто используется «фантомное» питание постоянным напряжением, которое подается по микрофонному кабелю. В то же время микрофон записывает переменные сигналы, такие как человеческий голос или музыка. Постоянное напряжение не должно появляться на выходе микрофона и не должно поступать на вход микрофонного усилителя, поэтому для его блокировки используется фильтр верхних частот.

Простой полосовой фильтр, собранный из двух каскадов — фильтра нижних частот (C2, R2) и фильтра высоких частот (C1, R1)

Если фильтр нижних частот и фильтр верхних частот стоят друг за другом, они образуют полосовой фильтр, который пропускает частоты только в определенной полосе частот и не пропускает частоты за пределами этой полосы. Такие фильтры широко используются в радиоприемниках и радиопередатчиках. В приемниках полосовые фильтры используются только для селективного пропускания и усиления сигналов радиостанции в требуемой узкой полосе частот. При этом сигналы других радиостанций за пределами этой полосы подавляются. Передатчики могут передавать радиосигналы только в определенном разрешенном для них диапазоне частот. Поэтому в них используются полосовые фильтры для ограничения полосы передаваемого сигнала таким образом, что он вписывался в допустимые пределы.

Автор статьи: Анатолий Золотков

Конденсаторы последовательное калькулятор онлайн. Последовательное соединение конденсаторов. Способы соединения конденсаторов

Содержание:

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4 .

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .

Если рассмотреть три конденсатора С 1 , С 2 и С 3 , соединенные в последовательную цепь, то выясняется, что средний конденсатор С 2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/C общ = 1/C 1 + 1/C 2 + 1/C 3 .

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости.

То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, С общ = С 1 + С 2 + С 3 .

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов при­меняется для увеличения емкости.

4)Если параллельно включены т одинаковых конденсаторов ем­костью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис. 3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденса­торов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих кон­денсаторов.

При последовательном включении двух конденсаторов их об­щая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конден­саторов емкостью С каждый, то общая емкость этих конденса­торов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. по­следовательное включение конденсаторов приводит к уменьше­нию общей емкости батареи конденсаторов.

На практике может оказаться, что допустимое ра­бочее напряжение U p конденсатора меньше напряжения, на кото­рое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить не­сколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется мень­ше его допустимого рабочего

U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) кон­денсаторов применяют тогда, когда необходимо увеличить ем­кость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на ниже­приведенных примерах.

Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым при­ложено напряжение U ; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .

Таким образом, конденсаторы служат для накопления и сохра­нения электрического поля и его энергии.

15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис.

3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего со­противления в расчет вводится внутренняя проводимостьg =1/ r .

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r — I ,

где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K — ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис.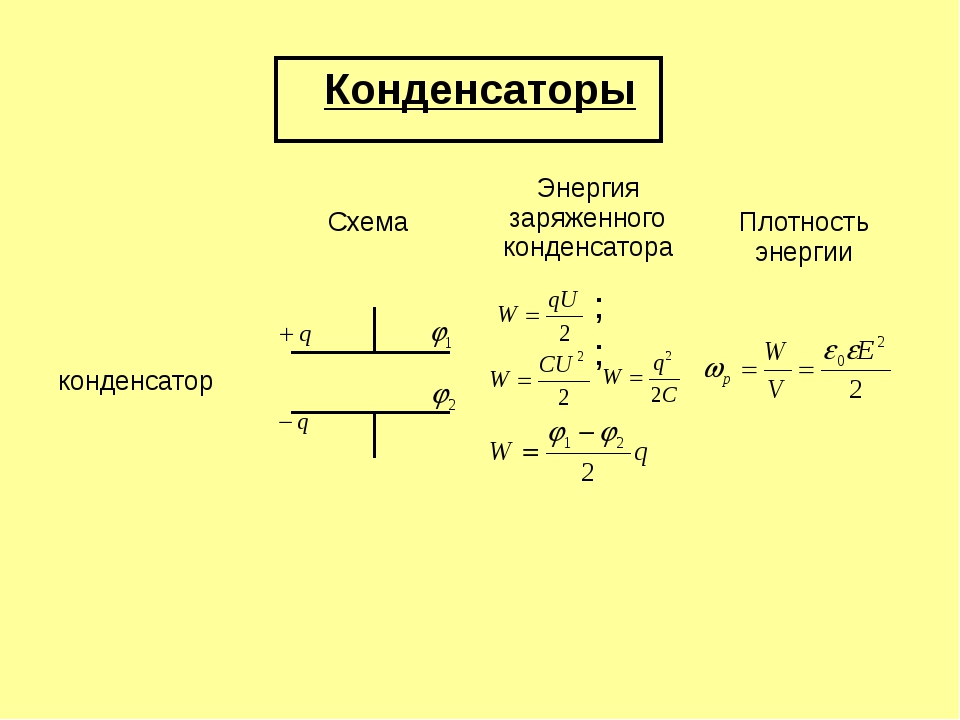 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.

В соответствии со вторым правилом Кирхгофа, падения напряжения V₁ , V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:

По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость C eq всех трех конденсаторов, соединенных последовательно, определяется как

Для группы из n соединенных последовательно конденсаторов эквивалентная емкость C eq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:

Эта формула для C eq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:

Если конденсаторов только два, то их общая емкость определяется по формуле

Если имеется n соединенных последовательно конденсаторов с емкостью C , их эквивалентная емкость равна

Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов .

Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.

Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки. На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.

Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.

Если несколько конденсаторов соединены параллельно , разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁ , Q₂ and Q₃ тоже будут различными. Общий заряд определяется как

Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?

Что необходимо знать для правильного соединения?

Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.

Зачем так делают?

Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К 1 =К 2 =К 3 . КЕ — конечная емкость, К — пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:

• ОЕ — общая емкость;
• Н — напряжение;
• КЕ — конечная емкость.

Что ещё необходимо знать, чтобы правильно соединить конденсаторы?

Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.

Ток при последовательном соединении

Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.

Падение напряженности и общая емкость

Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.

Пример № 1

Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.

Пример № 2

Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.

Заключение

Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.

У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью 470 мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на 1000 мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.

Схема последовательного соединения

Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:

q = q1 = q2 = q3 = …

Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.

Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:

U = U1 + U2 + U3,

при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.

Подставляя значения для напряжений в обе части уравнения, получается:

q/C = q/C1 + q/C2 + q/C3.

Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.

Результирующая формула для емкостей конденсаторов:

1/С = 1/С1 + 1/С2 + 1/С3.

Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей.

Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:

1. 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
2. С = 1/27,5 = 0,036 мкФ.

Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента.

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

С = (С1 х С2)/(С1 + С2).

В случае создания цепи из двух конденсаторов с идентичным емкостным значением:

С = (С х С)/(2 х С) = С/2.

Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.

Формула для емкостного делителя напряжения:

U1 = U x C/C1, U2 = U x C/C2, где:

• U – напряжение питания схемы;
• U1, U2 – падение напряжения на каждом элементе;
• С – итоговая емкость схемы;
• С1, С2 – емкостные показатели единичных элементов.

Вычисление падений напряжения на конденсаторах

К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:

• первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
• вторая – С1 = С2 = 400 нФ.

Первый вариант

1. Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
2. Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
3. На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант

1. Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
2. Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.

Параллельное и комбинированное соединение

Параллельное соединение конденсаторов представляется иным уравнением. Для определения общего емкостного значения надо просто найти совокупность всех величин по отдельности:

С = С1 + С2 + С3 + …

Напряжение к каждому элементу будет прикладываться идентичное. Следовательно, для усиления емкости надо соединить несколько деталей параллельно.

Если соединения смешанные, последовательно-параллельные, то для таких контуров применяют эквивалентные, или упрощенные, электросхемы. Каждую область цепи рассчитывают отдельно, а затем, представляя их вычисленными емкостями, объединяют в простую цепь.

Особенности замены конденсаторов

К примеру, в наличии сеть переменного тока 12 В и две альтернативных группы последовательных конденсаторных элементов.

Конденсаторы подсоединяются в последовательный контур для увеличения напряжения, под которым они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.

Часто применяется смешанное соединение конденсаторов, чтобы создать нужную емкостную величину и увеличить напряжение, которое детали способны выдержать.

Можно привести вариант, как соединить несколько компонентов, чтобы выйти на нужные параметры. Если требуется конденсаторный элемент 80 мкФ при напряжении 50 В, но есть только конденсаторы 40 мкФ на 25 В, необходимо образовать следующую комбинацию:

1. Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
2. Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
3. Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.

Важно! Для того чтобы усилить конденсаторы по напряжению, возможно их объединить в последовательную электросхему. Увеличение общей емкостной величины достигается параллельным подключением.

Что необходимо учитывать при создании последовательной цепи:

1. При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
2. Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.

Включение в последовательную цепь всегда должно происходить с соблюдением «плюса» и «минуса» конденсаторов. Если их соединить одноименными полюсами, то такое сочетание уже теряет поляризованность. При этом емкость созданной группы будет равна половине от емкостного значения одной из деталей. Такие конденсаторы возможно применять в качестве пусковых на электромоторах.

Видео

Энергия конденсатора, теория и примеры

Определение и общие сведения о энергии конденсатора

В том случае, если обкладки заряженного конденсатора замыкают при помощи проводника, то в проводнике появляется электрический ток, и через некоторое время конденсатор разряжается. При прохождении тока по проводнику выделяется некоторое количество теплоты, следовательно, конденсатор, обладающий зарядом, имеет энергию.

Определим энергию заряженного конденсатора. Будем считать, что конденсатор заряжают и этот процесс происходит очень медленно. Мгновенное значение напряжения между его обкладками обозначим как u. Так как процесс зарядки считаем квазистатическим, между обкладками увеличивается бесконечно медленно. Тогда потенциал каждой обкладки в каждый момент времени можно считать одинаковым в любом месте обкладки. При увеличении заряда обкладки на величину dq, совершается внешняя работа (работа источника) равная :

   

Используем формулу, которая связывает заряд, емкость и напряжение, получим:

   

В том случае, если емкость не зависит от напряжения электрического поля, то работа идет на увеличение энергии конденсатора (dW). Проинтегрируем выражение (2), учитывая, что напряжение изменяется от 0 до величины U, имеем:

   

Применяя формулу:

   

выражение для энергии поля конденсатора можно преобразовать к виду:

   

Именно благодаря своей способности запасать энергию, конденсаторы имеют большое значение в радиотехнике и электронике.

Энергия поля плоского конденсатора

Напряжение между обкладками плоского конденсатора может быть найдено как:

   

где d — расстояние между пластинами конденсатора. Учитывая, что для плоского конденсатора емкость определена выражением:

   

имеем:

   

где – объем конденсатора; E – напряженность электрического поля в конденсаторе. Объемная плотность энергии (w) может быть найдена как:

   

Примеры решения задач

Расчет реактивной мощности КРМ

Спасибо за интерес, проявленный к нашей Компании

Расчет реактивной мощности КРМ

Отправить другу

НЕОБХОДИМА КОНСУЛЬТАЦИЯ?

Теория расчета реактивной мощности КРМ

Q = P_{a· ( tgφ1-tgφ2)-  реактивная мощность установки КРМ (кВАр)}

Q = P_a · K

P_a -активная мощность (кВт)

K- коэффициент из таблицы

P_{a= S· cosφ}

S -полная мощность(кВА)

cos φ — коэффициент мощности

tg(φ₁+φ₂) согласуются со значениями cos φ в таблице. 

Таблица определения реактивной мощности конденсаторной установки  — КРМ (кВАр), необходимой для достижения заданного cos(φ).

Текущий (действующий)		Требуемый (достижимый) cos (φ)
tan (φ)	cos (φ)	0.80	0.82	0.85	0.88	0.90	0.92	0.94	0.96	0.98	1.00
		Коэффициент K
3.18	0.30	2.43	2.48	2.56	2.64	2.70	2.75	2.82	2.89	2.98	3.18
2.96	0.32	2.21	2.26	2.34	2.42	2.48	2.53	2.60	2.67	2.76	2.96
2.77	0.34	2.02	2.07	2.15	2.23	2.28	2.34	2.41	2.48	2.56	2.77
2.59	0.36	1.84	1.89	1.97	2.05	2.10	2.17	2.23	2.30	2.39	2.59
2.43	0.38	1.68	1.73	1.81	1.89	1.95	2.01	2.07	2.14	2.23	2.43
2.29	0.40	1.54	1.59	1.67	1.75	1.81	1.87	1.93	2.00	2.09	2.29
2.16	0.42	1.41	1.46	1.54	1.62	1.68	1.73	1.80	1.87	1.96	2.16
2.04	0.44	1.29	1.34	1.42	1.50	1.56	1.61	1.68	1.75	1.84	2.04
1.93	0.46	1.18	1.23	1.31	1.39	1.45	1.50	1.57	1.64	1.73	1.93
1.83	0.48	1.08	1.13	1.21	1.29	1.34	1.40	1.47	1.54	1.62	1.83
1.73	0.50	0.98	1.03	1.11	1.19	1.25	1.31	1.37	1.45	1.63	1.73
1.64	0.52	0.89	0.94	1.02	1.10	1.16	1.22	1.28	1.35	1.44	1.64
1.56	0.54	0.81	0.86	0.94	1.02	1.07	1.13	1.20	1.27	1.36	1.56
1.48	0.56	0.73	0.78	0.86	0.94	1.00	1.05	1.12	1.19	1.28	1.48
1.40	0.58	0.65	0.70	0.78	0.86	0.92	0.98	1.04	1.11	1.20	1.40
1.33	0.60	0.58	0.63	0.71	0.79	0.85	0.91	0.97	1.04	1.13	1.33
1.30	0.61	0.55	0.60	0.68	0.76	0.81	0.87	0.94	1.01	1.10	1.30
1.27	0.62	0.52	0.57	0.65	0.73	0.78	0.84	0.91	0.99	1.06	1.27
1.23	0.63	0.48	0.53	0.61	0.69	0.75	0.81	0.87	0.94	1.03	1.23
1.20	0.64	0.45	0.50	0.58	0.66	0.72	0.77	0.84	0.91	1.00	1.20
1.17	0.65	0.42	0.47	0.55	0.63	0.68	0.74	0.81	0.88	0.97	1.17
1.14	0.66	0.39	0.44	0.52	0.60	0.65	0.71	0.78	0.85	0.94	1.14
1.11	0.67	0.36	0.41	0.49	0.57	0.63	0.68	0.75	0.82	0.90	1.11
1.08	0.68	0.33	0.38	0.46	0.54	0.59	0.65	0.72	0.79	0.88	1.08
1.05	0.69	0.30	0.35	0.43	0.51	0.56	0.62	0.69	0.76	0.85	1.05
1.02	0.70	0.27	0.32	0.40	0.48	0.54	0.59	0.66	0.73	0.82	1.02
0.99	0.71	0.24	0.29	0.37	0.45	0.51	0.57	0.63	0.70	0.79	0.99
0.96	0.72	0.21	0.26	0.34	0.42	0.48	0.54	0.60	0.67	0.76	0.96
0.94	0.73	0.19	0.24	0.32	0.40	0.45	0.51	0.58	0.65	0.73	0.94
0.91	0.74	0.16	0.21	0.29	0.37	0.42	0.48	0.55	0.62	0.71	0.91
0.88	0.75	0.13	0.18	0.26	0.34	0.40	0.46	0.52	0.59	0.68	0.88
0.86	0.76	0.11	0.16	0.24	0.32	0.37	0.43	0.50	0.57	0.65	0.86
0.83	0.77	0.08	0.13	0.21	0.29	0.34	0.40	0.47	0.54	0.63	0.83
0.80	0.78	0.05	0.10	0.18	0.26	0.32	0.38	0.44	0.51	0.60	0.80
0.78	0.79	0.03	0.08	0.16	0.24	0.29	0.35	0.42	0.49	0.57	0.78
0.75	0.80		0.05	0.13	0.21	0.27	0.32	0.39	0.46	0.55	0.75
0.72	0.81			0.10	0.18	0.24	0.30	0.36	0.43	0.52	0.72
0.70	0.82			0.08	0.16	0.21	0.27	0.34	0.41	0.49	0.70
0.67	0.83			0.05	0.13	0.19	0.25	0.31	0.38	0.47	0.67
0.65	0.84			0.03	0.11	0.16	0.22	0.29	0.36	0.44	0.65
0.62	0.85				0.08	0.14	0.19	0.26	0.33	0.42	0.62
0.59	0.86				0.05	0.11	0.17	0.23	0.30	0.39	0.59
0.57	0.87					0.08	0.14	0.21	0.28	0.36	0.57
0.54	0.88					0.06	0.11	0.18	0.25	0.34	0.54
0.51	0.89					0.03	0.09	0.15	0.22	0.31	0.51
0.48	0.90						0.06	0.12	0.19	0.28	0.48
0.46	0.91						0.03	0.10	0.17	0.25	0.46
0.43	0.92							0.07	0.14	0.22	0.43
0.40	0.93							0.04	0.11	0.19	0.40
0.36	0.94								0.07	0.16	0.36
0.33	0.95									0.13	0.33

Пример:

Активная мощность двигателя : P=100 кВт

Действующий cos φ = 0.61 

Требуемый cos φ = 0.96

Коэффициент K из таблицы = 1.01

Необходимая реактивная мощности КРМ (кВАр):

Q = 100 · 1.01=101 кВАр

НЕОБХОДИМА КОНСУЛЬТАЦИЯ?

Возврат к списку

2

Об энергии, хранящейся в конденсаторе

Энергия, хранящаяся в конденсаторе, представляет собой потенциальную электростатическую энергию. Таким образом, это связано с зарядом Q и напряжением V между пластинами конденсатора. Заряженный конденсатор накапливает энергию в электрическом поле между своими пластинами. По мере зарядки конденсатора нарастает электрическое поле. Когда заряженный конденсатор отсоединяется от батареи, его энергия остается в поле в пространстве между пластинами.2 для расчета электростатической потенциальной энергии. Энергия, накопленная в конденсаторе с учетом емкости и напряжения, представляет собой полную электростатическую потенциальную энергию конденсатора при условии, что указаны значение емкости и напряжения. Электростатический потенциал энергии и обозначается символом U _e .

Как рассчитать энергию, запасенную в конденсаторе, с учетом емкости и напряжения с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для накопленной в конденсаторе энергии с учетом емкости и напряжения, введите емкость (C) и напряжение (В) и нажмите кнопку расчета.2 .

Калькулятор импеданса конденсатора

• Калькулятор электрического, радиочастотного и электронного оборудования • Онлайн-преобразователи единиц измерения

Обратите внимание, что величина импеданса идеального конденсатора равна его реактивному сопротивлению. Однако они не идентичны из-за фазового сдвига между напряжением и током в емкостной цепи. Для расчета используется следующая формула:

где:

X _C — реактивное сопротивление конденсатора в Ом (Ом),

Z _C — реактивное сопротивление конденсатора в Ом (Ом. ),

ω = 2πf — угловая частота в рад / с,

j — мнимая единица,

f — частота в герцах (Гц), а

C — это емкость в фарадах (Ф).

Для расчета введите емкость и частоту, выберите единицы измерения, и результат будет показан в омах.

График зависимости реактивного сопротивления идеального конденсатора X _C от частоты f для заданной емкости показывает обратную пропорциональность частоте

Конденсатор представляет собой пассивный обычно двухконтактный электрический компонент, состоящий в основном из двух электрических проводников, часто в форма тонких металлических пластин, разделенных диэлектриком, например пластиковой пленкой, керамикой, бумагой или даже воздухом.Конденсаторы используются для хранения энергии в виде электрического заряда.

Когда первоначально незаряженный конденсатор подключен к источнику постоянного напряжения постоянного тока, он заряжается до приложенного напряжения, а его зарядный ток экспоненциально спадает от максимального значения в начальной точке зарядки до нуля. При этом напряжение на конденсаторе увеличится до напряжения источника постоянного тока.

Итак, когда напряжение достигает своего максимума, ток достигает своего минимума.Скорость зарядки определяется постоянной времени цепи, к которой подключен конденсатор. Полностью заряженный конденсатор блокирует ток и действует как временное запоминающее устройство.

Идеальный конденсатор будет поддерживать этот заряд неопределенно долго, даже если напряжение зарядки постоянного тока будет снято. Однако в реальной жизни конденсаторы, особенно электролитические, не могут действовать как постоянные накопители из-за их относительно низкого сопротивления утечке и, следовательно, высокого тока утечки.

Если на конденсатор подается переменное синусоидальное напряжение, он заряжается то в одном направлении, то в противоположном. Его полярность изменяется с той же скоростью, что и напряжение переменного тока. Как мы упоминали выше, когда напряжение достигает своего максимума, ток достигает своего минимума, а когда напряжение достигает своего минимума, ток достигает своего максимума. Ток пропорционален скорости изменения напряжения , и ток является наибольшим, когда изменение напряжения является самым быстрым, то есть когда синусоидальное напряжение пересекает нулевую точку.На рисунке показан график напряжения V на конденсаторе, его заряда Q и тока в нем I.

В чисто емкостной схеме протекание тока зависит от скорости изменения напряжения. Ток заряжает конденсатор, и когда ток медленно приближается к нулю, конденсатор полностью заряжен и напряжение на нем достигает максимума. В _C — напряжение, Q _C — заряд, I _C — ток, φ = –90 ° = — π /2 — фазовый сдвиг.1 — конденсатор начинает заряжаться, ток достигает своего положительного максимума, скорость его изменения равна нулю, а напряжение и заряд конденсатора равны нулю; 2 — конденсатор полностью заряжен, ток равен нулю, скорость его изменения максимальная, а напряжение и заряд конденсатора находятся на своих положительных максимумах; 3 — конденсатор заряжается в обратном направлении, ток имеет отрицательный максимум, скорость его изменения равна нулю, а напряжение и заряд конденсатора равны нулю; 4 — конденсатор полностью заряжен, ток равен нулю, скорость его изменения максимальна, а напряжение и заряд конденсатора имеют отрицательный максимум

Как мы видим, напряжение отстает от тока по времени и фазе (90 °), потому что в конденсаторе должен течь ток, чтобы на нем повышалось напряжение.Или мы можем сказать, что ток опережает напряжение. Насколько это отставание или опережение зависит от значения реактивного сопротивления цепи по отношению к ее сопротивлению? Если в цепи вообще нет сопротивления, запаздывание или опережение могут достигать 90 ° (ток равен нулю, когда напряжение максимально). Этот угол называется разностью фаз.

Рассмотрим следующую аналогию: Солнце (солнечный свет — ток) наиболее мощно в астрономический полдень, но самая жаркая часть дня (температура — напряжение) обычно наступает на несколько часов позже.Или зимнее солнцестояние в Северном полушарии (самый короткий день) приходится на конец декабря, но самые холодные месяцы еще впереди — в зависимости от того, где вы живете, это январь или даже февраль. Причина этого «сезонного запаздывания» или «фазового сдвига» заключается в поглощении энергии Солнца массивными океанами Земли. Позже они выпускают его медленно — точно так же, как это делают конденсаторы.

День зимнего солнцестояния

Расчетное сопротивление — это мера сопротивления конденсатора сигналу на определенной частоте , который проходит через него.Емкостное реактивное сопротивление обратно пропорционально изменению частоты приложенного переменного напряжения. Формула показывает, что реактивное сопротивление конденсатора X _C велико на низких частотах и ​​мало на высоких частотах. При нулевой частоте (постоянное напряжение) емкостное сопротивление становится бесконечным или полностью противоположным току. Конденсатор блокирует постоянное напряжение и ток. С другой стороны, на очень высоких частотах конденсатор проводит очень хорошо — отсюда правило, которое мы усвоили в средней школе: конденсаторы пропускают переменный ток и блокируют постоянный ток.Если частота очень высокая, конденсаторы очень хорошо пропускают сигналы.

Импеданс измеряется в омах, как и сопротивление. Так же, как сопротивление, импеданс показывает величину сопротивления компонента потоку электрического тока. Но чем импеданс отличается от простого сопротивления? Разница заключается в зависимости импеданса от частоты сигнала. Сопротивление не зависит от частоты и от нее зависит полное сопротивление конденсаторов. Импеданс конденсаторов увеличивается с уменьшением частоты.Емкость конденсатора оказывает такое же влияние на импеданс, как и частота. Чем выше емкость, тем ниже сопротивление и наоборот.

Этот калькулятор разработан для идеальных конденсаторов. Настоящие конденсаторы всегда имеют некоторую индуктивность и сопротивление. Используйте наш калькулятор импеданса RLC, чтобы рассчитать импеданс реальных конденсаторов.

Винтажные конденсаторы, произведенные в СССР в конце 1960-х

Эту статью написал Анатолий Золотков

Capacitor Energy — AP Physics 2

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Калькулятор параллельной и последовательной емкости

Параллельный и последовательный

Емкость

Параллельная емкость	XXXX Фарад
Емкость серии	XXXX Фарад

Рассчитать Прозрачный

Конденсаторы — важные компоненты электрических цепей.Конденсаторы хранят электрическую энергию в виде электрического поля. Конденсатор состоит из двух параллельных проводящих пластин с диэлектрической средой между ними. Диэлектрик похож на изолятор, но обладает свойством поляризуемости.

Свойства конденсатора

• Конденсатор препятствует изменению напряжения.
• Ток, возникающий в конденсаторе, опережает напряжение; Это означает, что ток на 90 градусов опережает напряжение на конденсаторе.
• Конденсатор — идеальный электрический элемент; это означает, что теоретически он не поглощает и не рассеивает

Применение конденсатора

Свойство конденсатора накапливать электрическую энергию в виде напряжения, а также его другое свойство производить опережающий ток делает его полезным во многих электрических приложениях.

• Во время выработки электричества небольшой конденсатор подключается в конце цепи генератора, чтобы обеспечить опережающий коэффициент мощности, который идеально подходит для снижения потерь мощности и получения более качественной формы волны тока.
• При передаче и приеме радиосигналов конденсаторы используются в цепях фильтров.
• В схемах таймера или колебательных цепях конденсаторы являются существенными элементами.
Конденсаторы
• — хороший выбор для хранения энергии. Например, в автомобилях есть встроенные огромные конденсаторы для питания автомобильной аудиосистемы и обеспечения необходимого усиления звука.
• Два основных аспекта конструкции конденсатора — расстояние между параллельными пластинами и используемый диэлектрик, позволяют использовать конденсаторы в качестве механических датчиков.
Конденсаторы
• также используются для регулирования мощности и в выпрямительных цепях для преобразования переменного тока в постоянный.

Последовательные и параллельные соединения емкости

В зависимости от способа соединения их концов различают два основных типа емкостных цепей:

Цепи измерения емкости серии

• Параллельные схемы измерения емкости

По мере продвижения в этом посте мы будем понимать работу, сравнение, вычисления и различия между этими последовательными цепями и параллельными емкостными цепями.

Цепи измерения емкости серии

Считается, что две или более емкости соединены последовательно, если они соединены встык. Когда два конденсатора C1 и C2 соединены последовательно, полезная емкость равна обратной сумме обратных величин отдельных конденсаторов.

1 / C _net = 1 / C = 1 / C ₁ + 1 / C ₂

При последовательном соединении емкостей чистая емкость цепи меньше, чем значение любой емкости в цепи. схема.

Параллельные емкостные цепи

Два или более конденсатора считаются подключенными параллельно, если все их положительные полярности подключены к одному концу, а все отрицательные полярности подключены к другому концу цепи.

В параллельной цепи ток, исходящий от источника, или полный ток будет ветвиться в месте соединения, где встречаются положительные полярности емкостей, а затем течет в разных количествах в каждом конденсаторе, а затем снова объединяется вместе в точке встречи отрицательных стык полярностей и поток по направлению к началу координат.

При параллельном соединении емкостей чистая емкость представляет собой сумму всех емкостей, подключенных в цепи.

C _чистая = C ₁ + C ₂

Комбинация последовательной и параллельной емкостей

Если в цепи есть конденсаторы, включенные последовательно и параллельно, то вам нужно решить комбинацию конденсаторов шаг за шагом, учитывая, включены ли они последовательно или параллельно соседним, а затем вычислить конечную емкость цепи.

Чем вам может помочь калькулятор последовательной и параллельной емкости CalculatorHut?

Емкости — важные компоненты любых электронных схем. Любой студент-электронщик или студент-физик должен знать расчеты, связанные с подключением конденсаторов.

CalculatorHut, надежное место для размещения научных и ненаучных онлайн-калькуляторов, предлагает бесплатный онлайн-калькулятор последовательной и параллельной емкости, который решит все ваши потребности в онлайн-калькуляторе бесплатно.Вы можете рассчитать чистую емкость до десяти емкостей, подключенных последовательно или параллельно, с помощью этого простого в использовании бесплатного онлайн-калькулятора последовательной и параллельной емкости. Это очень удобный инструмент для студентов, который помогает им проверить правильность расчетов емкости.

CalculatorHut бесплатно ответит на любые ваши онлайн-вычисления. Он имеет огромный выбор более 100 калькуляторов по различным темам — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, физические калькуляторы, химические калькуляторы, математические калькуляторы и многие другие бесплатные онлайн-калькуляторы для научных расчетов.

CalculatorHut также предлагает бесплатный виджет любого калькулятора из широкого спектра калькуляторов для встраивания в качестве виджетов на другие веб-сайты. Для этого напишите нам на [email protected].

Если вы обнаружите, что какой-либо калькулятор отсутствует, и если вы хотите увидеть его на CalculatorHut, сообщите нам об этом. Мы будем более чем счастливы удовлетворить ваши потребности в бесплатном онлайн-калькуляторе бесплатно и всегда!

Вы также можете бесплатно носить с собой в кармане этот широкий ассортимент онлайн-калькуляторов.Да! Приложение CalculatorHut бесплатное и станет вашим другом, которое сделает любые вычисления проще и удобнее на ходу! Удачных расчетов!

Конденсаторная батарея в кВАр и мкФ Калькулятор для коррекции коэффициента мощности

Как рассчитать конденсаторную батарею в кВАр и микрофарадах для улучшения коэффициента мощности? Калькулятор и пример

Калькулятор конденсаторной батареи

Следующий калькулятор повышения коэффициента мощности рассчитает необходимое значение конденсаторной батареи в кВАр реактивной мощности «Q» и микрофарадах «мкФ».Конденсатор коррекции коэффициента мощности должен быть подключен параллельно каждой фазной нагрузке. Кроме того, как кВАр, так и мкфарад — это термины, используемые в конденсаторных батареях, а также в улучшении и коррекции коэффициента мощности для устранения реактивных компонентов со стороны нагрузки, что имеет множество преимуществ.

Чтобы рассчитать значение емкости конденсаторной батареи в кВАр и мкФ, просто введите значения реальной или активной мощности в кВт, существующий коэффициент мощности и целевой коэффициент мощности «Необходимо скорректировать коэффициент мощности» и нажмите кнопку «Рассчитать». чтобы получить результат емкости конденсаторной батареи в мкФ и кВАр.

Значение напряжения в вольтах и ​​частоты в Гц (50 или 60 Гц) является необязательным, если вы хотите только рассчитать номинальное значение в кВАр конденсаторной батареи. Если вам нужно рассчитать емкость конденсаторной батареи в микрофарадах, вы должны ввести известное значение частоты и напряжения.

Связанные калькуляторы:

Конденсаторная батарея в кВАр и мкФ Формула расчета

Конденсаторная батарея в кВАр

Следующие формулы можно использовать для расчета необходимой конденсаторной батареи в кВАр для улучшения коэффициента мощности.

Требуемый блок конденсаторов в кВАр = P в кВт (Tan θ ₁ — Tan θ ₂ )

Также

• кВАр = C x f ÷ В (159,155 x 10 ⁶ )… в кВАр
• кВАр = C x 2π x f x V ² x 1014313… 9018 кВАр 903

Где:

• кВАр = Требуемая реактивная вольт-амперная характеристика в килограммах.
• C = значение емкости конденсатора в мкФ
• f = частота в герцах «Гц»
• V = напряжение в вольтах
• θ ₁ = Cos ^-1 = существующий коэффициент мощности
• θ ₂ = Cos ^-1 = Целевой или желаемый коэффициент мощности, «который необходимо скорректировать».

Конденсаторная батарея в микрофарадах «мкФ»

Следующие формулы можно использовать для расчета необходимой конденсаторной батареи в мкФ для коррекции коэффициента мощности.

Требуемый конденсаторный блок в мкФ = кВАр x 10 ⁹ ÷ (2π x f x В ² )

Также

9018 10 ⁶ x Q в кВАр ÷ f x В ² … в микрофарадах
• C = кВАр x 10 ⁹ ÷ (2π x

  f V ² )… в микрофарадах

Где:

• C = значение емкости конденсатора в мкФ
• kVAR = Требуемая реактивная вольт-амперная характеристика в кило.
• f = частота в Гц
• V = напряжение в вольтах

Полезно знать:

Ниже приведены полезные формулы и уравнения для расчета коэффициента мощности, активной мощности, реактивной мощности и полной мощности.

Где:

• кВт = Активная мощность = P = V x I x Cosθ
• kVAR = Реактивная мощность = Q = V x I x Sinθ
• kVA = Полная мощность = S = V x I

Похожие сообщения:

Как рассчитать батарею конденсаторов в кВАр и мкФ для P.F Correction

В следующем примере показано, как рассчитать требуемый номинал конденсаторной батареи коррекции в микрофарадах и кВАр. Вы можете сравнить результат решенного примера с результатами калькулятора коэффициента мощности.

Пример 1:

A Однофазный 480 В, 60 Гц, двигатель потребляет ток питания 55,5 А при коэффициенте мощности «p.f» 0,60. Коэффициент мощности двигателя необходимо скорректировать до 0,98, подключив параллельно ему конденсатор. Рассчитайте требуемую емкость конденсатора как в кВАр, так и в мкФ.

Решение:

Нагрузка в кВт = P = V x I x Cosθ ₁

P = 480 В x 55,5 A x 0,60

P = 16 кВт

Требуемый блок конденсаторов в кВАр 9000

Требуемый конденсатор, кВАр = P в кВт (Tan θ ₁ — Tan θ ₂ )

θ ₁ = Cos ^-1 = (0,60) = 53 ° .130; Tan θ ₁ = Tan (53 ° .130) = 1,333

θ ₂ = Cos ^-1 = (0.98) = 11 ° .478; Tan θ ₂ = Tan (11 ° .478) = 0,203

кВАр = 16 кВт x (1,333 — 0,203)

ВАр = 1808 ВАр

Требуемый кВАр = 18.08 кВАр

µF Требуемый блок конденсаторов

C = кВАр x 10 ⁹ ÷ (2π x f x V ² )… в микрофарадах

C = 18,08 кВАр x 10 ⁹ ÷ (2π x 60 Гц x 480 ² В)

C = 208,2 мкФ

Похожие сообщения:

Пример 2:

Завод имеет нагрузку 300 кВт при 0.6 П.Ф. Если им необходимо повысить коэффициент мощности с 0,65 до 0,97, найдите емкость конденсаторной батареи в кВАр и микрофарадах, которую они должны установить параллельно с фазами нагрузки.

Решение:

Заданные данные:

• Активная нагрузка = 300 кВт
• Существующий коэффициент мощности Cosθ ₁ = 0,65
• Целевой коэффициент мощности Cosθ ₂ = 0,97

кВ Требуемый конденсатор в кВт x Tan (Cos ^-1 (θ ₁ ) — Cos ^-1 (θ ₂ ))

кВАр = 300 кВт x Tan (Cos ^-1 (0.65) — Cos ^-1 (0,97))

кВАр = 300 кВт xx Tan (49 ° .458 — 14 ° 0,069)

кВАр = 300 кВт x (1,169 — 0,250)

кВАр = 275,7 кВАр

Сопутствующие электротехнические и электронные калькуляторы:

Калькулятор коэффициента мощности

Калькулятор коэффициента мощности. Вычислить коэффициент мощности, полную мощность, реактивную мощность и емкость корректирующего конденсатора.

Калькулятор предназначен для образовательных целей.

Конденсатор коррекции коэффициента мощности должен быть подключен параллельно каждой фазной нагрузке.

При вычислении коэффициента мощности не различаются опережающие и запаздывающие коэффициенты мощности.

Расчет коррекции коэффициента мощности предполагает индуктивную нагрузку.

Расчет однофазной цепи

Расчет коэффициента мощности:

PF = | cos φ | = 1000 × P _(кВт) / ( V _(V) × I _(А) )

Расчет полной мощности:

| S _(кВА) | = В _(В) × I _(А) /1000

Расчет реактивной мощности:

Q _(кВАр) = √ ( | S _(кВА) | ² — P _(кВт) ² )

Расчет емкости конденсатора коррекции коэффициента мощности:

S _{с поправкой (кВА)} = P _(кВт) / PF _{с поправкой}

Q _{с поправкой (кВАр)} = √ ( S _{с поправкой (кВА)} ² — P _(кВт) ² )

Q _{c (кВАр)} = Q _(кВАр) — Q _{с поправкой (кВАр)}

C _(F) = 1000 × Q _{c (кВАр)} / (2π f _(Гц) × V _(V) ² )

Расчет трехфазной цепи

Для трех фаз со сбалансированной нагрузкой:

Расчет при межфазном напряжении

Расчет коэффициента мощности:

PF = | cos φ | = 1000 × P _(кВт) / ( √ 3 × V _{L-L (В)} × I _(A) )

Расчет полной мощности:

| S _(кВА) | = √ 3 × V _{L-L (V)} × I _(A) /1000

Расчет реактивной мощности:

Q _(кВАр) = √ ( | S _(кВА) | ² — P _(кВт) ² )

Расчет емкости конденсатора коррекции коэффициента мощности:

Q _{c (кВАр)} = Q _(кВАр) — Q _{с поправкой (кВАр)}

C _(F) = 1000 × Q _{c (кВАр)} / (2π f _(Гц) × V _{L-L (V)} ² )

Расчет с линейным напряжением

Расчет коэффициента мощности:

PF = | cos φ | = 1000 × P _(кВт) / (3 × V _{L-N (V)} × I _(A) )

Расчет полной мощности:

| S _(кВА) | = 3 × В _{L-N (В)} × I _(A) /1000

Расчет реактивной мощности:

Q _(кВАр) = √ ( | S _(кВА) | ² — P _(кВт) ² )

Расчет емкости конденсатора коррекции коэффициента мощности:

Q _{c (кВАр)} = Q _(кВАр) — Q _{с поправкой (кВАр)}

C _(F) = 1000 × Q _{c (кВАр)} / (3 × 2π f _(Гц) × V _{LN (V)} ² )

Калькулятор мощности ►

---

См. Также

Серии

и параллельный калькулятор емкости Apogeeweb

Часто задаваемые вопросы

1.Как рассчитать параллельную емкость?

Общее значение емкости конденсаторов, соединенных параллельно, фактически вычисляется путем сложения площадей пластин. Другими словами, общая емкость равна сумме всех отдельных емкостей, включенных параллельно.

2. Как отличить последовательный конденсатор от параллельного?

Когда разность потенциалов на пластинах одинакова, они параллельны. Когда ток через них равен, они включены последовательно.

3. Зачем нужно последовательно включать конденсаторы?

Причина, по которой вы можете соединять конденсаторы последовательно, заключается в том, чтобы увеличить эффективное управление напряжением цепи. Конденсаторы имеют номинальное напряжение пробоя, превышение которого значительно увеличивает вероятность отказа. Два одинаковых конденсатора будут иметь половину напряжения на каждом.

4. Последовательные или параллельные конденсаторы накапливают больше энергии?

Энергия, запасенная в конденсаторе, является функцией напряжения на конденсаторе.Напряжение будет выше, когда они подключены параллельно, поэтому при параллельном подключении сохраняется больше энергии.

5. Какова основная функция конденсатора?

Конденсатор — это электронный компонент, который накапливает и выделяет электричество в цепи. Он также пропускает переменный ток, не пропуская постоянный ток. Конденсатор является неотъемлемой частью электронного оборудования и поэтому почти всегда используется в электронных схемах.

6.В чем разница между последовательной и параллельной схемой?

В последовательной цепи сумма напряжений, потребляемых каждым отдельным сопротивлением, равна напряжению источника. Компоненты, соединенные параллельно, соединяются несколькими путями, так что ток может разделяться; одинаковое напряжение приложено к каждому компоненту.

7. Почему последовательно подключенные конденсаторы уменьшают емкость?

Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов.Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.

8. Что произойдет, если резистор и конденсатор соединить параллельно?

Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °. Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.

9. Как узнать, включен ли последовательный конденсатор параллельно?

Если у каждого конденсатора ОБЕ клеммы подключены к ОБЕИМ клеммам других, то они включены параллельно. Если у каждого конденсатора только одна клемма, подключенная к одной клемме другого конденсатора, они подключены последовательно.

10. Почему последовательно подключенные конденсаторы уменьшают емкость?

Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов.Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.

11. Как соединить параллельно конденсаторы и резисторы?

Детальная операция начинается с 1:42.

12. Почему мы используем конденсаторы в цепях постоянного тока?

При использовании в цепи постоянного или постоянного тока конденсатор заряжается до напряжения питания, но блокирует прохождение тока через него, потому что диэлектрик конденсатора непроводящий и в основном является изолятором.

13. Преобразует ли конденсатор переменный ток в постоянный?

Конденсатор не может самостоятельно преобразовывать переменный ток в постоянный ток, но хороший синхронизированный переключатель, который пропускает выбранные пики и отклоняет части формы волны переменного тока, сделает это.

14. Что происходит, когда конденсатор подключен к постоянному току?

Когда конденсаторы подключаются к источнику постоянного напряжения постоянного тока, они становятся заряженными до значения приложенного напряжения, действуя как устройства временного хранения и сохраняя или удерживая этот заряд неопределенно долго, пока присутствует напряжение питания.

15. Есть ли у конденсаторов положительная и отрицательная сторона?

Большинство электролитических конденсаторов поляризованного типа, то есть напряжение, подключенное к клеммам конденсатора, должно иметь правильную полярность, то есть положительную полярность и отрицательную отрицательную.

16. Как решить проблемы, связанные с подключением конденсаторов последовательно и параллельно?

Видео ниже показывает, как рассчитать емкость в последовательной и параллельной цепи, а также дает лабораторный пример, демонстрирующий математические действия.

Серия Подключение конденсаторов

На рис. 1 (а) показано, что два конденсатора подключены последовательно. Для каждого конденсатора он имеет одинаковый ток, а соотношение тока и напряжения соответствует

.

«

(а) (б)

Рисунок 1. Последовательное соединение

Итак, два конденсатора соединены последовательно, эквивалентная емкость составляет

.

Эквивалентная схема показана на рисунке 1 (б).При последовательном соединении конденсаторов напряжение на каждом конденсаторе соответствует

.

Параллельное соединение конденсаторов

На рис. 2 (а) показано, что два конденсатора подключены параллельно. Для каждого конденсатора оно имеет одинаковое напряжение, а соотношение тока и напряжения соответствует

.

Рисунок 2. Cicuit параллельных конденсаторов

Два конденсатора подключены параллельно, эквивалентная емкость

Эквивалентная схема показана на рисунке 2 (б).При параллельном соединении конденсаторов ток на каждом конденсаторе соответствует

.

Разница между последовательными конденсаторами и параллельными конденсаторами

При последовательном соединении конденсаторов емкость уменьшается (для расчета общей емкости после последовательного соединения см. Метод параллельного подключения резисторов), а выдерживаемое напряжение увеличивается.

Конденсаторы подключаются параллельно, емкость увеличивается (добавление каждой емкости), а выдерживаемое напряжение наименьшее.Последовательный конденсатор: чем больше число последовательно, тем меньше емкость, но выше выдерживаемое напряжение. Отношение емкости: 1 / C = 1 / C1 + 1 / C2 + 1 / C3 Параллельная емкость: чем больше параллельное соединение, тем больше емкость, но выдерживаемое напряжение не изменяется, отношение емкости: C = C1 + C2 + C3

См. Более подробную информацию о конденсаторах, включенных последовательно и параллельно. Кликните сюда!

.