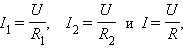Вопрос 15. Энергия электрического поля (системы электрических зарядов, заряженного конденсатора, запас энергии заряженного тела, энергия электростатического поля).
Во всех трех случаях математическая формула будет одинакова. В чем же соль? Где же сосредоточена энергия? Что является ее носителем?
Электростатика не отвечает на этот вопрос. Заряд и поле обладает энергией. Они могут существовать отдельно от породивших систем электрических зарядов.
Энергия систем неподвижных точечных зарядов.
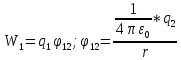

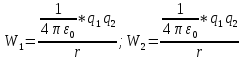
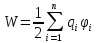
Энергия заряженного уединенного проводника.
Имеется проводник, заряд, емкость и потенциал. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, затратив работу
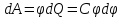
Чтобы
зарядить тело от ненулевого потенциала
до 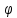 ,
нужно совершить работу:
,
нужно совершить работу:
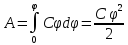
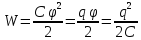
Энергия конденсатора – всякий конденсатор обладает энергией
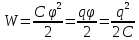
Энергия электростатического поля – преобразуем формулу, воспользовавшись выражением для емкости плоского конденсатора
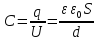
И разности потенциалов между обкладками:
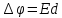
Тогда:
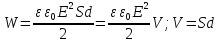
Объёмная плотность энергии электростатического поля:
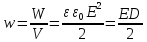
Вопрос 16. Постоянный электрический ток.
Сила тока I — скалярная величина, равная отношению заряда, прошедшего через поперечное сечение проводника, промежутку времени, в течение которого шел ток.
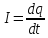
Ток называют постоянным, если сила тока не меняется со временем. Для того чтобы ток через проводник был постоянным необходимо, чтобы разность потенциалов на концах проводника была постоянной.
Если заряженная частица q движется со скоростью v (скорость направленного (!) движения), то:
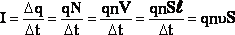 .
.Т.о. при увеличении площади сечения проводника скорость направленного движения частиц, создающих ток, уменьшается.
Плотность тока j — отношение силы тока к площади поперечного сечения проводника. Измеряется в А/м2. Вектор плотности тока сонаправлен с вектором напряженности поля. Т.о. плотность тока не зависит от размеров проводника.
Вопрос 17. Эдс и напряжение.
Для существования тока необходимо: наличие свободных зарядов, наличие поля с разностью потенциалов.
Положительный заряд движется в электростатическом поле по вектору напряженности от большего потенциала к меньшему. И в конце концов это приведет к выравниванию потенциалов и прекращению тока. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создаваться и поддерживать разность потенциалов. Эти устройства – источники тока.
Силы неэлектрического происхождения называют сторонними. Их природа различна.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда по всей цепи, называется электродвижущей силой источника.
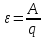
Физическая величина, численно равная работе, совершаемой сторонними и Кулоновскими силами на участке цепи, называется напряжением на данном участке.
Если ЭДС отсутствует, то 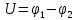 .
.
Вопрос 18. Последовательное и параллельное соединение проводников.
Проводники в электрических цепях могут соединяться последовательно и параллельно.
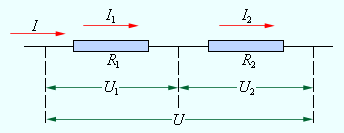
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
|
Рисунок 1.9.1. Последовательное соединение проводников |
По
закону Ома, напряжения U1 и U
U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд
|
Рисунок 1.9.2. Параллельное соединение проводников |
Записывая на основании закона Ома
|
где R – электрическое сопротивление всей цепи, получим
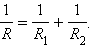
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
1.15. Энергия электрического поля заряженного проводника и конденсатора
При сообщении
проводнику с электроемкостью С заряда 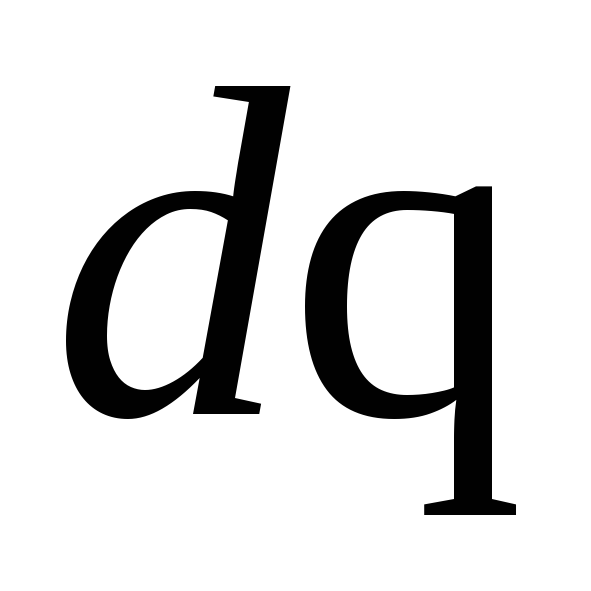
 ,
совершенной внешними силами при
перемещении заряда из бесконечности
на поверхность проводника
,
совершенной внешними силами при
перемещении заряда из бесконечности
на поверхность проводника 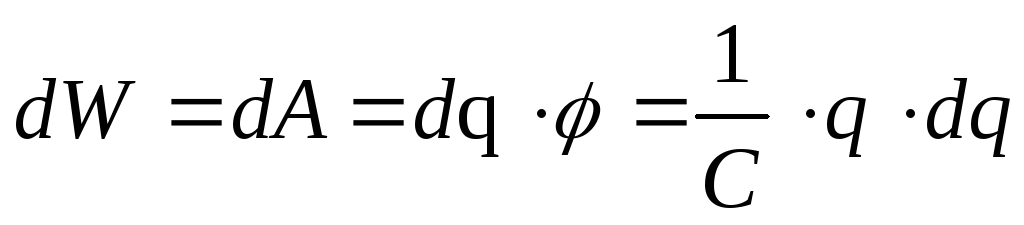 ,
,
Где  и
и соответственно
потенциал электрического поля и заряд
на поверхности проводника.
соответственно
потенциал электрического поля и заряд
на поверхности проводника.
Энергия проводника 
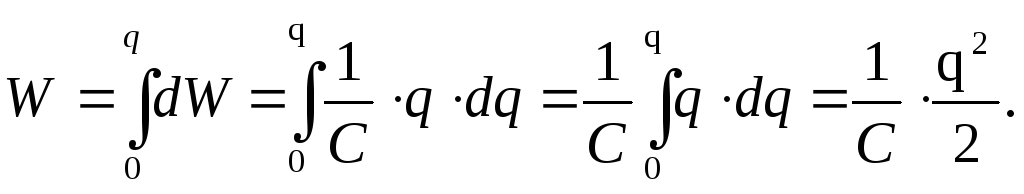 (1.40)
(1.40)
Для плоского конденсатора энергия электрического поля
 .
(1.41)
.
(1.41)
Подставляя в
последнее равенство 

где  — объем конденсатора.
— объем конденсатора.
Объемная плотность энергии электрического поля обкладками плоского конденсатора
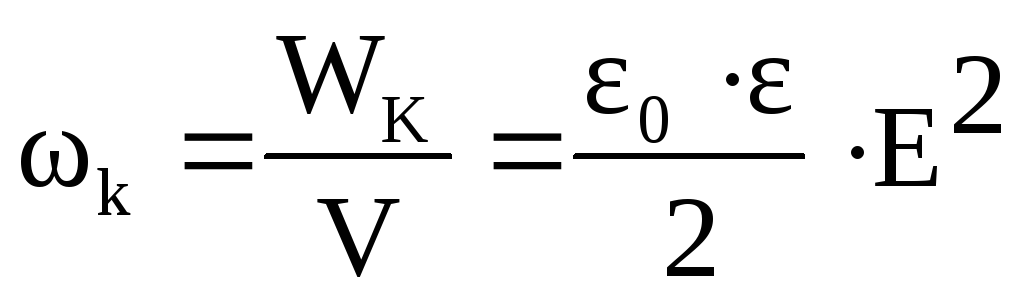 .
(1.43)
.
(1.43)
Вопросы и задания для самостоятельного изучения
Определить потенциал электрического поля на поверхности шара радиусом 1 м, зарядом 1 Кл.
Определить электроемкость шара радиусом 1 м.
От каких геометрических параметров зависит электроемкость плоского конденсатора.
Определить электроемкость батареи 10 конденсаторов 1 нФ. Соединенных последовательно.
Определить электроемкость батареи 10 конденсаторов 1 нФ соединенных параллельно.
Определить плотность энергии плоского конденсатора с расстоянием между пластинами 1мм и напряжением 100 В.
Лекция 4
Глава 2. Постоянный ток.
2.1. Электрический ток
Электрический ток – это направленное движение зарядов. Электрический ток называется конвекционным, когда заряды перемещаются в пространстве; током проводимости, когда заряды движутся внутри проводника; током в вакууме, когда заряды движутся в вакууме.
Рассмотрим ток проводимости как наиболее часто встречающийся в технике.
Для определения тока в проводнике используют понятие сил тока
 ,
(2.1)
,
(2.1)
где 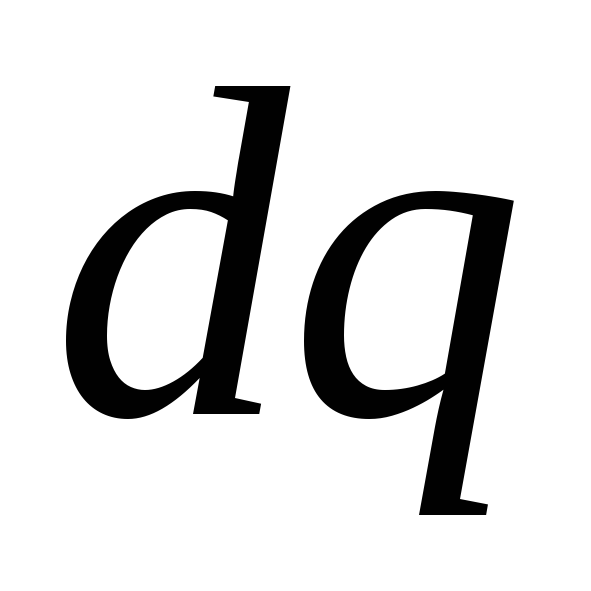 – количество заряда, прошедшее через
выбранное сечение проводника за
промежуток времени
– количество заряда, прошедшее через
выбранное сечение проводника за
промежуток времени .
.
Сила тока – определяет интенсивность направленного движения заряженных частиц и равна заряду, переносимому через поперечное сечение проводника в единицу времени. Если сила тока не зависит от времени, то ток будет называться постоянным
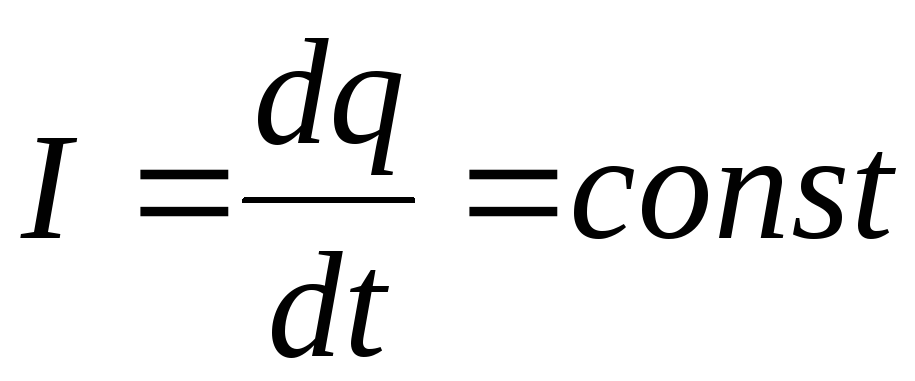 .
.
Заряды обоих знаков перемещаются в противоположных направлениях при прохождении тока в проводнике. Исторически сложилось так, что за направление электрического тока считают направление движения положительных зарядов, или направление, обратное движению отрицательных зарядов. Величина тока в системе СИ измеряется в амперах (А).
2.2. Закон Ома. Сопротивление и электропроводность проводника
Рассмотрим
цилиндрический проводник длиной 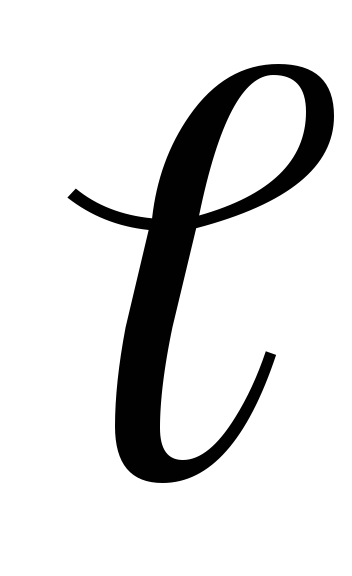 .
.
Для того, чтобы в
проводнике существовал постоянный ток  ,
необходимо внутри проводника создать
постоянное электрическое поле с
напряженностью
,
необходимо внутри проводника создать
постоянное электрическое поле с
напряженностью .
Напряженность электрического поля в
проводнике существует тогда, когда в
нем имеется градиент потенциала:
.
Напряженность электрического поля в
проводнике существует тогда, когда в
нем имеется градиент потенциала:
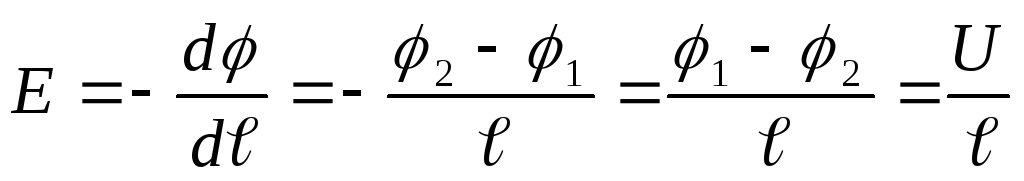 (2.2)
(2.2)
Где 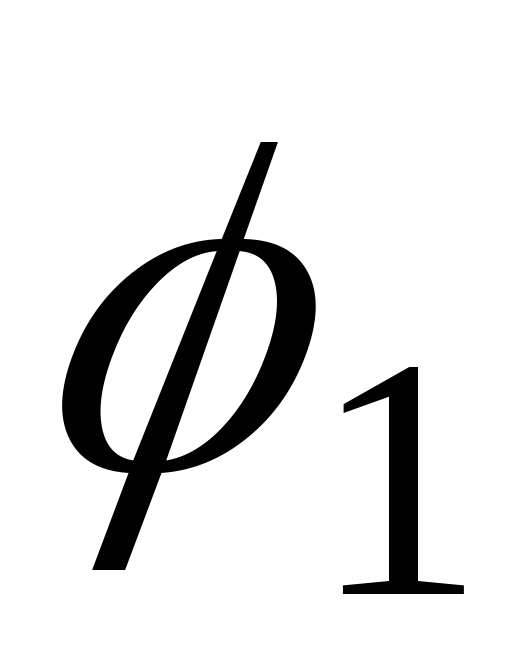 и
и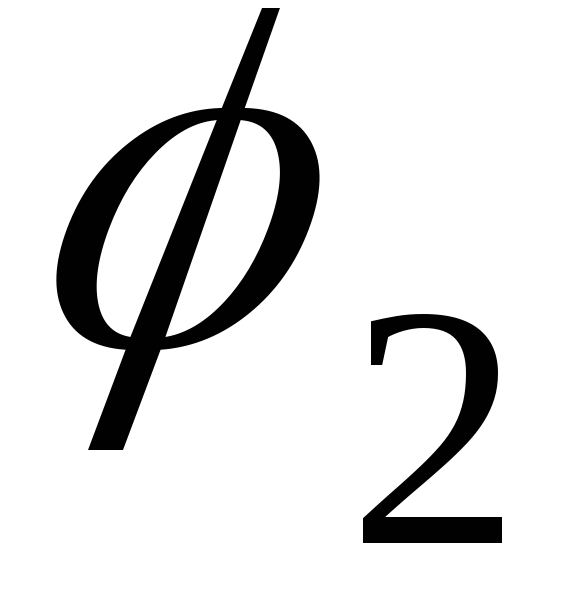 — электрические потенциалы на концах
проводникаU
— напряжение, приложенное к проводнику.
При изменении напряжения U
изменяется ток в проводнике по закону
Ома
— электрические потенциалы на концах
проводникаU
— напряжение, приложенное к проводнику.
При изменении напряжения U
изменяется ток в проводнике по закону
Ома
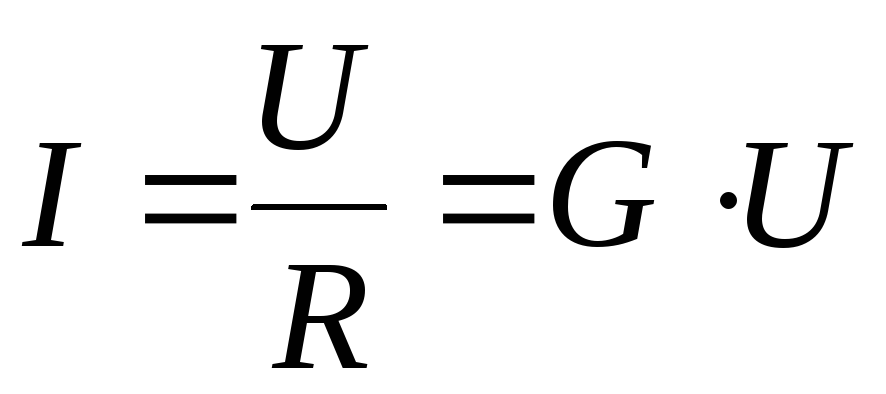 (2.3)
(2.3)
где R – электрическое сопротивление
проводника; 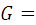
 – проводимость
проводника.
– проводимость
проводника.
В системе СИ сопротивление измеряется в Ом. 1 Ом – сопротивление такого проводника, в котором при напряжении 1В идет ток в 1 А. Сопротивление R зависит от материала, из которого сделан проводник, его геометрических размеров и формы. Для цилиндрических проводников справедливо соотношение
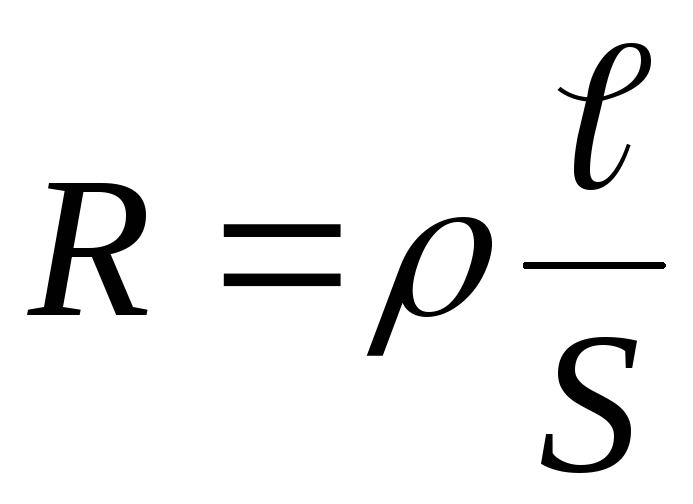 ,
(2.4)
,
(2.4)
где —  удельное сопротивление материала
проводника,
удельное сопротивление материала
проводника, ,
, соответственно
длина и площадь сечения проводника.
соответственно
длина и площадь сечения проводника.
Подставим (2.4) в (2.3),
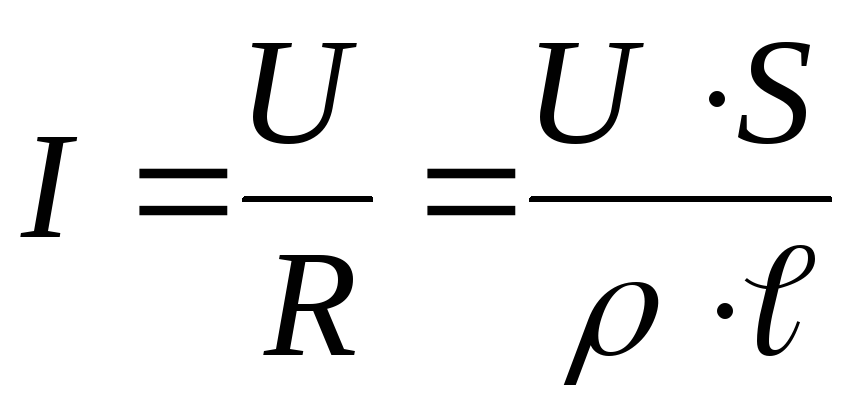 .
(2.5)
.
(2.5)
Введем понятие плотности тока j
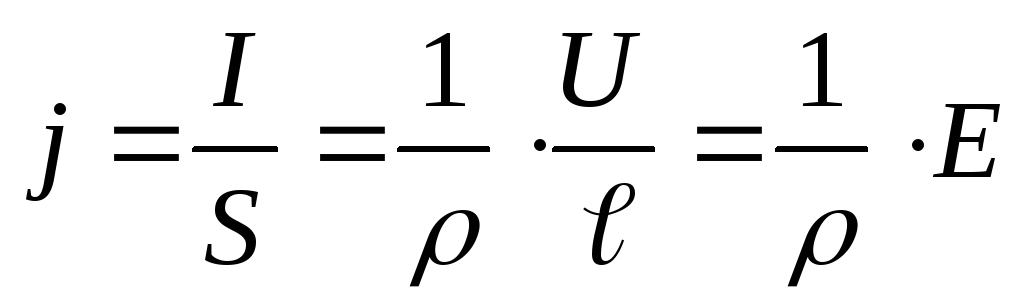 ,
(2.6)
,
(2.6)
где  удельная проводимость, или
электропроводность, проводника.
удельная проводимость, или
электропроводность, проводника.
Учитывая векторный
характер напряженности электрического
поля  ,
,
 (2.7)
(2.7)
Плотность тока 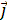 – вектор, совпадающий с вектором
напряжённости
– вектор, совпадающий с вектором
напряжённости  электрического
поля.
электрического
поля.
Для поддержания постоянной разности потенциалов на концах проводника необходимо подключать его к источнику напряжения, или источнику тока.(ИТ)
Сторонние силы действуют на заряды только в источнике тока. В замкнутой цепи, имеющей источник тока, помимо сторонних сил действуют электростатические силы (силы Кулона).
Электрическая
цепь постоянного тока (рис.2.1) включает
сопротивление нагрузки (резистор) R,
сопротивление внутренних деталей
источника тока r
(внутреннее сопротивление), ЭДС (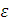 ).
).
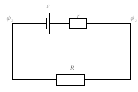
Рис. 2.1.
В источнике тока за счёт его внутренних сил (не Кулоновского происхождения) разделяются положительные и отрицательные заряды, которые скапливаются у его выходных электродов, и создают разность потенциалов на клеммах.
Так как к резистору R приложена разность потенциалов U, то, согласно закону Ома, через него будет идти ток за счёт Кулоновских сил.
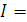
 (2.8)
(2.8)
По внутренним деталям ИТ проходит ток
 (2.9)
(2.9)
Токи 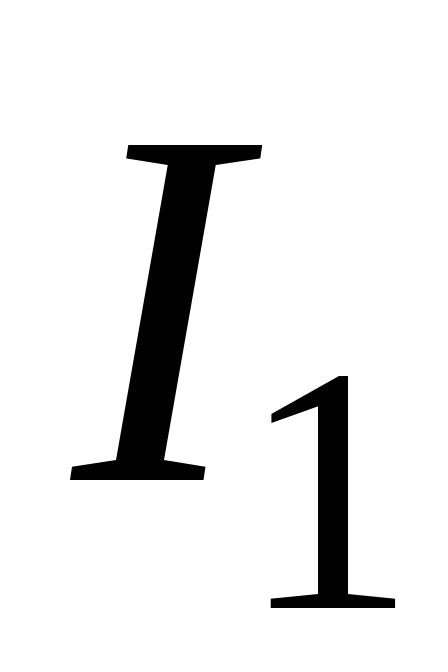 и
и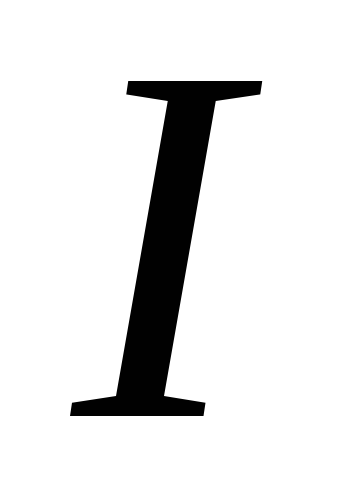 приводят
к разряду ИТ и уменьшению количества
положительных и отрицательных зарядов
на его электродах. Сторонние силы
непрерывно восстанавливают количество
этих зарядов на выходных электродах,
т.е. непрерывно восстанавливают
противоположные заряды на электродах
и создают ток
приводят
к разряду ИТ и уменьшению количества
положительных и отрицательных зарядов
на его электродах. Сторонние силы
непрерывно восстанавливают количество
этих зарядов на выходных электродах,
т.е. непрерывно восстанавливают
противоположные заряды на электродах
и создают ток ,
противоположный току
,
противоположный току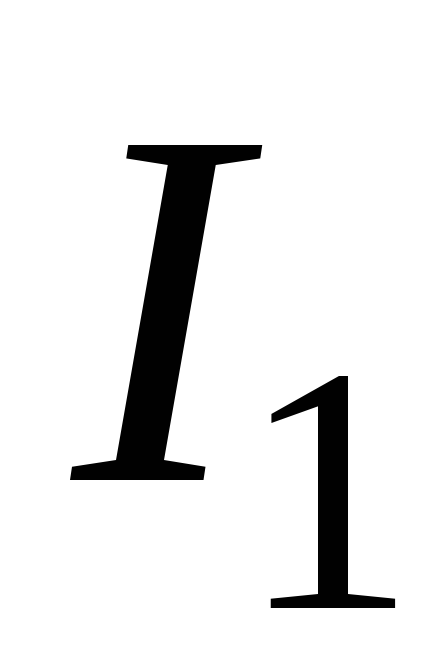 (рис.2.2).
(рис.2.2).

В стационарном процессе, когда токи постоянны
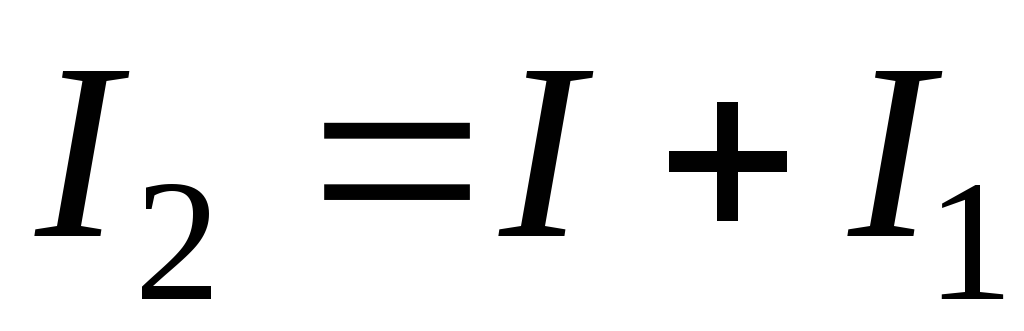 ,или
,или
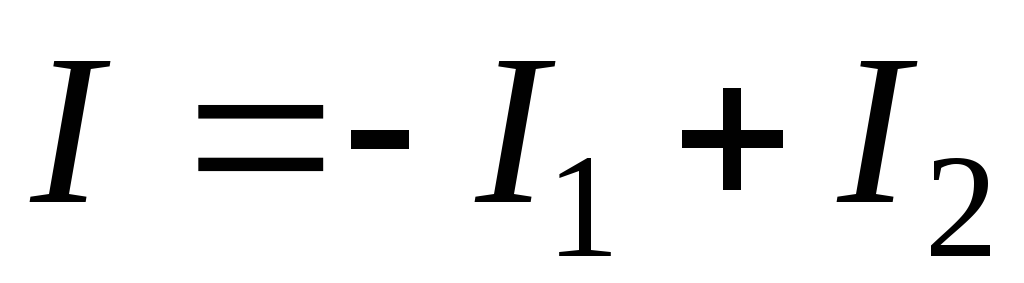 .
(2.10)
.
(2.10)
Рис. 2.2
Сторонние силы
источника тока, вызывающие ток  ,
появляются в результате действия
химических реакций или других явлений
и называют электродвижущей силой
,
появляются в результате действия
химических реакций или других явлений
и называют электродвижущей силой (ЭДС).
(ЭДС).
Для написания закона Ома для замкнутой цепи запишем уравнение (2.10) в виде:
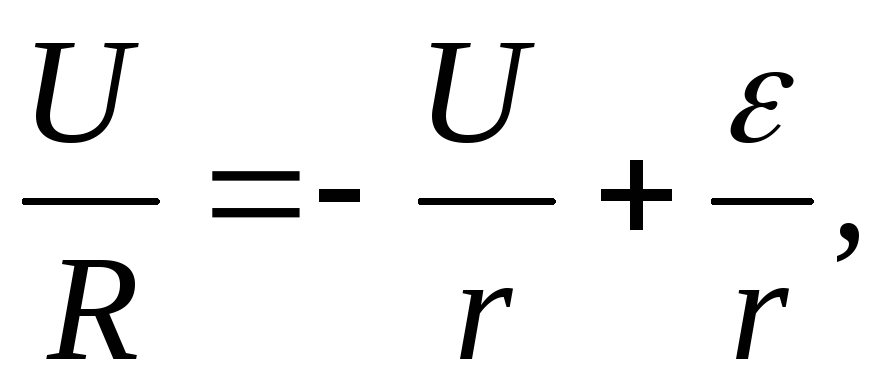 (2.11)
(2.11)
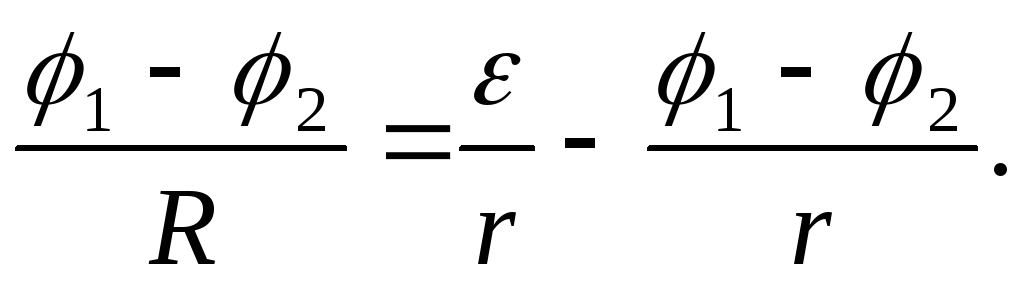
После алгебраических преобразований
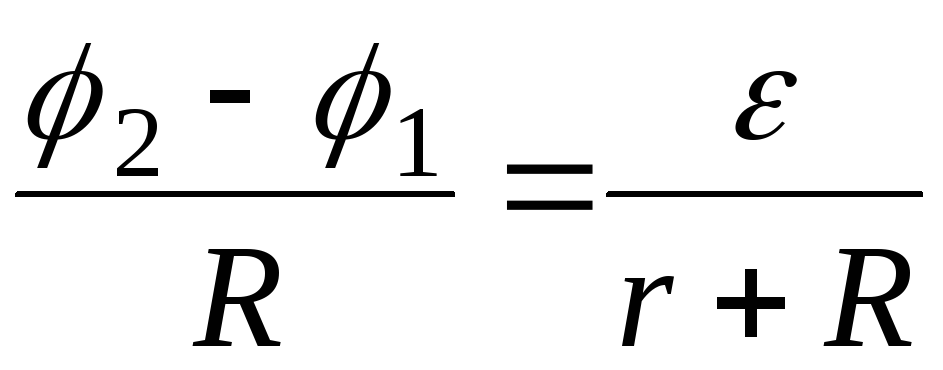 (2.12)
(2.12)
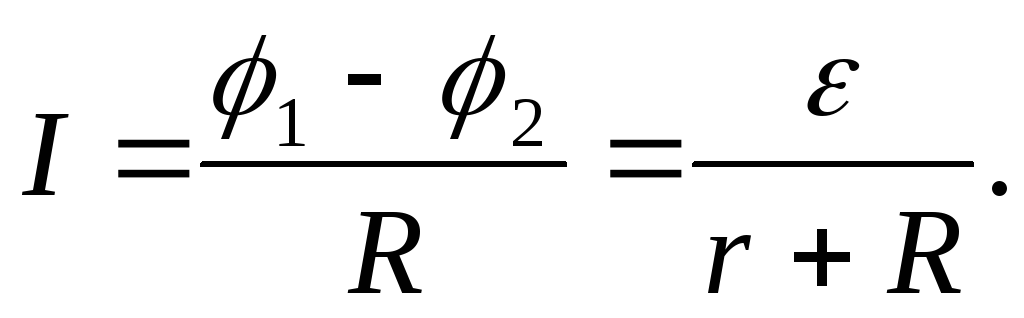 (2.13)
(2.13)
Закон Ома для замкнутой цепи.
Перепишем уравнение 2.13 в виде:
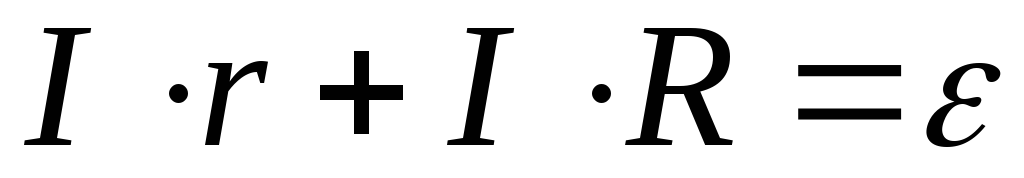 (2.14)
(2.14)
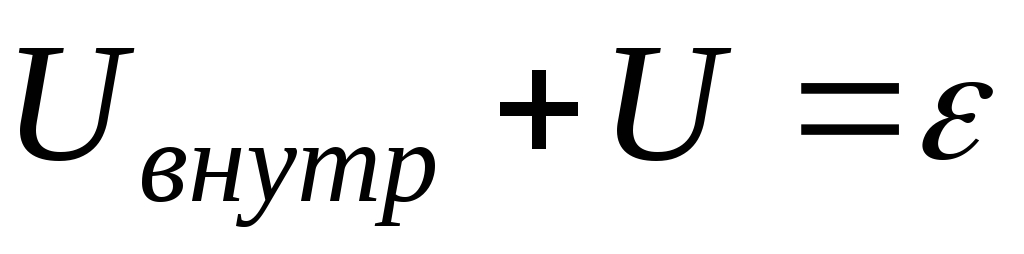
где 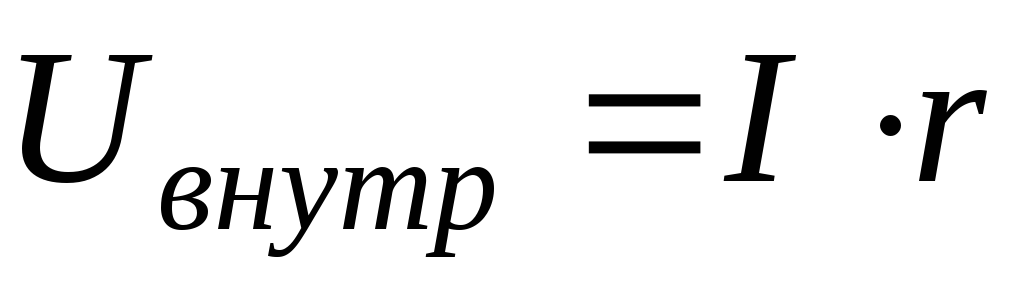 падение напряжения на внутренних
деталях источника тока;
падение напряжения на внутренних
деталях источника тока;
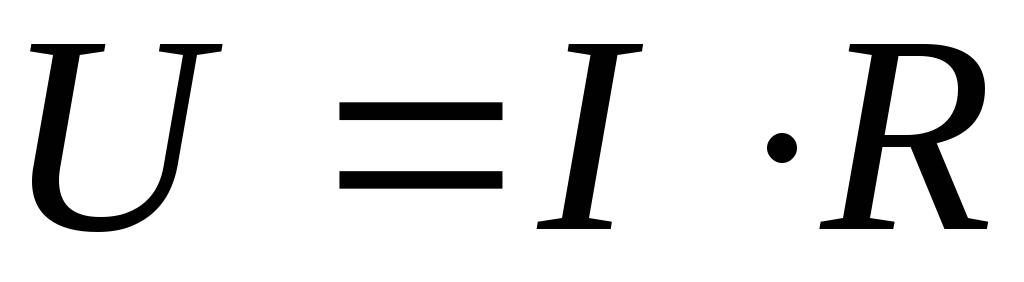 падение напряжения
на внешнем сопротивлении R.
падение напряжения
на внешнем сопротивлении R.
Из уравнения (2.14) следует, что
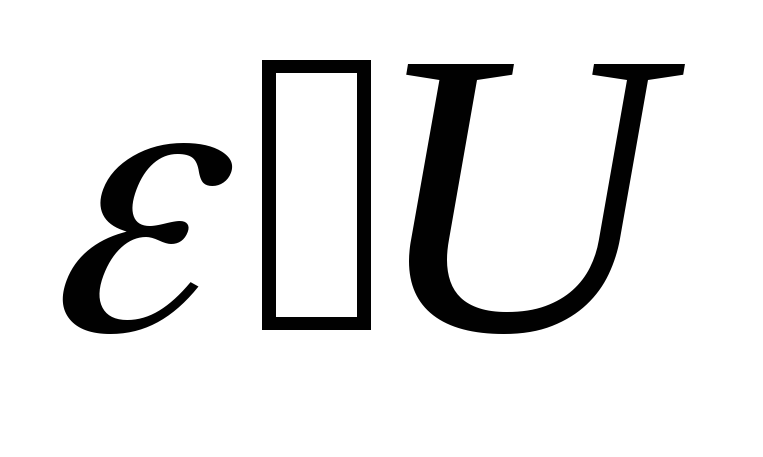 (2.15)
(2.15)
Если 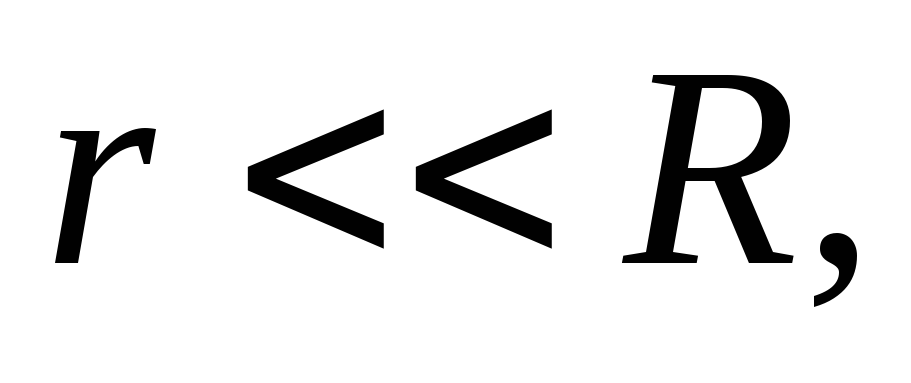 то
то
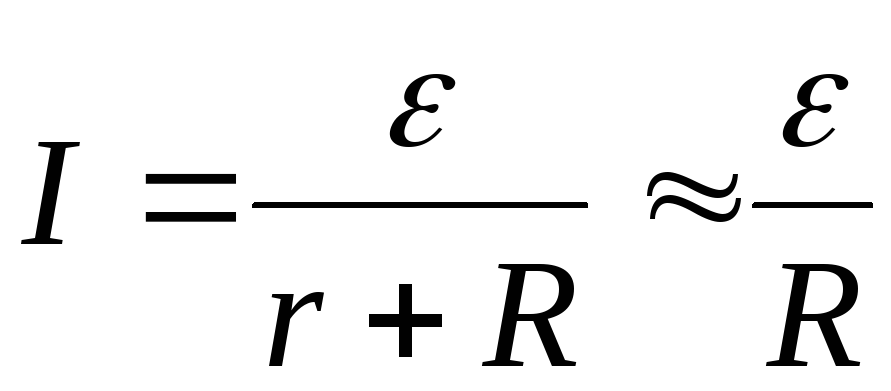 (2.16)
(2.16)
и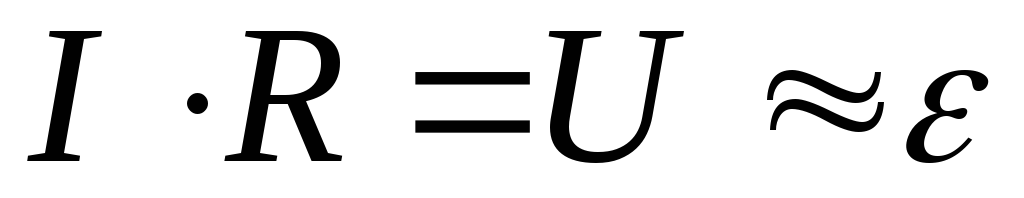 Если
Если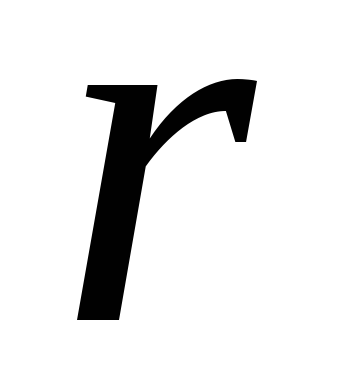 соизмеримо сR (т.е.
соизмеримо сR (т.е. 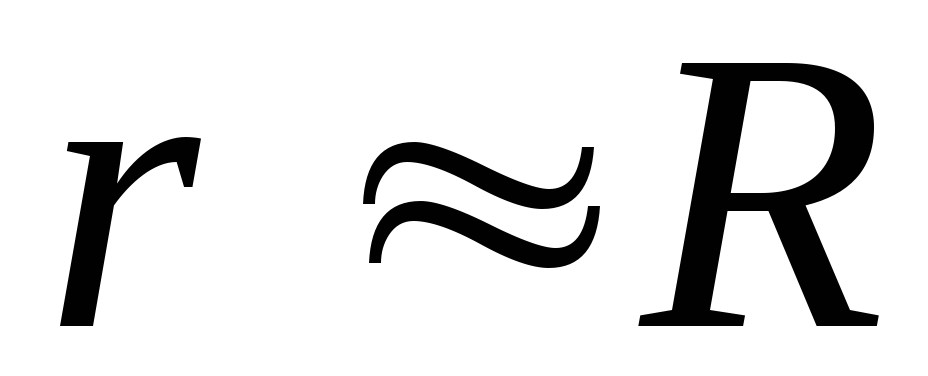 ), то
), то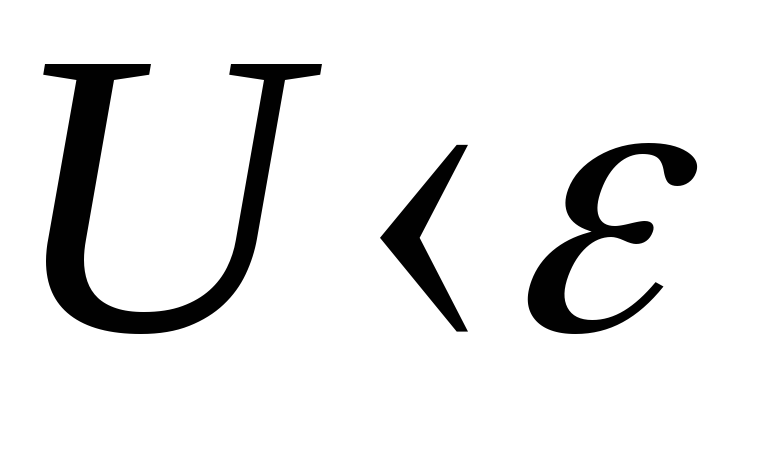 (именно поэтому говорят, что источник
тока «подсаживается» при подключении
к нему мощного потребителя тока,
обладающего малымR,
так как:
(именно поэтому говорят, что источник
тока «подсаживается» при подключении
к нему мощного потребителя тока,
обладающего малымR,
так как:  .
.
Сопротивления  и
и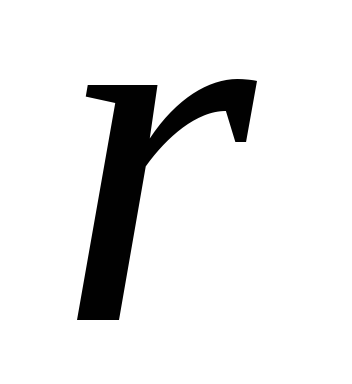 в цепи (рис.2.1) включены последовательно,
и следовательно, полное сопротивление
в цепи (рис.2.1) включены последовательно,
и следовательно, полное сопротивление
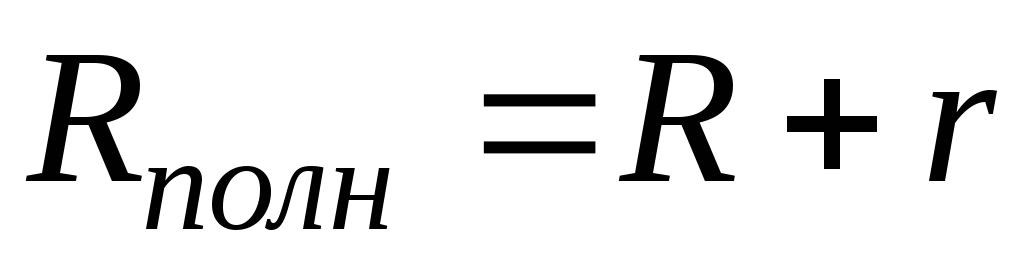 ,
( 2.17)
,
( 2.17)
. ( 2.18)
Из уравнения
(2.13) следует, что ток  у любого источника тока ограничены
из-за его внутреннего сопротивления
у любого источника тока ограничены
из-за его внутреннего сопротивления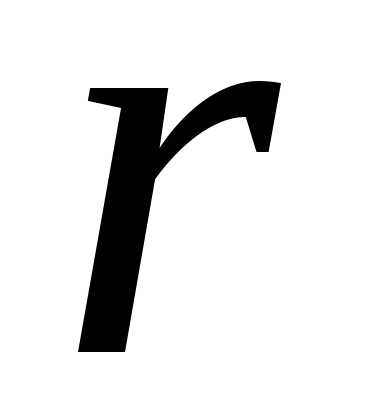 .
Максимальный ток
.
Максимальный ток возникает в результате короткого
замыкание (
возникает в результате короткого
замыкание (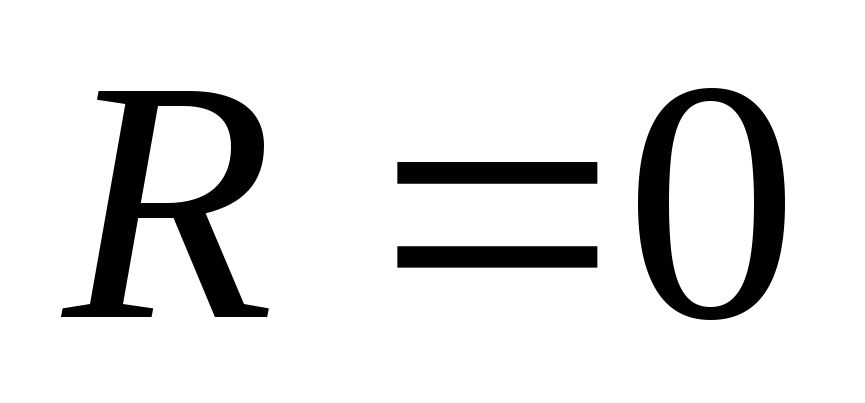 )
)
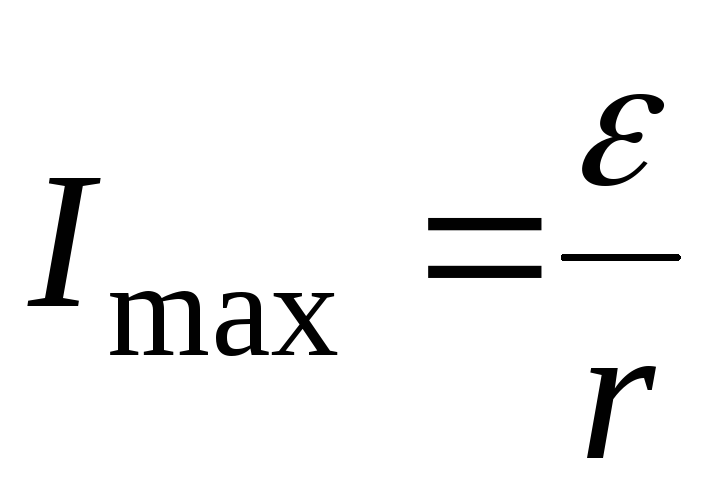 .
( 2.19 )
.
( 2.19 )
Например, для
батареи  =1,5
В и
=1,5
В и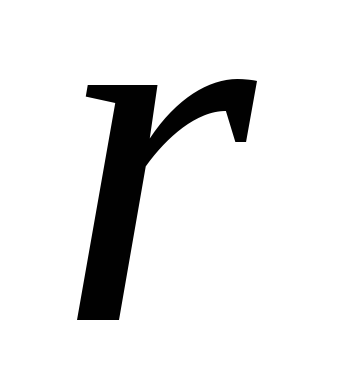 =0,1
Ом
=0,1
Ом
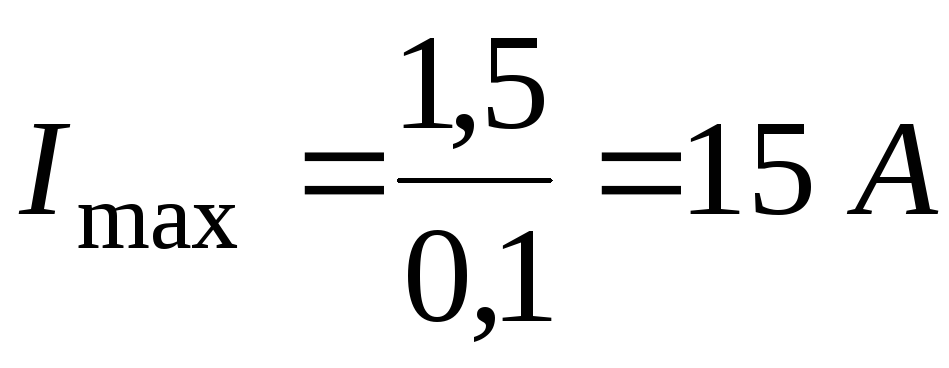 .
.
Лекция 5.
ФИЗИКА Ч1 / Лекции_Цаплин / Лекция 22 / Лекция 5
8
Лекция 5
Проводники в электрическом поле
Вопросы
Проводники в электростатическом поле.
Электроемкость заряженного проводника. Конденсаторы.
Энергия заряженного проводника, конденсатора и электростатического поля.
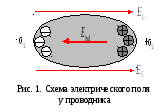
1. Проводники в электростатическом поле
Проводником называется среда, в которой имеется достаточное число свободных электрических зарядов. Например, в металлах в 1 см3 содержится около 1023 свободных электронов. В диэлектриках свободных электронов менее 106 в 1 см3, а в хороших диэлектриках менее 103 в 1 см3.
Хорошими проводниками электрического тока являются не только металлы, но еще растворы электролитов и ионизованные газы.
Металлы имеют кристаллическую структуру. В узлах кристаллических решеток металлов находятся положительно заряженные ионы, а валентные электроны могут свободно передвигаться между ними в различных направлениях по всему объему. Совокупность свободных электронов в металле называют электронным газом.
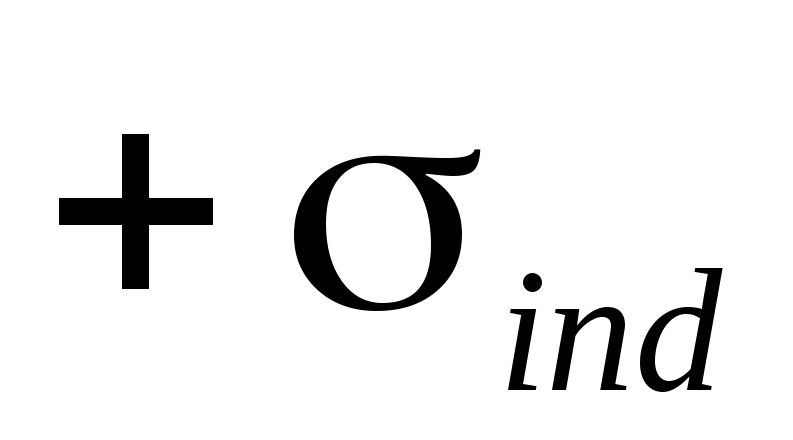 и
и  .
Электрическое поле индуцированных
зарядов компенсирует внешнее электрическое
поле, т.е.
.
Электрическое поле индуцированных
зарядов компенсирует внешнее электрическое
поле, т.е. 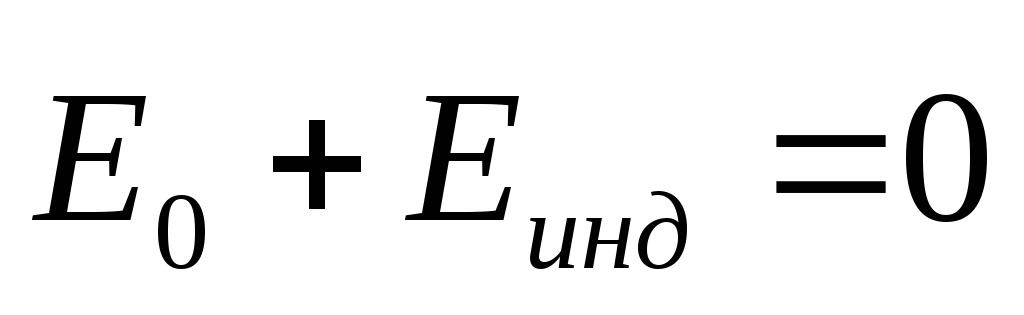 ,
т.к.
,
т.к. 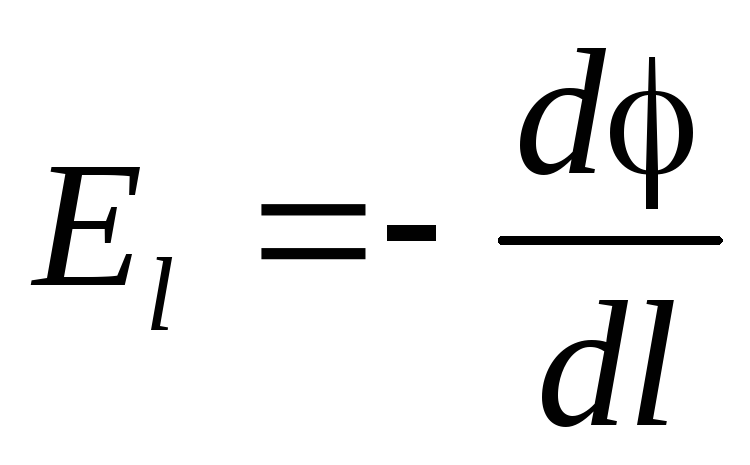 , то
, то 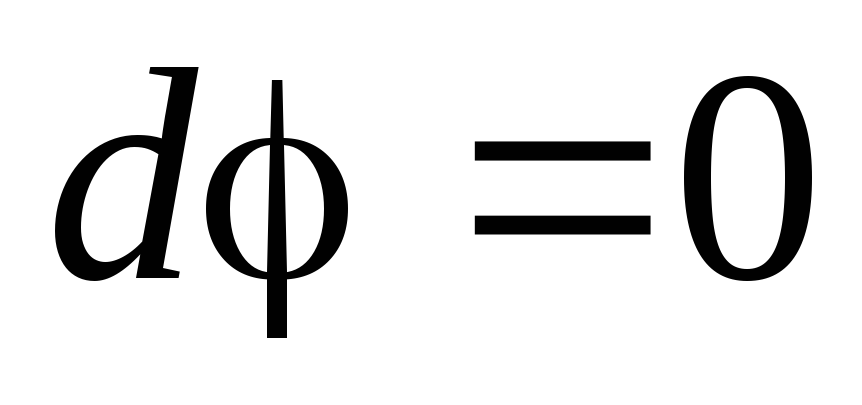
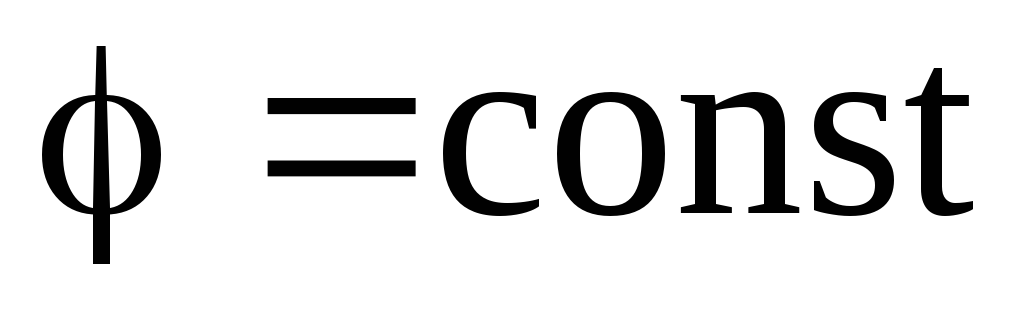 , (1)
, (1)
т.е. электростатическое поле внутри проводника отсутствует, а потенциал проводника является постоянным (проводник эквипотенциален).
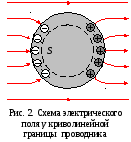
У криволинейной поверхности проводника
силовая линия напряженности
электростатического поля должна быть
направлена по нормали к этой поверхности,
иначе под действием тангенциальной
составляющей поля 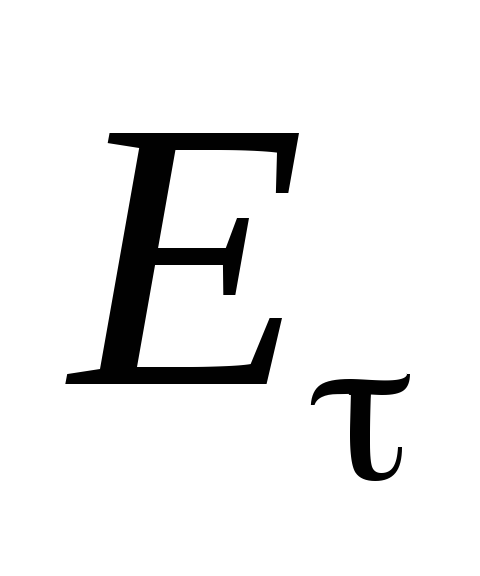 заряды перемещались бы по проводнику,
что противоречит условию (1).
заряды перемещались бы по проводнику,
что противоречит условию (1).
В заряженном проводнике избыточный заряд располагается только на поверхности, т.к. согласно теореме Гаусса для замкнутой области S внутри проводника заряд отсутствует.
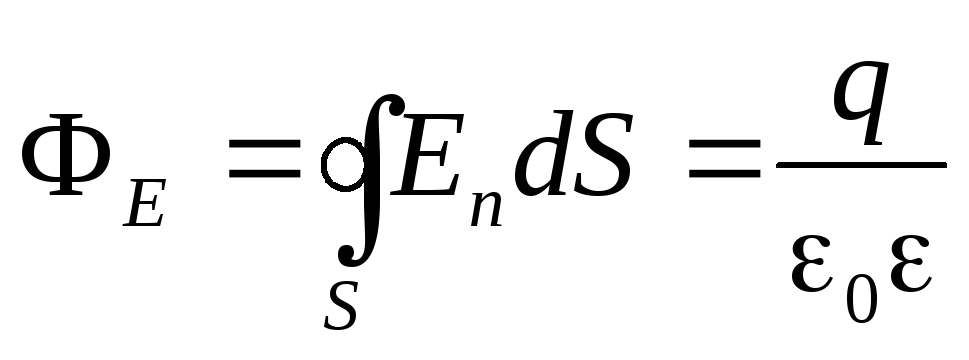

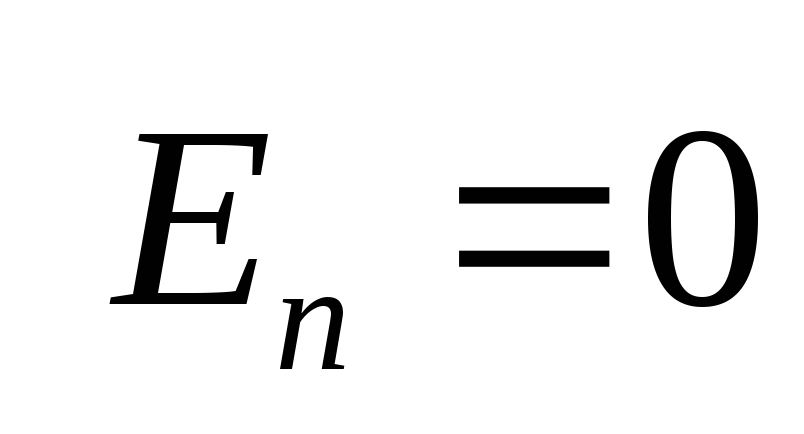

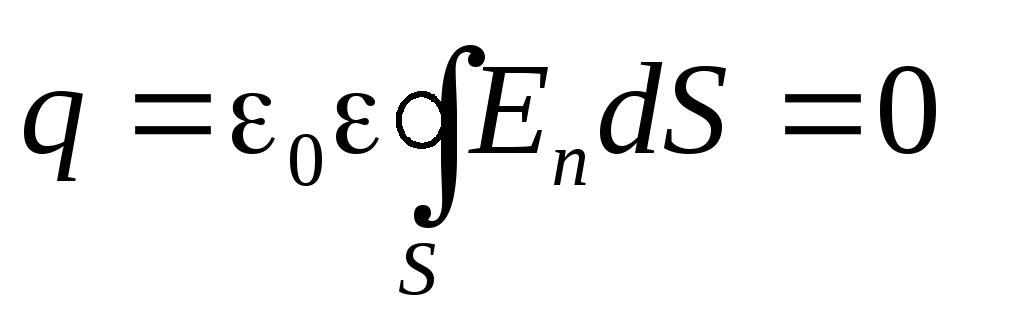 .
(2)
.
(2)
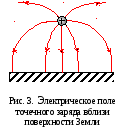
Пример. Точечный заряд у поверхности Земли. Поскольку силовые линии перпендикулярны эквипотенциальным поверхностям, электрическое поле вблизи проводника должно быть нормально к его поверхности. (Это понятно, так как если бы поле имело касательную составляющую, то электроны двигались бы вдоль поверхности проводника). В качестве примера на рис. 3 показано электрическое поле точечного заряда вблизи поверхности Земли (Земля – проводник).
Электростатическая индукция
При внесении незаряженного проводника в электростатическое поле носители зарядов приходят в движение. Перераспределение идет до тех пор, пока внутри проводника не будет Е=0, а на поверхности Е=Еn.
Явление, состоящее в электризации незаряженного проводника во внешнем электростатическом поле путем разделения в этом проводнике уже имеющихся в нем в равных количествах положительных и отрицательных зарядов, называется электризацией через влияние или электростатической индукцией.
И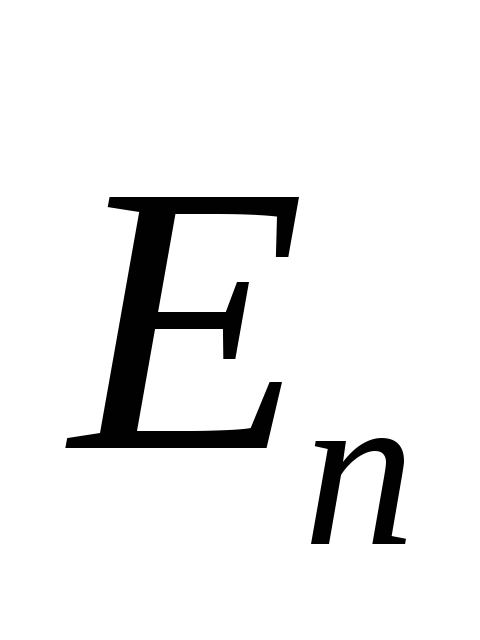
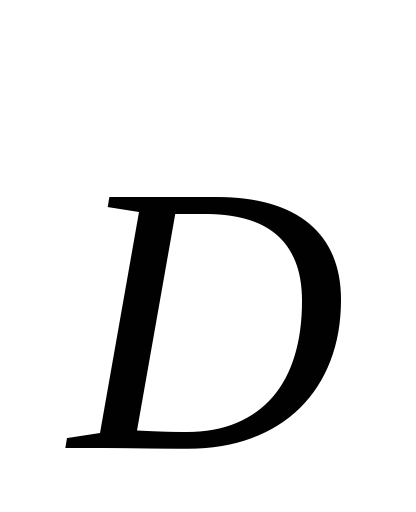 ндуцированные
заряды появляются на проводнике
вследствие смещения их под действием
поля. При замыкании концов проводника
с разноименными зарядами может появиться
ток смещения, поэтому вектор на
поверхности проводника называется
вектором электрического смещения .
ндуцированные
заряды появляются на проводнике
вследствие смещения их под действием
поля. При замыкании концов проводника
с разноименными зарядами может появиться
ток смещения, поэтому вектор на
поверхности проводника называется
вектором электрического смещения .
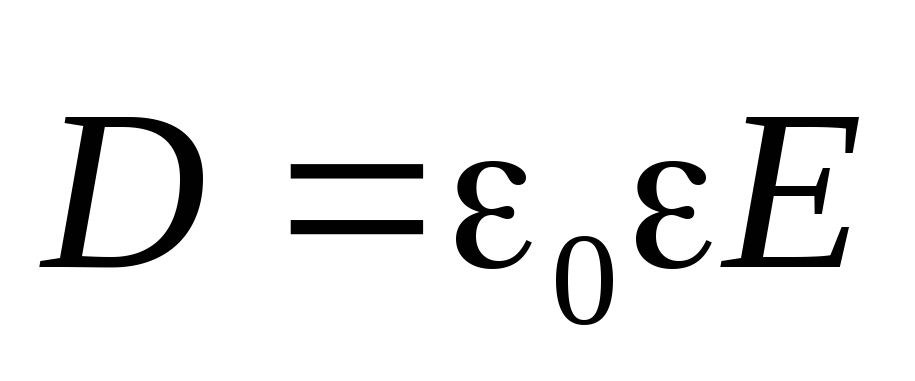 .
(2)
.
(2)
Электростатическая защита
Электростатическая защита объектов (например, приборов) от влияния внешних электростатических полей основана на том, что заряды располагаются на поверхности, а полость в замкнутом проводнике не заряжена (экранирована от внешнего поля). Для электростатической защиты можно использовать не сплошной проводник, а металлическую сетку, которую заземляют, т.е. соединяют с нулевым потенциалом Земли.
Свойство зарядов располагаться на внешней поверхности используется в электростатических генераторах, применяемых в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.
2. Электроемкость заряженного проводника. Конденсаторы
Электроемкостью заряженного проводника называется скалярная физическая величина С, характеризующая способность проводника накапливать заряды и численно равная заряду, изменяющему потенциал проводника на один Вольт.
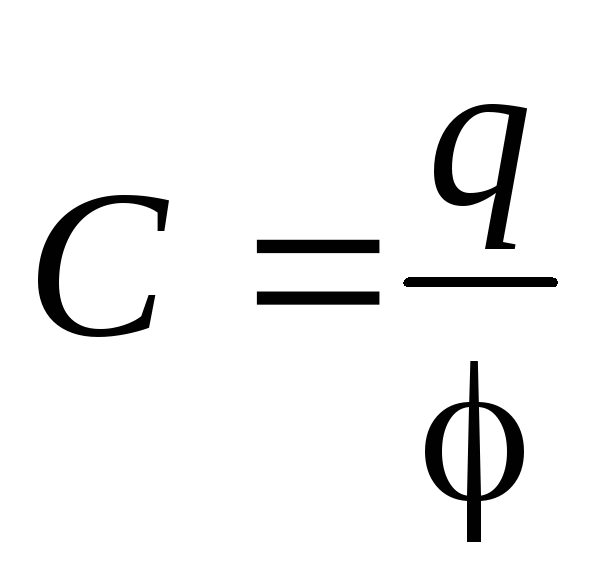 , 1 Фарад = 1 Кулон / 1 Вольт
. (3)
, 1 Фарад = 1 Кулон / 1 Вольт
. (3)
Так как заряды в проводнике располагаются только на поверхности, то электроемкость не зависит от материала проводника, его агрегатного состояния, но зависит от формы и размеров.
Фарад – большая единица. Например, используя потенциал проводящей поверхностно заряженной сферы и формулу (3), получим




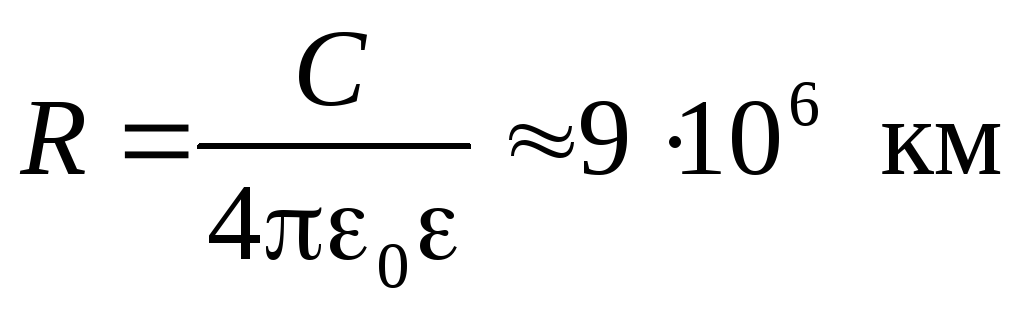 ,
,
что в 1400 раз больше радиуса Земли. Электроемкость Земли — 711 мкФ.
Единицы измерения в технике:
1 мФ = 10-3Ф; 1 мкФ = 10-6Ф; 1 нФ = 10-9Ф; 1 пФ = 10-12Ф.
Конденсатором называется система из двух изолированных
друг от друга проводников. Эти проводники
обычно называют пластинами, хотя они
могут иметь любую форму. На практике
конденсаторы используются как «накопители
зарядов» или «резервуары», в которых
содержится энергия электрического
поля. Если на пластины поместить
одинаковые по величине, но противоположные
по знаку заряды  и
и 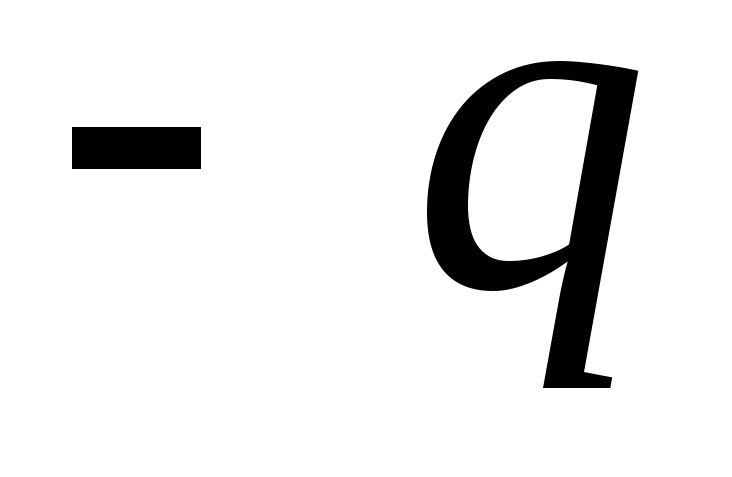 ,
то между пластинами возникнет разность
потенциалов
,
то между пластинами возникнет разность
потенциалов 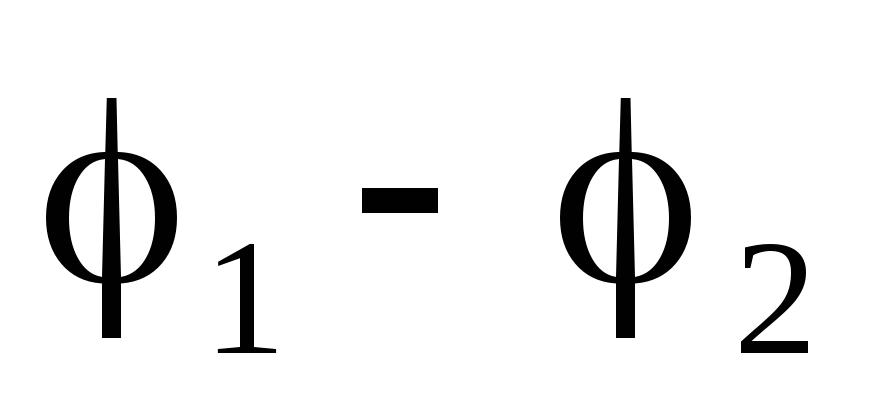 . Емкостью конденсатора называется величина:
. Емкостью конденсатора называется величина:
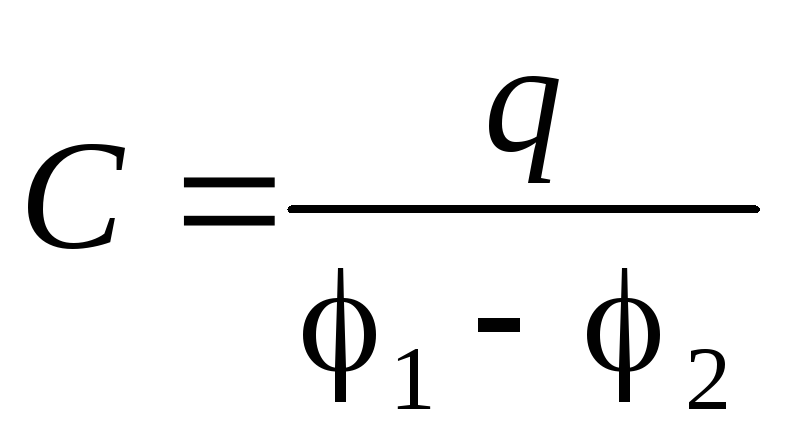 . (4)
. (4)

 ;
;  ;
;
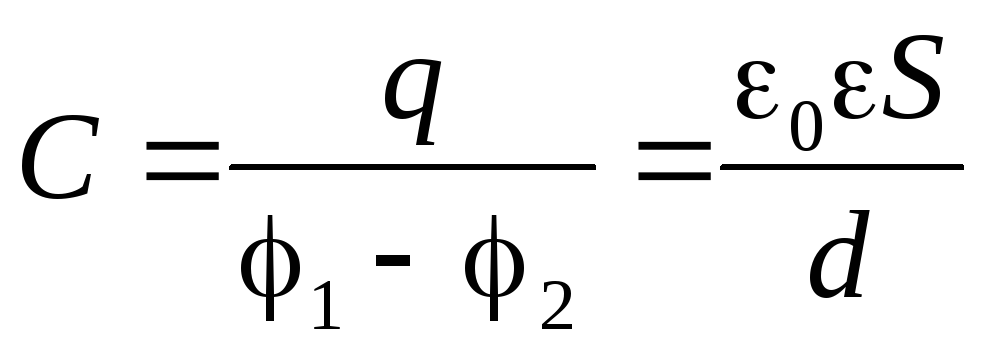 ,
(5)
,
(5)
т.е. ёмкость конденсатора зависит только от его геометрических характеристик, вида диэлектрика между пластинами, и не зависит от сообщаемых ему зарядов.
Для того чтобы получить заданную емкость, можно использовать не один, а несколько конденсаторов. Систему из нескольких конденсаторов называют батареей конденсаторов. Емкостью батареи конденсаторов называется величина
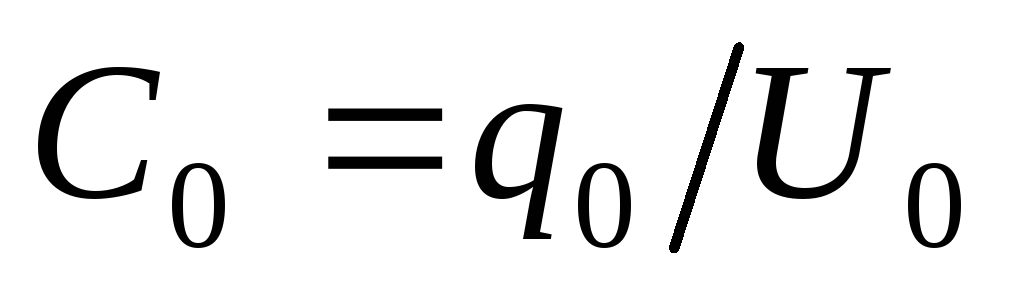 ,
,
где 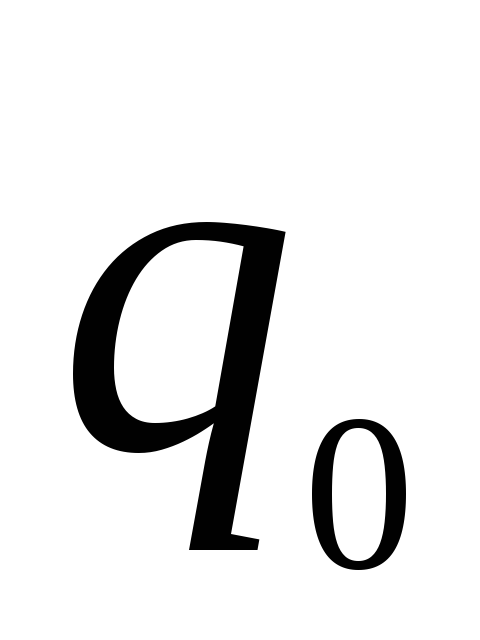 — полный заряд батареи, полученный от
источника, а
— полный заряд батареи, полученный от
источника, а 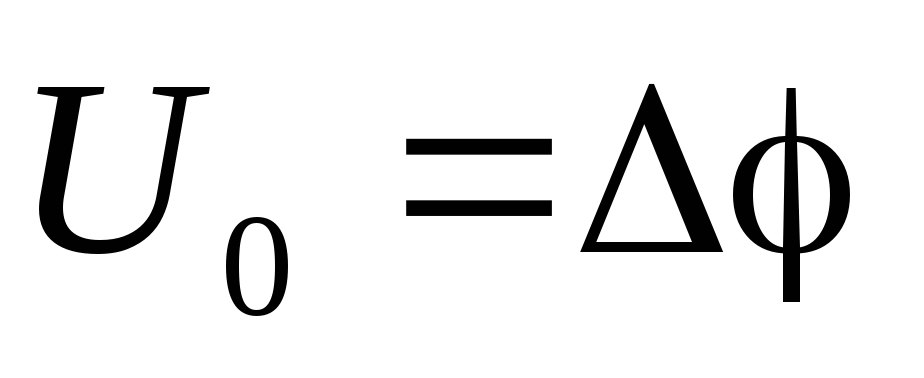 — напряжение, поданное на батарею
конденсаторов.
— напряжение, поданное на батарею
конденсаторов.
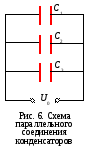
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов
между собой соединены все положительные
и отрицательные обкладки. В этом случае
все конденсаторы заряжаются до одной
и той же разности потенциалов 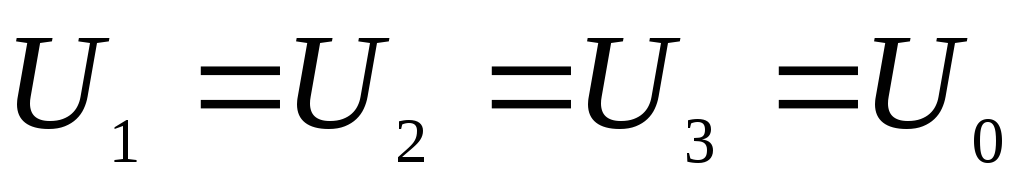 ,
общий заряд такой батареи:
,
общий заряд такой батареи:
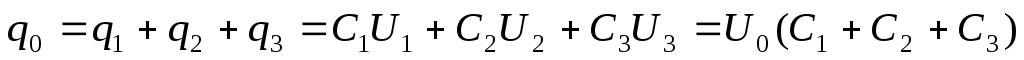
и, следовательно, емкость всей системы:


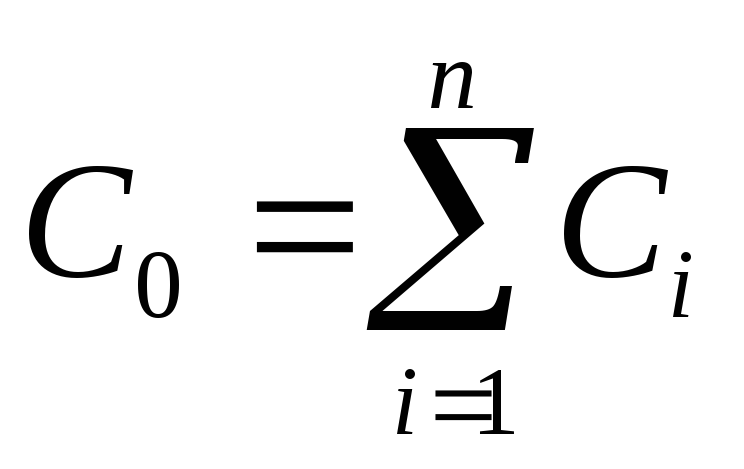 . (6)
. (6)
Ёмкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов. При С1 = С2 = С3 = 1 С0= 3.
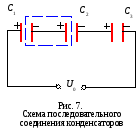
При последовательном соединении конденсаторов отрицательная обкладка первого конденсатора соединена с положительной обкладкой второго и т. д. В этом случае на всех конденсаторах заряды одинаковы:
 ,
,
а выделенная часть цепи нейтральна, так как она не соединена с источником напряжения.
Общее напряжение на батарее конденсаторов складывается из напряжений на каждом конденсаторе:


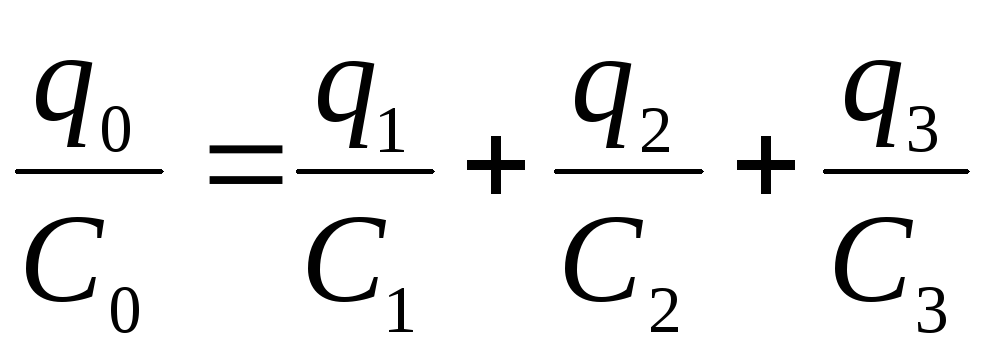 .
.
Из-за равенства зарядов
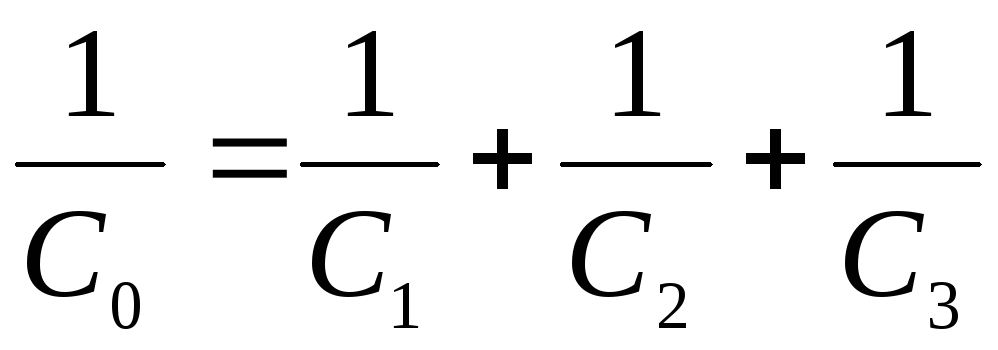

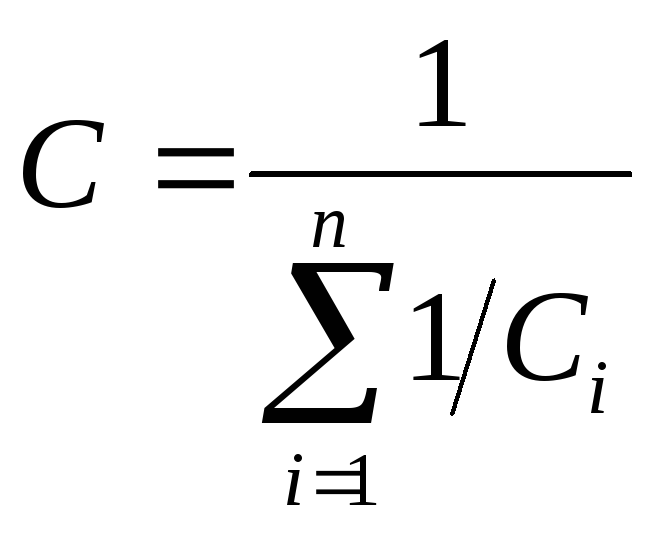 . (7)
. (7)
При С1 = С2 = С3 = 1 С0 = 1/3, т.е. ёмкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.
3. Энергия заряженного проводника, конденсатора
и электростатического поля
Для зарядки проводника нужно совершить работу против сил кулоновского отталкивания одноименных зарядов.
Если незаряженному проводнику сообщать
заряд малыми порциями dq,
переносимыми из бесконечности, где
0=0. По мере
зарядки проводника ёмкостью 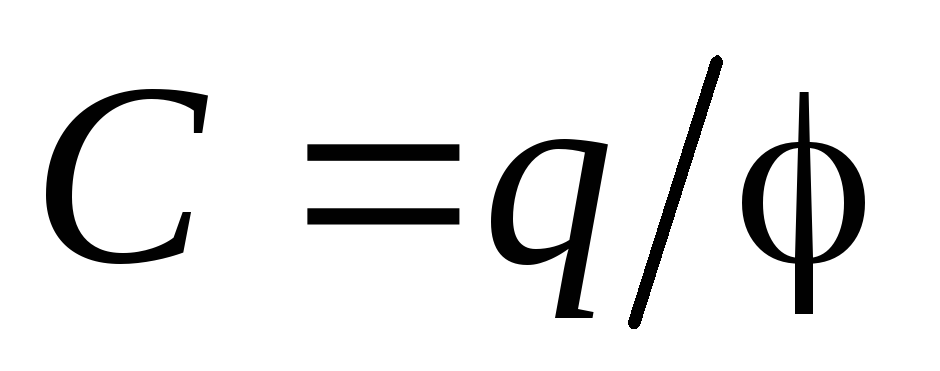 его потенциал возрастает
его потенциал возрастает
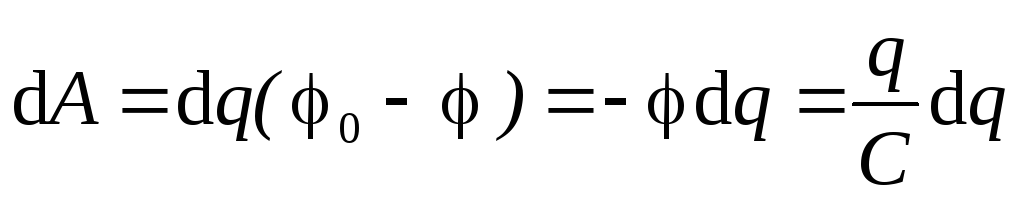

 .
.
Энергия заряженного проводника равна совершенной работе
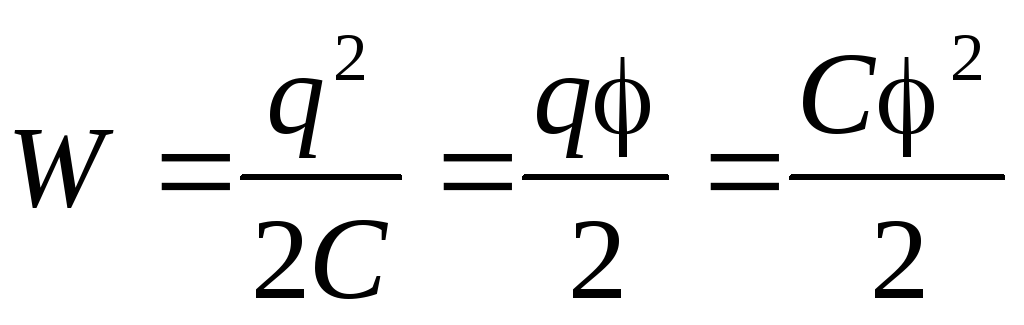 . (8)
. (8)
При зарядке конденсатора малыми
порциями 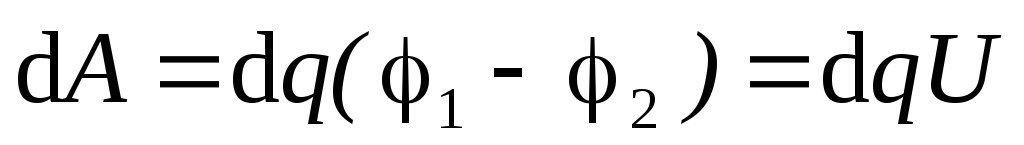 по аналогии с зарядкой проводника имеем
энергию заряженного конденсатора
по аналогии с зарядкой проводника имеем
энергию заряженного конденсатора
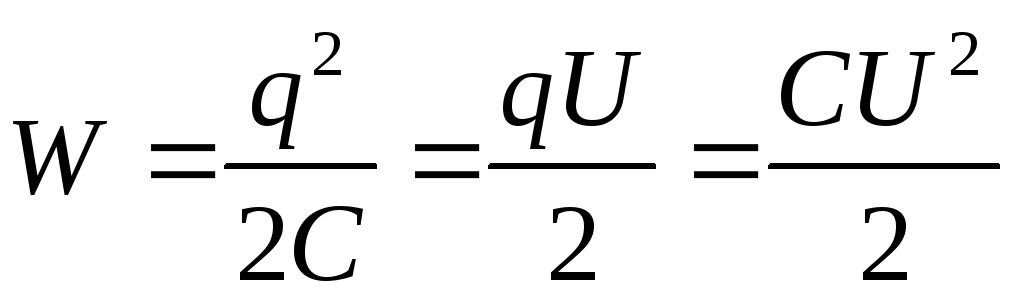 . (9)
. (9)
Используя формулу (9), можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. При изменении расстояния x между пластинами эта сила совершает работу

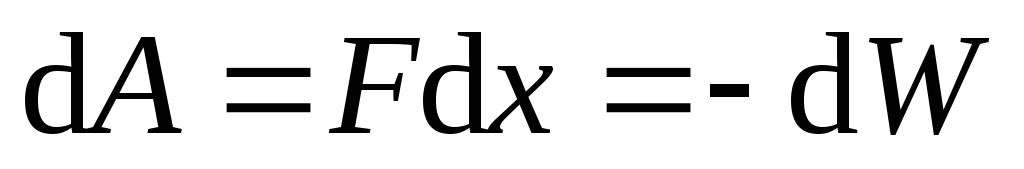




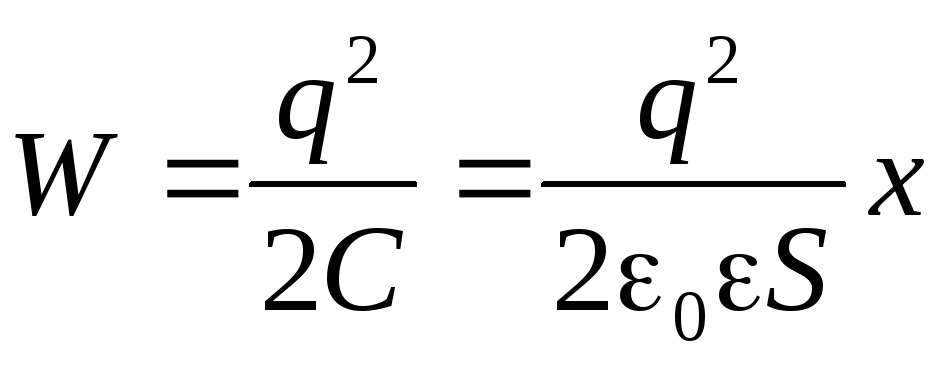
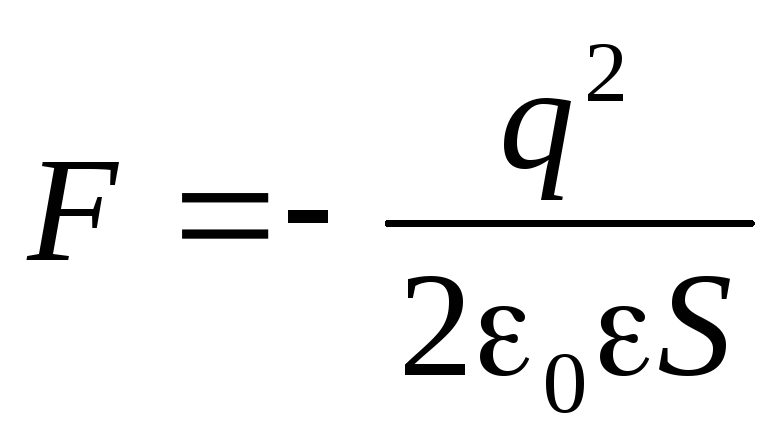 .
.
Выразим энергию (9) через характеристики электростатического поля
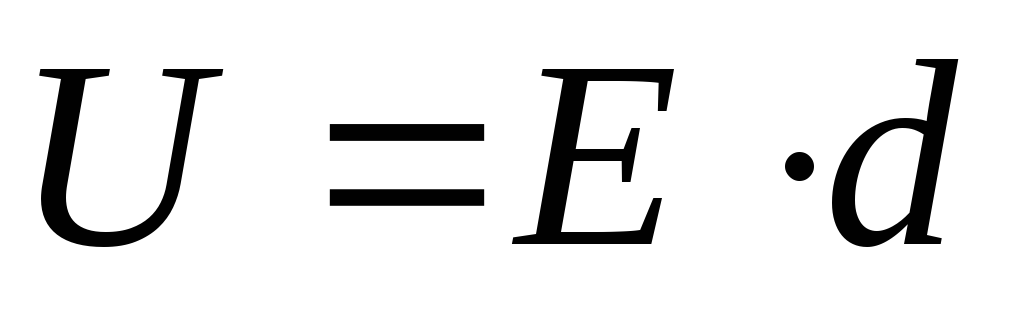 ,
, 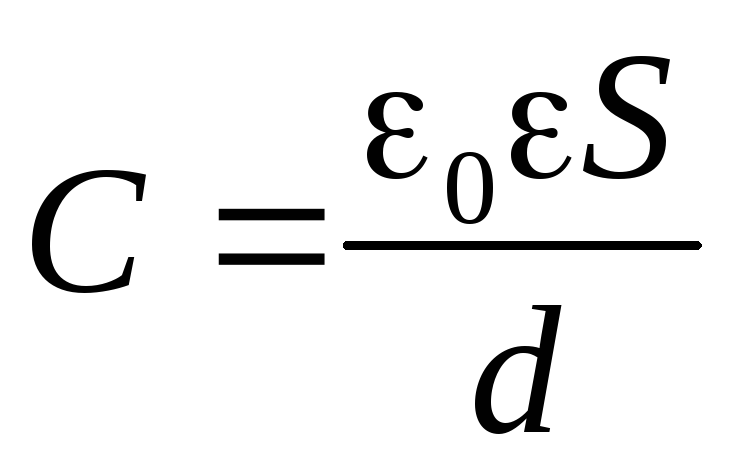 ,
,
 — объём между обкладками конденсатора.
— объём между обкладками конденсатора.
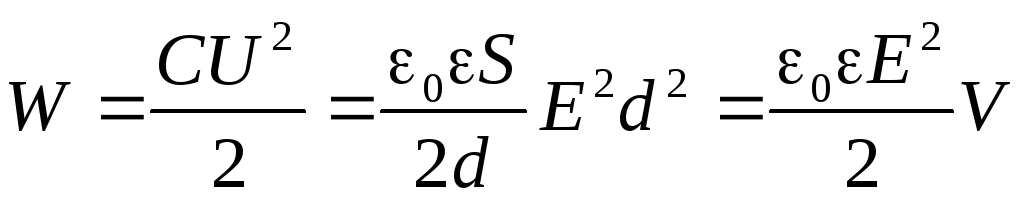

 . (10)
. (10)
Объёмная плотность энергии
 .
.
Используя связь (2) между напряженностью
электрического поля  и вектором электрического смещения
и вектором электрического смещения  полученный результат можно записать
так:
полученный результат можно записать
так:
 .
(11)
.
(11)
Объемная плотность энергии конденсатора уже не зависит от каких-либо его геометрических характеристик. Она выражается лишь через характеристики электрического поля конденсатора. Таким образом, энергия конденсатора – это энергия электрического поля, заключенного между его обкладками.
Выражение (11) для плотности электрического поля в какой-либо точке пространства, доказанное нами в случае электрического поля конденсатора, является универсальным. В общем случае энергия неоднородного электрического поля, заключенная в некотором объеме V, рассчитывается через объемный интеграл:
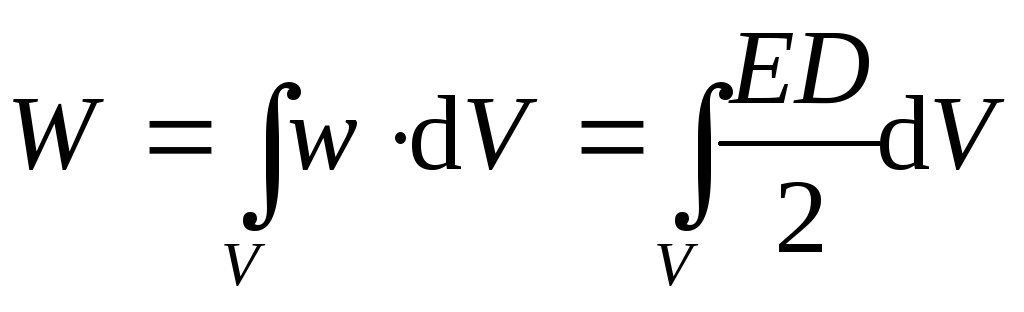 ,
(12)
,
(12)
т.е. носителем энергии является электростатическое поле.
17.Энергия заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии.
Энергия заряженного конденсатораравна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс
зарядки конденсатора можно представить
как последовательный перенос достаточно
малых порций заряда Δq > 0 с одной
обкладки на другую. При этом одна
обкладка постепенно заряжается
положительным зарядом, а другая –
отрицательным. Поскольку каждая порция
переносится в условиях, когда на
обкладках уже имеется некоторый заряд
q, а между ними существует некоторая
разность потенциалов  ,
при переносе каждой порции Δq внешние
силы должны совершить работу
,
при переносе каждой порции Δq внешние
силы должны совершить работу
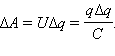
(С – емкость)
Энергия We конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:
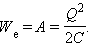
Энергия заряженного плоского конденсатора Eк равна работе A, которая была затрачена при его зарядке, или совершается при его разрядке.
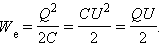 =Eк
=Eк
Поскольку напряжение на конденсаторе может быть рассчитано из соотношения:
U=E*d,
где E- напряженность поля между обкладками
конденсатора,d- расстояние
между пластинами конденсатора, то
энергия заряженного конденсатора
равна:
где V- объем пространства между обкладками конденсатора.
Энергия заряженного конденсатора сосредоточена в его электрическом поле.
Объемная плотность энергии электростатического поля (энергия единицы объема)
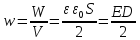
18. Электрический ток. Сила и плотность тока.
Ток — направленное движение электрически заряженных частиц. Величина тока измеряется так называемой силой тока, которая в системе СИ измеряется в амперах.
Токбывает постоянный и переменный. Постоянный ток — это ток, имеющий постоянную величину. Переменный ток периодически изменяет направление своего движения по синусоиде с определенной частотой, измеряемой в герцах (Гц). Переменный ток высокой частоты вытесняется на поверхность проводника
Материал, в котором течёт ток, называется проводником
Сила тока в проводнике — скалярная величина, численно равная заряду, протекающему в единицу времени через сечение проводника. Обозначается буквой :I
I=q/t
Плотность тока — векторная величина, имеющая смысл силы тока, протекающего через единицу площади. Например, при равномерном распределении плотности jтока по сечениюSпроводника |j|=I/S
19.Сторонние силы. Электродвижущая сила и напряжение.
Сторонние силы —силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока.
Сторонними считаются все силы отличные от кулоновских сил.
Электродвижущая сила
(эдс), физическая величина, характеризующая действие сторонних (непотенциальных) сил в источниках постоянного или переменного тока; в замкнутом проводящем контуре равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил (Eex). В замкнутом контуре (L) тогда ЭДС будет равна:
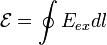 где dl — элемент длины контура.
где dl — элемент длины контура.
Напряжение (разность потенциалов) между точками A и B — это отношение работы электрического поля при переносе пробного электрического заряда из точки A в точку B к величине пробного заряда.
Ф1-Ф2=U12
При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля.
Альтернативное определение (для электростатического поля) —
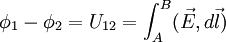
(интеграл от проекции поля на траекторию между точками AиBвдоль любой траектории, идущей изAвB)
Единицей измерения напряжения в системе СИ является Вольт.
1.4.2. Энергия заряженного проводника
Будем считать среду, в которой находятся электрические заряды и заряженные тела, однородной и изотропной, не обладающей сегнетоэлектрическими свойствами.
Заряжая некоторый проводник, необходимо совершить определенную работу против кулоновских сил отталкивания между одноименными электрическими зарядами. Эта работа идет на увеличение электрической энергии заряженного проводника, которая в данном случае аналогична потенциальной энергии в механике.
Рассмотрим
проводник, имеющий электроемкость  ,
заряд
,
заряд и потенциал
и потенциал .
Работа, совершаемая против сил
электростатического поля при перенесении
заряда
.
Работа, совершаемая против сил
электростатического поля при перенесении
заряда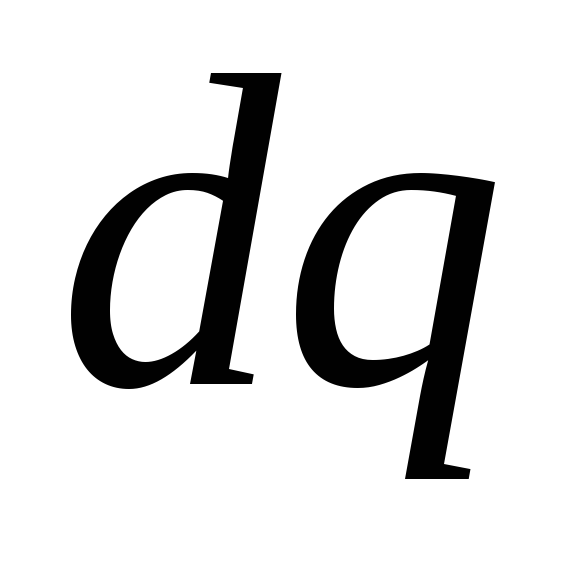 из бесконечности на проводник равна
из бесконечности на проводник равна
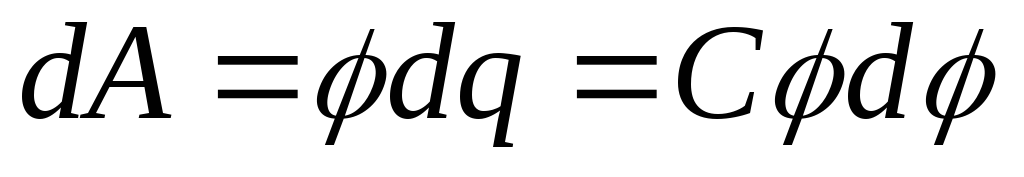 .
.
Для того, чтобы
зарядить тело от нулевого потенциала
до потенциала  ,
необходимо совершить работу
,
необходимо совершить работу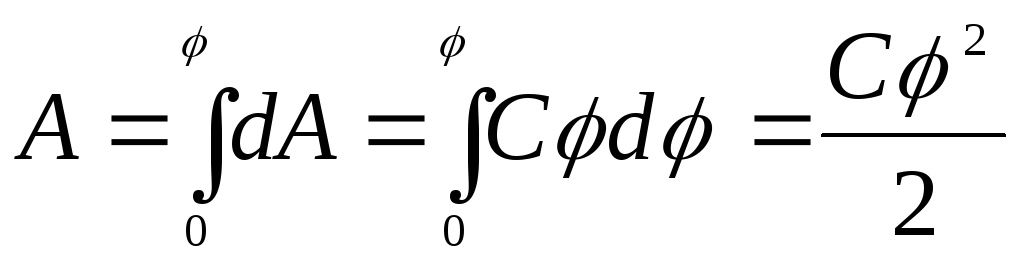 .
Ясно, что энергия заряженного тела равна
той работе, которую нужно совершить,
чтобы зарядить это тело:
.
Ясно, что энергия заряженного тела равна
той работе, которую нужно совершить,
чтобы зарядить это тело: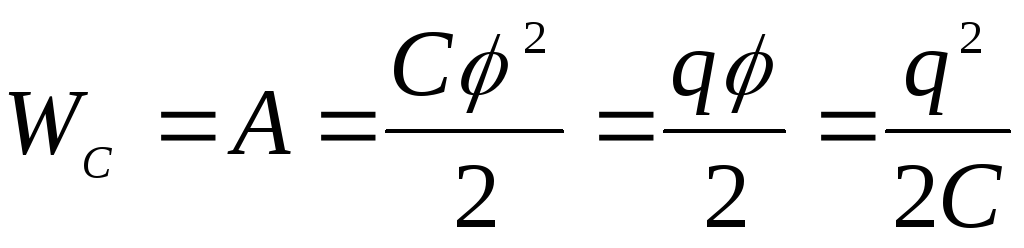 .
.
Энергию 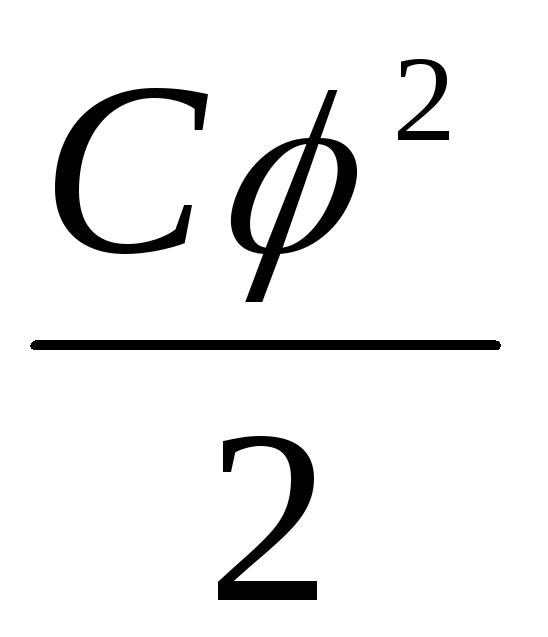 называют собственной энергией заряженного
тела. Ясно, что собственная энергия есть
не что иное, как энергия электростатического
поля этого тела.
называют собственной энергией заряженного
тела. Ясно, что собственная энергия есть
не что иное, как энергия электростатического
поля этого тела.
1.4.3. Энергия заряженного конденсатора. Объемная плотность энергии электростатического поля
Пусть
потенциал обкладки конденсатора, на
которой находится заряд 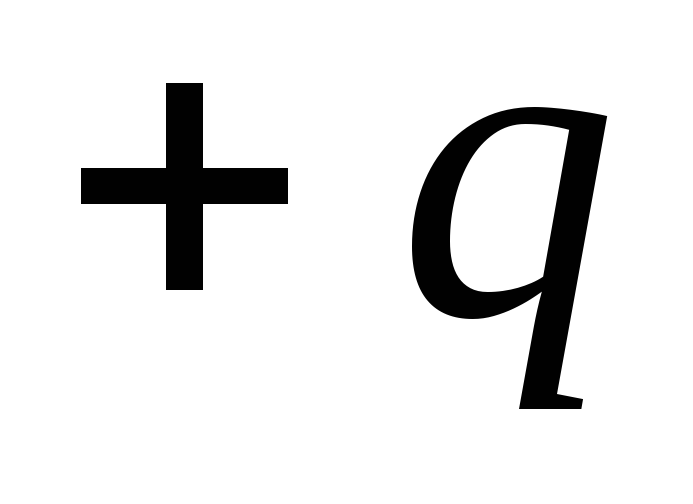 ,
равен
,
равен ,
а потенциал обкладки, на которой находится
заряд
,
а потенциал обкладки, на которой находится
заряд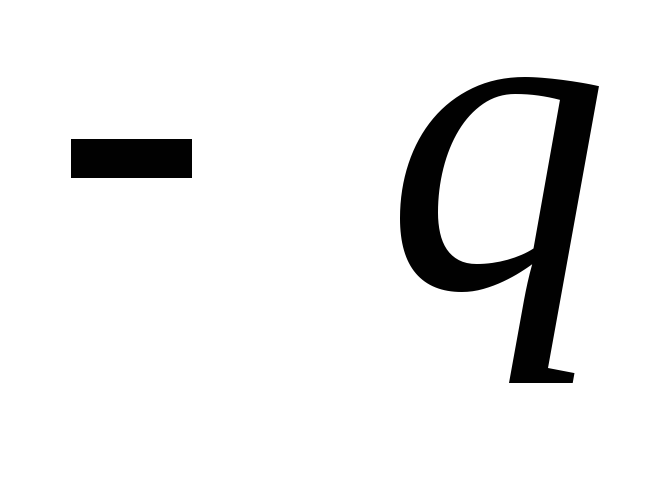 ,
,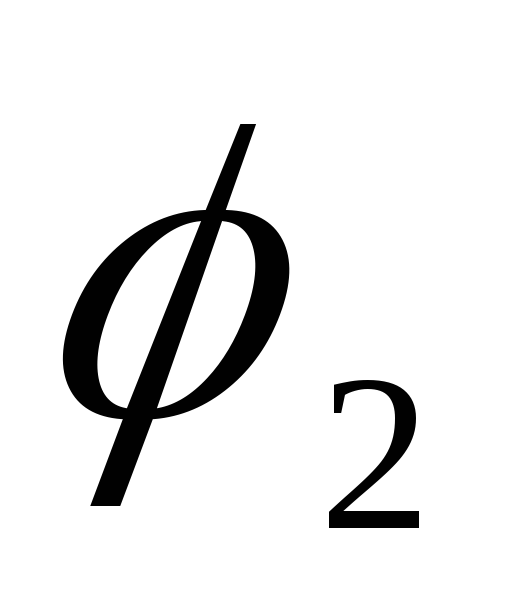 .
Энергия такой системы зарядов
.
Энергия такой системы зарядов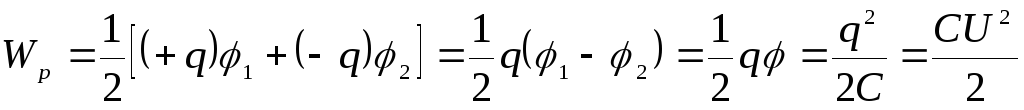 ,
то есть равна собственной энергии
системы зарядов, где
,
то есть равна собственной энергии
системы зарядов, где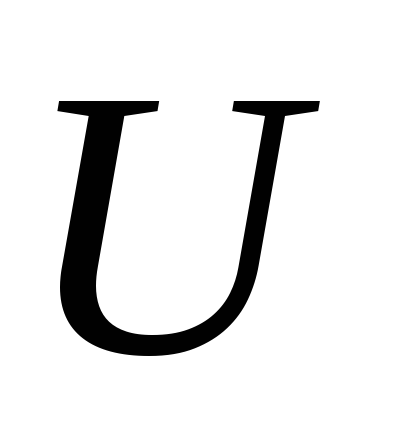 — напряжение между обкладками конденсатора,
— напряжение между обкладками конденсатора,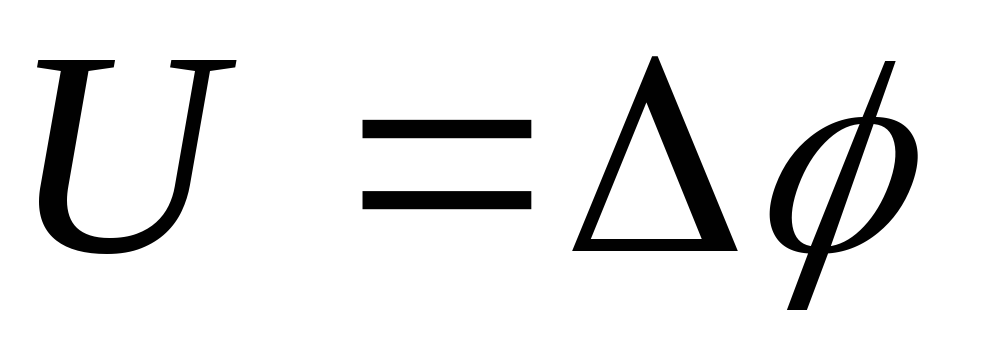 .
.
Рассмотрим
плоский конденсатор. Энергия, заключенная
в единице объема электростатического
поля называется объемной плоскостью
энергии. Эта объемная плоскость должна
быть одинаковой во всех точках однородного
поля, а полная энергия поля пропорциональна
его объему. Известно, что 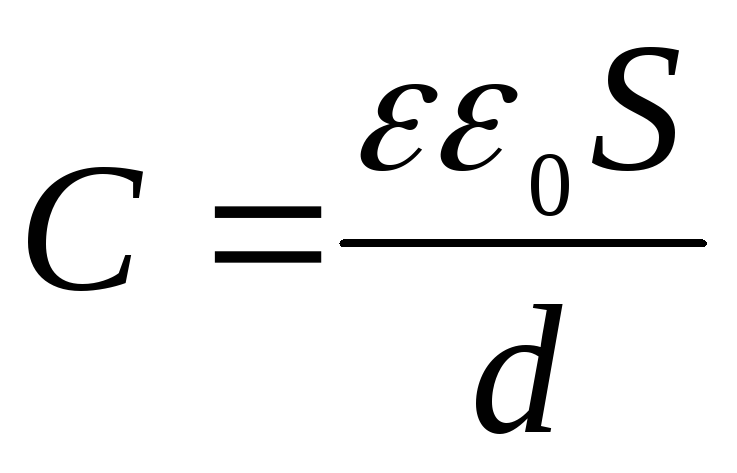 ,
,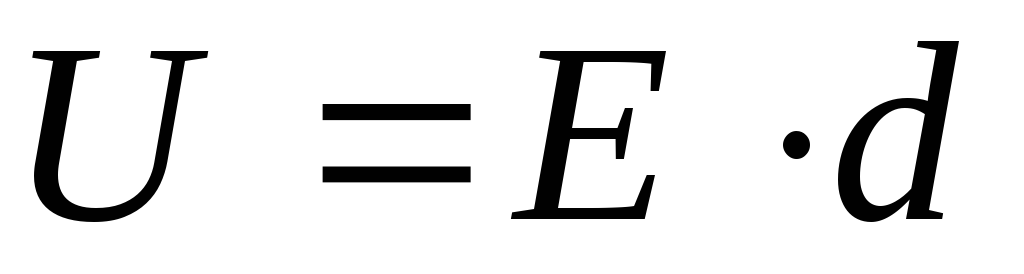 ,
тогда для энергии имеем:
,
тогда для энергии имеем: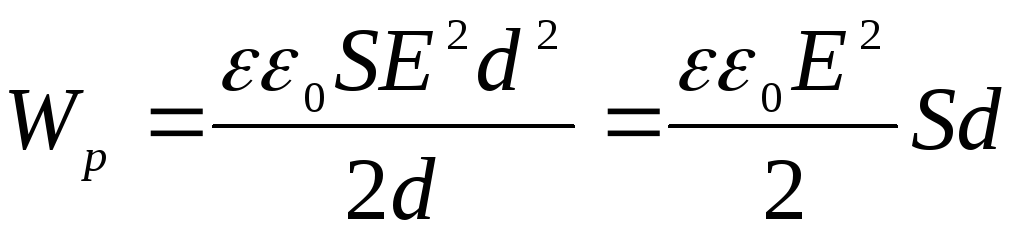 ,
но
,
но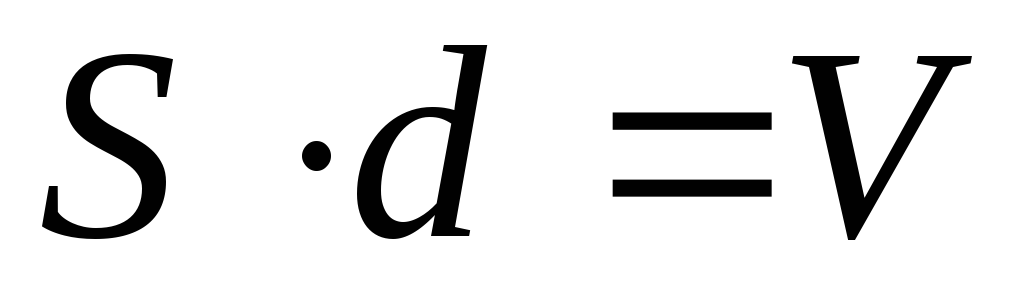 — объем электростатического поля между
обкладками конденсатора, то есть
— объем электростатического поля между
обкладками конденсатора, то есть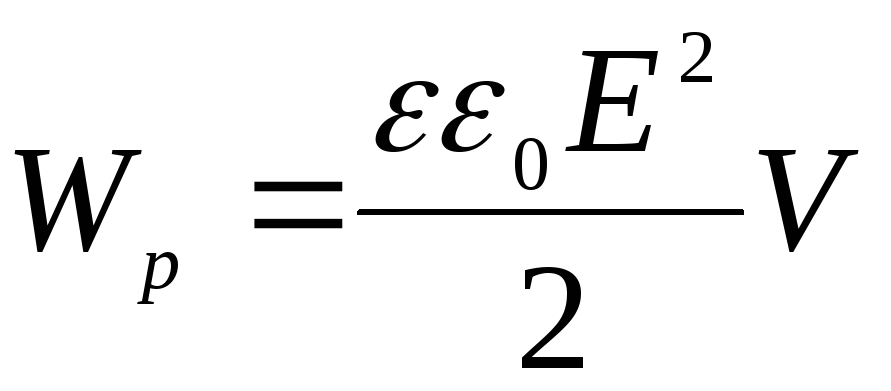 .
Тогда объемная плотность энергии
.
Тогда объемная плотность энергии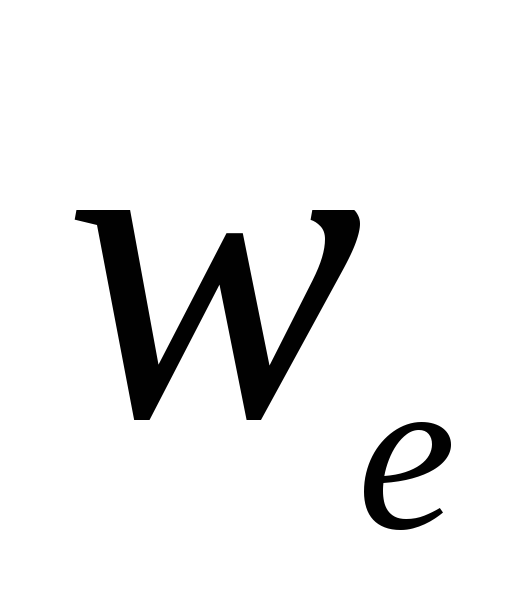 однородного электростатического поля
конденсатора равна
однородного электростатического поля
конденсатора равна ,
и определяется его напряженностью или
смещением. В случае неоднородных
электрических полей
,
и определяется его напряженностью или
смещением. В случае неоднородных
электрических полей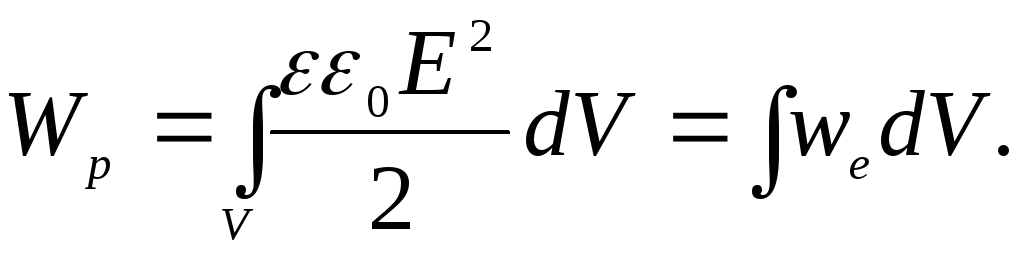
Найдем
энергию сферического конденсатора. На
расстоянии  от центра заряженного шара напряженность
его электростатического поля равна
от центра заряженного шара напряженность
его электростатического поля равна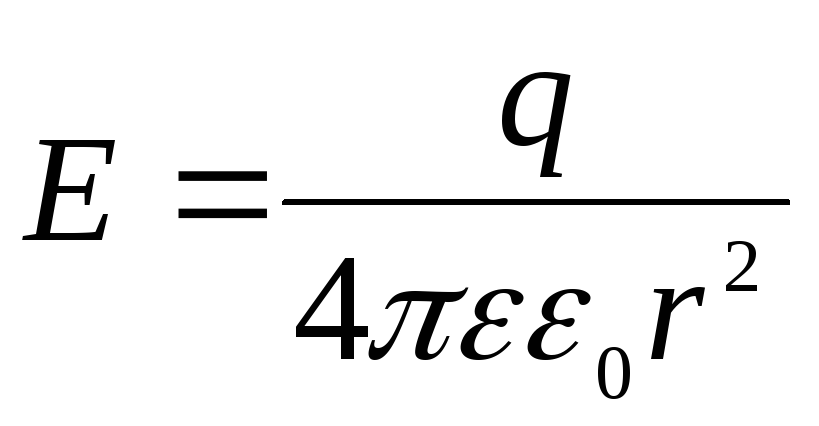 .
Рассмотрим бесконечно тонкий шаровой
слой, заключенный между сферами радиусов
.
Рассмотрим бесконечно тонкий шаровой
слой, заключенный между сферами радиусов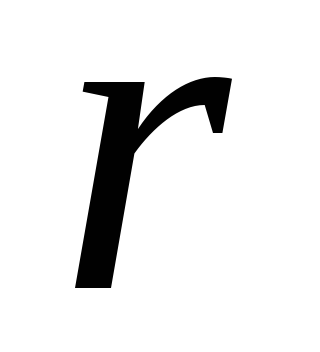 и
и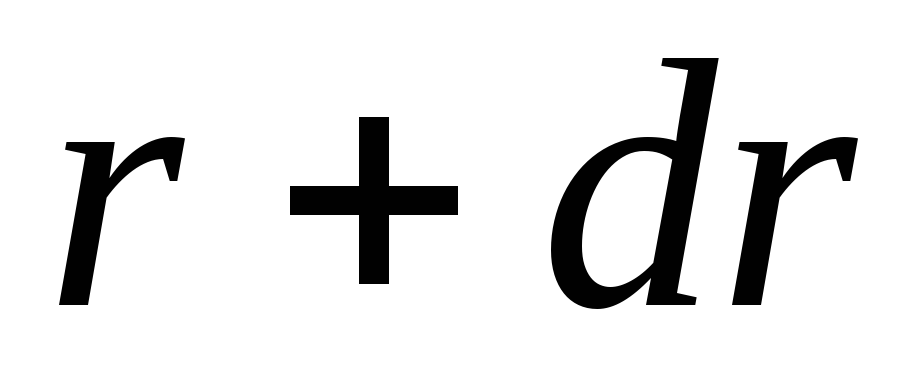 .
Объем такого слоя:
.
Объем такого слоя: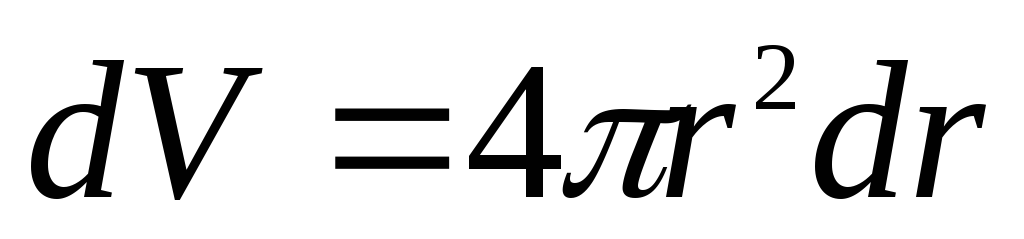 .
Энергия слоя
.
Энергия слоя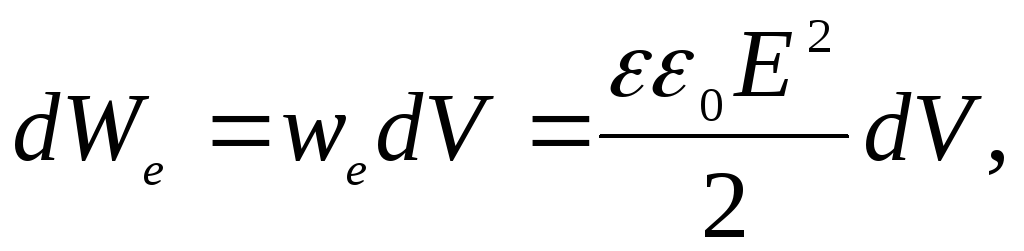 следовательно,
следовательно,
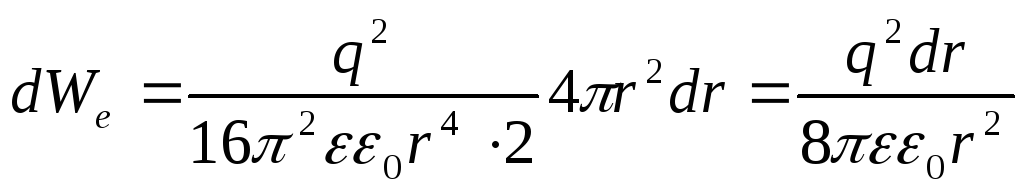 .
.
Тогда полная энергия заряженного шара равна:
 ,
,
где  — радиус шара. Емкость шара
— радиус шара. Емкость шара ,
следовательно,
,
следовательно,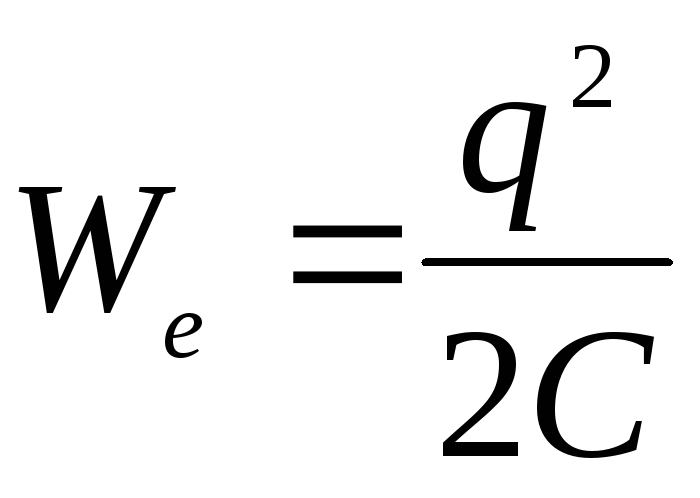 — энергия электростатического поля
сферического конденсатора равна его
собственной энергии, так как заряженное
тело потому и обладает электрической
энергией, что при его зарядке была
совершена работа против сил создаваемого
им электростатического поля.
— энергия электростатического поля
сферического конденсатора равна его
собственной энергии, так как заряженное
тело потому и обладает электрической
энергией, что при его зарядке была
совершена работа против сил создаваемого
им электростатического поля.
1.4.4.Энергия поляризованного диэлектрика. Объемная плотность энергии электрического поля в диэлектрике
Рассмотрим однородный изотропный диэлектрик, находящийся во внешнем электрическом поле. Процесс поляризации связан с работой по деформации электронных орбит в атомах и молекулах и по повороту осей молекул-диполей вдоль поля. Ясно, что поляризованный диэлектрик должен обладать запасом электрической энергии.
Если
поле напряженностью  создано в вакууме,
создано в вакууме, ,
то объемная плотность энергии этого
поля в точке с напряженностью
,
то объемная плотность энергии этого
поля в точке с напряженностью равна:
равна:
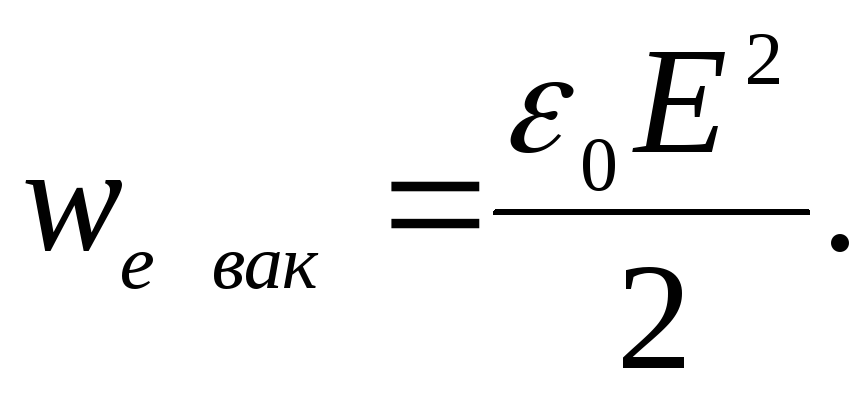
Докажем, что
объемная плотность энергии поляризованного
диэлектрика в этой точке выражается
формулой: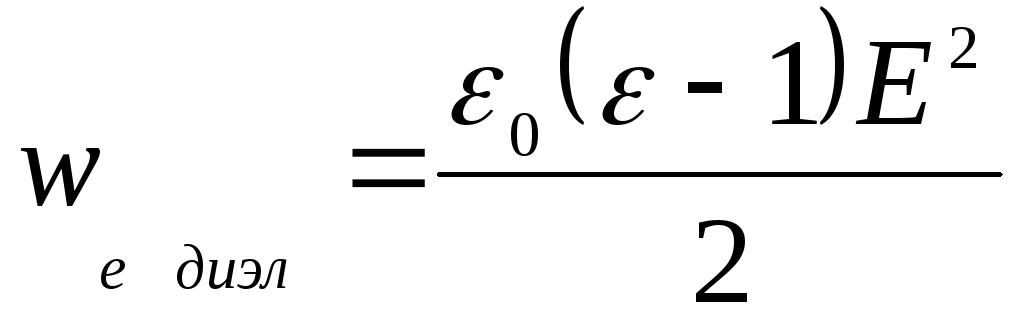 .
.
Рассмотрим
диэлектрик с неполярными молекулами.
Молекулы такого диэлектрика являются
упругими диполями. Электрический момент
упругого диполя, находящегося в поле с
напряженностью
,
равен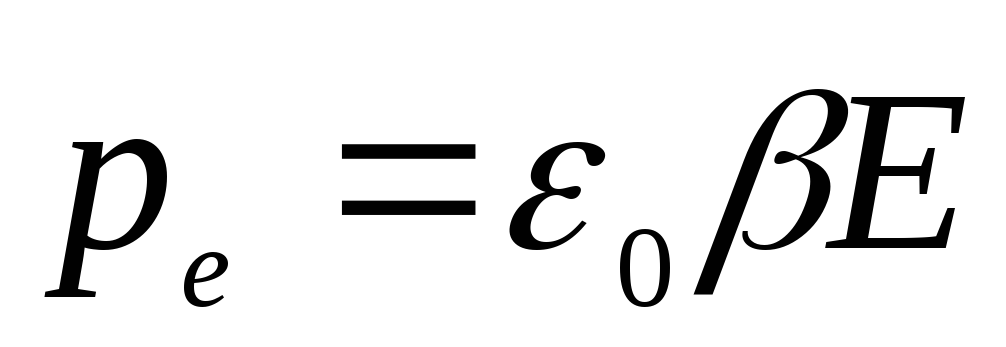 ,
где
,
где — поляризуемость диполя, или в скалярной
форме:
— поляризуемость диполя, или в скалярной
форме:
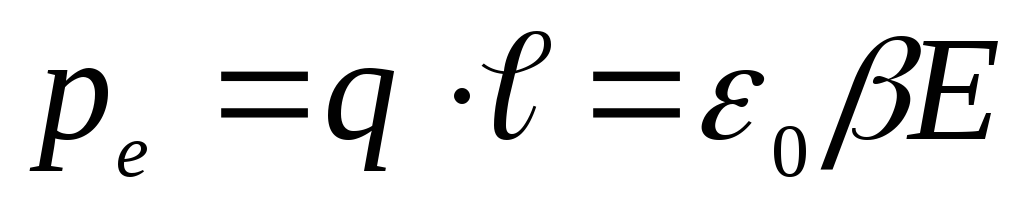 , (1.4.1)
, (1.4.1)
где 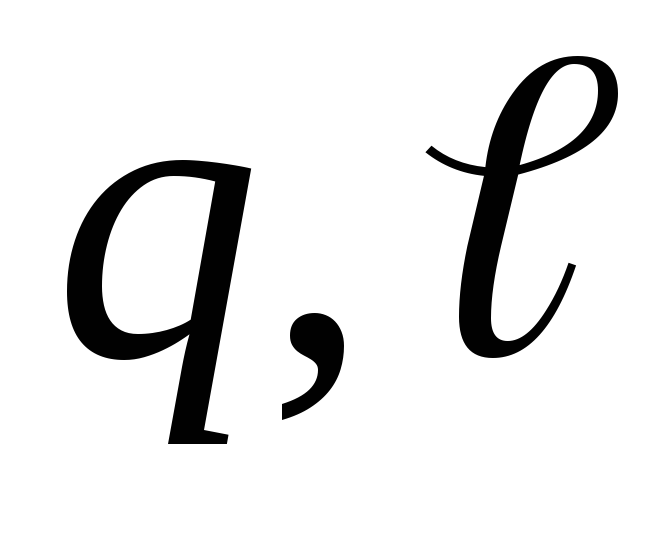 — заряд и плечо диполя.
— заряд и плечо диполя.
На
заряд  со стороны поля действует сила
со стороны поля действует сила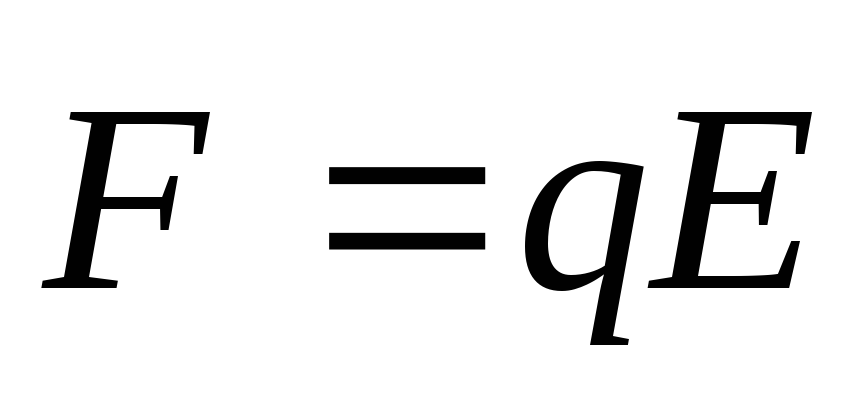 ,
которая при увеличении длины диполя на
,
которая при увеличении длины диполя на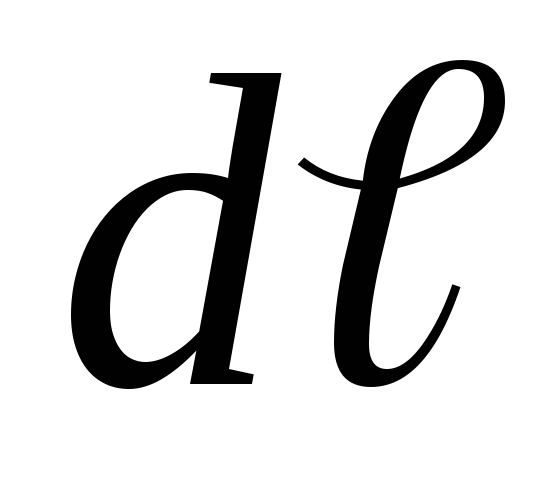 совершает работу
совершает работу .
Из выражения (1.4.1) получаем:
.
Из выражения (1.4.1) получаем: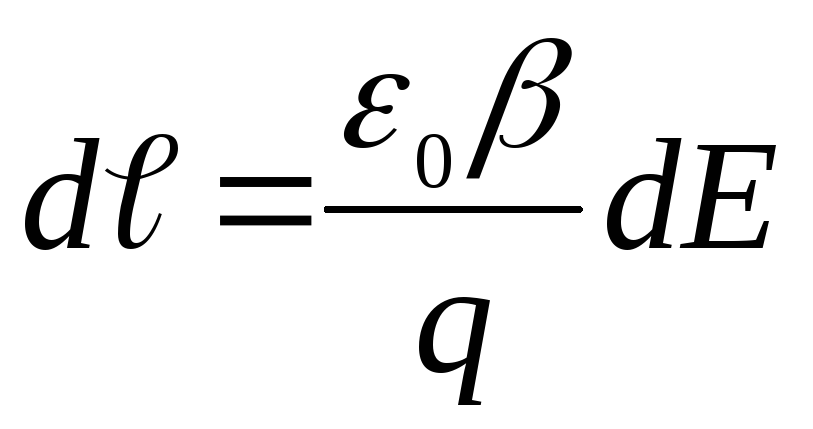 ,
поэтому
,
поэтому
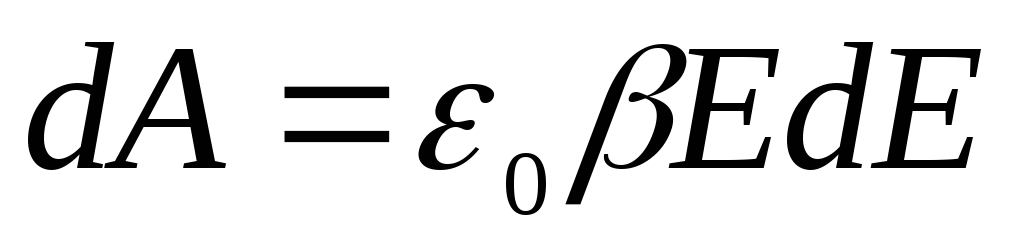 . (1.4.2)
. (1.4.2)
Чтобы
найти работу  поля при деформации одного упругого
диполя, надо проинтегрировать выражение
(1.4.2):
поля при деформации одного упругого
диполя, надо проинтегрировать выражение
(1.4.2):
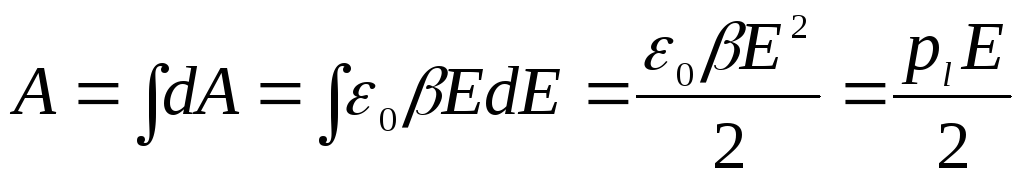 .
.
Работа  равна той потенциальной энергии, которой
обладает упругий диполь в электрическом
поле напряженностью
равна той потенциальной энергии, которой
обладает упругий диполь в электрическом
поле напряженностью .
Пусть
.
Пусть — число диполей в единице объема
диэлектрика. Тогда потенциальная энергия
всех этих диполей, то есть объемная
плотность энергии поляризованного
диэлектрика равна:
— число диполей в единице объема
диэлектрика. Тогда потенциальная энергия
всех этих диполей, то есть объемная
плотность энергии поляризованного
диэлектрика равна: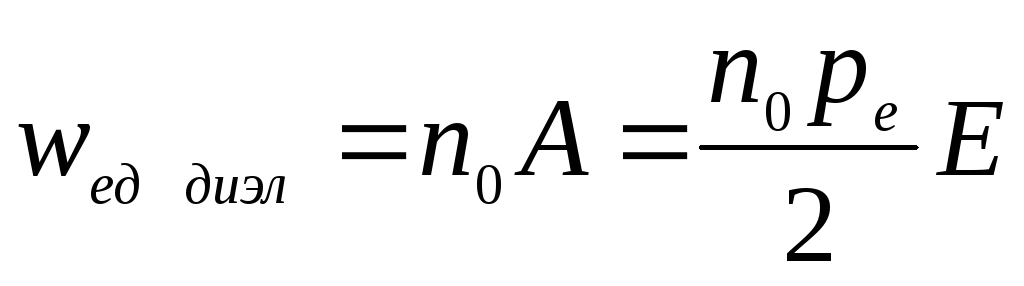 .
Однако
.
Однако — модуль вектора поляризации, тогда
— модуль вектора поляризации, тогда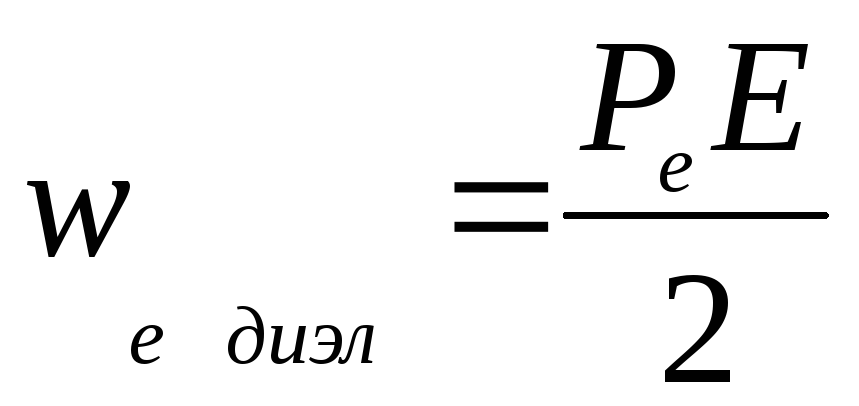 .
Известно, что
.
Известно, что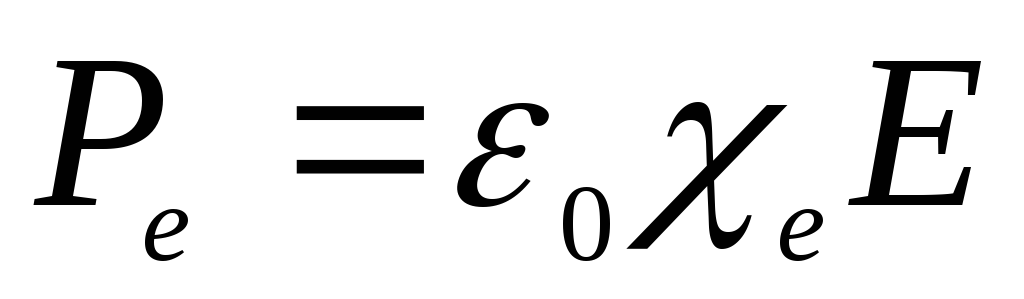 ,
и
,
и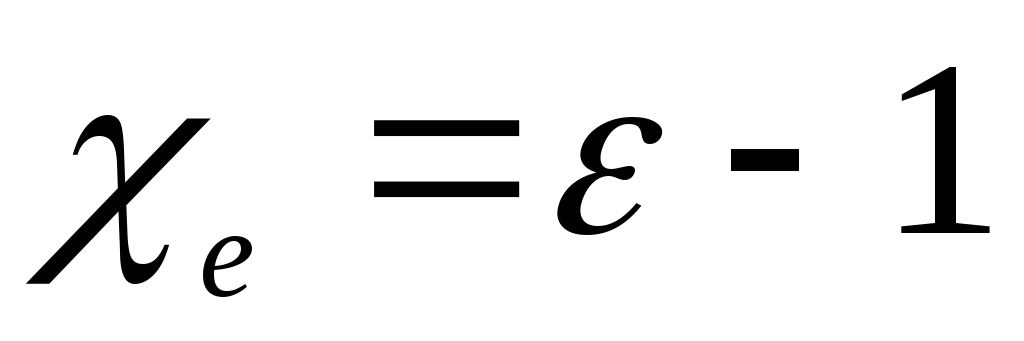 ,
тогда
,
тогда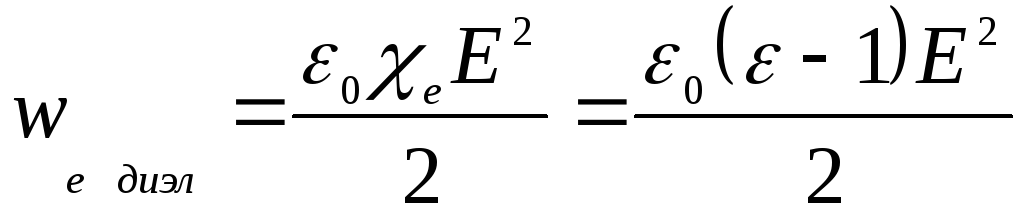 ,
что и требовалось доказать.
,
что и требовалось доказать.
Соединение конденсаторов.
Соединение конденсаторов бывает последовательным и параллельным.
1) Последовательное соединение.
При последовательном соединении заряды на всех конденсаторах одинаковые, а напряжения разные (рисунок).
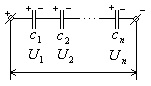
Рисунок. Последовательное соединение конденсаторов.
Мы имеем:
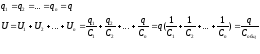
В итоге получаем

2) Параллельное соединение.
При параллельном
соединении напряжения на всех конденсаторах
одинаковые 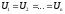 =U,
а заряды – разные (рисунок ниже).
=U,
а заряды – разные (рисунок ниже).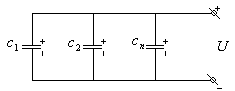
Рисунок. Параллельное соединение конденсаторов.
В итоге имеем:
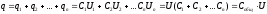
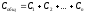
Энергия системы неподвижных точечных зарядов.
Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.
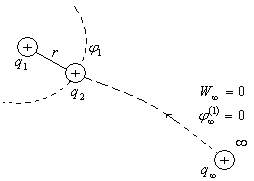
Рисунок. К определению энергии системы зарядов.
Рассмотрим сначала систему, состоящую из двух точечных зарядов (рисунок). Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q2 к q1 либо q1 к q2. В обоих случаях совершается одинаковая работа:
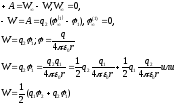
В последней формуле 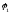 — потенциал поля 1-го заряда в том месте,
где находится второй заряд;
— потенциал поля 1-го заряда в том месте,
где находится второй заряд;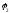 — потенциал поля второго заряда в том
месте, где находится первый заряд. С
учетом сказанного, эту формулу можно
записать также в виде:
— потенциал поля второго заряда в том
месте, где находится первый заряд. С
учетом сказанного, эту формулу можно
записать также в виде:
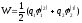 .
.
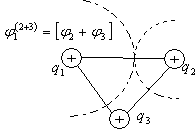
Рисунок. Система трех неподвижных точечных зарядов.
Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов (рисунок выше) может быть представлена в виде:
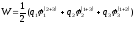
В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле:

Энергия заряженного проводника и заряженного конденсатора.
Поверхность
заряженного проводника (рисунок ниже)
при равновесии зарядов является
эквипотенциальной (φi=φ = const).
Следовательно, энергия
заряженного проводника: 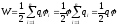 ,
гдеq — заряд проводника.
,
гдеq — заряд проводника.

Рисунок. Заряженный проводник.
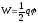
Конденсатор представляет собой пару заряженных проводников (рисунок), поэтому имеем:
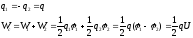
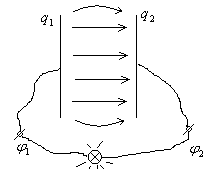
Рисунок. Заряженный конденсатор.
А поскольку заряд 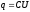 ,
тоэнергия
заряженного конденсатора может быть представлена одной из трех
формул:
,
тоэнергия
заряженного конденсатора может быть представлена одной из трех
формул:
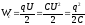
Энергия электростатического поля.
Выразим энергию заряженного конденсатора через величины, характеризующие электрическое поле, локализованное в пространстве между его обкладками – напряженность поля Е и объем V, занятый полем. Имеем для напряженности поля:
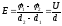 ,
где
,
где 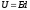 .
.
Воспользовавшись
формулой для емкости плоского конденсатора  ,
находим:
,
находим:

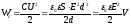 ,
где
,
где  — объём конденсатора, откуда следует,
что
— объём конденсатора, откуда следует,
что
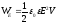
Мы видим, что энергия электрического поля прямо пропорциональна квадрату его напряженности Е и объёму V, занятому полем. Величину энергии поля, отнесенной к единице объема, называют плотностью энергии:
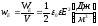 — плотность энергии
электрического поля.
— плотность энергии
электрического поля.
Энергия электрического поля, заряженного конденсатора — Мегаобучалка
1. Электроемкость проводника.
Если в процессе электризации проводнику сообщать заряды, то заряды распределяются по поверхности проводника так, что потенциалы точек поверхности любого заряженного проводника будут одинаковыми, т.е. поверхность проводника является эквипотенциальной поверхностью. Установлено, что между величиной заряда, на поверхности проводника и потенциалами точек поверхности проводника, прямая пропорциональная зависимость
С – электроемкость проводника
— формула расчета электроемкости проводника.
С – зависит от формы проводника, его геометрических размеров и окружающей среды. И не зависит от того, из какого вещества изготовлен проводник, сплошной проводник или полый (пустой). Электроемкость проводника рассчитать очень сложно, т.к. для каждого проводника должна быть своя формула расчета. Проще электроемкость измерить.
В «СИ» |C| = = 1 Ф (Фарад)
1 Фарад – электроемкость проводника, при сообщении которому заряда в 1 Кл потенциалы точек поверхности меняются на 1В.
Практические единицы измерения электроемкости.
2. Конденсаторы
Система проводников разделенных слоем диэлектрика называется КОНДЕНСАТОРОМ.
Проводники называются обкладками конденсатора. Если обкладки представляют собой плоскости, то конденсатор называется плоским.
Если конденсатор зарядить, то заряды располагаются по внутренним сторонам обкладок. Внешние стороны остаются электронейтральными, поэтому электрическое поле, создаваемое этими зарядами, полностью сосредоточено в диэлектрике между обкладками. Внешнее поле внутрь конденсаторов проникнуть не может, т.к. проводники для этого поля являются экраном. По этой причине конденсатор в течение определенного времени может сохранять энергию в электрическом поле.
Конденсаторы в электрорадиосхемах используются как накопители энергии. Заряды на обкладках равны по величине и противоположны по знаку. Заряд конденсатора в целом определяется величиной заряда одной из его обкладок. Выясним, как можно рассчитать электроемкость конденсатора.
С = — формула расчета электроемкости конденсатора.
От заряда и напряжения электроемкость конденсатора не зависит, а она зависит от рода диэлектрика, от толщины слоя диэлектрика и от площади обкладок.
формула расчета электроемкости конденсатора.
Название конденсаторов часто соответствует роду диэлектрика, например бумажный, керамический.
Такие конденсаторы можно использовать, как в цепях постоянного, так и переменного токов.
3. Соединение конденсаторов в батарею.
Конденсаторы можно соединять между собой и такое соединение называют конденсаторной батареей. При этом возможны варианты:
1. Последовательное
2. Параллельное
3. Смешанное соединение.
При ( 1 ) этом левая обкладка одного конденсатора соединяется с правой обкладкой другого. При последовательном соединении независимо от электроемкости заряд на конденсаторе одинаковый.
При последовательном соединении напряжение на всей конденсаторной батарее равно сумме напряжений на отдельных конденсаторах этой батареи.
3 ) ; ;
— формула расчета электроемкости конденсаторной батареи при последовательном соединении.
При последовательном соединении конденсаторов увеличивается рабочее напряжение конденсаторной батареи, а электроемкость – уменьшается и она становится меньше электроемкости самого маленького конденсатора, включенного в данную батарею.
И – одинаковое.
При параллельном соединении не зависимо от электроемкости напряжение на конденсаторах одинаковое
Заряд конденсаторной батареи равен сумме зарядов отдельных конденсаторов.
— формула расчета электроемкости при параллельном соединении.
При параллельном соединении конденсаторов в батарею электроемкость увеличивается , а рабочее напряжение берется по самому маленькому рабочему напряжению конденсаторов этой батареи.
3. Смешанное соединение
Если необходимо увеличить рабочее напряжение и электроемкость , то конденсаторы соединяют смешанно. При этом за счет последовательного соединения увеличивается рабочее напряжение, а за счет параллельного — увеличивается электроемкость.
Пример: даны 4 конденсатора с напряжением по 100 В и электроемкостью 4 мкФ каждый, как их соединить , что бы получить рабочее Е в 2 раза больше, а С осталось прежней.
3. Энергия электрического поля, заряженного конденсатора.
При зарядке конденсатора источником тока совершается работа, в результате которой на обкладках конденсатора появляются электрические заряды, а между обкладками в диэлектрике – электрическое поле, которое обладает энергией. Совершенная работа при зарядке и энергия электрического поля конденсатора численно равны, поэтому энергию электрического поля конденсатора можно рассчитать по совершенной работе при зарядке конденсатора.
— формула расчета энергии электрического поля, заряженного конденсатора