Энергия электрического поля конденсатора

Содержание:

Формула расчета энергии конденсаторов, как зарядить плоский конденсатор

Конденсаторы являются неотъемлемой частью электрических схем. В большинстве случаев оперируют такими понятиями, как емкость и рабочее напряжение. Эти параметры являются основополагающими.

Конденсаторы различных типов

В некоторых случаях для более полного понимания работы упомянутого элемента необходимо иметь представление, что означает энергия заряженного конденсатора, как она вычисляется и от чего зависит.

Определение понятия энергии

Наиболее просто вести рассуждения применительно к плоскому конденсатору. В основе его конструкции лежат две металлических обкладки, разделенные тонким слоем диэлектрика.

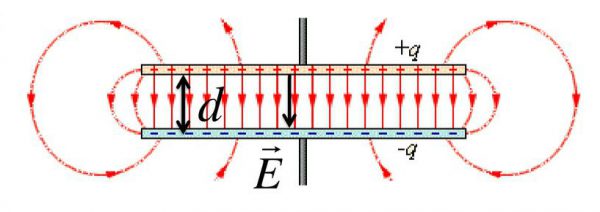
Плоский конденсатор

Если подключить емкость к источнику напряжения, то нужно обратить внимание на следующее:

• На разделение зарядов по обкладкам электрическим полем затрачивается определенная работа. В соответствии с законом сохранения энергии, эта работа равняется энергии заряженного конденсатора;
• Разноименно заряженные обкладки притягиваются друг к другу. Энергия заряженного конденсатора в этом случае равняется работе, затраченной на сближение пластин друг к другу вплотную.

Данные соображения позволяют сделать вывод, что формулу энергии заряженного конденсатора можно получить несколькими способами.

Вывод формулы

Энергия заряженного плоского конденсатора наиболее просто определяется, исходя из работы по сближению обкладок.

Рассмотрим силу притяжения единичного заряда одной из обкладок к противоположной:

F=q0E.

В данном выражении q0 – величина заряда, E – напряженность поля обкладки.

Поскольку напряженность электрического поля определяется из выражения:

E=q/(2ε0S), где:

• q – величина заряда,
• ε0 – электрическая постоянная,
• S – площадь обкладок,

формулу силы притяжения можно записать как:

F=q0 q/(2ε0S).

Для всех зарядов сила взаимодействия между обкладками, соответственно, составляет:

F=q2/(2ε0S).

Работа по сближению пластин равняется произведению силы взаимодействия на пройденное расстояние. Таким образом, энергия заряженного конденсатора определяется выражением:

W=A=Fd.

Важно! В приведенном выражении должна быть разница в положениях пластин. Записывая только одну величину d, подразумеваем, что конечным результатом будет полное сближение, то есть d2=0.

С учетом предыдущих выражений можно записать:

W=d q2/(2ε0S).

Известно, что емкость плоского конденсатора определяется из такого выражения:

C=d/(ε0S).

В результате энергия определяется как:

W=q2/(2С).

Полученное выражение неудобно тем, что вызывает определенные затруднения определения заряда на обкладках. К счастью, заряд, емкость и напряжение имеют строгую взаимосвязь:

q = С U.

Теперь выражение принимает полностью понятный вид:

W=CU2/2.

Полученное выражение справедливо для конденсаторов любых типов, не только плоских, и позволяет без затруднений в любой момент времени определять накопленную энергию. Емкость обозначается на корпусе и является величиной постоянной. В крайнем случае ее несложно измерять, используя специальные приборы. Напряжение измеряется вольтметром с необходимой точностью. К тому же очень просто зарядить конденсатор не полностью (меньшим напряжением), снизив, таким образом, запасенную энергию.

Для чего необходимо знать энергию

В большинстве случаев применения емкостей в электрических цепях понятие энергии не употребляется. Особенно это относится к время,- и частотозадающим цепям, фильтрам. Но есть области, где необходимо использовать накопители энергии. Наиболее яркий пример –фотографические вспышки. В накопительном конденсаторе энергия источника питания накапливается сравнительно медленно – несколько секунд, но разряд происходит практически мгновенно через электроды импульсной лампы.

Конденсатор, подобно аккумулятору, служит для накопления электрического заряда, но между этими элементами есть много различий. Емкость аккумулятора несравненно выше, чем у конденсатора, но последний способен отдать ее практически мгновенно. Лишь недавно, с появлением ионисторов, это различие несколько сгладилось.

Ионистор

Какова же ориентировочная величина энергии? Можно для примера вычислить ее для уже упомянутой фотовспышки. Пускай, напряжение питания составляет 300 В, а емкость накопительного конденсатора – 1000 мкФ. При полном заряде величина энергии составит 45 Дж. Это довольно большая величина. Прикосновение к выводам заряженного элемента может привести к несчастному случаю.

Конденсатор фотовспышки

Важно! Принудительный разряд путем закорачивания выводов металлическими предметами чреват выходом устройства из строя. Накопленная энергия конденсатора способна за долю секунды расплавить выводы внутри элемента и вывести его из строя.

Видео

28. Электроемкость. Конденсаторы и их соединение. Энергия электрического поля заряженного конденсатора. Виды конденсаторов.

5. Электроемкость

Электроемкость уединенного проводника – отношение заряда проводника к его потенциалу.

Электроемкость характеризует способность тела накапливать электрические заряды.При большой электроемкоститело может накопить большой заряд при небольшом значении потенциала.

Единица измерения электроемкости Фарад, Ф.

Ф = Кл/В

1 мкФ = 10^-6Ф

1 нФ = 10^-9Ф

1 пФ = 10^-12Ф

Конденсатор – система двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Плоский конденсатор –

две параллельные проводящие пластины, расположенные параллельно и разделенные

слоем диэлектрика.

Электрическое поле заряженного конденсатора

Вне пластин напряженность поля равна нулю

Напряженность поля внутри плоского конденсатора вдвое больше напряженности поля одной пластины

Напряженность поля внутри плоского

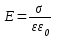
Электроемкость конденсатора – отношение заряда на одной из обкладок к разности потенциалов между пластинами.

С = Q/U

Для однородного поля внутри конденсатора напряженность поля и разность потенциалов между обкладками связаны соотношением

U = Ed

электроемкость плоского конденсатора определятся формулой

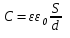
Энергия заряженного конденсатора

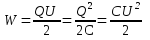
7. Последовательное и параллельное соединение конденсаторов

Последовательное соединение

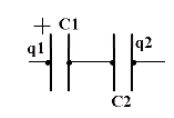
q=const

1/C =1/C₁ + 1/C₂

U = U₁₊U₂

Параллельное соединение

q=q₁₊q₂

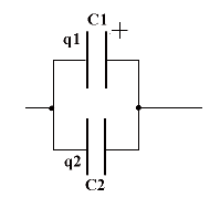
U=const

C= С₁+С₂

При последовательном соединении

При параллельном соединении емкость конденсаторов увеличивается

29. Физические основы проводимости металлов. Постоянный электрический ток, его

характеристики. Закон Ома для участка цепи.

Согласно классической электронной теории,электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла.

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев силы притяжения со стороны кристаллической решетки. Минимальная энергия, необходимая электрону для того, чтобы покинуть металл, называется работой выхода.

Допущения классической электронной теории являются весьма приближенными, однако она объясняетзаконы электрического тока в металлических проводниках.

При прохождении тока по проводнику переноса вещества не происходит

Электрическим током называется упорядоченное движение заряженных частиц.

Электрический ток возникает при упорядоченном перемещении свободных электронов или ионов.

При прохождении электрического тока через вещество всегда проявляется его магнитное действие. Могут проявляться также химическое и тепловое действия тока.

Направлением электрического тока считается направ­ление упорядоченного движения положительно заряженных частиц.

Если ток образован движением отрицательных зарядов (например, электронов), то направление тока противоположно направлению движения частиц.

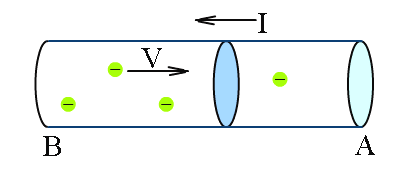
φА>φB;

Ток течет в сторону убывания потенциала.

Силой тока называется скалярная физическая величина I, равная элек­трическому заряду, который переносится через поперечное сечение проводника за единицу времени.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока

где Δq — заряд, который переносится сквозь поперечное сечение проводника за время Δt.

В самом общем случае сила тока определяется как производная от электрического заряда по времени.

I = q^/

Единица измерения силы тока Ампер, А – основная единица в системе СИ

Кл=А*с

Измерения показывают, что в металлах скорость электронов мала – порядка 10^-5 м/с (для меди).

Условие протекания постоянного тока на участке электрической цепи: – наличие постоянной разности потенциалов (напряжения) на этом участке.

5.Энергия электрического поля

Если обкладки заряженного конденсатора замкнуть металлической про­волокой, то в ней возникает электрический ток, а конденсатор разрядится. Электрический ток разряда конденсатора выделяет в проволоке определённое количество тепла, а это значит, что заряженный конденсатор обладает энергией.

Вычислим энергию заряженного конденсатора С. Для этого обозначим через U мгновенное значение напряжения на обкладках конденсатора в процессе разряда. Если малое количество заряда dq проходит в процессе разряда с одной обкладки на другую, то работа электрических сил dА будЕТ dА =U dq.

Выражая в этой формуле заряд обкладок q через напряжение Q = CU, получим dA = CU dU.

Полную работу, совершаемую электрическими силами за все время разряда, равную энергии кон­денсатора W, мы получим, интегрируя это выражение между значениями напряжения U (начало разряда) и 0 (конец разряда). Это дает:

A= — W = C= — CU²/2. (1)

Можно (1) переписать:

W = CU²/2 = q²/2C = qU/2. (2)

А где именно, т.е. в каком месте в конденсаторе локализована эта энергия? — На об­кладках конденсатора, т.е. на электрических зарядах, или в его электрическом поле, т.е. в пространстве между обкладками. В дальнейшем мы сможем ответить на этот вопрос, что энергия сосредоточена в электрическом поле. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию.

Учитывая это, мы можем преобразовать (2) т.о., чтобы в него входила характеристи­ка поля — его напряженность.

Рассмотрим вначале однородное поле и применим формулу (1) к плоскому конденсатору. Мы получим

W = ee₀SU²/2d = ee₀(U/d)²Sd/2, но

U/d=E, a Sd — объём, занимаемый полем.

Мы видим, что энергия однородного электрического поля пропорциональна объёму, занимаемому полем. Поэтому целесообразно говорить об энергии каждой единицы объёма, или об объёмной плотности энергии электрического поля. Она равна

W₁ = ee₀E²/2 = ED/2, т.к. V = Sd = 1.

Последнее выражение справедливо только для изотропного диэлектрика.

Если электрическое поле неоднородно, то его можно разбить на элементарные объемы dV и считать, что в пределах бесконечно малого объема это поле однородно. Поэтому энергия, заключенная в объеме поля dV, будет W₁dV, а полная энергия любого электрического поля может быть представлена в виде

W = (e₀/2)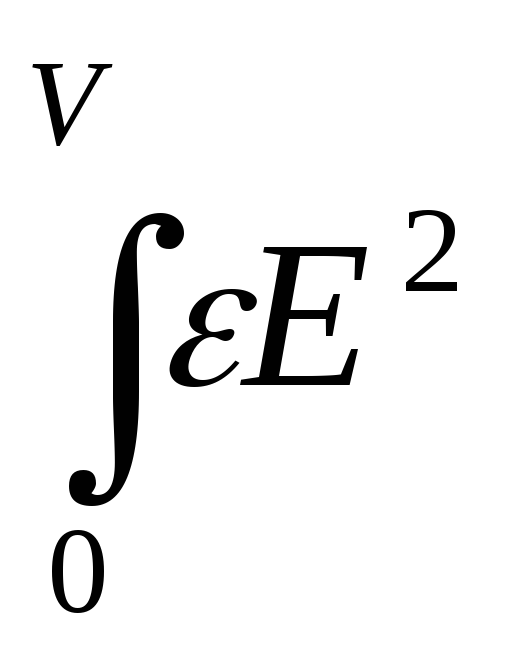dV,

Причем интегрирование проводится по всему объему V, где имеется электрическое поле.

6.Постоянный электрический ток

Электрическим током называется направленное движение электрических зарядов. Ток, воз­никающий в проводнике вследствие того, что в нем создастся электрическое поле, называется током проводимости. При движении зарядов нарушается их равновесное распределение: поверхность проводника уже не является эквипотенциальной и электрические силовые линии не на­правлены ^ ей, т.к. для движения зарядов необходимо, чтобы на поверхности провод­ника тангенциальная составляющая напряженности электрического поля не равнялась нулю (E_t¹ 0). Но тогда и внутри проводника должно существовать электрическое поле, ибо, как известно из электростатики, внутри проводника нет поля лишь в случае равновесного распределения зарядов по поверхности этого проводника. Перемещение зарядов — электрический ток — продолжается до тех пор, пока все точки проводника не станут эквипотенциаль­ными.

Т.о., для появления и существования электрического тока проводимости необходимы два условия.

Первое- наличие в данной среде носителей заряда, т.е. заряженных частиц, которые могли бы в ней перемещаться. Такими частицами, как мы убедимся далее, в металлах являются электроны проводимости, в жидких проводниках (электролитах) — положи­тельные и отрицательные ионы; в газах — положительные ионы и электроны, а также иногда и отрицательные ионы.

Второе — наличие в данной среде электрического поля, энергия которого затрачивалась бы на пе­ремещение электрических зарядов. Для того чтобы ток был длительным, энергия поля должна все время пополняться, иными словами, нужен источник электрической энергии -устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В зависимости от свойств этих источников в электротехнике различают источники напряжения и источники тока. Поэтому во избежание неточностей мы будем в дальнейшем пользоваться только термином «источник электрической энергии».

Упорядоченное движение зарядов можно осуществить и другим способом — перемещением в пространстве заряженного тела (проводника или диэлектрика). Такой электрический ток называется конвекционным током. Например, движение по орбите Земли, обладающей избыточным отрицательным зарядом, можно рассматривать как конвекционный ток.

За направление тока условно принимают направление движения положительных заря­дов.

Для характеристики электрического тока через какую либо поверхность (например, в случае тока проводимости — через поперечное сечение проводника) вводится понятие силы тока.

Силой тока называется физическая величина I, равная отношению заряда dq, переносимого через рассматриваемую поверхность S за малый промежуток времени dt, к величине этого промежутка:

I=dq/dt (1)

Если сила тока и его направление не изменяются с течением времени, то ток называется по­стоянным. Сила постоянного тока

I=q/t, (2)

где q — заряд, переносимый через поверхность S за конечный промежуток t.

Для того чтобы ток проводимости был постоянным, заряды не должны накапливаться или убывать ни в одной части проводника. Поэтому цепь постоянного тока должна быть замкнутой, а суммарный электрический заряд, который поступает за 1 секунду. сквозь по­верхность S₁ в объем проводника, заключенный между двумя произвольно выбранными поперечными сечениями S₁ и S₂ (рис.1), должен быть равным суммарному заряду, выхо­дящему из этого объема за то же время сквозь поверхность S₂ Т.о., сила постоянного тока I во всех сечениях проводника одинакова.

Рис.1

Единица силы тока в СИ — ампер (А) — определяется на основании электромагнитного взаимодействия двух параллельных прямолинейных проводников, по которым протекает постоянный ток. Из (2) следует, что 1А — равен силе постоянного электрического тока, при котором через поперечное сечение проводника в 1секунду переносится заряд, равный 1К:

1А=1К/с.

Для характеристики направления электрического тока в различных точках рассматриваемой по­верхности вводится вектор плотности электрического тока, который совпадает по направлению с движением положительно заряженных частиц — носителей заряда и численно равен от­ношению силы тока dI сквозь малый элемент поверхности, нормальный к направлению движения заряженных частиц, к площади dS_^ этого элемента:

`J = dI/ dS_^, (3)

В СИ плотность тока измеряется в (А/м²).

Очевидно, что dI = Jсоsa dS = J_n dS , или dI = J 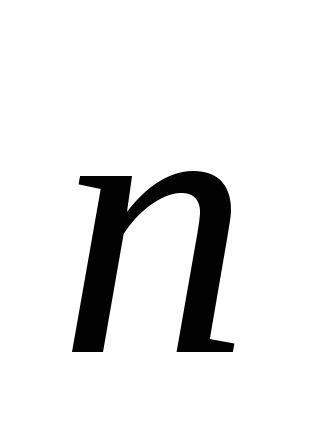dS,

где `n — единичный вектор, перпендикулярный площадке dS, J<sub>n</sub> – проекции J на направление нормали `n.

Сила тока через произвольную поверхность S равна

I = òJ_n dS = ò J dS,

где интегрирование проводится по всей площади этой поверхности. В дальнейшем S- это поперечное сечение проводника. Для постоянного тока

I = JS (4)

В цепи постоянного тока, состоящей из проводников с переменной площадью поперечного сечения, рис. 1, плотности тока в различных сечениях S₁ и S₂ обратно пропорциональны площадям этих сечений: J₁: J₂ = S₂ : S₁.

ЗАКОН ОМА

Рассмотрим отрезок однородного цилиндрического проводника длиной l

Рис.2.

Для того чтобы в этом проводнике шел постоянный электрический ток I, необходимо внутри провод­ника поддерживать постоянное электрическое поле Е. Т.к. E=dU/dI=- (U₂— U₁)/I=(U₁-U₂)/I= U/I, где U = U₁— U₂ — падение потенциала на участке 1-2, наз. напряжением, приложенным к проводнику.

При изменении U меняется и ток I. В 1826 г. Ом установил

I = GU = U/R, (5)

где G — электрическая проводимость, а R = 1/G — электрическое сопротивление проводника. Формула (5) выражает закон Ома в интегральной форме: ток, идущий в проводнике, численно равен отношению приложенного напряжения к сопротивлению проводника. Если U = 1В, I = 1А, то R = 1 Oм — сопротивление такого проводника, в котором при напряжении 1В идет электрический ток в 1А.

Сопротивление проводника зависит от геометрических размеров и формы, а также материала, из которого сделан.Где р – удельное сопротивление в-ва.

R = r1/S, (6)

Подставляя (6) в (5), преобразуем закон Ома

I = U/R = US/rl к виду I/S = U/l)/r.

Величина, обратная удельному сопротивлению, 1/r = g — называется удельной проводимостью или электропроводимостью данного вещества. Тогда j = g`E -закон Ома в дифференциальной форме.

Опыт показывает, что в первом приближении сопротивление металлических провод­ников линейно возрастает с температурой по закону R = R₀(1+at), где a» 4× 10^-3 град-¹— температурный коэффициент. При Т®0 и R®0.

Для некоторых металлов и сплавов вблизи абсолютного нуля температуры наблю­дается (при некоторой характерной для каждого из них температуре) скачкообразное падение сопротивления практически до нуля. Проводник при этом переходит в так называемое сверхпроводящее состояние. Если в замкнутом контуре из сверхпроводника создать электрический ток, то этот ток будет неделями течь в сверхпроводнике, практически не уменьшаясь по величине. Температуры перехода в сверхпроводящее состояние для различных металлов раз­личны и лежат в интервале примерно от 2К до 10К. Несколько лет назад открыта сверхпроводимость при более высоких температурах (азотные температуры).

Зависимость R = R(Т) широко используется в технике для создания термометров со­противлений.

Вернемся опять к электрическому току. Очевидно, что для поддержания постоянного тока в цепи на сво­бодные заряды должны действовать помимо кулоновских сил еще какие — то иные, не­ электростатические силы. Эти силы носят название сторонних сил. Если кулоновские силы вызывают соединение разноименных зарядов, что ведет к выравниванию потен­циалов и исчезновению электрического поля в проводнике, то сторонние силы вызывают разделение разноименных зарядов и поддерживают разность зарядов на концах проводника. Доба­вочное поле сторонних сил в цепи создается источниками электрической энергии (гальваническими элементами, аккумуляторами, электрическими генераторами). За счет поля сторонних сил электрические заряды движутся внутри источника электрической энергии против сил электростатического поля. В следствие это го на концах внешней цепи поддерживается разность потенциалов и в цепи идет постоянный ток. Перемещая заряды, сторонние силы совершают работу за счет энергии, затрачиваемой в источнике электрической энергии. Так, например, в электромагнитном ге­нераторе работа сторонних сил производится за счет механической энергии, расходуе­мой на вращение ротора генератора, а в гальванических элементах — за счет энергии, ко­торая выделяется при хим. процессах растворения электродов в электролите.

Для любой точки внутри проводника напряженность Е результирующего поля равна

`Е = `Е_стор. + `Е_кул., (8)

Энергия поля конденсатора — Основы электроники

Вся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накоп­ленную в конденсаторе, можно определить следующим обра­зом. Представим себе, что мы заряжаем конденсатор не сра­зу, а постепенно, перенося электрические заряды с одной его пластины на другую.

При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последую­щий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое коли­чество электричества, которое мы обозначим буквой Q.

Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U.

Как мы уже заметили, разность потенциалов в процессе за­ряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U.

Для упрощения вычисления энергии допустим, что мы пе­ренесли весь электрический заряд Q с одной пластины кон­денсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пласти­нами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запа­сенная в электрическом поле конденсатора, будет равна поло­вине напряжения U, умноженной на общее количество пере­несенного электричества Q.

Полученный результат мы можем записать в виде сле­дующей математической формулы:

W = UQ/2                                                                  (1)

Если напряжение в этой формуле будет выражено в воль­тах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накоп­ленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде:

W = CU²/2                                                                  (2)

Выражение (2) говорит нам о том, что энергия, со­средоточенная в поле конденсатора, равна по­ловине произведения емкости конденсатора на квадрат напряжения между его пласти­нами.

Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

§11. Электрическая емкость. Энергия электрического поля Основные формулы

Электрическая ёмкость уединенного проводника или конденсатора определяется соотношением

, или ,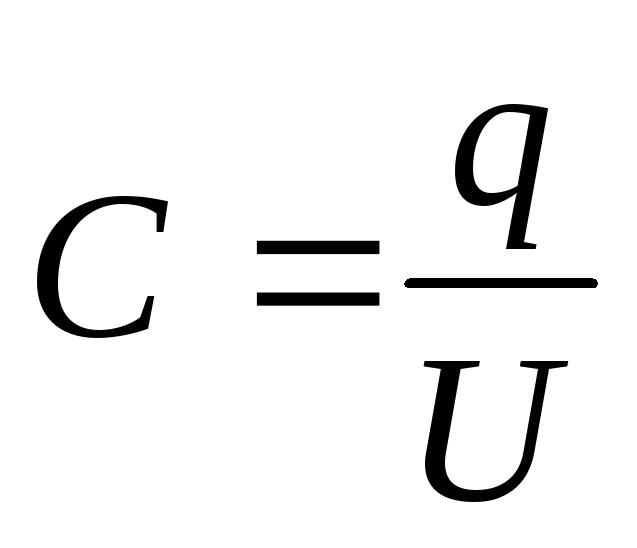

где φ – потенциал уединённого проводника; U – разность потенциалов между пластинами конденсатора; q – заряд проводника или конденсатора.

Электроемкость уединенной проводящей сферы радиуса R равна

.

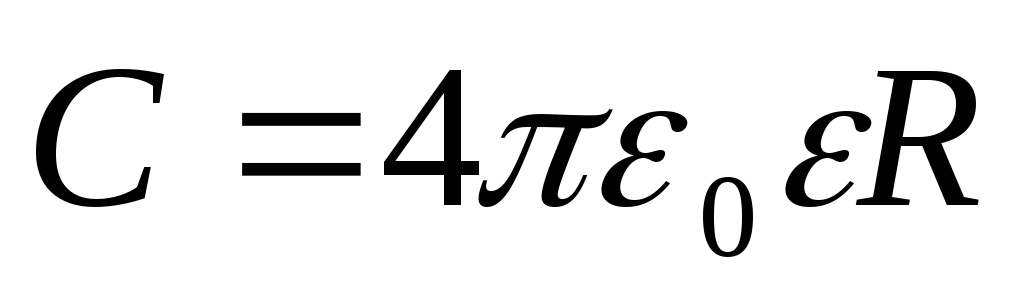Электроемкость плоского конденсатора равна

,

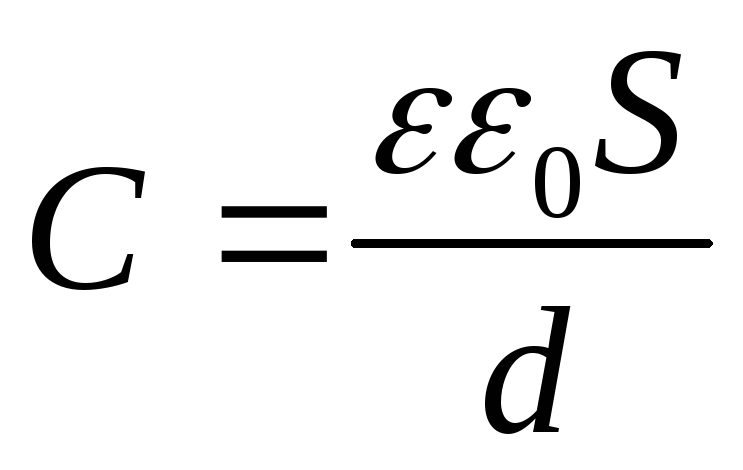где S – площадь каждой пластины конденсатора; d – расстояние между пластинами.

Электроемкость сферического конденсатора определяется формулой

,

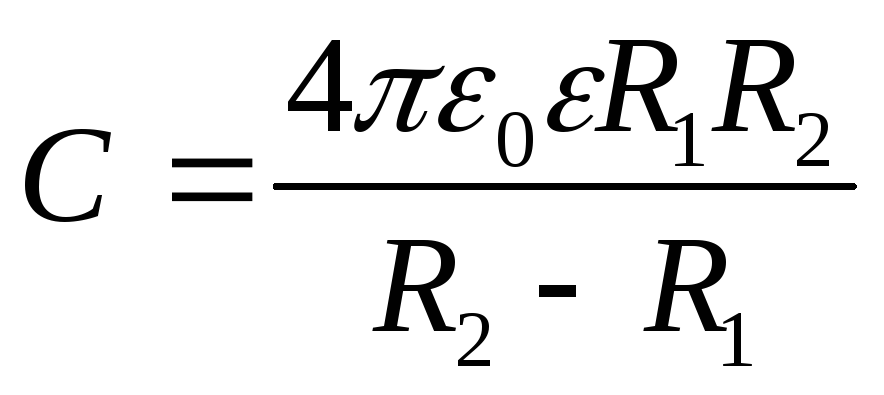где R₁ и R₂ – радиусы концентрических сфер, являющихся обкладками конденсатора; – диэлектрическая проницаемость вещества, находящегося между обкладками.

Электроемкость цилиндрического конденсатора определяется формулой

,

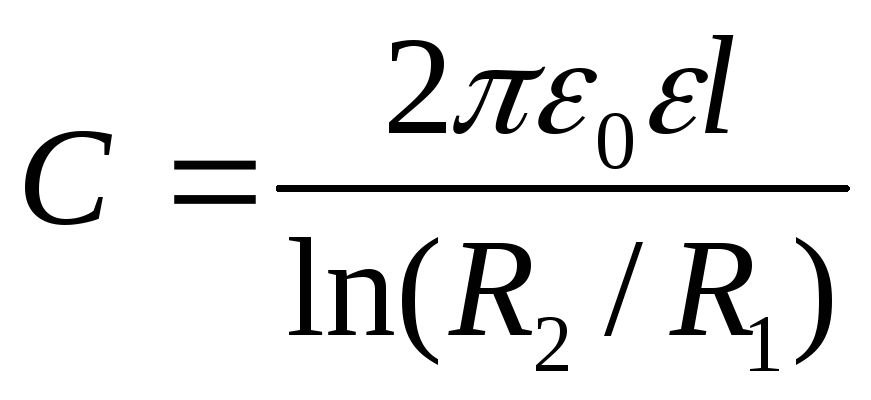где R₁ и R₂ – радиусы двух коаксиальных цилиндров длины l, являющихся обкладками конденсатора, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε.

Электроемкость батареи конденсаторов определяется по формулам:

а) при последовательном соединении

;

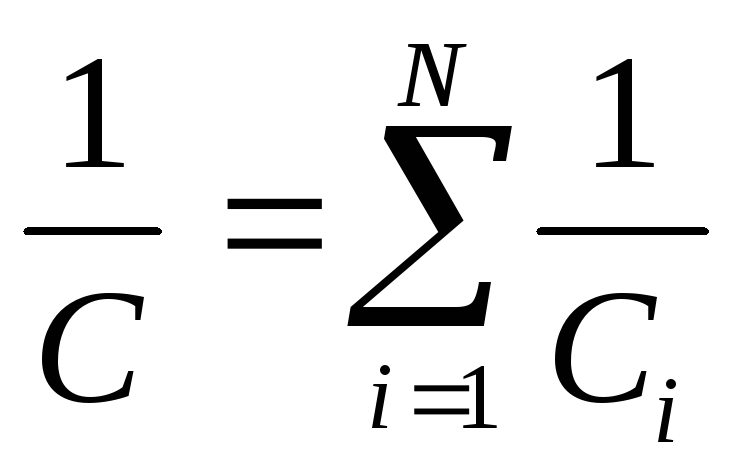б) при параллельном соединении

,

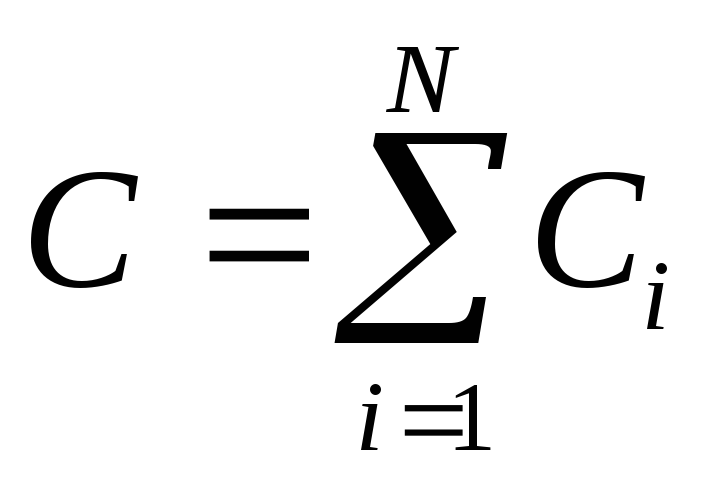где N – число конденсаторов в батарее.

Энергия электрического поля W уединенного заряженного проводника равна

,

где q – заряд проводника; φ– потенциал проводника; С – его электрическая емкость.

Энергия электрического поля заряженного конденсатора равна

,

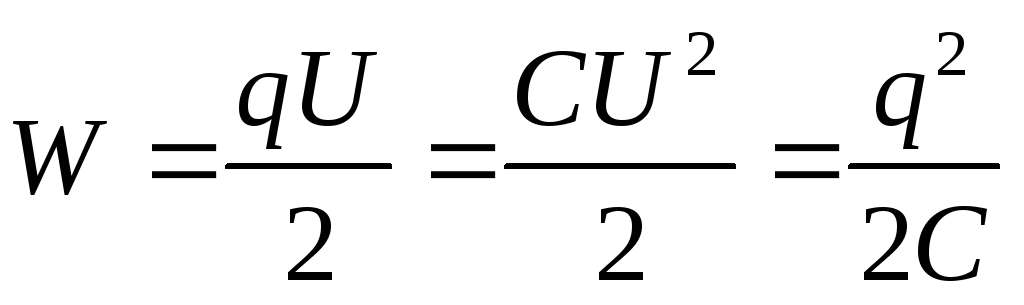где q – заряд конденсатора; U – разность потенциалов его обкладок; С – электрическая емкость конденсатора.

Объемная плотность энергии электростатического поля равна

,

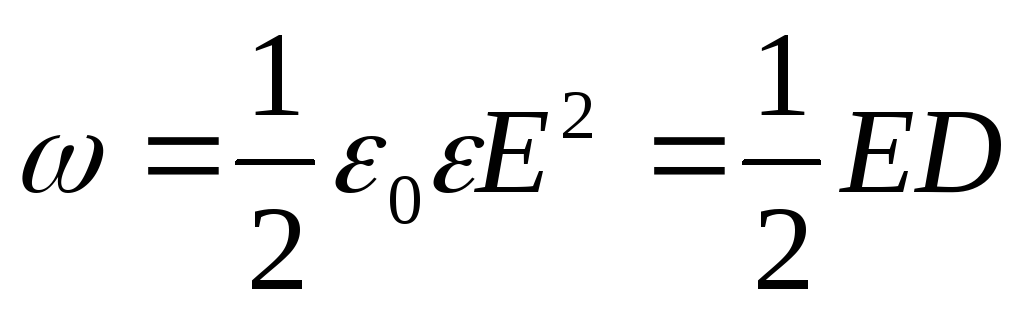где E и D – напряженность и смещение электростатического поля, находящегося в среде с диэлектрической проницаемостью ε.

Задачи

11.1. Найти электроемкость С уединенного металлического шара радиусом R = 1 см, находящегося в вакууме.

11.2. Определить электроемкость С металлической сферы радиу­сом R = 2 см, погруженной в воду.

11.3. Определить электроемкость С Земли, принимая ее за шар радиусом R = 6400 км.

11.4. Два металлических шара радиусами R₁ = 2 см и R₂ = 6 см соединены проводником, емкостью которого можно пренебречь. Шарам сообщен заряд q = l нКл. Найти поверхностную плотность зарядов на шарах.

11.5. Шар радиусом R₁ = 6 см заряжен до потенциала = 300 В, а шар радиусом R₂ = 4 см – до потенциала 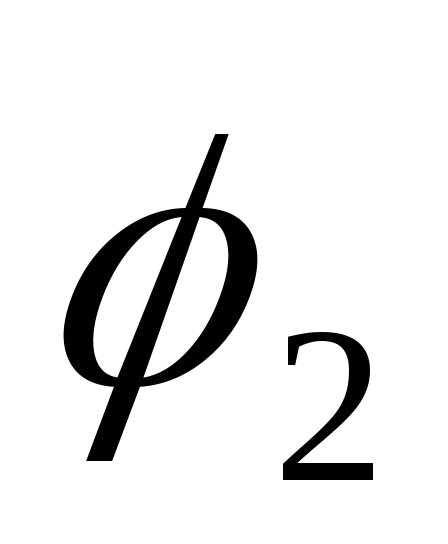= 500 В. Определить потенциал шаров после того, как их соединили металлическим проводником. Емкостью соединительного проводника пренебречь.

11.6. Определить электроемкость С плоского слюдяного конден­сатора, площадь S пластин которого равна 100 см², а расстояние между ними равно 0,1 мм.

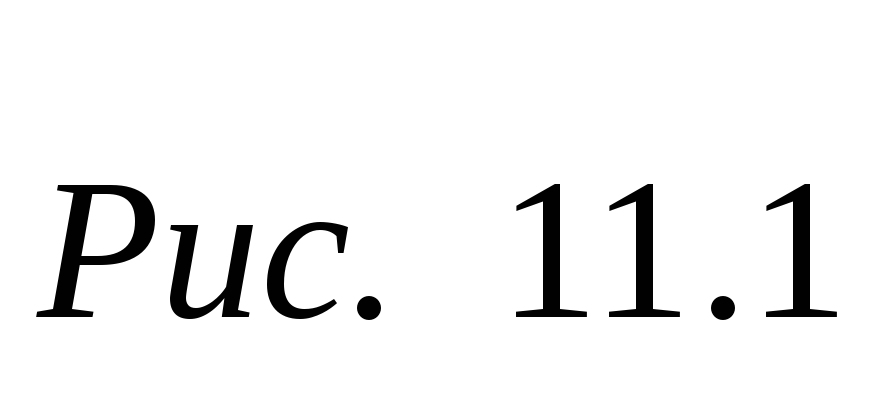
11.7. Найти емкость системы одинаковых конденсаторов между точками А и В, которая показана: а) на рис. 11.1; б) на рис. 11.2.

11.8. Четыре одинаковые металлические пластины расположены в воздухе на расстоянии d = 1 мм друг от друга. Площадь каждой пластины S = 220 см². Найти емкость системы между точками А и В, если пластины соединены так, как показано: а) на рис. 11.3; б) на рис. 11.4.

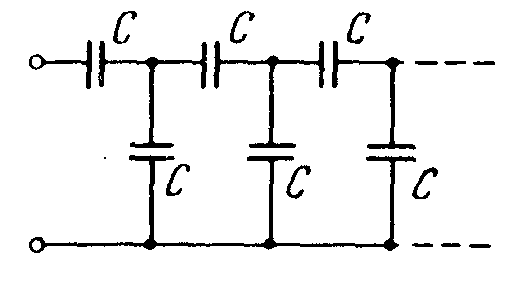
11.9. Найти емкость бесконечной цепи, которая образована повторением одного и того же звена из двух одинаковых конденсаторов, каждый емкости С (рис. 11.5).

11.10. Между пластинами плоского конденсатора, заряженного до разности потенциалов U = 600 В, находятся два слоя диэлектриков: стекла толщиной d₁ = 7 мм и эбонита толщиной d₂ = 3 мм. Площадь S каждой пластины конденсатора равна 200 см². Найти: 1) электроемкость С конденсатора; 2) смещение D, напряженность Е поля и падение потенциала Δφ в каждом слое.

11.11. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью = 0,2 мкКл/м². Расстояние d между пластинами равно 1 мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм?

11.12. В плоский конденсатор вдвинули плитку парафина толщиной d = 1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?

11.13. Электроемкость С плоского конденсатора равна 1,5 мкФ. Расстояние d между пластинами равно 5 мм. Какова будет электроемкость С конденсатора, если на нижнюю пластину положить лист эбонита толщиной d₁ = 3 мм?

11.14. Между пластинами плоского конденсатора находится плотно прилегающая стеклянная пластинка. Конденсатор заряжен до разности потенциалов U₁ = 100 В. Какова будет разность потенциалов U₂, если вытащить стеклянную пластинку из конденсатора?

11.15. Две концентрические металлические сферы радиусами R₁ = 2 см и R₂ = 2,1 см образуют сферический конденсатор. Определить его электроемкость С, если пространство между сферами за­полнено парафином.

11.16. К воздушному конденсатору, заряженному до разности потенциалов U = 600 В и отключённому от источника напряжения, присоединили параллельно второй, незаряженный конденсатор таких же размеров и формы, но с диэлектриком (фарфор). Определить диэлектрическую проницаемость фарфора, если после присоединения второго конденсатора разность потенциалов уменьшилось до U₁= 100 В.

11.17. Два конденсатора электроёмкостями С₁= 3 мкФ и С₂ = 6 мкФ соединены между собой и присоединены к батарее с ЭДС Е = 120 В. Определить заряды q₁и q₂конденсаторов и разности потенциалов U₁и U₂ между их обкладками, если конденсаторы соединены: 1) параллельно; 2) последовательно.

11.18. Конденсатор электроёмкостью С₁ = 0,2 мкФ был заряжен до разности потенциалов U₁ = 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U₂ = 450 В, напряжение U на нём изменилось до 400 В. Вычислить ёмкость С₂ второго конденсатора.

11.19. Конденсатор электроёмкостью С₁ = 0,6 мкФ был заряжен до разности потенциалов U₁ = 300 В и соединён параллельно со вторым конденсатором электроёмкостью С₂ = 0,4 мкФ, заряженным до разности потенциалов U₂ = 150 В. Найти заряд Δq, перетекший с пластин первого конденсатора на второй.

11.20. Три одинаковых плоских конденсатора соединены последовательно. Электроемкость С такой батареи конденсаторов равна 89 пФ. Площадь S каждой пластины равна 100 см². Диэлектрик – стекло. Какова толщина d стекла?

11.21. Конденсатор емкости С₁ = 1мкФ, заряженный до напряжения U=110B, подключили параллельно к концам системы из двух последовательно соединенных конденсаторов, емкости которых С₂ = 2 мкФ и С₃ = 3мкФ. Какой заряд протечет при этом по соединительным проводам?

11.22. Конденсатору, электроемкость С которого равна 10 пФ, сообщен заряд q = 1 пКл. Определить энергию W конденсатора.

11.23. Расстояние d между пластинами плоского конденсатора равно 2 см, разность потенциалов U = 6 кВ. Заряд q каждой пластики равен 10 нКл. Вычислить энергию W поля конденсатора и силу F взаимного притяжения пластин.

11.24. Какое количество теплоты Q выделится при разряде плоского конденсатора, если разность потенциалов U между пластинами равна 15 кВ, расстояние d = 1 мм, диэлектрик – слюда и площадь S каждой пластины равна 300 см²?

11.25. Сила F притяжения между пластинами плоского воздушного конденсатора равна 50 мН. Площадь S каждой пластины равна 200 см². Найти объемную плотность энергии ω электрического поля конденсатора.

11.26. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние d₁ между пластинами равно 1 см. Конденсатор зарядили до разности потенциалов U = 1,2 кВ и отключили от источника тока. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d₂ = 3,5 см?

11.27. Плоский воздушный конденсатор электроемкостью С = 1,11 нФ заряжен до разности потенциалов U = 300 В. После отключения от источника тока расстояние между пластинами конденсатора было увеличено в пять раз. Определить: 1) разность потенциалов U₁ на обкладках конденсатора после их раздвижения; 2) работу А внешних сил по раздвижению пластин.

11.28. Внутри плоского конденсатора находится параллельная обкладкам пластина, толщина которой составляет 0,6 расстояния между обкладками. Емкость конденсатора в отсутствие пластины С = 20нФ. Конденсатор сначала подключили к источнику постоянного напряжения U = 200 В, затем отключили и после этого медленно извлекли пластину из зазора. Найти работу, совершенную против электрических сил при извлечении пластины, если она: а) металлическая; б) стеклянная.

11.29. Конденсатор электроемкостью С₁ = 666 пФ зарядили до разности потенциалов U = 1,5 кВ и отключили от источника тока. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью С₂ = 444 пФ. Определить энергию, израсходованную на образование искры, проскочившей при соединении конденсаторов.

11.30. Конденсаторы электроемкостями С₁ = 1 мкФ, С₂ = 2 мкФ и С₃ = 3мкФ включены в сеть с напряжением U = 1,1 кВ. Определить энергию каждого конденсатора в случаях: 1) последовательного соединения; 2) параллельного соединения.

11.31. Электроемкость С плоского конденсатора равна 111 пФ. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U = 600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденсатора? Трение пренебрежимо мало.

11.32. Найти энергию W уединенной сферы радиусом R = 4 см, заряженной до потенциала φ = 500 В.

11.33. Вычислить энергию W электростатического поля металлического шара, которому сообщен заряд q = 100 нКл, если диаметр d шара равен 20 см.

11.34. Сферическую оболочку радиуса R₁, равномерно заряженную зарядом q, расширили до радиуса R₂. Найти работу, совершенную при этом электрическими силами.

11.35. Сферическая оболочка заряжена равномерно с повер­ хностной плотностью σ. Найти модуль электрической силы на единицу повер­хности оболочки.

Энергия поля конденсатора

При решении задач, связанных с определением энергии поля, важно помнить, что при отключении конденсатора от источника питания он сохраняет заряд, а если конденсатор остается подключенным к источнику, то напряжение будет постоянно.

Задача 1. Расстояние между пластинами плоского конденсатора уменьшили в 2 раза. Во сколько раз изменятся: заряд на пластинах, напряжение между пластинами, напряженность поля между пластинами и энергия конденсатора. Рассмотреть два случая: а) конденсатор отключен от источника напряжения; б) конденсатор остается присоединенным к источнику постоянного напряжения.

а) Если конденсатор отключен от питания, то он сохраняет заряд. Следовательно, в этом случае заряд не изменится. Емкость же вырастет вдвое, так как

Энергия

уменьшится вдвое (ведь емкость выросла).

Напряженность поля зависит только от заряда и поэтому тоже не изменится.

б) Если конденсатор подключен к источнику питания, то , и

– энергия увеличится вдвое. Так как емкость выросла вдвое, следовательно, вдвое вырос и заряд конденсатора. А это значит, что и напряженность поля также вдвое увеличится.

Задача 2. Заряженный конденсатор подключили параллельно к такому же, незаряженному. Во сколько раз изменилась энергия поля первого конденсатора?

При параллельном подключении заряд поделится между двумя конденсаторами поровну. Поэтому, так как

То энергия изменится в 4 раза:

Задача 3. Плотность энергии заряженного конденсатора Дж/м. С какой силой взаимодействуют обкладки конденсатора, если их площадь м?

Сила взаимодействия пластин:

Ответ: 3 Дж

Задача 4. Определить энергию заряженного плоского конденсатора с твердым диэлектриком по следующим данным: объем диэлектрика м, относительная диэлектрическая проницаемость , напряженность поля в диэлектрике В/м.

Ответ: мДж.

Задача 5. Определить энергию, перешедшую в тепло при соединении конденсаторов одноименно заряженными обкладками. Емкость первого конденсатора мкФ, второго мкФ. Напряжение на первом конденсаторе до соединения В, а на втором – В.

Энергия первого конденсатора:

Второго:

А после соединения заряд перераспределится и поэтому энергия системы будет равна

Где . Заряд первого конденсатора

Заряд второго

Заряд обоих конденсаторов

Тогда энергия системы равна

Таким образом, выделившееся тепло равно

Ответ: 0,5 мДж