Определение емкости конденсатора с помощью вольтметра
Цель работы: определение емкости конденсаторов и проверка законов последовательного и параллельного соединений конденсаторов.
Приборы и оборудование: источник питания, вольтметр, потенциометр (R), эталонный конденсатор (Сэт), исследуемые конденсаторы (Сх1 и Сх2), переключатели.
Теоретические сведения
Опытным путем было установлено, что в природе существует два типа электрических зарядов, условно названных положительными и отрицательными. Одноименные заряды отталкиваются друг от друга, разноименные притягиваются.
Р. Милликен доказал, что электрический заряд дискретен, т.е. величина заряда любого тела составляет целое число, кратное элементарному электрическому заряду е (e=1,6∙10-19 Кл). Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.
В результате обобщения опытных данных был сформулирован фундаментальный закон природы — закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри нее.
Единица электрического заряда, 1 кулон (Кл), — это электрический заряд, проходящий через поперечное сечение проводника при силе тока в 1 А за время, рапное 1с :
1Кл=1 А∙1с.
Закон
взаимодействия неподвижных точечных
электрических зарядов был открыт
Кулоном: сила взаимодействия F
двух точечных зарядов прямо пропорциональна
величине зарядов q
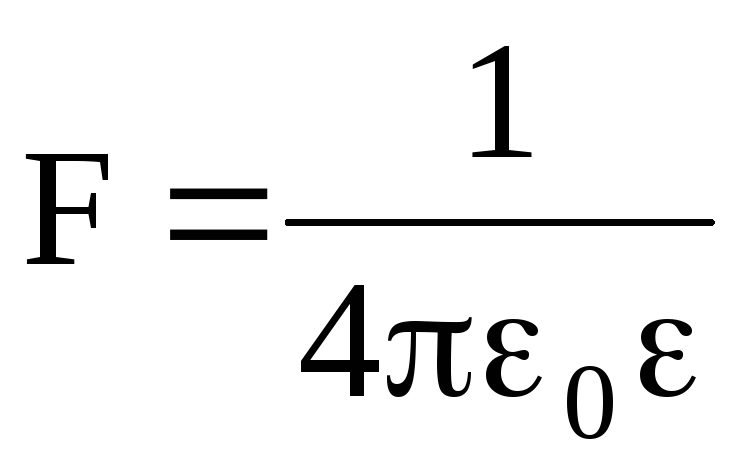 ∙
∙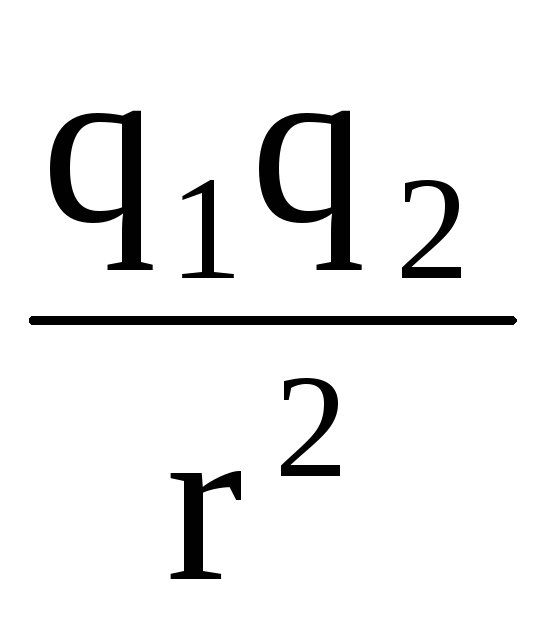 (1)
(1)
где 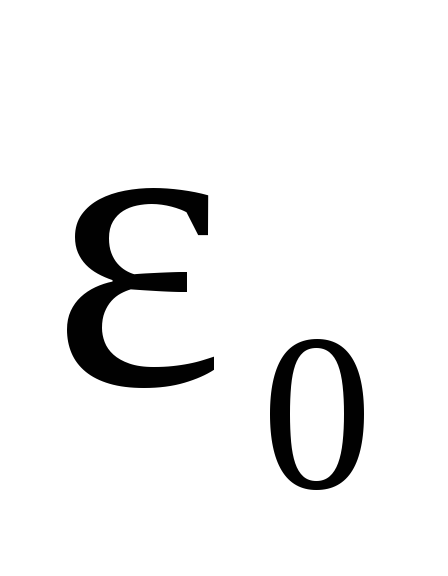 =8,8510-12 Ф/м — электрическая постоянная;
=8,8510-12 Ф/м — электрическая постоянная;  — диэлектрическая проницаемость среды
(безразмерная
величина).
— диэлектрическая проницаемость среды
(безразмерная
величина).
Напряженность  электрического
поля в данной точке есть физическая
величина, определяемая силой, действующей
на единичный положительный заряд,
помещенный в эту точку:
электрического
поля в данной точке есть физическая
величина, определяемая силой, действующей
на единичный положительный заряд,
помещенный в эту точку:
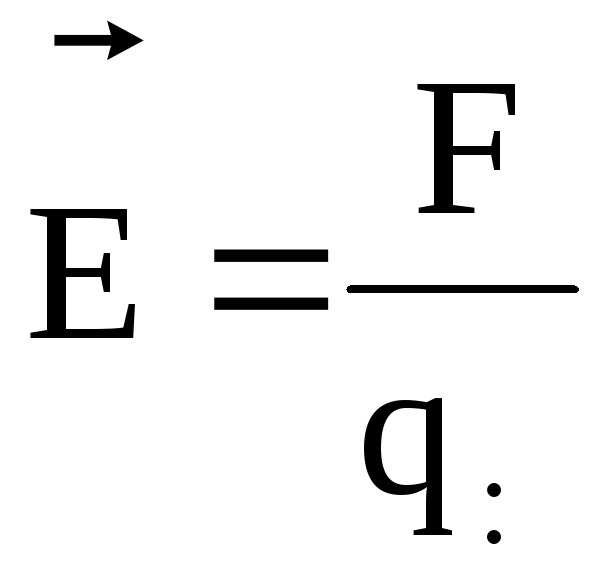 .
(2)
.
(2)
Направление
вектора  совпадает с направлением силы, действующей
на положительный
заряд. Выражение для определения единицы
напряженности
электрического поля:
совпадает с направлением силы, действующей
на положительный
заряд. Выражение для определения единицы
напряженности
электрического поля:
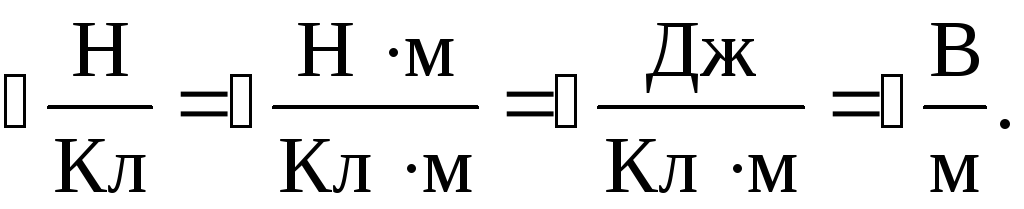 (3)
(3)
Графически электростатическое поле изображают с помощью линий напряженности (силовых линий), которые проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором напряженности (рис. I).
Величина

называется
потоком вектора напряженности через
площадку dS.
Здесь 
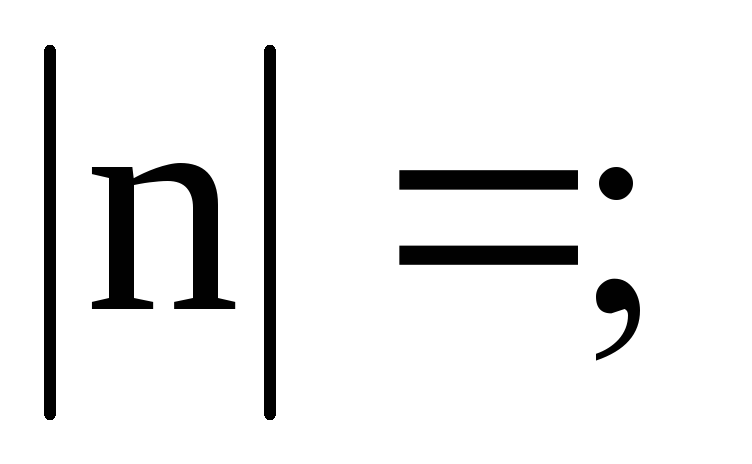 ).
). Электростатические
поля подчиняются принципу суперпозиции:
напряженность  результирующего поля, созданного
системой зарядов, равна геометрической
сумме напряженностей полей, созданных
в данной точке каждым из зарядов в
отдельности:
результирующего поля, созданного
системой зарядов, равна геометрической
сумме напряженностей полей, созданных
в данной точке каждым из зарядов в
отдельности:
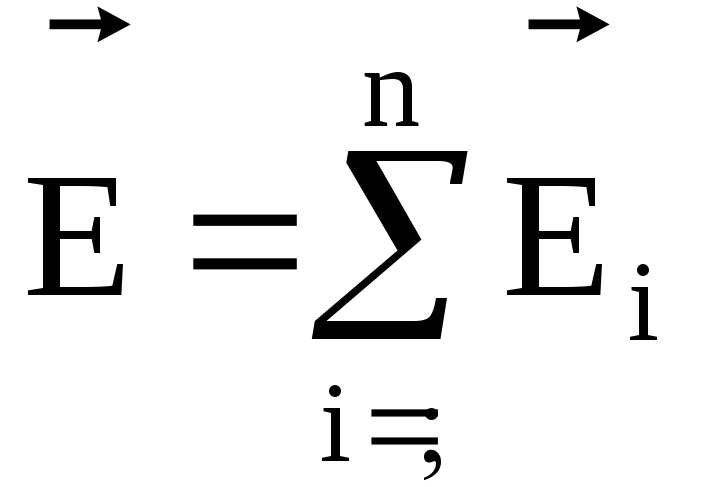
где  —
напряженность электростатического
поля, созданного i-м
зарядом.
—
напряженность электростатического
поля, созданного i-м
зарядом.
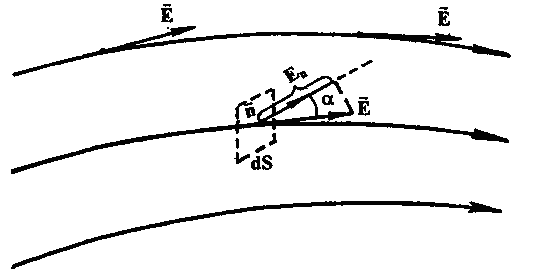
Рис. 1
Теорема Остроградского-Гаусса для электростатического поля в вакууме звучит так: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 0:
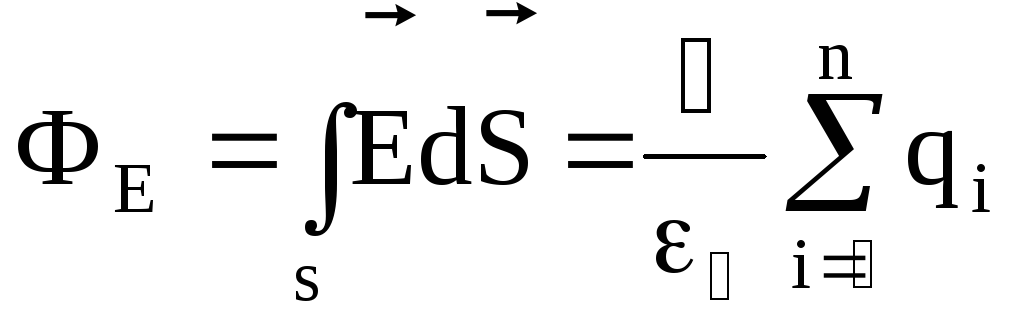
Из теоремы Гаусса следует, что напряженность электростатического поля между двумя бесконечными параллельными и разноименно заряженными плоскостями в вакууме будет равна
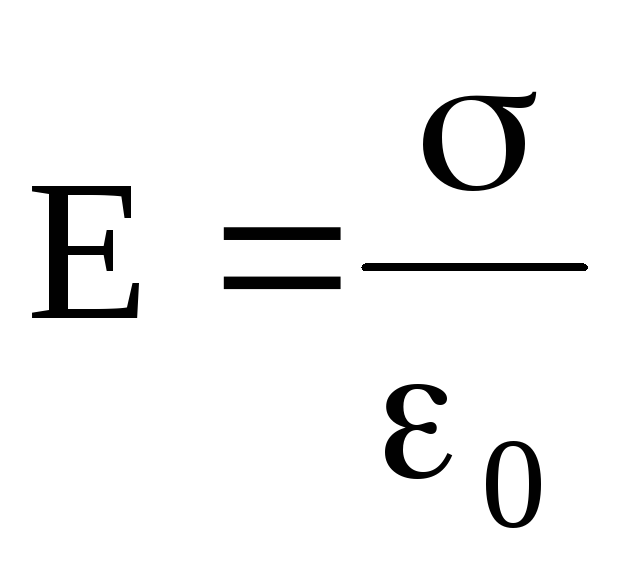 ,
(6)
,
(6)
где 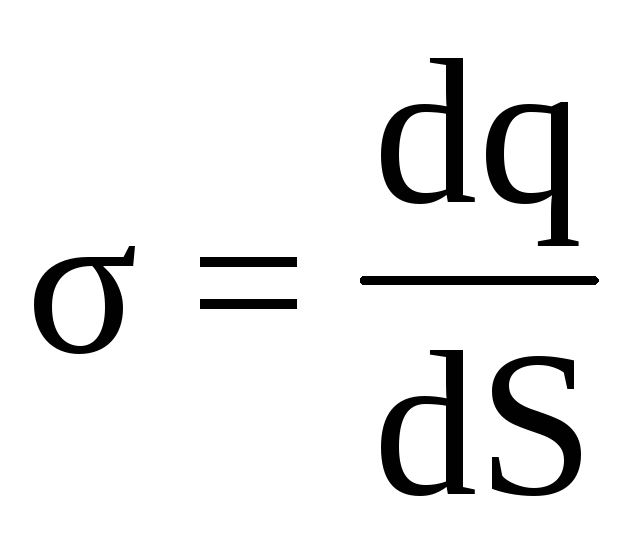 —
поверхностная плотность заряда
плоскостей.
—
поверхностная плотность заряда
плоскостей.
Если
между заряженными плоскостями находится
изолятор с диэлектрической
проницаемостью 
 раз (рис. 2):
раз (рис. 2): 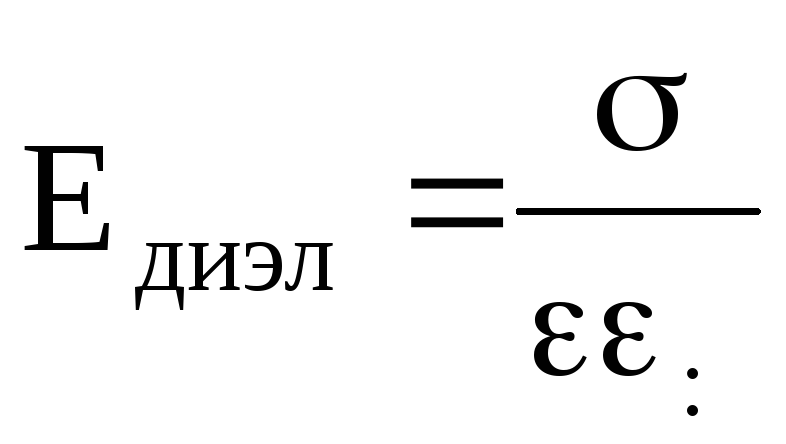 (7)
(7)
Электростатическое поле является полем консервативных сил, т.е. работа, совершаемая силами поля по перемещению электрического заряда из одной точки пространства в другую, не зависит от траектории движения заряда, а определяется только его начальным и конечным положениями. Для такого рода полей можно ввести понятие потенциальной энергии заряда, численно равной работе, совершаемой силами электростатического поля по перемещению его из данной точки пространства в другую (ту, в которой потенциальная энергия заряда равна нулю).
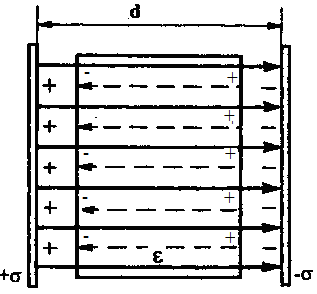
Рис. 2
Как правило, потенциальная энергия заряда, удаленного в бесконечность, считается равной нулю. Поэтому она будет равна
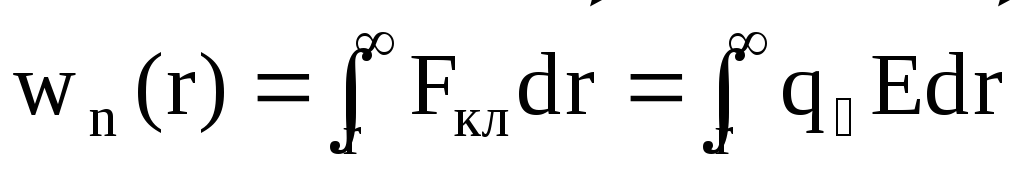
где 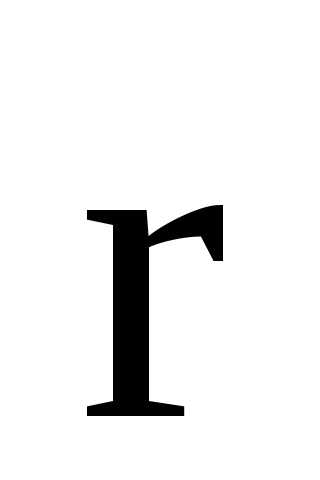 — радиус-вектор;
— радиус-вектор; 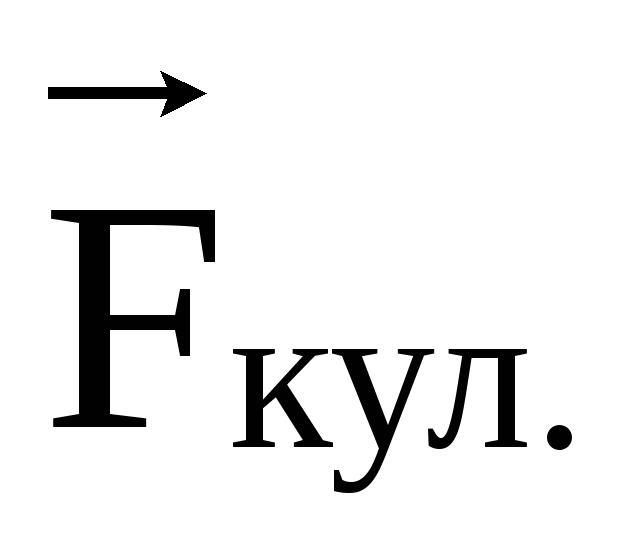 —
кулоновская сила;
—
кулоновская сила;  — напряженность электростатического
поля; q0 — электрический заряд.
— напряженность электростатического
поля; q0 — электрический заряд.
Если
заряд q0 перемещается из первой точки во
вторую(определяются соответственно
радиус-векторами 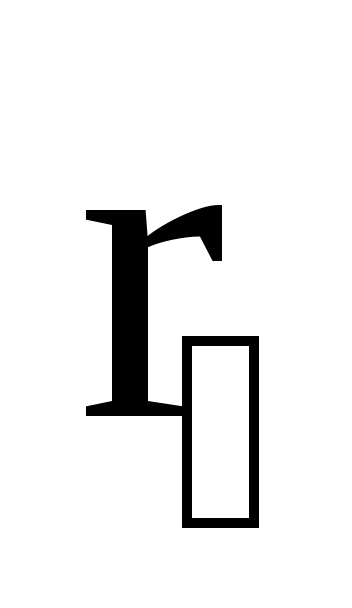 и
и 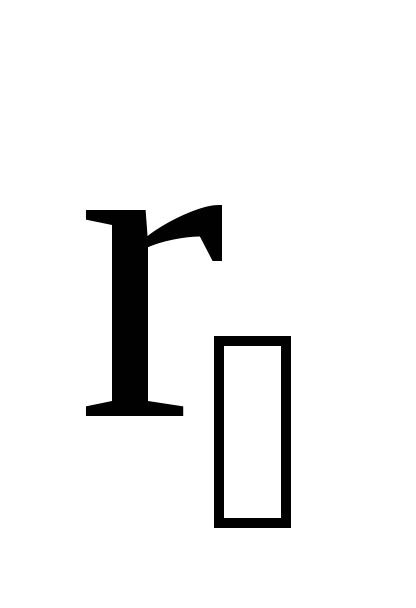
A (9)
(9)
где 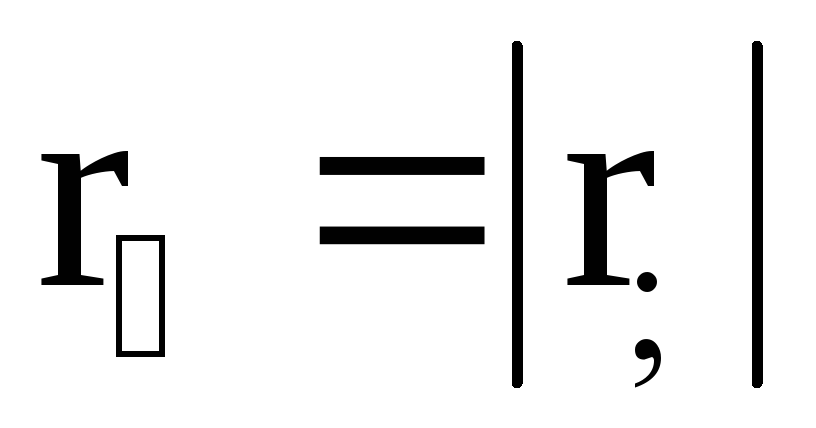 и
и 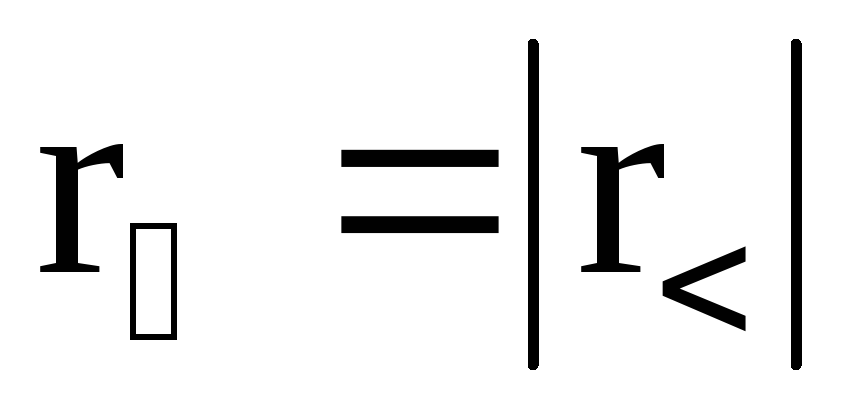 ;
;  и
и 
Потенциал – физическая величина, определяемая работой сил поля по перемещению единичного положительного заряда из данной точки в бесконечность:
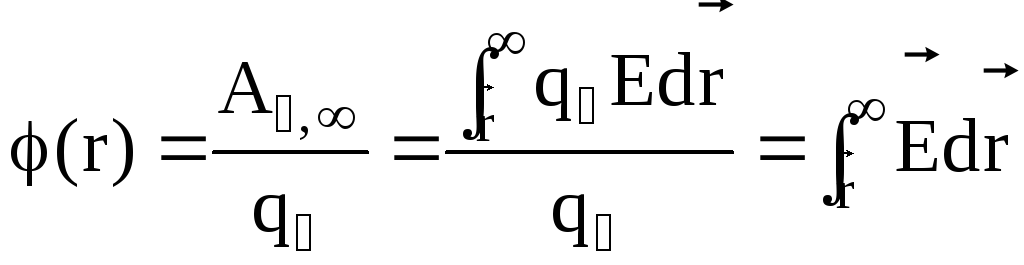 .
(10)
.
(10)
Единица потенциала — вольт (В): 1 В — потенциал такой точки поля, в которой заряд в 1Кл обладает потенциальной энергией в 1 Дж:
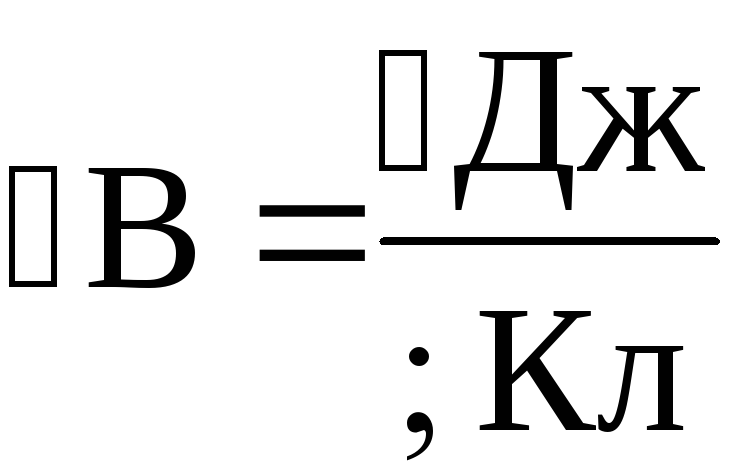
Поскольку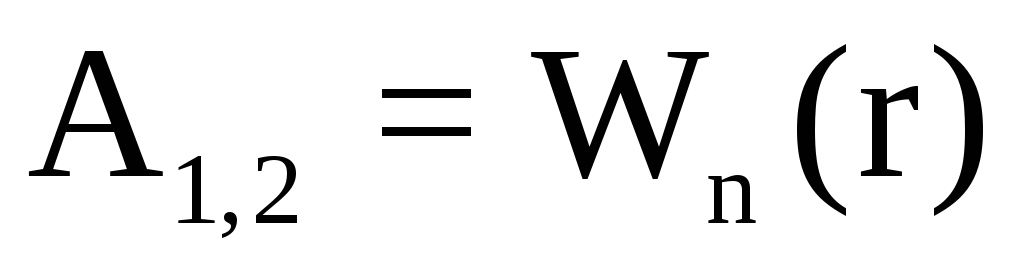 ,
то
,
то
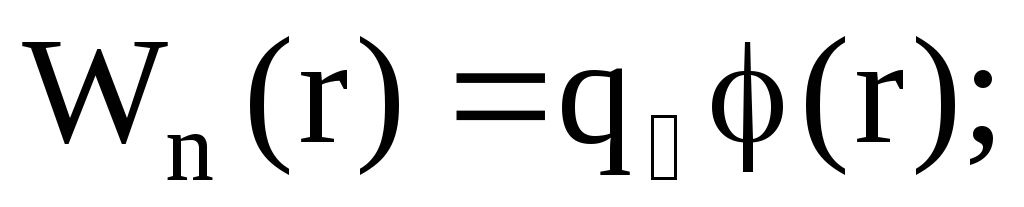
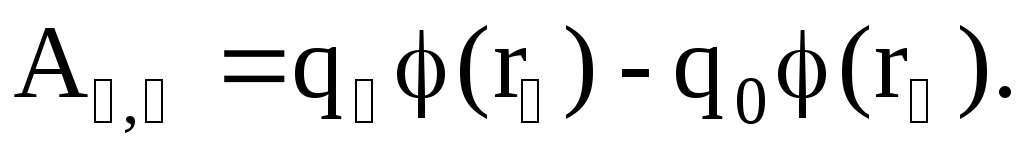 (11)
(11)
Отсюда
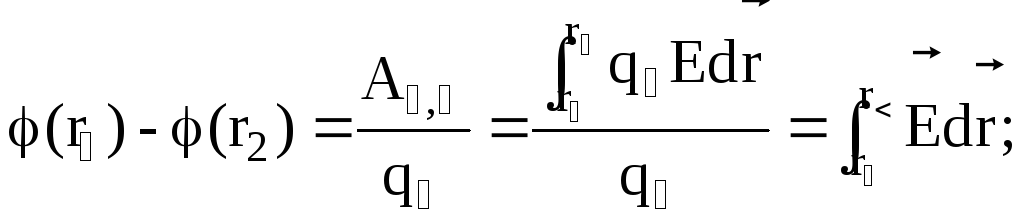
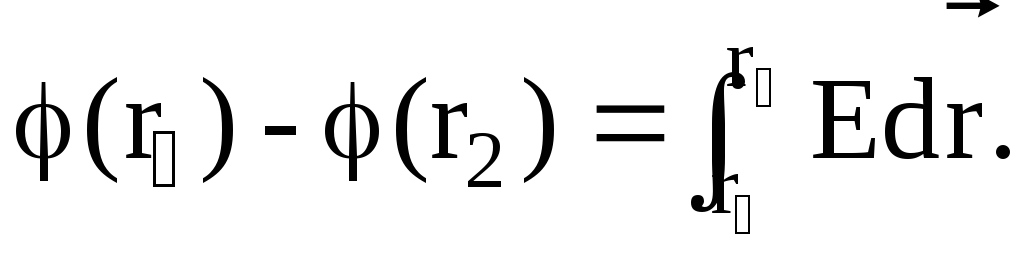 (12)
(12)
Зная
потенциал в каждой точке пространства  можно
найти напряженность
электростатического поля:
можно
найти напряженность
электростатического поля:
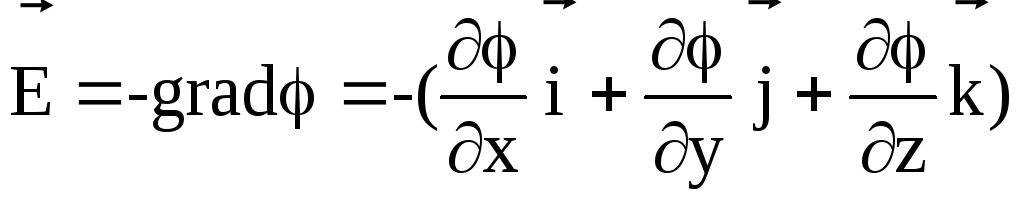 (13)
(13)
Знак «минус» указывает на то, что вектор напряженности Ё направлен в сторону убывания потенциала.
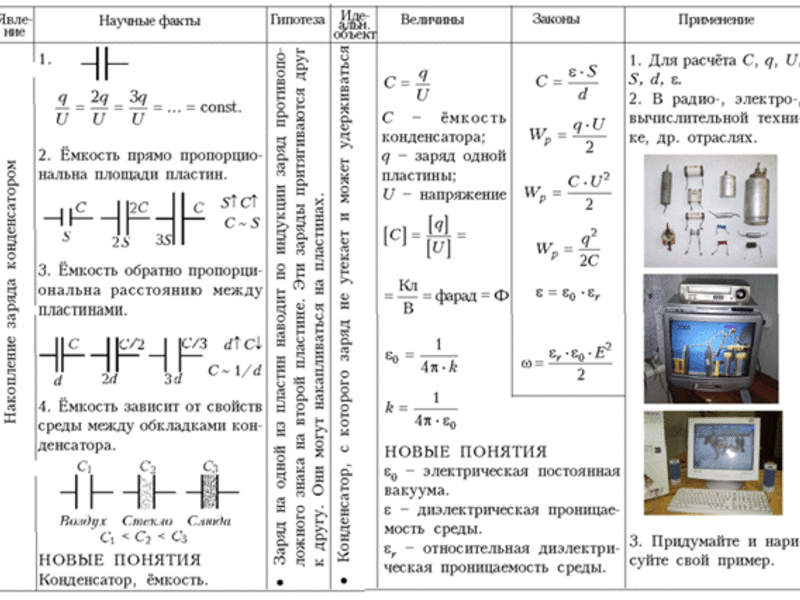
Потенциал уединенного проводника прямо пропорционален его заряду;
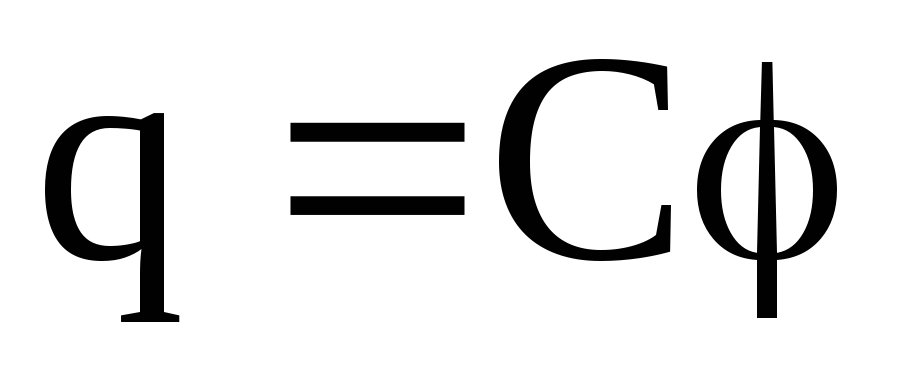
При
этом величину 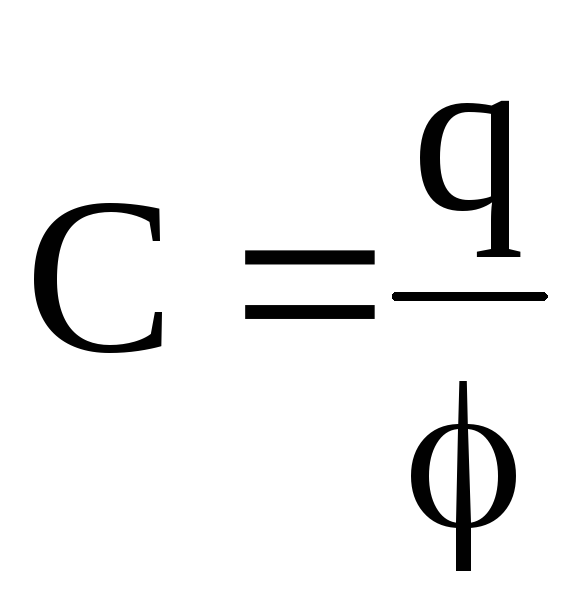 (14)
(14)
называют электроемкостью уединенного проводника. Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1Кл, т.е.
 .
(15)
.
(15)
Для
накопления значительных зарядов служат
конденсаторы, состоящие из
двух проводников (обкладок), разделенных
диэлектриком. В зависимости от формы
обкладок конденсаторы подразделяются
на плоские, цилиндрические и сферические.
Под емкостью конденсатора понимается
физическая величина, равная
отношению накопленного заряда q
к разности потенциалов 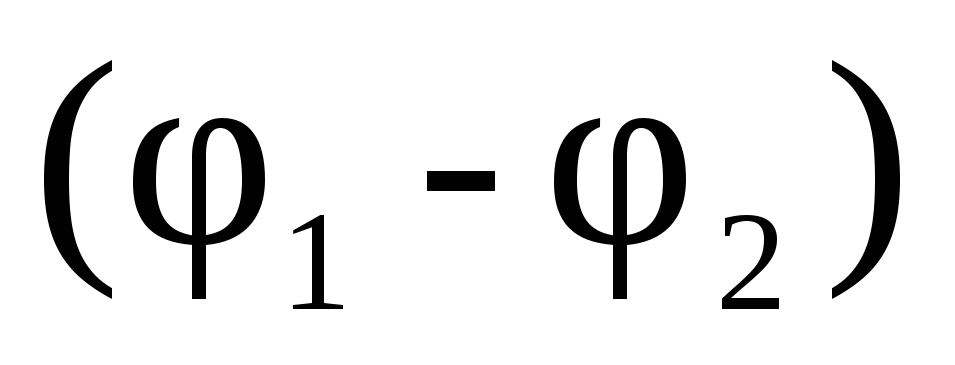 между
обкладками:
между
обкладками:
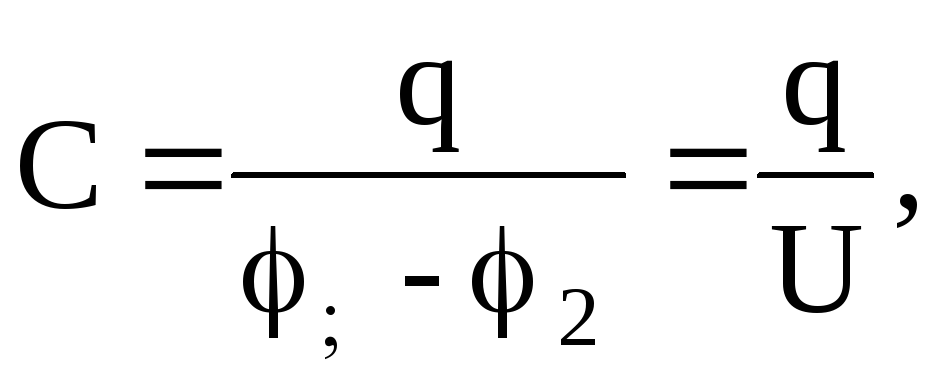 (16)
(16)
где 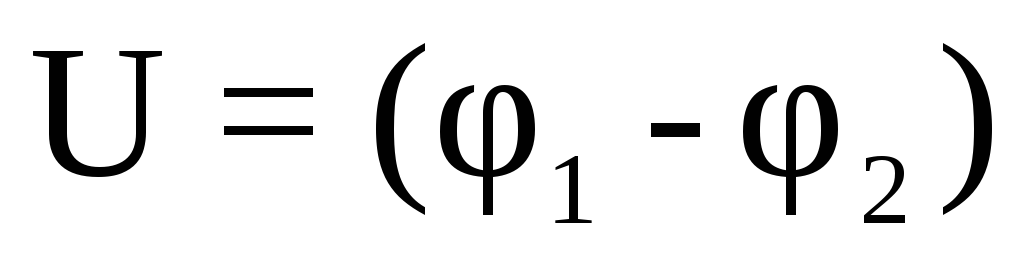 напряжение между обкладками. Плоский
конденсатор обладает емкостью
напряжение между обкладками. Плоский
конденсатор обладает емкостью
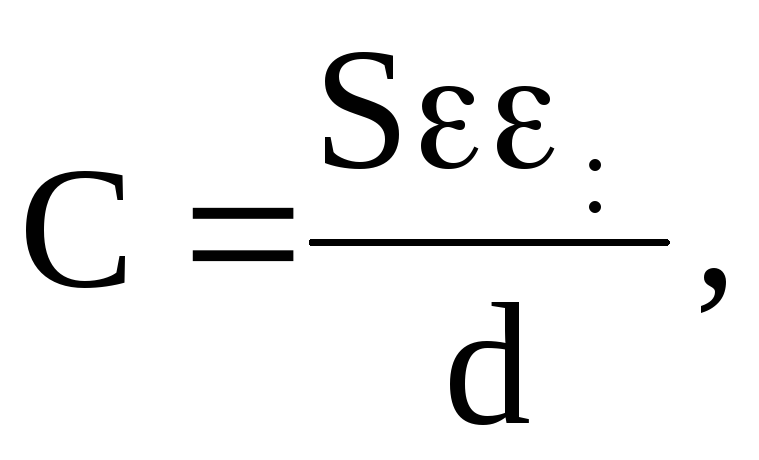 (17)
(17)
где  —
диэлектрическая проницаемость изолятора;
—
диэлектрическая проницаемость изолятора; 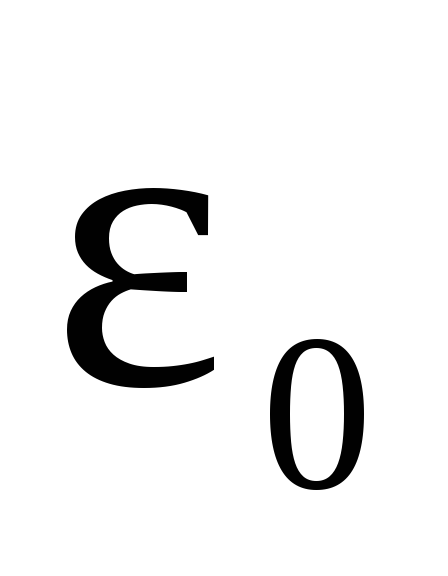 —
электрическая постоянная;
S
— площадь обкладки; d
— расстояние между обкладками.
—
электрическая постоянная;
S
— площадь обкладки; d
— расстояние между обкладками.
Для
увеличения емкости и варьирования ее
возможных значений конденсаторы
соединяют в батареи параллельно или
последовательно. У параллельно соединенных
конденсаторов разность потенциалов на
обкладках одинакова и равна 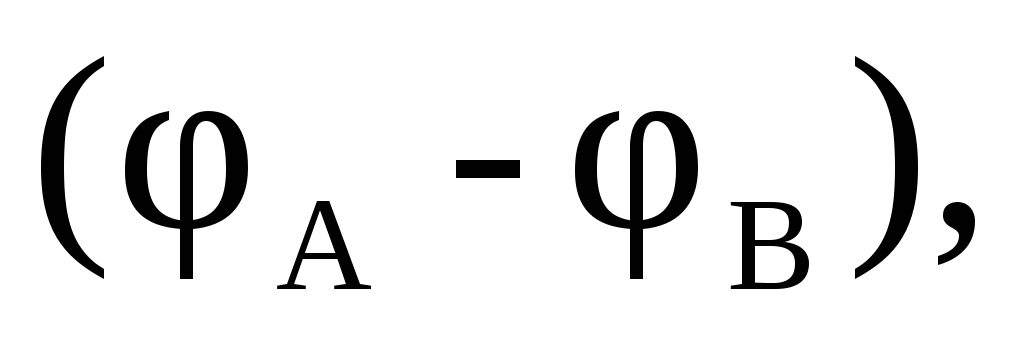 см рис. 3.
см рис. 3.
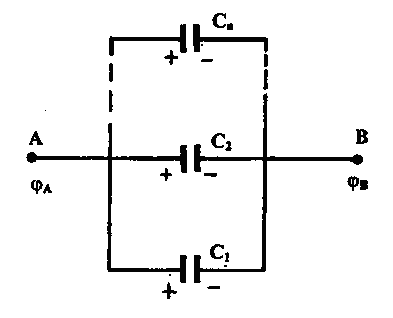
Рис. 3
Если
емкости отдельных конденсаторов  то их заряды равны соответственно
то их заряды равны соответственно
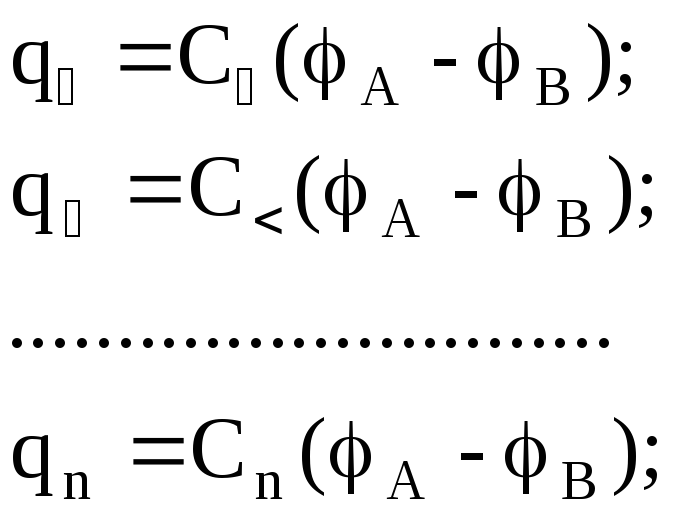 (18)
(18)
а заряд батареи конденсаторов-
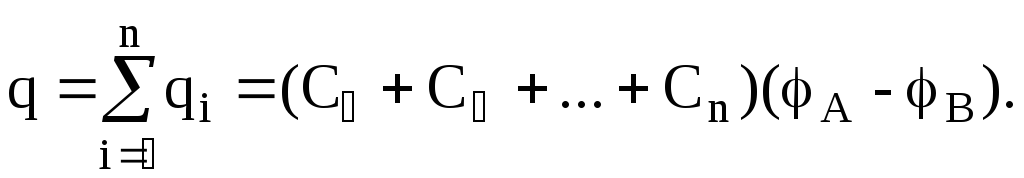
Полная емкость батареи –
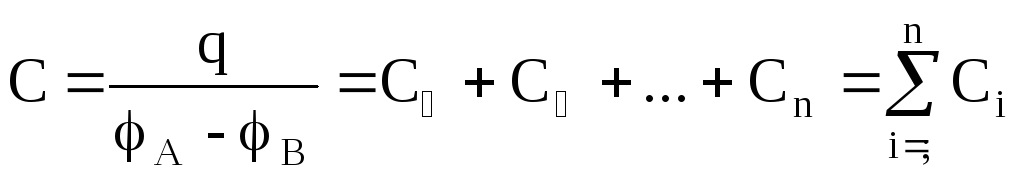 ,
(19)
,
(19)
т.е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи, см. рис. 4, равна
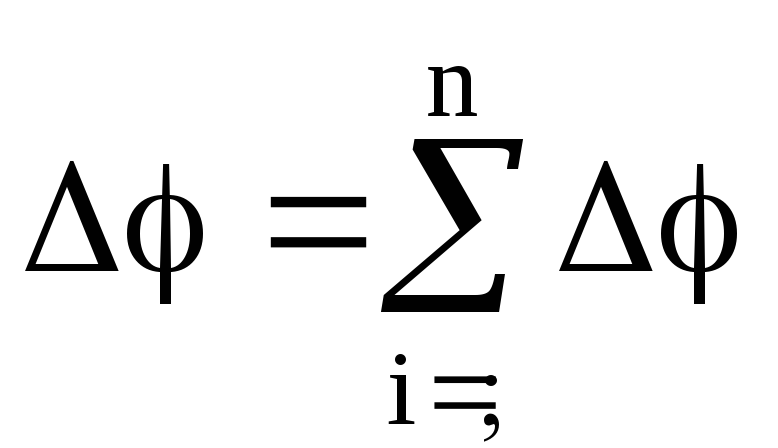 .
(20)
.
(20)
Причем для любого из рассматриваемых конденсаторов
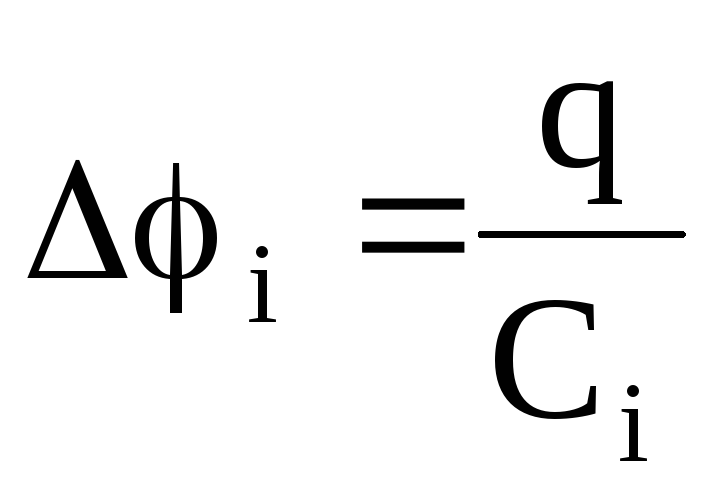 .
.
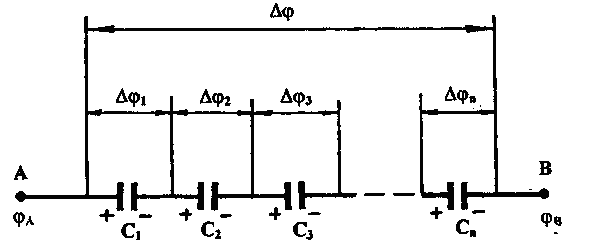
Рис. 4
С другой стороны,
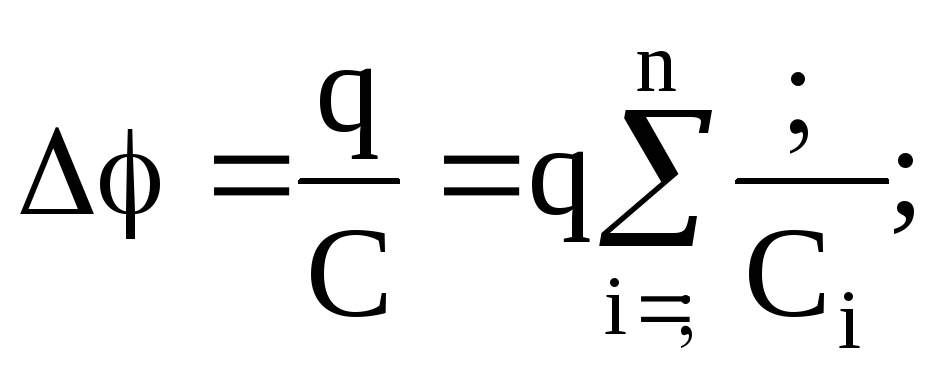 (21)
(21)
откуда 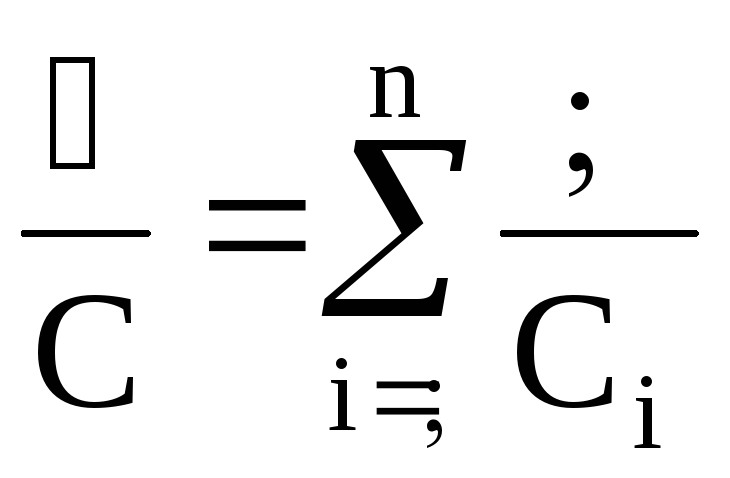 ,
(22)
,
(22)
т.е. при последовательном соединении конденсаторов суммируются обратные величины емкостей.
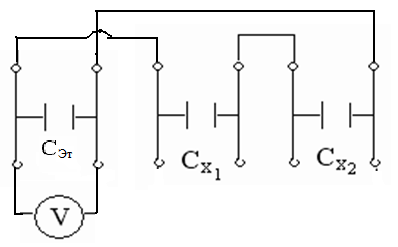
Если дана емкость эталонного конденсатора Сэт, то неизвестную емкость другого конденсатора Сх можно определить следующим образом.
Сначала конденсатор Сэт зарядить от источника постоянного тока (рис.5а). При этом накапливается заряд q. С помощью вольтметра измерить напряжение на обкладках конденсатора:
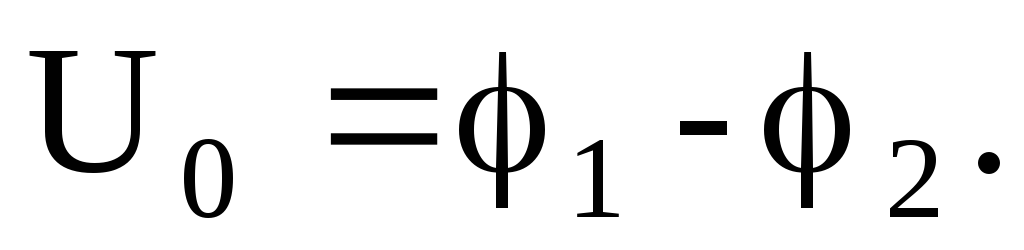
Тогда
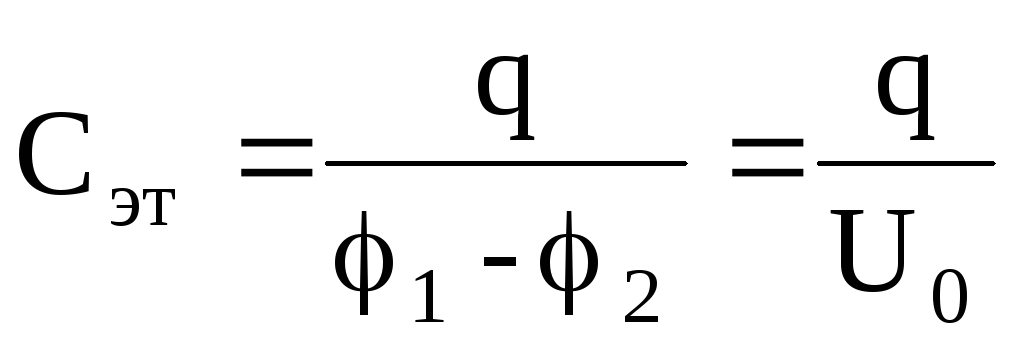 .
.
Отсюда
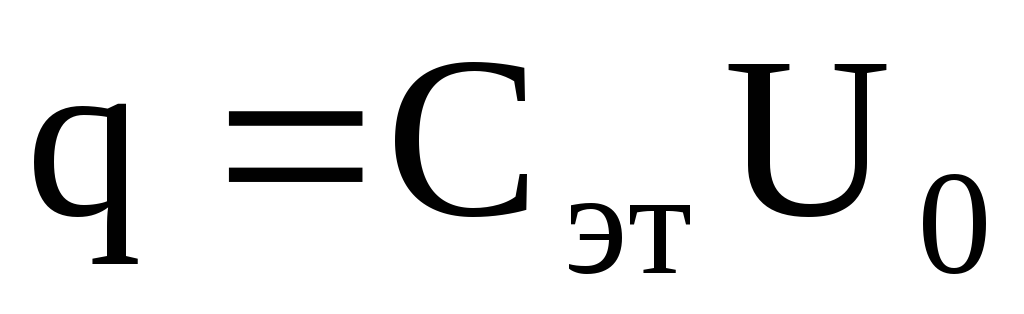 . (23)
. (23)
Затем эталонный конденсатор отключить от источника питания и к нему параллельно присоединить конденсатор неизвестной емкости Сх (рис. 5б). Электрический заряд q распределится по конденсаторам Сэт и Сх.
Согласно закону сохранения зарядов в замкнутой системе
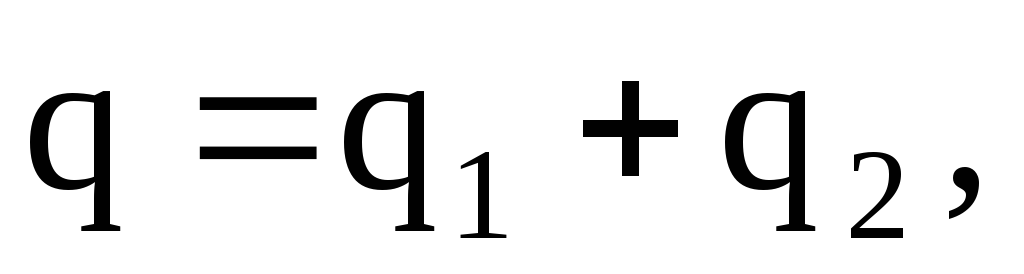 (24)
(24)
где q1, q2— электрические заряды на конденсаторах Сэт и Сх.
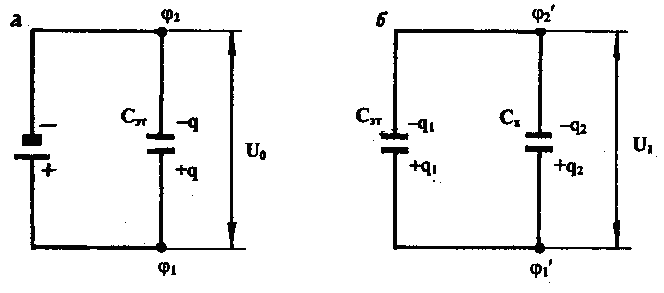
Рис. 5, а Рис. 5, б
После
этого измерить напряжение 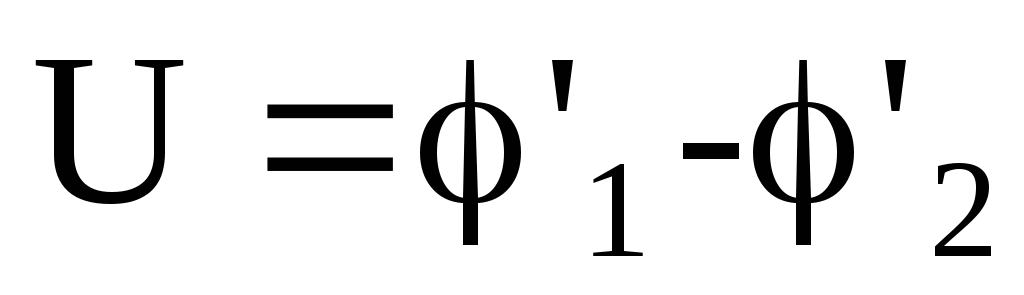 на
обкладках конденсаторов, причем
на
обкладках конденсаторов, причем
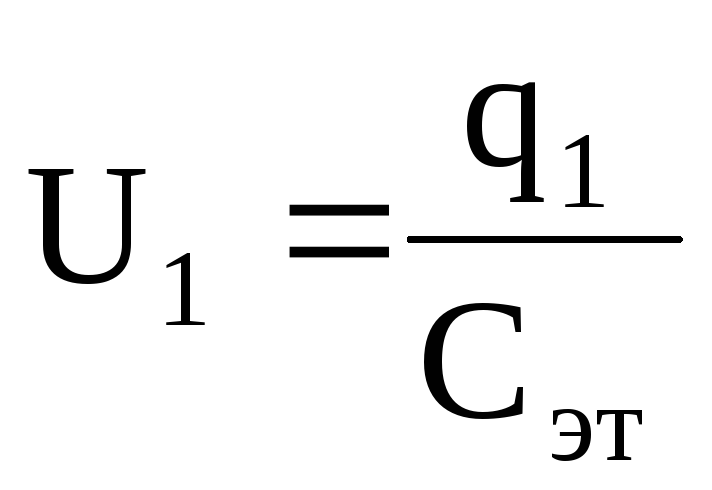 и
и 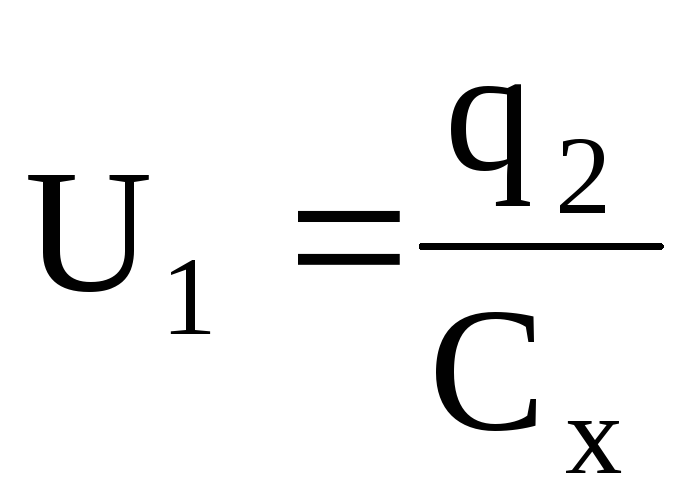 .
.
Отсюда
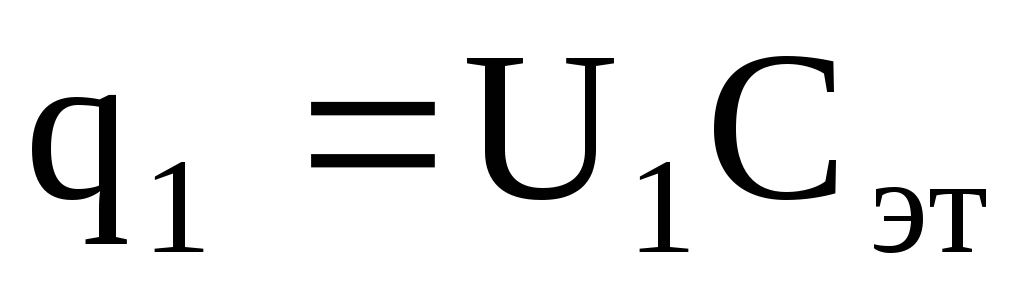 и
и 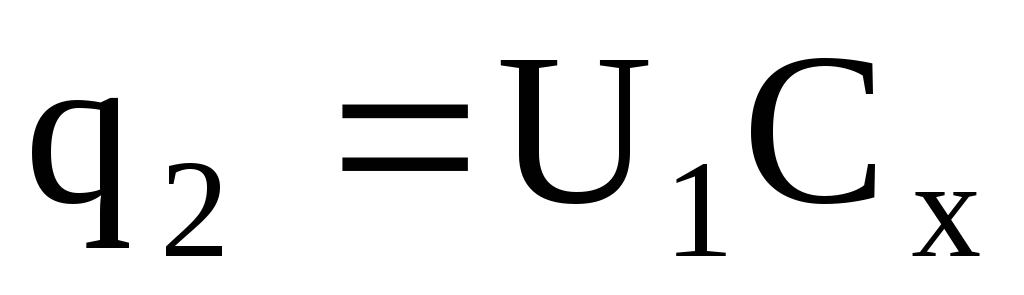 .
(25)
.
(25)
Поэтому
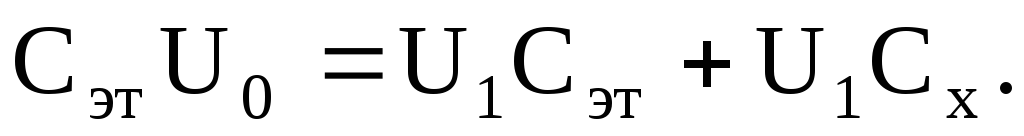
В
результате 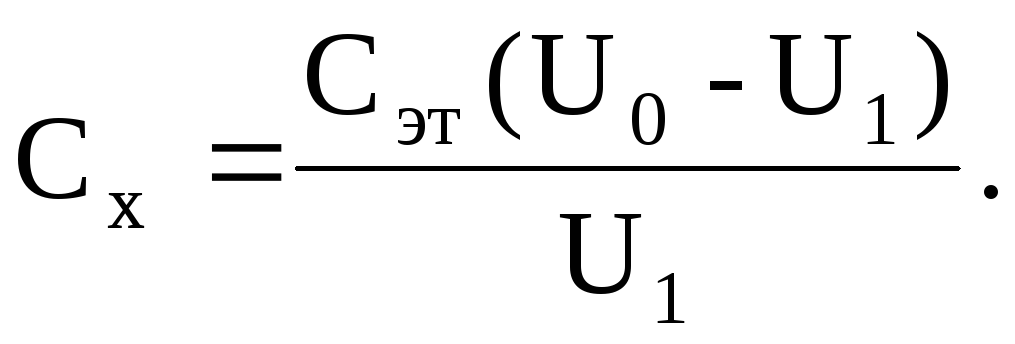 (26)
(26)
Порядок выполнения работы
1. Тумблером S1 включить установку собранную по схеме (рис. 6).
2. Переключателем S2 включить напряжение от источника питания на эталонном конденсаторе.
3. Установить движком потенциометра R напряжение U0=(1±0,2) В. Снять показания вольтметра.
4. Переключателем S2 отключить эталонный конденсатор от источника питания.
5. Соединить проводниками Сэт и Сх1 параллельно и снять показания вольтметра U1.
6. Тумблером S3 разрядить конденсаторы.
7. Подавая на эталонный конденсатор напряжение от 1 В до 3 В, провести измерения 3 раза. Данные занести в таблицу.
8. Для каждой пары значений напряжений U0 и U1 найти электроемкость по формуле
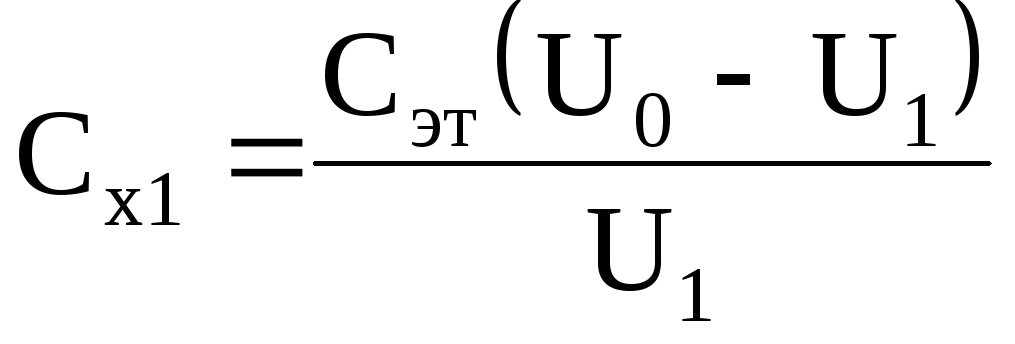 .
.
Затем определить среднюю величину электроемкости Сх1(ср). Результаты вычислений занести в таблицу.
9. По п.п. 3-9 найти электроемкость Сх2.
Таблица
1 | 2 | 3 | 4 | ||||||||
U0 | U1 | Cx1 | U0 | U2 | Cx2 | U0 | Uпар | Cпосл | U0 | Uпосл | Cпар |
|
|
|
| ||||||||
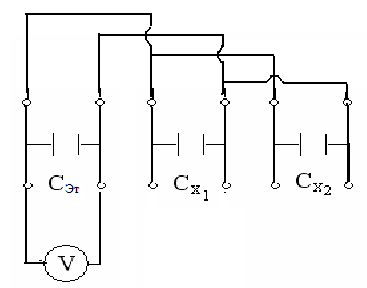
10. Соединить конденсаторы Сх1 и Сх2 последовательно (рис. 7).
11. По п.п. 3-9 найти электроемкость батареи Спосл.
12. Соединить конденсаторы Сх1 и Сх2 параллельно (рис. 8).
13. По п.п. 3-9 найти электроемкость батареи Спар.
По формулам 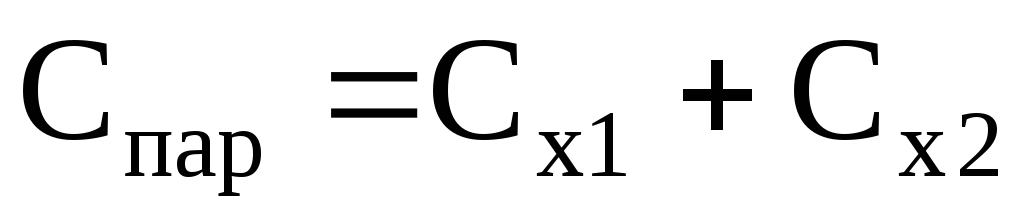 и
и 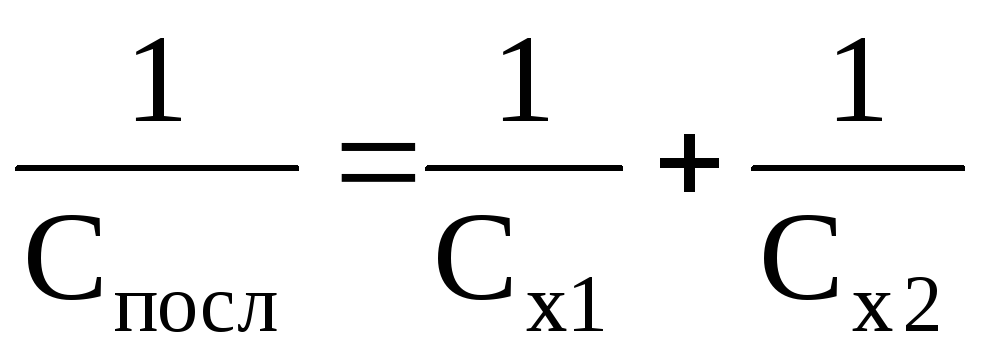 вычислить емкость батареи последовательно
и параллельно соединенных конденсаторов
и сравнить результаты с экспериментальными
значениями.
вычислить емкость батареи последовательно
и параллельно соединенных конденсаторов
и сравнить результаты с экспериментальными
значениями.
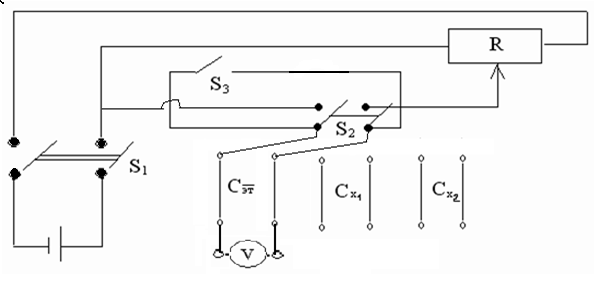
Рис. 6
| Последовательно Рис. 7 |
| Параллельно Рис. 8 |
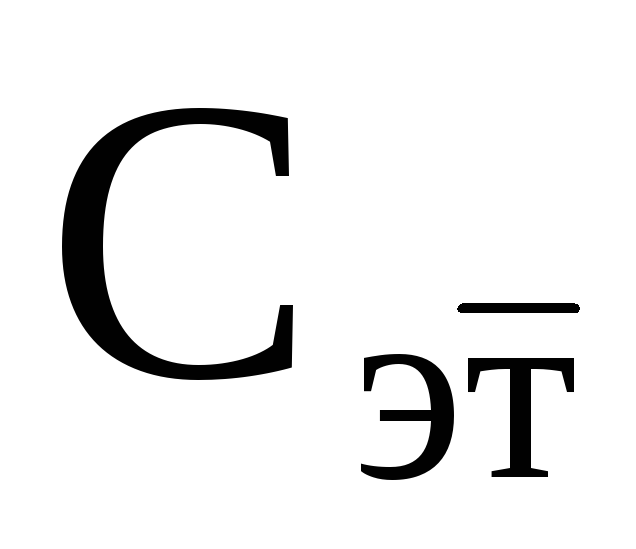 =1000
мкФ.
=1000
мкФ.
Контрольные вопросы
Как взаимодействуют электрические заряды? Закон кулона. Единица электрического заряда в системе СИ.
Закон сохранения электрического заряда.
Что такое напряженность электрического поля, силовые линии электростатического поля, поток вектора напряженности? В чем состоит принцип суперпозиции электрических полей.
Сформулировать теорему Остроградского-Гаусса для электростатического поля в вакууме. Как определяется напряженность электрического поля между двумя бесконечными параллельными и разноименно заряженными плоскостями?
Что такое потенциальная энергия электрического заряда, потенциал данной точки электростатического поля? Как найти работу, совершаемую силами поля по перемещению электрического заряда из одной точки в другую? единица потенциала и напряжения в системе СИ.
Какова связь между потенциалом и напряженностью электрического поля в данной точке?
Чему равна электроемкости уединенного проводника и конденсатора? Единица электроемкости в системе СИ.
Рассказать о параллельном и последовательном соединении конденсаторов. Вывести формулы.
ЛАБОРАТОРНАЯ РАБОТА 5
Емкость конденсатора: виды и применение; принципы работы и маркировка
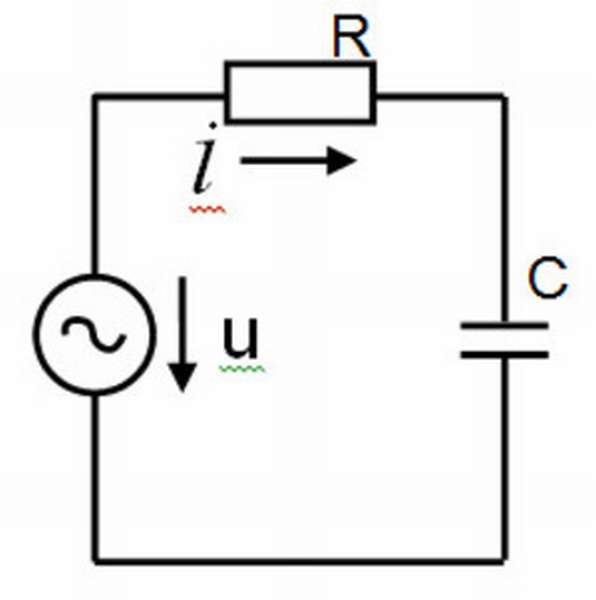 Конденсатором называется элемент электрической цепи, служащий в качестве накопителя заряда.
Конденсатором называется элемент электрической цепи, служащий в качестве накопителя заряда.
Областей применения этого устройства сейчас много, чем и обусловлен их большой ассортимент. Они различаются по материалам, из которых изготовлены, назначению, диапазону основного параметра. Но главной характеристикой конденсатора является его емкость.
Принцип работы конденсатора
Конструкция
На схемах конденсатор обозначается в виде двух параллельных линий, не связанных между собой:
Это соответствует его простейшей конструкции — двум пластинам (обкладкам), разделенным диэлектриком. Фактическое исполнение этого изделия чаще всего представляет собой завернутые в рулон обкладки с прослойкой диэлектрика или иные причудливые формы, но суть остается той же самой.
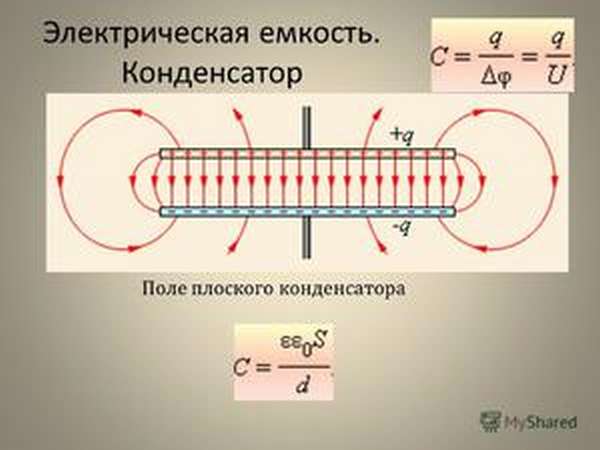
Емкость конденсатора
Электрическая ёмкость – способность проводника накапливать электрические заряды. Чем больше заряд вмещает проводник при данной разности потенциалов, тем больше ёмкость. Зависимость между зарядом Q и потенциалом φ выражается формулой:
C=Q/φ
где Q заряд в кулонах (Кл), φ потенциал в вольтах (В).
 Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Накопительная способность зависит от геометрических параметров проводника, диэлектрической проницаемости среды, где он находится. Так, для сферы из проводящего материала она будет выражаться формулой:
C=4πεε0R
где ε0—8,854·10^−12 Ф/м, электрическая постоянная, а ε диэлектрическая проницаемость среды (табличная величина для каждого вещества).
В реальной жизни нам чаще приходится иметь дело не с одним проводником, а с системами таковых. Так, в обычном плоском конденсаторе емкость будет прямо пропорциональна площади пластин и обратно — расстоянию между ними:
C=εε0S/d
ε здесь — диэлектрическая проницаемость прокладки между пластинами.
Емкость параллельных и последовательных систем
Параллельное соединение емкостей представляет собой один большой конденсатор с тем же слоем диэлектрика и суммарной площадью пластин, поэтому общая емкость системы представляет собой сумму таковых у каждого из элементов. Напряжение при параллельном соединении будет одним и тем же, а заряд распределится между элементами схемы.
C=C1+C2+C3
Последовательное соединение конденсаторов характеризуется общим зарядом и распределенным напряжением между элементами. Поэтому суммируется не емкость, а обратная ей величина:
1/C=1/С1+1/С2+1/С3
Из формулы емкости одиночного конденсатора можно вывести, что при одинаковых элементах, соединенных последовательно, их можно представить в виде одного большого с той же площадью обкладки, но с суммарной толщиной диэлектрика.
Свойства конденсатора
Реактивное сопротивление
Конденсатор не может проводить постоянный ток, что видно из его конструкции. В такой цепи он может только заряжаться. Зато в цепях переменного тока он прекрасно работает, постоянно перезаряжаясь. Если не ограничения, исходящие из свойств диэлектрика (его можно пробить при превышении предела напряжения), этот элемент заряжался бы бесконечно (т. н. идеальный конденсатор, что-то вроде абсолютно черного тела и идеального газа) в цепи постоянного тока, а ток через него проходить не будет. Проще говоря, сопротивление конденсатора в цепи постоянного тока бесконечно.
При переменном токе ситуация иная: чем выше частота в цепи, тем меньше сопротивление элемента. Такое сопротивление называется реактивным, и оно обратно пропорционально частоте и емкости:
Z=1/2πfC
где f частота в герцах.
Накопитель энергии
Энергия, запасенная заряженным конденсатором, может быть выражена формулой:
E=(CU^2)/2=(q^2)/2C
где U напряжение между обкладками, а q накопленный заряд.
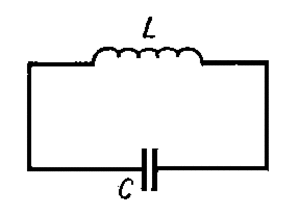
Конденсатор в колебательном контуре
В замкнутом контуре, содержащем катушку и конденсатор, может быть сгенерирован переменный ток.
После зарядки конденсатора он начнет саморазряжаться, давая возрастающий по силе ток. Энергия разряженного конденсатора станет равной нулю, зато магнитная энергия катушки — максимальной. Изменение величины тока вызывает ЭДС самоиндукции катушки, и она по инерции пропустит ток в сторону второй обкладки, пока та полностью не зарядится. В идеальном случае такие колебания бесконечны, а в реальности они быстро затухают. Частота колебаний зависит от параметров как катушки, так и конденсатора:
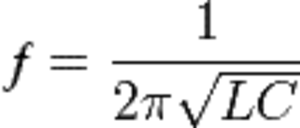
где L индуктивность катушки.
Паразитная индуктивность
Конденсатор может обладать собственной индуктивностью, что можно наблюдать при повышении частоты тока в цепи. В идеальном случае эта величина незначительна, и ей можно пренебречь, но в реальности, когда обкладки представляют собой свернутые пластинки, не считаться с этим параметром нельзя, особенно если речь идет о высоких частотах. В таких случаях конденсатор совмещает в себе две функции, и представляет собой своеобразный колебательный контур с собственной резонансной частотой.
Чтобы добиться корректной работы схемы, рекомендуется применять конденсаторы, у которых резонансная f больше собственной частоты в цепи.
Эксплуатационные характеристики
Помимо указанных выше емкости, собственной индуктивности и энергоемкости, реальные конденсаторы (а не идеальные) обладают еще рядом свойств, которые нужно учитывать при выборе этого элемента для цепи. К ним относятся:
 номинальное напряжение,
номинальное напряжение,- полярность,
- ток утечки,
- сопротивление материала обкладок,
- диэлектрические потери,
- зависимость емкости от температуры.
Чтобы понять, откуда берутся потери, необходимо разъяснить, что представляют собой графики синусоидальных тока и напряжения в этом элементе. Когда конденсатор заряжен максимально, ток в его обкладках равен нулю. Соответственно, когда ток максимален, напряжение отсутствует. То есть напряжение и ток сдвинуты по фазе на угол 90 градусов. В идеале конденсатор обладает только реактивной мощностью:
Q=UIsin 90
В реальности же обкладки конденсатора обладают собственным сопротивлением, а часть энергии расходуется на нагрев диэлектрика, что обуславливает ее потери. Чаще всего они незначительны, но иногда ими пренебрегать нельзя. Основной характеристикой этого явления служит тангенс угла диэлектрических потерь, представляющий собой отношение активной мощности (даваемой малыми потерями в диэлектрике) и реактивной. Измерить эту величину можно теоретически, представив реальную емкость в виде эквивалентной схемы замещения — параллельной или последовательной.
Определение тангенса угла диэлектрических потерь

При параллельном соединении величина потерь определяется отношением токов:
tgδ = Ir/Ic = 1/(ωCR)
В случае последовательного соединения угол вычисляется соотношением напряжений:
tgδ = Ur/Uc = ωCR
В реальности для замеров tgδ пользуются прибором, собранным по мостовой схеме. Его применяют для диагностики потерь в изоляции у высоковольтного оборудования. С помощью измерительных мостов можно измерять и другие параметры сетей.
Номинальное напряжение
Этот параметр указывается на маркировке. Он показывает предельную величину напряжения, которое может быть подано на обкладки. Превышение номинала может привести к пробою конденсатора и выходу его из строя. Зависит этот параметр от свойств диэлектрика и его толщины.
Полярность
Некоторые конденсаторы имеют полярность, то есть в схему его необходимо подключать строго определенным образом. Связано это с тем, что в качестве одной из обкладок используется какой-либо электролит, а диэлектриком служит оксидная пленка на другом электроде. При изменении полярности электролит просто разрушает пленку и конденсатор перестает работать.
Температурный коэффициент емкости
Он выражается отношением ΔC/CΔT где ΔT изменение температуры окружающей среды. Чаще всего эта зависимость линейна и незначительна, но для конденсаторов, работающих в агрессивных условиях, ТКЕ указывается в виде графика.
Разрушение конденсатора
 Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Перегрев обусловлен как внешними причинами (нагреванием соседних элементов схемы), так и внутренними, в частности, последовательным эквивалентным сопротивлением обкладок. В электролитических конденсаторах он приводит к испарению электролита, а в оксиднополупроводниковых — к пробою и химической реакции между танталом и оксидом марганца.
Опасность разрушения в том, что часто оно происходит с вероятностью взрыва корпуса.
Техническое исполнение конденсаторов
Классифицировать конденсаторы можно по нескольким группам. Так, в зависимости от возможности регулировать емкость их разделяют на постоянные, переменные и подстроечные. По своей форме они могут быть цилиндрическими, сферическими и плоскими. Можно делить их по назначению. Но самой распространенной классификацией является таковая по типу диэлектрика.
Бумажные конденсаторы
В качестве диэлектрика используется бумага, очень часто промасленная. Как правило, такие конденсаторы отличает большой размер, но были варианты и в небольшом исполнении, без промасливания. Используются в качестве стабилизирующих и накопительных устройств, а из бытовой электроники постепенно вытесняются более современными пленочными моделями.
При отсутствии промасливания имеют существенный недостаток — реагируют на влажность воздуха даже при герметичной упаковке. Промокшая бумага увеличивает энергопотери.
Диэлектрик в виде органических пленок
Пленки могут быть выполнены из органических полимеров, таких как:
- полиэтилентерифталат,
- полиамид,
- поликарбонат,
- полисульфон,
- полипропилен,
- полистирол,
- фторопласт (политетрафторэтилен).
По сравнению с предыдущими, такие конденсаторы имеют более компактные размеры, не увеличивают диэлектрические потери при увеличении влажности, но многие из них подвергаются риску выхода из строя при перегреве, а те, что этого недостатка лишены, отличаются более высокой стоимостью.
Твердый неорганический диэлектрик
Это может быть слюда, стекло и керамика.
Преимуществом этих конденсаторов считается их стабильность и линейность зависимости емкости от температуры, приложенного напряжения, а у некоторых — даже от радиации. Но иногда сама такая зависимость становится проблемой, и чем она менее выражена, тем дороже изделие.
Оксидный диэлектрик
С ним выпускаются алюминиевые, твердотельные и танталовые конденсаторы. Они имеют полярность, поэтому выходят из строя при неправильном подключении и превышении номинала напряжения. Но при этом они обладают хорошей емкостью, компактны и стабильны в работе. При правильной эксплуатации могут работать около 50 тыс. часов.
Вакуум
Такие устройства представляют собой стеклянную или керамическую колбу с двумя электродами, откуда выкачан воздух. В них практически отсутствуют потери, но малая емкость и хрупкость ограничивают сферу их применения радиостанциями, где величина емкости не так важна, а вот устойчивость к нагреву имеет принципиальное значение.
Двойной электрический слой
Если посмотреть, для чего нужен конденсатор, то можно понять, что этот тип — не совсем он. Скорее, это дополнительный или резервный источник питания, в качестве чего они и используются. Одни категория таких устройств — ионисторы — содержат в себе активированный уголь и слой электролита, другие работают на ионах лития. Емкость этих приборов может составлять до сотен фарад. К их недостаткам можно отнести высокую стоимость и активное сопротивление с токами утечки.
Маркировка конденсаторов
 Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Помимо этого, на большинстве из них существует цифро-буквенное обозначение его характеристик. В соответствии с российскими стандартами конденсаторы маркируются четырьмя знаками.
Первая буква К означает «конденсатор», следующая цифра — вид диэлектрика, далее следует указатель назначения в виде буквы, последний значок может означать как тип конструкции, так и номер разработки, это уже зависит от завода-изготовителя. Третий пункт часто пропускается. Используется такая маркировка на достаточно крупных изделиях, где ее можно разместить. По ГОСТ расшифровка будет выглядеть так:
Первые буквы:
- К — конденсатор постоянной емкости.
- КТ — подстроечник.
- КП — конденсатор переменной емкости.
Вторая группа — тип диэлектрика:
 1, 61 вакуум,
1, 61 вакуум,- 2, 60 воздух,
- 3 газ,
- 4 твердый,
- 10, 15 керамика,
- 20 кварц,
- 21 стекло,
- 22 стеклокерамика,
- 23 стеклоэмаль,
- 31, 32 слюда,
- 40, 41, 42 бумага,
- 50 алюминиевый электролитический,
- 51 танталовый,
- 52 объемно-пористый,
- 53, 54 оксидные,
- 71 полистирол,
- 72 фторопласт,
- 73 ПЭТ,
- 75 комбинированный,
- 76 лак и пленка,
- 77 поликарбонат.
На маленьких конденсаторах всего этого не разместить, поэтому там применяется сокращенная маркировка, которая с непривычки может даже потребовать калькулятора, а иногда — лупу. В этой маркировке зашифрованы емкость, номинал напряжения и отклонения от основного параметра. Остальные параметры наносить нет смысла: это, как правило, керамические конденсаторы.
Маркировка керамических конденсаторов
 Иногда с ними все просто — емкость отмечена числом и единицами: pF — пикофарад, nF — нанофарад, μF микрофарад, mF — миллифарад. То есть, надпись 100nF можно читать прямо. Номинал, соответственно, числом и буквой V. Но иногда не умещается и это, потому применяют сокращения. Так, часто емкость умещается в трех цифрах (103, 109 и т. д.), где последняя означает число нулей, а первые две — емкость в пикофарадах. Если в конце стоит цифра 9, значит, нулей нет, а между первыми двумя ставят запятую. При цифре 8 на конце запятую переносят еще на один знак назад.
Иногда с ними все просто — емкость отмечена числом и единицами: pF — пикофарад, nF — нанофарад, μF микрофарад, mF — миллифарад. То есть, надпись 100nF можно читать прямо. Номинал, соответственно, числом и буквой V. Но иногда не умещается и это, потому применяют сокращения. Так, часто емкость умещается в трех цифрах (103, 109 и т. д.), где последняя означает число нулей, а первые две — емкость в пикофарадах. Если в конце стоит цифра 9, значит, нулей нет, а между первыми двумя ставят запятую. При цифре 8 на конце запятую переносят еще на один знак назад.
Например, обозначение 109 расшифровывается как 1 пикофарад, а 100–10 пикофарад, 681–680 пикофарад, или 0,68 нанофарад, а 104- 100 тыс. пФ или 100нФ
Часто можно встретить первую букву единицы измерения в качестве запятой: p50–0,5 пФ, 1n5–1,5 нФ, 15μ – 15 мкФ, 15m – 15 мФ. Иногда вместо p пишется R.
После трех цифр может стоять буква, означающая разброс параметра емкости:
 B +/-0,1 пФ.
B +/-0,1 пФ.- C +/-0,25 пФ.
- D- +/-0,5 пФ.
- F +/-1%.
- G +/-2%.
- J +/-5%.
- K +/-10%.
- M +/-20%.
- Z до 80% отклонение.
Если вы высчитываете характеристику цепи в единицах СИ, то для того, чтобы найти емкость в фарадах, необходимо помнить показатели степеней числа 10:
- -3 миллифарады,
- -6 микрофарады,
- -9 нанофарады,
- -12 пикофарады.
Таким образом, 01 пФ — это 0,1 *10^-12 Ф.
На устройствах SMD емкость в пикофарадах обозначает буква, а цифра после нее — степень 10, на которую надо умножить это значение.
| буква | C | буква | C | буква | C | буква | C |
| A | 1 | J | 2,2 | S | 4,7 | a | 2,5 |
| B | 1,1 | K | 2,4 | T | 5,1 | b | 3,5 |
| C | 1,2 | L | 2,7 | U | 5,6 | d | 4 |
| D | 1,3 | M | 3 | V | 6,2 | e | 4,5 |
| E | 1,5 | N | 3,3 | W | 6,8 | f | 5 |
| F | 1,6 | P | 3,6 | X | 7,5 | m | 6 |
| G | 1,8 | Q | 3,9 | Y | 8,2 | n | 7 |
| Y | 2 | R | 4,3 | Z | 9,1 | t | 8 |
Номинальное рабочее напряжение таким же образом может маркироваться буквой, если полностью его написать проблематично. В России принят следующий стандарт буквенного обозначения номинала:
| буква | V | буква | V |
| I | 1 | K | 63 |
| R | 1,6 | L | 80 |
| M | 2,5 | N | 100 |
| A | 3,2 | P | 125 |
| C | 4 | Q | 160 |
| B | 6,3 | Z | 200 |
| D | 10 | W | 250 |
| E | 16 | X | 315 |
| F | 20 | T | 350 |
| G | 25 | Y | 400 |
| H | 32 | U | 450 |
| S | 40 | V | 500 |
| J | 50 |
Несмотря на списки и таблицы, лучше все-таки изучить кодировку конкретного производителя — в разных странах они могут отличаться.
К некоторым конденсаторам прилагается более развернутое описание их характеристик.
Емкость конденсатора 



14. Раскройте понятие электрическая емкость. Расскажите о назначении, видах конденсаторов и способах их соединения.
Э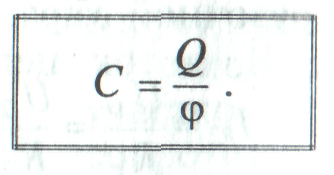 лектрическая
емкость проводника характеризуется
зарядомQ,
который необходимо сообщить проводнику,
чтобы его потенциал изменился на
единицу:
лектрическая
емкость проводника характеризуется
зарядомQ,
который необходимо сообщить проводнику,
чтобы его потенциал изменился на
единицу:
Единицей измерения емкости является фарад. Фарад — большая единица. На практике емкость измеряется в микрофарадах, нанофарадах и пикофарадах. 1мкФ = 1· 10-6Ф
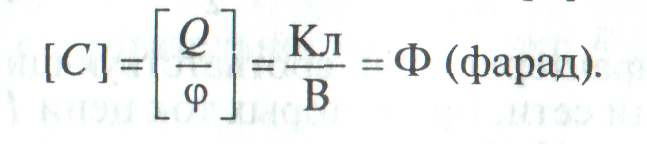
Электрическая емкость проводника характеризует способность проводника накапливать электрический заряд, изменяющий его потенциал на единицу (на 1 В).
Емкость проводника не зависит от заряда Q, сообщенного проводнику, так как изменение заряда Q вызовет пропорциональное изменение потенциала проводника φ, а их отношение остается неизменным .
Емкость проводника не зависит также от материала и массы проводника. Емкость проводника зависит от:
1) площади поверхности проводника, так как заряды располагаются на поверхности проводника;
2) среды, в которой находится проводник. Например, если проводник перенести из воздуха в минеральное масло, его емкость увеличится в 2,2 раза, так как диэлектрическая проницаемость минерального масла εг=2,2
3) близости других проводников. Если рядом с проводником в определенной среде расположен еще один проводник, то емкость системы этих двух проводников будет гораздо больше, чем сумма емкостей каждого из этих проводников в этой среде. На этом принципе устроены электрические конденсаторы.
Конденсаторы
Конденсатор представляет собой два проводника, разделенных диэлектриком.
Емкость конденсатора характеризуется зарядом, который нужно сообщить одному из проводников конденсатора для того, чтобы разность потенциалов между проводниками конденсатора (напряжение) изменилась на единицу.
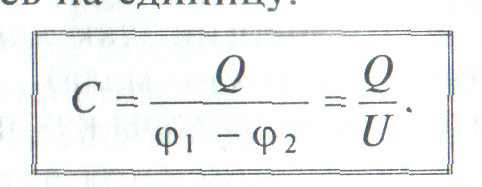
(3)
Различают естественные и искусственные конденсаторы.
Естественными конденсаторами являются провода электрической сети, две жилы кабеля, жила кабеля и его броня, провода воздушной линии электропередачи относительно земли, электроды электронной лампы и др. Естественные конденсаторы специально не создаются, их емкость определяется конструкцией электрических устройств, но ее необходимо учитывать при расчетах, монтаже и эксплуатации электротехнических и радиотехнических устройств.
Искусственные конденсаторы изготавливают специально. В зависимости от диэлектрика различают воздушные, бумажные, керамические, слюдяные, электролитические и другие виды конденсаторов. Каждый искусственный конденсатор обладает определенной емкостью С и рассчитан на определенное рабочее напряжение Up (оба параметра указаны на корпусе конденсатора). Искусственные конденсаторы нашли широкое применение в энергетике, автоматике, радиотехнике, электронике, в схемах электрических фильтров, усилителей, стабилизаторов, колебательного контура, улучшения коэффициента мощности и т.д.
Емкость
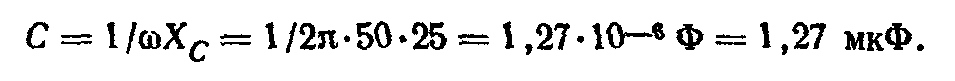
При
резонансе ХC=
ХL, поэтому 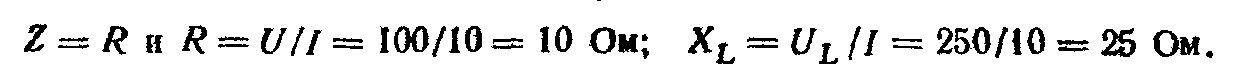 из
формулы XL=
ωL
индуктивность
из
формулы XL=
ωL
индуктивность
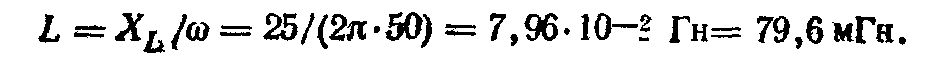
П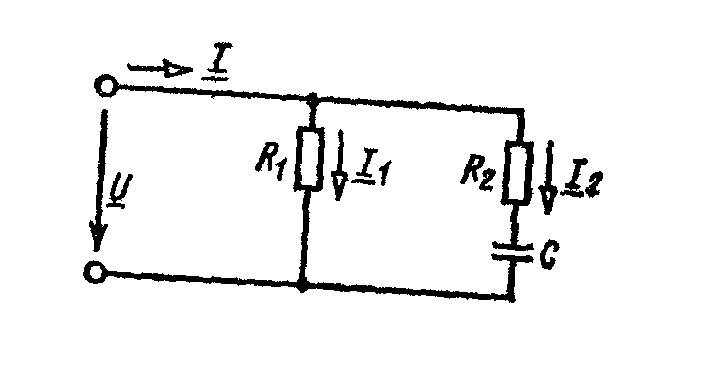 ример
2.6. Заданы
параметры цепи с двумя параллельными
ветвями (рис. а):
R1 = 10 Ом, R2 = 8 Ом, Хс=6 Ом. Напряжение питания U
= 127 В. Определить токи в ветвях и общий
ток. Построить векторную диаграмму, на
которой показать активную и реактивную
составляющие общего тока.
ример
2.6. Заданы
параметры цепи с двумя параллельными
ветвями (рис. а):
R1 = 10 Ом, R2 = 8 Ом, Хс=6 Ом. Напряжение питания U
= 127 В. Определить токи в ветвях и общий
ток. Построить векторную диаграмму, на
которой показать активную и реактивную
составляющие общего тока.
Рисунок к примеру 2.6.а)
Решение.
Начальную фазу напряжения примем равной
нулю (φu=0),
.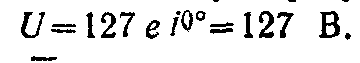
Комплексные сопротивления ветвей:
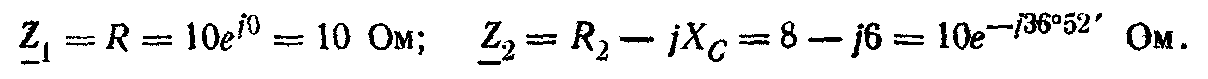
Токи в ветвях
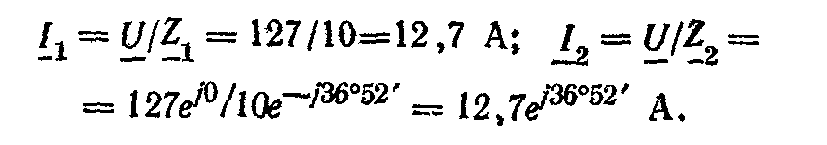
Общий ток
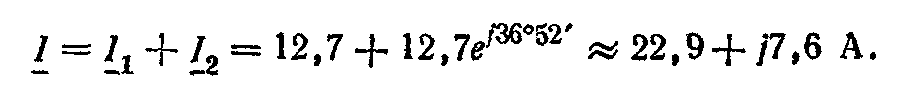
Для построения векторной диаграммы выберем масштаб для напряжения и тока. Проведем оси комплексной плоскости и построим векторы напряжения и токов в выбранном масштабе (рис. б). Активную и реактивную составляющие общего тока найдем разложением вектора тока на две составляющие, одна из которых совпадает по направлению с вектором напряжения, а другая перпендикулярна ему: Iа= I cosφ; Ip =I sin φ.
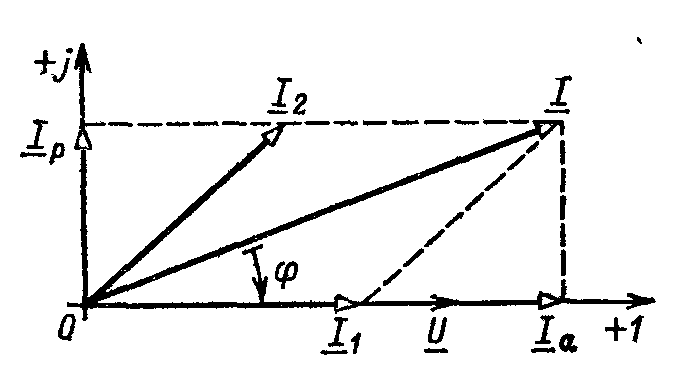
Рисунок к примеру 2.6. б)
Пример 2.7. В цепи синусоидального тока (рис. а) частотой 50 Гц включены параллельно катушка и конденсатор. Измерительные приборы показывают действующие значения напряжения и токов: U =40 В; I=0,13 А, I1=0,18 А, I2=0,115 А. Активное сопротивление катушки R=90 Ом. Определить сопротивления ветвей и их общее сопротивление, полную, активную и реактивную проводимости, углы сдвига фаз в двух ветвях и между напряжением и общим током, индуктивность катушки L и емкость конденсатора С. Построить векторную диаграмму.
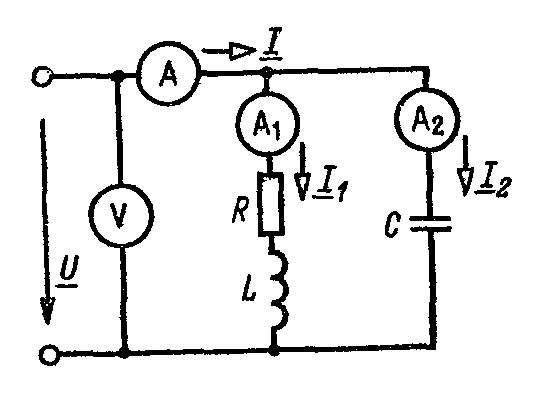
Рисунок к примеру 2.7.a)
Решение. Начальную фазу напряжения примем равной нулю, т. е.
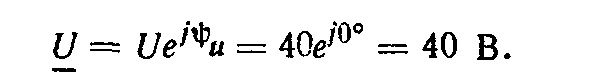
Полное сопротивление катушки
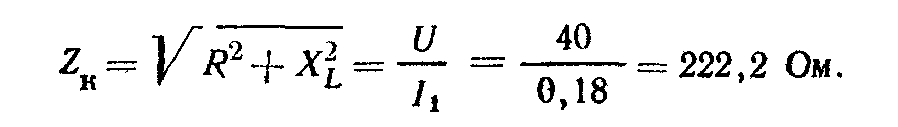
Индуктивное сопротивление
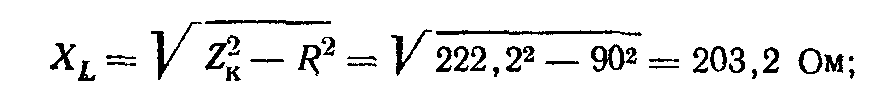
угол сдвига фаз в катушке
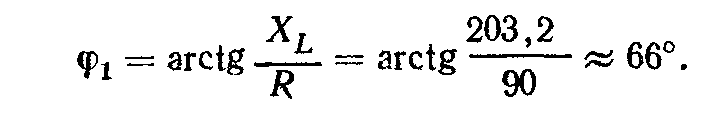
Комплексное сопротивление катушки
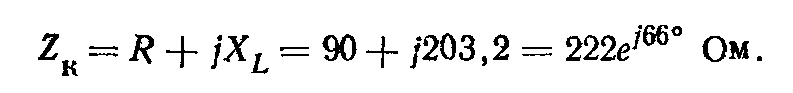
Полное сопротивление конденсатора равно его емкостному сопротивлению
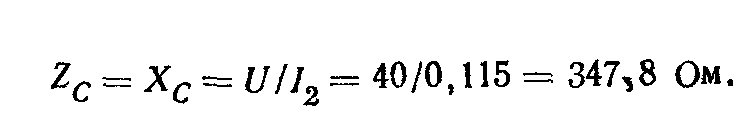
Комплексное сопротивление конденсатора
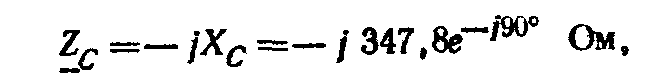
т. е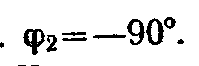
Комплексное сопротивление двух ветвей
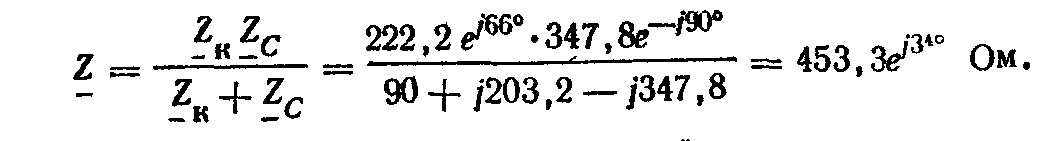
комплексная проводимость двух ветвей
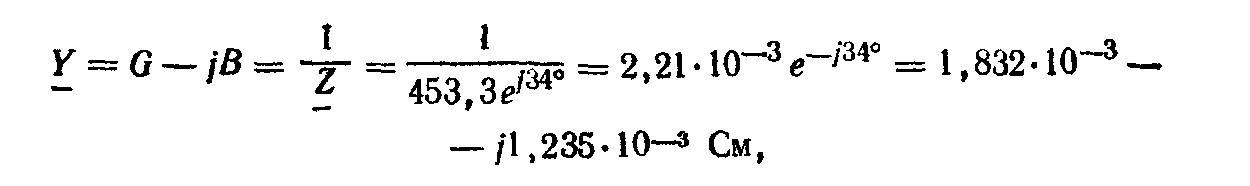
т.е. активная проводимость G =1,832.10-3 См, реактивная проводимость В= -1,235.10-3 См.
Общий ток
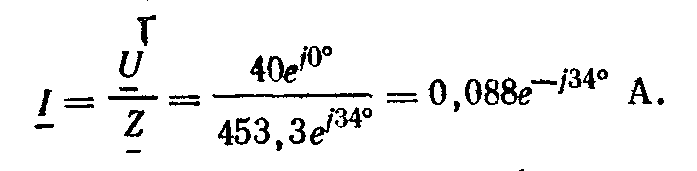
Угол сдвига фаз между напряжением и общим током
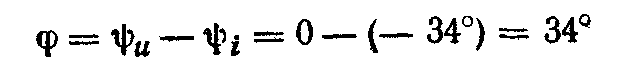
(равен аргументу Z).
Индуктивность катушки
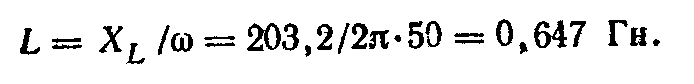
Емкость конденсатора
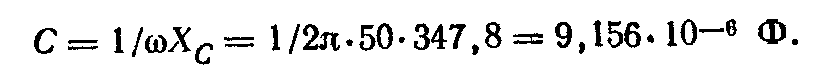
Выбрав масштабы для напряжения mU и тока mI, построение векторной диаграммы начнем с вектора U (рис. б). Ток I1 отстает по фазе от напряжения U на угол φ = — 66 0 .Ток I2 опережает по фазе напряжение U на угол φ = 90 0. Общий ток
отстает по фазе от напряжения на угол φ = — 340 .
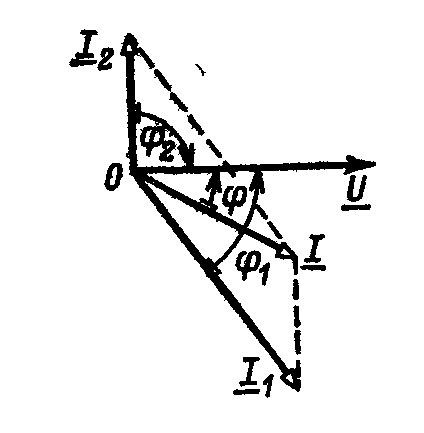
Рисунок к примеру 2.7.б)
Контрольные вопросы
Запишите формулы для расчета комплекса полного сопротивления при последовательном соединении элементов R, L и С.
Объясните, в каком контуре и при каких условиях возможен резонанс напряжений.
Покажите, как будет изменяться характер последовательного контура при плавном изменении емкости от 0 до ∞.
Объясните, почему, при каких условиях и во сколько раз напряжение на емкости при резонансе напряжений может быть больше, чем напряжение питания контура.
Объясните, почему при резонансе напряжений ток максимален.
84




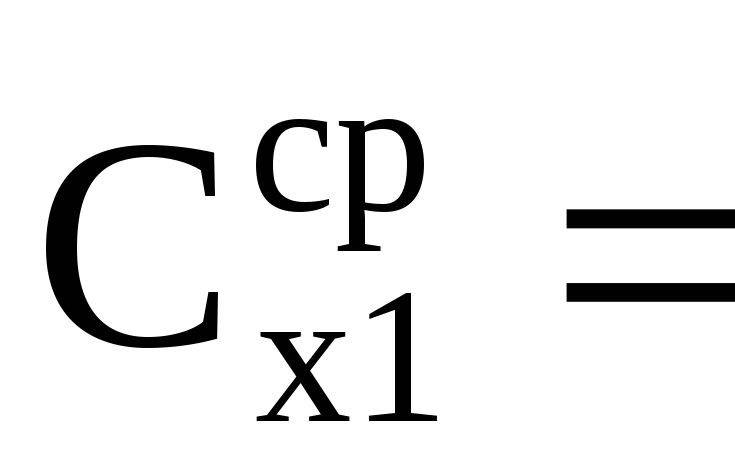
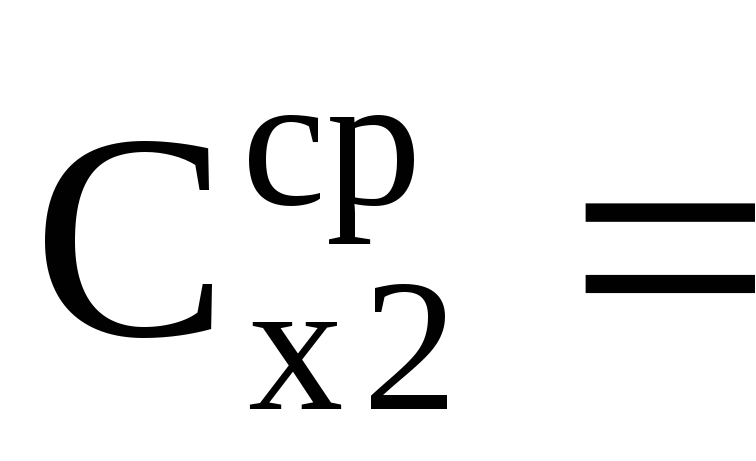
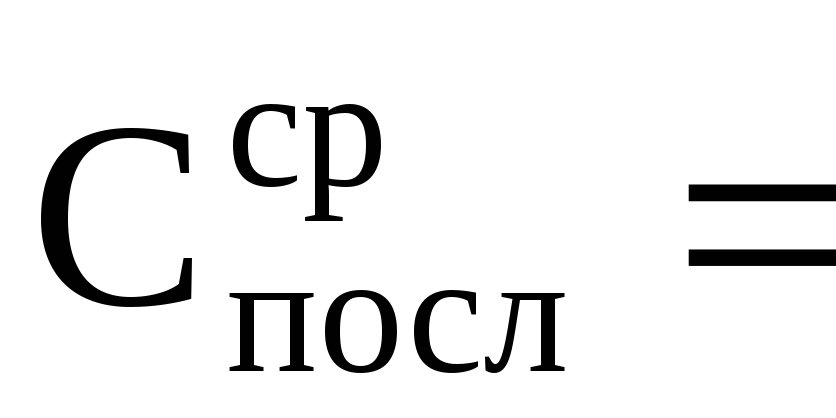
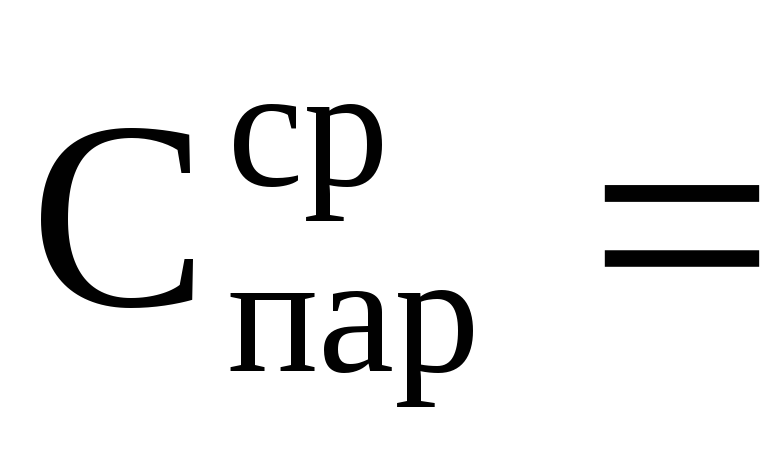
 номинальное напряжение,
номинальное напряжение, 1, 61 вакуум,
1, 61 вакуум, B +/-0,1 пФ.
B +/-0,1 пФ.