Электроемкость. Конденсаторы. Энегия конденсатора — Класс!ная физика
Электроемкость. Конденсаторы. Энегия конденсатора
Электроемкость — характеризует способность двух проводников накапливать электрический заряд.
— не зависит от q и U.
— зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.
Единицы измерения в СИ: ( Ф — фарад )
КОНДЕНСАТОРЫ
— электротехническое устройство, накапливающее заряд ( два проводника, разделенных слоем диэлектрика ).
где d много меньше размеров проводника.
Обозначение на электрических схемах:
Все электрическое поле сосредоточено внутри конденсатора.
Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.
Виды конденсаторов:
1. по виду диэлектрика: воздушные, слюдяные, керамические, электролитические
2. по форме обкладок: плоские, сферические.
Электроемкость плоского конденсатора
где S — площадь пластины (обкладки) конденсатора
d — расстояние между пластинами
eо — электрическая постоянная
e — диэлектрическая проницаемость диэлектрика
Включение конденсаторов в электрическую цепь
Параллельное
Последовательное
Тогда общая электроемкость (С):
при параллельном включении
при последовательном включении
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
Конденсатор — это система заряженных тел и обладает энергией.
Энергия любого конденсатора:
где С — емкость конденсатора
q — заряд конденсатора
Энергия конденсатора равна работе, которую совершит электрическое поле при сближении пластин конденсатора вплотную, или равна работе по разделению положительных и отрицательных зарядов, необходимой при зарядке конденсатора.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА
Энергия конденсатора приблизительно равна квадрату напряженности электрического поля внутри конденсатора.
Плотность энергии электрического поля конденсатора:
Электростатика и законы постоянного тока — Класс!ная физика
Электрический заряд. Электризация. Закон сохранения электрического заряда. Закон Кулона. Единица электрического заряда —
Близкодействие и дальнодействие. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии электрического поля —
Проводники и диэлектрики в электростатическом поле. Поляризация диэлектриков
Конденсаторы.Электроемкость конденсатора. Применение конденсаторов. — КиберПедия
План ответа
1. Определение конденсатора. 2. Обозначение. 3. Электроемкость конденсатора. 4. Электроемкость плоского конденсатора. 5. Соединение конденсаторов. 6. Применение конденсаторов.
Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы.Конденсатор — это система двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные диэлектриком, образуют плоский конденсатор. Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность между пластинами будет в два раза больше, чем напряженность одной пластины. Вне пластин напряженность равна нулю.
 Обозначаются конденсаторы на схемах так: — конденсатор постоянной емкости и
Обозначаются конденсаторы на схемах так: — конденсатор постоянной емкости и

— конденсатор переменной емкости.
Электроемкостью конденсатора называют величину, равную отношению величины заряда одной из пластин к напряжению между ними. Электроемкость обозначается С.
По определению С =q/U. Единицей электроемкости является фарад (Ф). 1 фарад — это электроемкость такого конденсатора, напряжение между обкладками которого равно 1 вольту при сообщении обкладкам разноименных зарядов по 1 кулону.
Электроемкость плоского конденсатора находится по формуле:
С=εε0•S/d
 где ε0— электрическая постоянная, ε — диэлектрическая постоянная среды, S — площадь обкладки конденсатора, d — расстояние между обкладками (или толщина диэлектрика).
где ε0— электрическая постоянная, ε — диэлектрическая постоянная среды, S — площадь обкладки конденсатора, d — расстояние между обкладками (или толщина диэлектрика).

Если конденсаторы соединяются в батарею, то при параллельном соединении
При последовательном соединении 1/C0= 1/C1 + 1/С2 (рис.).
В зависимости от типа диэлектрика конденсаторы бывают воздушные, бумажные, слюдяные.
Конденсаторы применяются для накопления электроэнергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного токов, в выпрямителях, колебательных контурах и других радиоэлектронных устройствах.
Билет № 14
Силы и энергия межмолекулярного взаимодействия. Строение газообразных, жидких и твёрдых тел. Опыт Штерна.
Межмолекулярные силы– силы взаимодействия между молекулами. Имеют электрическую природу, взаимодействие положительных и отрицательных зарядов.
 |











F
Силы отталкивания
 |
 0 dor
0 dor

Сила молекулярного взаимодействия
Силы притяжения
График зависимости межмолекулярных сил от расстояния между молекулами
· do— поперечник молекулы, r- расстояние между центрами молекул.
· Если r = do
· Если r<do сила отталкивания больше силы притяжения. Молекулы отталкиваются друг от друга.
· Если r >do сила отталкивания меньше силы притяжения. Молекулы притягиваются друг другу.

Энергия молекул.
Молекулы находятся в состоянии хаотического движения, молекулы взаимодействуют друг с другом, следовательно, они обладают кинетической и потенциальной энергией: 
· В газообразном состоянии потенциальная энергия взаимодействия молекул пренебрежимо мала по сравнению с кинетической. Поэтому газы не имеют постоянной формы и объема, заполняют весь предоставленный им объем.
· В жидкостях величина потенциальной энергии приблизительно равна кинетической энергии. Поэтому в жидкости молекулы могут скачкообразно перемещаться относительно друг друга. Время “оседлой” жизни 10-8c. C ростом температуры это время уменьшается. Жидкость имеет свойство текучести: сохраняя объем легко меняет форму, принимая форму сосуда.
В твердых телах величина потенциальной энергии взаимодействия молекул значительно больше кинетической энергии. Поэтому в твердых телах молекулы не могут свободно перемещаться, образуют кристаллическую решетку. Твердые тела сохраняют форму и объем. В кристаллической решетке молекулы обладают наименьшей потенциальной энергией 
Опыт Штерна
О. Штерн, воспользовавшись методом молекулярных пучков, изобретенным французским физиком Луи Дюнойе (1911г.) измерил скорость газовых молекул и на опыте подтвердил полученное Д. К. Максвеллом распределение молекул газа по скоростям. Результаты опыта Штерна подтвердили правильность оценки средней скорости атомов, которая вытекает из распределения Максвелла.
По графику можно было определить смещение для середины изображения щели и, соответственно, вычислить среднюю скорость движения атомов.

 При Т2<Т1 максимум кривой распределения смещается в область больших значений скоростей.
При Т2<Т1 максимум кривой распределения смещается в область больших значений скоростей.
· Вначале была высказана гипотеза о том, что молекулы движутся с разными скоростями.
· Эти скорости связаны с температурой и существует определенный закон распределения молекул по скоростям, что следовало из наблюдений, в частности, броуновского движения.
· Затем Д. К. Максвелл теоретически получил закон распределения молекул по скоростям, который носит название распределения Максвелла.
Закон получил экспериментальное подтверждение в опытах Максвелла.
Билет №15
Идеальный газ. Параметры состояния идеального газа
Идеальным газом называется газ, при рассмотрении свойств которого соблюдаются следующие условия:
а) соударения молекул такого газа происходят как соударения упругих шаров, размеры которых пренебрежимо малы;
б) от столкновения до столкновения молекулы движутся равномерно и прямолинейно;
в) пренебрегают силами взаимодействия между молекулами.
Реальные газы при комнатной температуре и нормальном давлении ведут себя как идеальные газы. Идеальными газами можно считать такие газы как гелий, водород, свойства которых уже при обычных условиях отвечают закономерностям идеального газа.
Состояние некоторой массы идеального газа будет определяться значениями трех параметров: P, V, T. Эти величины, характеризующие состояние газа, называются параметрами состояния. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение другого. Эта связь аналитически может быть задана в виде функции:

Соотношение, дающее связь между параметрами какого-либо тела, называется уравнением состояния. Следовательно, данное соотношение является уравнением состояния идеального газа.
1) Давление (P). В газе давление возникает в результате хаотического движения молекул, в результате которого молекулы сталкиваются друг с другом и со стенками сосуда. Давление – это физическая величина, численно равная силе, действующей на единицу площади поверхности, нормальную к ней. Если сила равномерно распределена по поверхности, то  . В системе СИ давление измеряется в 1Па=1Н/м2.
. В системе СИ давление измеряется в 1Па=1Н/м2.
2) Температура (Т).
Температура тела – это термодинамическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
Температура одинакова для всех частей изолированной системы, находящейся в состоянии термодинамического равновесия. Т.е., если соприкасающиеся тела находятся в состоянии теплового равновесия, т.е. не обмениваются энергией путем теплопередачи, то этим телам приписывается одинаковая температура. Если при установлении теплового контакта между телами одно из них передает энергию другому посредством теплопередачи, то первому телу приписывается большая температура, чем второму. Любое из свойств тела (температурный признак), зависящее от температуры может быть использовано для количественного определения (измерения) температуры.
Билет № 16
Внутренняя энергия. Теплоёмкость. Удельная теплоёмкость. Первое начало термодинамики. Адиабатный процесс.
1. Любое тело (газ, жидкость или твердое) обладает энергией, даже если кинетическая и потенциальные энергии самого тела нулевые. То есть тело не имеет скорости и находится на Земле. Эта энергия называется внутренней, обусловлена она движением и взаимодействием частиц, из которых состоит тело.
Внутренняя энергия состоит из кинетической и потенциальной энергии частиц поступательного и колебательного движений, из энергии электронных оболочек атомов, из внутриядерной энергии и энергии электромагнитного излучения.


Внутренняя энергия зависит от температуры. Если изменяется температура, значит, изменяется внутренняя энергия.
2. Количество теплоты — это энергия, которую получает или отдает система в процессе теплообмена. Обозначается символом Q, измеряется, как любая энергия, в Джоулях. В результате различных процессов теплообмена энергия, которая передается, определяется по-своему.
Нагревание и охлаждение. Этот процесс характеризуется изменением температуры системы. Количество теплоты определяется по формуле


Удельная теплоемкость вещества с измеряется количеством теплоты, которое необходимо для нагревания единицы массы данного вещества на 1К. Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость — известная, уже вычисленная для всех веществ величина, значение смотреть в физических таблицах.
Теплоемкость вещества С — это количество теплоты, которое необходимо для нагревания тела без учета его массы на 1К.


3. Закон сохранения энергии управляет всеми явлениями природы и связывает их воедино. Он всегда выполняется абсолютно точно, неизвестно ни одного случая, когда бы этот великий закон не выполнялся.
Этот закон был открыт в середине XIX в. немецким ученым, врачом по образованию Р. Майером (1814—1878), английским ученым Д. Джоулем (1818—1889) и получил наиболее точную формулировку в трудах немецкого ученого Г. Гельмгольца (1821 — 1894).
Закон сохранения и превращения энергии, распространенный на тепловые явления, носит название первого закона термодинамики.
В термодинамике рассматриваются тела, положение центра тяжести которых практически не меняется. Механическая энергия таких тел остается постоянной, изменяться может лишь внутренняя энергия каждого тела.
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
∆U=A+Q.
Часто вместо работы А внешних тел над системой рассматривают работу А’ системы над внешними телами. Учитывая, что А’=-А, первый закон термодинамики можно записать так:
Q=∆U+A′
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
4.Процесс в теплоизолированной системе называютадиабатным.
При адиабатном процессе Q=0 и согласно уравнению изменение внутренней энергии происходит только за счет совершения работы:
∆U=A.
Конечно, нельзя окружить систему оболочкой, абсолютно не допускающей теплопередачу. Но в ряде случаев можно считать реальные процессы очень близкими к адиабатным. Для этого они должны протекать достаточно быстро, так, чтобы за время процесса не произошло заметного теплообмена между системой и окружающими телами.
Билет № 17
Электроемкость. Конденсаторы и их соединение.
⇐ ПредыдущаяСтр 12 из 13Следующая ⇒
Электроемкостьюсистемы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

В системе СИ единица электроемкости называется фарад (Ф):

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками . Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля

Электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:

 (Сферический и цилиндрический)
(Сферический и цилиндрический)
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует 
Таким образом, при параллельном соединении электроемкости складываются.
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.
33.Электрическое поле в диэлектриках. Модели диэлектриков. Поляризация диэлектриков, вектор поляризации. Напряженность поля в диэлектриках.
Типы диэлектриков
Диэлектриками называются вещества, которые при обычных условиях практически не проводят электрический ток. Удельное электрическое сопротивление диэлектриков ρ ~ 106 – 1015 Ом·м, тогда как у металлов ρ ~ 10-8 – 10-6 Ом·м.
Согласно представлениям классической физики, в диэлектриках в отличие от проводников, нет свободных носителей заряда – заряженных частиц, которые могли бы под действием электрического поля прийти в упорядоченное движение и образовать электрический ток проводимости.
К диэлектрикам относятся все газы, если они не подвергались ионизации, некоторые жидкости (дистиллированная вода, бензол и др.) и твердые тела (фарфор, слюда и др.). Твердые диэлектрики подразделяют на кристаллические, аморфные и тела сложного строения, состоящие из смеси монокристаллов, соединенных аморфной прослойкой (керамика, полимеры).
Все молекулы диэлектрика электрически нейтральны: суммарный заряд всех ядер молекулы равен суммарному заряду электронов
Вектор, направленный по оси диполя от отрицательного заряда к положительному, и равный расстоянию между ними, называется плечом диполя l. Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда  на плечо l, называется электрическим моментом диполя или дипольным моментом.
на плечо l, называется электрическим моментом диполя или дипольным моментом.

Диэлектрики подразделяются на три основные группы.
К полярным диэлектрикам (H2O, NH3, СО и др.) относятся вещества, молекулы которых имеют асимметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов не совпадают (положительный заряд ядер, и отрицательный заряд электронов находятся в различных точках пространства). Эти молекулы обладают постоянным дипольным моментом.
К неполярным диэлектрикам относят вещества (N2, CO2, H2 и др.), молекулы которых имеют симметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов совпадают, и их дипольный момент равен нулю.
Третью группу диэлектриков составляют вещества (NaCl, KCl, KBr и др.), молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельную молекулу, можно рассматривать как систему двух вдвинутых одна в другую ионных подрешеток. В таких диэлектриках дипольные моменты отсутствуют.
Во внешнем электрическом поле диэлектрик поляризуется. Диэлектрик поляризован, если он имеет результирующий дипольный момент отличный от нуля, а дипольные моменты молекул ориентированы по полю. Механизм поляризации различен для различных диэлектриков.
Электроннаяполяризация возникает в диэлектриках, состоящих из неполярных молекул. Если поместить диэлектрик во внешнее электрическое поле, то положительные заряды будут смещаться по направлению вектора напряженности электрического поля  , а отрицательные – в противоположном направлении. В результате неполярные молекулы приобретут наведенный (индуцированный) дипольный момент, направленный вдоль внешнего поля, т.е. диэлектрик поляризуется (рис. 2.2). Дипольный момент молекул пропорционален напряженности внешнего поля
, а отрицательные – в противоположном направлении. В результате неполярные молекулы приобретут наведенный (индуцированный) дипольный момент, направленный вдоль внешнего поля, т.е. диэлектрик поляризуется (рис. 2.2). Дипольный момент молекул пропорционален напряженности внешнего поля 
 , (2.1)
, (2.1)
Где α – поляризуемость молекулы, зависящая только от объема молекулы.
 Электронная поляризация:
Электронная поляризация:
а) – внешнее поле отсутствует, б) – молекула диэлектрика
во внешнем электрическом поле
Ионная поляризация возникает в диэлектриках с ионными кристаллическими решетками. При помещении диэлектрика во внешнее электрическое поле подрешетки положительных ионов смещаются по направлению напряженности электрического поля Е, а отрицательные – против поля. В результате возникают индуцированные дипольные моменты, ориентированные по полю.
В целом процессы электронной и ионной поляризации сходны между собой. Оба эти явления можно рассматривать как разновидность деформационной поляризации, представляющий собой сдвиг зарядов друг относительно друга. На деформационную поляризацию не оказывает влияния температура. Данный вид поляризации не вызывает возникновения диэлектрических потерь и отличается большой скоростью установления состояния поляризации.
Ориентационная (дипольная) поляризация возникает в полярных диэлектриках (рис. 2.3). На каждый из зарядов диполя, внесенного в однородное электрическое поле с напряженностью  , будут действовать равные по модулю силы
, будут действовать равные по модулю силы  и
и  , направленные в противоположные стороны. Они создадут момент сил М, стремящийся повернуть молекулу-диполь так, чтобы его дипольный момент совпадал по направлению с вектором напряженности электрического поля. Вектор момента сил равен
, направленные в противоположные стороны. Они создадут момент сил М, стремящийся повернуть молекулу-диполь так, чтобы его дипольный момент совпадал по направлению с вектором напряженности электрического поля. Вектор момента сил равен  или по модулю
или по модулю  . Таким образом, каждая молекула-диполь будет испытывать ориентирующее действие поля (рис. 2.3).
. Таким образом, каждая молекула-диполь будет испытывать ориентирующее действие поля (рис. 2.3).
 |
Рис. 2.3. Ориентационная поляризация
Ориентационная поляризация связана с тепловым движением молекул и зависит от температуры. При повышении температуры уменьшается степень упорядоченности их ориентации.
Степень поляризации диэлектрика характеризуется векторной величиной, называемой поляризованностью, которая определяется как дипольный момент единицы объема диэлектрика.

где  – суммарный дипольный момент всех молекул диэлектрика в объеме V,
– суммарный дипольный момент всех молекул диэлектрика в объеме V,  – дипольный момент одной молекулы.
– дипольный момент одной молекулы.
Поляризованность изотропного диэлектрика любого типа связана с напряженностью поля соотношением
 , (2.3)
, (2.3)
где  – диэлектрическая восприимчивость вещества,
– диэлектрическая восприимчивость вещества,  – электрическая постоянная.
– электрическая постоянная.
Диэлектрическая восприимчивость вещества характеризует способность диэлектрика к поляризации.
Электроёмкость. Конденсаторы
Изучение электрических явлений вы начали еще в восьмом классе, познакомившись с явлением электризации. Сегодня мы можем провести классический опыт. Возьмем две стеклянные банки разных размеров, предварительно изолировав их от земли. Поднесем к каждой из этих банок одинаковый заряженный шар на изолированной ручке.

Если теперь мы измерим потенциалы каждой из банок, с помощью электрометров, то убедимся, что эти потенциалы не равны. Это наводит на мысли о том, что на различных телах накопление заряда происходит по-разному. Другой опыт, который мы можем провести — это разноименно зарядить два проводника.

Как вы понимаете, с увеличением заряда, будет расти напряженность электрического поля между данными проводниками. При неизменном расстоянии между проводниками, с увеличением напряженности будет расти и разность потенциалов, то есть, электрическое напряжение. При достаточно большом напряжении, диэлектрик становится проводящим (поскольку не существует идеальных диэлектриков). Возникает явление, которое называется пробоем диэлектрика: между проводниками проскакивает искра, в результате чего они разряжаются. Это говорит нам о том, что чем меньше увеличивается напряжение с увеличением заряда, тем больший заряд можно накопить. Таким образом, мы можем заключить, что необходимо ввести физическую величину, которая характеризует способность накапливать электрический заряд. Эта величина называется электроемкостью или просто емкостью.
Поскольку напряжение между двумя проводниками пропорционально напряженности электрического поля, а напряженность, в свою очередь, пропорциональна зарядам на проводниках, можно сделать вывод, что напряжение пропорционально зарядам на проводниках:

Как мы уже сказали, чем меньше увеличивается напряжение с увеличением заряда, тем больший заряд можно накопить. Поэтому, определение электроемкости для двух проводников звучит так: электроемкость двух проводников — это отношение заряда одного из проводников к разности потенциалов между ними:

Единицей измерения электроемкости является фарад (в честь Майкла Фарадея):

Как видно из формулы электроемкость двух проводников равна 1 Ф, если при сообщении им зарядов 1 Кл и –1 Кл, между ними возникает напряжение в 1 В.
Как мы уже говорили, заряд в 1 Кл — это очень большой заряд, поэтому, электроемкость в 1 Ф — тоже очень большая. На практике используются такие величины, как микрофарады и нанофарады.
Итак, мы дали определение электроемкости для двух проводников. Система проводников, используемых для накопления электрического заряда, называется конденсатором. Конденсатор состоит из двух проводников, которые разделены слоем диэлектрика.

Толщина диэлектрика должна быть невелика по сравнению с размерами проводников. Проводники в конденсаторе называются обкладками. В качестве обкладок часто используют очень тонкие металлические пластины, а в качестве диэлектрика — бумагу или воздух.
На сегодняшнем уроке мы рассмотрим плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин, находящихся на малом расстоянии друг от друга.

Поле внутри такого конденсатора будет однородным. Для того, чтобы зарядить конденсатор, достаточно подключить его к полюсам источника тока. Накопив заряд, конденсатор может сам являться источником тока некоторое время. Но, надо сказать, что конденсатор разряжается очень быстро. Электроемкость плоского конденсатора характеризуется площадью пластин и расстоянием между этими пластинами:

Очевидно, что чем больше площадь пластин, тем больший заряд можно на них накопить. Тем не менее, чем больше расстояние между пластинами, тем выше напряжение между ними:

Поскольку электроемкость обратно пропорциональна напряжению, мы можем заключить, что чем больше расстояние между пластинами, тем меньше электроемкость плоского конденсатора:

Таким образом, мы выяснили, что электроемкость плоского конденсатора прямо пропорциональна площади пластин и обратно пропорциональна расстоянию между ними:

Конечно же, электроемкость зависит и от диэлектрика, который используется в конденсаторе, поэтому в формуле мы видим диэлектрическую проницаемость. Также, в формуле есть коэффициент пропорциональности, который называется электрической постоянной. Значение электрической постоянной соответствует диэлектрической проницаемости вакуума:

Конденсаторы классифицируются по нескольким признакам: по форме обкладок, по типу диэлектрика и по назначению.
В основном конденсаторы бывают трех форм: плоские, сферические и цилиндрические.

Также конденсаторы разделяют по типу диэлектрика на керамические, бумажные и электролитические конденсаторы.

Кроме этого, конденсаторы классифицируются по назначению.

Помимо конденсаторов с постоянной электроемкостью, существуют также конденсаторы, которые обладают переменной электроемкостью. В таком конденсаторе есть статор и ротор. Вращая ротор, можно изменять суммарную площадь перекрываемую пластинами и, таким образом, изменять электроемкость. Конденсаторы с переменной емкостью широко используются в радиотехнике. Например, изменяя емкость конденсатора, можно настраивать радиоприемник на нужную частоту (или, как мы говорим, на нужную волну).
Кроме этого, на практике нередко используются конденсаторные батареи. Конденсаторная батарея представляет собой набор из нескольких конденсаторов постоянной емкости, соединенных между собой параллельно или последовательно. В зависимости от соединения, между параметрами конденсатора наблюдаются различные закономерности, которые сведены в таблицу:

Пример решения задачи.
Задача. Когда конденсатор с постоянной электроёмкостью зарядили от источника тока, напряжение между пластинами конденсатора составило 300 В. После этого, к конденсатору подключили лампочку, которая прогорела ровно 1,5 с, а потом погасла. Предполагая, что в течение этих полутора секунд, по лампочке проходил постоянный ток в 20 мА, определите электроёмкость данного конденсатора.

Общая задача электростатики.
П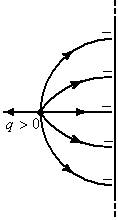 о
известному распределению зарядов
определить
о
известному распределению зарядов
определить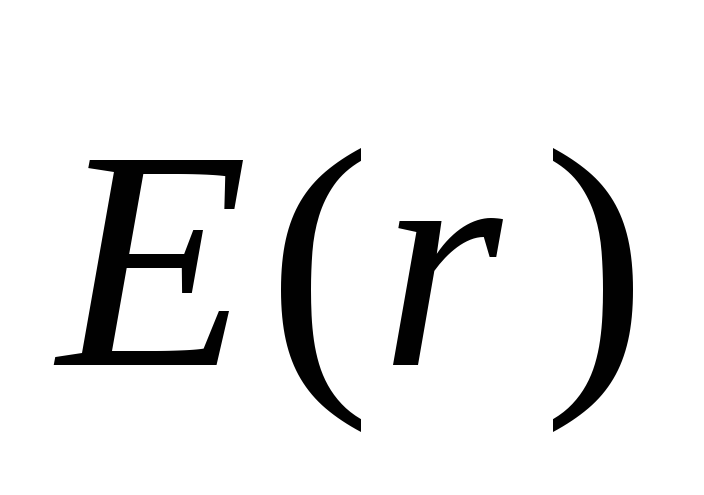 .
.
Очень часто встречаются задачи, в которых
распределение зарядов неизвестно, но
заданы потенциалы проводников, их форма
и относительное расположение, а требуется
определить 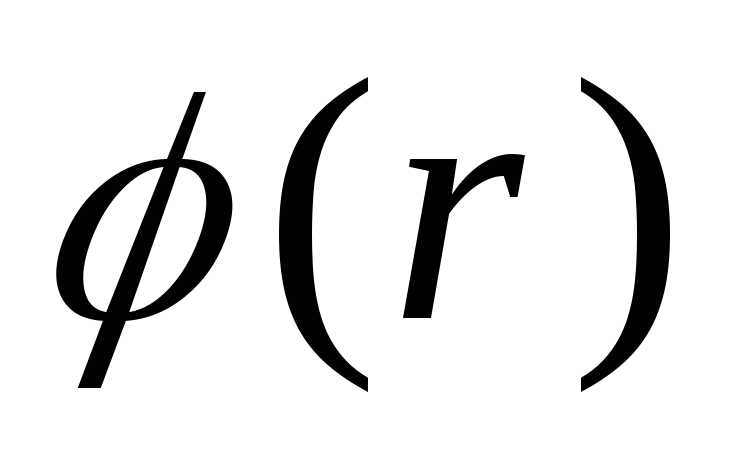 в
любой точке поля. Но как было показано,
зная
в
любой точке поля. Но как было показано,
зная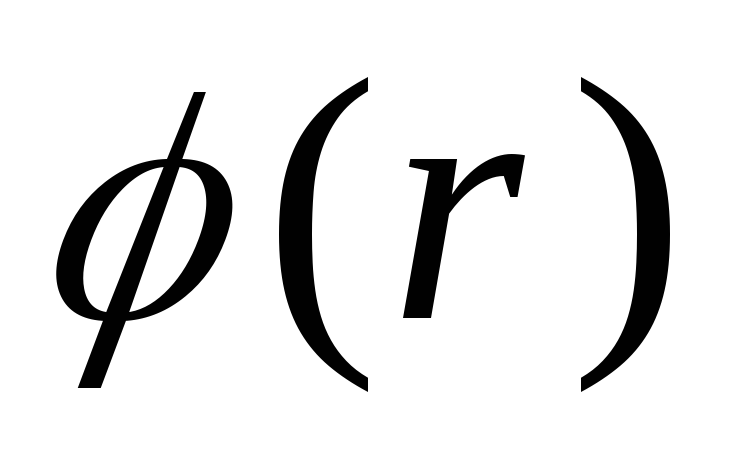 ,
можно определить
,
можно определить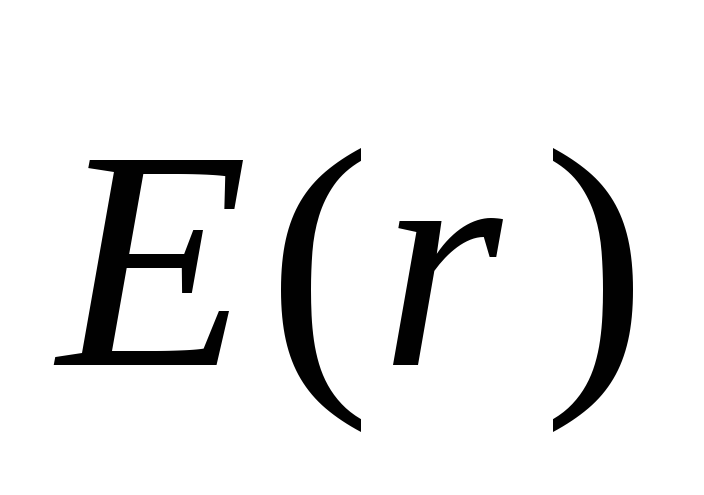 ,
а по значению
,
а по значению у поверхности проводников найти
распределение поверхностных зарядов
у поверхности проводников найти
распределение поверхностных зарядов .
.
Существует метод, который позволяет в
ряде случаев рассчитать электрическое
поле достаточно просто. Рассмотрим идею
этого метода на примере, когда точечный
заряд  находится около безграничной проводящей
плоскости (см. рисунок).
находится около безграничной проводящей
плоскости (см. рисунок).
И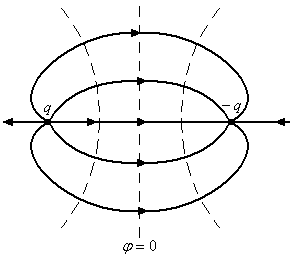 дея
заключается в том, чтобы найти другую
задачу, которая решается просто. В нашем
случае такой простой задачей является
задача с двумя точечными зарядами
дея
заключается в том, чтобы найти другую
задачу, которая решается просто. В нашем
случае такой простой задачей является
задача с двумя точечными зарядами и
и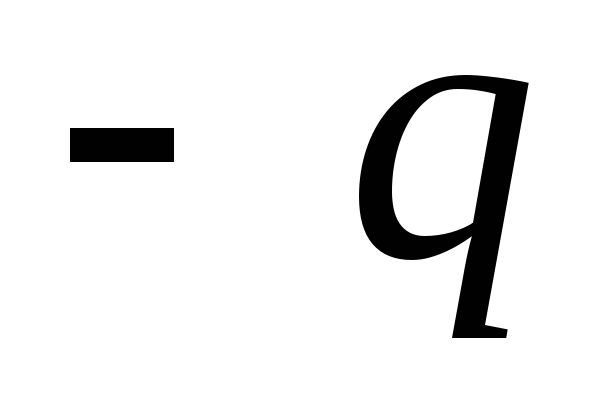 .
.
Если совместить с нулевой эквипотенциальной
поверхностью проводящую плоскость и
убрать заряд 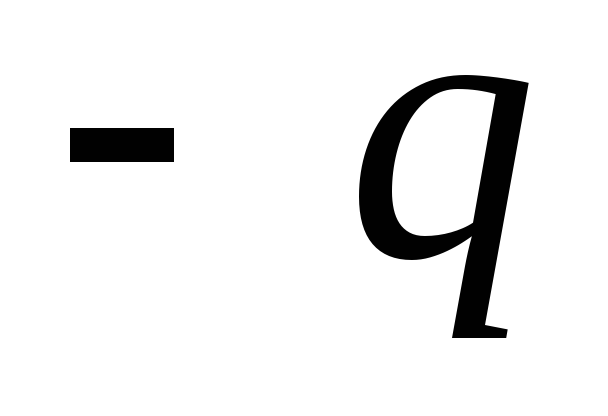 ,
структура в левой части полупространства
не изменится. Таким образом, взаимодействие
заряда с плоскостью можно свести к
взаимодействию точечных зарядов
,
структура в левой части полупространства
не изменится. Таким образом, взаимодействие
заряда с плоскостью можно свести к
взаимодействию точечных зарядов и
и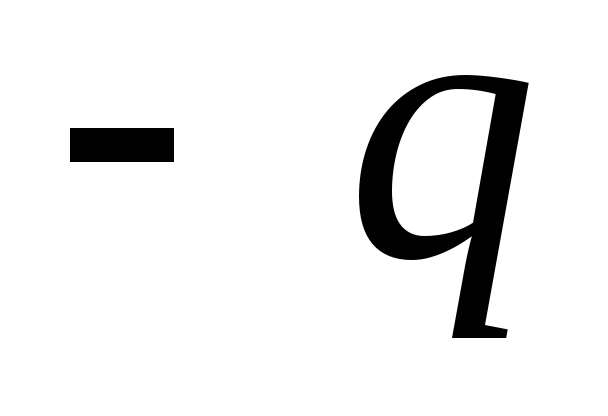 .
Фиктивный заряд
.
Фиктивный заряд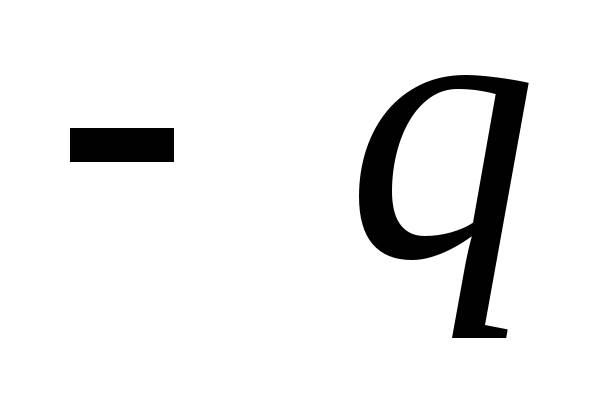 называется изображением заряда
называется изображением заряда .
Фиктивный заряд
.
Фиктивный заряд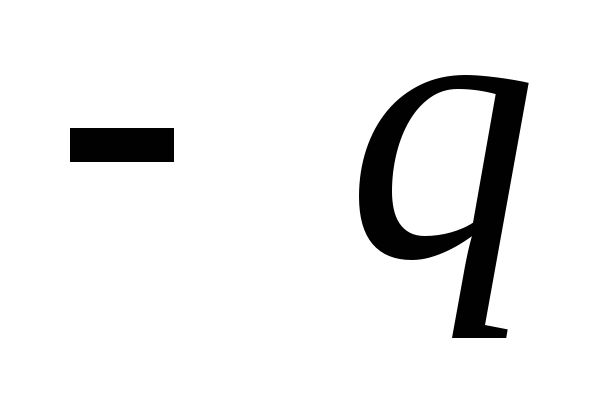 в левом полупространстве создает такое
же поле, как и индуцированные заряды на
плоскости. Поэтому он заменяет действие
всех индуцированных зарядов, в левой
части полупространства. Рассмотренный
пример, является иллюстрацией метода
изображений.
в левом полупространстве создает такое
же поле, как и индуцированные заряды на
плоскости. Поэтому он заменяет действие
всех индуцированных зарядов, в левой
части полупространства. Рассмотренный
пример, является иллюстрацией метода
изображений.
Понятие электроемкости. Конденсаторы.
Проводники способны накапливать электрический заряд и связанное с ними электрическое поле. Эта способность проводников называется электроемкостью (сокращенно ёмкостью).
Между зарядом уединенного проводника
и его потенциалом существует прямо
пропорциональная зависимость:  .
.
Следовательно, отношение 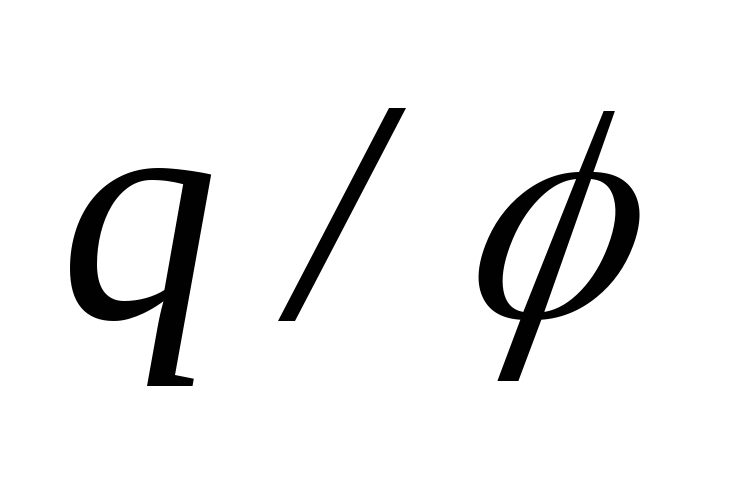 не зависит от заряда
не зависит от заряда ,
и для каждого уединенного проводника
имеет свое значение.
,
и для каждого уединенного проводника
имеет свое значение.
Величину
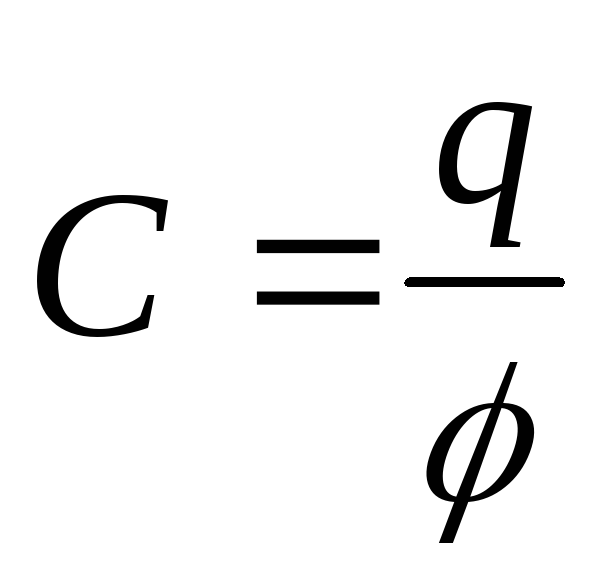
называют электроемкостью (ёмкостью) уединенного проводника. Она равна заряду, изменяющего потенциал проводника на единицу:
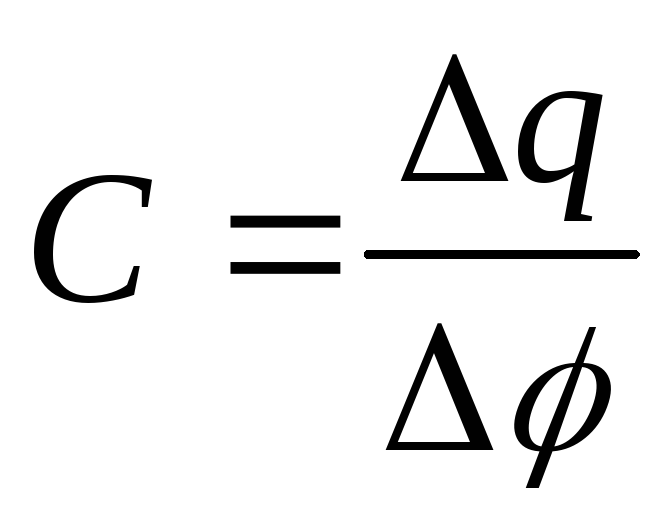 ,
,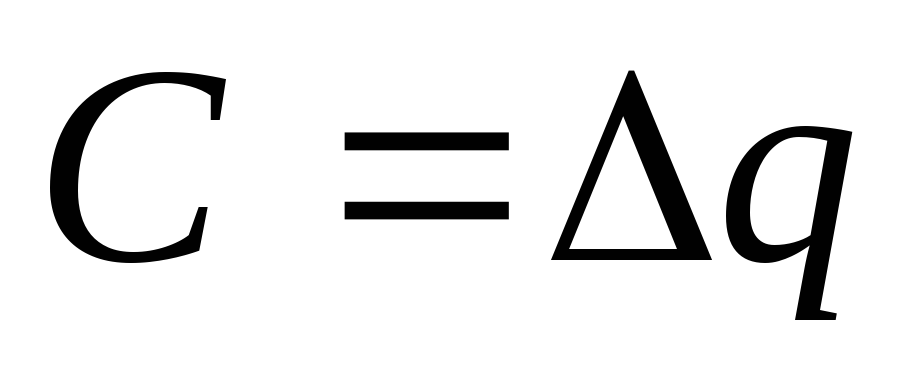 ,
если
,
если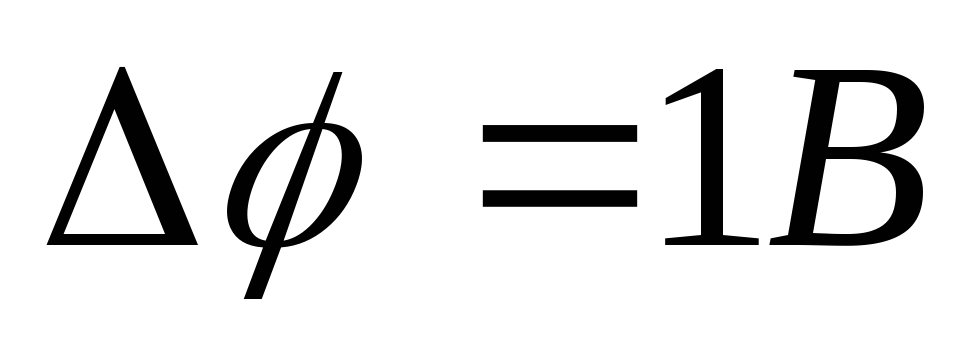 .
.
Единица измерения ёмкости Фарад 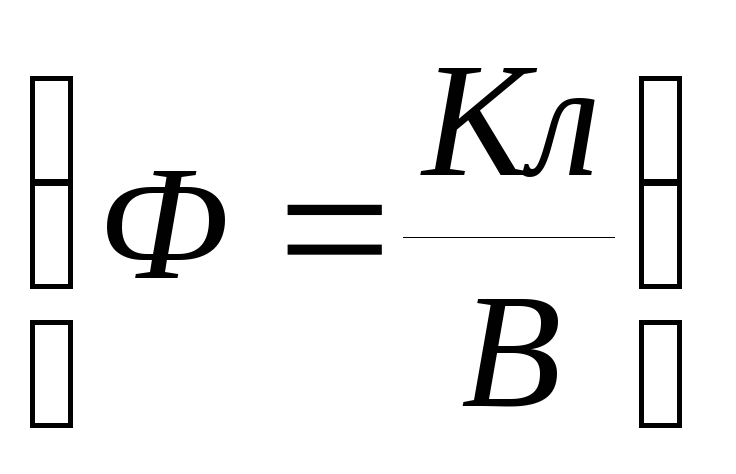 .
.
Фарад – очень большая величина. На
практике чаще всего применяются дольные
единицы: 1мкФ=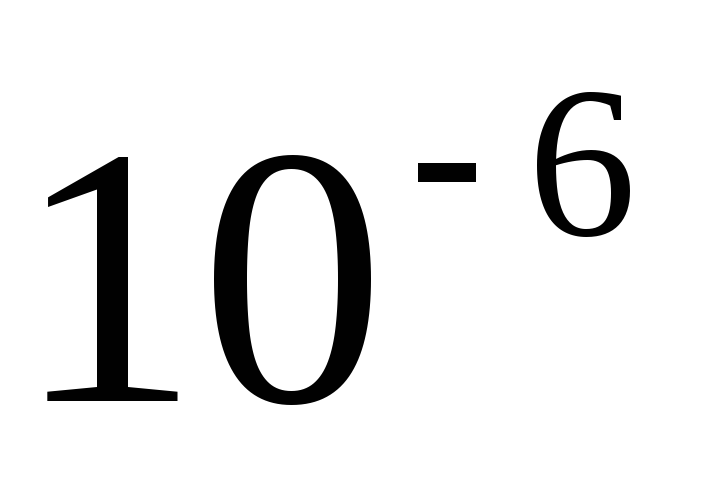 Ф,
1пФ=
Ф,
1пФ=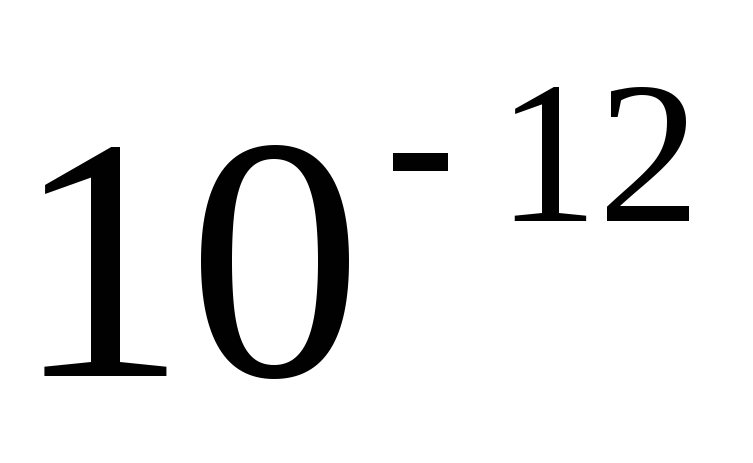 Ф.
Ф.
Электроемкость уединенного проводника зависит от его геометрических размеров и окружающего диэлектрика.
Рассмотрим электроемкость уединенного металлического шара.
Потенциал заряженного проводника в однородном диэлектрике равен:
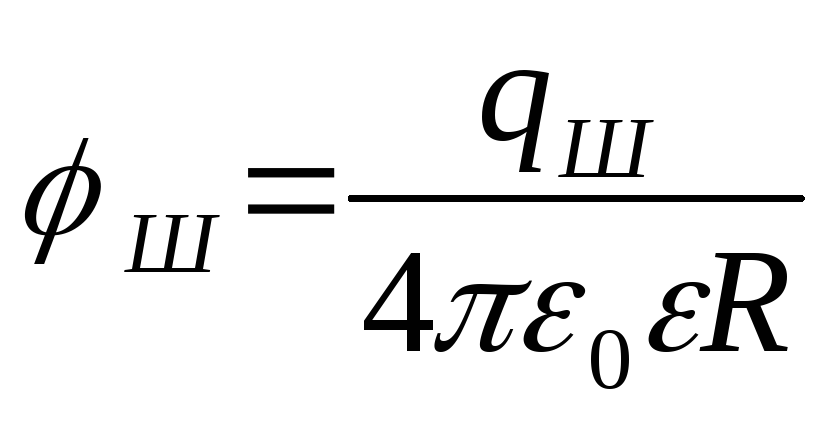 ,
,
где R– радиус шара, —
диэлектрическая проницаемость
диэлектрика.
—
диэлектрическая проницаемость
диэлектрика.
Из определения ёмкости получаем:
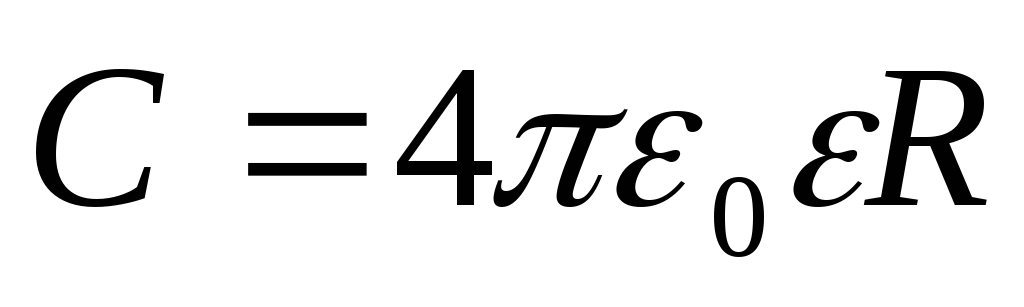 .
.
 ,
например, ёмкость Земли
,
например, ёмкость Земли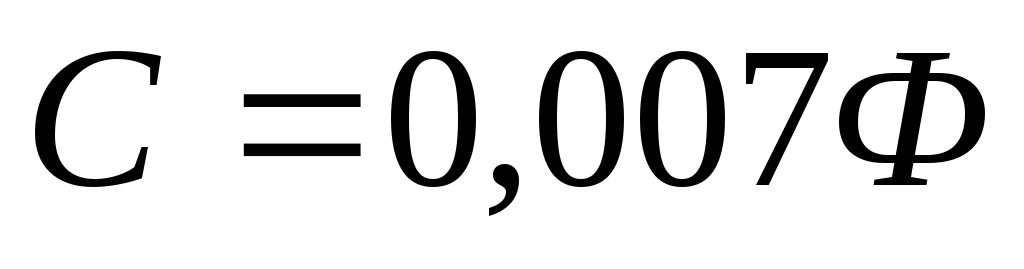 .
.
Как видно, ёмкость не зависит от природы проводника.
Конденсаторы.
Е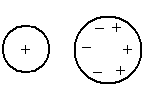 сли
проводник не уединен, то его ёмкость
будет увеличиваться при приближении к
нему других тел. Это связано с тем, что
поле данного заряженного проводника
вызывает перераспределение зарядов на
окружающих телах (см. рисунок).
сли
проводник не уединен, то его ёмкость
будет увеличиваться при приближении к
нему других тел. Это связано с тем, что
поле данного заряженного проводника
вызывает перераспределение зарядов на
окружающих телах (см. рисунок).
Индуцированные заряды вызывают, уменьшение потенциала данного проводника и увеличение его ёмкости.
Это обстоятельство позволяет создать такую систему проводников, которая обладает большей ёмкостью, чем уединенный проводник, и не зависящий от окружающих тел. Такую систему называют конденсатором.Простейший конденсатор состоит из двух пластин, расположенных на малом расстоянии.
Чтобы внешние тела не оказывали влияние на емкость конденсатора, его обкладки располагают так, чтобы поле заряженных обкладок, практически было полностью сосредоточено между обкладками. Это означает, что обкладки должны быть заряжены разноименными зарядами, одинаковыми по модулю.
Под ёмкостью конденсатора понимают отношение заряда конденсатора к разности потенциалов между обкладками, которую называют напряжением:
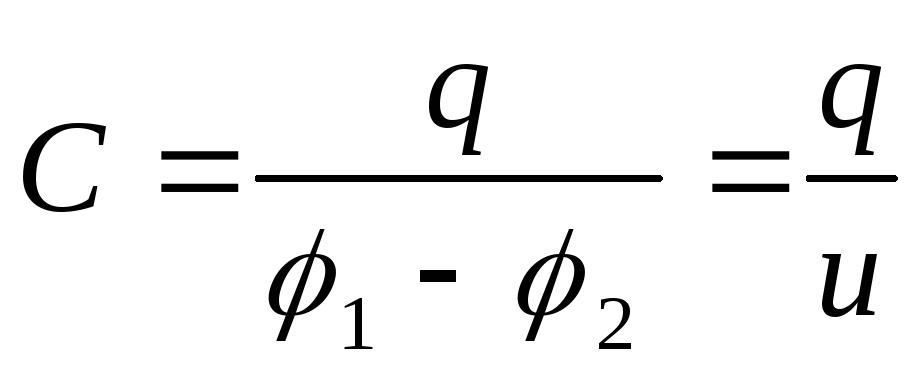 .
.
Зарядом конденсатора  считается заряд положительно заряженной
обкладки. Очевидно, что емкость
конденсатора измеряется в фарадах.
считается заряд положительно заряженной
обкладки. Очевидно, что емкость
конденсатора измеряется в фарадах.
Ёмкость конденсатора зависит от его геометрии. Найдём выражения для ёмкости некоторых конденсаторов.



