Электрическая емкость конденсатора формула: Емкость конденсаторов: определение, формулы, примеры. — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Емкость конденсаторов: определение, формулы, примеры.

Определение 1

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C=qφ1-φ2=qU.

Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.

Выделяют три большие группы: плоские, сферические, цилиндрические.

Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Определение 2

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.

Формула для расчета электроемкости записывается как

C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

Рисунок 1

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:

C=ε0Sd1ε1+d2ε2+…+dNεN.

Сферический конденсатор

Определение 3

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:

C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.

Рисунок 2

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C=2πεε0llnR2R1, где l — высота цилиндров, R1 и R2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.

Рисунок 3

Определение 4

Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.

Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:

C=∑i=1NCi.

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Пример 1

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.

Решение

Чтобы рассчитать электроемкость конденсатора, применяется формула:

C=εε0Sd.

Значения:

ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.

Подставим числовые выражения и вычислим:

C=8,85·10-12·10-410-3=8,85·10-13 (Ф).

Ответ: C≈0,9 пФ.

Пример 2

Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения — 103 В.

Решение

Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:

E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x — расстояние от центра сферы.

Нахождение заряда предполагает применение определения емкости конденсатора С:

q=CU.

Для сферического конденсатора предусмотрена формула вида

C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.

Производим подстановку выражений для получения искомой напряженности:

E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.

Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:

E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.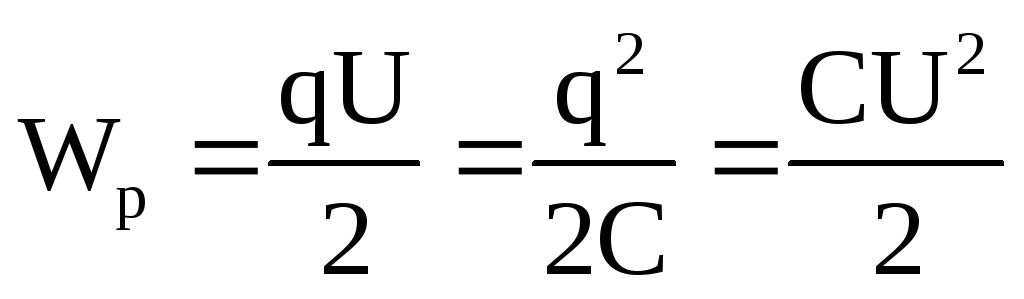

Ответ: E=3,45·104 Вм.

Формула емкости конденсатора, С

Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:

называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.

Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():

где – диэлектрическая проницаемость диэлектрика.

За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ).

Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).

Формула электрической емкости плоского конденсатора

Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:

где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:

Формула электрической емкости цилиндрического конденсатора

Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Формула электрической емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

где – радиусы обкладок конденсатора.

Примеры решения задач по теме «Емкость конденсатора»

По какой формуле найти ёмкость (объем) конденсаторов

Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.

Конденсаторы

Расчёт конденсаторов

Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:

C=q/U, где:

C – ёмкость,
q – заряд одной из обкладок элемента,
U – разность потенциалов между обкладками.

В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».

Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:

С=Co*ε, где:

С – реальная ёмкость,
Со – идеальная, при условии, что между пластинами вакуум или воздух,
ε – диэлектрическая проницаемость материала между ними.

Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.

Устройство конденсатора

Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).

Расчет плоской конструкции

Если нужно рассчитать плоский конденсатор, то необходимо учесть площадь обкладок и расстояние между ними. Это отражено в формуле, по которой рассчитывается ёмкость плоского конденсатора:

C=ε/d, где:

ε – диэлектрическая проницаемость изолирующего материала,
d – расстояние между пластинами.

Расчет конструкции цилиндрической формы

Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.

Вычисляются параметры такого устройства по формуле:

C=(2π*l*R*ε)/d, где:

l – длина устройства,
R – радиус цилиндра,
ε – диэлектрическая проницаемость изолятора,
d – его толщина.

Расчёт сферической конструкции

Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:

C=(4π*l*R1*R2*ε)/(R2-R1), где:

R1 – радиус внутренней сферы,
R2 – радиус внешней сферы,
ε – диэлектрическая проницаемость.

Формулы ёмкости конденсаторов различной формы

Ёмкость одиночного проводника

Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:

C=Q/φ, где:

Q – заряд,
φ – потенциал проводника.

Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.

Способы соединения элементов

Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.

Соединение конденсаторов

Параллельное соединение

Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.

При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:

C=C1+C2+…Cn,

где C1-Cn – параметры деталей, участвующих в параллельном соединении.

Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.

Последовательное соединение

Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.

При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.

Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.

Рассчитываются эти параметры следующим образом:

Допустимое напряжение:

Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;

Общая ёмкость:

1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.

Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).

Смешанное соединение

Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:

определяются группы элементов, соединённые параллельно;
для каждой группы в отдельности рассчитывается эквивалентные значения;
рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.

Видео

Оцените статью:

Урок 28.

электрическая ёмкость. конденсатор — Физика — 10 класс

Физика, 10 класс

Урок 28. Электрическая ёмкость. Конденсатор

Перечень вопросов, рассматриваемых на уроке:

Электрическая ёмкость
Плоский конденсатор
Энергия конденсатора

Глоссарий по теме:

Конденсатор – устройство для накопления электрического заряда.

Электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.

Под зарядом конденсатора понимают модуль заряда одной из его обкладок.

Последовательное соединение – электрическая цепь не имеет разветвлений. Все элементы цепи включают поочередно друг за другом. При параллельном соединении концы каждого элемента присоединены к одной и той же паре точек.

Смешанное соединение — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.

Энергия конденсатора

прямо пропорциональна квадрату напряжённости электрического поля внутри его:

Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения.

Основная и дополнительная литература по теме:

1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 321-330.

2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 97-100.

Теоретический материал для самостоятельного изучения

Конденсатор при переводе с латиницы означает, то что уплотняет, сгущает – устройство, предназначенное для накопления зарядов энергии электрического поля. Конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга. Главной характеристикой этого прибора, является его электроёмкость, которая зависит от площади его пластин, расстояния между ними и свойств диэлектрика.

Заряд конденсатора определяется – модулем заряда на любой одной из её обкладок. Заряд конденсатора прямо пропорционален напряжению между обкладками конденсатора. Коэффициент пропорциональности С называется электрической ёмкостью, электроёмкостью или просто ёмкостью конденсатора.

Электрической ёмкостью конденсатора называется физическая величина, которая численно равна отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.

Чем больше площадь проводников и чем меньше пространство заполняющего диэлектриком, тем больше увеличивается ёмкость обкладок конденсатора.

Измеряется электрическая ёмкость в Международной системе СИ в Фарадах. Эта единица имеет своё название в честь английского физика экспериментатора Майкла Фарадея который внёс большой вклад в развитие теории электромагнетизма. Один Фарад равен ёмкости такого конденсатора, между пластинами которого возникает напряжение, равное одному Вольту, при сообщении заряда в один Кулон.

Электрическая ёмкость конденсаторов определяется их конструкцией, самыми простыми из них являются плоские конденсаторы.

Чем больше площадь взаимного перекрытия обкладок и чем меньше расстояние между ними, тем значительнее будет увеличение ёмкости обкладок конденсатора. При заполнении в пространство между обкладками стеклянной пластины, электрическая ёмкость конденсатора значительно увеличивается, получается, что она зависит от свойств используемого диэлектрика.

Электрическая ёмкость плоского конденсатора зависит от площади его обкладок, расстояния между ними, диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками и определяется по формуле:

где – электрическая постоянная.

Для того чтобы получить необходимую определённую ёмкость, берут несколько конденсаторов и собирают их в батарею применяя при этом параллельное, последовательное или смешанное соединения.

Параллельное соединение:

q = q₁+ q₂+ q₃

u = u₁ = u₂ = u₃

с = с₁+с₂+с₃

с = n∙с

Последовательное соединение:

q = q₁= q₂= q₃

u = u₁ + u₂ + u₃

Энергия конденсатора равна половине произведения заряда конденсатора напряжённости поля и расстояния между пластинами конденсатора: u = Еd

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин, это поле совершает положительную работу. При этом энергия электрического поля уменьшается:

Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения:

Примеры и разбор решения заданий:

1. Плоский конденсатор, расстояние между пластинами которого равно 3 мм, заряжен до напряжения 150 В и отключен от источника питания. Разность потенциалов между пластинами возросла до 300 В.

Во сколько раз увеличилась разность потенциалов между пластинами?
Какое расстояние между пластинами конденсатора стало после того, как пластины были раздвинуты?
Во сколько раз изменилось расстояние между пластинами.

Решение:

Электрическая ёмкость конденсатора определяется по формуле:

1.По условию разность потенциалов увеличилось в два раза. U₁= 150В→ U₂ = 300В.

2.По условию d = 3 мм, если разность потенциалов увеличилось в два раза, по формуле соответственно и расстояние между пластинами увеличилось в два раза, и d =2·3 мм = 6 мм.

3.Расстояние между пластинами увеличилось в два раза.

Ответ:

1. 2

2. 6мм

3. 2

2. Конденсатор электроёмкостью 20 мкФ имеет заряд 4 мкКл. Чему равна энергия заряженного конденсатора?

Дано: С = 20 мкФ = 20 · 10^-6Ф, q = 4 мкКл = 4·10^-6Кл.

Найти: W.

Решение:

Энергия заряженного конденсатора W через заряд q и электрическую ёмкость С определяется по формуле:

Ответ: W = 0,4 мкДж.

формула для расчета электрической емкости

Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал. Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.

В чем измеряется емкость конденсатора

Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги. Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.

Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться. На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?

Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.). Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.

Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.

Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.

В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах.

Много это или мало — емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.

Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.

Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.

Рассмотрим пример.

В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.

Формула емкости плоского конденсатора

Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:

где Q – заряд,
φ – потенциал.

Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.

Для получения качественного конденсатора важны любые мелочи:

ровная поверхность каждой обкладки;
обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
размеры обкладок должны быть строго идентичными;
от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.

Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:

где S – площадь одной обкладки,
ε_r— диэлектрическая проницаемость диэлектрика,
ε₀ — электрическая постоянная,
d – расстояние между обкладками.

Электрическая постоянная выражается числом 8,854187817×10^-12.

Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.

Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м², точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.

В России это ε_r(также означает относительная проницаемость), в англоязычной литературе встречается ε_a(также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.

Дальше идет ε₀. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?

Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.

При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.

Есть другая формула для плоского переменного конденсатора:

Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.

Допустимая толщина диэлектрика d также зависит от ε_r, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.

Формула емкости цилиндрического конденсатора

Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой. Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:

Здесь видим несколько новых переменных:

l – высота цилиндра;
R₁и R₂ – радиус первого и второго (внешнего) цилиндров;
l_n – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.

Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).

Из нее видно, что все расстояния нужно приводить к метру.

Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.

Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.

Формула емкости сферического конденсатора

Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:

Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.

Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.

Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.

После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.

Примеры решения задач

Начнем с плоского конденсатора. Формула для этого вида:

Допустим, у нас есть следующие значения:

в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
конденсатор квадратный со сторонами в 7 мм.

Определяем площадь пластин: 7×7 = 49 мм².

Приводим к единой системе: 4,9×10^-5 = 0,000049 м². Толщина диэлектрика 0,02×10^-5= 0,00002 м. Электрическая постоянная 8,854187817×10^-12.

Подставляем в формулу и высчитываем числитель: 6×8,854187817×10^-12 ×4,9×10^-5, сокращаем и решаем 6×49×8,854187817×10^-17 = 2,603131218198×10^-14.

Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.

Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.

Формула для цилиндрического конденсатора:

Выбираем значения:

l = 1 см;
R₁ = 0,25 мм;
R₂ = 0,26 мм;
ε = 2.

Подгоняем под единую систему: l — 1 см = 1×10^-2 = 0,01 м; R₁ – 0,25 мм = 0,0025 м; R₂ – 0,26 мм = 0,0026 м.

Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10^-12×2×0,01 1,11×10^-12. Находим знаменатель: 0,26:0,25 = 1,04.

Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10^-12/0,39 = 2,85×10^-12.

Число с 12 нулями это приставка «пико», получаем 2,85 пФ.

Формула для сферического конденсатора:

Выбираем значения:

ε= 4;
r₁= 5 см;
r₂= 5,01 см.

Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10^-12×0,05×0,0501 1,11×10^-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10^-12×0,01 = 1,11×10^-10. Снова получили пикофарады, а именно 1,11 пФ.

Похожие материалы на сайте:

Понравилась статья — поделись с друзьями!

Электрическая ёмкость: определение, формулы, единицы измерения

Одним из важных параметров, учитываемых в электрических цепях, является электрическая емкость – способность проводников накапливать заряды. Понятие емкости применяется как для уединенного проводника, так и для системы, состоящей из двух и более проводников. В частности, емкостью обладают конденсаторы, состоящие из двух металлических пластин, разделенных диэлектриком или электролитом.

Для накопления зарядов широко применяютсяаккумуляторы, используемые в качестве источников постоянного тока для питания различных устройств. Количественной характеристикой, определяющей время работы аккумулятора, является его электроемкость.

Определение

Если диэлектрик, например, эбонитовую палочку, наэлектризовать трением то электрические заряды сконцентрируются в местах соприкосновения с электризующим материалом. При этом, другой конец палочки можно насытить зарядами противоположно знака и такая наэлектризованность будет сохраняться.

Совсем по-другому ведут себя проводники, помещенные электрическое поле. Заряды распределяются по их поверхности, образуя некий электрический потенциал. Если поверхность ровная, как у палочки, то заряды распределятся равномерно. Под действием внешнего электрического поля в проводнике происходит такое распределение электронов, чтобы внутри его сохранялся баланс взаимной компенсации негативных и позитивных зарядов.

Внешнее электрическое поле притягивает электроны на поверхность проводника, компенсируя при этом положительные заряды ионов. По отношению к проводнику имеет место электростатическая индукция, а заряды на его поверхности называются индуцированными. При этом на концах проводника плотность зарядов будет несколько выше.

На металлическом шаре заряды распределяются равномерно по всей поверхности. Наличие полости любой конфигурации абсолютно не влияет на процесс распределения.

Однако, если проводник убрать из зоны действия поля, то его заряды перераспределятся таким образом, что он снова станет электрически нейтральным.

На рисунке 1 изображена схема заряженного разнополюсного диэлектрика и проводника, удалённого из зоны действия электростатического поля. Благодаря тому, что диэлектрик сохраняет полученные заряды, уединенный проводник восстановил свою нейтральность.

Рис. 1. Распределение зарядов

Интересное явление наблюдается с двумя проводниками, разделенными диэлектриком. Если одному из них сообщить положительный заряд, а другому – отрицательный, то после убирания источника электризации заряды на поверхности проводников сохранятся. Заряженные таким образом проводники обладают разностью потенциалов.

Заряды, накопившиеся на диэлектрике, уравновешивают внутренние взаимодействие в каждом из проводников, не позволяя им разрядиться. Величина заряда зависит от площади поверхности параллельных проводников и от свойства диэлектрика, расположенного между ними.

Свойство сохранять накопленный заряд называется электроемкостью. Точнее говоря, – это характеристика проводника, физическая величина определяющая меру его способности в накоплении электрического заряда.

Накопленное электричество можно снять с проводников путем короткого замыкания их или через нагрузку. С целью увеличения емкости на практике применяют параллельные пластины или же длинные полоски тонкой фольги, разделённой диэлектриком. Полоски сворачивают в тугой цилиндр для уменьшения объема. Такие конструкции называют конденсаторами.

На рисунке 2 изображена схема простейшего конденсатора с плоскими обкладками.

Рис. 2. Схема простого конденсатора

Существуют конденсаторы других типов:

переменные;
электролитические;
оксидные;
бумажные;
комбинированные и другие.

Важной характеристикой конденсатора, как и других накопительных систем, является его электрическая емкость.

Формулы

На рисунке 3 наглядно показано формулы для определения емкости, в т. ч. и для сферы.

Рис. 3. Электроёмкость проводника

По отношению к конденсатору, для определения его емкости применяют формулу: C = q/U. То есть, эта величина прямо пропорциональна заряду одной из обкладок и обратно пропорциональна разнице потенциалов между обкладками (см. рис. 4).

Ёмкость конденсатора

О других способах определения ёмкости конденсатора читайте в нашей статье: https://www.asutpp.ru/kak-opredelit-emkost-kondensatora.html

Единицы измерения

За единицу измерения величины электроемкости принято фараду: 1 Ф = 1 Кл/1В. Поскольку фарада величина огромная, то для измерения емкости на практике она мало пригодна. Поэтому используют приставки:

мили (м) = 10^-3;
микро (мк) = 10^-6;
нано (н) = 10^-9;
пико (пк) = 10^-12;

Например, электрическая емкость 1 мкф = 0,000001 Ф. Параметр зависит от геометрических размеров, конфигурации проводника и материала диэлектрика.

Уединенный проводник и его емкость

Уединенным называют проводник, влиянием на который других элементов цепей можно пренебречь. Предполагается, что все другие проводники бесконечно удалены от него, а как известно, потенциал точки, бесконечно удаленной в пространстве, равен 0.

Электрическую емкость C уединенного проводника, определяют как количество электричества q, которое требуется для повышения электрического потенциала на 1 В: С = q/ϕ. Параметр не зависит от материала, из которого изготовлен проводник.

Конденсаторы постоянной и переменной емкости

Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).

Рис. 5. Конденсатор переменной емкости

Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.

Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.

Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.

Главные их преимущества электролитического конденсатора:

высокие показатели емкости при малом объеме;
применение в цепях с постоянным током.

Недостатки:

необходимо соблюдать полярность;
ограниченный срок службы;
чувствительность к повышенным напряжениям.

Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.

Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.

Конденсаторы различных типов

Аккумуляторы и электроемкость

Накопители электричества большой емкости (аккумуляторы) состоят из положительных и негативных пластин, погруженных в электролит. Во время зарядки часть атомов электролита распадается на ионы, которые оседают на пластине. Образуется разность потенциалов между пластинами, что является причиной возникновения ЭДС при подключении нагрузки.

С целью увеличения напряжения аккумуляторы последовательно соединяют в батареи. Разница потенциалов одной секции около 2 В. Для получения аккумулятора на 6 В необходимо создать батарею из трех секций, а на 12 В – батарею из 6 секций.

Для характеристики аккумуляторов (батарей) используются параметры:

емкости;
номинального напряжения;
максимального тока разряда.

Единицей емкости аккумулятора является ампер-час (А*ч) или кратные ей миллиампер-часы (мА*ч). Емкость аккумулятора зависит от площади пластин. Увеличить емкость можно путем параллельного подключения нескольких секций, но такой способ почти не применяется, так как проще и надежнее создать аккумулятор с большими пластинами.

Глава 20. Конденсаторы

Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.

Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):

(20.1)

Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.

Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):

(20.2)

Разность потенциалов между пластинами равна

(20.3)

где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора

(20.4)

Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает

(20.5)

Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.

Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов

(20.6)

Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .

Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов

(20.7)

Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна

(20.8)

С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:

(20.9)

Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.

Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).

Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).

Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4

(ответ 4).

Согласно определению электрической емкости имеем в задаче 20.1.5

(ответ 2).

Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).

При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул

где и — новый заряд конденсатора (ответ 3).

Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).

В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)

то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что

произведение от расстояния между пластинами не зависит (см. формулу (20.4)).

Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.

При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).

Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.8)

(1)

Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).

В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)

Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)

В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)

Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).

Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).

В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).

Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).

Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:

где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора

(ответ 4).

Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):

Емкость конденсатора Formula

Емкость конденсатора — это способность конденсатора накапливать электрический заряд на единицу напряжения на своих пластинах конденсатора. Емкость определяется делением электрического заряда на напряжение по формуле C = Q / V. Его единица — Фарад.

Формула

Его формула выглядит так:

C = Q / V

Где C — емкость, Q — напряжение, а V — напряжение. Мы также можем найти заряд Q и напряжение V, переписав приведенную выше формулу как:

Q =

В = Q / C

Фарад — единица измерения емкости.Один фарад — это величина емкости, когда один кулон заряда хранится с одним вольт на пластинах.

Большинство конденсаторов, которые используются в электронике, имеют значения емкости, которые указаны в микрофарадах (мкФ) и пикофарадах (пФ). Микрофарад — это одна миллионная фарада, а пикофарад — одна триллионная фарада.

Какие факторы влияют на емкость конденсатора?

Зависит от следующих факторов:

Площадь плит

Емкость прямо пропорциональна физическому размеру пластин, определяемому площадью пластины A.Большая площадь пластины дает большую емкость и меньшую емкость. На рисунке (а) показано, что площадь пластины конденсатора с параллельными пластинами равна площади одной из пластин. Если пластины перемещаются относительно друг друга, как показано на рис (b), площадь перекрытия определяет эффективную площадь пластины. Это изменение эффективной площади пластины является основным для определенного типа переменного конденсатора.

Тарелки разделительные

`Емкость обратно пропорциональна расстоянию между пластинами.Разделение пластин обозначено буквой d, как показано на рис. (А). Чем больше разделение пластин, тем меньше емкость, как показано на рис. (B). Как обсуждалось ранее, напряжение пробоя прямо пропорционально расстоянию между пластинами. Чем дальше разделены пластины, тем больше напряжение пробоя .

Диэлектрическая проницаемость материала

Как известно, изоляционный материал между пластинами конденсатора называется диэлектриком. Диэлектрические материалы имеют тенденцию уменьшать напряжение между пластинами при заданном заряде и, таким образом, увеличивать емкость.Если напряжение фиксировано, из-за наличия диэлектрика может храниться больше заряда, чем может храниться без диэлектрика. Мера способности материала создавать электрическое поле называется диэлектрической постоянной или относительной диэлектрической проницаемостью и обозначается как? _r.

Емкость прямо пропорциональна диэлектрической проницаемости. Диэлектрическая проницаемость вакуума определяется как 1, а диэлектрическая проницаемость воздуха очень близка к 1. Эти значения используются в качестве справочных, а для всех других материалов значения ∈r указаны по отношению к таковым для вакуума или воздуха.Например, материал с εr = 8 может иметь емкость в восемь раз большую, чем у воздуха, при прочих равных условиях.

Диэлектрическая проницаемость ∈r безразмерна, поскольку является относительной мерой. Это отношение абсолютной диэлектрической проницаемости материала, ∈r, к абсолютной диэлектрической проницаемости вакуума, ∈ ₀, выраженное следующей формулой:

∈ _r = ∈ / ∈ ₀

Ниже приведены некоторые общие диэлектрические материалы и типичные диэлектрические постоянные для каждого из них.Значения могут варьироваться, поскольку зависят от конкретного состава материала.

Материал Стандартные значения ∈r

Воздух 1.0
тефлон 2,0
Бумага 2.5
Масло 4.0
Слюда 5,0
Стекло 7,5
Керамика 1200

Диэлектрическая проницаемость ∈r безразмерна, поскольку является относительной мерой.Это отношение абсолютной диэлектрической проницаемости материала, ∈r, к абсолютной диэлектрической проницаемости вакуума, ∈0, которое выражается следующей формулой:

∈r = ∈ / ∈0

Значение ∈0 составляет 8,85 × 10-12 Ф / м.

Формула емкости по физическим параметрам

Вы видели, как емкость напрямую связана с площадью пластины, A, и диэлектрической проницаемостью, ∈r, и обратно пропорциональна расстоянию между пластинами, d. Точная формула для расчета емкости по этим трем величинам:

C = A ∈ _r ∈ / d

где ∈ = ∈ _r ∈ ₀ = ∈r (8.85 × 10-12Ф / м)

Емкость параллельного вывода конденсатора

Рассмотрим конденсатор с параллельными пластинами. Размер пластины большой, а расстояние между пластинами очень маленькое, поэтому электрическое поле между пластинами однородно.

Электрическое поле «E» между конденсаторами с параллельными пластинами составляет:

Емкость цилиндрических конденсаторов физика

Рассмотрим цилиндрический конденсатор длиной L, образованный двумя коаксиальными цилиндрами с радиусами «a» и «b».Предположим, что L >> b, такое, что на концах цилиндров нет окаймляющего поля.

Пусть «q» — это заряд конденсатора, а «V» — это разность потенциалов между пластинами. Внутренний цилиндр заряжен положительно, а внешний цилиндр — отрицательно. Мы хотим узнать выражение емкости для цилиндрического конденсатора. Для этого мы рассматриваем цилиндрическую гауссовскую поверхность радиуса «r», такую что a << b.

Если «E» — напряженность электрического поля в любой точке цилиндрической гауссовой поверхности, то по закону Гаусса:

Если «V» — разность потенциалов между пластинами, тогда

Это соотношение для емкости цилиндрического конденсатора.

Емкость сферического конденсатора

Емкость изолированного сферического конденсатора

Внешний источник
https://en.wikipedia.org/wiki/Capacitance

8.1 Конденсаторы и емкость — University Physics Volume 2

Задачи обучения

К концу этого раздела вы сможете:

Объясните понятие конденсатора и его емкости
Опишите, как оценить емкость системы проводников

Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии.Конденсаторы обычно состоят из двух электрических проводников, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но, точнее, они «обкладки конденсатора».) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор будет известен как «Вакуумный конденсатор». Однако пространство обычно заполнено изолирующим материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем накопителя в конденсаторе определяется свойством, называемым емкостью , емкостью , о котором вы узнаете больше чуть позже в этом разделе.

Конденсаторы

имеют различные применения: от фильтрации статического электричества, от радиоприема до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к первоначально незаряженному конденсатору, потенциал батареи перемещает небольшой заряд величиной Q с положительной пластины на отрицательную.Конденсатор в целом остается нейтральным, но с зарядами + Q + Q и −Q − Q, находящимися на противоположных пластинах.

Рисунок 8.2 Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них на пластинах есть заряды + Q + Q и −Q − Q (соответственно). (a) Конденсатор с параллельными пластинами состоит из двух пластин противоположного заряда с площадью A , разделенных расстоянием d . (b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).

Система, состоящая из двух идентичных параллельно проводящих пластин, разделенных расстоянием, называется конденсатором с параллельными пластинами (рис. 8.3). Величина электрического поля в пространстве между параллельными пластинами равна E = σ / ε0E = σ / ε0, где σσ обозначает поверхностную плотность заряда на одной пластине (напомним, что σσ — это заряд Q на площадь поверхности A ). Таким образом, величина поля прямо пропорциональна Q .

Рис. 8.3 Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности обкладок конденсатора.Линии электрического поля в конденсаторе с параллельными пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.

Конденсаторы с разными физическими характеристиками (такими как форма и размер пластин) накапливают разное количество заряда для одного и того же приложенного напряжения В на своих пластинах. Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В на его пластинах.Другими словами, емкость — это наибольшее количество заряда на вольт, которое может храниться на устройстве:

Единица измерения емкости в системе СИ — фарад (Ф), названная в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или

По определению, конденсатор емкостью 1,0 мкФ может сохранять заряд 1,0 К (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Следовательно, один фарад является очень большой емкостью.Типичные значения емкости варьируются от пикофарад (1пФ = 10−12Ф) (1пФ = 10−12Ф) до миллифарадов (1мФ = 10−3Ф) (1мФ = 10−3Ф), что также включает микрофарады (1мкФ = 10−6F1мкФ = 10− 6F). Конденсаторы могут быть разных форм и размеров (рис. 8.4).

Рисунок 8.4 Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно зависит от его емкости. (кредит: Windell Oskay)

Расчет емкости

Мы можем рассчитать емкость пары проводов с помощью следующего стандартного подхода.

Стратегия решения проблем

Расчет емкости

Предположим, что конденсатор заряжен Q .
Определить электрическое поле E → E → между проводниками. Если симметрия присутствует в расположении проводников, вы можете использовать закон Гаусса для этого расчета.
Найдите разность потенциалов между проводниками из VB − VA = −ABE → · dl →, VB − VA = −ABE → · dl →,
8,2
где путь интегрирования ведет от одного проводника к другому.Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |.
Зная В , определите емкость непосредственно из уравнения 8.1.

Чтобы показать, как работает эта процедура, мы теперь вычисляем емкости параллельных пластин, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.

Конденсатор с параллельными пластинами

Конденсатор с параллельными пластинами (рисунок 8.5) имеет две идентичные проводящие пластины, каждая с площадью поверхности A , разделенными расстоянием d . Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить.Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины расположены друг к другу, тем сильнее на них притяжение противоположных зарядов. Следовательно, C должно быть больше для меньшего d .

Рис. 8.5 В конденсаторе с параллельными пластинами с пластинами, разнесенными на расстояние d , каждая пластина имеет одинаковую площадь поверхности A .

Определим плотность поверхностного заряда σσ на пластинах как

Из предыдущих глав мы знаем, что, когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и что его величина определяется как

где постоянная ε0ε0 — диэлектрическая проницаемость свободного пространства, ε0 = 8.85 × 10–12Ф / м. Ε0 = 8,85 × 10–12Ф / м. Единица СИ в Ф / м эквивалентна C2 / N · m2.C2 / N · m2. Поскольку электрическое поле E → E → между пластинами однородно, разность потенциалов между пластинами составляет

. V = Ed = σdε0 = Qdε0A.V = Ed = σdε0 = Qdε0A.

Следовательно, уравнение 8.1 дает емкость конденсатора с параллельными пластинами как

C = QV = QQd / ε0A = ε0Ad.C = QV = QQd / ε0A = ε0Ad.

8,3

Обратите внимание на это уравнение, что емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора.Фактически, это верно не только для конденсатора с параллельными пластинами, но и для всех конденсаторов: емкость не зависит от Q или V . Если заряд изменяется, соответственно изменяется и потенциал, так что Q / V остается постоянным.

Пример 8.1

Емкость и заряд в конденсаторе с параллельными пластинами

(a) Какова емкость пустого конденсатора с параллельными пластинами с металлическими пластинами, каждая из которых имеет площадь 1,00 м 21.00м2, разделенных расстоянием 1,00 мм? (b) Сколько заряда хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 103 В3,00 × 103 В?

Стратегия

Определение емкости C является прямым применением уравнения 8.3. Найдя C , мы сможем найти накопленный заряд, используя уравнение 8.1.

Решение

Ввод заданных значений в уравнение 8.3 дает C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3м = 8,85 × 10−9F = 8,85nF.C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3m = 8 .85 × 10−9F = 8,85 нФ. Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью.
Обращение уравнения 8.1 и ввод известных значений в это уравнение дает Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл. Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл.

Значение

Этот заряд лишь немного больше, чем в типичных приложениях для статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3.0 МВ / м, на этом конденсаторе больше нельзя накапливать заряд при увеличении напряжения.

Пример 8.2

А, 1-Ф, конденсатор с параллельными пластинами

Предположим, вы хотите сконструировать конденсатор с параллельными пластинами емкостью 1,0 F. Какую площадь вы должны использовать для каждой пластины, если пластины разделены на 1,0 мм?

Решение

Преобразуя уравнение 8.3, получаем A = Cdε0 = (1.0F) (1.0 × 10−3m) 8.85 × 10−12F / m = 1.1 × 108m2 A = Cdε0 = (1.0F) (1.0 × 10−3m) 8,85 × 10−12F / m = 1,1 × 108 м2.

Каждая квадратная пластина должна быть 10 км в поперечнике.Раньше было обычным розыгрышем — попросить студента пойти в склад лаборатории и попросить конденсатор с параллельными пластинами 1F, пока обслуживающий персонал не устанет от шуток.

Проверьте свое понимание 8.1

Емкость конденсатора с параллельными пластинами составляет 2,0 пФ. Если площадь каждой пластины составляет 2,4 см 22,4 см2, каково расстояние между пластинами?

Проверьте свое понимание 8.2

Убедитесь, что у σ / Vσ / V и ε0 / dε0 / d одинаковые физические единицы.

Сферический конденсатор

Сферический конденсатор — это еще один набор проводников, емкость которых можно легко определить (Рисунок 8.dr) = Q4πε0∫R1R2drr2 = Q4πε0 (1R1−1R2).

В этом уравнении разность потенциалов между пластинами равна V = — (V2 − V1) = V1 − V2V = — (V2 − V1) = V1 − V2. Мы подставляем этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:

C = QV = 4πε0R1R2R2 − R1.C = QV = 4πε0R1R2R2 − R1.

8,4

Рисунок 8.6 Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды на проводнике находятся на его поверхности.

Пример 8.3

Емкость изолированной сферы

Вычислите емкость одиночной изолированной проводящей сферы радиуса R1R1 и сравните ее с уравнением 8.dr) = Q4πε0∫R1 + ∞drr2 = 14πε0QR1.

Таким образом, емкость изолированной сферы равна

. C = QV = Q4πε0R1Q = 4πε0R1.C = QV = Q4πε0R1Q = 4πε0R1.

Значение

Тот же результат можно получить, взяв предел уравнения 8.4 при R2 → ∞R2 → ∞. Таким образом, одиночная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.

Проверьте свое понимание 8.3

Радиус внешней сферы сферического конденсатора в пять раз превышает радиус его внутренней оболочки.Каковы размеры этого конденсатора, если его емкость 5,00 пФ?

Цилиндрический конденсатор

Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рисунок 8.7). Внутренний цилиндр радиуса R1R1 может быть либо оболочкой, либо полностью твердым. Внешний цилиндр представляет собой оболочку внутреннего радиуса R2R2. Мы предполагаем, что длина каждого цилиндра составляет l и что избыточные заряды + Q + Q и −Q − Q находятся на внутреннем и внешнем цилиндрах соответственно.dr) = Q2πε0l∫R1R2drr = Q2πε0llnr | R1R2 = Q2πε0llnR2R1.

Таким образом, емкость цилиндрического конденсатора составляет

C = QV = 2πε0lln (R2 / R1). C = QV = 2πε0lln (R2 / R1).

8,6

Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом.(Здесь мы предполагаем наличие вакуума между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком.) Эта конфигурация экранирует электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний проводник обычно заземлен. Теперь из уравнения 8.6 емкость коаксиального кабеля на единицу длины равна

. Cl = 2πε0ln (R2 / R1).Cl = 2πε0ln (R2 / R1).

В практических приложениях важно выбирать конкретные значения C / l . Это может быть достигнуто за счет соответствующего выбора радиусов проводников и изоляционного материала между ними.

Проверьте свое понимание 8.4

Когда цилиндрический конденсатор получает заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Какова емкость этой системы? (b) Если цилиндры 1.Длина 0 м, каково соотношение их радиусов?

Несколько типов конденсаторов, которые можно использовать на практике, показаны на рис. 8.4. Обычные конденсаторы часто состоят из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. Рисунок 8.2 (b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторые распространенные изоляционные материалы — это слюда, керамика, бумага и антипригарное покрытие Teflon ™.

Другой популярный тип конденсатора — электролитический конденсатор.Он состоит из окисленного металла в проводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость одного типа алюминиевого электролитического конденсатора может достигать 1,0 F. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста. Когда возникает обратная поляризация, электролитическое действие разрушает оксидную пленку.Этот тип конденсатора не может быть подключен к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет свою полярность (см. Схемы переменного тока в цепях переменного тока).

Конденсатор переменного тока (рисунок 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначается как «ротор»). Поворачивая вал, можно изменять площадь поперечного сечения в перекрытии пластин; следовательно, емкость этой системы может быть настроена на желаемое значение.Настройка конденсатора находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильное радио на любимую станцию, думайте о емкости.

Рисунок 8.8 В конденсаторе переменного тока емкость можно регулировать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спроул)

Символы, показанные на рисунке 8.9, представляют собой схемные изображения различных типов конденсаторов. Обычно мы используем символ, показанный на рисунке 8.9 (а). Символ на Рисунке 8.9 (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор представлен символом на рис. 8.9 (b), где изогнутая пластина обозначает отрицательный вывод.

Рисунок 8.9 Здесь показаны три различных схемных представления конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет конденсатор переменной емкости.

Интересный прикладной пример модели конденсатора взят из клеточной биологии и имеет дело с электрическим потенциалом в плазматической мембране живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым отобранным ионам проходить внутрь или из клетки. Разность потенциалов на мембране составляет около 70 мВ. Клеточная мембрана может иметь толщину от 7 до 10 нм. Рассматривая клеточную мембрану как наноразмерный конденсатор, оценка наименьшей напряженности электрического поля на ее « пластинах » дает значение E = Vd = 70 × 10−3V · 10 · 10−9m = 7 · 106V / m> 3MV / mE. = Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / m.

Этой величины электрического поля достаточно, чтобы вызвать электрическую искру в воздухе.

Рис. 8.10. Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней. Диффузия перемещает ионы K + K + (калий) и Cl – Cl– (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Таким образом, внешняя поверхность мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая разность потенциалов на мембране.Мембрана обычно непроницаема для Na + (ионов натрия).

Конденсаторы и диэлектрики | Физика

Цели обучения

К концу этого раздела вы сможете:

Опишите действие конденсатора и определите емкость.
Объясните, почему конденсаторы с параллельными пластинами и их емкости.
Обсудите процесс увеличения емкости диэлектрика.
Определите емкость при заданном заряде и напряжении.

Конденсатор — это устройство, используемое для хранения электрического заряда. Конденсаторы имеют различные применения: от фильтрации статического электричества при радиосигнале до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 1. (В большинстве случаев между двумя пластинами используется изолятор для обеспечения разделения — см. Обсуждение диэлектриков ниже). Клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, + Q и — Q , разделены на его две пластины.Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд Q .

Рис. 1. Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них разделены заряды + Q и — Q на своих двух половинах. (а) Конденсатор с параллельными пластинами. (b) Скрученный конденсатор с изоляционным материалом между двумя проводящими листами.

Конденсатор

Конденсатор — это устройство, используемое для хранения электрического заряда.

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Количество заряда

Q конденсатор может хранить

Рис. 2. Линии электрического поля в этом конденсаторе с параллельными пластинами, как всегда, начинаются с положительных зарядов и заканчиваются отрицательными.Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.

Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как на рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для конденсатора с параллельными пластинами, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поля будет больше. линии, если есть больше заряда.(Рисование одной силовой линии для каждого заряда — это только удобство. Мы можем нарисовать много силовых линий для каждого заряда, но их общее количество пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна Ом. .

Поле пропорционально начислению:

E ∝ Q ,

, где символ ∝ означает «пропорционально». Из обсуждения в разделе «Электрический потенциал в однородном электрическом поле» мы знаем, что напряжение на параллельных пластинах равно

V = Ed .

Таким образом, V ∝ E . Отсюда следует, что V ∝ Q , и, наоборот,

Q ∝ V .

В целом это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.

Различные конденсаторы будут накапливать разное количество заряда для одного и того же приложенного напряжения, в зависимости от их физических характеристик. Мы определяем их емкость C так, чтобы заряд Q , хранящийся в конденсаторе, был пропорционален C .Заряд, накопленный в конденсаторе, равен

Q = CV .

Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Изменив уравнение, мы видим, что емкость C — это количество заряда, сохраняемого на вольт, или

[латекс] C = \ frac {Q} {V} \\ [/ latex].

Емкость

Емкость C — величина накопленного заряда на вольт, или

[латекс] C = \ frac {Q} {V} \\ [/ latex]

Единица измерения емкости — фарад (Ф), названная в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или

[латекс] 1 \ text {F} = \ frac {1 \ text {C}} {1 \ text {V}} \\ [/ latex].

Конденсатор емкостью 1 фарад может хранить 1 кулон (очень большое количество заряда) при подаче всего 1 вольт. Таким образом, одна фарада — это очень большая емкость. Типичные конденсаторы варьируются от долей пикофарада (1 пФ = 10 ⁻¹² Ф) до миллифарадов (1 мФ = 10 ⁻³ Ф).

На рисунке 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.

Рисунок 3. Некоторые типичные конденсаторы. Размер и значение емкости не обязательно связаны. (Источник: Windell Oskay)

Конденсатор с параллельными пластинами

Рис. 4. Конденсатор с параллельными пластинами, разделенные пластинами на расстояние d. Каждая пластина имеет площадь A.

Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности A , разделенных расстоянием d (без материала между пластинами).Когда на конденсатор подается напряжение В , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость зависит от A и d , рассмотрев характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, в отличие от зарядов притягиваются, и сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут расходиться больше. Таким образом, C должен быть больше для большего A .Точно так же, чем ближе пластины расположены друг к другу, тем сильнее на них притяжение противоположных зарядов. Таким образом, C должен быть больше для меньшего d .

Можно показать, что для конденсатора с параллельными пластинами есть только два фактора ( A и d ), которые влияют на его емкость C . Емкость конденсатора с параллельными пластинами в форме уравнения равна

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].

Емкость параллельного пластинчатого конденсатора

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex]

A — это площадь одной пластины в квадратных метрах, а d — это расстояние между пластинами в метрах.Константа ε ₀ — диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε ₀ = 8,85 × 10 ⁻¹² Ф / м. Единицы измерения Ф / м эквивалентны C ² / Н · м ². Небольшое числовое значение ε ₀ связано с большим размером фарада. Конденсатор с параллельными пластинами должен иметь большую площадь, чтобы его емкость приближалась к фарадам. (Обратите внимание, что приведенное выше уравнение действительно, когда параллельные пластины разделены воздухом или свободным пространством.Когда между пластинами помещается другой материал, уравнение изменяется, как обсуждается ниже.)

Пример 1. Емкость и заряд в параллельном пластинчатом конденсаторе

Какова емкость конденсатора с параллельными пластинами, каждая из которых имеет площадь 1,00 м ², разделенных расстоянием 1,00 мм?
Какой заряд хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 10 ³ В?

Стратегия

Определение емкости C — это прямое приложение уравнения [латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].{-9} \ text {F} = 8.85 \ text {nF} \ end {array} \\ [/ latex]

Обсуждение части 1

Это небольшое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, например, использование тонких пленок очень большой площади, расположенных близко друг к другу.

Решение для Части 2

Заряд любого конденсатора определяется уравнением Q = CV . Ввод известных значений в это уравнение дает

[латекс] \ begin {array} {lll} Q & = & CV = \ left (8.{3} \ text {V} \ right) \\\ text {} & = & 26.6 \ mu \ text {C} \ end {array} \\ [/ latex]

Обсуждение части 2

Этот заряд лишь немного больше, чем у обычного статического электричества. Поскольку воздух разрывается при примерно 3,00 × 10 ⁶ В / м, на этом конденсаторе не может быть накоплено больше заряда за счет увеличения напряжения.

Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам выборочно входить и выходить из клетки.Существует разность потенциалов на мембране около –70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженных ионов натрия (Na ⁺) снаружи. {6} \ text {V / m} \\ [/ latex]

Этого электрического поля достаточно, чтобы вызвать пробой в воздухе.

Диэлектрик

Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если d сделать меньше, чтобы получить большую емкость, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [latex] E = \ frac {V} {d} \\ [/ latex]). Важным решением этой проблемы является размещение изоляционного материала, называемого диэлектриком , между пластинами конденсатора и обеспечение минимального размера d .Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем сломаться.

Есть еще одно преимущество использования диэлектрика в конденсаторе. В зависимости от используемого материала емкость больше, чем заданная уравнением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], на коэффициент κ , называемый диэлектрическая постоянная . Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex] (конденсатор с параллельными пластинами с диэлектриком).

Значения диэлектрической проницаемости κ для различных материалов приведены в таблице 1. Обратите внимание, что κ для вакуума равно 1, и поэтому приведенное выше уравнение справедливо и в этом случае. Если используется диэлектрик, например, путем размещения тефлона между пластинами конденсатора в примере 1, то емкость будет больше в κ раз, что для тефлона составляет 2,1.

Эксперимент на вынос: создание конденсатора

Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут из алюминиевой фольги, а разделитель (диэлектрик) между ними — из бумаги.

Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC
Материал	Диэлектрическая проницаемость κ	Диэлектрическая прочность (В / м)
Вакуум	1,00000	–
Воздух	1.00059	3 × 10 ⁶
Бакелит	4,9	24 × 10 ⁶
Плавленый кварц	3.78	8 × 10 ⁶
Неопреновый каучук	6,7	12 × 10 ⁶
Нейлон	3,4	14 × 10 ⁶
Бумага	3,7	16 × 10 ⁶
Полистирол	2,56	24 × 10 ⁶
Стекло Pyrex	5,6	14 × 10 ⁶
Кремниевое масло	2.5	15 × 10 ⁶
Титанат стронция	233	8 × 10 ⁶
Тефлон	2,1	60 × 10 ⁶
Вода	80	–

Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы с воздушным наполнением действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится равной. слишком большой.(Напомним, что [латекс] E = \ frac {V} {d} \\ [/ latex] для конденсатора с параллельными пластинами.) В таблице 1 также показаны максимальные напряженности электрического поля в В / м, которые называются диэлектрической прочностью , для нескольких материалов. Это поля, над которыми материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного расстояния между пластинами. 6 \ text {V / m} \ right) \ left ( 1.{-3} \ text {m} \ right) \\\ text {} & = & 3000 \ text {V} \ end {array} \\ [/ latex]

Однако предел для расстояния 1,00 мм, заполненного тефлоном, составляет 60 000 В, поскольку диэлектрическая прочность тефлона составляет 60 × 10 ⁶ В / м. Таким образом, тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для конденсатора с параллельными пластинами, заполненного воздухом, мы обнаружили, что конденсатор с тефлоновым заполнением может хранить максимальный заряд

[латекс] \ begin {array} {lll} Q & = & CV \\\ text {} & = & \ kappa {C} _ {\ text {air}} V \\\ text {} & = & (2.4 \ text {V}) \\\ text {} & = & 1.1 \ text {mC} \ end {array} \\ [/ latex]

Это в 42 раза больше заряда того же конденсатора, заполненного воздухом.

Диэлектрическая прочность

Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется его диэлектрической прочностью.

Микроскопически, как диэлектрик увеличивает емкость? За это отвечает поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость κ .Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды обуславливает ее относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации лучше всего объясняется характеристиками кулоновской силы. На рис. 5 схематично показано разделение зарядов в молекулах диэлектрического материала, помещенных между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень сильна, поскольку они расположены очень близко друг к другу.Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии d .

Рис. 5. (a) Молекулы изоляционного материала между пластинами конденсатора поляризованы заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (б) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к уменьшению напряжения между пластинами при одинаковом заряде.Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.

Другой способ понять, как диэлектрик увеличивает емкость, — это рассмотреть его влияние на электрическое поле внутри конденсатора. На рисунке 5 (b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются зарядами в диэлектрике, их меньше, идущих от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, даже если бы на пластинах был одинаковый заряд.Напряжение между пластинами составляет В, = Ед, , поэтому оно тоже снижается за счет диэлектрика. Таким образом, есть меньшее напряжение В для того же заряда Q ; поскольку [латекс] C = \ frac {Q} {V} \\ [/ latex], емкость C больше.

Диэлектрическая проницаемость обычно определяется как [латекс] \ kappa = \ frac {E_0} {E} \\ [/ latex], или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и в конечном итоге связанные с поляризуемостью материала.

Великие и малые вещи: субмикроскопическое происхождение поляризации

Поляризация — это разделение зарядов в атоме или молекуле. Как уже отмечалось, планетарная модель атома описывает его как имеющее положительное ядро, вращающееся вокруг отрицательных электронов, аналогично планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в других местах, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.

Рис. 6. Художественное представление о поляризованном атоме. Орбиты электронов вокруг ядра слегка смещены внешними зарядами (показаны в преувеличении). Получающееся разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что непохожий заряд теперь ближе к внешним зарядам, вызывая поляризацию.

В атомной физике мы обнаружим, что орбиты электронов более правильно рассматривать как электронные облака с плотностью облака, связанной с вероятностью обнаружения электрона в этом месте (в отличие от определенных местоположений и путей движения планет на их орбитах вокруг Солнца).Это облако сдвигается кулоновской силой, так что в среднем атом имеет разделенный заряд. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.

Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому они называются полярными молекулами. На рисунке 7 показано разделение зарядов в молекуле воды, которая имеет два атома водорода и один атом кислорода (H ₂ O).Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец слегка положительным. Внутреннее разделение зарядов в полярных молекулах облегчает их выравнивание с внешними полями и зарядами. Следовательно, полярные молекулы проявляют более сильные поляризационные эффекты и имеют более высокие диэлектрические проницаемости.Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды собирают ионы гораздо эффективнее, потому что у них есть электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как было показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

Рис. 7. Художественная концепция молекулы воды. Существует внутреннее разделение зарядов, поэтому вода — полярная молекула.Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда около двух ядер водорода. (Обратите внимание, что схема справа является приблизительной иллюстрацией распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)

Исследования PhET: лаборатория конденсаторов

Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.Измените напряжение и посмотрите, как на пластинах накапливаются заряды. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

Конденсатор — это устройство, используемое для хранения заряда.
Количество заряда Q , которое может хранить конденсатор, зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Емкость C — это количество накопленного заряда на вольт, или [латекс] C = \ frac {Q} {V} \\ [/ latex].
Емкость конденсатора с параллельными пластинами составляет [латекс] C = {\ epsilon} _ {0} \ frac {A} {d} \\ [/ latex], когда пластины разделены воздухом или свободным пространством. [latex] {\ epsilon} _ {\ text {0}} [/ latex] называется диэлектрической проницаемостью свободного пространства.
Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], где κ — диэлектрик. постоянная материала.
Максимальная напряженность электрического поля, при превышении которой изоляционный материал начинает разрушаться и становится проводником, называется диэлектрической прочностью.

Концептуальные вопросы

Зависит ли емкость устройства от приложенного напряжения? А как насчет хранящегося в нем заряда?
Используйте характеристики кулоновской силы, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора. Аналогичным образом объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
Объясните причину, по которой диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора.Какова независимая причина того, что диэлектрический материал также позволяет приложить большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C и допускает более В .)
Как полярный характер молекул воды помогает объяснить относительно большую диэлектрическую проницаемость воды? (См. Рисунок 7.)
Искры возникают между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем когда сухой. Объясните почему, учитывая полярный характер молекул воды.
Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
Мембраны в живых клетках, в том числе в человеческих, характеризуются разделением заряда через мембрану. Таким образом, мембраны представляют собой заряженные конденсаторы, важные функции которых связаны с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизм пищевой энергии или каким-либо другим источником?

Рисунок 8.Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K ⁺ (калий) и Cl ^— (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Это приводит к слою положительного заряда снаружи, слою отрицательного заряда внутри и, следовательно, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na ⁺ (ионы натрия).

Задачи и упражнения

Какой заряд сохраняется в конденсаторе 180 мкФ, когда к нему приложено 120 В?
Найдите накопленный заряд, когда 5.50 В подается на конденсатор емкостью 8,00 пФ.
Какой заряд хранится в конденсаторе в Примере 1?
Рассчитайте напряжение, приложенное к конденсатору 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
Какое напряжение необходимо приложить к конденсатору емкостью 8,00 нФ для накопления заряда 0,160 мкКл?
Какая емкость необходима для хранения 3,00 мкКл заряда при напряжении 120 В?
Какая емкость терминала большого генератора Ван-де-Граафа, учитывая, что он хранит 8?00 мкКл заряда при напряжении 12,0 МВ?
Найдите емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 5,00 м ², разделенных слоем тефлона 0,100 мм.
(a) Какова емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 1,50 м ², разделенных 0,0200 мм неопренового каучука? (b) Какой заряд он держит, когда к нему приложено 9,00 В?
Интегрированные концепции. Шутник подает 450 В на 80.Конденсатор 0 мкФ, а затем бросает его ничего не подозревающей жертве. Палец пострадавшего обожжен разрядом конденсатора через 0,200 г мяса. Какое повышение температуры мяса? Разумно ли предполагать отсутствие изменения фазы?
Необоснованные результаты. (a) Конденсатор с параллельными пластинами имеет площадь пластин 4,00 м ², разделенных нейлоном толщиной 0,0100 мм, и накапливает 0,170 Кл заряда. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие предположения являются ответственными или противоречивыми?

Глоссарий

конденсатор: устройство, накапливающее электрический заряд

емкость: количество заряда, хранимого на единицу вольт

диэлектрик: изоляционный материал

диэлектрическая прочность: максимальное электрическое поле, выше которого изоляционный материал начинает разрушаться и проводить

конденсатор с параллельными пластинами: две идентичные проводящие пластины, разделенные расстоянием

полярная молекула: молекула с внутренним разделением заряда

Избранные решения проблем и упражнения

1.21,6 мК

3. 80.0 мС

5. 20,0 кВ

7. 667 пФ

9. (а) 4,4 мкФ; (б) 4.0 × 10 ⁻⁵ C

11. (а) 14,2 кВ; (b) Напряжение неоправданно велико, более чем в 100 раз больше напряжения пробоя нейлона; (c) Предполагаемый заряд неоправданно велик и не может храниться в конденсаторе таких размеров.

Конденсаторы

и формулы для расчета емкости

Конденсаторы — это пассивные устройства. в электронных схемах для хранения энергии в виде электрического поля.Они комплимент индукторы, хранящие энергию в виде магнитного поля. Идеальный конденсатор является эквивалентом разомкнутой цепи (бесконечное сопротивление) для постоянного тока (DC) и представляет собой импеданс (реактивное сопротивление) для переменные токи (AC), зависящие от частоты тока (или напряжения). Реактивное сопротивление (сопротивление току расход) конденсатора обратно пропорционален частоте сигнала, воздействующего на него. Конденсаторы изначально были называемые «конденсаторами» по причине, восходящей к временам Лейденской банки, когда считалось, что электрические заряды накапливаться на пластинах в процессе конденсации.

Свойство емкости, которая препятствует изменению напряжения, используется для передачи сигналов с компонент с более высокой частотой, предотвращая прохождение сигналов компонентов с более низкой частотой. Обычное применение конденсатор в РЧ (радиочастотной) цепи — это место, где есть напряжение смещения постоянного тока, которое необходимо заблокировать от присутствия в цепи, позволяя РЧ-сигналу проходить. Источники питания постоянного тока используют большие значения емкости параллельно с выходом. клеммы для сглаживания низкочастотных пульсаций из-за выпрямления и / или переключения форм сигналов.

При использовании последовательно (левый рисунок) или параллельно (правый рисунок) с его комплемент цепи, индуктор, комбинация индуктора-конденсатора образует цепь, которая резонирует на определенной частоте это зависит от значений каждого компонента. В последовательной цепи сопротивление протеканию тока на резонансной частоте равен нулю с идеальными компонентами. В параллельной цепи (справа) сопротивление протеканию тока бесконечно с идеальными компонентами.

Реальные конденсаторы, состоящие из физических компонентов, демонстрируют больше, чем просто емкость, когда присутствует в цепи переменного тока.Слева показана модель симулятора общей схемы. Он включает в себя собственно идеальный конденсатор с параллельным резистивным подключением. компонент («Утечка»), реагирующий на переменный ток. Эквивалентный резистивный компонент постоянного тока (‘ESR’) последовательно с идеальным конденсатором и эквивалентной последовательной индуктивной составляющей. («ESL») присутствует из-за металлических выводов (если они есть) и характеристик поверхностей пластин. Эта индуктивность в сочетании с емкостью создает резонансную частоту, на которой конденсатор выглядит как чистое сопротивление.

Когда рабочая частота увеличивается за пределы резонанса (также известного как собственная резонансная частота или SRF), схема ведет себя как индуктивность, а не как емкость. Следовательно, требуется тщательное рассмотрение SRF, когда выбор конденсаторов. Симуляторы типа SPICE используют эту или даже более сложную модель для облегчения более точных расчетов. в широком диапазоне частот.

Уравнения для последовательного и параллельного объединения конденсаторов приведены ниже.Для конденсаторов приведены дополнительные уравнения. различной конфигурации. Как показывают эти цифры и формулы, емкость — это мера способности двух поверхностей. для хранения электрического заряда. Разделенный и изолированный диэлектриком (изолятором), чистый положительный заряд накапливается на одна поверхность и чистый отрицательный заряд хранится на другой поверхности. В идеальном конденсаторе заряд будет храниться бесконечно; однако реальные конденсаторы постепенно теряют свой заряд из-за токов утечки через неидеальный диэлектрик.

Суммарная емкость последовательно соединенных конденсаторов равна обратной величине сумма обратных величин индивидуальных емкостей. Держите единицы измерения постоянными.

Емкость (C в фарадах) двух параллельных пластин равной площади равна произведению площади (A, в метрах) одной пластины. расстояние (d, в метрах), разделяющее пластины, и диэлектрическая проницаемость (ε, в Фарадах на метр) пространства. разделение пластин.ε, полная диэлектрическая проницаемость, является произведением диэлектрической проницаемости свободного пространства, ε ₀, и относительная диэлектрическая проницаемость материала ε _r. Обратите внимание, что единицы измерения длины и площади могут быть метрическими. или английский, если они согласованы.

Коэффициент рассеяния (DF), также известный как тангенс потерь (tan δ), взаимозаменяемо определяется как величина, обратная коэффициенту качества (QF) или отношению эквивалентного последовательного сопротивления (ESR) и емкостного реактивного сопротивления (X _C).Это показатель степени потери накопленного заряда. DF обычно используется в низкочастотных приложениях, в то время как tan δ чаще используется в высокочастотных приложениях.

Общая емкость параллельно соединенных конденсаторов равна сумме индивидуальных емкости. Держите единицы измерения постоянными.

Следующие физические константы и механические размерные переменные применимы к уравнениям на этой странице.Единицы для уравнений показаны в скобках в конце уравнений; например, означает, что длина дана в дюймах, а индуктивность — в единицах Генри. Если единицы не указаны, то можно использовать любые, если они согласованы для всех объектов; т.е. все измерители, все мкФ, пр.

C = емкость
L = индуктивность
W = энергия
ε _r = относительная диэлектрическая проницаемость (безразмерная)
ε ₀ = 8,85 x 10 ^-12 Ф / м (диэлектрическая проницаемость свободного пространства)
µ _r = Относительная проницаемость (безразмерная)
µ ₀ = 4π x 10 ^-7 Гн / м (проницаемость свободного пространства)

1 метр = 3.2808 футов <—> 1 фут
= 0,3048 метра
1 мм = 0,03937 дюйма <—> 1 дюйм
= 25,4 мм

Кроме того, точки (не путать с десятичными знаками) используются для обозначения умножения. во избежание двусмысленности.

Емкостное реактивное сопротивление (X _C, в Ω) обратно пропорциональна частоте (ω в радианах / сек или f в Гц) и емкости (C в фарадах).Чистая емкость имеет фазовый угол -90 ° (напряжение отстает от тока с фазовым углом 90 °).

Заряд (Q, в кулонах) конденсатора Пластины — это произведение емкости (C в фарадах) и напряжения (V в вольтах) на устройстве.

Энергия (Вт, в Джоулях) хранится в конденсаторе представляет собой половину произведения емкости (C в фарадах) на напряжение (V в вольтах) на устройстве.

Ток действительно течет «через» идеальный конденсатор. Напротив, заряд, накопленный на его пластинах, передается в подключенную цепь, тем самым облегчая ток. поток. И наоборот, сетевое напряжение, приложенное к пластинам, вызывает протекание тока в подключенной цепи по мере накопления заряда. на тарелках.

Добротность безразмерная. отношение реактивного сопротивления к сопротивлению в конденсаторе.

Связанные страницы RF Cafe
— Конденсаторы и Расчет емкости
— Конденсатор Цветовой код
— Преобразование емкости
— Конденсатор Диэлектрики
— Стандартные значения конденсаторов
— Продавцы конденсаторов
— Благородное искусство разъединения

Заряд, разделение пластин и напряжение

Dynamics Track
Наклонная плоскость
Импульс

Конденсатор
Пластина Sep
Пластина Sep / Volt
Диэлектрики

Цепи
Закон Ом
Последовательный / Параллельный

Wave Tank
Частота / длина волны
Two Pt Interf.

Оптическая скамья
Рефракция
Фокусное расстояние

Параллельный пластинчатый конденсатор

Заряд конденсаторов, разделение пластин и напряжение

Конденсатор используется для хранения электрического заряда. Чем большее напряжение (электрическое давление) вы прикладываете к конденсатору, тем больше заряда нагнетается в конденсатор. Кроме того, чем большей емкостью обладает конденсатор, тем больший заряд будет вызван данным напряжением.Это соотношение описывается формулой q = CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение.

Глядя на эту формулу, можно спросить, что бы произошло, если бы заряд оставался постоянным, а емкость изменялась. Ответ, конечно, таков, что напряжение изменится! Это то, что вы будете делать в этой лаборатории.

Лабораторный конденсатор

Конденсатор с параллельными пластинами — это устройство, используемое для изучения конденсаторов.Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно скручены по спирали в небольших корпусах, поэтому конденсатор с параллельными пластинами значительно упрощает привязку функции к устройству.

Этот конденсатор работает, накапливая противоположные заряды на параллельных пластинах, когда напряжение подается с одной пластины на другую. Количество заряда, который перемещается в пластины, зависит от емкости и приложенного напряжения в соответствии с формулой Q = CV, где Q — заряд в кулонах, C — емкость в фарадах, а V — разность потенциалов между пластинами в вольт.

Конденсаторы накапливают энергию

Если напряжение подается на конденсатор, а затем отключается, заряд, накопленный в конденсаторе, сохраняется до тех пор, пока конденсатор не разрядится каким-либо образом. Между пластинами возникает электрическое поле, которое позволяет конденсатору накапливать энергию. Это один из полезных аспектов конденсаторов, способность накапливать энергию в электрическом поле, чтобы ее можно было использовать позже.

От чего зависит емкость?

Количество заряда, которое может храниться на один приложенный вольт, определяется площадью поверхности пластин и расстоянием между ними.Чем больше пластины и чем ближе они расположены, тем больше заряда может храниться на каждый вольт разности потенциалов между пластинами. Заряд, накопленный на приложенный вольт, представляет собой емкость, измеряемую в фарадах.

Может ли изменение емкости заряженного конденсатора изменить его напряжение?

Лабораторный конденсатор можно регулировать, поэтому мы можем провести интересный эксперимент с емкостью и напряжением. Если конденсатор имеет постоянный заряд, изменение емкости должно вызвать изменение напряжения.Раздвигание пластин приведет к уменьшению емкости, поэтому напряжение должно увеличиться.

Как можно математически определить емкость нашего конденсатора?
Для конденсатора с параллельными пластинами емкость определяется по следующей формуле:

С = ε 0 А / сут

Где C — емкость в Фарадах, ε 0 — постоянная диэлектрической проницаемости свободного пространства (8,85×10 -12), A — площадь пластин в квадратных метрах, а d — расстояние между пластинами в метрах.

Фарада — это очень большая величина емкости, поэтому мы будем использовать метрические префиксы для получения более удобных чисел. Емкость обычно измеряется в микрофарадах (мкФ), что составляет 1,0×10 -6F, или пикофарадах (пФ), что составляет 1,0×10 -12F. 1.0F = 1,000,000 мкФ = 1,000,000,000,000 пФ! Будьте очень внимательны с расчетами!

Этот расчет даст вам приблизительное значение емкости лабораторного конденсатора. Однако есть и другие факторы, которые вносят ошибки в реальные измерения емкости и напряжения.Вам нужно внимательно учитывать эти факторы.

Лабораторное оборудование:

Для получения хороших результатов эта лабораторная деятельность требует специального оборудования. Вам нужен хороший стабилизированный источник питания, чтобы напряжение, подаваемое на конденсатор, было одинаковым при каждом испытании.

Вам также понадобится очень точный способ измерения напряжения между пластинами без резистивной нагрузки на конденсатор. Количество накопленного заряда очень мало, поэтому обычный вольтметр не подойдет.Мельчайший заряд, накопленный в конденсаторе, просто разрядится через измеритель, делая любые измерения бесполезными. Вы будете использовать специальный прибор для измерения напряжения, называемый электрометром, который измеряет напряжение без разряда конденсатора.

Одна из проблем электрометра заключается в том, что он имеет некоторую собственную емкость. Поскольку эта емкость параллельна емкости конденсатора, встроенная емкость выводов должна быть добавлена к емкости конденсатора.

Назначение:

Целью данной лабораторной работы является исследование взаимосвязи между разделением пластин и напряжением в конденсаторе с параллельными пластинами, который поддерживается постоянным зарядом.

Оснащение:

Конденсатор переменной емкости
Электрометр
Регулируемый блок питания
Поводки для перемычек
Провода для электрометра

Осторожно:

Это хрупкое оборудование. Все должно сочетаться с легчайшими прикосновениями. Ничего не заставляйте!

Ваша первая задача — предсказать, что произойдет с напряжением конденсатора, когда вы зарядите его источником 10 В, а затем раздвинете пластины (что уменьшит емкость). Вы сделаете это в следующем разделе.

Теоретические расчеты:

Сначала необходимо рассчитать теоретическую емкость для каждого расстояния между пластинами. Мы сделаем первое, а потом вы сможете сделать все остальное! Самая сложная часть этого — правильно настроить юниты. Проще всего поставить все в метрах для расчетов:

Измерьте диаметр пластин конденсатора в сантиметрах. Ваш размер должен быть около 17,8 см
Разделите диаметр на 100, чтобы получить размер в метрах.Результат — 0,178 м. Разделите это на два, чтобы получить радиус: 0,089 м
Площадь пластины определяется по общей формуле A = πr 2. Подставьте числа, чтобы получить A = π (0,089) 2 = 0,0249 м 2
Преобразуйте расстояние между пластинами (1 мм) в метры, разделив на 1000. 1/1000 = 0,001 м.
Используйте это число в формуле C = ε 0A / d, чтобы определить расчетную емкость, таким образом: C = 8,85×10 -12 (0,0249) / 0,001 = 2,20×10 -10. Это равно 220×10 -12F или 220pF
Добавьте встроенную емкость электрометра (50 пФ) к теоретической емкости, чтобы получить 270 пФ.
Запишите этот результат (270 пФ) в столбец «Расчетная емкость» и строку 1 мм.
Повторите этот процесс для других расстояний между пластинами. Обратите внимание, что площадь пластины одинакова для всех, поэтому все, что вам нужно сделать, это повторить шаги 5, 6 и 7, вставляя правильные значения для интервала в каждом случае.
Теперь вы рассчитаете теоретическое напряжение для каждого интервала. Предположим, что для шага 1,0 мм напряжение составляет 10 В, поэтому вы можете просто указать это значение в таблице.Во-первых, вы определяете количество заряда в конденсаторе при таком расстоянии и напряжении. Используйте формулу Q = CV, чтобы определить заряд, таким образом: Q = 270×10 -12F (10V) = 2700×10 -12C. Этот заряд остается неизменным на всех расстояниях между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец Расчетный заряд! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V = Q / C, таким образом: V = 2700×10 -12C / 94,0×10 -12F = 28,7V. Введите это значение в столбец «Расчетное напряжение» в строке 5 мм.
Повторите тот же расчет напряжения для оставшихся расстояний между пластинами. Используйте рассчитанную емкость и постоянный заряд для каждого промежутка и введите значение напряжения в столбец «Расчетное напряжение» таблицы.
Поздравляем! Вы закончили предварительные расчеты! Все, что вам нужно сделать сейчас, это произвести измерения!

В следующих разделах вы проведете реальный эксперимент для проверки (или, возможно, не проверки!) Ваших теоретических расчетов.

Процедура настройки переменного конденсатора (если лаборатория уже настроена, переходите к следующему разделу!)

Поместите переменный конденсатор в середину лабораторного стола так, чтобы отметка 0 см находилась слева от вас. Не ставьте конденсатор слишком близко к краю стола!
Разместите блок питания за конденсатором переменной емкости. Подключите блок питания, но не включайте его.
Подключите красный и черный перемычки к красной и черной клеммам источника питания. Просто прикрепите зажим «крокодил» к отверстию и оставьте другой конец проводов свободным.
Поместите электрометр слева от конденсатора.
Присоедините плоские клеммы проводов электрометра к зажимным контактам на задней стороне каждой пластины конденсатора. Красный провод идет к правой пластине, черный — к левой пластине.
Вставьте разъем BNC в электрометр.
Установите пластины на расстоянии не менее 1 мм.Белые бамперы предотвращают сближение пластин. Если пластины не параллельны друг другу, используйте регулировочные ручки в середине правой опоры, чтобы выровнять пластины. Левый край пластикового язычка, выступающий к шкале, должен быть совмещен с отметкой 1 мм.

Сбор экспериментальных данных

Убедитесь, что оборудование настроено правильно и правильно.
Поверните все четыре регулятора на блоке питания против часовой стрелки до упора.
Поверните крайнюю левую ручку (Fine Current) в положение на 12 часов (прямо вверх!)
Включите источник питания. Дисплеи должны загореться.
Используйте ручки Fine и Coarse Voltage (две крайние правые ручки), чтобы установить напряжение на 10,0 В.
Установите пластины на минимальное значение
Установите электрометр на шкалу 30 В.
Нажмите кнопку питания на электрометре. Должен загореться светодиод 30 В.
Нажмите кнопку нуля на электрометре. Это обнуляет счетчик и обеспечивает нулевое напряжение на пластинах относительно друг друга.
На мгновение прикоснитесь к проводам от источника питания к пластинам, черный к левой пластине и красный к правой пластине.
Электрометр должен показать 12 В в этой точке (12 В — это первая маленькая отметка над «1» на нижней шкале. Если он не проверяет вашу настройку, попробуйте еще раз.Иногда вам нужно несколько раз прикоснуться проводами к пластинам, чтобы получить правильные показания 12 В.
С этого момента вы должны быть осторожны, чтобы не прикасаться к пластинам. Прикоснувшись к ним, вы измените заряд в пластинах и испортите данные!
Следите за электрометром, чтобы убедиться, что заряд сохраняется. Если вы видите падение напряжения более чем на вольт за 30 секунд, остановитесь и выясните, что не так, прежде чем продолжить.
Переключите электрометр на настройку 100 В. Счетчик должен по-прежнему показывать 12 В, но по шкале 100 В.
Осторожно раздвиньте пластины на расстояние 5 мм.
Снимите показание электрометра и запишите его в таблицу под столбцом «Измеренное напряжение».
Повторите два предыдущих шага для других расстояний между пластинами и запишите соответствующие данные.

Разделение пластин (мм)	Расчетная емкость (пФ)	Расчетный сбор (пКл)	Расчетное напряжение (В)	Измеренное напряжение (В)
1
5
10
15
20
25
30
35
40

Анализ данных:

На миллиметровой бумаге постройте расчетную емкость по оси x (горизонтальная) в зависимости от напряжения по оси y (вертикальная).Нанесите на график рассчитанное и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различать две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначили оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»).
Изучите свой график и ответьте на следующие вопросы:

Подтверждают ли ваши измеренные данные измеренные значения?

Две кривые имеют одинаковую форму? Если да, то на что это указывает?

Что бы вы сделали, чтобы повысить точность собираемых данных?
Формула для энергии, запасенной в конденсаторе, U e = ½CV 2.Сохраняется ли энергия, запасенная в конденсаторе, постоянной при изменении расстояния между пластинами? Он идет вверх или вниз? Обсудите, откуда пришла или ушла энергия.

8.3: Последовательные и параллельные конденсаторы

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях. Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения.Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы. Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:

\ [C = \ dfrac {Q} {V}.\]

Когда эта последовательная комбинация подключена к батарее с напряжением В , каждый из конденсаторов получает одинаковый заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю.Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.

Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно.Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен Q.

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны суммироваться с напряжением батареи, давая следующий баланс потенциалов:

\ [V = V_1 + V_2 + V_3.\]

Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \). Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем

\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]

Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}.\]

Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.

Комбинация серии

Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, равна сумме обратных величин индивидуальных емкостей:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]

Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны \ (1.000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.

Решение

Вводим указанные емкости в уравнение \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]

Теперь инвертируем этот результат и получаем

\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).Поскольку конденсаторы соединены параллельно, , все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:

\ [Q = Q_1 + Q_2 + Q_3. \]

В левой части этого уравнения используется соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем

\ [C_pV = C_1V + C_2V + C_3V. \]

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

\ [C_p = C_1 + C_2 + C_3. \]

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

Параллельная комбинация

Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]

Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети

Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая, что их индивидуальные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.

Решение

Ввод заданных емкостей в уравнение \ ref {capparallel} дает

\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (b) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \). Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).

Пример \ (\ PageIndex {3} \): эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех десятичных знаков.

Стратегия

Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, обозначенная \ (C_S \), параллельна \ (C_3 \).

Решение

Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]

Для этого

\ [C_S = 0,833 \ mu F. \ nonumber \]

Емкость \ (C_S \) подключена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:

\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]

Сеть конденсаторов

Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.

Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. Стратегия

Сначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \). Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.

Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет

\ [C_ {23} = C_2 + C_3 = 2.0 мк F + 4,0 мк F = 6,0 мк F. \]

Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,

\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому

\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12.0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]

Теперь разность потенциалов на конденсаторе 1 равна

\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48,0 \ mu C} {12,0 \ mu F} = 4,0 В. \]

Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:

\ [V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В. \]

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]

\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]

Значимость Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)

Упражнение \ (\ PageIndex {1} \)

Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12.0 В в каждой сети.

Ответьте на: \ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)
Ответ б: \ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)
Ответ c: \ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)

Емкость

: единицы и формулы — стенограмма видео и урока

Уравнения емкости

Определение емкости дается следующим уравнением: емкость C , измеренная в фарадах, равна заряду Q , измеренному в кулонах, деленному на напряжение В , измеренное в вольтах.Так, например, если вы подключаете батарею 12 В к конденсатору, и эта батарея заряжает конденсатор 4 кулонами заряда, она должна иметь емкость 4/12, что составляет 0,33 фарада.

Уравнение, определяющее емкость

Если бы конденсатор имел большую емкость, он бы накапливал больше заряда при подключении к той же батарее. Из этого уравнения мы можем видеть, что емкость измеряется в кулонах на вольт.Таким образом, он представляет, сколько кулонов заряда будет храниться в конденсаторе на один вольт, который вы приложите к нему.

Хорошо, но что физически заставляет конкретный конденсатор иметь другую емкость? От чего зависит, сколько заряда в нем хранится? Это основано на реальных физических характеристиках конденсатора. Итак, у нас есть еще одно уравнение для емкости, которое выглядит так:

Уравнение, основанное на физических характеристиках конденсатора

Емкость конденсатора с параллельными пластинами, простого конденсатора, состоящего всего из двух параллельных пластин, разделенных расстоянием, d , равна относительной диэлектрической проницаемости материала между местами, K , умноженной на диэлектрическая проницаемость свободного пространства, эпсилон-ноль, которая всегда равна 8.-12, умноженное на площадь пластин, A , измеренное в квадратных метрах, разделенное на расстояние между местами, d , измеренное в метрах.

Большая часть этого довольно очевидна, но K , относительная диэлектрическая проницаемость так называемого «диэлектрического» материала между пластинами обычно равна 1 или больше. Если между пластинами ничего нет, K = 1; если между пластинами воздух, то K почти все равно равен 1; и если это другой материал, это будет число больше единицы, в зависимости от конкретного материала.

Итак, это наши два основных уравнения для емкости, и, как обычно, пришло время попробовать их в примере задачи.

Пример расчета

Допустим, у вас есть конденсатор площадью 0,1 квадратный метр с пластинами на расстоянии 0,01 метра друг от друга, и между пластинами есть воздух. Если подключить к батарее 9В, сколько заряда останется на пластинах?

Ну, прежде всего, давайте запишем то, что мы знаем. Площадь равна 0,1 метра в квадрате, поэтому A = 0.1; пластины расположены на расстоянии 0,01 метра друг от друга, поэтому d = 0,01; и между пластинами находится воздух, поэтому K составляет примерно 1. У вас также есть напряжение, поэтому V = 9 вольт, и нас просят найти заряд, Q , поэтому Q равно знаку вопроса . Мы пока не можем решить для Q , потому что у нас есть V , но у нас нет C . Итак, нам нужно использовать другое уравнение, чтобы сначала найти емкость C .

Подставляя числа в это уравнение, мы получаем, что емкость равна 1, умноженному на 8.-10 кулонов. Вот и все — вот наш ответ.

Краткое содержание урока

Конденсатор — это компонент, который накапливает заряд (накапливает электрическую энергию) до тех пор, пока он не заполнится, а затем высвобождает его в виде всплеска. Есть много причин, по которым вы можете захотеть это сделать. Вы можете хранить заряд в конденсаторе на случай потери внешнего питания, чтобы устройство не умерло мгновенно, что позволило завершить процессы восстановления. Вы можете захотеть, чтобы схема получала регулярный «импульс» энергии каждые x раз.Вы найдете конденсаторы практически в любом электронном устройстве: компьютерах, телевизорах, автомобильных стартерах — что угодно.

Емкость — это мера способности конденсатора накапливать заряд, измеряемая в фарадах; конденсатор с большей емкостью будет накапливать больше заряда. Определение емкости дается следующим уравнением: емкость C , измеренная в фарадах, равна заряду Q , измеренному в кулонах, деленному на напряжение В , измеренное в вольтах. Емкость зависит от физических характеристик конденсатора.-12, умноженное на площадь пластин, A , измеренное в квадратных метрах, разделенное на расстояние между местами, d , измеренное в метрах. Значение K равно 1 для пустого пространства и довольно близко к 1 для воздуха. Эти два уравнения вместе позволяют решить множество простых задач, связанных с конденсаторами.

Результаты обучения

По завершении этого урока у вас будет возможность:

Вспомнить, что такое конденсатор, назначение конденсаторов и примеры конденсаторов
Определить емкость
Определите уравнение, которое обеспечивает определение емкости, и уравнение для емкости конденсатора с параллельными пластинами.